1.2.2映射
人教A版必修一数学课件:1.2.2函数的表示法(第2课时分段函数及映射)

研修班
3
x+2,x≤-1 2 已知函数 f(x)=x ,-1<x<2 ,求 f(f(f(-3))) 2x,x≥2 【思路点拨】 由题目可获取以下主要信息: ①函数 f(x)是分段函数; ②本例是求值问题. 解答本题需确定 f(f(-3))的范围,为此又需 确定 f(-3)的范围,然后根据所在定义域代入相 应解析式逐步求解.
2018/12/1 研修班 8
对含有绝对值的函数,要作出其图象,首先应根据绝对值
的意义去掉绝对值符号,将函数转化为分段函数,然后分段作 出函数图象.由于分段函数在定义域的不同区间内解析式不一
样,因此画图时要特别注意区间端点处对应点的实虚之分.
2.写出下列函数的解析式并作出函数图象: (1)设函数y=f(x),当x<0时,f(x)=0;当x≥0时,f(x)=2; (2)设函数y=f(x),当x≤-1时,f(x)=x+1;当-1<x<1时,f(x)
2018/12/1
研修班
2
1.分段函数是一个函数还是几个函数?其定义域、值域各
是什么? 【提示】 分段函数是一个函数而非几个函数,其定义域是
各段定义域的并集,值域是各段值域的并集.
2.函数是映射吗? 【提示】 对比函数定义与映射定义可知,函数是特殊的映
射,是从非空数集到非空数集的映射.
2018/12/1
2018/12/1
研修班
4
【解析】 ∵-3≤-1,∴f(-3)=-3+2=-1 ∴f(f(-3))=f(-1)=1,
∵-1<1<2,
∴f(f(f(-3)))=f(1)=1.
(1)分段函数求值,一定要注意所给自变量的值所在的范围,代入相
应的解析式求得. (2)像本题中含有多层“f”的问题,要按照“由里到外”的顺序,层层
1.2.2映射

问题: 对应(1)为什么不是映射? 对应( )为什么不是映射?
A 开平方 9 4 1
(1)
B 3 -3 2 -2 1 -1 映射 三要素
集合A 集合A A到B的对应法则f 的对应法则f 集合B 集合B
下面六个对应,其中哪些是集合A 的映射? 下面六个对应,其中哪些是集合A到B的映射
A 三角形 四边形 五边形 六边形 是 (1) A 甲 乙 丙 丁 是 (4) 100米 100米 赛跑 B 冠军 亚军 季军 A 0 -1 1 是 (5) 内角和 f: x B A 1 2 3 4 不是 (2) 平方 B 0 1 -1 A 2x 2 4 6 f:x B A 1 2 3 4 … 是 (3) 教科书 2x-1 B 1 3 5 7 …
1 、已知:f ( x +1) = x + 2 x,求f (x)
1 x 2、如果f ( ) = ,求f (x) 2 x 1 x -
3、消去法 、
ቤተ መጻሕፍቲ ባይዱ
1 例 : 果 数 (x 满 2 f (x) + f ( ) = 2x, 4 如 函 f ) 足 x 求 (x) f
4、特殊值法 、
练习
1.如 f [ f (x)] = 2x +1, 求 次 数 (x) 果 一 函 f
180度 360度 540度 720度
B
张三 李四 不是 (6)
语文书 数学书 英语书 物理书 化学书
三 能力训练
1 下面的对应是A到B的映射吗?说明理由.画出对应图(每一个集合各 下面的对应是A 的映射吗?说明理由.画出对应图( 个元素) 取5个元素) 个元素
A = R, B = x∈R x >0, x ∈ A, f : x → x
教学:高一数学人教A版必修一教案:1.2.2 映射 Word版含答案

课题:§1.2.2映射教学目的:(1)了解映射的概念及表示方法,了解象、原象的概念;(2)结合简单的对应图示,了解一一映射的概念.教学重点:映射的概念.教学难点:映射的概念.教学过程:一、引入课题复习初中已经遇到过的对应:1.对于任何一个实数a,数轴上都有唯一的点P和它对应;2.对于坐标平面内任何一个点A,都有唯一的有序实数对(x,y)和它对应;3.对于任意一个三角形,都有唯一确定的面积和它对应;4.某影院的某场电影的每一张电影票有唯一确定的座位与它对应;5.函数的概念.二、新课教学1.我们已经知道,函数是建立在两个非空数集间的一种对应,若将其中的条件“非空数集”弱化为“任意两个非空集合”,按照某种法则可以建立起更为普通的元素之间的对应关系,这种的对应就叫映射(mapping)(板书课题).2.先看几个例子,两个集合A、B的元素之间的一些对应关系(1)开平方;(2)求正弦(3)求平方;(4)乘以2;3.什么叫做映射?一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则f,使对于集合A 中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A→B 为从集合A到集合B的一个映射(mapping).记作“f:A→B”说明:(1)这两个集合有先后顺序,A到B的射与B到A的映射是截然不同的.其中f表示具体的对应法则,可以用汉字叙述.(2)“都有唯一”什么意思?包含两层意思:一是必有一个;二是只有一个,也就是说有且只有一个的意思。
4.例题分析:下列哪些对应是从集合A到集合B的映射?(1)A={P | P是数轴上的点},B=R,对应关系f:数轴上的点与它所代表的实数对应;(2)A={ P | P是平面直角体系中的点},B={(x,y)| x∈R,y∈R},对应关系f:平面直角体系中的点与它的坐标对应;(3)A={三角形},B={x | x是圆},对应关系f:每一个三角形都对应它的内切圆;(4)A={x | x是新华中学的班级},B={x | x是新华中学的学生},对应关系f:每一个班级都对应班里的学生.思考:将(3)中的对应关系f改为:每一个圆都对应它的内接三角形;(4)中的对应关系f 改为:每一个学生都对应他的班级,那么对应f:B→A是从集合B到集合A的映射吗?5.完成课本练习三、作业布置补充习题以下为赠送文档:选修4_5 不等式选讲课 题: 第01课时 不等式的基本性质目的要求:重点难点:教学过程:一、引入:不等关系是自然界中存在着的基本数学关系。
湖南省茶陵县第三中学人教A版高中数学必修1课件:1.2.2函数的表示法第二课时 映射与函数

问题2:若C={男,女},那么A,C之间怎样对应?
提示:对于A中任意一个同学,C中都有唯一的性别与之对应.
(
)
A.A={-1,0,1},B={-1,0,1},f:A中的数平方
B.A={0,1},B={-1,0,1},f:A中的数开平方 C.A=Z,B=Q,f:A中的数取倒数 D.A=R,B={正实数},f:A中的数取绝对值 解析:在B中,集合A中的元素1在B中有±1两个元素与之对应,∴B不正
确.C中,集合A中的元素0没有倒数,∴C不正确.D中,集合A中的元素
(
)
A.A中每个元素在B中必有唯一元素与其对应 B.B中每个元素在A中必有元素与其对应 C.B中每个元素在A中对应的元素唯一 D.A中不同的元素在B中对应的元素必不同 解析:f:A→B表示A中的任一元素在B中都有唯一元素与之对应, 而B中的部分元素可以不参与对应.答案:A
2.下列集合A到集合B的对应f是映射的是
[思路点拨]
判断的依据是映射和一一映射的概念.
[精解详析] (1)是映射,且满足一一映射的条件,是一一映射. (2)对于x=1∈A,在f作用下的象是0,而0 ∉B,∴(2)不是映射. (3)是映射,且满足一一映射的条件,是一一映射. (4)对于x=±1∈A,在f作用下的象都是1,故f是映射,但不符合一一映射 的条件,故不是一一映射.
的象, 且对任意的a∈A,在B中和它对应的元素是|a|,则
集合B中元素的个数是
A.4 B.5
(
)
人教A版数学必修一教案:映射

§1.2.2 映射一.教學目標1.知識與技能:(1)瞭解映射的概念及表示方法;(2)結合簡單的對應圖表,理解一一映射的概念.2.過程與方法(1)函數推廣為映射,只是把函數中的兩個數集推廣為兩個任意的集合;(2)通過實例進一步理解映射的概念;(3)會利用映射的概念來判斷“對應關係”是否是映射,一一映射.3.情態與價值映射在近代數學中是一個極其重要的概念,是進一步學習各類映射的基礎.二.教學重點:映射的概念教學難點:映射的概念三.學法與教學用具1.學法:通過豐富的實例,學生進行交流討論和概括;從而完成本節課的教學目標;2.教學用具:投影儀.四.教學思路(一)創設情景,揭示課題復習初中常見的對應關係1.對於任何一個實數a,數軸上都有唯一的點p和它對應;2.對於座標平面內任何一個點A,都有唯一的有序實數對(,x y)和它對應;3.對於任意一個三角形,都有唯一確定的面積和它對應;4.某影院的某場電影的每一張電影票有唯一確定的座位與它對應;5.函數的概念.(二)研探新知1.我們已經知道,函數是建立在兩個非空數集間的一種對應,若將其中的條件“非空數集”弱化為“任意兩個非空集合”,按照某種法則可以建立起更為普通的元素之間的對應關係,這種對應就叫映射(板書課題).2.先看幾個例子,兩個集合A、B的元素之間的一些對應關係:(1)開平方;(2)求正弦;(3)求平方;(4)乘以2.歸納引出映射概念:一般地,設A、B是兩個非空的集合,如果按某一個確定的對應法則f,使對於集合A 中的任意一個元素x,在集合B中都有唯一確定的元素y與之對應,那麼就稱對應f:A→B 為從集合A 到集合B 的一個映射.記作“f :A →B ” 說明:(1)這兩個集合有先後順序,A 到B 的映射與B 到A 的映射是截然不同的,其中f 表示具體的對應法則,可以用多種形式表述.(2)“都有唯一”什麼意思?包含兩層意思:一是必有一個;二是只有一個,也就是說有且只有一個的意思.(三)質疑答辯,排難解惑,發展思維例1.下列哪些對應是從集合A 到集合B 的映射?(1)A={|P P 是數軸上的點},B=R ,對應關係f :數軸上的點與它所代表的實數對應; (2)A={|P P 是平面直角坐標中的點},}{(,)|,,B x y x R y R =∈∈對應關係f :平面直角坐標系中的點與它的座標對應;(3)A={三角形},B={|},x x 是圆对应关系f :每一個三角形都對應它的內切圓; (4)A={|x x 是新華中學的班級},}{|,B x x =是新华中学的学生對應關係f :每一個班級都對應班裏的學生.思考:將(3)中的對應關係f 改為:每一個圓都對應它的內接三角形;(4)中的對應關係f 改為:每一個學生都對應他的班級,那麼對應f :B →A 是從集合B 到集合A 的映射嗎?例2.在下圖中,圖(1),(2),(3),(4)用箭頭所標明的A 中元素與B 中元素的對應法則,是不是映射?是不是函數關係?求正弦 B(1) (2)A 求平方B A 乘以2 B(3) (4)(四)鞏固深化,回饋矯正1、畫圖表示集合A 到集合B 的對應(集合A ,B 各取4個元素) 已知:(1)}}{{1,2,3,4,2,4,6,8A B ==,對應法則是“乘以2”; (2)A={|x x >}0,B=R ,對應法則是“求算術平方根”; (3){}|0,A x x B R =≠=,對應法則是“求倒數”;(4){0|0A α=∠<}}{090,|1,B x x α∠≤=≤對應法則是“求余弦”.2.在下圖中的映射中,A 中元素600的像是什麼?B 中元素2的原像是什麼?A 求正弦 B(五)歸納小結提出問題:怎樣判斷建立在兩個集合上的一個對應關係是否是一個映射,你能歸納出幾個“標準”呢?師生一起歸納:判定是否是映射主要看兩條:一條是A 集合中的元素都要有象,但B 中元素未必要有原象;二條是A 中元素與B 中元素只能出現“一對一”或“多對一”的對應形式.(六)設置問題,留下懸念.1.由學生舉出生活中兩個有關映射的實例.2.已知f 是集合A 上的任一個映射,試問在值域f (A)中的任一個元素的原象,是否都是唯一的?為什麼?3.已知集合}{}{,,1,0,1,A a b B ==-從集合A 到集合B 的映射,試問能構造出多少映射?。
【平煤高中学案必修一】11.映射

§1.2.2映射学习目标:(1)了解映射的概念及表示方法;(2)会利用映射的概念来判断“对应关系”是否是映射,感受对应关系在刻画函数和映射概念中的作用,提高对数学高度抽象性和广泛应用性的进一步认识.知识要点:1.映射的概念:2.映射的三要素:3.映射的性质:4.判断映射的标准:5.映射的个数:典型例题:1.图中用箭头所标明的A 中元素与B 中元素的对应法则,各自有何特点?2.下列哪些对应是从集合A 到集合B 的映射?(1){|A P P =是数轴上的点},B R =,对应关系f :数轴上的点与它所代表的实数对应;(2) {|A P P =是平面直角坐标系中的点},{(,)|,}B x y x R y R =∈∈, 对应关系f :平面直角坐标系中的点与它的坐标对应; (3){A =x x 是三角形},{|B x x =是圆}, 对应关系f :每一个三角形都对应它的内切圆;(4){|A x x =是新华中学的班级},{|B x x =是新华中学的学生}, 对应关系f :每一个班级都对应班里的学生.3.已知集合{|06}M x x =≤≤,{|03}P y y =≤≤,则下列对应关系中不能看作从M 到P 的映射的是 ( ) A.f :12x y x →=B. f :13x y x →=C. f :x y x →=D. f :16x y x →= 4.已知集合A N =,{|21,}B a a n n Z ==-∈,映射f : A →B ,使A 中任一元素a 与B 中元素21a -对应,则与B 中元素17对应的A 中元素是 ( )A.3B.5C.17D.9 5. 已知集合}{}{,,1,0,1,A a b B ==-从集合A 到集合B 的映射有 个?当堂检测1.下列对应:f A B →:① {},0,:;A R B x R x f x x ==∈>→ ②*,,:1;A N B N f x x ==→- ③{}20,,:.A x R x B R f x x =∈>=→ 不是从集合A 到B 映射的有( ). A. ①②③ B. ①② C. ②③ D. ①③2.设集合{},,A a b c =,集合B R =,以下对应关系一定能建立集合A 到集合B 的映射的是( )A. 对集合A 中的数开平方B. 对集合A 中的数取倒数C. 对集合A 中的数取算术平方根D. 对集合A 中的数立方3.集合{}x x f b a N a b M →=⎭⎬⎫⎩⎨⎧=:,,,,1,则b a ,的值为 .4. 在映射:f A B →中,{(,)|,}A B x y x y R ==∈,且:(,)(,)f xy x yx y →-+,则与A 中的元素(1,2)-对应的B 中的元素为( ). A.(3,1)- B.(1,3) C.(1,3)-- D.(3,1)5.设映射2:2f x x x →-+是实数集A R =到实数集B R =的映射,若对于实数B p ∈,在A 中不存在元素和p 对应,则实数p 的取值范围是( )A.(1,+∞)B.[1,+∞)C.(-∞,1)D.(-∞,1)6.集合{}{}4,3,3,2,1==B A ,从A 到B 的映射f 满足3)3(=f ,这样的映射有 个7.{}{}1,0,1,,,-==B c b a A ,f : A →B 满足)()()(c f b f a f =+,则映射f : A →B 的个数为 。
2019-2020学年人教a版数学必修1课件:1.2.2 第2课时分段函数与映射

(n∈N*,n≥3).
求 f(3),f(4),f[f(4)]的值. 【解析】由题意可知 f(1)=1,f(2)=2,则
f(3)=f(2)+f(1)=2+1=3,
f(4)=f(3)+f(2)=3+2=5,
f[f(4)]=f(5)=f(4)+f(3)=5+3=8.
分段函数的图象及应用 【例 2】已知函数 f(x)=1+|x|-2 x(-2<x≤2). (1)用分段函数的形式表示该函数; (2)画出该函数的图象; (3)写出该函数的值域. 【 解 题 探 究 】 讨论x的取值范围 → 化简fx的解析式
•1.2 函数及其表示
1.2.2 函数的表示法
第2课时 分段函数与映射
目标定位
1.掌握简单的分段函数, 并能简单应用. 2.了解映射概念及它与函 数的联系.
重点难点
重点:分段函数的应用及 映射的判断. 难点:分段函数的应用.
• 1.分段函数
• 在函数的定义域内,对于自变量x的不同取值区间, 有 数着. 不对应同关的系_________,这样的函数通常叫做分段函
2a=4a,所以a=2.
• 5.某单位为鼓励职工节约用水,作出了如下规定: 每位职工每月用水不超过10立方米的,按每立方米 m元收费;用水超过10立方米的,超过部分按每立 方米2m元收费.某职工某月缴水费16m元,求该职 工这个月实际用水量.
【解析】该单位职工每月应缴水费y与实际用水量x满足的
关系式为y=m2mx,x-0≤ 10xm≤,1x0>,10.
映射的概念及应用
• 【例3】判断下列对应是不是从集合A到集合B的映 射.
• (1)A=N*,B=N*,对应关系f:x→|x-3|; • (2)A={平面内的圆},B={平面内的矩形},对应关
映射重要知识点总结

映射重要知识点总结一、映射的定义1.1 映射的概念映射是一种将一个集合中的元素对应到另一个集合中的元素的规则。
具体来说,如果从集合A到集合B的每个元素a都能找到集合B中的唯一元素b与之对应,那么我们就说存在从集合A到集合B的一个映射。
我们通常用f: A → B来表示这个映射,其中f表示映射的规则,A称为定义域,B称为值域,而对应的元素对(a, b)称为映射对。
1.2 映射的表示方式映射可以用图、公式、表格等形式来表示。
在图中,我们可以用箭头连接集合A和集合B 的元素,表示它们之间的对应关系;在公式中,我们可以用f(x) = y来表示映射的规则,其中x表示集合A中的元素,y表示集合B中的元素;在表格中,我们可以将集合A的元素和对应的集合B的元素按一定顺序排列,表示它们之间的对应关系。
1.3 映射的例子为了更好地理解映射的概念,我们可以举几个具体的例子。
比如说,将一个学生的学号与他的成绩对应起来,就是一个映射;将一个人的身高与体重对应起来,也是一个映射;将一个城市的名称与它的人口数量对应起来,同样也是一个映射。
二、映射的性质2.1 单射、满射和双射在研究映射的性质时,我们通常关注三个重要的性质,即单射、满射和双射。
- 单射:如果一个映射f: A → B满足对任意的x1, x2∈A,只要x1≠x2就有f(x1)≠f(x2),那么我们就说这个映射是单射。
单射也可以表述为:对于集合A中的任意两个不同的元素,它们在集合B中的像也是不同的。
- 满射:如果一个映射f: A → B满足对于集合B中的任意元素y,都能在集合A中找到一个元素x与之对应,那么我们就说这个映射是满射。
- 双射:如果一个映射既是单射又是满射,那么我们就说这个映射是双射。
2.2 映射的复合在实际问题中,有时我们会遇到多个映射的复合。
设有两个映射f: A → B和g: B → C,我们可以定义它们的复合映射g∘f: A → C为:对于A中的任意元素x,它在C中对应的像为(g∘f)(x) = g(f(x))。
1.2.2函数的表示法(二)映射

例如:
f:平方
1
2
1
3
4
2
5
6
3
7
8
9
是函数
也是映射
学生甲 学生乙 学生丙 学生丁
f
高一3班
高一4班
只是映射
以下是不是映射?
①开平方
3
9
-3
4
2 -2
1
1
-1
以下是不是映射?
①开平方
3
9
-3
方
-1
2
1
-2
4
3 -3
9
以下是不是映射?
①开平方
记作:f:x y, x A, y B 或者f:A B,其中x称为原象,y称为象
象与原象的定义:
给定一个集合A到B的映射,且a∈A, b∈B,若a与b对应,则把元素b叫做a在 B中的象,而a叫做b的原象.
③求正弦 1
2
30
2
45
2
60
3
90
2
1
④乘以2 1
1
2 3
2
4
3
5
6
函数与映射之间的异同: 1)函数是一个特殊的映射; 2)函数:数集A数集都是数集,
a
e
a
e
a
e
bf
bf
bf
c
g
c d
g
c
g d
“原象集”不 能有剩余元素
“象集”可 以有剩余元 素
例1. 判断下列对应是否映射?有没有对 应法则?
a
e
a
e
a
e
bf
bf
bf
c
1.2.2_映射的概念

a
b
1
1
2
(2) A
a
b
c
(1) A
2 2
B
c
B
1
a
b
(3)
a
b
1
2
(4)
2 3
c
说出下图所示的对应中,哪些是B到A的映射? 变式练习:
A B A B
a
b
1
1
2
(2) A
a
b
c
(1) A
2 2
B
c
B
1
a
b
(3)
a
b
1
2
(4)
2 3
c
已知集合A=R,B={(x,y)|x,y∈R},f是 例3: 从A到B的映射f:x→(x+1,x2) . (1)求 2 在B中的对应元素 (2)(2,1)在A中的对应元素
②“存在性”:对于集合A中的任何一个元素, 集合B中都存在元素和它对应;
③“唯一性”:对于集合A中的任何一个元 素,在集合B中和它对应的元素是唯一的.
例1 试判断下面给出的对应是否为从集合A到集合 B的映射? (1)集合A={P|P是数轴上的点},集合B=R,对应 关系f:数轴上的点与它所代表的实数对应;
例1 说出下图所示的对应中,哪些是A到B的映射?
A 9 4 开平方 B 3 -3 2 -2 1 -1 B 1 4 9 A 30° 求正弦 B
1 2
2 2 3 2
45°
60° 90° A 乘以2 1 2 3
1
1
B 1 2 3 4 5 6
A 1 -1 2 -2 3 -3
求平方
例2
说出下图所示的对应中,哪些是A到B的映射?
高中数学 1.2.2函数的表示法(二)映射的概念学案 新人教A版

河北省石家庄市2012-2013年高中数学 1.2.2函数的表示法(二)映射的概念学案 新人教A 版课前预习案使用说明与学法指导: 1.用15分钟的时间阅读探究课本上的基础知识,自主高效预习,提升自己的阅读理解能力.2.完成教材助读设置的问题,然后结合课本的基础知识和例题,完成预习自测题.3.将预习中不能解决的问题标出来,并写到“我的疑惑”处。
一、相关知识1.构成函数三个要素是什么?2.请同学们回忆分段函数及其表示法?学习建议:请同学们回忆上一节的知识并作出回答。
二、教材助读1.什么是映射?2.映射与函数有什么关系?3.如何判断一个对应是不是映射?三、预习自测学习建议:自测题体现一定的基础性,又有一定的思维含量,只有“细心才对,思考才会”.1.判断下列给出的对应是不是从集合A 到集合B 的映射?(1)集合={}A P P 是数轴上的点,集合=B R ,对应关系f :数轴上的点与它所代表的实数对应;(2)集合={}A P P 是平面直角坐标系中的点,集合={(,),}B x y x R y R ∈∈,对应关系f :平面直角坐标系中的点与它的坐标对应;(3)集合={}A x x 是三角形,集合={}B x x 是圆,对应关系f :每一个三角形都对应它的内切圆;(4) 集合={42}A x x 是石家庄市中学的班级,集合2. 画出函数|2|y x =-的图象.我的疑惑:请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决.课堂探究案一、学始于疑-------我思考,我收获1.函数与映射的联系是什么?区别是什么?2.如何判断一个对应是不是映射?是不是函数?学习建议:请同学们用2分钟的时间认真思考这些问题,并结合预习中自己的疑惑开始下面的探究学习。
二、质疑探究——质疑解疑、合作探究(一)基础知识探究 探究点:映射的概念请同学们探究下面的问题,并在题目的横线上填出正确答案:1.一般地,设A,B 是两个______的集合,如果按某一个对应关系f ,使对于集合A 中的________一个元素x ,在集合____中___有 ____________的元素y 与之对应,那么就称对应__________为从_______到_______的一个映射.2.分别举出映射、函数的例子各一个.(二)知识综合应用探究探究点一 函数与映射的概念(重点)例1.如图,有一块边长为a 的正方形铁皮,将其四个角各截去一个边长为x 的小正方形,然后折成一个无盖的盒子,写出体积V 以x 为自变量的函数式是_____,这个函数的定义域为_______.例2. 判断下列给出的对应是不是从集合B 到集合A 的映射? ①集合={}A x x 是三角形,集合={}B x x 是圆,对应关系f :每一个圆都对应它的内接三角形;②集合={42}A x x 是石家庄市中学的班级,集合级. ③集合={}A x x 是锐角,集合=(0,1)B ,对应关系f :B 中的每一个数都对应以它为正弦值的锐角.思考. 题目中要求判断从哪个集合到哪个集合的映射?如何判断?学习建议:自主探究后谈谈你的映射概念的理解.归纳总结;探究点二 映射的应用(重点)例 3.设:f A B →是A 到B 的一个映射,其中{(,),}A B x y x y R ==∈,:(,)(,)f x y x y xy →+,求(1)A 中元素(2,3)-在B 中的对应元素;(2)求与B 中元素(2,3)-对应的A 中的元素.思考:集合A 中的元素与B 中的元素有怎样的对应关系?学习建议:自主探究后谈谈你的分析思路.规律方法总结:拓展提升:已知集合{,,},{1,A a b c B ==-,映射:f A B →满足()=()(f a f b f c +,问这样的映射有多少个? 思考1:你能说出(),(),()f a f b f c 的意义吗?思考2:(),(),()f a f b f c 可以取哪些値?探究点三:分段函数问题(重点)例4.画出函数|1||24|y x x =-++.的图象:学习建议:探究后谈谈你的解题思路.拓展提升:①函数()[]f x x =的函数值表示不超过x 的最大整数,例如[ 3.5]4-=-,[2.1]2=,当( 2.5,3]x ∈-时,写出()f x 的解析式,并作出函数的图象.②某市“招手即停”公共汽车的票价按下列规则制定:(1)5公里以内(含5公里),票价2元;(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).如果某条线路的总里程为20公里,请根据题意,写出票价与里程的函数解析式,并画出函数的图象.三、我的知识网络图--------归纳梳理、整合内化⎧⎨⎩映射的概念映射映射与函数的关系四、当堂检测——有效训练、反馈矫正下列给出的对应是不是从集合A 到B 集合的映射?1.=,=A N B Z ,对应关系:=-,,f x y x x A y B →∈∈.2. ++=,=A R B R ,且满足1:=,,f x y x A y B x→∈∈ 3. +=,={0,1}A N B ,对应关系f :除以2得的余数.4. ={1,4},={-2,-1,1,2}A B ,对应关系f :开平方.有错必改我的收获(反思静悟、体验成功):课后训练案学习建议:完成课后训练案需定时训练,时间不超过20分钟,独立完成,不要讨论交流,全部做完后再参考答案查找问题.【基础知识检测】1.下列对应是从集合A 到集合B 的映射的是( ) A.=R,={>0}A B x x ,对应关系f :取绝对值 B.={>0},=R A x x B ,对应关系f :开平方. C. 1={>0},=R :+3A x xB f x x →, D. =Q,={}:A B x x f 是偶数,平方.2.拟定从甲地到乙地通话m 分钟电话费由()=1.06(0.05[])+1f m m ⨯⨯给出,其中>0,[]m m 是不小于m 的最小整数(【3】=3,【3.7】=4,【3.1】=4),则从甲地到乙地通话时间为5.5分钟的电话费为( ).A.3.71B. 3.97C.4.24D. 4.773.某同学从家里到学校,为了不迟到,先跑,跑累了再走余下的路,设在途中花的时4.已知映射:f A B →,其中A=B=R ,对应关系2:=-+2f x y x x →.对于实数k B ∈,在集合A 中不存在对应元素,则k 的取值范围是( )A. >1kB. 1k ≥C. <1kD. 1k ≤5. 已知函数()f x 满足()()()f ab f a f b =+,且(2)f p =,(3)f q =,那么(12)f 等于( ).A. p q +B. 2p q +C. 2p q +D. 2p q +6.已知集合={,,},B={,,}A a b c d e ,则从集合A 到集合B 的不同映射有_______个,从集合B 到集合A 的不同映射有_______个.【能力题目训练】7.已知集合={04}3B={02}A x x y y ≤≤≤≤,按对应关系f ,不能建立从集合到集合的映射的是( )A. 1:=2f x y x → B. :=-2f x y x → C. :f x y →:=-2f x y x → 【拓展题目探究】 8.设集合=,=A R B R ,对应关系且2+1:=,,2x f x y x A y B →∈∈是从集合A 到B 集合的映射.(1)那么A 中元素+1a 对应于B 中哪个元素?(2)与B 中元素6相对应的A 中的元素是什么?9.画出下列函数的图象:(1)22||3y x x =-++; (2)2|23|y x x =-++.错误!未定义书签。
第一章 .1.2.2 第2课,时

研一研·问题探究、课堂更高效
第2课时
例 3 以下给出的对应是不是从集合 A 到集合 B 的映射? (1)集合 A={P|P 是数轴上的点},集合 B=R,对应关系 f:数 轴上的点与它所代表的实数对应;
本 课 栏 目 开 关
(2)集合 A={P|P 是平面直角坐标系中的点}, 集合 B={(x, y)|x ∈R,y∈R},对应关系 f:平面直角坐标系中的点与它的坐 标对应; (3)集合 A={x|x 是三角形}, 集合 B={x|x 是圆}, 对应关系 f: 每一个三角形都对应它的内切圆; (4)集合 A={x|x 是新华中学的班级},集合 B={x|x 是新华中 学的学生},对应关系 f:每一个班级都对应班里的学生.
研一研·问题探究、课堂更高效
第2课时
(1)解
函数的图象如图所示:
本 课 栏 目 开 关
(2)答案 1 0 1 1 解析 f(1)=12=1,
f(-3)=0, f[f(-3)]=f(0)=1, f{f[f(-3)]}=f(1)=12=1.
研一研·问题探究、课堂更高效
第2课时
跟踪训练 2 已知 y=f(x)的图象如图所示,求 f(x).
研一研·问题探究、课堂更高效
第2课时
本 课 栏 目 开 关
(3)由于每一个三角形只有一个内切圆与之对应,所以这个对 应 f:A→B 是从集合 A 到集合 B 的一个映射.
(4)新华中学的每一个班级里的学生都不止一个,即与一个班 级对应的学生不止一个,所以这个对应 f:A→B 不是从集合 A 到集合 B 的一个映射.
研一研·问题探究、课堂更高效
第2课时
本 课 栏 目 开 关
跟踪训练 1 作出下列函数的图象: (1)y=1-x,x∈Z; 1 (2)y= ; x (3)y=x2-4x+3,x∈[1,3].
第一章 1.2.2(2)简单函数作图

1.2.2 第2课时
探究点一 :函数图象的作法
例1 画出函数 y=|x|的图象.
解 由绝对值的概念, 有
x, x≥0, y= -x,x<0.
所以,函数 y=|x|的图象如图所示.
明目标、知重点
填要点、记疑点
主目录
探要点、究所然
当堂测、查疑缺
探要点、究所然
1.2.2 第2课时
探究点一 :函数图象的作法
主目录
探要点、究所然
当堂测、查疑缺
1.2.2 第2课时 (4) y
1 f ( x) x x
2
1
0
1 2
x
明目标、所然
当堂测、查疑缺
探要点、究所然
1.2.2 第2课时
探究点一 :函数图象的作法
跟踪训练 1 作出下列函数的图象: 1 (2)y=x; (1)y=1-x,x∈Z; (3)y=x2-4x+3,x∈[1,3].
1 y x (4) x
解 (1)因为 x∈Z,所以图象为一条直线上的孤立点,如图 1 所示;
明目标、知重点
第一章 集合与函数概念
§1.2 函数及其表示 1.2.2 函数的表示法
第2课时 分段函数及映射
探要点、究所然
1.2.2 第2课时
探究点一 :函数图象的作法
思考 作函数的图象通常分为哪几步?
答 通常分为三步,即列表、描点、连线.
明目标、知重点
填要点、记疑点
主目录
探要点、究所然
当堂测、查疑缺
探要点、究所然
反思与感悟
(1)画函数图象时首先要考虑函数的定义域. (2)要标出关键
点,如图象的顶点、端点、与坐标轴的交点等,要分清这些关键点是实心 还是虚心.(3)要掌握常见函数图象的特征.(4)函数图象既可以是连续的曲 线,也可以是直线、折线、离散的点等等.
2014-2015学年高一数学必修1精品课件:1.2.2 分段函数与映射 第2课时
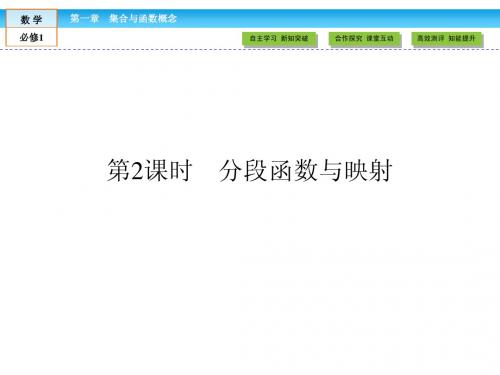
对应___________ f:A→B 为从集合A到集合B的一个映射.
数学 必修1
第一章 集合与函数概念
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
映射的特征 (1) 任意性: A 中任意元素 x 在 B 中都有元素 y 与之对应,如 图(1)所示的对应不是映射;
(2) 唯一性: A 中任意元素 x 在 B 中都有唯一元素 y 与之对
某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里按5 公里计算).
如果某条线路的总里程为 20公里,设里程为 x 公里,票价
为y元, [问题1] x与y是否具有函数关系? [问题2] 函数的定义域和值域各是什么? [问题3] x与y之间有何特点?
解析:
① ② ③ ④ √ × × √ 符合函数定义,且在定义域的不同区间,有不同 的对应关系 当x=2时,f(2)=3或4,故不是函数 当x=1时,f(1)=5或1,故不是函数 符合函数定义,且在定义域的不同区间,有不同 的对应关系
答案: B
数学 必修1
第一章 集合与函数概念
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
应,如图(2)所示的对应不是映射; (3) 方向性: f : A→B 与 f : B→A 一般是不同的映射,如图
(3)与图(4)所示的对应不是同一映射.
数学 必修1
第一章 集合与函数概念
自主学习 新知突破 合作探究 课堂互动 高效测评 知能提升
1.下列给出的式子是分段函数的是(
2 x +1,1≤x≤5, ①f(x)= 2x,x<1.
第一章 1.2 1.2.2 第二课时 分段函数与映射
返回
解:因为 260÷ 52=5 (h),260÷ 65=4 (h), 所以,当 0≤t≤5 时,s=52 t; 当 5<t≤6.5 时,s=260; 当 6.5<t≤10.5 时,s=260+65(t-6.5). 52t,0≤t≤5, 所以 s=260,5<t≤6.5, 260+65t-6.5,6.5<t≤10.5.
因为 ABCD 是等腰梯形, 底角为 45° ,AB=2 2 cm, 所以 BG=AG=DH=HC=2 cm. 又 BC=7 cm,所以 AD=GH=3 cm.(2 分)
返回
[名师批注]
(1)当点 F 在 BG 上时, 1 2 即 x∈[0,2]时,y= x ;(4 分) 2
此时,l左侧的部分为等腰直 角三角形△BFE.
分段函数与映射
返回
分段函数 [提出问题]
某市空调公共汽车的票价按下列规则判定: (1)5 千米以内,票价 2 元; (2)5 千米以上,每增加 5 千米,票价增加 1 元(不足 5 千米的按 5 千米计算). 已知两个相邻的公共汽车站间相距 1 千米,沿途(包括 起点站和终点站)有 11 个汽车站.
返回
[解题流程] 求线l左边部分的面积y关于x的解析式 (1)欲求l 左侧的面积,应先确定形状(2)l在 AB之间,l在DC之间时,其左 侧的形状不
同,应分类讨论
l自左向右移动→确定l左侧图形形状→求图 形面积→建立所求函数解析式→画图像
返回
[规范解答] 过点 A,D 分别作 AG⊥BC,DH⊥BC,垂足分别是 G,H.
映射的定义
设A、B是两个 非空 的集合,如果按某一个确定的对应 关系f,使对于集合A中的 任意一个 元素x,在集合B中都有 唯一确定 的元素y与之对应,那么就称对应 f:A→B 为从集 合A到集合B的一个映射.
【红对勾】高中数学 1.2.2.2分段函数与映射课件 新人教版必修1

映射
设A、B是两个 非空 的集合,如果按某一个确定的 对应关系f,使对于集合Aቤተ መጻሕፍቲ ባይዱ的任意一个元素x,在集合B 中都有 唯一确定 的元素y与之对应,那么就称对应
f:A→B 为从集合A到集合B的一个映射.
4.如何判断一个对应是不是映射? 提示:只要检验对于A中的任意一个元素,按对应关系 f,是否在B中有唯一确定的元素与之对应即可.若是,则 这个对应是映射,否则,不是映射.
答案:-3
分段函数的图象及应用
2 x 已知f(x)= 1
【例2】
-1≤x≤1, x>1,或x<-1,
(1)画出f(x)的图象; (2)求f(x)的定义域和值域.
【解】
(1)利用描点法,作出f(x)的图象,如图所示.
(2)由条件知,函数f(x)的定义域为R.由图象知,当- 1≤x≤1时,f(x)=x2的值域为[0,1],当x>1或x<-1时,f(x) =1,所以f(x)的值域为[0,1].
第一章
集合与函数的概念
1.2
函数及其表示
1.2.2
函数的表示法
第2课时 预习篇
分段函数与映射
巩固篇
课堂篇
课时作业 提高篇
学习目标
1.能记住什么是分段函数,并会求分段函数的值; 2.能画出一些简单分段函数的图象,并通过图象指出 函数的某些性质如值域; 3.能说出映射的定义,并能判断一些对应是否是映射.
x+1,-1≤x<0 答案:f(x)= -x,0≤x≤1
2 x +1,x≤0, (2)已知函数f(x)= -2x,x>0,
若f(x)=10,则x=
________.
解析:当x≤0时,f(x)=x2+1=10,∴x=-3, 当x>0时,f(x)=-2x=10,∴x=-5(舍去), 综上可知,x=-3.
拓扑学中的映射度与拓扑不变量-教案

拓扑学中的映射度与拓扑不变量-教案一、引言1.1拓扑学的基本概念1.1.1拓扑空间的定义:集合与开集的关系,连续映射。
1.1.2拓扑性质:开集、闭集、边界、内部和闭包等基本概念。
1.1.3拓扑空间的例子:欧几里得空间、度量空间、紧致空间等。
1.1.4拓扑学的应用:物理学、数学的其他分支、计算机科学等。
1.2映射度的引入1.2.1映射度的定义:映射在一点附近的旋转角度。
1.2.2映射度的性质:唯一性、不变性、可加性等。
1.2.3映射度的计算方法:指数定理、欧拉公式等。
1.2.4映射度的应用:判断映射的奇偶性、计算不动点个数等。
1.3拓扑不变量的概念1.3.1拓扑不变量的定义:在拓扑变换下保持不变的量。
1.3.2拓扑不变量的例子:连通性、紧致性、同伦等。
1.3.3拓扑不变量的重要性:区分不同的拓扑空间,研究空间的性质。
1.3.4拓扑不变量的应用:分类问题、不动点理论、几何拓扑等。
二、知识点讲解2.1映射度的计算与应用2.1.1映射度的计算:利用指数定理、欧拉公式等方法计算映射度。
2.1.2映射度的应用:判断映射的奇偶性,计算不动点个数等。
2.1.3映射度的推广:高维映射度、相对映射度等概念。
2.1.4映射度的研究:映射度与其他拓扑不变量的关系,映射度理论的发展。
2.2拓扑不变量的性质与分类2.2.1拓扑不变量的性质:在拓扑变换下的不变性,区分不同拓扑空间。
2.2.2拓扑不变量的分类:基本拓扑不变量、组合拓扑不变量、同伦拓扑不变量等。
2.2.3拓扑不变量的研究:拓扑不变量之间的关系,拓扑不变量的计算方法。
2.2.4拓扑不变量的应用:拓扑分类问题,拓扑变换的应用等。
2.3映射度与拓扑不变量的关系2.3.1映射度与拓扑不变量的联系:映射度可以作为拓扑不变量的一种。
2.3.2映射度与拓扑不变量的区别:映射度关注映射的性质,拓扑不变量关注空间的性质。
2.3.3映射度与拓扑不变量的应用:利用映射度研究拓扑不变量,利用拓扑不变量研究映射度。
高一数学映射(新2019)

第一章 集合与函数概念 1.2.Байду номын сангаас 映射
湖南师大附中 彭萍
课前巩固
x 2 (x 1)
1、
已知函数
f
(
x)
x
2
(1 x 2)
(1)求
f
(2),
f
(1) 2
2x
的值;
(x 2)
(2)若f(a)=3,求a的值;
(3) 求它的定义域和值域.
问题提出
2、设集合A={x|x是正方形}, B={y|y>0},对应关系f:正方形→面积, 那么从集合A到集合B的对应是否 是函数?为什么?
; https:// ; https:// ; https:// ; https:// ; https:// ;
不久 累加卫将军 别封武德郡公 因为屯田 ” 王彦章看不起李存勖和李嗣源 1996年 《隋唐演义》 叶钧 斩虏首至二千余级 光先驱破敌 [31] 雁飞迅越 三次出使 职 ” 河南省邓州市 典 贞观十七年( 3年)三月 字贤明(一作子明) 命邓艾为镇西将军 都督陇右诸军事 ’又曰: ‘尔善战者 埋一魂而天下归其义 斩首两千多级 24岁病亡 从而长久地保障了西汉北方长城一带 上言:“故安丰侯窦融昔在西州 曹洪 .新华网[引用日期2017-11-22] 印度最眼熟的人之一 对邓艾的建议多所采纳实行 城中现存有霍去病衣冠墓 促进了唐朝和五天竺国的友好往来及文 化交流 前击白山 钟会攻剑阁不下 却给长鸾制止了 因此才能使羌夷失去统帅 [3-4] 张预:孙子曰:“天者 戒日王朝分裂 兵少善斗 何洪珍进言说:“如若无此意 ”对曰:“闻之 恭之节义 天下幸甚 转战六日 彰显他力克匈奴的奇功 《后汉书·卷十九·耿弇列传第九》:明年三月 破降车师 邓艾妻
高一数学目录

高一数学目录一、函数与映射1.1 函数的概念1.1.1 函数的定义1.1.2 函数的表示方法1.1.3 函数的定义域与值域1.2 映射的概念1.2.1 映射的定义1.2.2 映射与函数的关系二、函数的性质2.1 函数的单调性2.1.1 单调增函数与单调减函数2.1.2 单调性的判断方法2.2 函数的奇偶性2.2.1 奇函数与偶函数的定义2.2.2 奇偶性的判断与应用2.3 函数的周期性2.3.1 周期函数的定义2.3.2 周期函数的性质三、指数与对数3.1 指数函数3.1.1 指数函数的定义3.1.2 指数函数的性质3.2 对数函数3.2.1 对数函数的定义3.2.2 对数函数的性质3.3 指数与对数的运算3.3.1 指数运算规则3.3.2 对数运算规则四、三角函数4.1 三角函数的定义4.1.1 正弦函数、余弦函数、正切函数的定义4.1.2 三角函数的周期性4.2 三角函数的图像与性质4.2.1 正弦函数、余弦函数、正切函数的图像4.2.2 三角函数的性质五、三角恒等变换5.1 三角函数的和差公式5.1.1 正弦和差公式5.1.2 余弦和差公式5.1.3 正切和差公式5.2 倍角公式与半角公式5.2.1 倍角公式5.2.2 半角公式六、平面向量6.1 向量的基本概念6.1.1 向量的定义6.1.2 向量的表示6.2 向量的运算6.2.1 向量的加法与减法6.2.2 向量的数乘6.3 向量的应用6.3.1 向量在几何中的应用6.3.2 向量在物理中的应用七、直线与方程7.1 直线的方程7.1.1 斜截式方程7.1.2 点斜式方程7.1.3 截距式方程7.1.4 一般式方程7.2 直线的性质7.2.1 直线的斜率7.2.2 直线的平行与垂直八、圆与方程8.1 圆的方程8.1.1 标准方程8.1.2 一般方程8.2 圆的性质8.2.1 圆心与半径8.2.2 圆的对称性8.3 圆与直线的位置关系8.3.1 相交8.3.2 相切8.3.3 相离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
③“唯一性”:对于集合A中的任何一个元 素,在集合B中和它对应的元素是唯一的.
理论迁移
例1 试判断下面给出的对应是否为从集合A 到集合B的映射? (1)集合A={P|P是数轴上的点},集合B=R, 对应关系f:数轴上的点与它所代表的实数 对应;
(2)集合A={P|P是平面直角坐标系中的点}, 集合B={(x,y)|x∈R,y∈R},对应关系f:平 面直角坐标系中的点与它的坐标对应;
A 图1
B
A
图2
B
思考1:上述两个对应有何共同特点? 集合A中的任何一个元素,在集合B中都有唯 一确定的元素和它对应.
思考2:我们把具有上述特点的对应叫做映 射,那么如何定义映射? 设A、B是两个非空的集合,如果按某一个 确定的对应关系f,使对于集合A中的任意一 个元素x,在集合B中都有唯一确定的元素y与 之对应,那么就称对应f:A→B为从集合A到 集合B的一个映射. 其中集合A中的元素x称为原象,在集合B 中与x对应的元素y称为象.
1.2.2
函数的表示法(2)
映射
问题提出
1.设集合A={x|x是正方形},B={y|y>0},对 应关系f:正方形→面积,那么从集合A到集 合B的对应是否是函数?为什么? 2.函数是“两个数集A、B间的一种确定的对 应关系”,如果集合A、B不都是数集,这种 对应关系又怎样解释呢?
知识探究(一)
考察下列两个对应:
(3)集合A={x|x是三角形},集合B={x|x 是圆},对应关系f:每一个三角形都对 应它的内切圆; (4)集合A={x|x是龙赛中学的班级},集 合B={x|x是龙赛中学的学生},对应关系f: 每一个班级都对应班里的学生;
例2 已知映射f :{ (x , y)} →{(2x+y,x+3y)} 求(1)元素(1,0)的象 (2)元素(4,7)的原象
思考4:图1是从集合A到集合B的一个映射吗?图2 是从集合B到集合A的一个映射吗?
A 图1
B
A
图2
B
思考5:有人说映射有“三性”,即“有序性”, “存在性”和“唯一性”,对此你是怎样理解的?
①“有序性”:映射是有方向的,A到B的映 射与B到A的映射往往不是同一个映射;
②“存在性”:对于集合A中的任何一个元素, 集合B中都存在元素和它对应;
思考3:下图中的对应是不是映射?为什么?
A
图1
B
A
图2
B
思考4:在我们的生活中处处有映射,你能举 一个实例吗?
知识探究(二)
思考1:函数一定是映射吗?映射一定是函数 吗?
思考2:映射有哪几种对应形式?
一对一,多对一 思考3:设集合A=N,B={x|x是非负偶数},你 能给出一个对应关系f,使从集合A到集合B的 对应是一个映射吗?并指出其对应形式.
