2016年普通高等学校招生全国统一考试(正文)
2016年普通高等学校招生全国统一考试(正文)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理综物理第Ⅰ卷二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14—18题只有一项符合题目要求,第19—21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.关于行星运动的规律,下列说法符合史实的是()A.开普勒在牛顿定律的基础上,导出了行星运动的规律B.开普勒在天文观测数据的基础上,总结出了行星运动的规律C.开普勒总结出了行星运动的规律,找出了行星按照这些规律运动的原因D.开普勒总结出了行星运动的规律,发现了万有引力定律15.关于静电场的等势面,下列说法正确的是()A.两个电势不同的等势面可能相交B.电场线与等势面处处相互垂直C.同一等势面上各点电场强度一定相等D.将一负的试探电荷从电势较高的等势面移至电势较低的等势面,电场力做正功16.一质点做速度逐渐增大的匀加速直线运动,在时间间隔t内位移为s,动能变为原来的9倍。
该质点的加速度为()A.st2B.3s2t2C.4st2D.8st217.如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m的小球。
在a和b之间的细线上悬挂一小物块。
平衡时,a、b间的距离恰好等于圆弧的半径。
不计所有摩擦。
小物块的质量为()A.m2B.√32m C.m D.2m18.平面OM和平面ON之间的夹角为30°,其横截面(纸面)如图所示,平面OM上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外。
一带电粒子的质量为m,电荷量为q(q>0)。
粒子沿纸面以大小为v的速度从OM的某点向左上方射入磁场,速度与OM成30°角。
已知该粒子在磁场中的运动轨迹与ON只有一个交点,并从OM上另一点射出磁场。
不计重力。
粒子离开磁场的出射点到两平面交线O的距离为()A.mv2qB B.√3mvqBC.2mvqBD.4mvqB19.如图,理想变压器原、副线圈分别接有额定电压相同的灯泡a和b。
2016普通高等学校招生全国统一考试(新课标I)(含答案)

高考真题及答案2016普通高等学校招生全国统一考试(新课标I)英语试卷类型A第Ⅰ 卷第一部分听力(共两节,满分30 分)做题时,现将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共 5 小题;每小题 1.5 分,满分7.5 分)听下面 5 段对话,每段对话后有一个小题。
从题中所给的A、 B、 C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例: How much is the shirt?A. £19. 15B.9£.18C.9£.15答案是C。
1. What are the speakers talking about?A. Having a birthday party.B. Doing some exercise.C. Getting Lydia a gift.2. What is the woman going to do?3. What does the woman suggest the man do?A. Tell Kate to stop.B. Call Kate, s friends.C. Stay away from Kate.4. Where does the conversation probably take place?5. What does the woman mean?A. Keep the window closed.B. Go out for fresh air.C. Turn on the fan.听第 6 段材料,回答第 6 、 7 题。
6. What is the man going to do this summer?7. How will the man use the money?A. To hire a gardener.B. To buy books.C. To pay for a boat trip.听第 7 段材料,回答第8 、 9 题。
2016年普通高等学校招生全国统一考试(正文)

2016年普通高等学校招生全国统一考试课标全国卷Ⅰ语文本卷满分150分,考试时间150分钟。
第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1—3题。
殷墟甲骨文是商代晚期刻在龟甲兽骨上的文字,是商王室及其他贵族利用龟甲兽骨占卜吉凶时写刻的卜辞和与占卜有关的记事文字。
殷墟甲骨文的发现对中国学术界产生了巨大而深远的影响。
甲骨文的发现证实了商王朝的存在。
历史上,系统讲述商史的是司马迁的《史记·殷本纪》,但此书撰写的时代距商代较远;即使公认保留了较多商人语言的《尚书·盘庚》篇,其中亦多杂有西周时的词语,显然是被改造过的文章。
因此,胡适曾主张古史作为研究对象,可“缩短二三千年,从诗三百篇做起”。
甲骨文的发现,将商人亲手书写、契刻的文字展现在学者面前,使商史与传说时代分离而进入历史时代。
特别是1917年王国维写了《殷卜辞中所见先公先王考》及《续考》,证明《史记·殷本纪》与《世本》所载殷王世系几乎皆可由卜辞资料印证,是基本可靠的。
论文无可辩驳地证明《殷本纪》所载的商王朝是确实存在的。
甲骨文的发现也使《史记》之类的历史文献中有关中国古史记载的可信性增强。
因为这一发现促使史学家们想到,既然《殷本纪》中的商王世系基本可信,司马迁的《史记》也确如刘向、扬雄所言是一部“实录”,那么司马迁在《史记·夏本纪》中所记录的夏王朝与夏王世系恐怕也不是向壁虚构。
特别是在20世纪20年代疑古思潮流行时期,甲骨文资料证实了《殷本纪》与《世本》的可靠程度,也使历史学家开始摆脱困惑,对古典文献的可靠性恢复了信心。
甲骨文的发现同时引发了震撼中外学术界的殷墟发掘。
“五四运动”促使中国的历史学界发生两大变化:一是提倡实事求是的科学态度,古史辨派对一切经不住史证的旧史学的无情批判,使人痛感中国古史上科学的考古资料的极端贫乏;二是历史唯物主义在史学界产生了巨大影响。
1925年王国维在清华国学研究院讲授《古史新证》,力倡“二重证据法”,亦使中国历史学研究者开始注重地下出土的新材料。
2016普通高等学校招生全国统一考试甲乙丙卷详解版

2016普通高等学校招生全国统一考试(新课标Ⅰ卷)我国是世界闻名的陶瓷古国,明清时期,“瓷都”景德镇是全国的瓷业中心,产品远销海内外,20世纪80年代初,广东省佛山市率先引进国外现代化陶瓷生产线,逐步发展成为全国乃至世界最大的陶瓷生产基地。
2003年,佛山陶瓷主产区被划入中心城区范围,陶瓷产业向景德镇等陶瓷产地转移。
据此完成1-3题。
1.与景德镇相比,20世纪80年代佛山瓷业迅速发展的主要原因是A.市场广阔B.原材料充足C.劳动力素质高D.国家政策倾斜2.促使佛山陶瓷产业向外转移的主要原因是佛山A.产业结构调整B.原材料枯竭C.市场需求减小D.企业竞争加剧3.景德镇吸引佛山陶瓷产业转移的主要优势是A.资金充足B.劳动力成本低C.产业基础好D.交通运输便捷【答案】1.D 2.A 3.C试题分析:1.注意抓住时间,20世纪80年,结合材料“20世纪80年代初,广东省佛山市率先引进国外现代化陶瓷生产线,逐步发展成为全国乃至世界最大的陶瓷生产基地。
”注意不要错选“市场广阔”,虽然材料中提到“全国乃至世界最大的陶瓷生产基地”,但是材料中是“逐步发展成为全国乃至世界最大的陶瓷生产基地”,这是佛山瓷业迅速发展的结果,获得了广阔的市场,不是佛山瓷业迅速发展的原因。
结合所学知识,在20世纪80年代初,珠三角的是我国改革开放的前沿,政策优势明显,国家政策倾斜使得佛山市率先引进国外现代化陶瓷生产线。
佛山瓷业发展的原材料并不充足,20世纪80年代,劳动力素质也不高。
2.材料“佛山陶瓷主产区被划入中心城区范围,陶瓷产业向景德镇等陶瓷产地转移”,这说明原来佛山陶瓷产业区变成发展以第三产业为主的中心城区,即佛山市的产业结构调整促使佛山陶瓷产业向外转移;原材料和市场需求并没有发生明显变化,企业竞争加剧不是促使佛山陶瓷产业向外转移的主要原因。
3、景德镇陶瓷发展历史悠久,明清时期,“瓷都”景德镇是全国的瓷业中心,产业基础好是吸引佛山陶瓷产业转移的主要优势,相比佛山市,景德镇在资金和交通方面没有优势,劳动力成本低是景德镇相对佛山一个优势,但不是主要优势,因为还有比景德镇劳动力成本更低的地区,所以景德镇吸引佛山陶瓷产业转移的主要优势是陶瓷产业基础好。
2016年普通高等学校招生全国统一考试(答案)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅲ)第二部分阅读理解第一节A21.A细节理解题。
根据文章第一段中的Opera和电话号码可知答案为A。
22.B细节理解题。
根据第二段中的which offers several concerts from March through June可知五月符合题意。
23.C细节理解题。
根据第四段中的前两句和Students with I.D.cards can attend the events for free.可知选C。
24.A细节理解题。
根据最后一段中的Large outdoor theater with the closest seats under cover 可知这个剧场有户外的座位。
B25.A细节理解题。
根据文章第三段...the woman joined the Welty party. When her dinner partner showed up...可以得知选A。
干扰项为C项,虽然有大雨,但是没有破坏他们的晚餐,所以排除C选项。
26.D词义猜测题。
根据上文中的Now we believe your stories可以推断出选D。
27.C推理判断题。
根据第八段中的I don’t make them up和最后一段,可以推断出她的小说中的人物来自真实的生活。
C28.D细节理解题。
根据第二段第一句Visiting an apple event is a good chance to see,and often taste,a wide variety of apples.可知可以品尝到很多品种的苹果。
故选D。
29.C细节理解题。
根据第二段中的it can be quite an eye opener to see the range of classical apples still in existence,such as Decio which was grown by the Romans可知选C。
2016年普通高等学校招生全国统一考试(答案)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅰ)1.B 核糖体不具有膜结构,A错误;酵母菌属于真核生物,其细胞核中含有DNA和RNA,B正确;蓝藻属于原核生物,细胞中不具有线粒体,C错误;叶绿体类囊体薄膜上进行的光反应过程中有ATP的合成,D错误。
2.C 由题意知,离子泵参与的跨膜运输方式属于主动运输,需要载体蛋白协助,需要消耗能量,是逆浓度梯度进行的,A、B错误;动物一氧化碳中毒会影响血液中氧气的运输,影响有氧呼吸产生ATP,从而降低离子泵跨膜运输离子的速率,C正确;蛋白质变性剂可使离子泵变性失活,会降低离子泵跨膜运输离子的速率,D错误。
3.C 测定酶活力的实验中缓冲液可维持溶液的pH,所以缓冲液应在底物与酶混合之前加入,反应时间的测定则应在底物与酶混合之后开始,据此可判断C项符合题意。
4.B 线粒体内膜上进行有氧呼吸的第三阶段,可产生ATP,A正确;突触间隙中的组织液属于细胞外液,神经递质通过扩散的方式在突触间隙中移动,不需要消耗ATP,B错误;蛋白质的合成需要消耗ATP,C正确;神经细胞兴奋后恢复为静息状态的过程中有K+外流和排钠吸钾(钠钾泵)过程,其中后者为逆浓度梯度运输,需要消耗ATP,D正确。
5.B 生态系统中生产者固定的能量最终以热能的形式散失,而散失的热能不能被生态系统重新利用,故生态系统中的能量具有单向流动的特点,B错误。
6.D 理论上,若常染色体隐性遗传病的致病基因频率为p,则男性和女性中的发病率均为p2,A错误;若常染色体显性遗传病的致病基因频率为q,则正常基因频率为1-q,男性和女性中正常的概率均为(1-q)2,患病概率均为1-(1-q)2=2q-q2,B错误;若X染色体隐性遗传病的致病基因频率为n,则男性(X-Y)中的发病率为n,D正确;若X染色体显性遗传病的致病基因频率为m,则正常基因频率为1-m,女性中正常的概率为(1-m)2,患病概率为1-(1-m)2=2m- m2,C错误。
2016年普通高等学校招生全国统一考试 试卷及答案(极品word版)

2016年普通高等学校招生全国统一考试理科数学注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成,答在本试题上无效. 4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合2{|430}A x x x =-+<,{|230}B x x =->,则A B = ( ) (A )3(3,)2--(B )3(3,)2-(C )3(1,)2(D )3(,3)2(2)设(1i)1i x y +=+,其中x y ,是实数,则i =x y +( )(A )1(B C D )2(3)已知等差数列{}n a 前9项的和为27,10=8a ,则100=a ( )(A )100(B )99(C )98(D )97(4)某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( ) (A )13(B )12(C )23(D )34(5)已知方程222213x y m n m n+=+-表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( )(A )(–1,3) (B )(–1,3) (C )(0,3) (D )(0,3)(6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( ) (A )17π(B )18π(C )20π(D )28π(7)函数y =2x 2–e |x |在[–2,2]的图像大致为( )(A )(B )(C )(D )(8)若101a b c >><<,,则( ) (A )c c a b <(B )c cab ba <(C )log log b a a c b c <(D )log log a b c c <(9)执行下面的程序图,如果输入的011x y n ===,,,则输出x ,y 的值满足( ) (A )2y x =(B )3y x =(C )4y x =(D )5y x =(10)以抛物线C 的顶点为圆心的圆交C 于A 、B 两点,交C 的准线于D 、E 两点.已知|AB |=|DE|=C 的焦点到准线的距离为( ) (A)2 (B)4 (C)6 (D)8(11)平面α过正方体ABCD -A 1B 1C 1D 1的顶点1A ,α//平面CB 1D 1,α⋂平面ABCD =m ,α⋂平面ABB 1A 1=n ,则m 、n 所成角的正弦值为( )(B (D)13 (12).已知函数()s i n ()(0),24f x x+x ππωϕωϕ=>≤=-,为()f x 的零点,4x π=为()y f x =图像的对称轴,且()f x 在51836ππ⎛⎫⎪⎝⎭,单调,则ω的最大值为( )(A )11 (B )9 (C )7 (D )5第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答. 二、填空题:本大题共3小题,每小题5分(13)设向量a =(m ,1),b =(1,2),且|a +b |2=|a |2+|b |2,则m =.(14)5(2x 的展开式中,x 3的系数是.(用数字填写答案)(15)设等比数列满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为。
2016年高考真题——全国Ⅰ卷(扫描版含答案).doc

2016年普通高等学校招生全国统一考试理科综合能力测试(化学)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束后,将本试题和答题卡一并交回。
第Ⅰ卷(选择题共126分)本卷共21小题,每小题6分,共126分。
可能用到的相对原子质量:一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
7.化学与生活密切相关,下列有关说法错误的是A.用灼烧的方法可以区分蚕丝和人造纤维B.食用油反复加热会产生稠环芳香烃等有害物质C.加热能杀死流感病毒是因为蛋白质受热变性D.医用消毒酒精中乙醇的浓度为95%8.设N A为阿伏加德罗常数值。
下列有关叙述正确的是A.14 g乙烯和丙烯混合气体中的氢原子数为2N AB.1 molN2与4 molH2反应生成的NH3分子数为2N AC.1 molFe溶于过量硝酸,电子转移数为2N AD.标准状况下,2.24 LCCl4含有的共价键数为0.4N A9.下列关于有机化合物的说法正确的是A.2-甲基丁烷也称异丁烷B.由乙烯生成乙醇属于加成反应C.C4H9Cl有3中同分异构体D.油脂和蛋白质都属于高分子化合物10.下列实验操作能达到实验目的的是A.用长颈漏斗分离出乙酸与乙醇反应的产物B.用向上排空气法收集铜粉与稀硝酸反应产生的NOC.配制氯化铁溶液时,将氯化铁溶解在较浓的盐酸中再加水稀释D.将Cl2与HCl混合气体通过饱和食盐水可得到纯净的Cl211.三室式电渗析法处理含Na2SO4废水的原理如图所示,采用惰性电极,ab、cd均为离子交换膜,在直流电场的作用下,两膜中间的Na +和可通过离子交换膜,而两端隔室中离子被阻挡不能进入中间隔室。
下列叙述正确的是 A.通电后中间隔室的24SO -离子向正极迁移,正极区溶液pH 增大B.该法在处理含Na 2SO 4废水时可以得到NaOH 和H 2SO 4产品C.负极反应为2H 2O –4e –=O 2+4H +,负极区溶液pH 降低D.当电路中通过1mol 电子的电量时,会有0.5mol 的O 2生成 12.298K 时,在20.0mL 0.10mol24SO-氨水中滴入0.10mol24SO-的盐酸,溶液的pH 与所加盐酸的体积关系如图所示。
教育部关于印发《2016年普通高等学校招生全国统一考试考务工作规定》的通知

教育部关于印发《2016年普通高等学校招生全国统一考试考务工作规定》的通知作者:来源:《云南教育·视界》2016年第05期各省、自治区、直辖市高等学校招生委员会、教育厅(教委):按照我部做好普通高等学校招生全国统一考试工作的要求和部署,现将《2016年普通高等学校招生全国统一考试考务工作规定》印发给你们,请遵照执行。
2016年普通高等学校招生全国统一考试考务工作规定第一章总则第一条为健全普通高等学校招生全国统一考试(以下简称全国统考)考务工作制度,规范考试管理,保障考试的正常实施,根据《教育法》《高等教育法》及有关法律、法规,制定本规定。
第二条除经教育部批准外,普通高等学校招生实行全国统考(包含“分省命题”的统一考试)。
全国统考的基本原则是公平、安全、科学、规范。
第三条全国统考的试题(包括副题、带试题内容的答题卡,下同)在启封并使用完毕前按国家绝密级事项管理;答案及评分参考在考试结束前按国家绝密级事项管理。
第四条全国统考考务工作由教育部领导,教育部考试中心负责管理,地方各级教育考试机构组织实施。
教育部和各省(区、市)设立考试安全类突发事件应急处置工作组,负责考试中突发事件的处置。
根据教育部的部署,各省级教育考试机构在省级人民政府及其招生委员会的领导下,组织实施和管理本地区的考试工作。
第五条各级教育考试机构应采用现代化技术手段管理全国统考工作。
第二章考试工作人员第六条各级教育考试机构应当配备与所承担的全国统考考务工作任务相适应的专职与兼职相结合的考试工作人员。
第七条考试工作人员的基本条件是:拥护党的路线、方针、政策,遵纪守法,熟悉业务,工作认真负责,身体健康。
第八条考试工作人员实行岗位聘任制,经培训、考核合格后持证上岗。
第九条专职考试工作人员如有直系亲属或者利害关系人参加当次全国统考的,应回避接触考试的试题、答案及评分参考、答卷等涉密材料;兼职人员如有直系亲属或者利害关系人参加当次全国统考的,不得参加考试工作。
2016年普通高等学校招生全国统一考试(答案)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅱ)一、选择题-⇒-3<m<1.故选A.1.A由已知可得-⇒2.C由(x+1)(x-2)<0⇒-1<x<2,又x∈Z,∴B={0,1},∴A∪B={0,1,2,3}.故选C.3.D由题可得a+b=(4,m-2),又(a+b)⊥b,∴4×3-2×(m-2)=0,∴m=8.故选D.4.A圆的方程可化为(x-1)2+(y-4)2=4,则圆心坐标为(1,4),圆心到直线ax+y-1=0的距离为=1,解得a=-.故选A.5.B分两步,第一步,从E→F,有6条可以选择的最短路径;第二步,从F→G,有3条可以选择的最短路径.由分步乘法计数原理可知有6×3=18条可以选择的最短路径.故选B.6.C由三视图可得圆锥的母线长为=4,∴S圆锥侧=π×2×4=8π.又S圆柱侧=2π×2×4=16π,S圆柱底=4π,∴该几何体的表面积为8π+16π+4π=28π.故选C.7.B将函数y=2sin 2x的图象向左平移个单位长度得到函数y=2sin2=2sin的图象,由2x+=kπ+(k∈Z),可得x=+(k∈Z).则平移后图象的对称轴为x=+(k∈Z),故选B.8.C k=0,s=0,输入a=2,s=0×2+2=2,k=1;输入a=2,s=2×2+2=6,k=2;输入a=5,s=6×2+5=17,k=3>2,输出s=17.故选C.9.D解法一:sin 2α=cos-=cos 2-=2cos2--1=2×-1=-.故选D.解法二:cos-=(cos α+sinα)=⇒cos α+sinα=⇒1+sin 2α=,∴sin2α=-.故选D. 10.C如图,数对(x i,y i)(i=1,2,…,n)表示的点落在边长为1的正方形OABC内(包括边界),两数的平方和小于1的数对表示的点落在半径为1的四分之一圆(阴影部分)内,则由几何概型的概率公式可得=⇒π=.故选C.11.A解法一:由MF1⊥x轴,可得M-,∴|MF1|=.由sin∠MF2F1=,可得cos∠MF2F1=-=,又tan∠MF2F1==,∴=,∴b2=ac,∵c2=a2+b2⇒b2=c2-a2,∴c2-a2-ac=0⇒e2-e-1=0,∴e=.故选A.解法二:由MF1⊥x轴,得M-,∴|MF1|=,由双曲线的定义可得|MF2|=2a+|MF1|=2a+,又sin∠MF2F1===⇒a2=b2⇒a=b,∴e==.故选A.12.B由f(-x)=2-f(x)可知f(x)的图象关于点(0,1)对称,又易知y==1+的图象关于点(0,1)对称,所以两函数图象的交点成对出现,且每一对交点都关于点(0,1)对称,则x1+x m=x2+x m-1=…=0,y1+y m=y2+y m-1=…=2,∴(x i+y i)=0×+2×=m.故选B.二、填空题13.答案解析由已知可得sin A=,sin C=,则sin B=sin(A+C)=×+×=,再由正弦定理可得=⇒b==.14.答案②③④解析由m⊥n,m⊥α,可得n∥α或n在α内,当n∥β时,α与β可能相交,也可能平行,故①错.易知②③④都正确.15.答案1和3解析由丙说的话可知丙的卡片上的数字一定不是2和3.若丙的卡片上的数字是1和2,则乙的卡片上的数字是2和3,甲的卡片上的数字是1和3,满足题意;若丙的卡片上的数字是1和3,则乙的卡片上的数字是2和3,此时,甲的卡片上的数字只能是1和2,不满足题意.故甲的卡片上的数字是1和3.16.答案1-ln 2解析直线y=kx+b与曲线y=ln x+2,y=ln(x+1)均相切,设切点分别为A(x 1,y1),B(x2,y2),由y=ln x+2得y'=,由y=ln(x+1)得y'=,∴k==,∴x1=,x2=-1,∴y1=-ln k+2,y2=-ln k.即A-,B--,∵A、B在直线y=kx+b上,∴---⇒-三、解答题17.解析(Ⅰ)设{a n}的公差为d,据已知有7+21d=28, 解得d=1.所以{a n}的通项公式为a n=n.b1=[lg 1]=0,b11=[lg 11]=1,b101=[lg 101]=2.(6分)(Ⅱ)因为b n=(9分)所以数列{b n}的前1 000项和为1×90+2×900+3×1=1 893.(12分)18.解析(Ⅰ)设A表示事件:“一续保人本年度的保费高于基本保费”,则事件A发生当且仅当一年内出险次数大于1,故P(A)=0.2+0.2+0.1+0.05=0.55.(3分)(Ⅱ)设B表示事件:“一续保人本年度的保费比基本保费高出60%”,则事件B发生当且仅当一年内出险次数大于3,故P(B)=0.1+0.05=0.15.又P(AB)=P(B),故P(B|A)====.因此所求概率为.(7分)(Ⅲ)记续保人本年度的保费为X元,则X的分布列为EX=0.85a×0.30+a×0.15+1.25a×0.20+1.5a×0.20+1.75a×0.10+2a×0.05=1.23a.因此续保人本年度的平均保费与基本保费的比值为1.23.(12分)19.解析(Ⅰ)由已知得AC⊥BD,AD=CD.又由AE=CF得=,故AC∥EF.因此EF⊥HD,从而EF⊥D'H.(2分)由AB=5,AC=6得DO=BO=-=4.由EF∥AC得==.所以OH=1,D'H=DH=3.于是D'H2+OH2=32+12=10=D'O2,故D'H⊥OH.(4分)又D'H⊥EF,而OH∩EF=H,所以D'H⊥平面ABCD.(5分)(Ⅱ)如图,以H为坐标原点,的方向为x轴正方向,建立空间直角坐标系H-xyz.则H(0,0,0),A(-3,-1,0),B(0,-5,0),C(3,-1,0),D'(0,0,3),=(3,-4,0),=(6,0,0),=(3,1,3).(6分)设m=(x1,y1,z1)是平面ABD'的法向量,-则即所以可取m=(4,3,-5).(8分)设n=(x2,y2,z2)是平面ACD'的法向量,则即所以可取n=(0,-3,1).(10分)于是cos<m,n>===-.sin<m,n>=.因此二面角B-D'A-C的正弦值是.(12分)20.解析(Ⅰ)设M(x 1,y1),则由题意知y1>0.当t=4时,E的方程为+=1,A(-2,0).(1分)由已知及椭圆的对称性知,直线AM的倾斜角为.因此直线AM的方程为y=x+2.(2分)将x=y-2代入+=1得7y2-12y=0.解得y=0或y=,所以y1=.(4分)因此△AMN的面积S△AMN=2×××=.(5分)(Ⅱ)由题意,t>3,k>0,A(-,0).将直线AM的方程y=k(x+) 代入+=1得(3+tk2)x2+2tk2x+t2k2-3t=0.(7分)由x1(-)=-得x1=-,故|AM|=|x1+ |=.(8分)由题设,直线AN的方程为y=-(x+),故同理可得|AN|=.(9分)由2|AM|=|AN|得=,即(k3-2)t=3k(2k-1).当k=时上式不成立,因此t=--.(10分)t>3等价于---=--<0,即--<0.(11分)由此得--或--解得<k<2.因此k的取值范围是(,2).(12分)21.解析(Ⅰ)f(x)的定义域为(-∞,-2)∪(-2,+∞).(2分)f '(x)=---=≥0,且仅当x=0时, f '(x)=0,所以f(x)在(-∞,-2),(-2,+∞)单调递增.因此当x∈(0,+∞)时, f(x)>f(0)=-1.所以(x-2)e x>-(x+2),(x-2)e x+x+2>0.(4分)(Ⅱ)g'(x)=-=(f(x)+a).(5分)由(Ⅰ)知, f(x)+a单调递增.对任意a∈[0,1), f(0)+a=a-1<0, f(2)+a=a≥0.因此,存在唯一x a∈(0,2],使得f(x a)+a=0,即g'(x a)=0.(6分)当0<x<x a时, f(x)+a<0,g'(x)<0,g(x)单调递减;当x>x a时, f(x)+a>0,g'(x)>0,g(x)单调递增.(7分)因此g(x)在x=x a处取得最小值,最小值为g(x a)=-==.(8分)于是h(a)=,由'=>0,得y=单调递增.所以,由x a∈(0,2],得=<h(a)=≤=.(10分)因为y=单调递增,对任意λ∈,存在唯一的x a∈(0,2],a=-f(x a)∈[0,1),使得h(a)=λ.所以h(a)的值域是.综上,当a∈[0,1)时,g(x)有最小值h(a),h(a)的值域是.(12分)22.解析(Ⅰ)因为DF⊥EC,所以△DEF∽△CDF,则有∠GDF=∠DEF=∠FCB,==,所以△DGF∽△CBF,由此可得∠DGF=∠CBF.因此∠CGF+∠CBF=180°,所以B,C,G,F四点共圆.(5分)(Ⅱ)由B,C,G,F四点共圆,CG⊥CB知FG⊥FB.连结GB.由G为Rt△DFC斜边CD的中点,知GF=GC,故Rt△BCG≌Rt△BFG,因此,四边形BCGF的面积S是△GCB面积S△GCB的2倍,即S=2S△GCB=2×××1=.(10分)23.解析(Ⅰ)由x=ρcosθ,y=ρsinθ可得圆C的极坐标方程ρ2+12ρcosθ+11=0.(3分) (Ⅱ)在(Ⅰ)中建立的极坐标系中,直线l的极坐标方程为θ=α(ρ∈R).(4分)设A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入C的极坐标方程得ρ2+12ρcos α+11=0.于是ρ1+ρ2=-12cos α,ρ1ρ2=11.(6分)|AB|=|ρ1-ρ2|=-=-.(8分)由|AB|=得cos2α=,tan α=±.(9分)所以l的斜率为或-.(10分)24.解析(Ⅰ)f(x)=---(2分)当x≤-时,由f(x)<2得-2x<2,解得x>-1;(3分) 当-<x<时, f(x)<2;(4分)当x≥时,由f(x)<2得2x<2,解得x<1.(5分)所以f(x)<2的解集M={x|-1<x<1}.(6分)(Ⅱ)证明:由(Ⅰ)知,当a,b∈M时,-1<a<1,-1<b<1,从而(a+b)2-(1+ab)2=a2+b2-a2b2-1=(a2-1)(1-b2)<0.因此|a+b|<|1+ab|.(10分)。
2016年普通高等学校招生全国统一考试(答案)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅱ)一、选择题1.D 由已知得B={x|-3<x<3},∵A={1,2,3},∴A∩B={1,2},故选D.2.C z=3-2i,所以=3+2i,故选C.3.A 由题图可知A=2,=-=,则T=π,所以ω=2,则y=2sin(2x+φ),因为题图经过点,所以2sin=2,所以+φ=2kπ+,k∈Z,即φ=2kπ-,k∈Z,当k=0时,φ=-,所以y=2sin,故选A.4.A 设正方体的棱长为a,则a3=8,解得a=2.设球的半径为R,则2R=a,即R=,所以球的表面积S=4πR2=12π.故选A.5.D 由题意得点P的坐标为(1,2).把点P的坐标代入y=(k>0)得k=1³2=2,故选D.6.A 由圆的方程可知圆心为(1,4).由点到直线的距离公式可得=1,解得a=-,故选A.7.C 由三视图知圆锥的高为2,底面半径为2,则圆锥的母线长为4,所以圆锥的侧面积为³4π³4=8π.圆柱的底面积为4π,圆柱的侧面积为4³4π=16π,从而该几何体的表面积为8π+16π+4π=28π,故选C.8.B 行人在红灯亮起的25秒内到达该路口,即满足至少需要等待15秒才出现绿灯,根据几何概型的概率公式知所求事件的概率P==,故选B.9.C 执行程序框图,输入a为2时,s=0³2+2=2,k=1,此时k>2不成立;再输入a为2时,s=2³2+2=6,k=2,此时k>2不成立;再输入a为5,s=6³2+5=17,k=3,此时k>2成立,结束循环,输出s为17,故选C.10.D 函数y=10lg x的定义域、值域均为(0,+∞),而y=x,y=2x的定义域均为R,排除A,C;y=lg x的值域为R,排除B,故选D.11.B f(x)=1-2sin2x+6sin x=-2+,当sin x=1时, f(x)取得最大值5,故选B.f(x)=cos 2x+6cos转化为关于12.B 由题意可知f(x)的图象关于直线x=1对称,而y=|x2-2x-3|=|(x-1)2-4|的图象也关于直线x=1对称,所以两个图象的交点关于直线x=1对称,且每对关于直线x=1对称的交点的横二、填空题13.答案-6解析因为a∥b,所以=,解得m=-6.14.答案-5解析由约束条件画出可行域,如图中阴影部分所示(包括边界).当直线x-2y-z=0过点B(3,4)时,z取得最小值,z min=3-2³4=-5.15.答案解析由cos C=,0<C<π,得sin C=.由cos A=,0<A<π,得sin A=.所以sin B=sin[π-(A+C)]=sin(A+C)=sin Acos C+sin Ccos A=,根据正弦定理得b==.16.答案1和3解析丙的卡片上的数字之和不是5,则丙有两种情况:①丙的卡片上的数字为1和2,此时乙的卡片上的数字为2和3,甲的卡片上的数字为1和3,满足题意;②丙的卡片上的数字为1和3,此时乙的卡片上的数字为2和3,甲的卡片上的数字为1和2,这时甲与乙的卡片上有相同的数字2,与已知矛盾,故情况②不符合,所以甲的卡片上的数字为1和3.三、解答题17.解析(Ⅰ)设数列{a n}的公差为d,由题意有2a1+5d=4,a1+5d=3.解得a1=1,d=.(3分)所以{a n}的通项公式为a n=.(5分)(Ⅱ)由(Ⅰ)知,b n=.(6分)当n=1,2,3时,1≤<2,b n=1;当n=4,5时,2≤<3,b n=2;当n=6,7,8时,3≤<4,b n=3;当n=9,10时,4≤<5,b n=4.(10分)所以数列{b n}的前10项和为1³3+2³2+3³3+4³2=24.(12分)18.解析(Ⅰ)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为=0.55,故P(A)的估计值为0.55.(3分)(Ⅱ)事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为=0.3,故P(B)的估计值为0.3.(6分)(Ⅲ)由所给数据得(10分) 调查的200名续保人的平均保费为0.85a³0.30+a³0.25+1.25a³0.15+1.5a³0.15+1.75a³0.10+2a³0.05=1.192 5a.因此,续保人本年度平均保费的估计值为1.192 5a.(12分)19.解析(Ⅰ)证明:由已知得AC⊥BD,AD=CD.又由AE=CF得=,故AC∥EF.(2分)由此得EF⊥HD,EF⊥HD',所以AC⊥HD'.(4分)(Ⅱ)由EF∥AC得==.(5分)由AB=5,AC=6得DO=BO==4.所以OH=1,D'H=DH=3.于是OD'2+OH2=(2)2+12=9=D'H2,故OD'⊥OH.由(Ⅰ)知AC⊥HD',又AC⊥BD,BD∩HD'=H,所以AC⊥平面BHD',于是AC⊥OD'.又由OD'⊥OH,AC∩OH=O,所以OD'⊥平面ABC.(8分)又由=得EF=.五边形ABCFE的面积S=³6³8-³³3=.(10分)所以五棱锥D'-ABCFE的体积V=³³2=.(12分)20.解析(Ⅰ)f(x)的定义域为(0,+∞).当a=4时,f(x)=(x+1)ln x-4(x-1), f '(x)=ln x+-3, f '(1)=-2,f(1)=0.曲线y=f(x)在(1, f(1))处的切线方程为2x+y-2=0.(3分)(Ⅱ)当x∈(1,+∞)时, f(x)>0等价于ln x->0.(4分)设g(x)=ln x-,则g'(x)=-=,g(1)=0.(6分)(i)当a≤2,x∈(1,+∞)时,x2+2(1-a)x+1≥x2-2x+1>0,故g'(x)>0,g(x)在(1,+∞)单调递增,因此g(x)>0;(8分)(ii)当a>2时,令g'(x)=0得x1=a-1-,x2=a-1+.(10分)由x2>1和x1x2=1得x1<1,故当x∈(1,x2)时,g'(x)<0,g(x)在(1,x2)单调递减,因此g(x)<0.(11分)综上,a的取值范围是(-∞,2].(12分)21.解析(Ⅰ)设M(x 1,y1),则由题意知y1>0.由已知及椭圆的对称性知,直线AM的倾斜角为.又A(-2,0),因此直线AM的方程为y=x+2.(2分)将x=y-2代入+=1得7y2-12y=0.解得y=0或y=,所以y1=.因此△AMN的面积S△AMN=2³³³=.(4分)(Ⅱ)将直线AM的方程y=k(x+2)(k>0)代入+=1得(3+4k2)x2+16k2x+16k2-12=0.由x1²(-2)=得x1=,故|AM|=|x1+2|=.由题设,直线AN的方程为y=-(x+2),故同理可得|AN|=.(7分)由2|AM|=|AN|得=,即4k3-6k2+3k-8=0.(9分)设f(t)=4t3-6t2+3t-8,则k是f(t)的零点, f '(t)=12t2-12t+3=3(2t-1)2≥0,所以f(t)在(0,+∞)单调递增.又f()=15-26<0, f(2)=6>0,因此f(t)在(0,+∞)有唯一的零点,且零点k在(,2)内,所以<k<2.(12分)22.解析(Ⅰ)证明:因为DF⊥EC,所以△DEF∽△CDF,则有∠GDF=∠DEF=∠FCB,==,所以△DGF∽△CBF,由此可得∠DGF=∠CBF.因此∠CGF+∠CBF=180°,所以B,C,G,F四点共圆.(5分)(Ⅱ)由B,C,G,F四点共圆,CG⊥CB知FG⊥FB,连结GB.由G为Rt△DFC斜边CD的中点,知GF=GC,故Rt△BCG≌Rt△BFG,因此,四边形BCGF的面积S是△GCB面积S△GCB的2倍,即S=2S△GCB=2³³³1=.(10分)23.解析(Ⅰ)由x=ρcos θ,y=ρsin θ可得圆C的极坐标方程为ρ2+12ρcos θ+11=0.(3分)(Ⅱ)在(Ⅰ)中建立的极坐标系中,直线l的极坐标方程为θ=α(ρ∈R).设A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入C的极坐标方程得ρ2+12ρcos α+11=0.(6分)于是ρ1+ρ2=-12cos α,ρ1ρ2=11.|AB|=|ρ1-ρ2|==.(8分)由|AB|=得cos2α=,tan α=±.(9分)所以l的斜率为或-.(10分)24.解析(Ⅰ)f(x)=(2分)当x≤-时,由f(x)<2得-2x<2,解得x>-1;(3分)当-<x<时, f(x)<2;(4分)当x≥时,由f(x)<2得2x<2,解得x<1,(5分)所以f(x)<2的解集M={x|-1<x<1}.(6分)(Ⅱ)证明:由(Ⅰ)知,当a,b∈M时,-1<a<1,-1<b<1,从而(a+b)2-(1+ab)2=a2+b2-a2b2-1=(a2-1)(1-b2)<0,因此|a+b|<|1+ab|.(10分)。
2016年普通高等学校招生全国统一考试(答案)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅰ)第Ⅰ卷第二部分阅读理解第一节A21.A细节理解题。
根据文章第二段第一句和第二句可知Jane Addams帮助穷人,为和平而努力,做出了很大的贡献,因此判断选A项。
B项“她的教学技能”。
C项“她得奖的努力”。
D 项“她的社区背景”。
这三项文中均未提及。
22.C细节理解题。
根据文章第四段第一句可知:Sandra Day O’Connor 1952年在斯坦福法学院毕业之后,因为是一位女士而不能在律师事务所找到工作,由此可判断当时社会对妇女的歧视,故选C项。
A项,根据文中信息“她从法学院毕业”可知她不缺乏法律的培训。
B项,她法庭经验的缺乏不是找不到工作的理由,原因是她是妇女。
D项,贫穷的经济状况,文中未提及。
discrimination n.歧视。
23.D细节理解题。
根据文章第五段第四句中的kicked off the civil-rights movement可判断Rosa Parks为民权运动做出了贡献,故选D项。
其他三项均和民权运动无关。
24.C推理判断题。
根据全文中四名女士在不同领域做出的贡献可知,她们是自己领域中的先锋人物,故选C项。
A项,文中只提及一人受到了高等教育。
B项,显然几人均和创造性无关。
D项,只有一人的贡献与和平有关。
B25.A细节理解题。
根据文章第一段最后一句中的giving them a closer relationship可知选择A项。
B、C、D三项均为文中未提及的内容。
26.D推理判断题。
根据文章第二段第四句可知,83%的人们说Robinson夫人的决定将会影响美国家庭的祖父母们,由此可判断这些人认为这是一个趋势,故选D项,注意C项错在bad,文中未提及是坏的影响。
27.C细节理解题。
根据文章第三段第一句可知,在20世纪60年代,我们有点野,总想离家更远更快来证明自己可以独立,由此可判断选择C项。
A项,根据他们想离家来证明自己可判断是非常自信的,因此可排除。
2016年普通高等学校招生全国统一考试(正文)(1)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅰ)文 数本卷满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B=( ) A.{1,3}B.{3,5}C.{5,7}D.{1,7}2.设(1+2i)(a+i)的实部与虚部相等,其中a 为实数,则a=( ) A.-3B.-2C.2D.33.为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( ) A.13 B.12C.23D.564.△ABC 的内角A,B,C 的对边分别为a,b,c.已知a=√5,c=2,cos A=23,则b=( )A.√2B.√3C.2D.35.直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为( ) A.13 B.12C.23D.346.将函数y=2sin (2x +π6)的图象向右平移14个周期后,所得图象对应的函数为( ) A.y=2sin (2x +π4)B.y=2sin (2x +π3)C.y=2sin (2x -π4)D.y=2sin (2x -π3)7.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A.17πB.18πC.20πD.28π8.若a>b>0,0<c<1,则( ) A.log a c<log b cB.log c a<log c bC.a c <b cD.c a >c b9.函数y=2x 2-e |x|在[-2,2]的图象大致为( )10.执行下面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y 的值满足( )A.y=2xB.y=3xC.y=4xD.y=5x11.平面α过正方体ABCD-A 1B 1C 1D 1的顶点A,α∥平面CB 1D 1,α∩平面ABCD=m,α∩平面ABB 1A 1=n,则m,n 所成角的正弦值为( ) A.√32B.√22C.√33D.1312.若函数f(x)=x-13sin 2x+asin x 在(-∞,+∞)单调递增,则a 的取值范围是( ) A.[-1,1]B.[-1,13]C.[-13,13]D.[-1,-13]第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分.13.设向量a=(x,x+1),b=(1,2),且a⊥b,则x= .14.已知θ是第四象限角,且sin(θ+π4)=35,则tan(θ-π4)= .15.设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若|AB|=2√3,则圆C的面积为.16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知{a n}是公差为3的等差数列,数列{b n}满足b1=1,b2=13,a n b n+1+b n+1=nb n.(Ⅰ)求{a n}的通项公式;(Ⅱ)求{b n}的前n项和.如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6.顶点P在平面ABC内的正投影为点D,D 在平面PAB内的正投影为点E,连结PE并延长交AB于点G.(Ⅰ)证明:G是AB的中点;(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),n表示购机的同时购买的易损零件数.(Ⅰ)若n=19,求y与x的函数解析式;(Ⅱ)若要求“需更换的易损零件数不大于n”的频率不小于0.5,求n的最小值;(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.;(Ⅰ)求|OH||ON|(Ⅱ)除H以外,直线MH与C是否有其他公共点?说明理由.21.(本小题满分12分)已知函数f(x)=(x-2)e x+a(x-1)2.(Ⅰ)讨论f(x)的单调性;(Ⅱ)若f(x)有两个零点,求a的取值范围.请考生在第22~24题中任选一题作答,如果多做,则按所做的第一题计分. 22.(本小题满分10分)选修4—1:几何证明选讲如图,△OAB 是等腰三角形,∠AOB=120°.以O 为圆心,12OA 为半径作圆. (Ⅰ)证明:直线AB 与☉O 相切;(Ⅱ)点C,D 在☉O 上,且A,B,C,D 四点共圆,证明:AB ∥CD.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy 中,曲线C 1的参数方程为{x =acost ,y =1+asint (t 为参数,a>0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=4cos θ. (Ⅰ)说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(Ⅱ)直线C 3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C 1与C 2的公共点都在C 3上,求a.24.(本小题满分10分)选修4—5:不等式选讲已知函数f(x)=|x+1|-|2x-3|.(Ⅰ)画出y=f(x)的图象;(Ⅱ)求不等式|f(x)|>1的解集.。
2016年普通高等学校招生全国统一考试(正文)
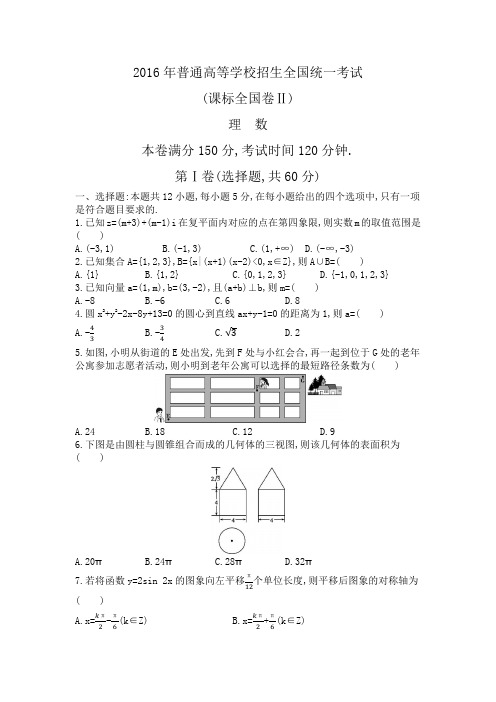
2016年普通高等学校招生全国统一考试(课标全国卷Ⅱ)理数本卷满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知z=(m+3)+(m-1)i在复平面内对应的点在第四象限,则实数m的取值范围是( )A.(-3,1)B.(-1,3)C.(1,+∞)D.(-∞,-3)2.已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=()A.{1}B.{1,2}C.{0,1,2,3}D.{-1,0,1,2,3}3.已知向量a=(1,m),b=(3,-2),且(a+b)⊥b,则m=( )A.-8B.-6C.6D.84.圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=( )A.-B.-C.D.25.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )A.24B.18C.12D.96.下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A.20πB.24πC.28πD.32π7.若将函数y=2sin 2x的图象向左平移个单位长度,则平移后图象的对称轴为( )A.x=-(k∈Z)B.x=+(k∈Z)C.x=-(k∈Z)D.x=+(k∈Z)8.中国古代有计算多项式值的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )A.7B.12C.17D.349.若cos-=,则sin 2α=( )A. B. C.- D.-10.从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为( )A. B. C. D.11.已知F1,F2是双曲线E:-=1的左,右焦点,点M在E上,MF1与x轴垂直,sin∠MF2F1=,则E的离心率为( )A. B. C. D.212.已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(xm,ym),则 (xi+yi)=( )A.0B.mC.2mD.4m第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分.13.△ABC的内角A,B,C的对边分别为a,b,c,若cos A=,cos C=,a=1,则b= .14.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)15.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2.”乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1.”丙说:“我的卡片上的数字之和不是5.”则甲的卡片上的数字是.16.若直线y=kx+b是曲线y=ln x+2的切线,也是曲线y=ln(x+1)的切线,则b= .三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)S n 为等差数列{an}的前n项和,且a1=1,S7=28.记bn=[lg an],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg 99]=1.(Ⅰ)求b1,b11,b101;(Ⅱ)求数列{bn}的前1 000项和.18.(本小题满分12分)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;(Ⅲ)求续保人本年度的平均保费与基本保费的比值.19.(本小题满分12分)如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=,EF交BD于点H.将△DEF沿EF折到△D'EF的位置,OD'=.(Ⅰ)证明:D'H⊥平面ABCD;(Ⅱ)求二面角B-D'A-C的正弦值.20.(本小题满分12分)已知椭圆E:+=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.(Ⅰ)当t=4,|AM|=|AN|时,求△AMN的面积;(Ⅱ)当2|AM|=|AN|时,求k的取值范围.21.(本小题满分12分)(Ⅰ)讨论函数f(x)=-e x的单调性,并证明当x>0时,(x-2)e x+x+2>0;(Ⅱ)证明:当a∈[0,1)时,函数g(x)=--(x>0)有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.请考生在第22~24题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4—1:几何证明选讲如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D 点作DF⊥CE,垂足为F.(Ⅰ)证明:B,C,G,F四点共圆;(Ⅱ)若AB=1,E为DA的中点,求四边形BCGF的面积.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.(Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;(Ⅱ)直线l的参数方程是,(t为参数),l与C交于A,B两点,|AB|=,求l的斜率.24.(本小题满分10分)选修4—5:不等式选讲已知函数f(x)=-+,M为不等式f(x)<2的解集.(Ⅰ)求M;(Ⅱ)证明:当a,b∈M时,|a+b|<|1+ab|.。
2016年普通高等学校招生全国统一考试(正文)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅰ)理综生物第Ⅰ卷一、选择题:本题共6小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列与细胞相关的叙述,正确的是( )A.核糖体、溶酶体都是具有膜结构的细胞器B.酵母菌的细胞核内含有DNA和RNA两类核酸C.蓝藻细胞的能量来源于其线粒体有氧呼吸过程D.在叶绿体中可进行CO2的固定但不能合成ATP2.离子泵是一种具有ATP水解酶活性的载体蛋白,能利用水解ATP释放的能量跨膜运输离子。
下列叙述正确的是( )A.离子通过离子泵的跨膜运输属于协助扩散B.离子通过离子泵的跨膜运输是顺着浓度梯度进行的C.动物一氧化碳中毒会降低离子泵跨膜运输离子的速率D.加入蛋白质变性剂会提高离子泵跨膜运输离子的速率3.若除酶外所有试剂已预保温,则在测定酶活力的实验中,下列操作顺序合理的是( )A.加入酶→加入底物→加入缓冲液→保温并计时→一段时间后检测产物的量B.加入底物→加入酶→计时→加入缓冲液→保温→一段时间后检测产物的量C.加入缓冲液→加入底物→加入酶→保温并计时→一段时间后检测产物的量D.加入底物→计时→加入酶→加入缓冲液→保温→一段时间后检测产物的量4.下列与神经细胞有关的叙述,错误..的是( )A.ATP能在神经元线粒体的内膜上产生B.神经递质在突触间隙中的移动消耗ATPC.突触后膜上受体蛋白的合成需要消耗ATPD.神经细胞兴奋后恢复为静息状态消耗ATP5.在漫长的历史时期内,我们的祖先通过自身的生产和生活实践,积累了对生态方面的感性认识和经验,并形成了一些生态学思想,如:自然与人和谐统一的思想。
根据这一思想和生态学知识,下列说法错误..的是( )A.生态系统的物质循环和能量流动有其自身的运行规律B.若人与自然和谐统一,生产者固定的能量便可反复利用C.“退耕还林、还草”是体现自然与人和谐统一思想的实例D.人类应以保持生态系统相对稳定为原则,确定自己的消耗标准6.理论上,下列关于人类单基因遗传病的叙述,正确的是( )A.常染色体隐性遗传病在男性中的发病率等于该病致病基因的基因频率B.常染色体显性遗传病在女性中的发病率等于该病致病基因的基因频率C.X染色体显性遗传病在女性中的发病率等于该病致病基因的基因频率D.X染色体隐性遗传病在男性中的发病率等于该病致病基因的基因频率第Ⅱ卷三、非选择题:本卷包括必考题和选考题两部分。
2016年普通高等学校招生全国统一考试(正文)

2016年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理数本卷满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合S={x|(x-2)(x-3)≥0},T={x|x>0},则S∩T=()A.[2,3]B.(-∞,2]∪[3,+∞)C.[3,+∞)D.(0,2]∪[3,+∞)2.若z=1+2i,则=( )-A.1B.-1C.iD.-I3.已知向量=,,=,,则∠ABC=()A.30°B.45°C.60°D.120°4.某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15 ℃,B点表示四月的平均最低气温约为5 ℃.下面叙述不正确的是( )A.各月的平均最低气温都在0 ℃以上B.七月的平均温差比一月的平均温差大C.三月和十一月的平均最高气温基本相同D.平均最高气温高于20 ℃的月份有5个5.若tan α=,则cos2α+2sin 2α=( )A. B. C.1 D.6.已知a=,b=,c=2,则( )A.b<a<cB.a<b<cC.b<c<aD.c<a<b7.执行下面的程序框图,如果输入的a=4,b=6,那么输出的n=( )A.3B.4C.5D.68.在△ABC中,B=,BC边上的高等于BC,则cos A=( )A. B. C.- D.-9.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A.18+36B.54+18C.90D.8110.在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )A.4πB.C.6πD.11.已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )A. B. C. D.12.定义“规范01数列”{a n}如下:{a n}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,a k中0的个数不少于1的个数,若m=4,则不同的“规范01数列”共有( ) A.18个 B.16个 C.14个 D.12个第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本题共4小题,每小题5分.13.若x,y满足约束条件-,-,-,则z=x+y的最大值为.14.函数y=sin x-cos x的图象可由函数y=sin x+cos x的图象至少向右平移个单位长度得到.15.已知f(x)为偶函数,当x<0时, f(x)=ln(-x)+3x,则曲线y=f(x)在点(1,-3)处的切线方程是.16.已知直线l:mx+y+3m-=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点.若|AB|=2,则|CD|= .三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知数列{a n}的前n项和S n=1+λa n,其中λ≠0.(Ⅰ)证明{a n}是等比数列,并求其通项公式;(Ⅱ)若S5=,求λ.18.(本小题满分12分)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量. 附注:参考数据:y i=9.32,t i y i=40.17,(-)=0.55,≈2.646.(-)(-)参考公式:相关系数r=,(-)(-)(-)(-)回归方程=+t中斜率和截距的最小二乘估计公式分别为:=,=-.(-)19.(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(Ⅰ)证明MN∥平面PAB;(Ⅱ)求直线AN与平面PMN所成角的正弦值.20.(本小题满分12分)已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.(Ⅰ)若F在线段AB上,R是PQ的中点,证明AR∥FQ;(Ⅱ)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.21.(本小题满分12分)设函数f(x)=αcos 2x+(α-1)(cos x+1),其中α>0,记|f(x)|的最大值为A.(Ⅰ)求f '(x);(Ⅱ)求A;(Ⅲ)证明|f '(x)|≤2A.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4—1:几何证明选讲如图,☉O中的中点为P,弦PC,PD分别交AB于E,F两点.(Ⅰ)若∠PFB=2∠PCD,求∠PCD的大小;(Ⅱ)若EC的垂直平分线与FD的垂直平分线交于点G,证明OG⊥CD.23.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系xOy中,曲线C1的参数方程为,(α为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin=2.(Ⅰ)写出C1的普通方程和C2的直角坐标方程;(Ⅱ)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.24.(本小题满分10分)选修4—5:不等式选讲已知函数f(x)=|2x-a|+a.(Ⅰ)当a=2时,求不等式f(x)≤6的解集;(Ⅱ)设函数g(x)=|2x-1|.当x∈R时, f(x)+g(x)≥3,求a的取值范围.。
2016普通高等学校招生全国统一考试

2016普通高等学校招生全国统一考试(新课标I)第二节(共 5 小题,每小题 2 分,满分10 分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项,选项中有两项为多余选项。
Secret codes (密码)keep messages private。
Banks, companies, and government agencies use secret codes in doing business, especially when information is sent by computer.People have used secret codes for thousands of years. 36 Code breaking never lags(落后) far behind code making. The science of creating and reading coded messages is called cryptography.There are three main types of cryptography. 37 For example, the first letters of “My elephant eats too many eels” Spell out the hidden message “Meet me.”38 You might represent each letter with a number, For example, Let’s number the letters of the alphabet, in order, from 1 to 26. If we substitute a number for each letter, the message “Meet me” would read “13 5 20 13 5.”A code uses symbols to replace words, phrases, or sentences. To read the message of a real code, you must have a code book. 39 For example, ”bridge“ might stand for “meet” and “out”might stand for “me.” The message “bridge out” would actually mean “Meet me.”40 However, it is also hard to keep a code book secret for long. So codes must be changed frequently.A.It is very hard to break a code without the code book.B.In any language, some letters are used more than others.C.Only people who know the keyword can read the message.D.As long as there have been codes, people have tried to break them.E.You can hide a message by having the first letters of each word spell it out.F.With a code book, you might write down words that would stand for other words.G.Another way to hide a message is to use symbols to stand for specific letters of the alphabet. 第三部分英语知识运用(共两节,满分45)第一节完形填空(共20 小题;每小题 1.5 分,满分30 分)A Heroic DriverLarry works with Transport Drivers. Inc. One morning in 2009. Larry was __41__along 165 north after delivering to one of his 42 . suddenly, he saw a car with its bright lights on. 43 he got closer, he found 44 vehicle upside down on the road. One morelook and he noticed 45 shooting out from under the 46 vehicle. Larry pulled over, set the brake and 47 the fire extinguisher (灭火器). Two good bursts from the extinguisher and the fire was put out.The man who had his bright lights on 48 and told Larry he had 49 an emergency call. They 50 heard a woman’s voice coming from the wrecked (毁坏的) vehicle. 51 the vehicle, they saw that a woman was trying to get out of the broken window. They told her to stay 52 until the emergency personnel arrived, 53 she thought the car was going to 54 . Larry told her that he had already put out the fire and she should not move 55 she injured her neck.Once fire and emergency people arrive, Larry and the other man 56 and let them go to work. Then, Larry asked the 57 if he was needed or 58 to go. They let him and the other man go.One thing is 59 —Larry went above and beyond the call of duty by getting so close to the burning vehicle! His 60 most likely saved the woman’s life.41. A. walking B. touring C.traveling D.rushing42. A. passengers B. colleagues C. employers D. customers43. A. Since B. Although C. As D. If44. A. each B. another C. that D. his45. A. flames B. smoke C. water D. steam46. A. used B. disabled C. removed D. abandoned47. A. got hold of B. prepared C. took charge of D. controlled48. A. came down B. came through C. came in D. came over49. A. returned B. received C. made D. confirmed50. A. then B. again C. finally D. even51. A. Starting B. Parking C. Passing D. Approaching52. A. quiet B. still C. away D. calm53. A. for B. so C. and D. but54. A. explode B. slip away C. fall apart D. crash55. A. as if B. unless C. in case D. after56. A. stepped forward B. backed off C. moved on D. set out57. A. woman B. police C. man D. driver58. A. forbidden B. ready C. asked D. free59. A.for certain B. for consideration C. reported D.checked60. A.patience B. skills C. efforts D.promise第II 卷第三部分英语知识运用第二节(共10小题;每小题1.5分,满分15分)阅读下面材料,在空白处填入适当的内容(1个单词)或括号内单词的正确形式。
2016年普通高等学校招生全国统一考试

绝密★启用前2016年普通高等学校招生全国统一考试语文注意事项:1.本试卷分第I卷(阅读题)和第Ⅱ卷(表达题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上.写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第I卷阅读题甲必考题―、现代文阅读(9分,每小题3分)阅读下面的文宇,完成1〜3題.人们常说“小说是讲故事的艺术”,但故事不等于小说,故事讲述人与小说家也不能混为一谈。
就传统而言,讲故事的讲述亲身经历或道题听途说的故事,口耳相传,吧它们转化为听众的经验;小说家则通常记录见闻传说,虚构故事,经过艺术处理,把它们变成小说交给读者。
除流传形式上的简单差异外,早起小说和故事的本质区别并不明显,经历和见闻是它们的共同要素,在传统较为落后的过去,作为远行者的商人和税收最适合充当故事讲述人的角色,故事的丰富程度与远行者的游历成比。
受此影响,国外古典小说也常以人物的经历为主线组织故事,《荷马史诗》《一千零一夜》都是描述某种特殊的经历和遭遇,《唐吉可德》中的故事是唐吉可德的行侠其余和所见所闻,17世纪欧洲的流浪汉小说也体现游历见闻的连缀。
在中国民间传说和历史故事为志怪录类的小说提供了用之不竭的素材,话本等古典小说形式也显示出小说和传统故事的亲密关系。
虚构的加强使小说和传统质检的区别清晰起来。
小说中的故事可以来自想象。
不一定是作者的亲历亲闻。
小说家常闭门构思,作品大多诞生于他们的离群索居的时候,小说家可以闲坐在布宜诺斯艾利斯的图书馆中,或者在巴黎一间终年不见阳光的阁楼里,杜撰他们想象中的历险故事,但是,一名水手也许礼金千辛万苦才能把在东印度群岛听到的故事带回伦敦;一个匠人瓢泼一生,积攒下无数的见闻、掌故或趣事,当他晚年作在火炉旁给孩子们讲述这一切的时候,他本人就是故事的一部分,传统故事是否值得转述,往往只取决于故事本事的趣味性和可流传性,与传统的故事方式不同,小说家一般并不单纯转述故事,他是在从事故事的制作和生产,有深思熟虑的讲述目的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年普通高等学校招生全国统一考试
(课标全国卷Ⅱ)
文数
本卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={1,2,3},B={x|x2<9},则A∩B=( )
A.{-2,-1,0,1,2,3}
B.{-2,-1,0,1,2}
C.{1,2,3}
D.{1,2}
2.设复数z满足z+i=3-i,则=( )
A.-1+2i
B.1-2i
C.3+2i
D.3-2i
3.函数y=Asin(ωx+φ)的部分图象如图所示,则( )
A.y=2sin
B.y=2sin
C.y=2sin
D.y=2sin
4.体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )
A.12π
B.π
C.8π
D.4π
5.设F为抛物线C:y2=4x的焦点,曲线y=(k>0)与C交于点P,PF⊥x轴,则k=( )
A. B.1 C. D.2
6.圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=( )
A.-
B.-
C.
D.2
7.下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π
B.24π
C.28π
D.32π
8.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )
A. B. C. D.
9.中国古代有计算多项式值的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
A.7
B.12
C.17
D.34
10.下列函数中,其定义域和值域分别与函数y=10lg x的定义域和值域相同的是( )
A.y=x
B.y=lg x
C.y=2x
D.y=
11.函数f(x)=cos 2x+6cos的最大值为( )
A.4
B.5
C.6
D.7
12.已知函数f(x)(x∈R)满足f(x)=f(2-x),若函数y=|x2-2x-3|与y=f(x)图象的交点为
(x1,y1),(x2,y2),…,(x m,y m),则=( )
A.0
B.m
C.2m
D.4m
第Ⅱ卷(非选择题,共90分)
本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.
二、填空题:本题共4小题,每小题5分.
13.已知向量a=(m,4),b=(3,-2),且a∥b,则m= .
14.若x,y满足约束条件则z=x-2y的最小值为.
15.△ABC的内角A,B,C的对边分别为a,b,c,若cos A=,cos C=,a=1,则b= .
16.有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
等差数列{a n}中,a3+a4=4,a5+a7=6.
(Ⅰ)求{a n}的通项公式;
(Ⅱ)设b n=[a n],求数列{b n}的前10项和,其中[x]表示不超过x的最大整数,如[0.9]=0,[2.6]=2.
18.(本小题满分12分)
某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(Ⅲ)求续保人本年度平均保费的估计值.
19.(本小题满分12分)
如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D'EF的位置.
(Ⅰ)证明:AC⊥HD';
(Ⅱ)若AB=5,AC=6,AE=,OD'=2,求五棱锥D'-ABCFE的体积.
20.(本小题满分12分)
已知函数f(x)=(x+1)ln x-a(x-1).
(Ⅰ)当a=4时,求曲线y=f(x)在(1, f(1))处的切线方程;
(Ⅱ)若当x∈(1,+∞)时, f(x)>0,求a的取值范围.
21.(本小题满分12分)
已知A是椭圆E:+=1的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA ⊥NA.
(Ⅰ)当|AM|=|AN|时,求△AMN的面积;
(Ⅱ)当2|AM|=|AN|时,证明:<k<2.
请考生在第22~24题中任选一题作答,如果多做,则按所做的第一题计分.
22.(本小题满分10分)选修4—1:几何证明选讲
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(Ⅰ)证明:B,C,G,F四点共圆;
(Ⅱ)若AB=1,E为DA的中点,求四边形BCGF的面积.
23.(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.
(Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;
(Ⅱ)直线l的参数方程是(t为参数),l与C交于A,B两点,|AB|=,求l的斜率.
24.(本小题满分10分)选修4—5:不等式选讲
已知函数f(x)=+,M为不等式f(x)<2的解集.
(Ⅰ)求M;
(Ⅱ)证明:当a,b∈M时,|a+b|<|1+ab|.。
