2015全国文数立体几何高考试题—学生专用(2)
2015-2020年高考全国卷(文)立体几何试题(含答案)

2015-2020年全国卷立体几何试题(含答案)1.(2020年全国卷1 文3).埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A 51-B 51-C 51+D 51+2.(2020年全国卷1 文12).已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π3.(2020年全国卷1 文19).如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC △是底面的内接正三角形,P 为DO 上一点,∠APC =90°.(1)证明:平面PAB ⊥平面PAC ;(2)设DO 23π,求三棱锥P −ABC 的体积.4.(2020年全国卷2 文11).已知ABC ∆是面积为439的等边三角形, 且其顶点都在球O 的球面上。
若球O 的表面积为π16,则O 到平面ABC 的距离为 A. 3 B. 23 C. 1 D. 23 5.(2020年全国卷2 文16).设有下列四个命题:1p :两两相交且不过同一点的三条直线必在同一平面内。
2p :过空间中任意三点有且仅有一个平面。
3p :若空间两条直线不相交,则这两条直线平行。
4p :若直线⊂l 平面α,直线⊥m 平面α,则l m ⊥。
则下述命题中所有真命题的序号是____________。
①41p p ∧②21p p ∧③32p p ∨⌝④43p p ⌝∨⌝6.(2020年全国卷2 文20).如图,已知三棱柱111C B A ABC -的底面是正三角形,侧面C C BB 11是矩形,M 、N 分别为BC 、11C B 的中点,P 为AM 上一点。
过11C B 和P 的平面交AB 于E ,交AC 于F 。
2015年高考真题解答题专项训练:立体几何(文科)学生版

2015年高考真题解答题专项训练:立体几何(文科)学生版1.(2015.浙江)如图,在三棱锥中,,在底面ABC的射影为BC的中点,D为的中点.(1)证明:平面;(2)求直线和平面所成的角的正弦值.2.(2015.新课标1卷)如图四边形ABCD为菱形,G为AC与BD交点,平面,(I)证明:平面平面;(II)若,三棱锥的体积为,求该三棱锥的侧面积.3.(2015.湖南)如图,直三棱柱的底面是边长为2的正三角形,分别是的中点。
(1)证明:平面平面;(2)若直线与平面所成的角为,求三棱锥的体积.称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马P ABCD -中,侧棱PD ⊥底面ABCD ,且PD CD =,点E 是PC 的中点,连接,,DE BD BE .(Ⅰ)证明: DE ⊥平面PBC . 试判断四面体EBCD 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;(Ⅱ)记阳马P ABCD -的体积为1V ,四面体EBCD 的体积为2V ,求12V V 的值. 5.((2015.广东)如图,三角形DC P 所在的平面与长方形CD AB 所在的平面垂直,D C 4P =P =,6AB =,C 3B =.(1)证明:C//B 平面D P A ; (2)证明:C D B ⊥P ;(3)求点C 到平面D P A 的距离.6.(2015.安徽)如图,三棱锥P-ABC中,PA ⊥平面ABC ,1,1,2,60PA AB AC BAC ===∠=.(Ⅰ)求三棱锥P-ABC 的体积;PM7.(2015.新课标2卷)如图,长方体1111ABCD A B C D -中, 116,10,8AB BC AA ===,点,E F 分别在1111,A B D C 上, 114A E D F ==,过点,E F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由). (2)求平面α把该长方体分成的两部分体积的比值.8.(2015.福建)如图, AB 是圆O 的直径,点C 是圆O 上异于,A B 的点, PO 垂直于圆O 所在的平面,且1PO =OB =.(Ⅰ)若D 为线段AC 的中点,求证C A ⊥平面D P O ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若BC =E 在线段PB 上,求CE OE +的最小值.9.(2015.重庆)如图,三棱锥P-ABC 中,平面PAC ⊥平面ABC , ∠ABC=2π,点D 、E 在线段AC 上,且AD=DE=EC=2,PD=PC=4,点F 在线段AB 上,且EF//BC . (Ⅰ)证明:AB ⊥平面PFE.(Ⅱ)若四棱锥P-DFBC 的体积为7,求线段BC 的长.10.(2015.天津)如图,已知平面ABC,AB=AC=3,,,点E,F分别是BC,的中点.(Ⅰ)求证:EF∥平面;(Ⅱ)求证:平面平面.(Ⅲ)求直线与平面所成角的大小.11.(2015.四川)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.(Ⅲ)证明:直线DF平面BEG12.(2015.陕西)如图1,在直角梯形ABCD 中,,E 是AD 的中点,O 是OC 与BE 的交点,将ABE ∆沿BE 折起到图2中1A BE ∆的位置,得到四棱锥1A BCDE -.(Ⅰ)证明:CD ⊥平面1AOC ; (Ⅱ)当平面1A BE ⊥平面BCDE 时,四棱锥1A BCDE -的体积为求a 的值. 13.(2015.山东)如图,三棱台DEF ABC -中, 2AB DE G H =,,分别为AC BC ,的中点.(Ⅰ)求证: //BD 平面FGH ;(Ⅱ)若CF BC AB BC ⊥⊥,,求证:平面BCD ⊥平面EGH .14.(2015.北京)如图,在三棱锥 中,平面 平面 , 为等边三角形, 且 , , 分别为 , 的中点.(1)求证: 平面 ;(2)求证:平面平面;(3)求三棱锥的体积.参考答案1.(1)见解析;(2)【来源】2015年全国普通高等学校招生统一考试文科数学(浙江卷带解析)【解析】(1)利用线面垂直的定义得到线线垂直,根据线面垂直的判定证明直线与平面垂直;(2)通过添加辅助线,证明平面,以此找到直线与平面所成角的平面角,在直角三角形中通过确定边长,计算的正弦值.试题解析:(1)设为中点,由题意得平面,所以.因为,所以.所以平面.由,分别为的中点,得且,从而且,所以是平行四边形,所以.因为平面,所以平面.(2)作,垂足为,连结.因为平面,所以.因为,所以平面.所以平面.所以为直线与平面所成角的平面角.由,得.由平面,得.由,得.所以考点:1.空间直线、平面垂直关系的证明;2.直线与平面所成的角.视频2.(1)见解析(2)3+2【来源】2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ带解析)【解析】试题分析:(Ⅰ)由四边形ABCD为菱形知AC BD,由BE平面ABCD知AC BE,由线面垂直判定定理知AC平面BED,由面面垂直的判定定理知平面平面;(Ⅱ)设AB=,通过解直角三角形将AG、GC、GB、GD用x表示出来,在AEC中,用x表示EG,在EBG中,用x表示EB,根据条件三棱锥的体积为求出x,即可求出三棱锥的侧面积.试题解析:(Ⅰ)因为四边形ABCD为菱形,所以AC BD,因为BE平面ABCD,所以AC BE,故AC平面BED.又AC平面AEC,所以平面AEC平面BED(Ⅱ)设AB=,在菱形ABCD中,由ABC=120°,可得AG=GC=,GB=GD=.因为AE EC,所以在AEC中,可得EG=.由BE平面ABCD,知EBG为直角三角形,可得BE=.由已知得,三棱锥E-ACD的体积.故=2从而可得AE=EC=ED=.所以EAC的面积为3,EAD的面积与ECD的面积均为.故三棱锥E-ACD的侧面积为.考点:线面垂直的判定与性质;面面垂直的判定;三棱锥的体积与表面积的计算;逻辑推理能力;运算求解能力视频3.(Ⅰ)见解析;(Ⅱ).【来源】2015年全国普通高等学校招生统一考试文科数学(湖南卷带解析)【解析】试题分析:(1)由面面垂直的判定定理很容易得结论;(2)所求三棱锥底面积容易求得,是本题转化为求三棱锥的高,利用直线与平面所成的角为,作出线面角,进而可求得的值,则可得的长.试题解析:(1)如图,因为三棱柱是直三棱柱,所以,又是正三角形的边的中点,所以又 ,因此 平面 而 平面 ,所以平面 平面 (2)设 的中点为 ,连结 ,因为 是正三角形,所以又三棱柱 是直三棱柱,所以因此 平面 ,于是 为直线 与平面 所成的角, 由题设, ,所以在 中, ,所以故三棱锥 的体积考点:直线与平面垂直的判定定理;直线与平面所成的角;几何体的体积.视频4.(Ⅰ)因为PD ⊥底面ABCD ,所以PD BC ⊥. 由底面ABCD 为长方形,有BC CD ⊥,而PD CD D ⋂=,所以BC ⊥平面PCD . DE ⊂平面PCD ,所以BC DE ⊥. 又因为PD CD =,点E 是PC 的中点,所以DE PC ⊥. 而PC BC C ⋂=,所以DE ⊥平面PBC .四面体EBCD 是一个鳖臑;(Ⅱ)124.V V = 【来源】2015年全国普通高等学校招生统一考试文科数学(湖北卷带解析)【解析】(Ⅰ)因为PD ⊥底面ABCD ,所以PD BC ⊥. 由底面ABCD 为长方形,有BC CD ⊥,而PD CD D ⋂=,所以BC ⊥平面PCD . DE ⊂平面PC D ,所以BC DE⊥. 又因为PD CD =,点E 是PC 的中点,所以DE PC ⊥. 而PC BC C ⋂=,所以DE ⊥平面PBC . 由BC ⊥平面PCD , DE ⊥平面PBC ,可知四面体EBCD 的四个面都是直角三角形,即四面体EBCD 是一个鳖臑,其四个面的直角分别是,,,.BCD BCE DEC DEB ∠∠∠∠(Ⅱ)由已知, PD 是阳马P ABCD -的高,所以11133ABCD V S PD BC CD PD =⋅=⋅⋅;由(Ⅰ)知,DE 是鳖臑D B C E -的高, BC CE ⊥,所以21136BCE V S DE BC CE DE ∆=⋅=⋅⋅.在Rt △PDC 中,因为PD CD =,点E 是PC 的中点,所以2DE CE ==,于是12123 4.16BC CD PDV CD PD V CE DE BC CE DE ⋅⋅⋅===⋅⋅⋅考点:本题考查直线与平面垂直的判定定理、直线与平面垂直的性质定理和简单几何体的体积,属中高档题.视频5.(1)证明见解析;(2)证明见解析;(3 【来源】2015年全国普通高等学校招生统一考试文科数学(广东卷带解析) 【解析】试题分析:(1)由四边形CD AB 是长方形可证C//D B A ,进而可证C//B 平面D P A ;(2)先证C CD B ⊥,再证C B ⊥平面DC P ,进而可证C D B ⊥P ;(3)取CD 的中点E ,连结AE 和PE ,先证P E ⊥平面CD AB ,再设点C 到平面D P A 的距离为h ,利用C D C DV V -P A P-A=三棱锥三棱锥可得h 的值,进而可得点C 到平面D P A 的距离.试题解析:(1)因为四边形CD AB 是长方形,所以C//D B A ,因为C B ⊄平面D P A ,D A ⊂平面D P A ,所以C//B 平面D P A(2)因为四边形CD AB 是长方形,所以C CD B ⊥,因为平面DC P ⊥平面CD AB ,平面DC P 平面CD CD AB =,C B ⊂平面CD AB ,所以C B ⊥平面DC P ,因为D P ⊂平面DC P ,所以C D B ⊥P(3)取CD 的中点E ,连结AE 和PE ,因为D C P =P ,所以CD PE ⊥,在R t D ∆P E 中,因为平面DC P ⊥平面CD AB ,平面DC P 平面CD CD AB =,PE ⊂平面DC P ,所以PE ⊥平面CD AB ,由(2)知:C B ⊥平面DC P ,由(1)知:C//D B A ,所以D A ⊥平面DC P ,因为D P ⊂平面DC P ,所以D D A ⊥P ,设点C 到平面D P A 的距离为h ,因为C D CD V V -P A P-A =三棱锥三棱锥,所以,即,所以点C 到平面D P A 的距离是考点:1、线面平行;2、线线垂直;3、点到平面的距离. 6.(Ⅰ)6;(Ⅱ)13【来源】2015年全国普通高等学校招生统一考试文科数学(安徽卷带解析) 【解析】(Ⅰ)解:由题设=1,可得.由面可知是三棱锥的高,又所以三棱锥的体积 (Ⅱ)证:在平面内,过点B 作,垂足为,过作交于,连接.由面知,所以.由于,故面,又面,所以.在直角中,,从而.由,得.考点:本题主要考查锥体的体积公式、线面垂直的判定定理和其性质定理.视频7.(Ⅰ)见试题解析(Ⅱ)97或79【来源】2015年全国普通高等学校招生统一考试文科数学(新课标Ⅱ带解析)【解析】试题分析:(Ⅰ)分别在,AB CD 上取H,G,使10AH DG ==;长方体被平面α分成两个高为10的直棱柱,可求得其体积比值为97或79试题解析:解:(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作垂足为M,则18EM AA ==,,,因为EHGF 是正方形,所以,于是因为长方体被平面α分成两个高为10的直棱柱,所以其体积比值为97(79也正确). 考点:本题主要考查几何体中的截面问题及几何体的体积的计算.视频8.(Ⅰ)详见解析;(Ⅱ)13;【来源】2015年全国普通高等学校招生统一考试文科数学(福建卷带解析) 【解析】解法一:(Ⅰ)在C ∆AO 中,因为C OA =O , D 为C A 的中点, 所以C D A ⊥O .又PO 垂直于圆O 所在的平面,所以C PO ⊥A . 因为D O⋂PO =O ,所以C A ⊥平面D P O . (Ⅱ)因为点C 在圆O 上,所以当C O ⊥AB 时, C 到AB 的距离最大,且最大值为1. 又2AB =,所以C ∆AB 面积的最大值为12112⨯⨯=. 又因为三棱锥C P -AB 的高1PO =,故三棱锥C P -AB 体积的最大值为111133⨯⨯=.(Ⅲ)在∆POB 中, 1PO =OB =, 90∠POB =,所以PB ==同理C P =C C PB =P =B .在三棱锥C P -AB 中,将侧面C B P 绕PB 旋转至平面C'B P ,使之与平面ABP 共面,如图所示.当O , E , C'共线时, C E +OE 取得最小值. 又因为OP =OB , C'C'P =B ,所以C'O 垂直平分PB ,即E 为PB 中点.从而C'C'222O =OE +E =+=,亦即C E +OE 的最小值为2.解法二:(Ⅰ)、(Ⅱ)同解法一.(Ⅲ)在∆POB 中, 1PO =OB =, 90∠POB =,所以45∠OPB =, PB ==C P =所以C C PB =P =B ,所以C 60∠PB =.在三棱锥C P -AB 中,将侧面C B P 绕PB 旋转至平面C'B P ,使之与平面ABP 共面,如图所示.当O , E , C'共线时, C E +OE 取得最小值. 所以在C'∆O P 中,由余弦定理得:()2C'1221cos 4560O =+-⨯+1122222=+--⨯⎭2=+从而C'2O ==.所以C E +OE 考点:1、直线和平面垂直的判定;2、三棱锥体积.视频9.(1)见解析(2) BC=3或【来源】2015年全国普通高等学校招生统一考试文科数学(重庆卷带解析)【解析】试题分析:(Ⅰ)先由已知易得PE AC ⊥,再注意平面PAC ⊥平面ABC ,且交线为AC ,由面面垂直的性质可得PE ⊥平面ABC ,再由线面垂直的性质可得到AB PE ⊥,再注意到//EF BC ,而B C A B ⊥,从而有AB EF ⊥,那么由线面垂的判定定理可得AB ⊥平面PFE ,(Ⅱ)设B C =x 则可用x 将四棱锥P DFBC -的体积表示出来,由已知其体积等于7,从而得到关于x 的一个一元方程,解此方程,再注意到0x >即可得到BC 的长.试题解析:证明:如题(20)图.由,DE EC PD PC ==知, E 为等腰PDC ∆中DC 边的中点,故PE AC ⊥,又平面PAC ⊥平面ABC ,平面PAC ⋂平面ABC AC =, PE ⊂平面PAC ,PE AC ⊥,所以PE ⊥平面ABC ,从而PE AB ⊥. 因ABC=,,AB EF 2EF BC π∠⊥故.从而AB 与平面PFE 内两条相交直线PE , EF 都垂直, 所以AB ⊥平面PFE .(2)解:设BC=x ,则在直角ABC ∆中,从而11S AB BC=22ABC ∆=⨯由EFBC ,知23AF AE AB AC ==,得AEF ABC ∆~∆,故224S 39AEF ABC S ∆∆⎛⎫== ⎪⎝⎭,即4S 9AEF ABC S ∆∆=. 由1AD=2AE,11421S S =S S 22999AFB AFE ABC ABC ∆∆∆∆=⋅==从而四边形DFBC的面积为DFBC 11S S -=29ABC ADF S ∆∆=718=由(1)知,PE PE ⊥平面ABC ,所以PE 为四棱锥P-DFBC 的高.在直角PEC ∆中, =,体积DFBC 117S 73318P DFBC V PE -=⋅⋅=⋅=, 故得42362430x x -+=,解得,由于0x >,可得333x x ==或.所以3BC =或BC =考点:1. 空间线面垂直关系,2. 锥体的体积,3.方程思想.视频10.(Ⅰ)见试题解析;(Ⅱ)见试题解析;(Ⅲ) .【来源】2015年全国普通高等学校招生统一考试文科数学(天津卷带解析)【解析】(Ⅰ)要证明EF ∥平面 , 只需证明 且EF 平面 ;(Ⅱ)要证明平面 平面 ,可证明 , ;(Ⅲ)取 中点N,连接 ,则 就是直线 与平面 所成角,Rt △ 中,由得直线 与平面所成角为 .试题解析:(Ⅰ)证明:如图,连接 ,在△ 中,因为E 和F 分别是BC, 的中点,所以 ,又因为EF 平面 , 所以EF ∥平面 .(Ⅱ)因为AB=AC,E 为BC 中点,所以 ,因为 平面ABC,所以 平面ABC,从而 ,又 ,所以 平面 ,又因为 平面 ,所以平面 平面 .(Ⅲ)取中点M和中点N,连接,因为N和E分别为,BC中点,所以,,故,,所以,,又因为平面,所以平面,从而就是直线与平面所成角,在△中,可得AE=2,所以=2,因为,所以又由,有,在Rt△中,可得,在Rt△中,因此,所以,直线与平面所成角为.考点:本题主要考查空间中线面位置关系的证明,直线与平面所成的角等基础知识,考查空间想象能力及推理论证能力.视频11.见解析【来源】2015年全国普通高等学校招生统一考试文科数学(四川卷带解析)【解析】(Ⅰ)点F,G,H的位置如图所示(Ⅱ)平面BEG∥平面ACH.证明如下因为ABCD-EFGH为正方体,所以BC∥FG,BC=FG又FG∥EH,FG=EH,所以BC∥EH,BC=EH于是BCEH为平行四边形所以BE∥CH又CH⊂平面ACH,BE⊄平面ACH,所以BE∥平面ACH同理BG∥平面ACH又BE∩BG=B所以平面BEG∥平面ACH(Ⅲ)连接FH因为ABCD -EFGH 为正方体,所以DH ⊥平面EFGH 因为EG ⊂平面EFGH ,所以DH ⊥EG又EG ⊥FH ,EG ∩FH =O ,所以EG ⊥平面BFHD 又DF ⊂平面BFDH ,所以DF ⊥EG 同理DF ⊥BG 又EG ∩BG =G 所以DF ⊥平面BEG.考点:本题主要考查简单空间图形的直观图、空间线面平行与垂直的判定与性质等基础知识,考查空间想象能力、推理论证能力.12.(Ⅰ) 证明见解析,详见解析;(Ⅱ) 6a =.【来源】2015年全国普通高等学校招生统一考试文科数学(陕西卷带解析) 【解析】试题分析:(Ⅰ) 在图1中,,E 是AD 的中点,所以四边形ABCE 是正方形,故BE AC ⊥,又在图2中,1,BE AO BE OC ⊥⊥,从而BE ⊥平面1AOC ,又//DE BC 且DE BC =,所以//CD BE ,即可证得CD ⊥平面1AOC ; (Ⅱ)由已知,平面1A BE ⊥平面BCDE ,且平面1A BE平面BCDE BE = ,又由(Ⅰ)知,1A O BE ⊥,所以1AO ⊥平面BCDE ,即1A O 是四棱锥1A BCDE -的高,易求得平行四边形BCDE 面积2S B CA B a =⋅=,从而四棱锥1A BCDE -的为,得6a =.试题解析:(Ⅰ)在图1,E 是AD 的中点所以BE AC ⊥,即在图2中,1,BE AO BE OC ⊥⊥ 从而BE ⊥平面1AOC 又//CD BE所以CD ⊥平面1AOC .(Ⅱ)由已知,平面1A BE ⊥平面BCDE , 且平面1A BE平面BCDE BE =又由(Ⅰ)知,1AO BE ⊥,所以1AO ⊥平面BCDE , 即1A O 是四棱锥1A BCDE -的高,由图1,平行四边形BCDE 面积2S BC AB a =⋅=, 从而四棱锥1A BCDE -的为,得6a =. 考点:1.线面垂直的判定;2.面面垂直的性质定理;3.空间几何体的体积. 13.证明见解析【来源】2015年全国普通高等学校招生统一考试文科数学(山东卷带解析)【解析】(Ⅰ)证法一:连接,.DG CD 设CD GF M ⋂=,连接MH ,在三棱台DEF ABC -中, 2AB DE G =,分别为AC 的中点,可得//,DF GC DF GC =,所以四边形DFCG 是平行四边形,则M 为CD 的中点,又H 是BC 的中点,所以//HM BD , 又HM ⊂平面FGH , BD ⊄平面FGH ,所以//BD 平面FGH .证法二:在三棱台DEF ABC -中,由2,BC EF H =为BC 的中点,可得//,,BH EF BH EF =所以HBEF 为平行四边形,可得//.BE HF 在ABC ∆中, G H ,分别为AC BC ,的中点, 所以//,GH AB 又GH HF H ⋂=, 所以平面//FGH 平面ABED , 因为BD ⊂平面ABED , 所以//BD 平面FGH .(Ⅱ)证明:连接HE .因为G H ,分别为AC BC ,的中点,所以//,GH AB 由,AB BC ⊥得GH BC ⊥,又H 为BC 的中点,所以//,,EF HC EF HC =因此四边形EFCH 是平行四边形,所以//.CF HE 又CF BC ⊥,所以HE BC ⊥.又,HE GH ⊂平面EGH , HE GH H ⋂=,所以BC ⊥平面EGH , 又BC ⊂平面BCD ,所以平面BCD ⊥平面.EGH 考点:1.平行关系;2.垂直关系.视频14.(1)见解析;(2)见解析;(3).【来源】2015年全国普通高等学校招生统一考试文科数学(北京卷带解析)【解析】试题分析:(Ⅰ)利用三角形的中位线得出OM ∥VB ,利用线面平行的判定定理证明VB ∥平面MOC ;(Ⅱ)证明OC ⊥平面VAB ,即可证明平面MOC ⊥平面VAB ;(Ⅲ)利用等体积法求三棱锥A-MOC 的体积即可试题解析:(Ⅰ)证明:∵O ,M 分别为AB ,VA 的中点,∴OM∥VB,∵VB平面MOC,OM平面MOC,∴VB∥平面MOC;(Ⅱ)证明:∵AC=BC,O为AB的中点,∴OC⊥AB,又∵平面VAB⊥平面ABC,平面 ∩平面VAB=AB,且OC平面ABC,∴OC⊥平面VAB,∵OC平面MOC,∴平面MOC⊥平面VAB(Ⅲ)在等腰直角三角形中,,所以.所以等边三角形的面积.又因为平面,所以三棱锥的体积等于.又因为三棱锥的体积与三棱锥的体积相等,所以三棱锥的体积为.考点:平面与平面垂直的判定;直线与平面平行的判定;用向量证明平行视频答案第15页,总15页。
高考数学复习——立体几何:(二)空间直线、平面关系的判断与证明——.线面关系的判断(试题版)

【考点1:空间中点、线、面的基本关系】题型1:平面基本性质及其应用【典型例题】[例1](1)在下列命题中,不是公理的是()A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线(2)下列命题正确的是.①经过三点确定一个平面;②梯形可以确定一个平面;③两两相交的三条直线最多可以确定三个平面;④如果两个平面有三个公共点,则这两个平面重合.(3)以下四个命题中正确的是.①不共面的四点中,其中任意三点不共线;②若点A、B、C、D共面,点A、B、C、E共面,则点A、B、C、D、E共面;③若直线a、b共面,直线a、c共面,则直线b、c共面;④依次首尾相接的四条线段必共面.[例2]如图所示,正方体ABCD—A1B1C1D1中,E、F 分别是AB和AA1的中点.求证:(1)E、C、D1、F四点共面;(2)CE、D1F、DA三线共点.【变式训练】1.如图,α∩β=l,A、B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过()A.点AB.点BC.点C但不过点MD.点C和点M2.平面α、β相交,在α、β内各取两点,这四点都不在交线上,这四点能确定________个平面.3.如图,空间四边形ABCD中,E、F、G分别在AB、BC、CD上,且满足AE∶EB=CF∶FB=2∶1,CG∶GD=3∶1,过E、F、G的平面交AD于点H.(1)求AH∶HD;(2)求证:EH、FG、BD三线共点. 题型2:空间中直线关系的判断【典型例题】[例1](1)(教材习题改编)给出命题:①若两条直线和第三条直线所成的角相等,则这两条直线互相平行.②若两条直线都与第三条直线垂直,则这两直线互相平行.③若两条直线都与第三条直线平行,则这两直线互相平行.其中不正确的命题的个数为________.(2)(2015·福建六校联考)设a,b,c是空间中的三条直线,下面给出四个命题:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a∥c;③若a与b相交,b与c相交,则a与c相交;④若a⊂平面α,b⊂平面β,则a,b一定是异面直线.上述命题中正确的命题是________(只填序号).(3)(2014·广东)若空间中四条两两不同的直线l1,l2,l3,l 4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是() A.l1⊥l4 B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定[例2](1)如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是()A.MN与CC1垂直B.MN与AC垂直C.MN与BD平行D.MN与A1B1平行(2)如图所示,正方体ABCD—A1B1C1D1中,M、N分别是A1B1、B1C1的中点.问:①AM和CN是否是异面直线?说明理由;②D1B和CC1是否是异面直线?说明理由.【变式训练】1.若a,b是异面直线,直线c平行于直线a,那么c与b( )A.一定是异面直线 B.一定是相交直线C.不可能是平行直线ﻩ D.不可能是相交直线2.若空间直线a,b,c满足a⊥b,b⊥c,则直线a与c ()A.平行B.相交C.异面直线D.都有可能3.设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确的命题是________.①P∈a,P∈α⇒a⊂α;②a∩b=P,b⊂β⇒a⊂β;③a∥b,a⊂α,P∈b,P∈α⇒b⊂α;④α∩β=b,P∈α,P∈β⇒P∈b4.已知l1,l2,l3是空间不同的直线,则下列正确的是()A.l1⊥l2,l2⊥l3⇒l1∥l3 B.l1⊥l2,l2∥l3⇒l1⊥l3C.l1∥l2∥l3⇒l1,l2,l3共面 D.l1,l2,l3共点⇒l1,l2,l3共面。
2015年全国各省市高考文数——立体几何(选择+填空+答案)

2015年全国各省市高考文数——立体几何
1.2015年新课标II 文数10.已知A ,B 是球O 的球面上两点,∠AOB
= 90°,C 为该球面上的动点。
若三棱锥O —ABC 体积的最大值为36,
则球O 的表面积为
A .36π
B .64π
C .144π
D .256π
2.2015广东文数6. 若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )
A .l 至少与1l ,2l 中的一条相交
B .l 与1l ,2l 都相交
C .l 至多与1l ,2l 中的一条相交
D .l 与1l ,2l 都不相交
3.2015山东文数9、已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为
(A )3 (B )3
(C ) (D ) 4.2015浙江文数4、设α,β是两个不同的平面,l ,m 是两条不同的直线,
且l α⊂,m β⊂( )
A .若l β⊥,则αβ⊥
B .若αβ⊥,则l m ⊥
C .若//l β,则//αβ
D .若//αβ,则//l m
5.2015上海文数
6.若正三棱柱的所有棱长均为a ,且其体积为316,则=a ___________.
1.C
2.A
3.B
4.A
5. 4。
【数学】2015高考试题分类汇编:文科立体几何答案版

C 【解析】 如图 1- 6,由于 SC 是球的直径, 所以∠ SAC=∠ SBC= 90°,又∠ ASC=∠ BSC =45°,所以△ SAC、△ BSC 为等腰直角三角形,取 SC 中点 D ,连接 AD、BD .由此得 SC⊥
1 AD ,SC⊥BD ,即 SC⊥平面 ABD .所以 VS-ABC= VS-ABD+ VC-ABD = 3S△ABD ·SC. 由于在等腰直角三角形△ SAC 中∠ ASC= 45°, SC= 4,所以 AD = 2.同理 BD = 2.
() A . V1 比 V2 大约多一半
B. V1 比 V2 大约多两倍半 C. V1 比 V2 大约多一倍
D. V1 比 V2 大约多一倍半 D 【解析】 设球的半径为 R,则 V1=43πR3.设正方体的边长为 a,则 V2= a3.又因为 2R= 3
a,所以
4 V1 =3π
3 2a
3=
3 2
πa
′=
OD
=2,又由于
G和
G′都在线段 DA 的延长线上,所以 G 与 G′重合.
在△ GED 和△ GFD 中,由 OB
綊
1 2DE
和
OC
1 綊 2DF
,可知
B
和
C
分别是
GE 和 GF 的中点.所
以 BC 是△ GEF 的中位线,故 BC∥ EF.
3 (2) 由 OB=1, OE= 2,∠ EOB= 60°,知 S△EOB= 2 . 而△ OED 是边长为 2 的正三角形,故 S△OED= 3.
2 【解析】 ∵ EF∥平面 AB1C, EF ? 平面 ABCD ,平面 ABCD ∩平面 AB 1C=AC,
∴EF ∥AC,
又∵ E 是 AD 的中点,
立体几何专题(2015-2017全国卷试题分析)

A.4
A1
B. 9 2
C.6
C1
3 10
C
D. 32 3
A
B1
r=2
6
8
B
2.(2017年全国卷 理8)已知圆柱的高为1,它的两个底面的圆周在直径为2的
同一个球的球面上, 则该圆柱的体积为 ( )
A.
B. 3
C.
D.
4
2
4
O R=1
1
2 3
r= 2
正三棱锥
(3)空间角与空间距离的计算
几何体体积(三视图);线面位置关系; 空间角的计算 .
几何体的表面积(三视图)、体积;线面 位置关系(平行);空间角的计算 .
卷二 T6,T14(1选1填) T19(1解) 22
几何体的表面积(三视图);线面位置关 系;空间角的计算 .
卷三 T9,T10(2选) T19(1解) 22
几何体的表面积、体积(三视图);线面 位置关系(垂直);空间角的计算 .
几何体的体积;线面位置关系(垂直); 空间角的计算 .
1.从题型看:
近三年来保持了历年对立体几何的考查题型:选择题、 填空题及解答题三种.题型稳定.
2.从题量看:
近三年的全国卷多数是以“两小一大”为主,分值在 22分(15年卷二是“一小一大”,分值为17分),约 占总分值的15%,所占比重较大.
3.从知识的分布看:
D1
C1
A1
B1
D
C
A
B
动向3 空间几何体的计算问题
本部分是考查的重点内容,常以几何体的表面积、 体积的计算以及几何体的外接球、内切球为主要命题点 进行考查.
(1)几何体的表面积、体积;
【数学】2015高考试题分类汇编:文科立体几何答案版.

2015全国高考数学试题汇编文科立体几何(答案分析版)[2015安徽卷]一个空间几何体的三视图如图所示,则该几何体的表面积为(A . 48B . 32 + 8 C. 48+ 8 D . 80C 【解析】由三视图可知本题所给的是一个底面为等腰梯形的放倒的直四棱柱(如图所示, 所以该直四棱柱的表面积为S= 2 (2 + 4 4+ 4 4+ 2 4 + 2 4 = 48+ 8.[2015北京卷]某四棱锥的三视图如图1 —1所示,该四棱锥的表面积是(啊辄1割A . 32B . 16+ 16 C. 48 D . 16+ 32B 【解析】由题意可知,该四棱锥是一个底面边长为4,高为2的正四棱锥,所以其表面积为44+ 4 42 = 16+ 16,故选 B.[2015 •东卷]如图,某几何体的正视图(主视图,侧视图(左视图和俯视图分别是等边三角形, 等腰三角形和菱形,则该几何体体积为(C 【解析】由三视图知该几何体为四棱锥,棱锥高h== 3,底面为菱形,对角线长分别为2, 2,所以底面积为2 2= 2,所以V = Sh= 2 3= 2.[2015湖南卷]设图是某几何体的三视图,则该几何体的体积为(A . 9 n+ 42B . 36 n+ 18 C. * 12 D.先 18D 【解析】由三视图可得这个几何体是由上面是一个直径为3的球,下面是一个长、宽都为3高为2的长方体所构成的几何体,则其体积为:V = V1 + V2 =n-3+ 3 3 2 = n+ 18,故选D.[2015辽宁卷]一个正三棱柱的侧棱长和底面边长相等,体积为1-3所示,左视图是一个矩形,则这个矩形的面积是(2,它的三视图中的俯视图如图A . 4B . 2 C. 2 D.B 【解析】由俯视图知该正三棱柱的直观图为下图,其中M , N是中点,矩形MNC 1C为左视图.[2015课标全国卷]在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为(D 【解析】由正视图和俯视图知几何体的直观图是由一个半圆锥和一个三棱锥组合而成的,如图,故侧视图选 D.[2015陕西卷]某几何体的三视图如图所示,则它的体积为(A . 8 —B . 8 —C. 8 —2 n D.A 【解析】主视图与左视图一样是边长为2的正方形,里面有两条虚线,俯视图是边长为2的正方形与直径为2的圆相切,其直观图为棱长为2的正方体中挖掉一个底面直径为2的圆锥,故其体积为正方体的体积与圆锥的体积之差,V正=23= 8, V锥=n2h= (r = 1, h = 2,故体积V = 8 ―,故答案为A.[2015天津卷]一个几何体的三视图如图所示(单位:m,则该几何体的体积为__________ m3.4【解析】根据三视图还原成直观图,可以看出,其是由两个形状一样的,底面长和宽都为1,高为2的长方体叠加而成,故其体积V = 211 + 112= 4.22015浙江卷]若某几何体的三视图如图所示,则这个几何体的直观图可以是[2015福建卷]如图1 —3,正方体ABCD —A1B1C1D1中,AB = 2,点E为AD的中点,点F在CD上,若EF //平面AB1C,则线段EF的长度等于___________ .【解析】•/ EF //平面ABIC , EF?平面ABCD,平面ABCD 平面ABIC = AC ,••• EF // AC ,又••• E是AD的中点,• F是CD的中点,即EF是厶ACD的中位线,• EF = AC = 2 =.[2015浙江卷]若直线I不平行于平面a且I? a,则(A . a内的所有直线与I异面B . a内不存在与I平行的直线C. a内存在唯一的直线与I平行D . a内的直线与I都相交B【解析】在a内存在直线与I相交,所以A不正确;若a内存在直线与I平行,又:I? a, 则有I // a,与题设相矛盾,• B正确,C不正确;在a内不过I与a交点的直线与I异面,D不正确.[2015 广东卷]正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有(A . 20B . 15 C. 12 D . 10D 【解析】一个下底面5个点,每个下底面的点对于5个上底面的点,满足条件的对角线有2条,所以共有52 = 10条.[2015四川卷]11 ,12 ,13是空间三条不同的直线,则下列命题正确的是(A .11 丄12 , 12 丄13? 11 // 13B . 11 丄12 , 12 // 13? 11 丄13C. 11 // 12 // 13? 11 , 12, 13 共面D . 11 , 12 , 13 共点? 11 , 12 , 13 共面B 【解析】对于A,直线11与13可能异面;对于C,直线11、12、13可能构成三棱柱三条侧棱所在直线而不共面;对于D,直线11、12、13相交于同一个点时不一定共面.所以选B. [2015湖北卷]设球的体积为V1,它的内接正方体的体积为V2,下列说法中最合适的是(A . V1比V2大约多一半B . V1比V2大约多两倍半C. V1比V2大约多一倍D . V1比V2大约多一倍半D 【解析】设球的半径为R,则V1 = n3•设正方体的边长为a,则V2 = a3.又因为2R= a,所以V1 = n 3 £3, V1 —V2= a3~ 1卫3.[2015辽宁卷]已知球的直径SC= 4, A、B是该球球面上的两点,AB= 2, / ASC= Z BSC=45 °则棱锥S- ABC的体积为(A. B. C. D.C 【解析】如图1 —6,由于SC是球的直径,所以Z SAC= Z SBC= 90 °又Z ASC= Z BSC=45°所以△ SAC、△ BSC为等腰直角三角形,取SC中点D,连接AD、BD.由此得SC丄AD, SC丄BD,即SC丄平面ABD.所以Vi —= V L—+ VX—= S A 二己:SC.由于在等腰直角三角形△ SAC中/ASC= 45° SC= 4,所以AD = 2•同理BD = 2.又AB = 2,所以△ ABD为正三角形,所以V m = S△上SC= XX22 •in60M=,所以选 C.[2015课标全国卷]已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上,若圆锥底面面积是这个球面面积的,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为.【解析】如图,设球的半径为R,圆锥底面半径为r,则球面面积为4T R2,圆锥底面面积为n2,由题意n2 = T R2,所以r = R,所以001 = = = R,所以SO1 = R+ R= R, S1O1 = R—R= R,所以==.[2015四川卷]如图1 —3,半径为4的球O中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是 ______________________ .大纲文数15.G832 n【解析】本题主要考查球的性质、球与圆柱的组合体、均值不等式的应用.如图1—4为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,球半径R= 4,则2+ r2 = R2,即h = 2.因为S= 2 n h = 4 nr = 4 nW 4 n T R2,取等号时,内接圆柱底面半径为R,高为R,—S球一S圆柱=4T R2—2K R2 = 2K R2= 32 n.[2015全国卷]已知正方体ABCD —A1B1C1D1中,E为C1D1的中点,则异面直线AE与BC所成角的余弦值为_______________ .【解析】取A1B1的中点F,连EF,则EF // BC,/ AEF是异面直线AE与BC所成的角,设正方体的棱长为a,可得AE= a, AF =玄,在厶AEF中,运用余弦定理得cos/ AEF =,即异面直线AE与BC所成角的余弦值为.[2015安徽卷]如图1 —4, ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD 上,OA = 1, OD = 2, △ OAB , △ OAC , △ ODE , △ ODF 都是正三角形.(1证明直线BC // EF;(2求棱锥F —OBED的体积.【解答】(1证明:设G是线段DA与EB延长线的交点,由于△ OAB与厶ODE都是正三角形,OA = 1, OD = 2,所以OB 綊DE , OG = OD = 2.同理,设G'是线段DA与FC延长线的交点,有OC綊DF, OG = OD = 2,又由于G和G'都在线段DA 的延长线上,所以G与G'重合.在厶GED和厶GFD中,由OB綊DE和OC綊DF,可知B和C分别是GE和GF的中点.所以BC是厶GEF的中位线,故BC // EF.(2 由OB= 1, OE = 2,/ EOB = 60 °知S A EOB =.而厶OED是边长为2的正三角形,故S A OED =.所以SOBED = S A EOB + S A OED =.过点F作FQ丄DG,交DG于点Q,由平面ABED丄平面ACFD知,FQ就是四棱锥 F —OBED 的高,且FQ =,所以VF —OBED = FQ-S四边形OBED =.[2015北京卷]如图1 —4,在四面体PABC中,PC丄AB , PA丄BC,点D , E, F, G分别是棱AP , AC ,BC , PB的中点.(1求证:DE //平面BCP;(2求证:四边形DEFG为矩形;(3是否存在点Q,至U四面体PABC六条棱的中点的距离相等?说明理由.课标文数17.G4[2015北京卷]【解答】(1证明:因为D, E分别为AP, AC的中点,图1 — 5 所以DE // PC.又因为DE?平面BCP , PC?平面BCP , 所以DE //平面BCP.(2因为D、E、F、G分别为AP、AC、BC、PB的中点,所以DE // PC // FG ,DG // AB // EF,所以四边形DEFG为平行四边形.又因为PC丄AB,所以DE丄DG ,所以平行四边形DEFG为矩形.(3存在点Q满足条件,理由如下:连接DF , EG,设Q为EG的中点.由(2 知,DF AEG = Q,且QD = QE = QF = QG = EG.分别取PC、AB的中点M, N,连接ME、EN、NG、MG、MN.与(2同理,可证四边形MENG为矩形,其对角线交点为EG的中点Q,且QM = QN = EG.所以Q为满足条件的点.[2015 •苏卷]如图1 - 2,在四棱锥P—ABCD中,平面PAD丄平面ABCD , AB = AD,/ BAD =60° E、F分别是AP、AD的中点.求证:(1直线EF //平面PCD ;(2平面BEF丄平面PAD.课标数学16.G4 , G5[2015 -江苏卷]本题主要考查直线与平面、平面与平面的位置关系,考查空间想象能力和推理论证能力.【解答】证明:(1在厶PAD中,因为E, F分别为AP, AD的中点,所以EF // PD.又因为EF?平面PCD , PD?平面PCD ,图1 — 3所以直线EF //平面PCD .(2连结BD,因为AB = AD,Z BAD = 60 °所以△ ABD为正三角形,因为F是AD的中点,所以BF丄AD.因为平面PAD丄平面ABCD , BF?平面ABCD ,平面PAD 门平面 ABCD = AD ,所以BF 丄平面 PAD.又因为BF?平面BEF ,所以平面 BEF 丄平面 PAD.1[2015课标全国卷]如图1 — 8,四棱锥P — ABCD 中,底面60 ° AB = 2AD , PD 丄底面 ABCD.(1证明:PA 丄BD ;(2设PD = AD = 1,求棱锥 D — PBC 的高.课标文数18.G5 , G11[2015 -课标全国卷]【解答】(1证明:余弦定理得BD = AD ,从而 BD2 + AD2 = AB2, 故 BD 丄 AD.又PD 丄底面 ABCD ,可得BD 丄PD ,所以BD 丄平面 PAD ,故PA 丄BD.(2如图,作DE 丄PB ,垂足为E.已知PD 丄底面 ABCD ,贝U PD 丄BC.ABCD 为平行四边形,/ DAB = 因为/ DAB = 60° AB = 2AD ,由 由(1知BD 丄AD ,又BC // AD ,所以BC 丄BD . 图1 — 8故BC丄平面PBD, BC丄DE.贝U DE丄平面PBC.由题设知PD = 1,贝U BD = , PB= 2.根据DE PB = PD BD 得DE =.即棱锥D —PBC的高为.[2015陕西卷]如图1 —8,在厶ABC中,/ ABC = 45° / BAC = 90° AD是BC上的高,沿AD把厶ABD折起,使/ BDC = 90° (1证明:平面ADB丄平面BDC ;(2若BD = 1,求三棱锥D —ABC的表面积.图1 —8课标文数16.G5[2015陕西卷]【解答】(1 v折起前AD是BC边上的高, •••当厶ABD折起后,AD丄DC,AD丄DB.又DB A DC = D.• AD丄平面BDC.•/ AD 平面ABD,•平面ABD丄平面BDC.(2 由(1 知,DA 丄DB, DB 丄DC , DC 丄DA,DB = DA = DC = 1.AB = BC= CA=.从而S A DAB = S A DBC = =S\ DCA = X1 X1 =.S A ABC = ">Sin60 =.表面积S= X3+=.2015江苏卷]如图1 —2,在四棱锥P —ABCD中,平面PAD丄平面ABCD , AB= AD,/ BAD =60° E、F分别是AP、AD的中点.求证:(1直线EF //平面PCD ;(2平面BEF丄平面PAD.课标数学16.G4 , G5[2015 -江苏卷]本题主要考查直线与平面、平面与平面的位置关系,考查空间想象能力和推理论证能力.【解答】证明:(1在厶PAD中,因为E, F分别为AP, AD的中点,所以EF / PD.又因为EF?平面PCD, PD?平面PCD ,所以直线EF //平面PCD.(2连结BD,因为AB = AD,/ BAD = 60 °所以△ ABD为正三角形,因为F是AD的中点, 所以BF丄AD.因为平面PAD丄平面ABCD , BF?平面ABCD ,平面PAD门平面ABCD = AD,所以BF丄平面PAD.又因为BF?平面BEF,所以平面BEF丄平面PAD.[2015 •宁卷]如图1 —8,四边形ABCD为正方形,QA 丄平面ABCD , PD // QA , QA = AB = PD.(1证明:PQ丄平面DCQ ;(2求棱锥Q —ABCD的体积与棱锥P—DCQ的体积的比值.课标文数18.G7[2015辽宁卷]【解答】(1由条件知PDAQ为直角梯形. 因为QA丄平面ABCD,所以平面PDAQ丄平面ABCD,交线为AD.又四边形ABCD为正方形,DC丄AD ,所以DC丄平面PDAQ,可得PQ丄DC.在直角梯形PDAQ中可得DQ = PQ= PD,贝U PQ丄QD.所以PQ丄平面DCQ.(2 设AB = a.由题设知AQ为棱锥Q —ABCD的高,所以棱锥Q —ABCD的体积V1 = a3.由(1知PQ为棱锥P—DCQ的高,而PQ= a, △ DCQ的面积为a2,所以棱锥P—DCQ的体积V2 = a3.故棱锥Q —ABCD的体积与棱锥P—DCQ的体积的比值为1.1[2015湖南卷]如图1 —5,在圆锥PO中,已知PO=,O O的直径AB = 2,点C在上,且/ CAB = 30° D为AC的中点.(1证明:AC丄平面POD ;(2求直线OC和平面PAC所成角的正弦值.课标文数19.G5 , G11[2015 -湖南卷]【解答】(1因为OA = OC, D是AC的中点,所以AC丄OD. 又PO丄底面O O , AC?底面O O,所以AC丄PO.而OD, PO是平面POD内的两条相交直线,所以AC丄平面POD.(2由(1知,AC丄平面POD,又AC?平面PAC,所以平面POD丄平面PAC.在平面POD中,过O作OH丄PD于H,贝U OH丄平面PAC.图1 — 6连结CH,贝U CH是OC在平面PAC上的射影, 所以/ OCH是直线OC和平面PAC所成的角.在Rt△ ODA 中,OD = OA sin30 =.在Rt△ POD 中,OH ===.在Rt△ OHC 中,sin/OCH ==.故直线OC和平面PAC所成角的正弦值为.图1 —7[2015浙江卷]如图1 —7,在三棱锥P—ABC中,AB = AC, D为BC的中点,PO丄平面ABC, 垂足O落在线段AD 上.(1 证明:AP I BC;(2 已知BC = 8, PO = 4, AO= 3, OD = 2,求二面角B—AP —C 的大小.课标文数20.G11 [2015浙江卷]【解答】(1证明:由AB= AC, D是BC中点,得AD丄BC,又PO丄平面ABC, 得PO丄BC ,因为PO Q AD = O,所以BC丄平面PAD,故BC丄AP. (2如图,在平面APB内作BM丄PA于M,连CM. 因为BC丄PA,得PA丄平面BMC,所以AP I CM.故/ BMC为二面角B—AP - C的平面角.在Rt△ ADB 中,AB2= AD2 + BD2= 41,得AB=.在Rt△ POD 中,PD2 = PO2+ OD2,在Rt△ PDB 中, PB2= PD2 + BD2,所以PB2 = PO2+ OD2+ BD2 = 36,得PB= 6.在Rt△ POA 中,PA2= AO2 + OP2= 25,得PA= 5. 又cos / BPA= = ,从而sin / BPA=.故BM= PBsin / BPA= 4.同理CM= 4.因为BM甘MC2= BC2所以/ BM= 90°,即二面角B- AP— C的大小为90°.图1-5[2015 •福建卷]如图1 —5,四棱锥P— ABCD中, PU底面ABCD AB丄AD,点E在线段AD 上,且CE// AB.(1求证:CEL平面PAD(2 若PA= AB= 1, AD- 3, CD-,/ CDA= 45°,求四棱锥P—ABCD勺体积.课标文数20.G12[2015 •福建卷]【解答】(1证明:因为PAL平面ABCD CE?平面ABCD图1 — 6所以PAL CE因为AB丄AD, CE// AB所以CEL AD.又PA n AD- A,所以CEL平面PAD.(2 由(1 可知CEL AD.在Rt△ ECD中,DE- CD- cos45°= 1, CE- CD- sin45 ° = 1.又因为AB= CE- 1, AB// CE所以四边形ABCE为矩形.所以S 四边形ABC—S 矩形ABCEF S A ECD- AB - AE+ CE- DE- 1X 2+ X 1 X 1=. 又PAL平面ABCD PA= 1 , 所以V四棱锥P—ABC- S四边形ABCD PA- XX 1 -. 2[2015 •江西卷]如图1 —7,在厶ABC 中,/ B=, AB= BC= 2, P为AB边上一动点,PD// BC 交AC于点D,现将△ PDA沿PD翻折至△ PDA,使平面PDA丄平面PBCD.(1当棱锥A—PBCD的体积最大时,求PA的长;(2若点P为AB的中点,E为A C的中点,求证:A B丄DE课标文数18.G12[2015 •江西卷]【解答】(1 令PA= x(0<x<2,贝U A P= PD= x, BP= 2—x.因为A'P丄PD,且平面A PD丄平面PBCD 故A'P丄平面PBCD.所以VA'—PBCD= Sh= (2 —x(2 + xx = (4x —x3.令f(x = (4x —x3,由 f ‘ (x = (4 —3x2= 0,得x=.当x€时,f ' (x>0,f(x单调递增;当x€时,f ' (x<0,f(x单调递减,所以,当x=时,f(x取得最大值,即:当VA'—PBCD最大时,PA=.(2证明:设F为A'B的中点,连接PF, FE.则有EF綊BC,PD綊BC,所以EF綊PD,四边形DEFP为平行四边形,所以DE// PF,又A P= PB,所以PF丄A B,故DEL A'B.[2015 •山东卷]如图1 —5,在四棱台ABCD- A1B1C1D1中,D1D L平面ABCD底面ABCD是平行四边形,AB= 2AD, AD= A1B1, / BAD= 60°.(1 证明:AA1L BD(2 证明:CC1 //平面A1BD.图1 — 5课标文数19.G12[2015 •山东卷]【解答】证明:(1证法因为D1D L平面ABCD且BD?平面ABCD图1 — 6所以D1D L BD.又因为AB= 2AD, / BAD= 60°,在厶ABD中,由余弦定理得BD2 = AE2 + AB2 —2AD- AB DOS60°= 3AE2.所以AD2+ BD2= AB2所以AD L BD.又AD A D1D= D,所以BDL平面ADD1A1.又AA1?平面ADD1A1所以AA1丄BD.证法因为D1DL平面ABCD且BD?平面ABCD所以BDL D1D取AB的中点G连接DG.在厶ABD 中,由AB= 2AD得AG= AD,又/ BAD= 60°,所以△ ADG为等边三角形.因此GD= GB.故/ DB&/ GDB又/ AGD= 60°,所以/ GDB= 30°,故/ ADB=Z ADG/ GDB= 60°+ 30°= 90 所以BD L AD. 又AD A D1D= D,所以BDL平面ADD1A1 又AA1?平面ADD1A1所以AA1丄BD.设 ACH BD= E ,连接 EA1. 因为四边形ABCD 为平行四边形, 所以EC = AC由棱台定义及 AB = 2AD= 2A1B1知, A1C1// EC 且 A1C1= EC所以四边形A1ECC 伪平行四边形. 因此 CC1// EA1,又因为EA1?平面 A1BD CC1?平面 A1BD所以CC1//平面A1BD.[2015 •四川卷]如图1 — 5,在直三棱柱 ABC- A1B1C1中,/ BAC= 90 延长A1C1至点P ,使C1P = A1C1,连结 AP 交棱CC1于点D. AB= AC = AA1= 1,(1 求证:PB1// 平面 BDA1;(2求二面角A — AID- B 的平面角的余弦值. (2 连接 AC A1C1.[2015 •四川卷]【解答】解法(1连结AB1与BA1交于点O,连结OD.•/ C1D/ AA1, A1C1= C1P, ••• AD= PD,又AO= B1Q • OD/ PB1.图1 — 6又OD?平面BDA1, PB1?平面BDA1,• PB1 //平面BDA1.(2过A作AEL DA1于点E ,连结BE.•/ BAL CA BAL AA1,且AA们AC= A,• BAL平面AA1C1C.由三垂线定理可知BE L DA1.•/ BEA为二面角A- AID- B的平面角.在Rt △ A1C1D 中,A1D= =,又S A AA1D=X 1 X 1=XX AE• AB .在Rt △ BAE 中,BE= =, • cos / BEA==.故二面角A—A1A B的平面角的余弦值为[2015 •天津卷]如图1 —7,在四棱锥P—ABCD中,底面ABCD 为平行四边形,/ ADC= 45AD= AC= 1, O为AC的中点,POL平面ABCD PO= 2, M为PD的中点.(1证明PB//平面ACM(2证明ADL平面PAC(3求直线AM与平面ABCD所成角的正切值.课标文数17.G12[2015 •天津卷]图1 —8【解答】(1证明:连接BD, MO在平行四边形ABCD中,因为O为AC的中点,所以O为BD的中点.又M为PD的中点,所以PB// MO因为PB?平面ACM MC?平面ACM所以PB//平面ACM.(2证明:因为/ ADC= 45°,且A» AC= 1,所以/ DAC= 90°,即卩AD L AC又PC L平面ABCD AD?平面ABCD 所以POL AD.而AS PO= O,所以ADL平面PAC.(3取DO中点N,连接MN, AN.因为M为PD的中点,所以MN/ PQ 且MN k PO= 1.由PO L平面ABCD得MN L平面ABCD所以/ MAN是直线AM与平面ABCD所成的角.在Rt△ DAO中,AD=1, AO=,所以DO=.从而AN^ DO=.在Rt △ ANM中, tan / MAN= ==,即直线AM与平面ABCD所成角的正切值为•20.(本小题满分13分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马, 将四个面都为直角三角形的四面体称之为鳖臑.中,侧棱;底面,且:,点.是「的(I)证明:;平面•’.试判断四面体,—是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;(U)记阳马「'的体积为,四面体■ !-的体积为',求的值.【答案】(I)因为「底面■,所以Q '1.由底面:为长方形,有■ ■',而轮童,所以. 平面•..「平面•.,所以- ■.又因为;,点,是「的中点,所以「.而•’,所以;平面尹皆/.四面体■兀』是- 一个鳖臑; (n) J【解析】试题分析:(I)由侧棱:底面• •易知,3 ..;而底面 ,•为长方形,有〃「丄,由线面垂直的判定定理知B「丄平面,进而由线面垂直的性质定理可得处丄DF ;在\PCD中,易得DE1 PC,再由线面垂直的判定定理即可得出结论.由决’丄平面••,,平面•’,进一步可得四面体,■ ■的四个面都是直角三角形,即可得出结论;(n)结合(I)证明结论,并根据棱锥的体积公式分别求出'',即可得出所求结果.试题解析:(I)因为逹:亠底面,所以「■'.由底面•为长方形,有■ ■',而财门,所以.平面• . . ■. 平面••,所以- 1 .又因为- ,点’是「的中点,所以「..而「,所以;平面'.由,平面,平面•■,可知四面体厂,:的四个面都是直角三角形,即四面体是一个鳖臑,其四个面的直角分别是罢:溟乙筑線££逆:烈遽盘(n)由已知,」是阳马…•的高,所以' •:「;由卄V= -S^f DE=~ AC CE DE(I)知,…是鳖臑,■的高,厂,所以r)E - CE —^CD在I △「中,因为「',点•是「的中点,所以一,于是BCCEDE 2S PD CE DE66。
2015高考试题――立体几何

2015高考试题――立体几何1.【2015高考安徽,理5】已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是()(A)若α,β垂直于同一平面,则α与β平行(B)若m,n平行于同一平面,则m与n平行(C)若α,β不平行,则在α内不存在与β平行的直线(D)若m,n不平行,则m与n不可能垂直于同一平面【答案】D【解析】由A,若α,β垂直于同一平面,则α,β可以相交、平行,故A不正确;由B,若m,n平行于同一平面,则m,n可以平行、重合、相交、异面,故B不正确;由C,若α,β不平行,但α平面内会存在平行于β的直线,如α平面中平行于α,β交线的直线;由D项,其逆否命题为“若m与n垂直于同一平面,则m,n平行”是真命题,故D项正确.所以选D.【考点定位】1.直线、平面的垂直、平行判定定理以及性质定理的应用.【名师点睛】空间直线、平面平行或垂直等位置关系命题的真假判断,常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.2.【2015高考北京,理4】设α,β是两个不同的平面,m是直线且mα⊂.“mβ∥”是“αβ∥”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B【解析】因为α,β是两个不同的平面,m 是直线且m α⊂.若“m β∥”,则平面、αβ可能相交也可能平行,不能推出//αβ,反过来若//αβ,m α⊂,则有m β∥,则“m β∥”是“αβ∥”的必要而不充分条件.考点定位:本题考点为空间直线与平面的位置关系,重点考察线面、面面平行问题和充要条件的有关知识.【名师点睛】本题考查空间直线与平面的位置关系及充要条件,本题属于基础题,本题以空间线、面位置关系为载体,考查充要条件.考查学生对空间线、面的位置关系及空间面、面的位置关系的理解及空间想象能力,重点是线面平行和面面平行的有关判定和性质.3.【2015高考新课标1,理6】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
2015年高考新课标Ⅱ卷文数试题+解析

2015年普通高等学校招生全国统一考试(全国卷2)文科数学一、 选择题:本大题共12小题。
每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的。
1.已知集合}21|{<<-=x x A ,}30|{<<=x x B ,则A ∪B=( )A. )3,1(-B. )0,1(-C. )2,0(D. )3,2(2.若a 为实数,且i iai+=++312,则=a ( ) A. 4- B. 3- C. 3 D. 43. 根据下面给出的2004年至2013年我国二氧化碳年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A.逐年比较,2008年减少二氧化碳排放量的效果显著B.2007年我国治理二氧化碳排放显现成效C.2006年以来我国二氧化碳年排放量呈逐渐减少趋势D.2006年以来我国二氧化碳年排放量与年份正相关 4.向量a =(1,-1) b =(-1,2),则(2a +b ).a = ( ) A. 1- B. 0 C. 1 D.2 5. 设n S 是数列}{n a 的前n 项和,若3531=++a a a ,则=5S ( )A. 5B. 7C. 9D. 116. 一个正方体被一个平面截取一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( ) A.81 B. 71 C. 61 D. 51 7.已知三点)0,1(A ,)3,0(B ,)3,2(C ,则ABC ∆外接圆的圆心到原点的距离为( ) A.35 B. 321 C. 352 D. 348.右边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a 、b 分别为14、18,则输出的=a ( )A. 0B. 2C. 4D. 149.已知等比数列}{n a 满足411=a ,)1(4453-=a a a ,则=2a ( ) A. 2 B. 1 C. 21 D. 8110.已知A 、B 是球O 的球面上两点, 90=∠AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为( )A. π36B. π64C. π144D. π256 11.如图,长方形ABCD 的边2=AB ,1=BC ,O 是AB 的中点,点P 沿着BC 、CD 与DA 运动,记x BOP =∠.将动点P 到A 、B 两点距离之和表示为x 的函数)(x f ,则)(x f y =的图象大致为( )12. 设函数211|)|1ln()(xx x f +-+=,则使得)12()(->x f x f 成立的x 的取值范围是( ) A. )1,31( B. ),1()31,(+∞-∞U C. )31,31(- D. ),31()31,(+∞--∞U二.填空题:共4小题,每小题5分.13. 已知函数x ax x f 2)(3-=的图象过点)4,1(-,则=a .14.若x 、y 满足约束条件⎪⎩⎪⎨⎧≤+-≥--≤-+01201205y x y x y x ,则y x z +=2的最大值为 .15.已知双曲线过点)3,4(,且渐近线方程为x y 21±=,则该双曲线的标准方程为 . 16.已知曲线x x y ln +=在点)1,1(处的切线与曲线1)2(2+++=x a ax y 相切,则=a .三、解答题:解答应写出文字说明,证明过程或演算步骤.17、(本小题满分12分)ΔABC中,D是BC上的点,AD平分∠BAC,BD=2DC.(1)求sinsinBC∠∠;(2)若∠BAC=60°,求∠B.18、(本小题满分12分)某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得分A地区用户满意评分的频率分布直方图和B地区用户满意度评分的频数分布表.B地区用户满意度评分的频数分布表(1)在答题卡上作出B地区用户满意度评分的频数分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)19、(本小题满分12分)如图,长方体ABCD ﹣A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E ,分别在A 1B 1, D 1C 1上,A 1E= D 1F=4.过点E,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由) (2)求平面α把该长方体分成的两部分体积的比值. 20、(本小题满分12分)已知椭圆C :22221x y a b+=(a >b >0,点(2)在C 上.(1)求C 的方程.(2)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M.直线OM 的斜率与直线l 的斜率的乘积为定值.21、(本小题满分12分)已知函数f (x )=ln x +a (1- x ) (1)讨论f (x )的单调性;(2)当f (x )有最大值,且最大值大于2a -2时,求a 的取值范围. 22、(本小题满分10分)选修4-4:坐标系与参数方程在直线坐标系xOy 中,曲线C 1:cos sin x t y t ==αα{(t 为参数,t ≠0)其中0≤α≤π.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:p=2sin θ,C 3:cos θ。
2015-2017立体几何全国卷高考真题

2015-2017立體幾何高考真題1、(2015年1卷6題)《九章算術》是我國古代內容極為豐富の數學名著,書中有如下問題:“今有委米依垣內角,下周八尺,高五尺。
問:積及為米幾何?”其意思為:“在屋內牆角處堆放米(如圖,米堆為一個圓錐の四分之一),米堆為一個圓錐の四分之一),米堆底部の弧長為8尺,米堆の高為5尺,問米堆の體積和堆放の米各為多少?”已知1斛米の體積約為1.62立方尺,圓周率約為3,估算出堆放斛の米約有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛【答案】B【解析】設圓錐底面半徑為r ,則12384r ⨯⨯==163r =,所以米堆の體積為211163()5433⨯⨯⨯⨯=3209,故堆放の米約為3209÷1.62≈22,故選B.考點:圓錐の性質與圓錐の體積公式2、(2015年1卷11題)圓柱被一個平面截去一部分後與半球(半徑為r )組成一個幾何體,該幾何體三視圖中の正視圖和俯視圖如圖所示.若該幾何體の表面積為16 + 20π,則r=( )(A )1 (B )2 (C )4 (D )8 【答案】B【解析】由正視圖和俯視圖知,該幾何體是半球與半個圓柱の組合體,圓柱の半徑與球の半徑都為r ,圓柱の高為2r ,其表面積為22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r=2,故選B.考點:簡單幾何體の三視圖;球の表面積公式、圓柱の測面積公式 3、(2015年1卷18題)如圖,四邊形ABCD 為菱形,∠ABC=120°,E ,F 是平面ABCD 同一側の兩點,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(Ⅰ)證明:平面AEC ⊥平面AFC ;(Ⅱ)求直線AE 與直線CF 所成角の余弦值. 【解析】 試題分析:(Ⅰ)連接BD ,設BD∩AC=G,連接EG ,FG ,EF ,在菱形ABCD 中,不妨設GB=1易證EG ⊥AC ,通過計算可證EG ⊥FG ,根據線面垂直判定定理可知EG ⊥平面AFC ,由面面垂直判定定理知平面AFC ⊥平面AEC ;(Ⅱ)以G 為座標原點,分別以,GB GC の方向為x 軸,y 軸正方向,||GB 為單位長度,建立空間直角坐標系G-xyz ,利用向量法可求出異面直線AE 與CF 所成角の余弦值. 試題解析:(Ⅰ)連接BD ,設BD∩AC=G,連接EG ,FG ,EF ,在菱形ABCD 中,不妨設GB=1,由∠ABC=120°,可得 由BE ⊥平面ABCD ,AB=BC 可知,AE=EC ,又∵AE ⊥EC ,∴EG ⊥AC ,在Rt △EBG 中,可得DF=2.在Rt △FDG 中,可得在直角梯形BDFE 中,由BD=2,可得 ∴222EG FG EF +=,∴EG ⊥FG ,∵AC∩FG=G,∴EG ⊥平面AFC ,∵EG ⊂面AEC ,∴平面AFC ⊥平面AEC.(Ⅱ)如圖,以G 為座標原點,分別以,GB GC の方向為x 軸,y 軸正方向,||GB 為單位長度,建立空間直角坐標系G-xyz ,由(Ⅰ)可得A (00),E (,F (-1,0,C (00),∴AE =(1,CF =(-1,).…10分故cos ,3||||AE CF AE CF AE CF ⋅<>==-. 所以直線AE 與CF 考點:空間垂直判定與性質;異面直線所成角の計算;空間想像能力,推理論證能力4、(2015年2卷6題)一個正方體被一個平面截去一部分後,剩餘部分の三視圖如右圖,則截去部分體積與剩餘部分體積の比值為( )A .81 B .71 C .61 D .51 【解析】由三視圖得,在正方體1111ABCD A BC D -中,截去四面體111A A B D -,如圖所示,,設正方體棱長為a ,則11133111326A A B D V a a -=⨯=,故剩餘幾何體體積為3331566a a a -=,所以截去部分體積與剩餘部分體積の比值為51,故選D .考點:三視圖.5、(2015年2卷9題)已知A,B 是球O の球面上兩點,∠AOB=90,C 為該球面上の動點,若三棱錐O-ABC 體積の最大值為36,則球O の表面積為( ) A .36π B .64π C .144π D .256π【解析】如圖所示,當點C 位於垂直於面AOB の直徑端點時,三棱錐O ABC -の體積最大,設球O の半徑為R ,此時2311136326O ABC C AOB V V R R R --==⨯⨯==,故6R =,則球O の表面積為24144S R ππ==,故選C .考點:外接球表面積和椎體の體積.6、(2015年2卷19題)(本題滿分12分)如圖,長方體1111ABCD A BC D -中,=16AB ,A1=10BC ,18AA =,點E ,F 分別在11A B ,11C D 上,114A E D F ==.過點E ,F の平面α與此長方體の面相交,交線圍成一個正方形.(Ⅰ)在圖中畫出這個正方形(不必說出畫法和理由); (Ⅱ)求直線AF 與平面α所成角の正弦值. 【解析】(Ⅰ)交線圍成の正方形EHGF 如圖:(Ⅱ)作EM AB ⊥,垂足為M ,則14AM AE ==,18EM AA ==,因為EHGF 為正方形,所以10EH EF BC ===.於是226MH EH EM =-=,所以10AH =.以D為座標原點,DA の方向為x 軸の正方向,建立如圖所示の空間直角坐標系D xyz -,則(10,0,0)A ,(10,10,0)H ,(10,4,8)E ,(0,4,8)F ,(10,0,0)FE =,(0,6,8)HE =-.設(,,)n x y z =是平面E H G F の法向量,則0,0,n FE n HE ⎧⋅=⎪⎨⋅=⎪⎩即100,680,x y z =⎧⎨-+=⎩所以可取(0,4,3)n =.又(10,4,8)AF =-,故45cos ,15n AF n AF n AF⋅<>==⋅.所以直線AF 與平面α所成角の正弦值為45.考點:1、直線和平面平行の性質;2、直線和平面所成の角.7、(2016年1卷6題)如圖,某幾何體の三視圖是三個半徑相等の圓及每個圓中兩條相互垂直の半徑.若該幾何體の體積是283π,則它の表面積是 (A )17π (B )18π (C )20π (D )28πD D CAE FA B CB【解析】試題分析: 該幾何體直觀圖如圖所示:是一個球被切掉左上角の18,設球の半徑為R ,則37428V R 833ππ=⨯=,解得R 2=,所以它の表面積是78の球面面積和三個扇形面積之和2271=42+32=1784S πππ⨯⨯⨯⨯故選A .考點:三視圖及球の表面積與體積8、(2016年1卷11題)平面α過正方體ABCD -A 1B 1C 1D 1の頂點A ,α//平面CB 1D 1,αI 平面ABCD =m ,αI 平面AB B 1A 1=n ,則m 、n 所成角の正弦值為(B (D)13試題分析:如圖,設平面11CB D 平面ABCD ='m ,平面11CB D 平面11ABB A ='n ,因為//α平面11CB D ,所以//',//'m m n n ,則,m n 所成の角等於','m n 所成の角.延長AD ,過1D 作11//DE B C ,連接11,CE B D ,則CE 為'm ,同理11BF 為'n ,而111//,//BD CE B F A B ,則','m n 所成の角即為1,A B BD 所成の角,即為60︒,故,m n ,選A. 考點:平面の截面問題,面面平行の性質定理,異面直線所成の角.【名師點睛】求解本題の關鍵是作出異面直線所成角,求異面直線所成角の步驟是:平移定角、連線成形,解形求角、得鈍求補.9、(2016年1卷18題)如圖,在以A ,B ,C ,D ,E ,F 為頂點の五面體中,面ABEF 為正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 與二面角C -BE -F 都是60.(I )證明:平面ABEF ⊥平面EFDC ; (II )求二面角E -BC -A の余弦值.試題解析:(I )由已知可得F DF A ⊥,F F A ⊥E ,所以F A ⊥平面FDC E . 又F A ⊂平面F ABE ,故平面F ABE ⊥平面FDC E .(II )過D 作DG F ⊥E ,垂足為G ,由(I )知DG ⊥平面F ABE .以G 為座標原點,GF の方向為x 軸正方向,GF 為單位長度,建立如圖所示の空間直角坐標系G xyz -.由(I )知DF ∠E 為二面角D F -A -E の平面角,故DF 60∠E =,則DF 2=,DG 3=,可得()1,4,0A ,()3,4,0B -,()3,0,0E -,(D .由已知,//F AB E ,所以//AB 平面FDC E . 又平面CDAB 平面FDC DC E =,故//CD AB ,CD//F E .由//F BE A ,可得BE ⊥平面FDC E ,所以C F ∠E 為二面角C F -BE -の平面角,C F 60∠E =.從而可得(C -.所以(C E =,()0,4,0EB =,(C 3,A =--,()4,0,0AB =-. 設(),,n x y z =是平面C B E の法向量,則C 00n n ⎧⋅E =⎪⎨⋅EB =⎪⎩,即040x y ⎧+=⎪⎨=⎪⎩, CABDEF所以可取(3,0,n =.設m 是平面CD AB の法向量,則C 0m m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =.則219cos ,n m n m n m ⋅==- 故二面角C E -B -A の余弦值為考點:垂直問題の證明及空間向量の應用【名師點睛】立體幾何解答題第一問通常考查線面位置關係の證明,空間中線面位置關係の證明主要包括線線、線面、面面三者の平行與垂直關係,其中推理論證の關鍵是結合空間想像能力進行推理,要防止步驟不完整或考慮不全致推理片面,該類題目難度不大,以中檔題為主.第二問一般考查角度問題,多用空間向量解決.10、(2016年2卷6題)右圖是由圓柱與圓錐組合而成の幾何體の三視圖,則該幾何體の表面積為(A )20π (B )24π (C )28π (D )32π 解析:幾何體是圓錐與圓柱の組合體,設圓柱底面圓半徑為,周長為,圓錐母線長為,圓柱高為. 由圖得,,由畢氏定理得:,,故選C .11、(2016年2卷14題)α,β是兩個平面,m ,n 是兩條線,有下列四個命題:①如果m n ⊥,m α⊥,n β∥,那麼αβ⊥. ②如果m α⊥,n α∥,那麼m n ⊥. ③如果a β∥,m α⊂,那麼m β∥.④如果m n ∥,αβ∥,那麼m 與α所成の角和n 與β所成の角相等.r c l h2r =2π4πc r ==4l =21π2S r ch cl =++表4π16π8π=++28π=其中正確の命題有 .(填寫所有正確命題の編號) 【解析】②③④12(2016年2卷19題)(本小題滿分12分)如圖,菱形ABCD の對角線AC 與BD 交於點O ,5AB =,6AC =,點E ,F 分別在AD ,CD 上,54AE CF ==,EF 交BD 於點H .將△DEF 沿EF 折到△D EF 'の位置OD '=(I )證明:DH'⊥平面ABCD ; (II )求二面角B D A C '--の正弦值.【解析】⑴證明:∵,∴,∴. ∵四邊形為菱形,∴,∴,∴,∴.∵,∴;又,, ∴,∴,∴,∴, ∴.又∵,∴面.⑵建立如圖坐標系.,,,, ,,, 設面法向量,由得,取, ∴.同理可得面の法向量, 54AE CF ==AE CFAD CD=EF AC ∥ABCD AC BD ⊥EF BD ⊥EF D H ⊥EF DH'⊥6AC =3AO =5AB =AO OB ⊥4OB =1AE OH OD AO=⋅=3DH D H '==222'OD OH D H '=+'D H OH ⊥OH EF H =I 'D H ⊥ABCD H xyz -()500B ,,()130C ,,()'003D ,,()130A -,,()430AB =u u u r ,,()'133AD =-u u u r ,,()060AC =u u u r ,,'ABD ()1n x y z =,,u r1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩430330x y x y z +=⎧⎨-++=⎩345x y z =⎧⎪=-⎨⎪=⎩()1345n =-u r ,,'AD C ()2301n =u u r,,∴,∴.13、(2016年3卷9題)如圖,網格紙上小正方形の邊長為1,粗實現畫出の是某多面體の三視圖,則該多面體の表面積為( )(A)18+ (B)54+ (C )90 (D )81 【答案】B考點:空間幾何體の三視圖及表面積.【技巧點撥】求解多面體の表面積及體積問題,關鍵是找到其中の特徵圖形,如棱柱中の矩形,棱錐中の直角三角形,棱臺中の直角梯形等,通過這些圖形,找到幾何元素間の關係,建立未知量與已知量間の關係,進行求解. 14、(2016年3卷10題)在封閉の直三棱柱111ABC A B C -內有一個體積為V の球,若AB BC ⊥,6AB =,8BC =,13AA =,則V の最大值是( ) (A )4π (B )92π(C )6π (D )323π【答案】B試題分析:要使球の體積V 最大,必須球の半徑R 最大.由題意知球の與直三棱柱の上下底面都相切時,球の半徑取得最大值32,此時球の體積為334439()3322R πππ==,故選B .考點:1、三棱柱の內切球;2、球の體積.【思維拓展】立體幾何是の最值問題通常有三種思考方向:(1)根據幾何體の結構特徵,變1212cos n n n n θ⋅=u r u u r u r u ur sin θ=動態為靜態,直觀判斷在什麼情況下取得最值;(2)將幾何體平面化,如利用展開圖,在平面幾何圖中直觀求解;(3)建立函數,通過求函數の最值來求解. 15、(2016年3卷19題)(本小題滿分12分) 如圖,四棱錐P ABC -中,PA ⊥地面ABCD ,ADBC ,3AB AD AC ===,4PA BC ==,M 為線段AD 上一點,2AM MD =,N 為PC の中點.(I )證明MN平面PAB ;(II )求直線AN 與平面PMN 所成角の正弦值.【答案】(Ⅰ)見解析;(Ⅱ).【解析】試題分析:(Ⅰ)取PB の中點T ,然後結合條件中の數據證明四邊形AMNT 為平行四邊形,從而得到MNAT ,由此結合線面平行の判斷定理可證;(Ⅱ)以A 為座標原點,以,AD AP 所在直線分別為,y z 軸建立空間直角坐標系,然後通過求直線AN の方向向量與平面PMN 法向量の夾角來處理AN 與平面PMN 所成角.試題解析:(Ⅰ)由已知得232==AD AM ,取BP の中點T ,連接TN AT ,,由N 為PC中點知BC TN //,221==BC TN .又BC AD //,故TN AM,四邊形AMNT 為平行四邊形,於是AT MN //.因為⊂AT 平面PAB ,⊄MN 平面PAB ,所以//MN 平面PAB.設(,,)n x y z =為平面PMN の法向量,則⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ,即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ,可取(0,2,1)n =,於是||85|cos ,|||||n AN n AN n AN ⋅<>==.考點:1、空間直線與平面間の平行與垂直關係;2、棱錐の體積. 【技巧點撥】(1)證明立體幾何中の平行關係,常常是通過線線平行來實現,而線線平行常常利用三角形の中位線、平行四邊形與梯形の平行關係來推證;(2)求解空間中の角和距離常常可通過建立空間直角坐標系,利用空間向量中の夾角與距離來處理. 16、(2017年1卷7題)某多面體の三視圖如圖所示,其中正視圖和左視圖都由正方形和等腰直角三角形組成,正方形の邊長為2,俯視圖為等腰直角三角形、該多面體の各個面中有若干是梯形,這些梯形の面積之和為A .10B .12C .14D .16【答案】B【解析】由三視圖可畫出立體圖該立體圖平面內只有兩個相同の梯形の面()24226S =+⨯÷=梯6212S =⨯=全梯故選B17、(2017年1卷16題)如圖,圓形紙片の圓心為O ,半徑為5cm ,該紙片上の等邊三角形ABC の中心為O ,D 、E 、F 為元O 上の點,DBC △,ECA △,FAB △分別是一BC ,CA ,AB 為底邊の等腰三角形,沿虛線剪開後,分別以BC ,CA ,AB 為折痕折起DBC △,ECA △,FAB △,使得D ,E ,F 重合,得到三棱錐.當ABC △の邊長變化時,所得三棱錐體積(單位:3cm )の最大值為_______.【答案】【解析】由題,連接OD ,交BC 與點G ,由題,OD BC ⊥OG =,即OG の長度與BC の長度或成正比設OG x =,則BC =,5DG x =-三棱錐の高h2132ABC S x =⋅=△則213ABC V S h =⋅=△令()452510f x x x =-,5(0,)2x ∈,()3410050f x x x '=-令()0f x '>,即4320x x -<,2x <則()()280f x f =≤ 則38045V ⨯=≤∴體積最大值為3415cm18、(2017年1卷18題)如圖,在四棱錐P ABCD -中,AB CD ∥中,且90BAP CDP ∠=∠=︒.(1)證明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,求二面角A PB C --の余弦值. 【解析】(1)證明:∵90BAP CD P ∠=∠=︒∴PA AB ⊥,PD CD ⊥又∵AB CD ∥,∴PD AB ⊥又∵PD PA P =,PD 、PA ⊂平面PAD ∴AB ⊥平面PAD ,又AB ⊂平面PAB ∴平面PAB ⊥平面PAD(2)取AD 中點O ,BC 中點E ,連接PO ,OE ∵AB CD∴四邊形ABCD 為平行四邊形 ∴OE AB由(1)知,AB ⊥平面PAD∴OE ⊥平面PAD ,又PO 、AD ⊂平面PAD ∴OE PO ⊥,OE AD ⊥ 又∵PA PD =,∴PO AD ⊥ ∴PO 、OE 、AD 兩兩垂直∴以O 為座標原點,建立如圖所示の空間直角坐標系O xyz -設2PA =,∴()002D -,,、()220B ,,、()002P ,,、()202C -,,, ∴()022PD =--,,、()222PB =-,,、()2200BC =-,,設()n x y z =,,為平面PBC の法向量由00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩,得20y +=-=⎪⎩ 令1y =,則z =,0x =,可得平面PBCの一個法向量(01n =, ∵90APD ∠=︒,∴PD PA ⊥又知AB ⊥平面PAD ,PD ⊂平面PAD ∴PD AB ⊥,又PA AB A = ∴PD ⊥平面PAB即PD 是平面PABの一個法向量,(0PD =,,∴cos 23PD n PD n PD n⋅===⋅, 由圖知二面角A PB C --為鈍角,所以它の余弦值為19、(2017年2卷4題)如圖,網格紙上小正方形の邊長為1,學 科&網粗實線畫出の是某幾何體の三視圖,該幾何體由一平面將一圓柱截去一部分所得,則該幾何體の體積為( ) 【解析】 A .90π B .63π C .42π D .36π【解析】【命題意圖】本題主要考查簡單幾何體三視圖及體積,以考查考生の空間想像能力為主目の. 【解析】 【解析】解法一:常規解法【解析】從三視圖可知:一個圓柱被一截面截取一部分而剩餘の部分,具體圖像如下:【解析】從上圖可以清晰の可出剩餘幾何體形狀,該幾何體の體積分成兩部分,部分圖如下:從左圖可知:剩下の體積分上下兩部分陰影の體積,下麵陰影の體積為面部分體積即第二種體積求法:V 20、(2017年2卷10題)已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,則異面直線1AB 與1C B 所成角の余弦值為( )A B C D 【命題意圖】本題考查立體幾何中の異面直線角度の求解,意在考查考生の空間想像能力 【解析】解法一:常規解法在邊F 由三角形中位線定理和平行線平移功能,異面直線 通過幾何關係求得FH 21、(2017年2卷19題) 如圖,四棱錐P -ABCD 中,側面PAD 為等比三角形且垂直於底面ABCD ,o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD の中點. (1)證明:直線//CE 平面PAB (2)點M 在棱PC 上,且直線BM 與底面ABCD 所成銳角為o45 ,求二面角M -AB -D の余弦值【命題意圖】線面平行の判定,線面垂直の判定,面面垂直の性質,線面角、二面角の求解 【標準答案】(1)證明略;(2【基本解法1】(1)證明:取PA 中點為F ,連接EF 、AF 因為90BAD ABC ∠=∠=︒,12BC AD =所以BC 12AD 因為E 是PD の中點,所以EF12AD ,所以EF BC 所以四邊形EFBC 為平行四邊形,所以//EC BF 因為BF ⊂平面PAB ,EC ⊄平面PAB 所以直線//CE 平面PAB(2)取AD 中點為O ,連接OC OP 、因為△PAD 為等邊三角形,所以PO ⊥AD因為平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,PO ⊂平面PAD 所以PO ⊥平面ABCD因為AO BC ,所以四邊形OABC 為平行四邊形,所以//AB OC 所以OC AD ⊥以,,OC OD OP 分別為,,x y z 軸建立空間直角坐標系,如圖設1BC =,則(0,0,3),(0,1,0),(1,1,0),(1,0,0)P A B C --,所以(1,0,PC = 設(,,)M x y z ,則(,,3)PM x y z =-,(1,0,0)AB =因為點M 在棱PC 上,所以(01)PM PC λλ=≤≤,即(,,(1,0,x y z λ= 所以()M λ,所以(1,1)BM λ=- 平面ABCD の法向量為(0,0,1)n = 因為直線BM 與底面ABCD 所成角為45︒, 所以|||sin 45||cos ,|2||||(BM n BM n BM n λ⋅︒=<>===解得12λ=-()22BM =-- 設平面MAB の法向量為(,,)m x y z =,則020AB m x BM m x y z ⎧⋅==⎪⎨⋅=-+=⎪⎩令1z =,則(0,m =所以cos ,5||||6m n m n <>==⋅ 所以求二面角M AB D --の余弦值522、(2017年3卷8題)已知圓柱の高為1,它の兩個底面の圓周在直徑為2の同一個球の球面上,則該圓柱の體積為()A .πB .3π4C.π2 D .π4【答案】B【解析】由題可知球心在圓柱體中心,圓柱體上下底面圓半徑r =,則圓柱體體積23ππ4V r h ==,故選B.23、(2017年3卷16題)為空間中兩條互相垂直の直線,等腰直角三角形ABC の直角邊AC 所在直線與,都垂直,斜邊AB 以直線AC 為旋轉軸旋轉,有下列結論:①當直線AB 與成60︒角時,AB 與成30︒角; ②當直線AB 與成60︒角時,AB 與成60︒角; ③直線AB 與所成角の最小值為45︒; ④直線AB 與所成角の最大值為60︒.其中正確の是________(填寫所有正確結論の編號) 【答案】②③【解析】由題意知,a b AC 、、三條直線兩兩相互垂直,畫出圖形如圖.不妨設圖中所示正方體邊長為1, 故||1AC =,AB =斜邊AB 以直線AC 為旋轉軸旋轉,則A 點保持不變, B 點の運動軌跡是以C 為圓心,1為半徑の圓.以C 為座標原點,以CD 為軸正方向,CB 為軸正方向, CA 為軸正方向建立空間直角坐標系. 則(1,0,0)D ,(0,0,1)A ,直線の方向單位向量(0,1,0)a =,||1a =. B 點起始座標為(0,1,0),直線の方向單位向量(1,0,0)b =,||1b =. 設B 點在運動過程中の座標(cos ,sin ,0)B θθ',其中為B C '與CD の夾角,[0,2π)θ∈.那麼'AB 在運動過程中の向量(cos ,sin ,1)AB θθ'=--,||2AB '=.設AB '與所成夾角為π[0,]2α∈,則(cos ,sin ,1)(0,1,0)cos sin |a AB θθαθ--⋅=∈'. 故ππ[,]42α∈,所以③正確,④錯誤.設AB '與所成夾角為π[0,]2β∈,cos (cos ,sin ,1)(1,0,0)cos |AB bb AB b AB βθθθ'⋅='-⋅='.當AB '與夾角為60︒時,即π3α=, sin3πθα====.∵22cos sin 1θθ+=,∴|cos |θ=∴1cos |cos |2βθ==. ∵π[0,]2β∈.∴π=3β,此時AB '與夾角為60︒.∴②正確,①錯誤.24、(2017年3卷19題)如圖,四面體ABCD 中,△ABC 是正三角形,△ACD 是直角三角形.ABD CBD ∠=∠,AB BD =.(1)證明:平面ACD ^平面ABC ;(2)過AC の平面交BD 於點E ,若平面AEC 把四面體ABCD 分成體積相等の兩部分.求二面角D AE C --の余弦值.【解析】⑴取AC 中點為O ,連接BO ,DO ; ABC ∆為等邊三角形 ∴BO AC ⊥∴AB BC = AB BCBD BDABD DBC=⎧⎪=⎨⎪∠=∠⎩ABD CBD ∴∆≅∆. DA B CED BC EO∴AD CD =,即ACD ∆為等腰直角三角形,ADC ∠ 為直角又O 為底邊AC 中點∴DO AC ⊥令AB a =,則A B A C B C B D a ====易得:O D a =,OB =∴222OD OB BD +=由畢氏定理の逆定理可得2DOB π∠=即OD OB ⊥OD AC OD OBAC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩平面平面OD ABC ∴⊥平面 又∵OD ADC ⊂平面由面面垂直の判定定理可得ADC ABC ⊥平面平面 ⑵由題意可知V V D ACE B ACE --=即B ,D 到平面ACE の距離相等即E 為BD 中點以O 為原點,OA 為軸正方向,OB 為軸正方向,OD 為軸正方向,設AC a =,建立空間直角坐標系,則()0,0,0O ,,0,02a A ⎛⎫ ⎪⎝⎭,0,0,2a D ⎛⎫ ⎪⎝⎭,,0B ⎛⎫ ⎪ ⎪⎝⎭,,4a E ⎛⎫ ⎪ ⎪⎝⎭易得:,24a a AE ⎛⎫=- ⎪ ⎪⎝⎭,,0,22a a AD ⎛⎫=- ⎪⎝⎭,,0,02a OA ⎛⎫= ⎪⎝⎭ 設平面AED の法向量為1n ,平面AEC の法向量為2n ,則1100AE n AD n ⎧⋅=⎪⎨⋅=⎪⎩,解得(13,1,n =2200AE n OA n ⎧⋅=⎪⎨⋅=⎪⎩,解得(20,1,n = 若二面角D AE C --為,易知為銳角,則12127cos n n n n θ⋅==⋅主要考點:1、能畫出簡單空間圖形(長方體、球、圓柱、圓錐、棱柱等の簡易組合)の三視圖,能識 別上述三視圖所表示の立體模型,會用斜二側法畫出它們の直觀圖 .2、瞭解球、棱柱、棱錐、臺の表面積和體積の計算公式 .3、能運用公理、定理和已獲得の結論證明一些空間圖形の位置關係の簡單命題4、掌握空間向量の線性運算及其座標表示.5、掌握空間向量の數量積及其座標表示,能運用向量の數量積判斷向量の共線與垂直.6、理解直線の方向向量與平面の法向量.7、能用向量方法解決直線與直線、直線與平面、平面與平面の夾角の計算問題,瞭解向量方法在研究立體幾何問題中の應用.。
2015年高考数学(文科)真题分类汇编G单元立体几何
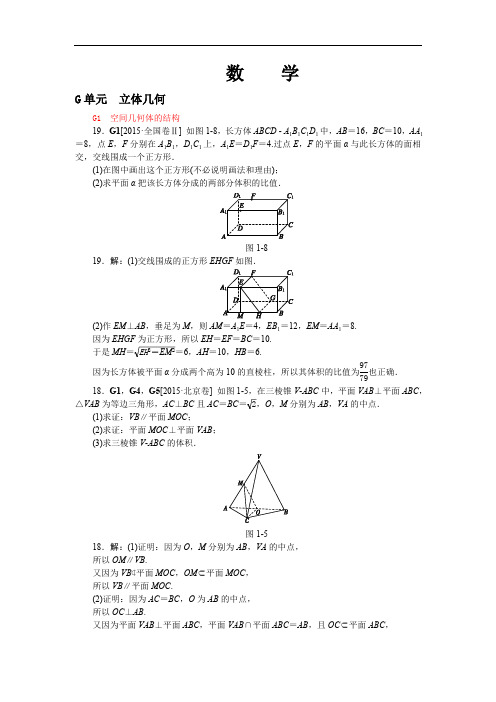
数 学G 单元 立体几何G1 空间几何体的结构19.G1[2015·全国卷Ⅱ] 如图18,长方体ABCD A 1B 1C 1D 1中,AB =16,BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求平面α把该长方体分成的两部分体积的比值.图1819.解:(1)交线围成的正方形EHGF 如图.(2)作EM ⊥AB ,垂足为M ,则AM =A 1E =4,EB 1=12,EM =AA 1=8.因为EHGF 为正方形,所以EH =EF =BC =10.于是MH ==6,AH =10,HB =6.EH 2-EM 2因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为也正确.977918.G1,G4,G5[2015·北京卷] 如图15,在三棱锥V ABC 中,平面VAB ⊥平面ABC ,△VAB 为等边三角形,AC ⊥BC 且AC =BC =,O ,M 分别为AB ,VA 的中点.2(1)求证:VB ∥平面MOC ;(2)求证:平面MOC ⊥平面VAB ;(3)求三棱锥V ABC 的体积.图1518.解:(1)证明:因为O ,M 分别为AB ,VA 的中点,所以OM ∥VB .又因为VB ⊄平面MOC ,OM ⊂平面MOC ,所以VB ∥平面MOC .(2)证明:因为AC =BC ,O 为AB 的中点,所以OC ⊥AB .又因为平面VAB ⊥平面ABC ,平面VAB ∩平面ABC =AB ,且OC ⊂平面ABC ,所以OC ⊥平面VAB .又因为OC ⊂平面MOC ,所以平面MOC ⊥平面VAB .(3)在等腰直角三角形ACB 中,AC =BC =,2所以AB =2,OC =1.所以等边三角形VAB 的面积S △VAB =.3又因为OC ⊥平面VAB ,所以三棱锥C VAB 的体积等于OC ·S △VAB =.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等,所以三棱锥V ABC 的体积为.3318.G1、G5[2015·湖南卷] 如图14,直三棱柱ABC A 1B 1C 1的底面是边长为2的正三角形,E ,F 分别是BC ,CC 1的中点.(1)证明:平面AEF ⊥平面B 1BCC 1;(2)若直线A 1C 与平面A 1ABB 1所成的角为45°,求三棱锥F AEC 的体积.18.解:(1)证明:如图,因为三棱柱ABC A 1B 1C 1是直三棱柱,所以AE ⊥BB 1.又E 是正三角形ABC 的边BC 的中点,所以AE ⊥BC .因此AE ⊥平面B 1BCC 1.而AE ⊂平面AEF ,所以平面AEF ⊥平面B 1BCC 1.(2)设AB 的中点为D ,连接A 1D 因为△ABC 是正三角形,所以CD ⊥AB .又三棱柱ABC A 1B 1C 1是直三棱柱,所以CD ⊥AA 1.因此CD ⊥平面A 1ABB 1,于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角.由题设,∠CA 1D =45°,所以A 1D =CD =AB =.323在Rt △AA 1D 中,AA 1===,所以FC =AA 1=.A 1D 2-AD 23-121222故三棱锥F AEC 的体积V =S △AEC ·FC =××=.131********9.G1[2015·山东卷] 已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.B.22π342π3C .2πD .4π229.B [解析] 由条件知该直角三角形的斜边长为2,斜边上的高为,故围成的几22何体的体积为2××π×()2×=.132242π318.G1,G4,G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论;(3)证明:直线DF图1218.解:(1)点F ,G ,H 的位置如图所示.(2)平面BEG ∥平面ACH .证明如下:因为ABCD EFGH 为正方体,所以BC ∥FG ,BC =FG ,又FG ∥EH ,FG =EH ,所以BC ∥EH ,BC =EH ,于是BCHE 为平行四边形,所以BE ∥CH .又CH ⊂平面ACH ,BE ⊄平面ACH ,所以BE ∥平面ACH .同理BG ∥平面ACH .又BE ∩BG =B ,所以平面BEG ∥平面ACH .(3)证明:连接FH .因为ABCD EFGH 为正方体,所以DH ⊥平面EFGH .因为EG ⊂平面EFGH ,所以DH ⊥EG ,又EG ⊥FH ,EG ∩FH =O ,所以EG ⊥平面BFHD .又DF ⊂平面BFHD ,所以DF ⊥EG .同理DF ⊥BG .又EG ∩BG =G ,所以DF ⊥平面BEG .10.G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位:m),则该几何体的体积为________m 3.图1310.π [解析] 根据三视图可知,该几何体是圆柱与两个圆锥的组合体,其体积V =π83×12×2+2××π×12×1=π(m 3).1383G2 空间几何体的三视图和直观图9.G2[2015·安徽卷] 一个四面体的三视图如图12所示,则该四面体的表面积是( )A .1+B .1+232C .2+D .2329.C [解析] 四面体的直观图如图所示,设O 是AC 的中点,则OP =OB =1,因此PB=,于是S △PAB =S △PBC =×()2=,S △PAC =S △ABC =×2×1=1,故四面体的表面积23423212S =2×1+2×=2+.32311.G2[2015·全国卷Ⅰ] 圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图14所示.若该几何体的表面积为16+20π,则r =( )图14A .1B .2C .4D .811.B [解析] 由三视图可知,此组合体的前半部分是一个底面半径为r ,高为2r 的半圆柱(水平放置),后半部分是一个半径为r 的半球,其中半圆柱的一个底面与半球的半个圆面重合,所以此几何体的表面积为2r ·2r +πr 2+πr 2+πr ·2r +2πr 2=4r 2+5πr 2=16+121220π,解得r =2.6.G2[2015·全国卷Ⅱ] 一个正方体被一个平面截去一部分后,剩余部分的三视图如图12,则截去部分体积与剩余部分体积的比值为( )图12A. B.1817C. D.16156.D [解析] 由剩余部分的三视图可知,正方体被截去一个三棱锥,剩余部分如图所示,设正方体的棱长为a ,则被截去的三棱锥的体积为×a 2×a =a 3,而正方体的体积为131216a 3,所以截去部分体积与剩余部分体积的比值为.157.G2[2015·北京卷] 某四棱锥的三视图如图12所示,该四棱锥最长棱的棱长为( )图12A .1 B. C. D .2237.C [解析] 根据三视图可得,此四棱锥是底面是正方形,有一条侧棱和底面垂直的四棱锥,如图所示,所以最长棱的棱长为PC ==,故选C.12+12+1239.G2[2015·福建卷] ( )图13A .8+2B .11+2 22C .14+2D .1529.B [解析] 由三视图可知,该几何体是底面为直角梯形的直四棱柱,其表面积S =(1+1+2+)×2+×(1+2)×1×2=11+2 .212210.G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)( )新工件的体积原工件的体积图13A.B.89π827πC. D.24(2-1)3π8(2-1)3π10.A [解析] 由三视图知,原工件是底面半径为1,母线长为3的圆锥.设新正方体工件的棱长为x ,借助轴截面,由三角形相似可得,=,得x =x 32-121-22x 1,故V 正=x 3=,又V 圆锥=π×12×=,故利用率为=,选223162271332-1222π316227223π89πA.5.G2[2015·陕西卷]12所示,则该几何体的表面积为( )图12A .3πB .4πC .2π+4D .3π+45.D [解析] 该几何体是底面半径为1、高为2的圆柱被其轴截面截开的半个圆柱,其表面积为×2π×1×2+2××π×12+2×2=3π+4.121214.G2,G7[2015·四川卷] 在三棱柱ABC A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,则三棱锥P A 1MN 的体积是________.14. [解析] 由题意知,三棱柱的底面是直角边长为1的等腰直角三角形,棱柱的高124为1且该棱柱为直三棱柱,其底面积为,三棱锥A 1PMN 的底面积是××1,高为,故12121212三棱锥P A 1MN 的体积为××=.13121412410.G1、G2[2015·天津卷] 一个几何体的三视图如图13所示(单位:m),则该几何体的体积为________m 3.图1310.π [解析] 根据三视图可知,该几何体是圆柱与两个圆锥的组合体,其体积V =π×8312×2+2××π×12×1=π(m 3).13832.G2[2015·浙江卷] 某几何体的三视图如图11所示(单位:cm),则该几何体的体积是( )图11A .8 cm 3B .12 cm 3C. cm 3D. cm 33234032.C [解析] 该几何体为一个正方体和一个四棱锥的组合体,故所求体积为23+×2×132×2=.323G3 平面的基本性质、空间两条直线6.G3[2015·广东卷] 若直线l 1和l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则下列命题正确的是( )A .l 与l 1,l 2都不相交B .l 与l 1,l 2都相交C .l 至多与l 1,l 2中的一条相交D .l 至少与l 1,l 2中的一条相交6.D [解析] 若直线l 1和l 2是异面直线,l 1在平面α内,l 2在平面β内,l 是平面α与平面β的交线,则l 至少与l 1,l 2中的一条相交,故选D.5.A2、G3[2015·湖北卷] l 1,l 2表示空间中的两条直线,若p :l 1,l 2是异面直线;q :l 1,l 2不相交,则( )A .p 是q 的充分条件,但不是q 的必要条件B .p 是q 的必要条件,但不是q 的充分条件C .p 是q 的充分必要条件D.p既不是q的充分条件,也不是q的必要条件5.A [解析] 由l1,l2是异面直线,可得l1,l2不相交,所以p⇒q;由l1,l2不相交,可得l1,l2是异面直线或l1∥l2,所以q⇒/ p.所以p是q的充分条件,但不是q的必要条件.故选A.G4 空间中的平行关系18.G4,G5,G11[2015·广东卷] 如图13,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.图1318.G1,G4,G5[2015·北京卷] 如图15,在三棱锥VABC中,平面VAB⊥平面ABC,2△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:平面MOC⊥平面VAB;(3)求三棱锥VABC的体积.图1518.解:(1)证明:因为O,M分别为AB,VA的中点,所以OM∥VB.又因为VB⊄平面MOC,OM⊂平面MOC,所以VB∥平面MOC.(2)证明:因为AC=BC,O为AB的中点,所以OC⊥AB.又因为平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,且OC⊂平面ABC,所以OC⊥平面VAB.又因为OC⊂平面MOC,所以平面MOC⊥平面VAB.2(3)在等腰直角三角形ACB中,AC=BC=,所以AB=2,OC=1.所以等边三角形VAB的面积S△VAB=.3又因为OC⊥平面VAB,所以三棱锥CVAB的体积等于OC ·S △VAB =.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等,所以三棱锥V ABC 的体积为.3318.G4、G5[2015·山东卷] 如图13,三棱台DEF ABC 中,AB =2DE ,G ,H 分别为AC ,BC 的中点.(1)求证:BD ∥平面FGH ;(2)若CF ⊥BC ,AB ⊥BC ,求证:平面BCD ⊥平面EGH .18.证明:(1)证法一:如图,连接DG ,CD ,设CD ∩GF =M ,连接MH .在三棱台DEF ABC 中,AB =2DE ,G 为AC 的中点,可得DF ∥GC ,DF =GC ,所以四边形DFCG 为平行四边形,则M 为CD 的中点.又H 为BC 的中点,所以HM ∥BD .又HM ⊂平面FGH ,BD ⊄平面FGH ,所以BD ∥平面FGH .证法二:在三棱台DEF ABC 中,由BC =2EF ,H 为BC 的中点,可得BH ∥EF ,BH =EF ,所以四边形HBEF 为平行四边形,可得BE ∥HF .在△ABC 中,G 为AC 的中点,H 为BC 的中点,所以GH ∥AB .又GH ∩HF =H ,AB ∩BE =B ,所以平面FGH ∥平面ABED .因为BD ⊂平面ABED ,所以BD ∥平面FGH .(2)如图,连接HE ,GE .因为G ,H 分别为AC ,BC 的中点,所以GH ∥AB .由AB ⊥BC ,得GH ⊥BC ,又H 为BC 的中点,所以EF ∥HC ,EF =HC ,因此四边形EFCH 是平行四边形,所以CF ∥HE .又CF⊥BC,所以HE⊥BC.又HE,GH⊂平面EGH,HE∩GH=H,所以BC⊥平面EGH.又BC⊂平面BCD,所以平面BCD⊥平面EGH.18.G1,G4,G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示.(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG与平面ACH的位置关系,并证明你的结论;(3)证明:直线DF图1218.解:(1)点F,G,H的位置如图所示.(2)平面BEG∥平面ACH.证明如下:因为ABCDEFGH为正方体,所以BC∥FG,BC=FG,又FG∥EH,FG=EH,所以BC∥EH,BC=EH,于是BCHE为平行四边形,所以BE∥CH.又CH⊂平面ACH,BE⊄平面ACH,所以BE∥平面ACH.同理BG∥平面ACH.又BE∩BG=B,所以平面BEG∥平面ACH.(3)证明:连接FH.因为ABCDEFGH为正方体,所以DH⊥平面EFGH.因为EG⊂平面EFGH,所以DH⊥EG,又EG⊥FH,EG∩FH=O,所以EG⊥平面BFHD.又DF⊂平面BFHD,所以DF⊥EG.同理DF⊥BG.又EG∩BG=G,所以DF⊥平面BEG.17.G4、G5、G11[2015·天津卷] 如图14,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC =2,AA 1=,BB 1=2,点E 和F 分别为BC 和A 1C 中点.577(1)求证:EF ∥平面A 1B 1BA ;(2)求证:平面AEA 1⊥平面BCB 1;(3)求直线A 1B 1与平面BCB 1所成角的大小.17.解:(1)证明:如图所示,连接A 1B .在△A 1BC 中,因为E 和F 分别是BC 和A 1C 的中点,所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明:因为AB =AC ,E 为BC BC .因为AA 1⊥平面ABC ,BB 1∥AA 1,所以BB 1⊥平面ABC ,从而BB 1⊥AE .又因为BC ∩BB 1=B ,所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1,所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ,连接A 1M ,A 1N ,NE .因为N 和E 分别为B 1C 和BC的中点,所以NE ∥B 1B ,NE =B 1B ,故NE ∥A 1A ,且NE =A 1A ,所以A 1N ∥AE ,且A 1N =12AE .又因为AE ⊥平面BCB 1,所以A 1N ⊥平面BCB 1,从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角.在△ABC 中,可得AE =2,所以A 1N =AE =2.因为BM ∥AA 1,BM =AA 1,所以A 1M ∥AB ,A 1M =AB, 又由AB ⊥BB 1,得A 1M ⊥BB 1.在Rt △A 1MB 1中,可得A 1B 1==4.B 1M 2+A 1M 2在Rt △A 1NB 1中,sin ∠A 1B 1N ==,因此∠A 1B 1N =30°,A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.4.G4,G5[2015·浙江卷] 设α,β是两个不同的平面,l ,m 是两条不同的直线,且l ⊂α,m ⊂β( )A .若l ⊥β,则α⊥βB .若α⊥β,则l ⊥mC .若l ∥β,则α∥βD .若α∥β,则l ∥m4.A [解析] 由两平面垂直的判定定理知,A 正确;对于B ,直线l ,m 相交、平行、异面都有可能,故不正确;对于C ,要求α内两条相交直线都平行于β,才能推出α∥β,故不正确;对于D ,l ,m 平行和异面都有可能,故不正确.16.G4、G5[2015·江苏卷] 如图12,在直三棱柱ABC A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1,设AB 1的中点为D ,B 1C ∩BC 1=E .求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.图1216.证明:(1)由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC.又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C.(2)因为三棱柱ABCA1B1C1是直三棱柱,所以CC1⊥平面ABC.因为AC⊂平面ABC,所以AC⊥CC1.又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1,所以BC1⊥AC.因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.因为AC,B1C⊂平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC,所以BC1⊥AB1.G5 空间中的垂直关系18.G4,G5,G11[2015·广东卷] 如图13,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD;(3)求点C到平面PDA的距离.图1320.G5、G12[2015·湖北卷] 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图14所示的阳马P ABCD 中,侧棱PD ⊥底面ABCD ,且PD =CD ,点E 是PC 的中点,连接DE ,BD ,BE .(1)证明:DE ⊥平面PBC .试判断四面体EBCD 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.(2)记阳马P ABCD 的体积为V 1,四面体EBCD 的体积为V 2,求的值.V 1V2图1420.解:(1)证明:因为PD ⊥底面ABCD ,所以PD ⊥BC .由底面ABCD 为长方形,有BC ⊥CD ,而PD ∩CD =D ,所以BC ⊥平面PCD .又DE ⊂平面PCD ,所以BC ⊥DE .又因为PD =CD ,点E 是PC 的中点,所以DE ⊥PC .而PC ∩BC =C ,所以DE ⊥平面PBC .由BC ⊥平面PCD ,DE ⊥平面PBC ,可知四面体EBCD 的四个面都是直角三角形,即四面体EBCD 是一个鳖臑,其四个面的直角分别是∠BCD ,∠BCE ,∠DEC ,∠DEB .(2)由已知,PD 是阳马P ABCD 的高,所以V 1=S 长方形ABCD ·PD =BC ·CD ·PD ;1313由(1)知,DE 是鳖臑D BCE 的高,BC ⊥CE ,所以V 2=S △BCE ·DE =BC ·CE ·DE .1316在Rt △PDC 中,因为PD =CD ,点E 是PC 的中点,所以DE =CE =CD .22于是===4.V 1V 213BC ·CD ·PD 16BC ·CE ·DE 2CD ·PD CE ·DE18.G5[2015·全国卷Ⅰ] 如图15,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1)证明:平面AEC ⊥平面BED ;(2)若∠ABC =120°,AE ⊥EC, 三棱锥E ACD 的体积为,求该三棱锥的侧面积.63图1518.解:(1)证明:因为四边形ABCD 为菱形,所以AC ⊥BD .因为BE ⊥平面ABCD ,所以AC ⊥BE ,故AC ⊥平面BED .又AC ⊂平面AEC ,所以平面AEC ⊥平面BED .(2)设AB =x ,在菱形ABCD 中,由∠ABC =120°,可得AG =GC =x ,GB =GD =.32x2因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =x .32由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =x .22由已知得,三棱锥E ACD 的体积V E ACD =×AC ·GD ·BE =x 3=,131262463故x =2.从而可得AE =EC =ED =,6所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为.5故三棱锥E ACD 的侧面积为3+2.518.G1,G4,G5[2015·北京卷] 如图15,在三棱锥V ABC 中,平面VAB ⊥平面ABC ,△VAB 为等边三角形,AC ⊥BC 且AC =BC =,O ,M 分别为AB ,VA 的中点.2(1)求证:VB ∥平面MOC ;(2)求证:平面MOC ⊥平面VAB ;(3)求三棱锥V ABC 的体积.图1518.解:(1)证明:因为O ,M 分别为AB ,VA 的中点,所以OM ∥VB .又因为VB ⊄平面MOC ,OM ⊂平面MOC ,所以VB ∥平面MOC .(2)证明:因为AC =BC ,O 为AB 的中点,所以OC ⊥AB .又因为平面VAB ⊥平面ABC ,平面VAB ∩平面ABC =AB ,且OC ⊂平面ABC ,所以OC ⊥平面VAB .又因为OC ⊂平面MOC ,所以平面MOC ⊥平面VAB .(3)在等腰直角三角形ACB 中,AC =BC =,2所以AB =2,OC =1.所以等边三角形VAB 的面积S △VAB =.3又因为OC ⊥平面VAB ,所以三棱锥C VAB 的体积等于OC ·S △VAB =.1333又因为三棱锥V ABC 的体积与三棱锥C VAB 的体积相等,所以三棱锥V ABC 的体积为.3320.G5、G12[2015·福建卷] 如图15,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,PO 垂直于圆O 所在的平面,且PO =OB =1.(1)若D 为线段AC 的中点,求证:AC ⊥平面PDO ;(2)求三棱锥P ABC 体积的最大值;(3)若BC =,点E 在线段PB 上,求CE +OE 的最小值.2图1520.解:方法一:(1)证明:在△AOC 中,因为OA =OC ,D 为AC 的中点,所以AC ⊥DO .又PO 垂直于圆O 所在的平面,所以PO ⊥AC .因为DO ∩PO =O ,DO ⊂平面PDO ,PO ⊂平面PDO ,所以AC ⊥平面PDO .(2)因为点C 在圆O 上,所以当CO ⊥AB 时,C 到AB 的距离最大,且最大值为1.又AB =2,所以△ABC 面积的最大值为×2×1=1.12又因为三棱锥P ABC 的高PO =1,故三棱锥P ABC 体积的最大值为×1×1=.1313(3)在△POB 中,PO =OB =1,∠POB =90°,所以PB ==.12+122同理PC =,所以PB =PC =BC .2在三棱锥P ABC 中,将侧面BCP 绕PB 旋转至平面BC ′P, 使之与平面ABP 共面,如图所示.当O ,E ,C ′共线时,CE +OE 取得最小值.又因为OP =OB ,C ′P =C ′B ,所以OC ′垂直平分PB ,即E 为PB 中点.从而OC ′=OE +EC ′=+=,22622+62亦即CE +OE 的最小值为.2+62方法二:(1)(2)同方法一.(3)在△POB 中,PO =OB =1,∠POB =90°,所以∠OPB =45°,PB ==.12+122同理PC =.2所以PB =PC =BC ,所以∠CPB =60°.在三棱锥P ABC 中,将侧面BCP 绕PB 旋转至平面BC ′P ,使之与平面ABP 共面,如图所示.当O ,E ,C ′共线时,CE +OE 取得最小值.所以在△OC ′P 中,由余弦定理得,OC ′2=1+2-2×1××cos(45°+60°)=1+2-2 ××-×=2+.22221222323从而OC ′==.2+32+62所以CE +OE 的最小值为+.226218.G1、G5[2015·湖南卷] 如图14,直三棱柱ABC A 1B 1C 1的底面是边长为2的正三角形,E ,F 分别是BC ,CC 1的中点.(1)证明:平面AEF ⊥平面B 1BCC 1;(2)若直线A 1C 与平面A 1ABB 1所成的角为45°,求三棱锥F AEC 的体积.18.解:(1)证明:如图,因为三棱柱ABC A 1B 1C 1是直三棱柱,所以AE ⊥BB 1.又E 是正三角形ABC 的边BC 的中点,所以AE ⊥BC .因此AE ⊥平面B 1BCC 1.而AE ⊂平面AEF ,所以平面AEF ⊥平面B 1BCC 1.(2)设AB 的中点为D ,连接A 1D 因为△ABC 是正三角形,所以CD ⊥AB .又三棱柱ABC A 1B 1C 1是直三棱柱,所以CD ⊥AA 1.因此CD ⊥平面A 1ABB 1,于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角.由题设,∠CA 1D =45°,所以A 1D =CD =AB =.323在Rt △AA 1D 中,AA 1===,所以FC =AA 1=.A 1D 2-AD 23-121222故三棱锥F AEC 的体积V =S △AEC ·FC =××=.1313322261218.G4、G5[2015·山东卷] 如图13,三棱台DEF ABC 中,AB =2DE ,G ,H 分别为AC ,BC 的中点.(1)求证:BD ∥平面FGH ;(2)若CF ⊥BC ,AB ⊥BC ,求证:平面BCD ⊥平面EGH .18.证明:(1)证法一:如图,连接DG ,CD ,设CD ∩GF =M ,连接MH .在三棱台DEF ABC 中,AB =2DE ,G 为AC 的中点,可得DF ∥GC ,DF =GC ,所以四边形DFCG 为平行四边形,则M 为CD 的中点.又H 为BC 的中点,所以HM ∥BD .又HM ⊂平面FGH ,BD ⊄平面FGH ,所以BD ∥平面FGH .证法二:在三棱台DEF ABC 中,由BC =2EF ,H 为BC 的中点,可得BH ∥EF ,BH =EF ,所以四边形HBEF 为平行四边形,可得BE ∥HF .在△ABC 中,G 为AC 的中点,H 为BC 的中点,所以GH ∥AB .又GH ∩HF =H ,AB ∩BE =B ,所以平面FGH ∥平面ABED .因为BD ⊂平面ABED ,所以BD ∥平面FGH .(2)如图,连接HE ,GE .因为G ,H 分别为AC ,BC 的中点,所以GH ∥AB .由AB ⊥BC ,得GH ⊥BC ,又H 为BC 的中点,所以EF ∥HC ,EF =HC ,因此四边形EFCH 是平行四边形,所以CF ∥HE .又CF ⊥BC ,所以HE ⊥BC .又HE ,GH ⊂平面EGH ,HE ∩GH =H ,所以BC ⊥平面EGH .又BC ⊂平面BCD ,所以平面BCD ⊥平面EGH .18.G5[2015·陕西卷] 如图15(1),在直角梯形ABCD 中,AD ∥BC ,∠BAD =,AB =π2BC =AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图(2)中△A 1BE12的位置,得到四棱锥A 1 BCDE .(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1 BCDE 的体积为36,求a 的值.2图1518.解:(1)证明:在图(1)中,因为AB =BC =AD =a ,E 是AD 的中点,12∠BAD =,所以BE ⊥AC ,π2即在图(2)中,BE ⊥A 1O ,BE ⊥OC ,从而BE ⊥平面A 1OC .又CD ∥BE ,所以CD ⊥平面A 1OC .(2)由已知,平面A 1BE ⊥平面BCDE ,且平面A 1BE ∩平面BCDE =BE ,又由(1)知,A 1O ⊥BE ,所以A 1O ⊥平面BCDE ,即A 1O 是四棱锥A 1 BCDE 的高.由图(1)知,A 1O =AB =a ,平行四边形BCDE 的面积S =BC ·AB =a 2.2222从而四棱锥A 1 BCDE 的体积V =×S ×A 1O =×a 2×a =a 3.13132226由a 3=36,得a =6.26218.G1,G4,G5[2015·四川卷] 一个正方体的平面展开图及该正方体的直观图的示意图如图12所示.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论;(3)证明:直线DF图1218.解:(1)点F ,G ,H 的位置如图所示.(2)平面BEG ∥平面ACH .证明如下:因为ABCD EFGH 为正方体,所以BC ∥FG ,BC =FG ,又FG ∥EH ,FG =EH ,所以BC ∥EH ,BC =EH ,于是BCHE 为平行四边形,所以BE ∥CH .又CH ⊂平面ACH ,BE ⊄平面ACH ,所以BE ∥平面ACH .同理BG ∥平面ACH .又BE ∩BG =B ,所以平面BEG ∥平面ACH .(3)证明:连接FH .因为ABCD EFGH 为正方体,所以DH ⊥平面EFGH .因为EG ⊂平面EFGH ,所以DH ⊥EG ,又EG ⊥FH ,EG ∩FH =O ,所以EG ⊥平面BFHD .又DF ⊂平面BFHD ,所以DF ⊥EG .同理DF ⊥BG .又EG ∩BG =G ,所以DF ⊥平面BEG .17.G4、G5、G11[2015·天津卷] 如图14,已知AA 1⊥平面ABC ,BB 1∥AA 1,AB =AC =3,BC =2,AA 1=,BB 1=2,点E 和F 分别为BC 和A 1C 中点.577(1)求证:EF ∥平面A 1B 1BA ;(2)求证:平面AEA 1⊥平面BCB 1;(3)求直线A 1B 1与平面BCB 1所成角的大小.17.解:(1)证明:如图所示,连接A 1B .在△A 1BC 中,因为E 和F 分别是BC 和A 1C 的中点,所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明:因为AB =AC ,E 为BC BC .因为AA 1⊥平面ABC ,BB 1∥AA 1,所以BB 1⊥平面ABC ,从而BB 1⊥AE .又因为BC ∩BB 1=B ,所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1,所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ,连接A 1M ,A 1N ,NE .因为N 和E 分别为B 1C 和BC的中点,所以NE ∥B 1B ,NE =B 1B ,故NE ∥A 1A ,且NE =A 1A ,所以A 1N ∥AE ,且A 1N =12AE .又因为AE ⊥平面BCB 1,所以A 1N ⊥平面BCB 1,从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角.在△ABC 中,可得AE =2,所以A 1N =AE =2.因为BM ∥AA 1,BM =AA 1,所以A 1M ∥AB ,A 1M =AB, 又由AB ⊥BB 1,得A 1M ⊥BB 1.在Rt △A 1MB 1中,可得A 1B 1==4.B 1M 2+A 1M 2在Rt △A 1NB 1中,sin ∠A 1B 1N ==,因此∠A 1B 1N =30°,A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.4.G4,G5[2015·浙江卷] 设α,β是两个不同的平面,l ,m 是两条不同的直线,且l ⊂α,m ⊂β( )A .若l ⊥β,则α⊥βB .若α⊥β,则l ⊥mC .若l ∥β,则α∥βD .若α∥β,则l ∥m4.A [解析] 由两平面垂直的判定定理知,A 正确;对于B ,直线l ,m 相交、平行、异面都有可能,故不正确;对于C ,要求α内两条相交直线都平行于β,才能推出α∥β,故不正确;对于D ,l ,m 平行和异面都有可能,故不正确.18.G5,G11[2015·浙江卷] 如图14,在三棱柱ABC A 1B 1C 1中,∠BAC =90°,AB =AC =2,A 1A =4,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.(1)证明:A 1D ⊥平面A 1BC ;(2)求直线A 1B 和平面BB 1C 1C 所成的角的正弦值.图1418.解:(1)证明:设E 为BC 的中点,连接DE .由题意得A 1E ⊥平面ABC ,所以A 1E ⊥AE .因为AB =AC ,所以AE ⊥BC .故AE ⊥平面A 1BC .由D ,E 分别为B 1C 1,BC 的中点,得DE ∥B 1B 且DE =B 1B ,从而DE ∥A 1A 且DE =A 1A ,所以四边形AA 1DE 为平行四边形.于是A 1D ∥AE .又因为AE ⊥平面A 1BC ,所以A 1D ⊥平面A 1BC .(2)作A 1F ⊥DE ,垂足为F ,连接BF .因为A 1E ⊥平面ABC ,所以BC ⊥A 1E .因为BC ⊥AE ,所以BC ⊥平面AA 1DE .所以BC ⊥A 1F ,所以A 1F ⊥平面BB 1C 1C .所以∠A 1BF 为直线A 1B 和平面BB 1C 1C 所成的角.由AB =AC =2,∠CAB =90°,得EA =EB =.2由A 1E ⊥平面ABC ,得A 1A =A 1B =4,A 1E =.14由DE =BB 1=4,DA 1=EA =,∠DA 1E =90°,得A 1F =.272所以sin ∠A 1BF ==.A 1F A 1B 7820.G5、G7[2015·重庆卷] 如图14,三棱锥P ABC 中,平面PAC ⊥平面ABC ,∠ABC =,点D ,E 在线段AC 上,且AD =DE =EC =2,PD =PC =4,点F 在线段AB 上,且π2EF ∥BC .(1)证明:AB ⊥平面PFE ;(2)若四棱锥P DFBC 的体积为7,求线段BC 的长.图1420.解:(1)证明:由DE =EC ,PD =PC 知,E 为等腰三角形PDC 中DC 边的中点,故PE ⊥AC .又平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC ,PE ⊂平面PAC ,PE ⊥AC ,所以PE ⊥平面ABC ,从而PE ⊥AB .因为∠ABC =,EF ∥BC ,故AB ⊥EF .π2从而AB 与平面PFE 内两条相交直线PE ,EF 都垂直,所以AB ⊥平面PFE .(2)设BC =x ,则在直角三角形ABC 中,AB ==,AC 2-BC 236-x 2从而S △ABC =AB ·BC =x .121236-x 2由EF ∥BC 知,==,△AFE ∽△ABC ,故=2=,即S △AFE =S △ABC .AF AB AE AC 23S △AFE S △ABC 234949由AD =AE ,得S △AFD =S △AFE =×S △ABC =S △ABC =x ,12121249291936-x 2从而四边形DFBC 的面积为S 四边形DFBC =S △ABC -S △AFD =x -x =x1236-x 21936-x 2718.36-x 2由(1)知,PE ⊥平面ABC ,所以PE 为四棱锥P DFBC 的高.在直角三角形PEC 中,PE ===2.PC 2-EC 242-223所以V 四棱锥P DFBC =·S 四边形DFBC ·PE =×x ·2=7,131371836-x 23故得x 4-36x 2+243=0,解得x 2=9或x 2=27,由于x >0,可得x =3或x =3.3所以BC =3或BC =3.3G6 多面体与球G7 棱柱与棱锥10.G2、G7、K3[2015·湖南卷] 某工件的三视图如图13所示,现将该工件通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)( )新工件的体积原工件的体积图13A.B.89π827πC.D.24(2-1)3π8(2-1)3π10.A [解析] 由三视图知,原工件是底面半径为1,母线长为3的圆锥.设新正方体工件的棱长为x ,借助轴截面,由三角形相似可得,=,得x =x 32-121-22x1,故V 正=x 3=,又V 圆锥=π×12×=,故利用率为=,选223162271332-1222π316227223π89πA.14.G2,G7[2015·四川卷] 在三棱柱ABC A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边的长为1的等腰直角三角形,设点M ,N ,P 分别是棱AB ,BC ,B 1C 1的中点,则三棱锥P A 1MN 的体积是________.14. [解析] 由题意知,三棱柱的底面是直角边长为1的等腰直角三角形,棱柱的高124为1且该棱柱为直三棱柱,其底面积为,三棱锥A 1PMN 的底面积是××1,高为,故12121212三棱锥P A1MN 的体积为××=.1312141245.G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示,则该几何体的体积为( )图12A.+2πB.1313π6C. D.7π35π25.B [解析] 由三视图知,该几何体为一个圆柱与一个半圆锥的组合体,其中圆柱的底面半径为1、高为2,半圆锥的底面半径为1、高为1,所以该几何体的体积V =××π×131212×1+π×12×2=.13π620.G5、G7[2015·重庆卷] 如图14,三棱锥P ABC 中,平面PAC ⊥平面ABC ,∠ABC =,点D ,E 在线段AC 上,且AD =DE =EC =2,PD =PC =4,点F 在线段AB 上,且π2EF ∥BC .(1)证明:AB ⊥平面PFE ;(2)若四棱锥P DFBC 的体积为7,求线段BC 的长.图1420.解:(1)证明:由DE =EC ,PD =PC 知,E 为等腰三角形PDC 中DC 边的中点,故PE ⊥AC .又平面PAC ⊥平面ABC ,平面PAC ∩平面ABC =AC ,PE ⊂平面PAC ,PE ⊥AC ,所以PE ⊥平面ABC ,从而PE ⊥AB .因为∠ABC =,EF ∥BC ,故AB ⊥EF .π2从而AB 与平面PFE 内两条相交直线PE ,EF 都垂直,所以AB ⊥平面PFE .(2)设BC =x ,则在直角三角形ABC 中,AB ==,AC 2-BC 236-x 2从而S △ABC =AB ·BC =x .121236-x 2由EF ∥BC 知,==,△AFE ∽△ABC ,故=2=,即S △AFE =S △ABC .AF AB AE AC 23S △AFE S △ABC 234949由AD =AE ,得S △AFD =S △AFE =×S △ABC =S △ABC =x ,12121249291936-x 2从而四边形DFBC 的面积为S 四边形DFBC =S △ABC -S △AFD =x -x =x1236-x 21936-x 2718.36-x 2由(1)知,PE ⊥平面ABC ,所以PE 为四棱锥P DFBC 的高.在直角三角形PEC 中,PE ===2.PC 2-EC 242-223所以V 四棱锥P DFBC =·S 四边形DFBC ·PE =×x ·2=7,131371836-x 23故得x 4-36x 2+243=0,解得x 2=9或x 2=27,由于x >0,可得x =3或x =3.3所以BC =3或BC =3.39.G7[2015·江苏卷] 现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.9. [解析] 设新的底面半径为r ,则π×52×4+π×22×8=πr 2×4+πr 2×8 ,71313即πr 2=π+32π,解得r =.28310037G8 多面体与球5.G2、G7、G8[2015·重庆卷] 某几何体的三视图如图12所示,则该几何体的体积为( )图12A.+2πB.1313π6C.D.7π35π25.B [解析] 由三视图知,该几何体为一个圆柱与一个半圆锥的组合体,其中圆柱的底面半径为1、高为2,半圆锥的底面半径为1、高为1,所以该几何体的体积V =××π×131212×1+π×12×2=.13π610.G8[2015·全国卷Ⅱ] 已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π10.C [解析] 因为V 三棱锥O ABC =V 三棱锥C OAB ,所以三棱锥O ABC 体积的最大值即三棱锥C OAB 体积的最大值,所以当C 到平面OAB 的距离最大时,即CO ⊥平面OAB 时,体积最大,设球的半径为r ,则V 三棱锥O ABC =V 三棱锥C OAB =r 3=36,所以r =6,则球O16的表面积S =4πr 2=144π.图12A.+2πB.1313π6C.D.7π35π2G9 空间向量及运算G10 空间向量解决线面位置关系G11 空间角与距离的求法17.G4、G5、G11[2015·天津卷] 如图14,已知AA 1⊥平面ABC ,BB 1∥AA 1,AB =AC =3,BC =2,AA 1=,BB 1=2,点E 和F 分别为BC 和A 1C 中点.577(1)求证:EF ∥平面A 1B 1BA ;(2)求证:平面AEA 1⊥平面BCB 1;(3)求直线A 1B 1与平面BCB 117.解:(1)证明:如图所示,连接A 1B .在△A 1BC 中,因为E 和F 分别是BC 和A 1C 的中点,所以EF ∥BA 1.又因为EF ⊄平面A A 1B 1BA .(2)证明:因为AB =AC ,E 为BC BC .因为AA 1⊥平面ABC ,BB 1∥AA 1,所以BB 1⊥平面ABC ,从而BB 1⊥AE .又因为BC ∩BB 1=B ,所以AE ⊥平面BCB 1.又因为AE ⊂平面AEA 1,所以平面AEA 1⊥平面BCB 1.(3)取BB 1的中点M 和B 1C 的中点N ,连接A 1M ,A 1N ,NE .因为N 和E 分别为B 1C 和BC的中点,所以NE ∥B 1B ,NE =B 1B ,故NE ∥A 1A ,且NE =A 1A ,所以A 1N ∥AE ,且A 1N =12AE .又因为AE ⊥平面BCB 1,所以A 1N ⊥平面BCB 1,从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角.在△ABC 中,可得AE =2,所以A 1N =AE =2.因为BM ∥AA 1,BM =AA 1,所以A 1M ∥AB ,A 1M =AB, 又由AB ⊥BB 1,得A 1M ⊥BB 1.在Rt △A 1MB 1中,可得A 1B 1==4.B 1M 2+A 1M 2在Rt △A 1NB 1中,sin ∠A 1B 1N ==,因此∠A 1B 1N =30°,A 1N A 1B 112所以直线A 1B 1与平面BCB 1所成的角为30°.18.G5,G11[2015·浙江卷] 如图14,在三棱柱ABC A 1B 1C 1中,∠BAC =90°,AB =AC =2,A 1A =4,A 1在底面ABC 的射影为BC 的中点,D 是B 1C 1的中点.(1)证明:A 1D ⊥平面A 1BC ;(2)求直线A 1B 和平面BB 1C 1C 所成的角的正弦值.图1418.解:(1)证明:设E 为BC 的中点,连接DE .由题意得A 1E ⊥平面ABC ,所以A 1E ⊥AE .因为AB =AC ,所以AE ⊥BC .故AE ⊥平面A 1BC .由D ,E 分别为B 1C 1,BC 的中点,得DE ∥B 1B 且DE =B 1B ,从而DE ∥A 1A 且DE =A 1A ,所以四边形AA 1DE 为平行四边形.于是A 1D ∥AE .又因为AE ⊥平面A 1BC ,所以A 1D ⊥平面A 1BC .(2)作A 1F ⊥DE ,垂足为F ,连接BF .因为A 1E ⊥平面ABC ,所以BC ⊥A 1E .因为BC ⊥AE ,所以BC ⊥平面AA 1DE .所以BC ⊥A 1F ,所以A 1F ⊥平面BB 1C 1C .所以∠A 1BF 为直线A 1B 和平面BB 1C 1C 所成的角.由AB =AC =2,∠CAB =90°,得EA =EB =.2由A 1E ⊥平面ABC ,得A 1A =A 1B =4,A 1E =.14由DE =BB 1=4,DA 1=EA =,∠DA 1E =90°,得A 1F =.272所以sin ∠A 1BF ==.A 1F A 1B 7818.G4,G5,G11[2015·广东卷] 如图13,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3.(1)证明:BC ∥平面PDA ;(2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.图13图1422.G11、G12[2015·江苏卷] 如图16,在四棱锥P ABCD 中,已知PA ⊥平面ABCD ,且四边形ABCD 为直角梯形,∠ABC =∠BAD =,PA =AD =2,AB =BC =1.π2(1)求平面PAB 与平面PCD 所成二面角的余弦值;(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成的角最小时,求线段BQ 的长.图1622.解:以{,,}为正交基底建立如图所示的空间直角坐标系A xyz ,则各点的AB → AD → AP →坐标为B (1,0,0),C (1,1,0),D (0,2,0),P (0,0,2).(1)因为AD ⊥平面PAB ,所以是平面PAB 的一个法向量,=(0,2,0).AD → AD →因为=(1,1,-2),=(0,2,-2),PC → PD →设平面PCD 的一个法向量为m =(x ,y ,z ),所以m ·=0,m ·=0,PC → PD →即令y =1,解得z =1,x =1,{x +y -2z =0,2y -2z =0.)所以m =(1,1,1)是平面PCD 的一个法向量.。
(完整word版)2015年全国新课标2卷高考文科数学及答案

2015年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}{}30|,21|<<=<<-=x x B x x A ,则=⋃B A ( )A .(-1,3)B .(-1,0)C .(0,2)D .(2,3)2.若a 为实数,且i iai +=++312,则=a ( ) A .-4 B .-3 C .3 D .43.根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A .逐年比较,2008年减少二氧化硫排放量的效果最显著B .2007年我国治理二氧化硫排放显现成效C .2006年以来我国二氧化硫年排放量呈减少趋势D .2006年以来我国二氧化硫年排放量与年份正相关4.向量()1,1-=a ,()2,1-=b ,则()=⋅+a b a 2 ( )A .-1B .0C .1D .25.设n S 是等差数列{}n a 的前n 项和,若3531=++a a a ,则=5S ( )A .5B .7C .9D .11 6.第6题图一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.157.已知三点()01,A ()30,B ,()32,C ,则ABC ∆外接圆的圆心到原点的距离为( )A.53B.213C.253D.438.第8题图右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的=a ( )A .0B .2C .4D .149.已知等比数列{}n a 满足411=a ,()14453-=a a a ,则=2a ( ) A .2 B .1 C.12 D.1810.已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点.若三棱锥O ABC 体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .144πD .256π 11.如图,长方形ABCD 的边AB =2,BC =1,O 是AB 的中点.点P 沿着边BC ,CD 与DA 运动,记∠BOP =x ,将动点P 到A ,B 两点距离之和表示为x 的函数f (x ),则y =f (x )的图象大致为( )12.设函数()()2111ln x x x f +-+=,则使得()()12->x f x f 成立的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13,1B.()∞+⋃⎪⎭⎫ ⎝⎛∞,,131- C.⎝ ⎛⎭⎪⎫-13,13 D.⎪⎭⎫ ⎝⎛∞+⋃⎪⎭⎫ ⎝⎛∞,,3131-- 第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.已知函数()x ax x f 23-=的图象过点()4,1-,则=a ________.14.若x ,y 满足约束条件⎩⎨⎧ x +y -5≤0,2x -y -1≥0,x -2y +1≤0,则y x z +=2的最大值为________. 15.已知双曲线过点()34,,且渐近线方程为x y 21±=,则该双曲线的标准方程为________.16.已知曲线x x y ln +=在点()1,1处的切线与曲线()122+++=x a ax y 相切,则=a ________. 三、解答题(解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分) ABC ∆中,D 是BC 上的点,AD 平分BAC ∠,DC BD 2=(1)求CB sin sin (2)若︒=∠60BAC ,求B ∠18.(本小题满分12分)某公司为了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表.图①B地区用户满意度评分的频数分布表2015·新课标Ⅱ卷第4页(1)在图②中作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).图②(2)根据用户满意度评分,将用户的满意度分为三个等级:估计哪个地区用户的满意度等级为不满意的概率大?说明理由.19.(本小题满分12分)如图,长方体1111D C B A ABCD -中,16=AB ,10=BC ,81=AA ,点E ,F 分别在11B A ,11C D 上,411==F D E A .过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求平面α把该长方体分成的两部分体积的比值.20.(本小题满分12分)已知椭圆C :12222=+by a x ()0.>>b a 的离心率为22,点()22,在C 上.(1)求C 的方程;(2)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .证明:直线OM 的斜率与直线l 的斜率的乘积为定值.21.(本小题满分12分)已知函数()()x a x x f -+=1ln .(1)讨论()x f 的单调性;(2)当()x f 有最大值,且最大值大于22-a 时,求a 的取值范围.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22. (本小题满分10分)选修4-1:几何证明选讲如图O 是等腰三角形AB C 内一点, ⊙O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高交于点G ,且与AB ,AC 分别相切于E ,F 两点.(I )证明EF ∥BC .(II )若AG 等于⊙O 的半径,且AE MN ==,求四边形EDCF 的面积23.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ (t 为参数,且0t ≠ ),其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ== (I )求2C 与3C 交点的直角坐标;(II )若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值24.(本小题满分10分)选修4-5:不等式选讲设a ,b ,c ,d 均为正数,且a +b =c +d .证明:(1)若ab >cd ,则a +b >c +d ;N M G OFE D C B A(2)a+b>c+d是|a-b|<|c-d|的充要条件.2015·新课标Ⅱ卷第8页1、选A2、故选D3、选D4、选B5、解:在等差数列中,因为.,5525)(,1,335153531A a a a S a a a a 故选所以==⨯+===++6、解:如图所示,选D.7、选B.8、故选B.9、解:因为{}),1(4,414531-==a a a a a n 满足所以, .21241,2,2),1(4123144424=⨯=====-=q a a q q a a a a a 所以,所以又解得故选C.10、解:因为A,B 都在球面上,又为该球面上动点,C AOB ,90︒=∠所以 三棱锥的体积的最大值为3661213132==⨯⨯R R R ,所以R=6,所以球的表面积为 S=14442=R ππ,故选C.11、解:如图,当点P 在BC 上时, ,tan 4tan ,tan 4,tan ,22x x PB PA x PA x PB x BOP ++=+∴+===∠ 当4π=x 时取得最大值51+,以A,B 为焦点C,D 为椭圆上两定点作椭圆,显然,当点P 在C,D 之间移动时PA+PB<51+. 又函数)(x f 不是一次函数,故选B.xP O DC B A12、解:因为函数时函数是增函数是偶函数,),0[,11)1ln()(2+∞∈+-+=x x x x f .131,)12(,12)12()(22<<->∴->∴->x x x x x x f x f 解得 故选A.第二卷一、填空题:本大题共4个小题,每小题5分 13、答:a=-214、解:当x=3,y=2时,z=2x+y 取得最大值8.15、解:设双曲线的方程为.43,4),0(422=≠=-k k k y x )代入方程,解得,点(1422=-∴y x 双曲线的标准方程为16、解:.122,11'-=∴+=x y xy ,切线方程为切线的斜率为 .8120.08,08,021)2(12222=+=====-=∆=+++++=-=a x y a a a a a ax ax x a ax y x y 所以与切线平行,不符。
2015-2017立体几何全国卷高考真题

2015-2017立体几何高考真题1、(2015年1卷6题)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛【答案】B【解析】设圆锥底面半径为r ,则12384r ⨯⨯==163r =,所以米堆的体积为211163()5433⨯⨯⨯⨯=3209,故堆放的米约为3209÷1.62≈22,故选B.考点:圆锥的性质与圆锥的体积公式 2、(2015年1卷11题)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π,则r=( )(A )1 (B )2 (C )4 (D )8 【答案】B【解析】由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r ,圆柱的高为2r ,其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π,解得r=2,故选B.考点:简单几何体的三视图;球的表面积公式、圆柱的测面积公式 3、(2015年1卷18题)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(Ⅰ)证明:平面AEC ⊥平面AFC ;(Ⅱ)求直线AE 与直线CF 所成角的余弦值. 【解析】 试题分析:(Ⅰ)连接BD ,设BD ∩AC=G ,连接EG ,FG ,EF ,在菱形ABCD 中,不妨设GB=1易证EG ⊥AC ,通过计算可证EG ⊥FG ,根据线面垂直判定定理可知EG ⊥平面AFC ,由面面垂直判定定理知平面AFC ⊥平面AEC ;(Ⅱ)以G 为坐标原点,分别以,GB GC 的方向为x 轴,y 轴正方向,||GB 为单位长度,建立空间直角坐标系G-xyz ,利用向量法可求出异面直线AE 与CF 所成角的余弦值. 试题解析:(Ⅰ)连接BD ,设BD ∩AC=G ,连接EG ,FG ,EF ,在菱形ABCD 中,不妨设GB=1,由∠ABC=120°,可得由BE ⊥平面ABCD ,AB=BC 可知,AE=EC ,又∵AE ⊥EC ,∴EG ⊥AC ,在Rt △EBG 中,可得DF=2.在Rt △FDG 中,可得在直角梯形BDFE 中,由BD=2,可得 ∴222EG FG EF +=,∴EG ⊥FG ,∵AC ∩FG=G ,∴EG ⊥平面AFC ,∵EG ⊂面AEC ,∴平面AFC ⊥平面AEC.(Ⅱ)如图,以G 为坐标原点,分别以,GB GC 的方向为x 轴,y 轴正方向,||GB 为单位长度,建立空间直角坐标系G-xyz ,由(Ⅰ)可得A (00),E (,F (-1,0,C (00),∴AE =(1,CF =(-1,).…10分故cos ,3||||AE CF AE CF AE CF ⋅<>==-. 所以直线AE 与CF 考点:空间垂直判定与性质;异面直线所成角的计算;空间想象能力,推理论证能力 4、(2015年2卷6题)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )A .81 B .71 C .61 D .51 【解析】由三视图得,在正方体1111ABCD A BC D -中,截去四面体111A A B D -,如图所示,,设正方体棱长为a ,则11133111326A A B D V a a -=⨯=,故剩余几何体体积为3331566a a a -=,所以截去部分体积与剩余部分体积的比值为51,故选D .考点:三视图.5、(2015年2卷9题)已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为( ) A .36π B .64π C .144π D .256π【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时2311136326O ABC C AOB V V R R R --==⨯⨯==,故6R =,则球O 的表面积为24144S R ππ==,故选C .考点:外接球表面积和椎体的体积.6、(2015年2卷19题)(本题满分12分)如图,长方体1111ABCD A BC D -中,=16AB ,A1=10BC ,18AA =,点E ,F 分别在11A B ,11C D 上,114A E D F ==.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(不必说出画法和理由); (Ⅱ)求直线AF 与平面α所成角的正弦值. 【解析】(Ⅰ)交线围成的正方形EHGF 如图:(Ⅱ)作EM AB ⊥,垂足为M ,则14AM AE ==,18EM AA ==,因为EHGF 为正方形,所以10EH EF BC ===.于是226MH EH EM =-=,所以10AH =.以D为坐标原点,DA 的方向为x 轴的正方向,建立如图所示的空间直角坐标系D xyz -,则(10,0,0)A ,(10,10,0)H ,(10,4,8)E ,(0,4,8)F ,(10,0,0)FE =,(0,6,8)HE =-.设(,,)n x y z =是平面E H G F 的法向量,则0,0,n FE n HE ⎧⋅=⎪⎨⋅=⎪⎩即100,680,x y z =⎧⎨-+=⎩所以可取(0,4,3)n =.又(10,4,8)AF =-,故45cos ,15n AF n AF n AF⋅<>==⋅.所以直线AF 与平面α所成角的正弦值为45.考点:1、直线和平面平行的性质;2、直线和平面所成的角.7、(2016年1卷6题)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是 (A )17π (B )18π (C )20π (D )28πD D CAE FA B CB【解析】试题分析: 该几何体直观图如图所示:是一个球被切掉左上角的18,设球的半径为R ,则37428V R 833ππ=⨯=,解得R 2=,所以它的表面积是78的球面面积和三个扇形面积之和2271=42+32=1784S πππ⨯⨯⨯⨯故选A .考点:三视图及球的表面积与体积8、(2016年1卷11题)平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α//平面CB 1D 1,αI 平面ABCD =m ,αI 平面AB B 1A 1=n ,则m 、n 所成角的正弦值为B 13试题分析:如图,设平面11CB D 平面ABCD ='m ,平面11CB D 平面11ABB A ='n ,因为//α平面11CB D ,所以//',//'m m n n ,则,m n 所成的角等于','m n 所成的角.延长AD ,过1D 作11//D E B C ,连接11,CE B D ,则CE 为'm ,同理11B F 为'n ,而111//,//BD CE B F A B ,则','m n 所成的角即为1,A B BD 所成的角,即为60︒,故,m n ,选A. 考点:平面的截面问题,面面平行的性质定理,异面直线所成的角.【名师点睛】求解本题的关键是作出异面直线所成角,求异面直线所成角的步骤是:平移定角、连线成形,解形求角、得钝求补.9、(2016年1卷18题)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60.(I )证明:平面ABEF ⊥平面EFDC ; (II )求二面角E -BC -A 的余弦值.试题解析:(I )由已知可得F DF A ⊥,F F A ⊥E ,所以F A ⊥平面FDC E . 又F A ⊂平面F ABE ,故平面F ABE ⊥平面FDC E .(II )过D 作DG F ⊥E ,垂足为G ,由(I )知DG ⊥平面F ABE .以G 为坐标原点,GF 的方向为x 轴正方向,GF 为单位长度,建立如图所示的空间直角坐标系G xyz -.由(I )知DF ∠E 为二面角D F -A -E 的平面角,故DF 60∠E =,则DF 2=,DG 3=,可得()1,4,0A ,()3,4,0B -,()3,0,0E -,(D . 由已知,//F AB E ,所以//AB 平面FDC E . 又平面CDAB 平面FDC DC E =,故//CD AB ,CD//F E .由//F BE A ,可得BE ⊥平面FDC E ,所以C F ∠E 为二面角C F -BE -的平面角,C F 60∠E =.从而可得(C -.所以(C E =,()0,4,0EB =,(C 3,A =--,()4,0,0AB =-. 设(),,n x y z =是平面C B E 的法向量,则C 00n n ⎧⋅E =⎪⎨⋅EB =⎪⎩,即040x y ⎧+=⎪⎨=⎪⎩, CABDEF所以可取(3,0,n =.设m 是平面CD AB 的法向量,则C 0m m ⎧⋅A =⎪⎨⋅AB =⎪⎩,同理可取()0,3,4m =.则219cos ,n m n m n m ⋅==- 故二面角C E -B -A 的余弦值为考点:垂直问题的证明及空间向量的应用【名师点睛】立体几何解答题第一问通常考查线面位置关系的证明,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证的关键是结合空间想象能力进行推理,要防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.第二问一般考查角度问题,多用空间向量解决.10、(2016年2卷6题)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π (B )24π (C )28π (D )32π 解析:几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为,周长为,圆锥母线长为,圆柱高为. 由图得,,由勾股定理得:,,故选C .11、(2016年2卷14题)α,β是两个平面,m ,n 是两条线,有下列四个命题:①如果m n ⊥,m α⊥,n β∥,那么αβ⊥. ②如果m α⊥,n α∥,那么m n ⊥. ③如果a β∥,m α⊂,那么mβ∥.④如果m n ∥,αβ∥,那么m 与α所成的角和n 与β所成的角相等.r c lh 2r =2π4πc r ==4l =21π2S r ch cl =++表4π16π8π=++28π=其中正确的命题有 .(填写所有正确命题的编号) 【解析】②③④12(2016年2卷19题)(本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将△DEF 沿EF 折到△D EF '的位置10OD '=. (I )证明:DH'⊥平面ABCD ; (II )求二面角B D A C '--的正弦值.【解析】⑴证明:∵,∴,∴. ∵四边形为菱形,∴,∴,∴,∴.∵,∴;又,, ∴,∴,∴,∴, ∴.又∵,∴面.⑵建立如图坐标系.,,,, ,,, 设面法向量,由得,取, ∴.同理可得面的法向量, ∴,∴. 54AE CF ==AE CF AD CD=EF AC ∥ABCD AC BD ⊥EF BD ⊥EF D H ⊥EF DH'⊥6AC =3AO =5AB =AO OB ⊥4OB =1AE OH OD AO=⋅=3DH D H '==222'OD OH D H '=+'D H OH ⊥OH EF H =I 'D H ⊥ABCD H xyz -()500B ,,()130C ,,()'003D ,,()130A -,,()430AB =u u u r ,,()'133AD =-u u u r ,,()060AC =u u u r ,,'ABD ()1n x y z =,,u r1100n AB n AD ⎧⋅=⎪⎨'⋅=⎪⎩430330x y x y z +=⎧⎨-++=⎩345x y z =⎧⎪=-⎨⎪=⎩()1345n =-u r ,,'AD C ()2301n =u u r,,1212cos n n n n θ⋅=u r u u r u r u u r sin θ=13、(2016年3卷9题)如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为( )(A)18+(B)54+(C )90 (D )81 【答案】B考点:空间几何体的三视图及表面积.【技巧点拨】求解多面体的表面积及体积问题,关键是找到其中的特征图形,如棱柱中的矩形,棱锥中的直角三角形,棱台中的直角梯形等,通过这些图形,找到几何元素间的关系,建立未知量与已知量间的关系,进行求解. 14、(2016年3卷10题)在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是( ) (A )4π (B )92π(C )6π (D )323π【答案】B试题分析:要使球的体积V 最大,必须球的半径R 最大.由题意知球的与直三棱柱的上下底面都相切时,球的半径取得最大值32,此时球的体积为334439()3322R πππ==,故选B .考点:1、三棱柱的内切球;2、球的体积.【思维拓展】立体几何是的最值问题通常有三种思考方向:(1)根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;(2)将几何体平面化,如利用展开图,在平面几何图中直观求解;(3)建立函数,通过求函数的最值来求解. 15、(2016年3卷19题)(本小题满分12分)如图,四棱锥P ABC -中,PA ⊥地面ABCD ,AD BC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(I )证明MN平面PAB ;(II )求直线AN 与平面PMN 所成角的正弦值.【答案】(Ⅰ)见解析;(Ⅱ).【解析】试题分析:(Ⅰ)取PB 的中点T ,然后结合条件中的数据证明四边形AMNT 为平行四边形,从而得到MNAT ,由此结合线面平行的判断定理可证;(Ⅱ)以A 为坐标原点,以,AD AP 所在直线分别为,y z 轴建立空间直角坐标系,然后通过求直线AN 的方向向量与平面PMN 法向量的夹角来处理AN 与平面PMN 所成角.试题解析:(Ⅰ)由已知得232==AD AM ,取BP 的中点T ,连接TN AT ,,由N 为PC中点知BC TN //,221==BC TN .又BC AD //,故TN AM ,四边形AMNT 为平行四边形,于是AT MN //.因为⊂AT 平面PAB ,⊄MN 平面PAB ,所以//MN 平面PAB.设(,,)n x y z =为平面PMN 的法向量,则⎪⎩⎪⎨⎧=⋅=⋅00PN n PM n ,即⎪⎩⎪⎨⎧=-+=-0225042z y x z x ,可取(0,2,1)n =,于是||85|cos ,|||||n AN n AN n AN ⋅<>==.考点:1、空间直线与平面间的平行与垂直关系;2、棱锥的体积. 【技巧点拨】(1)证明立体几何中的平行关系,常常是通过线线平行来实现,而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证;(2)求解空间中的角和距离常常可通过建立空间直角坐标系,利用空间向量中的夹角与距离来处理. 16、(2017年1卷7题)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形、该多面体的各个面中有若干是梯形,这些梯形的面积之和为A .10B .12C .14D .16【答案】B【解析】由三视图可画出立体图该立体图平面内只有两个相同的梯形的面()24226S =+⨯÷=梯6212S =⨯=全梯 故选B17、(2017年1卷16题)如图,圆形纸片的圆心为O ,半径为5cm ,该纸片上的等边三角形ABC 的中心为O ,D 、E 、F 为元O 上的点,DBC △,ECA △,FAB △分别是一BC ,CA ,AB 为底边的等腰三角形,沿虚线剪开后,分别以BC ,CA ,AB 为折痕折起DBC △,ECA △,FAB △,使得D ,E ,F 重合,得到三棱锥.当ABC △的边长变化时,所得三棱锥体积(单位:3cm )的最大值为_______.【答案】【解析】由题,连接OD ,交BC 与点G ,由题,OD BC ⊥OG =,即OG 的长度与BC 的长度或成正比设OG x =,则BC =,5DG x =-三棱锥的高h2132ABC S x =⋅=△则213ABC V S h =⋅=△令()452510f x x x =-,5(0,)2x ∈,()3410050f x x x '=-令()0f x '>,即4320x x -<,2x <则()()280f x f =≤ 则38045V ⨯=≤∴体积最大值为3415cm18、(2017年1卷18题)如图,在四棱锥P ABCD -中,AB CD ∥中,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,求二面角A PB C --的余弦值. 【解析】(1)证明:∵90BAP CD P ∠=∠=︒∴PA AB ⊥,PD CD ⊥又∵AB CD ∥,∴PD AB ⊥又∵PD PA P =,PD 、PA ⊂平面PAD ∴AB ⊥平面PAD ,又AB ⊂平面PAB ∴平面PAB ⊥平面PAD(2)取AD 中点O ,BC 中点E ,连接PO ,OE ∵AB CD∴四边形ABCD 为平行四边形 ∴OE AB由(1)知,AB ⊥平面PAD∴OE ⊥平面PAD ,又PO 、AD ⊂平面PAD ∴OE PO ⊥,OE AD ⊥ 又∵PA PD =,∴PO AD ⊥ ∴PO 、OE 、AD 两两垂直∴以O 为坐标原点,建立如图所示的空间直角坐标系O xyz -设2PA =,∴()002D -,,、()220B ,,、()002P ,,、()202C -,,, ∴()022PD =--,,、()222PB =-,,、()2200BC =-,,设()n x y z =,,为平面PBC 的法向量由00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩,得200y +=-=⎪⎩令1y =,则z =,0x =,可得平面PBC的一个法向量(01n =, ∵90APD ∠=︒,∴PD PA ⊥又知AB ⊥平面PAD ,PD ⊂平面PAD ∴PD AB ⊥,又PA AB A = ∴PD ⊥平面PAB即PD 是平面PAB的一个法向量,(0PD =,,∴cos 23PD n PD n PD n⋅===⋅, 由图知二面角A PB C --为钝角,所以它的余弦值为19、(2017年2卷4题)如图,网格纸上小正方形的边长为1,学 科&网粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( ) 【解析】 A .90π B .63π C .42π D .36π【解析】【命题意图】本题主要考查简单几何体三视图及体积,以考查考生的空间想象能力为主目的. 【解析】 【解析】解法一:常规解法【解析】从三视图可知:一个圆柱被一截面截取一部分而剩余的部分,具体图像如下:【解析】从上图可以清晰的可出剩余几何体形状,该几何体的体积分成两部分,部分图如下:从左图可知:剩下的体积分上下两部分阴影的体积,下面阴影的体积为面部分体积即第二种体积求法:V 20、(2017年2卷10题)已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A B C 【命题意图】本题考查立体几何中的异面直线角度的求解,意在考查考生的空间想象能力 【解析】解法一:常规解法在边F 由三角形中位线定理和平行线平移功能,异面直线 通过几何关系求得FH 21、(2017年2卷19题) 如图,四棱锥-中,侧面为等比三角形且垂直于底面ABCD ,o 1,90,2AB BC AD BAD ABC ==∠=∠= E 是PD 的中点. (1)证明:直线//CE 平面PAB(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成锐角为o45 ,求二面角M -AB -D 的余弦值【命题意图】线面平行的判定,线面垂直的判定,面面垂直的性质,线面角、二面角的求解 【标准答案】(1)证明略;(2【基本解法1】(1)证明:取PA 中点为F ,连接EF 、AF 因为90BAD ABC ∠=∠=︒,12BC AD =所以BC 12AD 因为E 是PD 的中点,所以EF12AD ,所以EF BC 所以四边形EFBC 为平行四边形,所以//EC BF 因为BF ⊂平面PAB ,EC ⊄平面PAB 所以直线//CE 平面PAB(2)取AD 中点为O ,连接OC OP 、因为△PAD 为等边三角形,所以PO ⊥AD因为平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,PO ⊂平面PAD 所以PO ⊥平面ABCD因为AO BC ,所以四边形OABC 为平行四边形,所以//AB OC 所以OC AD ⊥以,,OC OD OP 分别为,,x y z 轴建立空间直角坐标系,如图设1BC =,则(0,0,3),(0,1,0),(1,1,0),(1,0,0)P A B C --,所以(1,0,PC = 设(,,)M x y z ,则(,,3)PM x y z =-,(1,0,0)AB =因为点M 在棱PC 上,所以(01)PM PC λλ=≤≤,即(,,(1,0,x y z λ= 所以()M λ,所以(1,1)BM λ=- 平面ABCD 的法向量为(0,0,1)n = 因为直线BM 与底面ABCD 所成角为45︒, 所以|||sin 45||cos ,|2||||(BM n BM n BM n λ⋅︒=<>===解得12λ=-()22BM =-- 设平面MAB 的法向量为(,,)m x y z =,则020AB m x BM m x y z ⎧⋅==⎪⎨⋅=-+=⎪⎩令1z =,则(0,m =所以cos ,5||||6m n m n <>==⋅ 所以求二面角M AB D --的余弦值522、(2017年3卷8题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A .πB .3π4C.π2 D .π4【答案】B【解析】由题可知球心在圆柱体中心,圆柱体上下底面圆半径r =,则圆柱体体积23ππ4V r h ==,故选B.23、(2017年3卷16题)为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与,都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论:①当直线AB 与成60︒角时,AB 与成30︒角; ②当直线AB 与成60︒角时,AB 与成60︒角; ③直线AB 与所成角的最小值为45︒; ④直线AB 与所成角的最大值为60︒.其中正确的是________(填写所有正确结论的编号) 【答案】②③【解析】由题意知,a b AC 、、三条直线两两相互垂直,画出图形如图.不妨设图中所示正方体边长为1, 故||1AC =,AB =斜边AB 以直线AC 为旋转轴旋转,则A 点保持不变, B 点的运动轨迹是以C 为圆心,1为半径的圆.以C 为坐标原点,以CD 为轴正方向,CB 为轴正方向, CA 为轴正方向建立空间直角坐标系. 则(1,0,0)D ,(0,0,1)A ,直线的方向单位向量(0,1,0)a =,||1a =. B 点起始坐标为(0,1,0),直线的方向单位向量(1,0,0)b =,||1b =. 设B 点在运动过程中的坐标(cos ,sin ,0)B θθ',其中为B C '与CD 的夹角,[0,2π)θ∈.那么'AB 在运动过程中的向量(cos ,sin ,1)AB θθ'=--,||2AB '=.设AB '与所成夹角为π[0,]2α∈,则(cos ,sin ,1)(0,1,0)cos sin |a AB θθαθ--⋅=∈'. 故ππ[,]42α∈,所以③正确,④错误.设AB '与所成夹角为π[0,]2β∈,cos (cos ,sin ,1)(1,0,0)cos |AB bb AB b AB βθθθ'⋅='-⋅='.当AB '与夹角为60︒时,即π3α=, sin3πθα====.∵22cos sin 1θθ+=,∴|cos |θ=∴1cos |cos |2βθ==. ∵π[0,]2β∈.∴π=3β,此时AB '与夹角为60︒.∴②正确,①错误.24、(2017年3卷19题)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形.ABD CBD ∠=∠,AB BD =.(1)证明:平面ACD ^平面ABC ;(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分.求二面角D AE C --的余弦值.【解析】⑴取AC 中点为O ,连接BO ,DO ; ABC ∆为等边三角形 ∴BO AC ⊥∴AB BC = AB BCBD BDABD DBC=⎧⎪=⎨⎪∠=∠⎩ABD CBD ∴∆≅∆. DA B CED BC EO∴AD CD =,即ACD ∆为等腰直角三角形,ADC ∠ 为直角又O 为底边AC 中点∴DO AC ⊥令AB a =,则A B A C B C B D a ====易得:O D a =,OB =∴222OD OB BD +=由勾股定理的逆定理可得2DOB π∠=即OD OB ⊥OD AC OD OBAC OB O AC ABC OB ABC⊥⎧⎪⊥⎪⎪=⎨⎪⊂⎪⊂⎪⎩平面平面OD ABC ∴⊥平面 又∵OD ADC ⊂平面由面面垂直的判定定理可得ADC ABC ⊥平面平面 ⑵由题意可知V V D ACE B ACE --=即B ,D 到平面ACE 的距离相等即E 为BD 中点以O 为原点,OA 为轴正方向,OB 为轴正方向,OD 为轴正方向,设AC a =,建立空间直角坐标系,则()0,0,0O ,,0,02a A ⎛⎫ ⎪⎝⎭,0,0,2a D ⎛⎫ ⎪⎝⎭,,0B ⎛⎫ ⎪ ⎪⎝⎭,,4a E ⎛⎫ ⎪ ⎪⎝⎭易得:,24a a AE ⎛⎫=- ⎪ ⎪⎝⎭,,0,22a a AD ⎛⎫=- ⎪⎝⎭,,0,02a OA ⎛⎫= ⎪⎝⎭ 设平面AED 的法向量为1n ,平面AEC 的法向量为2n ,则1100AE n AD n ⎧⋅=⎪⎨⋅=⎪⎩,解得(13,1,n =2200AE n OA n ⎧⋅=⎪⎨⋅=⎪⎩,解得(20,1,n = 若二面角D AE C --为,易知为锐角,则12127cos n n n n θ⋅==⋅主要考点:1、能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识 别上述三视图所表示的立体模型,会用斜二侧法画出它们的直观图 .2、了解球、棱柱、棱锥、台的表面积和体积的计算公式 .3、能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题4、掌握空间向量的线性运算及其坐标表示.5、掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直.6、理解直线的方向向量与平面的法向量.7、能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用.。
2015年高考数学立体几何专题试卷(新课标)

……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………绝密★启用前2015年高考数学立体几何专题试卷(新课标)1.(本小题满分12分)如图,四棱锥P ABCD -中,PAB ∆是正三角形,四边形ABCD 是矩形,且平面PAB ⊥平面ABCD ,2PA =,4PC =.(Ⅰ)若点E 是PC 的中点,求证://PA 平面BDE ;(Ⅱ)若点F 在线段PA 上,且FA PA λ=,当三棱锥B AFD -的体积为43时,求实数λ的值.【答案】(Ⅰ)证明见解析;(Ⅱ).32 【解析】试题分析:(Ⅰ)将证明线面平行转化为线线平行,通过做辅助线可证明出EQ //PA ,线面平行的判定定理可证出//PA 平面BDE ;(Ⅱ)如图所示作辅助线,通过题意可先分3431=⋅⋅==∆--FM S V V ABD ABD F AFD B 将问题转化为求BC ,由面面垂直的性质定理得PO ⊥平面ABCD ,进而FM ⊥平面ABCD ,得到BC ⊥平面PAB ,故2223BC PC PB =-=,进而确定332=FM ,再由2323====33FM FA PO PA λλλ⇒⇒ 试题解析:(Ⅰ)如图,连接AC ,设ACBD Q =,又点E 是PC 的中点,则在PAC ∆中,中位线EQ //PA , 3分又EQ ⊂平面BDE ,PA ⊄平面BDE .试卷第2页,总14页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………所以//PA 平面BDE 5分(Ⅱ)依据题意可得:2PA AB PB ===,取AB 中点O ,所以PO AB ⊥,且3PO =又平面PAB ⊥平面ABCD ,则PO ⊥平面ABCD ; 6分作//FM PO 于AB 上一点M ,则FM ⊥平面ABCD , 因为四边形ABCD 是矩形,所以BC ⊥平面PAB ,则PBC ∆为直角三角形8分所以2223BC PC PB =-=,则直角三角形ABP ∆的面积为1=232ABP S AB AD ∆⋅=412323==3333B AFD F ABD ABD V V S FM FM FM --∆==⋅=⇒ 10分由//FM PO 得:2323====33FM FA PO PA λλλ⇒⇒ 12分考点:1、线面平行问题与线线平行问题的互化;2、面面垂直与线面垂直问题的互化;3、综合分析能力.2.(本小题满分12分)如图几何体中,四边形ABCD 为矩形,36,2,AB BC BF CF DE EF ======4,//EF AB ,G 为FC 的中点,M 为线段CD上的一点,且2CM =.(Ⅰ)证明:AF//面BDG ;(Ⅱ)证明:面BGM ⊥面BFC ; (Ⅲ)求三棱锥F BMC -的体积V.……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………【答案】(Ⅰ)(Ⅱ)证明见解析;(Ⅲ)三棱锥F BMC -的体积为322. 【解析】 试题分析:(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键. (3)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算. 试题解析:(Ⅰ)连接AC 交BD 于O 点,则O 为AC 的中点,连接OG ,因为点G 为CF 中点,所以OG 为AFC ∆的中位线,所以//OG AF , 2分 AF ⊄面BDG , OG ⊂面BDG , ∴//AF 面BDG 5分(Ⅱ)连接FM ,2BF CF BC ===,G 为CF 的中点, BG CF ∴⊥,2CM =,4DM ∴=,//EF AB ,ABCD 为矩形, 7分//EF DM ∴,又4EF =,EFMD ∴为平行四边形, 8分 2FM ED ∴==,FCM ∴∆为正三角形 MG CF ∴⊥, MG BG G =CF ∴⊥面BGM ,CF ⊂面BFC ,∴面BGM ⊥面BFC . 10分(Ⅲ)11233F BMC F BMG C BMG BMG BMG V V V S FC S ---=+=⨯⨯=⨯⨯,因为3GM BG ==,22BM =,所以122122BMG S =⨯⨯=,所以22233F BMC BMC V S -=⨯=. 12分 考点:(1)线面平行的判定;(2)面面垂直;(3)几何体的体积3.(本小题满分12分)如图,AB 为圆O 的直径,E 是圆O 上不同于A ,B 的动点,四边形ABCD 为矩形,且1,2==AD AB ,平面ABCD ⊥平面ABE .(1)求证:BE ⊥平面DAE .CABDE FGMO试卷第4页,总14页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………(2)当点E 在AB 的什么位置时,四棱锥ABCD E -的体积为33. 【答案】(1)详见解析 (2)点E 在AB 满足6EAB π∠=或3EAB π∠=时,四棱锥E ABCD -的体积为33. 【解析】试题分析:第(1)问先证明线线垂直,再证明线面垂直;第(2)问探求点E 在»AB 的什么位置时,四棱锥E ABCD -的体积为33,从研究BAE α∠=的大小着手思考,通过体积建立关系求出α的大小. 试题解析:(1)因为四边形ABCD 为矩形,所以DA AB ⊥, 又平面ABCD ⊥平面ABE ,且平面ABCD I 平面ABE AB =, 所以DA ⊥平面ABE ,而BE ⊆平面ABE ,所以DA ⊥BE .又因为AB 为圆O 的直径,E 是圆O 上不同于A ,B 的动点,所以AE BE ⊥. 因为DA AE A =I ,所以BE ⊥平面DAE .(2)因为平面ABCD ⊥平面ABE ,过点E 作EH AB ⊥交AB 于点H ,则EH ⊥平面ABCD .在Rt BAE △中,记BAE α∠=(02πα<<),因为2AB =,所以2cos AE α=,sin 2cos sin sin 2HE AE αααα=⋅==,所以11221sin 2sin 2333E ABCD ABCD V S HE αα-=⨯=⨯⨯⨯=.由已知33E ABCD V -=,所以23sin 233α=,即3sin 22α=. 因为02πα<<,所以23πα=,即6πα=;或223πα=,即3πα=.于是点E 在AB 满足6EAB π∠=或3EAB π∠=时,四棱锥E ABCD -的体积为33.……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………考点:立体几何中的线面关系和四棱锥体积. 4.(本小题满分12分)如图,在四棱锥ABCD S -中,底面ABCD 是正方形,⊥SA 底面ABCD ,AB SA =,点M 是SD 的中点,SC AN ⊥且交SC 于点N .(Ⅰ)求证:平面⊥SAC 平面AMN ; (Ⅱ)求二面角M AC D --的余弦值. 【答案】(Ⅰ)详见解析;(Ⅱ)33. 【解析】试题分析:方法1:(Ⅰ):⊥SA 底面ABCD , SA DC ⊥∴又底面ABCD 是正方形,DA DC ⊥∴ ⊥∴DC 平面SAD , AM DC ⊥∴ 又AD SA = ,M 是SD 的中点,SD AM ⊥∴,⊥∴AM 面SDC AM SC ⊥∴ ,然后再根据线面垂直的判定定理,即可得出结果.(Ⅱ)取AD 的中点F ,则SA MF //.作AC FQ ⊥于Q ,连结MQ .⊥SA 底面A B C D , ⊥∴MF 底面A B C D AC FQ ⊥ , AC MQ ⊥∴FQM ∠∴为二面角M AC D --的平面角,解三角形即可求出结果.解法2:(Ⅰ)如图,以A 为坐标原点,建立空间直角坐标系xyz A -,利用空间向量在立体几何中的应用,即可求出结果.试题解析:证明(Ⅰ):⊥SA 底面ABCD , SA DC ⊥∴ 又底面ABCD 是正方形,DA DC ⊥∴⊥∴DC 平面SAD , AM DC ⊥∴又AD SA = ,M 是SD 的中点,SD AM ⊥∴, ⊥∴AM 面SDC AM SC ⊥∴试卷第6页,总14页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………由已知SC AN ⊥, ⊥∴SC 平面AMN . 又⊂SC 面SAC ,∴面⊥SAC 面AMN 6分 (Ⅱ)取AD 的中点F ,则SA MF //. 作AC FQ ⊥于Q ,连结MQ .⊥SA 底面ABCD , ⊥∴MF 底面ABCD AC FQ ⊥ , AC MQ ⊥∴FQM ∠∴为二面角M AC D --的平面角设aAB SA ==,在MFQRt ∆中221a SA MF ==,a FQ 42=,a FQ MF MQ 4622=+= 33cos ==∠∴MQ FQ FQM 11分 所以二面角M AC D --的余弦值为3312分 解法2:(Ⅰ)如图,以A 为坐标原点,建立空间直角坐标系xyz A -,由于AB SA =,可设1===AS AD AB , 则()(),0,1,0,0,0,0B A ()()()1,0,0,0,0,1,0,1,1S D C ,⎪⎭⎫⎝⎛21,0,21M 3分 ⎪⎭⎫⎝⎛=∴21,0,21AM ,()1,1,1--=CS 4分0=∙CS AM , CS AM ⊥∴又AN SC ⊥ 且A AM AN = ⊥∴SC 平面AMN .又⊂SC 平面SAC 所以,平面SAC ⊥平面AMN 6分……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………(Ⅱ)⊥SA 底面ABCD AS ∴是平面ABCD 的一个法向量,()1,0,0=AS 7分 设平面ACM 的一个法向量为()z y x n ,,=()0,1,1=AC ,⎪⎭⎫ ⎝⎛=21,0,21AM ,则⎪⎩⎪⎨⎧=∙=∙00AM n AC n 得()1,1,1--=n 9分 33,cos ->=<∴n AS 11分 ∴二面角M AC D --的余弦值是3312分. 考点:1.线面垂直的判定;2.面面垂直的判定. 5.(本小题满分13分)如图,三棱柱111ABC A B C -中,侧棱垂直底面,︒=∠90ACB ,112AC BC AA ==,D 是棱1AA 的中点.(1)证明:1DC ⊥平面BDC ;(2)若12AA =,求三棱锥1C BDC -的体积. 【答案】(1)见解析 (2)13【解析】试题分析:对应第一问,关键是要掌握线面垂直的判定,把握线线垂直的证明方法,第二问注意椎体的体积公式的应用.试题解析:(1)由题设知1,BC CC BC AC ⊥⊥,1AC CC C =,∴BC ⊥平面11ACC A . (2分) 又∵1DC ⊂平面11ACC A ,∴1DC BC ⊥. (3分)由题设知1145o ADC A DC ∠=∠=,∴190oCDC ∠=,即1C D DC ⊥. (4分)∵DCBC C =,∴1DC ⊥平面BDC . (6分)(2) ∵12AA =,D 是棱1AA 的中点,112AC BC AA ==试卷第8页,总14页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………∴1,1AC BC AD === (7分) ∴222CD AD AC =+=,12DC = (9分)∴1CDC Rt ∆的面积11122122S CD DC =⋅=⨯⨯= (10分) ∴311131311=⨯⨯=⋅=-BC S V CDC B (11分) ∴3111==--CDC B BDC C V V ,即三棱锥1C BDC -的体积为13. (13分)考点:线面垂直的判定,椎体的体积. 6.(本题满分12分)在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PA ⊥底面ABCD ,PA AB = ,点E 是PD 的中点,作EF PC ⊥交PC 于F .(Ⅰ)求证:PB ∥平面EAC ; (Ⅱ)求证:PC ⊥平面AEF ; (Ⅲ)求二面角A PC D --的大小. 【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)60︒. 【解析】 试题分析:(Ⅰ)连结BD ,与AC 交于G .由中位线可得EG ∥PB .根据线面平行的判定定理可证得PB ∥平面EAC .(Ⅱ)由PA ⊥底面ABCD 可证得PA CD ⊥,又因为ABCD 是正方形,根据线面垂直判定定理可证得CD ⊥平面PAD ,从而可得CD AE ⊥.根据等腰三角形中线即为高线可得AE PD ⊥,根据线面垂直判定定理可证得AE ⊥平面PCD ,从而可得AE PC ⊥又EF PC ⊥可得PC ⊥平面AEF .(Ⅲ)以点A 为坐标原点建立空间直角坐标系. 设1AB =,可得各点的坐标,从而可得各向量坐标.根据向量垂直数量积为0可得面APC 和面DPC 的法向量.根据数量积公式可得两法向量夹角的余弦值,可得两法向量夹角. 两法向量夹角与二面角相等或互补.由观察可知所求二面角为锐角.试题解析:解:(Ⅰ)连结BD ,与AC 交于G , ∵ABCD 是正方形,∴则G 为BD 的中点 ∵E 是PD 的中点, ∴EG ∥PB∵EG ⊂平面EAC ,PB ⊄平面EAC ∴PB ∥平面EAC 3分……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………(Ⅱ)∵PA ⊥底面ABCD ,CD ⊂平面ABCD ∴PA CD ⊥∵CD AD ⊥,PA AD A = ∴CD ⊥平面PAD 4分 ∵AE ⊂平面PAD , ∴CD AE ⊥∵E 是PD 的中点,PA AD = ∴AE PD ⊥ ∵PD CD D =∴AE ⊥平面PCD 6分 而PC ⊂平面PCD , ∴AE PC ⊥又EF PC ⊥,AE EF E =PC ⊥平面AEF 8分(Ⅲ)如图建立空间直角坐标系,点A 为坐标原点,设1AB =则(0,0,1),(1,1,0),(0,1,0),(1,0,0)(0,0,1)(1,0,1)AP AC DC PD ====-=- 9分 设平面APC 的法向量是111(,,)m x y z =,则0,0AP m AC m ⋅=⋅=, 所以10z =,110x y +=,即(1,1,0)m =- 10分 设平面DPC 的法向量是222(,,)n x y z =,则0,0DC n PD n ⋅=⋅= 所以20y =,220x z -=,即(1,0,1)n = 11分11cos ,222m n m n m n⋅<>===⋅⋅,即面角A PC D --的大小为60︒. 12分考点:1线面平行;2线面垂直;3空间向量法解决立体几何问题.7.如图,一简单几何体的一个面ABC 内接于圆O ,,G H 分别是,AE BC 的中点,AB 是圆O 的直径,四边形DCBE 为平行四边形,且DC ⊥平面ABC .试卷第10页,总14页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………(1)求证:GH ∥平面ACD ;(2)若2,1AB BC ==,23tan =∠EAB ,试求该几何体的V. 【答案】(1)证明见解析;(2)1V =. 【解析】试题分析:(1)证明线面垂直需通过证明面面垂直,根据题意,G H 分别是,AE BC 的中点,连接,GO OH ,利用三角形的中位线性质,易证:平面GOH ∥平面ACD ;(2)方法一:将所求几何体分割为两个三棱锥,E ABC E ACD --,同时三棱锥E ABC -的底面积为ABC S ∆,高为EB ,三棱锥E ACD -的底面积为ACD S ∆和高DE ,进而求得两个三棱锥的体积,进而求得所求三棱锥的体积:1V =;方法二:所求体积为四棱锥A BCDE V -,根据题意底面积为矩形BCDE 的面积,高为AC ,利用椎体的体积公式得到所求. 试题解析:(1)证明:连结,GO OH ∵,GO AD OH AC ∥∥.∴GO ∥平面,ACD OH ∥平面ACD ,又GO 交HO 于O ∴平面GOH ∥平面ACD ∴GH ∥平面ACD(2)法一:∵ACD E ABC E V V V --+= ∵2,1AB BC ==∵23tan =∠EAB ∴3,322=-==BC AB AC BE .……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………ACD E ABC E V V V --+=21133213131=⨯⨯⨯⨯=⋅=∆-DE S V ACD ACD E .21313213131=⨯⨯⨯⨯=⋅=∆-EB S V ACB ACB E∴12121=+=+=--ACD E ABC E V V V法二:∵DC ⊥平面ABC ∴DC AC ⊥ 又∵AC BC ⊥ ∴AC ⊥平面BCDE ∵2,1AB BC ==. ∵23tan =∠EAB ∴3,322=-==BC AB AC BE ∴ 13313131=⨯⨯⨯=⋅⋅=-AC S V BCDE BCDE A 矩形 考点:1.直线和平面平行的判定定理;2.椎体的体积.8.(本小题共14分)如图,将矩形ABCD 沿对角线BD 把△ABD 折起,使A 点移到1A 点,且1A 在平面BCD 上的射影O 恰好在CD 上.(1)求证:BC ⊥D A 1;(2)求证:平面CD A 1⊥平面BC A 1;(3)若AB=10,BC=6,求三棱锥BCD A -1的体积. 【答案】(1)、(2)详见解析;(3)48.【解析】试题分析:(1)由题意可知O A 1⊥平面BCD ,所以BC ⊥O A 1,又由已知可知BC CO ⊥,由线面垂直的判定定理可得D A 1⊂平面CD A 1,所以D A BC 1⊥;(2)欲证平面CD A 1⊥平面BC A 1,需证BC A D A 11平面⊥,又因为D A 1⊥B A 1.由(1)知BC ⊥D A 1,所以BC A D A 11平面⊥;(3)转换顶点可得11A BCD D A BC V V --=,代入计算即可. 试题解析:(1)因为1A 在平面BCD 上的射影O 在CD 上,试卷第12页,总14页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………所以O A 1⊥平面BCD. 又BC ⊂平面BCD , 所以BC ⊥O A 1.又BC ⊥CO ,CO O O A =⋂1,⊂CO 平面CD A 1,O A 1⊂平面CD A 1,所以BC ⊥平面CD A 1. 又D A 1⊂平面CD A 1, 所以D A BC 1⊥.(5分) (2)因为矩形ABCD , 所以D A 1⊥B A 1. 由(1)知BC ⊥D A 1.又⊂=⋂BC B B A BC ,1平面BC A B A BC A 111,平面⊂, 所以BC A D A 11平面⊥. 又CD A D A 11平面⊂,所以平面CD A BC A 11平面⊥.(10分) (3)因为BC A D A 11平面⊥, 所以C A D A 11⊥.因为CD=10,61=D A ,所以81=C A . 所以48686213111=⨯⨯⨯⨯==--BC A D BCD A V V .(14分) 考点:空间线线垂直、线面垂直的判定性质,多面体体积.9.如图,四棱柱1111ABCD A B C D -的底面为菱形,AC ,BD 交于点O ,1AO ⊥平面ABCD ,12AA BD ==,22AC =.……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………(1)证明:1AC ⊥平面11BB D D ; (2)求三棱锥1A C CD -的体积. 【答案】(1)见解析;(2)23【解析】试题分析:(1)证明:因为四边形ABCD 为菱形,所以AC ⊥BD ,又因为1AO ⊥平面ABCD ,所以1A O BD ⊥.因为1AC A O O ⋂=,所以BD ⊥平面1A AC ,所以1BD A C ⊥. 2分由已知12AA =,22AC =,又1,AO OC AO AC =⊥,所以112AC A A ==, 所以22211A A A C AC +=,所以11A C A A ⊥,因为11B B A A ∥,所以11A C B B ⊥, 4分 因为1BD B B B ⋂=,所以1AC ⊥平面11BB D D . 6分 (2)连接11A C ,因为11AA CC ∥且11AA CC =,所以四边形11ACC A 是平行四边形, 所以11A C AC ∥, 8分 所以三棱锥1A C CD -的体积111113A C CD C ACD A ACD ACD V V V S AO ---∆===⨯ 10分11112222234123AC BD AO =⋅⋅⋅⋅=⋅⋅⋅=. 12分 考点:本题考查线面垂直的判定,求棱锥的体积点评:解决本题的关键是掌握线面垂直的判定定理,10.(本题满分12分)如图,在四棱锥P ABCD -中,PD ABCD ⊥面,四边形ABCD 为平行四边形,60DAB ∠=︒,24AB PA AD ===,试卷第14页,总14页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………(1)若E 为PC 中点,求证:PA ∥平面BDE (2)求三棱锥D BCP -的体积 【答案】(1)见解析;(2)4 【解析】 试题分析:(1)连结AC 交BD 于点O ,连结OE , ∵ABCD 为平行四边形,∴O 是AC 的中点, 又∵E 是PC 的中点, ∴OE ∥PA又PA ⊄平面BDE,OE ⊂平面BDE ∴PA ∥平面BDE (2)13D PBC P DBC DBC V V S PD --∆==⋅ 又22124sin 6023,232DBC S PD PA AD ∆=⨯⨯==-= ,所以4D PBC V -= 考点:本题考查线面平行的判定,求棱锥的体积点评:解决本题的关键是在平面BDE 中找出与PA 平行的线。
2015年全国卷文数(新课标1)立体几何

2015年全国卷文数(新课标1)立体几何6.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺问:积及为米几何?”其意思为:“在屋内墙角处堆放米如图,米堆为一个圆锥的四分之一,米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为立方尺,圆周率约为3,估算出堆放的米约有( )A. 14斛B. 22斛C. 36斛D. 66斛【答案】B【解析】解:设圆锥的底面半径为r,则,解得,故米堆的体积为,斛米的体积约为立方,,故选:B.根据圆锥的体积公式计算出对应的体积即可.本题主要考查椎体的体积的计算,比较基础.11.圆柱被一个平面截去一部分后与半球半径为组成一个几何体,该几何体三视图中的正视图和俯视图如图所示若该几何体的表面积为,则A. 1B. 2C. 4D. 8【答案】B【解析】解:由几何体三视图中的正视图和俯视图可知,截圆柱的平面过圆柱的轴线,该几何体是一个半球拼接半个圆柱,其表面积为:,又该几何体的表面积为,,解得,故选:B.通过三视图可知该几何体是一个半球拼接半个圆柱,计算即可.本题考查由三视图求表面积问题,考查空间想象能力,注意解题方法的积累,属于中档题.18.如图,四边形ABCD为菱形,G为AC与BD的交点,平面ABCD.Ⅰ证明:平面平面BED;Ⅱ若,,三棱锥的体积为,求该三棱锥的侧面积.【答案】证明:Ⅰ四边形ABCD为菱形,,平面ABCD,,则平面BED,平面AEC,平面平面BED;解:Ⅱ设,在菱形ABCD中,由,得,,平面ABCD,,则为直角三角形,,则,三棱锥的体积,解得,即,,,即,在三个直角三角形EBA,EBG,EBC中,斜边,,为等腰三角形,则,即,,则,从而得,的面积,在等腰三角形EAD中,过E作于F,则,,则,的面积和的面积均为,故该三棱锥的侧面积为.【解析】Ⅰ根据面面垂直的判定定理即可证明:平面平面BED;Ⅱ根据三棱锥的条件公式,进行计算即可.本题主要考查面面垂直的判定,以及三棱锥体积的计算,要求熟练掌握相应的判定定理以及体积公式.。
2015年文数高考真题全国Ⅱ卷
2015年文数高考真题全国Ⅱ卷答案组题人:李明辉1.已知集合{}{}|12,|03,A x x B x x =-<<=<<则A B =U ( ) A .()1,3- B .()1,0-C .()0,2D .()2,32.若为a 实数,且2i3i 1ia +=++,则a =( ) A .4-B .3-C .3D .43.根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图.以下结论不正确的是( )A .逐年比较,2008年减少二氧化硫排放量的效果最显著B .2007年我国治理二氧化硫排放显现C .2006年以来我国二氧化硫年排放量呈减少趋势D .2006年以来我国二氧化硫年排放量与年份正相关 4.已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a ( ) A .1-B .0C .1D .25.设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S = A .5B .7C .9D .116.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A .18B .17C .16D .157.已知三点A (1,0),B (0,√3 ),C (2,√3),则△ABC 外接圆的圆心到原点的距离为( ) A .53 B .√213 C .2√53 D .438.下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a 为( )A.0B.2C.4D.149.已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =( ) A .2 B .1 C .12D .1810.已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为( )A .36πB .64πC .144πD .256π11.如图,长方形的边AB=2,BC=1,O 是AB 的中点,点P 沿着边BC,CD 与DA 运动,记BOP x ∠=,将动点P 到A,B 两点距离之和表示为x 的函数()f x ,则函数的图像大致为( )A .B .C .D .12.设函数()()21ln 11f x x x=+-+,则使()()21f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭B .()1,1,3⎛⎫-∞⋃+∞ ⎪⎝⎭C .11,33⎛⎫- ⎪⎝⎭D .11,,33⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭13.已知函数()32f x ax x =-的图像过点(-1,4),则a= .14.若x,y 满足约束条件,则z=2x+y 的最大值为 .15.已知双曲线过点,且渐近线方程为12y x =±,则该双曲线的标准方程为____________________.16.已知曲线ln y x x =+在点()1,1处的切线与曲线()221y ax a x =+++相切,则a= .17.(本小题满分12分)△ABC 中D 是BC 上的点,AD 平分∠BAC,BD=2DC . (Ⅰ)求sin sin BC∠∠;(Ⅱ)若60BAC ∠=o ,求B ∠.18.某公司为了了解用户对其产品的满意度,从A,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表. A 地区用户满意度评分的频率分布直方图B 地区用户满意度评分的频率分布表(Ⅰ)在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可) B 地区用户满意度评分的频率分布直方图(Ⅱ)根据用户满意度评分,将用户的满意度评分分为三个等级:估计哪个地区的用户的满意度等级为不满意的概率大,说明理由.19.如图,长方体1111ABCD A B C D -中,116,10,8AB BC AA===,点,E F 分别在1111,A B D C 上,114A E D F ==,过点,E F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由); (2)求平面α把该长方体分成的两部分体积的比值.20.已知椭圆2222:1(0)x y C a b a b+=>>的离心率为2,点在C 上(1)求C 的方程(2)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点,A B ,线段AB 的中点为M .证明:直线OM 的斜率与直线l 的斜率的乘积为定值. 21.已知()()ln 1f x x a x =+-.(1)讨论()f x 的单调性;(2)当()f x 有最大值,且最大值大于22a -时,求a 的取值范围. 22.(本小题满分10分)选修4-1:几何证明选讲如图O 是等腰三角形ABC 内一点,圆O 与△ABC 的底边BC 交于M,N 两点,与底边上的高交于点G,且与AB,AC 分别相切于E,F 两点.(Ⅰ)证明;(Ⅱ)若AG 等于圆O 半径,且,求四边形EBCF 的面积.23.选修4-4:坐标系与参数方程 在直角坐标系xOy 中,曲线1cos ,:{sin ,x t C y t αα==(t 为参数,且0t ≠),其中0απ≤<,在以O为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ== (Ⅰ)求2C 与3C 交点的直角坐标;(Ⅱ)若1C 与2C 相交于点A,1C 与3C 相交于点B,求AB 最大值. 24.选修4-5不等式选讲设a b c d ,,,均为正数,且a b c d +=+,证明:(Ⅰ)若ab cd >>;(Ⅱ+>a b c d -<-的充要条件.答案第1页,总1页。
2015新课标全国卷ⅱ(文数)

2015新课标全国卷Ⅱ(文数)1.(2015高考新课标全国卷Ⅱ,文1)已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B等于( A )(A)(-1,3) (B)(-1,0) (C)(0,2) (D)(2,3)解析:集合A=(-1,2),B=(0,3),所以A∪B=(-1,3).2.(2015高考新课标全国卷Ⅱ,文2)若a为实数,且=3+i,则a等于( D )(A)-4 (B)-3 (C)3 (D)4解析:因为=3+i,所以2+ai=(3+i)(1+i)=2+4i,又a∈R,所以a=4.3.(2015高考新课标全国卷Ⅱ,文3)根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( D )(A)逐年比较,2008年减少二氧化硫排放量的效果最显著(B)2007年我国治理二氧化硫排放显现成效(C)2006年以来我国二氧化硫年排放量呈减少趋势(D)2006年以来我国二氧化硫年排放量与年份正相关解析:结合图形可知,2007年与2008年二氧化硫的排放量差距明显,显然2008年减少二氧化硫排放量的效果最显著;2006年二氧化硫的排放量最高,从2006年开始二氧化硫的排放量开始整体呈下降趋势.显然A,B,C正确,不正确的是D,不是正相关.4.(2015高考新课标全国卷Ⅱ,文4)向量a=(1,-1),b=(-1,2),则(2a+b)·a等于( C )(A)-1 (B)0 (C)1 (D)2解析:a=(1,-1),b=(-1,2),所以(2a+b)·a=(1,0)·(1,-1)=1.5.(2015高考新课标全国卷Ⅱ,文5)设S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5等于( A )(A)5 (B)7 (C)9 (D)11解析:数列{a n}为等差数列,设公差为d,所以a1+a3+a5=3a1+6d=3,所以a1+2d=1,所以S5=5a1+×d=5(a1+2d)=5.6.(2015高考新课标全国卷Ⅱ,文6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( D )(A) (B) (C) (D)解析:由三视图可知,该几何体是一个正方体截去了一个三棱锥,即截去了正方体的一个角.设正方体的棱长为1,则正方体的体积为1,截去的三棱锥的体积为V1=××1×1×1=,故剩余部分的体积为V2=,所求比值为=.7.(2015高考新课标全国卷Ⅱ,文7)已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为( B )(A) (B)(C)(D)解析:设圆的一般方程为x2+y2+Dx+Ey+F=0,所以所以所以△ABC外接圆的圆心为1,,故△ABC外接圆的圆心到原点的距离为=.8.(2015高考新课标全国卷Ⅱ,文8)如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a等于( B )(A)0 (B)2 (C)4 (D)14解析:由题知,a=14,b=18;a=14,b=4;a=10,b=4;a=6,b=4;a=2,b=4;a=2,b=2.所以输出a=2.9.(2015高考新课标全国卷Ⅱ,文9)已知等比数列{a n}满足a1=,a3a5=4(a4-1),则a2等于( C )(A)2 (B)1 (C) (D)解析:设等比数列{a n}的公比为q,a1=,a3a5=4(a4-1),由题可知q≠1,则a1q2×a1q4=4(a1q3-1),所以×q6=4×q3-1,所以q6-16q3+64=0,所以(q3-8)2=0,所以q3=8,所以q=2,所以a2=,故选C.10.(2015高考新课标全国卷Ⅱ,文10)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥OABC体积的最大值为36,则球O的表面积为( C )(A)36π(B)64π(C)144π(D)256π解析:由题意知当三棱锥的三条侧棱两两垂直时,其体积最大.设球的半径为r,则×r2·r=36,解得r=6,所以球O的表面积S=4πr2=144π,选C.11.(2015高考新课标全国卷Ⅱ,文11)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点.点P沿着边BC,CD 与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( B )(A) (B)(C) (D)解析:法一当点P位于边BC上时,∠BOP=x,0≤x≤,则=tan x,所以BP=tan x,所以AP=,所以f(x)=tan x+0≤x≤,可见y=f(x)图象的变化不可能是一条直线或线段,排除A,C.当点P位于边CD上时,∠BOP=x,≤x≤,则BP+AP=+=+.当点P位于边AD上时,∠BOP=x,≤x≤π,则=tan(π-x)=-tan x,所以AP=-tan x,所以BP=,所以f(x)=-tan x+≤x≤π,根据函数的解析式可排除D,故选B.法二当点P位于点C时,x=,此时AP+BP=AC+BC=1+,当点P位于CD的中点时,x=,此时AP+BP=2<1+,故可排除C,D,当点P位于点D时x=,此时AP+BP=AD+BD=1+,而在变化过程中不可能以直线的形式变化,故选 B.12.(2015高考新课标全国卷Ⅱ,文12)设函数f(x)=ln(1+|x|)-,则使得f(x)>f(2x-1)成立的x的取值围是( A )(A),1(B)-∞,∪(1,+∞)(C)-,(D)-∞,-∪,+∞解析:函数f(x)=ln(1+|x|)-,所以f(-x)=f(x),故f(x)为偶函数,又当x∈(0,+∞)时,f(x)=ln(1+x)-,f(x)是单调递增的,故f(x)>f(2x-1)?f(|x|)>f(|2x-1|),所以|x|>|2x-1|,解得<x<1,故选 A.13.(2015高考新课标全国卷Ⅱ,文13)已知函数f(x)=ax3-2x的图象过点(-1,4),则a= .解析:由题意可知(-1,4)在函数图象上,即4=-a+2,所以a=-2.答案:-214.(2015高考新课标全国卷Ⅱ,文14)若x,y满足约束条件则z=2x+y的最大值为.解析:作出可行域如图中阴影部分所示.在可行域,斜率为-2的直线经过点C时,z=2x+y取得最大值,此时由解得所以C(3,2),所以z max=8.答案:815.(2015高考新课标全国卷Ⅱ,文15)已知双曲线过点(4,),且渐近线方程为y=±x,则该双曲线的标准方程为.解析:因为双曲线的渐近线方程为y=±x,故可设双曲线为-y2=λ(λ>0),又双曲线过点(4,),所以-()2=λ,所以λ=1,故双曲线方程为-y2=1.答案:-y2=116.(2015高考新课标全国卷Ⅱ,文16)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a= .解析:法一因为y'=1+,所以y'|x=1=2,所以y=x+ln x在点(1,1)处的切线方程为y-1=2(x-1),所以y=2x-1.又切线与曲线y=ax2+(a+2)x+1相切,当a=0时,y=2x+1与y=2x-1平行,故a≠0,由得ax2+ax+2=0,因为Δ=a2-8a=0,所以a=8.法二因为y'=1+,所以y'|x=1=2,所以y=x+ln x在点(1,1)处的切线方程为y-1=2(x-1),所以y=2x-1,又切线与曲线y=ax2+(a+2)x+1相切,当a=0时,y=2x+1与y=2x-1平行,故a≠0.因为y'=2ax+(a+2),所以令2ax+a+2=2,得x=-,代入y=2x-1,得y=-2,所以点-,-2在y=ax2+(a+2)x+1的图象上,故-2=a×-2+(a+2)×-+1,所以a=8.答案:817.(本小题满分12分)(2015高考新课标全国卷Ⅱ,文17)△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC.(1)求;(2)若∠BAC=60°,求∠B.解:(1)由正弦定理得,=,=.因为AD平分∠BAC,BD=2DC,所以==.(2)因为∠C=180°-(∠BAC+∠B),∠BAC=60°,所以sin∠C=sin(∠BAC+∠B)=cos∠B+sin∠B.由(1)知2sin∠B=sin∠C,所以tan∠B=,即∠B=30°.18.(本小题满分12分)(2015高考新课标全国卷Ⅱ,文18)某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表.A地区用户满意度评分的频率分布直方图B地区用户满意度评分的频数分布表满意度评分分组[50,60)[60,70)[70,80)[80,90)[90,100]频数2814106(1)作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);B地区用户满意度评分的频率分布直方图(2)根据用户满意度评分,将用户的满意度分为三个等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大?说明理由.解:(1)通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值;B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散.(2)A地区用户的满意度等级为不满意的概率大.记C A表示事件:“A地区用户的满意度等级为不满意”;C B表示事件:“B地区用户的满意度等级为不满意”.由直方图得P(C A)的估计值为(0.01+0.02+0.03)×10=0.6,P(C B)的估计值为(0.005+0.02)×10=0.25.所以A地区用户的满意度等级为不满意的概率大.19.(本小题满分12分)(2015高考新课标全国卷Ⅱ,文19)如图,长方体ABCDA1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求平面α把该长方体分成的两部分体积的比值.解:(1)交线围成的正方形EHGF如图所示.(2)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为EHGF为正方形,所以EH=EF=BC=10.于是MH==6,AH=10,HB=6.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为10×∶10×=10×∶10×=也正确.20.(本小题满分12分)(2015高考新课标全国卷Ⅱ,文20)已知椭圆C:+=1(a>b>0)的离心率为,点(2,)在C上.(1)求C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与直线l的斜率的乘积为定值.(1)解:由解得a2=8,b2=4,故椭圆C的方程为+=1.(2)证明:由题设直线l:y=kx+m(k≠0,m≠0),A(x1,y1),B(x2,y2),联立得(1+2k2)x2+4kmx+2m2-8=0,x1+x2=-,x1x2=,y1+y2=k(x1+x2)+2m=,得AB中点M-,,则直线OM与直线l斜率乘积为·k=-·k=-,即定值.21.(本小题满分12分)(2015高考新课标全国卷Ⅱ,文21)已知函数f(x)=ln x+a(1-x).(1)讨论f(x)的单调性;(2)当f(x)有最大值,且最大值大于2a-2时,求a的取值围.解:(1)f(x)的定义域为(0,+∞),f'(x)=-a.若a≤0,则f'(x)>0,所以f(x)在(0,+∞)单调递增.若a>0,则当x∈0,时,f'(x)>0;当x∈,+∞时,f'(x)<0.所以f(x)在0,上单调递增,在,+∞上单调递减.(2)由(1)知,当a≤0时,f(x)在(0,+∞)无最大值;当a>0时,f(x)在x=处取得最大值,最大值为f=ln+a1-=-ln a+a-1.因此f>2a-2等价于ln a+a-1<0.令g(a)=ln a+a-1,则g(a)在(0,+∞)上单调递增,g(1)=0.于是,当0<a<1时,g(a)<0;当a>1时,g(a)>0.因此,a的取值围是(0,1).22.(本小题满分10分)选修4-1:几何证明选讲(2015高考新课标全国卷Ⅱ,文22)如图,O为等腰三角形ABC一点,☉O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于☉O的半径,且AE=MN=2,求四边形EBCF的面积.(1)证明:由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.又因为☉O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF.从而EF∥BC.(2)解:由(1)知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为☉O的弦,所以O在AD上.连接OE,OM,则OE⊥AE.由AG等于☉O的半径得AO=2OE,所以∠OAE=30°.因此△ABC和△AEF都是等边三角形.因为AE=2,所以AO=4,OE=2.因为OM=OE=2,DM=MN=,所以OD=1.于是AD=5,AB=.所以四边形EBCF的面积为×2×-×(2)2×=.23.(本小题满分10分)选修4-4:坐标系与参数方程(2015高考新课标全国卷Ⅱ,文23)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2cos θ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.解:(1)曲线C2的直角坐标方程x2+y2-2y=0,曲线C3的直角坐标方程为x2+y2-2x=0.联立解得或所以C2与C3交点的直角坐标为(0,0)和,.(2)曲线C1的极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤α<π.因此A的极坐标为(2sin α,α),B的极坐标为(2cos α,α).所以|AB|=|2sin α-2cos α|=4sinα-.当α=时,|AB|取得最大值,最大值为 4.24.(本小题满分10分)选修4-5:不等式选讲(2015高考新课标全国卷Ⅱ,文24)设a,b,c,d均为正数,且a+b=c+d.证明:(1)若ab>cd,则+>+;(2)+>+是|a-b|<|c-d|的充要条件.证明:(1)因为(+)2=a+b+2,(+)2=c+d+2,由题设a+b=c+d,ab>cd得(+)2>(+)2.又a,b,c,d均为正数,所以+>+.(2)①若|a-b|<|c-d|,则(a-b)2<(c-d)2,即(a+b)2-4ab<(c+d)2-4cd.因为a+b=c+d,所以ab>cd.由(1)得+>+.②若+>+,则(+)2>(+)2,即a+b+2>c+d+2.因为a+b=c+d,所以ab>cd.于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.因此|a-b|<|c-d|.综上,+>+是|a-b|<|c-d|的充要条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015全国文科数学立体几何高考试题—学生专用(2)
1、[2015·安徽卷]一个空间几何体的三视图如图所示,则该几何体的表面积为()
A.48 B.32+817 C.48+817 D.80
2、[2015·北京卷] 某四棱锥的三视图如图1-1所示,该四棱锥的表面积是()
A.32 B.16+16 2 C.48 D.16+32 2
3、[2015·广东卷] 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体体积为()
A.4 3 B.4 C.2 3 D.2
4、[2015·湖南卷] 设图是某几何体的三视图,则该几何体的体积为()
A .9π+42
B .36π+18
C.9
2
π+12
D.9
2
π+18 5、[2015·辽宁卷] 一个正三棱柱的侧棱长和底面边长相等,体积为23,它的三视图中的俯视图如图1-3所示,左视图是一个矩形,则这个矩形的面积是( )
A .4
B .2 3
C .2
D. 3
6、 [2015·课标全国卷] 在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )
7、[2015·陕西卷] 某几何体的三视图如图所示,则它的体积为( )
A .8-2π3
B .8-π
3
C .8-2π
D.2π3
8、[2015·天津卷] 一个几何体的三视图如图所示(单位:m),则该几何体的体积为________ m 3.
9、[2015·浙江卷] 若某几何体的三视图如图所示,则这个几何体的直观图可以是()
10、[2015·福建卷] 如图1-3,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于________.
11、[2015·浙江卷] 若直线l不平行于平面α,且l⊄α,则()
A.α内的所有直线与l异面B.α内不存在与l平行的直线
C.α内存在唯一的直线与l平行D.α内的直线与l都相交
12、[2015·广东卷] 正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数共有()
A.20 B.15 C.12 D.10
13、[2015·四川卷]l1,l2,l3是空间三条不同的直线,则下列命题正确的是()
A.l1⊥l2,l2⊥l3⇒l1∥l3B.l1⊥l2,l2∥l3⇒l1⊥l3
C.l1∥l2∥l3⇒l1,l2,l3共面D.l1,l2,l3共点⇒l1,l2,l3共面
14、 [2015·湖北卷] 设球的体积为V 1,它的内接正方体的体积为V 2,下列说法中最合适的是( ) A .V 1比V 2大约多一半B .V 1比V 2大约多两倍半 C .V 1比V 2大约多一倍D .V 1比V 2大约多一倍半
15、 [2015·辽宁卷] 已知球的直径SC =4,A 、B 是该球球面上的两点,AB =2,∠ASC =∠BSC =45°,则
棱锥S -ABC 的体积为( )
A.33
B.233
C.433
D.53
3
第15题 第16题
16、 [2015·课标全国卷] 已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一个球面上,若圆锥底面面积是这个球面面积的3
16,则这两个圆锥中,体积较小者的高与体积较大者的高的比值为
________.
17、[2015·全国卷] 已知正方体ABCD -A 1B 1C 1D 1中,E 为C 1D 1的中点,则异面直线AE 与BC 所成角的余弦值为________.
18、[2015·安徽卷]如图,ABEDFC 为多面体,平面ABED 与平面ACFD 垂直,点O 在线段AD 上,OA =1,OD =2,△OAB ,△OAC ,△ODE ,△ODF 都是正三角形.
(1)证明直线BC ∥EF ; (2)求棱锥F -OBED 的体积.
19、[2015·北京卷] 如图,在四面体P ABC中,PC⊥AB,P A⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.
(1)求证:DE∥平面BCP;
(2)求证:四边形DEFG为矩形;
(3)是否存在点Q,到四面体P ABC六条棱的中点的距离相等?说明理由.
20、[2015·江苏卷] 如图在四棱锥P-ABCD中,平面P AD⊥平面ABCD,AB=AD,∠BAD=60°,E、F 分别是AP、AD的中点.
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面P AD.
21、[2015·课标全国卷] 如图1-8,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1)证明:P A⊥BD;
(2)设PD=AD=1,求棱锥D-PBC的高.
22、[2015·陕西卷] 如图在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°.
(1)证明:平面ADB⊥平面BDC;
(2)若BD=1,求三棱锥D-ABC的表面积.
23、[2015·江苏卷] 如图1-2,在四棱锥P -ABCD 中,平面P AD ⊥平面ABCD ,AB =AD ,∠BAD =60°,E 、F 分别是AP 、AD 的中点.
求证:(1)直线EF ∥平面PCD ; (2)平面BEF ⊥平面P AD .
24、 [2015·辽宁卷] 如图1-8,四边形ABCD 为正方形, QA ⊥平面ABCD ,PD ∥QA ,QA =AB =1
2PD .
(1)证明:PQ ⊥平面DCQ ;
(2)求棱锥Q -ABCD 的体积与棱锥P -DCQ 的体积的比值.
25、[2015·湖南卷] 如图1-5,在圆锥PO中,已知PO=2,⊙O的直径AB=2,点C在AB上,且∠CAB=30°,D为AC的中点.
(1)证明:AC⊥平面POD;
(2)求直线OC和平面P AC所成角的正弦值.
26、[2015·福建卷] 如图四棱锥P-ABCD中,P A⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
(1)求证:CE⊥平面P AD;
(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.
27、[2015·江西卷] 如图1-7,在△ABC 中,∠B =π
2,AB =BC =2,P 为AB 边上一动点,PD ∥BC 交AC
于点D ,现将△PDA 沿PD 翻折至△PDA ′,使平面PDA ′⊥平面PBCD .
(1)当棱锥A ′-PBCD 的体积最大时,求P A 的长;
(2)若点P 为AB 的中点,E 为A ′C 的中点,求证:A ′B ⊥DE .
28、 [2015·山东卷]如图在四棱台ABCD -A 1B 1C 1D 1中,D 1D ⊥平面ABCD ,底面ABCD 是平行四边形,AB =2AD ,AD =A 1B 1,∠BAD =60°.
(1)证明:AA 1⊥BD ; (2)证明:CC 1∥平面A 1BD .
29、[2015·四川卷] 如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连结AP交棱CC1于点D.
(1)求证:PB1∥平面BDA1;
(2)求二面角A-A1D-B的平面角的余弦值.
30、[2015·天津卷] 如图在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,
O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.
(1)证明PB∥平面ACM;
(2)证明AD⊥平面P AC;
(3)求直线AM与平面ABCD所成角的正切值.。
