【计算机应用】_mathematica_期刊发文热词逐年推荐_20140726
数学软件Mathematica简介

图形渲染
Mathematica可以生成高质量的图形和动画,用于工程 设计的可视化展示。这有助于工程师更好地理解设计原 理和性能特点,提高设计效率。
数据科学中的应用
数据挖掘
Mathematica提供了强大的数据分析和挖 掘工具,可以帮助数据科学家从大量数据中 提取有价值的信息。例如,聚类分析、关联 规则挖掘等。
提供交互式编程环境, 方便用户进行编程和调 试。
Mathematica的起源与发展
起源
Mathematica最初由美国数学家 Stephen Wolfram于1988年开发, 旨在提供一个强大的数学工具包,以 简化复杂的数学计算和可视化。
发展
经过多年的不断更新和完善, Mathematica已经成为一款功能强大 、易用性强的数学软件,广泛应用于 科研、教育、工程等领域。
支持多种类型的2D和3D图形,如散点图、 线图、曲面图、等高线图等。
数据可视化工具
提供丰富的数据可视化工具,如直方图、饼 图、热力图等。
可视化动画
可以创建动态的视觉效果和动画,以更好地 展示数据和过程。
可视化交互
用户可以通过交互式界面与图形进行交互, 以获取更多信息。
编程语言的高级特性
函数式编程
Mathematica采用函数式编程语言,支持高阶函数、匿名函数等特性。
数和微分方程求解方面更优秀。
与MATLAB的比较
MATLAB主要面向工程和科学计算,特别适合矩阵计算和数值分析。Mathematica在 符号计算、公式推导和数据可视化方面更胜一筹,而MATLAB在实时控制系统设计和信
号处理方面更具优势。
与其他编程语言的比较
要点一
与Python的比较
Python是一种通用的高级编程语言,广泛用于数据科学、 机器学习和Web开发等领域。Mathematica在数学计算和 符号推导方面更强大,而Python在灵活性和开放性方面更 优秀,两者在某些领域可以相互补充。
数学运算软件Mathematica

第一章 绪论随着电子计算机的普及,数学软件也相继发展,选择一个合适的数学软件,以辅助庞大的数学运算也变得日益重要。
被美国Macworld 杂志誉为“不只是一套软件,更是一次划时代的革命”的Mathematica ,将改变我们对数学学习的感受,对日后数学及其它学科和工程计算的发展也将有深远的影响。
对Mathematica 而言,它不仅可以轻松地应付数值计算的任务,而且还能进行符号式的运算与有关图形的绘制。
除了一般的计算之外,Mathematica 还能做微分、积分、包括微分方程在内的方程和方程组的求解、数学式的化简和展开、因式分解、数据分析等等,从前被人们认为极为困难的数学问题都能在Mathematica 的辅助之下轻易解决。
国际上众多大学、研究所早已有计划地全面推广Mathematica 教学,国内也有多家大学做了这方面的尝试,将Mathematica 的学习加入到高等数学的学习中。
Mathematica 的独特功能和相对于Matlab 等软件较小的内存占用空间,使其在数学软件领域有很强的竞争力。
本讲义是基于Mathematica4.1版写成的,在各章节中均有相应的例题,供读者练习。
Mathematica 涉及的数学领域很多,本书的编写是为已经学习了高等数学和数值分析课程的非数学和计算机专业的研究生提供一本入门的教材。
因此,如果将来工作需要,同学们可以选读其它介绍更详细的书籍。
§1.1 数值计算与符号计算计算机的诞生源于数值计算,“计算(Calculation )”一词在过去仅仅是数值计算的意思。
现在的计算机除了传统的数值计算外,还可以进行数学符号的演算,Mathematica 的运算类型就包含了这两类计算,即数值计算(numerical calculation )和符号计算(symbolic calculation )。
如果计算过程和计算结果不包含任何未知数(代数),而是以具体的数值形式进行的,则称这一计算为数值计算,反之,如果运算过程中包含有代数的运算,则为符号计算。
mathematica软件简介

数据清洗
02
03
数据统计和分析
Mathematica可以方便地导入和 导出各种数据格式,如CSV、 Excel、数据库等。
Mathematica可以进行数据清洗 ,包括缺失值处理、异常值处理 等。
Mathematica可以进行各种数据 统计和分析,如描述性统计、回 归分析、聚类分析等。
图形和可视化
丰富的可视化功能
Mathematica软件具有丰富的可视化功能,可以生成各 种类型的图表和图形,包括二维和三维图形、动画、图像 处理等。
灵活的编程环境
Mathematica软件提供了一个灵活的编程环境,用户可 以使用Mathematica的编程语言(Wolfram Language )编写自定义函数和程序,扩展软件的功能。
THANK YOU
01
Mathematica可以进行各种代数运算,包括多项式
运算、矩阵运算、微积分运算等。
符号求解方程
02 Mathematica可以求解各种符号方程,如线性方程
、非线性方程、微分方程等。
符号化简
03
Mathematica可以将复杂的数学表达式进行符号化
简,得到最简形式。
数据处理和分析
01
数据导入导出
02
mathematica的基本操作
mathematica的基本操作
• Mathematica是一款由Wolfram Research公司开发的数学软 件,它以符号计算为核心,广泛用于科学计算、数值计算、数 学建模、数据分析和可视化等领域。
03
mathematica的功能介绍
符号计算
代数运算
mathematica的主要特点和优势
符号计算
mathematica简介

求函数 f 对自变量 x1,x2,混合偏导数 求函数 f 对自变量 x1,x2,的 n1,n2,阶混合偏导数
求导数(偏导数)
D[f , var]
D[f , x1, x2 ,]
D[f , {x1,n1},{ x2 ,n2},]
NUDT
Mathematica软件简介
NUDT
Mathematica软件简介
1
0.5
t1 -0.5
t3 1
t2
2
3
-1
NUDT
Mathematica软件简介
可选参数 PlotStyle(曲线的线型、颜色) PlotPoints(规定作图时取的最小点数)
GridLines(用于加网格线,可以在指定位置或默认)
Background(用于指定背景颜色,或灰度GreyLevel)
NUDT
Mathematica软件简介
表的操作 Join[ t1 , t2] Union[ t1 , t2] 将表 t1 和表 t2连接成一个表 将表 t1 和表 t2 的并集组成一个表
某些特殊属性表的建立 Table[ f , {i,imin , imax , stepi} , { j , jmin , jmax , stepj}]
绘制f(x)在区间[a, b]范围的图形
Plot[{f1(x), f2(x),}, {x, a, b}] 绘制多个函数图形 可选参数 PlotRange(绘图范围)、AspectRatio(高宽比)、
Axes(坐标)、AxesLabel(坐标名称)、
Ticks(坐标刻度标记)、AxesStyle(坐标轴颜色、线宽)
解方程(组) Solve[ eqns , vars ] 对系数按常规约定求解出方程(组)
Mathematica

expr/.x->value将 expr里所有的x均代换成value expr/.{x->value1,y->value2,…}执行数个不同变数的代换 expr/.{{x->value1},{x->value2},…}将 expr代入不同的x值 expr//.{x->value1,y->value2,…}重复代换到 expr不再改变为止
Collect[expr,x]将 expr表示成x的多项式, 如 Collect[expr,{x,y,…}]将 expr分别表示成 x,y,…的多项式 FactorTerms[expr]将 expr的数值因子提出, 如 4x+2=2(2x+1) FactorTerms[expr,x]将 expr中把所有不包含x项的因子提出 FactorTerms[expr,{x,y,…}]将 expr中把所有不包含{x,y,...}项的因子提出
D[f,x]函数f对x作微分 D[f,x1,x2,…]函数f对x1,x2,…作微分 D[f,{x,n}]函数f对x微分n次 D[f,x,NonConstants->{y,z,…}]函数f对x作微分,将y,z,…视为x的函数
Dt[f]全微分df Dt[f,x]全微分 Dt[f,x1,x2,…]全微分 Dt[f,x,Constants->{c1,c2,…}]全微分,视c1,c2,…为常数
高性能计算
Mathematica系统已经支持高性能计算。在Mathematica 5.2版本中,它已经支持自动多线程计算。在2002 年,gridMathematica的引入使得用户级的并行编程可以在不同的集群和多处理器系统中进行。在2008年,在所 有的Mathematica许可证中囊括了并行计算技术,包括支持网格技术如Windows HPC Server 2008、Microsoft Compute Cluster Server和Sun Grid。2010年,Mathematica增加了对CUDA和OpenCLGPU硬件的支持。另外, 第8版还可以生成C代码,它可以自动由系统C编译器进行编译,比如Intel C++编译器或者Visual Studio 2010 编译器。
Mathematica

四、 Mathematica4.0的球面距离功能 首先进入子程序软件包,运行命令: <<Miscellaneous`Geodesy`,然后运行其他与 之有关的命令与功能。 例6:求美国纽约到北京的球面最短距离 SphericalDistance[{40,-74},{39,116}] 求美国纽约到北京的椭球面最短距离 SpheroidalDistance[{40,-74},{39,116}]
二、平面函数作图
例10:在区间[0,2Pi]中画sinx的图像。 Plot[Sin[x],{x,0,2Pi}] 为图像加上背景颜色: Plot[Sin[x],{x,0,2Pi}, Background RGBColor[0,1,1]] 例11:在区间[-10,10]中画x^3的图像。 Plot[x^3,{x,-10,10}]
(4)若在Mathematica4.0的程序后面打分号“;“, 则机器正常运算,但不显示运算结果。 (5)若在Mathematica4.0的程序的最后面加 //Timing,则机器不但显示运算结果,而且显示 运算时间。 (6)若多次调用同一个字母,例如x,最好在调用 后使用清空命令 Clear[x]. (7)依次点击File,Palettes,BasicInput就可以出 现一个基本输入模板,将会大大方便使用者输入 数字符号和公式。 (8)进入子程序软件包的格式:例如,进入 Graphics子程序软件包的命令如下: <<Graphics`Graphics`.
动画功能
第一步,进入子程序包: <<Graphics`Animation` 第二步,制作动画,大只有三种情况: (1)围绕曲面的一个轴旋转一个曲面; (2)制作单一图像的动画,在作图的过程中, 添加一个控制变量,由控制变量的变化得 到一系列图像,然后将这些图像像放电影 一样连续显示,得到的效果就是动画; (3)制作多个图像的动画,将程序模块化。
《数学软件Mathematica应用浅谈》

数学软件Mathematica应用浅谈摘要我们在科学、工程和数学问题中常常会遇到求解类似方程f x 的情况。
高等数学中的许多重要方法,如求极限、导数和积()0分等,只靠笔算去实现是相当困难的,然而在实际的应用过程中,我们往往只关心这些问题的实际结果。
同时线性规划问题在生产和生活中都起到了重大作用,因此线性规划的求解方法也成为了一个备受关注的话题。
面对这种种不宜笔算的难题,我们需要一个强大的数学工具帮助我们解决这些问题。
针对于上述亟待解决的问题,数学软件Mathematica正是求解这些问题的一个实用系统也就是所谓的数学实验。
在该论文中我们将具体介绍两种利用Mathematica求解方程近似根的方法,分别为“利用牛顿法求解方程的根”和“利用对分区间法求解方程的根”。
另外,Mathematica有很强的图形功能,它对微积分中的问题,可以给出精彩的几何解释。
当然还能利用Mathematica来求解线性规划问题。
Mathematica的各项应用无论是在科学研究还是在生产实践中都有着举足轻重的地位。
关键词:Mathematica;求解方程近似根;微积分;线性规划BRIEF DISCUSSION ON THE APPLICATION OFMATHEMATICAL SOFTWAREMATHEMATICAABSTRACTIn science, engineering and mathematical problems often encountered in solving a similar equation . Higher mathematics in many important ways, such as seeking to limit, d erivative and integral, it is very difficult to rely on written calculation to achieve,in the actual application process, however, we tend to only care about the actual results of these methods. Linear programming problem in the production and living played a major role in the method of linear programming has also become a topic of concern. Faced with all these should not be written calculation problems,we need a powerful mathematical tool to help us solve these difficulties. For these problems to be solved mathematical software Matllematica, precisely to solve these problems of a practical system is the so-called mathematical experiment.In this paper we will specifically introduce two Mathematica solving equations approximate root, respectively, using Newton's law and equation root "and use the partition method and the root of the equation". Of Mathematica have strong graphics capabilities of the problems in the calculus can be given a wonderful geometric interpretation. Of course also use Mathematica to solve linear programming problems. The application of Mathematica have a pivotal position in the practice of scientific research is still in production.KEY WORDS:Mathematica , Approx imately solving equation root, Calculus , The Linear Programming目录第一章数学软件Mathematica简介 (1)(一)Mathematica简介 (1)(二)Mathematica的影响 (1)第二章利用Mathematica求解方程的近似根 (3)(一)利用牛顿法求解方程的根 (3)(二)利用对分区间法求方程的根 (5)第三章用数学软件Mathematica求解微积分 (8)(一)运用Mathematica求解运动学问题1 (8)(二)运用Mathematica求解运动学问题2 (10)第四章线性规划模型的建立及Mathematica求解 (13)(一)Mathematica在求解不等式约束问题的应用举例 (13)(二)线性规划模型的建立及Mathematica求解 (16)结束语 (20)参考文献 (22)致谢 (24)第一章数学软件Mathematica简介(一)Mathematica简介Mathematica是一款科学计算软件,很好地结合了数值和符号计算引擎、图形系统、编程语言、文本系统、和与其他应用程序的高级连接。
数学软件Mathematica简介

基本代数运算(太多,不介绍)
方程求解
Solve是Mathematica的通用求解命令,它 不但能求出精确的数值解或代数解,还可 求出复数解。 基本格式: 基本格式: Solve[eqn,x] 解方程eqn,其中x为变量 Solve[{eqn1,eqn2,…},{x,y, …}] 解方程组
例 作函数z=sin(xy)的三维图形
例 作二垂直相交圆柱面的三维图形(参数极限、微分、 极限 Limit[f,x->x0] Limit[f,x->x0,Direction->1] Limit[f,x->x0,Direction->-1] 左极限 右极限
sin x 例 求极限 lim x→0 x 解:输入Limit[Sin[x]/x,x>0]
微分 D[f,x] D[f,x1,x2,…,xn] D[f,{x,n}] Dt[f]
例 已知
dy y = x sin x, 求导数 ,y(20) . dx
积分 Integrate[f,x] 例 求不定积分
空间(三维)图形
Plot3D ParametricPlot3D
命令格式: Plot3D[f,{x,xmin,xmax},{y,ymin, ymax}] ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}] (空间曲线) ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}, {u,umin,umax}] (空间曲面)
方程求解示例
绘图
平面图形 Plot ParametricPlot Show 若载入相应的程序包,还可进行极坐标 绘图和隐函数绘图。
图形函数中最有代表性的函数为Plot,格式为 Plot[表达式,{变量,下限,上限},可选项] (其中表达式还可以是一个"表达式表",这样可 以在一个图里画多个函数);变量为自变量;上 限和下限确定了作图的范围;可选项可要可不 要,不写系统会按默认值作图,它表示对作图 的具体要求。
Mathematica在大学数学教学中的应用

GAOJIAO SHIYE高教视野17数学学习与研究2019.17Mathematica 在大学数学教学中的应用◎蔡浩江1房敏1王婧嘉2(1.西安石油大学理学院,陕西西安710065;2.中南大学交通运输工程学院,湖南长沙410075)【摘要】随着现代信息技术以及计算机辅助教学的蓬勃发展,最新的信息技术已经在高等院校的日常教学中越来越普及.在大学数学的教学领域中,信息技术的应用,可以使艰深、复杂的数学理论和公式变得简单直观.将Mathematica 这款非常实用的数学软件与传统教学相结合,构建符合学生认知规律的教学模式是提高大学数学教学质量的有效方法.实践证明这种教学模式的建立对培养学生的数学思维,激发学生的学习主动性,提高教学效果有着非常重要的作用.【关键词】计算机辅助教学;数学软件;Mathematica 一、目的与意义高校的数学教学中,传统的教学方法强调数学理论的连续与严谨,采用以教师为主导的灌输式的数学教学模式,使原本就比较抽象难懂的数学定义与概念变得难上加难.信息时代的到来,移动终端的使用,使传统教学模式受到了强烈冲击.当前,学生获取知识的渠道变得更为丰富,各种MOOC 、微课学习视频及其他丰富的网络教学资源都为学生的课外学习提供了条件.但是与传统教学相似,各种网络教学资源仍注重于学生掌握严谨的数学理论和计算能力,忽略了理论知识的推导以及创新思维的培养,淡化了理论推导过程中的猜想、观察、实验、归纳、类比、抽象等环节,忽视了学生的主体地位,弱化了学生自主探索的学习过程,不利于培养学生的应用与创新能力.对大多数学生而言,这些资源的利用虽然能够在一定程度上提高他们的学习效率,但仍然无法将所学的数学知识应用于其他课程及解决实际问题,学生的逻辑思维能力、创新与应用能力并没有显著提高.教学实践证明,数学软件与传统课堂教学的有机结合,是提高学生创新思维和应用能力的一条行之有效的途径.一方面,数学软件可以使用图像展现数学深奥的理论,可以加强学生对抽象知识的理解.另一方面,为了贯彻实施素质教育,教师还可以设计数学课程的实验教学环节:提出典型实际问题,引发学生思考,培养学生的数学思维;在教师的启发下分析问题、探索问题,从而提高学生的创新精神和实践能力;利用数学软件进行数学实验,使学生对教学内容有了直观认识,从而提升学习兴趣,提高研究能力.学生在使用数学软件解决问题的过程中找到了理论与实际的结合点,体验到了“学”和“用”的和谐统一,获得了学习带来的成就感,学习兴趣和动力会得到长效的保持.二、计算机辅助教学的可行性教学硬件的改善为软件的使用提供了保障条件.Matlab 、Mathematica 、Maple 并称为三大数学软件.Matlab 是Math Works 公司出品的数学软件,用于算法开发、数据分析以及数值计算;Mathematica 是由美国的Wolfram Research 公司开发的数学软件,其在图形、数值、代数等方面应用广泛;Maple 是由加拿大Waterloo 大学开发的科学计算软件,拥有优秀的符号计算和数值计算能力.它们各有所长,但就高校计算机辅助教学及实验教学而言,Mathematica 更具优势,原因有:第一,Mathematica 有与数学教材完全相同的基本数学符号输入界面,见图1,不需要太多的课堂时间讲解,学生即可上手使用;第二,自定义函数的写法,各类函数的输入和输出,更接近语言的表达顺序,简单易懂;第三,绘制的三维图形可以方便地调整观察视角,有利于学生对空间图形的直观认识;第四,符号运算方便、简洁,容易掌握.图1Mathematica 数学符号输入界面因此,将Mathematica 数学软件引入数学教学中具有很好的可行性.通过它,可以将复杂抽象的计算问题按照人们习惯的书写格式输入和输出,学生容易掌握,还可将复杂的函数关系用图形的形式展现出来,便于将抽象的问题具体化、可视化.本文将以Mathematica 的几个辅助实验为例说明与传统教学相结合的教学模式对提高大学数学教学效果的积极作用.三、Mathematica 软件在辅助教学的应用(一)在观察数列变化趋势中的使用在高等数学的教学过程中,极限作为微积分学的基础,无疑是最重要、最基础的环节.但在通常的教学中,大部分学生并不容易发现数列规律.借助Mathematica 程序给出的直观图示,可以帮助他们发现数列的规律,进而理解数列收敛的本质.例如,可以从复利问题引入重要极限lim n →ɕ1+1()nn,激发学生的学习兴趣,再借助Mathematica 程序绘出数列变化的直观图示,如图2所示:图2数列变化图示学生从图像中观察到了数列变化的特点,直观的感受使学生对公式首先有了感性认识,以此为基础,再利用二项展开式进行公式的推导和理论证明,从而使学生上升到理性认识.此过程遵循了猜想、观察、实验、归纳、类比、抽象的环节,重在思维方式的启发与培养,引导学生独立思考并提升了学生学习的积极性和主动性.(二)在函数绘图中的使用在传统的高数课堂教学中,由于缺乏对复杂函数图像的描绘等教学环节,对很多学生而言,曲线的直角坐标方程、极坐标方程及参数方程3种表达方式之间相互转化;不同坐标系下的三重积分的计算;线、面积的计算;隐函数的概念等知识点一直以来是都是难点问题.“数”与“形”之间不能完美的结合,使得部分学生缺乏直观认知,造成概念混淆,无法深入理解相关知识.但是在计算机辅助教学中,我们就可以借助Mathematica 中的绘图软件,在教学过程中绘制复杂函数的图像,“数”与“形”的有机结合,可以使抽象函数具体化,加深学生对函数以及相关知识的理解.使用高教视野GAOJIAO SHIYE18数学学习与研究2019.17Plot 、PolarPlot 、ParametricPlot 函数绘制一元函数、极坐标函数、参数方程表示的二维图形,使用Plot3D 、RevolutionPlot3D 、SphericalPlot3D 、ParametricPlot3D 函数绘制二元函数、柱坐标函数、球坐标函数、参数方程表示的三维图形,使用ContourPlot 绘制隐函数图形.还可以通过CoordinateTransform 函数实现直角坐标Cartesian ,极坐标Polar ,柱坐标Cylindrical ,球坐标Spherical 之间的相互转换.如图3绘制了极坐标方程ρ=cos2θ表示的四叶玫瑰线和方程x 3+y 3-3xy =0确定的函数曲线.图3图形图示还可以通过Animate 函数绘制动画,演示摆线、旋转曲面等图形的形成过程,如图4所示,帮助学生更好地理解所学内容并增强学生的学习兴趣.图4旋转曲面示例(三)在定积分和二重积分定义中的使用积分在数学、物理、机械、电子、军事等方面均有着广泛应用,但积分的概念对大部分学生而言却是难以理解的.在教学中,我们一般通过求曲边梯形面积和曲顶柱体体积的问题引入,需要经过“分割、近似代替、求和、取极限”四个步骤进行.其中“取极限”这一环节,课堂教学仅通过语言描述表达,没有相关的实验环节,学生缺乏直观的感性认知以及从具体到抽象的思维过程,无法深入、透彻地理解相关概念,难以获得较好的教学效果.通过Mathematica 绘制具体例子的图示,如图5所示,以图形直观的方式呈现,远胜于教师的口头讲解,有助于学生加深印象并理解概念.图5定积分与二重积分引例图示(四)在大数定律中的使用大数定律是概率统计中的重要定理,揭示了n 个相互独立的随机变量的算术平均值当n →ɕ时依概率收敛于其数学期望.为了帮助学生更好地理解大数定律,可以利用Mathematica 给出直观演示.例如,在讲授辛钦大数定律时,利用Mathematica 的Random 和NormalDistribution 函数,产生n 个相互独立且服从正态分布N (1,22)的随机变量X 1,X 2,…,X n ,考查当随机变量个数n 逐渐增多时,它们的算术平均值的变化情况.图6分别给出了当n =10,100,1000,10000四种情况下,重复试验50次,n 个随机变量的算术平均值的分布情况.图6大数定律图示从图6可以明显看出,当n =10时,10个相互独立的随机变量的算术平均值与μ=1有很大偏差,但随着n 越来越大,n 个相互独立的随机变量的算术平均值越来越密集在μ=1这条直线附近.由此可见,传统教学中复杂、艰深的数学定理,借助于数学软件的帮助,以直观易懂的图形图像展示给学生,使得复杂抽象的理论知识变得简单、具体,让学生印象深刻,从而取得较好的教学效果.四、计算机辅助教学的优点(一)有利于学生自主学习数学课程的教学强调进行交互式教学以及以学生为中心的自主学习,在课前、课中和课后都以学生为主体、教师为主导.数学软件辅助教学,使得作为主体的学生,对课程知识的获取和掌握不再完全依赖于任课教师的课堂教学,可以利用更多的课外时间自主学习.(二)有利于学习成绩的提高在运用计算机辅助的交互教学过程中,将Mathematica 软件引入到数学课堂,使抽象的概念、函数、公式变得直观形象,学生在数学模型的动态展现中更加深刻地理解理论知识,提高课堂的教学效率,提升学生的学习兴趣.学生在学习过程中遇到难题,也可以通过讨论,查找资料,编写程序等多种方式加以解决.(三)有利于实践能力的培养在课程教学中,我们运用Mathematica 软件进行交互教学,让学生通过自主学习的方式不仅掌握有关定理、公式,而且能够熟练掌握一门数学软件.既增强了学生的自学能力,还提高了学生的动手能力,也培养了学生的实践应用能力.五、结束语在数学课程中运用Mathematica 软件进行辅助教学,充分利用数学软件的计算和绘图功能,加强了数学教学的简便性和直观性,使得“数”与“形”有机结合,“教”与“学”相得益彰,不仅有助于提高课堂教学效果,还有助于培养学生利用数学软件探究问题的意识.学生在课后利用课外教学资源自主学习、表达和解决实际问题时,也可以方便地使用软件辅助,既促进了学生学习成绩的提高,也培养了学生理论联系实际的能力.教学实践证明,在数学教学中充分利用辅助软件是一种比较科学有效的教学方法,能够激发学生的学习兴趣,活跃课堂氛围,提高课堂教学效果.【参考文献】[1]同济大学数学系.高等数学(上册):第7版[M ].北京:高等教育出版社,2014.[2]同济大学数学系.高等数学(下册):第7版[M ].北京:高等教育出版社,2014.[3]朱开永,王升瑞,李媛.概率论与数理统计[M ].上海:同济大学出版社,2013.[4]Wolfram S.Mathematica 全书[M ].赫孝良,周仓义,译.西安:西安交通大学出版社,2002.[5]王绍恒,王艺静.Mathematica 软件在大学数学课程教学中的应用[J ].教育理论与实践,2013(21):39-40.[6]刘雄伟.基于Mathematica 的高等数学教学过程研究与实践[J ].大学教育,2016(2):136-138.。
Mathematica在数学分析中的应用探究

Mathematica在数学分析中的应用探究【摘要】本文先简单介绍Mathematica的背景与基本信息,再介绍如何Mathematica中的基本量,接着结合数学分析介绍Mathematica在微积分中的应用,给出如何有Mathematica解微分方程,最后是用Mathematica作函数图象的方法关键词:Mathematica 数学分析微积分函数一、导言有人曾将数学、哲学、自然科学间的关系做了如下的比喻:数学是大地,哲学是天空,在天与地之间的是一切自然科学。
将数学比作大地,我想这是要表明数学的基础性地位,数学更贴近我们所生活的世界吧。
如果将数学的学科结构比作一座大厦,那么作为基座,无疑就是微积分和线性代数了。
微积分作为高等数学的基础,首先将我们引领进了高等数学这座神秘的宫殿,让我们能窥探这颗王冠上的钻石。
数学分析包括了函数、极限、微分、积分等多方面的内容。
在计算机飞速发展的今天,我们拥有越来越多的工具来帮助我们解决与数学相关的问题。
其中Mathematica便是一款功能强大又面向大众的软件。
从牛顿泛黄的演算稿纸,到今天黑色键盘的敲击,计算机的普及也帮助高等数学走进千家万户,更贴近人们的生活。
本文分为七节。
第一节是导言。
第七节是结语。
本文的主要贡献是:第二节介绍Mathematicad的背景与基本信息。
第三节介绍如何Mathematica中的基本量。
第四节结合数学分析介绍Mathematica在微积分中的应用。
第五节给出如何有Mathematica解微分方程。
第六节是介绍用Mathematica作函数图象的方法。
二、Mathematica的背景与基本信息1.Mathematica的概述Mathematica是美国Wolfram研究公司生产的一种数学分析型的软件,以符号计算见长也具有高精度的数值计算功能和强大的图形功能。
Mathematica7.0的使用界面:表达式的输入:Mathematica 提供了多种输入数学表达式的方法。
Mathematica简介

数学软件Mathematica简介本文简要介绍该软件的基本使用方法,通过学习,初步了解Mathematica的功能及其使用方法.Mathematica是美国Wolfram Research公司开发的数学软件,主要用于解决科学研究、数学教学、工程技术等领域的符号运算、数值计算、程序设计、函数图形绘制等方面的问题.Mathematica是目前世界上最流行的数学软件之一,它是从事数学和其它科学研究的科研人员、高校师生,以及工程技术人员的得力助手和不可缺少的计算工具.一、算术运算进入Mathematica 系统后,显示在面前的是如图1-1所示的窗口,右边是基本工具板,我们立即可以在空白的窗口内进行预想的数学计算了.图1-1Mathematica中,空白窗口称为Notebook(记事本),窗口上端“Untitled-1”表示当前的记事本尚无标题,我们可以像使用普通计算器一样来进行数学运算. 计算结束后,执行File/Save as 命令,指定文件名称(扩展名为 *.nb)和路径将此记事本文件保存.算术与代数运算是数学中最基本的运算,我们先从最简单的算术运算做起.做数学计算,离不开加、减、乘、除和乘方,单击键盘上“+”、“-”、“*”、“/”和“^”输入这些运算符,其中乘号“*”可以用空格代替. 如果要计算图1-1所示的工具板上提供的某种数学运算,可用鼠标左键单击相应的按钮,便可将该运算符输入到窗口中,例如25+34*525+34*5然后用组合键Shift + Enter 或直接按小键盘上的Enter键(本书中,我们一律称这一操作为“执行”),便可输出计算结果. 屏幕上显示为In[1]:=25+34*5Out[1]=195这里“In[1]:=”和“Out[1]=”是由系统自动加上去的,表示输入和输出的编号. 此后的输入和输出,系统都会按照执行顺序自动加上“In[n]:=”和“Out[n]=”.本书中一般不再显示这些编号,而使用灰色底纹突出输入命令行,接在该行下面的式子、数值等则表示执行命令后的输出结果,并将二者用边框线框住. 输出的图形考虑到印刷的便利,一般予以编号.如果要计算较复杂的式子,需要按照运算顺序添加括号,例如计算3314(3523)23521+⋅+-⋅⎡⎤+⋅⎢⎥-⎣⎦,在窗口内输入(输入的式子中用乘号用空格代替):2+(18/5) (1+4 (3+5-2 3))/(2^3-1) 输出计算结果为23235又如计算(103.54+12.25)*1.2-3.3^5/5.263.68765(a+3)^3/(b-1)^2325 (3+a)(-1+b)对每一输入行和输出行,系统在Notebook 窗口的右边缘分别添加一个形如“”和“”的标记(图1-1),它随着输入行和输出结果行的宽度扩展,它标记的行称之为“Cell ”,即“细胞”或“单元”. 系统根据输入和相应输出的关系将有关的“细胞”组合起来形成多级细胞单元显示运算的层次.Mathematica 可以做任意位数的整数或分子分母为任意大整数的有理数的精确计算,也可以做具有任意位精度的数值(实、复数值)的近似计算. 一般使用 N[expr] 命令输出表达式expr 的近似值,用N[expr ,n]命令输出表达式expr 的n 位近似值,例如计算圆周率π的近似值,顺次输入Pi N[Pi] N[Pi,50]输出结果依次为π的精确值、近似值和精确到50位的近似值Pi3.141593.1415926535897932384626433832795028841971693993751也可以使用后缀格式“expr//N ”求表达式expr 的近似值,如求Sqrt[5]//N2.23607复数运算与实数运算一样,只需在输入复数时,虚数单位“i ”必须使用大写字母I ,输出结果中,显示为 ™ . 例如要计算复数123z i =-+⋅与复数232z i =--⋅的积、商以及1z 的3次方,则应输入(-2+3 I)(-3-2 I) (-2+3 I)/(-3-2 I) (-2+3 I)^312 -5 ™ -™ 46 +9 ™二、常数、变量和函数1.系统常数Mathematica系统中的数学常数列于表1-1.表1-1 数学常数∞2.变量和函数名Mathematica系统中,定义变量和函数名应遵从如下规则:变量或函数名必须以英文字母起头,后面接任意长度的字符或数字,各字符间不得有空格和其他运算符,如x、x1、xy2、T2x、data、Alpha、delta都是合法变量.系统区分变量中的大小写,X和x、xy1和Xy1视为不同的变量.系统内置函数名都以表示函数意义的完整英文单词为名,且起头的第一个字符必为大写字母,其余为小写字符,例如Sin[x]为x的正弦,Expand[expr]表示将表达式expr展开.如果函数名是几个英文单词复合而成,各单词的每个词头要大写,例如,FindRoot[eq1==eq2,{x,x0}]表示求方程式“eq1==eq2”的根. 用完整意义的单词作为函数名定义函数,常使用户能够“望文生义”,根据函数名就大致明确函数的意义. 不过,自定义函数时尽量不要与系统内置函数同名,因为系统内置函数的名称是受保护的.函数必须表示为“函数名[x]”的形式,自变量放在方括号内.3.系统内置函数Mathematica系统中的内置函数(Built-in Function),包括基本初等函数、特殊函数,还有众多旨在完成某项特定数学运算的功能函数,有时也称这类函数为“命令”.表1-2列出了常用的初等函数,它们与普通数学中的形式基本相同,只不过函数名的首字必须大写.表1-2 Mathematica的部分内置初等函数表1-2 续读者要了解更多的内置函数,可参阅书末的附录.4.自定义函数大量的数学问题还需要根据问题的具体意义,借助软件提供的运算功能自行定义函数加以解决,Mathematica 提供了两种自定义函数的方法:立即定义和延迟定义.立即定义,格式为:f[x_]=expr . 延迟定义,格式为:f[x_]:=expr .这里自变量x 右边的下划线“_”是非常重要的,称之为“空白”(blank ),x _表示定义的函数中的自变量,称为哑变量,可以用任何形式的参数或表达式去替代它.使用等号“=”和延迟赋值号“:=”定义的函数是不同的,二者的区别主要在于何时对表达式expr 进行计算,前者在定义f[x_ ]的同时就计算了expr ,而后者则是在需要计算函数 f 的值时才进行计算. 定义多元函数的方法也是相同的.我们用下面的例子来比较二者的区别,输入 f[x_]=Expand[(x +1)^3] 1+3 x+3 x 2 +x 3 f[x^2+1]1+3(1+x 2)+3(1+x 2)2+(1+x 2)3用立即定义法定义一个将多项式展开的函数:f[x_]=Expand[(x +1)^3],执行后,系统会立即输出(x+1)^3的展开式.而再输入f[x^2+1]时,输出的是1+3(1+x 2)+3(1+x 2)2+3(1+x 2)3.接下来用延迟定义法定义:g[x_]:=Expand[(x+1)^3],执行后,系统则不输出任何结果,只有再次调用g[x]时,系统才输出展开式.g[x_]:=Expand[(x+1)^3] g[x]1+3 x +3 x 2+x 3g[x^2+1]8+12 x 2+6 x 4+x 6g[2 a -3 b]1+6 a +12 a 2+8 a 3-9 b -36 a b-36 a 2 b +27 b 2+54 a b 2-27 b 35. 变量赋值、变量值的清除Mathematica 中,用等号“=”给变量赋值,也可以将一个表达式赋予一个变量,格式为 x = value 将值value 赋予变量x x = y = value 将值valu e 同时赋予变量x ,y x =.或 Clear[x]清除x 的值例1 使用一元二次方程求根公式求22230x x +-=的根.解 输入和输出结果为a =b =2;c =-3; Delta=b^2-4 a cx1 =(-b +Sqrt[Delta])/2/a x2 =(-b -Sqrt[Delta])/2/a 输出结果为28142142这里,把2、2、-3分别赋予变量a 、b 、c ,后面用“;”隔开,Mathematica 中,如果一个完整的输入语句之后面接分号“;”,该表达式的运算结果屏幕将不予显示. 把表达式b^2-4 a c 赋予变量Delta ,把计算根的表达式分别赋予变量x1和x2,执行后输出并显示出Delta 的值为28,两个根分别为1(24-±,而变量a 、b 、c 的值却没有显示出来. 如果接着输入 -b /2a Delta 则输出28对于赋了值的变量,如果在接下来的运算中不再使用,可以使用命令:“Clear[变量名]”或“变量=.”将它们清除,以免影响后续的数学运算. 例如,输入Clear[a ,B ,C ,Delta,x1,x2]执行后,这些变量便被清除了. 不再使用的自定义函数可使用同样的方法加以清除:Clear[f ,g]. 在Mathematica 运行期间,将不使用的变量及时加以清除,对保证后续运算结果的准确性是至关重要的,初学者应给予足够的重视.6. 括号的使用Mathematica 中,可以使用四种括号:方括号“[ ]”:仅用在函数表达式中,如f[x]、Sin[Pi/3]、Sqrt[3] 等; 圆括号“()”:用来表示运算项的结合顺序,例如,数学表达式223{5[2(2)]sin()}yx x x y x y⋅⋅++++⋅-应输入成如下形式:3(5(2 x + y /(x -y )+(2+x )^2)+Sin[x ^2] y)此外,在语句行的任何地方可以加入形如 (* …… *)”的括号,其中两星号之间可以输入一段注释语句意义的文字或其他, 其内容系统是不执行的.花括号“{ }”:用于定义一个“表”,如{a ,b ,c}; 双方括号“[[ ]]”:用于提取表中元素. 7. 变量替换Mathematica 提供了变量替换运算,其基本格式为:expr/.x →value以value 替代expr 中的xexpr/.{x →value1,y →value2,…} 以value 1和value 2等替代expr 中的x 、y Replace [expr,rules ] 按规则rules 替代expr例如x ^2+2x +3/.x →211x +y /.y →S in[x ]/.x →π/2Replace[x ^2+b ^2,x →a ]a ^2+b ^2{a ,b ,c }/.a →b /.b →d /.d →c{c ,c ,c }以上输入中的箭头“→”可以依次输入减号键“-”和大于号键“>”得到. 8. 先前变量值的调用在计算过程中,我们常常需要使用先前已经计算出来的结果,使用“%”、“%%”、“%...%”等分别来调出最后一个、倒数第二个和倒数第k 个计算结果. 例如,x +y /.{x →a ,y →b }a +b%+ca +b +c{%+d ,%%+d }{a +b +c +d ,a +b +c }三、 符号运算代数运算,即对使用字符代表数值的代数式进行运算,各种形式的代数式,在Mathematica 中,统称为表达式,如计算33()()a b a b +--,在计算机里做这种运算,称为“符号运算”. Mathematica 强大的符号运算功能,可以完成从初等数学到高等数学中众多的运算,如各种代数式运算、三角函数变换、函数求导、不定积分、级数展开、函数变换、向量矩阵运算等等. 在Mathematica 中,符号运算可以像普通数学运算一样进行,例如将代数式33232322a a a b ab b -++-化简,可以输入2 a^3-a ^3-3a ^2 b +3a b ^2-b ^3 输出为a 3-3 a 2b +3 a b 2-b 3在Notebook 中作符号运算时,有一点必须加以注意,参与运算的表达式中使用的字母符号(实际上,都是所谓的“变量”)必须是没有赋过值的,否则系统将把它当作数值对待,运算后,输出的将是表达式的值,而非预想的运算结果. 为了保证不出错误,应该在符号运算之前,先执行清除命令Clear[a ,x ,...].在大多数场合下,要完成代数运算,需要使用执行符号运算的命令,如表达式化简(Simplify )、分解因式(Factor)等等. 表1-3列出了几个常用的处理符号运算的命令(或称为函数).表1-3 处理符号运算的函数例如下面几个代数式的运算: Expand[(2 x +3 y-1)^2]1+4 x+4 x 2-6 y+12 x y+9 y 22 x^2+x -1//Factor(1+x )(-1+2 x)Together[x ^2/(x +2)-(x ^2-3)/(3x +1)] (*通分合并*)236+3 x -x +2 x (2+x) (1+3 x)Apart[(3 x^2-1)/(x^2+3 x +2)]321又如下列三角式的展开和化简: Sin[α-2β]//TrigExpandCos[β]2 Sin [α]-2 Cos[α] Cos[β] Sin[β]-Sin[α] Sin[β]2TrigReduce[%]Sin [α-2 β]将sin z 转化为指数型函数: TrigToExp[Sin[z]]12z将ln(/)m n a b 展开:PowerExpand[Log[a ^m /b ^n ]]m Log[a]-n Log[b]四、表与表的操作1. 表的概念“表”(List)是Mathematica中一个灵活、独特而重要的数据结构,它可以表示数学中点的坐标、向量、矩阵、集合、自变量取值范围、方程组等,其基本结构是{a,b,c,...},其中a,b,c,...称为表的元素,它们可以是数字、字符、表达式、函数、图形命令,甚至是表(子表),这时的表称为嵌套的表. Mathematica 中众多运算的输出结果也以表的形式给出.可以使用“表名[[num]]”提取该表中的第num个元素.对于嵌套表,用“表名[[num1,num2]]”提取该表中的第num1个子表中的第num2个元素,多层嵌套表也称为多维表.2. 建表方法Mathematica中有多种方法建表方法,可以直接定义法,输入一个花括号,将元素放在括号内,各元素之间用逗号分开即可.例如a={1,2,3}{1,2,3}a[[2]]2如下定义的嵌套表b代表一个23阶矩阵:b={{1,2,-2},{3,4,1}}; (* 定义表b,不做屏幕显示 *){b[[1]], b[[1,3]]} (* 输出表b的第一个子表,和第一个自表中的第三个元素 *){{1,2,-2},-2}b[[1]]相当于b的第一个元素,即矩阵的第一行. b[[1,3]]相当于13b.表作为一个整体可以参与相关的运算,也可以对表的元素进行相关的运算,例如a={1,2,3,4,5};a^2(* a的各元素平方组成的表 *){1,4,9,16,25}%+2a(* 上一个表加上a的各元素的2倍组成的表 *){3,8,18,24,35}10+a(* 将数10加到a的各个元素上去 *){11,12,13,14,15}Sum[a[[i]]^2,{i,5}] (* 计算a中各元素的平方和 *)55Sin[{Pi/6,Pi/3,Pi/2}] (* 将正弦函数作用到表的每个元素上 *)1 2,2使用建表函数Table、Range、Array等,可以建立元素具有某种规则的表,它们的最简单的使用格式为Table[expr,range] 产生一个指定范围内,元素按表达式expr计算出的表.Range[n] 产生一个从1到n的整数组成的表.Array[f,{m,n}] 产生一个以f[i,j]为元素的m n⨯阶数组.Table[ ]是一个非常有用的函数,在生成函数表、作图、制作动画等都会用到它. 例如a=Table[x^i,{i,5}](* 产生以函数i x为元素的表 *){x,x2,x3,x4,x5}Table[{i,Log[10,i]},{i,1,5}]//N(* 产生1-5的常用对数表 *){{1.,0.},{2.,0.30103},{3.,0.477121},{4.,0.60206},{5.,0.69897}}例2利用Table函数输出九九表.Table[i j,{i,9},{j,9}]{{1,2,3,4,5,6,7,8,9},{2,4,6,8,10,12,14,16,18},...,{9,18,27,36,45,54,63,72,81}} (注:此处略去部分输出结果)Range[n]函数的用法.例如,要产生一个从1到10的整数集合,输入b=Range[10]{1,2,3,4,5,6,7,8,9,10}Array[ ]函数的用法. 例如,要产生一个23⨯阶数组,输入Array[a,{2,3}]{{a[1,1],a[1,2],a[1,3]},{a[2,1],a[2,2],a[2,3]}}输出一个两行三列的数组a[i,j].例3用Array[]函数输出一个九九表.f[x_,y_]:=x y; c=Array[f,{9,9}]输出结果与例2的结果相同.有关表的更多的用法和操作,我们将在以后的相关章节中详细介绍.五、图形函数Mathematica有很多图形函数,利用它们可以方便地绘制各种数学函数的图形.其中,最常用的图形函数是产生平面曲线图形的函数命令为Plot[expr,{var,min,max},options]这里expr为函数表达式,var为自变量,min,max分别为自变量取值的下限和上限,它确定作图的自变量取值范围,options为针对输出图形或图元给出的各种控制选项. 也可以使用如下命令把几个函数图形在同一张图中显示出来,Plot[{expr1,expr2,...},{var,min,max},options]例4 做出函数sin()xf xx=的图形,可以输入f[x_]:=Sin[x]/xPlot[f[x],{x,-Pi,Pi},AspectRatio →0.4,PlotStyle →{RGBColor[0,0,1],Thickness[.01]}]Graphics 这里选项AspectRatio→0.4,表示图形的高和宽的比例为0.4 ,即高为宽的40%. 一般地,如果不输入这个选项,则系统默认图形的高和宽之比为黄金分割比,即1/GoldenRatio=0.618. 图形风格选项PlotStyle→{RGBColor[0, 0,1], Thickness[.01]}中,RGBColor[0, 0, 1] 表示图形中曲线的颜色为蓝色,RGBColor[1,0,0]和RGBColor[0,1,0]则分别表示颜色为红和绿,方括号中的三个数取0与1之间的数值.在Mathematica5.1以上的版本中,它们分别可以用Blue,Red和Green取代,Thickness[.01]表示曲线的粗细,方括号中的数值越大,曲线越粗.Mathematica中,凡是输出图形的下方,系统将输出一个字符串“ Graphics ”,如果在图形命令末尾加上分号“;”,则该字符串将不再显示.当函数图形绘制出来以后,用鼠标单击图形,它就被一个矩形框框住,鼠标指向该框内,鼠标变成一个纵横交叉的十字丝,这时按住Ctrl键,移动鼠标,跟踪平面上点的位置,在屏幕左下方的花括号内显示十字丝位置上点的坐标.不妨用这个函数并选择有关选项做出你所熟悉的一元函数的图形. 输出函数图形可用选项有很多,可以查阅帮助文件,也可以在Notebook中使用Option[]函数来了解:Options[Plot]执行后输出所有可用选项,由于选项太多,这里略去.要产生三维空间的曲面图形,最常用的函数为Plot3D[expr,{x,xmin,xmax},{y,ymin,ymax},options]Mathematica还提供了产生由参数方程确定的平面曲线、空间曲线、空间曲面的图形函数,产生极坐标系下曲线的图形函数等等. 图形函数以及它们的具体使用方法,这里不再介绍.此外,Mathematica也提供了利用一些基本图元作图的函数,其中,最常用的命令格式为Graphics[primitives,options]基本图元(primitives)包括: 点(Point)、线段(Line)、圆(Circle)、圆盘(Disk)、多边形(Polygon)、矩形(Rectangle)等,这样的图形需要调用如下的Show函数才将它显示出来.Show[plot,options]例 5 绘制单位圆和以圆与坐标轴的交点为顶点的内接正方形. 输入p=Graphics[{Thickness[0.01],Circle[{0,0},1]}];r=Graphics[{Thickness[0.01],Line[{{0,-1},{1,0},{0,1},{-1,0},{0,-1}}]}];Show[{p,r},Axes→True,AspectRatio→ Automatic];Show函数中,设置选项Axes→True,表示显示坐标轴,图形的显示比例为“自动”. 执行后输出的图形如图1-2所示.例6 利用图元“Circle ”绘制一幅奥林匹克五环标志图,并选取适当选项,显示“Beijing 2008”字样. 可以使用多种方法绘制出五环标志图,下面我们给出如下的命令,执行后输出如图1-3所示的五环标志. Apply[Circle,{{{0,0},1},{{2.4,0},1},{{4.8,0},1},{{1.2,-1.0},1},{{3.6,-1.0},1}},{1}];Show[Graphics[Table[{Blue,Thickness[0.03],%[[i ]]},{i ,5}]],AspectRatio → Automatic,PlotRange →{-3,2},PlotLabel →StyleForm["Beijing 2008",FontFamily →"Times", FontSize →28,FontWeight →"Bold",FontColor →Blue]];这里,使用Apply(应用)函数将Circle 命令作用到五个位置不同上去,产生包含五个圆环的表. 再用Table 函数将画圆的选项“Blue,Thickness[0.03]”分配给五圆表的每个元素,最后使用Show 函数将这五个圆环显示出来. 选择的选项中有:PlotRange →{-3,2}表示图形纵向范围,PlotLabel →StyleForm[]指出图形标签的风格形式,方括号内依次列出:字样“Beijing 2008”、字体、字号、字形和字体颜色等.作业:利用Mathematica 绘制一个尽量真实的奥林匹克五环标志图图1-2图1-3六、程序与编程Mathematica提供了众多可以解决各种数学问题的功能函数,但是,大量的数学问题仅靠这些函数来解决,还是远远不够的,需要自己编写计算机程序来解决. Mathematica系统为用户提供了一个功能非常强大的编程平台和编程语言,其语言结构简单、灵活,凡学过计算机语言(如C、Fortran等)的用户都能很快地掌握它.同任何程序语言的结构一样,Mathematica程序流程也分成顺序结构、循环结构、条件分支结构.1. 关系运算与逻辑运算在程序流程的控制中,需要用到关系运算和逻辑运算. 这些运算由相应的关系运算符和逻辑运算符完成,如果关系表达式和逻辑表达式成立,其输出结果为True,否则为False.关系运算符和逻辑运算符列于表1-4和表1-5中.表1-4 关系运算符及运算结果表1-5 逻辑运算符及运算结果2. 全局变量与局部变量当Mathematica开启并首次执行一个运算后,系统立即启动一个叫做“Mathematica Kernel”程序,它负责变量和函数的计算,并将计算结果暂时存储在这里.凡先前定义的变量的值,在Mathematica运行期间,该变量的值始终被保存,所以,在Mathematica中称这种变量为“全局(Global)变量”,全局变量的值只要没有及时地清除,很可能会影响后续的运算的结果.相对全局变量,Mathematica允许定义一种所谓的“局部(Local)变量”,不过这种变量必须放在一个由Module引起的模块中,用Module模块可以定义一个函数或者旨在完成某项具体任务的程序. 这个模块中定义的变量叫做局部变量. 局部变量的值仅在该模块内起作用,模块外的全局变量值与模块内定义的局部变量,即使它们同名也互不影响.Module模块的基本格式:Module[{x,y...},body],局部变量为x,y,...的模块.Module[{x=x0,y=y0,...},body],局部变量为x,y,...赋予初始值的模块.例如,输入x=10 (* x为全局变量,定义其值为 10*)f=Module[{x},x=(2 t-3 s)^2;x=Expand[x]](* Module中的变量x为局部变量*)不难看出,这里用Module模块定义的变量f,执行后输出结果为109 s2-12 s t+4 t2显然,输出的10为全局变量x的值,而模块内的变量x为局部变量,将(2 t-3 s)^2赋予x,再将它展开并输出展开式.这里须注意Module模块中最后一个语句为输出语句.3. 循环结构程序,实质上就是一系列有序的计算机指令组成的集合.大多数情况下,Mathematica程序,就是将一系列的命令组合在一起,按照先后顺序从前向后执行,当一个命令语句之后添加“;”时,计算结果不做屏幕显示,继续计算下一条命令,直到这组命令全部计算完备为止,这种程序结构,叫做顺序结构.但是,许多数学问题,需要利用计算机的高速运算多次循环计算才能得到结果,即需要编写一个循环结构的程序来完成. Mathematica中有多种建立循环结构程序的方法,我们仅介绍其中几种常用的方法.(1) Do循环Do循环的格式为Do[expr,{i,i min,i max}] 循环变量i从i min到i max,重复计算expr的值Do[expr,{i,i min,i max,di}] 循环变量i从i min到i max,以di为步长,重复计算expr的值.Do[expr,{i,i min,i max},{j,j min,j max}] 二重循环例7用Do循环计算前n个自然数的平方和,输出前15个自然数的平方和.Sqsum[n_Integer]:=Module[{s=0},Do[s+=k^2,{k,n}];s]Sqsum[15]1240输出结果为1240. 程序中k为循环变量,循环表达式“s+=k^2”,即“s=s+k^2”,循环变量的初值如果是1的话,可以省略.(2) For循环Fro循环的格式为For[start,test,incr,body] start为循环变量初值,test为检验条件,incr 为步进量,body为循环体.使用For循环作例6的问题:Sqsum1[n_]:=Module[{s=0},For[i=1,i<=n,i++,s+=i^2];s]Sqsum1[15]其中,循环变量i的初值为1,终值为n,i++表示步进量为1(它可以用i=i+1,或者i+=1代替),此程序的输出结果也是1240.(3) While循环While循环的格式为While[test, body]test为检验条件,body为循环体当检验条件满足,计算循环体,直到检验条件不满足为止.使用While循环作例6的问题,输入如下程序Sqsum2[n_]:=Module[{s=0,i=1},While[i<=n,s+=i^2;i+=1];s]Sqsum2[15]不难看出,这个程序的输出结果仍然是1240.4. 条件分支结构在数值或者非数值运算中,常常需要对给定的条件作逻辑判断,并根据判断结果控制程序的流向,这要用到分支结构.Mathematica中使用If、Which等命令控制程序的分支,下面简要介绍它们的用法.(1) If 语句格式If[cond,t,f],cond为检验条件,当cond为真时计算t,否则计算f.例8 编写程序从任意给出的3个数中挑选最大的数. 输入maxf[x_,y_,z_]:=Module[{m},If[x>y,m=x,m=y];If[z>m,m=z];Print[m,"i s the maximal number."]]程序中“Print”函数表示打印,其中引号中的字符串照原样打印.如果求ππee, 3,π中最大的数. 调用此程序并输出结果为maxf[E^Pi,3^Pi,Pi^E]π3is the maximal number.数学中的分段函数,常常要使用If命令来定义,我们将在实验1中详细讨论.,(2) Which 语句格式Which[cond1,expr1,cond2,expr2,...] 顺次检验条件cond i,当首次遇到某个条件cond k成立时,返回对应的表达式expr k的值.例9 用Which命令定义符号函数1 , 0 sgn[] 0 , 01 , 0xx xx-<⎧⎪==⎨⎪<⎩.sgn[x_]:=Which[x<0,-1,x==0,0,x>0,1]如果输入sgn[2.5],输出1,输入sgn[-3.1],则输出-1.为了解决复杂的问题,在计算机程序中,常常需要在适当的地方中改变程序的流向,例如在循环中,当循环结果符合要求以后,中断循环,跳出循环执行下面的语句,或控制程序转入下一轮循环. Mathematica 中提供了一些控制程序流程的命令函数,如Break[]、Continue[]、Return[expr]、Goto[name]等等. Mathematica 程序的语法与C语言语法基本相同,读者可以在所掌握的计算机语言的基础上,逐步熟悉程序的编写方法.例10 3N+1问题是数论中的一个有趣问题,任意给定一个正整数内 N ,如果它是偶数,则除以2,否则,将它乘以3再加上1,再将所得到的数当作新的N,重复上述计算步骤,经过有限次计算后,最后一定得到数1. 编写Mathematica程序验证这一事实.ThreeNPlus1[n_]:=Module[{m=n},For[i=1,i≤10^10,i++,{If[m==1,Break[],If[Mod[m,2]==0,m=m/2,m=3 m+1]]}]; Return[m]]程序里,对任意给定的正整数n,由于事前并不知道需要计算多少次,最后可以返回数1,故选取循环变量的终值为一个很大的数,这里取为1010.循环过程中,经过若干次计算后,一旦得到数1,程序执行到终止循环命令Break[](注:Break之后的方括号内不填任何值),则跳出循环,Return[m]表示返回到m的最后值. 可以验证,对于任何整数n调用这个函数,其返回值都是1.七、帮助与查询查阅软件提供的帮助是迅速掌握软件功能的重要途径,选择Help菜单下的Help Browser...菜单项(可单击F1) 打开帮助浏览器,其中介绍系统内置函数(Build-in Functions)、学习教科书(The Mathematica Book)、功能演示(Demos)、索引(Master Index)等内容,从中了解系统功能、函数与基本使用方法.Mathematica还提供了获取帮助的简便方法,要了解某个具体函数或者命令的意义,可以在Notebook中先输入“? 函数名”,例如,输入?Expand执行此命令,系统输出该函数的简要信息.Expand[expr] expands out products and positive integerpowers in expr. Expand[expr, patt] leaves unexpanded anyparts of expr that are free of the pattern patt. More...要了解更多的信息,可以单击上面这段文字末尾的“More...”按钮. 如果输入“??Expand”,执行后则输出该函数的详尽信息.如果忘记了某个函数或命令的英文拼写,可以输入?Ex*则会输出系统中所有以“Ex”起头的Mathematica命令的名称.八、加载程序包Mathematica提供的内置函数中,有一部分可以直接调用.还有些功能相对专业的函数,Mathematica将它们集中在一个个的程序包中,要使用这些函数首先必须调入包含着该函数的程序包,否则,若直接输入这些函数,系统并不能识别.加载程序包的方法是输入:<<程序包`子程序包名称` (或者Get[“程序包`子程序包名称`”])或者输入Needs[“程序包`子程序包名称`”]例如我们要做统计中线性回归方面的计算,就需要调入统计(Statistics)程序包中的线性回归子程序包,输入<<Statistics`LinearRegression`执行后就可以使用该程序包中的有关函数或命令做线性回归了. 注意,上面的命令中,要输入单引号“`”,需单击数字键1左边的那个键.Mathematica系统提供了代数、几何、微积分、数论、图形、统计等领域中的许多程序包,要了解这些程序包,从帮助浏览器的“Add-Ones&Link”卡中的标准程序包(Standard Packages)去查找.除了做数学的程序包外,有一个特殊的杂项(Miscellaneous)程序包,其中包括可以输出化学元素、物理常数、日历、城市数据等方面资料的子程序包. 例如,要想知道某年某月是星期几,需要加载中的日历(Calendar)子程序包,输入<<Miscellaneous`Calendar`执行后,比如要想知道2016奥运会的开幕日是星期几,输入DayOfWeek[{2016,8,5}]Friday即当天是星期五. 要想知道从2014年3月1日到2016奥运会开幕还有多少天,输入并执行后得到DaysBetween[{2014, 3, 1}, {2016, 8, 5}]888。
Mathematica_intro Mathematica 简介

MATHEMATICA用法简介前言Mathematica是美国Wolfram Research公司开发的数学软件。
它的主要使用者是从事理论研究的数学工作者和其它科学工作者、从事实际工作的工程技术人员、学校里的学生和教师。
Mathematica可以用于解决各种领域的涉及复杂的符号计算和数值计算的问题。
它可以完成许多复杂的工作,如求不定积分、做多项式的因式分解等等。
它代替了许多以前仅仅只能靠纸和笔解决的工作,这种思维和解题工具的革新可能对各种研究领域和工程领域产生深远的影响。
Mathematica可以做许多符号演算工作:它能做多项式的计算、因式分解、展开等,做各种有理式计算,求多项式、有理式方程和超越方程的精确解和近似解,做数值的或一般代数式的向量、矩阵的各种计算,求极限、导数、积分,做幂级数展开,求解某些微分方程等。
Mathematica还可以做任意位数的整数或分子分母为任意大整数的有理数的精确计算,做具有任意位精度的数值(实、复数值)的计算。
所有Mathematica系统内部定义的整函数、实(复)函数也具有这样的性质。
使用Mathematica可以很方便地画出用各种方式表示的一元和二元函数的图形。
通过这样的图形,我们常可以立即形象地把握住函数的某些特性,而这些特征一般很难从函数的符号表达式中看清楚。
Mathematica的能力不仅仅在于上面说的这些功能,更重要的在于它把这些功能有机地结合在一个系统里。
在使用这个系统时,人们可以根据自己的需要,一会儿从符号演算转去画图形,一会又转去做数值计算。
这种灵活性能带来极大的方便,常使一些看起来非常复杂的问题变得易如反掌。
在学习和使用Mathematica的过程中读者会逐步体会这些。
Mathematica还是一个很容易扩充和修改的系统,它提供了一套描述方法,相当于一个编程语言,用这个语言可以写程序,解决各种特殊问题。
第一节 Mathematica基本使用方法1.1 Mathematica的使用方法Mathematica系统已经被移植到许多不同的计算机和运行环境上。
mathematica

mathematica⼀、Mathematica⼊门1.Mathematica简介Mathematica是⼀个功能强⼤的计算机应⽤软件,由美国Wolfram Research公司开发,⾃1988年Mathematica1.0推出后,在计算技术领域引起了很⼤震动,使得Wolfram Research公司成为世界软件⼯业的先驱,并被⼴泛认为是技术和商业领域的佼佼者。
Mathematica是⼀个完全集成环境下的符号运算系统,具有强⼤的数值运算功能、符号运算功能、绘图功能。
利⽤Mathematica可以做任意位精度的数值计算。
如今,Mathematica 已⼴泛应⽤于数学、物理学、化学以及⼯程领域,被认为是现代技术的标志。
2. mathematica界⾯简介⼯作区窗⼝,基本输⼊模版,主菜单3. 会⾃制模版4.Mathematica的数值计算与符号运算使⽤Mathematica可以像使⽤标准科学计算器⼀样进⾏算术运算。
启动Mathematica后即可进⼊Mathematica系统集成界⾯,Mathematica集成界⾯可以输⼊⽂本、动画和实际的Mathematica输⼊。
加、减、乘、除、乘⽅的算符依次为+、-、*、/、^。
其中乘可以⽤空格来代替,减号可⽤来表⽰⼀个数的符号,并直接写在数的前边。
例1计算5.2+7.9。
解在Mathematica⼯作区输⼊:5.2+7.9,按Shift+Enter键后得结果:In[1]:=5.2+7.9Out[1]=13.1其中In[1]:=和Out[1]=是系统⾃动加上的,In后⾯代表输⼊的表达式,Out后⾯代表输出的结果。
Out[1]表⽰输⼊In[1]的输出结果,该结果可以被其它输⼊引⽤。
在Mathematica⼯作区输⼊命令后,按Shift+Enter键可以执⾏该命令,并输出结果。
本书各例中当有结果输出时,均需按Shift+Enter键。
In[2]:=Out[1]+10Out[2]=23.1但Mathematica⼜与计算器不同,它能给出精确的计算结果。
数学软件Mathematica的应用

数学软件Mathematica的应用一、数学软件Mathematica简介★ Mathematica是由美国Wolfram公司研究开发的一款着名的数学软件;★ Mathematica能够完成符号运算、数学图形的绘制等,功能非常强大;★ Mathematica能够做精确计算;★ Mathematica的界面操作非常友好;★ Mathematica是数学建模常用的数学软件之一。
二、利用模板进行微积分运算File(文件)→Palettes(模板)→BasicInput(基本输入)File(文件)→Palettes(模板)→BasicCalculations(基本计算)三、Mathematica中一些常用的函数(1(2(3((5(6(8)数值分析函数在Mathematica中,一个逻辑表达式的值有三个:真(True)、假(False)和“非真非假”。
条件控制函数If(1)If语句的结构与一般的程序设计语言中的If的结构类似。
它有三种情况: If[逻辑表达式,表达式1]当逻辑表达式的值为真时则计算表达式1,表达式1的值就是整个If结构的值;If[逻辑表达式,表达式1,表达式2]当逻辑表达式的值为真时则计算表达式1,为假时则计算表达式2;If[逻辑表达式,表达式1,表达式2,表达式3]当逻辑表达式的值为真时则计算表达式1,为假时则计算表达式2,其它情况则计算表达式3。
循环控制语句Mathematica中有3种描述循环的语句,它们是Do,While和For语句。
下面是其一般形式:For[初值,条件,修正,循环体]While[条件,循环体]Do[循环体,{循环范围}]四、结合图形进行分析1.作出函数xx f y 1sin )(==在区间]1,1[-上的图像,观察当0→x 时函数的变化情况;作出函数xx x f y 1sin )(==在区间]1,1[-上的图像,观察当0→x 时函数的变化情况;2.作出双曲抛物面xy z =的图形; 3.作weierstracs 函数)13cos(21)(1x x f nn nπ∑∞==(处处连续但处处不可导)的图像;4x ∈(-5,5), y ∈(-5,5)内的所有根;五、验证与探索1.x sin 的泰勒级数2.x sin 的无穷乘积猜想六、算法与程序1.分形图(迭代)2.将矩阵化为行最简形(步骤)七、实际问题的Mathematica 求解1.椭圆弧长的计算问题计算椭圆βα≤≤⎩⎨⎧==t t b y ta x ,sin cos 的弧长及近似值。
Mathematica入门及基础应用实例

Mathematica 入门一、引 言Mathematica 是美国Wolfram 公司开发的一个功能强大的数学软件系统,它主要包括:数值计 算、符号计算、图形功能和程序设计. 本指导书力图在不大的篇幅中给读者提供该系统的一个简 要的介绍. 指导书是按Mathematica 4.0版本编写的, 但是也适用于Mathematica 的任何其它图形 界面的版本.Mathematica 在数值计算、符号运算和图形表示等方面都是强有力的工具,并且其命令句法惊 人地一致, 这个特性使得Mathematica 很容易使用.不必担心你还不太熟悉计算机.本入门将带你 迅速了解Mathematica 的基本使用过程, 但在下面的介绍中,我们假定读者已经知道如何安装及启动Mathematica. 此外,始终要牢记的几点是:● Mathematica 是一个敏感的软件. 所有的Mathematica 函数都以大写字母开头;● 圆括号( ),花括号{ },方括号[ ]都有特殊用途, 应特别注意;● 句号“.”,分号“;”,逗号“,”感叹号“!”等都有特殊用途, 应特别注意;● 用主键盘区的组合键Shfit+Enter 或数字键盘中的Enter 键执行命令.二、一般介绍1. 输入与输出例1 计算 1+1:在打开的命令窗口中输入1+2+3并按组合键Shfit+Enter 执行上述命令,则屏幕上将显示:In[1] : =1+2+3Out[1] =6这里In[1] : = 表示第一个输入,Out[1]= 表示第一个输出,即计算结果.2. 数学常数Pi 表示圆周率π; E 表示无理数e; I 表示虚数单位i ;Degree 表示π/180; Infinity 表示无穷大.注:Pi,Degree,Infinity 的第一个字母必须大写,其后面的字母必须小写.3. 算术运算Mathematica 中用“+”、“-”、“*”、“/” 和“^”分别表示算术运算中的加、减、乘、除和 乘方.例2 计算 π⋅⎪⎭⎫ ⎝⎛⋅+⎪⎭⎫ ⎝⎛⋅--213121494891100. 输入 100^(1/4)*(1/9)^(-1/2)+8^(-1/3)*(4/9)^(1/2)*Pi则输出 3103π+ 这是准确值. 如果要求近似值,再输入N[%]则输出 10.543这里%表示上一次输出的结果,命令N[%]表示对上一次的结果取近似值. 还用 %% 表示上 上次输出的结果,用 %6表示Out[6]的输出结果.注:关于乘号*,Mathematica 常用空格来代替. 例如,x y z 则表示x*y*z,而xyz 表示字符 串,Mathematica 将它理解为一个变量名. 常数与字符之间的乘号或空格可以省略.4. 代数运算例3 分解因式 232++x x输入 Factor[x^2+3x+2]输出 )x 2)(x 1(++例4 展开因式 )2)(1(x x ++输入 Expand[(1+x)(2+x)]输出 2x x 32++例5 通分 3122+++x x 输入 Together[1/(x+3)+2/(x+2)]输出 )x 3)(x 2(x 38+++ 例6 将表达式)3)(2(38x x x +++ 展开成部分分式 输入 Apart[(8+3x)/((2+x)(3+x))]输出 3x 12x 2+++ 例7 化简表达式 )3)(1()2)(1(x x x x +++++输入 Simplify[(1+x)(2+x)+(1+x)(3+x)] 输出 2x 2x 75++三、函数1. 内部函数Mathematica 系统内部定义了许多函数,并且常用英文全名作为函数名,所有函数名的第一个 字母都必须大写,后面的字母必须小写. 当函数名是由两个单词组成时,每个单词的第一个字母都 必须大写,其余的字母必须小写. Mathematica 函数(命令)的基本格式为函数名[表达式,选项]下面列举了一些常用函数: 算术平方根x Sqrt[x]指数函数x eExp[x] 对数函数x a logLog[a,x] 对数函数x lnLog[x] 三角函数Sin[x], Cos[x], Tan[x], Cot[x], Sec[x], Csc[x] 反三角函数 ArcSin[x], ArcCos[x], ArcTan[x],ArcCot[x], AsrcSec[x], ArcCsc[x]双曲函数 Sinh[x], Cosh[x], Tanh[x],反双曲函数 ArcSinh[x], ArcCosh[x], ArcTanh[x]四舍五入函数 Round[x] (*取最接近x 的整数*)取整函数 Floor[x] (*取不超过x 的最大整数*)取模 Mod[m,n] (*求m/n 的模*)取绝对值函数 Abs[x]n 的阶乘 n!符号函数 Sign[x]取近似值 N[x,n] (*取x 的有n 位有效数字的近似值,当n 缺省时,n 的默认值 为6*)例8 求π的有6位和20位有效数字的近似值.输入 N[Pi] 输出 3.14159输入 N[Pi, 20] 输出 3.1415926535897932285注:第一个输入语句也常用另一种形式:输入 Pi//N 输出 3.14159例9 计算函数值(1) 输入 Sin[Pi/3] 输出23 (2) 输入 ArcSin[.45] 输出 0.466765(3) 输入 Round[-1.52] 输出 -2 例10 计算表达式)6.0arctan(226sin 2ln 1132+-+-e π 的值 输入 1/(1+Log[2])*Sin[Pi/6]-Exp[-2]/(2+2^(2/3))*ArcTan[.6]输出 0.2749212. 自定义函数在Mathematica 系统内,由字母开头的字母数字串都可用作变量名,但要注意其中不能包含空 格或标点符号.变量的赋值有两种方式. 立即赋值运算符是“=”,延迟赋值运算符是“: =”. 定义函数使用 的符号是延迟赋值运算符“: =”.例11 定义函数 12)(23++=x x x f ,并计算)2(f ,)4(f ,)6(f .输入Clear[f,x]; (*清除对变量f 原先的赋值*)f[x_]:=x^3+2*x^2+1; (*定义函数的表达式*)f[2] (*求)2(f 的值*)f[x]/.{x->4} (*求)4(f 的值,另一种方法*)x=6; (*给变量x 立即赋值6*)f[x] (*求)6(f 的值,又一种方法*)输出1797289注:本例1、2、5行的结尾有“;”,它表示这些语句的输出结果不在屏幕上显示.四、解方程在Mathematica 系统内,方程中的等号用符号“==”表示. 最基本的求解方程的命令为 Solve[eqns, vars]它表示对系数按常规约定求出方程(组)的全部解,其中eqns 表示方程(组),vars 表示所求未知变量.例12 解方程0232=++x x输入 Solve[x^2+3x+2==0, x]输出 }}1x {},2x {{-→-→例13 解方程组 ⎩⎨⎧=+=+10dy cx by ax 输入 Solve[{a x + b y == 0,c x + d y ==1}, {x,y}]输出 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+-→-→ad bc a y ,ad bc b x 例14 解无理方程a x x =++-11输入 Solve[Sqrt[x-1]+ Sqrt[x+1] == a, x]输出 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+→24a 4a 4x 很多方程是根本不能求出准确解的,此时应转而求其近似解. 求方程的近似解的方法有两种, 一种是在方程组的系数中使用小数,这样所求的解即为方程的近似解;另一种是利用下列专门用于 求方程(组)数值解的命令:NSolve[eqns, vars] (*求代数方程(组)的全部数值解*)FindRoot[eqns, {x, x0}, {y, y0}Λ,]后一个命令表示从点),,(00Λy x 出发找方程(组)的一个近似解,这时常常需要利用图像法先大 致确定所求根的范围,是大致在什么点的附近.例15 求方程013=-x 的近似解输入 NSolve[x^3-1== 0, x]输出 {{→x -0.5-0.866025ii},{→x -0.5+0.866025ii},{→x 1.}}输入 FindRoot[x^3-1==0,{x, .5}]输出 {→x 1.}下面再介绍一个很有用的命令:Eliminate[eqns, elims] (*从一组等式中消去变量(组)elims*)例16从方程组 ⎪⎩⎪⎨⎧=+=-+-+=++11)1()1(1222222y x z y x z y x 消去未知数y 、z .输入Eliminate[{x^2+y^2+z^2 ==1,x^2+(y-1)^2 + (z-1)^2 ==1, x + y== 1},{y, z}]输出 0x 3x 22==+-注:上面这个输入语句为多行语句,它可以像上面例子中那样在行尾处有逗号的地方将行与行 隔开, 来迫使Mathematica 从前一行继续到下一行在执行该语句. 有时候多行语句的意义不太明 确,通常发生在其中有一行本身就是可执行的语句的情形,此时可在该行尾放一个继续的记号“\”, 来迫使Mathematica 继续到下一行再执行该语句.五、保存与退出Mathematica 很容易保存Notebook中显示的内容,打开位于窗口第一行的File菜单,点击Save 后得到保存文件时的对话框,按要求操作后即可把所要的内容存为*.nb文件. 如果只想保存全部输入的命令,而不想保存全部输出结果,则可以打开下拉式菜单Kernel,选中Delete All Output,然后再执行保存命令. 而退出Mathematica与退出Word的操作是一样的.六、查询与帮助查询某个函数(命令)的基本功能,键入“?函数名”,想要了解更多一些,键入“??函数名”,例如, 输入?Plot则输出Plot[f,{x,xmin,xmax}] generates a plot of f as a functionof x from xmin to xmax. Plot[{f1,f2,…},{x,xmin,xmax}] plots several functions fi它告诉了我们关于绘图命令“Plot”的基本使用方法.例17 在区间]1,1y=的图形.[-上作出抛物线2x输入Plot[x^2,{x,-1,1}]则输出例18 .输入Plot[{Sin[x],Cos[x]},{x,0,2Pi}]则输出??Plot则Mathematica会输出关于这个命令的选项的详细说明,请读者试之.此外,Mathematica的Help菜单中提供了大量的帮助信息,其中Help菜单中的第一项Help Browser(帮助游览器)是常用的查询工具,读者若想了解更多的使用信息,则应自己通过Help菜单去学习.实验一一元函数微分学实验1 一元函数的图形(基础实验)实验目的 通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析 函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Mathematica 作平面曲线图性的方法与技巧.基本命令1. 在平面直角坐标系中作一元函数图形的命令Plot:Plot[f[x],{x,min,max},选项]Plot 有很多选项(Options), 可满足作图时的种种需要, 例如,输入Plot[x^2,{x,-1,1},AspectRatio->1,PlotStyle->RGBColor[1,0,0],PlotPoints->30]则输出2x y =在区间11≤≤-x 上的图形. 其中选项AspectRatio->1使图形的高与宽之比为1. 如 果不输入这个选项, 则命令默认图形的高宽比为黄金分割值. 而选项PlotStyle->RGBColor[1,0,0] 使曲线采用某种颜色. 方括号内的三个数分别取0与1之间. 选项PlotPoints->30令计算机描点作 图时在每个单位长度内取30个点, 增加这个选项会使图形更加精细.Plot 命令也可以在同一个坐标系内作出几个函数的图形, 只要用集合的形式{f1[x],f2[x],…} 代替f[x].2.利用曲线参数方程作出曲线的命令ParametricPlot:ParametricPlot[{g[t],h[t]},{t,min,max},选项]其中)(),(t h y t g x ==是曲线的参数方程. 例如,输入ParametricPlot[{Cos[t],Sin[t]},{t,0,2 Pi},AspectRatio->1]则输出单位圆t y t x sin ,cos ==的图形.3. 利用极坐标方程作图的命令PolarPlot如果想利用曲线的极坐标方程作图, 则要先打开作图软件包. 输入<<Graphics`Graphics`执行以后, 可使用PolarPlot 命令作图. 其基本格式为PolarPlot[r[t],{t,min,max},选项]例如曲线的极坐标方程为,3cos 3t r =要作出它的图形. 输入PolarPlot[3 Cos[3 t], {t,0,2 Pi}]便得到了一条三叶玫瑰线.4. 隐函数作图命令ImplicitPlot这里同样要先打开作图软件包, 输入<<Graphics\ImplicitPlot.m命令ImplicitPlot 的基本格式为ImplicitPlot[隐函数方程, 自变量的范围, 作图选项]例如方程22222)(y x y x -=+确定了y 是x 的隐函数. 为了作出它的图形, 输入ImplicitPlot[(x^2+y^2)^2==x^2-y^2,{x,-1,1}]输出图形是一条双纽线.5. 定义分段函数的命令Which命令Which 的基本格式为Which[测试条件1, 取值1, 测试条件2, 取值2,…]例如, 输入w[x_]=Which[x<0,-x,x>=0,x^2]虽然输出的形式与输入没有改变, 但已经定义好了分段函数:⎪⎩⎪⎨⎧≥<-=0,0,)(2x x x x x w 现在可以对分段函数)(x w 求函数值, 也可作出函数)(x w 的图形.实验举例初等函数的图形例1.1 作出指数函数x e y =和对数函数x y ln =的图形.输入命令Plot[Exp[x],{x,-2,2}]则输出指数函数xy =输入命令Plot[Log[x],{x,0.001,5},PlotRange->{{0,5},{-2.5,2.5}},AspectRatio->1]则输出对数函数x y ln =的图形. 注①:是描述x 的, 第二组数{-2.5,2.5}是描述y 的.注②:有时要使图形的x 轴和y 轴的长度单位相等, 需要同时使用PlotRange 和AspectRatio两个选项. 本例中输出的对数函数的图形的两个坐标轴的长度单位就是相等的.例1.2 作出函数x y sin =和x y csc =的图形观察其周期性和变化趋势.为了比较, 我们把它们的图形放在一个坐标系中. 输入命令Plot[{Sin[x],Csc[x]},{x,-2 Pi,2 Pi},PlotRange->{-2 Pi,2 Pi},注:.例1.3 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势.输入命令Plot[{Tan[x],Cot[x]},{x,-2 Pi,2 Pi},PlotRange->{-2 Pi,2 Pi},例 1.4 将函数观察直接函数和反函数的图形间的关系.输入命令p1=Plot[ArcSin[x],{x,-1,1}];p2=Plot[Sin[x],{x,-Pi/2,Pi/2},PlotStyle->GrayLeve1[0.5]];px=Plot[x,{x,-Pi/2,Pi/2},PlotStyle->Dashing[{0.01}]];.注 Show[…]命令把称为p1,p2和px 的三个图形叠加在一起显示. 选项PlotStyle->Dashing[{0.01}]使曲线的线型是虚线.例1.5 (教材 例1.1) 给定函数24325555)(x x x x x x f +++++= (a) 画出)(x f 在区间]4,4[-上的图形;(b) 画出区间]4,4[-上)(x f 与)()sin(x f x 的图形.输入命令f[x_]=(5+x^2+x^3+x^4)/(5+5x+5x^2);g1=Plot[f[x],{x,-4,4},PlotStyle->RGBColor[1,0,0]];则输出)(x f 在区间]4,4[-上的图形.输入命令g2=Plot[Sin[x]f[x],{x,-4,4},PlotStyle->RGBColor[0,1,0]]; Show[g1,g2];则输出区间]4,4[-上与的图形.注: Show[…]例1.6 在区间]1,1[-画出函数x y 1sin=的图形. 输入命令Plot[Sin[1/x],{x,-1,1}];则输出所求图形,从图中可以看到函数x y 1sin =在0=x 附近来回震荡.二维参数方程作图例1.7 作出以参数方程)20(sin ,cos 2π≤≤==t t y t x 所表示的曲线的图形.输入命令ParametricPlot[{2 Cos[t],Sin[t]},{t,0,2 Pi},AspectRatio->Automatic]注 在ParametricPlot 命令中选项AspectRatio->Automatic 与选项AspectRatio->1是等效的. 例 1.8分别作出星形线)20(sin 2,cos 233π≤≤==t t y t x 和摆线),sin (2t t x -=)40)(cos 1(2π≤≤-=t t y 的图形.输入命令ParametricPlot[{2 Cos[t]^3,2 Sin[t]^3},{t,0,2 Pi},AspectRatio->Automatic] ParametricPlot[{2*(t-Sin[t]),2*(1-Cos[t])},{t,0,4 Pi},AspectRatio->Automatic]则可以分别得到星形线和摆线的图形.例1.9 画出参数方程⎩⎨⎧==tt t y tt t x 3cos sin )(5cos cos )(的图形:输入命令ParametricPlot[{Cos[5 t]Cos[t],Sin[t]Cos[3t]},{t,0,Pi}, AspectRatio->Automatic];则分别输出所求图形.例1.10 (教材 例1.2) 画出以下参数方程的图形.(1) ⎪⎪⎩⎪⎪⎨⎧+⎪⎭⎫ ⎝⎛-=+⎪⎭⎫⎝⎛-=tt t y tt t x sin 7511sin 5)(cos 7511cos 5)( (2) ⎩⎨⎧-+=-+=t t t t y t t t t x sin )4cos 2sin 1()(cos )4cos 2sin 1()(分别输入以下命令:ParametricPlot[{5Cos[-11/5t]+7Cos[t],5Sin[-11/5t]+7Sin[t]},{t,0,10Pi},AspectRatio->Automatic];ParametricPlot[(1+Sin[t]-2 Cos[4*t])*{Cos[t],Sin[t]},{t,0,2*Pi},AspectRatio->Automatic,Axes->None]; 则分别输出所求图形例1.11 作出极坐标方程为)cos 1(2t r -=的曲线的图形.曲线用极坐标方程表示时, 容易将其转化为参数方程. 故也可用命令ParametricPlot[…]来作极坐标方程表示的图形.输入命令r[t_]=2*(1-Cos[t]);ParametricPlot[{r[t]*Cos[t],r[t]*Sin[t]},{t,0,2 Pi},AspectRatio->1]极坐标方程作图例1.12 (教材 例1.3) 作出极坐标方程为10/t e r =的对数螺线的图形. 输入命令<<Graphics`执行以后再输入PolarPlot[Exp[t/10],{t,0,6 Pi}]则输出为对数螺线的图形.隐函数作图例1.13 (教材 例1.4) 作出由方程xy y x 333=+所确定的隐函数的图形(笛卡儿叶形线). 输入命令<<Graphics\ImplicitPlot.m执行以后再输入ImplicitPlot[x^3+y^3==3x*y,{x,-3,3}]分段函数作图例1.14 分别作出取整函数][x y =和函数][x x y -=的图形. 输入命令Plot[Floor[x],{x,-4,4}]可以观察到取整函数的图形是一条阶梯形曲线.输入命令Plot[x-Floor[x],{x,-4,4}]得到函数][x x y -=.)例1.15 作出符号函数x y sgn =的图形. 输入命令Plot[Sign[x],{x,-2,2}]g[x_]: = -1/; x<0; g[x_]: = 0/; x=0; g[x_]: = 1/; x>0; Plot[g[x],{x,-2,2}]便得到上面符号函数的图形. 其中组合符号“/;”的后面给出前面表达式的适用条件例1.16 (教材 例1.5) 作出分段函数⎪⎩⎪⎨⎧>≤=0,,0,cos )(x e x x x h x 的图形.输入命令h[x_]:=Which[x<=0,Cos[x],x>0,Exp[x]] Plot[h[x],{x,-4,4}]则输出所求图形.注:一般分段函数也可在组合符号“/;”的后面来给出前面表达式的适用条件.例1.17 (教材 例1.6) 作出分段函数⎪⎩⎪⎨⎧=≠=0,00,1sin )(2x x xx x f 的图形. 输入命令f[x_]:=x^2Sin[1/x]/;x!=0;f[x_]:=0/; x=0;Plot[f[x],{x,-1,1}];则输出所求图形.函数性质的研究例1.18 研究函数)3(log 3)(35x e x x f x -++=在区间]2,2[-上图形的特征. 输入命令Plot[x^5+3E^x+Log[3,3-x],{x,-2,2}];则输出所求图形..例1.19 判断函数x x x f ππ2cos 2sin )(+=是否为周期函数.任选一个较大的范围, 如取]4,4[-, 在此区间上画出函数)(x f 的图形如图所示.Plot[Sin[2Pi x]+Cos[2Pi x],{x,-4,4}];例 1.20 判断函数133)(23+++==x x x x f y 的反函数的存在性. 若存在, 求反函数的表达式, 并画出起图形.先解方程,13323+++=x x x y 求x . 输入命令Solve[y==x^3+3x^2+3x+1,x]; 因此, 所求反函数为.13x y +-= 再输入命令Plot[-1+x^(1/3),{x,-3,3}];则输出反函数在区间]3,3[-内的图形.注:若一个函数满足: 一个y 对应着一个x , 则其反函数一定存在,且在表达式中将y 换成常量求解x , 即将所的表达式中y 换成x , x 换成y 即得到反函数的表达式.作函数图形的动画例1.21 制作函数cx sin 的图形动画, 观察参数c 对函数图形的影响. 输入命令.Do[Plot[Sin[c x],{x,-Pi,Pi},PlotRange->{-1,1}],{c,1,4,1/3}];则输出图形动画.例1.22 (教材 例1.7) 作出函数cx x x f sin )(2+=的图形动画,观察参数c 对函数图形的影响. 输入命令Do[Plot[x^2+Sin[c x],{x,-3,3},PlotRange->{-1,5}],{c,1,5,1/3}];则输出所求动画图形.实验习题1. 把正切函数x tan 和反正切函数x arctan 的图形及其水平渐近线2/,2/ππ=-=y y 和直线 x y =用不同的线型画在同一个坐标系内.2. 作出双曲正切函数x tanh 的图形.3. 输入以下命令Plot[{Sin[x],Sin[2 x],Sin[3 x]},{x,0,2 Pi}, PlotStyle->{RGBColor[1,0,0], RGBColor[0,1,0],RGBColor[0,0,1]}]理解选项的含义.4. 为观察复合函数的情况,分别输入以下命令:Plot[Sqrt[1+x^2],{x,-6,6},PlotStyle->{Dashing[{0.02,0.01}]}] Plot[Sin[Cos[Sin[x]]],{x,-Pi,Pi}]Plot[Sin[Tan[x]]-Tan[Sin[x]]/x^2,{x,-5,5}] Plot[{E^x,ArcTan[x],E^ArcTan[x]},{x,-5,5}]5. 观察函数的叠加, 输入以下命令:a1=Plot[x,{x,-5,5},PlotStyle->{RGBColor[0,1,0]}]a2=Plot[2 Sin[x],{x,-5,5},PlotStyle->{RGBColor[1,1,0]}] a3=Plot[x+2 Sin[x],{x,-5,5},PlotStyle->{RGBColor[1,0,0]}] Show[a1,a2,a3]6. 分别用ParametricPlot 和PolarPlot 两种命令, 作出五叶玫瑰线θ5sin 4=r 的图形.7. 用ImplicitPlot 命令作出椭圆322+=+xy y x 的图形.8. 选择以下命令的一部分输入, 欣赏和研究极坐标作图命令输出的图形.PolarPlot[Cos[t/2],{t,0,4 Pi}] PolarPlot[1-2 Sin[5 t],{t,0,2 Pi}] PolarPlot[Cos[t/4],{t,0,8 Pi}] PolarPlot[t*Cos[t],{t,0,8,Pi}] PolarPlot[t^(-3/2),{t,0,8 Pi}] PolarPlot[2 Cos[3 t],{t,0,Pi}] PolarPlot[1-2 Sin[t],{t,0,2 PI}] PolarPlot[4-3 Cos[t],{t,0,2 Pi}]PolarPlot[Sin[3 t]+Sin[2 t]^2,{t,0,2 Pi}] PolarPlot[3 Sin[2 t],{t,0,2 Pi}] PolarPlot[4 Sin[4 t],{t,0,2 Pi}]PolarPlot[Cos[2 t]+Cos[4 t]^2,{t,0,2 Pi}] PolarPlot[Cos[2 t]+Cos[3 t]^2,{t,0,2 Pi}]PolarPlot[Cos[4 t]+Cos[4 t]^2,{t,0,2 Pi},PlotRange->All]实验2 极限与连续(基础实验)实验目的 通过计算与作图, 从直观上揭示极限的本质,加深对极限概念的理解. 掌握用 Mathematica 画散点图, 以及计算极限的方法. 深入理解函数连续的概念,熟悉几种间断点的图形 特征,理解闭区间上连续函数的几个重要性质.基本命令1.画散点图的命令ListPlot:ListPlot[{{x1,y1},{x2,y2},…{xn,yn}},选项]或者ListPlot[{y1,y2,…yn},选项]前一形式的命令,在坐标平面上绘制点列),(,),,(),,(2211n n y x y x y x Λ的散点图;后一形式的命令, 默认自变量i x 依次取正整数,,,2,1n Λ作出点列为),(,),,2(),,1(21n y n y y Λ的散点图. 命令ListPlot 的选项主要有两个:(1) PlotJoined->True, 要求用折线将散点连接起来; (2) PlotStyle->PointSize[0.02], 表示散点的大小. 2.产生集合或者数表的命令Table:命令Table 产生一个数表或者一个集合. 例如, 输入Table[j^2,{j,1,6}]则产生前6个正整数的平方组成的数表{1,4,9,16,25,36}.3.连加求和的命令Sum:命令Sum 大致相当于求和的数学符号∑. 例如, 输入Sum[1/i,{i,100}]//N执行后得到1001312111++++Λ的近似值.与Sum 类似的还有连乘求积的命令Product. 4. 求函数多次自复合的命令Nest: 例如, 输入Nest[Sin,x,3]则输出将正弦函数自己复合3次的函数Sin[Sin[Sin[x]]]5.求极限的命令Limit: 其基本格式为Limit[f[x],x->a]其中f(x)是数列或者函数的表达式, x->a 是自变量的变化趋势. 如果自变量趋向于无穷, 用 x->Infinity.对于单侧极限, 通过命令Limit 的选项Direction 表示自变量的变化方向. 求右极限, 0+→a x 时, 用Limit[f[x],x->a,Direction->-1]; 求左极限, 0-→a x 时, 用Limit[f[x],x->a,Direction->+1]; 求+∞→x 时的极限, 用Limit[f[x],x->Infinity,Direction->+1]; 求-∞→x 时的极限, 用Limit[f[x],x->Infinity,Direction->-1]。
Mathematica软件介绍及其应用

可见,使用表达式”x=.”可以消除变量的赋值
17
Mathematica软件还可以定义函数
(1): f[x_]=Sin[x] (*被定义的函数的自变量后需跟下划线“_”*) (2)?f (*此命令用来查看f的含义*)
18
? 的其他用途
1、获取帮助信息
2、获取更多的帮助信息
3、获取更多的帮助信息
2
Mathematica的进一步说明
它吸取了不同类型软件的一些优点: (1)具有BASIC的简单易学的交互式方法 (2)具有MathCAD\Matlab那样强的数值计算能力 (3)具有Maple的和SMP那样的符号计算能力 (4)具有APL和LISP那样的人工智能列表处理能力 (5)像C和PASCAL那样的结构化设计语言 Mathematica的开发者 Stephen Wolfram是Mathematica的创始人,并被公认为是 当今科学计算的先驱。 Wolfram1959年出生于伦敦。他曾在 牛津大学和加州理工学院接受教育,15岁发表了第一篇科技 论文,1979年20岁时在加州理工学院获得理论物理学博士学 位。 他从1973年开始使用计算机,1981年主持开发了第一个计算 机代数系统SMP。
28
数的类型和精度
在Mathematica中,有四种类型的数据类型: 类型 说明
Integer
Rational Real
任意长度的整数
有理数 实数,可以具有一定的精 度
Complex
复数,a+bI的形式
29
整数,不用解释 有理数:可以看成两个整数的比 实数可以用小数点来区分(在Mathematica中实数可以 有任意精度的。Mathematica的一大特点就是符号计算 功能强大,数值运算不限精度。)
Mathematica 软件使用简介
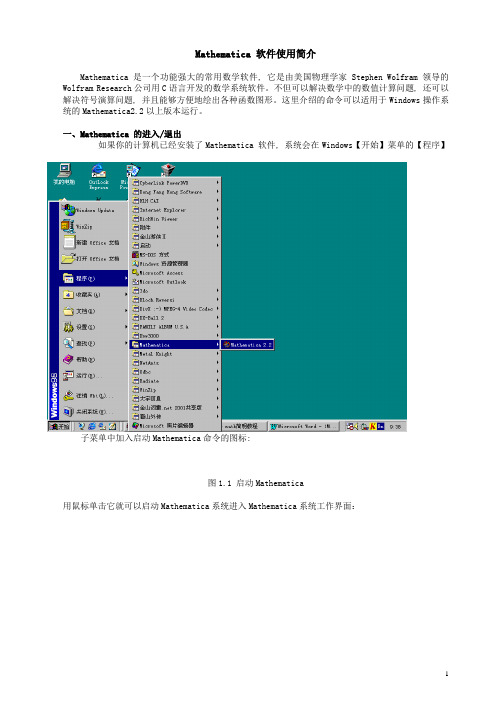
Mathematica 软件使用简介Mathematica 是一个功能强大的常用数学软件, 它是由美国物理学家Stephen Wolfram领导的Wolfram Research公司用C语言开发的数学系统软件。
不但可以解决数学中的数值计算问题, 还可以解决符号演算问题, 并且能够方便地绘出各种函数图形。
这里介绍的命令可以适用于Windows操作系统的Mathematica2.2以上版本运行。
一、Mathematica 的进入/退出如果你的计算机已经安装了Mathematica 软件, 系统会在Windows【开始】菜单的【程序】子菜单中加入启动Mathematica命令的图标:图1.1 启动Mathematica用鼠标单击它就可以启动Mathematica系统进入Mathematica系统工作界面:图1.2 Mathematica2.2工作界面图图1.3 Mathematica4.0工作界面图Mathematica系统工作界面是基于Windows 环境下的Mathematica 函数或程序运行与结果显示的图形用户接口, 是Mathematica的工作屏幕。
界面上方的主菜单和工具条的功能类似于Windows中的Word软件。
其中的空白位置称为Notebook用户区, 在这里可以输入文本、实际的Mathematica命令和程序等来达到使用Mathematica的目的。
在用户区输入的内容被 Mathematica用一个具有扩展名为“.ma”(Mathematica2.2)或“.mb”(Mathematica4.0)在的文件名来纪录,该文件名是退出Mathematica时保存在用户区输入内容的默认文件名,一般是文件名:“Newn b-1.ma”或“Newnb-1.mb”。
退出Mathematica系统像关闭一个Word文件一样, 只要用鼠标点击Mathematica系统集成界面右上角的关闭按钮即可。
关闭前, 屏幕会出现一个对话框, 询问是否保存用户区的内容, 如果单击对话框的“否(N)”按钮, 则关闭Notebook窗口, 退出Mathematica系统; 如果单击对话框的“是(Y)”按钮, 则先提示你用一个具有扩展名为 .ma或.mb的文件名来保存用户区内的内容, 再退出Mathematica系统。
科研的有力工具--Mathematica

科研的有力工具--Mathematica
倪致祥
【期刊名称】《阜阳师范学院学报(自然科学版)》
【年(卷),期】2005(022)002
【摘要】介绍了Mathematica的特点、功能和使用方法.
【总页数】4页(P7-10)
【作者】倪致祥
【作者单位】阜阳师范学院,物理系,安徽,阜阳,236032
【正文语种】中文
【中图分类】O41
【相关文献】
1.Mathematica软件在数学教学与科研中的应用 [J], 王兵贤;胡康秀
2.一个基于Mathematica平台的程序安全性自动验证工具 [J], 田丰;邢建英
3.STEAM教育深度学习的好工具r——Mathematica [J], 孟延豹;李想
4.良好的科研环境是科研的有力保障 [J], 王妮
5.完善的注册表工具Reg——一个强有力的注册表命令行工具就在你手中 [J], MarkMinasi;吴幼安
因版权原因,仅展示原文概要,查看原文内容请购买。
