传统和旋转交错网格有限差分在双相介质中模拟对比
地震波场的高阶交错网格有限差分模拟

地震波场的高阶交错网格有限差分模拟霍凤斌;李振鹏;徐发;张涛【摘要】This paper analyzes the stability and convergence of the seismic wave ifeld by using the high-order staggered-grid limited differential method of joining the absorbing boundary condition and attenuating zone to simulate the elastic wave equation. The results of the simulation of both isotropic-and anisotropic-medium models show that the grid frequency dispersion of the high-order differential wave equation simulation is smaller and more accurate. Therefore, this method should improve the efifciency of seismic prospecting and of the associated data interpretation.%应用高阶交错网格有限差分算法,并加入吸收边界条件和衰减带,对弹性波方程进行模拟,分析了其稳定性和收敛性。
通过对各向同性和各向异性介质模型的模拟表明,高阶差分波动方程模拟的网格频散较小、精度较高、效果较好,可为地震勘探及其资料解译提供技术手段。
【期刊名称】《上海国土资源》【年(卷),期】2014(000)001【总页数】4页(P97-100)【关键词】地震波场;波动方程;有限差分;边界条件;交错网格【作者】霍凤斌;李振鹏;徐发;张涛【作者单位】中海石油中国有限公司上海分公司,上海200030;中海石油中国有限公司上海分公司,上海200030;中海石油中国有限公司上海分公司,上海200030;中海石油中国有限公司上海分公司,上海200030【正文语种】中文【中图分类】P315.01随着地震波动理论在天然地震和油气地震中的应用,以及计算机技术的飞速发展,在现代地震数值模拟领域逐渐形成了有限差分法、有限元法、虚谱法和积分方程法等求解波动方程的方法。
基于交错网格有限差分弹性波正演模拟及波场特征分析

基于交错网格有限差分弹性波正演模拟及波场特征分析【摘要】为研究和认识多种储层中弹性波的波场特征,以利于多波地震资料解释,高精度数值模拟是有效的方法之一。
本文在弹性波方程基础上,采用高阶交错网格有限差分技术模拟地震波在各向同性介质和各向异性介质中的传播,可得到不同类型介质的弹性波场。
同时,文中也分析了各向异性系数对多波波场特征的影响。
通过对高精度数值模拟得到的波场快照对比研究表明,该方法可有效获得高精度弹性波正演结果,为研究各种复杂介质中弹性波的波场特征和传播规律奠定了基础。
【关键词】多波多分量波场特征各向异性弹性波正演1 引言随着油气田勘探技术的不断发展[1][2],人们对地震资料的认识也不断加深,纵波地震资料在含油气的显示上存在一些不确定性,单一纵波资料解释的多解性问题尤为突出。
在地震勘探领域中,过去一直把各向同性弹性体理论作为研究地下介质的前提,但是在实际地层中普遍存在各向异性,地下介质的各向异性(如周期薄互层引起的各向异性、以及裂隙引起的各向异性)产生的弹性波场与各向同性介质产生的弹性波场存在着不可忽略的差异。
由此,多波地震勘探作为油储地球物理的主要方法之一应运而生。
在多波资料解释过程中,要求搞清楚储层的岩性与多波的波场特征之间的关系,因此,多波波场数值模拟技术显得非常重要。
高精度数值模拟技术是联系地震、地质、测井以及油藏工程的纽带,其作用主要体现在提高人们对各种复杂介质中地震波传播规律的认知,并可为新技术、新方法提供试验数据,以满足方法技术研究的需要,同时也可以检验解释结果的正确性。
弹性波波动方程高精度数值模拟可以得到全波场信息,包含了地震波的动力学和运动学特点,为准确描述地震波场特征和波的传播规律奠定基础,本文在弹性波方程基础上,采用高阶交错网格有限差分技术模拟地震波在各向同性介质和各向异性介质中的传播,比较地震波在各向同性介质和各向异性介质中的波场响应异同,并分析了各向异性系数对多波波场特征的影响,这对研究各种复杂介质中弹性波的波场特征和传播规律有着重要的意义。
211064860_基于双相介质弹性波波场分离的逆时偏移方法

第45卷 第1期2023年1月物探化探计算技术COMPUTINGTECHNIQUESFORGEOPHYSICALANDGEOCHEMICALEXPLORATIONVol.45 No.1Jan.2023收稿日期:2021 10 23基金项目:国家自然科学基金创业创新发展联合基金(U19B603)第一作者:王鸣谦(1995-),男,硕士,主要研究方向为地震波正演及偏移成像,E mail:285639863@qq.com。
文章编号:1001 1749(2023)01 0001 07基于双相介质弹性波波场分离的逆时偏移方法王鸣谦1,张胜寒1,张济东1,付继有2(1.中国石油化工股份有限公司 石油物探技术研究院,南京 2111032.中国石油 长庆油田页油岩开发分公司,甘肃 745000)摘 要:随着地震勘探的发展,以单相介质模型为基础的声波逆时偏移和弹性波逆时偏移很难比较精确地描述地下介质和满足复杂的工程要求,尤其是在处理地下含流体多孔介质时,所以需要引入双相介质模型。
首先基于Biot理论双相介质一阶速度-应力弹性波方程,利用散度场和旋度场的波场分离理论将固相和流相中的纵横波场解耦分离,并由波场快照图得出固相与流相中的纵波波场与横波波场均完成分离,而快纵波与慢纵波相互耦合均存在于纵波波场中。
采用高阶交错网格有限差分方法,结合PML吸收边界条件,推导了具有波场分离的双相介质弹性波正传与反传的偏移延拓算子,结合互相关成像条件,可以得到双相介质弹性波固相与流相中的各分量偏移成像剖面。
最后对模型使用该双相介质弹性波波场分离的逆时偏移方法进行偏移成像试算并取得成功,效果较常规双相介质弹性波逆时偏移成像效果有了明显提升。
关键词:Biot理论;双相介质;波场分离;弹性波逆时偏移中图分类号:P631.4 文献标志码:A 犇犗犐:10.3969/j.issn.1001 1749.2023.01.010 前言由于实际情况中含有油气的储层是具有固体与流体两种状态的双相介质,因此建立在均匀各向同性的理论基础上研究波动传播规律并不是十分准确的,只是将储层简化为单相弹性介质,从而忽略了固相和流相之间的耦合作用,因此对地震波的传播描述有所偏差,所以建立更加符合实际地层情况的双相介质模型具有重大意义。
二维声波方程交错网格有限差分数值模拟研究

在对介质模型进行离散化处理的过程中,网格
是一种常用手段。对波动方程进行网格离散,可以
利用交错网格的差分形式。交错网格就是把速度和
应力分配到两套不同的网格中,这样可以使速度、应
力得到很好的耦合[2]。利用交错网格有限差分法对
一阶速度—应力波动方程进行求解时,应力、速度等
分量在模型交错网格节点中的位置分布如图 1所示。
-U ] k+1/2 i,j-n+1
其中 x=iΔx,z=jΔz,t=kΔt,i、j、k分别表示空 间和时间网格点。Uki,+j1/2,Wki++11//22,j+1/2,Pki,+j+11/2/2,Qki,j+1/2 和 Ski+1/2,j分别是速度 Vx、Vz与应力 σxx、σzz、σxz的离 散值。
数的问题转化为求解网格节点上的差分方程组的问
题,得到数值解。在波动方程网格离散化的过程中,
可以利用交错网格的差分形式。
1.1 均匀各向同性介质二维声波方程
均匀各向同性介质二维声波方程可表示为:
2u(x,xy2,z,t)+2u(x,zy2,z,t)=
v2(1x,z)2u(x,ty2,z,t)
(1)
应力 Pxx: Pki++11/2,j=Pki+1/2,j+C11ΔΔxtnΣN=1CNn[Uki++n1,/j2-Uik-+n1+/21,j]+
C13ΔΔztnΣN=1CNn[Wik++11//22,j+n-1/2
-W ] k+1/2 i+1/2,j-n1/2
应力 Qzz: Qik++11/2,j=Qki+1/2,j+C13ΔΔxtnΣN=1C(nN)[Uik++n1,/j2-Uik-+n1+/21,j]+
C33ΔΔztnΣN=1C(nN)[Wki++11//22,j+n-1/2-Wik++11//22,j-n+1/2]
一种基于全局优化的交错网格有限差分法

一种基于全局优化的交错网格有限差分法印兴耀;刘博;杨凤英【摘要】在地震波场数值模拟中,交错网格有限差分技术得到了广泛的应用,但是在弹性模量变化较大时,通常会因插值而导致模拟误差增大。
旋转交错网格可以很好地克服这个缺点,因而适合于各向异性介质正演模拟。
但是对于同样大小的网格单元,旋转交错网格需要的步长比常规交错网格要大,这会使梯度和散度算子的误差增大因而更易产生空间数值频散。
针对这些问题,本文提出了旋转交错网格与紧致有限差分相结合的方法,并基于模拟退火算法进行全局优化,压制数值频散,拓宽波数范围。
数值模拟结果表明,此方法可以有效地压制数值频散,且具有较高的模拟精度。
%Staggered grid finite difference techniques have been widely used in numerical simulation of seismic wave field,but the interpolation might enlarge the simulation errors when the elastic moduli change dramatically.Rotated staggered grid can overcome this drawback thus be more applicable for modeling the anisotropic media.However,for the grid cells with the same size,rotated staggered grid needs larger step than conventional staggered grid does,conse-quently,the gradient operator and divergence operator generate larger errors which are more likely to cause spatial numerical dispersion.Aiming at the above problems,a combination of rotated staggered grid and compact finite difference method is proposed,simultaneously,global optimization is preformed based on simulated annealing algorithm to suppress numerical dispersion and to broaden the range of wavenumber.Numerical simulation results show thatthis method can effectively suppress the numerical dispersion and exhibits high simulation accuracy at the same time.【期刊名称】《地震学报》【年(卷),期】2015(000)002【总页数】11页(P278-288)【关键词】全局优化;旋转交错网格;紧致有限差分;数值频散;正演模拟【作者】印兴耀;刘博;杨凤英【作者单位】中国山东青岛 266580 中国石油大学华东地球科学与技术学院;中国山东青岛 266580 中国石油大学华东地球科学与技术学院;中国山东青岛 266580 中国石油大学华东地球科学与技术学院【正文语种】中文【中图分类】P315.3+1引言地震波数值模拟是在地震波传播理论的基础上,通过数值计算来模拟地震波在地下介质中的传播(董良国,2003),是研究地震波传播特性与地球介质参数关系的重要手段.交错网格有限差分技术已经广泛应用于各向异性介质(Igel et al,1995;Collino,Tsogka,2001;裴正林,王尚旭,2005;殷文等,2006;何燕,2008)、孔隙介质(Dai et al,1995;Zeng et al,2001;孙林洁,2012)、黏弹性介质(白晓寅,2008;孙成禹等,2010)的波动方程模拟中,但是常规交错网格在模拟非均匀性较强的介质和各向异性介质时需对介质参数进行平均或内插(陈浩等,2006),低阶插值可能会导致精度降低,高阶插值则会导致计算量增大.Gold等(1997)提出了旋转交错网格有限差分算法,Saenger等进一步研究了旋转交错网格的稳定性与频散的关系(Saenger et al,2000;Saenger,Bohlen,2004).在旋转交错网格中采用沿网格对角线差分的方式,可以避免弹性模量的平均与插值,因而更准确.随后一些研究人员通过旋转交错网格的完全匹配层(perfectly matched layer,简写为PML)边界条件的实现,利用旋转交错网格技术对各向异性介质(李敏,刘洋,2012)和黏弹介质(严红勇,刘洋,2012)等进行了数值模拟.但由于旋转交错网格中差分是沿对角线进行,步长是同等条件下常规交错网格的■2倍(网格是正方形的情况下),若用常规的差分格式会导致离散的梯度算子和散度算子在计算时误差增大,因而容易出现数值频散.而如果使用高阶有限差分则会因需要更多的网格点而增大计算量与内存.紧致有限差分是一种隐式差分格式,在同等网格数的条件下,具有比常规差分格式更高的精度以及更低的数值频散,故成为目前关注的热点.Lele(1992)分析了紧致差分格式的分辨率特性;王书强等(2002)对弹性波方程的紧致差分格式及其与中心差分的误差进行了研究;Du等(2009)基于交错网格紧致有限差分进行了横向各向同性介质的正演模拟;Boersma(2011)利用6阶紧致有限差分求解了Navier-Stokes方程.实现有限差分时,差分系数的确定会影响数值模拟的精度.有限差分系数的求取一般包括泰勒展开和最优化算法两种方法(Liu,2013).基于泰勒展开得到的差分系数在波数较小时精度高,但随波数增大其精度会降低;基于最优化算法的差分系数求取方法是在给定精度与差分算子长度的情况下尽可能拓宽波数范围(Holberg,1987).Shan(2009),Kosloff等(2010),Zhou和Zhang(2011)以及Liu(2013)等对基于最小二乘算法的差分算子优化方法进行了深入研究;Zhang 和Yao(2012)则基于模拟退火算法对中心差分算子进行了优化.本文拟结合旋转交错网格与紧致有限差分技术,基于模拟退火全局优化算法对紧致差分算子进行优化,拓宽数值模拟的波数范围,在此基础上进行频散分析,最后通过数值模拟验证该方法的可行性和有效性.1 旋转交错网格紧致有限差分方法1.1 一阶速度-应力方程在弹性波正演模拟中,除了使用二阶方程外,还常常采用一阶速度-应力弹性波方程,其主要优点是无需对弹性常数进行空间差分(Virieux,1984).这里根据运动平衡方程和本构关系给出二维情况下体力为零时各向异性介质的一阶速度-应力方程:式中:v,σ分别代表速度和应力,1表示x方向,3表示z方向;cij为介质弹性张量矩阵的元素,当极端各向异性介质时,该矩阵有21个独立参数;当二维时,不考虑y分量,故张量矩阵中与y分量有关参数为0,只有5个独立参数(c11,c13=c31,c15=c51,c33,c35=c53,c55).1.2 紧致有限差分在地震波正演模拟中,采用常规的中心有限差分往往需要较多的网格点才能比较有效地压制数值频散,不利于边界的处理(王书强等,2002).紧致有限差分是一种隐式差分格式,只需要较少的网格点即可有效地压制数值频散,且同等阶次的精度要比常规中心有限差分格式高,因此本文采用紧致有限差分格式,弥补旋转交错网格因差分步长大导致梯度和散度算子在计算时误差增大因而更容易产生数值频散的不足.常规的2(M-1)点2 M阶紧致有限差分格式(Kim,Lee,1996)为式中,Δx为网格的空间步长,a和bn分别为差分的权系数,可以通过在第i个网格点的泰勒展开,然后对比对应系数来求解即可得到2(M-1)点2 M阶紧致有限差分格式的差分系数(Liu,Sen,2009),例如当M=5时,可以得到8点10阶的紧致差分格式系数为a=0.257 894 74,b1=0.889 871 16,b2=0.216 121 16,b3=-0.004 701 2,b4=0.000 151 55.1.3 旋转交错网格及完全匹配层吸收边界条件在二维旋转交错网格上,密度和速度的各个分量定义在相同位置,弹性模量和应力的各个分量定义在另外的相同位置上,如图1所示.旋转交错网格在计算时分为两步(陈浩等,2006):首先,计算沿着对角线方向即˜x,˜z方向进行差分,得到相关物理量的对角线方向的空间一阶导数;然后,通过坐标旋转的换算关系,将得到的两个对角线方向的差分进行线性组合从而获得坐标轴方向即x,z方向的一阶空间导数,其换算关系为(Saenger et al,2000):图1 旋转交错网格及完全匹配层吸收边界示意图x,z为坐标轴方向,x˜,z˜为对角线方向;灰色区域表示沿着x和z方向均进行衰减,白色区域表示只沿着x方向或者z方向进行衰减Fig.1 Schematic diagram of rotated staggeredgridand perfectly matched layer(PML)absorbing boundary xand zare the coordinate directions,andx˜andz˜ are the diagonal directions.Gray areas indicate that waves are absorbed along both xand z directions and white areas indicate that waves are absorbed only along the xor zdirection式中,∂/∂x˜和∂/∂z˜是沿对角线方向的导数;∂/∂x和∂/∂z是沿坐标轴方向的导数.利用波动方程进行数值模拟,一个关键问题就是边界条件.为了解决边界反射问题,引入弹性波方程的PML边界条件.陈浩等(2006)指出,在旋转交错网格中,PML吸收边界条件的处理方式及吸收效果与常规交错网格中几乎是一样的.为此,引入图1所示的PML吸收层.PML边界的基本做法是在研究区域四周引入PML,波在PML中传播时不会产生反射,并且随传播距离按一定规律衰减.当波传播到PML边界时,波场近似为零,也不会产生反射(王守东,2003).以式(1)中的vx为例来说明旋转交错网格紧致有限差分算法PML的实现方法:式中表示n+1/2时刻vx 在网格点(i,j)处沿坐标轴x方向的分量,表示n-1/2时刻的x方向分量,di为衰减因子,表示n 时刻σxx在网格点(i,j)处沿坐标轴x方向的导数.根据式(5)可推导出式中沿着所在对角线˜x与斜对角线˜z方向的导数值,根据求出.其中类似地可以推导出其它分量的旋转交错网格紧致有限差分下的PML控制方程. 1.4 紧致有限差分的全局优化根据平面波理论,令式中,β=kΔx/2,0≤β≤π/2.为了使式(2)左右两边的误差尽可能小,须满足β-β*≈0的β取值范围应尽可能地大.本文中,采用模拟退火全局最优算法(Kirkpatrick et al,1983)来优化旋转交错网格紧致有限差分算子.为此,建立以下目标函数:Kim和Lee(1996)指出,当θ接近最大值π/2时,会出现很多难以控制的误差,从而导致优化效果不佳,因此本文选择θ=rπ/2,其中0<r<1.表1列出了优化的8点10阶,10点12阶,12点14阶以及14点16阶的紧致有限差分系数.表1 优化的10—16阶紧致有限差分系数Table 1 Optimized coefficients of 10—16-order compact finite-difference阶次 r a b1 b2 b3 b4/10-2 b5/10-5 b6/10-3 b7/10-5 10 0.85 0.384 0.728 0.369 -0.015 0.152 12 0.87 0.390 0.720 0.376 -0.016 0.171 -6.49 14 0.89 0.434 0.658 0.434 -0.022 0.361 -74 0.138 16 0.85 0.452 0.633 0.458 -0.0252 0.452 -114 0.322 -7.792 频散分析由式(12)可以看出,β接近于β*的程度表征了优化的紧致有限差分算子的精度,故定义使α≈1的β取值范围越大,数值频散越小.图2给出了常规的基于泰勒展开得到的差分算子与本文提出的全局优化算子的精度对比.可以看出,对于常规的基于泰勒展开得到的紧致有限差分算子,随着空间阶次的增大,使α≈1的波数范围变得越宽,即数值模拟的精度随阶次的增大而增大.显然,本文得到的全局优化的紧致有限差分算子在相同最大误差下使α≈1的波数范围比常规紧致有限差分算子还要大.从图2中还可以看出,优化的8点10阶紧致有限差分算子的频散比常规14点16阶紧致有限差分算子小,即优化的10阶精度要高于常规的16阶精度,从而可以使用较少的网格点来达到较高的精度,节省计算内存.图2 10阶常规有限差分,10—16阶常规紧致有限差分及对应的优化紧致有限差分的频散对比(k代表波数,Δx表示空间网格间距)Fig.2 Dispersion comparison by 10-order conventional finite-difference,10—16-order conventional compact finite-difference and the corresponding optimized compact finitedifference.k denotes the wavenumber,andΔxis spatial grid spacing由图2中的10阶常规有限差分、10阶常规紧致有限差分与10阶优化紧致有限差分的频散曲线可以看出,10阶常规紧致有限差分格式的波数范围较10阶常规有限差分要宽,而经过优化的10阶紧致有限差分格式的波数范围则更进一步拓宽.设最大允许误差为εmax=|α-1|0≤β≤βmax,取εmax=0.2%,分别计算得到10阶常规有限差分、10阶常规紧致有限差分及10阶优化紧致有限差分的最大波数范围βmax分别为0.847 5,1.037 5,1.458 0,即10阶常规紧致有限差分的波数范围比常规差分格式拓宽了1.22倍,而经过全局优化后,波数范围提升至1.72倍.考虑到正演模拟中最常采用Δx=Δz的情况,则对于旋转交错网格,Δr比常规交错网格差分步长Δx及Δz增大了2倍,因而可以采用优化系数的紧致有限差分来弥补这一不足,从而有效地压制数值频散.需要指出的是,优化系数的紧致有限差分格式也可以很方便地应用于PML边界条件,而不需要特殊的处理.3 模型试算3.1 模型1为了验证全局优化的旋转交错网格紧致有限差分的精度比常规旋转交错网格有限差分方法有所提升,首先采用一个简单的各向同性模型进行测试(模型大小为3 000m×3 000m,在测试中并未添加任何边界条件),震源采用主频30Hz的雷克子波,z方向集中力源激发,网格大小为Δx=Δz=10m,时间采样为Δt=1ms.纵横波速度分别为4 000m/s和2 600m/s,模型密度为2 300kg/m3.图3给出了3种有限差分条件下400ms时刻x分量波场快照,均采用旋转交错网格系统.图3a采用常规10阶常规有限差分格式;图3b采用8点10阶,10点12阶,12点14阶,14点16阶常规紧致有限差分格式;图3c采用优化的8点10阶紧致有限差分格式.可以看出,10阶常规有限差分与10阶紧致有限差分对比,后者频散要小;而对于图3b中的紧致有限差分格式,随着空间阶次的增大,其精度越高,频散越小;对比图3b与图3c可以看出,优化的8点10阶紧致有限差分的数值频散甚至比常规14点16阶紧致有限差分还要小,这与图2所示是一致的.图4给出了从图3中提取的z=500m处(即50个网格点处)的波形曲线,以此来对比以上3种差分格式的数值频散.可以看出,10阶常规有限差分算法在波形外出现了数值抖动,说明数值频散比较高,模拟精度相对较低,而10阶紧致有限差分和优化的10阶紧致差分精度较高,从虚线框中可以进一步看出优化的10阶紧致有限差分算法的精度更高一些.图3 10阶常规有限差分(a),10—16阶常规紧致有限差分(b)与优化的10阶紧致有限差分(c)得到的波场快照Fig.3 Snapshots of wave field by using 10-order conventional finite-difference(a),10-16-order conventional compact finite-difference(b)and optimized 10-order compact finite-difference(c)3.2 模型2图4 10阶常规有限差分,10阶常规紧致有限差分及10阶优化紧致有限差分波形对比图Fig.4 Comparison of waveforms by using 10-order conventional finite-difference(FD)(dark line),10-order conventional compact FD (blue line)and optimized 10-order compact FD (red line)模型2的几何构造如图5所示,其中凹陷构造上部及下部均为各向同性介质,最下层为横向各向同性(VTI)介质.模型纵向和横向长为3 000m,具体参数见表2.采用优化的旋转交错网格紧致有限差分方法进行正演模拟,网格大小为Δx=Δz=10m,时间采样为Δt=1ms.震源采用30Hz雷克子波,在模型的(1 150m,1 500m)处以纵波源形式激发.模拟过程中,采用PML边界条件(PML层部分同样采用优化的旋转交错网格紧致有限差分算法),厚度层为30个网格点.为体现吸收效果包含了PML层,图6给出了600ms时刻x及z分量的波场快照.可以看出,震源激发的纵波传播至分界面时,发生了反射与透射,可以见到PP波、PS波等,并可在凹陷处看到断面波,波场复杂,但波前面清晰,数值频散小.从图7所示的单炮记录中也可以看出优化的旋转交错网格紧致有限差分算法具有较高的模拟精度,各类波均可得到清晰体现,并且能够证明所加PML边界条件的吸收效果很好,无明显人为边界反射产生.图5 凹陷模型示意图Fig.5 Schematic diagram of the depression model图6 600ms时刻优化的旋转交错网格紧致有限差分正演x分量(左)和z分量(右)的波场快照(虚线框外围代表PML层)Fig.6 Wavefield snapshots of x-(left)and z-component(right)at 600ms using optimized rotated staggered-grid compact finite-difference method(PML layers are outside the dashed box)表2 凹陷模型参数Table 2 Parameters of the depression model序号介质类型 c11/GPa c13/GPa c33/GPa c55/GPa 密度/(kg·m-3)31.77 42.68 31.77 13.75 2200第二层各向同性 42.33 47.04 42.34 18.82 2400第三层横向各向同性第一层各向同性87.88 21.22 67.60 22.56 2500图7 凹陷模型优化的旋转交错网格紧致有限差分正演x分量(左)和z分量(右)单炮记录Fig.7 Records of x-(left)and z-component(right)of the depression model using optimized rotated staggered-grid compact finite-difference method4 讨论与结论旋转交错网格在地震波正演模拟中由于其可以避免在模拟中因弹性模量插值或平均而产生的误差和其对边界条件处理的便捷性而被广泛应用.但由于其差分方向是沿网格的对角线方向,因此相对于常规的交错网格而言,其差分步长较大,梯度算子、散度算子在计算时更容易产生误差,这意味着旋转交错网格更容易产生数值频散,从而影响模拟的精度.若采用小网格,虽然可以压制数值频散,却又大大增加了运算量及内存.因此本文采用旋转交错网格与紧致有限差分技术相结合的方法来提高模拟精度,并在此基础上,基于模拟退火算法对紧致有限差分进行全局优化,进一步提高计算精度,压制数值频散.数值频散分析结果表明,优化的旋转交错网格紧致有限差分算法相对于普通旋转交错网格有限差分算法具有更宽的波数范围,这意味着优化的旋转交错网格有限差分算法可以在采用更大的空间采样间隔或者更高的震源主频时依然有较高的精度和较低的数值频散;且经过全局优化的10阶紧致有限差分算子比常规的16阶紧致有限差分算子具有更高的精度,即可以采用较少的网格点来达到较高的模拟精度,因此可以节省计算内存.数值模拟实验进一步证实了本文提出的优化的旋转交错网格紧致有限差分算法的正确性与可行性.凹陷模型中,各类波均具有比较清晰的响应,揭示了波场的传播规律.同时波场快照与单炮记录中无明显的人为边界反射产生,也证明了模拟采用的PML吸收边界条件的有效性.但是本文提出的方法亦存在不足之处.在求解紧致差分格式时需要解三角矩阵线性方程,较常规显式有限差分格式增加额外的计算负担,且不利于在GPU等平台直接并行,例如图3a和图3c中的400ms时长的计算时间分别为46.5s和85.6s,后者计算耗时约为前者的1.8倍.在科学计算中,效率与计算精度常常不可兼得,随着计算机科学计算能力的提高,可以采用GPU加速的LU分解算法或者使用LAPACK等优化程序包来克服求解大型矩阵的计算效率问题.在实际应用中需权衡利弊,选择适合的算法.衷心感谢审稿专家提出的宝贵意见和建议.参考文献白晓寅.2008.基于地震波衰减理论的地层吸收参数提取方法研究[D].东营:中国石油大学(华东)地球科学与技术学院:24-54.Bai X Y.2008.The Study on Method of Layer Absorbing Parameters Extraction Based on the Theory of Seismic Wave Attenuation[D].Dongying:School of Geosciences,China University of Petroleum:24-54(in Chinese).陈浩,王秀明,赵海波.2006.旋转交错网格有限差分及其完全匹配层吸收边界条件[J].科学通报,51(17):1985-1994.Chen H,Wang X M,Zhao H B.2006.Rotated staggered grid finite-difference and the PML boundary[J].Chinese Science Bulletin,51(17):1985-1994(in Chinese).董良国.2003.地震波数值模拟与反演中几个关键问题研究[D].上海:同济大学海洋与地球科学学院:1-2.Dong L G.2003.Several Key Problems in Seismic Wave Numerical Simulation and Inversion[D].Shanghai:School of Ocean and Earth Science,Tongji University:1-2(in Chinese).何燕.2008.正交各向异性弹性波高阶有限差分正演模拟研究[D].东营:中国石油大学(华东)地球科学与技术学院:45-80.He Y.2008.High-Order Finite-Difference Forward Modeling of Elastic-Wavein Orthorhombic Anisotropic Media[D].Dongying:School of Geosciences,China University of Petroleum:45-80(in Chinese).李敏,刘洋.2012.高阶旋转交错网格有限差分方法模拟TTI介质中横波分裂[J].物探与化探,36(6):934-940.Li M,Liu Y.2012.Modeling of the S-wave splitting in TTI media using high-order rotated staggered grid scheme[J].Geophysical and Geochemical Exploration,36(6):934-940(in Chinese).裴正林,王尚旭.2005.任意倾斜各向异性介质中弹性波波场交错网格高阶有限差分法模拟[J].地震学报,27(4):441-451.Pei Z L,Wang S X.2005.A staggered-grid high-order finite-difference modeling for elastic wave field in arbitrary tilt anisotropic media[J].Acta Seismologica Sinica,27(4):441-451(in Chinese).孙成禹,肖云飞,印兴耀,彭洪超.2010.黏弹介质波动方程有限差分解的稳定性研究[J].地震学报,32(2):147-156.Sun C Y,Xiao Y F,Yin X Y,Peng H C.2010.Study on the stability of finite difference solution of visco-elastic wave equations[J].Acta Seismologica Sinica,32(2):147-156(in Chinese).孙林洁.2012.非均匀孔隙介质有限差分正演模拟方法研究[D].青岛:中国石油大学(华东)地球科学与技术学院:64-108.Sun L J.2012.Finite-Difference Modeling Research in Heterogeneous Porous Media[D].Qingdao:School of Geosciences,China University of Petroleum:64-108(in Chinese).王守东.2003.声波方程完全匹配层吸收边界[J].石油地球物理勘探,38(1):31-34.Wang S D.2003.Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J].Oil Geophysi-cal Prospecting,38(1):31-34(in Chinese).王书强,杨顶辉,杨宽德.2002.弹性波方程的紧致差分方法[J].清华大学学报:自然科学版,42(8):1128-1131.Wang S Q,Yang D H,Yang K pact finite difference scheme for elastic equations[J].Journal of Tsinghua University:Science and Technology,42(8):1128-1131(in Chinese).严红勇,刘洋.2012.黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J].地球物理学报,55(4):1354-1365.Yan H Y,Liu Y.2012.Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media [J].Chinese Journal of Geophysics,55(4):1354-1365(in Chinese). 殷文,印兴耀,吴国忱,梁锴.2006.高精度频率域弹性波方程有限差分方法及波场模拟[J].地球物理学报,49(2):561-568.Yin W,Yin X Y,Wu G C,Liang K.2006.The method of finite difference of high precision elastic wave equations in the frequency domain and wave field simulation[J].Chinese Journal of Geophysics,49(2):561-568(in Chinese).Boersma B J.2011.A 6th order staggered compact finite difference method for the incompressible Navier-Stokes and scalar transport equations[J].J Comput Phys,230(12):4940-4954.Collino F,Tsogka C.2001.Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropicheterogeneous media[J].Geophysics,66(1):294-307.Dai N,Vafidis A,Kanasewich E R.1995.Wave propagation in heterogeneous,porous media:A velocity-stress,finitedifference method [J].Geophysics,60(2):327-340.Du Q Z,Li B,Hou B.2009.Numerical modeling of seismic wavefields in transversely isotropic media with a compact staggered-grid finite difference scheme[J].Appl Geophys,6(1):42-49.Gold N,Shapiro S A,Burr E.1997.Modelling of high contrasts in elastic media using a modified finite difference scheme[C]∥SEG Technical Program Expanded Abstracts.Dallas,Texas:SEG:1850-1853.Holberg putational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena[J].Geophys Prospect,35(6):629-655.Igel H,Mora P,Riollet B.1995.Anisotropic wave propagation through finite-difference grids[J].Geophysics,60(4):1203-1216.Kim J W,Lee D J.1996.Optimized compact finite difference schemes with maximum resolution[J].AIAA J,34(5):887-893.Kirkpatrick S,Gelatt C D Jr,Vecchi M P.1983.Optimization by simulated annealing[J].Science,220(4598):671-680.Kosloff D,Pestana R C,Tal-Ezer H.2010.Acoustic and elastic numerical wave simulations by recursive spatial derivative operators[J].Geophysics,75(6):T167-T174.Lele S pact finite difference schemes with spectral-like resolution[J].J Comput Phys,103(1):16-42.Liu Y,Sen M K.2009.An implicit staggered-grid finite-difference method for seismic modelling[J].Geophys J Int,179(1):459-474.Liu Y.2013.Globally optimal finite-difference schemes based on least squares[J].Geophysics,78(4):T113-T132.Saenger E H,Bohlen T.2004.Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid[J].Geophysics,69(2):583-591.Saenger E H,Gold N,Shapiro S A.2000.Modeling the propagation of elastic waves using a modified finite-difference grid[J].Wave Motion,31(1):77-92.Shan G.2009.Optimized implicit finite-difference and Fourier finite-difference migration for VTI media[J].Geophysics,74(6):WCA189-WCA197.Virieux J.1984.SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method[J].Geophysics,49(11):1933-1957. Zeng Y Q,He J Q,Liu Q H.2001.The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media [J].Geophysics,66(4):1258-1266.Zhang J H,Yao Z X.2012.Optimized finite-difference operator for broadband seismic wave modeling[J].Geophysics,78(1):A13-A18. Zhou H B,Zhang G Q.2011.Prefactored optimized compact finite-difference schemes for second spatial derivatives[J].Geophysics,76(5):WB87-WB95.。
非均匀介质地震波传播交错网格高阶有限差分法模拟

·18 ·
石油大学学报 (自然科学版) 2003 年 12 月
图 6 所示的是图 3 模型速度为 1 500 m/ s ,3 层
对该模型用精度为 O (Δt2 ,Δ x 10) 的一阶全声波方 密度分别为 1. 0 ,2. 0 和 2. 8 g/ cm3 时所模拟的地面
程交错网格高阶差分法和常规网格下的二阶声波方 单炮记录 。
程伪谱法进行了模拟 。
图 7 (a) 所示是 Marmousi 速度模型 ,取密度为
5 数值模拟
为了比较一阶全声波方程交错网格高阶差分法 与常规网格下的二阶声波方程伪谱法的模拟效果 , 分别对均匀模型 、横向非均匀模型和 Marmousi 模型 进行了二维地震波场模拟 。 交错网格高阶差分法均匀模型的计算区域为 1 000 m ×1 000 m ;伪谱法均匀模型的计算区域为 1 280 m ×1280 m 。模型的地震波速度为 2000 m/ s , 密度为常数 ;震源为点震源 ,主频为 30 Hz ,位于模 型中央 。网格大小为Δx =Δz = 10 m ,时间步长为 Δt = 1 ms。图 2 (a) , ( b) , (c) , ( d) 分别为四阶 、六 阶 、十阶交错网格差分法和伪谱法所模拟的 t = 200 ms 时瞬时波场快照 。可以看出 ,交错网格高阶差分 法当差分阶数较低时 ,频散严重 ;随着阶数的增加 , 频散降低 ,模拟波场的精度逐渐提高 。当采用十阶 差分格式时 ,其模拟结果与伪谱法的相当 。伪谱法 的优点是精度高 ,缺点是所需内存和计算量大 。交 错网格差分法主要优点是计算效率高 ,计算时间约 为伪谱法的 0. 65 倍 ,且所需内存小 。
【国家自然科学基金】_pml吸收边界_基金支持热词逐年推荐_【万方软件创新助手】_20140803
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
2011年 科研热词 推荐指数 完全匹配层 6 时域有限差分 2 数值模拟 2 卷积完全匹配层 2 近似完全匹配层 1 超宽带信号 1 超宽带 1 衰减系数 1 衰减函数 1 横向各向同性介质 1 有限差分 1 时域有限差分法 1 时域有限差分方法 1 多极点debye模型 1 多极点debye介质 1 声波散射 1 声波 1 地面回波 1 回波仿真 1 吸收边界条件 1 吸收边界 1 各向同性介质 1 交替方向隐式-时域有限差分 1 npml 1
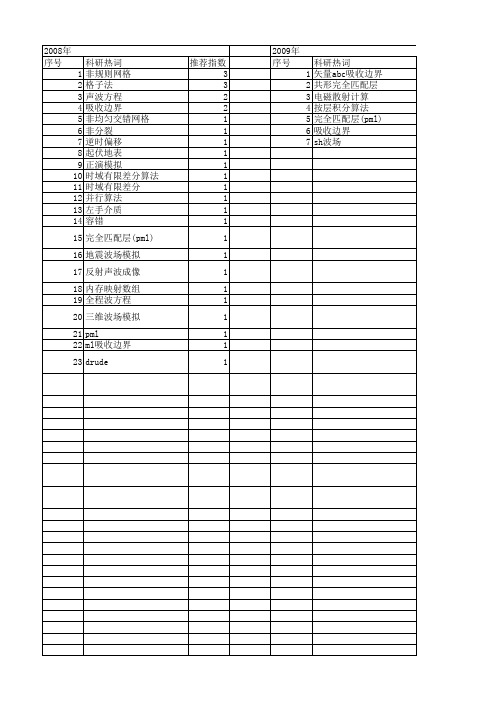
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词 非规则网格 格子法 声波方程 吸收边界 非均匀交错网格 非分裂 逆时偏移 起伏地表 正演模拟 时域有限差分算法 时域有限差分 并行算法 左手介质 容错 完全匹配层(pml) 地震波场模拟 反射声波成像 内存映射数组 全程波方程 三维波场模拟 pml ml吸收边界 drude
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
科研热词 完全匹配层 高斯制 超声波声场 褶积微分算子 色散介质 粒子模拟 时域有限差分法(fdtd) 时域有限差分法 旋转交错网格 数值模拟 探地雷达 常规完全匹配层 完全匹配层(pml) 孔隙介质 吸收边界 各向异性pml吸收边界 反射率 不分裂卷积完全匹配层 三维正演模拟 upml吸收边界 pml吸收边界 fdtd
利用高阶交错网格有限差分法数值模拟VTI 介质井孔声场

利用高阶交错网格有限差分法数值模拟VTI 介质井孔声场岳崇旺;王飞【摘要】Transversely isotropic(TI) media is a common petrophysical media. It is important to study the propa-gation characteristics of the acoutic field in the well for sonic logging theory, and it can provide the basis for the sonic log interpretation. This paper derived velocity–stress staggered-grid finite-difference equations of the elas-tic wave propagation in cylindrical coordinates for vertical transversely isotropic(VTI) media. Furthermore, it numeri-cally simulated acoustic propagation in the VTI media using finite–difference technique with two orders in time and ten orders in space. It gave the snapshots of borehole acoustic wave field in the homogeneous media at different times and calculated the full wave trains with acoustic sources located at the well axis. The calculated results show that if the coefficient of anisotropy of VTI media increases, the change of shear wave propagation has little effect, but the velocity of longitudinal wave propagation has been reduced relatively in the longitudinal direction, and has little change in the radial direction. And if the coefficient of anisotropy of VTI media increases, the first wave slowness of sonic logging will increase, and the acoustic amplitude will be slightly reduced.%横向各向同性(TI)介质是岩石地球物理中常见的一种现象,研究其井孔声场传播特征对声波测井理论以及为声波测井解释提供依据具有重要意义。
可变网格多尺度有限差分模拟方法

可变网格多尺度有限差分模拟方法作者:郭轩矫睿张洪雨来源:《价值工程》2014年第02期摘要:针对典型各项同性地质模型,地震波波动方程和有限差分法对交错网格地震波场进行模拟仿真研究。
为了得到一阶速度应力弹性波方程,首先对地震波波动方程原始形式进行推演,然后用时空二元高阶交错差分网格的方法对其进行离散化,最后对地质模型模拟仿真实验,并获取了对应的波场快照。
最后由仿真结果表明,算法计算精度准确,计算效率高,而且可变网格的变换对地质模型的研究起到了很重要的作用。
Abstract: Aiming at the typical gay geological model, the seismic wave equation and finite difference method are used to do simulation research to the staggered grid seismic wave field. In order to get a first order rate of seismic wave equation, the original form of the seismic wave equation is deduced firstly. Then space-time dual higher order difference staggered grid method is used to do discretization. Finally the geological model simulation experiment is done and the corresponding wave field snapshots are obtained. The simulation results show that the algorithm is accurate with high computational efficiency, and the varision of variable grid is of important significance for the study geological model.关键词:有限差分;地震模型;波动方程;正演模型Key words: finite difference;seismic model;wave equation;forward model中图分类号:O241.82 文献标识码:A 文章编号:1006-4311(2014)02-0315-020 引言随着地震勘探面临的勘探任务越来越复杂,地震勘探成效在很大程度上,取决于对基于符合实际介质模型的方法理论研究。
双相各向同性介质弹性波高精度波场分离数值模拟方法

文献标识码 : A
双 相 各 向 同性 介 质 弹 性 波 高 精 度 波 场 分 离 数 值 模 拟 方 法
陈可洋
( 中国 石 油 大 庆 油 田有 限 责 任 公 司勘 探 开发 研 究 院 , 龙 江 大 庆 13 1 ) 黑 6 7 2
摘要 : 了便: 研究双相介质 固流相混合 弹性 波场 中纵横 波波场的传 播规律 , 出了基于交 错 网格 为 于 二 提 的 Bo 双相各向同性介质 弹性 波动方程高精 度波 场分离正演数值模 拟方法 。采用高 阶交错网格有 l t 限差 分法来构建一阶双曲型双相各 向同性介质弹性波动方程正演算子实现波场正 演 , 并在每一步递
波强 衰减 和 高 频 散 的 主 要 原 因 。考 虑 多 相 介 质 组 合 情 况 形 成 了 S no 相 介 质 理 论 模 a ts三 型 明 , 介质 除 了考虑 固相外 , 考虑 了油 气水 等 流相 在 介质 孔 隙 的组 合 情 况 , 而形 成 了 J该 还 从
未饱 和孑 隙介 质: 的理 论 基础 等 L 面
出快 慢纵 波 相 互伴 生 因 而 无 法 实 现 分 离 。
关键 词 :i 双相各 向同性介质 ; Bo t 纯快 慢纵 波 ;纯横 波 ;波场分 离 ;正演 数值模 拟 ;散度 场和 旋度
场 ;固相 和流 相
目前 , 弹性波 场正 演数 值模 拟技 术在 地球 物理 勘 探 和 开发 以及超 声 检 测 中发 挥 着 重 要 的 作用¨ , 由人工 合成 的 弹性 波 数值模 拟 数据 有助 于 实 际 弹性 资 料 的处 理 和解 释 , 以深 化对 可 弹性波场 在 复杂介 质 中传播 的机 理 的认识 , 检验 地 震 资料 处 理 方法 和观 测 系统 设 计 的合理 并 性 等 。近些年 来对 复杂 孑 隙介 质 的研 究 已成 为 当 今 的前 沿 热 点 内容 , L 其应 用 领域 包 括 岩 土工程 、 地震 灾 害预 防 、 洋 工 程 、 油 勘 探 与 开发 地 球 物理 等 , 应 用 于 解 决 如 封 存 C 海 石 并 O 的动态监 测 、 提高 石油采 收率 以及 评价 洋底 似反 射层 下 的 天然 气 ( 括 可燃 冰 ) 量 等 。通 常 包 储 认 为孔 隙介 质是 由 固体 颗 粒 和 孔 隙 流 体共 同 构 成 , 由此 而 构 建 的 理 论 包 括 Bo 双 相 介 质 理 l t
各向异性介质数值模拟的算法研究

各向异性介质数值模拟的算法研究随着科技的不断发展,数值模拟在各个领域的应用越来越广泛。
各向异性介质数值模拟作为其中的重要分支之一,具有广泛的应用前景。
本文将对各向异性介质数值模拟的算法进行深入研究,以期提出更加高效、准确的模拟方法。
一、介绍各向异性介质是指其性质在各个方向上不尽相同的介质。
例如,在地质勘探领域,岩石的渗透率在不同方向上会有所差异。
这种差异性给数值模拟带来了更大的难度。
因此,研究各向异性介质数值模拟的算法显得尤为重要。
二、现有算法综述目前已有多种各向异性介质数值模拟的算法被提出并得到了广泛应用。
其中较为常见的算法包括有限差分法(Finite Difference Method,FDM)、有限体积法(Finite Volume Method,FVM)、有限元法(Finite Element Method,FEM)等。
这些算法各具特点,在满足不同条件下的应用具有一定优势。
1. 有限差分法有限差分法是将连续的方程通过差分近似的方法离散化,然后利用离散方程进行求解的一种常见数值模拟方法。
在各向异性介质数值模拟中,有限差分法可以通过适当的差分格式来处理不同方向上的差异性,从而得到较为准确的结果。
2. 有限体积法有限体积法是将连续介质分割成小的控制体积,然后在控制体积上进行积分,通过对守恒定律的离散化来进行求解的数值方法。
由于有限体积法在空间上的离散化较为自由,因此能够较好地适应各向异性介质的模拟需求。
3. 有限元法有限元法是将区域分割成小的单元,然后在每个单元上进行逼近,通过拟合的方式来对原方程进行求解的数值方法。
有限元法适用于较为复杂的几何形状,能够较好地处理各向异性介质的模拟问题。
三、改进算法研究尽管目前已有多种算法可以用于各向异性介质的数值模拟,但仍然存在一些问题和挑战。
接下来,本文将探讨一些改进算法的研究方向,以期能够提高模拟的准确性和效率。
1. 多网格方法多网格方法是一种多尺度的数值求解方法,通过在不同尺度上进行迭代求解,能够有效地提高计算效率。
双相TI介质中弹性波交错网格高阶有限差分法数值模拟

意义。
格技 术 , 建立 了各 向异 性孔 隙介 质 波动方 程 的高精 度差 分格 式 , 并对 这类 差分 格式 的频 散特 性 和稳定 性作 了详 细分 析讨 论 , 解决 了计 算稳 定性 和边 界反 射 问题 ; 裴正 林 l9基于 Bo 理 论 给 出 了三 维 双 相 8l 、 it 各 向异性 介 质应 力 ~ 速度 弹性 波 方 程 交 错 网格 任
经典的地震波理论只适合 于研究 固体或流体 单相介质中地震波传播规律 。然而 , 无论是砂岩储 层 还是 碳酸 盐储 层 , 者是 海 底 沉 积 物 , 是 由 固 或 都
体 和流 体两 种部 份组 成 , 由 固体 和 流体 组成 的双 即
相介 质 或多 相 介 质 。 由于 地 震 波在 双相 或 多相 介
( ) 长远 大 于 颗粒 尺 寸 , 粒 粒 径 又大 于 孔 1波 颗 隙尺 寸 。
e e 是应 变 矩 阵 的列 矩 阵 表 达式 ; ] S是 流
于 Bo 理论 的非均匀 孔 隙弹 性介 质 的高 阶交错 网 it
者仍 在进 行 对 于双 相 介 质模 型 和高 性 能 算 法 的研 究 。Gas n E提 出 了关 于弹性 波 在 多孔 介 质 中 sman1 ] 的传 播理 论 , 并建 立 了著 名 的 G sman方 程 ; i as n B—
相介 质理 论 , 奠定 了双 相 介 质 波 动 理论 的基 础 , 但
由于 B o 双相 介质 波动 方程 在 复 杂地 质 环 境 下没 it
各向异性介质弹性波高阶交错网格有限差分模拟

Ab s t r a c t : Th e e l a s t i c wa v e e q u a t i o n i s s i mu l a t e d b y t h e h i g h — o r d e r s t a g g e r e d — g r i d i f n i t e d i f f e r e n c e , t h e s t a b i l i t y a n d a s t r i n g e n c y a r e a n a l y z e d , i n wh i c h t h e a b s o r b i n g b o u n d a r y c o n d i t i o n s a n d a t t e n u a t i o n r e g i o n s a r e a d d e d i n . T he r e - s ui t s o f t h e ni a s o t r o p i c a n d i s o t r o p i c me d i a s h o w t h a t t h e h i g h - o r d e r d i f f e r e n c e e l a s t i c wa v e s i mu l a t i o n c a n ma k e a g o o d e f f e c t b e c a u s e o f l e s s g r i d d i s p e r s i o n a n d h i g h e r a c c u r a c y .
双相介质有限差分数值模拟代码

双相介质有限差分数值模拟代码(原创实用版)目录1.双相介质有限差分数值模拟的概念和背景2.双相介质有限差分数值模拟的实现方法3.双相介质有限差分数值模拟的应用案例4.双相介质有限差分数值模拟的发展前景正文一、双相介质有限差分数值模拟的概念和背景随着油气勘探、开发工作的不断发展,面临的勘探对象和开发条件越来越复杂,对储层预测的精度要求也越来越高。
由于储层实际上是双相介质,即由固相和液相组成,传统的单一介质地球物理勘探方法无法满足对储层参数的精确预测要求。
因此,研究双相介质有限差分数值模拟方法具有重要的现实意义。
二、双相介质有限差分数值模拟的实现方法双相介质有限差分数值模拟是通过构建有限差分网格,将双相介质模型离散化,然后求解离散化后的波动方程,得到地震波在双相介质中的传播特性。
具体实现方法包括以下几个步骤:1.建立双相介质模型:根据地质条件和物性参数,建立固相和液相的弹性模型,并考虑它们之间的相互作用。
2.构建有限差分网格:将双相介质模型划分为有限个小网格,每个小网格内的物质属性和物理参数可以看作是恒定的。
3.离散化波动方程:将双相介质模型中的波动方程离散化,得到一组线性或非线性代数方程组。
4.求解离散化后的方程组:利用有限差分方法求解离散化后的方程组,得到地震波在双相介质中的传播特性。
三、双相介质有限差分数值模拟的应用案例双相介质有限差分数值模拟方法在地球物理勘探领域有广泛的应用,例如:1.储层参数预测:通过模拟地震波在储层中的传播特性,反演储层的弹性模型和物性参数,从而为储层参数预测提供依据。
2.地震波传播特性分析:研究地震波在双相介质中的传播特性,有助于分析地震波在地下的衰减规律和传播路径。
3.地质结构解释:根据地震波在双相介质中的传播特性,解释地下的地质结构和构造背景。
四、双相介质有限差分数值模拟的发展前景随着计算机技术的不断发展,双相介质有限差分数值模拟方法在计算效率和模拟精度方面都将得到进一步提高。
VTI介质交错网格FCT有限差分数值模拟

VTI介质交错网格FCT有限差分数值模拟张省;何兵寿;王玉凤【期刊名称】《工程地球物理学报》【年(卷),期】2012(009)005【摘要】波动方程有限差分数值模拟是研究地震波在地下介质中的波场特征和传播机理的重要手段.对于常规有限差分技术,当采用大网格对计算空间进行差分离散时会出现严重的数值频散问题,降低了计算精度.通量校正(Flux- corrected transport method,FCT)技术能够有效压制粗网格情况下有限差分的数值频散.本文研究了具有垂直对称轴横向各向同性(Vertical Transverse Isotropy,VTI)介质的交错网格FCT有限差分技术.首先从一阶速度一应力弹性波方程出发,在交错网格空间中给出了该方程的高阶有限差分法格式及稳定性条件,在此基础上研究了波动方程正演过程中的数值频散FCT压制技术,二者结合实现了该方程的高精度有限差分数值模拟.同常规算法相比,本文算法不额外增加内存需求,少量增加计算量,但可有效压制VTI介质中弹性波动方程正演的数值频散现象.当采用大网格进行数值模拟时,本文方法明显提高了波场模拟精度.【总页数】7页(P565-571)【作者】张省;何兵寿;王玉凤【作者单位】中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100;中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100;中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100【正文语种】中文【中图分类】P631.4【相关文献】1.基于波动方程有限差分数值模拟及FCT消频散分析 [J], 赵威;李伟波;桂志先;周游;于晓东2.基于优化有限差分和混合吸收边界条件的三维VTI介质声波和弹性波数值模拟[J], 徐世刚;刘洋3.基于最小范数优化交错网格有限差分系数的波动方程数值模拟 [J], 唐超;文晓涛;王文化4.基于煤层的改进的旋转交错网格有限差分数值模拟 [J], 李勤;马随波;赵斌;章薇5.基于时空域交错网格有限差分法的应力速度声波方程数值模拟 [J], 彭更新;刘威;郭念民;胡自多;徐凯驰;裴广平因版权原因,仅展示原文概要,查看原文内容请购买。
基于旋转交错网格的双相各向异性介质二维三分量波场模拟

基于旋转交错网格的双相各向异性介质二维三分量波场模拟林朋;彭苏萍;卢勇旭;王攀【摘要】基于Biot双相介质模型,推导了双相TTI介质二维三分量一阶速度-应力弹性波方程,采用旋转交错网格(RSG)技术建立了各向异性孔隙介质波动方程的二维三分量高精度有限差分格式(FDTD),并引入不分裂卷积完全匹配层(CPML)作为吸收边界条件.为了验证算法可行性,对均匀双相TTI介质中的弹性波场进行了模拟.结果表明:使用旋转交错网格有限差分技术能够模拟出双相TTI介质中存在的快横波、慢横波、快纵波和慢纵波;双相各向异性介质中存在明显的横波分裂、波前面尖角和三分叉现象;不分裂卷积完全匹配层对边界反射的吸收效果较好.通过对比传统交错网格(SSG)和旋转交错网格有限差分技术,证明了旋转交错网格有限差分算法稳定性较强,精度较高,是一种实用的地震波场数值模拟方法.【期刊名称】《煤炭学报》【年(卷),期】2016(041)005【总页数】9页(P1203-1211)【关键词】双相各向异性介质;旋转交错网格;传统交错网格;不分裂卷积完全匹配层【作者】林朋;彭苏萍;卢勇旭;王攀【作者单位】中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京100083;中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京100083;中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京100083;中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京100083【正文语种】中文【中图分类】P631林朋,彭苏萍,卢勇旭,等.基于旋转交错网格的双相各向异性介质二维三分量波场模拟[J].煤炭学报,2016,41(5):1203-1211. doi:10. 13225/ j. cnki. jccs. 2015. 1561Lin Peng,Peng Suping,Lu Yongxu,et al. Study on 2D/3C wave propagation in two-phase anisotropic media using the rotated staggered-grid method[J]. Journal of China Coal Society,2016,41(5):1203-1211. doi:10. 13225/ j. cnki. jccs. 2015. 1561地球内部分布不均的岩石裂缝和孔隙在地震尺度上往往表现为各向异性性质,而传统的地震波传播理论仅仅适用于单相介质。
平板收缩流动的同位和交错网格FVM模拟及比较

平板收缩流动的同位和交错网格FVM模拟及比较王利业;欧阳洁;赵智峰;刘德峰【摘要】本文分别用同位和交错网格有限体积法模拟了4:1平板收缩流动过程,并将两种方法所得结果进行了比较分析,其中同位网格有限体积法采用动量插值方法解决速度与压力的失耦问题.算例表明,同位网格有限体积法和交错网格有限体积法对于4∶1平板收缩流动过程的模拟结果吻合.这说明同位网格有限体积法不仅算法简洁、实现方便,结果可靠,而且容易扩展应用于非结构网格及高维问题的模拟.【期刊名称】《工程数学学报》【年(卷),期】2009(026)001【总页数】9页(P85-93)【关键词】颗4;1平板收缩流;同位网格;交错网格;有限体积;动量插值【作者】王利业;欧阳洁;赵智峰;刘德峰【作者单位】西北工业大学理学院数学系,西安,710072;西北工业大学理学院数学系,西安,710072;西北工业大学理学院数学系,西安,710072;西北工业大学理学院数学系,西安,710072【正文语种】中文【中图分类】O3731 引言有限差分法、边界元法、有限元法、有限体积法等数值方法都已广泛地用于复杂流体流动过程的数值模拟,且有限元法和有限体积法也在众多领域中得到应用。
有限体积法计算时生成带状稀疏矩阵,CPU的计算时间和未知数个数成线性关系,计算效率优于其它数值方法。
文献[1]表明有限体积法的计算速度约为有限元法的两倍。
由于有限体积法计算效率高,因而特别适用于复杂流体流动的数值模拟。
有限体积法为了解决速度与压力的失耦问题,通常采用交错网格技术。
交错网格有限体积法已在很多领域发挥了重要作用[2-6]。
但由于交错网格固有的缺点,各种数值技术如多重网格、非结构网格、并行计算及扩展到高维等均很难实现,从而限制了有限体积法在流体模拟中的应用。
自1988年Peric等[7]确认同位网格技术以后,这种各个变量和物性值均置于同一套网格上的方法便迅速发展起来。
在动量方程的离散中,同位网格有限体积法得到的系数矩阵对于所有变量全部相同,从而减少了变量的存储;而且对于各种复杂情况以及不同网格坐标系的计算,同位网格有限体积法可以使离散方程相对简单,从而简化问题的求解。
高阶旋转交错网格有限差分方法模拟TTI介质中横波分裂

高阶旋转交错网格有限差分方法模拟TTI介质中横波分裂李敏;刘洋【期刊名称】《物探与化探》【年(卷),期】2012(36)6【摘要】笔者给出了一种能够模拟弹性波在任意各向异性介质中传播的二维三分量高阶有限差分算法.相对于常规交错网格有限差分方法,旋转交错网格有限差分方法在介质具有强差异性时能更精确地模拟地震波的传播,避免常规交错网格中因对弹性系数进行插值而带来的误差.采用高阶旋转交错网格有限差分方法模拟并分析了零偏移距横波分裂现象随裂缝介质方位角和倾角变化的响应特征.结果表明:结合完全匹配层(PML)吸收边界条件的高阶旋转交错网格有限差分方法能获得高精度的地震波场模拟数据,并且在边界具有良好的吸收效果;横波分裂现象主要受裂缝走向与波的极化方向之间的夹角影响,受裂缝倾角影响较小,且快慢横波的能量也跟裂缝走向与波极化方向间的夹角有关.具有倾斜对称轴的横向各向同性(TTI)介质倾角的变化可能会导致记录中波到达时的变化,影响快慢横波的时差.利用横波分裂的能量分布和方位各向异性特征,可以帮助检测裂缝的方位角和倾角.横波在多层TTI介质中传播时会发生多次分裂的现象.%A high-order rotated staggered grid scheme ( RSG) has been implemented to simulate the shear-wave splitting in tilted transversely isotropic (TTI) media. The high-order RSG can simulate wave propagation in media that contain high-contrast discontinuities like cracks more precisely than the standard staggered grid scheme (SSG) by avoiding the unstableness of the staggered grid scheme (SSG). The authors conducted a study of zero-offset S-wave splitting withthe high-order RSG. The S-wave splitting study was mainly focused on fractured media which, on the scale of seismic wavelength, could be regarded as transversely isotropic (TI) media. The results of numerical modeling show that the high-order RSG scheme can be used to simulate waves' propagation in general anisotropic media. The perfect matched layer (PML) absorbing boundary condition combined with the high order RSG scheme can well attenuate reflections from the artificial boundary. The S-wave splitting is mainly affected by the angle between polarization direction of incoming wave and strike of the TTI media, and the energy of fast and slow shear waves is also associated with this angle. The dipping angle of ITI media may affect time lag between the fast and slow waves, which may result in variation of arrival time of waves from the same interface. Thus, the analysis of energy distribution of the fast and slow waves and the variation of arrival time may help detect the strike and dipping angle of the fracture. Besides, when propagating in the media that contain more than one layer of TTI media, the S-wave splitting will occur more than once.【总页数】7页(P934-940)【作者】李敏;刘洋【作者单位】中国石油大学油气资源与探测国家重点实验室,北京102249;中国石油大学CNPC物探重点实验室,北京102249;中国石油大学油气资源与探测国家重点实验室,北京102249;中国石油大学CNPC物探重点实验室,北京102249【正文语种】中文【中图分类】P631.4【相关文献】1.黏弹TTI介质旋转交错网格微地震波场模拟 [J], 姚振岸;孙成禹;谢俊法;唐杰2.黏弹TTI介质中旋转交错网格高阶有限差分数值模拟 [J], 严红勇;刘洋3.旋转交错网格在横波分裂和再分裂模拟与分析中的应用 [J], 张建利;刘志斌;周超;田小波;李维新;王赟4.基于卷积完全匹配层的旋转交错网格高阶差分法模拟弹性波传播 [J], 冯德山;王向宇5.基于CPML-RML组合边界条件粘弹TTI介质旋转交错网格有限差分正演模拟[J], 张奎涛;顾汉明;刘少勇;刘春成;陈宝书;张立;肖逸飞因版权原因,仅展示原文概要,查看原文内容请购买。
基于有限差分的部分饱和双重孔隙介质弹性波模拟与分析

基于有限差分的部分饱和双重孔隙介质弹性波模拟与分析石志奇;何晓;刘琳;陈德华
【期刊名称】《物理学报》
【年(卷),期】2024(73)10
【摘要】双重孔隙介质模型考虑了岩石非均质性诱发的介观流对弹性波频散和衰减的影响,在非均质储层地震资料定量解释中取得良好的应用效果.基于双重孔隙介质理论模型,利用数值算法开展弹性波模拟工作不仅可以直观显示波的传播特征,同时也为后期地震反演成像工作奠定基础.本文基于Santos-Rayleigh部分饱和双重孔隙介质模型,利用交错网格有限差分算法模拟并分析了双重孔隙介质中的波场快照和波形曲线.采用Zener黏弹性模型近似表征介观流机制,结果表明Zener模型能够较好地反映快纵波传播特征,却无法表征慢纵波P3波在低频段的衰减特征.利用时间分裂法解决波动方程的刚性问题,提高计算效率.利用解析解验证了有限差分算法正确性的基础上,模拟了均匀介质和分层介质中的波场快照和波形曲线,清晰直观地反映了快纵波在地震频段的强衰减特征,与双重孔隙理论模型预测结果一致.模拟结果有助于进一步理解非均匀部分饱和孔隙介质中的弹性波传播特征.
【总页数】10页(P20-29)
【作者】石志奇;何晓;刘琳;陈德华
【作者单位】中国科学院声学研究所;中国科学院大学;北京市海洋深部钻探测量工程技术研究中心
【正文语种】中文
【中图分类】TP3
【相关文献】
1.双相介质和弹性介质混合模型的有限差分声波模拟
2.黏弹性介质瑞雷波有限差分模拟与特性分析
3.基于BISQ模型的各向同性孔隙介质弹性波三维交错网格高阶有限差分数值模拟
4.黏弹性流体饱和孔隙介质动力反应分析的显式有限元法
5.黏弹性介质中瑞雷波有限差分数值模拟与波场分析
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收稿日期:XXXX -XX -XX基金项目:国家重大科学仪器设备开发专项(2012YQ030126);国家自然基金煤炭联合项目(U1261203);中国地质调查局项目(12120115102101) 传统和旋转交错网格有限差分在双相介质中模拟对比林朋,卢勇旭(中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京 100083)摘要:以Biot 双相介质模型为背景,推导了双相各向同性介质二维三分量一阶速度—应力弹性波方程方程,建立了各向同性双相介质波动方程的二维三分量有限差分格式。
分别采用传统交错网格有限差分技术和旋转交错网格有限差分技术对均匀和非均匀双相各向同性介质进行了波场模拟。
结果表明:旋转交错网格有限差分技术能够有效模拟双相各向同性介质中弹性波的传播情况;通过传统和旋转交错网格有限差分技术的对比,说明了旋转交错网格有限差分算法在稳定性更强,避免了插值带来的误差,是一种有效的地震波场模拟方法。
关键词:双相介质;传统交错网格;旋转交错网格;波场模拟随着人们对地球内部认识的逐步加深和地球物理学的快速发展,含饱和流体的孔隙介质被认为是与含油气储层最为接近的介质模型,其是由固体骨架颗粒和孔隙中的流体(如气、水等)组成双相或多相介质。
双相介质中弹性波传播规律的正确认识,对于油气的开采具有重要意义。
地震波数值模拟是人们用来描述和认识地震波传播规律的有效途径。
交错网格有限差分技术作为地震波场模拟的常用方法之一,在地球物理中一直被广范应用。
Biot 理论描述了饱和流体空隙介质中地震波的传播,是双相介质波动理论的基础[1-3];Schmitt 讨论了柱坐标系下地震波在横向各向异性介质中的传播问题[4];Crampin 通过一系列实验研究发现,双相各向异性介质中存在横波分裂现象[5];王尚旭研究了双相介质地震波传播规律,并利用有限元法实现了双相介质地震波场模拟[6];牟永光应用有限差分技术对孔隙各向同性介质进行了波场分析[7];刘洋等通过虚谱法对双相各向异性介质中弹性波的传播特征[8];王秀明等使用高阶交错网格有限差分技术实现了非均匀孔隙介质的正演模拟[9];裴正林通过交错网格有限差分法实现了双相各向异性介质和三维横向各向同性介质弹性波的高阶波场模拟[10-11]。
本文使用传统和旋转交错网格两种有限差分技术对双相介质进行了波场模拟,通过对比,说明了旋转交错网格有限差分技术的有效性和优越性。
1 方法原理1.1 双相各向异性介质二维三分量弹性波方程根据双相介质地震波传播理论[2],可得到饱和流体孔隙介质运动方程[11] 21111221122112212222112222111211121112() ()() () ()() i ij i ij i ij i ij i ij i ij v b v b V s t V b v b V s tρρρρρρρρρτρρρρρρρρρτ∂-=+-++∇-∇∂∂-=+-++∇-∇∂ (1)(2) 式中,i 、j 表示x,y,z 三个不同方向分量,b ij 表示耗散系数,ij τ为固相应力分量,s 为作用在流体上的有效应力,(),,x y z υυυT =ν为介质固体骨架速度矢量,(),,x y z V V V T =V 为介质流体速度矢量。
令φ为孔隙度,11ρ和22ρ分别表示单位体积内固体骨架和流体部分的有效质量,12ρ为流体相对固体骨架运动时的视质量[12]。
三者与固相密度s ρ和流相密度f ρ之间满足[2]()11121222 = 1 = sf ρρφρρρφρ+-+ (3)(4) 由饱和流体孔隙介质传播理论,易得双相各向同性介质二维三分量一阶速度—应力表达式。
令Q i 表示固体骨架和流体空隙之间体积变化的耦合参数,R 表示描述流体的弹性参数,即将一定体积流体注入孔隙介质体积元,为保持总体积不变时在流体上施加的一种力的度量[12]。
对于双相各向同性介质,固相部分速度与应力之间的关系为()()()()111211331112++00++xx xz x x x x xz zz z z z z V V b x z t t b V V t t x z ττρυρυττρυρυ∂∂∂∂⎡⎤⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎡⎤∂∂∂∂=+⎢⎥⎢⎥⎢⎥⎢⎥∂∂∂∂⎢⎥⎢⎥⎢⎥⎣⎦-⎢⎥⎢⎥⎢⎥∂∂⎣⎦⎣⎦∂∂⎣⎦ (5) 由广义达西定律可得Biot 介质流相部分速度和应力关系式 ()()()()122211331222+00+x x x x z z z z s V V b x t t b s V V z t t ρυρυρυρυ∂∂∂⎡⎤⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎡⎤∂∂∂=-⎢⎥⎢⎥⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥⎢⎥⎣⎦-⎢⎥⎢⎥⎢⎥∂∂∂⎣⎦⎣⎦⎣⎦ (6)1.2 交错网格有限差分技术交错网格有限差分技术是一种有效的地震波正演模拟方法。
传统交错网格是将网格剖分成整网格点和半网格点,在相邻的两个时间层上的网格点处分别定义速度和应力分量,并且在空间分布上相邻的两个时间层上的物理量恰好交错半个网格,导数值在半网格点处计算,以实现时间和空间的交错[13]。
由于速度和应力的相对关系,对于不同的介质模型,在计算过程中需要对部分场量和模型参数进行插值,增加了计算误差,降低了计算精度。
网格定义、波场分量及弹性参数位置如图1(a )所示。
旋转交错网格由传统交错网格发展而来,通过旋转对网格进行了重新划分和定义。
与传统交错网格相比,不同之处在于,在同一网格点处仅定义同一物理量(速度、应力),通过计算沿网格对角线物理量的差分来计算微分,由于速度分量和应力分量各定义整网格点和半网格点上,避免了部分场量和模型参数的插值[14],降低了计算误差,提高了计算精度[15-16]。
网格定义、波场分量及弹性参数位置如图1(b )所示[17]。
(a )传统交错网格(b )旋转交错网格 图1 交错网格示意图 1.3 稳定性分析稳定性问题是地球物理学科研究中所必须解决的难题,直接关系到数值模拟方法的成败。
对于传统交错网格有限差分技术,在步长相等的情况下,时间域二阶、空间2M 阶的稳定性条件如下:max 11/n k k tV C h =∆⎫≤⎪∆⎭ (7)式中,t ∆是时间步长,D 是空间维数,h ∆为空间步长,V max 为最大相速度,C k 时是空间差分系数。
对于旋转交错网格有限差分技术,Saenger [14]在Neumann 稳定性条件下,给出了在空间步长相等时,时间域二阶、空间2M 阶的稳定性条件为:max 11/n k k tV C h =∆⎛⎫≤ ⎪∆⎝⎭∑ (8)式中参数意义同(7)式。
通过对比两种交错网格的稳定性条件可知,相较于传统交错网格,旋转交错网格有明显的优点,在理论上有更宽松的稳定性条件。
2数值模拟及分析2.1 均匀双相各向同性介质波场模拟为观察旋转交错网格有限差分技术在双相各向同性介质中的模拟效果,采用均匀各向同性介质为背景,模型大小为256256m m ,网格间距1m ,采样间隔0.1ms ,震源采用Ricker 子波,位于模型中间位置,加载于固相正应力处。
模型如图2所示。
取t=40ms 时的波场快照,使用传统和旋转交错网格有限差分技术所得波场快照如图3、4所示。
图2 均匀双相各向同性介质模型(a )固相X 分量 (b )流相X 分量(c )固相Z 分量 (d )流相Z 分量 图3 均匀双相各向同性介质传统交错网格数值模拟波场快照(a)固相X分量(b)流相X分量(c)固相Z分量(d)流相Z分量图4 均匀双相各向同性介质旋转交错网格波场快照结合图3和图4可知,使用传统和旋转交错网格有限差分技术对均匀双相各向同性介质模拟时,均可以得到清晰的波场快照,均匀双相介质中存在的快纵波、慢纵波和快横波都清晰可见,波场特征十分明显,波场分布符合地震波传播规律。
说明了旋转交错网格有限差分技术可以较好的模拟地震波在均匀双相介质中的传播规律,是一种有效的地震波场模拟方法。
2.2 非均匀双相各向同性介质波场模拟为进一步验证传统和旋转交错网格有限差分技术在双相各向同性介质模拟中的差异,以非均匀双相各向同性介质为背景,模型分为A、B两个区域,B是一密度和速度极小的地质异常区块,其参数与均匀情况下相同。
模型如图5所示。
对非均匀双相各向同性介质分别使用传统交错网格技术和旋转交错网格技术进行波场模拟,取t=40ms时的波场快照进行对比,所得波场快照如图6、7所示。
图5非均匀双相各向同性介质模型(a)固相X分量(b)流相X分量(c)固相Z分量(d)流相Z分量图6非均匀双相各向同性介质传统交错网格数值模拟波场快照(a)固相X分量(b)流相X分量(c)固相Z分量(d)流相Z分量图7非均匀双相各向同性介质旋转交错网格波场快照从图6可知,当使用传统交错网格有限差分技术对双相介质进行波场模拟时,除地质异常体外,波场均可以正常传播,符合双相介质波动理论,而在地质异常体附近,由于波场分量和模型参数的插值,导致波场出现了振幅异常现象,不能正确表示波场传播情况;从图7可以观察到,使用旋转交错网格有限差分技术模拟时,波场传播均符合双相介质地震波传播规律,在地质异常体附近有反射波和绕射波产生,可以正确表示波场在双相介质中的传播。
3结论(1)相对传统交错网格,旋转交错网格有限差分技术在理论上具有更宽松的稳定性条件。
(2)在均匀双相各向同性介质的波场模拟中,旋转交错网格有限差分技术能够得到清晰的波场快照,且波场特征十分明显,可以有效模拟双相各向同性介质中弹性波的传播情况。
(3)对存在地质异常体的非均匀双相各向同性介质,传统交错网格有限差分技术稳定性不足,具有明显的局限性;而旋转交错网格有限差分技术适应性较强,稳定性更好,是一种有效的地震波场数值模拟方法。
参考文献[1]Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, I: Low-frequency range [J]. The Journal ofthe Acoustic Society of America, 1956a, 28:168-178.[2]Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, II: High-frequency range [J]. The Journal ofthe Acoustic Society of America, 1956b, 28:179-191.[3]Biot M A. Mechanics of deformations and acoustic propagation in porous media [J]. J. Appl. Phys, 1962a, 33: 1482-1498.[4]Schmitt P D. Acoustic multipole logging in the transversely isotropic poroelastic formations. The Journal of the AcousticSociety of America, 1989, 86(6): 2397-2421.[5]Crampin S, Yedlin M. Shear-wave singularities of wave propagation in anisotropic media. J Geophys, 1981, 49: 43-46.[6]王尚旭. 双相介质中弹性波问题有限元数值解和A VO问题[D].北京:中国石油大学(北京)博士学位论文,1990.[7]牟永光,裴正林. 三维复杂地震数值模拟[M]. 石油工业出版社,2005-1.[8]刘洋,李承楚. 双相各向异性介质中弹性波传播特征研究[J]. 地震学报,1999,21(4):367-373.[9]杨顶辉. 双相各向异性介质中弹性波方程的有限元解法及波场模拟[J]. 地球物理学报,2002,45(4):575-583.[10]裴正林. 三维各向同性介质弹性波方程交错网格高阶有限差分法模拟[J]. 石油物探,2005,44(4):308-316.[11]裴正林. 双相各向异性介质弹性波传播交错网格高阶有限差分法模拟[J]. 石油地球物理勘探,2006,41(2):137-143.[12]孙卫涛,杨慧珠. 双相各向异性介质弹性波场有限差分正演模拟[J]. 固体力学学报,2004,25(1):21-28.[13]孙瑞艳. TTI介质旋转交错网格有限差分及其组合边界条件[D]. 东营:中国石油大学(华东)硕士学位论文,2010.[14]Saenger E. H., Gold N., Shapiro S. A.. Modeling the propagation of elastic waves using a modified finite-difference grid[J].Wave Motion, 2010, 31:77-92.[15]王亚妮,李长江,李庆春. 旋转交错网格VTI介质波场模拟与波场分解[J]. 物探化探计算技术,2015,37(2):198-202.[16]李长江,李庆春,王亚妮. 旋转交错网格TTI介质波场模拟与波场分解[J]. 物探与化探,2015,39(3):553-557.[17]Bohlen T, Saenger E H. Accuracy of heterogeneous staggered-grid finite-difference modeling of Rayleigh waves [J].Geophysical Prospecting, 1995, 43(6):805-829.The contrast of simulation in the two-phase media betweenthe traditionaland rotated staggered gridLIN Peng, Lu Yong-Xu(State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology(Beijing),Beijing 100083,China)Abstract:Starting from the model of the Biottwo-phase media theory, it is deduced that the 2D/3C velocity-stress elastic wave equation of the two-phase isotropic media and the finite difference time domain scheme is set up. The wave field simulation is based on the two-phase homogeneous and inhomogeneous isotropic media using the traditional staggered-grid method and the rotated staggered-grid method. The results show that the rotated staggered grid difference scheme performs perfect for the two-phase isotropic media. By comparing rotated stagger-grid and traditional stagger-grid, it can be proved that the finite difference algorithm of rotating staggered-grid is more stable, avoiding errors caused by interpolation, so the rotated staggered-grid difference scheme is a numerical simulation of seismic wave field method with a strong effectiveness.Key words: two-phase media; traditional staggered-grid; rotated staggered-grid; wave field simulation作者简介:林朋(1990—),男,在读硕士研究生,地球探测与信息技术专业,中国矿业大学(北京)煤炭资源与安全开采国家重点实验室。
