六角古亭木结构模拟与分析 (张永娟 09土木)
亭廊的设计_实例分析

从形状上看:功能形、抽象形、具象形和动物形等
从材料上看:铁制、合金钢、塑胶、玻璃钢、木 材、竹制、砼制、陶制及组合制等 从取出方式看:回转式、抽出内笼式、拆除支撑 配件、清出下部式及拆盖式等
实验三 园林建筑小品的设计 (6学时)
一、目的 1、了解园林建筑小品在环境中的平面布局、 造型设计和空间组合; 2、熟悉人体活动尺度与室外空间的关系, 掌握园林建筑小品设计中的比例与尺度的推敲方 法; 3、掌握园林建筑小品设计的步骤与基本方 法,分析和比较方案,并用平、立、剖面图进行 表现。
§3.3 园林小品
--以垃圾箱为例
在保持园林环境 整洁中,垃圾箱 扮演着重要角色。 在园林设计中占 有重要位置,好 的垃圾箱给人一 种美感,为园林 增添景致。
南京的一些公 共场所,出现 了一批具有生 态美感的垃圾 箱,这些另类 木制垃圾箱内 不仅设置了不 锈钢分类环保 投放筒,而且 拥有鲜花铺罩 的外表,令人 耳目一新
泉州:中山公园环保公厕,一座投资40多万元, 具有节能、低碳、环保等特点的生态公厕
园厕
紧凑园厕
实验二 公园厕所的设计(6学时)
一、目的 了解公园厕所建筑设计中场地设计的基本要求,即 基于人流路线的组织及功能分区的平面布局;了解简单 的形体组合、建筑的立面划分、朝向要求、建筑材料与 构造的基本做法等。 二、设计要求 1、在某城市公园内建一中小型公厕,供游人使用。 公园性质及地形自定,占地面积150~200m2,层次结构 形式不限; 2、图纸要求: (1)局部环境总平面图1:500; (2)公厕平面图、入口立面及侧立面图、剖面图1:100; (3)透视图
第三章 实例分析
§3.1 亭廊榭舫 3.1.1 亭
请到图书馆或网上参阅《中国亭全览》 亭是供游人休息、赏景的地方,又是园中 一景,一般四面透空,多数为斜屋面。
文档 1

建筑学论文标题:论古建筑结构班级:建筑112班姓名:宋旱雨学号:6001111052日期:2013.8.25摘要:本文对杭州、苏州园林建筑,西塘古镇古建筑民居楼以及南昌滕王阁进行了现状的调查,针对建筑内部的流线以及功能分区和外部流线做了系统的研究。
还有对古建筑的结构材料进行了调研。
同时对建筑规模,功能分区,布局方式,建筑,外表面做了一些调研。
还有在网上查了些资料对古建筑与西方的一个对比。
正文:一:前言中国可谓是个历史悠久的国家,所以在迄今为止也保留下来许许多多的古建筑,不过古建筑有着许多的不同之处,有南方的,也有北方的,他们都具有着各自的特色。
以前的建筑师也是根据每个地方的气候、地域等建筑出不同的建筑,所以他们在各处的建筑也有着不同的结构与特征。
中国建筑是世界上传统延续最长的建筑体系。
这一方面是因为中国的封建社会时期特别长,社会变化缓慢,另一方面是中国的地理环境比较封闭,周边有大海、高山、沙漠的阻隔,在交通不便的古代,很少受到很大的外来影响。
更因为中国的文化一般地高于相邻国家或民族的文化,即使某些外来因素传人中国,也会很自然地融人,而成为中国自己的东西。
中国建筑自其萌芽,直到今世,一脉相承,可以说是具有很大的稳定性,与历史上西欧建筑的剧烈变化大不相同。
中国古代建筑是中国传统文化的重要组成部分,与中医、国画、等相似,有中国自己特有的传统,是延续数千年的独特体系。
从都城的规划建设,到建筑的设计施工,乃至于装修装饰,都有自己的理论与方法,在世界上独树一帜,有着很卓越的成就。
它不仅是珍贵的历史文化遗产,认真加以研究总结,还可以为当今的建设提供可贵的借鉴。
建筑与人类的关系是十分密切的,人自一出生就是生活在建筑所构成的空间。
而建筑又是一种即有艺术形象,又同时具有不同物质功能的构筑物。
中国的古建筑无论是宫殿、坛庙、还是园林、住宅,它们的个体和群体形象都与一个时期的政治、经济、文化、技术等诸方面的条件有关。
本文有着自己亲身经历过的一些地方古建筑进行了调研,在实地结合自己在书上所学的一些知识在进行一些实际上的对比。
2022年湖北省恩施州中考数学试卷(解析版)

2022年湖北省恩施州中考数学试卷(真题)一、选择题(本大题共有12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.(3分)(2022•恩施州)8的相反数是()A.﹣8 B.8 C.D.﹣2.(3分)(2022•恩施州)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.3.(3分)(2022•恩施州)函数y=的自变量x的取值范围是()A.x≠3 B.x≥3 C.x≥﹣1且x≠3 D.x≥﹣1 4.(3分)(2022•恩施州)如图是一个正方体纸盒的展开图,将其折叠成一个正方体后,有“振”字一面的相对面上的字是()A.“恩”B.“乡”C.“村”D.“兴”5.(3分)(2022•恩施州)下列运算正确的是()A.a2•a3=a6B.a3÷a2=1 C.a3﹣a2=a D.(a3)2=a6 6.(3分)(2022•恩施州)为了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如下表所示:月用水量(吨) 3 4 5 6 户数 4 6 8 2 关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的()A.众数是5 B.平均数是7 C.中位数是5 D.方差是1 7.(3分)(2022•恩施州)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=()A.120°B.130°C.140°D.150°8.(3分)(2022•恩施州)一艘轮船在静水中的速度为30km/h,它沿江顺流航行144km与逆流航行96km所用时间相等,江水的流速为多少?设江水流速为vkm/h,则符合题意的方程是()A.=B.=C.=D.=9.(3分)(2022•恩施州)如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于BD的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC 交于点M、N,连接BM、DN.若AD=4,AB=2.则四边形MBND的周长为()A.B.5 C.10 D.2010.(3分)(2022•恩施州)如图1是我国青海湖最深处的某一截面图,青海湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=kh+P0,其图象如图2所示,其中P0为青海湖水面大气压强,k为常数且k≠0.根据图中信息分析(结果保留一位小数),下列结论正确的是()A.青海湖水深16.4m处的压强为188.6cmHgB.青海湖水面大气压强为76.0cmHgC.函数解析式P=kh+P0中自变量h的取值范围是h≥0D.P与h的函数解析式为P=9.8×105h+7611.(3分)(2022•恩施州)如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是()A.当t=4s时,四边形ABMP为矩形B.当t=5s时,四边形CDPM为平行四边形C.当CD=PM时,t=4sD.当CD=PM时,t=4s或6s12.(3分)(2022•恩施州)已知抛物线y=x2﹣bx+c,当x=1时,y<0;当x =2时,y<0.下列判断:①b2>2c;②若c>1,则b>;③已知点A(m1,n1),B(m2,n2)在抛物线y=x2﹣bx+c上,当m<m2<b时,n1>n2;④若方程x2﹣bx+c=0的两实数1根为x1,x2,则x1+x2>3.其中正确的有()个.A.1 B.2 C.3 D.4二、填空题(本大题共有4小题,每小题3分,共12分).13.(3分)(2022•恩施州)9的算术平方根是.14.(3分)(2022•恩施州)因式分解:a3﹣6a2+9a=.15.(3分)(2022•恩施州)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π).16.(3分)(2022•恩施州)观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为a n,且满足+=.则a4=,a2022=.三、解答题(本大题共有8个小题,共72分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).17.(8分)(2022•恩施州)先化简,再求值:÷﹣1,其中x=.18.(8分)(2022•恩施州)如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.19.(8分)(2022•恩施州)2022年4月29日,湖北日报联合夏风教室发起“劳动最光荣,加油好少年”主题活动.某校学生积极参与本次主题活动,为了解该校学生参与本次主题活动的情况,随机抽取该校部分学生进行调查.根据调查结果绘制如下不完整的统计图(如图).请结合图中信息解答下列问题:(1)本次共调查了名学生,并补全条形统计图.(2)若该校共有1200名学生参加本次主题活动,则本次活动中该校“洗衣服”的学生约有多少名?(3)现从参与本次主题活动的甲、乙、丙、丁4名学生中,随机抽取2名学生谈一谈劳动感受.请用列表或画树状图的方法,求甲、乙两人同时被抽中的概率.20.(8分)(2022•恩施州)如图,湖中一古亭,湖边一古柳,一沉静,一飘逸,碧波荡漾,相映成趣.某活动小组赏湖之余,为了测量古亭与古柳间的距离,在古柳A处测得古亭B位于北偏东60°,他们向南走50m到达D点,测得古亭B位于北偏东45°.求古亭与古柳之间的距离AB的长(参考数据:≈1.41,≈1.73,结果精确到1m).21.(8分)(2022•恩施州)如图,在平面直角坐标系中,O为坐标原点,已知∠ACB=90°,A(0,2),C(6,2).D为等腰直角三角形ABC的边BC上一点,且S△ABC=3S△ADC.反比例函数y1=(k≠0)的图象经过点D.(1)求反比例函数的解析式.(2)若AB所在直线解析式为y2=ax+b(a≠0),当y1>y2时,求x的取值范围.22.(10分)(2022•恩施州)某校计划租用甲、乙两种客车送180名师生去研学基地开展综合实践活动.已知租用一辆甲型客车和一辆乙型客车共需500元,租用2辆甲型客车和3辆乙型客车共需1300元.甲型客车每辆可坐15名师生,乙型客车每辆可坐25名师生.(1)租用甲、乙两种客车每辆各多少元?(2)若学校计划租用8辆客车,怎样租车可使总费用最少?23.(10分)(2022•恩施州)如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.(1)求证:∠ADE=∠PAE.(2)若∠ADE=30°,求证:AE=PE.(3)若PE=4,CD=6,求CE的长.24.(12分)(2022•恩施州)在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+c与y轴交于点P(0,4).(1)直接写出抛物线的解析式.(2)如图,将抛物线y=﹣x2+c向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y 轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)直线BC与抛物线y=﹣x2+c交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)若将抛物线y=﹣x2+c进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出抛物线y=﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标.2022年湖北省恩施州中考数学试卷参考答案与试题解析一、选择题(本大题共有12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.(3分)(2022•恩施州)8的相反数是()A.﹣8 B.8 C.D.﹣【分析】根据相反数的定义进行解答即可.【解答】解:8的相反数是﹣8,故选:A.【点评】本题考查相反数,掌握相反数的定义是正确解答的前提.2.(3分)(2022•恩施州)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据各个选项中的图形,可以写出是否为中心对称图形或轴对称图形,然后即可判断哪个选项符合题意.【解答】解:选项A中的图形是轴对称图形,不是中心对称图形,故选项A 不符合题意;选项B中的图形既是轴对称图形又是中心对称图形,故选项B符合题意;选项C中的图形是轴对称图形,不是中心对称图形,故选项C不符合题意;选项D中的图形是中心对称图形,不是轴对称图形,故选项D不符合题意;故选:B.【点评】本题考查中心对称图形、轴对称图形,解答本题的关键是明确题意,写出各个图形是否为中心对称图形或轴对称图形.3.(3分)(2022•恩施州)函数y=的自变量x的取值范围是()A.x≠3 B.x≥3 C.x≥﹣1且x≠3 D.x≥﹣1【分析】利用分式有意义的条件和二次根式有意义的条件得到不等式组,解不等式组即可得出结论.【解答】解:由题意得:,解得:x≥﹣1且x≠3.故选:C.【点评】本题主要考查了函数自变量的取值范围,二次根式,分式有意义的条件,依据题意列出不等式组是解题的关键.4.(3分)(2022•恩施州)如图是一个正方体纸盒的展开图,将其折叠成一个正方体后,有“振”字一面的相对面上的字是()A.“恩”B.“乡”C.“村”D.“兴”【分析】根据正方体表面展开图的特征进行判断即可.【解答】解:由正方体表面展开图的“相间、Z端是对面”可知,“振”与“兴”是对面,故选:D.【点评】本题考查正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确判断的前提.5.(3分)(2022•恩施州)下列运算正确的是()A.a2•a3=a6B.a3÷a2=1 C.a3﹣a2=a D.(a3)2=a6【分析】分别根据同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,合并同类项,只把系数相加减,字母与字母的次数不变,对各选项计算后利用排除法求解.【解答】解:A、a2•a3=a5,故本选项错误;B、a3÷a2=a,故本选项错误;C、a3和a2不是同类项,不能合并,故本选项错误;D、(a3)2=a6,故本选项正确.故选:D.【点评】本题考查了同底数幂的乘法,同底数幂的除法,合并同类项的法则,幂的乘方,熟练掌握运算性质是解题的关键.6.(3分)(2022•恩施州)为了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如下表所示:月用水量(吨) 3 4 5 6 户数 4 6 8 2 关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的()A.众数是5 B.平均数是7 C.中位数是5 D.方差是1【分析】根据众数、中位数、平均数、方差的计算方法分别进行计算即可.【解答】解:这组数据出现次数最多的是5吨,共出现8次,所以用水量的众数是5吨,因此选项A符合题意;这组数据的平均数为=4.4(吨),因此选项B不符合题意;将这20户的用水量从小到大排列,处在中间位置的两个数的平均数为=4.5(吨),因此选项C不符合题意;这组数据的方差为[(3﹣4.4)2×3+(4﹣4.4)2×6+(5﹣4.4)2×8+(6﹣4.4)2×2]≈0.46,因此选项D不符合题意;故选:A.【点评】本题考查平均数、中位数、众数、方差,掌握平均数、中位数、众数以及方差的计算方法是正确解答的前提.7.(3分)(2022•恩施州)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=()A.120°B.130°C.140°D.150°【分析】过点B作BF∥l1,交AC于点F,利用三角形的外角的性质,平行线的性质定理和对顶角相等的性质解答即可.【解答】解:过含30°角的直角三角板的直角顶点B作BF∥l1,交AC于点F,∵∠C=30°,∴∠A=90°﹣∠C=60°.∵∠1=∠A+∠ADE,∴∠ADE=60°.∵BF∥l1,∴∠ABF=∠ADE=60°,∴∠FBG=90°﹣∠ABF=30°.∵BF∥l1,l1∥l2,∴BF∥l2,∴∠BGH+∠FBG=180°,∴∠BGH=180°﹣∠FBG=150°,∴∠2=∠BGH=150°.故选:D.【点评】本题主要考查了直角三角形的两个锐角互余,平行线的性质定理,三角形的外角的性质,对顶角相等,过点B作BF∥l1,交AC于点F是解题的关键.8.(3分)(2022•恩施州)一艘轮船在静水中的速度为30km/h,它沿江顺流航行144km与逆流航行96km所用时间相等,江水的流速为多少?设江水流速为vkm/h,则符合题意的方程是()A.=B.=C.=D.=【分析】根据“顺流航行144km与逆流航行96km所用时间相等”列分式方程即可.【解答】解:根据题意,可得,故选:A.【点评】本题考查了分式方程的应用,理解题意并根据题意建立等量关系是解题的关键.9.(3分)(2022•恩施州)如图,在矩形ABCD中,连接BD,分别以B、D为圆心,大于BD的长为半径画弧,两弧交于P、Q两点,作直线PQ,分别与AD、BC 交于点M、N,连接BM、DN.若AD=4,AB=2.则四边形MBND的周长为()A.B.5 C.10 D.20【分析】利用作图过程可得PQ为BD的垂直平分线,利用垂直平分线的性质和全等三角形的判定与性质证明四边形MBND为菱形,利用勾股定理求得BM,则结论可得.【解答】解:由作图过程可得:PQ为BD的垂直平分线,∴BM=MD,BN=ND.设PQ与BD交于点O,如图,则BO=DO.∵四边形ABCD是矩形,∴AD∥BC,∴∠MDO=∠NBO,∠DMO=∠BNO,在△MDO和△NBO中,,∴△MDO≌△NBO(AAS),∴DM=BN,∴四边形BNDM为平行四边形,∵BM=MD,∴四边形MBND为菱形,∴四边形MBND的周长=4BM.设MB=x,则MD=BM=x,∴AM=AD﹣DM=4﹣x,在Rt△ABM中,∵AB2+AM2=BM2,∴22+(4﹣x)2=x2,解得:x=,∴四边形MBND的周长=4BM=10.故选:C.【点评】本题主要考查了基本作图,作线段的垂直平分线,矩形的性质,线段垂直平分线的性质,菱形的判定与性质,勾股定理,全等三角形的判定与性质,判定四边形MBND为菱形是解题的关键.10.(3分)(2022•恩施州)如图1是我国青海湖最深处的某一截面图,青海湖水面下任意一点A的压强P(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为P=kh+P0,其图象如图2所示,其中P0为青海湖水面大气压强,k为常数且k≠0.根据图中信息分析(结果保留一位小数),下列结论正确的是()A.青海湖水深16.4m处的压强为188.6cmHgB.青海湖水面大气压强为76.0cmHgC.函数解析式P=kh+P0中自变量h的取值范围是h≥0D.P与h的函数解析式为P=9.8×105h+76【分析】由图象可知,直线P=kh+P0过点(0,68)和(32.8,309.2).由此可得出k和P0的值,进而可判断B,D;根据实际情况可得出h的取值范围,进而可判断C;将h=16.4代入解析式,可求出P的值,进而可判断A.【解答】解:由图象可知,直线P=kh+P0过点(0,68)和(32.8,309.2),∴,解得.∴直线解析式为:P=7.4h+68.故D错误,不符合题意;∴青海湖水面大气压强为68.0cmHg,故B错误,不符合题意;根据实际意义,0≤h≤32.8,故C错误,不符合题意;将h=16.4代入解析式,∴P=7.4×16.4+68=188.6,即青海湖水深16.4m处的压强为188.6cmHg,故A正确,符合题意.故选:A.【点评】本题主要考查一次函数的实际应用,涉及一次函数的图象和性质,待定系数法等知识.关键是计算过程中需要结合实际意义.11.(3分)(2022•恩施州)如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是()A.当t=4s时,四边形ABMP为矩形B.当t=5s时,四边形CDPM为平行四边形C.当CD=PM时,t=4sD.当CD=PM时,t=4s或6s【分析】根据题意,表示出DP,BM,AD和BC的长,当四边形ABMP为矩形时,根据AP=BM,列方程求解即可;当四边形CDPM为平行四边形,根据DP=CM,列方程求解即可;当CD=PM时,分两种情况:①四边形CDPM是平行四边形,②四边形CDPM是等腰梯形,分别列方程求解即可.【解答】解:根据题意,可得DP=t,BM=t,∵AD=10cm,BC=8cm,∴AP=10﹣t,CM=8﹣t,当四边形ABMP为矩形时,AP=BM,即10﹣t=t,解得t=5,故A选项不符合题意;当四边形CDPM为平行四边形,DP=CM,即t=8﹣t,解得t=4,故B选项不符合题意;当CD=PM时,分两种情况:①四边形CDPM是平行四边形,此时CM=PD,即8﹣t=t,解得t=4,②四边形CDPM是等腰梯形,过点M作MG⊥AD于点G,过点C作CH⊥AD于点H,如图所示:则∠MGP=∠CHD=90°,∵PM=CD,GM=HC,∴△MGP≌△CHD(HL),∴GP=HD,∵AG=AP+GP=10﹣t+,又∵BM=t,∴10﹣t+=t,解得t=6,综上,当CD=PM时,t=4s或6s,故C选项不符合题意,D选项符合题意,故选:D.【点评】本题考查了矩形的判定,平行四边形的判定,全等三角形的判定和性质,涉及动点问题,用含t的代数式表示出各线段的长是解题的关键.12.(3分)(2022•恩施州)已知抛物线y=x2﹣bx+c,当x=1时,y<0;当x =2时,y<0.下列判断:①b2>2c;②若c>1,则b>;③已知点A(m1,n1),B(m2,n2)在抛物线y=x2﹣bx+c上,当m<m2<b时,n1>n2;④若方程x2﹣bx+c=0的两实数1根为x1,x2,则x1+x2>3.其中正确的有()个.A.1 B.2 C.3 D.4【分析】利用一元二次方程的根的判别式可判断①;把x=1、x=2,分别代入,得到不等式,求得即可判断②;求得抛物线的对称轴为直线x=b,利用二次函数的性质即可判断③;利用根与系数的关系即可判断④.【解答】解:∵a=>0,∴抛物线开口向上,当x=1时,y<0;当x=2时,y<0,∴抛物线与x轴有两个不同的交点,∴Δ=b2﹣4ac=b2﹣2c>0,故①正确;∵当x=1时,y<0;当x=2时,y<0,∴﹣b+c<0;∴b>+c,当c>1时,则b>,故②正确;抛物线的对称轴为直线x=b,且开口向上,当x<b时,y的值随x的增大而减小,∴当m1<m2<b时,n1>n2,故③正确;∵方程x2﹣bx+c=0的两实数根为x1,x2,∴x1+x2=2b,又∵b<,∴x1+x2<3,故④错误;综上,正确的有①②③,共3个,故选:C.【点评】本题考查了二次函数的性质,一元二次方程的根的判别式以及根与系数的关系等知识,掌握二次函数的性质是解题关键.二、填空题(本大题共有4小题,每小题3分,共12分).13.(3分)(2022•恩施州)9的算术平方根是 3 .【分析】9的平方根为±3,算术平方根为非负,从而得出结论.【解答】解:∵(±3)2=9,∴9的算术平方根是3.故答案为:3.【点评】本题考查了数的算术平方根,解题的关键是牢记算术平方根为非负.14.(3分)(2022•恩施州)因式分解:a3﹣6a2+9a=a(a﹣3)2.【分析】先提公因式a,再利用完全平方公式进行因式分解即可.【解答】解:原式=a(a2﹣6a+9)=a(a﹣3)2,故答案为:a(a﹣3)2.【点评】本题考查提公因式法、公式法分解因式,掌握完全平方公式的结构特征是正确解答的关键.15.(3分)(2022•恩施州)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,⊙O为Rt△ABC的内切圆,则图中阴影部分的面积为(结果保留π)5﹣π.【分析】根据题意,先作出相应的辅助线,然后求出内切圆的半径,再根据图形可知:阴影部分的面积=△ABC的面积﹣正方形CEOD的面积﹣⊙O面积的,代入数据计算即可.【解答】解:作OD⊥AC于点D,作OE⊥CB于点E,作OF⊥AB于点F,连接OA、OC、OB,如图,∵∠C=90°,OD=OE=OF,∴四边形CEOD是正方形,∵AC=4,BC=3,∠C=90°,∴AB===5,∵S△ABC=S△AOC+S△COB+S△BOA,∴=,解得OD=OE=OF=1,∴图中阴影部分的面积为:﹣1×1﹣π×12×=5﹣π,故答案为:5﹣π.【点评】本题考查三角形的内切圆、勾股定理、扇形面积的计算,解答本题的关键是求出内切圆的半径.16.(3分)(2022•恩施州)观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为a n,且满足+=.则a4=,a2022=.【分析】由题意可得a n=,即可求解.【解答】解:由题意可得:a1=2=,a2==,a3=,∵+=,∴2+=7,∴a4==,∵=,∴a5=,同理可求a6==,•∴a n=,∴a2022=,故答案为:,.【点评】本题考查了数字的变化类,找出数字的变化规律是解题的关键.三、解答题(本大题共有8个小题,共72分.请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).17.(8分)(2022•恩施州)先化简,再求值:÷﹣1,其中x=.【分析】先根据分式的除法法则把除法变成乘法,算乘法,再根据分式的减法法则进行计算,最后代入求出答案即可.【解答】解:÷﹣1=•﹣1=﹣1==,当x=时,原式==.【点评】本题考查了分式的化简求值,能正确根据分式的运算法则进行化简是解此题的关键,注意运算顺序.18.(8分)(2022•恩施州)如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.【分析】由“AAS”可证△CBE≌△DCF,可得CF=BE,CE=DF,可得结论.【解答】证明:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∵CE⊥BG,DF⊥CE,∴∠BEC=∠DFC=90°,∴∠BCE+∠CBE=90°=∠BCE+∠DCF,∴∠CBE=∠DCF,在△CBE和△DCF中,,∴△CBE≌△DCF(AAS),∴CF=BE,CE=DF,∵CE=EF+CF,∴DF=BE+EF.【点评】本题考查了正方形的性质,全等三角形的判定和性质,证明三角形全等是解题的关键.19.(8分)(2022•恩施州)2022年4月29日,湖北日报联合夏风教室发起“劳动最光荣,加油好少年”主题活动.某校学生积极参与本次主题活动,为了解该校学生参与本次主题活动的情况,随机抽取该校部分学生进行调查.根据调查结果绘制如下不完整的统计图(如图).请结合图中信息解答下列问题:(1)本次共调查了200 名学生,并补全条形统计图.(2)若该校共有1200名学生参加本次主题活动,则本次活动中该校“洗衣服”的学生约有多少名?(3)现从参与本次主题活动的甲、乙、丙、丁4名学生中,随机抽取2名学生谈一谈劳动感受.请用列表或画树状图的方法,求甲、乙两人同时被抽中的概率.【分析】(1)从两个统计图中可知,样本中参与“做饭”的有40人,占调查人数的20%,由频率=可以求出调查人数,进而求出参与“扫地”的频数,补全条形统计图;(2)用样本中参与“洗衣服”的所占的百分比估计总体中参与“洗衣服”的百分比,进而求出相应的人数;(3)用列表法表示从甲、乙、丙、丁四个人中选择2个人所有可能出现的结果情况,进而求出相应的概率即可.【解答】解:(1)40÷20%=200(人),200﹣40﹣50﹣30﹣20=60(人),故答案为:200,补全条形统计图如下:(2)1200×=300(人),答:该校1200名学生中参与“洗衣服”的学生约有300名;(3)从甲、乙、丙、丁四个人中选择2个人所有可能出现的结果情况如下:共有12种可能出现的结果,其中甲、乙同时被抽中的有2种,所以甲、乙同时被抽中的概率为=.【点评】本题考查条形统计图、扇形统计图以及样本估计总体,列举出所有可能出现的结果是解决问题的关键.20.(8分)(2022•恩施州)如图,湖中一古亭,湖边一古柳,一沉静,一飘逸,碧波荡漾,相映成趣.某活动小组赏湖之余,为了测量古亭与古柳间的距离,在古柳A处测得古亭B位于北偏东60°,他们向南走50m到达D点,测得古亭B位于北偏东45°.求古亭与古柳之间的距离AB的长(参考数据:≈1.41,≈1.73,结果精确到1m).【分析】过点B作BC⊥AD,交DA的延长线于点C,设AC=x米,则CD=(x+50)米,在Rt△ABC中,利用锐角三角函数的定义求出BC的长,再在Rt△BCD中,利用锐角三角函数的定义可得BC=DC,从而列出关于x的方程,进行计算即可求出AC的长,最后在Rt△ABC中,利用锐角三角函数的定义求出AB的长,即可解答.【解答】解:过点B作BC⊥AD,交DA的延长线于点C,设AC=x米,∵AD=50米,∴CD=AC+AD=(x+50)米,在Rt△ABC中,∠CAB=60°,∴BC=AC•tan60°=x(米),在Rt△BCD中,∠BDC=45°,∴tan45°==1,∴BC=CD,∴x=x+50,∴x=25+25,∴AC=(25+25)米,∴AB===50+50≈137(米),∴古亭与古柳之间的距离AB的长约为137米.【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.21.(8分)(2022•恩施州)如图,在平面直角坐标系中,O为坐标原点,已知∠ACB=90°,A(0,2),C(6,2).D为等腰直角三角形ABC的边BC上一点,且S△ABC=3S△ADC.反比例函数y1=(k≠0)的图象经过点D.(1)求反比例函数的解析式.(2)若AB所在直线解析式为y2=ax+b(a≠0),当y1>y2时,求x的取值范围.【分析】(1)根据等腰直角三角形的性质得出AC=BC=6,由S△ABC=3S△ADC得到CD=2,即可求得D(6,4),代入y1=(k≠0)即可求得k的值;(2)利用待定系数法求得y2的解析式,然后解析式联立,解方程组求得交点坐标,根据图形即可求得.【解答】解:(1)∵A(0,2),C(6,2),∴AC=6,∵△ABC是∠C为直角的等腰直角三角形,∴BC=AC=6,∵D为等腰直角三角形ABC的边BC上一点,且S△ABC=3S△ADC.∴CD=2,∴D(6,4),∵反比例函数y1=(k≠0)的图象经过点D,∴k=6×4=24,∴反比例函数的解析式为y=;(2)∵A(0,2),B(6,8),∴把A、B的坐标代入y2=ax+b得,解得,∴y2=x+2,解得或,∴两函数的交点为(﹣6,﹣4),(4,6)∴当y1>y2时,x的取值范围是x<﹣6或0<x<4.【点评】本题是反比例函数与一次函数的交点问题,考查了等腰直角三角形的性质,待定系数法求反比例函数的解析式,一次函数的解析式,数形结合是解题的关键.22.(10分)(2022•恩施州)某校计划租用甲、乙两种客车送180名师生去研学基地开展综合实践活动.已知租用一辆甲型客车和一辆乙型客车共需500元,租用2辆甲型客车和3辆乙型客车共需1300元.甲型客车每辆可坐15名师生,乙型客车每辆可坐25名师生.(1)租用甲、乙两种客车每辆各多少元?(2)若学校计划租用8辆客车,怎样租车可使总费用最少?【分析】(1)设租用甲种客车每辆x元,租用乙种客车每辆y元,根据题意建立二元一次方程组,再解方程即可得出结论.(2)设租甲型客车m辆,总费用为w元,则租乙型客车(8﹣m)辆,根据总费用=每辆车的租金×租车数量,即可得出w关于x的函数关系式,由师生总人数结合甲、乙两种型号客车的载客量,可求出x的取值范围,再利用一次函数的性质即可解决最值问题.【解答】解:(1)设租用甲种客车每辆x元,租用乙种客车每辆y元,根据题意可得,,解得.∴租用甲种客车每辆200元,租用乙种客车每辆300元.(2)设租用甲型客车m辆,则租用乙型客车(8﹣m)辆,租车总费用为w元,根据题意可知,w=200m+300(8﹣m)=﹣100m+2400,∵15m+25(8﹣m)≥180,∴0<m≤2,∵﹣100<0,∴w随m的增大而减小,∴当m=2时,w的最小值为﹣100×2+2400=2200.∴当租用甲型客车2辆,租用乙型客车6辆,租车总费用最少为2200元.【点评】本题考查了一次函数的应用、二元一次方程组的应用、一次函数的性质以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据总费用=每辆车的租金×租车数量,找出w 关于x的函数关系式.23.(10分)(2022•恩施州)如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.(1)求证:∠ADE=∠PAE.(2)若∠ADE=30°,求证:AE=PE.(3)若PE=4,CD=6,求CE的长.【分析】(1)连接OA,利用切线的性质定理,圆周角定理,同圆的半径相等,等腰三角形的性质和等角的余角相等解答即可;(2)利用(1)的结论,直径所对的圆周角为直角,三角形的外角的性质和等腰三角形的判定定理解答即可;(3)CE=x,则DE=CD+CE=6+x,OA=OE=,OC=OE﹣CE=,OP=OE+PE =,利用相似三角形的判定与性质得出比例式即可求得结论.【解答】(1)证明:连接OA,如图,∵PA为⊙O的切线,∴AO⊥PA,∴∠OAE+∠PAE=90°.∵DE是⊙O的直径,∴∠DAE=90°,∴∠ADE+∠AED=90°.∵OA=OE,∴∠OAE=∠AED,∴∠ADE=∠PAE;(2)证明:由(1)知:∠ADE=∠PAE=30°,∵∠DAE=90°,∴∠AED=90°﹣∠ADE=60°.∵∠AED=∠PAE+∠APE,∴∠APE=∠PAE=30°,∴AE=PE;(3)解:设CE=x,则DE=CD+CE=6+x,∴OA=OE=,∴OC=OE﹣CE=,OP=OE+PE=.∵PA、PB为⊙O的切线,∴PA=PB,PO平分∠APB,∴PO⊥AB.∵PA为⊙O的切线,∴AO⊥PA,∴△OAC∽△OPA,∴,∴,即:x2+10x﹣24=0.解得:x=2或﹣12(不合题意,舍去),∴CE=2.【点评】本题主要考查了圆的切线的性质,切线长定理,等腰三角形的判定与性质,圆周角定理,垂径定理,相似三角形的判定与性质,连接OA是解决此类问题常添加的辅助线.24.(12分)(2022•恩施州)在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+c与y轴交于点P(0,4).(1)直接写出抛物线的解析式.(2)如图,将抛物线y=﹣x2+c向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y 轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)直线BC与抛物线y=﹣x2+c交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)若将抛物线y=﹣x2+c进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出抛物线y=﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标.。
亭子结构力学大体分析

亭子结构力学大体分析亭子按角分类:三角亭、四角亭、五角亭、六角亭、八角亭、十二角亭、圆亭。
亭子按层(檐)分类:单檐四角亭、重檐四角亭、真上层四角亭、假上层四角亭;单檐六角亭、重檐六角亭、真上层六角亭、假上层六角亭;单檐八重檐、重檐八重檐、真上层八角亭、假上层八角亭;单檐圆亭、重檐圆亭。
亭子按形体分类:单体亭、鸳鸯(重体)亭、方形亭、圆形亭传统的木亭和中国古代大多数建筑一样,其构造体系可以分为:承重台基层、柱网层及屋架结构三部分。
屋架结构在亭的整体构造中最为重要,不同的屋顶表现形式正是有由不同的屋架结构所组成的。
它包括屋架层、屋面层两部分组成。
斗拱、房梁、檩条等组成屋架层;椽子、望板、屋瓦和屋脊组成屋面层。
亭子的构造做法相对别的建筑形式来讲比较简单,但是构造上“造无定式”,比较灵活。
由于亭的外部形体较小,多为单个开间,所以其屋顶多为攒尖式和歇山式的屋顶。
当然,还有硬山和悬山式的,但这里主要对前两种形式的屋顶构造做一分析。
(1)攒尖式。
由于地理分布不同传统亭的攒尖式做法,又分为南北两种。
北方属于官式做法,主要是抹角梁和扒梁法。
例如,四角的攒尖亭,都是先现在柱头上面安装箍头枋,造成圈梁,利用圏梁连接的柱子形成梁架。
接着在箍头枋的上面加上垫板和搭交檐檩,并在转交处装上角云,在角云上安装垫板和搭交檐檩,最后在搭交檐檩上使用扒梁或者抹角梁。
第一,抹角梁法。
这种方法主要是在檐檩上按照45°的轴线把抹角梁搭放在檐檩条上,形成一圈抹角梁。
然后再抹角梁上搭金枋。
金檩,由每个转交安装角梁,再在角梁上安装戗,再把戗搭落在中央的雷公柱上,这样就形成了攒尖顶的主要骨架结构。
若亭子体量较大,可在雷公柱下安装“太平梁”,使雷公柱的落于“太平梁”上分散压力。
(见图 4.23北方亭屋顶做法)例如,北京的颐和园内的廓如亭,就是使用的抹角梁。
抹角梁适用于所有的有角的亭子,但是像扇形亭和园亭就没法使用这种构造手法,只能用井口扒梁的手法。
2023-2024学年北京市大兴区高三(上)期末数学试卷【答案版】

2023-2024学年北京市大兴区高三(上)期末数学试卷一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U ={x |x >1},集合A ={x |x ≥2},则∁U A =( ) A .{x |1<x ≤2}B .{x |x <2}C .{x |1<x <2}D .{x |x ≤1}2.若复数z 满足i •(z +i )=1,则复数z 的虚部是( ) A .﹣2B .2C .﹣1D .03.(x 2−1x)6的展开式中的常数项为( )A .20B .﹣20C .15D .﹣154.设向量a →,b →,若|a →|=1,b →=(−3,4),b →=λa →(λ>0),则a →=( ) A .(45,−35)B .(−45,35)C .(35,−45)D .(−35,45)5.已知函数f (x )=2x ﹣1,则不等式f (x )≤x 的解集为( ) A .(﹣∞,2]B .[0,1]C .[1,+∞)D .[1,2]6.在△ABC 中,“C =π2”是“sin 2A +sin 2B =1”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.已知定点M (1,3)和抛物线C :x 2=8y ,F 是抛物线C 的焦点,N 是抛物线C 上的点,则|NF |+|NM |的最小值为( ) A .3B .4C .5D .68.已知a >b >0且ab =10、则下列结论中不正确的是( ) A .lga +lgb >0 B .lga ﹣lgb >0 C .lga ⋅lgb <14D .lga lgb>19.木楔在传统木工中运用广泛.如图,某木楔可视为一个五面体,其中四边形ABCD 是边长为2的正方形,且△ADE ,△BCF 均为等边三角形,EF ∥CD ,EF =4,则该木楔的体积为( )A .√2B .2√2C .2√23D .8√2310.设无穷等差数列{a n }的公差为d ,集合T ={t |t =sin a n ,n ∈N *}.则( ) A .T 不可能有无数个元素B .当且仅当d =0时,T 只有1个元素C .当T 只有2个元素时,这2个元素的乘积有可能为12D .当d =2πk,k ≥2,k ∈N ∗时,T 最多有k 个元素,且这k 个元素的和为0 二、填空题共5小题,每小题5分,共25分.11.设{a n }是等比数列,a 1=1,a 2•a 4=16,则a 5= . 12.若双曲线x 2−y 2b2=1(b >0)的一条渐近线方程为2x ﹣y =0,则b = . 13.能够说明“设a ,b ,c 是任意实数.若a >b >c ,则ab >c 2”是假命题的一组整数a ,b ,c 的值依次为 .14.如图是六角螺母的横截面,其内圈是半径为1的圆O ,外框是以为O 中心,边长为2的正六边形ABCDEF ,则O 到线段AC 的距离为 ;若P 是圆O 上的动点,则AC →⋅AP →的取值范围是 .15.设函数f (x )的定义域为R ,且f (x )满足如下性质:(i )若将f (x )的图象向左平移2个单位,则所得的图象关于y 轴对称,(ii )若将f (x )图象上的所有点的纵坐标不变,横坐标缩短为原来的12,再向左平移12个单位,则所得的图象关于原点对称.给出下列四个结论:①f (1)=f (3);②f (0)=0;③f (2)+f (4)=0;④f(−12)f(112)≤0.其中所有正确结论的序号是 .三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程,16.(14分)如图.在三棱柱ABC ﹣A 1B 1C 1中,BB 1⊥平面ABC ,CA =CB =√5,AA 1=AB =2,D 、E 分别为AB ,AA 1的中点.(1)求证:平面CDE ⊥平面ABB 1A 1;(2)求直线CE 与平面BCC 1B 1所成角的正弦值.17.(13分)在△ABC中,a=1,b=2.(1)若c=2√2,求△ABC的面积:(2)在下列三个条件中选择一个作为已知,使△ABC存在,求∠A.条件①:∠B=2∠A;条件②:∠B=π3+∠A;条件③:∠C=2∠A.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.18.(13分)为了解客户对A,B两家快递公司的配送时效和服务满意度情况,现随机获得了某地区客户对这两家快递公司评价的调查问卷,已知A,B两家公司的调查问卷分别有120份和80份,全部数据统计如下:假设客户对A,B两家快递公司的评价相互独立.用频率估计概率,(1)从该地区选择A快递公司的客户中随机抽取1人,估计该客户对A快递公司配送时效的评价不低于75分的概率;(2)分别从该地区A和B快递公司的样本调查问卷中,各随机抽取1份,记X为这2份问卷中的服务满意度评价不低于75分的份数,求X的分布列和数学期望;(3)记评价分数x≥85为“优秀”等级,75≤x<85为“良好”等级,65≤x<75为“一般”等级、已知小王比较看重配送时效的等级,根据该地区A,B两家快递公司配送时效的样本评价分数的等级情况.你认为小王选择A,B哪家快递公司合适?说明理由.19.(15分)已知椭圆C的两个顶点分别为A(﹣2,0),B(2,0),焦点在x轴上,离心率为√3 2.(1)求椭圆C 的方程;(2)设O 为原点,过点T (4,0)的直线l 交椭圆C 于点M ,N ,直线BM 与直线x =1相交于点P ,直线AN 与y 轴相交于点Q .求证:△OAQ 与△OTP 的面积之比为定值. 20.(15分)已知函数f(x)=ax +ln1−x1+x. (1)若曲线y =f (x )在点(0,f (0))处的切线斜率为0,求a 的值; (2)当a =4时,求f (x )的零点个数;(3)证明:0≤a ≤2是f (x )为单调函数的充分而不必要条件.21.(15分)若各项为正的无穷数列{a n }满足:对于∀n ∈N *,a n+12−a n 2=d ,其中d 为非零常数,则称数列{a n }为D 数列.记b n =a n +1﹣a n .(1)判断无穷数列a n =√n 和a n =2n 是否是D 数列,并说明理由; (2)若{a n }是D 数列,证明:数列{b n }中存在小于1的项; (3)若{a n }是D 数列,证明:存在正整数n ,使得∑ n i=11a i>2024.2023-2024学年北京市大兴区高三(上)期末数学试卷参考答案与试题解析一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U ={x |x >1},集合A ={x |x ≥2},则∁U A =( ) A .{x |1<x ≤2}B .{x |x <2}C .{x |1<x <2}D .{x |x ≤1}解:U ={x |x >1},集合A ={x |x ≥2},则∁U A ={x |1<x <2}. 故选:C .2.若复数z 满足i •(z +i )=1,则复数z 的虚部是( ) A .﹣2B .2C .﹣1D .0解:∵i •(z +i )=1,∴z +i =1i=−i ,解得z =﹣2i ,∴z 的虚部为﹣2. 故选:A .3.(x 2−1x)6的展开式中的常数项为( )A .20B .﹣20C .15D .﹣15解:通项公式T r +1=∁6r (x 2)6﹣r(−1x)r =(﹣1)r ∁6r x 12﹣3r , 令12﹣3r =0,解得r =4.∴展开式中的常数项=∁64=15. 故选:C .4.设向量a →,b →,若|a →|=1,b →=(−3,4),b →=λa →(λ>0),则a →=( ) A .(45,−35)B .(−45,35)C .(35,−45)D .(−35,45)解:设a →=(m ,n ),∵若|a →|=1,b →=(−3,4),b →=λa →(λ>0), ∴λm =﹣3,λn =4,且m 2+n 2=1,即9λ2+16λ2=1,∴λ2=25,又λ>0, ∴λ=5,∴m =−35,n =45,∴a →=(m ,n )=(−35,45).故选:D .5.已知函数f (x )=2x ﹣1,则不等式f (x )≤x 的解集为( )A.(﹣∞,2]B.[0,1]C.[1,+∞)D.[1,2]解:令g(x)=f(x)﹣x=2x﹣x﹣1,则g′(x)=2x ln2﹣1,令g′(x)=0,得2x=1ln2=log2e,即x=log2(log2e),当x∈(﹣∞,log2(log2e))时,g′(x)<0,当x∈(log2(log2e),+∞)时,g′(x)>0,∴g(x)在区间(﹣∞,log2(log2e))上单调递减,在区间(log2(log2e),+∞)上单调递增,又g(0)=0,g(1)=0,∴当x∈[0,1]时,g(x)=f(x)﹣x=2x﹣x﹣1≤0,∴不等式f(x)≤x的解集为[0,1].故选:B.6.在△ABC中,“C=π2”是“sin2A+sin2B=1”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件解:在△ABC中,当C=π2时,则A+B=π2,故sin2A+sin2B=sin2A+sin2(π2−A)=sin2A+cos2A=1,故充分性成立,当A=120°,B=30°,满足sin2A+sin2B=1,但C≠π2,故必要性不成立,综上所述,在△ABC中,“C=π2”是“sin2A+sin2B=1”的充分不必要条件.故选:A.7.已知定点M(1,3)和抛物线C:x2=8y,F是抛物线C的焦点,N是抛物线C上的点,则|NF|+|NM|的最小值为()A.3B.4C.5D.6解:作出抛物线C:x2=8y的图象如图:点M(1,3)在抛物线C:x2=8y内,抛物线的准线方程为y=﹣2,过M作准线的垂线,垂足为K,垂线交抛物线于N,则此时|NF|+|NM|取最小值为|MK|=3﹣(﹣2)=5.8.已知a >b >0且ab =10、则下列结论中不正确的是( ) A .lga +lgb >0 B .lga ﹣lgb >0 C .lga ⋅lgb <14D .lga lgb>1解:∵a >b >0且ab =10,∴a b>1,b =10a ,a >√10(若a ≤√10,则b <√10,ab <10,与已知矛盾),∴lgab =lga +lgb =lg 10=1>0,A 正确; ∴lg ab =lga ﹣lgb >lg 1=0,B 正确;由a >√10,得lga >12,∴(lga −12)2>0,∴lga •lgb =lga •lg 10a=lga (1﹣lga )=﹣(lga −12)2+14<14,C 正确;∵lga lgb −1=lga−lgb lgb 中,分子lga ﹣lgb >0,但分母lgb 的符号不确定,故lga lgb−1的符号不确定,D 错误. 故选:D .9.木楔在传统木工中运用广泛.如图,某木楔可视为一个五面体,其中四边形ABCD 是边长为2的正方形,且△ADE ,△BCF 均为等边三角形,EF ∥CD ,EF =4,则该木楔的体积为( )A .√2B .2√2C .2√23D .8√23解:如图,分别过点A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH ,由四边形ABCD 是边长为2的正方形,且△ADE ,△BCF 均为正三角形,EF ∥CD ,EF =4, 得EG =HF =1,AG =GD =BH =HC =√3. 取AD 的中点O ,连接GO ,可得GO =√2, ∴S △ADG =S △BCH =12×√2×2=√2. ∴该木楔子的体积V =V E ﹣ADG +V F ﹣BCH +V AGD ﹣BHC =2V E ﹣ADG +V AGD ﹣BHC =2×13×√2×1+√2×2=8√23.10.设无穷等差数列{a n }的公差为d ,集合T ={t |t =sin a n ,n ∈N *}.则( ) A .T 不可能有无数个元素B .当且仅当d =0时,T 只有1个元素C .当T 只有2个元素时,这2个元素的乘积有可能为12D .当d =2πk,k ≥2,k ∈N ∗时,T 最多有k 个元素,且这k 个元素的和为0 解:对于A ,不妨令a n =n ,则d =1,则t =sin a n ,由于y =sin x 的周期为2π,且对称轴为x =π2+kπ,k ∈Z ,则对任意的a i ,a j ,i ,j ∈N *,i ≠j ,必有sin a i ≠sin a j ,当a n 有无穷项时,T 中有无数元素,A 错误;对于B ,令a n =n π,此时d =π,此时sin n π=0,T 中只有一个元素0,B 错误;对于C ,若T 中只有两个元素,根据y =sin x 的周期性与中心对称性,sin a n 的值必一正一负,因为若两个值都为正,必不满足等差数列的定义,所以该两个数的乘积必为负,C 错误; 对于D ,当d =2πk ,k ≥2,k ∈N ∗时,在y =sin x 的一个周期[0,2π)内,取a 1=0,此时k ×2πk=2π,比如取k =5,此时sin a 1,sin a 2,⋯,sin a 5两两不相等,此时T 有5个元素;而结合y =sin x 的周期为2π可知,必有sin a i 必周期性重复出现,所以T 中最多有k 个元素; 再证明和为0,∑ k−1i=0sin(α+2iπk )=12sin πk ∑ k−1i=0[sin(α+2iπk )sin πk ]=12sin πk ∑ k−1i=0[cos(α+2i−1k π)−cos(α+2i+1k π)]=12sin πk[cos(α−πk )−cos (α+2k−1k π)]=0,D 正确. 故选:D .二、填空题共5小题,每小题5分,共25分.11.设{a n }是等比数列,a 1=1,a 2•a 4=16,则a 5= 16 .解:因为等比数列{a n }中,a 1=1,a 2a 4=a 12⋅q 4=16,则q 4=16,所以a 5=a 1⋅q 4=16.故答案为:16.12.若双曲线x 2−y 2b2=1(b >0)的一条渐近线方程为2x ﹣y =0,则b = 2 .解:双曲线x 2−y 2b2=1(b >0),则渐近线为y =±ba =±b , 双曲线x 2−y 2b2=1(b >0)的一条渐近线方程为2x ﹣y =0,即y =2x ,b >0,则b =2. 故答案为:2.13.能够说明“设a ,b ,c 是任意实数.若a >b >c ,则ab >c 2”是假命题的一组整数a ,b ,c 的值依次为 ﹣1,﹣2,﹣3(答案不唯一) .解:当a =﹣1,b =﹣2,c =﹣3时,满足a >b >c , 但ab =2,c 2=9,ab <c 2,故“设a ,b ,c 是任意实数.若a >b >c ,则ab >c 2”是假命题. 故答案为:﹣1,﹣2,﹣3(答案不唯一).14.如图是六角螺母的横截面,其内圈是半径为1的圆O ,外框是以为O 中心,边长为2的正六边形ABCDEF ,则O 到线段AC 的距离为 1 ;若P 是圆O 上的动点,则AC →⋅AP →的取值范围是 [6﹣2√3,6+2√3] .解:如图以O 为坐标原点,AD 所在直线为x 轴,AD 的垂直平分线所在直线为y 轴,建立平面直角坐标系,设点P (cos θ,sin θ)(0≤θ≤2π),由题意知,A (﹣2,0),O (0,0),C (1,−√3),直线AC 的斜率k =−√31−(−2)=−√33,AC 的方程为y ﹣0=√33(x +2),即x +√3y +2=0,故O 到线段AC 的距离d =2√1+(√3)2=1;又AC →=(3,−√3),AP →=(2+cos θ,sin θ),AC →⋅AP →=6+3cos θ−√3sin θ=6+2√3(√32cos θ−12sin θ)=6+2√3sin (π3−θ)∈[6﹣2√3,6+2√3].故答案为:1;[6﹣2√3,6+2√3].15.设函数f (x )的定义域为R ,且f (x )满足如下性质:(i )若将f (x )的图象向左平移2个单位,则所得的图象关于y 轴对称,(ii )若将f (x )图象上的所有点的纵坐标不变,横坐标缩短为原来的12,再向左平移12个单位,则所得的图象关于原点对称.给出下列四个结论:①f (1)=f (3);②f (0)=0;③f (2)+f (4)=0;④f(−12)f(112)≤0.其中所有正确结论的序号是 ①③④ .解:∵将f (x )的图象向左平移2个单位,则所得的图象关于y 轴对称,∴f (x )的图象关于x =2对称,∴f (﹣x )=f (x +4),∴f (1)=f (3),∴①正确;∵将f (x )图象上的所有点的纵坐标不变,横坐标缩短为原来的12,再向左平移12个单位,则所得的函数为f (2x +1),又f (2x +1)的图象在R 上关于原点对称,∴f (﹣2x +1)+f (2x +1)=0,∴2f (1)=0,∴f (1)=0, ∴f (x )关于(1,0)对称,∴f (﹣x )=﹣f (x +2),又f (﹣x )=f (x +4), ∴f (x +4)=﹣f (x +2),∴f (x +2)=﹣f (x ), ∴f (x +4)=f (x ),∴f (x )的周期T =4,∵f (﹣x )=﹣f (x +2),∴f (0)=﹣f (2),而x =2是f (x )的对称轴,∴f (2)不一定为0, ∴f (0)=0不一定成立,∴②错误;∵f (0)=﹣f (2),∴f (2)+f (0)=0,由周期性可知f (0)=f (4), ∴f (2)+f (4)=0,∴③正确; ∵f (x )的周期T =4,∴f (112)=f (4+32)=f (32),又f (x +2)=﹣f (x ),∴f (32)=﹣f (−12),∴f (112)=f (4+32)=f (32)=﹣f (−12),∴f (−12)f (112)=−[f(−12)]2≤0,∴④正确.故答案为:①③④.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程,16.(14分)如图.在三棱柱ABC ﹣A 1B 1C 1中,BB 1⊥平面ABC ,CA =CB =√5,AA 1=AB =2,D 、E 分别为AB ,AA 1的中点.(1)求证:平面CDE ⊥平面ABB 1A 1;(2)求直线CE 与平面BCC 1B 1所成角的正弦值.(1)证明:由BB 1⊥平面ABC ,CD ⊂平面ABC ,可得BB 1⊥CD , 由CA =CB ,D 为AB 中点,可得CD ⊥AB , 又AB ∩BB 1=B ,AB ,BB 1⊂平面ABB 1A 1, 所以CD ⊥平面ABB 1A 1,又CD ⊂平面CDE , 所以平面CDE ⊥平面ABB 1A 1;(2)解:由(1)知:DA ,DC ,BB 1两两垂直, 过D 作Dz ∥BB 1,则DA ,DC ,Dz 两两垂直, 故以D 为坐标原点,建立如图所示空间直角坐标系,由CA =CB =√5,AA 1=AB =2,D 、E 分别为AB ,AA 1的中点, 可得B (﹣1,0,0),C (0,2,0),C 1(0,2,2),E (1,0,1), 则CE →=(1,−2,1),CB →=(−1,−2,0),CC 1→=(0,0,2), 设平面BCC 1B 1的法向量为n →=(x ,y ,z),则有{n →⋅CB →=−x −2y =0n →⋅CC 1→=2z =0,令x =2,则y =﹣1,z =0,可得平面BCC 1B 1的一个法向量为n →=(2,−1,0),设直线CE 与平面BCC 1B 1所成角为θ,则有sinθ=|cos <CE →,n →>|=|CE →⋅n →||CE →||n →|=4√6×√5=2√3015,故直线CE 与平面BCC 1B 1所成角的正弦值为2√3015.17.(13分)在△ABC中,a=1,b=2.(1)若c=2√2,求△ABC的面积:(2)在下列三个条件中选择一个作为已知,使△ABC存在,求∠A.条件①:∠B=2∠A;条件②:∠B=π3+∠A;条件③:∠C=2∠A.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.解:(1)在△ABC中,a=1,b=2,c=2√2,由余弦定理,可得cos C=a2+b2−c22ab=1+4−82×2×1=−34,又C∈(0,π),可得sin C=√1−916=√74,故S△ABC=12ab⋅sinC=12×1×2×√74=√74;(2)若选条件①:由题意有B=2A,a=1,b=2,则由正弦定理,可得sinBsinA=ba,即sin2AsinA=2cos A=2,即cos A=1,又A∈(0,π),cos A≠1,故△ABC不存在;若选条件②:由题意有B=π3+A,a=1,b=2,则由正弦定理,可得sinBsinA=ba,即sin(π3+A)sinA=2,即32sinA−√32cosA=0,即√3sin(A−π6)=0,所以sin(A−π6)=0,又A∈(0,π),所以A−π6∈(−π6,5π6),故A−π6=0,即A=π6;若选条件③:由题意有C=2A,a=1,b=2,则由正弦定理,可得sinCsinA=ca,即sin2AsinA=2cosA=ca,由余弦定理,可得b2+c2−a22bc=c2a,即4+c2﹣1=2c2,解得c=√3,故cos A=c2a=√32,又A∈(0,π),所以A=π6;综上,只能选择条件②或③,解得A=π6.18.(13分)为了解客户对A,B两家快递公司的配送时效和服务满意度情况,现随机获得了某地区客户对这两家快递公司评价的调查问卷,已知A,B两家公司的调查问卷分别有120份和80份,全部数据统计如下:假设客户对A ,B 两家快递公司的评价相互独立.用频率估计概率,(1)从该地区选择A 快递公司的客户中随机抽取1人,估计该客户对A 快递公司配送时效的评价不低于75分的概率;(2)分别从该地区A 和B 快递公司的样本调查问卷中,各随机抽取1份,记X 为这2份问卷中的服务满意度评价不低于75分的份数,求X 的分布列和数学期望;(3)记评价分数x ≥85为“优秀”等级,75≤x <85为“良好”等级,65≤x <75为“一般”等级、已知小王比较看重配送时效的等级,根据该地区A ,B 两家快递公司配送时效的样本评价分数的等级情况.你认为小王选择A ,B 哪家快递公司合适?说明理由.解:(1)根据题中数据,该地区参与A 快递公司调查的问卷共120份,样本中对A 快递公司配送时效的评价不低于75分的问卷共29+47=76 份,所以样本中对A 快递公司配送时效的评价不低于75分的频率为76120=1930,估计该地区客户对A 快递公司配送时效的评价不低于75分的概率1930; (2)X 的所有可能取值为0,1,2,记事件C 为“从该地区A 快递公司的样本调查问卷中随机抽取1份,该份问卷中的服务满意度评价不低于75分”,事件D 为“从该地区B 快递公司的样本调查问卷中随机抽取1份,该份问卷中的服务满意度评价不低于75分”,由题设知,事件C ,D 相互独立,且P(C)=24+56120=23,P(D)=12+4880=34, 所以P (X =0)=P (CD )=(1−23)×(1−34)=112,P (X =1)=P (CD ∪C D )=(1−23)×34+23×(1−34)=512,P (X =2)=P (CD )=23×34=12,所以X的分布列为:故X的数学期望E(X)=0×112+1×512+2×12=1712;(3)答案不唯一,答案示例1:小王选择A快递公司合适,理由如下:根据样本数据,估计A快递公司配送时效评价为“优秀”的概率是29120,估计B快递公司配送时效评价为“优秀”的概率是1 5,因为29120>15,故小王选择A快递公司合适,答案示例2:小王选择B快递公司合适,理由如下:由(1)知,估计A快递公司配送时效评价为“良好”以上的概率是1930,由样本数据可知,估计B快递公司配送时效评价为“良好”以上的概率是16+4080=5680=710,因为1930<710,故小王选择B快递公司合适.19.(15分)已知椭圆C的两个顶点分别为A(﹣2,0),B(2,0),焦点在x轴上,离心率为√3 2.(1)求椭圆C的方程;(2)设O为原点,过点T(4,0)的直线l交椭圆C于点M,N,直线BM与直线x=1相交于点P,直线AN与y轴相交于点Q.求证:△OAQ与△OTP的面积之比为定值.解:(1)由题意可得a=2,e=ca=√32,可得c=√3,所以b2=a2﹣c2=4﹣3=1,所以椭圆C的方程为:x24+y2=1;证明:(2)显然直线l的斜率存在且不为0,由题意设直线l的方程为x=my+4,设M(x1,y1),N(x2,y2),联立{x=my+4x24+y2=1,整理可得:(4+m2)y2+8my+12=0,则Δ=82m2﹣4×12×(4+m2)>0,即m2>12,且y1+y2=−8m4+m2,y1y2=124+m2,可得y1y2y1+y2=−128m=−32m,即2my1y2=﹣3(y1+y2),设直线BM的方程为y=y1x1−2(x﹣2),令x=1,可得y P=−y1x1−2=−y1my1+2,直线AN 的方程为y =y 2x 2+2(x +2),令x =0,可得y Q =2y 2x 2+2=2y 2my 2+6, 所以S △OAQ S OTP=12|OA|⋅|y Q |12|OT|⋅|y P |=24•|2y 2my 2+6y 1my 1+2|=|my 1y 2+2y 2my 1y 2+6y 1|=|−32(y 1+y 2)+2y 2−32(y 1+y 2)+6y 1|=13•|y 2−3y 1−y 2+3y 1|=13,为定值. 即证得:△OAQ 与△OTP 的面积之比为定值,且定值为13.20.(15分)已知函数f(x)=ax +ln1−x1+x. (1)若曲线y =f (x )在点(0,f (0))处的切线斜率为0,求a 的值; (2)当a =4时,求f (x )的零点个数;(3)证明:0≤a ≤2是f (x )为单调函数的充分而不必要条件. 解:(1)函数f(x)=ax +ln1−x 1+x 的导数为f ′(x )=a +1+x 1−x •−2(1+x)2=a +2x 2−1, 可得曲线y =f (x )在点(0,f (0))处的切线斜率为a ﹣2=0,解得a =2; (2)当a =4时,f (x )=4x +ln 1−x 1+x ,由1−x1+x>0,解得﹣1<x <1,f (x )的定义域为(﹣1,1),关于原点对称,f (﹣x )+f (x )=﹣4x +ln 1+x 1−x +4x +ln 1−x1+x=0+ln 1=0,即f (﹣x )=﹣f (x ),可得f (x )为奇函数,则f (0)=0, 当0<x <1时,f (x )的导数为f ′(x )=4+2x 2−1=4x 2−2x 2−1, 当0<x <√22时,f ′(x )>0,f (x )递增;当√22<x <1时,f ′(x )<0,f (x )递减, 可得f (x )在x =√22处取得最大值,又x →1时,f (x )→﹣∞,所以0<x <1时,f (x )有一个零点;由奇函数的性质可得﹣1<x <0时,f (x )有一个零点, 则当a =4时,f (x )的零点个数为3;(3)证明:由f (x )=ax +ln 1−x1+x为单调函数,即f (x )在(﹣1,1)内递增,或递减.由f ′(x )=a +2x 2−1,若f (x )在(﹣1,1)内递增,则f ′(x )≥0,即a ≥21−x 2恒成立. 由g (x )=21−x 2∈[2,+∞),则a ≥21−x 2不恒成立,即f (x )在(﹣1,1)内不为递增函数. 若f (x )在(﹣1,1)内递减,则f ′(x )≤0,即a ≤21−x 2恒成立. 由g (x )=21−x 2∈[2,+∞),则a ≤2, 所以,f (x )为单调函数的充要条件为a ≤2, 而{a |0≤a ≤2}⫋(﹣∞,2],则0≤a ≤2是f (x )为单调函数的充分而不必要条件.21.(15分)若各项为正的无穷数列{a n }满足:对于∀n ∈N *,a n+12−a n 2=d ,其中d 为非零常数,则称数列{a n }为D 数列.记b n =a n +1﹣a n .(1)判断无穷数列a n =√n 和a n =2n 是否是D 数列,并说明理由; (2)若{a n }是D 数列,证明:数列{b n }中存在小于1的项; (3)若{a n }是D 数列,证明:存在正整数n ,使得∑ n i=11a i>2024. 解:(1)数列a n =√n 是D 数列.理由如下:a n+12−a n 2=(√n +1)2−(√n)2=1满足D 数列定义,数列a n =2n 不是D 数列.理由如下:a n+12−a n 2=(2n+1)2−(2n )2=22n+2−22n =3⋅22n 不是常数;(2)以下证明:d >0.假设d <0,由a n+12−a n 2=d 知{a n 2}为等差数列,故a n 2=a 12+(n −1)d ,因为{a n }是各项为正的无穷数列,当n 取大于[−a 12d ]+1 的整数时,a n 2≤a 12+([−a 12d]+2−1)d <0,与已知矛盾,所以假设不成立,所以d >0,以下证明{a n } 是递增数列.因为d >0,a n+12=a n 2+d >a n 2,且{a n }是各项为正的无穷数列,所以a n +1>a n , 所以{a n } 是递增数列,以下证明:∀t >0,∃k ∈N *,当n ≥k 时,a n >t , 若t <a 1,当n >1时,显然a n >t , 若t ≥a 1,取k =[t 2−a 12d]+2, 当n ≥k时,a n2≥a 12+([t 2−a 12d ]+2−1)d >t 2,即a n >t 成立, 因为b n =a n+1−a n =d a n+1+a n <d2a n,取t =d 2,当m ≥k 时,a n >t ,此时,b n <d2⋅d 2=1.所以若{a n } 是D 数列,则数列{b n }中存在小于1的项; (3)由(2)知,∃k ∈N ,当n ≥k 时,b n <1,即a π+1<a n +1, 以此类推,0<a k +m <a k +m ﹣1+1<a k +m ﹣2+2<…<a k +m ,m ∈N , 所以1a k+m>1a k +m,m ∈N *,设此时 2s−1≤a k <2s ,s ∈N *,令 n =k +m ,所以∑n i=11a i>∑k+mi=k1a i>1a k>1a k+1+1a k+2+⋯+1a k+m>12s+12s+1+12s+2+⋯+12s+m,因为12s+12s+1+12s+2+⋯+1s2s+(2s−1)>12s+2s=12,所以当m=2s+2×2024﹣1,m∈N*,∑n i=11a i >∑k+mi=k1a i>12s+12s+1+12s+2+⋯+12s+(2s+2×2024−1)=(12s+12s+1+⋯+12s+(2s−1))+(12s+1+12s+1+1+⋯+12s+1+(2s+1−1))+...+(12s+2×2024+12s+2×2024+1+⋯+12s+2×2024+(2s+2×2024−1))>2×20242=2024.所以存在正整数n,使得∑n i=11a n>2024.。
浙江大学建筑工程学院

浙江大学建筑工程学院2003年年鉴二OO四年一月目录1、本科生教育工作 (1)2、研究生教育及学科建设工作 (11)3、科学研究与实验室建设工作 (17)4、人事工作 (36)5、继续教育工作 (40)6、其他工作 (47)本科教学工作一、各类数据1、目前在校本科生人数为1340名(截止日期:2003年12月31日)2、2003年(2002)各系在浙江省招生情况3、2003届各系学生英语四级、六级通过率情况4、2003届各系学生获得学位情况5、2003届各系学生分配情况及一次性就业率情况6、2002级学生转入我院各专业情况7、土木工程专业六个专业方向学生人数二、2003年本科教学改革立项情况三、主要工作1、给本科生上课的教师人数为153名,占全院教师总人数的66.5%,其中教授31人,占全院总教授人数的81.6%。
本科教学业绩点为140.88,教师人均业绩点为0.92。
目前,本科的师生比为1:8.76。
2、有57名研究生分别担任2003级本科生的导师和联络员,其中有30名教授担任导师。
3、本学年为23门次本科课程设置了23个助教岗位。
4、组织有关教师向学校申报了《工程管理》本科新专业。
5、2项21世纪初校级本科教学改革项目通过了学校的结题验收。
同时,6、学院的6门精品课程和18门重点课程通过了学校的中期检查验收。
7、承办了浙江大学第四届大学生结构设计竞赛,全校共有161支队伍参赛,涉及十几个院系的480多位学生。
2003年11月9日,学院与校教务部承办了浙江省第二届“杭萧钢构杯”大学生结构设计竞赛,来自浙江省11所高校的36支队伍参加了决赛。
我院有5支参赛队代表浙江大学参加了决赛,分别获得特等奖1个、一等奖1个、二等奖2个、三等奖1个和创意奖1个。
8、我院城规2000级学生丁睐荣获2003年城市规划专业“居住区规划设计”作业优秀奖。
指导教师为王士兰研究员。
9、第六期大学生科研训练计划(SRTP)立项共有18项,其中学校立项12项(教师7项,学生5项),学院立项6项(教师3项,学生3项)。
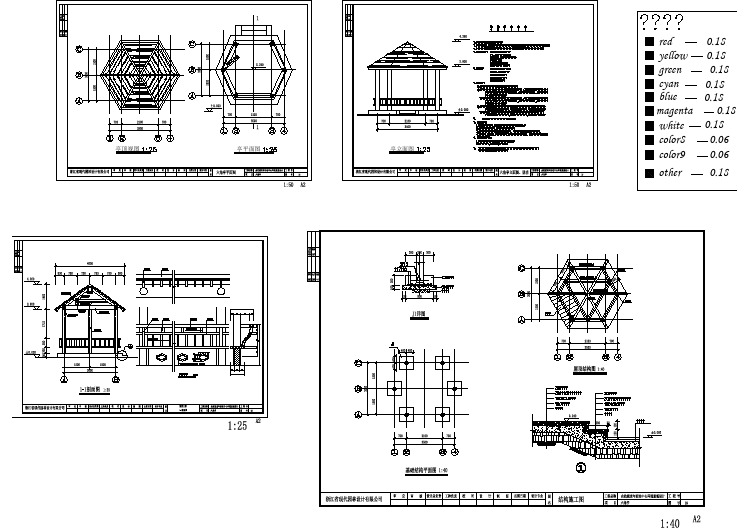
某地郊区老年人活动中心六角亭全套建筑施工设计cad图
盘活榫卯,仿建故宫亭

“隐居”山野,将东方美学带入生活今年28岁的苏清吾是浙江温州人。
受母亲影响,她从小就喜欢手作,会剪纸,喜欢给玩具娃娃做衣服。
考入浙江万里学院后,虽然学的是广告文案策划,但苏清吾对各种手工艺感兴趣,大三就开始买服装裁剪与缝纫方面的书学习。
她还曾上山砍竹子做鱼灯,搭泥窑烧小火炉。
大学毕业后,苏清吾从事房地产文案工作。
因为不想每天做重复的事,2016年,她辞职回老家,成为一名独立摄影师。
她平时会接一些广告拍摄之类的单子,每单收入从两三千元到七八千元不等。
此后,苏清吾搬到老家的山里居住,希望有更多时间做自己喜欢的事。
期间,她开始探索传统文化。
比如,她学会用“金缮”工艺修补残缺器物,用水彩仿画“岩彩画”。
她还会在兴致来临时自己烧制陶瓷,并为白瓷添釉上彩。
2018年,苏清吾将这些做成视频分享到网络上。
其中,她对笋衣的一系列处理最具巧思:用渐变的笋衣、嫩黄的绒毛做出一朵盛开的荷花,还做了一个戴花帽、着披风的侠女。
视频里的风筝也是她亲手制作的,裁布、画画、搭骨架,然后鼓捣做出自己喜欢的样子。
自己动手,把故宫亭“搬”回家虽然活得悠哉游哉,但周遭的压力很快就涌向了她。
“读书到头来还是跑山里,也不工作。
”“年纪不小了,也不考虑嫁人生娃。
”……苏清吾说,坚持到现在几乎全是靠喜欢撑着。
一次,苏清吾无意间在网上看到故宫的亭子,觉得配色非常好看,而且看上去构造也不算太复杂,就突发奇想:为何不自己建造一个?2020年5月,苏清吾决定在自家后院里仿造一座故宫亭。
她一边阅读大量书籍,查资料了解相关建筑知识,观看相关视频,一边积极地寻找建筑原材料。
苏清吾虽然一直喜欢捣鼓手工艺,但没有学过木工,真正动手后,才体会到这个活计的繁杂与艰难。
起初,她面对的只是一面水泥墙和一堆简单的木材。
后来,她开始对着木材进行画、锯、凿、挖、磨……仿造故宫亭,苏清吾采用的是古老的传统榫卯技艺。
在那个没有钉子的时代,各个零部件就是通过榫卯来连接的。
简单来说,就是一端长(榫头),一端被挖出一个与榫头相同尺寸的口子(卯口),盘活榫卯,仿建故宫亭文/张德强“”26然后将榫头插入卯口,形成榫卯连接。
基于响应面法与MOGA算法的竹集成材榫接合椅子节点力学分析及优化

DOI:10.13360 / j.issn.2096-1359.202302007
基于响应面法与 MOGA 算法的竹集成材榫 接合椅子节点力学分析及优化
杨越淳1,王雨凡1,杨洋1,张蕾2,张仲凤1∗
(1. 中南林业科技大学,国家林业和草原局绿色家具工程技术研究中心,湖南省绿色 家居工程技术研究中心,长沙 410004; 2. 东阳市家具研究院,东阳 322100)
摘 要:竹集成材是符合“双碳”目标的可持续发展绿色材料,具有“以竹代木” 的巨大潜力。 本研究借助竹集成 材优良材料性能,基于榫卯结构特性,以竹集成材榫接合椅子为例,运用有限元法( FEM) 进行椅子静载荷及耐久 性分析,探究竹集成材求解竹集成材 T 型椭圆榫接合节点 榫卯尺寸与其最大等效应力、总形变和最小安全系数的关系,并运用 MOGA 多目标遗传算法以形变最小化、安 全系数最大化为优化目标,进行榫卯尺寸优化。 结果表明:竹集成材榫接合椅子静载荷分析所得椅子最大等效 应力为 6.818 MPa,位于座面大边与椅后腿榫接合节点;最大等效应变值为 4.245× 10-3 ,位于椅子扶手与椅后腿 榫接合节点;椅子发生的最大形变为 4.433 mm,分布在椅子靠背位置。 椅子耐久性分析所得最大等效应力及最 大等效应变均位于椅子扶手与椅后腿榫接合节点,分别为 4.999 MPa 和 3.113×10-3 ;椅子整体发生的最大形变为 3.251 mm,位于椅子靠背上端。 由竹集成材 T 型榫接合节点响应面分析可知,椭圆榫接合节点的最大等效应力 及最大形变随着榫头厚度 a 及榫头长度 l 的增大而减小,安全系数随之增大,榫卯尺寸对 T 型榫接合节点力学 强度的影响以榫头厚度 a 和榫头长度 l 为主,榫头宽度 b 影响不显著。 运用 MOGA 算法优化竹集成材椭圆榫尺 寸,优化结果与实际试验结果的相对误差为 3.93%,相对误差较小,证明优化方法及结果有效。 本研究为竹集成 材椭圆榫的加工生产提供参考,并为竹集成材榫接合椅子的榫卯尺寸设计提供科学优化方法。 关键词:竹集成材;椅子;榫接合节点;响应面分析;MOGA 算法;有限元法( FEM) 中图分类号:TS664 文献标志码:A 文章编号:2096-1359(2024)01-0184-08
建筑受力构件中压力与拉力的工程案例和合理配置研究

SAVING能53墙材革新与建筑节能 2019.03建筑受力构件中压力与拉力的工程案例和合理配置研究0 引言压力和拉力是建筑受力构件最基本的两种受力形式。
有些学者,如苏黎世高等工业大学的结构教授席沃兹(Prof. Dr. Joseph Schwartz )甚至认为,仅通过拉力和压力的分析与计算即可涵盖所有的结构形式设计,而不需要引入弯矩的概念[1]。
压力与拉力在建筑结构设计中至关重要,但是在建筑发展的历史长河中,压力和拉力的分析应用却并不一直是并驾齐驱的。
本文通过按时间先后顺序梳理了工程史上6个典型案例的结构受力构件中的压力和拉力配置,分析说明受力构件中压力的应用和拉力的应用是一种此消彼长的关系,并尝试解释这种趋势的形成原因,以此来探讨在未来结构设计中压力与拉力的合理配置。
1 案例分析按照时间顺序选取6个具有代表性的建筑物,包括希腊、罗马时期的代表作品帕提农神庙和万神庙,20世纪重要的两座桥梁——萨尔基纳峡谷桥(1929~1930年)和意大利莫兰迪大桥(1967年),21世纪的两个概念性设计——苏黎世高等工业大学团队设计的东京奥林匹克体育场馆竞赛方案、东南大学和苏黎世高等工业大压力和拉力是建筑受力构件中最基本的两种受力形式。
本文按时间先后顺序梳理了工程史上6个典型案例,通过分析其结构受力构件中的压力和拉力配置,总结出在发展趋势上,建筑受力构件中的压力运用逐渐减少,拉力运用越来越重要。
试从材料发展、技术发展、方向性和审美因素等方面分析形成这一现象的原因,在此基础上,讨论总结出在建筑构件受力中应合理配置压力和拉力的比例,展现出建筑的形式和力学性能的和谐一致。
受力构件;拉力;压力;合理配置张军军1 张宏1 曹婷2 季翔3 王海宁1摘 要:关键词:(1.东南大学建筑学院,江苏 南京210096;2.苏黎世高等工业大学,瑞士8093;3.中国矿业大学,江苏 徐州221116)学2018年的联合教学成果双曲洞亭,分析在这些设计中压力和拉力的运用比例。
木结构六角亭构件介绍

木结构六角亭构件介绍一、基础木结构六角亭的基础通常采用石材或混凝土材料,其主要作用是承载整个亭子的重量,并防止亭子在风、雨等自然环境下的倾覆。
基础的设计和施工应考虑到地形、地质、气候等多方面因素,以确保亭子的安全性。
二、柱子木结构六角亭的柱子采用木材制作,常见的有松木、杉木、柏木等。
柱子的选择应考虑其材质、尺寸、形状等因素,以确保亭子的稳定性和耐久性。
柱子的安装应与基础连接牢固,确保承载力的传递。
三、梁和枋梁和枋是木结构六角亭中的重要构件,其主要作用是连接柱子,组成亭子的框架,并承受和传递荷载。
梁和枋的材质、尺寸、形状等应符合设计要求,以确保亭子的整体稳定性和承载能力。
四、斗拱斗拱是中国传统建筑中的独特构件,用于支撑屋檐和屋面,具有美观和承重的作用。
在木结构六角亭中,斗拱通常由多个斗、拱、昂等构件组成,形状和尺寸因时代和地区而异。
斗拱的设计和施工应考虑到其承重能力和美观性,以确保亭子的整体效果和质量。
五、屋顶木结构六角亭的屋顶采用木材制作,常见的有瓦片、石板等材料。
屋顶的设计应考虑其防水、保温、防风等因素,以确保亭子的使用效果和安全性。
屋顶的施工应与柱子、梁、枋等构件连接牢固,确保承载能力的传递。
六、门窗木结构六角亭的门窗采用木材制作,常见的有格子窗、推拉门等样式。
门窗的设计应考虑其通风、采光、保温等因素,以满足亭子的使用功能和视觉效果。
门窗的施工应与柱子、梁等构件连接牢固,确保其稳定性和安全性。
七、装饰木结构六角亭的装饰元素包括雕刻、彩绘、挂落等,用于增加亭子的美观性和文化内涵。
装饰的设计和施工应考虑到整体效果和材质选择,以展现出六角亭的独特风格和传统特色。
浅析苏州古典园林中小木作的类型与功能

浅析苏州古典园林中小木作的类型与功能付立婷;王玲【摘要】苏州古典园林里的小木作性质优良易于加工,代表了苏州当时建筑装饰里的最高水平.文章首先对小木作的类型进行了总结,并针对各种类型结合苏州古典园林里的实例进行说明.其次,对小木作的功能和作用进行了探讨,结合其在园林中的位置、图形纹样、文化寓意等进行了分析.苏州古典园林中的小木作作为一种设计资源在现代设计中值得保护和发展.【期刊名称】《福建建筑》【年(卷),期】2017(000)006【总页数】3页(P62-64)【关键词】苏州古典园林;小木作;装饰功能;实用功能;文化功能【作者】付立婷;王玲【作者单位】苏州大学金螳螂建筑学院江苏苏州221500;苏州大学金螳螂建筑学院江苏苏州221500【正文语种】中文【中图分类】TU855苏州古典园林是江南私家园林的代表,特征鲜明,讲究宅园合一,面积虽都较小,却可“咫尺之内,再造乾坤”。
其建筑离不开木材,装饰装修也离不开木材。
装修在建筑中适用范围广、内容多。
梁思成所著的《清式营造则例》中有关于“装修”一章,他将中国古代建筑中,除了梁、柱等承重木结构之外的门、窗、挂落、纱隔、天花等非承重结构的木构件称作装修,即指木装修[1]。
可以理解成平时所说的大木作和小木作,大木作主要指柱、梁等具有承重功能的木质结构,小木作在建筑中不属于承重结构的木构件,本文主要讨论研究的是苏州园林中主要起装饰作用的小木作。
苏州古典园林建筑中的装饰主次分明、种类多样,小木作总体上指建筑装饰中非承重结构的木构件,主要分为外檐装饰和内檐装饰。
具体来说,外延装饰有花格窗、挂落和栏杆,花格窗又分为隔扇和槛窗两大类,具体分类讨论见下文。
内檐装饰则主要有纱窗(又名纱槅)、天花和罩。
2.1 花格窗花格窗是苏州园林建筑中重要的装饰,种类丰富多样,可分隔空间,也可串联景物,功能性、观赏性都较强,具体来说因不同的位置和不同的图形可以分为多种类型,主要为以下两种。
宋式古建筑殿堂模型(八架椽前後乳栿用四柱,檐柱用六鋪作單抄雙昂)

宋式古建筑殿堂模型(八架椽前後乳栿用四柱,檐柱用六鋪作單抄雙昂)宋式古建筑殿堂模型(八架椽前後乳栿用四柱,檐柱用六鋪作單抄雙昂)尚未完工,待续。
(此作品完成后只发后续帖,就不再发新帖了,如有不便请见谅!)但凡喜爱中国古建筑的人,都会不同程度地关注中国古代木构建筑。
我为了更进一步地深入了解大木作结构特点,掌握斗栱、梁、柱等相互关系与演变的基本脉络,即着手制作基本上符合《营造法式》中宋式殿堂木构模型。
我的制作思路:首先经历由实践到认识的过程;其次尽可能还原具备宋代特征的大木作结构;第三可拆装组合。
主要参考书目:梁思成《中国建筑史》、《〈营造法式〉注释》;陈明达《营造法式大木作制度研究》;马炳坚《中国古建筑木作营造技术》;潘德华《斗拱》;王贵祥等《中国古代木构建筑比例与尺度研究》等等。
主要参考实例资料(注明:以上都是查阅相关实例资料作为参考,非实地考查。
):福建福州华林寺大殿、浙江宁波保国寺大殿、河南少林寺初祖庵、河北蓟县独乐寺山门、山西五台山佛光寺大殿、山西平遥镇国寺大殿等等。
手机拍摄图像质量一般,或许完成后再安装时补拍图片及视频,还请各位网友见谅先期回答网友几个问题:一、我没有什么专业“标签”,是个地地道道的DIY爱好者,喜爱中国古建筑,我的木工水平根本上不了台面,只是喜欢琢磨然后动手实践。
前面两段文字不是我在晒“专业”,请不要误解。
我仅想说明,我的古建筑模型制作的几年之路,就是这样走过来的。
如今是互联网时代,只要用心,总能找到你所需要的资料。
如果没有接触过古建学理知识,就不能玩古建模型了吗?我回答:当然可以玩,但至少要会些木工的基本技能吧!我之前发过一两个作品帖子后,许多网友表示非常喜欢古建筑模型制作,想学又不知从何入手。
我说:“脑热、盲从、趋利,三不学”。
因为“脑热”总会凉下来,“盲从”是不知道自己要什么,“趋利”的成本太高周期太长。
所以,想玩古建模型至少二者备其一:一是先学后做。
了解一些古建学理知识且爱动手做,这是认识到实践的过程。
【中国古建筑论文】略谈对木结构建筑的研究

【中国古建筑论文】略谈对木结构建筑的研究1应县木塔的建模与分析全塔采用了四百多组构筑奇巧的斗栱,是木塔最具特色的组成部分。
木塔始建于公元1056年,经历了近千年的环境侵蚀和多次强地震作用,结构变形和损伤严重,亟待修缮加固。
应县木塔的维修加固是中国文物保护工作的重大课题。
自1991年国家文物局批准成立“山西省应县木塔修缮工程领导小组”以来,国家已组织了大量的人力、财力对应县木塔进行了勘测、试验和研究。
目前,应县木塔修缮方案的研究论证工作仍在继续开展,运用现代分析模拟技术进行木塔保护研究,已取得了一批较丰硕的成果。
徐燊等对应县木塔进行了计算机建模方法的研究,提出了可动态修改的三维建模方法,以提高模型制作的效率。
该方法由四个步骤实现:将木塔的构件按斗栱、柱、梁栿进行分类,找出相应的规律性;以现有测绘数据为基准并依据《营造法式》的尺寸制度,以层为单位,构建主体结构的三维复原模型;将实测的变形值编入程序,对复原模型的坐标位置进行动态修改,得到符合现状的残损模型;将各层模型叠合,配上楼梯、栏杆、屋檐、塔顶等构件,完成全部三维复原工作。
张舵等在应县木塔有限元分析模型的研究中,通过引入梁单元组模拟斗栱连接,以解决虚拟半刚性单元难于反映实际构造的问题。
在有限元模型中,把斗栱设为一个在结构上与实际构造相似的梁单元组合,斗栱的各个构件均简化为梁单元杆件并在端部采用刚性连接,通过调整梁单元的刚度来改变斗栱构件的连接刚度。
在此基础上,他们建立了以梁单元为基本单元的木塔有限元模型,并结合木塔的实测模态结果确定了斗拱的刚度。
杜雷鸣等在应县木塔的抗震性能研究中,将斗拱节点域简化为刚接和铰接两种类型。
采用有限元软件ANSYS分别建立了节点域为刚接和铰接的木塔整体有限元模型,并对这两种简化模型开展动力特性分析。
模型分析结果与木塔实测值的对比表明,两种简化模型的分析振型与实测振型基本吻合,且实测频率介于两种简化模型的分析值之间,因此,可用两种简化模型的分析值来界定木塔地震响应的范围。
“中国传统木结构建筑影响深远”非连续性文本阅读训练及答案

阅读下面的文字,完成1~5题。
材料一:在世界传统建筑体系中,东亚与东南亚地区的建筑是以木结构建筑为主,其中又以中国的木结构建筑发展最早也最为成熟,影响深远。
其营造技艺一直传承至今,2009年被联合国教科文组织列入人类非物质文化遗产名录。
北京四合院、山西大院、徽派民居等,都是这一技艺的代表作。
①中国传统木结构营造技艺源远流长。
在距今约7000年的河姆渡文化遗址中,传统木结构建筑标志性的榫卯技术就已经出现。
在距今3800-3550年的河南偃师二里头文化遗址中,出现了大型木构架夯土建筑。
西汉时期,以“抬梁式”和“穿斗式”为代表的两种主要形式的木结构体系已经形成,并传承至今。
从隋唐至北宋,中国传统木结构建筑营造技艺逐渐变得程式化、标准化和模数化。
以宋代《营造法式》的出现为标志,一整套包括设计原则、类型等级、加工标准、施工规范、造价定额等的完整制度被总结出来,并以斗拱构件八等级的“材”作为模数标准。
这套制度起到了统一规格、简化程序的功效。
这是中国传统木结构建筑营造技艺的一个里程碑。
元末明初开始,官式建筑和部分城市民居普遍采用了砖墙,建筑挑檐和斗拱尺寸进一步缩小。
这一阶段比较重要的著作如明代《鲁班营造正式》清代工部《工程做法则例》,分别总结和规定了江南民居建筑、官式建筑等通行的设计标准。
单体建筑组合体现空间美学巧妙组合单体建筑,使之关系和谐,是中国传统建筑体系营造空间美学的重要方法。
不同历史时期、不同建筑体系,如宫廷、公署、礼制、合院式民居和园林等,组合方式均有差异。
院落空间的变化、建筑间的烘托与对比、室内外空间的交融与过渡、各种空间要素的虚实相应、天际线的变化……多样化的组合形态,产生了独特而丰富的艺术特征。
例如,曾作为皇家宫殿的北京故宫,需要在建筑体系空间中体现皇家的威严和秩序,具有强烈的象征性。
因此在整个建筑群中,就要特别突出中轴线建筑序列的视觉冲击力。
而一般的园林营造,则要着重避免各种内容与形态的对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、预期成果(有预期成果的填写) 根据设计思路和步骤,认真完成实验。希望达到预期结果,做出完整的六角 亭结构模型和制作图纸,同时对相关问题和结论进行深入分析和研究,做出项目 结题报告。
6
五、经费预算 资料费:包括纸张费、打印费等 200 元;相关书籍 500 元;调研费:2800 元; 材料费:3000 元;辅助工具:3300 元
器材名称 木质材料 美工刀 木刻刀 三角板 三棱比例尺 钢板尺 钢板角尺 钢丝锯 板锉 台虎钳 桌虎钳 木工刨 手锤 钢丝钳 圆规 铅笔 镊子 鸭嘴笔 各种曲线板 便携箱 板刷 木料胶水 各色油料 规格数量 2套 5个 5个 2套 2把 2个 2个 2把 5个 2个 2个 5个 2个 2个 2个 10 根 5个 5个 2只 2台 5个 30 瓶 20 瓶 总价(元) 3000 200 200 200 200 100 100 200 100 100 100 100 100 100 20 30 50 50 100 500 50 500 500 用于制作成品 用于切割木质板材 用于切割木板 用于测量平行线、平面、直角 按比例绘图和下料画线时不可缺少的工具 用于测量尺寸 用于画垂直线、平行线与直角 切割材料 修正材料 加工的辅助工具 用于夹持小型工件 用于刨平木材的平面及毛边 击打用的工具 弯折金属板、切丝以及夹持板材 用来在材料上画出所需要的圆形或等分线 用于材料上画线或写记号 制作细小构件时特别需要镊子来辅助工作 画墨线的工具 用于画、割曲线的工具 用于装各种工具 用于材料清洁 用于材料的粘合 用于材料上色 用途
主要成果
3
一、 申请理由(包括自身具备的知识条件、自己的特长、兴趣、已有的实践创 新基础等) 亭是我国极富特色的一种建筑形式,式样丰富,造型多变,是我国传统园林 建筑之一。在古典园林、现代园林、自然风景区以及城市园林绿化中,都可见到 各种各样的亭子悠然伫立。在园林和绿地中,亭是不可缺少的组成部分,常起着 画龙点睛的作用。经过时代的发展和人们物质及精神的进步,亭子的用途有了比 较大的变化。人们把它建在了自己家的院子里或者风景秀丽的地区。如西安世园 会中风格独特的格式风景亭、公园里形态各异的植物凉亭、佛教建筑景真八角亭 等等。 本次实验主要是在图纸的基础上进行六角古亭模型的制作,通过模型把平面 图纸与实际立体实物有机的联系在一起,这种三维的立体模式,有助于对建筑的 设计和推敲,可以直观地体现设计意图,弥补图纸在表现上的局限性。在本次试 验中使用木材制作模型,一直以来木结构建筑因其优越的抗震性能而备受关注, 除此之外木结构建筑还有节省空间、潮气控制、隔音、居住舒适度、低碳等方面 也具有明显优势,目前,国内国外木结构混合建筑已非常普遍。希望通过本次模 拟实验可以对木结构有很好的了解与分析。 本次的实验内容以团队兴趣为主导,以参加学校结构模型比赛的经验以及对 相关课程、专业知识、课外理论知识的学习为基础,想通过此次的创新实验进一 步加强自己的实践动手能力、增强创新能力和团队协作能力,同时培养每一位成 员的兴趣爱好,不断扩展每一位成员的视野,努力争取让团队成员成为优秀的大 学生。 此前,我组成员均已参加过农牧学院创新型实验和模型结构大赛以及许多其 他的实践动手活动,并积累了一定的实践动手能力和相关的经验。另外,我组成 员对本次的创新实验有较浓厚的兴趣和很高的激情,都比较喜欢此次创新实验的 内容。因此我们组建了团队来申报此次创新实验,希望能将所学的知识付诸于实 践,用实践来校验我们的学习成果进而提高每一位成员的创新意识和实践动手能 力,为大家以后的工作打下坚实的基础。对此次项目我们满怀激情,坚信我们的 付出一定能出色的完成实验项目,希望学校老师给我们一次锻炼和展现自我与团 队能力的机会。
项目选题名称
六角古亭木结构模拟与分析
项目选题所属 专业门类
项目选题类型
项目来源
( ) 校企联合项目 11 月
实施时间
完成时间:2012 年 本人签名
所在院系、年级、专业 2009 级土木工程本科 班
联系电话
成 员
2008 级电气工程及自 动化本科班
姓名
何强 西 藏 农 牧 学 院
西藏自治区
大学生创新性实验训练计划项目
申报书
项目名称: 项目主持人: 所在二级学院: 指导教师: 填表日期:
六角古亭木结构模拟与分析 张永娟
水利土木工程学院
何强
2011-10-5
1
附件一: 西藏自治区大学生创新性实验训练计划项目申请表
学校名称:西藏大学农牧学院 建 筑 模 型 类 ( )个人项目 (√ )团队项目 起始时间:2011 年 12 月 姓名 主持 张永娟 (√ )校内项目
4
二、实施方案(包括选题的训练目标、组织实施、过程管理、实践环节、教师指 导、项目结题等) 训练目标:通过此次的创新实验进一步加强团队成员的实践动手能力、创新能力 和相互协作能力, 同时培养每一位成员的兴趣爱好, 不断扩展每一位成员的视野, 争取让团队成员成为优秀的大学生。 前期准备:1.制作模型材料的准备。 2.制作模型辅助设备的准备。 组织实施: 技术路线紧紧围绕古建筑六角亭模型,以具体的古建筑为制作的灵感,然后用 木制材料进行结构模拟,用模型结构来分析木结构古建筑六角亭.
联系电话
指 导 教 师
单位
水 利 土 木 工 程 学 院
行政职务/专业 技术职务
教研室主 任/讲师
2
1、连续指导我院学生参加全国第三届和第四届结构模 型大赛,并取得优异成绩; 2、参与各级科研项目 4 项; 3、主持和参与多项对外社会服务项目; 4、发表学术论文 6 篇; 5、参与多项重点学科以及重点实验室建设。
调 查 分 确定模拟对象和分析内容 析 阶 木结构现状调查与分析 段
掌握古建亭子相关资料
模 型 制 构想六角古亭三视图 作 阶 确定最佳方案并绘画图纸 段
购买材料和相关辅助工具
实地考察古建亭子结构 模型分析研究
模型制作与优化
做出结题报告
5
过程管理: 1.由项目主持人制定总体规划。 2.由项目主持人分配成员各阶段的任务。 3.由项目主持人组织模型的制作和检验。 实践环节:1.构思草图方案,选取最佳方案。 2.绘制三视图。 3.选择材料并确定比例。 4.进行构件制作及加工。 5.进行结构成型并上色。 教师指导:在准备阶段、制作阶段、检验阶段加强与指导老师进的交流和有关问 题的请教,保证实验项目保质保量按时完成。 项目结题:在模型和图纸的基础上,对各阶段的情况和出现的有关问题与结论以 结题报告形式汇报,保证实验内容的真实和完整。 三、学校提供条件(包括项目开展所需的实验实训情况、配套经费、相关扶持政 策等) 1.实验室、实验材料和相关辅助工具。 2.自治区 5000 元和学校 5000 元配套经费。
