抛物线恒过定点
(完整版)函数图像过定点问题

函数图像过定点的研究题1:求证:拋物线y=(3-k)x2+(k-2)x+2k-1(k≠3)过定点,并求出定点的坐标.归纳:第一步:对含有变系数的项集中;第二步:然后将这部分项分解因式,使其成为一个只含系数和常数的因式与一个只含x和常数的因式之积的形式;第三步:令后一因式等于0,得到一个关于自变量x的方程(这时系数如何变化,都“失效”了);第四步:解此方程,得到x的值x0(定点的横坐标),将它代入原函数式(也可以是其变式),即得到一个y 的值y0(定点的纵坐标),于是,函数图象一定过定点(x0,y0);第五步:反思回顾,查看关键点、易错点,完善解题步骤.题2:(2001年北京市西城区中考题)无论m为任何实数,二次函数的图像总过的点是()A. (1,3)B. (1,0)C. (-1,3)D. (-1,0)巩固练习:1.无论m为何实数,二次函数y=x2﹣(2﹣m)x+m的图象总是过定点()A.(1,3)B.(1,0)C.(﹣1,3)D.(﹣1,0)2.对于关于x的二次函数y=ax2﹣(2a﹣1)x﹣1(a≠0),下列说法正确的有()①无论a取何值,此二次函数图象与x轴必有两个交点;②无论a取何值,图象必过两定点,且两定点之间的距离为;③当a>0时,函数在x<1时,y随x的增大而减小;④当a<0时,函数图象截x轴所得的线段长度必大于2.A.1个B.2个C.3个D.4个3.(2012•鼓楼区一模)某数学兴趣小组研究二次函数y=mx2﹣2mx+3(m≠0)的图象发现,随着m的变化,这个二次函数的图象形状与位置均发生变化,但这个二次函数的图象总经过两个定点,请你写出这两个定点的坐标:_________ .4.某数学小组研究二次函救y=mx2﹣3mx+2(m≠0)的图象发现,随着m的变化,这个二次函数图象的形状与位置均发生变化,但这个二次函数的图象总经过两个定点.请你写出这两个定点的坐标:_________ .5.(2009•宜宾县一模)二次函数y=x2+bx+c满足b﹣c=2,则这个函数的图象一定经过某一个定点,这个定点是_________ .6.无论m为何实数,二次函数y=x2﹣(2﹣m)x+m的图象总是过定点_________ .7.已知一个二次函数具有性质(1)图象不经过三、四象限;(2)点(2,1)在函数的图象上;(3)当x>0时,函数值y随自变量x的增大而增大.试写出一个满足以上性质的二次函数解析式:_________ .8.证明无论m为何值,函数y=mx-(4m-3)图像过定点,求出该定点坐标9.(南京2011年24题7分)已知函数y=mx2-6x+1(m是常数).⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;⑵若该函数的图象与x轴只有一个交点,求m的值.10.已知二次函数的顶点坐标为(﹣,﹣),与y轴的交点为(0,n﹣m),其顶点恰好在直线y=x+12(1﹣m)上(其中m、n为正数).(1)求证:此二次函数的图象与x轴有2个交点;(2)在x轴上是否存在这样的定点:不论m、n如何变化,二次函数的图象总通过此定点?若存在,求出所有这样的点;若不存在,请说明理由.函数图像过定点的研究题1:求证拋物线y=(3-k)x2+(k-2)x+2k-1(k≠3)过定点,并求出定点的坐标.审题视角有些函数的图象具有过定点的性质,这是由函数式中的一些系数的取值特点所决定的,例如,直线y=kx+b(k≠0),当b确定时,无论k取不等于0的任何值,它总过定点(0,b);物线线y=ax2+bx+c(a≠0),当c确定时,无论a、b取何值,它总过定点(o,c).本题中可以把函数解析式整理变形,使含字母k的项组合于一组,赋值为零,可以求的自变量的值,而后代入函数解析式,再求得相对应的函数值,即得定点的坐标.解:整理抛物线的解析式,得y=(3-k)x2+(k-2)x+2k-1=3x2-2x-1-kx2+kx+2k=3x2-2x-1-k(x2 -x-2)(k≠3),上式中令x2-x-2=0,得x1=-1,x2=2.将它们分别代入y=3x2-2x-1-k(x2-x-2),解得y1=4,y2=7,把点(-1,4)、(2,7)分别代入y=3x2-2x-1-k(x2-x-2),无论k取何值,等式总成立,即点(-1,4)、(2,7)总在抛物线y=(3-k)x2+(k-2)x+2k-1(k≠3)上,即拋物线y=(3-k)x2+(k-2)x+2k-1(k≠3)过定点(-1,4)、(2,7).归纳:第一步:对含有变系数的项集中;第二步:然后将这部分项分解因式,使其成为一个只含系数和常数的因式与一个只含x和常数的因式之积的形式;第三步:令后一因式等于0,得到一个关于自变量x的方程(这时系数如何变化,都“失效”了);第四步:解此方程,得到x的值x0(定点的横坐标),将它代入原函数式(也可以是其变式),即得到一个y 的值y0(定点的纵坐标),于是,函数图象一定过定点(x0,y0);第五步:反思回顾,查看关键点、易错点,完善解题步骤.题2:(2001年北京市西城区中考题)无论m为任何实数,二次函数的图像总过的点是()A. (1,3)B. (1,0)C. (-1,3)D. (-1,0)解法一、特殊值法依据:二次函数的图像随着m的取值不同,它的位置也随之变化,可见这是一个抛物线群。
直线或曲线恒过定点问题

直线或曲线恒过定点问题凰在人生的道路上灵活多变,另辟蹊径,岂不快哉!尾声:人们追求理想的道路就如同这三只蚂蚁,既要勇往直前,矢志不移;又要独辟蹊径,灵活变通.不管怎样,奋斗的人生总是美好的.请记住高尔基的名言吧:在停止努力之前,你永远不会是个失败者!简评这篇习作由材料整体人手,从三个不同的角度,生动地阐释了生活哲理.作者采用三幕剧的形式,新颖别致,条理清晰,令人耳目一年糠j新.每一幕(一个画面)之后再配以"画外音",简短的议论起到了画龙点睛的作用.文末以"尾声"作结,总述全文,高度概括,文章主旨显得更加深刻,集中.作者简介韩延明,高级教师,执教于陕西省商南高级中学,陕西省学科带头人,陕西省商洛市骨干教师,发表论文多篇.责任编辑刘静直线或曲线僵过定点问题口童其林例已知函数—log(一2)+1(a>0,a≠1)的图像恒过定点A,若点A在直线mx4- 1"+l一0上,其中>0,则旦+的最大IfL}L值为——.分析我们知道对数函数===log图像恒过点(1,O),由此可知—log(z一2)+1(以>0,.≠1)恒过定点(3,1),到此问题便不难求解.解析容易求得定点A的坐标是(3,1),代入直线方程得3+"+1—0,所以3.1—3(--3m—--n)——J—一一10—3(n+)≤一lO一6√旦一mmm7"/一\/,/ 一16,当且仅当m一.时等号成立.故+的最大值为一16.定点问题近年来频频出现在各地的高考试题中,定点问题理论依据是什么?究竞有哪些类型呢?举例说明如下.~,直线或曲线恒过定点的证明或应用例1求证:直线(2m4-1)z+(+1)一7m+4(m∈R)恒过某一定点P,并求该定点的坐标.解法一特殊引路法分析因直线(2+1)+(Ⅲ+1)一7m+4随取不同的值而变化,但是由题意分析可知应该是嗣绕某一定点在旋转,而这一定点l....高考_ll斌~题设…计版0凰我们只需两条相交直线即可求得,但是需要我们将点代入原直线方程来证明该点永远在直线上,这样就使得解法更为完备.证明直线(2m+1)x+(+1)一7m+4,取2+1一O===一÷.此时直线方程为=7X(一丢)+4一1①取m+1—0一一1,此时z一3②由①②得点P(3,1).将点P(3,1)代入直线方程得(2m+1)-z+(+1)y===(2m+1)×3+(+1)一7优+4,即方程对任意TnER恒成立.故直线(2m+1)x+(m+1)一7+4恒过定点P(3,1).解法二换元法分析众所周知,直线方程中的点斜式—k(x--xo)可以表明直线过点P(xo,yo),因此我们可以将直线(2m-~1)x+(+1)一7m+4的一般式通过换元法转化为直线方程的点斜式,从而证明该直线恒过定点,并且可直接求得该定点. 证明m--F-1=/=0~",===~2m+1z+.令一一km一高垒.由此可得—7m+T4一一3k~1.即原直线方程可化为—kx一3k+1一1一是(一3).由直线的点斜式方程可知该直线过点P(3,1).当m+1—0即m一一1时,原直线可化为一一7×(一1)+4一3,此时点P(3,1)仍然在直线上.综上,直线(2m+1)x+(仇+1)一7m4-4恒过定点P(3,1).解法三参数分离法分析对于直线方程(2m+1)z+(m+1)一7m+4来说,如果我们将其中的m看作参数,并将其分离得(2z+一7)+z+一4一O,此时我们令2z+一7===0,z+一4=0,则这两条直线的交点P(x.,Y.)一定满足直线方程(2+一7)+'z+一4—0,即P(0,y.)在直线(2+1)lz+(+1)一7m+4上,这样就将直线恒过定点转化为两条直线的交点了.证明(2m+1)z+(+1)一7m+4(2x+~7)+z+一4一O.令2z+一7—0,z+一4一O,解方程组f2+一7=0,lz+一4一o,得x=3,一1,因点P(3,1)满足2z+一7一O,z+一4一o.所以也满足(2z+一7)十Lz+一4—0.进一步得点P(3,1)满足(2m+1)z+(m+1)一7m4-4.故直线(2m+1)z+(m+1)一7m+4恒过定点P(3,1).解法四利用方程船一b有无穷多解的充要条件"关于z的方程ax—b有无穷多解的充要条件是:a—b:0".其实我们高中所学的含参数的多项式函数,含参数的分式函数,以及含参数的二次曲线图像过定点问题均可仿照该种方法求定点坐标.把方程化为(2x+一7)一一—+4.令2z+一7一O且一—+4—0,得x=3,Y一1,因此定点坐标为(3,1).例2函数Y一+2kx一3k+1图像过定点,则定点坐标为——.厨锻分析可将二次函数变形为以k为未知数的一次函数ak—b的形式,或利用方程理论求解.解将函数Y—kx.+2kx一3k+1化为fr+2z3—0(+2z3一Y一,令{v一.1一ofx一]fz一一3解此方程组得或,所以函数lVl【V=lY—+2kx一3k+1图像过定点(1,1)和(一3,1).例3函数Y—ax~2ax+2图像过定点,则定点坐标为——.分析这是含参数的指数函数图像过定点的问题,可利用指数函数Y一图像恒过点(0,1)这一性质来解决.解设函数Y—aXz-2图像过定点(1z.,Y.),则Y.~--axO一"o一,利用指数函数Y一图像恒过点(0,1)这一性质知:方程组z.一2axoq-2a--1=0(1)关于口恒成立,将<lll十r日h,,,(Y o—l(1)化为2z.口一【Y.一1f2z.一2一O再令z..一1=0(2),l一1llzn===l解(2)得.,所以函数—axZ2ax+2(yo—l图像过定点(1,1)如有含参数的对数函数图像过定点的问题,可利用对数函数Y—log.z图像恒过点(1, O)这一性质来解决.例4已知抛物线C:Y一去z与直线z:一走z一1没有公共点,设点P为直线上的案期动点,过P作抛物线C的两条切线,A,B为切点.(1)证明:直线AB恒过定点Q;(2)若点P与(1)中的定点Q的连线交抛物线c于M,N两点,证明:一.证明(1)设A(x1,Y1),则Y一去z.由一1z.得Y一z,所以Y『===z1.于是抛物线C在A点处的切线方程为—l—z1(z—z1),即—z1z—1.设P(z0,尼z0—1),贝Ⅱ有忌o~1一z.z ——Yl?设B(x2,2),同理有kxo一1一-z0Iz2--y2.所以AB的方程为kx.1一.z—Y,即lzo(z一是)(一1)一O,所以直线AB恒过定点Q(尼,1).(2)略.二,利用直线或曲线恒过定点解题有些问题并没有明确告诉你要求定点,但问题本身隐含着直线或曲线过定点,如果能够挖掘出这个隐蔽因素,问题便可迎刃而解或能够开辟解题的新天地.例5设点A和B为抛物线一4px(p>0)上原点以外的两个动点,已知OA_LOB, (=lM上AB,求点M的轨迹方程,并说明它表示什么曲线.t).一?._⑧_高~"试黟设许凰锻分析本题有很多解法,其中利用直线恒过定点求解是最快的一种.设OA的方程为一z,代入Y=4px得A(,),则oB的方程为一一1z,代入Y.=4px得B(4pk.,--4pk).'AB的方程为y—(一4户),过定点N(4P,0).由0M上AB,得M在以ON为直径的圆上(0点除外)故动点M的轨迹方程为.27.+一4z—O(1z≠O),它表示以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.例6对任意实数志,直线—b.x+3k一2(k∈R)与椭圆+一1(以>oKn≠4)恒有公共点,则倪的取值范围是分析直线方程中含参数k,则该直线过定点,求出定点以后,再利用定点在椭圆内或在椭圆上即可解决.解将直线Y一/ca:q-3k一2(k∈R)整理得(z+3)k=Y+2,f+3—0令2—0f.z一一3解之得IY一一2故一如+3k一2(k∈R)过定点(--3,一2),欲使对任意实数k,直线Y—+3志一2(k∈R)与椭圆+一l(a>oft口≠4).专避媾Il_恒有公共点,必须定点在椭圆内或在椭圆上, 所以有+≤1(n>o且n≠4)解之得a≥2且口≠4.作者简介童其林,高级教师,福建省永定县城关中学教务处主任,发表文章多篇,主要从事教学管理研究与教育教学研究.责任编辑李婷婷上海世博会之吉祥物。
利用几个常用结论解决抛物线垂直焦点弦问题

利用几个常用结论解决抛物线垂直焦点弦问题kuing近几日,在群内连续两次出现抛物线焦点弦问题,且我发现两题很相似,都可以用一些常用的熟知结论,几何化地去解决,不需要麻烦的代数化去解。
现整理如下。
先以引理结出这些常用结论,其详细证明这里略去,有兴趣可以自己试试证。
引理一:过抛物线焦点F 的直线交抛物线于两点A 、B 两点,过这两点分别作抛物线的切线,两切线交于点M ,则有:(1)AM BM ⊥;(2)FM AB ⊥;(3)点M 必在抛物线的准线上;引理二:(光学性质——抛物线)过抛物线焦点F 的光线经抛物线反射后的光线必定平行于抛物线的对称轴;引理三:过离心率为e ,焦准距为p 的圆锥曲线的焦点F 作两条互相垂直的直线,若这两条直线分别交圆锥曲线于A 、B 及C 、D ,且F 在A 、B 之间,F 在C 、D 之间,则有:21122e AB CD ep−+=; 引理四:梯形ABCD 中,AD 平行BC ,AC 与BD 交于点P ,过P 作与梯形两底边平行的直线交梯形两腰于E 、F ,则有211EF AD BC=+。
(注:前三个引理我均在人教论坛中某收集解释几何常用结论的贴中结出过;引理三我在论坛中贴过详细证明,用的是极坐标方法,搜索我的主题可以找到;引理四是初中内容)题一:解:(I )如图所示:由引理一,可知AMB ∆为直角三角形,M 为直角,点M 在准线上,过A ,B 分别作准线的垂线,垂足分别为A 1,B 1,取AB 的中点G ,连结GM 。
由于AMB ∆为直角三角形且M 为直角且GM 为其斜边上的中线,于是易得12∠=∠,引理二,可知234∠=∠=∠,因此得到14∠=∠,于是易知GM 也与准线垂直,即GM 为直角梯形AA 1B 1B 的中位线,所以显然A 、M 、B 三点的横坐标成等差数列,得证。
(II )由引理一,可知FM AB ⊥,因此由引理三以及抛物线离心率是e=1以及本题中易知焦准距为p=2,代入即知1114AB CD +=, 又易知四边形ABCD 的面积为12S AB CD =⋅,又由基本不等式有4111AB CD AB CD AB CD≥⋅+===+, 即得32S ≥,且等号成立当且仅当AB=CD 可取到,即四边形ABCD 的面积的最小值为32。
圆锥曲线专题:恒过定点问题的4种常见考法(原卷版)

圆锥曲线专题:恒过定点问题的4种常见考法一、常用方法技巧1、参数无关法把直线或者曲线方程中的变量x ,y 当作常数看待,把方程一端化为零,既然是过定点,那么这个方程就要对任意参数都成立,这时的参数的系数就要全部为零,这样就得到一个关于x ,y 的方程组,这个方程组的解所确定的点就是直线或曲线所过的定点。
2、特殊到一般法根据动点或动直线、动曲线的特殊情况探索出定点,再证明该定点与变量无关。
3、关系法对满足一定条件上的两点连结所得直线定点或满足一定条件的曲线过定点问题,可设直线(或曲线)上两点的坐标,利用坐标在直线(或曲线)上,建立点的坐标满足方程(组),求出相应的直线(或曲线),然后再利用直线(或曲线)过定点的知识求解。
二、手电筒模型解题步骤1、概念:只要任意一个限定AP 与BP 条件(如AP BP k k ⋅=定值,+AP BP k k =定值),直线AB 依然会过定点,因为三条直线形似手电筒,故称为手电筒模型。
2、解题步骤:第一步:由AB 直线y kx m =+,联立曲线方程得根与系数关系,∆求出参数范围;第二步:由AP 与BP 关系,得到一次函数()k f m =或()m f k =;第三步:将()k f m =或()m f k =代入y kx m =+,得到()y y k x x =-+定定.三、交点弦的中点所在直线恒过定点解题步骤第一步:设其中一条直线的斜率为1k ,求出直线方程;第二步:直线与曲线进行联立,出现韦达定理的形式,或者直接求出坐标,表示出这条弦的中点,并且类比出另外一条的中点坐标;第三步:由上述两部,根据点斜式写出两个中点所在直线的方程;第四步:化直线为点斜式,确定定点坐标。
四、圆锥曲线的切点弦方程1、过抛物线()220y px p =>外一点()00,M x y 作抛物线的切线,切点弦方程为()00yy p x x =+;2、过椭圆()222210x y a b a b+=>>外一点()00,M x y 作椭圆的切线,切点弦方程为00221x x y ya b +=;3、过双曲线()222210,0x y a b a b-=>>外一点()00,M x y 作双曲线的切线,切点弦方程为00221x x y ya b-=;五、几个重要的定点模型1、过椭圆()222210x y a b a b +=>>的左焦点(),0F c -作两条相互垂直的弦AB ,CD ,若弦AB ,CD 的中点分别为M ,N ,则直线MN 恒过定点222,0ac a b ⎛⎫- ⎪+⎝⎭.(双曲线与抛物线也有类似结论)2、动点()00,P x y 在直线0Ax By C ++=上,由P 引椭圆22221x y a b +=的两条切线,切点分别是M ,N ,则直线MN 恒过定点22,a A b B C C ⎛⎫-- ⎪⎝⎭.(双曲线与抛物线也有类似结论)3、(1)过椭圆()222210x y a b a b +=>>上的一定点()00,P x y 作两条斜率之和为m 的直线1l ,2l ,分别交椭圆于A ,B 两点,则直线AB 必过定点20000222,y b x x y m ma ⎛⎫--- ⎪⎝⎭;(2)过抛物线()220y px p =>上的一定点()00,P x y 作两条斜率之和为m 的直线1l ,2l ,分别交抛物线于A ,B 两点,则直线AB 必过定点0002,2y y x p m m ⎛⎫-- ⎪⎝⎭4、(1)过椭圆()222210x y a b a b +=>>上的一定点()00,P x y 作两条斜率之积为m 的直线1l ,2l ,分别交椭圆于A ,B 两点,则直线AB 必过定点()()2222002222,b ma x b ma y b ma b ma ⎛⎫++ ⎪- ⎪--⎝⎭(2)过抛物线()220y px p =>上的一定点()00,P x y 作两条斜率之积为m 的直线1l ,2l ,分别交抛物线于A ,B 两点,则直线AB 必过定点002,p x y m ⎛⎫-- ⎪⎝⎭(3、4两个结论对于圆与双曲线也成立,当22b a =时就是圆中的结论,用2b -替代2b 就可得到双曲线中的结论)题型一手电筒模型恒过定点问题【例1】已知圆22:(2)1M x y ++=,圆22:(2)49N x y -+=,动圆P 与圆M 外切并且与圆N 内切,圆心P 的轨迹为曲线C .(1)求曲线C 的方程;(2)设不经过点Q 的直线l 与曲线C 相交于A,B 两点,直线QA 与直线QB 的斜率均存在且斜率之和为-2,证明:直线l 过定点.【变式1-1】已知直线2y =与双曲线C :()222210,0x ya b a b-=>>交于A ,B 两点,F 是C 的左焦点,且AF AB ⊥,2BF AF =.(1)求双曲线C 的方程;(2)若P ,Q 是双曲线C 上的两点,M 是C 的右顶点,且直线MP 与MQ 的斜率之积为23-,证明直线PQ 恒过定点,并求出该定点的坐标.【变式1-2】已知F 为抛物线22y px =(0)p >的焦点,过F 且倾斜角为45︒的直线交抛物线于A,B 两点,||8AB =.(1)求抛物线的方程:(2)已知()0,1P x -为抛物线上一点,M,N 为抛物线上异于P 的两点,且满足2PM PN k k ⋅=-,试探究直线MN 是否过一定点?若是,求出此定点;若不是,说明理由.【变式1-3】已知动点(,)P x y (0)x ≥到定点(1,0)的距离比它到y 轴的距离大1.(1)求动点P 的轨迹E 的方程;(2)设点(,0)Q m (m 为常数),过点Q 作斜率分别为12,k k 的两条直线1l 与2l ,1l 交曲线E 于,A B 两点,2l 交曲线E 于,C D 两点,点,M N 分别是线段,AB CD 的中点,若121k k +=,求证:直线MN 过定点.题型二切点弦恒过定点问题【例2】在平面直角坐标系xOy 中,已知椭圆()2222:10x y C a b a b +=>>的右焦点与抛物线2y =的焦点重合,且椭圆的四个顶点围成的四边形面积为(1)求椭圆C 的标准方程;(2)已知点P 是直线420y x =-+上的动点,过点P 做椭圆C 的两条切线,切点分别为M ,N ,问直线MN 是否过定点?若是,求出该定点;若不是,请说明理由.【变式2-1】如图,已知椭圆2222:1(0)x y C a b a b +=>>的上顶点为(0,1)A ,离心率为2.(1)求椭圆C 的方程;(2)若过点A 作圆222:(1)(01)M x y r r ++=<<的两条切线分别与椭圆C 相交于点,B D (不同于点A ).当r 变化时,试问直线BD 是否过某个定点若是,求出该定点;若不是,请说明理由.【变式2-2】抛物线2:2(0)C x py p =>的焦点F 是椭圆22134x y +=的一个焦点.(1)求C 的准线方程;(2)若P 是直线240x y --=上的一动点,过P 向C 作两条切线,切点为M ,N ,试探究直线MN 是否过定点?若是,请求出定点,若否,请说明理由.【变式2-3】在平面直角坐标系xOy 中,已知点(0,2)F ,点P 到点F 的距离比点P 到直线3y =-的距离小1,记P 的轨迹为C .(1)求曲线C 的方程;(2)在直线2y =-上任取一点M ,过M 作曲线C 的切线12l l 、,切点分别为A 、B ,求证直线AB 过定点.题型三相交弦中恒过定点问题2:2(0)C x py p =>上.(1)求抛物线C 的方程;(2)过点(0,)T p 作两条互相垂直的直线1l 和2l ,1l 交抛物线C 于A 、B 两点,2l 交抛物线C 于D ,E 两点,若线段AB 的中点为M ,线段DE 的中点为N ,证明:直线MN 过定点.【变式3-1】在平面直角坐标系xOy 中,已知动点P 到点()2,0F 的距离与它到直线32x =的P 的轨迹为曲线C .(1)求曲线C 的方程;(2)过点F 作两条互相垂直的直线1l ,2l .1l 交曲线C 于A ,B 两点,2l 交曲线C 于S ,T 两点,线段AB 的中点为M ,线段ST 的中点为N .证明:直线MN 过定点,并求出该定点坐标.【变式3-2】已知椭圆()2222:10x y E a b a b +=>>A ,右顶点为B ,上顶点为C ,ABC 的内切圆的半径为4-.(1)求椭圆E 的标准方程;(2)点M 为直线:1l x =上任意一点,直线AM ,BM 分别交椭圆E 于不同的两点P ,Q .求证:直线PQ 恒过定点,并求出定点坐标.【变式3-3】已知M ⎝,N ⎫⎪⎪⎝⎭是椭圆2222:1(0)x yE a b a b +=>>上的两点.(1)求椭圆E 的方程;(2)过椭圆E 的上顶点A 和右焦点F 的直线与椭圆E 交于另一个点B ,P 为直线5x =上的动点,直线AP ,BP 分别与椭圆E 交于C (异于点A ),D (异于点B )两点,证明:直线CD 经过点F .题型四动圆恒过定点问题【例4】已知椭圆C :223412x y +=.(1)求椭圆C 的离心率;(2)设,A B 分别为椭圆C 的左右顶点,点P 在椭圆C 上,直线AP ,BP 分别与直线4x =相交于点M ,N .当点P 运动时,以M ,N 为直径的圆是否经过x 轴上的定点?试证明你的结论.【变式4-1】已知椭圆C :22221x y a b +=(0a b >>)的离心率为22,其左、右焦点分别为1F ,2F ,T 为椭圆C 上任意一点,12TF F △面积的最大值为1.(1)求椭圆C 的标准方程;(2)已知()0,1A ,过点10,2⎛⎫⎪⎝⎭的直线l 与椭圆C 交于不同的两点M ,N ,直线AM ,AN 与x 轴的交点分别为P ,Q ,证明:以PQ 为直径的圆过定点.【变式4-2】设A ,B 为双曲线C :22221x y a b-=()0,0a b >>的左、右顶点,直线l 过右焦点F 且与双曲线C 的右支交于M ,N 两点,当直线l 垂直于x 轴时,AMN 为等腰直角三角形.(1)求双曲线C 的离心率;(2)已知直线AM ,AN 分别交直线2ax =于P ,Q 两点,当直线l 的倾斜角变化时,以PQ 为直径的圆是否过定点,若过定点,求出定点的坐标;若不过定点,请说明理由.【变式4-3】已知抛物线()2:20C y px p =>与直线:20l x y +=交于M ,N 两点,且线段MN的中点为()8,p P y .(1)求抛物线C 的方程;(2)过点P 作直线m 交抛物线于点A ,B ,是否存在定点M ,使得以弦AB 为直径的圆恒过点M.若存在,请求出点M 坐标;若不存在,请说明理由.。
完整版函数图像过定点问题

函数图像过定点的研究题1:2+(k-2)x+2k(3求证:拋物线y=-k)x-1(k≠3)过定点,并求出定点的坐标.归纳:第一步:对含有变系数的项集中;第二步:然后将这部分项分解因式,使其成为一个只含系数和常数的因式与一个只含x和常数的因式之积的形式;第三步:令后一因式等于0,得到一个关于自变量x的方程(这时系数如何变化,都“失效”了);第四步:解此方程,得到x的值x0(定点的横坐标),将它代入原函数式(也可以是其变式),即得到一个y的值y(定点的纵坐标),于是,函数图象一定过定点(x,y);000第五步:反思回顾,查看关键点、易错点,完善解题步骤.题2:(2001年北京市西城区中考题)无论m为任何实数,二次函数的图像总)过的点是()0,1 31 C. 01B. ),( A. 13 (,)(-,)(-D.巩固练习:2)﹣m)x+m的图象总是过定点为何实数,二次函数1.无论my=x(﹣(2 )(﹣D. 1,0,10) C.(﹣1,3) 3 A.(1,) B.(2)1(a≠0),下列说法正确的有( 2.对于关于x的二次函数y=ax)﹣(2a﹣1x﹣取何值,图象必过两定②无论取何值,此二次函数图象与x轴必有两个交点;a①无论a的增大而减小;④当1时,y随x点,且两定点之间的距离为;③当a>0时,函数在x< x轴所得的线段长度必大于2.a<0时,函数图象截 4个..3 个 D A .1个 B. 2个C2(m≠0)的图象发现,随﹣2mx+33.(2012?鼓楼区一模)某数学兴趣小组研究二次函数y=mx的变化,这个二次函数的图象形状与位置均发生变化,但这个二次函数的图象总经过两着m .个定点,请你写出这两个定点的坐标:_________2的变化,这个二次函(m≠0)的图象发现,随着4.某数学小组研究二次函救y=mxm﹣3mx+2数图象的形状与位置均发生变化,但这个二次函数的图象总经过两个定点.请你写出这两个.定点的坐标:_________2,则这个函数的图象一定经过某一个﹣c=2+bx+c满足by=x5.(2009?宜宾县一模)二次函数.定点,这个定点是 _________2.的图象总是过定点 _________ y=x)﹣(2﹣mx+mm6.无论为何实数,二次函数)在函数的图象12,1)图象不经过三、四象限;(2)点(.已知一个二次函数具有性质(7的增大而增大.试写出一个满足以上性质的二次函x时,函数值y随自变量03上;()当x> _________ .数解析式:8.证明无论m为何值,函数y=mx-(4m-3)图像过定点,求出该定点坐标2.(m是常数)-6x+1y.9(南京2011年24题7分)已知函数=mx轴上的一个定点;m为何值,该函数的图象都经过y⑴求证:不论的值.轴只有一个交点,求m⑵若该函数的图象与x,﹣),与y轴的交点为(0.已知二次函数的顶点坐标为(﹣,n﹣m),其顶点恰101(好在直线1y=x+﹣m)上(其中m、n为正数).2(1)求证:此二次函数的图象与x轴有2个交点;(2)在x轴上是否存在这样的定点:不论m、n如何变化,二次函数的图象总通过此定点?若存在,求出所有这样的点;若不存在,请说明理由.函数图像过定点的研究题1:2+(k-2)x+-k)x2k-1(k≠3)过定点,并求出定点的坐标.求证拋物线y=(3审题视角有些函数的图象具有过定点的性质,这是由函数式中的一些系数的取值特点所决定的,例如,直线y=kx+b(k≠0),当b确定时,无论k取不等于0的任何值,它总过定点(0,b);物线线y=ax2+bx+c(a≠0),当c确定时,无论a、b取何值,它总过定点(o,c).本题中可以把函数解析式整理变形,使含字母k的项组合于一组,赋值为零,可以求的自变量的值,而后代入函数解析式,再求得相对应的函数值,即得定点的坐标.解:整理抛物线的解析式,得2+(k-2)x+2k-1 y=(3-k)x2-2x-1-kx2+=3xkx+2k2-2x-1-k(x2 -=3xx-2)(k≠3),2-x-2=0,得x=-1,x=上式中令x2. 2122-x-2),-2x-1-将它们分别代入y=3xk(x解得y=4,y=7,2122-x-2)1-k(x,3x(2,7)分别代入y=-2x -4)把点(-1,、无论k取何值,等式总成立,2+(k-2)x+2k-1(k≠3)上,(3,7)总在抛物线y=-k)x 4)即点(-1,、(22+(k-2)x+2k-1(k≠3)过定点(-1,4)、-即拋物线y=(3k)x(2,7).归纳:第一步:对含有变系数的项集中;第二步:然后将这部分项分解因式,使其成为一个只含系数和常数的因式与一个只含x和常数的因式之积的形式;第三步:令后一因式等于0,得到一个关于自变量x的方程(这时系数如何变化,都“失效”了);第四步:解此方程,得到x的值x0(定点的横坐标),将它代入原函数式(也可以是其变式),即得到一个y的值y(定点的纵坐标),于是,函数图象一定过定点(x,y);000第五步:反思回顾,查看关键点、易错点,完善解题步骤.题2:(2001年北京市西城区中考题)无论m为任何实数,二次函数的图像总过的点是()A. (1,3)B. (1,0))0,1(-D. )3,1(- C.解法一、特殊值法依据:二次函数的图像随着m的取值不同,它的位置也随之变化,可见这是一个抛物线群。
初中数学定点问题知识点与常考难题和培优提高练习压轴题(含解析)

初中数学定点问题知识点与常考难题和培优提高练习压轴题(含解析)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初中数学定点问题提高练习与常考难题和培优题压轴题(含解析)定点题型定点问题,初中一般是直线或抛物线恒过定点的问题,这类问题一般解法是根据直线或抛物线的动因,先选择适当的参数,用参数表示出直线或抛物线方程,然后按参数整理,并令参数的系数为0得方程组,解方程方程组求出定点坐标.解题思路:这类问题通常有两种处理方法:①第一种方法:是从特殊入手,通过考查极端位置,探索出“定值”是多少,再证明这个点(值)与变量无关;②第二种方法:是直接推理、计算;并在计算的过程中消去变量,从而得到定点(定值)。
具体地说,就是将要证明或要求解的量表示为某个合适变量的函数,化简消去变量即得定值。
一、直线过定点问题:解法1:取特殊值法给方程中的参数取定两个特殊值,这样就得到关于x,y的两个方程,从中解出x,y即为所求的定点,然后再将此点代入原方程验证即可。
例1:求直线(m+1)x+(m-1)y-2=0所通过的定点P的坐标。
解:令m=-1,可得y=-1;令m=1,可得x=1。
将(1,-1)点代入原方程得:(m+1)· 1+(m-1)(-1)-2=0 成立,所以该定点P为(1,-1)。
解法2:由“y-y0=k(x-x0)”求定点把含有参数的直线方程改写成y-y0=k(x-x0)的形式,这样就证明了它所表示的所有直线必过定点(x0,y0)。
例2:已知(k+1)x-(k-1)y-2k=0为直线l的方程,求证不论k取任何实数值时,直线l必过定点,并求出这个定点的坐标。
证明:由已知直线l的方程得(k+1)x=(k-1)y+2k,∴(k+1)x-(k+1)=(k-1)y+(k-1),不论k 取任何实数值时,直线l必过定点M(1,-1)。
解法3:方程思想若方程的解有无穷多个,则方程的系数均为0,利用这一方法的思路是将原方程整理为以参数为主元的方程,然后利用系数为零求得。
抛物线及其性质知识点大全
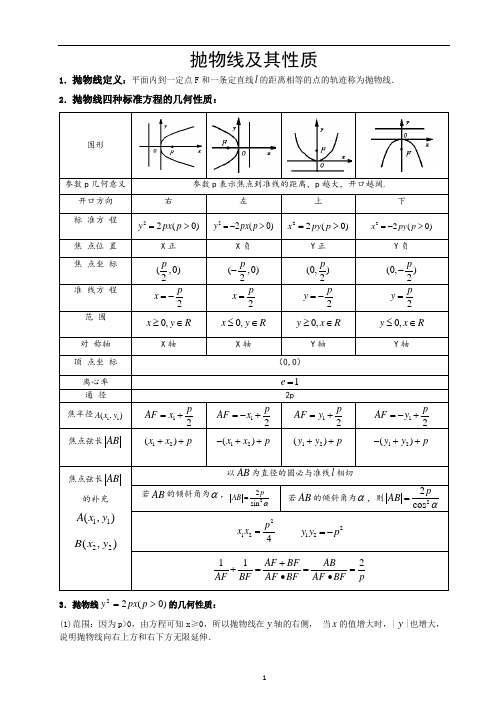
抛物线及其性质1.抛物线定义:平面内到一定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线. 2.抛物线四种标准方程的几何性质:图形参数p 几何意义 参数p 表示焦点到准线的距离,p 越大,开口越阔.开口方向 右左上下 标 准方 程 22(0)y px p => 22(0)y px p =-> 22(0)x py p =>22(0)x py p =->焦 点位 置 X 正X 负Y 正Y 负焦 点坐 标 (,0)2p (,0)2p -(0,)2p(0,)2p -准 线方 程 2p x =-2p x =2p y =-2p y =范 围 0,x y R ≥∈0,x y R ≤∈0,y x R ≥∈0,y x R ≤∈对 称轴 X 轴X 轴Y 轴Y 轴顶 点坐 标 (0,0)离心率 1e =通 径 2p焦半径11(,)A x y 12p AF x =+12p AF x =-+12p AF y =+12p AF y =-+焦点弦长AB12()x x p ++ 12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦长AB 的补充11(,)A x y22(,)B x y以AB 为直径的圆必与准线l 相切若AB 的倾斜角为α,22sin p AB α=若AB 的倾斜角为α,则22cos pAB α=2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 3.抛物线)0(22>=p px y 的几何性质:(1)范围:因为p>0,由方程可知x ≥0,所以抛物线在y 轴的右侧, 当x 的值增大时,|y |也增大,说明抛物线向右上方和右下方无限延伸.(2)对称性:对称轴要看一次项,符号决定开口方向. (3)顶点(0,0),离心率:1=e ,焦点(,0)2p F ,准线2px -=,焦准距p . (4) 焦点弦:抛物线)0(22>=p px y 的焦点弦AB ,),(11y x A ,),(22y x B ,则p x x AB ++=21||. 弦长|AB|=x 1+x 2+p,当x 1=x 2时,通径最短为2p 。
抛物线的有关结论

圆锥曲线中抛物线的有关结论山东省德州市实验中学 肖成荣由于抛物线的离心率是常数,导致了许多自身具有的规律性,再加上抛物线的方程比较简单,所以灵活性就更加显现,了解了抛物线的规律性后在处理抛物线的相关问题时会起到事半功倍的效果。
下面就抛物线的结论作以归整,供参考! 一、焦点)0,2(pF 处的结论 1、焦半径长:),(11y x A ,)0,2(p F ,2||1p x AF +=;2、焦点弦长:),(11y x A 、),(22y x B 在抛物线上,且AB 过焦点F ,则p x x AB ++=21||,或θ2sin 2||pAB =(θ为直线l 与抛物线对称轴的夹角);3、过焦点的直线与抛物线相交于A 、B 两点,分别过A 、B 两点作准线的垂线,垂足分别为M 、N ,MN 的中点为G 。
(1)两相切:①以焦半径AF 为直径的圆与y 轴相切;②以焦点弦AB 为直径的圆与抛物线的准线相切.(2)三直角:①∠AGB ②090=∠MFN ③GF (3)六定值:),(11y x A 、),(22y x B 的乘积是定值:21x x =243p OB OA -=⋅;②n BF m AF ==,mn GF =||.③22sin AOBp S θ∆= 二、点)0,(p D 处的结论例:抛物线px y 22=上的点到)0,(a A 的最近距离是多少?结论:)0,(p D 是抛物线px y 22=上到点)0,(a A 的距离最近的点为顶点的分界点,)0,(a A 在)0,(p D 左边顶点到点)0,(a A 的距离最近,右边横坐标为p a -的那两个抛物线上的点到点)0,(a A 的距离最近. 三、点)0,2(p E 处的结论B A ,是抛物线)0(22>=p px y 上的两点,OB OA ⊥,),(11y x A ,),(22y x B ,则ⅰ.2214p x x =,2214p y y -=;ⅱ.直线AB 过定点)0,2(p ;ⅲ.求AB 中点的轨迹方程;ⅳ.过O 向AB 引垂线,求垂足T 的轨迹方程;ⅴ.求AOB ∆面积的最小值.结论:),(11y x A 、),(22y x B 是抛物线)0(22>=p px y 上的两点,O 为抛物线的顶点,(1)090=∠AOB ⇔直线AB 过点)0,2(p E .(2)2214p x x =,2214p y y -=.四、准线上的有关结论过抛物线的焦点的直线交抛物线于两点B A ,,再以B A ,为切点作抛物线的切线,其交点在抛物线的准线上,且两切线垂直。
抛物线讲义(含知识点、例题、变式及答案)

第七节 抛 物 线 2019考纲考题考情1.抛物线的概念平面内与一个定点F 和一条定直线l (F ∉l )的距离相等的点的轨迹叫做抛物线,点F 叫做抛物线的焦点,直线l 叫做抛物线的准线。
2.抛物线的标准方程与几何性质 标准 方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y =0x =0焦点 F ⎝ ⎛⎭⎪⎫p 2,0 F ⎝ ⎛⎭⎪⎫-p 2,0 F ⎝ ⎛⎭⎪⎫0,p 2 F ⎝ ⎛⎭⎪⎫0,-p 2 离心率e =100抛物线焦点弦的6个常用结论设AB是过抛物线y2=2px(p>0)焦点F的弦,若A(x1,y1),B(x2,y2),则(1)x1x2=p24,y1y2=-p2。
(2)弦长|AB|=x1+x2+p=2psin2α(α为弦AB的倾斜角)。
(3)以弦AB为直径的圆与准线相切。
(4)过焦点垂直于对称轴的弦长等于2p(通径)。
(5)S△AOB=p22sinθ(θ为AB的倾斜角).(6)1|AF|+1|BF|为定值2p.考点一抛物线的定义及应用【例1】(1)已知抛物线x2=4y上一点A纵坐标为4,则点A到抛物线焦点的距离为()A.10B.4C.5D.15(2)已知抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l 于点Q,M,N分别为PQ,PF的中点,MN与x轴相交于点R,若∠NRF=60°,则|FR|等于()A.12B.1C.2 D.4解析(1)抛物线x2=4y的准线方程为y=-1,点A到准线的距离为5,根据抛物线定义可知点A到焦点的距离为5。
故选C。
(2)因为M,N分别是PQ,PF的中点,所以MN∥FQ,且PQ∥x轴。
又∠NRF=60°,所以∠FQP=60°。
由抛物线定义知|PQ|=|PF|,所以△FQP为正三角形。
证明抛物线原点张角90°恒过定点

证明抛物线原点张角90°恒过
定点
证明抛物线原点张角90°恒过定点
抛物线是一种几何图形,它是一条二次曲线,其形状取决于它的原点和张角。
本文将证明,抛物线原点张角90°恒过定点。
首先,我们来看一下抛物线的定义。
抛物线是一条二次曲线,它的方程为y=ax2+bx+c,其中a,b,c是常数。
抛物线的原点是它的几何中心,它的张角是抛物线的斜率。
接下来,我们来看一下抛物线原点张角90°恒过定点的证明。
首先,我们假设抛物线的原点为P,它的张角为90°,它恒过定点Q。
根据抛物线的定义,我们可以得出抛物线的方程为y=ax2+bx+c,其中a,b,c是常数。
接下来,我们来看一下抛物线原点张角90°恒过定点的证明。
根据抛物线的定义,我们可以得出抛物线的斜率为0,
即抛物线的张角为90°。
因此,抛物线原点张角90°恒过定点Q。
最后,我们来看一下抛物线原点张角90°恒过定点的结论。
根据上述证明,我们可以得出结论:抛物线原点张角90°恒过定点Q。
综上所述,本文证明了抛物线原点张角90°恒过定点Q的结论。
通过对抛物线的定义和证明,我们可以得出结论:抛物线原点张角90°恒过定点Q。
抛物线的有关结论

抛物线的有关结论由于抛物线具有常数离心率,因此具有许多自身规律性。
加上抛物线方程相对简单,使得其灵活性更加突出。
了解这些规律性可以在处理相关问题时事半功倍。
下面整理了抛物线的结论以供参考。
一、焦点F(p22sin二、点D(p,)处的结论对于抛物线y2=2px,点D(p,)是到点A(a,)距离最近的点,其中A为抛物线上的一点,且A为顶点的分界点。
当A(a,)在D(p,)左侧时,右侧横坐标为a-p的两个点到点A(a,)的距离最近。
三、点E(2p,)处的结论设A(x1,y1)和B(x2,y2)是抛物线y2=2px上的两点,且OA 垂直于OB。
则有以下结论:1.焦半径长:AF为直线FB上的点到焦点F的距离。
2.焦点弦长:AB为过点A和B的直线,且过焦点F。
|AB|=x1+x2+p或2psinθ。
3.过焦点F的直线与抛物线相交于A和B两点,分别过A和B两点作准线的垂线,垂足分别为M和N,MN的中点为G。
1) 两相切:以焦半径AF为直径的圆与y轴相切。
以焦点弦AB为直径的圆与抛物线准线相切。
2) 三直角:①∠AGB=90°;②直线AB过定点(2p,);③求AB中点的轨迹方程。
3) 六定值:焦点弦两端点MA和RA;直线AB与抛物线的交点C;过O向AB引垂线,垂足T的轨迹方程;求ΔAOB 面积的最小值。
四、准线上的有关结论对于抛物线y2=2px,点P(x,y)在准线上,其横坐标为p2/x,纵坐标为-py/2x+p。
其中x和y的乘积为定值:x1x2=4p2.过抛物线焦点的直线与抛物线交于两点A、B,以A、B 为切点作抛物线的切线,交点在抛物线的准线上,并且两条切线垂直。
反过来,准线上任意一点做抛物线的切线有两条,且两条切线垂直,两切点连线过抛物线的焦点。
下面对上述结论进行证明。
一、焦点F(p/2,0)处的结论1.焦半径长:设点A(x1,y1),则|AF|=x1+ p/2.证明:根据抛物线的定义,|AF|=AM=x1+ p/2.2.焦点弦长:设点A(x1,y1)、B(x2,y2)在抛物线上,且AB 过焦点F,则|AB|=x1+x2+p,或|AB|=2p*sinθ(θ为直线l与抛物线对称轴的夹角)。
抛物线的简单几何性质
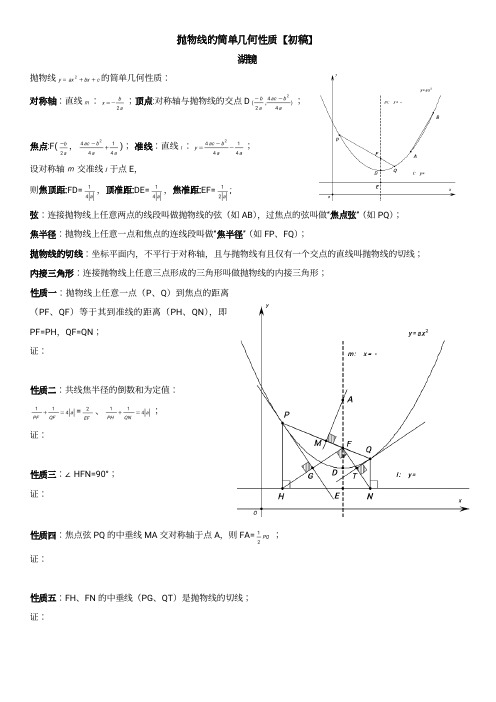
抛物线的简单几何性质【初稿】湖镜抛物线的简单几何性质:对称轴:直线:;顶点:对称轴与抛物线的交点D;焦点:F(,);准线:直线:;设对称轴交准线于点E,则焦顶距:F D=,顶准距:D E=,焦准距:E F=;弦:连接抛物线上任意两点的线段叫做抛物线的弦(如A B),过焦点的弦叫做“焦点弦”(如P Q);焦半径:抛物线上任意一点和焦点的连线段叫做“焦半径”(如F P、F Q);抛物线的切线:坐标平面内,不平行于对称轴,且与抛物线有且仅有一个交点的直线叫抛物线的切线;内接三角形:连接抛物线上任意三点形成的三角形叫做抛物线的内接三角形;性质一:抛物线上任意一点(P、Q)到焦点的距离(P F、Q F)等于其到准线的距离(P H、Q N),即P F=P H,Q F=Q N;证:性质二:共线焦半径的倒数和为定值:=、;证:性质三:∠H F N=90°;证:性质四:焦点弦P Q的中垂线M A交对称轴于点A,则F A=;证:性质五:F H、F N的中垂线(P G、Q T)是抛物线的切线;证:性质一证明:设P(x,y),则H(x,)练习:1、抛物线C1:y=,则C1的对称轴为,顶点坐标为,焦点为,准线为;2、如右图,抛物线y=-,直线l:y=a,点F(3,b),P为抛物线上任意一点,P H⊥l于H,连接P F,若P H=P F恒成立,求a、b的值(不允许用焦点和准线的概念及相关计算公式)。
性质二证明:补充知识:已知A(x1,y1)、B(x2,y2)是直线y=k x+b上不同两点,则A B=|x1-x2|(此结论如何证明?)证:设P(x1,y1)、Q(x2,y2),F(,),设P Q:y=k x+t练习:3、如图,抛物线y=-,直线l:y=4,直线P Q交抛物线于P、Q两点,直线P Q解析式为:y=k x-3k+1,作P H⊥l于H,作Q N⊥l于N,请问是否为定值,若是,请求出其值,若不是,请求出其取值范围。
抛物线性质归纳、证明和应用

抛物线性质归纳、证明和应用抛物线是平面内到定点距离等于到定直线(定点在定直线外)距离点轨迹,它是椭圆过渡到双曲线瞬间曲线,它只有一支(双曲线有两支),只有一条对称轴,没有渐近线和对称中心,属于无心曲线.抛物线焦半径、焦点弦性质丰富多彩,此外还有定点、定值、定弦、最值等问题也值得探讨,抛物线许多性质也是历年高考重点和热点,这里就它一些性质加以归纳,说明和证明,及其在历年高考和模拟考试出现典例. 一、焦半径、焦点弦性质如图,是过抛物线 y 2=2(p >0)焦点F 弦,、是准线垂线,垂足分别为D 、C ,M 是中点,N 是中点.设点A (x 1,y 1)、点B (x 2,y 2),直线交y 轴于点K (0,y 3),则:⑴ ① y 1y 2=-p 2;② x 1x 2=;③ +=;④ | |=x 1+x 2+p = (为倾斜角);⑤ S △=,S 梯形=.. ⑵ |)+|)=; ⑶ ∠=∠=∠; ⑷ 、是抛物线切线;⑸ 、分别是∠和∠平分线;⑹ 、、y 轴三线共点,、、y 轴三线共点;⑺ A 、O 、C 三点共线,B 、O 、D 三点共线; ⑻ 若| |:| |=m :n ,点A 在第一象限,为直线倾斜角. 则= ; K (0,y 3)C M DB (x 2,y 2)ROF ( ,0)A (x 1,y 1)xyHG x =-N Q⑼以为直径圆及y轴相切,以为直径圆及y轴相切;以为直径圆及准线相切.⑽交抛物线于点Q,则,Q是中点.★⑴①y1y2=-p2;②x1x2=;③+=④ | |=x1+x2+p=(为倾斜角);⑤S△=,S梯形=.【证明】设过焦点F(,0)直线方程为x=+,代入抛物线方程y2=2得y2-2-p2=0,因此①y1y2=-p2,y1+y2=2.另由⑶得在△中,⊥,有| |2=| |·| |,而| |=| y1 |,| |=| y2 |,| |=p,且y1 y2<0∴y1y2=-p2.②又点A、B在抛物线上,有x1=,x2=,因此x1x2=·==.③+===-,在直线方程x=+中令x=0,得y3=-,代入上式得+=④【证法一】根据抛物线定义,| |=| |=x1+,| |=| |=x2+,| |=| |+| |=x1+x2+p又| |==| y2-y1 |===2p(1+m2)当m≠0时,m===,有1+m2=1+=(k为直线斜率)当m=0时,=90,1+m2=1也满足D A(x1,y1)yθB1CDB(x2,y2)RA(x1,y1)xyO F(,0)θ图11+m2=∴| |=2p(1+m2)= .【证法二】如图2,过A、B引x轴垂线1、1,垂足为A1、B1,那么| |=| |-| 1 |=| |-| ,∴| |=|,1-)=同理,| |=|,1+)=∴| |=| |+| |=+= .【证法三】极坐标法,设抛物线极坐标方程为=,则| |=1=,| |=2=))= .∴| |=| |+| |=+= .⑤S△=S△+S△=| y1 |+| y1 |=··(| y1 |+| y1 |)∵y1y2=-p2,则y1、y2异号,因此,| y1|+| y1|=| y1-y2|∴S△=| y1-y2 |==== .又∵| |=| =,| |+| |=| |=.∴S梯形=(| |+| |)·| |=××=.【例1】(2001年新课程高考文)设坐标原点为O,抛物线y2=2x及过焦点直线交于A、B两点,则·=·······()A. B. - C. 3 D. -3【解】设A(x1,y1),B(x2,y2),则·=x1x2+y1y2=-p2=-,故选B.【例2】(2009年福建理)过抛物线y2=2(p>0)焦点F作倾斜角为45直线交抛物线于A、B两点,若线段长为8,则p= .【解】由性质⑴得| |===8,∴p==4.★⑵ |)+|)=【证法一】由⑴x 1x 2=,且| |=x 1+,| |=x 2+.∴|)+|)=+===p 24+p 2(x 1+x 2)+p 24 )=p2(x 1+x 2+p ) )=【证法二】由| |=1= ,| |=2=))= .∴|)+|)=+=+=【例3】(2000全国)过抛物线y =2(a >0)焦点F 用一直线交抛物线于P 、Q 两点,若线段及长分别是p 、q ,则+等于 · ( )A. 2aB.C.4aD.【解】由y =2得x 2= y ,(抛物线焦点到准线距离为),由此得+=4a ,故选C.★⑶ ∠=∠=∠,先证明:∠=∠ 【证法一】延长交延长线于E ,如图3,则△≌△,∴| |=| |,| |=| | ∴| |=| |+| |=| |+| | =| |+| |=| | ∴△为等腰三角形,又M 是中点, ∴⊥,即∠=∠【证法二】取中点N ,连结,则| |=(| |+| |)=(| |+| |)=| |,∴| |=| |=| |CD B (x 2,y 2)RA (x 1,y 1)xy OF EN M 图3∴△为直角三角形,为斜边,故∠=∠.【证法三】由已知得C (-,y 2)、D (-,y 1),由此得M (-,).∴=====,同理= ∴·=·===-1 ∴⊥,即∠=∠.【证法四】由已知得C (-,y 2)、D (-,y 1),由此得M (-,).∴=(x 1+,),=(x 3+,)∴·=(x 1+)(x 2+)+=x 1x 2+(x 1+x 2)+- =+(+)+- =+=+=0∴⊥,故∠=∠. 【证法五】由下面证得∠=90,连结,则=.又=,故△≌△,如图4 ∴∠1=∠2,同理∠3=∠4 ∴∠2+∠3=×180=90∴∠=∠.接着证明:∠=∠【证法一】如图5,由于| |=| |,∥,故可设∠=∠=∠=, 同理,设∠=∠=∠=,而∠+∠+∠+∠=180 ∴2(+)=180,即+=90,故∠=90图5C D B (x 2,y 2)R A (x 1,y 1)xy O F ( ,0) ααα ββ βCD BRAxyO F 图41 2 3 4M【证法二】取中点M ,即M (-,)由前知=,=== ∴=,∥,同理,∥ ∴∠=∠=90.【证法三】∵=(p ,-y 1),=(p ,-y 2),∴·=p 2+y 1y 2=0∴⊥,故∠=90.【证法四】由于| |2=p 2=-y 1y 2=| |·| |,即|)=|),且∠=∠=90∴ △∽△∴∠=∠,而∠+∠=90 ∴∠+∠=90 ∴∠=90【例4】(2009年湖北文)如图7,过抛物线y 2=2(P >0)焦点F 直线及抛物线相交于M 、N 两点,自M 、N 向准线l 作垂线,垂足分别为M 1、N 1,求证:1⊥1★⑷ 、是抛物线切线C D B (x 2,y 2)R A (x 1,y 1)xy O FM 图6G HD 1N 1NMxyO F图7M 1l D R A (x 1,y 1) xy OFM D 1【证法一】∵=,直线方程为y -y 1=(x -)及抛物线方程y 2=2联立消去x 得y -y 1=(-),整理得y 2-2y 1y +=0可见△=(2y 1)2-4=0, 故直线及抛物线y 2=2相切, 同理也是抛物线切线,如图8.【证法二】由抛物线方程y 2=2,两边对x 求导,=,得2y ·=2p ,=,故抛物线y 2=2在点A (x 1,y 1)处切线斜率为k 切=| y =y 1=.又=,∴k 切=,即是抛物线在点A 处切线,同理也是抛物线切线. 【证法三】∵过点A (x 1,y 1)切线方程为y 1y =p (x +x 1),把M (-,)代入左边=y 1·===1-,右边=p (-+x 1)=-+1,左边=右边,可见,过点A 切线经过点M , 即是抛物线切线,同理也是抛物线切线.★⑸ 、分别是∠和∠平分线【证法一】延长交延长线于E ,如图9,则△≌△,有∥,=, ∴∠=∠=∠, 即平分∠,同理平分∠.【证法二】由图9可知只须证明直线倾斜角是直线倾斜角2倍即可,即=2. 且M (-,)∵===错误!=错误!. ======.CD B (x 2,y 2)R A (x 1,y 1)xyO F EN M图9∴ 2======∴=2,即平分∠,同理平分∠.★⑹ 、、y 轴三线共点,、、y 轴三线共点 【证法一】如图10,设及相交于点G 1,由以上证明知| |=| |,平分∠,故1也是边上中线, ∴G 1是中点.设及y 轴交于点D 1,及y 轴相交于点G 2, 易知,| 1 |=| |,1∥, 故△1G 2≌△2∴| 2 |=| 2 |,则G 2也是中点.∴G 1及G 2重合(设为点G ),则、、y 轴三线共点,同理、、y 轴也三线共点.【证法二】直线方程为y -y 1=(x -),令x =0得及y 轴交于点G 1(0,),又直线方程为y =-(x -),令x =0得及y 轴交于点G 2(0,) ∴、及y 轴相交同一点G (0,),则、、y 轴三线共点, 同理、、y 轴也三线共点H .由以上证明还可以得四边形是矩形.★⑺ A 、O 、C 三点共线,B 、O 、D 三点共线 【证法一】如图11,==错误!=错误!,=-p2 )=-=-=-=∴=,则A 、O 、C 三点共线,CDB (x 2,y 2)R A (x 1,y 1)xyOF C D B (x 2,y 2)R A (x 1,y 1)xy O FM 图10G HD 1同理D 、O 、B 三点也共线. 【证法二】设及x 轴交于点O,∵∥∥∴|)=|)=|),O F |)=|),又| |=| |,| |=| |,∴ |)=O F |)∴||=| O F |,则O及O 重合,即C 、O 、A 三点共线,同理D 、O 、B 三点也共线. 【证法三】设及x 轴交于点O,∥,OF |)=|),∴| O F |=|·| |)=|·| |+| |)=错误!=错误!【见⑵证】∴O及O 重合,则即C 、O 、A 三点共线,同理D 、O 、B 三点也共线.【证法四】∵=(-,y 2),=(x 1,y 1),∵-·y 1-x 1 y 2=-·y 1- y 2=--=-+=0 ∴∥,且都以O 为端点∴A 、O 、C 三点共线,同理B 、O 、D 三点共线.【推广】过定点P (m ,0)直线及抛物线y 2=2(p >0)相交于点A 、B ,过A 、B 两点分别作直线l :x =-m 垂线,垂足分别为M 、N ,则A 、O 、N 三点共线,B 、O 、M 三点也共线,如下图:OyNMBAPxOy NM BAP x【例5】(2001年高考)设抛物线y 2=2(p >0)焦点为F ,经过点F 直线交抛物线于A 、B 两点,点C 在抛物线准线上,且∥x 轴. 证明直线经过原点O .【证法一】因为抛物线y 2=2(p >0)焦点为F (-,0),所以经过点F 直线方程可设为x =+; 代入抛物线方程得y 2-2-p 2=0设A (x 1,y 1),B (x 2,y 2),则y 1,y 2是该方程两个根, ∴y 1y 2=-p 2因为∥x 轴,且点C 在准线x =-上,故C (-,y 2),∴直线斜率为 =-p2 )===.∴直线经过原点O .【证法二】如图13,过A 作⊥l ,D ∥∥连结及相交于点N ,则|, | | )=|, | | )=|, | | ),|, | | )=|, | | )由抛物线定义可知:| |=| |,| |=| | ∴| |=|·| |, | | )=|·| |, | | )=| |. 即N 是中点,及抛物线顶点O 重合,所以直线经过原点O . ★⑻ 若| |:| |=m :n ,点A 在第一象限,为直线倾斜角. 则=;【证明】如图14,过A 、B 分别作准线l 垂线,垂足分别为D ,C ,过BCB (x 2,y 2)R A (x 1,y 1)xyOF 图12C D B (x 2,y 2)E A (x 1,y 1)xyO F图13N作⊥于E ,设| |=,| |=,则| |=| |,| |=| |,| |=| |-| |=(m -n )t∴在△中,∠=|)=(m -n )t ,(m +n )t )= ∴=∠=.【例6】设经过抛物线y 2=2焦点F 直线及抛物线相交于两点A 、B ,且| |:| |=3:1,则直线倾斜角大小为 . 【答案】60或120.★⑼ 以为直径圆及y 轴相切,以为直径圆及y 轴相切;以为直径圆及准线相切.【说明】如图15,设E 是中点,则E 坐标为(p2+x 1 ,2),),则点E 到y 轴距离为d =p2+x 1 ,2)=| |故以为直径圆及y 轴相切, 同理以为直径圆及y 轴相切.【说明】如图15,设M 是中点,作⊥准线l 于N ,则| |=(| |+| |)=(| |+| |)=| | 则圆心M 到l 距离| |=| |, 故以为直径圆及准线相切.★⑽ 交抛物线于点Q ,则Q 是中点.C DBR A xy O EF图14lC DBR A xy O F 图15lM N E【证明】设A(,y1),B(,y1),则C(-,y2),D(-,y1),M(-,),N(,),设中点为Q,则Q (错误!,错误!)∵错误!=错误!=错误!=错误!∴点Q在抛物线y2=2上,即Q是中点.二、定点、定值、定直线问题(共9个结论)★⑴平行于抛物线对称轴光线,被抛物面反射后会聚焦于抛物线焦点,如图17.【证明】如图17,设抛物线方程为y 2=2(p >0),直线∥x 轴,点A 坐标为(x 0,y 0),则过A 点切线方程为y 0y =p (x +x 0),直线l 斜率为k 0=,设直线到l 角为,则=,设直线斜率为k 1,则k 1=x 0-p2 )= ,设直线l 到角为,则==错误!=错误!=错误!. ∴=,又、∈[0,),则=,也就是说平行于抛物线对称轴光线,被抛物面反射后会聚焦于抛物线焦点.【例7】(2004年福建省质检)如图18,从点M (x 02)发出光线沿平行于抛物线y 2=4x 轴方向射向抛物线点P ,反射后经焦点F 又射向直线l :x -2y -7=0上点N ,再反射后又设回点M ,则x 0= .【解】∥x 轴,点P 在抛物线上,得P 坐标为(1,2),经过F (1,0)点后反射在Q 点,则Q 坐标为(1,-2),经Q 反射后点N 坐标为(3,-2),设M 关于l 对称点为M ,依题意,Q 、N 、M 共线.故可设M(x 1,-2),图17FA B xOTl图18FPMxO QNyM由此得 ,解得x 0=6.【另解】若设Q 关于直线l 对称点为Q,设Q(a ,b ),由于Q 、Q关于直线l 对称,由此得,解得则Q坐标为(,-),又M 、N 、Q 三点共线,=,即=,∴x 0=6.★⑵若C (x 0,y 0)是抛物线y 2=2(p >0)上任一点,过C 引两条互相垂直直线交抛物线于A 、B ,则直线过定点(2p +x 0,-y 0).【证明】设A (,s )、B (,t )(s ,t ,y 0互不相等)那么,由⊥得·=x 0-s 22p )·x 0-t22p)=错误!·错误!=错误!=-1 ∴4p 2=-(y 0+s )(y 0+t ) ∴=-4p 2-(s +t )y 0- ①又直线方程为=t 22p -s 22p),整理得,y = ②把①代入②得 y ==-y 0=(x -2p -x 0)-y 0 令x -2p -x 0=0,即x =2p +x 0,得y =-y 0. 故直线过定点(2p +x 0,-y 0).特别地,当C 是抛物线顶点时,定点P 坐标为(2p ,0).【拓展】C (x 0,y 0)是抛物线y 2=2(p >0)上一定点,直线及抛物线相交于A 、B 两点(都异于C ),若直线、斜率、乘积为定值m ,那么,直线过定点(x 0-,-y 0).xy OA (,s )图19B (,t )C (x 0,y 0)【例8】(2000京皖春季高考)如图20,设点A和B 为抛物线y 2=4(p >0)上原点以外两个动点,已知⊥,⊥,求点M 轨迹方程,并说明它表示什么曲线.【解法一】点A ,B 在抛物线y 2=4上,设A (,),B (,),、斜率分别为、.∴=错误!=错误!,=错误!,=错误!=错误!. 由⊥,得·==-1 ······· ①∴直线方程为,y -=(x -),即(+)(y -)=4p (x -) ② 由⊥,得直线方程y =+ ,4p ) ···· ③设点M (x ,y ),则x ,y 满足②、③两式,将②式两边同时乘以-,并利用③式整理得,2+-(x 2+y 2)=0 ········ ④ 由③、④两式得-+-(x 2+y 2)=0, 由①式知,=-16p 2,所以x 2+y 2-4=0. 因为A 、B 是原点以外两点,所以x ≠0. 所以点M 轨迹是以(2p ,0)为圆心,以2p 为半径圆,去掉坐标原点.【解法二】由性质(2)易知经过定点P (4p ,0),由于⊥,那么,M 轨迹以(2p ,0)为圆心,以2p 为半径圆,去掉坐标原点.其轨迹方程为x 2+y 2-4=0(x ≠0).★⑶抛物线y 2=2(p >0)弦中点D 恰好在定直线l :x =m (m >0)上,图20图21则线段垂直平分线过定点M(m+p,0).【证明】如图22,设A(x1,y1),B(x2,y2),D(m,y0),那么①-②得-=2p(x1-x2)∴直线斜率===∴直线斜率=-=-图22∴直线方程为y-y0=-(x-m)令y=0,得x=m+p∴直线垂直平分线恒过定点(m+p,0).【例9】(2008湖南理科高考)若A、B是抛物线y2=4x上不同两点,弦(不平行于y轴)垂直平分线及x轴相交于点P,则称弦是点P一条“相关弦”.已知当x>2时,点P(x,0)存在无穷多条“相关弦”.给定x0>2.⑴证明:点P(x0,0)所有“相关弦”中点横坐标相同;⑵(略)【说明】应用性质⑶,由已知得p=2,由定点P(x0,0)得m+p=x0,故m=x0-2∴“相关弦”中点横坐标为x0-2.★⑷设直线l 及抛物线y 2=2(p >0)相交于点A (x 1,y 1)、B (x 2,y 2),那么①若直线l 过抛物线对称轴定点M (a ,0),则y 1y 2=-2,x 1x 2=a 2;反之②若y 1y 2=k (定值),则直线l 恒过定点N (-,0). ③若直线l 及y 轴相交于点(0,y 3),则+=.【证明】①设过点M (a ,0)直线方程为x =+a ,代入抛物线方程y 2=2得y 2-2-2=0,因此y 1y 2=-2,x 1x 2=·===a 2.②设直线l 方程为x =+b ,代入抛物线方程y 2=2得y 2-2-2=0,即方程根y 1、y 2是P 、Q 两点纵坐标∴y 1y 2=-2,又y 1y 2=k .∴-2=k ,即b =-,则直线l 方程为x =- 令y =0,得x =-,则直线l 恒过定点N (-,0). ③由l 方程x =+a 中,令x =0得y 3=-,y 1+y 2=2 ∴+===-=.【例10】(北京2005年春季高考理科)如图24,O 为坐标原点,直线l 在x 轴和y 轴上截距分别为a 和b (a >0,b ≠0),且交抛物线y 2=2(p >0于M (x 1,y 1)、N (x 2,y 2)两点.图23⑴写出直线l截距式方程;⑵证明:+=.⑴【解】直线l截距式方程为+=1.⑵由上面性质⑶证明可得+=.★⑸过抛物线y 2=2(p >0)焦点F 作直线l 及抛物线交于A 、B 两点,且及准线交于点M ,设=,=,则+=0.【证法一】设过点F (,0)直线方程为x =+,代入抛物线方程y 2=2得y 2-2-p 2=0,因此y 1y 2=-p 2,y 1+y 2=2令x =-,得=- 由=得(x 1+,y 1+)=(-x 1,-y 1)∴y 1+=- y 1,=1+,同理,=1+∴+=2++=2+y 2)=2+=2-2=0.【证法二】由已知=,=,得·<0.则错误!=-错误! ···· ①过点A ,B 分别作准线l 垂线,垂足分别为A 1,B 1,则有:错误!=错误!=错误! ② 由①②得-错误!=错误!,即+=0.【例11】(2007年福建理科高考)如图27,已知点F (1,0),直线l :x =-1,P 为平面上动点,过P 作直线l 垂线,垂足为点Q ,且·=·. ⑴求动点P 轨迹C 方程;⑵过点F 直线交轨迹C 于A ,B 两点,交直线l 于点M ,已知 =1,=2,求1+2值; B (x 2,y 2)A (x 1,y 1)xyOF 图25MB (x 2,y 2)A (x 1,y 1)xyO F 图26MA 1BOyx1-1 l F图27【略解】⑴动点P轨迹C方程为:y2=4x;⑵1+2=0.★⑹定长为l 弦两个端点在抛物线y 2=2上,M 是 中点,M 到y 轴距离为d ,那么,M 轨迹方程为:4(y 2+p 2)(2-y 2)=p 2l 2,且①当0<l <2p 时,d 最小值为,此时,∥y 轴;②当l ≥2p 时,d 最小值为,此时,弦过焦点F .【解】设A (x 1,y 1),B (x 2,y 2),弦中点M 坐标为(x 0,y 0),直线方程为x =+b ,代入抛物线方程y 2=2得y 2-2-2=0. ∴y 1+y 2=2,y 1y 2=-2. 又中点为M (x 0,y 0),且点M 在直线上, ∴y 0==,x 0=0+b ,m =,b =x 0-0=x 0-.∴| |2=l 2=(x 1-x 2)2+(y 1-y 2)2=(1+b -2-b )2+(y 1-y 2)2=(1+m 2)(y 1-y 2)2=(1+m 2)[(y 1+y 2)2-4y 1y 2] =(1+)[4+8]=(1+)[4+8p (x 0-)]整理得,4(+p 2)(20-)=p 2l 2. 故中点M 轨迹方程为:4(y 2+p 2)(2-y 2)=p 2l 2.由上可知d =x =+,令t =y 2+p 2≥p 2,即y 2=t -p 2,则d =x =+=+-(t ≥p 2).令=,得t =.①当0<l <2p 时,p 2>,d 在t ∈[ p 2,+∞)上是增函数, ∴当t =p 2,即y =0时,=+-=,此时,m =0,即∥y 轴. ②当l ≥2p 时,p 2≤,∴d =+-≥2-=.当且仅当=,即t =≥p 2时取等号,故d 最小值为.图28②【证法二】当l ≥2p 时,过A 、B 、M 作准线x =-垂线,垂足为A 、B 、M ,则||=d +=(| |+| |)=(| |+| |)≥| |=l .上式当且仅当| |+| |=| |,即弦过抛物线焦点M 时取等号,则d 最小值为l -=.【说明】经过焦点F 最短弦是通经2p ,因此当弦长l <2p 时,不能用证法二证明d 最小值为.【例12】长度为a 线段两个端点在抛物线x2=2(a ≥2p >0)上运动,以中点C 为圆心作圆及抛物线准线相切,求圆C 最小半径.【解】依题意,问题转化为定长弦两个端点在抛物线上,弦中点C 到y轴距离最值问题,由上面性质可知当弦经过焦点F 时,点C 到准线距离为最小值. 如图30. ∴圆C 最小半径为r =.★⑺过抛物线y 2=2(p >0)对称轴上定点M (m ,0)(m >0),作直线及抛物线相交于A ,B 两点.点N 是定直线l :x =-m 上任一点,则直线,,斜率成等差数列.【证明】设A (x 1,y 1),B (x 2,y 2),N (-m ,n ),由性质⑶有y 1y 2=-2,BAx y OF图29M A ' M ' B 'BAx yO图30C FBN(-m ,n )y则直线、斜率为=,= ∴+=错误!+错误!=+ =+=====- 又∵直线斜率为==-. ∴+=2∴直线,,斜率成等差数列.★⑻抛物线一组平行弦中点共线,且所在直线平行于对称轴或及对称轴重合.【证明】设斜率为k (k 为常数)一组平行线及抛物线y 2=2(p >0)交于点、(i =1,2,…)弦中点为,(即M 1,M 2,…,),且直线方程为y =+(为直线在y 轴上截距),(x 1,y 1),(x 2,y 2)(,).联立方程组,消去x 得y 2-y +=0 ∴y 1+y 2=,又是中点∴==,则M 1,M 2,…,在平行于x 轴直线y =上.当直线及x 轴垂直(即直线斜率不存在时),易知M 1,M 2,…,在x 轴上.【例13】(2009年陕西卷理20文21)已知抛物线C :y =2x 2,直线y =+2交C 于A ,B 两点,M 是线段中点,过M 作x 轴垂线交C 于点N .⑴证明:抛物线C 在点N 处切线及平行;【证明】如图34,设A(x1,2),B(x1,2),把y=+2代入y=2x2得2x2--2=0,由韦达定理得x1+x2=,x1x2=-1,∴===,即N点坐标为(,)设抛物线在点N处切线l方程为y-=m(x-),将y=2x2代入上式得2x2-+-=0,∵直线l及抛物线C相切,∴=m2-8(-)=0,解得m=k,即l∥.【说明】其实,也就是及平行弦,它们中点在过中点且及对称轴(x轴)平行直线上,它及C交点N,此时切点就是这些弦缩点,故过N点抛物线C切线及平行.★⑼过定点P(x0,y0)作任一直线l及抛物线y2=2(p>0)相交于A、B 两点,过A、B两点作抛物线切线l1、l2,设l1,l2相交于点Q,则点Q 在定直线-y0y+0=0上.【证明】设A(x1,y1)、B(x2,y2),因为过点P及x轴平行直线及抛物线只有一个交点,所以直线及x轴不平行,故可设方程为x-x0=m(y-y0).联立方程组,消去x得y2-+0-x0=0∴y1y2=2p(0-x0)PABQOx y图35又过A 、B 两点抛物线切线方程为y 1y =p (x +x 1)和y 2y =p (x +x 2),联立方程组解得 ==-错误!=错误!=0-x 0 ····· ① =p ·= ·············· ②由②得m = 代入①得= y 0-x 0,∴点Q 在直线-y 0y +0=0上.【例14】(2007年重庆文科高考题)如图36,对每个正整数 n ,(,)是抛物线x 2=4y 上点,过焦点F 直线交抛物线于另一点(,). ⑴试证:=-4(n ≥1);⑵取=2n,并记为抛物线上分别以及为切点两条切线交点.试证:| 1 |+| 2 |+…+| |=2n-2-n +1+1.【说明】本题第⑴小题就是抛物线焦点弦性质y 1y 2=-p 2.第⑵小题两条切线交点就是上面抛物线性质,即点必在直线y =-1上.【例15】(2008年山东理科高考)如图,设抛物线方程为x 2=2(p >0),M 为 直线y =-2p 上任意一点,过M 引抛物线切线,切点分别为A ,B . ⑴求证:A ,M ,B 三点横坐标成等差数列;⑵⑶略.【证明】由题意设A (x 1,),B (x 2,),x 1<x 2,M (x 0,-2p )由x 2=2得y =,y =A 2A 1B 1 B 2F Oxy图36yBAO M-2p图37所以,=,=,因此直线方程为y+2p=(x-x0),直线方程为y+2p=(x-x0),所以,+2p=(x1-x0)…………①,+2p=(x2-x0)…………②,①-②得,=-∴=x1+x2-x0,即2x0=x1+x2所以A,M,B三点横坐标成等差数列.★⑽过抛物线y2=2(p>0)焦点F直线l及抛物线交于A、B两点,线段垂直平分线交x轴于点M,则|)=2.(m≠0),且A(x1,y1)、B(x2,y2),把x=+代入y2=2,得y2=2+p2,即y2-2-p2=0∴y1+y2=2,y1·y2=-p2∴x 1+x 2=m (y 1+y 2)+p =22+p , ∴中点N 坐标为(2+,)垂直平分线方程为y -=-m (x -2-) 令y =0,得M 横坐标为x =2+∴| |=| - |=2+p =p (m 2+1),又| |=x 1+x 2+p =2p (m 2+1).∴|)==2【证法二】设A (x 1,y 1)、B (x 2,y 2),过A 、B 分别作准线垂线,垂足分别为C 、D ,则C (-,y 1)、D (-,y 2),则中点E 坐标为(-,),由证法一知y 1+y 2=2, ∴E (-,),所以=-p 2-p2 )=-m又=,所以·=(-m )·=-1 ∴⊥,又⊥,所以∥又∥x 轴,所以四边形为平行四边形 ∴| |=| |=(| |+| |)=| | 所以|)=2★⑾P 是过抛物线y 2=2(p >0)上一定点,过P 作及x 轴平行直线m ,过直线为n ,直线l ⊥x 轴,l 及m 、n 分别相交于A 、B 两点,则中点M 在点P 处切线.【证明】设P (,t ),则m 方程为y =t ,直线n (即)方程为y =x , 设直线l 方程为x =s (s ≠),那么A 坐标为(s ,t ),B 坐标为(s ,),中点M 坐标为(t ,),即(t ,) 又过点P (,t )抛物线切线方程为=p (x+) ∴y =(x +)当x ==s 时,y =(s +)=+== 可见点M 在点P 处切线n 上.★⑿点P (a ,0)(a ≠0)是抛物线y 2=2(p >0)对称轴上一点,过P 直线l 及抛物线相交于两点A 、B ,A 关于x 轴对称点为A ,又点Q (-a ,0),那么A、B 、Q 三点共线.【证明】设直线l 方程为x =+a ,A (x 1,y 1),B (x 2,y 2)则A(x 1,-y 1),联立方程组 ,消去x 得--a =0,那么y 1 y 2=-2, 又=(x 1+a ,-y 1),=(x 2+a ,y 2), ∵(x 1+a )y 2+(x 2+a )y 1 =(+a )y 2+(+a )y 1=++a (y 1+y 2)=+a (y 1+y 2)=(y 1+y 2)(+a )=(y 1+y 2)(+a )=0 ∴∥l nmyxMABOFPyO xQ PBA'A∴Q、A、B三点共线.【例16】给出一个抛物线,根据其性质,用尺规作图求出该抛物线对称轴、顶点和焦点.2图a 图b 【作法】1.任意作两条平行弦A1B1和A2B2;2.分别取A1B1和A2B2中点M、N,过M、N作直线m;3.作直线⊥m,交抛物线于C、D;4.取中点E;5.过E作直线l∥m,交抛物线于点O.则直线l为抛物线对称轴,O为抛物线顶点,如图a.6.过顶点O作两条互相垂直弦、;7.设及对称轴l相交于点G;8.取靠近O四等分点F.则F为抛物线焦点.【说明】1.根据性质⑻,平行弦中点共线,且及对称轴平行;2.垂直于对称轴弦中点在对称轴上,故l为抛物线对称轴;3.根据性质⑵得过顶点(2p,0),故F为抛物线焦点.31 / 31。
高考数学讲义抛物线之切线与定点问题

2014年二轮复习抛物线之切线与定点问题内容明细内容要求层次了解理解 掌握 圆锥曲线椭圆的定义与标准方程 √ 椭圆的简单几何意义 √ 抛物线的定义及其标准方程√ 抛物线的简单几何意义 √ 双曲线的定义及标准方程 √ 双曲线的简单几何性质 √ 直线与圆锥曲线的位置关系√北京三年高考两年模拟统计中点弦 垂直角度弦长面积范围定点定值 共线比例其它 高考试题 4 1 1 模拟试题 7 8 11 14 4 4 共计78151455抛物线之切线与定点2014年高考怎么考自检自查必考点抛物线22y px =分为上下两支,可以分别看成函数求导 对于22y px =求导得2'2yy p =,则'p y y=抛物线22y px =在11(,)A x y 的切线的斜率为1AT p k y = 故切线AT 为111()py y x x y -=- 化简得到11()py x x y =+ 同理切线BT 为22()py x x y =+抛物线切线性质总结(老师带领学生证明)性质1:过抛物线一弦AB 的中点平行于对称轴的直线与抛物 线交于点P ,若过P 的切线为PT ,则PT //AB性质2:过抛物线上一点P 的切线交其对称轴于点T ,则PF TF =性质3:过抛物线焦点弦的两端点作抛物线的切线,两切线交点在准线上TPQBAOyxFOyxA自检自查必考点TF BAOyx性质4:过抛物线的准线上任一点所作的两条切线必须相互垂直性质5:过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点 性质6:切线交点与弦中点连线平行于对称轴性质7:过抛物线准线上的一点引抛物线的两条切线,则准线上这点与焦点连线与准线的夹角被切线平分 性质8:过准线上任一点作抛物线的切线,过两切点的弦最短时,即为通径性质9:从抛物线的焦点向它的任意切线作垂线,则其垂足必在抛物线顶点的切线上性质10:过抛物线的焦点作直线与抛物线的任意切线垂直,则此直线与准线的交点和切线的连线必平行于此抛物线的对称轴性质11:抛物线的三切线围成的三角形的垂心必在准线上【例1】 证明:过抛物线上一点00M x y (,)的切线方程是:00y y p x x =+()【例2】 设抛物线2y =2px 的焦点弦AB 在其准线上的射影是11A B ,证明:以11A B 为直径的圆必过一定点22y px =例题精讲【例3】 在平面直角坐标系xoy 中,直线l 与抛物线24y x =相交于不同的,A B 两点.⑴如果直线l 过抛物线的焦点,求OA OB ⋅u u u r u u u r的值;⑵如果4OA OB ⋅=-u u u r u u u r证明直线l 必过一定点,并求出该定点.【例4】 如图,过抛物线()220y px p =>上一定点()()000,0,P x y y >作两条直线分别交抛物线于()()1122.,,.A x y B x y(I)求该抛物线上纵坐标为2p的点到其焦点F 的距离; (II)当PA 与PB 的斜率存在且倾斜角互补时,求12y y y +的值,并证明直线AB 的斜率是非零常数.yPO xAB【例5】 如图,抛物线关于x 轴对称,它的顶点在坐标原点,点()()()11221,2,,,,P A x y B x y 均在抛物线上. (I )写出该抛物线的方程及其准线方程;(II )当PA PB 与的斜率存在且倾斜角互补时,求12y y +的值及直线AB 的斜率.x【例6】 如图,在平面直角坐标系xoy 中,过y 轴正方向上一点(0,c)C 任作一直线,与抛物线2y x =相交于AB 两点,一条垂直于x 轴的直线,分别与线段AB 和直线:l y c =-交于,P Q(Ⅰ)若2OA OB ⋅=u u u r u u u r,求c 的值;(Ⅱ)若P 为线段AB 的中点,求证:QA 为此抛物线的切线; (Ⅲ)试问(Ⅱ)的逆命题是否成立?说明理由。
函数图像恒过定点问题

函数恒过定点问题1. 方程“ OX=0'的理解:若方程的解有无穷多个,贝U方程的系数均为02. 若方程mx=n有无数个解,则m= ____ ,n= ____ 方法:解决函数恒过定点问题,最常用的方法是将函数看成方程,则这个方程有无穷个解。
方程的解有无穷多个,则方程的系数均为0,利用这一方法的思路是将原方程整理为以参数为主元的方程,然后利用系数为零求得。
一、直线过定点问题由“y-y / =k (x-x x)”求定点把含有参数的直线方程改写成“ y-y / =k (x-x x)的形式,这样就证明了它所表示的所有直线必过定点(X,, y/)例1:已知(k+1)x- (k-1 )y-2k=0为直线I的方程,求证不论k取任何实数值时,直线I必过定点,并求出这个定点的坐标例2:若实数满足2a-3b=1,求证:直线ax+by=5必过定点练习题1 .直线I : kx - y+2k+1=0必过定点__________2 .直线y=mx+2m+1过定点_________3 .直线kx+3y+k - 9=0过定点 ________4 .设a+b=3,则直线ax+by=1恒过定点 __________5 .当a+b+c=0时,直线ax+by+c=0必过定点_________6 .直线(m- 1)x+y+2m+1=0S定点________7. 直线(2a- 1)x+2ay+3=0恒过的定点是________8. 对于任意实数m n,直线(m+n x+12my- 2n=0恒过定点的坐标是__________9. 若p,q满足条件3p- 2q=1,直线px+3y+q=0必过定点___________10 .直线(m- 1)x+ (2m+3 y -(m- 2)=0 恒过定点________二、抛物线过定点问题将解析式中除自变量和因变量之外的参数(设为 m 集中,形成(ax 2+bx+c ) m 的形式,根据题意可得ax 2+bx+c=0,解得定点的横坐标x o ,带入解析式求得纵 坐标y o ,函数图象一定过定点(x 0,y o )例1 •已知抛物线不论m 取何值,抛物线恒过某定点P ,则P 点的坐标为(A.( 2,- 5)B.( 2, 5)C. (- 2, 5)D.不能确定例2.兴趣小组研究二次函数化,这个二次函数的图象形状与位置均发生变化,两个定点,请你写出这两个定点的坐标: 练习题1. 抛物线y=kx 2+ (2k+1) x+2恒过定点,请直接写出定点坐标 _________2. 抛物线y=x 2+mx- 2m 通过一个定点,则这个定点的坐标是 ____________ 的图象发现,m 的变 但这个二次函数的图象总经过。
抛物线知识点与性质大全

抛物线与方程【知识讲解】 1、定义平面,到定点的距离与到定直线距离相等的点的轨迹(定点不在定直线上).其中定点称为抛物线的焦点,定直线称为抛物线的准线.【注】若定点在直线上,则轨迹为过该点垂直于直线的一条直线.2、抛物线的方程与其简单性质3、通径过抛物线的焦点F 作直线⊥l x 轴,交抛物线22y px =于,A B 两点,弦长2=AB p ,此时的弦长称为通径,此为所有的焦点弦中最短的弦.4、焦点弦的性质(1)过抛物线()220y px p =>的焦点F 的直线交抛物线于()()1122,,,A x y B x y 两点,则①12p AF x =+,22p BF x =+;②12x x ⋅=定值24p ,12y y ⋅=定值2p -;③11||||FA FB +=定值2p ;④()1221122p x y x y y y +=-+. (2)过抛物线()220y px p =>的焦点F 作倾斜角为θ(斜率为k )的直线交抛物线于,A B (A 在B 上方)两点,则 ①1cos p A F θ=-上;②1cos p B F θ=+下;③2222s 1i 1n p k AB p θ⎛⎫+ =⎪⎝⎭=. (3)过抛物线()220y px p =>的焦点F 作直线1l 交抛物线于,A B 两点,分别过,A B 作准线l 的垂线,垂足分别为,P Q ,设AB 中点为M ,过M 作准线的垂线,垂足为N ,则①AN BN ⊥;②PF QF ⊥;③NF AB ⊥;④PF AN ⊥;⑤QF BN ⊥;⑥以AB 为直径的圆与准线相切,切点即为N ; ⑦以()AF BF 为直径的圆与y 轴相切;⑧24PQ AF BF =;24PQF APF BQF S S S ∆∆∆=⋅;⑨232sin ABQPp S θ=四边形. (4)过抛物线()220y px p =>的焦点F 作直线1l 交抛物线于,A B 两点,分别过,A B 作准线l 的垂线,垂足分别为,P Q ,准线l 与x 轴交于H 点,O①AHF BHF ∠=∠; ②,,A O Q 三点共线; ③,,B O P 三点共线;(5)过抛物线()220y px p =>的焦点F 作直线1l 交抛物 线于,A B 两点,线段AB 的垂直平分线交x 轴于E 点,则12EF AB =. (6)过抛物线()220y px p =>的焦点F 作直线1l 交抛物线于,A B 两点,G 为准线上的一动点,且直线GA 、GF 、GB 的斜率均存在,则直线GA 、GF 、GB 的斜率成等差数列,即2GA GB GF k k k +=.5、过点()(),00M m m >的直线交抛物线()220y px p =>于()()1122,,,A x y B x y 两点,则 ①12x x ⋅=定值2m ;②12y y ⋅=定值2pm -; ③2OA OB m p ⊥⇔=;④m p =时,2211||||MA MB +=定值21p . 6、设点是抛物线()220y px p =>的焦点,12,,,n P P P 是抛物线上的n 个不同的点,若120n FP FP FP +++=,则12n FP FP FP np +++=.【典型例题】例1、已知动点M 的坐标满足方程3412x y +-,则动点M 的轨迹是() A .椭圆B. 双曲线C. 抛物线D. 圆【变式】已知动点M 的坐标满足方程3412x y +-,则动点M 的轨迹是()A .椭圆B. 双曲线C. 抛物线D. 直线例2、点P 与点()20F ,的距离比它到直线40x +=的距离小2,则P 的轨迹方程为_______.【变式】动圆M 与定直线2y =相切且与定圆C :22(3)1x y ++=相外切,则动圆圆心M 的轨迹方程为_______.【变式2】到y 轴的距离比到点()2,0F 的距离小2的动点P 的轨迹方程为_______.例3、抛物线24y x =的焦点坐标为_______.【变式】1【2014】若抛物线22y px =的焦点与椭圆22195x y +=的右焦点重合,则该抛物线的准线方程为_______.【变式2】抛物线C 恒过定点()0,2A ,C 的准线为轴,则C 的顶点M 的轨迹方程为_______.例4、在抛物线24y x =上一点P ,使它到定点()2,2M 和焦点F 的距离之和最小,并求出距离之和的最小值.【变式1】设P 是抛物线28y x =上的一个动点,则点P 到直线4360x y -+=与点P 到y 轴的距离之和的最小值为________.【变式2】设P 是抛物线24y x =上的一个动点.(1)求点P 到点()1,1A -的距离与点P 到直线1x =-的距离之和的最小值; (2)求点P 到直线220x y ++=的距离d 与点P 到抛物线焦点F 距离之和的最小值.【变式3】已知FAB ∆,点F 的坐标为(1,0),点A 、B 分别在图中抛物线24y x =与圆22(1)4x y -+=的实线部分上运动,且AB 总是平行于x 轴,那么FAB ∆的周长的取值围为.例5、已知抛物线26y x =上存在三点,,A B C ,且ABC ∆的重心为抛物线的焦点为F ,则=FA FB FC ++_______.【变式】已知抛物线26y x =的焦点为F ,若该抛物线上存在四点123P P P 、、、4P ,满足1234=0FP FP FP FP +++,则1234=FP FP FP FP +++_______.例6、直线l 过()1,2A ,且与抛物线212y x =交于,M N 两点,且MA AN =,则直线l 的方程为_________;MN =_______.例7、抛物线24y x =的焦点为F ,若过F 点的直线与抛物线相交于,M N 两点,若4FM FN =-,则直线MN 的斜率为_______.【变式】【2014新课标】已知抛物线2:8C y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若4FP FQ =, 则QF =_______.例8、过抛物线x y 82=的焦点作弦AB ,点()11,A x y 、()22,B x y ,且1021=+x x ,则=AB _____.【变式1】已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点()02,M y ,若点M 到该抛物线焦点的距离为3,则OM =_____.【变式2】过抛物线x y 82=的焦点作弦AB ,点()11,A x y 、()22,B x y ,且10AB =,则ABO ∆重心的横坐标为_____.【变式3】过抛物线x y 82=的焦点作弦AB ,点()11,A x y 、()22,B x y ,且128y y +=,则=AB _____.例9、抛物线()220y px p =>的动弦AB 长为()2a a p ≥,求弦中点M 到y 轴的最短距离.【变式】抛物线()220y px p =>的动弦AB 长为()02a a p <<,求弦中点M 到y 轴的最短距离.例10、若抛物线2:1C y ax =-上存在关于直线20x y -=对称两点A 和B ,数a 的取值围.例11、【2014】已知F 是抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,2OA OB ⋅=(其中O 为坐标原点),则ABO ∆与AFO ∆面积之和的最小值是____.例12、已知抛物线()220y px p =>,过定点(),0p 作两条互相垂直的直线12l l 、,1l 与抛物线交于,P Q 两点,2l 与抛物线交于,M N 两点,设1l 的斜率为k ,若已知弦PQ 的中垂线在y 轴上的截距为32p pk k+,则弦MN 的中垂线在y 轴上的截距为__________. 例13、设M 为抛物线2:4(0)C x py p =>准线上的任意一点,过点M 作曲线C 的两条切线,设切点为,A B .直线AB 是否过定点?如果是,求出该定点,如果不是,请说明理由.例14、过抛物线()220y px p =>的焦点F 作相互垂直的两条直线12,l l ,抛物线与1l 交于点12,,P P 与2l 交于点12,Q Q .证明:无论如何取直线12,l l ,都有121211PP Q Q +为一常数.例15、抛物线()2:20C y px p =>的焦点恰是椭圆22143x y +=的一个焦点,过点,02p F ⎛⎫⎪⎝⎭的直线与抛物线C 交于点,A B . (1)求抛物线C 的方程;(2)O 是坐标原点,求AOB ∆的面积的最小值; (3)O 是坐标原点,证明:OA OB ⋅为定值.【变式1】已知定点(2,0)F ,直线:2l x =-,点P 为坐标平面上的动点,过点P 作直线l 的垂线,垂足为点Q ,且FQ PF PQ ⊥+().设动点P 的轨迹为曲线C .(1)求曲线C 的方程;(2)过点F 的直线1l 与曲线C 有两个不同的交点A 、B ,求证:111||||2AF BF +=; (3)记OA 与OB 的夹角为θ(O 为坐标原点,A 、B 为(2)中的两点),求cos θ的取值围.【变式2】已知抛物线()2:20C y px p =>,直线l 交此抛物线于不同的两个点()11,A x y 、()22,B x y ,且OA OB ⊥.(1)证明21y y ⋅和12x x ⋅均为定值;(2)证明直线l 恒过定点P ; (3)求AB 的中点M 的轨迹方程;(4)过原点作AB 的垂线,垂足为N ,求N 的轨迹方程.(5)对于C 上除原点外的任意一定点()00,Q x y ,若仍有PA PB ⊥,请问是否还有直线l 恒过定点,若是,请求出定点'P ;若否,请说明理由.【变式3】设抛物线2:2(0)C y px p =>的焦点为F ,经过点F 的动直线交抛物线C 于点11(,)A x y ,22(,)B x y 且124y y =-.(1)求抛物线C 的方程;(2)若()2OE OA OB =+(O 为坐标原点),且点E 在抛物线C 上,求直线倾斜角.(3)若点M 是抛物线C 的准线上的一点,直线,,MF MA MB 的斜率分别为012,,k k k .求证: 当0k 为定值时,12k k +也为定值.例16、在平面直角坐标系xOy 中,点M 到点()1,0F 的距离比它到y 轴的距离多1,记点M 的轨迹为C .(1)求轨迹为C 的方程(2)设斜率为k 的直线过定点()2,1P -,求直线与轨迹C 恰好有一个公共点,两个公共点,三个公共点时k 的相应取值围.例17、已知抛物线()2:20C y px p =>,直线交此抛物线于不同的两个点()11,A x y 、()22,B x y .(1)当直线过点(),0M p 时,证明21y y ⋅为定值;(2)如果直线过点(),0M p ,过点M 再作一条与直线垂直的直线l '交抛物线C 于两个不同点D 、E .设线段AB 的中点为P ,线段DE 的中点为Q ,记线段PQ 的中点为N .问是否存在一条直线和一个定点,使得点N 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.例18、动圆C 过定点F ,02p ⎛⎫⎪⎝⎭,且与直线2p x =-相切,其中0p >.设圆心C 的轨迹Γ的程为()0,=y x F (1)求()0,=y x F ;(2)曲线Γ上的一定点()00,y x P (0y ≠0) ,方向向量()p y d -=,0的直线(不过P 点)与曲线Γ交与A 、B 两点,设直线PA 与PB 的斜率分别为PA k ,PB k ,计算PB PA k k +;(3)曲线Γ上的两个定点()000,y x P 、⎪⎭⎫ ⎝⎛''000,y x Q ,分别过点00,Q P 作倾斜角互补的两条直线N Q M P 00,分别与曲线Γ交于N M ,两点,求证直线MN 的斜率为定值.例19、已知抛物线()2:20C y px p =>和:M 228120x y x +-+=,过抛物线C 上一点()()000,0P x y y ≥作两条直线与M 相切与,A B 两点,圆心M 到抛物线准线的距离为92. (1)求抛物线C 的方程;(2)当P 点坐标为()2,2时,求直线AB 的方程;(3)设切线PA 与PB 的斜率分别为12,k k ,且1212k k ⋅=,求点()00,P x y 的坐标.例20、过抛物线()220y px p =>的对称轴上一点()(),00A a a >的直线与抛物线交于,M N 两点,自,M N 向直线:l x a =-作垂线,垂足分别为1M 、1N . (1)当2pa =时,求证:11AM AN ⊥; (2)记1AMM ∆、11AM N ∆、1ANN ∆的面积分别为123,,S S S ,是否存在实数λ,使得对任意的,都有2213S S S λ=成立,若存在,求出λ的值;若不存在,说明理由.M。
专题27:抛物线的定点问题20页

专题27:抛物线的定点问题1.已知抛物线()2:20C y px p =>的焦点为F ,过点F 且垂直于x 轴的直线与C 交于A ,B 两点,AOB (点O 为坐标原点)的面积为2. (1)求抛物线C 的方程;(2)设不经过原点O 的直线l 与抛物线交于P 、Q 两点,设直线OP 、OQ 的倾斜角分别为α和β,证明:当4παβ+=时,直线l 恒过定点.2.已知点()0,1A -,()0,1B ,动点P 满足PB AB PA BA =⋅.记点P 的轨迹为曲线C . (1)求C 的方程;(2)设D 为直线2y =-上的动点,过D 作C 的两条切线,切点分别是E ,F .证明:直线EF 过定点.3.设抛物线22y px =()0p >的焦点为F ,已知直线1l :20mx y m --=,圆E :222440x y x y +---=.(1)设直线1l 与圆E 的交点分别为P ,Q ,求当PQ 取得最小值时,直线1l 的方程;(2)若抛物线过圆E 的圆心,直线1l ,2l 过同一定点且与抛物线相交于A ,B 和C ,D 点,12l l ⊥,设M 是AB 的中点,N 是CD 的中点,证明:直线MN 恒过定点.4.已知抛物线()21:20C y px p =>的焦点F 是椭圆222:21C x y +=的一个顶点.(1)求抛物线1C 的方程;(2)若点()1,2P ,M 、N 为抛物线1C 上的不同两点,且PM PN ⊥,问:直线MN 是否过定点?若过定点,求出该定点坐标;若不过定点,请说明理由.5.在平面直角坐标系xOy 中,已知直线y x =被抛物线2:2(0)C y px p =>截得的弦长为直线l 与抛物线C 相交于点M ,N ,点()1,2A ,且直线AM ,AN 的斜率之和为4.(1)求抛物线C 的方程;(2)求证:直线l 过定点,并求出定点坐标.6.已知抛物线()2:20E x py p =>的焦点为F ,()02,A y 是E 上一点,且2AF =.(1)求抛物线E 的方程;(2)设点B 是E 上异于点A 的一点,直线AB 与直线3y x =-交于点P ,过点P 作x 轴的垂线交抛物线E 于点M,证明:直线BM 过定点,并求出该定点坐标.7.在平面直角坐标系xOy 中,M 为直线3y x =-上的动点,过点M 作抛物线2:2C x y =的两条切线,MA MB ,切点分别为,,A B N 为AB 的中点.(1)证明MN x ⊥轴;(2)直线AB 是否恒过定点?若是,求出这个定点的坐标;若不是,请说明理由.8.已知点1,0A ,E ,F 为直线1x =-上的两个动点,且AE AF ⊥,动点P 满足//EP OA ,//FO OP (其中O 为坐标原点). (1)求动点P 的轨迹C 的方程;(2)若直线l 与轨迹C 相交于两不同点M 、N ,如果4OM ON ⋅=-,证明直线l 必过一定点,并求出该定点的坐标.9.平面上动点M 到定点()1,0F 的距离比M 到直线2x =-的距离小1.(1)求动点M 满足的轨迹方程C ﹔(2)若A ,B 是(1)中方程C 表示的曲线上的两点,且OA OB ⊥(O 为坐标原点).试问直线AB 是否经过定点,并说明理由. 10.设抛物线C :22y px =(0p >)的焦点为F ,点()4,P m 是抛物线C 上一点,且5PF=.(1)求抛物线C 的方程;(2)设直线l 与抛物线C 交于A ,B 两点,若6AF BF +=,求证:线段AB 的垂直平分线过定点.11.已知F 是抛物线()2:20C y px p =>的焦点,()1,M t 是抛物线上一点,且32MF. (1)求抛物线C 的方程;(2)已知斜率存在的直线l 与抛物线C 交于A ,B 两点,若直线AF ,BF 的倾斜角互补,则直线l 是否会过某个定点?若是,求出该定点坐标,若不是,说明理由.12.在直角坐标系xOy 中,已知一动圆经过点()3,0,且在y 轴上截得的弦长为6,设动圆圆心的轨迹为曲线C . (1)求曲线C 的方程;(2)过点3(,0)2作相互垂直的两条直线1l ,2l ,直线1l 与曲线C 相交于A ,B 两点,直线2l 与曲线C 相交于E ,F 两点,线段AB ,EF 的中点分别为M 、N ,求证:直线MN 恒过定点,并求出该定点的坐标.参考答案1.(1)24y x =;(2)证明见解析.【分析】(1)根据焦点,02pF ⎛⎫ ⎪⎝⎭,求得点A ,B 的坐标,然后由1222AOB pS AB =⋅⋅=△求解;(2)易知直线l 的斜率存在,记为k ,设直线:l y kx m =+,与24y x =联立, 由tan OP k α=,tan OQ k β=,结合4παβ+=,由()tan tan tan 1tan tan 1OQ Q O P P O O k k B k k ααβαβ+++==-⋅⋅-14tan π== 求解.【解析】(1)因为焦点,02pF ⎛⎫ ⎪⎝⎭,所以点A ,B 的坐标分别为,2pp ⎛⎫ ⎪⎝⎭,,2p p ⎛⎫- ⎪⎝⎭.所以12222AOBpS p =⋅⋅=△, 故2p =.故抛物线C 的方程为24y x =. (2)由题设()11,P x y ,()22,Q x y , 易知直线l 的斜率存在,记为k ,则设直线:l y kx m =+,与24y x =联立得2440ky y m -+=, 得124y y k+=,124my y k⋅=, 则()2221212121221422444y y m x x y y y y k k ⎡⎤+=+=⨯+-=-⎣⎦, 2221212244y y m x x k⋅=⋅=,121212164OP OQ y y k k k x x y y m ⋅=⋅==⋅,()()2112121112OP OQ x kx m x kx m y y k k x x x x +++=+=+ ()12121224k x m x x x x m++==.又知tan OP k α=,tan OQ k β=,()tan tan tan 1tan tan 1OQ Q O P P O O k k Bk k ααβαβ+++==-⋅⋅-, 41441m tan k mπ===-,解得44m k =+,所以直线():4444l y kx k k x =++=++,恒过定点()4,4-.【点评】 定点问题的常见解法:①假设定点坐标,根据题意选择参数,建立一个直线系或曲线系方程,而该方程与参数无关,故得到一个关于定点坐标的方程组,以这个方程组的解为坐标的点即所求定点;②从特殊位置入手,找出定点,再证明该点适合题意. 2.(1)24x y =;(2)证明见解析.【分析】(1)把已知条件用坐标表示,并化简即得C 的方程; (2)设(),2D t -,()11,E x y ,()22,F x y ,利用导数得出切线,DE DF 的方程,由D 在切线上,从而可得直线EF 的方程,由直线方程可得定点坐标.【解析】(1)设(),P x y ,则(),1PA x y =---,(),1PB x y =--,()0,2AB =,()0,2BA =-,所以,PB AB PA BA =⋅()10,2y AB =+=,化简得24x y =.所以,C 的方程为24x y =.(2)由题设可设(),2D t -,()11,E x y ,()22,F x y , 由题意知切线DE ,DF 的斜率都存在,由24x y =,得24x y =,则2y x '=, 所以12DE x k =, 直线DE 的方程为()1112x y y x x -=-,即211122x x y y x -=-,①因为()11,E x y 在24x y =上,所以2114x y =,即21122x y =,②将②代入①得11220x x y y --=, 所以直线DE 的方程为11220x x y y --= 同理可得直线DF 的方程为22220x x y y --=. 因为(),2D t -在直线DE 上,所以11240tx y -+=, 又(),2D t -在直线DF 上,所以22240tx y -+=, 所以直线EF 的方程为240tx y -+=, 故直线EF 过定点()0,2.【点评】 本题考查直接法求动点轨迹方程,考查抛物线中的直线过定点问题,解题方法是设出切线坐标,由导数的几何意义写出切线方程,再由D 在切线上,根据直线方程的意义得出直线EF 方程,然后得定点坐标.3.(1)220x y --=;(2)证明见解析.【分析】(1)先判断直线1l :20mx y m --=过定点()2,0T ,由垂径定理表示出PQ =PQ ET ⊥时,当d 最大时,PQ 最小,求出PQ斜率m ,得到直线方程;(2)联立方程组表示出点M 、N ,进而表示出直线MN 的方程,利用点斜式方程说明直线过定点.【解析】 (1)由题意得直线1l :20mx y m --=过定点()2,0T , 由222440x y x y +---=得()()22129x y -+-=. 因为()()2221029-+-<,所以点()2,0T 在圆E 内.设圆心()1,2到直线1l 的距离为d ,PQ =d 最大时,PQ 最小,此时PQ ET ⊥,所以112PQ ETm k k ==-=,此时直线1l 的方程为220x y --=.(2)证明:因为抛物线过圆E 的圆心()1,2, 所以222p =,解得2p =, 所以抛物线的方程为24y x =.由直线1l 的方程为20mx y m --=,可得直线1l :12x y m=+,且过定点()2,0T ,由12l l ⊥可得直线2l :2x my =-+,联立24,2,y x x my ⎧=⎨=-+⎩,消x 整理得2480y my +-=.设点()11,C x y ,()22,D x y ,则124y y m +=-, 所以2Ny m =-,则222Nx m =+,即点()222,2N m m+-,同理得点2222,M m m ⎛⎫+ ⎪⎝⎭, 当1m ≠时, 直线MN 的斜率2222212112MNmm m k m m mm m +===---,则直线MN 的方程为222221m y x m m m ⎛⎫-=-- ⎪-⎝⎭, 即22222121m m y x m m m m-=--+⋅-,所以直线MN 的方程为()241my x m =--, 即直线MN 恒过定点()4,0;当1m =时,()4,2N -,()4,2M ,直线MN 的方程为4x =,也过定点()4,0. 综上,直线MN 恒过定点()4,0.【点评】证明直线过定点,通常有两类:(1)直线方程整理为斜截式y=kx+b ,过定点(0,b ); (2)直线方程整理为点斜式y - y o =k (x- x 0),过定点(x 0,y 0) . 4.(1)24y x =;(2)过定点()5,2-.【分析】(1)根据已知条件求出p 的值,可得出抛物线1C 的方程; (2)设直线MN 的方程x my n =+,设点()11,M x y 、()22,N x y ,将直线MN 的方程与抛物线的方程联立,列出韦达定理,由PM PN ⊥得出0PM PN ⋅=,代入韦达定理可得出m 、n 所满足的关系式,由此可得出直线MN 所过定点的坐标.【解析】(1)把椭圆2C 的方程化为标准方程是221112x y +=,椭圆的左、右顶点分别为()1,0-、()1,0, 依题意12p=,解得2p =,所以抛物线1C 的方程为24y x =; (2)若直线MN 与y 轴垂直,则直线MN 与抛物线1C 只有一个交点,不合乎题意.设直线MN 的方程为x my n =+,与抛物线方程联立并化简得2440y my n --=.则216160m n ∆=+>,可得20m n +>,设()11,M x y 、()22,N x y ,则124y y m +=,124y y n =-.因为PM PN ⊥,()()()21111111221,21,2,244y y y PM x y y y -+⎛⎫⎛⎫=--=--=- ⎪ ⎪⎝⎭⎝⎭, 同理可得()()22222,24y y PN y -+⎛⎫=-⎪⎝⎭, 所以,()()()()()()121212222222016y y y y PM PN y y --++⋅=+--=,所以,()()()()12122222160y y y y --+++=⎡⎤⎣⎦, 显然12y ≠且22y ≠,所以,()()()121212221622048200y y y y y y n m +++=+++=-++=,所以,25n m =+,所以,直线MN 的方程为25x my m =++,即()250x m y -+-=,因此,直线MN 过定点()5,2-.【点评】 求解直线过定点问题常用方法如下:(1)“特殊探路,一般证明”:即先通过特殊情况确定定点,再转化为有方向、有目的的一般性证明;(2)“一般推理,特殊求解”:即设出定点坐标,根据题设条件选择参数,建立一个直线系或曲线的方程,再根据参数的任意性得到一个关于定点坐标的方程组,以这个方程组的解为坐标的点即为所求点; (3)求证直线过定点()00,x y ,常利用直线的点斜式方程()00y y k x x -=-或截距式y kx b =+来证明.5.(1)24y x =;(2)直线l 过定点,定点坐标为()0,1-,证明见解析. 【分析】(1)联立直线方程和抛物线方程,求出交点的坐标后利用弦长公式可求p 的值,从而可求抛物线的方程.(2)设直线l 的方程为x my b =+,联立直线方程和抛物线方程,消去x 后利用韦达定理化简斜率之和,从而可得b m =,故可求定点坐标.我们也可以设211,4y M y ⎛⎫ ⎪ ⎪⎝⎭,222,4y N y ⎛⎫ ⎪⎝⎭,用坐标表示斜率之和,再用该两点的坐标表示直线l ,化简后可得直线过定点.【解析】(1)由2,2,y x y px =⎧⎨=⎩解得10x =,22x p =,因为直线y x =被抛物线()2:20C y px p =>截得的弦长为0p -=,0p >,解得2p =, 所以抛物线C 的方程为24y x =.(2)法一: 设直线l 的方程为x my b =+,()11,M x y ,()22,N x y ,由2,4,x my b y x =+⎧⎨=⎩得2440y my b --=, 所以124y y m +=,124y y b =-,因为点()1,2A ,且直线AM ,AN 的斜率之和为4,所以121222411y y x x --+=--,而2114y x =,2224y x =,化简得12120y y y y ++=, 所以440m b -=,即b m =, 所以直线l 的方程为()1x m y =+, 所以直线l 过定点,定点坐标为()0,1-. 法二:设211,4y M y ⎛⎫ ⎪ ⎪⎝⎭,222,4y N y ⎛⎫ ⎪⎝⎭, 因为点()1,2A ,且直线AM ,AN 的斜率之和为4,所以1222122241144y y y y --+=--,即12120y y y y ++=,①当210y y +≠时,直线l 的方程为221112221444y yy y y x y y ⎛⎫--=- ⎪⎝⎭- 即2141y x y y =--, 所以直线l 过定点,定点坐标为()0,1-;②当210y y +=时,120y y =,所以120y y ==,不满足题意. 所以直线l 过定点,定点坐标为()0,1-.【点评】直线与抛物线的位置关系中的定点、定值、最值问题,一般可通过联立方程组并消元得到关于x 或y 的一元二次方程,再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式,该关系中含有1212,x x x x +或1212,y y y y +,最后利用韦达定理把关系式转化为若干变量的方程(或函数),从而可求定点、定值、最值问题,也可以设出交点坐标,用交点坐标表示目标代数式,从而解决定点、定值、最值问题.6.(1)24x y =;(2)证明见解析,定点为()2,3. 【分析】(1)根据抛物线的性质即可得到042py =,022py +=,解得即可;(2)设1(B x ,1)y ,2(M x ,2)y .由题意,可设直线BM 的方程为y kx b =+,由根与系数的关系.得124x x k +=,124x x b =-,再根据A ,P ,B 三点共线,化简整理可得(2)3y k x =-+.即可求出直线BM 过定点. 【解析】(1) 根据题意知,042py =,① 因为||2AF =,所以022py +=.②. 联立①②解的01y =,2p =. 所以E 的方程为24x y =.(2)证明:设1(B x ,1)y ,2(M x ,2)y .由题意,可设直线BM 的方程为y kx b =+,代入24x y =,得2440x kx b --=.由根与系数的关系.得124x x k +=,124x x b =-.③ 由MP x ⊥轴及点P 在直线3y x =-上,得2(P x ,23)x -,则由A ,P ,B 三点共线,得21214122x kx b x x -+-=--,整理,得1212(k 1)(24)(1)260x x k x b x b ---++--=. 将③代入上式并整理,得1(2)(23)0x k b -+-=.由点B 的任意性,得230k b +-=,所以32(2)3y kx k k x =+-=-+. 即直线BM 恒过定点(2,3).【点评】 证明直线过定点,一般有两种方法.(1)特殊探求,一般证明:即可以先考虑动直线或曲线的特殊情况,找出定点的位置,然后证明该定点在该直线或该曲线上(定点的坐标直线或曲线的方程后等式恒成立).(2)分离参数法:一般可以根据需要选定参数R λ∈,结合已知条件求出直线或曲线的方程,分离参数得到等式2123(,)(,)(,)0f x y f x y f x y λλ++=,(一般地,(,)(1,2,3)i f x y i =为关于,x y 的二元一次关系式)由上述原理可得方程组123(,)0(,)0(,)0f x y f x y f x y =⎧⎪=⎨⎪=⎩,从而求得该定点.7.(1)证明见解析;(2)直线AB 恒过定点(1,3).【分析】(1)设切点211,2x A x ⎛⎫ ⎪⎝⎭,222,2x B x ⎛⎫ ⎪⎝⎭,求出导数y x '=,由此可得切线斜率,得切线MA 方程()21112x y x x x -=-,同时设(,3)M t t -,代入切线方程并整理,同理得MB 方程,从而可得12,x x 是方程22360x tx t -+-=的两根,利用韦达定理得1212,x x x x +,求出N 点横坐标可证得结论; (2)利用(1)再求得N 点纵坐标,由,A B 两点坐标求得直线AB 的斜率,然后得出直线AB 方程后可得定点坐标.【解析】(1)设切点211,2x A x ⎛⎫ ⎪⎝⎭,222,2x B x ⎛⎫ ⎪⎝⎭,y x '=,∴切线MA 的斜率为1x ,切线()2111:2x MA y x x x -=-,设(,3)M t t -,则有()211132x t x t x --=-,化简得2112360x tx t -+-=,同理可的2222260x tx t -+-=∴1x ,2x 是方程22360x tx t -+-=的两根,∴122x x t +=,1226x x t =-,122N M x x x t x +===,∴MN x ⊥轴. (2)∵()()22221212121113442N y x x x x x x t t =+=+-=-+,∴()2,3N t t t -+. .()221212121122ABx x k x x t x x -=⋅=+=-, ∴直线()2:3()AB y t t t x t --+=-,即3(1)y t x -=-, ∴直线AB 过定点(1,3).【点评】本题考查直线与抛物线相交问题,考查导数的几何意义,方法是设切点211,2x A x ⎛⎫ ⎪⎝⎭,222,2x B x ⎛⎫ ⎪⎝⎭,设动点坐标(,3)M t t -,把M 点坐标代入两切线方程得出12,x x 是一元二次方程的根,利用韦达定理得出1212,x x x x +,这样可得中点N 坐标,由中点N 坐标写出直线AB 方程可得定点坐标.是设而不求思想的运用.8.(1)()240y x x =≠;(2)证明见解析,定点为()2,0.【分析】(1)设点(),P x y ,()1,E a -,()1,F b -,由AE AF ⊥可得出4ab =-,由//EP OA ,//FO OP 可得出y a =,y bx =-,代入4ab =-化间可得出动点P 的轨迹C 的方程;(2)设直线l 的方程为()0x ty n n =+≠,设点()11,M x y 、()22,N x y ,联立直线l 与曲线C 的方程,列出韦达定理,由4OM ON ⋅=-可求得n 的值,可得出直线l 的方程,进而可得出直线l 所过定点的坐标. 【解析】(1)设(),P x y 、()1,E a -、()1,F b -,则()2,AE a =-,()2,AF b =-,()1,EP x y a =+-,()1,0OA =,()1,FO b =-,(),OP x y =.由AE AF ⊥,得40AE AF ab ⋅=+=,且点E 、F 均不在x 轴上,故4ab =-,且0a ≠,0b ≠. 由//EP OA ,得0y a -=,即y a =. 由//FO OP ,得0bx y +=,即y bx =-.所以24y abx x =-=,所以动点P 的轨迹C 的方程为:()240y x x =≠;(2)若直线l 的斜率为零时,则直线l 与曲线C 至多只有一个公共点,不合乎题意.可设直线l 的方程为()0x ty n n =+≠.由24y ty n y x=+⎧⎨=⎩,得2440y ty n --=. 设()11,M x y 、()22,N x y ,则124y y t +=,124y y n =-.()21221212124416y y OM ON x x y y y y n n ∴⋅=+=+=-=-,0n ≠,解得2n =,所以,直线l 的方程为2x ty =+,即直线l 恒过定点()2,0.【点评】 直线过定点:根据题中条件确定直线方程y kx m =+中的k 与、所满足的等量关系或等式,然后再代入直线方程,即可确定直线所过定点的坐标9.(1)24y x =;(2)直线AB 经过定点()4,0,证明见解析. 【分析】(1)利用抛物线的定义可得动点M 满足的轨迹方程C ﹔ (2)设直线OA 的方程为:y kx =,则直线OB 的方程为:1=-y x k,联立直线与抛物线方程解出交点坐标,进而可得直线AB 的方程,可得直线AB 经过的定点坐标.【解析】(1)由题意易得:点M 到定点()1,0F 的距离等于点M 到直线1x =-的距离由抛物线定义可得:动点M 满足的轨迹方程C 为24y x =.(2)设直线OA 的方程为:y kx =,则直线OB 的方程为:1=-y x k.联立方程24y kx y x =⎧⎨=⎩可得244(,)A k k ,同理可得:24,4()B k k -.∴()222441414kk k k k k k k+===±-- 直线AB 的方程为224(4)1k y k x k k +=--即2(4)1ky x k =--. 特别的,当1k =或1-时,点A 与点B 的横坐标都是4. 综上可知,直线AB 经过定点()4,0.【点评】 本题考查抛物线的定义的应用,考查直线与抛物线的位置关系,解决本题的关键点是设出直线OA 和OB 的方程,分别与抛物线联立解出交点坐标,即可写出直线AB 的方程,进而得出定点坐标,考查了学生计算能力,属于中档题. 10.(1)24y x =;(2)证明见解析. 【分析】(1)由条件可得542pPF==+,解出即可; (2)当直线l 的斜率存在时,设:l y kx m =+,()()1122,,,A x y B x y ,联立直线与抛物线的方程联立消元,然后韦达定理可得12242kmx x k -+=,由6AF BF +=可得12242242km x m k k kx -+==⇒=-,然后表示出线段AB 的垂直平分线方程可得答案.【解析】(1)由抛物线的焦半径公式可得542pPF ==+,解得2p = 即抛物线C 的方程为24y x =(2)当直线l 的斜率存在时,设:l y kx m =+,()()1122,,,A x y B x y由24y x y kx m⎧=⎨=+⎩可得()222240k x km x m +-+= 所以0k ≠,()2222440km k m ∆=-->,即1km <12242kmx x k -+=因为6AF BF +=,所以1226x x ++=,所以12242242km x m k k kx -+==⇒=- 所以线段AB 的中点坐标为()2,2k m +所以线段AB 的垂直平分线方程为()122x ky k m ---=-, 即()1214124x k m x x k k k k ky +++=+=--=--,所以过定点()4,0 当直线l 的斜率不存在时也满足综上:线段AB 的垂直平分线过定点()4,0【点评】 定点问题的常见解法:①假设定点坐标,根据题意选择参数,建立一个直线系或曲线系方程,而该方程与参数无关,故得到一个关于定点坐标的方程组,以这个方程组的解为坐标的点即所求定点;②从特殊位置入手,找出定点,再证明该点适合题意.11.(1)22y x =;(2)过定点,定点为1,02⎛⎫- ⎪⎝⎭.【分析】(1)根据抛物线的定义可知3122p MF =+=,求出p 后可得抛物线方程.(2) 设直线l 的方程为y kx m =+,设()11,A x y ,()22,B x y ,由条件可得0AF BF k k +=,化简即得()()1212121202kx x m x x y y ++-+=,联立直线与抛物线方程,利用韦达定理代入可得2k m =,从而得出答案. 【解析】(1)根据抛物线的定义,31122p MF p =+=⇒=, 抛物线的方程为22y x =,(2)设直线l 的方程为y kx m =+,设()11,A x y ,()22,B x y ,直线l 与抛物线的方程联立得()22222202y kx mk x km x m y x =+⎧⇒+-+=⎨=⎩, 12222km x x k -+=,2122m x x k =,则122y y k +=,122m y y k =, 又0AF BF k k +=,即12121122y y x x --+=--,()122112102x y x y y y +-+=,()()1212121202kx x m x x y y ++-+=,即22222120m km k m k k k-⋅+⋅-=,整理得:2k m =, 所以直线的方程为()21y m x =+, 即直线经过定点1,02⎛⎫- ⎪⎝⎭.【点评】关键点睛:本题考查求抛物线的方程和直线与抛物线的位置关系,考查直线过定点问题,解答本题的关键是由0AF BF k k +=,得到()()1212121202kx x m x x y y ++-+=,然后由方程联立韦达定理代入,属于中档题.12.(1)26y x =;(2)证明见解析,9(,0)2.【分析】(1)设圆心(),C x y ,然后根据条件建立方程求解即可;(2)设直线1l 的方程为3()2y k x =-,然后算出22363(,)2k M k k+,236(,3)2k N k +-,然后表示出直线MN 的方程即可.【解析】(1)设圆心(),C x y ,由题意得2229(3)x x y =-++,即26y x = 所以曲线C 的方程为26y x =(2)由题意可知,直线12,l l 的斜率均存在,设直线1l 的方程为3()2y k x =-,()11,A x y ,()22,B x y 联立方程组2632y x y k x ⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩得22224(1224)90k x k x k -++=, 所以212236k x x k ++=,12126(3)y y k x x k +=+-= 因为点M 是线段AB 的中点,所以22363(,)2k M k k + 同理,将k 换成1k -得236(,3)2k N k +-, 当222363622k k k ++≠,即1k ≠±时 2222333636122MNkk k k k k k k +-==++-- 所以直线MN 的方程为22363()12k k y k x k -++=-- 即29()12k y x k -=--, 所以直线MN 恒过定点9(,0)2当1k =±时,直线MN 的方程为92x =,也过点9(,0)2所以直线MN 恒过定点9(,0)2【点评】 定点问题的常见解法:①假设定点坐标,根据题意选择参数,建立一个直线系或曲线系方程,而该方程与参数无关,故得到一个关于定点坐标的方程组,以这个方程组的解为坐标的点即所求定点;②从特殊位置入手,找出定点,再证明该点适合题意.。
中考数学复习指导:图象过定点问题和“思维模式”

图象过定点问题和“思维模式”关于函数图象过定点的问题,很多同学感到棘手.本文将应用“模式化”思维求解与按照常规思维求解进行比较,表明数学问题“模式化”的优越性,供同学们在学习中参考.一、“模式化”思维例析例1 若m是不为零的任意实数,求证:一次函数y=mx-3m+1的图象必通过一定点,并求出此定点坐标.证明由于y=mx-3m+1=m(x-3)+1,而m是不为零的任意实数,要使该函数图象通过一个定点,则此时y的值一定与m值无关,显然,当且仅当x-3=0时,y的值与m的值无关,此时,x=3.y=m(x-3)+1=1.所以一次函数y=mx-3m,+1的图象必通过一定点(3,1).注常规方法为特殊值法,即取m1=1,m2=-1,然后构建方程组求解并检验.求解时往往容易出错.例2 求证抛物线y=x2-(k+4)x-(2k+12)(k为参数,且k≠0)恒过一定点,并求出此定点.证明要使抛物线恒过一定点,则该定点坐标必与k值无关.所以.y=x2-(k+4)x-(2k+12)=k(x+2)+x2-4x-12中,与k相关的因式值必为零(k≠0),即:k+2=0.∴x=-2.将x=-2代入,函数y=0,则该抛物线恒过定点(-2,0).注常规法用参数法,令k的值分别为k1、k2,且k1≠k2,得方程组求之,但由于该方法有别于取特殊值法,不需验证交点是否满足原函数解析式,初学者不易掌握.例3 已知二次函数y=ax2+(6-a)x-6a-1(a≠0),证明无论a为何值,抛物线恒过定点,并求定点坐标.证明要使抛物线恒过定点,则定点处的x,y值必与a的值无关,即y =ax 2+(6-a )x -6a -1=a(x 2-x -6)+6x -1(a ≠0),必有x 2-x -6=0,解得x 1=3,x 2=-2,∴y 1=17,y 2=-13.所以不论a 为何值(a ≠0),抛物线恒过定点(3,17)与点(-2,-13).注 常规法用主元法,以a 为主元,得a(x 2-x -6)=-6x +y +1.根据一元一次方程的解的性质,a 为任意非零实数,即说明关于a 的方程有无穷解,由0·a =0的模式可得260610x x x y ⎧--=⎨-++=⎩解之即得. 若应用上述模式求证另辟蹊径,较为方便.例4 若a =b -2求证函数f(x)=ax 2+bx +2的图象过两定点.证明 因为a =b -2,所以f(x )=b (x 2+x )-2x 2+2.若函数f(x )的图象过两定点,则定点处的x 、y 值必与b 的值无关,此时必有x 2+x =0,解得x 1=0,x 2=-1.故不论a ,b 为何值但只需满足a =b -2时,函数f(x)的图象必过两定点(-1,0)与点(0,2).注 常规法用观察法,因为a =b -2,所以a -b +2=0,则f(-1)=0,f(0)=2,即得所求.但初学者往往不易把握,例5 已知二次函数y =x 2-(m 2+6)x +2m 2+8,求证不论m 为何值,抛物线与x 轴正方向都有两交点,且其中一个交点为定点.证明 因为无论m 为何值,要使抛物线与x 轴正方向恒有两交点,且其中一个交点为定点,于是抛物线y =m 2(2-x )+x 2-6x +8在定点处的函数值与m 值无关,此时2-x =0,x =2,求得y =0.若抛物线与x 轴正方向恒有两交点,则y=0时有x2-(m2+6)x+2m2+8=0,分解因式得(x-2)(x-m2-4)=0,∴x1=2>0,x2=m2+4>0.所以不论m为何值,抛物线与x轴的正方向恒有两交点(2,0),(m2+4,0),且恒交定点(2,0).注常规法用直接求根法,因为交点在x轴上,所以令y=0,直接求元.由于该问题存在一个非定点,所以用常规法较方便.二、发散思维例析例6 设a、b为任意实数,且2a+b=1,关于x,y的方程ax+by=3有一个解恒定不变,求方程的这个解.解∵2a+b=1,则b=1-2a,∴原方程变形为ax+y-2ay-3=0,即a(x-2y)+(y-3)=0.由于a、b为任意实数,且方程ax+by=3有一个解恒定不变,则说明方程的解不因a、b的变化而变化.只有当x-2y=0时,原方程的解才与a、b的值无关,所以x=2y,解得y=3,x=6,即为方程的定解.例7 已知m为一切非零实数,代数式my+(m2-4m,)x2-2m2x-3的值恒为一个常数,求这个常数,并求此时x,y的值.解原式变形为m(y-4x2)+m2(x2-2x)-3.由上述思维模式,得224020y x x x ⎧-=⎪⎨-=⎪⎩ 解得00x y =⎧⎨=⎩或216x y =⎧⎨=⎩ 所以当x =0,y =0或x =2y =16时,原代数式的值恒为-3.例8 已知a =-3x 2-2xy +3x +1,b =2x 2+xy -1,且2a +3b 的值与x 无关,求y 的值.解 由上述思维模式,求得2a +3b=-6x 2-4xy +6x +2+6x 2-3xy -3=x (6-y )-1.由于2a +3b 的值与x 无关,所以得6-y =0,y =6.三、小结(1)解决函数图象过定点问题时,我们可以抓住定点的不变性与参数的可变性,将函数解析式转化为以参数字母为主元的形式,从而可知与参数字母相乘的另一因式的值必为零.如上面例析,利用此“思维模式”能找到捷径,也可将此“模式”引申到方程与代数式的定解、定值问题中.(2)当函数图象除过定点外还过另一不定点,或问题中待定字母较多时,则需全面考 虑,另辟蹊径,如上面例5所述,又如已知二次函数y =ax 2+bx +c ,(a ≠0)当a +b +c =2时,图像过一定点,求谈定点的坐标时,则须用观察法,由a +b +c =2可知x =1,得y =2.所以对具体问题要具体分析,切记不要被思维定势所局限.。
怎样证明曲线(直线)恒过定点

4
-
2 1
=
(y 1 +
16 2) (y 2 +
2)
=-
1,
化简得 - y 1y 2 - 2 (y 1 + y 2) = 20. ②
联立 ①② 消去 y 1y 2 , 得
4x - 20 - (y 1 + y 2) (y + 2) = 0.
这是“l1 + Κl2 = 0”的直线系方程, 所以必
4x - 2 0 = 0 x = 5 ,
∴ 定点(3 , 1) 在圆 C 的内部.
故直线 l 必与圆 C 相交.
说明 本题也可以通过证明圆心到直线
的距离小于圆的半径, 完成问题的解答. (收稿日期: 2000208201)
明曲线必过定点, 这时可这样分析: 假设曲线
经过的定点是 P (x 0 , y0 ) , 这样 x 0、y 0 必满足方
程, 即对于任何 m 值, F (x 0 , y0 , m ) = 0 总成
立. 这时如果将 F (x 0 , y0 , m ) = 0 看作是关于
m 的方程, 那么这个方程就有无穷多个解. 我
2 直线或曲线恒过定点的证明举例
例 1 已知 (k + 1 ) x - (k - 1) y - 2k = 0
为直线 l 的方程, 求证: 不论 k 取何实数值, 直
线 l 必过定点, 并求出这个定点坐标. 证法 1 整理直线 l 的方程, 得
(x + y ) + k (x - y - 2) = 0 ,
y = - 1.
把 x = 1 , y = - 1 代入原方程, 得
k + 1 + k + 1 - 2 k = 0,
