Workbench屈曲分析总结
非线性屈曲分析

ansys workbench非线性屈曲分析(2013-08-26 21:26:29)转载▼标签:ansys很多旋转受压结构必须进行屈曲分析,常规结构屈曲分析软件有nastran、abaqus和ansys,nastran对线性大型模型分析效率较高;abaqus屈曲分析使用较少;ansys使用比较频繁,其快速建模,与CAD软件的良好借口及有限元模型前处理的便捷性(WB界面)很有吸引力,屈曲分析功能较为完善,可以进行线性、非线性和后屈曲分析。
ansys学习资料中介绍较多的是线性屈曲分析。
线性屈曲分析在工业实际中预测的值偏高,有的甚至超过实际实验测试值的几十倍,线性分析唯一优势是其分析速度较快。
但在实际中其预测值参考价值不大,仅给定结构屈曲失效的上限值。
非线性屈曲分析考虑其他因素,包括结构加工缺陷(几何),材料非线性等,因此较为接近实际情况,但计算耗时较长。
针对最艰难学习情况归纳总结非线性屈曲分析时技术要点及应注意事项。
对于规则旋转壳,承受外压载荷作用,进行非线性屈曲分析时,必须加上几何缺陷,关键步是添加APDL语句/prep7upgeom,0.1,1,1,file,rstcdwrite,db,file,cdb/solu该步引入屈曲模态情况下的几何缺陷,缺陷为屈曲模态变形相对值的0.1倍,该值可以根据实际加工水平等其他条件确定,上述语句保存在txt文档中,在workbench流程APDL模块调用。
分析详细流程为,static structure模块导入几何,施加载荷和边界条件,分析求解,将linear buckling拖入流程中,共享static structure模块数据,进行线性屈曲模块分析,Mechanial APDL模块调用屈曲分析结果,并调入(addinput)上面内含几何缺陷命令语句命令的txt文件,更新,将Mechanical结果导入Finite Element modeler模块,更新,此时在缺陷附近的单元节点位置发生改变。
屈曲梁Workbench仿真与试验分析

李 爱 民
(江 苏 建 筑 职 业 技 术 学 院 机 电 ] 程 学 院 ,江 苏 徐 州I 221116)
M
摘 要 :研 究 弹 性 直 梁 在 受 轴 向 力 作 用 下 大 变 形 非 线 性 屈 曲 分 析 的 方 法 ,并 对 两 端
固 支的 梁 进 行 非 线 性 屈 曲 分 析 与 仿 真 实 验 : 根 据 材 料 力 学 ,当 此 弹 性 直 梁 所 受 轴a
.
Aeeol’(1ing to the mechanirs of m aterials,when axiaI toree of elastic beam is greater than a el·iticaJ value it will produce .
large detormation, and beeoine the post buckled beam . Firstly. a m athematical m odel of tile buckling beam is established,and the them‘etieal fol·nlUla of the axially 1oaded beam is derive(1 the malhematieal nl0del is solv (1 by using
g n
C
W orkbench Simulation and Experimental Analysis of Buckling Beam
C
Abstract:This paper studies the analysis m ethod tor nonlinear buckling ot’elastic straight bgea m under the action of axial fin’ce.and nonlillear but’kling analysis and silnulation experinlent are ‘-al’ried ()tit 【ln the beam with clam ped ends
最新Workbench屈曲分析总结资料

Workbe nch屈曲分析1、基础概念结构在载荷作用下由于材料弹性性能发生变形,若变形后结构上的载荷保持平衡,这种状态称为弹性平衡。
如果结构在平衡状态时,受到扰动而偏离平衡位置,当扰动消除后仍能恢复原来平衡状态,这种平衡状态称为稳定平衡状态,反之,如果受到扰动而偏离平衡位置,即使扰动消除,结构仍不能恢复原来的平衡状态,而结构在新的状态下平衡,则原来的平衡状态就成为不稳定平衡状态。
当结构所受载荷达到某一值时,若增加一微小的增量,则结构平衡状态将发生很大的改变,这种现象叫做结构失稳或结构屈曲。
根据失稳的性质,结构稳定问题可分为以下三类:第一类失稳是理想化情况,即达到某个载荷时,除结构原来的平衡状态存在外,出现第二个平衡状态,故又叫做平衡分叉失稳,数学上就是求解特征值问题,又叫做特征值屈曲分析。
第二类失稳是结构失稳,变形将大大发展,而不会出现新的变形形式,即平衡状态不发生质变,也叫极顶失稳,结构失稳时,相应载荷叫做极限载荷,理想结构或完善结构不存在,总是存在这样那样的缺陷,大多数问题属于第二类失稳问题。
第三类失稳是当在和达到某值时,结构平衡状态发生一明显跳跃,突然过渡到非临近的另一具有较大位移的平衡状态,称为跳跃失稳,跳跃失稳没有平衡分叉点,也没有极值点,如坦拱、扁壳、二力杆的失稳都属于此类。
结构弹性稳定分析属于第一类失稳对应workbench的线性特征值分析(Eigenvalue Buckling),考虑缺陷,非线性影响的第二类结构属于workbe nch的非线性特征值分析( Eige nvalue Buckling),第三类的失稳对应workbench的Static Structural,无论前屈曲平衡状态或后屈曲平衡状态均可一次计算求出,即全过程分析。
1.1屈曲分析基础理论在平衡状态,考虑到轴向力或中面内力对弯曲变形的影响,根据势能驻值原理得到结构平衡方程为kJ K G〕U—p:式中K E 1为结构弹性刚度矩阵,K G I为结构几何刚度矩阵,也称为初应力刚度矩阵,<U '为节点位移向量;"P*为节点载荷向量,上式也为几何非线性分析平衡方程。
屈曲分析

屈曲分析屈曲分析是一种在工程力学中常见的分析方法,用于研究杆件在受力作用下的屈曲性能。
屈曲指的是杆件在受到压力作用时,由于材料的强度不足或几何形状的不合理,导致杆件发生弯曲或破坏的现象。
屈曲分析的目的是确定杆件的屈曲载荷和屈曲形态,以保证结构的安全可靠性。
屈曲分析主要涉及材料力学、结构力学和数值计算等方面的知识。
首先,我们需要了解材料的力学性能,包括材料的弹性模量、屈服强度和断裂韧性等。
这些参数将决定杆件是否具备抵抗屈曲的能力。
其次,结构力学的知识是进行屈曲分析的基础。
我们需要掌握静力学的基本原理,了解杆件在受力作用下的受力分布和相应的应力状态。
最后,数值计算方法可以帮助我们通过计算机模拟杆件的受力情况,得出屈曲载荷和屈曲形态。
在进行屈曲分析时,我们可以采用不同的理论模型,例如欧拉理论、托列密理论和von Mises理论等。
欧拉理论是最常用的屈曲分析方法之一,适用于长、细杆件的屈曲分析。
托列密理论则适用于短、粗杆件的屈曲分析。
von Mises理论是一种较为通用的屈曲分析方法,考虑了材料的屈服特性,适用于多种类型的杆件。
在进行屈曲分析时,我们需要首先确定杆件的几何形状和边界条件。
然后,在已知杆件的几何参数、材料参数和加载条件的情况下,可以利用力学理论和数值计算方法求解杆件的屈曲载荷和屈曲形态。
在求解过程中,需要进行数值模型的建立、边界条件的施加和求解方法的选择。
通过合理的假设和较为准确的计算,可以得到较为可靠的屈曲分析结果。
屈曲分析在工程设计中具有重要的意义。
通过屈曲分析,我们可以评估杆件的屈曲性能,确定结构的安全使用范围。
在设计过程中,我们可以调整材料的选择、几何形状的设计和支撑结构的设置等,以提高结构的屈曲承载能力。
此外,屈曲分析还可以为结构优化设计提供参考,以实现结构的轻量化和高效化。
总之,屈曲分析是研究杆件受力情况的重要方法之一。
通过屈曲分析,我们可以了解杆件的屈曲载荷和屈曲形态,为结构的设计和使用提供参考。
workbench屈服分析ANSYS接触分析及四个强度理论文件

14. 在结果明细窗口中显示 “Load Multiplier” 值为 65610. 记得我 们曾经施加过一个单位力,所以,此结果与我们精确计算的结果 65648非常接近
14 13
July 3, 2006 Inventory #002022 WS2-11
线性屈曲
. . .作业7 – 结果
• 将力的大小变为预定的载荷 (10000 lbf).
作业7
线性屈曲
线性屈曲
作业7 – 目标
• • •
Workshop Supplement
ANSYS Workbench - Simulation ANSYS Workbench - Simulation ANSYS Workbench - Simulation ANSYS Workbench - Simulation
线性屈曲
作业7 - Solution
• 在求解命令条中插入屈曲工具:
11. 点击求解命令条. 12. “RMB > Insert > Buckling”.
Workshop Supplement
ANSYS Workbench - Simulation ANSYS Workbench - Simulation ANSYS Workbench - Simulation ANSYS Workbench - Simulation
July 3, 2006 Inventory #002022 WS2-5
线性屈曲
作业7 – 前处理
1. 将工作单位设置为 U.S. customary单位制:
– “Units > U.S. Customary (in, lbm, psi, F, s)”.
Workshop Supplement
workbench屈曲计算失稳结果

workbench屈曲计算失稳结果引言在工程设计和结构分析中,对于工作台(w o rk be nc h)的屈曲计算与失稳结果分析是非常重要的。
本文将介绍w or kb en ch屈曲计算的基本原理和方法,并深入探讨失稳结果的分析。
1.屈曲计算的基本原理和方法屈曲是指杆件或板件在受到压力作用时,由于其几何形状和受力状态的特殊性,产生的一种失稳现象。
wo rk be n ch的屈曲计算主要有以下几个基本原理和方法:1.1欧拉公式欧拉公式是屈曲计算的基本公式,它描述了杆件或板件的临界屈曲载荷与其几何形状和边界条件的关系。
1.2边界条件的选择边界条件的选择对于屈曲计算结果的准确性和可靠性至关重要。
不同的边界条件会对杆件或板件的屈曲载荷产生影响,并决定了其失稳形态。
1.3数值计算方法数值计算方法是实际进行wo rk be nc h屈曲计算的常用手段。
常见的数值计算方法包括有限元方法、薄壁理论等。
2.失稳结果分析屈曲计算中得到的失稳载荷只是一个基本的结果,真正重要的是对失稳结果进行分析和判断。
失稳结果分析主要从以下几个方面展开:2.1稳定性分析稳定性分析是判断wo r kb en ch在失稳后是否能保持稳定的过程。
稳定性分析需要考虑材料的应变硬化特性、几何形态的变化等因素。
2.2失效模式分析失效模式分析旨在确定w or kb en ch失稳后可能产生的各种失效模式。
通过失效模式分析,可以进一步评估w ork b en ch的可靠性和安全性。
2.3失稳形态分析失稳形态分析是对wo r kb en ch失稳后的变形形态进行研究和分析。
失稳形态分析可以帮助工程师了解w or kb en c h失稳的机制和影响因素。
结论本文介绍了w or kb en c h屈曲计算的基本原理和方法,以及失稳结果的分析。
在工程设计和结构分析中,对于wo r kb en ch的屈曲计算和失稳结果的分析至关重要。
工程师们可以根据本文提供的内容进行深入研究和应用,以确保工作台的稳定性和安全性。
ANSYS Workbench 17·0有限元分析:第13章-特征值屈曲分析

第13章 特征值屈曲分析
屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,屈曲分析包括线性屈曲分析和非线性屈曲分析。
线性屈曲分析可以考虑固定的预载荷,也可使用惯性释放;非线性屈曲分析包括几何非线性失稳分析、弹塑性失稳分析、非线性后屈★ 了解线性屈曲分析。
13.1 屈曲分析概述
特征值屈曲分析(Eigenvolue Buckling)是以特征值为研究对象的,特征值或线性屈曲分析预测的是理想线性结构的理论屈曲强度(分歧点),特征值方程决定了结构的分歧点。
然而,非理想和非线性行为阻止了许多真实的结构达到它们理论上的弹性屈曲强度。
线性屈曲通常产生非保守的结果,应当谨慎使用。
尽管屈曲分析是非保守的,但是也有许多优点。
屈曲分析比非线性屈曲分析计算省时,并且应当作第一步计算来评估临界载荷(屈曲开始时的载荷)。
通过线性屈曲分析可以预知结构的屈曲模型形状,结构可能发生屈曲的方法可以作为设计中的向导。
13.1.1 关于欧拉屈曲
结构的丧失稳定性称为(结构)屈曲或欧拉屈曲。
L.Euler
从一端固定、另一端自由的受压理想柱出发,给出了压杆的临
界载荷。
所谓理想柱,是指起初完全平直而且承受中心压力的
受压杆,如图13-1所示。
设此柱完全是弹性的,且应力不超过比例极限,若轴向外
载荷P小于它的临界值,则此杆将保持直的状态而只承受轴向图13-1 受压杆。
基于ANSYS Workbench变截面压杆屈曲分析方法

摘要 : 以工 程 应 用 中 变 截 面 压 杆 为 例 , 用 AN YS Wok e c 中概 念 建 模 方 法 进 行 3 运 S rb n h D建 模 , 据 实 际 根 应 用 条 件 对 压 杆 两 端 施 加 约 束 , 在 A YS Wok e c NS rb n h的 屈 曲分 析 模 块 中通 过 施 加 单 位 载 荷 计 算 出 变 截 面
在 机 械 工 程 中 ,有 不 少 构 件 属 于 变 截 面 压 杆 形
式 , 起 重 机 吊臂 、 幅 油 缸 等 承 受 压 力 作 用 的 支 柱 如 变 都 可 简化 为 阶梯 形 状 的受 压 件来 分 析 其 承载 能 力 。 这 类 构 件 在 受 到 轴 向压 力 作 用 时 容 易 出 现 弯 曲 或 失
文 章 编 号 : 6 2 0 2 ( 01 ) 4 0 7 — 3 17 — 1 12 2 0 — 0 0 0
基 于 ANS o k e c YS W r b n h变 截 面 压 杆 屈 曲分 析 方 法
闵 加 丰 ,阚 伟 良 ,朱 海 清
( 南 大 学 机 械 工 程 学 院 , 苏 无 锡 21 1 2 江 江 42 )
即 设 该 构 件 中各 个 不 同横
硕 士在读 , 主攻机械设计 及理论 学习
论 为 基 础 ,分 析 中 不 考 虑 结 构 在 受 载 变 形 过 程 中 结
构构形 的变 化 , 就是在 外力施 加 的各个 阶段 , 是 也 总
步 求 解 这 些 方 程 往 往 遇 到数 学 上 的 困 难 , 因此 对 这 类 问 题 进 行 深 入 研 究 很 有 必 要 。 本 文 应 用 ANS YS
算 简 便 , 有 较 强 的 通 用 性 , 对 于 截 面 变 化 较 大 或 具 但
基于ANSYS Workbench的真空管道屈曲分析

书山有路勤为径,学海无涯苦作舟基于ANSYS Workbench 的真空管道屈曲分析利用ANSYS Workbench 对某装置中设计的真空管道进行了屈曲分析,并把有限元分析结果和解析法计算结果进行对比,验证了有限元屈曲分析的可靠性。
同时,提出真空管道优化设计方法,并对优化结果进行校核。
计算结果表明:通过合理设置加强圈,既能有效提高真空管道抗外压失稳能力,又能减轻管道重量,从而显著降低制造成本。
大型真空管道为薄壁结构件,其主要失效形式不是强度失效而是失稳失效。
所谓的压力容器失稳是指压力容器所承受的载荷超过某一临界值时突然失去原有几何形状的现象。
研究外压容器稳定性的目的在于研究容器的临界压力及相应的失稳模态,以改进加强措施,提高结构的抗失稳能力。
由于外压容器很难进行外压试验,直接考核大型外压容器承受外压时的稳定性是不现实的,因此大型外压容器的稳定性计算往往多采用理论或有限元分析方法。
ANSYS 软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件,在压力容器的屈曲稳定分析中有着广泛的应用,它提供了两种预测结构屈曲临界载荷和屈曲模态的技术,一种是特征值屈曲分析,可以预测结构屈曲形状,得到失稳临界载荷的上限。
另一种是非线性屈曲(包括几何非线性和几何及材料双非线性)分析。
使用非线性技术,模型中就可以包括诸如初始缺陷、塑性行为、间隙、大变形响应等特征,因此,非线性屈曲分析更接近工程实际的真实情况。
本文利用特征值屈曲分析和非线性屈曲分析方法,对某装置中设计的真空管道进行屈曲分析,并把有限元分析结果和解析法计算结果进行对比,得出真空管道稳定性的分析结论。
同时,提出真空管道优化设计方法,为提高真空。
Workbench屈曲分析总结

Workbench 屈曲分析1、基础概念结构在载荷作用下由于材料弹性性能发生变形,若变形后结构上的载荷保持平衡,这种状态称为弹性平衡。
如果结构在平衡状态时,受到扰动而偏离平衡位置,当扰动消除后仍能恢复原来平衡状态,这种平衡状态称为稳定平衡状态,反之,如果受到扰动而偏离平衡位置,即使扰动消除,结构仍不能恢复原来的平衡状态,而结构在新的状态下平衡,则原来的平衡状态就成为不稳定平衡状态。
当结构所受载荷达到某一值时,若增加一微小的增量,则结构平衡状态将发生很大的改变,这种现象叫做结构失稳或结构屈曲。
根据失稳的性质,结构稳定问题可分为以下三类:第一类失稳是理想化情况,即达到某个载荷时,除结构原来的平衡状态存在外,出现第二个平衡状态,故又叫做平衡分叉失稳,数学上就是求解特征值问题,又叫做特征值屈曲分析。
第二类失稳是结构失稳,变形将大大发展,而不会出现新的变形形式,即平衡状态不发生质变,也叫极顶失稳,结构失稳时,相应载荷叫做极限载荷,理想结构或完善结构不存在,总是存在这样那样的缺陷,大多数问题属于第二类失稳问题。
第三类失稳是当在和达到某值时,结构平衡状态发生一明显跳跃,突然过渡到非临近的另一具有较大位移的平衡状态,称为跳跃失稳,跳跃失稳没有平衡分叉点,也没有极值点,如坦拱、扁壳、二力杆的失稳都属于此类。
结构弹性稳定分析属于第一类失稳对应workbench 的线性特征值分析(Eigenvalue Buckling ),考虑缺陷,非线性影响的第二类结构属于workbench 的非线性特征值分析(Eigenvalue Buckling ),第三类的失稳对应workbench 的Static Structural ,无论前屈曲平衡状态或后屈曲平衡状态均可一次计算求出,即全过程分析。
1.1屈曲分析基础理论在平衡状态,考虑到轴向力或中面内力对弯曲变形的影响,根据势能驻值原理得到结构平衡方程为[][](){}{}P U K K G E =+式中[]E K 为结构弹性刚度矩阵,[]G K 为结构几何刚度矩阵,也称为初应力刚度矩阵,{}U 为节点位移向量;{}P 为节点载荷向量,上式也为几何非线性分析平衡方程。
ansys-workbench-屈曲分析讲义

• 与线性静力分析类似,任何DS支持的类型的几何体都可以使用:
– 实体 – 壳体 (确定适当的厚度) – 线体(定义适当的横截面)
• 只有屈曲模式和位移结果可用于线体。 • 尽管模型中可以包含点质量,但是由于点质量只受惯性载荷的作用,因此在应用中有
一些限制。
• 材料属性,杨氏模量和泊松比是必须有的。
Actual _ Load
线性屈曲分析 Analysis
… 检查结果
• 屈曲载荷因子可以在“线性屈曲分析”分析分支下“Timeline”的结果中进行 检查。
– 这是求解多个屈曲模态的一个很好的方法,以便观察结构屈曲在给定的施加载 荷下的多个屈曲模态。
线性屈曲分析 Analysis
C. Workshop 7.1 – 线性屈曲
线性屈曲分析 Analysis
简介
• 本章将介绍线性屈曲分析。
• 内容:
A. 屈曲的背景知识 B. 屈曲分析步骤 C. Workshop 7-1
• 本章所述的功能,一般可用于ANSYS DesignSpace Entra及以上版本的 许可。
– 本章讨论的某些选项可能需要更高级的许可,但这些都指出相应的许可。
线性屈曲分析 Analysis
… 线性屈曲基础
• 对于线性屈曲分析求解特征值要用到屈曲载荷因子li和屈曲模态yi:
假设:
– [K] 和 [S] 不变:
• 假定为线弹性材料 • 利用小变形理论并没有包括非线性
• 重要的是要记住与进行线性屈曲分析模拟有关的这些假设。
线性屈曲分析 Analysis
B. 屈曲分析步骤
• 特征值或线性屈曲分析预测理想线弹性结构的理论屈曲强度。
• 此方法相当于教科书上线弹性屈曲分析的方法。
workbench19.2屈曲分析
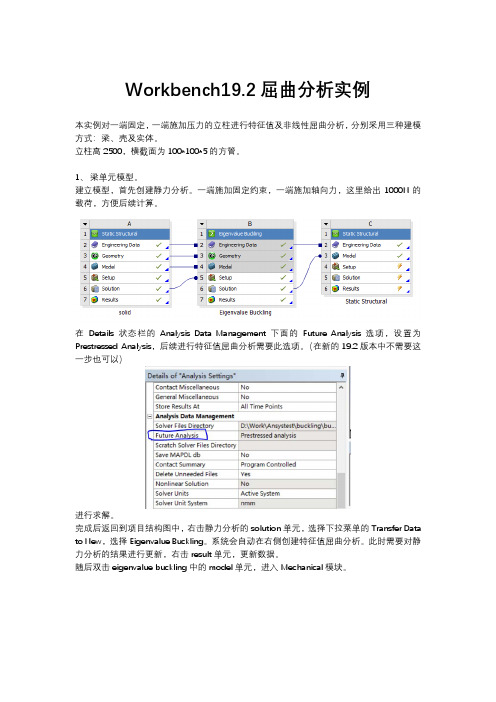
Workbench19.2屈曲分析实例本实例对一端固定,一端施加压力的立柱进行特征值及非线性屈曲分析,分别采用三种建模方式:梁、壳及实体。
立柱高2500,横截面为100*100*5的方管。
1、梁单元模型。
建立模型,首先创建静力分析。
一端施加固定约束,一端施加轴向力,这里给出1000N的载荷,方便后续计算。
在Details状态栏的Analysis Data Management下面的Future Analysis选项,设置为Prestressed Analysis,后续进行特征值屈曲分析需要此选项。
(在新的19.2版本中不需要这一步也可以)进行求解。
完成后返回到项目结构图中,右击静力分析的solution单元,选择下拉菜单的Transfer Data to New,选择Eigenvalue Buckling。
系统会自动在右侧创建特征值屈曲分析。
此时需要对静力分析的结果进行更新,右击result单元,更新数据。
随后双击eigenvalue buckling中的model单元,进入Mechanical模块。
此时在Static Structural下方会多出一个Eigenvale buckling。
在Details中设置Analysis setting,Options中的max modes to find(最大模态数)。
一般设置为1阶即可,通常在非线性分析中会将第一阶屈曲模态作为结构的初始缺陷。
来获得应力及应变结果。
这里我选择提取二阶模态一阶特征值为225.47,则其特征值载荷为2.25e5 N .下一步进行非线性屈曲分析。
回到项目结构图中,在右侧创建静力分析,将Engineer Data和Solution的数据传递到Static中。
点击Eigenvalue的 Solution单元,可以在右边的Properties窗体中看到一个Scale factor,这是被传递的模态的放大系数。
特征值计算的模态会按照这个放大系数将模态的位移施加给非线性分析的模型上。
基于ANSYS Workbench变截面压杆屈曲分析方法

基于ANSYS Workbench变截面压杆屈曲分析方法I. 绪论A. 研究背景B. 研究问题C. 研究目的D. 研究方法E. 预期结果II. 变截面压杆屈曲理论分析A. 压杆的屈曲基本理论B. 变截面压杆的屈曲形式与影响因素C. 基于ANSYS Workbench的变截面压杆屈曲分析方法III. ANSYS Workbench变截面压杆屈曲仿真建模A. ANSYS Workbench基本介绍B. 变截面压杆的建模方式C. 加载条件与分析过程IV. 实验数据分析与结果比对A. 实验数据采集B. 屈曲载荷与形变数据分析C. 模拟结果与实验结果的比对V. 结论与展望A. 结论总结B. 未来研究方向第一章:绪论A. 研究背景随着工程领域的发展,越来越多的设计师和工程师开始采用轻量化的设计方案,以减少材料成本和节约能源。
压杆作为一种常用的结构元件,在许多机械结构和建筑结构中起着重要的作用。
而变截面压杆,则是压杆结构中一种重要的设计方案。
B. 研究问题在实际工程设计中,变截面压杆的屈曲分析是一项非常重要的工作。
由于其结构的复杂性和曲率变化的巨大性,传统的理论计算方法难以进行准确的分析。
因此,为了能够更好地理解和优化该结构,需要采用一种有效的数值仿真分析方法进行计算、分析和优化。
C. 研究目的本篇论文的研究目的是探究在ANSYS Workbench软件平台下,采用有限元分析方法进行变截面压杆屈曲分析的可行性,并进一步探讨优化设计策略和建议,以提高压杆的屈曲强度和性能。
D. 研究方法本研究将采用文献研究与数值仿真方法相结合的实验研究方法,首先对变截面压杆的相关理论背景进行探讨。
接着,将基于ANSYS Workbench的有限元分析方法建立变截面压杆屈曲模型,进行屈曲载荷的模拟计算。
然后,将通过分析模拟结果和实验数据的比对,验证计算的准确性和可信度,并提出相应的结论和建议。
E. 预期结果本研究预期将为工程设计师和研究者提供一种有效的变截面压杆屈曲分析方法,并为改进和优化该结构提供有理有据的数据和理论支持。
workbench屈服分析ANSYS接触分析及四个强度理论文件

⎡ π 2 • 30e6 • 12.771 ⎤ P' = 0.25 • ⎢ ⎥ = 65648.3lbf 2 (120) ⎣ ⎦
(
)
July 3, 2006 Inventory #002022 WS2-4
线性屈曲
作业7 – 开始页
• • • • 选取 “A link to a geometry file on my computer or network” 浏览文件 “pipe.x_t”. 点击文件 “Pump_housing” 按照指导教师的要求 更改工作路径 “Open a new simulation based on the selected geometry” 启动DS,关闭模板菜单
July 3, 2006 Inventory #002022 WS2-5
线性屈曲
作业7 – 前处理
1. 将工作单位设置为 U.S. customary单位制:
– “Units > U.S. Customary (in, lbm, psi, F, s)”.
Workshop Supplement
ANSYS Workbench - Simulation ANSYS Workbench - Simulation ANSYS Workbench - Simulation ANSYS Workbench - Simulation
对于应力结果进行快速检查表明,模型在受载荷后仍保持在材料允 许的力学性能范围内。 正如前面所述,这一步在屈曲分析中并不是必要的,但却被认为是 比较符合工程实际情况的。
模型是一个钢管,一端固定,另一端自由,并在这个自由端施加 了纯压缩载荷。管的尺寸和材料属性如下: OD = 4.5 in ID = 3.5 in. E = 30e6 psi, I = 12.7 in^4, L = 120 in. 在这样的情况下,我们假设管子遵循手册中的如下公式:
工字梁Workbench非线性屈曲分析

工字梁Workbench非线性屈曲分析本文由Workbench小学授权转载1.失稳介绍根据失稳的性质,结构稳定性问题分为三类:①线性屈曲问题:当结构承受载荷达到某个值后,结构的平衡状态可能存在的同时,出现了第二个平衡状态。
压杆稳定性也属于这类问题。
②极限失稳点问题:当结构承受达到极限值后,结构的平衡状态可能存在的同时,不会出现新的平衡点③跳跃失稳问题:当结构承受达到极限值后,结构的平衡状态出现新的平衡状态。
本次仿真的主题是一个长度为1m的工字钢非线性屈曲分析。
2.建立模块关联3.建立模型注意:材料默认结构钢,也可以在材料库更改为存在双线性的结构钢。
4.划分网格注意:通过Mesh中的Edge sizing一Number of division选项将整个梁划分为100份。
5.边界条件添加边界条件说明:选择为节点过滤器,上端施加向下200N的力与远端约束,下端设置简支约束。
6.远端约束细节7.求解,后处理8.屈曲后处理查看其中在Eigenvalue Buckling的后处理中可以看到上图中的工字钢的屈曲载荷因子。
屈曲状态一般发生在低阶模态中,高阶不考虑该问题。
得到工字钢的屈曲载荷极限:屈曲载荷因子(5.29)x施加的力(200N)=1058N,退出并保存文件。
9.复制静力学模块注意:选择Duplicate选项进行复制,改变边界条件,将Force设置为1200N,并插入command设置初始缺陷,其他不变,设置1200N的原因是需要得到该工字钢是否在1058N处发生极限跳跃失稳。
注意:这里的初始缺陷施加为0.0001,具体值根据实际工程应用确定,command中的地址为源文件的存放地址。
10.分析设置注意:为了更清晰地捕捉到失稳点,将子步设置尽量大,并打开大变形与稳定性开关,如下图所示。
11.求解,后处理设置为总形变,Z方向形变与下端点的支座反力总变形图:最后通过chart功能建立变形与支座反力的图表,如下图所示:结论:从上图结果可以看出,工字型钢在1020N的逐渐开始失稳。
workbench 线体 屈曲计算

Workbench 是 ANSYS 提供的一种集成仿真环境,它允许工程师对各种工程问题进行结构、流体、热分析等多物理场耦合仿真。
在 Workbench 中进行线体(Beam)屈曲计算时,通常需要遵循以下步骤:
1.几何建模:在 Workbench 界面中创建几何模型,包括线体的几何形状、截
面尺寸等信息。
你可以使用 Workbench 中的几何建模工具创建线体模型。
2.材料属性定义:为线体指定材料属性,包括弹性模量、泊松比、密度等。
你可以在 Workbench 中定义材料属性,并将其应用于线体模型。
3.边界条件设置:定义加载和约束条件,包括受力边界条件、支撑约束等。
在 Workbench 中,你可以使用加载和约束工具来设置这些边界条件。
4.屈曲分析设置:设置屈曲分析的参数和求解器选项,包括加载类型、分析
类型、求解器选项等。
在 Workbench 中,你可以选择适当的分析类型和求解器来执行屈曲分析。
5.求解和后处理:运行屈曲分析,并对计算结果进行后处理。
Workbench 提
供了丰富的后处理工具,可以用来可视化和分析屈曲分析的结果,包括模态形态、位移、应力等。
通过遵循上述步骤,在 Workbench 中进行线体屈曲计算时,你可以利用其强大的建模、分析和后处理工具来评估线体结构的屈曲性能,并根据分析结果进行设计优化和改进。
注意,在进行屈曲分析时,应该仔细考虑材料特性、几何形状和边界条件等因素,以确保分析结果的准确性和可靠性。
ANSYSWorkbench基础教程与工程分析详解第六章屈曲分析

工程中很多结构需要进行结构稳定性计算,如细长杆、压缩部件、真空容器等,这些构件在不稳定(屈曲)开始时,结构本质上没有变化的载荷作用下(超过一个很小的动荡),在x 方向上的微小位移会使得结构有一个很大的改变,这类问题除了要考虑强度之外,还要分析其屈曲稳定性的问题。
本章所要学习的内容包括: ¾ 了解线性屈曲分析基础¾ 掌握ANSYS Workbench 屈曲分析的操作流程 ¾ 了解线性屈曲分析的应用场合 ¾ 理解屈曲分析的结果6.1 线性屈曲分析基础特征值或线性屈曲分析预测的是理想线弹性结构的理论屈曲强度(分歧点);而非理想和非线性行为阻止许多真实的结构达到它们的理论上的弹性屈曲强度。
线弹性通常产生非保守的结果,但也是有优点的。
(1)它比非线性屈曲计算省时间,并且应当做第一步计算来评估临界载荷(屈曲开始的载荷)。
(2)线性屈曲分析可以用来作为决定产生什么样的屈曲模型形状的设计工具,为设计做指导。
线性屈曲的分析方程为:{}([][])0i i K S λΨ+=式中各个符号的含义如下。
S 表示应力刚度矩阵; i λ表示屈曲载荷乘子;i Ψ表示屈曲模态。
实际上,线性屈曲方程和自由振动方程很相似,两者都是利用相似的矩阵方法来求解特征值问题的。
线性屈曲的分析步骤与之前的静力学分析非常相似,过程如下。
(7)求解计算并保存。
ANSYS Workbench1 4.5屈曲模态分析步骤与其他有限元分析步骤大同小异,软件支持模态分析中存在接触对,但因为屈曲分析是线性分析,所以接触行为不同于非线性接触行为,接触设置的线性屈曲分析设置如表6-1所示。
表6-1 存在接触设置的线性屈曲分析设置Linear Buckling Analysis(线性屈曲分析)Contact Type (接触类型) Initially Touching (初始接触) Inside Pinball Region (Pinball 区域内) Outside Pinball Region (Pinball 区域外) Bonded (绑定) Bonded (绑定) Bonded (绑定) Free (自由) No Separation (不分离) No Separation (不分离) No Separation (不分离) Free (自由) Rough (粗糙) Bonded (绑定) Free (自由) Free (自由) Frictionless (光滑)No Separation (不分离)Free (自由)Free (自由)6.2 案例图解6.2.1 斜撑杆受压屈曲分析分析起落架中承受轴向压力的斜撑杆,杆为空心圆管,外径为52mm ,内径为44mm ,L =950mm 。
9 Workbench DS屈曲分析

BucklingLoad = λ *Unit _ Load
BucklingLoad = λ * Actual _ Load
第一个算例,屈曲载荷乘子(λ)就是屈曲载荷 第一个算例,屈曲载荷乘子( 第二个算例,屈曲载荷乘子(λ)可以解释为安全因子。 第二个算例,屈曲载荷乘子( 可以解释为安全因子。
ANSYS BASIC TRAINING
载荷和约束
至少要施加一个能够引起屈曲的结构载荷到模型上: 至少要施加一个能够引起屈曲的结构载荷到模型上: – 所有的结构载荷都要乘上载荷系数来决定屈曲载荷.因此不支持不 所有的结构载荷都要乘上载荷系数来决定屈曲载荷. 成比例或常值的载荷(常数载荷见后面的片子) 成比例或常值的载荷(常数载荷见后面的片子) – 允许刚性约束(即无位移约束) 允许刚性约束(即无位移约束) – 允许无热载荷 – 仅有压缩的约束是非线性,因此不推荐使用在屈曲分析中 仅有压缩的约束是非线性,
ANSYS BASIC TRAINING
屈曲分析实例
目标: 目标: – 校验下面管子模型在ANSYSY Workbench中的线性屈曲分析结果. 校验下面管子模型在ANSYSY Workbench中的线性屈曲分析结果 中的线性屈曲分析结果. 结果将与使用手册上的计算结果想比较. 结果将与使用手册上的计算结果想比较.
ANSYS BASIC TRAINING
求解选项
求解下拉菜单提供了详细的将要执行分析的类型 – 对于屈曲分析,求解下拉菜单的详细选项通常都不需要改变. 对于屈曲分析,求解下拉菜单的详细选项通常都不需要改变. 在大多情况下,“Solver Type 通常在默认的“Program 在大多情况下, Type”通常在默认的 通常在默认的“ Controlled”选项的左边 选项的左边. Controlled 选项的左边.它仅仅控制在初始静力分析中的求解 器而不是屈曲求解方法. 器而不是屈曲求解方法. 屈曲分析不支持“Large Deflection . 屈曲分析不支持“ Deflection”. – “Analysis Type 在线性屈曲分析情况下可以显示“Buckling . 在线性屈曲分析情况下可以显示“ Analysis Type”在线性屈曲分析情况下可以显示 Buckling”.
线性屈曲分析

Workbench -Mechanical Introduction Introduction作业7线性屈曲分析Workshop Supplement •本作业的目标是在ANSYS Workbench中审查线性屈曲结果,并同手册中的封闭形式的解进行对比。
然后给模型施加个的力并给出它的安全因子•然后给模型施加一个10,000 lbf的力,并给出它的安全因子。
•最后,确定结果在屈曲发生前不会发生破坏失效。
Workshop SupplementWorkshop SupplementWorkshop Supplement1.双击Toolbox 下的Static Structural创建一个新系统2.把Linear Buckling 系统拖放到static1.structural 系统中的Solution 模块2.Workshop Supplement •当schematic 设置正确时,它将显示如下:“Drop Target”•上一页的drop target(拖放目标)表示了拖放操作的结果。
A系统中的A2 到A4 是和系统B共享的。
同样把solution (A6)移到系统B设置中。
实际结构进行的是屈曲分析上,结构进行的是屈曲分析。
Workshop Supplement •确定项目单位设为US Customary (lbm, in, s, F, A, lbf, V)•确定选择了Display Values in Project UnitsWorkshop Supplementb.c.Workshop Supplement5.在A 系统static structural 的Geometry 上点击鼠标右键选择Import Geometry Import Geometry 导入文件Pipe.x_t5.6.双击Model 启动Mechanical.6.•当Mechanical application 打开时,project pp p jschematic 会随着改变设置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Workbench 屈曲分析
1、基础概念
结构在载荷作用下由于材料弹性性能发生变形,若变形后结构上的载荷保持平衡,这种状态称为弹性平衡。
如果结构在平衡状态时,受到扰动而偏离平衡位置,当扰动消除后仍能恢复原来平衡状态,这种平衡状态称为稳定平衡状态,反之,如果受到扰动而偏离平衡位置,即使扰动消除,结构仍不能恢复原来的平衡状态,而结构在新的状态下平衡,则原来的平衡状态就成为不稳定平衡状态。
当结构所受载荷达到某一值时,若增加一微小的增量,则结构平衡状态将发生很大的改变,这种现象叫做结构失稳或结构屈曲。
根据失稳的性质,结构稳定问题可分为以下三类:
第一类失稳是理想化情况,即达到某个载荷时,除结构原来的平衡状态存在外,出现第二个平衡状态,故又叫做平衡分叉失稳,数学上就是求解特征值问题,又叫做特征值屈曲分析。
第二类失稳是结构失稳,变形将大大发展,而不会出现新的变形形式,即平衡状态不发生质变,也叫极顶失稳,结构失稳时,相应载荷叫做极限载荷,理想结构或完善结构不存在,总是存在这样那样的缺陷,大多数问题属于第二类失稳问题。
第三类失稳是当在和达到某值时,结构平衡状态发生一明显跳跃,突然过渡到非临近的另一具有较大位移的平衡状态,称为跳跃失稳,跳跃失稳没有平衡分叉点,也没有极值点,如坦拱、扁壳、二力杆的失稳都属于此类。
结构弹性稳定分析属于第一类失稳对应workbench 的线性特征值分析(Eigenvalue Buckling ),考虑缺陷,非线性影响的第二类结构属于workbench 的非线性特征值分析(Eigenvalue Buckling ),第三类的失稳对应workbench 的Static Structural ,无论前屈曲平衡状态或后屈曲平衡状态均可一次计算求出,即全过程分析。
1.1屈曲分析基础理论
在平衡状态,考虑到轴向力或中面内力对弯曲变形的影响,根据势能驻值原理得到结构平衡方程为
[][](){}{}P U K K G E =+
式中为结构弹性刚度矩阵,为结构几何刚度矩阵,也称为初应力刚度矩阵,为节点位移向量;为节点载荷向量,上式也为几何非线性分析平衡方程。
为得到随遇平衡状态,应是系统势能的二阶变分为零。
即:
[][](){}0=+U K K G E δ
因此必有: [][]()0K E =+G K
式中结构弹性刚度矩阵已知,结构外载荷也就是要求得屈曲载荷未知,结构几何刚度矩
阵未知,为了求得该屈曲载荷,假设有一组载荷[]0P ,对应的几何刚度矩阵为[]0G K ,并假定
屈曲时的载荷是[]0P 的λ倍,固有λ[]
0G K =[]G K ,上式可变为 []E K []G K {}U {}P
[][]()00=+G
E K K λ 写成特征值的方式为
[][](){}0=+ιιφλG E K K
式中ιλ为第ι阶的特征值,{}ιφ为ιλ对应的特征向量,是该阶载荷下结构的变形形状,即屈曲模态或失稳模态。
在workbench 中计算出的是ιλ和{}ιφ,即屈曲载荷系数和模态,而屈曲载荷为λ[]
0P .
2.1、Linear-based Eigenvalue Buckling Analysis
线性屈曲分析应注意以下几点
●线性屈曲分析只能在静力分析模块中定义边界
●通过特征值屈曲分析计算的结果是在静态结构分析中应用所有载荷的屈曲载荷因
子。
例如,如果在静态分析中对结构应用10 N压缩负载,如果特征值屈曲分析计算
负载系数为1500,则预测的屈曲载荷为1500×10 = 15000N。
因此,在屈曲分析之
前的静态分析中应用单位载荷是一种典型的方法。
●在静态分析中所使用的所有载荷都适用于屈曲负载系数
●请注意,负载系数表示所有负载的比例因子。
如果某些负载是恒定的(例如,自重
重力负载),而其他负载是可变的(例如,外部施加的负载),则需要采取特殊步骤
确保准确的结果。
为了实现这一目,可以使用一个策略,就是是迭代特征值,调整可变载荷,直到屈
曲因子变为1.0(或接近1.0,在一些收敛公差内)
特征值屈曲分析案例
材料:结构钢
模型:r=1mm L=50mm的圆柱
边界:一端固定,一端施加10N集中力。
1.创建分析系统
首先创建一个结构静力分析分析系统,再创建特征值分析系统将他们数据共享。
2、静力分析边界
3.求解静力分析
3.求解特征值
在总变形中可以查看1阶变形模态和1阶特征值,可以看出一阶特征值为15.534,则屈曲
载荷为10*15.534=155.34N,如果将静力分析中集中力改为155.34,计算出特征值为0.9997,约等于1,集中力155.34就是此结构的屈曲载荷。
2.2、Nonlinear-based Eigenvalue Buckling Analysis
非线性屈曲分析要点
●至少有一个非线性属性在静力分析中被定义。
●除了在静态结构分析中定义的荷载之外,还必须在屈曲分析中至少定义一个载荷来
进行求解。
要启用此功能,将“保持预应力加载模式”属性设置为“是”(默认设置)将在“特征值屈曲”分析中保留静态结构分析中的加载模式。
将属性设置为否需要您
定义特征值屈曲分析的新加载模式。
这种新的加载模式可以与预应力分析完全不同
●在基于非线性的特征值屈曲分析中,负载乘数仅对屈曲分析中的负载进行了缩放。
在估计结构的极限屈曲载荷时,必须考虑静态结构中的载荷和特征值分析。
用于计
算非线性特征值屈曲的极限屈曲载荷的方程是
F BUCKLING= F RESTART+ λi· F PERTRUB where:
FBUCKLING = The ultimate buckling load for the structure.
FRESTART = Total loads in Static Structural analysis at the specified restart load step.
λi = Buckling load factor for the "i'th" mode.
FPERTRUB = Perturbation loads applied in buckling analysis
●例如:如果在静力分析中施加100N集中力,在屈曲分析中加10N力,你得到载荷因
子位15,则结构的极限屈曲力位100+(15*10)=250
●注意:可以使用一维柱的屈曲来验证上述方程的极限屈曲载荷。
然而,对于在静态
结构和特征值屈曲分析中应用的不同负载组合,计算2D和3D问题的极限屈曲载荷可
能不如1D列示例那么直接,这是因为FRESTART和FPERTRUB的值基本上是分别在静态
和屈曲分析中的有效载荷值。
●举个例子,一个悬臂梁的理论极限弯曲强度为1000N,它受到了影响对250 n的压
缩力(a)。
根据负载因素计算极限屈曲载荷(F)的过程用力学方法对线性和非线性
特征值屈曲分析进行了计算,如下图所示示意图
非线性屈曲分析案例
分析模型与前文特征值分析一样,只是在求解设置中打开大变形开关。
1.静力分析结果
2.屈曲分析设置
设置中Keep Pre-Stress Load-Pattern为YES,这时只能在静力分析中施加载荷,不允许在屈曲分析中施加载荷。
3.屈曲分析结果
在总变形中可以查看1阶变形模态和1阶特征值,可以看出一阶特征值为14.535,则屈曲载荷为10+10*14.534=155.34N,如果将静力分析中集中力改为155.34,计算出特征值为7.877e-4
155.34+155.34*7.877e-4 155.34,集中力155.34就是此结构的屈曲载荷。
若屈曲分析设置中Keep Pre-Stress Load-Pattern为NO,此时在静力分析中可以施加载荷,允屈曲分析中也可以施加载荷。
屈曲分析中的载荷只能施加节点力。
首先在施加集中力的端面创建一个节点集合
在屈曲分析中设置集中力
屈曲分析结果
在总变形中可以查看1阶变形模态和1阶特征值,可以看出一阶特征值为7.2672,则屈曲载荷为10+20*7.2672=155.34N。
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
