人教版小学数学五年级上册 《简易方程》知识点梳理 复习资料
小学五年级数学上学期《简易方程》知识点

小学五年级数学上学期《简易方程》知识点小学五年级数学上学期《简易方程》知识点知识点是网络课程中信息传递的基本单元,研究知识点的表示与关联对提高网络课程的学习导航具有重要的作用。
下面是店铺整理的小学五年级数学上学期《简易方程》知识点,一起来看看吧。
小学五年级数学上学期《简易方程》知识点11、用字母表运算定律。
加法交换律:a+b=b+a加法结合律:a+b+c=a+(b+c)乘法交换律:ab=ba乘法结合律:abc=a(bc)乘法分配律:(ab)c=acbc2、用字母表示计算公式。
长方形的周长公式:c=(a+b)2长方形的面积公式:s=ab正方形的周长公式:c=4a正方形的面积公式:s=3、读作:x的平方,表示:两个x相乘。
2x表示:两个x相加,或者是2乘x。
4、①含有未知数的等式称为方程。
②使方程左右两边相等的未知数的值叫做方程的解。
③求方程的解的过程叫做解方程。
5、把下面的数量关系补充完整。
路程=(速度)(时间)速度=(路程)(时间)时间=(路程)(速度)总价=(单价)(数量)单价=(总价)(数量)数量=(总价)(单价)总产量=(单产量)(数量)单产量=(总产量)(数量)数量=(总产量)(单价)工作总量=(工作效率)(工作时间)工作效率=(工作总量)(工作时间)工作时间=(工作总量)(工作效率)大数-小数=相差数大数-相差数=小数小数+相差数=大数一倍量倍数=几倍量几倍量倍数=一倍量几倍量一倍量=倍数被减数=减数+差减数=被减数-差加数=和-另一个加数被除数=除数商除数=被除数商因数=积另一个因数小学五年级数学上学期《简易方程》知识点21、方程的意义含有未知数的等式,叫做方程。
2、方程和等式的关系3、方程的解和解方程的区别使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
4、列方程解应用题的一般步骤(1)弄清题意,找出未知数,并用表示。
(2)找出应用题中数量之间的相等关系,列方程。
人教版五年级上册数学简易方程整理和复习(课件)

4x+8×5=60
三、方 程 法 解 题 和 算 术 方 法 解 题 混 淆
四年级少先队员去敬老院慰问老人,其中参加劳动的有24人,比表演节目的人
数的2倍多4人,表演节目的有多少人?
解:设表演节目的有x人。 2x+4=24 x=10
四、等 量 关 系 找 错
甲、乙两ห้องสมุดไป่ตู้相距360km,一辆汽车由甲城开往乙城,一辆摩托车同时从乙城开往
二、方 程 的 意 义
梳理解读:含有未知数的(等式)叫做方程。 温馨提示:方程一定是等式,等式不一定是方程。
三、解 方 程
梳理解读:1.等式的性质:(1)等式的两边同时加上或减去(相同)的数,等 式仍然成立;(2)等式的两边同时乘一个数或除以一个(不为0的 数),等式仍然成立。
2.方程的解:使方程两边相等的未知数的(值)叫做方程的解。 3.解方程:求方程的解的(过程)叫做解方程。
甲城。摩托车每小时行45km,3小时后两车相距15km。汽车每小时行驶多少千米 ?
解:设汽车每小时行驶xkm。 3 (45+x) +15 = 360 x = 70
四、等 量 关 系 找 错
小明的画片数是小乐的3倍,如果小明给小乐8张,则两人的画片数正好相等,
原来各有多少张?
解:设原来小乐有x张画片,小明有3x张画片。 3x-x = 8×2 x=8
简易方程
知识盘点 易错练习
一、用字母表示数
知识清单
二、方程的意义 三、解方程
四、列方程解决实际问题
一、用 字 母 表 示 数
梳理解读:1.用字母表示运算定律 加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c) 乘法交换律:ab=ba 乘法结合律:(axb)xc=ax(bxc) 乘法分配律:(a+b)c=ac+bc
2023-2024年小学数学五年级上册期末考点复习 第五单元《简易方程》(人教版含详解)
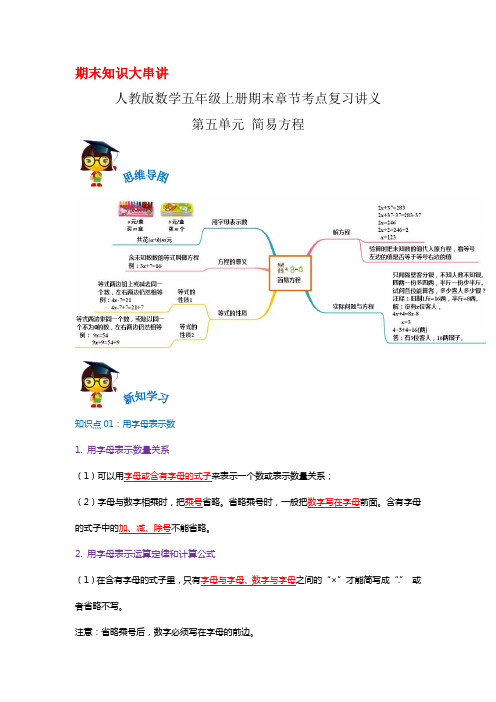
期末知识大串讲人教版数学五年级上册期末章节考点复习讲义第五单元简易方程知识点01:用字母表示数1. 用字母表示数量关系(1)可以用字母或含有字母的式子来表示一个数或表示数量关系;(2)字母与数字相乘时,把乘号省略。
省略乘号时,一般把数字写在字母前面。
含有字母的式子中的加、减、除号不能省略。
2. 用字母表示运算定律和计算公式(1)在含有字母的式子里,只有字母与字母、数字与字母之间的“×”才能简写成“.”或者省略不写。
注意:省略乘号后,数字必须写在字母的前边。
(2)应用公式求值解决问题的步骤:第一步:写出字母公式第二步:把字母表示的数值代入公式第三步:计算出结果,记住写单位3. 用字母表示复杂的数量关系(1)不同的式子可以表示相同的数量关系。
(2)将字母的具体数值代入含有字母的式子中,即可求得相应式子的值。
4. 化简含有字母的式子并代入数据求值计算含有字母的式子的时候,可以先运用运算定律将含有字母的式子进行化简,再求值。
知识点02:解简易方程1.方程的意义(1)方程的意义:含有未知数的等式是方程。
(2)方程必须具备的两个条件:一是等式;二含有未知数。
2.方程一定是等式;但等式不一定是方程。
3. 所有的方程都是等式,但等式不一定都是方程。
4.等式的性质等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
5.方程的解使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
考点01:用字母表示数1.(2022秋•龙口市月考)静静今年10岁,妈妈比她大a岁,再过m年,妈妈比静静大()岁。
A.10+a B.a C.m【思路引导】不管过多少年,两人的年龄差是不会变的。
【完整解答】解:静静今年10岁,妈妈比她大a岁,再过m年,妈妈比静静大a岁。
故选:B。
2.(2022春•遂平县期末)妈妈今年a岁,比笑笑年龄的3倍少5岁,笑笑今年()岁。
人教版数学五年级上册教案-五《简易方程》整理和复习

人教版数学五年级上册教案-五《简易方程》整理和复习一、课时安排•本节课所需时间:1课时•教学内容:简易方程的整理和复习•教学目标:能够熟练应用简易方程解决相关问题•教学重点:理解简易方程的概念,熟练应用简易方程进行计算•教学难点:巩固简易方程的解题方法二、教学内容1. 复习简易方程的基本概念•简易方程的定义:一元一次方程,通常表示形式为a*x + b = c•解决简易方程的步骤:去括号、去分母、合并同类项、移项求解•简易方程的解的含义:求出使等式成立的未知数的值2. 简易方程的练习1.已知方程 a*x + b = c,其中a=2,b=3,c=9,求x的值。
2.如果一个数等于它的三分之一再加上5,求这个数是多少?3. 拓展练习1.若一个数等于它的三倍再加上10,求这个数是多少?2.我们班共有40名同学,男生人数是女生人数的2倍,求男生和女生的人数各是多少?三、教学方法•教师讲解与示范•学生练习与讨论•小组合作解决问题•师生互动,激发学生思维四、教学过程1.引入:通过提出实际问题引导学生认识简易方程的应用价值。
2.复习:让学生回顾简易方程的基本概念,并解释解题步骤。
3.练习:让学生尝试解决简易方程的练习题,巩固知识。
4.拓展:提出拓展练习,鼓励学生思考,激发学生解决问题的兴趣。
5.总结:帮助学生总结本节课的教学要点,强化知识记忆。
五、教学反思本节课设计了复习简易方程的内容,并通过练习和拓展练习的方式帮助学生巩固和拓展知识。
教学过程中,学生表现积极,能够熟练运用简易方程解决问题,但在拓展练习中仍存在一定挑战。
在今后的教学中,需要更加重视拓展练习的设计,培养学生解决问题的能力。
以上为本节课的教案内容,希望能够帮助大家更好地理解和应用简易方程的知识。
小学五年级数学上册第四单元《简易方程》概念与公式汇总

小学五年级数学上册第四单元《简易方程》概念与公式汇总1.在含有字母的式子里,乘号可以记做“·”,也可以省略不写。
(1)数字与字母相乘,省略乘号,要将数字写在字母的前面。
(2)字母与字母相乘,直接省略乘号。
(3)括号与数字相乘,要将数字写在括号的前面,再省略乘号。
2.长方形的周长=(长+宽)×2 C长=2(a+b)长方形的面积=长×宽S长=ab正方形的周长=边长×4 C正=4a方形的面积=边长×边长S正=a23.表示相等关系的式子叫做等式。
4.含有未知数的等式是方程。
5.方程一定是等式,等式不一定是方程。
6.等式两边同时加上、减去、乘或除以同一个数(0除外),所得结果仍然是等式。
方程左右两边同时加上(或减去)相同的数,方程左右两边依然相等。
方程左右两边同时乘以(或除以“0”除外)相同的数,方程左右两边依然相等。
7.使方程左右两边相等的未知数的值叫做方程的解。
求方程的解的过程,叫做解方程。
解方程的根据是天平平和的道理,还可以根据方程各部分之间的关系。
8.解方程时常用的关系式:一个加数=和-另一个加数被减数=差+减数减数=被减数-差一个因数=积÷另一个因数被除数=商×除数除数=被除数÷商注意:解完方程,要养成检验的好习惯。
9.三个或五个连续的自然数(或连续的奇数,连续的偶数)的和,等于中间的一个数的3倍或5倍。
10.列方程解应用题的思路:A、审题并弄懂题目的已知条件和所求问题。
B、理清题目的数量关系C、设未知数,一般是把所求的数用X表示。
D、根据数量关系列出方程E、解方程F、检验G、作答。
人教版小学数学五年级上册简易方程知识点总结

5简易方程
特别注意:
加号、减号、除号及数与
数之间的乘号不能省略。
提示:
2a与a2的区别:
2a表示a+a,a2表示a×a。
提示:
省略乘号时,一般把数字写
在字母的前面。
举例:x×6可以写成6x。
提示:
1×a省略乘号时,不能写成
1a,要写成a,这里的“1”我们要
省略不写。
温馨提示:
用含有字母的式子表示数
量关系,是加减关系时,如果后
面加单位,必须把这个含有字母
的式子用括号括起来。
注意:
方程必须满足的条件:必须
是等式,必须有未知数,二者缺
一不可。
易错点:
误认为含有未知数的式子
是方程。
举例:
3x-2>18是方程。
( )
正确解答:(✕)
提示:
等式的性质是解方程的重。
人教版-数学-五年级-上册-第五章-简易方程-知识点

第五单元《简易方程》一.用字母表示数1.用字母表示数。
在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。
数和字母相乘时,省略乘号后,一律将数写在字母前面。
加号、减号除号以及数与数之间的乘号不能省略。
2.用字母表示运算定律。
加法交换律是a+b=b+a;加法结合律是(a+b)+c=a+(b+c);乘法交换律是ab=ba;乘法结合律是(ab)c=a(bc);乘法分配律是(a+b)c=ac+bc。
3.用字母表示常见的数量关系及计算公式。
用含有字母的式子表示指定的数量,再把字母的取值代入式子中求值,只要在答中写出得数即可。
4、a×a可以写作a•a或a2,a2 读作a的平方。
2a表示a+a二.方程的意义1.方程与等式的区别。
含有未知数的等式叫做方程;方程一定是等式,而等式不一定是方程。
2.等式的性质。
等式两边同时加上或减去相同的数,同时乘或除以相同的数(0除外),左右两边仍然相等。
3、两个数相加,和都相同,一个加数越小,另一个加数就越大。
两个数相减,差都相同,减数越大,被减数也越大。
两个数相乘,积都相同,一个因数越小,另一个因数就越大。
两个数相除,商都相同,除数越大,被除数就越大。
三.解方程1.方程的解与解方程。
“方程的解”是一个数,是使等号左右两边相等的未知数的值;“解方程”是指演算过程。
2.解形如±a=b 和a=b 的方程。
依据等式性质来解此类方程。
解方程时要注意写清步骤,等号对齐。
3.验算。
检验是不是方程的解,把解代入原方程的左边算出得数,再算出右边的得数,如果左右两边的得数相等,那么这个解就是原方程的解。
4、解方程原理:1)、等式两边同时加或减相等的数,等式不变。
2)、等式两边同时乘或除以相同的数(0 除外),等式不变。
5、在列方程解决问题时,我们应统一单位,在方程求出的解的后面不写单位名称。
“三看两原则”三看:一看含有未知数的式子前面是否有“- ”(减号),若有,先处理;二看含有未知数的式子前面是否有“÷”(除号),若有,先处理;三看是否含有小括号“()”,若有优先选择整体法;两原则:1、未知数前面的符合要为“+ ”(加号);2、未知数前面的数字(系数)要为“1 ”。
人教版五年级上册数学 简易方程(整理和复习)

第四单元:简易方程整理和复习(一)一、填空.1、果园里有苹果树和梨树共45棵,其中梨树有a棵,苹果树比梨树多( )棵.2、2a表示( )或者( ),a2表示( )3、一个正方形周长是m米,这个正方形的边长是( )这个正方形的面积是( )4、某工厂每月用水a吨,全年用水( )吨5、三角形在面积公式用字母表示是( ),当a=3.6厘米,h=4厘米时,s=( )二、判断(对的打”√”,错的打”×”)1、a2>2a ( )2、2x+3=11的解是x=4. ( )3、4x+5>10是方程( )4、当a=3,b=5时,2a+3b=21 ( )5、42+3=2x,不是方程是等式.( )三、解下列方程.4x-18×2=20 2.5x-0.5x=0.4×8 x-4.5+10=17.8四、列方程解文字题.1、一个数的5倍加上这个数的8倍等于169,求这个数?2、9个0.6比x的2倍多2.7,求x?整理和复习(二)一、选择合适的方法解下列应用题.1、一个三角形面积是24.8平方米,底是12.4米高是多少米?2、小青家今年养了50只鸡,比鹅的3倍还多5只,小青家今年养鹅多少只?3、甲乙两辆汽车分别从相距800千米的两城相向开出,8小时相遇,已知甲车每小时行驶45千米, 乙车每小时会驶多少千米?4、香蕉每千克4.50元,梨每千克4元,小红的妈妈买了4千克香蕉,给了营业员30元,剩下的钱去买梨,能买梨多少千克?5、小红和小军一共储蓄了235元,已知小红储蓄的是小军的1.5倍,小红和小军各储蓄多少元?6、三个数的平均数是120,甲数是乙数的2倍,丙数比甲数多5,甲, 乙,丙三个数各是多少?第四单元测试题(A卷)一、填空.1、平行四边形底长a米,高是底的1.8倍,面积是( )2、货车每小时行S千米,客车每小时行m千米,客车3小时后和货车5小时一共行驶了( )千米.3、食堂买来200千克煤,已烧了a天,还剩b千克,平均每天烧了( )千克.4、每个足球x元,买4个足球,付出200元,应找回( )元.5、三个连续自然数,已知中间一个数是m,那么前一个数是( ),后一个数是( ),三数之和是( )6、当x=5时,x2=( ),2x+8=( )7、用字母表示梯形面积公式是( )8、一种商品降价a元后是80元,原价是( )元.二、判断.(对的打”√”,错的打”×”)(1)、方程一定是等式,等式不一定是方程.( )(2)、小明今年a岁,哥哥比他大b岁,c年后,哥哥比他大b+c岁.( )(3)、x的3倍与3x相等. ( )(4)、3x+4x=7x, 3a+4b=7ab ( )(5)、含有x的等式叫方程. ( )三、选择题.(填序号)(1)、下列式子中是方程的是( )①、4a=0.8 ②、0.17x+2.5 ③、3x+7>15 ④、3.5x-1.7x<8(2)、47除一个数所得的商是6余5,求这个数的方程是( )①、6x+5=47 ②、6x-5=47 ③、47÷6-5=x(3)、当a=8,b=6时,2a+3b等于( )①、36 ②、34 ③、240(4)、甲数是a,是乙数的3倍, 乙数是( )①、3a ②、a÷3 ③、2a(5)、一个正方形边长是8米,若边长增加2米,面积增加( )①、4平方米②、16平方米③、36平方米④、100平方米四、解下列方程.5.5x+6.7=7.8 28-x+3.6=20 3.5x-0.8x=11.348x-27.54÷2.7=1.8 6.2x-x=41.6 9x-14×5.5=58五、列式计算.1、20.3被2.9除的商去乘0.67与1.33的和,积是多少?2、15个8比一个数的4倍多10,求这个数.(列方程解答)3、甲数是x,乙数是甲数的3倍少0.2, 乙数是5.8,甲数是多少?(列方程解答)六、看图列方程.X本文艺术X本X本16本91本故事书七、应用题.1、汽车站有480箱货物,一辆货车运了5次,还剩30箱,平均每次运多少箱?(列方程解答)2、A,B两城相距150千米,甲乙两人同时骑自行车从两地相对出发,甲每小时行16千米,4小时后,两人还相距30千米, 乙每小时行多少千米?3、果园里有桃树和杏树一共1080棵,已知杏树经桃树的棵数多180棵,杏树和桃树各有多少棵?4、一个长方形操场周长是348米,宽是69米,它的面积是多少平方米?5、龟兔赛跑,全程200米,龟每分钟跑2.5米,兔每分钟跑32米,兔自以为是,在途中睡了一觉,当龟到达终点时,兔子离终点还有40米,兔子在途中睡了几分钟?第四单元测试(B 卷)一、 填空.1、长方形周长计算公式用字母表示是( )2、李师傅每天做m 个零件,比张师傅多做8个,两人一天共做( )3、每本练习本x,买了6本,付出10元,应找回( )元.4、甲数是乙数的a 倍,甲数比乙数多( )倍.5、( )叫方程.6、甲乙两数之差是14,两数之和是108,甲数是( ), 乙数是( ).7、a ×(7+b),当a =5时,b=( )才能使a ×(7+b) =52.58、一个正方形周长是a 厘米,用字母表示它面积的式子是( ),当a =24时,正方形面积应是( )平方厘米.二、把左右两边意义相等的用直线连起来.a 与a 相乘 a +2ba 与相加 a 2a 的2倍 2a +3aa 的二分之一 2a比a 的2倍多3的数 a +aa 与b 的和的2倍 21a a 与b 的2倍的和 (a +b)×2三、判断(对的打”√”,错的打”×”)(1)、等式就是方程. ( )(2)、42=4×2 ( )(3)、4x -20=4与50-5x =20的解是相同的. ( )(4)、光明商店上午卖出a 台冰箱,下午卖出b 台冰箱,这天一共卖了ab 台.( )(5)、2.5a +b =2.5ab ( )(6)、2b ×(b +c)=2b 2+2c ( )四、选择(填序号)1、a 除150的商再减去20的差,列式为( )①、a÷150-20 ②、150÷a-20③、a÷(150-20) ④、150÷(a -20)2、下列式子里是方程的有( )①、x+3 ②、3+15=18 ③、4a+27=78 ④、4x-15<203、0.75x-4×1.8=0.3的解是( )①、x=8 ②、x=10 ③、x=1004、根据8x-6=50,可推得3x+7的值是( )①、50 ②、28 ③、215、m是三个连续自然数中间一个数,三个数之和是( )①、3m+2 ②、3m ③、3m+1 ④、3m-1五、当a=4,b=5,c=6时,求下列各式的值.a+3b-2c abc÷12 bc÷a-b六、列方程并求出方程的解.1、5x减去3.2与9的积差是2.7.2、一个数的7.5倍与这个数的4.5倍多24,这个数是多少?七、应用题.1、同学们植树,一班比二班多植63棵,一班42人,平均每人植8棵,二班39人,平均每人植多少棵?(用方程解答)2、买3张桌子和4把椅子一共用了308元,每把椅子32元,每张桌子多少元?(用方程解答)3、一个长方形周长和一个正方形周长相等,已知长方形长24厘米,宽16厘米,求正方形面积?4、两辆汽车从相距400千米的两地同时相对开出,3小时后还相距10千米,已知一辆汽车每小时行驶55千米,求另一辆汽车速度?(用两种方法解答)1、鸡兔同笼,共有35个头,94条腿,求鸡兔各有几只?总复习(一)一、直接写出得数.8-0.72=0.72×2.5×4=7.2÷0.8=0.64÷1.6=8.7÷2.9×2.9= 4.2÷0.1=7.2+6.5+2.8= 1.5×0.75+1.5×0.25=二、用自己喜欢的方法计算下列各题.12.7-(8.65+2.7) 92.5×0.25×4 6.7×0.9+6.7×0.18.25×9.9+0.825 3.4×8.7+34×0.13 6.5×1.1三、笔算下列各题.7.89×4.27 28.56÷5.1 102.6÷3.8四、列式计算.1、8.5与4.2的积比17.8的一半多多少?2、26.34比3.4与4.6的积多多少?总复习(二)一、填空.1、0.78+0.78+0.78+0.78改写成简便算式是( ),这个算式表示的意义是( ),也表示( ).2、5小时24分=( )小时 2.3小时=( )小时( )分3、12.53里面有( )个0.01 125个0.1是( )4、8.789保留整数是( ),保留一位小数是( ),精确到百分位是( )5、20÷6的商是一个( )小数,写成简便记法是( )6、求6.25的十分之三是多少?列式是( )7、在3.6262,3.62,3.62,3.626中,是有限小数的( );是无限小数的有( );纯循环小数是( ),混循环小数是( ).二、判断(1)、8.25×4.7与82.5×0.47的积相等. ( )(2)、无限小数一定比有限小数大. ( )(3)、两个小相等,积一定比其中任何一个因数大.( )(4)、循环小数一定是无限小数.( )(5)、一个数除以小数,商一定比被除数小.( )(6)、3.26的循环节是26.( )三、计算下面各题(得数保留两位小数)3.03÷(0.25×68) 16.06÷5.7×1.74.65×5.73÷3.9总复习(三)一、填空.1、加法、减法叫做( )运算, 乘法,除法叫做( )运算2、只含同一级运算的要( )计算,含有两级运算的要先算( )运算,再算( )运算.3、8.2+4.5×0.3÷1.5这道算式含有( )级运算,要先算( )法,再算( )法,最后算( )法,如果把这道算式改写成先算加,再算除,最后算乘法,列式为( )二、按顺序计算,然后列成综合算式.列综合算式:______________ 列综合算式:______________三、列式计算.1、5.2与3.5的差去除10.5,所得商再加上20.9,和是多少?2、1.28减去1.54与0.31的差,所得的差再乘9.4,积是多少?总复习(四)一、 填空.1、7.2公顷=( )平方米 3.04平方米=( )平方米( )方分米2、两个完全一样的( )梯形可拼成一个长方形,这个拼成的长方形面积是每个梯形面积的( )倍.3、一个三角形与一个平行四边形等底等高,这个三角形面积一定是这个平行四边形面积的( )4、一个平行四边形的面积是63平方米,现在底缩小3倍,高不变,面积是( )平方米.二、计算下面每个图形的面积(单位:厘米)5.2 5.8 4.7 3.4 4.2 4.5 4.8 5.5 3.2三、应用题.1、有一块三角形小麦地,高30米,比底长18米,这块地面积是多少平方米?2、有一个平行四边形底是15分米,高8分米,它和另一个三角形的面积,底相等,这个三角形的高是多少分米?3、如右图,用篱笆围一块菜地,利用了一面墙.篱笆全长40米,这块菜地面积是多少平方米?9米总复习(五)一、填空.1、一个三角形,它的底是a米,高是2米,它的面积是( )2、a+b比a大( ),a-s比a小( )3、a+a+a+a+a=( ) a×a×a=( )4、a、b、c 三数的平均数是( )5、甲数比乙数大5,如果乙数是m,那么甲数是( ),如果甲数是m,那么乙数是( )6、当x=5时,2x-1.7×4的值是( )二、判断题.(对的打”√”,错的打”×”.)1、等式一定是方程.( )2、只含有未知数x的等式才是方程.( )3、a×b×2=2ab,a×2b=2ab. ( )4、2×2=4,22=4,所以a2=a×2. ( )三、解下列方程1.8×2-0.3x=2.4 15x-8x+30=135 8x+0.4×1.2=1.2四、列方程并求出方程的解.1、12.5减去一个数的2.5倍,等于这个数的3.5倍,求这个数?2、3.5除17.5的商比一个数的4倍多0.2,求这个数?总复习(六)应用题.1、梯形上底是a米,下底是b米,高是h米,(1)用字母表示出梯形的面积S.(2)当a=2.5,b=4.8,h=2.4时这个梯形面积是多少?2、一枝钢笔的价钱是一枝圆珠笔的2.5倍,现各买2支,一共用了10.5元,每支钢笔和圆珠笔各是多少元?3、AB两城相距720千米,一列客车从A城开往B城,行2小时后,另一辆货车从B城开往A城,4小时后与客车相遇,已知客车每小时行80千米,货车平均每小时行多少千米?4、一根绳子长13.4米,第一次剪去3.2米,第二次剪去多少米才能使剩下的长度刚好是第一次剪去的2倍?5、甲乙丙三数之和是183,甲数比乙数的2倍多7,丙数比乙数的3倍少4,求甲乙丙三数各是多少?。
人教版数学五年级上册教案-五《简易方程》整理和复习

人教版数学五年级上册教案-五《简易方程》整理和复习一. 教材分析《简易方程》是五年级上册数学的一个重要内容,主要让学生初步接触和理解方程的概念,学会用字母表示数,以及简单的一元一次方程的解法。
本节课的内容为方程的概念、字母表示数、解一元一次方程等,这些内容对于学生来说具有一定的挑战性,需要学生掌握一定的数学思维和方法。
二. 学情分析五年级的学生已经具备了一定的数学基础,能够理解和掌握一些基本的数学概念和运算方法。
但是,对于方程这一概念,学生可能比较陌生,需要通过实例和操作来理解和掌握。
同时,学生对于字母表示数和一元一次方程的解法可能存在一定的困难,需要教师进行详细的讲解和引导。
三. 教学目标1.让学生理解方程的概念,能够找出生活中的方程。
2.学会用字母表示数,理解字母表示数的意义。
3.掌握一元一次方程的解法,能够解一些简单的一元一次方程。
4.培养学生的逻辑思维和解决问题的能力。
四. 教学重难点1.方程的概念和字母表示数的理解。
2.一元一次方程的解法。
五. 教学方法1.实例教学:通过生活中的实例,让学生理解和掌握方程的概念和字母表示数的方法。
2.引导发现:教师引导学生发现方程的解法和步骤,培养学生的逻辑思维。
3.练习巩固:通过大量的练习,让学生巩固和掌握一元一次方程的解法。
六. 教学准备1.PPT课件:制作相关的PPT课件,展示实例和练习题目。
2.练习题:准备一些相关的练习题目,用于巩固和检测学生的学习效果。
七. 教学过程导入(5分钟)教师通过一个生活中的实例,如“小明买书”的问题,引入方程的概念。
引导学生发现其中的数量关系,并尝试用字母表示未知数。
呈现(10分钟)教师通过PPT课件,展示一些简单的方程,如2x + 3 = 7等,引导学生理解方程的概念,并讲解方程的解法。
操练(10分钟)教师给出一些方程,如3x - 7 = 13等,引导学生独立解方程,并在黑板上展示解题过程。
巩固(10分钟)教师给出一些练习题目,让学生独立完成,并互相检查答案。
(2017)新人教版小学数学五年级上册 《简易方程》知识点梳理 复习资料

第五单元《简易方程》知识点梳理一、用字母表示数1.在含有字母的式子里,字母中间的乘号可以记作“•”,也可以省略不写,字母和数字相乘一般要把数字写在前面。
加号、减号、除号以及数与数之间的乘号不能省略。
2.a2读作a的平方,表示2个a相乘或a×a。
2a表示2个a相加或a+a 或2×a 。
3.用字母表运算定律。
加法交换律:a+b=b+a 加法结合律:a+b+c=a+(b+c)乘法交换律:ab=ba 乘法结合律:abc=a(bc)乘法分配律:(a+b)c=ac+bc4.用字母表示计算公式。
长方形的周长公式:c=2(a+b) 长方形的面积公式:s=ab正方形的周长公式:c=4a 正方形的面积公式:s= a2二、等式和方程1.等式:表示相等关系的式子叫等式。
2.等式的性质1:等式两边加上(或减去)同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
3.方程:(1)方程:含有未知数的等式叫做方程。
(2)使方程左右两边相等的未知数的值,叫做方程的解。
(3)求方程的解的过程叫做解方程。
(4)所有的方程都是等式,但等式不一定都是方程。
(5)方程的解是一个数,解方程是一个计算过程。
4.四则运算的10个关系式:加法:和=加数+加数一个加数=和-另一个加数减法:差=被减数-减数被减数=差+减数减数=被减数-差乘法:积=因数×因数一个因数=积÷另一个因数除法:商=被除数÷除数被除数=商×除数除数=被除数÷商8、方程的检验过程:方程左边=……=……=方程右边所以,X=……是方程的解。
9.方程与实际问题中常用的等量关系式。
路程=速度X 时间速度=路程÷时间时间=路程÷速度总价=单价X 数量单价=总价÷数量数量=总价÷单价工作总量=工作效率X 工作时间工作效率=工作总量÷工作时间工作时间=工作总量÷工作效率总产量=单产量X 数量单产量=总产量÷数量数量=总产量÷单产量大数-小数=相差数大数-相差数=小数小数+相差数=大数一倍量X倍数=几倍量几倍量÷倍数=一倍量几倍量÷一倍量=倍数评价测试样例一、填空题。
汇总五年级人教版数学简易方程的相关知识点知识点总结

汇总五年级人教版数学简易方程的相关知识点知识点总结小学是我们整个学业生涯的基础,所以小朋友们一定要培养良好的学习习惯,为同学们特别提供了五年级人教版数学简易方程的相关知识点,希望对大家的学习有所帮助!
1、方程的意义
含有未知数的等式,叫做方程。
2、方程和等式的关系
3、方程的解和解方程的区别
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
4、列方程解应用题的一般步骤
(1) 弄清题意,找出未知数,并用_表示。
(2) 找出应用题中数量之间的相等关系,列方程。
(3) 解方程。
(4) 检验,写出答案。
5、数量关系式
加数=和 - 另一个加数减数=被减数–差被减数= 差 + 减数
因数=积÷ 另一个因数除数=被除数÷ 商被除数= 商 _除数
为大家整理的五年级人教版数学简易方程的相关知识点,更多小学生辅导相关内容请随时关注!。
人教版小学五年级上册数学《简易方程》知识点及练习题

【篇一】小學五年級上冊數學《簡易方程》知識點1、方程的意義含有未知數的等式,叫做方程。
2、方程和等式的關係3、方程的解和解方程的區別使方程左右兩邊相等的未知數的值,叫做方程的解。
求方程的解的過程叫做解方程。
4、列方程解應用題的一般步驟(1)弄清題意,找出未知數,並用表示。
(2)找出應用題中數量之間的相等關係,列方程。
(3)解方程。
(4)檢驗,寫出答案。
5、數量關係式加數=和-另一個加數減數=被減數–差被減數=差+減數因數=積另一個因數除數=被除數商被除數=商除數【篇二】小學五年級上冊數學《簡易方程》練習題一、填空。
1、某廠計畫每月用煤a噸,實際用煤b噸,每月節約用煤( )噸。
2、一本書100頁,平均每頁有a行,每行有b個字,那麼,這本書一共有( )個字。
3、用字母表示長方形的周長公式()4、根據運算定律寫出:9n+5n=( + )n= a×0.8×0.125=( ×)ab=ba運用()定律。
5、實驗小學六年級學生訂閱《希望報》186份,比五年級少訂a份。
186+a表示()6、一塊長方形試驗田有4.2公頃,它的長是420米,它的寬是()米。
7、一個等腰三角形的周長是43釐米,底是19釐米,它的腰是()。
8、甲乙兩數的和是171.6,乙數的小數點向右移動一位,就等於甲數。
甲數是();乙數是()。
二、判斷題。
(對的打√,錯的打×)1、含有未知數的算式叫做方程。
()2、5x表示5個x相乘。
()3、有三個連續自然數,如果中間一個是a,那麼另外兩個分別是a+1和a-1。
()4、一個三角形,底a縮小5倍,高h擴大5倍,面積就縮小10倍。
()三、解下列方程。
3.5x=140 2x+5=40 15x+6x=1685x+1.5=4.5 13.7—x=5.29 4.2×3—3x=5.1(寫出檢驗過程)四、列出方程並求方程的解。
(1)、一個數的5倍加上3.2,和是38.2,求這個數。
五年级上册数学5 简易方程解简易方程之方法及难点归纳

五年级上册解简易方程之方法及难点归纳重点概念:方程,方程的解,解方程,等式的基本性质(详见“知识点汇总”)要点回顾:“解方程”就是要运用“等式的基本性质”,对“方程”的左右两边同时进行运算,以求出“方程的解”的过程。
(方程的解即是如同“X=6”的形式)“解方程”就好像是要把复杂的绳结解开,因此一般要按照“绳结”形成的过程逆向操作(逆运算)。
过程规范:先写“解:”,“=”号对齐往下写,同时运算前左右两边要照抄,解的未知数写在左边。
注意事项:以下内容除了标明的外,全都是正确的方程习题示例,且没有跳步,请仔细观看其中每步的解题意图。
带“*”号的题目不会考查,但了解它们有助于掌握解复杂方程的一般方法,对简单的方程也就自然游刃有余了。
一、一步方程只有一步计算的方程,直接逆运算除未知数外的部分。
难点:当未知数出现在减数和除数时,要先逆运算含未知数的部分。
二、两步方程两步方程中,若是只有同级运算,也可以先计算,后当做一步方程求解。
注意要“带符号移动”,增添括号时还要注意符号的变化。
如果含有两级运算,就“逆着运算顺序”同时变化,如含有未知数的一边是“先乘后减”,则先逆运算减法(即两边同加),再逆运算乘法(即两边同时除以),依此类推。
难点:当未知数出现在减数和除数时,要先把含有未知数的部分看作一个整体(可以看成是一个新的未知数),就相当于简化成了一步方程。
例题中,“64÷x”、“7.2-x”和“6÷x”被看成新的未知数(y),因此原方程就可以看成是6+y=10,5y=6和10-y=8的形式。
三、三步方程(一)应用乘法分配律,共同因数是已知数的具有乘法分配律的形式,即两个有共同因数的乘积(或具有相同除数的除法式子)相加或相减,而共同因数(或除数)是已知数的,既可以逆用乘法分配律提取共同因数而将其简化为两步方程,也可以直接算出已知部分而化简。
通过比较可以看出,一般来说提取共同因数的方法确实计算量要少一些,不容易算错。
五年级数学上册《简易方程》知识点汇总.doc

五年级数学上册《简易方程》知识点汇总1、在含有字母的式子里,数字和字母中间的乘号,字母和字母之间的乘号,可以记作“·”,也可以省略不写。
加号、减号,除号以及数与数之间的乘号不能省略。
2、a×a可以写作a·a或a ,a 读作a的平方。
2a表示a+a3、方程:含有未知数的等式称为方程。
方程一定是等式,但等式不一定是方程。
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
(解方程要先写“解”)方程的解是一个数;解方程是一个计算过程。
4、解方程的原理:(1)等式的基本性质等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立。
(2)10个数量关系式:加法:和=加数+加数一个加数=和-两一个加数减法:差=被减数-减数被减数=差+减数减数=被减数-差乘法:积=因数×因数一个因数=积÷另一个因数除法:商=被除数÷除数被除数=商×除数除数=被除数÷商5、方程的检验过程:检验:方程左边=…… =方程右边所以,x=…是方程的解。
6、列方程解应用题的步骤:(1)弄清题意,找出未知数,用x表示。
(2)分析、找出数量之间的等量关系,列出方程;(3)解方程。
(4)检验,写出答案。
根据倍数关系表示为几x。
再根据两个量的和或差列出方程。
2019-04-081、在含有字母的式子里,数字和字母中间的乘号,字母和字母之间的乘号,可以记作“·”,也可以省略不写。
加号、减号,除号以及数与数之间的乘号不能省略。
2、a×a可以写作a·a或a ,a 读作a的平方。
2a表示a+a3、方程:含有未知数的等式称为方程。
方程一定是等式,但等式不一定是方程。
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
(解方程要先写“解”)方程的解是一个数;解方程是一个计算过程。
4、解方程的原理:(1)等式的基本性质等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立。
人教版五年级上册《简易方程复习》

7X+2=30 7X+2-2=30-2 7X=28 7X÷7=28÷7 X=4
答:地球赤道大约有4万千米。
3、食堂运来12筐土豆和15筐茄子,一共 重600千克,每筐茄子重20千克,每筐土 豆重多少千克? 解:设每筐土豆重x千克。 土豆的重量+茄子的重量=总重量 12x+15×20=600 12x+300=600 12x=600-300 12x=300 注意: x=300÷12 无单位! x=25 答:每筐土豆重25千克。
×
√
(3)方程一定是等式。
(4)a的平方等于2个a相加。 (5)a÷b中,a、b可以是任何数。
×
×
×
等量关系哪里找
• 一、“倍”、“共”、“比”中 找等量。 • 二、公式。
(1)五年级同学捐书a本,六年级同学捐 的比五年级的2倍还多12本,六年级捐书 ( 2a+12 )本。
(2)修路队x天修2.4千米的公路,平均 每天修(2.4÷x )千米。
例:7x=21
(1)25-x=15 解: x=25-15 x=10
(2) 4x=26.4 解: x=26.4÷4 x=6.6
解方程注意: 1.要写解字 2.等号对齐 3.运用等式的基本性质解题或者 运用各部分的关系解题
(3)3x-10.5=15 解:3x=10.5+15 3x=25.5 x=25.5÷3 x=8.5
15x-17 (3)x的15倍与17的差,列式为( )
(4)小红今年a岁,她的妈妈比她大25岁, 她妈妈今年( a+25 )岁,当小红15岁时, 她妈妈( 40 )岁。
含有未知数的等式叫做方程。
含有未知数
必须是等式 11.4= x+9 7-x>4 不是方程 20-13=7
人教版五年级数学上册 简易方程 知识点归纳

简易方程知识点归纳
知识点一、用字母表示数
1、在含有字母的式子中,字母与字母、数字与字母之间的乘号可以记为“.” ,也可以省略不写。
加号、减号、除号不能省略,数字与数字之间的乘号也不能省略。
例:2×a 可以写作2a ;a ×b 可以写作ab ;但2×3不能..写作2.3,也不能..
写作23 。
2、如果字母前面的数字是1,则省略这个1。
例:1a 要写成a ;1x 要写成x 。
知识点二、方程的概念
1、含有未知数的等式叫做方程。
2、使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
知识点三、天平原理
1、等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
2、等式的性质2:等式两边乘以同一个数,或除以同一个不为0的数,左右两边仍然相等。
知识点四、解简易方程的步骤
①去括号
②运用等式的性质,将带有未知数的放在左边,不带未知数的放在右边
③合并
④求出未知数的值
解方程格式的注意事项:①一开始要写上“解”字、②上下的“=”要对齐。
温馨提示:如果时间充裕,解完方程后可以将未知数的值代入原方程进行验算。
知识点五、运用方程解应用题
解题步骤:
①设x来表示未知数。
一般可以设“是”、“比”、“占”后面的量为x,或者“的”字前面的量为x,有时候也可以根据题目问什么,就设什么为x 。
②找出等量关系,列方程。
③解答。
新人教版五年级上册简易方程整理与复习

乘法方程:
5X = 21
运算方法:方程两边同时除以已知的因数
0.4x=1.2 0.6x=0.36 1.4x=0.532 2.5x=10
0.12x=2.4 2.5x=48
除法方程: (1) X ÷ 4 = 15 运算方法:方程两边同时乘除数 x÷3=2.1 x÷3.5=17 x÷21.3=0.5 x÷7.9=74
比 a 多 2的数 比a 少 2 的数 2个a相加的和
2个a相乘的积 a的2倍
a
2
2a
a+2 a-2
4.填空。
(1) a与b的和的一半是( (a+b)÷2 )。
(2) 有三个连续自然数,如果中间一个是a , 那么另外两个分别是( a-1 )和( a+1 )。 (3) 食堂买来 x千克大米,吃了 y 千克,还 剩( x- y )千克。如果 x =45, y =28,上面 的式子的值是( 17 )。 (4)一辆客车每小时行驶50km,行驶 x 小 时,共行驶了150km,请用含有字母的式 子表示三个数量之间的关系 ( 50 x =150 )。
两个未知数的方程
5.4x + x =12.8 x – 0.36x = 16
运算方法:运用乘法分配率进行运算
13.2x+9x=3.33 8x-3x=105 5.4x+x=12.8 X-0.36x=16 x+2.1x=0.775 x-0.27x=22.63
7.解方程。(任选两题检验)
10.2-5X=2.2 0.5(x+2)=3 3×1.5+6X=33 3x+1.5=13.5
数学五年级上简易方程知识点总结

总结:数学五年级上简易方程是指在一个未知数参与的方程中仅包含简单的运算符号和数值,要求学生根据题意求解出未知数的值。
简易方程是学生在初步接触代数的阶段,为培养学生逻辑思维和分析问题的能力铺垫。
下面将对数学五年级上的简易方程知识点进行总结,包括解一元一次方程和运算中的应用。
一、解一元一次方程1.一元一次方程的定义:一元一次方程是指只含有一个未知数的等式,且未知数的指数为1、例如:3x+4=72.解一元一次方程的方法:a)凑方程法:通过移项将所有未知数放在方程的一边,将常数项放在方程的另一边,然后通过具体的计算求解未知数的值。
b)记号法:通过一个符合等式的记号代替未知数,然后通过观察数值间的关系求解未知数的值。
c)试数法:根据题意,通过试探不同的数值,逐个验证是否满足方程,并找出使等式成立的未知数的值。
二、运算中的应用1.运算符号的运用:在方程中,加法、减法、乘法、除法等运算符号的使用范围广泛,学生需要根据题意适当运用运算符号完成方程。
2.带有简易方程的应用题:a)两数之和是一些数的问题:根据题意,建立方程求解未知数。
b)均分问题:将一组数均分成若干份,求解每份的数值。
c)加分问题:根据题意,通过方程解算学生其中一科成绩的得分。
d)买卖问题:根据题意,通过方程解算买卖商品的数值。
三、解题策略1.分析题意:仔细阅读题目,理解题目所给的信息,确定已知条件和未知数。
3.解方程:通过凑方程法、记号法、试数法等方法解方程,求出未知数的值。
4.检验答案:将求得的未知数代入原方程,验证是否满足等式,确保答案的正确性。
总结起来,数学五年级上简易方程的知识点包括解一元一次方程和运算中的应用。
通过掌握解方程的方法和运算符号的应用,学生可以运用数学知识解决一些实际问题,培养数学思维和逻辑推理的能力。
小学五年级数学上年末简易方程复习知识点

小学五年级数学上年末简易方程复习知识点小学是我们整个学业生涯的基础,因此大伙儿一定要培养良好的学习适应,查字典数学网为大伙儿专门提供了五年级数学上期末简易方程复习知识点。
1、(P45)在含有字母的式子里,字母中间的乘号能够记作“”,也能够省略不写。
加号、减号除号以及数与数之间的乘号不能省略。
2、a×a能够写作aa或a ,a 读作a的平方。
2a表示a+a3、方程:含有未知数的等式称为方程。
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
4、解方程原理:天平平稳。
等式左右两边同时加、减、乘、除相同的数(0除外),等式依旧成立。
5、10个数量关系式:加法:和=加数+加数一个加数=和-两一个加数减法:差=被减数-减数被减数=差+减数减数=被减数-差乘法:积=因数×因数一个因数=积÷另一个因数除法:商=被除数÷除数被除数=商×除数除数=被除数÷商6、所有的方程差不多上等式,但等式不一定差不多上等式。
7、方程的检验过程:方程左边=……8、方程的解是一个数;观看内容的选择,我本着先静后动,由近及远的原则,有目的、有打算的先安排与幼儿生活接近的,能明白得的观看内容。
随机观看也是不可少的,是相当有味的,如蜻蜓、蚯蚓、毛毛虫等,小孩一边观看,一边提问,爱好专门浓。
我提供的观看对象,注意形象逼真,色彩鲜亮,大小适中,引导幼儿多角度多层面地进行观看,保证每个幼儿看得到,看得清。
看得清才能说得正确。
在观看过程中指导。
我注意关心幼儿学习正确的观看方法,即按顺序观看和抓住事物的不同特点重点观看,观看与说话相结合,在观看中积存词汇,明白得词汇,如一次我抓住时机,引导幼儿观看雷雨,雷雨前天空急剧变化,乌云密布,我问幼儿乌云是什么模样的,有的小孩说:乌云像大海的波浪。
有的小孩说“乌云跑得飞速。
”我加以确信说“这是乌云滚滚。
”当幼儿看到闪电时,我告诉他“这叫电光闪闪。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五单元《简易方程》知识点梳理
一、用字母表示数
1.在含有字母的式子里,字母中间的乘号可以记作“•”,也可以省略不写,字母和数字相乘一般要把数字写在前面。
加号、减号、除号以及数与数之间的乘号不能省略。
2.a2读作a的平方,表示2个a相乘或a×a。
2a表示2个a相加或a+a 或2×a 。
3.用字母表运算定律。
加法交换律:a+b=b+a 加法结合律:a+b+c=a+(b+c)
乘法交换律:ab=ba 乘法结合律:abc=a(bc)
乘法分配律:(a+b)c=ac+bc
4.用字母表示计算公式。
长方形的周长公式:c=2(a+b) 长方形的面积公式:s=ab
正方形的周长公式:c=4a 正方形的面积公式:s= a2
二、等式和方程
1.等式:表示相等关系的式子叫等式。
2.等式的性质1:等式两边加上(或减去)同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
3.方程:
(1)方程:含有未知数的等式叫做方程。
(2)使方程左右两边相等的未知数的值,叫做方程的解。
(3)求方程的解的过程叫做解方程。
(4)所有的方程都是等式,但等式不一定都是方程。
(5)方程的解是一个数,解方程是一个计算过程。
4.四则运算的10个关系式:
加法:和=加数+加数一个加数=和-另一个加数
减法:差=被减数-减数被减数=差+减数减数=被减数-差乘法:积=因数×因数一个因数=积÷另一个因数
除法:商=被除数÷除数被除数=商×除数除数=被除数÷商8、方程的检验过程:
方程左边=……
=……
=方程右边
所以,X=……是方程的解。
9.方程与实际问题中常用的等量关系式。
路程=速度X 时间速度=路程÷时间时间=路程÷速度
总价=单价X 数量单价=总价÷数量数量=总价÷单价
工作总量=工作效率X 工作时间工作效率=工作总量÷工作时间工作时间=工作总量÷工作效率
总产量=单产量X 数量单产量=总产量÷数量数量=总产量÷单产量大数-小数=相差数大数-相差数=小数小数+相差数=大数一倍量X倍数=几倍量几倍量÷倍数=一倍量几倍量÷一倍量=倍数
评价测试样例
一、填空题。
1.在横线里填上“>”“<”或“=”.
(1)当x=1时,6+8xО14,(2)当x=0.8时,x﹣0.5x О0.04,(3)当x=2.5时,7x﹣3О10。
2.一本练习本b元,小强买了5本,小莹买了4本,2人一共花了()元,小强比小莹多花了()元。
3.桃子重x千克,西瓜的质量是桃子的3倍,那么3x表示的是();如果桃子和西瓜共重300千克,列成等式是()。
4.小军有m本课外书,如果分给小明4本,两人的书就一样多,小明原来有()本。
5.我们所穿的尺码通常用”码“或”厘米“作单位,它们之间的换算关系是b=2a﹣10(b表示尺码数,a表示厘米数).那么25厘米的鞋子用”码“作单位就是()码.
6.a、b都是自然数,并且a+b=26,那么a、b两数最多相差()。
7.2a表示( )或者( ),a2表示( )。
8.水果店运来x箱苹果,每箱重10千克,卖出75千克,还剩下5千克。
等量关系:(),方程:() =5 。
9.小冬兰家养了a只黑兔,养的白兔比黑兔只数的4倍还多2只。
养了()只白兔。
10.奶奶今年a岁,小玲今年(a-50)岁,过3年后,奶奶和小玲相差()岁。
11.一个两位数,它的个位上的数字是a,十位上的数字是b,那么这个两位数可写()。
12.如果A+B=35;B+C=46;A+C=59,那么A+B+C= (),A= ()。
13.用方程表示数量关系。
(1)比a多2.4的数是3.8。
()
(2)7.8除以a,商是0.6。
()
二、选择题。
1.丁丁比平平小,丁丁今年a岁,平平今年b岁,2年后丁丁比平小()岁。
A.2 B.b﹣a C.a﹣b D.b﹣a+2
2.电影院第一排有m个座位,后面一排都比前一排多1个座位.第n排有()个座位。
A.m+n
B.m+n+1
C.m+n﹣1
D.mn
3. 4x+8错写成4(x+8)结果比原来()
A.多4
B.少4
C.多24
D.少6
4.甲、乙、丙、丁四人参加某次电脑技能比赛.甲、乙两人的平均成绩为a 分,他们两人的平均成绩比丙的成绩低9分,比丁的成绩高3分,那么他们四人的平均成绩为()分。
A.a+6
B.4a+1.5
C.4a+6
D.a+1.5
5.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出8千克放入乙袋,那么甲、乙两袋质量相等.列成等式是()。
A.a+8=b﹣8
B.a﹣b=8×2
C.(a+b)÷2=8
D.a﹣8=b
三、判断题。
1.方程的解和解方程的意义相同。
()
2.如果a﹣b=5,b﹣c=2,那么a﹣c=7.()
3.方程一定是等式,但等式不一定是方程.()
4.13除a与b的和,商是多少?列式为13÷a+b。
()
四、计算题。
1.直接写得数。
0.27×5= 2.8÷0.7= 12.5×8= 0.25×4= 9.9÷99=
0.42×100= 6÷1000= 14.7÷7= 0.6×0.5= 2-0.23= 2.解方程。
2.7×2-1.5x=0 13x-6.8x+x=46.8
2.6x-6.5+
3.5=10 2×(x-0.7)=
4.8
3.用简便方法计算。
①4×0.8×2.5×12.5 ②0.65×14+87×65%-65%
③42÷[14-(50-39)] ④2.25×4.8+77.5×0.48
五、用方程解决问题。
1.“摄氏度”和“华氏度”都是用来计量温度的单位.它们之间的换算关系式是“华氏度=32+摄氏度×1.8”,如果某人的体温测得是华氏温度101.48度,那么也就是多少摄氏度呢?
2.鸡兔同笼,共有头71个,鸡的脚比兔的脚少98只,问鸡、兔各几只?
3.手机付费有下面两种方式,请你帮爸爸选一选。
A种:无月租费,每分0.10元
B种:月租费20元,每3分0.20元
(1)假设爸爸每月通话时间是a分,请分别表示出爸爸每月的通话费用。
(2)假设爸爸每月通话450分,他应选择哪种付费方式?需要多少元?(3)假设爸爸每月通话为750分,他应选择哪种付费方式?需要多少元?
4.南京到上海距离312km,一列快车从南京开往上海,一列慢车从上海开往南京,慢车比快车早1.4小时出发,快车走了2.2小时相遇到慢车,已知快车比慢车每小时多行10km,相遇时两车各行多少km?。
