求下面图形阴影部分的面积(单位CM)
五年级数学上册期中专项练习:求阴影部分的面积(解析版)苏教版

2022-2023学年五年级数学上册典型例题系列之期中专项练习:求阴影部分的面积(解析版)一、填空题。
1.下图中阴影都分的面积是( )平方厘米。
(单位:厘米)【答案】52【分析】观察图可知:题中阴影部分的面积=梯形面积-空白三角形的面积,根据梯形面积公式S=(a+b)×h÷2和三角形面积公式S=ah÷2,代入数值计算即可。
【详解】(9+13)×8÷2-9×8÷2=22×8÷2-36=88-36=52(平方厘米)【点睛】本题考查梯形面积公式和三角形面积公式的应用,关键是熟记公式。
2.图中的ABCD是长方形,长BC=8厘米,宽AB=5厘米,ABDE是梯形,△BDE的面积是()平方厘米。
【答案】20【分析】通过观察图形可知,三角形ABE与三角形AED是同底等高的三角形,所以面积相等,因此,阴影面积为长方形ABCD面积的一半,根据长方形的面积公式:S=ab,把数据代入公式解答即可。
【详解】长方形ABCD的面积为:8×5=40(平方厘米)三角形ABE与三角形AED是同底等高的三角形,所以面积相等,即三角形ABD 的面积等于阴影面积,因此,阴影面积为长方形ABCD面积的一半。
所以阴影部分的面积是:40÷2=20(平方厘米)【点睛】此题解答的关键是根据同底等高的三角形的面积相等,推出三角形ABE与三角形AED相等,进而推出阴影部分的面积是长方形ABCD面积的一半。
3.下图中长方形的面积是24cm²,那么阴影部分的面积是( )cm²。
【答案】12【分析】长方形的面积=长×宽,三角形的面积=底×高÷2;图中长方形的长相当于三角形的底,长方形的宽相当于三角形的高,据此可知,阴影部分的面积等于长方形面积的一半;据此计算即可。
【详解】24÷2=12(平方厘米)4.如图,平行四边形的底是12厘米,高是8厘米,图中阴影部分的面积是( )平方厘米。
五年级数学上册《阴影图形面积》练习题带答案

五年级数学上册《阴影图形面积》练习题带答案1、求梯形中阴影部分的面积。
(单位:厘米)(32+18)×15÷2-32×15÷2=375-240=135(平方厘米)答:阴影部分的面积是135平方厘米。
2、求图中阴影部分的面积。
(单位:厘米)已知平行四边形面积是24平方厘米。
24-(5+6)×4÷2=2(平方厘米)答:阴影部分的面积是2平方厘米。
3、求图中阴影部分的面积。
(单位:厘米)6×6+4×4-6×6÷2-4×10÷2=14(平方厘米)答:阴影部分的面积是14平方厘米。
4、下图是平行四边形,面积是36平方米,求阴影部分的面积。
(单位:米)36÷6=6(米)6-1.5=4.5(米)4.5×6÷2=13.5(平方米)答:阴影部分的面积是13.5平方米。
5、如图,一个梯形的上、下底分别是6厘米、10厘米,已知阴影部分的面积是24平方厘米,这个梯形的面积是?三角形的高:24×2÷10=4.8(厘米),梯形面积:(6+10)×4.8÷2=38.4(平方厘米)答:这个梯形的面积是38.4平方厘米。
6、求下图阴影部分的面积(单位:厘米)阴影部分面积=大三角形面积+ 小三角形面积= (6×6÷2)+(3×6÷2)=(36÷2)+(18÷2)= 18 + 9= 27(cm²)7、求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×2²-2×1=1.14(平方厘米)8、正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以r²=7,所以阴影部分的面积为:7-r²=7-×7=1.505平方9、求阴影部分的面积。
小升初数学几何求阴影部分面积题带解析
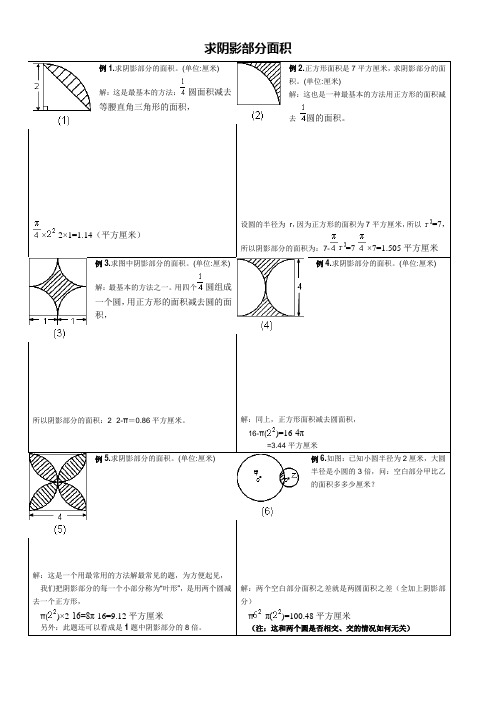
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
小学六年级-阴影部分面积及答案完整
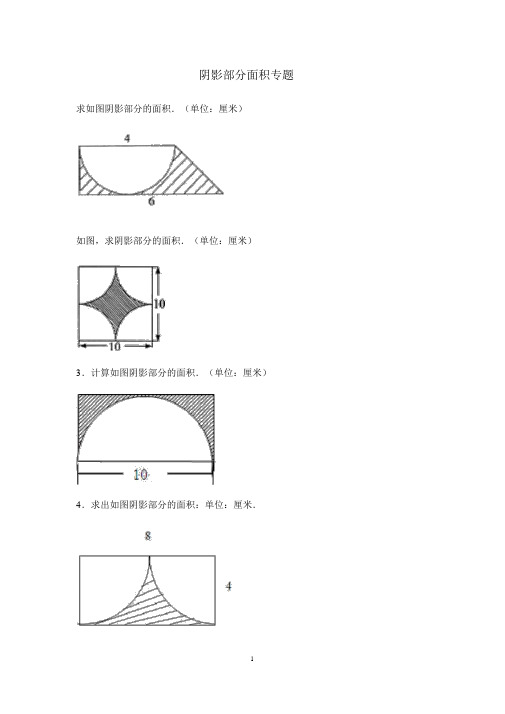
阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.1526356分析阴影部分的面积等于梯形的面积减去直径为 4 厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:( 4+6)× 4÷2÷2﹣3.14 ×÷2,=10﹣3.14 ×4÷2,=10﹣6.28 ,=3.72 (平方厘米);答:阴影部分的面积是 3.72 平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析根据图形可以看出:阴影部分的面积等于正方形的面积减去 4 个扇形的面积.正方形的面积等于( 10×10)100 平方厘米, 4 个扇形的面积等于半径为( 10÷2) 5 厘米的圆的面积,即: 3.14 ×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14 ×5×5,100﹣78.5 ,=21.5 (平方厘米);答:阴影部分的面积为21.5 平方厘米.点评解答此题的关键是求 4 个扇形的面积,即半径为 5 厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析分析图后可知, 10 厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解: 10÷2=5(厘米),长方形的面积 =长×宽 =10×5=50(平方厘米),22(平方厘米),半圆的面积 =πr÷2=3.14×5÷2=39.25阴影部分的面积 =长方形的面积﹣半圆的面积,=50﹣39.25 ,=10.75 (平方厘米);答:阴影部分的面积是10.75 .点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积. 1526356专题平面图形的认识与计算.分析由题意可知:阴影部分的面积 =长方形的面积﹣以 4 厘米为半径的半圆的面积,代入数据即可求解.2解答解: 8×4﹣3.14 ×4÷2,=32﹣25.12 ,=6.88 (平方厘米);答:阴影部分的面积是 6.88 平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.考点圆、圆环的面积. 15263564个直径为 4厘分析由图可知,正方形的边长也就是半圆的直径,阴影部分由米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1 个圆的面积,然后根据“阴影部分的面积 =2×圆的面积”算出答案.2解答解: S=πr2=3.14 ×( 4÷2)阴影部分的面积 =2 个圆的面积,=2×12.56 ,=25.12 (平方厘米);答:阴影部分的面积是25.12 平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积. 1526356 分析图一中阴影部分的面积 =大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积 =梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积 =(8+15)×( 48÷8)÷ 2﹣ 48=21(平方厘米);答:图一中阴影部分的面积是 6 平方厘米,图二中阴影部分的面积是 21 平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积= 圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径: 15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14 ×122,=×3.14 ×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04 平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积. 1526356 分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积 =圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:( 1)阴影部分面积:3.14 ×﹣3.14×,=28.26 ﹣3.14 ,=25.12 (平方厘米);(2)阴影部分的面积:23.14 ×3﹣×(3+3)× 3,=28.26 ﹣9,=19.26 (平方厘米);答:圆环的面积是25.12 平方厘米,阴影部分面积是19.26 平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积. 1526356专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5 厘米为半径的半圆的面积﹣以3÷2=1.5 厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长: 3.14 ×( 10+3),=3.14 ×13,=40.82 (厘米);面积:×3.14 ×[(10+3)÷2] 2﹣×3.14 ×(10÷2)2﹣×3.14 ×(3÷2)2,=×3.14 ×( 42.25 ﹣25﹣2.25 ),=×3.14 ×15,=23.55 (平方厘米);答:阴影部分的周长是40.82 厘米,面积是 23.55 平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长 =πr ,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积. 1526356分析先用“ 3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积 =阴影部分的面积”解答即可.解答解: r=3 , R=3+3=6, n=120,,=,=37.68 ﹣9.42 ,=28.26 (平方厘米);答:阴影部分的面积是28.26 平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析先求出半圆的面积 3.14 ×( 10÷2)2÷2=39.25 平方厘米,再求出空白三角形的面积 10×( 10÷2)÷ 2=25 平方厘米,相减即可求解.2=39.25 ﹣25=14.25 (平方厘米).答:阴影部分的面积为14.25 平方厘米.点评考查了组合图形的面积,本题阴影部分的面积 =半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积. 1526356分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.2解答解:( 4+10)× 4÷2﹣3.14 ×4 ÷4,=15.44 (平方厘米);答:阴影部分的面积是15.44 平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积. 1526356专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为 10 厘米和 15 厘米,三角形①的底和高分别为 10 厘米和( 15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解: 10×15﹣10×( 15﹣7)÷ 2,=150﹣ 40,=110(平方厘米);答:阴影部分的面积是110 平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积. 1526356分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:( 6+10)× 6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48 平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积. 1526356分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解: 2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是 3 平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答2=13×4÷2﹣3.14 ×4,=26﹣12.56 ,=13.44 (平方厘米);答:阴影部分的面积是13.44 平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积 =梯形的面积﹣圆的面积.17.( 2012?长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积. 1526356分析由图可知,阴影部分的面积 =梯形的面积﹣半圆的面积.梯形的面积 = (a+b)2h,半圆的面积 = πr,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2= ×14×3﹣×3.14×9,=21﹣14.13 ,=6.87 (平方厘米);答:阴影部分的面积为 6.87 平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
求下列图形阴影部分的面积

一、阴影部分的面积=总面积—空白在一长方形草地里有一条宽1米的曲折小路,如图所示,小路的面积是平方米.• A. 10• B. 20• C. 301、如图是创意广告公司为某商品设计的商标图案,图中阴影部分为红色,若每个小长方形面积是1,则阴影面积是8.如图所示,每个小正方格的面积都是1平方厘米,阴影部分的面积是.2、求下列图形阴影部分的面积.3、如图,已知长方形面积是56平方厘米,A、B分别是长和宽的中点,则阴影部分的面积是多少平方厘米.4、.如图,阴影部分的面积为.(单位:厘米).5、如图,图中阴影的面积是3 .6、小丽用一张黄色纸剪了一个大写英文字母“M”,求它的面积是多少?(单位:cm)7、.如图,B、C分别是正方形边上的中点,己知正方形的周长是80厘米.阴影部分的面积是多少平方厘米.8、图中长方形的面积是180平方厘米,S1与S2的面积都是60平方厘米,阴影部分的面积是多少平方厘米?二、等量代换1、.某小区有一块如图所示的梯形空地,根据图中的数据计算,空地的面积是多少平方米.2.如图,四边形ABCD的面积是多少平方厘米?2.如图是两个一样的直角三角形重叠在一起,图中阴影部分面积是多少?3.如图,长方形ABCD中,AB=12厘米,BC=8厘米,平行四边形BCEF的一边BF交CD于G,若梯形CEFG的面积为64平方厘米,则DG长为多少厘米?4、如图,在平行四边形中,已知甲的面积8平方厘米,丙的面积15平方厘米,那么乙的面积是23平方厘米.5.如图是两个一样的直角三角形重叠在一起,图中阴影部分面积是多少?6、如图,长方形ABCD中,AB=12厘米,BC=8厘米,平行四边形BCEF的一边BF交CD于G,若梯形CEFG的面积为64平方厘米,则DG长为_____.7.如图所示是两个相同的直角梯形重叠在一起,求阴影部分的面积.(单位:厘米)8、如图中阴影甲的面积比阴影乙的面积大多少三、同加同减差不变1、如图,甲、乙两个阴影部分的面积比较,结果是()4.在图中的平行四边形中,甲的面积()乙的面积.如图梯形ABCD中,两个阴影部分的面积关系是A. s1=s2B. s1>s2C. s1<s22、如图,边长为4cm的正方形将边长为3cm的正方形遮住了一部分,则空白部分的面积的差等于多少cm2.3、.如图中阴影甲的面积比阴影乙的面积大多少?4、如图ABCD是长方形,已知AB=4厘米,BC=6厘米,三角形EFD的面积比三角形ABF的面积大6平方厘米,求ED=()厘米.5.如图,BCEF是平行四边形,三角形ABC是直角三角形,BC长8厘米,AC长7厘米,阴影部分面积比三角形ADH的面积大12平方厘米.求HC的长度.四、巧添辅助线1.如图,已知一个四边形的两条边的长度和它的三个角的度数.那么这个四边形的面积是多少平方厘米.五、巧妙利用“一半”1.比大小.(1)甲的周长()乙的周长;(2)甲的面积()乙的面积.2、如图:平行四边形的面积是16cm2,阴影部分的面积是多少cm2.3.如图所示,甲、乙两图中的两个大正方形和两个小正方形的边长分别相等,甲和乙两幅图的阴影面积相比,甲()乙4、如图,涂色部分面积是长方形面积的()5.如图阴影部分的面积与空白部分的面积相比较,它们()6.如图,平行四边形的面积是3.6平方厘米,阴影部分的面积是7、图中阴影部分的面积是空白部分面积的()8.如图,空白部分面积是阴影部分面积的()9、如图,平行四边形的面积是28平方厘米,阴影部分的面积是多少平方厘米.10.如图,星星家有一块平行四边形的菜地,面积是124平方米,其中阴影部分种黄瓜,那么黄瓜的种植面积是多少平方米.11.如图正方形边长为5厘米,长方形的面积是多少平方厘米.12.如图,正方形ABCD的边长是8厘米,长方形DEFG的长DG=10厘米,则它的宽DE的长是六、推导法1、求图中阴影部分的面积.(1)如图1(2)如图2 已知梯形的面积是60平方米.2、.如图,大小两个正方形拼在一起,阴影部分面积为28平方厘米,小正方形边长为4厘米,则图中空白部分的面积是()平方厘米.3.如图,正方形的周长是16厘米,三角形的面积是多少平方厘米.4、如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少平方厘米?5、将边长为8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面积是43.2平方厘米.6、.已知△ABC的面积是180平方厘米,AC长18厘米,CE长8厘米,则阴影部分的面积是多少平方厘米.7.把一个梯形分成一个三角形和一个平行四边形(如图).已知平行四边形的面积是12平方厘米,三角形的面积是平方厘米.8、如图,梯形的上底是8厘米,下底6厘米,阴影部分的面积是12平方厘米,空白部分的面积是多少平方厘米.9、求右图中直角三角形ABC中阴影部分面积以及BD长度(cm),AE=EF=FC.10、比较下面三个图形中阴影部分的面积大小,则A.甲与丙相等B.甲与乙相等C.乙与丙相等D.无法比较11、如图三个图都是由边长为4厘米和3厘米的两个正方形组成的,阴影部分的面积是A.①>③>②B.②>①>③C.③>①>②13、下图中的两个正方形的边长分别为8厘米和5厘米,求阴影部分的面积.14、如图,阴影部分的面积是多少平方厘米.15、.图中,将两个正方形放在一起,大正方形面积为94,则△ABC的面积为多少16、如图中,两个正方形的边长分别是5厘米和3厘米,阴影部分的面积是A.19平方厘米B.20平方厘米17、图中的两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积.18.已知如图阴影部分的面积是3平方厘米,则两个正方形中较小的正方形的面积为.6.如图中,小正方形边长为1分米,大正方形边长为2分米,阴影部分面积是多少?9.大正方形的边长10厘米,小正方形的边长5厘米,下面的图形中阴影部分面积一样大的图形有19.如图,直角梯形A BCD的上底与高相等,正方形DEFH的边长等于6厘米,阴影部分的面积是多少平方厘米.20.如图,甲和乙是两个正方形,阴影部分的面积是平方厘米.21、在长方形ABCD中,E是AD边上的三等分点,DE=2AE,BD、CE将长方形分成四部分,两个三角形的面积已给出,则阴影部分的面积是多少?(答案11)21、如图所示:E、F、G和H分别是梯形每条边的中点,那么下面有图形的阴影部分面积是原来梯形面积的一半.A.4个B.3个C.2个D.1个22、长方形ABCD周长为16米,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积之和是68平方米,求长方形ABCD的面积.4.边长为8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面积是多少平方厘米.26.下面哪些图形的阴影部分面积是相等的?(每个小正方形的边长相等)7.图中阴影部分的面积是.8.求图形面积.(单位:厘米)6.求下列阴影部分的面积.(单位:厘米)四个正方形A 、B 、C 、D 如图放置,其中正方形A 的周长是12厘米,正方形D 的周长是60厘米,则阴影部分的面积会为多少平方厘米.5.如图,长方形ABCD 中,AB=67,BC=30.E 、F 分别是AB 、BC 边上的两点,BE+BF=49.那么,三角形DEF 面积的最小值是( ).设AE=x ,则BE=67-x ,BF=49-(67-x )=x-18,CF=30-(x-18)=48-x . 三个直角三角形面积和是21[30x+(67-x)(x-18)+(48-x)67]=21[2010+x(48-x)],要想让三角形DEF 面积最小,只需三个直角三角形面积之和最大,显然x=24,则三个直角三角形面积和是21(2010+242)=1293,进行解答即可.解答设AE=x ,则BE=67-x ,BF=49-(67-x )=x-18,CF=30-(x-18)=48-x . 三个直角三角形面积和是21[30x+(67-x)(x-18)+(48-x)67]=21[2010+x(48-x)], 当x=24,则三个直角三角形面积和是21(2010+242)=1293,则三角形DEF 面积是2010-1293=717;故答案为:717.点评此题较难,解答此题的关键是:要想让三角形DEF 面积最小,只需三个直角三角形面积之和最大,进而解答即可.。
(完整版)小学六年级求阴影部分面积试题和答案
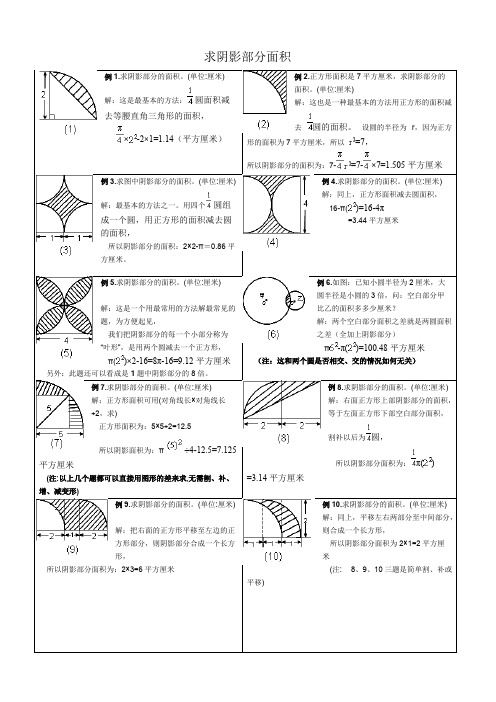
tat i me an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法: 圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r ,因为正方形的面积为7平方厘米,所以 =7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个 圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积, 16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形, π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
小学六年级圆_阴影部分面积含答案
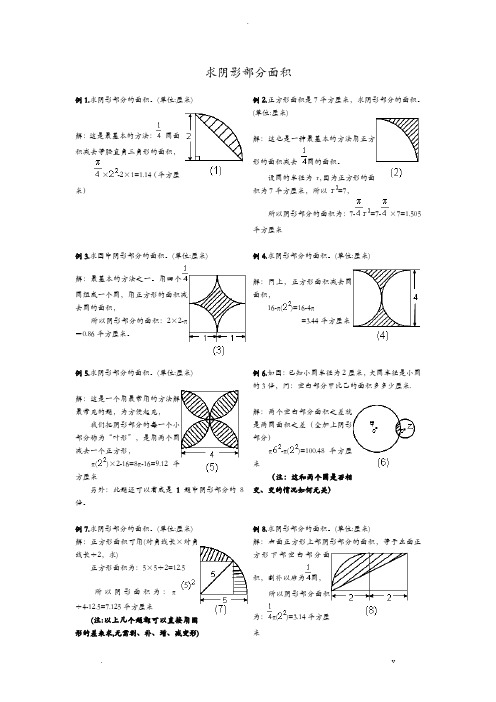
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米.解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
五年级上册苏教版第二单元多边形的面积图形计算易错题(附带答案及解析)

五年级上册苏教版第二单元多边形的面积图形计算易错题一、图形计算1.求下面组合图形的面积(单位:cm).(1)(2)(3)(4)2.计算下面三角形的面积.(1)(2)(3)(4)3.计算下面梯形的面积.(1)(2)4.求下面组合图形的面积。
(单位:cm)(1)(2)5.如下图,梯形的面积是156平方厘米,你能求出阴影三角形的面积吗?6.求下图阴影部分的面积.7.看图计算面积(单位:厘米)8.求图中阴影部分的面积.(单位:米)(1)(2)9.计算下面图形的面积.10.11.下面图形中阴影部分的面积是25平方厘米,求出梯形的面积.12.计算下面图形阴影部分的面积.(单位:米)13.已知如图梯形中阴影部分的面积是10平方厘米,试求梯形的面积。
(单位:厘米)14.求下面图形中阴影部分的面积.15.计算下面图形中阴影部分的面积。
(单位:厘米)16.计算下列图形的面积.(单位:cm)1. 2.17.求下图阴影部分面积.18.下图中每个小方格的面积表示1 cm2,请你估估阴影部分的面积.(1)(2)参考答案:1.(1)25×18+25×15÷2=637.5(cm2)(2)(20+45)×36÷2-20×10÷2=1070(cm2)(3)(15+20)×10÷2+20×10÷2=275(cm2)(4)20×15-12×9÷2=246(cm2)【解析】【详解】略2.(1)45 cm2(2)24 cm2(3)140 dm2(4)135 m2【解析】【详解】略3.(1)81 dm2(2)180 m2【解析】【详解】略4.(1)800cm2(2)109cm2【解析】【分析】(1)把图形分成一个底是32cm,高是20cm的平行四边形面积+底是32cm,高是10cm的三角形面积,根据平行四边形面积公式:底×高,三角形面积公式:底×高÷2,代入数据,即可解答;(2)把图形面积分成长是12cm,宽是10cm的长方形面积-上底是3cm,下底是8cm,高是2cm的梯形面积,根据长方形面积公式:长×宽,梯形面积公式:(长+宽)×高÷2,代入数据,即可解答。
小学六年级阴影部分面积及答案完整

阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012?长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
小学六年级阴影部分面积及答案完整

阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3。
14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3。
72(平方厘米);答:阴影部分的面积是3。
72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3。
14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78。
求阴影部分面积(五年级,含答案)
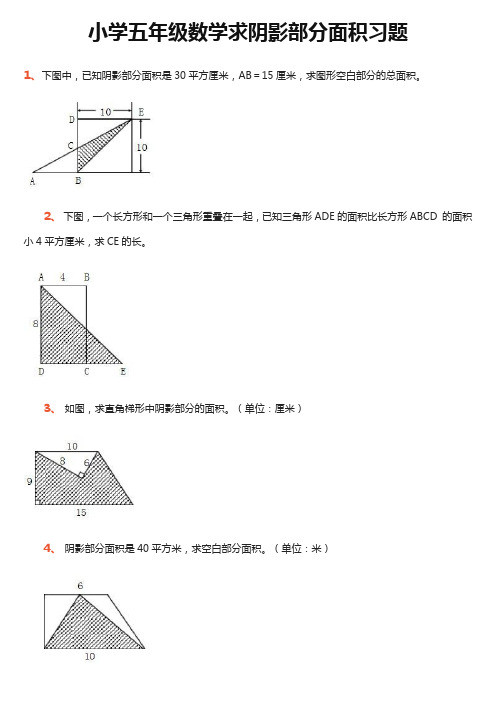
小学五年级数学求阴影部分面积习题1、下图中,已知阴影部分面积是30平方厘米,AB=15厘米,求图形空白部分的总面积。
2、下图,一个长方形和一个三角形重叠在一起,已知三角形ADE的面积比长方形ABCD 的面积小4平方厘米,求CE的长。
3、如图,求直角梯形中阴影部分的面积。
(单位:厘米)4、阴影部分面积是40平方米,求空白部分面积。
(单位:米)5、求下图阴影部分的面积。
(单位:厘米)6、下图,ABCD是直角梯形,已知AE=EF=FD,AB为6厘米,BC为10厘米,阴影部分面积为6平方厘米。
求直角梯形ABCD的面积。
7、下图是由一个三角形和一个梯形组成,已知三角形的面积是1平方分米,求这个图形的面积。
(单位:分米)8、如图,平行四边形面积240平方厘米,求阴影部分面积。
9、下图ABCD是梯形,它的面积是140平方厘米,已知AB=15厘米,DC=5厘米。
求阴影部分的面积。
10、求下面阴影部分的面积(单位:厘米)11、如图,求长方形中的梯形面积。
(单位:厘米)12、求下图阴影部分的面积(单位:厘米)13、求梯形的面积。
(单位:厘米)14、如图,已知梯形ABCD的面积为37.8平方厘米,BE长7厘米,EC长4厘米,求平行四边形ABED 的面积。
15、求空白部分面积。
(单位:厘米)16、如图,已知平行四边形ABCD中,阴影部分面积为72平方厘米,求三角形BCD的面积。
17、求梯形中阴影部分的面积。
(单位:cm)18、下图,ABCD是一个等腰梯形,ADFE是边长为4厘米的正方形,CF=2厘米,求阴影部分的面积。
19、下图ABCD是梯形,它的面积是200平方厘米,已知AB=20厘米,DC=5厘米,求阴影部分的面积。
(单位:厘米)20、在平行四边形ABCD中,CE上的高是6厘米,AD=8厘米,BE=11厘米,求三角形ABC 的面积。
21、在下图中,已知直角梯形ABCD的面积是60平方厘米,DC长6厘米,AB长24厘米,求:三角形AED的面积。
人教版小学数学五年级上册6.《求阴影部分面积》重点考点(含答案)

人教版小学数学五年级上册6.《求阴影部分面积》重点考点(含答案)五年级上册数学重点考点求阴影部分面积(知识点:平行四边形的面积三角形的面积梯形的面积组合图形的面积)1.计算下面图形的面积。
2.求下图阴影部分的面积。
(单位:厘米)3.如图是两个正方形,求阴影部分的面积(单位:厘米)。
4.将一张长方形纸如图折叠,求图中阴影部分面积。
(单位:cm)5.计算图中阴影部分的面积。
(单位:cm)6.有一张长方形纸,把纸的一角如图那样折叠,求图中阴影部分的面积。
7.寻找合适的条件,求出下图中涂色部分的面积。
(单位:cm)8.下图梯形中,阴影部分面积是24平方分米,求梯形面积。
9.求如图中阴影部分的面积。
(单位:厘米)10.已知阴影部分面积是24cm2,求梯形面积。
11.求阴影部分的面积。
(单位:米)12.计算阴影部分的面积。
(单位:dm)13.计算图形中阴影部分的面积。
14.求出阴影部分的面积。
(单位:cm)15.求涂色部分的面积。
16.计算阴影部分的面积。
(1)(2)17.求下列阴影部分的面积。
(单位:cm)18.求阴影部分面积。
19.求下面图形中阴影部分的面积。
(单位:cm)20.求阴影部分的面积。
21.求阴影部分的面积。
(单位:分米)22.求阴影部分的面积。
(单位:cm)23.求阴影部分的面积。
(单位:分米)24.求阴影部分的面积。
参考答案:1.100平方厘米【分析】要求的图形面积可以看作是一个长为15厘米,宽为10厘米的长方形面积减去两个底为5厘米,高为5厘米的三角形面积和一个边长为5厘米的正方形的面积之和,再根据长方形面积=长×宽,正方形面积=边长×边长,三角形面积=底×高÷2,代入相应数值计算,即可解答。
【详解】(平方厘米)【点睛】本题主要考查的是组合图形面积的计算,解题关键是先分析都是由哪些基本图形组成,再根据相应图形面积的计算公式,代入数值计算即可。
2.144平方厘米【分析】用长方形的面积减去梯形的面积即是阴影部分的面积,分别利用长方形的面积=长×宽和梯形的面积=(上底+下底)×高÷2求解。
100例圆图形中阴影部分的面积附答案

图形中阴影部分的面积1.求阴影部分的面积(1)(2)2.求下面各图中阴影部分的面积。
(单位:cm)(1)(2)3.求图中阴影部分的周长和面积。
(单位:cm)4.计算下面各图形中阴影部分的周长与面积(1)(2)5.求阴影部分的面积。
6.求阴影部分的周长和面积。
7.计算下图阴影部分的面积。
8.求阴影部分的面积。
(单位:厘米)9.求阴影部分的面积。
10.计算下面图形阴影部分的面积。
11.计算下列图形阴影部分的面积。
12.求阴影部分的周长和面积。
(单位:cm)13.求左图阴影部分的周长,右图阴影部分的面积。
14.求图中阴影①比阴影②少多少平方厘米?(单位:厘米)15.认真观察下图,求出图1的周长,图2阴影部分的面积。
(1)(2)16.通过计算,比较下面两图阴影部分的周长和面积。
(单位:cm)①②17.下图中阴影部分的周长是多少cm?(单位:cm)18.下图中圆的面积与长方形的面积相等.已知圆的周长是6.28厘米,图中阴影部分的面积你会求吗?19.求阴影部分面积。
20.求阴影部分面积。
(单位:米)21.计算阴影部分的面积。
(1)(2)22.求下面图形阴影部分的面积。
(1)(2)23.求阴影部分的面积。
(1)(2)24.求下图阴影部分的周长。
25.求阴影部分的面积。
(单位:cm)26.求阴影部分的面积。
(单位:cm)27.求阴影部分的面积(单位:cm)28.求出阴影部分的面积。
(单位:厘米)29.求下图中阴影部分的面积。
30.求阴影部分的面积。
(单位:分米)31.看图求阴影部分的面积。
32.求下面图形阴影部分的面积(单位:cm)。
33.求阴影部分的周长和面积。
34.求图中阴影部分的面积。
(单位:m)35.计算下侧图形阴影部分的面积。
36.求下列图中阴影部分面积。
(单位:分米)37.求阴影部分的面积。
38.求阴影部分的面积。
39.求阴影部分面积。
40.求下图中阴影部分的面积。
(单位:厘米)41.求阴影部分的面积。
100例小学数学图形中阴影部分的面积附答案
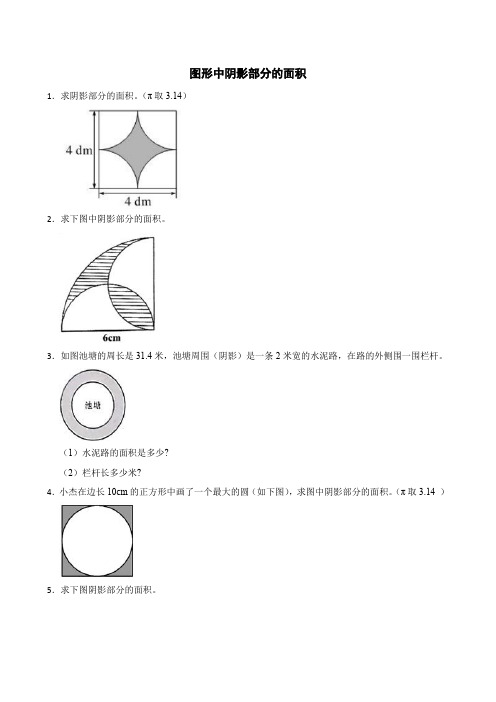
图形中阴影部分的面积1.求阴影部分的面积。
(π取3.14)2.求下图中阴影部分的面积。
3.如图池塘的周长是31.4米,池塘周围(阴影)是一条2米宽的水泥路,在路的外侧围一围栏杆。
(1)水泥路的面积是多少?(2)栏杆长多少米?4.小杰在边长10cm的正方形中画了一个最大的圆(如下图),求图中阴影部分的面积。
(π取3.14 )5.求下图阴影部分的面积。
6.求图中阴影部分的面积.(单位:厘米)7.求阴影部分的面积。
(单位:厘米)8.求下图阴影部分的面积。
(单位:分米)9.求下图中阴影部分的面积。
(单位:米)10.如下图,求阴影部分的面积。
11.求下图阴影部分的面积.(单位:厘米)12.求出下图阴影部分的面积。
13.下图中三个圆的周长都是25.12厘米,不用测量。
计算图中阴影部分的总面积。
14.计算图中阴影部分的面积.(单位:厘米)15.求各图中阴影部分的面积.(单位:cm)(1)(2)16.求阴影部分的面积。
17.求下列图形阴影部分的面积。
(单位:厘米,π≈3.14)(1)(2)18.求下面图形阴影部分的周长和面积。
19.计算如图中阴影部分的面积.20.甲、乙两图中正方形的面积都是40cm2,阴影部分的面积哪一块大?大多少?21.求下图中阴影部分的面积。
(单位:m)(1)(2)22.求阴影部分的面积。
(1)(2)23.求阴影部分的面积。
24.求阴影部分的面积。
25.如图:圆的直径是6dm,阴影部分的面积是多少?26.计算阴影部分的周长和面积27.求下图中阴影部分的面积。
(1)R=10cm,r=4cm (2)28.计算阴影部分的周长和面积29.求阴影部分的周长。
(单位:cm)30.下图中,正方形的边长是4cm,求阴影部分的面积。
31.在半径为4厘米的圆中有两条直线垂直相交(如图),比较该图中阴影部分的面积与空白部分面积的大小,谁大?大多少?32.分别以直角三角形ABC的三条边为直径画了三个半圆,得到下图。
小学六年级数学面积计算讲解提高练习(附答案及解析)

面积计算(一)一、知识要点计算平面图形的面积时,有些问题乍一看,在已知条件与所求问题之间找不到任何联系,会使你感到无从下手。
这时,如果我们能认真观察图形,分析、研究已知条件,并加以深化,再运用我们已有的基本几何知识,适当添加辅助线,搭一座连通已知条件与所求问题的小“桥”,就会使你顺利达到目的。
有些平面图形的面积计算必须借助于图形本身的特征,添加一些辅助线,运用平移旋转、剪拼组合等方法,对图形进行恰当合理的变形,再经过分析推导,方能寻求出解题的途径。
二、精讲精练【例题1】已知如图,三角形ABC的面积为8平方厘米,AE=ED,BD=2/3BC,求阴影部分的面积。
练习1:1、如图,AE=ED,BC=3BD,S△ABC=30平方厘米。
求阴影部分的面积。
2、如图所示,AE=ED,DC=1/3BD,S△ABC=21平方厘米。
求阴影部分的面积。
3、如图所示,DE=1/2AE,BD=2DC,S△EBD=5平方厘米。
求三角形ABC的面积。
【例题2】两条对角线把梯形ABCD分割成四个三角形,如图所示,已知两个三角形的面积,求另两个三角形的面积各是多少?练习2:1、两条对角线把梯形ABCD分割成四个三角形,(如图所示),已知两个三角形的面积,求另两个三角形的面积是多少?2、已知AO=1/3OC,求梯形ABCD的面积(如图所示)。
【例题3】四边形ABCD的对角线BD被E、F两点三等分,且四边形AECF的面积为15平方厘米。
求四边形ABCD的面积(如图所示)。
练习3:1、四边形ABCD的对角线BD被E、F、G三点四等分,且四边形AECG的面积为15平方厘米。
求四边形ABCD的面积(如图)。
2、如图所示,求阴影部分的面积(ABCD为正方形)。
【例题4】如图所示,BO=2DO,阴影部分的面积是4平方厘米。
那么,梯形ABCD的面积是多少平方厘米?练习4:1、如图所示,阴影部分面积是4平方厘米,OC=2AO。
求梯形面积。
2、已知OC=2AO,S△BOC=14平方厘米。
