BP神经网络PID控制器流程图
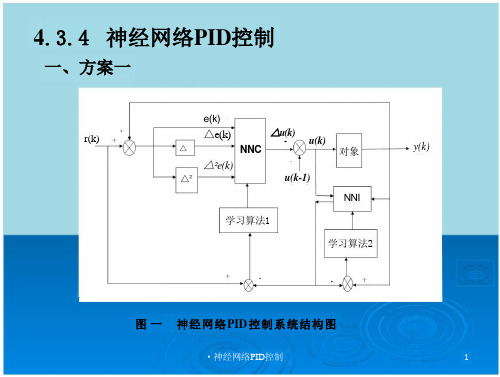
神经网络PID控制
NNI
十
十
x₁(k)=e(k)x₂(k)=△e(k)=e(k)-e(k-1)x₃(k)=△²e(k)=e(k)-2e (k-1)+e(k-2)e(k)=r(k)-y(k)NNC 的输出为:△u(k)=k₁x₁(k)+k₂x₂(k)+k₃x₃(k)式中,}i=1,2,3 为权系数,△u(k) 为输入信号的加权和。由此可见,NNC 具有增量D 控制的结构
i=1,2,…,Q-1
BP网络的输入层节点的输为
网络的隐含层输入、输为
·神经网络PID控制 20
o(k)=1
(13)
(14)
式中o 为输出层权系数 阈值,
网络的输出层的输入输出为
·神经网络PID控制 21
图二 神经网络PID控制系统结构图
·神经网络PID控制 17
二、方案二
被控对象
u
个
经典PID控制算式为u(k)=u(k-1)+Kp[e(k)-e(k-1)]+K,e(k)+K,[e(k)-2e(k-1) + e(k-2)1
7.由(20)式,计算修正输出层敝系数。(k);8.由(21)式,计算修正隐含层敝系数。)(k);9.置k=k+1, 返回到“3”,直到性能指标J 满足要求。
·神经网络PID控制 26
系数a(k)是慢时变的,a(k)=1.2(1-0.8e -01k),神经网络结构为4—5—3,输入层的个神经元分别为模型翰入r(k)、 输 出(k)、误 差(k)和常量。学习速率=0.25,动量系数=0.05,加权系数初始值取随[=0.50.5]上的随机数。当输入信号为幅值是的正弦信号(t)sin(2πt)时,取采样时间为.001s,仿真结果如图所示。·神经网络PID控制 27
基于BP神经网络的PID控制器的设计

基于BP神经网络的PID控制器的研究与实现课程名称:人工神经网络目录前言 (2)一、BP神经网络 (3)二、模拟PID控制系统 (5)三、基于BP神经网络的PID控制器 (6)四、仿真程序 (10)五、运行结果 (17)六、总结 (18)参考文献 (19)前言人工神经网络是以一种简单神经元为节点,采用某种网络拓扑结构构成的活性网络,可以用来描述几乎任意的非线性系统。
不仅如此,人工神经网络还具有学习能力、记忆能力、计算能力以及各种智能处理能力,在不同程度和层次上模仿人脑神经系统的信息处理、存储和检索的功能。
不同领域的科学家,对人工神经网络有着不同的理解、不同的研究内容,并且采用不同的研究方法。
对于控制领域的研究工作者来说,人工神经网络的魅力在于:①能够充分逼近任意复杂的非线性关系,从而形成非线性动力学系统,以表示某种被控对象的模型或控制器模型;②能够学习和适应不确定性系统的动态特性;③所有定量或定性的信息都分布储存于网络内的各神经单元,从而具有很强的容错性和鲁棒性;④采用信息的分布式并行处理,可以进行快速大量运算。
对于长期困扰控制界的非线性系统和不确定性系统来说,人工神经网络无疑是一种解决问题的有效途径。
正因为如此,把人工神经网络引入传统的 PID 控制,将这两者结合,则可以在一定程度上解决传统 PID 调节器不易在线实时整定参数、难于对一些复杂过程和参数慢时变系统进行有效控制的不足。
一、BP神经网络BP神经网络是一种有隐含层的多层前馈网络,其结构如图1-1所示。
如果把具有M个输入节点和L个输出节点的BP神经网络看成是从M 维欧氏空间到L维欧氏空间的非线性映射,则对于具有一定非线性因数的工业过程被控对象,采用BP网络来描述,不失为一种好的选择。
在BP神经网络中的神经元多采用S型函数作为活化函数,利用其连续可导性,便于引入最小二乘学习算法,即在网络学习过程中,使网络的输出与期望输出的误差边向后传播边修正加权系数,以期使误差均方值最小。
pid控制原理框图

pid控制原理框图PID就是比例微积分调整,详细你可以参照自动掌握课程里有具体介绍!正作用与反作用在温控里就是当正作用时是加热,反作用是制冷掌握。
PID掌握简介目前工业自动化水平已成为衡量各行各业现代化水平的一个重要标志。
同时,掌握理论的进展也经受了古典掌握理论、现代掌握理论和智能掌握理论三个阶段。
智能掌握的典型实例是模糊全自动洗衣机等。
自动掌握系统可分为开环掌握系统和闭环掌握系统。
一个控掌握系统包括掌握器﹑传感器﹑变送器﹑执行机构﹑输入输出接口。
掌握器的输出经过输出接口﹑执行机构﹐加到被控系统上﹔掌握系统的被控量﹐经过传感器﹐变送器﹐通过输入接口送到掌握器。
不同的掌握系统﹐其传感器﹑变送器﹑执行机构是不一样的。
比如压力掌握系统要采纳压力传感器。
电加热掌握系统的传感器是温度传感器。
目前,PID掌握及其掌握器或智能PID掌握器(仪表)已经许多,产品已在工程实际中得到了广泛的应用,有各种各样的PID掌握器产品,各大公司均开发了具有PID参数自整定功能的智能调整器(intelligentregulator),其中PID掌握器参数的自动调整是通过智能化调整或自校正、自适应算法来实现。
有利用PID掌握实现的压力、温度、流量、液位掌握器,能实现PID掌握功能的可编程掌握器(plc),还有可实现PID掌握的PC系统等等。
1、开环掌握系统开环掌握系统(open-loopcontrolsystem)是指被控对象的输出(被掌握量)对掌握器(controller)的输出没有影响。
在这种掌握系统中,不依靠将被控量反送回来以形成任何闭环回路。
2、闭环掌握系统闭环掌握系统(closed-loopcontrolsystem)的特点是系统被控对象的输出(被掌握量)会反送回来影响掌握器的输出,形成一个或多个闭环。
闭环掌握系统有正反馈和负反馈,若反馈信号与系统给定值信号相反,则称为负反馈(NegativeFeedback),若极性相同,则称为正反馈,一般闭环掌握系统均采纳负反馈,又称负反馈掌握系统。
基于BP神经网络的PID控制器设计

Abstract
Classical PID control algorithm,as a general method of industrial process control,application scope is broad-ranged.In principle,it does not depend on the specificmathematical model of the controlled plant,but tuning algorithm parameters is a verydifficult task.To moreimportant,even if tuning the parameter is completed,asparameters do not have adaptive capacity,due to a change in environment,PID controlof the response of the system deviation get worse,parameters need to be re-tumed.Inresponse to these problems,people have been using theadaptive method of fuzzy,neural networks to adjust PID parameters,try hard to overcome this problem.Under normal circumstances,an adaptive control system can be capable of running,and the corresponding parameters should adapt to tlle change in status of the scene,so the corresponding parameters must be based on the data of the scene to conduct onlineidentification orestimated.Non-time—varyingparameters can beconfirmed for a period of on-line identification,but the time-varying parameters system will be necessary to continue this ongoing process,so the requirement of fast identification or the relative slow pace of change of parameters,greatly limits the application of adaptive technology.To overcome this limitation,this paper uses the ideology of literature[1],thetechnology of neural network will be used in the process of parameter identification,combining classical PID control algorithm,forms an adaptive PlD control algorithmbased on BP neural network.The essence of this algorithm applies neural network tobuild the model of system parameters,change the change law of the parameters of time-varying parameters systems into the Parametric model of neural network,reflectingthe law that the parameters change with the state,that is,when the system changes,itcan get the time-varying parameters of system from the model directly,without the process ofidentification.On the basis of me parameters model of neural network,combining the computation of PID controI parameters in the known system model of literature[1],derived an adaptive PID controlalgorithm.Through the simulation of linear and non-1inear systems in the computer,the result indicates that this adaptive PID control algorithm is effective.
基于BP神经网络的自适应PID控制器设计

基于BP 神经网络的自适应PID 控制器设计一.基于BP 神经网络的自适应PID 控制器的原理PID 控制是最早发展起来的、 应用领域至今仍然广泛的控制策略之一,它是基于对象数学模型的方法,尤其适用于可建立精确数学模型的确定性控制系统。
其优点是算法简单、 鲁棒性好和可靠性高。
但是,由于实际工业生产过程往往具有非线性,许多非线性系统难以确定精确的数学模型,常规的PID 控制器就不能达到理想的控制效果,由于受到参数整定方法烦杂的困扰,参数往往整定不良、 性能欠佳。
神经网络所具有的任意非线性表达能力,可以通过对系统性能的学习来实现具有最佳组合的PID 控制。
基于BP 网络的自适应PID 控制器,通过BP 神经网络调整自身权系数,对PID 控制参数进行调节,以达到某种性能指标的最优。
二.基于BP 神经网络的自适应PID 控制器的控制器结构基于BP 神经网络的PID 控制系统结构图如图1所示:此控制器由两部分组成:(1)经典的PID 控制器,直接对被控对象进行闭环控制,并且三个参数p K ,i K ,d K 为在线调整方式;图1 BP 网络结构p ki kd ki(2)神经网路,根据系统的运行状态,调节PID 控制器的参数,以期达到某种性能指标的最优化,是输出层神经元的输出状态对应于PID 控制器的一个可调参数p K ,i K ,d K 。
通过神经网络的自学习、加权系数调整,使神经网络输出对应于某种最优控制率下的PID 控制器参数。
基于BP 神经网络的自适应PID 控制器的控制器如图2所示:该控制器的算法如下:(1)确定BP 神经网络的结构,即确定输入节点数M 和隐含层节点数Q ,并给各层加权系数的初值)0(1ij w 和)0(2ij w ,选定学习速率η和惯性系数α,此时k=1; (2)采样得到rin(k)和yout(k),计算该时刻误差error(k)=rin(k)-yout(k);(3)计算神经网络NN 各层神经元的输入、输出,NN 输出层的输出即为PID 控制器的三个可调参数p K ,i K ,d K ;(4)根据经典增量数字PID 的控制算法(见下式)计算PID 控制器的输出u(k); ))2()1(2)(()())1()(()1()(-+--++--+-=k error k error k error K k error K k error k error K k u k u d i p (5)进行神经网络学习,在线调整加权系数)(1k w ij 和)(2k w ij 实现PID 控制参数的自适应调整;(6)置k=k+1,返回到(1)。
基于BP神经网络的PID控制器设计

基于BP神经网络的PID控制器设计班级:21班学号:姓名:常临妍摘要常规PID控制技术是工业控制中一种常用的控制方法。
其结构简单、容易实现、控制效果良好,且能对相当一些工业对象或过程进行有效的控制,已得到广泛应用。
但其局限性在于:当控制对象不同,或被控对象具有复杂的非线性特性时,难以建立精确的数学模型。
控制器的参数难以自动调整以适应外界环境的变化。
且由于对象和环境的不确定性,往往难以达到满意的控制效果。
为了使控制器具有较好的自适应性,实现控制器参数的自动调整,可以借助BP神经网络控制的方法。
BP神经网络已被证明具有逼近任意连续有界非线性函数的能力,给非线性控制带来了新的思路。
利用人工神经网络的自适应能力,并结合传统的PID控制理论,构造神经网络PID控制器,实现控制器参数的自动调整。
本文研究了基于BP神经网络的PID控制器设计,利用BP神经网络的自适应能力进行在线参数整定。
其实现具有自适应性等特点,网络的收敛速度快,能够对非线性对象有很好的控制,系统的跟踪性能好。
其参数设定无需知道被控对象的具体参数及其数学模型,对不同的对象具有适应性。
关键词:PID控制BP神经网络控制器设计一.绪论1.1神经元网络PID的发展历程1934年,美国心理学家W.McCulloch和数学家W.Pitts用数学模型对神经系统中的神经元进行理论建模,建立了MP神经元模型。
MP神经元模型首次用简单的数学模型模仿出生物神经元活动功能,并揭示了通过神经元的相互连接和简单的数学计算,可以进行相当复杂的逻辑运算这一事实。
1957年,美国计算机学家F.Rosenblatt提出了著名的感知器模型。
它是一个具有连续可调权值矢量的MP神经网络模型,经过训练可达到对一定输入矢量模型进行识别的目的。
1959年,美国工程师B.Widrow和M.Hoff提出了自适应线性元件。
它与感知器的主要不同之处在于其神经元有一个线性激活函数,这允许输出可以是任意值,而不仅仅只是像感知器中那样只能取0或1。
基于BP_神经网络的PID_控制算法参数优化

- 22 -高 新 技 术从本质上来看,PID 控制算法就是对比例、积分和比例微分间的关系进行控制的一种算法。
PID 控制调节器具有适应性强、鲁棒性良好的特征,因此被广泛应用于工业控制领域。
但是,随着科学技术、控制理论发展,在工业生产中被控对象逐渐向复杂化和抽象化的趋势发展,并呈现滞后性、时变性和非线性的特征,这使传统PID 控制器难以精准调控这种较复杂的控制系统。
为了解决该问题,研究人员将控制理论与其他先进的算法相结合,形成全新的控制理论,包括神经网络控制、遗传算法以及模糊控制等。
对神经网络算法来说,由于其具有较高的鲁棒性和容错性,因此适用于复杂的非线性控制系统中,并且具有广阔的应用前景和较大的发展潜力。
1 BP 神经网络结构及算法BP 神经网络将网络视为一个连续域,在这个网络中,输入层和输出层都是任意时刻、任意数目的样本值,网络输出层值与输入层值间也可以具有任意关系,这个学习过程就称为BP 神经网络学习过程。
作为一种被广泛应用的神经网络模型,BP 神经网络由输入层、输出层和隐含层组成:1) 输入层。
从第i 个输入向量中产生相应的输出值。
2) 输出层。
在输出值的作用下将其转换为输入数据。
3) 隐含层。
在输出值的作用下对数据进行隐含处理,将处理后的结果反馈给输入层,3个输入层构成1个BP 神经网络。
当输入数据在时间域内经过多次的误差传播时,最后被一个误差源作为输出信号,即经过输入单元和输出组的中间信息。
如果该误差源的误差小于输出单元和输出组中各单元间的误差,那么这些单元在计算输出时就会有很大的变化;如果超过了期望值,那么这一单元被认为是输入量存在误差(也就是输入信号存在误差),将不再使用该单元;如果仍然超过期望值,那么输出量又会存在误差[1]。
通过分析输入与输出量间的关系可以得出BP 网络中各个隐藏层上节点数与该输出量间的关系。
BP 神经网络的拓扑结构如图1所示。
为了对BP 神经网络进行运算和优化,该文设定了中间层的加权和结点临界,以便将全部采样的真实输出量与预期的输出量的偏差控制在一个很低的区间,并且通过调节这个区间来保证它的稳定性。
BP神经网络与PID控制的结合

神经网络可以指向两种,一个是生物神经网络,一 个是人工神经网络。
生物神经网络主要是指人脑的神经网络。人脑是人 类思维的物质基础,思维的功能定位在大脑皮层, 后者含有大约1011个神经元,每个神经元又通过神 经突触与大约103个其它神经元相连,形成一个高度 复杂高度灵活的动态网络。作为一门学科,生物神 经网络主要研究人脑神经网络的结构、功能及其工 作机制,意在探索人脑思维和智能活动的规律。
周而复始的信息正向传播和误差反向传播过程,是 各层权值不断调整的过程,也是神经网络学习训练 的过程,此过程一直进行到网络输出的误差减少到 可以接受的程度,或者预先设定的学习次数为止。
PID控制
PID控制器(比例-积分-微分控制器)是一个在 工业控制应用中常见的反馈回路部件,由比例单元 P 、积分单元I 和微分单元D 组成。PID 控制的基础 是比例控制;积分控制可消除稳态误差,但可能增 加超调;微分控制可加快大惯性系统响应速度以及 减弱超调趋势。
人工神经网络(Artificial Neural Network, 即ANN ),是20世纪80年代以来人工智能领域兴起 的研究热点。它从信息处理角度对人脑神经元网络 进行抽象,建立某种简单模型,按不同的连接方式 组成不同的网络。所以它的技术原型就是自然神经 网络。在工程与学术界也常直接简称为神经网络或 类神经网络。人工神经网络是一种运算模型,由大 量的节点(或称神经元)之间相互联接构成。
(3) 置k=k+1,返回到(1)。
总结
将神经网络与PID控制相结合,利用神经网络的 自学习能力和逼近任意函数的能力,可在线进行PID 参数调整,有效地控制较复杂的被控对象,大大改 善了常规PID控制器的性能,同时也显示了神经网络 在解决高度非线性和严重不确定系统方面的潜能。 所以BP神经网络PID控制比传统的PID控制具有更好 的控制特性。
毕业设计(论文)_基于BP神经网络的PID控制器设计

(2)汽车行业。汽车自动驾驶系统、保险行为分析。
(3)银行业。支票和其他文档阅览器贷款评估器。
(4)国防领域。武器操纵控制、目标跟踪、物体识别、各种新的传感器。
(5)电子领域。编码序列预测、集成电路芯片的设计、过程控制芯片、故障分析、机器视觉声音合成、非线性建模。
(6)娱乐领域。动画、特效设计、市场预测。
阶跃响应是指将一个阶跃输入加到系统上时,系统的输出。稳态误差是指系统的响应进入稳态后,系统的期望输出与实际输出之差。控制系统的性能可以用稳、准、快三个字来描述。稳是指系统的稳定性,一个系统要能正常工作,首先必须是稳定的,从阶跃响应上看应该是收敛的;准是指控制系统的准确性、控制精度,通常用稳态误差来描述,它表示系统输出稳态值与期望值之差;快是指控制系统响应的快速性,通常用上升时间来定量描述。
在模拟控制系统中,控制器最常用的控制规律是PID控制。PID的控制规律为:
(2.1)
式中, —比例系数; —积分时间常数; —微分时间常数[4]。
比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差。
基于BP神经网络的PID控制器的设计

基于BP神经网络的PID控制器的研究与实现课程名称:人工神经网络目录前言 (3)一、BP神经网络 (3)二、模拟PID控制系统 (5)三、基于BP神经网络的PID控制器 (6)四、仿真程序 (10)五、运行结果 (16)六、总结 (17)参考文献 (18)前言人工神经网络是以一种简单神经元为节点,采用某种网络拓扑结构构成的活性网络,可以用来描述几乎任意的非线性系统。
不仅如此,人工神经网络还具有学习能力、记忆能力、计算能力以及各种智能处理能力,在不同程度和层次上模仿人脑神经系统的信息处理、存储和检索的功能。
不同领域的科学家,对人工神经网络有着不同的理解、不同的研究内容,并且采用不同的研究方法。
对于控制领域的研究工作者来说,人工神经网络的魅力在于:①能够充分逼近任意复杂的非线性关系,从而形成非线性动力学系统,以表示某种被控对象的模型或控制器模型;②能够学习和适应不确定性系统的动态特性;③所有定量或定性的信息都分布储存于网络内的各神经单元,从而具有很强的容错性和鲁棒性;④采用信息的分布式并行处理,可以进行快速大量运算。
对于长期困扰控制界的非线性系统和不确定性系统来说,人工神经网络无疑是一种解决问题的有效途径。
正因为如此,把人工神经网络引入传统的PID 控制,将这两者结合,则可以在一定程度上解决传统PID 调节器不易在线实时整定参数、难于对一些复杂过程和参数慢时变系统进行有效控制的不足。
一、BP神经网络BP神经网络是一种有隐含层的多层前馈网络,其结构如图1-1所示。
如果把具有M个输入节点和L个输出节点的BP神经网络看成是从M维欧氏空间到L维欧氏空间的非线性映射,则对于具有一定非线性因数的工业过程被控对象,采用BP网络来描述,不失为一种好的选择。
在BP神经网络中的神经元多采用S型函数作为活化函数,利用其连续可导性,便于引入最小二乘学习算法,即在网络学习过程中,使网络的输出与期望输出的误差边向后传播边修正加权系数,以期使误差均方值最小。
基于BP算法的神经网络PID控制器设计及仿真
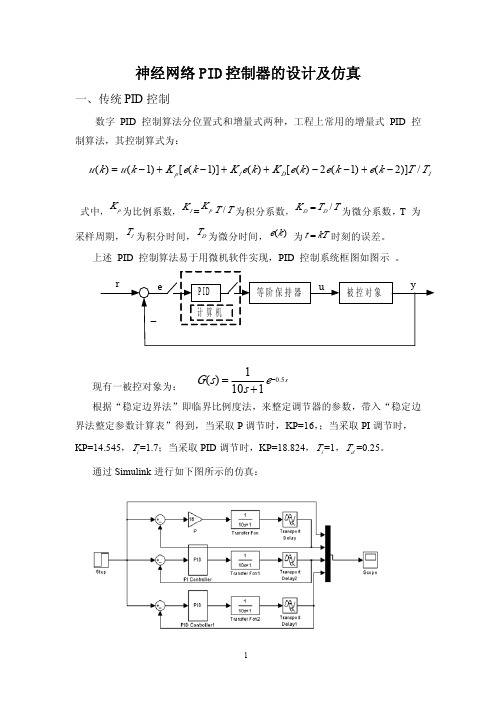
se s s G 5.01101)(−+=()(1)[(1)]()[()2(1)(2)]/p I D Iu k u k K e k K e k K e k e k e k T T =−+−++−−+−神经网络PID 控制器的设计及仿真一、传统PID 控制数字PID 控制算法分位置式和增量式两种,工程上常用的增量式PID 控制算法,其控制算式为:式中,pK 为比例系数,I K =p K /T T为积分系数,/D D K T T =为微分系数,T 为采样周期,IT 为积分时间,DT 为微分时间,()e k 为t kT =时刻的误差。
上述PID 控制算法易于用微机软件实现,PID 控制系统框图如图示。
现有一被控对象为:根据“稳定边界法”即临界比例度法,来整定调节器的参数,带入“稳定边界法整定参数计算表”得到,当采取P 调节时,KP=16,;当采取PI 调节时,KP=14.545,i T =1.7;当采取PID 调节时,KP=18.824,i T =1,d T =0.25。
通过Simulink 进行如下图所示的仿真:仿真结果如下图所示:二、基于BP算法的PID控制基于BP神经网络的PID控制系统结构如下图所示,控制器由两个部分组成:①经典的PID控制器:直接对被控对象进行闭环控制,并且KP,KI,KD三个参数为在线P,I,D整定;②神经网络NN:根据系统的运行状态,调节PID控制器的参数,以期达到某种性能指标的最优化。
即使神经网络的输出层神经元的输出状态对应于PID控制器的三个可调参数KP,KI,KD,通过神经网络的自学习、调整权系数,从而使其稳定P,I,D状态对应于某种最优控制规律下的PID控制器参数。
在这里设计的BP网络采用结构简单的三层BP神经网络,其结构如下图所示,有m个输入节点、Q个隐含层节点、3个输出节点。
输入节点对应所选的系统运行状态量,如系统不同时刻的输入量和输出量等,必要时要进行归一化K K K。
基于BP神经网络的PID控制器的设计资料

基于BP神经网络的PID控制器的研究与实现课程名称:人工神经网络目录前言 (3)一、BP神经网络 (4)二、模拟PID控制系统 (5)三、基于BP神经网络的PID控制器 (6)四、仿真程序 (10)五、运行结果 (17)六、总结 (18)参考文献 (19)前言人工神经网络是以一种简单神经元为节点,采用某种网络拓扑结构构成的活性网络,可以用来描述几乎任意的非线性系统。
不仅如此,人工神经网络还具有学习能力、记忆能力、计算能力以及各种智能处理能力,在不同程度和层次上模仿人脑神经系统的信息处理、存储和检索的功能。
不同领域的科学家,对人工神经网络有着不同的理解、不同的研究内容,并且采用不同的研究方法。
对于控制领域的研究工作者来说,人工神经网络的魅力在于:①能够充分逼近任意复杂的非线性关系,从而形成非线性动力学系统,以表示某种被控对象的模型或控制器模型;②能够学习和适应不确定性系统的动态特性;③所有定量或定性的信息都分布储存于网络内的各神经单元,从而具有很强的容错性和鲁棒性;④采用信息的分布式并行处理,可以进行快速大量运算。
对于长期困扰控制界的非线性系统和不确定性系统来说,人工神经网络无疑是一种解决问题的有效途径。
正因为如此,把人工神经网络引入传统的PID 控制,将这两者结合,则可以在一定程度上解决传统PID 调节器不易在线实时整定参数、难于对一些复杂过程和参数慢时变系统进行有效控制的不足。
一、BP神经网络BP神经网络是一种有隐含层的多层前馈网络,其结构如图1-1所示。
如果把具有M个输入节点和L个输出节点的BP神经网络看成是从M维欧氏空间到L维欧氏空间的非线性映射,则对于具有一定非线性因数的工业过程被控对象,采用BP网络来描述,不失为一种好的选择。
在BP神经网络中的神经元多采用S型函数作为活化函数,利用其连续可导性,便于引入最小二乘学习算法,即在网络学习过程中,使网络的输出与期望输出的误差边向后传播边修正加权系数,以期使误差均方值最小。
基于BP神经网络PID整定原理和算法步骤-精品

虽然人工神经网络存在着以上的许多优点及广泛的应用,但同时也存在着一些不足,由于神经网络的不足阻碍了神经网络的发展,在现实应用中BP神经网络是最为广泛的神经网络模型,BP神经网络是在1986年被提出的,因其系统地解决了多层网络中隐含单元连接权的学习问题,它同样具有人工神经网络所具有的特点。本课题是以BP神经网络模型研究为主。BP神经网络的缺点主要表现在以下几个方面:
Nowadays, the neural network has wide application fields and prospects in the national economy and modernization of national defense science.It mainly applies in information, automation, economical and so on.
90年代初,对神经网络的发展产生了很大的影响是诺贝尔奖获得者Edelamn提出Darwinism模型。他建立了一种神经网络系统理论,例如,Darwinism的结构包括Dawin网络和Nallance网络,并且这两个网络是并行的,而他们又包含了不同功能的一些子网络。他采用了Hebb权值修正规则,当一定的运动刺激模式作用后,系统通过进化,学会扫描跟踪目标。Narendra和Parthasarathy(1990年)提出了一种推广的动态神经网络系及其连接权的学习算法,它可表示非线性特性,增强了鲁棒性。神经网络理论有较强的数学性质和生物学特性,尤是神经科学、心理学和认识科学等方面提出一些重大问题,是向神经网络理论研究的新挑战,因而也是它发展的最好的机会。
毕设 利用BP神经网络PID控制器进行优化

引言PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好和可靠性高,被广泛应用于工业控制过程,尤其适用于可建立精确数学模型的确定性控制系统。
而实际工业生产过程中往往具有非线性,时变不确定性,因而难以建立精确的数学模型,应用常规PID控制器不能达到到理想的控制效果,在实际生产过程中,由于受到参数整定方法繁杂的困扰,常规PID控制器参数往往整定不良,性能欠佳,对运行工况的适应性很差[1]。
因此常规PID控制的应用受到很大的限制和挑战。
人们对PID应用的同时,也对其进行各种改进,主要体现在两个方面:一是对常规PID本身结构的改进,即变结构PID控制。
另一方面,与模糊控制、神经网络控制和专家控制相结合,扬长避短,发挥各自的优势,形成所谓智能PID控制。
这种新型控制器己引起人们的普遍关注和极大的兴趣,并已得到较为广泛的应用。
它具有不依赖系统精确数学模型的特点,对系统参数变化具有较好的鲁棒性。
主要算法有:基于规则的智能PID自学习控制算法、加辨识信号的智能自整定PID控制算法、专家式智能自整定PID控制算法、模糊PID控制算法、基于神经网络的PID控制算法、自适应PID预测智能控制算法和单神经元自适应PID 智能控制等多种控制算法。
本设计正是利用BP神经网络PID控制器对一个单闭环调速系统进行仿真研究,并和常规的PID控制进行对比,从而得出BP神经网络PID控制器具有较强的自整定、自适应的优点。
第1章绪论1.1课题背景随着科学技术的迅速发展和进步,对控制系统提出了新的更高要求。
由于各种实际工程系统的发展规模越来越大,复杂性越来越高,常规控制的理论和技术已无法满足工程上对提高自动化水平和扩大自动化范围的要求,因此,科学技术的进步促使了智能控制技术的建立与发展。
智能控制是一类无需人的干预就能够独立的驱动智能机器实现其目标的自动控制。
目前的智能控制技术包括:神经元网络技术、模糊控制技术、遗传算法优化技术、专家控制系统、基于规则的仿人智能控制技术等已进入工程化和实用化的时代,并已有商品出售。
基于BP神经网络的自整定PID控制的MATLAB程序代码
基于BP神经网络的自整定PID控制仿真在工业控制中,PID控制是工业控制中最常用的方法。
这是因为PID控制器结构简单、实现简单,控制效果良好,已得到广泛应用。
但是,PID具有一定的局限性:被控制对象参数随时间变化时,控制器的参数难以自动调整以适应外界环境的变化。
为了使控制器具有较好的自适应性,实现控制器参数的自动调整,可以采用神经网络控制的方法。
利用人工神经网络的自学习这一特性,并结合传统的PID控制理论,构造神经网络PID控制器,实现控制器参数的自动调整。
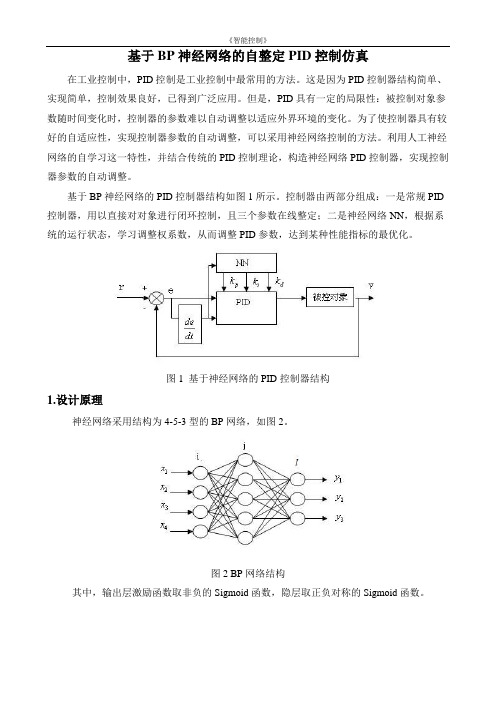
基于BP神经网络的PID控制器结构如图1所示。
控制器由两部分组成:一是常规PID 控制器,用以直接对对象进行闭环控制,且三个参数在线整定;二是神经网络NN,根据系统的运行状态,学习调整权系数,从而调整PID参数,达到某种性能指标的最优化。
图1 基于神经网络的PID控制器结构1.设计原理神经网络采用结构为4-5-3型的BP网络,如图2。
图2 BP网络结构其中,输出层激励函数取非负的Sigmoid函数,隐层取正负对称的Sigmoid函数。
被控对象为一时变非线性对象,数学模型可表示为: 2()(1)()(1)1(1)a k y k y k u k y k -=+-+- 式中,系数a(k)是慢时变的,。
为保证控制器有一定的动态跟踪能力,选定神经网络的输入层输入为[(),(1),(2),1]T in X e k e k e k =--网络的学习过程由正向和反向传播两部分组成。
如果输出层不能得到期望输出,那么转入反向传播过程,通过修改各层神经元的权值,使得输出误差信号最小。
输出层节点分别对应三个可调参数(3)1(3)2(3)3p I D O K O K O K ⎫=⎪=⎬⎪=⎭取性能指标函数为: 21()(()())2E k r k y k =-设其中:()()()r k y k e k -=若PID 控制器采用采用增量式数字PID 控制算法,则有(3)1(3)2(3)3()()(1)()()()()2(1)(2)u k e k e k O u k e k O u k e k e k e k O ⎫∂=--⎪∂⎪⎪∂=⎬∂⎪⎪∂=--+-⎪∂⎭2.网络权系数调整网络权系数的修正采用梯度下降法。
神经网络PID

神经网络PIDBP神经网络PID控制方法研究3.1引言所谓“神经网络”是以一种简单计算处理单元(即神经元)为节点,采用某种网络拓扑结构构成的活性网络,可以用来描述几乎任意的非线性系统;不仅如此,神经网络还具有学习能力、记忆能力、计算能力以及各种智能处理能力,在不同程度和层次上模仿人脑神经系统的信息处理、存储和检索功能。
神经网络在控制系统中的应用提高了整个系统的信息系统处理能力和适应能力,提高了系统的智能水平。
由于神经网络己具有逼近任意连续有界非线性函数的能力,对于长期困扰控制界的非线性系统和不确定性系统来说,神经网络无疑是一种解决问题的有效途径。
采用神经网络方法设计的控制系统具有更快的速度(实时性)、更强的适应能力和更强的鲁棒性。
正因为如此,近年来在控制理论的所有分支都能够看到神经网络的引入及应用,对于传统的PID控制当然也不例外,以各种方式应用于PID控制的新算法大量涌现,其中有一些取得了明显的效果。
传统的控制系统设计是在系统数学模型己知的基础上进行的,因此,它设计的控制系统与数学模型的准确性有很大的关系。
神经网络用于控制系统设计则不同,它可以不需要被控对象的数学模型,只需对神经网络进行在线或离线训练,然后利用训练结果进行控制系统的设计。
神经网络用于控制系统设计有多种类型,多种方式,既有完全脱离传统设计的方法,也有与传统设计手段相结合的方式。
一般来说,基于神经网络的PID控制器的典型结构主要有两种,单神经元网络PID控制器和神经网络PID控制器两种控制算法。
本章将详细介绍基于BP神经网络的PID控制算法,然后对单闭环调速系统的进行设计,对其进行Matlab 算法仿真。
3.2基于BP神经网络的PID整定原理PID控制要取得好的控制效果,就必须通过调整好比例、积分和微分三种控制作用在形成控制量中相互配合又相互制约的关系,这种关系不一定是简单的“线性组合”,而是从变化无穷的非线性组合中找出最佳的关系。
PID神经网络控制-医学课件

r
P
v
(2) 经 k 步训练后,输入层至隐层 权值调整算法:
u
I
P
y
1 w ij
(k
1) 1w ij
(k )
1
E 1w ij
R
D
x'
x q NNC
1w ij ( k ) 1 i (k )r j ( k )
i ( k ) ' ( k )( 2 w i ) sgn
rn
2w P
u1
un
v1
y1
vn
yn
x'
R
xq
NNC
图 4-7-2 PID 神经网络多变量控制结构 6
q s2(k 1 ) x s2(k ), 1 q s2(k ) 1
q s2(k ) 1 ,
q s2 1
1 ,
q s2 1
x s3(k ) x s3(k 1 ), 1 q s3(k ) 1
控制器输出计算,见节 2-8,不同点:
(1)网络输入层输入输出相等
1W 2W
R(k ) [r1 (k ), r2 (k )] [r(k ), y(k )] ;
r
P
v
(2)输出层神经元用线性模型,输入=输出: u(k ) x' (k ) , u(k) :控制量
u
I
P
y
(3)控制器与被控对象一起作为广义网络考虑;
q i (k ) q i (k 1) xi (k ) xi (k 1)
图 4 -7-1 PID 神经网络单变量控制结构
2
4-7-2 PID神经网络多变量控制
