数据结构java第07章
JAVA 07 数组

Arrays as Objects (cont’d)
As with other objects, the declaration creates only a reference, initially set to null. An array must be created before it can be used. One way to create an array:
In Java, an array is an object. If the type of its elements is anyType, the type of the array object is anyType[ ]. Array declaration:
• anyType [ ] arrName;
1.39 c[0]
1.69 ቤተ መጻሕፍቲ ባይዱ[1]
1.74 c[2]
0.0 c[3]
c is array’s name
下标 (Subscripts)
In Java, an index is written within square brackets following array’s name (for example, a[k]). Indices start from 0; the first element of an array a is referred to as a[0] and the n-th element as a[n-1]. An index can have any int value from 0 to array’s length - 1.
• 例:
int [ ] scores = new int [10] ; private double [ ] gasPrices = { 3.05, 3.17, 3.59 }; String [ ] words = new String [10000]; String [ ] cities = {"Atlanta", "Boston", "Cincinnati" };
数据结构课后习题答案第七章
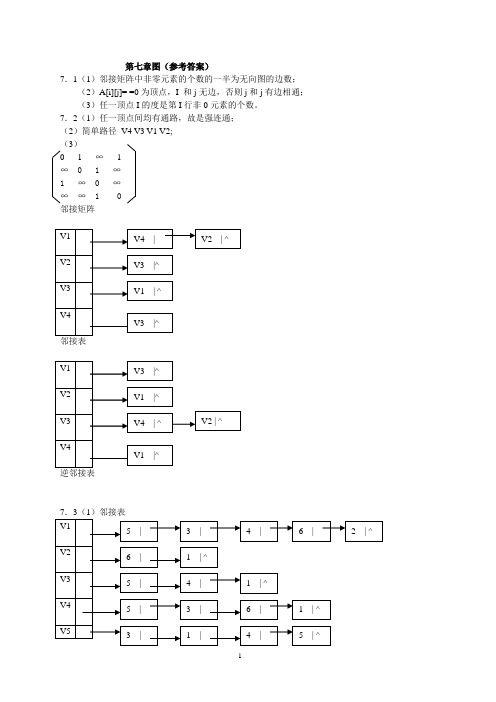
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
第7章树和二叉树(2)-数据结构教程(Java语言描述)-李春葆-清华大学出版社

二叉树也称为二分树,它是有限的结点集合,这个集合或者是空,或者由 一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成。 二叉树中许多概念与树中的概念相同。 在含n个结点的二叉树中,所有结点的度小于等于2,通常用n0表示叶子结 点个数,n1表示单分支结点个数,n2表示双分支结与度为2的树是不同的。
度为2的树至少有3个结点,而二叉树的结点数可以为0。 度为2的树不区分子树的次序,而二叉树中的每个结点最多有 两个孩子结点,且必须要区分左右子树,即使在结点只有一棵 子树的情况下也要明确指出该子树是左子树还是右子树。
2/35
归纳起来,二叉树的5种形态:
Ø
4/35
3. 满二叉树和完全二叉树
在一棵二叉树中,如果所有分支结点都有左孩子结点和右孩子结点,并且 叶子结点都集中在二叉树的最下一层,这样的二叉树称为满二叉树。
可以对满二叉树的结点进行层序编号,约定编号从树根为1开始,按照层 数从小到大、同一层从左到右的次序进行。
满二叉树也可以从结点个数和树高度之间的关系来定义,即一棵高度为h 且有2h-1个结点的二叉树称为满二叉树。
R={r} r={<ai,aj> | ai,aj∈D, 1≤i,j≤n,当n=0时,称为空二叉树;否则其中
有一个根结点,其他结点构成根结点的互不相交的左、右子树,该 左、右两棵子树也是二叉树 } 基本运算: void CreateBTree(string str):根据二叉树的括号表示串建立其存储结构。 String toString():返回由二叉树树转换的括号表示串。 BTNode FindNode(x):在二叉树中查找值为x的结点。 int Height():求二叉树的高度。 … }
5
E
数据结构第七章参考答案

习题71.填空题(1)由10000个结点构成的二叉排序树,在等概率查找的条件下,查找成功时的平均查找长度的最大值可能达到(___________)。
答案:5000.5(2)长度为11的有序序列:1,12,13,24,35,36,47,58,59,69,71进行等概率查找,如果采用顺序查找,则平均查找长度为(___________),如果采用二分查找,则平均查找长度为(___________),如果采用哈希查找,哈希表长为15,哈希函数为H(key)=key%13,采用线性探测解决地址冲突,即d i=(H(key)+i)%15,则平均查找长度为(保留1位小数)(___________)。
答案:6,3,1.6(3)在折半查找中,查找终止的条件为(___________)。
答案:找到匹配元素或者low>high?(4)某索引顺序表共有元素275个,平均分成5块。
若先对索引表采用顺序查找,再对块元素进行顺序查找,则等概率情况下,分块查找成功的平均查找长度是(___________)。
答案:31(5)高度为8的平衡二叉树的结点数至少是(___________)。
答案: 54 计算公式:F(n)=F(n-1)+F(n-2)+1(6)对于这个序列{25,43,62,31,48,56},采用的散列函数为H(k)=k%7,则元素48的同义词是(___________)。
答案:62(7)在各种查找方法中,平均查找长度与结点个数无关的查找方法是(___________)。
答案:散列查找(8)一个按元素值排好的顺序表(长度大于2),分别用顺序查找和折半查找与给定值相等的元素,平均比较次数分别是s和b,在查找成功的情况下,s和b的关系是(___________);在查找不成功的情况下,s和b的关系是(___________)。
答案:(1)(2s-1)b=2s([log2(2s-1)]+1)-2[log2(2s-1)]+1+1(2)分两种情况考虑,见解答。
java 数据结构第七章2

数组二叉树的优缺点
二叉树数组表示法的优点是: 二叉树数组表示法的优点是: 对于任一个节点都能很容易的找到其父节点、子节点及兄弟,而且每 对于任一个节点都能很容易的找到其父节点、子节点及兄弟, 个节点的存储空间不大,只占用数组的一个内存空间。 个节点的存储空间不大,只占用数组的一个内存空间。 二叉树数组表示法的缺点是: 二叉树数组表示法的缺点是: 当二叉树的深度和节点数的比例偏高时(二叉树分布平均, 当二叉树的深度和节点数的比例偏高时(二叉树分布平均,如歪斜 ),内存的利用率会偏低 容易造成空间的浪费。 内存的利用率会偏低, 树),内存的利用率会偏低,容易造成空间的浪费。
二叉树的遍历
二叉树的遍历通常分解为三个任务: 二叉树的遍历通常分解为三个任务:
1.访问根节点 2.遍历左子树(即依次遍历左子树上的所有节点) 遍历左子树(即依次遍历左子树上的所有节点) 3.遍历右子树(即依次遍历右子树上的所有节点) 遍历右子树(即依次遍历右子树上的所有节点)
可见,上述三个任务的顺序就是遍历二叉树的顺序。通常用 、 、 可见,上述三个任务的顺序就是遍历二叉树的顺序。通常用N、L、R 表示上述三个步骤,则遍历二叉树的顺序就有NLR、LNR、LRN、 表示上述三个步骤,则遍历二叉树的顺序就有 、 、 、 NRL、RNL、RLN。通常限定“先左后右”,这样就只剩下前三种次 、 、 。通常限定“先左后右” 按这三种次序进行的遍历分别称为先根遍历(或前序便利)、 )、中 序。按这三种次序进行的遍历分别称为先根遍历(或前序便利)、中 或中序)遍历和后根(或后序)遍历。 根(或中序)遍历和后根(或后序)遍历。
public class Node { private Person person; private Node leftChild; private Node rightChild; public Person getPerson() { return person; } public Node getLeftChild() { return leftChild; } public Node getRightChild() { return rightChild; } public void setLeftChild(Node leftChild) { this.leftChild=leftChild; } public void setRightChild(Node rightChild) {
java语言程序设计(基础篇) 第七章

7.2. 为对象定义类
例如一个圆对象(circle),有数据域圆半径( radius)(标识了圆的属性),圆的行为就是 其面积可以通过方法getArea计算而得。同类型 的对象使用一个公共的类来定义。类就是定义 对象的数据和方法的模板.。一个对象是类的实 例(instance)。你可以生成一个类的很多个实 例,产生一个实例也叫做实例化(instantiation
To distinguish between object reference variables and primitive data type variables (§7.4).
To use classes in the Java library (§7.5).
To declare private data fields with appropriate get and set methods to make class easy to maintain (§7.6-7.8).
第7章 对象和类
在前一部分(2到6章),我们学习了编程基础,学会 使用基本数据类型、控制语句、方法以及数组 ,这些都是所有的面向过程的语言都具有的特 征,但, Java,是个面向对象的语言,不但具有 面向过程语言的要素,也具有抽象、封装、继 承、多态等特征以实现强大的灵活性、模块化 、以及可重用性以开发软件,在这一部分,我 们将学习如何定义、扩展以及使用类与对象
).术语对象、实例通常可互用,类和对象的关
系类似于书版和从书版印刷出很多的书。 下面是个圆的例子。
4
对象
类名: Circle
数据域: radius is _______
方法: getArea
一个类模板
圆对象 1
数据域: radius is 10
数据结构第七章课后习题答案 (1)

7_1对于图题7.1(P235)的无向图,给出:(1)表示该图的邻接矩阵。
(2)表示该图的邻接表。
(3)图中每个顶点的度。
解:(1)邻接矩阵:0111000100110010010101110111010100100110010001110(2)邻接表:1:2----3----4----NULL;2: 1----4----5----NULL;3: 1----4----6----NULL;4: 1----2----3----5----6----7----NULL;5: 2----4----7----NULL;6: 3----4----7----NULL;7: 4----5----6----NULL;(3)图中每个顶点的度分别为:3,3,3,6,3,3,3。
7_2对于图题7.1的无向图,给出:(1)从顶点1出发,按深度优先搜索法遍历图时所得到的顶点序(2)从顶点1出发,按广度优先法搜索法遍历图时所得到的顶点序列。
(1)DFS法:存储结构:本题采用邻接表作为图的存储结构,邻接表中的各个链表的结点形式由类型L_NODE规定,而各个链表的头指针存放在数组head中。
数组e中的元素e[0],e[1],…..,e[m-1]给出图中的m条边,e中结点形式由类型E_NODE规定。
visit[i]数组用来表示顶点i是否被访问过。
遍历前置visit各元素为0,若顶点i被访问过,则置visit[i]为1.算法分析:首先访问出发顶点v.接着,选择一个与v相邻接且未被访问过的的顶点w访问之,再从w 开始进行深度优先搜索。
每当到达一个其所有相邻接的顶点都被访问过的顶点,就从最后访问的顶点开始,依次退回到尚有邻接顶点未曾访问过的顶点u,并从u开始进行深度优先搜索。
这个过程进行到所有顶点都被访问过,或从任何一个已访问过的顶点出发,再也无法到达未曾访问过的顶点,则搜索过程就结束。
另一方面,先建立一个相应的具有n个顶点,m条边的无向图的邻接表。
第七章-数据结构教程(Java语言描述)-李春葆-清华大学出版社

第二阶段通常用C语言完成,以便实现更复杂的功能, 也使程序有更好的可读性和可移植性。这个阶段的任 务有: 初始化本阶段要使用到的硬件设备。 检测系统内存映射。 将内核映像和根文件系统映像从Flash读到RAM。 为内核设置启动参数。 调用内核。
ห้องสมุดไป่ตู้
7.1.4常见的BootLoader
(1)Redboot Redboot (Red Hat Embedded Debug and Bootstrap)是Red Hat公司开发的一个独立运行在嵌入式系统上的BootLoader程序, 是目前比较流行的一个功能、可移植性好的BootLoader。 Redboot是一个采用eCos开发环境开发的应用程序,并采用了 eCos的硬件抽象层作为基础,但它完全可以摆脱eCos环境运行, 可以用来引导任何其他的嵌入式操作系统,如Linux、Windows CE等。
BootLoader是嵌入式系统在加电后执行的第一段代码, 在它完成CPU和相关硬件的初始化之后,再将操作系 统映像或固化的嵌入式应用程序装载到内存中然后跳 转到操作系统所在的空间,启动操作系统运行。
对于嵌入式系统而言,BootLoader是基于特定硬件平 台来实现的。因此,几乎不可能为所有的嵌入式系统 建立一个通用的BootLoader,不同的处理器架构都有 不同的BootLoader。
第7章 嵌入式Linux系统移植及调试
目录
7.1 Boot Loader基本概念与典型结构 7.2 U-Boot 7.3 交叉开发环境的建立 7.4 交叉编译工具链 7.5 嵌入式Linux系统移植过程 7.6 Gdb调试器 7.7 远程调试 7.8 内核调试
一个嵌入式linux系统通常由引导程序及参数、 linux内核、文件系统和用户应用程序组成。 由于嵌入式系统与开发主机运行的环境不同, 这就为开发嵌入式系统提出了开发环境特殊化 的要求。交叉开发环境正是在这种背景下应运 而生。
数据结构(Java

7.2 内部排序法——交换式排序
内部排序法中的交换式排序,是运用数据值比较后,依判断规则对数据位置进行交换, 以达到排序的目的。 交换式排序法又可分为两种: 冒泡排序法(Bubble sort) 快速排序法 (Quick sort)
7.2.1 冒泡排序法(sort-01.java)
冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从后向前(从下标较大 的元素开始) ,依次比较相邻元素的排序码,若发现逆序则交换,使排序码较小的元素逐渐 从后部移向前部(从下标较大的单元移向下标较小的单元) ,就象水底下的气泡一样逐渐向 上冒。 因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换, 就说明序列有序,因此要在排序过程中设置一个标志 flag 判断元素是否进行过交换。从而 减少不必要的比较。 下图演示了一个冒泡过程的例子。
7.1.2 排序的分类
排序的分类大致上可分为两种: 1) 内部排序(Internal sort):将欲处理的数据整个存放到内部存储器中做排序,数据可被随 机存取。内部排序法依排序的方式可分为三种: ◆交换式排序法 ◆选择式排序法 ◆插入式排序法 2) 外部排序(External Sort):欲处理的数据量过于庞大,无法全部存放到内部存储器,必须 借助外部的辅助存储器(比如:磁盘,磁带),由于数据是存在外存中,故数据不可随机 被存取。外部排序又分为两种: ◆合并排序法 ◆直接合并排序法 以上各种内部排序法及外部排序法将在后续小节中按重要程度进行讲解。
7.1.1 排序的特性——稳定性与不稳定性
2
因为排序关键字不一定是记录的关键字, 同一关键字值可能对应多个记录。 对于具有同 一排序关键字值的多个记录来说, 若采用的排序方法使排序后记录的相对次序不变, 则称此 排序方法是稳定的,否则称为不稳定的。如果一种排序方法使排序后的结果稳定,则称此方 法是稳定的;若一种排序方法使排序后的结果不稳定,则称此方法是不稳定的。
数据结构(Java语言描述)第七章 查找

第七章 查找
目录
1 查找
2 静态查找表
第七章 查找
动态查找表 哈希表 小结
总体要求
•掌握顺序查找、折半查找的实现方法; •掌握动态查找表(包括:二叉排序树、二叉平衡树 、B-树)的构造和查找方法; •掌握哈希表、哈希函数冲突的基本概念和解决冲突 的方法。
7.1基本概念
1、数据项 数据项是具有独立含义的标识单位,是数据不可分 割的最小单位。 2、数据元素 数据元素数是据由项若(名干) 数据项构成的数据单位,是在某
}
性能分析:i 0 1 2 3 4
5 13 19 21 37
Ci 3 4 2 3 4
查找成功:
比较次数 = 路径上的结点数
比较次数 = 结点 4 的层数
比较次数
2
56 7 56 64 75 1 34
判定树
5
8 9 10 80 88 92 2 34
查找37 8
树的深度
0
3
6
9
≤=
log2n +1
1
4
}
【算法7-1】初始化顺序表 public SeqTable(T[] data,int n){
elem=new ArrayList<ElemType<T>>(); ElemType<T> e; for(int i=0;i<n;i++){
e=new ElemType<T>(data[i]); elem.add(i, e); } length=n; }
前者叫作最大查找长度(Maximun Search Length),即 MSL。后者叫作平均查找长度(Average Search Length) ,即ASL。
java习题及答案第7章 习题参考答案
第7章多线程编程1.什么是线程?与进程有何不同?答:线程是操作系统中重要概念之一,是程序运行的基本执行单元,与进程一样,也有创建、销毁和切换等状态,但负荷远小于进程,又称为轻量级进程。
与进程不同的是:占用的资源少,不像进程那样可由几个线程组成,在Java语言中,用ng.Thread类创建和管理线程,而进程是由ng.Process类等类创建和管理。
2.使用多线程的优势何在?答:使用多线程具有很多优势,这主要表现在如下五方面:充分利用CPU资源;简化编程模型;简化异步事件的处理;使GUI程序更有效率;节约成本。
3.主要的线程状态有哪些?它们之间是如何转换的?答:线程主要有如下5个状态:New(新)、Runnable(可运行、就绪)、Running(运行)、Blocked(被阻塞、挂起)和Dead(死亡),它们之间转换如下图所示:4.简述创建线程的两种方法及各自的步骤。
答:第一种方法是通过继承Thread类编写用户自己的线程类,而后创建实例,步骤为:➢定义自己的线程类MyThread,并覆盖Thread类的run(),实现所需功能;➢实例化MyThread类,并用start()方法启动。
第二种方法是通过实现Runnable接口来创建线程,使用Runnable接口创建线程的步骤为:➢实现Runnable接口,如实现了该接口的类为MyRunnable,并在MyRunnable类的run()方法里编写想让线程执行的代码;➢创建实现了Runnable接口类的实例,如创建MyRunnable类的实例为myRunnable;➢创建线程类Thread的实例,并用构造方法Thread(Runnable)将myRunnable赋值给target。
5.简述sleep()方法的作用,并修改例7.10中休眠部分,体会线程有无休眠的差异。
答:sleep()作为休眠方法,可让线程休眠一段时间,此期间线程不消耗CPU资源。
传入参数是休眠的时间,单位为毫秒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(a) 在G3的邻接表存储结构中删除顶点C
1 3 6∧ 2 4 3∧ 328
3 4 9∧
未删除的边结点更改 某些顶点序号
A2D
9
5
6
E
0A 1B 2D
015 105 202
0 2 2∧ 1 2 6∧ 216
2 3 9∧
B
3E
3 2 9∧
(b) 删除顶点C之后
16
可编辑版(Java版)(第2版)》
7.3 图的遍历
可编辑版(Java版)(第2版)》
2.顶点的度
deg(A)=indeg(A)+outdeg(A) 3.子图
6
可编辑版(Java版)(第2版)》
4.路径 5.连通性
7
可编辑版(Java版)(第2版)》
7.1.2 图抽象数据类型
public interface GGraph<E> { //图接口
int vertexCount();
➢ 第11章 Jav可a编开辑版发运行环境
2
第7章 图
7.1 7.2 7.3 7.4 7.5
图及其抽象数据类型 图的表示和实现 图的遍历 最小生成树 最短路径
▪ 目的:理解图结构。
▪ 要求:掌握图的存储结构和操作实现。
▪ 重点:图的两种存储结构,遍历算法,最小生成 树,最短路径。
▪ 难点:图的存储和操作实现,最小生成树,最短
路径。
3
可编辑版(Java版)(第2版)》
7.1 图及其抽象数据类型
7.1.1 图的基本概念
1. 图的定义和术语
G=(V, E)
V={A | A∈某个数据元素集合}
E={(A, B) | A, B∈V}
① 无向图
② 有向图
4
可编辑版(Java版)(第2版)》
③ 完全图 ④ 带权图 ⑤ 邻接顶点
5
4 3 9 调整 4 1 3 再选
A
D
4
m st数 组 024
C
9
247
TE
7
413
B
3
E
i
439
(c) U ={A ,C,E}, TE={(0,2,4),(2,4,7)}
(d) U ={A ,C,E,B}, TE={(0,2,4),(2,4,7),(4,1,3)}
A
D
4
C
9
7
B
3
E
m st数 组 024 247 413 439
20
可编辑版(Java版)(第2版)》
7.4.2 最小生成树的构造算法
1. Prim算法
21
可编辑版(Java版)(第2版)》
A
in
E
m st数 组
起点 终点 权
0 0 1 25 权 值 1 0 2 4 最小 2 0 3 22 的 边
30 4 ∞
A 4
D 18
C
16
7
B
E
数据结构(Java版)
(第2版)
叶核亚
可编辑版
1
数据结构(Java版)(第2版)
➢ 第0章 Java程序设计基础
➢ 第1章 绪论
➢ 第2章 线性表
➢ 第3章 栈与队列
➢ 第4章 串
➢ 第5章 数组和广义表
➢ 第6章 树和二叉树
➢ 第7章 图
➢ 第8章 查找
➢ 第9章 排序
➢ 第10章 综合应用设计
② 图的插入操作
11
可编辑版(Java版)(第2版)》
③ 图的删除操作 ④ 带权值的边类 ⑤ 邻接矩阵表示的带权图类
12
可编辑版(Java版)(第2版)》
7.2.2 图的邻接表表示
1. 邻接表
① 无向图的邻接表表示
13
可编辑版(Java版)(第2版)》
② 有向图的邻接表表示
14
可编辑版(Java版)(第2版)》
2.邻接表表示的带权图类
① 顶点表元素类 ② 邻接表表示的带权图类的声明及构造方法 ③ 图的插入操作
15
可编辑版(Java版)(第2版)》
④ 图的删除操作 ⑤ 邻接表表示的图类
A2D
9
5
6
8
E
B
C3
7
0A 1B 2C
删除顶点及 边单链表
3D 4E
015 105 217 302 423
0 3 2∧ 127 238 316 4 3 9∧
2.邻接矩阵表示的带权图类
① 邻接矩阵表示的带权图类的声明及构造方法
顶点集合{"A","B","C","D","E"}; 边集合{ (0,1,5), (0,3,2), (1,0,5), (1,2,7), (1,3,6), (2,1,7), (2,3,8), (2,4,3),
(3,0,2),(3,1,6), (3,2,8), (3,4,9), (4,2,3), (4,3,9)};
//返回顶点数
E get(int i);
//返回顶点vi元素
boolean insertVertex(E vertex); //插入顶点
boolean insertEdge(int i, int j, int weight); //插入边
boolean removeVertex(int v); //删除顶点
boolean removeEdge(int i, int j); //删除边
int getFirstNeighbor(int v);
//返回邻接顶点序号
int getNextNeighbor(int v, int w); //返回下一个邻接顶点
}
8
可编辑版(Java版)(第2版)》
7.2 图的表示和实现
7.2.1 图的邻接矩阵表示 7.2.2 图的邻接表表示
9
可编辑版(Java版)(第2版)》
7.2.1 图的邻接矩阵表示
1. 邻接矩阵
aij 1 0
① 不带权图的邻接矩阵
若 (vi,vj)E或 vi,vj E 若 (vi,vj)E或 vi,vj E
① 带权图的邻接矩阵
10
可编辑版(Java版)(第2版)》
m st数 组 起点 终点 权
024
i
2 1 16
2 3 18
m in
247
已加入 TE的 边
调整后再 选最小权 值的边
(a) U={A}, TE={}, m st中 是 起 点 为 A的 边
(b) U={A,C}, TE={(0,2,4)}
A
D
4
C
9
7
i
B
3
E min
m st数 组
024 TE
247
7.3.1 图的深度优先搜索遍历 7.3.2 图的广度优先搜索遍历
17
可编辑版(Java版)(第2版)》
7.3.1 图的深度优先搜索遍历
18
可编辑版(Java版)(第2版)》
7.3.2 图的广度优先搜索遍历
19
可编辑版(Java版)(第2版)》
7.4 最小生成树 7.4.1 生成树
1. 树 2. 生成树和生成森林 3. 最小生成树
(e) U ={A ,C,E,B,D }=V , TE={(0,2,4),(2,4,7),(4,1,3),(4,3,9)}
22
可编辑版(Java版)(第2版)》
2.Kruskal算法
