一次函数与反比例函数练习

合集下载

九年级数学一次函数及反比例函数练习题(含答案)

一次函数及反比例函数专题训练一、填空题：（每题 3 分，共 36 分）１、函数 y ＝x －2 自变量 x 的取值范围是＿＿＿＿。

２、如图，在直角坐标系中，矩形ABOC 的长为 3，宽为 2，则顶点A 的坐标是＿＿＿＿。

３、点 P （3，－4）关于原点对称的点是＿＿＿＿＿＿＿＿。

４、直线 y ＝4x －3 过点（＿＿＿＿，0）（0，＿＿＿＿）５、已知反比例函数 y ＝－4x 的图像经过P （－2，m ），则 m ＝＿＿＿＿。

６、函数 y ＝2x，当 x ＜0 时，y 随 x 的增大而＿＿＿＿。

７、将直线 y ＝3x －1 向上平移 3 个单位，得到直线＿＿＿＿＿＿＿＿。

８、已知：y 是 x 的反比例函数，且当 x ＝3 时，y ＝8。

则 y 与 x 的函数关系式为＿＿＿。

９、一次函数 y ＝－3x ＋4 的图象与坐标轴所围成的三角形面积是＿＿＿＿。

10、如果直线 y ＝ax ＋b 不经过第四象限，那么 ab ＿＿＿0（填“≥”、“≤”或“＝”）。

11、近视眼镜的度数 y （度）与镜片焦距 x （m ）成反比例，已知 400°近视眼镜片的焦距为0.25m ，则眼镜度数 y 与镜片焦距 x 之间的函数关系式为＿＿＿＿＿＿＿＿。

12、某书定价 8 元，如果购买 10本以上，超过 10 本的部分打八折。

请写出购买数量 x （本）与付款金额 y （元）之间的关系式＿＿＿＿＿＿＿＿＿＿＿＿。

二、选择题：（每题 4 分，共 24 分）１、点 P （a ，a －2）在第四象限，则 a 的取值范围是（）A 、－2＜a ＜0B 、0＜a ＜2C 、a ＞2D 、a ＜0２、在函数 y ＝3x －2，y ＝1x＋3，y ＝－2x ，y ＝－x 2＋7 是正比例函数的有（）A 、0 个B 、1 个C 、2 个D 、3 个３、王大爷饭后出去散步，从家中走 20 分钟到一个离家 900 米的公园，与朋友聊天10分钟后，然后用15分钟返回家里。

反比例函数与一次函数专项练习30题(有答案)ok

反比例函数和一次函数专项练习30题（有答案）1．如图，已知一次函数与反比例函数的图象交于A，B两点，且点A的横坐标为4．（1）求k的值；（2）根据正比例函数与反比例函数的性质直接写出B点坐标；（3）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．2．正比例函数y=kx和反比例函数的图象相交于A，B两点，已知点A的横坐标为1，纵坐标为3．（1）写出这两个函数的表达式；（2）求B点的坐标；（3）在同一坐标系中，画出这两个函数的图象．3．反比例函数与一次函数y=2x+1的图象都过点（1，a）．（1）确定a的值以及反比例函数解析式；（2）求反比例函数和一次函数的图象的另一个交点坐标．4．已知一次函数y=kx+b的图象经过点A（0，1）和点B（a，﹣3a）（a＞0），且点B在反比例函数的图象上，求a的值和一次函数的解析式．5．如图正比例函数与反比例函数的图象在第一象限内的交点A的横坐标为4．（1）求k值；（2）求它们另一个交点B的坐标；（3）利用图象直接写出：当x在什么范围内取值时，y1＞y2．6．已知一次函数y=kx+b与反比例函数的图象交于点（﹣1，﹣1），求这两个函数的解析式及它们图象的另一个交点的坐标．7．如图所示，一次函数y=kx+b的图象与反比例函数的图象交于M、N两点．（1）根据图中条件求出反比例函数和一次函数的解析式；（2）当x为何值时一次函数的值大于反比例函数的值．8．如图，已知反比例函数的图象与一次函数y2=k2x+b的图象交于A，B两点，且A（2，n），B（﹣1，﹣2）．（1）求反比例函数和一次函数的关系式；（2）利用图象直接写出当x在什么范围时，y1＞y2．9．如图，正比例函数y1=k1x的图象与反比例函数的图象相交于A、B两点，其中点A的坐标为（1，2）．（1）分别求出这两个函数的表达式；（2）请你观察图象，写出y1＞y2时，x的取值范围；（3）在y轴上是否存在点P，使△AOP为等腰三角形？若存在，请你直接写出点P的坐标；若不存在，请说明理由．10．已知反比例函数y=﹣和一次函数y=kx﹣2都经过点A（m，﹣3）．（1）求m的值和一次函数的关系式．（2）若点M（a，y1）和N（a+2，y2）都在这个反比例函数的图象上，试通过计算或利用反比例函数的图象性质比较y1与y2的大小．11．如图，函数y=3x的图象与反比例函数的图象的一个交点为A（1，m），点B（n，1）在反比例函数的图象上．（1）求反比例函数的解析式；（2）求n的值；（3）若P是y轴上一点，且满足△POB的面积为6，求P点的坐标．12．如图，已知反比例函数的图象经过点A（﹣2，1），一次函数y2=kx+b（k≠0）的图象经过点C（0，3）与点A，且与反比例函数的图象相交于另一点B．（1）分别求出反比例函数与一次函数的解析式；（2）求点B的坐标．（3）根据图象写出使y1＞y2的x的取值范围．13．直线y1=2x﹣7与反比例函数的图象相交于点P（m，﹣3）．（1）求反比例函数的解析式．（2）试判断点Q是否在这个反比例函数的图象上？14．如图，一次函数y=kx+b的图象与反比例函数y=的图象相交于A（1，a）、B（﹣2，1）两点．（1）求反比例函数和一次函数的解析式；（2）求△AOB的面积．15．如图，一次函数y=kx+b的图象与反比例函数的图象相交于A、B两点．（1）根据图象，分别写出点A、B的坐标；（2）求出反比例函数的解析式；（3）求出线段AB的长度．16．如图，已知A（n，2），B（2，﹣4）是一次函数y1=kx+b的图象和反比例函数y2=的图象的两个交点．（1）求反比例函数和一次函数的解析式；（2）当x取何值时，y1＜y2？17．已知反比例函数的图象，经过一次函数y=x+1与的交点，求反比例函数的解析式．18．如图，一次函数y=kx+2与x轴交于点A（﹣4，0），与反比例函数y=的图象的一个交点为B（2，a）．（1）分别求出一次函数与反比例函数的解析式；（2）作BC⊥x轴，垂足为C，求S△ABC．19．如图，一次函数y1=kx+b与反比例函数．（m、k≠0）图象交于A（﹣4，2），B（2，n）两点．（1）求m、n的值及反比例函数的表达式；（2）当x取非零的实数时，试比较一次函数值与反比例函数值的大小．20．一次函数y1=kx+b与反比例函数的图象相交于点A（﹣1，4）、B（﹣4，n），（1）求n的值；（2）连接OA、OB，求△OAB的面积；（3）利用图象直接写出y1＞y2时x的取值范围．21．已知：如图，一次函数y=ax+b的图象与反比例函数的图象交于点A（m，4）和点B（﹣4，﹣2）．（1）求一次函数y=ax+b和反比例函数的解析式；（2）求△AOB的面积；（3）根据图象，直接写出不等式的解集．22．如图，一次函数y=kx+b的图象与反比例函数的图象相交于A、B两点．（1）利用图中条件，求反比例函数和一次函数的解析式；（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围；（3）你能求出图中△AOB的面积吗？若不能，请说明理由；若能，请写出求解过程．23．如图，直线y=kx+2k（k≠0）与x轴交于点B，与双曲线y=交于点A、C，其中点A在第一象限，点C在第三象限．（1）求点B的坐标；（2）若，求点A的坐标．24．已知一次函数与反比例函数y=﹣的图象交于点P（﹣3，m），Q（2，﹣3）．求一次函数的解析式．25．已知正比例函数y=k1x（k1≠0）的图象经过A（2，﹣4）、B（m，2）两点．（1）求m的值；（2）如果点B在反比例函数（k2≠0）的图象上，求反比例函数的解析式．26．如图，已知正比例函数y=﹣3x与反比例函数的图象相交于A和B两点，如果有一个交点A的横坐标为2．（1）求k的值；（2）求A，B两点的坐标；（3）当_________时，．27．如图，已知A（﹣4，2）、B（n，﹣4）是一次函数y=kx+b的图象与反比列函数的图象的两个交点．（1）求m、n的值；（2）求一次函数的关系式；（3）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．28．如图，一次函数y=x+3的图象与x轴、y轴分别交于点A、点B，与反比例函数的图象交于点C，CD⊥x轴于点D，求四边形OBCD的面积．29．如图，已知反比例函数的图象与一次函数y=k2+b的图象交于A、B两点，A（2，n），B（﹣l，﹣2）．（1）求反比例函数和一次函数的关系式；（2）试证明线段AB分别与x轴、y轴分成三等分；（3）利用图象直接写出不等式的解集．30．如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数的图象交于二、四象限内的A、B两点，点B的坐标为（6，n）．线段OA=5，E为x轴负半轴上一点，且sin∠AOE=，求该反比例函数和一次函数的解析式．参考答案：1．（1）由x=4，得y=2；则k=xy=4×2=8；（2）∵A，B两点是正比例函数和反比例函数的交点，点A（4，2），∴B（﹣4，﹣2）；（3）由图象可得在两个交点的左边，一次函数的值小于反比例函数的值，∴x＜﹣4或0＜x＜42．（1）∵正比例函数y=kx 与反比例函数，的图象都过点A（1，3），则k=3，∴正比例函数是y=3x ，反比例函数是．（2）∵点A与点B关于原点对称，∴点B的坐标是（﹣1，﹣3）．（3）∵正比例函数的图象过原点，所以令x=1，则y=3，图象过（1，3），描出此点即可；∵反比例函数的图象是双曲线，∴应在每一个双曲线上描出3各点，即可画出函数图象．3．（1）由题意得，2+1=a，解得，a=3，（1分）由题意得，，解得，k=3．（2分）反比例函数解析式为．（3分）（2）由题意得，，（4分）解得，，∴反比例函数和一次函数图象的另一个交点坐标是（﹣4．∵点B（a，﹣3a）在反比例函数图象上，∴﹣=﹣3a，解得a=1，a=﹣1（舍去），∴点B的坐标为（1，﹣3），∵一次函数y=kx+b图象经过点A（0，1），B（1，﹣3），∴，解得，∴一次函数解析式为y=﹣4x+1．5．（1）将A的横坐标4代入y1=x，得y1=×4=2，由题意可得A点坐标为（4，2），由于反比例函数y=的图象经过点A，∴k=2×4=8．（5分）（2）将两个函数的解析式组成方程组得：，解得，．所以A（4，2），B（﹣4，﹣2）．所以B点坐标为B（﹣4，﹣2）．（3分）（3）由于A点横坐标4，B点横坐标为﹣4，由图可知：当x＞4或﹣4＜x＜0时，y1＞y2．6．由已知得，（2分）解得．（4分）∴一次函数的解析式为y=2x+1，（5分）反比例函数的解析式为．（6分）由，解得x=﹣1或．（7分）当时，y=2．∴函数图象的另一个交点的坐标为（）∴m=6，a=﹣6即N（﹣1，﹣6）且，解得∴反比例函数和一次函数的解析式的解析式分别为y=．y=2x﹣4．（2）由图象可知，当﹣1＜x＜0或x＞3时一次函数的值大于反比例函数的值．8．（1）∵双曲线过点（﹣1，﹣2），∴k1=﹣1×（﹣2）=2．∵双曲线y1=，过点（2，n），∴n=1．由直线y2=k2x+b过点A，B 得，解得．∴反比例函数关系式为y1=，一次函数关系式为y2=x﹣1．（2）当x＜﹣1或0＜x＜2时，y1＞y2．9．（1）解：∵y1=k1x过点A（1，2），∴k1=2．（2分）∴正比例函数的表达式为y1=2x．（3分）∵反比例函数过点A（1，2），∴k2=2．（5分）∴反比例函数的表达式为y=．（6分）（2）﹣1＜x＜0或x＞1．（8分）（3）∵点A的坐标为（1，2），∴OA=，当OA为腰时，OA=OP2=，P2点坐标为（0，4），当AP1=OA=，可知P1坐标为（0，），当OA=OP3=时，可得P3坐标为（0，﹣）由图可知，P1（0，），P2（0，﹣），P3（0，4），当OA为底时，OP4==，故P1（0，），P2（0，﹣），P3（0，4），P4（0，）．10．（1）∵反比例函数y=﹣经过点A（m，﹣3）．∴﹣3m=﹣6，∴m=2；∵一次函数y=kx﹣2经过点A（m，﹣3）．∴2k﹣2=﹣3，∴k=﹣，∴一次函数的关系式为y=﹣x﹣2．（2）当a＞0时，则a＜a+2，∵反比例函数y=﹣的图象在第四象限内是增函数，∴y1＜y2；当﹣2＜a＜0时，则a+2＞0，由图象知y1＞y2；当a＜﹣2时，则a＜a+2，∵反比例函数y=﹣的图象在第二象限内是增函数，∴y1＜y211．（1）∵函数y=3x的图象过点A（1，m），∴m=3，∴A（1，3）；∵点A（1，3）在反比例函数的图象上，∴k=1×3=3，∴反比例函数的解析式为y=；（2）∵点B（n，1）在反比例函数的图象上，（3）依题意得PO•3=6∴OP=4，∴P点坐标为（0，4）或（0，﹣4）．12．（1）∵点A（﹣2，1）在反比例函数y1=mx的图象上，∴1=m﹣2，即m=﹣2，又A（﹣2，1），C（0，3）在一次函数y2=kx+b图象上，∴即k=1，b=3，∴反比例函数与一次函数解析式分别为：y=与y=x+3；（2）由得x+3=﹣，即x2+3x+2=0，∴x=﹣2或x=﹣1，∴点B的坐标为（﹣1，2）．（3）当x＜﹣2或﹣1＜x＜0时，反比例函数在一次函数图象的上方，即y1＞y2…13．（1）把（m，﹣3）分别代入和y1=2x﹣7，得，解得m=2，k=﹣6，∴反比例函数的解析式．（2）把点Q代入反比例函数的解析式中，即=﹣=．故点Q在反比例函数的图象上14．（1）把B（﹣2，1）代入得：m=﹣2×1=﹣2，∴y=﹣，把A（1，a）代入得：a=﹣2，∴A（1，﹣2），把A（1，﹣2），B（﹣2，1）代入得：，解得：k=﹣1，b=﹣1，∴y=﹣x﹣1，答：一次函数和反比例函数的解析式分别是y=﹣，y=﹣x﹣1．（2）令y=0，则0=﹣x﹣1，∴x=﹣1，∴C（﹣1，0），∴OC=1，∴S△AOB=S△AOC+S△BOC =×1×2+×1×1=1.5 15．（1）A点坐标为（﹣6，﹣2），B点坐标为（4，3）；（2）把B（4，3）代入y=得m=3×4=12，所以反比例函数的解析式为y=；（3）分别过点A、点B作y轴、x轴的垂线，两线交于点C，即AC⊥BC，如图，则点C的坐标为C（4，﹣2），在Rt△ACB中，AC=10，BC=5，∵AB2=BC2+AC2，∴AB==5．16．（1）∵B（2，﹣4）在函数y2=的图象上，∴m=﹣8．∴反比例函数的解析式为：y2=﹣．∵点A（n，2）在函数y2=﹣的图象上∴n=﹣4∴A（﹣4，2）∵y1=kx+b经过A（﹣4，2），B（2，﹣4），∴，解得．∴一次函数的解析式为：y1=﹣x﹣2（2）由交点坐标和图象可知，当﹣4＜x＜0或x＞2取何值时，y1＜y217．把y=x+1代入得：x+1=x+，解得：x=1，把x=1代入y=x+1得：y=2，把（1，2）代入y=得：k=2，即反比例函数的解析式是y=18．（1）将A（﹣4，0）代入y=kx+2得：﹣4k+2=0，即k=0.5，∴一次函数解析式为y=0.5x+2，将B（2，a）代入一次函数解析式得：a=1+2=3，即B （2，3），将B（2，3）代入反比例解析式得：m=2×3=6，则反比例解析式为y=；（2）∵OC=2，OA=4，∴AC=OC+OA=2+4=6，∵BC=3，∴S△ABC =AC•BC=919．（1）∵A（﹣4，2）在上，∴m=﹣8，∴反比例函数的解析式是y=﹣，∵B（2，n ）在上，∴n=﹣4．（2）当x＜﹣4或0＜x＜2时，y1＞y2；当x=﹣4或x=2时，y1=y2；当﹣4＜x＜0或x＞2时，y1＜y2．20．（1）根据题意，反比例函数y2=的图象过（﹣1，4），（﹣4，n），易得m=﹣4，n=1；则y1=kx+b的图象也过点（﹣1、4），（﹣4，1）；代入解析式可得k=1，b=5；∴y1=x+5；（2）设直线AB交x轴于C点，由y1=x+5得，∴C（﹣5，0），∵S△AOC =×5×4=10，S△BOC =×5×1=2.5，∴S△AOB=S△AOC﹣S△BOC=10﹣2.5=7.5；（3）根据图象，两个图象只有两个交点，根据题意，找一次函数的图象在反比例函数图象上方的部分；易得当x＞0或﹣4＜x＜﹣1时，有y1＞y2，故当y1＞y2时，x的取值范围是x＞0或﹣4＜x＜﹣1 21．（1）∵点B（﹣4，﹣2）在反比例函数的图象上，∴，k=8．∴反比例函数的解析式为．﹣﹣﹣﹣﹣﹣﹣﹣（1分）∵点A（m，4）在反比例函数的图象上，∴，m=2．∵点A（2，4）和点B（﹣4，﹣2）在一次函数y=ax+b 的图象上，∴解得∴一次函数的解析式为y=x+2．（2）设一次函数y=x+2的图象与y轴交于点C，分别作AD⊥y轴，BE⊥y轴，垂足分别为点D，E．（如图）∵一次函数y=x+2，当x=0时，y=2，∴点C的坐标为（0，2）．∴S△AOB=S△AOC+S△BOC ===6（3）﹣4＜x＜0或x＞2．阅卷说明：第（3）问两个范围各（1分）22．（1）设反比例函数的解析式是y=（a≠0），把A（﹣2，1）代入得：k=﹣2，即反比例函数的解析式是y=﹣；把B（1，n）代入反比例函数的解析式得：n=﹣2，即B的坐标是（1，﹣2），把A（﹣2，1）和B（1，﹣2）代入y=kx+b得：，解得：k=﹣1，b=﹣1．即一次函数的解析式是y=﹣x﹣1；（2）根据图象可知：一次函数的值大于反比例函数的值的x的取值范围是x＜﹣2或0＜x＜1；（3）能求出△AOB的面积，把y=0代入y=﹣x﹣1得：0=﹣x﹣1，x=﹣1，即C的坐标是（﹣1，0），OC=1，∵A（﹣2，1），B（1，﹣2），∴△AOB的面积S=S△AOC+S△BOC=×1×1+×1×|﹣2|=1.523．（1）当y=0时，则kx+2k=0，又∵k≠0∴x=﹣2，∴点B坐标为（﹣2，0）；（2）设点A的坐标为（x、y），∴S△AOB =•|﹣2|•|y|=，∴y=±，∵点A在第一象限，∴y=，把y=代入y=得x=，∴点A 的坐标为（，）24．∵把P（﹣3，m）代入反比例函数y=﹣得：m=2，∴点P的坐标为（﹣3，2），设一次函数的关系式为y=kx+b，∴把Q和P 的坐标代入得：，解得：k=﹣1，b=﹣1．故所求一次函数的关系式为y=﹣x﹣125．（1）因为函数图象经过点A（2，﹣4），所以2k1=﹣4，得k1=﹣2．（2分）所以，正比例函数解析式：y=﹣2x．（1分）（2）根据题意，当y=2时，﹣2m=2，得m=﹣1．（1分）于是，由点B 在反比例函数的图象上，得，解得k2=﹣2．所以，反比例函数的解析式是．26．（1）把x=2代入y=﹣3x得：y=﹣6，即A的坐标是（2，﹣6），把A的坐标代入y=得：﹣6=，解得：k=﹣13；（2）解方程组得：，，即A的坐标是（2，﹣6），B的坐标是（﹣2，6）；（3）当﹣2＜x＜0或x＞2时，＞﹣3x，故答案为：﹣2＜x＜0或x＞227．（1）把A（﹣4，2）代入y=得：m=﹣8，即反比例函数的解析式为y=﹣，把B（n，﹣4）代入得：n=2，即B（2，﹣4），即m=﹣8，n=2；（2）把A、B的坐标代入一次函数的解析式得：解得：k=﹣1，b=﹣2，即一次函数的解析式是y=﹣x﹣2；（3）一次函数的值小于反比例函数的值的x的取值范围是x＞2或﹣4＜x＜028．解方程组得或，∴C点坐标为（1，4），∵CD⊥x轴，∴D点坐标为（1，0）对y=x+3，令x=0，y=3，∴B点坐标为（0，3），∴四边形OBCD的面积=（OB+CD）•OD=（3+4）×1=29．1）解：把B（﹣1，﹣2）分别代入反比例函数∴k1=﹣1×（﹣2）=2，∴反比例函数的解析式为y=；把A（2，n）代入上式，得n=1，∴A点坐标为（2，1），把A（2，1）和B（﹣l，﹣2）分别代入一次函数y=k2x+b 得，2k2+b=1，﹣k2+b=﹣2，解得k2=1，b=﹣1，∴一次函数的关系式为y=x﹣1；（2）证明：过A作AE⊥x轴于E，BF⊥y轴与F，AB 与坐标轴相交于C、D，如图，对于y=x﹣1，令x=0，y=﹣1；令y=0，x=1，∴C（1，0），D（0，﹣1），AC===，CD===，BD===，∴AC=CD=BD，∴线段AB分别与x轴、y轴分成三等分；（3）解：x＜﹣1或0＜x＜230．过点A作AC⊥x轴于点C．∵sin∠AOE=，OA=5，∴AC=OA•sin∠AOE=4，由勾股定理得：CO==3，∴A（﹣3，4），把A（﹣3，4）代入到中得m=﹣12，∴反比例函数解析式为，∴6n=﹣12，∴n=﹣2，∴B（6，﹣2），∴有，解得：，∴，一次函数的解析式为。

一次函数与反比例函数的综合应用训练

一次函数与反比例函数的综合应用训练例1：已知一次函数y=（3-k）x-2k2+18.（1）k为时，它的图象经过原点；（2）k为时，它的图象经过点（0，-2）；（3）k为时，它的图象平行于直线y=-x；（4）k为时，它的图象垂直于直线y=2x+1；（5）k为时，y随x的增大而减小,=+的图象经过M(0，2)，N(1，3)两点．例2：已知一次函数y kx b(l) 求k、b的值；=+的图象与x轴和y轴的交点坐标(2) 求一次函数y kx b=+的图象与坐标轴围成的三角形面积。

(3) 求一次函数y kx b例3：一家小型放映厅的盈利额y元同售票数x之间的关系如图所示，其中保险部门规定：超过150人时，要缴纳公安消防保险费50元，据图回答：（1）当0＜x≤150时，y与x的关系式。

（2）当150＜x≤200时，y与x的关系式。

（3）当售票数x为时，不赔不赚；当售票数x为时，赔本；若获得最大利润200元x为。

基础巩固小训练：一、选择题1、一次函数y=（m-2）x+（3-2m ）的图像经过点（-1，-4），则m 的值为（）．A ．-3B ．3C ．1D ．-12、若一次函数y=（2-m ）x+m 的图像经过第一、•二、•四象限，•则m•的取值范围是（）3、一次函数y=kx+b 满足x=0时y=-1；x=1时，y=1，则一次函数的表达式为（）．A ．y=2x+1B ．y=-2x+1C ．y=2x-1D ．y=-2x-14、如图，线段AB 对应的函数表达式为（）A ．y=-32x+2B ．y=-23x-2C ．y=-23x+2（0≤x ≤3）D ．y=-23x+2（0<x<3） 5、已知函数y=x-3，若当x=a 时，y=5；当x=b 时，y=3，a 和b 的大小关系是（）A ．a>bB ．a=bC ．a<bD ．不能确定6、已知正比例函数y ＝kx （k ≠0），y 随x 的增大而减小，则一次函数y ＝x ＋k 的图像大致是（）。

一次函数与反比例函数综合练习题

一次函数与反比例函数综合练习题1.如图是反比率函数 y ＝的图象的一支，依据图象回答以下问题：( 1) 图象的另一支在哪个象限？常数 n 的取值范围是什么？( 2) 若函数图象经过点( 3，1) ，求 n 的值；( 3) 在这个函数图象的某一支上任取点 A( a 1 ， b 1 ) 和点 B( a 2 ，b 2 ) ，假如 a 1＜ a 2 ，试比较 b 1 和 b 2 的大小．y2 如图，已知反比率函数yk与一次函数 y x b 的图象在第一象限订交于点4A(1, k4) ．x2（ 1）试确立这两个函数的表达式；（ 2）求出这两个函数图象的另一个交点B 的坐标，并依据图象写出使反比率函数的值大于一次函数的值的 x 的取值范围．3 如图，在直角坐标系中，矩形 OABC 的极点 O 与坐标原点重合，极点O24xA ， C 分别在座标轴上，极点B 的坐标为（ 4， 2）．过点 D （ 0， 3）和 E（ 6， 0）的直线分别与AB ，BC 交于点 M ， N ．（ 1）求直线 DE 的分析式和点M 的坐标；（m （ x2）若反比率函数 yx＞ 0）的图象经过点 M ，求该反比率函数的分析式，并经过计算判断点N能否在该函数的图象上；（3）若反比率函数 ymy（x ＞0）的图象与△D．．xMABMNB 有公共点，请直接写出 m 的取值范围．ykx 2mN4.如图，一次函数的图象与反比率函数的图象交于点 P ，点 PyExxOC在第一象限． PA ⊥x 轴于点 A ， PB ⊥ y 轴于点 B ．一次函数的图象分别交x 轴、 y 轴于点 C 、 D ，且 S PBD =4， OC 1 ．（ 1）求点 D 的坐标；（ 2）求一次函数与反比率函数的分析式；△OA 2x 的取值范围 .（ 3）依据图象写出当x 0 时，一次函数的值大于反比率函数的值的5 已知：如图，在平面直角坐标系xOy 中，直线 AB 分别与 x 、y 轴交于点 B 、 A ，与反比率函数的图象分别交于点 C 、 D ， CE ⊥ x 轴于点 E ， tan ABO1，OB4， OE 2 ．2（ 1）求该反比率函数的分析式；（ 2）求直线 AB 的分析式．6．如图，在平面直角坐标系 xOy 中，一次函数 y=kx+ b 与反比率函数ymA ，与 x的图象交于点3x轴交于点 B ， AC ⊥ x 轴于点 C ， tanABC， AB=10 ， OB=OC ．4（ 1）求反比率函数和一次函数的分析式；（2）若一次函数与反比率函数的图象的另一交点为D ，连结 OA 、 OD ，求 △ AOD 的面积．yA7．如图，直线 AB : ykx b 与反比率函数ym交于 B ，与 x 轴交于点 A ，4,C( 6,0), BCxtan OABBO 5 .5m (1) 求直线 AB 和反比率函数y的分析式；x(2) 求线段 AB 的长 .8．如图，一次函数yx 1 与反比率函数 ymA.一次函数 yx 1 与坐标交于第二象限点x1 轴分别交于 B 、 C 两点，连结 AO ，若 tanAOB.3(1) 求反比率函数的分析式；(2) 求 AOC 的面积 .9．如图 ,已知在平面直角坐标系xOy 中，一次函数mykx b(k0) 的图象与反比率函数yx (m 0) 的图象订交于 A 、B 两点，且点B 的纵坐标为6，过点 A 作AEx 轴于点 E,tan ∠ AOE=1， AE=2.求：（ 1）求反比率3函数与一次函数的分析式；(2) 求 △ AOB 的面积；10 ．如图，一次函数y 1 ax b 的图象与反比率函数y 2k的yx图象交于A, B 两点，已知OA10, tan AOC1,点B 的3 3A坐标为 (, m).2OC x(1) 求反比率函数的分析式和一次函数的分析式；B(2) 察看图象，直接写出使函数值y 1 y 2 建立的自变量 x 的取值范围 .11 ．如图，一次函数 y ax b 的图象与反比率函数 yk A ， B 两点，与 y 轴交的图象订交于x于点 C ，与 x 轴交于点 D ，点 D 的坐标为2,0 ，点 A 的横坐标是（ 1）求点 A 的坐标；（ 2）求一次函数和反比率函数的分析式；（ 3）求△ AOB 的面积；2， tan ∠ CDO = 1.2yACDBO x12 ．如图，已知反比率函数my的图象经过点A(1, 3),一次函数xy kx b 的图象经过点A与点C(0,4), 且与反比率函数的图象订交于另一点B(3, n).(1)试确立这两个函数的分析式；(2)求 AOB 的面积；(3)依据图象直接写出反比率函数值大于一次函数值时自变量的取值范围 .13 ．如图，若直线y kx b( k 0) 与 x 轴交于点A(5m,0) ，与双曲线 y(m 0) 在第二象OAB 的面积为52x限交于点 B ，且 OA OB ，2（1）求直线AB的分析式及双曲线的分析式；（2）求∠ ABO值 .14. 如图，在平面直角坐标系中，一次函数y kx b(k0) 与反比率函数y mm 0 的图象x分别交于一、三象限的A，B 两点，与x轴交于点 C ，与 y 轴交于点 D ，线段OC=2，点A的坐标为 n,3，且 cos ∠ACO =4. （1）求该反比率函数和一次函数的分析式；（ 2）求△AOB的面积 .5yk1 x b 的图象分别与 x 轴、y轴的正半轴交于15 ．如图，已知一次函数y A 、 B 两点，且与反比例函数 y k2交于 C、 E 两点，点 C 在第二象限，过点C 作 CD ⊥x轴于点 D ， OD=1, OE＝A x D10 ,cos∠AOE=3 10．(1)求反比率函数与一次函数的分析式；CO 10B(2)求△ OCE 的面积；k过面积为y16 ．若反比率函数y19 的正方形 AMON 的极点 A ，且过点 A 的直线y2mx n 的x1, a ）图象与反比率函数的另一交点为B（M A（ 1）求出反比率函数与一次函数的分析式；（ 2）求AOB 的面积；Ok 17 、如图，四边形OABC 是面积为 4 的正方形，函数yxN x (x ＞ 0)的图象经过点B．B(1)求 k 的值；(2) 将正方形 OABC 分别沿直线AB 、 BC 翻折，获得正方形MABC′、 NA′ BC．设线段 MC′、 NA′分别与函数y k E、 F ，求线段 EF 所在直线的分析式．(x＞ 0) 的图象交于点x18 、如图，RtVABO的极点 A 是反比率函数y k与一次xy函数 yx ( k1) 的图象在第四象限的交点，AB x轴于 B，且S V ABO 5 。

一次函数反比例函数练习题完整

一次函数反比例函数练习题(可以直接使用，可编辑优秀版资料，欢迎下载）B ′ AB CEOxy中考考点练习《一次函数与反比例函数》1、反比例函数xk y 的图像经过A （－23，5）点、B （a ，－3），则k ＝，a ＝．2、如图是一次函数y 1＝kx ＋b 和反比例函数y 2＝＝m x的图象，•观察图象写出y 1>y 2时，x 的取值范围是_________．3、已知点A 的坐标为(13)，，点B 的坐标为(31)，．⑴ 写出一个图象经过A B ，两点的函数表达式；⑵ 指出该函数的两个性质．4、如图，在直角坐标系中放入一个边长OC 为9的矩形纸片ABCO ．将纸片翻折后，点B 恰好落在x 轴上，记为B ′，折痕为CE ，已知tan ∠OB ′C ＝34．（1）求B ′点的坐标；（2）求折痕CE所在直线的解析式．y32 1O 1 2 xA B3（A）（B）（C）5、若反比例函数kyx=的图象经过点（-1,2)，则这个函数的图象一定经过点（）A、(2,-1) B、(12-,2) C、(-2,-1) D、(12,2)7、下列各图象中，不能表示y是x的函数的是（）8、把直线y=x向左平移一个单位长度后，其表达式为（）（A）y=x+1 (B)y=x-1 (C)y=x (D)y=x-2 9、如图，一次函数图象经过点A，且与正比例函数y x=-的图象交于点B，则该一次函数的表达式为（）（A）2y x=-+(B)2y x=+(C)22+=xy(D)2y x=--2乙甲乙甲815101.510.5Oy/千米10、在全民健身环城越野赛中，甲乙两选手的行程y （千米）随时间（时）变化的图象（全程）如图所示.有下列说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米.其中正确的说法有（）（A ） 1 个 (B) 2 个 (C)3 个 (D)4个11、点P 1（x 1，y 1），点P 2（x 2，y 2）是一次函数y ＝－4x + 3 图象上的两个点，且 x 1＜x 2，则y 1与y 2的大小关系是（）．12、一次函数y=(2-a)x+a 中，y 随x 的增大而减小，且︱a ︱=4，则该函数关系式为______.13、如图，过原点的一条直线与反比例函数y ＝k x（k<0）的图像分别交于A 、B 两点，若A 点的坐标为（a ，b ），则B 点的坐标为（）14、函数2y kx =-与k y x=（k ≠0）在同一坐标系内的图象可能是（）15、点P(1，a)在反比例函数y=kx的图象上，它关于y轴的对称点在一次函数y=2x+4的图象上，求此反比例函数的解析式.16、如图,1 已知在平面直角坐标系xOy中，一次函数y=kx+b (k≠0)的图象与反比例函数y=mx(m≠0)的图象相交于A、B两点，且点B的纵坐标为-12，过点A作AC⊥x轴于点C，AC=1,OC=2．求：（1）求反比例函数的解析式；（2）求一次函数的解析式．图17、一次函数y=kx+b 的图象与反比例函数y=mx 的图象交于点A （2，1），B （－1，n ）两点。

经典一次函数、反比例函数练习(附详细答案)

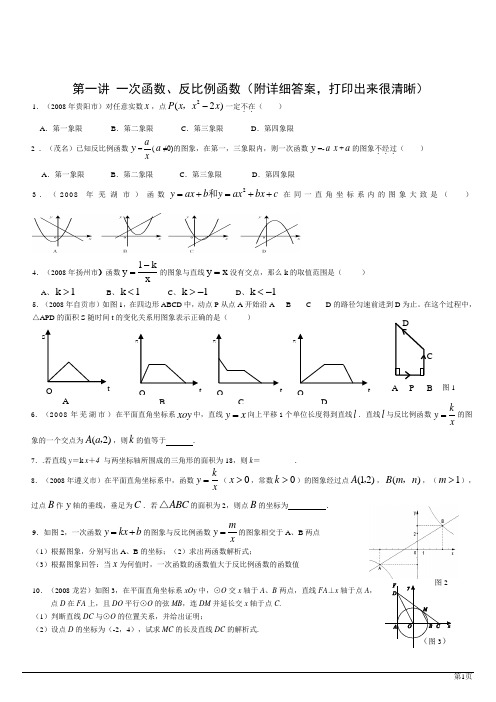
第一讲一次函数、反比例函数（附详细答案，打印出来很清晰）1．（2008年贵阳市）对任意实数x ，点2(2)P x x x -，一定不在．．（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限2 ．（茂名）已知反比例函数y =xa (a ≠0)的图象，在第一，三象限内，则一次函数y =-a x +a 的图象不经过．．．（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3．（2008年芜湖市）函数2y a x b y a x b x c =+=++和在同一直角坐标系内的图象大致是（）4．（2008年扬州市）函数xk1y-=的图象与直线x y =没有交点，那么k 的取值范围是（） A 、1k > B 、1k < C 、1k -> D 、1k -<5．（2008年自贡市）如图1，在四边形ABCD 中，动点P 从点A 开始沿A B C D 的路径匀速前进到D 为止。

在这个过程中，的变化关系用图象表示正确的是（）6．（2008年芜湖市）在平面直角坐标系xoy 中，直线y x =向上平移1个单位长度得到直线．直线l 与反比例函数ky x=的图象的一个交点为(2)A a ，，则k 的值等于．7．.若直线y ＝k x ＋4 与两坐标轴所围成的三角形的面积为18，则k ＝_________． 8．（2008年遵义市）在平面直角坐标系中，函数ky x=（0x >，常数0k >）的图象经过点(12)A ，，()B m n ，，（1m >），过点B 作y 轴的垂线，垂足为C ．若ABC △的面积为2，则点B 的坐标为．9．如图2，一次函数y kx b =+的图象与反比例函数my x=的图象相交于A 、B 两点（1）根据图象，分别写出A 、B 的坐标；（2）求出两函数解析式；（3）根据图象回答：当x 为何值时，一次函数的函数值大于反比例函数的函数值10．（2008龙岩）如图3，在平面直角坐标系xOy 中，⊙O 交x 轴于A 、B 两点，直线FA ⊥x 轴于点A ，点D 在FA 上，且DO 平行⊙O 的弦MB ，连DM 并延长交x 轴于点C . （1）判断直线DC 与⊙O 的位置关系，并给出证明；（2）设点D 的坐标为（-2，4），试求MC 的长及直线DC 的解析式.图111．（2008年泰州市）2008年5月12日14时28分四川汶川发生里氏8.0级强力地震．某市接到上级通知，立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区．乙组由于要携带一些救灾物资，比甲组迟出发1.25小时（从甲组出发时开始计时）．图中的折线、线段分别表示甲、乙两组的所走路程y 甲（千米）、y 乙（千米）与时间x （小时）之间的函数关系对应的图像．请根据图像所提供的信息，解决下列问题：（1）由于汽车发生故障，甲组在途中停留了小时；（2分）（2）甲组的汽车排除故障后，立即提速赶往灾区．请问甲组的汽车在排除故障时，距出发点的路程是多少千米？（6分）（3）为了保证及时联络，甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米，请通过计算说明，按图3所表示的走法是否符合约定．（4分）12．（2008年巴中市）已知：如图，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ．（1）写出直线BC 的解析式．（2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？13．（2008黄冈市）已知：如图，在直角梯形COAB 中，OC ∥AB ，以O 为原点建立平面直角坐标系，A ，B ，C 三点的坐标分别为A(8，0)，B(8，10)，C(0，4)，点D 为线段BC 的中点，动点P 从点O 出发，以每秒1个单位的速度，沿折线OABD 的路线移动，移动的时间为t 秒．（1）求直线BC 的解析式；（2）若动点P 在线段OA 上移动，当t 为何值时，四边形OPDC 的面积是梯形COAB 面积的27？（3）动点P 从点O 出发，沿折线OABD 的路线移动过程中，设△OPD 的面积为S ，请直接写出S 与t 的函数关系式，并指出自变量t 的取值范围；（4）当动点P 在线段AB 上移动时，能否在线段OA 上找到一点Q ，使四边形CQPD 为矩形？若能，请求出此时动点P 的坐标；若不能，请说明理由．14．（河南12分）如图，直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ，点A 的坐标是（-2，0）．（1）试说明△ABC 是等腰三角形；（2）动点M 从A 出发沿x 轴向点B 运动，同时动点N 从点B 出发沿线段BC 向点C 运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M 运动t 秒时，△MON 的面积为S ．① 求S 与t 的函数关系式；② 设点M 在线段OB 上运动时，是否存在S =4的情形？若存在，求出对应的t 值；若不存在请说明理由； ③在运动过程中，当△MON 为直角三角形时，求t 的值．（图3）第一讲一次函数、反比例函数答案1~5 C C C A B 6. 2 7. 49- 或 49 8. (3, 23) 9.（1）A （-6，-2），B （4，3） ,（2）12y x =，112y x =+,（3）-6<x<0或x>410．（13分）（1）答：直线DC 与⊙O 相切于点M . 证明如下：连OM ， ∵DO ∥MB ，∴∠1=∠∵OB =OM ，∴∠1=∠3 ，∴∠2=∠4 . 在△DAO 与△DMO 中，⎪⎩⎪⎨⎧DO=DO =∠∠AO=OM42∴△DAO ≌△DMO . ∴∠OMD =∠OAD .由于FA ⊥x 轴于点A ，∴∠OAD =90°.∴∠OMD =90°. 即OM ⊥DC . ∴DC 切⊙O 于M .（2）解：由D （－2，4）知OA =2（即⊙O 的半径），AD =4 .由（1）知DM =AD =4，由△OMC ∽△DAC ，知MC AC = OM AD = 24 = 12 .∴AC =2MC . 在Rt △ACD 中，CD =MC ＋4.由勾股定理，有(2MC )2＋42=(MC ＋4)2，解得MC = 83 或MC =0（不合，舍去）。

反比例函数和一次函数的综合练习题

反比例函数和一次函数的综合练习题————————————————————————————————作者：————————————————————————————————日期:ﻩ1．已知直线1y k x =(10k ≠）和双曲线2k y x=(20k ≠)的一个交点是(2-,5)，求它们的另一个交点坐标．２.直线()0y ax a =>与双曲线3y x=交于()()1122A x y B x y ，、，两点，则122143x y x y -= .3.已知正比例函数与反比例函数图象交点到x 轴的距离是3,到y 轴的距离是4,求它们的解析式．4．若一次函数3y x b =+和反比例函数3b y x-=的图像有两个交点，当b =______时，有一个交点的纵坐标为6.5.如图,直线43y x =与双曲线()0k y x x =>交于点A .将直线43y x =向右平移92个单位后，与双曲线()0k y x x =>交于点B ，与x 轴交于点C ,若2AOBC=，则k =_____＿___. CABOyx6.已知一次函数y kx b =+(0k ≠）的图象与x 轴、y 轴分别交于点A 、B ,且与反比例函数my x=(0m ≠)的图象在第一象限交于C 点，CD 垂直于x 轴，垂足为D .若1OA OB OD ===, （1）点A 、B 、D 的坐标；（2）求一此函数与反比例函数的解析式.xyOC B A D7.在平面直角坐标系Oxy 中,直线y x =-绕点O 顺时针旋转90︒得到直线l ．直线l 与反比例函数ky x=的图像的一个交点为()3A a ，,试确定反比例函数的解析式．8.在平面直角坐标系xOy 中,直线y x =向上平移1个单位长度得到直线l .直线l 与反比例函数ky x=的图象的一个交点为()2A a ，,则k 的值等于．9．在平面直角坐标系xOy 中,直线y x =-绕点O 顺时针旋转90的到直线l .直线l 与反比例函数ky x=的图象的一个交点为()3A a ，,试确定反比例函数的解析式.1０．已知反比例函数ky x =（0k <)的图像经过点A (3-,m )，过点A 作AB ⊥x 轴于点B ，且AOB ∆的面积为3.（1）求k 和m 的值．（2）若一次函数1y ax =+的图象经过点A ,并且与x 轴相交于点C ,求:AO AC 的值.CBAxy O1１.如图，反比例函数ky x=的图像与一次函数y mx b =+的图像交于()13A ，,()1B n -，两点.（1）求反比例函数与一次函数的解析式;（2）根据图像回答:当x 取何值时,反比例函数的值大于一次函数的值．O ABxy1２.如图7,已知一次函数1y x m =+（m 为常数）的图象与反比例函数2ky x =（k 为常数,0k ≠)的图象相交于点()13A ，．（１）求这两个函数的解析式及其图象的另一交点B 的坐标; （2）观察图象,写出使函数值12y y ≥的自变量x 的取值范围．13O ABxy13.如图,已知()()424A B n --，，，是一次函数y kx b =+的图象与反比例函数的图象的两个交点.（1）求此反比例函数和一次函数的解析式;（2）根据图象写出使一次函数的值小于反比例函数的值的x 的取值范围.OABxyOA （-2，1）B （1，n ）xy14.如图,已知：一次函数y kx b =+的图像与反比例函数my x=的图像交于A 、B 两点．（１）利用图中条件,求反比例函数和一次函数的解析式；（2）根据图像写出使一次函数的值大于反比例函数的值的x 取值范围．１5.如图,已知()()424A n B --，，，是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点.（1)求反比例函数和一次函数的解析式；（2)求直线AB 与x 轴的交点C 的坐标及AOB ∆的面积;(3）求方程0mkx b x+-=的解(请直接写出答案）；（3）求不等式0mkx b x+-=的解集（请直接写出答案）. O ABxy1６.已知一次函数与反比例函数的图象交于点P (3-,m )，Q （2，3-). （1）求这两个函数的函数关系式;(2)在给定的直角坐标系(如图)中，画出这两个函数的大致图象;(３)x 为何值时,一次函数的值大于反比例函数的值?x 为何值时，一次函数的值小于反比例函数的值？1７.已知正比例函数1y k x =1(0)k ≠与反比例函数22(0)k y k x=≠的图象交于A B 、两点，点A 的坐标为(21)，. （１）求正比例函数、反比例函数的表达式；（2）求点B 的坐标．18.已知一次函数y x m =+与反比例函数1m y x+=（1m ≠-）的图象在第一象限内的交点为P (0x ,3)（1)0x 的值．（2）一次函数和反比例函数的解析式.１9.直线y kx =（0k >）与双曲线4y x=交于A()11x y ，,B ()22x y ，两点,求122127x y x y -的值．BA xyO20.如图,一次函数122y x =-的图象分别交x 轴、y 轴于A B P ，，为AB 上一点且PC 为AOB ∆的中位线,PC 的延长线交反比例函数()0k y k x =>的图象于Q ,32OQC S ∆=,则k 的值和Q 点的坐标分别为_＿_____＿_＿_＿_＿.２1.已知反比例函数y=k2x和一次函数ｙ=2ｘ－1，其中一次函数的图象经过(ａ，b),(a+1，b ＋k ）两点。

一次函数和反比例函数测试题(含答案)

一次函数和反比例函数测试题(考试时间70分钟试卷满分100分)一、选择题（每题4分，共24分）1．如图，已知直线y ＝k 1x (k 1≠0)与反比例函数y ＝k 2x (k 2≠0)的图象交于M ，N 两点．若点M 的坐标是(1，2)，则点N 的坐标是( )A ．(－1，－2)B ．(－1，2)C ．(1，－2)D ．(－2，－1)2．如图，已知反比例函数y ＝－3x 与正比例函数y ＝kx (k ＜0)的图象相交于A ，B 两点，AC 垂直x 轴于点C ，则△ABC 的面积为( )A ．3B ．2C ．kD ．k 2 3. 已知函数1y x=的图象如图所示，当1x -≥时，y 的取值范围是（） A. 1y <- B. 1y -≤ C. 1y -≤或0y > D. 1y -<或0y ≥ 4．若点A(－6，y 1)，B(－2，y 2)，C(3，y 3)在反比例函数y ＝2k 2＋3x (k 为常数)的图象上，则y 1，y 2，y 3的大小关系为( )A ．y 1＞y 2＞y 3B ．y 2＞y 3＞y 1C ．y 3＞y 2＞y 1D ．y 3＞y 1＞y 2 5．在同一直角坐标系中，函数y ＝kx 和y ＝kx －3的图象大致是( )y xO 1-1-第3题图6．如图，已知一次函数y ＝ax ＋b 和反比例函数y ＝kx 的图象相交于A (－2，y 1)，B (1，y 2)两点，则不等式ax ＋b ＜kx 的解集为( )A ．x ＜－2或0＜x ＜1B ．x ＜－2C ．0＜x ＜1D ．－2＜x ＜0或x ＞1 二、填空题（每小题4分，共16分）7．已知反比例函数y ＝k －1x (k 是常数，k ≠1)的图象有一支在第二象限，那么k 的取值范围是 .8．已知A(－4，y 1)，B(－1，y 2)是反比例函数y ＝－4x 图象上的两个点，则y 1与y 2的大小关系为 .9．如果一次函数y ＝kx ＋3(k 是常数，k ≠0)的图象经过点(1，0)，那么y 的值随x 值的增大而 .(填“增大”或“减小”) 10．（2018•东营）如图，B （3，﹣3），C （5，0），以OC ，CB 为边作平行四边形OABC ，则经过点A 的反比例函数的解析式为 .三、解答题（共6小题，共60分）11．（8分）正比例函数 y ＝kx 和一次函数 y ＝ax ＋b 的图象都经过点A(1,2)，且一次函数的图象交 x 轴于点 B(4,0)．求正比例函数和一次函数的表达式．12．（12分）已知函数y ＝(2m ＋1)x ＋m －3 （1）若函数图象经过原点，求m 的值；第6题图第10题图（2）若函数的图象平行直线y ＝3x －3，求m 的值；（3）若这个函数是一次函数，且y 随着x 的增大而减小，求m 的取值范围．13.（12分）如图，一次函数y =kx +b 的图象与反比例函数y =xm的图象交于A （－2，1）B （1，n ）两点．(1)试确定上述反比例函数和一次函数的表达式； (2)求△ABO 的面积；(3)根据图像直接写出当一次函数的值大于反比例函数的值时x 的取值范围。

反比例函数与一次函数综合练习题(总复习用)

y x 0反比例函数与一次函数综合练习题1.如图是反比例函数 y=m+2x 的图象的一支，根据图象回答下列问题： (1)图象的另一支在哪个象限?常数m 的取值范围是什么? (2)已知点（－3，y 1）, （－1，y 2）, （2，y 3）, 则函数值y 1、y 2、y 3的大小关系怎样？2.已知：如图，一次函数的图象经过第一、二、三象限，与y 轴交于点C ，与x 轴交于点D ．OB ＝10 ，tan ∠DOB ＝13． ⑴求反比例函数的解析式：⑵设点A 的横坐标为m ，△ABO 的面积为S ，求S 与m的函数关系式，并写出自变量m 的取值范围；3.如图所示，已知反比例函数y= k x的图象经过点A （－ 3 ，b ），过点A 作AB ⊥x 轴于点B ，△AOB 的面积为 3 。

⑴求k 、b 的值；⑵若一次函数y=ax+1的图象经过点A ，并且与x 轴相交于点M ，求AO ∶AM ； ⑶如果以AM 为一边的正三角形AMP 的顶点P 在二次函数y=－x 2+ 3 mx+m －9的图象上，求m 的值。

4.如图，已知C 、D 是双曲线y= m x 在第一像限内的分支上的两点，直线CD 分别交x 轴、y 轴于A 、B 两点，设C 、D 的坐标分别是(x 1，y 1)，(x 2，y 2)，连结OC 、OD 。

⑴求证：y 1<OC<y 1+ 1y m ； ⑵若∠BOC=∠AOD=α，tan α=13，OC=10 ，求直线CD 的解析式； ⑶在⑵的条件下，双曲线上是否存在一点P ，使得S △POC =S △POD ？若存在，请给出证明；若不存在，请说明理由。

5.已知一次函数y=mx+b 与反比例函数y= m x(m ≠0) ⑴k 满足什么条件时，这两个函数在同一坐标系xOy 中的图象有两个公共点？⑵设⑴中的两个公共点为A ，B ，试判断∠AOB 是锐角还是钝角？6.已知A （m ，2）是直线l 与双曲线y= 3x的交点。

一次函数及反比例函数难题(含答案)

专题训练7 一次函数及反比例函数一、选择题（每小题3分，共24分）1．函数y kx =-与y kx =（k ≠0）的图象的交点个数是（）A. 2B.1C. 0D.不确定2．若点（3，4）是反比例函数xm m y 122++=图象上一点，则此函数图象必经过点（）A.（3，－4）B.（2，－6）C.（4，－3）D. （2，6） 3. 函数y kx b =+与y kxkb =≠()0的图象可能是（）A B C D4．已知反比例函数)0(<=k xky 的图像上有两点A(1x ，1y )，B(2x ，2y )，且21x x <，则21y y -的值是（）A.正数B.负数C.非正数D. 不能确定5．．在同一坐标系中，函数x ky =和3+=kx y 的图像大致是（）A B C D6．骆驼被称为“沙漠之舟”，它的体温随时间的变化而发生较大的变化，其体温（℃）与时间（时）之间的关系如右图所示．若y （℃）表示0时到t 时内骆驼体温的温差（0时到t 时最高温度与最低温度的差）．则y 与t 之间的函数关系用图象表示，大致正确的是（）（A ）（B ）（C ）（D ）（第6题）7．李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，结果准时到校。

在课堂上，李老师请学生画出自行车行进路程s 千米与行进时间t 的函数图像的示意图，同学们画出的示意图如下，你认为正确的是（）A B C D8．正比例函数与反比例函数的图象都经过点（1，4），在第一象限内正比例函数的图象在反比例函数图象上方的自变量x 的取值范围是（）（A ）1x >．（B ）01x <<．（C ）4x >．（D ）04x <<．二、填空题（每小题3分，共18分）9．函数4y x =-与4y x=-的图象交于A 、B 两点，过点A 作AC 垂直于y 轴，垂足为点C ，则△BOC 的面积为___________． 10、若函数y=4x 与y=x 1的图象有一个交点是（21，2），则另一个交点坐标是 _。

中考数学总复习《反比例函数》练习题(附答案)

中考数学总复习《反比例函数》练习题（附答案）班级:___________姓名：___________考号：_____________一、单选题1．一次函数y1=k1x+b(k1≠0)与反比例函数y2=k2x(k2≠0)的图象交于点A(−1，−2)，点B(2，1)．当y1<y2时，x的取值范围是（）A．x<−1B．−1<x<0或x>2 C．0<x<2D．0<x<2或x<−12．关于函数y=−2x，下列说法中正确的是（）A．图像位于第一、三象限B．图像与坐标轴没有交点C．图像是一条直线D．y的值随x的值增大而减小3．如图，在直角坐标系中，点A是双曲线y= 3x（x＞0）上的一个动点，点B是x轴正半轴上的一个定点，当点A的横坐标逐渐增大时，△OAB的面积将会（）A．逐渐减小B．不变C．逐渐增大D．先减小后增大4．在同一平面直角坐标系中，反比例函数y=-8x与一次函数y=-x+2交于A，B两点，O为坐标原点，则△AOB的面积为()A．2B．6C．10D．85．如图，△ABC的三个顶点分别为A（1，2），B（4，2），C（4，4）．若反比例函数y= k x在第一象限内的图象与△ABC有交点，则k的取值范围是（）A．1≤k≤4B．2≤k≤8C．2≤k≤16D．8≤k≤166．如图，过反比例函数y= 1x（x＞0）的图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接OA、OB，设AC与OB的交点为E，△AOE与梯形ECDB的面积分别为S1、S2，比较它们的大小，可得（）A．S1＞S2B．S1=S2C．S l＜S2D．大小关系不能确定7．某村耕地总面积为50公顷，且该村人均耕地面积y（单位：公顷/人）与总人口x（单位：人）的函数图象如图所示，则下列说法正确的是（）A．该村人均耕地面积随总人口的增多而增多B．该村人均耕地面积y与总人口x成正比例C．若该村人均耕地面积为2公顷，则总人口有100人D．当该村总人口为50人时，人均耕地面积为1公顷8．在同一直角坐标系中，函数y=kx+1与y=−k x(k≠0)的图象大致是（）A．B．C．D．9．如图，在平面直角坐标系xOy中，函数y=kx+b（k≠0）与y= mx（m≠0）的图象相交于点A（-2，3），B（6，-1），则不等式kx+b＞mx的解集为（）A．x<−2B．−2<x<0或x>6 C．x<6D．0<x<6或x<−210．已知两个函数y1=k1x+b与y2= k2x的图象如图所示，其中A（-1，2），B（2，-1），则不等式k1x+b＞k2x的解集为（）A．x<−1或x>2B．x<−1或0<x<2 C．−1<x<2D．−1<x<0或0<x<211．在反比例函数y=−3x图象上有三个点A(x1，y1)、B(x2，y2)、C(x3，y3)，若x1<0<x2<x3，则下列结论正确的是（）A．y3<y2<y1B．y1<y3<y2C．y2<y3<y1D．y3<y1<y2 12．图所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的是A．当x=3时，EC＜EM B．当y=9时，EC＞EMC．当x增大时，EC·CF的值增大。

中考数学总复习《反比例函数与一次函数综合》专题训练-附答案

中考数学总复习《反比例函数与一次函数综合》专题训练-附答案学校:___________班级：___________姓名：___________考号：___________1．如图，已知反比例函数()10cy c x=≠和一次函数()20y kx b k =+≠的图象相交于点()2,3A -和()3,B a ．(1)求反比例函数和一次函数的表达式；(2)将一次函数2y 向下平移5个单位长度后得到直线3y ，当213y y y >>时，求x 的取值范围． 2．如图，反比例函数()0ky k x=>的图象经过正方形OABC 的顶点B ，一次函数1y x =+经过BC 的中点D ．(1)求反比例函数的表达式；(2)将ABD △绕点A 顺时针旋转90︒，点D 的对应点为E ，判断E 点是否落在双曲线上． 3．如图，反比例函数()0ky k x=< 的图象与矩形ABCO 的边相交于D 、E 两点()51E -，，且23AD BD =∶∶,一次函数经过D 、E 两点．(1)求反比例函数与一次函数的解析式； (2)求BDE △的面积．4．对于实数,a b ，我们可以用{}min ,a b 表示,a b 两数中较小的数，例如{}min 3,11-=- {}min 2,22=，类x x⎩⎭(1)求反比例函数的解析式；(2)请直接写出不等式2kx x -＞的解集；(3)点P 为反比例函数ky x=图像的任意一点，若3POC AOC S S =△△，求点P 的坐标． 7．如图，一次函数y mx n =+()0m ≠的图象与反比例函数ky x=()0k ≠的图象交于第二、四象限内的点(),3A a 和点()6,B b ．过点A 作x 轴的垂线，垂足为点C ，AOC 的面积为3(1)分别求出一次函数y mx n =+()0m ≠与反比例函数ky x=()0k ≠的表达式； (2)结合图象直接写出kmx n x>＋的解集； (3)在x 轴正半轴上取点P ，使PA PB -取得最大值时，求出点P 的坐标．8．如图，直线y ＝2x ＋6与反比例函数=ky x(k ＞0)的图象交于点A (1，m )，与x 轴交于点B ，平行于x 轴的直线y ＝n (0＜n ＜6)交反比例函数的图象于点M ，交AB 于点N ，连接BM ．x，求AOB 的面积；根据图象，请直接写出满足不等式1y kx b =+C ，点A 的坐标为(2)若点E 是点C 关于x 轴的对称点，求ABE 的面积． 11．已知平面直角坐标系中，直线AB 与反比例函数(0)ky x x=>的图象交于点()1,3A 和点()3,B n ，与x 轴交于点C ，与y 轴交于点D ．(1)求反比例函数的表达式及n 的值；(2)将OCD 沿直线AB 翻折，点O 落在第一象限内的点E 处，EC 与反比例函数的图象交于点F ． △请求出点F 的坐标；△将线段BF 绕点B 旋转，在旋转过程中，求线段OF 的最大值． 12．如图，正比例函数(0)y kx k =≠与反比例函数my (m 0)x=≠的图象交于A 、B 两点，A 的横坐标为4-，B 的纵坐标为6-．(1)求反比例函数的表达式． (2)观察图象，直接写出不等式mkx x<的解集． (3)将直线AB 向上平移n 个单位，交双曲线于C 、D 两点，交坐标轴于点E 、F ，连接OD 、BD ，若OBD 的面积为20，求直线CD 的表达式．13．某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y （微克/毫升）与服药时间x 小时之间函数关系如图所示．②的面积是OCD．如图，已知一次函数y轴交于点，若ACD的面积为16．如图，菱形ABCD 的边AB 在x 轴上，点A 的坐标为()1,0，点()44D ,在反比例函数()0k y x x=>的图象上，直线23y x b =+经过点C ，与y 轴交于点E ，与x 轴交于点M ，连接AC 、AE ．(1)求k 、b 的值； (2)求ACE △的面积；(3)在x 轴上取点P ，求出使PC PE -取得最大值时点P 的坐标． 17．已知反比例函数1k y x=图象经过点(3,2)A ，直线:(0)l y kx b k =+<，经过点(2,0)C -，经过点A 且垂直于x 轴的直线与直线l 相交于B ．(1)求1k 的值；(2)若ABC 的面积等于15，求直线l 的解析式；(3)点G 在反比例函数的图象上，点Q 在x 轴上，问是否存在点G 和点Q ，使以G ．Q 及（2）中的C ．B 四点为顶点的四边形是平行四边形，若存在，请求出点Q 的坐标，若不存在，请说明理由． 18．（综合与探究）如图，在平面直角坐标系中，已知反比例函数()0ky x x=<的图象过点()4,2C -，点D 的纵坐标为4，直线CD 与x 轴，y 轴分别交于点,A B ．Rt AOB直角边上的一个动点，当16PCD AOBS S=时，求点关于y轴的对称点为x轴的对称点为,N 使得以点,,M N为顶点的四边形是平行四边形？若存在，标；若不存在，请说明理由．．如图，已知直线y=x参考答案：3．(1)5y x =- 1722y x =+(2)944．(1)B (2)直线1x = 5．(1)1y x =- 2y x= (2)(1,0)C 12x <≤6．(1)3y x= (2)10x -＜＜或3＞x (3)()1,3或()1,3--7．(1)反比例函数的表达式为6y x =-，一次函数表达式为122y x =-+．(2)2x <－或06x << (3)()10,0P 8．(1)8y x= (2)39．(1)反比例函数的表达式为：22y x=-(2)32AOBS=(3)20x -<<或1x >10．(1)一次函数解析式1y x 4=-，反比例函数解析式212y x= (2)32ABE S =△11．(1)3y x= 1n =(2)△F 点坐标为3(4,)4；△线段OF 的最大值为17104+12．(1)24y x=-(2)40x -<<或>4x。

一次函数与反比例函数的综合专题练习

一次函数与反比例函数的综合专题练习1. 如图，反比例函数ky x=（k ＜0）与一次函数y =x +4的图象交于A 、B 两点的横坐标分别为﹣3，﹣1．则关于x 的不等式4kx x<+（x ＜0）的解集为（）A ．x ＜﹣3B ．﹣3＜x ＜﹣1C ．﹣1＜x ＜0D ．x ＜﹣3或﹣1＜x ＜02. 如图，直线6y =-分别交x 轴，y 轴于A ，B ，M 是反比例函数ky x=（x ＞0）的图象上位于直线上方的一点，MC ∥x 轴交AB 于C ，MD ⊥MC 交AB 于D ，AC •BD =k 的值为（）A ．﹣3B ．﹣4C ．﹣5D ．﹣63．在平面直角坐标系内，直线AB 垂直于x 轴于点C （点C 在原点的右侧），并分别与直线y =x 和双曲线1y x=相交于点A 、B ，且AC +BC =4，则△OAB 的面积为（）A ．或3B +1﹣1C ．3D 14.一次函数y =﹣x +1（0≤x ≤10）与反比例函数1y x=（﹣10≤x ＜0）在同一平面直角坐标系中的图象如图所示，点（x 1，y 1），（x 2，y 2）是图象上两个不同的点，若y 1=y 2，则x 1+x 2的取值范围是（）A ．﹣8910≤x ≤1 B ．﹣8910≤x ≤899 C ．﹣899≤x ≤8910 D ．1≤x ≤89105.如图，P 为反比例函数ky x=（k ＞0）在第一象限内图象上的一点，过点P 分别作x 轴，y 轴的垂线交一次函数y =﹣x ﹣4的图象于点A 、B ．若∠AOB =135°，则k 的值是（）学-科网A ．2B ．4C ．6D ．86. 如图，已知点A 是一次函数12y x =（x ≥0）图象上一点，过点A 作x 轴的垂线l ，B 是l 上一点（B 在A 上方），在AB 的右侧以AB 为斜边作等腰直角三角形ABC ，反比例函数ky x=（x ＞0）的图象过点B ，C ，若△OAB 的面积为6，则△ABC 的面积是．7.如图，直线333--=x y 与x ，y 轴分别交于点A ，B ，与反比例函数xky =的图象在第二象限交于点C ，过点A 作x 轴的垂线交该反比例函数图象于点D ．若AD =AC ，则点D 的坐标为．8.如图，过C （2，1）作AC ∥x 轴，BC ∥y 轴，点A ，B 都在直线y =﹣x +6上，若双曲线ky x=（x ＞0）与△ABC 总有公共点，则k 的取值范围是．9.如图，在平面直角坐标系xOy 中，已知直线y =kx （k ＞0）分别交反比例函数1y x =和9y x=在第一象限的图象于点A ，B ，过点B 作 BD ⊥x 轴于点D ，交1y x=的图象于点C ，连结AC ．若△ABC 是等腰三角形，则k 的值是．10.如图，直线y =kx （k 为常数，k ≠0）与双曲线my x=（m 为常数，m ＞0）的交点为A 、B ，AC ⊥x 轴于点C ，∠AOC =30°，OA =2．（1）求m 的值；（2）点P 在y 轴上，如果3ABP S k ∆=，求P 点的坐标．11.如图，一次函数y =ax +b 的图象与反比例函数ky x=的图象交于C ，D 两点，与x ，y 轴交于B ，A 两点，且tan ∠ABO =12，OB =4，OE =2．（1）求一次函数的解析式和反比例函数的解析式；（2）求△OCD 的面积；（3）根据图象直接写出一次函数的值大于反比例函数的值时，自变量x 的取值范围．12.有这样一个问题：探究同一平面直角坐标系中系数互为倒数的正、反比例函数1y x k =与ky x=（k ≠0）的图象性质．小明根据学习函数的经验，对函数1y x k =与ky x=，当k ＞0时的图象性质进行了探究．下面是小明的探究过程：（1）如图所示，设函数1y x k =与ky x=图象的交点为A ，B ，已知A 点的坐标为（﹣k ，﹣1），则B 点的坐标为；（2）若点P 为第一象限内双曲线上不同于点B 的任意一点． ①设直线P A 交x 轴于点M ，直线PB 交x 轴于点N ．求证：PM =PN ．证明过程如下，设P （m ，k m），直线P A 的解析式为y =ax +b （a ≠0）．则1ka b kma b m -+=-⎧⎪⎨+=⎪⎩，解得：__________a b =⎧⎨=⎩ ∴直线P A 的解析式为请你把上面的解答过程补充完整，并完成剩余的证明． ②当P 点坐标为（1，k ）（k ≠1）时，判断△P AB 的形状，并用k 表示出△P AB 的面积．13.如图，在平面直角坐标系中，Rt △AOB 的斜边OA 在x 轴的正半轴上，∠OBA =90°，且tan ∠AOB =12，OB=反比例函数ky x=的图象经过点B ．（1）求反比例函数的表达式；（2）若△AMB 与△AOB 关于直线AB 对称，一次函数y =mx +n 的图象过点M 、A ，求一次函数的表达式．14. 如图，一次函数y =kx +b 与反比例函数ay x=的图象在第一象限交于A 、B 两点，B 点的坐标为（3，2），连接OA 、OB ，过B 作BD ⊥y 轴，垂足为D ，交OA 于C ，若OC =CA ．（1）求一次函数和反比例函数的表达式；（2）求△AOB 的面积．15. 如图，一次函数15y k x =+（10k <）的图象与坐标轴交于A ，B 两点，与反比例函数2k y x=（20k >）的图象交于M ，N 两点，过点M 作MC ⊥y 轴于点C ，已知CM =1．（1）求21k k -的值；（2）若14AM AN =，求反比例函数的解析式；（3）在（2）的条件下，设点P 是x 轴（除原点O 外）上一点，将线段CP 绕点P 按顺时针或逆时针旋转90°得到线段PQ ，当点P 滑动时，点Q 能否在反比例函数的图象上？如果能，求出所有的点Q 的坐标；如果不能，请说明理由．。

一次函数和反比例函数练习题

《一次函数和反比例函数》练习题姓名：1. （2012四川成都8分）如图，一次函数y=－2x+b（b为常数）的图象与反比例函数ky=x（k为常数，且k≠0）的图象交于A，B两点，且点A的坐标为(1，4)．（1）分别求出反比例函数及一次函数的表达式；（2）求点B的坐标．2. （2012四川乐山10分）如图，直线y=2x+2与y轴交于A点，与反比例函数ky=x（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO=2．（1）求k的值；（2）点N（a，1）是反比例函数ky=x（x＞0）图象上的点，在x轴上是否存在点P，使得PM+PN最小？若存在，求出点P的坐标；若不存在，请说明理由．3. （2012四川宜宾8分）如图，在平面直角坐标系中，已知四边形ABCD为菱形，且A（0，3）、B（﹣4，0）．（1）求经过点C的反比例函数的解析式；（2）设P是（1）中所求函数图象上一点，以P、O、A顶点的三角形的面积与△COD的面积相等．求点P的坐标．4. （2012四川广安6分）如图，已知双曲线ky=x和直线y=mx+n交于点A和B，B点的坐标是（2，﹣3），AC垂直y轴于点C，AC=32．（1）求双曲线和和直线的解析式．（2）求△AOB的面积．5. （2012四川巴中10分）如图，在平面直角坐标系中，一次函数11y k x 1=+的图象与y 轴交于点A ，与x 轴交于点B ，与反比例函数22k y x=的图象分别交于点M ，N ，已知△AOB 的面积为1，点M 的纵坐标为2，（1）求一次函数和反比例函数的解析式；（2）直接写出12y y >时x 的取值范围。

6. （2012四川泸州7分）如图，一次函数y=ax+b的图象与y轴、x轴分别交于点A(0、B(3，0)，与反比例函数ky=x的图象在第一象限交于C、D两点。

(1)求该一次函数的解析式。

(2)若AC×k的值。

如果我是山，就要站成一种尊严，让山花灿烂，山风拂面，让每一处角落都渗透梦语言，让我价值在太阳底下展现；如果我是水，就要流成一种磅礴，让小船远航，鱼儿欢畅，让每一股细流都一往无前，让我价值迎风吟唱。

专题26.17 反比例函数与一次函数专题(基础篇)(专项练习)-2022-2023学年九年级数学下册

专题26.17 反比例函数与一次函数专题（基础篇）（专项练习）一、单选题（本大题共10小题，每小题3分，共30分） 1．一次函数y ax a =-与反比例函数(0)ay a x=≠在同一坐标系中的图象可能是（） A ． B ．C ．D ．2．在平面直角坐标系中，反比例函数(0)ky k x=≠的图象的两个分支分别位于第一、三象限，则一次函数y =kx +k 的图象大致是（）A ．B ．C ．D ．3．如图，正比例函数y kx =与反比例函数6y x=的图象交于,A B 两点，BC x ∥轴，AC y ∥轴，则ABCS=（）A ．10B ．11C ．12D ．134．如图，一次函数11y k x b =+与反比例函数22k y x=的图象相交于A ，B 两点，点A 的横坐标为2，点B 的横坐标为1-，则不等式21k k x b x+<的解集是（）A ．10x -<<或2x >B ．1x <-或02x <<C ．1x <-或2x >D ．12x -<<5．小亮为了求不等式3x >x +2的解集，绘制了如图所示的反比例函数y =3x与一次函数y =x +2的图像，观察图像可得该不等式的解集为（）A ．3x <-B ．1x >C ．31x -<<D ．3x <-或01x <<6．某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y （微克/毫升）与服药时间x 小时之间函数关系如图所示（当410x ≤≤时，y 与x 成反比例）．血液中药物浓度不低于6微克毫升的持续时间为（）A ．73B ．3C ．4D ．1637．在同一直角坐标系中，函数y ＝kx -k 与ky x=（k ≠0）的大致图象是（） A ． B ．C ．D ．8．如图，反比例函数ky x=（x ＜0）的图象经过正方形ABCD 的顶点A ，B ，连接AO ，BO ，作AF ⊥y 轴于点F ，与OB 交于点E ，E 为OB 的中点，且3AOE S =△，则k 的值为（）A ．4B ．4-C ．8D ．8-9．已知正比例函数y ＝2x 与反比例函数y ＝2x 的图象交于A 、B 两点，若A 点的坐标为（1，2），则B 点的坐标为（）A ．（1，－2）B ．（－1，2）C ．（－1，－2）D ．（2，1）10．如图，函数()10y x x =≥与()20,0ky x k x=>≠的图像相交于点()4,A m ，直线2x =与1y 和2y 分别交点B ，C ，则下列说法中错误的是（）A ．16k =B ．当4x >时，12y y <C ．当2x =时，6BC =D ．当x 逐渐增大时，1y 随着x 的增大而增大，2y 随着x 的增大而减小二、填空题（本大题共8小题，每小题4分，共32分）11．一次函数11y k x b =+与反比例函数22k y x=的图像交于(),2A n 和()4,1B --两点，若12y y >，则x 的取值范围是_______．12．如图，函数y 1＝x +1与函数y 2＝2x 的图象相交于点M （1，m ），N （﹣2，n ）．若y 1＜y 2，则x 的取值范围是x ＜﹣2或 _____．13．直线AB ：y =－43x +4交坐标轴于A 、B 两点，若P 是线段AB 的三等分点，且双曲线y =kx过点P ，则k =________．14．如图，正比例函数y =-x 与反比例函数y =kx的图象交于A ， C 两点，过点A 作AB ⊥x轴于点B ，过点C 作CD ⊥x 轴于点D ，若△ABD 的面积为6，则k ＝ ____15．点(),A a b 是一次函数1y x =+与反比例函裂4y x=图像的交点，其22a b ab -=_____________．16．如图所示，在平面直角坐标系中，直线443y x =-+分别与x 轴、y 轴交于B 、A 两点，点P 是线段AB 上一点，连接OP ，且3POB POA S S =△△，若双曲线y =kx过点P ，则k =________．17．已知点P（m，n）在直线y=-x+3上，也在双曲线y=-1x上，则m2+n2=___________18．已知反比例函数5yx=与一次函数6y x=-+的图象交于点(),.a b则11a b+的值为______．三、解答题（本大题共6小题，共58分）19．（8分）如图，直线y＝ax＋b与x轴交于点A（4，0），与y轴交于点B（0，﹣2），与反比例函数y＝kx（x＞0）的图象交于点C（6，m）．(1) 求直线和反比例函数的表达式；(2) 连接OC，在x轴上找一点P，使S△POC＝2S△AOC，请求出点P的坐标．20．（8分）如图，在平面直角坐标系中，一次函数y=ax+b(a≠0)的图象分别交x轴，y轴于A，B两点，与反比例函数y=kx(k≠0)的图象交于C，D两点，DE⊥x轴于点E，点C的坐标为(6，−1) ，DE=3．(1) 求反比例函数与一次函数的表达式；(2) 若点P在反比例函数图象上，且△POA的面积等于8，求P点的坐标．21．（10分）如图，已知反比例函数ky x=的图像与一次函数y x b =-+的图像交于点()1,4A ，点()4,B n ．(1) 求n 和b 的值； (2) 求⊥OAB 的面积； (3) 观察图像，不等式kx b x>-+的解集为________．22．（10分）如图，在平面直角坐标系中，一次函数()1y kx b k 0=+≠ 图象与反比例函数()2my m 0x=≠图象交于A ，B 两点，与x 轴交于点C ，已知点()4,1A ，点B 的横坐标为2-．(1) 求一次函数与反比例函数的解析式， (2) 若点D 是x 轴上一点，且6ABDS=，求点D 坐标；(3) 当12y y ≥时，直接写出自变量x 的取值范围．23．（10分）已知一次12y x a =-+的图象与反比例函数()20ky k x=≠的图象相交． (1)判断2y 是否经过点(),1k ．(2)若1y 的图象过点(),1k ，且25a k +=． ⊥求2y 的函数表达式．⊥当0x >时，比较1y ，2y 的大小．24．（12分）如图，已知一次函数y ＝x ﹣2与反比例函数3y x=的图象交于A 、B 两点．（1）求A 、B 两点的坐标；（2）求⊥AOB 的面积；（3）观察图象，可知一次函数值小于反比例函数值的x 的取值范围是．参考答案1．A【分析】根据一次函数与反比例函数图象的性质进行判断即可得解．解：当0a >时，0a -<，则一次函数y ax a =-经过一、三、四象限，反比例函数(0)ay a x=≠经过一、三象限，故排除C ，D 选项；当0a <时，0a ->，则一次函数y ax a =-经过一、二、四象限，反比例函数(0)ay a x=≠经过二、四象限，故排除B 选项，故选：A ．【点拨】本题主要考查了一次函数与反比例函数图象的性质，熟练掌握相关性质与函数图象的关系是解决本题的关键．2．C【分析】直接利用反比例函数的性质得出k 的取值范围，进而结合一次函数的性质得出答案．解：⊥反比例函数y =kx（k ≠0）图象的两支分别位于第一、三象限，⊥k ＞0，⊥一次函数y =kx +k 的图象大致是：．故选：C ．【点拨】此题主要考查了反比例函数以及一次函数的性质，正确得出k 的取值范围是解题关键．3．C【分析】设出A 点坐标，根据题意得出B 、C 点的坐标，再根据面积公式刚好消掉未知数求出面积的值；解：根据题意设6,A t t ⎛⎫⎪⎝⎭，正比例函数y kx =与函数6y x=的图象交于,A B 两点， 6,B t t ⎛⎫∴-- ⎪⎝⎭，BC x ∥轴，AC y ∥轴，6,C t t ⎛⎫∴- ⎪⎝⎭，()11661222ABCSBC AC t t t t ⎡⎤⎛⎫⎡⎤∴=⋅=⨯--⨯--= ⎪⎢⎥⎣⎦⎝⎭⎣⎦；故选：C ．【点拨】本题考查了反比例函数和一次函数的交点问题，求三角形面积等知识点，熟练掌握反比例函数的性质是解题的关键．4．A【分析】根据不等式21k k x b x+<的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围进行求解即可．解：由题意得不等式21k k x b x+<的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围，⊥不等式21k k x b x+<的解集为10x -<<或2x >，故选A ．【点拨】本题主要考查了一次函数与反比例函数综合，利用数形结合的思想求解是解题的关键．5．D【分析】结合函数图像的上下位置关系结合交点的坐标，即可得出不等式的解集．解：观察函数图像，发现：当x ＜-3或0＜x ＜1时，反比例函数图像在一次函数图像的上方， ⊥不等式3x>x +2的解集为x ＜-3或0＜x ＜1．故选：D ．【点拨】本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图像的交点坐标满足两函数解析式．6．A【分析】先分别利用正比例函数以及反比例函数解析式，再利用y ＝6分别得出x 的值，进而得出答案．解：当0≤x ≤4时，设直线解析式为：y ＝kx ，将（4，8）代入得：8＝4k ，解得：k ＝2，故直线解析式为：y ＝2x ，当4≤x ≤10时，设反比例函数解析式为：y ＝a x，将（4，8）代入得：8＝4a，解得：a ＝32，故反比例函数解析式为：y ＝32x；因此血液中药物浓度上升阶段的函数关系式为y ＝2x （0≤x ≤4），下降阶段的函数关系式为y ＝32x（4≤x ≤10）．当y ＝6，则6＝2x ，解得：x ＝3，当y ＝6，则6＝32x ，解得：x ＝163， ⊥163−3＝73（小时），⊥血液中药物浓度不低于6微克/毫升的持续时间73小时故选A ．【点拨】此题主要考查了反比例函数的应用，根据题意得出函数解析式是解题关键． 7．B【分析】根据k 的取值范围，分别讨论k ＞0和k ＜0时的情况，然后根据一次函数和反比例函数图象的特点进行选择正确答案．解：当k ＞0时，一次函数y =kx -k 经过一、三、四象限，函数y =kx（k ≠0）的图象在一、二象限，观察各选项，没有选项符合要求．当k ＜0时，一次函数y =kx -k 经过一、二、四象限，函数y =kx（k ≠0）的图象经过三、四象限，只有选项B 的图象符合要求．故选：B ．【点拨】此题考查一次函数的图象和反比例函数的图象，数形结合是解题的关键． 8．D【分析】过点B 作BG ⊥y 轴交于点G ，得到EF 是⊥BOG 的中位线，EF =12BG ，设A （a ，k a ），B （b ，k b ），得到E 点坐标为（2b ，ka），设OB 的解析式为y =k 1x ，代入E ，B 坐标得到a =2b ，根据S △AOE =12AE GF ⨯得到S △AOE =83k -，故可求出k 的值．解：过点B 作BG ⊥y 轴交于点G ， ⊥AF ⊥y 轴，BG ⊥y 轴， ⊥AF //BG⊥E 点是OB 的中点 ⊥EF 是⊥BOG 的中位线 ⊥EF =12BG设A （a ，k a ），B （b ，kb），⊥BG =-b ，EF =2b-则E 点坐标为（2b ，ka），设OB 的解析式为y =k 1x ，（k 1≠0），过E 点 ⊥k a =2bk 1 ⊥k 1=2k ab⊥OB 的解析式为y =2kabx ，代入B 点，即k b =2kab×b ⊥a =2b⊥S △AOE =111222222b k k k bk ak AE GF a k b a a b ⎛⎫⎛⎫⎛⎫⨯=⨯-⨯-=⨯--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭把a =2b 代入得S △AOE =1822243k k k k k ⎛⎫⨯--+=- ⎪⎝⎭=3⊥k =-8 故选D ．【点拨】此题主要考查反比例函数与几何综合，解题的关键是熟知反比例函数的图像与性质、待定系数法、三角形中位线的性质．9．C【分析】解答这类题一般解这两个函数的解析式组成的方程组即可．解：由已知可得22y xy x =⎧⎪⎨=⎪⎩，解这个方程组得，1211x x -＝，＝，则得1222y y -＝，＝，则这两个函数的交点为（1，2），（﹣1，﹣2），因为已知A 点的坐标为（1，2），故B 点的坐标为（﹣1，﹣2）．故选：C ．【点拨】正比例函数与反比例函数的交点关于原点对称，同学们要熟记才能灵活运用． 10．B【分析】把()4,A m 代入()10y x x =≥解得(4,4)A ，再代入()20,0ky x k x=>≠可解得k 的值，把2x =代入两个解析式，分别解得点B ,C 的坐标，即可求出BC 的长，最后根据图像的性质，可判断函数值的大小，及函数的增减性．解：由题意，把点()4,A m 代入()10y x x =≥得，4=m(4,4)A ∴把(4,4)A 代入()20,0ky x k x=>≠得， 16k =216y x∴=，故A 正确；由图像可知，当4x >时，12y y >，故B 错误；当x =2时， 12162,82y y === (2,2),(2,8)B C ∴826BC ∴=-=，故C 正确；由图像可知，在第一象限内，当x 逐渐增大时，1y 随着x 的增大而增大，2y 随着x 的增大而减小故D 正确，故选：B ．【点拨】本题考查反比例函数与一次函数的交点、一元二次方程的根与系数的关系、一次函数的性质、掌握相关知识是解题关键．11．40x -<<或2x > 【分析】把（-4，-1）代入22k y x =得24y x =，把(,2)n 代入24y x=得n =2，即点A 坐标为（2，2），把A 、B 坐标代入11y k x b =+，得1112y x =+，作出1y ，2y 的图像即可得．解：把（-4，-1）代入22k y x=得，2(4)(1)4k =-⨯-=， ⊥24y x=，把(,2)n 代入24y x =得，42n= 解得，n =2，⊥点A 坐标为（2，2），把A 、B 坐标代入11y k x b =+，112241k b k b +=⎧⎨-+=⎩ 解得，1121k b ⎧=⎪⎨⎪=⎩， ⊥1112y x =+，如图所示：⊥12y y >，⊥40x -<<或2x >，故答案为：40x -<<或2x >．【点拨】本题考查了一次函数与反比例函数，解题的关键是掌握一次函数的性质，反比例函数的性质．12．0＜x ＜1【分析】观察函数图象，找出一次函数图象在反比例函数图象的下方时对应的x 的取值范围即可．解：由图象可知，y 1＜y 2时的x 的取值范围为：x ＜−2或0＜x ＜1，故答案为：0＜x ＜1．【点拨】本题主要考查了反比例函数图象与一次函数图象的交点问题，能利用数形结合求出不等式的解集是解答此题的关键．13．83【分析】根据直线解析式求得点,A B 的坐标，根据P 是线段AB 的三等分点求得P （1,83）或（2，43）根据反比例数的k 的意义即可求解．解：⊥直线AB ：y =－43x +4交坐标轴于A 、B 两点，⊥A （0,4），B （3,0） ⊥P 是线段AB 的三等分点 ⊥P （1,83）或（2，43） ⊥双曲线y =kx过点P ，⊥k =1×83=83或k =2×43=83，即k=83．【点拨】本题考查了一次函数与反比例函数综合，求得点P的坐标是解题的关键．14．-6【分析】首先由正比例函数y=-x的图象与反比例函数y=kx的图象交于A、C两点，可得O为线段AC的中点，O为线段BD的中点，然后由反比例函数y=kx的比例系数k的几何意义，可知△AOB的面积等于12|k|，从而求出k的值．解：⊥反比例函数与正比例函数的图象相交于A、C两点，⊥A、C两点关于原点对称，⊥OA=OC，⊥AB⊥x轴，CD⊥x轴，⊥△AOB⊥△COD(AAS)，⊥OB=OD，即O为线段BD的中点，⊥⊥AOB的面积=12△ABD的面积=3，⊥△AOB的面积=12|k|，⊥12|k|=3，⊥k<0，⊥k=-6．故答案为：-6．【点拨】此题考查了一次函数与反比例函数的交点问题以及待定系数法求解析式．做此类题一定要正确理解k的几何意义．图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=12|k|．15．-4【分析】把点A（a，b）分别代入一次函数y=x-1与反比例函数4yx=，求出a-b与ab的值，代入代数式进行计算即可．解：⊥点A(a，b)是一次函数y=x+1与反比例函数4yx=的交点，⊥b=a+1，4=ba，即a−b=-1，ab=4，⊥()22414a b b ab a a b --==⨯-=-（）．故答案为：-4．【点拨】反比例函数与一次函数的交点问题，对于本题我们可以先分别把点代入两个函数中，在对函数和所求的代数式进行适当变形，然后整体代入即可．16．94【分析】：设P （m ，43-m +4），然后利用一次函数的性质求出A 、B 的坐标，进而求出OA ，OB 的长，再根据3POB POA S S =△△，得到34POB AOB S S =△△，由此利用三角形面积公式列出方程求解即可．解：设P （m ，43-m +4），⊥直线443y x =-+分别与x 轴、y 轴交于B 、A 两点，⊥点A 的坐标为（0，4），点B 的坐标为（3，0）， ⊥OA =4，OB =3， ⊥3POB POA S S =△△， ⊥34POB AOB S S =△△， ⊥12×3×（43-m +4）=34×12×3×4，解得：m =34，即P （34，3）⊥双曲线y =kx过点P ，⊥k =34×3=94．故答案为：94．【点拨】本题主要考查了反比例函数与一次函数综合，求出A 、B 的坐标，进而利用三角形面积公式建立方程求解是解题的关键．17．11【分析】直接利用一次函数图象上点的坐标特征以及反比例函数图象上点的特征得出n +m 以及mn 的值，再利用完全平方公式将原式变形得出答案．解：⊥点P （m ，n ）在直线y =-x +3上，⊥n +m =3，⊥点P （m ，n ）在双曲线y =-1x上，⊥mn =-1，⊥m 2+n 2=（n +m ）2-2mn =9+2=11．故答案为：11．【点拨】此题主要考查了一次函数图象上点的坐标特征以及反比例函数图象上点的特征，正确得出m ，n 之间关系是解题关键．18．65【分析】把图象的交点a b （，）分别代入反比例函数5y x=与一次函数6y x =-+，得到a 和b 的两个关系式，就可以求出答案．解：把a b （，）分别代入反比例函数5y x=与一次函数6y x =-+，得 5ab =，6a b +=，1165a b a b ab +∴+==．故答案为：65．【点拨】本题考查了两个函数的交点问题，交点坐标就是两个解析式组成方程组的解，关键是分式是化简和整体思想的应用．19．(1)122y x =-；6y x =(2)（8,0）或（-8,0）【分析】（1）用待定系数法直接求表达式即可．（2）先求出⊥AOC 的面积，再求出⊥POC ，根据三角形的面积公式求解即可．（1）解：将A （4，0）B （0，﹣2）代入y ＝ax ＋b 得：042a bb=+⎧⎨-=⎩ 解得：122a b ⎧=⎪⎨⎪=-⎩ ⊥直线的表达式为：122y x =- 点C （6，m ）在直线上16212m =⨯-= ⊥k =6m =6⊥反比例函数的表达式为：6yx =．（2）解：设P点坐标为：（p，0）S△AOC=12cOA y⋅=14122⨯⨯=⊥S△POC＝2S△AOC⊥12cOP y⋅=1142p⨯=⊥p=8⊥P点坐标为（8,0）或（-8,0）．【点拨】本题考查反比例函数与一次函数的综合应用．正确的求出一次函数与反比例函数的表达式是解题的关键．20．(1)反比例函数的关系式为y=-6x；一次函数的关系式为y=-12x+2；(2)点P的坐标是（-32，4）或（32，-4）．【分析】（1）用待定系数法求出反比例函数表达式，进而求出点D的坐标，再利用待定系数法求出一次函数表达式即可求解；（2）设点P的坐标是（m，n），根据三角形面积公式求得即可．（1）解：⊥点C（6，-1）在反比例函数y=kx（k≠0）的图象上，⊥k=6×（-1）=-6，⊥反比例函数的关系式为y=-6x，⊥点D在反比例函数y=-6x上，且DE=3，⊥y=3，代入求得：x=-2，⊥点D的坐标为（-2，3）．⊥C、D两点在直线y=ax+b上，则6123a ba b+=-⎧⎨-+=⎩，解得122ab⎧=-⎪⎨⎪=⎩，⊥一次函数的关系式为y=-12x+2；（2）解：设点P的坐标是（m，n）．把y=0代入y=-12x+2，解得x=4，即A（4，0），则OA=4，⊥⊥POA 的面积等于8， ⊥12×OA ×|n |=8，解得：|n |=4， ⊥n 1=4，n 2=-4，⊥点P 的坐标是（-32，4）或（32，-4）．【点拨】此题考查了一次函数与反比例函数的交点问题，涉及的知识有：坐标与图形性质，待定系数法确定函数解析式，一次函数与坐标轴的交点，三角形面积，熟练掌握待定系数法是解本题的关键．21．(1)1n =，5b =(2)152(3)01x <<或4x > 【分析】（1）将点()1,4A 代入一次函数的解析式可得b 的值，从而可得一次函数的解析式，再将点()4,B n 代入求解即可得；（2）设一次函数5y x =-+与x 轴的交点为点C ，先根据一次函数的解析式求出点C 的坐标，再根据OAB 的面积等于OAC 的面积减去OBC 的面积即可得；（3）找出反比例函数ky x=的图像位于一次函数y x b =-+的图像的上方时，x 的取值范围即可得．（1）解：由题意，将点()1,4A 代入y x b =-+得：14b -+=，解得5b =，则一次函数的解析式为5y x =-+，将点()4,B n 代入得：451n =-+=．（2）解：如图，设一次函数5y x =-+与x 轴的交点为点C ，当0y =时，50x -+=，解得5x =，即()5,0,5C OC =，()()1,4,4,1A B ，OAB ∴的面积为11155451222OAC OBCS S -=⨯⨯-⨯⨯=．（3）解：不等式k x b x >-+表示的是反比例函数k y x =的图像位于一次函数y x b =-+的图像的上方，则由函数图像得：01x <<或4x >，故答案为：01x <<或4x >．【点拨】本题考查了反比例函数与一次函数的综合、一次函数的几何应用，熟练掌握待定系数法是解题关键．22．(1)一次函数解析式为1112y x =-，反比例函数解析式为24y x=(2)（-2，0）或（6，0）；(3)20x -≤<或4x ≥【分析】（1）把点()4,1A 代入()2m y m 0x =≠可得反比函数解析式，从而得到点B 的坐标为（-2，-2），再把点()4,1A ，B （-2，-2）代入()1y kx b k 0=+≠，可求出一次函数解析式，即可求解，（2）设直线AB 交x 轴于点E ，根据ABD AED BED SS S =+，即可求解；（3）根据图象即可求得．（1）解：把点()4,1A 代入()2m y m 0x =≠得：4m =，⊥反比例函数解析式为24y x =； ⊥点B 的横坐标为2-，⊥2422y ==--， ⊥点B 的坐标为（-2，-2），把点()4,1A ，B （-2，-2）代入()1y kx b k 0=+≠，得：4122k b k b +=⎧⎨-+=-⎩，解得：121k b ⎧=⎪⎨⎪=-⎩， ⊥一次函数解析式为1112y x =-；（2）解：如图，设直线AB 交x 轴于点E ，对于1112y x =-，当y 1=0时，x =2， ⊥点E （2，0），设点D 的坐标为（a ，0），则2DE a =-，⊥ABD AED BED S S S =+，6ABD S =， ⊥111222622a a ⨯⨯-+⨯⨯-=，解得：a =-2或6，⊥点D 的坐标为（-2，0）或（6，0）；（3）解：观察图象得：当20x -≤<或4x ≥时，一次函数的图象位于反比例函数图象的上方或两图象相交，⊥当12y y ≥时，自变量x 的取值范围为20x -≤<或4x ≥．【点拨】本题主要考查了一次函数和反比例函数的交点问题，待定系数法求函数的解析式，函数图象上点的坐标特征，三角形的面积，数形结合是解题的关键．23．(1)过(2)⊥21=y x ；⊥当01x <<时，12y y <，当1x >时，12y y >，当1x =时，12y y = 【分析】（1）根据()20k y k x =≠，把点(),1k 代入反比例函数，即可；（2）①把点(),1k 代入12y x a =-+，得12k a =-+，根据25a k +=，解出k 和a 的值，即可得到2y 的表达式；②根据函数图象，即可比较1y ，2y 的大小．解：（1）⊥()20k y k x =≠⊥把点(),1k 代入反比例函数，得1k k =⊥2y 经过点(),1k ．（2）①⊥1y 的图象过点(),1k⊥把点(),1k 代入12y x a =-+，得12k a =-+又⊥25a k +=⊥解得2a =，1k = ⊥21=y x⊥2y 的函数表达式为：21=y x ②如图所示：由函数图象得，当01x <<时，12y y <；当1x >时，12y y >；当1x =时，12y y =．【点拨】本题考查一次函数和反比例函数的知识，解题的关键是掌握一次函数与反比例函数图象的性质，交点的综合问题．24．（1）点A 坐标（3，1），点B 坐标（﹣1，﹣3）；（2）S △AOB ＝4；（3）0＜x ＜3或x ＜﹣1【分析】（1）联立一次函数与反比例函数解析式进行求解即可；（2）如图，设直线AB 与y 轴的交点为C ，由题意可得点C （0，-2），进而根据割补法求解三角形的面积即可；（3）根据函数图象可直接进行求解．解：（1）由题意可联立一次函数与反比例函数解析式得：23y x y x =-⎧⎪⎨=⎪⎩，解得13x y =-⎧⎨=-⎩或31x y =⎧⎨=⎩， ⊥点A 坐标（3，1），点B 坐标（﹣1，﹣3）．（2）设直线AB 与y 轴的交点为C ，如图所示：⊥直线AB 为y ＝x ﹣2，⊥令x=0时，则有y=-2，⊥点C（0，﹣2），⊥S△AOB＝S△OCB+S△OCA＝12×2×1+12×2×3＝4．（3）由图象可知：0＜x＜3或x＜﹣1时，一次函数值小于反比例函数值．故答案为0＜x＜3或x＜﹣1．【点拨】本题考查一次函数与反比例函数的有关知识，掌握用方程组求交点坐标，求三角形面积时关键找到特殊点，用分割法解决面积问题，属于中考常考题型．。

一次函数和反比例函数的练习题

函数综合复习例题讲解：1．已知y 与x+3成正比例，并且x=1时，y=8，那么y 与x 之间的函数关系式为（）（A ）y=8x （B ）y=2x+6 （C ）y=8x+6 （D ）y=5x+3 2．若直线y=kx+b 经过一、二、四象限，则直线y=bx+k 不经过（）（A ）一象限（B ）二象限（C ）三象限（D ）四象限 3．直线y=-2x+4与两坐标轴围成的三角形的面积是（）（A ）4 （B ）6 （C ）8 （D ）164．设b>a ，将一次函数y=bx+a 与y=ax+b 的图象画在同一平面直角坐标系内，•则有一组a ，b 的取值，使得下列4个图中的一个为正确的是（）5．无论m 为何实数，直线y=x+2m 与y=-x+4的交点不可能在（）（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限 6．要得到y=-32x-4的图像，可把直线y=-32x （）．（A ）向左平移4个单位（B ）向右平移4个单位（C ）向上平移4个单位（D ）向下平移4个单位7．若直线y=3x-1与y=x-k 的交点在第四象限，则k 的取值范围是（）．（A ）k<13 （B ）13<k<1 （C ）k>1 （D ）k>1或k<138．已知一次函数y=-6x+1，当-3≤x ≤1时，y 的取值范围是________．9．已知一次函数y=（m-2）x+m-3的图像经过第一，第三，第四象限，则m 的取值范围是________． 10．已知直线y=-2x+m 不经过第三象限，则m 的取值范围是_________．11．已知y=p+z ，这里p 是一个常数，z 与x 成正比例，且x=2时，y=1；x=3时，y=-1．（1）写出y 与x 之间的函数关系式；（2）如果x 的取值范围是1≤x ≤4，求y 的取值范围．12．已知：如图一次函数y=12x-3的图象与x 轴、y 轴分别交于A 、B 两点，过点C （4，0）作AB 的垂线交AB 于点E ，交y 轴于点D ，求点D 、E 的坐标．综合练习：1.如图，直线y=kx+b 经过点A （-2，0），和B （1，3）两点，则不等式组-2x+5≥kx+b ＞0的解集为2.已知，一次函数y kx b =+的图像与正比例函数13y x =交于点A ，并与y 轴交于点(0,4)B -，△AOB 的面积为6，则kb = 。