2020中考数学专题6——几何模型之”12345及答案
2020中考数学专题6——几何模型之”12345“-含答案
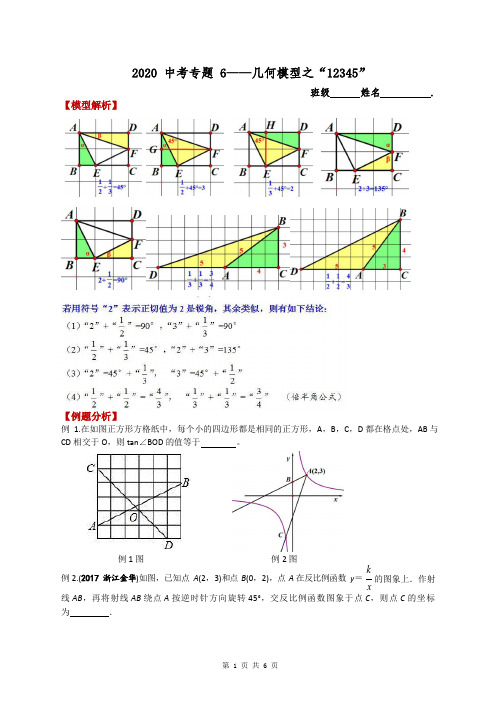
【模型解析】2020 中考专题 6——几何模型之“12345”班级姓名.【例题分析】例 1.在如图正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D 都在格点处,AB 与CD 相交于O,则tan∠BOD 的值等于。
例1 图例2 图k例2.(2017 浙江金华)如图,已知点A(2,3)和点B(0,2),点A 在反比例函数y=x的图象上.作射线AB,再将射线AB 绕点A 按逆时针方向旋转45°,交反比例函数图象于点C,则点C 的坐标为.3 2 例 3.如图,正方形 ABCD 中,P 是 BC 的中点,把△PAB 沿着 PA 翻折得到△PAE ,过 C 作 CF ⊥DE 于 F ,若 CF =2,则 DF = .【巩固训练】1. 如图 1,∠AOB 是放置在正方形网格中的一个角,则 cos ∠AOB 的值是.图 1 图 2图 32. 如图 2 是由边长相同的小正方形组成的网格,A ,B ,P ,Q 四点均在正方形网格的格点上,线段AB,PQ 相交于点 M ,则图中∠QMB 的正切值是( ) 1 A.B.1C. 2D.23. 如图 3,把一个矩形纸片 OABC 放入平面直角坐标系中,使 OA 、OC 分别落在 x 轴、y 轴上,连接 OB,将纸片 OABC 沿 OB 折叠,使点 A 落在 A'的位置上.若 OB= ,BC 1,求点 A'的坐标为 .OC 24. 如图 4,半圆 O 的直径 AB=10cm ,弦 AB=10cm ,弦 AC=6cm ,AD 平分∠BAC ,则 AD 的长为()A. 4 cmB. 3 cmC. 5 cmD.4 cm图 4图 55.如图 5,在四边形 ABCD 中,∠BAC =∠BDC=90°,AB=AC=则 DM= (),CD=1 ,对角线的交点为 M ,A.B. 2 3 1C.D.2235 5 5 5 5 55 6. 如图6,在平面直角坐标系xOy 中,点A (-1,0),B (0,2),点C 在第一象限,∠ABC =135°,kAC 交y 轴于D ,CD =3AD ,反比例函数y =的图象经过点C ,则k 的值为 .xADFBEC图 6图 7图 87(2017 浙江丽水)如图 7,在平面直角坐标系 xOy 中,直线 y =-x +m 分别交 x 轴,y 轴于 A ,B 两点,已知点 C (2,0). (1) 当直线 AB 经过点 C 时,点 O 到直线 AB 的距离是 ; (2) 设点 P 为线段 OB 的中点,连结 PA ,PC ,若∠CPA =∠ABO ,则 m 的值是 .8.(2018山东滨州)如图8,在矩形ABCD 中,AB =2,BC =4,点E ,F 分别在BC ,CD 上,若AE = , ∠EAF=45°,则AF 的长为 .9.如图 9,在四边形 ABCD 中 BC⊥AB,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E 是 AB 上一点,且∠ DCE=45°,BE=4, 则 DE= .图 9 图 10 图 1110.(2018 山东泰安)如图 10,在矩形 ABCD 中, AB = 6 ,BC = 10 ,将矩形 ABCD 沿 BE 折叠, 点 A 落在 A ' 处,若 EA ' 的延长线恰好过点C ,则sin ∠ABE 的值为 .11. 如图 11,正方形 ABCD 的边长 AB=2,E 为 AB 的中点,F 为 BC 的中点,AF 分别与 DE 、BD相交于点 M ,N ,则 MN 的长为( )A.B .﹣1C .D .12.如图12,抛物线y =-x2 +bx +c 与直线y =1x + 2 交于C、D 两点,其中点C 在y 轴上,27点D 的坐标为(3,2F。
初中数学-12345模型

初中数学——模型12345数学解题五境界第一个境界:正确解题.很多同学以为如果一道题目做错,订正一下,知道哪里错了,怎么做,就行了,其实这只是最低境界.第二个境界:一题多解.我们要养成的良好习惯是,不要满足于用一种做法和思路解题.一道题目做完之后想一想还有没有其它方法,哪种方法更简单.对于最后的结果,是不是可以有其它的合理解释.第三个境界:多题一解.完成一道题目的分析后,尝试推而广之,或把其中的数字换成字母,或把一些条件做一些改变,从这道题目延伸出去,探究与此相关的一类题目.第四个境界:发现定理.到了这个境界,可以自己发现一些结论或定理、规律。
这些结论、定理规律都是解题的有用工具。
解题高手都有自己的定理库.第五个境界:自己编题.解题的最高境界是能够编题。
不是所有的老师都具备编题的能力。
解题高手拿到一道题目,会知道出题者的意图,会发现出题者的陷阱。
即便出题者粗心出现了一个错误,他也能够很快地纠正纠偏.刘俊勇:如果没有真正消化吸收为自己的东西,过一段时间就忘却了,真正弄清楚更重要,远胜于蜻蜓点水式浏览一遍.一方面重视技巧,尤其是考试技巧学习技巧,另一方面回归数学本质,回归教育意义当我们听到一个技巧的时候,除了拿来使用之外,还需要去体会专家在思考、总结过程的数学思考,这个我觉得更加重要和有意义。
因为专家的本意也正是立足于思想的交流,而不是一招一式的传递,在本地方的一些小型的培训中,我注意到活动中最最怕的就是坐在下面的教师一直把自己当成听众、容器,同时,相当一部教师的都有简单的拿来主义和简单的怀疑主义倾向,这个也特别可怕数学是思维的体操,没有绝技想拿冠军是不可能的。
以教材为主对大部分学生适用,但在我们这光靠教材的知识点,中考想考满分概率为零。
学灵魂在于积累、创新、规纳而不是照搬的模仿和接受,要有自己的数学大格局,适合自己的就是最好的!版块一引入问题1.如图1-1,在3×3 的网格中标出了∠1 和∠2,则∠1+∠2=图1-1 图1-22.如图1-2,在△ABC 中,∠BAC=45°,AD 是BC 边上的高,BD=3,DC=2,则AD 的长为.版块二“1 2 3”+“4 5”的来源一般化结论:若α+β= 45︒则有tanα=a - 1,a + 1tanβ=1(a>1),a当 a =3时,则得到tanα=2tan β=1(了解)2 3 5当a=2 时,则得到tanα=1tan β=1(重要)2 3当a =5时,则得到tanα=2tan β=3(了解);2 5 7当a = 4 时,则得到tanα=1tan β=3(次重要)4 55510【例 1】(济南市中考题)如图2-1, ∠AOB 是放置在正方形网络中的一个角,则cos ∠AOB 的值是 .图 2-1【例 2】(2015 湖北十堰)如图 2-2,正方形 ABCD的边长为 6,点 E ,F 分别在 AB ,AD 上,若 CE = 3 ,且∠ECF =45°,则 CF 的长为( )A . 2B . 3C .5103图 2-2倍角与半角构造D .10 53当出现等腰三角形或翻折的背景问题时,解决策略“ 顶角⇔ 底角⇔ 顶角”解题依据“ 90︒ 1 - 顶角=底角”. 2如图,在等腰三角形 ABC 中,AB =AC . ⑴若 tan ∠BCA = 2 ,则 tan ∠BAC =.⑵若 tan ∠BAC = 4,则 tan ∠ABC =.3【例3】如图2-3,已知正方形ABCD 中,E 为BC 上一点.将正方形折叠起来,使点A 和点E 重合,折痕为MN.若tan ∠AEN =1,DC+CE=10.3⑴求△ANE 的面积;⑵求sin ∠ENB 的值.图2-3【例4】如图2-4,已知正方形ABCD 的边长为,对角线AC、BD 交于点O,点E 在BC 上,且CE=2BE,过B 点作BF ⊥AE 于点F,连接OF,则线段OF 的长度为。
完整版)初中数学几何模型大全+经典题型(含答案)

完整版)初中数学几何模型大全+经典题型(含答案)通过将倍长中点相关线段进行旋转变换,可以构造出旋转全等模型。
这种模型的特点是,将相邻等线段所成角的一半旋转后拼接在一起,形成对称全等。
同时,也可以通过将两个等腰三角形或正多边形的夹角进行变化,来构造出模型变形。
如果遇到复杂图形找不到旋转全等,可以先找到两个正多边形或等腰三角形的公共极点,然后围绕公共极点找到两组相邻等线段,分组组成三角形证全等。
幂定理可以用等线段、等比值、等乘积进行代换,从而将两个数之间的比值转换成乘积。
在相似证明中,常用的辅助线是平行线,根据题目条件来确定比值并做出相应的平行线。
题目一:在半圆中,圆心为O,圆上有点C、E,CD垂直于AB,EF垂直于AB,EG垂直于CO。
证明CD等于GF。
题目二:在正方形ABCD内部,点P满足∠PAD=∠PDA=15度。
证明△PBC是正三角形。
题目三:在图中,ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点。
证明A2B2C2D2是正方形。
题目四:在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F。
证明∠DEN=∠F。
题目五:在△ABC中,H为垂心,O为外心,且OM垂直于BC于M。
1)证明AH等于2OM;2)如果∠BAC等于60度,证明AH等于AO。
1.设P为正三角形ABC内任意一点,连接PA,PB,PC,由三角形不等式可得PA+PB>AB。
PB+PC>BC。
PC+PA>CA。
将三式相加得到2PA+2PB+2PC>AB+BC+CA=3,即PA+PB+PC>3/2.又由于P到三角形三边的距离不超过1,所以PA+PB+PC<3,综上可得1.5≤PA+PB+PC<3,即所求不等式成立。
2.设P为正方形ABCD内任意一点,连接PA,PB,PC,PD。
由于正方形四边相等,所以PA+PC=2,PB+PD=2.又由于P到四边的距离不超过1,所以PA+PB+PC+PD<4.将前两式相加得到PA+PB+PC+PD=2(PA+PB)/2+2(PC+PD)/2≥2√(PA·PB)+2√(PC·P D)。
(完整版)初中数学几何模型大全+经典题型(含答案).docx

初中数学几何模型大全+ 经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是 45 °、30 °、22.5 °、15 °及有一个角是 30 °直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2 角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60 度旋 60 度,造等边三角形遇90 度旋 90 度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋 180 度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“ 8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
2020中考专题6——几何模型之”12345“
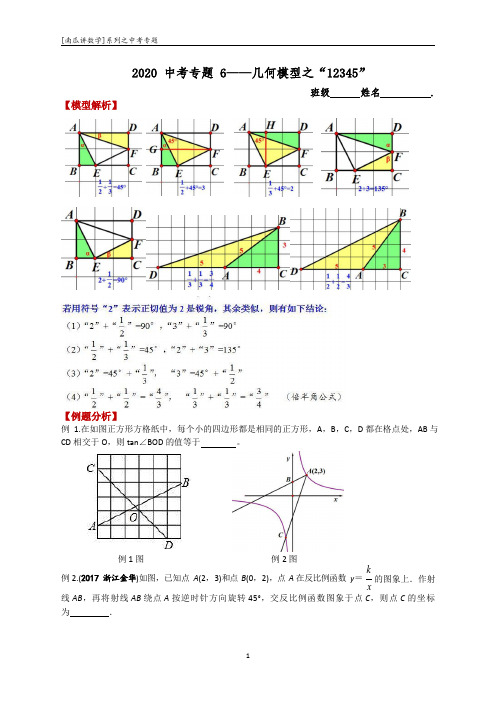
【模型解析】2020 中考专题 6——几何模型之“12345”班级姓名.【例题分析】例 1.在如图正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D 都在格点处,AB 与CD 相交于O,则tan∠BOD 的值等于。
例1 图例2 图k例2.(2017 浙江金华)如图,已知点A(2,3)和点B(0,2),点A 在反比例函数y=x的图象上.作射线AB,再将射线AB 绕点A 按逆时针方向旋转45°,交反比例函数图象于点C,则点C 的坐标为.3 2 例 3.如图,正方形 ABCD 中,P 是 BC 的中点,把△PAB 沿着 PA 翻折得到△PAE ,过 C 作 CF ⊥DE 于 F ,若 CF =2,则 DF = .【巩固训练】1. 如图 1,∠AOB 是放置在正方形网格中的一个角,则 cos ∠AOB 的值是.图 1 图 2图 32. 如图 2 是由边长相同的小正方形组成的网格,A ,B ,P ,Q 四点均在正方形网格的格点上,线段AB,PQ 相交于点 M ,则图中∠QMB 的正切值是( ) 1 A.B.1C. 2D.23. 如图 3,把一个矩形纸片 OABC 放入平面直角坐标系中,使 OA 、OC 分别落在 x 轴、y 轴上,连接 OB,将纸片 OABC 沿 OB 折叠,使点 A 落在 A'的位置上.若 OB= ,BC 1,求点 A'的坐标为 .OC 24. 如图 4,半圆 O 的直径 AB=10cm ,弦 AB=10cm ,弦 AC=6cm ,AD 平分∠BAC ,则 AD 的长为()A. 4 cmB. 3 cmC. 5 cmD.4 cm图 4图 55.如图 5,在四边形 ABCD 中,∠BAC =∠BDC=90°,AB=AC=则 DM= (),CD=1 ,对角线的交点为 M ,A.B. 2 3 1C.D.2235 5 5 5 5 55 6. 如图6,在平面直角坐标系xOy 中,点A (-1,0),B (0,2),点C 在第一象限,∠ABC =135°,kAC 交y 轴于D ,CD =3AD ,反比例函数y =的图象经过点C ,则k 的值为 .xADFBEC图 6图 7图 87(2017 浙江丽水)如图 7,在平面直角坐标系 xOy 中,直线 y =-x +m 分别交 x 轴,y 轴于 A ,B 两点,已知点 C (2,0). (1) 当直线 AB 经过点 C 时,点 O 到直线 AB 的距离是 ; (2) 设点 P 为线段 OB 的中点,连结 PA ,PC ,若∠CPA =∠ABO ,则 m 的值是 .8.(2018山东滨州)如图8,在矩形ABCD 中,AB =2,BC =4,点E ,F 分别在BC ,CD 上,若AE = , ∠EAF=45°,则AF 的长为 .9.如图 9,在四边形 ABCD 中 BC⊥AB,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E 是 AB 上一点,且∠ DCE=45°,BE=4, 则 DE= .图 9 图 10 图 1110.(2018 山东泰安)如图 10,在矩形 ABCD 中, AB = 6 ,BC = 10 ,将矩形 ABCD 沿 BE 折叠, 点 A 落在 A ' 处,若 EA ' 的延长线恰好过点C ,则sin ∠ABE 的值为 .11. 如图 11,正方形 ABCD 的边长 AB=2,E 为 AB 的中点,F 为 BC 的中点,AF 分别与 DE 、BD相交于点 M ,N ,则 MN 的长为( )A.B .﹣1C .D .12.如图12,抛物线y =-x2 +bx +c 与直线y =1x + 2 交于C、D 两点,其中点C 在y 轴上,27点D 的坐标为(3,2F。
2020中考数学专题6——几何模型之”12345“-含答案
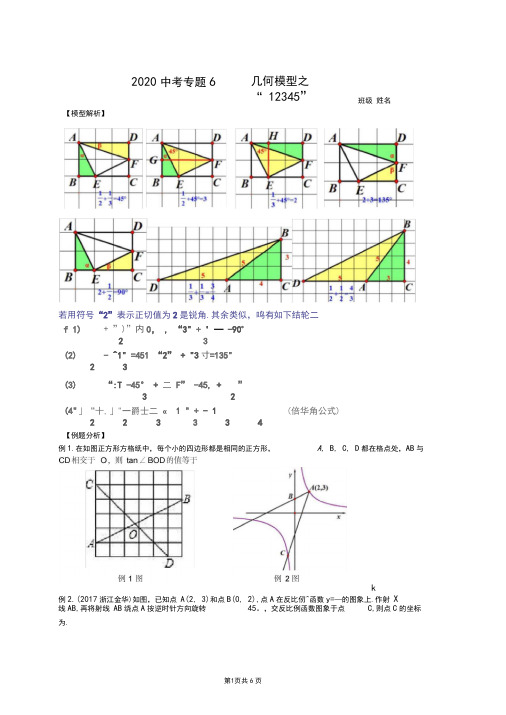
若用符号“2”表示正切值为2是锐角.其余类似,鸣有如下结轮二 f 1) + ”)”内0, , “3" + ' — -90c2 3 (2) - ^1" =451 “2” + "3寸=135"2 3(3)“:T -45° + 二 F” -45, + ”3 2(4"」“十,」"一爵士二 « 1 " + - 1(倍华角公式)2 23 3 34【例题分析】例1.在如图正方形方格纸中,每个小的四边形都是相同的正方形,A, B, C, D 都在格点处,AB 与k例2.(2017浙江金华)如图,已知点 A(2, 3)和点B(0, 2),点A 在反比仞^函数y=—的图象上.作射 X线AB,再将射线 AB 绕点A 按逆时针方向旋转 45。
,交反比例函数图象于点 C,则点C 的坐标 为.2020中考专题6几何模型之“ 12345”【模型解析】 班级 姓名例3.如图,正方形ABCD中,P是BC的中点,把^ PAB沿着PA翻折得到^ PAE过C作C。
DE于F,若C已2,贝U DF=.DD.4 cm5. 如图5,在四边形AB=AC=ABCD 中,/ BAC = / BDC=90 J5, CD=1 ,对角线的交点为M,则DM=( )A 3 B,5A. B.2 3D.【巩固训练】1.如图1, / AOB是放置在正方形网格中的一个角,则cos/ AOB的值是2.如图2是由边长相同的小正方形组成的网格,A, B, P, Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中/ QMB的正切值是( )1A. -B.1 C- 3 D.223.如图3,把一个矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB, 将纸片OABC 沿OB折叠,使点A落在A'的位置上.若OB=岳_B£1 ,求点A'的坐标为.OC 24.如图4,半圆O的直径AB=10cm ,弦AB=10cm ,弦AC=6cm , AD平分/ BAC ,则AD的长为C. cmA. 4 5 cmB. 3- 5 cm图4 图5,点C 在第一象限,/ ABC= 135 则k 的值为.y=—x+ m 分别交x 轴,y 轴于A, B两点,已知点 C (2, 0)(1)当直线AB 经过点C 时,点O 到直线AB 的距离是 ;⑵设点P 为线段OB 的中点,连结 PA, PC,若/ CPA= /ABO,则m 的值是8.(2018山东滨州)如图8,在矩形ABCDK /EA 已45° ,则 AF 勺长为.9.如图 9,在四边形 ABCDP BC± AB,AD // BC(BC>AD), / B=90° ,AB=BC=12 E 是 AB 上一点,且/ DCE=45 , BE=4,贝U DE=.6.如图6,在平面直角坐标系xOy 中,点A( —1, 0) , B (0, 2)AB= 2, BC= 4,点 E, 吩另।J 在 BC CDh,若 AE=岳,图9 图10 10 . (2018山东泰安)如图10,在矩形ABCD 中,AB 点A 落在A'处,若EA'的延长线恰好过点 C ,则sin图116 , BC 10,将矩形ABCD 沿BE 折叠, ABE的值为.11 .如图11 ,正方形 ABCD 的边长 AB=2 , E 为AB 的中点, F 为BC 的中点,AF 分别与DE 、BD相交于点M , N ,则MN 的长为()A. k由AC 交y 轴于D, CD- 3AD,反比例函数y=—的图象经过点C,图6 图77 (2017浙江丽水)如图7,在平面直角坐标系 xOy 中,直线 B.13.如图13,抛物线y = x 2-4x+3与坐标轴交于 A 、B 、C 三点,点P 在抛物线上,PDXBC 于点D, 垂足D 在线段BC 上.若CD 二,求点P 的坐标.PD 212.如图12,抛物线yx 2bx c 与直线y lx 2交于2C 、D 两点,其中点C 在y 轴上,点D 的坐标为(3,7)。
中考数学必会几何模型(含答案)

MATH微信:beijingdaxue777QQ:1456770148中考必会几何模型目录专题一角平分线相关问题模型 (3)模型1角平分线相关模型 (3)专题二8字模型与飞镖模型 (6)模型1:角的8字模型 (6)模型2:角的飞镖模型 (8)模型3边的“8”字模型 (10)模型4边的飞镖模型 (11)专题三半角模型 (15)专题四将军饮马模型 (23)模型1:直线与两定点 (23)模型2角与定点 (28)模型3两定点一定长 (31)专题五角平分线四大模型 (34)模型1角平分线的点向两边作垂线 (34)模型2截取构造对称全等 (35)模型3角平分线+垂线构造等腰三角形 (37)模型4角平分线+平行线 (39)专题六截长补短辅助线模型 (42)模型1截长补短 (42)专题七蚂蚁行程 (48)模型1立体图形展开的最短路径 (48)专题八三垂直全等模型 (55)模型1三垂直全等模型 (55)专题九手拉手模型 (62)模型1手拉手 (62)专题十相似模型 (68)模型1A、8模型 (68)模型2共边共角型 (72)模型3一线三等角型 (75)模型4倒数型 (79)模型5与圆有关的简单相似 (82)模型6相似和旋转 (85)专题十一圆中的辅助线 (89)模型1连半径构造等腰三角形 (89)模型2构造直角三角形 (90)模型3与圆的切线有关的辅助线 (94)专题十二中点四大模型 (97)模型1倍长中线或类中线(与中点有关的线段)构造全等三角形 (97)模型2已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”. (99)模型3已知三角形一边的中点,可考虑中位线定理 (102)模型4已知直角三角形斜边中点,可以考虑构造斜边中线 (107)专题一角平分线相关问题模型模型1角平分线相关模型(1)如图1,若点P是∠ABC和∠ACB的角平分线的交点,则∠P=90°+∠A;(2)如图2,若点P是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣∠A;(3)如图3,若点P是∠ABC和外角∠ACE的角平分线的交点,则∠P=∠A.图1图2图3针对训练1.(2016•枣庄)如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为()A.15°B.17.5°C.20°D.22.5°【小结】本题若不套用模型,则需要通过三角形的外角性质证明得到∠A、∠D的数量关系.2.(2018•巴中)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=.【分析】由解题模型一中的(1)可知,∠BOC=90°+∠A,把∠BOC=110°代入计算可得到∠A的度数.【详解】∵∠BOC=90°+∠A,∠BOC=110°,∴90°+∠A=110°.∴∠A=40°.【小结】本题若不套用模型,需要利用三角形的内角和定理、角平分线的定义得到∠BO C、∠A的数量关系.3.(2018•济南历城区模拟)如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2018=.【详解】∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,∴∠A1BC=∠ABC,∠A1CD=∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,【小结】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义,熟记性质然后推出后一个角是前一个角的一半是解题的关键。
“12345模型”

【中考数学专题】特殊角的妙用——“12345模型”几何图形中经常会出现一些特殊角,熟悉的有30°、45°、60°等等,特殊角往往伴随着固有属性运用于题目中,也是解题思路来源之一。
比如看到30°角我们会想到1:2,45°角总是跟等腰直角三角形说不清道不明,60°甚至能牵出一只等边三角形。
关于特殊角,除了用角度表示,诸如15°角的倍数,还可以用三角函数表示,只要最终的结果是:(1)好看;(2)好用,就可以将其归为特殊角。
比如tanA=1/2,诚然我并不知道∠A的度数到底是多少,而且∠A也一定不是一个整数度数,但这并不妨碍∠A的特殊性,∠A所对的直角边是邻边的两倍,这与30°角的直角三角形三边比值并无本质区别。
打开三角函数的大门,打开新世界。
从一道中考题说起如图所示的网格是正方形网格,则∠PAB+∠PBA=___°.(点A、B、P是网格线交点)解法有很多,这里就根据现有的方格纸来构造一下:∠PAB+∠PBA=∠BPQ=45°这里的∠PAB和∠PBA便是今天要说的特殊角,除了它们的和为45°之外,用三角函数的观点来看:tan∠PAB=1/2,tan∠PBA=1/3这个正切值可以说很好看了。
“12345模型”对于这里的数据,为了便于记忆,老师总结为“12345”模型。
上文所举的中考题已经足够说明这个结论,考虑到使用这个结论的多样性,以下用3种方法给出证明:法一:方格纸中的构造小学的时候我们可能就遇到过这样一个题目:求∠1+∠2.考虑∠1和∠2的正切值,这不正是刚刚所说的α和β吗?构造等角,将α和β组合到一起:根据这里的等腰直角△ABC,可得∠1+∠2=45°此外,模型还可变式为:法二:勾三股四弦五如图,AC=4,BC=3,AB=5,这个三角形我们再熟悉不过了。
在这里:分别延长CB、CA可构造构造此处我们还可得:这个也是在解题中常用的结论。
中考数学备考一题一课三45度角和12345模型

45°---等腰直角三角形中的“夹半角”模型
X
6
K
6
Y
12 A
B
Q 12
6+x 12-x
D N x
C
方法一:平移FE到BQ,则QE=4.5,AQ=3,QBN=45° 将ABCD补形成为正方形,如图所示,这样就转化为了 8年级非常重要的模型,夹半角(45°) 有:(6+x)2=62+(12-x)2
x=4 即CN=4 点评:此方法简介明了,和8年级几何模型关联很大 是很好的方法。
3
α
45°
β
B
12-x
α
45° Yx
D 方法五:构造相似:这个构造方法还是很高级的,
其本质是12345模型,同学们可以再次深刻体会
用好此模型,一类45°角的问题真的可以做到口答。
由 BQX NBY
BX XQ
3 32
N YN = BY , 2x = 12-x
x=4
x 即CN=4
1
1
点评:12345,即tanα= 2,tanβ= 3
X
a
K
x
z
45° B
Y
c
N b y C
半角模型基本结论: 1、a+b=c 2、x2+y2=z2
45°---等腰直角三角形中的“一线三垂直”模型1
A
3
Qx
3+x 6
45°
B
3+x
Px G
D
方法二:构造一线三垂直的全等和相似: 平移后AQ=3
有3+x+x=6,x=1.5 PG=1.5
由 BGP BCN
PG BG 3 9
中考数学难点突破与经典模型精讲练解直角三角形中的拥抱模型和12345模型(解析版)

专题16 解直角三角形中的拥抱模型和12345模型【模型展示】 分别解两个直角三角形,其中公共边BC 是解题的关键.在Rt△ABC 和Rt△DCB 中,BC=BC.一、单选题1.如图,某学校大楼顶部有一个LED 屏AB ,小明同学在学校门口C 处测得LED 屏底部A 的仰角为53°,沿大门楼梯CD 向上走到D 处测得LED 屏顶部B 的仰角为30°,D 、E 、F 在同一水平高度上,已知大门楼梯CD 的坡比i =80CD =米,30EF =米,大楼AF 和大门楼梯CD 的剖面在同一平面内,则LED 屏AB 的高度为( ) 1.73≈,sin 5345︒≈,cos5335︒≈,tan 5343︒≈)A .24.6米B .30.6米C .34.6米D .44.6米 【答案】C【分析】如图,过D 作DH ⊥水平线于H ,延长AF 交水平线于,G 则,AG CH ⊥ 过C 作CO DE ⊥于,O 则,,DH CO CH DO 利用坡度的含义求解30,40,cos 30403,CDOOC OD CD 再求解30,tan53OC OE 60403,tan 5340,DF AF EF tan3074.6,BF DF 从而可得答案.【详解】解:如图,过D 作DH ⊥水平线于H ,延长AF 交水平线于,G 则,AG CH ⊥ 过C作CO DE ⊥于,O 则,,DH CO CH DO 由题意得:1:3,80,CD i CD 13tan ,33DHCO CDO CHDO 30,40,cos 30403,CDO OC ODCD53,ACG 而,DF HG ∥53,OEC AEF ACG ∴∠=∠=∠=︒4030,4tan 533OC OE 30,EF 4403303060403,tan533040,3DF AFEF 30,,BDFBF DF·tan 30604074.6,BF DF ∴=︒=+=≈ 74.64034.6.AB BF AF故选C【点睛】本题考查的是解直角三角形的应用,坡度的含义,熟练的构建直角三角形是解本题的关键.2.如图,某建筑物AB 在一个坡度为i =1:0.75的山坡BC 上,建筑物底部点B 到山脚点C 的距离BC =20米,在距山脚点C 右侧同一水平面上的点D 处测得建筑物顶部点A 的仰角是42°,在另一坡度为i =1:2.4的山坡DE 上的点E 处测得建筑物顶部点A 的仰角是24°,点E 到山脚点D 的距离DE =26米,若建筑物AB 和山坡BC 、DE 的剖面在同一平面内,则建筑物AB 的高度约为( )(参考数据:sin 24°≈0.41,cos 24°≈0.91,tan 24°≈0.45,sin 42°≈0.67.cos 42°≈0.74,tan 42°≈0.90)A .36.7米B .26.3 米C .15.4米D .25.6 米 【答案】D【分析】如图所示,过E 点做CD 平行线交AB 线段为点H ,标AB 线段和CD 线段相交点为G 和H 由坡度为i =1:0.75,BC =20可得BG =16,GC =12,由坡度为 i =1:2.4,DE =26可得DF =24,EF =10,分别在在AGB 中满足tan 42AG GD =︒,在AEH △中满足tan 24AH HE =︒化简联立得AB =25.6.【详解】如图所示,过E 点做CD 平行线交AB 线段为点H ,标AB 线段和CD 线段相交点为G 和H△在BGC 中BC =20,坡度为i =1:0.75,△222BG GC BC +=, △2223()4BG BG BC +=, △222916BG BG BC +=, △22252016BG =, △22540016BG =, △21640025BG =⨯, △2256BG =,△16BG =, △3124CG BG ==. 在BGC 中DE =26,坡度为 i =1:2.4,△222DF EF DE +=,△22212()5EF EF DE +=, △22214425EF EF DE +=, △221692625EF =, △225676169EF =⨯, △2100EF =,△10EF =, △12245DF EF ==, △在AGB 中满足tan 42AG GD =︒,在AEH △中满足tan 24AH HE =︒, 即0.9AB BG GC CD +=+,0.45AB BH GC CD DF+=++ 其中BG =16、BG =12、BH =BG -EF =6、DF =24,代入化简得160.9(12)60.45(36)AB CD AB CD +=+⎧⎨+=+⎩①②, 令2②-①有2261620.45360.91220.450.9AB AB CD CD -+⨯-=⨯⨯-⨯+⋅⋅-△421.6AB -=,△AB =25.6.故选:D .【点睛】本题考查了解直角三角形的应用,利用三角形的坡度和斜边长通过勾股定理可以求得三角形各边长度,再根据角度列含两个未知数的二元一次方程组,正确的列方程求解是解题的关键.3.数学实践活动课中小明同学测量某建筑物CD 的高度,如图,已知斜坡AE 的坡度为i =1:2.4,小明在坡底点E处测得建筑物顶端C处的仰角为45°,他沿着斜坡行走13米到达点F 处,在F测得建筑物顶端C处的仰角为35°,小明的身高忽略不计.则建筑物的CD高度约为()(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)A.28.0米B.28.7米C.39.7米D.44.7米【答案】D【分析】过点F作FG△BD于G,FH△CD于H,设FG=x米,则EG=2.4x米,在Rt△FGE 中,由勾股定理解得FG=5,EG=12,证明△CDE是等腰直角三角形,则CD=DE,设CD=y 米,在Rt△CHF中,由三角函数定义求解即可.【详解】过点F作FG△BD于G,FH△CD于H则△CFH=35°,四边形DGFH是矩形,△HF=DG,DH=FG,△斜坡AE的坡度为i=1:2.4,△设FG=x米,则EG=2.4x米,在Rt△FGE中,由勾股定理得:EF2FG2+EG2,即:132=x2+(2.4x)2,解得:x=5,△FG=5,EG=12,△△CED=45°,△△CDE是等腰直角三角形,△CD=DE,设CD=y米,则CH=(y﹣5)米,Rt△CHF中,tan△CFH=CH HF,即tan35°=512yy-+,则y﹣2=tan35°×(y+12),解得:y≈44.7,即建筑物的CD高度约为44.7米;故选:D.【点睛】本题考查的是解直角三角形的应用-仰角俯角问题以及坡度坡角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键4.我校兴趣小组同学为测量校外“御墅临枫”的一栋电梯高层AB的楼高,从校前广场的C处测得该座建筑物顶点A的仰角为45°,沿着C向上走到D点.再测得顶点A 的仰角为22°,已知CD的坡度:i=1:2,A、B、C、D在同一平面内,则高楼AB的高度为()(参考数据;sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)A.60B.70C.80D.90【答案】D【分析】作AH△ED交ED H,根据坡度的概念分别求出CE、DE,根据正切的定义求出AB.【详解】解:作AH△ED交ED的延长线于H,设DE=x米,△CD的坡度:i=1:2,△CE=8x米,由勾股定理得,DE2+CE2=CD8,即x2+(2x)2=(2,解得,x=30,则DE=30米,CE=60米,设AB=y米,则HE=y米,△DH=y﹣30,△△ACB=45°,△BC=AB=y,△AH=BE=y+60,在Rt△AHD中,tan△DAH=tan22DH AH︒=则3060yy-+≈0.4,解得,y=90,△高楼AB的高度为90米,故选:D.【点睛】本题考查的是解直角三角形的应用-仰角俯角问题、坡度坡角问题,掌握仰角俯角的概念、坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.5.如图,某大楼DE楼顶挂着“众志成城,抗击疫情”的大型宣传牌,为了测量宣传牌的高度CD,小江从楼底点E向前行走30米到达点A,在A处测得宣传牌下端D的仰角为60°.小江再沿斜坡AB行走26米到达点B,在点B测得宣传牌的上端C的仰角为43°,已知斜坡AB的坡度i=1:2.4,点A、B、C、D、E在同一平面内,CD△AE,宣传牌CD的高度约为()(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)A.8.3米B.8.5米C.8.7米D.8.9米【答案】A【分析】过B分别作AE、DE的垂线,设垂足为F、G.分别在Rt△ABF和Rt△ADE中,通过解直角三角形求出BF、AF、DE的长,再求出EF即BG的长;在Rt△CBG中求出CG的长,根据CD=CG+GE-DE即可求出宣传牌的高度.【详解】解:过B作BF△AE,交EA的延长线于F,作BG△DE于G.Rt△ABF 中,i =tan△BAF =BF AF =12.4,AB =26米, △BF =10(米),AF =24(米),△BG =AF +AE =54(米),Rt△BGC 中,△CBG =43°,△CG =BG •tan43°≈54×0.93=50.22(米),Rt△ADE 中,△DAE =60°,AE =30米,,△CD =CG +GE -DE =50.22+10-(米).故选:A .【点睛】此题考查了仰角、坡度的定义,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答此类题的关键.6.如图,小明在距离地面30米的P 处测得A 处的俯角为15︒,B 处的心角为60︒,若斜面坡度为,则斜面AB 的长是( )米.A.B .C .D .【答案】B【分析】过点A 作AF BC ⊥于点F ,根据三角函数的定义得到30ABF ∠=︒,根据已知条件得到3045HPB APB ∠∠=︒=︒,,求得60HBP ∠=︒,解直角三角形即可得到结论.【详解】如图所示:过点A 作AF BC ⊥于点F ,斜面坡度为,AF tan ABF BF ∠∴== 30ABF ∠∴=︒,在P 处进行观测,测得山坡上A 处的俯角为15︒,山脚B 处的俯角为60︒,3045HPB APB ∠∠∴=︒=︒,,60HBP ∠∴=︒,9045PBA BAP ∠∠∴=︒=︒,,PB AB ∴=,303060PH PH m sin PB PB =︒===,,解得:)PB m =,故AB =,故选:B .【点睛】此题主要考查了解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题,正确得出PB AB =是解题关键.7.如图,某人在山坡坡脚C 处测得一座建筑物顶点A 的仰角为63.4︒,沿山坡向上走到P 处再测得该建筑物顶点A 的仰角为53︒.已知BC =90米,且B 、C 、D 在同一条直线上,山坡坡度i =5:12,求此人从所在位置点P 走到建筑物底部B 点的路程( )米.(结果精确到0.1米)(测倾器的高度忽略不计,参考数据:4tan533︒≈,tan63.42︒≈)A .119.2B .137.1C .129.2D .127.1【答案】D 【分析】首先过点P 作PE △AB 于E ,PH △BD 于H ,由题意可知i =PH :CH =5:12,然后设PH =5x 米,CH =12x 米,在Rt △ABC 中,63.4ACB ∠=︒,BC =90米,则可得tan63.4AB BC︒=,利用正切函数的知识可求AB ,在Rt △AEP 中,53APE ∠=︒,利用正切函数可得关于x 的方程,从而得出PH ,在Rt △PHC 中,利用勾股定理可求CP 的长度,进一步可求此人从所在位置点P 走到建筑物底部B 点的路程.【详解】解:如图:过点P 作PE △AB 于E ,PH △BD 于H ,设PH =BE =5x 米,CH =12x 米,在Rt △ABC 中,63.4ACB ∠=︒,BC =90米,则tan63.4AB BC ︒=, 即=290AB , △AB =180(米),在Rt △AEP 中,53APE ∠=︒,AE =AB -BE =180-5x ,BH =EP =BC +CH =90+12x , △18054tan5390123AE x EP x -︒===+, 解得207x =, 经检验207x =是原方程的解,且符合题意, △201005577PH x ==⨯=(米),在Rt △PHC 中,260371PC x ===(米), 故此人从所在位置点P 走到建筑物底部B 点的路程是:26089090127.177+=≈(米),故选:D .【点睛】本题考查了仰角的定义,以及解直角三角形的实际应用问题,解题的关键是要能借助仰角构造直角三角形并解直角三角形,注意数形结合思想的应用,注意辅助线的作法.二、填空题8.一名高山滑雪运动员沿着斜坡FC 滑行,他在点D 处相对大树顶端A 的仰角为30︒,从D点再滑行米到达坡底的C 点,在点C 处相对树顶端A 的仰角为45︒,若斜坡CF 的坡比为1:3i =(点E ,C ,B 在同一水平线上),则大树AB 的高度___________米(结果保留根号).【答案】【分析】作DH △CE 于H ,解Rt △CDH ,即可求出DH ,CH ,过点D 作DG △AB 于点G ,设BC =a 米,用a 表示出AG 、DG ,根据tan△ADG =AG DG列式计算得到答案. 【详解】解:过点D 作DH △CE 于点H ,过点D 作DG △AB 于点G ,设BC =a 米,由题意知CD =△斜坡CF 的坡比为i =1:3, △13DH CH =, 设DH =x 米,则CH =3x 米,△DH 2+CH 2=DC 2,△()(2223x x +=,△x =2,△DH =2米,CH =6米,△△DHB =△DGB =△ABC =90°,△四边形DHBG 为矩形,△DH =BG =2米,DG =BH =(a +6)米,△△ACB =45°,△BC =AB =a (米),△AG =(a −2)米,△△ADG =30°,△tan 30AG DG ︒==△26a a -=+△a =6+△AB =6+,故答案为:6+【点睛】本题考查的是解直角三角形的应用−仰角俯角问题,掌握锐角三角函数的定义、仰角俯角的概念是解题的关键.9.如图,小明在P 处测得A 处的俯角为15°,B 处的俯角为60°,PB =30m .若斜面AB 坡度为AB 的长是______m .【答案】30【分析】根据斜面AB 坡度为30ABF ∠=︒,再利用角之间的关系求出601545∠=︒-︒=︒APB ,PAB 45∠=︒,进一步得到=30m =PB AB .【详解】解:△斜面AB 坡度为1:,△tan∠ABF 30ABF ∠=︒,△在P 处测得A 处的俯角为15°,B 处的俯角为60°,△906030∠=︒-︒=︒HPB ,△60HBP ∠=︒,△90PBA ∠=︒,△601545∠=︒-︒=︒APB ,∠=︒,△PAB45=,△PB ABPB=,△30mAB=,△30m故答案为:30【点睛】此题主要考查了解直角三角形的应用,正确得出PB=AB是解题关键.三、解答题10.大楼AB是某地标志性建筑,如图所示,某校九年级数学社团为测量大楼AB的高度,一小组先在附近一楼房CD的底端C点,用高为1.5米的测杆CE在E处观测AB大楼顶端B 处的仰角是72°,另一小组到该楼房顶端D点处观测AB大楼底部A处的俯角是30°,已知楼房CD高约是45米,根据以上观测数据求AB大楼的高(精确到0.1米).(,sin72°≈0.951,cos72°≈0.034,tan72°≈3.08)【答案】241.3米【分析】过E作EF△AB于F,则四边形ACEF是矩形,得到EF=AC,AF=CE,利用三角函数在Rt△ACD中求出AC,在Rt△BEF中求出BF,即可得到AB大楼的高.【详解】解:过E作EF△AB于F,则四边形ACEF是矩形,△EF=AC,AF=CE,在Rt △ACD 中,△DAC =30°,CD =45,△AC =tan30CD =︒在Rt △BEF 中,△BEF =72°,EF =AC =△BF =EF ∙tan72°=,△AB =AF +BF =239.78+1.5≈241.3(米),答:AB 大楼的高为241.3米.【点睛】此题考查了解直角三角形的实际应用,正确理解题意构造直角三角形解决问题是解题的关键.11.如图,坡AB 的坡度为1:2.4,坡面长26米,BC AC ⊥,现计划在斜坡中点D 处挖去部分坡体(用阴影表示)修建一个平行于水平线CA 的平台DE 和一条新的斜坡(BE 请将下面两小题的结果都精确到0.1 1.732)≈.(1)若修建的斜坡BE 的坡角(即)BEF ∠恰为45︒,则此时平台DE 的长为______米;(2)坡前有一建筑物GH ,小明在D 点测得建筑物顶部H 的仰角为30︒,在坡底A 点测得建筑物顶部H 的仰角为60︒,点B 、C 、A 、G 、H 在同一平面内,点C 、A 、G 在同一条水平直线上,问建筑物GH 高为多少米?【答案】(1)7.0(2)建筑物GH 高约为17.9米【分析】(1)先利用勾股定理解直角BCA ∆求出10BC =,24AC =,再证BCA BFD ∆∆,推出12BF FD BD BC AC AB ===,代入数值即可求解; (2)过点D 作DP AC ⊥,垂足为P ,利用矩形的性质求出12PA AC PC =-=,5MG DP ==,12DM PG AP AG AG ==+=+,解Rt DMH ∆可得()tan3012HM DM AG =⋅︒=+,进而得出()125GH HM MG AG =+=++,再解Rt HGA ∆,列等式求出AG ,则HG =. 【详解】(1)解:由题意知,90BCA ∠=︒,26AB =,12.4BC AC =,△设BC x =,则 2.4AC x =,由勾股定理得:222BC AC AB +=,即()2222.426x x +=,解得10x =,△10BC =,24AC =.△45BEF ∠=︒,90BFE ∠=︒,△45FBE BEF ∠=∠=︒,△BF FE =.由题意,DF AC ∥,△BDF BAC ∠=∠,又△90BCA BFE ∠=∠=︒,△BCA BFD ∆∆, △12BF FD BD BC AC AB ===, △1132AD BD AB ===,152BF CF EF BC ====,1122DF AC ==, △1257.0(DE DF EF =-=-=米);则平台DE 的长为7.0m ,(2)解:过点D 作DP AC ⊥,垂足为P .在矩形FDPC 中,5DP CF ==,12PC DF ==,△12PA AC PC =-=.在矩形DPGM 中,5MG DP ==,12DM PG AP AG AG ==+=+,在Rt DMH ∆中,()tan3012HM DM AG =⋅︒=+,△()125GH HM MG AG =+=++, 60HAG ∠=︒,)1253tan60AG HG AG AG++∴︒===解得:AG =,17.9HG ∴==≈(米), 即建筑物GH 高约为17.9米.【点睛】本题考查解直角三角形的实际应用,涉及勾股定理、相似三角形的判定与性质、矩形的判定与性质、特殊角的三角函数值等知识点,解题的关键是构造直角三角形,利用特殊角的三角函数值求解.12.在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C 处测得该建筑物顶端B 的仰角为60°,沿山坡向上走20m 到达D 处,测得建筑物顶端B 的仰角为30°.已知山坡坡度3:4i =,即3tan 4θ=,请你帮助该小组计算建筑物的高度AB .(结果精确到0.1m ,1.732≈)【答案】该建筑物AB 的高度约为31.9m【分析】如图,作DE AC ⊥交AC 于点E ,作DF AB ⊥交AB 于点F ,作CH DF ⊥交DF 于点H ,根据题意分别求出BF 和AF 的长,再根据AB AF BF =+即可求解.【详解】作DE AC ⊥交AC 于点E ,作DF AB ⊥交AB 于点F ,作CH DF ⊥交DF 于点H 则DE AF =,HF AC =,DH CE = △3tan 4θ= △设3DE x =,则4CE x =在Rt CDE △中,90E ∠=︒△222DE CE CD +=△222(3)(4)20x x +=△4x =(负值舍去)△12DE =,16CE =△12AF DE ==,16DH CE ==设BF y =,则(12)AB y =+在Rt BDF 中,30BDF ∠=︒ △tan BF BDF DF ∠=△DF =在Rt ABC 中,60ACB ∠=︒ △tan AB ACB AC ∠=△12)AC y =+即12)HF AC y ==+ △DF FH DH -=12)16y +=△(6y =+△6121831.9(m)AB BF FA =+=+=+≈答:该建筑物AB 的高度约为31.9m .【点睛】本题考查解直角三角形的应用,熟练掌握坡角坡度,仰角的定义,添加合适的辅助线构造直角三角形是解题的关键.13.如图,在建筑物DF 的左边有一个小山坡,坡底B 、C 同建筑底端F 在同一水平线上,斜坡AB 的坡比为5:12i = ,小李从斜坡底端B 沿斜坡走了26米到达坡顶A 处,在坡顶A处看建筑物的顶端D 的仰角α为35︒,然后小李沿斜坡AC 走了C 点,已知建筑物上有一点E ,在C 处看点E 的仰角为18︒,(点A 、B 、C 、D 、E 、F 在同一平面内)建筑物顶端D 到E 的距离DE 长度为28.8米,求建筑物DF 的高度.(参考数据:4cos355︒≈, 7tan35?10≈,9cos1810︒≈,1tan183︒≈)【答案】40.8米【分析】如图AG BC ⊥于G ,AH DF ⊥于H ,连接AD CE ,根据比例设5AG x =,12BG x =,结合勾股定理求出=2x ,得到10AG =,再次由勾股定理求出8GC =,设EF m =,然后利用解直角三角形,求出12m =,即可得到答案.【详解】解:如图AG BC ⊥于G ,AH DF ⊥于H ,连接AD 、CE ,△AB 的坡比5:12i =,设5AG x =,12BG x =,△在Rt ABG 中,1326AB x ===, △=2x ,△10AG =,在Rt ACG 中,8GC ,设EF m =,在Rt CEF 中,1tan =tan18?=3EF CF β≈, △3CF m =,△四边形AGFH 是矩形,△83AH GF GC CF m ==+=+,又△()28.81018.8DH DE EH DE EF HF m m =+=+-=+-=+,在Rt AHD 中,7tan tan 3510DH AH α=︒=≈, 18.878310m m +∴≈+,12m =∴,△28.81240.8DF DE EF =+=+=,答:建筑物DF 的高度为40.8米.【点睛】本题考查了解直角三角形的应用——仰角俯角问题,也考查了勾股定理,根据题意作出正确的辅助线是解答此题的关键.14.某工程队计划测量一信号塔OC 的高度,由于特殊原因无法直达到信号塔OC 底部,因此计划借助坡面高度来测量信号塔OC C 的高度.如图,在信号塔OC 旁山坡脚A 处测得信号塔OC 顶端C 的仰角为70︒,当从A 处沿坡面行走13米到达P 处时,测得信号塔OC 顶端C 的仰角为45︒.已知山坡的坡度1:2.4i =,且O ,A ,B 在同一条直线上.请根据以上信息求信号塔OC 的高度.(侧倾器高度忽略不计,参考数据:sin700.94︒≈,cos700.34︒≈,tan70 2.7︒≈)【答案】信号塔OC 的高度约为27.0米【分析】过点P 作PE △OB 于点E ,PF △OC 于点F ,设PE =5x ,则AE =12x ,在Rt △AEP 中根据勾股定理可得(5x )2+(12x )2=132,解方程求出x ,设CF =PF =m 米,则OC = (m +5) 米,OA =(m -12)米,在Rt △AOC 中,由5tan 7012OC m OA m +︒==-求得m 的值,继而可得答案. 【详解】解:如图,过点P 作PE △OB 于点E ,PF △OC 于点F ,则四边形OFPE 是矩形, △OF =PE ,OE =PF ,△i =1:2.4,13AP =, △15tan 2.412PE PAE AE ∠===, △设PE =5x ,则AE =12x ,在Rt △AEP 中,由勾股定理得:(5x )2+(12x )2=132,解得:1x =或=1x -(舍去),△PE =5,则AE =12,△△CPF =45°,PF △CF ,△△CPF =△PCF = 45°,△CF PF =,设CF =PF =m 米,则OC = (m +5) 米,OA =(m -12)米,在Rt △AOC 中,5tan 7012OC m OA m +︒==-, 解得:22.0m ≈,△22.0527.0OC ≈+=(米)△信号塔OC 的高度约为27.0米.【点睛】本题考查的是解直角三角形的应用,仰角、坡度的定义,矩形的性质与判定,解题的关键是要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形. 15.感恩回馈,传播文化.2022年3月份,河南省绝大部分景点实施免门票政策,其中去嵩山少林寺的人数量巨大.如图,王林进入景区之后沿直线BD 行至山坡坡脚C 处,测得检票大厅顶点A 的仰角为60︒,沿山坡向上走到山门E 处再测得检票大厅顶点A 的仰角为37︒,已知山坡的坡比1:1.5i =,48BC =米.求王林所在山门E 处的铅直高度.(结果精确到0.1.参考数据:sin 370.60,cos 370.80,tan 37 1.73≈≈≈°°°)【答案】22.1米【分析】根据解直角三角形求得tan60AB BC =⋅︒=,如图,过点E 作EF AB ⊥于点F ,EG BD ⊥于点G ,则四边形EFBG 是矩形,设EG BF x ==米,求得()48 1.5EF BG x ==+米,列方程()0.7548 1.5x x +=,求解即可.【详解】解:在Rt ABC 中,48BC =米,60ACB ∠=︒, △tan60AB BC =⋅︒=.如图,过点E 作EF AB ⊥于点F ,EG BD ⊥于点G ,则四边形EFBG 是矩形,△,EF BG BF GE ==,设EG BF x ==米.在Rt EGC 中,1tan 1.5EG i ECG CG =∠==, △ 1.5CG x =(米),△()48 1.5EF BG x ==+米.在Rt AFE 中,37AEF ∠=︒,△()tan370.7548 1.5AF EF x =⋅︒≈+米.又△()AF AB BF x =-=米,△()0.7548 1.5x x +=,解得22.1x ≈,即22.1EG ≈(米).答:王林所在山门E 处的铅直高度约为22.1米.【点睛】本题考查了解直角三角形的应用问题,坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.16.如图,某测绘小组在山坡坡脚A 处测得信号发射塔尖C 的仰角为56.31°,沿着山坡向上走到P 处再测得点C 的仰角为36.85°,已知AP =米,山坡的坡度1:3i =(坡度指坡面的铅直高度与水平宽度的比),且D 、A 、B 三点在同一条直线上,求塔尖C 到地面的高度CD 的长.(测角仪的高度忽略不计,参考数据:sin56.310.83︒≈,cos56.310.55︒≈,tan56.31 1.50︒≈,sin36.850.60︒≈,cos36.850.80︒≈,tan36.850.75︒≈)【答案】约为130米【分析】过点P 作PM CD ⊥垂足为M ,则四边形DBPM 是矩形,得DM BP =,MP DB =,根据1:3i =,且AP =,求出PB ,AB 的长度;在Rt CPM 中,36.85CPM ∠=︒,设CM x =,由三角函数值求出3443PM CM x ==,在Rt ACD 中56.31CAD ∠=︒,20CD x =+,()2203AD x =+,根据PM BD AB AD ==+列方程求出x ,即可得到CD 长度. 【详解】解:过点P 作PM CD ⊥垂足为M ,则四边形DBPM 是矩形DM BP ∴=,MP DB =, 1:3i =,且AP =20PB ∴=,60AB =,在Rt CPM 中,36.85CPM ∠=︒,设CM x =,3tan 36.854CM PM ︒==, 3443PM CM x ∴==, 在Rt ACD 中,56.31CAD ∠=︒,20CD x =+,203tan 56.312CD x AD AD +∴︒===, ()2203AD x ∴=+, PM BD AB AD ==+,即()42206033x x =++, 110x ∴=,130CD CM DM ∴=+=,答:塔尖到地面的高度CD 约为130米.【点睛】本题考查了解直角三角形的应用,仰角俯角问题,以及坡角问题,本题要求学生借助仰角关系,构造直角三角形,并结合图形利用三角函数解直角三角形.17.在一次数学课外实践活动中,某小组要测量一幢大楼MN 的高度,如图,在山坡的坡脚A 处测得大楼顶部M 的仰角是58︒,沿着山坡向上走75米到达B 处.在B 处测得大楼顶部M 的仰角是22︒,已知斜坡AB 的坡度3:4i =(坡度是指坡面的铅直高度与水平宽度的比)求大楼MN 的高度.(图中的点A ,B ,M ,N ,C 均在同一平面内,N ,A ,C 在同一水平线上,参考数据:tan220.4,tan58 1.6︒≈︒≈)【答案】大楼MN 的高度为92米【分析】过点B 分别作BE △AC ,BF △MN ,垂足分别为E 、F ,通过解直角三角形表示出BF 、AN 、AE 的长度,利用BF =NE 进行求解即可.【详解】过点B 分别作BE △AC ,BF △MN ,垂足分别为E 、F ,90BEA BFN BFM MNA ∴∠=∠=∠=∠=︒∴四边形BENF 为矩形,,BE AN BF NE ∴==设MN x =,在Rt ABE 中,斜坡AB 的坡度3:4i =,即34BE AE =, 3sin 5BE BAE AB ∴∠== 75AB =45,60BE AE ∴==45FN ∴=45MF x ∴=-在Rt AMN △中,tan ,58MN MAN MAN AN∠=∠=︒ tan 58 1.6x AN∴︒=≈ 58AN x ∴≈ 5608NE AN AE x ∴=+=+ 在Rt BMF △中,tan ,22MF MBF MBF BF∠=∠=︒ 45tan 220.4x BF-∴︒=≈ 5(45)2BF x ∴≈- 5560(45)82x x ∴+=- 解得92x =,所以,大楼MN 的高度为92米.【点睛】本题考查了解直角三角形的应用—仰角俯角问题,准确理解题意,能添加辅助线构造直角三角形是解题的关键.18.如图,公园内有一个垂直于地面的立柱AB ,其旁边有一个坡面CQ ,坡角30QCN ∠=.在阳光下,小明观察到在地面上的影长为120cm ,在坡面上的影长为180cm .同一时刻,小明测得直立于地面长60cm 的木杆的影长为90cm (其影子完全落在地面上).求立柱AB 的高度.【答案】【分析】延长AD交BN于点E,过点D作DF△BN于点F,根据直角三角形的性质求出DF,根据余弦的定义求出CF,根据题意求出EF,再根据题意列出比例式,计算即可.【详解】解:延长AD交BN于点E,过点D作DF△BN于点F,在Rt△CDF中,△CFD=90°,△DCF=30°,则DF=12CD=90(cm),CF=CD•cos△DCF cm),由题意得:DFEF=6090,即90EF=6090,解得:EF=135,△BE=BC+CF+EF,6090,解得:AB答:立柱AB的高度为.【点睛】此题考查了解直角三角形的应用-坡度坡角问题、平行投影的应用,解题的关键是数形结合,正确作出辅助线,利用锐角三角函数和成比例线段计算.19.如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度AB,在居民楼前方有一斜坡,坡长15m CD =,斜坡的倾斜角为α,4cos 5α=.小文在C 点处测得楼顶端A 的仰角为60︒,在D 点处测得楼顶端A 的仰角为30︒(点A ,B ,C ,D 在同一平面内).(1)求C ,D 两点的高度差;(2)求居民楼的高度AB .(结果精确到1m 1.7≈)【答案】(1)9m(2)24m【分析】(1)过点D 作DE BC ⊥,交BC 的延长线于点E ,在Rt DCE 中,可得()4cos 1512m 5CE CD α=⋅=⨯=,再利用勾股定理可求出DE ,即可得出答案.(2)过点D 作DF AB ⊥于F ,设m AF x =,在Rt ADF 中,30AF x tan DF DF ︒===,解得DF =,在Rt ABC 中,()9m AB x =+,)12m BC =-,tan60AB BC ︒===x 的值,即可得出答案. (1)解:过点D 作DE BC ⊥,交BC 的延长线于点E ,在Rt DCE 中,4cos 5α=,15m CD =, ()4cos 1512m 5CE CD α∴=⋅=⨯=.()9m DE ∴===.答:C ,D 两点的高度差为9m .(2)过点D 作DF AB ⊥于F ,由题意可得BF DE =,DF BE =,设m AF x =,在Rt ADF 中,tan tan30AF x ADF DF DF ∠=︒===解得DF =,在Rt ABC △中,()9m AB AF FB AF DE x =+=+=+,)12m BC BE CE DF CE =-=-=-,tan60AB BC ︒===解得92x =, ()9924m 2AB ∴=+≈. 答:居民楼的高度AB 约为24m .【点睛】本题考查解直角三角形的应用-仰角俯角问题、坡度坡角问题,熟练掌握锐角三角函数的定义是解答本题的关键.20.在一次课外活动中,某数学兴趣小组测量一棵树CD 的高度.如图所示,测得斜坡BE 的坡度1:4i =,坡底AE 的长为8米,在B 处测得树CD 顶部D 的仰角为30°,在E 处测得树CD 顶部D 的仰角为60°,求树高CD .(结果保留根号)【答案】(3)米【分析】作BF CD ⊥于点F ,设DF x =米,则BF =米,(2)CD x =+米,从而计算出2)EC x =+米,结合AC EC AE -=,得到BF EC AE -=,建立起等式计算即可.【详解】解:作BF CD ⊥于点F ,根据题意可得四边形ABFC 是矩形,△,AB FC AC BF ==,△斜坡BE 的坡度1:4i =,坡底AE 的长为8米,△2AB FC ==,设DF x =米,在Rt DBF 中,tan DF DBF BF ∠=, 则3tan 30DF BF ==(米), 在Rt DCE 中,(2)CD DF CF x =+=+米,tan DC DEC EC ∠=, △32)tan 603CD EC x ==+米.△AC EC AE -=, △BF EC AE -=,8=.解得:1x =,则12)3)CD =+=米.答:CD 的高度是3)米.【点睛】本题考查的是解直角三角形的应用﹣仰角俯角问题,坡度坡角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.21.如图,株洲市炎陵县某中学在实施“五项管理”中,将学校的“五项管理”做成宣传牌(CD ),放置在教学楼A 栋的顶部(如图所示)该中学数学活动小组在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°,沿芙蓉小学围墙边坡AB 向上走到B 处测得宣传牌顶部C 的仰角为45°.已知山坡AB 的坡度为i =1:3,AB m ,AE =8m .(1)求点B距水平面AE的高度BH.(2)求宣传牌CD的高度.(结果精确到0.1)【答案】(1)点B距水平面AE的高度BH是2米(2)广告牌CD的高度约为2.1米【分析】(1)根据山坡AB的坡度为i=1:3,可设BH=a,则AH=3a,然后在Rt△ABH中,利用勾股定理进行计算即可解答;(2)过点B作BF△CE,垂足为F,则BH=EF=2米,BF=HE=14米,然后在Rt△ADE中,利用锐角三角函数的定义求出DE的长,再在Rt△BFC中,利用锐角三角函数的定义求出CF的长,最后进行计算即可解答.【详解】(1)解:在Rt△ABH中,BH:AH=1:3,△设BH=a,则AH=3a,△AB由勾股定理得BH=2,答:点B距水平面AE的高度BH是2米;(2)解:在Rt△ABH中, BH=2,△AH =6,在Rt△ADE中, tan△DAE=DE AE.,即DE=tan60 ·AE,如图,过点B作BF△CE ,垂足为F,BF= AH + AE=6+8 =14,DF= DE-EF= DE-BH,在Rt△BCF中,△C=△CBF=45°,△ CF= BF= 14,△CD=CF-DF =14—()答:广告牌CD的高度约为2.1米.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.。
12345模型

12345模型1.12345模型 (1)原理若α+β=45°,且tan α=12,则tan β=13;反之,亦然. 即一个45°的角可以分成两个角之和,其中一个角的正切值为12,另一个角的正切值为13.(2)证明方法1:已知等腰Rt △ABC ,∠B =90°,延长BC 至点D ,使得CD =BC ,则tan α=12,过点C 作CE ⊥AD 于点E ,易证tan β=13.方法2:已知正方形ABCD 中,E 、F 分别为AB 、CD 的中点,则tan α=12,过点F 作FG ⊥AC 于点G ,易证tan β=13.(3)应用:知二推一若tan α=12,tan β=13,则α+β=45°.若α+β=45°,tan α=12,则tan β=13.若α+β=45°,tan β=13,则tan α=12.βαDABBAECDαβABCDF E αβααβαE FGDCB A2.二倍角问题若tanα=12,则tan2α=43.若tanβ=13,则tan2β=34.若tanα=12,则tan(α+45°)=3.若tanβ=13,则tan(β+45°)=2.52ββ2αααβ453类型1:12345模型【例题1】(1)如图,A、B、C、D都在方格纸的格点上,则∠AOC的度数为___________.【答案】45°.(2)如图,在矩形ABCD中,∠EAF=45°,AB=4,BC=8,BE=2,则DF=___________.【答案】83.(提示:∵∠EAF=45°,tan∠BAE=12,∴tan∠DAF=13)(3)如图,在正方形ABCD中,AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长为__________.【答案】2.(提示:连接AE,易证△AEF≌△AED(HL),∴∠EAG=45°,又∵tan∠BAG=12,∴tan∠DAE=13)(4)如图,在正方形ABCD中,AB=6,BE=2AE,连接DE,在AD、BC上分别存在点G、F,连接GF交DE于点H,且∠GHD=45°,则FG的长度为__________.【答案】.(提示:过点D作DM∥CF交CB于点M,则∠EDM=45°,又∵tan∠ADE=13,∴tan∠CDM=12)ABCDOEFDCBAAB CDGFE EFGDCBAHA BCDGFEHEFGMD CBA【例题2】(1)如图,在平面直角坐标系中,一次函数y =2x -1的图象分别交x 轴、y 轴于点A 、B ,将直线AB 绕点B 顺时针旋转45°,交x 轴于点C ,则直线BC 的函数解析式为___________________.【答案】y =13x -2.(提示:tan ∠OCB =13,∴OC =3OB =6)(2)如图,在平面直角坐标系中,点A (0,6),B (3,0),在x 轴上有一动点P ,若∠P AB =45°,则点P 的坐标为_______________.【答案】(-2,0)或(9,0). 【例题3】(1)如图,正方形ABCD 中,点P 是BC 的中点,把△P AB 沿着P A 翻折得到△P AE ,过点C 作CF ⊥DE 交DE 的延长线于点F ,若CF =2,则DF =_______.【答案】6.(提示:过点A 作AG ⊥DE 于点G ,则△ADG ≌△AEG ,∵tan ∠BAP =12,∴tan ∠CDF =tan ∠DAG =13,∴DF =6)(2)如图,已知正方形ABCDAC 、BD 交于点O ,点E 在BC 上,且CE =2BE ,过点B 作BF ⊥AE 于点F ,连接OF ,则线段OF 的长为________.xxxABCDF EPPEF GDC BAABCDF EOO EF G HDCB A.(提示:过点O作OG⊥AE于点G,则tan∠GOB=tan∠OAG=12,∴OG=1,AG=2,∵tan∠BAE=13,∴AF=3,∴GF=3-2=1,∴OF)(3)如图,已知正方形ABCD的边长为3,E是边BC上一点,BE=1,将△ABE、△ADF分别沿折痕AE、AF向内折叠,点B、D在点G处重合,过点E作EH⊥AE,交AF的延长线于点H,则线段FH的长为___________.(提示:AE AH=,AF FH)(4)如图,矩形ABCD中,AB=2,AD=4,E、F分别在边AD、BC上,点A与点C关于EF所在的直线对称,P是边DC上的一动点.连接BP交EF于点M,当∠EMP=45°时,CP的长为___________.【答案】43.(提示:由对称可知,∠MON=90°,∴∠ONM=45°,∵tan∠ACB=12,∴tan∠PBC=13,∴CP=43)【例题4】如图,在△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=9,BD=3,EA=EC,∠ECD=45°,则BE的长为____________..(提示:BC=DF=FB∴CF,∴tan∠DCF=13,∵∠ECD=45°,∴tan∠GCE=12,∵CG=∴AE=CE,∵tan∠EAH=13,∴EH=32,AH=92,∴HB=152,∴BEAB CDHGFEAB CDFEPMOMNPEFDCBAEDCBAHA BCDFGE类型2:二倍角问题【例题5】(1)如图,将矩形ABCD 沿BE 折叠,使得点C 落在点G 处,若DE =1,CE =2,BC =6,则AF 的长为___________.【答案】4.(提示:tan ∠AFB =tan ∠GBC =34) (2)如图,已知正方形ABCD 的边长为6,E 为BC 的中点,将△ABE 沿直线AE 折叠后,点B 落在点F 处,AF 交对角线BD 于点G ,则FG 的长为___________.【答案】127.(提示:过点G 作GH ⊥AB 于点H ,则tan ∠HAG =43,设AG =3x ,则HG =HB =4x ,∴x =67,∴AG =307,∴AF =6-=127) (3)如图,将一张矩形纸片ABCD 的边BC 斜着向AD 边对折,使点B 落在AD 边上,记为B ′,折痕为CE ,再将CD 边斜向下对折,使点D 落在B ′C 边上,记为D ′,折痕为CG ,若B ′D ′=2,BE =13BC ,则矩形纸片ABCD 的面积为__________.【答案】15.(提示:∵tan ∠ECB =13,∴tan ∠GB ′D ′=34,tan ∠DCG =12,∵B ′D ′=2,∴GD =GD ′=1.5,∴CD =3,∴B ′C =5,∴矩形ABCD 的面积=3×5=15)(4)如图,在正方形ABCD 中,E 是AB 边上一点,G 是AD 延长线上一点,BE =DG ,CF ⊥EG 于点H ,交AD 于点F ,连接CE 、BH ,若BH =8,tan ∠FCB =2,则FG =___________.ABCD GFEABC D GFEEFGHDCBA D ′B ′A BCDGE ABCDHGFE E FGHDCBA【答案】.(提示:连接GC ,则△EBC ≌△GDC ,∴∠GCH =∠GEC =45°,∵tan ∠FCB =2,∴tan ∠FCD =12,∴tan ∠DCG =tan ∠ECB =13)【例题6】(1)如图,Rt △ABC 内接于⊙O ,BC 为直径,AB =4,AC =3,D 是弧AB 的中点,CD 与AB 的交点为E ,则CEDE的值为___________.【答案】3.(提示:法1,∵tan ∠ACB =43,D 是弧AB 的中点,∴tan ∠DCB =tan ∠ABD =12;法2,OE =1.5,DF =2.5-1.5=1)(2)如图,四边形ABCD 内接于O ,AB 为直径,AD =CD ,过点D 作DE ⊥AB 于点E ,连接AC 交DE于点F ,若sin ∠CAB =35,DF =5,则BC 的长为_________.【答案】12.(提示:∵DO ∥CB ,∴sin ∠DOE =sin ∠DFG =45,又∵AD =CD ,∴tan ∠DAG =12,∵DF =5,∴DG =4,FG =3,AG =8,∴OG =6,∴BC =12)。
中考数学:初中数学几何模型大全+经典题型含答案

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
(完整版)初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
初中数学几何模型大全+经典题型(含答案)

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
2020年江苏省中考数学试题分类汇编(6)——四边形(含答案)

2020年江苏省中考数学试题分类(6)——四边形一.多边形内角与外角(共2小题)1.(2020•扬州)如图,小明从点A 出发沿直线前进10米到达点B ,向左转45°后又沿直线前进10米到达点C ,再向左转45°后沿直线前进10米到达点D …照这样走下去,小明第一次回到出发点A 时所走的路程为( )A .100米B .80米C .60米D .40米2.(2020•无锡)正十边形的每一个外角的度数为( )A .36°B .30°C .144°D .150°二.平行四边形的性质(共2小题)3.(2020•扬州)如图,在▱ABCD 中,∠B =60°,AB =10,BC =8,点E 为边AB 上的一个动点,连接ED 并延长至点F ,使得DF =14DE ,以EC 、EF 为邻边构造▱EFGC ,连接EG ,则EG 的最小值为 . 4.(2020•扬州)如图,▱ABCD 的对角线AC 、BD 相交于点O ,过点O 作EF ⊥AC ,分别交AB 、DC 于点E 、F ,连接AF 、CE .(1)若OE =32,求EF 的长;(2)判断四边形AECF 的形状,并说明理由.三.平行四边形的判定与性质(共1小题)5.(2020•淮安)如图,在▱ABCD 中,点E 、F 分别在BC 、AD 上,AC 与EF 相交于点O ,且AO =CO .(1)求证:△AOF ≌△COE ;(2)连接AE 、CF ,则四边形AECF (填“是”或“不是”)平行四边形.四.菱形的性质(共4小题)6.(2020•盐城)如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,H 为BC 中点,AC =6,BD =8.则线段OH 的长为( ) A .125 B .52 C .3 D .57.(2020•常州)数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形ABCD 中,AB =2,∠DAB =120°.如图,建立平面直角坐标系xOy ,使得边AB 在x 轴正半轴上,点D 在y 轴正半轴上,则点C 的坐标是 .8.(2020•无锡)如图,在菱形ABCD 中,∠B =50°,点E 在CD 上,若AE =AC ,则∠BAE = °.9.(2020•淮安)菱形的两条对角线长分别为6和8,则这个菱形的边长为 .五.菱形的判定(共1小题)10.(2020•南通)下列条件中,能判定▱ABCD 是菱形的是( )A .AC =BDB .AB ⊥BC C .AD =BD D .AC ⊥BD六.菱形的判定与性质(共1小题)11.(2020•连云港)如图,在四边形ABCD 中,AD ∥BC ,对角线BD 的垂直平分线与边AD 、BC 分别相交于点M 、N .(1)求证:四边形BNDM 是菱形;(2)若BD =24,MN =10,求菱形BNDM 的周长.七.矩形的性质(共2小题)12.(2020•连云港)如图,将矩形纸片ABCD 沿BE 折叠,使点A 落在对角线BD 上的A '处.若∠DBC =24°,则∠A'EB等于()A.66°B.60°C.57°D.48°13.(2020•宿迁)如图,在矩形ABCD中,AB=1,AD=√3,P为AD上一个动点,连接BP,线段BA与线段BQ关于BP所在的直线对称,连接PQ,当点P从点A运动到点D时,线段PQ在平面内扫过的面积为.八.正方形的性质(共4小题)14.(2020•镇江)如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.15.(2020•常州)如图,点C在线段AB上,且AC=2BC,分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG=.16.(2020•连云港)如图,将5个大小相同的正方形置于平面直角坐标系中,若顶点M、N的坐标分别为(3,9)、(12,9),则顶点A的坐标为.17.(2020•宿迁)如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.九.四边形综合题(共5小题)18.(2020•南通)【了解概念】有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.【理解运用】(1)如图①,对余四边形ABCD 中,AB =5,BC =6,CD =4,连接AC .若AC =AB ,求sin ∠CAD 的值;(2)如图②,凸四边形ABCD 中,AD =BD ,AD ⊥BD ,当2CD 2+CB 2=CA 2时,判断四边形ABCD 是否为对余四边形.证明你的结论;【拓展提升】(3)在平面直角坐标系中,点A (﹣1,0),B (3,0),C (1,2),四边形ABCD 是对余四边形,点E 在对余线BD 上,且位于△ABC 内部,∠AEC =90°+∠ABC .设AA AA =u ,点D 的纵坐标为t ,请直接写出u 关于t 的函数解析式.19.(2020•盐城)木门常常需要雕刻美丽的图案.(1)图①为某矩形木门示意图,其中AB 长为200厘米,AD 长为100厘米,阴影部分是边长为30厘米的正方形雕刻模具,刻刀的位置在模具的中心点P 处,在雕刻时始终保持模具的一边紧贴木门的一边,所刻图案如虚线所示,求图案的周长;(2)如图②,对于(1)中的木门,当模具换成边长为30√3厘米的等边三角形时,刻刀的位置仍在模具的中心点P 处,雕刻时也始终保持模具的一边紧贴木门的一边,使模具进行滑动雕刻.但当模具的一个顶点与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.再滑动模具进行雕刻,如此雕刻一周,请在图②中画出雕刻所得图案的草图,并求其周长.20.(2020•扬州)如图1,已知点O 在四边形ABCD 的边AB 上,且OA =OB =OC =OD =2,OC 平分∠BOD ,与BD 交于点G ,AC 分别与BD 、OD 交于点E 、F .(1)求证:OC ∥AD ;(2)如图2,若DE =DF ,求AA AA 的值;(3)当四边形ABCD 的周长取最大值时,求AA AA 的值.21.(2020•南京)如图①,要在一条笔直的路边l 上建一个燃气站,向l 同侧的A 、B 两个城镇分别铺设管道输送燃气.试确定燃气站的位置,使铺设管道的路线最短.(1)如图②,作出点A 关于l 的对称点A ',线段A 'B 与直线l 的交点C 的位置即为所求,即在点C 处建燃气站,所得路线ACB 是最短的.为了证明点C 的位置即为所求,不妨在直线l 上另外任取一点C ',连接AC '、BC ',证明AC +CB <AC ′+C 'B .请完成这个证明.(2)如果在A 、B 两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域.请分别给出下列两种情形的铺设管道的方案(不需说明理由).①生态保护区是正方形区域,位置如图③所示;②生态保护区是圆形区域,位置如图④所示.22.(2020•泰州)如图,正方形ABCD 的边长为6,M 为AB 的中点,△MBE 为等边三角形,过点E 作ME的垂线分别与边AD 、BC 相交于点F 、G ,点P 、Q 分别在线段EF 、BC 上运动,且满足∠PMQ =60°,连接PQ .(1)求证:△MEP ≌△MBQ .(2)当点Q 在线段GC 上时,试判断PF +GQ 的值是否变化?如果不变,求出这个值,如果变化,请说明理由.(3)设∠QMB =α,点B 关于QM 的对称点为B ',若点B '落在△MPQ 的内部,试写出α的范围,并说明理由.2020年江苏省中考数学试题分类(6)——四边形参考答案与试题解析一.多边形内角与外角(共2小题)1.【解答】解:∵小明每次都是沿直线前进10米后向左转45度,∴他走过的图形是正多边形,∴边数n =360°÷45°=8,∴他第一次回到出发点A 时,一共走了8×10=80(m ).故选:B .2.【解答】解:正十边形的每一个外角都相等,因此每一个外角为:360°÷10=36°,故选:A .二.平行四边形的性质(共2小题)3.【解答】解:作CH ⊥AB 于点H ,∵在▱ABCD 中,∠B =60°,BC =8,∴CH =4√3,∵四边形ECGF 是平行四边形,∴EF ∥CG ,∴△EOD ∽△GOC ,∴AA AA=AA AA =AA AA , ∵DF =14DE , ∴AA AA =45, ∴AA AA =45, ∴AA AA =45,∴当EO 取得最小值时,EG 即可取得最小值,当EO ⊥CD 时,EO 取得最小值,∴CH =EO ,∴EO =4√3,∴GO =5√3,∴EG 的最小值是9√3,故答案为:9√3.4.【解答】解:(1)∵四边形ABCD 是平行四边形,∴AB ∥CD ,AO =CO ,∴∠FCO =∠EAO ,又∵∠AOE =∠COF ,∴△AOE ≌△COF (ASA ),∴OE =OF =32,∴EF =2OE =3;(2)四边形AECF 是菱形,理由:∵△AOE ≌△COF ,∴AE =CF ,又∵AE ∥CF ,∴四边形AECF 是平行四边形,又∵EF ⊥AC ,∴四边形AECF 是菱形.三.平行四边形的判定与性质(共1小题)5.【解答】(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠OAF =∠OCE ,在△AOF 和△COE 中,{∠AAA =∠AAAAA =AA AAAA =AAAA,∴△AOF ≌△COE (ASA )(2)解:四边形AECF 是平行四边形,理由如下:由(1)得:△AOF ≌△COE ,∴FO =EO ,又∵AO =CO ,∴四边形AECF 是平行四边形;故答案为:是.四.菱形的性质(共4小题)6.【解答】解:∵四边形ABCD 为菱形,∴AC ⊥BD ,OB =OD =12BD =4,OC =OA =12AC =3,在Rt △BOC 中,BC =√AA 2+AA 2=√32+42=5,∵H 为BC 中点,∴OH =12BC =52.故选:B .7.【解答】解:∵四边形ABCD 是菱形,且AB =2,∴CD =AD =AB =2,∵∠DAB =120°,∴∠OAD =60°,Rt △AOD 中,∠ADO =30°, ∴OA =12AD =12×2=1,OD =√22−12=√3, ∴C (2,√3),故答案为:(2,√3).8.【解答】解:∵四边形ABCD 是菱形,∴CA 平分∠BCD ,AB ∥CD ,∴∠BAE +∠AEC =180°,∠B +∠BCD =180°,∴∠BCD =180°﹣∠B =180°﹣50°=130°,∴∠ACE =12∠BCD =65°,∵AE =AC ,∴∠AEC =∠ACE =65°,∴∠BAE =180°﹣∠AEC =115°;故答案为:115.9.【解答】解:∵菱形ABCD 中,AC =6,BD =8,∴AC ⊥BD ,OA =12AC =3,OB =12BD =4,∴AB =√AA 2+AA 2=5.即这个菱形的边长为:5.故答案为:5.五.菱形的判定(共1小题)10.【解答】解:∵四边形ABCD 是平行四边形,∴当AC ⊥BD 时,四边形ABCD 是菱形;故选:D .六.菱形的判定与性质(共1小题)11.【解答】(1)证明:∵AD ∥BC ,∴∠DMO =∠BNO ,∵MN 是对角线BD 的垂直平分线,∴OB =OD ,MN ⊥BD ,在△MOD 和△NOB 中,{∠AAA =∠AAA AAAA =AAAA AA =AA,∴△MOD ≌△NOB (AAS ),∴OM =ON ,∵OB =OD ,∴四边形BNDM 是平行四边形,∵MN ⊥BD ,∴四边形BNDM 是菱形;(2)解:∵四边形BNDM 是菱形,BD =24,MN =10,∴BM =BN =DM =DN ,OB =12BD =12,OM =12MN =5,在Rt △BOM 中,由勾股定理得:BM =√AA 2+AA 2=√52+122=13,∴菱形BNDM 的周长=4BM =4×13=52.七.矩形的性质(共2小题)12.【解答】解:∵四边形ABCD 是矩形,∴∠A =∠ABC =90°,由折叠的性质得:∠BA 'E =∠A =90°,∠A 'BE =∠ABE ,∴∠A 'BE =∠ABE =12(90°﹣∠DBC )=12(90°﹣24°)=33°, ∴∠A 'EB =90°﹣∠A 'BE =90°﹣33°=57°;故选:C .13.【解答】解:∵当点P 从点A 运动到点D 时,PQ =P A ,∴点Q 运动轨迹是圆弧,如图,阴影部分的面积即为线段PQ 在平面内扫过的面积,∵矩形ABCD 中,AB =1,AD =√3,∴∠ABC =∠BAC =∠C =∠Q =90°.∴∠ADB =∠DBC =∠ODB =∠OBQ =30°, ∴∠ABQ =120°,由矩形的性质和轴对称性可知,△BOQ ≌△DOC ,S △ABD =S △BQD , ∴S 阴影部分=S 四边形ABQD ﹣S 扇形ABQ =2S △ABD ﹣S 扇形ABQ ,=S 矩形ABCD ﹣S 扇形ABQ =1×√3−120A ×12360=√3−A 3.故答案为:√3−A 3. 八.正方形的性质(共4小题)14.【解答】解:∵四边形ABCD 是正方形, ∴∠ACB =∠BAC =45°,∴∠2+∠BCP =45°,∵∠1=∠2,∴∠1+∠BCP =45°,∵∠BPC =180°﹣∠1﹣∠BCP ,∴∠BPC =135°,故答案为:135.15.【解答】解:连接CG ,在正方形ACDE 、BCFG 中,∠ECA =∠GCB =45°,∴∠ECG =90°,∵AC =2BC ,∴设AC =2a ,BC =a ,∴CE =2√2a ,CG =√2a ,∴tan ∠CEG =AA AA =12,故答案为:12.16.【解答】解:如图,∵顶点M 、N 的坐标分别为(3,9)、(12,9),∴MN ∥x 轴,MN =9,BN ∥y 轴,∴正方形的边长为3,∴BN =6,∴点B (12,3),∵AB ∥MN ,∴AB ∥x 轴,∴点A (15,3)故答案为(15,3).17.【解答】证明:∵四边形ABCD 是正方形,∴AB =AD =CD =BC ,∠DAE =∠BAE =∠BCF =∠DCF =45°,在△ABE 和△ADE 中,{AA =AA AAAA =AAAA AA =AA ,∴△ABE ≌△ADE (SAS ),∴BE =DE ,同理可得△BFC ≌△DFC ,所以BF =DF ,在△ABE 和△CBF 中,{AA =AA AAAA =AAAA AA =AA ,∴△ABE ≌△CBF (SAS ),∴BE =BF ,∴BE =BF =DE =DF ,∴四边形BEDF 是菱形.九.四边形综合题(共5小题)18.【解答】解:(1)过点A 作AE ⊥BC 于E ,过点C 作CF ⊥AD 于F .∵AC =AB ,∴BE =CE =3, 在Rt △AEB 中,AE =√AA 2−AA 2=√52−32=4,∵CF ⊥AD ,∴∠D +∠FCD =90°,∵∠B +∠D =90°,∴∠B =∠DCF ,∵∠AEB =∠CFD =90°,∴△AEB ∽△DFC ,∴AA AA =AA AA , ∴3AA =54, ∴CF =125, ∴sin ∠CAD =AA AA =1255=1225.(2)如图②中,结论:四边形ABCD 是对余四边形.理由:过点D 作DM ⊥DC ,使得DM =DC ,连接CM .∵四边形ABCD 中,AD =BD ,AD ⊥BD ,∴∠DAB =∠DBA =45°,∵∠DCM =∠DMC =45°,∴∠CDM =∠ADB =90°,∴∠ADC =∠BDM ,∵AD =DB ,CD =DM ,∴△ADC ≌△BDM (SAS ),∴AC =BM ,∵2CD 2+CB 2=CA 2,CM 2=DM 2+CD 2=2CD 2,∴CM 2+CB 2=BM 2,∴∠BCM =90°,∴∠DCB =45°,∴∠DAB +∠DCB =90°,∴四边形ABCD 是对余四边形.(3)如图③中,过点D 作DH ⊥x 轴于H .∵A (﹣1,0),B (3,0),C (1,2),∴OA =1,OB =3,AB =4,AC =BC =2√2,∴AC 2+BC 2=AB 2,∴∠ACB =90°,∴∠CBA =∠CAB =45°,∵四边形ABCD 是对余四边形,∴∠ADC +∠ABC =90°,∴∠ADC =45°,∵∠AEC =90°+∠ABC =135°,∴∠ADC +∠AEC =180°,∴A ,D ,C ,E 四点共圆,∴∠ACE =∠ADE ,∵∠CAE +∠ACE =∠CAE +∠EAB =45°,∴∠EAB =∠ACE ,∴∠EAB =∠ADB ,∵∠ABE =∠DBA ,∴△ABE ∽△DBA ,∴AA AA =AA AA , ∴AA AA =AA AA , ∴u =AA 4, 设D (x ,t ),由(2)可知,BD 2=2CD 2+AD 2,∴(x ﹣3)2+t 2=2[(x ﹣1)2+(t ﹣2)2]+(x +1)2+t 2,整理得(x +1)2=4t ﹣t 2,在Rt △ADH 中,AD =√AA 2+AA 2=√(A +1)2+A 2=2√A ,∴u =AA 4=√A 2(0<t <4),即u =√A 2(0<t <4).19.【解答】解:(1)如图①,过点P 作PE ⊥CD 于点E ,∵点P 是边长为30厘米的正方形雕刻模具的中心,∴PE =15cm ,同理:A ′B ′与AB 之间的距离为15cm ,A ′D ′与AD 之间的距离为15cm ,B ′C ′与BC 之间的距离为15cm ,∴A ′B ′=C ′D ′=200﹣15﹣15=170(cm ),B ′C ′=A ′D ′=100﹣15﹣15=70(cm ),∴C 四边形A ′B ′C ′D ′=(170+70)×2=480cm ,答:图案的周长为480cm ;(2)连接PE、PF、PG,过点P作PQ⊥CD于点Q,如图②∵P点是边长为30√3cm的等边三角形模具的中心,∴PE=PG=PF,∠PGF=30°,∵PQ⊥GF,∴GQ=FQ=15√3cm,∴PQ=GQ•tan30°=15cm,PG=AAAAA30°=30cm,当△EFG向上平移至点G与点D重合时,由题意可得,△E′F′G′绕点D顺时针旋转30°,使得E′G′与AD边重合,∴DP′绕点D顺时针旋转30°到DP″,∴A A′A″̂=30A×30180=5AAA,同理可得其余三个角均为弧长为5πcm的圆弧,∴A=(200−30√3+100−30√3)×2+5A×4=600﹣120√3+20π(cm),答:雕刻所得图案的周长为(600﹣120√3+20A)cm.20.【解答】(1)证明:∵AO=OD,∴∠OAD=∠ADO,∵OC平分∠BOD,∴∠DOC=∠COB,又∵∠DOC+∠COB=∠OAD+∠ADO,∴∠ADO=∠DOC,∴CO∥AD;(2)解:如图1,∵OA=OB=OD,∴∠ADB=90°,设∠DAC=α,则∠ACO=∠DAC=α.∵OA=OD,DA∥OC,∴∠DFE =3α,∵DF =DE ,∴∠DEF =∠DFE =3α,∴4α=90°,∴α=22.5°,∴∠DAO =45°,∴△AOD 和△ABD 为等腰直角三角形,∴AD =√2AO ,∴AA AA =√2,∵DE =DF ,∴∠DFE =∠DEF ,∵∠DFE =∠AFO ,∴∠AFO =∠AED ,又∠ADE =∠AOF =90°,∴△ADE ∽△AOF ,∴AA AA =AA AA =√2.(3)解:如图2,∵OD =OB ,∠BOC =∠DOC ,∴△BOC ≌△DOC (SAS ),∴BC =CD ,设BC =CD =x ,CG =m ,则OG =2﹣m ,∵OB 2﹣OG 2=BC 2﹣CG 2,∴4﹣(2﹣m )2=x 2﹣m 2,解得:m =14A 2,∴OG =2−14A 2, ∵OD =OB ,∠DOG =∠BOG ,∴G 为BD 的中点,又∵O 为AB 的中点,∴AD =2OG =4−12A 2,∴四边形ABCD 的周长为2BC +AD +AB =2x +4−12A 2+4=−12A 2+2x +8=−12(A −2)2+10, ∵−12<0, ∴x =2时,四边形ABCD 的周长有最大值为10.∴BC =2,∴△BCO 为等边三角形,∴∠BOC =60°,∵OC ∥AD ,∴∠ADF =∠DOC =60°,∠DAE =30°,∴∠AFD =90°,∴AA AA =√33,DF =12DA , ∴AA AA =2√33.21.【解答】证明:(1)如图②,连接A 'C ',∵点A ,点A '关于l 对称,点C 在l 上,∴CA =CA ',∴AC +BC =A 'C +BC =A 'B ,同理可得AC '+C 'B =A 'C '+BC ',∵A 'B <A 'C '+C 'B ,∴AC +BC <AC '+C 'B ;(2)如图③,在点C 处建燃气站,铺设管道的最短路线是AC +CD +DB ;(其中点D 是正方形的顶点);如图④,在点C 处建燃气站,铺设管道的最短路线是AC +CD +AA ̂+EB ,(其中CD ,BE 都与圆相切)22.【解答】证明:(1)∵正方形ABCD 的边长为6,M 为AB 的中点,∴∠A =∠ABC =90°,AB =BC =6,AM =BM =3,∵△MBE 是等边三角形,∴MB =ME =BE ,∠BME =∠PMQ =60°,∴∠BMQ =∠PME ,又∵∠ABC =∠MEP =90°,∴△MBQ ≌△MEP (ASA );(2)PF +GQ 的值不变,理由如下:如图1,连接MG ,过点F 作FH ⊥BC 于H ,∵ME=MB,MG=MG,∴Rt△MBG≌Rt△MEG(HL),∴BG=GE,∠BMG=∠EMG=30°,∠BGM=∠EGM,∴MB=√3BG=3,∠BGM=∠EGM=60°,∴GE=√3,∠FGH=60°,∵FH⊥BC,∠C=∠D=90°,∴四边形DCHF是矩形,∴FH=CD=6,∵sin∠FGH=AAAA=√32=6AA,∴FG=4√3,∵△MBQ≌△MEP,∴BQ=PE,∴PE=BQ=BG+GQ,∵FG=EG+PE+FP=EG+BG+GQ+PF=2√3+GQ+PF,∴GQ+PF=2√3;(3)如图2,当点B'落在PQ上时,∵△MBQ≌△MEP,∴MQ=MP,∵∠QMP=60°,∴△MPQ是等边三角形,当点B'落在PQ上时,点B关于QM的对称点为B',∴△MBQ≌△MB'Q,∴∠MBQ=∠MB'Q=90°∴∠QME=30°∴点B'与点E重合,点Q与点G重合,∴∠QMB=∠QMB'=α=30°,如图3,当点B'落在MP上时,同理可求:∠QMB=∠QMB'=α=60°,∴当30°<α<60°时,点B'落在△MPQ的内部.。
初中数学-12345模型(于新华)

纪博士数数12345于特讲题主讲:纪东旭于新华整理:郑梦前【研修团队】郑梦前、顾永清、焦建林、黄萍学悟有别,你我自取,教学践行,适切至上!(林福凯)数学解题五境界第一个境界:正确解题.很多同学以为如果一道题目做错,订正一下,知道哪里错了,怎么做,就行了,其实这只是最低境界.第二个境界:一题多解.我们要养成的良好习惯是,不要满足于用一种做法和思路解题.一道题目做完之后想一想还有没有其它方法,哪种方法更简单.对于最后的结果,是不是可以有其它的合理解释.第三个境界:多题一解.完成一道题目的分析后,尝试推而广之,或把其中的数字换成字母,或把一些条件做一些改变,从这道题目延伸出去,探究与此相关的一类题目.第四个境界:发现定理.到了这个境界,可以自己发现一些结论或定理、规律。
这些结论、定理规律都是解题的有用工具。
解题高手都有自己的定理库.第五个境界:自己编题.解题的最高境界是能够编题。
不是所有的老师都具备编题的能力。
解题高手拿到一道题目,会知道出题者的意图,会发现出题者的陷阱。
即便出题者粗心出现了一个错误,他也能够很快地纠正纠偏.刘俊勇:如果没有真正消化吸收为自己的东西,过一段时间就忘却了,真正弄清楚更重要,远胜于蜻蜓点水式浏览一遍.一方面重视技巧,尤其是考试技巧学习技巧,另一方面回归数学本质,回归教育意义当我们听到一个技巧的时候,除了拿来使用之外,还需要去体会专家在思考、总结过程的数学思考,这个我觉得更加重要和有意义。
因为专家的本意也正是立足于思想的交流,而不是一招一式的传递,在本地方的一些小型的培训中,我注意到活动中最最怕的就是坐在下面的教师一直把自己当成听众、容器,同时,相当一部教师的都有简单的拿来主义和简单的怀疑主义倾向,这个也特别可怕数学是思维的体操,没有绝技想拿冠军是不可能的。
以教材为主对大部分学生适用,但在我们这光靠教材的知识点,中考想考满分概率为零。
学灵魂在于积累、创新、规纳而不是照搬的模仿和接受,要有自己的数学大格局,适合自己的就是最好的!版块一引入问题1.如图1-1,在3×3的网格中标出了∠1和∠2,则∠1+∠2=图1-1图1-22.如图1-2,在△ABC 中,∠BAC =45°,AD 是BC 边上的高,BD =3,DC =2,则AD 的长为_________.版块二“123”+“45”的来源一般化结论:若45αβ+=︒则有1tan 1a a α-=+,1tan a β=(1a >),当32a =时,则得到21tan tan =35αβ=(了解)当a =2时,则得到11tan tan =23αβ=(重要)当52a =时,则得到23tan tan =57αβ=(了解);当4a =时,则得到13tan tan =45αβ=(次重要)【例1】(济南市中考题)如图2-1,AOB ∠是放置在正方形网络中的一个角,则cos AOB ∠的值是.图2-1【例2】(2015湖北十堰)如图2-2,正方形ABCD 的边长为6,点E ,F 分别在AB ,AD 上,若CE =53,且∠ECF =45°,则CF 的长为()A .102B .53C .5103D .1053图2-2倍角与半角构造当出现等腰三角形或翻折的背景问题时,解决策略“⇔⇔顶角底角顶角”解题依据“1902︒-顶角=底角”.如图,在等腰三角形ABC 中,AB =AC .⑴若tan 2BCA ∠=,则tan BAC ∠=.⑵若4tan 3BAC ∠=,则tan ABC ∠=.【例3】如图2-3,已知正方形ABCD 中,E 为BC 上一点.将正方形折叠起来,使点A 和点E 重合,折痕为MN .若31tan =∠AEN ,DC +CE =10.⑴求△ANE 的面积;⑵求ENB ∠sin 的值.图2-3【例4】如图2-4,已知正方形ABCD ,对角线AC 、BD 交于点O ,点E 在BC 上,且CE=2BE ,过B 点作BF ⊥AE 于点F ,连接OF ,则线段OF 的长度为。
特殊角的妙用-“12345”模型

感谢观看
中考数学专题
此处我们还可得: tan(α+45°)=3 tan(β+45°)=2
Hale Waihona Puke 中考数学专题【2018湖北中考第9题】
如图,正方形ABCD中,AB=6,G是BC的中点,将△ABG沿AG对折至△AFG,延长
GF交DC于点E,则DE长是( )
A.1
B.1.5
C.2
D.2.5
【分析解答】
根据BG是AB的一半,可得tan∠BAG=1/2, 连接AE,易证△AEF≌△AED, ∴tan∠DAE=1/3,∴DE=2,
根据这里的等腰直角△ABC,可得∠1+∠2=45°
中考数学专题
法二:勾三股四弦五 如图,AC=4,BC=3,AB=5,这个三角形我们再熟悉不过了。在这里: tanA=3/4,tanB=4/3
分别延长CB、CA使得AD=BE=AB可构造构造: 2α=∠ABC,2β=∠BAC,α+β=45°
法三:构造矩形 直角中夹一个45°角也是一种常见的构图。
中考数学专题
特殊角的妙用-“12345”模型
中考数学专题
一、几何图形中经常会出现一些特殊角,熟悉的有30°、45°、60°等等,特殊角往 往伴随着固有属性运用于题目中,也是解题思路来源之一。
比如看到30°角我们会想到直角三角形,45°角总是跟等腰直角三角形有着说不清道 不明的联系,60°甚至能牵出一只等边三角形。
M 【分析解答】 观察发现tan∠ADE=1/3,且∠GHD=45°, 条件已经具备,考虑GF可动,平移GH,将 α、β、45°汇于直角处。可知CF=3, 所以DF长度为3倍根号5.
2019-2020学年度
做题从来都不是靠题目告诉我什么,而是结合已知信息,分析这里需要什么 已知45°+α寻β、已知45°+β寻α 留意题中给的45°角以及由正切值确定的α和β。
12345模型,平面几何不得不说的几何模型
A
FB
A
5
E
3 2 5
B
2
4C
tan 1 , tan 1 , 454
5
D
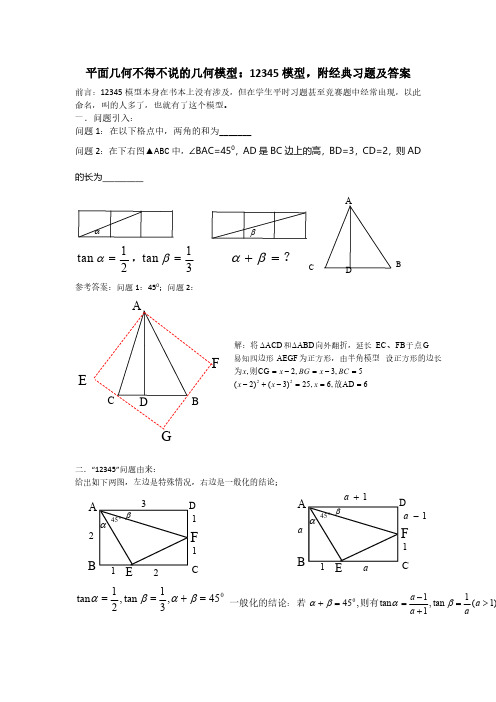
已知正方形 ABCD中,E为BC上一点,将正方形折叠 起来,使点 A与点E重合 折痕为MN,若tanAEN 1 , DC CE 10; (1)求ANE的面积;(2)求 sin ENB的值
平面几何不得不说的几何模型:12345 模型,附经典习题及答案
前言:12345 模型本身在书本上没有涉及,但在学生平时习题甚至竞赛题中经常出现,以此 命名,叫的人多了,也就有了这个模型。 一.问题引入: 问题 1:在以下格点中,两角的和为_______ 问题 2:在下右图▲ABC 中,∠BAC=450,AD 是 BC 边上的高,BD=3,CD=2,则 AD
DEG EDF 450 , 故tanEDF 1 3
C EF : FD 10 :10
如图,等腰RtABC中,C 900,D为BC的中点,将ABC折叠,使A 与点D重合,若EF为折痕,则sinBED的值为 ______
C
F
A
E
D
BA
C
tanCAD 1 ,CAD BAD 450
2
F
D
则tanBAD 1 ,又DEH 2BAD
2
B O
A
B PO
A
连接 OA ,则 AOE 2ABE
P tan ABE 1 , 则 tan AOE 4
2
3
故 sin E 4 5
E
E
正方形ABCD中,点P是BC的中点,把PAB沿着PA翻折得到PAE 过C作CF DE交DE延长线于点F,若CF 2,则DF _______
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【模型解析】
2020 中考数学专题 6——几何模型之“12345”
班级姓名.
【例题分析】
例 1.在如图正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D 都在格点处,AB 与CD 相交于O,则tan∠BOD 的值等于。
例1 图例2 图
k
例2.(2017 浙江金华)如图,已知点A(2,3)和点B(0,2),点A 在反比例函数y=
x
的图象上.作射线AB,再将射线AB 绕点A 按逆时针方向旋转45°,交反比例函数图象于点C,则点C 的坐标为.
3 2 例 3.如图,正方形 ABCD 中,P 是 BC 的中点,把△PAB 沿着 PA 翻折得到△PAE ,过 C 作 CF ⊥DE 于 F ,若 CF =2,则 DF = .
【巩固训练】
1. 如图 1,∠AOB 是放置在正方形网格中的一个角,则 cos ∠AOB 的值是
.
图 1 图 2
图 3
2. 如图 2 是由边长相同的小正方形组成的网格,A ,B ,P ,Q 四点均在正方形网格的格点上,线段
AB,PQ 相交于点 M ,则图中∠QMB 的正切值是( ) 1 A.
B.1
C. 2
D.2
3. 如图 3,把一个矩形纸片 OABC 放入平面直角坐标系中,使 OA 、OC 分别落在 x 轴、y 轴上,连接 OB,
将纸片 OABC 沿 OB 折叠,使点 A 落在 A'的位置上.若 OB= ,
BC 1
,求点 A'的坐标为 .
OC 2
4. 如图 4,半圆 O 的直径 AB=10cm ,弦 AB=10cm ,弦 AC=6cm ,AD 平分∠BAC ,则 AD 的长为
(
)
A. 4 cm
B. 3 cm
C. 5 cm
D.4 cm
图 4
图 5
5.
如图 5,在四边形 ABCD 中,∠BAC =∠BDC=90°,
AB=AC=
则 DM= (
)
,CD=1 ,对角线的交点为 M ,
A.
B.
2 3 1 C.
D.
2
2
3
5 5 5 5 5 5
5 6. 如图6,在平面直角坐标系xOy 中,点A (-1,0),B (0,2),点C 在第一象限,∠ABC =135°,
k
AC 交y 轴于D ,CD =3AD ,反比例函数y =
的图象经过点C ,则k 的值为 .
x
A
D
F
B
E
C
图 6
图 7
图 8
7(2017 浙江丽水)如图 7,在平面直角坐标系 xOy 中,直线 y =-x +m 分别交 x 轴,y 轴于 A ,B 两点,已知点 C (2,0). (1) 当直线 AB 经过点 C 时,点 O 到直线 AB 的距离是 ; (2) 设点 P 为线段 OB 的中点,连结 PA ,PC ,若∠CPA =∠ABO ,则 m 的值是 .
8.(2018山东滨州)如图8,在矩形ABCD 中,AB =2,BC =4,点E ,F 分别在BC ,CD 上,若AE = , ∠EAF=45°,则AF 的长为 .
9.如图 9,在四边形 ABCD 中 BC⊥AB,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E 是 AB 上一点,且∠ DCE=45°,BE=4, 则 DE= .
图 9 图 10 图 11
10.(2018 山东泰安)如图 10,在矩形 ABCD 中, AB = 6 ,BC = 10 ,将矩形 ABCD 沿 BE 折叠, 点 A 落在 A ' 处,若 EA ' 的延长线恰好过点C ,则sin ∠ABE 的值为 .
11. 如图 11,正方形 ABCD 的边长 AB=2,E 为 AB 的中点,F 为 BC 的中点,AF 分别与 DE 、BD
相交于点 M ,N ,则 MN 的长为( )
A.
B .
﹣1
C .
D .
12.如图12,抛物线y =-x2 +bx +c 与直线y =1
x + 2 交于C、D 两点,其中点C 在y 轴上,2
7
点D 的坐标为(3,
2
F。
)。
点P 是y 轴右侧的抛物线上一动点,过点P 作PE⊥x 轴于点E,交CD 于点(1)求抛物线的解析式。
(2)若存在点P,使∠PCF=45°,请直接写出相应的点P 的坐标。
图12
13.如图13,抛物线y=x2-4x+3 与坐标轴交于A、B、C 三点,点P 在抛物线上,PD⊥BC 于点D,
垂足D 在线段BC 上.若CD
=
1
,求点P 的坐标.PD 2
图13
2 2020 中考专题 6——几何模型之“12345” 参考答案
1
例 1.解:如图,∠BOD=∠OAD+∠OED,易得 tan ∠OAD= 2
∠BOD=3.
1 ,∠OED=45°,由“3”=“ 2
”+45°得 tan
例2.解:如图,作AE⊥y轴于E ,作AF⊥CF,垂足为F ,且AF∥y轴.由点A (2,3)和点B (0,2),可得 1 BE=1.AE=2,所以tan∠BAE= 2 1 .因为∠BAC=45°,所以∠BAE+∠CAF=45°,由“ 2 1
”+“ 3
”=45°
1 CF 1
可得tan∠CAF= ,即 = .设CF=a,则AF=3a,所以C 点坐标可表示为(2-a,3-3a ).把C (2-a,3-3a )
3 AF 3 代入 y = 6
得(2-a)(3-3a)=6.解得a=3(a=0舍去).所以点C 的坐标为(-1,-6).
x
1 例 3.解:因为在正方形 ABCD 中 P 是 BC 的中点,所以 tan ∠BAP=
2
1
,由翻折可知∠EAP=∠BAP.由“ ”
2
1 4 +“ ”=“ 2
3 4 ”可知 tan ∠BAE= 3
3
,所以 tan ∠DAE= 4
,又因为 AE=AD ,作 AH ⊥DE ,则∠DAH=∠EAH. 1 1
由“ ”+“ 3 3 3 ”=“ 4 1
”可知 tan ∠DAH= 3
1 ,所以 tan ∠CDF= 3
,所以 DF=3CF=6.
【巩固训练】答案
1. 3
; 2.D 3.( - 3 , 4 )
4.A
5.D
6. 9
7.(1) (2)12
8.
4 10
5
5 5
3
1 9. 10. 3 10
11. C 12.(1) y = -x 2 + 7 x + 2 (2)P( 1 , 7
)
2 2 2
简析:易得tan ∠DCG= 1 ,因为∠PCF =45°,所以∠DCG+∠PCH=45°,由“ 1 ”+“ 1
”=45°,
2 2 3
1 PH 1 7 可得tan ∠PCH = .所以 = ,设PH=a.则CH=3a.所以设 P (a,2+3a ).所以- a 2
+ a + 2 = 2 + 3a ,
3 CH 3 2
所以 a = 0(舍去)或a = 1 .所以 P ( 1 , 7
)。
2 2 2
10
13.P(
13 , 40 ) 3 9
简析:易得 tan ∠PCD=2,因为∠DCH =135°,所以 tan ∠PCH=3.设 CH=a,则 PH=3a. 所以 P(3a,3+a) 代入抛物线解析式得9a 2
-12a + 3 = 3 + a ,所以 a = 0(舍去)或a =
13 .所以 P ( 13 ,
40 )。
9
3 9。
