2011年北京市朝阳区高三二模数学(理)试题及答案
北京市朝阳区高三数学第二次高考模拟考试(理) 新人教版

朝阳区2009~2010学年度高三年级第二学期统一考试(二)数学学科测试(理工类)(考试时间120分钟 满分150分)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分第I 卷(选择题 共40分)注意事项:1.答第I 卷前,考生务必将自己的姓名、考试科目涂写在答题卡上。
考试结束时,将试题卷和答题卡一并交回。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
一、选择题:本大题共8小题,每小题5分,共40分. 在每小题的4个选项中,只有一项是符合题目要求的.(1)已知集合1{ 2 }2x A x -=?-,{4, 2, 0, 1 }B =--,则A B I 等于(A ){4,2,0,1}-- (B ){2,0,1}- (C ){4}- (D )Æ(2)已知向量(1, 2)=a ,(3, 2)=-b ,如果k +a b 与3-a b 垂直,那么实数k 的值为(A )19- (B )13-(C )119(D )19 (3)一个几何体的三视图如图所示,则此几何体的体积是(A )112 (B )80 (C )72 (D )64(第3题图)(第4题图)俯视图 侧视图(4)某程序框图如图所示,该程序运行后,输出的x 值为31,则a 等于(A )1- (B )0 (C )1 (D )2 (5)已知平面a ,b ,直线l a ^,直线m b Ì,有下面四个命题:①a b∥Þl m ^ ② a b ^Þl m ∥③ l m∥Þa b ^④ l m ^Þa b ∥其中正确的命题是 (A )①与② (B )③与④ (C )①与③ (D )②与④(6)函数2()(2)e xf x x x =-的图象大致是(7)已知椭圆2222 1 (0)x y a b a b+=>>,A 是椭圆长轴的一个端点,B 是椭圆短轴的一个端点,F 为椭圆的一个焦点. 若AB BF ⊥,则该椭圆的离心率为(A(B(C(D(8)已知函数222()(1)2f x a x bx b =--+(11b a -<-<). 用()card A 表示集合A中元素的个数,若使得()0f x >成立的充分必要条件是x A Î,且()4c a r d A =Z I ,则实数a 的取值范围是(A )(1, 2)- (B )(1, 2) (C )(2, 3) (D )(3, 4)(A ) (B ) (C ) (D )第II 卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.(9)不等式组0,10,3260x x y x y ìïïï--íïï--ïïî≥≥≤所表示的平面区域的面积等于 .(10)已知圆4cos :3sin x C y q q ì=+ïïíï=+ïî(q 为参数),直线:230l x y -+=,则圆心C 到直线l 的距离为 .(11)如右图,从圆O 外一点P 引两条直线分别交圆O 于点、A B , 、C D ,且PA AB =,5PC =,9CD =,则AB 的长等于 .(12)如果1()nx x+展开式中,第四项与第六项的系数相等,则n = ,展开式中的常数项的值等于 .(13)上海世博园中的世博轴是一条1000m 长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为120. 据此数据计算,中国馆到世博轴其中一端的距离是m .(14)已知数列{}n a 为等差数列,若m a a =,n a b =(1n m -≥,, m n *ÎN ),则m n nb maa n m+-=-. 类比等差数列{}n a 的上述结论,对于等比数列{}n b (0n b >,n *ÎN )若m b c =,n b d =(n m -≥2,, m n *ÎN ),则可以得到m n b += .CB世博轴·A 中国馆120º三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤. (15)(本小题满分13分)设函数()2sin cos cos(2)6f x x x x π=--.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)当2[0,]3x π∈时,求函数()f x 的最大值及取得最大值时的x 的值.(16)(本小题满分13分)袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取球.(Ⅰ)若有放回地取3次,每次取1个球,求取出1个红球2个黑球的概率; (Ⅱ)若无放回地取3次,每次取1个球,①求在前2次都取出红球的条件下,第3次取出黑球的概率; ②求取出的红球数X 的分布列和均值(即数学期望).(17)(本小题满分14分)如图,在四棱锥S ABCD -中,底面ABCD 是正方形,其他四个侧面都是等边三角 形,AC 与BD 的交点为O ,E 为侧棱SC(Ⅰ)当E 为侧棱SC 的中点时,求证:SA (Ⅱ)求证:平面BDE ⊥平面SAC ; (Ⅲ)当二面角E BD C --的大小为45︒时,试判断点E 在SC 上的位置,并说明理由(18)(本小题满分13分) 已知函数22()ln axf x x e=-,(a e R,∈为自然对数的底数). (Ⅰ)求函数()f x 的递增区间;(Ⅱ)当1a =时,过点(0, )P t ()t ∈R 作曲线()y f x =的两条切线,设两切点为111(,())P x f x ,222(,())P x f x 12()≠x x ,求证:120x x +=.(19)(本小题满分13分)已知动点M 到点(1, 0)F 的距离,等于它到直线1x =-的距离. (Ⅰ)求点M 的轨迹C 的方程;(Ⅱ)过点F 任意作互相垂直的两条直线12,l l ,分别交曲线C 于点,A B 和,M N .设线段AB ,MN 的中点分别为,P Q ,求证:直线PQ 恒过一个定点; (Ⅲ)在(Ⅱ)的条件下,求FPQ ∆面积的最小值.(20)(本小题满分14分)已知{}n a 是递增数列,其前n 项和为n S ,11a >,且10(21)(2)n n n S a a =++,*n ∈N .(Ⅰ)求数列{}n a 的通项n a ;(Ⅱ)是否存在*, , m n k N ∈,使得2()m n k a a a +=成立?若存在,写出一组符合条件的,,m n k 的值;若不存在,请说明理由; (Ⅲ)设32n n n b a -=-,2(3)51n n n a c n +=-,若对于任意的*n ∈N ,不等式12031(1)(1)(1)nb b b +++≤恒成立,求正整数m 的最大值.(考生务必将所有题目的答案答在答题卡上,在试卷上作答无效)朝阳区2009~2010学年度高三年级第二学期统一考试(二)数学学科测试答案(理工类) 2010.5一、选择题:三、解答题:(15)(本小题满分13分)解:(Ⅰ)因为()2sin cos cos(2)6f x x x x π=-+sin 2(cos 2cossin 2sin )66x x x ππ=--3sin 222x x = )6x π=-,所以())6f x x π=-. …………5分所以函数()f x 的最小正周期为π. …………7分 (Ⅱ)由222()262k x k k p p p p p --+?Z ≤≤得,()63k x k k p pp p -+?Z ≤≤.又因为[0, ]x π∈,所以函数()f x 在[0,]p 上的递增区间为[0,]3π和5[, ]6ππ.…………13分 (16)(本小题满分13分) 解:(1)记“取出1个红球2个黑球”为事件A ,根据题意有12334144()()()77343P A C =⨯=;答:取出1个红球2个黑球的概率是144343. …………4分(2)①方法一:记“在前2次都取出红球”为事件B ,“第3次取出黑球”为事件C ,则321()767P B ⨯==⨯,3244()76535P BC ⨯⨯==⨯⨯,所以4()435(|)1()57P BC P C B P B ===.方法二:()3244(|)()3255n BC P C B n B ⨯⨯===⨯⨯. 答:在前2次都取出红球的条件下,第3次取出黑球的概率是45. …………7分 ②随机变量X 的所有取值为0, 1, 2, 3.3343374(0)35C A P X A ⋅===,2134333718(1)35C C A P X A ⋅===, 1234333712(2)35C C A P X A ⋅===,3333371(3)35C A P X A ⋅===.所以418121459012335353535357EX =⨯+⨯+⨯+⨯==. …………13分 (17)(本小题满分14分) 解法一:证明:(Ⅰ)连接OE ,由条件可得SA ∥OE .因为SA Ë平面BDE ,OE Ì平面BDE ,所以SA ∥平面BDE . …………4分(Ⅱ)由已知可得,SB SD =,O 是BD 中点,所以BD SO ^,又因为四边形ABCD 是正方形,所以BD AC ^. 因为ACSO O =,所以BD SAC ⊥面.又因为BD BDE ⊂面,所以平面BDE ⊥平面SAC . …………8分 (Ⅲ)解:连接OE ,由(Ⅱ)知BD SAC ⊥面.而OE SAC ⊂面, 所以BD OE ⊥. 又BD AC ⊥.所以EOC ∠是二面角E BD C --的平面角,即45EOC ∠=︒. 设四棱锥S ABCD -的底面边长为2,在SAC ∆中,2SA SC ==, AC =又因为12OC AC ==SO OC ⊥, 所以SOC ∆是等腰直角三角形.由45EOC ∠=︒可知,点E 是SC 的中点. 解法二:(Ⅰ)同解法一 …………4分(Ⅱ)证明:由(Ⅰ)知SO ABCD ⊥面,AC 建立如图所示的空间直角坐标系. 设四棱锥S ABCD -的底面边长为2, 则(0, 0, 0)O ,(0, 0,S ,) 0, 0A,()0, 0B ,()0, 0C ,()0, 0D .所以()0, 0AC =-,()0, 0BD =-. 设CE a =(02a <<),由已知可求得45ECO ∠=︒. 所以(, 0, )22E a ,(, )22BE a =. 设平面BDE 法向量为(, , )x y z =n ,则0,0BD BE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0, ()0.22y a x =⎧⎪⎨+=⎪⎩ 令1z =,得(, 0, 1)2aa=-n . 易知()0, 0BD =-是平面SAC 的法向量. 因为(, 0, 1)(0, 0)02aBD a⋅=⋅-=-n , 所以BD ⊥n ,所以平面BDE ⊥平面SAC . …………8分(Ⅲ)解:设CE a =(02a <<),由(Ⅱ)可知,平面BDE 法向量为(, 0, 1)2aa=-n . 因为SO ABCD ⊥底面,所以(0, 0,OS =是平面SAC 的一个法向量. 由已知二面角E BD C --的大小为45︒.所以cos , cos 45OS 〈〉=︒=n ,2=,解得1a =. 所以点E 是SC 的中点. …………14分 (18)(本小题满分13分)解:(Ⅰ)函数()f x 的定义域是(, 0)(0, )-∞+∞.222()()a e ax f x x e ex-'=-=. 当0a =时,由2()0f x x'=>,解得0x >;当0a >时,由2()()0e ax f x ex -'=>,解得0ex a<<; 当0a <时,由2()()0e ax f x ex-'=>,解得0x >,或e x a <. 所以当0a =时,函数()f x 的递增区间是(0, )+∞; 当0a >时,函数()f x 的递增区间是(0, )ea;当0a <时,函数()f x 的递增区间是(, )e a-∞,(0, )+∞. …………8分 (Ⅱ)因为222()()e x f x x e ex-'=-=, 所以以111(,())P x f x 为切点的切线的斜率为112()e x ex -; 以222(,())P xf x 为切点的切线的斜率为222()e x ex -. 又因为切线过点(0, )P t ,所以21111122()ln (0)x e x t x x e ex --+=-; 22222222()ln (0)x e x t x x e ex --+=-. 解得,221t x e += ,222t x e +=. 则2212x x =. 由已知12x x ¹所以,120x x +=. ……………………………13分(19)(本小题满分13分)解:(Ⅰ)设动点M 的坐标为(,)x y ,|1|x +,化简得24y x =,所以点M 的轨迹C 的方程为24y x =.……4分(Ⅱ)设,A B 两点坐标分别为11(, )x y ,22(,)x y ,则点P 的坐标为1212(,)22x x y y ++. 由题意可设直线1l 的方程为(1)y k x =- (0)k ≠,由24, (1),y x y k x ⎧=⎨=-⎩得2222(24)0k x k x k -++=. 2242(24)416160k k k D =+-=+>.因为直线1l 与曲线C 于,A B 两点,所以12242x x k +=+,12124(2)y y k x x k+=+-=. 所以点P 的坐标为222(1, )k k+.由题知,直线2l 的斜率为1k -,同理可得点Q 的坐标为2(12,2)k k +-.当1k ≠±时,有222112k k +≠+,此时直线PQ 的斜率2222221112PQ kk k k k k k+==-+--.所以,直线PQ 的方程为222(12)1k y k x k k +=---, 整理得2(3)0yk x k y +--=.于是,直线PQ 恒过定点(3, 0)E ;当1k =±时,直线PQ 的方程为3x =,也过点(3, 0)E .综上所述,直线PQ 恒过定点(3, 0)E . …………10分 (Ⅲ)可求的||2EF =,所以FPQ ∆面积121||(2||)2(||)42||||S FE k k k k =+=+≥. 当且仅当1k =±时,“=”成立,所以FPQ ∆面积的最小值为4.…………13分(20)(本小题满分14分)解:(Ⅰ)11110(21)(2)a a a =++,得2112520a a -+=,解得12a =,或112a =. 由于11a >,所以12a =.因为10(21)(3)n n n S a a =++,所以210252n n n S a a =++.故221111101010252252n n n n n n n a S S a a a a ++++=-=++---,整理,得22112()5()0n n n n a a a a ++--+=,即11()[2()5]0n n n n a a a a +++--=. 因为{}n a 是递增数列,且12a =,故10n n a a ++≠,因此152n n a a +-=. 则数列{}n a 是以2为首项,52为公差的等差数列. 所以512(1)(51)22n a n n =+-=-.………………………………………………5分 (Ⅱ)满足条件的正整数, , m n k 不存在,证明如下:假设存在*, , m n k N ∈,使得2()m n k a a a +=, 则15151(51)2m n k -+-=-. 整理,得3225m n k +-=, ① 显然,左边为整数,所以①式不成立.故满足条件的正整数, , m n k 不存在. …………9分(Ⅲ)313(51)21222n n n n b a n n --=-=--=+, 2(3)2(3)51351512n n n a n n c n n n ++-==⋅=+--.不等式12011131(1)(1)(1)n mb b b+++可转化为 111(1)(1)(1)b +++3121231111n n b b b bb b b b ++++=⋅⋅⋅4682235721n n +=⋅⋅⋅⋅⋅+. 设46822()35721n f n n +=⋅⋅⋅⋅⋅+, 则 (1)21()35721f n n f n n ⋅⋅⋅++=⋅⋅⋅⋅⋅+2423n n +=+ 24124n n +=>===+. 所以(1)()f n f n +>,即当n 增大时,()f n 也增大. 要使不等式12031(1)(1)(1)n b b b +++对于任意的*n ∈N 恒成立,只需min ()31m f n ≤即可. 因为min 4()(1)315f n f ===, 即43112448151515m ⨯==≤. 所以,正整数m 的最大值为8. …………14分。
2011朝阳高三三模数学理

朝阳区2010~2011学年度第二学期高三年级保温测试数 学 试 卷(理工类)(考试时间120分钟,满分150分) 2011.5一、选择题(本大题共8小题,每小题5分,共40分)1.若集合{}A=|1x x x R ≤∈,,{}2B=|y y x x R =∈,,则A B I = ( )A .{}|11x x -≤≤B .{}|0x x ≥C .{}|01x x ≤≤D . ∅2.设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是 ( ) A .若l m ⊥,m α⊂,则l α⊥ B .若l α⊥,l m //,则m α⊥ C .若l α//,m α⊂,则l m //D .若l α//,m α//,则l m//3.已知ξ~N (0, s 2),若P (ξ >2) = 0.023,则P (-2≤ξ≤2) = ( )A .0.477B .0.628C .0.954D .0.9774.6的展开式中常数项是( )A .-160B .-20C .20D .1605.一空间几何体的三视图如图所示,则该几何体的体积为( ) A .13B .23C .53D .436.a ,b 为非零向量,“函数2()()f x x =+a b 为偶函数”是“⊥a b ”的 ( )A .充分但不必要条件B .必要但不充分条件C .充要条件D .非充非要条件7.设等差数列{}n a 的前n 项和为n S ,若111a =-,466a a +=-,则当n S 取最小值时,n 等于( ) A .6B .7C .8D .98.已知平面上不重合的四点P ,A ,B ,C 满足0PA PB PC ++= ,且AB AC mAP +=,那么实数m 的值为 ( ) A .5 B .4 C .3 D .2二、填空题(本大题共6小题,每小题5分,共30分)9.由直线x y =与曲线2x y =所围图形的面积=S ________.10.样本中共有五个个体,其值分别为a ,0,1,2,3.若该样本的平均值为1,则样本方差为________. 11.已知某程序框图如图所示,则执行该程序后输出的结果是________.12.如图,已知⊙O 的直径5A B =,C 为圆周上一点,4=BC ,过点C 作⊙O 的切线l ,过点A 作l 的垂线AD ,垂足为D ,则C D =________.正视图侧视图俯视图13.若直线l 的参数方程为31,545x t y t ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数),则直线l 的斜率为________;在极坐标系中,直线m 的方程为sin()42πρθ+=,则点7(2,)4A π到直线m 的距离为________.14.已知点(4, 1)A 和坐标原点O ,若点(,)B x y 满足1133x y x y x y -≥-⎧⎪+≥⎨⎪-≤⎩,则OA OB ⋅ 的最大值是________. 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤) 15.(13分)设函数()cos(2)6f x x π=+sin 2x +.(Ⅰ)求函数()f x 的单调递增区间;(Ⅱ)设A ,B ,C 为∆ABC 的三个内角,若AB=1,sinB=31,()22C f =,求AC 的长.16.(13分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为23.现有10件产品,其中6件是一等品,4件是二等品.(Ⅰ)随机选取1件产品,求能够通过检测的概率;(Ⅱ)随机选取3件产品,其中一等品的件数记为X ,求X 的分布列; (Ⅲ)随机选取3件产品,求这三件产品都不能通过检测的概率.开始a =2,i =1 i ≥2010i =i +1结束输出a是否lOADCB17.(13分)如图,在四棱锥P-ABCD 中,底面ABCD 为直角梯形,AD//BC ,∠ADC=90°,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M 是棱PC 上的点,PA=PD=2,BC=12AD=1,(Ⅰ)若点M 是棱PC 的中点,求证:PA//平面BMQ ; (Ⅱ)求证:平面PQB ⊥平面PAD ;(Ⅲ)若二面角M-BQ-C 为30°,设PM = tMC ,试确定t 的值.18.(13分)已知数列}{n a ,其前n 项和为237()22n S n n n N *=+∈.(Ⅰ)求数列}{n a 的通项公式,并证明数列}{n a 是等差数列;(Ⅱ)如果数列}{n b 满足n n b a 2log =,请证明数列}{n b 是等比数列,并求其前n 项和.19.(14分)已知函数()ln a xf x x x-=+,其中a 为大于零的常数.(Ⅰ)若曲线()y f x =在点(1,(1)f )处的切线与直线12y x =-平行,求a 的值;(Ⅱ)求函数()f x 在区间[1,2]上的最小值.20.(14分)已知椭圆C:22221(0)x y a b ab+=>>的长轴长为,离心率22=e .(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若过点B (2,0)的直线l (斜率不等于零)与椭圆C 交于不同的两点E ,F (E 在B ,F 之间),且∆OBE 与∆OBF 的面积之比为12,求直线l 的方程.PABCD QM高三数学练习题参考答案 (理科)一、选择题:(本大题共8小题,每小题5分,共40分)(1)C (2)B (3)C (4)A (5)D (6)C (7)A (8)C 二、填空题:(本大题共6小题,每小题5分,共30分)(9)61(10) 2 (11)-1 (12)125(13)43-;2(14)11三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15(本小题共13分) 解:()cos(2)6f x x π=+sin 2x +=1cos 2cossin 2sinsin 22sin 2sin(2)66223x x x x x x πππ-+=+=+......3分(I )令222,232k x k k Z πππππ-≤+≤+∈,则5,1212k x k k Z ππππ-≤≤+∈所以函数f(x)的单调递增区间为5[,]().1212k k k Z ππππ-+∈ .............6分(II)由已知()sin()3C f C π+==22, ……………………………………………….8分因为40,333C C ππππ<<∴<+<所以233C ππ+=,3C π=,所以2. ……10分在∆ABC 中,由正弦定理,sin sin AC AB BC=,得1sin sin 92AB B AC C ⋅===. …..13分 16(本小题共13分)解:(Ⅰ)设随机选取一件产品,能够通过检测的事件为A . …………………………1分事件A 等于事件 “选取一等品都通过检测或者是选取二等品通过检测” ……………2分151332104106)(=⨯+=A p …………………………4分(Ⅱ) 由题可知X 可能取值为0,1,2,3.3463101(0)30C C P X C ===,21463103(1)10C C P X C ===,12463101(2)2C C P X C ===,03463101(3)6C C P X C ===. ………………8分……………9分C(Ⅲ)设随机选取3件产品都不能通过检测的事件为B , ……………10分 事件B 等于事件“随机选取3件产品都是二等品且都不能通过检测” 所以,3111()()303810P B =⋅=. ………………………………………………………13分 17(本小题共13分)证明:(Ⅰ)连接AC ,交BQ 于N ,连接MN . ………………………………………1分∵BC ∥AD 且BC=12AD ,即BC //AQ ,∴四边形BCQA 为平行四边形,且N 为AC 中点,又∵点M 在是棱PC 的中点,∴ MN // PA. ……………………………………………………………………2分 ∵ MN ⊂平面MQB ,PA ⊄平面MQB , …………………………………3分 ∴ PA // 平面MBQ . …………………………………………………………………4分 (Ⅱ)∵AD // BC ,BC=12AD ,Q 为AD 的中点,∴四边形BCDQ 为平行四边形,∴CD // BQ .……………………………………6分 ∵∠ADC=90° ∴∠AQB =90° 即QB⊥AD. 又∵平面PAD ⊥平面ABCD且平面PAD ∩平面ABCD=AD , ………………………………………………7分 ∴BQ ⊥平面PAD . …………………………………………………………8分 ∵BQ ⊂平面PQB ,∴平面PQB ⊥平面PAD . …………………………………………………………9分 另证:AD // BC ,BC=12AD ,Q 为AD 的中点∴ BC // DQ 且BC= DQ ,∴ 四边形BCDQ 为平行四边形,∴CD // BQ .∵ ∠ADC=90° ∴∠AQB =90° 即QB⊥AD. …………………………………6分 ∵ PA=PD , ∴PQ ⊥AD . …………………………………………………7分 ∵ PQ ∩BQ=Q ,∴AD ⊥平面PBQ . ………………………………………………8分 ∵ AD ⊂平面PAD ,∴平面PQB ⊥平面PAD . ……………………………………………………9分 (Ⅲ)∵PA=PD ,Q 为AD 的中点, ∴PQ ⊥AD.∵平面PAD ⊥平面ABCD ,且平面PAD ∩平面ABCD=AD , ∴PQ⊥平面ABCD .…10分(不证明PQ⊥平面ABCD 直接建系扣1分) 如图,以Q 为原点建立空间直角坐标系.则平面BQC 的法向量为(0,0,1)n = ;(0,0,0)Q ,(0,0,P ,0)B,(0)C -.………设(,,)M x y z ,则(,,PM x y z =-,(1,)M C x y z=---,∵PM t M C = ,∴(1))(x tx y t yz t z =--⎧⎪=⎨⎪-=-⎩), ∴ 111t x tyt z t ⎧=-⎪+⎪⎪=⎨+⎪⎪=⎪+⎩……12分在平面MBQ 中,0)Q B = ,(,111t Q M t t t=-+++ ,∴ 平面MBQ法向量为0,)m t =.∵二面角M-BQ-C 为30°,cos 302n m t n m ︒⋅===3t =.…………13分 18(本小题共13分)解:(Ⅰ)当1n =时,115a S ==, ……………………………………………………1分当2n ≥时,22137[(1)][(1)]22n n n a S S n n n n -=-=--+--37(21)3222n n =-+=+. ……………………………3分又15a =满足32n a n =+, ……………………………………………………5分 32()n a n n N *∴=+∈. ………………………………………………………6分∵132[3(1)2]3n n a a n n --=+--+= (2,)n n N *≥∈,∴数列{}n a 是以5为首项,3为公差的等差数列. ……………………………7分(Ⅱ)由已知得2na nb = ()n N *∈, …………………………………………8分∵+1+13+12==2=2=82n n nna a -a n a nb b ()n N *∈, ……………………10分又11232a b ==, ∴数列}{n b 是以32为首项,8为公比的等比数列. …………12分∴数列}{n b 前n 项和为32(18)32(81)187nn-=--. …………………………13分19(本小题共14分) 解:2221()1'()x a x ax af x x x x x x----=+=-=(0x >) ………………………………..4分 (I )因为曲线()y f x =在点(1,(1)f )处的切线与直线1-2y x =平行,所以'(1)-2f =,即12, 3.a a -=-=解得 ……………………………………6分(II)当01a <≤时,'()0f x >在(1,2)上恒成立,这时()f x 在[1,2]上为增函数 min ()(1)1f x f a ∴==-. ………………………………………………….8分当12a <<时,由'()0f x =得,(1,2)x a =∈对于(1,)x a ∈有'()0,f x <()f x 在[1,a]上为减函数, 对于(,2)x a ∈有'()0,f x >()f x 在[a ,2]上为增函数,min ()()ln f x f a a ∴==. …………………………………………………..11分当2a ≥时,'()0f x <在(1,2)上恒成立, 这时()f x 在[1,2]上为减函数,m in ()(2)ln 212af x f ∴==+-.综上,()f x 在[1,2]上的最小值为①当01a <≤时,m in ()1f x a =-,②当12a <<时,min ()ln f x a =,③当2a ≥时,m in ()ln 212a f x =+-.…………….14分20(本小题共14分).解:(I )椭圆C 的方程为)0(12222>>=+b a bya x,由已知得22222c e a a a b c ⎧==⎪⎪⎪=⎨⎪=+⎪⎪⎩……..3分解得 1,1a b c ===∴所求椭圆的方程为1222=+yx. ………………………………………………… 5分(II)由题意知l 的斜率存在且不为零,设l 方程为2(0)x my m =+≠ ①,将①代入1222=+yx,整理得22(2)420m y m y +++=,由0>∆得2 2.m > ………….……………….……….7分设),(11y x E ,),(22y x F ,则1221224222m y y m y y m -⎧+=⎪⎪+⎨⎪=⎪+⎩②. …………………………8分由已知,12OBEOBF S S ∆∆=, 则||1||2BE BF =由此可知,2BF BE =,即212y y =. …………………………………………….10分 代入②得,12212432222m y m y m -⎧=⎪⎪+⎨⎪=⎪+⎩,消去1y 得222221629(2)2m m m ⋅=++ 解得,2187m =,满足22.m >即7m =±. ………………………………………………………….13分所以,所求直线l的方程为71407140x x --=+-=或. …….14分。
2011年北京市各城区数学二模试题汇总 注意:是5个城区的哦!!
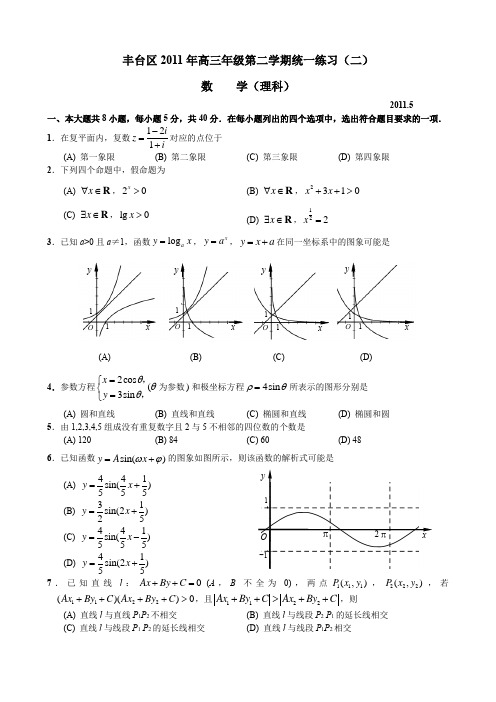
xyO π2π1-1丰台区2011年高三年级第二学期统一练习(二)数学(理科)2011.5一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.在复平面内,复数121iz i-=+对应的点位于 (A) 第一象限 (B)第二象限 (C) 第三象限(D)第四象限2.下列四个命题中,假命题为(A) x ∀∈R ,20x > (B) x ∀∈R ,2310x x ++> (C) x ∃∈R ,lg 0x >(D) x ∃∈R ,122x =3.已知a >0且a ≠1,函数log a y x =,x y a =,y x a =+在同一坐标系中的图象可能是(A)(B) (C) (D)4.参数方程2cos (3sin x y θθθ=⎧⎨=⎩,,为参数)和极坐标方程4sin ρθ=所表示的图形分别是(A) 圆和直线 (B) 直线和直线 (C) 椭圆和直线 (D)椭圆和圆 5.由1,2,3,4,5组成没有重复数字且2与5不相邻的四位数的个数是(A) 120 (B) 84 (C) 60 (D) 486.已知函数sin()y A x ωϕ=+的图象如图所示,则该函数的解析式可能是(A) 441sin()555y x =+(B) 31sin(2)25y x =+(C) 441sin()555y x =-(D) 41sin(2)55y x =+7.已知直线l :0Ax By C ++=(A ,B 不全为0),两点111(,)P x y ,222(,)P x y ,若1122()()0Ax By C Ax By C ++++>,且1122Ax By C Ax By C ++>++,则(A) 直线l 与直线P 1P 2不相交(B) 直线l 与线段P 2P 1的延长线相交 (C) 直线l 与线段P 1P 2的延长线相交(D) 直线l 与线段P 1P 2相交OO O O x xxxyyyy1 11 1111 18.已知函数2()2f x x x =-,()2g x ax =+(a >0),若1[1,2]x ∀∈-,2[1,2]x ∃∈-,使得f (x 1)= g (x 2),则实数a 的取值范围是 (A) 1(0,]2(B) 1[,3]2(C) (0,3] (D)[3,)+∞二、填空题:本大题共6小题,每小题5分,共30分.9.圆C :222220x y x y ++--=的圆心到直线3x +4y +14=0的距离是. 10.如图所示,DB ,DC 是⊙O 的两条切线,A 是圆上一点,已知 ∠D =46°,则∠A =.11.函数2cos sin y x x x =-的最小正周期为,最大值 为.12.一个几何体的三视图如图所示,则该几何体的体积是.13.如果执行右面的程序框图,那么输出的a =___.14.如图所示,∠AOB =1rad ,点A l ,A 2,…在OA 上,点B 1,B 2,…在OB 上,其中的每一个实线段和虚线段的长均为1个长度单位,一个动点M 从O 点出发,沿着实线段和以O 为圆心的圆弧匀速运动,速度为l 长度单位/秒,则质点M 到达A 3点处所需要的时间为__秒,质点M 到达A n 点处所需要的时间为__秒.OA 1A 2 A 3 A 4B 1 B 2 B 3 B 4 AB正视图侧视图俯视图A三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知等差数列{}n a 的前n 项和为n S ,a 2=4,S 5=35. (Ⅰ)求数列{}n a 的前n 项和n S ;(Ⅱ)若数列{}n b 满足n a n b e =,求数列{}n b 的前n 项和n T .16.(本小题共14分)张先生家住H 小区,他在C 科技园区工作,从家开车到公司上班有L 1,L 2两条路线(如图),L 1路线上有A 1,A 2,A 3三个路口,各路口遇到红灯的概率均为12;L 2路线上有B 1,B 2两个路口,各路口遇到红灯的概率依次为34,35.(Ⅰ)若走L 1路线,求最多..遇到1次红灯的概率; (Ⅱ)若走L 2路线,求遇到红灯次数X 的数学期望;(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.17.(本小题共13分)已知平行四边形ABCD 中,AB =6,AD =10,BD =8,E 是线段AD 的中点.沿BD 将△BCD 翻折到△BC D ',使得平面BC D '⊥平面ABD . (Ⅰ)求证:C D '⊥平面ABD ; (Ⅱ)求直线BD 与平面BEC '所成角的正弦值; (Ⅲ)求二面角D BE C '--的余弦值.12A B D E C ' C18.(本小题共13分)已知函数2()ln (2)f x x ax a x =-+-. (Ⅰ)若()f x 在1x =处取得极值,求a 的值; (Ⅱ)求函数()y f x =在2[,]a a 上的最大值.19.(本小题共14分)已知抛物线P :x 2=2py (p >0).(Ⅰ)若抛物线上点(,2)M m 到焦点F 的距离为3.(ⅰ)求抛物线P 的方程;(ⅱ)设抛物线P 的准线与y 轴的交点为E ,过E 作抛物线P 的切线,求此切线方程; (Ⅱ)设过焦点F 的动直线l 交抛物线于A ,B 两点,连接AO ,BO 并延长分别交抛物线的准线于C ,D 两点,求证:以CD 为直径的圆过焦点F .20.(本小题共13分) 用[]a 表示不大于a 的最大整数.令集合{1,2,3,4,5}P =,对任意k P ∈和N*m ∈,定义51(,)[]i f m k ==∑,集合{N*,}A m k P =∈∈,并将集合A 中的元素按照从小到大的顺序排列,记为数列{}n a . (Ⅰ)求(1,2)f 的值; (Ⅱ)求9a 的值;(Ⅲ)求证:在数列{}n a中,不大于m 00(,)f m k 项.(考生务必将答案答在答题卡上,在试卷上作答无效)海淀区高三年级第二学期期末练习数学(理科) 2011.5选择题 (共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.复数11i+在复平面上对应的点的坐标是A .(1,1) B. (1,1)- C. (1,1)-- D. (1,1)-2. 已知全集R,U =集合{}1,2,3,4,5A =,{|2}B x x =∈≥R ,下图中阴影部分所表示的集合为 A {1}B.{0,1} C. {1,2}D. {0,1,2} 3.函数21()log f x x x=-的零点所在区间 A .1(0,)2 B.1(,1)2C.(1,2)D.(2,3) 4.若直线l 的参数方程为13()24x tt y t =+⎧⎨=-⎩为参数,则直线l 倾斜角的余弦值为A .45-B .35-C .35D .455. 某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下:甲 乙 9 8 8 1 7 7 9 9 6 1 0 2 2 5 6 7 9 9 5 3 2 0 3 0 2 3 7 1 0 4根据上图,对这两名运动员的成绩进行比较,下列四个结论中,不正确...的是 A .甲运动员得分的极差大于乙运动员得分的极差B .甲运动员得分的的中位数大于乙运动员得分的的中位数C .甲运动员的得分平均值大于乙运动员的得分平均值D .甲运动员的成绩比乙运动员的成绩稳定6.一个锥体的主视图和左视图如图所示,下面选项中,不.可能是...该锥体的俯视图的是7.若椭圆1C :1212212=+b ya x(011>>b a )和椭圆2C :1222222=+b ya x(022>>b a )的焦点相同且12a a >.给出如下四个结论:① 椭圆1C 和椭圆2C 一定没有公共点; ②1122a b a b >; ③22212221b b a a -=-; ④1212a a b b -<-.其中,所有正确结论的序号是A .②③④B. ①③④C .①②④D.①②③8. 在一个正方体1111A B C D A B C D -中,P 为正方形1111A B C D 四边上的动点,O 为底面正方形ABCD 的中心,,M N 分别为,AB BC 中点,点Q 为平面ABCD 内一点,线段1D Q 与OP 互相平分,则满足M Q λ=的实数λ的值有A. 0个B. 1个C. 2个D. 3个非选择题(共110分)二、填空题:本大题共6小题,每小题5分,共30分.9.点(,)P x y 在不等式组2,,2y x y x x ≤⎧⎪≥-⎨⎪≤⎩表示的平面区域内,则z x y =+的最大值为_______.主视图左视图B ACDA1D 1A 1C 1B DCBOPNQ10.运行如图所示的程序框图,若输入4n =,则输出S 的值为 . 11.若4234512345(1)x mx a x a x a x a x a x -=++++, 其中26a =-,则实数m 的值为;12345a a a a a ++++的值为.12.如图,已知O 的弦AB 交半径OC 于点D ,若3AD =,2BD =,且D 为OC 的中点,则CD 的长为 .13.已知数列{}n a 满足1,a t =,120n n a a +-+=(,)t n ∈∈**N N ,记数列{}n a 的前n 项和的最大值为()f t ,则()f t = .14. 已知函数sin ()xf x x=(1)判断下列三个命题的真假: ①()f x 是偶函数;②()1f x <;③当32x π=时,()f x 取得极小值. 其中真命题有____________________;(写出所有真命题的序号) (2)满足()()666n n f f πππ<+的正整数n 的最小值为___________. 三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.(本小题共13分)已知函数2()coscos f x x x x ωωω=(0)ω>的最小正周期为π.(Ⅰ)求2()3f π的值;(Ⅱ)求函数()f x 的单调区间及其图象的对称轴方程.16.(本小题共13分)某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客,假设每位乘客在2、3、4层下电梯是等可能的.(Ⅰ)求这4位乘客中至少有一名乘客在第2层下电梯的概率;(Ⅱ)用X 表示4名乘客在第4层下电梯的人数,求X 的分布列和数学期望. 17.(本小题共14分)如图,四棱锥P ABCD -的底面是直角梯形,//AB CD ,AB AD ⊥,PAB ∆和PAD ∆是两个边长为2的正三角形,4DC =,O 为BD 的中点,E 为PA 的中点. (Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求证://OE 平面PDC ;(Ⅲ)求直线CB 与平面PDC 所成角的正弦值.18. (本小题共14分)已知函数221()()ln 2f x ax x x ax x =--+.()a ∈R . (I )当0a =时,求曲线()y f x =在(e,(e))f 处的切线方程(e 2.718...=); (II )求函数()f x 的单调区间.19.(本小题共13分)在平面直角坐标系xOy 中,设点(,),(,4)P x y M x -,以线段PM 为直径的圆经过原点O .(Ⅰ)求动点P 的轨迹W 的方程;(Ⅱ)过点(0,4)E -的直线l 与轨迹W 交于两点,A B ,点A 关于y 轴的对称点为'A ,试判断直线'A B 是否恒过一定点,并证明你的结论.20. (本小题共13分)对于数列12n A a a a :,,,,若满足{}0,1(1,2,3,,)i a i n ∈=⋅⋅⋅,则称数列A 为“0-1数列”.定义变换T ,T 将“0-1数列”A 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如A :1,0,1,则():0,1,1,0,0,1.T A 设0A 是“0-1数列”,令1(),k k A T A -= 12k = ,,3,.(Ⅰ)若数列2A :1,0,0,1,0,1,1,0,1,0,0,1.求数列10,A A ;(Ⅱ) 若数列0A 共有10项,则数列2A 中连续两项相等的数对至少有多少对?请说明理由;A D OC PBE(Ⅲ)若0A 为0,1,记数列k A 中连续两项都是0的数对个数为k l ,1,2,3,k =⋅⋅⋅.求k l 关于k 的表达式.北京市朝阳区高三年级第二次综合练习数学测试题(理工类)2011.5(考试时间120分钟满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题共40分)注意事项:1.答第一部分前,考生务必将自己的姓名、考试科目涂写在答题卡上.考试结束时,将试题卷和答题卡一并交回.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. (1)已知全集U =R ,集合{|021}xA x =<<,3{|log 0}B x x =>,则U ()A B I ð=(A ){|1}x x >(B ){|0}x x >(C ){|01}x x <<(D ){|0}x x <(2)设,x y ∈R ,那么“0>>y x ”是“1>yx”的 (A )必要不充分条件(B )充分不必要条件 (C )充分必要条件 (D )既不充分又不必要条件(3)三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则侧视图的面积为(A ) 8 (B ) 4(C)D(4)已知随机变量X 服从正态分布(, 4)N a ,且(1)0.5P X >=,则实数a 的值为(A )1 (BC )2(D )4(5)若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”.现从正视图1,2,3,4,5,6这六个数字中任取3个数,组成无重复数字的三位数,其中“伞数”有 (A )120个(B )80个(C )40个(D )20个(6)点P 是抛物线x y 42=上一动点,则点P 到点(0,1)A -的距离与到直线1-=x 的距离和的最小值是 (ABC )2 (D )2(7)已知棱长为1的正方体1111ABCD A BC D -中,点E ,F 分别是棱1BB ,1DD 上的动 点,且1BE D F λ==1(0)2λ<≤.设EF 与AB 所成的角为α,与BC 所成的角为β,则αβ+的最小值(A )不存在(B )等于60︒(C )等于90︒(D )等于120︒(8)已知点P 是ABC ∆的中位线EF 上任意一点,且//EF BC ,实数x ,y 满足PA xPB yPC ++=0 .设ABC ∆,PBC ∆,PCA ∆,PAB ∆的面积分别为S ,1S ,2S ,3S ,记11SSλ=,22S S λ=,33S Sλ=.则23λλ⋅取最大值时,2x y +的值为(A )32(B )12(C ) 1 (D )2 第二部分(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.(9)已知复数z 满足1iz i =-,则z =. (10)曲线C :cos 1,sin 1x y θθ=-⎧⎨=+⎩(θ为参数)的普通方程为.(11)曲线233y x =-与x 轴所围成的图形面积为________.(12)已知数列{}n a 满足12a =,且*1120,n n n n a a a a n +++-=∈N ,则2a =;并归纳出数列{}n a 的通项公式n a =.(13)如图,PA 与圆O 相切点A ,PCB 为圆O 的割线,并且不过圆心O ,已知30BPA ∠=,PA =1PC =,则PB =;圆O 的 半径等于.(14)已知函数2()(1)1f x ax b x b =+++-,且(0, 3)a ∈,则对于任意 的b ∈R ,函数()()F x f x x =-总有两个不同的零点的概率是.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. (15)(本小题满分13分)已知函数2()2sin sin()2sin 12f x x x x π=⋅+-+()x ∈R . (Ⅰ)求函数()f x 的最小正周期及函数()f x 的单调递增区间;(Ⅱ)若0()23x f =,ππ(, )44x ∈-,求0cos 2x 的值.(16)(本小题满分13分)为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为16,第二轮检测不合格的概率为110,两轮检测是否合格相互没有影响. (Ⅰ)求该产品不能销售的概率;(Ⅱ)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利-80元).已知一箱中有产品4件,记一箱产品获利X 元,求X 的分布列,并求出均值E (X ).(17)(本小题满分13分)在长方形11AA B B 中,124AB AA ==,C ,1C 分别是AB ,11A B 的中点(如图1). 将此长方形沿1CC 对折,使二面角11A CC B --为直二面角,D ,E 分别是11A B ,1CC 的中点(如图2).(Ⅰ)求证:1C D ∥平面1A BE ; (Ⅱ)求证:平面1A BE ⊥平面11AA B B ; (Ⅲ)求直线1BC 与平面1A BE 所成角的正弦值.(18)(本小题满分13分)设函数2()ln ()f x x x a =+-,a ∈R . (Ⅰ)若0a =,求函数()f x 在[1,]e 上的最小值;(Ⅱ)若函数()f x 在1[, 2]2上存在单调递增区间,试求实数a 的取值范围; (Ⅲ)求函数)(x f 的极值点.(19)(本小题满分14分)已知椭圆2222:1(0)x y C a b a b +=>>经过点(2, 1)A ,离心率为2.过点(3, 0)B 的直线l 与椭圆C交于不同的两点,M N . (Ⅰ)求椭圆C 的方程; (Ⅱ)求BM BN ⋅的取值范围;(Ⅲ)设直线AM 和直线AN 的斜率分别为AM k 和AN k ,求证:AM AN k k +为定值.(20)(本小题满分14分)对于正整数, a b ,存在唯一一对整数q 和r ,使得a bq r =+,0r b <≤.特别地,当0r =时,称b 能整除a ,记作|b a ,已知{1, 2, 3,,23}A =⋅⋅⋅.(Ⅰ)存在q A ∈,使得201191 (091)q r r =+<≤,试求,q r 的值;图(1)(Ⅱ)求证:不存在这样的函数:{1,2,3}f A →,使得对任意的整数12,x x A ∈,若12||{1,2,3}x x -∈,则12()()f x f x ≠;(Ⅲ)若B A ⊆,12)(=B card (()card B 指集合B 中的元素的个数),且存在,a b B ∈,b a <,|b a ,则称B 为“和谐集”.求最大的m A ∈,使含m 的集合A 的有12个元素的任意子集为“和谐集”,并说明理由.北京市西城区2011年高三二模试卷数学(理科)2011.5第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知集合{0,1}A =,{1,0,3}B a =-+,且A B ⊆,则a 等于 (A )1(B )0(C )2-(D )3-2.已知i 是虚数单位,则复数23z i+2i 3i =+所对应的点落在(A )第一象限 (B )第二象限 (C )第三象限(D )第四象限3.在ABC ∆中,“0AB BC ⋅>”是“ABC ∆为钝角三角形”的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件(D )既不充分又不必要条件4.已知六棱锥P ABCDEF -的底面是正六边形,PA ⊥平面ABC .则下列结论不正确...的是 (A )//CD 平面PAF (B )DF ⊥平面PAF (C )//CF 平面PAB (D )CF ⊥平面PAD5.双曲线22221x y a b-=的渐近线与圆22(2)1x y +-=相切,则双曲线离心率为(A(B(C )2(D )3 6.函数sin()(0)y x ϕϕ=π+>的部分图象如右图所示,设P 是图象的最高点,,A B 是图象与x 轴的交点,则tan APB ∠=(A )10 (B )8 (C )87(D )77.已知数列{}n a 的通项公式为13n a n =-,那么满足119102k k k a a a +++++= 的整数k(A )有3个 (B )有2个 (C )有1个(D )不存在8.设点(1,0)A ,(2,1)B ,如果直线1ax by +=与线段AB 有一个公共点,那么22a b +(A )最小值为15 (B )最小值为5 (C )最大值为15(D第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.在中,若2B A =,:a b =A =_____. 10.在521()x x+的展开式中,2x 的系数是_____. 11.如图,AB 是圆O 的直径,P 在AB 的延长线上,PD切圆O 于点C .已知圆O 2OP =,则PC =______;ACD ∠的大小为______.12.在极坐标系中,点(2,)2A π关于直线:cos 1l ρθ=的对称点的一个极坐标为_____.13.定义某种运算⊗,a b ⊗的运算原理如右图所示.ABC ∆设()(0)(2)f x x x x =⊗-⊗. 则(2)f =______;()f x 在区间[2,2]-上的最小值为______.14.数列{}n a 满足11a =,11n n n a a n λ+-=+,其中λ∈R , 12n = ,,.①当0λ=时,20a =_____;② 若存在正整数m ,当n m >时总有0n a <,则λ的取值范围是_____.三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数cos 2()sin()4x f x x π=+.(Ⅰ)求函数()f x 的定义域; (Ⅱ)若4()3f x =,求s i n 2x 的值.16.(本小题满分13分)如图,已知菱形ABCD 的边长为6,60BAD ∠=,AC BD O = .将菱形ABCD 沿对角线AC 折起,使BD =B ACD -.(Ⅰ)若点M 是棱BC 的中点,求证://OM 平面ABD ; (Ⅱ)求二面角A B D O --的余弦值;(Ⅲ)设点N 是线段BD 上一个动点,试确定N点的位置,使得CN =.17.(本小题满分13分)甲班有2名男乒乓球选手和3名女乒乓球选手,乙班有3名男乒乓球选手和1名女乒乓球选手,学校计划从甲乙两班各选2名选手参加体育交流活动.M(Ⅰ)求选出的4名选手均为男选手的概率.(Ⅱ)记X 为选出的4名选手中女选手的人数,求X 的分布列和期望.18.(本小题满分14分)已知函数()(1)e (0)xa f x x x=->,其中e 为自然对数的底数.(Ⅰ)当2a =时,求曲线()y f x =在(1,(1))f 处的切线与坐标轴围成的面积;(Ⅱ)若函数()f x 存在一个极大值点和一个极小值点,且极大值与极小值的积为5e ,求a 的值.19.(本小题满分14分)已知椭圆2222:1x y M a b +=(0)a b >>且椭圆上一点与椭圆的两个焦点构成的三角形周长为246+.(Ⅰ)求椭圆M 的方程;(Ⅱ)设直线l 与椭圆M 交于,A B 两点,且以AB 为直径的圆过椭圆的右顶点C , 求ABC ∆面积的最大值.20.(本小题满分13分)若m A A A ,,,21 为集合2}(,,2,1{≥=n n A 且)n ∈*N 的子集,且满足两个条件: ①12m A A A A = ;②对任意的A y x ⊆},{,至少存在一个},,3,2,1{m i ∈,使}{},{x y x A i = 或}{y . 则称集合组m A A A ,,,21 具有性质P .如图,作n 行m 列数表,定义数表中的第k 行第l 列的数为⎩⎨⎧∉∈=)(0)(1l l kl A k A k a .(Ⅰ)当4n =时,判断下列两个集合组是否具有性质P ,如果是请画出所对应的表格,如果不是请说明理由;集合组1:123{1,3},{2,3},{4}A A A ===; 集合组2:123{2,3,4},{2,3},{1,4}A A A ===. (Ⅱ)当7n =时,若集合组123,,A A A 具有性质P ,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合123,,A A A ;(Ⅲ)当100n =时,集合组12,,,t A A A 是具有性质P 且所含集合个数最小的集合组,求t 的值及12||||||t A A A ++ 的最小值.(其中||i A 表示集合i A 所含元素的个数)北京市东城区2010-2011学年第二学期高三综合练习(二)数学 (理科)第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分。
朝阳区高考二模数学理试题目及答案word精品文档9页

北京市朝阳区高三年级第二次综合练习数学测试题(理工类)2019.5(考试时间120分钟满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题共40分)注意事项:1.答第一部分前,考生必将自己的姓名、考试科目涂写在答题卡上。
考试结束时,将试题卷和答题卡一并交回。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题卷上。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项。
(1)已知全集U=R,集合A={x︱0<2x<1},B={x︱log3x>0},则A∩(C U B)=(A){x︱x>1} (B){x︱x>0} (C){x︱0<x<1} (D){x︱x<0}(2)设x,y∈R那么“x>y>0”是“xy>1”的(A)必要不充分条件(B)充分不必要条件(C)充分必要条件(D)既不充分又不必要条件(3)三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则侧视图的面积为(A)8 (B)4 (C)43(D)3(4)已知随机变量X服从正态分布N(a,4),且P(X>1)=0.5,则实数a的值为(A)1 (B)3(C)2 (D)4(5)若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”。
现从1,2,3, 4,5, 6 这六个数字中任取3个数,组成无重复数字的三位数,其中“伞数”有(A)120个(B)80个(C)40个(D)20个(6)点P是抛物线y2=4x上一动点,则点P到点A(0,–1)的距离与到直线x=–1的距离和最小值是(A)5(B)3(C)2 (D)2(7)已知棱长为1的正方体ABCD–A1 B1 C1 D1中,点E,F分别是棱BB1 ,DD1上的动点,且BE=D1 F=λ(0<λ≤12)。
2011年朝阳区高三二模数学(文、理)试卷及答案无水印

2011届高考二模数学试卷文科数学命题人:胡全新 何春阳注意:本试题卷包括选择题、填空题和解答题三部分。
时量120分钟。
满分150分。
一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设合集{0,1,2,3,4},{0,3,4},{1,3},()U U A B C A B === 则= ( )A .{2}B .{1,2,3}C .{1,3}D .{0,1,2,3,4}2.在样本的频率分布直方图中,共有5个长方形,若正中间一个小长方形的面积等于其它4个小长方形的面积和的14,且样本容量为100,则正中间的一组的频数为( ) A .80B .0.8C .20D .0.23.一组数据4,5,12,7,11,9,8,则下面叙述正确的是 ( ) A .它们的中位数是7,总体均值是8 B .它们的中位数是7,总体方差是52 C .它们的中位数是8,总体方差是528D .它们的中位数是8,总体方差是5274.在区间[,]22ππ-上随机取一个,sin x x 的值介于1122-与之间的概率为( )A .13B .2π C .12D .235.已知实数m 是2,8的等比中项,则双曲线221yx m-=的离心率为( )A .5B .52C .3D .26.设抛物线28y x =的焦点为F ,准线为,l P 为抛物线上一点,,P A l A ⊥为垂足,如果直线AF 斜率为3-,那么|PF|=( )A .43B .8C .83D .167.若0,0,4a b a b >>+=且,则下列不等式恒成立的是 ( )A .112a b> B .111ab+≤ C .2ab ≥ D .228a b +≥8.若函数s i n ()(0,0,||)2y A x A πωϕωϕ=+>><在一个周期内的 图象如图所示,M ,N 分别是这段图象的最高点和最低点,且O MO N ⋅=(O 为坐标原点),则A= ( ) A .6π B .712π C .76π D .73π二、填空题:本大题共8小题,每小题5分,满分35分。
2011年北京市各区二模试题分类解析(6):数列

六、数列1、(2011昌平二模理6). 已知等差数列{}n a 的公差为3,若431,,a a a 成等比数列,则2a 等于(D )A .9B .3C . -3D .-92、(2011东城二模理5)已知正项数列{}n a 中,11=a ,22=a ,222112(2)n n n a a a n +-=+≥,则6a 等于( D )(A )16 (B )8 (C )22 (D )4 3、(2011顺义二模理4).已知等比数列{}n a 中,各项都是正数,且2312,21,a a a 成等差数列,则9876a a a a ++等于(D )A 21+B 21-C 223+D 223-4、(2011西城二模理7).已知数列{}n a 的通项公式为13n a n =-,那么满足119102k k k a a a +++++= 的整数k ( B )(A )有3个(B )有2个(C )有1个(D )不存在 5、(2011西城二模理14).数列{}n a 满足11a =,11n n n a a n λ+-=+,其中λ∈R , 12n = ,,.①当0λ=时,20a =_120____; ②若存在正整数m ,当n m >时总有0n a <,则λ的取值范围是__(21,2),k k k -∈*N ___. 6、(2011昌平二模文3)数列{}n a 对任意*N n ∈ ,满足13n n a a +=+,且38a =,则10S 等于( A )A .155B . 160C .172D .240 7、(2011丰台二模文4)已知数列{}n a 中,135a =,111(2)n n a n a -=-≥,则2011a =(C) (A) 12-(B) 23-(C)35(D)528、(2011顺义二模文4)已知等比数列{}n a 中,各项都是正数,且2312,21,a a a 成等差数列,则7698a a a a ++等于(C)A 21+B 21-C 223+D 223- 9、1(2011朝阳二模理12)已知数列{}n a 满足12a =,且*1120,n n n n a a a a n +++-=∈N ,则2a =43 ;并归纳出数列{}n a 的通项公式n a = 221n n - 2、(2011海淀二模理13)已知数列{}n a 满足1,a t =,120n n a a +-+= (,)t n ∈∈**N N ,记数列{}n a 的前n 项和的最大值为()f t ,则()f t = 222, (4(1), (4t tt t t ⎧+⎪⎪⎨+⎪⎪⎩为偶数)为奇数) .3、(2011东城二模文14)已知等差数列{}n a 首项为a ,公差为b ,等比数列{}n b 首项为b ,公比为a ,其中,a b 都是大于1的正整数,且1123,a b b a <<,那么a = 2 ;若对于任意的*N n ∈,总存在*N m ∈,使得 3n m b a =+成立,则n a = 5n-34、(2011海淀二模文13)已知数列}{n a 满足,11=a 且)(1n n n a a n a -=+(*n ∈N ),则2a ;n a =__n_.5、(2011西城二模文9) 已知}{n a 为等差数列,341a a +=,则其前6项之和为__3___.6、(2011西城二模文14)数列{}n a 满足11a =,11n n n a a n λ+-=+,其中λ∈R ,12n = ,,.给出下列命题:①λ∃∈R ,对于任意i ∈*N ,0i a >;②λ∃∈R ,对于任意2()i i ≥∈*N ,10i i a a +<;③λ∃∈R ,m ∈*N ,当i m >(i ∈*N )时总有0i a <.其中正确的命题是__①③____.(写出所有正确命题的序号) 解答1(2011昌平二模理20). (本小题满分13分)已知数列{}n a 满足125a =,且对任意n *∈N ,都有11422n n n n a a a a +++=+. (Ⅰ)求证:数列1n a ⎧⎫⎨⎬⎩⎭为等差数列;(Ⅱ)试问数列{}n a 中()1k k a a k *+⋅∈N 是否仍是{}n a 中的项?如果是,请指出是数列的第几项;如果不是,请说明理由. (Ⅲ)令21(5),3n nb a =+证明:对任意2*,2n b n n N b ∈>都有不等式成立.解: (Ⅰ)111242n n n n n n a a a a a a ++++=+,即11223n n n n a a a a ++-=, ……1分所以11132n n a a +-=, ……. 2分 所以数列1n a ⎧⎫⎨⎬⎩⎭是以52为首项,公差为32的等差数列. ……3分 (II )由(Ⅰ)可得数列1n a ⎧⎫⎨⎬⎩⎭的通项公式为1322n n a +=,所以232n a n =+.…… 4分 ()122243231292110k k a a k k k k +⋅=⋅=+++++ …….5分22921622k k =+++22372322k k =++⋅+. …… 7分因为()2213723122k k k k k k +++=+++, …… 8分当k *∈N 时,()12k k +一定是正整数,所以23722k k ++是正整数.(也可以从k 的奇偶性来分析)所以1k k a a +⋅是数列{}n a 中的项,是第23722k k ++项. …… 9分(Ⅲ)证明:由(2)知:232n a n =+,21232(5)(5)4332n n n b n a +=+=+=+…..10分下面用数学归纳法证明:422(4)n n +>+对任意*n N ∈都成立。
北京市朝阳区2011年第二学期高三综合练习(一)

北京市朝阳区2011年第二学期高三综合练习(一)数学(理科)(朝阳一模)(时间:120分钟总分: 150分)第1卷(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小 题列出的四个选项中,选出符合题目要求的一项.1.若集合},,2{{},,|{2R x x y y N R x x y y M ∈+==∈==则=N M ( )),0.[+∞A ),.(∝+-∞B ∅.C )1,1()4,2.(- D2.某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从这两个班抽出16人参加军训表演,则一班和二班分别被抽取的人数是 ( )8,8.A 6,10.B 7,9.C 4,12.D3.极坐标方程θρcos 4=化为直角坐标方程是 ( )4)2.(22=+-y x A 4.22=+y x B 4)2(.22=-+y x C 4)1()1.(22=-+-y x D4.已知}{n a 是由正数组成的等比数列,n s 表示 }{n a 的前n 项和.若,144,3421==a a a 则10s 的值是( )511.A 1023.B 1533.C 3069.D5.函数)2(cos 2π+=x y 的单调递增区间是 ( )Z k k k A ∈+),2,.(πππ z k k k B ∈++),,2.(ππππZ k k k C ∈+),2,2.(πππ z k k k D ∈++),22,2.(ππππ6.已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积等于 ( )126.A 33.B 46.C 332.D7.如图,双曲线的中心在坐标原点0,A ,C 分别是双曲线虚轴的上、下顶点,B 是双曲线的左顶点,F 为双曲线的左焦点,直线AB 与FC 相交于点D.若双曲线的离心率为2,则∠BDF 的余弦值是 ( )77.A 775.B 147.C 1475.D 8.定义区间(a ,b ),k ,b ),(a ,b],k ,b]的长度均为,a b d -=多个区间并集的长度为各区间长度之和.例如, )2,1()5,3[的长度.3)35()12(=-+-=d 用][x 表示不超过x 的最大整数,记 ],[||x x x -=其中.R x ∈设=)(x f ,1)(|,|][-=⋅x x g x x 若321,,d d d 分别表示不等式),()(x g x f > 方程),()(x g x f =不等式)()(x g x f <解集区间的长度,则当20110≤≤x 时,有 ( )2008,2,1.321===d d d A 2009,1,1.321===d d d B2003,5,3.321===d d d C 2006,3,2.321===d d d D第Ⅱ卷(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.复数,1,321i z i z -=+=则21z z等于 10.在二项式6)2(+x 的展开式中,第四项的系数是11.如下图,在三角形ABC 中,D ,E 分别为BC ,AC 的中点,F 为AB 上的点,且.4=若 ,AE y AF x AD +=则实数=x =y ,12.执行下图所示的程序框图,若输入,2.5-=x 则输出y 的值为13.如下图,在圆内接四边形ABCD 中,对角线AC ,BD 相交于点 E.已知=∠===D B C EC AE CD BC ,2,32=∠C A B 则,30 ,AC 的长是14.对于各数互不相等的整数数组n i i i i n (),,,,(321 ⋅是不小于3的正整数),对于任意},,,3,2,1{,n q P ∈ 当P q <时,有,q P i i >则称q P i i ,是该数组的一个“逆序”,一个数据中所有“逆序”的个数称为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于____;若数组,,(21i i ),,3n i i 中的逆序数为n ,则数组),,,(11i i i n n -中的逆序数为三、解答题:本大题共6小题,共80分,解答应写在文字说明,演算步骤或证明过程:15.(本小题共13分)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知⋅-=432cos C (I)求sinC ;(Ⅱ)当C=2a ,且73=b 时,求a .16.(本小题共13分)如图,在四棱雉P- ABCD 中,底面ABCD 为直角梯形,且=∠=∠PAD ABC BC AD ,// ,90 侧面PAD ⊥底面ABCD.若BC AB PA ==.21AD = (I)求证:CD ⊥平面PAC .(Ⅱ)侧棱PA ⊥是否存在点E ,使得BE∥平面PCD? 若存在,指出点E 的位置并证明;若不存在,请说明理由.(Ⅲ)求二面角A-PD-C 的余弦值.17.(本小题共13分)在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进 4个球且最后.2个球都投 进者获奖,否则不获奖,已知教师甲投进每个球的概率都是⋅32 (I)记教师甲在每场的6次投球中投进球的个数为X , 求X 的分布列及数学期望;(Ⅱ)求教师甲在一场比赛中获奖的概率;(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙 在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?18.(本小题共13分)已知函数>-+=a x a xZ x f (2ln )().0 (I)若曲线)(x f y =在点))1(,1(f P 处的切线与直线2+=x y 垂直,求函数)(x f y =的单调区间; (Ⅱ)若对于),0(+∞∈∀x 都有)1(2)(->a x f 成立,试求a 的取值范围;(Ⅲ)记).()()(R b b x x f x g ∈-+=当1=a 时,函数)(x g 在区间].,[1e e -上有两个零点,求实数b的取值范围.19.(本小题共14分)已知A (-2,0),B(2,O)为椭圆C 的左、右顶点,F 为其右焦点,P 是椭圆C 上异于A ,B 的动点,且△APB 面积的最大值为.32(I )求椭圆C 的方程及离心率;(Ⅱ)直线AP 与椭圆在点B 处的切线交于点D ,当直线AP 绕点A 转动时,试判断以BD 为直径的圆与直 线PF 的位置关系,并加以证明.20.(本小题共14分)有n 个首项都是1的等差数列,设第m 个数列的第k 项为),3,,,3,2,1,(≥=n n k m a nk 公差为,m d 并且*,,,,32ln r n n a a a a 成等差数列.(I)证明212211,,3(1P P n m d p d p d m ≤≤+==是m 的多项式),并求21P P +的值; (Ⅱ)当3,121==d d 时,将数列}{m d 分组如下:),(1d ),,,,,(),,,(98765432d d d d d d d d …(每组数的个数构成等差数列),设前m 组中所有数之和为m m c c ()(4),0>求数列}*2{m c d 的前挖项和n s . (Ⅲ)设N 是不超过20的正整数,当N n >时,对于(Ⅱ)中的,n s 求使得不等式n n d S >-)6(501成立的所有N 的值.。
朝阳高三二模数学理含答案

北京市朝阳区高三年级第二次综合练习数学学科测试 (理工类)2018.5(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知集合2{log 1}A x x =>,{}1B x x =≥,则A B U = A .(1,2] B .(1+)∞, C .(1)2, D .[1+)∞, 2.在ABC △中,π=1,==6AB AC C ∠,则B ∠= A .4π B .4π或2πC .43π D .4π或43π 3.执行如图所示的程序框图,则输出的S 值为A .10B .13C .40D .1214.在极坐标系中,直线:cos sin 2l ρθρθ+=与圆:2cos C ρθ=的位置关系为A .相交且过圆心B .相交但不过圆心C .相切D .相离5.如图,角α,β均以Ox 为始边,终边与单位圆O 分别交于点A ,B ,则OA OB ⋅u u u r u u u r=A .)sin(βα-B .)sin(βα+C .)cos(βα-D .)cos(βα+ 6.已知函数22,,(),,x x a f x x x a ⎧≥=⎨<⎩则“0a ≤”是“函数()f x 在[0,)+∞上单调递增”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.某校象棋社团组织中国象棋比赛.采用单循环赛制,即要求每个参赛选手必须且只须和其他选手各比赛一场,胜者得2分,负者得0分,平局两人各得1分.若冠军获得者得分比其他人都多,且获胜场次比其他人都少,则本次比赛的参赛人数至少为A .4B .5C .6D .78.若三个非零且互不相等的实数123,,x x x 成等差数列且满足123112x x x +=,则称123,,x x x 成一个“β等差数列”.已知集合{}100,M x x x =≤∈Z ,则由M 中的三个元素组成的所有数列中,“β等差数列”的个数为A .25B .50C .51D .100第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上. 9.计算21=(1i)+______. 10.双曲线22(0)x y λλ-=≠的离心率是_____;该双曲线的两条渐近线的夹角是______. 11.若31()n x x -展开式的二项式系数之和为8,则n =____,其展开式中的含31x项的系数为______.(用数字作答)12.已知某三棱锥的三视图如图所示,则该三棱锥底面和三个侧面中,直角三角形个数是___.13.已知不等式组0,2,1(1)y x y y k x ≥⎧⎪+≤⎨⎪+≥+⎩在平面直角坐标系xOy 中所表示的平面区域为D ,D 的面积为S ,则下面结论:①当0k >时,D 为三角形; ②当0k <时,D 为四边形;③当13k =时,4S =; ④当103k <≤时,S 为定值.其中正确的序号是______.14.如图,已知四面体ABCD 的棱AB //平面α,且AB =其余的棱长均为1.四面体ABCD 以AB 所在的直线为轴旋转x正视图侧视图俯视图弧度,且始终在水平放置的平面α的上方.如果将四面体ABCD 在平面α内正投影面积看成关于x 的函数,记为()S x ,则函数()S x 的最小值为 ;()S x 的最小正周期为 . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)已知函数()2sin (sin cos )f x x x x a =+-的图象经过点(,1)2π,a ∈R . (Ⅰ)求a 的值,并求函数()f x 的单调递增区间;(Ⅱ)若当[0,]2x π∈时,不等式()f x m ≥恒成立,求实数m 的取值范围. 16.(本小题满分13分)某市旅游管理部门为提升该市26个旅游景点的服务质量,对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分.每项评分最低分0分,最高分100分.每个景点总分为这五项得分之和.根据考核评分结果,绘制交通得分与安全得分散点图、交通得分与景点总分散点图如下:请根据图中所提供的信息,完成下列问题:(Ⅰ)若从交通得分前5名的景点中任取1个,求其安全得分大于90分的概率;(Ⅱ)若从景点总分排名前6名的景点中任取3个,记安全得分不大于90分的景点个数为ξ,求随机变量ξ的分布列和数学期望;(Ⅲ)记该市26个景点的交通平均得分为1x ,安全平均得分为2x ,写出1x 和2x 的大小关系? (只写出结果) 17.(本小题满分14分)如图,在四棱锥P ABCD -中,平面PBC ⊥平面ABCD .△PBC 是等腰三角形,且3PB PC ==;在梯形ABCD 中,AB DC P ,AD DC ⊥,5,4,3AB AD DC ===.(Ⅰ)求证://AB 面PDC ;(Ⅱ)求二面角A PB C --的余弦值;(Ⅲ)在线段AP 上是否存在点H ,使得BH ⊥平面ADP ?请说明理由.18.(本小题满分13分)已知函数2()e 2x f x x ax ax =++()a ∈R .(Ⅰ)若曲线()y f x =在点(0,(0))f 处的切线方程为30x y +=,求a 的值; (Ⅱ)当102a -≤<时,讨论函数()f x 的零点个数. 19. (本小题满分14分)已知抛物线2:2C y x =.(Ⅰ)写出抛物线C 的准线方程,并求抛物线C 的焦点到准线的距离;(Ⅱ)过点(2,0)且斜率存在的直线l 与抛物线C 交于不同两点,A B ,且点B 关于x 轴的对称点为D ,直线AD 与x 轴交于点M .(ⅰ)求点M 的坐标;(ⅱ)求OAM ∆与OAB ∆面积之和的最小值. 20. (本小题满分13分)若无穷数列{}n a 满足:存在*(,,)p q a a p q p q =∈>N ,并且只要p q a a =,就有(1,2,3,p i q i a ta i ++==L ;t 为常数),则称{}n a 具有性质T .(Ⅰ)若{}n a 具有性质T ,且3t =,12454,5,1,5a a a a ====,78936a a a ++=,求3a ;(Ⅱ)若无穷数列{}n a 的前n 项和为n S ,且2nn S b =+(b ∈R ),证明存在无穷多个b 的不同取值,使得数列{}n a 具有性质T ;(Ⅲ)设{}n b 是一个无穷数列,数列{}n a 中存在p q a a =*(,,)p q p q ∈>N ,且*1cos ()n n n a b a n +=∈N .求证:“{}n b 为常数列”是“对任意正整数1,{}n a a 都具有性质T ”的充分不必要条件.北京市朝阳区高三年级第二次综合练习数学学科测试答案(理工类)2018.5三、解答题:(本题满分80分) 15. (本小题满分13分) 解:(Ⅰ)根据题意得2sin(sin cos )1222a πππ+-=. 即2(10)1a ⨯+-=,解得1a =.又()2sin (sin cos )1f x x x x =+-22sin 2sin cos 1x x x =+-sin 2cos2x x =-)4x π=-由222242k x k πππ-+π≤-≤+πk (∈)Z ,得322244k x k ππ-+π≤≤+π,所以388k x k ππ-+π≤≤+π, 所以函数()f x 的单调递增区间是3[,88k k k ππ-+π+π](∈)Z . ……7分(Ⅱ)由(Ⅰ)可知())4f x x π=-.当[0,]2x π∈时,2[,]444x ππ3π-∈-,所以sin(2)124x π-≤-≤.所以1()f x -≤≤当244x ππ-=-,即0x =时,()f x 取得最小值1-. 因为不等式()f x m ≥恒成立等价于()m f x ≤最小值, 所以 1m ≤-.故实数m 的取值范围是(,1]-∞-. ……13分16.(本小题满分13分)解:(Ⅰ)由图可知,交通得分前5名的景点中安全得分大于90分的景点有3个. 故从交通得分前5名的景点中任取1个,其安全得分大于90分的概率为35.……3分 (Ⅱ)由图可知,景点总分前6名的景点中安全得分不大于90分的景点有2个. 设从景点总分前6名的景点中任取3个,安全得分不大于90分的个数为ξ,则ξ的取值为0,1,2.所以343641(0)205C P C ξ====; 122436123(1)205C C P C ξ====;21243641(2)205C C P C ξ====.故ξ的分布列为所以130121555E ξ=⨯+⨯+⨯=. ……10分 (Ⅲ)12x x >. ……13分17.(本小题满分14分) 证明:(Ⅰ)因为AB DC P ,又因为AB PDC ⊄平面,DC PDC ⊂平面, 所以//AB 平面PDC . ……3分(Ⅱ)取BC 中点F ,在PBC △中,因为PB PC =,所以PF BC ⊥.又易知5,AC AB ==所以AF BC ⊥.又因为平面PBC ⊥平面ABCD ,且平面PBC I 平面=ABCD BC , 所以PF ⊥平面ABCD .所以PF AF ⊥.以F 为原点,建立如图所示的空间直角坐标系F xyz -.在梯形ABCD 中,因为AB DC P ,AD DC ⊥,4,3AD DC ==,5AB =,所以BC =,AF =又因为3PB =,所以2PF =.于是有(0,0,2),(0,P A B C .所以FA =u u u r,(AB =-u u u r,2)PB =-u u u r.因为AF ⊥平面PBC,所以FA =u u u r是平面PBC 的一个法向量.设平面PBA 的一个法向量为(,,)x y z =m ,则0,0,AB PB ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u r m m即0,20.z ⎧-+=⎪-=所以2,2.y x z =⎧⎪= 令2y =,则=m .所以cos ,FA <>=u u u r m . 由图可知,二面角A PB C --为锐角,所以二面角A PB C --. ……9分 (Ⅲ)因为5,3AB DC ==,且(AB =-u u u r ,所以35CD AB =-u u u r u u ur .所以25AD AB BC CD AB BC =++=+u u u r u u u r u u u r u u u r u u u r u u u r2((0,(5=-+-=.设平面ADP 的一个法向量为111(,,)x y z =n ,则0,0,AD AP ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n即11110,20.y z ⎧=⎪⎨⎪-+=⎩所以11112,.x y z =-⎧⎪= 令12x =,则(2,=-n .假设线段AP 上存在点H ,使得BH ⊥平面ADP ,且设([0,1])AH AP λλ=∈u u u r u u u r.所以((,0,2)AH AP λλλ==-=-u u u r u u u r.所以(,0,2)),)BH BA AH λλλ=+=+-=-u u u r u u u r u u u r. 因为BH ⊥平面ADP ,所以//BH u u u rn .=λ不存在. 所以假设不成立,故线段AP 上不存在点H ,使得BH ⊥平面ADP .……14分 18.(本小题满分13分)解:由题意可知()(1)(e 2)xf x x a '=++.(Ⅰ)因为曲线()y f x =在点(0,(0))f 处的切线方程为30x y +=,所以(0)0,f =(0) 3.f '=- 由0e 23a +=-得2a =-. ……4分 (Ⅱ)当102a -≤<时,令()(1)(e 2)0x f x x a '=++=得1x =-或ln(2)x a =-. ①当ln(2)1a -<-,即1(,0)2ea ∈-时, 当x 变化时,()f x ',()f x 的变化情况如下表:所以函数()f x 在(ln(2),1)a --上单调递减,在(,ln(2))a -∞-和(1,)-+∞上单调递增.又因为2(ln(2))ln (2)0f a a a -=-<, (0)0f =,所以函数()f x 有一个零点. ②当ln(2)1a -=-,即12ea =-时, 当x 变化时,()f x ',()f x 的变化情况如下表:所以函数()f x 在(,+)-∞∞上单调递增. 又因为(0)0f =,所以函数()f x 有一个零点. ③当1ln(2)0a -<-<,即11(,)22ea ∈--时, 当x 变化时,()f x ',()f x 的变化情况如下表:所以函数()f x 在(1,ln(2))a --上单调递减,在(,1)-∞-和(ln(2),)a -+∞上单调递增.又因为22(2)2e +442e0f a a ---=--=-<,1(1)ef a -=--,2(ln(2))ln (2)0f a a a -=-<,(0)0f =,所以当11(,)e 2e a ∈--时,此时1(1)0e f a -=--<,函数()f x 有一个零点;当1ea =-时,此时(1)0f -=,函数()f x 有两个零点;当11(,)2e a ∈--时,此时1(1)0ef a -=-->,函数()f x 有三个零点.④当ln(2)0a -=,即12a =-时,显然函数()f x 有两个零点.综上所述,(1)当1(,0)e a ∈-时,函数()f x 有一个零点;(2)当11{,}e 2a ∈--时,函数()f x 有两个零点;(3)当11(,)2ea ∈--时,函数()f x 有三个零点. ……13分 另外的解法提示:()(e 2)xf x x ax a =++,易知(0)0f =.即可考虑()e 2x g x ax a =++的零点.19.(本小题满分14分)解:(Ⅰ)由题意可知,抛物线的准线方程为12x =-. 抛物线C 的焦点到准线的距离为1. ……4分(Ⅱ)由已知设直线:(2)l y k x =-,显然0k ≠;11(,)A x y ,22(,)B x y ,12x x ≠.由22,(2),y x y k x ⎧=⎨=-⎩得2240ky y k --=. 所以122y y k+=, 124y y =-. (ⅰ)因为点,B D 关于x 轴对称,所以22(,)D x y -.所以直线AD 的方程为121112()y y y y x x x x +-=--.令0y =,得11211212211212()()x y y y x x x y x y x y y y y +--+==++2212211212122()2y y y y y y y y +===-+. 所以(2,0)M -. ……10分(ⅱ)记OAM ∆与OAB ∆面积分别为OAM S ∆,OAB S ∆,设(2,0)P则11211+()22OAM OAB S S OM y OP y y ∆∆=⨯+⨯+ 122y y =+≥==当且仅当212y y =,即12y y ==mOAM ∆与OAB ∆面积之和的最小值是. ……14分20. (本小题满分13分)解:(Ⅰ)因为{}n a 具有性质T ,且3t =,525a a ==,所以633,a a =7433,a a ==85315,a a ==96339,a a a ==由78936a a a ++=,得3315936,a ++=所以32a =,经检验符合题意. ……3分 (Ⅱ)证明:因为无穷数列{}n a 的前n 和为n S ,且2n n S b =+,所以12a b =+,当2n ≥时,11222n n n n a --=-=.若存在()p q a a p q =>,则1q =.取122(,p b p -=-∈N 且2p ≥,p 为常数),则112p p a a -==,对12p t -=,有111122(1,2,3,)p i p p i i i a a ta i +--+++====L ,所以{}n a 具有性质T ,且b 的不同取值有无穷多个. ……8分 (Ⅲ)证明:当{}n b 为常数列时,有n b m =(常数),*1cos ()n n a m a n +=∈N , 对任意的正整数1a ,因为存在p q a a =,则由cos cos p q m a m a =,必有11p q a a ++=,进而有(1,2,3,p i q i a a i ++==L ),这时1t =,(1,2,3,p i q i a ta i ++==L ), 所以{}n a 都具有性质T .所以,“{}n b 为常数列”是“对任意正整数1,{}n a a 都具有性质T ”的充分条件. 取,21,20,2n n k b k n k *π⎧=-⎪=∈⎨⎪=⎩N (),,对任意正整数1a ,由11cos (2,)n n n a b a n n --=≥∈N 得,2111cos cos 2a b a a π==,因为1a 为正整数,所以20a ≠,且12a a ≠. 322cos 0a b a ==,433cos 2a b a π==,…, 即,当3n ≥时,0,21,,22,2n n k a k n k *=+⎧⎪=∈⎨π=+⎪⎩N (). 对任意,p q ,则,p q 同为奇数或同为偶数.① 若,p q 同为偶数,则(1,2,3,)p i q i a a i ++==L 成立;② 若,p q 同为奇数,则(1,2,3,)p i q i a a i ++==L 成立.所以对于任意,p q 满足p q a a =,则取1t =,1p i q i a a ++=⨯.故{}n a 具有性质T ,但{}n b 不为常数列,所以“{}n b 为常数列”是“对任意正整数1,{}n a a 都具有性质T ”的不必要条件. 证毕 ……13分。
北京市朝阳区年高三二模数学理科答案

(Ⅰ)由已知得 f (x) 2e2x1 a .
……………14 分
因为曲线在点处的切线与直线 x ey 1 0 垂直,
所以 f (0) e .所以 f (0) 2e a e .
所以 a e .
……………3 分
(Ⅱ)函数的定义域是, f (x) 2e2x1 a .
所以从全市高中学生中任意选取一人,其参加社区服务时间不少于 90 小时的
概率估计为 P 60 20 80 2 . 200 200 5
……………5 分
(Ⅱ)由(Ⅰ)可知,从全市高中生中任意选取 1 人,其参加社区服务时间不少于 90
2 小时的概率为 .
5
中国权威高考信息资源门户
0.
(8km)2 4(3 4k 2 )(4m2 12) 0 ,化简得 3 4k 2 m2 .
设 A(x1, y1), B(x2 , y2 ) ,则
x1
x2
8km 3 4k 2
,
x1x2
4m2 12 3 4k 2
.
若 OA 2OB OA 2OB 成立,
2 2
k
k 1
k
由Tk
x1k r x2r ,得 Tk 1
x x k 1r r
1
2
x1
x1k r x2r x2k 1 .
r0
r0
r0
即 Tk 1
x1Tk
xk 1 2
.
所以 Tk x1Tk1 x2k , x2Tk x1x2Tk 1 x2k 1 .
所以 Tk1 x1Tk (x2Tk x1x2Tk1) (x1 x2 )Tk x1x2Tk1 .
则 FG = (x1, y1 1, z1) . 由(Ⅱ)可知平面 EDF 的一个法向量是 n = (1, 1, 3)
北京朝阳高考二模数学理高中教育文档

北京市朝阳区高三年级第二次综合练习数学学科测试(理工类)第一部分(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知集合}{|230A x x =∈-R ≥,集合}{2|320B x x x =∈-+<R ,则A B = ( ).A .3|2x x ⎧⎫⎨⎬⎭⎩≥B .3|22x x ⎧⎫<⎨⎬⎭⎩≤C .}{|12x x <<D .3|22x x ⎧⎫<<⎨⎬⎭⎩2.如果0a b >>,那么下列不等式一定成立的是( ).A .33log log a b <B .11()()44a b >C .11a b< D .22a b <3.执行如右图所示的程序框图,若输出的结果为2,则输入的正整数a 的可能取值的集合是( ).A .}{1,2,3,4,5B .}{1,2,3,4,5,6C .}{2,3,4,5D .}{2,3,4,5,64.已知函数π()sin()(0,0,)2f x A x A ωϕωϕ=+>><的部分图像如右图所示,则ϕ=( ).A .π6-B .π6C .π3-D .π35.已知命题:p 复数1iiz +=在复平面内所对应的点位于第四象限;命题:q 0x ∃>,cos x x =,则下列命题中为真命题的是( ).A .()()p q ⌝∧⌝B .()p q ⌝∧C .()p q ∧⌝D .p q ∧(P )M NDCBA 6.若双曲线2221(0)y x b b-=>的一条渐近线与圆22(2)1x y +-=至多有一个交点,则双曲线离心率的取值范围是( ).A .(1,2]B .[2,)+∞C .(1,3]D .[3,)+∞7.某工厂分别生产甲、乙两种产品1箱时所需要的煤、电以及获得的纯利润如下表所示.煤(吨) 电(千度) 纯利润(万元)1箱甲产品 31 2 1箱乙产品11 1若生产甲、乙两种产品可使用的煤不超过120吨,电不超过60千度,则可获得的最大纯利润和是( ). A .60万元 B .80万元 C .90万元 D .100万元8.如图放置的边长为1的正PMN △沿边长为3的正方形ABCD 的各边内侧逆时针方向滚动.当PMN △沿正方形各边滚动一周后,回到初始位置时,点P 的轨迹长度是( ). A .8π3 B .16π3C .4πD .5π第二部分(非选择题共110分)二、填空题(本大题共6小题,每小题5分,共30分)9.已知平面向量a ,b 满足1=a ,2=b ,a 与b 的夹角为60︒,则2+=a b __________.10.5(12)x -的展开式中3x 项的系数为___________.(用数字表示)11.如图,AB 为圆O 的直径,2AB =,过圆O 上一点M 作圆O 的切线,交AB 的延长线于点C ,过点M作MD AB ⊥于点D ,若D 是OB 中点.则•AC BC =___________.12.由两个四棱锥组合而成的空间几何体的三视图如图所示,则其体积是________;表面积是_________.13.已知数列{}n a 的前n 项和为n S ,且满足24n n S a =-*()n ∈N ,则n a =_________;数列{}2log n a 的前n 项和为_____________.ODMCBA14.若存在正实数M ,对于任意(1,)x ∈+∞,都有()≤f x M ,则称函数()f x 在(1,)+∞上是有界函数.下列函数① 1()1f x x =-;②2()1x f x x =+;③ln ()x f x x=;④()sin f x x x =, 其中“在(1,)+∞上是有界函数”的序号为__________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)在ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,且2π3A =,3b =,ABC △的面积为1534. (I )求边a 的边长;(II )求cos 2B 的值.16.(本题满分13分)某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200学生参加社区服务的数据,按时间段[)75,80,[)80,85,[)85,90,[)90,95,[]95,100(单位:小时)进行统计,其频率分布直方图如图所示.(I )求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率; (II )从全市高中学生(人数很多)中任意选取3位学生,记ξ为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量ξ的分布列和数学期望E ξ.17.(本小题满分14分)-中,底面ABCD是正方形,侧面PAD⊥底面ABCD,,E F分别为PA,BD中如图,在四棱锥P ABCD点,2===.PA PD ADEF平面PBC;(I)求证://(II)求二面角E DF A--的余弦值;(III)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.18.(本小题满分13分)已知函数21()e 1,x f x ax a +=-+∈R .(I )若曲线()y f x =在点(0,(0))f 处的切线与直线e 10x y ++=垂直,求a 的值; (II )求函数()f x 的单调区间;(III )设32e a <,当[0,1]x ∈时,都有()1f x …成立,求实数a 的取值范围.19.(本小题满分14分)已知椭圆C 的中心在原点O ,焦点在x 轴上,离心率为12,右焦点到到右顶点的距离为1. (I )求椭圆C 的标准方程;(II )是否存在与椭圆C 交于A ,B 两点的直线l :()y kx m k =+∈R ,使得22OA OB OA OB +=-uu r uu u r uu r uu u r成立?若存在,求出实数m 的取值范围,若不存在,请说明理由.20.(本小题满分13分)已知12,x x 是函数2()f x x mx t =++的两个零点,其中常数,m t ∈Z ,设120nn r rn r T x x -==∑(*n ∈N ).(I )用,m t 表示1T ,2T ; (II )求证:543T mT tT =--;(III )求证:对任意的*n ∈N ,n T ∈Z .北京市朝阳区高三年级第二次综合练习数学学科测试(理工类)2014.5一、选择题(满分40分)题号1 2 34 5 6 7 8 答案B C C DDACB二、填空题(满分30分)题号 9 10 11121314答案2380- 382383 12n +(3)2n n + ②③三、解答题(满分80分) 15.(本小题满分13分) 解:(Ⅰ)由1sin 2ABC S bc A ∆=得,11533sin 234ABC S c ∆2π=⨯⨯=. 所以5c =.由2222cos a b c bc A =+-得,22235235cos493a 2π=+-⨯⨯⨯=, 所以7a =.……………7分(Ⅱ)由sin sin a bA B=得,73sin 32B =, 所以33sin 14B =. 所以271cos 212sin 98B B =-=.……………13分 16.(本小题满分13分) 解:(Ⅰ)根据题意,参加社区服务时间在时间段[)90,95小时的学生人数为2000.060560⨯⨯=(人), 参加社区服务时间在时间段[]95,100小时的学生人数为2000.020520⨯⨯=(人). 所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为80人. 所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率估计为6020802.2002005P +===……………5分(Ⅱ)由(Ⅰ)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为2.5由已知得,随机变量ξ的可能取值为0,1,2,3.所以00332327(0)()()55125P C ξ==⋅=; 11232354(1)()()55125P C ξ==⋅=;22132336(2)()()55125P C ξ==⋅=;3303238(3)()()55125P C ξ==⋅=.随机变量ξ的分布列为ξ0 1 2 3P27125 54125 36125 8125 因为ξ~2(3)5B ,,所以26355E ξ=⨯=.……………13分 17.(本小题满分14分)证明:(Ⅰ)如图,连结AC . 因为底面ABCD 是正方形,所以AC 与BD 互相平分. 又因为F 是BD 中点, 所以F 是AC 中点.在△PAC 中,E 是PA 中点,F 是AC 中点, 所以EF ∥PC .又因为EF ⊄平面PBC ,PC ⊂平面PBC , 所以EF ∥平面PBC .……………4分(Ⅱ)取AD 中点O .在△PAD 中,因为PA PD =, 所以PO AD ⊥.因为面PAD ⊥底面ABCD , 且面PAD 面=ABCD AD , 所以PO ⊥面ABCD .因为OF ⊂平面ABCD 所以PO OF ⊥. 又因为F 是AC 中点,所以OF AD ⊥.如图,以O 为原点,,,OA OF OP 分别为,,x y z 轴建立空间直角坐标系.OxyzFA BC DP E E P DCBAF因为2PA PD AD ===,所以3OP =,则(,0)O ,(1,0,0)A ,(1,2,0)B ,(1,2,0)C -,(1,0,0)D -,(0,0,3)P ,13(,0,)22E ,(0,1,0)F . 于是(0,2,0)AB = ,33(,0,)22DE = ,(1,1,0)DF = . 因为OP ⊥面ABCD ,所以(0,0,3)OP = 是平面FAD 的一个法向量.设平面EFD 的一个法向量是000=(,,)x y z n .因为0,0,DF DE ⎧⋅=⎪⎨⋅=⎪⎩ n n 所以00000,330,22x y x z +=⎧⎪⎨+=⎪⎩即0000,3.y x z x =-⎧⎪⎨=-⎪⎩ 令01x =则=(1,1,3)--n . 所以315cos ,535OP OP OP ⋅-<>===⋅⋅ n n n. 由图可知,二面角E-DF-A 为锐角,所以二面角E-DF-A 的余弦值为155.…10分 (Ⅲ)假设在棱PC 上存在一点G ,使GF ⊥面EDF .设111(,,)G x y z , 则111=(,1,)FG x y z - .由(Ⅱ)可知平面EDF 的一个法向量是=(1,1,3)--n .因为GF ⊥面EDF ,所以=FG λ n . 于是,111,1,3x y z λλλ=-=-=-,即111,1,3x y z λλλ==-=-.又因为点G 在棱PC 上,所以GC 与PC 共线. 因为(1,2,3)PC =-- ,111(+1,2,)CG x y z =- , 所以11112123x y z +---==. 所以113123λλλ+-----==,无解. 故在棱PC 上不存在一点G ,使GF ⊥面EDF 成立.……………14分18.(本小题满分13分)(Ⅰ)由已知得21()2e x f x a +'=-.因为曲线()f x 在点(0,(0))f 处的切线与直线e 10x y ++=垂直,所以(0)e f '=.所以(0)2e e f a '=-=.所以e a =.……………3分(Ⅱ)函数()f x 的定义域是(),-∞+∞,21()2e x f x a +'=-.(1)当0a ≤时,()0f x '>成立,所以)(x f 的单调增区间为(),-∞+∞.(2)当0a >时,令()0f x '>,得11ln 222a x >-,所以()f x 的单调增区间是11(ln ,)222a -+∞; 令()0f x '<,得11ln 222a x <-,所以()f x 的单调减区间是11(,ln )222a -∞-. 综上所述,当0a ≤时,)(x f 的单调增区间为(),-∞+∞; 当0a >时,()f x 的单调增区间是11(ln ,)222a -+∞, ()f x 的单调减区间是11(,ln )222a -∞-.……………8分 (Ⅲ)当0x =时,(0)e 11f =+≥成立,a ∈R .“当(0,1]x ∈时,21()e 11x f x ax +=-+≥恒成立” 等价于“当(0,1]x ∈时,21e x a x+≤恒成立.” 设21e ()x g x x+=,只要“当(0,1]x ∈时,min ()a g x ≤成立.” 212(21)e ()x x g x x+-'=. 令()0g x '<得,12x <且0x ≠,又因为(0,1]x ∈,所以函数()g x 在1(0, )2上为减函数; 令()0g x '>得,12x >,又因为(0,1]x ∈,所以函数()g x 在1(,1]2上为增函数. 所以函数()g x 在12x =处取得最小值,且21()2e 2g =. 所以22e a ≤.又因为a 32e <,所以实数a 的取值范围22(,e ]-∞.……………13分(Ⅲ)另解:(1)当0a ≤时,由(Ⅱ)可知,()f x 在[0,1]上单调递增,所以()(0)e 1f x f ≥=+.所以当0a ≤时,有()1f x ≥成立.(2)当02e a <≤时,可得11ln 0222a -≤. 由(Ⅱ)可知当0a >时,()f x 的单调增区间是11(ln,)222a -+∞, 所以()f x 在[0,1]上单调递增,又()(0)e 1f x f ≥=+,所以总有()f x ≥1成立.(3)当32e 2e a <<时,可得110ln 1222a <-<. 由(Ⅱ)可知,函数()f x 在11[0,ln )222a -上为减函数,在11(ln ,1]222a -为增函数, 所以函数()f x 在11ln 222a x =-处取最小值, 且ln 211(ln )e ln 1ln 122222222a a a a a a a f a -=-++=-+.当[0,1]x ∈时,要使()f x ≥1成立,只需ln 1122a a a -+≥, 解得22e a ≤.所以22e 2e a <≤.综上所述,实数a 的取值范围22(,e ]-∞.19.(本小题满分14分) (Ⅰ)设椭圆C 的方程为22221x y a b+=()0a b >>,半焦距为c . 依题意12c e a ==,由右焦点到右顶点的距离为1,得1a c -=. 解得1c =,2a =.所以2223b a c =-=.所以椭圆C 的标准方程是22143x y +=.……………4分 (Ⅱ)解:存在直线l ,使得22OA OB OA OB +=- 成立.理由如下: 由22,1,43y kx m x y =+⎧⎪⎨+=⎪⎩得222(34)84120k x kmx m +++-=. 222(8)4(34)(412)0km k m ∆=-+->,化简得2234k m +>. 设1122(,),(,)A x y B x y ,则122834km x x k +=-+,212241234m x x k -=+. 若22OA OB OA OB +=- 成立, 即2222OA OB OA OB +=- ,等价于0OA OB ⋅= .所以12120x x y y +=.1212()()0x x kx m kx m +++=,221212(1)()0k x x km x x m ++++=,222224128(1)03434m km k km m k k-+⋅-⋅+=++, 化简得,2271212m k =+. 将227112k m =-代入2234k m +>中,22734(1)12m m +->, 解得,234m >. 又由227121212m k =+≥,2127m ≥, 从而2127m ≥,2217m ≥或2217m ≤-. 所以实数m 的取值范围是22(,21][21,)77-∞-+∞ .……………14分 20.(本小题满分13分)解:(Ⅰ)由12x x m +=-,12x x t =.因为120n n r r n r T xx -==∑,所以11112120r r r T x x x x m -===+=-∑. 222222212112212120()r r r T x x x x x x x x x x m t -===++=+-=-∑.…………3分(Ⅱ)由120k k r r k r T x x -==∑,得 545455512112214200r r r r r r T xx x x x x x T x --====+=+∑∑. 即55142T x T x =+,同理,44132T x T x =+.所以5241232x T x x T x =+.所以5142412312412343()()T x T x T x x T x x T x x T mT tT =+-=+-=--.……………8分 (Ⅲ)用数学归纳法证明.(1)当1,2n =时,由(Ⅰ)问知k T 是整数,结论成立. (2)假设当1,n k =-n k =(2k ≥)时结论成立,即1,k k T T -都是整数. 由120k k r r k r T xx -==∑,得111112112200k k k r r k r r k k r r T x x x x x x ++--++====+∑∑. 即1112k k k T x T x ++=+.所以112k k k T xT x -=+,121212k k k x T x x T x +-=+.所以11212112121()()k k k k k k T x T x T x x T x x T x x T +--=+-=+-. 即11k k k T mT tT +-=--.由1,k k T T -都是整数,且m ,t ∈Z ,所以1k T +也是整数. 即1n k =+时,结论也成立.由(1)(2)可知,对于一切n *∈N ,120n n r r r x x -=∑的值都是整数.………13分。
高考数学 答案

最新整理北京市朝阳区2011年高三一模试卷
数学(理科)参考答案及评分标准2011.4
北京市朝阳区2011年高三二模试卷
数学(理科)参考答案及评分标准2011.5
北京市朝阳区2012年高三一模试卷
数学(理科)参考答案及评分标准2012.4
北京市朝阳区2012年高三二模试卷
数学(理科)参考答案及评分标准2012.5
北京市朝阳区2013年高三一模试卷
数学(理科)参考答案及评分标准2013.4
北京市朝阳区2013年高三二模试卷
数学(理科)参考答案及评分标准2013.5
北京市朝阳区2014年高三一模试卷
数学(理科)参考答案及评分标准2014.4
北京市朝阳区2014年高三二模试卷
数学(理科)参考答案及评分标准2014.5
.。
2011年北京市各区二模试题分类解析(12)圆锥曲线

此时AS的方程为 , ,
所以 ,要使 的面积为 ,
只需点T到直线AS的距离等于 ,
所以点T在平行于AS且与AS距离等于 的直线 上
设 ,则由 ,解得
1当 时,由 得
由于 ,故直线 与椭圆C有两个不同交点
② 时,由 得
由于 ,故直线 与椭圆C没有交点
综上所求点T的个数是2.…
所以 (此时直线 经过定点 ,与椭圆有两个交点),
所以
.……………12分
设 ,
则 .
所以当 时, 取得最大值 .
8、(2011昌平二模文19)(本小题满分14分)
已知椭圆C: 的左焦点为 (-1,0),离心率为 ,过点 的直线 与椭圆C交于 两点.
(Ⅰ)求椭圆C的方程;
(II)设过点F不与坐标轴垂直的直线交椭圆C于A、 B两点,线段AB的垂直平分线与 轴交于点G,求点G横坐标的取值范围.
则 , ,………………………………………10分
, .
所以 ………………………………………12分
.
所以 为定值 .…
11、(2011丰台二模文19)(本小题共14分)
已知椭圆C的长轴长为 ,一个焦点的坐标为(1,0).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l:y=kx与椭圆C交于A,B两点,点P为椭圆的右顶点.
设 ,
则 ,………………13分
当且仅当 时取等号,
所以 面积的最大值为 .………………14分
方法二:不妨设直线 的方程 .
由 消去 得 ,………………6分
设 , ,
则有 , . ①………………7分
因为以 为直径的圆过点 ,所以 .
由 ,
北京市朝阳区高三数学第二次综合练习试题 理 (朝阳二模)新人教A版

北京市朝阳区2011-2012学年度高三年级第二次综合练习数学试卷(理工类)(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)注意事项:考生务必将答案答在答题卡上,在试卷上答无效。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知全集R U =,集合{}21x A x =>,{}2340B x x x =-->,则U AB ð=A .{}04x x ≤< B .{}04x x <≤ C .{}10x x -≤≤ D .{}14x x -≤≤ 2.复数z 满足等式(2i)i z -⋅=,则复数z 在复平面内对应的点所在的象限是 A .第一象限 B .第二象限 C .第三象限 D . 第四象限3.已知双曲线2215x y m -=(0m >)的右焦点与抛物线212y x =的焦点相同,则此双曲线的离心率为A .6B .32 D . 344.在△ABC 中, 2AB =,3AC =,0AB AC ⋅<,且△ABC 的面积为32,则BAC ∠ 等于A .60或120B .120C .150D .30或150 5.在直角坐标系xOy 中,直线l 的参数方程为,4x t y t=⎧⎨=+⎩(t 为参数).以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为)4ρθπ=+,则直 线l 和曲线C 的公共点有A .0个B .1个C .2个D .无数个 6.下列命题::p 函数44()sin cos f x x x =-的最小正周期是π;:q 已知向量(1)λ,=a ,2(1),λ=-b ,(11)-,=c ,则(+)//a b c 的充要条件是1λ=-;:r 若111adx =x⎰(1a >),则e =a . 其中所有的真命题是A .rB .,p qC .,q rD .,p r 7.直线y x =与函数22,,()42,x m f x x x x m >⎧=⎨++≤⎩的图象恰有三个公共点,则实数m 的取 值范围是A .[1,2)-B .[1,2]-C .[2,)+∞D .(,1]-∞- 8.有一个棱长为1的正方体,按任意方向正投影, 其投影面积的最大值是A. 1第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在答题卡上. 9.二项式25(+ax 展开式中的常数项为5,则实数a =_______.10.执行如图所示的程序框图,输出的结果是_______.11.若实数,x y 满足10,0,x y x -+≤⎧⎨≤⎩则22x y +的最小值是 .(第10题图)12.如图,AB 是圆O 的直径,CD AB ⊥于D ,且2AD BD =,E 为AD 的中点,连接CE 并延长交圆O 于F .若CD =则AB =_______, EF =_________.13. 一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加 投资1万元,年产量为x (x *∈N )件.当20x ≤时,年销售总收入为(233x x -)万元;当20x >时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y 万元,则y (万元)与x (件)的函数关系式为 ,该工厂的年产量为 件时,所得年利润最大.(年利润=年销售总收入-年总投资)14.在如图所示的数表中,第i 行第j 列的数记为,i j a ,且满足11,,12,j j i a a i -==,1,1,1,(,)N i j i j i j a a a i j *+++=+∈,则此数表中的 第5行第3列的数是 ;记第3行的 数3,5,8,13,22, ⋅⋅⋅ 为数列{}n b ,则数列 {}n b 的通项公式为 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.把答案答在答题卡上.15. (本小题满分13分)已知函数()2cos cos f x x x x m =-+()R m ∈的图象过点π(,0)12M . (Ⅰ)求m 的值;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c .若cos +cos =2cos c B b C a B , 求()f A 的取值范围.16. (本小题满分13分)一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.(Ⅰ)求取出的3个球颜色相同且编号是三个连续整数的概率; (Ⅱ)求取出的3个球中恰有2个球编号相同的概率;(Ⅲ)记X 为取出的3个球中编号的最大值,求X 的分布列与数学期望.第1行 1 2 4 8 … 第2行 2 3 5 9 … 第3行 3 5 8 13 …17. (本小题满分14分)在如图所示的几何体中,四边形ABCD 为正方形,⊥EA 平面ABCD ,//EF AB , =4,=2,=1AB AE EF .(Ⅰ)若点M 在线段AC 上,且满足14CM CA =, 求证://EM 平面FBC ; (Ⅱ)求证:⊥AF 平面EBC ; (Ⅲ)求二面角--A FB D 的余弦值. 18. (本小题满分14分)已知函数22()ln (0)a f x a x x a x=++≠.(Ⅰ)若曲线()y f x =在点(1,(1))f 处的切线与直线20x y -=垂直,求实数a 的值; (Ⅱ)讨论函数()f x 的单调性;(Ⅲ)当(,0)a ∈-∞时,记函数()f x 的最小值为()g a ,求证:21()e 2g a ≤. 19. (本小题满分13分)在平面直角坐标系xOy中,已知点(A,B ,E 为动点,且直线EA 与直线EB 的斜率之积为12-. (Ⅰ)求动点E 的轨迹C 的方程;(Ⅱ)设过点(1,0)F 的直线l 与曲线C 相交于不同的两点M ,N .若点P 在y 轴上,且 PM PN =,求点P 的纵坐标的取值范围. 20.(本小题满分13分) 已知数列12:,,,n n A a a a (,2)n n ∈≥*N 满足01==n a a ,且当n k ≤≤2()*N k ∈时,1)(21=--k k a a ,令1()nn i i S A a ==∑.(Ⅰ)写出)(5A S 的所有可能的值; (Ⅱ)求)(n A S 的最大值;(Ⅲ)是否存在数列n A ,使得2(3)()4n n S A -=?若存在,求出数列n A ;若不存在,说明理由.E CBDMA F北京市朝阳区高三年级第二次综合练习 数学答案(理工类) 2012.5二、填空题:9. 1 10. 13 11.1212. 3 ,3 13. 2**32100,020,,160,20,,N N x x x x y x x x ⎧-+-<≤∈=⎨->∈⎩16 14. 16,121n n a n -=++三、解答题:15. (本小题满分13分) 解:(Ⅰ)由()12(cos 21)22f x x x m =-++π1sin(2)62x m =--+.……3分因为点π(,0)12M 在函数()f x 的图象上, 所以ππ1sin(2)01262m ⋅--+=, 解得12m =. ……5分(Ⅱ) 因为cos +cos =2cos c B b C a B ,所以sin cos sin cos C B B C +=2sin cos A B ,所以sin(+)2sin cos B C A B =,即sin 2sin cos A A B =. ……7分 又因为(0,A ∈π),所以sin 0A ≠,所以1cos 2B =. ……8分 又因为(0,B ∈π),所以π3B =,2π3A C +=. ……10分所以2π03A <<, ππ7π2666A -<-<,所以πsin(2)6A -∈1(,1]2-.…12分所以()f A 的取值范围是1(,1]2-. ……13分16. (本小题满分13分) 解:(Ⅰ)设“取出的3个球颜色相同且编号是三个连续整数”为事件A ,则39325()84P A C +==.答:取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率为584.…4分 (Ⅱ)设“取出的3个球中恰有两个球编号相同”为事件B ,则114739281()843C C P B C ===.答:取出的3个球中恰有两个球编号相同的概率为13. ……8分 (Ⅲ)X 的取值为2,3,4,5.12212222391(2)21C C C C P X C +===, 12212424394(3)21C C C C P X C +===,12212626393(4)7C C C C P X C +===, 1218391(5)3C C P X C ===. ……11分所以X 的分布列为X 的数学期望234521217321EX =⨯+⨯+⨯+⨯=. ……13分17. (本小题满分14分)证明:(Ⅰ)过M 作MN BC ⊥于N ,连结FN ,则MN //AB ,又14CM AC =,所以14MN AB =.又EF //AB 且14EF AB =,所以EF //MN ,且EF MN =, 所以四边形EFNM 为平行四边形,所以EM //FN .又FN ⊂平面FBC ,EM ⊄平面FBC ,所以//EM 平面FBC . ……4分(Ⅱ)因为⊥EA 平面ABCD ,⊥AB AD ,故以A 为原点,建立如图所示的空间直角坐标系-A xyz .由已知可得(0,0,0),(4,0,0),(4,4,0),(0,4,0),A B C D (0,0,2),(1,0,2)E F .显然=(1,0,2),=(0,4,0),=(4,0,-2)AF BC EB . 则=0,=0⋅⋅AF BC AF EB , 所以,⊥⊥AF BC AF EB .即,⊥⊥AF BC AF EB ,故⊥AF 平面EBC .EDCM AF BN(Ⅲ)因为EF//AB ,所以EF 与AB 确定平面EABF ,由已知得,=(0,4,0),=(3,0,-2)BC FB ,=(4,4,0)-BD . ……9分 因为⊥EA 平面ABCD ,所以⊥EA BC . 由已知可得⊥AB BC 且=EA AB A ,所以⊥BC 平面ABF ,故BC 是平面ABF 的一个法向量. 设平面DFB 的一个法向量是()n =x,y,z .由0,0,n n ⎧⋅=⎪⎨⋅=⎪⎩BD FB 得440,320,-+=⎧⎨-=⎩x y x z 即32=⎧⎪⎨=⎪⎩y x,z x, 令2=x ,则(2,2,3)n =.所以cos <,n n n⋅>==⋅BC BC BC 由题意知二面角A-FB-D 锐角,故二面角A-FB-D . ……14分 18. (本小题满分14分)解:(I )()f x 的定义域为{|0}x x >.()()22210a a f x x x x '=-+>.根据题意,有()12f '=-,所以2230a a --=,解得1a =-或32a =. ……3分 (II )()()22222222()(2)10a a x ax a x a x a f x x x x x x+--+'=-+==>. (1)当0a >时,因为0x >,由()0f x '>得()(2)0x a x a -+>,解得x a >; 由()0f x '<得()(2)0x a x a -+<,解得0x a <<. 所以函数()f x 在(),a +∞上单调递增,在()0,a 上单调递减. (2)当0a <时,因为0x >,由()0f x '>得 ()(2)0x a x a -+>,解得2x a >-;由()0f x '<得()(2)0x a x a -+<,解得02x a <<-.所以函数()f x 在()0,2a -上单调递减,在()2,a -+∞上单调递增. ……9分 (III )由(Ⅱ)知,当(,0)a ∈-∞时,函数()f x 的最小值为()g a ,且22()(2)ln(2)2ln(2)32a g a f a a a a a a a a =-=-+-=---.2()ln(2)3ln(2)22g a a aa a -'=-+-=---, 令()0g a '=,得21e 2a =-.当a 变化时,()g a ',()g a 的变化情况如下表:2e 2-是()g a 在(,0)-∞上的唯一极值点,且是极大值点,从而也是()g a 的最大值点. 所以()22221111(e )e ln[2(e )]3(e )2222最大值g a g =-=--⨯---2222131e ln e e e 222=-+=.所以,当(,0)a ∈-∞时,21()e 2g a ≤成立. ……14分19. (本小题满分13分)解:(Ⅰ)设动点E 的坐标为(,)x y 12=-,整理得221(2x y x +=≠. 所以动点E 的轨迹C 的方程为221(2x y x +=≠. ………5分 (II )当直线l 的斜率不存在时,满足条件的点P 的纵坐标为0. ………6分 当直线l 的斜率存在时,设直线l 的方程为(1)y k x =-.将(1)y k x =-代入2212x y +=并整理得,2222(21)4220k x k x k +-+-=. 2880k ∆=+>.设11(,)M x y ,22(,)N x y ,则2122421k x x k +=+, 21222221k x x k -=+.设MN 的中点为Q ,则22221Q k x k =+,2(1)21Q Q k y k x k =-=-+, 所以2222(,)2121k kQ k k -++. ………9分由题意可知0k ≠,又直线MN 的垂直平分线的方程为22212()2121kk y x k k k +=--++. 令0x =解得21212P k y k k k==++. .………10分当0k >时,因为12k k +≥04P y <≤=; 当0k <时,因为12k k +≤-04P y >≥=-………12分 综上所述,点P纵坐标的取值范围是[. .………13分 20.(本小题满分13分)解:(Ⅰ)由题设,满足条件的数列5A 的所有可能情况有: (1)01210,,,,.此时5()=4S A ;(2)01010,,,,.此时5()=2S A ; (3)01010,,,,.-此时5()=0S A ;(4)01210,,,,.---此时5()=4S A -; (5)01010,,,,.-此时5()=0S A ;(6)01010,,,,.--此时5()=2S A -; 所以,)(5A S 的所有可能的值为:4,2,0,2-,4-. ……4分(Ⅱ)由1)(21=--k k a a ,可设11k k k a a c ---=,则11k c -=或11k c -=-(n k ≤≤2,k ∈*N ),因为11n n n a a c ---=,所以 11221n n n n n n a a c a c c -----=+=++11221n n a c c c c --==+++++.因为01==n a a ,所以1210n c c c -+++=,且n 为奇数,121,,,n c c c -是由21-n 个1和21-n 个1-构成的数列.所以112121()()()n n S A c c c c c c -=+++++++1221(1)(2)2n n n c n c c c --=-+-+++.则当121,,,n c c c -的前21-n 项取1,后21-n 项取1-时)(n A S 最大, 此时)(n A S 11(1)(2)(21)22n n n n +-=-+-++-+++2(1)4n -=.证明如下:假设121,,,n c c c -的前21-n 项中恰有t 项12,,t m m m c c c 取1-,则 121,,,n c c c -的后21-n 项中恰有t 项12,,,t n n n c c c 取1,其中112n t -≤≤, 112i n m -≤≤,112i n n n -<≤-,1,2,,i t =. 所以()n S A 1211212211(1)(2)222n n n n n n n c n c c c c c -+--+-=-+-++++++11(1)(2)(21)22n n n n +-=-+-++-+++122[()()()]t n m n m n m --+-++-122[()()()]t n n n n n n +-+-++-221(1)(1)2()44ti i i n n n m =--=--<∑. 所以)(n A S 的最大值为2(1)4n -. ……9分(Ⅲ)由(Ⅱ)可知,如果121,,,n c c c -的前21-n 项中恰有t 项12,,,t m m m c c c 取1-,121,,,n c c c -的后21-n 项中恰有t 项12,,,t n n n c c c 取1,则21(1)()2()4tn i ii n S A n m =-=--∑,若2(3)()4n n S A -=,则122()ti i i n n m =-=-∑,因为n 是奇数,所以2-n 是奇数,而12()tiii n m =-∑是偶数,因此不存在数列nA ,使得4)3()(2-=n A S n . ……13分。
2011北京朝阳中考二模数学(含解析)

5 / 15
五、解答题(本题共 22 分,第 23 题 7 分,第 24 题 7 分,第 25 题 8 分) 23.若 △ABC 和 △ADE 均为等边三角形, M 、 N 分别是 BE 、 CD 的中点. (1)当 △ADE 绕 A 点旋转到如图①的位置时,求证: CD BE , △AMN 是等边三角形; (2)如图②,当 EAB 30 , AB 12 , AD 2 3 时,求 AM 的长.
1 6 4 3 2 1 4 5 3
8.如图(甲) ,扇形 OAB 的半径 OA 6 ,圆心角 AOB 90 ,C 是弧 AB 上不同于 A 、 B 的动点, 2 E O B 于点 E , 过点 C 作 CD OA 于点 D , 作C 连结 DE , 点 H 在线段 DE 上, 且 EH DE . 设 3 EC 的长为 x , △CEH 的面积为 y ,图(乙)中表示 y 与 x 的函数关系式的图象可能是( ) .
1 16.解: (1)令 y 0 ,则 x 3 0 ,解得 x 6 . 2 ∴ A(6 , 0) .
令 x 0 ,则 y 3 . ∴ B(0 , 3) . (2)∵点 P 在直线 y ∴ P(2 , 2) . ∴过点 P 的反比例函数图象的解析式为 y 17. (1)证明:连接 AH , 依题意,正方形 ABCD 与正方形 AEFG 全等,
1 / 15
图(甲)
A.
B.
图(乙)
C.
D.
二、填空题(本题共 16 分,每小题 4 分) 9.若二次根式 2 x 4 有意义,则 x 的取值范围是 10.若等腰三角形两边长分别为 2 和 5 ,则它的周长是
. . .
11.若关于 x 的一元二次方程 kx2 2 x 1 0 有实数根,则 k 的取值范围是
数学_2011年北京市朝阳区高考数学二模试卷(理科)(含答案)

2011年北京市朝阳区高考数学二模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1. 已知全集U =R ,集合A ={x|0<2x <1},B ={x|log 3x >0},则A ∩(∁U B)=( ) A {x|x >1} B {x|x >0} C {x|0<x <1} D {x|x <0}2. 设x ,y ∈R ,那么“x >y >0”是“xy >1”的( )A 必要不充分条件B 充分不必要条件C 充分必要条D 既不充分又不必要条件3. 三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形.若三棱柱的正视图(如图所示)的面积为8,则侧视图的面积为( )A 8B 4C 4√3D √34. 已知随机变量X 服从正态分布N(a, 4),且P(X >1)=0.5,则实数a 的值为( ) A 1 B √3 C 2 D 45. 若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”.现从1,2,3,4,5,6这六个数字中任取3个数,组成无重复数字的三位数,其中“伞数”有( ) A 120个 B 80个 C 40个 D 20个6. 点P 是抛物线y 2=4x 上一动点,则点P 到点A(0, −1)的距离与到直线x =−1的距离和的最小值是( )A √5B √3C 2D √27. 已知棱长为1的正方体ABCD −A 1B 1C 1D 1中,点E ,F 分别是棱BB 1,DD 1上的动点,且BE =D 1F =λ(0<λ≤12).设EF 与AB 所成的角为α,与BC 所成的角为β,则α+β的最小值( )A 不存在B 等于60C 等于90D 等于1208. 已知点P 是△ABC 的中位线EF 上任意一点,且EF // BC ,实数x ,y 满足PA →+xPB →+yPC →=0.设△ABC ,△PBC ,△PCA ,△PAB 的面积分别为S ,S 1,S 2,S 3,记S 1S =λ1,S 2S =λ2,S3S=λ3.则λ2⋅λ3取最大值时,2x +y 的值为( )A 32 B 12 C 1 D 2二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上. 9. 已知复数z 满足iz =1−i ,则z =________.10. 曲线C:{x =cosθ−1y =sinθ+1(θ为参数)的普通方程为________.11. 曲线y =3−3x 2与x 轴所围成的图形面积为________.12. 已知数列{a n }满足a 1=2,且a n+1a n +a n+1−2a n =0,n ∈N ∗,则a 2=________;并归纳出数列{a n }的通项公式a n =________.13. 如图,PA 与圆O 相切点A ,PCB 为圆O 的割线,并且不过圆心O ,已知∠BPA =30∘,PA =2√3,PC =1,则PB =________;圆O 的半径等于________.14. 已知函数f(x)=ax 2+(b +1)x +b −1,且a ∈(0, 3),则对于任意的b ∈R ,函数F(x)=f(x)−x 总有两个不同的零点的概率是________.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. 已知函数f(x)=2sinx ⋅sin(π2+x)−2sin 2x +1(x ∈R).(1)求函数f(x)的最小正周期及函数f(x)的单调递增区间; (2)若f(x02)=√23,x 0∈(−π4,π4),求cos2x 0的值.16. 为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为16,第二轮检测不合格的概率为110,两轮检测是否合格相互没有影响. (1)求该产品不能销售的概率;(2)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损80元(即获利−80元).已知一箱中有产品4件,记一箱产品获利X 元,求X 的分布列,并求出均值E(X).17. 在长方形AA 1B 1B 中,AB =2AA 1=4,C ,C 1分别是AB ,A 1B 1的中点(如图1).将此长方形沿CC 1对折,使二面角A 1−CC 1−B 为直二面角,D ,E 分别是A 1B 1,CC 1的中点(如图2).(1)求证:C 1D // 平面A 1BE ;(2)求证:平面A 1BE ⊥平面AA 1B 1B ;(3)求直线BC 1与平面A 1BE 所成角的正弦值. 18. 设函数f(x)=lnx +(x −a)2,a ∈R .(1)若a =0,求函数f(x)在[1, e]上的最小值;(2)若函数f(x)在[12,2]上存在单调递增区间,试求实数a 的取值范围;(3)求函数f(x)的极值点. 19. 已知椭圆C :x 2a2+y 2b 2=1(a >b >0)经过点A(2, 1),离心率为√22.过点B(3, 0)的直线l与椭圆C 交于不同的两点M ,N . (1)求椭圆C 的方程; (2)求BM →⋅BN →的取值范围;(3)设直线AM 和直线AN 的斜率分别为k AM 和k AN ,求证:k AM +k AN 为定值.20. 对于正整数a ,b ,存在唯一一对整数q 和r ,使得a =bq +r ,0≤r <b .特别地,当r =0时,称b 能整除a ,记作b|a ,已知A ={1, 2, 3, ..., 23}.(Ⅰ)存在q ∈A ,使得2011=91q +r(0≤r <91),试求q ,r 的值;(Ⅱ)求证:不存在这样的函数f:A →{1, 2, 3},使得对任意的整数x 1,x 2∈A ,若|x 1−x 2|∈{1, 2, 3},则f(x 1)≠f(x 2);(Ⅲ)若B ⊆A ,card(B)=12(card(B)指集合B 中的元素的个数),且存在a ,b ∈B ,b <a ,b|a ,则称B 为“和谐集”.求最大的m ∈A ,使含m 的集合A 的有12个元素的任意子集为“和谐集”,并说明理由.2011年北京市朝阳区高考数学二模试卷(理科)答案1. D2. B3. C4. A5. C6. D7. C8. A9. −1−i10. (x +1)2+(y −1)2=1 11. 4 12. 43,2n 2n −113. 12,7 14. 1315. 解:(1) f(x)=2sinx ⋅cosx −2sin 2x +1… =sin2x +cos2x… =√2sin(2x +π4).… 故函数f(x)的最小正周期T =2π2=π.…令2kπ−π2≤2x +π4≤2kπ+π2(k ∈Z),…可得2kπ−3π4≤2x ≤2kπ+π4,即kπ−3π8≤x ≤kπ+π8,k ∈z ,所以,函数f(x)的单调递增区间为[kπ−3π8,kπ+π8](k ∈Z).…(2)解法一:由已知得f(x02)=sinx 0+cosx 0=√23,… 两边平方,可得1+sin2x 0=29,所以,sin2x 0=−79. …因为x 0∈(−π4,π4),所以2x 0∈(−π2,π2), 所以,cos2x 0=√1−(−79)2=4√29.… 解法二:因为x 0∈(−π4,π4),所以x 0+π4∈(0,π2).… 又因为f(x02)=√2sin(2⋅x 02+π4)=√2sin(x 0+π4)=√23, 解得 sin(x 0+π4)=13.…所以,cos(x 0+π4)=√1−(13)2=2√23.… 所以,cos2x 0=sin(2x 0+π2)=sin[2(x 0+π4)]=2sin(x 0+π4)cos(x 0+π4) =2⋅13⋅2√23=4√29.… 16. 解 (1)记“该产品不能销售”为事件A ,则P(A)=1−(1−16)×(1−110)=14.所以,该产品不能销售的概率为14.…(2)由已知,可知X 的取值为−320,−200,−80,40,160.… P(X =−320)=(14)4=1256,P(X =−200)=C 41⋅(14)3⋅34=364, P(X =−80)=C 42⋅(14)2⋅(34)2=27128, P(X =40)=C 43⋅14⋅(34)3=2764,P(X =160)=(34)4=81256.…所以X 的分布列为E(X)=−320×1256−200×364−80×27128+40×2764+160×81256=40 所以,均值E(X)为40.…17.(1)证明:由已知,将长方形AA 1B 1B 沿CC 1对折后,二面角A 1−CC 1−B 为直二面角,因为在长方形AA 1B 1B 中,C ,C 1分别是AB ,A 1B 1的中点,所以CC 1⊥BC ,CC 1⊥AC .即∠ACB 是二面角A 1−CC 1−B 的平面角. 所以∠ACB =90∘.所以BC ⊥AC . 所以CA ,CB ,CC 1两两垂直.以点C 为原点,分别以CA ,CB ,CC 1为x ,y ,z 轴,建立空间直角坐标系.… 因为AB =2AA 1=4,且D ,E 分别是A 1B 1,CC 1的中点,所以C 1(0, 0, 2),D(1, 1, 2),A 1(2, 0, 2),B(0, 2, 0),E(0, 0, 1).… 所以C 1D →=(1,1,0),A 1B →=(−2,2,−2),BE →=(0,−2,1). 设平面A 1BE 的法向量为n =(x, y, z), 所以{n ⋅A 1B →=0n ⋅BE →=0所以{−2x +2y −2z =0−2y +z =0令y =1,则z =2,x =−1. 所以n =(−1, 1, 2).…又因为C 1D →⋅n =(1,1,0)⋅(−1,1,2)=0. 所以C 1D →⊥n .又因为C 1D ⊄平面A 1BE , 所以C 1D // 平面A 1BE .…(2)证明:由(1)知A(2, 0, 0),A 1(2, 0, 2),B(0, 2, 0),AA 1→=(0,0,2),AB →=(−2,2,0). 设平面AA 1B 1B 的法向量为m =(x, y, z),所以{m ⋅AA 1→=0m ⋅AB →=0所以{2z =0−2x +2y =0令y =1,则x =1,z =0,所以m =(1, 1, 0).… 由(1)知,平面A 1BE 的法向量为n =(−1, 1, 2). 所以m ⋅n =(1, 1, 0)⋅(−1, 1, 2)=0.所以m ⊥n .所以平面A 1BE ⊥平面AA 1B 1B .…(3)解:由(1)知,B(0, 2, 0),C 1(0, 0, 2).所以BC 1→=(0,−2,2). 又由(1)知,平面A 1BE 的法向量为n =(−1, 1, 2).…设直线BC 1与平面A 1BE 所成角为θ,则sinθ=|cos <n,BC 1→>|=|n⋅BC 1→|n|⋅|BC 1→||=2√2⋅√6=√36. 所以直线BC 1与平面A 1BE 所成角的正弦值为√36.… 18. 解:(1)f(x)的定义域为(0, +∞).… 因为f′(x)=1x +2x >0,所以f(x)在[1, e]上是增函数,当x =1时,f(x)取得最小值f(1)=1. 所以f(x)在[1, e]上的最小值为1.… (2)解法一:f′(x)=1x +2(x −a)=2x 2−2ax+1x设g(x)=2x 2−2ax +1,…依题意,在区间[12,2]上存在子区间使得不等式g(x)>0成立.…注意到抛物线g(x)=2x 2−2ax +1开口向上, 所以只要g(2)>0,或g(12)>0即可.…由g(2)>0,即8−4a +1>0,得a <94,由g(12)>0,即12−a +1>0,得a <32, 所以a <94,所以实数a 的取值范围是(−∞,94).…解法二:f′(x)=1x +2(x −a)=2x 2−2ax+1x,…依题意得,在区间[12, 2]上存在子区间使不等式2x 2−2ax +1>0成立. 又因为x >0,所以2a <(2x +1x ).…设g(x)=2x +1x ,所以2a 小于函数g(x)在区间[12, 2]的最大值.又因为g′(x)=2−1x 2,由g′(x)=2−1x 2>0,解得x >√22; 由g′(x)=2−1x 2<0,解得0<x <√22. 所以函数g(x)在区间(√22,2)上递增,在区间(12,√22)上递减. 所以函数g(x)在x =12,或x =2处取得最大值. 又g(2)=92,g(12)=3,所以2a <92,a <94所以实数a 的取值范围是(−∞,94).… (3)因为f′(x)=2x 2−2ax+1x,令ℎ(x)=2x 2−2ax +1①显然,当a ≤0时,在(0, +∞)上ℎ(x)>0恒成立,这时f ′(x)>0,此时,函数f(x)没有极值点; … ②当a >0时,(1)当△≤0,即0<a ≤√2时, 在(0, +∞)上ℎ(x)≥0恒成立, 这时f ′(x)≥0,此时,函数f(x)没有极值点; … (2)当△>0,即a >√2时, 易知,当a−√a 2−22<x <a+√a 2−22时,ℎ(x)<0,这时f ′(x)<0; 当0<x <a−√a 2−22或x >a+√a 2−22时,ℎ(x)>0,这时f ′(x)>0; 所以,当a >√2时,x =a−√a 2−22是函数f(x)的极大值点;x =a+√a 2−22是函数f(x)的极小值点.…综上,当a ≤√2时,函数f(x)没有极值点; 当a >√2时,x =a−√a 2−22是函数f(x)的极大值点;x =a+√a 2−22是函数f(x)的极小值点.…19. 解:(1)由题意得{4a 2+1b 2=1a 2=b 2+c 2c a =√22.,解得a =√6,b =√3.故椭圆C 的方程为x 26+y 23=1.(2)由题意显然直线l 的斜率存在,设直线l 方程为y =k(x −3), 由{y =k(x −3)x 26+y 23=1得(1+2k 2)x 2−12k 2x +18k 2−6=0.因为直线l 与椭圆C 交于不同的两点M ,N ,所以△=144k 4−4(1+2k 2)(18k 2−6)=24(1−k 2)>0,解得−1<k <1.设M ,N 的坐标分别为(x 1, y 1),(x 2, y 2),则x 1+x 2=12k 21+2k 2,x 1x 2=18k 2−61+2k 2,y 1=k(x 1−3),y 2=k(x 2−3). 所以BM →⋅BN →=(x 1−3)(x 2−3)+y 1y 2 =(1+k 2)[x 1x 2−3(x 1+x 2)+9]=3+3k 21+2k 2=32+32(1+2k 2).因为−1<k <1,所以2<32+32(1+2k 2)≤3.故BM →⋅BN →的取值范围为(2, 3]. (3)由(2)得k AM +k AN =y 1−1x 1−2+y 2−1x 2−2=(kx 1−3k −1)(x 2−2)+(kx 2−3k −1)(x 1−2)(x 1−2)(x 2−2)=2kx 1x 2−(5k +1)(x 1+x 2)+12k +4x 1x 2−2(x 1+x 2)+4=2k(18k 2−6)−(5k+1)⋅12k 2+(12k+4)(1+2k 2)18k 2−6−24k 2+4(1+2k 2)=−4k 2+42k 2−2=−2.所以k AM +k AN 为定值−2.20. (1)因为2011=91×22+9,所以q =22,r =9.(2)证明:假设存在这样的函数f:A →{1, 2, 3},使得对任意的整数x ,y ,若|x −y|∈{1, 2, 3},则f(x)≠f(y).设f(1)=a ,a ∈{1, 2, 3},f(2)=b ,b ∈{1, 2, 3},由已知a ≠b ,由于|3−1|=2,|3−2|=1,所以f(3)≠f(1),f(3)≠f(2).不妨令f(3)=c ,c ∈{1, 2, 3},这里c ≠a ,且c ≠b ,同理,f(4)≠b ,且f(4)≠c ,因为{1, 2, 3}只有三个元素,所以f(4)=a .即f(1)=f(4),但是|4−1|=3,与已知矛盾. 因此假设不成立,即不存在这样的函数f:A →{1, 2, 3},使得对任意的整数x ,y ,若|x −y|∈{1, 2, 3},则f(x)≠f(y).(Ⅲ)当m =8时,记M ={7+i|i =1, 2, ..., 16},N ={2(7+i)|i =1, 2, 3, 4}记P =∁M N ,则card(P)=12,显然对任意1≤i <j ≤16,不存在n ≥3,使得7+j =n(7+i)成立.故P 是非“和谐集”,此时P ={8, 9, 10, 11, 12, 13, 14, 15, 17, 19, 21, 23}.同样的,当m =9,10,11,12时,存在含m 的集合A 的有12个元素的子集为非“和谐集”.因此m ≤7. 下面证明:含7的任意集合A 的有12个元素的子集为“和谐集”.设B ={a 1, a 2, ..., a 11, 7},若1,14,21中之一为集合B 的元素,显然为“和谐集”. 现考虑1,14,21都不属于集合B ,构造集合B 1={2, 4, 8, 16},B 2={3, 6, 12},B 3={5, 10, 20},B 4={9, 18},B 5={11, 22},B ′={13, 15, 17, 19, 23}.以上B 1,B 2,B 3,B 4,B 5每个集合中的元素都是倍数关系.考虑B ′⊆B 的情况,也即B ′中5个元素全都是B的元素,B中剩下6个元素必须从B1,B2,B3,B4,B5这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,即集合B中至少有两个元素存在倍数关系.综上所述,含7的任意集合A的有12个元素的子集B为“和谐集”,即m的最大值为7.。
