应用MATLAB建模实例---吊门过程仿真
如何通过MATLAB进行模拟与仿真

如何通过MATLAB进行模拟与仿真MATLAB是一种用于科学计算、数据分析和可视化的强大工具,它也是进行模拟和仿真的理想选择。
通过MATLAB,用户可以编写脚本或函数来描述和模拟各种现象,并通过可视化结果来验证和分析模拟过程。
在本文中,我们将介绍如何使用MATLAB进行模拟和仿真,包括建模、求解、可视化和分析。
首先,建立一个模型是进行模拟和仿真的第一步。
在MATLAB中,可以使用符号计算工具箱或数值计算方法来建立模型。
符号计算工具箱提供了一种使用符号表达式而不是数值进行计算的方法,这对于一些复杂系统的建模非常有用。
数值计算方法则使用数值解来近似求解模型。
在MATLAB中,可以通过定义变量和方程来建立模型。
例如,假设我们要建立一个简单的弹簧振动系统的模型,可以使用如下的方程:m*x''+k*x=0其中,m是质量,x是位移,k是弹簧常数。
我们可以使用MATLAB的符号计算工具箱来定义这个方程:syms x(t) m keqn = m * diff(x, t, t) + k * x == 0这样,我们就建立了一个描述弹簧振动系统的方程。
接下来,我们需要求解这个方程。
在MATLAB中,可以使用ode45函数来求解常微分方程。
例如,使用ode45函数求解上面的方程,并绘制振动的位移随时间的变化曲线:tspan = [0 10]; % 时间范围x0=1;%初始位移v0=0;%初始速度parameters = {m, k}; % 参数figure;plot(t, x(:, 1))xlabel('时间')ylabel('位移')title('弹簧振动')function dxdt = spring_ode(t, x, m, k)dxdt = [x(2); -k/m * x(1)];end在上面的代码中,我们定义了一个名为spring_ode的函数来描述弹簧振动的常微分方程。
自动实验一——典型环节的MATLAB仿真 报告
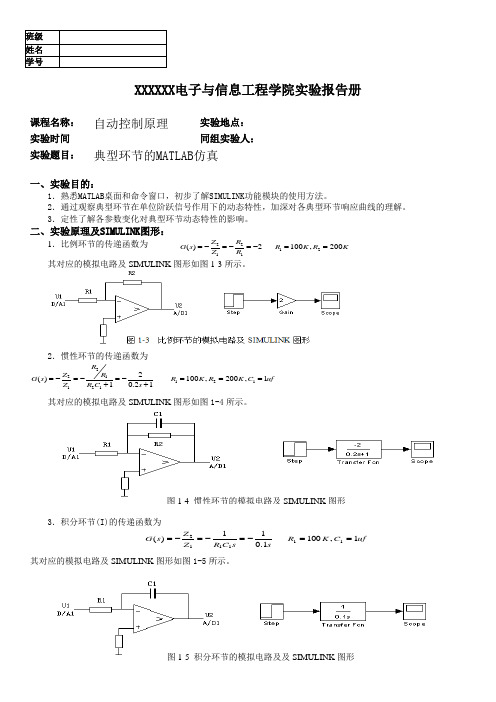
班级 姓名 学号XXXXXX 电子与信息工程学院实验报告册课程名称:自动控制原理 实验地点: 实验时间同组实验人: 实验题目: 典型环节的MATLAB 仿真一、实验目的:1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理及SIMULINK 图形:1.比例环节的传递函数为 221211()2100,200Z R G s R K R K Z R =-=-=-==其对应的模拟电路及SIMULINK 图形如图1-3所示。
2.惯性环节的传递函数为2211211212()100,200,110.21R Z R G s R K R K C uf Z R C s =-=-=-===++其对应的模拟电路及SIMULINK 图形如图1-4所示。
3.积分环节(I)的传递函数为uf C K R s s C R Z Z s G 1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK 图形如图1-5所示。
图1-5 积分环节的模拟电路及及SIMULINK 图形 图1-4 惯性环节的模拟电路及SIMULINK 图形4.微分环节(D)的传递函数为uf C K R s s C R Z Z s G 10,100)(111112==-=-=-= uf C C 01.012=<<其对应的模拟电路及SIMULINK 图形如图1-6所示。
5.比例+微分环节(PD )的传递函数为)11.0()1()(111212+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<=== 其对应的模拟电路及SIMULINK 图形如图1-7所示。
6.比例+积分环节(PI )的传递函数为)11(1)(11212s R s C R Z Z s G +-=+-=-= uf C K R R 10,100121===其对应的模拟电路及SIMULINK 图形如图1-8所示。
如何利用Matlab进行模拟和仿真实验

如何利用Matlab进行模拟和仿真实验Matlab是一种功能强大的数学计算和数据可视化软件。
它不仅可以进行数学模拟和仿真实验,还可以处理数据、绘制图表和实施算法。
在工程、物理学、生物学等领域,Matlab被广泛用于解决各种实际问题。
本文将介绍如何利用Matlab进行模拟和仿真实验,并探讨其在实验设计和结果分析中的应用。
一. Matlab的基本功能Matlab具有很多基本功能,如矩阵操作、数值计算、符号计算等。
这些功能使得Matlab成为进行模拟和仿真实验的理想选择。
在Matlab中,可以定义和操作矩阵,进行线性代数运算,如求解方程组、矩阵求逆等。
此外,Matlab还提供了许多内置函数,可以进行数值计算和符号计算,如求解微分方程、积分、数值优化等。
二. 模拟实验的设计在进行模拟实验之前,首先需要设计实验方案。
实验设计包括选择合适的模型和参数设置,确定实验变量和观测指标等。
在Matlab中,可以使用函数或脚本来定义模型和参数,通过修改参数值来观察实验结果的变化。
比如,可以使用Matlab的模型库来选择合适的模型,然后使用函数传入参数值进行求解。
此外,Matlab还提供了绘图功能,可以绘制实验结果的图表,以便更直观地分析数据。
三. 仿真实验的实施在设计好实验方案后,就可以开始进行仿真实验了。
在Matlab中,可以使用已定义的模型和参数进行仿真计算。
可以通过Matlab的编程功能来实现计算过程的自动化。
比如,可以使用循环语句来迭代计算,以观察参数变化对结果的影响。
此外,Matlab还提供了随机数生成和统计分析函数,可以用于生成随机变量和分析实验数据。
四. 实验结果的分析在完成仿真实验后,需要对实验结果进行分析。
Matlab提供了丰富的数据处理和分析工具,可以对实验数据进行统计分析、绘图和可视化展示。
可以使用Matlab的数据处理函数来计算均值、标准差、相关系数等统计指标。
此外,Matlab还可以通过绘图函数来绘制直方图、散点图、线图等图形,以便更好地理解和展示数据。
基于Matlab的吊车-双摆系统控制

2
一、吊车-双摆系统控制的描述 吊车 双摆系统控制的描述
吊车-双摆系统是一个非线性、多变量的复 杂系统,是检验各种控制理论的理想模型。 实际的吊车需要将货物尽可能快地运送到目 的地,并在移动过程中不能有大的晃动,这 就要求吊车在移动过程中保持上下摆角平稳 而且小车本身又要达到指定的位置,这些要 求可通过电机的控制来实现。
(
) (
)
10
对系统在平衡点附近做线性化处理,进行受力分析,结合以上系统的拉格朗 日方程然后进行线性化处理,取状态变量
x x ɺ α x= ɺ α β ɺ β
可得关于小车、上摆角、下摆角的状态方程:
1 0 0 −(m1 + m2 )gr 2 −KeKt 0 Ra(Mr 2 + J ) Mr 2 + J 0 0 0 ɺ x= −KeKt −[(M + m1 + m2 )r 2 + J ]g 0 2 (Mr 2 + J )L1 Ra(Mr + J ) 0 0 0 [(M + m1 + m2 )r 2 + J ]g KeKt 0 2 (Mr 2 + J )L1 Ra(Mr + J )
17
主程序: 主程序 cdp.m %control for Crane Double Pendulum clear all; close all; global K A=[ 0 1.0000 0 0 0 0;0 -58.1558 -13.3099 0 0 0 ;0 0 0 1.0000 0 0;0 -73.7445 -112.7311 0 79.6748 0;0 0 0 0 0 1.0000;0 73.7445 112.7311 0 -247.1962 0] B=[0;9.48888;0;46.275;0;-46.275] C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0;0 0 0 1 0 0;0 0 0 0 1 0; 0 0 0 0 0 1] D=[0 0 0 0 0 0]' Q=[1000 0 0 0 0 0;0 1 0 0 0 0;0 0 100 0 0 0;0 0 0 1 0 0;0 0 0 0 100 0;0 0 0 0 0 1]; R=[0.1]; K=lqr(A,B,Q,R); cdpsim;
MatlabSimulink系统建模和仿真

图:电容的充电、放电过程的仿真结果。在充电仿真中,输出信号 为系统的零状态响应。在放电过程仿真中,输出信号为系统的零输 入响应。 如果要仿真系统输入信号为任意函数的情况,只需要修改仿 真程序中的输入信号设臵即可。
“实例2.3”单摆运动过程的建模和仿真。 (1)单摆的数学模型 设单摆摆线的固定长度为l ,摆线的质量忽略不计,摆锤质 量为m ,重力加速度为g ,设系统的初始时刻为t=0 ,在任 意 t 0 时刻摆锤的线速度为v(t) ,角速度为 w(t ) ,角位移 为 (t ) 。以单摆的固定位臵为坐标原点建立直角坐标系, 水平方向为x 轴方向。如下图所示。
图:电容的充电电路以及等价系统
(1)数学分析
首先根据网络拓扑和元件伏安特性建立该电路方程组
dy (t ) i (t ) C dt
dy (t ) 1 1 x(t ) y (t ) dt RC RC
y(t ) x(t ) Ri (t )
并化简得
该方程也称为系统的状态方程。在方程中,变量y 代表电 容两端的电压,是电容储能的函数。本例中它既是系统的 状态变量,又是系统的输出变量。
7.1 Matlab编程仿真的方法
7.1.1 概述 通过编程的形式建立计算机仿真模型是最基本的 计算机建模方法。Matlab编程仿真过程就是用编 写脚本文件或函数文件来描述数学模型,并实现 计算机数值求解的过程。 我们把外界对系统产生作用的物理量称为输入 信号或激励,把由于系统内部储存的能量称为系 统的状态,而将系统对外界的作用物理量称为系 统的输出信号或响应。
图:模拟真实示波器显示的调幅仿真波形,仿真中考虑了输 入信号与示波器扫描不同步,载波相位噪声以及加性信道噪 声的影响
7.1.3 连续动态系统的Matlab编程仿真 7.1.3.1 几个实例
如何在Matlab中进行模拟和仿真

如何在Matlab中进行模拟和仿真引言:模拟和仿真是数字化时代不可替代的工具,在众多领域具有广泛的应用。
Matlab作为一种强大的数学计算软件,提供了丰富的工具和函数,可以帮助我们进行各种模拟和仿真分析。
本文将介绍如何在Matlab中进行模拟和仿真,以及一些常用的技巧和注意事项。
一、Matlab中的模拟和仿真工具1. Matlab的基本特性Matlab具有高效的计算能力和友好的用户界面,支持多种数学运算、绘图和数据处理功能。
它提供了丰富的工具箱,可以满足不同领域的模拟和仿真需求。
2. Matlab SimulinkMatlab Simulink是Matlab中的一款强大的系统仿真工具,可用于建立各种复杂的动态系统模型。
通过使用Simulink中的模块和线路连接,可以直观地建立并仿真各种系统,如电路、机械系统、控制系统等。
3. Matlab中的其他工具箱除了Simulink,Matlab还提供了许多其他工具箱,如Signal Processing Toolbox、Control System Toolbox、Communication Toolbox等,可以用于处理和分析特定领域的信号、控制和通信问题。
这些工具箱提供了丰富的函数和算法,大大简化了模拟和仿真的过程。
二、Matlab模拟和仿真的基本步骤1. 建立模型在进行模拟和仿真之前,首先需要明确模型的目标和要求。
然后,根据模型的特点和公式,使用Matlab提供的函数和工具箱,建立相应的数学模型。
可以根据需要将模型分为多个子系统,以便更好地组织和管理模型。
2. 参数设置模型建立完成后,需要设置各个参数的数值。
这些参数可能包括模型的物理特性、控制参数等。
根据具体情况,可以通过手工输入、数据拟合或对已有数据的分析来确定参数的取值。
3. 运行仿真参数设置完成后,即可运行仿真。
Matlab提供了多种仿真方法,如连续仿真、离散仿真、Monte Carlo仿真等。
第五讲 基于MATLAB-Simulink的建模与仿真

MATLAB软件简介?
MATLAB软件的典型应用领域:
❖科学研究; ❖工程技术应用研究 ❖CAI(Computer Aided Instruct) ❖数学实验(Mathematical Experiment) ❖数学建模(Mathematical Modeling)
模型 Transfer-Fcn:线性传递函数模型 Zero-Pole:以零极点表示的传递
函数模型 Memory:存储上一时刻的状态值 Transport Delay:输入信号延时 一个给定时间再输出 Variable Transport Delay:输入 信号延时一个可变时间再输出
✓ 离散模块(Discrete)
For循环不能用For循环内重新赋值循环变
量n来终止。
在For循环中循环控制量的范围可以是任
何有效的MATLAB矩阵。比如
data=[11 9 45 6; 7 16 -1 5];
for n=data
x=n(1)-n(2)
end 这时程序的输出有四个数值,分别是矩阵
data的两列相减的结果
x = 4 x = -7
x = 46 x = 1
For循环可按需要嵌套,即For循环体内的命 令组中可以出现另一个For循环体,这体现了 For循环体也是命令组。比如 for n=1:5
for m=5:-1:1
A(n,m)=n^2+m^2; End
end
MATLAB软件简介?
While-end循环以不定的次数求一组语句的值。 Whil-end 循环的一般形式是: while expression(控制表达式) {commands} end 只要在控制表达式(expression)里的所有元 素为真,就执行While和end语句之间的命令 串({commands})。
matlab的仿真流程总结

matlab的仿真流程总结下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!1. 问题定义与分析明确仿真的目的和要解决的问题。
确定系统的输入、输出和关键参数。
如何在Matlab中进行模拟仿真

如何在Matlab中进行模拟仿真在科学和工程领域中,模拟仿真是一种非常重要的工具,可以帮助实现对现实世界复杂问题的理解和分析。
而在这方面,Matlab是一个功能强大且广泛使用的软件平台,它提供了丰富的工具和函数,便于进行模拟仿真。
本文将介绍如何在Matlab中进行模拟仿真,并探讨其中的一些关键技巧和注意事项。
首先,要进行模拟仿真,我们需要有一个模型。
模型是对待研究问题的一种简化和抽象,它可以是数学方程、系统方程或者演化规则等形式。
在Matlab中,可以使用符号计算工具箱对模型进行推导和建立。
通过定义变量、方程和初始条件,可以将实际问题转化为计算机可以处理的形式。
一旦建立了模型,就可以开始进行仿真了。
在Matlab中,可以使用数值计算工具箱中的函数来求解微分方程、差分方程和代数方程等。
例如,ode45函数可以用于求解常微分方程,而ode15s函数则适合求解刚性方程。
此外,还有丰富的工具函数可以用于求解常微分方程组、偏微分方程和随机过程等。
除了求解方程,Matlab还提供了许多其他的工具和函数,用于分析和处理仿真结果。
例如,可以使用绘图函数来可视化仿真结果,帮助我们更好地理解问题。
Matlab中的绘图函数可以实现各种类型的图形,包括线图、散点图、柱状图、等高线图等。
此外,还可以使用统计工具箱中的函数进行数据分析和参数估计。
在进行模拟仿真时,我们还需要注意一些技巧和注意事项。
首先,要注意选择合适的数值方法和精度。
不同的问题可能需要不同的数值方法,而选择适当的数值方法可以提高求解效率和准确性。
此外,要注意数值方法的稳定性和收敛性。
有时候,仿真结果可能会出现数值误差,这时可以考虑使用更高精度的方法或者增加计算步长来改善结果。
其次,要注意仿真中的参数选择和设置。
参数的选择会影响仿真结果的准确性和可靠性。
有时候,我们需要进行参数敏感性分析,即通过改变参数的值来观察仿真结果的变化情况。
这可以帮助我们了解模型的行为和性质,并指导进一步的研究和设计。
悬吊式起重机动力学仿真

Simulink仿真系统的的具体要求:1.根据以下悬吊式起重机结构建立系统动力学方程。
2.在Simuilink环境下建立仿真系统。
3.在MATLAB命令窗口输入相对应程序,点击运行。
4.设置系统初始值,保存之后点击按钮Start simulation进行查看scope具体步骤如下:1.悬吊式起重机动力学方程小车水平方向受力方程:吊绳垂直方向受力方程:小车的力矩平衡方程:())1(sin22θlxdtdmx cFxmpt---=())2(cos22θldtdmgmPpp=-)3(sincos)sin(22θθθθ IPllxdtdlmp=--式中,mt 、mp 、I 、c 、l 、F 、x 、 分别为起重机的小车质量、吊重、吊重惯量、等价粘性摩擦系数、钢丝绳长(不计绳重),小车驱动力、小车位移以及钢丝绳的摆角。
由(2)、(3)式去掉P ,则有在MATLAB 中建立Simulink仿真系统模型如下图:())74.9(sin 22----=θl x dt d m x c F x m p t ())84.9(cos sin 2-=++θθθx l m gl m l m I p p p2.在双击X2中弹出以下窗口设置摆动角度初始值0.01如下图:设置仿真时间为200s ,启动Simulink 仿真,则由小车位移示波器和吊重摆角示波器,可观察到系统在初始状态x(0)=0,,(0)=0.01rad/s, 作用下x 、θ的变化过程曲线:3.在运行仿真模型前,须先计算出k1、k2和lmp 。
设mt =50kg ,mp=270kg ,l=4m,0)0(=x 0)0(=θc=20N/m s,在MATLAB指令窗输入以下指令:l=4;c=20;mp=270;mt=50;I=mp*l^2; %计算吊重转动惯量lmp=l*mp;k1=1/(mt+mp);k2=mp*l/(I+mp*l^2);在simulink中点击保存运行之后查看两个scope视图如下所示:1.悬吊式起重机小车位移图:2.悬吊式起重机重摆角图:。
第三章 matlab的simulink建模与仿真

nonlinear control
4、提供仿真库的扩充和定制功能
5、应用领域
通信与卫星系统 航空航天
生物系统
汽车系统
船舶系统
金融系统
3、simulink在matlab家族中的位置
Stateflow Blockset Toolboxes coder RTW compiler
simulink MATLAB
第三章 matlab的simulink建模 与仿真
3.1 绪论
一、系统与模型
1、系统
系统是指具有某些特定功能,相互联系、相互作 用的元素集合。 系统的两个基本特征:整体性、相关性
对系统的研究从以下三个方面入手:
1)实体:组成系统的元素,对象
2)属性:实体的特征
3)活动:系统状态变化的过程
系统仿真是研究系统的一种重要手段,而系统模 型是仿真所研究的直接对象。 2、系统模型 实体模型:根据相似性建立 模型 数学模型:原始系统数学模型;仿真系统数学模型
连续系统的输入输出方程为: y(t ) u(t ) sin u(t ) u(t)与y(n)的数学关系为: u(t ) y(n), nTs t (n 1)Ts 整个系统的方程描述:
y (t ) u (n) n / 2, n 1,2,3... y (n) u (n) 1, y (n) sin( y (n)),n t n 1
Function&Tables(函数与表库)
表数据选择器(从表中选择数据) 求取输入信号的数学函数值 对输入信号进行内插运算 输入信号的一维线性内插 输入信号的二维线性内插
输入信号的n维线性内插
M函数(对输入进行运算输出结果) 多项式求值 查找输入信号所在范围 S-函数模块 S-函数生成器
实验一典型环节的MATLAB仿真

实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB 中SIMULINK 是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK 功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB 软件,在命令窗口栏“>>”提示符下键入simulink 命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK 仿真环境下。
2.选择File 菜单下New 下的Model 命令,新建一个simulink 仿真环境常规模板。
3.在simulink 仿真环境下,创建所需要的系统三、实验内容按下列各典型环节的传递函数,建立相应的SIMULINK 仿真模型,观察并记录其单位阶跃响应波形。
① 比例环节1)(1=s G 和2)(1=s G 实验处理:1)(1=s G SIMULINK 仿真模型波形图为:实验处理:2)(1=s G SIMULINK 仿真模型波形图为:实验结果分析:增加比例函数环节以后,系统的输出型号将输入信号成倍数放大.② 惯性环节11)(1+=s s G 和15.01)(2+=s s G 实验处理:11)(1+=s s GSIMULINK 仿真模型波形图为:实验处理:15.01)(2+=s s GSIMULINK 仿真模型波形图为:实验结果分析:当11)(1+=s s G 时,系统达到稳定需要时间接近5s,当15.01)(2+=s s G 时,行动达到稳定需要时间为2.5s,由此可得,惯性环节可以调节系统达到稳定所需时间,可以通过惯性环节,调节系统达到稳定输出的时间。
③ 积分环节s s G 1)(1=实验处理: SIMULINK 仿真模型实物图为:实验结果分析:由以上波形可以的出,当系统加入积分环节以后,系统的输出量随时间的变化成正比例增加。
MATLAB建模与仿真工具箱的使用指南

MATLAB建模与仿真工具箱的使用指南绪论近年来,建模与仿真技术在各个领域的应用越来越广泛。
MATLAB作为一款强大的科学计算软件,拥有丰富的工具箱,其中建模与仿真工具箱是其中一项重要的功能。
本文将从初学者角度出发,指导读者如何使用MATLAB建模与仿真工具箱进行模型的构建和仿真。
一、建模与仿真简介1.1 建模的概念与意义建模是指利用已有的数据或者基础理论,通过建立数学或物理模型来描述和解决实际问题的过程。
建模能够对复杂的系统或现象进行抽象和简化,从而更好地理解和分析问题。
通过建模,我们可以预测系统的行为、优化系统性能、辅助决策等。
1.2 仿真的概念与应用仿真是指通过对建立的模型进行计算机模拟,以模拟实际系统或现象的行为。
仿真可以提供系统的动态演化信息,帮助我们理解系统行为,并且可以进行参数调整和优化。
仿真还可以用于产品开发、系统设计、风险评估等方面。
二、MATLAB建模与仿真工具箱简介2.1 工具箱的作用与组成MATLAB建模与仿真工具箱是为了方便用户进行系统建模与仿真而开发的一系列工具集合。
它包含了各种用于建模与仿真的函数、算法和工具,涵盖了多个领域的建模需求,如控制系统、信号处理、通信系统等。
2.2 常用工具箱的功能介绍2.2.1 SimulinkSimulink是MATLAB中最常用的建模与仿真工具,它提供了一个图形化的界面,可以通过将各种预定义的模块进行连接来构建系统模型。
Simulink支持多种类型的模型,如连续时间系统、离散时间系统、混合系统等。
Simulink还提供了丰富的仿真和分析工具,如参数扫描、优化、系统响应分析等。
2.2.2 Control System ToolboxControl System Toolbox是用于控制系统建模与仿真的工具箱,它提供了大量的函数和算法,用于设计和分析线性控制系统。
Control System Toolbox支持多种控制器设计方法,如PID控制器、先进的模型预测控制器等。
MATLAB在建模仿真中的应用

悬浮Scope模块 使用悬浮Scope模块的方法有如下两种:
(1) 直接将Sinks模块库中的Floating Scope模块拖动到指定的系 统模型之中。然后选择需要显示的信号并进行适当的设置,最后进 行系统仿真并显示系统中指定的信号。
(2) 设置普通的Scope模块为Floating Scope模块。
简单系统进行仿真时,影响仿真结果输出的因素有仿真起始时间、 结束时间和仿真步长。对于简单系统仿真来说,不管采用何种求解 器,Simulink总是在仿真过程中选用最大的仿真步长。 如果仿真时间区间较长,而且最大步长设置采用默认取值auto,则 会导致系统在仿真时使用大的步长,因为Simulink的仿真步长是通 过下式得到的:
(1) 系统输出连续变化。变化的间隔为无穷小量。 (2) 对系统的数学描述来说,存在系统输入或输出的微分项 (导数项)。 (3) 系统具有连续的状态。在离散系统中,系统的状态为时间 的离散函数,而连续系统的状态为时间连续量。
南华大学数理学院 管 亮
例12.4 蹦极者系着一根弹力绳从高处的桥梁(或是山崖等)向下 跳,整个蹦极跳系统的数学描述为:
打印输出
参数设置
视图整体缩放 X 轴缩放 Y 轴缩放
视图自动缩放 保存当前坐标轴设置 恢复坐标轴设置
悬浮时信号选择 去除坐标轴选择 悬浮 Scope 开关
南华大学数理学院 管 亮
坐标系数目 悬浮 Scope 开关 显示时间范围
坐标系标签
南华大学数理学院 管 亮
信号显示点数限制
保存信号至工作空 间变量
Z u 1 ( n ) u 2 ( n ) Z u 1 ( n ) Z u 2 ( n )
(2) 设离散信号u(n)的Z变换为U(z) ,则的Z变换为z-1 U(z) 。 如:
如何在Matlab中进行模拟与仿真

如何在Matlab中进行模拟与仿真Matlab作为一款广泛应用于工程和科学领域的软件,为用户提供了丰富的模拟与仿真工具,以帮助他们有效地研究和解决实际问题。
本文将介绍如何在Matlab中进行模拟与仿真的基本步骤和常用技巧,以及如何优化仿真结果和改进仿真模型。
一、概述在深入探讨Matlab中的模拟与仿真之前,我们先来了解一下这两个概念的含义。
模拟是指通过对实际系统进行数学建模和计算机仿真,以预测系统的行为和性能。
而仿真则是指通过设计和实现计算机模型,以模拟实际系统的运行情况。
二、模拟与仿真的基本步骤1. 确定模拟目标:在进行模拟与仿真之前,我们需要明确模拟的目标是什么。
例如,是为了分析系统的动态响应,还是为了优化某个过程的效率等。
2. 建立数学模型:模型是模拟与仿真的基础,它反映了实际系统的行为和性能。
在建立数学模型时,我们需要根据系统的特性和要求,选择合适的数学方法和模型类型,如方程、函数、状态空间模型等。
3. 编写Matlab程序:在Matlab中,我们可以使用脚本和函数来实现模型的数学表达式和计算过程。
脚本通常用于执行一系列的计算操作,而函数则用于封装特定的计算功能,以便在不同的场景下复用。
4. 调试和验证:在运行模拟程序之前,我们需要对其进行调试和验证,以确保程序的正确性和可靠性。
在调试过程中,我们可以使用Matlab提供的调试工具,如断点调试、变量跟踪等。
5. 运行模拟程序:在调试和验证完成后,我们可以开始运行模拟程序,以获取系统的模拟结果。
在运行过程中,我们可以通过Matlab的图形界面或命令行窗口,实时查看和分析模拟结果。
三、模拟与仿真的常用技巧1. 参数优化:在进行模拟与仿真时,系统的参数选择对结果的准确性和可靠性至关重要。
通过分析系统的特性和要求,我们可以使用Matlab提供的优化工具,如遗传算法、粒子群优化等,来寻找最优的参数组合。
2. 可视化分析:Matlab提供了丰富的绘图和可视化函数,可以帮助我们直观地分析和展示模拟结果。
如何通过MATLAB进行模拟与仿真

如何通过MATLAB进行模拟与仿真引言:MATLAB(Matrix Laboratory)是一种用于数值分析和数据可视化的高级编程语言和环境。
它被广泛应用于科学研究、工程设计和教育培训等领域。
本文将介绍如何利用MATLAB进行模拟与仿真,从而加强理论学习、验证设计方案以及优化算法等方面发挥作用。
一、了解MATLAB的基本概念和功能MATLAB是一种多范式的编程语言,可进行数据分析、算法开发和数值计算等多种任务。
它具有强大的矩阵操作能力和丰富的函数库,可以进行各种数学运算、统计分析和信号处理等操作。
此外,MATLAB还支持快速绘图、动态可视化和图像处理等功能,有助于直观展示仿真结果。
二、建立仿真模型在进行仿真前,首先需要建立仿真模型。
仿真模型是指根据实际问题所设定的数学模型,并将其转化为MATLAB可以识别和处理的形式。
在建模过程中,可以利用MATLAB提供的各种函数和工具箱,如Simulink、Control System Toolbox等进行辅助。
确定好模型的输入、输出和参数等,以便后续的仿真和分析。
三、选择适当的仿真方法MATLAB提供了多种仿真方法,根据具体问题的特点选择合适的仿真方法非常重要。
常用的仿真方法包括Monte Carlo方法、有限元法和迭代求解等。
Monte Carlo方法适用于随机变量的模拟,有限元法用于解决结构、电磁和热力等问题,而迭代求解则适用于非线性方程组的求解。
根据问题的需求和复杂度,选择相应的仿真方法能够提高仿真的准确性和效率。
四、进行仿真实验在进行仿真实验前,需要根据仿真模型设定好实验参数和条件,如初始状态、仿真时间和外部输入等。
然后,利用MATLAB提供的仿真函数对模型进行仿真,并得到仿真结果。
仿真结果可以是一组数据、图形或动态模拟等形式,根据需要进行相应的处理和分析。
五、仿真结果的可视化与分析仿真结果的可视化与分析是评估仿真效果和提取有价值信息的重要环节。
MATLAB提供了丰富的绘图函数和工具,可以将仿真结果以直观、易理解的方式展示出来。
