求一次函数的表达式

合集下载

17.3.4求一次函数的表达式

类型六：根据面积求表达式
如图，一次函数的图象过点A(3,0).与y轴交于点B，若
△AOB的面积为6，求这个一次函数的解析式
y B
o
A
解：∵A（3，0）.∴OA=3，
∵S= 1 OA×OB= 1×3×OB=6
2
2
∴OB=4， B点的坐标为（0,4），
x
B'
第20页，共35页。
类型六：根据面积求表达式
1
1.一次函数的一般形式是什么?
y=kx+b(k,b为常数,k≠0) y=kx （k≠0）
2、一次函数图像是什么？
3、直线y=-2x+4与x轴交于点_____，与y轴交于点________.
4、直线y=kx+4与正比例函数y=-2x图像平行，则
k= _____ ，此直线的关系式为。 _____
第1页，共35页。
③解方程组，求出k，b；
④把求出的k、b代回表达式ห้องสมุดไป่ตู้可。
待定系数法．
第7页，共35页。
像这样先设出函数表达式（其中含有待定系数），再根据
条件列出方程或者方程组，
求出待定系数，
从而得到所求结果的方法，
叫做待定系数法．
第8页，共35页。
确定正比例函数的表达式,就是要确定哪个值？
K的值 (自变量的系数)
第28页，共35页。
2.某地长途汽车客运公司规定
旅客可随身携带一定质量的行李，如果超过规定，则需要购 y
买行李票，行李票费用y元是
行李质量x（千克）的一次函
数，其图象如下图所示：
①写出y与x之间的函数关系 10
式；
6
②旅客最多可免费携带多少

待定系数法求一次函数表达式

根据题意，得 10k+.2 解得, b＝8
∴ 函数的解析式为 y= 0.2x ＋8 (-20≤x≤100)
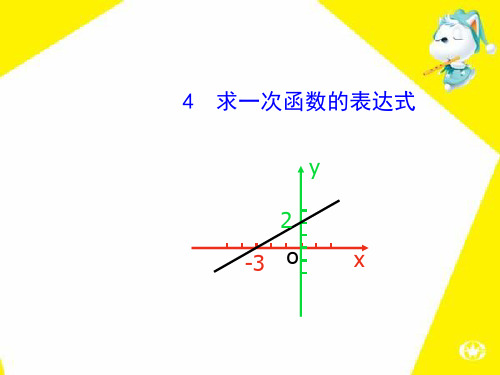
变式2 ：求下图中直线的函数表达式
解：设这个一次函数的解析式为y=kx+b. ∵y=kx+b的图象过点（0，3）与（1，0）.
y
∴ b=3 k+b=0
解得 k=-3 b=3
Page 4
练习1：已知一次函数的图象经过点(1,5)与（-1，－1）.求这个函数的表达式。解：设这个一次函数的表达式为y=kx+b （k≠0）. ∵根据题意，得： k+b=5 -k+b=-1 解得 k=3 b=2
∴这个一次函数的解析式为y=3x+2
Page 5
变式1：已知一次函数y=kx+b，当x=1时， y=1，当x=2时，y=3.求这个一次函数的解析式。
• • • •
例3、已知温度计中水银（或酒精）柱的高度y（厘
米）是温度x（℃）的一次函数。某型号的实验用水银温度计能测量-20℃至100℃的温度，当温度为10℃时水银柱高10厘米；温度为50℃水银柱高18厘米。求这个函数的表达式。
y=kx+b(k≠0) , 解：设这个函数的表达式为_______________
k
b
步骤概括：设、代、求、写注意：对于是实际问题时所求的结果还得考虑自
变量的取値范围。
Page 10
思考1：已知一次函数y=kx+b 的图象与y=2x平行且过点(2,-1).求这个函数 x=5时的函数值.
∵ y=kx+b 的图象与y=2x平行. 解：
∴ k=2 ∴
∴ y=2x-b
b=-5

华东师大版八年级下册17.求一次函数的表达式课件

根据实际情况收集信息求函数关系式
1.如下图，两摞相同规格的碗整齐地放在桌面上，请根据图中的数据信息，解答下列问题：（1）求整齐摆放在桌面上的碗的高度y(cm)与碗的个数x(个) 之间的函数关系式；（y与x成一次函数关系）（2）把这两摞碗整齐地摆成一摞时，碗的高度是多少？
11c m
14c m
解：（1）设y=kx+b ，
利用表格信息确定函数关系式
某型号汽车进行耗油实验，y(耗油量)是t(时间)的一次函数，函数关系如下表，请确定函数表达式。
t (时间) 0
12Leabharlann 3…y(耗油量) 100
84
68
52
…
解：设一次函数的解析式为y=kt+b 取t=0,y=100; t=1,y=84.
｛得方程组
b=100
k+b=84
解得：k=-16, b=100 ∴这个一次函数的表达式为y=-16t+100
的两点
(x1,y1)与
解出 (x2,y2)
画出一次函数的
图象直线L
选取
从形到数体现了“数形结合”的数学思想
利用点的坐标求函数关系式
1.已知一次函数的图象经过点(3,5)与（－4，－9）. 求这个一次函数的解析式．
解：设这个一次函数的解析式为y=kx+b ∵图象经过点(3,5)与（－4，－9）
∴
b=2
∴｛ 4k+b=0
解得：k=-
1 2
,b=2.
∴直线AB的表达式为y=- 1 x+2.
2
像这样先设出函数解析式，再根据条件确定解析式中未知的系数，从而具体写出这个式子的方法，叫做待定系数法．

一次函数1

2.（2006河北中考25题）有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．图11是反映所挖河渠长度y（米）与挖掘时间x（时）之间关系的部分图象．请解答下列问题：
（1）乙队开挖到30米时，用了_____小时．开挖6小时时，甲队比乙
队多挖了______米；
（2）请你求出：
4.当b=0时(即 y=kx)，一次函数图像变为正比例函数，正比例函
数是特殊的一次函数.
5.函数图像性质：当k相同，且b不相等，图像平行；当k不同，且b相等，图像相交于Y轴；当k互为负倒数时，两直线垂直；
图像性质：
1．作法与图形：通过如下3个步骤：
（1）列表：每确定自变量x的一个值，求出因变量y的一个值，并列表，（2）描点：一般取两个点,根据“两点确定一条直线”的道理；（3）连线：可以作出一次函数的图像——一条直线。因此，作一次函数的图像只需知道2点，并连成直线即可。（通常找函数图像与x轴和y轴
走平路到达学校，所用的时间与路返回，且走平路、上坡路、下坡路的速度分别保持和去上学时一致，那么他从学校到家需要的时间是( A.14分钟 ) B.17分钟 C.18分钟 D.20分钟
某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程，其中进水、清洗、排水时洗衣机中的水量y（升）与时间x（分钟）之间的关系如图所示：根据图象解答下列问题：
(1)汽车共行驶了___________ km； (2)汽车在行驶途中停留了___________ h； (3)汽车在整个行驶过程中的平均速度为___________ km/h；
(4)汽车自出发后3h至4.5h之间行驶的方向是___________.
6、图中，射线l甲、l乙分别表示甲、乙两运动员在自行车比赛中所走的路程s与时间t的函数关系，求它们行进的速度关系。 7、（2011四川内江）小高从家骑自行车去学校上学，先走上坡路到达点A，再走下坡路到达点B，最后

待定系数法求一次函数表达式

例4：在弹性限度内，弹簧长度y（cm）是所挂物体质量x（g）的一次函数.已知一根弹簧挂10g物体时的长度为10cm，挂30g物体时的长度为15cm，试求y与x的函数表达式
Hale Waihona Puke 拓展探究1.已知： y与x成正比例，且当 x=3时 y=7，求y与x的函数解析式．
变式1 ： y与x-1成正比例，且当 x=3时 y=7，求y与x的函数解析式．变式2 ： y+3与x-1成正比例，且当 x=3时 y=7，求y与x的函数解析式．
（1）求这个函数的解析式（2）求当x=3时,y的值。
例3：（1）已知y是 x的一次函数，当 x=-1时 y=3，当 x =2 时 y=-3，求y关于 x 的函数解析式．
（2）已知y是 x的正比例函数，当x=2时，y=－4, 求这个函数的解析式.
练：已知y是x的一次函数，又表给出了部分对应值，则m的值是_______．
练：已知：y－1与x成正比例，当x＝1时，y＝3．写出y与x之间的函数关系式
拓展探究：
2.已知y=y1+y2 ，y1与x成正比例，y2与x-1成正比例，且 x=3时 y=4; x=1时 y=2. 求y与x的函数解析式．
练：已知y=y1+y2 ，y1与x成正比例，y2与x-2成正比例，且 x=-1时 y=2; x=3时 y=-2. 求y与x的函数解析式．
例1：已知一次函数y=kx+b。当x=3时，y= 0；当x=0时，y=-4。（1）求k，b的值（2）求当x=2时,y的值
例2：已知正比例函数y=kx，当x=3时，y=4. 求当x=2时，y的值
练1：在一次函数y=kx-3中，当x=3时，y=6。则k= 练2：已知一次函数y=kx+b中，当x=1时，y=3，当x=-1时，y=7。

确定一次函数的表达式

确定一次函数的表达式在数学的世界里，一次函数就像是一座桥梁，连接着不同的数量关系。

而确定一次函数的表达式，则是我们能够顺利通过这座桥梁，解决各种实际问题的关键钥匙。

一次函数的一般形式是 y ＝ kx ＋ b（其中 k、b 是常数，k ≠ 0）。

这里的 k 被称为斜率，它决定了函数图像的倾斜程度；b 则是截距，也就是函数图像与 y 轴的交点。

要确定一次函数的表达式，实际上就是要找出 k 和 b 的值。

那怎么来找呢？通常有两种常见的方法：待定系数法和利用函数图像的特征。

先说待定系数法。

假设我们知道一次函数上的两个点的坐标，比如（x₁, y₁）和（x₂, y₂），把这两个点代入函数表达式 y ＝ kx ＋ b 中，就可以得到一个关于 k 和 b 的方程组。

举个例子，如果已知点（1, 3）和（2, 5）在某个一次函数上，那么把（1, 3）代入函数表达式得到 3 ＝ k×1 ＋ b，即 k ＋ b ＝ 3；把（2, 5）代入得到 5 ＝ k×2 ＋ b，即 2k ＋ b ＝ 5。

接下来解这个方程组，就能求出 k 和 b 的值。

从第一个方程 k ＋ b ＝ 3 可以得到 b ＝ 3 k，把它代入第二个方程2k ＋ b ＝ 5 中，就有 2k ＋ 3 k ＝ 5，解得 k ＝ 2。

再把 k ＝ 2 代入 b＝ 3 k ，得到 b ＝ 1。

所以这个一次函数的表达式就是 y ＝ 2x ＋ 1。

再来说说利用函数图像的特征来确定表达式。

如果我们能从图像中直接看出函数与 y 轴的交点，那这个交点的纵坐标就是 b 的值。

而斜率 k 呢，可以通过图像上任意两个点的坐标来计算。

比如说，函数图像与 y 轴交于（0, －2），并且还经过点（2, 4）。

那么 b ＝－2，而斜率 k ＝（4 （－2））÷（2 0）＝ 3 。

所以这个一次函数的表达式就是 y ＝ 3x 2 。

在实际应用中，确定一次函数的表达式非常有用。

华师大版数学八下17.求一次函数的表达式课件

变式练习
“黄金 1 号”玉米种子的价格为 5 元/kg.如果一次购买 2 kg 以上的种子，超过 2 kg 部分的种子价格打 8 折.
（1）填写下表
购买量/kg 0.5 1 1. 2 2.5 3 3.5 4 … 2.5 5 75.5 10 12 14 16 18 …
付（款2金）额写/元出购买量关于付款金额的函数解析式.
1234
待定系数法.
-1
叫做
-2
例 4 温度计是利用水银（或酒精）热胀冷缩的原理制作的，温度计中水银（或酒精）柱的高度 y（厘米）是温度 x（℃）的一次函数. 某种型号的实验用水银温度计能测量 – 20℃ 至 100℃的温度，已知 10℃ 时水银柱高 10 厘米，50℃时水银柱高 18 厘米. 求这个函数的表达式.
解设所求函数表达式是 y = kx + b (k ≠ 0)，设
根据题意，得
列
10k + b = 10，解得 k = 0.2，解
50k + b = 18.
b = 8.
所以，所求函数表达式是 y = 0.2x + 8，代
其中 x 的取值范围是 – 20 ≤ x ≤ 100.
待定系数法：先设待求的函数关系式(其中含有待定
4 求一次函数的表达式
华东师大版八年级数学下册
我们在画函数y=2x,y=3x-1时，至少应选取几个点？为什么？
两点法——两点确定一条直线
前面我们学习了给定一次函数解析式，可以说
出它的性质，反过来给出有关的信息，能否求出解析式呢？
目标导学一：用待定系数法求一次函数解析式
求下图中直线的函数解析式.
的系数)，再根据条件列出方程或方程组, 求出待定系数,从而得到所求结果的方法, 叫做待定系数法.

求一次函数的表达式

第17章函数及其图象3.—次函数的性质学习目标【知识与技能】1. 掌握一次函数y=kx + b（k工0）的性质.2. 能根据k与b的值说出函数的有关性质.【过程与方法】经历探索一次函数图象性质的过程，感受一次函数中k与b的值对函数性质的影响【情感态度】观察图象，体会一次函数k、b的取值和直线位置的关系，提高学生数形结合能力【教学重点】掌握一次函数y=kx + b（k工0）的性质【教学难点】利用一次函数的有关性质解决有关问题教学过程一、情境导入：1•一次函数的图象是什么形状呢？2. 正比例函数y=kx（k工0）的图象是经过哪一点的一条直线？3. 画一次函数图象时，只要取几点？4. 在同一直角坐标系中画出下列函数的图象.并说出它们有什么关系.y=4x y=4x + 2【教学说明】对相关知识进行复习，为本节课的教学做准备.二、探究展示：探究：一次函数的性质一21. 在同一直角坐标系中，画出函数y=§x+1和y=3x-2的图象.观察图象，回答下列问题：(1)在你所画的一次函数图象中，直线经过几个象限？2(2)直线y=2x+1的图象上，当一个点在直线上从左向右移动时，(即自3变量x从小到大时)，点的位置也在逐步从低到高变化，那么函数y的值是如何变化的？(3)函数y=3x-2的图象是否也有这种变化？一22. 在同一坐标系中，画出函数y=-x + 2和y=- x-1的图象(图略).3根据上面分析的过程，请同学们研究这两个函数图象是否也有相应的变化？你能发现什么规律？【归纳结论】一次函数y=kx + b有下列性质：⑴当k>0时，y随x的增大而增大，这时函数的图象从左到右上升；(2)当k v0时，y随x的增大而减小，这时函数的图象从左到右下降.【教学说明】通过观察，总结结论.提高学生观察能力和概括能力.三、运用新知，深化理解1. 已知一次函数y=(2m-1)x + m + 5,当m是什么数时，函数值y随x的增大而减小？分析:一次函数y=kx + b(k M0)，若k v 0，则y随x的增大而减小. 解:因为一次函数y=(2m-1)x + m + 5，函数值y随x的增大而减小.1所以，2m-1v 0,即m<—.22. 已知一次函数y=(1-2m)x + m-1,若函数y随x的增大而减小，并且函数的图象经过二、三、四象限，求m的取值范围.分析：一次函数y=kx + b(k工0),若函数y随x的增大而减小，则k v 0,若函数的图象经过二、三、四象限，贝U k v 0,b v 0.解：由题意得：「1-2m<0I m-1<0,1解得，—<m<123. 已知一次函数y=(3m-8)x + 1-m图象与y轴交点在x轴下方，且y随x的增大而减小，其中m为整数.(1) 求m的值；(2) 当x取何值时，0v y v 4?分析：一次函数y=kx + b(k工0)与y轴的交点坐标是(0,b)，而交点在x轴下方，则b v 0,而y随x的增大而减小，则k v 0.解：⑴由题意得：j 3m-8<01-m<0，8解之得，1<m<-，又因为m为整数,所以m=2.3(2)当m=2 时，y=-2x-1.又由于0v y v4.所以O v-2x-1 v4.5 1解得：-—<x<-—.2 24. 画出函数y=-2x + 2的图象，结合图象回答下列问题：⑴这个函数中，随着x的增大，y将增大还是减小？它的图象从左到右怎样变化？(2)当x取何值时，y=0?⑶当x取何值时，y> 0?分析：(1)由于k=-2 v 0,y随着x的增大而减小.(2)y=0,即图象上纵坐标为0的点,所以这个点在x轴上.(3)y >0,即图象上纵坐标为正的点，这些点在x 轴的上方.-2 -3 -4解:⑴由于k=-2 v 0,所以随着x 的增大，y 将减小.当一个点在直线上从左向右移动时，点的位置也在逐步从高到低变化，即图象从左到右呈下降趋势.⑵当x=1时,y=0.(3) 当 x v 1 时,y >0.【教学说明】通过实际问题的应用，加深学生对本节知识的巩固.提高学生解决问题的能四、归纳拓展：1. (1)当k >0时，y 随x 的增大而增大，这时函数的图象从左到右上升；(2)当k v 0时，y 随x 的增大而减小，这时函数的图象从左到右下降.当b>0,直线与y 轴交于正半轴；当b v 0时，直线与y 轴交于负半轴；当b=0时，直线与y 轴交于坐标原点.2. k >0,b >0时，直线经过一、二、三象限；k >0,b v 0时，直线经过一、三、四象限；k v 0,b >0时，直线经过一、二、四象限；k v 0,b v 0时，直线经过二、三、四象限.课后作业1. 布置作业：教材P 50 “练习”.2. 完成本课时对应练习.v=-2x+2——教学反思本节课的难点是性质的应用，学生都能记住一次函数的性质，但在应用中不能灵活的应用，所以，课后还应该在性质的应用上多花时间，多做练习，使学生都能够掌握.。

一次函数法线方程公式

一次函数法线方程公式
一次函数的法线方程可以通过以下步骤来推导和计算。

首先，我们知道一次函数的一般表达式为y = mx + c，其中m是斜率，c 是y轴截距。

设一次函数为y = mx + c，其斜率为m。

一次函数的导数即为其斜率，因此导数为m。

而法线的斜率是原函数斜率的负倒数，即-1/m。

接下来，我们需要确定法线的截距。

设过点P(x1, y1)的直线的法线方程为y y1 = -1/m(x x1)。

将原函数y = mx + c 带入，得到c = y1 + x1/m。

因此，一次函数的法线方程为y y1 = -1/m(x x1)，其中m为原函数的斜率，(x1, y1)为直线上的一点。

这就是一次函数的法线方程公式。

希望这个解答能够帮到你。

17.求一次函数的表达式PPT课件(华师大版)

【解析】（1）15 （2）由图象可知，s是t的正比例函数设所求函数的关系式为s=kt (k≠0) 代入（45，4）得：4=45k 解得：k= ∴s与t的函数关系式为s= t(0≤t≤45).
由图象可知，小聪在30≤t≤45的时段内 s是t的一次函数，设函数关系式为s=mt+n(m≠0) 代入（30，4），（45，0）得：
2.
3.
4.（宁波·中考)小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料，学校与天一阁的路程是4千米.小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达天一阁.图中折线O→A→B→C和线段OD分别表示两人离学校的路程s （千米）与所经过的时间t(分钟)之间的函数关系，请根据图象回答下列问题：（1）小聪在天一阁查阅资料的时间为_____分钟，小聪返回学校的速度为______千米/分钟；（2）请你求出小明离开学校的路程s（千米）与所经过的时间 t(分钟)之间的函数关系式；（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
图象必经过二、四象限
常数项 b 决定一次函数图象与 y轴交点的位置.
1.确定一次函数的表达式需要几个条件？确定一次函数的表达式需要两个条件：分别求出k和b的值.
2.确定正比例函数的表达式需要几个条件？确定正比例函数的表达式需要一个条件：只要求出k的值.
【例题】
例1 已知y与x成正比例，且当x=-1时，y=-6，求y与 x之间的函数表达式.
用待定系数法解题一般分为几步？一设、二列、三解、四还原
1.设一次函数的一般情势y=kx+b(k≠0);
2.根据已知条件列出关于k ,b的二元一次方程组; 3.解这个方程组,求出k, b; 4.将已经求出的 k,b的值代入关系式.

求一次函数表达式的方法：23招经典解法

第五、六课时一次函数表达式的方法解法（23招）安徽省池州市贵池区梅龙初级中学黄老师（QQ ：495014580）四、求一次函数的表达式基本解法1、待定系数法（1）图象过原点：函数为正比例函数，可设表达式为y =kx ，再找图象上除原点外的一个点的坐标代入表达式，即可求出k .（2）图象不过原点：函数为一般的一次函数，可设表达式为y =kx +b ，再找图象上的两个点的坐标代入表达式，即可求出k ，b 。

例：（中考常州）已知一次函数y =kx +b （k ，b 为常数且0≠k ）的图象经过点A （0，－2）和点B （1，0），则k =______，b =______.答案：k =2，b =－2例：（中考重庆）已知正比例函数)0(≠=k kx y 的图象经过点（1，－2），则这个正比例函数的表达式为______答案：y =－2x常见解法：1、定义式例，已知函数3)3(82+-=-mx m y 是一次函数，求其解析式。

解析：该函数是一次函数 ∴182=-m解得，m =±3,又m ≠3∴m =－3故解析式为：y =－6x +32、点斜式要点：如何求k ？（1）公式：1212x x y y k --= （2）图象（比值）：|k |=BCAB (两直角边的比）（3）增量：V （速度）、P （电功率）（4）每每（美美题）：（5）平移变换：k 值相等（6）垂直变换：121-=k k（7）对称变换：|k |、|b |不变（8）相似比：(略)（9）正切值：tanα（斜率）（10）旋转变换：（略）例，已知一次函数y =kx －3的图象过点（2，－1），求这个函数解析式。

解析：方法一：（代入法）将点（2,－1）代入y =kx －3得，－1=2k －3，解得，k =1故解析式为：y =x －3方法二：（一点式）解析：一次函数y =kx －3的图象过点（2，－1）∴可令y =k (x －2)－1=kx －2k －1∴－2k －1=－3,解得，k =1∴这个函数解析式为y =x －33、两点式例，一次函数经过（－2，0)、(0，4),求此函数的解析式。

一次函数表达式的确定

一次函数表达式的确定一次函数是指函数的最高次数为一次的函数，其表达式的一般形式为y=ax+b，其中a和b是常数。

一次函数的图像呈现为一条直线，其中a决定了直线的斜率（即直线的倾斜程度），b决定了直线在y轴上与原点的位置关系。

在确定一次函数表达式时，关键是要有足够的信息来确定a和b的值。

以下是几种常见的确定一次函数表达式的方法：1. 已知两个点的坐标：假设已知直线上的两个点A(x1, y1)和B(x2, y2)，则可以通过计算斜率k=(y2-y1)/(x2-x1)来确定a的值，然后再利用其中一个点的坐标，代入y=ax+b的表达式，解方程得到b的值。

例如，已知直线上两个点A(2,4)和B(5,10)，则斜率k=(10-4)/(5-2)=2、代入点A的坐标，可得4=2a+b，代入任意一个点的坐标，如5=5a+b。

解这个方程组，可以得到a=2，b=0，即y=2x的一次函数表达式。

2. 已知斜率和一点坐标：有时候可能已知直线的斜率k和其中一个点的坐标，可以直接代入y=ax+b的表达式，然后解方程得到b的值。

例如，已知一次函数的斜率为3，且经过点(1, 4)，代入y=ax+b的表达式，可得4=3*1+b，解方程得到b=1、因此，一次函数的表达式为y=3x+13.已知函数图像上的一些特征：有时候，可能通过观察函数图像上的一些特征，来确定一次函数的表达式。

-如果直线与y轴平行，则直线在y轴上的截距为b，且斜率为无穷大。

此时，一次函数的表达式为y=b。

- 如果直线与x轴平行，则直线在x轴上的截距为b，且斜率为零。

此时，一次函数的表达式为y=ax+b，其中a为零。

- 如果直线经过原点，则直线在y轴上的截距为零，即b为零。

此时，一次函数的表达式为y=ax。

4.利用最小二乘法拟合数据：如果已知一些数据点，但不确定是否符合一次函数的形式，可以使用最小二乘法来拟合数据点，以确定最优的一次函数表达式。

最小二乘法通过最小化实际数据与拟合函数之间的误差来确定最优的a和b的值。

求一次函数的表达式

k=-1 b=3
第一步第二步第三步第四步
1=2k+b 4= -k+b
所以这个一次函数的表达式为所以这个一次函数的表达式为 y=-x+3
探究2 探究
已知一次函数的对应值如下表：已知一次函数y=kx+b，x与y的对应值如下表：一次函数，与的对应值如下表

x y
-3 2
0 4
3 6
9 10
2、已知一次函数、已知一次函数y=kx+b，x与y的对应值如下表：的对应值如下表：一次函数，与的对应值如下表
x y -3 2 0 4 3 6 9 10 24 20 99 ？ y 120 84 ？ 144 … …
L1 L2
3、已知两个函数的图象如图，、已知两个函数的图象如图，函数的图象如图根据图上的数据能否求出这两个函数的解析式？如果能，个函数的解析式？如果能，请求出它们的解析式。求出它们的解析式。寻找两个点的坐标或两对对应值
4
O
P x
-4
3
找点(坐标建立方程找点坐标),建立方程组),解方程组坐标建立方程(组解方程组分段函数如何求表达式，分段函数如何求表达式，注意每个函数的自变量的取值范围
作业
试题单 1题——6题题题
下节专题
求一次函数的表达式（求一次函数的表达式（二） ——实际问题实际问题
x y
-3 2
0 4
3 6 (24,20)
9 10
24 20
99
120 ？
210
…
20=24k+b 84= 120k+b
？ 84 70 (120,84) k= 2 3 b= 4