导数解曲线公切线问题
高考:导数题型归类,分类解题方法举例,如极值点偏移、隐零点运用

高考:导数题型归类,分类解题方法举例,如极值点偏移、隐零点运用高考压轴题:导数题型及解题方法一、切线问题题型1:求曲线y=f(x)在x=x处的切线方程。
方法:f'(x)为在x=x处的切线的斜率。
题型2:过点(a,b)的直线与曲线y=f(x)的相切问题。
方法:设曲线y=f(x)的切点(x,f(x)),由(x-a)f'(x)=f(x)-b求出x,进而解决相关问题。
注意:曲线在某点处的切线若有则只有一条,曲线过某点的切线往往不止一条。
例题:已知函数f(x)=x-3x。
1)求曲线y=f(x)在点x=2处的切线方程;(答案:9x-y-16=0)2)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围。
提示:设曲线y=f(x)上的切点(x,f(x)),建立x,f(x)的等式关系。
将问题转化为关于x,m的方程有三个不同实数根问题。
答案:m的范围是(-3,-2))练1:已知曲线y=x-3x。
1)求过点(1,-3)与曲线y=x-3x相切的直线方程。
(答案:3x+y=0或15x-4y-27=0)2)证明:过点(-2,5)与曲线y=x-3x相切的直线有三条。
题型3:求两个曲线y=f(x)、y=g(x)的公切线。
方法:设曲线y=f(x)、y=g(x)的切点分别为(x1,f(x1))、(x2,g(x2)),建立x1,x2的等式关系,(x2-x1)f'(x1)=g(x2)-f(x1),(x2-x1)f'(x2)=g(x2)-f(x1);求出x1,x2,进而求出切线方程。
解决问题的方法是设切点,用导数求斜率,建立等式关系。
例题:求曲线y=x与曲线y=2elnx的公切线方程。
(答案:2ex-y-e=0)练1:求曲线y=x与曲线y=-(x-1)的公切线方程。
(答案:2x-y-1=0或y=0)2.设函数f(x)=p(x-2)-2lnx,g(x)=x,直线l与函数f(x),g(x)的图象都相切,且与函数f(x)的图象相切于(1,0),求实数p的值。
(完整版)导数解曲线公切线问题

导数解公切线专题3 2151. (2009年江西文12)若存在过点(1,0)的直线与曲线y X和y ax x 9都相切,4则a等于25亠217亠257亠A. 1或B. 1或C. 或-D.—或764446442.(2016年全国II理16)若直线y kx b是曲线y ln x2的切线,也是曲线y In (x1)的切线,则b .3•求曲线y=x3+x2- 2X在点A(1,0)处的切线方程•变式:求曲线y=x3+x2—2x过点A(1,0)的切线方程【答案】1 In2【解析】试题分析;对因数y=lnx+2求导得y (=-f 对> =ln (x+l )求导得#=丄,设直线y =与圉数X x+1y=}nx+2相切于点号口小),与函埶y = ln (x +1)相切于点占(花jJ :则时=Ln 珂+ 2= In 任+1),则点的g'J 在切线上得$-(1口珂+2)=丄(工-珂),由Eg/J 在切线上得3•求曲线y=x 3+x 2— 2x 在点A(1,0)处的切线方程• 解:T y ' =x 2+2x — 2,•••切线斜率 k= y'x =1=3. •••切线方程为y=3(x — 1), 即 3x — y — 3=0.变式:求曲线y=x 3+x 2— 2x 过点A(1,0)的切线方程.y-ln (^ + 1) = —-—(x-x,),这两芳立绫表示同一牛世戈,所以“ ja + 1ln(x n +1) =1口叫’解之得X ; 叼+131. (2009年江西文12)若存在过点(1,0)的直线与曲线y x 和yax 215 x 49都相切,则a 等于A .1或-64B .1 或 214C .-或-244 641.设过(1,0)的直线与y33x 相切于点(x 0 , x 0 ),所以切线方程为x o3x o 2(x X o )23x 0 x 2x 0,又(1,0)在切线上,则X 。
0或X 。
21525当X 0时,由y0与y axx 9相切可得 a4643」丄27 27 一2 15当X )—时,由yx 与y ax X 9相切可得a24 442. ( 2016 年全国II理16) 若直线ykx b 是曲线 y In xy In (x 1)的切线,则b所以选A .考点:导数的几何意义•1,2的切线,也是曲线解设切点P (X。
导数的应用切线与极值问题

导数的应用切线与极值问题导数的应用:切线与极值问题导数是微积分中的重要概念,它在各个科学领域中都有着广泛的应用。
其中,切线与极值问题是导数应用的两个常见问题。
本文将探讨如何使用导数解决切线和极值问题,并通过实例解释其应用。
一、切线问题切线是曲线上某一点处与该点相切的直线。
通过导数,我们可以确定曲线上某点的切线方程。
设曲线方程为y=f(x),点P(x,y)处的切线斜率k即为函数f(x)在该点的导数,即k=f'(x)。
例子1:求曲线y=x^2+2x+1在点P(1,4)处的切线方程。
解:首先求导数:f'(x)=(x^2+2x+1)'=2x+2。
然后求点P(1,4)处的斜率:k=f'(1)=2(1)+2=4。
由切线斜率和点可确定切线方程,即y-4=4(x-1)。
将其化简,得到切线方程为y=4x。
二、极值问题在求解极值问题时,我们可以利用导数为0的点来确定函数的最大值或最小值。
设函数f(x)在[a,b]区间上连续且在区间内可导,若f'(c)=0且c∈(a,b),则c称为f(x)在[a,b]上的临界点。
临界点和区间端点都有可能是函数的极值点。
例子2:求函数f(x)=x^3-3x^2的极小值。
解:首先求导数:f'(x)=(x^3-3x^2)'=3x^2-6x。
然后求导函数的临界点:3x^2-6x=0。
化简得到x(x-2)=0,解得x=0或x=2。
接下来,我们通过判断临界点和区间端点的函数值来确定极小值。
计算f(0)=-0、f(2)=-4,因此f(x)=x^3-3x^2的极小值为-4,在x=2处取得。
综上,我们通过求解导数和判断临界点来确定函数的极值。
三、切线和极值问题的应用切线问题和极值问题在实际应用中有着广泛的运用。
例子3:一辆汽车在某段时间内行驶的路程和时间的关系如图所示。
求该段时间内汽车的平均速度,以及汽车行驶的最快和最慢速度。
图表:时间(小时) 0 2 4 6 8 10路程(公里)***********解:我们可以通过导数来求解这个问题。
导数中的公切线问题--2024年新高考数学一轮复习题型归纳与方法总结 解析版
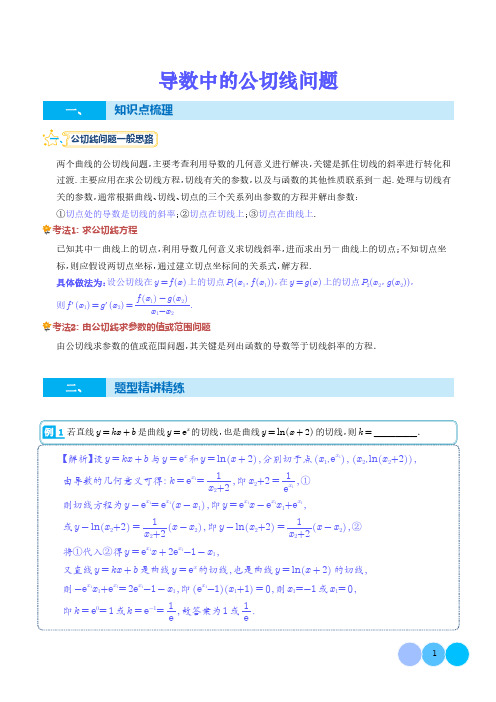
导数中的公切线问题知识点梳理一、公切线问题一般思路两个曲线的公切线问题,主要考查利用导数的几何意义进行解决,关键是抓住切线的斜率进行转化和过渡.主要应用在求公切线方程,切线有关的参数,以及与函数的其他性质联系到一起.处理与切线有关的参数,通常根据曲线、切线、切点的三个关系列出参数的方程并解出参数:①切点处的导数是切线的斜率;②切点在切线上;③切点在曲线上.考法1:求公切线方程已知其中一曲线上的切点,利用导数几何意义求切线斜率,进而求出另一曲线上的切点;不知切点坐标,则应假设两切点坐标,通过建立切点坐标间的关系式,解方程.具体做法为:设公切线在y =f (x )上的切点P 1(x 1,f (x 1)),在y =g (x )上的切点P 2(x 2,g (x 2)),则f ′(x 1)=g ′(x 2)=f x 1 -g x 2x 1-x 2.考法2:由公切线求参数的值或范围问题由公切线求参数的值或范围问题,其关键是列出函数的导数等于切线斜率的方程.题型精讲精练1若直线y =kx +b 是曲线y =e x 的切线,也是曲线y =ln x +2 的切线,则k =______.【解析】设y =kx +b 与y =e x 和y =ln x +2 ,分别切于点x 1,e x 1,x 2,ln x 2+2 ,由导数的几何意义可得:k =e x 1=1x 2+2,即x 2+2=1ex 1,①则切线方程为y -e x 1=e x 1x -x 1 ,即y =e x 1x -e x 1x 1+e x 1,或y -ln x 2+2 =1x 2+2x -x 2 ,即y -ln x 2+2 =1x 2+2x -x 2 ,②将①代入②得y =e x 1x +2e x 1-1-x 1,又直线y =kx +b 是曲线y =e x 的切线,也是曲线y =ln x +2 的切线,则-e x 1x 1+e x 1=2e x 1-1-x 1,即e x 1-1 x 1+1 =0,则x 1=-1或x 1=0,即k =e 0=1或k =e -1=1e ,故答案为1或1e.2已知直线y =kx +b 与函数y =e x 的图像相切于点P x 1,y 1 ,与函数y =ln x 的图像相切于点Q x 2,y 2 ,若x 2>1,且x 2∈n ,n +1 ,n ∈Z ,则n =______.【解析】依题意,可得e x 1=k =1x 2y 1=e x 1=kx 1+by 2=ln x 2=kx 2+b,整理得x 2ln x 2-ln x 2-x 2-1=0令f x =x ln x -ln x -x -1x >1 ,则f x =ln x -1x在1,+∞ 单调递增且f 1 ⋅f 2 <0,∴存在唯一实数m ∈1,2 ,使f m =0f x min =f m <f 1 <0,f 2 =ln2-3<0,f 3 =2ln3-4<0,f 4 =3ln4-5<0,f 5 =4ln5-6>0,∴x 2∈4,5 ,故n =4.【题型训练】1.求公切线方程一、单选题1(2023·全国·高三专题练习)曲线y =1x与曲线y =-x 2的公切线方程为()A.y =-4x +4B.y =4x -4C.y =-2x +4D.y =2x -4【答案】A【分析】画出图象,从而确定正确选项.【详解】画出y =1x,y =-x 2以及四个选项中直线的图象如下图所示,由图可知A 选项符合.故选:A2(2023·全国·高三专题练习)对于三次函数f (x ),若曲线y =f (x )在点(0,0)处的切线与曲线y =xf (x )在点(1,2)处点的切线重合,则f ′(2)=()A.-34B.-14C.-4D.14【答案】B【分析】由f(0)=0得d=0,然后求得f (x),由f (0)=2-01-0求得c=2,设g(x)=xf(x),由g(1)=2得f(1)=2及a+b=0,再由g (1)=2得3a+2b+2=0,解得a,b后可得f (2).【详解】设f(x)=ax3+bx2+cx+d(a≠0),∵f(0)=d=0,∴f(x)=ax3+bx2+cx,∴f′(x)=3ax2+2bx+c∴f′(0)=c=2-01-0=2,设g(x)=xf(x),则g(1)=f(1)=a+b+2=2,即a+b=0⋯⋯①又∵g′(x)=f(x)+xf′(x),∴g′(1)=f(1)+f′(1)=2,∴f′(1)=0,即3a+2b+2=0⋯⋯②由①②可得a=-2,b=2,c=2,∴f′(2)=-14.故选:B.3(2023·全国·高三专题练习)已知函数f x =x ln x,g x =ax2-x.若经过点A1,0存在一条直线l与曲线y=f x 和y=g x 都相切,则a=()A.-1B.1C.2D.3【答案】B【分析】先求得f(x)在A(1,0)处的切线方程,然后与g x =ax2-x联立,由Δ=0求解【详解】解析:∵f x =x ln x,∴f x =1+ln x,∴f 1 =1+ln1=1,∴k=1,∴曲线y=f x 在A1,0处的切线方程为y=x-1,由y=x-1y=ax2-x得ax2-2x+1=0,由Δ=4-4a=0,解得a=1.故选:B4(2023·全国·高三专题练习)已知函数f(x)=x2-4x+4,g(x)=x-1,则f(x)和g(x)的公切线的条数为A.三条B.二条C.一条D.0条【答案】A【分析】分别设出两条曲线的切点坐标,根据斜率相等得到方程8n3-8n2+1=0,构造函数f x =8x3-8x2+1,f x =8x3x-2,研究方程的根的个数,即可得到切线的条数.【详解】设公切线与f x 和g x 分别相切于点m,f m,n,f n,f x =2x-4,g x =-x -2,gn =fm =g n -f m n -m ,解得m =-n -22+2,代入化简得8n 3-8n 2+1=0,构造函数f x =8x 3-8x 2+1,f x =8x 3x -2 ,原函数在-∞,0 ↗,0,23 ↘,23,+∞ ↗,极大值f 0 >0,极小值,f 23<0故函数和x 轴有交3个点,方程8n 3-8n 2+1=0有三解,故切线有3条.故选A .【点睛】这个题目考查了利用导数求函数在某一点处的切线方程;步骤一般为:一,对函数求导,代入已知点得到在这一点处的斜率;二,求出这个点的横纵坐标;三,利用点斜式写出直线方程.考查了函数零点个数问题,即转化为函数图像和x 轴的交点问题.5(2023·全国·高三专题练习)已知函数f x =x 2-2m ,g x =3ln x -x ,若y =f x 与y =g x在公共点处的切线相同,则m =()A.-3B.1C.2D.5【答案】B【分析】设曲线y =f x 与y =g x 的公共点为x 0,y 0 ,根据题意可得出关于x 0、m 的方程组,进而可求得实数m 的值.【详解】设函数f x =x 2-2m ,g x =3ln x -x 的公共点设为x 0,y 0 ,则f x 0 =g x 0 f x 0 =g x 0 ,即x 20-2m =3ln x 0-x 02x 0=3x 0-1x 0>0,解得x 0=m =1,故选:B .【点睛】本题考查利用两函数的公切线求参数,要结合公共点以及导数值相等列方程组求解,考查计算能力,属于中等题.6(2023·全国·高三专题练习)函数f (x )=ln x 在点P (x 0,f (x 0))处的切线与函数g (x )=e x 的图象也相切,则满足条件的切点的个数有A.0个B.1个C.2个D.3个【答案】C【分析】先求直线l 为函数的图象上一点A (x 0,f (x 0))处的切线方程,再设直线l 与曲线y =g (x )相切于点(x 1,e x 1),进而可得ln x 0=x 0+1x 0-1,根据函数图象的交点即可得出结论.【详解】解:∵f (x )=ln x ,∴f ′(x )=1x ,∴x =x 0,f ′(x 0)=1x 0,∴切线l的方程为y-ln x0=1x0(x-x0),即y=1x0x+ln x0-1,①设直线l与曲线y=g(x)相切于点(x1,e x1),∵g (x)=e x,∴e x1=1x0,∴x1=-ln x0.∴直线l也为y-1x0=1x0(x+ln x0)即y=1x0x+ln x0x0+1x0,②由①②得ln x0=x0+1 x0-1,如图所示,在同一直角坐标系中画出y=ln x,y=x+1x-1的图象,即可得方程有两解,故切点有2个.故选:C二、填空题7(2023·吉林长春·长春吉大附中实验学校校考模拟预测)与曲线y=e x和y=-x24都相切的直线方程为.【答案】y=x+1【分析】分别设出直线与两曲线相切的切点,然后表示出直线的方程,再根据切线是同一条直线建立方程求解.【详解】设直线与曲线y=e x相切于点x1,e x1,因为y =e x,所以该直线的方程为y-e x1=e x1x-x 1,即y=e x1x+e x11-x1,设直线与曲线y=-x24相切于点x2,-x224,因为y =-x2,所以该直线的方程为y+x224=-x22x-x2,即y=-x22x+x224,所以e x1=-x22e x11-x1=x224,解得x1=0,x2=-2,所以该直线的方程为y=x+1,故答案为:y=x+1.8(2023·全国·高三专题练习)已知f x =e x-1(e为自然对数的底数),g x =ln x+1,请写出f x 与g x 的一条公切线的方程.【答案】y=ex-1或y=x【分析】假设切点分别为m,e m-1,n,ln n+1,根据导数几何意义可求得公切线方程,由此可构造方程求得m,代入公切线方程即可得到结果.【详解】设公切线与f x 相切于点m,e m-1,与g x 相切于点n,ln n+1,∵f x =e x,g x =1x,∴公切线斜率k=e m=1n;∴公切线方程为:y-e m+1=e m x-m或y-ln n-1=1nx-n,整理可得:y=e m x-m-1e m-1或y=1nx+ln n,∴e m=1nm-1e m+1=-ln n,即m=-ln nm-1e m +1=-ln n,∴m-1e m+1-m=m-1e m-1=0,解得:m=1或m=0,∴公切线方程为:y=ex-1或y=x.故答案为:y=ex-1或y=x.9(2023春·安徽·高三合肥市第六中学校联考开学考试)已知直线l与曲线y=e x、y=2+ln x都相切,则直线l的方程为.【答案】y=x+1或y=ex【分析】分别求出两曲线的切线方程是y=e x1x+e x11-x1和y=1x2x+1+ln x2,解方程e x1=1x2,e x11-x1=1+ln x2,即得解.【详解】解:由y=e x得y =e x,设切点为x1,e x1,所以切线的斜率为e x1,则直线l的方程为:y=e x1x+e x11-x1;由y =2+ln x 得y =1x ,设切点为x 2,2+ln x 2 ,所以切线的斜率为1x 2,则直线l 的方程为:y =1x 2x +1+ln x 2.所以e x 1=1x 2,e x 11-x 1 =1+ln x 2,消去x 1得1x 2-11+ln x 2 =0,故x 2=1或x 2=1e,所以直线l 的方程为:y =x +1或y =ex .故答案为:y =x +1或y =ex 10(2023春·浙江金华·高三浙江金华第一中学校考阶段练习)已知直线y =kx +b 是曲线y =ln 1+x 与y =2+ln x 的公切线,则k +b =.【答案】3-ln2【分析】分别设两条曲线上的切点,写出切线方程,建立方程组,解出切点,计算k +b .【详解】设曲线y =ln 1+x 上切点A x 1,ln 1+x 1 ,y =11+x,切线斜率k =11+x 1,切线方程y -ln 1+x 1 =11+x 1x -x 1 ,即y =11+x 1x -x 11+x 1+ln 1+x 1同理,设曲线y =2+ln x 上切点B x 2,2+ln x 2 ,y =1x,切线斜率k =1x 2,切线方程y -2+ln x 2 =1x 2x -x 2 ,即y =1x 2x +1+ln x 2,所以11+x 1=1x 2-x11+x 1+ln (1+x 1)=1+ln x 2,解得x 1=-12x 2=12,所以k =2,b =1-ln2,k +b =3-ln2.故答案为:3-ln2.2.公切线中的参数问题一、单选题1(2023·陕西渭南·统考一模)已知直线y =ax +b (a ∈R ,b >0)是曲线f x =e x 与曲线g x =ln x +2的公切线,则a +b 等于()A.e +2B.3C.e +1D.2【答案】D【分析】由f x 求得切线方程,结合该切线也是g x 的切线列方程,求得切点坐标以及斜率,进而求得直线y =ax +b ,从而求得正确答案.【详解】设t ,e t 是f x 图象上的一点,f x =e x ,所以f x 在点t ,e t 处的切线方程为y -e t =e t x -t ,y =e t x +1-t e t ①,令g x =1x=e t ,解得x =e -t ,g e -t=ln e -t+2=2-t ,所以2-t -e te -t-t=e t ,1-t =1-t e t ,所以t =0或t =1(此时①为y =ex ,b =0,不符合题意,舍去),所以t =0,此时①可化为y -1=1×x -0 ,y =x +1,所以a +b =1+1=2.故选:D2(2023·陕西榆林·校考模拟预测)若直线l 与曲线y =e x 相切,切点为M x 1,y 1 ,与曲线y =x +32也相切,切点为N x 2,y 2 ,则2x 1-x 2的值为()A.-2B.-1C.0D.1【答案】B【分析】根据导数求出切线的斜率,得到切线方程,根据两切线方程即可得解.【详解】因为直线l 与曲线y =e x 相切,切点为M x 1,y 1 ,可知直线l 的方程为y =e x 1x -x 1 +e x 1=e x 1x +1-x 1 e x 1,又直线l 与曲线y =x +3 2也相切,切点为N x 2,y 2 ,可知直线l 的方程为y =2x 2+3 x -x 2 +x 2+3 2=2x 2+3 x -x 22+9,所以e x 1=2x 2+3 1-x 1 e x 1=-x 22+9,两式相除,可得21-x 1 =3-x 2,所以2x 1-x 2=-1.故选:B3(2023春·河南·高三校联考阶段练习)已知曲线y =x 在点x 0,x 0 0<x 0<14处的切线也与曲线y =e x 相切,则x 0所在的区间是()A.0,14e 4B.14e 4,14e 2C.14e 2,14eD.14e ,14【答案】C【分析】设切线l与曲线y=e x的切点为m,e m,通过导数分别写出切线方程,由两条切线重合得出方程,再通过此方程有解得出结果.【详解】设该切线为l,对y=x求导得y =12x,所以l的方程为y-x0=12x0x-x0,即y=12x0x+x02.设l与曲线y=e x相切的切点为m,e m,则l的方程又可以写为y-e m=e m x-m,即y=e m x+1-me m.所以e m=12x0,x02=1-me m.消去m,可得x0=1+ln2x0,0<x0<1 4,令t=2x0∈0,1,则ln t-t24+1=0.设h t =ln t-t24+1,当0<t<1时,h t =1t-t2>0,所以h t 在0,1上单调递增,又h1e=-14e2<0,h1e=12-14e>0,所以t0=2x0∈1e,1e,所以x0∈14e2,14e.故选:C.4(2023·全国·高三专题练习)若函数f x =2a ln x+1与g x =x2+1的图像存在公共切线,则实数a的最大值为()A.eB.2eC.e22D.e2【答案】A【分析】分别设公切线与g x =x2+1和f(x)=2a ln x+1的切点x1,x21+1,x2,2a ln x2+1,根据导数的几何意义列式,再化简可得a=2x22-2x22ln x2,再求导分析h(x)=2x2-2x2⋅ln x(x >0)的最大值即可【详解】g x =2x,f x =2a x,设公切线与g x =x2+1的图像切于点x1,x21+1,与曲线f(x)=2a ln x+1切于点x2,2a ln x2+1,所以2x1=2ax2=2a ln x2+1-x21+1x2-x1=2a ln x2-x21x2-x1,故a=x1x2,所以2x1=2x1x2ln x2-x21x2-x1,所以x1=2x2-2x2⋅ln x2,因为a=x1x2,故a=2x22-2x22ln x2,设h(x)=2x2-2x2⋅ln x(x>0),则h (x)=2x(1-2ln x),令h (x)=0⇒x=e当h (x)>0时,x∈(0,e),当h (x)<0时,x∈(e,+∞),所以h x 在(0,e)上递增,在(e,+∞)上递减,所以h(x)max=h(e)=e,所以实数a的最大值为e,故选:A.5(2023·湖南郴州·统考模拟预测)定义:若直线l与函数y=f x ,y=g x 的图象都相切,则称直线l为函数y=f x 和y=g x 的公切线.若函数f x =a ln x a>0和g x =x2有且仅有一条公切线,则实数a的值为()A.eB.eC.2eD.2e【答案】C【分析】设直线与g x =x2的切点为x1,x21,然后根据导数的几何意义可推得切线方程为y=2x1x-x21,y=ax2x+a ln x2-1.两条切线重合,即可得出a=4x22-4x22ln x2有唯一实根.构造h x =4x2-4x2ln x x>0,根据导函数得出函数的性质,作出函数的图象,结合图象,即可得出答案.【详解】设直线与g x =x2的切点为x1,x21,因为g x =2x,根据导数的几何意义可知该直线的斜率为2x1,即该直线的方程为y-x21=2x1x-x1,即y=2x1x-x21.设直线与f x =a ln x的切点为(x2,a ln x2),因为f x =ax,根据导数的几何意义可知该直线的斜率为ax2,即该直线的方程为y-a ln x2=ax2x-x2,即y=ax2x+a ln x2-1.因为函数f x =a ln x a>0和g x =x2有且只有一条公切线,所以有2x1=ax2a ln x2-1=-x21 ,即a=4x22-4x22ln x2有唯一实根.令h x =4x2-4x2ln x x>0,则h x =8x-8x ln x-4x=4x1-2ln x.解h x =0,可得x= e.当4x1-2ln x>0时,0<x<e,所以h x 在0,e上单调递增;当4x1-2ln x<0时,x>e,所以h x 在e,+∞上单调递减.所以h x 在x=e处取得最大值h e=4e-4e×12=2e.当x→0时,h x →0,h e =4e2-4e2ln e=0,函数h x 图象如图所示,因为a>0,a=4x2-4x2ln x有唯一实根,所以只有a=2e.故选:C6(2023春·广东汕头·高三汕头市潮阳实验学校校考阶段练习)已知函数f x =2+ln x,g x = a x,若总存在两条不同的直线与函数y=f x ,y=g x 图象均相切,则实数a的取值范围为()A.0,1B.0,2C.1,2D.1,e【答案】B【分析】设函数y=f x ,y=g x 的切点坐标分别为x1,2+ln x1,x2,a x2,根据导数几何意义可得a2=4ln x1+4x1,x1>0,即该方程有两个不同的实根,则设h x =4ln x+4x,x>0,求导确定其单调性与取值情况,即可得实数a的取值范围.【详解】解:设函数f x =2+ln x上的切点坐标为x1,2+ln x1,且x1>0,函数g x =a x 上的切点坐标为x2,a x2,且x2≥0,又f x =1x,g x =a2x,则公切线的斜率k=1x1=a2x2,则a>0,所以x2=a24x21,则公切线方程为y-2+ln x1=1x1x-x1,即y=1x1x+ln x1+1,代入x 2,a x 2 得:a x 2=1x 1x 2+ln x 1+1,则a 22x 1=1x 1⋅a 24x 21+ln x 1+1,整理得a 2=4ln x 1+4x 1,若总存在两条不同的直线与函数y =f x ,y =g x 图象均相切,则方程a 2=4ln x 1+4x 1有两个不同的实根,设h x =4ln x +4x,x >0,则h x =4x⋅x -4ln x +4x2=-4ln xx,令h x =0得x =1,当x ∈0,1 时,h x >0,h x 单调递增,x ∈1,+∞ 时,h x <0,h x 单调递减,又h x =0可得x =1e,则x →0时,h x →-∞;x →+∞时,h x →0,则函数h x 的大致图象如下:所以a >00<a 2<4,解得0<a <2,故实数a 的取值范围为0,2 .故选:B .【点睛】本题考查了函数的公切线、函数方程与导数的综合应用,难度较大.解决本题的关键是,根据公切线的几何意义,设切点坐标分别为x 1,2+ln x 1 ,且x 1>0,x 2,a x 2 ,且x 2≥0,可得k =1x 1=a 2x 2,即有x 2=a 24x 21,得公切线方程为y =1x 1x +ln x 1+1,代入切点x 2,a x 2 将双变量方程a x 2=1x 1x 2+ln x 1+1转化为单变量方程a 22x 1=1x 1⋅a 24x 21+ln x 1+1,根据含参方程进行“参变分离”得a 2=4ln x 1+4x 1,转化为一曲一直问题,即可得实数a 的取值范围.7(2023·全国·高三专题练习)若曲线y =ln x +1与曲线y =x 2+x +3a 有公切线,则实数a 的取值范围()A.2ln2-36,3-ln22B.1-4ln212,3-ln22C.2ln2-36,+∞ D.1-4ln212,+∞【答案】D【分析】分别求出两曲线的切线方程,则两切线方程相同,据此求出a 关于切点x 的解析式,根据解析式的值域确定a 的范围.【详解】设x 1,y 1 是曲线y =ln x +1的切点,设x 2,y 2 是曲线y =x 2+x +3a 的切点,对于曲线y =ln x +1,其导数为y =1x ,对于曲线y =x 2+x +3a ,其导数为y =2x +1,所以切线方程分别为:y -ln x 1+1 =1x 1x -x 1 ,y -x 22+x 2+3a =2x 2+1 x -x 2 ,两切线重合,对照斜率和纵截距可得:1x 1=2x 2+1ln x 1=-x 22+3a,解得3a =ln x 1+x 22=ln 12x 2+1+x 22=-ln 2x 2+1+x 22x 2>-12 ,令h x =-ln 2x +1 +x 2x >-12,hx =-22x +1+2x =4x 2+2x -22x +1=2x +1 2x -1 2x +1=0,得:x =12,当x ∈-12,12时,h x <0,h x 是减函数,当x ∈12,+∞时,h x >0,h x 是增函数,∴h min x =h 12 =14-ln2且当x 趋于-12时,,h x 趋于+∞;当x 趋于+∞时,h x 趋于+∞;∴3a ≥14-ln2,∴a ≥1-4ln212;故选:D .8(2023·河北·统考模拟预测)若曲线f (x )=3x 2-2与曲线g (x )=-2-m ln x (m ≠0)存在公切线,则实数m 的最小值为()A.-6eB.-3eC.2eD.6e【答案】A【分析】求出函数的导函数,设公切线与f x 切于点x 1,3x 21-2 ,与曲线g x 切于点x 2,-2-m ln x 2 ,x 2>0 ,即可得到m =-6x 1x 2,则x 1=0或x 1=2x 2-x 2ln x 2,从而得到m =12x 22ln x 2-12x 22,在令h x =12x 2ln x -12x 2,x >0 ,利用导数求出函数的最小值,即可得解;【详解】因为f (x )=3x 2-2,g (x )=-2-m ln x (m ≠0),所以f (x )=6x ,g (x )=-mx,设公切线与f x 切于点x 1,3x 21-2 ,与曲线g x 切于点x 2,-2-m ln x 2 ,x 2>0 ,所以6x 1=-m x 2=-2-m ln x 2-3x 21-2 x 2-x 1=-m ln x 2-3x 21x 2-x 1,所以m =-6x 1x 2,所以6x 1=6x 1x 2ln x 2-3x 21x 2-x 1,所以x 1=0或x 1=2x 2-x 2ln x 2,因为m ≠0,所以x 1≠0,所以x 1=2x 2-x 2ln x 2,所以m =-62x 2-x 2ln x 2 x 2=12x 22ln x 2-12x 22,令h x =12x 2ln x -12x 2,x >0 ,则h x =12x 2ln x -1 ,所以当0<x <e 时h x <0,当x >e 时h x >0,所以h x 在0,e 上单调递减,在e ,+∞ 上单调递增,所以h x min =h e =-6e ,所以实数m 的最小值为-6e.故选:A【点睛】思路点睛:涉及公切线问题一般先设切点,在根据斜率相等得到方程,即可找到参数之间的关系,最后构造函数,利用导数求出函数的最值.二、多选题9(2023·湖北·统考模拟预测)若存在直线与曲线f x =x 3-x ,g x =x 2-a 2+a 都相切,则a 的值可以是()A.0B.-24C.log 27D.e π+πe【答案】ABC【分析】设该直线与f x 相切于点x 1,x 31-x 1 ,求出切线方程为y =3x 21-1 x -2x 31,设该直线与g x 相切于点x 2,x 22-a 2+a ,求出切线方程为y =2x 2x -x 22-a 2+a ,联立方程组,得到-a 2+a =94x 41-2x 31-32x 21+14,令h x =94x 4-2x 3-32x 2+14,讨论h x 的单调性,从而得到最值,则可得到-a 2+a ≥-1,解出a 的取值范围,四个选项的值分别比较与区间端点比较大小即可判断是否在区间内.【详解】设该直线与f x 相切于点x 1,x 31-x 1 ,因为f x =3x 2-1,所以f x 1 =3x 21-1,所以该切线方程为y -x 31-x 1 =3x 21-1 x -x 1 ,即y =3x 21-1 x -2x 31.设该直线与g x 相切于点x 2,x 22-a 2+a ,因为g x =2x ,所以g x 2 =2x 2,所以该切线方程为y -x 22-a 2+a =2x 2x -x 2 ,即y =2x 2x -x 22-a 2+a ,所以3x 21-1=2x 2-2x 31=-x 22-a 2+a ,所以-a 2+a =x 22-2x 31=3x 21-122-2x 31=94x 41-2x 31-32x 21+14,令h x =94x 4-2x 3-32x 2+14,∴h x =9x 3-6x 2-3x ,所以当x ∈-∞,-13 ∪0,1 时,hx <0;当x ∈-13,0 ∪1,+∞ 时,h x >0;∴h x 在-∞,-13和0,1 上单调递减;在-13,0 和1,+∞ 上单调递增;又h -13 =527,h 1 =-1,所以h x ∈-1,+∞ ,所以-a 2+a ≥-1,解得1-52≤a ≤1+52,所以a 的取值范围为1-52,1+52,所以A 正确;对于B ,-24-1-52=25-2+2 4>0,所以1-52<-24<0,所以B 正确;对于C ,因为0<log 27<log 222=32<1+52,所以C 正确;对于D ,因为e π+πe>2e π⋅πe=2>1+52,所以D 不正确.故选:ABC10(2023·全国·高三专题练习)函数f x =ln x +1,g x =e x -1,下列说法正确的是( ).(参考数据:e 2≈7.39,e 3≈20.09,ln2≈0.69,ln3≈1.10)A.存在实数m ,使得直线y =x +m 与y =f x 相切也与y =g x 相切B.存在实数k ,使得直线y =kx -1与y =f x 相切也与y =g x 相切C.函数g x -f x 在区间23,+∞ 上不单调D.函数g x -f x 在区间23,+∞上有极大值,无极小值【答案】AB【分析】对AB ,设直线与y =f x 、y =g x 分别切于点P x 1,y 1 ,Q x 2,y 2 ,利用点在线上及斜率列方程组,解得切点即可判断;对CD ,令h x =g x -f x ,由二阶导数法研究函数单调性及极值.【详解】对AB ,设直线l 与y =f x 、y =g x 分别切于点P x 1,y 1 ,Q x 2,y 2 ,f x =1x,gx =ex,则有y1=f x1=ln x1+1y2=g x2=e x2-1y1-y2x1-x2=1x1=e x2⇒ln x1+1-e x2-1x1-x2=e x2⇒-x2+1-e x2-11e x2-x2=e x2⇒e x2-1x2-1=0,解得x2=0或x2=1.当x2=0,则y2=0,x1=1,y1=1,公切线为y=x,此时存在实数m=0满足题意;当x2=1,则y2=e-1,x1=1e,y1=0,公切线为y=e x-1e=ex-1,此时存在实数k=1满足题意,AB对;对CD,令h x =g x -f x =e x-ln x-2,x∈0,+∞,则m x =h x =e x-1 x,由m x =e x+1x2>0得h x 在0,+∞单调递增,由h23=e23-32=e2-278e232+32e23+94>0得,x∈23,+∞时,h x >0,h x 单调递增,CD错.故选:AB.三、填空题11(2023·全国·高三专题练习)若曲线y=ax2与y=ln x有一条斜率为2的公切线,则a= .【答案】1ln2e【分析】根据导数的几何意义以及切线方程的求解方法求解.【详解】设公切线在曲线y=ax2与y=ln x上的切点分别为A(x1,y1),B(x2,y2),由y=ln x可得y =1x,所以1x2=2,解得x2=12,所以y2=ln x2=-ln2,则B12,-ln2 ,所以切线方程为y+ln2=2x-1 2,又由y=ax2,可得y =2ax,所以2ax1=2,即ax1=1,所以y1=ax21=x1,又因为切点A(x1,y1),也即A(x1,x1)在切线y+ln2=2x-1 2上,所以x1+ln2=2x1-1 2,解得x1=ln2+1,所以a =1x 1=1ln2+1=1ln2e .故答案为:1ln2e.12(2023·河北唐山·统考三模)已知曲线y =ln x 与y =ax 2a >0 有公共切线,则实数a 的取值范围为.【答案】12e,+∞【分析】设公切线与曲线的切点为x 1,ln x 1 ,x 2,ax 22 ,利用导数的几何意义分别求y =ln x 和y =ax 2上的切线方程,由所得切线方程的相关系数相等列方程求参数关系,进而构造函数并利用导数研究单调性求参数范围.【详解】设公切线与曲线y =ln x 和y =ax 2的切点分别为x 1,ln x 1 ,x 2,ax 22 ,其中x 1>0,对于y =ln x 有y =1x ,则y =ln x 上的切线方程为y -ln x 1=1x 1x -x 1 ,即y =xx 1+ln x 1-1 ,对于y =ax 2有y =2ax ,则y =ax 2上的切线方程为y -ax 22=2ax 2x -x 2 ,即y =2ax 2x -ax 22,所以1x 1=2ax 2ln x 1-1=-ax 22,有-14ax21=ln x 1-1,即14a=x 21-x 21ln x 1x 1>0 ,令g x =x 2-x 2ln x ,g x =x -2x ln x =x 1-2ln x ,令gx =0,得x =e 12,当x ∈0,e12时,g x >0,g x 单调递增,当x ∈e 12,+∞ 时,g x <0,g x 单调递减,所以g x max =g e12=12e ,故0<14a ≤12e ,即a ≥12e.∴正实数a 的取值范围是12e,+∞.故答案为:12e,+∞.13(2023·浙江金华·统考模拟预测)若存在直线l 既是曲线y =x 2的切线,也是曲线y =a ln x 的切线,则实数a 的最大值为.【答案】2e【分析】设切线与两曲线的切点分别为(n ,n 2),(m ,a ln m ),根据导数的几何意义分别求出切线方程,可得a4m2=1-ln m,由题意可知a4=m2(1-ln m)有解,故令g(x)=x2(1-ln x),(x>0),利用导数求得其最值,即可求得答案.【详解】由题意知两曲线y=x2与y=a ln x,(x>0)存在公切线,a=0时,两曲线y=x2与y=0,(x>0),不合题意;则y=x2的导数y =2x,y=a ln x的导数为y =a x,设公切线与y=x2相切的切点为(n,n2),与曲线y=a ln x相切的切点为(m,a ln m),则切线方程为y-n2=2n(x-n),即y=2nx-n2,切线方程也可写为y-a ln m=am(x-m),即y=amx-a+a ln m,故2n=am-n2=-a+a ln m,即a24m2=a-a ln m,即a4m2=1-ln m,即a4=m2(1-ln m)有解,令g(x)=x2(1-ln x),(x>0),则g (x)=2x(1-ln x)+x2-1 x=x(1-2ln x),令g (x)=0可得x=e,当0<x<e时,g (x)>0,当x>e时,g (x)<0,故g(x)在(0,e)是增函数,在(e,+∞)是减函数,故g(x)的最大值为g(e)=e 2,故a4≤e2,所以a≤2e,即实数a的最大值为2e,故答案为:2e。
用导数求切线方程的四种类型

用导数求切线方程的四种类型在微积分中,切线是曲线上某一点的切线。
通过使用导数,我们可以求解给定曲线上某一点的切线方程。
在本文中,我们将探讨四种使用导数求解切线方程的常见类型。
1. 曲线方程已知的情况首先,我们考虑的是当曲线方程已知时求解切线方程的情况。
假设我们有一个曲线y=f(x),其中f(x)是一个可导函数。
要求解曲线上某一点(x1,y1)处的切线方程,我们可以执行以下步骤:1.计算函数f(x)在点(x1,y1)处的导数f′(x1)。
2.使用点斜式或一般式等方程形式得到切线方程。
点斜式切线方程的一般形式为y−y1=m(x−x1),其中m是斜率。
一般式切线方程的一般形式为ax+by=c,其中a,b,c是常数。
2. 给定两个点的情况其次,我们考虑的是当曲线上两个点已知时求解切线方程的情况。
与上一种情况不同,我们不知道曲线的具体方程,但我们已知曲线上的两个点(x1,y1)和(x2,y2)。
为了求解这种情况下的切线方程,我们可以按照以下步骤进行:1.使用点斜式求解斜率。
2.写出点斜式的一般方程形式y−y1=m(x−x1)。
3.将另一个点(x2,y2)替代初始点(x1,y1)。
4.解方程得出切线方程。
3. 已知切线方程的情况接下来,我们讨论已知切线方程的情况。
假设我们已经知道了曲线上某一点处的切线方程,我们的目标是求解曲线方程。
我们可以按照以下步骤进行操作:1.确定切线方程的斜率m。
2.使用导数的定义f′(x)=m来设置方程。
3.解方程以获得曲线方程。
4. 求解切线与坐标轴的交点最后,我们研究切线与坐标轴相交的情况。
为了求解切线与x轴和y轴的交点,我们可以按照以下步骤进行:1.求解切线与x轴的交点:将y值设为0,然后解方程得到x坐标的值。
2.求解切线与y轴的交点:将x值设为0,然后解方程得到y坐标的值。
通过上述四种类型的方法,我们可以使用导数来求解切线方程。
这些方法在解决微积分问题以及实际问题中的应用非常广泛。
2023届高考数学导数满分通关:曲线的公切线方程

专题03 曲线的公切线方程【方法总结】解决此类问题通常有两种方法(1)利用其中一曲线在某点处的切线与另一曲线相切,列出关系式求解;(2)设公切线l 在y =f (x )上的切点P 1(x 1,f (x 1)),在y =g (x )上的切点P 2(x 2,g (x 2)),则f ′(x 1)=g ′(x 2)=f (x 1)-g (x 2)x 1-x 2.注意:求两条曲线的公切线,如果同时考虑两条曲线与直线相切,头绪会比较乱,为了使思路更清晰,一般是把两条曲线分开考虑,先分析其中一条曲线与直线相切,再分析另一条曲线与直线相切,直线与抛物线相切可用判别式法.【例题选讲】[例1](1)(2020·全国Ⅲ)若直线l 与曲线y =x 和圆x 2+y 2=15都相切,则l 的方程为( )A .y =2x +1B .y =2x +12C .y =12x +1D .y =12x +12答案 D 解析 易知直线l 的斜率存在,设直线l 的方程y =kx +b ,则|b |k 2+1=55①.设直线l 与曲线y =x 的切点坐标为(x 0,x 0)(x 0>0),则y ′|x =x 0=12x 0-12=k ②,x 0=kx 0+b ③,由②③可得b =12x 0,将b =12x 0,k =12x 0-12代入①得x 0=1或x 0=-15(舍去),所以k =b =12,故直线l 的方程y =12x +12.(2)已知f (x )=e x (e 为自然对数的底数),g (x )=ln x +2,直线l 是f (x )与g (x )的公切线,则直线l 的方程为 .答案 y =e x 或y =x +1 解析 设l 与f (x )=e x 的切点为(x 1,y 1),则y 1=1e x ,f ′(x )=e x ,∴f ′(x 1)=1e x,∴切点为(x 1,1e x),切线斜率k =1e x,∴切线方程为y -1e x=1e x(x -x 1),即y =1e x·x -11e xx +1e x,①,同理设l 与g (x )=ln x +2的切点为(x 2,y 2),∴y 2=ln x 2+2,g ′(x )=1x ,∴g ′(x 2)=1x 2,切点为(x 2,ln x 2+2),切线斜率k =1x 2,∴切线方程为y -(ln x 2+2)=1x 2(x -x 2),即y =1x 2·x +ln x 2+1,②,由题意知,①与②相同,∴111122121e e , e e ln 1,x x x x x x x x -⎧=⇒=⎪⎨⎪-+=+⎩③④把③代入④有-11e x x +1e x =-x 1+1,即(1-x 1)(1e x -1)=0,解得x 1=1或x 1=0,当x 1=1时,切线方程为y =e x ;当x 1=0时,切线方程为y =x +1,综上,直线l 的方程为y =e x 或y =x +1.(3)曲线C 1:y =ln x +x 与曲线C 2:y =x 2有________条公切线.答案 1 解析 由y =ln x +x 得y ′=1x+1,设点(x 1,ln x 1+x 1)是曲线C 1上任一点,∴曲线C 1在点(x 1,ln x 1+x 1)处的切线方程为y -(ln x 1+x 1)=⎝⎛⎭⎫1x 1+1(x -x 1),即y =⎝⎛⎭⎫1x 1+1x +ln x 1-1.同理可得曲线C 2在点(x 2,x 22)处的切线方程为y -x 22=2x 2(x -x 2),即y =2x 2x -x 22.依题意知两切线重合,∴⎩⎪⎨⎪⎧1x 1+1=2x 2,ln x 1-1=-x 22,消去x 2得1x 21+2x 1+4ln x 1-3=0,①,令f (x )=1x 2+2x +4ln x -3(x >0),则f ′(x )=-2x 3-2x 2+4x =4x 2-2x -2x 3=2(2x +1)(x -1)x 3,当x ∈(0,1)时,f ′(x )<0;当x ∈(1,+∞)时,f ′(x )>0,∴f (x )在(0,1)上单调递减,在(1,+∞)上单调递增,∴f (x )min =f (1)=0,∴f (x )只有一个零点.即方程①只有一个解,故曲线C 1与C 2只有1条公切线.(4)已知曲线y =x +ln x 在点(1,1)处的切线与曲线y =ax 2+(a +2)x +1相切,则a = . 答案 8 解析 方法一 因为y =x +ln x ,所以y ′=1+1x ,y ′|x =1=2.所以曲线y =x +ln x 在点(1,1)处的切线方程为y -1=2(x -1),即y =2x -1.因为y =2x -1与曲线y =ax 2+(a +2)x +1相切,所以a ≠0(当a =0时曲线变为y =2x +1与已知直线平行).由⎩⎪⎨⎪⎧y =2x -1,y =ax 2+(a +2)x +1,消去y ,得ax 2+ax +2=0.由Δ=a 2-8a =0,解得a =8.方法二 同方法一得切线方程为y =2x -1.设y =2x -1与曲线y =ax 2+(a +2)x +1相切于点(x 0,ax 20+(a +2)x 0+1).因为y ′=2ax +(a +2),所以0|x x y '==2ax 0+(a +2).由⎩⎪⎨⎪⎧2ax 0+(a +2)=2,ax 20+(a +2)x 0+1=2x 0-1,解得⎩⎪⎨⎪⎧x 0=-12,a =8.(5) (2016·课标全国Ⅱ)若直线y =kx +b 是曲线y =ln x +2的切线,也是曲线y =e x 的切线,则b =________. 答案 0或1 解析 设直线y =kx +b 与曲线y =ln x +2的切点为(x 1,y 1),与曲线y =e x 的切点为(x 2,y 2),y =ln x +2的导数为y ′=1x ,y =e x 的导数为y ′=e x ,可得k =e x 2=1x 1.又由k =y 2-y 1x 2-x 1=e x 2-ln x 1-2x 2-x 1,消去x 2,可得(1+ln x 1)·(x 1-1)=0,则x 1=1e 或x 1=1,则直线y =kx +b 与曲线y =ln x +2的切点为⎝⎛⎭⎫1e ,1或(1,2),与曲线y =e x 的切点为(1,e)或(0,1),所以k =e -11-1e =e 或k =1-20-1=1,则切线方程为y =e x 或y =x +1,可得b =0或1.(6)已知曲线f (x )=ln x +1与g (x )=x 2-x +a 有公共切线,则实数a 的取值范围为 .答案 8 解析 设切线与f (x )=ln x +1相切于点P (x 0,ln x 0+1),f ′(x 0)=1x 0,∴切线方程为y -(ln x 0+1)=1x 0(x -x 0),即y =1x 0x +ln x 0,联立⎩⎪⎨⎪⎧y =1x 0x +ln x 0,y =x 2-x +a ,得x 2-⎝⎛⎭⎫1+1x 0x +a -ln x 0=0,∴Δ=⎝⎛⎭⎫1+1x 02-4(a -ln x 0)=0,即1x 20+2x 0+1-4a +4ln x 0=0,即4a =1x 20+2x 0+1+4ln x 0有解,令φ(x )=1x 2+2x +1+4ln x (x >0),φ′(x )=-2x 3-2x 2+4x =4x 2-2x -2x 3=2(2x +1)(x -1)x 3,当x ∈(0,1)时,φ′(x )<0,当x ∈(1,+∞)时,φ′(x )>0,∴φ(x )在(0,1)上单调递减,在(1,+∞)上单调递增,∴φ(x )min =φ(1)=4,又x →+∞时,φ(x )→+∞,故φ(x )的值域为[4,+∞),所以4a ≥4,即a ≥1,故实数a 的取值范围是[1,+∞).【对点训练】1.若直线l 与曲线y =e x 及y =-14x 2都相切,则直线l 的方程为________.1.答案 y =x +1 解析 设直线l 与曲线y =e x 的切点为(x 0,0x e ),直线l 与曲线y =-14x 2的切点为⎝⎛⎭⎫x 1,-x 214,因为y =e x 在点(x 0,0x e )处的切线的斜率为y ′|x =x 0=0x e ,y =-x 24在点⎝⎛⎭⎫x 1,-x 214处的切线的斜率为y ′|x =x 1=⎝⎛⎭⎫-x 2|x =x 1=-x 12,则直线l 的方程可表示为y =0x e x -x 0e 0x e +0x e 或y =-12x 1x +14x 21,所以⎩⎨⎧0x e =-x 12,-x 0x e+0x e =x 214,所以0x e =1-x 0,解得x 0=0,所以直线l 的方程为y =x +1.2.已知函数f (x )=x 2的图象在x =1处的切线与函数g (x )=e xa的图象相切,则实数a 等于( )A .eB .e e 2C .e2D .e e2.答案 B 解析 由f (x )=x 2,得f ′(x )=2x ,则f ′(1)=2,又f (1)=1,所以函数f (x )=x 2的图象在x =1处 的切线方程为y -1=2(x -1),即y =2x -1.设y =2x -1与函数g (x )=e xa 的图象相切于点(x 0,y 0),由g ′(x )=e x a ,可得00000e 2,e 21,x x g x a g x x a ⎧()==⎪⎪⎨⎪()===-⎪⎩′解得x 0=32,a =321e 2=e e 2. 3.已知函数f (x )=x +1,g (x )=a ln x ,若在x =14处函数f (x )与g (x )的图象的切线平行,则实数a 的值为( )A .14B .12C .1D .43.答案 A 解析 由题意可知f ′(x )=12x -12,g ′(x )=a x ,由f ′(14)=g ′(14),得12×(14)-12=a 14,可得a =14,经检验,a =14满足题意.4.若f (x )=ln x 与g (x )=x 2+ax 两个函数的图象有一条与直线y =x 平行的公共切线,则a 等于( ) A .1 B .2 C .3 D .3或-14.答案 D 解析 设在函数f (x )=ln x 处的切点为(x ,y ),根据导数的几何意义得到k =1x =1,解得x =1,故切点为(1,0),可求出切线方程为y =x -1,此切线和 g (x )=x 2+ax 也相切,故x 2+ax =x -1,化简得到x 2+(a -1)x +1=0,只需要满足Δ=(a -1)2-4=0,解得a =-1或a =3.5.若直线y =kx +b 是曲线y =ln x +2的切线,也是曲线y =ln(x +1)的切线,则b =________.5.答案 1-ln 2 解析 y =ln x +2的切线为y =1x 1·x +ln x 1+1(设切点横坐标为x 1).y =ln(x +1)的切线为y =1x 2+1x +ln(x 2+1)-x 2x 2+1(设切点横坐标为x 2).∴⎩⎨⎧1x 1=1x 2+1,ln x 1+1=ln(x 2+1)-x2x 2+1,解得x 1=12,x 2=-12,∴b =ln x 1+1=1-ln2.6.已知f (x )=ln x ,g (x )=12x 2+mx +72(m <0),直线l 与函数f (x ),g (x )的图象都相切,与f (x )图象的切点为(1,f (1)),则m =________.6.答案 -2 解析 ∵f ′(x )=1x ,∴直线l 的斜率k =f ′(1)=1.又f (1)=0,∴切线l 的方程为y =x -1.g ′(x )=x +m ,设直线l 与g (x )的图象的切点为(x 0,y 0),则有x 0+m =1,y 0=x 0-1,y 0=12x 20+mx 0+72,m <0,∴m =-2.7.已知定义在区间(0,+∞)上的函数f (x )=-2x 2+m ,g (x )=-3ln x -x ,若以上两函数的图象有公共点, 且在公共点处切线相同,则m 的值为( )A .2B .5C .1D .07.答案 C 解析 根据题意,设两曲线y =f (x )与y =g (x )的公共点为(a ,b ),其中a >0,由f (x )=-2x 2+ m ,可得f ′(x )=-4x ,则切线的斜率为k =f ′(a )=-4a ,由g (x )=-3ln x -x ,可得g ′(x )=-3x -1,则切线的斜率为k =g ′(a )=-3a -1,因为两函数的图象有公共点,且在公共点处切线相同,所以-4a =-3a -1,解得a =1或a =-34(舍去),又g (1)=-1,即公共点的坐标为(1,-1),将点(1,-1)代入f (x )=-2x 2+m ,可得m =1.8.若直线y =kx +b 是曲线y =e xe 2的切线,也是曲线y =e x -1的切线,则k +b 等于( )A .-ln 22B .1-ln 22C .ln 2-12D .ln 228.答案 D 解析 设直线y =kx +b 与曲线y =e x e 2相切于点P (x 1,y 1),y ′=e x e2=e x -2,k 1=12e x -;直线y =kx +b 与曲线y =e x -1相切于点Q (x 2,y 2),y ′=e x ,k 2=2e x ,∴l 1:y =1112221e e e x x x x x ---+-,l 2:y =2222e e 1e x x x x x +--,12112222212e e e e e e 1x x x x x x x x ⎧=⎪⎨=⎪⎩---,∴---,∴x 2=-ln 2,∴k +b =2222e e 1e x x x x +--=12+12-1-(-ln 2)×12=ln 22.9.设曲线y =e x 在点(0,1)处的切线与曲线y =1x (x >0)在点P 处的切线垂直,则P 的坐标为________.9.答案 (1,1) 解析 y ′=e x ,曲线y =e x 在点(0,1) 处的切线的斜率k 1=e 0=1.设P (m ,n ),y =1x (x>0)的导数为y ′=-1x 2(x >0),曲线y =1x (x >0)在点P 处的切线斜率k 2=-1m 2(m >0),因为两切线垂直,所以k 1k 2=-1,所以m =1,n =1,则点P 的坐标为(1,1).10.已知曲线f (x )=x 3+ax +14在x =0处的切线与曲线g (x )=-ln x 相切,则a 的值为 .10.答案 -e34- 解析 由f (x )=x 3+ax +14,得f ′(x )=3x 2+a .∵f ′(0)=a ,f (0)=14,∴曲线y =f (x )在x =0处的切线方程为y -14=ax .设直线y -14=ax 与曲线g (x )=-ln x 相切于点(x 0,-ln x 0),又∵g ′(x )=-1x,∴⎩⎪⎨⎪⎧-ln x 0-14=ax 0,①a =-1x,②将②代入①得ln x 0=34,∴x 0=e 34,∴a =-1e 34=-e 34-.11.已知曲线y =e x 在点(x 1,1e x )处的切线与曲线y =ln x 在点(x 2,ln x 2)处的切线相同,则(x 1+1)(x 2-1)=( ) A .-1 B .-2 C .1 D .211.答案 B 解析 已知曲线y =e x 在点(x 1,1e x )处的切线方程为y -1e x =1e x (x -x 1),即y =1111e e e x x x x x -+ ,曲线y =ln x 在点(x 2,ln x 2)处的切线方程为y -ln x 2=1x 2(x -x 2),即y =1x 2x -1+ln x 2,由题意得⎩⎪⎨⎪⎧1e x =1x 2,1e x -1e x x 1=-1+ln x 2,得x 2=11e x ,111e e x x x -=-1+ln x 2=-1+1ln 1e x =-1-x 1,则1e x =x 1+1x 1-1.又x 2=11e x ,所以x 2=x 1-1x 1+1,所以x 2-1=x 1-1x 1+1-1=-2x 1+1,所以(x 1+1)(x 2-1)=-2. 12.曲线C 1:y =x 2与曲线C 2:y =a e x (a >0)存在公切线,则a 的取值范围是________.12.答案 ⎝⎛⎦⎤0,4e 2 解析 设公切线在y =x 2上的切点为(x 1,x 21),在y =a e x (a >0)上的切点为(x 2,2e x a ).函 数y =x 2,y =a e x (a >0)的导数分别为y ′=2x ,y ′=a e x,则公切线的斜率为2x 1=222112e e x x x a a x x =--,整理得a=2241e x x ()-.由a >0可知,x 2>1,令f (x )=4x -1e x ,x ∈(1,+∞),则f ′(x )=4e x 2-x e x 2=8-4xe x,f ′(x )>0⇒1<x <2;f ′(x )<0⇒x >2,∴f (x )在区间(1,2)上单调递增,在区间(2,+∞)上单调递减,f (x )max =f (2)=4e 2;当x →+∞时,f (x )→0,即0<f (x )≤4e2,∴a ∈⎝⎛⎦⎤0,4e 2. 13.若存在过点O (0,0)的直线l 与曲线y =x 3-3x 2+2x 和y =x 2+a 都相切,求a 的值. 13.解析 易知点O (0,0)在曲线y =x 3-3x 2+2x 上.(1)当O (0,0)是切点时,由y ′=3x 2-6x +2,得y ′|x =0=2,即直线l 的斜率为2,故直线l 的方程为y =2x .由⎩⎪⎨⎪⎧y =2x ,y =x 2+a ,得x 2-2x +a =0,依题意Δ=4-4a =0,得a =1.(2)当O (0,0)不是切点时,设直线l 与曲线y =x 3-3x 2+2x 相切于点P (x 0,y 0), 则y 0=x 30-3x 20+2x 0,且k =y ′|x =x 0=3x 20-6x 0+2,①,又k =y 0x 0=x 20-3x 0+2,②, 联立①②,得x 0=32(x 0=0舍去),所以k =-14,故直线l 的方程为y =-14x .由⎩⎪⎨⎪⎧y =-14x ,y =x 2+a ,得x 2+14x +a =0,依题意,Δ=116-4a =0,得a =164.综上,a =1或a =164.14.已知函数f (x )=ax 3+3x 2-6ax -11,g (x )=3x 2+6x +12和直线m :y =kx +9,且f ′(-1)=0.(1)求a 的值;(2)是否存在k ,使直线m 既是曲线y =f (x )的切线,又是曲线y =g (x )的切线?如果存在,求出k 的值;如果不存在,请说明理由.14.解析 (1)由已知得f ′(x )=3ax 2+6x -6a ,∵f ′(-1)=0,∴3a -6-6a =0,∴a =-2.(2)存在.由已知得,直线m 恒过定点(0,9),若直线m 是曲线y =g (x )的切线,则设切点为(x 0,3x 20+6x 0+12). ∵g ′(x 0)=6x 0+6,∴切线方程为y -(3x 20+6x 0+12)=(6x 0+6)(x -x 0), 将(0,9)代入切线方程,解得x 0=±1.当x 0=-1时,切线方程为y =9;当x 0=1时,切线方程为y =12x +9. 由(1)知f (x )=-2x 3+3x 2+12x -11,①由f ′(x )=0得-6x 2+6x +12=0,解得x =-1或x =2.在x =-1处,y =f (x )的切线方程为y =-18;在x =2处,y =f (x )的切线方程为y =9, ∴y =f (x )与y =g (x )的公切线是y =9.②由f ′(x )=12得-6x 2+6x +12=12,解得x =0或x =1.在x =0处,y =f (x )的切线方程为y =12x -11;在x =1处,y =f (x )的切线方程为y =12x -10; ∴y =f (x )与y =g (x )的公切线不是y =12x +9.综上所述,y=f(x)与y=g(x)的公切线是y=9,此时k=0.。
利用导数解决曲线切线问题的技巧

利用导数解决曲线切线问题的技巧导数是微积分中一个重要的概念,它可以帮助我们解决曲线切线问题。
在本文中,我们将介绍一些利用导数解决曲线切线问题的技巧。
第一部分:导数的定义与意义在引入导数之前,我们先来了解一下导数的定义与意义。
导数可以理解为函数在某一点处的变化率,表示函数在该点附近的斜率。
导数的计算公式为:f'(x) = lim(h -> 0) [f(x + h) - f(x)] / h第二部分:计算导数的方法有很多种方法可以计算导数,下面我们将介绍几种常用的方法。
1. 使用导数定义计算根据导数的定义,我们可以通过求函数在某一点的斜率来计算导数。
这种方法通常适用于简单的多项式函数或基本三角函数。
2. 使用求导法则求导法则是一些用来计算导数的常用规则。
这些规则包括求和法则、常数法则、乘积法则、商法则以及复合函数法则等。
通过应用这些法则,我们可以更快速地计算导数。
3. 使用隐函数求导对于一些复杂的函数表达式,我们可能无法直接通过求导法则计算导数。
这时,我们可以使用隐函数求导的方法。
通过对方程两边同时求导,然后解方程组,我们可以求得导函数。
第三部分:曲线切线问题与导数曲线切线问题是指在给定函数图像上找到曲线某点处的切线方程。
利用导数可以帮助我们解决曲线切线问题。
1. 切线的斜率首先,根据导数的定义,我们知道函数在某点的导数就是切线的斜率。
因此,要求解曲线切线的斜率,我们只需要计算函数在该点处的导数。
2. 切线的方程根据点斜式的定义,切线的方程可以表示为:y - y1 = f'(x1)(x - x1)其中,(x1, y1)是切线上的一点,f'(x1)是函数在该点处的导数。
通过求得导数和已知点坐标,我们可以得到切线的方程。
第四部分:实例分析为了更好地理解利用导数解决曲线切线问题的技巧,我们来看一个具体的实例。
例:求函数f(x) = x^2在点(1, 1)处的切线方程。
首先,我们需要计算函数在x = 1处的导数。
高中数学课件-第1讲 导数的概念及运算-链接高考1 破解两条曲线的公切线问题

链接高考1破解两条曲线的公切线问题[问题解读]在近几年高考导数试题的命制过程中,求曲线的公切线问题成为高考的热点题型之一.学生在做题过程中,解决单一曲线的切线问题相对比较熟练,求解方法也较容易理解.但是对于两条曲线的公切线问题的求解,显然就比单一曲线的切线问题要复杂得多,灵活得多,难度也大得多.下面通过典型例题分析一下常见的三类公切线问题.类型1两曲线相切时切点处的公切线方程如果两条曲线1与2有且仅有一个公共点,且在处有且仅有一条公切线,则称1与2相切于点(如图).典例1已知曲线1:==ln ,曲线2:==1−1,求证:1与2相切,并求其公切线的方程.【解】由&=ln ,&=1−1,得ln −+1=0.令=En −+1>0,则′=ln .当∈0,1时,′<0,∈1,+∞时,′>0,所以在0,1上单调递减,在1,+∞上单调递增,故min=1=0.即函数=En −+1有且仅有一个零点1,即方程ln −+1=0仅有唯一根=1,故方程组&=ln ,&=1−1仅有一组解&=1,&=0.又′=1,′1=1,′=12,′1=1,所以′1=y1,所以1与2相切于点1,0,所以其公切线方程为=−1,即−−1=0(如图).类型2两曲线相交时的公切线方程若两条曲线1与2至少有一个公共点,且在点处的切线不相同,则称1与2相交于点.典例2已知曲线1:==ln+1,曲线2:==−142−1.(1)求证:1与2相交;【解】证明:由&=ln+1,&=−142−1,得l n+1+142+1=0.令=ln+1+142+1>−1,则′=1r1+2=2+r22r1>0.所以在−1,+∞上单调递增,所以存在0(例如0=e−2−1)使0<0,又0=1>0,所以有唯一零点=∈−1,0,即方程组&=ln+1,&=−142−1有唯一解又′=1r1>0,′=−2>0.若′=y,则1r1=−2,所以2++2=0.因为方程2++2=0无实根,所以′≠y.所以1与2相交.(2)求 1 与 2的公切线方程.【解】 方法一:设 1 与 2 的公切线 :=B + 分别与 1 , 2 相切于点 1,ln 1+1 , 2,−1422−1 ,则 &=11+1=−22,&l n 1+1 =B 1+,&−1422−1=B 2+, 消去 , , 2,得 l n 1+1 −11+1 2+11+1=0 ,令 =1+1>0 ,则 l n −12+1=0 .设 =ln −12+1 ,则 ′ =2−r23>0 ,又 1 =0 ,即=ln −12+1 只有一个零点1,即方程l n −12+1=0 有唯一的根 =1 ,所以 1+1=1 ,解得1=0 , 2=−2 , =1 , =0 .所以切点分别为 0,0 , −2,−2 ,公切线 的方程为 −=0.(如图)故 在 0,+∞上单调递增,方法二:设1与2的公切线:=B+,代入=−142−1得2+4B+4+1=0,所以=42−4×1×4+1=0,即2−−1=0.①设与曲线=ln+1相切于点1,ln1+1,由=ln+1得,′=1r1,则=11+1,②l n1+1=B1+.③由①,②,③得l n1+1−11+12+11+1=0.(下同方法一)方法三:设公切线与曲线=ln+1和曲线分别相切于点1,ln1+1,2,−1422−1 .由=ln+1与=−142−1得,′=1r1,′=−12.由是曲线=在=1处的切线得,:−ln1+1=11+1−1,①由是曲线=在=2处的切线得,:− −1422−1 =−122−2,②由此得&11+1=−122,&l n1+1−11+1=1422−1.消去2,得l n1+1+11+1−11+12=0.(下同方法一).类型3两曲线相离时的公切线问题已知两曲线1:=,2:=,若方程组&=,&=无解,则1与2相离.典例3已知曲线1:==,曲线2:==log.(1)若1与2相离,求的取值范围;【解】假设方程组&=,&=log有解,即=log有解.因为函数=与函数=log互为反函数,所以=log的解满足=,即l n =ln .令=ln ,则′=1−ln 2,当∈0,e时,′>0,当∈e,+∞时,′<0,所以在0,e上单调递增,在e,+∞上单调递减,所以max=e=1e.又1=0,∈0,1时,<0,∈1,+∞时,>0,故函数=ln 的大致图象如图,所以当l n ≤1e,即≤e1e时,=log有解,故当>e1e时,1与2相离.(2)若 =e ,曲线 1 与 2 的公切线 与 1 , 2 分别相切于点 =1 和 =2 处,求 1−2−12 的值.【解】 当 =e 时,由(1)知, 1 与 2 相离(如图).设公切线 :=B + 与 1 , 2 分别相切于点1,e 1 , 2,ln 2, 由 =e ,得 ′ =e,由 =ln ,得 ′ =1,由题意得 &=e 1=12,①&e 1=B 1+,②&l n 2=B 2+,③将①代入②,③并消去得,1−2+2ln 2=1,由①得,l n 2=−1,所以1−2−12=1.[归纳总结]一般地,求1:=与2:=的公切线的方程有以下三种思路:思路1:设切点分别为1,1,2,2,公切线的方程为=B+,则&=′1=′2,&1=B1+,&2=B2+,研究方程组解的情况.思路2:设切点分别为1,1,2,2,′1=y2=1−21−21≠2.研究方程组解的情况,解的情况对应着公切线的情况.但要注意,求解方程时,一般可转化为研究函数的零点问题.2024版高考总复习思路3:设切点分别为1,1,2,2,公切线:−1= y1−1,−2=y2⋅−2,则&′1=′2,&1−1′1=2−2′2,研究方程组解的情况.。
导数专题:导数与曲线切线问题(6大题型)(解析版)

第1页共14页
导数与曲线切线问题
一、求曲线“在”与“过”某点的切线
1、求曲线“在”某点处的切线方程步骤
第一步(求斜率):求出曲线在点()()00,x f x 处切线的斜率0()
f x '第二步(写方程):用点斜式000()()()
y f x f x x x '-=-第三步(变形式):将点斜式变成一般式。
2、求曲线“过”某点处的切线方程步骤(此类问题的点不一定是切点)
第一步:设切点为()()00,Q x f x ;
第二步:求出函数()y f x =在点0x 处的导数0()f x ';
第三步:利用Q 在曲线上和0()PQ f x k '=,解出0x 及0()f x ';
第四步:根据直线的点斜式方程,得切线方程为000()()()y f x f x x x '-=-.
二、切线条数问题
求曲线的切线条数一般是设出切点()(),t f t ,由已知条件整理出关于t 的方程,把切线问条数问题转化为关于t 的方程的实根个数问题。
三、公切线问题
研究曲线的公切线,一般是分别设出两切点,写出两切线方程,然后再使用这两个方程表示同一条直线,但要注意以下两个方面:
(1)两个曲线有公切线,且切点是同一点;
(2)两个曲线有公切线,但是切点不是同一点。
四、已知切线求参数问题
此类问题常见的考查形式有两种,一是判断符合条件的切线是否存在,二是根据切线满足条件求参数的值或范围。
常用的求解思路是把切线满足条件转化为关于斜率或切点的方程或函数,再根据方程的
根的情况或函数性质去求解。
利用导数求曲线的切线和公切线以及切线条数专题总结.doc

导数中的切线问题专题总结一、求切线方程1.过曲线上一点求切线方程的三个步骤2.求过曲线y =f (x )外一点P (x 1,y 1)的切线方程的六个步骤(1)设切点(x 0,f (x 0)).(2)利用所设切点求斜率k =f ′(x 0)=li m Δx →0f x 0+Δx-f x 0Δx .(3)用(x 0,f (x 0)),P (x 1,y 1)表示斜率.(4)根据斜率相等求得x 0,然后求得斜率k .(5)根据点斜式写出切线方程.(6)将切线方程化为一般式.例1.已知曲线y =1x .(1)求曲线在点P (1,1)处的切线方程;(2)求曲线过点Q (1,0)处的切线方程.例2.已知曲线y=1 x .(1)求曲线在点P(1,1)处的切线方程;(2)求曲线过点Q(1,0)处的切线方程.3.(2016全国卷Ⅲ)已知f(x)为偶函数,当x<0时,f(x)=f(-x)+3x,则曲线y=f(x)在点(1,-3)处的切线方程是二、求切点坐标【小结】求切点坐标可以按以下步骤进行(1)设出切点坐标;(2)利用导数或斜率公式求出斜率;(3)利用斜率关系列方程,求出切点的横坐标;(4)把横坐标代入曲线或切线方程,求出切点纵坐标例1.已知抛物线y =2x 2+1分别满足下列条件,请求出切点的坐标.(1)切线的倾斜角为45°.(2)切线平行于直线4x -y -2=0.(3)切线垂直于直线x +8y -3=0..变式练习直线l :y =x +a (a ≠0)和曲线C :y =x 3-x 2+1相切,则a 的值为___________,切点坐标为____________.三、求两个函数公切线公切线问题:切点相同。
()()00x g x f =()()00''x g x f =切点不同。
()()()()k x g x f mkx x g m kx x f ==+=+=212211'',例1、 已知直线b kx y +=是曲线2ln +=x y 的切线,也是曲线x e y =的切线,求k 和b 的值解析:例2.若直线b kx y +=是曲线2ln +=x y 的切线,也是y =ln(x +1)的切线,求b 的值例3.已知函数f (x )=lnx ,g (x )=2﹣(x >0)(1)试判断当f (x )与g (x )的大小关系;(2)试判断曲线 y=f (x )和 y=g (x )是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;变式练习1.两曲线y =x 2−1和y =alnx −1存在公切线,则正实数a 的取值范围变式练习2.若曲线y =12e x 2与曲线y =alnx 在它们的公共点P (s,t )处有公切线,则实数a =变式练习 3.已知函数()()1263,1163223++=--+=x x x g ax x ax x f 和直线m:9+=kx y ,又()01'=-f ,是否存在k,使直线m 既是曲线()x f y =的切线,又是曲线()x g y =的切线?如果存在,求出k 的值四、切线条数切线的条数问题====以切点0x 为未知数的方程的根的个数例1.已知函数32()f x ax bx cx =++在点0x 处取得极小值-4,使其导数'()0f x >的x 的取值范围为(1,3),求:(1)()f x 的解析式;(2)若过点(1,)P m -可作曲线()y f x =的三条切线,求实数m 的取值范围.例2.已知函数f (x )=2x 3﹣3x+1,g (x )=kx+1﹣lnx .(1)设函数,当k <0时,讨论h (x )零点的个数;(2)若过点P (a ,﹣4)恰有三条直线与曲线y=f (x )相切,求a 的取值范围.变式练习.已知函数f (x )=x 2+2(1﹣a )x ﹣4a ,g (x )=﹣(a+1)2,则f (x )和g (x )图象的公切线条数的可能值是 .。
高考数学导数公切线问题、切线数量问题的一般解法及题型细分

函数的公切线与切线数量问题问题概述:函数的公切线问题,指的是直线b kx y +=同时与两个函数()x f y =与()x g y =同时相切,并在此基础上讨论直线和函数的性质的问题。
解法探究:公切线问题主要关注两个点,(1)两个切点均在函数和切线上;(2)切线斜率满足导数公式。
根据以上两个点,列出等式,即可进行计算求解。
具体公式如下:()()()()⎪⎩⎪⎨⎧'='=+⋅=+⋅=212211x g x f k b x k x g b x k x f 一般的,公切线问题都可以转换为解方程组求参数问题,或者是讨论方程组解的个数问题。
一、已知两个函数的解析式求公切线【例1】曲线21:C y x =与曲线2:C y lnx =公切线的条数是( )A .0B .1C .2D .3分析:最基本的求公切线问题,直接套用基本解法,进行计算即可。
解:设与曲线2y x =和曲线y lnx =相切的切点分别为()2a a ,,()b b ln ,,0>b ,设切线为m kx y +=由题可知2()2x x '=,1()lnx x'=,………………………………准备工作 根据公切线的解法可知:⎪⎪⎩⎪⎪⎨⎧==+=+=b a k m kb b m ka a 12ln 2………………………………列方程 把k 和a 消去,用b 表示剩下的式子,有⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+⋅=+==m m b b b m b b b a 11ln 21412122,把m 消去有141ln 02-+=b b………………………………方程组消元想求公切线的条数,相当于求这个方程的解的个数设()141ln 2-+=x x x f ,()33222222211x x x x x x f ⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-=-=', 所以()x f y =在⎪⎪⎭⎫⎝⎛220,上递减,在⎪⎪⎭⎫ ⎝⎛∞+,22上递增。
导数法求切线方程的三种题型

题目:导数法求切线方程的三种题型求曲线的切线方程是导数的重要应用之一。
用导数求切线方程的关键在于清楚导数的几何意义:切线的斜率确实是函数y=f(x)在切点处的导数。
下面举出长建的题型及解法:题型一:已知切点,求曲线的切线方程。
例1:求函数y=f(x)=2x3在x=1处的切线方程。
解:先求y’=f’(x)=6x2f’(1)=6×1=6=k当x=1时y=2∴切点为(1,2)y-2=6(x-1)y=6x-4题型二:已知曲线外一点,求曲线的切线方程。
例2:已知函数f(x)=x3-3x,过点A(0,16)做曲线y=f(x)的切线,求切线方程。
解:带入可知点A不在曲线上。
设切点M(x0,y0),且点M位于曲线上,知足y0=x03-3x0①f’(x)=3x2-3f’(x0)=3x02-3=k ②又有k=(Y0-16)/(x0-0) ③①带入③,且②=③,取得3x02-3=(x03-3x0)/x0解得x0=-2 ∴y0=-2∴M坐标为(-2,-2)K=3×(-2)2-3=9∴y+2=9(x+2)Y=9x+16题型三:弄清“过某点的切线”与“在某点的切线”例3:(1)求曲线y=x3-2x在点A(1,-1)处的切线方程。
(2)求过曲线y=x3-2x上的点A(1,-1)处的切线方程。
解:(1)做法仿照例1可得切线方程为x-y-2=0(2)设切点为(x0,y0),那么有y0=x03-3x0f’(x0)=3x02-23x02-2=k=(y0+1)/(X0-1)3x02-2= (x03-3x0+1)/ (X0-1)解得x0=1或x0=-1/2当x0=1时y0=-1 切点为(1,-1)现在切线方程为x-y-2=0当x0=-1/2时y0=7/8 切点为(-1/2,7/8) 对结果进行分析可知:“在点A处”实际是指A点确实是切点,而“过点A”包括了A点是切点和A点不是切点两种情形。
以上确实是要紧的三种题型,咱们发觉求切线方程最关键的确实是求出切点,利用切线的斜率等于切点处函数的导数,但假设函数在(x0,y0)处的导数不存在时,该切线方程为y= y0。
利用导数求曲线地切线和公切线

利用导数求曲线的切线和公切线【例1】.曲线f(x)=x3-2x2+1.(1)求在点P〔1,0〕处的切线l1的方程;(2)求过点Q〔2,1〕与曲线f(x)相切的直线l2的方程.提醒:注意是在某个点处还是过某个点!二.有关切线的条数【例2】.〔2014•〕函数f〔x〕=2x3﹣3x.〔Ⅰ〕求f〔x〕在区间[﹣2,1]上的最大值;〔Ⅱ〕假如过点P〔1,t〕存在3条直线与曲线y=f〔x〕相切,求t的取值X 围;〔Ⅲ〕问过点A〔﹣1,2〕,B〔2,10〕,C〔0,2〕分别存在几条直线与曲线y=f〔x〕相切?〔只需写出结论〕【解答】解:〔Ⅰ〕由f〔x〕=2x3﹣3x得f′〔x〕=6x2﹣3,令f′〔x〕=0得,x=﹣或x=,∵f〔﹣2〕=﹣10,f〔﹣〕=,f〔〕=﹣,f〔1〕=﹣1,∴f〔x〕在区间[﹣2,1]上的最大值为.〔Ⅱ〕设过点P〔1,t〕的直线与曲线y=f〔x〕相切于点〔x0,y〕,如此y0=2﹣3x,且切线斜率为k=6﹣3,∴切线方程为y﹣y0=〔6﹣3〕〔x﹣x〕,∴t﹣y0=〔6﹣3〕〔1﹣x〕,即4﹣6+t+3=0,设g〔x〕=4x3﹣6x2+t+3,如此“过点P〔1,t〕存在3条直线与曲线y=f〔x〕相切〞,等价于“g〔x〕有3个不同的零点〞.∵g′〔x〕=12x2﹣12x=12x〔x﹣1〕,∴g〔0〕=t+3是g〔x〕的极大值,g〔1〕=t+1是g〔x〕的极小值.∴g〔0〕>0且g〔1〕<0,即﹣3<t<﹣1,∴当过点过点P〔1,t〕存在3条直线与曲线y=f〔x〕相切时,t的取值X围是〔﹣3,﹣1〕.〔Ⅲ〕过点A〔﹣1,2〕存在3条直线与曲线y=f〔x〕相切;过点B〔2,10〕存在2条直线与曲线y=f〔x〕相切;过点C〔0,2〕存在1条直线与曲线y=f〔x〕相切.【例3】.函数f〔x〕=lnax〔a≠0,a∈R〕,.〔Ⅰ〕当a=3时,解关于x的不等式:1+e f〔x〕+g〔x〕>0;〔Ⅱ〕假如f〔x〕≥g〔x〕〔x≥1〕恒成立,某某数a的取值X围;〔Ⅲ〕当a=1时,记h〔x〕=f〔x〕﹣g〔x〕,过点〔1,﹣1〕是否存在函数y=h〔x〕图象的切线?假如存在,有多少条?假如不存在,说明理由.【解答】解:〔I〕当a=3时,原不等式可化为:1+e ln3x+>0;等价于,解得x,故解集为〔Ⅱ〕∵对x≥1恒成立,所以,令,可得h〔x〕在区间[1,+∞〕上单调递减,故h〔x〕在x=1处取到最大值,故lna≥h〔1〕=0,可得a=1,故a的取值X围为:[1,+∞〕〔Ⅲ〕假设存在这样的切线,设切点T〔x,〕,∴切线方程:y+1=,将点T坐标代入得:即,①设g〔x〕=,如此∵x>0,∴g〔x〕在区间〔0,1〕,〔2,+∞〕上是增函数,在区间〔1,2〕上是减函数,故g〔x〕极大=g〔1〕=1>0,故g〔x〕极,小=g〔2〕=ln2+>0,.又g〔〕=+12﹣6﹣1=﹣ln4﹣3<0,由g〔x〕在其定义域上的单调性知:g〔x〕=0仅在〔,1〕内有且仅有一根,方程①有且仅有一解,故符合条件的切线有且仅有一条.【作业1】.〔2017•某某一模〕函数f 〔x 〕=2x 3﹣3x+1,g 〔x 〕=kx+1﹣lnx . 〔1〕设函数,当k <0时,讨论h 〔x 〕零点的个数;〔2〕假如过点P 〔a ,﹣4〕恰有三条直线与曲线y=f 〔x 〕相切,求a 的取值X 围. 三. 切线与切线之间的关系【例4】.〔2018•某某模拟〕a ,b ,c ∈R ,且满足b 2+c 2=1,如果存在两条互相垂直的直线与函数f 〔x 〕=ax+bcosx+csinx 的图象都相切,如此a+c的取值X 围是.23a b c ++=则23b c +,∵b 2+c 2=1,∴sin ,cos b a ββ==设,∴235sin()b c βϕ+=+,故a+c ∈[﹣,],【例5】.函数f 〔x 〕=lnx ﹣a 〔x ﹣1〕,g 〔x 〕=e x ,其中e 为自然对数的底数.〔Ⅰ〕设,求函数t 〔x 〕在[m ,m+1]〔m >0〕上的最小值;〔Ⅱ〕过原点分别作曲线y=f 〔x 〕与y=g 〔x 〕的切线l 1,l 2,两切线的斜率互为倒数,求证:a=0或.【解答】〔Ⅰ〕解:,令t'〔x〕>0得x>1,令t'〔x〕<0得x<1,所以,函数t〔x〕在〔0,1〕上是减函数,在〔1,+∞〕上是增函数,∴当m≥1时,t〔x〕在[m,m+1]〔m>0〕上是增函数,∴当0<m<1时,函数t〔x〕在[m,1]上是减函数,在[1,m+1]上是增函数,∴t〔x〕min=t〔1〕=e.〔Ⅱ〕设l2的方程为y=k2x,切点为〔x2,y2〕,如此,∴x2=1,y2=e∴k2=e.由题意知,切线l1的斜率,∴切线l1的方程为,设l1与曲线y=f〔x〕的切点为〔x1,y1〕,∴,∴,,又y1=lnx1﹣a〔x1﹣1〕,消去y1,a后整理得,令,如此,∴m〔x〕在〔0,1〕上单调递减,在〔1,+∞〕上单调递增,假如x1∈〔0,1〕,∵,,∴,而,在单调递减,∴.假如x1∈〔1,+∞〕,∵m〔x〕在〔1,+∞〕上单调递增,且m〔e〕=0,∴x1=e,∴综上,a=0或.【作业2】.〔2017•某某二模〕函数f〔x〕=〔ax2+x﹣1〕e x+f'〔0〕.〔1〕讨论函数f〔x〕的单调性;〔2〕假如g〔x〕=e﹣x f 〔x〕+lnx,h〔x〕=e x,过O〔0,0〕分别作曲线y=g〔x〕与y=h〔x 〕的切线l1,l2,且l1与l2关于x 轴对称,求证:﹣<a<﹣.四.求公切线的方程【例6】.〔2018•某某一模〕函数,g〔x〕=3elnx,其中e为自然对数的底数.〔Ⅰ〕讨论函数f〔x〕的单调性.〔Ⅱ〕试判断曲线y=f〔x〕与y=g〔x〕是否存在公共点并且在公共点处有公切线.假如存在,求出公切线l的方程;假如不存在,请说明理由.【解答】解:〔Ⅰ〕由,得,令f′〔x〕=0,得.当且x≠0时,f′〔x〕<0;当时,f′〔x〕>0.∴f〔x〕在〔﹣∞,0〕上单调递减,在上单调递减,在上单调递增;〔Ⅱ〕假设曲线y=f〔x〕与y=g〔x〕存在公共点且在公共点处有公切线,且切点横坐标为x>0,如此,即,其中〔2〕式即.记h〔x〕=4x3﹣3e2x﹣e3,x∈〔0,+∞〕,如此h'〔x〕=3〔2x+e〕〔2x﹣e〕,得h〔x〕在上单调递减,在上单调递增,又h〔0〕=﹣e3,,h〔e〕=0,故方程h〔x0〕=0在〔0,+∞〕上有唯一实数根x=e,经验证也满足〔1〕式.于是,f〔x0〕=g〔x〕=3e,f′〔x〕=g'〔x〕=3,曲线y=g〔x〕与y=g〔x〕的公切线l的方程为y﹣3e=3〔x﹣e〕,即y=3x.【作业3】.函数f 〔x 〕=lnx,g〔x〕=2﹣〔x>0〕〔1〕试判断当f〔x〕与g〔x〕的大小关系;〔2〕试判断曲线 y=f〔x〕和 y=g〔x〕是否存在公切线,假如存在,求出公切线方程,假如不存在,说明理由;〔3〕试比拟〔1+1×2〕〔1+2×3〕…〔1+2012×2013〕与 e4021的大小,并写出判断过程.五.与公切线有关的参数取值X围问题【例7】.函数f〔x〕=blnx,g〔x〕=ax2﹣x〔a∈R〕.〔Ⅰ〕假如曲线f〔x〕与g〔x〕在公共点A〔1,0〕处有一样的切线,某某数a、b的值;〔Ⅱ〕当b=1时,假如曲线f〔x〕与g〔x〕在公共点P处有一样的切线,求证:点P唯一;〔Ⅲ〕假如a>0,b=1,且曲线f〔x〕与g〔x〕总存在公切线,求正实数a的最小值.【解答】解:〔Ⅰ〕f′〔x〕=,g'〔x〕=2ax﹣1.∵曲线f〔x〕与g〔x〕在公共点A〔1,0〕处有一样的切线,∴,解得a=b=1.〔Ⅱ〕设P〔x0,y〕,如此由题设有lnx=ax2﹣x…①,又在点P有共同的切线,∴f′〔x0〕=g′〔x〕,∴,∴a=,代入①得lnx0=x,设h〔x〕=lnx ﹣+x,如此h′〔x〕=+〔x>0〕,如此h′〔x〕>0,∴h〔x〕在〔0,+∞〕上单调递增,所以 h〔x〕=0最多只有1个实根,从而,结合〔1〕可知,满足题设的点P只能是P〔1,0〕.〔Ⅲ〕当a>0,b=1时,f〔x〕=lnx,f′〔x〕=,f〔x〕在点〔t,lnt 〕处的切线方程为y﹣lnt=〔x﹣t〕,即y=x+lnx﹣1.与y=ax2﹣x,联立得ax2﹣〔1+〕x﹣lnt+1=0.∵曲线f〔x〕与g 〔x〕总存在公切线,∴关于t〔t>0〕的方程△=+4a〔lnt﹣1〕=0,即=4a〔1﹣lnt〕〔*〕总有解.假如t>e,如此1﹣lnt<0,而>0,显然〔*〕不成立,所以 0<t<e,从而,方程〔*〕可化为4a=.令H〔t〕=〔0<t<e〕,如此H′〔t〕=.∴当0<t<1时,h'〔t〕<0;当1<t<e时,h'〔t〕>0,即 h〔t〕在〔0,1〕上单调递减,在〔1,e〕上单调递增.∴h〔t〕在〔0,e〕上的最小值为h〔1〕=4,∴要使方程〔*〕有解,只须4a≥4,即a≥1.∴正实数a的最小值为1.【例8】.〔2017•某某模拟〕.函数f〔x〕=ae x〔a≠0〕,g〔x〕=x2〔Ⅰ〕假如曲线c1:y=f〔x〕与曲线c2:y=g〔x〕存在公切线,求a最大值.〔Ⅱ〕当a=1时,F〔x〕=f〔x〕﹣bg〔x〕﹣cx﹣1,且F〔2〕=0,假如F〔x〕在〔0,2〕内有零点,某某数b的取值X围.【解答】解:〔Ⅰ〕设公切线l与c1切于点〔x1,a〕与c2切于点〔x2,〕,∵f′〔x〕=ae x,g′〔x〕=2x,∴,由①知x2≠0,①代入②:=2x2,即x2=2x1﹣2,由①知a=,设g〔x〕=,g′〔x〕=,令g′〔x〕=0,得x=2;当x<2时g′〔x〕>0,g〔x〕递增.当x>2时,g′〔x〕<0,g〔x〕递减.∴x=2时,g〔x〕max =g〔2〕=,∴amax=.〔Ⅱ〕F〔x〕=f〔x〕﹣bg〔x〕﹣cx﹣1=e x﹣bx2﹣cx﹣1,∵F〔2〕=0=F〔0〕,又F〔x〕在〔0,2〕内有零点,∴F〔x〕在〔0,2〕至少有两个极值点,即F′〔x〕=e x﹣2bx﹣c在〔0,2〕内至少有两个零点.∵F″〔x〕=e x﹣2b,F〔2〕=e2﹣4b﹣2c﹣1=0,c=,①当b≤时,在〔0,2〕上,e x>e0=1≥2b,F″〔x〕>0,∴F″〔x〕在〔0,2〕上单调增,F′〔x〕没有两个零点.②当b≥时,在〔0,2〕上,e x<e2≤2b,∴F″〔x〕<0,∴F″〔x〕在〔0,2〕上单调减,F′〔x〕没有两个零点;③当<b<时,令F″〔x〕=0,得x=ln2b,因当x>ln2b时,F″〔x〕>0,x<ln2b时,F″〔x〕<0,∴F″〔x〕在〔0,ln2b〕递减,〔ln2b,2〕递增,所以x=ln2b时,∴F′〔x〕最小=F′〔ln2b〕=4b﹣2bln2b﹣+,设G〔b〕=F′〔ln2b〕=4b﹣2bln2b﹣+,令G′〔b〕=2﹣2ln2b=0,得2b=e,即b=,当b<时G′〔b〕>0;当b>时,G′〔b〕<0,当b=时,G〔b〕最大=G〔〕=e+﹣<0,∴G〔b〕=f′〔ln2b〕<0恒成立,因F′〔x 〕=e x﹣2bx﹣c在〔0,2〕内有两个零点,∴,解得:<b<,综上所述,b的取值X围〔,〕.【作业4】.函数f〔x〕=a〔x﹣〕﹣blnx〔a,b∈R〕,g〔x〕=x2.〔1〕假如a=1,曲线y=f〔x〕在点〔1,f〔1〕〕处的切线与y轴垂直,求b 的值;〔2〕假如b=2,试探究函数f〔x〕与g〔x〕在其公共点处是否有公切线,假如存在,研究a的个数;假如不存在,请说明理由.六.公切线的条数问题【例9】.函数f〔x〕=lnx,g〔x〕=e x.〔1〕确定方程f〔x〕=实数根的个数;〔2〕我们把与两条曲线都相切的直线叫作这两条曲线的公切线,试确定曲线y=f 〔x〕,y=g〔x〕公切线的条数,并证明你的结论.【解答】解:〔1〕由题意得lnx==1+,即lnx﹣1=.分别作出y=lnx﹣1和y=的函数图象,由图象可知:y=lnx﹣1和y=的函数图象有两个交点,∴方程f〔x〕=有两个实根;〔2〕解:曲线y=f〔x〕,y=g〔x〕公切线的条数是2,证明如下:设公切线与f〔x〕=lnx,g〔x〕=e x的切点分别为〔m,lnm〕,〔n,e n〕,m≠n,∵f′〔x〕=,g′〔x〕=e x,∴,化简得〔m﹣1〕lnm=m+1,当m=1时,〔m﹣1〕lnm=m+1不成立;当m≠1时,〔m﹣1〕lnm=m+1化为lnm=,由〔1〕可知,方程lnm=有两个实根,∴曲线y=f〔x〕,y=g〔x〕公切线的条数是2条.【作业5】.函数f〔x〕=x2+2〔1﹣a〕x﹣4a,g〔x〕=﹣〔a+1〕2,如此f〔x〕和g〔x〕图象的公切线条数的可能值是.【作业1解答】解:〔1〕f′〔x〕=〔2x+1〕〔x﹣1〕2=0,x=﹣或1,∴x=﹣是h〔x〕的零点;∵g′〔x〕=k﹣,k<0,g′〔x〕<0,g〔x〕在[1,+∞〕上单调递减,g〔x〕的最大值为g〔1〕=k+1.k<﹣1,g〔1〕<0,g〔x〕在[1,+∞〕上无零点;k=﹣1,g〔1〕=0,g〔x〕在[1,+∞〕上有1个零点;﹣1<k<0,g〔1〕>0,g〔e1﹣k〕=ke1﹣k+k<0,g〔x〕在[1,+∞〕上有1个零点;综上所述,k<﹣1时,h〔x〕有1个零点;﹣1≤k<0时,h〔x〕有两个零点;〔2〕设切点〔t,f〔t〕〕,f′〔x〕=6x2﹣6x,∴切线斜率f′〔t〕=6t2﹣6t,∴切线方程为y﹣f〔t〕=〔6t2﹣6t〕〔x﹣t〕,∵切线过P〔a,﹣4〕,∴﹣4﹣f〔t〕=〔6t2﹣6t〕〔a﹣t〕,∴4t3﹣3t2﹣6t2a+6ta﹣5=0①由题意,方程①有3个不同的解.令H〔t〕=4t3﹣3t2﹣6t2a+6ta﹣5,如此H′〔t〕=12t2﹣6t﹣12at+6a=0.t=或a.a=时,H′〔t〕≥0,H〔t〕在定义域内单调递增,H〔t〕不可能有两个零点,方程①不可能有两个解,不满足题意;a时,在〔﹣〕,〔a,+∞〕上,H′〔t〕>0,函数单调递增,在〔,a〕上,H′〔t〕<0,函数单调递减,H〔t〕的极大值为H〔〕,极小值为H 〔a〕;a时,在〔﹣∞,a〕,〔,+∞〕上,H′〔t〕>0,函数单调递增,在〔a,〕上,H′〔t〕<0,函数单调递减,H〔t〕的极大值为H〔a〕,极小值为H 〔〕;要使方程①有三个不同解,如此H〔〕H〔a〕<0,即〔2a﹣7〕〔a+1〕〔2a2﹣5a+5〕>0,∴a>或a<﹣1.【作业2解答】解:由得f'〔x〕=[ax2+〔2a+1〕x]e x,f'〔0〕=0,所以f〔x〕=〔ax2+x﹣1〕e x.〔1〕f'〔x〕=[ax2+〔2a+1〕x]e x=[x〔ax+2a+1〕]e x.①假如a>0,当或x>0时,f'〔x〕>0;当时,f'〔x〕<0,所以f〔x〕的单调递增区间为;单调递减区间为.②假如a=0,f〔x〕=〔x﹣1〕e x,f'〔x〕=xe x,当x>0时,f'〔x〕>0;当x <0时,f'〔x〕<0,所以f〔x〕的单调递增区间为〔0,+∞〕;单调递减区间为〔﹣∞,0〕.③假如,当或x<0时,f'〔x〕<0;当时,f'〔x〕>0,所以f〔x〕的单调递增区间为;单调递减区间为.④假如,故f〔x〕的单调递减区间为〔﹣∞,+∞〕.⑤假如,当或x>0时,f'〔x〕<0;当时,f'〔x〕>0,所以f〔x〕的单调递增区间为;单调递减区间为.当a>0时,f〔x〕的单调递增区间为;单调递减区间为.当a=0时,f〔x〕的单调递增区间为〔0,+∞〕;单调递减区间为〔﹣∞,0〕.,当时,f〔x〕的单调递增区间为;单调递减区间为.当时,f〔x〕的单调递减区间为〔﹣∞,+∞〕;当时,f〔x〕单调递增区间为;单调递减区间为,〔0,+∞〕;〔2〕证明:g〔x〕=e﹣x f〔x〕+lnx=﹣e﹣x〔ax2+x﹣1〕e x+lnx=ax2+x﹣1+lnx,设l2的方程为y=k2x,切点为〔x2,y2〕,如此,所以x2=1,y2=e,k2=e.由题意知k1=﹣k2=﹣e,所以l1的方程为y=﹣ex,设l1与y=g〔x〕的切点为〔x1,y1〕,如此.又,即,令,在定义域上,u'〔x〕>0,所以〔0,+∞〕上,u〔x〕是单调递增函数,又,所以,即,令,如此,所以,故.【作业3解答】解:〔1〕证明:设F〔x〕=f〔x〕﹣g〔x〕,如此F′〔x〕=﹣,由F'〔x〕=0,得x=3,当0<x<3时,F'〔x〕<0,当x>3时F'〔x〕>0,可得F〔x〕在区间〔0,3〕单调递减,在区间〔3,+∞〕单调递增,所以F〔x〕取得最小值为F〔3〕=ln3﹣1>0,∴F〔x〕>0,即f〔x〕>g〔x〕;〔2〕假设曲线f〔x〕与g〔x〕有公切线,切点分别为P〔x0,lnx〕和Q〔x1,2﹣〕.因为f′〔x〕=,g′〔x〕=,所以分别以P〔x0,lnx〕和Q〔x1,2﹣〕为切线的切线方程为y=+lnx﹣1,y=+2﹣.令,即2lnx1+﹣〔3+ln3〕=0.令h〔x〕=2lnx1+﹣〔3+ln3〕.所以由h′〔x〕=﹣=0,得x1=3.显然,当0<x1<3时,h'〔x〕<0,当x1>3时,h'〔x〕>0,所以h〔x〕min=ln3﹣1>0,所以方程2lnx1+﹣〔3+ln3〕=0无解,故二者没有公切线.所以曲线y=f〔x〕和y=g〔x〕不存在公切线;〔3〕〔1+1×2〕〔1+2×3〕•…•〔1+2012×2013〕>e4021.理由:由〔1〕可得lnx>2﹣〔x>0〕,可令x=1+n〔n+1〕,可得ln〔1+n〔n+1〕〕>2﹣>2﹣=2﹣3〔﹣〕,如此ln〔1+1×2〕+ln〔1+2×3〕+…+ln〔1+2012×2013〕>2×2012﹣3〔1﹣+﹣+…+﹣〕=4024﹣3+>4021.即有〔1+1×2〕〔1+2×3〕…〔1+2012×2013〕>e4021.【作业4解答】解:〔Ⅰ〕∵f〔x〕=x﹣﹣blnx,∴f′〔x〕=1+﹣,由于曲线y=f〔x〕在点〔1,f〔1〕〕处的切线垂直于y轴,故该切线斜率为0,即f′〔1〕=0,即1+1﹣b=0,∴b=2;〔2〕假设f〔x〕,g〔x〕的图象在其公共点〔x0,y〕处存在公切线,由f〔x〕=a〔x﹣〕﹣2lnx,得f′〔x〕=,g′〔x〕=2x,由f′〔x0〕=g′〔x〕,得=2x,即2x3﹣ax2+2x﹣a=0,即〔x02+1〕〔2x﹣a〕=0,如此x=,又函数的定义域为〔0,+∞〕,当a≤0时,x0=≤0,如此f〔x〕,g〔x〕的图象在其公共点〔x,y〕处不存在公切线;当a>0时,令f〔〕=g〔〕,﹣2ln﹣2=,即=ln,令h〔x〕=﹣ln〔x>0〕,h′〔x〕=x﹣=,如此h〔x〕在〔0,2〕递减,〔2,+∞〕递增.且h〔2〕=﹣<0,且当x→0时,h〔x〕→+∞;当x→+∞时,h〔x〕→+∞,∴h〔x〕在〔0,+∞〕有两个零点,∴方程=ln在〔0,+∞〕解的个数为2.综上:当a≤0时,函数f〔x〕与g〔x〕的图象在其公共点处不存在公切线;当a>0时,函数f〔x〕与g〔x〕的图象在其公共点处存在公切线,a的值有2个.在导数的练习中,常见这一类题型:含有的一个不等式,以与的一些其他性质,让解不等式或者比拟大小。
第5讲利用导数研究函数的公切线问题 高考数学

试卷讲评课件
练2
若曲线f x = acosx与曲线g x = x 2 + bx + 3在交点 0, m 处有
6
公切线,则a + b + m =___.
【分析】若曲线 与曲线 在交点 , 处有公切线,则切点的
坐标相等且切线的斜率(切点处的导函数值)均相等,由此构造关于,
当 , 不是 的切点时,
设切点为 , − + ≠ ,
则 ′ = − + ,
试卷讲评课件
− +
所以
= − + ,得 = ,
所以
= − ,所以直线的方程为 = − .
=
+
= .
故选:
− = + − +
,则
= +
,即
试卷讲评课件
例2
已知f x =1 lnx,g x = x a ,若f x 与g x 的图象在交点处的切
−1
/e
线重合,则a =______.
e
【分析】设 与 的图象交点为 , ,再根据导数的几何意义
第5讲 利用导数求解函数的切线(3)
主讲人:某某某老师
某某学校
知识点一 利用导数求解公切线问题
知识点二 与公切线有关的参数问题
知识点一 利用导数求解公切线问题
试卷讲评课件
例1
若直线y = kx + b是曲线y = lnx + 2的切线,也是曲线
y = ln x + 1 的切线,则k =(
导数中公切线问题

导数中的公切线问题一、公切线的定义公切线是指与一个函数的所有切线都相切的直线。
在数学上,公切线被定义为在函数图像上与多个切线相交的直线。
这些切线的斜率是无穷大,因此公切线与每个切线的距离是无穷小的。
二、公切线的求法求函数的公切线,需要找到与该函数相切的所有切线的切点,然后通过这些切点来求得公切线的方程。
首先,我们需要找到函数上的所有极值点,因为极值点可能是公切线与函数的切点。
然后,我们可以利用导数来求得切线的斜率,再根据切点求得切线的方程。
最后,我们可以将所有切线的方程进行线性组合,得到公切线的方程。
三、公切线与极值公切线与极值有密切的关系。
当函数在某一点上取得极值时,该点处的导数必定为零,即该点的切线斜率为零。
因此,极值点一定是公切线与函数的切点。
此外,公切线的斜率与该点处的二阶导数有关,如果二阶导数为正,则公切线在该点处的斜率为正,函数在该点处取得极小值;如果二阶导数为负,则公切线在该点处的斜率为负,函数在该点处取得极大值。
四、公切线与单调性函数的单调性与公切线也有关。
如果函数在某个区间内单调增加(或减少),则该区间内的所有切线的斜率都大于(或小于)零,因此该区间内的所有公切线的斜率也大于(或小于)零。
此外,如果函数在某个区间内单调增加,则该区间内的所有公切线的斜率都小于(或大于)零;如果函数在某个区间内单调减少,则该区间内的所有公切线的斜率都大于(或小于)零。
五、公切线与曲线形状公切线的形状可以反映函数的曲线形状。
例如,如果一个函数的公切线都是直线,则该函数是一个多项式函数;如果一个函数的公切线都是圆弧,则该函数是一个正弦或余弦函数。
此外,如果一个函数的公切线既有直线又有圆弧,则该函数可能是具有跳跃点的函数。
导数中公切线问题

设曲线方程为y=f x ,切线方
程为y g(x)斜率为k,则切点
(x0 , f
x )满足: 0
f
k (x0 )
f'
( x0 g(
) x0
)
曲线y f (x)在x x0处的切线 方程为:
y f x0 f ' x0 (x x0)
“重一法”解两曲线公切线
设切点 求k
点斜式写出切线方程
例1:若直线l与曲线C1 : y x2 1及C2 : y 求直线l 的方程.
f (x) ex
g(x) ln x 2
解析:设y kx b与y ex和y ln x 2分别切于点 P(x1, ex1)和Q(x2 , ln x2 2)
对y ex求导得y' ex,则在点P处 切线方程为:y ex1 x (1 x1)ex1……①
设切点
对y ln x 2求导得y' 1 ,则在点Q处
本源 课 微
“重一法”解两曲线公切线
艺术家关注画面,文学家关注情 感,而数学家则本能关注对象的 数量关系和空间形式。
切线
本源 课 微
“重一法”解两曲线公切线
南昌市外国语学校 袁夏荣
“重一法”解两曲线公切线
切 点 几 何 特 征 ①切点处的导数即为
在该点处切线斜率k
②切点在曲线上也在 切线上
数的特征
【法二】
①②重合
1 x0
et
=1
ln x01et tet m
斜率相等 纵截距相等
x0 1,t 0,m 2
即两切点坐标:(1,0)(0,1 )
代入y x b ,b 1
“重一法”解两曲线公切线
例3:若函数f (x) ex , g(x) ln x 2,若直线y kx b与 曲线y f (x)和曲线y g(x) 相切,求k , b.
导数解曲线公切线问题

导数解公切线专题1.(2009年江西文12)若存在过点(1,0)的直线与曲线3y x =和21594y ax x =+-都相切,则a 等于A .1-或25-64B .1-或214C .74-或25-64D .74-或7 2.(2016年全国II 理16)若直线y kx b =+是曲线ln 2y x =+的切线,也是曲线ln(1)y x =+的切线,则b = .3.求曲线y =x 3+x 2-2x 在点A (1,0)处的切线方程.变式:求曲线y =x 3+x 2-2x 过点A (1,0)的切线方程.1.(2009年江西文12)若存在过点(1,0)的直线与曲线3y x =和21594y ax x =+-都相切,则a 等于A .1-或25-64B .1-或214C .74-或25-64D .74-或7 1.设过(1,0)的直线与3y x =相切于点300(,)x x ,所以切线方程为320003()y x x x x -=-即230032y x x x =-,又(1,0)在切线上,则00x =或032x =-, 当00x =时,由0y =与21594y ax x =+-相切可得2564a =-, 当032x =-时,由272744y x =-与21594y ax x =+-相切可得1a =-,所以选A . 2.(2016年全国II 理16)若直线y kxb =+是曲线ln 2y x =+的切线,也是曲线ln(1)y x =+的切线,则b = .【答案】1ln2-考点:导数的几何意义.3.求曲线y=x3+x2-2x在点A(1,0)处的切线方程. 解:∵y′=3x2+2x-2,∴切线斜率k= y′|x=1=3.∴切线方程为y=3(x-1),即3x-y-3=0.变式:求曲线y=x3+x2-2x过点A(1,0)的切线方程.解设切点P(x0, x03+x02-2x0),∵y′=3x2+2x-2,∴切线斜率k=3x02+2x0-2.∴切线方程为y-(x03+x02-2x0)=(3x02+2x0-2)(x-x0) .∵点A在切线上,∴0-(x03+x02-2x0)=(3x02+2x0-2)(1-x0).即x03-x02-x0+1=0.故(x0-1)2 ( x0+1)=0.解得x0=-1 或x0= 1 .∴当x0=-1时,切线方程为x+y-1=0;当x0=1时,切线方程为3x-y-3=0.综上,曲线过点A(1,0)的切线方程为3x-y-3=0,或x+y-1=0.·AO x y。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数解曲线公切线问题 Prepared on 24 November 2020
导数解公切线专题
1.(2009年江西文12)若存在过点(1,0)的直线与曲线3y x =和21594
y ax x =+-都相切,则a 等于
A .1-或25-64
B .1-或214
C .74-或25-64
D .74-或7 2.(2016年全国II 理16)若直线y kx b =+是曲线ln 2y x =+的切线,也是曲线ln(1)y x =+的切线,则b = .
3.求曲线y =x 3+x 2-2x 在点A (1,0)处的切线方程. 变式:求曲线y =x 3+x 2-2x 过点A (1,0)的切线方程.
1.(2009年江西文12)若存在过点(1,0)的直线与曲线3y x =和21594
y ax x =+-都相切,则a 等于
A .1-或25-64
B .1-或214
C .74-或25-64
D .74-或7 1.设过(1,0)的直线与3y x =相切于点300(,)x x ,所以切线方程为
320003()y x x x x -=-
即230032y x x x =-,又(1,0)在切线上,则00x =或032
x =-, 当00x =时,由0y =与21594y ax x =+-相切可得2564
a =-, 当032x =-时,由272744y x =-与21594
y ax x =+-相切可得1a =-,所以选A . 2.(2016年全国II 理16)若直线y kx b =+是曲线ln 2y x =+的切线,也是曲线ln(1)y x =+的切线,则b = .
【答案】1ln2-
考点:导数的几何意义.
3.求曲线y=x3+x2-2x在点A(1,0)处的切线方程. 解:∵y′=3x2+2x-2,
∴切线斜率k= y′|x=1=3.
∴切线方程为y=3(x-1),
即 3x-y-3=0.
变式:求曲线y=x3+x2-2x过点A(1,0)的切线方程. 解设切点P(x0, x03+x02-2x0),
∵y′=3x2+2x-2,
∴切线斜率k=3x02+2x0-2.
∴切线方程为
y-(x03+x02-2x0)=(3x02+2x0-2)(x-x0) .
∵点A在切线上,
∴0-(x03+x02-2x0)=(3x02+2x0-2)(1-x0).即x03-x02-x0+1=0.
·
A
O x y
故 (x0-1)2 ( x0+1)=0.
解得x0=-1 或x0= 1 .
∴当x0=-1时,切线方程为x+y-1=0;当x0=1时,切线方程为3x-y-3=0.综上,曲线过点A(1,0)的切线方程为 3x-y-3=0,或x+y-1=0.。
