2010年九年级文理科联赛试卷12(20101025)
2010年各中考数学试题12套打包江苏南京

南京市2010年初中毕业生学业考试注意事项:1本试卷共6页•全卷满分120分,考试时间为120分钟•考生答题全部答在答题卡上,答在本试卷上 无效。
2 •请认真核对监考教师在答题卡所粘贴条形码上的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.3 •答选择题必须用2B 铅笔将答题卡上对应的答案标号涂黑•如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用 0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.5.作图必须用2B 铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共有6小题,每小题2分,共12分•在每小题给出的四个选项中,恰有一项是符合 题目要求的,请将正确选择项前的字母代号填涂在答题卡相应位置上)1.— 3的倒数是A . — 3B . 3C — 1 C•3D . 1A*丄”JL- — *A S=2. 计算a 3 • a 4 5的结果是-2 -10 1 J J6 7A . aB . a 8C . aD . 12 a3.如图,下列各数中,数轴点 A 表示的可能是A . 4的算术平方根B . 4的立方根C . 8的算术平方根D . 8的立方根二、填空题(本大题共10个小题,每小题2分,共20分•不需写出解答过程,请把正确答案直接填写在答题卡相应位置上)7. — 2的绝对值的结果是 ___________ .4 甲各蔬菜保鲜适宜的温度是1C 〜5C,乙种蔬菜保鲜适宜的温度是3C 〜8C,将这两种蔬菜放在一起同时保鲜,适宜的温度是 A • 1C 〜3 C B • 3 C 〜5 C C . 5 C 〜8 CD . 1C 〜8C 5 如图,在平面直角坐标系中,菱形 OABC 的顶点C 的坐标是(3, 4),则顶点A 、B 的坐标分别是A • (4,0)、( 7,4)B . ( 5,0)、( 8,4)C . ( 4,0)、( 7,4)D • (5,0)、( 8,4)6.,如图,夜晚,小亮从点A 经过路灯C 的正下方沿直线走到点B ,他的影长y 随他与点A 之间的距离x的变化而变化,那么表示 y 与x 之间的函数关系的图象大致为ABD.18函数y =—中,自变量x 的取值范围是 --------------------9. 南京地铁2号线(含东延线)、1号线南延线开通后,南京地铁总里程约为记数法表示为 ___________10. _____________________________________________________________ 如图,O 是直线 I 上一点,/ AOB = 100°,则/ 1 + Z 2 = __________________________________________________ 11 .计算诅a •畅 (a > 0)的结果是 ___________ .则这两人5次射击命中的环数的平均数X 甲 = 乂乙=8,方差S 甲14.如图,以O 为圆心的两个同心圆中, 大圆的弦AB 是小圆的切线,C 为切点.若两圆的半径分别为 3cm 和5cm ,贝U AB 的长为 __________________ cm .15 .如图,点C 在O O 上,将圆心角/ AOB 绕点O 按逆时针方向旋转到/ A'OB '旋转角为a (0°V a V16. 如图,AB 丄BC , AB = BC = 2cm , OA 与OC 关于点 O 中心对称,则 AB 、BC 、CO 、OA 所围成的图 形的面积是 ______________ c m 2.三、解答题(本大题共12小题,共88分,请在答题卡指定区域内作答,解答时应写出文字说明、证明过 程或演算步骤)17. (6分)解方程组丿2乂十‘—4,£ +2y =5.11 a 2— b 2(6分)计算(a - j 十w19. (6分)为了估计西瓜、苹果和香蕉三种水果一个月的销售量,某水果店对这三种水果行了统计,统计结果如图所示.(1) 若西瓜、苹果和香蕉的售价分别为 6元/千克、8元/千克和3元/千克.则这7天销售额最大的小果品种是( )A .西瓜B .苹果C .香蕉(2) 估计一个月(按 30天计算)该水果店可销售苹果多少千克?85 000m ,将85 000用科学甲7 9 86 10 乙789 8 818.7天的销售量进12•若反比例函数的图象经过点(一 2, — 1),则这个函数的图象位于第 13.甲、乙两人5次射击命中的环数如下:氛木卓店三科水天的価■■煉计圈贰且翠弟 鲁画貳黒孫弹20. (7分)如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离 为1.5m ,测得树顶A 的仰角为33°,求树的高度 AB .(参考数据:sin33 °~ 0. 54, cos33°~ 0. 84, tan33°~ 0. 65)如图,四边形 ABCD 的对角线AC 、 求证:(1) OA = OB ; (2) AB // CD .22. ( 7分)已知点 A (1, 1)在二次函数 y = x 2— 2ax — b 的图象上(1)用含a 的代数式表示b ; 2)如果该二次函数的图象与x 轴只有一个交点,求这个二次函数的图象的顶点坐标.23. (9分)某厂为新型号电视机上市举办促销活动,顾客每购买一台该型号电视机, 可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖.厂家设计的抽奖方案是:在一个不透明的盒子中,放入 10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出 1个球,摸到黄球的顾客获得大奖在,摸到白球的顾客获得小奖.(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖•该抽奖文案符合厂家的设奖要求吗?请说明理由; (2)下图是一个可以自由转动的转盘,请你将转盘分为 2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:24. ( 8分)甲车从 A 地出发以60km/h 的速度沿公路匀速行驶,0.5h 后,乙车也从 A 地发出,以80km/h的速度沿该公路与甲车同向匀速行驶求乙车出发后几小时追上甲车.请建立一次函数关系解决上述问题.25. ( 8 分)如图,AB 是O O 的直径,点 D 在O O 上,/ DAB = 45°, BC // AD , CD // AB . (1)判断直线CD 与O O 的位置关系,并说明理由; (2)若O O 的半径为1,求图中阴影部分的面积(结果保留n ).BC 为10m ,测角仪的高度 CD21.1•在转盘上用文字注明颜色和扇形圆心角的度数.2.结合转盘简述获奖方式,不需说明理由.)DC第25题26. (8分)学习《图形的相似》后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探 索两个直角三角形相似的条件(1“对于两个直角三角形,满足一边一锐角对应相等, 或两直角边对应相等,两个直角三角形全等” •类 似地,你可以得到"满足 _____________________ 或 __________________ ,两个直角三角形相似” ; (2) “满足斜边和一条直角边对应相等的两个直角三角形全等” ,类似地,你可以得到“满足 ___________的两个直角三角形相似” •请你结合下列所给图形,写出已知,并完成说理过程. 已知:如图, _____________________________________ 求证:Rt △ ABC 也 Rt △ A'B'C '.27. (8分)某批发商以每件50元的价格购进800件T 恤.第一个月以单价 80元销售,售出了 200件;第 二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩 余的T 恤一性清仓,清仓时单价为 40元.设第二个月单价降低 x 元. (1)填表(不需化简): 时间 第一个月第二个月清仓 单价(元) 8040销售量(件)200那么第二个月的单价应是多少元?(8分)如图,正方形ABCD 的边长是 接EM 并延长交射线 CD 于点F , (1) 设AE = x 时,△ EGF 的面积为y .求y 关于x 的函数关系式,并写出自变量(2) P 是MG 的中点,请直接写出点 P 运动路线的长.2, M 是AD 的中点.点E 从点A 出发,沿AB 运动到点B 停止.连 过M 作EF 的垂线交射线 BC 于点G ,连接EG 、FG .x 的取值范围;28. 第28题南京市2010年初中毕业生学业考试数学注■事琐:1.宣试■共6页.全矗H分120分.考试时简为120分神.才生答通全■答aWH卡上•答在* 试矗上无效.2.谓认11核对监*教簿在答題卡上所帖贴築殖岳的姓名、考试证号矗否与本人相将合.葬将自己的姓名、帝■证号用0.5 «**色■水签字笔填乌衽答fit卡及*试輪上.3.答选择用2B1G鑑将答■卡上对虫的答*标号涂H.如摘改劝,谓用•皮療干RJS. 再选涂真饱答寒.答&选择用0.5豪米JR色■水签字卡上的播定位■.衽其他位■答& 一停无效.4.作图必珈用2B诒笔作答•并请加舄尬粗,搭月漬整・一、送择11(本大11共6小BL毎小《! 2分■共12分.左毎小&所恰出的四个遶项中.怙科一項是杆合13目要求的,请将正■选项曲的字毋代号填涂在上)1.-3的倒數是A. a e B o r C.J D.a113. toffl.T列各敢中•数紬匕点A衷示的可能是A•)-2-10123A. 4的算术平方権B. 4的立方根(938)C.8的算术平方郴D.8的立方根4.甲种罠菜保鲜适宜的温度是1 9~5・C・乙幹茂菜保鲜适宜的SI度是3・C~8・C.梅这两斡蔬菜放在一起同财保解•进宜的温度是A. FC~3・CB. 39〜5・C C 5*C-8*C D. 1*C-8*C5. 平面血角坐标疑中•芟形OABC的3AC的坐标处(3・4》•则頂点A、B的樂标分蹈殳B. (4.0)«(8.4)D.<S«0)X8.4)数孚试題« 1 «(共6页)A. (4,0)*(7.4)C.<5.0),(7.4)(95ft)・9・效学试■疥2页(共6页〉6•如图•夜晚•小亮从点A 经过踣灯C 的正下方沿直线走到点〃•他的老长yRI 他与点A 之何的距离工的变化而变化•那么液示,与工之何函效关麻的图◎大致为二■填空•(*大理共10小題•毎小題2分•共20分•不需坊出解答过程■请把答幕直接填耳衽上)7. 一2的龟对值的结果是 ▲・8•两数,■占中・白变■工的取値范屬媳▲・則Z 】 + Z2・ ▲ ••H •计算庙・yS7(a>0)的结果是 ▲ •12•若反比例鬲散的阳食竝过点(一2• —1〉・则这个蹟效的田役位于第 ▲ 象限. 13•甲、乙两人5次射击命中的环tttoT :甲 7 9 8 6】0 乙 78988JH 这卿人5次射击命中的环数的平均ttx»-x^-8.方程松 ▲4>5">・、・V 或14.如图•以0为18心的两个间心空中•大18的荻AB 址小齡的切线・C 为切点.若斷08的半径 .分别为3 em 和5 em •则AB 的长为 A cm.(Men)10•如图・O 是直8U 上一点.ZAOB-100\yB.A BA.C.D.85 000用科鼻记散法农示为快总W WW 为85 000 m •将(miofl)lS.teffl-点C往©O上•将01心角ZAOB绕点O技連时什方向鬓转利ZA0B'•離转角为a WVaV】80•人若ZAOB・3(T・ZBCA'・40・・则Za・16. 如阳・AB丄BC.AB-BC-2 cm>6X与6&关于点O中心对称•则AB.BC&&所曲成的阳形的面枳2 ▲ cm'・三■■答JH(*大1■共】2小■•共88分•请在答JH卡拒定区域内作答■解答时应*出文字农朗. 证朗过林成演尊步口)[2x+y—<•17. (6分)解方稅组,U+2y-5.的mwft进行了统计•忱计结果如图所示.<1〉若西瓜■卑果和香蕉的鲁价分别为6元/千克.8元/千克和3元/千克•则这7天• • • 大的水果品▲ >1A・药瓜 B.草果aw«(2>ttit一个月(按30天卄算)谈水果店可柄害草杲各少千克?数孑试・第3JU共6頁〉(91160)•臬水果店对这三种水果7天• 11 •数学试题第4页(共6页》20. <7分)如用•小明软利用测角仪Atm 的离度•巳知他鳥树的水平距声BC 为10 m ■测角仪 的髙度CD 为1.5 m.M 得I4DI A 的仰角为33\^树的离度AB.21. <7分〉如田•四边形ABCD 的对角红AC.BD 相交于点O.^ABOOi^BAD. 求证:(l )OA-OB»(2)AB/7Ca《1》用含a 的代数式农示趴《2)如果谏二次丙数的图象与工紬只材一个交点•求这个二次函数的阳役的広点坐标.23. <9分)篥厂为新型号电視机上市券办促的活动•窝客每购买一台谈虫号电視机•可获得一 次抽奖机会•谏厂拟按10%设大奖•其余90%为小奖.厂家设计的抽奖方案是,左一个不进期的盒子中•放入10个黄球和90个白球•这铁球除・ 色外都相同•搅匀后从中任韋蟆出1个球,複到黄球的H 甞获得大奖•摸到白球的wwaw 小奖・(i )r»请枚了一位敷学老溥•他设什的抽奖方案趕:左一个不透期的盒子中•敖入2个黄 球和3个白球•这整球除瀬色外挪相同•技匀后从中任倉換出2个球•換到的2个球祁 是黄球的顒專获猫大奖•其余的1RWRW 小奖.谏抽奖方案符合厂家的设奖JFW 吗?请■说朗理由)22. «7 分〉巳M A(l>l )az散亍试題*5«(共6貝)(2)Tffl«-个可以(I 由转动的转盘•请你将轻盘分为2个廉形区域•分别涂上触■白两种 ■色•并设廿捕奖方褰・*其符合厂家的设奖在转fit 上用文字注明 ■色和电形的》1心角的度数・2•结合转盘简述获奖方式•不需说明理由•>(M23S )24.《8分〉甲车从A 地岀发以60 km/h 的速度沿公路匀速行校・0.5h 斤•乙车也从A 地出发. 以80 km/h 的連度沿涣公路与甲车阖向匀連行肢・求乙车出发后几小时ill 上甲车.圻建宜一次甬散关系解决t 注何越・26. «8分〉孕习《阳形的相似》后•我幻可以侪助探发网个山角三角形全务的条件所获得的经 穀•堆续棵索彌个立介三角形相册的条件.d 广対于何个血角三丸形•雷足一边一仪角对应相舒•戍两血角边对应相务•两个0角三角形全簽・•类似地•你可以得到•摘足▲ •或 ▲ •两个f [角三角形(2)-m 足貝边和一条逍角边対应相第的烤个"角三角形全铮-•类似地・你可以足▲ 的购个A 角三角形相or •请结合下列所恰田形・卑出已知•井完成说理过程・ 巳知&如图•_▲一. 试说朗 RiAABCsRtAA'ffC :21. (8分)某就发裔以毎件50元的价格科进800件T 憧•疥一个月以炉价80元的■•侮出了 200件;第二个月如果承价不变•預计仍可鲁出200件•批发商为堆加MW*.决定降价桥 19 •根掘市场■査•越价毎薛低1元•可多售出10件•但最低小价应离于购进的价第二25. (8 分〉如用・AB 是©O 的在QO 上.^DAB^^\BC//AD.CD//AB.(弟 26Q个月结束后•批发裔林对剧余的TH一次性清仓的售•清仓时草价为40元•设第二个月如价降低■元.(!>««<不需化簡八(228. (8分)如图•正方形ABCD的壬长@2・M萨AD的中点•点E从点A岀发•沿AB运动到点B序止.连接EM并圧乎诒的乘蛻交射找BC于启G・连按《1〉设AE-x时•△EGF的面稅为y.^y关于工的两数关杲式•并埒出白变債z的取(ft范ffh (2)P^MG的中点•请立接耳岀点P运动殆线的长•数学试■第6页(共6 50• 14 •南京市2010年初中毕业生学业右试数学试题参考答案及评分标准说朗:本评分标准他題倍出了一种或几种解虫供•弓•如果弓生的解法与本解袴不同•參廉本评分标准的分.一•透择&(毎小題2分•共12分)二•填空&(毎小题2分•共20分)7.2& 工#1 9.8.5X10 ・ 10.80 11.4a12•—•三13・> 14.8 15.110 16.2三■解答題(*大題共12小JH •共88分)17. (*« 6 分》解法一QX2•得2x + 4y-10. ®© —①•鮒3y・6.第这个方稅•得>-2. .................................................................................. 3分«y-2代人①•御”■】・............................................ 5分所以原方程组的朋是*::; ......................................... 6分館这个方昶•魁厂# ---------- —------- ............................ 3分1代入③•得,・2・ ................................................................................. 5分所以脈方程粗的解趕 ................................................. 6分ly-2.18•《本題6分)_b—a . (a4-6)(a~6>"■ST*------------ 7b --------_b_a . ubab (<i4-6)(a —6>._a_b . ________ ______ab (a + 6)(a~6)■—一・ ..............................Q^b^19.(^tf 6 分〉Mi<l>A ......................................................................(2)140+7X30-600(千克人祥:估计一个月诛水果店可钥傅単果600千克.放学衿案Ml J«共4 JO20•《本18 7分)•"如图•过点D作DE丄川3・乘足为£在RtAADE 中• DE-BC- 10.ZADE・33\unZADE-^ ・AAE-DE> tanZADE *10X0.65-6.5. ................. 5 分A AB-AE+BE-AK+CD-6.5+1.5-8( m).F,树的高度AB约为8m. ...................................... 7分21.«本題7分)证明:(1)V^ABCMABAD>AZCAB-ZI>B^. AOA-OB. ............................................................. 3 分<2) •••△ABCXZiBAD. .\AC-BD.又VOA-OB..\oc・()D. :・zocD・zmc.・・・^AOB-/:COD.^CAB^ 朋•-孑AOB“g■咆一产。
2010年初三联考试卷

为 ▲ m/s.如果水平推力为 12N,在此过程中小强对该物体做的功的功率为 ▲ W. 16.如下图所示,跑车在车尾安装了一种“气流偏导器” ,它的上表面平直,底部呈弧形 突出,相当于一个倒置的翅膀如图所示,这主要是为了让跑车高速行驶时,偏导器上方空 气流速较小,压强较 ▲,从而形成向▲(选填“上或下” )的压力差,增大了对地面的压 力,从而增大了车对地面的摩擦力,使车轮能很好的抓住地面。
丁 23 题 24. (4 分) “海宝”是 2010 年世博会的吉祥物,其形象如图所示。在点缀上海街头的各种 “海宝”中,有一座“海宝” (材质均匀、实心)的质量为 3.0×103 千克,密度为 1.5×103 千克/米 3,与水平地面的接触面积为 1m2. (g 取 10N/kg) 求其: ①体积 V ②重力大小 G ③对地面的压强 P 25. (7 分)位于某市海滨的田湾核电站,至今已有两台机组先 题 24 后并网发电。 (1)先期并网发电的两台机组年发电量约为 1.6×1010kWh,这些电能相当于该市新海 电厂完全燃烧多少吨标准煤放出的能量?(标准煤的热值为 3.0×107J/kg) (2)与新海电厂的火力发电相比,核能发电具有哪些优点?(说出两点即可) (3)若电厂通过供电系统,用 220V 的电压给离电厂较远的小明家所在的小区供电。某
2009-2010 中考模拟考试
物 理 试 卷
说明: 1.本试卷共 6 页,包含选择题(第 1 题~第 12 题,共 12 题) 、非选择题(第 13 题~ 第 30 题,共 18 题)两部分。本卷满分 100 分,考试时间为 100 分钟。考试结束后,请将 答题卡交回。 2.答题前,考生务必将本人的姓名、准考证号、座位号填写在答题卡相应的位置上。 3.作图题必须用 2B 铅笔作答,并请加黑、加粗。 一、选择题(本题共 12 小题,每小题 2 分,共 24 分.每小题给出的四个选项中只有一个 .... 选项正确) 1.速度是表示物体运动快慢的物理量,它是用路程和时间的比值来定义的.初中物理经 常用到这种定义物理量的方法,下列物理量中所采用的定义方法与速度不同的是 A.密度 B.压强 C. 功 D. 功率 2.关于力和运动的关系,下列说法正确的是 A.轿车上装有安全气囊,可以防止惯性。 B.桌子不推就不动,所以力是维持物体运动的原因。 C.正在弯道匀速拐弯的汽车,如果把作用在汽车上的一切外力撤消,汽车将继续拐弯。 D.扔出去的铅球在空中作抛物线运动时,铅球受力一定不平衡。 3.把图 3 中的凸透镜看作眼睛的晶状体,光屏看作是视 网膜.给凸透镜“戴”上近视眼镜,使烛焰在“视网膜” 上成一清晰的像.若“取下”近视眼镜,为使光屏上的像 清晰,在保持烛焰和透镜位置不变的条件下,应将光屏 A.保持在原来位置 B.靠近透镜 C.远离透镜 D.无论怎样移动光屏都不能使像清晰 4.下列设备的运行与电磁波无关的是 A.汽车上安装有 GPS(全球卫星定位系统)以确定行驶路线和距离 B.“嫦娥一号”接收地面指挥中心的运行指令实现变轨而奔向月球 C.医院里,医生利用 B 超可观察到母体内的婴儿情况 D.在生活中人们利用手机可以方便地取得联系 5.如图所示的电路中,电源电压恒定.闭合开关 S 后,电路正常工作.过了一会儿,两 电表的示数突然都变为零,则该电路中出现的故障可能是 A. 电阻 R 断路 B.电阻 R 短路 C.灯 L 断路 D.灯 L 短路 6.下列数值最不接近实际情况的是 A.让人感觉舒适的房间温度约为 25℃ B.两个鸡蛋的质量约为 100g C.初中生立正站立时对地压强约为 1000Pa. D.初中生的体积约为 50dm3 7.魔术表演常给人以震撼的视觉冲击,如图所示,魔术师刘谦的爱徒先将一标有“PZ220
2010——2012年中山市初三数学竞赛试题真题以及详细答案

中山市2010年初三数学竞赛试题一、选择题(共5小题,每小题7分,共35分. 每道小题有且只有一个选项是正确的. 请将正确选项代号填入题后的括号里,不填、多填或错填都得0分)1.若20 10a b b c ==,,则a b b c ++的值为 ( ) (A )1121 (B )21011 (C )11021 (D )21112.若实数a ,b 满足21202a ab b -++=,则a 的取值范围是 ( )(A )a ≤2- (B )a ≥4 (C )2-≤a ≤4 (D )a ≤2-或 a ≥43.如图,在四边形ABCD 中,∠B =135°,∠C =120°,AB =BC =4-CD =则AD 边的长为 ( )(A )(B )64 (C )622+(D )64+4.在一列数123x x x ,,,……中,已知11=x ,且当k ≥2时,1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,(取整符号[]a 表示不超过实数a 的最大整数,例如[]2.62=,[]0.20=),则2010x 等于 ( ) (A) 1 (B) 2 (C) 3 (D) 45.如图,在平面直角坐标系xOy 中,等腰梯形ABCD 的顶点坐标分别为A (1,1),B (2,-1),C (-2,-1),D (-1,1).y 轴上一点P (0,2)绕点A 旋转180°得点P 1,点P 1绕点B 旋转180°得点P 2,点P 2绕点C 旋转180°得点P 3,点P 3绕点D 旋转180°得点P 4,……,重复操作依次得到点P 1,P 2,…, 则点P 2010的坐标是 ( ) (A )(2010,2) (B )(2012,2-)(C )(2010,2-) (D )(0,2) 二、填空题(共5小题,每小题7分,共35分)6.已知a =5-1,则2a 3+7a 2-2a -11 的值等于 .7.一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶.在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间.过了10分钟,小轿车追上了货车;又过了5分钟,小轿车追上了客车;再过t 分钟,货车追上了客车,则t = .8.如图,在平面直角坐标系xOy 中,多边形OABCDE 的顶点坐标分别是O (0,0),A (0,6),B (4,6),C (4,4),D (6,4),E (6,0).若直线l 经过点M (2,3),且将多边形OABCDE 分割成面积相等的两部分,则直线l 的函数表达式是 .9.如图,射线AM ,BN 都垂直于线段AB ,点E 为AM 上一点,过点A 作BE 的垂线AC 分别交BE ,BN 于点F ,C ,过点C 作AM 的垂线CD ,垂足为D .若CD =CF ,则AEAD= . 10.对于i =2,3,…,k ,正整数n 除以i 所得的余数为i -1.若n 的最小值0n 满足020003000n <<,则正整数k 的最小值为 . 三、解答题(共4题,每题20分,共80分)11.设实数a ,b 满足:2231085100a ab b a b -++-=,求u =29722a b ++的最小值.12.如图,AB 为⊙O 的直径,C 为圆上一点,AD 平分∠BAC 交⊙O 于点D ,DE ⊥AC 交AC 的延长线于点E ,FB 是⊙O 的切线交AD 的延长线于点F . (1)求证:DE 是⊙O 的切线. (2)若DE = 3,⊙O 的半径为5,求BF 的长.13.设1x ,2x ,…,008 2x 是整数,且满足下列条件: (1)21≤≤-n x (n =1,2,…,2 008); (2)++21x x …+008 2x =200;(3)++2221x x …+2008 2x =2 008. 求++3231x x …+3008 2x 的最小值和最大值.14.如图,已知直线b x y l +=31:经过点)41 0(,M ,一组抛物线的顶点11(1, y )B ,22(2, y )B ,33(3, y )B ,…,n (, y )n B n (n 为正整数)依次是直线l 上的点,这组抛物线与x 轴正半轴的交点依次是:11(, 0)A x ,22(, 0)A x ,33(, 0)A x ,…,11(,0)n n A x ++(n 为正整数),设d x =1(0<d <1). (1)求经过点1A 、1B 、2A 的抛物线的解析式(用含d 的代数式表示);(2)定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为“美丽抛物线”. 探究:当d (0<d <1)的大小变化时,这组抛物线中是否存在“美丽抛物线”?若存在,请求出相应的d 的值.中山市2010年初三数学竞赛试题参考答案一、选择题1.B 解:由题设得12012101111110a ab bc b c b +++===+++. 2.D 解:因为b 是实数,所以关于b 的一元二次方程21202b ab a -++= 21()41(2)2a a ∆--⨯⨯+=≥0, 解得a≤2-或 a≥4.3.C 解:如图,过点A ,D 分别作AE ,DF 垂直于直线BC ,垂足分别为E ,F . 由已知可得CF=DF =于是 EF =4过点A 作AG ⊥DF ,垂足为G .在Rt △ADG 中,根据勾股定理得AD ==2+4.B 解:由11=x 和1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭可得 11x =,22x =,33x =,44x =, 51x =,62x =,73x =,84x =,……因为2010=4×502+2,所以2010x =2.5.C 解:由已知可以得到,点1P ,2P 的坐标分别为(2,0),(2,2-). 记222 )P a b (,,其中222,2a b ==-.根据对称关系,依次可以求得: 322(42)P a b --,--,422(2)P a b ++,4,522(2)P a b ---,,622(4)P a b +,. 令662(,)P a b ,同样可以求得,点10P 的坐标为(624,a b +),即10P (2242,a b ⨯+), 由于2010=4⨯502+2,所以点2010P 的坐标为(2010,2-). 二、填空题6.1解:由已知得 (a +1)2=5,所以a 2+2a =4,于是2a 3+7a 2-2a -12=2a 3+4a 2+3a 2-2a -11=3a 2+6a -11=17.15解:设在某一时刻,货车与客车、小轿车的距离均为S 千米,小轿车、货车、客车的速度分别为a b c ,,(千米/分),并设货车经x 分钟追上客车,由题意得 ()10a b S -=, ① ()152a c S -=, ② ()x b c S -=. ③由①②,得30b c S -=(),所以,x=30. 故 3010515t =--=(分).8. 11133y x =-+ 解:如图,延长BC 交x 轴于点F ;连接OB ,AF ;连接CE ,DF ,且相交于点N .由已知得点M (2,3)是OB ,AF 的中点,即点M 为矩形ABFO 的中心,所以直线l 把矩形ABFO 分成面积相等的两部分.又因为点N (5,2)是矩形CDEF 的中心,所以,过点N (5,2)的直线把矩形CDEF 分成面积相等的两部分.于是,直线MN 即为所求的直线l .设直线l 的函数表达式为y kx b =+,则2352k b k b =⎧⎨+=⎩+,,解得 1311.3k b ⎧=-⎪⎪⎨⎪=⎪⎩, 故所求直线l 的函数表达式为11133y x =-+. 9.215- 解:见题图,设,FC m AF n ==.因为Rt △AFB ∽Rt △ABC , 所以2AB AF AC =⋅. 又因为 FC =DC =AB ,所以 2()m n n m =+,即2()10n n m m +-=,解得n m =,或n m =(舍去). 又Rt △AFE ∽Rt △CFB ,所以AE AE AF n AD BC FC m ====12,即AE AD=12. 10.9解:因为1n +为2 3 k ,,,的倍数,所以n 的最小值0n 满足 []012 3 n k +=,,,,其中[]2 3 k ,,,表示2 3 k ,,,的最小公倍数. 由于[][]2 3 88402 3 92520 ==,,,,,,,, [][]2 3 1025202 3 1127720==,,,,,,,, 因此满足020003000n <<的正整数k 的最小值为9.三、解答题11.解:由2231085100a ab b a b -++-= 可得()()23450a b a b --+=,(6分)所以 20a b -=,或 3450a b -+=. …………(8分)(i )当20a b -=时, ()22297223672236134u a b b b b =++=++=+-,于是1b =-时,u 的最小值为34-,此时2a =-,1b =-. …………(13分)(ii )当3450a b -+=时,()222972216322716111u a b b b b =++=++=++,于是1b =-时,u 的最小值为11,此时3a =-,1b =-. …………(18分)综上可知,u 的最小值为34-. …………(20分) 12、解:(1)如图,连接OD .因为AD 平分∠BAC ,所以∠1=∠2.又因为OA =OD ,所以∠1=∠3.所以∠2=∠3.所以OD ∥AE .因为DE ⊥AE ,所以DE ⊥OD .而点D 在⊙O 上,所以DE 是⊙O 的切线. …………(7分)(2)如图,连接BE 与OD 交于点H ,作OG ⊥AE 于点G . 则 OG = DE =3, EG = DO =5,所以AG=4,AE = 4+5= 9…………(10分),因为EA ∥OD , AO=OB ,所以HO=12AE =92,HD = 5-92=12,故HE = =(20分)13.解:设1x ,2x ,…,008 2x 中有q 个0,r 个-1,s 个1,t 个2. …………(2分) 则220042008r s t r s t -++=⎧⎨++=⎩① …………(5分)两式相加得31104s t +=.故0368t ≤≤. …………(10分)由33312200886200x x x r s t t ++⋅⋅⋅+=-++=+, …………(12分)得33312200820063682002408x x x ≤++⋅⋅⋅+≤⨯+=.…………(15分)由方程组①知:当0,1104,904t s r ===时,++3231x x …+3008 2x 取最小值200; ……(17分) 当368,0,536t s r ===时, ++3231x x …+3008 2x 取最小值2408. …………(20分)14.解:(1)易得14b =,B 1(7121,),…………(3分) 设其解析式为27(1)(0),12y a x a =-+≠由1(,0),A d 得2712(1)a d =--,…………(7分) 于是2277(1)12(1)12y x d =--+-为所求;…………(8分)(或者由12(,0),(2,0)A d A d -为该抛物线与x 轴的两个交点,设其解析式为()(2)(0)y a x d x d a =--+≠,再代入点17(1,)12B ,同样可得) (2)根据对称性易得12345...A A A A A 、、、、的横坐标依次为d,2-d,2+d,4-d,4+d,6-d,…(10分)1223344522,2,22,2...A A d A A d A A d A A d=-==-=,(12分) 要使三角形为直角三角形,则斜边上中线等于斜边的一半,因为0<d <1,斜边长都小于2,所以只要高123,,...y y y 小于1才能构成直角三角形,…………(14分)当>3x 时,所对应的函数值都大于1,可以得到符合要求的顶点为1B 、2B ,………(16分) 再求得相应的d 的值为512或1112.…………(20分)(B )3MN =(C )若MN 与⊙O 相切,则∠MON =90°(D )若MN 与⊙O 相交,则AM ≥二、填空题(共5小题,每小题7分,共35分)6.一个密码箱的密码, 每个数位上的数都是从0到9的自然数, 若要使不知道密码的人一次拨对密码的概率小于12011, 则密码的位数至少需要 4 位. 7.已知非负数a b c ,,满足条件75a b c a +=-=,,设S a b c =++的最大值为m ,最小值为n ,则m n -的值为 7 .8.已知二次函数()()221y x a a =-+-(a 为常数),当a 取不同的值时,其图像构成一个“抛物线系”.下图分别是当1a =-,0a =,1a =,2a =时二次函数的图像.它们的顶点在一条直线上,这条直线的解析式是xy 12=-.(第8题图 ) (第9题 图)9.如图,在平面直角坐标系中,边长为1的正方形11OA B C 的对角线1AC 和1OB 交于点1M ,以11M A 为对角线作第二个正方形2121A A B M ,对角线11A M 和22A B 交于点2M ;以21M A 为对角线作第三个正方形3132A A B M ,对角线12A M 和33A B 交于点3M ;……依此类推,这样作的第n 个正方形对角线交点n M 的坐标为n n11122(,)-. 10.如图,一次函数y ax b =+的图像与x 轴,y 轴交于A ,B 两点,与反比例函数ky x=的图像相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE ,EF .有下列四个结论:①△CEF 与△DEF 的面积相等; ②△AOB ∽△FOE ; ③△DCE ≌△CDF ;④AC BD =.其中正确的结论是 ①②④ .(把你认为正确结论的序号都填上)(第10题图)三、解答题(共4题,每题20分,共80分)11.设关于x 的方程0212482=-+-+-a x a x x 恰有两个实根.求实数a 的取值范围.解:原方程变形为.0)2(2442=+--+-a x a x ……………………………(5分) 令).0(4≥-=y x y 则0)2(22=+-+a ay y0)2)](2([=-++⇒y a y ,2),2(21=+-=⇒y a y ……………………………(10分)即x 4a 2()-=-+或.24=-x 故原方程恰有两实根2)2(=+-⇔a 或)2(+-a <0. ……………………………(15分)因此,4-=a 或a >-2 ……………………………(20分)12.已知a 、b 、c 是三角形的三边长,实数p 、q 满足1=+q p .判断代数式222p q c qb pa -+的符号并写出理由.解:令.222pqc qb pa y -+= 将p q -=1代入上式得222)1()1(c p p b p pa y ---+=.)(222222b p c b a p c +--+= ……………………………(5分) 将上式视为关于p 的二次函数,图像开口向上,则.4)(222222c b c b a ---=∆ ])(][)([2222c b a c b a +---=).( )( )( )(c b a c b a c b a c b a --+++--+= ……………………………(10分) 由于a 、b 、c 是三角形三边,则有c b a -+>0,c b a +->0,c b a ++>0,c b a --<0, ……………………………(15分)于是,∆<0y ⇒>0. ……………………………(20分)13.在凹四边形ABCD 中,∠A=∠C=o 40,∠B=o50,E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点.判断四边形EFGH 的形状并证明你的结论.解:四边形EFGH 是矩形. ………………(5分) 如右图,联结AC 、BD.由三角形中位线定理得,21//BD EH .21//BD FG则.//FG EH 故四边形EFGH 是平行四边形. ……………………………(10分)由∠BAD+∠ABC=o90,∠BCD+∠ABC=o90, 得AD ⊥BC,CD ⊥AB.于是,D 是△ABC 的垂心,BD ⊥AC. ……………………………(15分) 又GH ∥AC,则BD ⊥GH. 从而,FG ⊥GH.故四边形EFGH 是矩形. ……………………………(20分) 14.对于每个正整数n ,设)(n f 表示1+2+⋅⋅⋅+n 的末位数字(如,1)1(=f ,3)2(=f 6)3(=f ),试计算)2011()2()1(f f f +⋅⋅⋅++的值。
湖北省武汉市2010年九年级数学中考模拟试题12
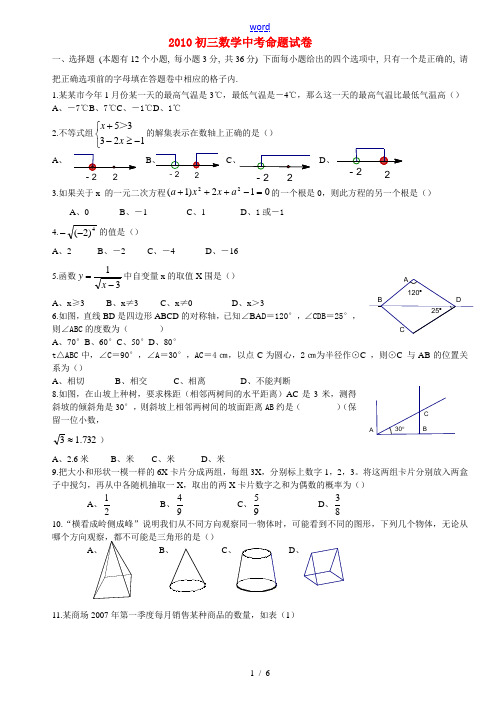
2-22-22-22DC BA 25︒120︒30︒CBA2010初三数学中考命题试卷一、选择题 (本题有12个小题, 每小题3分, 共36分) 下面每小题给出的四个选项中, 只有一个是正确的, 请把正确选项前的字母填在答题卷中相应的格子内.1.某某市今年1月份某一天的最高气温是3℃,最低气温是-4℃,那么这一天的最高气温比最低气温高() A 、-7℃B 、7℃C 、-1℃D 、1℃2.不等式组⎩⎨⎧-≥-+12335x x >的解集表示在数轴上正确的是()A 、BCD 、 3.如果关于x 的一元二次方程012)1(22=-+++a x x a 的一个根是0,则此方程的另一个根是()A 、0B 、-1C 、1D 、1或-1 4.4)2(--的值是()A 、2B 、-2C 、-4D 、-16 5.函数31-=x y 中自变量x 的取值X 围是()A 、x ≥3B 、x ≠3C 、x ≠0D 、x >36.如图,直线BD 是四边形ABCD 的对称轴,已知∠BA D =120°,∠CDB =25°,则∠ABC 的度数为( )A 、70°B 、60°C 、50°D 、80°t △ABC 中,∠C =90°,∠A =30°,AC =4㎝,以点C 为圆心,2㎝为半径作⊙C ,则⊙C 与AB 的位置关系为()A 、相切B 、相交C 、相离D 、不能判断8.如图,在山坡上种树,要求株距(相邻两树间的水平距离)AC 是3米,测得斜坡的倾斜角是30°,则斜坡上相邻两树间的坡面距离AB 约是( )(保留一位小数,732.13≈)A 、2.6米B 、米C 、米D 、米9.把大小和形状一模一样的6X 卡片分成两组,每组3X ,分别标上数字1,2,3。
将这两组卡片分别放入两盒子中搅匀,再从中各随机抽取一X ,取出的两X 卡片数字之和为偶数的概率为()A 、21 B 、94 C 、95 D 、83 10.“横看成岭侧成峰”说明我们从不同方向观察同一物体时,可能看到不同的图形,下列几个物体,无论从哪个方向观察,都不可能是三角形的是()A 、B 、C 、D 、11.某商场2007年第一季度每月销售某种商品的数量,如表(1)图232121.622.022.8月份销售额(万元)0yx-2-12Py=ax+b y=kx+m 第1个第2个第3个第4个第5个PDCByx月份 1 2 3 销售额(件)100120144其销售额如图(2)由表(1)和图(2)获取的信息中正确的有() ①每月销售量是逐月增长的,且增长率是相等的 ②2月份的销售额最高,这个月的零售价也是最高的 ③该商品的零售价在逐月降低④3月份该商品的零售价下降的幅度比2月份零售价下降的幅度大 A 、1个 B 、2个 C 、3个 D 、4个1212、如图,AB 为⊙O 的直径,AC 交⊙O 于E 点,BC 交⊙O 于D 点,CD=BD ,∠C=70°.现给出以下四个结论:①∠A=45°;②AC=AB ;③AE BE =;④CE·AB=2BD 2.其中正确的结论是( ) A .只有①② B .只有②③ C .只有②④ D .只有③④第Ⅱ卷(非选择题 共84 分)二、填空题(本题有4个小题, 每小题3分, 共12分) 13.已知22)(9n x mx x +=++,则m =14.如图,函数m kx y +=与)<0(a b ax y +=的图像交于点P ,则根据图像可得不等式组⎩⎨⎧+++mkx b ax m kx >>0的解集为15.观察下列各图中小圆圈的摆放规律,并按这样的规律继续摆放下去,则第十个图形中小圆圈的个数为FEDCBA16.如图,点P 为双曲线x y 8=(x >0)上一点,PA ⊥x 轴于A ,PB ⊥y 轴于B ,,PA 、PB 分别交双曲线xk y =(x >0)于C 、D ,连接CD ,若1=∆PCD S ,则k = 三、解答题(72分)17.(6分)解方程:142=-x x18.(6分)先化简,再求值:)331(922+-+÷-x x x x ,其中x =4.19.(6分)如图,A 、D 、F 、B 在同一直线上,AD =BF ,AE =BC ,且AE ∥BC ,求证EF ∥CD 。
桐乡市2010年九年级文理科联赛模拟试卷(十)及答案

2010年九年级文理科联赛模拟试卷(十)(20101125)班级___________________ 姓名_____________一、选择题(每题3分,共27分) 1.下列各式运算中,正确的是( )A 、222()a b a b +=+ B 、2(3)3-= C 、3412a a a ⋅=D 、2236()(0)a a a =≠ 2.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x ,掷第二次,将朝上一面的点数记为y ,则点(x y ,)落在直线5y x =-+上的概率为:( ) A、118 B、112 C 、19 D、413.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ).A .2+10B .2+210C .12D .18 4.已知抛物线2y ax bx c =++(a <0)过A (2-,0)、O (0,0)、 B (3-,1y )、C (3,2y )四点,则1y 与2y 的大小关系是( ). A .1y >2yB .1y 2y =C .1y <2yD .不能确定5.如图,菱形ABCD 由6个腰长为2,且全等的等腰梯形镶嵌而成, 则线段AC 的长为( ). A .3B .6C .33D .636. 二次函数2y ax bx c =++的图象如图所示,则一次函数ac bx y -=与反比例函数x cb a y +-=在同一坐标系内的图象大致为( )① ②3 4101- 1O xy(第6题图)第9题图ABC7、y=x 2+(1-a )x +1是关于x 的二次函数,当x 的取值范围是1≤x≤3时,y 在x =1时取得最大值,则实数a 的取值范围是( )。
A .a=5B .a≥5C .a =3D .a≥38.在某次聚会上,每两人都握了一次手,所有人共握手10次,设有x 人参加这次聚会,则列出方程正确的是( ). A .(1)10x x -= B .(1)102x x -= C .(1)10x x += D .(1)102x x += 9.如图,在△ABC 中,AB = AC ,AB = 8,BC = 12,分别以 AB 、AC 为直径作半圆,则图中阴影部分的面积是( ) A .64127π- B .1632π-C .16247π-D .16127π-二、填空题10.如图,在直径AB =12的⊙O 中,弦CD ⊥AB 于M ,且M 是半径OB 的中点,则弦CD 的长是_______(结果保留根号). 11.甲、乙、丙、丁四支足球队在世界杯预选赛中的进球数分别为:9、9、11、7,则这组数据的:①众数为_____________;②中位数为____________;③平均数为__________.12.已知关于x 的一元二次方程x 2 +kx +1 =0有两个相等的实数根,则k = .13. 在平面直角坐标系中,点A 1(1,1),A 2(2,4),A 3(3,9),A 4(4,16),…,用你发现的规律 确定点A 9的坐标为 。
2010——2012年中山市初三数学竞赛试题真题以及详细答案

2010——2012年中山市初三数学竞赛试题真题以及详细答案中山市2010年初三数学竞赛试题一、选择题(共5小题,每小题7分,共35分)1.若 a/(ba+c) = 20.c/(cb+a) = 10,则 b 的值为(B)。
2.若实数 a,b 满足 a - ab + b + 2 = 0,则 a 的取值范围是(C)。
3.如图,在四边形 ABCD 中,∠B = 135°,∠C = 120°,AB = 23,BC = 4 - √22,CD = 42,则 AD 边的长为2 + 2√6.4.在一列数 x1,x2,x3,…… 中,已知 x1 = 1,且当k ≥ 2 时,xk = xk-1 + [k-1/4] - [k-2/4],(取整符号 [a] 表示不超过实数 a 的最大整数),则 x2010 等于(B)。
5.如图,在平面直角坐标系 xOy 中,等腰梯形 ABCD 的顶点坐标分别为 A(1,1),B(2,-1),C(-2,-1),D (-1,1)。
y 轴上一点 P(0,2)绕点 A 旋转 180°得点 P1,点 P1 绕点 B 旋转 180°得点 P2,点 P2 绕点 C 旋转 180°得点P3,点 P3 绕点 D 旋转 180°得点 P4,……,重复操作依次得到点 P2010,P2010 的坐标是(A)(2010,2)。
二、填空题(共5小题,每小题7分,共35分)6.已知 a = 5 - √2,则 2a^3 + 7a^2 - 2a - 11 的值等于 267 - 94√2.7.一辆客车、一辆货车和一辆小轿车在一条笔直的公路上朝同一方向匀速行驶。
在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间。
过了 10 分钟,小轿车追上了货车;又过了 5 分钟,小轿车追上了客车;再过 t 分钟,货车追上了客车,则 t = 15.8.在平面直角坐标系xOy中,有一个五边形OABCDE,其顶点坐标分别为O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0)。
2010年初中理科综合模拟试题(二)

2010年初中毕业生升学考试理科综合模拟试卷(二)本试卷分卷I 和卷II 两部分;卷I 为选择题,卷II 为非选择题。
本试卷满分为120分,考试时间为120分钟。
卷Ⅰ(选择题,共44分)注意事项:1、答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上。
考试结束,监考人员将试卷和答题卡一并收回。
2、每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
答在试卷上无效。
一、选择题(本大题共22个小题;每小题2分,共44分。
在每小题给出的四个选项中,只有一个选项符合题意)1.胆矾是一种蓝色晶体(化学式是CuSO 4·5H 2O ),受热时易失去结晶水,成为白色的无水CuSO 4粉末,无水CuSO 4易吸收水份又变成蓝色。
在工业上精炼铜、镀铜等都要用胆矾。
上述对胆矾的描述中,没有涉及到的是A .物理性质B .制法C .用途D .化学性质2. 下列实验操作,正确的是① 粗盐提纯的操作步骤是:溶解、过滤、蒸发② 用托盘天平称量药品时,把药品放在左盘,砝码放在右盘③ 用酒精灯的焰心给物质加热④ 配制一定质量分数的溶液时,其操作步骤是:溶解、量取、称量、计算A 、④B 、②④C 、①③D 、 ①②3.已知某两种物质在光照条件下能发生化学反应,其微观示意图如下:(说明:一种小球代表一种元素的原子) 则下列说法中正确的是 A 、图示中共有3种物质 B 、该反应属于置换反应C 、图示中的反应物都是单质D 、该图示符合质量守恒定律4.下列实验现象描述错误..的是 A 、红磷在空气中燃烧,产生大量白色烟雾B 、将二氧化碳通入紫色石蕊溶液中,溶液变红色C 、红亮的铜丝在酒精灯火焰上灼烧,铜丝表面变黑D 、氢氧化钠溶液中加入硫酸铜溶液,产生蓝色沉淀5.下列是几种粒子的结构示意图,有关说法不正确...的是 ①②③ ④A 、①和②属同种元素B 、②属于稀有气体元素C 、①和③的化学性质相似D 、④属于金属元素6.修筑三峡大坝时用混凝土(成分中含有氧化钙)浇筑,为防止浇筑过程中混凝土水化放出的热量使坝体温度升高,技术人员在仓内埋设了许多管道,一旦温度升高,则通水冷却。
2010年河北中考试题及答案解析

河北省2010年初中毕业生升学文化课考试理科综合试卷及答案本试卷分卷I 和卷II 两部分;卷I 为选择题,卷II 为非选择题。
本试卷满分为120分,考试时间为120分钟。
卷Ⅰ(选择题,共44分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上。
考试结束,监考人员将试卷和答题卡一并收回。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
答在试卷上无效。
一、选择题(本大题共22个小题;每小题2分,共44分。
在每小题给出的四个选项中,只有一个选项符合题意)1.下列物质不能..为人类生命活动提供能量的是 A .米饭 B .水 C .鸡蛋D .花生油2.下列有关氧气的说法正确的是A .能供给呼吸B .化学性质比较稳定C .具有可燃性D .是空气中含量最多的物质3.医疗上可以用含有氢氧化镁的药物治疗胃酸过多,其反应的化学方程式为:Mg(OH)2 + 2HCl =MgCl 2 + 2H 2O ,该反应属于 A .化合反应B .分解反应C .置换反应D .复分解反应4.图1是钠元素的原子结构示意图,下列叙述不正确...的是A .钠原子的质子数为11 B .钠原子的最外层电子数为1 C .钠原子易失去电子形成阳离子 D .钠元素为非金属元素5.推理是一种重要的研究和学习方法。
下列推理正确的是 A .碱中都含有氢氧根,所以碱中一定含有氢元素 B .分子是构成物质的微粒,因此物质都是由分子构成的C .中和反应有盐和水生成,因此有盐和水生成的反应一定是中和反应D .铁丝能在氧气中燃烧,空气中有氧气,所以铁丝也能在空气中燃烧 6.利用图2所示装置,能完成实验室制取气体的是A .用①③制取氧气B .用②③制取二氧化碳C .用②④制取氧气D .用①⑤制取二氧化碳7.图3所示的四个图象,能正确反映对应变化关系的是溶质质量分数 二氧化碳质量氧气质量生成气体质量ggg图2 ③① ②④ ⑤A .①水的电解B .②木炭在密闭的容器内燃烧C .③加热一定量的高锰酸钾制氧气D .④20 ℃时,向一定量接近饱和的硝酸钾溶液中加入硝酸钾固体 8.下列过程中发生化学变化的是 A .铁丝弯曲B .西瓜榨汁C .食物腐烂D .灯丝熔断9.“低碳生活”是指生活中所耗用的能量、材料要尽量减少,从而减低二氧化碳的排放量。
2010年河北省初中毕业生升学文化课考试理科综合试题和参考答案

题号
二
得分
四
三
36
37
38
以下数据可供解题时参考: 相对原子质量:H-1 C-12 O-16 Na-23 Cl-35.5
得 分 评卷人 二、填空及简答题(本大题共 9 个小题;每空 1 分,共 34 分)
23.电冰箱在结构上和工作过程中应用了许多物理知识(如图 9 所示)。
(1)问题:为什么要使用三脚插头? 回答:
J。热水
器消耗的电能比水吸收的热量多,其原因是:
(答出
一种即可)。[c水 = 4.2×103 J/(kg·℃)]
26.阅读短文,回答问题。
海水的利用
地球表面的 70%以上是海洋,开发利用海洋有广阔的前景。
潮汐是一种海平面周期性变化现象,海平面每昼夜有两次涨落。人们在靠近海的河口或海
湾深处建大坝,在大坝中间装上水轮发电机组。涨潮时,海水通过大坝流进河口,带动水轮发
河北省初中毕业生升学文化课考试
理科综合试卷
本试卷分卷 I 和卷 II 两部分;卷 I 为选择题,卷 II 为非选择题。 本试卷满分为 120 分,考试时间为 120 分钟。
卷Ⅰ(选择题,共 44 分)
注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上。考试结束, 监考人员将试卷和答题卡一并收回。
②火车刹车后不能马上停下来,是由于火车具有惯性
③高速飞行的子弹具有惯性,穿入木头静止后惯性消失
④将锤子的木柄在硬地上撞击几下,锤头便套紧了,利用了物体的惯性
A.①②
B.①③
C.②④
D.③④
19.图 5 是直流电铃的原理图。关于电铃工作时的说法 不.正.确.的是 A.电流通过电磁铁时,电磁铁有磁性且 A 端为 N 极 B.电磁铁吸引衔铁,弹性片发生形变具有弹性势能 C.小锤击打铃碗发出声音,是由于铃碗发生了振动 D.小锤击打铃碗时,电磁铁仍具有磁性
2010年全国卷新课标理科试题与详细答案

2010年普通高等学校招生全国统一考试数学理工农医类(新课标卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题.其他题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.参考公式:样本数据x 1,x 2,…,x n 的标准差s其中x 为样本平均数 柱体体积公式V =Sh其中S 为底面面积,h 为高 锥体体积公式V =13Sh 其中S 为底面面积,h 为高 球的表面积,体积公式 S =4πR 2,V =43πR 2 其中R 为球的半径第Ⅰ卷(选择题共50分)一、选择题:本大题共12小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x ||x |≤2,x ∈R },B ={x≤4,x ∈Z },则A ∩B =( ) A .(0,2) B .[0,2] C .{0,2} D .{0,1,2} 答案:D ∵A ={-2,-1,0,1,2},B ={0,1,2,3,…,16},∴A∩B ={0,1,2}. 2.已知复数z,z 是z 的共轭复数,则z ·z =( ) A.14 B.12C .1D .2 答案:A z·z =|z|2而|z|=221=24=12,∴|z|2=14,∴z·z =14. 3.曲线y =2x +x在点(-1,-1)处的切线方程为( ) A .y =2x +1 B .y =2x -1 C .y =-2x -3 D .y =-2x -2 答案:A ∵y ′=22(2)x x x ++-=22(2)x +,∴在点(-1,-1)处的切线方程的斜率为2)21(22=+-.∴切线方程为y +1=2(x +1), 即y =2x +1.4.如图,质点P 在半径为2的圆周上逆时针运动,其初始位置为P 0),角速度为1,那么点P 到x 轴的距离d 关于时间t 的函数图像大致为( )答案:C 法一:P 从P 0出发,逆时针运动,t =0时,d ,t 与d 满足关系式d =2sin(t -π4)(t ≥0).所以选择C 项. 法二:(排除法)当t =0时,P )到x ,排除A 、D 两项,当t =π4时, P (2,0)到x 轴的距离为0,排除B.故选C 项. 5.已知命题:p 1:函数y =2x -2-x 在R 上为增函数,p 2:函数y =2x +2-x 在R 上为减函数,则在命题q 1:p 1∨p 2,q 2:p 1∧p 2,q 3:(p 1)∨p 2和q 4:p 1∧(p 2)中,真命题是( )A .q 1,q 3B .q 2,q 3C .q 1,q 4D .q 2,q 4 答案:C 对于p 1:y ′=2x ln2-(12)x ln 12=ln2(2x +2-x ),∴y ′>0,∴函数为增函数, ∴p 1为真.对于p 2:y ′=2x ln2+(12)x ln 12=ln2[2x -(12x ],y ′<0不一定成立,∴p 2为假,∴q 1为真,q 2为假,q 3为假,q 4为真.6.某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X ,则X 的数学期望为( )A .100B .200C .300D .400 答案:BE (X )=1 000×0.9×0+1 000×0.1×2=200.7.如果执行下面的框图,输入N =5,则输出的数等于 ()A.54 B.45 C.65 D.56答案:D 由框图可知,输出的S 为 S =112⨯+123⨯+134⨯+145⨯+156⨯=1-12+12-13+13-14+14-15+15-16=1-16=56.8.设偶函数f (x )满足f (x )=x 3-8(x ≥0),则{x |f (x -2)>0}=( )A .{x |x <-2或x >4}B .{x |x <0或x >4}C .{x |x <0或x >6}D .{x |x <-2或x >2 答案:B ∵f (x )为偶函数,∴f (x -2)=f (|x -2|),∴f (x -2)>0等价于f (|x -2|)>0=f (2),又∵f (x )=x 3-8(x ≥0)为增函数, ∴|x -2|>2.解得x >4或x <0.9.若cos α=-45,α是第三象限的角,则1tan21tan 2αα+-=( ) A .-12 B.12C .2D .-2答案:A ∵cos α=-45,α为第三象限角,∴sin α=-35.∵sin211tancos 221tansin 221cos2αααααα++=--=2cossin(cossin )2222cos sin(cos sin )(cos sin )222222αααααααααα++=+--=2231()1sin 1sin 54cos cos sin 225ααααα+++==---=-12. 10.设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为( )A .πa 2 B.73πa 2 C.113πa 2 D .5πa 2 答案:B 如图,O 1,O 分别为上、下底面的中心,D 为O 1O 的中点,则DB 为球的半径,有r =DBS 表=4πr 2=4π×2712a =73πa 2. 11.已知函数f (x )=|lg |,010,16,10.2x x x x <≤⎧⎪⎨+>⎪⎩-若a ,b ,c 互不相等,且f (a )=f (b )=f (c ),则abc 的取值范围是( )A .(1,10)B .(5,6)C .(10,12)D .(20,24) 答案:C 由图知a ,b ,c 有两个在(0,10]上,假设a ,b ∈(0,10],并有一个大于1一个小于1,不妨设a <1,b >1,则f (a )=|lg a |=-lg a =lg1a,f (b )=|lg b |=lg b ,∴1a=b .∴a ·b ·c =c ,由图知c ∈(10,12).12已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为N (-12,-15),则E 的方程为( )A.23x -26y =1B.24x -25y =1C.26x -23y =1D.25x -24y =1答案:B 由c =3,设双曲线方程为22x a -229y a -=1,k AB =k NF =015312++=1, 设A (x 1,y 1),B (x 2,y 2),则212x a -2129y a -=1, ①222x a -2229y a-=1, ② ①-②,得12122()()x x x x a +--12122()()9y y y y a +--=0.又N (-12,-15)为AB 中点,∴x 1+x 2=-24,y 1+y 2=-30. ∴122()x x a -24-=122()9y y a -30--.∴1212y y x x --=22(9)5a a 4-=1. ∴a 2=4.∴双曲线方程为24x -25y =1. 第Ⅱ卷(非选择题共100分)二、填空题:本大题共4小题,每小题5分,共20分.13.设y =f (x )为区间[0,1]上的连续函数,且恒有0≤f (x )≤1,可以用随机模拟方法近似计算积分1⎰f(x)d x.先产生两组(每组N 个)区间[0,1]上的均匀随机数x 1,x 2,…,x N 和y 1,y 2,…,y N ,由此得到N 个点(x i ,y i )(i =1,2,…,N).再数出其中满足y i ≤f(x i )(i =1,2,…,N)的点数N 1,那么由随机模拟方法可得积分1⎰f(x)d x 的近似值为__________.答案:1N N解析:由题意可知01,01,x y ≤≤⎧⎨≤≤⎩它所围成的区域面积为S =1,结合积分的几何意义和几何模型可知,1()f x dx S⎰=1N N ,即10⎰f(x)d x =1NN.14.正视图为一个三角形的几何体可以是__________.(写出三种)答案:三棱锥、圆锥、四棱锥(答案不唯一)15.过点A(4,1)的圆C 与直线x -y -1=0相切于点B(2,1),则圆C 的方程为__________.答案: (x -3)2+y 2=2解析:法一:设圆C 方程:(x -a)2+(y -b)2=r 2, 圆心(a ,b)到直线x -y -1=0的距离 d=r , ①又圆C 过点A(4,1),B(2,1),∴(4-a)2+(1-b)2=r 2, ② (2-a)2+(1-b)2=r 2, ③由①②③,得a =3,b =0,r,∴圆的方程为(x -3)2+y 2=2.法二:∵圆过A 、B 两点,∴圆心C 在线段AB 的中垂线上.而k AB =1142--=0 AB 中点M(3,1),∴AB 中垂线方程为x =3.又∵圆C 与直线x -y -1=0,相切于点B(2,1),所以圆心在过点B 且与x -y -1=0垂直的直线x +y -3=0上.由330x x y =⎧⎨+=⎩-得圆心C(3,0),∴r =|CA|∴圆的方程为:(x -3)2+y 2=2.16.在△ABC 中,D 为边BC 上一点,BD =12DC ,∠ADB =120°,AD =2.若△ADC 的面积为3,则∠BAC =__________. 答案:60°解析:S △ADC =12×2×DC×2=3解得DC =1),∴BD -1,BC =1).在△ABD 中,AB 2=4+1)2-2×2×1)×cos 120°=6,∴AB .在△ACD 中,AC 2=4+-1)]2-2×2×1)×cos 60°=24-∴AC 1),则cos ∠BAC =222AB +AC BC 2AB AC ⋅-12,∴∠BAC =60°.三、解答题:共80分.解答应写出文字说明、证明过程或演算步骤. 17.(12分)设数列{a n }满足a 1=2,a n +1-a n =3·22n -1.(1)求数列{a n }的通项公式;(2)令b n =na n ,求数列{b n }的前n 项和S n . 解析: (1)由已知,当n≥1时,a n +1=[(a n +1-a n )+(a n -a n -1)+…+(a 2-a 1)]+a 1=3(22n -1+22n -3+…+2)+2=22(n +1)-1. 而a 1=2,所以数列{a n }的通项公式为a n =22n -1.(2)由b n =na n =n·22n -1知S n =1·2+2·23+3·25+…+n·22n -1. ① 从而22·S n =1·23+2·25+3·27+…+n·22n +1. ②①-②,得(1-22)S n =2+23+25+…+22n -1-n·22n +1, 即S n =19[(3n -1)22n +1+2]. 18.(12分)如图,已知四棱锥P —ABCD 的底面为等腰梯形,AB ∥CD ,AC ⊥BD ,垂足为H ,PH 是四棱锥的高,E 为AD 中点.(1)证明PE ⊥BC ;(2)若∠APB =∠ADB =60°,求直线PA 与平面PEH 所成角的正弦值.解析:以H 为原点,HA ,HB ,HP 分别为x ,y ,z 轴,线段HA 的长为单位长,建立空间直角坐标系如图,则A(1,0,0),B(0,1,0).(1) 证明:设C(m,0,0),P(0,0,n)(m <0,n >0),则D(0,m,0),E(12,2m,0).可得PE =(12,m2,-n),BC =(m ,-1,0).因为PE ·BC=m 2-m 2+0=0,所以PE ⊥BC. (2) 解:由已知条件可得m=-3,n =1,故C(-3,0,0),D(0,-3,0), E(12,-6,0),P(0,0,1).设n =(x ,y ,z )为平面PEH 的法向量,则10,0,20,0.HE x y HP z ⎧⎧⋅==⎪⎪⎨⎨⋅=⎪⎪⎩=⎩n n 即 因此可以取n =(10).由PA =(1,0,-1),可得|cos 〈PA ,n 〉|,所以直线P A 与平面PEH 所成角的正弦值为4. 19.(12分)为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.附:K 2=2n(ad bc)(a+b)(c+d)(a+c)(b+d)-解析: (1)调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估计值为70500=14%. (2)K 2=2500(4027030160)20030070430⨯⨯⨯⨯⨯⨯-≈9.967.由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关. (3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.20.(12分)设F 1,F 2分别是椭圆E :22x a +22y b=1(a >b >0)的左、右焦点,过F 1斜率为1的直线l 与E 相交于A ,B 两点,且|AF 2|,|AB|,|BF 2|成等差数列.(1)求E 的离心率;(2)设点P(0,-1)满足|PA|=|PB|,求E 的方程.解析:得|AB |=43a . l 的方程为y =x +c ,其中c 设A (x 1,y 1),B (x 2,y 2), 则A ,B 两点坐标满足方程组2222,1.y x c x y ab =+⎧⎪⎨+=⎪⎩ 化简得(a 2+b 2)x 2+2a 2cx +a 2(c 2-b 2)=0,则x 1+x 2=2222a c a b +-,x 1x 2=22222()a c b a b+-. 因为直线AB 斜率为1,所以|AB |x 2-x 1|=得43a =2224ab a b +,故a 2=2b 2. 所以E 的离心率e =ca=2a =. (2)设AB 的中点为N (x 0,y 0),由(1)知x 0=122x x +=22223a c a b =+--c ,y 0=x 0+c =3c. 由|P A |=|PB |得k PN =-1. 即001y x +=-1, 得c =3,从而a =,b =3.故椭圆E 的方程为22189x y +=1. 21.(12分)(理)设函数f(x)=e x -1-x -ax 2.(1)若a =0,求f(x)的单调区间;(2)若当x≥0时f(x)≥0,求a 的取值范围. 解析: (1)a =0时,f (x )=e x -1-x ,f ′(x )=e x -1.当x ∈(-∞,0)时,f ′(x )<0;当x ∈(0,+∞)时,f ′(x )>0.故f (x )在(-∞,0)上单调减少,在(0,+∞)上单调增加. (2)f ′(x )=e x -1-2ax .由(1)知e x ≥1+x ,当且仅当x =0时等号成立, 故f ′(x )≥x -2ax =(1-2a )x , 从而当1-2a ≥0,即a ≤12时,f ′(x )≥0(x ≥0),而f (0)=0, 于是当x ≥0时,f (x )≥0.由e x >1+x (x ≠0)可得e -x >1-x (x ≠0).从而当a >12时,f ′(x )<e x -1+2a (e -x -1)=e -x (e x -1)(e x -2a ),故当x ∈(0,ln2a )时,f ′(x )<0,而f (0)=0,于是当x ∈(0,ln2a )时,f (x )<0.综合得a 的取值范围为(-∞,12]. 方法二,分离参数法:当0≥x 时,0)(≥x f ,由012≥---ax x e x,即x e ax x--≤12,(1)当0=x 时,R a ∈,(2)当0≠x 时,21x x e a x --≤,令21)(x xe x g x --=,则322)(xx e xe x g x x ++-=' 令22)(++-=x e xe x h xx,则,1)(+-='xxe xe x h 令,1)(+-=xxe xe x m 则0)(>='x xe x m ,∴)(x m 为增函数,则0)0()(=>m x m ,∴0)(>'x h ,∴)(x h 为增函数,则0)0()(=>h x h ,∴0)(>'x g ,)(x g 为增函数,则)0()(g x g >,∴)0(g a ≤ 可是)0(g 不存在,只能求极限,由洛比达法则得,212lim )2()1(lim )()1(lim )(lim 00200==''-=''--=++++→→→→x x x x x x x e x e x x e x g ,故21≤a 22.(10分)选修4-1:几何证明选讲如图,已知圆上的弧,过C 点的圆的切线与BA 的延长线交于E 点,证明:(1)∠ACE =∠BCD ;(2)BC 2=BE×CD. 解析: (1)因为,所以∠BCD =∠ABC .又因为EC 与圆相切于点C , 故∠ACE =∠ABC , 所以∠ACE =∠BCD .(2)因为∠ECB =∠CDB ,∠EBC =∠BCD , 所以 △BDC ∽△ECB , 故BC CDBE BC=,即BC 2=BE ×CD .23.(10分)选修4-4:坐标系与参数方程已知直线C 1:1cos sin x t y t αα=+⎧⎨=⎩ (t 为参数),圆C 2:cos sin x y θθ=⎧⎨=⎩(θ为参数). (1)当α=3π时,求C 1与C 2的交点坐标; (2)过坐标原点O 作C 1的垂线,垂足为A ,P 为OA 的中点,当α变化时,求P 点轨迹的参数方程,并指出它是什么曲线.解析: (1)当α=3π时,C 1的普通方程为y(x -1),C 2的普通方程为x 2+y 2=1.联立方程组221),1,y x x y ⎧=⎪⎨+=⎪⎩-解得C 1与C 2的交点为)0,1(,(12,-2). (2)C 1的普通方程为0sin cos sin =--αααy xA 点坐标为)sin cos ,(sin 2ααα- 故当α变化时,P 点轨迹的参数方程为21sin 21sin cos 2x y ααα⎧=⎪⎪⎨⎪=⎪⎩- (α为参数). P 点轨迹的普通方程为(x -14)2+y 2=116. 故P 点轨迹是圆心为(14,0),半径为14的圆. 24.(10分)选修4-5:不等式选讲设函数1|42|)(+-=x x f(1)画出函数)(x f y =的图像;(2)若不等式ax x f ≤)(的解集非空,求a 的取值范围.解析:(1)由于⎩⎨⎧≥-<+-=2322,52)(x x x x x f 则函数)(x f y =的图像如图所示.(2)由函数)(x f y =与函数ax y =的图像可知,当且仅当21≥a 或2-<a 时,函数)(x f y =与函数ax y =的图像有交点.故不等式ax x f ≤)(的解集非空时,a 的取值范围为),21[)2,(+∞⋃--∞。
2010年九年级数学文理联赛模拟试卷10
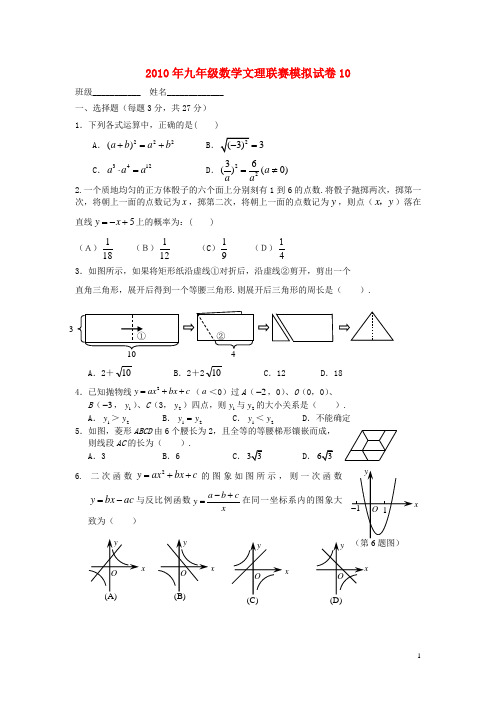
2010年九年级数学文理联赛模拟试卷10班级___________ 姓名_____________ 一、选择题(每题3分,共27分) 1.下列各式运算中,正确的是( )A .222()a b a b +=+ B3=C .3412a a a ⋅=D .2236()(0)a aa=≠ 2.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x ,掷第二次,将朝上一面的点数记为y ,则点(x y ,)落在直线5y x =-+上的概率为:( ) (A)118 (B)112 (C )19 (D)41 3.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个 直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ).A .2+10 B .2+210 C .12 D .18 4.已知抛物线2yax bx c =++(a <0)过A (2-,0)、O (0,0)、 B (3-,1y )、C (3,2y )四点,则1y 与2y 的大小关系是( ). A .1y >2y B .1y 2y = C .1y <2y D .不能确定 5.如图,菱形ABCD 由6个腰长为2,且全等的等腰梯形镶嵌而成, 则线段AC 的长为( ). A .3B .6C .D .6. 二次函数2y ax bx c =++的图象如图所示,则一次函数ac bx y -=与反比例函数xcb a y +-=在同一坐标系内的图象大致为( )②3 4xxx第9题图7、(2010年四川省自贡市).y=x 2+(1-a )x +1是关于x 的二次函数,当x 的取值范围是1≤x ≤3时,y 在x=1时取得最大值,则实数a 的取值范围是( )。
A .a=5B .a ≥5C .a =3D .a ≥38.在某次聚会上,每两人都握了一次手,所有人共握手10次,设有x 人参加这次聚会,则列出方程正确的是(). A .(1)10x x -= B .(1)102x x -= C .(x x +9.如图,在△ABC 中,AB = AC ,AB = 8,BC = 12AB 、AC A .64π- B .1632π-C .16π-D .16π-二、填空题10.如图,在直径AB =12的⊙O 中,弦CD ⊥AB 于M ,且M 是半径OB 的中点,则弦CD 的长是_______(结果保留根号).11.甲、乙、丙、丁四支足球队在世界杯预选赛中的进球数分别为:9、9、11、7,则这组数据的:①众数为_____________;②中位数为____________;③平均数为__________. 12.已知关于x 的一元二次方程x 2+kx +1 =0有两个相等的实数根,则k = .13. 在平面直角坐标系中,点A 1(1,1),A 2(2,4),A 3(3,9),A 4(4,16),…,用你发现的规律 确定点A 9的坐标为 。
2010年九年级数学文理联赛模拟试卷12

2010年九年级数学文理联赛模拟试卷12班级___________ 某某_____________ 一、选择题1、(2007某某某某)已知反比例函数xky =的图象在第二、第四象限内,函数图象上有两点A (72,y 1)、B (5,y 2),则y 1与y 2的大小关系为( )。
A 、y 1>y 2B 、y 1=y 2C 、y 1<y 2D 、无法确定2、(2007某某省)对于反比例函数2y x=,下列说法不正确...的是( ) A .点(21)--,在它的图象上 B .它的图象在第一、三象限 C .当0x >时,y 随x 的增大而增大D .当0x <时,y 随x 的增大而减小3、(2007某某眉山)如图,A 、B 是反比例函数y =x2的图象上的两点.AC 、BD 都垂直于x 轴,垂足分别为C 、D .AB 的延长线交x 轴于点E .若C 、D 的坐标分别为(1,0)、(4,0),则ΔBDE 的面积与ΔACE 的面积的比值是( ). A .21 B .41 C.81 D .161 4、(2007某某某某)如图,是一次函数y=kx+b 与反比例函数y=2x的图像,则关于x 的方程kx+b=2x的解为( ) (A)x l =1,x 2=2 (B)x l =-2,x 2=-1 (C)x l =1,x 2=-2 (D)x l =2,x 2=-15、(2007某某某某)已知正比例函数x k y 11=和反比例函授xk y 22=的图像都经过点(2,1),则1k 、2k 的值分别为:( ) A.1k =21,2k =2 B.1k =2,2k =21 C.1k =2,2k =2 D.1k =21,2k =21 6、(2007某某内江)用配方法解方程2420x x -+=,下列配方正确的是( )A .2(2)2x -=B .2(2)2x +=C .2(2)2x -=-D .2(2)6x -=7、(2007某某)若关于x 的一元二次方程22430x kx k ++-=的两个实数根分别是12,x x ,且满足1212x x x x +=.则k 的值为( )(A )-1或34(B )-1(C )34(D )不存在 8、(2007某某某某)已知关于x 的一元二次方程22x m x -= 有两个不相等的实数根,则m 的取值X 围是( )A . m >-1B . m <-2C .m ≥0 D.m <0 9、(2007某某某某)已知01b 2a =-++,那么2007)b a (+的值为( ).A 、-1B 、1C 、20073D 、20073-10、(2007某某某某)直线l 1:y =k 1x +b 与直线l 2:y =k 2x 在同一平面直角坐标系中的图象如图所示,则关于x 的不等式k 1x +b >k 2x 的解为( )。
2010年九年级数学文理联赛模拟试卷5

D2010年九年级数学文理联赛模拟试卷5班级___________ 姓名_____________ 一、选择题(每题3分,共27分)1、(2010宁波市)4.据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为A .0.82×1011B .8.2×1010C .8.2×109D .82×1082、(2010宁波市)17.若x +y =3,xy =1,则x 2+y 2=_________________.7 3、已知反比例函数xy 1=,下列结论不正确的是( ) A 、图象经过点(1,1) B 、图象在第一、三象限C 、当1>x 时,10<<yD 、当0<x 时,y 随着x 的增大而增大4、骰子是一种特的数字立方体(见图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )A 、B 、C 、D 、5C .1.2元/支,2.6元/本 D .1.2元/支,3.6元/本6.若自然数n 使得三个数的加法运算“n +(n +1)+(n +2)”产生进位现象,则称n 为“连加进位数”.例如:2不是“连加进位数”,因为2+3+4=9不产生进位现象;4是“连加进位数”,因为4+5+6=15产生进位现象;51是“连加进位数”,因为51+52+63=156产生进位现象.如果从0,1,2,…,99这100个自然数中任取一个数,那么取到“连加进位数”的概率是( )A .0.88B .0.89C .0.90D .0.91 7.反比例函数xy 6=图象上有三个点)(11y x ,,)(22y x ,,)(33y x ,,其中3210x x x <<<, 则1y ,2y ,3y 的大小关系是( )A .321y y y <<B .312y y y <<C .213y y y <<D .123y y y <<8.如图,矩形ABCD 中,AB >AD ,AB =a ,AN 平分∠DAB ,DM ⊥AN 于点M ,CN ⊥AN 于点N .则DM +CN 的值为(用含a 的代数式表示)( )A .aB .a 54C .a 22D . a 23∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(第11题) 9.如图,将三角形纸片ABC 沿DE 折叠,使点A 落在BC 边上的点F 处,且DE ∥BC ,下列结论中,一定正确的个数是 ①BDF ∆是等腰三角形 ②BC DE 21=③四边形ADFE 是菱形 ④2BDF FEC A ∠+∠=∠A .1B .2C .3D .4 二、填空题 (本大题有5小题,每小题4分,共20分)10.因式分解:2mx 2-4mx +2m = .11.如图,已知菱形ABCD 的一个内角∠BAD =80º,对角线AC 、BD 相交于点O ,点E 在AB 上且BE =BO ,则∠BAD =_______.12.在直角坐标系中,横坐标和纵坐标都是整数的点称为格点.已知一个圆的圆心在原点,半径等于5,那么这个圆上的格点有 个. 13.学校组织一次有关世博的知识竞赛共有20道题,每一题答对得5分,答错或不答都倒扣1分.小明最终得76分,那么他答对 题. 14.因为cos30º=32,cos210º=-32,所以cos210º=cos(180º+30º)=-cos30º=-32; 因为cos45º=22,cos225º=-22,所以cos225º=cos(180º+45º)=-cos45º=-22. 猜想:一般地,当α为锐角时,有cos(180º+α)=-cos α.由此可知cos240º= . 三、解答题(本大题共4个小题,满分28分)15.(1)解不等式:3x -2>x +4; (2)解方程:1x x ++1x x -=216.果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树产量把杨梅树划分成A ,B ,C ,D ,E 五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下:(第21题)A B C DE F(1)补齐直方图,求a 的值及相应扇形的圆心角度数;(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果; (3)若在甲地块随机抽查1棵杨梅树,求该杨梅树产量等级是B 的概率.17.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+(2-)=1. 若坐标平面上的点作如下平移:沿x 轴方向平移的数量为a (向右为正,向左为负,平移a 个单位),沿y 轴方向平移的数量为b (向上为正,向下为负,平移b 个单位),则把有序数对{a ,b }叫做这一平移的“平移量”;“平移量”{a ,b }与“平移量”{c ,d }的加法运算法则为}{}{}{d b c a d c b a ++=+,,,. 解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.(2)①动点P 从坐标原点O 出发,先按照“平移量”{3,1}平移到A ,再按照“平移量”{1,2}平移到B ;若先把动点P 按照“平移量”{1,2}平移到C ,再按照“平移量” {3,1}平移,最后的位置还是点B 吗? 在图1中画出四边形OABC . ②证明四边形OABC 是平行四边形.(3)如图2,一艘船从码头O 出发,先航行到湖心岛码头P (2,3),再从码头P 航行到码头Q (5,5),最后回到出发点O . 请用“平移量”加法算式表示它的航行过程.(第22图118、(沈阳)如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=3,矩形ABOC绕点O按顺时针方向旋转600后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.(1)判断点E是否在y轴上,并说明理由;(2)求抛物线的函数表达式;(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上,若存在,请求出点P,点Q的坐标;若不存在,请说明理由.2010年九年级文理科联赛模拟试卷5答案 一. 仔细选一选 (每小题3分, 共27分)二 、填空题(每小题4分,共20分)10、2)1(2-x m ; 11、025; 12、 12 ;13、 16 ; 14、21-; 三、简答题 16.(10分)(1)画直方图 …………………………………………………………………2分a =10, 相应扇形的圆心角为:360°×10%=36°. ………………………………2分 (2)5.8020155365575685595=⨯+⨯+⨯+⨯+⨯=甲x ,7520255465975285395=⨯+⨯+⨯+⨯+⨯=乙x , …………………………………2分甲x >乙x ,由样本估计总体的思想,说明通过新技术管理甲地块杨梅产量高于乙地块杨梅产量. ……………………………………………………………………………1分 (若没说明“由样本估计总体”不扣分) (3)P =3.0206=. ………………………………………………………………………3分 17.(12分)(1){3,1}+{1,2}={4,3}. ……………………………………………2分 {1,2}+{3,1}={4,3}. …………………………………………………………………2分(2)①画图 …………………………………………………2分最后的位置仍是B .……………………………………1分 ② 证明:由①知,A (3,1),B(4,3),C (1,2) ∴OC=AB =2221+=5,OA=BC =2213+=10, ∴四边形OABC 是平行四边形.…………………………3分(3){2,3}+{3,2}+{-5,-5}={0, 0}.……………………2分18、解:(1)点E 在y 轴上 ························· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO ,2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ····················· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=∴在Rt DOM △中,12DM =,OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ························· 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ·························· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将()A,122D ⎛⎫ ⎪ ⎪⎝⎭,代入22y ax bx =++中得321312422a a ⎧-+=⎪⎨++=⎪⎩解得899a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴所求抛物线表达式为:2829y x x =-+ ················ 9分 (3)存在符合条件的点P ,点Q . ····················· 10分 理由如下:矩形ABOC 的面积3AB BO ==∴以O B P Q ,,,为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边, 又3OB =OB ∴边上的高为2 ····························· 11分依题意设点P 的坐标为(2)m ,点P在抛物线2829y x x =-+上282299m m ∴--+=解得,10m =,2m = 1(02)P ∴,,22P ⎛⎫⎪ ⎪⎝⎭以O B P Q ,,,为顶点的四边形是平行四边形,PQ OB ∴∥,PQ OB ==,∴当点1P 的坐标为(02),时, 点Q的坐标分别为1(Q,2Q ; 当点2P的坐标为2⎛⎫⎪ ⎪⎝⎭时,点Q的坐标分别为32Q ⎛⎫ ⎪ ⎪⎝⎭,42Q ⎫⎪⎪⎝⎭.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年九年级文理科联赛试卷12(20101025)班级___________ 姓名_____________一、选择题1、(2007山东临沂)已知反比例函数xky =的图象在第二、第四象限内,函数图象上有两点A (72,y 1)、B (5,y 2),则y 1与y 2的大小关系为( )。
A 、y 1>y 2 B 、y 1=y 2 C 、y 1<y 2 D 、无法确定2、(2007江西省)对于反比例函数2y x=,下列说法不正确...的是( ) A .点(21)--,在它的图象上 B .它的图象在第一、三象限 C .当0x >时,y 随x 的增大而增大D .当0x <时,y 随x 的增大而减小3、(2007四川眉山)如图,A 、B 是反比例函数y =x2的图象上的两点.AC 、BD 都垂直于x 轴,垂足分别为C 、D .AB 的延长线交x 轴于点E .若C 、D 的坐标分别为(1,0)、(4,0),则ΔBDE 的面积与ΔACE 的面积的比值是( ). A .21 B .41 C.81 D .161 4、(2007浙江宁波)如图,是一次函数y=kx+b 与反比例函数y=2x 的图像,则关于x 的方程kx+b=2x的解为( )(A)x l =1,x 2=2 (B)x l =-2,x 2=-1 (C)x l =1,x 2=-2 (D)x l =2,x 2=-15、(2007湖南益阳)已知正比例函数x k y 11=和反比例函授xk y 22=的图像都经过点(2,1),则1k 、2k 的值分别为:( ) A. 1k =21,2k =2 B. 1k =2,2k =21 C. 1k =2,2k =2 D. 1k =21,2k =21 6、(2007四川内江)用配方法解方程2420x x -+=,下列配方正确的是( ) A .2(2)2x -=B .2(2)2x +=C .2(2)2x -=-D .2(2)6x -=7、(2007山东)若关于x 的一元二次方程22430x kx k ++-=的两个实数根分别是12,x x ,且满足1212x x x x += .则k 的值为( )(A )-1或34 (B )-1(C )34(D )不存在8、(2007安徽芜湖)已知关于x 的一元二次方程22x m x -= 有两个不相等的实数根,则m 的取值范围是( )A . m >-1B . m <-2C .m ≥0D .m <0 9、(2007山东济宁)已知01b 2a =-++,那么2007)b a (+的值为( ).A 、-1B 、1C 、20073D 、20073-10、(2007山东临沂)直线l 1:y =k 1x +b 与直线l 2:y =k 2x 在同一平面直角坐标系中的图象如图所示,则关于x 的不等式k 1x +b >k 2x 的解为( )。
A 、x >-1B 、x <-1C 、x <-2D 、无法确定 二、填空题1、(2007山东德州)不等式组2752312x x x x -<-⎧⎪⎨++>⎪⎩的整数解是.22、(2007湖北天门)已知关于x 的不等式组⎩⎨⎧--0x 230a x >>的整数解共有6个,则a 的取值范围是 。
3.若关于x 得一元二次方程x 2-3x +m =0有实数根,则m 的取值范围是 。
4.若0)1(32=++-n m ,则m +n 的值为 。
5.用“☆”定义新运算: 对于任意实数a 、b , 都有a ☆b =b 2+1。
例如7☆4=42+1=17,那么5☆3= ;当m 为实数时,m ☆(m ☆2)= 。
6、(2007浙江省萧山中学自主招生考试)已知方程()0332=+-+x a x 在实数范围内恒有解,并且恰有一个解大于1小于2,则a 的取值范围是 . 7、(2007山东烟台)观察下列各式:==请你将发现的规律用含自然数n (n ≥1)的等式表示出来__________________________. 8、(2007四川巴中)先阅读下列材料,然后解答问题:从A B C ,,三张卡片中选两张,有三种不同选法,抽象成数学问题就是从3个元素中选取2个元素组合,记作2332C 321⨯==⨯. 一般地,从m 个元素中选取n 个元素组合,记作:(1)(1)C (1)321nm m m m n n n --+=-⨯⨯⨯例:从7个元素中选5个元素,共有5776543C 2154321⨯⨯⨯⨯==⨯⨯⨯⨯种不同的选法.问题:从某学习小组10人中选取3人参加活动,不同的选法共有 种.y k 2x9.直线y = 2x +6与两坐标轴围成的三角形面积是 10.符号“f ”表示一种运算,它对一些数的运算结果如下: (1)f (1)=0,f (2) = 1,f (3)=2,f (4)= 3,…… (2)1111()()()()23452,3,4,5f f f f ====……利用以上规律计算:1(2010)()2010ff -=三、简答题1、已知抛物线y =4x 2-11x -3. (Ⅰ)求它的对称轴;(Ⅱ)求它与x 轴、y 轴的交点坐标. 2、(2007重庆)我市某镇组织20辆汽车装运完A 、B 、C 三种脐橙共100吨到外地销售。
按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满。
根据下表提供的信息,解答以下问题:之间的函数关系式;(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值。
3、(2007云南双柏)阅读下列材料,并解决后面的问题.材料:一般地,n 个相同的因数a 相乘:n n a a a a 记为个⋅.如23=8,此时,3叫做以2为底8的对数,记为()38log 8log 22=即.一般地,若()0,10>≠>=b a a b a n 且,则n 叫做以a 为底b 的对数,记为()813.log log 4==如即n b b a a ,则4叫做以3为底81的对数,记为)481log (81log 33=即.问题:(1)计算以下各对数的值:(3分) ===64log 16log 4log 222 .(2)观察(1)中三数4、16、64之间满足怎样的关系式?64log 16log 4log 222、、 之间又满足怎样的关系式?(2分)(3)由(2)的结果,你能归纳出一个一般性的结论吗?(2分)()0,0,10l o g l o g >>≠>=+N M a a N M a a 且(4)根据幂的运算法则:m n mna aa +=⋅以及对数的含义证明上述结论.(3分)4、已知抛物线y =ax 2+bx +c 与y 轴交于点A (0,3),与x 轴分别交于B (1,0)、C (5,0)两点。
(1)求此抛物线的解析式;(2)若点D 为线段OA 的一个三等分点,求直线DC 的解析式;(3)若一个动点P 自OA 的中点M 出发,先到达x 轴上的某点(设为点E ),再到达抛物线的对称轴上某点(设为点F ),最后运动到点A 。
求使点P 运动的总路径最短的点E 、点F 的坐标,并求出这个最短总路径的长。
2010年九年级文理科联赛试卷12答案(20100914)一、选择题(每小题3分,共30分)二 、填空题(每小题3分,共30分)11、 ; 12、 ; 13、 ; ; 14、 ; 15 ;16、 ; 17、 ;18、 ;19、 ; 20、 。
2、解:(1)根据题意,装运A 种脐橙的车辆数为x ,装运B 种脐橙的车辆数为y ,那么装运C 种脐橙的车辆数为()y x --20,则有:()10020456=--++y x y x 整理得:202+-=x y(2)由(1)知,装运A 、B 、C 三种脐橙的车辆数分别为x 、202+-x 、x ,由题意得:⎩⎨⎧≥+-≥42024x x ,解得:4≤x ≤8,因为x 为整数,所以x 的值为4、5、6、7、4,所以安排方案共有5种。
方案一:装运A 种脐橙4车,B 种脐橙12车,C 种脐橙4车; 方案二:装运A 种脐橙5车,B 种脐橙10车,C 种脐橙5车; 方案三:装运A 种脐橙6车,B 种脐橙8车,C 种脐橙6车; 方案四:装运A 种脐橙7车,B 种脐橙6车,C 种脐橙7车; 方案五:装运A 种脐橙8车,B 种脐橙4车,C 种脐橙8车; (3)设利润为W (百元)则:()160048104162025126+-=⨯+⨯+-+⨯=x x x x W∵048<-=k ∴W 的值随x 的增大而减小 要使利润W 最大,则4=x ,故选方案一1600448+⨯-=最大W =1408(百元)=14.08(万元)答:当装运A 种脐橙4车,B 种脐橙12车,C 种脐橙4车时,获利最大,最大利润为14.08万元。
5、证明:解:(1)24log 2= , 416log 2= ,664log 2=(2)4×16=64 ,4log 2 + 16log 2 = 64log 2 (3)M a log + N a log = )(log MN a (4)证明:设M a log =b 1 , N a log =b 2 则M ab =1,N a b =2∴2121b b b b a a a MN+=⋅=∴b 1+b 2=)(log MN a 即M a log + N a log = )(log MN a。
