用Matlab画出信号的时域波形及频谱,观察它们的关系。
matlab软件仿真实验(信号与系统)(1)
matlab软件仿真实验(信号与系统)(1)《信号与系统实验报告》学院:信息科学与⼯程学院专业:物联⽹⼯程姓名:学号:⽬录实验⼀、MATLAB 基本应⽤实验⼆信号的时域表⽰实验三、连续信号卷积实验四、典型周期信号的频谱表⽰实验五、傅⽴叶变换性质研究实验六、抽样定理与信号恢复实验⼀MATLAB 基本应⽤⼀、实验⽬的:学习MATLAB的基本⽤法,了解 MATLAB 的⽬录结构和基本功能以及MATLAB在信号与系统中的应⽤。
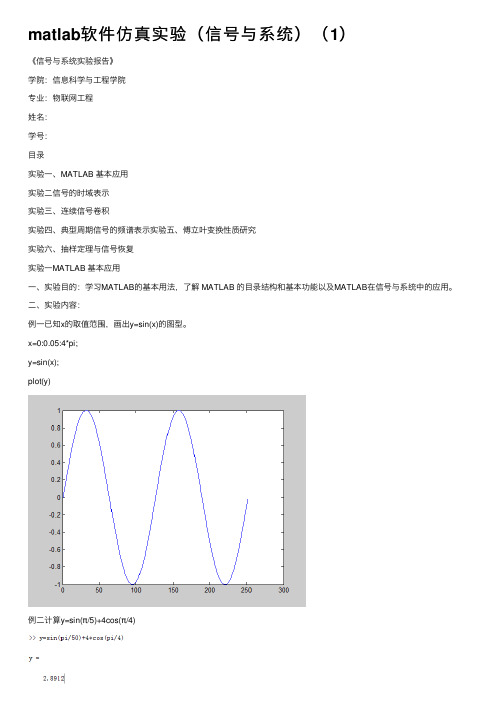
⼆、实验内容:例⼀已知x的取值范围,画出y=sin(x)的图型。
x=0:0.05:4*pi;y=sin(x);plot(y)例⼆计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,⽤subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表⽰1、指数信号:指数信号Ae at在MATLAB中可⽤exp函数表⽰,其调⽤形式为:y=A*exp(a*t) (例取 A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;2、正弦信号:正弦信号Acos(w0t+?)和Asin(w0t+?)分别由函数cos和sin表⽰,其调⽤形式为:A*cos(w0t+phi) ;A*sin(w0t+phi) (例取A=1,w0=2π,?=π/6) 参考程序:A=1;w0=2*pi; phi=pi/6; t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on ;3、抽样函数:抽样函数Sa(t)在MATLAB中⽤sinc函数表⽰,其定义为:sinc(t)=sin(πt)/( πt)其调⽤形式为:y=sinc(t)参考程序:t=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft);grid on;4、矩形脉冲信号:在MATLAB中⽤rectpuls函数来表⽰,其调⽤形式为:y=rectpuls(t,width),⽤以产⽣⼀个幅值为1,宽度为width,相对于t=0点左右对称的矩形波信号,该函数的横坐标范围由向量t决定,是以t=0为中⼼向左右各展开width/2的范围,width的默认值为1。
熟悉MATLAB软件的相关函数的使用方法、各种信号的时域波形

实验目的:熟悉MA TLAB 软件的相关函数的使用方法、各种信号的时域波形。
实验内容:1、用MA TLAB 软件绘制各类典型信号的时域波形并且给出程序源代码。
(1)指数信号、 指数序列; (2)单位阶跃函数、 单位阶跃序列; (3)单位脉冲信号; 单位抽样序列;(4)矩形信号,矩形序列信号, 矩形宽度自定; (5)正弦信号、 正弦序列,其中振幅和频率自选; 2、 假设存在一个单边离散指数序列][n s , 参数自选; ][n d 为随机噪声,方差和均值自选; 绘制][n s ,][n d 和][][][n d n s n x +=的图形3、绘制你所采集的电信号的时域波形(部分即可), 进行必要的说明和分析4、选作提高: 编写一个程序, 运行后可以在键盘上依次任意输入两个序列,计算两个序列的线性卷积,并输出计算结果。
(相关函数:input , conv )实现方案:(1)指数信号、指数序列1、指数信号分为实指数信号和复指数信号,其中实指数信号的基本形式为 atKe =f(t)。
其中,K 、a 为实数。
当a>0时,实指数信号随时间按指数式增长;当a<0时,实指数信号随时间按指数式衰减;当a=0时,实指数信号不随时间变化,转化为直流信号。
MATLAB 中用exp 函数来表示实指数信号,语句表示为 y=K*exp(a*t).下面用MA TLAB 命令产生单边递增指数信号)(32t u e t ,当0<=t<=5的波形图。
MATLAB 源程序为:K=3;a=2; t=0:0.01:5; y=K*exp(a*t); plot(t,y),grid on程序运行后,产生如下图所示的波形。
2、复指数信号复指数信号的基本形式为)sin()cos()()(t jKe t Ke Ke Ke t f t t j st ωωσσωσ+===+其中, ωσj s += 是复变量;σ、ω为实数。
当 ω=0 时,st Ke 为一个实指数信号;当0>σ 0≠ω时,stKe 的实部和虚部分别是按指数规律衰减的正弦振荡;当0<σ0≠ω时,stKe 的实部和虚部均为等幅的正弦振荡。
利用Matlab绘制正弦信号的频谱图并做相关分析

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求:1、信号可变(信号的赋值、相位、频率可变);2、采样频率fs可变;3、加各种不同的窗函数并分析其影响;4、频谱校正;5、频谱细化。
二、采用matlab编写如下程序:clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1:fs=100,N=1024');grid on;%两种信号叠加,x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2:fs=100,N=1024,两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3:fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4:fs=100,N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5:fs=400,N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6:fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7:fs=100,N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8:fs=100,N=1024,加汉宁窗函数');grid on;三、运行结果如下:四、分析与结论:1)从所做图像可以看出,信号的幅值均小于真实值,说明在截断信号时存在泄露。
用matlab画出声音的频谱

一.实验内容
任选一个声音文件,画出其波形图和频谱图。
二.算法分析和描述
(1)选择一个wav文件作为分析的对象
(2)读取音频信号的数据,并画出其时域波形和频谱图。
所使用到的几个函数如下:
1.[x,fs,bits]=wavread('filename')这是一个matlab中读取wav文件的
数据的函数。
2.[d]=fft(w,l)这是matlab中fft函数的一种输入输出形式。
3.sound(w,fs,bits)函数它将数列的数据通过声卡转化为声音。
三.实现方法(含实现思路、程序流程图和源程序列表等)clear
[y,fs,bits]=wavread(‘声音');
sound(y,fs,bits);
Y=fft(y,4096);
subplot(211);
plot(y);
title('声音信号的波形');
subplot(212)
plot(abs(Y));
title('声音信号的频谱');
四.实验结果分析(含执行结果验证、输出显示信息和图形等)通过编程实现得到下列图形:。
信号波形的产生与频谱的MATLAB程序(DOC)

目录目录………………………………………………………………………………………………正文…………………………………………………………………………………………………1 基本波形………………………………………………………………………………1.1正弦波…………………………………………………………………………1.2三角波和锯齿波………………………………………………………………1.3方波和不对称方波……………………………………………………1.4伪码……………………………………………………………………………………2调幅………………………………………………………………………………2.1常规双边带调幅(AM)……………………………………………………………2.2抑制载波双边带调幅(DSB)……………………………………………………………2.3 单边带调幅(SSB)…………………………………………………………………3.4振幅键控(ASK)……………………………………………………………………3调频………………………………………………………………………………3.1单音频调频……………………………………………………………………………3.2锯齿波调频……………………………………………………………………………3.3 三角波调频…………………………………………………………………………3.4 移频键控(FSK)………………………………………………………………………4 调相……………………………………………………………………………………………4.1 方波调相…………………………………………………………………………………4.2 伪码调相…………………………………………………………………………………一、 基本波形(1)正弦波)t 2sin()(θ+***=m f pi t sm f 为正弦波频率,θ为初始相位理论频谱:)]()([)(m m j S ωωδωωδπω--+=m ω为正弦波角频率,且m m f *2πω= 时域波形:图1-1-1 正弦波的时域波形(横坐标为时间t ,纵坐标为幅度) 图1-1-1为正弦波的时域波形。
基于MATLAB的信号波形与频谱分析

基于MATLAB的信号波形与频谱分析摘要本文利用MATLAB软件进行信号频谱分析的设计,并通过GUI界面(图形用户界面)实现信号频谱分析的动态设计。
用户可与计算机交互式地进行对象参数的设置、控制算法的选取、以及对离散信号与连续信号的动态频谱分析。
并利用MATLAB内嵌的Simulink模块,实现系统的信号频谱分析,满足不同用户的不同要求。
MATLAB的GUIDE是专门用于图形用户界面(GUI)程序设计的快速开发环境,本文从介绍GUIDE入手结合具体的软件图形界面实例,给出了利用GUIDE制作图形用户界面的基本方法。
通过本文的研究得出利用GUIDE设计的仿真界面不仅可以对离散信号与连续信号的动态频谱进行相关分析,而且还可以对此问题作进一步的预测和分析。
基于GUIDE技术制作的图形用户界面,具有友好性,开放性,方便科研人员不断地研究和扩充。
关键词频谱分析;GUI;SIMULINK;MATLABAbstractUsing MATLAB software for signal spectrum analysis of the design, and through the GUI interface (graphical user interface) signal spectrum analysis of the dynamic design. Users can interactively with the computer targeting parameters for the establishment, control algorithm selection, and the discrete signals and continuous signal analysis of the dynamic spectrum. MATLAB and Simulink embedded module, the signal system to achieve spectral analysis, meet the needs of different users with different needs.MATLAB GUIDE is devoted to the graphical user interface (GUI) design procedures for the rapid development environment, This paper introduced GUIDE start from the context of the specific examples of graphical interface software, GUIDE is produced using a graphical user interface methods. Through this paper, the study of the use of simulation GUIDE interface design can not only right for discrete signal and the signal dynamic spectrum analysis, but also the issue for further analysis and forecasts. GUIDE technology based on the production of graphical user interface is friendly and open, facilitate researchers continue to study and expanded.Keywords Spectrum Analysis ;GUI;SIMULINK;MATLAB目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 MATLAB应用软件简介 (1)1.2课题研究的内容 (2)1.2.1信号的频谱分析 (2)1.2.2信号频谱分析的原理 (3)1.2.3频谱分析与显示原理 (3)1.2.4对三阶交调进行模拟分析 (3)1.2.5伪彩色编码的动态频谱图显示 (4)1.2.6宽带频谱图与窄带频谱图 (5)1.3 GUI界面设计实现 (5)1.4 SIMULINK (6)1.4.1 SIMULINK模型与文件 (7)1.4.2 SIMULINK仿真原理 (7)第2章MATLAB工具箱的概述及GUI界面的简介 (8)2.1引言 (8)2.2句柄图形及图形用户界面 (8)2.3 GUIDE (8)2.4编制回调程序 (10)2.5主界面 (10)2.6子界面 (11)2.7基于MATLAB信号处理工具箱的数字滤波器设计与仿真 (11)2.8带通滤波器设计实例 (12)第3章GUI界面下噪声信号的频谱分析与实现 (14)3.1概述 (14)3.2 MATLAB信号处理工具箱介绍及功能 (14)3.2.1MATLAB工具箱介绍 (14)3.2.2工具箱功能 (15)3.3通风机噪声信号的采集方法 (17)3.4噪声信号的频谱分析 (18)3.5 GUI界面下噪声频谱分析的实现 (19)结论 (22)致谢 (23)参考文献 (24)附录A (25)附录B (27)第1章绪论1.1 MATLAB应用软件简介MATLAB是一种功能强大的科学计算和工程仿真软件,它的交互式集成界面能够帮助用户快速地完成数值分析、矩阵运算、数字信号处理、仿真建模、系统控制和优化等功能。
实验三 信号的时域运算Matlab实现

向量,f 和 k 为返回的和序列及其的时间序列向量
k=min(min(k1),min(k2)):max(max(k1),max(k2)); %构造和序列的长度
s1=zeros(1,length(k));s2=s1;
%初始化新向量
s1(find((k>=min(k1))&(k<=max(k1))==1))=f1;
2) f4 (t) = −[ f1(−t) + f1(t)]
3) f5 (t) = f2 (t) × f3 (t)
4) f6 (t) = f1 (t) × f2 (t)
4. 已知离散序列 f (k ) = {3,0,1,2, 3,3,3,3,0,3},用 MATLAB 绘出下列 ↑ 序列的波形。
1) f (k − 2)ε (k)
2) f (−k)
3) f (−k + 2)
4) f (k − 2)ε (k − 2)
【四】 思考题
实验三 信号的时域运算、时域变换及 MATLAB 实现
在对信号进行平移、反折和尺度变换时,运算顺序对结果是否有影响?在运算中应该注 意什么?
【五】 实验报告要求
1.简述实验目的及实验原理; 2.实验内容及结果分析:
~ n1 + m1 +( L1 + L2 )- 2 非零。因此,对于 f1 (k ) 和均为有限期间非零的情况,我们只
需要计算序列 f (k ) 在区间( n1 + m1 )~ n1 + m1 +( L1 + L2 )- 2 的序列值,便可以表征
根据前面的介绍,我们可用符号运算来实现上述过程,MATLAB 命令如下: syms t; f=sym('(t/2+1)*(heaviside(t+2)-heaviside(t-2))'); subplot(2,3,1),ezplot(f,[-3,3]); y1=subs(f,t,t+2); subplot(2,3,2),ezplot(y1,[-5,1]); y2=subs(f,t,t-2); subplot(2,3,3),ezplot(y2,[-1,5]); y3=subs(f,t,-t); subplot(2,3,4),ezplot(y3,[-3,3]); y4=subs(f,t,2*t); subplot(2,3,5),ezplot(y4,[-2,2]); y5=-f; subplot(2,3,6),ezplot(y5,[-3,3]); 运行结果如图 3.1 所示。
用MATLAB进行FFT频谱分析

用MATLAB进行FFT频谱分析假设一信号:()()292.7/2cos1.0996.2/2sin1.06.0+++=ttRππ画出其频谱图。
分析:首先,连续周期信号截断对频谱的影响。
DFT变换频谱泄漏的根本原因是信号的截断。
即时域加窗,对应为频域卷积,因此,窗函数的主瓣宽度等就会影响到频谱。
实验表明,连续周期信号截断时持续时间与信号周期呈整数倍关系时,利用DFT变换可以得到精确的模拟信号频谱。
举一个简单的例子:()ππ2.0100cos+=tY其周期为。
截断时不同的持续时间影响如图一.1:(对应程序)140.0160.0180.02截断时,时间间期为周期整数倍,频谱图0.0250.0320406080100截断时,时间间期不为周期整数倍,频谱图图错误!文档中没有指定样式的文字。
.1其次,采样频率的确定。
根据Shannon 采样定理,采样带限信号采样频率为截止频率的两倍以上,给定信号的采样频率应>1/,取16。
再次,DFT 算法包括时域采样和频域采样两步,频域采样长度M 和时域采样长度N 的关系要符合M ≧N 时,从频谱X(k)才可完全重建原信号。
实验中信号R 经采样后的离散信号不是周期信号,但是它又是一个无限长的信号,因此处理时时域窗函数尽量取得宽一些已接近实际信号。
实验结果如图一.2:其中,0点位置的冲激项为直流分量造成(对应程序为)0204060801001201401601802000.40.50.60.70.800.050.10.150.20.250.30.350.40.450.550100150图 错误!文档中没有指定样式的文字。
.2♣ARMA (Auto Recursive Moving Average )模型:将平稳随机信号x(n)看作是零均值,方差为σu 2的白噪声u(n)经过线性非移变系统H(z)后的输出,模型的传递函数为()()()∑∑=-=-+==Pk kk Qr r rza zb z A z B z H 111用差分方程表示为()()()∑∑==-+--=Qr r P k k r n u b k n x a n x 01AR (Auto Recursive )自回归模型,即ARMA 模型中系数b 只有在r=0的情况下为1,其余都是零,获得一个全极点模型:()()()∑=-+==Pk kk za z A z B z H 111差分方程表示为:()()()n u k n x a n x Pk k +--=∑=1AR 模型的功率谱估计为:()()()Ω-ΩΩ=j j uj x e A e A eS 12σ程序:%%------------------------------------------------------------------------%%功能:利用MATLAB 的FFT 函数做双正弦信号频谱分析 %%------------------------------------------------------------------------ fs=16; t=0:1/fs:200;x6=+sin(2*pi*t/*+cos(2*pi*t/+2)*;subplot(2,1,1);plot(t,x6);N=length(t);subplot(212);plot((-N/2:N/2-1)*fs/N,abs(fftshift(fft(x6,N)))) %绘制信号的频谱,横轴对应实际频率axis([0 0 160]);例子:%%------------------------------------------------------------------------%%功能:连续周期信号截断对频谱的影响%%------------------------------------------------------------------------fs=8000;n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,1);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,2);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期为周期整数倍,频谱图');n1=;n=0:1/fs:n1;n=n(1,1:end-1);N=length(n);y=cos(100*pi*n+*pi);subplot(2,2,3);plot(n,y);title('函数y=cos(100{\pi}t+{\pi})');subplot(2,2,4);stem((-N/2:N/2-1)*fs/N,abs(fftshift(fft(y,N))));axis([0 1000 0 100]);grid on;title('截断时,时间间期不为周期整数倍,频谱图');。
基于MATLAB的信号波形与频谱分析

中文摘要利用DFT分析信号频谱的基本流程,阐述了频谱分析过程中误差形成的原因及减小分析误差的主要措施。
实例列举了基于MATLAB GUI编制的信号分析系统,集成了常用的信号分析方法,系统界面友好,使用方便,与传统处理方法相比效率更高。
关键词:MATLAB GUI;信号分析;频谱分析Analysis of Signal Waveform and FrequencySpectrum Based on MATLABAbstractThe use of DFT analysis of signal spectrum basic process , elaborated spectral analysis in the process of formation and reduce error analysis error measures. The examples cited MATLAB GUI system based on the signal analysis system, integrated with the commonly used method of signal analysis, the system friendly interface, convenient use, compared with the traditional processing approaches more efficient.Key words: MATLAB GUI; signal analysis; spectrum analysisI目录中文摘要 (I)Abstract (I)引言 (3)1.信号的概述 (3)1.3 信号频谱的误差分析 (5)2.信号的频谱分析 (6)2.1 软件介绍 (7)2.1.1 MATLAB软件介绍 (7)2.1.2 GUI软件介绍 (7)2.2 信号的频谱分析 (7)2.2.1 信号谱分析的原理 (7)2.2.2 信号谱编程思路 (8)3.信号系统频谱分析实例 (9)3.1系统设计 (9)4.结论 (17)参考文献 (18)致谢 (19)II引言信号的频谱分析是利用傅里叶分析的方法,求出与时域描述相对应的频域描述,从中找出信号时域波形相对应的频率函数,从中找出描述该信号频谱结构的变化规律,以达到特征提取的目的。
频谱的分析实验报告

一、实验目的1. 理解频谱分析的基本原理和方法;2. 掌握FFT(快速傅里叶变换)在频谱分析中的应用;3. 分析不同信号在时域和频域的特性;4. 学习利用MATLAB进行频谱分析。
二、实验原理频谱分析是信号处理中的重要手段,通过对信号的频谱进行分析,可以了解信号的频率成分、能量分布等信息。
傅里叶变换是频谱分析的核心,它可以将信号从时域转换为频域,揭示信号的频率特性。
FFT是一种高效的傅里叶变换算法,它可以将N点的DFT计算复杂度从O(N^2)降低到O(NlogN),在信号处理领域得到广泛应用。
三、实验内容1. 实验一:时域信号与频域信号的关系(1)利用MATLAB生成一个简单的正弦波信号,观察其时域波形和频谱;(2)改变正弦波的频率和幅度,观察时域波形和频谱的变化;(3)分析正弦波信号的频率成分和能量分布。
2. 实验二:利用FFT进行频谱分析(1)利用MATLAB生成一个含有多个频率成分的复合信号;(2)对复合信号进行FFT变换,观察其频谱;(3)分析复合信号的频率成分和能量分布;(4)对比不同FFT点数对频谱分析结果的影响。
3. 实验三:窗函数对频谱分析的影响(1)利用MATLAB生成一个矩形窗和汉宁窗,观察它们的时域波形;(2)对信号进行矩形窗和汉宁窗处理,分别进行FFT变换;(3)比较两种窗函数对频谱分析结果的影响。
四、实验结果与分析1. 实验一结果与分析实验结果显示,正弦波信号的时域波形为周期性的正弦波形,其频谱为离散的频率成分,频率为正弦波的频率。
改变正弦波的频率和幅度,时域波形和频谱相应地发生变化。
2. 实验二结果与分析实验结果显示,复合信号的频谱为多个频率成分的叠加,通过FFT变换可以清晰地观察到各个频率成分。
对比不同FFT点数对频谱分析结果的影响,FFT点数越多,频谱分辨率越高,但计算复杂度也随之增加。
3. 实验三结果与分析实验结果显示,矩形窗和汉宁窗的时域波形具有不同的形状,对信号进行窗函数处理可以降低边缘效应,提高频谱分析精度。
基于MATLAB仿真分析频谱信号的误差

时域信号经过FFT 变换后可以得到信号在频域的频率分布和相应的幅值信息,在频域中只需要关注特定频率的信号,可以有效排除其他频率信号的干扰,从而利用频谱信息恢复出该频率的时域信号。
因此,频谱的信息准确与否会影响到恢复的时域信号。
本文利用MATLAB 软件,从时域正弦信号的初相位和采样频率出发,对FFT 变换后的频域信息误差进行了仿真分析。
1时域与频域信息之间的相互转换对于时域信号,如正弦信号y=Asin (2πft+ψ)+B ,其直流分量为B ,交流分量的幅值为A 、频率为f ,初始相位为ψ。
当模拟信号转化为数字信号时需要进行采样,采样频率f s 需满足采样定理,即f s >2f 。
对于采集的N 点序列,离散傅里叶变换(DFT )公式如下[1]:X (k )=N-1n =0∑x n e-2πNkn (k=0,1,…,N-1)(1)可由欧拉公式变形为:X (k )=N-1n =0∑x (n )(cos (2πkn N )-isin (2πkn N ))(2)X (k )=N-1n =0∑x (n )cos (2πkn N )-i N-1n =0∑x (n )sin (2πkn N )(k=0,1,…,N-1)(3)通过以上公式计算可以得到N 点序列的DFT 结果,从而得到信号在频域的信息。
本文在MATLAB 软件中使用的是FFT 算法。
FFT 是一种实现DFT 的快速算法,其采用分而治之的思想,利用复数形式的离散傅里叶变换来计算实数形式的离散傅里叶变换,使DFT 的计算量降低了一个或几个数量级,使得DFT 得到广泛的应用[2]。
从频域到时域的转换可以通过对频谱信息进行相应的计算得到。
以下以正弦信号y=2sin (2π×2000t+14π)+3为例,图1a为该信号的时域波形,图1b 为该信号的频谱。
该信号在时域的信息有:直流分量B=3,交流分量幅值A=2,频率f=2000Hz ,初相位ψ=14π。
用Matlab画出信号的时域波形及频谱,观察它们的关系。

A
7
实验结果
A
8
f2(t)u(t2)u(t2)
f(t)F(j) F2(j)F2j4sa (2)
四 实验内容 1. 根据对称性得出: → MATLAB编程 R=0.05; t=-3:R:3; f2=(t>=-2)-(t>=2); subplot(1,2,1),plot(t,f2) grid on;
10
实验结果
A
11
f 3 (t) t[u (t 1) u (t 1)] f '3 (t ) f 4 (t)
MATLAB编程 R=0.05; h=0.001; t=-1.2:R:1.2; y=t.*(t>=-1)-t.*(t>=1); f4=diff(y)/h; subplot(1,2,1),plot(t,f1) Xlabel('t'),ylabel('f4') axis([-2,2,-0.5,1.5]); N=1000; k=-N:N; W1=40; W=k*W1/N; F=y*exp(-j*t'*W)*R; F=real(F); subplot(1,2,2),plot(W,F) Xlabel('W'),ylabel('F(jw)')
1 正确运用傅立叶变换
2用Matlab编程观察周期信 号的合成过程。进一步理 解周期信号的傅里叶级数 分解特性。
3.学习用Matlab绘制周期 信号频谱的方法。
A
3
三 实验原理 1. 周期矩形脉冲信号 的傅里叶展开系 数为sin 2x/2x的函数称为“采样函数”, 这个函数数据有以下特性 (1)Sa(2t)为偶函数 (2)当t→0时,Sa(t)=1是以1/t为振幅 的“正弦函数”;因而对于x的正负两半 轴都为衰减的正弦震荡; (3)在x=nπ处(n=1,2,3,…),sin x=0即Sa(t)=0;而在x=0处Sa(t)在 t→0时等于1。
利用Matlab绘制正弦信号的频谱图并做相关分析

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求:1、信号可变(信号的赋值、相位、频率可变);2、采样频率fs可变;3、加各种不同的窗函数并分析其影响;4、频谱校正;5、频谱细化。
二、采用matlab编写如下程序:clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1:fs=100,N=1024');grid on;%两种信号叠加,x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2:fs=100,N=1024,两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3:fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4:fs=100,N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5:fs=400,N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6:fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7:fs=100,N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8:fs=100,N=1024,加汉宁窗函数');grid on;三、运行结果如下:四、分析与结论:1)从所做图像可以看出,信号的幅值均小于真实值,说明在截断信号时存在泄露。
频谱matlab程序

频谱matlab程序
频谱matlab程序是一种用于对信号进行频域分析的工具。
该程序可以将信号转换成频谱图,以便进一步分析信号的特性。
频谱matlab程序通常包含以下步骤:
1. 载入信号数据,例如音频文件。
2. 对信号进行预处理,例如去噪、滤波等。
3. 对信号进行时域分析,例如绘制时域波形和频率响应图。
4. 进行傅里叶变换,将信号转换成频谱图。
5. 绘制频谱图,例如绘制功率谱密度图和频谱时序图。
6. 对频谱进行分析,例如计算主频、谐波、失真等特性参数。
频谱matlab程序是一种强大的工具,可以帮助工程师和科学家分析各种类型的信号,例如音频、视频、传感器数据等。
该程序的设计和实现需要深入了解信号处理和傅里叶分析的原理和方法。
- 1 -。
ssch4_6利用MATLAB进行信号频域分析

X 工程 (
j)
1 2p
p
- 100p
100p
Sa
2
2
Sa
-
100p
2
Sa
100p
2
X 工程 (j)
2
-100p
0
100p
利用MATLAB分析信号频谱
例:利用MATLAB分析余弦信号x(t) cos(100pt)的频谱。
%compute the spectrum of x(t) =cos(100*pi*t)
利用MATLAB分析信号频谱
%compute the spectrum of speech signal
[x,Fs,Nbits]=wavread('为什么要进行频域分析_男声.wav');
x=x(:,1);
N =length(x); t=(0:N-1)/Fs;
女生声音信号频谱
figure(1);
plot(t,x);
信号处理课程组 电子信息工程学院
2015.12
信号的频域分析
➢ 连续周期信号的频域分析 ➢ 连续非周期信号频域分析 ➢ 离散周期信号的频域分析 ➢ 离散非周期信号频域分析 ➢ 连续时间信号的时域抽样 ➢ 利用MATLAB分析信号频谱
利用MATLAB分析信号频谱
※ 男女语音信号的频谱分析 ※ 频谱近似值与理论值比较 ※ 频谱工程值与理论值比较 ※ 利用有限项分析Gibbs现象
N=32; L=512; f0=50; fs=300;
T=1/fs;
t=(0:N-1)*T;
x=cos(2*pi*f0*t);
ws=2*pi*fs; X=fftshift(fft(x,L));
matlab课程设计参考题目

课题一:连续时间信号和系统时域分析及MATLAB实现课题要求:深入研究连续时间信号和系统时域分析的理论知识。
利用MATLAB强大的图形处理功能、符号运算功能以及数值计算功能,实现连续时间信号和系统时域分析的仿真波形。
课题内容:一、用MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
1、单位阶跃信号,2、单位冲激信号,3、正弦信号,4、实指数信号,5、虚指数信号,6、复指数信号。
二、用MATLAB实现信号的时域运算1、相加,2、相乘,3、数乘,4、微分,5、积分三、用MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
给出几个典型例子,要求可以改变激励的参数,分析波形的变化。
课题二:离散时间信号和系统时域分析及MATLAB实现。
课题要求:深入研究离散时间信号和系统时域分析的理论知识。
利用MATLAB强大的图形处理功能、符号运算功能以及数值计算功能,实现离散时间信号和系统时域分析的仿真波形。
课题内容:一、用MATLAB绘制常用信号的时域波形(通过改变参数分析其时域特性)1、单位序列,2、单位阶跃序列,3、正弦序列,4、离散时间实指数序列,5、离散时间虚指数序列,6、离散时间复指数序列。
二、用MATLAB实现信号的时域运算1、相加,2、相乘,3、数乘。
三、用MATLAB实现信号的时域变换(参数变化,分析波形的变化)1、反转,2、时移(超时,延时),3、展缩,4、倒相。
熟悉MATLAB软件的相关函数的使用方法各种信号的时域波形

实验目的:熟悉MATLAB 软件的相关函数的使用方法、各种信号的时域波形。
实验容:1、用MATLAB 软件绘制各类典型信号的时域波形并且给出程序源代码。
(1)指数信号、 指数序列;(2)单位阶跃函数、 单位阶跃序列;(3)单位脉冲信号; 单位抽样序列;(4)矩形信号,矩形序列信号, 矩形宽度自定;(5)正弦信号、 正弦序列,其中振幅和频率自选;2、 假设存在一个单边离散指数序列][n s , 参数自选;][n d 为随机噪声,方差和均值自选; 绘制][n s ,][n d 和 ][][][n d n s n x +=的图形3、绘制你所采集的电信号的时域波形(部分即可), 进行必要的说明和分析4、选作提高: 编写一个程序, 运行后可以在键盘上依次任意输入两个序列,计算两个序列的线性卷积,并输出计算结果。
(相关函数:input , conv )实现方案:(1)指数信号、指数序列1、指数信号分为实指数信号和复指数信号,其中实指数信号的基本形式为 。
其中,K 、a 为实数。
当a>0时,实指数信号随时间按指数式增长;当a<0时,实指数信号随时间按指数式衰减;当a=0时,实指数信号不随时间变化,转化为直流信号。
MATLAB 中用exp函数来表示实指数信号,语句表示为 y=K*exp(a*t).下面用MATLAB 命令产生单边递增指数信号,当0<=t<=5的波形图。
MATLAB 源程序为:K=3;a=2;t=0:0.01:5;y=K*exp(a*t);plot(t,y),grid on程序运行后,产生如下图所示的波形。
2、复指数信号复指数信号的基本形式为)sin()cos()()(t jKe t Ke Ke Ke t f t t j st ωωσσωσ+===+其中,ωσj s += 是复变量;、为实数。
当 =0 时,为一个实指数信号;当 时, 的实部和虚部分别是按指数规律衰减的正弦振荡;当 时,的实部和虚部均为等幅的正弦振荡。
利用Matlab绘制正弦信号的频谱图并做相关分析

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求:1、信号可变(信号的赋值、相位、频率可变);2、采样频率fs可变;3、加各种不同的窗函数并分析其影响;4、频谱校正;5、频谱细化。
二、采用matlab编写如下程序:clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1:fs=100,N=1024');grid on;%两种信号叠加,x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2:fs=100,N=1024,两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3:fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4:fs=100,N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5:fs=400,N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6:fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7:fs=100,N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8:fs=100,N=1024,加汉宁窗函数');grid on;三、运行结果如下:四、分析与结论:1)从所做图像可以看出,信号的幅值均小于真实值,说明在截断信号时存在泄露。
数字信号处理上机报告-一

数字信号处理上机报告-一数字信号处理第一次上机实验报告实验一:设给定模拟信号()1000t a x t e -=,的单位是ms 。
(1) 利用MATLAB 绘制出其时域波形和频谱图(傅里叶变换),估计其等效带宽(忽略谱分量降低到峰值的3%以下的频谱)。
(2) 用两个不同的采样频率对给定的进行采样。
○1。
○2。
比较两种采样率下的信号频谱,并解释。
实验一MATLAB 程序:(1)N=10; Fs=5; Ts=1/Fs;n=[-N:Ts:N];xn=exp(-abs(n)); w=-4*pi:0.01:4*pi; X=xn*exp(-j*(n'*w)); subplot(211) plot(n,xn);title('x_a(t)时域波形');xlabel('t/ms');ylabel('x_a(t)');t ()a x t ()()15000s a f x t x n =以样本秒采样得到。
()()11j x n X e ω画出及其频谱()()11000s a f x t x n =以样本秒采样得到。
()()11j x n X e ω画出及其频谱axis([-10, 10, 0, 1]);subplot(212);plot(w/pi,abs(X));title('x_a(t)频谱图');xlabel('\omega/\pi');ylabel('X_a(e ^(j\omega))');ind = find(X >=0.03*max(X))*0.01; eband = (max(ind) -min(ind));fprintf('等效带宽为 %fKHZ\n',eband); 运行结果:等效带宽为 12.110000KHZ(2).N=10;omega=-3*pi:0.01:3*pi;%Fs=5000Fs=5;Ts=1/Fs;n=-N:Ts:N;xn=exp(-abs(n));X=xn*exp(-j*(n'*omega));subplot(221);stem(n,xn);grid on;axis([-10, 10, 0, 1.25]);title('时域波形(f_s=5000)');xlabel('n');ylabel('x_1(n)');subplot(222);plot(omega/pi,abs(X));title('频谱图(f_s=5000)');xlabel('\omega/\pi');ylabel('X_1(f)');%Fs=1000Fs=1;Ts=1/Fs;n=-N:Ts:N;xn=exp(-abs(n));X=xn*exp(-j*(n'*omega));subplot(223);stem(n,xn);grid on;axis([-10, 10, 0, 1.25]);title('时域波形(f_s=1000)');xlabel('n');ylabel('x_2(n)');subplot(224);plot(omega/pi,abs(X));title('频谱图(f_s=1000)');xlabel('\omega/\pi');ylabel('X_2(f)');运行结果:实验二:给定一指数型衰减信号,采样率,为采样周期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
病假条范文
安觅柔檲
实验结果
四 实践心得 通过实践,使我受益匪浅,知道如何在实 践中更加深入的对理论知识进行了解,更加 巩固了我的理论知识和我对信号与系统的了 解 实践考察通是过对平时学习的一个考验,使 我们能充分的了解到自己学到的东西,使我 们把学到的东西进行充分的运用,让我们把 学到的东西在实践考察课题中充分的发挥出 来,可以说是对我们的一个考验。
Xlabel('t'),ylabel('f1') axis([-2,2,-0.5,1.5]); N=1000; k=-N:N; W1=40; W=k*W1/N; F=f1*exp(-j*t'*W)*R; F=real(F); subplot(1,2,2),plot(W,F) grid on; Xlabel('W'),ylabel('F(jw)')
试用MATLAB画出它们的时域波形及频谱,观 察它们的关系。
二
实验目的 1 正确运用傅立叶变换 2用Matlab编程观察周期信 号的合成过程。进一步理 解周期信号的傅里叶级数 分解特性。 3.学习用Matlab绘制周期 信号频谱的方法。
三 实验原理 1. 周期矩形脉冲信号 的傅里叶展开系数 为sin 2x/2x的函数称为“采样函数”,这个 函数数据有以下特性 (1)Sa(2t)为偶函数 (2)当t→0时,Sa(t)=1是以1/t为振幅 的“正弦函数”;因而对于x的正负两半 轴都为衰减的正弦震荡; (3)在x=nπ处(n=1,2,3,…),sin x=0即 Sa(t)=0;而在x=0处Sa(t)在t→0时等 于1。
信号与系统课程实践考察 班级: 学号: 姓名: 指导老师:
f1 (t ) sa(2t )
一 实验题目
f1 (t ) sa(2t )
f2 (t ) u(t 2) u(t 2)
df 3 (t ) f 4 (t ) dt
f3 (t ) t[u(t 1) u(t 1)]
2f ( )
1. 根据对称性 MATLAB编程 R=0.05; t=-1.2:R:1.2; t1=2*t; f1=sinc(t1); subplot(1,2,1),plot(t,f1) Xlabel('t'),ylabel('f1') axis([-2,2,-0.5,1.5]); N=1000; k=-N:N; W1=40; W=k*W1/N; F=f1*exp(-j*t'*W)*R; F=real(F); subplot(1,2,2),plot(W,F) Xlabel('W'),ylabel('F(jw)')
实验结果
f2 (t ) u(t 2) u(t 2)
f (t ) F ( j ) F2 ( j ) F2 j 4sa (2 )
四 实验内容 1. 根据对称性得出: → MATLAB编程 R=0.05; t=-3:R:3; f2=(t>=-2)-(t>=2); subplot(1,2,1),plot(t,f2) grid on;
Xlabel('t'),ylabel('f2') axis([-3,3,-0.5,1.5]); N=1000; k=-N:N; W1=40; W=k*W1/N; F=f2*exp(-j*t'*W)*R; F=real(F); subplot(1,2,2),plot(W,F) grid on;
实验结果
实验结果
MATLAB程序
f 4 (t )
d f3 (t ) dt
R=0.005; t=-1.2:R:1.2; f3=t.*(t>=-1)-t.*(t>=1); subplot(1,2,1),plot(t,f3) Xlabel('t'),ylabel('f3') axis([-2,2,-1.5,1.5]); N=1000; k=-N:N; W1=40; W=k*W1/N; F=f3*exp(-j*t'*W)*R; F=real(F); subplot(1,2,2),plot(W,F) Xlabel('W'),ylabel('F(jw)')
1.f(t)的傅里叶变换
f(t) →F(w) f(at) → 1/abs(a)F(w/a) f(at+b) →1/abs(a)* ej*(b/a)w *F(j*w/a) U(t) → πδ(w)+1/jw U(at+b) → ej*(b/a)w*(πδ(w/a)+a/jw)
f2(t)=u(t+2)-u(t-2) → ( e jw+e-jw)*(πδ(w)+jw)
R=0.001;t=-4:R:4; f1=(t>=-2)-(t>=2); f2=f1.*t; N=1000;k=-N:N; W1=40;W=k*W1/N; F1=f1*exp(j*t'*W)*R;F1=real(F1); plot(W,F1);xlabel('w');ylabel('F 1(jw)')
f 3 (t) t[u (t 1) u (t 1)] f ' 3 (t ) f 4 (t )
MATLAB编程 R=0.05; h=0.001; t=-1.2:R:1.2; y=t.*(t>=-1)-t.*(t>=1); f4=diff(y)/h; subplot(1,2,1),plot(t,f1) Xlabel('t'),ylabel('f4') axis([-2,2,-0.5,1.5]); N=1000; k=-N:N; W1=40; W=k*W1/N; F=y*exp(-j*t'*W)*R; F=real(F); subplot(1,2,2),plot(W,F) Xlabel('W'),ylabel('F(jw)')
f3(t)=t[u(t+1)-u(t-1)] → [πð(w)+1/jw] (ejw-e-jw)
f4(t)=df3(t)/dt →【πð(w)+1/jw】(ejw-e-jw)-2πð(w)
f1 (t ) sa(2t )
Eg (t ) Esa (
z
2
)
F (t `)
