Genetic Algorithms for Free-Form Surface Matching
人工智能 遗传算法

人工智能遗传算法英文回答:Genetic Algorithms for Artificial Intelligence.Genetic algorithms (GAs) are a class of evolutionary algorithms that are inspired by the process of natural selection. They are used to solve optimization problems by iteratively improving a population of candidate solutions.How GAs Work.GAs work by simulating the process of natural selection. In each iteration, the fittest individuals in thepopulation are selected to reproduce. Their offspring are then combined and mutated to create a new population. This process is repeated until a satisfactory solution is found.Components of a GA.A GA consists of the following components:Population: A set of candidate solutions.Fitness function: A function that evaluates thequality of each candidate solution.Selection: The process of choosing the fittest individuals to reproduce.Reproduction: The process of creating new individuals from the selected parents.Mutation: The process of introducing random changes into the new individuals.Applications of GAs.GAs have been used to solve a wide variety of problems, including:Optimization problems.Machine learning.Scheduling.Design.Robotics.Advantages of GAs.GAs offer several advantages over traditional optimization methods, including:They can find near-optimal solutions to complex problems.They are not easily trapped in local optima.They can be used to solve problems with multiple objectives.Disadvantages of GAs.GAs also have some disadvantages, including:They can be computationally expensive.They can be sensitive to the choice of parameters.They can be difficult to terminate.中文回答:人工智能中的遗传算法。
详解Python结合Genetic

详解Python结合Genetic Algorithm算法破解⽹易易盾拼图验证⾸先看⼀下⽬标的验证形态是什么样⼦的是⼀种通过验证推理的验证⽅式,⽤来防⼈机破解的确是很有效果,但是,But,这⾥⾯已经会有⼀些破绽,⽐如:(以上是原图和⼆值化之后的结果)(这是正常图⽚)像划红线的这些地⽅,可以看到有明显的突变,并且⼆值化之后边缘趋于直线,但是正常图像是不会有这种这么明显的突变现象。
初识潘多拉后来,我去翻阅了机器视觉的相关⽂章和论⽂,发现了⼀个⽜逼的算法,这个算法就是——Genetic Algorithm遗传算法,最贴⼼的的是,作者利⽤这个算法实现了⼀个功能,“拼图⾃动还原”(不是像什么A*算法寻找最优路线解那种哈,就是单纯的拼图)项⽬仓库地址⾸先来介绍下如何使⽤跑起来这个项⽬吧,坑是真的很多,接下来感受⼀下pyCham的⼀路报错!这⾥我⽤的是python3.10的版本,⽬前是最新的版本⽂档中这⼀步执⾏是会报错的pip3 install -r requirements.txt解决⽅案:单独对requirements.txt⽂件下的每个包单独下载,然后根据当前下载的包的最新版本替换旧版本号。
我⽬前每个包最新使⽤的是这些版本号全部替换完了之后,再执⾏⼀次下⾯的代码,他就不会报错了pip3 install -r requirements.txt然后下⼀步,执⾏下⾯代码pip3 install -e .进⼊潘多拉然后我们按照官⽹的提⽰来执⾏,先创建⼀个拼图出来,命令是这样的(这⾥的⽂件名我改了)create_puzzle images/starry.jpg --size=60 --destination=puzzle.jpg会发现,好像不⾏,因为我们没有在正确的位置上执⾏,他的脚本位置是在bin⽂件夹下⾯,你可能会遇到如下问题成功之后的话,会在bin⽬录下⽣成⼀个拼图图⽚以上是介绍如何⽣成图⽚,接下来是重头戏,如何还原图⽚gaps --image=puzzle.jpg --generations=20 --population=600对于参数的解释官⽹是这样的:Option :--image Path to puzzle(需要被还原的图⽚)--size Puzzle piece size in pixels (拼图的⼤⼩)--generations Number of generations for genetic algorithm (遗传算法的代数)--population Number of individuals in population--verbose Show best solution after each generation (显⽰每⼀代后的最佳解决⽅案)--save Save puzzle solution as image (拼图结果另存为图像)先按照官⽅的⾛⼀遍很好,很舒服,继续报错,⽽且语法拼写上我们也没有拼写错,没关系!我已经帮你找到解决⽅案了。
几种仿生优化算法综述

几种仿生优化算法综述仿生优化算法(Bio-inspired optimization algorithm)是一类基于生物系统中某些行为特征或机理的优化算法。
这些算法通过模拟生物个体、种群或进化过程来解决各种优化问题。
以下将对几种常见的仿生优化算法进行综述。
1. 遗传算法(Genetic Algorithm)是仿生优化算法中最为经典的一种。
它受到遗传学理论中的基因、染色体、遗传交叉和变异等概念的启发。
遗传算法通过对候选解进行不断的遗传操作,如选择、交叉和变异,逐步优化解的质量。
它适用于多维、多目标和非线性优化问题。
2. 粒子群优化算法(Particle Swarm Optimization,简称PSO)是一种群体智能算法,受到鸟群、鱼群等群体行为的启发。
PSO算法通过模拟粒子在解空间中的搜索和信息交流过程来优化解。
每个粒子代表一个可能的解,并根据自身和群体的历史最优解进行位置调整。
PSO算法具有收敛速度快和易于实现的特点,适用于连续优化问题。
3. 蚁群算法(Ant Colony Optimization,简称ACO)是一种仿生优化算法,受到蚂蚁在寻找食物和回家路径选择行为的启发。
ACO算法通过模拟蚂蚁在解空间中的搜索、信息素的跟踪和更新过程来优化解。
每只蚂蚁通过选择路径上的信息素浓度来决定下一步的移动方向。
蚁群算法适用于组合优化问题和离散优化问题。
4. 免疫优化算法(Immune Optimization Algorithm,简称IOA)是一种仿生优化算法,受到免疫系统中的免疫机制和抗体选择过程的启发。
IOA算法通过模拟抗体的生成和选择过程来优化解。
每个解表示一个抗体,根据解的适应度和相似度选择和改进解。
免疫优化算法具有较强的全局搜索能力和鲁棒性。
genetic algorithm 计算量

题目:遗传算法在计算量中的应用与优势分析一、概述随着科学技术的不断发展和计算机技术的飞速进步,大规模的计算问题已经成为了许多领域中不可或缺的一部分。
在处理这些大规模计算问题时,传统的优化方法可能会显得效率不高,一些新的算法被研究人员提出,其中遗传算法就是其中之一。
本文将针对遗传算法在计算量中的应用和优势进行详细分析。
二、遗传算法的基本原理1. 遗传算法的起源和发展遗传算法是一种模拟自然界生物进化过程的优化算法,它起源于达尔文的进化论,通过模拟生物的自然选择、交叉和变异等过程来实现优化。
遗传算法最初是由美国的约翰·霍兰德教授于20世纪60年代提出的,自提出以来,遗传算法一直在人工智能领域得到了广泛的应用和深入的研究。
2. 遗传算法的基本原理遗传算法是一种通过模拟自然界的进化过程来解决优化问题的方法。
其基本原理包括个体编码、选择、交叉和变异四个步骤。
个体编码是将问题空间中的解表示为一定长度的二进制串或其他形式的编码;选择是根据适应度函数从种裙中选择个体;交叉是模拟生物的交叉繁殖过程,产生新的个体;变异是在个体的基础上进行一定概率的随机变化。
通过不断迭代,种裙中的个体会趋向于最优解。
三、遗传算法在计算量中的应用1. 遗传算法在函数优化中的应用在处理数学函数优化问题时,传统的优化方法如梯度下降可能存在局部最优解的问题,而遗传算法能够全局搜索解空间,在寻找全局最优解时具有一定的优势。
对于多峰函数、非线性函数等复杂函数的优化问题,遗传算法能够给出较为满意的结果。
2. 遗传算法在组合优化中的应用在组合优化问题中,例如旅行商问题、背包问题等,传统的动态规划方法可能面临组合数目过大的问题难以解决。
而遗传算法不同于传统优化方法,通过种裙的进化过程,能够找到较好的组合解,使得在组合优化问题中具有较好的适用性。
3. 遗传算法在机器学习中的应用在机器学习领域,特征选择、参数优化等问题也经常涉及到优化问题。
遗传算法可以作为一种基于自然进化的算法,用于搜索最优的特征子集或参数组合,克服了传统的特征选择和参数优化方法的局限性。
遗传算法(GeneticAlgorithm)..

被选定的一组解 根据适应函数选择的一组解 以一定的方式由双亲产生后代的过程 编码的某些分量发生变化的过程
遗传算法的基本操作
➢选择(selection):
根据各个个体的适应值,按照一定的规则或方法,从 第t代群体P(t)中选择出一些优良的个体遗传到下一代 群体P(t+1)中。
等到达一定程度时,值0会从整个群体中那个位上消失,然而全局最 优解可能在染色体中那个位上为0。如果搜索范围缩小到实际包含全局 最优解的那部分搜索空间,在那个位上的值0就可能正好是到达全局最 优解所需要的。
2023/10/31
适应函数(Fitness Function)
➢ GA在搜索中不依靠外部信息,仅以适应函数为依据,利 用群体中每个染色体(个体)的适应值来进行搜索。以染 色体适应值的大小来确定该染色体被遗传到下一代群体 中的概率。染色体适应值越大,该染色体被遗传到下一 代的概率也越大;反之,染色体的适应值越小,该染色 体被遗传到下一代的概率也越小。因此适应函数的选取 至关重要,直接影响到GA的收敛速度以及能否找到最优 解。
2023/10/31
如何设计遗传算法
➢如何进行编码? ➢如何产生初始种群? ➢如何定义适应函数? ➢如何进行遗传操作(复制、交叉、变异)? ➢如何产生下一代种群? ➢如何定义停止准则?
2023/10/31
编码(Coding)
表现型空间
基因型空间 = {0,1}L
编码(Coding)
10010001
父代
111111111111
000000000000
交叉点位置
子代
2023/10/31
111100000000 000011111111
APS算法分析之五基因算法

APS算法分析之五基因算法基因算法 GA (Genetic Algorithm)是基于自然系统的进化过程,算法创立一初始化方案的人种,基于初始化方案, 算法再产生新的一个人种,通过许多代的连续过程,方案的质量被改善,算法结束于当达到一特别的中断规则 (如. 当加工时间已经达到),它实际上是随机搜寻算法。
它已经用于许多优化问题,如销售员旅行问题,货柜包装问题,排程问题,顺序问题,设施布局问题等。
和本地搜索策略不同的是,GA和 Tabu 搜索 (TS) 在搜索中比较一最较差的目标函数值,接受临时的方案来克服本地优化,找到全局优化。
然而,因为,GA 和TS 是探索法,可能不是最佳的方案,但是,大部分情况下,至少可以找到一个非常好可行的方案。
GA是随机搜寻算法,因为用较差目标函数值的方案用特别的可能性是可以接受的。
因此,用一个一样的初始方案开始,和一样的参数设置,也可能导致不同的方案。
而用确定性搜索算法如TS就会导致同样的方案。
基本概念:人种保持在内存为进一步改善的一列数字集,新列数字使用特别的基因运作产生。
选择是根据它们的适应性来选择出“父代”基本基因运作:∙复制∙交叉∙变异一人种的数字串选择可以用一特别的数字串的进化函数产生后一代。
进化函数反映染色体的“适应”。
比如:在车间流水线排序问题∙N 任务必须在 M 机器排程∙每一任务包含 m 工序∙每一工序需要不同的机器∙所有任务在同样的加工订单上处理特别假设 :1,所有任务在零时间可以得到2,工序的准备时间包含在加工时间里 3,对所有机器所有工序的顺序已定义 4,目标: 最小化时间跨度适应函数:对一人种的目标函数值的所有成员,如计算跨度。
从这个较低的跨度被决定和得到最高的适应值fmax.,从不同的人种结果中的每一成员的适应值到它的前辈的索引清单中的适应值。
这个作法就保证了为一较低跨度的排程选择的可能性是高的。
缩减规模d影响到选择的可能性。
必须的条件是: fmin > 0.适应值 (用 fmax=20, d=5 => fmin=5):*f(13452) = 20*f(12345) = 15*f(24531) = 10*f(23541) = 5*整个人种的适应值: 50 (在人种里的所有个体的适应合计)复制 / 选择∙大部分公用的复制/选择概率是给定的。
遗传算法原理(英文)

Soft Computing Lab.
WASEDA UNIVERSITY , IPS
2
Evolutionary Algorithms and Optimization:
Theory and its Applications
Part 2: Network Design
Network Design Problems Minimum Spanning Tree Logistics Network Design Communication Network and LAN Design
Book Info
Provides a comprehensive survey of selection strategies, penalty techniques, and genetic operators used for constrained and combinatorial problems. Shows how to use genetic algorithms to make production schedules and enhance system reliability.
Soft Computing Lab.
WASEDA UNIVERSITY , IPS
4
Evolutionary Algorithms and Optimization:
Theory and its Applications
Part 4: Scheduling
Machine Scheduling and Multi-processor Scheduling Flow-shop Scheduling and Job-shop Scheduling Resource-constrained Project Scheduling Advanced Planning and Scheduling Multimedia Real-time Task Scheduling
genetic

geneticGenetic Algorithms: An IntroductionIntroductionGenetic algorithms are a class of optimization algorithms that mimic the process of natural selection in order to find solutions to complex problems. They are based on the concept of evolution and genetics and have been successfully applied in various fields such as engineering, computer science, biology, and economics. This document aims to provide an introduction to genetic algorithms, explaining their basic principles, components, and applications.1. Basics of Genetic Algorithms1.1 Evolutionary NatureGenetic algorithms are inspired by the process of natural evolution. They start with a population of potential solutions (individuals) representing different points in the search space. These individuals undergo a series of iterations called generations, during which they are evaluated based on afitness function that quantifies how good they are as solutions to the problem.1.2 Genetic RepresentationIn a genetic algorithm, each individual is represented as a string of genes, where a gene corresponds to a certain characteristic or variable of the solution. The collection of genes forms a chromosome, and the complete set of chromosomes constitutes the population.1.3 Genetic OperatorsGenetic algorithms utilize three main genetic operators to create new individuals:1.3.1 SelectionDuring selection, individuals with higher fitness values have a higher chance of being chosen for reproduction. This mimics the survival of the fittest principle in nature.1.3.2 CrossoverCrossover involves swapping genetic information between pairs of individuals. It is performed at a random crossoverpoint to create offspring with characteristics inherited from both parents.1.3.3 MutationMutation introduces small random changes to the genetic material of an individual. This helps explore new areas of the search space and prevent premature convergence to suboptimal solutions.2. Genetic Algorithm Workflow2.1 InitializationThe algorithm begins by initializing a population of individuals randomly or based on prior knowledge about the problem. Each individual is represented by a chromosome encoded with genes.2.2 EvaluationEach individual in the population is evaluated using the fitness function, which measures how well the individual solves the problem. The fitness function determines the reproductive success of each individual.2.3 SelectionBased on their fitness values, individuals are selected for reproduction. The selection process can be done using various strategies such as tournament selection, roulette wheel selection, or rank-based selection.2.4 CrossoverSelected individuals undergo crossover, where genetic information is exchanged between pairs of individuals. This generates a new population of offspring.2.5 MutationTo add diversity to the population and prevent convergence to a local optimum, a small fraction of the offspring undergoes mutation. Random changes are introduced to their genes.2.6 ReplacementThe new population, consisting of offspring and mutated individuals, replaces the previous population. This ensures the survival of the fittest individuals.2.7 TerminationThe algorithm continues to iterate through the steps of selection, crossover, mutation, and replacement until a termination condition is met. This condition can be a maximum number of generations, a desired fitness level, or any other predefined criterion.3. Applications of Genetic AlgorithmsGenetic algorithms have been applied to solve a wide range of optimization problems, including:3.1 Engineering DesignGenetic algorithms are widely used in engineering design optimization, such as in determining optimum parameters for complex systems, designing efficient structures, and optimizing production processes.3.2 Scheduling and RoutingThey have been utilized to solve complex scheduling and routing problems, such as job scheduling, vehicle routing, and airline crew scheduling.3.3 Machine LearningGenetic algorithms have been combined with machine learning algorithms to optimize the performance of machine learning models. They can be used for feature selection, parameter optimization, and model fitting.3.4 Financial ModelingIn finance, genetic algorithms are used for portfolio optimization, risk management, and trading strategy development. They can identify the optimal portfolio allocation based on historical data and risk preferences.ConclusionGenetic algorithms offer a powerful and flexible approach to solving complex optimization problems. By mimicking the process of natural evolution, they generate high-quality solutions and can handle a wide range of problem domains. By understanding the basic principles and workflow of genetic algorithms, practitioners can apply this technique to various real-world problems and achieve improved results.。
基于自然梯度的噪声自适应变分贝叶斯滤波算法

基于自然梯度的噪声自适应变分贝叶斯滤波算法胡玉梅 1, 2, 3 潘 泉 1, 2 胡振涛 4 郭 振 1, 2, 5摘要 考虑到运动目标跟踪系统机动、隐身等人为对抗特征以及非视距、干扰、遮挡等环境因素, 其系统建模、估计与辨识过程中越来越无法回避非线性、非高斯以及参数未知等复杂系统特征的影响. 针对过程噪声先验信息不准确以及量测噪声非高斯环境下运动目标的非线性状态估计问题, 提出一种基于自然梯度的噪声自适应变分贝叶斯(Variational Bayes, VB)滤波算法. 首先, 利用指数族分布具有统一表达形式的优势, 构建参数化逆威沙特(Inverse-Wishart, IW)分布作为状态一步预测误差协方差的共轭先验分布, 同时选取学生t分布重构因量测随机缺失导致的具有非高斯特点的似然函数; 其次, 在变分贝叶斯优化框架下采用平均场理论将状态变量联合后验分布近似分解为独立的变分分布, 在此基础上, 结合坐标上升方法更新各变量的变分分布参数; 进而, 结合 Fisher 信息矩阵推导置信下界最大化关于状态估计及其估计误差协方差的自然梯度, 使非线性状态后验分布的近似分布沿梯度下降, 以实现对状态后验概率密度函数(Probability density function, PDF)的“紧密”逼近. 理论分析和仿真实验表明: 相对传统的非线性滤波方法, 本文算法对噪声不确定问题具有较好的自适应能力, 并且能够获得较高的状态估计精度.关键词 非线性滤波, 自适应滤波, 变分贝叶斯推断, 自然梯度, Fisher 信息矩阵引用格式 胡玉梅, 潘泉, 胡振涛, 郭振. 基于自然梯度的噪声自适应变分贝叶斯滤波算法. 自动化学报, 2023, 49(10): 2094−2108DOI 10.16383/j.aas.c210964A Novel Noise Adaptive Variational Bayesian Filter Using Natural GradientHU Yu-Mei1, 2, 3 PAN Quan1, 2 HU Zhen-Tao4 GUO Zhen1, 2, 5Abstract Considering the increasing complexity and changeability of characteristics such as maneuvering and stealth in moving target tracking system and the influence of adverse factors such as non-line-of-sight, interference and occlusion in measurement environment. State estimation is likely to be confronted with complex system charac-teristics such as nonlinearity, non-Gaussian noise and unknown parameters. Aiming at nonlinear adaptive state es-timation of moving target in a system with unknown process noise and non-Gaussian measurement noise, a novel noise adaptive variational Bayesian (VB) filter using natural gradient is proposed. Firstly, a parameterized inverse-Wishart (IW) distribution and a student's t distribution are constructed as the conjugate prior distribution of pre-dicted state error covariance and measurement likelihood respectively. Then, in the framework of variational Bayesian optimization, the joint a posteriori distribution of estimation variables is approximately decomposed into independent variational distributions by using mean-field theory. On this basis, the variational distribution para-meters of each variable are updated by combining coordinate ascend method and the characteristics of exponential distributions. Furthermore, under the condition of maximizing evidence lower bound, the natural gradients with re-spect to state estimation and its error covariance are derived by combining with Fisher information matrix. So that the variational distribution of nonlinear state gradually approaches the posteriori probability density function (PDF) of state along the natural gradient direction. Finally, simulation results show that the proposed algorithm has better adaptive ability to the problem of noise uncertainty and can obtain higher estimation accuracy com-pared to traditional algorithms.Key words Nonlinear filtering, adaptive filtering, variational Bayesian inference, natural gradient, Fisher informa-tion matrixCitation Hu Yu-Mei, Pan Quan, Hu Zhen-Tao, Guo Zhen. A novel noise adaptive variational Bayesian filter using natural gradient. Acta Automatica Sinica, 2023, 49(10): 2094−2108收稿日期 2021-10-13 录用日期 2022-03-01Manuscript received October 13, 2021; accepted March 1, 2022国家自然科学基金(61790552, 61976080), 西北工业大学博士论文创新基金(CX201915)资助Supported by National Natural Science Foundation of China (61790552, 61976080) and Innovation Foundation for Doctor Dis-sertation of Northwestern Polytechnical University (CX201915)本文责任编委 段海滨Recommended by Associate Editor DUAN Hai-Bin1. 西北工业大学自动化学院 西安 7100722. 信息融合技术教育部重点实验室 西安 7100723. 中国航空工业集团公司西安航空计算技术研究所 西安 710065 4. 河南大学人工智能学院 郑州450046 5. 湖北航天技术研究院总体设计所 武汉 4300401. School of Automation, Northwestern Polytechnical Uni-versity, Xi'an 7100722. Key Laboratory of Information Fu-sion Technology, Ministry of Education, Xi'an 7100723. Xi'an Aeronautical Computing Technique Research Institute, Aviation Industry Corporation of China, Ltd., Xi'an 7100654. School of Artificial Intelligence, Henan University, Zhengzhou 4500465. Sy-stem Design Institute, Hubei Aerospace Technology Academy, Wuhan 430040第 49 卷 第 10 期自 动 化 学 报Vol. 49, No. 10 2023 年 10 月ACTA AUTOMATICA SINICA October, 2023非线性滤波器设计与实现因其普适性及重要性一直是国内外学者研究的热点问题, 近年来非线性状态估计理论已成功应用于陆、海、空、天中运动目标的预警与防御, 智能交通的精确导航与制导, 无人机定位与遥感监测、工业过程监控与故障诊断等众多领域[1−3]. 考虑到运动目标跟踪系统机动、隐身等复杂多变的人为对抗特征以及非视距、干扰、遮挡等环境因素无法避免, 其系统建模、估计与辨识过程中越来越无法回避非线性、非高斯以及参数未知等复杂系统特征的影响[4]. 在对复杂环境下运动目标系统噪声先验信息进行建模时, 建模误差存在于状态演化模型中, 并通常假设其满足一定的参数化统计特性[5]. 然而, 在实际工程中, 由于先验建模信息的不足导致难以对此类参数进行准确赋值. 例如, 在现代目标跟踪系统中出现的欺骗、干扰、杂波、未知分布特性的量测噪声和系统噪声等情形, 尤其在非合作运动目标强机动场景中, 因难以对其运动过程进行精细化建模, 常造成目标跟踪航迹间断甚至无法正常起始的现象.针对系统噪声未知问题, 其解决思路通常选取逆伽马分布和逆威沙特(Inverse-Wishart, IW) 分布等具有统一参数表达形式的指数族分布作为共轭先验分布. Särkkä 等[6] 在变分贝叶斯 (Variational Bayes, VB) 推断框架下利用指数族分布构建共轭先验分布近似未知量测噪声的后验概率密度函数(Probability density function, PDF), 进而结合贝叶斯滤波机理实现时变噪声方差和目标状态的联合估计, 其滤波效果达到与交互式多模型方法相接近的估计精度, 并且凭借 VB 便于结合平均场近似解耦理论将高维变量求解转化为多个低维变量计算的特点, 使其在解决多未知扰动问题方面更具有优势.随后, 文献[7] 采用IW分布近似多变量噪声后验PDF的思想, 给出变分推断框架下噪声方差估计的一般实现形式. 在此基础上, 变分贝叶斯方法在未知量测/系统噪声估计方面得到了进一步的发展[8−9], 并成功推广应用于多目标跟踪环境[10−11]. 在文献[12−13]中滤波器的构建均建立在量测噪声和系统噪声统计特性未知的假设条件下, 其中, 文献[12] 在状态和量测扩维基础上通过采用批处理方式实现对未知噪声矩阵的估计, 然而这种扩维方式不可避免造成计算复杂度的急剧增加; 文献[13] 给出两类噪声统计特性均未知条件下噪声方差的在线估计方法, 并且为避免系统噪声和状态相互独立假设的不合理性,采用独立于当前状态的前一时刻状态预测误差协方差代替系统噪声的统计特性, 进而利用平均场理论近似解耦计算边缘后验 PDF 的变分分布, 以迭代递推方式求解其估计变量期望的解析解, 同时, 将状态一步预测误差协方差的先验分布建模为参数化IW分布, 以实现状态后验概率分布的更新.tααt tttt 考虑到外界环境干扰以及非线性传播等因素的影响, 量测数据概率分布往往呈现出重尾和非对称等非高斯特征. 例如, 在基于电磁信号的距离估计中, 障碍物遮挡造成的非视距量测误差往往远大于其他来源服从对称分布的误差, 导致量测分布呈现非对称非高斯现象. 其次, 受传感器精度和灵敏度的限制, 当运动目标发生强机动时, 雷达极化反射不稳定性将导致的量测随机缺失现象, 也将造成量测产生非高斯特征. 针对量测噪声非高斯问题的处理, 文献[14]采用莱斯分布构建非共轭指数族变换点检测模型, 并将其成功应用于雷达目标跟踪系统中. 文献[15]则提出一种通过构建状态演化模型和量测模型的条件矩实现非线性非高斯系统的状态估计方法. 为了进一步提升滤波器对不同分布形状噪声的鲁棒性, 文献[16] 将 Skew-分布作为非高斯量测似然的近似分布形式, 在此基础上设计了一种鲁棒变分贝叶斯估计器. 文献[17] 考虑在散度最小化准则下, 利用变分分布实现对后验 PDF 的近似. 散度对异常数据具有较好的抑制作用, 但是也打破了对数边缘概率与变分置信下界 (Eviden-ce lower bound, ELBO)、KL 散度(Kullback-Lei-bler divergence) 之和的等式约束关系, 其实质是一种伪 VB 推断方法. 考虑到学生分布和 Skew-分布对因量测异常导致的量测重尾现象和非对称性具有较好鲁棒性[18−19], 文献[20] 针对系统噪声和量测噪声均具有重尾特性的线性系统采用学生分布对状态预测概率密度函数和量测似然函数进行建模, 进而提出了一种基于高斯−学生混合分布的线性滤波器, 与传统高斯假设条件下滤波器估计效果相比进一步提升了系统的状态估计的精度和鲁棒性. 在系统噪声未知且时变和量测噪声重尾条件下,文献[21] 构建参数化IW分布作为状态一步预测误差协方差的共轭先验分布, 同时, 选取参数化学生分布刻画具有厚尾特点的量测似然函数. 然而, 上述噪声自适应方法未考虑非线性滤波器自身的优化问题和如何衡量后验分布近似程度的问题.考虑到在非线性滤波器设计过程中, 参数化变分分布对系统状态后验近似的程度是提高估计精度的关键因素之一, 基于采样的随机优化和基于拟牛顿、高斯牛顿和梯度上升等确定性优化方法的非线性滤波器相继提出. 在随机性优化方面, MCMC (Markov chain Monte Carlo)[22−23] 和序贯蒙特卡罗(Sequential Monte Carlo, SMC) 利用随机样本来逼近后验概率, 并以样本分布近似未知变量后验分布. 随机优化方法的优点是在大量样本的条件下能10 期胡玉梅等: 基于自然梯度的噪声自适应变分贝叶斯滤波算法2095够保证较高精度的估计, 但要承担较大的计算负担[24]. 在确定性优化方面, 文献[25] 以最小二乘准则为目标函数, 采用牛顿法推导给出一种迭代卡尔曼滤波器. 文献[26] 综合梯度法和牛顿法提出一种无噪声条件下的滚动时域估计器, 并证明其渐进收敛性和稳定性. 文献[27] 针对非线性状态空间的状态估计及其估计误差协方差的迭代更新问题, 利用正则化的非线性最小二乘思想提出一种随机增量近端梯度算法. VB 方法通过求解参数化的目标函数,利用参数优化结果逼近后验分布, 是一种确定性近似方法. 因此, VB 具有确定性优化方法特有的计算量较小的优势, 同时由于 VB 便于结合平均场理论近似解耦联合概率分布, 进一步减小了计算代价.α非线性状态估计优化的实质是对多维状态后验PDF 的近似逼近, 并且其近似程度不能简单地采用欧氏距离进行度量. 因此, 选取合理度量准则将有利于提高后验 PDF 的近似程度, KL 散度作为分布之间“差异”的度量在后验分布近似性衡量中具有天然优势. 文献[17]给出状态估计的变分迭代优化实现形式, 获得 散度和 KL 散度下对后验 PDF 更紧密的近似. 同时, 从信息几何角度出发, 概率分布是统计流形上点, 在一定条件下两概率分布之间的 KL 散度与作为统计流形度规的 Fisher 信息满足一定的数学关系. 基于信息几何理论, Amari [28]利用自然梯度优化方式实现统计流形空间中目标函数的最速梯度下降(或上升). 文献[29] 结合自然梯度策略和卡尔曼滤波框架设计一种非线性状态估计方法, 在文献[30] 中, 该方法进一步推广应用于传感器网络目标跟踪系统. 文献[31] 中作者证明了针对非线性状态估计优化的自然梯度方法在克拉美罗下界意义下是渐进最优的. 考虑自然梯度优化的优势, 以变分置信下界最大化条件下状态估计及其估计误差协方差的自然梯度为切入点, 从信息几何角度实现对状态后验概率密度函数的“紧密”逼近, 进而提高状态估计精度.t 在过程噪声先验不准确和由于量测随机丢失导致的量测噪声分布非高斯的情况下, 针对非线性系统状态估计精度和鲁棒性提升问题, 本文提出一种基于自然梯度的噪声自适应变分贝叶斯滤波算法.本文结构如下: 第 1 节结合IW 分布和学生 分布分别实现对状态预测误差协方差和量测似然的参数化建模; 第 2 节结合平均场近似和坐标上升方法给出了变分贝叶斯框架下未知变量变分分布的迭代更新方式; 第 3 节推导给出 ELBO 关于系统状态估计及其误差协方差的自然梯度, 进而构建并设计一种基于自然梯度的噪声自适应非线性变分贝叶斯滤波器; 第 4 节给出仿真验证与分析; 第 5 节总结全文, 并展望了后续研究方向.1 预备知识Ξk z k q (Ξk |ψk )假设动态系统隐变量 的量测为 , 根据变分贝叶斯理论可知, 在变分贝叶斯框架下以变分分布 作为桥梁可将难以积分的问题转化为ELBO 的优化问题.L (ψk )D KL [q (Ξk |ψk )∥p (Ξk |z k )]q (Ξk |ψk )p (Ξk |z k )其中, 表示具有单调递增特性的变分 ELBO, 表示变分分布 与后验分布之间的 KL 散度, 其表达式分别为q (Ξk |ψk )ψk 其中, 表示以 为参数的变分分布.p (Ξk |z k )p (Ξk |z k )t 未知变量的估计实际是对状态后验分布 的近似逼近, 当非线性状态后验分布难以获取时, 变分贝叶斯方法能够通过构建简单的变分分布实现对 的近似逼近. 变分分布选取需考虑先验分布和后验分布具有相同的函数形式, 一般情况下具有共轭特性的指数族分布满足这一条件. 本文考虑系统噪声未知情况, 根据标准卡尔曼滤波实现结构可知, 系统噪声的统计特性仅影响状态预测误差协方差, 因此可直接对状态预测误差协方差进行先验建模. 并且当系统噪声假设服从均值已知但方差未知的多变量高斯分布假设时, 可选取IW 分布作为其分布方差矩阵的共轭先验分布; 此外, 针对量测缺失导致量测噪声出现重尾问题, 考虑选取能够有效表征这一现象的学生 分布对量测似然函数进行建模.1.1 IW 分布共轭先验模型n ×n A 在贝叶斯滤波框架下, 对于系统噪声高斯分布参数未知问题的处理, 可转化为状态预测误差协方差的估计问题. 这里选取IW 分布作为共轭先验分布, 以保证后验分布与先验分布具有相同的函数形式. 一个服从IW 分布的 维随机对称正定矩阵 的概率密度函数可以表示为2096自 动 化 学 报49 卷t T n ×n tr (·)Γn (·)n P k |k −1其中, 和分别表示IW 分布的自由度参数和 维逆尺度矩阵, 表示矩阵的迹, 表示 维的伽马函数. 进而状态预测误差协方差 的先验分布表示为t k ≥n +1E [P k |k −1]对于逆威沙特分布, 当 时, 其变量期望即状态预测误差协方差的均值 表示为t k 令先验分布参数 表示为式 (6) 进一步转化为τ其中, 表示调谐参数[7]. 根据式 (5) ~ (8) 计算得到状态预测协方差的先验分布及其分布参数.t 1.2 学生 分布量测似然模型t υk 0R k t 当量测噪声分布由于量测值随机异常或缺失呈现重尾特征时, 传统高斯噪声分布模型难以对噪声分布特性进行有效刻画. 考虑学生 分布能够更好地体现这一特征, 并且对异常值具有较好的鲁棒性.当量测噪声 满足均值为 、方差为 的分布参数时, 建立参数化学生 分布模型, 即v t R k 其中, 表示学生 分布的自由度参数, 噪声方差 是该分布的尺度矩阵. 在此条件下量测似然函数可表示为t λk t 通常学生 分布的概率密度函数难以求得封闭解, 为了解决这个问题, 引入服从伽马分布的辅助随机变量 , 从而进一步将学生 分布转化为服从参数化高斯分布的伽马分布的积分,式 (10) 中量测似然函数可转化为G (λk ;αk ,βk )λk αk βk 其中, 表示辅助变量服从伽马分布, 和 分别为形状参数和逆尺度参数[20]. 综合上述特点, 在传感器量测存在随机异常值情况下量测似然函数表示为如下结构化形式:p (λk )=G (λk ;αk ,βk )(13)G (λk ;αk ,βk )E [λk ]并且 及其均值分别表示为λk αk βk 最后, 通过对辅助变量 及其超参数 和 更新确定量测似然的表达式.1.3 平均场近似ΞkΞk =(x k ,P k |k −1,λk )根据以上分析建模, 式 (2) 中的系统隐变量 定义为. 考虑到联合后验分布形式的复杂性以及参数相互耦合的问题, 无法直接求得其解析解. 在假设各未知变量相互独立的前提下, 通过引入平均场近似策略实现联合变分分布的近似解耦, 即q (x k )q (P k |k −1)q (λk )x k P k |k −1λk 其中, , 和 分别表示状态 ,状态一步预测协方差 和辅助变量 的变分分布, 通过平均场理论对待估计变量联合分布进行分解, 有助于在变分贝叶斯迭代框架结合坐标上升和各类优化方法实现多变量的联合优化. 结合上述第1.1节和第1.2节中的共轭先验模型和量测似然模型, 相应的变分分布分别表示为q (λk )=G (λk ;αk ,βk )(17)q (P k |k −1)=IW (P k |k −1;t k |k −1,T k |k −1)(18)q (x k )=N (x k ;x k |k ,P k |k )(19)αk βk λk t k |k −1T k |k −1P k |k −1x k |k P k |k x k 其中, 和 为辅助随机变量 的超参数, 同理, 和 为随机未知变量 的超参数; 和 为隐变量 的超参数. 在变分贝叶斯优化过程中, 可结合平均场理论将联合后验的变分分布近似解耦为多个单变量变分分布, 并利用坐标上升方法分别对每个变量进行迭代更新.2 未知变量的变分分布更新Ξk x k P k |k −1λk Ξk Ξk =(x k ,P k |k −1,λk )根据上述构建的共轭先验模型和量测似然模型, 变分置信下界中隐变量 包括状态 , 状态一步预测协方差 和辅助变量 , 可定义为. 采用变分分布近似上述多未知变量的联合后验分布, 即10 期胡玉梅等: 基于自然梯度的噪声自适应变分贝叶斯滤波算法2097()进而, 相应变分置信下界转化为x kP k |k −1λk 在变分置信下界最大化约束下, 结合坐标上升方法, 变量 , 和 概率分布的对数形式的更新分别表示为c P k |k −1,λk c x k ,λk c x k ,P k |k −1其中, , 和 分别表示在迭代过程中产生的实常数.结合建模信息和各变量变分分布的特点, 联合后验分布及其对数形式分别表示为c Ξk D zn z k P k |k −1(x k −xk |k −1)T P −1k |k −1(·)(x k −x k |k −1)T P −1k |k −1(x k −x k |k −1)t λk P k |k −1x k 其中, 表示迭代过程中与变量相关的实常数, 和 分别表示向量 和矩阵 的维数, 表示 的缩写形式(下文中类似情况不再一一说明). 根据式(26)可知, 由于高斯分布、学生 分布和伽马分布均属于指数分布族而具有简单的对数形式, 因此便于采用迭代更新的方式计算其解析解.以下给出 、 以及 的迭代估计的具体实现原理和步骤.λk 2.1 迭代更新i +1λk 根据式 (22)和式 (26), 在第 次变分迭代更新过程中, 的变分分布对数形式可表示为c λk x k P k |k −1x k =x i k |k +˜x k x i k |k˜xk i 其中, 表示 和 积分后相关的实常数.根据贝叶斯无偏估计理论, , 其中 和 分别表示第 次估计值及其估计偏差. 同时,结合局部线性化技术, 式 (27)中期望部分可进一步改写为H ik =∂h k (x k )∂x k |x k =x i k |k x k =x i k |k 其中, 表示量测函数在处的雅克比矩阵.i +1λi +1k αi +1k βi +1k 计算式 (14) 中伽马分布的对数表达式, 并结合式 (27)和式 (28), 不难看出, 第 次更新后参数 的变分分布中超参数 和 的更新过程可表示为Υi k =(z k −H i k x i k |k )T (z k −H i k x ik |k )+(H i k )T P i k |k H i k .其中,λk i +1λi +1k 根据式 (15)中伽马分布的均值表达式, 同时结合式 (29) 和式 (30), 参数 的第 次变分迭代更新 可表示为λkΥi k Υik Υi k i 由式 (31) 可以清晰地看出, 辅助随机变量 的更新与 负相关, 并且在迭代过程中 的变化与上一次迭代的状态估计值及量测函数在此估计值处的局部线性化矩阵有关. 根据 表达式, 第 次2098自 动 化 学 报49 卷i +1Υi k λi +1k i Υi k λi +1k (z k −H i k x ik |k )Υi k 252/E [λ]E [λ]=α/βαβββ迭代的估计值(可理解为第 次迭代估计的先验) 越接近真实状态, 值越小, 根据式 (31) 可知 则越大; 相反, 第 次的估计状态距真实状态较远, 值越大, 则越小. 其物理意义是, 当发生量测随机缺失时导致滤波更新的新息 增大, 同时 值将随之增大, 从而造成式 (11) 中实际量测噪声方差增大, 这种情况将反馈于滤波过程中状态估计的自适应更新. 为了直观地解释这种现象, 结合式 (11) 和式 (13), 采用一维高斯分布和伽马分布说明其相关关系. 图1 给出伽马分布参数对量测似然的影响示意图. 在图1 中, 假设高斯分布的均值和方差分别为 和 , 并且 ,伽马分布参数 和 的值分别在图1(a)和图1(b)中注明. 当量测未发生丢失时, 的值较小, 高斯分布比较集中(如图1(a)所示); 当量测发生随机丢失, 的值增大, 高斯分布比较分散(如图1(b)所示).010********x(a) a = 10, b = 20.020.040.060.080.10概率密度伽马分布高斯分布伽马分布高斯分布1020304050x(b) a = 10, b = 600.0050.0100.0150.0200.0250.0300.035概率密度图 1 伽马分布参数对量测似然函数的影响示意图Fig. 1 The diagram of the influence of Gammadistribution parameters on likelihoodP k |k −12.2 迭代更新i 假设第 次迭代状态估计值已知, 根据式 (23)i +1P k |k −1和式 (26), 在第 次变分贝叶斯迭代更新过程中, 的变分分布的对数形式表示为c P k |k −1x k λk E i x k ,λk [(x k −xk |k −1)(x k −x k |k −1)T ]其中, 参数 表示 和 积分后的相关性实常数. 式 (32)中的期望 可转化为K ik i i t i kT i k P k |k −1其中, 表示在第 次变分贝叶斯迭代中卡尔曼滤波的增益. 令第 次迭代中IW 分布参数分别为 和 , 根据IW 分布表达式 (4), 同时结合式 (32)和式 (33), 则状态预测误差协方差 更新后变分分布的超参数分别为P k |k −1i +1P i +1k |k −1因此, 根据式 (6)中 均值表达式, 同时结合式 (34) 和式 (35), 状态预测误差协方差的第次变分迭代更新 表示为z k −h k (x k |k −1)P i +1k |k −1根据卡尔曼滤波实现原理可知, 当过程噪声方差建模不准确时, 状态预测误差协方差较大, 并且导致量测预测不精确而产生较大的量测新息 . 同时, 由式 (33)可知, 的迭代更新与量测新息正相关, 进而从物理意义上说明状态预测协方差建模的合理性.x k |k 2.3 迭代更新i +1根据式 (24) 和式 (26), 在第 次迭代更新过程中, 系统状态的变分分布对数形式表示为10 期胡玉梅等: 基于自然梯度的噪声自适应变分贝叶斯滤波算法2099{c x k P k |k −1λk i +1P k |k −1λk 其中, 表示与 和 积分后相关性的实常数. 在第 次迭代中, 依据式 (31) 和式 (36) 已经获取状态预测误差协方差 和辅助变量 的估计值由贝叶斯滤波理论可知, 状态后验分布的近似变分分布应具有以下形式C i +1k 其中,表示归一化常数结合高斯分布表达式, 式 (40) 可进一步改写为x i +1k |k P i +1k |k 综合式 (37) ~ (42), 目标状态后验分布的近似变分分布分别是以 和 为期望和协方差的高斯分布, 即()λi +1P i +1k |k x i +1k |k P i +1k |k 针对非线性系统状态估计问题, 现有贝叶斯滤波方法在实现式 (43) 中状态估计及其误差协方差的迭代更新过程中, 往往难以获得与真实后验“紧密”近似的变分分布. 虽然在多个变量坐标迭代优化过程中能够弥补部分由于线性化和参数不精确带来的误差, 但估计精度提升效果受限, 有时难以满足实际工程需求. 因此, 考虑在获得 和 估计值的基础上, 在置信下界最大化条件下结合自然梯度方法和 Fisher 信息矩阵, 推导给出 和 迭代更新解析表达式的具体实现.3 基于自然梯度的噪声自适应变分贝叶斯滤波器3.1 变分置信下界的自然梯度i λk P k |k −1λi k P ik |k −1x k 第 次变分迭代后, 在分别获取参数 和 的估计值 和 的基础上, 式 (2) 可转化为仅包含未知变量 的形式ψk =(x k |k ,P k |k )L (ψk)ψk 定义此时变分参数 , 通过最大化式(44)中的置信下界即可获得状态估计及其误差协方差. 自然梯度通过信息几何方法寻找统计流形空间的目标函数最速下降/上升方向, 给出了一种实现式 (44)置信下界求解的可行性方案[25]. 下面以置信下界 最大化为目标函数, 同时结合Fisher 信息矩阵推导关于变分参数 的自然梯度.式 (44)的置信下界可以进一步表示为i i +1p (x k )p (x k )≈q (x k |ψik),ψk 假设第 次迭代是第 次迭代的先验, 即式(45)中的先验信息 可以近似为 则变分参数 的最优估计值表示为ψk ψ∗k 通过计算式 (46)等号右边关于 线性化函数,可获取置信下界的自然梯度以及相应的最优 .E q [log p (z k |x k )]ψk =ψik D KL [q (x k |ψk )∥q (x k |ψik)]ψk =ψik i +1定理 1. 假设系统状态演化满足高斯分布特性,并且对数似然期望 在 的邻域内一阶可导, 同时, 在 的邻域内二阶可导, 则第 次迭代过2100自 动 化 学 报49 卷。
遗传算法Genetic Algorithm

Optimization
Stochastic Optimization
Good at dealing with problems that:
• affected by many variables • have many possible solutions • the results may make a big difference because of the combination
• It was first proposed by Professor J.Holland from the United States in 1975.
• A randomized search algorithm that evolved from the evolutionary laws of the biological world (物竞天择,适者生存)
• Random Searching 随机搜索 • Hill Climbing 爬山法 • Simulated Annealing 模拟退火算法 • Genetic Algorithm 遗传算法
NWU - IPMI
7
What is Genetic Algorithm?
Genetic Algorithm
NWU - IPMI
21
Genetic Algorithm
Basic Elements
Control Parameter(控制参数)
1. Encoding 2. Adaptive Function 3. Initial Population 4. Genetic Operation 5. Control Parameter
3. Initial Population
遗传算法在生物信息学中的应用

遗传算法在生物信息学中的应用在当今时代,生物信息学逐渐得到广泛关注,已经成为了现代生命科学的重要分支之一。
在生物信息学中,遗传算法已经被广泛应用,并取得了很多有意义的成果。
本文将着重探讨遗传算法在生物信息学中的应用。
一、遗传算法简介遗传算法(GA,Genetic Algorithm)是应用生物进化思想(遗传学、进化论)来解决优化问题的一种搜索算法。
遗传算法首先将种群进行初始化,然后通过选择、交叉、变异等操作,不断优化种群的适应性,最终找到最优解或最优逼近解。
遗传算法的优点在于其具有快速性、自适应性和高可靠性等特点。
在许多复杂问题的解决中,遗传算法已经成为了最有效的方法之一。
二、遗传算法在基因序列比对中的应用基因序列比对是生物信息学的重要研究方向之一。
在进行基因序列比对时,遗传算法被广泛应用。
传统的基因序列比对算法包括Smith-Waterman算法和Needleman-Wunsch算法等。
这些算法在精度方面表现很好,但时间复杂度比较高。
对于大量数据的比对,传统算法已经无法满足需求。
遗传算法通过不断调整基因序列的适应度,从而得到基因的最优匹配。
这种方法可以大大减少比对时间和资源耗费。
目前已经有很多基于遗传算法的基因序列比对软件,例如BLAST、FASTA等。
三、遗传算法在蛋白质结构预测中的应用蛋白质结构预测是生物信息学中的重要问题之一。
在蛋白质结构预测中,遗传算法也被广泛应用。
蛋白质结构预测的难点在于蛋白质的复杂性和多样性。
传统的蛋白质结构预测算法需要大量的时间和资源,而且精度也难以保证。
遗传算法通过不断优化蛋白质的结构,从而得到最优的蛋白质结构,具有极高的准确性和快速性。
目前已经有很多基于遗传算法的蛋白质结构预测软件,例如Rosetta、SwissModel等。
这些软件已经被广泛应用于生命科学研究和临床治疗中。
四、遗传算法在基因表达数据分析中的应用基因表达数据分析是生物信息学中的一个热门领域。
在基因表达数据分析中,遗传算法也得到了广泛应用。
优化算法之手推遗传算法(GeneticAlgorithm)详细步骤图解
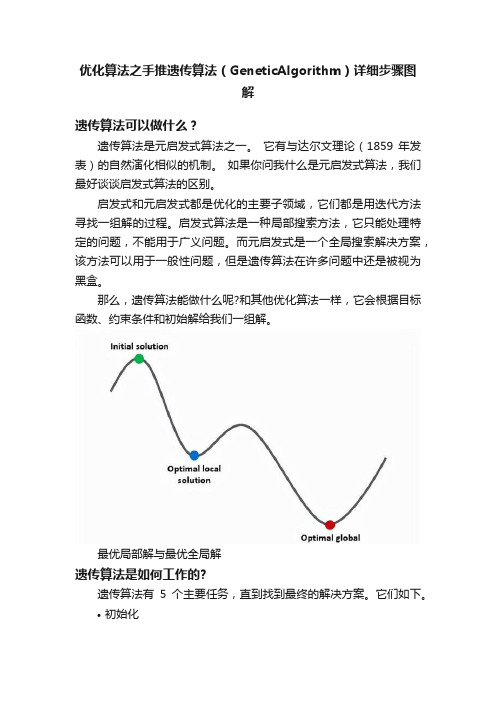
优化算法之手推遗传算法(GeneticAlgorithm)详细步骤图解遗传算法可以做什么?遗传算法是元启发式算法之一。
它有与达尔文理论(1859 年发表)的自然演化相似的机制。
如果你问我什么是元启发式算法,我们最好谈谈启发式算法的区别。
启发式和元启发式都是优化的主要子领域,它们都是用迭代方法寻找一组解的过程。
启发式算法是一种局部搜索方法,它只能处理特定的问题,不能用于广义问题。
而元启发式是一个全局搜索解决方案,该方法可以用于一般性问题,但是遗传算法在许多问题中还是被视为黑盒。
那么,遗传算法能做什么呢?和其他优化算法一样,它会根据目标函数、约束条件和初始解给我们一组解。
最优局部解与最优全局解遗传算法是如何工作的?遗传算法有5个主要任务,直到找到最终的解决方案。
它们如下。
•初始化•适应度函数计算•选择•交叉•突变定以我们的问题我们将使用以下等式作为遗传算法的示例。
它有 5 个变量和约束,其中 X1、X2、X3、X4 和 X5 是非负整数且小于 10(0、1、2、4、5、6、7、8、9)。
使用遗传算法,我们将尝试找到X1、X2、X3、X4 和 X5 的最优解。
将上面的方程转化为目标函数。
遗传算法将尝试最小化以下函数以获得 X1、X2、X3、X4 和 X5 的解决方案。
由于目标函数中有 5 个变量,因此染色体将由 5 个基因组成,如下所示。
初始化在初始化时,确定每一代的染色体数。
在这种情况下,染色体的数量是 5。
因此,每个染色体有 5 个基因,在整个种群中总共有 25 个基因。
使用 0 到 9 之间的随机数生成基因。
在算法中:一条染色体由几个基因组成。
一组染色体称为种群下图是第一代的染色体。
适应度函数计算它也被称为评估。
在这一步中,评估先前初始化中的染色体。
对于上面示例,使用以下的计算方式。
这是第一代种群中的第一个染色体。
将 X1、X2、X3、X4 和 X5 代入目标函数,得到 53。
适应度函数是 1 除以误差,其中误差为 (1 + f(x))。
遗传算法

遗传算法(Genetic Algorithm)遗传算法(Genetic Algorithm)1 原理遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。
它是由美国的J.Holland教授1975年首先提出,其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。
遗传算法的这些性质,已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
它是现代有关智能计算中的关键技术之一。
遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。
它的思想源于生物遗传学和适者生存的自然规律,是具有“生存+检测”的迭代过程的搜索算法。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。
其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
作为一种新的全局优化搜索算法,遗传算法以其简单通用、鲁棒性强、适于并行处理以及高效、实用等显著特点,在各个领域得到了广泛应用,取得了良好效果,并逐渐成为重要的智能算法之一。
遗传算法的基本步骤:我们习惯上把Holland1975年提出的GA称为传统的GA。
它的主要步骤如下:编码:GA在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合便构成了不同的点。
初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了一个群体。
GA以这N个串结构数据作为初始点开始迭代。
适应性值评估检测:适应性函数表明个体或解的优劣性。
不同的问题,适应性函数的定义方式也不同。
笛卡尔遗传规划CartesianGeneticProgramming(CGP)简单理解(1)

笛卡尔遗传规划CartesianGeneticProgramming(CGP)简单理解(1)初识遗传算法Genetic Algorithm(GA) 遗传算法是计算数学中⽤于解决最优化的搜索算法,是进化算法的⼀种。
进化算法借鉴了进化⽣物学中的⼀些现象⽽发展起来的,这些现象包括遗传、突变、⾃然选择以及杂交等,是⼀个通过计算机模拟解决最优化问题的过程,遗传算法从代表问题可能存在的⼀个解集的⼀个种群(population)开始的,⼀个种群由⼀定数量的候选解也称为个体(individual)组成,个体由基因(gene)编码⽽成,基因的表现形式实际上是每个个体上带有的染⾊体(chromosome) 染⾊体即为基因的集合,应⽤遗传算法的⼀般步骤是:1.需要实现表现形到基因型的编码⼯作,常⽤编码⽅法有⼆进制编码、格雷码编码、浮点编码和符号编码。
2.进化从随机个体(初代种群)的种群开始,之后⼀代⼀代进化。
按照优胜劣汰的准则在每⼀代中,评价整个种群的适应度(fitness),从当前种群中选择(selection)多个个体(基于它们的适应度)。
3.借助于⾃然遗传学的遗传算⼦(genetic operators)进⾏组合交叉(crossover)和变异(mutation) 产⽣新的种群,该种群在算法的下⼀次迭代中成为新的种群。
4.在末代种群中的最优个体通过解码(decoding)产⽣最优解笛卡尔遗传规划介绍 笛卡尔遗传规划源⾃ Miller 等⼈对进化数字电路的发展。
1999 年出现了专门研究笛卡尔遗传规划的团队2000 年由 Miller 等⼈发表了Cartesian Genetic Programming,正式提出了笛卡尔遗传规划的⼀般形式。
笛卡尔遗传规划由⼀个带索引节点的有向图表⽰,这是⼀个有n 个输⼊m个输出的有向图(directed graph),其中输⼊节点的下标为 0 到 n-1,输出由最后⼀列的m个节点得到。
遗传算法中主要的变异算法

遗传算法中主要的变异算法Genetic algorithms, at their core, rely on mutation operators as a key mechanism for introducing diversity and exploring the search space. Mutation algorithms play a crucial role in the optimization process, as they randomly alter the genetic information of individuals in the population, potentially leading to the discovery of better solutions.在遗传算法中,变异算法作为引入多样性和探索搜索空间的关键机制,起着至关重要的作用。
优化过程中,变异算法随机改变种群中个体的遗传信息,有可能发现更好的解决方案。
One of the most common mutation algorithms is the uniform mutation, where each gene in an individual's chromosome has a small probability of being mutated. This type of mutation randomly selects a gene and replaces it with a new value from the allowed range, effectively introducing a random change to the individual's genetic makeup.最常见的变异算法之一是均匀变异,其中个体染色体中的每个基因都有较小的概率发生变异。
Generative Fluid Dynamics Integration of Fast Fluid

Generative Fluid Dynamics: Integration of Fast Fluid Dynamics and Genetic Algorithms for wind loading optimizationof a free form surfaceAngelos Chronis1, Alasdair Turner1 and Martha Tsigkari11University College London, Gower Street,London, UK, WC1E 6BTangelos.chronis.09@, a.turner@, mtsigkar@Keywords:Computational Fluid Dynamics (CFD), Fast Fluid Dynamics (FFD), Genetic Algorithms (GA), wind load, optimization.AbstractThe integration of simulation environments in generative, performance-driven form-finding methods is expected to enable an exploration into performative solutions of unprecedented complexity in architectural design problems. Computational fluid dynamics simulations have a wide range of applications in architecture, yet they are mainly applied at final design stages for evaluation and validation of design intentions, due to their computational and expertise requirements.This paper investigates the potential of a fast fluid dynamics simulation scheme in a generative optimization process, through the use of a genetic algorithm, for wind loading optimization of a free form surface. A problem-specific optimization environment has been developed for experimentation. The optimization process has provided valuable insight on both the performance objectives and the representation of the problem. The manipulation of the parametric description of the problem has enabled control over the solution space highlighting the relation of the representation to the performance outcome of the problem.1.INTRODUCTIONThe recent advancements of digital fabrication and the continuous development of computer aided design tools have not only liberated architecture from its geometrical constraints but they have also infused in it a computational realm of experimentation into form and function of unprecedented complexity. With parametric design systems being only the start point and computationally simulated dynamical systems of form finding the quintessence of this exploration, architecture has in part shifted from the design and drafting to the creation of the generative systems from which the final form emerges (Kolarevic 2003). The architectural discourse has lately been rigorously engaged in embodying the potential of this achievable complexity not only in the aesthetic but also in the performative aspects of contemporary architecture.The integration of simulation environments in the architectural computational framework has been a key factor in this exploration, as they provide the test bed for experimentation with the various aspects of architectural performance. This has led to a substantial development of both the simulation algorithms and their interfacing tools as well as their applicability in the building industry, facilitated also through the increase of available computational resources but also significantly through novel computational approaches and paradigms (Malkawi 2004). Although it is expected that the incorporation of these simulation environments in computational generative processes will enable a critical and systemic thinking into performance driven architecture and shape innovative performative solutions, their integration in a streamlined computational framework throughout all stages of the design process remains a challenge (Shea et al 2005).One of the areas that are still largely unexplored, in terms of its integration into generative design approaches is that of computational fluid dynamics (CFD). CFD simulations have a vast variety of applications in architecture, ranging from wind load analysis on buildings to ventilation and energy performance, contamination dispersion or even acoustical analyses (Malkawi 2004). However due to the complexity of the simulated phenomenaand the consequent computational demand of the simulation algorithms available, their use is restricted to final design stages for evaluation and validation of design intentions. There is evidence though, as it will be argued here, that through the use of less accurate but also computationally less demanding approaches, CFD simulations may be able to be applied not only at earlier design stages to inform preliminary design decisions, but even more to be integrated in generative form finding processes. In our approach we aim to explore the potential of a real-time fluid dynamics simulation scheme in the optimization of the wind loading of a free form surface canopy, through the use of a genetic algorithm (GA). It has to be stated, that the aim of this approach is not to attempt to simulate the physical phenomena with the maximum possible accuracy, but rather to investigate the potential of a resource effective simulation scheme in a conceptual stage generative approach.2.BACKGROUNDThe phenomena of fluid dynamics are described by the Navier Stokes equations and are considered one of the most challenging engineering problems. Navier-Stokes are notoriously difficult to approach analytically and therefore numerical methods are used to approximate their solution. This approximation introduces an amount of error in the simulation, the tolerance of which depends on the application and the goals of the simulation (Lomax et al 1999). The computational approaches to the simulation of fluids have been continuously expanding the past decades and there is a great variety of available simulation algorithms today, ranging from particle to mesh based approaches and from lower to higher accuracy models. Despite their continuous development though, the available simulation tools have not yet reached the expectations of researchers in combining accuracy with speed (Chen 2009). The computational timeframe of the simulations ranges from hours and days to even weeks, when involved in optimization processes (Hanna et al 2010).The areas of application of CFD in architecture are numerous and include among many others the analysis of indoor climate (Hartog et al 2000), ventilation performance (Chen 2009) and heating, ventilation and air conditioning (HVAC) systems (Hien & Mahdavi 1999) as well as the analysis of urban scale conditions, such as street layout configurations (Xiaomin et al 2006) and airflow analysis in dense urban environments (Chung & Malone-Lee 2010). In a number of these studies (Chung & Malone-Lee 2010; Hartog et al 2000; Hien & Mahdavi 1999) it is highlighted that there is a need to incorporate CFD simulations at earlier design stages. More specifically, what is pointed out is the inconsistency between the synthetic and the analytic design stages and therefore it is suggested that optimization needs to be initiated at early design stages to be more effective. The suggestions include parametric design systems, hybrid simulation approaches and visualization schemes to approach the simulation data sets.In the field of wind engineering, the applications of CFD simulations are also numerous and span all scales of the urban environment, from high rise buildings (Huang et al 2007) to building roofs (Kumar & Stathopouloos 1997). Although in most cases the study of wind loads is validated through wind tunnel experiments, the CFD simulations are considered a fundamental tool in wind load analysis (Baker 2007). Again the integration of CFD simulations in earlier design stages is attempted through different approaches, such as the development of tools that streamline the pre and post processing of the simulation (Kerklaan and Coenders 2007) or the use of special effect visualization-oriented tools, similarly to the approach taken here, to dynamically sketch and assess the performance of design alternatives of tension membrane structures, before formally assessing them through wind tunnel tests (Mark 2007).2.1.Fast Fluid DynamicsThe numerical scheme used in our approach was developed for the computer graphics industry (Stam 1999) and therefore the visual aspect but most importantly the speed of the simulation are more crucial than the accuracy of the solver. Although the simulation scheme does not disregard the physics of the fluid mechanics, due to the lower order numerical solvers used to approximate the solution, the solver suffers from an amount of numerical dissipation. Indeed recent experiments with the specific fluid simulation scheme show that the solver cannot accurately predict turbulent flows by comparing the results to standard experimental data for a number of different cases, i.e. flow in a lid-driven cavity, fully developed channel flow, forced convective flow and natural convective flow in a room (Zuo and Chen 2007; 2009; 2010). The same studies however consider the solver’s accuracy as adequate for a number of cases and objectives, such as building emergency management, preliminary sustainable design and real-time indoor environment control. The results on the speed of the simulations, on the other hand, are outstanding,with a timeframe that ranges from 4 to 100 times faster than real time. Moreover, when implemented on a parallel computing scheme the fast fluid dynamics (FFD) simulation timeframe are reported to be 500 to 1500 times faster than a CFD simulation. It is not aimed to attempt a validation of these results, here, but on the contrary to explore the potential of the fluid solver in a generative preliminary design optimization process.2.2.GAs and CFDGenetic algorithms have been widely used for optimization in many engineering fields and lately they have been increasingly applied in architectural oriented optimization problems. Very briefly, a GA is mimicking the natural selection process through a population of candidates that represent a solution to the given problem by assessing their fitness and reproducing their genetic material. One significant advantage of GAs that makes them inherently useful in architectural context is their effectiveness in searching through very large and complex solution spaces, where deterministic methods cannot perform that well. The integration of CFD simulations and GA optimization techniques is also not a novelty in other engineering areas. In the automotive, aerospace and nautical industries, the use of CFD in optimization techniques is fully integrated and automated (Duvigneau & Visonneau 2003) and falls under the general category of shape optimization (Roy et al 2008).In architectural related research though, there are very few attempts to couple CFD and GAs. These are mainly limited in the analysis of indoor environments and more specifically the optimization of HVAC systems. Malkawi et al (Choudhary & Malkawi 2002; Malkawi et al 2003; Malkawi et al 2005) have combined GAs and CFD to study the performance of a mechanically ventilated room, through the integration of a parametric model and the partial automation of the optimization process, which is also assisted by the user. Although the intervention of the user in the optimization procedure in this case is significant in driving the optimization procedure towards the desired solution space, the use of a commercial fluid solver does not allow for the adaptation of the simulation environment. Other approaches include the use of GAs and CFD for the optimization of HVAC systems in office spaces (Lee 2007; Kim et al 2007) as well as other performance criteria, such as the optimization of window design problems (Suga et al 2010) and smoke-control systems in buildings (Huang et al 2009). Again with a few exceptions these approaches do not significantly adapt the simulation environment to the needs of each problem or attempt to optimize the computational framework of the simulation. Furthermore most of these studies are considered with orthogonal geometries, thus limiting their applicability in form finding methods.3.THE OPTIMIZATION FRAMEWORKAs already mentioned, the aim of this approach is to explore the potential of a faster but less accurate CFD simulation scheme in the optimization of the performance, in terms of wind loading of a free form surface. The computational efficiency of the process was overall an important driver in the development of the simulation framework and therefore certain simplifications and compromises had to be made to make the attempt feasible. The free form surface was deliberately vaguely defined, and material and site specific parameters were not considered, in order to reduce the complexity of the problem and shift the interest mostly towards the potential of the solver in providing valuable insight on a simple problem, through a generative design process.Moreover the study was constrained to one constant wind direction to further reduce the problem’s complexity, although the use of a range of wind directions is strongly considered as a further step. Finally the wind loading calculation is also restricted to the mean wind load on the surface for simplification, while at a further stage more complex wind loading functions could be taken into account.The fluid solver used here is based on a three dimensional implementation (Ash 2006) of Stam’s (1999) fluid solver. The main simulation routines of the solver are the advection, diffusion and projection routines (see also Stam 2003) and as they form the core of the simulation algorithm they have not been significantly changed. Other parts of the simulation scheme have been adapted and developed to suit the needs of the study. Stam’s fluid solver is a grid-based method, i.e. the solution is derived by resolving the equations for each cell in a grid over each time step. The solver is based on a fixed-size grid cell, which does not allow the adaptation of the mesh resolution in areas of interest, but facilitates the integration of other parts of the simulation scheme. The implementation of the fluid solver, as well as all other parts of the optimization framework were developed by the authors in the Processing open-source programming language (Figure 1).Figure 1 Fluid domain section - velocity field3.1. BoundariesOne important aspect of the CFD simulations is the handling of the domain boundaries. As the fluid solver was developed for visualization purposes, the external boundary routines of the solver had to be adjusted to simulate a continuous channel flow instead of the original bounding box domain. Again, more complex and sophisticated boundaries that would take into account site parameters, such as the ground surface roughness, would increase the complexity of the problem and therefore were avoided. The modeling of a more complex urban environment was indeed attempted but dropped due to computational resource requirements.The internal boundaries of the fluid domain are derived by the free form surface and are therefore more complex to handle as they need to be redefined for each instance of the GA population. For this reason a meshing algorithm had to be developed. To describe the internal boundary meshing algorithm a description of the free form surface needs to be given. The surface is defined as a B-Spline (URBS) surface, which is controlled by a set of 25 control points, arranged in a two dimensional grid of 5 control points in each direction. To impose some constructability on the scheme, the 4 corners of the control grid are fixed to the ground, as they could serve as anchor points for the structure. The remaining control points are freely movable by the optimization algorithm inside a certain range of height, width and length, depending on the degrees of freedom which have varied during each optimization scheme, as it will be described further on. The range of movement is also constrained by the adjacency of the points, to avoid folding and distortion of the surface. This configuration defines the parametric range of movement of the surface inside the fluid domain and consequently the range of the solution space (Figure 2).Figure 2 Free form surface configuration (a) and movement range forone (b) and three (c) degrees of freedom.To set up the internal boundaries of the domain, for each parametric instance of the surface, a meshing algorithm had to be developed. For internal boundaries, at least two cells of the fluid domain in each dimension have to be occupied to counteract the velocity and density fields of the fluid in both directions normal to the surface. The meshing algorithm runs for every (u , v ) position on the surface (at given intervals) and assigns a solid boolean for the corresponding pair of cells of the fluid domain in each dimension. This boolean is used inside the boundary routine of the solver to adjust the condition at the boundary cells at each time step of the simulation. The boundary cells are also used for the calculation of the wind loading of the surface which is implicitly calculated from the density and velocity fields (Figures 3, 4).Figure 3 Internal boundaries generated by the meshing algorithm for one instance of the surface.Figure 4 Wind loading calculation – three time steps.3.2. The genetic algorithmEach member of the GA population represents an instance of the parametric surface and corresponds to a set of genes which define its parameters. Three different encoding schemes for the GA genes were used in our experiments, each with different results. Two of these schemes were a direct encoding of the moving position of the control points of the surface, movable in one (z component only) and three dimensions (x,y,z) respectively.To reduce the searchable solution space and increase the convergence of the optimization process, a topological description of the surface was also introduced as an encoding scheme. In this scheme, the control points of the surface were derived from a sine function, whose parameters were encoded in the genes in order to preserve the topological relation between the control points (Figure 5).Figure 5 The genotype and phenotype correspondence in two encoding schemes .In the scope of this effort two different gene crossover methods were also used, i.e. a multiple point and a single point crossover method which is also helpful in preserving the topology of the surface. In the multiple point crossover method each new member of the population inherits the genes from each of its parents in random order, therefore loosing the topological relationship between adjacent control points of the surface. In the single point crossover method, on the other hand, each new member inherits a uniform portion of its parents’ chromosomes, preserving the topological relationship between adjacent points.The population size of the GA in our experiments ranged from 36 to 64 members and the number of offspring did not exceed the 1500 generations, due to computation time limitations. As it has already been mentioned, the time efficiency of the process was an important factor in the development process therefore the optimization process did not reach its full potential in many of the experiments as it was restricted by the timeframe which has reached up to 8 hours on a typical configurations computer. One thing worth mentioning is that although the GA is able to generate multiple instances of the surface in no time, each of them has to be evaluated individually, in a serial manner, throughthe CFD simulation engine, as the generation of multiple CFD domains to parallelize the optimization process would exceed the capabilities of any machine. However a further step could involve the distribution of the optimization process over a network.The steps of the optimization process were the following:1) An initial population of surfaces is randomlygenerated by the GA. 2) For each member of the initial population the CFDdomain is preprocessed and the internal boundaries are defined. 3) The simulation engine runs until it converges andthe fitness of the member is evaluated as the mean wind load on the surface in a given time period. 4) The fluid domain and the internal boundaries arereset. 5) When the whole of the initial population has beenevaluated and ranked, a new member is generated by the GA and steps 2 to 4 are repeated for each new member (Figure 6).Figure 6 The optimization flowchart.4. RESULTSThe results of the experiments with the first two (direct) encoding schemes were, as expected, similar, with a slight increase in the performance range achieved by the three degrees of freedom scheme. In both cases the optimization process was successful in optimizing the performance of the surface, steadily decreasing the wind loads, though not reaching its full potential, in the given timeframe. The optimum range of generated surfaces in both schemes presented significant uniformity in their form, characterizedby symmetry in the vertical to the wind direction as well as by a wave-like profile in the parallel direction leading to an overall aerodynamic shape. In both schemes however the optimum forms did not converge to a single trend, but were divided into two schemes, almost inverted from each other in form but both performing equally in the CFD domain. This lack of uniformity could be indicative of a possible preliminary convergence to local optima, also due to the computational demands of the process, or possibly of an under-constrained problem set up which leads to multiple solutions. Therefore it led to further experimentation in an effort to constrain the solution space through both a different crossover method and a different encoding scheme (Figures 7-12).Figures 7, 8 Three degrees of freedom - Optimization screenshot and 4fittest membersFigures 9, 10 Fitness plots for one and three degrees of freedom. Figures 11, 12 One degree of freedom - 4 fittest members of the twooptimization trendsThe single crossover method introduced was effective in reducing the time frame of the optimization, achieving a similar performance range in almost half the amount of generations, without though effectively converging to one uniform solution. The shape of the optimal surfaces followed again two distinct trends with two inverted shape patterns similar to the ones observed with the multiple crossover method (Figures 13, 14).On the contrary, through the topological description scheme, the optimization process converged to one single optimal trend throughout all the experiments, without though reaching the same performance range, indicating that the preservation of the surface topology was effective in the restriction of the solution space but also in the restriction of the achievable performance (Figures 15, 16).Figures 13, 14 Single crossover method - 4 fittest members and fitness graphFigures 15, 16 Topological description scheme- 4 fittest members and fitness graph5.DISCUSSIONThe incorporation of the FFD solver in the optimization process has been effective in providing an experimentation platform for generative techniques. Although the computational demand of the process remains high, it has been feasible not only to integrate the complex CFD simulations in a generative approach but furthermore to generate results, with regards to the objectives of this study, in a complex solution space. More importantly the implementation of the fluid solver in an object-oriented programming environment has enabled the adaptation of the simulation environment to the study’s objectives.In terms of the problem-specific generated results, the optimization process has provided valuable insight on the problem, through the identification of performance trends, in relation to the different encoding schemes. The manipulation of the problem’s representation has provided control over the generated solution space, highlightingtherelationship between the parametric definition range and the resulting performance range. This control though can by no means be regarded as a way to a deterministic solution to the studied problem, if not properly assessed in relation to more realistic design parameters. In the scope of this study, several inseparable parameters of what would constitute a realistic architectural problem are deliberately omitted, for simplification. Nevertheless the focus of the study was on the potential of the implementation of the solver in a preliminary design stage and thus it can be regarded as a starting point for further experimentation.It needs to be mentioned that for these results to be useful one essential further step is the formal assessment of their performance using standard simulation packages, or potentially physical tests, as the inaccuracy caused by the numerical dissipation of the solver could possibly be misleading. Moreover, the use of generic parameters, in both the simulation framework and the description of the problem, does not facilitate the assessment of the results in an architectural context. A more thorough modeling of the simulation environment as well as the incorporation of other important optimization constraints, such as pedestrian comfort or other types of loading, are important further steps as well. Further work in progress also includes the use of multi-objective GAs to incorporate other optimization constraints in the problem, the use of artificial neural networks, trained by the solution space to increase the time efficiency and achieve a two-step optimization process as well as the implementation of further developed versions of the fluid solver to produce more accurate results.6.CONCLUSIONIn this study we explored the potential of a fast fluid dynamics simulation scheme in a generative optimization process. The implementation of the fluid solver in a problem-specific optimization framework has been effective in providing informative insight on the representation of the problem. Although more complex representations and objectives as well as a formal validation of the generated results would be required to address real architectural problems, this implementation is considered as a proof of concept and further experimentation with the simulation framework is expected to yield more interesting results. ReferencesA SH,M.2006. 'Fluid Simulation for Dummies', [online] Available at: /pyblog/fluid-simulation-for-dummies.html [Accessed01 September 2010].B AKER,C.2007. 'Wind engineering-Past, present and future', in Journal of Wind Engineering and Industrial Aerodynamics 95(9-11), 843-870.C HEN,Q.2009. 'Ventilation performance prediction for buildings: A method overview and recent applications', in Building and Environment 44(4), 848-858.C HOUDHARY,R.,M ALKAWI,A.M.,2002. 'Integration of CFD and genetic algorithms', in Proceedings of the Eighth International Conference on Air Distribution in Rooms, Copenhagen, Denmark.C HUNG,D.H.J.AND L.C.M ALONE-L EE 2010. 'Computational Fluid Dynamics for Urban Design', in Proceedings of the 15th International Conference on Computer-Aided Architectural Design Research in Asia CAADRIA, April 2010, Hong Kong, China, 357–366.D UVIGNEAU,R.&V ISONNEAU,M.2003. 'Shape optimization strategies for complex applications in Computational Fluid Dynamics', in Proceedings 2nd International Conference on Computer Applications and Information Technology in the Maritime Industries, May 2003, Hamburg, Germany.H ANNA,S.,H ESSELGREN,L.,G ONZALEZ,V.&V ARGAS,I.2010. 'Beyond Simulation: Designing for Uncertainty and Robust Solutions', in Proceedings of the Symposium on Simulation for Architecture and Urban Design at the 2010 Spring Simulation Multiconference, April 2010, Orlando, USA.H ARTOG,J.P. D.,K OUTAMANIS, A.AND L USCUERE,P.G.2000. 'Possibilities and limitations of CFD simulation for indoor climate analysis', available from: Repository of Delft University of Technology.H IEN,W.N.&M AHDAVI,A.1999. 'Computational Air Flow Modeling for Integrative Building Design', in Proceedings of the 6th International Building Performance Simulation Association Conference –'Building Simulation 1999', September 1999, Kyoto, Japan.H UANG,S.,L I,Q.&X U,S.2007. 'Numerical evaluation of wind effects on a tall steel building by CFD', in Journal of Constructional Steel Research 63(5), 612-627.K ERKLAAN,R. A.G.&C OENDERS,J.2007. 'Geometrical modeling strategies for wind engineering', in Proceedings of the IASS Symposium on Shell and Spatial Structures –'Structural Architecture: Towards the future, looking to the past', Venice 2007, Italy, 81-82K IM,T.;S ONG,D.;K ATO,S.&M URAKAMI,S.2007. 'Two-step optimal design method using genetic algorithms and CFD-coupled simulation for indoor thermal environments', in Applied Thermal Engineering 27(1), 3-11.K OLAREVIC,B.2003. 'Computing the Performative in Architecture', in Proceedings of the 21st eCAADe Conference –'Digital Design', Graz 2003, Austria.。
遗传算法2017-7

适应度收敛曲线
遗传算法工具箱
遗传算法的工具箱有很多种: Genetic Algorithm Tool 简称GATOOL->GADS Genetic Algorithm Optimization Tool 简称GAOT Genetic Algorithm Toolbox 简称GATBX Simple Genetic Algorithm 1002 简称SGA1002 …………
度较高的个体按某种规则或模型遗传到下一代群体 中,一般适应度较高的个体将有更多的机会遗传到 下一代群体中。 选择是一个概率选择的过程,基因 差的不一定会被淘汰。
2019/9/7
19
5 交叉
为了产生新的个体,种群中进行交叉繁殖。以某一 概率选出两个个体,相互交换一部分基因,就形成 了两个新的个体。
2019/9/7
Y
y=x2
0
31 X
将每一个自然数看成一个生命体,通过进化,看谁 能生存下来,谁就是所寻找的数字,即问题的解。
2019/9/7
12
1 编码
求解过程
将每一个数作为一个生命体,就必须给其赋予一定
的基因,这个过程叫做编码。可以将变量x编码成5 位长的二进制无符号整数表达形式,例如:x=13 (01101), 即数13的基因为 01101。
步3 计算S 中每个个体的适应度 f( ) ; 步4 若终止条件满足,则取S中适应度最大的个体作为所求 结果,算法结束。
步5 否则,按选择概率P(xi)所决定的选中机会,每次从S 中随机选定1个个体并将其染色体复制,共做 N 次,然后将复制 所得的 N 个染色体组成群体 S1 ;
基本遗传算法步骤
步6 按交叉率Pc所决定的参加交叉的染色体数c,从S1中 随机确定c 个染色体,配对进行交叉操作,并用产生的新染色 体代替原染色体,得群体 S2 ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Genetic Algorithms for Free-Form Surface MatchingK.Brunnstr¨o m and A.J.StoddartDept.of Electronic and Electrical EngineeringUniversity of SurreyGuildford,Surrey GU25XH,UKAbstractThe free-form surface matching problem is important inseveral practical applications,such as reverse engineering.An accurate,robust and fast solution is,therefore,of greatsignificance.Recently genetic algorithms have attractedgreat interest for their ability to robustly solve hard opti-mization problems.In this work we investigate the perfor-mance of such an approach forfinding the initial guess ofthe transformation,a translation and a rotation,between theobject and the model surface.This would be followed by alocal gradient descent method such as ICP to refine the es-timate.Promising results are demonstrated on accurate realdata.1.IntroductionThe free-form surface matching problem remains a diffi-cult problem.Apart from being interesting in its own right,there are a number of direct applications.These include in-spection and recognition of free-form surfaces from densedepth data.In these problems correspondences need to beestablished between models and the data.For example inreverse engineering processes range data is acquired by arange scanner.Separate views need to be registered andfused[11].The registration is usually based on gradient-descent e.g.the iterative closest point(ICP)algorithm.Tofind the right solution the user must input an initial guess.For these applications an accurate,robust and fast solutionis of vital importance.The problem of matching two free-form surfaces can becast as a search or an optimization problem.This leads toa6dimensional optimization problem with many local ex-trema.Hence,a gradient-descent method would most likelyThere are very few algorithms on the market that con-vincingly address the problem of free-form surface match-ing without an initial guess.One algorithm that apparently does solve the problem is based on a multi stage algorithm of some complexity[1].It requires in the region of30min-utes to compute a solution.Besl’s survey article[2]on free-form surface matching convincingly specifies the problem.It cites111other arti-cles almost none of which actually address the general free-form matching problem.Those that do,assume that reliable features(e.g.zero crossings of curvature)can be extracted. We make no such assumption.This paper,which is a shortened version of the technical report[4],is organized as follows.First we present the ge-netic algorithm for free-form surface matching,assuming that the reader is familiar with how a genetic algorithm is working in general.For such a description see e.g.Goldberg [6].We then describe our experiments and results.Finally we conclude with a discussion.2.The genetic algorithmTo use a genetic algorithm for solving our problem,it must be formulated in a suitable way.First we need to con-vert the continuous problem of free-form surface matching to discrete form.This is done by randomly sampling the model surface to a‘sufficient’density,and randomly sam-pling the scene surface to some other density.We now pose the problem as a point matching problem.We wish to la-bel(associate)each point in the scene with a point from the model,or a null label.Because the points are randomly chosen we do not expect an exact match.However,when sampled to a sufficient density we hope to match to a rela-tively close point.We also need a way to measurefitness of the chromosomes.The chromosomes represents an assign-ment of model points to scene points.Thefitness function used will be described in detail below.It is based on a func-tion that counts the number of good matches,by using the translational and rotational invariants such as relative ori-entation of surface normals and relative distances between points.Finally,we must decide on when a suitable result has been obtained.Thefitness function measures the num-ber of good matches.Ideally when all points are correctly matched,it will correspond to the number of scene points. However,due to the random sampling,noise and occlusion this cannot be achieved in practise.Furthermore,there is no way from within the genetic algorithm to check whether we have found the right solution or not.In thefield of GA’s the choice of termination is still an open question.We have investigated three different approaches:the optimization is stopped when a certain percentage of the total number of correct matches have been found;the maximumfitness has not increased for afixed number of generations;or it is ter-minated after a certain number of generations.There are a few free parameters that need to be selected. The number is small compared to many other methods1. The parameters are:population size i.e.the number of chro-mosomes;the crossover probability;the mutation probabil-ity;the stopping criteria;and one parameter in thefitness function,which we call the temperature.The problem of selecting parameters for the GA’s is an open question.They are usually chosen heuristically based on experience of the user community.This has guided us in our choice of parameters.2.1.Thefitness functionA genetic algorithm needs a cost function orfitness func-tion to be defined for a given problem.In this Section we develop afitness function appropriate for the free-form sur-face matching problem.Because thefitness must measure match quality in corre-spondence space it is designed to be invariant to translation or rotation of either the scene or model.It should be robust in the presence of clutter as well.Because of the random sampling we can never achieve an exact match but there will usually be reasonably“good”approximate matches.The quality of the best match will be a function of the average spacing between the randomly selected points on the surface.In genetic algorithms the choice of afitness function needs careful consideration.The convergence of the algo-rithm depends crucially on relative sizes of this over solu-tion space.A choice we make is to build up a cost that has some meaning,in particular we aim tofind an interme-diate quality measure which counts the number of good matches.This will then be transformed into which will be thefitness passed to the GA.We suppose that the model points are labeled by and the scene points are labeled by or .If scene point takes on label this is denotedby.We denote a joint labeling of all objects by the set.As a shorthand we define the multi-index.Now suppose that we choose2points from the scene surface.They will contain4vectors(2positions and2nor-mal vectors)of information between them,i.e.. There are10independent parameters and4invariants under rigid translation and rotation.We are interested in features that remain invariant to rotation and translation.The most obvious is the length of the vector from point to point ,i.e..Pairwise relative orientation is also an invariant.Finally,there will be a twist angle between thetwo normals representing the extent to which they are out of plane.Thus the four invariants are(1)(2)(3)(4)Now consider two model points and two scene points. We wish to define a pairwise match quality which will be a product over four terms.Thefirst termcan then be expressed as.Where is the density of points on the sur-face,which we estimate to be the area of the surface divided by the number of randomly sampled points.This agrees well with the empirical average closest distance.The angular quality measure is defined as(10)The form of the expression and the parameter(tempera-ture)are intended to bear a close resemblance to the formal-ism of the simulated annealing method of optimization.We believe that this is a good form for thefitness func-tion.Evolutionary pressure in GA’s is exerted by the ratio of costs,and the exponential form of thefitness ensures that each gain of correct matches is accompanied by an in-crease infitness of a factor.A few values of were tested,with decreasing performance for and no real improvement for values,so we have used the value throughout this work.2.2.Finding the transformationThe result of the GA is a good labeling,but we actually want a transformation,a translation and a rotation,which takes the object data set into the model.When the genetic algorithm are stopped,the chromosome of the best scoring individual will contain both good and bad matches.If we can pick out the subset that just contain good matches we could use a standard method tofind the transformation.This could indeed be done by looking at the point-wise matching 3score,Equation8.If this is close to we can use it for calculating the transformation.In this work we have simply been using a threshold,typically set to about30%of.The transformation is then found by least-squaresfitting, which is solved using a SVD-based based method[8].plexityThe core computation is thefitness function which is evaluated for each individual in the population,to deter-mine its relative strength.As can be seen by equation9, this computation will be of.Consider the situation that we have a population of in-dividuals and the algorithm is stopped after generations. This will give an overall complexity of .(g)(h)(i)(j)(k)(l)Figure2.High precision3D data of a bust of Beethoven produced by Viewpoint Animation Engineering.3.Experiments and ResultsWe will here present a few experiments illustrating the strengths and weaknesses of the presented approach to free-form surface matching.It should be stressed that our ob-jective is not accurate registration,rather it is to develop a technique tofind an approximate pose.The parameters of the algorithm have been kept constant throughout the exper-iments.In one case the number of points has been increased to obtain a better match.Both results are presented.In the standard case the population has consists of individu-als,each having points i.e.(see Section2.1). The genetic algorithm searches for matches among la-bel points i.e..The crossover probability was and the mutation rate per label.The temperature has beenfixed at.In all cases the GA was run for1000gen-erations.The GA specific parameters have been obtained by testing a few values around those given in Goldberg’s book about GA’s and selecting the set with the fastest con-vergence for a particular example.The computation time in the examples with these parameters is about2minutes on a AlphaStation 250.(a)(b)(c)(d)(e)(f)(g)(h)(i)Figure3.High precision3D data of a cow produced by Viewpoint Animation Engineering.d)-f)Shows the re-sult when using the above described set of parameters, except that the number of labels for the GA have been doubled to reflect that the model surface has double the area.g)-i)The result when usingand.In thefirst example,Figure1,an image of a rabbit ob-tained by a laser rangefinder,Cyberware,have been used. The scene,1(a),and the model,1(b),have been taken from different directions,with a more than50%overlap,1(c). The resulting transformation applied to the scene is shown in Figure1(d),and in1(e)and1(f)it is shown together with the model from two different viewing directions.The data was used in Turk and Levoy[11]and made available by ftp. It has been registered with an ICP based algorithm starting from a user supplied initial position.The ICP transforma-tion is given as comparison to the GA computed transfor-mation in the table of Figure5(a).As can be seen there are good agreement between the values computed by the two methods.In the next example,Figure2,we have been using3D data of a bust of Beethoven.The object or the scene is shown in Figure2(a).The model is a translated and rotated version of the object,Figure2(b).This data was produced by Viewpoint Animation Engineering using point measure-ments of high accuracy.The two data sets are shown to-gether in Figure2(c).Applying the computed transforma-tion to the object,the result can be seen in Figures2(d)-(f). The table in Figure5(b)gives the computed transformation and the errors in these parameters.In Figure3the model is a cow2,3(b).The scene,3(a), has been generated by cutting out half the cow from head to tail and then adding a rotation and a translation to its posi-tion.The match in thefirst example has been obtained byusing the same parameters as above,except that we have increased the number of labels to reflect the fact that the size of the model is double that of the object. The transformation found was not very good,Figure3(d)-(f)and5(c)(Estimate1).This is improved considerably, Figure3(g)-(i)and5(c)(Estimate2),by increasing the num-ber of points on the object surface as well as the number of labels points on the model surface.In thefinal example,Figure4and5(d),the front legs of the cow above have been cutout and rotated relative to each other.A rather surprising solution is found,even though we expected the algorithm to have problems in this case.The points around the cylindrical part of the body will dominate the solution,which make the algorithm stuck in a local op-timum.(a)(b)(c)(d)(e)(f)Figure4.High precision3D data of a cow produced by Viewpoint Animation Engineering.The scene and model are cut out pieces from the front leg region of the cow.Note the near cylindrical shape of most of the data.4.DiscussionWe have in this paper presented a simple approach,with promising results,based on genetic algorithm,forfinding the initial guess for the free-form matching problem.The basic steps of the algorithm are:1)Randomly sampling the object and model surface.2)Search for a solution with a genetic algorithm.3)Calculating the transformation from the matched points.Our goal is tofind a pose in the close vicinity of the global ually thefitness function has many lo-cal optima.We use a stochastic search technique that can in principle locate the global optimum to any desired prob-ability.In this sense it resembles Simulated Annealing.Naturally there is a tradeoff between the success rate and the resources allocated.On the datasets we studied we ob-tain good results in2-10minutes on a workstation.The results fall short of the performance that would be desired in practical applications such as multi view fusion of range images.However we believe that there is consider-able scope for refinement of the algorithm.Recent advancesin thefield of Genetic Algorithms suggest that small modi-fications can significantly improve their performance.On the other hand almost all optimization algorithms benefit from the inclusion of domain-specific knowledge into the basic algorithm.This we have not yet done,but seems likely to lead to a much more efficient algorithm.Work is in progress on these points.ParameterICP estimate0.000.019-0.0130.0380.039-1.0031.4b) 4.00-1.830.00180.0Estimate8.95-0.99-0.091True0.71 1.000.00-0.91-2.43-0.08521.2 Estimate2 1.15 1.000.010True 2.00-1.000.003.40 2.74-0.91171.5Figure5.The computed transformation for the example shown in Figure1,2,3and4.Thefirst three columns represent the computed translation.The next three the rotation axis and the last the rotation angle.a)Result for the example in Figure1b)Figure2c)Figure3d) Figure4References[1]R.Bergevin,urendeau,and D.Poussart.Registeringrange view of multipart objects.IEEE Trans.Pattern Analysisand Machine Intell.,61(1):1–16,Jan.1995.[2]P.Besl.The free-form surface matching problem.In H.Free-man,editor,Machine Vision for Three-Dimensional Scenes,pages25–69.Academic,New York,1990.[3]P.Besl and N.McKay.A method for registration of3-dshapes.IEEE Trans.Pattern Analysis and Machine Intell.,14(2):239–256,1992.[4]K.Brunnstr¨o m and A.J.Stoddart.Genetic algorithmsfor free-form surface matching.Technical Report ISRNKTH/NA/P--95/19--SE,Dept.of Numerical Analysis andComputing Science,KTH(Royal Institute of Technology),Oct.1995.[5] A.Cross and E.Hancock.Genetic search for structuralmatching.In R.Cipolla,editor,Proc.4th European Confer-ence on Computer Vision,volume1064of Lecture Notes inComputer Science,pages514–525,Cambridge,United King-dom,Apr.1996.Springer Verlag,New York.[6] D.Goldberg.Genetic algorithms in search,optimization andmachine learning.Addison-Wesley,Reading,Mass.,1988.[7]J.-J.Jacq and C.Roux.Registration of3-d images by geneticoptimization.Pattern Recognition,16(8):823–856,1995.[8]K.Kanatani.Analysis of3-d rotationfitting.IEEE Trans.Pattern Analysis and Machine Intell.,16(5):543–549,1994.[9] A.Papoulis.Probability,Random Variables,and StochasticProcesses.McGraw-Hill,Inc.,Singapore,1984.[10] A.J.Stoddart,J.Illingworth,and T.Windeatt.Optimal pa-rameter selection for derivative estimation in range images.Image and Vision Computing,13(8):629–635,1995.[11]G.Turk and M.Levoy.Zippered polygon meshes from rangeimages.In Proc.SIGGRAPH’94,In Computer GraphicsProceedings,Annual Conference Series,pages311–318,Or-lando,Florida,1994.5。
