指数函数经典练习题

合集下载

指数函数练习题及答案

(指数函数练习题及答案1．设y 1＝，y 2＝，y 3＝(12)－，则( )A ．y 3>y 1>y 2B ．y 2>y 1>y 3C ．y 1>y 2>y 3D ．y 1>y 3>y 2 解析：选＝＝，y 2＝＝，y 3＝(12)－＝，∵y ＝2x在定义域内为增函数，且>>， %∴y 1>y 3>y 2.2．若函数f (x )＝⎩⎪⎨⎪⎧a x，x >14－a2x ＋2，x ≤1是R 上的增函数，则实数a 的取值范围为( )A ．(1，＋∞)B ．(1,8)C ．(4,8)D ．[4,8)解析：选D.因为f (x )在R 上是增函数，故结合图象(图略)知⎩⎪⎨⎪⎧a >14－a 2>04－a 2＋2≤a，解得4≤a <8.3．函数y ＝(12)1－x的单调增区间为( )A ．(－∞，＋∞)B ．(0，＋∞)C ．(1，＋∞)D ．(0,1)@解析：选A.设t ＝1－x ，则y ＝⎝ ⎛⎭⎪⎫12t ，则函数t ＝1－x 的递减区间为(－∞，＋∞)，即为y ＝⎝ ⎛⎭⎪⎫121－x的递增区间．4．已知函数y ＝f (x )的定义域为(1,2)，则函数y ＝f (2x)的定义域为________．解析：由函数的定义，得1＜2x＜2⇒0＜x ＜1.所以应填(0,1)．答案：(0,1)1．设13<(13)b <(13)a<1，则( )A ．a a <a b <b aB ．a a<b a<a bC ．a b <a a <b aD ．a b <b a <a a、解析：选C.由已知条件得0<a <b <1，∴a b <a a ，a a <b a ，∴a b <a a <b a .2．若(12)2a ＋1<(12)3－2a，则实数a 的取值范围是( )A ．(1，＋∞)B ．(12，＋∞)C ．(－∞，1)D ．(－∞，12)解析：选B.函数y ＝(12)x在R 上为减函数，∴2a ＋1>3－2a ，∴a >12.3．下列三个实数的大小关系正确的是( )；A ．(12011)2＜212011＜1B ．(12011)2＜1＜212011C ．1＜(12011)2＜212011D ．1＜212011＜(12011)2解析：选B.∵12011＜1，∴(12011)2＜1,212011＞20＝1.4．设函数f (x )＝a －|x |(a ＞0且a ≠1)，f (2)＝4，则( )A ．f (－1)＞f (－2)B ．f (1)＞f (2)C ．f (2)＜f (－2)D ．f (－3)＞f (－2)解析：选D.由f (2)＝4得a －2＝4，又a ＞0，∴a ＝12，f (x )＝2|x |，∴函数f (x )为偶函数，在(－∞，0)上单调递减，在(0，＋∞)上单调递增．5．函数f (x )＝12x ＋1在(－∞，＋∞)上( ) X k b 1 . c o m$A ．单调递减无最小值B ．单调递减有最小值C ．单调递增无最大值D ．单调递增有最大值解析：选＝2x＋1为R 上的增函数且u ＞0，∴y ＝1u在(0，＋∞)为减函数．即f (x )＝12x ＋1在(－∞，＋∞)上为减函数，无最小值．6．若x ＜0且a x ＞b x＞1，则下列不等式成立的是( ) A ．0＜b ＜a ＜1 B ．0＜a ＜b ＜1 C ．1＜b ＜a D ．1＜a ＜b …解析：选B.取x ＝－1，∴1a ＞1b＞1，∴0＜a ＜b ＜1.7．已知函数f (x )＝a －12x ＋1，若f (x )为奇函数，则a ＝________.解析：法一：∵f (x )的定义域为R ，且f (x )为奇函数，∴f (0)＝0，即a －120＋1＝0.∴a ＝12.法二：∵f (x )为奇函数，∴f (－x )＝－f (x )，即a －12－x ＋1＝12x ＋1－a ，解得a ＝12.—答案：128．当x ∈[－1,1]时，f (x )＝3x－2的值域为________．解析：x ∈[－1,1]，则13≤3x ≤3，即－53≤3x－2≤1.答案：⎣⎢⎡⎦⎥⎤－53，1 9．若函数f (x )＝e －(x －u )2的最大值为m ，且f (x )是偶函数，则m ＋u ＝________. 解析：∵f (－x )＝f (x )， ∴e －(x ＋u )2＝e －(x －u )2，∴(x ＋u )2＝(x －u )2，^∴u ＝0，∴f (x )＝e －x 2.∵x 2≥0，∴－x 2≤0，∴0＜e －x 2≤1， ∴m ＝1，∴m ＋u ＝1＋0＝1. 答案：110．讨论y ＝(13)x 2－2x的单调性．解：函数y ＝(13)x 2－2x的定义域为R ，令u ＝x 2－2x ，则y ＝(13)u .列表如下：&)uy ＝(13)x 2－2xx ∈(－∞，1]x ∈(1，∞)|由表可知，原函数在(－∞，1]上是增函数，在(1，＋∞)上是减函数．11．已知2x≤(14)x －3，求函数y ＝(12)x 的值域．解：由2x ≤(14)x －3，得2x ≤2－2x ＋6，∴x ≤－2x ＋6，∴x ≤2.∴(12)x ≥(12)2＝14，即y ＝(12)x 的值域为[14，＋∞)．12．已知f (x )＝(12x －1＋12)x .\(1)求函数的定义域；(2)判断函数f (x )的奇偶性； (3)求证：f (x )>0.解：(1)由2x－1≠0，得x ≠0，∴函数的定义域为{x |x ≠0，x ∈R }．在定义域内任取x ，则－x 在定义域内，f (－x )＝(12－x －1＋12)(－x )＝(2x1－2x ＋12)(－x )＝－1＋2x 21－2x ·x ＝2x＋122x－1·x ， $函数单调性区间而f (x )＝(12x －1＋12)x ＝2x＋122x－1·x ， ∴f (－x )＝f (x )，∴函数f (x )为偶函数．(3)证明：当x <0时，由指数函数性质知， 0<2x <1，－1<2x－1<0，∴12x －1<－1， ∴12x －1＋12<－12. 又x <0，∴f (x )＝(12x －1＋12)x >0.由f (x )为偶函数，当x >0时，f (x )>0. 综上，当x ∈R ，且x ≠0时，函数f (x )>0.。

(完整版)指数函数经典习题大全

指数函数习题新泰一中闫辉一、选择题1．下列函数中指数函数的个数是 ( ).①②③④A．0个 B．1个 C．2个 D．3个2．若，，则函数的图象一定在（）A．第一、二、三象限 B．第一、三、四象限C．第二、三、四象限 D．第一、二、四象限3．已知，当其值域为时，的取值范围是（）A． B．C． D．4．若，，下列不等式成立的是（）A． B． C． D．5．已知且，，则是（）A．奇函数 B．偶函数C．非奇非偶函数 D．奇偶性与有关6．函数（）的图象是（）7．函数与的图象大致是( ).8．当时，函数与的图象只可能是（）9．在下列图象中，二次函数与指数函数的图象只可能是（）10．计算机成本不断降低,若每隔3年计算机价格降低 ,现在价格为8100元的计算机,则9年后的价格为( ).A．2400元 B．900元 C．300元 D．3600元二、填空题1．比较大小：（1）；（2） ______ 1；（3） ______2．若，则的取值范围为_________．3．求函数的单调减区间为__________．4．的反函数的定义域是__________．5．函数的值域是__________ ．6．已知的定义域为 ,则的定义域为__________.7．当时, ,则的取值范围是__________.8．时，的图象过定点________ ．9．若 ,则函数的图象一定不在第_____象限.10．已知函数的图象过点 ,又其反函数的图象过点(2,0),则函数的解析式为____________.11．函数的最小值为____________.12．函数的单调递增区间是____________.13．已知关于的方程有两个实数解,则实数的取值范围是_________.14．若函数（且）在区间上的最大值是14，那么等于_________．三、解答题1．按从小到大排列下列各数：，，，，，，，2．设有两个函数与，要使（1）；（2），求、的取值范围．3．已知 ,试比较的大小.4．若函数是奇函数，求的值．5．已知，求函数的值域．6．解方程：（1）；（2）．7．已知函数（且）（1）求的最小值；（2）若，求的取值范围．8．试比较与的大小,并加以证明.9．某工厂从年到年某种产品的成本共下降了19%，若每年下降的百分率相等，求每年下降的百分率10．某工厂今年1月、2月、3月生产某产品分别为1万件、1.2件、1.3万件，为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量与月份数的关系，模拟函数可以选用二次函数或函数（其中、、为常数），已知四月份该产品的产量为1.37万件，请问用以上哪个函数作为模拟函数较好？请说明理由．11．设，求出的值．12．解方程．参考答案：一、1．B 2．A 3．D 4．B 5．A 6．B 7．D 8．A 9．A 10．A二、1．（1）（2）（3）2． 3． 4．（0，1） 5．6． 7．8．恒过点（1，3） 9．四 10．11． 12． 13． 14．或三、1．解：除以外，将其余的数分为三类：（1）负数：（2）小于1的正数：，，（3）大于1的正数：，，在（2）中，；在（3）中，；综上可知说明：对几个数比较大小的具体方法是：（1）与0比，与1比，将所有数分成三类：，，，（2）在各类中两两比2．解：（1）要使由条件是，解之得（2）要使，必须分两种情况：当时，只要，解之得；当时，只要，解之得或说明：若是与比较大小，通常要分和两种情况考虑．3．4．解：为奇函数，，即，则，5．解：由得，即，解之得，于是，即，故所求函数的值域为6．解：（1）两边同除可得，令，有，解之得或，即或，于是或（2）原方程化为，即，由求根公式可得到，故7．解：（1），当即时，有最小值为（2），解得当时，；当时，．8．当时, > ,当时, > .9．解：设每年下降的百分率为，由题意可得，，，故每年下降的百分率为10%10．解：设模拟的二次函数为，由条件，，，可得，解得又由及条件可得，解得下面比较，与1.37的差，比的误差较小，从而作为模拟函数较好11．解：故12．解：令，则原方程化为解得或，即或（舍去），习题二1. 求不等式2741(0x x aa a -->>，1)a ≠且中x 的取值范围．2. . 指数函数xb y a ⎛⎫= ⎪⎝⎭的图象如图所示，求二次函数2y ax bx =+的顶点的横坐标的取值范围．3. 函数()xf x a =（0a >，且1a ≠）对于任意的实数x ，y 都有（）Ａ．()()()f xy f x f y =Ｂ．()()()f xy f x f y =+ Ｃ．()()()f x y f x f y +=Ｄ．()()()f x y f x f y +=+oyx14. 若11()()23x x <，则x 满足（）Ａ．0x > Ｂ．0x < Ｃ．0x ≤Ｄ．0x ≥5. (1)已知12()3a a -+=，求33a a -+；(2)已知21xa=，求33x xx xa a a a--++； (3)已知31xa -+=，求2362a ax x ---+的值．6. 已知函数()xf x a =（0a >，1a ≠）在[]22-，上函数值总小于2，求实数a 的取值范围． 7 已知函数()xxf x a a -=+（0a >，1a ≠），且(1)3f =，则(0)(1)(2)f f f ++的值是． 8. 若关于x 的方程22210xx a a +++=g 有实根，试求a 的取值范围．9. 当0a >且1a ≠时，函数2()3x f x a-=-必过定点．10. 设311x y a +=，22x y a -=其中0a >，且1a ≠．确定x 为何值时，有：（１）12y y =；（２）12y y >．11 当0a ≠时，函数y ax b =+和axy b =的图象是（）12. 函数()y f x =的图象与2xy =的图象关于x 轴对称，则()f x 的表达式为． 13. 若函数()()()21021x F x f x x ⎛⎫=+≠ ⎪-⎝⎭g 是偶函数，且()f x 不恒等于0，则()f x 为（）Ａ．奇函数Ｂ．偶函数Ｃ．可能是奇函数，也可能是偶函数Ｄ．非奇非偶函数14. 已知函数()()2211xf xg x x =-=-，，构造函数()F x 定义如下：当()()f x g x ≥时，()()F x f x =；当()()f x g x <时，()()F x g x =-，那么()F x （）Ａ．有最大值1，无最小值Ｂ．有最小值0，无最大值Ｃ．有最小值1-，无最大值Ｄ．无最小值，也无最大值15. 当0x >时，函数()()21xf x a =-的值总大于1，则实数a 的取值范围是．16. 已知函数()f x 满足对任意实数12x x <有()()12f x f x <且()()()1212f x x f x f x +=g 若写出一个满足这些条件的函数则这个函数可以写为．习题三一、选择题（每小题4分，共计40分） 1．下列各式中成立的一项是（）A ．7177)(m n mn = B ．3339= C ．43433)(y x y x +=+ D ．31243)3(-=-2．化简)31()3)((656131212132b a b a b a ÷-的结果（）A ．a 9-B ．a -C ．a 6D ．29a3．设指数函数)1,0()(≠>=a a a x f x，则下列等式中不正确．．．的是（）A ．f (x +y )=f(x )·f (y )B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)]([+∈=N n y f x f xy f nnn4．函数210)2()5(--+-=x x y（）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或 5．若指数函数xa y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于（）A ．215+ B ．215- C ．215± D ．251± 6．方程)10(2||<<=a x ax 的解的个数为（）A. 0个B. 1个C. 2个D. 0个或1个 7．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R8．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围（）A ．)1,1(-B ． ),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或9．已知2)(xx e e x f --=，则下列正确的是（）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 10．函数22)21(++-=x x y 得单调递增区间是（）A ．]1,(--∞B ．),2[+∞C ．]2,21[D ． ]21,1[-二、填空题（每小题4分，共计28分）11．已知0.622,0.6a b ==，则实数a b 、的大小关系为．12：不用计算器计算48373271021.097203225.0+-⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛--π=___________． 13．不等式x x 283312--<⎪⎭⎫ ⎝⎛的解集是__________________________．14．已知{}2,1,0,1,2,3n ∈--，若11()()25n n ->-，则=n ___________．15．不等式2221212-++⎪⎭⎫ ⎝⎛<⎪⎭⎫⎝⎛a x axx 恒成立，则a 的取值范围是．16．定义运算：⎩⎨⎧>≤=⊗)()(b a b b a a b a ，则函数()xx x f -⊗=22的值域为_________________17.如图所示的是某池塘中的浮萍蔓延的面积(2m )与时间t (月)的关系:ty a =,有以下叙述: ① 这个指数函数的底数是2；② 第5个月时,浮萍的面积就会超过230m ； ③ 浮萍从24m 蔓延到212m 需要经过1.5个月； ④ 浮萍每个月增加的面积都相等；⑤ 若浮萍蔓延到22m 、23m 、26m 所经过的时间分别为1t 、2t 、3t ，则123t t t +=. 其中正确的是．三、解答题：（10+10+12=32分） 18．已知17a a -+=，求下列各式的值: （1）33221122a a a a----；（2）1122a a-+；（3）22(1)a a a -->.19.已知函数)1(122>-+=a a a y x x在区间[－1，1]上的最大值是14，求a 的值.t/月20.（1）已知m x f x+-=132)(是奇函数，求常数m 的值；（2）画出函数|13|-=xy 的图象，并利用图象回答：k 为何值时，方程|31|x k -=无解？有一解？有两解？参考答案题号 1 2 3 4 5 6 7 8 9 10 答案BADDCCADAC二、填空题（4*7=28分）11.b a >； 12.100； 13.}24|{-<>x x x 或； 14.－1或2 15.(-2, 2) ； 16.]1,0( 17.①②⑤ 三、解答题：（10+10+12=32分） 18．解: （1）原式=11113312222111112222()()()(1)1718a a a a a a a a a aa a--------++==++=+=--。

指数函数练习题

指数函数练习题
1. 指数函数基础概念
指数函数是数学中常见的一种函数形式，通常表示为f(x)=a x，其中a是一个常数且a>0,a eq1。

指数函数具有一些特殊的性质，例如在x=0时函数值为1，函数图像以指数速率增加或减小等。

2. 指数函数的性质
•当a>1时，指数函数呈增长趋势，函数图像在x轴的右侧无上界。

•当0<a<1时，指数函数呈下降趋势，函数图像在x轴的右侧趋近于0。

•指数函数在x=0处必过点(0,1)。

•指数函数在不同的底数a下，增长或减小的速率有所差异。

3. 指数函数练习题
1.计算23的值。

2.求解方程3x=9。

3.指数函数f(x)=2x的图像经过点(0,1)和(1,2)，试求f(2)的值。

4.若指数函数g(x)=4x，求g(−1)的值。

4. 解答
1.$2^3 = 2 \\times 2 \\times 2 = 8$，所以23的值为8。

2.化简方程3x=9可得x=2，因为32=9。

3.由已知条件可知，f(1)=2，f(0)=1，根据指数函数的性质f(2)=
22=4。

4.$g(-1) = 4^{-1} = \\frac{1}{4}$。

5. 总结
通过以上练习题，我们对指数函数的基本概念和性质有了更深入的理解。

在计算指数函数值时，可以利用指数函数的性质和常用计算方法来简化计算过程。

熟练掌握指数函数的求值方法有助于提高数学解题的效率，加深对指数函数的认识。

以上是关于指数函数练习题的相关内容，希望对读者有所帮助。

指数函数的运算法则练习题

指数函数的运算法则练习题1. 求解以下指数函数的运算结果：a) 如果f(x) = 2^x 和 g(x) = 2^(2x+1)，求f(x) × g(x)的结果。

解析：根据指数函数的运算法则，当底数相同时，指数相加表示两个函数相乘。

所以f(x) × g(x)可以简化为 2^x × 2^(2x+1)。

利用指数函数的运算法则，我们可以将这个乘法式简化为一个式子，即2^(x + (2x+1))。

进一步化简，可以得出f(x) × g(x) = 2^(3x+1)。

b) 如果h(x) = 3^x 和 k(x) = (3^x)^2，求h(x) ÷ k(x)的结果。

解析：根据指数函数的运算法则，当一个指数函数的指数再次取指数时，等效于指数相乘。

所以k(x)可以简化为 3^(x × 2)。

利用指数函数的运算法则，我们可以将这个除法式简化为一个式子，即3^x ÷ 3^(2x)。

根据指数函数的运算法则，当两个指数相减时，等效于两个函数相除。

所以h(x) ÷ k(x)可以简化为 3^x ÷ (3^x × 3^(2x))。

进一步化简，可以得出h(x) ÷ k(x) = 3^x ÷ 3^(3x)。

2. 计算以下指数函数的值：a) 如果f(x) = 5^2x，求f(3)的值。

解析：将x替换为3，可以得出f(3) = 5^(2×3) = 5^6。

通过计算，可以得出f(3)的值为15625。

b) 如果g(x) = (1/4)^x，求g(-2)的值。

解析：将x替换为-2，可以得出g(-2) = (1/4)^(-2) = 4^2。

通过计算，可以得出g(-2)的值为16。

3. 给定一个指数函数f(x) = (1/2)^(x+2)，求解方程f(x) = 1。

解析：将f(x)替换为1，可以得出(1/2)^(x+2) = 1。

指数函数的练习题

指数函数的练习题指数函数是高中数学中的重要内容，它在数学和实际生活中都有广泛的应用。

通过练习题的形式，我们可以更好地理解和掌握指数函数的相关概念和性质。

下面，我将给大家提供一些指数函数的练习题，希望能够对大家的学习有所帮助。

练习题一：简单指数函数计算1. 计算 $2^3$ 和 $(-3)^2$ 的值。

2. 计算 $10^{-2}$ 和 $\left(\frac{1}{2}\right)^{-3}$ 的值。

练习题二：指数函数的性质1. 如果 $a > 1$，那么 $a^x$ 是否是递增函数？为什么？2. 如果 $0 < a < 1$，那么 $a^x$ 是否是递增函数？为什么？3. 如果 $a > 1$，那么 $a^x$ 是否有上界？为什么？练习题三：指数函数的图像1. 画出函数 $y = 2^x$ 和 $y = \left(\frac{1}{2}\right)^x$ 的图像。

2. 画出函数 $y = 3^x$ 和 $y = \left(\frac{1}{3}\right)^x$ 的图像。

练习题四：指数函数的应用1. 假设某种细菌的数量每小时增加50%，现在有1000个细菌，经过多少小时后细菌的数量会达到5000个？2. 一笔投资每年以5%的利率复利计算，如果初始投资为10000元，经过多少年后投资会翻倍？练习题五：指数函数的方程1. 解方程 $2^x = 8$。

2. 解方程 $3^{2x-1} = \frac{1}{9}$。

通过以上的练习题，我们可以加深对指数函数的理解和运用。

在计算指数函数的值时，我们需要注意底数的正负以及指数的大小。

指数函数的性质也是我们需要掌握的重要内容，它们对于理解函数的增减性和图像的变化有着重要的影响。

通过绘制指数函数的图像，我们可以更直观地观察函数的特点和变化趋势。

指数函数在实际生活中也有广泛的应用。

在金融领域中，复利计算常常使用指数函数的概念。

指数函数经典例题(答案)

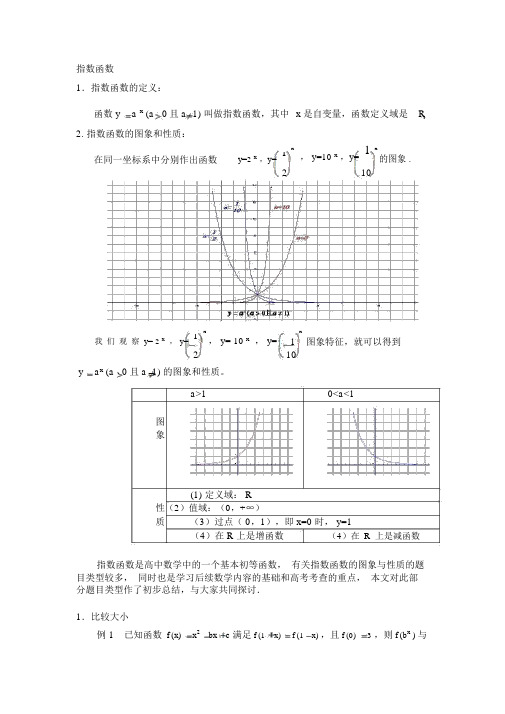
指数函数1．指数函数的定义：函数 y a x (a 0且a 1) 叫做指数函数，其中 x 是自变量，函数定义域是 R2. 指数函数的图象和性质：x ， y=10 x ，y=1x在同一坐标系中分别作出函数y=2 x，y=1的图象 .2 10x x我们观察 y= 2 x ， y=1， y= 10 x ， y=1 图象特征，就可以得到 210y a x (a 0且a 1) 的图象和性质。

a>10<a<1图象11(1) 定义域： R性（2）值域：（0，+∞）质（3）过点（ 0，1），即 x=0 时， y=1（4）在 R 上是增函数（4）在 R 上是减函数指数函数是高中数学中的一个基本初等函数，有关指数函数的图象与性质的题目类型较多，同时也是学习后续数学内容的基础和高考考查的重点，本文对此部分题目类型作了初步总结，与大家共同探讨． 1．比较大小例 1 已知函数 f (x)x 2 bx c 满足 f (1 x) f (1 x) ，且 f (0) 3 ，则 f (b x ) 与f ( c x ) 的大小关系是_____．分析：先求 b， c 的值再比较大小，要注意b x， c x的取值是否在同一单调区间内．解：∵ f (1 x) f (1 x) ，∴函数 f ( x) 的对称轴是x 1 ．故 b 2，又 f (0) 3 ，∴c 3 ．∴函数 f ( x) 在∞，1 上递减，在1，∞上递增．若 x ≥ 0 ，则 3x≥ 2x≥ 1 ，∴f(3x)≥f(2x)；若 x 0 ，则3x 2 x 1 ，∴f (3x) f (2x ) ．综上可得 f (3x )≥ f (2x ) ，即 f (c x ) ≥ f (b x ) ．评注：①比较大小的常用方法有：作差法、作商法、利用函数的单调性或中间量等．②对于含有参数的大小比较问题，有时需要对参数进行讨论．2．求解有关指数不等式例 2 已知(a22a5)3 x(a22a 5)1 x，则x的取值范围是___________．分析：利用指数函数的单调性求解，注意底数的取值范围．解：∵ a22a 5 ( a 1)24≥4 1，∴函数 y(a22a5)x在(∞，∞)上是增函数，∴ 3x 1x ，解得x 1．∴ x 的取值范围是1，∞．44评注：利用指数函数的单调性解不等式，需将不等式两边都凑成底数相同的指数式，并判断底数与 1 的大小，对于含有参数的要注意对参数进行讨论．3．求定义域及值域问题例 3求函数 y 1 6x 2的定义域和值域．解：由题意可得 16x2≥ 0 ，即 6x 2≤ 1 ，∴ x 2 ≤ 0 ，故 x ≤ 2．∴函数 f (x) 的定义域是∞，2 ．令 t6x 2，则 y1t ，又∵ x≤ 2 ，∴ x 2 ≤ 0 ．∴ 0 6x 2≤ 1 ，即 0 t ≤ 1 ．∴ 0 ≤ 1 t 1，即 0 ≤ y 1 ．∴函数的值域是01，．评注：利用指数函数的单调性求值域时，要注意定义域对它的影响．4．最值问题例 4函数y a2x2a x1(a 0且a 1)在区间[ 11]，上有最大值14，则 a 的值是 _______．分析：令 t a x可将问题转化成二次函数的最值问题，需注意换元后t 的取值范围．解：令t a x，则t0 ，函数y a2 x2a x 1 可化为y(t1)2 2 ，其对称轴为t1．∴当 a 1 时，∵x11，，∴1≤ a x≤ a ，即1≤ t ≤ a ．a a∴当 t a 时，y max(a1)2214．解得 a 3 或 a 5 （舍去）；当 0 a 1 时，∵x11，，∴ a ≤ a x≤1，即 a ≤ t ≤1，a a1时， y max12∴ t1214 ，a a解得 a 1或 a1（舍去），∴ a 的值是 3 或1．353评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．5．解指数方程例 5 解方程3x 232x80 ．解：原方程可化为9 (3x )280 3x9 0 ，令 t3x (t0)，上述方程可化为9t 280t 9 0 ，解得t9或 t1（舍去），∴ 3x9，∴ x 2 ，经检验原方程的9解是 x 2 ．评注：解指数方程通常是通过换元转化成二次方程求解，要注意验根．6．图象变换及应用问题例 6 为了得到函数y 9 3x 5 的图象，可以把函数y3x的图象（）．A．向左平移 9 个单位长度，再向上平移 5 个单位长度B．向右平移 9 个单位长度，再向下平移 5 个单位长度C．向左平移 2 个单位长度，再向上平移 5 个单位长度D．向右平移 2 个单位长度，再向下平移 5 个单位长度分析：注意先将函数 y9 3x 5 转化为t3x 2 5 ，再利用图象的平移规律进行判断．解：∵ y 9 3x 5 3x 2 5 ，∴把函数y 3 x的图象向左平移2个单位长度，再向上平移 5 个单位长度，可得到函数y 93x 5 的图象，故选（C）．评注：用函数图象解决问题是中学数学的重要方法，利用其直观性实现数形结合解题，所以要熟悉基本函数的图象，并掌握图象的变化规律，比如：平移、伸缩、对称等．习题1、比较下列各组数的大小：（1）若，比较与；（2）若，比较与；（3）若，比较与；（）若，且，比较 a 与 b；4 a 与 b．（）若，且，比较5解：（1）由，故，此时函数为减函数．由，故．（ 2）由，故．又，故．从而．而（3）由．，因，故．又，故．从（4）应有．又因．因若，故，则．从而．又，故，这与已知，这样矛盾．（5）应有．又因．因若，且，则，故．又．从而，故，这样有，这与已知矛盾．小结：比较通常借助相应函数的单调性、奇偶性、图象来求解．2，曲线则分别是指数函数与 1 的大小关系是 ( ).,和的图象 ,(分析 : 首先可以根据指数函数单调性 , 确定, 在轴右侧令, 对应的函数值由小到大依次为 ,故应选 .小结 : 这种类型题目是比较典型的数形结合的题目 , 第(1) 题是由数到形的转化 , 第(2) 题则是由图到数的翻译 , 它的主要目的是提高学生识图 , 用图的意识 . 求最值3，求下列函数的定义域与值域 .1(1)y ＝2 x 3 ; (2)y＝4x +2x+1+1.11解：(1) ∵ x-3 ≠0，∴ y ＝2 x 3 的定义域为｛ x ｜ x ∈R 且 x ≠3｝. 又∵ ≠x 310，∴ 2 x 3 ≠1，1∴y ＝2 x 3 的值域为｛ y ｜y>0 且 y ≠1｝.(2)y ＝ 4x +2x+1+1 的定义域为 R. ∵ 2x >0, ∴ y ＝ 4x +2x+1+1＝ (2 x ) 2+2· 2x +1＝x2(2 +1) >1.∴ y ＝4x +2x+1 +1 的值域为｛ y ｜ y>1｝.4，已知-1≤x ≤2, 求函数 f(x)=3+2 ·3x+1-9 x 的最大值和最小值解：设 t=3 x, 因为 -1 ≤ x ≤ 2，所以1t 9 ，且 f(x)=g(t)=-(t-3)2+12, 故当 t=33即 x=1 时， f(x) 取最大值 12，当 t=9 即 x=2 时 f(x) 取最小值 -24 。

指数函数习题（经典含答案及详细解析）

2．函数f (x )＝x 2－bx ＋c 满足f (1＋x )＝f (1－x )且A ．f (b x )≤f (c x) B ．f (b x )≥f (c x) lg(a x －2x－5 ≥5 [9，(9，1，，1[1，[1，，1)上的最大值比最小值大，则234x x ---+11．(2011·银川模拟)若函数y ＝a 2x ＋2a x－1(a >0且a ≠1)在x ∈[－1,1]上的最大值为14，求a 的值．的值．12．已知函数f (x )＝3x ，f (a ＋2)＝18，g (x )＝λ·3ax －4x的定义域为[0,1]． (1)求a 的值；的值；(2)若函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．的取值范围．指数函数答案指数函数答案1.1.解析：由解析：由a ⊗b ＝îïíïìa a ≤bba >b得f (x )＝1⊗2x＝îïíïì2xx，1x答案：答案：A A 2. 2. 解析：∵解析：∵f (1(1＋＋x )＝f (1(1－－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)(0)＝＝3，∴c ＝3.3.∴∴f (x )在(－∞，－∞，1)1)1)上递减，在上递减，在上递减，在(1(1(1，＋∞)上递增．，＋∞)上递增．，＋∞)上递增．若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x)．若x <0<0，则，则3x<2x<1<1，∴，∴f (3x)>f (2x)． ∴f (3x )≥f (2x )．答案：答案：A A3.3.解析：由于函数解析：由于函数y ＝|2x－1|1|在在(－∞，－∞，0)0)0)内单调递减，在内单调递减，在内单调递减，在(0(0(0，＋∞)内单调递增，而函数在，＋∞)内单调递增，而函数在区间区间((k －1，k ＋1)1)内不单调，所以有内不单调，所以有k －1<0<k ＋1，解得－，解得－1<1<k <1. 答案：答案：C C4. 4. 解析：由题意得：解析：由题意得：A ＝(1,2)(1,2)，，a x －2x >1且a >2>2，由，由A ⊆B 知a x －2x>1在(1,2)(1,2)上恒成立，即上恒成立，即a x －2x －1>0在(1,2)(1,2)上恒成立，令上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0ln2>0，所以函数，所以函数u (x )在(1,2)(1,2)上单调递增，则上单调递增，则u (x )>u (1)(1)＝＝a －3，即a ≥3.≥3. 答案：答案：B B5. 5. 解析：数列解析：数列解析：数列{{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数，为增函数，注意a 8－6>(3>(3－－a )×7－)×7－33，所以îïíïìa >13－a >0a8－6－a －3，解得2<a <3.答案：答案：C C6. 6. 解析：解析：f (x )<12⇔x 2－a x <12⇔x 2－12<a x ，考查函数y ＝a x 与y ＝x 2－12的图象，的图象，当a >1时，必有a －1≥12，即1<a ≤2，≤2，当0<a <1时，必有a ≥12，即12≤a <1<1，，综上，12≤a <1或1<a ≤2.≤2.答案：答案：C C7. 7. 解析：当解析：当a >1时，y ＝a x 在[1,2][1,2]上单调递增，故上单调递增，故a 2－a ＝a 2，得a ＝32.当0<a <1时，y ＝ax 在[1,2][1,2]上单调递减，故上单调递减，故a －a 2＝a 2，得a ＝12.故a ＝12或32.答案：12或328. 8. 解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线曲线||y |＝2x＋1与直线y ＝b 的图象如图所示，由图象可得：如果的图象如图所示，由图象可得：如果||y |＝2x＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]1,1]．．答案：答案：[[－1,1]9. 9. 解析：如图满足条件的区间解析：如图满足条件的区间解析：如图满足条件的区间[[a ，b ]，当a ＝－＝－11，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－＝－11，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：答案：1 110. 10. 解：要使函数有意义，则只需－解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.≤1. ∴函数的定义域为∴函数的定义域为{{x |－4≤x ≤1}．≤1}．令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－＝－((x ＋32)2＋254，∴当－4≤x ≤1时，t max ＝254，此时x ＝－32，t min ＝0，此时x ＝－＝－44或x ＝1.∴0≤t ≤254.∴0≤－x 2－3x ＋4≤52.∴函数y ＝2341()2x x ---+的值域为的值域为[[28，1]1]．．＋)＋(≤－时，≤234()2x x ---+在，－32]－32，－32，，－32][1a，，1a ]＝1a，即(1a＋＝13或－15(或13.。

指数函数习题及答案完整版

指数函数习题及答案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】指数函数习题一、选择题1．定义运算ab＝，则函数f(x)＝12x的图象大致为( )2．函数f(x)＝x2－bx＋c满足f(1＋x)＝f(1－x)且f(0)＝3，则f(b x)与f(c x)的大小关系是( )A．f(b x)≤f(c x)B．f(b x)≥f(c x)C．f(b x)>f(c x)D．大小关系随x的不同而不同3．函数y＝|2x－1|在区间(k－1，k＋1)内不单调，则k的取值范围是( ) A．(－1，＋∞)B．(－∞，1)C．(－1,1) D．(0,2)4．设函数f(x)＝ln[(x－1)(2－x)]的定义域是A，函数g(x)＝lg(－1)的定义域是B，若AB，则正数a的取值范围( )A．a>3 B．a≥3C．a> D．a≥5．已知函数f(x)＝若数列{a n}满足a n＝f(n)(n∈N*)，且{a n}是递增数列，则实数a的取值范围是( )A．[，3) B．(，3)C．(2,3) D．(1,3)6．已知a>0且a≠1，f(x)＝x2－a x，当x∈(－1,1)时，均有f(x)<，则实数a 的取值范围是( )A．(0，]∪[2，＋∞)B．[，1)∪(1,4]C．[，1)∪(1,2]D．(0，)∪[4，＋∞)二、填空题7．函数y＝a x(a>0，且a≠1)在[1,2]上的最大值比最小值大，则a的值是________．8．若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是________．9．(2011·滨州模拟)定义：区间[x1，x2](x1<x2)的长度为x2－x1.已知函数y＝2|x|的定义域为[a，b]，值域为[1,2]，则区间[a，b]的长度的最大值与最小值的差为________．三、解答题10．求函数y＝211．(2011·银川模拟)若函数y＝a2x＋2a x－1(a>0且a≠1)在x∈[－1,1]上的最大值为14，求a的值．12．已知函数f(x)＝3x，f(a＋2)＝18，g(x)＝λ·3ax－4x的定义域为[0,1]．(1)求a的值；(2)若函数g(x)在区间[0,1]上是单调递减函数，求实数λ的取值范围．指数函数答案1.解析：由ab＝得f(x)＝12x＝答案：A2.解析：∵f (1＋x )＝f (1－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)＝3，∴c ＝3.∴f (x )在(－∞，1)上递减，在(1，＋∞)上递增．若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x )．若x <0，则3x <2x <1，∴f (3x )>f (2x )． ∴f (3x )≥f (2x )．答案：A3.解析：由于函数y ＝|2x －1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1. 答案：C4.解析：由题意得：A ＝(1,2)，a x －2x >1且a >2，由AB 知a x －2x >1在(1,2)上恒成立，即a x －2x －1>0在(1,2)上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0，所以函数u (x )在(1,2)上单调递增，则u (x )>u (1)＝a －3，即a ≥3. 答案：B5.解析：数列{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数，注意a 8－6>(3－a )×7－3，所以，解得2<a <3. 答案：C6.解析：f (x )<x 2－a x <x 2－<a x ，考查函数y ＝a x 与y ＝x 2－的图象，当a >1时，必有a －1≥，即1<a ≤2，当0<a <1时，必有a ≥，即≤a <1，综上，≤a <1或1<a ≤2. 答案：C7.解析：当a >1时，y ＝a x 在[1,2]上单调递增，故a 2－a ＝，得a ＝.当0<a <1时，y ＝a x 在[1,2]上单调递减，故a －a 2＝，得a ＝.故a ＝或. 答案：或8.解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线|y |＝2x ＋1与直线y ＝b 的图象如图所示，由图象可得：如果|y |＝2x ＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]．答案：[－1,1]9.解析：如图满足条件的区间[a ，b ]，当a ＝－1，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－1，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：110.解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1.∴函数的定义域为{x |－4≤x ≤1}．令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－(x ＋)2＋，∴当－4≤x ≤1时，t max ＝，此时x ＝－，t min ＝0，此时x ＝－4或x ＝1. ∴0≤t ≤.∴0≤≤.∴函数y ＝2341()2x x --+[，1]．由t ＝－x 2－3x ＋4＝－(x ＋)2＋(－4≤x ≤1)可知，当－4≤x ≤－时，t 是增函数，当－≤x ≤1时，t 是减函数．根据复合函数的单调性知：y ＝1()2[－4，－]上是减函数，在[－，1]上是增函数．∴函数的单调增区间是[－，1]，单调减区间是[－4，－]．11.解：令a x ＝t ，∴t >0，则y ＝t 2＋2t －1＝(t ＋1)2－2，其对称轴为t ＝－1.该二次函数在[－1，＋∞)上是增函数．①若a >1，∵x ∈[－1,1]，∴t ＝a x ∈[，a ]，故当t ＝a ，即x ＝1时，y max ＝a 2＋2a －1＝14，解得a ＝3(a ＝－5舍去)． ②若0<a <1，∵x ∈[－1,1]，∴t ＝a x∈[a ，]，故当t ＝，即x ＝－1时， y max ＝(＋1)2－2＝14. ∴a ＝或－(舍去)．综上可得a ＝3或.12.解：法一：(1)由已知得3a ＋2＝183a ＝2a ＝log 32. (2)此时g (x )＝λ·2x －4x ，设0≤x 1<x 2≤1，因为g (x )在区间[0,1]上是单调减函数，所以g (x 1)－g (x 2)＝(2x 1－2x 2)(λ－2x 2－2x 1)>0恒成立，即λ<2x 2＋2x 1恒成立．由于2x 2＋2x 1>20＋20＝2，所以实数λ的取值范围是λ≤2. 法二：(1)同法一．(2)此时g (x )＝λ·2x －4x ，因为g (x )在区间[0,1]上是单调减函数，所以有g ′(x )＝λln2·2x －ln4·4x ＝ln2[－2·(2x )2＋λ·2x ]≤0成立．设2x ＝u ∈[1,2]，上式成立等价于－2u 2＋λu ≤0恒成立．因为u ∈[1,2]，只需λ≤2u 恒成立，所以实数λ的取值范围是λ≤2.。

指数练习题及答案

指数练习题及答案一、选择题1. 计算下列哪个指数表达式的值等于32：A. $2^5$B. $4^3$C. $5^2$D. $3^4$2. 如果 $a^m = b^n$，且 $a$ 和 $b$ 都是正整数，$m$ 和$n$ 都是正整数，那么下列哪个选项是正确的？A. $a = b$B. $m = n$C. $a = b^{\frac{1}{n}}$D. 无法确定3. 指数函数 $y = 2^x$ 的图像在 x 轴上的截距是：A. 0B. 1C. -1D. 没有截距4. 以下哪个表达式是正确的：A. $(a^m)^n = a^{mn}$B. $(a^m)^n = a^{n^m}$C. $(a^m)^n = a^{n/m}$D. $(a^m)^n = a^{m/n}$5. 如果 $x$ 和 $y$ 是正数，且 $x^2 = y^3$，那么 $x$和 $y$ 的关系是：A. $x = y$B. $x = y^{\frac{3}{2}}$C. $x = y^{\frac{2}{3}}$D. $x = y^2$二、填空题6. 计算 $3^3$ 的结果是______。

7. 如果 $2^6 = 64$，那么 $2^{12}$ 等于______。

8. 根据指数法则，$(a \cdot b)^n = a^n \cdot b^n$，那么 $(3 \cdot 5)^2$ 等于______。

9. 如果 $4^x = 16$，那么 $x$ 的值是______。

10. 计算 $(\frac{1}{2})^{-2}$ 的结果是______。

三、解答题11. 证明：$(a^m)^n = a^{mn}$。

12. 给定 $a = 2$，$m = 3$，$n = 4$，计算 $(a^m)^n$。

指数函数精典习题

指数函数精典习题姓名函数图象：作出以下函数图象（1）2xy=（2）1()2xy=（3）12xy+=（4）21xy=+（5）2xy-=（6）||2xy=（7）||2xy-=（8）221xy-=+解析式、定义域、值域、识图问题1、若集合{}{}23,,2,xA y y x RB y y x x R==∈==-+∈，A B⋂=________.2、若3()(),012xf x x=<<，则有（）A、()1f x> B、0()1f x<< C、1() 1.5f x<< D、0() 1.5f x<<3、函数12xy+=的图象是下图中的（）、4、函数y=）A、(,0]-∞ B、(,1]-∞ C、[0,)+∞ D、[1,)+∞5、函数2xy-=的值域是（）A、(0,1)B、(0,1]C、(0,)+∞ D、(,)-∞+∞6、01,1a b<<<-，则函数()xf x a b=+的图象不经过（）A、第一象限B、第二象限C、第三象限D、第四象限7、若13()273x<<，则（）A、13x-<< B、1x<-或3x> C、31x-<<- D、13x<<8．函数⎪⎩⎪⎨⎧>≤-=-,,12)(21xxxxfx，满足1)(>xf的x的取值范围（）A．)1,1(-B．),1(+∞- C．}2|{-<>xxx或 D．}11|{-<>xxx或9、已知0a>_________________.10、已知指数函数()y f x=，且3()225f-=()y f x=的解析式是（）A、32y x= B、5xy-= C、5y x= D、5xy=11、求函数11()()()1,[3,2]42x xf x x=-+∈-的值域画出函数|13|-=xy的图象，并利用图象回答：k为何值时，方程|3x－１｜＝k无解？有一解？有两解？比较大小问题1、比较下列各组数的大小：（1）0.2_______25 ; （2）0.63()4-_______343()4-；（3）134()5-_______0.35()4；（4）0.53()2_______2、设1.50.90.4812314,8,2y y y-⎛⎫=== ⎪⎝⎭，则（）A、312y y y>> B、213y y y>> C、132y y y>> D、123y y y>>3、设.)32(,)32(2.15.1-==ba那么实数a、b与1的大小关系正确的是 ( )A. 1<<ab B. 1<<ba C. ab<<1 D. ba<<14、311213,32,2-⎪⎭⎫⎝⎛的大小顺序有小到大依次为_____________。

指数函数练习题

指数函数练习题1. 计算下列指数函数的值：- $ f(x) = 2^x $ 当 $ x = 3 $- $ g(x) = 3^x $ 当 $ x = -2 $- $ h(x) = 5^x $ 当 $ x = 0.5 $2. 确定下列指数函数的单调性：- $ f(x) = 4^x $- $ g(x) = (1/2)^x $3. 给定函数 $ y = a^x $，其中 $ a > 0 $ 且 $ a \neq 1 $，求当 $ x $ 增加时，函数值 $ y $ 的变化趋势。

4. 用指数函数表示下列数列的通项公式：- $ 2, 4, 8, 16, \ldots $- $ 1/8, 1/4, 1/2, 1, \ldots $5. 已知 $ f(x) = 2^x $，求 $ f(-2) $ 和 $ f(2) $ 的值。

6. 给定 $ y = 3^x $，求 $ x $ 使得 $ y = 27 $。

7. 证明指数函数 $ y = a^x $（其中 $ a > 0 $ 且 $ a \neq1 $）在其定义域内是连续的。

8. 一个细菌种群每分钟翻倍，初始时有 100 个细菌。

使用指数函数描述 30 分钟后细菌的数量。

9. 一个投资账户的本金为 $ P $，年利率为 $ r $（以小数形式表示），假设每年复利一次，求该账户 $ t $ 年后的金额。

10. 已知 $ f(x) = 10^x $，求 $ f(-1) $，$ f(0) $，和$ f(1) $ 的值。

11. 给定 $ y = 2^x $，求 $ x $ 使得 $ y = 32 $。

12. 证明对于所有 $ x > 0 $，指数函数 $ y = e^x $ 总是大于$ y = x $。

13. 一个物体从高度 $ h $ 落下，忽略空气阻力，其下落距离$ s $ 可以用 $ s = 0.5gt^2 $ 表示，其中 $ g $ 是重力加速度，$ t $ 是时间。

指数函数专题训练

指数函数专题训练1. 指数函数的定义和特性- 指数函数可以用如下形式表示：f(x) = a^x，其中a是一个常数，称为底数，x是指数。

- 指数函数的定义域是所有实数，值域是正实数。

- 当底数a大于1时，指数函数是增长函数；当0 < a < 1时，指数函数是减少函数。

- 指数函数的图像为一个逐渐增长或减少的曲线，且不会与x 轴相交。

- 指数函数有以下的性质：- a^0 = 1，任何数的0次方都等于1。

- a^x * a^y = a^(x+y)，指数相加时，底数相乘。

- a^x / a^y = a^(x-y)，指数相减时，底数相除。

2. 指数函数的图像和性质探究- 结合实际情境，探究指数函数的图像和性质。

例如，比较a 为2和a为0.5时的指数函数图像，观察它们的变化趋势。

- 使用计算工具绘制指数函数的图像，并根据图像，讨论指数函数在不同区间上的增长或减少速度。

- 研究指数函数的性质，例如指数函数的导数和二阶导数，沿着它的图像观察变化趋势，并探究导数和二阶导数与指数函数相关的规律。

3. 指数函数的应用- 研究指数函数在实际问题中的应用，如金融领域中的复利计算，人口增长模型等。

- 研究指数函数在自然科学中的应用，如放射性衰变的模型，生态系统中的物种扩张模型等。

- 研究指数函数在工程领域中的应用，如电路中的电流增长和衰减模型，生物医学工程中的光强度计算模型等。

4. 指数函数的变形和拓展- 研究具有不同底数和指数的指数函数，探索它们的图像和性质。

- 研究含有常数和其他函数的指数函数，例如f(x) = a^x + b，探讨对图像和性质造成的影响。

- 考虑复数底数和指数的指数函数，研究它们的图像和性质。

5. 指数函数的计算和求解问题- 学习如何计算和化简含有指数函数的复合函数。

- 学习如何解指数函数的方程和不等式，例如a^x = b，a^x > b 等。

- 学习如何利用指数函数求解实际应用问题，例如利用指数函数计算复利、模拟人口增长等。

指数函数练习题(包含详细答案)

1．给出下列结论： ②n a n ＝|a |(n >1，n ∈N *，n 为偶数)；④若2x ＝16,3y ＝127，则x ＋y ＝7.其中正确的是( )A ．①②B ．②③C ．③④D ．②④答案 B解析 ∵2x ＝16，∴x ＝4，∵3y ＝127，∴y ＝－3.∴x ＋y ＝4＋(－3)＝1，故④错．2．函数y ＝16－4x 的值域是( )A ．[0，＋∞)B ．[0,4]C ．[0,4)D ．(0,4)答案 C3．函数f (x )＝3－x －1的定义域、值域是( )A ．定义域是R ，值域是RB ．定义域是R ，值域是(0，＋∞)C ．定义域是R ，值域是(－1，＋∞)D ．以上都不对答案 C解析 f (x )＝(13)x －1，∵(13)x >0，∴f (x )>－1.4．设y 1＝40.9，y 2＝80.48，y 3＝(12)－1.5，则( )A ．y 3>y 1>y 2B ．y 2>y 1>y 3C ．y 1>y 2>y 3D ．y 1>y 3>y 2 答案 D解析 y 1＝21.8，y 2＝21.44，y 3＝21.5，∵y ＝2x 在定义域内为增函数，∴y 1>y 3>y 2.5．函数f (x )＝a x －b 的图像如图，其中a ，b 为常数，则下列结论正确的是( )A ．a >1，b <0B ．a >1，b >0C ．0<a <1，b >0D ．0<a <1，b <0 答案 D6．(2014·成都二诊)若函数f (x )＝(a ＋1e x －1)cos x 是奇函数，则常数a 的值等于( ) A ．－1B ．1C ．－12D.12 答案 D7．(2014·山东师大附中)集合A ＝{(x ，y )|y ＝a }，集合B ＝{(x ，y )|y ＝b x ＋1，b >0，b ≠1}，若集合A ∩B 只有一个子集，则实数a 的取值范围是( )A ．(－∞，1)B ．(－∞，1]C ．(1，＋∞)D ．R 答案 B8．函数f (x )＝3·4x －2x 在x ∈[0，＋∞)上的最小值是( )A ．－112B ．0C ．2D ．10 答案 C解析设t ＝2x ，∵x ∈[0，＋∞)，∴t ≥1.∵y ＝3t 2－t (t ≥1)的最小值为2，∴函数f (x )的最小值为2.9．已知函数f (x )＝⎩⎨⎧x －1，x >0，2－|x |＋1，x ≤0.若关于x 的方程f (x )＋2x －k ＝0有且只有两个不同的实根，则实数k 的取值范围为( )A ．(－1,2]B ．(－∞，1]∪(2，＋∞)C ．(0,1]D ．[1，＋∞) 答案 A解析在同一坐标系中作出y ＝f (x )和y ＝－2x ＋k 的图像，数形结合即可．10．函数y ＝2|x |的定义域为[a ，b ]，值域为[1,16]，当a 变化时，函数b ＝g (a )的图像可以是( ) 答案 B解析函数y ＝2|x |的图像如图．当a ＝－4时，0≤b ≤4；当b ＝4时，－4≤a ≤0.11．若函数y ＝(a 2－1)x 在(－∞，＋∞)上为减函数，则实数a 的取值范围是________．答案 (－2，－1)∪(1，2)解析函数y ＝(a 2－1)x 在(－∞，＋∞)上为减函数，则0<a 2－1<1，解得1<a <2或－2<a <－1.12．函数y ＝a x 在[0,1]上的最大值与最小值的和为3，则a ＝________.答案 2解析 ∵y ＝a x 在[0,1]上为单调函数，∴a 0＋a 1＝3，∴a ＝2.13．(2014·沧州七校联考)若函数f (x )＝a |2x －4|(a >0，a ≠1)满足f (1)＝19，则f (x )的单调递减区间是________．答案 [2，＋∞)解析 f (1)＝a 2＝19，a ＝13，f (x )＝⎩⎪⎨⎪⎧ (13)2x －4，x ≥2，(13)4－2x ， x <2.∴单调递减区间为[2，＋∞)．14．若0<a <1,0<b <1，且，则x 的取值范围是________．答案 (3,4)解析 log b (x －3)>0，∴0<x －3<1，∴3<x <4.15．若函数y ＝2－x ＋1＋m 的图像不经过第一象限，则m 的取值范围是______．答案 m ≤－216．是否存在实数a ，使函数y ＝a 2x ＋2a x －1(a >0且a ≠1)在[－1,1]上的最大值是14?答案 a ＝3或a ＝13解析令t ＝a x ，则y ＝t 2＋2t －1.(1)当a >1时，∵x ∈[－1,1]，∴a x ∈[1a ，a ]，即t ∈[1a ，a ]．∴y ＝t 2＋2t －1＝(t ＋1)2－2在[1a ，a ]上是增函数(对称轴t ＝－1<1a )．∴当t ＝a 时，y max ＝(a ＋1)2－2＝14.∴a ＝3或a ＝－5.∵a >1，∴a ＝3.(2)当0<a <1时，t ∈[a ，1a]． ∵y ＝(t ＋1)2－2在[a ，1a ]上是增函数， ∴y max ＝(1a ＋1)2－2＝14.∴a ＝13或a ＝－15.∵0<a <1，∴a ＝13.综上，a ＝3或a ＝13.17．(2011·上海)已知函数f (x )＝a ·2x ＋b ·3x ，其中a ，b 满足a ·b ≠0.(1)若a ·b >0，判断函数f (x )的单调性；(2)若a ·b <0，求f (x ＋1)>f (x )时的x 的取值范围．答案 (1)a >0，b >0时，f (x )增函数；a <0，b <0时，f (x )减函数(2)a <0，b >0时，x >log 1.5⎝ ⎛⎭⎪⎫－a 2b ；a >0，b <0时，x <log 1.5⎝ ⎛⎭⎪⎫－a 2b 解析 (1)当a >0，b >0时，任意x 1，x 2∈R ，x 1<x 2，∴f (x 1)－f (x 2)<0，∴函数f (x )在R 上是增函数．当a <0，b <0时，同理，函数f (x )在R 上是减函数．(2)f (x ＋1)－f (x )＝a ·2x ＋2b ·3x >0.当a <0，b >0时，⎝ ⎛⎭⎪⎫32x >－a 2b ，则x >log 1.5⎝ ⎛⎭⎪⎫－a 2b ；当a >0，b <0时，⎝ ⎛⎭⎪⎫32x <－a 2b ，则x <log 1.5⎝ ⎛⎭⎪⎫－a 2b .18．已知函数f (x )＝－2x2x ＋1. (1)用定义证明函数f (x )在(－∞，＋∞)上为减函数；(2)若x ∈[1,2]，求函数f (x )的值域；(3)若g (x )＝a 2＋f (x )，且当x ∈[1,2]时g (x )≥0恒成立，求实数a 的取值范围．答案 (1)略 (2)[－45，－23] (3)a ≥85(2)∵f (x )在(－∞，＋∞)上为减函数，∴f (x )的值域为[－45，－23]．(3)当x ∈[1,2]时，g (x )∈[a 2－45，a 2－23]．∵g (x )≥0在x ∈[1,2]上恒成立，∴a 2－45≥0，∴a ≥85.。

指数函数练习题

指数函数练习题1.指数函数的基本概念指数函数是数学中一类重要的函数，常用于描述指数增长或指数衰减的情况。

其一般形式为：$y = a \cdot b^x$，其中 $a$ 和$b$ 是常数，$b。

0$ 且 $b \neq 1$。

指数函数的特点包括：当 $b。

1$ 时，函数呈指数增长趋势；当 $0 < b < 1$ 时，函数呈指数衰减趋势；当 $b = 1$ 时，函数退化为常数函数。

2.指数函数的求解与应用指数函数的求解主要涉及确定常数 $a$ 和 $b$ 的值，以及利用函数的性质进行计算。

示例1.已知函数 $y = 3 \cdot 2^x$，求当 $x = 2$ 时的函数值。

解答：将 $x = 2$ 代入函数表达式中，得到 $y = 3 \cdot 2^2 = 12$。

因此，当 $x = 2$ 时，函数值为 12.示例2.某车辆的初始价格为 10 万元，每年贬值 5%，求经过 5 年后车辆的价格。

示例2.某车辆的初始价格为 10 万元，每年贬值5%，求经过 5 年后车辆的价格。

解答：设经过 $x$ 年后车辆的价格为 $y$，则满足指数衰减的函数关系为 $y = 10 \times (1-0.05)^x$。

代入 $x = 5$，得到 $y = 10 \times (1-0.05)^5 \approx 7.788$ 万元。

因此，经过 5 年后车辆的价格约为 7.788 万元。

指数函数在实际生活中有广泛的应用，例如金融领域的复利计算、生物学中的指数增长模型、电子电路中的放大器响应曲线等。

3.指数函数的练习题练习题1.若指数函数 $y = a \cdot b^x$ 过点 $(1,4)$，并且在$x = 2$ 处的斜率为 1，求函数的表达式。

练习题1.若指数函数 $y = a \cdot b^x$ 过点 $(1,4)$，并且在 $x = 2$ 处的斜率为 1，求函数的表达式。

指数函数(经典题、易错题)

指数函数（经典题、易错题）指数函数（经典题、易错题）一．选择题（共22小题）1．若函数，且0≤x≤1，则有（）A．f（x）≥1B．C．D．2．函数y=（）x2+2x﹣1的值域是（）A．（﹣∞，4）B．（0，+∞）C．（0，4]D．[4，+∞）3．函数的值域为（）A．（0，1]B．（0，+∞）C．（1，+∞）D．（﹣∞，+∞）4．函数y=4x+2x+1+5，x∈[1，2]的最大值为（）A．20B．25C．29D．315．函数y=3|x|﹣1的定义域为[﹣1，2]，则函数的值域为（）A．[2，8]B．[0，8]C．[1，8]D．[﹣1，8]6．函数的值域是（）A．（0，+∞）B．（0，1）C．（0，1]D．[1，+∞）7．（2011?山东）若点（a，9）在函数y=3x的图象上，则tan的值为（）A．B．C．1D．8．设a、b、c、d都是大于零且不等于1的实数，y=ax、y=bx、y=cx、y=dx在同一坐标系中的图象如图（1）所示，则a、b、c、d的大小关系是（）A．a＞b＞c＞dB．a＞b＞d＞cC．a＞d＞c＞bD．a＞c＞b＞d9．如图，设a，b，c，d＞0，且不等于1，y=ax，y=bx，y=cx，y=dx在同一坐标系中的图象如图，则a，b，c，d的大小顺序（）A．a＜b＜c＜dB．a＜b＜d＜cC．b＜a＜d＜cD．b＜a＜c＜d10．（2012?四川）函数y=ax﹣a（a＞0，a≠1）的图象可能是（）A．B．C．D．11．把函数y=2x﹣2+3的图象按向量平移，得到函数y=2x+1﹣1的图象，则向量=（）A．（﹣3，﹣4）B．（3，4）C．（﹣3，4）D．（3，﹣4）12．函数y=3x﹣1的图象大致是（）A．B．C．D．13．函数f（x）=4x+5×2x﹣1+1的值域是（）A．（0，1）B．[1，+∞）C．（1，+∞）D．[0，1]14．已知a=，b=，c=，则下列关系中正确的是（）A．a＜b＜cB．c＜a＜bC．a＜c＜bD．b＜a＜c15．若a＞0，a≠1，则函数y=ax﹣1的图象一定过点（）A．（0，1）B．（1，1）C．（1，0）D．（0，﹣1）16．已知a，b∈R，且a＞b，则下列不等式中恒成立的是（）A．a2＞b2B．（）a＜（）bC．lg（a﹣b）＞0D．＞117．函数的单调增区间为（）A．[﹣1，+∞）B．（﹣∞，﹣1]C．（﹣∞，+∞）D．（﹣∞，0]18．函数y=ax﹣1+1（0＜a≠1）的图象必经过点（）A．（0，1）B．（1，1）C．（1，2）D．19．已知a=30.2，b=0.2﹣3，c=3﹣0.2，则a，b，c的大小关系是（）A．a＞b＞cB．b＞a＞cC．c＞a＞bD．b＞c＞a20．（2005?山东）下列大小关系正确的是（）A．0.43＜30.4＜log40.3B．0.43＜log40.3＜30.4C．log40.3＜0.43＜30.4D．log40.3＜30.4＜0.4321．设，则a，b，c的大小关系是（）A．a＞b＞cB．b＞a＞cC．b＞c＞aD．c＞b＞a22．比较a，b，c的大小，其中a=0.22，b=20.2，c=log0.22（）A．B．c＞a＞bC．a＞b＞cD．b＞a＞c二．填空题（共2小题）23．函数的单调递增区间是_________ ．24．（2005?上海）方程4x+2x﹣2=0的解是_________ ．指数函数（经典题、易错题）参考答案与试题解析一．选择题（共22小题）1．若函数，且0≤x≤1，则有（）A．f（x）≥1B．C．D．考点：指数函数的定义、解析式、定义域和值域．1091931专题：计算题．分析：结合指数函数数在[0，1]上的单调性可求．解答：解：∵0≤x≤1且函数单调递减∴故选D点评：本题主要考查了指数函数的单调性的应用，属于基础试题．2．函数y=（）x2+2x﹣1的值域是（）A．（﹣∞，4）B．（0，+∞）C．（0，4]D．[4，+∞）考点：指数函数的定义、解析式、定义域和值域．1091931专题：计算题．分析：本题是一个复合函数，求其值域可以分为两步来求，先求内层函数的值域，再求函数的值域，内层的函数是一个二次型的函数，用二次函数的性质求值域，外层的函数是一个指数函数，和指数的性质求其值域即可．解答：解：由题意令t=x2+2x﹣1=（x+1）2﹣2≥﹣2∴y=≤=4∴0＜y≤4故选C点评：本题考查指数函数的定义域和值域、定义及解析式，解题的关键是掌握住复合函数求值域的规律，由内而外逐层求解．以及二次函数的性质，指数函数的性质．3．函数的值域为（）A．（0，1]B．（0，+∞）C．（1，+∞）D．（﹣∞，+∞）考点：指数函数的定义、解析式、定义域和值域．1091931专题：计算题．分析：画出f（x）的图象，由f（x）图象f（x）可得的值域．解答：解：函数的图象如图：由f（x）的图象可得：f（x）的值域为（0，+∞）．故选B．点评：本题考查指数函数的值域，用到了指数函数的图象．4．函数y=4x+2x+1+5，x∈[1，2]的最大值为（）A．20B．25C．29D．31考点：指数函数的定义、解析式、定义域和值域；函数的最值及其几何意义．1091931专题：计算题．分析：由x∈[1，2]，知2≤2x≤4，把y=4x+2x+1+5转化为y=（2x+1）2+4，当2x=4时，ymax=（4+1）2+4=29．解答：解：∵x∈[1，2]，∴2≤2x≤4，∴y=4x+2x+1+5=（2x）2+2×2x+5=（2x+1）2+4，当2x=4时，ymax=（4+1）2+4=29．故选C．点评：本题考查指数函数的性质和应用，解题时要认真审题，注意配方法的合理运用．5．函数y=3|x|﹣1的定义域为[﹣1，2]，则函数的值域为（）A．[2，8]B．[0，8]C．[1，8]D．[﹣1，8]考点：指数函数的定义、解析式、定义域和值域．1091931专题：计算题．分析：设t=|x|可得出t∈[0，2]，根据指数函数的单调性求出值域即可．解答：解：设t=|x|∵函数y=3|x|﹣1的定义域为[﹣1，2]，∴t∈[0，2]∴y=3t﹣1∴y=3t﹣1在t∈[0，2]的值域为[0，8]故选B．点评：本题考查了指数函数的定义域和值域，求出函数y=3t﹣1的定义域是解题的关键，属于基础题．6．函数的值域是（）A．（0，+∞）B．（0，1）C．（0，1]D．[1，+∞）考点：指数函数的定义、解析式、定义域和值域．1091931专题：计算题．分析：本题是一个复合函数，求其值域可以分为两步来求，先求内层函数的值域，再求函数的值域，内层的函数是一个二次型的函数，用二次函数的性质求值域，外层的函数是一个指数函数，和指数的性质求其值域即可．解答：解：由题意令t=x2≥0∴y=≤=1∴0＜y≤1故选C点评：本题考查指数函数的定义域和值域、定义及解析式，解题的关键是掌握住复合函数求值域的规律，由内而外逐层求解．以及二次函数的性质，指数函数的性质．7．（2011?山东）若点（a，9）在函数y=3x的图象上，则tan的值为（）A．B．C．1D．考点：指数函数的图像与性质．1091931专题：计算题．分析：先将点代入到解析式中，解出a的值，再根据特殊三角函数值进行解答．解答：解：将（a，9）代入到y=3x中，得3a=9，解得a=2．∴=．故选D．点评：对于基本初等函数的考查，历年来多数以选择填空的形式出现．在解答这些知识点时，多数要结合着图象，利用数形结合的方式研究，一般的问题往往都可以迎刃而解．8．设a、b、c、d都是大于零且不等于1的实数，y=ax、y=bx、y=cx、y=dx在同一坐标系中的图象如图（1）所示，则a、b、c、d的大小关系是（）A．a＞b＞c＞dB．a＞b＞d＞cC．a＞d＞c＞bD．a＞c＞b＞d考点：指数函数的图像与性质．1091931专题：综合题．分析：通过作直线x=1与图象交于四点，利用这几个点的位置关系，从而确定a，b，c，d的大小关系．解答：解：∵a1=a，∴作直线x=1与图象分别交于A，B，C，D点，则它们纵坐标分别为：a，b，c，d由图a＞b＞c＞d故选A．点评：本题考查了指数函数的图象与性质，同时考查了数形结合的思想方法，是个基础题．9．如图，设a，b，c，d＞0，且不等于1，y=ax，y=bx，y=cx，y=dx在同一坐标系中的图象如图，则a，b，c，d的大小顺序（）A．a＜b＜c＜dB．a＜b＜d＜cC．b＜a＜d＜cD．b＜a＜c＜d考点：指数函数的图像与性质．1091931专题：数形结合．分析：要比较a、b、c、d的大小，根据函数结构的特征，作直线x=1，与y=ax，y=bx，y=cx，y=dx 交点的纵坐标就是a、b、c、d，观察图形即可得到结论．解答：解：作辅助直线x=1，当x=1时，y=ax，y=bx，y=cx，y=dx的函数值正好是底数a、b、c、d直线x=1与y=ax，y=bx，y=cx，y=dx交点的纵坐标就是a、b、c、d观察图形即可判定大小：b＜a＜d＜c故选：C．点评：本题主要考查了指数函数的图象与性质，同时考查了数形结合的数学思想，分析问题解决问题的能力，属于基础题．10．（2012?四川）函数y=ax﹣a（a＞0，a≠1）的图象可能是（）A．B．C．D．考点：指数函数的图像变换．1091931专题：计算题．分析：a＞1时，函数y=ax﹣a在R上是增函数，且图象过点（1，0），故排除A，B．当1＞a＞0时，函数y=ax﹣a在R上是减函数，且图象过点（1，0），故排除D，由此得出结论．解答：解：函数y=ax﹣a（a＞0，a≠1）的图象可以看成把函数y=ax的图象向下平移a个单位得到的．当a＞1时，函数y=ax﹣a在R上是增函数，且图象过点（1，0），故排除A，B．当1＞a＞0时，函数y=ax﹣a在R上是减函数，且图象过点（1，0），故排除D，故选C．点评：本题主要考查指数函数的图象变换，指数函数的单调性和特殊点，体现了分类讨论的数学思想，属于中档题．11．把函数y=2x﹣2+3的图象按向量平移，得到函数y=2x+1﹣1的图象，则向量=（）A．（﹣3，﹣4）B．（3，4）C．（﹣3，4）D．（3，﹣4）考点：指数函数的图像变换．1091931专题：计算题．分析：我们可以用待定系数法解答本题，先设出平移向量的坐标，根据函数图象的平移法则，我们可以求出平移后函数的解析式，根据已知我们可构造出一个关于h，k的二元一次方程组，解方程组即可求出平移向量的坐标．解答：解：设平移向量=（h，k）则函数y=2x﹣2+3的图象平移后得到的函数解析式为：y=2x﹣h﹣2+3+k即x﹣h﹣2=x+1且3+k=﹣1解得h=﹣3，k=﹣4故向量=（﹣3，﹣4）故选A点评：本题考查的知识点是函数图象的平移变换，其中根据平移法则“左加右减，上加下减”构造关于h，k的二元一次方程组，是解答本题的关键．12．函数y=3x﹣1的图象大致是（）A．B．C．D．考点：指数函数的图像变换．1091931专题：作图题．分析：可利用排除法解此选择题，由特殊点（0，0）在函数图象上可排除A、B；由特殊性质函数的值域为（﹣1，+∞），排除C，即可得正确选项解答：解：由函数y=3x﹣1的图象过（0，0）点，排除A、B，由函数y=3x﹣1的值域为（﹣1，+∞），排除C故选 D点评：本题考查了指数函数的图象变换，排除法解选择题13．函数f（x）=4x+5×2x﹣1+1的值域是（）A．（0，1）B．[1，+∞）C．（1，+∞）D．[0，1]考点：指数函数的单调性与特殊点．1091931专题：计算题．分析：令2x=t，t＞0，则函数f（x）=t2+t+1，利利用二次函数的性质求出值域．解答：解：令2x=t，t＞0，则函数f（x）=t2+t+1=﹣＞﹣=1，且由二次函数的性质知，函数f（x）=﹣无最大值，故值域为（1，+∞）．故选 C．点评：本题考查指数函数的单调性和值域，二次函数的值域的求法，体现了换元的思想．14．已知a=，b=，c=，则下列关系中正确的是（）A．a＜b＜cB．c＜a＜bC．a＜c＜bD．b＜a＜c考点：指数函数的单调性与特殊点．1091931专题：常规题型．分析：利用幂的运算性质将a化简；由于三个数同底；研究指数函数的单调性，判断出三个数的大小．解答：解：∵∵是同底数的幂考查指数函数是减函数故选D点评：本题考查指数函数的单调性取决于底数的范围、考查利用指数函数的单调性比较幂的大小．15．若a＞0，a≠1，则函数y=ax﹣1的图象一定过点（）A．（0，1）B．（1，1）C．（1，0）D．（0，﹣1）考点：指数函数的单调性与特殊点．1091931专题：计算题．分析：令令x﹣1=0求出x的值，代入解析式求出定点的坐标．解答：解：令x﹣1=0得，x=1，代入数y=ax﹣1=1，∴函数y=ax﹣1的图象一定过点（1，1），故选B．点评：本题考查了指数函数的图象过定点（0，1）的应用，令指数为零求解即可，是基础题．16．已知a，b∈R，且a＞b，则下列不等式中恒成立的是（）A．a2＞b2B．（）a＜（）bC．lg（a﹣b）＞0D．＞1考点：指数函数的单调性与特殊点．1091931专题：计算题．分析：不妨设 a=﹣1，b=﹣2，代入各个选项进行检验可得 A、C、D 都不正确，只有B正确，从而得到结论．解答：解：令 a=﹣1，b=﹣2，代入各个选项进行检验可得 A、C、D 都不正确，只有B正确，故选B．点评：本题考查不等式的性质，通过给变量取特殊值，举反例来说明某个命题不正确，是一种简单有效的方法．17．函数的单调增区间为（）A．[﹣1，+∞）B．（﹣∞，﹣1]C．（﹣∞，+∞）D．（﹣∞，0]考点：指数函数的单调性与特殊点．1091931专题：计算题．分析：分别判断出各段函数在其定义区间的单调性，根据同增异减口诀，先判断内层函数的单调性，再判断外层函数单调性，若两函数单调性相同，则此复合函数在此定义域上为增函数，反之则为减函数．解答：解：外层函数是，内层函数是y=x2+2x由题意可得外层函数是减函数∵根据复合函数同增异减的性质∴只要找到y=x2+2x的减区间即可∵y=x2+2x的对称轴是x=﹣1∴它的减区间为（﹣∞，﹣1）∴函数的增区间为（﹣∞，﹣1）．点评：复合函数的单调性一般是看函数包含的两个函数的单调性（1）如果两个都是增的，那么函数就是增函数（2）一个是减一个是增，那就是减函数（3）两个都是减，那就是增函数．18．函数y=ax﹣1+1（0＜a≠1）的图象必经过点（）A．（0，1）B．（1，1）C．（1，2）D．（0，2）考点：指数函数的单调性与特殊点．1091931专题：计算题．分析：由a0=1，可得当x=1时，函数y=ax﹣1+1=a0+1=2，从得到函数y=ax﹣1+1（0＜a≠1）的图象必经过的定点坐标．解答：解：由a0=1，可得当x=1时，函数y=ax﹣1+1=a0+1=2，故函数y=ax﹣1+1（0＜a≠1）的图象必经过点（1，2），故选C．点评：本题主要考查指数函数的单调性及特殊点，属于基础题．19．已知a=30.2，b=0.2﹣3，c=3﹣0.2，则a，b，c的大小关系是（）A．a＞b＞cB．b＞a＞cC．c＞a＞bD．b＞c＞a考点：指数函数单调性的应用．1091931专题：计算题．分析：先取中间量1，利用指数函数的图象性质，判断c最小，排除C、D；再将a、b两数变形比较，即可得正确选项解答：解：利用指数函数的图象性质知a＞1，b＞1，而c＜1，故c最小，排除C、D∵a=＜31=3，b==53=125∴b＞a故选B点评：本题主要考查了幂的大小的比较，利用指数函数图象和幂的运算性质比较大小的技巧20．（2005?山东）下列大小关系正确的是（）A．0.43＜30.4＜log40.3B．0.43＜log40.3＜30.4C．log40.3＜0.43＜30.4D．log40.3＜30.4＜0.43考点：指数函数单调性的应用．1091931专题：常规题型．分析：结合函数y=0.4x，y=3x，y=log4x的单调性判断各函数值与0和1的大小，从而比较大小．解答：解：∵0＜0.43＜0.40=1，30.4＞30=1，log40.3＜log0.41=0∴log40.3＜0.43＜30.4故选C点评：本题是指数函数与对数函数的单调性的简单应用，在比较指数（对数）式的大小时，若是同底的，一般直接借助于指数（对数）函数的单调性，若不同底数，也不同指（真）数，一般与1（0）比较大小．21．设，则a，b，c的大小关系是（）A．a＞b＞cB．b＞a＞cC．b＞c＞aD．c＞b＞a考点：指数函数单调性的应用．1091931专题：证明题．分析：先利用指数函数y=为R上的单调减函数，比较a、b的大小，排除A、B，再利用幂函数y=x3在R上为增函数，比较b、c的大小，即可得正确选项解答：解：考察函数y=为R上的单调减函数，∴，即a＜b，排除A、B；∵b3=，c3==，∴b3＞c3，考察幂函数y=x3在R上为增函数，∴b＞c，排除D；故选 C点评：本题主要考查了指数函数、幂函数的图象和性质，利用函数的单调性比较大小的方法和技巧，属基础题22．比较a，b，c的大小，其中a=0.22，b=20.2，c=log0.22（）A．b＞c＞aB．c＞a＞bC．a＞b＞cD．b＞a＞c考点：指数函数单调性的应用；不等式比较大小．1091931专题：计算题．分析：将log0.22看作函数y=log0.2x当x=2时所对应的函数值小于零，将a=0.22看作函数y=0.2x 当x=2时所对应的函数值小于1，将b=20.2看作函数y=2x当x=0.2时所对应的函数值大于1．解答：解：根据对数函数的性质可知c=log0.22＜0根据指数函数的性质可知0＜0.22＜1，20.2＞1∴b＞a＞c故选D点评：本题主要考查在数的比较中，我们要注意函数思想的应用．二．填空题（共2小题）23．函数的单调递增区间是（﹣1，+∞）．考点：指数函数综合题．1091931专题：计算题．分析：令t=x2+2x﹣3，则y=3t，本题即求函数t=x2+2x﹣3的增区间，由二次函数的性质可得函数t=x2+2x﹣3的增区间为（﹣1，+∞）．解答：解：函数=，令t=x2+2x﹣3，则y=3t．故本题即求函数t=x2+2x﹣3的增区间．由二次函数的性质可得函数t=x2+2x﹣3的增区间为（﹣1，+∞），故答案为（﹣1，+∞）．点评：本题主要考查指数型复合函数的单调性的应用，二次函数的性质，属于中档题．24．（2005?上海）方程4x+2x﹣2=0的解是0 ．考点：指数函数综合题．1091931专题：计算题；转化思想．分析：先换元，转化成一元二次方程求解，进而求出x的值．解答：解：令t=2x，则t＞0，∴t2+t﹣2=0，解得t=1或t=﹣2（舍）即2x=1；即x=0；故答案为0．点评：考查了指数运算，对于不是同底的指数问题，首先换成同一底数，体现了换元的思想，在换元中注意新变量的取值范围．属容易题．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一,填空题1有下列四个命题：其中正确的个数是（）①正数的偶次方根是一个正数；②正数的奇次方根是一个正数； ③负数的偶次方根是一个负数；④负数的奇次方根是一个负数。

A ．0B ．1C ．2D ．3 2、38-的值是（）A ．2B ．-2 C ．2±D ．8 3、给出下列等式：①2a a =；②2()a a =；③33a a =；④33()a a =.其中不一定正确的是()A ．①B ．②C ．③D ．④4、042(4)a a -+-有意义，则实数a 的取值范围是（） A ．2a ≥B ．24a ≤<或4a >C ．2a ≠D ．4a ≠5、若233441(12)a a a -+=-，则实数a 的取值范围是（） A ．12a ≥B ．12a ≤C ．1122a -≤≤D ．R6、1216-的值为（）A ．4B ．14C ．2D ．127、下列式子正确的是()A ．1236(1)(1)-=-B ．3355(2)2-=-C ．255()a a -=-D ．120-=8、将322-化为分数指数幂的形式为（）A ．122-B ．122--C ．132-D ．562-9.函数13x y =-的定义域是（）A 、(,0]-∞B 、(,1]-∞C 、[0,)+∞D 、[1,)+∞10.01,1a b <<<-，则函数()xf x a b =+的图象不经过（）A 、第一象限B 、第二象限C 、第三象限D 、第四象限 11.设137x=，则（） A 、21x -<<-B 、32x -<<-C 、10x -<<D 、01x << 12、若13()273x<<，则（） A 、13x -<<B 、1x <-或3x >C 、31x -<<-D 、13x <<二,填空题1、已知0a >，将a a a 化为分数指数幂的形式为_________________.2、计算或化简：（1）238()27-=___________（2）12113342(2)(3)x y x y --=_________________；3、已知38,35ab==，则233a b -=________________；4、若416,x =且x R ∈，则x =_________________. 5、求下列各式的值：（1）4823=____________；（2）425625=_________ （3）3313630.12548--=____________6.若0a >，且1a ≠，则函数21x y a -=+的图象一定过定点___________.7.比较下列各组数的大小：（1）0.2(3)_______25(3);（2）0.63()4-_______343()4-；（3）134()5-_______0.35()4；（4）0.53()2_______22()5 8.已知0.80.81m n>>,则m 、n 、0的大小关系为___________.9.0.70.50.80.8,0.8, 1.3,ab c ===则a 、b 、c 的大小关系为___________.10.函数121x y =-的定义域是___________，值域是___________.11.某厂2004年的产值为a 万元，预计产值每年以5%递增，该厂到2016年的产值是（）A 、13(15%)a +万元B 、12(15%)a +万元 C 、11(15%)a +万元D 、1210(15%)9+万元 6、函数2282x x y -++=的定义域是___________，值域是___________，增区间是___________，减区间是___________. 一、选择题 1、下列各式中，正确的是＿＿＿.(填序号) ①12()a a -=-;②133aa -=-；③2(0)a a a =-<；④3443()()()a aa b b=≠、b 0.2、已知a b R ∈、，则等式22()()()a b a b b a --=--成立的条件是＿＿＿.A ．a b > B.a b < C.a b = D.a b ≤ 3、下列运算正确的是＿＿＿.A.2332()()a a -=-B.235()a a -=-C.235()a a -=D.236()a a -=- 4、函数xa x f )1()(2-=是R 上的减函数，则a 的取值范围是() A.1 B.12 C.2 D.2a a a a ><<<>5、下列关系式中正确的是（）C.211233331.51.511112 D.22222--⎛⎫⎛⎫⎛⎫⎛⎫<<<< ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭6、当[]1,1-∈x 时函数23)(-=xx f 的值域是（）7、函数xa y =在[]1,0上的最大值与最小值的和为3，则a =() A.21B.2 C.4D.41 8、下列函数中指数函数的个数是(???). ?①23x y =－②13x y +=?③3x y =??④3y x =A 。

0个?????B 。

1个?????C 。

2个???????D .3个9、计算机成本不断降低,若每隔3年计算机价格降低13,现在价格为8100元的计算机,则9年后的价格为（） 2 y 20 x y-2A 2400元?????B 900元?????C 300元?????D 3600元二、填空题 10.已知234x -=，则x =＿＿＿.11.设0.90.48 1.512314,8,()2y y y -===，则123,,y y y 的大小关系是＿＿＿.12.函数()f x 的定义域为[1,4],则函数(2)xf -的定义域为＿＿＿.13.已知函数()f x 是定义在R 上的奇函数，当0x >时，()2xf x =，则(2)f -=＿＿＿. 三、解答题1.计算141030.7533270.064()[(2)]160.012-----+-++- 2.画出函数121x y -=-图像,并求定义域与值域。

3.求函数y =1151x x--的定义域.练习题2一、选择题1．下列函数中指数函数的个数是(). ①②?③??④A ．0个?B ．1个??C ．2个?D ．3个 2．若，，则函数的图象一定在（）A ．第一、二、三象限?B ．第一、三、四象限C ．第二、三、四象限?D ．第一、二、四象限 3．已知，当其值域为时，的取值范围是（）A ．?B ．C ．??D ．4．若，，下列不等式成立的是（） A ．??B ．?C ．??D ．5．已知且，，则是（）A．奇函数?B．偶函数C．非奇非偶函数?D．奇偶性与有关6．函数（）的图象是（）7．函数与的图象大致是(?).8．当时，函数与的图象只可能是（）9．在下列图象中，二次函数与指数函数的图象只可能是（）10．计算机成本不断降低,若每隔3年计算机价格降低,现在价格为8100元的计算机,则9年后的价格为().??A．2400元B．900元??C．300元?D．3600元二、填空题1．比较大小：（1）；??（2）______1；??（3）______2．若，则的取值范围为_________．3．求函数的单调减区间为__________．4．的反函数的定义域是__________．5．函数的值域是__________．6．已知的定义域为,则的定义域为__________.7．当时,,则的取值范围是__________.8．时，的图象过定点________．9．若,则函数的图象一定不在第_____象限.10．已知函数的图象过点,又其反函数的图象过点(2,0),则函数的解析式为____________.11．函数的最小值为____________.12．函数的单调递增区间是____________.13．已知关于的方程有两个实数解,则实数的取值范围是_________.14．若函数（且）在区间上的最大值是14，那么等于_________．三、解答题1．按从小到大排列下列各数：，，，，，，，2．设有两个函数与，要使（1）；（2），求、的取值范围．3．已知,试比较的大小.4．若函数是奇函数，求的值．5．已知，求函数的值域．6．解方程：（1）；?（2）．7．已知函数（且）（1）求的最小值；?（2）若，求的取值范围．8．试比较与的大小,并加以证明.9．某工厂从年到年某种产品的成本共下降了19%，若每年下降的百分率相等，求每年下降的百分率10．某工厂今年1月、2月、3月生产某产品分别为1万件、1.2件、1.3万件，为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量与月份数的关系，模拟函数可以选用二次函数或函数（其中、、为常数），已知四月份该产品的产量为1.37万件，请问用以上哪个函数作为模拟函数较好？请说明理由．11．设，求出的值．12．解方程．练习题3一、选择题（每小题4分，共计40分） 1．下列各式中成立的一项是（）A ．7177)(m n mn =B ．3339=C ．43433)(y x y x +=+D ．31243)3(-=-2．化简)31()3)((656131212132b a b a b a ÷-的结果（）A ．a 9-B ．a -C ．a 6D ．29a3．设指数函数)1,0()(≠>=a a a x f x，则下列等式中不正确．．．的是（）A ．f (x +y )=f(x )·f (y )B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)]([+∈=N n y f x f xy f nnn4．函数21)2()5(--+-=x x y（）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或5．若指数函数xa y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于（）A ．215+ B ．215- C ．215± D ．251± 6．方程)10(2||<<=a x ax 的解的个数为（）A.0个B.1个C.2个D.0个或1个 7．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R8．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围（）A ．)1,1(-B ．),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或9．已知2)(xx e e x f --=，则下列正确的是（）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 10．函数22)21(++-=x x y 得单调递增区间是（）A ．]1,(--∞B ．),2[+∞C ．]2,21[D ．]21,1[- 二、填空题（每小题4分，共计28分）11．已知0.622,0.6a b ==，则实数a b 、的大小关系为．12．不用计算器计算：48373271021.097203225.0+-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛--π=__________________． 13．不等式x x 283312--<⎪⎭⎫⎝⎛的解集是__________________________．14．已知{}2,1,0,1,2,3n ∈--，若11()()25nn->-，则=n ___________．15．不等式2221212-++⎪⎭⎫ ⎝⎛<⎪⎭⎫⎝⎛a x axx 恒成立，则a 的取值范围是．16．定义运算：⎩⎨⎧>≤=⊗)()(b a b b a a ba ，则函数()xx x f -⊗=22的值域为_________________ 17.如图所示的是某池塘中的浮萍蔓延的面积(2m )与时间t (月)的关系:ty a =,有以下叙述: ①这个指数函数的底数是2；②第5个月时,浮萍的面积就会超过230m ； ③浮萍从24m 蔓延到212m 需要经过1.5个月； ④浮萍每个月增加的面积都相等；⑤若浮萍蔓延到22m 、23m 、26m 所经过的时间分别为1t 、2t 、3t ，则123t t t +=. 其中正确的是．三、解答题：（10+10+12=32分） 18．已知17a a -+=，求下列各式的值:2 1 0 y/m 2 t/月2 3814（1）33221122a a a a----；（2）1122a a-+；（3）22(1)a a a -->.19.已知函数)1(122>-+=a a a y x x在区间[－1，1]上的最大值是14，求a 的值.20.（1）已知m x f x +-=132)(是奇函数，求常数m 的值；（2）画出函数|13|-=xy 的图象，并利用图象回答：k 为何值时，方程|31|x k -=无解？有一解？有两解？。