抽象语法树_图文-课件PPT(演示稿)-课件
注释语法分析树

注释语法分析树概念语法制导翻译的基本思想在语法分析基础上边分析边翻译•翻译的依据:语义规则或语义子程序•翻译的结果:相应的中间代码•翻译的做法:为每个产生式配置相应的语义子程序,每当使用某个产生式进行规约或推导时,就调用语义子程序,完成一部分翻译工作•语法分析完成时,翻译工作也告结束sdd && sdt•语法制导定义 syntax-directed definitions(sdd)o将文法符号和某些属性相关联规则与产生式相关联o并通过语义规则来描述如何计算属性的值 e → e 1+ t e . v a l = e 1. v a l + t . v a l e→e1+t e.val=e1.val + t.vale→e1+te.val=e1.val+t.val•语法制导的翻译方案 syntax-directed translationscheme(sdt)o在产生式体中加入语义动作,并在适当的时候执行这些语义动作o e → e 1 + t { e . v a l = e 1. v a l + t . va l ; } e → e1+t \{e.val=e1.val + t.val;\}e→e1+t{e.val=e1.val+t.val;}语义规则•描述一个产生式所对应的翻译工作,如:o改变某些变量的值;o填/查各种符号表;o发现并报告源程序错误;o产生中间代码•决定于翻译的目的,例如:产生什么样的中间代码文法属性(s,l)•综合属性:分析树节点n上的非终结符的综合属性只能通过该节点或子节点的属性来定义。
终结符可以具有综合属性,值由词法分析器提供。
•继承属性分析树节点n上的非终结符的继承属性只能通过该节点或父节点或兄弟节点的属性来定义。
终结符没有继承属性sdd•只包含综合属性的sdd称为s属性的sdd•含有继承属性的sdd在对sdd的求值过程中,如果结点n的属性a依赖于结点m1的属性a1, m2的属性a2,…。
抽象语法树(AST)

抽象语法树(AST)抽象语法树(AST)最近在做一个类JAVA语言的编译器,整个开发过程,用抽象语法树(Abstract SyntaxTree,AST)作为程序的一种中间表示,所以首先就要学会建立相对应源代码的AST和访问AST。
Eclipse AST是Eclipse JDT的一个重要组成部分,定义在包org.eclipse.jdt.core.dom中,用来表示JAVA语言中的所有语法结构。
Eclipse AST的总体结构1、org.eclipse.jdt.core.dom.AST(AST节点类)Eclipse AST的工厂类,用于创建表示各种语法结构的节点。
2、org.eclipse.jdt.core.dom.ASTNode及其派生类(AST类)用于表示JAVA语言中的所有语法结构,在实际使用中常作为AST 上的节点出现。
3、org.eclipse.jdt.core.dom.ASTVisitor(ASTVisitor类)Eclipse AST的访问者类,定义了统一的访问AST中各个节点的方法。
详细介绍:一、AST节点类整体结构包括CompilationUnit类(编译单元)、TypeDeclaration类(类型声明)、MethodDeclaration类(方法声明);语句包括Block类(语句块)、ExpressionStatement类(表达式)、IfStatement(if语句)、WhileStatement类(while语句)、EmptyStatement类(空语句)、BreakStatement类和ContinueStatement类;表达式包括MethodInvocation类(方法调用)、Assignment 类(赋值表达式)(“=”、“+=”、“-=”、“*=”、“/=”)、InfixExpression类(中缀表达式)(“+”、“-”、“*”、“/”、“%”、“==”、“!=”、“<"、“<=”、“>=”、“&&”、“||”。
抽象语法树(AST)

抽象语法树(AST)AST描述 在计算机科学中,抽象语法树(AST)或语法树是⽤编程语⾔编写的源代码的抽象语法结构的树表⽰。
树的每个节点表⽰在源代码中出现的构造。
语法是“抽象的”,因为它不代表真实语法中出现的每个细节,⽽只是结构,内容相关的细节。
例如,分组括号在树结构中是隐式的,并且可以通过具有三个分⽀的单个节点来表⽰类似于if-condition-then表达式的句法结构。
这将抽象语法树与传统上指定的解析树区分开来,这些语法树通常由解析器在源代码转换和编译过程中构建。
⼀旦构建,通过后续处理(例如,上下⽂分析)将附加信息添加到AST 。
抽象语法树也⽤于程序分析和程序转换系统。
参考:[维基百科]()解析器Parser JavaScript Parser是把js源码转化为抽象语法树的解析器,⼀般分为词法分析、语法分析及代码⽣成或执⾏。
词法分析 词法分析阶段会把字符串形式的代码转换为令牌(Tokens)流。
可将令牌看作是⼀个扁平的语法⽚段数组。
var answer = 6 * 7;//Tokens[{"type": "Keyword","value": "var","range": [34,37],"loc": {"start": {"line": 2,"column": 0},"end": {"line": 2,"column": 3}}},{"type": "Identifier", "value": "answer", "range": [38,44],"loc": {"start": {"line": 2,"column": 4},"end": {"line": 2,"column": 10 }}},{"type": "Punctuator", "value": "=","range": [45,46],"loc": {"start": {"line": 2,"column": 11 },"end": {"line": 2,"column": 12 }}},{"type": "Numeric", "value": "6","range": [47,48],"loc": {"start": {"line": 2,"column": 13 },"end": {"line": 2,"column": 14 }}},{"type": "Punctuator", "value": "*","range": [49,50],"loc": {"start": {"line": 2,"column": 15 },"end": {"line": 2,"column": 16 }}},{"type": "Numeric", "value": "7","range": [51,52],"loc": {"start": {"line": 2,"column": 17},"end": {"line": 2,"column": 18}}},{"type": "Punctuator","value": ";","range": [52,53],"loc": {"start": {"line": 2,"column": 18},"end": {"line": 2,"column": 19}}}]语法分析 语法分析阶段会把⼀个令牌流转换成抽象语法树(AST)的形式,这个阶段会使⽤令牌中的信息把它们转换成⼀个AST的树结构。
语法树

抽象语法树 Abstract Syntax Tree, AST
Tom 2015/02/25
Agenda
• 编译步骤(Compile step) • 抽象语法树(Abstract Syntax Tree(AST)) • Eclipse AST • JavaCC AST • Clang AST
翻译步骤
操作。
2022/3/23
访问者模式(Visitor Pattern)
package com.tom.vistor;
public abstract class Node { /** * 接受操作 */ public abstract void accept(Visitor visitor);
}
package com.tom.vistor;
2022/3/23
抽象语法树 Abstract Syntax Tree(AST)
语法分析程序从扫描程序中获取记号形式的源代码, 并完成定义程序结构的语法分析(syntax analysis)。 语法分析定义了程序的结构元素及其关系。通常将语 法分析的结果表示为分析树( parse tree)或语法树 (syntax tree)
访问者模式涉及到的角色如下: ● 抽象访问者(Visitor)角色:声明了一个或者多个方法操作,形 成所有的具体访问者角色必须实现的接口。 ● 具体访问者(ConcreteVisitor)角色:实现抽象访问者所声明的 接口,也就是抽象访问者所声明的各个访问操作。 ● 抽象节点(Node)角色:声明一个接受操作,接受一个访问者对 象作为一个参数。 ● 具体节点(ConcreteNode)角色:实现了抽象节点所规定的接受 操作。 ● 结构对象(ObjectStructure)角色:有如下的责任,可以遍历结 构中的所有元素;如果需要,提供一个高层次的接口让访问者对象可以 访问每一个元素;如果需要,可以设计成一个复合对象或者一个聚集, 如List或Set。
离散数学——树ppt课件

(1)(2)
如果G是树,则G中任意两个顶点之间存在唯一的路径。
存在性。 由G的连通性及定理14.5的推论(在n阶图G中,若从顶点vi到 vj(vivj)存在通路,则vi到vj 一定存在长度小于等于n-1的初级 通路(路径))可知,
u,v∈V,u与v之间存在路径。
唯一性(反证法)。 若路径不是唯一的,设Г1与Г2都是u到v的路径, 易知必存在由Г1和Г2上的边构成的回路, 这与G中无回路矛盾。
ij,i, j互不为前缀,则称A为前缀码。
若i(i=1,2,…,m)中只出现0与1两个符号,则称A为二元前缀码。 (2)如何产生二元前缀码? 定理16.6 由一棵给定的2叉正则树,可以产生唯一的一个二元前缀
码。
35
方法:
将每个分支点引出的两条边分别标上0和1。
结果:
图所示树产生的前缀码为{00, 10, 11, 011, 0100, 0101}。
r叉完全正则有序树——r叉完全正则树是有序的
30
最优二叉树
定义16.9 设2叉树T有t片树叶v1, v2, …, vt,权分别为w1, w2,
t
…, wt,称 W (t) wil(vi ) 为T的权,其中l(vi)是vi的层数, i 1
在所有有t片树叶、带权w1, w2, …, wt的2叉树中,权最小的 2叉树称为最优2叉树。
1,1,1,2,2,2,3
由度数列可知,Ti中有一个3度顶点vi,vi的邻域N(vi)中有3个 顶点,这3个顶点的度数列只能为以下三种情况之一:
1,1,2
1,2,2
2,2,2
设它们对应的树分别为T1,T2,T3。此度数列只能产生这三棵 非同构的7阶无向树。
15
例16.2
抽象语法树对应的代码
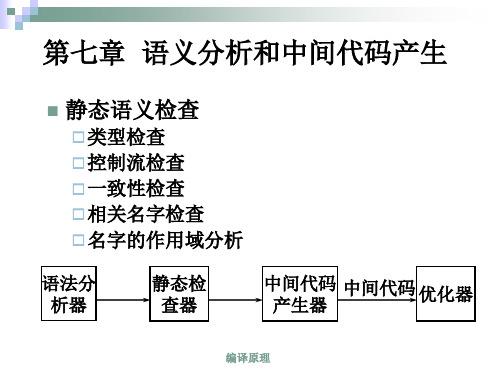
1. 如果E是一个变量或常量,则E的后缀式是E 自身。
2. 如果E是E1 op E2形式的表达式,其中op是任 何二元操作符,则E的后缀式为E1 E2 op,其 中E1 和E2 分别为E1 和E2的后缀式。
3. 如果E是(E1)形式的表达式,则E1 的后缀式就 是E的后缀式。
•把表达式翻译成后缀式的语义规则描述
产生式 E→E(1)op E(2) E→ (E(1)) E→id
语义动作 E.code:= E(1).code || E(2).code ||op E.code:= E(1).code E.code:=id
• E.code表示E后缀形式 • op表示任意二元操作符 • “||”表示后缀形式的连接。
{POST[k]:=op;k:=k+1} {}
E→i
{POST[k]:=i;k:=k+1}
例:输入串a+b+c的分析和翻译 POST: 1 2 3 4 5
a b + c +…
编译原理
7.1.2 图表示法
图表示法
DAG 抽象语法树
编译原理
7.1.2 图表示法
无循环有向图(Directed Acyclic Graph, 简称DAG)
+
*
b
uminus
c DAG
assign
抽象语法树对应的代码:
a
+
*
*
b uminus b uminus
c 抽象语法树
c
编译原理
T1:=-c T2:=b*T1 T3:=-c T4:=b*T3 T5:=T2+T4 a:=T5
assign
tiny语法及其抽象语法树

第15讲
TINY语言的语法
3.7 TINY语言的语法
3.7.l TINY的上下文无关文法 P97程序清单3-1
3.3.2 抽象语法树
根据翻译的需要,对分析树的必要信息的浓缩。 抽象语法树的构成方法: 操作符作为中间结点,而它的各个操作数是它的 孩子结点。 表达式3 + 4的分析树: 抽象语法树:
3.7.2 TINY编译器的语法树结构
TINY语法树举例
计算一个整型阶乘的语法树:
{TINY语言范例-计算阶乘} read x;{输入一个整数} if 0<x then {若 x<=0则不计算} fact:=1; repeat fact:=fact*x; x:=x-1 until x=0; write fact {输出x的阶乘} end
3.7.2明
typedef enum{Stmtk,ExpK}NodeKind; typedef enum{Ifk,RepeatK,AssingK,ReadK,WriteK}StmtKind; typedef enum{Opk,ConstK,IdK}ExpKind; /*ExpType用于类型检查*/ typedef enum{Void,Integer,Boolean}ExpType; #define MAXCHILDREN 3
3.7.2 TINY编译器的语法树结构
TINY语法树举例
3.3.2 抽象语法树
If语句只需要3个附属结构就可以翻译:测试表达式、 then部分和else部分。因此上例对应的语法树是: if
0
other
other
3.3.2 抽象语法树
例11:用分号分隔开的语句序列的文法: stmt-sequence → stmt ; stmt-sequence | stmt stmt → s 串s; s; s关于这个文法的分析树和语法树:
语法树

扫描程序(s c a n n e r)
记号
Lexical analysis
语法分析程序
语法树
语义分析程序
注释树
源代码优化程序
中间代码
代码生成器
目标代码
目标代码优化程序
前端 (front end)
目标代码
编译器
在现代编译器的构造过程中,前端主要实现从源程序到中间形式(Intermediate Representation)的转换,而编译器的后端用来完成从中间形式到具体目标机代码 的转换,这是一种广泛采用的编译器构造模型。
抽象语法树 Abstract Syntax Tree, AST
Tom 2014/11/29
工程师 vs 程序猿
This is a placeholder
text.
This is a placeholder
text.
任重而道远
代码优化
代码重构
代码修复
代码自动分析
代码漏洞
Agenda
• Compile step • Abstract Syntax Tree(AST) • Eclipse AST • JavaCC AST • Clang AST
2022/3/23
编译步骤
源代码
a [index] = 4 + 2
扫描程序(s c a n n e r) Lexical analysis
a 标识符 [ 左括号 i n d e x 标识符 ] 右括号 = 赋值 4 数字 + 加号 2 数字
(t o k e n)
翻译步骤
语法分析程序(p a r s e r)
中间代码( I R)
抽象语法树Abstractsyntaxtree

抽象语法树Abstractsyntaxtree什么是抽象语法树?在计算机科学中,抽象语法和抽象语法树其实是源代码的抽象语法结构的树状表现形式我们常⽤的浏览器就是通过将js代码转化为抽象语法树来进⾏下⼀步的分析等其他操作。
所以将js转化为抽象语法树更利于程序的分析。
如图:如上图中的变量声明语句,转化为AST之后就是右图的样⼦。
先来分析⼀下左图:var 是⼀个关键字AST是⼀个定义者= 是Equal 等号的叫法有很多形式,在后⾯我们还会看到“is tree” 是⼀个字符串;就是 Semicoion再来对应⼀下右图:⾸先⼀段代码转化成的抽象语法树是⼀个对象,该对象会有⼀个顶级的type属性'Program',第⼆个属性是body是⼀个数组。
body数组中存放的每⼀项都是⼀个对象,⾥⾯包含了所有的对于该语句的描述信息type:描述该语句的类型 --变量声明语句kind:变量声明的关键字 -- vardeclaration: 声明的内容数组,⾥⾯的每⼀项也是⼀个对象type: 描述该语句的类型id: 描述变量名称的对象type:定义name: 是变量的名字init: 初始化变量值得对象type: 类型value: 值 "is tree" 不带引号row: "\"is tree"\" 带引号抽象语法树有哪些⽤途?代码语法的检查,代码风格的检查,代码的格式化,代码的⾼亮,代码错误提⽰,代码⾃动补全等等如:JSLint、JSHint 对代码错误或风格的检查,发现⼀些潜在的错误IDE的错误提⽰,格式化,⾼亮,⾃动补全等等代码的混淆压缩如:UglifyJS2等优化变更代码,改变代码结构达到想要的结构代码打包⼯具webpack,rollup等等CommonJS、AMD、CMD、UMD等代码规范之间的转化CoffeeScript、TypeScript、JSX等转化为原⽣Javascript通过什么⼯具或库来实现源码转化为抽象语法树?那就是javascript Parser 解析器,他会把js源码转化为抽象的语法树。
编译原理语法推导与语法树PPT学习教案

第6页/共25页
例5.2 文法G E → T | E +T T → F|T*F F → i |(E)
i1*i2+i3 是文法G的一个句型吗?
如果是,求出其句柄。
第7页/共25页
3.2 推导 与语法 树
推导与短语 – 4、素短语
• 含有终结符的短语,如果它不存在也具有同样性质的真子 串(不能包含有另一个素短语),则该短语为素短语 (1)是短语 (2)至少包含一个终结符 (3)不再包含其它素短语
图3-4 句子i+i*i的语法树
第12页/共25页
3.2 推导 与语法 树
语法树与二义性
– 2、子树与短语
• 语法树某个结点连同它的所有后代组成了一棵子树。只含 有单层分枝的子树称为简单子树。
• 子树与短语的关系十分密切,根据子树的概念,句型的短
语、直接短语、句柄和素短语的直观解释如下:
S
(1) 短语:子树的末端结点(即树叶)
3.2 推导 与语法 树
推导与短语 – 3、句柄
*
S αAδ 且
A β
•
举 例 : 文法G[E]:S → AB A → bB B → Sb | a 句型“baSb”的短语和句柄?
一个句型的最左直接短语称为该句型的句柄。注意,一个 句型的直接短语可能不只一个,但最左直接短语则是惟一 的。
[解 答 ]: ( 1)
• 对于文法(3.1),句子i+i*i存在两种最左(最右)推导,形成 两棵不同的语法树:
最左推导 1
E EE iE iE*E ii*E ii*i
最左推导 2
E E*E EE*E iE*E ii*E ii*i
第16页/共25页
3.2 推导 与语法 树
SUIF 抽象语法树

SUIF抽象语法树1.概述本次实验中实验三的目标是通过解析语法分析的输出文件来生成中间代码。
至于中间代码的形式,我们要求采用抽象语法树。
抽象语法树的结构则是借鉴SUIF的中间表示。
2.SUIF编译系统中间表示总体上来说,SUIF中间表示由三部分组成:抽象语法树(AST)、符号表、和指令表达式。
2.1.SUIF的层级结构SUIF中间表示组织成4级层次结构,包括:文件级,过程级,高级结构控制级和指令表达式树级。
SUIF中间表示的主要部分是一个混合式的抽象语法树(AST)。
从层次结构上来看,包括高级结构控制级和指令表达式树级,即除了传统的指令级别的操作,它还包含三个高级的结构:循环,条件声明和数组访问。
循环和条件表示类似于抽象语法树,但却是语言无关的。
图2-1展示了SUIF中间表示的层级结构:图2-1:SUIF中间表示的层次结构2.2.SUIF的符号表示SUIF的符号表分为global symbal table,file symbal table,proc symbal table和block symbal table这4种。
它们也是高到低,逐级的贯穿在了SUIF中间表示前3个层级中。
图2-2则表明了这个层次结构:图2-2:SUIF的符号表示2.3.SUIF的面向对象实现SUIF系统的内核提供了一个面向对象的SUIF中间表示的实现。
SUIF库对每个程序表示元素定义了一个C++类,允许我们对隐藏了细节的数据结构提供接口。
在这个系统中,各个类之间存在若干相互联系和共享的属性,这由类的继承和动态邦定功能实现。
例如:变量、标号和过程都是符号,他们共享相同的符号接口,但过程除了符号还有函数体。
除了基本的SUIF数据结构,SUIF的内核中还定义了很多基本的数据结构,包括哈希表,可扩展数组等。
对每个类来说,经常需要用到的函数都被定义为成员函数。
图2-3给出了主要的SUIF数据结构的类层次,所有的类都从suif_object基类继承。
第三章 抽象语法树

第三章抽象语法树在现代编译器的构造过程中,前端主要实现从源程序到中间形式(Intermediate Representation)的转换,而编译器的后端用来完成从中间形式到具体目标机代码的转换,这是一种广泛采用的编译器构造模型。
虽然源程序到目标程序的直接转换是可行的,但是使用独立于具体目标平台的中间形式有以下优点:(1)使用中间形式可以比较容易地构造面向不同目标平台和不同语言的编译器。
在不改动已有编译器前端的情况下,为新的目标平台构造一个生成该平台目标程序的后端,就可以构造出新平台的编译器。
同样对于一个新的语言,在不改动已有编译器后端的情况下,为新语言构造一个识别该语言的前端,就可以构造出新语言的编译器。
(2)针对中间形式,可以进行独立于目标平台的代码优化。
这样可以生成较高质量的目标代码,在此基础上可以对目标代码进行平台相关的优化,进而生成更高质量的目标代码。
使用中间形式的主要缺点是,产生中间代码的编译过程与不产生中间代码的编译过程相比在效率上会显得有些低。
这是因为中间代码还要进行再一次的翻译才能生成目标代码。
但是,增加一层中间形式可以使编译器更好地模块化,并且可以在中间形式上做很多优化,这些足以抵消两次翻译所带来的低效率。
所以,很多现代的编译器都使用了中间形式,比较常见的中间形式有逆波兰表示,N元表示和树形表示三种。
由于,在本系统中,我们使用抽象语法树作为中间形式,所以不再对前两种中间形式做以介绍,感兴趣的读者可以参考《编译原理》(Alfred V.Aho编著)。
3.1 树形表示树形表示是一种非常流行的中间形式,它与三元式表示有着密切的关系,三元式表示可以看成是树形表示的直接形式。
例如,表达式W*X+(Y+Z)的树形表示如图3.1所示:图3.1 表达式W*X+(Y+Z)的树形表示在现代编译器的构造过程中,经常使用抽象语法树(Abstract Syntax Tree)作为一种中间形式,这样做可以把翻译过程从语法分析过程中分离出来,使得层次非常清晰。
离散数学PPT课件 5树与生成树(ppt文档)
(b)
4.森林:一个无向图的每个连通分支都是树.如(b)
5.与树定义等价的几个命题
定理8-9.1给定图T,以下关于树的定义是等价的.
⑴无回路的连通图.
⑵无回路且e=v-1 其中e是T的边数,v是T的结点数.
⑶连通的且e=v-1.
⑷无回路但添加一条新边则得到一条仅有的回路.
⑸连通的,但删去任一条边,T便不连通.
v2 71
2 3 2
v3 51
v1 8 v8 7 v5 3 v4
4 2 v7 4
34 6 6 v6
Kruskal算法: 设G是有n个结点,m条边(m≥n-1)的连通图. S=Φ i=0 j=1
将所有边按照权升序排序: 43;1
⑹每对结点之间有一条且仅有一条路.
证明:⑴⑵:已知T是连通无回路图,通过不断地增加T中
的结点数,归纳证明.
当 v=2时, T如右图所示,e=1 显然e=v-1.
以后对T在保证连通又无回路的前提下每增加一个结点,
也增加一条边. 设最后T有v个结点e条边, 所以 e=v-1.
⑵⑶: 已知T是无回路的,且e=v-1.(推出T是连通的) 假设T不是连通的,设T有k个连通分支, T1,T2,...,Tk,(k≥2) 因为它的每个连通分支都是连通无回路的,所以都是树, 设Ti有结点数vi,边数ei, 所以边数 ei =vi-1 设T有v个结点,e条边. 所以
边 e78 e56 e35 e46 e67 e58 e12 e18
权4 4 5 6 6 7 7 8
v2
2 3
7 12
v3 51
v1 8 v8 7 v5 3 v4
