立体几何初步空间几何与点线面三轮复习考前保温专题练习(六)含答案人教版高中数学
立体几何初步空间几何与点线面强化训练专题练习(六)含答案人教版高中数学高考真题汇编

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.若l 为一条直线,α、β、γ为三个互不重合的平面,给出下面三个命题:①,;αγβγαβ⊥⊥⇒⊥ ②,;αγβγαβ⊥⇒⊥∥ ③.l αβαβ⊥⇒⊥∥,l其中正确的命题有(A )0个 (B )1个 (C )2个 (D )3个(2020天津文)2.正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 ( )A .26 B .6C .66 D .36(2020全国4文3)3.给出下列四个命题:①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行.③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行.④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线. 其中假.命题的个数是(A)1 (B)2 (C)3 (D)4(2020辽宁理)4.已知m 、l 是直线,α、β是平面,给出下列命题 ①若l 垂直于α内的两条相交直线,则l ⊥α ②若l 平行于α,则l 平行于α内的所有直线 ③若m ⊂α,l ⊂β,且l ⊥m ,则α⊥β ④若l ⊂β,且l ⊥α,则α⊥β⑤若m ⊂α,l ⊂β,且α∥β,则m ∥l其中正确的命题的序号是_____(注:把你认为正确的命题的序号都填上). (2020全国19)5.如图,在体积为1的三棱锥A —B CD 侧棱AB 、AC 、AD 上分别取点E 、F 、G , 使AE : EB=AF : FC=AG : GD=2 : 1,记O 为三平面BCG 、CDE 、DBF 的交点,则三棱锥O —BCD 的体积等于 ( )OGFABCDEA .91B .81 C . 71 D .41(2020重庆理)6.如图,若Ω是长方体1111ABCD-A B C D 被平面EFGH 截去几何体11EFGH B C 后得到的几何体,其中E 为线段11A B 上异于1B 的点,F 为线段1B B 上异于1B 的点,且EH ∥11A D ,则下列结论中不正确...的是( )A .EH ∥FGB .四边形EFGH 是矩形C .Ω是棱柱D .Ω是棱台(2020福建理)7.如图,在正方体ABCD A B C D -1111中,P 是侧面BB C C 11内一动点,若P 到直线BC 与直线C D 11的距离相等,则动点P 的轨迹所在的曲线是( )AB CD A 1B 1C 1D 1PA. 直线B. 圆C. 双曲线D. 抛物线(2020北京理)(4) 8.以下命题(其中a ,b 表示直线,α表示平面)①若a ∥b ,b ⊂α,则a ∥α ②若a ∥α,b ∥α,则a ∥b ③若a ∥b ,b ∥α,则a ∥α ④若a ∥α,b ⊂α,则a ∥b 其中正确命题的个数是( ) (A )0个(B )1个(C )2个(D )3个9.1.异面直线a b 、分别在平面α和β内,若l αβ=,则直线l 必定-----------------------( )(A)分别与a b 、相交 (B )与a b 、都不相交 (C)至多与a b 、中的一条相交 (D)至少与a b 、中的一条相10.点A 在直线l 上,l 在平面α外,用符号表示正确的是-------------------------------------( )(A),A l l α∈∉ (B),A l l α∈⊄ (C),A l l α⊂⊄ (D),A l l α⊂∉第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题11.如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,底面各边都相等,M 是PC 上的一动点,当点M 满足 时,平面MBD ⊥平面PCD .(只需写出一种情形)12.设1AA 是正方体的一条棱,这个正方体中与1AA 平行的棱共有 ▲ 条.13.正方体ABCD -A 1B 1C 1D 1的棱长为23,则四面体11A B CD -的外接球的体积为 .14.有一个各条棱长均为a 的正四棱锥形礼品(如图所示),现用一张正方形包装纸将其完全包住,要求包装时不能剪裁,但可以折叠,则包装纸的最小边长应为 ▲ .15.下列命题中,正确命题的序号是________. ①若直线l 上有无数个点不在平面α内,则l ∥ α;②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行;③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点. 解析:①错误,l 上有无数个点不在平面α内,不等于所有点都不在平面α内,直线l与平面α相交时就是这样的情形;②错误,l ∥α只是说线面无公共点,α内的线与直线l 有平行和异面两种关系;③错误,有线面平行、线在面内两种位置关系;④符合直线与平面平行的定义.只有④对.16.在空间四边形ABCD 中,两条对边3AB CD ==,,E F 分别是另外两条对边A BCDPM,AD BC 上的点,且::1:2,3AE ED BF FCEF ===,求AB 和CD 所成的角。
立体几何初步空间几何与点线面40分钟限时练(六)含答案人教版新高考分类汇编

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分 一、选择题1.已知正四棱锥S ABCD 的侧棱长与底面边长都相等,E 是SB 的中点,则AE SD ,所成的角的余弦值为( )A .13B .23C .33D .23(2020全国2理)2.如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题...是( B )A.等腰四棱锥的腰与底面所成的角都相等 B.等腰四棱锥的侧面与底面所成的二面角都相等或互补C.等腰四棱锥的底面四边形必存在外接圆D.等腰四棱锥的各顶点必在同一球面上(2020江西文)3.如图,在四面体AB CD 中,截面A EF 经过四面体的内切球(与四个面都相切的球)球心O ,且与BC ,DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A -BEFD 与三棱锥A -EF C 的表面积分别是S 1,S 2,则必有( )A. S 1<S 2B. S 1>S 2C. S 1=S 2D.S 1,S 2的大小关系不能确定(2020江西理) DB A OC EF4.对于平面α和共面的直线m 、,n 下列命题中真命题是(A )若,,m m n α⊥⊥则n α∥ (B )若m αα∥,n ∥,则m ∥n (C )若,m n αα⊂∥,则m ∥n (D )若m 、n 与α所成的角相等,则m ∥n (2020福建理)5.在下列关于直线l 、m 与平面α、β的命题中,真命题是( )(A)若l ⊂β且α⊥β,则l ⊥α. (B) 若l ⊥β且α∥β,则l ⊥α.(C) 若l ⊥β且α⊥β,则l ∥α. (D) 若α∩β=m 且l ∥m ,则l ∥α. (2020上海理)6.如图,在多面体AB CDEF 中,已知ABCD 是边长为1的正方形,且BCF ADE ∆∆、均为正三角形,EF ∥AB ,EF=2,则该多面体的体积为( )A B C DE F(A )32 (B )33 (C )34 (D )23(2020全国1文) 7.已知m 、n 是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:①若βαβα//,,则⊥⊥m m ;②若βααβγα//,,则⊥⊥;③若βαβα//,//,,则n m n m ⊂⊂; ④若m 、n 是异面直线,βααββα//,//,,//,则n n m m ⊂⊂其中真命题是( )A .①和②B .①和③C .③和④D .①和④(2020辽宁)8. 一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是 ( )A .334; B .34; C . 312;D .33. 9.A 、B 是直线l 外的两点,过A 、B 且和l 平行的平面的个数是( )(A )0个 (B )1个 (C )无数个 (D )以上都有可能10.1.直线与平面平行的充要条件是----------------------------------------------------------------------( )(A)直线与平面内的一条直线平行 (B)直线与平面内两条直线不相交(C)直线与平面内任一条直线都不相交 (D)直线与平面内的无数条直线平 第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分 二、填空题11.如图, 在空间四边形SABC 中, SA ⊥平面ABC , ∠ABC = 90︒, AN ⊥SB 于N ,AM ⊥SC 于M 。
立体几何初步空间几何与点线面强化训练专题练习(六)含答案人教版高中数学考点大全

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于 ( )A .23 B .33C .23D .13(2020年普通高等学校招生统一考试大纲版数学(理)WOR D 版含答案(已校对)) 2.过平行六面体1111D C B A ABCD -任意两条棱的中点作直线, 其中与平面11D DBB 平行的直线共有A .4条B .6条C .8条D .12条(2020湖南理)3.设三棱柱ABC-A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B-A PQC 的体积为( ) (A )16V (B )14V (C )13V (D )12V (2020全国3文)4.若三棱锥A-BC D 的侧面ABC 内一动点P 到底面BCD 的面积与到棱AB 的距离相等,则动点P 的轨迹与ABC 组成图形可能是:( )(2020重庆理)ABCABCABCABCPPPP5.到两互相垂直的异面的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是 (A ) 直线 (B ) 椭圆(C ) 抛物线(D ) 双曲线(2020重庆理)6.已知m 、n 是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题: ①若βαβα//,,则⊥⊥m m ;②若βααβγα//,,则⊥⊥; ③若βαβα//,//,,则n m n m ⊂⊂;④若m 、n 是异面直线,βααββα//,//,,//,则n n m m ⊂⊂其中真命题是( )A .①和②B .①和③C .③和④D .①和④(2020辽宁)7.高为24的四棱锥S -ABCD 的底面是边长为1的正方形,点S 、A 、B 、C 、D 均在半径为1的同一球面上,则底面ABCD 的中心与顶点S 之间的距离为(2020年高考重庆卷理科9) (A )24 (B )22(C )1 (D )28.分别和两条异面直线都相交的两条直线的位置关系是---------------------------------------( )(A)异面 (B)相交 (C)平行 (D)异面或相9.空间四点A B C D 、、、共面而不共线,那么这四点中----------------------------------------( )(A)必有三点共线 (B)必有三点不共线 (C)至少有三点共线 (D)不可能有三点共10.线a 、b 和平面α,下面推论错误的是A. b a ⊥⇒⎭⎬⎫⊆⊥ααb a B αα⊥⇒⎭⎬⎫⊥b b // a aC ααα⊆⇒⎭⎬⎫⊥⊥a //a b b a 或D b //a b //a ⇒⎭⎬⎫⊆αα第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题11.设,m n 为空间的两条直线,,αβ为空间的两个平面,给出下列命题: ①若m ∥α,m ∥β , 则α∥β; ②若m ⊥α,m ⊥β,则α∥β; ③若m ∥α,n ∥α,则m ∥n ; ④若m ⊥α,n ⊥α,则m ∥n ; 上述命题中,其中假命题...的序号是 ▲ . 12. 下列说法不正确的....是______________A. 空间中,一组对边平行且相等的四边形是一定是平行四边形; B .同一平面的两条垂线一定共面;C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;D. 过一条直线有且只有一个平面与已知平面垂直.13. 设平面,,βα直线b a ,,集合{}{}垂直的平面与,垂直的平面与βα==B A ,{}垂直的直线与a M =,{}垂直的直线与b N =,给出下列命题:①若∅≠B A ,则;//βα ②若βα//,则B A =;③若b a ,为异面直线,则∅=N M ;④若b a ,相交,则;N M = 其中不正确的命题序号是___ ★ .(1),(3),(4)14.设l ,m 表示两条不同的直线,α表示一个平面,从“∥、⊥”中选择适当的符号填入下列空格,使其成为真命题,即: ________⎫⇒⎬⎭l m l αm ▲ α. ∥,⊥,⊥15.若直线l 上有两点到平面α的距离相等,则直线l 与平面α的位置关系是___________16.如图,∠BAD =90°的等腰直角三角形ABD 与正三角形CBD 所在平面互相垂直,E 是BC 的中点,则AE 与CD 所成角的大小为 .AECDB评卷人得分三、解答题17.如图,在三棱锥V -ABC 中,VC ⊥底面ABC ,AC ⊥BC ,D 是AB 的中点,且第8题图AC =BC =a ,∠VDC =θ⎪⎭⎫⎝⎛<<20πθ。
立体几何初步空间几何与点线面三轮复习考前保温专题练习(六)带答案人教版高中数学高考真题汇编

高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
1.给出以下四个命题
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;
③如果两条直线都平行于一个平面,那么这两条直线互相平行;
④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直. 其中真命题的个数是
A.4
B.3
C.2
D.1(2020广东)
①②④正确,故选B.
2.设三棱柱ABC-A 1B 1C 1的体积是V ,P.Q 分别是侧棱AA 1上的点,且PA=QC 1,则四棱锥B-A PQC 的体积为( )
A.V 61
B.V 41
C.V 31
D.V 21 (2020全国3理)。
立体几何初步空间几何与点线面章节综合学案练习(六)带答案人教版高中数学新高考指导
高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
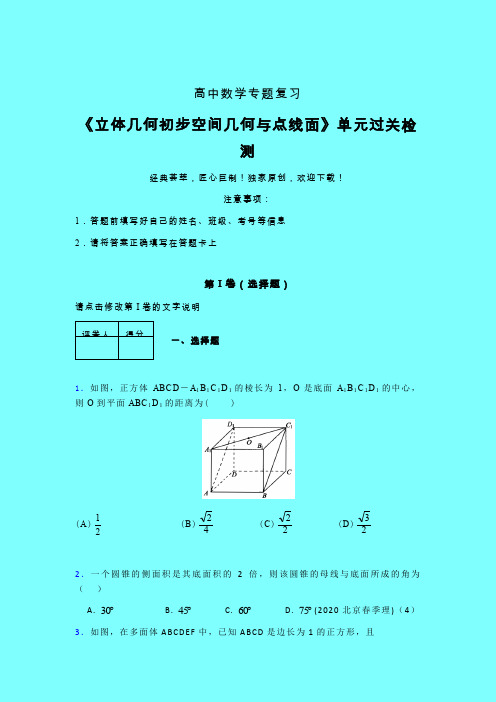
1.如图,正方体ABC D -A 1B 1C 1D 1的棱长为1,O 是底面A 1B 1C 1D 1的中心,则O 到平面ABC 1D 1的距离为( )
(A )
21 (B )42 (C )22 (D )2
3
2.一个圆锥的侧面积是其底面积的2倍,则该圆锥的母线与底面所成的角为( )
A. 30︒
B. 45︒
C. 60︒
D. 75︒(2020北京春季理)(4) 3.如图,在多面体AB CDEF 中,已知ABCD 是边长为1的正方形,且。
立体几何初步空间几何与点线面章节综合检测专题练习(六)带答案人教版高中数学考点大全

高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
1.设m.n 是两条不同的直线,α.β是两个不同的平面,
( ) A .若m∥α,n∥α,则m∥n
B .若m∥α,m∥β,则α∥β
C .若m∥n,m⊥α,则n ⊥α
D .若m∥α,α⊥β,则m⊥β(2020年高考浙江卷(文))
2.已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94
,底面是边长为3的正三角形.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为
( ) A .512π B .3π C .4π D .6
π(2020年普通高等学校招生统一考试山东数学(理)试题(含答案))
3.若l 为一条直线,α、β、γ为三个互不重合的平面,给出下面三个命题: ①,;αγβγαβ⊥⊥⇒⊥ ②,;αγβγαβ⊥⇒⊥∥ ③.l αβαβ⊥⇒⊥∥,l
其中正确的命题有。
立体几何初步空间几何与点线面考前冲刺专题练习(六)带答案新高考高中数学

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.如图,在四面体AB CD 中,截面A EF 经过四面体的内切球(与四个面都相切的球)球心O ,且与BC ,DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A -BEFD 与三棱锥A -EF C 的表面积分别是S 1,S 2,则必有( ) A.S 1<S 2 B. S 1>S 2 C. S 1=S 2 D.S 1,S 2的大小关系不能确定(2020江西理)DBAOCEF2.若三棱锥A-BC D 的侧面ABC 内一动点P 到底面BCD 的面积与到棱AB 的距AB CAB CAB CAB CP PP P离相等,则动点P的轨迹与ABC组成图形可能是:()(2020重庆理)3.设α、β为两个不同的平面,l、m为两条不同的直线,且l⊂α,m⊂β,有如下的两个命题:①若α∥β,则l∥m;②若l⊥m,则α⊥β.那么()(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题(C) ①②都是真命题(D) ①②都是假命题(2020浙江文)4.到两互相垂直的异面的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是(A)直线(B)椭圆(C)抛物线(D)双曲线(2020重庆理)5. 设γβα,,为两两不重合的平面,n m l ,,为两两不重合的直线,给出下列四个命题:①若γα⊥,γβ⊥,则//αβ; ②若//αβ,α⊂l ,则//l β;③若α⊂m ,α⊂n ,//m β,//n β,则//αβ;④若l αβ=I ,m βγ=I ,n γα=I ,//l γ,则//m n 。
其中命题正确的是 ▲ .(填序号) 6.1.已知平面α与平面βγ、都相交,则这三个平面可能的交线有( ) (A) 1条或2条 (B ) 2条或3条 (C) 1条或3条 (D) 1条,或2条,或3 7.α、β表示平面,a 、b 表示直线,则α//a 的一个充分条件是 ( )()A βα⊥,且β⊥a ()B b =βα ,且b a //)(C b a //,且α//b ()D βα//,且β⊂a8.如果用a 记某三角形两边中点的连线,用α记过该三角形第三边的一个平面,那么必有( )(A)a α∥ (B)a α⊂ (C)a α⊄ (D)a a αα⊂∥或 9.正方体的两条对角线相交所成角的正弦值等于------( ) (A)22 (B)13(C)223 (D)101010.如图所示的直观图,其平面图形的面积是_______________A OB22 045B 1A 1EDAC BC 111.在长方体ABCD -A 1B 1C 1D 1中,AB =AD =3 cm ,AA 1=2 cm ,则四棱锥A -BB 1D 1D 的体积 为 ▲ cm 3.12.底面边长为2 ,高为1 的正三棱锥的全面积为:_____▲ .13. 已知直线⊥a 平面α,直线//b 平面α,则直线b a ,的位置关系是 ▲_14.已知平面,,αβγ,直线,l m 满足:,,,αγγαγβ⊥==⊥m l l m ,那么①m β⊥; ②l α⊥; ③βγ⊥; ④αβ⊥.可由上述条件可推出的结论有 ▲ (请将你认为正确的结论的序号都填上). 15.已知一个圆锥的展开图如图所示,其中扇形的圆心角为120°,底面圆的半径为1,则该圆锥的体积为__________.(第9题)16.棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的 中点,则直线EF 被球O 截得的线段长为 评卷人得分三、解答题17.如图,在正三棱柱111A B C A B C -中,D 是BC 的中点.(1)求证:1AD DC ⊥;(2)如果E 是11C B 的中点,求证:1//A E 平面1ADC .18.设,,αβγ表示不同的平面,,a b 表示不同的直线,给出下列四个命题: (1)若,,αβαγ⊥⊥则β∥γ;(2)若α∥β,且β与γ无公共点,则α与γ无公共点;(3)若,,αβγ两两相交,则有三条交线;(4),,,a b αγβαβγ⊥⋂=⋂=则a b ⊥。
立体几何初步空间几何与点线面考前冲刺专题练习(六)附答案新教材高中数学

高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
1.若l 为一条直线,α、β、γ为三个互不重合的平面,给出下面三个命题: ①
,;
αγβγαβ⊥⊥⇒⊥ ②,;αγβγαβ⊥⇒⊥∥ ③.l αβαβ⊥⇒⊥∥,l
其中正确的命题有 (A )0个 (B )1个 (C )2个 (D )3个(2020天津文)
2.设有直线m 、n 和平面α、β。
下列四个命题中,正确的是
A.若m ∥α,n ∥α,则m ∥n
B.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β
C.若α⊥β,m ⊂α,则m ⊥β
D.若α⊥β,m ⊥β,m ⊄α,则m ∥α
(2020湖南理)
(D ) 3.正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 ( )。
立体几何初步空间几何与点线面强化训练专题练习(六)附答案人教版高中数学高考真题汇编

高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
1.若l 为一条直线,α、β、γ为三个互不重合的平面,给出下面三个命题: ①
,;
αγβγαβ⊥⊥⇒⊥ ②,;αγβγαβ⊥⇒⊥∥ ③.l αβαβ⊥⇒⊥∥,l
其中正确的命题有 (A )0个 (B )1个 (C )2个 (D )3个(2020天津文)
2.正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 ( )
A .26
B . 6
C .66
D . 3
6(2020全国4文3)
3.给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行.。
立体几何初步空间几何与点线面一轮复习专题练习(六)附答案新人教版高中数学名师一点通
高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
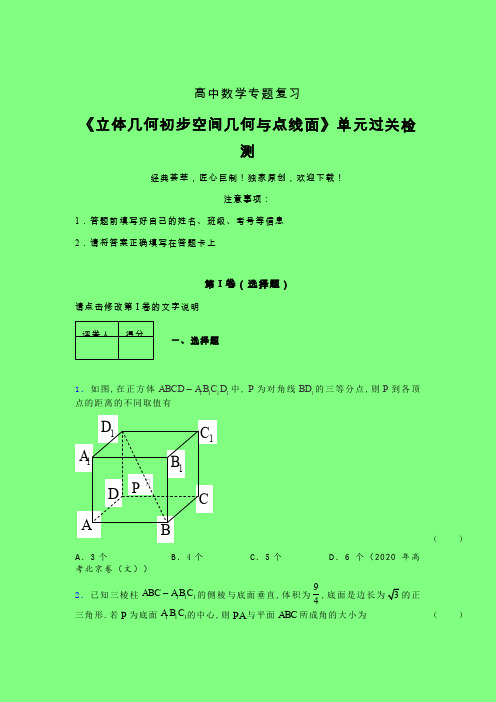
1.如图,在正方体1111ABCD A B C D -中,P 为对角线1BD 的三等分点,则P 到各顶点的距离的不同取值有 ( ) A .3个
B .4个
C .5个
D .6个(2020年高考北京卷(文))
2.已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94
,底面是边长为3的正三角形.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为 ( ) 1D 1B P
D 1C
C B
A 1A。
立体几何初步空间几何与点线面晚练专题练习(六)含答案新高考高中数学

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.一平面截一球得到直径是6cm 的圆面,球心到这个平面的距离是4cm ,则该球的体积是 ( ) (A)33π100cm (B) 33π208cm (C) 33π500cm (D) 33π3416cm (2020江苏) 2.木星的体积约是地球体积的30240倍,则它的表面积约是地球表面积的( ) A .60倍 B .6030倍C .120倍D .12030倍(2020湖北文)3.已知m 、l 是直线,α、β是平面,给出下列命题 ①若l 垂直于α内的两条相交直线,则l ⊥α ②若l 平行于α,则l 平行于α内的所有直线 ③若m ⊂α,l ⊂β,且l ⊥m ,则α⊥β ④若l ⊂β,且l ⊥α,则α⊥β⑤若m ⊂α,l ⊂β,且α∥β,则m ∥l其中正确的命题的序号是_____(注:把你认为正确的命题的序号都填上). (2020全国19)4.在空间,下列命题正确的是_____(注:把你认为正确的命题的序号都填上).①如果两直线a 、b 分别与直线l 平行,那么a ∥b . ②如果直线a 与平面β内的一条直线b 平行,那么a ∥β. ①果直线a 与平面β内的两条直线b 、c 都垂直,那么a ⊥β.④如果平面β内的一条直线a 垂直平面γ,那么β⊥γ. (2020北京安徽春季18)5.已知正四棱锥S ABCD -中,23SA =,那么当该棱锥的体积最大时,它的高为A .1B .3C . 2D .3(2020全国II 理 【答案解析】C6.已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为( ) ()A 26 ()B 36 ()C 23 ()D 227.给出下列四个命题:①一个角是平面图形;②三条直线两两相交,它们必在同一平面内;③两个平面有三个公共点,它们必重合;④四边形是平面图形。
立体几何初步空间几何与点线面强化训练专题练习(六)含答案新人教版高中数学名师一点通

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.设四面体的六条棱的长分别为1,1,1,1,2和a ,且长为a 的棱与长为2的棱异面,则a 的取值范围是 ()A .(0,2)B .(0,3)C .(1,2)D .(1,3)(2020重庆理)2.设有直线m 、n 和平面α、β。
下列四个命题中,正确的是 A.若m ∥α,n ∥α,则m ∥nB.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥βC.若α⊥β,m ⊂α,则m ⊥βD.若α⊥β,m ⊥β,m ⊄α,则m ∥α (2020湖南理)(D )3.对于平面α和共面的直线m 、,n 下列命题中真命题是 (A )若,,m m n α⊥⊥则n α∥ (B )若m αα∥,n ∥,则m ∥n(C )若,m n αα⊂∥,则m ∥n (D )若m 、n 与α所成的角相等,则m ∥n (2020福建理)4.设三棱柱ABC-A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B-A PQC 的体积为( ) (A )16V (B )14V (C )13V (D )12V (2020全国3文)5.正三棱柱侧面的一条对角线长为2,且与底面成45°角,则此三棱柱的体积为 ( )A .26 B .6C .66 D .36(2020全国4文3)6.如果直线l 、m 与平面α、β、γ满足:l =β∩γ,l ∥α,m ⊂α和m ⊥γ,那么必有( )A .α⊥γ且l ⊥mB .α⊥γ且m ∥βC .m ∥β且l ⊥mD .α∥β且α⊥γ(2020全国文7理5)7.ABC ∆的顶点在平面α内,A 、C 在α的同一侧,AB 、BC 与α所成的角分别是30和45.若AB =3,BC =42,AC =5,则AC 与α所成的角为( )(A )60(B )45(C )30(D )15(2020全国2文) 8.1.下面给出四个命题中正确命题的个数是----------------------------------------------------------( )①若a b ∥,b c ∥,则a c ∥;②若a b ⊥,b c ⊥,则a c ⊥;③若a b 、相交,b c 、相交,则a c 、也相交;④若a b 、是异面直线,b c 、是异面直线,则a c 、也是异面直线(A) 1 (B) 2 (C) 3 (D) 9.下列说法中正确的是A 经过两条平行直线,有且只有一个平面直线B 如果两条直线同平行于同一个平面,那么这两条直线平行C 三点唯一确定一个平面D 不在同一平面内的两条直线相互垂直,则这两个平面也相互垂直10.如图所示的直观图,其平面图形的面积是_______________A OB22 04511.如图,在三棱锥ABC P -中,⊥PA 底面ABC ,90=∠ABC ,1===BC AB PA ,则PC 与底面ABC 所成角的正切值...为 .12.给出下列关于互不相同的直线,,m l n 和平面,αβ的四个命题: ①若,,m lA A m αα⊂=∉,则l 与m 不共面②若,m l 是异面直线, //,//,,,l m n l n m n ααα⊥⊥⊥且则 ③若//,//,//,//l m l m αβαβ则 ④若,,,//,//,l m lm A l m ααββαβ⊂⊂=则//其中为真命题的是13.设,m n 为空间的两条直线,,αβ为空间的两个平面,给出下列命题: (1)若m ∥α,m ∥β , 则α∥β; (2)若m ⊥α,m ⊥β,则α∥β; (3)若m ∥α,n ∥α,则m ∥n ; (4)若m ⊥α,n ⊥α,则m ∥n ; 上述命题中,所有真命题的序号是 .14. 已知三棱台111A B C A B C -中,三棱锥111B A B C -、1A ABC -的体积分别为2、18,则此三棱台的体积的值等于______________.15.已知某四面体的六条棱长分别为5,3,2,2,2,2,则两条较长棱所在直线所成PABC(第8题)角的余弦值为 ▲ .16. 设α、β、γ表示是三个不同的平面,a 、b 、c 表示是三条不同的直线,给出下列 五个命题:(1)若a ∥α,b ∥β,a ∥b ,则α∥β;(2)若a ∥α,b ∥α,ββαβ⊂⊂=⋂b a c ,,,则b a //; (3)若ααα⊥⇒⊂⊂⊥⊥a c b c a b a ,,,; (4)若,,γβγα⊥⊥则βα//或βα⊥;(5)若a 、b 在平面α内的射影互相垂直,则a ⊥b . 其中正确命题的序号是 ▲ . 评卷人得分三、解答题17.【2020高考天津第17题】如图,在四棱锥P ABCD -中,PA ^底面ABCD ,AD AB ^,//AB DC ,2AD DC AP ===,1AB =,点E 为棱PC 的中点.(Ⅰ)证明:BE DC ^;(Ⅱ)求直线BE 与平面PBD 所成角的正弦值;(Ⅲ)若F 为棱PC 上一点,满足BF AC ^,求二面角F AB P --的余弦值.平面FAB 的法向量,则110,0,n AB n BFìï?ïíï?ïî即0,1130.222x x y z ì=ïïïíï-++=ïïî不妨令1z =,可得()10,3,1n =-为平面FAB 的一个法向量.取平面ABP 的法向量()20,1,0n =,则1212113310cos ,10101n n n n n n ×´-===-×.易知,二面角F AB P --是锐角,∴其余弦值为31010.18.如图所示,在四棱锥P —ABCD 中,侧面PAD 是正三角形,且垂直于底面ABCD ,底面ABCD 是边长为2的菱形,︒=∠60BAD ,M 为PC 上一点,且PA ∥平面BDM .⑴求证:M 为PC 中点;⑵求平面ABCD 与平面PBC 所成的锐二面角的大小. (理)PCDM19.设S 为ABC ∆平面外的一点,SA=SB=SC ,γβα2,2,2=∠=∠=∠ASC BSC ASB ,若γβα222s in s in s in =+,(1)求证:平面ASC ⊥平面ABC;(2)若αβ=,且S A 与面AB C 所成角为450,求异面直线AB 与SC 所成的角。
立体几何初步空间几何与点线面一轮复习专题练习(六)含答案人教版高中数学考点大全

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I卷(选择题)请点击修改第I卷的文字说明评卷人得分一、选择题1.设四面体的六条棱的长分别为1,1,1,1,2和a,且长为a的棱与长为2的棱异面,则a的取值范围是()A.(0,2)B.(0,3)C.(1,2)D.(1,3)(2020重庆理)2.表面积为23的正八面体的各个顶点都在同一个球面上,则此球的体积为()A.23πB.13π C.23πD.223π(2020安徽理)3.已知正方体外接球的体积是323π,那么正方体的棱长等于.4.在正四面体P —ABC 中,D ,E ,F 分别是AB ,BC ,CA 的中点,下面四个结论中不成立的是(A)BC∥平面PDF (B )DF ⊥平面PAE(C)平面PDF ⊥平面ABC (D)平面PAE ⊥平面ABC(2020北京理) 5.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 是A 1B 1的中点,则E 到平面AB C 1D 1的距离为( ) A .23 B .22 C .21 D .33(2020湖南文) 6.已知a 、b 、c 是直线,β是平面,给出下列命题:①若c a c b b a //,,则⊥⊥; ②若c a c b b a ⊥⊥则,,//; ③若b a b a //,,//则ββ⊂;④若a 与b 异面,且ββ与则b a ,//相交;⑤若a 与b 异面,则至多有一条直线与a ,b 都垂直. 其中真命题的个数是( ) A .1B .2C .3D .4(2020湖北文)7.对于不重合的两个平面βα与,给定下列条件: ①存在平面γ,使得α、β都垂直于γ; ②存在平面γ,使得α、β都平等于γ; ③存在直线α⊂l ,直线β⊂m ,使得m l //; ④存在异面直线l 、m ,使得.//,//,//,//βαβαm m l l 其中,可以判定α与β平行的条件有( ) A .1个B .2个C .3个D .4个(2020重庆文)8.已知矩形ABCD ,AB =1,BC =2.将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中, ( )A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直(2020浙江理)9.如图正方体1111EFGH E F G H -中,下列四对截面中,彼此平行的一对截面是-------------------------------------------------------( ) (A)面11E FG 与面1EGH (B)面1FHG 与面11F H G (C)面11F H H 与面1FHE (D)面11E HG 与面1EH G 10.1.直线与平面平行的充要条件是----------------------------------------------------------------------( )(A)直线与平面内的一条直线平行 (B)直线与平面内两条直线不相交 (C)直线与平面内任一条直线都不相交 (D)直线与平面内的无数条直线平第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题11.设1AA 是正方体的一条棱,则这个正方体中与1AA 垂直的棱共有 条. 12.已知正四棱柱AB CD - A 1B 1C 1D 1的对角线AC 1的长为6,且AC 1与底面所成角的余弦值为33,则该正四棱柱的体积为 ▲ .(第9题)13.如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .14.体积为8的一个正方体,其表面积与球O 的表面积相等,则球O 的体积等于________.15.如图边长为a 的等边三角形ABC 的中线A F 与中位线DE 交于点G ,已知△A 'DE 是△ADE 绕DE 旋转过程中的一个图形(点A '∉平面ABC ),则下列命题中正确的是 .①动点A ' 在平面ABC 上的射影在线段AF 上;②BC ∥平面A 'DE ;③三棱锥A '-FED 的体积有最大值.16.设l ,m 表示两条不同的直线,α表示一个平面,从“∥、⊥”中选择适当的符号填入下列空格,使其成为真命题,即: ________⎫⇒⎬⎭l m l αm ▲ α. ∥,⊥,⊥评卷人得分三、解答题17. 在四棱锥P A B C D -中,底面A B C D为直角梯形,//BC AD ,90ADC ∠=,12BC CD AD ==,PA PD =,,E F 分别为,AD PC 中点,证明: (1)AD PB ⊥; (2)//PA 平面BEF .18.如图所示,长方体1111ABCD A B C D -的对角线1AC 的长为a ,0145BAC ∠=,0160DAC ∠=,求这个长方体的体积.19.如图1所示,在ABC Rt ∆中,6=AC ,3=BC ,︒=∠90ABC ,CD 为ACB ∠的平分线,点E 在线段AC 上,4=CE .如图2所示,将BCD ∆沿CD 折起,使得平面⊥BCD 平面ACD ,连结AB ,设点F 是AB 的中点. (1)求证:⊥DE 平面BCD ;(2)若//EF 平面B D G ,其中G 为直线AC 与平面B D G 的交点,求三棱锥DEG B -的体积.PBCDE AF20.已知点O 是正方形ABCD 两对角线的交点,DE ⊥平面ABCD ,BF ⊥平面ABCD ,且2AB BF DE==. (Ⅰ)求证:EO ⊥平面AFC ;(5分) (Ⅱ)在线段EF 上找一点M ,使三棱锥M ACF -为正三棱锥;(5分)(Ⅲ)试问在线段DF (不含端点)上是否存在一点R , 使得CR ∥平面ABF ,若存在,请指出点R 的位置; 若不存在,请说明理由.(5分)【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.A 2.A解析:A 此正八面体是每个面的边长均为a 的正三角形,所以由238234a ⨯=A BCDE FO知,1a =,则此球的直径为2,故选A 。
立体几何初步空间几何与点线面午练专题练习(六)含答案人教版新高考分类汇编

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为 ( ) A .6π B .43πC .46πD .63π(2020课标文)2.如图,平面α⊥平面β,,,A B AB αβ∈∈与两平面α、β所成的角分别为4π和6π。
过A 、B 分别作两平面交线的垂线,垂足为'A 、',B 则:''AB A B =(A) A'B'A B βα(A )2:1 (B )3:1 (C )3:2 (D )4:3(2020全国2理)3.棱长为2的正四面体的四个顶点都在同一个球面上, 若过该球球心的一个截面如图1,则图中三角形(正四面体的截面)的面积是图1A .22 B .23 C .2 D .3 (2020湖南理)4.设,m n 是平面α内的两条不同直线,1l ,2l 是平面β内的两条相交直线,则α//β的一个充分而不必要条件是A .m //β且//l αB . 1//m l 且2//n lC .//m β且//n βD . //m β且2//n l (2020福建理)5.已知矩形ABCD ,AB =1,BC =2.将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中, ( )A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直(2020浙江理)6.α、β是两个不同的平面,m 、n 是平面α及β之外的两条不同直线, 给出四个论断:① m ⊥ n ②α⊥β ③ m ⊥β ④ n ⊥α以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:___________________.7.正三棱柱的侧面展开图是边长分别为6和4的矩形,则它的体积为 ( )A.89 3 B .4 3 C.29 3 D .43或83 3 解析:分侧面矩形长、宽分别为6和4或4和6两种情况8.已知a b c 、、是直线,α是平面,b 、c ≠⊂α,则“⊥a 平面α”是“b a ⊥且c a ⊥”的…………………………………………………………………………………………( )A .充要条件.B .充分非必要条件.C .必要非充分条件.D .非充分非必要条件.9.点A 是等边三角形BCD 所在平面外一点,AB AC AD BC a ====,E F 、分别在AB CD 、上,且(0)AE CFEB FDλλ==>。
立体几何初步空间几何与点线面章节综合学案练习(六)含答案人教版高中数学

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.已知n m ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则 ( )A .βα//,且α//lB .βα⊥,且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l (2020年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案)) 2.对于平面α和共面的直线m 、,n 下列命题中真命题是 (A )若,,m m n α⊥⊥则n α∥ (B )若m αα∥,n ∥,则m ∥n(C )若,m n αα⊂∥,则m ∥n (D )若m 、n 与α所成的角相等,则m ∥n (2020福建理)3.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 是A 1B 1的中点,则E 到平面AB C 1D 1的距离为( ) A .23 B .22 C .21 D .33(2020湖南文)4.对于不重合的两个平面βα与,给定下列条件: ①存在平面γ,使得α、β都垂直于γ; ②存在平面γ,使得α、β都平等于γ; ③存在直线α⊂l ,直线β⊂m ,使得m l //; ④存在异面直线l 、m ,使得.//,//,//,//βαβαm m l l 其中,可以判定α与β平行的条件有( ) A .1个B .2个C .3个D .4个(2020重庆文)5.已知m 、n 是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题: ①若βαβα//,,则⊥⊥m m ;②若βααβγα//,,则⊥⊥; ③若βαβα//,//,,则n m n m ⊂⊂;④若m 、n 是异面直线,βααββα//,//,,//,则n n m m ⊂⊂其中真命题是( )A .①和②B .①和③C .③和④D .①和④(2020辽宁)6.一个正方体的顶点都在球面上,它的棱长为2cm,则球的表面积是A 28cm πB 212cm πC 216cm πD 220cm π7.正方体各棱所在的直线中,与此正方体的一条对角线异面的共有( ) A .2条 B 。
立体几何初步空间几何与点线面课后限时作业(六)含答案新高考高中数学

高中数学专题复习《立体几何初步空间几何与点线面》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.设l 为直线,,αβ是两个不同的平面,下列命题中正确的是 ( )A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥(2020年高考广东卷(文))2.如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上.过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于M N ,.设BP x =,MN y =,则函数()y f x =的图象大致是( )(2020北京理)3.若三棱锥A-BC D 的侧面ABC 内一动点P 到底面BCD 的面积与到棱AB 的距A B CD MNP A 1B 1C 1D 1 yxA .OyxB .OyxC .OyxD .OAB CAB CAB CAB CP PP P离相等,则动点P的轨迹与ABC组成图形可能是:()(2020重庆理) 4.已知平面βα与所成的二面角为80°,P为α、β外一定点,过点P的一条直线与α、β所成的角都是30°,则这样的直线有且仅有()A.1条B.2条C.3条D.4条(2020湖北理)5.已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:①若m⊂α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是()A.0 B.1 C.2 D.3(2020福建理) 6.已知m、l是直线,α、β是平面,给出下列命题①若l垂直于α内的两条相交直线,则l⊥α②若l 平行于α,则l 平行于α内的所有直线 ③若m ⊂α,l ⊂β,且l ⊥m ,则α⊥β ④若l ⊂β,且l ⊥α,则α⊥β⑤若m ⊂α,l ⊂β,且α∥β,则m ∥l其中正确的命题的序号是_____(注:把你认为正确的命题的序号都填上). (2020全国19)7.关于直线a 、b 、l 及平面M 、N ,下列命题中正确的是( ) A .若a ∥M ,b ∥M ,则a ∥b B .若a ∥M ,b ⊥a ,则b ⊥MC .若a M ,b M ,且l ⊥a ,l ⊥b ,则l ⊥MD .若a ⊥M ,a ∥N ,则M ⊥N (2020上海春13) 8.以下命题(其中a ,b 表示直线,α表示平面)①若a ∥b ,b ⊂α,则a ∥α ②若a ∥α,b ∥α,则a ∥b ③若a ∥b ,b ∥α,则a ∥α ④若a ∥α,b ⊂α,则a ∥b 其中正确命题的个数是( ) (A )0个(B )1个(C )2个(D )3个9.在ABC ∆中,︒=∠90ACB ,AB=8,︒=∠60BAC ,PC ⊥面ABC ,PC =4,M 是AB 边上的一动点,则PM 的最小值为( ) A .72 B .7C .19D .510.空间两直线平行是指它们--------------------------------------------------( )(A)无交点 (B)共面且无交点 (C)和同一直线垂直 (D)以上都不对第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题CAP11.如图,在正三棱锥A BCD -中,底面BCD ∆的边长为2,点,E F 分别是CD 和AD 的中点,且EF BF ⊥,则正三棱锥A BCD -的外接球的表面积为▲ .12.如图,在四棱锥P ABCD -中,侧面PAD 是正三角形,且与底面ABCD 垂直,底面ABCD 是边长为2的菱形,60BAD ∠=,N 是PB 中点,截面DAN 交PC 于M .(Ⅰ)求证://AD MN ;(Ⅱ)求证:PB ⊥平面ADMN ;13.如果a ,b 是异面直线,且a ∥平面α,那么b 与α的位置关系可能是__________;14.设,m n 为空间的两条直线,,αβ为空间的两个平面,给出下列命题: (1)若m ∥α,m ∥β , 则α∥β; (2)若m ⊥α,m ⊥β,则α∥β; (3)若m ∥α,n ∥α,则m ∥n ; (4)若m ⊥α,n ⊥α,则m ∥n ; 上述命题中,所有真命题的序号是 .15.如图,已知 PA ⊥Rt △ABC 所在的平面,且AB ⊥BC ,连结PB 、PC ,则图中直角三角形的个数是__________个.第11题EFDACBACBDMNP16.如果三棱锥的三个侧面两两垂直,它们面积分别为6cm 2、4cm 2、3cm 2,那么它的外接球体积是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学专题复习
《立体几何初步空间几何与点线面》单元过关检
测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分
一、选择题
1.已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于 ( )
A .
23 B .
33
C .
23
D .
1
3
(2020年普通高等学校招生统一考试大纲版数学(理)WOR D 版含答案(已校对))
2.如图,AB 是平面α的斜线段...,A 为斜足,若点P 在平面α内运动,使得ABP △的面积为定值,则动点P 的轨迹是( )
A .圆
B .椭圆
C .一条直线
D .两条平行直线
(2020浙江理)
A
B P
α
(第10题)
3.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是
A .16π
B .20π
C .24π
D .32π(2020全国1理)
4.设,m n 是平面α内的两条不同直线,1l ,2l 是平面β内的两条相交直线,则α//β的一个充分而不必要条件是
A .m //β且//l α
B . 1//m l 且2//n l
C .//m β且//n β
D . //m β且2//n l (2020福建理)
5.已知三条直线m 、n 、l ,三个平面α、β、γ.下面四个命题中,正确的是( ) A .
⇒⎭
⎬⎫
⊥⊥γβγαα∥β B .
⇒⎭
⎬⎫
⊥m l m β//l ⊥β C .⇒⎭⎬⎫γγ////n m m ∥n D .⇒⎭
⎬⎫⊥⊥γγn m m ∥n (2020北京春2)
6.已知矩形ABCD ,AB =1,BC =2.将∆ABD 沿矩形的对角线BD 所在的直线进行翻着,在翻着过程中, ( )
A .存在某个位置,使得直线AC 与直线BD 垂直
B .存在某个位置,使得直线AB 与直线CD 垂直
C .存在某个位置,使得直线A
D 与直线BC 垂直
D .对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直(2020浙江理)
7.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,
且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、
三棱锥、三棱柱的高分别为1h ,2h ,h ,则12::h h h = ( ). (A)3:1:1 (B)
3:2:2
(C)
3:2:2
(D)3:2:3
8.设m 、n 是两条不同的直线,,,αβγ是三个不同的平面,给出下列四个命题: ①若,,则 ②若,,,则
③若,,则 ④若αγ⊥,βγ⊥,则//αβ
其中正确命题的序号是 A ①和② B ②和③ C
③
和
④
D ①和④ 9.
1.直线与平面平行的充要条件是----------------------------------------------------------------------( )
(A)直线与平面内的一条直线平行 (B)直线与平面内两条直线不相交 (C)直线与平面内任一条直线都不相交 (D)直线与平面内的无数条直线平 10.点A 在直线l 上,l 在平面α外,用符号表示正确的是-------------------------------------( )
(A),A l l α∈∉ (B),A l l α∈⊄ (C),A l l α⊂⊄ (D),A l l α⊂∉
第II 卷(非选择题)
请点击修改第II 卷的文字说明 评卷人
得分
二、填空题
11.在正方体1111ABCD A B C D -中,E 分为1DD 的中点,则1BD 与平面AEC 的位置关系是
12.四棱锥P ABCD -的底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD DC =,E 是PC 的中点,则二面角B DE C --的平面角为 .
13.已知n m ,是两条不同直线,βα,是两个不同平面,有下列4个命题: ①若//,m n n α⊂,则m ∥α; ②若,,m n m n αα⊥⊥⊄,则//n α; ③若,,m n αβαβ⊥⊥⊥,则m n ⊥;
④若m n 、是异面直线,,,//m n m αββ⊂⊂,则//n α. 其中正确的命题序号是 ▲ .
14.过平面外一点只能作一条直线与这个平面平行
( )
15.若长方体的长、宽、高分别是2、2、1,则长方体的外接球的表面积为 ▲ .
16.若直线a ∥平面α,AB CD 、为夹在a 与α间的等长线段,
,,,A a D a B C αα∈∈∈∈,则AB 与CD 的位置关系是______________ 评卷人
得分
三、解答题
17.(本小题满分14分)
如图,在三棱柱111ABC A B C -中,侧面11AA B B 为菱形, 且160A AB ∠=︒,AC BC =,D 是AB 的中点.
(1)求证:平面1A DC ⊥平面ABC ; (2)求证:1BC ∥平面1A DC .
18.已知:平行六面体1111D C B A ABCD -的底面ABCD 是菱形,且满足:
6011=∠=∠=∠BCD CD C CB C
(1)面C 1BD//面AB 1D 1 (2)证明 BD C C ⊥1; (3)当1
CC CD
的值为多少时,能使BD C C A 11平面⊥?请给出证明.
19.已知直线a 和b 是异面直线,直线c a ∥,直线b 与c 不相交,求证:b 和c 是异面直线。
1
1
1
D
C B A
C B
A (第16
B 1
A 1
C 1
D 1
A
B
C
D
20.已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、选择题
1.A 2.B 3.C 4.B 解析::B
[解析]若1212//,//,.,.m l n l m n αλλβ⊂⊂,则可得//αβ.若//αβ则存在1221
,//,//m l n l λλ 5.D 6.B 7.B 8.A ; 9. 10.
第II 卷(非选择题)
请点击修改第II 卷的文字说明 评卷人
得分
二、填空题
11. 12.
13.②③ 14.× 15.π9 16. 评卷人
得分
三、解答题
17. (1)证明:∵ 11ABB A 为菱形,且160A AB ∠=︒,
∴△1A AB 为正三角形. …………………2分
D 是AB 的中点,∴1AB A D ⊥.
∵AC BC =,D 是AB 的中点,∴ AB CD ⊥. …………………4分 1A D CD D =,∴AB ⊥平面1A DC . …………………6分
∵AB ⊂平面ABC ,∴平面1A DC ⊥平面ABC . …………………8分 (2)证明:连结1C A ,设1
1
AC AC E =,连结DE . ∵三棱柱的侧面11AA C C 是平行四边形,∴E 为1AC 中点. …………………
10分
在△1ABC 中,又∵D 是AB 的中点,∴DE ∥1BC . …………………12分
∵DE ⊂平面1A DC ,1BC ⊄平面1A DC ,∴ 1BC ∥平面1A D C . …………………14分
18.解:(1)略
(2)证明:连结A 1C 1、AC ,AC 和BD 交于点O ,连结C 1O ,∵四边形ABCD 是菱形,∴AC ⊥BD ,BC =CD
又∵∠BCC 1=∠DCC 1,C 1C 是公共边,∴△C 1BC ≌△C 1DC ,∴C 1B =C 1D ∵DO =OB ,∴C 1O ⊥BD ,但AC ⊥BD ,AC ∩C 1O =O ∴BD ⊥平面AC 1,又C 1C ⊂平面AC 1,∴C 1C ⊥BD .
(3)由(2)知BD ⊥平面AC 1,∵A 1O ⊂平面AC 1,∴BD ⊥A 1C ,当
1
CD
CC =1时,平行六面体的六个面是全等的菱形,同理可证BC 1⊥A 1C ,又∵BD ∩BC 1=B ,∴A 1C ⊥平面C 1BD . 19.
20.解:设圆台的母线长为l ,则 1分
圆台的上底面面积为2
24S ππ=⋅=上 3分
圆台的上底面面积为2
525
S ππ=⋅=下 5分 所以圆台的底面面积为29S S S π=+=下上 7分
又圆台的侧面积(25)
7S l l ππ=+=侧 9分 于是725l ππ= 10分 即29
7
l =为所求. 12分。
