人教A版高中数学必修第一册三角函数的概念课件
合集下载
人教A版高中数学必修第一册 第5章 三角函数 课件(1)(共38张PPT)

图象图正象弦特曲征线、余弦曲线、正切曲线
三角函数
三角函数的图象与性质
周 奇期 偶性 性 性质
单调性
最大、最小值
A,ω,φ对函数图象的影响
函数y=Asinωx+φ的图象 图象画法五 变点 换法 法
三角函数模型的简单应用
专题训练
专题一 正弦函数与余弦函数的对称性问题 正弦函数 y=sinx,余弦函数 y=cosx,在教材中已研究了 它们的定义域、值域、单调性、奇偶性、周期性.除了上述有 关内容之外,近年来有关正弦函数、余弦函数等对称性问题在 高考中有所出现,有必要对其作进一步的探讨.
第五章
人教2019A版必修 第一册
三角函数
小结与复习
知识框图
三 角 函 数
பைடு நூலகம்
公式一~四:α+2kπk∈Z,-α,π±α的三角函数值等于α的同名函数值, 前面加上一个把α看成锐角时原函数值的符号
三角函数的诱导公式
公式五、六:π2±α的正余弦函数值,分别等于α的余弦正弦函数值, 前面加上一个把α看成锐角时原函数值的符号
解得ab= =- -41, .
∴a、b 的取值分别是 4、-3 或-4、-1.
[点拨] 本题是先由定义域确定正弦函数 y=sin(2x+6π)的 值域,但对整个函数的最值的取得与 a 有关系,故对 a 进行分 类讨论.
设 a≥0,若 y=cos2x-asinx+b 的最大值为 0,最 小值为-4,试求 a、b 的值.
[分析] 通过换元化为一元二次函数最值问题求解.
[解析] 原函数变形为 y=-(sinx+a2)2+1+b+a42. 当 0≤a≤2 时,-a2∈[-1,0], ∴ymax=1+b+a42=0.① ymin=-(1+a2)2+1+b+a42=-4② 由以上两式①②,得 a=2,b=-2,舍 a=-6(与 0≤a≤2 矛盾).
人教A版高中数学必修一《5.2.1三角函数的概念》精品课件(39页)

D.第四象限
解析:由sin α<0可知α在第三或第四象限,由tan α>0可知α在第一或第三象
限,综上,α在第三象限. 答案:C
3.已知角
α
的终边与单位圆的交点
P
55,-2
5Hale Waihona Puke 5,则sinα+cos
α=(
)
5 A. 5
B.-
5 5
25 C. 5
D.-2 5 5
解析:由三角函数的定义知 sin α=-255,cos α= 55,所以 sin α+cos α=-255
所以 1100x=
x x2+9 .
又 x≠0,所以 x=±1,所以 r= 10.又 y=3>0,
所以 θ 是第一或第二象限角.
当 θ 为第一象限角时,sin θ=31010,tan θ=3,
则 sin θ+tan θ=3 1100+30;
当 θ 为第二象限角时,sin θ=31010,tan θ=-3,
+
55=-
5 5.
答案:B
知识点二 诱导公式一 (一)教材梳理填空 (1)终边相同的角的同一三角函数的值 _相__等___. (2)公式
[微思考] 同一三角函数值相等时,角是否一定相等或相差周角的整数倍? 提示:不一定,如 sin 30°=sin 150°=12.
(二)基本知能小试
1.判断正误
(1)若α=β+720°,则cos α=cos β.
3.三角函数值的符号: 如图所示:
正弦: 一二 象限正, 三四 象限负; 余弦: 一四 象限正, 二三 象限负; 正切: 一三 象限正, 二四 象限负. 简记口诀:一全正、二正弦、三正切、四余弦. [微思考] 三角函数值在各象限的符号由什么决定? 提示:由α的终边所在的象限决定.
5.2.1三角函数的概念(第一课时)人教A版高中数学必修第一册课件

立德树人 和谐发展
例2 如图,设α是一个任意角,它的终边上任意一点P(不与原点O
重合)的坐标为(x,y),点P与原点的距离为r.
y
=tanα ( ).
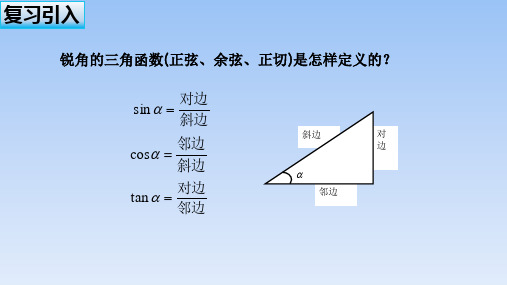
y x y 【探究】当 时,点P的坐标是什么?当 或 时,点P的坐标又是什么?给 求证:sin α ,cos α ,tan α . 请同学们回忆一下:在直角三角形中,如何表示角的正弦、余弦和正切值.
(2)把点P的横坐标 叫做α的余弦函数,记作cosα,即 =cosα
旋转角α,终止位置为OP.
于是
,即 △.OMP∽△OM0P0.于是
M 0P0 1
MP r
,即 y0
y r
.
因为y0与y同号,所以 y0
y r
,即sin α
y r
.
同理可得 cosα x,tan α y.
r
x
定义推广:
立德树人 和谐发展
旋转角α,终止位置为OP.
【探究】当
时,点P的坐标是什么?当 或 时,点P的坐标又是什么?给
定一个角α,它的终边OP与单位圆的交点P的坐标是唯一确定的吗?
探求新知
立德树人 和谐发展
【分析】利用勾股定理可以发现,当
时,点P的坐标是
;当
或
时,点P的坐标分别是
和
,它们都是唯一确定的(如图).
【结论】一般地,任意给定一个角α∈R,它的终边OP与单位圆的交点P的坐标,无 论是横坐标 还是纵坐标 ,都是唯一确定的.所以,点P的横坐标 和 纵坐标 都是角α的函数.
).
可以看出,当
时,α的终边始终在y轴上,这时
,
即此时tanα无意义.除此之外,正切tanα与实数α是一一对应的,所以它们之间
人教高中数学必修一A版 《三角函数的概念》三角函数(第1课时三角函数的概念)PPT课件

PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 范文下载:/fanwen/ 教案下载:/jiaoan/ PPT课件:/kejian/ 数学课件:/kejian/shu xue/ 美术课件:/kejian/me ishu/ 物理课件:/kejian/wul i/ 生物课件:/kejian/she ngwu/ 历史课件:/kejian/lish i/
试卷下载:/shiti/
历史课件:/kejian/lish i/
预
习
3
探新知
栏目导航
4
1.单位圆
PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ PPT论坛: 语文课件:/kejian/yuw en/ 英语课件:/kejian/ying yu/ 科学课件:/kejian/kexu e/ 化学课件:/kejian/huaxue/ 地理课件:/kejian/dili/
科学课件:/kejian/kexue/ 物理课件:/kejian/wul i/
化学课件:/kejian/huaxue/ 生物课件:/kejian/she ngwu/
地理课件:/kejian/dili/
②x
叫做
α 的余弦函数,记作 PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 范文下载:/fanwen/
PPT教程: /powerpoint/
资料下载:/ziliao/
范文下载:/fanwen/
数学人教A版必修第一册5.2.1三角函数的概念课件

作业
1、完成练习册第130-131页
必做:例1、例2、跟踪2、3、4,A级1-5、9
选做:6-8、10
2、在导学案完成表格数据
谢谢大家,欢迎批评指正
T H A N K
Y O U
A L L
r
x
0
O
y
又 y0与y同号,
y0
r
0
M
0
M
新知探索 —— 三角函数第二定义
设α是一个任意角,Px, y 是终边上的任意一点,
点P与原点的距离为:r x 2 y 2 >0
y
sin α
r
x
cos α
r
y
tan α x 0
x
比较三角函数第一定义:设α是一个任意
7
、
的正弦值、余
2
6
y
x
探究二
(, ),把按锐角三角函数定义求得的锐角x的正弦记为 ,并把按
设 ∈
本节三角函数定义求得的锐角x记为 。 和 相等吗?对于余弦和正
切也有相同的结论吗?
1
AB
OA
1
sin x
z
1
A
OA
A1 B1 y sin x
1
1
AB
O
由三角函数的性质得: 1
角,它的终边与单位圆相交于点P(x,y)
sinα=y cosα=x tanα =
(x≠0)
05 课堂探究 -例题讲授
例3、已知角α的终边过点P(-12,5),求角α
的三角函数值。
课堂小结
1、三角函数的第一定义
2、三角函数的第二定义
3、求任意角的三角函数值的方法:先寻求
人教A版高中数学必修一课件 《任意角和弧度制》三角函数PPT(第一课时任意角)

理解与角的概念有关问题的关键 正确理解象限角与锐角、直角、钝角、平角、周角等概念,弄清角 的始边与终边及旋转方向与大小.另外需要掌握判断结论正确与否 的技巧,判断结论正确需要证明,而判断结论不正确只需举一个反 例即可.
经过 2 个小时,钟表的时针和分针转过的角度分
别是( )
A.60°,720°
B.-60°,-720°
D.-390°
解析:选 D.-390°=330°-720°,所以与 330°角终边相同 的角是-390°.
3.若角 α 的终边与 75°角的终边关于直线 y=0 对称,且-360° <α<360°,则角 α 的值为____________. 解析:如图,设 75°角的终边为射线 OA,射线 OA 关于直线 y= 0 对称的射线为 OB,则以射线 OB 为终边的一个角为-75°,所 以以射线 OB 为终边的角的集合为{α|α=k·360°-75°,k∈Z}.又 -360°<α<360°,令 k=0 或 1,得 α=-75°或 285°.
-110°是( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角 答案:C
与 30°角终边相同的角的集合是( ) A.{α|α=30°+k·360°,k∈Z} B.{α|α=-30°+k·360°,k∈Z} C.{α|α=30°+k·180°,k∈Z} D.{α|α=-30°+k·180°,k∈Z}
本部分内容讲解结束
按ESC键退出全屏播放
象限角的条件是角的顶点与坐标原点重合,角的始边与 x 轴的非负 半轴重合.
3.终边相同的角 所有与角 α 终边相同的角,连同角 α 在内,可构成一个集合 S= _{_β_|β_=__α_+__k_·_3_6_0_°__,__k_∈__Z_}__,即任一与角 α 终边相同的角,都可以 表示成角 α 与_______整__数_个__周_角_____的和. ■名师点拨
人教A版高中数学:三角函数的概念【精品课件】

[教材解难]
正确认识三角函数线 (1)正弦线、余弦线、正切线分别是正弦、余弦、正切函数 的几何表示,三角函数线的长度等于三角函数值的绝对值,方向表 示三角函数值的正负,凡与 x 轴或 y 轴同向的为正值,反向的为负 值. (2)三角函数线的画法 定义中不仅定义了什么是正弦线、余弦线、正切线,同时也给 出了角 a 的三角函数线的画法,即先找到 P,M,T 点,再画出 MP, OM,AT. (3)三角函数线的作用 三角函数线的主要作用是解三角不等式及比较同角异名三角 函数值的大小,同时它也是以后学习三角函数的图象与性质的基 础.
知识点四 三角函数值在各象限的符号
状元随笔 对三角函数值符号的理解 三角函数值的符号是根据三角函数定义和各象限内坐标符号 导出的.从原点到角的终边上任意一点的距离 r 总是正值.根据三 角函数定义知: (1)正弦值符号取决于纵坐标 y 的符号; (2)余弦值的符号取决于横坐标 x 的符号; (3)正切值的符号是由 x,y 符号共同决定的,即 x,y 同号 为正,异号为负.
应用诱导公式一时,先将角转化到 0 ~2π 范围内的角,再求 值.对于特殊角的三角函数值一定要熟记.
最新课程标准: 理解同角三角函数的基本关系式:sin2x+cos2x=1,csoins xx=tan x.
知识点 同角三角函数的基本关系式
状元随笔 (1)利用 sin2α+cos2α=1 可实现 α 的正弦、余弦的互化,利 用csoins αα=tan α 可以实现角 α 的弦切互化. (2)关系式的逆用及变形用:1=sin2α+cos2α,sin2α=1- cos2α,cos2α=1-sin2α.
知识点二 正弦、余弦、正切函数在弧度制下的定义域
三角函数
定义域
sin α
高中数学新人教A版必修一三角函数的概念课件34张

【跟踪训练 3】 若角α的终边与直线 y=3x 重合,且 sin α<0,又 P(m,n)是角α终边
上一点,且|OP|= 10 ,则 m-n=
.
解析:由题,所以n=3m, 又m2+n2=10, 所以m2=1. 又sin α<0,所以m=-1,所以n=-3. 故m-n=2.
答案:2
考查角度2:三角函数值的符号 【例4】 (2018·石家庄质检)已知sin α<0,tan α>0. (1)求角α的集合;
(A) 4 5
(B)- 4 (C) 3
5
5
(D)- 3 5
解析:因为点 A 的纵坐标 yA= 4 ,且点 A 在第二象限,又因为圆 O 为单位圆,所以 A 5
点的横坐标 xA=- 3 ,由三角函数的定义可得 cos α=- 3 .故选 D.
5
5
【例2】 若角θ的终边过点P(-4a,3a)(a≠0). (1)求sin θ+cos θ的值;
(A)1 (B)-1 (C)±1 (D)±2
解析:sin α= 2 = 2 ,x=2,tan α= y = 2 =1.故选 A.
x2 22 x
x2
4.(教材改编题)若sin α<0且tan α<0,则α是( D ) (A)第一象限角 (B)第二象限角 (C)第三象限角 (D)第四象限角
解析:由sin α<0,得α在第三或第四象限;由tan α<0,得α在第二或第四象 限,故α在第四象限.故选D.
2.弧度制
(1)定义 长度等于 (2)公式
半径长
角α的弧度数公式
角度与弧度的换算 弧长公式
扇形面积公式
的弧所对的圆心角叫做1弧度的角.弧度记作rad.
|α|= ①1°=
高中数学人教A版必修第一册5.三角函数的概念-任意角的三角函数定义(PPT全文课件)

tan 45 1.
sin 60 3 , 2
cos 60 1 , 2
tan 60 3.
sin120 3 , 2
sin135 2 , 2
sin150 1 , 2
cos120 1 , 2
cos135 2 , 2
cos150 3 , 2
tan120 3. tan135 1.
tan150 3 . 3
② 45°
P( 2 , 2 ) 22
45
sin 45 2 , 2
cos 45 2 , 2
tan 45 1.
求三角函数值的方法(单位圆定义): 分别计算出30°,45°,60°;
120°,135°,150°; 0°, 90°, 180°的三个三角函数值:
③ 60°
P(1 , 3) 22
60
sin 60 3 , 2
又因为②式 tan 0 成立,所以角 的终边可能位于
第一或第三象限.
因为①②式都成立,所以角 的终边只能位于第三象限. 于是角 为第三象限角.
反过来(必要性)请同学们自己证明.
诱导公式一: 作用:大角化小角,负角化正角(化为0~2π范围内的角)
求三角函数值的方法(单位圆定义):
分别计算出30°,45°,60°;
求三角函数值的方法(单位圆定义):
分别计算出30°,45°,60°;
120°,135°,150°;
⑤ 135°
0°, 90°, 180°的三个三角函数值:
P( 2 , 2 ) 22
135
sin135 2 , 2
cos135 2 , 2
tan135 1.
求三角函数值的方法(单位圆定义): 分别计算出30°,45°,60°;
sin 60 3 , 2
cos 60 1 , 2
tan 60 3.
sin120 3 , 2
sin135 2 , 2
sin150 1 , 2
cos120 1 , 2
cos135 2 , 2
cos150 3 , 2
tan120 3. tan135 1.
tan150 3 . 3
② 45°
P( 2 , 2 ) 22
45
sin 45 2 , 2
cos 45 2 , 2
tan 45 1.
求三角函数值的方法(单位圆定义): 分别计算出30°,45°,60°;
120°,135°,150°; 0°, 90°, 180°的三个三角函数值:
③ 60°
P(1 , 3) 22
60
sin 60 3 , 2
又因为②式 tan 0 成立,所以角 的终边可能位于
第一或第三象限.
因为①②式都成立,所以角 的终边只能位于第三象限. 于是角 为第三象限角.
反过来(必要性)请同学们自己证明.
诱导公式一: 作用:大角化小角,负角化正角(化为0~2π范围内的角)
求三角函数值的方法(单位圆定义):
分别计算出30°,45°,60°;
求三角函数值的方法(单位圆定义):
分别计算出30°,45°,60°;
120°,135°,150°;
⑤ 135°
0°, 90°, 180°的三个三角函数值:
P( 2 , 2 ) 22
135
sin135 2 , 2
cos135 2 , 2
tan135 1.
求三角函数值的方法(单位圆定义): 分别计算出30°,45°,60°;
人教版高中数学必修第一册5.2三角函数的概念 课时3 三角函数的概念(1)【课件】

提高用定义解题的能力.
学习目标
课程目标
学科核心素养
经历三角函数概念的建构过程,体会
通过用单位圆上点的坐标定义ห้องสมุดไป่ตู้意角的三
用单位圆上点的坐标刻画任意角三角
角函数,培养数学抽象、直观想象素养
函数的方法
理解任意角的三角函数的概念,能根 通过运用任意角的三角函数的定义求任意
据定义求出任意角α的正弦、余弦和 角α的三角函数值,培养逻辑推理、数学运
初探新知
【活动1】从函数角度理解三角函数的定义
【问题1】对于一个任意角,如何定义它的三角函数呢?
【问题2】怎样从函数的角度理解三角函数的定义呢?
【活动2】探究角的终边上任意一点的坐标与该角三角函
数之间的关系
【问题4】能否找到一个方法计算当α∈(0,+∞)时,h的高度?
【问题5】如图,建立直角坐标系,随着点P位置的改变,∠AOP的
【解】
【方法规律】
根据角的终边上任意一点的坐标,便可求出该角的三角函数;当角的终边在
y轴上时,其正切函数值不存在;由于角既是图形,又可与实数建立一一对应
关系,因此三角函数是以实数为自变量的函数.在本题中,由于求出的m值有
两个,因此在求角θ的余弦和正切值时要分两种情况进行讨论.
课堂反思
1. 通过本节课的学习,你学到了哪些知识?
【方法规律】
当点P是角的终边与单位圆的交点时,横坐标x即为cos α,纵坐标y即为
sin α, 即为tan α(α≠ +kπ,k∈Z);当点P是角的终边上任意一点时,
需要先求出r=
α= ,tan
+ ,然后求出对应角的三角函数值:sin
学习目标
课程目标
学科核心素养
经历三角函数概念的建构过程,体会
通过用单位圆上点的坐标定义ห้องสมุดไป่ตู้意角的三
用单位圆上点的坐标刻画任意角三角
角函数,培养数学抽象、直观想象素养
函数的方法
理解任意角的三角函数的概念,能根 通过运用任意角的三角函数的定义求任意
据定义求出任意角α的正弦、余弦和 角α的三角函数值,培养逻辑推理、数学运
初探新知
【活动1】从函数角度理解三角函数的定义
【问题1】对于一个任意角,如何定义它的三角函数呢?
【问题2】怎样从函数的角度理解三角函数的定义呢?
【活动2】探究角的终边上任意一点的坐标与该角三角函
数之间的关系
【问题4】能否找到一个方法计算当α∈(0,+∞)时,h的高度?
【问题5】如图,建立直角坐标系,随着点P位置的改变,∠AOP的
【解】
【方法规律】
根据角的终边上任意一点的坐标,便可求出该角的三角函数;当角的终边在
y轴上时,其正切函数值不存在;由于角既是图形,又可与实数建立一一对应
关系,因此三角函数是以实数为自变量的函数.在本题中,由于求出的m值有
两个,因此在求角θ的余弦和正切值时要分两种情况进行讨论.
课堂反思
1. 通过本节课的学习,你学到了哪些知识?
【方法规律】
当点P是角的终边与单位圆的交点时,横坐标x即为cos α,纵坐标y即为
sin α, 即为tan α(α≠ +kπ,k∈Z);当点P是角的终边上任意一点时,
需要先求出r=
α= ,tan
+ ,然后求出对应角的三角函数值:sin
人教A版必修第一册5.2.1三角函数的概念课件

22
y
,
5
所以 sin 5 3
3 ,cos 5
2
3
1 2
,tan
5 3
3
3
o
﹒
A
x
﹒B
思考:若把角 5 改为 7 呢?
3
6
请看课本P180:练习2
sin 7 1 , cos 7 3 , tan 7 3
6
2
6
2
63
任意角的三角函数的定义的推广:
设角 是一个任意角,P(x, y) 是终边上的任意一点,
1.任意角的三角函数的定义
设 是一个任意角,它的终边与单位圆交于点P(x, y)
那么:(1)y 叫做 的正弦,记作 sin ,即 sin y ;
x (2) 叫做 的余弦,记作 cos,即 cos x ;
y
(3) 叫做
x
的正切,记作tan
,即
tan
y x
(x
0)
y
所以,正弦,余弦,正切都是以
(2)sin73π
cos
-23π 6
+tan
-15π 4
cos 133π.
y; r
cosα
x; r
tanα
y (x x
0)
请看课本P180:练习3
练习:3:已知角 的终边过点P12,5 ,
求 的三个三角函数值.
解: |OP|=r x2 y2 122 52 13
sinθ
y r
5 ,cosθ 13
x r
12 , 13
tanθ
y x
5 12
2.三角函数的定义域
点 P 与原点的距离 r x2 y 2 0
记 r | OP | x2 y2
y
,
5
所以 sin 5 3
3 ,cos 5
2
3
1 2
,tan
5 3
3
3
o
﹒
A
x
﹒B
思考:若把角 5 改为 7 呢?
3
6
请看课本P180:练习2
sin 7 1 , cos 7 3 , tan 7 3
6
2
6
2
63
任意角的三角函数的定义的推广:
设角 是一个任意角,P(x, y) 是终边上的任意一点,
1.任意角的三角函数的定义
设 是一个任意角,它的终边与单位圆交于点P(x, y)
那么:(1)y 叫做 的正弦,记作 sin ,即 sin y ;
x (2) 叫做 的余弦,记作 cos,即 cos x ;
y
(3) 叫做
x
的正切,记作tan
,即
tan
y x
(x
0)
y
所以,正弦,余弦,正切都是以
(2)sin73π
cos
-23π 6
+tan
-15π 4
cos 133π.
y; r
cosα
x; r
tanα
y (x x
0)
请看课本P180:练习3
练习:3:已知角 的终边过点P12,5 ,
求 的三个三角函数值.
解: |OP|=r x2 y2 122 52 13
sinθ
y r
5 ,cosθ 13
x r
12 , 13
tanθ
y x
5 12
2.三角函数的定义域
点 P 与原点的距离 r x2 y 2 0
记 r | OP | x2 y2
高中数学必修第一册人教A版5.2《三角函数的概念》名师课件
(2)∵角θ是第二象限角, ∴ cos<0,根据三角函数的定义可知,
当为第二象限角时,−1 < cos =
< 0. ∴
−
2
< cos < 0, ∴ sin(cos) < 0.
方法归纳
求三角函数值或相关式子的符号的步骤
对于判断含三角函数的代数式的值的符号问题,关键是要搞清楚三角函数中
解析
(1)原式 = cos 8
+
3
+ tan −4
+
4
=
cos
3
+
tan
4
1
2
= +1=
3
.
2
(2)原式 = sin 90° + 2 × 360° + tan 45° + 2 × 360° − cos360° = sin90° +
tan45° − 1 = 1 + 1 − 1 = 1
素养提炼
形式给出时,要根据问题的实际及解题的需要进行分类讨论.
典例讲授
例5、判断下列三角函数值的符号.
(1) sin3 − cos4 − tan5;
(2)sin(cos)(角为第二象限角).
解析
(1)∵
2
<3<<4<
3
2
< 5 < 2
∵3是第二象限角,4是第三象限角,5是第四象限角,
∴ sin 3>0,cos4 < 0, tan5 < 0. ∴ sin3 − cos4 − tan5 > 0.
+1
当为第二象限角时,−1 < cos =
< 0. ∴
−
2
< cos < 0, ∴ sin(cos) < 0.
方法归纳
求三角函数值或相关式子的符号的步骤
对于判断含三角函数的代数式的值的符号问题,关键是要搞清楚三角函数中
解析
(1)原式 = cos 8
+
3
+ tan −4
+
4
=
cos
3
+
tan
4
1
2
= +1=
3
.
2
(2)原式 = sin 90° + 2 × 360° + tan 45° + 2 × 360° − cos360° = sin90° +
tan45° − 1 = 1 + 1 − 1 = 1
素养提炼
形式给出时,要根据问题的实际及解题的需要进行分类讨论.
典例讲授
例5、判断下列三角函数值的符号.
(1) sin3 − cos4 − tan5;
(2)sin(cos)(角为第二象限角).
解析
(1)∵
2
<3<<4<
3
2
< 5 < 2
∵3是第二象限角,4是第三象限角,5是第四象限角,
∴ sin 3>0,cos4 < 0, tan5 < 0. ∴ sin3 − cos4 − tan5 > 0.
+1
高中数学人教A版必修第一册三角函数的概念课件

b
cos c
a
tan b
二 课堂探究
探究一:1、已知∠α的度数,如何求角的终边与单位圆交点P的坐标?
2
3
y
M
方法: 过点P向x轴做垂线,得到直角三角形 OPM,可以用锐角三角函数求点P;
PM sin 60 PM 3
OP
2
OM cos60 OM 1
x OP
2
点P的坐标为: -
1 2
人教A版2019高中数学必修第一册
OPM,可以用锐角三角函数求点P;
4 3 4 计算:当∠α变化的时候,点P的坐标情况
r 5 sin ,cos ,tan 由例题2可知,只要知道∠α终边上任意一点P的坐标,就可以求得∠α的三个三角函数值。
5 5 3 归纳:利用单位圆求任意角三角函数值的一般步骤
③求出角的终边与单位圆的交点坐标
即 终边与单位圆的交点P的坐标为
=,所ta以nα (
).
自主学习:课本P177—P179
探究一:1、已知∠α的度数,如何求角的终边与单位圆交点P的坐标?
计算:当∠α变化的时候,点P的坐标情况
我们把正弦函数、余弦函数和正切函数统称为三角函数. 探究一:1、已知∠α的度数,如何求角的终边与单位圆交点P的坐标?
2、会求∠α的三角函数值;
(3)把点P的纵坐标和横坐标的比值 叫做∠α的正切函数,记作tanα,
自主学习:课本P177—P179
由例题2可知,只要知道∠α终边上任意一点P的坐标,就可以求得∠α的三个三角函数值。
(2)把点P的横坐标x叫做∠α的余弦函数,记作cosα,即x=cosα
M 探究二:1、如图,∠α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r;
cos c
a
tan b
二 课堂探究
探究一:1、已知∠α的度数,如何求角的终边与单位圆交点P的坐标?
2
3
y
M
方法: 过点P向x轴做垂线,得到直角三角形 OPM,可以用锐角三角函数求点P;
PM sin 60 PM 3
OP
2
OM cos60 OM 1
x OP
2
点P的坐标为: -
1 2
人教A版2019高中数学必修第一册
OPM,可以用锐角三角函数求点P;
4 3 4 计算:当∠α变化的时候,点P的坐标情况
r 5 sin ,cos ,tan 由例题2可知,只要知道∠α终边上任意一点P的坐标,就可以求得∠α的三个三角函数值。
5 5 3 归纳:利用单位圆求任意角三角函数值的一般步骤
③求出角的终边与单位圆的交点坐标
即 终边与单位圆的交点P的坐标为
=,所ta以nα (
).
自主学习:课本P177—P179
探究一:1、已知∠α的度数,如何求角的终边与单位圆交点P的坐标?
计算:当∠α变化的时候,点P的坐标情况
我们把正弦函数、余弦函数和正切函数统称为三角函数. 探究一:1、已知∠α的度数,如何求角的终边与单位圆交点P的坐标?
2、会求∠α的三角函数值;
(3)把点P的纵坐标和横坐标的比值 叫做∠α的正切函数,记作tanα,
自主学习:课本P177—P179
由例题2可知,只要知道∠α终边上任意一点P的坐标,就可以求得∠α的三个三角函数值。
(2)把点P的横坐标x叫做∠α的余弦函数,记作cosα,即x=cosα
M 探究二:1、如图,∠α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们将正弦函数,余弦函数和正切函数统称为三角函数, 通常将它们记为:
正弦函数 余弦函数 正切函数
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三第一册三角函数 的概念 课件
1
人教A版高中数学必修第一册三角函数 的概念 课件
例题讲解
例2. 填表:
角 角的弧度数
0º 90º 180º 270º 360º 0
角与单位圆交点坐标 (1,0) (0,1)(-1,0)(0,-1)(1,0)
0
1
0
-1
0
1
0
-1
0
1
0 不存在 0
不存在
0
注:根据三角函数的定义,我们可以解决此类角的终边与坐标轴重合的三角函数问题.
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
人教A(2019版)高一上
5.2.1 三角函数的概念 (第一课时)
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习目标
1. 了解单位圆的概念; 2. 借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义; 3. 解决已知角的终边任意点坐标,求该角的三角函数等问题.
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
谢谢观看!
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
人教A版高中数学必修第一册三角函数 的概念 课件
探究学习
人教A版高中数学必修第一册三角函数 的概念 课件
1
-1
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
探究学习
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
课堂小结
任意角的三角函数
借助单位圆定义
求角的三角函数值
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
情景引入
P
O
在直角坐标系中,我们称以原点为圆心,以单位长度为半径的圆为单位圆 (unit circle).
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习新知——任意角的三角函数的定义
y
1
P
-1
x
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习新知——任意角的三角函数的定义
y
1
-1
x
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习新知——任意角的三角函数的定义
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
例题讲解
解:
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
正弦函数 余弦函数 正切函数
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三第一册三角函数 的概念 课件
1
人教A版高中数学必修第一册三角函数 的概念 课件
例题讲解
例2. 填表:
角 角的弧度数
0º 90º 180º 270º 360º 0
角与单位圆交点坐标 (1,0) (0,1)(-1,0)(0,-1)(1,0)
0
1
0
-1
0
1
0
-1
0
1
0 不存在 0
不存在
0
注:根据三角函数的定义,我们可以解决此类角的终边与坐标轴重合的三角函数问题.
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
人教A(2019版)高一上
5.2.1 三角函数的概念 (第一课时)
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习目标
1. 了解单位圆的概念; 2. 借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义; 3. 解决已知角的终边任意点坐标,求该角的三角函数等问题.
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
谢谢观看!
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
人教A版高中数学必修第一册三角函数 的概念 课件
探究学习
人教A版高中数学必修第一册三角函数 的概念 课件
1
-1
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
探究学习
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
课堂小结
任意角的三角函数
借助单位圆定义
求角的三角函数值
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
情景引入
P
O
在直角坐标系中,我们称以原点为圆心,以单位长度为半径的圆为单位圆 (unit circle).
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习新知——任意角的三角函数的定义
y
1
P
-1
x
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习新知——任意角的三角函数的定义
y
1
-1
x
人教A版高中数学必修第一册三角函数 的概念 课件
人教A版高中数学必修第一册三角函数 的概念 课件
学习新知——任意角的三角函数的定义
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
例题讲解
解:
人教A版( 高2中01数9)学高必中修数第学一必册修三第角一函册数 的5.概2.念1 三课角件函 数的概 念课件 第一课 时(共1 3张ppt )
