材料的热膨胀
各种材料热膨胀系数

食盐
40
不锈钢
14.4-16.0
苯
1.23
铍
12.3
碳纤维(HM 35 in L?ngsrichtung)
-0.5
钛
10.8
氯仿(三氯甲烷)
1.28
水泥
6 – 14
康铜
15.2
铋
14
果酸
1.07
铅
29.3
Kovar
~ 5
钨
4.5
乙醚
1.62
铜
17.5
铜
16.5
锌
36
乙酸乙酯
1.38
镉
41
镁
26
各种材料热膨胀系数
热膨胀系数(Coefficient of thermal expansion,簡稱CTE)是指物质在热胀冷缩效应作用之下,几何特性随着温度的变化而发生变化的规律性系数。
实际应用中,有两种主要的热膨胀系数,分別是:
线性热膨胀系数:a=1/L*△L/△T
体积热膨胀系数:γ=1/V0*(аV/аt)p
物质
α in 10-6/K 20 °C
物质
α in 10-6/K 20 °C
物质
γ in 10-3/K 20 °C
铝
23.2
木头, Eiche
8
银
19.5
酒精(乙醇)
1.1
纯铝
23.0(铝的热膨胀系数高达23μm/m.℃。)
不变钢
1.7-2.0
锡
2
丙酮
1.43
锑
10.5
铱
6.5
钢
13
汽油Байду номын сангаас
1.06
各种材料热膨胀系数

一些液体的体积热膨胀系数 γ
物质
α in 10-6/K 20 °C
物质
α in 10-6/K 20 °C
物质
α in 10-6/K 20 °C
3
玻璃 (派热克斯玻璃)
85
பைடு நூலகம்物质
γ in 10-3/K 20 °C
8
酒精(乙醇)
纯铝
(铝的热膨胀系数高达23μm/m.℃。)
2
13
40
氯仿(三氯甲烷)
6 – 14
14
~ 5
36
41
26
23
5
3
Minerall(Hydraulikl)
51
2
9
/柴油
6
18
13
玻璃陶瓷(Zerodur)
<
1
玻璃 (工业玻璃)
9
80
玻璃 (普通)
120
各种材料热膨胀系数
热膨胀系数(Coefficient of thermal expansion,简称CTE)是指物质在热胀冷缩效应作用之下,几何特性随着温度的变化而发生变化的规律性系数。
实际应用中,有两种主要的热膨胀系数,分别是:
线性热膨胀系数:a=1/L*△L/△T
体积热膨胀系数:γ=1/V0*(аV/аt)p
材料的热膨胀

无机材料的线膨胀 系数一般都不大
某些无机材料的热膨胀系数与温度之间的关系
精选ppt
7
三、 影响热膨胀的因素
1. 合金成分对热膨胀的影响
组成合金ቤተ መጻሕፍቲ ባይዱ溶质元素及含量对合金的热膨胀 的影响极为明显。固溶体中加人膨胀系数大
的溶质元素时, 膨胀系数增大; 反之, 加人溶质元素的膨胀系数 较小时, 固溶体的膨胀系数减小。
精选ppt
3
二、 热膨胀系数
定义:在等压(p一定)下,单位 温度变化所导致的体积变化, 即热膨胀系数。
精选ppt
4
线膨胀系数α:α=ΔL/(L*ΔT)
面膨胀系数β:β=ΔS/(S*ΔT) 体膨胀系数γ:γ=ΔV/(V*ΔT)
式中ΔL为所给长度变化ΔT下物体温度的改变,L为初始长度;ΔS 为所给面积变化ΔT下物体温度的改变,S为初始面积;ΔV为所给 体积变化ΔT下物体温度的改变,V为初始体积。
精选ppt
温度范围 303 ~ 573 153 ~ 1133 523 ~ 753 303 ~ 1123 693 ~ 1263
373 1573 293 ~ 373 273 ~ 473 293 ~ 573 273 ~ 373 273 ~1273 273 ~1273 273 ~1273 273 ~1273
αl
Cu-Au合金
膨胀系数
rE / %
精选ppt
8
2.相变对热膨胀的影响
当金属和合金发生一级或二级相变时, 其膨胀
量和膨胀系数都会发生变化。
一级相变:金属与合金中的大多数相变都属于
一级相变, 一级相变的特征是能量、体积和晶
体结构的不连续变化, 即是转变将伴随比容的
突变, 相应的膨胀系数将有不连续的变化, 其转
各种材料热膨胀系数

玻璃陶瓷(Zerodur)
< 0.1
金
14.2
花岗岩
3.0
石墨
2.0
灰铸铁
9.0
木头, Eiche
8.0
不变钢
1.7-2.0
铱
6.5
食盐
40.0
碳纤维(HM 35 in L?ngsrichtung)
-0.5
康铜
15.2
Kovar
~ 5
铜
16.5
镁
26.0
锰
23.0
砖
5.0
黄铜
18.4
钼
5.2
新银
18.0
镍
13.0
铂
9.0
尼龙
120.0
聚甲基丙烯酸甲酯(PMMA)
85.0
聚氯乙烯(PVC)
80.0
瓷器
3.0
银
19.5
锡
2.0
钢
13.0
不锈钢
14.4-16.0钛10ຫໍສະໝຸດ 8铋14.0钨
4.5
锌
36.0
锡
26.7
一些液体的体积热膨胀系数 γ
物质
γ in 10-3/K 20 °C
酒精(乙醇)
1.10
丙酮
1.43
汽油
1.06
苯
1.23
氯仿(三氯甲烷)
1.28
果酸
1.07
乙醚
1.62
乙酸乙酯
1.38
甘油(Propantriol)
0.49
甲醇
1.10
Mineral?l(Hydraulik?l)
0.70
石蜡
0.76
煤油
材料物理性能课件-1.3材料的热膨胀

V0[1(a
b
c)T]
V
a
b
c
由于膨胀系数是随温度变化的,所以上述各值都是指
定温度范围内的平均值,因此与平均热容一样,应用
时要注意适用的温度范围。膨胀系数的精确表达为:
dl
l lT dT
dV
V VT dT
continue
热膨胀的物理本质
在晶格振动中,曾近似地认为质点的热振动是 简谐振动。对于简谐振动,升高温度只能增大 振幅,并不会改变平衡位置。因此质点间平均 距离不会因温度升高而改变。热量变化不能改 变晶体的大小和形状,也就不会有热膨胀。这 样的结论显然是不正确的。
熔点越低,则热膨胀系数越大。由于单质的熔点与周 期表存在一定的规律性,所以热膨胀系数与周期表也 存在相应关系。
continue
格律乃森给出的金属热膨胀极限方程
V Tm C
对于大多数立方和六方结构的金属,C值在0.06~0.076
线膨胀系数与德拜温度的关系
l
A V 2/3M
1 2D
continue
5、X射线衍射法 是一种微观的检测方法。借助晶体对x射线的衍射, 测量晶格常数(原子间距)随温度的变化。
continue
热膨胀在工程中的意义
热膨胀系数是材料的一项重要热学性能指标,在实
际工程应用中具有重要意义。
1) 是决定材料抗热震性的主要因素。
2) 陶瓷坯上釉,二者α应匹配。釉α适当小于坯,烧结
谐振动,晶格振动中相邻质点间的作用力实际上是非 线性的,位能曲线也是非对称的。
导致热膨胀的次要因素
晶体中各种热缺陷的形成将造成局部点阵的畸变和 膨胀。随温度的升高,热缺陷浓度指数增加,所以 高温时,这方面的影响对某些晶体也就变得重要了。
材料的热膨胀

Copyright © Sino-i Technology Limited All rights reserved
Sino-i Technology Ltd.
ITSM / ITIL
部分材料的线性膨胀系数
材料名称
Al Ti Cr Fe Ni Cu W Invar合金6Ni-Fe 铸铁 黄铜
Si Al2O3 SiC Si3N4 石英玻璃
Sino-i Technology Ltd.
Copyright © Sino-i Technology Limited All rights reserved
Sino-i Technology Ltd.
ITSM / ITIL
材料热膨胀的本质: 在于晶格点阵实际上在作非 简谐振动,晶格振动中相邻质点间的作用力实际 上是非线性的,点阵能曲线也是非对称的。
Sino-i Technology Ltd.
ITSM / ITIL
3.晶体缺陷对热膨胀的影响
实际晶体中总是含有某些缺陷, 它们在室温处于“ 冻结” 状态, 但 它们可明显地影响晶体的物理性能。 Timmesfeld等人研究了空位对固体热膨胀的影响。由空位引起的晶 体附加体积变化为:
△ V = BV0exp[-Q/kT]
变点处a 将为无限大。
二级相变:相变时两相的化学势相等, 相变时
虽然没有体积的不连续变化, 但仍存在膨胀系
数的不连续变化。属于二级相变的磁性转变和
有序无序转变,在其相变处膨胀系数温度曲线上
有折点。 Copyright © Sino-i Technology Limited All rights reserved
式中,Q 是空位形成能,B 是常数, V0是晶体0k时的体积,k 是玻 耳兹曼常数,T 是温度( K )。这里的空位可以由辐射或高温淬火产 生。
热的膨胀和膨胀系数的计算

热的膨胀和膨胀系数的计算材料的热膨胀是指由于温度的升高,材料的长度、面积或体积增加的现象。
膨胀系数是一个材料的性质,用来描述其对温度变化的敏感度。
本文将介绍热膨胀的基本原理以及如何计算膨胀系数。
一、热膨胀的原理根据热力学原理,物质的温度升高会导致分子的热运动增强,分子之间的相互作用力减弱,使材料的体积、长度或面积增大。
不同材料的热膨胀性能可能有所不同,这取决于其结构、成分和弹性模量等因素。
热膨胀是一种普遍存在于物质中的现象,对于工程设计和材料选择具有重要意义。
二、线膨胀系数的计算线膨胀系数(α)是描述材料在一定温度下单位长度的膨胀量。
通常用公式表示为:ΔL = αL₀ΔT其中,ΔL是材料长度的变化量,L₀是初始长度,ΔT是温度的变化量。
根据单位换算,线膨胀系数的单位通常是1/℃或者K⁻¹。
线膨胀系数可以通过实验测量或者查阅资料获得,常见材料的线膨胀系数如下:- 钢:11x10⁻⁶ /℃- 铝:23x10⁻⁶ /℃- 铜:16x10⁻⁶ /℃- 玻璃:8x10⁻⁶ /℃三、体膨胀系数的计算体膨胀系数(β)用于描述材料在一定温度下单位体积的膨胀量。
通常用公式表示为:ΔV = βV₀ΔT其中,ΔV是材料体积的变化量,V₀是初始体积,ΔT是温度的变化量。
与线膨胀系数类似,体膨胀系数的单位也是1/℃或者K⁻¹。
体膨胀系数可以通过实验测量或者查阅资料获得,常见材料的体膨胀系数如下:- 钢:3x10⁻⁵ /℃- 铝:7x10⁻⁵ /℃- 铜:5x10⁻⁵ /℃- 玻璃:9x10⁻⁶ /℃四、应用实例假设我们有一根长度为1m的铁管,将其加热到100℃,我们可以根据铁的线膨胀系数计算出其长度的变化量:ΔL = αL₀ΔT= 11x10⁻⁶ /℃ x 1m x 100℃= 0.011m因此,铁管的长度将增加0.011m。
同样地,我们也可以计算铁管的体积变化量:ΔV = βV₀ΔT= 3x10⁻⁵ /℃ x (1m)³ x 100℃= 0.03m³铁管的体积将增加0.03m³。
第一章 材料的热学性能(热膨胀)

线膨胀系数和金属熔Байду номын сангаас的关系式
三、影响固体材料热膨胀系数的一些因素
3.晶体缺陷
格尔茨利坎、荻梅斯费尔德等人研究了空位对固体热膨胀的影响。 格尔茨利坎、荻梅斯费尔德等人研究了空位对固体热膨胀的影响。
空位引起的晶体附加体积变化
辐射空位引起热膨胀系数变化
三、影响固体材料热膨胀系数的一些因素
4.结构
结构紧密的晶体膨胀系数大, 结构紧密的晶体膨胀系数大,结构空敞的晶体膨 胀系数小。 胀系数小。这是由于开放结构能吸收振动能及调整 键角来吸收振动能所导致的。 键角来吸收振动能所导致的。
格律爱森( 定律指出: 格律爱森(Grueisen)定律指出:体膨胀 定律指出 与定容热容成正比, 与定容热容成正比,它们有相似的温度依 赖关系, 赖关系,在低温下随温度升高急剧增大 德拜T 定律),而到高温则趋于平缓。 ),而到高温则趋于平缓 (德拜 3定律),而到高温则趋于平缓。
金属材料
三、影响固体材料热膨胀系数的一些因素
简谐振动是指质点间的作用力与距离成正比,即微观弹性模量β 为常数。(平衡位置不变,只适用于热容分析。) 非简谐振动是指作用力并不简单地与位移成正比,热振动不是 左右对称的线性振动而是非线性振动。 固体材料热膨胀的本质是 源于材料内部的质点(分子或原子)之 间相互作用力关于质点平衡位置的不对称性。
晶格质点振动受力分析
晶格质点振动能量分析
双原子势能曲线: 双原子势能曲线:与合力变化相 对应, 对应,两原子相互势能成一个不 对称曲线变化。温度上升, 对称曲线变化。温度上升,势能 增高,不对称性越明显, 增高,不对称性越明显,导致振 动中心右移,原子间距增大。 动中心右移,原子间距增大。宏 观上表现为热膨胀。 观上表现为热膨胀。
各种材料热膨胀系数

各种材料热膨胀系数材料的热膨胀系数可以定义为单位温度变化时材料长度、体积或面积的变化量与初始尺寸的比值。
不同材料的热膨胀系数差异很大,以下是一些常见材料的热膨胀系数。
1.金属:铝:铝的线膨胀系数为24×10^-6/℃。
因此,当铝材料从摄氏0度升到100度时,材料长度将增加约0.24%。
铁:铁的线膨胀系数为11.7×10^-6/℃。
在相同条件下,铁材料的长度增加约0.117%。
铜:铜的线膨胀系数为16.6×10^-6/℃。
在相同条件下,铜材料的长度增加约0.166%。
2.塑料:聚乙烯:聚乙烯的线膨胀系数为105×10^-6/℃。
因此,当聚乙烯材料从摄氏0度升至100度时,材料长度将增加约1.05%。
聚丙烯:聚丙烯的线膨胀系数为125×10^-6/℃。
在相同条件下,聚丙烯材料的长度增加约1.25%。
聚四氟乙烯:聚四氟乙烯的线膨胀系数为12×10^-6/℃。
在相同条件下,聚四氟乙烯材料的长度增加约0.12%。
3.陶瓷:石英:石英的膨胀系数为0.5×10^-6/℃。
因此,当石英材料从摄氏0度升至100度时,材料长度将增加约0.005%。
氧化铝:氧化铝的线膨胀系数约为7.4×10^-6/℃。
在相同条件下,氧化铝材料的长度增加约0.074%。
4.玻璃:硼硅酸玻璃:硼硅酸玻璃的线膨胀系数约为3.3×10^-6/℃。
因此,当硼硅酸玻璃材料从摄氏0度升至100度时,材料长度将增加约0.033%。
钠钙玻璃:钠钙玻璃的线膨胀系数约为9×10^-6/℃。
在相同条件下,钠钙玻璃材料的长度增加约0.09%。
总结:不同材料的热膨胀系数可以很大程度上影响材料的热胀冷缩性能。
了解材料的热膨胀系数可以帮助工程师设计和预测材料在不同温度下的性能和变形情况。
常见材料热膨胀系数解析

常见材料热膨胀系数解析常见材料热膨胀系数解析引言:热膨胀是物体在温度变化时展现出的一种性质,也是工程设计和材料选择中不可忽视的因素。
随着温度的升高,物体的尺寸会发生改变,这可能会对工程结构的稳定性和性能产生重要影响。
理解和掌握常见材料的热膨胀系数是非常重要的。
一、热膨胀系数的概念和定义热膨胀系数是一个描述物体在温度变化时膨胀程度的物理量,通常用符号α表示。
它定义为单位温度变化下单位长度的线膨胀或体膨胀量。
常见的热膨胀系数单位是°C⁻¹。
二、常见材料的热膨胀系数1. 金属材料:金属是一类导热性能较好的材料,它的热膨胀系数一般比较大。
铝的热膨胀系数为22.2×10⁻⁶ °C⁻¹,而钢的热膨胀系数在10×10⁻⁶ - 13×10⁻⁶ °C⁻¹之间。
在工程设计中使用金属材料时,需要考虑温度变化对构件的影响。
2. 石材和混凝土:石材和混凝土是建筑工程中常用的材料,它们的热膨胀系数比金属要小。
石材的热膨胀系数在5×10⁻⁶ - 11×10⁻⁶ °C⁻¹之间,混凝土的热膨胀系数约为10×10⁻⁶ °C⁻¹。
这种相对较小的热膨胀系数使得石材和混凝土在温度变化下变形较小,更适用于建筑结构的使用。
3. 塑料和橡胶:塑料和橡胶是热膨胀系数较大的材料。
由于它们的热膨胀系数较高,温度变化会导致较大的变形。
在使用塑料和橡胶制品的工程中,需要考虑温度变化对构件的影响,特别是在高温环境下。
4. 玻璃:玻璃的热膨胀系数比较小,一般在8×10⁻⁶ - 10×10⁻⁶ °C⁻¹之间。
这使得玻璃在温度变化下变形较小,适用于长时间稳定性要求较高的工程结构和仪器设备。
三、热膨胀系数的影响和应用1. 工程设计中的考虑:在工程设计中,材料的热膨胀系数需要考虑作为一个重要的参数。
材料的热膨胀性能

(P230 5.2材料的热膨胀) 热胀冷缩现象,称为热膨胀。 当有组织变化时,会有一明显的体积效 应(一级相变)。
2018/11/20 1
§2-1 热膨胀系数
一、线膨胀系数 设一物体在TK温度下的真实长度为l,当温度升高 Δ TK后,其长度变为l+Δ l,则有下列关系式成立:
l T l l 1 dl 1 ( K 1或O C 1 ) 这里α 为材料的线膨胀系数。一般来说 α T l dT L
Al2TiO5: 垂直于C轴方向(层间): α=-2.6×10-6K-1 平行于C轴方向(层内): α=11.5×10-6K-1
10
1、多型性转变的影 响 属于一级相变, Δ l或Δ V有突变, α 产生明显变化, 若相变为等温转变, 则α 在转变点趋近 于无穷大。 2、有序—无序转变 属于二级相变,相 变时体积无突变, 但α 在相变温度区 间有变化。
由上述的位能理论可知,热膨胀与位能曲线的形状密切相关。而位能曲 线形状与质点间的结合力和熔点有关。结合能(力)越大,熔点越高,位 能曲线变得深而窄,升高同样的温度Δ T,质点的振幅增加得较少,平均 平衡位置的位移量亦较少,因此热膨胀系数较小。 格留奈申(Gruneisen)给出了固态金属膨胀的极限方程: VTM VO C VO
i K ( i )T
这里: i 为第i相的应力, 复合体的平均体积膨胀 系数, E K 3(1 2 ) 由于整体内应力之和为 0,则有
i 第i相的膨胀系数, T 从应力松弛状态算起的 温度变化。
i
K ( i )Vi T 0,
2018/胀机理
各种材料热膨胀系数

26。7
甘油(Propantriol)
0.49
铬
6.2
锰
23
金
14.2
甲醇
1。1
钻石
1。3
砖
5
花岗岩
3
Mineral?l(Hydraulik?l)
0.7
冰, 0 °C
51
黄铜
18.4
石墨
2
石蜡
0.76
铁
12.2
钼
5。2
灰铸铁
9
煤油/柴油
0。96/0.69
锗
6
新银
18
玻璃 (Quarzglas)
0.5
大多数情况之下,此系数为正值.也就是说温度升高体积扩大。但是也有例外,当水在0到4摄氏度之间,会出现反膨胀。而一些陶瓷材料在温度升高情况下,几乎不发生几何特性变化,其热膨胀系数接近0。
一些固体的线性热膨胀系数 α(单位:10—6/K)
一些液体的体积热膨胀系数 γ
物质
α in 10-6/K 20 °C
水银
0.18
玻璃 (窗玻璃)
7。6
镍
13
玻璃陶瓷(Zerodur)
< 0.1
松节油
1
玻璃 (工业玻璃)
4。5
铂
9
聚氯乙烯(PVC)
80
四氯化碳
1.22
玻璃 (普通)
7。1
尼龙
120
瓷器
3
甲苯
1。12
玻璃 (派热克斯玻璃)
3。25
聚甲基丙烯酸甲酯(PMMA)
85
水
0。21
—4。1
食盐
40
不锈钢
14.4-16。0
常见材料热膨胀系数

常见材料热膨胀系数
【实用版】
目录
1.热膨胀系数的定义和意义
2.常见材料的热膨胀系数
3.热膨胀系数在实际应用中的重要性
4.结论
正文
热膨胀系数是一个重要的物理量,它表征了物体在受热时,其长度、面积或体积变化的程度。
热膨胀系数包括线膨胀系数、面膨胀系数和体膨胀系数,这些系数可以用来描述物质在不同温度下的膨胀情况。
在日常生活中,我们常常会接触到各种材料,如金属、陶瓷、塑料等。
这些材料的热膨胀系数是不同的,因此,在实际应用中,我们需要根据材料的热膨胀系数来设计产品,以确保产品的稳定性和安全性。
例如,在制造金属器件时,我们需要选择具有相近热膨胀系数的金属材料,以避免因温度变化引起的器件变形或破裂。
同样,在焊接或熔接不同材料时,我们也需要选择具有相近热膨胀系数的材料,以确保焊接或熔接处的稳定性。
热膨胀系数在实际应用中的重要性不言而喻。
在工程设计、材料科学、物理学等领域,热膨胀系数都是一个重要的研究课题。
通过研究材料的热膨胀系数,我们可以更好地了解材料的性质和特点,从而更好地利用这些材料来满足我们的需求。
总的来说,热膨胀系数是一个重要的物理量,它对于我们了解和利用材料具有重要的意义。
在实际应用中,我们需要根据材料的热膨胀系数来设计产品,以确保产品的稳定性和安全性。
材料的热膨胀行为及其在工程中的应用

材料的热膨胀行为及其在工程中的应用材料的热膨胀行为是指当材料受热时,其体积、长度和面积会发生改变的现象。
热膨胀行为是由于物质内部原子的热运动引起的,随着温度的升高,原子的热振动增强,从而使材料的尺寸发生变化。
热膨胀在工程中有着广泛的应用,下面将从材料选择、结构设计和工程实践等方面进行论述。
1. 材料选择在工程设计中,我们需要考虑材料的热膨胀系数。
热膨胀系数是描述材料热膨胀行为的物理量,它表示在单位温度变化下,材料单位长度的形变量。
不同材料的热膨胀系数存在差异,因此在选材时需要根据具体的工程要求和环境条件来选择合适的材料。
例如,在建筑领域中,由于环境温度的变化以及建筑材料的特性差异,我们需要选择具有相似热膨胀系数的材料来减小热膨胀对结构的影响。
另外,在航空航天、核工程等领域,材料的低热膨胀系数是一个重要的考虑因素,以确保材料在极端温度环境下的稳定性与可靠性。
2. 结构设计在工程结构设计中,必须合理考虑材料的热膨胀行为,以避免由于热膨胀引起的变形、开裂等问题。
一种常见的应用是利用热膨胀行为来设计伸缩缝和隔热层。
伸缩缝可以有效地补偿材料由于温度变化而引起的体积变化,防止产生过大的应力,从而减小结构的变形和破坏风险。
在建筑物、桥梁、管道等工程中广泛采用伸缩缝的设计,以确保结构的稳定性与耐久性。
隔热层的设计也是基于材料的热膨胀行为。
在高温环境下,结构材料容易受到热膨胀的影响,从而导致材料性能的下降和破坏。
通过在结构表面覆盖一层隔热材料,可以减少热膨胀对结构的直接作用,提高结构的稳定性和耐用性。
3. 工程实践热膨胀行为在工程实践中的应用包括管道的伸缩补偿、高温设备的设计等。
管道的伸缩补偿是为了解决由于温度变化引起的管道变形和应力增大问题。
通过在管道中安装伸缩补偿器,可以有效地补偿热膨胀引起的管道变形,保证管道的正常运行。
在高温设备的设计中,必须考虑材料的热膨胀特性。
例如,在炉膛的设计中,需合理预留热膨胀空间,以避免设备由于热膨胀而产生应力集中和变形等问题。
第三节材料热膨胀
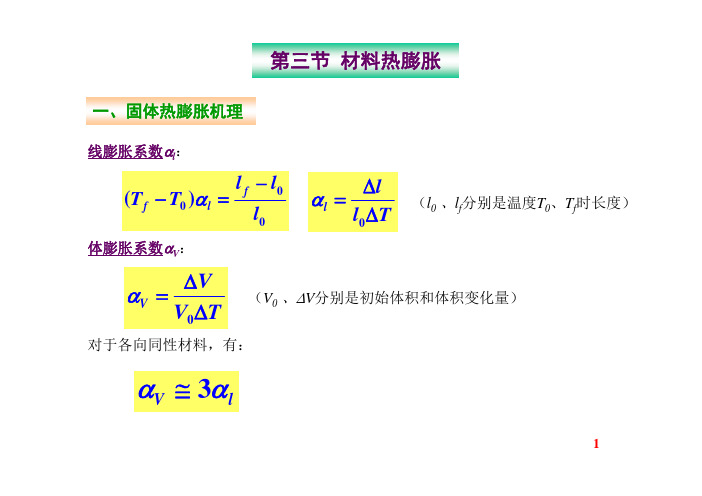
第三节材料热膨胀一、固体热膨胀机理线膨胀系数αl :体膨胀系数αV :对于各向同性材料,有:00()f f l l l T T l α−−=0l l l TαΔ=Δ(l 0、l f 0V V V TαΔ=Δ(V 0、ΔV 分别是初始体积和体积变化量)3V lαα≅热膨胀本质:从原子的观点看,热膨胀是点阵结构中的质点间平均距离随温度升高而增大现象的宏观反映质点的振动可分为简谐振动和非简谐振动材料热膨胀的物理本质是质点振动的非简谐效应简谐效应:质点围绕其平衡位置作简谐振动,质点之间相互作用势能对平衡位置是对称的,温度升高只能增大振幅,并不改变平衡位置。
质点间平均距离不会因温度升高而改变,即不改变晶体的大小和形状,晶体受热不膨胀非简谐效应:原子之间斥力项(玻恩斥力B/r n,n和原子的电子层有关,电子层越多,n越大,nHe =5,nNe=7,nAr=9)随原子间距的变化比引力项(库仑力A/r2)的变化更快。
热振动不是左右对称的线性振动,而是非线性振动23在质点平衡位置r 0的两侧,合力曲线的斜率是不相等的。
当r <r 0时,曲线的斜率较大;r >r 0时,斜率较小。
r <r 0时斥力随位移变化很快;r >r 0时引力随位移的变化要慢一些在这样的受力情况下,质点振动时的平均位置就不在r 0处,而要向右移。
因此相邻质点间平均距离增加温度越高,振幅越大,质点在r 0两侧受力不对称情况越显著,平衡位置向右移动越多,相邻质点间平均距离就增加得越多,以致晶胞参数增大,晶体膨胀从点阵能曲线的非对称性同样可以得到具体解释非对称势能曲线对称势能曲线T 1T 2T 3T 4T 5对于给定的点阵能曲线,r,β,β’均为常数,似乎α也为常数。
但如再考虑δ4,δ5,…时,则可得α随温度而变化的规律除了质点的非对称振动外,作为次要因素,晶体中的各种热缺陷的形成也将造成局部点阵的畸变和膨胀且随着温度升高,缺陷浓度按指数关系增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/3/10
讲解:XX
5
部分材料的线性膨胀系数
材料名称 Al Ti Cr Fe Ni Cu W Invar合金6Ni-Fe 铸铁 黄铜 Si Al2O3 SiC Si3N4 石英玻璃
2021/3/10
αl /10-6 K-1 24.9 9.2 10.60 16.7 17.1 17.18 5.19 0~2 10.5 ~ 12 18.5 ~ 21 6.95 8.8 4.7 2.7 0.5
Timmesfeld等人研究了空位对固体热膨胀的影 响。由空位引起的晶体附加体积变化为:
Q/kT]
△ V = BV0exp[-
式中,Q 是空位形成能,B 是常数, V0是晶体
0k时的体积,k 是玻耳兹曼常数,T 是温度( K
2021/3/10
讲解:XX
10
4.晶体各向异性对热膨胀的影响
由于晶体结构的不对称性, 在不同的晶轴上产生 不相等的热膨胀, 所以晶体的热膨胀量也需要用六 个独立的参数来表征。
2021/3/10
讲解:XX
11
Thank
You!
2021/3/10
讲解:XX
12
感谢您的阅读收藏,谢谢!
2021/3/10
13
讲解:XX
温度范围 303 ~ 573 153 ~ 1133 523 ~ 753 303 ~ 1123 693 ~ 1263
373 1573 293 ~ 373 273 ~ 473 293 ~ 573 273 ~ 373 273 ~1273 273 ~1273 273 ~1273 273 ~1273
6
无机材料的线膨胀 系数一般都不大
某些无机材料的热膨胀系数与温度之间的关系
2021/3/10
讲解:XX
7
三、 影响热膨胀的因素
1. 合金成分对热膨胀的影响
组成合金的溶质元素及含量对合金的热膨胀 的影响极为明显。固溶体中加人膨胀系数大
的溶质元素时, 膨胀系数增大; 反之, 加人溶质元素的膨胀系数 较小时, 固溶体的膨胀系数减小。
αl
Cu-Au合金
膨胀系数
r 2021/3/1E0 / %
讲解:XX
8
2.相变对热膨胀的影响
当金属和合金发生一级或二级相变时, 其膨胀
量和膨胀系数都会发生变化。
一级相变:金属与合金中的大多数相变都属于
一级相变, 一级相变的特征是能量、体积和晶
体结构的不连续变化, 即是转变将伴随比容的
突变, 相应的膨胀系数将有不连续的变化, 其转
材料的热膨胀
2021/3/10
讲解:XX
1
一、 热膨胀的本质
定义:通常是指外压强不变的 情况下,大多数物质在温度升 高时,其体积增大,温度降低 时体积缩小的现象。
2021/3/10
讲解:XX实际上在作非 简谐振动,晶格振动中相邻质点间的作用力实际 上是非线性的,点阵能曲线也是非对称的。
变点处a 将为无限大。
二级相变:相变时两相的化学势相等, 相变时
虽然没有体积的不连续变化, 但仍存在膨胀系
数的不连续变化。属于二级相变的磁性转变和
有序无序转变,在其相变处膨胀系数温度曲线上
有折点。 2021/3/10
讲解:XX
9
3.晶体缺陷对热膨胀的影响
实际晶体中总是含有某些缺陷, 它们在室温处 于“ 冻结” 状态, 但它们可明显地影响晶体 的物理性能。
原子间相互作用的势能曲线
2021/3/10
讲解:XX
3
二、 热膨胀系数
定义:在等压(p一定)下,单位 温度变化所导致的体积变化, 即热膨胀系数。
2021/3/10
讲解:XX
4
线膨胀系数α:α=ΔL/(L*ΔT)
面膨胀系数β:β=ΔS/(S*ΔT) 体膨胀系数γ:γ=ΔV/(V*ΔT)
式中ΔL为所给长度变化ΔT下物体温度的改变,L为初始长度;ΔS 为所给面积变化ΔT下物体温度的改变,S为初始面积;ΔV为所给 体积变化ΔT下物体温度的改变,V为初始体积。
固体中热膨胀的各向异性可以定性地从原子间结 合力的强弱来说明。在非立方晶系中, 特别是在具 有一次轴对称的晶系中,平行于轴向和垂直于轴向 的原子间结合力差别甚大。若在某一个方向上结合 力较其它方向为小,则晶体首先在该方向上受到热 激发,因此在该方向上的热膨胀迅速增加,与此同 时往往伴随着垂直于该方向上的收缩,因此出现膨 胀系数的负值。
