2020扬州中考时间安排
2024年江苏省扬州市中考英语试题(含答案)

扬州市2024年初中毕业升学考试英语一、单项选择(共15小题;每小题1分,计15分)在下列各题A、B、C、D四个选项中选择一个能填入题干空白处的最佳答案。
1.The Marco Polo Memorial Hall stands at the east end of Dongguan Street ________ Yangzhou.A. toB. onC. atD. in2.“What’s that?” is ________ of the first things that children say.A. someB. eachC. oneD. that 3.Teamwork doesn’t happen ________ in the workplace or school. It needs training.A. naturallyB. correctlyC. wildlyD. especially 4.Look! My sister ________ the table. Let’s give her a hand.A. setB. setsC. is settingD. was setting 5.China has made great efforts ________ other countries build high-speed railways.A. helpB. to helpC. helpingD. helped6.Our monitor is ________. He always spends a lot of time helping with our class projects.A. generousB. humorousC. nervousD. curious7.As we all k now, the Yangtze River ________ as a “mother river” of the Chinese nation.A. knowsB. knewC. is knownD. was known8.— How does this new washing machine work?—It’s easy. You ________ touch this icon.A. evenB. almostC. everD. just9.M any think SOS is short for “save our ship”, but it doesn’t really ________ anything.A. look forB. stand forC. pay forD. try for10.You can’t eat an elephant all at once. Eat it one bite ________.A. on timeB. at a timeC. all the timeD. at the same time 11.Since I was born, my family ________ in the same flat.A. liveB. will liveC. are livingD. have lived12.________ you are too tired to do all the things on your To-Do list, try a To-Don’t list.A. IfB. UntilC. AlthoughD. Unless13.— Do you know why zebrafish are taken to Shenzhou-18?— They have ________ like small size and short development cycle.A. stagesB. advantagesC. messagesD. passages 14.Teenagers don’t always understand ________ their parents have so ma ny rules.A. whyB. whichC. whereD. what15.—I hear you’re leaving for Guilin for your holiday?—________. And I’m looking forward to it.A. It doesn’t matterB. It’s a pleasureC. That’s rightD. Never mind二、完形填空(共15 小题;每小题1分,计15分)阅读下面短文,从文后各题所给的A、B、C、D四个选项中选出一个最佳答案。
扬州市教育局关于做好2020年全市义务教育阶段学校招生入学工作的通知

扬州市教育局关于做好2020年全市义务教育阶段学校招生入学工作的通知文章属性•【制定机关】扬州市教育局•【公布日期】2020.06.10•【字号】•【施行日期】2020.06.10•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】体育卫生与艺术教育正文扬州市教育局关于做好2020年全市义务教育阶段学校招生入学工作的通知-部门信息公开目录〉部门文件-教育局各县(市、区)教育(教体)局,开发区城乡管理局,市蜀冈—瘦西湖风景名胜区社会事业局,市生态科技新城社会事业局,市直各学校:为贯彻落实《中共中央国务院深化教育教学改革全面提高义务教育质量的意见》(中发﹝2019﹞26号)、省委省政府相关文件要求和《省教育厅关于做好2020年义务教育学校招生入学工作的通知》(苏教基〔2020〕4号)精神,规范办学与招生行为,依据相关法律政策规定,结合我市实际,现就做好2020年全市义务教育阶段学校招生入学工作通知如下。
一、招生对象、信息登记(一)招生对象1.全市义务教育学校招生对象。
今年小学一年级应招收年满6周岁(2014年8月31日前出生)的儿童入学。
今年初一年级应招收15周岁以下(2005年9月1日以后出生)的应届小学毕业生。
2.市教育局直属初中学校招生对象。
市教育局直属初中学校(以下简称“市直初中”)招收对象为:市直公办初中施教区范围内户籍小学毕业生(教育行政部门统筹安排的随迁子女除外),持有市直初中招生区域内居住证的随迁子女要求在市直初中就读的应届小学毕业生;市直民办初中招收市教育局批准的招生范围内自愿选择登记该校招生入学的应届小学毕业生。
(二)招生时间全市各地所有义务教育学校原则上于7月下旬开始招生,8月上中旬基本完成招生工作,县(市)、江都区具体招生步骤和时序安排可依据本通知要求确定。
市区(含邗江区、广陵区、经济技术开发区、景区和生态科技新城,不含江都区,下同)由市教育局统一规定入学条件、招生入学时间,在各区划定公办学校施教区基础上由市教育局统一公布。
邗江区普通高中招生政策解读

邗江区普通高中招生政策解读2017邗江区普通高中招生政策解读今天,2017邗江区普通高中招生政策出炉。
四星高中邗江中学和瓜洲中学享受热点高中待遇。
邗江中学今年招收共810人,其中面向市直、广陵区、开发区、蜀冈-瘦西湖风景名胜区和生态科技新城招收210人,面向邗江区招600人。
邗江中学定向指标生总计划按区内招生计划70%测算,定向指标生数的70%按照各初中学校中考考生数平均分配到各初中校;定向指标生数的30%参照教学质量录取。
下面是yjbys店铺为大家带来的关于邗江区普通高中招生政策解读的知识,欢迎阅读。
一、今年普通高中招生政策与去年一致的有哪些?1. 坚持招生计划管理。
各学校严格按照公布的招生计划招生,不得突破计划招收学生。
未经批准超计划招收学生的招生行为无效,教育局对违规招收的学生不予办理学籍。
各学校不得招收借读生、旁听生,坚持学生学籍与就读学校一致的原则,学生不得无故退学,其他学校也不得录取。
2. 坚持以中考成绩作为高中录取新生的依据。
所有应届初三学生都必须参加中考,任何学生都要根据中考成绩参加高中阶段各类学校录取。
3. 坚持普通高中录取最低控制线办法。
今年继续实行普通高中录取最低控制线办法,任何普通高中学校都不得录取市定生源地普通高中录取最低控制线下的学生,任何生源地普通高中录取最低控制线下的学生都不能被普通高中学校录取,不能建立普通高中学籍,不能参加省学业水平测试和高考。
4. 四星高中邗江中学和瓜洲中学享受热点高中待遇。
邗江中学定向指标生总计划按区内招生计划70%测算,定向指标生数的70%按照各初中学校中考考生数平均分配到各初中校;定向指标生数的30%参照教学质量录取。
瓜洲中学定向指标生总计划按招生计划50%测算平均分配到邗江实验学校、邗江中学(集团)北区校维扬中学、梅苑双语学校三所初中。
定向指标生的录取将根据各初中学校定向指标生分配数和考生志愿,从高分到低分依次录取,录取成绩控制线为中考成绩总分的85%。
扬州中考地理及生物会考方案

扬州中考地理及生物会考方案关于调整完善全市初中地理、生物会考方案的说明一、近年来地理、生物会考考试方式及其结果运用近年来,初中地理、生物作为毕业会考科目,考试统一安排在初二年级进行,具体考试时间分别为6月19日上午 8:00 —9:00 和10:00—11:00(中考结束的第二天),实行闭卷考试,由市教育局统一命题、制卷,统一组织考试,统一组织阅卷,考试结果以合格与不合格两种等级形式呈现。
会考是中考的重要组成部分,地理、生物会考科目成绩均合格者方可报考三星及以上普通高中,凡有会考科目成绩不合格者要求升入省三星及以上普通高中就读的,市教育局一律不予办理普通高中学籍。
二、调整完善的必要性调整完善初中会考方案,是进一步推进实施素质教育的需要,是维护国家课程的严肃性、开足开齐开好国家规定课程的需要,是维护学生受教育权、促进学生全面发展和可持续发展的需要,是为学生进入高中阶段后更好地学习地理、生物等国家必修课程和更好地适应高考改革的需要。
为强化学科均衡发展,我市从2013年开始进一步重视会考学科成绩的运用,强化“地理、生物会考科目成绩均合格者方可报考三星及以上普通高中”。
鉴于当前部分地区和部分学校对地理、生物会考学科仍然重视不够,未能做到开齐开足开好国家规定课程,以及省新的高考方案即将出台(上半年省教育厅已宣布新高考方案最迟于2017年公布实施,按照这一时间表,今年的初二年级学生以及后来的学生在升入高中后将按照新高考方案实施),根据国家高考改革方向,目前在浙江、上海已经试行新的高考方案,学生除要考语数外(计入总分)三门学科外,还须在物理、化学、生物、政治、历史、地理共6门学科中选择3门学科参加考试并计入总分,这3门学科每门学科的分值均在70分左右。
按照这一改革方向,学生在初中阶段生物、地理学科的学习基础也变得更加重要。
因此,迫切需要重视初中地理、生物学科的教学工作,按照课程建设要求配齐地理、生物学科专业教师,强化学生在初中阶段地理、生物学科的学业基础,全面实施素质教育,促进学生全面发展,为学生升入高中后更好地学好地理、生物学科做好必要的'准备,促进学生可持续升学和可持续发展。
全国各地中考时间

全国各地中考时间
2021年全国各地中考时间汇总
2021ቤተ መጻሕፍቲ ባይዱ中考的.号角已经吹响,初三的小伙伴们一定在奋力拼搏,为2021中考而战。在此,应届毕业生网考试频道店铺为广大中考生整理了2021全国各地中考时间,供大家参考。希望对广大师生能够有所帮助。
2021伊犁中考时间:6月19日至6月21日
【2021年全国各地中考时间汇总】
2021淮安中考时间:6月15日至6月17日
2021徐州中考时间:6月18日至6月20日
2021南通中考时间:6月16日至6月18日
2021苏州中考时间:6月17日至6月19日
2021镇江中考时间:6月15日至6月19日
宿迁2021中考时间:6月15日至6月17日
无锡2021中考时间:6月16至6月17日
2021广安中考时间:6月16日至6月18日
2021凉山中考时间:6月13日至6月15日
2021乐山中考时间:6月11日至6月13日
2021宜宾中考时间:7月11日至7月13日
2021绵阳中考时间:6月11日至6月12日
2021内江中考时间:6月11日至6月13日
2021巴中中考时间:6月11日至6月12日
2021株洲中考时间:6月18日至6月20日
内蒙古
2021呼和浩特中考时间:6月25日至6月27日
2021呼伦贝尔中考时间:6月25日至6月28日
2021锡林郭勒中考时间:6月25日至6月27日
2021鄂尔多斯中考时间:6月25日至6月28日
2021包头中考时间:6月25日至6月27日
2021巴彦淖尔中考时间:6月25日至6月28日
2023全国各省市中考时间汇总
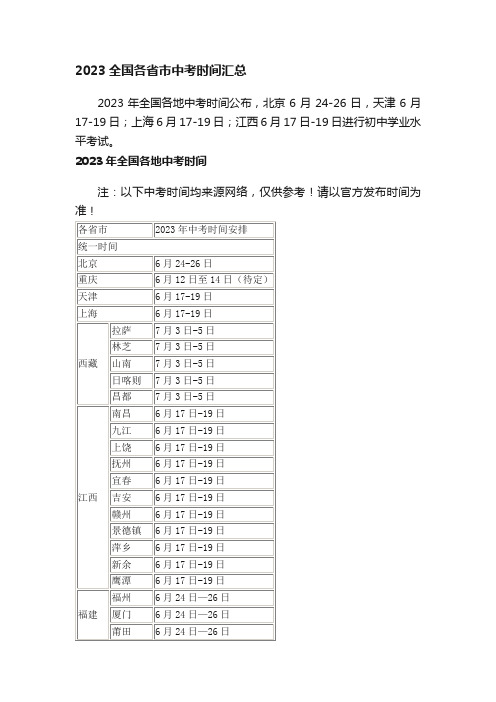
6月17-19日
苏州
6月17-19日
常州
6月18日-6月20日
广西
梧州
6月24-26日
贵港
6月24-26日
北海
6月24-26日
桂林
6月24-26日
南宁
6月24-26日
钦州
6月24-26日
柳州
6月24-26日
崇左
6月24-26日
玉林
6月24-26日
广东
江门
6月26日-6月28日
梅州
6月26日-6月28日
衡阳
6月18-20日
长沙
6月18-20日
株洲
6月17-19日
邵阳
6月18-20日
永州
6月18-20日
郴州
6月18-20日
常德
6月18-20日
岳阳
6月18-20日
浙江
金华
6月14-15日
衢州
6月14-15日
丽水
6月13-14日
义乌
6月14-15日
台州
6月15-17日
嘉兴
6月14-15日
宁波
6月16-17日
阜阳
6月14-16日
宿州
6月14-16日
巢湖
6月14-16日
六安
6月14-16日
亳州
6月14-16日
池州
6月14-16日
宣城
6月14-16日
青海
西宁
果洛
海北
海东
海南
海西
黄南
6月26-28日
玉树
黑龙江
哈尔滨
6月25-27日
齐齐哈尔
6月25-27日
2020年中考时间是几月几号

2020年中考时间是几月几号2020年中考时间宁夏:7月18日-20日西藏:7月18日-20日吉林:7月27日-29日内蒙古:7月21日-30日陕西:7月17日-19日天津:7月18日-19日广西:7月24日-26日重庆:7月12日-14日浙江:6月26日-27日广东:7月20日-22日广州:7月24日-26日海南:7月25日-27日江西:7月17日-19日北京:7月17日-19日山西:7月20日-22日福建:7月18日-20日安徽:7月14日-16日云南:7月25日-27日中考时间2020上海:考试项目考试日期考试时间考试科目中考6月27日(星期六)9:00—10:40 语文14:00—15:40 物理、化学6月28日(星期日)9:00—10:45外语(9:00-9:05为听力试音时间)14:00—15:40 数学初中学业考6月29日(星期一)9:00-9:40 历史(开卷)甘肃:兰州地区确定安排在7月16日-19日进行。
黑龙江:7月14日-16日。
中职对口升学考试时间为7月18日至19日。
专升本考试时间为7月18日。
河北省:7月18日-19日。
河南省:7月15-16日。
青海省:2020年初中毕业暨升学考试延期至7月15日至18日。
九年级考试集中安排在7月15日至17日三天进行,使用省卷和西宁市卷的考生同步开考。
新疆:乌鲁木齐(6月20日-22日);石河子(6月18日-22日)。
江苏:江苏南通:7月12-14日江苏无锡:7月12-13日江苏苏州:7月13-15日江苏宿迁:7月9-18日江苏常州:7月16-18日江苏盐城:7月14-16日江苏扬州:7月16-18日江苏连云港:7月14-16日江苏泰州:7月12-14日山东:山东济南:7月12-15日山东烟台中:7月14-16日山东滨州:7月12-14日山东威海中:7月16-18日山东菏泽:7月14-16日山东淄博中:7月12-15日山东青岛:7月13-16日山东潍坊:7月13-16日湖北:湖北武汉市:7月20-21日湖北天门:7月20-22日湖北随州:7月20-21日湖北襄阳:7月17-19日湖北宜昌:7月20-22日湖北神农架林区:7月20-22日湖北潜江:7月20-22日湖北恩施:7月20-22日湖北咸宁:7月20-21日湖北荆州:7月20-21日湖北荆门:7月20-22日湖北仙桃:7月20-22日湖北十堰:7月20-22日湖南:湘潭:7月16日—18日邵阳:7月18日—20日益阳:7月16日—18日郴州:7月18日—20日永州:7月18日—20日怀化:7月16日—19日娄底:7月16日—18日辽宁:地区2020辽宁中考时间安排沈阳7月18日-21日朝阳7月17日-19日营口7月17日-19日大连7月17日-19日抚顺7月17日-19日鞍山7月17日-19日阜新7月17日-19日四川:泸州市:7月11日-13日四川南充:7月12-13日四川攀枝花:7月12-15日四川内江:延期一个月四川甘孜州:7月13-15日阿坝州:7月13-15日四川宜宾:7月11-13日四川成都:7月14-15日眉州:7月12-14日四川眉山:7月12-14日四川德阳:7月11日开始四川乐山:7月12-14日四川绵阳:7月11-12日贵州:贵阳市:7月12日至14日遵义市:6月20日-22日毕节市:7月13日至15日安顺市:7月12日至14日。
2024各省市中考具体考试时间(一览)

2024各省市中考具体考试时间(一览)2024各省市中考具体考试时间一览6月11日:乐山、绵阳、内江、巴中、德阳、泸州6月12日:重庆、济南、枣庄、东营、滨州、眉山6月13日:淄博、潍坊、济宁、日照、泰安、德州、青岛、凉山、温岭、湖州、丽水6月14日:安徽、连云港6月15日:菏泽、临沂、聊城、烟台、绍兴、舟山、台州、淮安、镇江、宿迁、泰州6月16日:云南、甘肃、成都、广安、南充、达州、金华、义乌、温州、衢州、盐城、南通、无锡、扬州6月17日:江西、常熟、苏州、乌鲁木齐6月18日:湖南、宁波、徐州6月19日:上海、天津、陕西、岳阳、杭州、深圳、南京、咸宁、孝感、荆门、新疆、伊犁2024北京中考时间:6月24日至6月26日2024年上海中考时间:6月19至6月21日2024天津中考时间:6月19日至6月20日2024福建中考时间:6月25日至6月27日2024陕西中考时间:6月19日至6月21日安徽2024中考时间:6月14日至6月16日2024云南中考时间:6月16日至6月18日2024贵州中考时间:6月25日至6月27日2024西藏中考时间:6月25日至6月27日2024青海中考时间:6月21日至6月23日2024青海西宁中考时间:6月21日至6月23日2024重庆中考时间:6月12日至6月14日2024吉林中考时间安排:6月27日至6月29日2024长春中考时间:6月27日至6月29日2024江西中考时间安排:6月17日-6月19日河北2024中考时间:6月21日至6月22日2024山西中考时间:6月20日至6月22日2024河南省中考时间:6月25日至6月27日2024宁夏中考时间:6月28日至6月30日2024黑龙江龙东地区中考时间:6月25日-6月27日2024哈尔滨中考时间:6月25日至6月27日2024大庆中考时间:6月25日至6月27日2024甘肃中考时间:6月16日至6月18日2024淄博中考时间:6月13日至6月16日2024菏泽中考时间安排:6月15日至6月17日2024济宁中考时间安排:6月13日至6月15日2024日照中考时间:6月13日至6月15日2024临沂中考时间:6月15日至6月17日2024济南中考时间:6月12日至6月14日2024泰安中考时间:6月13日至6月16日2024聊城中考时间:6月15日至6月17日2024德州中考时间:6月13日至6月15日2024青岛中考时间:6月13日至6月15日2024烟台中考时间:6月15日至6月17日2024潍坊中考时间:6月13日至6月16日2024枣庄中考时间:6月12日至6月13日2024东营中考时间:6月12日至6月15日2024滨州中考时间:6月12日至6月14日2024威海中考时间:6月16日至6月18日2024甘孜中考时间:6月13日至6月15日2024广安中考时间:6月16日至6月18日2024凉山中考时间:6月13日至6月15日2024乐山中考时间:6月11日至6月13日2024宜宾中考时间:7月11日至7月13日2024绵阳中考时间:6月11日至6月12日2024内江中考时间:6月11日至6月13日2024巴中中考时间:6月11日至6月12日四川眉山2024中考时间:6月12日至14日2024德阳中考时间:6月11日至6月13日2024南充中考时间:6月16日至6月17日2024达州中考时间:6月16日至6月18日2024泸州中考时间:6月11日至6月13日2024益阳中考时间:6月18日至6月20日岳阳2024中考时间:6月19日至6月20日2024张家界中考时间:6月22日至6月24日2024衡阳中考时间:6月18日至6月20日2024永州中考时间:6月18日至6月20日2024长沙中考时间:6月18至6月20日2024怀化中考时间:6月18日至6月20日2024邵阳中考时间:6月18日至6月19日2024株洲中考时间:6月18日至6月20日2024呼和浩特中考时间:6月25日至6月27日2024呼伦贝尔中考时间:6月25日至6月28日2024锡林郭勒中考时间:6月25日至6月27日2024鄂尔多斯中考时间:6月25日至6月28日2024包头中考时间:6月25日至6月27日2024巴彦淖尔中考时间:6月25日至6月28日2024沈阳中考时间:6月26日至6月29日2024锦州中考时间:6月28日至6月30日2024葫芦岛中考时间:6月28日至6月30日2024鞍山中考时间:6月28日至6月30日2024大连中考时间:6月26日至6月27日2024绍兴中考时间:6月15日-6月17日2024宁波中考时间:6月18日至6月19日2024金华中考时间:6月16日至6月17日2024温岭中考时间:6月13日至6月15日2024温州中考时间:6月16日至6月17日2024湖州中考时间:6月13日至6月14日2024衢州中考时间:6月16日至6月17日2024舟山中考时间:6月15日至6月16日2024丽水中考时间:6月13日至6月14日2024杭州中考时间:6月19日至6月20日2024台州中考时间:6月15日至6月17日2024梅州中考时间:6月26日至6月28日2024揭阳中考时间:6月26日至6月28日2024东莞中考时间:6月26日至6月28日2024惠州中考时间:6月26日至6月28日深圳2024中考时间:6月19至6月20日汕头2024中考时间:6月26至6月28日2024清远中考时间:6月26日至6月28日2024中山中考时间:6月26日至6月28日常熟2024年中考时间:6月17日至6月19日2024年盐城中考时间:6月16日至6月18日2024徐州中考时间:6月18日至6月20日2024南通中考时间:6月16日至6月18日2024苏州中考时间:6月17日至6月19日2024镇江中考时间:6月15日至6月19日宿迁2024中考时间:6月15日至6月17日无锡2024中考时间:6月16至6月17日2024南京中考时间:6月19日至6月20日2024连云港中考时间:6月14日至6月16日2024泰州中考时间:6月15日至6月17日2024扬州中考时间:6月16日至6月18日2024十堰中考时间:6月20日至6月22日2024潜江中考时间:7月20日至7月22日2024宜昌中考时间:6月20日至6月22日2024荆州中考时间:6月20日至6月22日2024鄂州中考时间:6月20日至6月21日神农架2024年中考时间:6月20至21日2024咸宁中考时间:6月19日至6月21日2024黄冈中考时间:6月20日至6月21日2024孝感中考时间:6月19日至6月21日2024武汉中考时间:6月20日至6月21日2024仙桃中考时间:6月20日至6月22日2024黄石中考时间:6月20日至6月22日2024襄阳中考时间:6月20日至6月22日恩施2024中考时间:6月20日至6月22日2024荆门中考时间:6月19日至6月22日2024桂林中考时间:6月24日至6月26日2024贵港中考时间:6月24日至6月26日2024南宁中考时间:6月24日至6月26日梧州2024中考时间:6月23日至6月26日2024玉林中考时间:6月24日至6月26日2024来宾中考时间:6月24日至6月26日2024新疆中考时间:6月19日至6月21日2024乌鲁木齐中考时间:6月17日至6月21日2024伊犁中考时间:6月19日至6月21日中考填错志愿如何补救首先,不要慌张,打电话到填报志愿的学校招生办,告知对方填报志愿时没有看清楚,填错了学校。
扬州市教育局关于印发《2020全市教育工作要点》的通知

扬州市教育局关于印发《2020全市教育工作要点》的
通知
文章属性
•【制定机关】扬州市教育局
•【公布日期】2020.03.19
•【字号】扬教发〔2020〕13号
•【施行日期】2020.03.19
•【效力等级】地方规范性文件
•【时效性】现行有效
•【主题分类】教育综合规定
正文
扬州市教育局关于印发《2020全市教育工作要点》的通知各县(市、区)教育(教体)局、经济技术开发区城乡管理局、市蜀冈—瘦西湖风景名胜区社会事业局、市生态科技新城社会事业局,市直各学校:
现将《2020全市教育工作要点》印发给你们,请结合实际认真贯彻落实。
附件:1. 2020全市教育工作要点
2.市教育局2020年度重点工作重大活动行事历
扬州市教育局
2020年3月19日附件1
附件2
市教育局2020年度重点工作重大活动行事历(按完成时间排序)
注:排首位的处室(单位)为牵头处室(单位),该处室(单位)分管领导为牵头领导。
全国各地中考时间汇总

全国各地中考时间汇总2022年全国各地中考时间汇总↓↓↓01统考省份重庆:6月12日—14日北京:6月24日—26日天津:6月18日—20日河北:6月21日—22日山西:6月20日—22日吉林:6月27日—29日上海:7月11日—12日安徽:6月14日—16日福建:6月25日—27日江西:6月17日—19日河南:6月22日—24日海南:6月25日—27日西藏:7月3日—5日陕西:6月18日—20日青海:6月21日—23日宁夏:6月28日—30日新疆:6月18日—20日02内蒙古呼和浩特:6月25日—27日包头/乌海/巴彦淖尔/乌兰察布/锡林郭勒/阿拉善(统考):6月25日—27日赤峰:6月26日—28日通辽:6月26日—28日鄂尔多斯:6月25日—27日呼伦贝尔/兴安(统考):6月25日—27日03辽宁沈阳:6月25日—28日大连:6月25日—27日抚顺:6月28日—30日本溪:6月28日—30日丹东:7月26日—28日锦州:6月28日—29日营口:6月28日—30日阜新:6月28日—30日辽阳:6月28日—30日盘锦:6月28日—29日铁岭:6月28日—30日朝阳:6月28日—30日葫芦岛:6月28日—30日04黑龙江哈尔滨:6月25日—27日齐齐哈尔/黑河/大兴安岭(统考):6月25日—27日鸡西/牡丹江(统考):6月25日—27日鹤岗/双鸭山/伊春/佳木斯/七台河/(统考):6月25日—27日大庆:6月25日—26日05江苏南京:6月18日—19日无锡:6月16日—18日徐州:6月18日—20日常州:6月18日—20日苏州:6月17日—19日南通:6月16日—18日连云港:6月14日—16日淮安:6月15日—17日盐城:6月16日—18日扬州:6月16日—18日镇江:6月7日—19日泰州:6月15日—17日宿迁:6月17日—19日06浙江杭州:6月18日—19日温州:6月16日—17日嘉兴/舟山(统考):6月14日—15日湖州:6月18日—19日绍兴:6月15日—17日金华:6月14日—15日衢州:6月22日—23日台州:6月15日—17日丽水:6月13日—14日07山东济南:6月12日—14日青岛:6月13日—15日淄博:6月14日—17日东营:6月12日—14日烟台:6月14日—16日潍坊:6月13日—15日济宁:6月13日—15日泰安:6月13日—16日日照:6月13日—15日临沂:6月15日—17日德州:6月13日—15日聊城:6月14日—17日滨州:6月13日—15日菏泽:6月14日—16日08湖北武汉:6月20日—21日黄石:6月20日—22日十堰:6月20日—22日宜昌:6月20日—22日襄阳:6月20日—22日鄂州:6月20日—21日荆门:6月20日—22日孝感/黄冈/咸宁(统考):6月20日—21日荆州:6月20日—22日随州:6月20日—21日09湖南长沙:6月18日—20日株洲:6月17日—19日湘潭:6月18日—20日衡阳:6月18日—20日邵阳:6月18日—19日岳阳:6月18日—19日常德:6月18日—20日张家界:6月18日—20日益阳:6月18日—20日郴州:6月18日—20日永州:6月18日—20日怀化:7月16日—19日娄底:6月18日—20日湘西:6月18日—20日10广东广州:6月20日—22日深圳:6月26日—28日其它地市(统考):6月26日—28日11广西南宁/北海/钦州/防城港/来宾/崇左(统考):6月24日—26日柳州:6月24日—26日桂林:6月24日—26日梧州:6月24日—26日贵港:6月24日—26日玉林:6月24日—26日百色:6月24日—26日贺州:6月24日—26日河池:6月24日—26日12四川成都:6月13日—14日自贡:6月11日—13日攀枝花:6月12日—14日泸州:6月13日—15日德阳:6月11日—13日绵阳:6月11日—12日广元:6月13日—15日遂宁:6月11日—13日内江:6月11日—13日乐山:6月12日—14日南充:6月12日—13日眉山:6月12日—14日宜宾:6月14日—16日广安:6月27日—29日达州:6月13日—15日雅安:6月12日—14日巴中:6月11日—12日资阳:6月13日—15日阿坝:6月13日—15日甘孜:6月13日—15日凉山:6月13日—15日13贵州贵阳/六盘水/安顺(统考):6月24日—26日遵义:6月24日—26日毕节:6月24日—26日铜仁:6月24日—26日黔西南:6月24日—26日黔东南:6月24日—26日黔南:6月24日—26日14甘肃兰州:6月16日—18日天水:6月16日—18日其它地市(统考):6月16日—18日注:以上具体考试时间和科目安排请以考试当天为准!END文章来源:网络整合【免责声明】版权属于原。
江苏省扬州市2020年中考语文真题试题(含解析)

扬州市2020年初中毕业、升学统一考试语文试题(考试时间:150分钟满分:150分)说明:1.本试卷共6页,计22题(包含单项选择题:第1-5题、第11题,共6题),满分150分,考试时间150分钟。
考试结束后,请将本试卷和答题卡一并交回。
2.答题前,考生务必将本人的姓名、准考证号准确无误地填写在答题卡相应的位置上。
同时务必在试卷的装订线内将本人的姓名、准考证号、毕业学校填好,在试卷第一面的右下角填好座位号。
3.所有的试题都必须在专用的“答题卡”上作答,选择题用2B铅笔作答,非选择题在指定位置用0.5毫米黑色水笔作答。
在试卷或草稿纸上答题无效。
一、积累运用(32分)1.下列加点字注音,全部正确....的一项是(2分)(▲)A.踌躇.(chú)挑衅.(pàn)自诩.(xǔ)茅塞.顿开(sài)B.颓.唐(tuí)嫉.妒(jì)呜咽.(yàn)脍.炙人口(kuài)C.吮.吸(yǔn)惬.意(qiè)地壳.(ké)明眸善睐.(lài)D.恬.静(tián)豁.免(huò)愠.怒(yùn)争妍.斗艳(yán)1.(2分)D。
A选项中“衅”应读作xìn,“塞”应读作sè;B选项中“嫉”应读作jí,“咽”应读作yè;C选项中“吮”应读作shǔn,“壳”应读作qiào。
2.下列各句中,加点词语使用正确....的一项是(2分)(▲)A.李白笔下的蜀道雄奇险峻,峰回路转....,悬崖峭壁随处可见,令人胆战心惊。
B.个别同学对他这次考试取得的进步表示怀疑,他却忍辱负重....,依然刻苦学习。
C.瘦西湖是中国湖上园林的代表,这里的行云流水....让众多中外游客赞叹不已。
D.“扬州市汉字听写大赛”前夕,老师喋喋不休....地嘱咐我们一定要胆大细心。
全国全国各地中考时间
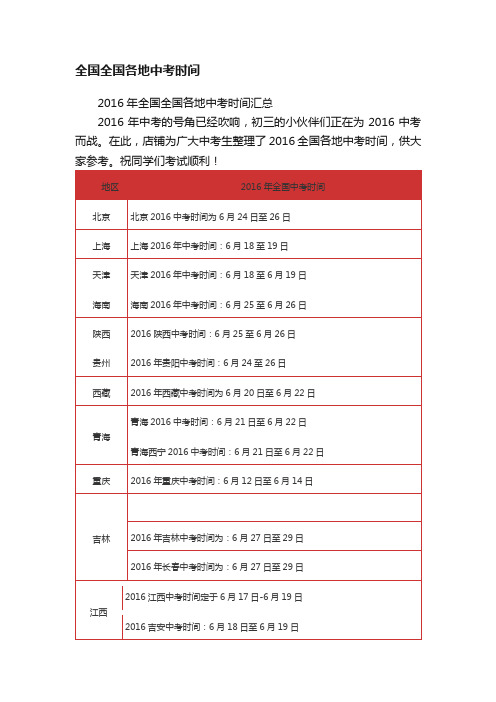
2015年齐齐哈尔中考时间:6月25日至6月28日
甘肃
甘肃兰州2016年中考时间:6月16日至6月19日
新疆
新疆2016中考时间:6月20至6月22日
2016年乌鲁木齐中考时间:6月20日至22日
2016伊犁中考时间:6月20日至22日
山东
淄博2016年中考时间:6月10日至6月12日
湖北仙桃2016中考时间:6月19日至22日
黄石2016中考时间:6月20日至22日
2016襄阳中考时间:6月20至6月22日
恩施2016年中考时间:6月19至22日
【2016年全国全国各地中考时间汇总】
江苏
盐城2016年中考时间:6月16至18日
2015年苏州中考时间:6月17日至19日
2015年江苏中考时间:6月18日至6月20日
2016年镇江中考时间:6月17至19日
徐州2014年中考时间:6月16至18日
无锡2016年中考时间:6月16至17日
2016南京中考时间:6月11日-6月12日
连云港2016年中考时间:6月14至16日
浙江
永康2016年中考时间:待定
宁波2016年中考时间:6月11日至6月12日
金华2016年中考时间:6月11至6月12日
2016温岭中考时间:6月13日至6月15日
温州2016中考时间:6月18至19日
2016湖州中考时间:6月18日-6月19日
衢州2016年中考时间:6月11日至6月12日
舟山2016年中考时间:6月11日至6月12日
泰州2016中考时间:6月15至17日
2016扬州中考时间:6月16日至18日
2020年年江苏省扬州市数学中考试题(解析版)

扬州市2020年初中毕业、升学统一考试数学试题说明:1.本试卷共6页,包含选择题(第1题~第8题,共8题)、非选择题(第9题~第28题,共20题)两部分.本卷满分150分,考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.2.答题前,考生务必将自己的姓名、准考证号填写在答题卡相应的位置上,同时务必在试卷的装订线内将本人的的姓名、准考证号、毕业学校填写好,在试卷第一面的右下角写好座位号.3.所有的试题都必须在考用的“答题卡”上作答,选择题用2B 铅笔作答、非选择题在指定位置用0.5毫米的黑色笔作答.在试卷或草稿纸上答题无效.4.如有作图需要,请用2B 铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共有8小题,每小题3分,共24分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答填卡相应位置上)1.的相反数是( )A .2 B . C . D .【答案】B .【考点】相反数。
【分析】利用绝对值的定义,直接得出结果。
2.下列计算正确的是( )A . B .C . D .【答案】C .【考点】积的乘方和幂的乘方运算法则。
【分析】利用积的乘方和幂的乘方运算法则,直接得出结果。
3.下列调查,适合用普查方式的是( )A .了解一批炮弹的杀伤半径B .了解扬州电视台《关注》栏目的收视率C.了解长江中鱼的种类 D .了解某班学生对“扬州精神”的知晓率【答案】D .【考点】普查方式的适用。
【分析】根据普查方式的适用范围,直接得出结果。
4.已知相交两圆的半径分别为4和7,则它们的圆心距可能是( )A .2 B .3 C .6 D .11【答案】C .【考点】两圆的位置与圆心距的关系。
【分析】根据两圆的位置与圆心距的关系知,相交两圆的圆心距在两圆的半径的差跟和之间,从而所求圆心距在3和11 之间,因此得出结果。
5.如图是由几个小立方块所塔成的几何的俯视图,小正方形中的数字表示该位置小立方块的个数,则该几何体的主视图是( )12-122-12-236a a a =·()()2222a b a b a b+-=-()2326aba b =523a a -=【答案】A .【考点】三视图。
2020年江苏省扬州市中考语文试卷及答案

A.读《蒹葭》,我们领略了金秋拂晓、清露为霜,瑟瑟秋风、苇丛起伏,茫茫秋水、清澈澄明的空灵意境之美;B.读《鱼我所欲也》,我们感动于孟子不为名利左右,坚守本心,舍生取义的情怀和担当;C.读《刘姥姥进大观园》,我们折服于曹雪芹高超的写作技巧,能于一席一饭之间,抓住瞬间,描绘出众多人物的反应,营造出强烈的喜剧效果;0 D.读《假如生活欺骗了你》,我们理解了普希金含蓄的劝告:其实没什么好忧愁的,只要保持积极乐观的心态,生活中所有的困难都将不复存在。
【致敬师长】(5分)您是勤劳的耕耘者,经年累月,使我们荒寂的心原上撒满希望的种子;您是长明的灯塔,久久伫立,把我们从无边的暗夜引向光明;您是平静的港湾,温情脉脉,目送我们驶向远方。
老师,谢谢您!我们将用汗水浇灌希望的种子,让它萌发生长;我们将常常拂拭自己的心灵,不让灰尘遮蔽真理的光芒;_______,_______。
3.(1)修改语段中画线的病句。
(写出修改意见即可,2分)(2)根据语境,补齐语段空缺处的内容。
(3分)【腹有诗书】(8分)4.默写。
(每空1分)(1)静以修身,_______________。
(诸葛亮《诫子书》)(2)采菊东篱下,_______________。
(陶渊明《饮酒<其五>》)(3) _______________,长河落日圆。
(王维《使至塞上》)(4)会当凌绝顶,_______________。
(杜甫《望岳》)(5)鸡声茅店月,_______________。
(温庭筠《商山早行》)(6)回首向来萧瑟处,归去,_______________。
(苏轼《定风波》)(7)中国秉持“人类命运共同体”的理念,推进新冠肺炎疫情防控国际合作,充分展现了“____________,___________”的大国担当。
(在《礼记·礼运》中选句填写)【时刻警醒】(6分)5.读下面题为“拉”的漫画,完成任务。
2024学年江苏省扬州中学高二上学期期中考数学试题及答案

江苏省扬州中学2023-2024学年第一学期期中考试高二数学2023.11试卷满分:150分 考试时间:120分钟注意事项:1.作答前,请考生务必将自己的姓名、考试证号等写在答题卡上并贴上条形码.2.将选择题答案填写在答题卡的指定位置上(使用机读卡的用2B 铅笔在机读卡上填涂),非选择题一律在答题卡上作答,在试卷上答题无效.3.考试结束后,请将机读卡和答题卡交监考人员.一.单项选择题:本大题共8小题,每小题5分,共40分.在每题给出的四个选项中,只有一项是最符合题意的.(请将所有选择题答案填到答题卡的指定位置中.)1.经过(A 、()1,0B -两点的直线的倾斜角为( )A.π6 B.π3C.2π3D.5π62. 抛物线22x py =的准线方程是2y =,则实数p 的值为( )A. 8- B. 4- C. 4D. 83. 已知(),P x y 是椭圆22114425x y +=上的点,则x y +的值可能是( )A. 13B. 14C. 15D. 164. 若点()2,1在圆220x y x y a +-++=的外部,则a 的取值范围是( )A. 1,2⎛⎫+∞⎪⎝⎭B. 1,2⎛⎫-∞ ⎪⎝⎭C. 14,2⎛⎫- ⎪⎝⎭D. ()1,4,2⎛⎫-∞-⋃+∞⎪⎝⎭5. 已知12,F F 是椭圆 221259x y +=的两个焦点,过1F 的直线交椭圆于,M N 两点,则2MNF 的周长为( )A. 10B. 16C. 20D. 266. 已知抛物线2:16C y x =,直线:4l x =与C 交于A ,B 两点,M 是射线BA 上异于A ,B 的动点,圆1C 与圆2C 分别是OMA 和OMB △的外接圆(O 为坐标原点),则圆1C 与圆2C 面积的比值为( )A 小于1B. 等于1C. 大于1D. 与M 点的位置有关.7. 由伦敦著名建筑事务所Steyn Studio 设计的南非双曲线大教堂惊艳世界,该建筑是数学与建筑完美结合造就的艺术品. 若将如图所示的大教堂外形弧线的一段近似看成双曲线22221y x a b-=(00)a b >>,下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )A. 221124y x -= B. 223144y x -=C. 22144x y -= D. 221164y x -=8. 已知点()2,4M ,若过点()4,0N 的直线l 与圆()22:69C x y -+=交于A 、B 两点,则MA MB +的最大值为( )A. 12B. C. 10D. 6二.多项选择题:本大题共4小题,每小题5分,共20分.在每题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.(请将所有选择题答案填到答题卡的指定位置中. )9. 已知直线2:(1)10l a a x y ++-+=,其中R a ∈,则( )A. 直线l 过定点(0,1)B. 当1a =-时,直线l 与直线0x y +=垂直C. 当0a =时,直线l 在两坐标轴上的截距相等D. 若直线l 与直线0x y -=10. 已知椭圆2222:1(0)x y E a b a b+=>>的两个焦点分别为12,F F ,与y 轴正半轴交于点B ,下列选项中给出的条件,能够求出椭圆E 标准方程的选项是( )A. 2,1a c ==B. 已知椭圆E 的离心率为12,短轴长为2C. 12BF F △是等边三角形,且椭圆E 的离心率为12D. 设椭圆E 的焦距为4,点B 在圆22()9x c y -+=上11. 抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.已知抛物线24y x =的焦点为F ,一束平行于x 轴的光线1l 从点()3,1M 射入,经过抛物线上的点()11,P x y 反射后,再经抛物线上另一点()22,Q x y 反射后,沿直线2l 射出,则下列结论中正确的是( )A. 34PQ k =- B. 121=x x C. 254PQ =D. 1l 与2l 之间的距离为412. 已知双曲线22:13y C x -=的左、右焦点分别为12,F F ,点P 是双曲线C 的右支上一点,过点P 的直线l 与双曲线C 的两条渐近线分别交于,M N ,则( )A. 2212PF PF -的最小值为8C. 若直线l 与双曲线C 相切,则点,M N 的纵坐标之积为2-;D. 若直线l 经过2F ,且与双曲线C 交于另一点Q ,则PQ 最小值为6.三.填空题:本大题共4小题,每小题5分,共20分.(请将所有填空题答案填到答题卡的指定位置中.)13. 若双曲线22221x y a b-=()0,0a b >>____.14. 若在抛物线y 2=-4x 上存在一点P ,使其到焦点F 的距离与到A (-2,1)的距离之和最小,则该点的坐标为________.15. 阿基米德是古希腊著名数学家、物理学家,他利用“逼近法”得到椭圆的面积除以圆周率π等于椭圆的长半轴长与短半轴长的乘积. 已知椭圆22221x y a b+=(a >b >0)的右焦点为(3,0)F ,过F 作直线l 交椭圆于A 、B 两点,若弦AB 中点坐标为(2,1)-,则该椭圆的面积为_____________.16. 已知圆1C 和圆2C 与x 轴和直线(0)y kx k =>相切,两圆交于,P Q 两点,其中P 点坐标为(3,2),已知两圆半径的乘积为132,则k 的值为___________.的的四.解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.(请将所有解答题答案填到答题卡的指定位置中.)17. 已知方程2214x y m+=(R m ∈且0m ≠)(1)若方程表示焦点在y 上的椭圆,且离心率为12,求m 的值;(2)若方程表示等轴双曲线,求m 的值及双曲线的焦点坐标.18. 已知直线l 经过直线12:34110, :2380l x y l x y +-=+-=的交点M .(1)若直线l 经过点(3,1)P ,求直线l 的方程;(2)若直线l 与直线3250x y ++=垂直,求直线l 的方程.19. 已知圆C 经过()()1,4,5,0A B 两点,且在x 轴上截距之和为2.(1)求圆C 的标准方程;(2)圆M 与圆C 关于直线10x y -+=对称,求过点()3,0且与圆M 相切的直线方程.20. 已知双曲线:()2211551x y m m m -=<<--的一个焦点与抛物线C :()220y px p =>的焦点重合.(1)求抛物线C 的方程;(2)若直线l :8xty =+交抛物线C 于A 、B 两点,O 为原点,求证:以AB 为直径的圆经过原点O .21.已知直线:R)l y kx k =+∈,与双曲线22:13x C y -=左支交于A ,B 两点.(1)求实数k 的取值范围;(2)若OAB(O 为坐标原点),求此时直线l 的斜率k 的值.22. 已知椭圆()2222:10x y C a b a b +=>>过点(2.(1)求椭圆C 方程;(2)点,A B 分别为椭圆C 的上下顶点,过点()04P ,且斜率为k 的直线与椭圆C 交于不同的两点,M N ,探究直线,BM AN 的交点是否在一条定直线0l 上,若存在,求出该直线0l 的方程;若不存在,请说明理由.的的江苏省扬州中学2023-2024学年第一学期期中考试高二数学2023.11试卷满分:150分 考试时间:120分钟注意事项:1.作答前,请考生务必将自己的姓名、考试证号等写在答题卡上并贴上条形码.2.将选择题答案填写在答题卡的指定位置上(使用机读卡的用2B 铅笔在机读卡上填涂),非选择题一律在答题卡上作答,在试卷上答题无效.3.考试结束后,请将机读卡和答题卡交监考人员.一.单项选择题:本大题共8小题,每小题5分,共40分.在每题给出的四个选项中,只有一项是最符合题意的.(请将所有选择题答案填到答题卡的指定位置中.)1. 经过(A 、()1,0B -两点的直线的倾斜角为( )A.π6 B.π3C.2π3D.5π6【答案】B 【解析】【分析】求出直线AB 的斜率,利用直线的斜率与倾斜角的关系可得出结果.【详解】设直线AB 的倾斜角为α,则0πα≤<,且tan α==,故π3α=.故选:B.2. 抛物线22x py =的准线方程是2y =,则实数p 的值为( )A. 8- B. 4- C. 4D. 8【答案】B 【解析】【分析】根据抛物线的准线求得p 的值【详解】由题意可得:22p-=,则4p =-故选:B3. 已知(),P x y 是椭圆22114425x y +=上的点,则x y +的值可能是( )A. 13B. 14C. 15D. 16【答案】A【解析】【分析】根据题意,可设12cos ,5sin x y θθ==,得到13sin()x y θϕ+=+,求得x y +的取值范围,即可求解.【详解】由椭圆22114425x y +=,可设12cos ,5sin x y θθ==,其中[]0,2πθ∈,则12cos 5sin 13sin()x y θθθϕ=+=++,其中12tan 5ϕ=,因为1sin()1θϕ-≤+≤,所以1313x y -≤+≤,即x y +的取值范围为[]13,13-,结合选项,可得A 符合题意.故选:A.4. 若点()2,1在圆220x y x y a +-++=的外部,则a 的取值范围是( )A 1,2⎛⎫+∞ ⎪⎝⎭B. 1,2⎛⎫-∞ ⎪⎝⎭C. 14,2⎛⎫- ⎪⎝⎭D. ()1,4,2⎛⎫-∞-⋃+∞⎪⎝⎭【答案】C 【解析】【分析】利用表示圆的条件和点和圆的位置关系进行计算.【详解】依题意,方程220x y x y a +-++=可以表示圆,则22(1)140a -+->,得12a <;由点()2,1在圆220x y x y a +-++=的外部可知:2221210a +-++>,得4a >-.故142a -<<.故选:C5. 已知12,F F 是椭圆 221259x y +=的两个焦点,过1F 的直线交椭圆于,M N 两点,则2MNF 的周长为( )A. 10 B. 16C. 20D. 26【答案】C 【解析】【分析】由椭圆的定义可得122MF MF a +=,122NF NF a +=,代入即可求出答案.【详解】由椭圆的定义可得:122MF MF a +=,122NF NF a +=,.则2MNF 的周长为:22112244520MN MF NF MF NF MF NF a ++=+++==⨯=.故选:C .6. 已知抛物线2:16C y x =,直线:4l x =与C 交于A ,B 两点,M 是射线BA 上异于A ,B 的动点,圆1C 与圆2C 分别是OMA 和OMB △的外接圆(O 为坐标原点),则圆1C 与圆2C 面积的比值为( )A. 小于1 B. 等于1C. 大于1D. 与M 点的位置有关【答案】B 【解析】【分析】求出,A B 的坐标,由对称性可得OB OA =,OBA OAB ∠=∠,设OAM △,OBM 的外接圆半径为12,R R ,由正弦定理得到12sin OM R OAB =∠,22sin OMR OBA=∠,故12R R =,故面积比值为1.【详解】由题意得,抛物线2:16C y x =的焦点坐标为()4,0F ,将4x =代入2:16C y x =中,8y =±,不妨令()()4,8,4,8A B -,由对称性可知,A B 两点关于y 轴对称,OB OA =,OBA OAB ∠=∠,设OAM △,OBM 的外接圆半径为12,R R ,当点M 在A 点上方时,()12sin sin πsin OM OM OM R OAM OAB OAB===∠-∠∠,当点M 在A 点上方时,12sin OMR OAB=∠,同理22sin OMR OBA=∠,因为OBA OAB ∠=∠,所以12R R =,所以圆1C 圆2C 面积的比值为1.故选:B7. 由伦敦著名建筑事务所Steyn Studio 设计的南非双曲线大教堂惊艳世界,该建筑是数学与建筑完美结合造就的艺术品. 若将如图所示的大教堂外形弧线的一段近似看成双曲线22221y x a b-=(00)a b >>,下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )A. 221124y x -= B. 223144y x -=C. 22144x y -= D. 221164y x -=【答案】B 【解析】【分析】首先根据题意得到22222b c a c a b=⎧⎪⎪=⎨⎪=+⎪⎩,再解方程组即可.【详解】设双曲线的一个焦点为()0,c ,一条渐近线方程为a y x b=,则焦点到渐近线的距离2d b ===,所以2222224234b a ca b c a b=⎧⎧⎪=⎪⎪=⇒⎨⎨⎪⎪=⎩=+⎪⎩,即双曲线方程为:223144y x -=.故选:B8. 已知点()2,4M ,若过点()4,0N 的直线l 与圆()22:69C x y -+=交于A 、B 两点,则MA MB + 的最大值为( )A. 12B. C. 10D. 6【答案】A 【解析】【分析】设AB 中点(),P x y ,根据垂径定理可得点P 的轨迹方程,进而可得MP的取值范围,又2MA MB MP +=,即可得解.【详解】设AB 中点(),P x y ,则()6,CP x y =- ,()4,NP x y =-,所以()()2640CP NP x x y ⋅=--+= ,即()2251x y -+=,所以点P 的轨迹为以()5,0E 为圆心,1为半径的圆,所以11ME MP ME -≤≤+,5ME ==,所以46MP ≤≤,又2MA MB MP +=,所以MA MB +的最大值为12,故选:A.二.多项选择题:本大题共4小题,每小题5分,共20分.在每题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.(请将所有选择题答案填到答题卡的指定位置中. )9. 已知直线2:(1)10l a a x y ++-+=,其中R a ∈,则( )A. 直线l 过定点(0,1)B. 当1a =-时,直线l 与直线0x y +=垂直C. 当0a =时,直线l 在两坐标轴上的截距相等D. 若直线l 与直线0x y -=【答案】ABD 【解析】【分析】坐标代入方程检验判断A ,根据垂直的条件判断B ,求出两坐标轴上截距判断C ,求出平行线间距离判断D .【详解】选项A ,把坐标(0,1)代入直线方程而立,A 正确;选项B ,1a =-时直线l 方程为10x y -+=,斜率是1,直线0x y +=斜率是1-,两直线垂直,B 正确;选项C ,0a =时直线方程为10x y -+=,在x 轴上截距为=1x -,在y 轴上截距为1y =,不相等,C 错;选项D ,211a a ++=即0a =或1-时,直线l 方程为10x y -+=与直线0x y -=平行,距离为d ==D 正确.故选:ABD .10. 已知椭圆2222:1(0)x y E a b a b+=>>的两个焦点分别为12,F F ,与y 轴正半轴交于点B ,下列选项中给出的条件,能够求出椭圆E 标准方程的选项是( )A 2,1a c ==B. 已知椭圆E 的离心率为12,短轴长为2C. 12BF F △是等边三角形,且椭圆E 的离心率为12D. 设椭圆E 的焦距为4,点B 在圆22()9x c y -+=上【答案】ABD.【解析】【分析】逐项代入分析即可求解.【详解】根据222a b c =+之间的关系即可求解,故选项A 正确;根据2221,22,2c e b a b c a ====+即可求解,故选项B 正确;12BF F △是等边三角形,且椭圆E 的离心率为12,只能确定12,2c a c e a ===,不能求椭圆E 标准方程,故选项C 不正确;设椭圆E 的焦距为4,点B 在圆22()9x c y -+=上,所以()2222224,09c c b c b a =-+=+==,即可求出椭圆E 标准方程,故选项D 正确.故选:ABD.11. 抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.已知抛物线24y x =的焦点为F ,一束平行于x 轴的光线1l 从点()3,1M 射入,经过抛物线上的点()11,P x y 反射后,再经抛物线上另一点()22,Q x y 反射后,沿直线2l 射出,则下列结论中正确的是( )A. 34PQ k =-B. 121=x xC. 254PQ = D. 1l 与2l 之间的距离为4【答案】BC【解析】【分析】由抛物线的光学性质可知,直线PQ 过焦点(1,0)F ,设直线:1PQ x my =+,代入24y x =,由韦达定理得124y y =-,进而求得121=x x ,可判断B ;先求点P 的坐标,再结合124y y =-可得点Q 的坐标,然后利用斜率公式即可判断A ;根据抛物线的定义可知12Q x p P x ++=,可判断C ;由于1l 与2l 平行,所以1l 与2l 之间的距离12d y y =-,可判断D .【详解】由抛物线的光学性质可知,直线PQ 过焦点(1,0)F ,设直线:1PQ x my =+,代入24y x =得2440y my --=,则124y y =-,所以()212121616y y x x ==,所以121=x x ,故B 正确;点P 与M 均在直线1l 上,则点P 的坐标为(1,14),由124y y =-得24y =-,则点Q 的坐标为(4,4)-,则4141344PQ k --==--,故A 错误;由抛物线的定义可知,121254244PQ x x p =++=++=,故C 正确;1l 与2l 平行,1l ∴与2l 之间的距离125d y y =-=,故D 错误.故选:BC.12. 已知双曲线22:13y C x -=的左、右焦点分别为12,F F ,点P 是双曲线C 的右支上一点,过点P 的直线l 与双曲线C 的两条渐近线分别交于,M N ,则( )A. 2212PF PF -的最小值为8B. 212PF PF OP -为定值C. 若直线l 与双曲线C 相切,则点,M N 的纵坐标之积为2-;D. 若直线l 经过2F ,且与双曲线C 交于另一点Q ,则PQ 的最小值为6.【答案】AB【解析】【分析】设00(,)P x y ,由2221208PF PF x -=,可判定A 正确;化简2122PF PF OP -=,可判定B 正确;设直线l 的方程为x my n =+,联立方程组,结合Δ0=,得到2213n m =-,在化简123y y =-,可判定C 不正确;根据通经长和实轴长,可判定D 错误.【详解】由题意,双曲线2213y x -=,可得1,a b ==2c ==,所以焦点12(2,0),(2,0)F F -,且1222PF PF a -==,设00(,)P x y ,则01x ≥,且220013y x -=,即220033=-y x ,双曲线C的两条渐近线的方程为y =,对于A 中,由()][()22222212000002288PF PF x y x y x ⎡⎤-=++--+=≥⎣⎦,所以A 正确;对于B中,2221200()PF PF OP x y -=-+2200(33)x x =-+-2000(21)(21)(43)2x x x =+---=(定值),所以B 正确;对于C 中,不妨设1122(,),(,)M x y N x y ,直线l 的方程为x my n =+,联立方程组2213x my n y x =+⎧⎪⎨-=⎪⎩,整理得222(31)6330m y mny n -++-=,若直线l 与双曲线C 相切,则22223612(31)(1)0m n m n ∆=---=,整理得2213n m =-,联立方程组x my n y =+⎧⎪⎨=⎪⎩,解得y =M的纵坐标为1y =,联立方程组x my n y =+⎧⎪⎨=⎪⎩,解得y =N的纵坐标为2y =,则点,M N的纵坐标之积为21222233(13)33113y n m mm y ---===-=--所以C 不正确;对于D 中,若点Q 在双曲线的右支上,则通经最短,其中通经长为226b a=,若点Q 在双曲线的左支上,则实轴最短,实轴长为226a =<,所以D 错误.故选:AB.三.填空题:本大题共4小题,每小题5分,共20分.(请将所有填空题答案填到答题卡的指定位置中.)13. 若双曲线22221x y a b-=()0,0a b >>____.【答案】y =【解析】【分析】由c e a ===b a =,即可求出双曲线的渐近线方程.【详解】因为双曲线22221x y a b-=()0,0a b >>c e a ===222b a =,所以b a =,双曲线22221x y a b-=()0,0a b >>渐近线方程为:b y x a =±=.故答案为:y =14. 若在抛物线y 2=-4x 上存在一点P ,使其到焦点F 的距离与到A (-2,1)的距离之和最小,则该点的坐标为________.【答案】1,14⎛⎫-⎪⎝⎭##()0.25,1-【解析】【分析】作出图象,结合题意可知A ,P 及P 到准线的垂足三点共线时,所求距离之和最小,此时P 点的纵坐标为1,代入抛物线即可求得P 点的坐标.【详解】根据题意,由y 2=-4x 得p =2,焦点坐标为(-1,0),作出图象,如图,.因为PF 等于P 到准线的距离PQ ,所以PF PA PQ PA AQ +=+≥,可知当A ,P 及P 到准线垂足三点共线时,点P 与点F 、点P 与点A 的距离之和最小,此时点P 的纵坐标为1,将y =1代入抛物线方程求得14x =-,所以点P 的坐标为1,14⎛⎫- ⎪⎝⎭.故答案为:1,14⎛⎫- ⎪⎝⎭.15. 阿基米德是古希腊著名的数学家、物理学家,他利用“逼近法”得到椭圆的面积除以圆周率π等于椭圆的长半轴长与短半轴长的乘积. 已知椭圆22221x y a b+=(a >b >0)的右焦点为(3,0)F ,过F 作直线l 交椭圆于A 、B 两点,若弦AB 中点坐标为(2,1)-,则该椭圆的面积为_____________.【答案】【解析】【分析】利用作差法构建斜率、中点坐标相关方程2121221212y y x x b x x y y a-+=-⋅-+,再结合222a c b -=即可求解出a 、b ,进而求出面积.【详解】设()11,A x y ,()22,B x y ,记AB 的中点为M ,即(2,1)M -,因为AB 的中点为M ,所以由中点坐标公式得121242x x y y +=⎧⎨+=-⎩,因为直线AB 过椭圆焦点()3,0F ,所以直线AB 斜率为121201132y y k x x --===--,又因为A ,B 在椭圆22221x y a b+=上,的所以22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减得22221212220x x y y a b --+=,整理得2121221212y y x x b x x y y a-+=-⋅-+,代值化简得222b a =,因为椭圆22221x y a b+=的焦点为()3,0F ,所以22a b 9-=,得a =,3b =,由题意可知,椭圆的面积为ab π=.故答案为:.16. 已知圆1C 和圆2C 与x 轴和直线(0)y kx k =>相切,两圆交于,P Q 两点,其中P 点坐标为(3,2),已知两圆半径的乘积为132,则k 的值为___________.【答案】【解析】【分析】根据题意可设1(,)C ma a ,2(,)C mb b ,(0)m >,由P 在两圆上,将坐标代入对应圆的方程整理,易知,a b 是22(64)130m r m r -++=的两个根,进而求直线12C C 的斜率,再根据直线12C C 、(0)y kx k =>倾斜角的关系求k 值.【详解】由题设,圆1C 和圆2C 与x 轴和直线(0)y kx k =>相切,且一个交点P (3,2),∴1C 和2C 在第一象限,若,a b 分别是圆1C 和圆2C 的半径,可令1(,)C ma a ,2(,)C mb b ,(0)m >,∴222222(3)+(2){(3)+(2)ma a a mb b b --=--=,易知:,a b 是22(64)130m r m r -++=的两个根,又132ab =,∴213132m =,可得m =12C C k =,而直线12C C 的倾斜角是直线(0)y kx k =>的一半,∴1212221C C C C k k k ==-.故答案为:【点睛】关键点点睛:分析圆心的坐标并设1(,)C ma a ,2(,)C mb b ,结合已知确定,a b 为方程的两个根,应用韦达定理求参数m ,进而求12C C 斜率,由倾斜角的关系及二倍角正切公式求k 值.四.解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.(请将所有解答题答案填到答题卡的指定位置中.)17. 已知方程2214x y m+=(R m ∈且0m ≠)(1)若方程表示焦点在y 上椭圆,且离心率为12,求m 的值;(2)若方程表示等轴双曲线,求m 的值及双曲线的焦点坐标.【答案】(1)163m = (2)4m =-,()±【解析】【分析】(1)根据题中条件及离心率公式直接计算即可;(2)根据题中条件得4m =-,进一步计算得到c 的值,即可求解.【小问1详解】因为方程为焦点在y 轴上的椭圆,所以22,4a m b ==则离心率12c e a ===,解得163m =故163m =【小问2详解】由题意得 4m =-,c ===故焦点坐标为()±18. 已知直线l 经过直线12:34110, :2380l x y l x y +-=+-=的交点M .(1)若直线l 经过点(3,1)P ,求直线l 的方程;(2)若直线l 与直线3250x y ++=垂直,求直线l 的方程.【答案】(1)250x y +-=(2)2340x y -+=【解析】的.【分析】(1)联立方程求得交点坐标,再由两点式求出直线方程.(2)根据直线垂直进行解设方程,再利用交点坐标即可得出结果.【小问1详解】由341102380x y x y +-=⎧⎨+-=⎩得12x y =⎧⎨=⎩,即直线1l 和2l 的交点为(1,2)M .直线l 还经过点()3,1P ,∴l 的方程为211231y x --=--,即250x y +-=.【小问2详解】由直线l 与直线3250x y ++=垂直,可设它的方程为230x y n -+=.再把点(1,2)M 的坐标代入,可得260n -+=,解得4n =,故直线l 的方程为2340x y -+=.19. 已知圆C 经过()()1,4,5,0A B 两点,且在x 轴上的截距之和为2.(1)求圆C 的标准方程;(2)圆M 与圆C 关于直线10x y -+=对称,求过点()3,0且与圆M 相切的直线方程.【答案】(1)()22116x y -+=(2)3x =或3490x y --=【解析】【分析】(1)根据题意,设圆的一般式方程,代入计算,即可得到结果;(2)根据题意,分直线的斜率存在与不存在讨论,结合点到直线的距离公式列出方程,即可得到结果.【小问1详解】设圆C 的方程为()2222040x y Dx Ey F D E F ++++=+->,令0y =,可得20x Dx F ++=,则122x x D +=-=,将()()1,4,5,0A B 代入可得,116402550D E F D F ++++=⎧⎨++=⎩,解得2015D E F =-⎧⎪=⎨⎪=-⎩,所以圆C 方程为222150x y x +--=,即()22116x y -+=.【小问2详解】圆C 的圆心()1,0C ,圆M 的圆心与()1,0C 关于10x y -+=对称,∴设圆M 的圆心为(),M a b 则11022111a b b a +⎧-+=⎪⎪⎨⎪⨯=-⎪-⎩,解得12a b =-⎧⎨=⎩,圆M 的标准方程为:()()221216x y ++-=,若过点()3,0的直线斜率不存在,则方程为3x =,此时圆心()1,2C -到直线3x =的距离为314r +==,满足题意;若过点()3,0且与圆C 相切的直线斜率存在,则设切线方程为()3y k x =-,即30kx y k --=,则圆心到直线30kx y k --=4,解得34k =,所以切线方程为39044x y --=,即3490x y --=,综上,过点()3,0且与圆C 相切的直线方程为3x =或3490x y --=.20. 已知双曲线:()2211551x y m m m -=<<--的一个焦点与抛物线C :()220y px p =>的焦点重合.(1)求抛物线C 的方程;(2)若直线l :8x ty =+交抛物线C 于A 、B 两点,O 为原点,求证:以AB 为直径的圆经过原点O .【答案】(1)28y x =(2)见解析.【解析】【分析】(1)根据双曲线方程求出其焦点坐标,即也是抛物线焦点,得到抛物线方程.(2)直线l 与抛物线联立后,利用韦达定理求出0OA OB ⋅= 即可得证.【小问1详解】由双曲线方程()2211551x y m m m -=<<--知其焦点在x 轴上且焦点坐标为1(2,0)F -,2(2,0)F ,所以2(2,0)F 为抛物线C :()220y px p =>的焦点,得242p p =⇒=,所以抛物线C 的方程为28y x =.【小问2详解】设11(,)A x y ,22(,)B x y 联立22886408x ty y ty y x=+⎧⇒--=⎨=⎩,2644640t ∆=+⨯>由韦达定理得128y y t +=,1264y y =-所以12121212(8)(8)OA OB x x y y ty ty y y ⋅=+=+++ 21212(1)8()64t y y t y y =++++2(1)(64)8(8)640t t t =+-++=所以OA OB ⊥ ,所以以AB 为直径的圆经过原点O .得证21. 已知直线:R)l y kx k =+∈,与双曲线22:13x C y -=的左支交于A ,B 两点.(1)求实数k 的取值范围;(2)若OAB (O 为坐标原点),求此时直线l 的斜率k 的值.【答案】(11k <<(2)k =【解析】【分析】(1)设点坐标,联立方程组,根据根与系数的关系求解;(2)通过OAB 面积求解出12x x -,从而求解出k 的值.【小问1详解】依题意,设()()1122,,,A x y B x y ,联立方程组22330y kx x y ⎧=+⎪⎨--=⎪⎩,整理得:()221390,k x ---=因为直线:R)l y kx k =∈,与双曲线22:13x C y -=的左支交于A ,B 两点,所以()2212212130361090130k k x x k x x ⎧-≠⎪=->⎪⎪⎪-⎨=>⎪-⎪⎪+=<⎪⎩ ,解得210,13k k ><<1k <<,【小问2详解】设点O到直线:R)l y kx k =∈的距离为d,则d =,212OAB S AB d x ==-=- ,又因为S =,所以1212,5x x -=又因为12125x x -==,代入12212913x x k x x -⎧=⎪-⎪⎨⎪+=⎪⎩125,整理得4236210k k+-=1k <<,解得k =,此时直线l的斜率k.22. 已知椭圆()2222:10x y C a b a b +=>>过点(2.(1)求椭圆C 方程;(2)点,A B 分别为椭圆C 的上下顶点,过点()04P ,且斜率为k 的直线与椭圆C 交于不同的两点,M N ,探究直线,BM AN 的交点是否在一条定直线0l 上,若存在,求出该直线0l 的方程;若不存在,请说明理由.【答案】(1)22:184x y C += (2)存在,1y =【解析】【分析】(1)由椭圆离心率可得222a b =,再将(2代入椭圆的方程可得228,4a b ==,即可求出椭圆的方程;(2)设()()1122,,,M x y N x y ,直线MN 的方程为:4y kx =+,联立直线MN 和椭圆的方程求出两根之积和两根之和,设直线AN 的方程和直线BM 的方程,两式联立求得交点的纵坐标的表达式,将两根之积和两根之和代入可证得交点在一条定直线上.【小问1详解】,即c e a ===,所以2212b a =,所以222a b =,又因为椭圆()2222:10x y C a b a b +=>>过点(2,所以224212b b +=,解得:228,4a b ==,所以椭圆C 方程为22184x y +=.【小问2详解】因为()()0,2,0,2A B -,设()()1122,,,M x y N x y ,直线MN 的方程为:4y kx =+,联立方程221844x y y kx ⎧+=⎪⎨⎪=+⎩,得()221216240k x kx +++=,()()222Δ164241264960,k k k =-⨯⋅+=->得232k >则1212221624,1212k x x x x k k -+=⋅=++直线AN 的方程为:2222y y x x --= ,直线BM 的方程为:1122y y x x ++=,联立两直线方程消元:()()2112112122222226y x kx x x y y y x kx x x -+-==+++ 法1:由()221216240k x kx +++=解得:12x x ==,代入化简,2123y y -===-+,解得:1y =,即直线,BM AN 的交点在定直线1y =上.法2:由韦达定理得1221612k x x k-=-+代入化简()()22222222224162824211212242324612612k k x k k x y k k k y k k x x k -⎛⎫+- ⎪--+-++⎝⎭===-+++++,得1y =,即直线,BM AN 的交点在定直线1y =上.法3:由1212221624,1212k x x x x k k -+=⋅=++,得()121232x x kx x -+=⋅代入化简()()1211223221232362x x x y y x x x -++-==-+-++,得1y =,即直线,BM AN 的交点在定直线1y =上.法4: 代()11,M x y 点进椭圆方程得2211184x y +=化简得()()221111221844y y x y +-=-=进而得到()()1111222y x y x -=+,代入化简()()121222222y y y y x x ----=+⋅转化为韦达定理代入()()()()1212121222222222y y kx kx y y x x x x ----++-==+⋅⋅()22221212122241622422412122412k k k k x x k x x k k x x k ⎛⎫-⋅-⋅+ ⎪⎡⎤-+++++⎣⎦⎝⎭==⋅+22222243248211224312k k k k k -++-⋅+=-+,得1y =,即直线,BM AN 的交点在定直线1y =上.【点睛】思路点睛:本题考查直线与椭圆综合应用中的定直线问题的求解,求解此类问题的基本思路如下:①假设直线方程,与椭圆方程联立,整理为关于x 或y 的一元二次方程的形式;②利用0∆>求得变量之间的关系,同时得到韦达定理的形式;③利用韦达定理表示出已知的等量关系,化简整理得到所求定直线.。
2023江苏扬州中考语文真题及答案

2023江苏扬州中考语文真题及答案试卷满分150分,考试时间150分钟一、积累运用(28分)亲爱的同学们:扬州是一座因水而兴的美丽古城。
为了让扬州走向更远的世界,现向大家发出如下倡议:做生活环境的保护者。
绿杨城郭,生态宜居。
“草树知春不久归,①”(韩愈《晚春》),是烟花三月园林巷陌的流韵;“起舞弄清影,②”(苏轼《水调歌头》),是八月中秋五亭桥上的浪漫。
【甲】。
文化遗产,享誉世界。
漆器玉器,刺绣剪纸,名匠倍出。
“ ③,④”(诸葛亮《诫子书》),先人们安清贫、守寂寞,传统工艺才得以延续至今,我们有责任将其传承下去。
做先贤精神的践行者。
苏中古城,人杰地灵。
五次东渡空折返,鉴真坚信“ ⑤,⑥”(李白《行路难》),宏旨精义终得远播;梅花岭上花似雪,“ ⑦,只有香如故”(陆游《卜算子·咏梅》),可法精神流芳百世。
扬州城的命运与长江、大运河【乙】,“ ⑧。
悠悠”(辛弃疾《南乡子·登京口北固亭有怀》)。
今天,长江、大运河上百舸争流,“潮平两岸阔,⑨ ”(王湾《次北固山下》),幸福扬州正成为世界向往的诗和远方。
1、结合语境,完成题目。
(5分)(1)给加点字注音:因水而兴()(1分)(2)指出加点短语中的错别字并修改:“”应改为“。
”(2分)(3)联系上下文,在【甲】处补写一句:。
(2分)2、在①—⑨处填写相应的名句。
(9分)3、填入【乙】处的成语最恰当的一项是()(2分)A.唇齿相依B.息息相关C.骨肉相连D.一脉相承4、语言综合实践(12分)班级开展“身边的文化遗产”学习实践活动,老师要求同学们实地采访,撰写新闻通讯稿。
(1)你约扬扬周末去漆器厂采访,可扬扬说何必那么辛苦,不如在家上网搜点资料,轻松又省时。
你劝说道:“。
”(3分)(2)扬扬同意前往。
请你针对他采访提纲中的“采访问题”提出修改意见。
(4分)采访提纲时间、地点:×月×日,××漆器厂采访对象:厂长采访目的:了解漆器的特点以及发展历史、现状和前景采访用具:纸、笔、相机采访问题:①你厂的环境怎么样,可以带我参观参观吗?②你厂有多少年历史了?产品现在受欢迎吗?打算开发哪些新产品?③你厂产品最贵的卖多少钱?④你现在一个月工资多少?(3)采访后,扬扬列出了通讯稿写作要点,请你提建议。
2023年江苏省各市中考时间汇总

2023年江苏省各市中考时间汇总2023年江苏省各市中考时间南京市2023年中考考试时间:6月18日至6月19日无锡市2023年中考考试时间:6月16日至6月18日徐州市2023年中考考试时间:6月18日至6月20日常州市2023年中考考试时间:6月18日至6月20日苏州市2023年中考考试时间:6月17日至6月19日南通市2023年中考考试时间:6月16日至6月18日连云港市2023年中考考试时间:6月14日至6月16日淮安市2023年中考考试时间:6月15日至6月17日盐城市2023年中考考试时间:6月16日至6月18日扬州市2023年中考考试时间:6月16日至6月18日镇江市2023年中考考试时间:6月7日至6月19日泰州市2023年中考考试时间:6月15日至6月17日宿迁市2023年中考考试时间:6月17日至6月19日江苏中考难度大吗不大。
江苏中考难度并不是很难,基础题70%,一般难度20%,较难题10%,大家只需要夯实基础,考试中正常发挥,基本上就能顺利升入高中。
江苏省,简称“苏”,是中华人民共和国省级行政区,省会南京,位于长江三角洲地区,中国大陆东部沿海。
中考如何备考1、课堂复习是核心现在进入中考紧张的复习阶段,课堂上老师会对重点的知识点进行归纳整理,系统地进行架构,帮助同学们在脑海里形成一个完整的体系。
这个时候,就要求同学们能够集中精力,跟上老师的步伐,掌握课堂中的重点内容。
中考网络家教会针对学生的学习情况量身定做复习方针。
2、提高效率完成关键作业同学们在做作业方面提高效率,把自己薄弱的学科作业放在最前面做,在自己的精力最充沛、最有耐心的时候做,充分调动自己的主动性;3、认清状态选择适合学习方法基础再牢的学生也有自己的薄弱点,学习成绩好的考生最容易在基础知识上丢分,做好查漏补缺的工作,不留知识盲点,还要放下偏题、难题,回归基础知识,注意归纳、总结;针对自己的薄弱学科或薄弱环节进行查缺补漏;还要注意归类复习,把典型题目做一遍,在精练的原则上多做题,开拓思维;4、课外补课要适合自己课外辅导现在很受欢迎的就是网络一对一在线辅导,无地域限制,全国各地的学子可以与清华北大状元一对一在线学习,学习状元们的的方法和学习技巧,根据网络家教制定的复习方法,弥补薄弱的学科;5、劳逸结合迎接挑战每节课间做好休息;午间休息时,可以到操场上散散步,呼吸一下新鲜的空气。
2020中考语文考点分析整理

2020中考语文考点分析整理试卷分为两部分,一卷为选择题部分,二卷为非选择题部分;试卷满分120分,考试时间120分钟,一般为中考第一科,时间为9:00-11:00;题型:第一卷一、选择题(共11小题,共计27分;1~4,6~7每题2分;第5题,8~11题每题3分)1.字音(2分)2.恰当词语填空(2分)3.语病(2分)4.标点符号(2分)5.诗词赏析(3分)任务型阅读《长在树上的“宝石”》6.文意的理解(2分)7.句子的说明方法及作用(2分)8.文章的生层次解读(3分)课内文言文阅读《岳阳楼记》9.加点词语的解释不正确的一项(3分)10.通假字的考察(3分)11.文章大意的理解,不正确的选项(3分)第二卷二、古诗文默写(8分,每空一分),要求每个字都对;根据语文中考考纲要求,初中背诵篇目要求61篇,目录如下:7~9年级(共计61篇)1 关雎(关关雎鸠)《诗经》2 蒹葭(蒹葭苍苍)《诗经》3 十五从军征(十五从军征)汉乐府4 观沧海(东临碣石)曹操5 饮酒(结庐在人境)陶潜6 木兰辞(唧唧复唧唧)北朝民歌7 送杜少府之任蜀州(城阙辅三秦)王勃8 登幽州台歌(前不见古人)陈子昂9 次北固山下(客路青山外)王湾10 使至塞上(单车欲问边)王维11 闻王昌龄左迁龙标遥有此寄(杨花落尽子规啼)李白12 行路难(金樽清酒斗十千)李白13 黄鹤楼(昔人已乘黄鹤去)崔颢14 望岳(岱宗夫如何)杜甫15 春望(国破山河在)杜甫16 茅屋为秋风所破歌(八月秋高风怒号)杜甫17 白雪歌送武判官归京(北风卷地白草折)岑参18 酬乐天扬州初逢席上见赠(巴山楚水凄凉地)刘禹锡19 卖炭翁(卖炭翁)白居易20 钱塘湖春行(孤山寺北贾亭西)白居易21 雁门太守行(黑云压城城欲摧)李贺22 赤壁(折戟沉沙铁未销)杜牧23 泊秦淮(烟笼寒水月笼沙)杜牧24 夜雨寄北(君问归期未有期)李商隐25 无题(相见时难别亦难)李商隐26 相见欢(无言独上西楼)李煜27 渔家傲(塞下秋来风景异)范仲淹28 浣溪沙(一曲新词酒一杯)晏殊29 登飞来峰(飞来峰上千寻塔)王安石30 江城子(老夫聊发少年狂)苏轼31 水调歌头(明月几时有)苏轼32 渔家傲(天接云涛连晓雾)李清照33 游山西村(莫笑农家腊酒浑)陆游34 南乡子(何处望神州)辛弃疾35 破阵子(醉里挑灯看剑)辛弃疾36 过零丁洋(辛苦遭逢起一经)文天祥37 天净沙•秋思(枯藤老树昏鸦)马致远38 山坡羊•潼关怀古(峰峦如聚)张养浩39 己亥杂诗(浩荡离愁白日斜)龚自珍40 满江红(小住京华)秋瑾41 《论语》12章(学而时习之;吾日三省吾身;吾十有五而志于学;温故而知新;学而不思则罔;贤哉回也;知之者不如好之者;不义而富且贵;三人行;子在川上曰;三军可夺帅也;博学而笃志)42 曹刿论战《左传》43 《孟子》三则(鱼我所欲也;富贵不能淫;天将降大任于是人也)44 《庄子》一则(北冥有鱼……亦若是则巳矣。
2021年江苏扬州中考政策有哪些

【导语】中考是中国重要的考试之⼀,参加中考的同学⼀定要调整好⼼态,做好考前⼼理准备与物质准备的⼤检查,以良好的⼼态、充沛的体⼒与精⼒去迎接考试。
那考⽣们知道2021年江苏扬州中考政策有哪些吗?如果还不清楚,⽆忧考为考⽣整理了2021年江苏扬州中考政策有哪些的资讯,欢迎阅读!2021年江苏扬州中考政策 问:2021年江苏扬州中考政策有哪些 答:根据《国务院办公厅关于新时代推进普通⾼中育⼈⽅式改⾰的指导意见》(国办发〔2019〕29号)、省委办公厅省政府办公厅《关于新时代推进普通⾼中育⼈⽅式改⾰和资源建设的意见》(苏办发〔2020〕15号)、《省教育厅关于做好2021年中⼩学招⽣⼊学⼯作的通知》(苏教基〔2021〕1号)精神,2021年全市⾼中阶段学校招⽣⼯作将有序开展。
普通⾼中招⽣录取⼯作由市教育局统⼀管理,市教育局和县(市、区)教育(教体)局分别组织实施。
继续实⾏市直、⼴陵区、开发区、景区、⽣态科技新城招⽣区域和邗江招⽣区域普通⾼中招⽣考试统⼀上报名、统⼀发布招⽣简章、统⼀上填报志愿和上更改志愿、统⼀考试阅卷成绩发布、统⼀录取“五统⼀”。
2021年全市普通⾼中招⽣计划⼈数与去年⼤致相当。
今年⾼中阶段学校招⽣对象为应届或往届初中毕业⽣(含随迁⼦⼥)、修业的社会青年,其中地理、⽣物毕业会考科⽬成绩均达到C等级及其以上⽅可报考三及以上普通⾼中,艺术素质测评C等级及以上考⽣⽅可报考四普通⾼中。
全市初中升学考试与初中毕业考试合并进⾏。
语⽂、数学、英语、物理、化学、道德与法治、历史和体育学科中考总成绩作为考⽣升学的依据,升学成绩总分满分为780分。
志愿填报时间为5⽉29—31⽇。
市直⼴陵招⽣区域和邗江招⽣区域的考⽣,6⽉20、21、22⽇可以到指定志愿更改地点进⾏更改志愿,普通⾼中录取时间为6⽉29—30⽇。
公办普通⾼中学校坚持属地招⽣原则,民办普通⾼中招⽣⼯作纳⼊所在地教育⾏政部门统⼀管理,招⽣范围与所在地公办普通⾼中保持⼀致,并在今年招⽣⼊学中实现同步招⽣,做到公办民办普通⾼中招⽣时间⼀致,同步登记报名、同步招⽣录取、同步注册学籍。
扬州市教育局关于公布2020年全市初中毕业升学考试文化科目考试时间的通知

扬州市教育局关于公布2020年全市初中毕业升学考试
文化科目考试时间的通知
文章属性
•【制定机关】扬州市教育局
•【公布日期】2020.04.23
•【字号】扬教发〔2020〕19号
•【施行日期】2020.04.23
•【效力等级】地方规范性文件
•【时效性】现行有效
•【主题分类】招生考试
正文
扬州市教育局关于公布2020年全市初中毕业升学考试文化科
目考试时间的通知
县(市、区)教育(教体)局,开发区城乡管理局,市蜀冈—瘦西湖风景名胜区社会事业局,市生态科技新城社会事业局,市直各初中学校:
经批准,今年全市初中毕业升学考试文化科目考试时间为7月16日—18日,具体文化考试日程见附表;初二地理、生物考试时间为7月15日上午,地理考试时间为9:00—10:00,生物考试时间为10:10—11:10。
望各地提前准备,精心做好中考文化科目考试各项准备工作;各初中学校在扎实做好疫情防控的同时,认真组织教育教学工作,全力做好今年初中毕业升学考试工作和初二年级地理、生物考试工作。
附表:2020年初中毕业升学考试文化科目考试日程
扬州市教育局
2020年4月23日附表
2020年初中毕业升学考试文化科目考试日程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020xxxx时间安排
延伸阅读:
xx考前必知5条注意事项
1、记清入场时间避免迟到
考生凭准考证进入考场,并对号入座,考生将准考证放在课桌的左上角。
开考15分钟后,不准迟到考生进入考场;所有学科开考30分钟后,方能交卷出考场。
2、试听听不清可当场提出
考生如在听力试听过程中遇到听不清的情况,可以当场提出,由监考员予以判断和反映,以便及时采取措施;播音结束没有提出问题,则视同认同播音效果正常。
分发试卷、答题卡时,考生不得离座,接卷后,在指定位置填写姓名、准考证号和座位号。
除此之外,考生卷面不得做任何其它标记。
开考铃响后,考生开始答题。
考生如遇试卷、答题卡分发错误或缺页、缺题、漏印和字迹模糊等问题,可举手询间。
3、答案写在草稿纸上无效
答题卡中选择题用2B铅笔在答题卡填涂作答,填涂要规范(涂匀、涂实、涂满、涂黑)。
答题卡中非选择题用0.5毫米黑色笔迹签字笔在答题卡上规定区域作答,字迹要工整、清晰,答案书写在试卷、草稿纸上一律无效。
答题卡要注意保持整齐、干净,切勿折叠破损。
试卷、草稿纸、答题卡不要带出考场,更不能将答题情况转抄后带出考室。
4、计算器手机不能带入考场
考生进入考场,除带2B铅笔、0.5毫米黑色笔迹签字笔、圆规、直尺、三角板、橡皮外,其它任何物品(涂改液、修正带、计算器、快译通、移动通信工
具等)均不准带入考场。
思想品德、历史科可带规定资料。
考试中,考生不要将手机、小灵通等通信工具带进考室。
一旦带入考室,无论作弊与否,都以违纪论处。
与高考不同,中考不要求所有考点对考生进行安检,考生也可以带手表入场。
5、试卷带出场当科记零分
中考时,考生将某科试卷带出考室,该科成绩作零分处理。
为确保中考公平,武汉市招考办昨日列出2013年中考考纪“高压线”,考生在考试时切莫触“线”。
