广东省广州市白云区汇侨中学九年级数学《弦切角定理》课件
九年级上人教新课标24.2弦切角及和圆有关的比例线段

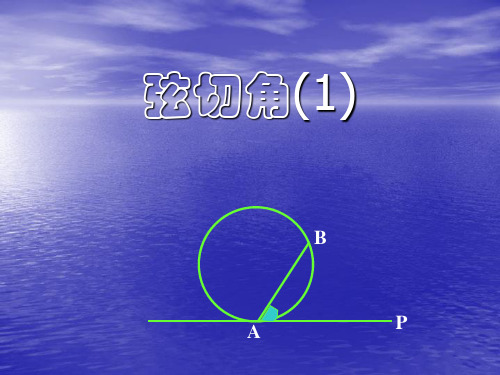
初三数学弦切角及和圆有关的比例线段知识精讲一. 本周教学内容:弦切角及和圆有关的比例线段二. 重点、难点:1. 弦切角的概念:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
注意:弦切角必须具备三个条件:(1)顶点在圆上(切点),(2)一边和圆相切,(3)一边和圆相交(弦),三者缺一不可。
2. 弦切角定理:弦切角等于它所夹的弧对的圆周角。
3. 弦切角定理的推论:如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。
弦切角是和圆有关的角之一,其他几种有圆心角、圆周角、圆内接四边形的外角。
这四种角之间的关系及转换是与圆有关的论证及计算的基础。
4. 相交弦定理:圆内两条相交弦,被交点分成的两条线段长的积相等。
5. 相交弦定理的推论:如果弦与直径相交,那么弦的一半是它分直径所成的两条线段的比例中项。
6. 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
7. 切割线定理的推论(或称割线定理):从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
本节是本章中综合性最强的部分,是本章及初中平面几何中难点之一。
其中,相交弦定理、切割线定理及割线定理在证明等积式、比例式和线段长度的计算中起着极其重要的作用。
这三个定理实际是一个整体,可以看做相交弦交点从圆内移到圆外,由割线旋转到切线时的结果。
应用定理和推论解题时,要注意数形结合的思想、方程思想的运用。
由于定理和推论的结论都是两条线段乘积的形式,所以一元二次方程更显威力。
例1. 如图,经过⊙O求证:∠ATC=∠证明一:∵TC为⊙∵∠TBC=∠A+∠∴∠TBC=∠BTC即∠ATC=∠TBC证明二:∵∠ETA又∵∠ATC=180°-∠ETA ∠TBC=180°-∠TBA104,==AB PABP6∴=OP OC CO =∴⨯=-∴=564549222,, CO CO >∴=07,答:⊙O 半径为7cmOD =24,进而求出例3. 如图,△ABC (1)求证:AE 2=PE (2)若AE =4,PE (1)证明:∵PA ∵PF//AC ,∴∠C 又∠∠ AEP = ∴=∴AE DE PEBE, BD DC PF AC =,// ∴=BE AE∴=⋅AE PE DE 2(2)解:根据相交弦定理:AE ·BE =GE ·EF AE EF GE GE ==∴4=⋅∴=48822,,, PE PG PE GE =∴=-=-=5523,∴=+=+=PF PE EF 5813 ∵PA 是⊙O 的切线∴=⋅=⨯=PA PG PF 23133939=15,sin C =35,求Rt △AD 、DB 的比值,又 解:连结OD 、DB∵CD 是⊙O 切线,∴OD ⊥CD 在中,Rt ODC C OD OC ∆sin ==35设,,则OD k OC k DC k ===354OD OB BC k k k AB k =∴=-==,,5326 ∠=∠∠=∠CDB A C C , ∴∆∆CDB CAD ~∴===DB AD BC CD k k 2412AD DB AD =∴==151275,.∵AB 是⊙O 直径 ∴∠=︒ADB 90 ()∴=+=+=AB AD DB 222215751525. ∴=61525k ∴==BC k 2525注意:将Rt △ADB 中,DB 、AD 两边的比转化为切线、割线的比,(即)在这类图形中常用。
九年级上数学《弦切角定理》课件
B
一边与圆相交,
另一边与圆相切 的角叫做弦切角
A
AmB 是弦切角∠PAB所夹的弧。
m
P
顶点在圆上,一边与圆相交,另一边 与圆相切的角叫做弦切角。 下面五个图中的∠BAC是不是弦切角?
C B A C C A
×
B
×
C
B
A
×
B
B C
×
A
A
√
从数学的角度看,弦切角能分成几大类? C C C .O .O .O P P P D A B A A B D
BAC为直角, 圆心在AC上。 BAC为锐角, 圆心在角外。
B
BAC为钝角, 圆心在角内。
上图中BAC所夹的弧分别是:半圆、劣弧、优弧。
猜想:弦切角BAC与圆周角APC的关系 现在分别作出他们所对的圆周角APC, 如上图
︵ 已知:AC是⊙O的弦,AB是⊙O的切线,AmC 是弦切角∠BAC所 ︵ 夹的弧,∠P是AmC所对的圆周角。 求证:∠BAC=∠P Q C
课堂练习:
1、已知AB是⊙O的切线A为切点,由图填空:
30º
O
70º
1 3
O
25º
O
2
80º 4 A ; B
A ∠1= 30º ∠4= 40º
B
A
B
;∠2= 70º ;∠3= 65º 。 弦切角等于它所夹的弧对的圆心角的一半.
2、选择: AB为⊙O直径,PC为⊙O的切线,C为切点, 若∠BPC=30°,则∠BCP=( A )。 A、 30°B、 60°C、 15°D、22. 5°
如图,DE切⊙O于点A,AB、AC是 ⊙O的弦,若 AB=AC,那么∠DAB 与∠EAC是否相等?为什么?
2020届一轮复习人教A版 弦切角定理 课件(22张)

1234 5
5.如图,AB是半圆O的直径,C是圆周上一点(异于点A,B),过点C作圆 O的切线l,过点A作直线l的垂线AD,垂足为点D.AD交半圆于点E.求 证:CB=CE.
分析转化为证明∠CBE=∠CEB.
题型一 题型二 题型三
证明连接BD,如图.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∠BCD=∠BAD,∠CBD=∠CAD,
∴∠BCD=∠CBD.∴BD=CD.
又BE为☉O的切线,
∴∠EBD=∠BAD,∠EBD=∠BCD.
故在△BED和△CEB中,
∠EBD=∠ECB,∠BED=∠CEB,
∴△BED∽△CEB.
题型一 题型二 题型三
题型二 线段成比例问题
【例2】 如图,已知△ABC内接于☉O,∠BAC的平分线交☉O于点 D,CD的延长线交过点B的切线于点E.
求证:������������������������22 = ������������������������.
分析直接证明此等式有一定的难度,可以考虑把它分解成两个比 例式的形式,然后借助相似三角形的性质得出结论.
又∠ACB=80°,
∴∠D=∠ACB-∠DAC=80°-35°=45°.
答案:A
对弦切角的理解 剖析弦切角的特点:(1)顶点在圆上;(2)一边与圆相交;(3)另一边与 圆相切.
弦切角定义中的三个条件缺一不可.如图①②③④中的角都不是 弦切角.图①中,缺少“顶点在圆上”的条件;图②中,缺少“一边和圆相 交”的条件;图③中,缺少“一边和圆相切”的条件;图④中,缺少“顶点
在圆上”和“另一边和圆相切”两个条件.
题型一 题型二 题型三
题型一
中考突破数学24224弦切角17页PPT

︵ 已知:AC是⊙O的弦,AB是⊙O的切︵线,AmC 是弦切角∠BAC所夹的弧,∠P是AmC所对的 圆周角。求证:∠BAC=∠P
( 1 ) 圆心O在∠BAC的外部 作⊙O的直径AQ,连结CQ
Q C
∵∠BAQ=∠ACQ=90°
P
O m
∴∠BAC=90°-∠CAQ
A
B
∠Q=90°-∠CAQ 弦切角等于所夹
若∠BPC=30°,则∠BCP=(A)。
A、 30°B、 60°C、 15°D、22. 5°
C
PB
O
A
3,如图:四边形ABCD为圆内接四边形,AB 是直径,MN切⊙O于C点,∠BCM=38° 那么∠ABC的度数是( B )。 A、38°B、52°C、68° D、42°
O
B
38°
M
C
A
D N
弦切角定理:弦切角等于它所夹的弧对的圆周角.
44、卓越的人一己知道。——苏联
∠DAC=∠Q
弦切角等于所夹
∴ ∠BAC=∠P
弧对的圆周角。
课堂练习: 1、已知AB是⊙O的切线A为切点,由图填空:
30º O 70º
21 AB
O
3
25º
A
B
O 80º
4
A
B
∠1= 30º;∠2= 70º;∠3= 65º ;∠4= 40º。
弦切角等于它所夹的弧对的圆心角的一半.
2、选择: AB为⊙O直径,PC为⊙O的切线,C为切点,
一般情况下,弦切角、圆周角、圆心角 都是通过它们夹的(或对的)同一条弧(或 等弧)联系起来,因此,当已知有切线时常 添线构建弦切角或添切点处的半径应用切线 的性质。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
【初中数学】圆中弦切角及弦切角定理

【初中数学】圆中弦切角及弦切角定理一、弦切角1、定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
如图:2、弦切角的三种情况(1)圆心在弦切角外;(2)圆心在弦切角的一条边上;(3)圆心在弦切角内;二、弦切角定理及证明定理:弦切角的度数等于它所夹的弧的圆周角;弦切角的度数等于它所夹的弧的圆心角度数的一半。
已知:如图,PQ是圆O的切线,切点为P。
求证:∠APQ=∠ABP,2∠APQ=∠AOP.(1)当圆心在弦切角外部时证明:连接OA,OP,在非弦切角所夹弧优弧PA上任取一点B,连接BP和BA。
∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠POA=180°∴2∠OPA+∠POA=180°∵ PO为圆的切线,OP为半径∴ ∠OPA+∠APQ=90°∴ ∠OPA=90°-∠APQ∴ 2(90°-∠APQ)+∠POA=180°∴∠POA=2∠APQ∵ ∠POA=2∠ABP(同弧所对的圆心角是圆周角的2倍)∴ ∠APQ=∠ABP(2)当圆心在弦切角的一边上时证明:在非弦切角所夹弧AP上任取一点B,连接AB、PB ∵ AP为直径∴ ∠ABP=90°∵ PQ为圆的切线,OP为半径∴ ∠APQ=90°∴∠APQ=∠ABP∴2∠APQ=∠AOP(同弧所对的圆心角是圆周角的2倍). (3)当圆心在弦切角的内部时证明:连接OA,OP,在非弦切角所夹弧劣弧PA上任取一点B,连接BP和BA。
∵ OA=OP∴ ∠OPA=∠OAP∵ ∠OPA+∠OAP+∠1=180°∴2∠OPA+∠1=180°∵ PO为圆的切线,OP为半径∴ ∠OPA=∠APQ-90°∴ 2(∠APQ-90°)+∠1=180°∴ ∠1+2∠APQ=360°∵ ∠1+∠2=360°∴∠2=2∠APQ∴ ∠POA=2∠APQ(这里的∠POA是大于180°的角,是优弧AP所对的圆心角)∵ ∠POA=2∠ABP(同弧所对的圆心角是圆周角的2倍)∴ ∠APQ=∠ABP三、例题例1、已知:如图,直线BC切⊙O于B点,AB=AC,AD=BD,求∠A.解:由弦切角定理可得,∠DBC=∠A∵ AD=BD∴ ∠A=∠ABD∵ AB=AC∴ ∠ABC=∠ACB=2∠A∵ ∠A+∠ABC+∠ACB=180°∴5∠A=180°∴ ∠A=36°例2、已知:如图,直线DC与⊙O相切于点C,AB为⊙O直径,AD⊥DC于D,∠DAC=28°,求∠CAB的值。
【人教版】九年级上册数学《弦切角》ppt教学课件

连结OC,由切线性质, 可得OC∥AD,于是 有∠2=∠3,又由于 B ∠1=∠3,可证得 ∠1=∠2
E
·O 1A 32 CD
小结:
1、概念的引入
顶点在圆上,一边与圆相交,另一边与圆相 切的角叫做弦切角。
2、定理的发现
弦切角定理:弦切角等于它所夹的弧对的圆周角。
推论:两个弦切角所夹的弧相等,
那么这两个弦切角相等。
的度数是( B )。
A、38°B、52° C、68° D、42°
O
A
B
38°
M
C
D N
弦切角定理:弦切角等于它所夹的弧对的圆周角。 推论:两个弦切角所夹的弧相等, 那么这两个弦切角相等。
如图,DE切⊙O于点A,AB、AC是 ⊙O的弦,若 AB=AC,那么∠DAB 与∠EAC是否相等?为什么?
∠ DAB= ∠EAC
C
B O
E
A
D
例题解析
例1:如图:已知AB是⊙O的直
径,AC是弦,直线CE和⊙O切于
点C,AD⊥CE于D。
B
O
求证:(1)AC平分∠BAD
(2)AC2=2AD·AO
A
你还能用其他方法解答 吗?试试看!
E
C
D
有弦切角,常连结弦切角 所夹弧所对的圆周角。
例题解析(思路2)
例1: 如图,已知AB是⊙O的直径,AC是弦,直 线CE和⊙O切于点C,AD⊥CE,垂足是D,求证: AC平分∠BAD.
4
A
B
∠1= 30º ;∠2= 70º ;∠3= 65º ; ∠4= 40º 。 弦切角等于它所夹的弧对的圆心角的一半.
2、选择: AB为⊙O直径,PC为⊙O的切线,C为切点,
高中数学 1.2.3弦切角定理课件 北师大版选修41

3.正确使用弦切角定理 剖析:要正确使用弦切角定理,第一步要找到弦切角,弦切角的特点是:(1)顶点在 圆上;(2)一边与圆相交;(3)一边与圆相切,这三个条件缺一不可,第二步要准确找到 弦切角所夹的弧,再看这段弧上的圆周角,然后用弦切角定理解题,如果没有圆周角, 有这段弧所对的圆心角也可以.
M Z Z 目标导航 UBIAODAOHANG
Байду номын сангаас
A.∠ADB
B.∠AOB
C.∠ABC D.∠BAO
解析:∠ADB 是圆周角,∠AOB 是圆心角,∠ABC 是弦切角,∠BAO 不是
弦切角.
答案:C
M Z Z 目标导航 UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
圆相切”两个条件.
M Z Z 目标导航 UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
2.圆心角、圆周角、弦切角的比较 剖析:如下表所示.
圆心角
圆周角
顶点在圆心的 定义
角
顶点在圆上,两边和 圆相交
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
12
1.弦切角 顶点在圆上,一边和圆相交,另一边和圆相切的角称为弦切角.
名师点拨弦切角可分为三类:(1)圆心在角的外部,如图①所示;(2)圆心在 角的一边上,如图②所示;(3)圆心在角的内部,如图③所示.
弦切角的性质 课件

连接 EF 并延长交⊙O 于点 A,求证:点 A 是BC 的中点.
[思路点拨] (1)由切线的性质定理,知△PCF 是等腰直角 三角形,因此求出 CF 的长,进而求出半径;
(2)中,利用弦切角定理,可以求出两个三角形中,有一组
︵︵
角相等,然后利用相似三角形的判定及性质,可证出AC 与AB
︵
所对的圆周角相等,从而证出点 A 是BC 的中点.
如图所示,因为∠BDE 与∠BED 所夹的弧是同一个弧,所
以∠BDE=∠BED;
︵
︵
如 果 EM = DM
__∠__C_E_M__=__∠__A_D__M___.
,也可以得出
利用弦切角解决与角有关的问题
如 图 甲 , 在 △ABC 中 , ∠B = 90° , O 是 AB 上 一 点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点 D,直线ED交BC的延长线于F.若AD∶AE=2∶1,求tan∠F.
[思路点拨]
[解题过程] 如图乙所示,连接 BD.
∵AC 为⊙O 的切线,∴∠1=∠2. ∵∠A=∠A,∴△ADE∽△ABD, ∴AADE=BDDE,即BDDE=21,∴DBDE=12. ∵BE 为⊙O 的直径,∴∠BDE=90°,∴tan∠2=DBDE=12. ∵∠F+∠BEF=90°,∠2+∠BEF=90°, ∴∠2=∠F,∴tan∠F=tan∠2=12.
3.弦切角定理 (1)文字语言叙述 弦切角等于它_所__夹__的__弧___所对的圆周角. (2)图形语言叙述
如图,AB与⊙O切于A点,则∠BAC=__∠__D___.
4.与弦切角定理有关的结论 (1)弦切角的度数等于它__所__夹__的__弧__的__度__数__的__一__半__. (2)弦切角的度数等于它__所__夹__的__弧__所__对__的__圆__心__角__度__数__的___ _一__半_____. (3) 如 果 两 个 弦 切 角 所 夹 的 __弧__相__等____ , 那 么 这 两 个 __弦__切__角__也__相__等____.
2.4 弦切角的性质 课件(人教A选修4-1)(2)

所以∠DCE=∠CBE.
所以∠CBE=∠CEB. 所以CE=CB.
法二:连接AC、BE,在DC延长线上取一点F. 因为AB是半圆O的直径,C为圆周上一点, 所以∠ACB=90°,即∠BCF+∠ACD=90°. 又因为AD⊥l,所以∠DAC+∠ACD=90°.
所以∠BCF=∠DAC.
又因为直线l是圆O的切线,所以∠CEB=∠BCF. 又∠DAC=∠CBE,所以∠CBE=∠CEB. 所以CE=CB.
OB于D.求证:∠DAC=∠CAB. 分析:本题考查弦切角定理的应用.解答本题需要
根据题意画出图形,然后利用相关定理解决.
证明:法一:如图,延长 AD 交⊙O 于 E,AB 切⊙O 于 A, ∵CD⊥AE, ∴ = CE . AC
又∵∠DAC 的度数等于 CE 度数的一
半,
AC ∠CAB 的度数等于 度数的一半,
提示:弦切角等于它所夹的弧所对的圆心角的一半.
[研一题] [例1] 如图,AB、CB分别切⊙O于D、
E,试写出图中所有的弦切角. 分析:本题考查弦切角的定义.解答本 题需要明确构成弦切角的三个条件,然后依
据定义作出判断.
解:由弦切角的定义可知, ∠ADE、∠BDE、∠BED、∠CED都是弦切角.
[悟一法]
[悟一法]
充分利用圆周角定理、圆内接四边形的性质、平行 四边形性质定理、弦切角定理等结论,架设与三角形有 关问题的桥梁,证明三角形相似是解决此类问题的有效
途径.
[通一类] 3.AB是圆O的直径,过A、B作两弦AC和BD相交于E,求 证:AB2=AE· AC+BE· BD. 证明:如图,AB是圆的直径. AC与BD相交于E,作EF⊥AB,F为垂足.
点击下图进入“创新演练”
《1.2.3弦切角定理》课件2-优质公开课-人教B版选修4-1精品

∴AC平分∠DAB.
【反思感悟】 本题方法一是课本证法,是利用切线性质以及
平行线性质,而方法二巧妙地使用弦切角以及直径所对圆周
角为直角达到证题目的,各有千秋.
【探究学习】 对弦切角与所夹弧的关系的探究 【例 4】 如图所示,DE 切⊙O 于 A,AB、AC 是⊙O 的弦,若 = ,那么∠DAB 和∠EAC 是否相等?为什么?
例1:判断下列各图形中的角是不是弦切角,并说明理由:
分析:此题利用弦切角的定义来判断.
解:以上各图中的角都不是弦切角.
图(1)中,缺少“顶点在圆上”的条件;
图(2)中,缺少“一边和圆相交”的条件; 图(3)中,缺少“一边和圆相切”的条件; 图 (4) 中,缺少“顶点在圆上”和“一边和圆相切”两个条 件. 【反思感悟】 弦切角的三要素:(1)顶点在圆周上; (2)一边与圆相交;(3)一边与圆相切.
由弦切角定理可直接得到角相等,在与弦切角有关的几何问
题中,往往还需借助其他几何知识来综合解答,由弦切角得 到的角相等只是推理论证中的一个条件.
(2)证明直线平行
弦切角定理构建了角与角的相等关系,
而直线的平行是以角的关系为基本条件 的,因而在圆中我们可以利用弦切角定 理来推理论证直线的平行.如图所示, 若 CD 切 圆 O 于 点 M , 弦 AM 与 弦 BM 相 等,则由∠ CMA =∠ B ,∠ A =∠ B 得到 ∠CMA=∠A,从而CD∥AB.
1.2.3 弦切角定理
关键词:弦切角定理、弦切角定理的推论
知识点一
弦切角的概念
定义:顶点在圆周上,一边和圆相交、另一边和圆相切的角 叫做弦切角.
如图所示,∠ACD和∠BCD都是弦切角.
【推敲引申】 弦切角必须具备三个条件: 1. (1)顶点在圆上(顶点为圆切线的切点);
弦切角课件包[上学期]-3
![弦切角课件包[上学期]-3](https://img.taocdn.com/s3/m/a62955743c1ec5da50e27040.png)
B
A
D
需要更完整的资源请到 新世纪教 育网 -
如图:DE切⊙O于点A ,AB、AC是⊙O的弦,若 AB=AC,且∠DAB=45°,则∠BAC= ( D ) A、45°;B、50°;C、60°;D、90°。
C
O
B
E
A
需要更完整的资源请到 新世纪教 育网 -
B
A
×
B
B C
×
A A 需要更完整的资源请到 新世纪教
育网 -
√
如图,说出图中所有的弦切角及其所夹的弧。 弦切角∠MAB和∠MBA 夹的弧都是 AB 弦切角∠ABQ和∠BAP 夹的弧都是 AmB
M
A
O · Q
P m
B
练习
需要更完整的资源请到 新世纪教 育网 -
如图,AB是⊙O的直径,DE切⊙O于点C。若 ∠ACD=40°,则∠BAC=( C ) A、30°;B、40°;C、50°;D、60°。
B O A
E
C
D
需要更完整的资源请到 新世纪教 育网 -
练习
如图,BC切⊙O于点B,圆心O在AC上,∠A =25°,那么∠ABC= .
需要更完整的资源请到 新世纪教 育网 -
A
·
O B
如图,BC切⊙O于点B,圆心O在AC上,∠A =25°,那么∠ABC= 115 ° .
连结OB A
·
O B
Байду номын сангаас
D
∵ ∴ ∵ C ∴ ∴
BC切⊙O于点B ∠OBC= 90° AO=BO ∠OAB= ∠OBA=25 °
∠ABC= ∠OBC+ ∠ABO = 90°+ 25 °=115 °
数学九年级下册正弦、余弦、正切函数的简单应用课件PPTPPT公开课

因为∠A=45°,则AC=BC,由勾 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB.
金紫山上有个道观,与顶峰的海拔差约为100米,除了迂回的登顶小路之外,还有一条70度左右的碎石坡可以登顶,是户外运动者青睐
之地.
股定理得AB =AC +BC =2BC . 如如下果图 出,水在的直高角度三为角50形m,中那,么我需们要把准锐备角多α长的的对水边管与?邻边的比叫作2 角α的正切2 ,记作ta2nα, 即 2
AB 10 5
AC 8 4
例3 如图,在平面直角坐标系内有一点P(3,4),
连接OP,求OP与x轴正方向所夹锐角 α 的正弦值.
解 如图,设点A(3,0),连接P A .
在△APO中,由勾股定理得
O P O A 2 A P 23 2 4 2 5 .
因此sin AP 4.
A
OP 5
归纳 结合平面直角坐标系求某角的正弦函数值,一般过已知点 向x轴或y轴作垂线,构造直角三角形,再结合勾股定理求解.
先利用勾股定理求
已知直角三角形的边长求正弦值
13
? 3 5 因为∠A=45°,则AC=BC,由勾股定理得AB2=AC2+BC2=2BC2.
当然是的,可以用类比探索正弦函数的方法,是有理可证的,这个证明大家下去自己证明。 因为∠A=45°,则AC=BC,由勾股定理得AB2=AC2+BC2=2BC2.
未知的斜边与直角 边的长.
因为∠A=45°,则AC=BC,由勾股定理得AB2=AC2+BC2=2BC2.
B 求锐角三角函数时,勾股定理的运用是很重要的.
如下图,在直角三角形中,我们把锐角α的对边与邻边的比叫作角α的正切,记作tanα, 即
