基于邻接矩阵的电路信号流图分析法

合集下载

《深入浅出图神经网络：GNN原理解析》随笔

《深入浅出图神经网络：GNN原理解析》阅读随笔目录一、前言 (2)1.1 本书的目的和价值 (3)1.2 图神经网络简介 (3)二、图神经网络基础 (5)2.1 图的基本概念 (6)2.2 神经网络的基本概念 (8)2.3 图神经网络与神经网络的结合 (9)三、图神经网络的分类 (10)3.1 基于消息传递的图神经网络 (12)3.2 基于能量函数的图神经网络 (12)3.3 基于图注意力机制的图神经网络 (14)四、图神经网络的训练方法 (15)4.1 迭代训练法 (16)4.2 随机梯度下降法 (17)4.3 动量法 (19)4.4 自适应学习率方法 (20)五、图神经网络的优化技术 (21)5.1 局部优化算法 (22)5.2 全局优化算法 (24)5.3 混合优化算法 (26)六、图神经网络的评估与可视化 (27)6.1 评估指标 (28)6.2 可视化方法 (29)6.3 实战案例分析 (31)七、图神经网络的未来发展方向与应用前景 (32)7.1 当前研究的热点和挑战 (34)7.2 未来可能的技术创新 (35)7.3 图神经网络在各个领域的应用前景 (37)八、结语 (38)8.1 对本书内容的总结 (39)8.2 对未来图神经网络发展的展望 (40)一、前言在人工智能领域，图神经网络（Graph Neural Networks, GNNs）作为一种强大的深度学习模型，近年来得到了广泛的关注和研究。

它们能够处理非结构化数据，如社交网络、分子结构、知识图谱等，因此在许多应用中具有重要的地位。

尽管GNNs在学术界和工业界都取得了显著的成功，但它们的原理和应用仍然是一个活跃的研究课题。

特别是对于初学者来说，理解和掌握GNN的原理解析及其在实际问题中的应用，是一个不小的挑战。

为了帮助读者更好地理解GNNs，本文将从基础到高级逐步展开，深入剖析GNN的核心概念、模型架构以及最新的研究进展。

结合具体的代码实现和实验结果，我们将展示GNN在实际应用中的强大能力。

邻接矩阵的实验原理及应用

邻接矩阵的实验原理及应用实验原理邻接矩阵是一种图的表示方法，通过矩阵的形式记录图中各个顶点之间的连接关系。

邻接矩阵可以用于描述有向图和无向图。

无向图的邻接矩阵无向图的邻接矩阵是一个方阵，其中的每个元素表示图中两个顶点之间是否存在边。

如果顶点i和顶点j之间存在边，则邻接矩阵的第i行第j列和第j行第i列的元素值都为1；否则，为0。

邻接矩阵的对角线上的元素表示各个顶点的度数。

有向图的邻接矩阵有向图的邻接矩阵同样是一个方阵，其中的每个元素表示从顶点i到顶点j是否存在边。

如果顶点i到顶点j存在边，则邻接矩阵的第i行第j列的元素值为1；否则，为0。

邻接矩阵的表示方法邻接矩阵可以用二维数组来表示，数组的大小为n×n，其中n为图中顶点的个数。

数组的下标表示顶点的编号，而数组中的元素表示邻接关系。

应用邻接矩阵在图的算法和应用领域有重要的应用。

图的遍历使用邻接矩阵可以进行图的遍历操作，包括深度优先遍历和广度优先遍历。

通过对邻接矩阵的遍历，可以访问图中所有的顶点和边。

最短路径算法邻接矩阵可以作为最短路径算法的基本数据结构。

通过邻接矩阵，可以方便地计算两个顶点之间的最短路径。

最小生成树算法最小生成树算法可以使用邻接矩阵作为数据结构。

通过构建邻接矩阵，并使用Prim算法或Kruskal算法，可以生成图的最小生成树。

图的连通性判断邻接矩阵可以用来判断图的连通性。

通过对邻接矩阵进行深度优先搜索或广度优先搜索，可以确定图中的连通分量。

图的可达性分析邻接矩阵可以用于分析图中顶点之间的可达性。

通过对邻接矩阵进行矩阵运算，可以得到图中任意两个顶点之间的可达性。

总结邻接矩阵是一种表示图的方法，通过矩阵的形式记录图中各个顶点之间的连接关系。

邻接矩阵具有简单、直观、易于操作等优点，在图的算法和应用中有广泛的应用。

通过对邻接矩阵的遍历、最短路径算法、最小生成树算法、连通性判断和可达性分析等操作，可以解决各种与图相关的问题。

以上就是邻接矩阵的实验原理及应用，希望对你有所帮助。

数字通信原理实验邻接矩阵

数字通信原理实验邻接矩阵邻接矩阵是数字通信中一种重要的数学工具，用于描述一个图形结构中各个节点之间的连通性。

在数字通信原理实验中，邻接矩阵被广泛应用于网络拓扑结构的分析和设计。

本文将详细介绍邻接矩阵在数字通信中的应用。

邻接矩阵通常是一个二维矩阵，其中的每个元素代表一个节点之间的连接状态。

如果节点i与节点j之间存在连通关系，则邻接矩阵中第i行第j列的元素为1，否则为0。

用邻接矩阵表示一个图形结构，可以清晰地体现各个节点之间的关系，有利于进行网络拓扑分析。

在数字通信中，邻接矩阵广泛应用于路由算法中。

路由算法是计算机网络中用于寻找最优路径的一种算法。

通过构建邻接矩阵，可以很方便地实现路由算法。

此外，邻接矩阵也被广泛应用于网络拓扑的设计中。

网络拓扑是指网络中各节点之间的物理连接结构。

通过构建邻接矩阵，可以快速地分析网络的连接状态，为网络拓扑的优化和设计提供依据。

例如，在无线传感器网络中，邻接矩阵可以用于描述节点之间的信号强度，有利于调整信号传输的强度和方向，从而提高网络的数据传输效率。

在实际的数字通信应用中，邻接矩阵还可以用于描述数据传输的各种参数。

例如，在传统的计算机网络中，邻接矩阵可以用于描述各个节点之间的数据传输速度和数据包传输的成功率等参数。

通过实时地监控这些参数，可以调整网络的数据流量，从而提高网络的数据传输效率和稳定性。

最后，需要指出的是，邻接矩阵虽然在数字通信中具有重要的应用，但也不可避免地存在一定的局限性。

例如，在大规模网络中，邻接矩阵的构建和存储会消耗大量的系统资源。

因此，在实际应用中需要综合考虑各种因素，选择适合的网络拓扑结构和数学工具，从而实现数字通信的高效、稳定和可靠。

2019年软考中级数据库系统工程师真题及答案解析

个元素是随机整数，现需查找某个整数是否在该数组那么a、b、c处应分别填( )。

打交道的软件模块。

B、集线器1、阅读下列说明和图，回答问题1至问题4，将解答填入答题纸的对应栏内。

解答学校欲开发一学生跟踪系统，以更自动化、更全面地对学生在校情况(到课情况和健康状态等相关信息)进行管理和追踪，使家长能及时了解子女的到课情况和健康状态，并在有健康问题时及时与医护机构对接。

该系统的主要功能是：(1)采集学生状态。

通过学生卡传感器，采集学生心率、体温(摄氏度)等健康指标及其所在位置等信息并记录。

每张学生卡有唯一的标识(ID)与一个学生对应。

(2)健康状态告警。

在学生健康状态出现向题时，系统向班主任、家长和医护机构健康服务系统发出健康状态警告，由医护机构健康服务系统通知相关医生进行处理。

(3)到课检查。

综合比对学生状态、课表以及所处校园场所之间的信息对学生到课情况进行判定。

对旷课学生，向其家长和班主任发送旷课警告。

(4)在校情况汇总。

定期汇总在校情况，并将报告发送给家长和班主任。

(5)家长注册。

家长注册使用该系统，指定自己子女，经学校管理人员审核后，向家长发送注册结果。

(6)基础信息管理。

学校管理人员对学生及其所用学生卡和班主任、课表(班级、上课时间及场所等)、校园场所(名称和所在位置区域)等基础信息进行管理，对家长注册申请进行审核，将家长ID 加入学生信息记录中使家长与其子女进行关联，一个学生至少有一个家长，可以有多个家长。

课表信息包括班级、班主任、时间和位置等。

现采用结构化方法对学生跟踪系统进行分析与设计，获得如图1-1所示的上下文数据流图和图1-2所示的0层数据流图。

1）使用说明中的词语，给出图1-1中的实体E1〜E5的名称。

(5分)2）使用说明中的词语，给出图1-2中的数据存储D1〜D4的名称。

(4分)3）据说明和图中术语，补充1-2中缺失的数据流及其起点和终点(三条即可)。

(3分) 4）根据说明中术语，说明图1-1中数据流“学生状态”和“学生信息”的组成。

线性网络的信号流图分析法

x5a5a1x1a2x2a4x4 x6a6a1x1a2x2a4x4(527)
与式（5-2-7）对应的SFG如图5-12所示。将图5-12 与图5-4相比较，可以看出，节点x3已被消去，支路发生移动。移动
的规则为：为消去节点x3,使与x3相联的每一条入支路的始端不动，而其末端分别沿着每一条出支路做正向移动，移至该出支路的末端，形成3×2=6条新支路。每条新支路的传输值为被移动支路与沿其移动支路二支路传输值之积。如果被消节点有m条入支路、n条出支路，则支路移动后的新支路数为m×n。
§ 5-1 信号流图
• 基本概念：信号流图是一种表示线性代数方程组变量关系的加权有向图，它由节点和联接在节点之间的有向支路构成。例如:在节点x、y之间有传输值为a的一条支路，箭头指向节点y，如图5-1所示。该信号流图所对应的方程是 y=ax
• 如果节点 x 有两条或两条以上的入支路，其对应方程为 xi i （入支路传输值×该入支路起始处的节点变量），其中求和是对节点x i 的所有入支路进
（1）从源节点出发的支路可以倒向；不是源节点出发的单支路不能倒向。
（2）将两节点之间的支路倒向后，支路传输值为原支路传输值的倒数；
（3）将原来终结在被倒向支路末端节点的其他支路全部改为终结在倒向后支路末端节点上，其传输值为原支路传输值乘以倒向支路传输值的负倒数。
§ 5-3 Mason公式
• Mason图增益公式（简称Mason公式）是求SFG图增益（传输值）的公式，它与用克莱姆法则求线性方程组解的方法相当。Mason公式直接根据SFG的结构给出传输值的解，应用更加方便。
自环消去规则
• 在绘制SFG和简化SFG的过程中，常有自环出现。在此情况下，必须消去自环，才能使SFG进一步化简。图5-16所示的SFG对应的线性方程组为

邻接矩阵求通路数和回路数

邻接矩阵求通路数和回路数一、概述邻接矩阵是图论中表示图的一种方式，它由一个二维数组表示，其中数组的行和列分别代表图中的顶点，而数组中的元素则表示两个顶点之间是否存在边。

邻接矩阵求通路数和回路数是图论中常见的问题之一，本文将详细介绍如何通过邻接矩阵来求解这两个问题。

二、邻接矩阵求通路数1.定义通路是指从一个顶点出发到达另一个顶点所经过的所有边构成的路径。

邻接矩阵求通路数即为求解从一个顶点到另一个顶点所有可能路径数量。

2.算法步骤（1）初始化：设置访问标记数组visited[]为false。

（2）递归遍历：从起始节点开始递归遍历图，对于每个节点进行如下操作：a.将当前节点标记为已访问。

b.如果当前节点为目标节点，则将计数器加1。

c.否则，对于当前节点所有未访问过的相邻节点进行递归遍历。

（3）返回结果：返回计数器值即可。

3.代码实现下面是使用C++语言实现邻接矩阵求通路数的代码：int countPaths(int graph[][V], int src, int dest) {bool visited[V] = {false};int count = 0;countPathsUtil(graph, src, dest, visited, count);return count;}void countPathsUtil(int graph[][V], int u, int dest, bool visited[], int &count) {visited[u] = true;if (u == dest) {count++;} else {for (int v = 0; v < V; v++) {if (graph[u][v] && !visited[v]) {countPathsUtil(graph, v, dest, visited, count);}}}visited[u] = false;}三、邻接矩阵求回路数1.定义回路是指从一个顶点出发，沿着若干条边走过一些顶点后又回到起点的路径。

邻接矩阵求通路数和回路数

邻接矩阵求通路数和回路数引言在图论中，邻接矩阵是一种常用的表示图的方法之一。

通过邻接矩阵，我们可以快速和方便地求解图中的一些问题，如通路数和回路数。

本文将深入探讨邻接矩阵的性质和应用，以及如何利用邻接矩阵求解图中的通路数和回路数。

什么是邻接矩阵邻接矩阵是一种用于表示图的二维矩阵。

对于图中的n个顶点，邻接矩阵就是一个n×n的矩阵，其中的元素表示顶点之间的连接关系。

如果两个顶点之间有边相连，则对应的元素为1；如果两个顶点之间没有边相连，则对应的元素为0。

邻接矩阵的性质邻接矩阵具有以下几个性质： 1. 邻接矩阵是对称的：如果图是无向图，那么邻接矩阵是对称的，即矩阵的第i行第j列元素与第j行第i列元素相等。

如果图是有向图，那么邻接矩阵不一定对称。

2. 对角线上的元素表示顶点的度：对于无向图，邻接矩阵对角线上的元素表示每个顶点的度，即与该顶点相连的边的数目。

对于有向图，矩阵的对角线上的元素分为两部分，其中左上方表示该顶点的出度，右下方表示该顶点的入度。

3. 邻接矩阵中相应位置的元素相乘是对应路径的长度：如果图中有边从顶点i到顶点j，那么矩阵的第i行第j列元素与第j行第i列元素的乘积即为这条边的长度。

如果两个顶点之间没有直接的边相连，那么对应的元素相乘为0。

邻接矩阵求通路数通路是指图中从一个顶点到另一个顶点的路径。

我们可以利用邻接矩阵来求解图中两个顶点之间的通路数。

理论基础假设有一个由n个顶点构成的图G，对应的邻接矩阵为A。

定义A k为邻接矩阵A的第k次幂，表示从一个顶点到另一个顶点通过k条边的通路数。

A0为对角线元素全为1，其余元素全为0的矩阵。

由此可知，邻接矩阵A的第k次幂矩阵的元素A_k[i][j]表示从顶点i到顶点j经过k条边的通路数。

通过计算A k可以求得两个顶点之间的通路数。

为了避免幂次的计算，我们可以使用矩阵乘法的方式来逐步计算A k。

实际应用以图G为例，假设邻接矩阵为A，我们要求图中顶点i到顶点j的通路数。

用邻接矩阵法输出图结构

图结构（设计性）4.1 实验目的1．熟练掌握图的两种存储结构（邻接矩阵和邻接表）的表示方法。

2．掌握图的基本运算及应用。

3．加深对图的理解，逐步培养解决实际问题的编程能力。

4.2 实验要求1 •对图的各项操作一定要编写成为C （C++ ）语言函数，组合成模块化的形式，每个算法的实现要从时间复杂度和空间复杂度上进行评价。

2．将本算法中的各个操作实现。

3．保存程序的运行结果，并结合程序进行分析。

4．上机过程中，能够熟练运用高级语言的程序调试器DEBUG 调试程序。

5．上机后，认真整理源程序及其注释，完成实验报告（包括源程序、实验结果、算法分析、心得体会等）。

4.3 实验内容在VC++环境下编写调试图深度优先和广度优先遍历的算法和函数，或者把已布置作业中的算法改成程序，进行运行。

问题描述：输入每条边的顶点u和v及其权值w,然后建立用邻接矩阵表示的图。

其相关操作如下：1. 创建一个可以随机确定结点数和弧（有向或无向）数的图。

2. 根据图结点的序号，得到该结点的值。

3. 根据图结点的位置的第一个邻接顶点的序号，以及下一个邻接顶点的序号。

4. 实现从第v 个顶点出发对图进行深度优先递归遍历。

5. 实现对图作深度优先遍历。

6. 编写主程序，实现对各不同的算法调用。

4.4 实验清单#include <stdio.h>#define MAX_VERTEX_NUM 10 /* 最多顶点个数*/#define INFINITY 32768 /* 表示极大值，即*/#define True 1#define False 0#define Error -1#define Ok 1typedef enum{DG, DN, UDG, UDN} GraphKind; /* 图的种类：DG 表示有向图,DN表示有向网,UDG表示无向图,UDN表示无向网*/typedef char VertexData; /* 假设顶点数据为字符型*/typedef struct ArcNode{// AdjType adj; /*对于无权图，用1或0表示是否相邻；对带权图，则为权值类型*/// OtherInfo info;int adj;} ArcNode;typedef struct{VertexData vexs[MAX_VERTEX_NUM]; /*顶点向量*/ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; /*邻接矩阵*/int vexnum,arcnum; /*图的顶点数和弧数*/GraphKind kind; /*图的种类标志*/}AdjMatrix; /*(Adjacency Matrix Graph)*/int LocateVertex(AdjMatrix *G ,VertexData v) /*求顶点位置函数*/{int j=Error,k;for(k=0;k<G->vexnum;k++)if(G->vexs[k]==v){j=k;break;}return(j);}int CreateDN(AdjMatrix *G) /*创建一个有向网*/{int i,j,k,weight;VertexData v1,v2;printf(" 输入图的弧数和顶点数\n");fflush(stdin);scanf("%d,%d",&G->arcnum,&G->vexnum); /* 输入图的顶点数和弧数*/ for(i=0;i<G->vexnum;i++) /*初始化邻接矩阵*/for(j=0;j<G->vexnum;j++)G->arcs[i][j].adj=INFINITY;for(i=0;i<G->vexnum;i++){printf(" 输入图的顶点\n"); fflush(stdin); scanf("%c",&G->vexs[i]); /* 输入图的顶点*/ } for(k=0;k<G->arcnum;k++){printf(" 输入一条弧的两个顶点及权值\n"); fflush(stdin);scanf("%c,%c,%d",&v1,&v2,&weight);/* 输入一条弧的两个顶点及权值*/i=LocateVertex(G,v1);j=LocateVertex(G,v2);G->arcs[i][j].adj=weight; /*建立弧*/}return(Ok);}void printf_adjmatrix(AdjMatrix *G){int i,j;printf(" ");for(i=0;i<G->vexnum;i++) {printf("%c",G->vexs[i]);printf(" ");} printf("\n");for(i=0;i<G->vexnum;i++) {printf("%c",G->vexs[i]);for(j=0;j<G->vexnum;j++){if(G->arcs[i][j].adj == INFINITY)printf(” x ")；elseprintf("%-4d", G->arcs[i][j].adj);}printf("\n");}}void main(){AdjMatrix G;CreateDN(&G);printf_adjmatrix(&G);4.5运行结果4.6实验心得对图结构和矩阵之间的概念和关系还不是很了解，在写程序是出现了很多错误我自己对输出图结构这方面还不是很了解，通过慢慢摸索，写出了程序，有很大的成就。

基于随机矩阵理论的网络图谱分析与优化方法

基于随机矩阵理论的网络图谱分析与优化方法随机矩阵理论是一门研究矩阵的随机性质和统计特性的学科，被广泛应用于各个领域，包括网络图谱分析与优化。

本文将介绍基于随机矩阵理论的网络图谱分析与优化方法的相关概念、原理和实际应用。

1. 网络图谱分析的基本概念网络图谱是指由节点和边组成的网络结构，用于描述复杂系统中不同实体之间的相互关系。

网络图谱分析旨在揭示网络结构和节点之间的特征和规律，从而帮助人们更好地理解和优化复杂系统。

2. 随机矩阵理论在网络图谱分析中的应用随机矩阵理论提供了一种量化网络图谱特性和性能的数学工具。

通过构建网络图谱的邻接矩阵，可以将网络图谱转化为一个随机矩阵，从而利用随机矩阵理论来分析网络的随机性质和统计特性。

3. 随机矩阵理论在网络图谱优化中的应用基于随机矩阵理论的网络图谱优化方法主要包括两个方面：一是通过分析网络图谱的特征值分布，进行网络结构优化；二是利用随机矩阵理论优化网络中的信号传输和信息量。

3.1 特征值分布分析与网络结构优化网络图谱的特征值分布包含了关于网络结构的重要信息。

通过分析特征值分布的统计特性，可以判断网络的连通性、聚类性和鲁棒性等指标。

例如，可以利用随机矩阵理论中的Marcenko-Pastur分布来识别网络中的主要特征值并去除噪声，从而优化网络的结构。

3.2 信号传输与信息量优化通过构建网络图谱的随机矩阵，并利用随机矩阵理论中的性质和方法，可以优化信号传输和信息量的传递效率。

例如，可以利用随机矩阵理论中的信号处理方法，对网络中的信号传输进行优化，提高网络通信的质量和速度。

4. 基于随机矩阵理论的网络图谱分析与优化方法应用案例基于随机矩阵理论的网络图谱分析与优化方法已经广泛应用于各个领域。

以社交网络为例，可以利用随机矩阵理论来分析社交网络中用户之间的关系和影响力，从而优化社交网络的推荐系统和信息传播效率。

另外，基于随机矩阵理论的网络图谱分析与优化方法也可以应用于金融市场、物流网络等领域，从而提升系统的效益和性能。

耦合邻接矩阵-概述说明以及解释

耦合邻接矩阵-概述说明以及解释1.引言1.1 概述耦合邻接矩阵是图论中的一种重要概念，用于描述图中各个节点之间的连接关系。

它是邻接矩阵的一种变体，旨在更准确地表示节点之间的耦合强度或紧密程度。

耦合邻接矩阵在各种领域中都有广泛的应用，如社交网络分析、交通流动模型和生物网络等。

在耦合邻接矩阵中，矩阵的每个元素代表了相应节点之间的耦合强度或关联程度。

通常情况下，矩阵的行和列代表不同的节点，而元素的值则反映了这些节点之间的连接强度。

如果节点之间存在连接，则相应元素的值为非零；反之，如果节点之间不存在连接，则元素的值为零。

通过这种方式，耦合邻接矩阵提供了一种直观清晰的表示方式，能够帮助我们更好地理解和分析图中各节点之间的关系。

耦合邻接矩阵在实际应用中具有许多优点和特点。

首先，它能够准确地描述节点间的连接状态，使得我们能够直观地观察到各节点之间的关联情况。

其次，耦合邻接矩阵可用于计算各节点的中心度、距离和分离度等重要指标，帮助我们深入研究节点的特性和网络的结构。

另外，耦合邻接矩阵还可以与其他图论算法和方法结合使用，从而提供更多的分析和应用可能性。

然而，耦合邻接矩阵也存在一些局限性和缺点。

首先，由于矩阵的规模随着节点数量的增加而增大，对于大型图而言，耦合邻接矩阵的存储和计算代价较高。

此外，耦合邻接矩阵的表示方式可能会损失一些与节点相关的属性信息，例如节点的度数或其他附加属性。

因此，在使用耦合邻接矩阵进行分析和建模时，需要充分考虑这些限制并选择合适的方法和技术。

综上所述，耦合邻接矩阵作为一种描述图中节点连接关系的工具，具有重要的应用价值。

它能够帮助我们深入研究图的结构和特性，并为各种领域的问题建模和解决提供有力支持。

在接下来的文章中，我们将详细讨论耦合邻接矩阵的定义、应用以及优缺点，以期更全面地了解和应用这一概念。

1.2 文章结构本文将通过以下几个部分来介绍耦合邻接矩阵的定义、应用以及它们存在的优缺点。

首先，在引言部分，将对本文要讨论的主题进行概述。

邻接矩阵检索-概述说明以及解释

邻接矩阵检索-概述说明以及解释1.引言1.1 概述：邻接矩阵是图论中一种常见的数据结构，用于描述图中各个顶点之间的连接关系。

在邻接矩阵中，图的顶点通常用矩阵的行和列来表示，矩阵的元素则表示顶点之间是否相连或具有何种关系。

邻接矩阵在图论中有着广泛的应用，可以用来表示网络结构、社交关系、路线规划等各种场景。

通过邻接矩阵，我们可以方便地进行图的遍历、查找、最短路径等操作，为解决各类实际问题提供了便利。

本文将重点介绍邻接矩阵的定义与概念，探讨邻接矩阵在图论中的应用，并详细介绍邻接矩阵检索算法，希望能够为读者提供对邻接矩阵及其应用的深入理解。

1.2文章结构1.2 文章结构本文主要分为三个部分，即引言、正文和结论。

在引言部分，将会对邻接矩阵进行概述，介绍文章的结构和目的。

其中，概述部分将对邻接矩阵的基本定义和概念进行简要介绍，为后续的正文部分做铺垫；文章结构部分将给出整篇文章的框架和布局，方便读者快速了解文章内容；而目的部分则会说明本文撰写的目的和意义。

在正文部分，将围绕着邻接矩阵展开讨论。

具体而言，将首先介绍邻接矩阵的定义与概念，让读者对其有一个清晰和全面的认识；接着将探讨邻接矩阵在图论中的应用，以便读者更深入地理解这一概念；最后将重点讨论邻接矩阵的检索算法，为读者提供一种快速高效地检索邻接矩阵信息的方法。

在结论部分，将对全文进行总结，回顾本文所涉及的内容和观点；同时也将展望邻接矩阵在未来的应用和发展方向，为读者呈现一幅邻接矩阵所展现出的无限可能；最后提出结论，总结本文的主要观点和贡献，为本文画上一个完整的句号。

1.3 目的邻接矩阵是图论中一种重要的数据结构，用于表示图中各个顶点之间的连通关系。

邻接矩阵检索算法则是基于邻接矩阵的数据结构，用于实现对图的快速检索和查询操作。

本文旨在探讨邻接矩阵检索算法的原理和实现方法，通过深入分析算法的逻辑结构和实用性，帮助读者更好地理解和应用邻接矩阵在图论中的作用。

通过本文的阐述，读者将能够了解邻接矩阵在图论中的重要性和应用价值，掌握邻接矩阵检索算法的具体实现方式，从而提升对图的处理和分析能力。

交通网络分析技术

给定权——两节点之间有边连接
1
2
3
j 12 3 4 5 6 7 8 9
i
1
02 ∞ 2 ∞ ∞ ∞ ∞ ∞
2
20 2 ∞ 2 ∞ ∞ ∞ ∞
4
5
63
∞2 0 ∞ ∞ 2 ∞ ∞ ∞
4
2∞ ∞ 0 1 ∞ 2 ∞ ∞
5
∞2 ∞ 1 0 1 ∞ 2 ∞
6
∞∞ 2 ∞ 1 0 ∞ ∞ 2
7
∞∞ ∞ 2 ∞ ∞ 0 2 ∞
C1、C2分别为机动车、非机动车路段实用通行能力。
t0 零L流u路0段行驶时间t0的确定：
3、基本参 L——路段长度
数的确定
u0——交通量为零时的行驶车速
u0 r1r1— r2—v自0 行车影响折减系数
r2——车道宽度影响系数
v0——路段设计车速
• 路段设计车速v0的确定可根据《城市道路交通规划设计规范》确定
三、出行路权的分析
城市0道1 路网规划：
出行路权为所有路段的行驶时间及所有交叉口的延误之和。
02 公路网规划：
可不考虑交叉口延误的影响，出行路权为路段行驶时间。
，息思
请却想
的精髓，否则容易造成观者的阅读压力，适得其反。
机动车道路段通行能力C1的确定
C1是通过对理论通行能力进行修正而得，修正包括：自行车影响折减系数(r1)、车道宽度影响折减系数(r2)、车道数修正(r3)、交叉口影响折减系数(r4)等。
C 115r 0 1r0 2r3r4
• 车道数修正系数r3的确定
行能力，W2——非机动车道宽，W1——机动车道宽。
车道宽度影响系数r2的确定
单
言千

基于邻接矩阵的电路信号流图分析法

定义 1 导纳矩阵 A ( [ aij ] n n ) , aij 表示节点 i与 j 间所有电源置零后的总导纳;
定义 2 独立电源关联导纳矩阵 B ( [ bij ] n n ) , 这个矩阵是保留原电路所有节点和只与独立电压源串联构成支路的导纳所得到的电路的导纳矩阵;
定义 3 独立电源矩阵 C ( [ cij ] n n ) , cij 表示节点 i与节点 j 间连入独立源的值;
K eywords A d jacency m atr ix SFG m atrix Sym bo l ana ly sis C ircu it ana lys is
0引言
长期以来, 应用于线性系统分析中的数值解求解方法日益成熟, 处理速度令人满意。而符号类型解, 尤其是高复杂度电路符号解的求解速度受制于计算机处理能力而不尽理想。符号解具有着数值解无法替代的重要价值 [ 1], 目前比较经典的求解方法有两种: 结合高斯消去法的节点电压方程法和应用梅逊公式的信号流图法 [ 2- 5] 。前者便于计算机编程实现, 但规模较大时, 处理速度较慢; 后者从信号流图拓扑结构直观角度处理是简便的, 但计算机处理不甚方便, 因为仅查找前向通路和回路, 就会给计算机带来极大开销。本文围绕线性电路符号类型解的求解过程, 提出了一种改进的电路处理方法, 旨在保证计算机处理可实现性的同时, 进一步提高计算速度。此方法以信号流图法为基础, 采用邻接矩阵表征原电路所携带的信息, 并使用有别于梅逊公式的方法处理信号流图。其性能与两个因素相关: 其一是采用的邻接矩阵数目; 其二是处理信号流图方法的效率。这也正是本文探讨的重点。

电网络-第六章信号流图分析解析

1
x1
a
c
x3
f
d
g
x4
1
x7
b
e
p
1
x2
x5
前向路（通路）说明图
h
x1
b
a
c
x3
f
d
g
x4
e
p
x2
有向回路说明图
（8）路径增益：一条有向路中各支路增益的乘积。用p表示。
h
x6
1
P2＝bd×1
1
x1
a
c
x3
f
d
g
x4
x7
b
e
p
1
x2
P1＝ace×1
x5
前向通路的路径增益说明图
（9）回路增益：有向回路中所有支路的增益乘积。用L表示。 L3＝h h
R2 gU1
R4
（2）列方程
U1 （I 3 gU1）对C1割集 R 1 U4 （I 2 gU1）对C2割集R 4 I2 （U S U 4）对l1回路 G2 I3 （U S U1）对l2回路 G 3 1 1 G , G 其中 3 R 2 R2 3
R1 U1 I3 1 gR1 U4 R （） R4 I 2 ( gR4 )U1 4 I 2 gU1
j

2
1
2
3
是唯一的。
（2）由线性方程组 SFG
设 X s [ xs1 xs 2 xsm ]T 为m维输入向量， X [ x1 x2 xn ]T 为n维待求向量，A为n n非奇异矩阵，
B是n m矩阵，X有唯一解。写成矩阵 AX BX S 。
改写成 X i Tij X j ，的形式， X X AX BX S ，（i 1 ， 2， n）

实验8图的邻接矩阵表示及遍厉算法

实验八图的邻接矩阵表示及遍厉算法科目：数据结构实验和课程设计班级：10信管姓名：戴丽学号：2010110401 实验目的：熟悉C语言程序的基本结构，掌握程序中的用户头文件、文件之间的相互关系及各自的作用。

熟悉图的邻接矩阵表示和遍历算法。

熟悉C语言操作环境的使用以及多文件程序的输入、编辑、调试和运行的全过程。

实验要求：认真阅读和掌握本实验内容所给的全部程序。

保存和输出程序运行结果，并结合程序进行分析。

按照你对图的邻接矩阵表示和遍历算法，编写程序代码然后运行，给出运行结果。

实验设备：每人一台安装VC6.0编写软件的计算机，公用打印机。

注意事项：要在硬盘上建立好自己的工作目录，专门用来存储自己所做的实验程序及相关数据，以后每次做实验最好仍采用这个目录。

认真编写算法及运行结果，针对本实验的具体算法，认真写出算法分析。

实验步骤：#include <iostream.h> //无向连通图的邻接矩阵表示以及无向连通图的深度优先搜索、广度优先搜索#define n 4 //图中的顶点数#define e 5 //图中的边数typedef char vertype; //设置图的顶点信息为整型struct graph{ vertype vexs[n]; //图的顶点信息表int a[n][n]; //图的邻接矩阵}; //图的邻接矩阵表示结构定义graph create() //建立无向连通图g的邻接矩阵表示{graph g;int i,j,k;for(k=0;k<n;k++)cin>>g.vexs[k];for(i=0;i<n;i++)for(j=0;j<n;j++)g.a[i][j]=0;for(k=0;k<e;k++){cin>>i>>j;g.a[i][j]=g.a[j][i]=1;}return g;}void dfs(graph g,int i) //对以邻接矩阵表示的无向连通图，以序号为i的顶点为出发点进行深度优先搜索{cout<<g.vexs[i];int flag[4]={1,1,1,1};for(int j=0;j<4;j++){if(g.a[i][j]!=0&&!flag[j])dfs(g,j);}}void bfs(graph g,int i) //对以邻接矩阵表示的无向连通图，以序号为i的顶点作为出发点进行广度优先搜索{int j,w,flag[4]={0};int s[100],front,rear=0;char p;cout<<g.vexs[i];flag[i]=1;rear++;s[rear]=i;while(front!=rear){front++;w=s[front];p=g.vexs[w];for(j=0;j<4;j++){if(g.a[i][j]!=0&&!flag[j]){cout<<g.vexs[j];flag[j]=1;rear++;s[rear]=j;}}}}void main(){graph g; //申请无向连通图g的邻接矩阵表示空间g=create(); //建立用邻接矩阵表示的无向连通图cout<<"对无向连通图g进行深度优先搜索得到的序列是:"; dfs(g,0);cout<<"对无向连通图g进行广度优先搜索得到的序列是:"; bfs(g,0);}算法分析：1、邻接矩阵是表示顶点之间相互关系的矩阵，用邻接矩阵方法存储图，很容易确定图中任意两个顶点之间是否有关联。

第二章信号流图

2
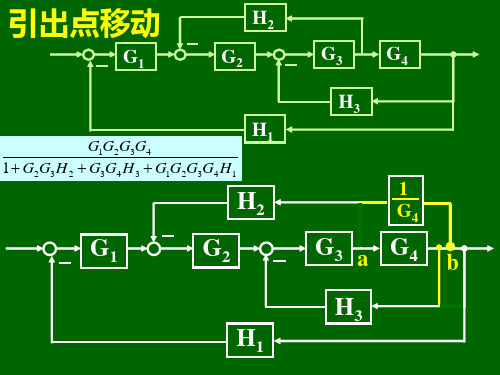
G 3G 4 H
3
16
例：求图示系统的传递函数。解：
R (s)
G1 (s)
G 4 (s)
C (s)
G 2 (s)

G 3 (s)

H 2 (s) H 1 (s)
G4
G1
R
H
G2 H
1
G3
C
2
1
17
G4
G1
R
H
G2 H
1
G3
C
2
1
L1 G 1 G 2 H 1 , L 2 G 2 G 3 H 2 , L 3 G 1 G 2 G 3 , L 4 G 4 H 2 , L 5 G 1 G 4 p1 G 1G 2 G 3 , p 2 G 1G 4 , 1 2 1 1 ( L1 L 2 L 3 L 4 L 5 ) C (s) R (s) p1 1 G 1G 2 G 3 G 4 1 G 1G 2 G 3 G 4 H 1 G 2 G 3 H
R (s) G 1 ( s )G 2 ( s ) H ( s )
（二）闭环系统的传递函数
R(s) ＋－ B(s) ＋ G1(s) ＋ H(s)
23
N(s) G2(s) C(s)
1.输入信号下的闭环传递函数
R(s) ＋
(s)
C (s) R (s)

G 1 ( s )G 2 ( s ) 1 G 1 ( s )G 2 ( s ) H ( s )
i2
C
R1
R2
u c (t )

7
进行拉氏变换。并考虑 1 Cs I 2 (s) 1 Cs i2

邻接矩阵求简单路径 -回复

邻接矩阵求简单路径-回复邻接矩阵是图论中一种主要的表示方式，它将图的结构以矩阵的形式展现出来。

在邻接矩阵中，节点之间的关系通过1和0来表示，1代表有边相连，0代表无边相连。

邻接矩阵的一个重要应用是求解图中的简单路径。

简单路径是指图中两个节点之间不包含重复节点的路径。

求解简单路径的方法有很多种，邻接矩阵是其中之一。

下面，我将一步一步解释如何利用邻接矩阵求解图中的简单路径。

首先，我们需要构建图的邻接矩阵。

假设我们有一个有向图，其中包含6个节点和一些边。

我们可以使用一个6×6的矩阵来表示这个图的邻接关系。

矩阵的每一行和每一列分别对应图中的一个节点，矩阵中的1和0表示节点之间是否有边相连。

接下来，我们需要确定起始节点和目标节点。

我们通过邻接矩阵来判断两个节点之间是否有边相连，如果有，我们可以沿着这条边继续寻找下一个节点。

如果没有，我们就需要回溯到上一个节点，尝试其他的路径。

为了记录已经遍历过的节点，我们可以使用一个数组或者栈来保存当前的路径。

每次遍历到一个新的节点时，我们将其添加到路径中，并标记为已访问。

当我们找到目标节点时，我们就找到了一条简单路径。

需要注意的是，在寻找路径的过程中，可能会遇到环路或者重复访问的问题。

为了解决这个问题，我们需要在每次访问节点时，标记它为已访问，并在继续深入之前检查该节点是否已经在路径中。

如果已经在路径中，我们就需要回溯到上一个节点，尝试其他的路径。

当我们找到一条简单路径后，我们可以保存它或者输出它。

如果需要找到所有的简单路径，我们可以继续寻找其他的路径，直到遍历完所有的节点。

总结起来，使用邻接矩阵求解简单路径的步骤如下：1. 构建图的邻接矩阵，将节点之间的关系以1和0表示。

2. 确定起始节点和目标节点。

3. 使用一个数组或者栈来保存当前的路径。

4. 遍历节点，检查节点之间是否有边相连。

如果相连，将下一个节点添加到路径中。

5. 检查新的节点是否已经在路径中，如果是，则回溯到上一个节点，尝试其他的路径。

邻接矩阵法

邻接矩阵法邻接矩阵法邻接矩阵法是图论中常用的一种表示图的方法，它利用一个二维数组来表示图中各个节点之间的关系，其中数组的行和列分别代表着图中的节点，而数组中的元素则表示着两个节点之间是否存在边。

邻接矩阵法的优点邻接矩阵法具有以下几个优点：1. 方便查找由于邻接矩阵法使用了二维数组来表示图中各个节点之间的关系，因此我们可以很方便地查找某两个节点之间是否存在边。

2. 易于实现相比其他表示图的方法，邻接矩阵法非常容易实现。

只需要使用一个二维数组即可。

3. 空间效率高如果一个图是稠密图（即节点之间存在大量边），那么使用邻接矩阵法可以节省空间。

因为在这种情况下，邻接矩阵法所需的空间比其他方法更小。

邻接矩阵法的缺点虽然邻接矩阵法有很多优点，但它也有以下几个缺点：1. 浪费空间如果一个图是稀疏图（即节点之间存在少量边），使用邻接矩阵法会浪费很多空间，因为在这种情况下，大部分数组元素都是0。

2. 不利于动态操作如果我们需要对一个图进行动态操作（如添加或删除节点或边），那么使用邻接矩阵法就不太方便。

3. 时间效率低在某些情况下，使用邻接矩阵法可能会导致时间效率较低。

比如，在查找某两个节点之间是否存在路径时，我们需要遍历整个二维数组。

邻接矩阵法的实现下面我们来看一下如何用代码实现邻接矩阵法。

1. 定义二维数组首先，我们需要定义一个二维数组来表示图中各个节点之间的关系。

假设有n个节点，则我们可以定义一个n*n的二维数组：int graph[n][n];2. 初始化数组为了方便起见，我们可以将所有元素都初始化为0：for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {graph[i][j] = 0;}}3. 添加边如果要向图中添加一条从节点i到节点j的有向边，则只需要将graph[i][j]设置为1即可：graph[i][j] = 1;如果要向图中添加一条无向边，则需要将graph[i][j]和graph[j][i]都设置为1：graph[i][j] = 1;graph[j][i] = 1;4. 删除边如果要从图中删除一条从节点i到节点j的有向边，则只需要将graph[i][j]设置为0即可：graph[i][j] = 0;如果要从图中删除一条无向边，则需要将graph[i][j]和graph[j][i]都设置为0：graph[i][j] = 0;graph[j][i] = 0;5. 判断是否存在边如果要判断从节点i到节点j是否存在有向边，则只需要查看graph[i][j]的值即可。

用信号流图求解矩阵全部特征值的方法及其实现

用信号流图求解矩阵全部特征值的方法及其实现
张仰森
【期刊名称】《计算机工程与设计》
【年(卷),期】1996(000)003
【摘要】探讨利用信号流图求解矩阵全部特征值的方法及其在计算机上的实现过程，是将图论方法与计算机结合起来求解矩阵全部特征值的一种新偿试。

【总页数】1页(P60)
【作者】张仰森
【作者单位】无
【正文语种】中文
【中图分类】O241.6
【相关文献】
1.基于动力学方程求解复矩阵特征值问题的并行实现 [J], 黄祖兰;蒋耀林;陈明敏;林小拉
2.迭代方法求解矩阵全部特征值问题 [J], 熊汉
3.一个求实对称矩阵的全部特征值及特征向量的新方法 [J], 李百浩;蒋长锦
4.求解矩阵特征值的GPU实现 [J], 夏健明;魏德敏
5.基于神经网络方法的对称矩阵特征值的求解 [J], 张丽丽
因版权原因，仅展示原文概要，查看原文内容请购买。

基于邻接矩阵的电路信号流图分析法

《深入浅出图神经网络：GNN原理解析》随笔

邻接矩阵的实验原理及应用

数字通信原理实验 邻接矩阵

2019年软考中级数据库系统工程师真题及答案解析

线性网络的信号流图分析法

邻接矩阵求通路数和回路数

邻接矩阵求通路数和回路数

用邻接矩阵法输出图结构

基于随机矩阵理论的网络图谱分析与优化方法

耦合邻接矩阵-概述说明以及解释

邻接矩阵 检索-概述说明以及解释

交通网络分析技术

基于邻接矩阵的电路信号流图分析法

电网络-第六章信号流图分析解析

实验8图的邻接矩阵表示及遍厉算法

第二章信号流图

邻接矩阵求简单路径 -回复

邻接矩阵法

用信号流图求解矩阵全部特征值的方法及其实现

数字通信原理实验邻接矩阵

邻接矩阵检索-概述说明以及解释