DFT章节仿真实验
MATLAB仿真实现DFT变换

数字信号处理 课程实验报告实验指导教师:黄启宏 实验名称MATLAB 仿真实现DFT 变换 专业、班级 电子与通信工程 姓 名 张帅 实验地点 仿古楼301 实验日期 2013.11.10一、实验内容对有限序列x(n),令其长度为N 点,把这N 点序列视为一个周期序列,从而实现序列x(n)的傅里叶变化。
二、实验目的(1)实现非周期,有限长序列(或无限长序列)x(n)的傅里叶变换;(2)加深对DFT 定义式的理解。
三、实验原理对N 点序列x(n),其DFT 变换定义为:10()()N nk N n X k x n W -==∑ 20,1,2,,1,j N Nk N W e π-=-=四、涉及实验的相关情况介绍(包含使用软件或实验设备等情况) 一台安装MATLAB 软件的电脑五、实验记录程序、相关的图形、相关数据记录及分析)(function mainxn=[1,2,3,4];%输入xn序列;N=4;Xk1=DFT(xn,N);L=0:1:N-1;subplot(3,1,1)stem(L,abs(Xk1))title('DFT N=4')N=8;Xk2=DFT(xn,N);L=0:1:N-1;subplot(3,1,2)stem(L,abs(Xk2))title('DFT N=8')N=16;Xk3=DFT(xn,N);L=0:1:N-1;subplot(3,1,3)stem(L,abs(Xk3))title('DFT N=16')*************************************************************** function [Xk]=DFT(xn,N)%定义DFT算法;xxn=zeros(1,N);xxn([1:length(xn)])=xn; %构造长度为N的序列;Xk=ones(1,N);Wn=exp(-j*2*pi/N);wn=ones(N,N);for k=0:1:N-1for n=0:1:N-1wn(k+1,n+1)=Wn^(k*n);endendXk=(wn*xxn')';六、实验总结00.51 1.52 2.530510DFT N=4012345670510DFT N=80510150510DFT N=16。
数字信号处理--实验五 用DFT(FFT)对信号进行频谱分析

subplot(3,1,3);stem(wk,abs(Xk32),'.'); %绘制32点DFT的幅频特性图
title('(e) 32点DFT的幅频特性图');
xlabel('\omega/\pi');
ylabel('幅度');
k=0:31;wk=2*k/32; %产生32点DFT对应的采样点频率(关于π归一化值)
subplot(2,2,4);stem(wk,abs(Xk32),'.'); %绘制32点DFT的幅频特性图
title('(d) 32点DFT的幅频特性图');
xlabel('\omega/\pi');
ylabel('幅度');
图5.1R(t)的波形及其幅度特性
对 ,选择采用频率 ,采样点数为16,32,64。
3.分别对它们转换成序列,按顺序用 表示。
4.分别对它们进行FFT。如果采样点数不满足2的整数幂,可以通过序列尾部加0满足。
5.计算幅度特性并进行打印。
五、实验过程原始记录(数据、图表、计算等)
(一)离散信号
%
n=0:1:10;
Xk3=fft(xn,32); %计算xn的32点DFT
k3=0:length(abs(Xk3))-1;wk3=2*k3/32; %产生32点DFT对应的采样点频率(关于π归一化值)
如果用FFT对模拟信号进行谱分析,首先要把模拟信号转换成数字信号,转换时要求知道模拟信号的最高截至频率,以便选择满足采样定理的采样频率。一般选择采样频率是模拟信号中最高频率的3~4倍。另外要选择对模拟信号的观测时间,如果采样频率和观测时间确定,则采样点数也确定了。这里观测时间和对模拟信号进行谱分析的分辨率有关,最小的观测时间和分辨率成倒数关系。最小的采样点数用教材相关公式确定。要求选择的采样点数和观测时间大于它的最小值。
实验二 离散傅里叶变换(DFT)实验

实验二 离散傅里叶变换(DFT )实验【实验目的】1.进一步熟悉CCS 集成开发环境的软硬件调试方法2.学习DFT 的基本原理3.掌握如何在DSP 中实现DFT 算法【实验内容】1. 了解DFT 的基本原理。
2.了解命令文件中伪指令MEMORY 和SECTIONS 的作用。
2. CCS 中的软硬件开发环境的熟悉。
3. 常用信号(包括正弦波,方波,三角波,锯齿波)的DFT 。
【实验器材】1.DSP 开发板2.DSP 仿真器3 .PC 机(软件:CCS ,全称:Code composer studio )三 实验原理。
傅里叶变换是一种将信号从时域变换到频域的变换形式,是信号处理的重要分析工具。
离散傅里叶变换(DFT )是傅里叶变换在离散系统中的表示形式。
本实验是在学生首先产生一信号后,对该信号进行DFT ,并在CCS 中利用其自带的观察窗口或Memory 菜单来查看变换前后的波形或频谱值,从而完成了一个简易频谱分析仪。
让学生更加直观形象地体会DFT 的整个过程假设信号为x (0),x(1),……,x (N),那么其离散傅立叶变换后的实部和虚部以及频谱幅度分别为:2()0()()()()N j k n N r i n X k x n eX k jX k π-===+∑ 0(0)()(0)0N r i i X x i X =∴==∑ 002 ()()cos(())2()()sin(())(0)Nr n N i i X k x n k n N X k x n k n k N ππ===⨯⨯⨯=-⨯⨯⨯>∑∑()A k =具体的实现过程的时候需要根据硬件的特性来实现。
比如cos和sin的值都可事先通过软件计算出结果,保存在两个数组中,直接对其进行查表操作。
若缓存数量为128,即N=128。
对于cos和sin的系数,根据需要可以首先计算出128点的sin值,而cos的值则可以通过sin表整体后移N/4点,也就是整体后移32点后得到。
验证dft的实验报告

验证dft的实验报告导言DFT(Discrete Fourier Transform)是一种将一个离散信号的时域表示转换为频域表示的数学变换方法。
本次实验旨在验证DFT的有效性和可靠性,以及了解它在信号处理领域的应用。
实验目的1. 了解DFT的原理和数学表达式;2. 熟悉DFT的运算过程;3. 验证DFT算法在信号处理中的效果。
实验步骤1. 实现DFT算法首先,我们需要实现DFT算法。
DFT将时域信号转换为频域信号,我们需要编写代码来执行这个转换过程。
以下是伪代码示例:function dft(signal):N = length(signal) 信号长度spectrum = []for k in range(N):real_part = 0imag_part = 0for n in range(N):angle = 2 * pi * k * n / Nreal_part += signal[n] * cos(angle)imag_part += signal[n] * sin(angle)spectrum[k] = complex(real_part, imag_part)return spectrum2. 生成测试信号为了验证DFT的准确性,我们需要生成一个已知频谱的测试信号。
我们可以使用一个简单的正弦函数和脉冲函数的组合作为测试信号,如下所示:signal = sin(2 * pi * f1 * t) * pulse(t, t_start, t_end)其中,`f1`是正弦函数的频率,`t`是时间,`pulse(t, t_start, t_end)`是一个单位脉冲函数。
3. 运行DFT算法将生成的测试信号输入DFT算法中,得到频域信号。
我们可以将频域信号进行绘图,观察其频谱分布。
4. 验证结果比较DFT算法得到的频谱和测试信号的已知频谱,检查它们是否吻合。
可以使用频谱图来进行对比分析。
实验结果与分析我们使用Python编程语言实现了DFT算法,并生成了一个具有已知频谱的测试信号。
实验二 DFT 和FFT实验报告

实验二DFT 和FFT1、实验目的认真复习周期序列DFS、有限长序列DFT 的概念、旋转因子的定义、以及DFS 和DFT的性质等有关内容;复习基2-FFT 的基本算法,混合基-FFT 的基本算法、Chirp-Z 变换的算法等快速傅立叶变换的方法。
掌握有限长序列的循环移位、循环卷积的方法,对序列共轭对称性的含义和相关内容加深理解和掌握,掌握利用DFT 分析序列的频谱特性的基本方法。
掌握FFT 算法的基本原理和方法、Chirp-Z 变换的基本原理和方法,掌握利用FFT 分析序列的频谱特性的方法。
熟悉利用MATLAB 进行序列的DFT、FFT 的分析方法。
2、实验内容a. 设周期序列( ) { x~(n) = …,0,1,2,3,0,1,2,3,0,1,2,3,….},求该序列的离散傅立叶级数X(k) = DFS[x~(n)],并画出DFS 的幅度特性。
function [Xk]=dfs(xn,N)n=0:1:N-1;k=0:1:N-1;Wn=exp(-j*2*pi/N);nk=n'*k;Wnk=Wn.^nk;Xk=xn*Wnk;xn=[0,1,2,3];k=0:1:3;N=4;Xk=dfs(xn,N);y=abs(Xk);stem(k,y);b . 设周期方波序列为 x(n)= ⎩⎨⎧+≤≤++≤≤)1-1)N (m n (01)-L mN n 1(mN L mN (m=0,,....2,1±±)其中 N 为基波周期,L/N 是占空比。
(1) 用L 和N 求| X (k ) |的表达式;(2) 当L 和N 分别为:L=5,N=20;L=5,N=40;L=5,N=60 以及L=7,N=60 时画出 DFS 的幅度谱;(3) 对以上结果进行讨论,总结其特点和规律L=5; N=20;k=[-N/2:N/2];xn=[ones(1,L),zeros(1,N-L)]; Xk=dfs(xn,N);y=abs([Xk(N/2+1:N) Xk(1:N/2+1)]); stem(k,y);c . 设有限长序列x (n ) = {0,1,2,3},计算DTFT[x(n)]=X(e j ω),并画出它的幅度谱;然后 利用kw 1=42πk,k=0,1,2,3对X(e j ω)进行采样,并证明它等于实验a 中的X ~(k )。
数字信号实验 DFT FFT

北京信息科技大学实验报告封面实验报告课程名称:数字信号实验题目:用DFT(FFT)对时域离散信号进行频谱分析系(院):光电学院专业:光信息科学与技术班级:光信0801学生姓名:靖鑫学号: 2008010750指导教师:罗倩开课时间: 2010--2011学年一学期实验五用DFT(FFT)对时域离散信号进行频谱分析一、实验目的:学习DFT的基本性质及对时域离散信号进行频谱分析的方法。
二、实验内容给定参考实验信号如下:x1(n)=R4(n)x5(n): 用x1(n)=R4(n)以8为周期进行周期性延拓形成的周期序列。
(1) 分别以变换区间N=8, 16, 32,对x1(n)=R4(n)进行DFT(FFT), 画出相应的幅频特性曲线;(2) 分别以变换区间N=8, 16, 对x2(n), x3(n)分别进行DFT(FFT), 画出相应的幅频特性曲线;(3) 分别以变换区间N=4, 8, 16, 对x4(n)分别进行DFT(FFT), 画出相应的幅频特性曲线;(4) 对x5(n)进行频谱分析, 并选择变换区间, 画出幅频特性曲线。
三、实验报告1. 分析讨论。
(1) 用实验内容中的(1)分析DFT的变换区间对频域分析的作用,并说明DFT的物理意义。
(2) 对于试验内容(2),分析当N=8时,两个信号的幅频特性为什么一样,而N=16时又不一样。
(3) 对于实验内容(3),x4(n)是一个周期信号,画出它的理论幅度频谱特性。
对照理论结果, 分析该周期信号的变换区间应该如何选取。
如果周期信号的周期预先不知道,如何用DFT分析它的频谱。
(4) 对于实验内容(4),对照理论结果分析实验结果。
2. 根据以上的实验内容和分析讨论,写出自己认为重要的几点结论。
内容1..分别以变换区间N=8, 16, 32,对x1(n)=R4(n)进行DFT(FFT),画出相应的幅频特性曲线;xn=[1 1 1 1 ];Xk8=fft(xn,8);Xk16=fft(xn,16);Xk32=fft(xn,32);k=0:7subplot(321);stem(k,abs(Xk8),'.');title('8点幅频');grid on;xlabel('k');ylabel('幅度');subplot(322);stem(k,angle(Xk8),'.');title('8点相频');grid on;xlabel('k');ylabel('相位');k=0:15subplot(323);stem(k,abs(Xk16),'.');title('16点幅频');grid on;xlabel('k');ylabel('幅度');subplot(324);stem(k,angle(Xk16),'.'); title('16点相频');grid on;xlabel('k');ylabel('相位');k=0:31subplot(325);stem(k,abs(Xk32),'.');title('32点幅频');grid on;xlabel('k');ylabel('幅度');axis([0,31,0,4]); subplot(326);stem(k,angle(Xk32),'.'); title('32点相频');grid on;axis([0,31,-3,3]); xlabel('k');ylabel('相位');2.分别以变换区间N=8, 16, 对x3(n)分别进行DFT(FFT), 画出相应的幅频特性曲线;xn=[4 3 2 1 1 2 3 4];Xk8=fft(xn,8);%计算8点fftXk16=fft(xn,16);%计算16点fftk=0:7subplot(221);stem(k,abs(Xk8),'.');title('8点幅频');grid on;xlabel('k');ylabel('幅度');subplot(222);stem(k,angle(Xk8),'.');title('8点相频');grid on;xlabel('k');ylabel('相位');k=0:15subplot(223);stem(k,abs(Xk16),'.');title('16点幅频');grid on;xlabel('k');ylabel('幅度');subplot(224);stem(k,angle(Xk16),'.');title('16点相频');grid on;xlabel('k');ylabel('相位');分别以变换区间N=8, 16, 对x2(n)分别进行DFT(FFT), 画出相应的幅频特性曲线;xn=[1 2 3 4 4 3 2 1];Xk8=fft(xn,8);%计算8点fftXk16=fft(xn,16);%计算16点fftk=0:7subplot(221);stem(k,abs(Xk8),'.');title('8点幅频');grid on;xlabel('k');ylabel('幅度');subplot(222);stem(k,angle(Xk8),'.');title('8点相频');grid on;xlabel('k');ylabel('相位');k=0:15subplot(223);stem(k,abs(Xk16),'.');title('16点幅频');grid on;xlabel('k');ylabel('幅度');subplot(224);stem(k,angle(Xk16),'.');title('16点相频');grid on;xlabel('k');ylabel('相位');3..分别以变换区间N=8, 16, 对x2(n), x3(n)分别进行DFT(FFT), 画出相应的幅频特性曲线;n=0:50;xn=cos(pi/4.*n);Xk4=fft(xn,4);Xk8=fft(xn,8);Xk16=fft(xn,16);k=0:3subplot(321);stem(k,abs(Xk4),'.');title('8点幅频');grid on;xlabel('k');ylabel('幅度');subplot(322);stem(k,angle(Xk4),'.'); title('8点相频');grid on;xlabel('k');ylabel('相位');k=0:7subplot(323);stem(k,abs(Xk8),'.'); title('8点幅频');grid on;xlabel('k');ylabel('幅度');subplot(324);stem(k,angle(Xk8),'.'); title('8点相频');grid on;xlabel('k');ylabel('相位');k=0:15subplot(325);stem(k,abs(Xk16),'.'); title('16点幅频');grid on;xlabel('k');ylabel('幅度');subplot(326);stem(k,angle(Xk16),'.'); title('16点相频');grid on;xlabel('k');ylabel('相位');4..对x5(n)进行频谱分析, 并选择变换区间, 画出幅频特性曲线。
DFT和FFT实验(上传)

DFT 和FFT 实验一、实验目的和要求 1、掌握DFT 变换 2、掌握DFT 性质3、掌握快速傅立叶变换(FFT ) 二、实验内容和原理 1、实验内容1)求有限长离散时间信号的离散时间傅立叶变换)(Ωj e X 并绘图。
∙已知nje n x ⎪⎪⎭⎫⎝⎛=39.0)(π 100≤≤n ∙ 已知10102)(≤≤-=n n x n2)已知序列)sin(2)82.0cos()(n n n x ππ+=,500≤≤n ,绘制)(n x 及其离散傅立叶变换)(k X 的幅度、相位图。
3)设)()2.0sin()(n randn n n x +=π,10-≤≤N n ,其中,randn(n)为高斯白噪声。
求出m N 4=,m=2,3,4的matlab 采用不同算法的执行时间。
4)研究高密度频谱和高分辨率频谱。
设有连续信号)1092cos()1072cos()105.62cos()(333t t t t x ⨯⨯+⨯⨯+⨯⨯=πππ∙以采样频率kHz f s 32=对信号x(t)采样,分析下列三种情况的幅频特性。
∙ 采集数据长度N=16点,做N=16点的FFT ,并画出幅频特性。
∙ 采集数据长度N=16点,补零到256点,做N=256点的FFT ,并画出幅频特性。
∙ 采集数据长度N=256点,做N=256点的FFT ,并画出幅频特性。
观察三种不同频率特性图,分析和比较它们的特点以及形成的原因。
2、实验原理 1)DFT序列x (n )的离散时间傅里叶变换(DTFT )表示为nj nj e n x eX Ω-∞-∞=Ω∑=)()(,如果x (n )为因果有限长序列,n =0,1,...,N-1,则x (n )的DTFT 表示为n j N n j e n x eX Ω--=Ω∑=10)()(x (n )的离散傅里叶变换(DFT )表达式为)1,...,1,0()()(210-==--=∑N k en x k X nk NjN n π序列的N 点DFT 是序列DTFT 在频率区间[0,2π]上的N 点灯间隔采样,采样间隔为2π/N 。
实验一 利用DFT进行信号分析实验报告

利用DFT进行信号分析一、实验目的1.通过编写程序加深对DFT/IDFT的理解;2.运用DFT/IDFT进行初步的频谱分析;3.对DFT/IDFT运行过程出现的现象进行解释二、实验内容给定信号如下:x(t)=2+3cos(100πt-π/6)+1.5cos(150πt-π/2)1.对给定信号进行频谱分析,画出时域、振幅谱、相位谱的图像;2.滤掉50HZ频率,反变换后观察图像,分析是否满足采样定理;3.对DFT出现的GIBBS效应、栅栏效应等的分析;4.进行傅式反变换观察能否将原信号恢复三、实验步骤1. 对给定信号进行频谱分析,画出时域、振幅谱、相位谱的图像;x(t)=2+3cos(100πt-π/6)+1.5cos(150πt-π/2)其中fm1=75Hz为主频,包含一个有效信号和一个干扰信号(fm=50Hz),。
将子波信号离散化,令t=i×dt ,则x(t)=x(i*dt),将子波信号变换到频率域进行滤波,取2560个采样点,采样间隔取0.001s生成给定信号的源程序为:clearclfN=2560;fm=50;fm1=75;dt=0.001;df=1/(N*dt);n=[1:N];k=[1:N];t=0:dt:(N-1)*dt;f=0:df:(N-1)*df;for i=1:Nx(i)=2+3*cos(fm*2*pi*dt*i-pi/6)+1.5*cos(fm1*2*pi*dt*i-pi/2); endq(k)=x*exp(-j*2*pi/N).^(n'*k);a=abs(q);p=angle(q);p=180/pi*p;subplot(3,1,1);plot(t,x,'k'),grid on,xlabel('时间t'),ylabel('信号x(t)'),title('给定信号的时域图像');subplot(3,1,2);plot(f,a,'k'),grid on,xlabel('频率f'),ylabel('振幅a'),title('给定信号的振幅谱');subplot(3,1,3);plot(f,p,'k'),grid on,xlabel('频率f'),ylabel('相位p'),title('给定信号的相位谱');运行程序,得给定信号的时域图像、振幅谱、相位谱如图:频率f=k×df ,其中频率采样间隔df=1,所以x(f)=x(k*df)。
实验四 验证DFT的相关性质
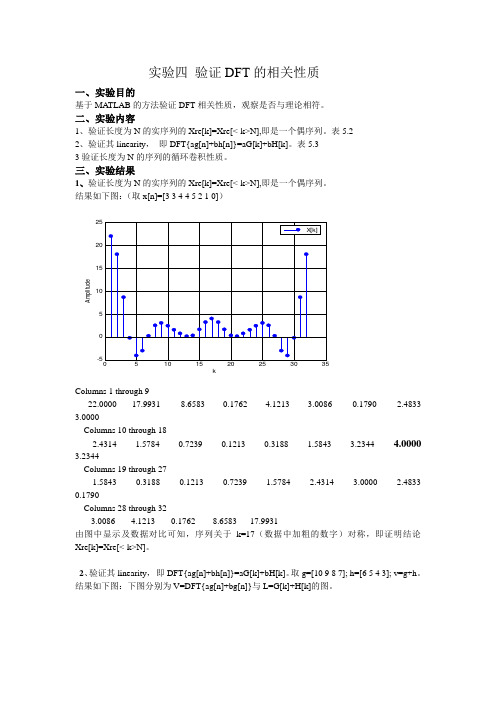
实验四 验证DFT 的相关性质一、实验目的基于MATLAB 的方法验证DFT 相关性质,观察是否与理论相符。
二、实验内容1、验证长度为N 的实序列的Xre[k]=Xre[<-k>N],即是一个偶序列。
表5.22、验证其linearity , 即DFT{ag[n]+bh[n]}=aG[k]+bH[k]。
表5.3 3验证长度为N 的序列的循环卷积性质。
三、实验结果1、验证长度为N 的实序列的Xre[k]=Xre[<-k>N],即是一个偶序列。
结果如下图:(取x[n]=[3 3 4 4 5 2 1 0])Columns 1 through 922.0000 17.9931 8.6583 -0.1762 -4.1213 -3.0086 0.1790 2.4833 3.0000Columns 10 through 182.4314 1.5784 0.7239 0.1213 0.3188 1.58433.23444.0000 3.2344Columns 19 through 271.5843 0.3188 0.1213 0.7239 1.57842.43143.0000 2.4833 0.1790Columns 28 through 32-3.0086 -4.1213 -0.1762 8.6583 17.9931由图中显示及数据对比可知,序列关于k=17(数据中加粗的数字)对称,即证明结论Xre[k]=Xre[<-k>N]。
2、验证其linearity , 即DFT{ag[n]+bh[n]}=aG[k]+bH[k]。
取g=[10 9 8 7]; h=[6 5 4 3]; v=g+h 。
结果如下图:下图分别为V=DFT{ag[n]+bg[n]}与L=G[k]+H[k]的图。
05101520253035kA m p l i t u d eV =Columns 1 through 552.0000 49.1322 -12.8792i 41.2464 -23.0816i 30.2819 -28.6724i 18.8284 -28.9706iColumns 6 through 109.3779 -24.6780i 3.6335 -17.5928i 2.0890 -10.0085i 4.0000 - 4.0000i 7.7379 - 0.8241i ……. L =Columns 1 through 552.0000 49.1322 -12.8792i 41.2464 -23.0816i 30.2819 -28.6724i 18.8284 -28.9706iColumns 6 through 109.3779 -24.6780i 3.6335 -17.5928i 2.0890 -10.0085i 4.0000 - 4.0000i 7.7379 - 0.8241i经过数据对比与图中的显示,两者完全相等。
DFT和FFT实验报告

1课程名称: 数字信号处理实验名称: DFT 和FFT专业班级: 姓名: 学号: 实验日期:2012.11.20一、实验目的:1.加深DFT 算法的原理和基本性质的理解;2.掌握DFT 、IDFT 的MATLAB 编程方法;3.学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT ;二、实验原理(一)由傅里叶分析可知,一个周期函数可以由其各个谱波分量的线性组合得到,这就是离散傅级数。
将其推广至有限持续时间序列,并产生一个新的变换,这就是离散傅里叶变换。
1. 离散傅立叶变换的定义如下所示:(1)IDFT 和DFT 的Matlab 实现函数:DFT.Mfunction[Xk]=dft(xn,N)%计算离散傅立叶变换%Xk 为在0<=n<=N-1间DFT 系数数组%xn 为N 点有限持续时间序列%N 为DFT 的长度n=0:N-1; k=0:N-1;10)(1)]([)(10)()]([)(1010-≤≤==-≤≤==∑∑-=--=N n W k X N k X IDFT n x N k W n x n x DFT k X N k nkN N n nk NWN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=xn*WNnk;IDFT.Mfunction[xn]=idft(Xk,N)%计算离散傅立叶变换%xn为在0<=n<=N-1间的N点有限持续时间序列%Xk为在0<=n<=N-1间DFT系数数组%N为DFT的长度n=0:N-1;k=0:N-1;WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^(-nk);xn=Xk*WNnk/N;三、实验内容:1.分析信号频谱:已知信号为: x(n)=cos(0.48*pi*n)+sin(0.52*pi*n) ,对该信号进行频谱分析。
(实验五利用DFT分析模拟信号频谱)

实验报告实验课程:数字信号处理实验开课时间:2020—2021 学年秋季学期实验名称:利用DFT分析模拟信号频谱实验时间: 2020年9月27日星期日学院:物理与电子信息学院年级:大三班级:182 学号:1843202000234 姓名:武建璋一、实验预习【例1.5.1】已知周期信号x(t)=cos(10*pi*t)+2sin(18*pi*t),计算其频谱。
解:信号基频ω0=2*pi rad/s,周期T=1;最高次谐频为9*ω0=18*pi rad/s,所以N≥(2*9+1=19),程序如下:%example 1_5_1……clc,clear,close allT0 = 1;N = 19;T = T0/N;t = 0:T:T0;x = cos(2*pi*5*t) +2*sin(2*pi*9*t);Xm = fft(x,N);f = (-(N - 1)/2:(N - 1)/2)/N/T;stem(f,abs(fftshift(Xm)));xlabel('f(Hz)');ylabel('f(Magnitube)');title('幅度谱');【例1.5.2】利用DFT近似分析连续信号x(t)=exp(-t)*u(t)的幅度谱并理论值比较。
fsam = 50;Tp = 6;N = 512;T = 1/fsam;t = 0:T:Tp;x = exp(-1*t);X = T*fft(x,N);subplot(2,1,1);plot(t,x);xlabel('t');title('时域波形');w = (-N/2:N/2 - 1)*(2*pi/N)*fsam;y = 1./(j*w+1);subplot(2,1,2);plot(w,abs(fftshift(X)),w,abs(y),'r-.');title('幅度谱');xlabel('w');legend('理论值','计算值',0);axis([-10,10,0,1.4])实验内容1. 利用FFT分析信号)x t-=的频谱。
dftatpg实验【可编辑】

实验一DFT Compiler1.实验目的:●熟悉DFT Compiler操作流程,完成对设计tcrm.v的自动扫描链插入。
●回顾使用Design Compile进行逻辑综合的流程。
2.实验内容:DFT Compiler是一款功能强大的用于可测性设计的工具,提供从前端逻辑域到后端物理域完整的可测性设计解决方案,自动综合为带有扫描链的可测性设计。
本文通过DFT Compiler 将设计tcrm.v综合为带有扫描链的门级网表tcrm_scan.vg,并输出测试协议文件tcrm_stil.spf,为进一步完成自动测试向量生成作数据准备。
设计的原理图如图2.1所示。
图2.1 tcrm原理图其Verilog代码形式详见tcrm.v3.DFT Compiler流程与基本命令set target_librarys et link_libraryread_verilogread_file -format verilogset_wire_load_modelcreate_clockset_max_areaset_input_delay...set_output_delayset_scan_styleset test_default_delayset test_default_bidir_delayset test_default_strobeset test_default_periodcompile -scancreate_test_protocoldft_drcInsert_dftwritewrite_test_protocol4.相关文件组织DFT/Lab1/script/ //脚本文件夹tcrm.con //设计约束tcrm.tmv //测试时间约束变量设置tcrm.tp //测试协议tcrm.tcl//实验完整流程与命令集SMIC_db/ //库文件夹typical.db //前端综合库src/ //设计文件夹tcrm.v //设计数据report/ //报告文件夹,用来存放生成的报告mapped/ //存放综合过的网表文件5.实验步骤A)启动DFT Compiler 是DC_Ultra中一个组件,因此其启动命令与DC相同,在DC中输入DFT 相关命令就可以使用DFT Compiler。
验证dft的实验报告

验证dft的实验报告实验名称:DFT(密度泛函理论)的验证实验目的:通过实验证明DFT的有效性和准确性引言:密度泛函理论(DFT)是一种量子力学计算方法,常用于研究原子与分子的电子结构和性质。
DFT使用能量密度作为基本变量,通过求解Schrödinger方程来计算系统的电子密度。
DFT具有计算效率高、适用范围广等优点,因此成为了现代计算化学的重要工具之一。
本实验旨在验证DFT的实用性和准确性。
实验步骤:1. 收集实验所需数据:选取已知结构的分子,如水分子或甲烷分子,并获取其实验测定的物理化学性质,如键长、键角等。
2. 配置计算机程序:在计算机上安装并配置相应的DFT计算软件(如VASP、Gaussian等),确保计算参数的准确性。
3. 进行DFT计算:使用选定的DFT软件对所选分子进行计算,得到分子的电子结构和性质的计算结果。
4. 比较实验数据与计算结果:将实验测定的数据与DFT计算得到的结果进行比较,验证DFT的准确性和可靠性。
5. 分析误差来源:分析实验与计算结果的差异,探讨误差来源,并讨论DFT方法的适用性和局限性。
结果与讨论:通过对比实验数据与DFT计算结果,我们发现DFT方法在预测分子的结构和性质方面表现出良好的准确性。
例如,对于水分子,实验测定的键长为O-H键长为0.958 Å,而DFT计算得到的结果为0.959 Å,两者非常接近。
类似地,对于甲烷分子,实验测定的C-H键长为1.087 Å,而DFT计算得到的结果为1.088 Å,也具有较高的精度。
然而,DFT方法在一些特殊情况下可能存在一定的误差。
例如,对于具有强关联电子性质的体系,如过渡金属和稀土元素化合物,DFT计算结果可能与实验数据存在较大程度的偏差。
这是因为DFT方法中一般使用的理论近似对于电子关联效应的描述不够准确。
此外,DFT对于分子中弱相互作用的精确性也有待改进。
在分析误差来源时,我们发现DFT计算中使用的交换关联泛函选择对结果的准确性起着关键作用。
DFT实验

1.点击菜单FILE->new->m-file
3.点击菜单FILE->open->work
2.输入子函数代码后save
4.运行程序
4
4
2.若有一有限长序列 序列长度 N=12,利用matlab计算它的DFT并画出图 形 程序清单:
x(n) cos(
nБайду номын сангаас ) 6
5
N=12; %序列长度 n=0:N-1; %时间抽样 xn=cos(pi*n/6); %产生序列x(n) k=0:N-1; %频率域抽样 WN=exp(-j*2*pi/N); %产生Wn nk=n'*k; %产生nk WNnk=WN.^nk; %产生DFT因子 Xk=xn*WNnk %DFT定义 %要画三幅图,所以分别用figure(1),(2), (3)标注 figure(1) stem(n,xn) %绘制离散数据图形(杆图),n横轴, x(n)的值为对应的纵轴 figure(2) stem(k,abs(Xk)) %绘制x(k)的图形 %figure(3) %IDFT103(Xk,N)
实验一 离散傅里叶变换DFT
1
一 实验目的
1.了解matlab软件及用matlab进行数字信号 处理 2.熟悉DFT离散傅里叶变换及逆变化的定义 3.掌握序列的DFT及IDFT的计算机实现方法
2
二 实验原理
1. 设长度为N的有限长序列x(n)是
(n)的一个周期 周期为N的周期序列x
X (k ) DFT [ x (n)] x (n)W
n 0 N 1
N 1
nk N
0 k N 1
1 nk x(n) IDFT [ X (k )] X (k )WN 0 n N 1 N k 0 3
数字信号处理实验DFT

数字信号处理实验(第七章DFT)一、实验内容利用DFT对信号(如由多个正弦信号组成的信号)进行频谱分析,并研究不同数据长度,补零,加窗等对频率分辨率的影响。
二、实验工具MATLAB2012b软件三、实验涉及知识1.加窗:通常情况下,信号都是无限长的。
而在运用计算机进行模拟时,这是无法操作的。
所以实际情况下,要把观测的信号限制在一定长的时间之内。
为了从无限长的信号中得到有限长的数据,在时域乘一个窗函数,将信号截短,叫做加窗。
2.补零:为了增加频域抽样点数N,在不改变时域数据的情况下,在时域数据末端加一些零值点,叫做补零。
3.频率分辨率:指对两个最近的频谱峰值能够分辨的能力。
四、实验设计思路实验要求是利用DFT进行频谱分析,并研究不同数据长度,补零,加窗等对频率分辨率的影响。
我们利用DFT计算频谱的目的在于,针对计算机只能计算有限个离散的点的取值这一特点,实现计算机对连续时间信号的频谱的模拟。
所以我们比较关心的是模拟频谱和原信号频谱的拟合程度,我们希望拟合程度越高越好。
这就需要增加频率分辨率,因为频率分辨率越高,根据公式,说明相同采样频率下,采样的长度就越长,也就是频谱采样的点数就越多,我们可以看到的模拟频谱图像就越清晰,这样与原信号的拟合程度就越好。
根据实验要求,我将实验定为五部分,用4个m文件分别研究不同数据长度,补零,加窗,采样频率对频率分辨率的影响。
在程序设计中,出现的一个问题是,如何计算DFT后的频域函数的值。
课堂用的参考书上曾经给出一个将DFT转换为矩阵运算的方法,查阅相关参考书后,我发现在MATLAB信号处理工具箱中自带了一个dftmtx的函数,这个函数的功能是可以计算出旋转因子,计算出旋转因子后再将时域函数也转换成矩阵的形式进行DFT就可以了。
这里说明一下,由于dftmtx这个函数默认取值间隔为1,所以在没有特意设定采样频率的值得情况下,我们将采样频率默认为 1 。
实验设计中,为了更好的理解频率分辨率的概念,我不仅采用了绘图的形式,还直接计算了频率的分辨率,从而更直观的得到频率分辨率的具体数值。
数字信号DFT算法实验报告

数字信号处理实验报告学号:078205130 姓名:张贤辉一、实验目的(1)进一步加深DFT算法原理和基本性质的理解(因为FFT只是DFT的一种快速算法,所以FFT的运算结果必然满足DFT的基本性质)(2)熟悉FFT算法原理(3)学习用FFT对连续信号和时域离散信号进行谱分析的方法分析误差及其原因,以便在实际中正确应用FFT二实验原理理解快速FFT算法的原理及推导过程并能熟练使用MATLAB计算快速傅里叶变换,第一题程序b=[1,sqrt(2),1];a=[1,-0.67,0.9];[H,w]=freqz(b,a);magH=abs(H);phaH=angle(H);figure(1);subplot(2,1,1);plot(w/pi,magH);xlabel('频率单位:pi');ylabel(' 幅度');title('幅度响应');grid on;subplot(2,1,2);plot(w/pi,phaH);xlabel('频率单位:pi');ylabel(' 相位单位:pi');title('相位响应');grid on第二题程序fs=1000;t=0:1/fs:0.1; %采集信号长度为0.1秒,时间间隔为1/fs,即采样频率足够高,采样周期足够短就可以逼近原信号。
A=444.128;a=50*sqrt(2)*pi;b=a;xa=A*exp(-a*t).*sin(b*t); %近似模拟信号k=0:511; w=2*pi*k/512;Xa=dtft(xa,w); %近似模拟信号频谱figure(2);subplot(3,2,1);plot(t,xa); %画出原始波形axis([0,max(t),min(xa),max(xa)]);title('模拟信号');xlabel('t(s)');ylabel('xa(t)');line([0,max(t)],[0,0]);f=fs*k/512; %模拟频率fsubplot(3,2,2);plot(f,abs(Xa));title('模拟信号的幅度频谱');axis([0,500,0,max(abs(Xa))]);xlabel('f(Hz)');ylabel('|Xa(jf)|');fs1=1000;t1=0:1/fs1:0.1; %采集信号长度为0.1秒x1=A*exp(-a.*t1).*sin(b*t1); %1kHZ采样序列x1(n)X1=dtft(x1,w); %x1(n)的512点dtftsubplot(3,2,3);stem(t1,x1,'.');axis([0,max(t1),min(x1),max(x1)]);title('采样序列x1(n)');xlabel('n');ylabel('x1(n)');line([0,max(t1)],[0,0]);subplot(3,2,4);plot(w/pi,abs(X1));title('x1(n)的幅度频谱');axis([0,2,0,max(abs(X1))]);xlabel('w/pi');ylabel('|X1(jw)|');fs2=300;t2=0:1/fs2:0.1; %采集信号长度为0.1秒x2=A*exp(-a.*t2).*sin(b*t2); %300HZ采样序列x2(n) X2=dtft(x2,w); %x2(n)的512点dtftsubplot(3,2,5);plot(w/pi,abs(X2));title('x2(n)的幅度频谱');axis([0,2,0,max(abs(X2))]);xlabel('w/pi');ylabel('|X2(jw)|');fs3=200;t3=0:1/fs3:0.1; %采集信号长度为0.1秒x3=A*exp(-a.*t3).*sin(b*t3); %200HZ采样序列x2(n) X3=dtft(x3,w); %x3(n)的512点dtftsubplot(3,2,6);plot(w/pi,abs(X3));title('x3(n)的幅度频谱');axis([0,2,0,max(abs(X3))]);xlabel('w/pi');ylabel('|X3(jw)|');第三题程序function [y,ny]=convm(x,nx,h,nh)nyb=nx(1)+nh(1);nye=nx(length(x))+nh(length(h));ny=[nyb:nye];y=conv(x,h);x=[11,7,0,-1,4,2];nx=[-2:3];h=[2,3,-5,2,1];nh=[-1:4];[y,ny]=convm(x,nx,h,nh)stem(ny,y);xlabel(‘序列n’);ylabel(输出响应y(n));function X=dtft(x,w)X=x*exp(-j*[0:(length(x)-1)]'*w);实验总结在实验中,要正确的做出该实验的内容,需要充分理解DFT离散傅里叶变换原理,频率采样定理。
云师大 数字信号处理实验 05 第一篇 实验五 利用DFT分析模拟信号频谱

本科学生实验报告学号124090380 姓名赵玲学院物电学院专业、班级12电子实验课程名称数字信号分析与处理教师及职称和伟开课学期2014 至2015学年下学期填报时间2015 年 4 月23 日云南师范大学教务处编印实验序号 第一篇 实验五 实验名称 利用DFT 分析模拟信号频谱实验时间2015-4-22实验室同析楼三栋313实验室1.实验目的应用离散傅里叶变换DFT 分析模拟信号()t x 的频谱,深刻理解利用DFT 分析模拟信号频谱的原理、分析工程中出现的现象及解决方法。
2. 实验原理、实验流程或装置示意图连续周期信号相对离散周期信号,连续非周期子信号相对于离散非周期信号,都可以通过时域抽样定理建立相互关系,因此,在离散信号DFT 分析方法的基础上,增加时域抽样的步骤,就可以实现连续信号的DFT 分析。
【例1.5.1】 已知周期信号()()()t t t x ππ18sin 210cos +=,计算其频谱。
[解]信号基频πω20= rad/s ,周期10=Ts ;最高次谐频为πω1890= rad/s ,所以()19192=+⨯≥N 。
T0=1;N=19;T=T0/N;%周期T0=1、FFT 的点数N 、时域抽样间隔Tt=0:T:T0;x=cos(2*pi*5*t)+2*sin(2*pi*9*t);%周期信号 Xm=fft(x,N)/N;%利用FFT 计算频谱 f=(-(N-1)/2:(N-1)/2)/N/T;%若N 为偶数f=1/T/N*(-N/2:(N/2-1)) stem(f,abs(fftshift(Xm)));% 画出幅度谱xlabel('f(Hz)');ylabel('Magnitude');title('幅度谱'); 运行结果如图1.5.1所示-10-8-6-4-2024681000.10.20.30.40.50.60.70.80.91f(Hz)M a g n i t u d e幅度谱图1.5.1 信号的幅度谱一、验设计方案【例1.5.2】 利用DFR 近似分析连续信号()()t u e t x t -=的幅度谱并与理论值比较。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
1
2
3
4
5
6
7
200 150 100 50 0
0
1
2
3
4
5
6
7
(3)与两序列线性卷积相比较 x1=[1 3 5 3 6 8 3 9]; x2=[2 4 3 6 7 9 0 2]; n=0:length(x1)-1; n1=0:length(x1)*2-2; w=-2*pi:0.01:2*pi; XX1=x1*exp(-j*n'*w); XX2=x2*exp(-j*n'*w); YY2=XX1.*XX2; y2=YY2*exp(j*w'*n1) stem((0:length(n1)-1),y2,'fill') 或者调用两序列线性卷积函数conv x1=[1 3 5 3 6 8 3 9]; x2=[2 4 3 6 7 9 0 2]; y=conv(x1,x2)
(1)x=[1,2,3,4]; w=-2*pi:0.01:2*pi; n=0:3; X=x*exp(-j*n'*w); plot(w,real(X)) hold on %根据DTFT公式直接计算离散序列的DTFT %注意图像不能同时表达出变换的模和相位,在作图时应 取DTFT的模或者实部
10
5
0
-5 -8
2、两组实序列x1(n)=[1 3 5 3 6 8 3 9],x2(n)=[2 4 3 6 7 9 0 2], 计算x1(n)和x2(n)的圆周卷积y(n),计算x1(n)和x2(n) X2( 的傅里叶变换 X1( )和X2( ) Y( )=X1( ) ) 求 Y( ) , 的反傅里叶变换y2(n),比较y1(n)和y2(n)。
-6
-4
-2
0
2
4
6
8
(2)计算DFT可以直接调用MATLAB中的fft函数,或者根据DFT 公式直接计算 stem(2*pi*n/length(n),fft(x),‘fill’,‘k’)%直接调用fft函数计算离散序 列的DFT,注意Matlab中提供的fft函数结果取序列DFT的实部 或者 w1=2*pi*n/length(n); X1=x*exp(-j*n'*w1); stem(w1,X1, 'fill','k')%根据DFT公式计算离散序列的DFT
(1)计算两个序列的圆周卷积可以直接调用Matlab中的cconv 函数 x1=[1 3 5 3 6 8 3 9]; x2=[2 4 3 6 7 9 0 2]; y=cconv(x1,x2,8) y =170 175 178 143 161 115 154 158 subplot(3,1,1); stem((0:length(x1)-1),y,'fill')
180 160 140 120 100 80 60 40 20 0
0
1
2
3
4
5
6
7
(2)通过计算序列x1(n)和x2(n)的DFT,验证 DFT乘积性质 X1=fft(x1); X2=fft(x2); y1=ifft(X1.*X2); subplot(3,1,2); stem((0:length(y1)-1),y1,'fill');
10
5
0
-5 -8
-6
-4
-2
0
2
4
6
8
(3)y=[x,zeros(1,28)]; n2=0:31; stem(2*pi*n2/length(n2),fft(y),'fill','b')
10
5
0
-5 -8
பைடு நூலகம்-6
-4
-2
0
2
4
6
8
(4)序列经过补零得到的DFT频谱更加密集, 从采样的角度分析是由于 减小!实验分析结 果是DFT可以实现DTFT的采样!
1、已知x(n)={1,2,3,4},完成下列要求: (1)、计算其DTFT,并画出 [- , ] 区间的波形; (2)、计算4点DFT,并把结果显示在(1)中所画的图形中; (3)、对x(n)补零,计算32点DFT,并显示结果; (4)、根据实验结果,分析是否可以由DFT计算DTFT, 如果可以,如何实现。
y= 2 10 25 41 64 109 136 158 168 165 153 102 97 6 18
200 100 0
0
1
2
3
4
5
6
7
200 100 0
0 x 10
5
1
2
3
4
5
6
7
4 2 0
0
2
4
6
8
10
12
14
圆周卷积可以认为是线性卷积周期延拓或者频谱采样时出现 时域混叠的结果
