习题解答_现控理论_第5章

合集下载

第5章习题解答

第5章思考题及习题5参考答案一、填空1．如果采用晶振的频率为3MHz，定时器/计数器T x（x=0,1）工作在方式0、1、2下，其方式0的最大定时时间为，方式1的最大定时时间为，方式2的最大定时时间为。

答：32.768ms，262.144ms，1024µs2．定时器/计数器用作计数器模式时，外部输入的计数脉冲的最高频率为系统时钟频率的。

答：1/243．定时器/计数器用作定时器模式时，其计数脉冲由提供，定时时间与有关。

答：系统时钟信号12分频后，定时器初值4．定时器/计数器T1测量某正单脉冲的宽度，采用方式可得到最大量程？若时钟频率为6MHz，求允许测量的最大脉冲宽度为。

答：方式1定时,131.072ms。

5. 定时器T2 有3种工作方式：、和，可通过对寄存器中的相关位进行软件设置来选择。

答：捕捉，重新装载（增计数或减计数），波特率发生器，T2CON6. AT89S52单片机的晶振为6MHz，若利用定时器T1的方式1定时2ms，则（TH1）= ，（TL1）= 。

答：FCH，18H。

二、单选1．定时器T0工作在方式3时，定时器T1有种工作方式。

A.1种B.2种 C．3种D．4种答：C2. 定时器T0、T1工作于方式1时，其计数器为位。

A.8位B.16位C.14位D.13位答：B3. 定时器T0、T1的GATE x=1时，其计数器是否计数的条件。

A. 仅取决于TR x状态B. 仅取决于GATE位状态C. 是由TR x和INT x两个条件来共同控制D. 仅取决于INT x的状态答：C4. 定时器T2工作在自动重装载方式时，其计数器为位。

A.8位B. 13位C.14位D. 16位答：D5. 要想测量INT0引脚上的正单脉冲的宽度，特殊功能寄存器TMOD的内容应为。

A.87HB. 09HC.80HD. 00H答：B三、判断对错1．下列关于T0、T1的哪些说法是正确的。

A.特殊功能寄存器SCON，与定时器/计数器的控制无关。

第5章习题解答

第五章可编程序控制器及其工作原理5-1 可编程序控制器具有哪些特点？答：可编程序控制器特点：1）抗干扰能力强，可靠性高；2）控制系统结构简单、通用性强、应用灵活；3）编程方便，易于使用；4）功能完善，扩展能力强；5）PLC控制系统设计、安装、调试方便；6) 维修方便，维修工作量小；7) 体积小、重量轻，易于实现机电一体化。

5-2 整体式PLC、组合式PLC由哪几部分组成？各有何特点？答：整体式结构的PLC是将中央处理单元（CPU）、存储器、输入单元、输出单元、电源、通信端口、I∕O扩展端口等组装在一个箱体内构成主机。

另外还有独立的I/O扩展单元等通过扩展电缆与主机上的扩展端口相连，以构成PLC不同配置与主机配合使用。

整体式结构的PLC结构紧凑、体积小、成本低、安装方便。

小型机常采用这种结构。

组合式结构的PLC是将CPU、输入单元、输出单元、电源单元、智能I∕O单元、通信单元等分别做成相应的电路板或模块，各模块可以插在带有总线的底板上。

装有CPU的模块称为CPU模块，其他称为扩展模块。

组合式的特点是配置灵活，输入接点、输出接点的数量可以自由选择，各种功能模块可以依需要灵活配置。

5-3 PLC控制与继电器控制比较，有何相同之处？有何不同之处？答：PLC控制与继电器控制的比较见下表：5-4 PLC的硬件指的是哪些部件？它们的作用是什么？答：PLC的基本结构由中央处理器（CPU），存储器，输入、输出接口，电源，扩展接口，通信接口，编程工具，智能I/O接口，智能单元等组成。

1）中央处理器（CPU）中央处理器（CPU）其主要作用有①接收并存储从编程器输入的用户程序和数据。

②诊断PLC内部电路的工作故障和编程中的语法错误。

③用扫描的方式通过I∕O部件接收现场的状态或数据，并存入输入映像存储器或数据存储器中。

④PLC进入运行状态后，从存储器逐条读取用户指令，解释并按指令规定的任务进行数据传送、逻辑或算术运算等；根据运算结果，更新有关标志位的状态和输出映像存储器的内容，再经输出部件实现输出控制、制表打印或数据通信等功能。

任彦硕《自动控制原理》全部答案

R1
R2
+
1 sC2
Ur (s) R1C2s
(d)
Ur (s) R1
=
Uc (s)
( R2
//
1 sC2
)
⇒ T(s) = Uc(s) Ur (s)
=
R2 R1
1 R2C2s +1
题 2-2：试用运算法建立题 2-2 图所示 LC、RLC 电网络的动态结构图，并求解
自 u i (t) 至 u o (t) 信号传输的传递函数。
b)
R 2 uc(t) C2 −
R1 u r(t)
Rb
R2 C2
− +
c)
− uc(t)
R1 u r(t)
Rb
题 2-1 图电网络
C3 R3 C2 R2
− +
d)
− uc(t)
(a) T (s) = Uc (s) =
R2
+
1 sC2
=
R2C1C2s + C1
Ur (s)
R1
+
R2
+
1 sC1
+
1 sC2
−
Ms2
X1(s)
=
ms2
X
2
⇒ X1(s) =
ms2 + ks + f
F (s) s2[Mms2 + (M + m)ks + (M + m) f ]
(b)
⎧ ⎪⎪m ⎨
⎪ ⎪⎩
f1
d 2 x1(t) + dt 2
d[x1(t) − dt
f1
d[
x1
(t) − dt

(完整版)自动控制原理课后习题及答案

第一章绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答：1开环系统(1) 优点:结构简单，成本低，工作稳定。

用于系统输入信号及扰动作用能预先知道时，可得到满意的效果。

(2) 缺点：不能自动调节被控量的偏差。

因此系统元器件参数变化，外来未知扰动存在时，控制精度差。

2 闭环系统⑴优点：不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值，都会产生控制作用去清除此偏差，所以控制精度较高。

它是一种按偏差调节的控制系统。

在实际中应用广泛。

⑵缺点：主要缺点是被控量可能出现波动，严重时系统无法工作。

1-2 什么叫反馈？为什么闭环控制系统常采用负反馈？试举例说明之。

解答：将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。

闭环控制系统常采用负反馈。

由1-1中的描述的闭环系统的优点所证明。

例如，一个温度控制系统通过热电阻（或热电偶）检测出当前炉子的温度，再与温度值相比较，去控制加热系统，以达到设定值。

1-3 试判断下列微分方程所描述的系统属于何种类型（线性，非线性，定常，时变）？（1）22()()()234()56()d y t dy t du t y t u t dt dt dt ++=+（2）()2()y t u t =+（3）()()2()4()dy t du t ty t u t dt dt +=+ （4）()2()()sin dy t y t u t tdt ω+=（5）22()()()2()3()d y t dy t y t y t u t dt dt ++= （6）2()()2()dy t y t u t dt +=（7）()()2()35()du t y t u t u t dt dt =++⎰解答：（1）线性定常（2）非线性定常（3）线性时变（4）线性时变（5）非线性定常（6）非线性定常（7）线性定常1-4 如图1-4是水位自动控制系统的示意图，图中Q1，Q2分别为进水流量和出水流量。

操作系统第三版第5章习题解答

第5章习题解答一、填空1．一个文件的文件名是在创建该文件时给出的。

2．所谓“文件系统”，由与文件管理有关的那部分软件、被管理的文件以及管理所需要的数据结构三部分组成。

3．块是辅助存储器与内存之间进行信息传输的单位。

4．在用位示图管理磁盘存储空间时，位示图的尺寸由磁盘的总块数决定。

5．采用空闲区表法管理磁盘存储空间，类似于存储管理中采用可变分区存储管理方法管理内存储器。

6．操作系统是通过文件控制块（FCB）感知一个文件的存在的。

7．按用户对文件的存取权限将用户分成若干组，规定每一组用户对文件的访问权限。

这样，所有用户组存取权限的集合称为该文件的存取控制表。

8．根据在辅存上的不同存储方式，文件可以有顺序、链接和索引三种不同的物理结构。

9．如果把文件视为有序的字符集合，在其内部不再对信息进行组织划分，那么这种文件的逻辑结构被称为“流式文件”。

10．如果用户把文件信息划分成一个个记录，存取时以记录为单位进行，那么这种文件的逻辑结构称为“记录式文件”。

二、选择1．下面的 B 不是文件的存储结构。

A．索引文件B．记录式文件C．串联文件D．连续文件2．有一磁盘，共有10个柱面，每个柱面20个磁道，每个盘面分成16个扇区。

采用位示图对其存储空间进行管理。

如果字长是16个二进制位，那么位示图共需A字。

A．200 B．128 C．256 D．1003．操作系统为每一个文件开辟一个存储区，在它的里面记录着该文件的有关信息。

这就是所谓的 B 。

A．进程控制块B．文件控制块C．设备控制块D．作业控制块4．文件控制块的英文缩写符号是 C 。

A．PCB B．DCB C．FCB D．JCB5．一个文件的绝对路径名总是以 C 打头。

A．磁盘名B．字符串C．分隔符D．文件名6．一个文件的绝对路径名是从 B 开始，逐步沿着每一级子目录向下，最后到达指定文件的整个通路上所有子目录名组成的一个字符串。

A．当前目录B．根目录C．多级目录D．二级目录7．从用户的角度看，引入文件系统的主要目的是D 。

《现代控制理论》课后习题答案2

( sI − A) −1 =
1 adj( sI − A) det( sI − A)
(1)
式（1）中的 adj( sI − A) 和 det( sI − A) 可分别写成以下形式：
adj( sI − A) = H n −1s n −1 + H n − 2 s n − 2 + " + H 0 det( sI − A) = s + an −1s
故
Φ (t ) = α 0 (t ) I + α1 (t ) A + α 2 (t ) A2
⎡ −2tet + e 2t ⎢ = ⎢ −2(1 + t )et + 2e 2t ⎢ −2(2 + t )et + 4e 2t ⎣
(3t + 2)et − 2e 2t (3t + 5)et − 4e 2t (3t + 8)et − 8e 2t
n n −1
(2) (3) (4)
+ " + a0
，可得将式（1）两边分别左乘 det( sI − A)( sI − A) ，并利用式（2）和（3）
Is n + an −1 Is n −1 + " + a0 I = H n −1s n + ( H n − 2 − AH n−1 ) s n − 2 + " + ( H 0 − AH1 )s − AH 0
e jt = a0 (t ) + a1 (t ) j ， e − jt = a0 (t ) − a1 (t ) j
而
e jt = cos t + j sin t ， e− jt = cos t − j sin t 因此， a0 (t ) = cos t ， a1 (t ) = sin t 。由此得到状态转移矩阵 ⎡ cos t sin t ⎤ Φ (t ) = e At = a0 (0) I + a1 (t ) A = ⎢ ⎥ ⎣ − sin t cos t ⎦

现代控制理论课后习题答案

前言本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。

本书对该教材中的习题给予了详细解答，可帮助同学学习和理解教材的内容。

由于习题数量较多，难易程度不同，虽然主要对象是研究型大学自动化专业本科学生，但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。

书中第5、6、8章习题由高立群教授组织编选和解答；第4、7 章由井元伟教授组织编选和解答，第1、2章由郑艳副教授组织编选和解答。

由于时间比较仓促，可能存在错误，请读者批评、指正。

另外有些题目解法和答案并不唯一，这里一般只给出一种解法和答案。

编者 2005年5月第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示，设输入为1u ，输出为2u ，试自选状态变量并列写出其状态空间表达式。

图P2.1解此题可采样机理分析法，首先根据电路定律列写微分方程，再选择状态变量，求得相应的系统状态空间表达式。

也可以先由电路图求得系统传递函数，再由传递函数求得系统状态空间表达式。

这里采样机理分析法。

设1C 两端电压为1c u ，2C 两端的电压为2c u ，则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =，22c x u =，由式(1)和(2)得：1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为：12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。

自动控制原理_第5章习题解答-

第5章频率特性法教材习题同步解析一放大器的传递函数为：G (s )=1+Ts K测得其频率响应，当ω=1rad/s 时，稳态输出与输入信号的幅值比为12/2，稳态输出与输入信号的相位差为－π/4。

求放大系数K 及时间常数T 。

解：系统稳态输出与输入信号的幅值比为A ==222172K T ω=+ 稳态输出与输入信号的相位差arctan 45T ϕω=-=-︒，即1T ω=当ω=1rad/s 时，联立以上方程得T =1，K =12放大器的传递函数为：G (s )=121s +已知单位负反馈系统的开环传递函数为5()1K G s s =+ 根据频率特性的物理意义，求闭环输入信号分别为以下信号时闭环系统的稳态输出。

（1）r （t ）=sin （t +30°）；（2）r （t ）=2cos （2t －45°）；（3）r （t ）= sin （t +15°）－2cos （2t －45°）；解：该系统的闭环传递函数为65)(+=Φs s 闭环系统的幅频特性为365)(2+=ωωA闭环系统的相频特性为6arctan )(ωωϕ-=（1）输入信号的频率为1ω=，因此有37375)(=ωA ，()9.46ϕω︒=- 系统的稳态输出537()sin(20.54)37ss c t t ︒=+ （2）输入信号的频率为2ω=，因此有10()A ω=，()18.43ϕω︒=- 系统的稳态输出10()cos(263.43)2ss c t t ︒=- （3）由题（1）和题（2）有对于输入分量1：sin （t +15°），系统的稳态输出如下5371()sin( 5.54)37ss c t t ︒=+ 对于输入分量2：－2cos （2t －45°），系统的稳态输出为102()cos(263.43)ss c t t ︒=-- 根据线性系统的叠加定理，系统总的稳态输出为)4363.632cos(210)537.5sin(37375)(︒︒--+=t t t c ss绘出下列各传递函数对应的幅相频率特性与对数频率特性。

单片机原理及接口技术(C51编程)(第2版)-习题答案 - 第5章习题解答

第5章思考题及习题5参考答案一、填空1. AT89S51单片机任何一个端口要想获得较大的驱动能力，要采用电平输出。

答：低2.检测开关处于闭合状态还是打开状态，只需把开关一端接到I/O端口的引脚上，另一端接地，然后通过检测来实现。

答： I/O端口引脚的电平3. “8”字型的LED数码管如果不包括小数点段共计段，每一段对应一个发光二极管，有和两种。

答：7，共阳极，共阴极4. 对于共阴极带有小数点段的数码管，显示字符“6”（a段对应段码的最低位）的段码为，对于共阳极带有小数点段的数码管，显示字符“3”的段码为。

答：7DH，B0H5. 已知8段共阳极LED数码显示器要显示某字符的段码为A1H(a段为最低位)，此时显示器显示的字符为。

答：d6. LED数码管静态显示方式的优点是：显示闪烁，亮度，比较容易，但是占用的线较多。

答：无，较高，软件控制，I/O口7. 当显示的LED数码管位数较多时，一般采用显示方式，这样可以降低，减少的数目。

答：动态，成本，I/O端口8. LCD 1602是型液晶显示模块，在其显示字符时，只需将待显示字符的由单片机写入LCD 1602的显示数据RAM（DDRAM），内部控制电路就可将字符在LCD上显示出来。

答：字符，ASCII码9. LCD 1602显示模块内除有字节的 RAM外，还有字节的自定义，用户可自行定义个5×7点阵字符。

答：80，显示数据，64，字符RAM，810．当按键数目少于8个时，应采用式键盘。

当按键数目为64个时，应采用式键盘。

答：独立，矩阵11．使用并行接口方式连接键盘，对独立式键盘而言，8根I/O口线可以接个按键，而对矩阵式键盘而言，8根I/O口线最多可以接个按键。

答：8，6412．LCD 1602显示一个字符的操作过程为：首先，然后，随后，最后。

答：读忙标志位BF，写命令，写显示字符，自动显示字符二、判断对错1．P0口作为总线端口使用时，它是一个双向口。

《现代控制理论》课后习题答案

=
3 2
， c2
=
2s + 5 lim s→−3 s + 1
=
1 2
。
从输入通道直接到输出通道上的放大系数 d = 1，由此可得:
⎡ x1
⎢ ⎣
x 2
⎤ ⎥ ⎦
=
⎡− 1
⎢ ⎣
0
0⎤ − 3⎥⎦
⎡ ⎢ ⎣
x1 x2
⎤ ⎥ ⎦
+
⎡1⎤ ⎢⎣1⎥⎦u
y
=
⎡ ⎢⎣
3 2
1 2
⎤ ⎥⎦
⎡ ⎢ ⎣
x1 x2
u
d
d
b2
dt
dt
d
b1
m
dt
b0
因此，两个环节调换后的系统状态变量图为
u
d
d
b2
dt
dt
d
b1
dt
b0
m
−∫
−∫
y −∫
a0
a1
a2
进一步简化，可得系统状态变量图为 u
b0
b1
b2
− ∫ x1
− ∫ x2
− ∫ x3 y
a0
a1
a2
3
取 y = x3 ， y = x2 ， y = x1 ，可以得到两个环节调换后的系统的状态空间模型为
a(s)
1 a(s)
=
s3
+
1 a2s2 +
a1s
+
a0
， b(s)
=
b2 s 2
+ b1s
+ b0
。
2
由于 s−3 y 相当于对 y 作 3 次积分，故 y = 1 可用如下的状态变量图表示： m a(s)

自动控制原理习题答案详解

自动控制原理习题详解（上册）第一章习题解答1-2日常生活中反馈无处不在。

人的眼、耳、鼻和各种感觉、触觉器官都是起反馈作用的器官。

试以驾车行驶和伸手取物过程为例，说明人的眼、脑在其中所起的反馈和控制作用。

答：在驾车行驶和伸手取物过程的过程中，人眼和人脑的作用分别如同控制系统中的测量反馈装置和控制器。

在车辆在行驶过程中，司机需要观察道路和行人情况的变化，经大脑处理后，不断对驾驶动作进行调整，才能安全地到达目的地。

同样，人在取物的过程中，需要根据观察到的人手和所取物体间相对位置的变化，调整手的动作姿势，最终拿到物体。

可以想象蒙上双眼取物的困难程度，即使物体的方位已知。

1-3水箱水位控制系统的原理图如图1-12所示，图中浮子杠杆机构的设计使得水位达到设定高度时，电位器中间抽头的电压输出为零。

描述图1-12所示水位调节系统的工作原理，指出系统中的被控对象、输出量、执行机构、测量装置、给定装置等。

图1-12水箱水位控制系统原理图答：当实际水位和设定水位不相等时，电位器滑动端的电压不为零，假设实际水位比设定水位低，则电位器滑动端的电压大于零，误差信号大于零（e>0），经功率放大器放大后驱动电动机M旋转，使进水阀门开度加大，当进水量大于出水量时（Q^>Q2），水位开始上升，误差信号逐渐减小，直至实际水位与设定水位相等时，误差信号等于零，电机停止转动，此时，因为阀门开度仍较大，进水量大于出水量，水位会继续上升，导致实际水位比设定水位高，误差信号小于零，使电机反方向旋转，减小进水阀开度。

这样，经反复几次调整后，进水阀开度将被调整在一适当的位置，进水量等于出水量，水位维持在设定值上。

在图1-12所示水位控制系统中，被控对象是水箱，系统输出量水位高，执行机构是功率放大装置、电机和进水阀门，测量装置浮子杠杆机构，给定和比较装置由电位器来完成。

1-4工作台位置液压控制系统如图1-13所示，该系统可以使工作台按照给定电位器设定的规律运动。

第5章习题解答控制工程

5.7 系统的传递函数方框图如图所示，已知25.0,1.021==T T ，试求：（1）系统稳定时K 值的取值范围；解：由题意可以写出系统的闭环传递函数为：()()()()K s s T T s T T K s T s T s K s T s T s Ks G B ++++=+++++=2213212121)(11111)( 系统的特征方程为：0)(221321=++++K s s T T s T T即：04040141)(232121221213=+++=++++K s s s T T Ks T T s T T T T s由特征方程写出根据Routh 判据，系统闭环稳定的充要条件为：⎩⎨⎧>>-040040560K K 即：014>>K5.9试根据下面开环频率特性，使用Nyquist 判据分析相应的闭环系统的稳定性()()110110)(++=ωωωωj j j j G K解：使用Nyquist 判据要求画出开环频率特性)(ωj G K 的Nyquist 轨迹)(ωj G K 的幅频特性函数与虚频特性函数分别为：)1100()1(10)(22++=ωωωωj G K110arctan1arctan20)(ωωπω---=∠j G K将)(ωj G K 表示成下式：)1100)(1()10100(110)1100)(1(10)101)(1()(22222++-+-=++⋅--⋅-=ωωωωωωωωωωωj j j j j G K可得其实频特性函数与虚频特性函数分别为：)1100)(1(110)}(Re{22++-=ωωωωωj G K)1100)(1()10100()}(Im{222++-=ωωωωωj G K考虑ω的几个特殊值当0=ω：∞=)(ωj G 2)(πω-=∠j G 当∞=ω： 0)(=ωj G πω23)(-=∠j G由于当ω从0变化至∞，)(ωj G ∠从2π-变化至23π-，因此该系统的Nyquist 轨迹必然从复平面的第三象限移动至第二象限，也即轨迹必然与负实轴相交。

第5章-习题解答

第5章-习题解答第5章习题与答案5-1 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则［］(A) 其振幅为3 m (B) 其周期为s 31 (C) 其波速为10 m/s (D) 波沿x 轴正向传播 [答案：B]5-2 一平面简谐波，波速u =5m · s －1. t = 3 s 时波形曲线如题5-2图所示. 则x =0处的振动方程为［］(A)y =2×10－2cos(πt /2－π/2) ( S I ) . (B) y =2×10－2cos(πt ＋π ) ( S I ) . (C) y =2×10－2cos(πt /2+π/2) ( S I ) . (D) y =2×10－2cos(πt －3π/2)( SI ) . [答案：A]5-3 如题5-3图所示，两相干波源s 1和s 2相距λ/4(λ为波长), s 1ux y (10· · · · · · · 0 5 1122－ PSS题5-2图题5-3图的位相比s 2的位相超前π/2 ,在s 1、s 2的连线上, s 1外侧各点(例如P 点)两波引起的两谐振动的位相差是［］(A) 0 . (B) π . (C) π /2 . (D) 3π/2 . [答案：B]5-4 一平面简谐波沿ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形如题5-5图中的哪一个？［］ [答案：B]5-5 横波以波速u 沿x 轴负方向传播．t 时刻波形曲线如题5-5图所示．则该时刻［］题5-4图-(A) A 点振动速度大于零 (B)B 点静止不动(C) C 点向下运动(D) D 点振动速度小于零 [答案：D]5-6 一平面简谐波沿x 轴正方向传播，t = 0 时刻的波形如题5-6图所示，则P 处质点的振动在t = 0时刻的旋转矢量图是［］[答案：A]5-7 一简谐波沿x 轴正方向传播，t = T /4时的波形曲线如题5-7图所示．若振动以余弦函数表示，且此题各点振动的初相取-π 到π 之间的值，则［］ (A) O 点的初相为0=φωS A O ′ωSA ωωSAO ′(A)(B)(C)(D)S题5-5图题5-6图(B) 1点的初相为π-=211φ(C) 2点的初相为π=2φ(D) 3点的初相为π-=213φ[答案：D]5-8 在驻波中，两个相邻波节间各质点的振动［］(A) 振幅相同，相位相同 (B) 振幅不同，相位相同(C) 振幅相同，相位不同 (D) 振幅不同，相位不同 [答案：B]5-9 一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：［］(A) 它的动能转化为势能. (B) 它的势能转化为动能. (C) 它从相邻的一段质元获得能量其能量逐渐增大.(D) 它把自己的能量传给相邻的一段质元，题5-7图其能量逐渐减小. [答案：D]5-10 一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π，则振幅是__________，波长是__________，频率是__________，波的传播速度是__________。

现代控制理论习题解答(第二章)

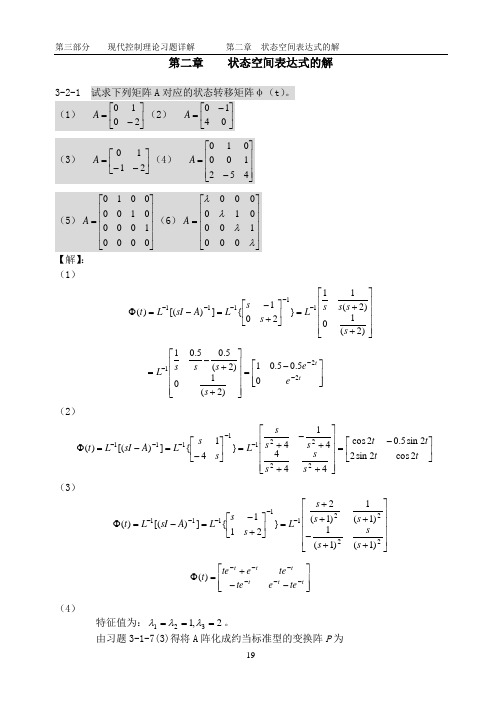
第二章状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ（t ）。

（1） ⎥⎦⎤⎢⎣⎡-=2010A（2） ⎥⎦⎤⎢⎣⎡-=0410A（3）⎥⎦⎤⎢⎣⎡--=2110A （4）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A（5）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=00100001000010A （6）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ0100010000A【解】：（1）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----)2(10)2(11}201{])[()(11111s s s s L s sL A sI L t⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-=---ttees s s s L 22105.05.01)2(10)2(5.05.01（2）⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎦⎤⎢⎣⎡-=-=Φ-----t tt ts s s s s s L s sL A sI L t 2cos 2sin 22sin 5.02cos 444414}41{])[()(222211111（3）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-+++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----222211111)1()1(1)1(1)1(2}211{])[()(s s s s s s L s s L A sI L t⎥⎥⎦⎤⎢⎢⎣⎡--+=Φ------tttttt teetete e te t )(（4）特征值为：2,1321===λλλ。

由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-20010011~1AP P A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=t tt ttA e ete e e2~0000⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===Φ-121132120000421211101)(21~t t tttA Ate te eePPeet⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--++-----++-----++--=Φt t ttt tt t t t t t t tt tt t ttt t tt t t e te eete ee te e e te e e te e ete e ete e e te e tee t 34838424225342222322)(222222222（5）为结构四重根的约旦标准型。

控制系统工程导论课后习题问题详解

第一章概论习题及及解答1-1 试列举几个日常生活中的开环控制和闭环控制系统实例，并说明它们的工作原理。

略1-2. 图1-17是液面自动控制系统的两种原理示意图。

在运行中，希望液面高度0H 维持不变。

1．试说明各系统的工作原理。

2．画出各系统的方框图，并说明被控对象、给定值、被控量和干扰信号是什么?()a 工作原理：出水量2θ与进水量一致，系统处于平衡状态，液位高度保持在0H 。

当出水量大于进水量，液位降低，浮子下沉，通过连杆使阀门1L 开大，使得进水量增大，液位逐渐回升；当出水量小于进水量，液位升高，浮子上升，通过连杆使阀门1关小，液位逐渐降低。

其中被控对象是水槽，给定值是液面高度希望值0H 。

被控量是液面实际高度，干扰量是出水量2θ。

()b 工作原理：出水量与进水量一致系统处于平衡状态，电位器滑动头位于中间位置，液面为给定高度0H 。

当出水量大于（小于）进水量，浮子下沉（上浮）带动电位器滑动头向上（下）移动，电位器输出一正（负）电压，使电动机正（反）转，通过减速器开大（关小）阀门1L ，使进水量增大（减小），液面高度升高（降低），当液面高度为0H 时，电位器滑动头处于中间位置，输出电压为零，电动机不转，系统又处于平衡状态。

其中被控对象是水槽，给定值为液面高度希望值0H ，被控量是液面实际高度，干扰量是出水量2θ。

()a ，()b 系统结构图如下图1-3 什么是负反馈控制?在图1-17(b)系统中是怎样实现负反馈控制的?在什么情况下反馈极性会误接为正，此时对系统工作有何影响?解：负反馈控制就是将输出量反馈到输入端与输入量进行比较产生偏差信号，利用偏差信号对系统进行调节，达到减小或消除偏差的目的。

图1-17()b系统的输出量液面实际高度通过浮子测量反馈到输入端与输入信号（给定液面高度）进行比较，如果二者不一致就会在电位器输出一电压值——偏差信号，偏差信号带动电机转动，通过减速器使阀门1开大或关小，从而进入量改变，当输出量——液面实际高度与给定高度一致偏差信号为0，电机，减速器不动，系统又处于平衡状态。

第5章电气自动控制技术习题与解答

第5章电气自动控制技术习题解答习题A 选择题5-1热继电器对三相异步电动机起（）的作用。

CA.零压保护B.短路保护C.过载保护 5-2 选择一台三相异步电动机的熔丝时，熔丝的额定电流（）。

CA ．等于电机的额定电流 B. 等于电机的起动电流 C. 大致等于电机的起动电流/2.5 5-3在电动机的继电接触器控制线路中的零压保护是（）。

BA．防止电源电压降低后电流增大而烧坏电机；B．防止停电后再恢复供电时电动机自行起动；C．防止电源断电后电动机立即停车而影响工作。

5-4在图5-和图5-中的联锁常闭（动断）触点KMR 和KMF 的作用是（）。

AA．保证两个触发器不同时动作；B．使两个触发器依次进行正反转运行；C．起自锁作用。

5-5 PLC 的工作方式为（）ＢＡ.等待命令工作方式Ｂ.循环扫描工作方式Ｃ.中断工作方式5-6 PLC 应用控制系统设计时所编制的程序是指（）。

ＢＡ.系统程序Ｂ.用户应用程序Ｃ.系统程序及用户应用程序5-7 PLC 的扫面周期与（）有关。

CA．该PLC 的扫面速度 B.用户程序的长短 C. A 和B5-8 PLC 输出端的状态（）。

CA.随输入信号的改变而立即发生变化B.随程序的执行不断在发生变化C.根据程序执行的最后结果在刷新输出阶段发生变化B基本题5-9 试画出三相异步电动机既能够连续工作又能够点动的继电接触器控制线路。

解：控制线路为：图中左边部分为主电路。

工作时，合上刀开关QS ，三相交流电经过QS ，熔断起FU ，接触器KM 主触点，热继电器FR 至三相交流电动机。

右边部分为控制电路，需要点动运行时，按下SB3点动按钮，其常闭触点先断开自锁电路，常开触发后闭合接通起动控制电路，KM 接触器线圈得电，主触点闭合，接通三相电源，电动机起动运转。

当松开点动按钮SB3 时，KM 线圈失电，KM 主触点断开，电动机停止运转。

若需要电动机连续运转，由停止按钮 SB 1 及起动按钮 SB 2 控制，接触器 KM 的辅助触点起自锁作用。

自动控制理论课后习题详细解答答案(夏德钤翁贻方版)第五章

第五章5-1 已知单位反馈系统的开环传递函数，试绘制其开环频率特性的极坐标图(1)解：幅频特性：相频特性：列表取点并计算。

0.5 1.0 1.5 2.0 5.010.01.790.7070.370.2240.0390.0095-116.6-135-146.3-153.4-168.7-174.2系统的极坐标图如下：(2)解：幅频特性：相频特性：列表取点并计算。

00.20.50.8 1.0 2.0 5.010.910.630.4140.3170.1720.01950-15.6-71.6-96.7-108.4-139.4-162.96系统的极坐标图如下：(3)解：幅频特性：相频特性：列表取点并计算。

0.20.30.51254.55 2.74 1.270.3170.0540.0039-105.6-137.6-161-198.4-229.4-253系统的极坐标图如下：(4)解：幅频特性：相频特性：列表取点并计算。

0.20.250.30.50.60.8122.7513.87.86 2.520.530.650.317-195.6-220.6-227.6-251.6-261.6-276.7-288.4系统的极坐标图如下：5-2 试绘制上题中各系统的开环对数频率特性（伯德图）。

(1)解：系统为Ⅰ型，伯德图起始斜率为－20dB/dec，在处与=20=0相交。

环节的交接频率，斜率下降20dB/dec，变为-40dB/de c。

系统的伯德图如图所示:(2)解：伯德图起始为0dB线，的交接频率，斜率下降20dB/dec，变为－20dB/de c。

的交接频率，斜率下降20dB/dec，变为－40dB/de c。

系统的伯德图如图所示。

（3）解：系统为Ⅰ型，伯德图起始斜率为－20dB/dec，其延长线在=1处与=20=0相交。

的交接频率，斜率下降20dB/dec，变为－40dB/de c。

的交接频率，斜率下降20dB/dec，变为－60dB/de c。

自动控制原理习题答案任彦硕主编习题解答-第5章

习题解答第5章题5-1：试绘制下列开环传递函数的幅相频率特性曲线。

(1) 10G(s)H(s)(s 1)(0.2s 1)=++ (2) 25(s 1)G(s)H(s)(s 3)(s 2s 2)+=+++(3) 100G(s)H(s)(s 1)(s 3)(s 4)=+++ 题5-6：试绘制题5-1各开环传递函数的对数幅频特性渐近线和半对数相频特性曲线。

(1) 2221010122()()(1)(0.21)(1)(10.04)j G j H j j j ωωωωωωω−−==++++ω 实频特性：)04.01)(1(210)(222ωωωω++−=P 虚频特性：)04.01)(1(12)(22ωωωω++−=Q 相频特性：()arctan arctan 0.2ϕωω=−−ωNyqist 曲线：起点：0ω=(0)10P ⇒=，(0)0Q =，(0)0ϕ=D 终点：ω=∞()0P ⇒∞=，()0Q ∞=， ()180ϕ∞=−D 与虚轴交点：()0P ω= 2.236ω⇒=() 3.73Q ω⇒=−Nyqist 曲线如下：转折频率1：111T ω==；转折频率2：215T ω==对数幅频特性：()20lg ()20lg10L A ωω==−− 半对数相频特性：()arctan arctan 0.2ϕωω=−−ωBode 图如下：(2) 25(1)()()(3)(22)j G j H j j j ωωωωωω+=+−+ 222222225(3)(2)202(12)(9)[(2)4]j ωωωωωωω+−+−+=+−+ω实频特性：]4)2)[(9(20)2)(3(5)(2222222ωωωωωωω+−++−+=P虚频特性：]4)2)[(9()21(10)(22222ωωωωωω+−++−=Q 相频特性：2()arctan arctanarctan310.5ωωϕωωω=−−−Nyqist 曲线：起点：0ω=5(0)6P ⇒=，(0)0Q =，(0)0ϕ=D 终点：ω=∞()0P ⇒∞=，()0Q ∞=， ()180ϕ∞=−D 与虚轴交点：()0P ω= 2.09ω⇒=()0.66Q ω⇒=−Nyqist 曲线如下：225(1)0.83(1)()()(3)(22)(0.331)[(0.7)1]j j G j H j j j j j j ωωωωωωωωωω++==+−++++ 转折频率1：11 1.414T ω==；转折频率2：213T ω== 对数幅频特性：5()20lg ()20lg 6L A ωω==+半对数相频特性：2()arctan arctanarctan310.5ωωϕωωω=−−−Bode 图如下：(3) 23222100100[128(19)]()()(1)(3)(4)(1)(3)(4)j G j H j j j j ωωωωωωωωωωω−+−==++++++ 实频特性：)4)(3)(1()812(100)(2222ωωωωω+++−=P 虚频特性：)4)(3)(1()19(100)(2223ωωωωωω+++−=Q相频特性：()arctan arctan 0.33arctan 0.25ϕωωω=−−−ωNyqist 曲线：起点：0ω=(0)8.33P ⇒=，(0)0Q =，(0)0ϕ=D 终点：ω=∞()0P ⇒∞=，()0Q ∞=， ()270ϕ∞=−D 与虚轴交点：()0P ω= 1.22ω⇒=() 4.77Q ω⇒=− 与实轴交点：()0Q ω= 4.36ω⇒=()0.71P ω⇒=−Nyqist 曲线如下：8.33()()(1)(0.331)(0.251)G j H j j j j ωωωωω=+++转折频率1：111T ω==；转折频率2：213T ω==；转折频率3：314T ω== 对数幅频特性：()20lg ()18.4L A ωω==−−半对数相频特性：()arctan arctan 0.33arctan 0.25ϕωωωω=−−−Bode 图如下：题5-2：已知某一控制系统的单位阶跃响应为4t 9t c(t)1 1.8e 0.8e −−=−+试求该系统的开环频率特性。