11-3磁通量 磁场的高斯定理
磁场高斯定理 知乎

磁场高斯定理
磁场的高斯定理是磁场理论中的一个重要定律,它表述为:磁场中通过任一封闭曲面的磁通量一定为零。
这里,磁通量表示的是通过某个曲面的磁感线的数量,磁感线是用来表示磁场分布的线。
高斯定理告诉我们,不论磁场如何分布,无论曲面如何取向,只要它是封闭的,通过这个曲面的磁通量总是为零。
这个定理反映了磁场的无源性质。
在磁场中,没有类似于电荷这样的源,磁场线是闭合的,从一处出发的磁场线会形成闭合回路,不会像电场线那样从一个正电荷出发终止于一个负电荷。
因此,磁场线不会从一个地方出发而终止于另一处,这就意味着磁场线不会穿越一个封闭的曲面,导致磁通量恒为零。
与静电场的高斯定理相比,磁场的高斯定理体现了磁场的本质差异。
在静电场中,由于电荷的存在,电场线会从正电荷出发终止于负电荷,因此,通过一个封闭曲面的电通量可以不为零。
而磁场的高斯定理表明磁场是无源的,不存在孤立的磁荷,磁场线总是闭合的。
这个定理在磁场的实际应用中具有重要意义,例如在电磁感应、磁场的能量传递等方面都是基于磁场的高斯定理的原理。
通过理解和应用磁场的高斯定理,我们可以更好地理解和预测磁场的行为和作用。
1。
11-2 磁通量 高斯定理 安培环路定理.
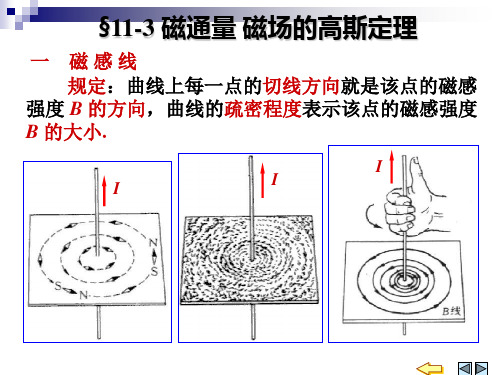
n v v 安培环路定理 ∫ B ⋅ dl = µ 0 ∑ I i L i =1
一闭合路径的积分的值,等于 µ 0 乘以该闭合路径 闭合路径的积分的值, 的积分的值 包围的各电流的代数和. 所包围的各电流的代数和
v 在真空的稳恒磁场中,磁感应强度 B 沿任 在真空的稳恒磁场中,
安培环路定理
n v v ∫ B ⋅ dl = µ 0 ∑ I i L i =1
令 当
2)选回路 . )
d
R
L = 2 πR
B = µ0 NI L
2R >> d 时,螺绕环内可视为均匀场 .
例3 无限长载流圆柱体的磁场 解 1)对称性分析 2)选取回路 ) )
I
r>R
2π rB = µ0 I
v v ∫ B ⋅ d l = µ0 I
l
R R
L
r
2π r 2 v v πr 0 < r < R ∫ B ⋅ d l = µ0 2 I l πR 2 µ0r µ0 Ir 2π rB = 2 I B= 2 R 2π R
v 方向不同, (2)若不同电流元在 点dB )若不同电流元在P点 方向不同,正交分解
B = ∫ dB
统一积 分变量
Bx = ∫ dBx
By = ∫ dBy
二、灵活选择微元,利用已有的结果用叠加原理求解 例3. 4
无限长载流 无限长载流 直导线
B=
µ0I
2πr
圆电流中心 圆电流中心
B =
µ0I
2R
三、安培环路定律 安培环路定律
v v ∫ B ⋅ dL = µ 0 ( I 1 − I 2 + 2 I 3 )
v v v ∫ B ⋅ dL = 0; 但:B ≠ 0
磁通量磁场的高斯定理教案

磁通量磁场的高斯定理教案一、教学目标1. 让学生了解磁通量的概念,理解磁通量与磁场之间的关系。
2. 引导学生掌握高斯定理的内容,理解高斯定理在磁场研究中的应用。
3. 培养学生的实验操作能力,通过实验观察磁通量的变化,进一步验证高斯定理。
二、教学内容1. 磁通量的定义及其计算公式。
2. 高斯定理的表述及其数学表达式。
3. 磁通量与磁场之间的关系。
4. 高斯定理在磁场研究中的应用。
5. 实验操作:观察磁通量的变化,验证高斯定理。
三、教学重点与难点1. 教学重点:磁通量的定义及其计算公式,高斯定理的表述及其数学表达式。
2. 教学难点:磁通量与磁场之间的关系,高斯定理在磁场研究中的应用。
四、教学方法1. 采用讲授法,讲解磁通量、磁场、高斯定理的概念和原理。
2. 采用实验法,让学生通过实验观察磁通量的变化,验证高斯定理。
3. 采用问题驱动法,引导学生思考磁通量与磁场之间的关系,提高分析问题和解决问题的能力。
五、教学过程1. 引入:通过展示磁铁吸引铁屑的实验,引导学生思考磁场的概念。
2. 讲解:讲解磁通量的定义及其计算公式,阐述磁通量与磁场之间的关系。
3. 讲解:介绍高斯定理的表述及其数学表达式,讲解高斯定理在磁场研究中的应用。
4. 实验:安排学生进行磁通量实验,观察磁通量的变化,验证高斯定理。
6. 作业:布置相关练习题,巩固所学知识。
7. 课后辅导:解答学生在课后遇到的问题,提供进一步的学习指导。
六、教学评估1. 课堂讲解评估:观察学生对磁通量、磁场和高斯定理的理解程度,以及学生能否正确运用相关概念解决问题。
2. 实验操作评估:检查学生在实验中的操作技能,观察学生是否能正确观察和记录磁通量的变化。
3. 作业完成情况评估:检查学生作业的完成质量,评估学生对课堂所学知识的掌握程度。
七、教学反思1. 反思教学内容:根据学生的反馈,调整和优化教学内容,确保学生能够更好地理解和掌握磁通量、磁场和高斯定理的知识。
2. 反思教学方法:根据学生的学习效果,调整和改善教学方法,提高教学质量和效果。
磁感应强度磁场的高斯定理

目 录
• 磁感应强度简介 • 磁场的高斯定理 • 磁场与电流的关系 • 磁场与物质相互作用 • 磁场的应用 • 总结与展望
01
磁感应强度简介
定义与物理意义
定义
磁感应强度是描述磁场强弱的物理量 ,表示磁场中某点单位面积上磁力线 的条数。
物理意义
磁感应强度是描述磁场对通电导体作 用力大小的物理量,也是描述磁场对 磁体作用力大小的物理量。
磁感应强度的测量方法
1 2
霍尔效应法
利用霍尔效应测量磁感应强度,通过测量霍尔电 压的大小来确定磁感应强度的大小。
磁通量法
通过测量穿过某一面积的磁通量,再根据磁通量 与磁感应强度的关系计算出磁感应强度的大小。
3
磁力线描绘法
利用磁力线描绘仪描绘出磁场分布,再根据磁力 线的疏密程度判断磁感应强度的大小。
磁感应强度的单位
特斯拉(T)
国际单位制中的基本单位,表 示垂直于磁场方向上单位面积
上所通过的磁力线数。
高斯(G)
辅助单位,表示垂直于磁场方 向上单位长度上所通过的磁力 线数。
毫特斯拉(mT)
常用单位,表示垂直于磁场方 向上单位面积上所通过的磁力 线数。
微特斯拉(μT)
常用单位,表示垂直于磁场方 向上单位面积上所通过的磁力
03
合曲面的磁通量密度。
03
磁场与电流的关系
安培环路定律
安培环路定律
描述磁场与电流之间的关系,指出磁场线总是围绕电流闭合 ,且磁感应线的积分与穿过某一闭合曲线的电流成正比。
安培环路定律的数学表达式
B·dS = μ₀I,其中B表示磁感应强度,dS表示微小面积元素,I 表示穿过该面积元素的电流。
第34讲稳恒磁场——磁通量高斯定理和安培环路定律第34讲稳恒

第34讲:稳恒磁场——磁通量、高斯定理和安培环路定律
内容:§11-3,§11-4 1.磁感应线 2.磁通量
3.高斯定理 (50分钟) 4.安培环路定律 (50分钟)
要求:
1.了解磁感应线的物理意义;
2.理解磁通量的物理意义计算方法; 3.掌握高斯定理及其物理意义;
4.掌握安培环路定律的物理意义并能用以解决磁感应强度的计算。
重点与难点:
1.高斯定理 2.安培环路定律
方法:
重点讲清中的物理意义与计算方法,在此基础上,讲清磁场高斯定理的物理意义,并由此阐明磁场的性质,对安培环路定理,要在讲清其它意义的基础上,通过例题的分析,使学员能掌握其应用方法。
作业:
问题:P173:7,8,9,10 习题:P179:10,13,16,18 预习:§11-5
复习:
1.磁场的概念:
2.Biot-Savart 定律: 3
04r r
l Id B d
⨯=πμ
3.载流长直导线:()120sin sin 4ββπμ-=a
I
B
4.圆形电流轴线:()
2/3222
02x R IR B +=μ 圆心处:R I B 20μ=
5.载流直螺线管: ()120cos cos 2
ββμ-=nI
B
无限长 nI B 0μ=
6.运动电荷的磁场:3
04r r
v q B ⨯=πμ
I 0
⎰
⎰∑⎰⎰⎰⎰⎰⎰⎰⎰
为积分回路L,绕行方向为
Cylinder 圆柱体很长,导体中部磁场是对称的(由电流的对称性可
r
均匀分布在圆柱面上,则由安培环路定
则由安培环路。
第2、3次_磁场高斯定理_安培环路定律讲解

通过曲面S的磁通量为
在国际单位制中,磁通量 的单位是Wb(韦伯)。
dm B dS BdS cos
m
BdS
s
BdS cos
s
二、磁场的高斯定理
对一封闭曲面来说,一般取向外的指向为正法线的指向。 这样从闭合面穿出的磁通量为正 ( / 2),穿入的磁通量为 负 ( / 2) ,由于磁感线是闭合线,那么穿过任一封闭曲 面的磁通量一定为零。
0 I
(r R) (r R)
0 (r R)
B
0
I
2 r
(r R)
0I B 2 R
O
I R
Rr
练 同轴的两筒状导线通有等值反向的电流 I , 习 求 B 的分布。
(1) r R2, B 0
R2
R1
(2)
R1
r
R2 ,
B
0 I 2 r
I
I
r
(3) r R1, B 0
电场、磁场中典型结论的比较
长直线
长 直
内
圆
柱 面
外
长 直
内
圆
柱 体
外
电荷均匀分布
E
2 0r
E0
E
2 0r r
E 2 0 R2 E
环 等于该闭合曲线所包围(套链)的电流的代数和与
路 定
真空中的磁导率的乘积。即
理
B dl 0 Ii
说 明
电流与环路成右旋关系
I4
I1 I 2
I3
如图 B dl 0 Ii
l
0 (I2 I3)
说
B dl 0 Ii 0 (I2 I3)
明
由环
环路
路上
简述磁场中的高斯定理

简述磁场中的高斯定理磁场是我们生活中常见的自然现象之一,它在物质中的运动和相互作用起着重要的作用。
而高斯定理则是描述磁场分布的一项重要定理,它能够帮助我们更好地理解和分析磁场的性质和特点。
高斯定理是由德国数学家卡尔·弗里德里希·高斯在19世纪初提出的。
它实际上是电磁学中的一个重要定理,用来描述磁场中的场线分布和磁通量的关系。
通过高斯定理,我们可以通过计算一个封闭曲面上的磁通量来确定磁场的分布情况。
在磁场中,我们可以通过放置一个封闭曲面来应用高斯定理。
这个封闭曲面可以是任意形状,但通常选择一个对称的形状,以便简化计算。
曲面内部的磁场可以是均匀的,也可以是非均匀的。
无论是哪种情况,高斯定理都适用。
高斯定理的数学表达形式如下:∮B·dA = 0其中,∮B·dA表示沿着曲面边界的磁场B与面元dA的点积之和,等于0。
这个等式告诉我们,封闭曲面上的磁场的总磁通量是零,即磁通量的进出平衡。
这是因为磁场是无源场,不存在磁荷,所以磁通量在封闭曲面上的总和为零。
高斯定理的应用可以帮助我们解决一些实际问题。
例如,当我们需要计算一个导线产生的磁场时,可以通过选择一个合适的封闭曲面来应用高斯定理。
由于封闭曲面上的磁通量为零,我们可以通过计算曲面内部的磁场分布来得到导线产生的磁场。
另一个应用高斯定理的例子是计算磁铁的磁场。
当我们想要知道一个磁铁的磁场分布时,可以使用高斯定理来计算磁通量。
通过选择一个合适的封闭曲面,我们可以得到磁铁的磁场分布情况。
需要注意的是,高斯定理只适用于静态磁场,即磁场不随时间变化。
对于变化的磁场,我们需要使用其他方法来描述和分析。
磁场中的高斯定理是描述磁场分布的重要定理,它通过计算封闭曲面上的磁通量来帮助我们理解和分析磁场的性质和特点。
通过选择合适的封闭曲面,我们可以应用高斯定理解决一些实际问题,如计算导线和磁铁的磁场分布。
高斯定理在电磁学中具有重要的应用价值,对于深入理解和研究磁场具有重要意义。
磁场的高斯定理

ΔN B ΔS
磁场中某点处垂直 B 矢量的单位面积上 通过的磁力线数目等于该点 B 的数值.
定义:通过任一曲面的磁力线的条数 称为通过这一面元的磁通量Φm 。
dΦm B dS
s
s
en
B
B
穿过某一曲面的磁通量
Φm
s
B dS
dΦm
dS
B
磁通量单位:韦伯,Wb
一致,
B 的方向与环路方向 (3)要求环路上各点 B 大小相等,
I 0 B d l I 写成 目的是将: B 0 L dl 或 B 的方向与环路方向垂直, B dl , cos 0 B dl 0
L
【例9-4 】求长直密绕螺线管内磁场.
R
B
2π R
dl
0 I l B dl 2π Rdl
B dl 0 I
l
l
设闭合回路 l 为圆 形回路( l 与 I成右螺 旋)
I
o
R
B
若回路绕向为逆时针
dl
l
dl
0 I l B d l 2 π
2π
0
dφ 0 I
l
r2
l
多电流情况
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
I1
I2
I3
推广: 安培环路定理
n B dl 0 Ii i 1
l
§9.2
安培环路定理
2.定理表述
在真空中的稳恒磁场内,磁感应强度沿闭合回路的 线积分等于环路所包围的电流代数和乘以 0。 数学表达式:
大学物理 磁场的高斯定理

在静电场中,由于自然界有单独存在的正、负电 荷,因此通过一闭合曲面的电通量可以不为零,这反 映了静电场是有源场。而在磁场中,磁力线的连续性 表明,像正、负电荷那样的磁单极是不存在的,磁场 是无源场。
上页
下页
思考问题!!
求穿过旋转曲面的磁通量, 是否可以通过求穿过平面圆的
磁通量来求呢?
m BS cos B r 2cos
S
n
B
上页
下页
dS
对于闭合曲面 SB dS
(2)磁通量是标量,其正负由角确定。与电场中一样,
对闭合曲面来说,我们规定取向外的方向为法线的正方向。
这样:
磁力线穿入: 0 磁力线穿出: 0
上页
下页
二、.磁场的高斯定理
由于磁力线是闭合曲线,因此通过任一闭合曲 面磁通量的代数和(净通量)必为零,亦即
sB dS 0
典型载流体磁场分布
磁力线的特征:
1)无头无尾的闭合曲线 2)与电流相互套合,服从右手螺旋定则
3)磁力线不相交
上页
下页
2. 磁通量
磁场中,通过一给定曲面的磁力线数目,称为通过
Байду номын сангаас
该曲面的磁通量。
m
B dS
s
BdS cos
s
dS
B
在国际单位制中,磁通量的单位为韦伯(wb)。
说明
(1)对于有限曲面 B dS
为什么?
BB
上页
下页
例1 在匀强磁场B中,有一半径为r的半球面S,S 边线所在平面的法线方向的单位矢量n和B的夹角为
,如图所示,则通过半球面S的磁通量为
-B r2cos
将半球面和圆面组成一个闭 合面,则由磁场的高斯定理知, 通过此闭合面的磁通量为零。
安培环路定理洛仑兹力

l
0
π π
r2 R2
I
2π
rB
0r2
R2
I
B
0Ir
2π R2
I
RR
L
r
B
I . dB
dI B
B I 的方向与 成右螺旋
0 r R, r R,
B
0Ir
2π R2
B 0I
2π r
I
0I B
2π R
R
oR r
例4 无限长载流圆柱面的磁场
L1
r
IR
L2 r
0I B
2π R
oR r
解
0 r R, B d l 0
B
线为B
2)选回路 .
l B dl 2π RB 0NI
B 0NI
d
2π R
R
令 L 2πR B 0 NI L
2R d 当
时,螺绕环内可视为均匀场 .
例3 无限长载流圆柱体的磁场
解 1)对称性分析
2)选取回路
rR
Bdl
l
0I
2π rB 0I
B 0I
2π r
0 r R
l
Bd
右螺旋)
lI
I
若回路绕向化为逆时针时,则
B
o
R
dl
l
Bdl
0I
2π
2π
0
d
0I
l
d
dl
B
Ir
l
l 与 I 成右螺旋
对任意形状的回路
B dl
0I
rd
0I
d
2π r
2π
B dl
l
0I
电流在回路之外
磁场中的高斯定理

高斯定理表明,在通电导线周 围的磁场中,穿过任意一个闭 合曲面的磁通量等于电流的代 数和。
通过高斯定理,可以计算出通 电导线周围的磁场分布和特点, 例如磁场的方向和强度。
磁通量的计算实例
磁通量是指穿过某个面的磁场的强弱和方向的量。通过计算磁通量,可 以了解磁场的分布和特点。
计算磁通量需要使用高斯定理,通过积分来计算穿过某个面的磁通量。
磁场矢量场
高斯定理的应用使得我们可以方便地处理磁场矢量场问题。通过计算矢量场的散度,我们可以得到特定区域内磁 场的变化情况,从而更好地理解磁场的行为和性质。
磁场中的高斯定理的推导
高斯定理推导
高斯定理在磁场中的推导基于磁场的高斯定理和安培环路定律。通过引入磁通量密度和磁通量等概念 ,我们可以利用微积分的方法推导出高斯定理在磁场中的形式。
磁场与电场的关系
磁场和电场是相互联系的,变化的电 场会产生磁场,变化的磁场也会产生 电场。因此,磁场和电场可以相互转 化,形成电磁波。
磁场的方向
磁场的方向
在磁场中任意一点,磁场都有一个特定的方向,称为该点的磁场方向。磁场方 向可以通过放入该点的磁针的指向来确定,磁针的北极指向磁场方向。
磁场方向的确定
高斯定理表明,在磁场中,穿过任意一个闭合曲面的磁通量等于零,即磁场是无源 场。
在地球磁场中,由于地球内部的物理过程,产生了磁场分布。高斯定理可以用来分 析地球磁场的分布和特点,例如地磁场的极性和强度分布。
通电导线周围的磁场高斯定理分析
当导线中电流发生变化时,会 在导线周围产生磁场。高斯定 理可以用来分析这个磁场的分 布和特点。
磁场大小的测量
测量磁场大小的方法有多种,如高斯计、特斯拉计等。这些 仪器通过测量磁感应线的密度或磁通量来计算磁场的大小。 在地球表面,地磁场的大小约为0.5-0.6特斯拉。
03磁场中的高斯定理-安培环路定理讲解

S
7
例1、如图 矩形线圈与载流无限长直导线共面,直导 线电流为I,求线圈的磁通量。 解:选距离电流r处,宽度为dr ,平 行于直导线的面积元 ds=ldr I
a
b
B
0 I dm Bldr ldr 2r a b 0 I m ldr 2r a
l
r
8
0 Il a b ln( ) 2 a
3
直线电流的磁感应线
磁感应线为一组环 绕电流的闭合曲线。
4
圆电流的磁感应线
I
5
通电螺线管的磁感应线
磁感应线的特点:
(1) 磁感应线是连续的,不会相交。 (2) 磁感应线是围绕电流的一组闭合曲线,没有 起点,没有终点。 (3)磁感线密处 B 大;磁感线疏处 B 小。 6
1.穿过一面积元dS的磁通量
得距电流垂直距离为r处的一点磁感应 强度的大小
r
L
0 I B 2r
18
问题:能否用安培环路定理求有限长直线电流的B?
设ab为闭合电流 I 中的一段直线电流, 长为 2R。取半径 为R 、圆心为 ab 的中点o、 且垂直于 ab 的圆为回路 L。 有人用安培环路定理求 L 上各点的 B: a 2R
I
0 R L
L
B d l 0 I
B Biblioteka B2 π R 0 I 0 I
2π R
b
对不对? 【答】不对。
19
检验:用毕-萨定理+叠加原理,可得
a
I
2
2R b
R
L
1
L
Bdl
4πr 0 I 0 I 0 0 P 4 π r cos45 cos135 4 π r 2 B的方向与圆周相切(右手定则)。 所以正确的环流应为:
磁通量 磁场的高斯定理
R
磁的高斯定理、安培环路定理
17
物理学
第五版
(2)选回路
l B dl 2π RB 0NI
B 0NI
2π R
d
令 L 2πR
R
B 0 NI L 0nI
当 2R d 时,螺绕环内可视为均匀场 。
磁的高斯定理、安培环路定理
18
物理学
第五版
例3 无限大均匀带电(单位长度电流密度为i)平
B dl ?
★ 安培环路定理的表述
在稳恒磁场中,磁感应强度 B 在任意闭合曲线上的环流,
等于该闭合曲线所包围的电流的代数和与真空中的磁导率
的乘积。即
B dl 0 Ii
L
i
当环路的方向与包围电流的方向满足右手螺旋关
系时,该电流为正;反之,则为负。
磁的高斯定理、安培环路定理
B 0I
2π r
IR
0I B
2π R
oR r
磁的高斯定理、安培环路定理
14
物理学
第五版 讨论1 无限长载流圆柱面的磁场
0
B
0I 2r
rR rR
0I B
2R
已知:I、R
r
Ir R
0R r
磁的高斯定理、安培环路定理
15
物理学
第五版
讨 论 2
同求轴B的无的限分长布两。筒状导线通有等值反向的电流I,
8
物理学
第五版
说
明
B • dl 0 Ii
I1
I2
由环 由
环
I3
环路 环
路
11-3 磁通量 磁场的高斯定理
B
I
o d1 d 2
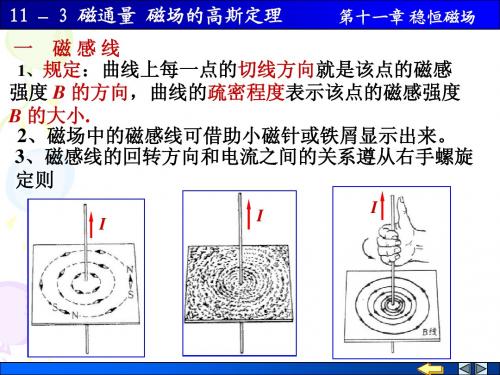
2π x µ0I l dΦ = BdS = ld x 2π x v v µ0 Il d2 dx x Φ = ∫S B ⋅ dS = ∫d1 2π x µ 0 Il d 2 Φ= ln 2π d1
B=
µ0 I
11 – 3 磁通量 磁场的高斯定理
第十一章 稳恒磁场
的均匀磁场中, 例2、 在磁感强度为 的均匀磁场中,有一半径为 的半球 、 在磁感强度为B的均匀磁场中 有一半径为R的半球 与半球面轴线的夹角为α, 面,B与半球面轴线的夹角为 ,求通过该半球面的磁通量 与半球面轴线的夹角为 。 B 由于磁感强度B与球面上的面 分析 由于磁感强度 与球面上的面 S 元外法线的夹角是个变量, 元外法线的夹角是个变量,直接 α 计算半球面内的磁通量难度较大。 计算半球面内的磁通量难度较大。 en 依照高斯定理, 依照高斯定理,穿过半球面的磁通 R 量等于穿过球面截圆的磁通量, 量等于穿过球面截圆的磁通量,由此 可求得穿过半球面的磁通量。 可求得穿过半球面的磁通量。 由磁场中的高斯定理, 解 由磁场中的高斯定理,穿过半球面的磁感线全部穿过 圆面S,因此有 圆面 因此有 v v
11 – 3 磁通量 磁场的高斯定理
第十一章 稳恒磁场
磁场高斯定理
v v ∫S B ⋅ d S = 0
物理意义: 物理意义:通过任意闭合曲面的磁通量必等于零 (故磁场是无源的 ) 故磁场是无源的.) 无源的
11 – 3 磁通量 磁场的高斯定理
第十一章 稳恒磁场
例 如图载流长直导线的电流为 I , 试求通过矩 v 形面积的磁通量. 形面积的磁通量 解 先求 B ,对变磁场 给出 dΦ 后积分求 Φ v
v B
v dS1 v θ1 B 1
磁通量磁场的高斯定理教案

磁通量磁场的高斯定理教案一、教学目标1. 让学生理解磁通量的概念,掌握磁通量的计算方法。
2. 让学生了解高斯定理在磁场中的应用,理解高斯定理的含义。
3. 培养学生运用高斯定理解决实际问题的能力。
二、教学内容1. 磁通量的定义及其计算方法2. 高斯定理的表述3. 高斯定理在磁场中的应用4. 磁通量与磁场强度之间的关系5. 实际问题分析与练习三、教学重点与难点1. 教学重点:磁通量的计算方法,高斯定理的表述及应用。
2. 教学难点:高斯定理在复杂磁场中的应用,磁通量与磁场强度之间的关系。
四、教学方法1. 采用讲授法,讲解磁通量的定义、计算方法及高斯定理的表述。
2. 利用示例和实际问题,引导学生运用高斯定理解决实际问题。
3. 通过讨论和小组合作,探讨磁通量与磁场强度之间的关系。
五、教学过程1. 引入:通过展示磁铁穿过线圈的实验,引导学生思考磁通量的概念。
2. 讲解磁通量的定义及计算方法,让学生理解磁通量的含义。
3. 讲解高斯定理的表述,让学生了解高斯定理在磁场中的应用。
4. 示例讲解:利用高斯定理计算闭合回路中的磁通量,让学生掌握高斯定理的应用。
5. 实际问题分析与练习:让学生运用高斯定理解决实际问题,巩固所学知识。
6. 课堂小结:回顾本节课所学内容,总结磁通量的计算方法和高斯定理的应用。
7. 布置作业:设计一些有关磁通量和磁场强度的问题,让学生课后思考和练习。
六、教学拓展1. 引导学生探讨磁通量的单位及转换关系,加深对磁通量概念的理解。
2. 分析高斯定理在不同磁场分布下的应用,如均匀磁场、非均匀磁场等。
七、课堂互动1. 提问:磁通量的计算方法有哪些?2. 提问:高斯定理在实际应用中有什么意义?3. 讨论:磁通量与磁场强度之间的关系如何理解?八、教学评价1. 课后作业:检查学生对磁通量计算和高斯定理应用的掌握情况。
2. 课堂表现:观察学生在讨论和解决问题时的参与程度和理解程度。
九、教学反思1. 总结本节课的教学效果,反思教学方法是否适合学生的学习需求。
磁场的高斯定理,说明

磁场的高斯定理,说明高斯定律(gauss' law),属物理定律。
在静电场中,穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关,且等于封闭曲面的电荷的代数和除以真空中的电容率。
该定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。
静电场中通过任意闭合曲面(称高斯面)s 的电通量等于该闭合面内全部电荷的代数和除以真空中的电容率,与面外的电荷无关。
物理定律由于磁力线总是闭合曲线,因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来,否则这条磁力线就不会闭合起来了。
如果对于一个闭合曲面,定义向外为正法线的指向,则进入曲面的磁通量为负,出来的磁通量为正,那么就可以得到通过一个闭合曲面的总磁通量为0。
这个规律类似于电场中的高斯定理,因此也称为高斯定理。
与静电场中的高斯定理相比较,两者有著本质上的区别。
在静电场中,由于自然界中存有着单一制的电荷,所以电场线存有起点和终点,只要闭合面内有净余的也已(或负)电荷,沿着闭合面的电通量就不等于零,即为静电场就是有源场;而在磁场中,由于自然界中没单独的磁极存有,n极和s极就是无法拆分的,磁感线都就是无头无尾的滑动线,所以通过任何闭合面的磁通量必等于零。
特别要强调两点: 1.关于电场线的方向的规定:电场线上每一点的切线方向就是该点电场的方向。
2.关于电场线的疏密的规定:电场线在某处的疏密要反映电场强度的大小,即在电场中通过某一点的电场线的数密度与该点电场强度的大小呈正相关,即: e=dn/ds,其中ds是在电场中的某一点取一个通过该点的且与电场线垂直的微分面,dn就是穿过该面ds的电场线的根数。
高斯定理来源于库仑定律,依赖场强共振原理,只有当电场线密度等同于场强悍小时场线通量就可以与场强通量等同于,并统一遵守高斯定理。
高斯面上的实际场强就是其内外所有电荷产生的场强共振而变成的合场强。
但利用高斯面所求出的场强则仅仅就是分析高斯面上场强原产时所牵涉的电荷在高斯面上产生的合场强,而不涵盖未牵涉的电荷所产生的场强。
11-3 磁通量磁场的高斯定理

B
N B S
11 – 3 磁通量 磁场的高斯定理
I I
第十一章 稳恒磁场 I
I
S
S N
I N
11 – 3 磁通量 磁场的高斯定理 性质: 任何两条磁感线不相交. ①
第十一章 稳恒磁场
②磁感线是闭合曲线,并与闭合载流导线相套合. ③磁感线密处 B 大,即磁场强,反之磁场弱 .
二 磁通量
第十一章 稳恒磁场
B
S
dS1 1 B1
闭合曲面:外法线方向为正
dS2
2
B2
dΦ B1 dS1 0 1 dΦ2 B2 dS 2 0
S
B cosdS 0
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通量必等于零 (故磁场是无源场.)
11 – 3 磁通量 磁场的高斯定理 一 磁 感 线(magnetic induction lines)
第十一章 稳恒磁场
规定: ① 曲线上每一点的切线方向就是该点的磁感强 度 B 的方向. ②磁感线的疏密程度表示该点的磁感强度的大小.
磁场中某点处垂直 B 矢量的单位面积上通过的 磁感线数目(磁感线密度)等于该点 B 的数值.
11 – 3 磁通量 磁场的高斯定理
第十一章 稳恒磁场
例 如图载流长直导线的电流为 I , 试求通过矩 形面积的磁通量. 解 先求 ,对变磁场
B
I
d1
d2
o
B // S 0 I dΦ BdS ldx l 2π x 0 Il d 2 dx Φ S B dS d1 2π x 0 Il d 2 x Φ ln 2π d1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dΦ m
B
= ∫ B cosθds
S
dS
单位:韦伯, 单位:韦伯,Wb (Weber 法国物理 学家 1804-1891) 为标量,只有大小正负之分。 Φm为标量,只有大小正负之分。
S
0 ≤θ <
π
2
,
Φm > 0
π
2 对于任意曲面,应先选择曲面正法向,通量才有确定的意义。 对于任意曲面,应先选择曲面正法向,通量才有确定的意义。
θ
B
∫ B ⋅ ds = 0
S
θ
B
θ < π / 2, Φ m > 0, 穿出为正
三、磁场的Gauss定理 磁场的Gauss定理
1. 定理表述 任何磁场中通过任意封闭曲面的 磁通量恒等于零, 磁通量恒等于零,即
∫ B ⋅ ds = 0
S
2. 讨论 1) 磁场 磁场Gauss定理与电场 定理与电场Gauss定理的对比 定理与电场 定理的对比 电场是有源、保守场,而磁场是无源、非保守场; 电场是有源、保守场,而磁场是无源、非保守场 如果有磁单极子存在,磁场的Gauss定理要修改为: 定理要修改为: 如果有磁单极子存在,磁场的 定理要修改为
B
2 磁力线性质
磁力线总是闭合的(磁场的无源性); 磁力线总是闭合的(磁场的无源性); 磁力线永不相交(磁场的唯一性); 磁力线永不相交(磁场的唯一性); 磁力线密处 B 大;磁力线疏处 B 小。
3 磁力线与点力线的比较(略) 磁力线与点力线的比较(
二、磁通量
磁通量——通过磁场中某一曲面的磁感线数,称为 通过磁场中某一曲面的磁感线数, 磁通量 通过磁场中某一曲面的磁感线数 通过该曲面的磁通量。 通过该曲面的磁通量。
∫ B ⋅ ds = µ ∑
S 0
内
g ⇔ ∫ E ⋅ ds =
S
1
ε0
∑
内
q
2) 成立条件:稳恒电流。但是进一步研究表明,上述磁场 成立条件:稳恒电流。但是进一步研究表明, 定理是普遍成立的; 的Gauss定理是普遍成立的; 定理是普遍成立的 3) 由于磁场是无源场,因而不能由Gauss定理计算磁场。 由于磁场是无源场,因而不能由 定理计算磁场。 定理计算磁场
<θ ≤π,
Φm < 0
3.穿过闭合曲面的磁通量
Φ m = ∫ dΦ m = ∫ B ⋅ ds
S
π / 2 < θ ≤ π , Φm < 0,穿入为负
n
对闭合曲面——Gauss面规定外法 闭合曲面 面规定外法 向为正。 向为正。 对于闭合曲面,由于磁力线是无 对于闭合曲面,由于磁力线是无 头无尾的闭合曲线,所以穿入、 头无尾的闭合曲线,所以穿入、穿出 的磁力线条数相等, 的磁力线条数相等,则对任意闭合曲 n 面的磁通量为零。 面的磁通量为零。
1 穿过一面元 的磁通量 穿过一面元dS的磁通量
dS
n
dΦ m B= dS ⊥
θ
dS ⊥
dΦ m = BdS ⊥ = BdS cosθ
dΦ m = B ⋅ d S
θ
B
பைடு நூலகம்
ˆ dS = dSn
n为法线方向单位矢量。 为法线方向单位矢量。 为法线方向单位矢量
2 穿过某一曲面的磁通量
Φ m = ∫ dΦ m = ∫ B ⋅ ds
磁场的Gauss定理 § 11.3 磁通量 磁场的 定理
同电场中引 入电力线来形象 地描述电场一样, 地描述电场一样, 可以引入磁力线 来形象地描述磁 场的分布及其特 点。
一、磁力线
1 规定
在磁场中画一系列曲线, 在磁场中画一系列曲线,并规定 方向:曲线上任一点的切线方向为该点的磁场方向。 方向:曲线上任一点的切线方向为该点的磁场方向。 大小:通过磁场中某点并垂直于磁场B的单位面积的 大小:通过磁场中某点并垂直于磁场 的单位面积的 磁力线数正比于该点的赤感应强度的大小。 磁力线数正比于该点的赤感应强度的大小。 dΦ m dS ⊥ B= dΦ m dS ⊥ 即磁感应强度大小为磁力线 的面密度。 的面密度。
