02数字信号处理2
数字信号处理 第2章.ppt

X e (ej ) FT[xr (n)] xi (n)e jn n
X o (ej ) FT[ jxi (n)] j xi (n)e jn n
第2章 时域离散信号和系统的频域分析
上面两式中,xr(n)和xi(n)都是实数序列。容易证明:Xe(ejω) 满足(2.2.20)式,具有共轭对称性,它的实部是偶函数, 虚部是奇函数;Xo(ejω) 满足(2.2.21)式,具有共轭反对 称性质,它的实部是奇函数,虚部是偶函数。
(2.2.1)
第2章 时域离散信号和系统的频域分析
FT为Fourier Transform的缩写。FT[x(n)]存在的充 分必要条件是序列x(n)满足绝对可和的条件,即满足下式:
| x(n) |
n
(2.2.2)
X(ejω)的傅里叶反变换为
x(n) IFT[X (ej )] 1 π X (ej )d (2.2.3) 2π π
n0 n0
n0
第2章 时域离散信号和系统的频域分析
第2章 时域离散信号和系统的频域分析
【例2.2.1】 设x(n)=RN(n),求x(n)的傅里叶变换。
解
N 1
x(e j )
RN (n)e jn e j
n
n0
1 e jN e jN / 2 (e jN / 2 e jN / 2 ) 1 e j e j / 2 (e j / 2 e j / 2 )
X o (ej )
1 [ X (ej ) 2
X *(e j )]
(2.2.23)
有了上面的概念和结论,下面研究FT
第2章 时域离散信号和系统的频域分析
(1) 将序列x(n)分成实部xr(n)与虚部xi(n),即 x(n)=xr(n)+jxi(n)
数字信号处理第2章

Z变换与拉氏变换的关系:
这一关系实际上是通过 到了Z平面。
若将Z平面用极坐标表示
标表示
,代入
将S平面的函数映射
,S平面用直角坐 ,得:
上述关系表明: z 的模 r 仅与 s 的实部 相对应, z 的幅角 则仅与 s 的虚部 对应。
映射关系:
Z变换与拉氏变换的关系
0 0,2 (S平面实轴映射到Z平面的正实轴)
解:
,求它的傅立叶变换。
其幅度谱和相位谱分别为:
典型例题
❖ 例2 已知序列的傅立叶变换如下,求它的反变换。
解:
显然序列 h(n)不是绝对可和的,而是平方可和 的 ,但其依然存在傅立叶变换。 Parseval定理
典型例题
❖ 例3 证明复指数序列 x(n) e j0n 的傅立叶变换为:
证:根据序列的傅立叶反变换定义,利用冲击函 数 的性质,有:
即序列绝对可和
某的有 立些序些叶既列序变不,列换满若虽依足引然然绝入不存对频满在可 域足。和的以见的冲上后条击条例件函件。也数,不但满满,足足其平平傅方方立可可叶和和变条,换件其傅
也存在。如
、某些周期序列,见后例。
序列傅立叶变换的定义
5.常用序列的傅立叶变换
序列
(n)
傅立叶变换
1
1
典型例题
❖ 例1 已知
A形k(式k=求0,X取1(…:z),N)B,(此z) A( z )
时
为了方bi 便z i通常利用
i0
N
1 ai z i
X(z)/z的
i 1
若序列为因果序列,且N≥M,当X(z)的N个极点都是单
极点时,可以展开成以下的部分分式的形式:
则其逆Z变换为:
数字信号处理第2章 Z变换综述

例4:求序列 x(n) a u (n)的Z变换及收敛域。
n
解: X ( z )
n
n n n n 1 n a u ( n ) z a z ( az ) n 0 n 0
1 az 1 (az 1 ) 2 (az 1 ) n
1 — 64
Z -
-2
-3 1 —— Z 256
1 -3 —— Z 256
...
极点分为:实极点、复极点 若为复极点必然是共轭极点,必然是成对出现
例:
z 1 z z X ( z) 2 1 2 1 z z z z 1 ( z 1 )2 ( 3 j)2 2 2
因为D(z)的系数是实数,所以复极点必然成对出现
§2.3
z变换性质1
一、线性: Z[a x (n)+a x (n)]=a Z[x (n)]+a Z[x (n)]
1 1 2 2 1 1 2 2
二、时移: Z[x(n)]=X(z)
Z[x(n-m)]=z-m· X(z)
意义:z-1:单位延迟器
z变换性质2
三、时域卷积:
x(n) h(n) y(n)
|a|<|z|<1/|a|
双边序列的收敛域是左边序列和右边序列z变换的 公共收敛区间。
课本P27表2.1
z nu(n) ~ ( z 1) 2
作业2.1(2)(6)
z 2 sin z sin(0 ) sin(n0 )u (n) ~ z 2 2 z cos0 1 sin z 1 sin(0 ) 1 2 z 1 cos0 z 2
z z 1 z z X ( z) 2 z 4 z 3 ( z 1)(z 3) 2 z 1 z 3
数字信号处理(第二版) 绪论

三、发展与运用
年代 60年代 70年代 80年代 90年代 21世纪
特点 大学探索 军事运用 商用成功 消费类电子 能源、居家
$/MIPS $100-$1,000 $10-$100 $1-$10 $0.1-$1 $0.01以下
三、发展与运用
上个世纪60年代计算机每秒可以完成百万 次操作,而1024点的DFT就需要百万次的复 数乘法运算。
三、发展与应用
1946年 宾夕法尼亚大学发明了第一代电子管计算 机
1957年 飞歌公司制造出第二代晶体管计算机 1964年 IBM公司制造出第三代集成电路计算机 1971年 Intel公司制造出第四代微型计算机―微处
理器 1975年 第一台PC机 1979年 苹果机问世 1982年 IBM—PC
数字信号处理
Digital Signal Processing 绪论
从模拟到数字
1、留声机诞生于1877年 。它的发明人就是誉满全球 的发明大王爱迪生。
2、模拟系统经历了一个世纪 的历程。留声机→电唱机→ 钢丝录音机→磁带录音机
3、 1982年问世的CD唱 盘,是数字技术取代模拟技 术的典型产品。 CD唱盘只用 了5年就淘汰了唱片。
3、可以实现模拟系统很难达 到的指标或特性
例如: 有限长单位脉冲响应数字滤波器可以实 现严格的线性相位; 在数字信号处理中可以将信号存储起来 ,用延迟的方法实现非因果系统,从而 提高了系统的性能指标; 数据压缩方法可以大大地减少信息传输 中的信道容量。
4、可以实现多维信号处理
利用庞大的存储单元,可以存储 二维的图像信号或多维的阵列信 号,实现二维或多维的滤波及谱 分析等。
信号可以由单个信号源产生,也可以由多个信号源产 生。前者是一标量信号(Scalar signal),而后者是一向 量信号通常也称作多通道信号(Multichannel signal),例 如,立体声信号是一种双通道信号。
(完整word版)数字信号处理第二章习题解答
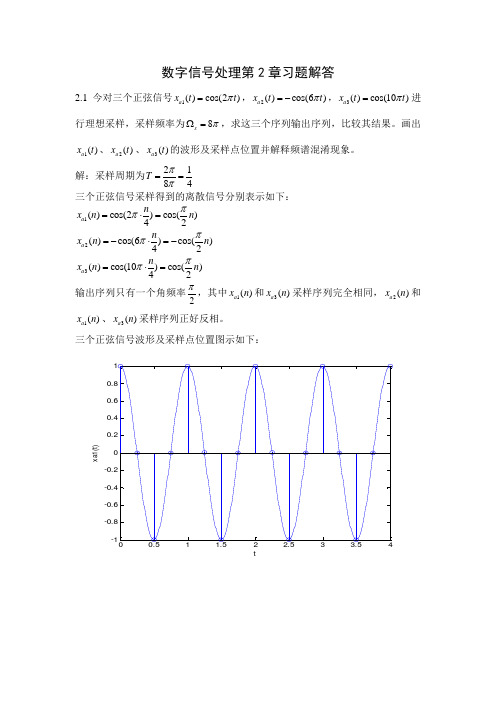
数字信号处理第2章习题解答2.1 今对三个正弦信号1()cos(2)a x t t π=,2()cos(6)a x t t π=-,3()cos(10)a x t t π=进行理想采样,采样频率为8s πΩ=,求这三个序列输出序列,比较其结果。
画出1()a x t 、2()a x t 、3()a x t 的波形及采样点位置并解释频谱混淆现象。
解:采样周期为2184T ππ== 三个正弦信号采样得到的离散信号分别表示如下:1()cos(2)cos()42a n x n n ππ=⋅=2()cos(6)cos()42a n x n n ππ=-⋅=-3()cos(10)cos()42a n x n n ππ=⋅=输出序列只有一个角频率2π,其中1()a x n 和3()a x n 采样序列完全相同,2()a x n 和1()a x n 、3()a x n 采样序列正好反相。
三个正弦信号波形及采样点位置图示如下:tx a 1(t )tx a 2(t )tx a 3(t )三个正弦信号的频率分别为1Hz 、3Hz 和5Hz ,而采样频率为4Hz ,采样频率大于第一个正弦信号频率的两倍,但是小于后两个正弦信号频率的两倍,因而由第一个信号的采样能够正确恢复模拟信号,而后两个信号的采样不能准确原始的模拟信号,产生频谱混叠现象。
2.3 给定一连续带限信号()a x t 其频谱当f B >时,()a X f 。
求以下信号的最低采样频率。
(1)2()a x t (2)(2)a x t (3)()cos(7)a x t Bt π解:设()a x t 的傅里叶变换为()a X j Ω(1)2()a x t 的傅里叶变换为22()[()]Ba a BX j X j d ππωωω-⋅Ω-⎰因为22,22B B B B πωππωπ-≤≤-≤Ω-≤ 所以44B B ππ-≤Ω≤即2()a x t 带限于2B ,最低采样频率为4B 。
数字信号处理-第2章-精品文档精选文档PPT课件

2.1、数字信号处理系统的基本组成
•大多数数字信号处理的应用中,信号为来自不同模拟信号源,这些模拟 信号(电压或电流)通常为连续时间信号。
•应用数字信号处理(DSP)主要有三个原因: 1)滤波:滤除信号中来自周围环境的干扰或噪声; 2)检测:检测淹没在噪声中的特定信号(如雷达或声纳系统中),当检测 到的信号超过给定的阈值则认为目标信号存在,反之认为不存在; 3)压缩:当信号转换到另外一个域后,在变换域上更容易分辨信息的重 要程度,对重要部分分配多的比特数,次要部分分配尽可能少的比特 数,达到压缩的目的(如DCT算法)。
的是离散时间信号。将连续时间信号转换成离散时间信号的过程叫抽样。
抽样可由称为A/D变换器的器件完成:
量化结果
声卡
5
模拟输入 xa (t)
Ts
抽样器
抽样输出
xˆa (t)
xˆa(t) xa(t)•P (t)
xa(t)(t nTs)
n
xˆa (t)
周期性抽样函数 P (t )
xˆa (t)
Ts
P(t) (tnTs)
是否可以根据抽样后的离散时间序列恢复原始信号? •奈奎斯特抽样频率:能够再恢复出原始信号的最低抽样频率(使 抽样后的信号频谱不发生混叠的最低抽样频率,即信号最高频率的 二倍)
0 s/2 s2 0
•满足奈奎斯特抽样频率的抽样信号可由理想低通滤波器恢复出原 始信号。此后将推导这个过程。
xˆa(t) G (j )/g (t( ) 低 通 y滤 (t) 波 xa) (t)
X a ( j)
xa
(t )e
jt dt
[xa
(t )
•
P
(t )]e
数字信号处理第2章Z变换

s=jΩ X(S)
z=esT
X(z) z=ejω
模拟:x(t)
X(j) =T
X(ejω)
t=nT
s
数字:x(n)
§2.6 离散系统的系统函数和 系统的频率响应
一、离散系统的系统函数
1、差分方程和系统函数的关系
系统的差分方程为:
对方程两边做z变换,得:
整理得系统函数为:
2、 H(z)和单位抽样响应h(n) 的关系
(2)与的关系(=T)
的取值范围是从-→(负频端无意义,只是
用于数学分析),而在圆周上变化,具有明显 的周期性,以2为周期,这样的对应关系非单值
关系,所以要把限制在一个周期内。
= T,从–→, 所以在一个周期内:为–/T→/T
=0,S平面的实轴,
=0,z平面正实轴;
=0(常数), S:平行实轴的直线,
意义:z-1:单位延迟器
z变换性质2
三、时域卷积:
系统函数:
§2.4 z反变换
部分分式法:
X(z)一般是z的有理分式,可写成X(z)=N(z)/D(z),而N(z)、
D(z)一般是实系数多项式,则X(z)可以写成部分分式之和的形 式
再利用已知的z变换:
结合收敛域写出反变换:
需要注意的问题:
①极点zk,为D(z)=0的根 ②计算系数Ak时,要写成:
③利用已知z变换时,注意收敛域
配分法: 例2-4-1:
(在滤波器的设计中,分子、分母通常写成负幂的形式)
求系数Ak
例2-4-2:
利用z变换的时移性质: 令: 则:
长除法-原理
即D(z)除以N(z)的商为z的多项式,多项式的系数即为序列x(n) 左边序列对应z的正次幂的系数,右边序列对应z的负次幂的系数
数字信号处理第2章

能,即白色白色、 白色黑色、 黑色白色、 黑色黑色。 如果
将上述实验视为一个信源,并用a1、 a2分别表示白色球和黑 色球,信源输出的消息就是一个符号序列,可以使用二维随
机矢量描述该信源,即
(a , a ) ( a1 , a2 ) X2 1 1 80 79 80 20 p( x) 100 99 100 99 ( a2 , a2 ) 20 80 20 19 100 99 100 99 ( a2 , a1 )
源输出的随机序列的统计特性与时间的推移无关,那么该序列是平稳的。
平稳随机序列分析相对简单,在实际中,为了分析问题方便起见,假设 分析的序列是平稳的。 如果信源输出的随机序列中,每个随机变量都
是离散的,而且随机矢量的各维概率分布都与时间无关,即任何时刻随
机矢量的各维概率分布相同,那么这样的信源称为离散平稳信源,可以 用N维概率空间描述。
第2章 信源与信源熵
表述的复杂程度将随序列的增加而增加。 而在实际信源中,
p( x1 , x2 ,...xN ) p( xN | x1 , x2 ..., xN 1 ) p ( x1 , x2 ,...xN 1 )
p( x N | x1 , x2 ,... x N 1 ) p ( x N 1 | x1 , x2 ,..., x N 2 ) p ( x1 , x2 ,..., x N 2 ) ...
取出一个球,记录球的颜色(用变量x2表示)。 如果将
这样两次取球实验视为信源输出符号,显然信源输出消息构 成二维随机序列,而构成消息的两个随机变量相互独立,所 以可以用随机变量的乘积加以描述。 在实际通信系统中, 也存在这样的信源。
第2章 信源与信源熵
数字信号处理实验二

实验二 快速傅里叶变换(FFT)及其应用一、思考题(1) 实验中的信号序列()c x n 和()d x n 在单位圆上的z 变换频谱()()c j j d X e X e ωω和会相同吗如果不同,说出哪一个低频分量更多一些,为什么答:设j Z r e ω=⨯ ()()n n G z g n z ∞-=-∞=⨯∑因为为单位圆,故r=1.因为()()j j n n G e g n eωω∞-=-∞=⨯∑,故3723456704()(8)23432j j n j n j j j j j j j c n n X e nen e e e e e e e e ωωωωωωωωωω---------===+-=++++++∑∑ 7235670()(4)43223j j n j j j j j j d n X e n ee e e e e e ωωωωωωωω-------==-=+++---∑比较可知频谱不相同,()c X n 的低频分量多。
(2) 对一个有限长序列进行DFT 等价于将该序列周期延拓后进行DFS 展开,因为DFS 也只是取其中一个周期来运算,所以FFT 在一定条件下也可以用以分析周期信号序列。
如果实正弦信号()sin(2),0.1x n fn f π== 用16点FFT 来做DFS 运算,得到的频谱是信号本身的真实谱吗为什么答:针对原来未经采样的连续时间信号来说,FFT 做出来的永远不会是信号本身的真实频谱,只能够是无限接近。
FFT 频谱泄露问题是一定会存在的,因为毕竟采样率再高,也不能完全达到原来的连续时间信号准确。
原题的采样率是1/10,就是将2*pi 分成10份,即每个正弦波周期进行10次采样,这样的采样率很低,而最后你只截取16个点来做分析,泄露一般会挺严重,看到的频谱,应该是一个上头尖,下面慢慢变宽的尖锥形,而纯正的正弦波的理想频谱应该是在某频点只有一个尖峰。
二.?实验原理:?(1)混叠:采样序列的频谱是被采样信号频谱的周期延拓,当采样频率不满足奈奎斯特采样定理的时候,就会发生混叠,使得刺痒后的序列信号的频谱不能真实的反映原采样信号的频谱。
数字信号处理第二章2

可加性:
2 T [ x1 n x2 n ] [ x1 (n) x2 (n)] sin( n ) 9 7 2 2 x1 (n) sin( n ) x2 (n) sin( n ) 9 7 9 7 y1 (n) y2 (n) 2 T [ax1 n ] ax1 (n) sin( n ) ay1 n 9 7
已知某线性移不变系统,其单位抽样响应h(n)为
h(n) a u (n)
n
讨论其因果性和稳定性
2.3常系数线性差分方程
一、差分方程的表示
二、差分方程的求解
三、系统结构
一.表示法
一个N阶常系数线性差分方程表示为
a
k 0
N
k
y (n k ) m 0b NhomakorabeaM
m
x ( n m)
三.系统结构
1.系统的输入与输出的运算关系的表述,非 实际结构。 2.差分方程可直接得到系统结构。 例:y(n)=b x(n)-a y(n-1)
0 1
用⊕表示相加器; 用 表示乘法器; 用 Z 1 表示一位延时单元。
例:差分方程y(n)= b0 x(n)-a1y(n-1)表示的系统结构为 : x(n)
线性移不变因果系统的充要条件为
h(n)=0,n< 0。或h(n)=h(n)u(n)
六、稳定系统
有界的输入产生有界的输出系统。(BIBO) 线性移不变稳定系统的充要条件是
n
h( n)
p
已知某线性移不变系统,其单位抽样响应h(n)为
h( n) a u ( n)
n
《数字信号处理》课件第2章 (2)

|z|>a的整个区域。
序列的性质决定了Z变换的收敛域。为了进一步搞清这种
关系,我们专门讨论几种特殊序列的情景。
第二章 Z 变 换
Z平面 Im
收敛 域
a
Re
图2.1 序列anu(n)的Z平面上的零、极点与收敛域
第二章 Z 变 换
1 假设该序列只有有限多个序列值不为零, 因而
n2
X (z) x(n)zn
n
n0
等式右边第一项的收敛域为0≤|z|<Rx+,第二项的收敛域为0<|z|≤∞, 所以X(z)的收敛域为0<|z|<Rx+,同样处于以Rx+为半径的一个圆的 里边, 但Z平面的原点已不包括在收敛域之内。
第二章 Z 变 换 4. 双边序列 双边序列是从n=-∞ 延伸到n=∞的序列, 通常可写成
1
X (z) x(n)zn x(n)zn x(n)zn (2-10)
(2-5)
nn1
对这个Z变换而言,z=0及z=∞有可能是它的极点, 这要视n的具
体取值而定。首先,如果n1≥0,x(n)为因果序列, 此时z=∞将不再 是极点,因而其收敛域应该是0<|z|≤∞,即z=∞ 也在其收敛域内。
其次,如果n2<0(即n<0),这时z=0已不是极点,收敛域将是 0≤|z|<∞,Z平面的原点也处于其收敛域内。最一般的情况可能是
x(n) 1 2πj
C'
X
1 p
pn1
p2dp
(2-22)
第二章 Z 变 换
第二章 Z 变 换
对于有理Z变换而言,围线积分用留数定理求值较方便。此时
x(n) 1 X (z)zk1dz [ X (z)zn1在C之内的极点上的留数 ]
数字信号处理(第2版)教学课件第2章 离散系统的变换域分析与系统结构

第 2 章 离散系统的变换域分析与系统结构
图 2-1 x(n) anu(n) 收敛域
图 2-2 x(n) anu(n 1) 收敛域
数字信号处理
3.收敛域与序列特性的关系 (1)有限长序列
【例 2-3】 求矩形序列 RN (n) 的 Z 变换及其收敛域。 解:
X (z)
∞
RN (n)z
n∞
n
N 1
zn
n0
1 zN 1 z1
由结果的分母可以看出,似乎 z = 1 是 X(z)的极
点, 但同时分子 多项式在 z = 1 时也有一个零
点,零、极点对消,因此收敛域为|z| > 0, 即
除原点外的整个 z 平面。
第 2 章 离散系统的变换域分析与系统结构
(2)右边序列 由【例 2-1】的结论可知,一般右边序列的收敛域为 Rx< | z | <∞, 即复平面上半径为 Rx的圆的外侧区域,Rx称为收敛 半径。
常 用的部分分式之和,这些分式都可以通过常用的 Z 变换对
确定 其反变换, 再根据线性性质将各部分分式相加即得到原
序列 x(n)。
各部分分式收敛域的确定,原则如下
(1) 收敛域以极点为边界。
(2)总收敛域为各分式收敛域的交集,或者说各分式的收敛域应 包含总收敛域。
第 2 章 离散系统的变换域分析与系统结构
所示。
第 2 章 离散系统的变换域分析与系统结构
图 2-3 x(n) = b|n|的收敛域
数字信号处理
4.常见序列的 Z 变换收敛域
【例 2-5】 求单位序列(n)、(n8)和(n+5)的 Z 变换和收敛域。
解:
∞
ZT[(n)] (n)zn z0 1
数字信号处理02

j
2 N
am N
2 N
n0
ak
1 N
N 1
~ (n )e x
j
kn
n0
由于
j 2 N ( k LN ) n
e
e
j
2 N
ak
kn
1 N
N 1
~ (n )e x
j
2 N
kn
n0
所以,ak是周期序列,它满足ak=ak+LN 令
~ X ( k ) Na
例 x1(n)=0.5δ(n+1)+δ(n)+ 0.5δ(n–1)
X 1 (e
j
)
n
x1 ( n )e
j n
1 2
e
j
1
1 2
e
j
1 cos
3、反变换式
X (e
j
)
n
x (n )e
j n
两端同乘ejωm并在-π~π(0~2π)内积分
1 N
N 1
~ X (k )
k 0
r
2
( k 0 2 r )
式中k=0,1,2,…,N-1,如果让k在-∞~∞之间 变化,上式可简化为
X (e
j
)
2 N
k
2 ~ X ( k ) ( k) N
基本序列的傅立叶变换举例:
e
j 0 n
2 ( 0 ) e
j n
d e
j 0 n
e
j 0 n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k=
x(k) zk =zmX(z)
一般收敛区不变,也有特例。
例2-11
x(n)= (n) X(z)=1
0 ≤ z ≤ 0 ≤ z < 0 <z≤
x(n+1)=(n+1) X1(z)=z x(n1)=(n1) X2(z)=z1
3、单边z变换的位移性
e
z = z ej0
cos(0n)u(n)= 1 (ej0n+ ej0n) u(n) 2
1 2
z z + j 0 z ej0 z e
z(z cos0) = 2 z 2z cos0+1
z>1
sin(0n)u(n)= 1 (ej0n ej0n) u(n) j2
1 A= 1az1 1 W(z) = 1a
1 = z 1 = 1 1 a
1 B= 1 z 1
a = z1 = 1/a 1a z>1
1 a 1z1 1az1
1 (1 an+1 ) u(n) w(n)= 1 a 应用:求离散系统的零状态响应。 x(n) X(z) y(n)= x(n) h(n) h(n ) H(z) Y(z) =X(z)H(z)
RX<z< RX+
x (n)z n 交换运算次序 nx(n) zn1
d n z = x(n) dz n=
n=
= n=
= z1 nx(n) zn = z1 Z[nx(n) ]
利用
z x(n)=u(n) X(z) = z 1
z>1
(z1) 1 z d z nu(n) z = z = 2 dz z 1 (z 1) (z 1)2 z(z+1) d z z = dz (z 1)2 (z 1)3 z2 z z (n 1)u(n)= nu(n)u(n) = 2 z 1 (z 1)2 (z 1) n 2u ( n ) 2z z ( z+ 1) z = n(n 1)u(n)=n2u(n)nu(n) 3 3 2 ( z 1) (z 1) (z 1)
(1) 若序列x(n)的单边z变换为 x(n)u(n) X(z)
则序列左移后单边z变换为 x(n+m) u(n) zm X(z) x(k) zk
k=0
m 1
m >0
证明 Z[x(n+m)u(n)]=
n=0
x(n+m) zn
令n+m=k
= x(n+m) z(n+m) zm
n=0
两式相乘得到z平面的收敛区为:
RXRY <z< RX + RY +
证明 W(z) =Z[x(n)y(n)] 将
= x(n)y(n)zn
n=
(1) 代入(1)
1 x(n)= j2 W(z) =
c
X(v)vn1dv
RX<v< RX+
n=
1 j2
c
Z{Re[x(n)]}= Z Z{jIm[x(n)]}= Z
1 1 [x(n)+x (n)] = [X(z)+ X(z)] 2 2 1 [x(n)x(n)] 1 [X(z) X(z)] = 2 2
7、初值定理 条件——因果序列 证明 X(z)= x(0)=lim X(z)
z→
(2.4-10)
k=m
序列右移后单边z变换的示意图如图2-7所示。
1
x(n )
X(z)
0
n
1
x(nm) u(n) zm X(z) 图2-7 n
加
0
特别的,
x(n1)u(n) z1 X(z)+x(1 ) x(n2) u(n) z2X(z)+z1 x(1)+zx(2)
(3) 若x(n)为因果序列
1 例2-13已知 x(n)=u(n) X(z)= 1 z 1 y(n)=an u(n) 1 (a<1) Y(z)= 1az1
z>1
z > a
求 w(n)= x(n) y(n) 1 1 解 W(z) =X(z) Y(z) = 1z1 1az1 A B = 1z1 1az1
n→
z →1
(2.4-11)
9、时域卷积定理
已知 x(n) X(z)
y(n) Y(z)
RX<z< RX+ RY<z< RY +
若 则
w(n)= x(n) y(n)
W(z)=X(z)Y(z) R<z<R+ R+ =min[RX +, RY+ ]
其中 R=max[RX , RY ]
z>max[e0, e0 ]
2、双边序列移位 若 则 证明 x(n)X(z) RX<z< RX+
x(n+m)zmX(z) Z[x(n+m)]=
RX<z< RX+
n=
x(n+m) zn
= x(n+m) z(n+m) zm
n=
令n+m=k ,代入上式 Z[x(n+m)]= zm
计算一般用留数法(作复变函数积分困难),即 W(z) = Res[X(v) Y(z/v)v1, ak] 其中ak是v平面上X(v) Y(z/v)v1在围线c内的全部极点。 应用时必须正确确定哪些极点位于积分围线内。
§2.5 z变换与拉普拉斯变换、傅里叶变换的关系 傅里叶变换、拉普拉斯变换以及z变换是在此之前学 习过的三种变换。下面讨论这三种变换之间的内在联 系与关系。 要讨论z变换与拉普拉斯变换的关系,先要研究z平面 与s平面的映射(变换)关系。§2.1节通过理想采样 将连续信号的拉普拉斯变换与采样序列的z变换联系 起来,引进了复变量z,它与复变量s有下面的映射
X(v)vn1dv y(n)zn 交换积分、求和次序
1 X(v)v1 = j2 c
n=
y(n)(z/v)n dv RY<z/v< RY+
1 X(v)v1 = j2 c 1 = j2
n=
y(n)(z/v)n dv
R<v<R+
c
X(v)Y(z/v)v1dv
关系
z=esT
1 或s= lnz T
式中T是采样间隔,对应的采样频率s=2/T 。 为了更清楚地说明(2.5-1)式的映射关系,将s=+j 代入(2.5-1),得
z=esT =e(+j)T = rej
因此得到 r=eT (2.5-2)
= T
式中是数字域频率。
由(2.5-2)式具体讨论s与z平面的映射关系。 (1)s平面的虚轴(=0)映射到z平面的单位圆ej , s平面 左半平面(<0)映射到z平面单位圆内(r=eT <1) ; s平面右半平面(>0)映射到z平面单位圆外(r=eT >1)。 (2) =0时, =0,s平面的实轴映射到z平面上的正 实轴。 s平面的原点( = =0),映射到z平面单位
6、复序列的共轭
若
则 x(n) X(z) x(n) X(z)
n=
RX<z< RX+
RX<z< RX+
n=
证 Z[x(n) ]
应用
n = x (n ) z =
[x(n)(z)n]
=[ x(n)(z)n] =X(z)
n=
10、序列相乘——复卷积定理
(2.4-13) 若w(n)= x(n) y(n) 则 1 W(z) = j2
c
X(v)Y(z/v)v1dv
R<v<R+
R=max[RX ,z/RY + ]<v<min[RX + ,z/RY ]=R+ 其中c是v平面收敛区内一条逆时针封闭曲线 即由 RX<v< RX + RY<z/v< RY +
X(z)= X1(z) + zN X1(z) + z2N X1(z) + = X1(z) (1+ zN + z2N +)
= X1(z)
zmN
m=0
1zmN = X1(z) lim m→ 1zN
1 zN = X1(z) = X1(z) N 1 z zN 1
n=0
x(n)zn =x(0)+ x(1)z1 + x(2)z 2 +
对等式两边取极限
z→
lim X(z) =lim[x(0)+ x(1)z1 + x(2)z 2 + ] = x(0)
z →
8、终值定理
若x(n)是因果序列、除单位圆上可有一个z=1的一阶
极点外,其余极点均在单位圆内。则 lim x(n)=lim (z1) X (z)
利用
z x(n)=u(n) X(z) = z 1
z>1
1z a z n 1 a x(n) X(a z)= = 1 a z 1 z a
a1z>1
+ j0 z) ej 0nu(n)X(e
=
e
j + 0
+ j0
z > a
z z 1 z>1
z(z cosh0) = 2 z 2z cosh0+1 z>max[e0, e0 ]
