第四章课后习题P106
计算机网络课后习题参考答案第四章

第四章网络层1.网络层向上提供的服务有哪两种?是比较其优缺点。
网络层向运输层提供“面向连接”虚电路(Virtual Circuit)服务或“无连接”数据报服务前者预约了双方通信所需的一切网络资源。
优点是能提供服务质量的承诺。
即所传送的分组不出错、丢失、重复和失序(不按序列到达终点),也保证分组传送的时限,缺点是路由器复杂,网络成本高;后者无网络资源障碍,尽力而为,优缺点与前者互易2.网络互连有何实际意义?进行网络互连时,有哪些共同的问题需要解决?网络互联可扩大用户共享资源范围和更大的通信区域进行网络互连时,需要解决共同的问题有:不同的寻址方案不同的最大分组长度不同的网络接入机制不同的超时控制不同的差错恢复方法不同的状态报告方法不同的路由选择技术不同的用户接入控制不同的服务(面向连接服务和无连接服务)不同的管理与控制方式3.作为中间设备,转发器、网桥、路由器和网关有何区别?中间设备又称为中间系统或中继(relay)系统。
物理层中继系统:转发器(repeater)。
数据链路层中继系统:网桥或桥接器(bridge)。
网络层中继系统:路由器(router)。
网桥和路由器的混合物:桥路器(brouter)。
网络层以上的中继系统:网关(gateway)。
4.试简单说明下列协议的作用:IP、ARP、RARP和ICMP。
IP协议:实现网络互连。
使参与互连的性能各异的网络从用户看起来好像是一个统一的网络。
网际协议IP是TCP/IP体系中两个最主要的协议之一,与IP协议配套使用的还有四个协议。
ARP协议:是解决同一个局域网上的主机或路由器的IP地址和硬件地址的映射问题。
RARP:是解决同一个局域网上的主机或路由器的硬件地址和IP地址的映射问题。
ICMP:提供差错报告和询问报文,以提高IP数据交付成功的机会因特网组管理协议IGMP:用于探寻、转发本局域网内的组成员关系。
5.IP地址分为几类?各如何表示?IP地址的主要特点是什么?分为ABCDE 5类;每一类地址都由两个固定长度的字段组成,其中一个字段是网络号net-id,它标志主机(或路由器)所连接到的网络,而另一个字段则是主机号host-id,它标志该主机(或路由器)。
第4章习题解答
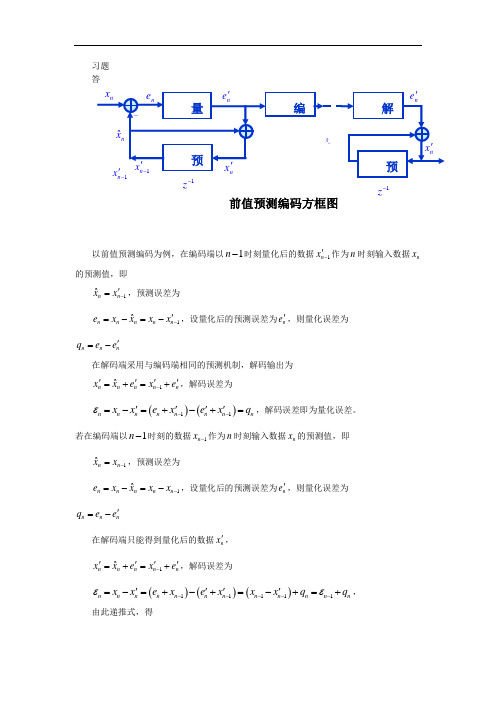
习题 答以前值预测编码为例,在编码端以1n -时刻量化后的数据1nx -'作为n 时刻输入数据n x 的预测值,即1ˆn n xx -'=,预测误差为 1ˆn n n n n e x x x x -'=-=-,设量化后的预测误差为n e ',则量化误差为 n n nq e e '=- 在解码端采用与编码端相同的预测机制,解码输出为1ˆnn n n n x x e x e -''''=+=+,解码误差为 ()()11n n nn n n n n x x e x e x q ε--''''=-=+-+=,解码误差即为量化误差。
若在编码端以1n -时刻的数据1n x -作为n 时刻输入数据n x 的预测值,即1ˆn n xx -=,预测误差为 1ˆn n n n n e x x x x -=-=-,设量化后的预测误差为n e ',则量化误差为 n n nq e e '=- 在解码端只能得到量化后的数据n x ', 1ˆnn n n n x x e x e -''''=+=+,解码误差为 ()()()11111n n nn n n n n n n n n x x e x e x x x q q εε-----''''=-=+-+=-+=+, 由此递推式,得1z -z 前值预测编码方框图01nn i i q εε==+∑,解码误差由量化误差的累积形成,造成信号的严重失真。
因此,在预测编码中用于预测的数据必须是量化后的数据而不能用量化前的数据。
习题设编码帧和已编码参考帧分别用(,)k f x y 和1(,)k f x y -'表示,(,)k f x y 包含P Q ⨯个宏块,每个宏块用,MB p q 表示,其中像素为,MB (,)(16,16), 0,,15; 0,,15; 0,,1; 0,,1p q k m n f p m q n m n p P q Q =++===-=-在已编码参考帧中与,MB p q 空间距离为(i,j )的16×16块中的像素为1(16,16)(16,16), -;-; 0,,15; 0,,15;k k f p m i q n j f p m q n M i M N j N m n -'++++=++≤≤≤≤==其中()()M N ±⨯±为搜索范围。
(整理)第四章能量衡算及热数据的估算习题解答
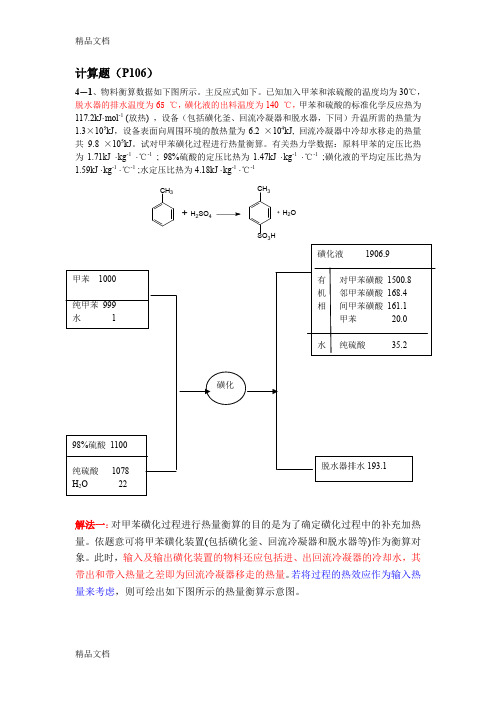
计算题(P106)4-1、物料衡算数据如下图所示。
主反应式如下。
已知加入甲苯和浓硫酸的温度均为30℃,脱水器的排水温度为65 ℃,磺化液的出料温度为140 ℃,甲苯和硫酸的标准化学反应热为117.2kJ·mol -1 (放热) ,设备(包括磺化釜、回流冷凝器和脱水器,下同)升温所需的热量为1.3×105kJ ,设备表面向周围环境的散热量为6.2 ×104kJ, 回流冷凝器中冷却水移走的热量共9.8 ×105kJ 。
试对甲苯磺化过程进行热量衡算。
有关热力学数据:原料甲苯的定压比热为1.71kJ ·kg -1 ·℃-1 ; 98%硫酸的定压比热为1.47kJ ·kg -1 ·℃-1 ;磺化液的平均定压比热为1.59kJ ·kg -1 ·℃-1 ;水定压比热为4.18kJ ·kg -1 ·℃-1解法一:对甲苯磺化过程进行热量衡算的目的是为了确定磺化过程中的补充加热量。
依题意可将甲苯磺化装置(包括磺化釜、回流冷凝器和脱水器等)作为衡算对象。
此时,输入及输出磺化装置的物料还应包括进、出回流冷凝器的冷却水,其带出和带入热量之差即为回流冷凝器移走的热量。
若将过程的热效应作为输入热量来考虑,则可绘出如下图所示的热量衡算示意图。
CH 3+H 2SO 4CH 33H+H 2O则热量平衡方程式可表示为 取热量衡算的基准温度为25o C (若取0 ℃作为基准,结果又如何?),则(1)(2)磺化过程热效应反应中共加入98%浓硫酸的质量为1100kg ,其中含水22kg 。
若以SO 3计,98%硫酸的质量分率为80%。
由式(4-44)得反应结束后,磺化液含硫酸35.2kg,水21.4kg 。
以SO 3计,硫酸的质量分率为50.8%。
则1234567Q Q Q Q Q Q Q ++=+++141000 1.71(3025)1100 1.47(3025) 1.6610Q kJ=⨯⨯-+⨯⨯-=⨯3p cQ Q Q =+1-122111 2.989(2515)110.20130.062 4773.4 kJ (kg H )s H m mm mO -∆=+--++=⋅2-122111 2.989(2515)10.50810.5080.20130.0620.5080.5081833.6 kJ (kg H )s H O ⨯-∆=+--++=⋅所以有反应消耗的甲苯量为979 kg ,则(3)反应产物(磺化液、脱水器排出的水)带走的热量Q 4 Q 4=1906.9 x 1.59 x (140-25)+193.1 x 4.18 x (65-25)=3.77 x 105 KJ (4)由题意知 Q 5=1.3 x 105 KJ Q 6=6.2 x 104 KJ Q 7=9.8 x 105 KJ 所以Q 2=Q 4+Q 5+Q 6+Q 7-Q 1-Q 3=2.12 x 105 KJ4224773.421.41833.6 6.610p Q kJ=⨯-⨯=⨯kJ1025.1 2.1179210979Q 63c ⨯=⨯⨯=kJ1032.1 1025.1106.6 Q Q Q 664cp 3⨯=⨯+⨯=+=解法二:对甲苯磺化过程进行热量衡算的目的是为了确定磺化过程中的补充加热量。
第4章全部习题参考答案

超流水线以增加流水线级数的方法来缩短机器周期,使相同时间内超流水线能执行更多的机器指令。
3.4第4章习题解答1、简要解释下列名词述语虚拟存储器:依靠操作系统的支持来实现的,为用户提供一个比实际内存大的可访问存储器空间,即在软件编程上可使用的存储器,称为虚拟存储器。
随机存储器RAM:按给定地址随机地访问任一存储单元,访问时间与单元位置无关。
只读存储器ROM:在正常工作中只能读出,不能写入的存储器。
存取周期:指存储器做连续访问操作过程中一次完整的存取操作所需的全部时间。
数据传输率:是数据传入或传出存储器的速率。
动态刷新:对动态存储器中原存信息为1的电容补充电荷,称为动态刷新。
直接映像Cache:将主存与Cache的存储空间划分为若干大小相同的页,每个主存页只能复制到某一个固定的Cache页中。
全相联映像Cache:将主存与Cache的存储空间划分为若干大小相同的页,主存的每一页可以映象到Cache的任一页上。
组相联映像Cache:将主存与Cache都分组,主存中一个组内的页数与Cache的分组数相同。
每一组Cache中含有若干页(一般页数较少);则主存中的各页与Cache的固定组号有映象关系,可自由映象到对应的Cache组中任一页。
段页式虚拟存储器:将程序按其逻辑结构分段,每段再分为若干大小相同的页,主存空间也划分为若干同样大小的页。
相应地建立段表与页表,分两级查表实现虚实地址的转换。
以页为单位调进或调出主存,按段共享与保护程序及数据。
相联存储器:是一种按内容寻址的存储器,它是根据所存信息的全部特征或部分特征进行存取的存储器,称为相联存储器。
2.请简计算机系统中的三级存储体系结构模式,并分析这种模式的优点和缺点。
答:三级存储体系包括缓存(cache)、内存和外存,这种模式的优点是层次体系清晰、便于设计实现,也利于系统调度管理,能提高存储系统性能;缺点是结构复杂,管理和控制都比较复杂,硬件成本高。
3.何谓随机存取?何谓顺序存取?何谓直接存取?请各举一例进行说明。
《道路勘测设计》第4章横断面设计课后习题及答案

第四章 横断面设计4-1 某新建三级公路,设计速度V =30km/h ,路面宽度B =7m ,路拱%2=G i ,路肩m b J 75.0=,路肩横坡%3=J i 。
某平曲线转角800534'''= α,半径m R 150=,缓和曲线m L s 40=,加宽值m b 7.0=,超高%3=h i ,交点桩号为K7+086.42。
试求平曲线上5个主点及下列桩号的路基路面宽度、横断面上的高程与设计高程之差:① K7+030;②K7+080;③K7+140;④K7+160。
解:已知:JD =K7+086.42,800534'''= α,m R 150=,m L s 40=⑴平曲线要素计算:)(m R L p s44.015024402422=⨯==)(m R L l q S s 99.191502404024024022323=⨯-=-=)(m tg q tg p R T 19.6799.192800534)0.44150(2)(=+'''⋅+=+⋅+== α)(21.13140800534150180L 180m R L s =+'''⨯⨯=+=παπ)(67.75012800534sec )0.44150(2sec )(m R p R E =-'''⋅+=-⋅+= α)(m L T D 17.321.13119.6722=-⨯=-= (2)主点里程桩号计算 JD K7+086.42 -T -67.19 ZH K7+019.23 +Ls +40 HY K7+059.23ZH K7+019.23+L/2 +131.21/2 QZ K7+84.84ZH K7+019.23+L +131.21 HZ K7+150.44-Ls -40YH K7+110.44⑶超高过渡及加宽计算:新建三级公路,设计速度V =30km/h ,无中间带,超高过渡采用采用内边线旋转,加宽线性过渡,路基边缘为设计高程,加宽值m b 7.0=,超高%3=h i ,临界断面距过渡段起点m L i i x c h G 67.2640%3%20=⨯=•=。
课后习题及答案第4章快速傅里叶变换习题答案.pdf

和共轭反对称分量, 即
F(k)=X(k)+jY(k)=Fep(k)+Fop(k) 计算一次 N 点 IFFT 得到
f(n)=IFFT[F(k)]=Re[f(n)]+j Im[f(n)] 由 DFT 的共轭对称性可知
Re[f(n)]=IDFT[Fep(k)]=IDFT[X(k)]=x(n) j Im[f(n)]=IDFT[Fop(k)]=IDFT[jY(k)]=jy(n)
X (k + N ) = X1(k) −W2kN X 2 (k)
k = 0,1,L, N −1
由上式可解出
X1(k)
=
1 2
[
X
(k)
+
X
(k
+
N )]
X
2
(k)
=
1 2
[X
(k)
+
X
(k
+
N
)]W2−Nk
k = 0,1, 2,L, N −1
由以上分析可得出运算过程如下:
(1)由 X(k)计算出 X1(k)和 X2(k):
Xk=conj(Xk);
%对 Xk 取复共轭
xn=conj(fft(Xk, N))/N; %按照所给算法公式计算 IFFT
分别对单位脉冲序列、 长度为 8 的矩形序列和三角序列进行 FFT, 并调
用函数 ifft46 计算 IFFT 变换, 验证函数 ifft46 的程序 ex406.m 如下:
%程序 ex406.m
Tc = 2TF +1024 次复数乘计算时间 = 2 × 0.1536×10−3 +10×10−9 ×1024
= 0.317 44 ms 可实时处理的信号最高频率 fmax 为
第四章习题答案

第4章习题4-1 对信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.010.015.017.018.019.02.0s s s s s s s P S 7654321进行二元编码,编码方案为(1)计算平均码长L ; (2)编码后信息传输率R ;(3)编码信息率R '; (4)编码效率η。
解:(1)()14.3Ls p L iq1i i=⋅=∑=(码元/信源符号)(2)()61.2S H =(比特/信源符号)()831.014.361.2L S ===H R (bit/码元) (3)logr L R ='=3.14( bit/信源符号) (4)831.0R Rmax==η 或者()831.0R S H ='=η 4-2 设离散无记忆信源的概率空间为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡4143s s S 21P ,若对信源采取等长二元编码,要求编码效率96.0=η,允许译码错误概率510-≤δ,试计算需要的信源序列长度N 为多少?解:信源熵为()811034log 434log 41S .Η=+=(bit/符号)自信息量的方差()()()[]22i q1i i 2S H logp p S -=∑=σ4715.0811.041log 4143log 43222=-⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛= 因为编码效率96.0=η,由()()ε+=S S H H η可得()3379.0811.096.004.0S H 1=⨯=-=ηηε 可得()752221013.4103379.04715.0S N ⨯=⨯=≥-δεσ 所以,信源序列长度达到71013.4⨯以上,才能实现给定的要求,因此等长编码没有实际的意义,一般统计编码都是采用不等长编码。
4-6设离散无记忆信源的概率空间为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1.09.0s s S 21P ,对信源进行N 次扩展,采用霍夫曼编码。
当N=1,2,∞时的平均码长和编码效率为多少?解:(1)N=1时,将1s 编成0,2s 编成1,则1L 1=又因为信源熵()469.0))logp(s p(s S H q1i i i =-=∑=bit/符号所以()469.0L S H 11==η (2)N=2时,编码过程如下2S概率 霍夫曼编码11s s 0.81121s s 0.09 01 12s s 0.09 000 22s s 0.01001所以()=+⨯+⨯+⨯=0.090.0130.0920.811L 2则645.02L 2= 所以()==0.645X H 2η (3)N=∞时,由香农第一定理可知,必然存在唯一可译码,使()S H N L limr NN =∞→而霍夫曼编码为最佳码,即平均码长最短的码,故()()469.0S H S H N L limr NN ===∞→即1lim N N =∞→η4-7已知信源共7个符号消息,其概率空间为()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.010.015.017.018.019.02.0s s s s s s s x P S 7654321试进行香农编码。
第四章习题答案

5 / 6 1 / 6 解 : 传递矩阵为 PY | X = , 输入信源符号的概率 3 / 4 1 / 4 分布可以写成行向量形 式, 即PX = [0.6 0.4] 由信道传递矩阵和输入 信源符号概率向量 , 求得输出符号 5 / 6 1 / 6 概率分布为 PY = PX PY | X = [0.6 0.4] = [0.8 0.2] 3 / 4 1 / 4 输入符号和输出符号的 联合概率分布为 PXY 0.6 0 5 / 6 1 / 6 0.5 0.1 = 3 / 4 1 / 4 = 0.3 0.1 0 0.4
(1) I ( x 1 ) = − log p( x1 ) = − log 2 0.6 = 0.737(bit ) I ( x 2 ) = − log p( x 2 ) = − log 2 0.4 = 1.322(bit ) p( y1 | x1 ) 5/6 ( 2) I ( x1 ; y1 ) = log = log 2 = 0.059(bit ) p( y1 ) 0.8 p( y 2 | x1 ) 1/ 6 I ( x 1 ; y 2 ) = log = log 2 = 0.269(bit ) p( y 2 ) 0.2 p( y1 | x 2 ) 3/4 I ( x 2 ; y1 ) = log = log 2 = 0.09(bit ) p( y1 ) 0.8 p( y 2 | x 2 ) 1/ 4 I ( x 2 ; y 2 ) = log = log 2 = 0.322(bit ) p( y 2 ) 0.2
解:每个字母占用2× 5ms=10ms ,每秒内发出 1000/10=100个字母的代码组(单位:字母/s)。 (1) 各个字母以等概率出现时,每个字母的代码组 含 2bit信息量,传输的平均信息速率R为: R=2×100=200(bit/s) (2) 各字母的出现概率不相等,
《道路勘测设计》第4章横断面设计课后习题及答案

第四章 横断面设计4-1 某新建三级公路,设计速度V =30km/h ,路面宽度B =7m ,路拱%2=G i ,路肩m b J 75.0=,路肩横坡%3=J i 。
某平曲线转角800534'''= α,半径m R 150=,缓和曲线m L s 40=,加宽值m b 7.0=,超高%3=h i ,交点桩号为K7+086.42。
试求平曲线上5个主点及下列桩号的路基路面宽度、横断面上的高程与设计高程之差:① K7+030;②K7+080;③K7+140;④K7+160。
解:已知:JD =K7+086.42,800534'''= α,m R 150=,m L s 40=⑴平曲线要素计算:)(m R L p s44.015024402422=⨯==)(m R L l q S s 99.191502404024024022323=⨯-=-=)(m tg q tg p R T 19.6799.192800534)0.44150(2)(=+'''⋅+=+⋅+== α)(21.13140800534150180L 180m R L s =+'''⨯⨯=+=παπ)(67.75012800534sec )0.44150(2sec )(m R p R E =-'''⋅+=-⋅+= α)(m L T D 17.321.13119.6722=-⨯=-= (2)主点里程桩号计算 JD K7+086.42 -T -67.19 ZH K7+019.23 +Ls +40HY K7+059.23ZH K7+019.23+L/2 +131.21/2 QZ K7+84.84ZH K7+019.23+L +131.21 HZ K7+150.44-Ls -40YH K7+110.44⑶超高过渡及加宽计算:新建三级公路,设计速度V =30km/h ,无中间带,超高过渡采用采用内边线旋转,加宽线性过渡,路基边缘为设计高程,加宽值m b 7.0=,超高%3=h i ,临界断面距过渡段起点m L i i x c h G 67.2640%3%20=⨯=•=。
谢希仁计算机网络第五版(第4章)课后习题答案

第4 章网络层4-01网络层向上提供的服务有哪两种?试比较其优缺点。
答案:虚电路服务和数据报服务。
虚电路的优点:虚电路服务是面向连接的,网络能够保证分组总是按照发送顺序到达目的站,且不丢失、不重复,提供可靠的端到端数据传输;目的站地址仅在连接建立阶段使用,每个分组使用短的虚电路号,使分组的控制信息部分的比特数减少,减少了额外开销;端到端的差错处理和流量控制可以由分组交换网负责,也可以由用户机负责。
虚电路服务适用于通信信息量大、速率要求高、传输可靠性要求高的场合。
虚电路的缺点:虚电路服务必须建立连接;属于同一条虚电路的分组总是按照同一路由进行转发;当结点发生故障时,所有通过出故障的结点的虚电路均不能工作。
数据报的优点:数据报服务不需要建立连接;每个分组独立选择路由进行转发,当某个结点发生故障时,后续的分组可以另选路由,因而提高了通信的可靠性。
数据报服务的灵活性好,适用于传输可靠性要求不高、通信子网负载不均衡、需要选择最佳路径的场合。
数据报的缺点:数据报服务是面向无连接的,到达目的站时不一定按发送顺序,传输中的分组可能丢失和重复,提供面向无连接的、不可靠的数据传输;每个分组都要有目的站的全地址;当网络发生故障是,出故障的结点可能会丢失数据,一些路由可能会发生变化;端到端的差错处理和流量控制只由主机负责。
4-02网络互连有何实际意义?进行网络互连时,有哪些共同的问题需要解决?答案:网络互连暗含了相互连接的计算机进行通信,也就是说从功能上和逻辑上看,这些相互连接的计算机网络组成了一个大型的计算机网络。
网络互连可以使处于不同地理位置的计算机进行通信,方便了信息交流,促成了当今的信息世界。
存在问题有:不同的寻址方案;不同的最大分组长度;不同的网络介入机制;不同的超时控制;不同的差错恢复方法;不同的状态报告方法;不同的路由选择技术;不同的用户接入控制;不同的服务(面向连接服务和无连接服务);不同的管理与控制方式;等等。
第四章总结习题

U 0 1
P(u)
1 4
1 4
2 3
1 4
1 4
接收符号为V={0,1,2,3},其失真矩阵为 0 1 1 1
D 1 0 1 1 1 1 0 1 1 1 1 0
求Dmax,Dmin及信源的R(D)函数,并作出其曲线(取4到5 个点)
2024/7/16
13
习题1
第四章 信息率失真函数
解答:四元对称信源在汉明失真矩阵下,它的平均失真度
信息率失真函数也是一个界限。只要信息率大于这个界限, 译码失真就可限制在给定的范围内。即通信的过程中虽然有 失真,但仍能满足要求,否则就不能满足要求。
2024/7/16
11
第四章 信息率失真函数
研究信道编码和率失真函数的意义
研究信道容量的意义:在实际应用中,研究信道容量是为 了解决在已知信道中传送最大信息率问题。目的是充分利 用已给信道,使传输的信息量最大而发生错误的概率任意 小,以提高通信的可靠性。这就是信道编码问题。
第四步:求D(S),将上述结果代入式(4.2.14)有
nm
D(S)
p(xi ) p( y j )d (xi , y j )ieSd (xi ,y j )
i1 j1
D(S)
p(x1) p( y1)d (x1,
y ) eSd (x1, y1 ) 11
p(x2 ) p( y1)d (x2 ,
y ) eSd (x2 , y1 ) 11
(4.2.10)
p( y1 / x1) p( y1 / x2 ) p( y2 / x1)
p( y1)1eSd (x1, y1) p( y1)2eSd (x2 , y1) p( y2 )1eSd (x1, y2 )
社会保障学作业

社会保障学作业第三章课后题第1、2、6题(p106页)第四章课后题第2、5、6题(p136页)第五章课后题第1、3、8题(p167页)第六章课后题第3、5题(p199页)第七章课后题第1、5题(p231页)第八章课后题第2、5题(p262页)第九章课后题第3题 (p286页)第十章课后题第1、3题(p320页)第十一章课后题第2、3、4题(p351页)第十二章课后题第2、3、6题(p387页)1、如何理解社会保障体系的含义及目标?答:社会保障体系,是指由社会保障各个有机组成部分所构成的整体,它强调的是社会保障制度内在结构、项目设臵等。
换言之,社会保障体系是国家依法建立起来的保障国民生活、维护社会稳定的系统,它是由保险、救助、福利、互助和个人自我保障等相互联系的子系统编结成的一个既相对独立、有相互联系的“社会安全网”。
无论以个国家或地区的社会保障体系建设是否已经完善,均会以完备的社会保障体系为其追求目标,这一目标又可以分解为社会保障体系的完整性、协调性与层次性。
2、中国现行社会保障体系框架包括哪些内容?答:第一,从现代社会保障制度所包括的业务内容看,构成社会保障体系的内容主要包括以下三类,社会救助、社会保险、社会福利。
第二对社会保障体系亦可作如下划分,与社会生产相关联的保障制度,普遍保障制度,全民的福利性保障制度。
3、中国适合采取哪种模式来发展自己的社会保障事业?答:如果不是以社会保障制度主体内容为依据,而是从社会保障制度的整体出发,那么,许多国家选择的或正在改革中的社会保障制度,其实是福利保障与保险保障乃至储蓄保障并存、现收现付与部分积累乃至完全积累并存的混合型保障模式。
中国在摒弃社会主义国家传统的国家保险模式后,经过20年来的改革正在逐渐形成中的即是一种混合型社会保障制度,其中既有个别全民性福利,也有社会保险,还引进了个人账户制,社会救助亦因需要者众多而与社会保险制度具有几乎同等重要的地位,从而只能是混合型保障模式。
信息论与编码第四章课后习题答案

−∫
1 − sin x d sin x 1 − sin x
因此有
h( X ) = −2 A log A −
A log e(2 ln 2 − 2 + 2 ln 2 − 2) 2Байду номын сангаас= −2 A log A + 2 A log e − 2 A log e ln 2 = −2 A log A + 2 A log e − 2 A 1 ,因此 2
试计算 h( X ) , h(Y ) , h( XY ) 和 I ( X ; Y ) 。 解: p( x) = ∫ p ( x, y )dy 1 =∫ dy (a 2 − a1 )(b2 − b1 ) = 1 a2 − a1
同理, p( y ) = 因此
1 。 b2 − b1
h( X ) = − ∫ p ( x ) log p ( x)dx = log(a 2 − a1 ) h(Y ) = − ∫ p( y ) log p( y )dy = log(b2 − b1 ) h( XY ) = − ∫ p ( x, y ) log p ( x, y )dxdy = log( a2 − a1 ) + log(b2 − b1 ) I ( X ; Y ) = h( X ) + h(Y ) − h( XY ) = 0 【4.7】在连续信源中,根据差熵、条件差熵和联合差熵的定义,证明 (1) h( X | Y ) ≤ h( X ) ,当且仅当 X 和 Y 统计独立时等号成立; (2)h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) ,当且仅当 X 1 X 2 L X N 彼此统计 独立时等式成立。 证明: (1) h( XY ) = − ∫ p( y )dy ∫ p( x | y ) log p ( x | y )dx ≤ − ∫ p ( y )dy ∫ p( x | y ) log p ( x )dx = − ∫ p( x, y ) log p ( x )dxdy = h( X ) 等号成立当且仅当 p( x | y ) = p ( x ) ,即 p( x, y ) = p( x ) p ( y ) ,因此仅当 X 和 Y 统计 独立时等号成立。 (2)根据条件概率密度的相关公式,有 h( X 1 X 2 X N ) = h( X 1 ) + h( X 2 | X 1 ) + h( X 3 | X 1 X 2 ) + L + h( X N | X 1 X 2 X N −1 ) 根据(1)的结论,条件差熵小于差熵,因此有 h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) 等号成立当且仅当
物理学简明教程第四章课后习题答案高等教出版社

物理学简明教程第四章课后习题答案高等教出版社第四章 机械振动与机械波4-1 一个质点作简谐运动,振幅为A ,在起始时刻质点的位移为2A -,且向x 轴正方向运动,代表此简谐运动的旋转矢量为( )题4-1图分析与解(B )图中旋转矢量的矢端在x 轴上投影点的位移为-A /2,且投影点的运动方向指向Ox 轴正向,即其速度的x 分量大于零,故满足题意.因而正确答案为(B ).4-2 一简谐运动曲线如图(a )所示,则运动周期是( )(A) 2.62 s (B) 2.40 s (C) 2.20 s (D )2.00 s题4-2图分析与解 由振动曲线可知,初始时刻质点的位移为A /2,且向x 轴正方向运动.图(b)是其相应的旋转矢量图,由旋转矢量法可知初相位为-.振动曲线上给出质点从A /2 处运动到x =0处所需时间为1 s ,由对应旋转矢量图可知相应的相位差65232πππϕ=+=∆,则角频率1s rad 65Δ/Δ-⋅==πϕωt ,周期s 40.22==ωπT .故选(B ).4-3 两个同周期简谐运动曲线如图(a )所示, x 1的相位比x 2的相位( )3/π2(A )落后2π(B )超前2π(C )落后π(D )超前π 分析与解 由振动曲线图作出相应的旋转矢量图(b )即可得到答案为(B ).题4 -3图4-4 两个同振动方向、同频率、振幅均为A 的简谐运动合成后,振幅仍为A ,则这两个简谐运动的相位差为( )(A )60 (B )90 (C )120 (D )180分析与解 由旋转矢量图可知两个简谐运动1和2的相位差为120 时,合成后的简谐运动3的振幅仍为A .正确答案为(C ).题4-4图4-5 若简谐运动方程为⎪⎭⎫ ⎝⎛+=4ππ20cos 10.0t x ,式中x 的单位为m ,t 的单位为s.求:(1)振幅、频率、角频率、周期和初相;(2)s 2=t 时的位移、速度和加速度.分析 可采用比较法求解.将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量.运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果.解 (1)将()()m π25.0π20cos 10.0+=t x 与()ϕω+=t A x cos 比较后可得:振幅A =0.10m ,角频率1s rad π20-⋅=ω,初相ϕ=0.25π,则周期s 1.0/π2==ωT ,频率Hz /1T =v .(2)s 2=t 时的位移、速度、加速度分别为()m 1007.7π25.0π40cos 10.02-⨯=+=t x()-1s m 44.4π25.0π40sin π2d /d ⋅-=+-==t x v()-22222s m 1079.2π25.0π40cos π40d /d ⋅⨯-=+-==t x a4-6 一放置在水平桌面上的弹簧振子,振幅A =2.0 ×10-2 m ,周期T =0.50s.当t =0 时,(1)物体在正方向端点;(2)物体在平衡位置、向负方向运动;(3)物体在x =-1.0×10-2m 处,向负方向运动;(4)物体在x =-1.0×10-2 m 处,向正方向运动.求以上各种情况的运动方程.分析 在振幅A 和周期T 已知的条件下,确定初相φ是求解简谐运动方程的关键.初相的确定通常有两种方法.(1)解析法:由振动方程出发,根据初始条件,即t =0 时,x =x 0和v =v 0来确定φ值.(2)旋转矢量法:如图(a )所示,将质点P 在Ox 轴上振动的初始位置x 0和速度v 0的方向与旋转矢量图相对应来确定φ.旋转矢量法比较直观、方便,在分析中常采用.题4-6图解 由题给条件知A =2.0 ×10-2 m ,1s π4/2-==T ω,而初相φ可采用分析中的两种不同方法来求.解析法:根据简谐运动方程()ϕω+=t A x cos ,当0t =时有()ϕω+=t A x cos 0,sin 0ϕωA -=v .当(1)A x =0时,1cos 1=ϕ,则01=ϕ;(2)00=x 时,0cos 2=ϕ,2π2±=ϕ,因00<v ,取2π2=ϕ;(3)m 100120-⨯=.x 时,50cos 3.=ϕ,3π3±=ϕ,由00<v ,取3π3=ϕ; (4)m 100120-⨯-=.x 时,50cos 4.-=ϕ,3ππ4±=ϕ,由00>v ,取3π44=ϕ. 旋转矢量法:分别画出四个不同初始状态的旋转矢量图,如图(b )所示,它们所对应的初相分别为01=ϕ,2π2=ϕ,3π3=ϕ,3π44=ϕ. 振幅A 、角频率ω、初相φ均确定后,则各相应状态下的运动方程为(1)()m t πcos4100.22-⨯=x(2)()()m /2πt π4cos 100.22+⨯=-x(3)()()m /3πt π4cos 100.22+⨯=-x(4)()()m /3π4t π4cos 100.22+⨯=-x 4-7 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ×10-2 m .若使物体上、下振动,且规定向下为正方向.(1)当t =0 时,物体在平衡位置上方8.0 ×10-2m处,由静止开始向下运动,求运动方程.(2)当t =0时,物体在平衡位置并以0.6m·s -1的速度向上运动,求运动方程.分析 求运动方程,也就是要确定振动的三个特征物理量A 、ω和φ.其中振动的角频率是由弹簧振子系统的固有性质(振子质量m 及弹簧劲度系数k )决定的,即ω=k 可根据物体受力平衡时弹簧的伸长来计算;振幅A 和初相φ需要根据初始条件确定.题4-7图解 物体受力平衡时,弹性力F 与重力P 的大小相等,即F =mg .而此时弹簧的伸长量Δl =9.8 ×10-2m .则弹簧的劲度系数k =F /Δl =mg /Δl .系统作简谐运动的角频率为1s 10-=∆==l g m k //ω(1)设系统平衡时,物体所在处为坐标原点,向下为x 轴正向.由初始条件t =0 时,x 10=8.0 ×10-2 m 、v 10=0 可得振幅()m 10082210210-⨯=+=./ωv x A ;应用旋转矢量法可确定初相π1=ϕ[图(a )].则运动方程为()()m π10t cos 100.821+⨯=-x(2)t =0时,x 20=0、v 20=0.6 m·s -1,同理可得()m 100622202202-⨯=+=./ωv x A ;2/π2=ϕ[图(b )].则运动方程为 ()()m π5.010t cos 100.622+⨯=-x4-8 某振动质点的x -t 曲线如图(a )所示,试求:(1)运动方程;(2)点P 对应的相位;(3)到达点P 相应位置所需的时间.分析 由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题.本题就是要通过x -t 图线确定振动的三个特征量A 、ω和0ϕ,从而写出运动方程.曲线最大幅值即为振幅A ;而ω、0ϕ通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比较方便.解 (1)质点振动振幅A =0.10 m.而由振动曲线可画出t 0=0 和t 1=4 s时旋转矢量,如图(b )所示.由图可见初相3/π0-=ϕ(或3/π50=ϕ),而由()3201//ππω+=-t t 得1s 24/π5-=ω,则运动方程为()m 3/π24π5cos 10.0⎪⎭⎫ ⎝⎛-=t x题4-8图(2)图(a )中点P 的位置是质点从A /2 处运动到正向的端点处.对应的旋转矢量图如图(c )所示.当初相取3/π0-=ϕ时,点P 的相位为()000=-+=p p t ωϕϕ(如果初相取成3/π50=ϕ,则点P 相应的相位应表示为()π200=-+=p p t ωϕϕ.(3)由旋转矢量图可得()3/π0=-p t ω,则s 61.=p t .4-9 质量为10 g 的物体沿x 的轴作简谐运动,振幅A =10 cm ,周期T =4.0 s ,t =0 时物体的位移为,cm 0.50-=x 且物体朝x 轴负方向运动,求(1)t =1.0 s时物体的位移;(2)t =1.0 s 时物体受的力;(3)t =0之后何时物体第一次到达x =5.0 cm 处;(4)第二次和第一次经过x =5.0 cm 处的时间间隔.分析:根据题给条件可以先写出物体简谐运动方程)cos(ϕω+=t A x .其中振幅A ,角频率Tπ2=ω均已知,而初相ϕ可由题给初始条件利用旋转矢量法方便求出. 有了运动方程,t 时刻位移x 和t 时刻物体受力x m ma F 2ω-==也就可以求出. 对于(3)、(4)两问均可通过作旋转矢量图并根据公式t ∆=∆ωϕ很方便求解.解由题给条件画出t =0时该简谐运动的旋转矢量图如图(a )所示,可知初相3π2=ϕ.而A =0.10 m ,1s 2ππ2-==T ω.则简谐运动方程为 m )3π22πcos(10.0+=t x (1)t =1.0 s 时物体的位移m 1066.8m )3π22π0.1cos(10.02-⨯-=+⨯=x(2)t =1.0 s 时物体受力N1014.2N )1066.8()2π(101032232---⨯=⨯-⨯⨯⨯-=-=x m F ω (3)设t =0时刻后,物体第一次到达x =5.0 cm 处的时刻为t 1,画出t =0和t =t 1时刻的旋转矢量图,如图(b )所示,由图可知,A 1与A 的相位差为π,由t ∆=∆ωϕ得s 2s 2/ππ1==∆=ωϕt (4)设t =0时刻后,物体第二次到达x =5.0 cm 处的时刻为t 2,画出t =t 1和t = t 2时刻的旋转矢量图,如图(c )所示,由图可知,A 2与A 1的相位差为3π2,故有 s 34s 2/π3/π212==∆=-=∆ωϕt t t题 4-9 图4-10 图(a )为一简谐运动质点的速度与时间的关系曲线,且振幅为2cm ,求(1)振动周期;(2)加速度的最大值;(3)运动方程.分析 根据v -t 图可知速度的最大值v max ,由v max =A ω可求出角频率ω,进而可求出周期T 和加速度的最大值a max =A ω2.在要求的简谐运动方程x =A cos(ωt +φ)中,因为A 和ω已得出,故只要求初相位φ即可.由v -t 曲线图可以知道,当t =0 时,质点运动速度v 0=v max /2 =A ω/2,之后速度越来越大,因此可以判断出质点沿x 轴正向向着平衡点运动.利用v 0=-A ωsin φ就可求出φ.解 (1)由ωA v =max 得1s 51-=.ω,则s 2.4/π2==ωT(2)222max s m 1054--⋅⨯==.ωA a(3)从分析中已知2/sin 0ωA ωA =-=v ,即21sin /-=ϕ6/π5,6/π--=ϕ因为质点沿x 轴正向向平衡位置运动,则取6/π5-=,其旋转矢量图如图(b )所示.则运动方程为()cm 6π55.1cos 2⎪⎭⎫ ⎝⎛-=t x题4-10图4-11 有一单摆,长为1.0m ,最大摆角为5°,如图所示.(1)求摆的角频率和周期;(2)设开始时摆角最大,试写出此单摆的运动方程;(3)摆角为3°时的角速度和摆球的线速度各为多少?题4-11图分析 单摆在摆角较小时(θ<5°)的摆动,其角量θ与时间的关系可表示为简谐运动方程()ϕωθθ+=t cos max ,其中角频率ω仍由该系统的性质(重力加速度g 和绳长l )决定,即l g /=ω.初相φ与摆角θ,质点的角速度与旋转矢量的角速度(角频率)均是不同的物理概念,必须注意区分.解 (1)单摆角频率及周期分别为s 01.2/π2;s 13.3/1====-ωT l g ω(2)由0=t 时o max 5==θθ可得振动初相0=ϕ,则以角量表示的简谐运动方程为t θ13.3cos 36π= (3)摆角为3°时,有()60cos max ./==+θθϕωt ,则这时质点的角速度为()()1max 2max max s 2180800cos 1sin /d d --=-=+--=+-=..ωθϕωωθϕωωθθt t t线速度的大小为1s m 218.0/d d -⋅-==t l v θ讨论 质点的线速度和角速度也可通过机械能守恒定律求解,但结果会有极微小的差别.这是因为在导出简谐运动方程时曾取θθ≈sin ,所以,单摆的简谐运动方程仅在θ较小时成立.4-12 如图(a )所示,质量为1.0 ×10-2kg 的子弹,以500m ·s -1的速度射入木块,并嵌在木块中,同时使弹簧压缩从而作简谐运动,设木块的质量为4.99 kg ,弹簧的劲度系数为8.0 ×103 N ·m -1,若以弹簧原长时物体所在处为坐标原点,向左为x 轴正向,求简谐运动方程.题4-12图分析 可分为两个过程讨论.首先是子弹射入木块的过程,在此过程中,子弹和木块组成的系统满足动量守恒,因而可以确定它们共同运动的初速度v 0,即振动的初速度.随后的过程是以子弹和木块为弹簧振子作简谐运动.它的角频率由振子质量m 1+m 2和弹簧的劲度系数k 确定,振幅和初相可根据初始条件(初速度v 0和初位移x 0)求得.初相位仍可用旋转矢量法求.解 振动系统的角频率为 ()121s 40-=+=m m k /ω 由动量守恒定律得振动的初始速度即子弹和木块的共同运动初速度v 0为12110s m 0.1-⋅=+=m m v m v 又因初始位移x 0=0,则振动系统的振幅为 ()m 105.2//202020-⨯==+=ωωx A v v 图(b )给出了弹簧振子的旋转矢量图,从图中可知初相位2/π0=ϕ,则简谐运动方程为()()m π0.540cos 105.22+⨯=-t x4-13 如图(a )所示,一劲度系数为k 的轻弹簧,其下挂有一质量为m 1的空盘.现有一质量为m 2的物体从盘上方高为h 处自由落入盘中,并和盘粘在一起振动.问:(1)此时的振动周期与空盘作振动的周期有何不同?(2)此时的振幅为多大?题4-13图分析 原有空盘振动系统由于下落物体的加入,振子质量由m 1变为m 1 + m 2,因此新系统的角频率(或周期)要改变.由于()2020/ωx A v +=,因此,确定初始速度v 0和初始位移x 0是求解振幅A 的关键.物体落到盘中,与盘作完全非弹性碰撞,由动量守恒定律可确定盘与物体的共同初速度v 0,这也是该振动系统的初始速度.在确定初始时刻的位移x 0时,应注意新振动系统的平衡位置应是盘和物体悬挂在弹簧上的平衡位置.因此,本题中初始位移x 0,也就是空盘时的平衡位置相对新系统的平衡位置的位移.解 (1)空盘时和物体落入盘中后的振动周期分别为k m ωT /π2/π21== ()k m m ωT /π2/π221+='='可见T ′>T ,即振动周期变大了.(2)如图(b )所示,取新系统的平衡位置为坐标原点O .则根据分析中所述,初始位移为空盘时的平衡位置相对粘上物体后新系统平衡位置的位移,即g km g k m m k g m l l x 2211210-=+-=-= 式中k g m l 11=为空盘静止时弹簧的伸长量,l 2=g km m 21+为物体粘在盘上后,静止时弹簧的伸长量.由动量守恒定律可得振动系统的初始速度,即盘与物体相碰后的速度gh m m m m m m 22122120+=+=v v 式中gh 2=v 是物体由h 高下落至盘时的速度.故系统振动的振幅为 ()gm m kh k g m x A )(21/2122020++='+=ωv 本题也可用机械能守恒定律求振幅A .4-14 质量为0.10kg 的物体,以振幅1.0×10-2 m 作简谐运动,其最大加速度为4.0 m·s -1求:(1)振动的周期;(2)物体通过平衡位置时的总能量与动能;(3)物体在何处其动能和势能相等?(4)当物体的位移大小为振幅的一半时,动能、势能各占总能量的多少?分析 在简谐运动过程中,物体的最大加速度2max ωA a =,由此可确定振动的周期T .另外,在简谐运动过程中机械能是守恒的,其中动能和势能互相交替转化,其总能量E =kA 2/2.当动能与势能相等时,E k =E P =kA 2/4.因而可求解本题.解 (1)由分析可得振动周期s 314.0/π2/π2max ===a A ωT(2)当物体处于平衡位置时,系统的势能为零,由机械能守恒可得系统的动能等于总能量,即J 100221213max 22k -⨯====.m Aa m A E E ω (3)设振子在位移x 0处动能与势能相等,则有42220//kA kx = 得m 100772230-⨯±=±=./A x(4)物体位移的大小为振幅的一半(即2x A =/)时的势能为4221212P /E A k kx E =⎪⎭⎫ ⎝⎛== 则动能为43P K /E E E E =-=4-15 已知两同方向、同频率的简谐运动的运动方程分别为()()m π75.010cos 05.01+=t x ;()()m π25.010cos 06.02+=t x .求:(1)合振动的振幅及初相;(2)若有另一同方向、同频率的简谐运动()()m 10cos 07033ϕ+=t x .,则3ϕ为多少时,x 1+x 3的振幅最大?又3ϕ为多少时,x 2+x 3的振幅最小?题4-15图分析 可采用解析法或旋转矢量法求解.由旋转矢量合成可知,两个同方向、同频率简谐运动的合成仍为一简谐运动,其角频率不变;合振动的振幅()12212221cos 2ϕϕ-++=A A A A A ,其大小与两个分振动的初相差12ϕϕ-相关.而合振动的初相位()()[]22112211cos cos sin sin arctanϕϕϕϕϕA A A A ++=/ 解 (1)作两个简谐运动合成的旋转矢量图(如图).因为2/πΔ12-=-=ϕϕϕ,故合振动振幅为 ()m 1087cos 2212212221-⨯=-++=.ϕϕA A A A A合振动初相位()()[]rad 1.48arctan11cos cos sin sin arctan22112211==++=ϕϕϕϕϕA A A A /(2)要使x 1+x 3振幅最大,即两振动同相,则由π2Δk =ϕ得,...2,1,0,π75.0π2π213±±=+=+=k k k ϕϕ要使x 1+x 3的振幅最小,即两振动反相,则由()π12Δ+=k ϕ得(),...2,1,0,π25.1π2π1223±±=+=++=k k k ϕϕ4-16 两个同频率的简谐运动1 和2 的振动曲线如图(a )所示,求(1)两简谐运动的运动方程x 1和x 2;(2)在同一图中画出两简谐运动的旋转矢量,并比较两振动的相位关系;(3)若两简谐运动叠加,求合振动的运动方程.分析 振动图已给出了两个简谐运动的振幅和周期,因此只要利用图中所给初始条件,由旋转矢量法或解析法求出初相位,便可得两个简谐运动的方程.解 (1)由振动曲线可知,A =0.1 m,T =2s,则ω=2π/T =πs-1.曲线1表示质点初始时刻在x =0 处且向x 轴正向运动,因此φ1=-π/2;曲线2 表示质点初始时刻在x =A /2 处且向x 轴负向运动,因此φ2=π/3.它们的旋转矢量图如图(b )所示.则两振动的运动方程分别为()()m 2/ππcos 1.01-=t x 和(2)由图(b )可知振动2超前振动1 的相位为5π/6.(3)()ϕω+'=+=t A x x x cos 21其中()m 0520cos 212212221.=-++='ϕϕA A A A A ()12π0.268arctan cos cos sin sin arctan 22112211-=-=++=ϕϕϕϕϕA A A A 则合振动的运动方程为 ()()m π/12πc o s 052.0-=t x题4-16 图4-17 图(a )表示t =0 时的简谐波的波形图,波沿x 轴正方向传播,图(b )为一质点的振动曲线.则图(a )中所表示的x =0 处振动的初相位与图(b )所表示的振动的初相位分别为( )()()m 3/ππcos 1.02+=t x题4-17 图(A)均为零 (B)均为2π (C)均为2π- (D)2π与2π-(E)2π-与2π 分析与解 本题给了两个很相似的曲线图,但本质却完全不同.求解本题要弄清振动图和波形图不同的物理意义.图(a )描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态.其中原点处质点位移为零,其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向,利用旋转矢量法可以方便的求出该质点振动的初相位为π/2.而图(b )是一个质点的振动曲线图,该质点在t =0 时位移为0,t >0 时,由曲线形状可知,质点向y 轴正向运动,故由旋转矢量法可判知初相位为-π/2,答案为(D ).4-18一横波以速度u 沿x 轴负方向传播,t 时刻波形曲线如图(a )所示,则该时刻()(A )A 点相位为π(B )B 点静止不动(C )C 点相位为2π3(D )D 点向上运动 分析与解由波形曲线可知,波沿x 轴负向传播,B 、D 处质点均向y 轴负方向运动,且B 处质点在运动速度最快的位置. 因此答案(B )和(D )不对. A 处质点位于正最大位移处,C 处质点位于平衡位置且向y 轴正方向运动,它们的旋转矢量图如图(b )所示.A 、C 点的相位分别为0和2π3.故答案为(C )题 4-18 图4-19 如图所示,两列波长为λ的相干波在点P 相遇.波在点S 1振动的初相是φ1,点S 1到点P 的距离是r 1.波在点S 2的初相是φ2,点S 2到点P 的距离是r 2,以k 代表零或正、负整数,则点P 是干涉极大的条件为( )()()()()()()π2/π2A π2/π2A π2A πA 211212121212k r r k r r k k r r =-+-=-+-=-=-λϕϕλϕϕϕϕ 分析与解 P 是干涉极大的条件为两分振动的相位差π2Δk =,而两列波传到P 点时的两分振动相位差为()λϕϕϕ/π2Δ1212r r ---=,故选项(D )正确.题4-19图4-20 一横波在沿绳子传播时的波动方程为()x y ππ5.2cos 20.0-=,式中y 的单位为m ,t 的单位为s .(1)求波的振幅、波速、频率及波长;(2)求绳上质点振动时的最大速度;(3)分别画出t =1s 和t =2 s 时的波形,并指出波峰和波谷.画出x =1.0 m处质点的振动曲线并讨论其与波形图的不同. 分析 (1)已知波动方程(又称波函数)求波动的特征量(波速u 、频率υ、振幅A 及波长λ等),通常采用比较法.将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y 书写,然后通过比较确定各特征量(式中u x 前“-”、“+”的选取分别对应波沿x 轴正向和负向传播).比较法思路清晰、求解简便,是一种常用的解题方法.(2)讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别.例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即v =d y /d t ;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质的性质决定.介质不变,波速保持恒定.(3)将不同时刻的t 值代入已知波动方程,便可以得到不同时刻的波形方程y =y (x ),从而作出波形图.而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程y =y (t ),从而作出振动图.解 (1)将已知波动方程表示为()[]()m 5.2/π5.2cos 20.0x t y -=与一般表达式()[]0cos ϕω+-=u x t A y /比较,可得0s m 52m 20001=⋅==-ϕ,.,.u A则m 0.2/,Hz 25.1π2/====v u λωv(2)绳上质点的振动速度()[]()1s m 5.2/π5.2sin π5.0d /d -⋅--==x t t y v则1max s m 57.1-⋅=v(3)t =1s和t =2s时的波形方程分别为 ()()()()m ππ5cos 20.0m ππ5.2cos 20.021x y x y -=-=波形图如图(a )所示. x =1.0m 处质点的运动方程为()()m π5.2cos 20.0t y -=振动图线如图(b )所示.波形图与振动图虽在图形上相似,但却有着本质的区别.前者表示某确定时刻波线上所有质点的位移情况,而后者则表示某确定位置的一个质点,其位移随时间变化的情况.题4-20图4-21 波源作简谐运动,其运动方程为()m t πcos240100.43-⨯=y ,它所形成的波形以30m·s-1的速度沿一直线传播.(1)求波的周期及波长;(2)写出波动方程.分析 已知波源运动方程求波动物理量及波动方程,可先将运动方程与其一般形式进行比较,求出振幅A 、角频率ω及初相φ0,而这三个物理量与波动方程的一般形式()[]0cos ϕω+-=u x t A y /中相应的三个物理量是相同的.再利用题中已知的波速u 及公式ω=2πν=2π/T 和λ=uT 即可求解.解 (1)由已知的运动方程可知,质点振动的角频率1s π240-=ω.根据分析中所述,波的周期就是振动的周期,故有s 1033.8/π23-⨯==ωT波长为λ=uT =0.25 m(2)将已知的波源运动方程与简谐运动方程的一般形式比较后可得A =4.0 ×10-3m ,1s π240-=ω,φ0=0故以波源为原点,沿x 轴正向传播的波的波动方程为()[]()()m π8π240cos 100.4/cos 30x t u x t ωA y -⨯=+-=-4-22 图示为平面简谐波在t =0 时的波形图,设此简谐波的频率为250Hz ,且此时图中质点P 的运动方向向上.求:(1)该波的波动方程;(2)在距原点O 为7.5 m 处质点的运动方程与t =0 时该点的振动速度.分析 (1)从波形曲线图获取波的特征量,从而写出波动方程是建立波动方程的又一途径.具体步骤为:1. 从波形图得出波长λ、振幅A 和波速u =λυ;2. 根据点P 的运动趋势来判断波的传播方向,从而可确定原点处质点的运动趋向,并利用旋转矢量法确定其初相φ0.(2)在波动方程确定后,即可得到波线上距原点O 为x 处的运动方程y =y (t ),及该质点的振动速度υ=d y /d t .解 (1)从图中得知,波的振幅A =0.10 m ,波长λ=20.0m ,则波速u =λυ=5.0 ×103m·s-1.根据t =0 时点P 向上运动,可知波沿Ox 轴负向传播,并判定此时位于原点处的质点将沿Oy 轴负方向运动.利用旋转矢量法可得其初相φ0=π/3.故波动方程为()[]()[]()m 3/π5000/π500cos 10.0/cos 0++=++=x t u x t A y ϕω()ϕω+=t cos A y(2)距原点O 为x =7.5m处质点的运动方程为()()m 12π13π5000.10cosy /t +=t =0 时该点的振动速度为 ()-10s m 40.6/12π13sin π50/d d ⋅=-===t t y v题4-22图4-23 平面简谐波的波动方程为()x t y π2π4cos 08.0-=,式中y 和x 的单位为m ,t 的单位为s,求:(1) t =2.1 s 时波源及距波源0.10m 两处的相位;(2)离波源0.80 m 及0.30 m 两处的相位差.解 (1)将t =2.1 s 和x =0 代入题给波动方程,可得波源处的相位π4.81=ϕ将t =2.1 s 和x ′=0.10 m 代入题给波动方程,得0.10 m 处的相位为π2.82=ϕ(2)从波动方程可知波长λ=1.0 m .这样,x 1=0.80 m 与x 2=0.30 m 两点间的相位差πΔπ2Δ=⋅=λϕx4-24 两相干波波源位于同一介质中的A 、B 两点,如图(a )所示.其振幅相等、频率皆为100 Hz ,B 比A 的相位超前π.若A 、B 相距30.0m ,波速为u =400 m ·s -1,试求AB 连线上因干涉而静止的各点的位置.题4-24图分析 两列相干波相遇时的相位差λϕϕϕr Δπ2Δ12--=.因此,两列振幅相同的相干波因干涉而静止的点的位置,可根据相消条件()π12Δ+=k ϕ获得.解 以A 、B 两点的中点O 为原点,取坐标如图(b )所示.两波的波长均为λ=u /υ=4.0 m .在A 、B 连线上可分三个部分进行讨论.1. 位于点A 左侧部分()π14π2ΔA B A B -=---=r r ϕϕϕ因该范围内两列波相位差恒为2π的整数倍,故干涉后质点振动处处加强,没有静止的点.2. 位于点B 右侧部分()π16π2ΔA B A B =---=r r ϕϕϕ显然该范围内质点振动也都是加强,无干涉静止的点.3. 在A 、B 两点的连线间,设任意一点P 距原点为x .因x r -=15B ,x r +=15A ,则两列波在点P 的相位差为()()π1/π2ΔA B A B +=---=x r r λϕϕϕ根据分析中所述,干涉静止的点应满足方程()()π152π1+=+k x x得()2,...1,0,k m 2±±==k x因x ≤15 m ,故k ≤7.即在A 、B 之间的连线上共有15 个静止点.4-25图(a )是干涉型消声器结构的原理图,利用这一结构可以消除噪声.当发动机排气噪声声波经管道到达点A 时,分成两路而在点B 相遇,声波因干涉而相消.如果要消除频率为300 Hz 的发动机排气噪声,则图中弯管与直管的长度差Δr =r 2-r 1至少应为多少?(设声波速度为340 m ·s -1)题4-25图分析 一列声波被分成两束后再相遇,将形成波的干涉现象.由干涉相消条件,可确定所需的波程差,即两管的长度差Δr .解 由分析可知,声波从点A 分开到点B 相遇,两列波的波程差Δr =r 2 - r 1,故它们的相位差为()λλϕ/Δπ2/π2Δ12r r r =-=由相消静止条件Δφ=(2k +1)π,(k =0,±1,±2,…)得 Δr =(2k +1)λ/2根据题中要求令k =0 得Δr 至少应为m 57022.//===∆v u r λ讨论 在实际应用中,由于噪声是由多种频率的声波混合而成,因而常将具有不同Δr 的消声单元串接起来以增加消除噪声的能力.图(b )为安装在摩托车排气系统中的干涉消声器的结构原理图.4-26 一警车以25 m ·s -1的速度在静止的空气中行驶,假设车上警笛的频率为v =800 Hz .求:(1)静止站在路边的人听到警车驶近和离去时的警笛声波频率;(2)如果警车追赶一辆速度为15m ·s -1的客车,则客车上人听到的警笛声波的频率是多少?(设空气中的声速u =330m ·s -1)分析 由于声源与观察者之间的相对运动而产生声多普勒效应,由多普勒频率公式可解得结果.在处理这类问题时,不仅要分清观察者相对介质(空气)是静止还是运动,同时也要分清声源的运动状态.解 (1)根据多普勒频率公式,当声源(警车)以速度υs =25 m ·s -1运动时,静止于路边的观察者所接收到的频率为su u v v υ =' 警车驶近观察者时,式中υs 前取“-”号,故有Hz 6.8651=-='su u v v υ 警车驶离观察者时,式中υs 前取“+”号,故有Hz 7.7432=+='su u v v υ (2)客车的速度为0υ=15m ·s -1,声源(警车)与客车上的观察者作同向运动时,观察者收到的频率为Hz 2.82603=--='su u v v υυ 4-27 蝙蝠在洞穴中飞来飞去,能非常有效地用超声波脉冲导航.假如蝙蝠发出的超声波频率为39 kHz ,当它以声速的401的速度朝着表面平直的岩壁飞去时,试求它听到的从岩壁反射回来的超声波频率为多少?分析:由题意可知,蝙蝠既是波的发出者,又是波的接收者.设超声波的传播速度为u .首先,蝙蝠是声源,发出信号频率为v ,运动速度为40s u =υ,岩壁是接收者,利用多普勒频率公式,即可求得岩壁接收到的信号频率v '.经岩壁反射后频率不变,即岩壁发射信号频率为v ',这时蝙蝠是波的接收者,其运动速度为400u =υ,再次利用多普勒频率公式,可求得蝙蝠接收到的信号频率v ''. 解:将蝙蝠看成波源,则由分析可知,岩壁接收到的信号频率为sυ-='u uv v ,在蝙蝠接收岩壁反射信号时,又将它看成接收者.则蝙蝠接收到的信号频率为 kHz 41kHz 3940/1140/11/1/1s 0s 00=⨯-+=-+=-+='+=''v u u v u u v u u v υυυυυ。
第4章习题解答

习题4.8 答以前值预测编码为例,在编码端以1n -时刻量化后的数据1nx -'作为n 时刻输入数据n x 的预测值,即1ˆn n xx -'=,预测误差为 1ˆn n n n n e x x x x -'=-=-,设量化后的预测误差为n e ',则量化误差为 n n nq e e '=- 在解码端采用与编码端相同的预测机制,解码输出为1ˆnn n n n x x e x e -''''=+=+,解码误差为 ()()11n n nn n n n n x x e x e x q ε--''''=-=+-+=,解码误差即为量化误差。
若在编码端以1n -时刻的数据1n x -作为n 时刻输入数据n x 的预测值,即1ˆn n xx -=,预测误差为 1ˆn n n n n e x x x x -=-=-,设量化后的预测误差为n e ',则量化误差为 n n nq e e '=- 在解码端只能得到量化后的数据n x ', 1ˆnn n n n x x e x e -''''=+=+,解码误差为 ()()()11111n n nn n n n n n n n n x x e x e x x x q q εε-----''''=-=+-+=-+=+, 由此递推式,得1z -z 前值预测编码方框图01nn i i q εε==+∑,解码误差由量化误差的累积形成,造成信号的严重失真。
因此,在预测编码中用于预测的数据必须是量化后的数据而不能用量化前的数据。
习题4.13设编码帧和已编码参考帧分别用(,)k f x y 和1(,)k f x y -'表示,(,)k f x y 包含P Q ⨯个宏块,每个宏块用,MB p q 表示,其中像素为,MB (,)(16,16), 0,,15; 0,,15; 0,,1; 0,,1p q k m n f p m q n m n p P q Q =++===-=-在已编码参考帧中与,MB p q 空间距离为(i,j )的16×16块中的像素为1(16,16)(16,16), -;-; 0,,15; 0,,15;k k f p m i q n j f p m q n M i M N j N m n -'++++=++≤≤≤≤==其中()()M N ±⨯±为搜索范围。
计算机组成与设计第三版 第四章课后答案

注意:最后一项操作中,移入通用寄存起R1最高位的不是状态触发器C的值,而是
ALU运算的符号位Cy的值,通用寄存器和Q联合右移时,不能支持与C的循环移位。
4.10 在浮点数中为什么采用隐藏位?在什么时刻处理隐藏 位?
原码尾数中使用隐藏位技术,是指把非“0”值的 规格化浮点数的尾数最高位上的1强行去掉(隐 藏起来),这是通过左移原来的尾数实现的,最 高位上的1看不见了,却可以使结果的表示精度 多出了一个二进制位,考虑到隐藏位和剩余尾数, 则此时它所代表的实际值在1~2之间。
4.6 运算器内的乘商寄存器的移位操作与通用寄存器的移 位操作之间应有什么样的关联关系吗作是联合 移位,没有乘除寄存器单独移位功能。当通用寄存器本 身移位时,乘除寄存器不受影响。
4.8.以教学计算机为例,说明应如何控制与操作运算器完成指定的数据运算、 传送功能,为什么必须在Am2901芯片之外解决向运算器提供最低位的进位信 号,最低、最高位的移位输入信号,以及状态位的接受与记忆问题。设计完 成如下操作功能的操作步骤和必须提供的信号:把100送入R0,R0的内容送入 R1,完成R0-R1并存入R0,R1的内容减1,R1的内容送入Q,R1和Q与C联合 右移一位。
在什么时刻处理隐藏原码尾数中使用隐藏位技术是指把非0值的规格化浮点数的尾数最高位上的1强行去掉隐藏起来这是通过左移原来的尾数实现的最高位上的1看不见了却可以使结果的表示精度多出了一个二进制位考虑到隐藏位和剩余尾数则此时它所代表的实际值在12之间
计算机组成原理第四章习题
4.1解释定点运算器的功能和组成部件?以Am2901芯片为 实例,来介绍定点运算器的有关知识,你的认知程度如何? 答:定点运算器的功能与组成 ⑴ 对数据进行算术运算和逻辑运算,给出结果某些特征; ⑵ 暂存参加运算的数据和中间结果; ⑶可用硬件完成乘除运算; ⑷ 接受外部数据的输入,送出运算结果; ⑸与计算机其他部件协同工作运算器的组成:①算术与 逻辑运算部件;②通用寄存器;③乘商寄存器;④多路 选择器;⑤输入/输出逻辑电路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
延期付款信用证对付款期限一般由如下两种规定: (1)运输单据开出后若干天付款 (Available at __ days after the date of transport documents) (2)见单后若干天付款 (Available at _____ days after presentation of the documents)
补充:各种单据的制作时间
各种单据的签发时间应符合逻辑性和国际惯例 ,通常提单日期是确定各单据日期的关键,汇 票日期应晚于提单、发票等其他单据,但不能 晚于信用证有效期。
各单据具体日期如下:
发票日期应在各单据之首; 箱单应等于或迟于发票日期,但必须在提单日 之前;ቤተ መጻሕፍቲ ባይዱ提单日期不能超过信用证规定的装运期也不得 早于信用证的最早装运期; 保单的签发日应早于或等于提单日期(一般早 于提单日期2天),但不能早于发票; 产地证不早于发票日期,不迟于提单日;
第四章课后习题P106
关于延期付款信用证的补充 说明
延期付款信用证 (Deferred Payment Credit)
特点:远期付款但不需要汇票的信用证,受益人 交单后要等到付款到期日才能取得付款。 表达:This credit is available by deferred payment with issuing bank or a nominated bank
商检证日期不晚于提单日期,但也不能过分早 于提单日,尤其是鲜活及容易变质的商品; 受益人证明:等于或者晚于提单日; 装船通知:等于或晚于提单日后三天内; 船公司证明:等于或早于提单日。
6.4.4 几种信用证的综合比较
即期付款 信用证
是否需要 汇票 汇票期限 指定兑现银行 指定兑现银行 的兑现责任 兑现方式 追索权 要或不要 即期 代付行 可以不予 付款 即期付款 无 开证行 必须付款
延期付款 信用证
一般不要 —— 代付行 可以不予 付款 延期付款 无 开证行 必须付款
承兑 信用证
一定要 远期 代付行 可以不予承 兑 开证行 必须承兑
议付 信用证
一般要 即期或者远期 议付行 可以不予议付
即期承兑远期付款 无
即期议付 有
