I型错误与II型错误的关系
卫生统计学试题及答案

医学统计学模拟试题(A)一、单选题:在A、B、C、D 和E 中选出一个最佳答案,将答案的字母填在相应下划线的空格里。
(每题1 分)1. 卫生统计工作的基本步骤包括_____。
A 动物实验、临床试验、全面调查和抽样调查B 资料整理、统计描述、参数估计和统计推断C 实验设计、资料收集、资料整理和统计分析D 资料收集、资料核对、资料整理和资料分析E 统计设计、统计描述、统计估计和统计推断2. 以下_____不属于定量资料。
A. 体块指数(体重/身高2)B. 白蛋白与球蛋白比值C. 细胞突变率(%)D. 中性核细胞百分比(%)E. 中学生中吸烟人数3. 关于频数表的制作, 以下_____论述是正确的。
A. 频数表的组数越多越好B. 频数表的下限应该大于最小值C. 频数表的上限应该小于最大值D. 一般频数表采用等距分组E. 频数表的极差是最小值与最大值之和4. 比较身高与坐高两组单位相同数据变异度的大小,宜采用_____。
A. 变异系数(CV)B.标准差(s)C.方差(s2)D.极差(R)E.四分位间距5. 从μ到μ+1.96s 范围外左右两则外正态曲线下的面积是_____ 。
A.2.5% B.95% C.5.0% D.99% E.52.5%6. 关于假设检验的以下论述中,错误的是_____。
A. 在已知A药降血压疗效只会比B 药好或相等时, 可选单侧检验B. 检验水准?定得越小, 犯I型错误的概率越小C. 检验效能1-?定得越小, 犯II型错误的概率越小D. P 值越小, 越有理由拒绝H0E. 在其它条件相同时, 双侧检验的检验效能比单侧检验低7. 两组数据中的每个变量值减同一常数后,做两个样本均数( )差别的t 检验,____。
A. t 值不变B. t 值变小C. t 值变大D. t 值变小或变大E. 不能判断8. 将90 名高血压病人随机等分成三组后分别用A、B 和C 方法治疗,以服药前后血压的差值为疗效,欲比较三种方法的效果是否相同,正确的是____ 。
东北师范大学秋心理统计学第一次作业及答案

单选题(共10道试题,共30分。
)1.已知n=10的两个相关样本的平均数差是10.5,其自由度为 A.92.用从总体抽取的一个样本统计量作为总体参数的估计值称为 B.点估计3.双侧检验是关于()的检验 B.只强调差异而不强调方向性4.某一事件在无限测量中所能得相对出现的次数是 C.概率5.从变量的测量水平来看,以下数据与其他不同类的变量取值 D.1克6.在3×2×2的设计当中有多少个一级交互作用 A.37.方差分析的基本原理是 C.综合的F检验8.进行分组次数分布统计时,关键的一点是 A.确定每组的取值范围9.()表明了从样本得到的结果相比于真正总体值的变异量 D.取样误差10.关于独立组和相关组的说法错误的是A.独立组问题往往来自组内设计B.相关组问题往往来自组内设计C.独立组的两个样本的容量可以不同D.相关组的两个样本容量必然相同满分:3分多选题(共10道试题,共30分。
)1.统计分组需要注意的问题是A.分组以被研究对象本质特征为基础B.分组以被研究对象的具体特征为基础C.分组标志要明确D.分组要包含所有数据E.分组要适当剔除极端数据满分:3分2.对于HSD检验和Scheffe检验,以下说法正确的是A.两种检验都是事后检验B.HSD 检验比Scheffe 检验更加敏感C.HSD 检验只能用于n 相等的情况D.只有Scheffe 检验控制了族系误差E.以上说法均正确3.次数分布图可以清晰直观的给出数据的分布趋势,有不同的类型A.直方图B.棒图C.折线图D.茎叶图E.饼图4.二项分布涉及的问题中A.个体要么具有某种特征,要么不具有某种特征B.要么发生事件X ,要么发生事件YC.一个事件具有两个特征D.XY 时间可以同时发生E.XY 可以同时发生,也可不同时发生5.次数分布图包括:A.直方图B.圆形图C.次数多边形图D.累加次数分布图E.折线图6.下列属于非参数检验的方法有 A.卡方检验B.符号检验C.符号等级检验法D.秩和检验E.中位数检验等。
第7章假设检验

判断结果:接受原假设,或拒绝原假设。
基本思想
参数的假设检验:已知总体的分布类型,对分布函数或 密度函数中的某些参数提出假设,并检验。
基本原则——小概率事件在一次试验中是不可能发生的。
思想:如果原假设成立,那么某个分布已知的统计 量在某个区域内取值的概率应该较小,如果样本的观 测数值落在这个小概率区域内,则原假设不正确,所以, 拒绝原假设;否则,接受原假设。
Hypothesis Testing
■ 假设检验
抗氧化剂
乙酰胆碱酯酶抑制剂 抗炎药物
假设检验是统计钙推通断的道另阻一重滞要剂内容。正是应用统计推断的 理论和方法,人们才能顺利地通过有限的样本信息去把握总体特征, 实现抽样研究的目的。
21
问题实质上都是希望通过样本统计量与 总体参数的差别,或两个样本统计量的 差别,来推断总体参数是否不同。这种 识别的过程,就是本章介绍的假设检验 (hypothesis test)。
假设检验——根据问题的要求提出假设,构造适当的统 计量,按照样本提供的信息,以及一定的 规则,对假设的正确性进行判断。
基本原则——小概率事件在一次试验中是不可能发生的。
1、假设检验的基本思想
假设检验是利用小概率反证法思想,从问
题的对立面(H0)出发间接判断要解决的问 题(H1)是否成立。然后在H0成立的条件下 计算检验统计量,最后获得P值来判断。
Hypothesis Testing
H0: 0 H1: 0
• H1 的内容反映了检验的单双侧。若 H1
为 0 或 < 0,则为单侧检验(onesided test)。若 H1 为 0,则为双侧
置信区间的I型错误和II型错误

置信区间的I型错误和II型错误
前⾔
本⽂主要分两部份,第⼀部分置信区间的定义和应⽤,第⼆部分是置信区间的⼀⼆型错误
⼀、置信区间
置信区间是指由样本统计量所构造的总体参数的估计区间。
在统计学中,⼀个概率样本的置信区间(Confidence interval)是对这个样本的某个总体参数的区间估计。
置信区间展现的是这个参数的真实值有⼀定概率落在测量结果的周围的程度,其给出的是被测量参数的测量值的可信程度,即前⾯所要求的“⼀个概率”。
⼆、错误类型
第⼀类错误:原假设是正确的,却拒绝了原假设。
第⼆类错误:原假设是错误的,却没有拒绝原假设
关系:①α与β是在两个前提下的概率,所以α+β不⼀定等于1,这是两类错误的关系中较为重要的⼀点。
②在其他条件不变的情况下,α与β不可能同时减⼩或增⼤,此消彼长的关系
是更怕I型错误还是II型错误?从风控的⾓度来回答,我觉得将换⼈放进来(第⼆类错误)会⽐将好⼈拒绝(第⼀类错误)要严重。
第五章 统计推断(1)

某一给定值。
检验程序:
(a) 确定假设H 0和H A: H 0:= 0;H A 有三种可能的形式: ( 1 ) 0 (2) 0 (若已知不可能小于 0 ) (3) 0 (若已知不可能大于 0 )
(b)计算检验的统计量:
1. 单个样本平均数检验
在实际研究中,常常要 检验一个样本平均数 x与已知的总体 平均数0是否有显著差异,即检 验该样本是否来自某一 已知 的总体。
已知的总体平均数一般 为一些公认的理论数值 。如畜禽正常 的生理指标、怀孕期、 生产性能指标等,都可 以样本平均数 与之比较,检验差异显 著性。
1.1 在σ已知的情况下,单个平均数的显著性 检验-u检验 检验程序:
• 两类错误之间的关系如何?
二者的区别是I型错误只有在否定H0的情况下发生,而 II型错误只有在接受H0时才会发生。 二者的联系是,在样本容量相同的情况下,I型错误减 小,II型错误就会增大;反之II型错误减小,I型错误就 会增大。比如,将显著性水平α从0.05提高到0.01,就 更容易接受H0,因此犯I型错误的概率就减小,但相应 地增加了犯II型错误的概率。
第一节 假设检验的基本步骤及原理
1. 假设检验的基本步骤
我们通过一个例子来介绍假设检验的基本步骤:
例一,已知某品种玉米 单穗重X ~ N (300,9.52 ),即单穗重 总体平均数0 300g,标准差 9.5 g。在种植过程中喷洒 了某种药剂的植株中随 机抽取9个果穗,测得平均单穗 重 x 308g,试问这种药剂对该品 种玉米的平均单穗重 有无真实影响?
• (一)提出假设
首先对样本所在的总体 作一假设。假设喷洒了 药剂的玉米单穗重 总体平均数与原来的玉米单穗重总 体平均数0之间没有真实差异, 即=0。也就是说表面差异( x 0)是由抽样误差造成的 。
医学统计学 思考题

第一章绪论1.举例说明总体和样本的概念。
研究人员通常需要了解和研究某一类个体,这个类就是总体。
总体是根据研究目的所确定的所有同质观察单位某种观察值(即变量值)的集合,通常有无限总体和有限总体之分,前者指总体中的个体是无限的,如研究药物疗效,某病患者就是无限总体,后者指总体中的个体是有限的,它是指特定时间、空间中有限个研究个体。
但是,研究整个总体一般并不实际,通常能研究的只是它的一部分,这个部分就是样本。
例如在一项关于2007年西藏自治区正常成年男子的红细胞平均水平的调查研究中,该地2007年全部正常成年男子的红细胞数就构成一个总体,从此总体中随即抽取2000人,分别测的其红细胞数,组成样本,其样本含量为2000人。
2.简述误差的概念。
误差泛指实测值与真实值之差,一般分为随机误差和非随机误差。
随机误差是使重复观测获得的实际观测值往往无方向性地围绕着某一个数值左右波动的误差;非随机误差中最常见的为系统误差,系统误差也叫偏倚,是使实际观测值系统的偏离真实值的误差。
3.举例说明参数和统计量的概念。
某项研究通常想知道关于总体的某些数值特征,这些数值特征称为参数,如整个城市的高血压患病率。
根据样本算得的某些数值特征称为统计量,如根据几百人的抽样调查数据所算得的样本人群高血压患病。
统计量是研究人员能够知道的,而参数是他们想知道的。
一般情况下,这些参数是难以测定的,仅能够根据样本估计。
显然,只有当样本代表了总体时,根据样本统计量估计的总体参数才是合理的。
4.简述小概率事件原理。
当某事件发生的概率小于或等于0.05时,统计学上习惯称该事件为小概率事件,其含义是该事件发生的可能性很小,进而认为它在一次抽样中不可能发生,这就是所谓的小概率事件原理,它是进行统计推断的重要基础。
第二章调查研究设计1.调查研究主要特点是什么?调查研究的主要特点是:①研究的对象及其相关因素(包括研究因素和非研究因素)是客观存在的,不能人为给予干预措施②不能用随机化分组来平衡混杂因素对调查结果的影响。
卫生统计学考试题(第二套)

卫生统计学考试题(第二套).统计推断的内容包括DA.点估计和区间估计B.集中趋势与离散趋势指标C.统计描述和统计图表D.参数估计和假设检验E.参数估计和统计预测.欲测量某地2002年正常成年男子的血糖值,其总体为BA.该地所有成年男子B.该地所有成年男子血糖值C.2002年该地所有正常成年男子血糖值2002年所有成年男子D.2002年所有成年男子的血糖值3. 一组观察值如果每个值都同时增加或减少一个不为0的常数,则CA.均数改变,几何均数不变B.均数改变,中位数不变C.均数,几何均数和中位数都改变D.均数不变,几何均数和中位数改变E.均数,几何均数和中位数都不变4.上四分位数即BA.第5百分位数B.第25百分位数C.第50百分位数D.第75百分位数E.第95百分位数E. F38.配对设计差值的符号秩和检验用正态近似法的条件是E<25A.n>30n>40B.n>50n>25A.实验对照B.空白对照C.安慰剂对照D.标准对照E.历史对照.某医师研究丹参预防冠心病的作用,实验组用丹参,对照组用无任何作用的糖丸,这属于C39.某医师研究乙酰半胱氨酸的祛痰效果,实验组用乙酰半胱氨酸,对照组用“疗效公认的”漠己新,这种对照称为D5.下列指标可较全面地描述正态分布资料特征的是DA.中位数和方差B.均数和中位数C.中位数和极差D.均数和标准差E.几何均数和标准差6.设随机变量X符合均数为四标准差为o (。
#1)的正态分布,作u =(X-|i)M 的变量变换,则和X的均数与标准差相比,其pi值的CA.均数不变,标准差变B.均数和标准差都不变C.均数变而标准差不变D.均数和标准差都改变E.均数与标准差的变化情况无法确定7.关于标准差与标准误,以下说法正确的是EA.标准误可用来估计医学参考值范围8.标准差可反映样本均数的变异程度C.标准误可描述正态(近似正态)分布资料的频数分布D.样本含量一定时,标准差越大,标准误越小E.标准误是表示抽样误差的大小的指标8.已知某地正常人某定量指标的总体均值M=5,今随机测得该地某人群中80 人该指标的数值,若资料满足条件使用,检验来推断该人群该指标的总体均值pi 与w之间是否有差别,则自由度为D4A.5C. 76D. 79E. 809.关于假设检验,下列说法中正确的是BA.单侧检验优于双侧检验B.采用配对t检验还是成组t检验取决于研究设计C.检验结果若P值小于0.05,则接受Ho,犯错误的可能性很小D.由于配对t检验的效率高于成组t检验,因此最好都用配对t检验E.进行假设检验时拒绝厅。
卫生统计学

(一)最佳选择题1.两样本均数比较的t 检验,差别有统计学意义时,P 越小,说明( )。
A.两样本均数差别越大B.两总体均数差别越大C.越有理由认为两总体均数不同D.越有理由认为两样本均数不同E.越有理由认为两总体均数相同2. 甲乙两人分别从同一随机数字表抽得30个(各取两位数字)随机数字作为两个样本,求得1X 和21S ;2X 和22S ,则理论上( )。
A.12XX =B.2212S S =C.作两样本均数比较的t 检验,必然得出无统计学意义的结论D.作两样本方差比较的F 检验,必然方差齐E.由甲、乙两样本均数之差求出的总体均数95%可信区间,很可能包括0 3. 在参数未知的正态总体中随机抽样,Xμ-≥( )的概率为5%。
A. 1.96σB. 1.96C. 2.58D.0.05/2, tSνE.0.05/2, XtS ν4. 某地1992年随机抽取100名健康女性,算得其血清总蛋白含量的均数为74g/L ,标准差为4g/L ,则其95%的参考值范围为( )。
A.74±4⨯4B.74±1.96⨯4C.74±2.58⨯4D.74±2.58⨯4÷10E. 74±1.96⨯4÷10 5. 关于以0为中心的t 分布,错误的是( )。
A. t 分布图是一簇曲线B. t 分布图是单峰分布C.当ν→∝时,t →zD. t 分布图以0为中心,左右对称E.相同ν时,|t|越大,P越大6. 在两样本均数比较的t检验中,无效假设是()。
A.两样本均数不等B.两样本均数相等C.两总体均数不等D.两总体均数相等E.样本均数等于总体均数7. 两样本均数比较作t检验时,分别取以下检验水准,以()所取第二类错误最小。
A.α=0.01B.α=0.05C.α=0.10D.α=0.20E.α=0.308. 正态性检验,按α=0.10水准,认为总体服从正态分布,此时若推断有错,其错误的概率()。
医学统计学整理

名词解释1.医学统计学是一门“运用统计学的原理和方法,研究医学科研中有关数据的收集、整理和分析的应用科学,研究对象为医学中具有不确定性结果的事物。
2.总体(population):根据研究目的所确定的同质观察单位的全体。
只包括(确定的时间和空间范围内)有限个观察单位的总体,称为有限总体(finite population)。
假想的,无时间和空间概念的,称为无限总体(infinite population)。
3.参数(parameter):总体的统计指标或特征值。
总体参数是事物本身固有的、不变的。
4.样本(sample):从总体中随机抽取的部分个体。
5.变量(variable):观察对象个体的特征或测量的结果。
由于个体的特征或指标存在个体差异,观察结果在测量前不能准确预测.变量的观察值称为数据。
6.定量资料:指构成其的变量值是定量的,其表现为数值大小,有单位。
对每个观察单位用定量的方法测定某项指标的数值,组成的资料。
7.计数资料:将全体观测单位按照某种性质或特征分组,再分别清点各组观察单位的个数。
8.有序数据:其取值是定性的,但各类别(属性)之间有程度或顺序上的差别。
9.变异(variation):同质事物间的差别.由于观察单位通常即为观察个体,故亦称为个体变异10.同质:指根据研究目的所确定的观察单位其性质应大致相同。
11.抽样误差(sampling error):由于抽样造成的统计量与参数之间的差别,特点是不能避免的,可用标准误描述其大小。
12.误差:统计上所说的误差泛指测量值与真值之差,样本指标与总体指标之差。
主要有系统误差和随机误差13.可信区间(confidence interval, CI):按一定的概率或可信度(1-α)用一个区间估计总体参数所在范围,这个范围称作可信度1-α的可信区间14.平均数:是一组(群)数据典型或有代表性的值.这个值趋向于落在根据数据大小排列的数据的中心,包括算术平均数(arithmetic mean)、几何平均数(geometric mean)、中位数(median)等。
医学统计学 必过重点

1.总体:是根据研究目的确定的同质的观察单位的全体,更确切的说,是同质的所有观察单位某种观察值(变量值)的集合。
总体可分为有限总体和无限总体。
总体中的所有单位都能够标识者为有限总体,反之为无限总体。
样本:从总体中随机抽取部分观察单位,其测量结果的集合称为样本。
样本应具有代表性。
所谓有代表性的样本,是指用随机抽样方法获得的样本。
2.随机抽样:随机抽样是指按照随机化的原则(总体中每一个观察单位都有同等的机会被选入到样本中),从总体中抽取部分观察单位的过程。
随机抽样是样本具有代表性的保证。
3.变异:在自然状态下,个体间测量结果的差异称为变异。
变异是生物医学研究领域普遍存在的现象。
严格的说,在自然状态下,任何两个患者或研究群体间都存在差异,其表现为各种生理测量值的参差不齐。
4.计量资料:对每个观察单位用定量的方法测定某项指标量的大小,所得的资料称为计量资料。
计量资料亦称定量资料、测量资料。
.其变量值是定量的,表现为数值大小,一般有度量衡单位。
如某一患者的身高(cm)、体重(kg)、红细胞计数(1012/L)、脉搏(次/分)、血压(KPa)等计数资料:将观察单位按某种属性或类别分组,所得的观察单位数称为计数资料(。
计数资料亦称定性资料或分类资料。
其观察值是定性的,表现为互不相容的类别或属性。
如调查某地某时的男、女性人口数;治疗一批患者,其治疗效果为有效、无效的人数;调查一批少数民族居民的A、B、AB、O 四种血型的人数等。
等级资料:将观察单位按测量结果的某种属性的不同程度分组,所得各组的观察单位数,称为等级资料(ordinal data)。
等级资料又称有序变量。
如患者的治疗结果可分为治愈、好转、有效、无效或死亡,各种结果既是分类结果,又有顺序和等级差别,但这种差别却不能准确测量;一批肾病患者尿蛋白含量的测定结果分为+、++、+++等。
等级资料与计数资料不同:属性分组有程度差别,各组按大小顺序排列。
等级资料与计量资料不同:每个观察单位未确切定量,故亦称为半计量资料。
统计学 假设检验

假设检验
雪儿·海蒂(Shere Hite)在1987年出版的《女性与爱情:前进中的文化之旅》一书中给
出了大量数据:
● 84%的女性“在情感上对两性关系不满意”(804页)。
● 95%的女性“在恋爱时会因男友而产生情感及心理上的烦恼”(810页)。
● 84%的女性“在与男友的恋爱中有屈尊感”(809页)。
他对这个问题很感兴趣。他兴奋地说道:“让我
们来检验这个命题吧!”并开始策划一个实验。
在实验中,坚持茶有不同味道的那位女士被奉上
一连串的已经调制好的茶,其中,有的是先加茶
后加奶制成的,有的则是先加奶后加茶制成的。
Hypothesis Testing
接下来,在场的许多人都热心地加入到实验中来。
几分钟内,他们在那位女士看不见的地方调制出
Hypothesis Testing
同样,即便这位女士能做出区分,她仍然有猜错的
可能。或者是其中的一杯与奶没有充分地混合,或
者是泡制时茶水不够热。即便这位女士能做出区分
,也很有可能是奉上了10杯茶,她却只是猜对了
其中的9杯。
Hypothesis Testing
是奶加到茶里,还是茶加到奶里?
假设:她没有这种分辨能力,是碰巧猜对的!
假设其中真有99个白球,摸出
红球的概率只有1/100,这是
小概率事件。
小概率事件在一次试验中竟然发生了,不能不
使人怀疑所作的假设。
这个例子中所使用的推理方法,可以称为
带概率性质的反证法
它不同于一般的反证法
一般的反证法要求在原假设成立的条件
下导出的结论是绝对成立的,如果事实与之
矛盾,则完全绝对地否定原假设。
…99个
6.3 假设检验的两类错误及注意事项

都有可能犯错误(I型错误或者II型错误),假设检验的结论不能绝对化。
二、假设检验需注意的问题
(3)单侧检验与双侧检验的选择
如果有信息(如专业知识)知某个偏离方向不会发生,那么备选假设就 只有一个偏离方向,就是单侧检验。
˙ 假设检验提供具体的P 值,P 值越小,
代表越有理由去拒绝零假设。
小结
一、假设检验的两类错误 ˙Ⅰ型错误 ˙Ⅱ型错误 ˙检验效能 二、假设检验的注意事项 ˙要有严密的研究设计
˙要正确理解P 值和统计结论的意义
˙注意单侧检验与双侧检验的选择 ˙理解参数估计与假设检验的异同点
双侧检验:
H0 : 0
H1 : 0
单侧检验:
①HH01: :
0 0
或
②
HH01: :
0 0
二、假设检验需注意的问题
(4)参数估计与假设检验的异同点
˙ 两者均可用于统计学推断,两者的统 计结论具有同等的效力。 ˙置信区间能够提供包含参数的范围宽 窄的信息。
比较的组间应具有可比性,即各对比组间 除了要比较的主要因素外,其他可能影响结果 的因素应尽可能相同或相近。
二、假设检验需注意的问题
(2)正确理解P值和统计结论的意义
P 值指当零假设成立时,出现当前样本结果以及更极端结果的概率。P
值越小,说明越有理由拒绝零假设,而非说明差异越大。 有统计学意义并不等于有实际临床意义,还应结合专业知识来分析,应
一、假设检验中的二类错误
Ⅰ型错误的概率大小用α 表示,是根据研究 者的要求在计算检验统计量之前设定的。
卫生统计学习题及答案(精华版)

统计学习题二、简答1。
简述描述一组资料的集中趋势和离散趋势的指标。
集中趋势和离散趋势是定量资料中总体分布的两个重要指标。
(1)描述集中趋势的统计指标:平均数(算术均数、几何均数和中位数)、百分位数(是一种位置参数,用于确定医学参考值范围,P50就是中位数)、众数。
算术均数:适用于对称分布资料,特别是正态分布资料或近似正态分布资料;几何均数:对数正态分布资料(频率图一般呈正偏峰分布)、等比数列;中位数:适用于各种分布的资料,特别是偏峰分布资料,也可用于分布末端无确定值得资料. (2)描述离散趋势的指标:极差、四分位数间距、方差、标准差和变异系数。
四分位数间距:适用于各种分布的资料,特别是偏峰分布资料,常把中位数和四分位数间距结合起来描述资料的集中趋势和离散趋势.方差和标准差:都适用于对称分布资料,特别对正态分布资料或近似正态分布资料,常把均数和标准差结合起来描述资料的集中趋势和离散趋势;变异系数:主要用于量纲不同时,或均数相差较大时变量间变异程度的比较。
2。
举例说明变异系数适用于哪两种形式的资料,作变异程度的比较?度量衡单位不同的多组资料的变异度的比较。
例如,欲比较身高和体重何者变异度大,由于度量衡单位不同,不能直接用标准差来比较,而应用变异系数比较. 3。
试比较标准差和标准误的关系与区别.区别:⑴标准差S:①意义:描述个体观察值变异程度的大小.标准差小,均数对一组观察值得代表性好;②应用:与均数结合,用以描述个体观察值的分布范围,常用于医学参考值范围的估计;③与n的关系:n越大,S越趋于稳定;⑵标准误S X:①意义:描述样本均数变异程度及抽样误差的大小.标准误小,用样本均数推断总体均数的可靠性大;②应用于均数结合,用以估计总体均数可能出现的范围以及对总体均数作假设检验;③与n的关系:n越大,S X越小.联系:①都是描述变异程度的指标;②由S X=s/n-1可知,S X与S成正比。
n一定时,s 越大,S X越大。
一类错误与二类错误

一类错误与二类错误:
第一类错误:原假设是正确的,却拒绝了原假设。
第二类错误:原假设是错误的,却没有拒绝原假设。
第一类错误即I 型错误是指拒绝了实际上成立的H0,为“弃真”的错误,其概率通常用α表示,这称为显著性水平。
α可取单侧也可取双侧,可以根据需要确定α的大小,一般规定α=0.05或α=0.01。
第二类错误即II 型错误是指不拒绝实际上不成立的H0,为“存伪”的错误,其概率通常用β表示。
β只能取单尾,假设检验时一般不知道β的值,在一定条件下(如已知两总体的差值δ、样本含量n和检验水准α)可以测算出来。
第一类错误和第二类错误的区别:
第一类错误就是事件直接引发的,而第二类错误由于一些隐藏的因素当时没有显示出来之后发现的或者由第一类错误导致发生的错误。
第一类错误(typeⅠerror),Ⅰ型错误,拒绝了实际上成立的H0,即错误地判为有差别,这种弃真的错误称为Ⅰ型错误。
其概率大小用即检验水准用α表示。
α可取单尾也可取双尾。
假设检验时可根据研究目的来确定其大小,一般取0.05,当拒绝H0时则理论上理论100次检验中平均有5次发生这样的错误。
第二类错误(typeⅡerror)。
Ⅱ型错误,接受了实际上不成立的H0 ,也就是错误地判为无差别,这类取伪的错误称为第二类错误。
第二类错误的概率用β表示,β的大小很难确切估计。
二者的关系是:当样本例数固定时,α愈小,β愈大;反之,α
愈大,β愈小。
因而可通过选定α控制β大小。
要同时减小α和β,唯有增加样本例数。
统计推断中的I型错误和II型错误是什么

统计推断中的I型错误和II型错误是什么在统计学中,当我们进行统计推断时,常常会面临两种类型的错误,即 I 型错误和 II 型错误。
这两种错误对于我们正确理解和解释统计结果至关重要。
首先,让我们来了解一下什么是 I 型错误。
简单来说,I 型错误也被称为“假阳性错误”或“α错误”。
想象一下,我们正在进行一项假设检验,比如检验一种新药物是否有效。
我们先提出一个零假设(通常表示没有效果或没有差异),然后通过收集数据来判断是否有足够的证据拒绝这个零假设。
但有时候,尽管实际上零假设是正确的(也就是说新药物确实没有效果),但由于样本的随机性或者其他因素,我们却错误地拒绝了零假设,得出了药物有效的结论。
这就像是法官在审判一个实际上无罪的人时,却误判他有罪。
这种错误就是 I 型错误。
为了控制 I 型错误的发生概率,我们通常会设定一个显著性水平(通常用α表示)。
例如,如果我们将显著性水平设定为 005,这意味着我们愿意接受 5%的可能性犯 I 型错误。
也就是说,在 100 次假设检验中,平均可能会有 5 次错误地拒绝了实际上正确的零假设。
接下来,我们再看看 II 型错误。
II 型错误也被称为“假阴性错误”或“β错误”。
还是以新药物的检验为例,如果新药物实际上是有效的,但我们的检验结果却没能发现这一点,接受了零假设(即认为药物无效),那么这就是 II 型错误。
这就好比法官在审判一个实际上有罪的人时,却误判他无罪。
II 型错误的发生概率受到多种因素的影响。
其中一个重要的因素是样本量。
通常情况下,样本量越大,我们越有可能发现真实的差异或效果,从而减少 II 型错误的发生概率。
另一个影响因素是效应大小。
如果实际的效应很大,我们更容易检测到,II 型错误的概率就会降低;反之,如果效应较小,就更难检测到,II 型错误的概率就会增加。
那么,I 型错误和 II 型错误之间有什么关系呢?它们之间存在一种权衡关系。
一般来说,如果我们想要减少 I 型错误的概率(降低α),那么往往会增加 II 型错误的概率(增加β);反之,如果我们想要减少 II 型错误的概率,可能就需要增加 I 型错误的概率。
i类误差和ii类误差

i类误差和ii类误差I 类误差和 II 类误差引言:在统计学中,我们经常需要进行各种类型的假设检验。
在这些检验中,我们通常会犯两种类型的错误,即 I 类误差和 II 类误差。
本文将详细介绍这两种错误的定义、原因、影响以及如何最小化它们。
一、I 类误差1. 定义:I 类误差也被称为“虚假阳性”或“α错误”。
它指的是在原假设为真时拒绝了原假设的情况。
2. 原因:I 类误差通常是由于样本数据产生的随机变异或实验设计不合理导致的。
过于宽松的显著性水平(α)也可能导致增加I 类错误发生的概率。
3. 影响:发生 I 类错误会导致我们错误地拒绝了一个真实的假设,即得出了一个虚假阳性结果。
这可能引起不必要的麻烦和浪费资源。
4. 最小化 I 类误差:为了最小化 I 类错误,我们可以采取以下措施:- 合理设计实验:确保实验设计符合科学原则,并尽量减少潜在影响结果的干扰因素。
- 选择适当的显著性水平:根据研究领域和问题的重要性,选择一个合适的显著性水平来控制 I 类错误的概率。
- 增加样本容量:通过增加样本容量可以减少随机误差对结果的影响,从而降低 I 类错误的概率。
二、II 类误差1. 定义:II 类误差也被称为“虚假阴性”或“β错误”。
它指的是在原假设为假时接受了原假设的情况。
2. 原因:II 类误差通常是由于样本数据不足或实验设计不合理导致的。
过于严格的显著性水平(α)也可能导致增加 II 类错误发生的概率。
3. 影响:发生 II 类错误会导致我们未能拒绝一个错误的假设,即得出了一个虚假阴性结果。
这可能导致错失发现真实效应或关联关系的机会。
4. 最小化 II 类误差:为了最小化 II 类错误,我们可以采取以下措施:- 增加样本容量:通过增加样本容量可以提高研究统计功效,从而减少 II 类错误的概率。
- 选择适当的显著性水平:根据研究领域和问题的重要性,选择一个合适的显著性水平来控制 II 类错误的概率。
- 使用更敏感的测量工具:选择更敏感的测量工具可以增加检测到真实效应或关联关系的机会。
卫生统计学

五、填空题1、统计工作的基本步骤是 设计 、 收集 、 整理 、 分析 。
2、统计分析包括 统计描述 和 统计推断 。
3、四分位数间距是(P75和P25)的差。
4、描述正态分布的计量资料两个参数是 u 和 6 。
5、常用的统计资料类型分 数值变量 、无序分类变量 和 有序分类 。
6、常用平均数有均数、(几何均数)和中位数。
7、常用相对数有率、 构成比 和相对比。
8、总体均数区间估计的两个要素是 可信度 和 精度 。
9、t 检验分布曲线的形状与(自由度)有关。
10、四格表资料的χ2检验的自由度为(1)。
11、成组t 检验的自由度为 n-1 ,2χ检验的自由度为 (c-1)(R-_1) 。
12、统计学上一般将P ≤ 0.05 或P ≤ 0.01 定为小概率事件。
13、随机区组设计的方差分析,可将总变异分解为(SS 总=SS 组间+SS 配伍+SS 误差) 14、医学统计中常用相对数有 率、 构成比 相对比15、血清学滴度资料最常用来表示其平均水平的指标是(几何均数)16、变异系数用于①(度量衡单位不同);②(两均数相差悬殊)。
17、横轴上,正态曲线下,从μ-1.96σ到μ+2.58σ的面积为 0.97 。
18、S — X 大小与 S 成正比。
19、用最小二乘法原理确定回归直线是使(∑(y-y ))为最小。
20、统计表的结构包括 标题 标目 线条 数字 四个方面。
21、确定医学正常值范围,习惯上以95%为界值。
若资料是正态分布,应计算(双侧)_x+-1.96s__,若资料呈偏态分布,应计算__p2.5____及___p97.5__。
22、X 服从N (5,22)的正态分布,X的50P 为(5 )。
24、对于任何分布的资料,955P ~P 的范围包含了 90% 变量值。
25、秩和检验的优点 使用范围 、 计算简单 、 不分变量的类型 。
27、比较甲乙两地血型的构成比有无差别,宜用(χ2)检验。
28、比较某地区某时期三种疾病的发病率在各年度的发展速度,应该绘制 半对数线图。
正确的选择数据统计分析方法:多组数据比较
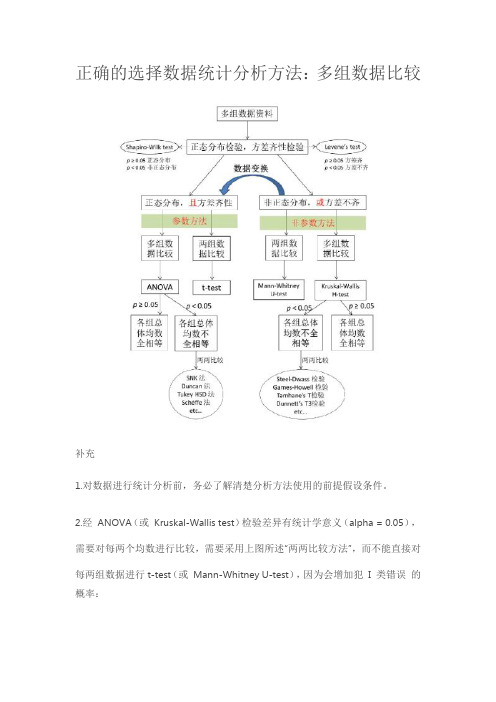
正确的选择数据统计分析方法:多组数据比较补充1.对数据进行统计分析前,务必了解清楚分析方法使用的前提假设条件。
2.经ANOVA(或Kruskal-Wallis test)检验差异有统计学意义(alpha = 0.05),需要对每两个均数进行比较,需要采用上图所述“两两比较方法”,而不能直接对每两组数据进行t-test(或Mann-Whitney U-test),因为会增加犯I 类错误的概率:例如三组数据资料,ANOVA结果显示p < 0.05;然后每两组均数t-test比较一次,则需比较3次,那么比较3次至少有一次犯I 类错误的概率就是alpha’ = 1-0.95^3 = 0.1426 > 0.05。
3.第一型及第二型错误(英语:Type I error & Type II error)或型一错误及型二错误:4.对于双样本t-test讨论:z-test:大样本;>30;z分布;t-test:小样本;<30;t分布;但是,对于> 30 的样本,Z-test检验要求知道总体参数的标准差,在理论上成立,事实上总体参数的标准差未知,实际应用中一般使用t-test.小知识:如何选取两两比较的方法?5-1、SNK 法最为常用,但当两两比较的次数极多时,该方法的假阳性很高,最终可以达到100%。
因此比较次数较多时,不推荐使用;5-2、若存在明显的对照组,要进行的是“验证性研究”,即计划好的某两个或几个组间的比较,宜用LSD 法;5-3、若设计了对照组,要进行k-1 个组与某个对照组之间的比较,宜用Dunnett 法;5-4、若需进行多个均数间的两两比较(探索性研究),且各组人数相等,宜用Tukey法;5-5、根据对所研究领域内相关研究的文献检索,参照所研究领域内的惯例选择适当的方法。
