管件展开图
断节下料展开图(管件)

在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个°的角,即∠AOK、∠KOC、∠COD与∠DOE。
各种管件放样图

在管道安装I:程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相%一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类.它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3・2任意角度马蹄弯1. 任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度).(1)按已知尺寸画出立面图,如图3・3所示。
(2)以D/2为半径画圆.然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2\ 3'、4\ 5\ 6\ 7\(4)作一水平线段,长为/D,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、Io(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1气2\ 3‘、4\ 5\ 6\ 7,引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3.3任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3・4直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成.有两个端节及若干个中节组成,端节为中节的一半,根据中节数的光少,虾壳弯分为单节、两节、三节等:节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难C 1、90。
单节虾壳弯展开方法、步骤:(1) 作NAOB = 90°,以。
为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2) 将ZAOB平分成两个45°,即图中ZAOC、ZCOB.再将ZAOC、匕COB各平分成两个22.5°的角,即ZAOK. ZKOC. ZCOD 与NDOE。
管件展开图画法(详细)

管件展开图画法(详细)⽬录⼀、展开原理⼆、展开放样的基本要求与⽅法三、⼏何展开法的三个要求与典型实例四、(实训项⽬⼀)展开放样训练五、展开实例选(参考)第⼀节展开原理1.展开放样的基本思路1) 什么是展开放样所谓展开,实际是把⼀个封闭的空间曲⾯沿⼀条特定的线切开后铺平成⼀个同样封闭的平⾯图形。
它的逆过程,即把平⾯图形作成空间曲⾯,通常叫成形过程。
实际⽣产⼯作中,往往是先设计空间曲⾯后再制作该曲⾯,⽽这个曲⾯的制造材料⼤都是平⾯板料。
因此,⽤平板做曲⾯,先要求得相应的平⾯图形,即根据曲⾯的设计参数把平⾯坯料的图样画出来。
这⼀⼯艺过程就叫展开放样。
实际⼯作中,有⼈把它简称为展开,也有⼈把它简称为放样,本书中采⽤前者的说法。
2) 展开的基本思路----换⾯逼近图2-1-0 换⾯逼近⽰意图如图2-1-0,我们按预先设定的经纬⽹络把曲⾯⽹格化,并在曲⾯上任取其⼀个四⾓⾯元abcd(A、B、C、D为其四个顶点,a、b、c、d为其四条边界弧线)。
连接它的四个顶点A、B、C、D和对⾓点B、C,将得到⼀个与四⾓⾯元abcd对应的四边形ABCD以及组成四边形ABCD的两个平⾯三⾓形△ABC和△BCD。
为了简化我们的研究,我们以三⾓形△ABC和△BCD代替对应的四⾓⾯元abcd,其中直线段AB、AC、CD、DB与a、b、c、d四条弧线分别对应。
对所有的⽹格都做同样的替代处理,我们就可以得到⼀个与曲⾯贴近的,由众多三⾓平⾯元构成的多棱⾯。
多棱⾯与原曲⾯当然会存在差别,但是,只要⽹格数⽬⾜够多,他们的误差可以⾜够⼩,⼩到我们允许的公差范围内。
把曲⾯换成与之相近、由⼩平⾯组成的多棱⾯,再⽤多棱⾯的展开图去近似替代该曲⾯的理论展开图,这就是换⾯逼近的基本思路。
多棱⾯的展开是容易的,只要在同⼀平⾯上把这些⼩平⾯元按相邻位置和共⽤边逐个画出来就得到了多棱⾯的展开图。
需要指出的是,如何⽹格化是个中关键,这⼀部分将在讲展开⽅法时详细介绍。
断节下料展开图(管件)

在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
管道弯头展开放样图作法

管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
各种管件放样图

在管道安装工程中,经常遇到转弯、分支与变径所需得管配件,这些管配件中得相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样就是管道工必须掌握得技能之一。
ﻫ一、弯头得放样弯头又称马蹄弯,根据角度得不同,可以分为直角马蹄弯与任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2任意角度马蹄弯1.任意角度马蹄弯得展开方法与步骤(己知尺寸a、b、D与角度).ﻫ (1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中得半圆6等分,等分点得顺序设为1、2、3、4、5、6、7。
ﻫ (3)由各等分点作侧管中心线得平行线,与投影接合线相交,得交点为1'、2'、3’、4'、5'、6'、7'.ﻫ(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段得垂直引上线,使其与投影接合线上得各点1'、2'、3’、4'、5’、6'、7’引来得水平线相交.ﻫ(6)用圆滑得曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯得展开放样图2、直角马蹄弯得展开放样(己知直径D)由于直角马蹄弯得侧管与立管垂直,因此,可以不画立面图与断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯得展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯得展开放样ﻫ虾壳弯由若干个带斜截面得直管段组成,有两个端节及若干个中节组成,端节为中节得一半,根据中节数得多少,虾壳弯分为单节、两节、三节等;节数越多,弯头得外观越圆滑,对介质得阻力越小,但制作越困难。
ﻫ1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯得中心线。
ﻫ(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22、5°得角,即∠AO K、∠KOC、∠COD与∠DOE。
管道弯头展开放样图作法

管道弯头展开放样图作法令狐采学在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
管道弯头展开放样图作法
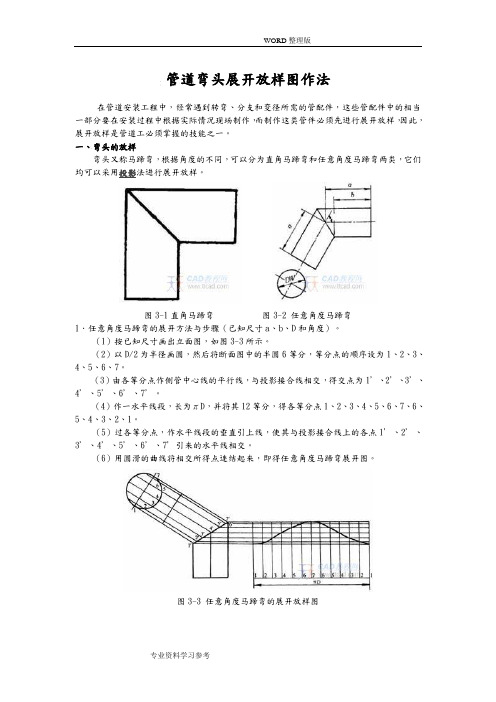
管道弯头展开放样图作法在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在管道安装工程中,经常遇到转弯、分支和变径所需的管配件,这些管配件中的相当一部分要在安装过程中根据实际情况现场制作,而制作这类管件必须先进行展开放样,因此,展开放样是管道工必须掌握的技能之一。
一、弯头的放样弯头又称马蹄弯,根据角度的不同,可以分为直角马蹄弯和任意角度马蹄弯两类,它们均可以采用投影法进行展开放样。
图3-1直角马蹄弯图3-2 任意角度马蹄弯1.任意角度马蹄弯的展开方法与步骤(己知尺寸a、b、D和角度)。
(1)按已知尺寸画出立面图,如图3-3所示。
(2)以D/2为半径画圆,然后将断面图中的半圆6等分,等分点的顺序设为1、2、3、4、5、6、7。
(3)由各等分点作侧管中心线的平行线,与投影接合线相交,得交点为1'、2'、3'、4'、5'、6'、7'。
(4)作一水平线段,长为πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(5)过各等分点,作水平线段的垂直引上线,使其与投影接合线上的各点1'、2'、3'、4'、5'、6'、7'引来的水平线相交。
(6)用圆滑的曲线将相交所得点连结起来,即得任意角度马蹄弯展开图。
图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样(己知直径D)由于直角马蹄弯的侧管与立管垂直,因此,可以不画立面图和断面图,以D/2为半径画圆,然后将半圆6等分,其余与任意角度马蹄弯的展开放样方法相似。
图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成,有两个端节及若干个中节组成,端节为中节的一半,根据中节数的多少,虾壳弯分为单节、两节、三节等;节数越多,弯头的外观越圆滑,对介质的阻力越小,但制作越困难。
1、90°单节虾壳弯展开方法、步骤:(1)作∠AOB=90°,以O为圆心,以半径R为弯曲半径,画出虾壳弯的中心线。
(2)将∠AOB平分成两个45°,即图中∠AOC、∠COB,再将∠AOC、∠COB各平分成两个22.5°的角,即∠AOK、∠KOC、∠COD与∠DOE。
(3)以弯管中心线与OB的交点4为圆心,以D/2为半径画半圆,并将其6等分。
(4)通过半圆上的各等分点作OB的垂线,与OB相交于1、2、3、4、5、6、7,与OD相交于1'、2'、3'、4'5'、6'、7',直角梯形11'77'就是需要展开的弯头端节。
(5)在OB的延长线的方向上,画线段EF,使EF=πD,并将EF 12等分,得各等分点l、2、3、4、5、6、7、6、5、4、3、2、1,通过各等分点作垂线。
(6)以EF上的各等分点为基点,分别截取11'、22′、33′、44′、55'、66′、77'线段长,画在EF相应的垂直线上,得到各交点1′、2′、3'、4′、5'、6'、7'、6′、5'、4′、3'、2′、1′,将各交点用圆滑的曲线依次连接起来,所得几何图形即为端节展开图。
用同样方法对称地截取11'、22′、33′、44′、55'、66′、77'后,用圆滑的曲线连接起来,即得到中节展开图,如图3-5所示。
图3-5 90°单节虾壳弯展开图2、90°两节虾壳弯展开图从展开图可以看出,其展开画法与单节虾壳弯的展开法相似,只是将∠AOB=90°等分成6等份,即∠COB=15°,其余请大家参考单节虾壳弯的展开画法。
图3-6 90°两节虾壳弯展开图三、三通管的展开1、等径直角三通管展开图作图步骤如下:1)按已知尺寸画出主视图和断面图,由于两管直径相等,其结合线为两管边线交点与轴线交点的连线,可直接画出。
2)6等分管I断面半圆周,等分点为l、 2、 3、 4、 3、2、l。
由等分点引下垂线,得与结合线1′-4'—l′的交点。
3)画管I展开图。
在CD延长线上取l-l等于管I断面圆周长度,并12等分。
由各等分点向下引垂线,与由结合线各点向右所引的水平线相交,将各对应交点连成曲线,即得所求管I展开图。
4)画管Ⅱ展开图。
在主视图正下方画一长方形,使其长度等于管断面周长,宽等于主视图AB。
在B′B〃线上取4-4等于断面1/2圆周。
6等分4-4,等分点为4、 3、2、 l、 2、 3、4,由各等分点向左引水平线,与由主视图结合线各点向下所引的垂线相交,将各对应交点连成曲线,即为管Ⅱ开孔实形。
A′B'B″A″即为所求管Ⅱ展开图。
图3-7 等径直角三通管展开图2、异径直交三通管展开作图方法和步骤:1)依据所给尺寸画出异径直交三通管的侧视图(主管可画成半圆),按支管的外径画半圆。
2)将支管上半圆弧6等分,标注号为4、3、2、1、2、3、4。
然后从各等分点向上向下引垂直的平行线,与主管圆弧相交,得出相应的交点4'、3'、2'、1'、2'、3'、4'。
3)将支管图上直线4--4向右延长得AB直线,在AB上量取支管外径的周长(πD),并12等分之,自左向右等分点的顺序标号是1、2、3、4、3、2、1、2、3、4、3、2、1。
4)由直线AB上的各等分点引垂直线,然后由主管圆弧上各交点向右引水平线与之相交,将对应点连成光滑曲线,即得到支管展开图(俗称雄头样板)。
5)延长支管圆中心的垂直线,在此直线上以点1°为中心,上下对称量取主管圆弧上的弧长,得交点1°、2°、3°、4°、3°、2°、1°。
6)通过这些交点作垂直于该线的平行线,同时,将支管半圆上的6根等分垂直线延长,并与这些平行直线相交,用光滑曲线连接各交点,此即为主管上开孔的展开图样。
图3-8 异径直交三通展开图3、同径斜交三通管的展开作图方法和步骤如下(已知主管与支管交角为α)(1)根据主管直径及相交角α画出同径斜三通的正面投影图(主视图)。
(2)在支管的顶端画半圆并6等分,得各等分点1、2、3、4、5、6、7,过各等分点作斜支管轴心线的平行线交支管与主管相交线于1'、2'、3'、4'、5'、6'、7'。
(3)在支管直径17线段的延长线的方向上,作直线AB=πD,并将其12等分,得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。
(4)过AB线段的各等分点1、2、3、4、5、6、7、6、5、4、3、2、1作AB的垂线,再过主管与支管的相交点1'、2'3'、4'、5'、6'、7'作线段AB的平行线,依次对应于各点1″、2″、3″、4″、5″、6″、7″,将所得交点用圆滑曲线连结起来,所得几何图形就是支管展开图(即雄头样板)。
(5)在主管右断面图上画半圆;由支管与主管的相交点1'、2'3'、4'向右引主管轴心线的平行线,将主管断面图的半圆分成6分,交于a、b、c、d点。
(此步也可省略)(6)在三通主管下面作一条线段7°1°平行于三通主管轴心线,以7°1°为中心上下依此截取ab、bc、cd的弧长,并作7°1°的平行线段,再过1'、2'、3'、4'、5'、6'、7'各点作三通主管轴线的垂直引下线,依此相交于1°、2°、3°、4°、5°、6°、7°将所得交点用圆滑曲线连结起来,所得几何图形就是主管开孔的展开图(即雌头样板)。
图3-9 同径斜交三通管的展开图四、大小头的展开1、同心大小头的展开方法一:放射线法展开步骤:(图3-10)(1)运用正投影原理画出同心大小头的立面图;(2)以ac为直径作大头的半圆并6等分,每一等分的弧长为A;(3)延长ab、cd交于O点;(4)以O为圆心,分别以Oa、Ob为半径画弧EF、GH,截取EF=12A,连结OE、OF,所得几何图形EFHG 即为要展开的大小头展开图。
图3-10 同心大小头展开图方法二:利用三角形求实长法的展开步骤:(1)按已知尺寸画出主视图和俯视图,将其上、下口分成12等分,使表面组成24个三角形。
(2)采用直角三角形法求出l-2'线的实长。
(3)按照已知三边作三角形的方法,即可得到如图3-11所示同心大小头的展开图。
图3-11 同心大小头展开图2、偏心大小头的展开步骤(图3-12):(1)运用正投影原理画出偏心大小头的立面图;(2)延长7-A及1-B交于O点;(3)以1-7为直径画半圆并6等分,得等分点1、2、3、4、、5、6、7;(4)以7为圆心,以7到半圆各等分点的距离为半径画同心圆弧,分别与直线17相交得交点为2'、3'、4'、5'、6';(5)自O点连接O6'、O5'、O4'、O3'、O2'的连结线交AB于6″、5″、4″、3″、2″各点;(6)以O为圆心,以O7、O6'、O5'、O4'、O3'、O2'、O1为半径作同心圆弧;(7)在O7为半径的圆弧上任取一点7',以7'为起点,以大头半圆等分的弧长为线段长,顺次阶梯地截得各同心圆弧交于6'、5'、4'、3'、2'、1'、2'、3'、4'、5'、6'、7';(8)以O为圆心,分别以OA、O6″、O5″、O4″、O3″、O2″、OB为半径,分别画圆弧顺次阶梯地与于O7'、O6'、O5'、O4'、O3'、O2'、O1'各条半径线相交于7″、6″、5″、4″、3″、2″、1″、2″、3″、4″、5″、6″、7″各点,用圆滑曲线连结所有交点,所得几何图形就是偏心大小头的展开图;图3-12 偏心大小头展开图五、天圆地方的展开步骤l)按已知尺寸画山主视图和俯视图,并3等分俯视图1/4圆周,得等分点为l、2、3、4,连接各等分点与B。
2)求实长线。
作EF、D'Η′延长线的公垂线GH,截取H-l(4)、H-2(3)等于俯视图中B—1(B -4)、B-2(B-3),连接G-l(4)、G-2(3),即得俯视图中的b、c线实长b'、c'。
3)画展开图。
画AB线段等于俯视图中的AB长,以A、B为圆心,实长b′为半径分别画圆弧相交于l点。
以B为圆心,实长c'为半径画圆弧,与以l为圆心,俯视图等分弧长为半径顺次画弧交于2、3 两点。
以 3为圆心,等分弧长为半径画圆弧,与以B为圆心,b'为半径画圆弧交于4点。
以4为圆心b'为半径画圆弧,与以B为圆心俯视图AB长为半径画圆弧交于C点;用同样方法求出3、2、1点。
以1为圆心,主视图h'为半径画弧,与以C为圆心,1/2CD为半径画圆弧交于J点;用同样方法求出左边各点,以直线或曲线连接各点,即得所求展开图。
图3-13 天圆地方展开图。
