meanshift1
均值漂移MeanShift

均值漂移Mean Shift均值漂移(Mean Shift)00均值漂移是一种有效的统计迭代算法。
均值漂移算法是一种基于密度梯度上升的非参数方法,通过迭代运算找到目标位置,实现目标跟踪。
它显著的优点是算法计算量小,简单易实现,很适合于实时跟踪场合;但是跟踪小目标和快速移动目标时常常失败,而且在全部遮挡情况下不能自我恢复跟踪。
通过实验提出应用核直方图来计算目标分布,证明了均值漂移算法具有很好的实时性特点。
Mean Shift 简介Mean Shift 这个概念最早是由Fukunaga等人[1]于1975年在一篇关于概率密度梯度函数的估计中提出来的,其最初含义正如其名,就是偏移的均值向量,在这里Mean Shift是一个名词,它指代的是一个向量,但随着Mean Shift理论的发展,Mean Shift的含义也发生了变化,如果我们说Mean Shift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其偏移均值,然后以此为新的起始点,继续移动,直到满足一定的条件结束.然而在以后的很长一段时间内Mean Shift并没有引起人们的注意,直到20年以后,也就是1995年,另外一篇关于Mean Shift的重要文献[2]才发表.在这篇重要的文献中,Yizong Cheng对基本的Mean Shift算法在以下两个方面做了推广,首先Yizong Cheng定义了一族核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同,其次Yizong Cheng还设定了一个权重系数,使得不同的样本点重要性不一样,这大大扩大了Mean Shift的适用范围.另外Yizong Cheng指出了Mean Shift可能应用的领域,并给出了具体的例子.Comaniciu等人[3][4]把Mean Shift成功的运用的特征空间的分析,在图像平滑和图像分割中Mean Shift都得到了很好的应用. Comaniciu等在文章中证明了,Mean Shift算法在满足一定条件下,一定可以收敛到最近的一个概率密度函数的稳态点,因此Mean Shift算法可以用来检测概率密度函数中存在的模态.Comaniciu等人[5]还把非刚体的跟踪问题近似为一个Mean Shift最优化问题,使得跟踪可以实时的进行.在后面的几节,本文将详细的说明Mean Shift的基本思想及其扩展,其背后的物理含义,以及算法步骤,并给出理论证明.最后本文还将给出Mean Shift在聚类,图像平滑,图像分割,物体实时跟踪这几个方面的具体应用.Mean Shift 的基本思想及其扩展基本Mean Shift给定d维空间中的n个样本点,i=1,…,n,在点的Mean Shift向量的基本形式定义为:k表示在这n个样本点中,有k个点落入区域中.我们可以看到是样本点相对于点的偏移向量,(1)式定义的Mean Shift向量就是对落入区域中的k个样本点相对于点的偏移向量求和然后再平均.从直观上看,如果样本点从一个概率密度函数中采样得到,由于非零的概率密度梯度指向概率密度增加最大的方向,因此从平均上来说, 区域内的样本点更多的落在沿着概率密度梯度的方向.因此,对应的, Mean Shift向量应该指向概率密度梯度的方向如上图所示, 大圆圈所圈定的范围就是 ,小圆圈代表落入区域内的样本点,黑点就是Mean Shift的基准点 ,箭头表示样本点相对于基准点的偏移向量,很明显的,我们可以看出,平均的偏移向量会指向样本分布最多的区域,也就是概率密度函数的梯度方向从前面关于Mean Shift和概率密度梯度的关系的论述,我们可以清楚的看到,Mean Shift算法本质上是一个自适应的梯度上升搜索峰值的方法,如下图所示,如果数据集服从概率密度函数f(x),给定一个如图初始点,Mean Shift算法就会一步步的移动,最终收敛到第一个峰值点.从这张图上,我们可以看到Mean Shift至少有如下三方面的应用:(1)聚类,数据集中的每一点都可以作为初始点,分别执行Mean Shift算法,收敛到同一个点算作一类;(2)模态的检测,概率密度函数中的一个峰值就是一个模态,Mean Shift在峰值处收敛,自然可以找到该模态.(3)最优化,Mean Shift可以找到峰值,自然可以作为最优化的方法,Mean Shift算法进行最优化的关键是要把最优化的目标转化成Mean Shift 隐含估计的概率密度函数.[1]The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition (1975)[2]Mean shift, mode seeking, and clustering (1995)[3]Mean Shift: a robust approach toward feature space analysis (2002)[4]Real-time tracking of non-rigid objects using mean shift (2000)[5]Mean-shift Blob Tracking through Scale Space (2003)[6]An algorithm for data-driven bandwidth selection(2003) 从直观上看,如果样本点从一个概率密度函数中采样得到,由于非零的概率密度梯度指向概率密度增加最大的方向,因此从平均上来说, 区域内的样本点更多的落在沿着概率密度梯度的方向.因此,对应的, Mean Shift向量应该指向概率密度梯度的方向。
meanshift算法简介

怎样找到数据集合中数据最密集的地方呢?
数据最密集的地方,对应于概率密度最大的地方。我们可 以对概率密度求梯度,梯度的方向就是概率密度增加最大 的方向,从而也就是数据最密集的方向。
令
,假设除了有限个点,轮廓函数 的梯度对所
有
均存在 。将 作为轮廓函数,核函数 为:
fh,K
x
2ck ,d n nhd 2 i1
Meanshift算法的概述及其应用
Meanshift的背景
Mean Shift 这个概念最早是由Fukunaga等人于 1975年在一篇关于概率密度梯度函数的估计中提出 来的,其最初含义正如其名,就是偏移的均值向量。
直到20年以后,也就是1995年,,Yizong Cheng发 表了一篇对均值漂移算法里程碑意义的文章。对基 本的Mean Shift算法在以下两个方面做了改进,首先 Yizong Cheng定义了一族核函数,使得随着样本与 被偏移点的距离不同,其偏移量对均值偏移向量的贡 献也不同,其次Yizong Cheng还设定了一个权重系 数,使得不同的样本点重要性不一样,这大大扩大了 Mean Shift的适用范围.另外Yizong Cheng指出了 Mean Shift可能应用的领域,并给出了具体的例子。
• 一维下的无参数估计 设X1,X2, …Xn是从总体中抽出的独立同分布
的样本,X具有未知的密度函数f(x),则f (x)的核估计为:
h为核函数的带宽。常用的核函数如下:
分别是单位均匀核函数 和单位高斯核函数
多维空间下的无参密度估计:
在d维欧式空间X中,x表示该空间中的一个点, 表示该空间中的
核函数,
(5)若
,则停止;否则y0←y1转步骤②。
限制条件:新目标中心需位于原目标中 心附近。
meanshift 算法matlab代码

一、Meanshift算法简介Meanshift算法是一种基于密度估计的聚类算法,它通过不断调整数据点的位置来找到数据集中的局部最大值。
该算法最初由Fukunaga 和Hostetler在上世纪70年代提出,后来由Dorin Comaniciu和Peter Meer在2002年进行了改进,成为了在计算机视觉和模式识别领域被广泛应用的算法之一。
Meanshift算法在图像分割、目标跟踪和特征提取等领域有着广泛的应用,其优点是不需要预先指定聚类的个数,能够自适应地发现数据中的聚类结构。
本文将介绍Meanshift算法的基本原理,并给出在Matlab中的实现代码。
二、Meanshift算法的基本原理1. 数据点的内核密度估计Meanshift算法基于密度估计的原理,它首先对数据点进行内核密度估计。
对于每一个数据点x,其内核密度估计可以表示为:\[ f(x)=\frac{1}{nh^d}\sum_{i=1}^{n}K\left(\frac{x-x_i}{h}\right)\]其中,n为数据点的数量,h为内核函数的带宽,K为内核函数,d为数据点的维度。
2. Meanshift向量的计算在得到数据点的密度估计之后,Meanshift算法通过不断调整数据点的位置来找到局部最大值。
对于数据点x,其Meanshift向量可以表示为:\[ m(x)=\frac{\sum_{i=1}^{n}K\left(\frac{x-x_i}{h}\right)x_i}{\sum_{i=1}^{n}K\left(\frac{x-x_i}{h}\right)}-x\]Meanshift向量的计算可以理解为将数据点向其密度估计的最大值方向移动,直至收敛于密度估计的局部最大值位置。
3. 聚类的形成Meanshift算法通过不断迭代调整数据点的位置,当数据点的移动趋于收敛之后,将在同一局部最大值处的数据点归为同一类,从而形成聚类。
三、Meanshift算法的Matlab代码实现在Matlab中,可以通过以下代码实现Meanshift算法的聚类:```matlabfunction [labels, centroids] = meanshift(data, bandwidth)[n, d] = size(data);labels = zeros(n, 1);stopThresh = 1e-3 * bandwidth;numClusters = 0;计算内核密度估计f = (x) exp(-sum((x - data).^2, 2) / (2 * bandwidth^2));迭代计算Meanshift向量for i = 1:nif labels(i) == 0x = data(i, :);diff = inf;while truex_old = x;weights = f(x);x = sum(repmat(weights, 1, d) .* data) / sum(weights); diff = norm(x - x_old);if diff < stopThreshbreak;endend将收敛的数据点归为同一类numClusters = numClusters + 1;idx = find(weights > 0.5);labels(idx) = numClusters;endend计算聚类中心centroids = zeros(numClusters, d);for i = 1:numClustersidx = find(labels == i);centroids(i, :) = mean(data(idx, :));endend```以上代码实现了对输入数据data进行Meanshift聚类,其中bandwidth为内核函数的带宽。
meanshif算法简介PPT课件

Meanshift的背景
Mean Shift 这个概念最早是由 Fukunaga等人于1975年在一篇关于概率密度梯度函 数的估计中提出来的,其最初含义正如其名,就是偏 移的均值向量。
直到20年以后,也就是1995年,,Yizong Cheng 发表了一篇对均值漂移算法里程碑意义的文章。对 基本的Mean Shift算法在以下两个方面做了改进, 首先Yizong Cheng定义了一族核函数,使得随着样 本与被偏移点的距离不同,其偏移量对均值偏移向 量的贡献也不同,其次Yizong Cheng还设定了一个 权重系数,使得不同的样本点重要性不一样,这大大 扩大了Mean Shift的适用范围.另外Yizong Cheng 指出了Mean Shift可能应用的领域,并给出了具体 的例子。
Mean shift向量的物理意义的什么呢?
为了更好地理解这个式子的物理意义,假设上式中g(x)=1 平均的偏移量会指向样本点最密的方向,也 就是概率密度函数梯度方向
下面我们看一下mean shift算法的步骤
mh x
给定一个初始点x,核函数G(x), 容许误差 ,Mean
Shift算法循环的执行下面三步,直至结束条件满足,
若再考虑到
这个表达式就是基于核函数
的概率密度函数的估计
怎样找到数据集合中数据最密集的地方呢?
数据最密集的地方,对应于概率密度最大的地方。我们可 以对概率密度求梯度,梯度的方向就是概率密度增加最大 的方向,从而也就是数据最密集的方向。
令 的梯度对所有 廓函数,核函数
,假设除了有限个点,轮廓函数
均存在 。将
Meanshift的应用
• Mean Shift可以应用在很多领域,比如聚类,图像平 滑,,图像分割。尤其是应用在目标跟踪领域,其跟踪
meanshift算法原理

meanshift算法原理
MeanShift(均值漂移)是一种非参数化的聚类算法,用于在数据集中发现数据点的密集区域。
它基于密度估计的原理,通过计算数据点的局部密度梯度来寻找数据点的聚集中心。
MeanShift 算法的原理如下:
1. 初始化:为每个数据点选择一个随机的聚集中心。
2. 密度估计:对于每个数据点,计算其与其他数据点之间的距离,并将距离定义为核函数的参数。
常用的核函数是高斯核函数。
3. 均值漂移:对于每个数据点,计算其局部密度梯度向量。
梯度向量的方向是从当前数据点指向密度更高的方向,梯度的大小代表密度的变化程度。
使用梯度向量来更新当前数据点的位置。
4. 更新聚集中心:将数据点移动到更新后的位置,并将其作为新的聚集中心。
5. 重复步骤2-4 直到满足停止条件(例如,聚集中心的移动小于某个阈值)。
MeanShift 算法的特点是不需要事先指定聚类的数量,它能够自动确定聚类的形状和数量。
它具有较好的收敛性和适应性,对于非凸形状的聚类问题也能有效地处理。
在应用中,MeanShift 算法可以用于图像分割、目标跟踪、图像压缩等领域。
它在计算复杂度上较高,但在一些特定的数据集和问题中表现出良好的效果。
meanshift计算方法

meanshift计算方法Meanshift是一种经典的非参数密度估计和聚类算法,常用于图像处理、目标跟踪和图像分割等任务。
Meanshift算法的核心思想是通过迭代寻找样本空间中的密度极大值点,从而找到数据的聚类中心。
该方法的基本原理如下:1.密度估计:首先,对于给定的数据集,通过核密度估计方法来估计数据集中每个样本点的密度。
核密度估计是一种非参数的密度估计方法,通过计算每个样本点周围的核密度来估计该样本点的密度。
常用的核函数有高斯核函数和均匀核函数等。
2.中心寻找:从样本空间中任意选择一个点作为初始中心点。
然后,计算该点与样本空间中其他点之间的距离,并根据距离来调整中心点的位置。
具体而言,可以使用欧氏距离或其他距离度量来计算中心点与样本点之间的距离。
调整中心点的位置是通过计算样本点对中心点的贡献度来实现的,贡献度是根据距离的远近来确定的。
距离越近的样本点对中心点的贡献度越大,距离越远的样本点对中心点的贡献度越小。
3.密度更新:根据样本空间中当前的中心点,计算每个样本点与中心点之间的距离,并根据距离的远近来更新样本点的密度。
即,距离越近的样本点密度越高,距离越远的样本点密度越低。
通过迭代更新样本点的密度,可以逐渐得到数据集在样本空间中的密度分布。
4.收敛判断:判断中心点的位置是否稳定(即中心点是否收敛)。
当中心点的移动距离小于设定的阈值时,算法停止迭代,并输出最终的聚类中心。
Meanshift算法的优点是可以适应任意形状和密度的数据集,并且不需要事先指定聚类的数量。
它能够自动发现数据集中的聚类中心,并将数据点聚集在它们周围。
同时,Meanshift算法对初始中心点的选择不敏感,因此较为稳定。
然而,Meanshift算法也存在一些缺点。
首先,该算法的时间复杂度较高,其计算复杂度为O(N^2),其中N为数据集的大小。
其次,Meanshift算法在处理高维数据时容易受到维数灾难的影响,数据点之间的距离随着维数的增加而呈指数增长,导致聚类结果不准确。
MeanShift算法
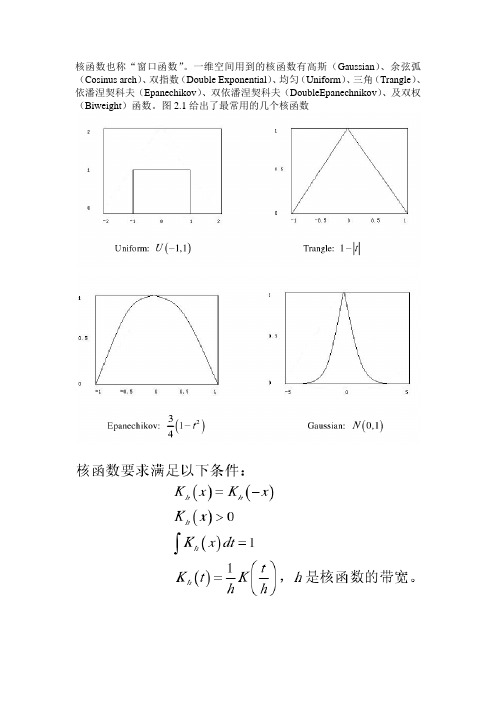
核函数也称“窗口函数”。
一维空间用到的核函数有高斯(Gaussian)、余弦弧(Cosinus arch)、双指数(Double Exponential)、均匀(Uniform)、三角(Trangle)、依潘涅契科夫(Epanechikov)、双依潘涅契科夫(DoubleEpanechnikov)、及双权(Biweight)函数。
图2.1给出了最常用的几个核函数给定一组一维空间的n个数据点集合令该数据集合的概率密度函数假设为f (x),核函数取值为,那么在数据点x处的密度估计可以按下式计算:上式就是核密度估计的定义。
其中,x为核函数要处理的数据的中心点,即数据集合相对于点x几何图形对称。
核密度估计的含义可以理解为:核估计器在被估计点为中心的窗口内计算数据点加权的局部平均。
或者:将在每个采样点为中心的局部函数的平均效果作为该采样点概率密度函数的估计值。
MeanShift实现:1.选择窗的大小和初始位置.2.计算此时窗口内的Mass Center.3.调整窗口的中心到Mass Center.4.重复2和3,直到窗口中心"会聚",即每次窗口移动的距离小于一定的阈值,或者迭代次数达到设定值。
meanshift算法思想其实很简单:利用概率密度的梯度爬升来寻找局部最优。
它要做的就是输入一个在图像的范围,然后一直迭代(朝着重心迭代)直到满足你的要求为止。
但是他是怎么用于做图像跟踪的呢?这是我自从学习meanshift以来,一直的困惑。
而且网上也没有合理的解释。
经过这几天的思考,和对反向投影的理解使得我对它的原理有了大致的认识。
在opencv中,进行meanshift其实很简单,输入一张图像(imgProb),再输入一个开始迭代的方框(windowIn)和一个迭代条件(criteria),输出的是迭代完成的位置(comp )。
这是函数原型:int cvMeanShift( const void* imgProb, CvRect windowIn,CvTermCriteria criteria, CvConnectedComp* comp )但是当它用于跟踪时,这张输入的图像就必须是反向投影图了。
meanshift算法学习笔记一

Mean shift算法学习周记一我所认知的什么是mean shift算法Mean Shift算法本质上是最优化理论中的最速下降法(亦称梯度下降法,牛顿法等),即沿着梯度下降方法寻找目标函数的极值。
在跟踪中,就是为了寻找到相似度值最大的候选目标位置。
Mean shift算法的基本思想从初始目标区域提取的特征,对于下一个的视频而言,其上任意位置都可以圈定出一个与初始化目标区域相同大小的区域,并提取该区域的颜色直方图特征与初始化目标区域提取的颜色直方图特征进行匹配,计算得到两个特征之间的相似度。
由此,可以得到一个由特征匹配程度构成的一个相似度概率密度分布图我们真正需要寻找的就是该概率密度分布图上的最大值(与初始目标特征最相似的位置)。
Mean Shift方法就是沿着概率密度的梯度方向进行迭代移动,最终达到密度分布的最值位置。
其迭代过程本质上是的最速下降法,下降方向为一阶梯度方向,步长为固定值。
但是,Mean Shift没有直接求取下降方向和步长,它通过模型的相似度匹配函数的一阶Talor展开式进行近似,直接推到迭代的下一个位置。
由此,沿着梯度方向不断迭代收敛到目标相似度概率目标分布的局部极大值。
Mean shift算法特点由于在实际中,我们不可能去求取下一帧中所有位置的相似度。
Mean Shift 是在不知道该概率密度分布的条件下,使用迭代过程中每次选定的目标区域的局部密度特征来进行迭代的,因此,它寻找的是目标的局部极大值。
这就导致目标运动过快或背景过于复杂时,迭代寻找的局部极值并不是目标在下一帧中的最佳匹配位置。
另外,Mean Shift作为最速下降法的一种,它的收敛速度并不快,且在接近最优值时,存在锯齿现象。
Mean shift算法的作用及特点(1)因为目标直方图具有特征稳定,抗部分遮挡,计算方法简单和计算量小的特点。
所以基于Mean Shift 的跟踪一般采用直方图对目标进行建模,然后通过相似度量,最终实现目标的匹配和跟踪。
基于MeanShift算法的目标跟踪

基于MeanShift算法的目标跟踪1 算法描述1.1 meanshift算法背景meanShift这个概念最早是由Fukunage在1975年提出的,Fukunage等人在一篇关于概率密度梯度函数的估计中提出这一概念。
其最初的含义正如其名:偏移的均值向量;但随着理论的发展,meanShift的含义已经发生了很多变化。
如今,我们说的meanShift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,然后以此为新的起始点,继续移动,直到满足一定的结束条件。
在很长一段时间内,meanShift算法都没有得到足够的重视,直到1995年另一篇重要论文的发表。
该论文的作者Yizong Cheng定义了一族核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。
其次,他还设定了一个权重系数,使得不同样本点的重要性不一样,这大大扩展了meanShift的应用范围。
此外,还有研究人员将非刚体的跟踪问题近似为一个meanShift的最优化问题,使得跟踪可以实时进行。
目前,利用meanShift进行跟踪已经相当成熟。
1.2 meanshift算法原理Meanshift可以应用在很多领域,比如聚类,图像平滑,图像分割,还在目标跟踪领域有重要的应用。
Meanshift跟踪算法是通过计算候选目标与目标模板之间相似度的概率密度分布,然后利用概率密度梯度下降的方向来获取匹配搜索的最佳路径,加速运动目标的定位和降低搜索的时间,因此其在目标实时跟踪领域有着很高的应用价值。
该算法由于采用了统计特征,因此对噪声具有很好的鲁棒性;由于是一个蛋参数算法,容易作为一个模块和其他算法集成;采用核函数直方图建模,对边缘阻挡、目标的旋转、变形以及背景运动都不敏感;同时该算法构造了一个可以用meanshift算法进行寻优的相似度函数。
Meanshift本质上是最陡下降法,因此其求解过程收敛速度快,使得该算法具有很好的实用性。
基于MeanShift算法的目标跟踪解析

基于MeanShift算法的目标跟踪1 算法描述1.1 meanshift算法背景meanShift这个概念最早是由Fukunage在1975年提出的,Fukunage等人在一篇关于概率密度梯度函数的估计中提出这一概念。
其最初的含义正如其名:偏移的均值向量;但随着理论的发展,meanShift的含义已经发生了很多变化。
如今,我们说的meanShift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,然后以此为新的起始点,继续移动,直到满足一定的结束条件。
在很长一段时间内,meanShift算法都没有得到足够的重视,直到1995年另一篇重要论文的发表。
该论文的作者Yizong Cheng定义了一族核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。
其次,他还设定了一个权重系数,使得不同样本点的重要性不一样,这大大扩展了meanShift的应用范围。
此外,还有研究人员将非刚体的跟踪问题近似为一个meanShift的最优化问题,使得跟踪可以实时进行。
目前,利用meanShift进行跟踪已经相当成熟。
1.2 meanshift算法原理Meanshift可以应用在很多领域,比如聚类,图像平滑,图像分割,还在目标跟踪领域有重要的应用。
Meanshift跟踪算法是通过计算候选目标与目标模板之间相似度的概率密度分布,然后利用概率密度梯度下降的方向来获取匹配搜索的最佳路径,加速运动目标的定位和降低搜索的时间,因此其在目标实时跟踪领域有着很高的应用价值。
该算法由于采用了统计特征,因此对噪声具有很好的鲁棒性;由于是一个蛋参数算法,容易作为一个模块和其他算法集成;采用核函数直方图建模,对边缘阻挡、目标的旋转、变形以及背景运动都不敏感;同时该算法构造了一个可以用meanshift算法进行寻优的相似度函数。
Meanshift本质上是最陡下降法,因此其求解过程收敛速度快,使得该算法具有很好的实用性。
MeanShift与基于MeanShift的目标跟踪算法及实现

MeanShift与基于MeanShift的目标跟踪算法及实现导论:无参密度估计也叫做非参数估计,和参数密度估计共同构成了概率密度估计方法。
参数密度估计方法要求特征空间服从一个已知的概率密度函数,在实际的应用中这个条件很难达到。
而无参数密度估计方法对先验知识要求最少,完全依靠训练数据进行估计,并且可以用于任意形状的密度估计。
所以依靠无参密度估计方法,即不事先规定概率密度函数的结构形式,在某一连续点处的密度函数值可由该点邻域中的若干样本点估计得出。
常用的无参密度估计方法有:直方图法、最近邻域法和核密度估计法。
MeanShift算法正是属于核密度估计法,它不需要任何先验知识而完全依靠特征空间中样本点的计算其密度函数值。
对于一组采样数据,直方图法通常把数据的值域分成若干相等的区间,数据按区间分成若干组,每组数据的个数与总参数个数的比率就是每个单元的概率值;核密度估计法的原理相似于直方图法,只是多了一个用于平滑数据的核函数。
采用核函数估计法,在采样充分的情况下,能够渐进地收敛于任意的密度函数,即可以对服从任何分布的数据进行密度估计。
MeanShift算法思想与物理含义:的采样点,无论其离中心x的此外,从公式1中可以看到,只要是落入Sh(x)计算的贡献是一样的。
然而在现实跟踪过程中,当跟踪目远近,对最终的Mh标出现遮挡等影响时,由于外层的像素值容易受遮挡或背景的影响,所以目标模型中心附近的像素比靠外的像素更可靠。
因此,对于所有采样点,每个样本点的重要性应该是不同的,离中心点越远,其权值应该越小。
故引入核函数和权重系数来提高跟踪算法的鲁棒性并增加搜索跟踪能力。
核函数:核函数也叫窗口函数,在核估计中起到平滑的作用。
常用的核函数有:Uniform,Epannechnikov,Gaussian等。
本文算法只用到了Epannechnikov,它数序定义如下:基于MeanShift的目标跟踪算法:基于均值漂移的目标跟踪算法通过分别计算目标区域和候选区域内像素的特征值概率得到关于目标模型和候选模型的描述,然后利用相似函数度量初始帧目标模型和当前帧的候选模版的相似性,选择使相似函数最大的候选模型并得到关于目标模型的Meanshift向量,这个向量正是目标由初始位置向正确位置移动的向量。
meanshift聚类算法的原理和特点

meanshift聚类算法的原理和特点
Mean Shift算法是一种非参数的统计方法,主要用于聚类和密度估计。
其基本原理是通过迭代的方式找到最终的聚类中心,即对每一个样本点计算其漂移均值,以计算出来的漂移均值作为新的起始点,重复以上的步骤,直到满足终止的条件,得到的最终的均值漂移点即为最终的聚类中心。
Mean Shift算法的特点如下:
1. 无需预先设定聚类数目:Mean Shift算法能够根据数据的分布自动进行聚类,无需预先设定聚类的数目。
2. 适用于任意形状的聚类:Mean Shift算法对聚类的形状没有特别的要求,可以适用于任意形状的聚类。
3. 对数据规模和分布不敏感:Mean Shift算法对数据规模和分布不敏感,可以在不同的数据规模和分布下进行聚类。
4. 适合处理大规模数据集:Mean Shift算法采用核函数来计算样本之间的相似度,可以在大规模数据集上进行快速聚类。
5. 可视化效果好:Mean Shift算法可以通过颜色来标记不同的聚类,使得聚类的结果更加直观和易于理解。
然而,Mean Shift算法也存在一些不足之处,例如对于高维数据的处理能力有限,容易受到噪声和异常值的影响等。
因此,在实际应用中,需要根据具体的数据和任务特点选择合适的聚类算法。
目标跟踪meanshift

Bhattacharyya 系数
q q1 , , qm
p y p1 y, , pm y
q
1
y
1
p y
f y cosy
p yT q p y q
m
u 1
• k表示在这n个样本点 中,有k个点落入Sh 区域中.
Mean Shift示意图
直观描述
感兴趣区域 质心
目的:找出最密集的区域 完全相同的桌球分布
Mean Shift 矢量
直观描述
感兴趣区域
质心
目的:找出最密集的区域 完全相同的桌球分布
Mean Shift 矢量
直观描述
感兴趣区域 质心
Objective : Find the densest region Distribution of identical billiard balls
数据最密集的地方,对应于概率密度最大的地方。我们可 以对概率密度求梯度,梯度的方向就是概率密度增加最大 的方向,从而也就是数据最密集的方向。
令
,假设除了有限个点,轮廓函数 的梯度对所
有
均存在 。将 作为轮廓函数,核函数 为:
fh,K
x
2ck ,d nhd 2
n i 1
目标跟踪——meanshift
Meanshift背景
Mean Shift 这个概念最早是由Fukunaga 于1975 年在一篇关于概率密 度梯度函数的估计中提出来的,其最初含义正如其名,就是偏移的均 值向量,在这里Mean Shift 是一个名词,它指代的是一个向量,但随着 Mean Shift 理论的发展,Mean Shift 的含义也发生了变化,如果我们说 Mean Shift 算法,一般是指一个迭代的步骤,即先算出当前点的偏移 均值,移动该点到其偏移均值,然后以此为新的起始点,继续移动,直到 满足一定的条件结束.
图像分割之meanshift

图像分割之meanshift
阅读⽬的:理解quick shift,同时理解mean shift原理,mean shift⽤于图像聚类,优点是不需要指定聚类中⼼个数,缺点是计算量太⼤(原因)。
mean shift主要⽤来寻找符合⼀些数据样本的模型,证明样本符合某⼀概率密度函数(PDF),是⼀种⾮参数迭代算法能够寻找模型和聚类。
数据经过⾮参数密度估计能够得到符合数据分布的概率密度函数,⽽mean shift是⾮参数的密度梯度估计,能够对概率密度函数进⾏分析,⽐如找到概率密度函数极值点。
⾯对的是什么样的⼀个问题,mean shift能够解决?
以聚类为例,⼀副图像需要进⾏分割,根据的是像素间的距离和像素的颜⾊,亮度相似性。
那么我们就将这些东西量化构建⼀个图像的特征空间。
这个特征空间包括像素在图像中的位置以及每个像素RGB三个分量。
在特征空间中位置相近,颜⾊相近会聚集在⼀起成为⼀类。
我们的⽬的是找到这样⼀个个聚类中⼼,将中⼼⼀定范围内的像素赋值给相同的标签。
mean shift将特征空间(连续的)中的点(如图像中的像素)当成抽样隐藏概率密度函数(可表⽰成曲⾯或超曲⾯)上的点(如上图),那么密集的区域或者某个聚类就相当于概率密度函数的模式(局部最⼤值)。
这样找聚类中⼼就转换成求隐含概率密度函数的模式。
mean shift 的流程
1.在特征空间中每个点上放置⼀个窗⼝
2.计算窗⼝中所有数据的均值
3.移动窗⼝到均值,直到窗⼝到达最密集的区域。
待更新。
meanshift方法

meanshift方法
meanshift方法是一种非参数密度估计和跟踪算法,主要用于图像处理和机器视觉领域。
该方法通过迭代的方式,将每个点的位置向其周围点的均值移动,从而实现密度估计和目标跟踪。
meanshift算法的基本流程如下:
1. 随机选择一个点作为初始点。
2. 以该点为中心,选择一个窗口大小(通常为固定值),计算窗口内的所有点的均值。
3. 将该点的位置更新为均值所对应的位置。
4. 重复步骤2和步骤3,直到所有点的位置不再发生明显的变化。
meanshift算法具有以下优点:
1. 非参数性:不需要预先设定任何参数,能够自动适应数据的分布。
2. 简单易行:算法实现简单,计算速度快,适合处理大规模数据。
3. 鲁棒性:对噪声和异常值具有较强的鲁棒性。
在图像处理中,meanshift算法可以用于图像分割、目标跟踪、特征提取等任务。
在机器视觉中,该算法可以用于行为识别、人脸识别、手势识别等领域。
《2024年基于MeanShift的运动目标跟踪算法研究》范文

《基于Mean Shift的运动目标跟踪算法研究》篇一一、引言随着计算机视觉技术的快速发展,运动目标跟踪作为计算机视觉领域的一个重要研究方向,已经得到了广泛的应用。
Mean Shift算法作为一种经典的跟踪算法,在实时性和准确性方面具有显著的优势。
本文将重点研究基于Mean Shift的运动目标跟踪算法,分析其原理、实现及优化方法,并探讨其在现实场景中的应用。
二、Mean Shift算法原理Mean Shift算法是一种基于概率密度的迭代方法,通过计算目标区域的均值偏移量来调整目标位置。
其基本思想是将当前帧中目标区域的特征提取出来,与上一帧中目标区域的特征进行匹配,从而实现对目标的跟踪。
具体而言,Mean Shift算法首先在目标区域周围设定一个窗口,然后计算窗口内所有像素的加权平均值,得到一个新的中心点。
如果新中心点与原中心点重合,则认为目标位置已经确定;否则,将窗口移动到新中心点附近,继续进行迭代计算,直到满足一定的收敛条件为止。
三、基于Mean Shift的运动目标跟踪算法实现基于Mean Shift的运动目标跟踪算法主要包括目标初始化、特征提取、匹配和迭代更新等步骤。
1. 目标初始化:在视频序列的第一帧中,通过手动或自动的方式确定目标的位置和大小,并设定一个初始的窗口。
2. 特征提取:提取目标区域的特征信息,如颜色直方图等。
这些特征信息将用于后续的匹配和跟踪。
3. 匹配:将当前帧中提取的目标特征与上一帧中对应区域内的特征进行匹配,计算两者的相似度。
4. 迭代更新:根据相似度结果和Mean Shift算法的原理,调整目标的位置和大小,并将新的位置作为下一次迭代的起点。
四、算法优化及改进为了提高Mean Shift算法的跟踪性能和实时性,可以采取以下优化和改进措施:1. 特征提取:采用更有效的特征提取方法,如基于SIFT、SURF等算法的局部特征描述符,以提高特征的区分度和匹配精度。
2. 多特征融合:将多种特征信息进行融合,以提高算法对复杂场景的适应能力。
meanshift公式

求出的q_temp用来作为的是hist1矩阵的列向量下标形式为
第四步:计算权重矩阵
hist1为1行4096列的矩阵
其中
中的ቤተ መጻሕፍቲ ባይዱ
当计算矩形区域中的第一个像素时
计算矩形区域中的坐标为(i,j)的像素时
也就是说,q_temp决定着hist1中的第一行第几列不为零,而hist1为q_temp中权重值相同的像素加到同一列上去。
扩展的meanshift形式:
G(x)是一个单位核函数
H是一个正定的对称dxd矩阵(带宽矩阵)
目标模型描述:
假设其中有n个像素用 表示其位置,对选中的区域灰度颜色空间均匀划分,得到由m个相等的区间构成的灰度直方图
目标模型的 概率密度可表示为:
表示以目标中心为原点的归一化像素的位置
为目标的中心坐标,k是核函数 的截断函数,常选用Epanechikov核函数。
候选模型描述:
在第t帧时,第t-!帧的目标中心位置为 ,以 为搜索窗口的中心得到候选目标的中心位置坐标f,计算当前帧的候选目标区域直方图,该区域的像素用 表示,则概率密度为:
h为核函数窗口大小
相似性度量:
Bhattacharyya系数作为相似性函数(对两个统计样本的重叠量的近似计算)
计算巴氏系数涉及到对两个样本的重叠部分进行基本形式的积分。
Bhattacharyya系数用来度量两个统计样本的重叠度。该系数可以用来度量两个样本集的可分性。
计算Bhattacharyya系数包含了一个基本的关于两个样本集重合度的积分运算。两个样本集中的定义域被分成了事前定义的几份,这种划分可以体现在下面的定义中:
a,b代表样本,n代表划分的数目, 和 分别代表两个样本集中在第i个划分中的样本之和。对于两个样本集来说,如果相同划分中的样本数越多,样本和越大,则该式的值越大。划分数的选择取决于每一个样本集中的样本数;太少的划分将因为过高估计了重叠区域而减小精度,而太多的划分将会因为在该本该有重叠的区域没有恰好重叠而减小精度(最精细的划分将会使每一个相同的区间中都没有重叠)。
传统meanshift跟踪算法流程

传统meanshift 跟踪算法实现流程一、 Meanshift 算法流程图视频流手动选定跟踪目标提取目标灰度加权直方图特征hist1提取候选目标区域提取候选目标的灰度加权直方图特征hist2均值漂移得到均值漂移向量及新的候选区域位置是否满足迭代结束条件第二帧之后图像第一帧图像得到当前帧目标位置是否图1 meanshift 流程图二、 各模块概述1、 手动选定目标区域:手动框出目标区域,并把该区域提取出来作为目标模板区域;2、 提取目标灰度加权直方图特征hist1;2.1构造距离权值矩阵m_wei ;使用Epanechnikov 核函数构造距离加权直方图矩阵:设目标区域中像素点(,)i j 到该区域中心的距离为dist ,则_(,)1/m wei i j dist h =-,这里h 是核函数窗宽,h 为目标区域中离区域中心最远的像素点到中心的距离:若所选目标区域为矩形区域,区域的半宽度为x h ,半高度为y h ,则22()x y h sqrt h h =+; 2.2得到归一化系数C ;1/C M =,其中M 是m_wei 中所有元素值之和; 2.3计算目标的加权直方图特征向量hist1;若图像为彩色图像,则把图像的,,r g b 分量归一化到[0,15]之间(分量值与16取余,余数即为归化后的分量值),然后为不同的分量值赋予不同的权值得到每个像素点的特征值_q temp :_256*16*q t e m p r g b =++ 对于像素点(,)i j ,设其特征值为_q temp ,则另1(_1)1(_1)_(,)hist q temp hist q temp m wei i j +=++;若图像是灰度图像,则直接利用每个像素的灰度值作为每个像素的特征值,然后统计得到hist1;把一维数组hist1归一化:11*hist hist C =;归一化后的数组hist1即为目标的加权直方图特征向量;3、 从第二帧开始的图像,通过迭代的方式找到该帧图像中目标的位置;3.1提取候选目标区域:以上一帧图像中目标的位置或上一次迭代得到的目标位置为中心提取出目标模板区域大小的区域;3.2提取候选目标区域的加权直方图特征向量hist2:提取方法同步骤2.3; 计算候选目标区域的特征值矩阵_1q temp :_1(,)256*(,)16*(,)q t e m p i j r i j g i j b i j=++; 3.3均值漂移到新的目标区域;3.3.1计算候选目标区域相对于目标区域的均值漂移权值w :(1()/2()),2(2w s q r t h i s t i h i s t ih i s t=≠ 2()0h i s t i =时,()0;w i = 3.3.2 根据每个像素点所占的均值漂移权值计算漂移矩阵xw : 11(_1(,)1)*[(1),(2)]abi j xw xw w q temp i j i y j y ===++--∑∑ 3.3.2得到权值归一化后的均值漂移向量Y :11/(_1(,)1)abi j Y xw w q temp i j ===+∑∑3.3.3得到下一个候选目标区域的中心位置y : ;y y Y =+二、算法总结对于输入的视频流,程序处理流程:1、获取第一帧图像,在第一帧图像中给出要跟踪的目标矩形模板区域A ,假定A 的高度为a ,宽度为b 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matchIterator=matches.begin(); matchIterator!=matches.end(); ++matchIterator )
{
if ( matchIterator->size()>1 )
bvertexpnt.copyTo(homovertexpnt);
for ( int i=0; i<2; i++ )
{
bvertexpnt.at<double>(0,0) = vertexpnt[i].x;
bvertexpnt.at<double>(1,0) = vertexpnt[i].y;
rotaroi = ObjInfo.roi;
StatisticsPnts(frame);
WeightAnisotroHist(ObjInfo.pu, EPANECHNIKOV_KERNEL);
double qq = ObjInfo.quality;
ClcQuality(EPANECHNIKOV_KERNEL);
{
if ( (*matchIterator)[0].distance/(*matchIterator)[1].distance < 0.6 )
{
//circle( frame, keypnt[(*matchIterator)[0].trainIdx].pt, 2, CV_RGB(0,255,0), -1 );
d = ransacmat.at<double>(0,2)*ransacmat.at<double>(1,1)
- ransacmat.at<double>(1,2)*ransacmat.at<double>(0,1);
s = sqrt((c*c+d*d)/(a*a+b*b));
cout<<"scale: "<<s<<endl;
{
Rect roi = ObjInfo.roi.boundingRect();
ObjInfo.sigmamat.at<double>(0,0) = (double)(roi.height*roi.height)/4.0;
ObjInfo.sigmamat.at<double>(1,1) = (double)(roi.width*roi.width)/4.0;
#include "stdafx.h"
#include "opencv2/opencv.hpp"
#include "AnisotroMS.h"
#include "def.h"
using namespace cv;
using namespace std;
CAnisotroMSTracker::CAnisotroMSTracker( void )
//{
// bvertexpnt.at<double>(0,0) = bmatchkeypnt[i].x; //ObjInfo.roi.center.x;
// bvertexpnt.at<double>(1,0) = bmatchkeypnt[i].y; //ObjInfo.roi.center.y;
ObjInfo.roi.size.width *= s;
ObjInfo.roi.size.height *= s;*/
bvertexpnt = Mat::ones(3,1,CV_64FC1);
bvertexpnt.copyTo(homovertexpnt);
// for ( int i=0; i<matchkeypnt.size(); i++ )
StatisticsPnts(frame);
WeightAnisotroHist( ObjInfo.qu, EPANECHNIKOV_KERNEL );
}
void CAnisotroMSTracker::ClcFea( Mat &frame, RotatedRect rroi, vector<KeyPoint> &keypnt, Mat &feadesp, int flag )
QueryPerformanceCounter(&stop);
timecost = (double)(stop.QuadPart - start.QuadPart) / freq.QuadPart * 1000;
cout<<"timecost----: "<<timecost<<"ms"<<endl;
Mat feadesp, ransacmat, bvertexpnt, homovertexpnt;
BruteForceMatcher<L2<float>> matcher;
vector<vector<DMatch>> matches;
vector<Point2f> matchkeypnt, bmatchkeypnt;
quality = ObjInfo.quality;
ObjInfo.roi = rroi;
ObjInfo.quality = qq;
return true;
/////////////////////////////////////////////
/*Rect roi = ObjInfo.roi.boundingRect()&Rect(0,0,frame.cols,frame.rows);
{
Mat mask;
LARGE_INTEGER start, stop, freq;
double timecost;
SiftFeatureDetector detector;
SiftDescriptorExtractor extractor;
QueryPerformanceFrequency(&freq);
}
}
}
int CAnisotroMSTracker::ClcRansac( Mat &frame, RotatedRect &rotaroi, double &quality )
{
RotatedRect rroi = ObjInfo.roi;
vector<KeyPoint> keypnt;
b = -ransacmat.at<double>(0,2);
c = ransacmat.at<double>(0,2)*ransacmat.at<double>(1,0)
- ransacmat.at<double>(1,2)*ransacmat.at<double>(0,0);
}
CAnisotroMSTracker::~CAnisotroMSTracker( void )
{
O运行此函数前roi要求已经完成了初始化
void CAnisotroMSTracker::InitAnisotroMStracker( Mat &frame )
// homovertexpnt = ransacmat*bvertexpnt;
// testpnt = Point2f(homovertexpnt.at<double>(0,0)/homovertexpnt.at<double>(2,0),
// homovertexpnt.at<double>(1,0)/homovertexpnt.at<double>(2,0));
mask = Mat::zeros(frame.rows, frame.cols, CV_8UC1);
ellipse( mask, rroi, CV_RGB(255,255,255), -1 );
QueryPerformanceCounter(&start);
detector.detect(frame, keypnt, mask );
homovertexpnt = ransacmat*bvertexpnt;
vertexpnt[i] = Point2f(homovertexpnt.at<double>(0,0)/homovertexpnt.at<double>(2,0),
homovertexpnt.at<double>(1,0)/homovertexpnt.at<double>(2,0));
//}
bvertexpnt.at<double>(0,0) = ObjInfo.roi.center.x;
bvertexpnt.at<double>(1,0) = ObjInfo.roi.center.y;
homovertexpnt = ransacmat*bvertexpnt;
vector<Point2f> vertexpnt;
double a,b,c,d,s;
Point2f testpnt;
ClcFea(frame, ObjInfo.roi, keypnt, feadesp, 0);
