50道解分式方程及答案
六年级解分式方程练习题及答案
(40)4X-3×9=29(41) X+ = (42)X- X=12
解:4X-3×9=29 X+ = X- X=12
4X-27=29 X= - X=12
4X=29+27 X= X=12÷
4X=56X= ÷ X=21
X=56÷4X=
X=14
(43)3X+5×0.3=4.5(44) X= (45)X-15%X=68
(22)X-0.25= (23)4+0.7X=102(24) X+ X=42
解:(22)X-0.25= 解:4+0.7X=102解: X+ X=42
X- = 0.7X=102-4 X=42
X= + 0.7X=98X=42÷
X= X=98÷0.7X=42×
X=140X=36
(25)4X-6× =2(26) ÷X= (27)9X÷0.7=9
X= 2X= - 6X=13.4-5
X= ÷ 2X= 6X=8.4
X= × X= ÷2X=8.4÷6
X= X= X=1.4
(49) X=20× (50)5X-2.4×5=8(51) (X-4.5)=6
解: X=20× 解:5X-2.4×5=8解: (X-4.5)=6
X=55X-12=8X-4.5=6÷
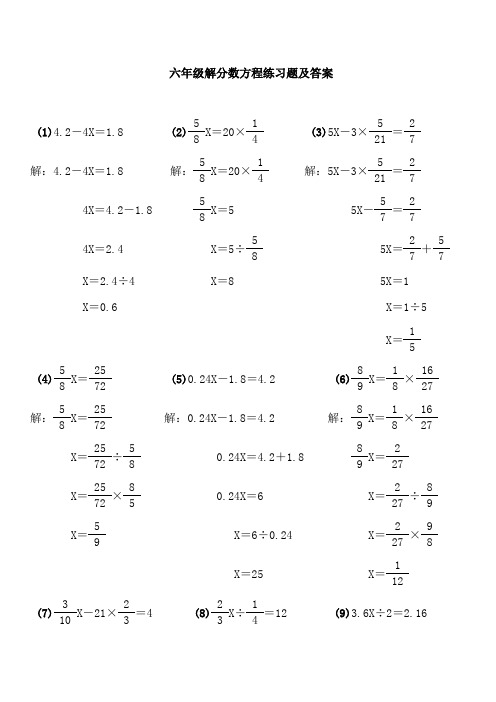
六年级解分数方程练习题及答案
(1)4.2-4X=1.8(2) X=20× (3)5X-3× =
解:4.2-4X=1.8解: X=20× 解:5X-3× =
4X=4.2-1.8 X=55X- =
4X=2.4 X=5÷ 5X= +
X=2.4÷4 X=85X=1
X=0.6 X=1÷5
X=
(4) X= (5)0.24X-1.8=4.2(6) X= ×
解:3X+5×0.3=4.5解: X= 解:X-15%X=68
初中数学:分式方程习题精选(附参考答案)

初中数学:分式方程习题精选(附参考答案)1.某学校组织七、八两个年级学生到黄河岸边开展植树造林活动,已知七年级植树900棵与八年级植树1 200棵所用的时间相同,两个年级平均每小时共植树350棵。
求七年级年级平均每小时植树多少棵?设七年级年级平均每小时植树x 棵,则下面所列方程中正确的是( ) A .900350−x =1 200xB .900x =1 200350+xC .900350+x =1 200xD .900x=1 200350−x2.若关于x 的方程2x =m2x+1无解,则m 的值为( ) A .0 B .4或6 C .6D .0或43.解分式方程2x −1x+1=0去分母时,方程两边同乘的最简公分母是_____________. 4.分式方程3−x x−4+14−x=1的解是________.5.甲、乙两人做某种机器零件,甲每小时比乙每小时多做10个,甲做160个所用时间与乙做140个所用时间相等,甲、乙两人每小时分别做多少个?设甲每小时做x 个,则可列分式方程为__________. 6.(1)解方程:xx+1=2x 2−1(2)解方程:1x−1+1=32x−27.为了让学生崇尚劳动,尊重劳动,在劳动中提升综合素质,某校定期开展劳动实践活动。
甲、乙两班在一次体验挖土豆的活动中,甲班挖1 500千克土豆与乙班挖1 200千克土豆所用的时间相同。
已知甲班平均每小时比乙班多挖100千克土豆,问:乙班平均每小时挖多少千克土豆?8.已知点P (1-2a ,a -2)关于原点的对称点在第一象限内,且a 为整数,则关于x 的分式方程x+1x−a =2的解是( ) A .x =5 B .x =1 C .x =3D .不能确定9.某工厂生产一种零件,计划在20天内完成,若每天多生产4个,则15天完成且还多生产10个。
设原计划每天生产x 个,根据题意可列分式方程为( ) A .20x+10x+4=15 B .20x−10x+4=15 C .20x+10x−4=15 D .20x−10x−4=1510.照相机成像应用了一个重要原理,用公式1f =1u +1v (v ≠f )表示,其中f 表示照相机镜头的焦距,u 表示物体到镜头的距离,v 表示胶片(像)到镜头的距离。
分式方程计算题50道及答案

分式方程计算题50道及答案1、计算:1/2 + 1/3答案:5/62、计算:2/3 + 3/6答案:13、计算:3/6 + 2/6答案:1/24、计算:3/5 - 2/5答案:1/55、计算:1/2 - 1/4答案:1/46、计算:3/8 - 1/4答案:1/47、计算:2/9 - 1/9答案:1/98、计算:3/4 x 1/3答案:1/49、计算:2/3 x 2/3答案:4/910、计算:5/6 x 1/5答案:1/611、计算:3/7 x 1/5答案:3/3512、计算:2/3 ÷ 1/2答案:4/313、计算:3/4 ÷ 1/2答案:3/214、计算:2/9 ÷ 2/3答案:1/315、计算:1/6 ÷ 1/2答案:1/316、计算:1/3 + 1/3 - 1/3答案:1/317、计算:2/3 x 2/3 - 2/3答案:2/918、计算:1/4 x 2/3 ÷ 1/2答案:1/319、计算:1/3 + 1/4 ÷ 2/3答案:7/1220、计算:2/5 - 1/5 ÷ 1/3答案:3/1521、计算:1/5 x 1/5 ÷ 1/2答案:1/2022、计算:1/3 x 1/3 - 1/3答案:1/923、计算:2/3 - 3/6 + 1/6答案:1/224、计算:1/4 + 2/3 - 1/3答案:3/425、计算:1/3 - 1/4 + 1/4答案:1/426、计算:1/2 x 3/4 ÷ 1/3答案:127、计算:1/2 ÷ 1/5 + 5/6答案:11/628、计算:2/3 x 2/3 ÷ 1/3答案:4/329、计算:1/6 + 2/3 - 1/2答案:1/330、计算:2/5 - 3/4 + 1/4答案:-3/2031、计算:1/4 x 1/5 ÷ 2/3答案:2/1532、计算:1/3 - 1/4 + 2/9答案:1/1233、计算:2/3 x 3/4 - 1/3答案:5/1234、计算:1/6 + 1/6 - 2/6答案:1/635、计算:1/5 x 5/6 ÷ 1/3答案:5/636、计算:2/3 - 1/5 + 5/6答案:11/1537、计算:1/4 x 1/4 ÷ 4/3答案:1/1238、计算:1/2 - 2/3 + 3/4答案:1/439、计算:2/3 x 3/4 ÷ 1/3答案:4/340、计算:2/9 - 1/4 + 3/4答案:5/641、计算:1/5 x 5/6 - 1/3答案:1/6答案:3/243、计算:1/8 - 1/4 + 1/2答案:3/844、计算:2/3 x 1/2 ÷ 5/6答案:2/945、计算:1/6 + 2/3 ÷ 1/2答案:5/346、计算:2/5 - 1/5 ÷ 3/4答案:5/1247、计算:1/5 x 1/5 ÷ 4/3答案:1/2048、计算:1/3 x 1/3 - 1/4答案:1/1249、计算:1/2 - 1/3 + 2/3答案:1/2答案:4/9。
初二50道分式方程练习题

初二50道分式方程练习题1. 解方程:(3x + 2)/(5 - x) = 7/92. 解方程:(2x - 1)/(x + 3) = 4/53. 解方程:(5x + 1)/(2x - 3) = 3/44. 解方程:(4 - 2x)/(7x + 1) = 2/35. 解方程:(3x - 4)/(4 - x) = 2/56. 解方程:(x + 1)/(2x - 3) = 5/87. 解方程:(3x - 2)/(x + 5) = 1/28. 解方程:(2x - 5)/(x + 1) = 3/49. 解方程:(4x - 3)/(7x + 2) = 2/510. 解方程:(3x + 1)/(2 - x) = 7/911. 解方程:(5x - 4)/(3x - 2) = 1/212. 解方程:(x - 2)/(4x + 3) = 3/513. 解方程:(3 - 4x)/(5x + 2) = 2/714. 解方程:(2x - 3)/(x + 4) = 1/215. 解方程:(4x + 1)/(3 - 2x) = 5/716. 解方程:(9 - 2x)/(6x - 1) = 3/418. 解方程:(3x + 4)/(5 + x) = 1/319. 解方程:(2x - 5)/(3x + 1) = 4/920. 解方程:(4x + 3)/(7 - x) = 2/521. 解方程:(7x - 1)/(x - 3) = 5/922. 解方程:(3x + 2)/(4 - 2x) = 1/323. 解方程:(x - 1)/(2x + 3) = 2/524. 解方程:(4 - 3x)/(x + 2) = 1/425. 解方程:(5x + 1)/(3x - 4) = 7/826. 解方程:(3 - 5x)/(x + 2) = 2/327. 解方程:(2x + 1)/(3 - 4x) = 1/528. 解方程:(4 - 3x)/(2 + x) = 5/729. 解方程:(5x + 2)/(7x - 3) = 3/430. 解方程:(3x - 2)/(5x + 1) = 5/731. 解方程:(6 - 2x)/(5x - 3) = 1/232. 解方程:(3x + 2)/(2 - 4x) = 1/733. 解方程:(x - 3)/(4x - 1) = 3/535. 解方程:(2x + 1)/(3 - 5x) = 7/836. 解方程:(4 - 2x)/(3x + 1) = 3/537. 解方程:(3x - 1)/(2x + 5) = 1/238. 解方程:(2x + 3)/(x - 4) = 7/939. 解方程:(3 - 2x)/(x + 3) = 4/540. 解方程:(4x - 1)/(2x + 3) = 3/441. 解方程:(5 - 3x)/(x + 4) = 2/542. 解方程:(2x + 1)/(5x - 2) = 3/743. 解方程:(3x - 2)/(4x + 1) = 1/344. 解方程:(x + 3)/(2 - 3x) = 2/545. 解方程:(5x - 1)/(2x + 3) = 4/946. 解方程:(4 - 3x)/(3x - 2) = 1/247. 解方程:(2x - 1)/(7x + 3) = 5/948. 解方程:(3x + 4)/(5 - x) = 7/849. 解方程:(x + 2)/(3x - 5) = 4/750. 解方程:(5x - 2)/(4 + 3x) = 1/2以上是初二50道分式方程练习题,请根据题目逐一解答,求出每道题的x值。
初三解分式方程专题练习(附答案)

初三解分式方程专题练习一.解答题(共30小题)1.解方程:.2.解关于的方程:.3.解方程.4.解方程:=+1.6.解分式方程:.5.解方程:.7.(2011•台州)解方程:.8.解方程:.9.解分式方程:.10.解方程:.11.解方程:.12.解方程:.14.解方程:.13.解方程:.15.解方程:16.解方程:.17.①解分式方程;18.解方程:.19.(1)计算:|﹣2|+(+1)0﹣()﹣1+tan60°;(2)解分式方程:=+1.20.解方程:21.解方程:+=123.解分式方程:22.解方程:.24.解方程:25.解方程:27.解方程:26.解方程:+=128.解方程:29.解方程:30.解分式方程:.初三解分式方程专题练习答案与评分标准一.解答题(共30小题)1.解方程:.解答:解:方程两边都乘以y(y﹣1),得2y2+y(y﹣1)=(y﹣1)(3y﹣1),2y2+y2﹣y=3y2﹣4y+1,3y=1,解得y=,检验:当y=时,y(y﹣1)=×(﹣1)=﹣≠0,∴y=是原方程的解,∴原方程的解为y=.2.解关于的方程:.解答:解:方程的两边同乘(x+3)(x﹣1),得x(x﹣1)=(x+3)(x﹣1)+2(x+3),整理,得5x+3=0,解得x=﹣.检验:把x=﹣代入(x+3)(x﹣1)≠0.∴原方程的解为:x=﹣.3.解方程.解答:解:两边同时乘以(x+1)(x﹣2),得x(x﹣2)﹣(x+1)(x﹣2)=3.(3分)解这个方程,得x=﹣1.(7分)检验:x=﹣1时(x+1)(x﹣2)=0,x=﹣1不是原分式方程的解,∴原分式方程无解.(8分)4.解方程:=+1.解答:解:原方程两边同乘2(x﹣1),得2=3+2(x﹣1),解得x=,检验:当x=时,2(x﹣1)≠0,∴原方程的解为:x=.5.(2011•威海)解方程:.解答:解:方程的两边同乘(x﹣1)(x+1),得3x+3﹣x﹣3=0,解得x=0.检验:把x=0代入(x﹣1)(x+1)=﹣1≠0.∴原方程的解为:x=0.6.(2011•潼南县)解分式方程:.解答:解:方程两边同乘(x+1)(x﹣1),得x(x﹣1)﹣(x+1)=(x+1)(x﹣1)(2分)化简,得﹣2x﹣1=﹣1(4分)解得x=0(5分)检验:当x=0时(x+1)(x﹣1)≠0,∴x=0是原分式方程的解.(6分)7.(2011•台州)解方程:.解答:解:去分母,得x﹣3=4x (4分)移项,得x﹣4x=3,合并同类项,系数化为1,得x=﹣1(6分)经检验,x=﹣1是方程的根(8分).8.(2011•随州)解方程:.解答:解:方程两边同乘以x(x+3),得2(x+3)+x2=x(x+3),2x+6+x2=x2+3x,∴x=6检验:把x=6代入x(x+3)=54≠0,∴原方程的解为x=6.9.(2011•陕西)解分式方程:.解答:解:去分母,得4x﹣(x﹣2)=﹣3,去括号,得4x﹣x+2=﹣3,移项,得4x﹣x=﹣2﹣3,合并,得3x=﹣5,化系数为1,得x=﹣,检验:当x=﹣时,x﹣2≠0,∴原方程的解为x=﹣.解答:解:方程两边都乘以最简公分母(x﹣3)(x+1)得:3(x+1)=5(x﹣3),解得:x=9,检验:当x=9时,(x﹣3)(x+1)=60≠0,∴原分式方程的解为x=9.11.(2011•攀枝花)解方程:.解答:解:方程的两边同乘(x+2)(x﹣2),得2﹣(x﹣2)=0,解得x=4.检验:把x=4代入(x+2)(x﹣2)=12≠0.∴原方程的解为:x=4.12.(2011•宁夏)解方程:.解答:解:原方程两边同乘(x﹣1)(x+2),得x(x+2)﹣(x﹣1)(x+2)=3(x﹣1),展开、整理得﹣2x=﹣5,解得x=2.5,检验:当x=2.5时,(x﹣1)(x+2)≠0,∴原方程的解为:x=2.5.13.(2011•茂名)解分式方程:.解答:解:方程两边乘以(x+2),得:3x2﹣12=2x(x+2),(1分)3x2﹣12=2x2+4x,(2分)x2﹣4x﹣12=0,(3分)(x+2)(x﹣6)=0,(4分)解得:x1=﹣2,x2=6,(5分)检验:把x=﹣2代入(x+2)=0.则x=﹣2是原方程的增根,检验:把x=6代入(x+2)=8≠0.∴x=6是原方程的根(7分).14.(2011•昆明)解方程:.解答:解:方程的两边同乘(x﹣2),得3﹣1=x﹣2,解得x=4.检验:把x=4代入(x﹣2)=2≠0.解答:(1)解:原方程两边同乘以6x,得3(x+1)=2x•(x+1)整理得2x2﹣x﹣3=0(3分)解得x=﹣1或检验:把x=﹣1代入6x=﹣6≠0,把x=代入6x=9≠0,∴x=﹣1或是原方程的解,故原方程的解为x=﹣1或(6分)16.(2011•大连)解方程:.解答:解:去分母,得5+(x﹣2)=﹣(x﹣1),去括号,得5+x﹣2=﹣x+1,移项,得x+x=1+2﹣5,合并,得2x=﹣2,化系数为1,得x=﹣1,检验:当x=﹣1时,x﹣2≠0,∴原方程的解为x=﹣1.17.(2011•常州)①解分式方程;解答:解:①去分母,得2(x﹣2)=3(x+2),去括号,得2x﹣4=3x+6,移项,得2x﹣3x=4+6,解得x=﹣10,检验:当x=﹣10时,(x+2)(x﹣2)≠0,∴原方程的解为x=﹣10;18.(2011•巴中)解方程:.解答:解:去分母得,2x+2﹣(x﹣3)=6x,∴x+5=6x,解得,x=1经检验:x=1是原方程的解.19.(2011•巴彦淖尔)(1)计算:|﹣2|+(+1)0﹣()﹣1+tan60°;(2)解分式方程:=+1.(2)方程两边同时乘以3(x+1)得3x=2x+3(x+1),x=﹣1.5,检验:把x=﹣1.5代入(3x+3)=﹣1.5≠0.∴x=﹣1.5是原方程的解.20.(2010•遵义)解方程:解答:解:方程两边同乘以(x﹣2),得:x﹣3+(x﹣2)=﹣3,解得x=1,检验:x=1时,x﹣2≠0,∴x=1是原分式方程的解.21.(2010•重庆)解方程:+=1解答:解:方程两边同乘x(x﹣1),得x2+x﹣1=x(x﹣1)(2分)整理,得2x=1(4分)解得x=(5分)经检验,x=是原方程的解,所以原方程的解是x=.(6分)22.(2010•孝感)解方程:.解答:解:方程两边同乘(x﹣3),得:2﹣x﹣1=x﹣3,整理解得:x=2,经检验:x=2是原方程的解.23.(2010•西宁)解分式方程:解答:解:方程两边同乘以2(3x﹣1),得3(6x﹣2)﹣2=4(2分)18x﹣6﹣2=4,18x=12,x=(5分).检验:把x=代入2(3x﹣1):2(3x﹣1)≠0,∴x=是原方程的根.∴原方程的解为x=.(7分)24.(2010•恩施州)解方程:经检验:当x=3时,x﹣4=﹣1≠0,所以x=3是原方程的解.(8分)25.(2009•乌鲁木齐)解方程:解答:解:方程两边都乘x﹣2,得3﹣(x﹣3)=x﹣2,解得x=4.检验:x=4时,x﹣2≠0,∴原方程的解是x=4.26.(2009•聊城)解方程:+=1解答:解:方程变形整理得:=1方程两边同乘(x+2)(x﹣2),得:(x﹣2)2﹣8=(x+2)(x﹣2),解这个方程得:x=0,检验:将x=0代入(x+2)(x﹣2)=﹣4≠0,∴x=0是原方程的解.27.(2009•南昌)解方程:解答:解:方程两边同乘以2(3x﹣1),得:﹣2+3x﹣1=3,解得:x=2,检验:x=2时,2(3x﹣1)≠0.所以x=2是原方程的解.28.(2009•南平)解方程:解答:解:方程两边同时乘以(x﹣2),得4+3(x﹣2)=x﹣1,解得:.检验:当时,,∴是原方程的解;29.(2008•昆明)解方程:解答:解:原方程可化为:,方程的两边同乘(2x﹣1),得2﹣5=2x﹣1,∴原方程的解为:x=﹣1.30.(2007•孝感)解分式方程:.解答:解:方程两边同乘以2(3x﹣1),去分母,得:﹣2﹣3(3x﹣1)=4,解这个整式方程,得x=﹣,检验:把x=﹣代入最简公分母2(3x﹣1)=2(﹣1﹣1)=﹣4≠0,∴原方程的解是x=﹣(6分)。
分式方程精选题答案

分式方程精选题参考答案与试题解析一.解答题(共30小题)1.(2016•常州)先化简,再求值(x﹣1)(x﹣2)﹣(x+1)2,其中x=.【分析】根据多项式乘以多项式先化简,再代入求值,即可解答.【解答】解:(x﹣1)(x﹣2)﹣(x+1)2,=x2﹣2x﹣x+2﹣x2﹣2x﹣1=﹣5x+1当x=时,原式=﹣5×+1=﹣.【点评】本题考查了多项式乘以多项式,解决本题的关键是熟记多项式乘以多项式.2.(2016•厦门校级模拟)化简:5x2y﹣2xy2﹣5+3xy(x+y)+1,并说出化简过程中所用到的运算律.【分析】先依据单项式乘多项式的法则进行计算,然后再依据同类项法则进行计算即可.【解答】解:原式=5x2y﹣2xy2﹣5+3x2y+3xy2+1(乘法的分配律)=8x2y+xy2﹣4(乘法的分配律).【点评】本题主要考查的是单项式乘多项式法则,合并同类项法则的应用,熟练掌握相关法则是解题的关键.3.(2016•濉溪县三模)计算:(x+3)(x﹣5)﹣x(x﹣2).【分析】根据多项式与多项式相乘的法则、单项式与多项式相乘的法则以及合并同类项法则计算即可.【解答】解:原式=x2﹣5x+3x﹣15﹣x2+2x=﹣15.【点评】本题考查的是多项式乘多项式,掌握多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加是解题的关键.4.(2016•南平模拟)化简:a(2﹣a)﹣(3+a)•(3﹣a)【分析】直接利用单项式乘以多项式以及平方差公式化简求出答案.【解答】解:a(2﹣a)﹣(3+a)•(3﹣a)=2a﹣a2﹣(9﹣a2)=2a﹣9.【点评】此题主要考查了单项式乘以多项式以及平方差公式,正确掌握运算法则是解题关键.5.(2016春•杨浦区期末)利用幂的运算性质计算:3××.【分析】根据同底数幂的乘法计算即可.【解答】解:原式=3×××=3×=3×2=6.【点评】本题考查了同底数幂的乘法,解题时牢记定义是关键.6.(2016春•长春校级期末)已知a x=5,a x+y=30,求a x+a y的值.【分析】首先根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,求出a y的值是多少;然后把a x、a y的值相加,求出a x+a y的值是多少即可.【解答】解:∵a x=5,a x+y=30,∴a y=a x+y﹣x=30÷5=6,∴a x+a y=5+6=11,即a x+a y的值是11.【点评】此题主要考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.7.(2016春•湘潭期末)已知a x=3,a y=2,求a x+2y的值.【分析】直接利用同底数幂的乘法运算法则将原式变形进而将已知代入求出答案.【解答】解:∵a x=3,a y=2,∴a x+2y=a x×a2y=3×22=12.【点评】此题主要考查了同底数幂的乘法运算以及幂的乘方运算,正确应用同底数幂的乘法运算法则是解题关键.8.(2016春•新化县期末)计算:(﹣2x2y)3•3(xy2)2.【分析】先依据积的乘方公式进行计算,然后再依据单项式乘单项式法则计算即可.【解答】(1)原式=﹣8x6y3•3x2y4=﹣24x8y7.【点评】本题主要考查的是单项式乘单项式、积的乘方、幂的乘方,掌握相关法则是解题的关键.9.(2016春•青岛校级期末)(﹣3x2y2)2•2xy+(xy)5.【分析】根据积的乘方等于乘方的积,可得单项式的乘法,根据单项式的乘法,可得同类项,根据合并同类项,可得答案.【解答】解:原式=9x4y4•2xy+x5y5=18x5y5+x5y5=19x5y5.【点评】本题考查了积的乘方、单项式的乘法、合并同类项,熟记法则并根据法则计算是解题关键.10.(2016春•石景山区期末)﹣6ab(2a2b﹣ab2)【分析】根据单项式与多项式相乘的运算法则计算即可.【解答】解:原式=﹣6ab•2a2b+6ab•ab2=﹣12a3b2+2a2b3.【点评】本题考查的是单项式乘多项式,单项式与多项式相乘的运算法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.11.(2016春•东阿县期末)观察下列各式(x﹣1)(x+1)=x2﹣1(x﹣1)(x2+x+1)=x3﹣1(x﹣1)(x3+x2+x+1)=x4﹣1…①根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)=x7﹣1.②你能否由此归纳出一般性规律:(x﹣1)(x n+x n﹣1+…+x+1)=x n+1﹣1.③根据②求出:1+2+22+…+234+235的结果.【分析】①观察已知各式,得到一般性规律,化简原式即可;②原式利用得出的规律化简即可得到结果;③原式变形后,利用得出的规律化简即可得到结果.【解答】解:①根据题意得:(x﹣1)(x6+x5+x4+x3+x2+x+1)=x7﹣1;②根据题意得:(x﹣1)(x n+x n﹣1+…+x+1)=x n+1﹣1;③原式=(2﹣1)(1+2+22+…+234+235)=236﹣1.故答案为:①x7﹣1;②x n+1﹣1;③236﹣1【点评】此题考查了多项式乘以多项式,弄清题中的规律是解本题的关键.12.(2016春•长春校级期末)若(x+a)(x+2)=x2﹣5x+b,则a+b的值是多少?【分析】根据多项式与多项式相乘的法则把等式的左边展开,根据题意列出算式,求出a、b的值,计算即可.【解答】解:(x+a)(x+2)=x2+(a+2)x+2a,则a+2=﹣5,2a=b,解得,a=﹣7,b=﹣14,则a+b=﹣21.【点评】本题考查的是多项式乘多项式,多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.13.(2016春•门头沟区期末)化简:(x+5)(2x﹣3)﹣2x(x2﹣2x+3)【分析】根据单项式乘多项式和多项式乘多项式法则把原式展开,根据合并同类项法则计算即可.【解答】解:(x+5)(2x﹣3)﹣2x(x2﹣2x+3)=2x2﹣3x+10x﹣15﹣2x3+4x2﹣6x=﹣2x3+6x2+x﹣15.【点评】本题考查的是单项式乘多项式和多项式乘多项式,多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.14.(2016春•扬州期末)计算:(x+2)(x﹣1)﹣3x(x+3)【分析】原式利用多项式乘以多项式,单项式乘以多项式法则计算,去括号合并即可得到结果.【解答】解:原式=x2﹣x+2x﹣2﹣3x2﹣9x=﹣2x2﹣8x﹣2.【点评】此题考查了多项式乘多项式,以及单项式乘多项式,熟练掌握运算法则是解本题的关键.15.(2016春•青岛校级期末)(2a+1)(a﹣1)﹣2a(a+1)【分析】根据多项式的乘法,可得整式的加减,根据整式的加减,可得答案;【解答】解:原式=2a2﹣2a+a﹣1﹣2a2﹣2a=﹣3a﹣1.【点评】本题考查了多项式的乘法、整式的加减,熟记法则并根据法则计算是解题关键.16.(2016春•埇桥区期末)已知x+1与x﹣k的乘积中不含x项,求k的值.【分析】根据多项式的乘法,可得整式,根据整式不含x项,可得关于k的方程,根据解方程,可得答案.【解答】解:由(x+1)(x﹣k)=x2+(1﹣k)x﹣k,得x的系数为1﹣k.若不含x项,得1﹣k=0,解得k=1.【点评】本题考查了多项式乘多项式,利用整式不含x项得出关于k的方程是解题关键.17.(2016春•常州期末)已知x+y=3,(x+3)(y+3)=20.(1)求xy的值;(2)求x2+y2+4xy的值.【分析】(1)先根据多项式乘以多项式法则展开,再把x+y=3代入,即可求出答案;(2)先根据完全平方公式变形,再代入求出即可.【解答】解:(1)∵x+y=3,(x+3)(y+3)=xy+3(x+y)+9=20,∴xy+3×3+9=20,∴xy=2;(2)∵x+y=3,xy=2,∴x2+y2+4xy=(x+y)2+2xy=32+2×2=13.【点评】本题考查了多项式乘以多项式的应用,能熟记多项式乘以多项式法则和乘法公式是解此题的关键.18.(2016春•户县期末)先化简,再求值.已知|m﹣1|+(n+)2=0,求(﹣m2n+1)(﹣1﹣m2n)的值.【分析】先根据非负数的性质,求出m,n的值,再根据多项式乘以多项式,即可解答.【解答】解:∵|m﹣1|+(n+)2=0,∴m﹣1=0,n+=0,∴m=1,n=﹣,∴(﹣m2n+1)(﹣1﹣m2n)=m2n+m4n2﹣1﹣m2n=m4n2﹣1==1×﹣1==﹣.【点评】本题考查了多项式乘以多项式,解决本题的关键是熟记多项式乘以多项式.19.(2016春•港南区期中)已知x m=5,x n=7,求x2m+n的值.【分析】根据同底数幂的乘法,即可解答.【解答】解:∵x m=5,x n=7,∴x2m+n=x m•x m•x n=5×5×7=175.【点评】本题考查了同底数幂的乘法,解决本题的关键是熟记同底数幂的乘法法则.20.(2016春•淮阴区期中)已知3×9m×27m=321,求m的值.【分析】先把9m×27m分解成32m×33m,再根据同底数幂的乘法法则进行计算即可求出m 的值.【解答】解:∵3×9m×27m=3×32m×33m=31+2m+3m=321,∴1+2m+3m=21,∴m=4.【点评】此题考查了同底数幂的乘法,幂的乘方与积的乘方,理清指数的变化是解题的关键.21.(2016•徐州)计算:(1)(﹣1)2016+x0﹣+(2)÷.【分析】(1)先计算负整数指数幂、零指数幂、化简二次根式然后计算加减法;(2)利用完全平方公式、平方差公式、化除法为乘法进行约分化简.【解答】解:(1)原式=1+1﹣3+2=1;(2)原式=×=x.【点评】本题考查了分式的乘除法、实数的运算以及负整数指数幂等知识点,属于基础题.22.(2016•南京)计算﹣.【分析】首先进行通分运算,进而合并分子,进而化简求出答案.【解答】解:﹣=﹣==.【点评】此题主要考查了分式的加减运算,正确进行通分运算是解题关键.23.(2016•青岛)(1)化简:﹣(2)解不等式组,并写出它的整数解.【分析】(1)原式通分并利用同分母分式的减法法则计算即可得到结果;(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,确定出整数解即可.【解答】解:(1)原式=﹣==;(2),由①得:x≤1,由②得:x≥﹣2,则不等式组的解集为﹣2≤x≤1,则不等式组的整数解为﹣2,﹣1,0,1.【点评】此题考查了分式的加减法,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.24.(2016•福州)化简:a﹣b﹣.【分析】先约分,再去括号,最后合并同类项即可.【解答】解:原式=a﹣b﹣(a+b)=a﹣b﹣a﹣b=﹣2b.【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.25.(2016•十堰)化简:.【分析】首先把第一个分式的分子、分母分解因式后约分,再通分,然后根据分式的加减法法则分母不变,分子相加即可.【解答】解:=++2=++2=++==【点评】本题考查了分式的加减法法则、分式的通分、约分以及因式分解;熟练掌握分式的通分是解决问题的关键.26.(2016•甘孜州)化简:+.【分析】先通分变为同分母分式,然后再相加即可解答本题.【解答】解法一:+=+==.解法二:+=+=+=.【点评】本题考查分式的加减法,解题的关键是明确分式的加减法的计算方法.27.(2016•毕节市)已知(1)化简A;(2)若x满足不等式组,且x为整数时,求A的值.【分析】(1)原式第一项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果;(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,确定出整数x的值,代入计算即可求出A的值.【解答】解:(1)A=(x﹣3)•﹣1=﹣1==;(2),由①得:x<1,由②得:x>﹣1,∴不等式组的解集为﹣1<x<1,即整数x=0,则A=﹣.【点评】此题考查了分式的混合运算,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.28.(2016•资阳)化简:(1+)÷.【分析】首先把括号内的式子通分相加,把除法转化为乘法,然后进行乘法运算即可.【解答】解:原式=÷=•=a﹣1.【点评】本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.29.(2016•陕西)化简:(x﹣5+)÷.【分析】根据分式的除法,可得答案.【解答】解:原式=•=(x﹣1)(x﹣3)=x2﹣4x+3.【点评】本题考查了分式混合运算,利用分式的除法转化成分式的乘法是解题关键.30.(2016•成都)化简:(x﹣)÷.【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.【解答】解:原式=•=•=x+1.【点评】此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.。
(完整版)50道解分式方程及答案

50道解分式方程1.解分式方程:13)1(2522-=--x x x x 2.解分式方程:xx x -=+--314323.解分式方程:x-3113x x 2+=--4.解分式方程:012132=---xx 5.解分式方程:212423=---x x x 6.解分式方程:2112323x x x -=-+7.解方程:221+=1x+1x 1-8.(2011•宁夏)解方程:.9.(本题10分)解方程:1422=---xx x x 10.(2011•綦江县)解方程:.11.(本小题满分8分)解方程:02311=-++xx 12.(11·孝感)解关于的方程:2131x x x =++-13.(2011•攀枝花)解方程:.14.解方程:.2x 1+=33x 19x 3--15.阅读理解 解分式方程+ = 3时,小云用了如下的方法:11+x 12+x 解:设 = y ,则原方程可化为y +2y = 311+x 解这个整式方程得 y= 1由= 1去分母,得x+1=1,∴x=011+x 经检验 x = 0 是原方程的根∴原方程的根为x = 0上面的方法叫换元法,请你用换元法解方程+ = 2 2-x x 634-x x 16.解分式方程312422x x x -=--17.(5分)解分式方程:22111x x =---18.解分式方程:.21221-=+--x x x19.解分式方程:.482222-=-+-+x x x x x 20.解分式方程:141212-=+--x x x x 21.解分式方程:.2353114=-+--xx x 22.解分式方程:.45251=+-++xx x 23. 解分式方程:.4112242x x x--=--24.解分式方程:22416222-+=--+x x x x x -25.解分式方程:2111x x x =-+-26.解分式方程:212423=---x x x 27.解分式方程:451+=x x 28.解分式方程.312422x x x -=--29.解分式方程:.12211x x x +=-+30.解分式方程:.225103x x x x-=+-31. 解分式方程:.11322x x x-+=--32. 解分式方程:223=124x x x --+-33.解分式方程:(本题6分)111142-+=+-x x x 34.(2011昭通,22,7分)解分式方程:212423=---x x x 35.解分式方程.123482---=-xxx 36.解分式方程:23222x x x -=+-37.解方程:.24x+2+=11xx 1---38.解方程:+3=21-x 21-x -x 39.解方程:21233x x x -=---40.解方程:.48122-=--x x x 41.1412132-=+--x x x 42.解方程:.213x x x +=+43.解分式方程.(1)(2) 11322x x x--=--222121393x x x x x =++--44.解方程:.13321++=+x xx x 45.解下列分式方程: (1); (2)0223=--xx xx x x +=++2111246.解方程:(1)+1=; (2)-=.32x x --32x -41x +11x -241x -47.解分式方程:(1)= (2)+1=23+x 11+x 35--x x x -3248.解分式方程(1)(2)35253=-+--x x x 114112=---+x x x 49.解方程(1) (2)23121x x x x +=++21124x x x -=--50.解方程:2511=+++x x x x参考答案1.无解2.解:2- x+4(x-3)=-1 , (2分) 3x=9, ∴x=3 (2分) 经检验:x=3是增根,舍去 (1分) 所以原方程无解 (1分)3.去分母:2-x=x-3-1x=3经检验x=3是方程增根,原方程无解。
分式方程计算30题(附答案、讲解)

郭氏数学公益教学博客中考分式方程计算30题(附答案、讲解)一.解答题(共30小题)1.(2011•自贡)解方程:.2.(2011•孝感)解关于的方程:.3.(2011•咸宁)解方程.4.(2011•乌鲁木齐)解方程:=+1.5.(2011•威海)解方程:.6.(2011•潼南县)解分式方程:.7.(2011•台州)解方程:.8.(2011•随州)解方程:.9.(2011•陕西)解分式方程:.10.(2011•綦江县)解方程:.11.(2011•攀枝花)解方程:.12.(2011•宁夏)解方程:.13.(2011•茂名)解分式方程:.14.(2011•昆明)解方程:.15.(2011•菏泽)解方程:16.(2011•大连)解方程:.17.(2011•常州)解分式方程;18.(2011•巴中)解方程:.(2)解分式方程:=+1.20.(2010•遵义)解方程:21.(2010•重庆)解方程:+=122.(2010•孝感)解方程:.23.(2010•西宁)解分式方程:24.(2010•恩施州)解方程:25.(2009•乌鲁木齐)解方程:26.(2009•聊城)解方程:+=1 27.(2009•南昌)解方程:28.(2009•南平)解方程:29.(2008•昆明)解方程:30.(2007•孝感)解分式方程:.答案与评分标准一.解答题(共30小题)1.(2011•自贡)解方程:.考点:解分式方程。
专题:计算题。
分析:方程两边都乘以最简公分母y(y﹣1),得到关于y的一元一方程,然后求出方程的解,再把y的值代入最简公分母进行检验.解答:解:方程两边都乘以y(y﹣1),得2y2+y(y﹣1)=(y﹣1)(3y﹣1),2y2+y2﹣y=3y2﹣4y+1,3y=1,解得y=,检验:当y=时,y(y﹣1)=×(﹣1)=﹣≠0,∴y=是原方程的解,∴原方程的解为y=.点评:本题考查了解分式方程,(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.2.(2011•孝感)解关于的方程:.考点:解分式方程。
分式方程计算题100道及答案优秀7篇

分式方程计算题100道及答案优秀7篇智力题推荐【51-60 篇一71 李先生到16层楼去谈生意,但他只乘电梯到14层楼,然后再步行爬楼梯上去,为什么?李先生个子太矮,按不到16楼的电梯按键72 一个小孩和一个大人在漆黑的夜晚走路,小孩是大人的儿子,大人却不是小孩的父亲,请问为什么?因为他们是母子关系73 什么字全世界通用?阿拉伯数字74 一个人的前面放了一本又厚又宽的大书,他想跨过去可怎么也跨不过去,你知道这是什么原因吗?因为书就放在墙角75 人的长寿秘诀是什么?保持呼吸,不要断气76 什么时候看到的月亮最大?登上月球时77 什么人一年中只工作一天?圣诞老人78 什么事睁一只眼闭一只眼比较好?射击79 为什么刚出生的小孩只有一只左眼睛?人本来就只有一只左眼睛80 哪颗牙最后长出来?假牙分式方程应用题答案篇二初中化学计算题1. 用氯酸钾和二氧化锰的混合物16g,加热制取氧气,待完全反应,冷却后称量,得到11.2g固体物质,计算原混合物中二氧化锰的质量(计算结果保留二位小数)。
1.解:设原混合物中KClO3质量为x,依题意可知完全反应后生成氧气的质量为:16g-11.2g=4.8g(1分)MnO2由2KClO3=====2KCl+3O2↑ (1分)△2.(5分)由硫元素和铜元素组成的一种化合物(硫化物)4.0g,高温条件下在空气中充分煅烧,只得到气体SO2和4.0g固体CuO 。
(1)要使煅烧后的固体CuO完全溶解,可加入适量稀硫酸。
计算至少需要溶质质量分数为10%的稀硫酸多少克?(要求写出计算所需的化学方程式)(2)运用所学知识和上述数据进行分析,这种硫化物的化学式为。
(1)解:设质量为x的这种稀硫酸可与4.0gCuO恰好完全反应CuO + H2SO4 = CuSO4 + H2O80 984.0g 10% xx =49g答:完全溶解这些固体产物至少需要溶质质量分数为10%的稀硫酸49g 。
(2)Cu2S3.侯德榜是我国著名的化学家。
初三解分式方程练习题及答案

初三解分式方程练习题及答案精品文档初三解分式方程练习题及答案一(解答题1(解方程:2(解关于的方程:3(解方程4(解方程:5(解方程:6(解分式方程:7(解方程:8(解方程:9(解分式方程:10(解方程:11(解方程:12(解方程:13(解分式方程:( ( ( ( ( ( ( ( ( =+1( ( ( (14(解方程:15(解方程: (解不等式组16(解方程:17(?解分式方程( ( ; ?解不等式组18(解方程:19(计算:|,2|+解分式方程:1 / 15精品文档20(解方程:21(解方程:22(解方程:23(解分式方程:24(解方程:25(解方程:26(解方程:( ( +1),+tan60?; 0,1=+1( +=1 ( +=127(解方程:28(解方程:29(解方程:30(解分式方程:(答案与评分标准一(解答题1(解方程:(考点:解分式方程。
专题:计算题。
分析:方程两边都乘以最简公分母y,得到关于y的一元一方程,然后求出方程的解,再把y的值代入最简公分母进行检验(解答:解:方程两边都乘以y,得2 / 15精品文档2y+y=,2222y+y,y=3y,4y+1,3y=1,解得y=,检验:当y=时,y=×=,?0,?y=是原方程的解,?原方程的解为y=(点评:本题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解(解分式方程一定注意要验根(2(解关于的方程:(考点:解分式方程。
专题:计算题。
分析:观察可得最简公分母是,方程两边乘最简公分母,可以把分式方程转化为整式方程求解( 解答:解:方程的两边同乘,得x=+2,整理,得5x+3=0,3 / 15精品文档解得x=,(检验:把x=,代入?0(?原方程的解为:x=,(点评:本题考查了解分式方程(解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解(解分式方程一定注意要验根(3(解方程(考点:解分式方程。
分式方程专项练习50题(有答案)

分式方程专项练习50题(有答案)1.$\frac{x}{x+2}=\frac{2}{x-1}$,改写为$x(x-1)=2(x+2)$。
2.$\frac{5x-3}{x^2}=0$,当 $5x-3=0$ 时成立,即$x=\frac{3}{5}$。
3.$\frac{x}{x}+\frac{1}{x}=1$,当 $x\neq 0$ 时成立。
4.$x^2+2x=0$,当 $x=0$ 或 $x=-2$ 时成立。
5.$\frac{13}{x(x-2)}=\frac{1}{x-1}$,改写为 $13(x-1)=x(x-2)$。
6.$\frac{1}{x-1}-\frac{2}{x+1}=\frac{1}{2}$,改写为$3x^2-2x-5=0$,当 $x=\frac{1}{3}$ 或 $x=-\frac{5}{3}$ 时成立。
7.$\frac{x+1}{x-1}=\frac{x}{x+1}$,改写为 $x^2-1=0$,当 $x=1$ 或 $x=-1$ 时成立。
8.$\frac{2x-5}{3-x}=\frac{2x-2}{x+1}$,改写为 $4x^2-13x+7=0$,当 $x=1$ 或 $x=\frac{7}{4}$ 时成立。
9.$\frac{2x-5}{x-2}-\frac{1}{x+2}=x$,改写为 $3x^2-4x-3=0$,当 $x=\frac{1\pm\sqrt{13}}{3}$ 时成立。
10.$\frac{2x-1}{x+1}=1-\frac{1}{x+1}$,改写为 $x^2+3x-2=0$,当 $x=-3+\sqrt{11}$ 或 $x=-3-\sqrt{11}$ 时成立。
11.$\frac{x}{x+1}+\frac{x}{x-1}=2$,改写为 $2x^2-2x-1=0$,当 $x=\frac{1\pm\sqrt{3}}{2}$ 时成立。
12.$\frac{1}{x-1}+\frac{1}{x+1}=\frac{4}{x^2-1}$,改写为 $3x^4-8x^2-5=0$,当 $x=\pm\sqrt{\frac{5}{3}}$ 或$x=\pm\sqrt{\frac{8}{3}}$ 时成立。
分式方程练习题及答案

分式方程练习题及答案一、填空题1. 将分式 $\frac{3}{4}$ 化为小数,计算结果保留两位小数。
解答:0.752. 若 $\frac{a}{3} = \frac{2}{5}$,求 $a$ 的值。
解答:$a = \frac{6}{5}$3. 已知 $\frac{x}{4} = \frac{5}{12}$,求 $x + 2$ 的值。
解答:$x + 2 = \frac{5}{3}$4. 若 $\frac{2}{x} = \frac{7}{16}$,求 $x$ 的值。
解答:$x = \frac{32}{7}$5. 解方程 $\frac{1}{2x} - \frac{3}{4} = \frac{1}{8}$,求 $x$ 的值。
解答:$x = \frac{5}{2}$二、选择题1. 若 $\frac{2}{3}x - 1 = \frac{5}{6}$,则 $x =$A. $-\frac{1}{4}$B. $\frac{1}{2}$C. $\frac{7}{9}$D.$\frac{9}{7}$解答:C. $\frac{7}{9}$2. 若 $x - \frac{2}{3} = \frac{x}{5}$,则 $x =$A. $-\frac{1}{4}$B. $\frac{3}{2}$C. $\frac{15}{17}$D.$\frac{5}{7}$解答:B. $\frac{3}{2}$3. 若 $\frac{x}{3} = \frac{2}{5x}$,则 $x =$A. $-2$B. $-\frac{1}{2}$C. $\frac{1}{2}$D. 2解答:D. 24. 若 $\frac{3}{2} - \frac{4}{x} = \frac{5}{6}$,则 $x =$A. $-\frac{8}{3}$B. $\frac{24}{15}$C. $\frac{35}{2}$D.$\frac{6}{5}$解答:B. $\frac{24}{15}$5. 若 $2 - \frac{3}{x} = \frac{1}{4}$,则 $x =$A. 4B. 5C. 6D. 8解答:C. 6三、解答题1. 解方程 $\frac{x}{4} + \frac{1}{3} = \frac{5}{6}$,求 $x$ 的值。
分式方程应用题总汇和答案

分式方程应用题总汇及答案1、A、B 两地的距离是 80 公里 . 一辆公共汽车从 A 地驶出 3 小时后 . 一辆小汽车也从 A 地出发 . 它的速度是公共汽车的 3 倍. 已知小汽车比公共汽车迟 20 分钟抵达 B 地 . 求两车的速度。
【提示】设共交车速度为x. 小汽车速度为3x. 列方程得: 80/(3x) +3=80/x +20/602、为加速西部大开发 . 某自治区决定新修一条公路. 甲、乙两工程队承包此项工程。
假如甲工程队独自施工. 则恰巧按期达成;假如乙工程队独自施工就要超出6 个月才能达成 . 此刻甲、乙两队先共同施工 4 个月 . 剩下的由乙队独自施工 . 则恰巧按期达成。
问本来规定修睦这条公路需多长时间【提示】设时间为x 个月 . 列方程得: [1/x+1/(x+6)]*4+(x-4)/(x+6)=13、某工人原计划在规准时间内恰巧加工1500 个部件 . 改良了工具和操作方法后.工作效率提升为本来的 2 倍. 所以加工 1500 个部件时 . 比原计划提早了五小时 .问原计划每小时加工多少个部件【提示】设原计划每小时加工x 个部件 . 列方程得: 1500/2x +5=1500/x4、甲、乙两组学生去距学校千米的敬老院打扫卫生. 甲组学生步行出发半小时后.乙组学生骑自行车开始出发 . 结果两组学生同时抵达敬老院 . 假如步行的速度是骑自行车的速度的 1/3. 求步行和骑自行车的速度各是多少【提示】设步行的速度是每小时x 千米 . 则 3x +=x5、某质检部门抽取甲、乙两个相同数目的产品进行质量检测. 结果甲厂有 48 件合格产品 . 乙厂有 45 件合格产品 . 甲厂合格率比乙厂高5%.求抽取查验的产品数量及甲厂的合格率。
【提示】设抽取查验的产品数目为x. 则 (48/x -45/x)*100%=5%6、某车间加工 1200 个部件后 . 采纳了新工艺 . 工效提升 50%.这样加工相同多的部件就少用 10 小时 . 采纳新工艺前后每小时分别加工多少个部件7、A、B 两地相距 48 千米 . 一艘轮船从 A 地顺水航行至 B 地. 又立刻从 B 地逆流返回 A地. 共用去 9 小时 . 已知水流速度为 4 千米 / 时. 若设该轮船在静水中的速度为 x 千米 / 时 . 则可列方程求解。
50道解分式方程及答案

50道解分式方程及答案1.解分式方程:$\frac{5x-23}{x(x^2-1)}=\frac{2-x}{1}+4$2.解分式方程:$\frac{2-x}{1}+4=\frac{x-3}{3-x}$3.解分式方程:$\frac{x-3}{3-x}-x=1$4.解分式方程:$\frac{x^2}{x-2}-\frac{4}{2x-3}=1$5.解分式方程:$\frac{1}{2x-4}-\frac{2}{2x+2}=\frac{1}{2x-3}$6.解分式方程:$\frac{2}{2x-3}-\frac{1}{2x+3}=1$7.解方程:$\frac{2}{x-1}-\frac{3}{x+1}=1$8.解方程:$\frac{2x+1}{x-1}-\frac{3x-1}{x+1}=2$9.解方程:$\frac{5}{x-1}-\frac{3}{x+2}=2$10.解方程:$\frac{x^2}{x-4}-1=\frac{x}{2x-3}$11.解方程:$\frac{13}{x+2}=\frac{x-1}{x+3}$12.解关于$x$的方程:$\frac{2}{x+1}-\frac{1}{x-2}=x$13.解方程:$\frac{x+1}{x^2+3x-1}=\frac{1}{x-1}$14.解方程:$\frac{x+1}{x-1}+\frac{2}{x+2}=3$15.阅读理解:小云用换元法解方程$\frac{x+1}{x+1+y}+\frac{2y}{x+1+y}=3$,得到$y=1$,从而解得$x=0$。
16.解分式方程:$\frac{x^4}{x-2x^3}+2=\frac{x}{2x-3}$17.解分式方程:$\frac{2x-1}{x-1}-\frac{2x+1}{x+1}=1$18.解分式方程:$\frac{1-x}{x-2}+2=\frac{1}{x-2}$19.解分式方程:$\frac{x-1}{x+1}-\frac{x+1}{x-1}=2$20.解分式方程:$\frac{1}{x^2-1}-\frac{1}{x+1}=1$21.解分式方程:$\frac{2x-1}{x+1}-\frac{x+2}{x-1}=3$22.解分式方程:$\frac{4x-1}{x-1}-\frac{1}{x+1}=\frac{3x+1}{x^2-1}$23.解分式方程:$\frac{x-3}{3-x}-\frac{x}{x-2}=1$24.解分式方程:$\frac{x}{x+2}-\frac{1}{x-1}=\frac{4}{x+5}$25.解分式方程:$\frac{x+1}{x-1}+\frac{1}{x+1}=2$26.解分式方程:$\frac{x+1}{x-1}-\frac{1}{x+1}=1$27.解分式方程:$\frac{x-1}{x+1}-\frac{1}{x-1}=1$28.解分式方程:$\frac{2}{x-1}-\frac{1}{x+1}=\frac{2x}{x^2-1}$29.解分式方程:$\frac{3x}{2x-4}-1=\frac{2}{2x-2}$30.解分式方程:$\frac{5}{2x+3}-\frac{1}{x-x^2}=\frac{1}{x}$31.解分式方程:$\frac{x+1}{x-2}-\frac{2}{x+1}=1$32.解分式方程:$\frac{x-1}{x-2}+\frac{1}{2-x}=1$9.解法一:首先,将原方程化简为 $\frac{x-2}{2}=\frac{1}{y-2}$,令$y-2=t$,则原方程变为 $\frac{x-2}{2}=\frac{1}{t}$。
100道解分式方程及答案

100道解分式方程练习题(带答案)解答:一、复习例解方程:(1)2x+xx+3=1; (2)15x=2×15 x+12;(3)2(1x+1x+3)+x-2x+3=1.解(1)方程两边都乘以x(3+3),去分母,得2(x+3)+x2=x2+3x,即2x-3x=-6所以x=6.检验:当x=6时,x(x+3)=6(6+3)≠0,所以x=6是原分式方程的根.(2)方程两边都乘以x(x+12),约去分母,得15(x+12)=30x.解这个整式方程,得x=12.检验:当x=12时,x(x+12)=12(12+12)≠0,所以x=12是原分式方程的根.(3)整理,得2x+2x+3+x-2x+3=1,即2x+2+x-2 x+3=1,即2x+xx+3=1.方程两边都乘以x(x+3),去分母,得2(x+3)+x2=x(x+3),即2x+6+x2=x2+3x,亦即2x-3x=-6.解这个整式方程,得x=6.检验:当x=6时,x(x+3)=6(6+3)≠0,所以x=6是原分式方程的根.二、新课例1 一队学生去校外参观,他们出发30分钟时,学校要把一个紧急通知传给带队老师,派一名学生骑车从学校出发,按原路追赶队伍.若骑车的速度是队伍进行速度的2倍,这名学生追上队伍时离学校的距离是15千米,问这名学生从学校出发到追上队伍用了多少时间?请同学根据题意,找出题目中的等量关系.答:骑车行进路程=队伍行进路程=15(千米);骑车的速度=步行速度的2倍;骑车所用的时间=步行的时间-0.5小时.请同学依据上述等量关系列出方程.答案:方法1 设这名学生骑车追上队伍需x小时,依题意列方程为15x=2×15 x+12.方法2 设步行速度为x千米/时,骑车速度为2x千米/时,依题意列方程为15x-15 2x=12.解由方法1所列出的方程,已在复习中解出,下面解由方法2所列出的方程.方程两边都乘以2x,去分母,得30-15=x,所以x=15.检验:当x=15时,2x=2×15≠0,所以x=15是原分式方程的根,并且符合题意.所以骑车追上队伍所用的时间为15千米30千米/时=12小时.答:骑车追上队伍所用的时间为30分钟.指出:在例1中我们运用了两个关系式,即时间=距离速度,速度=距离时间.如果设速度为未知量,那么按时间找等量关系列方程;如果设时间为未知量,那么按速度找等量关系列方程,所列出的方程都是分式方程.例2 某工程需在规定日期内完成,若由甲队去做,恰好如期完成;若由乙队去做,要超过规定日期三天完成.现由甲、乙两队合做两天,剩下的工程由乙独做,恰好在规定日期完成,问规定日期是多少天?分析;这是一个工程问题,在工程问题中有三个量,工作量设为s,工作所用时间设为t,工作效率设为m,三个量之间的关系是s=mt,或t=sm,或m=st.请同学根据题中的等量关系列出方程.答案:方法1 工程规定日期就是甲单独完成工程所需天数,设为x天,那么乙单独完成工程所需的天数就是(x+3)天,设工程总量为1,甲的工作效率就是x1,乙的工作效率是1x+3.依题意,列方程为2(1x+1x3)+x2-xx+3=1.指出:工作效率的意义是单位时间完成的工作量.方法2 设规定日期为x天,乙与甲合作两天后,剩下的工程由乙单独做,恰好在规定日期完成,因此乙的工作时间就是x天,根据题意列方程2x+xx+3=1.方法3 根据等量关系,总工作量—甲的工作量=乙的工作量,设规定日期为x天,则可列方程1-2x=2x+3+x-2x+3.用方法1~方法3所列出的方程,我们已在新课之前解出,这里就不再解分式方程了.重点是找等量关系列方程.三、课堂练习1.甲加工180个零件所用的时间,乙可以加工240个零件,已知甲每小时比乙少加工5个零件,求两人每小时各加工的零件个数.2.A,B两地相距135千米,有大,小两辆汽车从A地开往B地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟.已知大、小汽车速度的比为2:5,求两辆汽车的速度.答案:1.甲每小时加工15个零件,乙每小时加工20个零件.2.大,小汽车的速度分别为18千米/时和45千米/时.四、小结1.列分式方程解应用题与列一元一次方程解应用题的方法与步骤基本相同,不同点是,解分式方程必须要验根.一方面要看原方程是否有增根,另一方面还要看解出的根是否符合题意.原方程的增根和不符合题意的根都应舍去.2.列分式方程解应用题,一般是求什么量,就设所求的量为未知数,这种设未知数的方法,叫做设直接未知数.但有时可根据题目特点不直接设题目所求的量为未知量,而是设另外的量为未知量,这种设未知数的方法叫做设间接未知数.在列分式方程解应用题时,设间接未知数,有时可使解答变得简捷.例如在课堂练习中的第2题,若题目的条件不变,把问题改为求大、小两辆汽车从A地到达B地各用的时间,如果设直接未知数,即设,小汽车从A地到B地需用时间为x小时,则大汽车从A地到B地需(x+5-12)小时,依题意,列方程135 x+5-12:135x=2:5.解这个分式方程,运算较繁琐.如果设间接未知数,即设速度为未知数,先求出大、小两辆汽车的速度,再分别求出它们从A地到B地的时间,运算就简便多了.五、作业1.填空:(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这件工作的时间是______小时;(2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以比原计划多用天数是______;(3)把a千克的盐溶在b千克的水中,那么在m千克这种盐水中的含盐量为______千克.2.列方程解应用题.(1)某工人师傅先后两次加工零件各1500个,当第二次加工时,他革新了工具,改进了操作方法,结果比第一次少用了18个小时.已知他第二次加工效率是第一次的2.5倍,求他第二次加工时每小时加工多少零件?(2)某人骑自行车比步行每小时多走8千米,如果他步行12千米所用时间与骑车行36千米所用的时间相等,求他步行40千米用多少小时?(3)已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米?(4)A,B两地相距135千米,两辆汽车从A地开往B地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟.已知两车的速度之比是5:2,求两辆汽车各自的速度.答案:1.(1)mn m+n; (2)m a-b-ma; (3)ma a+b.2.(1)第二次加工时,每小时加工125个零件.(2)步行40千米所用的时间为40 4=10(时).答步行40千米用了10小时.(3)江水的流速为4千米/时.课堂教学设计说明1.教学设计中,对于例1,引导学生依据题意,找到三个等量关系,并用两种不同的方法列出方程;对于例2,引导学生依据题意,用三种不同的方法列出方程.这种安排,意在启发学生能善于从不同的角度、不同的方向思考问题,激励学生在解决问题中养成灵活的思维习惯.这就为在列分式方程解应用题教学中培养学生的发散思维提供了广阔的空间.2.教学设计中体现了充分发挥例题的模式作用.例1是行程问题,其中距离是已知量,求速度(或时间);例2是工程问题,其中工作总量为已知量,求完成工作量的时间(或工作效率).这些都是运用列分式方程求解的典型问题.教学中引导学生深入分析已知量与未知量和题目中的等量关系,以及列方程求解的思路,以促使学生加深对模式的主要特征的理解和识另别,让学生弄清哪些类型的问题可借助于分式方程解答,求解的思路是什么.学生完成课堂练习和作业,则是识别问题类型,能把面对的问题和已掌握的模式在头脑中建立联系,探求解题思路.3.通过列分式方程解应用题数学,渗透了方程的思想方法,从中使学生认识到方程的思想方法是数学中解决问题的一个锐利武器.方程的思想方法可以用“以假当真”和“弄假成真”两句话形容.如何通过设直接未知数或间接未知数的方法,假设所求的量为x,这时就把它作为一个实实在在的量.通过找等量关系列方程,此时是把已知量与假设的未知量平等看待,这就是“以假当真”.通过解方程求得问题的解,原先假设的未知量x就变成了确定的量,这就是“弄假成真”.解分式方程的例题及答案第2 篇一认识分式知识点一分式的概念1、分式的概念从形式上来看,它应满足两个条件:(1)写成的形式(A、B表示两个整式)(2)分母中含有这两个条件缺一不可2、分式的意义(1)要使一个分式有意义,需具备的条件是(2)要使一个分式无意义,需具备的条件是(3)要使分式的值为0,需具备的条件是知识点二、分式的基本性质分式的分子与分母都乘以(或除以)同一个分式的值不变用字母表示为= (其中M是不等于零的整式)知识点三、分式的约分1、概念:把一个分式的分子和分母中的公因式约去,这种变形称为分式的约分2、依据:分式的基本性质注意:(1)约分的关键是正确找出分子与分母的公因式(2)当分式的分子和分母没有公因式时,这样的分式称为最简分式,化简分式时,通常要使结果成为最简分式或整式。
分式方程50题 参考答案与试题解析

分式方程50题参考答案与试题解析一.解答题(共50小题)1.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:(x+1)2﹣4=x2﹣1,整理得:x2+2x+1﹣4=x2﹣1,解得:x=1,经检验x=1是增根,分式方程无解;(2)去分母得:(x﹣2)2=(x+2)2+16,整理得:x2﹣4x+4=x2+4x+4+16,解得:x=﹣2,经检验x=﹣2是增根,分式方程无解.2.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:3(x﹣1)=2x,去括号得:3x﹣3=2x,解得:x=3,经检验x=3是分式方程的解;(2)去分母得:(x﹣2)2﹣x2+4=16,整理得:x2﹣4x+4﹣x2+4=16,解得:x=﹣2,经检验x=﹣2是增根,分式方程无解.3.【分析】(1)方程两边同乘2(4+x),得关于x的一元一次方程,解方程可求解x值,最后验根即可;(2)方程两边同乘x2﹣1,得关于x的一元一次方程,解方程可求解x值,最后验根即可.【解答】解:(1)方程两边同乘2(4+x),得2(3﹣x)=4+x,解得x=,当x=时,2(4+x)≠0,∴x=是原方程的解.(2)方程两边同乘x2﹣1,得x﹣1+2=0解得x=﹣1,当x=﹣1时,x2﹣1=0,∴x=﹣1是方程的增根,∴原方程无解.4.【分析】分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程整理得:﹣=1﹣,方程两边同乘以(x+3)(x﹣3)得:x+3﹣8x=x2﹣9﹣x(x+3),解这个方程得:x=3,经检验,x=3是原方程的增根,所以原方程无解.5.【分析】(1)原式括号中两项通分并利用同分母分式的减法法则计算,约分即可得到结果;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)原式=•=•=;(2)分式方程整理得:=1+,去分母得:x=2x﹣1+2,解得:x=﹣1,检验:当x=﹣1时,2x﹣1≠0,则分式方程的解为x=﹣1.6.【分析】两方式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:3(x+1)=2(x﹣2),去括号得:3x+3=2x﹣4,解得:x=﹣7,经检验x=﹣7是分式方程的解;(2)去分母得:x2+2x+1=x2﹣1+4,解得:x=1,经检验x=1是增根,分式方程无解.7.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:2(x+2)=3(3x﹣1),去括号得:2x+4=9x﹣3,移项合并得:﹣7x=﹣7,解得:x=1,经检验x=1是分式方程的解.8.【分析】分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:原方程可化为:﹣=1,去分母,得3x﹣6=x﹣2,解得:x=2,经检验:x=2是原方程的增根,所以原方程无解.9.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:x+3=2x,解得:x=3,检验:把x=3代入得:x(x+3)=18≠0,则分式方程的解为x=3.10.【分析】分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:分式方程整理得:+=4,去分母得:x+4+2=4x﹣12,移项合并得:﹣3x=﹣18,解得:x=6,经检验x=6是分式方程的解.11.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:5x+7﹣2(x+5)=x2+4x﹣5,整理得:x2+x﹣2=0,即(x﹣1)(x+2)=0,解得:x=1或x=﹣2,经检验x=1是增根,则分式方程的解为x=﹣2.12.【分析】根据解分式方程的解法步骤求解即可.【解答】解:去分母得,(x+1)(x﹣2)﹣(x+2)(x﹣2)=3(x+2)去括号得,x2﹣x﹣2﹣x2+4=3x+6移项得,x2﹣x﹣x2﹣3x=6+2﹣4合并同类项得,﹣4x=4系数化为1得,x=﹣1经检验,x=﹣1是原方程的解,所以原方程的解为x=﹣1.13.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:最简公分母为(x﹣2)2,去分母得:x(x﹣2)﹣(x﹣2)2=4,整理得:x2﹣2x﹣x2+4x﹣4=4,解得:x=4,检验:把x=4代入得:(x﹣2)2=4≠0,∴分式方程的解为x=4.14.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到m的值,经检验即可得到方程的解.【解答】解:去分母得:5﹣m=m﹣2﹣3,移项合并得:2m=10,解得:m=5,检验:把m=5代入得:m﹣2=5﹣2=3≠0,∴分式方程的解为m=5.15.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:3+x2﹣9=x(x+3),解得:x=﹣2,检验:当x=﹣2时,x2﹣9≠0,∴原方程的解为x=﹣2.16.【分析】方程两边都乘以x﹣1得出3x+2=5,求出方程的解,再进行检验即可.【解答】解:方程两边都乘以x﹣1得:3x+2=5,解得:x=1,检验:当x=1时,x﹣1=0,所以x=1不是原方程的解,即原方程无解.17.【分析】方程两边都乘以x(x﹣1)得出x﹣8+3x=0,求出方程的解,再进行检验即可.【解答】解:方程两边都乘以x(x﹣1)得:x﹣8+3x=0,解得:x=2,检验:当x=2时,x(x﹣1)≠0,所以x=2是原方程的解,即原方程的解是:x=2.18.【分析】(1)方程两边都乘以x(x+1)得出5x+2=3x,求出方程的解,再进行检验即可;(2)方程两边都乘以2(x﹣1)得出2x=3﹣4(x﹣1),求出方程的解,再进行检验即可.【解答】解:(1)方程两边都乘以x(x+1)得:5x+2=3x,解得:x=﹣1,检验:当x=﹣1时,x(x+1)=0,所以x=﹣1是增根,即原方程无解;(2)方程两边都乘以2(x﹣1)得:2x=3﹣4(x﹣1),解得:x=,检验:当x=时,2(x﹣1)≠0,所以x=是原方程的解,即原方程的解是:x=.19.【分析】方程两边都乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:=+1,方程两边都乘(x﹣1)(x+1),得x(x+1)=4+(x﹣1)(x+1),解得x=3,检验:当x=3时,(x﹣1)(x+1)=8≠0.故x=3是原方程的解.20.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)方程两边同乘x(x﹣1)得:9(x﹣1)=8x,解得:x=9,经检验x=9是分式方程的解;(2)方程两边同乘x﹣2得:x﹣1﹣3(x﹣2)=1,解得:x=2,经检验x=2是增根,分式方程无解.21.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程﹣=1,去分母得:x2﹣4x+4﹣3x=x2﹣2x,解得:x=,经检验x=是分式方程的解.22.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)分式方程整理得:﹣=1,去分母得:1﹣2=x﹣2,解得:x=1,经检验x=1是分式方程的解;(2)去分母得:x2+x﹣x2+1=3,解得:x=2,经检验x=2是分式方程的解.23.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)=,去分母得:x﹣3=2x,解得:x=﹣3,经检验x=﹣3是分式方程的解;(2)方程整理得:﹣1=﹣,去分母得:x﹣2x+1=﹣3,解得:x=4,经检验x=4是分式方程的解.24.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:(x+3)(x﹣1)﹣x2+9=2,整理得:x2+2x﹣3﹣x2+9=2,即2x=﹣4,解得:x=﹣2,经检验x=﹣2是分式方程的解.25.【分析】(1)方程组整理后,利用加减消元法求出解即可;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)方程组整理得:,①×2+②得:11x=22,解得:x=2,把x=2代入①得:y=3,则方程组的解为;(2)去分母得:3x+3﹣4x=x﹣1,解得:x=2,经检验x=2是分式方程的解.26.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)+=0,去分母得:x﹣2+x+3=0,解得:x=﹣,经检验x=﹣是分式方程的解;(2)﹣=1,去分母得:(x+1)2﹣4=x2﹣1,解得:x=1,经检验x=1是增根,分式方程无解.27.【分析】(1)方程组利用加减消元法求出解即可;(2)分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1),①×2+②得:5x=10,解得:x=2,把x=2代入①得:y=1,则方程组的解为;(2)分式方程整理得:﹣2=﹣,去分母得:3x﹣2(x﹣3)=﹣3,去括号得:3x﹣2x+6=﹣3,解得:x=﹣9,经检验x=﹣9是分式方程的解.28.【分析】分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程整理得:+1=﹣,去分母得:2x﹣4+4x﹣2=﹣3,移项合并得:6x=3,解得:x=,经检验x=是增根,分式方程无解.29.【分析】(1)方程组利用加减消元法求出解即可;(2)分式方程去分母转化为整式方程,求出整式方程的解得到y的值,经检验即可得到分式方程的解.【解答】解:(1),①+②得:3x=9,解得:x=3,把x=3代入①得:y=0,则方程组的解为;(2)分式方程=+1,去分母得:3=1+y﹣2,解得:y=4,经检验y=4是分式方程的解.30.【分析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1)=,去分母得:3x=2x﹣2,解得:x=﹣2,经检验x=﹣2是分式方程的解;(2)方程组整理得:,①+②得:6y=6,解得:y=1,把y=1代入①得:x=3,则方程组的解为.31.【分析】(1)方程组利用加减消元法求出解即可;(2)分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1),①+②得:4x=12,解得:x=3,把x=3代入②得:y=1,则方程组的解为;(2)分式方程整理得:﹣=1,去分母得:4﹣3=x﹣2,解得:x=3,经检验x=3是分式方程的解.32.【分析】(1)方程组利用加减消元法求出解即可;(2)分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1),②×2﹣①得:7y=7,解得:y=1,把y=1代入②得:x=2,则方程组的解为;(2)分式方程整理得:﹣=﹣5,去分母得:﹣3=x﹣5(x﹣1),去括号得:﹣3=x﹣5x+5,移项合并得:4x=8,解得:x=2.33.【分析】(1)根据加减消元法解方程即可求解;(2)方程两边都乘最简公分母,可以把分式方程转化为整式方程求解.【解答】解:(1).②﹣①×2得:7x=﹣14,解得:y=﹣2,把y=﹣2代入①得:x=2.故方程组的解为;(2)+2=,方程两边都乘(x﹣2)得1﹣x+2(x﹣2)=﹣1,解得x=2,检验:当x=2时,x﹣2=0,是增根.故原方程无解.34.【分析】(1)利用加减消元法解方程组;(2)方程两边乘以(x+1)(x﹣1)得到整式方程,然后解整式方程后进行检验确定原方程的解.【解答】解:(1),②﹣①得4x=28,解得x=7,把x=7代入①得7﹣3y=﹣8,解得y=5,所以方程组的解为;(2)去分母得﹣2=2(x﹣1)﹣(x+1),解得x=1,经检验:原方程的解为x=1.35.【分析】(1)方程两边都乘最简公分母,可以把分式方程转化为整式方程求解;(2)根据加减消元法解方程即可求解.【解答】解:(1)=1+,方程两边都乘(x﹣2)得x=x﹣2+x+1,解得x=1,检验:当x=1时,x﹣2≠0.故x=1是原方程的解;(2),①+②×5得:17x=17,解得:x=1,把x=1代入②得:y=﹣5.故方程组的解为.36.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程+1=,去分母得:2+1+x=4x,解得:x=1,经检验x=1是分式方程的解.37.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:分式方程整理得:﹣1=,去分母得:(x﹣2)2﹣(x2﹣4)=12,整理得:x2﹣4x+4﹣x2+4=12,移项合并得:﹣4x=4,解得:x=﹣1,检验:把x=﹣1代入得:(x+2)(x﹣2)≠0,∴分式方程的解为x=﹣1.38.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:分式方程整理得:﹣=1,去分母得:(x+2)2﹣20=x2﹣4,整理得:x2+4x+4﹣20=x2﹣4,移项合并得:4x=12,解得:x=3,检验:把x=3代入得:(x+2)(x﹣2)≠0,则分式方程的解为x=3.39.【分析】(1)方程组利用加减消元法求出解即可;(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1),①+②得:6x=18,解得:x=3,①﹣②得:4y=8,解得:y=2,则方程组的解为;(2)分式方程整理得:﹣2=,去分母得:x﹣2(x﹣3)=3,去括号得:x﹣2x+6=3,移项合并得:﹣x=﹣3,解得:x=3,检验:把x=3代入得:x﹣3=0,∴x=3是增根,则分式方程无解.40.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程整理得:﹣=1,去分母得:x﹣2﹣4x+8=x2﹣4,即x2+3x﹣10=0,分解因式得:(x﹣2)(x+5)=0,解得:x=2或x=﹣5,经检验x=2是增根,则分式方程的解为x=﹣5.41.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:x+1=4(x﹣2),解得:x=3,检验:把x=3代入得:(x﹣2)(x+1)≠0,∴x=3是原方程的解.42.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:4﹣(x+2)=0,解得:x=2,经检验x=2是增根,分式方程无解.43.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:3﹣2(x+3)=x﹣3,去括号得:3﹣2x﹣6=x﹣3,移项合并得:﹣3x=0,解得:x=0,经检验x=0是分式方程的解.44.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:3x﹣6﹣2x=0,解得:x=6,经检验x=6是分式方程的解;(2)去分母得:x2+2x+1﹣4=x2﹣1,解得:x=1,经检验x=1是增根,分式方程无解.45.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:方程两边同时乘以(x+3)(x﹣3)得(x﹣3)+2(x+3)=12,去括号得:x﹣3+2x+6=12,移项得:x+2x=12+3﹣6,合并得:3x=9,解得:x=3,检验:把x=3代入(x+3)(x﹣3)=0,∴x=3是增根,原方程无解.46.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:x2+4x+4﹣3x2=2x2+4x,整理得:4x2=4,即x2=1,解得:x=1或x=﹣1,经检验x=1和x=﹣1都为分式方程的解.47.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:2x=3x﹣6,解得:x=6,经检验x=6是分式方程的解;(2)去分母得:x2+2x+1﹣4=x2﹣x,解得:x=1,经检验x=1是增根,则原方程无解.48.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:2=2x﹣1﹣3,解得:x=3,经检验x=3是分式方程的解;(2)去分母得:x﹣3﹣2=1,解得:x=6,经检验x=6是分式方程的解.49.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)方程两边同乘(3+x)(3﹣x),得9(3﹣x)=6(3+x),解这个方程,得x=,检验:当x=时,(3+x)(3﹣x)≠0,则x=是原方程的解;(2)方程两边同乘(x+1)(x﹣1),得4+x2﹣1=(x﹣1)2,解这个方程,得x=﹣1,检验:当x=﹣1时,(x+1)(x﹣1)=0,x=﹣1是增根,则原方程无解.50.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:x+3=5x,解得:x=,经检验x=是分式方程的根;(2)去分母得:3﹣x+1=x﹣4,解得:x=4,经检验x=4是增根,方程无解.。
(完整)初三解分式方程专题练习(附答案)

初三解分式方程专题练习一.解答题(共30小题)1.解方程:.2.解关于的方程:.3.解方程.4.解方程:=+1.6.解分式方程:.5.解方程:.7.(2011•台州)解方程:.8.解方程:.9.解分式方程:.10.解方程:.11.解方程:.12.解方程:.14.解方程:.13.解方程:.15.解方程:16.解方程:.17.①解分式方程;18.解方程:.19.(1)计算:|﹣2|+(+1)0﹣()﹣1+tan60°;(2)解分式方程:=+1.20.解方程:21.解方程:+=123.解分式方程:22.解方程:.24.解方程:25.解方程:27.解方程:26.解方程:+=128.解方程:29.解方程:30.解分式方程:.初三解分式方程专题练习答案与评分标准一.解答题(共30小题)1.解方程:.解答:解:方程两边都乘以y(y﹣1),得2y2+y(y﹣1)=(y﹣1)(3y﹣1),2y2+y2﹣y=3y2﹣4y+1,3y=1,解得y=,检验:当y=时,y(y﹣1)=×(﹣1)=﹣≠0,∴y=是原方程的解,∴原方程的解为y=.2.解关于的方程:.解答:解:方程的两边同乘(x+3)(x﹣1),得x(x﹣1)=(x+3)(x﹣1)+2(x+3),整理,得5x+3=0,解得x=﹣.检验:把x=﹣代入(x+3)(x﹣1)≠0.∴原方程的解为:x=﹣.3.解方程.解答:解:两边同时乘以(x+1)(x﹣2),得x(x﹣2)﹣(x+1)(x﹣2)=3.(3分)解这个方程,得x=﹣1.(7分)检验:x=﹣1时(x+1)(x﹣2)=0,x=﹣1不是原分式方程的解,∴原分式方程无解.(8分)4.解方程:=+1.解答:解:原方程两边同乘2(x﹣1),得2=3+2(x﹣1),解得x=,检验:当x=时,2(x﹣1)≠0,∴原方程的解为:x=.5.(2011•威海)解方程:.解答:解:方程的两边同乘(x﹣1)(x+1),得3x+3﹣x﹣3=0,解得x=0.检验:把x=0代入(x﹣1)(x+1)=﹣1≠0.∴原方程的解为:x=0.6.(2011•潼南县)解分式方程:.解答:解:方程两边同乘(x+1)(x﹣1),得x(x﹣1)﹣(x+1)=(x+1)(x﹣1)(2分)化简,得﹣2x﹣1=﹣1(4分)解得x=0(5分)检验:当x=0时(x+1)(x﹣1)≠0,∴x=0是原分式方程的解.(6分)7.(2011•台州)解方程:.解答:解:去分母,得x﹣3=4x (4分)移项,得x﹣4x=3,合并同类项,系数化为1,得x=﹣1(6分)经检验,x=﹣1是方程的根(8分).8.(2011•随州)解方程:.解答:解:方程两边同乘以x(x+3),得2(x+3)+x2=x(x+3),2x+6+x2=x2+3x,∴x=6检验:把x=6代入x(x+3)=54≠0,∴原方程的解为x=6.9.(2011•陕西)解分式方程:.解答:解:去分母,得4x﹣(x﹣2)=﹣3,去括号,得4x﹣x+2=﹣3,移项,得4x﹣x=﹣2﹣3,合并,得3x=﹣5,化系数为1,得x=﹣,检验:当x=﹣时,x﹣2≠0,∴原方程的解为x=﹣.解答:解:方程两边都乘以最简公分母(x﹣3)(x+1)得:3(x+1)=5(x﹣3),解得:x=9,检验:当x=9时,(x﹣3)(x+1)=60≠0,∴原分式方程的解为x=9.11.(2011•攀枝花)解方程:.解答:解:方程的两边同乘(x+2)(x﹣2),得2﹣(x﹣2)=0,解得x=4.检验:把x=4代入(x+2)(x﹣2)=12≠0.∴原方程的解为:x=4.12.(2011•宁夏)解方程:.解答:解:原方程两边同乘(x﹣1)(x+2),得x(x+2)﹣(x﹣1)(x+2)=3(x﹣1),展开、整理得﹣2x=﹣5,解得x=2.5,检验:当x=2.5时,(x﹣1)(x+2)≠0,∴原方程的解为:x=2.5.13.(2011•茂名)解分式方程:.解答:解:方程两边乘以(x+2),得:3x2﹣12=2x(x+2),(1分)3x2﹣12=2x2+4x,(2分)x2﹣4x﹣12=0,(3分)(x+2)(x﹣6)=0,(4分)解得:x1=﹣2,x2=6,(5分)检验:把x=﹣2代入(x+2)=0.则x=﹣2是原方程的增根,检验:把x=6代入(x+2)=8≠0.∴x=6是原方程的根(7分).14.(2011•昆明)解方程:.解答:解:方程的两边同乘(x﹣2),得3﹣1=x﹣2,解得x=4.检验:把x=4代入(x﹣2)=2≠0.解答:(1)解:原方程两边同乘以6x,得3(x+1)=2x•(x+1)整理得2x2﹣x﹣3=0(3分)解得x=﹣1或检验:把x=﹣1代入6x=﹣6≠0,把x=代入6x=9≠0,∴x=﹣1或是原方程的解,故原方程的解为x=﹣1或(6分)16.(2011•大连)解方程:.解答:解:去分母,得5+(x﹣2)=﹣(x﹣1),去括号,得5+x﹣2=﹣x+1,移项,得x+x=1+2﹣5,合并,得2x=﹣2,化系数为1,得x=﹣1,检验:当x=﹣1时,x﹣2≠0,∴原方程的解为x=﹣1.17.(2011•常州)①解分式方程;解答:解:①去分母,得2(x﹣2)=3(x+2),去括号,得2x﹣4=3x+6,移项,得2x﹣3x=4+6,解得x=﹣10,检验:当x=﹣10时,(x+2)(x﹣2)≠0,∴原方程的解为x=﹣10;18.(2011•巴中)解方程:.解答:解:去分母得,2x+2﹣(x﹣3)=6x,∴x+5=6x,解得,x=1经检验:x=1是原方程的解.19.(2011•巴彦淖尔)(1)计算:|﹣2|+(+1)0﹣()﹣1+tan60°;(2)解分式方程:=+1.(2)方程两边同时乘以3(x+1)得3x=2x+3(x+1),x=﹣1.5,检验:把x=﹣1.5代入(3x+3)=﹣1.5≠0.∴x=﹣1.5是原方程的解.20.(2010•遵义)解方程:解答:解:方程两边同乘以(x﹣2),得:x﹣3+(x﹣2)=﹣3,解得x=1,检验:x=1时,x﹣2≠0,∴x=1是原分式方程的解.21.(2010•重庆)解方程:+=1解答:解:方程两边同乘x(x﹣1),得x2+x﹣1=x(x﹣1)(2分)整理,得2x=1(4分)解得x=(5分)经检验,x=是原方程的解,所以原方程的解是x=.(6分)22.(2010•孝感)解方程:.解答:解:方程两边同乘(x﹣3),得:2﹣x﹣1=x﹣3,整理解得:x=2,经检验:x=2是原方程的解.23.(2010•西宁)解分式方程:解答:解:方程两边同乘以2(3x﹣1),得3(6x﹣2)﹣2=4(2分)18x﹣6﹣2=4,18x=12,x=(5分).检验:把x=代入2(3x﹣1):2(3x﹣1)≠0,∴x=是原方程的根.∴原方程的解为x=.(7分)24.(2010•恩施州)解方程:经检验:当x=3时,x﹣4=﹣1≠0,所以x=3是原方程的解.(8分)25.(2009•乌鲁木齐)解方程:解答:解:方程两边都乘x﹣2,得3﹣(x﹣3)=x﹣2,解得x=4.检验:x=4时,x﹣2≠0,∴原方程的解是x=4.26.(2009•聊城)解方程:+=1解答:解:方程变形整理得:=1方程两边同乘(x+2)(x﹣2),得:(x﹣2)2﹣8=(x+2)(x﹣2),解这个方程得:x=0,检验:将x=0代入(x+2)(x﹣2)=﹣4≠0,∴x=0是原方程的解.27.(2009•南昌)解方程:解答:解:方程两边同乘以2(3x﹣1),得:﹣2+3x﹣1=3,解得:x=2,检验:x=2时,2(3x﹣1)≠0.所以x=2是原方程的解.28.(2009•南平)解方程:解答:解:方程两边同时乘以(x﹣2),得4+3(x﹣2)=x﹣1,解得:.检验:当时,,∴是原方程的解;29.(2008•昆明)解方程:解答:解:原方程可化为:,方程的两边同乘(2x﹣1),得2﹣5=2x﹣1,∴原方程的解为:x=﹣1.30.(2007•孝感)解分式方程:.解答:解:方程两边同乘以2(3x﹣1),去分母,得:﹣2﹣3(3x﹣1)=4,解这个整式方程,得x=﹣,检验:把x=﹣代入最简公分母2(3x﹣1)=2(﹣1﹣1)=﹣4≠0,∴原方程的解是x=﹣(6分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
50道解分式方程1. 解分式方程:13)1(2522-=--x x x x2. 解分式方程:xx x -=+--314323. 解分式方程:x-3113x x 2+=--4. 解分式方程:012132=---x x5. 解分式方程:212423=---x x x6. 解分式方程:2112323x x x -=-+7. 解方程:221+=1x+1x 1-8.(2011?宁夏)解方程:.9.(本题10分)解方程:1422=---x x x x10.(2011?綦江县)解方程:.11.(本小题满分8分)解方程:02311=-++x x12.(11·孝感)解关于的方程:2131x x x =++-13.(2011?攀枝花)解方程:.14.解方程:2x 1+=33x 19x 3--.15.阅读理解 解分式方程11+x +12+x = 3时,小云用了如下的方法: 解:设 11+x = y ,则原方程可化为y +2y = 3解这个整式方程得 y= 1由 11+x = 1去分母,得x+1=1,∴x=0 经检验 x = 0 是原方程的根∴原方程的根为x = 0上面的方法叫换元法,请你用换元法解方程2-x x + 634-x x = 216.解分式方程312422x x x -=--17.(5分)解分式方程:22111x x =---18.解分式方程:21221-=+--x x x .19.解分式方程:20.解分式方程:141212-=+--x x x x21.解分式方程:2353114=-+--x x x .22.解分式方程:45251=+-++x x x .23.24.解分式方程:22416222-+=--+x x x x x - 2526.解分式方程:212423=---x x x27.解分式方程:451+=x x28.解分式方程312422x x x -=--.2930.解分式方程:225103x x x x-=+-.31. 解分式方程:32. 解分式方程:223=124x x x --+-33.解分式方程:(本题6分)111142-+=+-x x x34.(2011昭通,22,73536.解分式方程37.解方程:24x+2+=11x x 1---.38.解方程:21-x +3=21-x -x39.解方程:21233x x x -=---40.解方程:48122-=--x x x .41.1412132-=+--x x x4243.解分式方程.(44.解方程:13321++=+x x x x .45.解下列分式方程:(1) 0223=--xx ; (2) x x x x +=++2111246.解方程:(1)32x x --+1=32x -; (2)41x +-11x -=241x -.47.解分式方程:(1)23+x =11+x (2)35--x x +1=x -3248.解分式方程(1)35253=-+--x xx(2)114112=---+x x x49.解方程(1(250.解方程:2511=+++x xx x参考答案1.无解2.解:2- x+4(x-3)=-1 , (2分)3x=9, ∴x=3 (2分)经检验:x=3是增根,舍去 (1分)所以原方程无解 (1分)3.去分母:2-x=x-3-1x=3经检验x=3是方程增根,原方程无解。
4.1=x5.解:方程两边同乘以)2(2-x ,得223-=-x x322--=--x x53-=-x35=x 检验:当35=x 时,0)2(2≠-x ∴35=x 是原分式方程的解 6.x=-37.x=28.解:原方程两边同乘(x ﹣1)(x+2),得x (x+2)﹣(x ﹣1)(x+2)=3(x ﹣1),展开、整理得﹣2x=﹣5,解得x=2.5,检验:当x=2.5时,(x ﹣1)(x+2)≠0,∴原方程的解为:x=2.5.9.解法一 解:令y x x =-21分 原方程化为12=-y y 整理得 022=--y y 2分解得 1,221-==y y 2分当21=y 时 22=-x x解得41=x 2分当11-=y 时12-=-x x 解得12=x 2分 经检验:41=x ,12=x 是原方程的解 2分∴原方程的解是41=x 、12=x 1分解法二 解:原方程化为:1)2()2)(42()2(2=-----x x x x x x x 2分 当0)2(≠-x x 时,)2()2(222-=--x x x x整理得:0452=+-x x 3分解得:41=x 、12=x 2分(若前面无“当0)2(≠-x x 时”在此应当检验)∴原方程的解是41=x 、12=x 1分10.:解: 方程两边都乘以最简公分母(x ﹣3)(x+1)得:3(x+1)=5(x ﹣3),解得:x=9,检验:当x=9时,(x ﹣3)(x+1)=60≠0,∴原分式方程的解为x=9.11.解:332+=-x x ,5.2-=x .经检验知,5.2-=x 是原方程的解.12.解:方程两边同乘以(x -1)(x +3),得x (x -1)=(x -1) (x +3)+2 (x +3)……………………………………2分13.解:方程的两边同乘(x+2)(x ﹣2),得2﹣(x ﹣2)=0,解得x=4.检验:把x=4代入(x+2)(x ﹣2)=12≠0.∴原方程的解为:x=4.14.原方程无解15.解:设2-x x =Y 则原方程化为Y +34Y =2 解这个整式方程得 Y =76 因此2-x x =76 解得,X =-12,经检验,X =-12是原方程的根∴原方程的根是X =-1216.53x = 17.解:方程两边都乘以(x+1)(x —1),得:………………………1分2= —(x+1)解之得:x= —3………………………………3分检验:将x= —3代入(x+1)(x —1)≠0………………4分所以x= —3是原方程的解………………………………5分18.19.方程两边同乘以最简公分母)2)(2(-+x x ,得8)2()2(2=+--x x x844222=----x x x x 126=-x 2-=x 经检验:2-=x 不是原方程的根,原方程无解20.原方程变形为)1)(1(4121-+=+--x x x x x -------------------------2分 方程两边都乘以)1)(1(-+x x ,去分母并整理得022=--x x ,----------5分 解这个方程得1,221-==x x 。
--------------------------------------7分 经检验,2=x 是原方程的根,1-=x 是原方程的增根。
---------------9分 ∴原方程的根是2=x 。
21.解:方程两边同乘(3)x -,得 625114-=--x x . ---------------2分解得 5=x . -----------------------------------4分检验:5=x 时30x -≠,5=x 是原分式方程的解.22.解:方程两边同乘(5)x +,得 20421+=-+x x . -----------------2分解得 7-=x . -------------------------4分检验:7-=x 时50x +≠,7-=x 是原分式方程的解.23.24.22(2)16(2)x x --=+22441644x x x x -+-=++816x -=2x =-……………………4分经检验:2x =-不是方程的解……………………5分∴原方程无解……………………6分25.解:去分母,得:2(x-1)=x (x+1)-(x+1)(x-1)……………………………………….2分 2x-2=x 2+x- x 2+1……………………………………………………………3分x=3……………………………………………………………………………4分经检验x=3是原方程的解……………………………………………………5分26.原方程的解是x =35 【答案】解:两边同乘以)4(+x x 得:x x 54=+.解得:1=x .经检验:1=x 是原分式方程的解.所以原分式方程的解为x=1.28.53x = 29.x =330.解:方程两边同乘以x(x+3)(x -1),得5(x -1)-(x+3)=0.解这个方程,得2x =.检验:把x 代入最简公分母,得2×5×1=10≠0. ∴原方程的解是2x =.31.解:………………1分 去分母得 x-1+1=3(x-2)解得 x=3. ………………4分经检验:x=3是原方程的根.所以原方程的根为x=3.32.54x = 33.无解34 解得35……………………………1分 ()()()42382--+-=x x x ……………………………3分46822+---=x x x ……………………………4分∴10-=x经检验:10-=x 是原方程的根.………………………5分36.72=x 37.解:方程两边都乘以(x+1)(x ﹣1),得4﹣(x+1)(x+2)=﹣(x 2﹣1),整理,得,3x=1,解得1x=3。
经检验,1x=3是原方程的根。
∴原方程的解是1x=3。
38.见解析39.无解40.无解41.x=-1是增根,原方程无解42.x=643.(1) 3x =,(2) 原方程无解44.23-=x 7分 检验 1分45.(1) 3x-2(x-2)=0 2分3x-2x+4=0 4分x =-4 6分(2)2x+x+1=1 2分3x=0 4分0=x 无解 6分46.(1)1x = (2)3x =47.(1)21-=x (2)原方程无解 48.(1)4=x (2)1=x49.(1)1x =-是增根,原方程无解;(250.2,121-==x x (验根)。
