全国统考2022高考数学一轮复习高考大题专项三数列理含解析北师大版
全国统考2022高考数学一轮复习课时规范练31等比数列及其前n项和理含解析北师大版.docx

课时规范练31 等比数列及其前n 项和基础巩固组1.(2020安徽安庆二模,理5)等比数列{a n }的前n 项和为S n .若a 3a 6=2a 52,S 4=152,则a 2+a 4=( )A .32B .52C.32D.40 2.等比数列{a n }的前n 项和为S n ,若S 2n =4(a 1+a 3+…+a 2n-1)(n ∈N +),a 1a 2a 3=-27,则a 5=( ) A.81B.24C.-81D.-243.已知正项等比数列{a n }的前n 项和为S n ,且7S 2=4S 4,则公比q 的值为( ) A.1B.1或12C .√32D.±√324.(2020湖南郴州一模)在数列{a n }中,a 1=2,a n 2=a n-1·a n+1(n ≥2,n ∈N *),S n 为{a n }的前n 项和,若a 6=64,则S 7的值为( ) A.126 B.256 C.255 D.254 5.(2020广东惠州联考)已知数列{a n }为等差数列,且2a 1,2,2a 6成等比数列,则{a n }前6项的和为( ) A.15 B .212C.6D.3 6.设等比数列{a n }的前n 项和为S n ,若S 2=3,S 4=15,则S 6=( )A.63B.62C.61D.607.(2020辽宁大连24中一模,4)在公差不为零的等差数列{a n }中,a 1+a 2+a 5=13,且a 1,a 2,a 5成等比数列,则数列{a n }的公差等于( ) A.1B.2C.3D.48.(2019全国1,理14)记S n 为等比数列{a n }的前n 项和.若a 1=13,a 42=a 6,则S 5= .9.等比数列{a n }的各项均为实数,其前n 项和为S n .已知S 3=74,S 6=634,则a 8= . 10.(2020四川绵阳三模,理17)若数列{a n }的前n 项和为S n ,已知a 1=1,a n +1=23S n .(1)求S n ;(2)设b n =1S n,求证:b 1+b 2+b 3+…+b n <52.综合提升组11.(2020全国2,理6)数列{a n }中,a 1=2,a m+n =a m a n .若a k+1+a k+2+…+a k+10=215-25,则k=( )A.2B.3C.4D.512.(2020湖南常德一模,文7)等比数列{a n}的各项均为正数,已知向量n=(a5,a4),m=(a7,a8),且m·n=4,则log2a1+log2a2+…+log2a11=()A.5B.112C.132D.2+log2513.我国古代数学著作《算法统宗》中有这样一个问题(意为):“有一个人要走378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,那么,此人第4天和第5天共走路程是()A.24里B.36里C.48里D.60里14.(2020湖南常德一模,文17)在数列{a n}中,a1=1,a n+1=2a n+1(n∈N*).(1)证明:数列{a n+1}为等比数列;(2)求数列{a n}的前n项和S n.创新应用组15.(2020河南驻马店二模,文16)在数列{a n}中,a1=1,a n≠0,曲线y=x3在点(a n,a n3)处的切线经过点(a n+1,0),下列四个结论:①a2=23;②a3=13;③∑i=14a i=6527;④数列{a n}是等比数列,其中所有正确结论的编号是.16.(2020广东广州一模,理17)记S n为数列{a n}的前n项和,2S n-a n=12n-1(n∈N+).(1)求a n+a n+1;(2)令b n=a n+2-a n,证明数列{b n}是等比数列,并求其前n项和T n.参考答案课时规范练31等比数列及其前n项和1.B 设等比数列{a n }的公比为q ,因为a 3a 6=2a 52,所以a 4a 5=2a 52,所以q=a 5a 4=12.因为S 4=152,所以a 1(1-q 4)1-q=152,解得a 1=4,所以a 2=2,a 4=12,a 2+a 4=52.故选B.2.C 设等比数列{a n }的公比为q ,已知S 2n =4(a 1+a 3+…+a 2n-1)(n ∈N *),令n=1,则S 2=4a 1,可得a 2=3a 1,q=3.∵a 1a 2a 3=-27,∴a 23=-27,解得a 2=-3,∴a 1=-1,则a 5=-34=-81.3.C 因为7S 2=4S 4,所以3(a 1+a 2)=4(S 4-S 2)=4(a 3+a 4),故q 2=34,因为数列{a n }为正项的等比数列,故q>0,所以q=√32,故选C .4.D 在数列{a n }中,满足a n 2=a n-1a n+1(n ≥2),则数列{a n }为等比数列.设其公比为q ,由a 1=2,a 6=64,得q 5=a6a 1=32,则q=2,则S 7=2×(1-27)1-2=28-2=254.5.C 由2a 1,2,2a 6成等比数列,可得4=2a 1·2a 6=2a 1+a 6,即a 1+a 6=2,又数列{a n }为等差数列,所以{a n }前6项的和为12×6(a 1+a 6)=6.6.A 由等比数列的性质可知S 2,S 4-S 2,S 6-S 4成等比数列,即3,12,S 6-15成等比数列, 所以S 6-15=12×4,解得S 6=63. 7.B 设数列{a n }的公差为d ,且d ≠0.∵a 1+a 2+a 5=13,∴3a 1+5d=13. ①∵a 1,a 2,a 5成等比数列,∴(a 1+d )2=a 1(a 1+4d ),②解①②组成的方程组,可得d=2.故选B. 8.1213设等比数列{a n }的公比为q ,则a 4=a 1q 3=13q 3,a 6=a 1q 5=13q 5. ∵a 42=a 6,∴19q 6=13q 5.∵q ≠0,∴q=3. ∴S 5=a 1(1-q 5)1-q=13(1-35)1-3=1213.9.32 设该等比数列的公比为q ,则S 6-S 3=634−74=14,即a 4+a 5+a 6=14.①∵S 3=74,∴a 1+a 2+a 3=74. 由①得(a 1+a 2+a 3)q 3=14, ∴q 3=1474=8,即q=2.∴a 1+2a 1+4a 1=74,a 1=14, ∴a 8=a 1·q 7=14×27=32.10.(1)解由a n +1=23S n ,可得S n +1-S n =23S n ,即S n +1=53S n ,由a 1=1,可得S 1=1,所以数列{S n }是首项为1,公比为53的等比数列,则S n =53n-1;(2)证明因为b n =1S n=35n-1,所以b 1+b 2+b 3+…+b n =1-(35) n1-35=52−52×35n <52. 11.C ∵a m+n =a m ·a n ,令m=1,又a 1=2,∴a n+1=a 1·a n =2a n , ∴a n+1a n=2,∴{a n }是以2为首项,2为公比的等比数列,∴a n =2n .∴a k+1+a k+2+…+a k+10=2k+1+2k+2+…+2k+10=2k+1·1-2101-2=2k+11-2k+1=215-25.∴{k +11=15,k +1=5,解得k=4. 12.B 因为向量n =(a 5,a 4),m =(a 7,a 8),m ·n =4,所以m ·n =a 5a 7+a 4a 8=4,因为{a n }是等比数列,所以a 5·a 7=a 4·a 8=2,所以a 1·a 11=2, 所以log 2a 1+log 2a 2+…+log 2a 11=log 2(a 1·a 11)112=log 22112=112.故选B.13.B 记每天走的路程里数为{a n },可知{a n }是公比q=12的等比数列,由S 6=378,得S 6=a 1(1-126)1-12=378,解得a 1=192,∴a 4+a 5=192×(12)3+192×(12)4=24+12=36.所以此人第4天和第5天共走了36里,故选B . 14.(1)证明∵a n+1=2a n +1,∴a n+1+1=2(a n +1),又a 1+1=2,∴数列{a n +1}是以2为首项,2为公比的等比数列. (2)解由(1)得a n +1=2n , ∴a n =2n -1, ∴S n=(21-1)+(22-1)+…+(2n -1)=(21+22+…+2n )-n=2×(1-2n )1-2-n=2n+1-n-2.故S n =2n+1-n-2.15.①③④ ∵y'=3x 2,∴曲线y=x 3在点(a n ,a n 3)处的切线方程为y-a n 3=3a n 2(x-a n ),∵该切线经过点(a n+1,0),∴-a n 3=3a n 2(a n+1-a n ).∵a n ≠0,∴a n+1=23a n ,又a 1=1,∴{a n }是首项为1,公比为23的等比数列.∴a 2=23,a 3=49,∑i=14a i =1-(23)41-23=6527.故所有正确结论的编号是①③④. 16.解(1)由2S n -a n =12n -1,①则2S n+1-a n+1=12n ,②②-①,可得2a n+1-a n+1+a n =12n −12n -1=-12n ,所以a n +a n+1=-12n . (2)由(1)可知a n +a n+1=-12n ,③则a n+1+a n+2=-12n+1,④④-③,可得a n+2-a n =-12n+1--12n =12n+1, 则b n =12n+1,且b n+1=12n+2.令n=1,则b 1=14.又因为b n+1b n=12n+212n+1=12,所以数列{b n }是首项为14,公比为12的等比数列.所以T n =14(1-12n )1-12=121-12n =12−12n+1.。
2021-2022年高考数学一轮复习高考大题专项练3高考中的数列

2021年高考数学一轮复习高考大题专项练3高考中的数列1.已知等差数列{a n}的前n项和为S n,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.(1)求数列{a n}的通项公式;(2)设是首项为1,公比为3的等比数列,求数列{b n}的前n项和T n.2.设数列{a n}的前n项和为S n,已知a1=3,S n+1=3S n+3.(1)求数列{a n}的通项公式;(2)若b n=,求数列{b n}的前n项和T n.3.已知数列{a n}的首项为1,S n为数列{a n}的前n项和,S n+1=qS n+1,其中q>0,n∈N+.(1)若a2,a3,a2+a3成等差数列,求数列{a n}的通项公式;(2)设双曲线x2-=1的离心率为e n,且e2=2,求+…+.4.已知数列{a n}的首项a1=,a n+1=(n∈N+).(1)求证:数列是等比数列;(2)求数列的前n项和S n.5.(xx江苏,19)对于给定的正整数k,若数列{a n}满足:a n-k+a n-k+1+…+a n-1+a n+1+…+a n+k-1+a n+k=2ka n对任意正整数n(n>k)总成立,则称数列{a n}是“P(k)数列”.(1)证明:等差数列{a n}是“P(3)数列”;(2)若数列{a n}既是“P(2)数列”,又是“P(3)数列”,证明{a n}是等差数列.6.设S n为等差数列{a n}的前n项和,已知S3=a7,a8-2a3=3.(1)求a n;(2)设b n=,数列{b n}的前n项和为T n,求证:T n>(n∈N+).7.已知正项数列{a n}的首项a1=1,前n项和S n满足a n=(n≥2).(1)求证:{}为等差数列,并求数列{a n}的通项公式;(2)记数列的前n项和为T n,若对任意的n∈N+,不等式4T n<a2-a恒成立,求实数a的取值范围.8.(xx山东潍坊一模)已知数列{a n}是等差数列,其前n项和为S n,数列{b n}是公比大于0的等比数列,且b1=-2a1=2,a3+b2=-1,S3+2b3=7.(1)求数列{a n}和{b n}的通项公式;(2)令c n=求数列{c n}的前n项和T n.参考答案高考大题专项练三高考中的数列1.解(1)依题意得,解得故a n=a1+(n-1)d=3+2(n-1)=2n+1,即a n=2n+1.(2)由题意可知=3n-1,则b n=a n·3n-1=(2n+1)·3n-1.故T n=3+5×3+7×32+…+(2n+1)·3n-1, ①3T n=3×3+5×32+7×33+…+(2n-1)·3n-1+(2n+1)·3n, ②①-②得-2T n=3+2×3+2×32+…+2·3n-1-(2n+1)3n=3+2·-(2n+1)3n=-2n·3n,因此,T n=n·3n.2.解(1)(方法一)∵S n+1=3S n+3,∴S n+1+=3.∴S n+3n-1=×3n-1=.∴当n≥2时,a n=S n-S n-1==3n,a1也适合.∴a n=3n.(方法二)由S n+1=3S n+3(n∈N+),可知当n≥2时,S n=3S n-1+3,两式相减,得a n+1=3a n(n≥2).又a1=3,代入S n+1=3S n+3得a2=9,故a n=3n.(2)∵b n=,∴T n=, ①∴T n=, ②由①-②,得T n=,解得T n=.3.解(1)由已知,S n+1=qS n+1,S n+2=qS n+1+1,两式相减得到a n+2=qa n+1,n≥1.又由S2=qS1+1得到a2=qa1,故a n+1=qa n对所有n≥1都成立.所以,数列{a n}是首项为1,公比为q的等比数列.从而a n=q n-1.由a2,a3,a2+a3成等差数列,可得2a3=a2+a2+a3.所以a3=2a2,故q=2.所以a n=2n-1.(2)由(1)可知,a n=q n-1.所以双曲线x2-=1的离心率e n=.由e2==2,解得q=.所以+…+=(1+1)+(1+q2)+…+[1+q2(n-1)]=n+[1+q2+…+q2(n-1)]=n+=n+(3n-1).4.(1)证明∵a n+1=,∴.∴-1=.又a1=,∴-1=.∴数列是以为首项,以为公比的等比数列.(2)解由(1)知-1=,则+1.故+n.设T n=+…+, ①则T n=+…+, ②由①-②得T n=+…+=1-,∴T n=2-.又1+2+3+…+n=,∴数列的前n项和S n=2-.5.证明(1)因为{a n}是等差数列,设其公差为d,则a n=a1+(n-1)d,从而,当n≥4时,a n-k+a n+k=a1+(n-k-1)d+a1+(n+k-1)d=2a1+2(n-1)d=2a n,k=1,2,3, 所以a n-3+a n-2+a n-1+a n+1+a n+2+a n+3=6a n,因此等差数列{a n}是“P(3)数列”.(2)数列{a n}既是“P(2)数列”,又是“P(3)数列”,因此,当n≥3时,a n-2+a n-1+a n+1+a n+2=4a n, ①当n≥4时,a n-3+a n-2+a n-1+a n+1+a n+2+a n+3=6a n.②由①知,a n-3+a n-2=4a n-1-(a n+a n+1), ③a n+2+a n+3=4a n+1-(a n-1+a n).④将③④代入②,得a n-1+a n+1=2a n,其中n≥4,所以a3,a4,a5,…是等差数列,设其公差为d'.在①中,取n=4,则a2+a3+a5+a6=4a4,所以a2=a3-d',在①中,取n=3,则a1+a2+a4+a5=4a3,所以a1=a3-2d',所以数列{a n}是等差数列.6.(1)解设等差数列{a n}的公差为d,由题意得解得故a n=a1+(n-1)d=2n+1.(2)证明∵a1=3,d=2,∴S n=na1+d=n(n+2).∴b n=.∴T n=b1+b2+…+b n-1+b n=,故T n>.7.解(1)因为a n=,所以S n-S n-1=,即=1,所以数列{}是首项为=1,公差为1的等差数列,得=n,所以a n==n+(n-1)=2n-1(n≥2),当n=1时,a1=1也适合,所以a n=2n-1.(2)因为,所以T n=+…+.所以T n<.要使不等式4T n<a2-a恒成立,只需2≤a2-a恒成立,解得a≤-1或a≥2,故实数a的取值范围是(-∞,-1]∪[2,+∞).8.解(1)设等差数列{a n}的公差为d,等比数列{b n}的公比为q>0,且b1=-2a1=2,a3+b2=-1,S3+2b3=7.∴a1=-1,-1+2d+2q=-1,3×(-1)+3d+2×2×q2=7,解得d=-2,q=2.∴a n=-1-2(n-1)=1-2n,b n=2n.(2)c n=①当n=2k(k∈N+)时,数列{c n}的前n项和T n=T2k=(c1+c3+…+c2k-1)+(c2+c4+…+c2k)=2k++…+,令A k=+…+,∴A k=+…+,∴A k=+4+…++4×,可得A k=.∴T n=T2k=2k+.②当n=2k-1(k∈N+)时,数列{c n}的前n项和T n=T2k-2+a2k-1=2(k-1)++2=2k+.∴T n=k∈N+.。
数学一轮复习第四章三角函数解三角形4.2同角三角函数的基本关系及诱导公式学案理

4。
2同角三角函数的基本关系及诱导公式必备知识预案自诊知识梳理1。
同角三角函数的基本关系(1)平方关系:sin2α+cos2α=。
(2)商数关系:sinαcosα=(α≠π2+kπ,k∈Z)。
2.三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)π+α-απ-απ2-απ2+α正弦sin α余弦cos α正切tan α续表公式一二三四五六口诀函数名不变,符号看象限函数名改变,符号看象限1。
特殊角的三角函数值2.同角三角函数基本关系式的常用变形(1)(sin α±cos α)2=1±2sin αcos α;(2)sin α=tan αcos αα≠π2+kπ,k∈Z;(3)sin2α=sin2αsin2α+cos2α=tan2αtan2α+1;(4)cos 2α=cos 2αsin 2α+cos 2α=1tan 2α+1。
考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”。
(1)对任意的角α,β有sin 2α+cos 2β=1。
( ) (2)若α∈R ,则tan α=sinαcosα恒成立.( )(3)sin (π+α)=-sin α成立的条件是α为锐角。
( )(4)若cos(n π—θ)=13(n ∈Z ),则cos θ=13.( )2。
(2020河北衡水中学模拟一,理3)已知cos α-π2=-2√55,α∈π,3π2,则tan α=( )A 。
2B 。
32C.1D.123。
(2020河北唐山模拟,理4)已知角α的顶点在原点,始边与x 轴的正半轴重合,终边上一点A (2sin α,3)(sin α≠0),则cos α=( )A.12B 。
-12C 。
√32D.-√324。
函数f (x )=15sin x+π3+cos x —π6的最大值为( ) A.65B.1C.35D.15关键能力学案突破考点同角三角函数基本关系式的应用【例1】(1)若tan(α-π)=12,则sin 2α+1cos 2α-sin 2α=( )A。
2020版高考数学北师大版(理)一轮复习:高考大题专项三 高考中的数列

-21-
解 (1)由题意知当n≥2时,an=Sn-Sn-1=6n+5,
当n=1时,a1=S1=11,符合上式.
所以an=6n+5.
设数列{bn}的公差为d.
由
������1 ������2
= =
������1 ������2
+ +
������2 , ������3 ,
即
11 = 2������1 + ������, 17 = 2������1 + 3������,
高考大题专项三 高考中的数列
-2-
从近五年高考试题分析来看,高考数列解答题主要题型有:等差、 等比数列的综合问题;证明一个数列为等差或等比数列;求数列的 通项及非等差、等比数列的前n项和;证明数列型不等式.命题规律 是解答题每两年出现一次,命题特点是试题题型规范、方法可循、 难度稳定在中档.
题型一
=23=8(n∈N+),
又 b1=2������1=32,
所以数列{bn}是以 32 为首项,8 为公比的等比数列.
所以 Tn=32(11--88������) = 372(8n-1).
题型一
题型二
题型三
题型四
-10-
解题心得证明与判断一个数列是等差(或等比)数列的要求不同, 证明必须是严格的,只能用等差(或等比)数列的定义.用定义法证明 一个数列是等差数列,常采用的两个式子 an-an-1=d(n≥2)和 an+1-an =d,前者必须加上“n≥2”,否则 n=1 时 a0 无意义;在等比数列中也 有:n≥2 时,有���������������������-���1=q(常数 q≠0),或 n∈N+时,有������������������+������1=q(常数 q≠0).
2022高3统考数学文北师大版1轮教师文档:第5章 Word版含答案

[答案] B
(2)如果一个数列{an}的通项公式 an=n2+2n+3.
①求 a10; ②83 是否为该数列的项,如果是,是数列的第几项. [解 析] ①当 n=10,a10=100+2×10+3=123.
②如果 n2+2n+3=83,即 n2+2n-80=0. ∴(n+10)(n-8)=0,∴n=8(n=-10 舍),
.
3
bn 1 n 1 n
( ) ( ) 于是,an= =3 2
-2 3
2n 1 3an-1+1
. 11
11
(5)取倒数,得 =
an
an-1
{ =3+ .∴ an
an-1
}是等差数列,
= +3(n-1)=1
an a1
+
1
3(n-1)⇒an=
.
3n-2 lg an+1
(6)由题意知 an>0,将 an+1=a 2n两边取常用对数得到 lg an+1=2lg an,即 lg an =
an-1 an an
× ×…× × =
a1 a2
an-2 an-1 a1
由 an+1=pan+q 化为 an+1+ m=p(an+m),构造{an+m} 为等比数列
an+1 由 an+1=pan+qn 化为
qn+1 =
an+1-an=f(n)(f(n)可求和)
an+1 an
=f(n),f(n)可求积
∴Sn= =
1-q
1-2
=1-2n,
∴S6=1-26=-63. [答案] -63
(2)(2020·广东江门模拟)记数列{an}的前 n 项和为 Sn,若任意 n∈N+,2Sn=an+
1,则 a2 020=________. [解析] ∵2Sn=an+1, ∴2Sn-1=an-1+1(n≥2), ∴2Sn-2Sn-1=2an=an-an-1(n≥2), 即 an=-an-1(n≥2),又 2S1=2a1=a1+1, ∴a1=1,∴a2 020=a2=-a1=-1. [答案] -1
2022高三全国统考数学北师大版(理)一轮复习学案:11.1 分类加法计数原理与分步乘法计数原理

第十一章计数原理11.1分类加法计数原理与分步乘法计数原理必备知识预案自诊知识梳理1.两个计数原理名称分类加法计数原理分步乘法计数原理条件完成一件事,可以有.在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……在第n类方案中有m n种不同的方法完成一件事需要,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……做第n步有m n种不同的方法结论完成这件事共有N=m1+m2+…+m n种不同的方法完成这件事共有N=m1×m2×…×m n种不同的方法依据能否独立完成整个事件能否逐步完成整个事件2.两个计数原理的区别与联系名称分类加法计数原理分步乘法计数原理相同点用来计算完成一件事的方法种数不同点分类、相加分步、相乘每类方案中的每一种方法都能独立完成这件事每步依次完成才算完成这件事情(每步中的每一种方法都不能独立完成这件事)注意点类类独立,不重不漏步步相依,缺一不可考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)在分类加法计数原理中,某两类不同方案中的方法可以相同.()(2)在分类加法计数原理中,每类方案中的方法都能直接完成这件事.()(3)在分步乘法计数原理中,只有各步骤都完成后,这件事情才算完成.()(4)在分步乘法计数原理中,每个步骤中完成这个步骤的方法是各不相同的.()(5)如果完成一件事情有n个不同步骤,在每一步中都有若干种不同的方法m i(i=1,2,3,…,n),那么完成这件事共有m1m2m3·…·m n种不同的方法.()2.(2020江苏南京中华中学高三月考)体育场南侧有4个大门,北侧有3个大门,某人到该体育场晨练,则他进、出门的方案有()A.12种B.7种C.14种D.49种3.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为()A.24B.18C.12D.94.高二年级的三个班去甲、乙、丙、丁四个工厂参观学习,去哪个工厂可以自由选择,甲工厂必须有班级要去,则不同的参观方案有()A.16种B.18种C.37种D.48种5.算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:如果把5根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为()A.46B.44C.42D.40关键能力学案突破考点分类加法计数原理【例1】(1)三个人踢毽,互相传递,每人每次只能踢一下,由甲开始踢,经过4次传递后,毽又被踢回给甲,则不同的传递方式共有()A.4种B.6种C.10种D.16种(2)如果一个三位正整数如“a1a2a3”满足a1<a2且a2>a3,则称这样的三位数为凸数(如120,343,275等),那么所有凸数的个数为.解题心得使用分类加法计数原理应遵循的原则:分类的标准可能有多个,但不论是以哪一个为标准,都应遵循“标准要明确,不重不漏”的原则,且完成这件事情的任何一种方法必须属于某一类,不能同时属于两类.对点训练1(1)在所有的两位数中,个位数字大于十位数字的两位数的个数为.(2)已知椭圆x 2m +y2n=1的焦点在y轴上,且m∈{1,2,3,4,5},n∈{1,2,3,4,5,6,7},则这样的椭圆的个数为.考点分步乘法计数原理【例2】(1)将3张不同的演唱会门票分给10名同学中的3人,每人1张,则不同分法的种数是()A.2 160B.720C.240D.120(2)(2020北京东城质检)中国古代将物质属性分为“金、木、土、水、火”五种,其相互关系是“金克木,木克土,土克水,水克火,火克金”.将五种不同属性的物质任意排成一列,则属性相克的两种物质不相邻的排法种数为()A.8B.10C.15D.20解题心得利用分步乘法计数原理解决问题时,要按事件发生的过程合理分步,并且分步必须满足两个条件:一是完成一件事的各个步骤是相互依存的,二是只有各个步骤都完成了,才算完成这件事.对点训练2(1)一个旅游景区的游览线路如图所示,某人从点P处进,点Q处出,沿图中线路游览A,B,C三个景点及沿途风景,则不同(除交汇点O外)的游览线路有种.(2)西部五省,有五种颜色供选择涂色,要求每省涂一色,相邻省不同色,有种涂色方法.考两个计数原理的综点合应用【例3】(1)用0,1,2,3,4,5,6这7个数字可以组成个无重复数字的四位偶数.(2)如果一条直线与一个平面垂直,那么称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是.解题心得解决较为复杂的计数问题,一般要将两个计数原理综合应用.使用时要做到合理分类,准确分步:处理计数问题,应紧扣两个原理,根据具体问题首先弄清楚是“分类”还是“分步”,要搞清楚“分类”或者“分步”的具体标准.分类时需要满足两个条件:①类与类之间要互斥(保证不重复);②总数要完备(保证不遗漏),也就是要确定一个合理的分类标准.分步时应按事件发生的连贯过程进行分析,必须做到步与步之间互相独立,互不干扰,并确保连续性.对点训练3(1)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有()A.144个B.120个C.96个D.72个(2)(2020江苏盐城高三检测)有7张卡片分别写有数字1,1,1,2,2,3,4,从中任取4张,可排出不同的四位数的个数是.第十一章计数原理11.1分类加法计数原理与分步乘法计数原理必备知识·预案自诊知识梳理1.n类不同方案n个步骤考点自诊1.(1)×(2)√(3)√(4)√(5)√2.D由题意某人从体育场进门有7种方式,出门有7种方式,根据分步乘法计数原理可知他进、出门的方案有7×7=49(种).3.B由题意知,小明从街道的E处出发到F处的最短路径有6条,再从F处到G处的最短路径有3条,则小明到老年公寓可以选择的最短路径条数为6×3=18.故选B.4.C根据题意,若不考虑限制条件,每个班级都有4种选择,共有4×4×4=64(种)情况,其中工厂甲没有班级去,即每个班级都选择了其他三个工厂,此时每个班级都有3种选择,共有3×3×3=27(种)方案.则符合条件的有64-27=37(种)方案.故选C.5.B按每一位算筹的根数分类一共有15种情况,如下:(5,0,0),(4,1,0),(4,0,1),(3,2,0),(3,1,1),(3,0,2),(2,3,0),(2,2,1),(2,1,2),(2,0,3),(1,4,0),(1,3,1),(1,2,2 ),(1,1,3),(1,0,4),2根以上的算筹可以表示两个数字,运用分步乘法计数原理,则上述情况能表示的三位数字个数分别为2,2,2,4,2,4,4,4,4,4,2,2,4,2,2.根据分类加法计数原理,5根算筹能表示的三位数字个数为2+2+2+4+2+4+4+4+4+4+2+2+4+2+2=44.故选B.关键能力·学案突破例1(1)B(2)240(1)分两类:甲第一次踢给乙时,满足条件的有3种传递方式(如图),同理,甲先传给丙时,满足条件的也有3种传递方式.由分类加法计数原理可知,共有3+3=6(种)传递方式.(2)若a2=2,则百位数字只能选1,个位数字可选1或0,“凸数”为120与121,共2个.若a2=3,则百位数字有两种选择,个位数字有三种选择,则“凸数”有2×3=6(个).若a2=4,满足条件的“凸数”有3×4=12(个),…,若a2=9,满足条件的“凸数”有8×9=72(个).故所有凸数有2+6+12+20+30+42+56+72=240(个).对点训练1(1)36(2)20(1)按十位数字分类,十位可为1,2,3,4,5,6,7,8,共分成8类,在每一类中满足条件的两位数分别有8个,7个,6个,5个,4个,3个,2个,1个,则共有8+7+6+5+4+3+2+1=36(个)两位数.(2)焦点在y轴上的椭圆满足m<n,因此将m分类计数.以m的值为标准分类,分为五类,第一类:当m=1时,使n>m的n有6种选择;第二类:当m=2时,使n>m的n有5种选择;第三类:当m=3时,使n>m的n有4种选择;第四类:当m=4时,使n>m的n有3种选择;第五类:当m=5时,使n>m的n有2种选择.由分类加法计数原理知,符合条件的椭圆共有20个.例2(1)B(2)B(1)分步来完成此事.第1张有10种分法,第2张有9种分法,第3张有8种分法,共有10×9×8=720(种)分法.故选B.(2)由题意知,可看作五个位置排列五个元素,第一个位置有五种排列方法,不妨假设是金,则第二个位置只能从土与水两者中选一种排放,有两种选择,不妨假设排上的是水,第三个位置只能排上木,第四个位置只能排上火,第五个位置只能排上土,故总的排列方法种数有5×2×1×1×1=10.对点训练2(1)48(2)420(1)根据题意,从点P处进入后,参观第一个景点时,有6个路口可以选择,从中任选一个,有6种选法;参观完第一个景点,参观第二个景点时,有4个路口可以选择,从中任选一个,有4种选法;参观完第二个景点,参观第三个景点时,有2个路口可以选择,从中任取一个,有2种选法.由分步乘法计数原理知,共有6×4×2=48(种)不同游览线路.(2)对于新疆有5种涂色的方法,对于青海有4种涂色方法,对于西藏有3种涂色方法,对于四川,若与新疆颜色相同,则有1种涂色方法,此时甘肃有3种涂色方法;若四川与新疆颜色不相同,则四川只有2种涂色方法,此时甘肃有2种涂色方法;根据分步乘法、分类加法计数原理,则共有5×4×3×(2×2+1×3)=420(种)方法.故答案为420.例3(1)420(2)36(1)要完成的“一件事”为“组成无重复数字的四位偶数”,所以千位数字不能为0,个位数字必须是偶数,且组成的四位数中四个数字不重复,因此应先分类,再分步.(方法1)第1类,当千位数字为奇数时,即取1,3,5中的任意一个时,个位数字可取0,2,4,6中的任意一个,百位数字不能取与这两个数字重复的数字,十位数字不能取与这三个数字重复的数字.根据分步乘法计数原理,有3×4×5×4=240(个)数.第2类,当千位数字为偶数且不为0时,即取2,4,6中的任意一个时,个位数字可以取除首位数字外的任意一个偶数数字,百位数字不能取与这两个数字重复的数字,十位数字不能取与这三个数字重复的数字.根据分步乘法计数原理,有3×3×5×4=180(个)数.根据分类加法计数原理,共可以组成240+180=420(个)无重复数字的四位偶数.(方法2排除法)先定个位数有4种取法,再定另外3位数有A63=120(种)取法,共有480种.其中0作千位,其余数作个位不合题意,有3×A52=60(种)取法.故应有480-60=420(种)取法.故共可以组成420个无重复数字的四位偶数.(2)第1类,对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有2×12=24(个);第2类,对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有12个.所以正方体中“正交线面对”共有24+12=36(个).对点训练3(1)B(2)114(1)由题意可知,符合条件的五位数的万位数字是4或5.当万位数字为4时,个位数字从0,2中任选一个,共有2×4×3×2=48(个)偶数;当万位数字为5时,个位数字从0,2,4中任选一个,共有3×4×3×2=72(个)偶数.故符合条件的偶数共有48+72=120(个).(2)根据题意,分4类情况讨论:①取出的4张卡片中没有重复数字,即取出的4张卡片中的数字为1,2,3,4,此时有A44=24(种)顺序,可以排出24个四位数;②取出的4张卡片中有2个重复数字,则2个重复的数字为1或2,若重复的数字为1,在2,3,4中取出2个,有C32=3(种)取法,安排在四个位置中,有A42=12(种)情况,剩余位置安排数字1,可以排出3×12=36(个)四位数,同理,若重复的数字为2,也可以排出36个四位数;③若取出的4张卡片为2张1和2张2,在4个位置安排两个1,有C42=6(种)情况,剩余位置安排两个2,则可以排出6×1=6(个)四位数;④取出的4张卡片中有3个重复数字,则重复的数字为1,在2,3,4中取出1个卡片,有C31=3(种)取法,安排在四个位置中,有C41=4(种)情况,剩余位置安排1,可以排出3×4=12(个)四位数.故一共有24+36+36+6+12=114(个)四位数.。
全国统考2022高考数学一轮复习第十一章计数原理11.2排列与组合学案理含解析北师大版
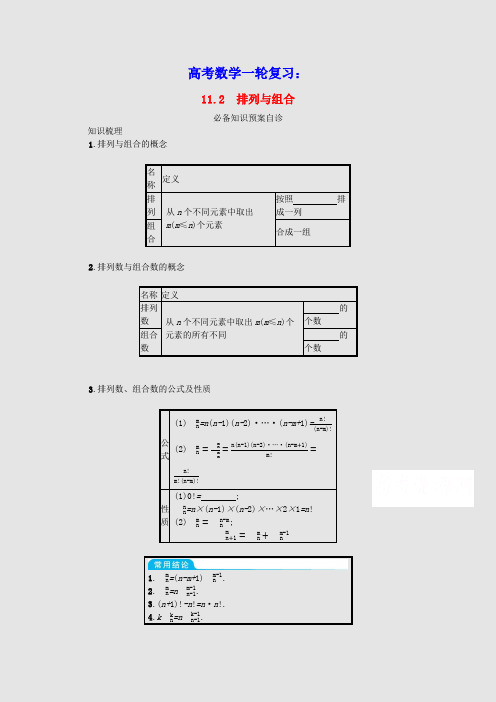
高考数学一轮复习:11.2 排列与组合必备知识预案自诊知识梳理1.排列与组合的概念名称定义 排列 从n 个不同元素中取出m (m ≤n )个元素 按照 排成一列 组合合成一组2.排列数与组合数的概念名称 定义排列数 从n 个不同元素中取出m (m ≤n )个元素的所有不同 的个数组合数的个数3.排列数、组合数的公式及性质公式(1)A n m =n (n-1)(n-2)·…·(n-m+1)=n!(n -m)!(2)A n m =A nm A m m =n(n -1)(n -2)·…·(n -m +1)m!=n!m!(n -m)!性质 (1)0!= ;A n n =n ×(n-1)×(n-2)×…×2×1=n !(2)A n m =A n n -m;A n +1m =A n m +A n m-11.A n m =(n-m+1)A n m -1.2.A n m =n A n -1m -1.3.(n+1)!-n !=n ·n !.4.k A n k =n A n -1k -1.5.A n m=nm An-1m-1=nn-mAn-1m=n-m+1mA n m-1.考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)所有元素完全相同的两个排列为相同排列.()(2)一个组合中取出的元素讲究元素的先后顺序.()(3)两个组合相同的充要条件是其中的元素完全相同.()(4)若组合式C A A=C A A,则x=m成立.()(5)排列中,给出的n个元素各不相同,被取出的元素也各不相同的情况.即如果某个元素已被取出,则这个元素就不再取了.()2.2019年5月22日具有“国家战略”意义的“长三角一体化”会议在芜湖举行,长三角城市群包括:上海市以及江苏省、浙江省、安徽省三省部分城市,简称“三省一市”.现有4名高三学生准备高考后到上海市、江苏省、浙江省、安徽省四个地方旅游,假设每名同学均从这四个地方中任意选取一个去旅游,则恰有一个地方未被选中的概率为()A.2764B.916C.81256D.7163.将A,B,C,D,E这5名同学从左至右排成一排,则A与B相邻且A与C之间恰好有一名同学的排法种数为()A.18B.20C.21D.224.2020年7月1日迎来了我国建党99周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为()A.20.5元B.21元C.21.5元D.22元5.(2020广西柳州抽测)将4名学生分别安排到甲、乙、丙三地参加社会实践活动,每个地方至少安排一名学生参加,则不同的安排方案共有种.关键能力学案突破考点简单的排列应用题(多考向探究)考向1在与不在问题——特殊元素(或位置)优先法【例1】6人站成一排,其中甲不能站在排头,乙不能站在排尾的不同排法共有种.解题心得解此类问题常用“元素分析法”“位置分析法”.元素分析法——即以元素为主,优先考虑特殊元素的要求,再考虑其他元素;位置分析法——即以位置为主,优先考虑特殊位置的要求,再考虑其他位置.变式发散6人站成一排,则甲既不站排头又不站排尾的站法有种.对点训练16个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有()A.192种B.216种C.240种D.288种考向2 相邻问题——捆绑法 【例2】3名男生、3名女生排成一排,男生必须相邻,女生也必须相邻的排法种数为( ) A.2 B.9 C.72 D.36解题心得在实际排列问题中,某些元素要求必须相邻时,可以先将这些元素看成一个整体,与其他元素排列后,再考虑相邻元素的内部排序,这种方法称为“捆绑法”.对点训练2某小区有排成一排的7个车位,现有3辆不同型号的车需要停放,如果要求剩余的4个车位连在一起,那么不同的停放方法的种数为( )A.16B.18C.24D.32 考向3 不相邻问题——插空法【例3】某校高三要安排毕业晚会的4个音乐节目,2个舞蹈节目和1个曲艺节目的演出顺序,要求2个舞蹈节目不连排,则不同排法的种数是( )A.1 800B.3 600C.4 320D.5 040解题心得某些元素要求不相邻时,可以先安排其他元素,再将这些不相邻元素插入已排好的元素的空隙或两端位置,这种方法称为“插空法”.对点训练3某次联欢会要安排3个歌舞类节目,2个小品类节目和1个相声类节目的演出顺序,同类节目不相邻的排法种数是( )A.72B.120C.144D.168 考向4 定序问题——等几率法【例4】有4名男生,3名女生,其中3名女生高矮各不相同,将7名学生排成一行,要求从左到右,女生从矮到高排列(不一定相邻),不同的排法共有 种.解题心得若有(m+n )个元素排成一列,其中有m 个元素之间的顺序固定不变,则将这(m+n )个元素排成一列,共有A A +A A +A种不同的排法,然后固定其他的n 个元素的位置不动,把这m 个元素变换顺序,共有A A A 种排法,其中只有一个排列是我们所需要的排列,因而共有A A +AA +A A AA 种不同的排法.对点训练47个人排成一队参观某项目,其中A ,B ,C 三人进入展厅的次序必须是先B 再A 后C ,则不同的列队方式种数为( )A.120B.240C.420D.840考点组合问题【例5】某市工商局对35种商品进行抽样检查,已知其中有15种不合格商品.现从35种商品中选取3种.(1)其中某一种不合格商品必须在内,不同的取法有多少种? (2)其中某一种不合格商品不能在内,不同的取法有多少种? (3)恰有2种不合格商品在内,不同的取法有多少种? (4)至少有2种不合格商品在内,不同的取法有多少种? (5)至多有2种不合格商品在内,不同的取法有多少种? 解题心得组合问题的两类题型及求解方法(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.对点训练5(1)从4男2女共6名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,不同选法共有()A.156种B.168种C.180种D.240种(2)2020年国庆假期,高三的8名同学准备拼车去旅游,其中(1)班、(2)班、(3)班、(4)班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学(乘同一辆车的4名同学不考虑位置),其中(1)班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有()A.18种B.24种C.48种D.36种考点分组与分配问题【例6】按下列要求分配6本不同的书,各有多少种不同的分配方法?(1)分成三份,1份1本,1份2本,1份3本;(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;(3)平均分成三份,每份2本;(4)平均分配给甲、乙、丙三人,每人2本;(5)分成三份,1份4本,另外两份每份1本;(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本.解题心得分组、分配问题的一般解题思路是先分组再分配.(1)分组问题属于“组合”问题.①对于整体均分,不管它们的顺序如何,都是一种情况,所以分组后一定要除以组数的阶乘;②对于部分均分,即若有m组元素个数相同,则分组时应除以m!;③对于不等分组,只需先分组,后排列.(2)分配问题属于“排列”问题.①相同元素的“分配”问题,常用的方法是采用“隔板法”;②不同元素的“分配”问题,利用分步乘法计数原理,分两步完成,第一步是分组,第二步是发放;③限制条件的分配问题常采用分类法求解.对点训练6(1)某科研单位准备把7名大学生分配到编号为1,2,3的三个实验室实习,若要求每个实验室分配到的大学生人数不小于该实验室的编号,则不同的分配方案的种数为()A.280B.455C.355D.350(2)(2020新高考全国1,3)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有()A.120种B.90种C.60种D.30种(3)在第二届乌镇互联网大会中,为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在a,b,c三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有()A.96种B.124种C.130种D.150种11.2排列与组合必备知识·预案自诊知识梳理1.一定的顺序2.排列组合3.(1)1考点自诊1.(1)×(2)×(3)√(4)×(5)√2.B4名同学去旅游的所有情况有44=256(种),恰有一个地方未被选中共有C41·C42C21A22·A33=144(种)情况,所以恰有一个地方未被选中的概率为p=144256=916.故选B.3.B当A,C之间为B时,看成一个整体进行排列,共有A22·A33=12(种),当A,C之间不是B时,先在A,C之间插入D,E中的任意一个,然后B在A之前或之后,再将这四个人看成一个整体,与剩余一个进行排列,共有C21·A22·A22=8(种),所以共有20种不同的排法.故选B.4.B利用捆绑法可求得照片的总数为A33A44=144,则每名老党员需要支付的照片费为144×0.5+72×0.756=21(元).故选B.5.36第一步,先从4名学生中任取两人组成一组,与剩下2人组成三组,有C42=6(种)不同的方法;第二步,将分成的三组安排到甲、乙、丙三地,则有A33=6(种)不同的方法.故共有6×6=36(种)不同的安排方案.关键能力·学案突破例1504(方法1特殊元素法)分两类:第1类,甲先从中间四个位置选一个站好,有A41种站法.乙不站排尾,则乙可从除排尾之外的4个位置中选一个站好,共有A41种站法.其余四人任意排,有A44种站法.故共有A41A41A44种站法.第2类,甲站排尾,此时,乙不再特殊,共有A55种站法.根据分类加法计数原理,共有A41A41A44+ A55=504(种)不同的站法.(方法2特殊位置法)排头与排尾特殊,故可以从排头与排尾入手.分三类:第1类,从除甲、乙之外的4人中选2人站排头、排尾,有A42A44种站法.第2类,甲站排尾,有A55种站法.第3类,乙站排头,有A55种站法(其中重合部分:乙站排头,甲站排尾,有A44种站法).根据分类加法计数原理,共有A42A44+A55+A55−A44=504(种)不同的站法.(方法3间接法)6人站成一排有A66种站法,甲站排头或乙站排尾有2A55种站法,甲站排头且乙站排尾有A44种站法,故共有A66-2A55+A44=504(种)不同的站法.变式发散480 先安排甲的位置(既不站排头又不站排尾),再安排其他5人的位置,分为两步:第1步,将甲排在除排头、排尾的任意位置上,有A 41种站法;第2步,余下5人站在剩下的5个位置上,有A 55种站法.由分步乘法计数原理可知,共有A 41A 55=480(种)不同的站法. 对点训练1B 分两类:第1类,甲在最左端,有A 55=5×4×3×2×1=120(种)不同的排法;第2类,乙在最左端,甲不在最右端,有4A 44=4×4×3×2×1=96(种)不同的排法.所以共有120+96=216(种)不同的排法.例2C 可分两步完成:第1步,把3名女生作为一个整体,看成一个元素,3名男生作为一个整体,看成一个元素,两个元素排成一排有A 22种排法;第2步,3名女生排在一起有A 33种排法,3名男生排在一起有A 33种排法,故排法种数为A 22A 33A 33=72.对点训练2C 将4个车位捆绑在一起,看成一个元素,先排3辆不同型号的车,在3个车位上任意排列,有A 33=6(种)方法,再将捆绑在一起的4个车位插入4个空位中,有4种方法,故共有4×6=24(种)方法.例3B 先排除舞蹈节目以外的5个节目,共A 55种排法,再把2个舞蹈节目插在6个空位中,有A 62种排法,所以共有A 55A 62=3600(种)排法.对点训练3B 先安排小品节目和相声节目,然后让歌舞节目去插空.安排小品节目和相声节目的顺序有三种:“小品,小品,相声”“小品,相声,小品”和“相声,小品,小品”.对于第一种情况,形式为“□小品歌舞小品□相声□”,有A 22C 31A 32=36(种)安排方法;同理,第三种情况也有36种安排方法;对于第二种情况,三个节目形成4个空,其形式为“□小品□相声□小品□”,有A 22A 43=48(种)安排方法,故共有36+36+48=120(种)安排方法.例4840 7名学生的排列共有A 77种,其中女生的排列共有A 33种,按照从左到右,女生从矮到高的排列只是其中的一种,故有A 77A 33=A 74=840(种)不同的排法.对点训练4D 根据题意,先将7人排成一列,有A 77种排法,其中A ,B ,C 三人进入展厅的次序必须是先B 再A 后C ,即A ,B ,C 三人顺序一定,则不同的列队方式有A 77A 33=840(种).例5解(1)从余下的34种商品中,选取2种,有C 342=561(种)取法,故某一种不合格商品必须在内的不同取法有561种.(2)从34种可选商品中,选取3种,有C 343种或者C 353−C 342=C 343=5984(种)取法.故某一种不合格商品不能在内的不同取法有5984种.(3)从20种合格商品中选取1种,从15种不合格商品中选取2种,有C 201C 152=2100(种)取法.故恰有2种不合格商品在内的不同的取法有2100种.(4)选取2种不合格商品有C 201C 152种取法,选取3种不合格商品有C 153种取法,共有C 201C 152+C 153=2100+455=2555(种)取法.故至少有2种不合格商品在内的不同的取法有2555种. (5)任意选取3种的总数为C 353,因此共有C 353−C 153=6545-455=6090(种)取法. 故至多有2种不合格商品在内的不同的取法有6090种.对点训练5(1)B (2)B (1)从4男2女共6名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队有C 61·C 51·C 42=6×5×4×32=180(种)选法,服务队中没有女生的选法有C 41·C 31·C 22=4×3×1=12(种),所以要求服务队中至少有1名女生,不同选法共有180-12=168(种)选法.故选B .(2)由题意,第一类,一班的2名同学在甲车上,甲车上剩下两个要来自不同的班级,从三个班级中选两个为C 32=3(种),然后分别从选择的班级中再选择一个学生为C 21C 21=4,故有3×4=12(种);第二类,一班的2名同学不在甲车上,则从剩下的3个班级中选择一个班级的两名同学在甲车上,为C 31=3,然后再从剩下的两个班级中分别选择一人为C 21C 21=4,这时共有3×4=12(种),根据分类加法计数原理得,共有12+12=24(种)不同的乘车方式.故选B . 例6解(1)先从6本书中选1本,有C 61种分配方法;再从剩余5本书中选择2本,有C 52种分配方法,剩余的就是3本书,有C 33种分配方法,所以总共有C 61C 52C 33=60(种)分配方法.(2)由(1)可知分组后共有60种方法,分别分给甲、乙、丙后的方法有C 61C 52C 33A 33=360(种).(3)从6本书中选择2本书,有C 62种分配方法;再从剩余4本书中选择2本书,有C 42种分配方法;剩余的就是2本书,有C 22种分配方法,所以有C 62C 42C 22=90(种)分配方法.但是,该过程有重复.假如6本书分别为A ,B ,C ,D ,E ,F ,若三个步骤分别选出的是(AB ),(CD ),(EF ).则所有情况为(AB ,CD ,EF ),(AB ,EF ,CD ),(CD ,AB ,EF ),(CD ,EF ,AB ),(EF ,AB ,CD ),(EF ,CD ,AB ).所以分配方法共有C 62C 42C 22A 33=15(种).(4)由(3)可知,将三份分别分给甲、乙、丙三人,则分配方法有C 62C 42C 22A 33×A 33=90(种).(5)从6本书中选4本书的方法有C 64种,从剩余2本书中选1本书有C 21种,因为在最后两本书的选择中发生了重复,所以分配方法总共有C 64C 21A 22=15(种).(6)由(5)可知,将三份分别分给甲、乙、丙三人即可,则分配方法有C 64C 21A 22×A 33=90(种).对点训练6(1)B (2)C (3)D (1)每个实验室人数分配有三种情况,即1,2,4;1,3,3;2,2,3.当实验室的人数为1,2,4时,分配方案有C 71C 62C 44=105(种);当实验室的人数为1,3,3时,分配方案有C 71C 63C 33=140(种);当实验室的人数为2,2,3时,分配方案有C 72C 52C 33=210(种).故不同的分配方案有455种.故选B.(2)甲场馆安排1名有C 61种方法,乙场馆安排2名有C 52种方法,丙场馆安排3名有C 33种方法,所以共有C 61·C 52·C 33=60(种)方法,故选C .(3)根据题意,分2步进行分析:①五个参会国要在a ,b ,c 三家酒店选择一家,且这三家至少有一个参会国入住, 所以可以把5个国家人分成三组,一种是1,1,3,另一种是1,2,2.当按照1,1,3来分时共有C 53=10(种)分组方法;当按照1,2,2来分时共有C 52C 32A 22=15(种)分组方法,则一共有10+15=25(种)分组方法;②将分好的三组对应三家酒店,有A 33=6(种)对应方法;则安排方法共有25×6=150(种).故选D .。
2022高三全国统考数学北师大版(理)一轮复习学案:11.3 二项式定理含解析

11.3二项式定理必备知识预案自诊知识梳理1.二项式定理2.续表3.二项式系数与项的系数的区别二项式系数是指C n0,C n1,…,C n n,它只与各项的项数有关,而与a,b的值无关;而项的系数是指该项中除变量外的常数部分,它不仅与各项的项数有关,而且也与a,b的值有关.如(a+bx)n的二项展开式中,第k+1项的二项式系数是C n k,而该项的系数是C n k a n-k b k.当然,在某些二项展开式中,各项的系数与二项式系数是相等的.1.C n0+C n1+C n2+…+C n n=2n.2.C n0+C n2+C n4+…=C n1+C n3+C n5+…=2n-1.考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)(a+b)n的展开式中的第r项是C n r a n-r b r.()(2)在二项展开式中,系数最大的项为中间的一项或中间的两项.()(3)在(a+b)n的展开式中,每一项的二项式系数都与a,b无关.()(4)通项T r+1=C n r a n-r b r中的a和b不能互换.()(5)在(a+b)n的展开式中,某项的系数与该项的二项式系数相同.()2.(2020浙江绍兴质量调测)x-1x5的展开式中的第2项为()A.-5x3B.-10x C.5x3D.10x3.已知C n03n+C n13n-1+C n23n-2+…+C n n-13+C n n=212,则n=()A.8B.6C.4D.24.若(x-1)4=a0+a1x+a2x2+a3x3+a4x4,则a0+a2+a4的值为()A.9B.8C.7D.65.若x3+√xn的展开式的所有二项式系数之和为128,则n=.6.(x-1)(3x2+1)3的展开式中x4的系数是.关键能力学案突破考点求二项展开式中的特定项(或系数)问题(多考向探究)考向1已知二项式求其特定项(或系数)【例1】(1)(2020天津,11)在(x+2x2)5的展开式中,x2的系数是.(2)(2020云南师大附中高三月考)若(ax-1x)6的展开式中常数项等于-20,则a=()A.12B.-12C.1D.-1解题心得求形如(a+b)n(n∈N+)的展开式中与特定项相关的量(常数项、参数值、特定项等)的步骤(1)利用二项式定理写出二项展开式的通项T r+1=C n r a n-r b r,常把字母和系数分离开来(注意符号不要出错);(2)根据题目中的相关条件(如常数项要求指数为零,有理项要求指数为整数)先列出相应方程(组)或不等式(组),再解出r;(3)把r代入通项中,即可求出T r+1,有时还需要先求n,再求r,才能求出T r+1或者其他量.对点训练1(1)(2020湖南衡阳八中高三月考)√x3−√x5的展开式中的常数项为()A.5B.10C.40D.-40(2)已知x-√x5的展开式中x5的系数为A,x2的系数为B,若A+B=11,则a=.考向2已知两个因式之积求其特定项(或系数)【例2】(1)(1+x2)1-1x6的展开式中,常数项为()A.-15B.16C.15D.-16(2)(2020山东泰安高三一模)已知(2-mx)1-1x3的展开式中的常数项为8,则实数m=()A.2B.-2C.-3D.3(3)(1-√x)8(1+√x)5的展开式中x2的系数是()A.-5B.10C.-15D.25解题心得求形如(a+b)m(c+d)n(m,n∈N+)的展开式中与特定项相关的量的步骤(1)根据二项式定理把(a+b)m与(c+d)n分别展开,并写出其通项;(2)根据特定项的次数,分析特定项可由(a+b)m与(c+d)n的展开式中的哪些项相乘得到;(3)把相乘后的项合并即可得到所求特定项或相关量.对点训练2(1)(1-√x)6(1+√x)4的展开式中x的系数是()A.-4B.-3C.3D.4(2)已知(x-1)(ax+1)6的展开式中含x2的项的系数为0,则正实数a=.考向3已知三项式求其特定项(或系数)【例3】(1)(x2+1x+√2)5的展开式中的常数项为.(2)(x2-x-2)4的展开式中x2的系数是.解题心得求三项展开式中某些特定项(或系数)的方法:(1)通过变形先把三项式转化为二项式,再用二项式定理求解;(2)两次利用二项式定理的通项求解;(3)由二项式定理的推证方法知,可用排列、组合的基本原理去求,即把三项式看作几个因式之积,要得到特定项看有多少种方法从这几个因式中取因式中的量.对点训练3(1)(x2+x+y)5的展开式中x5y2的系数为()A.10B.20C.30D.60(2)(1+x+√x)4的展开式中x2的系数为.考点二项式系数的性质与各项系数的和(多考向探究)考向1二项式系数的最值问题【例4】已知m为正整数,(x+y)2m的展开式的二项式系数的最大值为a,(x+y)2m+1的展开式的二项式系数的最大值为b.若13a=7b,则m=()A.5B.6C.7D.8解题心得二项式系数最大项的确定方法(1)若n是偶数,则中间一项T n2+1的二项式系数最大;(2)若n是奇数,则中间两项T n+12与T n+12+1的二项式系数相等并且最大.对点训练4在(x+ax)n(a>0)的二项展开式中,只有第5项的二项式系数最大,且所有项的系数和为256,则含x6的项的系数为.考向2项的系数的最值问题【例5】已知(√x3+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,则在(2x-1x)2n的展开式中,二项式系数最大的项为,系数的绝对值最大的项为.解题心得二项展开式系数最大项的求法如求(a+bx)n(a,b∈R)的展开式系数最大的项,一般是采用待定系数法,设展开式各项系数分别为A1,A2,…,A n+1,且第r项系数最大,应用{A r≥A r-1,A r≥A r+1,从而解得r.对点训练5在(x 3+1x 2)n 的展开式中,只有第4项的系数最大,则展开式中x 3项的系数为. 考向3求二项展开式中系数的和【例6】若(x-3)3(2x+1)5=a 0+a 1x+a 2x 2+…+a 8x 8,则a 0=,a 0+a 2+…+a 8=.解题心得求二项展开式系数和的常用方法是赋值法:(1)“赋值法”普遍适用于恒等式,对形如(ax+b )n ,(ax 2+bx +c )m(a ,b ∈R )的式子,求其展开式的各项系数之和,常用赋值法,只需令x=1即可;对形如(ax+by )n (a ,b ∈R )的式子求其展开式各项系数之和,只需令x=y=1即可.(2)一般地,若f (x )=a 0+a 1x+a 2x 2+…+a n x n ,则f (x )的展开式中各项系数之和为f (1),奇数项系数之和为a 0+a 2+a 4+…=f (1)+f (-1)2,偶数项系数之和为a 1+a 3+a 5+…=f (1)-f (-1)2. 对点训练6已知(1-2x )7=a 0+a 1x+a 2x 2+…+a 7x 7.求:(1)a 1+a 2+…+a 7;(2)a 1+a 3+a 5+a 7;(3)a 0+a 2+a 4+a 6;(4)|a 0|+|a 1|+|a 2|+…+|a 7|.考点 二项式定理的应用【例7】(1)设a ∈Z 且0≤a<13,若512 012+a 能被13整除,则a 等于()A.0B.1C.11D.12(2)0.996的计算结果精确到0.001的近似值是()A.0.940B.0.941C.0.942D.0.943(3)中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设a ,b ,m (m>0)为整数,若a 和b 被m 除所得的余数相同,则称a 和b 对模m 同余,记为a ≡b (mod m ).若a=C 200+C 201·2+C 202·22+…+C 2020·220, a ≡b (mod 10),则b 的值可以是()A.2 011B.2 012C.2 013D.2 014解题心得1.整除问题和求近似值是二项式定理中常见的两类应用问题,用二项式定理处理整除问题,通常把幂的底数写成除数与某数的和或差的形式,再用二项式定理展开,切记余数不能为负,求近似值则应关注展开式的前几项.2.二项式定理的应用的基本思路是正用或逆用二项式定理,注意选择合适的形式.对点训练7(1)1-90C 101+902C 102-903C 103+…+(-1)r 90r C 10r +…+9010C 1010除以88的余数是()A.-1B.1C.-87D.87(2)1.028≈(小数点后保留三位小数).指点迷津(四) 破解解题密码——排列、组合问题的解题策略排列、组合一直是学习中的难点,通过我们平时做的练习,不难发现排列、组合问题的特点是条件隐晦,不易挖掘,题目多变,解法独特,数字庞大,难以验证.在高考中极易丢分.策略一特殊元素与特殊位置优先策略考情分析位置分析法和元素分析法是解决排列、组合问题最常用也是最基本的方法,若以元素分析为主,需先安排特殊元素,再出来其他元素.若以位置分析为主需先满足特殊位置的要求,再处理其他位置,若多个约束条件,往往是考虑一个约束条件的同时,兼顾其他约束条件.【例1】若从0,1,2,3,4,5这六个数字中选3个数字,组成没有重复数字的三位偶数,则这样的三位数一共有()A.20个B.48个D.120个0不能在首位数字,则分2种情况讨论:①若0在个位,此时0一定不在首位,由排列公式即可得此时三位偶数的数目;②若0不在个位,要排除0在首位的可能,由分步乘法计数原理可得此情况下三位偶数的数目,综合2种情况,由分类加法计数原理计算可得答案.,分2种情况讨论:①若0在个位,此时只需在1,2,3,4,5中任取2个数字,作为十位和百位数字即可,有A52=20(个)没有重复数字的三位偶数;②若0不在个位,此时必须在2或4中任取1个,作为个位数字,有2种取法,0不能作为百位数字,则百位数字有4种取法,十位数字也有4种取法,此时共有2×4×4=32(个)没有重复数字的三位偶数,综合可得,共有20+32=52(个)没有重复数字的三位偶数.故选C.解题心得解题需要注意偶数的末位数字以及0不能在首位等性质,对于每一类还要注意分步完成.策略二相邻元素捆绑策略【例2】明年的今天,同学们已经毕业离校了,在离校之前,有三位同学要与语文、数学两位老师合影留念,则这两位老师必须相邻且不站两端的站法种数为()B.24C.36D.48,把两位老师看出一个元素,采用插空法,即可求解.,三位同学全排列,共有A33=6(种)不同的排法,把两位老师看出一个元素,采用插空法,且要求不站在两端,插到三位同学构成的两个空隙中,共有A33C21A22=24(种)不同的排法.故选B.解题心得关于相邻问题,要求某几个元素必须排在一起的问题,可以用捆绑法来解决,即将需要相邻的元素合并为一个元素,再与其他元素一起排列,同时要注意合并元素内部也必须排列.策略三不相邻问题插空策略【例3】若4名演讲比赛获奖学生和3名指导教师站在一排拍照,则其中任意2名教师不相邻的站法有种.4名演讲比赛获奖学生全排列,再根据不相邻问题插空位原则,安排三位指导教师,由分步乘法计数原理即可求得答案.,分两步分析:先将4名演讲比赛获奖学生全排列,有A44=24(种)站法, 站好后有5个空位,在其中选三个空位,安排指导教师,有A53=60(种)情况,则有24×60=1440(种)符合题意的站法.故答案为1440.解题心得对于不相邻问题,可以把没有位置要求的元素进行排列,再把不相邻的元素插入队列的中间或两端的空隙中.策略四定序问题倍缩、空位插入策略【例4】(经典例题)7人排队,其中甲、乙、丙3人顺序一定,共有多少种不同的排法?,再把剩余4人插入队列,或放7把椅子,让其他人坐好,再让甲乙丙按顺序入座.方法1)共有A 77A 33=840(种)不同的排法. (方法2)设想有7把椅子让除甲、乙、丙以外的4人坐,共有A 74种坐法,其余的三个位置给甲、乙、丙坐,有1种坐法,则坐法种数为A 74=840.故共有840种不同的排法.(方法3)先让甲、乙、丙排队,有1种排法,再把其余4人分别插入,不同排法的种数为4×5×6×7=840.故共有840种不同的排法.解题心得对于定序问题可以倍缩法,也可以转化为占为插空模型处理,只要选出有序元素所占的位置即可,相同元素的排列一般也按定序排列的方法处理.策略五重排问题求幂策略【例5】某校科技大楼电子阅览室在第8层,从下一层到上一层,每层均有2个楼梯,则由一楼上到电子阅览室的不同走法共有() 9种 B.28种 C.27种 D.82种.2种走法,从二楼到三楼有2种走法,…,从一楼到八楼分7步进行,每步都有2种不同的走法,所以根据分步乘法计数原理可得由一楼上到电子阅览室的不同走法共有27种.故选C .解题心得允许重复的排列问题的特点是以元素为研究对象,元素不受位置约束,可以逐一安排各个元素的位置,但一个元素只能安排一个位置,且不能同时安排在两个位置上.一般地,n 个不同的元素没有限制的安排在m 个位置上的排列数为m n 种.策略六分排问题直排策略【例6】有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这两人不左右相邻,那么不同的排法种数是()A.234B.346D.3631)一共可坐的位子有20个,2个人坐的方法数为A 202,还需排除两左右相邻的情况.把可坐的20个座位排成连续一行,将其中两个相邻座位看成一个整体,则相邻的坐法有A 191A 22,还应再加上2A 22,所以不同坐法的种数为A 202−A 191A 22+2A 22=346.(方法2)因为前排中间的3个座位不能坐,实际上可坐的位置是前排8个,后排12个,分成以下3种情况:①甲、乙2人一个前排,一个后排,有C 81C 121A 22种排法;②两人均在后排,共A 1212种排法,还需排除甲、乙2人相邻的情况,即A 111A 22种排法;故有(A 1212−A 111A 22)种排法;③甲、乙均在前排,又分两类:第一类,甲乙2人一左一右,有C 41C 41A 22种排法;第二类,甲乙2人同左同右,有2(A 42−A 31A 22)种排法.综上不同排法种数有C 81C 121A 22+A 1212−A 111A 22+C 41C 41A 22+2(A 42−A 31A 22)=346.解题心得一般地,对于元素分成多排的排列问题,可先转化成一排考虑,再分排研究.策略七元素相同问题隔板策略隔板法模型的构建是解决排列、组合中一类分装组合问题,它是求相同元素名额分配方案种数的一种处理策略.【例7】(1)从A ,B ,C ,D 4个班级中选10人组成卫生检查小组,每班至少选一人,每班人数的不同情况的种数为()A.42B.56C.84D.168(2)将十个相同的小球装入编号为1,2,3的三个盒子(每次要把十个球装完)中,要求每个盒子里的个数不少于盒子的编号数,则这样的装法种数为()A.9B.12C.15D.18(3)把1 995个不加区别的小球分别放在10个不同的盒子里,使得第i 个盒子中至少有i 个球(i=1,2,…,10),则不同放法的总数是()A.C 194010B.C 19409C.C 194910D.C 19499(4)8个相同的小球分别放入4个不同的盒子中,每盒可空,共有不同的放法() 种 B.56种 C.35种 D.20种将10个人排成一排,然后从中间形成的9个空中选3个,分别放入一个隔板,即可将10个人分为4个部分,且每部分至少1个人,由此可得每班人数的不同情况有C 93=9×8×73×2×1=84(种).故选C . (2)根据题意,先在编号为2,3的三个盒子中分别放入1,2个小球,编号为1的盒子里不放;再将剩下的7个小球放入3个盒子里,每个盒子里至少一个,分析可得,7个小球排好,有6个空位,在6个空位中任选2个,插入挡板,共C 62=15(种)放法,即可得符合题目要求的放法共15种.故选C .(3)先在第i 个盒里放入i 个球,i=1,2,…,10,即第1个盒里放1个球,第2个盒里放2个球,…,这时共放了1+2+…+10=55(个)球,还余下1995-55=1940(个)球.故转化为把1940个球任意放入10个盒子里(允许有的盒子里不放球).把这1940个球用9块隔板隔开,每一种隔法就是一种球的放法,1940个球连同9块隔板共占有1949个位置,相当于从1949个位置中选9个位置放隔板,有C 19499种放法.故选D.(4)首先设想每个盒子内放入1个小球,共用去4个小球,(添加4个这样的小球)将问题转化为把12个相同的小球分装到4个不同的盒子中求不同的放法的问题,利用隔板法,把12个小球排成一列,在11个空隙中插入3个隔板,即得不同的放法有C 113=165(种).故选A .解题心得将n 个相同的元素分成m 份(n ,m 为整数),每份至少一个元素,可以用(m-1)个隔板,插入n 个元素排成一排形成的(n-1)个空隙中,所有分法为C n -1m -1种.策略八小集团问题先整体后局部策略【例8】身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有()B.28种C.36种D.48种,共有A 55种结果,去掉相同颜色衣服的人都相邻的情况,再去掉仅穿红色衣服的人的相邻和仅穿黄色衣服的人相邻两种情况,从而求得结果.,共有A 55种结果.去掉同颜色衣服相的人都相邻的情况,再去掉仅穿红色相邻和仅穿黄色相邻的两种情况.穿相同颜色衣服的人都相邻的情况有A 22A 22A 33种(相邻的看成一整体),当穿红色衣服的相邻,而穿黄色衣服的人不相邻,共有A 22A 22A 33种(相邻的看成一整体,不相邻利用插空法),同理当穿黄色衣服的相邻,而穿红色衣服的人不相邻,也共有A 22A 22A 33种,所以穿相同颜色衣服的人不能相邻的排法种数是A 55−A 22A 22A 33-2A 22A 22A 33=48.故选D .解题心得小集团排列问题,先整体排列,后局部排列,再结合其他策略进行处理.策略九正难则反总体淘汰策略【例9】用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为()B.252C.261D.279,用0,1,…,9十个数字组成的三位数(含有重复数字的)共有9×10×10=900(个),组成无重复数字的三位数共有9×9×8=648(个),因此组成有重复数字的三位数共有900-648=252(个).故选B .解题心得有些排列组合问题,正面直接考虑比较复杂,而它的反面往往比较简单易求,分类情况也较简单明确,此时可以先求出它的反面,再从整体中淘汰.策略十排组混合问题先选后排策略【例10】将甲、乙、丙、丁四位老师分配到三个班级,每个班级至少一位老师,则共有分配方案()A.81种B.256种D.36种,先将四位老师分为三组,再分到三个班,由分步乘法计数原理求解即可计算出答案.,将4名老师分成三组,不同的分法种数是C 42=6;第二步,分到三个班的不同分法有A 3=6(种).故不同的分配方案为6×6=36(种).故选D .解题心得排列组合的应用问题,一般按先选再排,先分组再分配的处理原则.对于分配问题,解题的关键是要搞清楚事件是否与顺序有关,对于平均分组问题更要注意顺序,避免计数的重复或遗漏.策略十一平均分组除法策略【例11】某高校大一新生中的6名同学打算参加学校组织的“演讲团”“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法种数为() B.1 080 C.1 440 D.2 5203组与4组两类,再分组分配下去,均分问题要除序后再分配.1个社团且每个社团至多两人参加,所以可以将问题看成是将6名同学分配到除“演讲团”外的四个社团,或除“演讲团”外的四个社团中的三个社团,可以分成两类:第一类,当6名同学分成人数分别为1,1,2,2四个组时,应分配到除“演讲团”外的四个社团中,不同的参加方法种数为C 61C 51A 22·C 42C 22A 22·A 44=1080;第二类,当6名同学分成人数分别为2,2,2三个组时,应分配到除“演讲团”外的四个社团中的三个社团中,不同的参加方法种数为C 62C 42C 22A 33·C 43·A 33=360.综上,不同的参加方法种数为1080+360=1440.故选C .解题心得平均分成的组,不管它顺序如何,都是一种情况,所以分组以后一定要除以A n n (n 为均分组数),避免重复计数.策略十二合理分类与分步策略【例12】用五种不同颜色给三棱台ABC-DEF 的六个顶点涂色,要求每个点涂一种颜色,且每条棱的两个端点涂不同颜色.则不同的涂色方法有种.,先涂A ,B ,C ,再涂D ,E ,F ,然后分若5种颜色都用上、若5种颜色只用4种、若5种颜色只用3种这三种情况,分别求得结果,再相加,即可得结果.,先涂A,B,C,再涂D,E,F.第一类:若5种颜色都用上,先涂A,B,C,方法有A53种,再涂D,E,F中的两个点,方法有A32种,最后剩余的一个点只有2种涂法,故此时方法共有A53·A32×2=720(种).第二类:若5种颜色只用4种,首先选出4种颜色,方法有C54种;先涂A,B,C,方法有A43种,再涂D,E,F中的一个点,方法有3种,最后剩余的两个点只有3种涂法,故此时方法共有C54·A43×3×3=1080(种).第三类:若5种颜色只用3种,首先选出3种颜色,方法有C53种;先涂A,B,C,方法有A33种,再涂D,E,F,方法有2种,故此时方法共有C53·A33×2=120(种).综上可得,不同涂色方案共有720+1080+120=1920(种),故答案是1920.解题心得解决带约束条件的排列、组合问题,可按元素的性质进行分类,按事情发展的过程进行分步,应做到标准明确,分步层次清楚,不重不漏,分类标准一旦确定要贯穿于整个解题过程,不要一步一个标准.策略十三构造模型策略【例13】(1)方程x+y+z=10的正整数解的组数为()A.9B.12C.15D.18(2)某栋楼从2楼到3楼共10个台阶,上楼可以一步上一个台阶,也可以一步上两个台阶,若规定从2楼到3楼8步走完,则上楼方法种数为()B.16C.21D.28设方程x+y+z=10的正整数解依次为x1,x2,x3,则x1+x2+x3=10(x1≥1,x2≥2,x3≥3).记y1=x1,y2=x2-1,y3=x3-2,则y1+y2+y3=7(y1≥1,y2≥1,y3≥1).于是,问题转化为求方程y1+y2+y3=7的正整数解的组数.进而将问题转化为将7个相同的小球装入3个编号分别为1,2,3的盒子内,每个盒子中至少一个的问题,由隔板法易知其组数为C62=15.故选C.(2)(方法1)由于10÷8的余数为2,所以可以判定一步1个台阶共6次,一步2个台阶共2次.选定在这8步中一步1个台阶的位置或一步2个台阶的位置,则上楼的方法有C86=C82=28(种).(方法2)从结果入手,设计“插入法模型”,构建组合数求解.问题就是将6个1和2个2组合,不同的组合方案就构成了不同的走法,可分类完成.①若2个2不相邻,则先排6个1构成7个空位,在7个空位中选出2个插入2,有C72种方法;②若2个2相邻,则先排6个1构成7个空位,在7个空位中选出1个插入两个2,共有C71种方法,因此上楼的方法共有C71+C72=28(种).故选D.解题心得一些不易理解的排列、组合问题,如果能转化成非常熟悉的模型,如占位填空模型、组数模型、排队模型、装盒模型,相邻模型等可使问题直观,容易解决.策略十四实际操作穷举策略【例14】(1)将15个颜色、大小完全相同的球全部放入编号为1,2和3的三个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号数,则不同的放球方法有()A.15种B.182种C.91种D.120种(2)有红、黄、蓝色的球各5只,分别标有A,B,C,D,E五个字母,现从中取5只,要求各字母均有且三色齐备,则共有不同的取法()A.150种B.180种种 D.100种先放1,2,3的话,那么还剩下9个球,9个球放到3个不同的盒子里,情况有: 0,0,9,分别在1,2,3号盒子中的任意一个中放9个,共3种情况;0,1,8,分别在1,2,3号盒子中的任意两个中放8个和1个,共6种情况;0,2,7,分别在1,2,3号盒子中的任意两个中放2个和7个,共6种情况;1,1,7分别在1,2,3号盒子中的任意两个中放一个,共3种情况;依次讨论可得还有以下几种情况1,2,6;1,3,5;1,4,4;2,2,5;2,3,4;2,5,2;2,6,1;3,3,3;3,6,0;….所以共有91种.故选C.(2)共有C51C41+C51C42+C51C43535352=150(种),故选A.解题心得对于条件比较复杂的排列组合问题,不易用公式进行运算,往往利用穷举法或画出树状图会收到意想不到的结果,一些复杂的分类选取题,要满足的条件比较多,无从入手,经常出现重复遗漏的情况,用表格法,则分类明确,能保证题中须满足的条件,能达到好的效果.策略十五分解与合成策略【例15】30 030能被多少个不同的偶数整除?30030分解成质因数的乘积形式30030=2×3×5×7×11×13.依题意可知偶因数必先取2,再从其余5个因数中任取若干个组成乘积,所有的偶因数有C50+C51+C52+C53+C54+C55=32(个).解题心得分解与合成策略是排列组合问题的一种最基本的解题策略,把一个复杂问题分解成几个小问题逐一解决,然后依据问题分解后的结构,用分类加法计数原理和分步乘法计数原理将问题合成,从而得到问题的答案,每个比较复杂的问题都要用到这种解题策略.策略十六化归策略【例16】25人排成5×5方阵,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?9人排成3×3方阵,现从中选3人,要求3人不在同一行也不在同一列,有多少种选法.这样每行必有1人从其中的一行中选取1人后,把这人所在的行列都划掉,如此继续下去.从3×3方队中选3人的方法有C31C21C11种.再从5×5方阵选出3×3方阵便可解决问题.从5×5方队中选取3行3列有C53C53种选法,所以从5×5方阵选不在同一行也不在同一列的3人有C53C53C31C21C11=600(种)选法.解题心得处理复杂的排列组合问题时可以把一个问题转化成一个简要的问题,通过解决这个简要的问题的解决找到解题方法,从而进一步解决原来的问题.策略十七数字排序问题查字典策略【例17】由0,1,2,3,4,5六个数字可以组成多少个没有重复的比324 105大的数?324105大的数的个数为N=2A55+2A44+A33+A22+A11=297.解题心得数字排序问题可用查字典法,查字典的法应从高位向低位查,依次求出其符合要求的个数,根据分类加法计数原理求出其总数.11.3二项式定理必备知识·预案自诊知识梳理1.C n 0a n +C n 1a n-1b+…+C n r a n-r b r +…+C n n b nC n r a n-r b r r+1 2.C n m =C n n -m考点自诊1.(1)×(2)×(3)√(4)√(5)×2.A 因为x-1x5的展开式的通项为T r+1=C 5r x 5-r ·-1x r =(-1)r C 5r x 5-2r,令r=1,则可得x-1x5的展开式中的第2项为(-1)×C 51x 3=-5x 3.3.B C n 03n +C n 13n-1+…+C n n -13+C n n =C n 03n 10+C n 13n-111+…+C n n -1311n-1+C n n 301n=(3+1)n =4n =212,即22n =212,得n=6.故选B .4.B 令x=1,则a 0+a 1+a 2+a 3+a 4=0,令x=-1,则a 0-a 1+a 2-a 3+a 4=16,两式相加得a 0+a 2+a 4=8.. 5.7由题意,可知2n =128,解得n=7.6.-27(x-1)(3x 2+1)3展开式中x 4的系数,x-1中的x 与(3x 2+1)3展开式中x 3项相乘,但(3x 2+1)3展开式中没有x 3项,x-1中的-1与(3x 2+1)3展开式中x 4项相乘,C 31(3x 2)2=27x 4,所以x 4的系数是-27.关键能力·学案突破例1(1)10(2)C(1)(x+2x 2)5=(x+2·x -2)5,展开式通项T r+1=C 5r x 5-r (2x -2)r =2r C 5r x 5-3r,令5-3r=2,得r=1.∴x 2的系数为21·C 51=2×5=10.(2)∵(ax -1x )6的展开式的通项为T r+1=C 6r (-1)r a 6-r x 6-r-r =C 6r (-1)ra 6-r x 6-2r ,令6-2r=0得r=3,可得常数项为C 63(-1)3a 3=-20a 3=-20,得a=1.对点训练1(1)C(2)±1(1)√x 3−√x5的展开式的通项为T r+1=C 5r(√x 3)5-r ·-√xr=(-2)r C 5rx 10-5r 6.根据题意,得10-5r=0,r=2,因此,常数项为(-2)2C 52=40.(2)x-√x 5的展开式的通项为T r+1=C 5r x 5-r ·-√x r =C 5r(-a )r x 5-32r .由5-32r=5,得r=0,由5-32r=2,得r=2,所以A=C 50×(-a )0=1,B=C 52×(-a )2=10a 2,则由1+10a 2=11,解得a=±1.例2(1)B(2)A(3)A(1)因为(1+x 2)1-1x 6=(1+x 2)1-6x +15x 2−20x 3+15x 4−6x 5+1x 6,故它的展开式中的常数项是1+15=16.故选B .(2)1-1x3的展开式的通项为T r+1=C 3r ·13-r -1x r =C 3r·(-1)r x -r ,则(2-mx )1-1x 3的展开式中的常数项为2×C 30+(-m )×C 31×(-1)1=2+3m ,由题知2+3m=8,则m=2.(3)(1-√x )8(1+√x )5=(1-√x )3[(1-√x )(1+√x )]5=(1-√x )3(1-x )5,(1-√x )3的通项为C 3r(-√x )r ,其中r=0,1,2,3.(1-x )5的通项为C 5r(-x )r ,其中r=0,1,2,3,4,5.所以展开式中x 2的系数是C 30(-1)0×C 52(-1)2+C 32(-1)2×C 51(-1)1=10-15=-5,故选A .对点训练2(1)B(2)25(1)(方法1)(1-√x )6的展开式的通项为C 6m ·(-√x )m =C 6m(-1)m x m2,(1+√x )4的展开式的通项为C 4n ·(√x )n =C 4n x n2.令m 2+n2=1,得m+n=2,于是(1-√x )6(1+√x )4的展开式中x 的系数等于C 60×(-1)0×C 42+C 61×(-1)1×C 41+C 62×(-1)2×C 40=-3.(方法2)(1-√x )6(1+√x )4=[(1-√x )(1+√x )]4(1-√x )2=(1-x )4(1-2√x +x ).于是(1-√x )6(1+√x )4的展开式中x 的系数为C 40×1+C 41×(-1)1×1=-3.(2)(ax+1)6的展开式中含x 2的项的系数为C 64a 2,含x 的项的系数为C 65a ,由(x-1)(ax+1)6的展开式中含x 2的项的系数为0,可得-C 64a 2+C 65a=0,因为a 为正实数,所以15a=6,所以a=25.例3(1)63√22(2)-8(1)原式=(x 2+2√2x+22x)5=132x 5·[(x+√2)2]5=132x 5·(x+√2)10.求原展开式中的常数项,转化为求(x+√2)10的展开式中含x 5的项的系数,即C 105·(√2)5.所以所求的常数项为C 105·(√2)532=63√22. (2)由题意知,(x 2-x-2)4=(x-2)4(x+1)4,(x-2)4的通项为T r 1+1=C 4r1x 4-r 1(-2)r 1,(x+1)4的通项为T r 2+1=C 4r2x 4-r 21r 2,当r 1=2,r 2=4时,系数为24;当r 1=3,r 2=3时,系数为-128;当r 1=4,r 2=2时,系数为96.所以x 2的系数为24-128+96=-8.故答案为-8.对点训练3(1)C(2)19(1)(方法1)(x 2+x+y )5的展开式的通项为T r+1=C 5r (x 2+x )5-r·y r ,令r=2,则T 3=C 52(x 2+x )3y 2,又因为(x 2+x )3的展开式的通项为T r+1=C 3r (x 2)3-r ·x r =C 3r x 6-r ,令6-r=5,则r=1,所以(x 2+x+y )5的展开式中,x 5y 2的系数为C 52C 31=30.(方法2)(x 2+x+y )5表示5个x 2+x+y 之积.所以x 5y 2可从其中5个因式中,两个取x 2,剩余的3个因式中一个取x ,其余因式取y ,因此x 5y 2的系数为C 52C 31C 22=30.(2)由于x 2=x 2·(√x )0,x 2=x·(√x )2,x 2=x 0·(√x )4,据此结合排列、组合的性质可得x 2的系数为C 42C 20C 22+C 41C 32C 11+C 40C 44C 00=6+12+1=19.故答案为19.例4B 由题意可知,a=C 2m m ,b=C 2m+1m.∵13a=7b ,∴13·(2m )!m !m !=7·(2m+1)!m !(m+1)!,即137=2m+1m+1,解得m=6.故选B .对点训练48因为只有第5项的二项式系数最大,所以n=8.因为所有项的系数和为256,所以(1+a )8=256,所以a=1.x+1x8的通项为Tr+1=C 8r x 8-r (1x)r=C 8r x 8-2r,令8-2r=6,所以r=1.所以含x 6的项的系数为C 81=8.故答案为8.例5-8 064-15 360x 4由题意知,22n -2n =992,即(2n -32)(2n +31)=0,故2n =32,解得n=5.由二项式系数的性质知,(2x -1)10的展开式中第6项的二项式系数最大,故二项式系数最大的项为T 6=C 105(2x )5(-1)5=-8064.设第r+1项的系数的绝对值最大,则T r+1=C 10r ·(2x )10-r ·(-1x )r =(-1)r C 10r ·210-r ·x 10-2r,令{C 10r·210-r ≥C 10r -1·210-r+1,C 10r ·210-r≥C 10r+1·210-r -1,。
2022高三全国统考数学北师大版(理)一轮复习学案:1.2 简单不等式的解法含解析2

1.2简单不等式的解法 必备知识预案自诊知识梳理1.两个实数比较大小的方法 (1)作差法{a -b >0⇔a b ,a -b =0⇔a b ,a -b <0⇔a b .(2)作商法{ ab >1⇔a b (a ∈R ,b >0),ab =1⇔a b (a ∈R ,b ≠0),ab<1⇔a b (a ∈R ,b >0).2.不等式的性质(1)对称性:a>b ⇔b<a. (2)传递性:a>b ,b>c ⇒a>c.(3)可加性:a>b ⇔a+c>b+c ;a>b ,c>d ⇒a+c>b+d.(4)可乘性:a>b ,c>0⇒ac>bc ;a>b ,c<0⇒ac<bc ;a>b>0,c>d>0⇒ac>bd. (5)可乘方:a>b>0⇒a n >b n (n ∈N ,n ≥2). (6)可开方:a>b>0⇒√a n>√b n(n ∈N ,n ≥2). 3.三个“二次”Δ>0 Δ=0 Δ<0续表考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)a>b⇔ac2>bc2.()(2)a>b>0,c>d>0⇒ad >bc.()(3)若关于x的不等式ax2+bx+c<0的解集为(x1,x2),则必有a>0.()(4)不等式x-2x+1≤0的解集是[-1,2].()(5)若关于x的方程ax2+bx+c=0(a≠0)没有实数根,则关于x的不等式ax2+bx+c>0的解集为R.()2.设a,b,c,d∈R,且a>b,c>d,则下列结论中正确的是()A.ad >bcB.a-c>b-dC.ac>bdD.a+c>b+d3.(2020福建厦门期末检测)实数x,y满足x>y,则下列不等式恒成立的是()A.yx<1 B.2-x<2-yC.lg(x-y)>0D.x2>y24.(2020安徽马鞍山二模,理1)已知集合A={x|x2-2x-3≤0,x∈Z},B={x||x|≤2,x∈Z},则A∩B=()A.{-1,0,1}B.{-2,-1,0,1}C.{-1,0,1,2}D.{-2,-1,0,1,2,3}5.设a ,b ,c 是任意实数,能够说明“若c<b<a 且ac<0,则ab<ac ”是假命题的一组整数a ,b ,c 的值依次为.关键能力学案突破考点比较两个数(式)的大小【例1】(1)已知a 1,a 2∈(0,1),若M=a 1a 2,N=a 1+a 2-1,则M 与N 的大小关系是() A.M<N B.M>N C.M=N D.不确定 (2)若a=ln33,b=ln44,c=ln55,则()A.a<b<cB.c<b<a D.b<a<c(式)大小常用的方法有哪些?解题心得比较大小常用的方法有作差法、作商法、构造函数法.(1)作差法的一般步骤:①作差;②变形;③定号;④下结论.变形常采用配方、因式分解、有理化等方法把差式变成积式或者完全平方式.(2)作商法一般适用于分式、指数式、对数式,作商只是思路,关键是化简变形,从而使结果能够与1比较大小.(3)构造函数法:构造函数,利用函数的单调性比较大小.对点训练1(1)已知实数a ,b ,c 满足b+c=6-4a+3a 2,c-b=4-4a+a 2,则a ,b ,c 的大小关系是() A.c ≥b>a B.a>c ≥b C.c>b>a D.a>c>b(2)已知a ,b 是实数,且e <a<b ,其中e 是自然对数的底数,则a b 与b a 的大小关系是.考点不等式的性质及应用【例2】(1)(2020北京海淀一模,4)已知实数a ,b ,c 在数轴上对应的点如图所示,则下列式子中正确的是()A.b-a<c+aB.c 2<abC.cb >caD.|b|c<|a|c(2)(2020山西太原三模,理3)已知a>b>1,c<0,则 ()A.c a<c bB.c a <c bc c D.log a (b-c )>log b (a-c ),求由这些量组成的代数式的范围常用不等式的哪些性质?解题心得1.已知某些量的范围,在求由这些量组成的代数式的范围时,常用不等式同向可加性、同向同正可乘性;2.在应用可乘方性时要注意应用的条件,当不等式两边异号时,平方后不等号不确定;3.当ab>0时,对不等式a>b 两边取倒数,或两边同乘以1ab ,化简得1b >1a .对点训练2(1)(2020海南高三期末,4)已知实数a ,b 满足a>b>0,则下列不等式一定成立的有()A.a 2<b 2B.-a<-bC.b a +a b≥2D.a+b>ab(2)(2020山东青岛5月模拟,9改编)设a ,b ,c 为实数,且a>b>0,则下列不等式中正确的是() A.log 2(ab )<log 2b 2 B.ac 2>bc 2C.b a <1<a bD.(12)a>(12)b考点一元二次不等式的解法(多考向探究)考向1常系数一元二次不等式的解法【例3】解下列不等式: (1)2x 2-3x-2>0; (2)-3x 2+6x-2>0; (3)4x 2-4x+1≤0; 2x+2>0.?解题心得对于常系数一元二次不等式,可以用分解因式法求解,即把不等式分解成(x-a )(x-b )>0或(x-a )·(x-b )<0型不等式,再依据“大于取两边,小于取中间”的口诀写出解集;对难于因式分解的不等式可采用判别式法求解,先计算对应方程的判别式,若判别式不小于零,求出相应的一元二次方程的根,画出对应函数的简图,由图像得出不等式的解集,若判别式小于零,直接根据对应函数的图像确定不等式的解集.对点训练3解下列不等式: (1)x 2-3x+2<0; (2)3x 2+5x-2>0; (3)-2x 2+3x+2≤0.考向2含参数的一元二次不等式的解法【例4】解关于x 的不等式ax 2+2x+1<0.?解题心得含有参数的不等式的求解,需要对参数进行分类讨论,讨论有三层:第一,若二次项系数含参数,先讨论二次项系数是否为零,以确定不等式是一次不等式还是二次不等式;第二,当二次项系数不为零时,若不易分解因式,则依据判别式符号进行分类讨论;第三,对方程的根进行讨论,比较大小,以便写出解集.对点训练4解关于x 的不等式x 2-ax-2a 2<0.考点分式不等式的解法【例5】已知全集U=R ,集合A={x||x-1|<1},B={x |2x -5x -1≥1},则A ∩(∁U B )=() A.{x|1<x<2} B.{x|1<x ≤2} ≤x<2} D.{x|1≤x<4}?解题心得解分式不等式时,切忌直接去分母,一般先通过移项、通分,将分式不等式化简如化为f (x )g (x )>0或f (x )g (x )<0,再等价转化为整式不等式的形式(如化为{f (x )g (x )>0,g (x )≠0或{f (x )g (x )<0,g (x )≠0),即转化为一次、二次或高次不等式. 对点训练5不等式2x -33x -4≤2的解集为.考点 一元二次不等式恒成立问题 (多考向探究)考向1主元x 在R 上恒成立求参数范围【例6】若一元二次不等式2kx 2+kx-38<0对一切实数x 都成立,则k 的取值范围为() A.(-3,0]B.[-3,0)C.[-3,0]D.(-3,0)考向2主元x 在给定区间上恒成立求参数范围【例7】设对任意实数x ∈[-1,1],不等式x 2+ax-3a<0恒成立,则实数a 的取值范围是() A.a>0B.a>12C.a>0或a<-12D.a>14?3给定参数范围的恒成立问题【例8】已知对任意的k ∈[-1,1],函数f (x )=x 2+(k-4)x+4-2k 的值恒大于零,则x 的取值范围是.解题心得1.ax 2+bx+c ≥0(a ≠0)对任意实数x 恒成立的条件是{a >0,Δ≤0;ax 2+bx+c ≤0(a ≠0)对任意实数x 恒成立的条件是{a <0,Δ≤0.2.含参数的一元二次不等式在某区间内恒成立问题,常有两种解决方法:一是利用二次函数在区间上的最值来解决;二是先分离出参数,再通过求函数的最值来解决.3.已知参数范围求函数自变量的范围的一般思路是更换主元法.把参数当作函数的自变量,得到一个新的函数,然后利用新函数求解.对点训练6(1)已知a 为常数,任意x ∈R ,ax 2+ax+1>0,则a 的取值范围是() A.(0,4) B.[0,4) C.(0,+∞) D.(-∞,4)(2)已知函数f (x )=x 2+mx-1,若对于任意x ∈[m ,m+1],都有f (x )<0成立,则实数m 的取值范围是.(3)已知不等式xy ≤ax 2+2y 2对x ∈[1,2],y ∈[2,3]恒成立,则实数a 的取值范围是.1.比较法是不等式性质证明的理论依据,是不等式证明的主要方法之一.作差法的主要步骤为作差—变形—判断正负.2.判断不等式是否成立,主要有利用不等式的性质和特殊值验证两种方法,特别是对于有一定条件限制的选择题,用特殊值验证的方法更简单.3.简单的分式不等式可以等价转化,利用一元二次不等式的解法进行求解.4.“三个二次”的关系是解一元二次不等式的理论基础;一般可把a<0的情形转化为a>0的情形.5.(1)对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图像在给定的区间上全部在x 轴上方,恒小于0就是相应的二次函数的图像在给定的区间上全部在x 轴下方.另外常转化为求二次函数的最值或用分离参数法求最值.(2)解决恒成立问题一定要搞清谁是主元,谁是参数.一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.1.2 简单不等式的解法必备知识·预案自诊知识梳理1.(1)>=<(2)>=<3.{x|x>x 2或x<x 1}{x|x 1<x<x 2}∅∅考点自诊1.(1)×(2)√(3)√(4)×(5)×2.D ∵a ,b ,c ,d ∈R ,且a>b ,c>d ,根据同向不等式的可加性,得a+c>b+d ,故选D .3.B 由x>y ,得-x<-y.由y=2t 是增函数,得2-x <2-y .4.C 由题意,得A={-1,0,1,2,3},B={-2,-1,0,1,2},则A ∩B={-1,0,1,2},故选C.5.1,0,-1(答案不唯一)由c<b<a 且ac<0,可取a 为正数,c 为负数,由命题为假命题,得ab<ac 不成立,即ab ≥0,所以a ,b ,c 可取的一组分别为1,0,-1.关键能力·学案突破例1(1)B(2)B(1)M-N=a 1a 2-(a 1+a 2-1)=a 1a 2-a 1-a 2+1=(a 1-1)·(a 2-1).∵a 1∈(0,1),a 2∈(0,1), ∴a 1-1<0,a 2-1<0.∴(a 1-1)(a 2-1)>0,即M-N>0. ∴M>N.(2)(方法1)易知a ,b ,c 都是正数,ba =3ln44ln3=log 8164<1,所以a>b ;bc =5ln44ln5=log 6251024>1, 所以b>c.故c<b<a. (方法2)对于函数y=f (x )=lnx x ,y'=1-lnx x 2,易知当x>e 时,函数f (x )递减.因为e <3<4<5,所以f (3)>f (4)>f (5),即c<b<a.对点训练1(1)A(2)a b >b a (1)∵c-b=4-4a+a 2=(a-2)2≥0,∴c ≥b.又b+c=6-4a+3a 2, ∴2b=2+2a 2. ∴b=a 2+1.∴b-a=a2-a+1=(a -12)2+34>0,∴b>a.∴c ≥b>a. (2)令f (x )=lnx x,则f'(x )=1-lnxx 2,当x>e 时,f'(x )<0,所以f (x )在(e,+∞)上递减,因为e <a<b ,所以f (a )>f (b ),即lna a>lnb b⇒b ln a>a ln b ⇒a b >b a. 例2(1)D(2)C(1)(方法1)根据数轴可得c<b<a<0,且|c|>|b|>|a|,对于A:因为c<b ,a<0,所以c+a<c ,b-a>b ,则c+a<c<b<b-a ,即c+a<b-a ,故A 错误;对于B:因为c<b<a<0,|c|>|b|>|a|,所以c 2>b 2>a 2,且b 2>ab ,所以c 2>b 2>ab ,即c 2>ab ,故B 错误;对于C:因为b<a<0,所以1b >1a ,则cb<c a,故C 错误;对于D:因为|b|>|a|,且c<0,所以|b|c<|a|c ,故D 正确.(方法2)不妨令c=-5,b=-4,a=-1,则c+a=-6<b-a=-3,故A 错误;c 2=25>ab=4,故B 错误;cb =54<ca =5,故C 错误;|b|c=-20<|a|c=-5,故D 正确.故选D .(2)由于a>b>1,所以0<1a <1b ,又c<0,故ca >cb ,选项A 错误;当c=-2,a=4,b=3时,c a >c b ,故选项B 错误;由于a>b>1,c<0,故a c <b c ,选项C 正确;由于a>b>1,c<0,所以a-c>b-c ,故log a (b-c )<log b (a-c ),选项D 错误,故选C .对点训练2(1)B(2)C(1)因为a>b>0,于是a 2>b 2,故A 不正确;由a>b>0,得-a<-b ,故B 正确;由基本不等式可知ba +ab ≥2√b a ·a b =2,因为a>b ,所以等号取不到,故C 不正确;当a=3,b=2时,3+2<2×3,故D 不正确.故选B.(2)由a>b>0,得ab>b 2,所以log 2(ab )>log 2b 2,故A 不正确; 因为c 2≥0,当c 2=0时,ac 2=bc 2,故B 不正确;由a>b>0,两边同乘1b ,得ab >1,由a>b>0,两边同乘1a ,得ba <1,故C 正确;由a>b ,函数y=(12)x为减函数,得(12)a<12b,故D 不正确.故选C.例3解(1)由2x 2-3x-2=2(x-2)x+12>0,得不等式的解集是x x<-12,或x>2.(2)不等式可化为3x 2-6x+2<0.因为3x 2-6x+2=0的判别式Δ=36-4×3×2=12>0,所以方程3x 2-6x+2=0的解是x 1=1-√33,x 2=1+√33.因为函数y=3x 2-6x+2是开口向上的抛物线,所以不等式的解集是x 1-√33<x<1+√33.(3)方程4x 2-4x+1=0的解是x 1=x 2=12,函数y=4x 2-4x+1是开口向上的抛物线,所以原不等式的解集是x x=12.(4)因为x 2-2x+2=0的判别式Δ<0,所以方程x 2-2x+2=0无解.又因为函数y=x 2-2x+2是开口向上的抛物线,所以原不等式的解集为R .对点训练3解(1)∵(x-1)(x-2)<0,∴1<x<2.故原不等式的解集为(1,2).(2)方程3x 2+5x-2=0的两解是x 1=-2,x 2=13.函数y=3x 2+5x-2的图像是开口向上的抛物线,与x 轴有两个交点(-2,0)和13,0.不等式的解集为x x<-2,或x>13.(3)原不等式化为2x 2-3x-2≥0,∵2x 2-3x-2=0的两解为x 1=-12,x 2=2,∴不等式的解集是x x ≤-12,或x ≥2.例4解(1)当a=0时,不等式的解集为x x<-12,(2)当a>0时,Δ=4-4a ,①Δ>0,即0<a<1时,不等式的解集为x -1-√1-a a <x<-1+√1-aa ;②Δ≤0,即a ≥1时,不等式的解集为∅.(3)当a<0时,Δ=4-4a>0,不等式的解集为x x<-1+√1-aa,或x>-1-√1-aa.对点训练4解原不等式变形为(x-2a )(x+a )<0.①若a>0,则-a<x<2a ,此时不等式的解集为{x|-a<x<2a }; ②若a<0,则2a<x<-a ,此时不等式的解集为{x|2a<x<-a }; ③若a=0,则原不等式即为x 2<0,此时解集为∅. 例5C 由题意得A={x||x-1|<1}={x|-1<x-1<1}={x|0<x<2},B={x|2x -5x -1≥1}={x|x -4x -1≥0}={x|x<1或x ≥4},∴∁U B={x|1≤x<4},∴A ∩(∁U B )={x|1≤x<2}.故选C .对点训练5(-∞,54]∪(43,+∞)由2x -33x -4≤2,得4x -53x -4≥0,解得x>43或x ≤54. 例6D2kx 2+kx-38<0对一切实数x 都成立,则必有{2k <0,Δ=k 2-4×2k ×(-38)<0,解得-3<k<0.例7B(方法1)y=x 2+ax-3a 的对称轴是x=-a2.①当-a2≥1,即a ≤-2时,区间[-1,1]是函数y=x 2+ax-3a 的递减区间, 当x=-1时,函数有最大值,所以1-4a<0,得a>14,与a ≤-2相矛盾. ②当0<-a2<1,即-2<a<0时,当x=-1时,函数有最大值. 代入不等式得a>14,与-2<a<0矛盾.③当-1<-a 2≤0,即0≤a<2时,当x=1有最大值时,代入不等式得1-2a<0,即a>12,故12<a<2. 要使不等式x 2+ax-3a<0恒成立, ∴12<a<2.④当-a2≤-1,即a ≥2时,区间[-1,1]是函数y=x 2+ax-3a 的递增区间,x=1时有最大值,代入不等式得1-2a<0,a>12,∴a ≥2.综上所述,a>12.故选B .(方法2)设f (x )=x 2+ax-3a ,∵对任意实数x ∈[-1,1],不等式x 2+ax-3a<0恒成立, ∴{f (-1)=1-a -3a <0,f (1)=1+a -3a <0, 即{1-4a <0,1-2a <0,∴{a >14,a >12,故a>12.故选B . 例8{x|x<1或x>3}x 2+(k-4)x+4-2k>0恒成立,即g (k )=(x-2)k+(x 2-4x+4)>0在k ∈[-1,1]时恒成立.只需g (-1)>0,且g (1)>0,即{x 2-5x +6>0,x 2-3x +2>0,解得x<1或x>3.对点训练6(1)B(2)(-√22,0)(3)[-1,+∞)(1)因为任意x ∈R ,ax 2+ax+1>0,所以必有{a >0,Δ=a 2-4a <0或a=0,即0≤a<4. (2)对于任意x ∈[m ,m+1],都有f (x )<0,则有{f (m )<0,f (m +1)<0,即{m 2+m 2-1<0,(m +1)2+m (m +1)-1<0,解得-√22<m<0.(3)因为不等式xy ≤ax 2+2y 2对任意的x ∈[1,2],y ∈[2,3]恒成立, 所以a ≥yx -2(y x )2对任意的x ∈[1,2],y ∈[2,3]恒成立. 令t=y x ,由x ∈[1,2],y ∈[2,3],可知1≤t ≤3, 所以a ≥t-2t 2在区间[1,3]上恒成立. 令f (t )=-2t 2+t ,则f (t )=-2t 2+t=-2(t -14)2+18.因为f (t )在区间[1,3]上是减少的,所以f (t )max =f (1)=-1,所以a ≥-1.。
全国统考2022高考数学一轮复习第六章数列6.1数列的概念与表示学案理含解析北师大版

第六章数列6.1数列的概念与表示必备知识预案自诊知识梳理1.数列的有关概念概念含义数列按照排列的一列数数列的项数列中的通项公式如果数列{a n}的第n项a n与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫作这个数列的通项公式数列{a n}的前n项和把数列{a n}从第1项起到第n项止的各项之和,称为数列{a n}的前n项和,记作S n,即S n=2.数列的表示方法列表法列表格表达n与a n的对应关系图像法把点画在平面直角坐标系中公式法通项公式把数列的通项用表达的方法递推公式使用初始值a1和a n+1=f(a n)或a1,a2和a n+1=f(a n,a n-1)等表达数列的方法3.数列的函数特征数列的三种表示方法也是函数的表示方法,数列可以看作是定义域为正整数集(或它的有限子集{1,2,…,n})的函数a n=f(n),当自变量由小到大依次取值时所对应的一列.4.数列的性质单调性递增数列任意n∈N+,递减数列任意n∈N+,常数列任意n∈N+,a n+1=a n摆动数列 从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列 周期性任意n ∈N +,存在正整数常数k ,a n+k =a n5.a n 与S n 的关系若数列{a n }的前n 项和为S n ,则a n ={S 1,S =1,S S -S S -1,S ≥2.在数列{a n }中,若a n 最大,则{a n ≥a n -1,a n ≥a n +1.若a n 最小,则{a n ≤a n -1,a n ≤a n +1.考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”. (1)所有数列的第n 项都能使用公式表达. ( )(2)数列{a n }和集合{a 1,a 2,a 3,…,a n }是一回事. ( ) (3)若数列用图像表示,则从图像上看都是一群孤立的点. ( ) (4)一个确定的数列,它的通项公式只有一个. ( ) (5)若数列{a n }的前n 项和为S n ,则对任意n ∈N +,都有a n =S n -S n-1. ()2.已知数列{a n }的前n 项和为S n ,且S n =n 2+n ,则a 2的值是( ) A.2 B.4 C.5 D.63.(2020北京海淀期中,7)已知数列{a n }的前n 项和为S n ,且S n =a n (n=1,2,3,…),则a 2020=( )A.0B.1C.2 020D.2 0214.已知数列{a n }满足a n =S (S +1)2,则S 3= .5.(2020天津河东一模)设数列{a n }的前n 项和为S n ,且S n =S 1(4S -1)3,若a 4=32,则a 1= .关键能力学案突破考点由数列的前几项求数列的通项公式【例1】根据下面各数列前几项的值,写出数列的一个通项公式:(1)-1,7,-13,19,…; (2)-11×2,12×3,-13×4,14×5,…; (3)23,415,635,863,1099,…;(4)5,55,555,5 555,….思考如何由数列的前几项写出一个数列的通项公式?解题心得求数列通项公式或指定项,通常用观察法,观察出前几项与项数之间的关系,抽象出a n 与n 的关系,对于正、负项相间的数列,一般用(-1)n或(-1)S +1来区分奇偶项的符号.对点训练1根据下面各数列前几项的值,写出数列的一个通项公式: (1)12,2,92,8,252,…;(2)1,-3,5,-7,9,…; (3)1,2,1,2,1,2,…; (4)9,99,999,9 999,….考点由a n 与S n 的关系求通项a n【例2】(1)(2020辽宁大连模拟,文15)已知数列{a n }的前n 项和为S n ,且满足S n =2n+2-3,则a n = .(2)(2020山西太原三模,文15)已知数列{a n }的前n 项和为S n ,且S n +a n =-2,则数列{a n }的通项公式a n = .(3)设S n 是数列{a n }的前n 项和,且a 1=-1,S S +1=S n S S +1,则S n = .思考由a n 与S n 的关系求通项公式a n 的一般方法是什么? 解题心得1.已知数列的前n 项和S n =f (n ),则通项公式a n ={S 1,S =1,S S -S S -1,S ≥2.当n=1时,若a 1适合S n -S n-1,则n=1的情况可并入n ≥2时的通项公式a n ;当n=1时,若a 1不适合S n -S n-1,则用分段函数的形式表示.2.给出S n 与a n 的递推关系,求a n 的常用思路:一是利用S n -S n-1=a n (n ≥2)转化为a n 的递推关系,再求其通项公式;二是转化为S n 的递推关系,先求出S n 与n 之间的关系,再求a n .对点训练2(1)已知数列{a n }的前n 项和为S n ,a 1=2,S n+1=2S n -1,则a 10=( ) A.128 B.256 C.512 D.1 024(2)(2020山东烟台一模,14)已知数列{a n}的前n项和公式为S n=2n2-n+1,则数列{a n}的通项公式为.(3)已知S n为数列{a n}的前n项和,且log2(S n+1)=n+1,则数列{a n}的通项公式为.考点由数列的递推关系式求a n(多考向探究)考向1形如a n+1=a n f(n),求a n【例3】在数列{a n}中,已知a1=1,na n-1=(n+1)a n(n≥2),求数列{a n}的通项公式.思考已知在数列{a n}中,a n+1=a n f(n),利用什么方法求a n?考向2形如a n+1=a n+f(n),求a n【例4】(2020河北唐山一模,文15,理15)在数列{a n}中,已知a1=1,a n+1=a n+tn(n∈N+,t 为非零常数),且a1,a2,a3成等比数列,则a n= .思考已知在数列{a n}中,S S+1=a n+f(n),利用什么方法求a n?考向3形如a n+1=pa n+q,求a n【例5】已知数列{a n}满足a1=1,a n+1=3a n+2,求数列{a n}的通项公式.思考已知在数列{a n}中,a n+1=pa n+q(p,q均为常数),利用什么方法求a n?考向4由含a n+1与a n的二次三项式求a n【例6】已知各项都为正数的数列{a n}满足a1=1,S S2-(2a n+1-1)a n-2a n+1=0.(1)求a2,a3;(2)求{a n}的通项公式.思考已知含有a n+1与a n的二次三项式的递推公式,如何求a n?解题心得根据给出的初始值和递推关系求数列通项的常用方法(1)若递推关系为a n+1=a n +f (n )或a n+1=f (n )·a n ,则可以分别通过累加、累乘法求得通项公式,或用迭代法求得通项公式;(2)当递推公式为a n+1=pa n +q (其中p ,q 均为常数)时,通常解法是先把原递推公式转化为a n+1-t=p (a n -t ),其中t=S1-S ,再利用换元法转化为等比数列求解;(3)当递推公式含有a n+1与a n 的二次三项式时,通常先对递推公式进行化简、变形,转化为等差或等比数列,再用公式法求a n .对点训练3(1)(2020辽宁大连模拟,文11)在数列{a n }中,a 1=1,a =(n ,a n ),b =(a n+1,n+1),且a ⊥b ,则a 100= ( )A.10099B.-10099C.100D.-100(2)在数列{a n }中,a 1=2,a n+1=a n +1S (S +1),则数列a n = .(3)(2020山西太原二模,理15)已知数列{a n }满足SSS =S -1SS S +1S +1-1+1(n ∈N +),且a 2=6,则{a n }的通项公式为 .(4)(2020陕西宝鸡三模,文15)已知数列{a n },{b n }满足a 1=1.1,b 1=0.2,a n+1=S S +1+S S2,b n+1=13a n +23b n ,n ∈N ,令c n =a n -b n ,则数列{c n }的通项公式为 .(5)已知数列{a n }对任意的n ∈N +都有a n+1=a n -2a n+1a n ,若a 1=12,则a 8= .考点数列的性质 (多考向探究)考向1 数列的周期性【例7】在数列{a n }中,a 1=0,a n+1=√3+S S1-√3S S,则S 2 020= .解题心得解决数列周期性问题的方法先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值. 对点训练4数列{a n }满足a n+1={2S S ,0≤S S ≤12,2S S -1,12<S S <1,a 1=35,则数列的第2 019项为 .考向2 数列的单调性【例8】(1)已知等差数列{a n }的前n 项和为S n (n ∈N +),且a n =2n+λ,若数列{S n }(n ≥7,n ∈N +)为递增数列,则实数λ的取值范围为 .(2)已知f (x )={(2S -1)S +4,S ≤1,S S ,S >1的定义域为R ,数列{a n }(n ∈N +)满足a n =f (n ),且{a n }是递增数列,则实数a 的取值范围是( )A.(1,+∞)B.12,+∞C.(1,3)D.(3,+∞)解题心得解决数列的单调性问题的三种方法作差比较法 根据a n+1-a n 的符号判断数列{a n }是递增数列、递减数列或常数列续 表作商比较法根据an +1a n (a n >0或a n <0)与1的大小关系进行判断数形结合法结合相应函数的图像直观判断对点训练5已知数列{a n }满足a n ={(12-S )S +1,S <6,S S -5,S≥6,若对任意的n ∈N +都有a n >S S +1,则实数a 的取值范围是( )A.0,12B.12,712C.12,1D.712,1考向3 数列的最大(小)项【例9】(1)已知数列{a n }中,前n 项和为S n ,且S n =S +23a n ,则SS S S -1的最大值为( )A.-3B.-1C.3D.1(2)已知数列{a n }的通项公式为a n =12S-15,其最大项和最小项的值分别为( )A.1,-17B.0,-17C.17,-17D.1,-111解题心得求数列的最大项、最小项的常用思想 (1)利用“两边夹”思想设a n 为数列{a n }中的最大项,则有{S S ≥S S -1,S S ≥S S +1(n ≥2).若设a n 为数列{a n }中的最小项,则有{S S ≤S S +1,S S ≤S S -1(n ≥2).(2)利用函数思想①构造函数,确定函数的单调性,再求出数列的最大(小)项.②根据{a n }对应函数的单调性确定,递增数列:a 1<a 2<…<a n ,故(a n )min =a 1.递减数列:a 1>a 2>…>a n ,故(a n )max =a 1.对点训练6(1)数列{a n }的通项公式为a n =SS 2+90,则数列{a n }中的最大项的值是( ) A.3√10 B.19C.119D.√1060(2)若数列{a n }的前n 项和S n =n 2-10n (n ∈N +),则数列{na n }中数值最小的项是( ) A.第2项 B.第3项 C.第4项 D.第5项1.求数列通项公式或指定项,通常用观察法,观察出前几项与项数之间的关系,抽象出a n 与n 的关系,对于正、负项相间的数列,一般用(-1)n 或(-1)n +1来区分奇偶项的符号.2.已知递推关系求通项公式,一般有三种常见思路: (1)先算出前几项,再归纳、猜想;(2)形如“a n+1=pa n +q ”这种形式通常转化为a n+1+λ=p (a n +λ),由待定系数法求出λ,再化为等比数列;(3)递推公式化简整理后,若为a n+1-a n =f (n )型,则采用累加法;若为a n +1a n=f (n )型,则采用累乘法.3.求数列最大项的方法:(1)判断{a n }的单调性;(2)解不等式组{a k ≥a k -1,a k ≥a k +1.1.在利用函数观点研究数列时,一定要注意自变量的取值是正整数.2.数列的通项公式不一定唯一.3.注意a n =S n -S n-1中需n ≥2.4.由S n 求a n 时,利用a n ={S 1,n =1,S n -S n -1,n ≥2求出a n 后,要注意验证a 1是否适合求出的a n 的关系式.第六章 数列6.1 数列的概念与表示 必备知识·预案自诊知识梳理1.确定的顺序 每一个数 a 1+a 2+…+a n2.(n ,a n ) 公式3.函数值4.a n+1>a n a n+1<a n考点自诊1.(1)× (2)× (3)√ (4)× (5)×2.B 由题意,S 2=22+2=6,S 1=1+1=2,所以a 2=S 2-S 1=6-2=4.故选B.3.A 由S n =a n 得,当n ≥2时,a n =S n -S S -1=a n -S S -1,所以S S -1=0.当n=2021时,a 2020=0.4.10 因为a n =S (S +1)2,所以a 1=1,a 2=3,a 3=6,所以S 3=a 1+a 2+a 3=1+3+6=10.5.12 ∵S n =S 1(4S -1)3,a 4=32,则a 4=S 4-S 3=32.∴255S 13−63S 13=32,∴a 1=12.关键能力·学案突破例1解(1)偶数项为正,奇数项为负,故通项公式必含有因式(-1)n;观察各项的绝对值,后一项的绝对值总比它前一项的绝对值大6,故所求数列的一个通项公式a n =(-1)n(6n-5).(2)这个数列的前4项的绝对值都等于序号与序号加1的乘积的倒数,且奇数项为负,偶数项为正,故所求数列的一个通项公式a n =(-1)n·1S (S +1).(3)这是一个分数数列,其分子构成偶数数列,而分母可分解为1×3,3×5,5×7,7×9,9×11,…,即分母的每一项都是两个相邻奇数的乘积,故所求数列的一个通项公式a n =2S(2S -1)(2S +1).(4)将原数列改写为59×9,59×99,59×999,…,易知数列9,99,999,…的通项公式为10n-1,故所求的数列的一个通项公式a n =59(10n-1).对点训练1解(1)数列的项有的是分数,有的是整数,可先将各项都统一写成分数形式再观察:12,42,92,162,252,…,所以它的一个通项公式为a n =S 22.(2)数列各项的绝对值为1,3,5,7,9,…,是连续的正奇数,并且奇数项为正,偶数项为负,所以它的一个通项公式为a n =(-1)n+1(2n-1).(3)这是一个周期数列,奇数项是1,偶数项是2,所以此数列的一个通项公式为a n ={1,S 为奇数,2,S 为偶数.(4)这个数列的前4项可以写成10-1,100-1,1000-1,10000-1,所以它的一个通项公式为a n =10n -1.例2(1)a n ={5,S =1,2S +1,S ≥2(2)a n =-(12)S -1 (3)-1S (1)根据题意,数列{a n }满足S n =2n+2-3,当n ≥2时,有a n =S n -S n-1=(2n+2-3)-(2n+1-3)=2n+1,当n=1时,有a 1=S 1=8-3=5,不符合a n =2n+1,故a n ={5,S =1,2S +1,S ≥2.(2)当n=1时,S 1+a 1=-2,所以a 1=-1.由S n +S S =-2,得S S +1+S S +1=-2,两式相减得2S S +1=a n ,所以数列{a n }是以-1为首项,以12为公比的等比数列,所以a n =-(12)S -1.(3)因为a n+1=S n+1-S n ,a n+1=S n S n+1,所以由两式联立得S n+1-S n =S n S n+1.因为S n ≠0,所以1S S−1S S +1=1,即1SS +1−1S S=-1.又1S 1=-1,所以数列{1S S}是首项为-1,公差为-1的等差数列.所以1S S=-1+(n-1)×(-1)=-n ,所以S n =-1S .对点训练2(1)B (2)a n ={2,S =14S -3,S ≥2 (3)a n ={3,S =1,2S ,S ≥2.(1)∵S n+1=2S n -1,当n ≥2时,S n =2S n-1-1,两式相减得a n+1=2a n .当n=1时,a 1+a 2=2a 1-1,a 1=2,a 2=1.∴数列{a n }从第二项开始为等比数列,公比为2.则a 10=a 2×28=1×28=256,故选B .(2)由题意,当n=1时,a 1=S 1=2;当n ≥2时,a n =S n -S n-1=2n 2-n-2(n-1)2+n-1=4n-3.又因为a 1=2不满足a n =4n-3,所以a n ={2,S =1,4S -3,S ≥2.(3)由log 2(S n +1)=n+1,得S n +1=2n+1,当n=1时,a 1=S 1=3;当n ≥2时,a n =S n -S n-1=2n,显然当n=1时,不满足上式.所以数列{a n }的通项公式为a n ={3,S =1,2S ,S ≥2.例3解∵na n-1=(n+1)a n (n ≥2),∴S S S S -1=S S +1(n ≥2).∴a n =S S S S -1·S S -1S S -2·S S -2S S -3·…·S3S 2·S 2S 1·a 1=S S +1×S -1S ×S -2S -1×…×34×23×1=2S +1. 又a 1也满足上式,∴a n =2S +1. 例4S 2-S +22∵a 1=1,a n+1=a n +tn (n ∈N *,t 为非零常数),∴a 2=a 1+t=t+1,a 3=a 2+2t=3t+1.∵a 1,a 2,a 3成等比数列,∴S 22=a 1a 3,即(t+1)2=1×(3t+1),整理得t 2-t=0,解得t=1(t=0舍去).∴a n+1-a n =n ,∴a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n-1)=1+1+2+…+(n-1)=1+(1+S -1)(S -1)2=S 2-S +22.例5解∵a n+1=3a n +2,∴a n+1+1=3(a n +1).∴S S +1+1S S +1=3. ∴数列{a n +1}为等比数列,且公比q=3.又a 1+1=2,∴a n +1=2·3n-1.∴a n =2·3n-1-1.例6解(1)由题意得a 2=12,a 3=14.(2)由S S 2-(2a n+1-1)a n -2a n+1=0,得2a n+1(a n +1)=a n (a n +1). 因为{a n }的各项都为正数,所以S S +1S S=12.故{a n }是首项为1,公比为12的等比数列,因此a n =12S -1.对点训练3(1)D (2)3-1S (3)2n 2-n (4)c n =0.9×13S -1(5)116 (1)因为a =(n ,a n ),b =(a n+1,n+1),且a ⊥b ,所以na n+1+(n+1)a n =0,所以S S +1S S =-S +1S ,所以S 2S 1=-21,S 3S 2=-32,…,S 100S 99=-10099.以上各式左右分别相乘,得S 100S 1=-100,因为a 1=1,所以a 100=-100.故选D.(2)由题意,得a n+1-a n =1S (S +1)=1S−1S +1,a n =(a n -a n-1)+(a n-1-a n-2)+…+(a 2-a 1)+a 1=1S -1−1S +1S -2−1S -1+…+12−13+1-12+2=3-1S .又a 1也满足上式,∴a n =3-1S .(3)由题意,得S S S -1=S -1SS S +1S +1-1,当n ≥2时,S SS-1S -1=S S +1S +1-1S,所以数列{S SS-1S -1}从第二项开始是常数列,又S 22-12-1=2,所以S SS-1S -1=2,即a n =2n 2-n (n ≥2),又n=1也满足,所以a n =2n 2-n. (4)由题意,得a n+1-b n+1=S S +1+S S2-b n+1=-12b n+1+12a n =-1213a n +23b n +12a n =13(a n -b n ), 即S S +1-S S +1S S -S S=13,即S S +1S S=13.又因为a 1=1.1,b 1=0.2,所以c 1=a 1-b 1=0.9,故{c n }是首项为0.9,公比为13的等比数列,所以c n =0.9×13S -1.(5)由a n+1=a n -2a n+1a n ,得1S S +1−1S S=2,∴数列{1S S}是1S 1=2,公差d=2的等差数列,∴1S S=2+2(n-1)=2n ,a 8=116.例70 ∵a 1=0,a n+1=√3+S S 1-√3S S ,∴a 2=√31=√3,a 3=√3+√31-√3×√3=2√3-2=-√3,a 4=√3-√31+√3×√3=0,即数列{a n }为周期数列,周期为3,且a 1+a 2+a 3=0,则S 2020=S 3×673+1=a 1=0.对点训练425 由已知可得,a 2=2×35-1=15,a 3=2×15=25,a 4=2×25=45,a 5=2×45-1=35,∴{a n }为周期数列,且周期T=4, ∴a 2019=a 504×4+3=a 3=25.例8(1)(-16,+∞) (2)D (1)当n ≥7时,数列{S n }为递增数列,设S n+1>S n ,即S n+1-S n =a n+1>0,∴a n+1=2(n+1)+λ>0,则λ>-2n-2.又n ≥7,∴-2n-2≤-16,即λ>-16.(2)由于{a n }是递增数列,所以a>1,且a 2>a 1,即a 2>2a+3,解得a<-1或a>3,所以a>3.对点训练5B ∵a n >a n+1恒成立,∴a 满足{12-S <0,(12-S )×5+1>S ,0<S <1,解得12<a<712.例9(1)C (2)A (1)∵S n =S +23a n ,∴当n ≥2时,a n =S n -S n-1=S +23a n -S +13a n-1,可化为SS S S -1=S +1S -1=1+2S -1,由函数y=2S -1在区间(1,+∞)内单调递减,可得当n=2时,2S -1取得最大值2.∴SS S S -1的最大值为3.(2)因为n ∈N *,所以当1≤n ≤3时,a n =12S-15<0,单调递减,当n ≥4时,a n =12S -15>0,单调递减,所以最小项为a 3=18-15=-17,最大项为a 4=116-15=1,故选A . 对点训练6(1)C (2)B (1)a n =S S 2+90=1S +90S,令f (x )=x+90S (x>0),运用基本不等式得f (x )≥6√10,当且仅当x=3√10时,等号成立.因为a n =1S +90S,n ∈N *,所以1S +90S<16√10,即当n=9或n=10时,a n =119最大.(2)∵S n =n 2-10n ,∴当n ≥2时,a n =S n -S n-1=2n-11;当n=1时,a 1=S 1=-9也适合上式.∴a n =2n-11(n ∈N *).记f (n )=na n =n (2n-11)=2n 2-11n ,∴此函数图像的对称轴为直线n=114,又n ∈N *,∴当n=3时,f (n )取最小值.∴数列{na n }中数值最小的项是第3项.。
2022届高考数学一轮复习第八章8.3等比数列核心考点精准研析训练理含解析北师大版

第八章核心考点·精准研析考点一等比数列基本量的运算1.已知各项均为正数的等比数列{a n}的前n项和为S n,且S3=14,a3=8,则a6等于( )2.(2020·某某模拟)S n是等比数列{a n}的前n项和,若S4,S3,S5成等差数列,则{a n}的公比q的值为( )A.或13.已知等比数列{a n}满足a1=3,a1+a3+a5=21,则a3+a5+a7= ( )4.(2019·全国卷Ⅲ)已知各项均为正数的等比数列{a n}的前4项的和为15,且a5=3a3+4a1,则a3=( )5.已知S n是等比数列{a n}的前n项和,若存在m∈N*,满足=9,=,则数列{a n}的公比为( )【解析】1.选C.因为S3=14,a3=8,所以q≠1,所以, 解得a1=2,q=2或a1=18,q=-(舍),所以a6=a1q5=2×32=64.,S3,S5成等差数列知等比数列{a n}的公比q≠1,因此得2S3=S5+S4,即4=+,化简整理得q3(q+2)(q-1)=0,所以q=0(舍去),q=1(舍去)或q=-2.故q=-2.3.选B.设数列{a n}的公比为q,则a1(1+q2+q4)=21,又a1=3,所以q4+q2-6=0,所以q2=2(q2=-3舍去),所以a3=6,a5=12,a7=24,所以a3+a5+a7=42.,公比为q,1由已知得,a1q4=3a1q2+4a1,因为a1>0且q>0,则可解得q=2,又因为a1(1+q+q2+q3)=15,即可解得a1=1,则a3=a1q2=4.5.选B.设公比为q,若q=1,则=2,与题中条件矛盾,故q≠==q m+1=9,所以q m==q m=8=,所以m=3,所以q3=8,所以q=2.把T1条件“S3=14,a3=8”改为“a3=9,S3=27”其他条件不变,则公比q的值为( ) 或-或 -【解析】选C.当公比q=1时,a1=a2=a3=9,所以S3=3×9=27.符合题意.当q≠1时,S3=,所以27=,所以a1=27-18q,因为a3=a1q2,所以(27-18q)·q2=9,所以(q-1)2(2q+1)=0,所以q=-.综上q=1或q=-.解决等比数列有关问题的常用思想方法(1)方程的思想:等比数列中有五个量a1,n,q,a n,S n,一般可以“知三求二”,通过列方程(组)求出关键量a1和q,问题便可迎刃而解.(2)分类讨论的思想:等比数列的前n项和公式涉及对公比q的分类讨论,将q分为q=1和q≠1两种情况进行讨论.【秒杀绝招】1.应用转化法解T2选B.由S4,S3,S5成等差数列,得2S3=S5+S4,即2(a1+a2+a3)=2(a1+a2+a3+a4)+a5,整理得a5=-2a4,所以=-2,即q=-2.故选B.2.应用等比数列性质解T3:选B.设数列{a n}的公比为q,则a1(1+q2+q4)=21,又a1=3,所以q4+q2-6=0,所以q2=2(q2=-3舍去),所以a3+a5+a7=q2(a1+a3+a5)=2×21=42,所以a3+a5+a7=42.考点二等比数列的判断与证明【典例】1.已知数列{a n}中,a1=1,若a n=2a n-1+1(n≥2),则a5的值是________.【解题导思】序号联想解题(1) 由a n =2a n-1+1(n≥2)及a1=1,联想到数列的递推公式求a5(2) 由a n=2a n-1+1(n≥2)联想到转化法求通项公式【解析】因为a n=2a n-1+1,所以a n+1=2(a n-1+1),所以=2,又a1=1,所以{a n+1}是以2为首项,2为公比的等比数列,即a n+1=2×2n-1=2n,所以a5+1=25,即a5=31.答案:31【一题多解】由a n=2a n-1+1(n≥2)及a1=1,联想到数列的递推公式求a5,当n=2得a2=3,同理得a3=7,a4=15,a5=31.答案:312.已知数列{a n}的前n项和为S n,a1=1,S n+1=4a n+2(n∈N*),若b n=a n+1-2a n,求证:{b n}是等比数列.世纪金榜导学号【解题导思】序号题目拆解(1)①S n+1=4a n+2(n∈N*)②出现S n+2=4a n+1+2(n∈N*)(2)①b n=a n+1-2a n②证明{b n}是等比数列把n换为n+1左式和已知式子相减a n+2=4a n+1-4a n, 把n换为n+1得出b n+1转化为证明为常数【证明】因为a n+2=S n+2-S n+1=4a n+1+2-4a n-2=4a n+1-4a n, 所以====2.因为S2=a1+a2=4a1+2,所以a2=5.所以b1=a2-2a1=3.所以数列{b n}是首项为3,公比为2的等比数列.若本例2中的条件不变,试求{a n}的通项公式.【解析】由题知b n=a n+1-2a n=3·2n-1,所以-=,故是首项为,公差为的等差数列.所以=+(n-1)·=,所以a n=(3n-1)·2n-2.【继续探究】若将本例中“S n+1=4a n+2”改为“S n+1=2S n+(n+1)”,其他不变,求数列{a n}的通项公式.【解析】由已知得n≥2时,S n=2S n-1+n.所以S n+1-S n=2S n-2S n-1+1,所以a n+1=2a n+1,所以a n+1+1=2(a n+1),n≥2,(*)又a1=1,S2=a1+a2=2a1+2,即a2+1=2(a1+1),所以当n=1时(*)式也成立,故{a n+1}是以2为首项,以2为公比的等比数列,所以a n+1=2·2n-1=2n,所以a n=2n-1.1.等比数列的四种常用判定方法(1)定义法:若=q(q为非零常数,n∈N*)或=q(q为非零常数且n≥2,n∈N*),则{a n}是等比数列.(2)等比中项法:若数列{a n}中,a n≠0且=a n·a n+2(n∈N*),则{a n}是等比数列.(3)通项公式法:若数列{a n}的通项公式可写成a n=c·q n-1(c,q均是不为0的常数,n∈N*),则{a n}是等比数列.(4)前n项和公式法:若数列{a n}的前n项和S n=k·q n-k(k为常数且k≠0,q≠0,1),则{a n}是等比数列.2.证明某数列不是等比数列若证明某数列不是等比数列,则只要证明存在连续三项不成等比数列即可.(2018·全国卷Ⅰ改编)已知数列{a n}满足a1=1,na n+1=2(n+1)a n,设b n=.(1)求b1,b2,b3.(2)判断数列{b n}是否为等比数列,并说明理由.(3)求{b n}的前10项和S10.【解析】(1)由条件可得a n+1=a n.将n=1代入得a2=4a1,而a1=1,所以a2=4.将n=2代入得a3=3a2,所以a3=12.从而b1=1,b2=2,b3=4.(2){b n}是首项为1,公比为2的等比数列.理由:由条件可得=,即b n+1=2b n,又b1=1,所以{b n}是首项为1,公比为2的等比数列.(3)由(2)可得S n==2n-1,所以S10=210-1=1 023.考点三等比数列的性质及其应用命题精解读1.考什么:等比数列通项公式、前n项和公式、性质和最值问题2.怎么考:等比数列性质、等比数列前n项和的性质作为考查等比数列运算知识的最佳载体,试题常以选择题、填空题的形式出现,有时也会出现在解答题中3.新趋势:以数列为载体与函数、不等式知识结合等问题.解题过程中常常渗透数学运算核心素养.学霸好1.与等比数列性质有关的运算问题解题思路在等比数列中凡是涉及两项的乘积问题,首先考虑其项数和是否相等,若相等则利用等比数列的性质进行运算方法2.交汇问题以数列为载体与函数性质、不等式等知识结合考查,注意分类讨论思想的应用等比数列项的性质应用【典例】已知等比数列{a n }中,a4+a8=-2,则a6(a2+2a6+a10)的值为( )【解析】选6(a2+2a6+a10)=a6a2+2+a6a10=+2a4a8+=(a4+a8)2,因为a4+a8=-2,所以a6(a2+2a6+a10)=4.1.等比数列性质的应用可以分为哪些变形?提示:通项公式的变形、等比中项的变形、前n项和公式的变形.2.在解决等比数列项的性质的有关问题时,如何迅速挖掘隐含条件利用性质解题?提示:在等比数列中凡是涉及两项的乘积问题,首先考虑其项数和是否相等,若项数和相等,则利用等比数列的性质进行运算.提醒:根据题目条件,认真分析,发现具体的变化特征即可找出解决问题的突破口.等比数列中的最值与X围问题【典例】设等比数列{a n}满足a1+a3=10,a2+a4=5,则a1a2…a n的最大值为________.世纪金榜导学号【思路探究】利用等比数列通项公式求出首项a1与公比q,再将a1a2…a n的最值问题利用指数幂的运算法则转化为二次函数最值问题.【解析】设等比数列{a n}的公比为q,则由a1+a3=10,a2+a4=q(a1+a3)=5,知q=.又a1+a1q2=10,所以a1=8.故a1a2…a n==23n·==.记t=-+=-(n2-7n),结合n∈N*可知n=3或4时,t有最大值6.又y=2t为增函数,从而a1a2…a n的最大值为26=64.答案:64求等比数列中的最值与X围问题有哪些方法?提示:求解此类问题的常用思路是根据题目所给条件建立关于变量n的函数关系进行求解.有时也应用基本不等式.1.已知等比数列{a n}满足a1=,a3a5=4(a4-1),则a2= ( )A.2B.1C.D.【解析】选C.设公比为q,因为a3a5=,a3a5=4(a4-1),所以=4(a4-1),所以-4a4+4=0,所以a4=2.又因为q3===8,所以q=2,所以a2=a1q=×2=.2.已知正数组成的等比数列{a n},若a1·a20=100,那么a7+a14的最小值为( ) A.20 B.25C.50 D.不存在【解析】选A.(a7+a14)2=++2a7·a14≥4a7a14=4a1a20=400(当且仅当a7=a14时取等号).所以a7+a14≥20.1.已知数列{a n}满足log2a n+1=1+log2a n(n∈N*),且a1+a2+a3+…+a10=1,则log2(a101+a102+…+a110)=________.【解析】因为log2a n+1=1+log2a n,可得log2a n+1=log22a n,所以a n+1=2a n,所以数列{a n}是以a1为首项,2为公比的等比数列,又a1+a2+…+a10=1,所以a101+a102+…+a110=(a1+a2+…+a10)×2100=2100,所以log2(a101+a102+…+a110)=log22100=100.答案:1002.设等比数列{a n}的公比为q,前n项和S n>0(n=1,2,3,…),求q的取值X围.【解析】因为数列{a n}为等比数列,S n>0,所以a1=S1>0,q≠0.当q=1时,S n=na1>0;当q≠0且q≠1时,S n=>0,即>0,所以或所以-1<q<0或0<q<1或q>1.综上,q的取值X围为(-1,0)∪(0,+∞).。
2022届高考数学一轮复习专题提能透视数列高考热点探求应对策略学案理含解析北师大版202107072

透视数列高考热点,探求应对策略授课提示:对应学生用书第116页数列是一种特殊的函数,其考查的重点是数列的通项、数列的前n 项和、参数的取值X 围的探求、数列不等式的证明等,研究的数列主要是等比数列与等差数列.数列的最值、周期性、单调性的探究,以及递推数列的相关综合题目,也是历年高考考查的热点. (一)数列单调性及应用1.与等差数列的单调性有关的问题[例1] 已知数列{a n }的前n 项和为S n ,且满足:a 1=1,a n >0,a 2n +1=4S n +4n +1(n ∈N +),若不等式4n 2-8n +3<(5-m )2n ·a n 对任意的n ∈N +恒成立,则整数m 的最大值为( ) A .3 B .4 C .5D .6[解析] 当n ≥2时,⎩⎪⎨⎪⎧a 2n +1=4S n +4n +1,a 2n =4S n -1+4(n -1)+1,两式相减得a 2n +1-a 2n =4a n +4,即a 2n +1=a 2n +4a n +4=(a n +2)2,又a n >0,所以a n +1=a n+2(n ≥2).对a 2n +1=4S n +4n +1,令n =1,可得a 22=4a 1+4+1=9,所以a 2=3,则a 2-a 1=2,所以数列{a n }是以1为首项,2为公差的等差数列,故a n =2n -1.因为4n 2-8n +3=(2n -1)(2n -3),n ∈N +,2n -1>0,所以不等式4n 2-8n +3<(5-m )2n ·a n 等价于5-m >2n -32n .记b n =2n -32n ,则b n +1b n =2n -12n +12n -32n=2n -14n -6,当n ≥3时,b n +1b n <1,又b 1=-12,b 2=14,b 3=38,所以(b n )max =b 3=38.故5-m >38,得m <378,所以整数m 的最大值为4. [答案] B将a n 的表达式代入不等式4n 2-8n +3<(5-m )·2n ·a n ,约去公因式,从而简化了运算.在求解b n =2n -32n 的最大值时,通过作商与“1”比较大小判断数列的单调性,从而求得最大值.2.与等比数列的单调性有关的问题[例2] 已知数列{a n }满足:a 1=1,a n +1=a na n +2(n ∈N +),若b n +1=(n -λ)⎝⎛⎭⎫1a n +1,b 1=-λ,且数列{b n }是递增数列,则实数λ的取值X 围是( ) A .(2,+∞) B .(3,+∞) C .(-∞,2)D .(-∞,3)[解析] 由a n +1=a n a n +2知,1a n +1=2a n +1,即1a n +1+1=2⎝⎛⎭⎫1a n +1,所以数列⎩⎨⎧⎭⎬⎫1a n +1是首项为1a 1+1=2,公比为2的等比数列,所以1a n +1=2n ,所以b n +1=(n -λ)·2n ,因为数列{b n }是递增数列,所以b n +1-b n =(n -λ)2n -(n -1-λ)2n -1=(n +1-λ)2n -1>0对一切正整数n 恒成立,所以λ<n +1,因为n ∈N +,所以λ<2. [答案] C判断数列的单调性的方法函数法:构造函数,通过判断所构造函数的单调性,即可得出相应数列的单调性. 定义法:利用单调函数的定义判断数列的单调性.作差法:对于数列中任意相邻的两项a n +1,a n ,通过作差a n +1-a n ,判断其与0的大小,即可判断数列的单调性.作商法:数列的各项非零且同号(同正或同负),对于数列中任意相邻的两项a n +1,a n ,通过作商a n +1a n,判断其与1的大小,即可判断数列的单调性.[题组突破]1.已知数列{a n }的首项为a 1,{b n }是公比为23的等比数列,且b n =a n -2a n -1(n ∈N +),若不等式a n >a n +1对任意的n ∈N +恒成立,则a 1的取值X 围是( ) A .(-2,2)B .(-2,0)C .(0,2)D .(2,+∞)解析:∵b n =a n -2a n -1(n ∈N+),∴a n =b n -2b n -1,∴a n+1-a n =b n +1-2b n +1-1-b n -2b n -1=b n +1-b n(1-b n +1)(1-b n )=-13b n⎝⎛⎭⎫1-23b n (1-b n )<0,解得b n >32或0<b n <1.若b n >32,则b 1⎝⎛⎭⎫23n -1>32对任意的n ∈N +恒成立,显然不可能;若0<b n <1,则0<b 1⎝⎛⎭⎫23n -1<1对任意的n ∈N +恒成立,只需0<b 1<1,即0<a 1-2a 1-1<1,解得a 1>2.答案:D2.已知在等差数列{a n }中,a 1=120,公差d =-4,若S n ≤a n (n ≥2),其中S n 为该数列的前n 项和,则n 的最小值为( ) A .60 B .62 C .70D .72解析:由题意得a n =120-4(n -1)=124-4n ,S n =120n +n (n -1)2×(-4)=122n -2n 2.由S n ≤a n ,得122n -2n 2≤124-4n ,即n 2-63n +62≥0,解得n ≥62或n ≤1(舍去).所以n 的最小值为62. 答案:B3.(2021·某某高三监测)在数列{a n }中,a 1+a 22+a 33+…+a n n =2n -1(n ∈N +),且a 1=1,若存在n ∈N +使得a n ≤n (n +1)λ成立,即实数λ的最小值为________.解析:依题意得,数列⎩⎨⎧⎭⎬⎫a n n 的前n 项和为2n -1,当n ≥2时,a nn =(2n -1)-(2n -1-1)=2n -1,且a 11=21-1=1=21-1,因此a n n =2n -1(n ∈N +),a nn (n +1)=2n -1n +1.记b n =2n -1n +1,则b n >0,b n +1b n=2(n +1)n +2=(n +2)+n n +2>n +2n +2=1,b n +1>b n ,数列{b n }是递增数列,数列{b n }的最小项是b 1=12.依题意得,存在n ∈N +使得λ≥a n n (n +1)=b n 成立,即有λ≥b 1=12,λ的最小值是12.答案:12(二)数列中的新情境问题[例3] 已知{a n }是各项均为正数的等比数列,且a 1+a 2=3,a 3-a 2=2,等差数列{b n }的前n 项和为S n ,且b 3=5,S 4=16. (1)求数列{a n },{b n }的通项公式;(2)如图,在平面直角坐标系中,有点P 1(a 1,0),P 2(a 2,0),…,P n (a n ,0),P n +1(a n+1,0),Q 1(a 1,b 1),Q 2(a 2,b 2),…,Q n (a n ,b n ),若记△P n Q n P n +1的面积为,求数列{}的前n 项和T n .[解析] (1)设数列{a n }的公比为q ,因为a 1+a 2=3,a 3-a 2=2,所以⎩⎪⎨⎪⎧a 1+a 1q =3,a 1q 2-a 1q =2,得3q 2-5q -2=0,又q >0, 所以q =2,a 1=1,则a n =2n -1. 设数列{b n }的公差为d ,因为b 3=5,S 4=16,所以⎩⎪⎨⎪⎧b 1+2d =5,4b 1+6d =16,解得⎩⎪⎨⎪⎧b 1=1,d =2,则b n =2n -1.(2)由(1)得P n P n +1=a n +1-a n =2n -2n -1=2n -1, P n Q n =b n =2n -1,故=S △P n Q n P n +1=2n -1(2n -1)2=(2n -1)2n -2,则T n =c 1+c 2+c 3+…+=12×1+1×3+2×5+…+(2n -1)2n -2, ①2T n =1×1+2×3+4×5+…+(2n -1)2n -1, ②由①-②得,-T n =12+2(1+2+…+2n -2)-(2n -1)·2n -1=12+2(1-2n -1)1-2-(2n -1)2n -1=(3-2n )2n -1-32,故T n =(2n -3)2n -1+32(n ∈N +).数列中新情境问题的求解关键:一是观察新情境的特征,如本题中的各个直角三角形的两直角边长的特征;二是会转化,如本题,把数列{}的通项公式的探求转化为直角三角形的两直角边长的探求;三是活用数列求和的方法,如本题,活用错位相减法,即可得数列{}的前n 项和. [例4] 设数列{a n }的前n 项和为S n ,若S nS 2n为常数,则称数列{a n }为“幸福数列”.(1)等差数列{b n }的首项为1,公差不为零,若{b n }为“幸福数列”,求{b n }的通项公式;(2)数列{}的各项都是正数,其前n 项和为S n ,若c 31+c 32+c 33+…+c 3n =S 2n 对任意的n ∈N +都成立,试推断数列{}是否为“幸福数列”?并说明理由.[解析] (1)设等差数列{b n }的公差为d (d ≠0),前n 项和为T n ,则T nT 2n=k ,因为b 1=1, 所以n +12n (n -1)d =k [2n +12·2n (2n -1)d ],即2+(n -1)d =4k +2k (2n -1)d , 整理得(4k -1)dn +(2k -1)(2-d )=0. 因为对任意正整数n 上式恒成立,则⎩⎪⎨⎪⎧d (4k -1)=0,(2k -1)(2-d )=0,解得⎩⎪⎨⎪⎧d =2,k =14.故数列{b n }的通项公式是b n =2n -1. (2)数列{}不是“幸福数列”.理由如下:由已知,当n =1时,c 31=S 21=c 21.因为c 1>0,所以c 1=1.当n ≥2时,c 31+c 32+c 33+…+c 3n =S 2n ,c 31+c 32+c 33+…+c 3n -1=S 2n -1. 两式相减,得c 3n =S 2n -S 2n -1=(S n -S n -1)(S n +S n -1)=·(S n +S n -1). 因为>0,所以c 2n =S n +S n -1=2S n -.显然c 1=1适合上式,所以当n ≥2时,c 2n -1=2S n -1--1.于是c 2n -c 2n -1=2(S n -S n -1)-+-1=2-+-1=+-1.因为+-1>0,所以--1=1,所以数列{}是首项为1,公差为1的等差数列,所以=n ,S n =n (n +1)2. 所以S nS 2n =n (n +1)2n (2n +1)=n +14n +2不为常数,故数列{}不是“幸福数列”.遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使问题得以解决.[对点训练]“泥居壳屋细莫详,红螺行沙夜生光.”是宋代诗人欧阳修对鹦鹉螺的描述.假设一条螺旋线是用以下方法画成(如图):△ABC 是边长为1的正三角形,曲线CA 1,A 1A 2,A 2A 3分别是以A ,B ,C 为圆心,AC ,BA 1,CA 2为半径画的弧,曲线CA 1A 2A 3称为螺旋线,再以A 为圆心,AA 3为半径画弧……如此画下去,则所得弧CA 1,A 1A 2,A 2A 3,…,A 28A 29,A 29A 30的总长度为( )A .310πB .1103πC .58πD .110π解析:根据弧长公式知,弧CA 1,A 1A 2,A 2A 3,…,A n -2A n -1,A n -1A n 的长度分别为23π,2×23π,3×23π,…,(n -1)×23π,n ×23π,该数列是首项为23π,公差为23π的等差数列,所以该数列的前n 项和S n =π3n (n +1),所以所得弧CA 1,A 1A 2,A 2A 3,…,A 28A 29,A 29A 30的总长度为S 30=π3×30×(30+1)=310π.答案:A(三)数列与其他知识交汇应用数列在中学教材中既有相对独立性,又有较强的综合性,数列常与函数、向量、三角函数、解析几何、充分必要条件等知识相交汇,考查数列的基本运算与应用.[例5](2021·某某月考)已知等差数列{a n }的前n 项和为S n ,若OB →=a 1OA →+a 2 020OC →,且A ,B ,C 三点共线(该直线不过点O ),则S 2 020等于( ) A .1 008B .1 010C .2 017D .2 019[解析] ∵A ,B ,C 三点共线,∴a 1+a 2 020=1, ∴S 2 020=2 020(a 1+a 2 020)2=1 010.[答案] B本题巧妙地将三点共线条件(P A →=xPB →+yPC →且A ,B ,C 三点共线⇔x +y =1)与等差数列的求和公式结合,解决的关键是抓住整体思想求值.[题组突破]1.等差数列{a n }中的a 4,a 2 016是函数f (x )=x 3-6x 2+4x -1的极值点,则log 14a 1 010=( )A .12B .2C .-2D .-12解析:因为f ′(x )=3x 2-12x +4,而a 4和a 2 016为函数f (x )=x 3-6x 2+4x -1的极值点,所以a 4和a 2 016为3x 2-12x +4=0的根,所以a 4+a 2 016=4,又a 4,a 1 010,a 2 016成等差数列,所以2a 1 010=a 4+a 2 016,即a 1 010=2,所以log 14a 1 010=-12.答案:D2.已知数列{a n }为等差数列,数列{b n }为等比数列,且满足a 2 016+a 2 017=π,b 20b 21=4,则tan a 1+a 4 0322+b 19b 22=( )A .33B . 3C .1D .-1解析:依题意得a 1+a 4 032=a 2 016+a 2 017=π,b 19b 22=b 20b 21=4,所以tan a 1+a 4 0322+b 19b 22=tan π6=33.答案:A3.(2021·某某一中月考)已知函数f (x )=a x +b (a >0,a ≠1)的图像经过点P (1,3),Q (2,5).当n ∈N +时,a n =f (n )-1f (n )·f (n +1),记数列{a n }的前n 项和为S n ,当S n =1033时n 的值为( ) A .4 B .5 C .6D .7解析:∵f (x )的图像过点P (1,3),Q (2,5),∴易知f (x )=2x+1,∴a n =2n(2n+1)(2n +1+1)=(2n +1+1)-(2n +1)(2n +1)(2n +1+1)=12n +1-12n +1+1,∴S n =12+1-122+1+122+1-123+1+…+12n +1-12n +1+1=13-12n +1+1,∴13-12n +1+1=1033,∴12n +1+1=133,解得n =4. 答案:A4.(2021·某某一中月考)已知点A (1,0),B (0,1)和互不相同的点P 1,P 2,P 3,…,P n ,…满足OP n →=a n OA →+b n OB →(n ∈N +),其中{a n },{b n }分别为等差数列和等比数列,O 为坐标原点,若AP 1→=2P 1B →. (1)求P 1的坐标;(2)试判断点P 1,P 2,P 3,…,P n ,…能否共线?并证明你的结论. 解析:(1)设P 1(x ,y ),则AP 1→=(x -1,y ),P 1B →=(-x ,1-y ), 由AP 1→=2P 1B →得x -1=-2x ,y =2-2y ,得x =13,y =23,所以P 1⎝⎛⎭⎫13,23. (2)由OP n →=a n OA →+b n OB →,得OP n →=(a n ,b n ).设等差数列{a n }的公差为d ,等比数列{b n }的公比为q ,由题意知d =0,q =1不会同时成立.若d =0且q ≠1,则a n =a 1=13,则P 1,P 2,P 3,…,P n ,…都在直线x =13上;若q =1且d ≠0,则b n =b 1=23,则P 1,P 2,P 3,…,P n ,…都在直线y =23上;若d ≠0且q ≠1,假设P 1,P 2,P 3,…,P n ,…共线. 则=(a n -a n -1,b n -b n -1)与=(a n +1-a n ,b n +1-b n )共线(n >1,n ∈N+), 即⎩⎪⎨⎪⎧a n -a n -1=λ(a n +1-a n ),b n -b n -1=λ(b n +1-b n )(λ∈R ),则b n +1-b n =b n -b n -1,得q =1,与q ≠1矛盾, 故当d ≠0且q ≠1时,P 1,P 2,P 3,…,P n ,…不共线.。
最新高考一轮总复习北师版新教材《解答题专项三 数列中的综合问题》

(2)注意合理运用数列的相关性质以及整体思想,简化运算过程,注意数列
中“项数为正整数”等隐含条件.
对点训练(2021·新高考Ⅱ,17)记Sn是公差不为0的等差数列{an}的前n项和,
若a3=S5,a2a4=S4.
(1)求数列an的通项公式;
+2
. ...................................................................................2
3
+2
∴Sn= 3 an.
当 n≥2
+1
时,Sn-1= an-1.
3
分
①
②
+2
+1
an=Sn-Sn-1= an- an-1, .................................................................. 4 分
由 bn+1=a2n+2=a2n+1+1=a2n+2+1=a2n+3,
得 bn+1-bn=a2n+3-a2n=3.
所以{bn}是首项为 2,公差为 3 的等差数列,
所以 bn=2+(n-1)×3=3n-1. ...............................................................................5 分
例题(10 分)(2022·新高考Ⅰ,17)记 Sn 为数列{an}的前 n 项和,已知 a1=1,
1
公差为3的等差数列.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考大题专项(三) 数列
1.(2020广东天河区模拟)已知S n为数列{a n}的前n项和,且a1<2,a n>0,6S n=a n2+3a n+2,n∈N+.
(1)求数列{a n}的通项公式;
(2)若任意n∈N+,b n=(-1)n a n2,求数列{b n}的前2n项和T2n.
2.(2020湖南郴州二模,文17)设等差数列{a n}的公差为d(d>1),前n项和为S n,等比数列{b n}的公比为q.已知b1=a1,b2=3,2q=3d,S10=100.
(1)求数列{a n},{b n}的通项公式;
(2)记c n=a n·b n,求数列{c n}的前n项和T n.
3.(2020安徽合肥4月质检二,理17)已知等差数列{a n}的前n项和为S n,a2=1,S7=14,数列{b n}满足
b1·b2·b3·…·b n=2n2+n 2.
(1)求数列{a n}和{b n}的通项公式;
(2)若数列{c n}满足c n=b n cos(a nπ),求数列{c n}的前2n项和T2n.
4.(2020山西长治二模)S n 为等比数列{a n }的前n 项和,已知a 4=9a 2,S 3=13,且公比q>0. (1)求a n 及S n .
(2)是否存在常数λ,使得数列{S n +λ}是等比数列?若存在,求出λ的值;若不存在,请说明理由.
5.(2020天津,19)已知{a n }为等差数列,{b n }为等比数列,a 1=b 1=1,a 5=5(a 4-a 3),b 5=4(b 4-b 3). (1)求{a n }和{b n }的通项公式;
(2)记{a n }的前n 项和为S n ,求证:S n S n+2<S n+12
(n ∈N +);
(3)对任意的正整数n ,设c n ={(3a n -2)b n
a n
a n+2
,n 为奇数,
a n -1
b n+1
,n 为偶数.
求数列{c n }的前2n 项和.
参考答案
高考大题专项(三) 数列
1.解(1)当n=1时,6a 1=a 12
+3a 1+2,且a 1<2,解得a 1=1.
当n ≥2时,6a n =6S n -6S n-1=a n 2
+3a n +2-(a n -12+3a n-1+2).
化简,得(a n +a n-1)(a n -a n-1-3)=0,因为a n >0,所以a n -a n-1=3,
所以数列{a n }是首项为1,公差为3的等差数列,所以a n =1+3(n-1)=3n-2.
(2)b n =(-1)n a n 2=(-1)n (3n-2)2.
所以b 2n-1+b 2n =-(6n-5)2+(6n-2)2=36n-21.
所以数列{b n }的前2n 项的和T 2n =36×(1+2+…+n )-21n=36×n (n+1)2
-21n=18n 2-3n.
2.解(1)由题意,得{S 10=10a 1+45d =100,b 2=b 1q =3,
将b 1=a 1,q=3
2d 代入上式,
可得{2a 1+9d =20,a 1d =2,解得{a 1=9,d =29
(舍去),或{a 1=1,
d =2.
∴数列{a n }的通项公式为a n =1+2(n-1)=2n-1,n ∈N +. ∴b 1=a 1=1,q=3
2
d=3
2×2=3,
∴数列{b n }的通项公式为b n =1×3n-1=3n-1,n ∈N +. (2)由(1)知,c n =a n ·b n =(2n-1)·3n-1,
∴T n =c 1+c 2+c 3+…+c n =1×1+3×3+5×32+…+(2n-1)·3n-1, ① 3T n =1×3+3×32+…+(2n-3)·3n-1+(2n-1)·3n , ②
①-②,得-2T n
=1+2×3+2×32+…+2·3n-1-(2n-1)·3n =1+2×(3+32
+…+3n-1)-(2n-1)·3n =1+2×3-3n 1-3
-(2n-
1)·3n =-(2n-2)·3n -2,
∴T n =(n-1)·3n +1.
3.解(1)设数列{a n }的公差为d ,由a 2=1,S 7=14,得{a 1+d =1,
7a 1+21d =14.解得{a 1=1
2,d =12,
所以a n =n
2
.∵b 1·b 2·b 3·…·b n =2
n 2+n
2
=2
n (n+1)2
,∴b 1·b 2·b 3·…·b n-1=2
n (n -1)
2
(n ≥2),
两式相除,得b n =2n (n ≥2).
当n=1时,b 1=2适合上式.∴b n =2n . (2)∵c n =b n cos(a n π)=2n cos (n
2π),
∴T 2n =2cos π
2+22cos π+23cos 3π
2+24cos(2π)+…+22n-1cos (2n -1)π2
+22n cos(n π)
则T 2n
=22cos π+24cos(2π)+26cos(3π)+…+22n cos(n π)=-22+24-26+…+(-1)n ·22n =-4×[1-(-4)n
]1+4
=-4+(-4)
n+1
5
.
4.解(1)由题意可得{
a 1q 3=9a 1q ,
a 1(1-q 3)1-q
=13,q >0,
解得{a 1=1,
q =3,
所以a n
=3n-1,S
n =
1-3n 1-3
=3n -12
.
(2)假设存在常数λ,使得数列{S n +λ}是等比数列,因为S 1+λ=λ+1,S 2+λ=λ+4,S 3+λ=λ+13,所以(λ+4)2=(λ+1)(λ+13),解得λ=12,此时S n +12=1
2×3n
,则
S n+1+
12
S n +
12
=3,故存在常数λ=12,使得数列{S n +1
2}是等比
数列.
5.(1)解设等差数列{a n }的公差为d ,等比数列{b n }的公比为q.由a 1=1,a 5=5(a 4-a 3),可得d=1,从而{a n }的通项公式为a n =n.由b 1=1,b 5=4(b 4-b 3),又q ≠0,可得q 2-4q+4=0,解得q=2,从而{b n }的通项公式为b n =2n-1.
(2)证明由(1)可得S n =
n (n+1)2
,故S n S n+2=14
n (n+1)(n+2)(n+3),S n+12=1
4
(n+1)2(n+2)2,从而S n S n+2-S n+12
=-12
(n+1)(n+2)<0,所以S n S n+2<S n+12
.
(3)解当n 为奇数时,c n =
(3a n -2)b n a n a n+2=
(3n -2)2n -1n (n+2)
=
2n+1n+2
−
2n -1n
;当n 为偶数时,c n =
a n -1
b n+1
=
n -12n
.对任意的正整数
n ,有∑k=1n
c 2k-1=∑
k=1
n
22k
2k+1
−22k -22k -1=22n
2n+1-1,
∑k=1
n
c 2k =∑
k=1
n 2k -1
4k
=14
+
342+543
+…+
2n -14n
. ① 由①得14∑k=1n
c 2k =
1
4
2+
34
3+…+
2n -34n +
2n -14n+1.
②
由①②得34∑k=1n
c 2k =14+2
42+…+2
4n −2n -1
4n+1=
24(1-1
4
n )1-14
−1
4−2n -1
4n+1,从而得∑k=1
n
c 2k =5
9−6n+5
9×4n .
因此,∑k=1
2n
c k =∑k=1
n
c 2k-1+∑k=1
n
c 2k =4n
2n+1−6n+5
9×4n −4
9.所以,数列{c n }的前2n 项和为4n
2n+1−6n+5
9×4n −4
9.。
