相似三角形解答题难题含答案个人精心整理
(完整版)相似三角形难题集锦(含答案),推荐文档

2.如图,在△ABCABC,动点P以2m/s的速度从移动.同时,动点Q以1m/s的中,ACB90°,平分CDB点到达B点时,Q点随之的速度移动.如果P、Q同时出发,用<t<6)。
中,点A的坐标为(2,1),的图象与线段OA的夹角是45°,在△ABCAB=,为边在C建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙,∠ACB=90°,点M是AC上的一轴上,.那么D点的坐标为()A. B.C. D.10..已知,如图,直线y=﹣2x+——A、X字型上一点,AD=AC,BC边上的AE交CD于F求证:求证:中,AB∥CD,AB=b,CD=a,E为边上的任意一点,EF∥AB,且EF交BC于点F,某同学在研究这一问题时,发现如下事实:(1)当时,EF=;当时,;(3)当时,EF=.当时,参照上述研究结论,请你猜已知:如图,在△ABC中,M是AC的中点,E、建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙离等于该顶点对边上中线长的.)角平分线定理:三角形一个AB于点E、F.求证:.O,过O作EF//AB求证:.的四个顶点分别在△ABC 求证:.长为a.求证:.,点在平行延长线于点Q,S,交于点.求证:)如图2,图,当点在平行四边形ABCD的对角线或的延长线上时,是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图2为例进行证明或说明)建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙建议收藏下载本文,以便随时学习!、G、H.求证:为直角.求证:求证:的延长线交于点E.))求证:.是BC的中点,连接、CG,AE与CG相交于点证:.分别是△ABC的两边上的高,过D作BA的延长线于F、H。
;(2)BG·CG=GF·GH交于点M,EF与AC交于点旋转,使得DE与BA三角形并证明你的结论.)请写出图中各对相似三角形(相似比为1除外)建议收藏下载本文,以便随时学习!我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙中,AD⊥BC 于D 。
经典相似三角形练习题(附参考答案)

经典练习题相似三角形(附答案)一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=_________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问: (1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE. (1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t 的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是: _________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离O O′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S 1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S 3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点:相似三角形的判定;平行线的性质。
相似三角形难题

相似三角形难题难题1题目:在△ABC中,D、E分别是AB、AC的中点,BE、CD相交于点O,AO的延长线交BC于点F,求证:AF:AO=2:1。
解答思路:1.连接DE:由于D、E分别是AB、AC的中点,根据三角形的中位线定理,DE∥BC且DE=21BC。
2.利用相似三角形:由于DE∥BC,根据平行线的性质,我们有△ADE∼△ABC和△DOE∼△COB。
3.找出比例关系:由于DE=21BC,则BCDE=21。
由于△ADE∼△ABC,则AFAO=ACAE=21(因为E是AC的中点)。
4.计算AF:AO:由于AFAO=21,则AF:AO=2:1。
难题2题目:在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,DBAD=32,△ABC的面积为S,求△ADE的面积。
解答思路:1.利用相似三角形:由于DE∥BC,根据平行线的性质,我们有△ADE∼△ABC。
2.找出比例关系:由于DBAD=32,则ABAD=52。
3.计算面积比:由于△ADE∼△ABC,则S△ABC S△ADE=(ABAD)2=(52)2=254。
4.计算△ADE的面积:由于S△ABC=S,则S△ADE=254S。
难题3题目:在△ABC中,D、E分别是AB、AC上的点,且∠ADE=∠B,AE=6,AD=4,AC=9,求AB的长。
解答思路:1.利用相似三角形:由于∠ADE=∠B且∠A=∠A(公共角),根据相似三角形的判定定理,我们有△ADE∼△ACB。
2.找出比例关系:由于△ADE∼△ACB,则ACAD=ABAE。
3.代入已知值求解:代入已知值AE=6,AD=4,AC=9,得到94=AB6。
4.计算AB:解这个方程得到AB=227。
相似三角形试题及答案

相似三角形试题及答案
一、选择题
1. 已知两个三角形相似,下列说法正确的是()
A. 对应角相等
B. 对应边成比例
C. 对应角相等且对应边成比例
D. 面积相等
答案:C
2. 若两个三角形的相似比为2:3,则下列说法正确的是()
A. 周长比为2:3
B. 周长比为3:2
C. 面积比为4:9
D. 面积比为9:16
答案:C
二、填空题
1. 若三角形ABC与三角形DEF相似,且AB:DE=2:3,则BC:EF=______。
答案:2:3
2. 若三角形ABC与三角形DEF相似,且相似比为1:2,则三角形ABC
的面积是三角形DEF面积的______。
答案:1/4
三、解答题
1. 已知三角形ABC与三角形DEF相似,AB=6cm,DE=9cm,求BC和EF 的长度。
答案:由于三角形ABC与三角形DEF相似,根据相似三角形的性质,对应边成比例。
因此,BC:EF=AB:DE=6:9=2:3。
设BC=2x,则EF=3x。
由于AB:DE=2:3,所以2x/3x=6/9,解得x=3cm。
因此,BC=6cm,
EF=9cm。
2. 已知三角形ABC与三角形DEF相似,且三角形ABC的面积为24平方厘米,三角形DEF的面积为36平方厘米,求相似比。
答案:设相似比为k,则三角形ABC与三角形DEF的面积比为k^2。
因此,k^2=24/36=2/3,解得k=√(2/3)。
所以相似比为√(2/3)。
经典相似三角形练习题(附参考答案)

类似三角形一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延伸线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试解释:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,衔接BE,CD,M,N分离为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基本上,将△ADE绕点A按顺时针偏向扭转180°,其他前提不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的前提下,请你在图②中延伸ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延伸线上一点,衔接EC,交AD于点F.在不添加帮助线的情形下,请你写出图中所有的类似三角形,并任选一对类似三角形赐与证实.7.如图,在4×3的正方形方格中,△ABC和△DEF的极点都在边长为1的小正方形的极点上.(1)填空:∠ABC=_________°,BC=_________;(2)断定△ABC与△DEC是否类似,并证实你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点动身沿AB偏向以1cm/s的速度向B点匀速活动;同时,动点N从D点动身沿DA偏向以2cm/s的速度向A点匀速活动,问:(1)经由若干时光,△AMN的面积等于矩形ABCD 面积的?(2)是否消失时刻t,使以A,M,N为极点的三角形与△ACD类似?若消失,求t的值;若不消失,请解释来由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD.AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情形,并求出拔取到的两个三角形是类似三角形的概率是若干;(留意:全等算作类似的特例)(2)请你任选一组类似三角形,并给出证实.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,衔接AE.(1)写出图中所有相等的线段,并加以证实;(2)图中有无类似三角形?如有,请写出一对;若没有,请解释来由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的随意率性一点,过点M分离作AB.AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对类似三角形(不需证实);(3)M位于BC的什么地位时,四边形AQMP为菱形并证实你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试解释:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B动身,以1cm/s的速度,沿B⇒A⇒D⇒C偏向,向点C活动;动点Q从点C动身,以1cm/s的速度,沿C⇒D⇒A偏向,向点A活动,过点Q作QE⊥BC于点E.若P.Q 两点同时动身,当个中一点到达目标地时全部活动随之停止,设活动时光为t秒.问:①当点P在B⇒A上活动时,是否消失如许的t,使得直线PQ将梯形ABCD的周长等分?若消失,请求出t的值;若不消失,请解释来由;②在活动进程中,是否消失如许的t,使得以P.A.D为极点的三角形与△CQE类似?若消失,请求出所有相符前提的t的值;若不消失,请解释来由;③在活动进程中,是否消失如许的t,使得以P.D.Q为极点的三角形正好是以DQ为一腰的等腰三角形?若消失,请求出所有相符前提的t的值;若不消失,请解释来由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P.Q分离是AB.BC 上活动的两点.若P自点A动身,以1cm/s的速度沿AB偏向活动,同时,Q自点B动身以2cm/s的速度沿BC偏向活动,问经由几秒,以P.B.Q为极点的三角形与△BDC类似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开端沿AB边向B点以2cm/s的速度移动,点Q从点B开端沿BC边向点C以4cm/s的速度移动,假如P.Q分离从A.B同时动身,问经由几秒钟,△PBQ与△ABC类似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为若干时,这两个直角三角形类似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,可否在边AB上找一点N(不含A.B),使得△CDM与△MAN类似?若能,请给出证实,若不克不及,请解释来由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B动身,沿BC偏向以2cm/s的速度移动,点P从C动身,沿CA偏向以1cm/s的速度移动.若Q.P分离同时从B.C动身,试探讨经由若干秒后,以点C.P.Q为极点的三角形与△CBA类似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上肯定点P 的地位,使得以P,A,D为极点的三角形与以P,B,C为极点的三角形类似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的极点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E扭转,使得DE与BA的延伸线交于点M,EF与AC交于点N,于是,除(1)中的一对类似三角形外,可否再找出一对类似三角形并证实你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开端向B以2cm/s的速度移动;点Q沿DA边从点D开端向点A以1cm/s的速度移动.假如P.Q同时动身,用t (秒)暗示移动的时光,那么当t为何值时,以点Q.A.P为极点的三角形与△ABC类似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA地点的直线行走14米到B点时,身影的长度是变长了照样变短了?变长或变短了若干米?23.阳光亮媚的一天,数学兴致小组的同窗们去测量一棵树的高度(这棵树底部可以到达,顶部不轻易到达),他们带了以下测量对象:皮尺,标杆,一副三角尺,小平面镜.请你在他们供给的测量对象中选出所需对象,设计一种测量计划.(1)所需的测量对象是:_________;(2)请鄙人图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母暗示)求出x.24.问题布景在某次活动课中,甲.乙.丙三个进修小组于统一时刻在阳光下对校园中一些物体进行了测量.下面是他们经由过程测量得到的一些信息:甲组:如图1,测得一根竖立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得黉舍旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体其粗细疏忽不计)的高度为200cm,影长为156cm.义务请求:(1)请依据甲.乙两组得到的信息盘算出黉舍旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请依据甲.丙两组得到的信息,求景灯灯罩的半径.(友谊提醒:如图3,景灯的影长等于线段NG的影长;须要时可采取等式1562+2082=2602)25.阳光经由过程窗口照耀到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下漫步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的程度距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请解释来由;(3)若李华在点A朝着影子(如图箭头)的偏向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分离以直角三角形ABC三边为直径向外作三个半圆,其面积分离用S1,S2,S3暗示,则不难证实S1=S2+S3.(1)如图②,分离以直角三角形ABC三边为边向外作三个正方形,其面积分离用S1,S2,S3暗示,那么S1,S2,S3之间有什么关系;(不必证实)(2)如图③,分离以直角三角形ABC三边为边向外作三个正三角形,其面积分离用S1.S2.S3暗示,请你肯定S1,S2,S3之间的关系并加以证实;(3)若分离以直角三角形ABC三边为边向外作三个一般三角形,其面积分离用S1,S2,S3暗示,为使S1,S2,S3之间仍具有与(2)雷同的关系,所作三角形应知足什么前提证实你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD.CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两类似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.解答:证实:∵DE∥BC,∴DE∥FC,∴∠AED=∠C.又∵EF∥AB,∴EF∥AD,∴∠A=∠FEC.∴△ADE∽△EFC.点评:本题考核的是平行线的性质及类似三角形的剖断定理.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延伸线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.解答:(1)证实:∵梯形ABCD,AB∥CD,∴∠CDF=∠FGB,∠DCF=∠GBF,(2分)∴△CDF∽△BGF.(3分)(2)解:由(1)△CDF∽△BGF,又F是BC的中点,BF=FC,∴△CDF≌△BGF,∴DF=GF,CD=BG,(6分)∵AB∥DC∥EF,F为BC中点,∴E为AD中点,∴EF是△DAG的中位线,∴2EF=AG=AB+BG.∴BG=2EF﹣AB=2×4﹣6=2,∴CD=BG=2cm.(8分)3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.解答:证实:∵FD∥AB,FE∥AC,∴∠B=∠FDE,∠C=∠FED,∴△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试解释:△ABF∽△EAD.解答:证实:∵矩形ABCD中,AB∥CD,∠D=90°,(2分)∴∠BAF=∠AED.(4分)∵BF⊥AE,∴∠AFB=90°.∴∠AFB=∠D.(5分)∴△ABF∽△EAD.(6分)点评:考核类似三角形的剖断定理,症结是找准对应的角.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,衔接BE,CD,M,N分离为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基本上,将△ADE绕点A按顺时针偏向扭转180°,其他前提不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的前提下,请你在图②中延伸ED交线段BC于点P.求证:△PBD∽△AMN.解答:(1)证实:①∵∠BAC=∠DAE,∴∠BAE=∠CAD,∵AB=AC,AD=AE,∴△ABE≌△ACD,∴BE=CD.②由△ABE≌△ACD,得∠ABE=∠ACD,BE=CD,∵M.N分离是BE,CD的中点,∴BM=CN.又∵AB=AC,∴△ABM≌△ACN.∴AM=AN,即△AMN为等腰三角形.(2)解:(1)中的两个结论仍然成立.(3)证实:在图②中准确画出线段PD,由(1)同理可证△ABM≌△ACN,∴∠CAN=∠BAM∴∠BAC=∠MAN.又∵∠BAC=∠DAE,∴∠MAN=∠DAE=∠BAC.∴△AMN,△ADE和△ABC都是顶角相等的等腰三角形.∴△PBD和△AMN 都为顶角相等的等腰三角形,∴∠PBD=∠AMN,∠PDB=∠ANM,∴△PBD∽△AMN.6.如图,E是▱ABCD的边BA延伸线上一点,衔接EC,交AD于点F.在不添加帮助线的情形下,请你写出图中所有的类似三角形,并任选一对类似三角形赐与证实.剖析:依据平行线的性质和两角对应相等的两个三角形类似这一剖断定理可证实图中类似三角形有:△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.解答:解:类似三角形有△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.(3分)如:△AEF∽△BEC.在▱ABCD中,AD∥BC,∴∠1=∠B,∠2=∠3.(6分)∴△AEF∽△BEC.(7分)7.如图,在4×3的正方形方格中,△ABC和△DEF的极点都在边长为1的小正方形的极点上.(1)填空:∠ABC=135°°,BC=;(2)断定△ABC与△DEC是否类似,并证实你的结论.解答:解:(1)∠ABC=135°,BC=;(2)类似;∵BC=,EC==;∴,;∴;又∠ABC=∠CED=135°,∴△ABC∽△DEC.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点动身沿AB偏向以1cm/s的速度向B点匀速活动;同时,动点N从D点动身沿DA偏向以2cm/s的速度向A点匀速活动,问:(1)经由若干时光,△AMN的面积等于矩形ABCD面积的?(2)是否消失时刻t,使以A,M,N为极点的三角形与△ACD类似?若消失,求t的值;若不消失,请解释来由解:(1)设经由x秒后,△AMN的面积等于矩形ABCD面积的,则有:(6﹣2x)x=×3×6,即x2﹣3x+2=0,(2分)解方程,得x1=1,x2=2,(3分)经磨练,可知x1=1,x2=2相符题意,所以经由1秒或2秒后,△AMN的面积等于矩形ABCD面积的.(4分)(2)假设经由t秒时,以A,M,N为极点的三角形与△ACD类似,由矩形ABCD,可得∠CDA=∠MAN=90°,是以有或(5分)即①,或②(6分)解①,得t=;解②,得t=(7分)经磨练,t=或t=都相符题意,所以动点M,N同时动身后,经由秒或秒时,以A,M,N为极点的三角形与△ACD类似.(8分)9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD.AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情形,并求出拔取到的两个三角形是类似三角形的概率是若干;(留意:全等算作类似的特例)(2)请你任选一组类似三角形,并给出证实.解答:解:(1)任选两个三角形的所有可能情形如下六种情形:①②,①③,①④,②③,②④,③④(2分)个中有两组(①③,②④)是类似的.∴拔取到的二个三角形是类似三角形的概率是P=(4分)证实:(2)选择①.③证实.在△AOB与△COD中,∵AB∥CD,∴∠CDB=∠DBA,∠DCA=∠CAB,∴△AOB∽△COD(8分)选择②.④证实.∵四边形ABCD是等腰梯形,∴∠DAB=∠CBA,∴在△DAB与△CBA中有AD=BC,∠DAB=∠CAB,AB=AB,∴△DAB≌△CBA,(6分)∴∠ADO=∠BCO.又∠DOA=∠COB,∴△DOA∽△COB(8分).点评:此题考核概率的求法:假如一个事宜有n种可能,并且这些事宜的可能性雷同,个中事宜A消失m种成果,那么事宜A的概率P(A)=,即类似三角形的证实.还考核了类似三角形的剖断.10.附加题:如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,衔接AE.(1)写出图中所有相等的线段,并加以证实;(2)图中有无类似三角形?如有,请写出一对;若没有,请解释来由;(3)求△BEC与△BEA的面积之比.解答:解:(1)AD=DE,AE=CE.∵CE⊥BD,∠BDC=60°,∴在Rt△CED中,∠ECD=30°.∴CD=2ED.∵CD=2DA,∴AD=DE,∴∠DAE=∠DEA=30°=∠ECD.∴AE=CE.(2)图中有三角形类似,△ADE∽△AEC;∵∠CAE=∠CAE,∠ADE=∠AEC,∴△ADE∽△AEC;(3)作AF⊥BD的延伸线于F,设AD=DE=x,在Rt△CED中,可得CE=,故AE=.∠ECD=30°.在Rt△AEF中,AE=,∠AED=∠DAE=30°,∴sin∠AEF=,∴AF=AE•sin∠AEF=.∴.点评:本题重要考核了直角三角形的性质,类似三角形的剖断及三角形面积的求法等,规模较广.11.如图,在△ABC中,AB=AC=a,M为底边BC上的随意率性一点,过点M分离作AB.AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对类似三角形(不需证实);(3)M位于BC的什么地位时,四边形AQMP为菱形并证实你的结论.解答:解:(1)∵AB∥MP,QM∥AC,∴四边形APMQ是平行四边形,∠B=∠PMC,∠C=∠QMB.∵AB=AC,∴∠B=∠C,∴∠PMC=∠QMB.∴BQ=QM,PM=PC.∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a.(2)∵PM∥AB,∴△PCM∽△ACB,∵QM∥AC,∴△BMQ∽△BCA;(3)当点M中BC的中点时,四边形APMQ是菱形,∵点M是BC的中点,AB∥MP,QM∥AC,∴QM,PM是三角形ABC的中位线.∵AB=AC,∴QM=PM=AB=AC.又由(1)知四边形APMQ是平行四边形,∴平行四边形APMQ是菱形.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试解释:△ADM∽△MCP.解答:证实:∵正方形ABCD,M为CD中点,∴CM=MD=AD.∵BP=3PC,∴PC=BC=AD=CM.∴.∵∠PCM=∠ADM=90°,∴△MCP∽△ADM.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B动身,以1cm/s的速度,沿B⇒A⇒D⇒C偏向,向点C活动;动点Q从点C动身,以1cm/s的速度,沿C⇒D⇒A偏向,向点A活动,过点Q作QE⊥BC于点E.若P.Q 两点同时动身,当个中一点到达目标地时全部活动随之停止,设活动时光为t秒.问:①当点P在B⇒A上活动时,是否消失如许的t,使得直线PQ将梯形ABCD的周长等分?若消失,请求出t的值;若不消失,请解释来由;②在活动进程中,是否消失如许的t,使得以P.A.D为极点的三角形与△CQE类似?若消失,请求出所有相符前提的t的值;若不消失,请解释来由;③在活动进程中,是否消失如许的t,使得以P.D.Q为极点的三角形正好是以DQ为一腰的等腰三角形?若消失,请求出所有相符前提的t的值;若不消失,请解释来由.解答:解:(1)过D 作DH ∥AB交BC于H 点,∵AD∥BH,DH∥AB,∴四边形ABHD是平行四边形.∴DH=AB=8;BH=AD=2.∴CH=8﹣2=6.∵CD=10,∴DH2+CH2=CD2∴∠DHC=90°.∠B=∠DHC=90°.∴梯形ABCD是直角梯形.∴SABCD=(AD+BC)AB=×(2+8)×8=40.(2)①∵BP=CQ=t,∴AP=8﹣t,DQ=10﹣t,∵AP+AD+DQ=PB+BC+CQ,∴8﹣t+2+10﹣t=t+8+t.∴t=3<8.∴当t=3秒时,PQ将梯形ABCD周长等分.②第一种情形:0<t≤8若△PAD∽△QEC则∠ADP=∠C∴tan∠ADP=tan∠C==∴=,∴t=若△PAD∽△CEQ则∠APD=∠C∴tan∠APD=tan∠C==,∴=∴t=第二种情形:8<t≤10,P.A.D三点不克不及构成三角形;第三种情形:10<t≤12△ADP为钝角三角形与Rt△CQE不类似;∴t=或t=时,△PAD与△CQE类似.③第一种情形:当0≤t≤8时.过Q点作QE⊥BC,QH⊥AB,垂足为E.H.∵AP=8﹣t,AD=2,∴PD==.∵CE=t,QE=t,∴QH=BE=8﹣t,BH=QE=t.∴PH=t﹣t=t.∴PQ==,DQ=10﹣t.Ⅰ:DQ=DP,10﹣t=,解得t=8秒.Ⅱ:DQ=PQ,10﹣t=,化简得:3t2﹣52t+180=0解得:t=,t=>8(不合题意舍去)∴t=第二种情形:8≤t≤10时.DP=DQ=10﹣t.∴当8≤t<10时,以DQ为腰的等腰△DPQ恒成立.第三种情形:10<t≤12时.DP=DQ=t﹣10.∴当10<t≤12时,以DQ为腰的等腰△DPQ恒成立.综上所述,t=或8≤t<10或10<t≤12时,以DQ为腰的等腰△DPQ成立.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P.Q分离是AB.BC 上活动的两点.若P自点A动身,以1cm/s的速度沿AB偏向活动,同时,Q自点B动身以2cm/s的速度沿BC偏向活动,问经由几秒,以P.B.Q为极点的三角形与△BDC类似?解答:解:设经x秒后,△PBQ∽△BCD,因为∠PBQ=∠BCD=90°,(1)当∠1=∠2时,有:,即;(2)当∠1=∠3时,有:,即,∴经由秒或2秒,△PBQ∽△BCD.15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开端沿AB边向B点以2cm/s的速度移动,点Q从点B开端沿BC边向点C以4cm/s的速度移动,假如P.Q分离从A.B同时动身,问经由几秒钟,△PBQ与△ABC类似.解答:设经由秒后t秒后,△PBQ与△ABC类似,则有AP=2t,BQ=4t,BP=10﹣2t,当△PBQ∽△ABC时,有BP:AB=BQ:BC,即(10﹣2t):10=4t:20,解得t=2.5(s)(6分)当△QBP∽△ABC时,有BQ:AB=BP:BC,即4t:10=(10﹣2t):20,解得t=1.所以,经由2.5s或1s时,△PBQ与△ABC类似(10分).解法二:设ts后,△PBQ与△ABC类似,则有,AP=2t,BQ=4t,BP=10﹣2t分两种情形:(1)当BP与AB对应时,有=,即=(2)当BP与BC对应时,有=,即=,解得t=1s所以经由1s或2.5s时,以P.B.Q三点为极点的三角形与△ABC类似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为若干时,这两个直角三角形类似.解答:解:∵AC=,AD=2,∴CD==.要使这两个直角三角形类似,有两种情形:1)当Rt△ABC∽Rt△ACD时,2)有=,∴AB==3;3)当Rt△ACB∽Rt△CDA时,4)有=,∴AB==3.故当AB的长为3或3时,这两个直角三角形类似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,可否在边AB上找一点N(不含A.B),使得△CDM与△MAN类似?若能,请给出证实,若不克不及,请解释来由.解答:证实:分两种情形评论辩论:①若△CDM∽△MAN,则=.∵边长为a,M是AD的中点,∴AN=a.②若△CDM∽△NAM,则.∵边长为a,M是AD的中点,∴AN=a,即N点与B重合,不合题意.所以,能在边AB上找一点N(不含A.B),使得△CDM与△MAN类似.当AN=a时,N点的地位知足前提.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B动身,沿BC偏向以2cm/s的速度移动,点P从C动身,沿CA偏向以1cm/s的速度移动.若Q.P分离同时从B.C动身,试探讨经由若干秒后,以点C.P.Q为极点的三角形与△CBA类似?解答:解:设经由x秒后,两三角形类似,则CQ=(8﹣2x)cm,CP=xcm,(1分)∵∠C=∠C=90°,∴当或时,两三角形类似.(3分)(1)当时,,∴x=;(4分)(2)当时,,∴x=.(5分)所以,经由秒或秒后,两三角形类似.(6分)点评:本题分解考核了旅程问题,类似三角形的性质及一元一次方程的解法.19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上肯定点P 的地位,使得以P,A,D为极点的三角形与以P,B,C为极点的三角形类似.解答:解:(1)若点A,P,D分离与点B,C,P对应,即△APD∽△BCP,∴=,∴=,∴AP2﹣7AP+6=0,∴AP=1或AP=6,检测:当AP=1时,由BC=3,AD=2,BP=6,∴=,又∵∠A=∠B=90°,∴△APD∽△BCP.当AP=6时,由BC=3,AD=2,BP=1,又∵∠A=∠B=90°,∴△APD∽△BCP.(2)若点A,P,D分离与点B,P,C对应,即△APD∽△BPC.∴=,∴=,∴AP=.磨练:当AP=时,由BP=,AD=2,BC=3,∴=,又∵∠A=∠B=90°,∴△APD∽△BPC.是以,点P的地位有三处,即在线段AB距离点A的1..6处.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的极点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E扭转,使得DE与BA的延伸线交于点M,EF与AC交于点N,于是,除(1)中的一对类似三角形外,可否再找出一对类似三角形并证实你的结论.解答:证实:(1)∵△ABC是等腰直角三角形,∴∠MBE=45°,∴∠BME+∠MEB=135°又∵△DEF是等腰直角三角形,∴∠DEF=45°∴∠NEC+∠MEB=135°∴∠BEM=∠NEC,(4分)而∠MBE=∠ECN=45°,∴△BEM∽△CNE.(6分)(2)与(1)同理△BEM∽△CNE,∴.(8分)又∵BE=EC,∴,(10分)则△ECN与△MEN中有,又∠ECN=∠MEN=45°,∴△ECN∽△MEN.(12分)21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开端向B以2cm/s的速度移动;点Q沿DA边从点D开端向点A以1cm/s的速度移动.假如P.Q同时动身,用t(秒)暗示移动的时光,那么当t为何值时,以点Q.A.P为极点的三角形与△ABC类似.解答:解:以点Q.A.P为极点的三角形与△ABC类似,所以△ABC∽△PAQ或△ABC∽△QAP,①当△ABC∽△PAQ时,,所以,解得:t=6;②当△ABC∽△QAP时,,所以,解得:t=;③当△AQP∽△BAC时,=,即=,所以t=;④当△AQP∽△BCA时,=,即=,所以t=30(舍去).故当t=6或t=时,以点Q.A.P为极点的三角形与△ABC类似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA地点的直线行走14米到B点时,身影的长度是变长了照样变短了?变长或变短了若干米?解答:解:∵∠MAC=∠MOP=90°,∠AMC=∠OMP,∴△MAC∽△MOP.∴,即,解得,MA=5米;同理,由△NBD∽△NOP,可求得NB=1.5米,∴小明的身影变短了5﹣1.5=3.5米.23.阳光亮媚的一天,数学兴致小组的同窗们去测量一棵树的高度(这棵树底部可以到达,顶部不轻易到达),他们带了以下测量对象:皮尺,标杆,一副三角尺,小平面镜.请你在他们供给的测量对象中选出所需对象,设计一种测量计划.(1)所需的测量对象是:;(2)请鄙人图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母暗示)求出x.解答:解:(1)皮尺,标杆;(2)测量示意图如图所示;(3)如图,测得标杆DE=a,树和标杆的影长分离为AC=b,EF=c,∵△DEF∽△BAC,∴,∴,∴.(7分)24.问题布景在某次活动课中,甲.乙.丙三个进修小组于统一时刻在阳光下对校园中一些物体进行了测量.下面是他们经由过程测量得到的一些信息:甲组:如图1,测得一根竖立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得黉舍旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细疏忽不计)的高度为200cm,影长为156cm.义务请求:(1)请依据甲.乙两组得到的信息盘算出黉舍旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请依据甲.丙两组得到的信息,求景灯灯罩的半径.(友谊提醒:如图3,景灯的影长等于线段NG的影长;须要时可采取等式1562+2082=2602)解答:解:(1)由题意可知:∠BAC=∠EDF=90°,∠BCA=∠EFD.∴△ABC∽△DEF.∴,即,(2分)∴DE=1200(cm).所以,黉舍旗杆的高度是12m.(3分)(2)解法一:与①类似得:,即,∴GN=208.(4分)在Rt△NGH中,依据勾股定理得:NH2=1562+2082=2602,∴NH=260.(5分)设⊙O的半径为rcm,衔接OM,∵NH切⊙O于M,∴OM⊥NH.(6分)则∠OMN=∠HGN=90°,又∵∠ONM=∠HNG,∴△OMN∽△HGN,∴(7分),又ON=OK+KN=OK+(GN﹣GK)=r+8,∴,解得:r=12.∴景灯灯罩的半径是12cm.(8分)解法二:与①类似得:,即,∴GN=208.(4分)设⊙O的半径为rcm,衔接OM,∵NH切⊙O于M,∴OM⊥NH.(5分)则∠OMN=∠HGN=90°,又∵∠ONM=∠HNG,∴△OMN∽△HGN.∴,即,(6分)∴MN=r,又∵ON=OK+KN=OK+(GN﹣GK)=r+8.(7分)在Rt△OMN中,依据勾股定理得:r2+(r)2=(r+8)2即r2﹣9r﹣36=0,解得:r1=12,r2=﹣3(不合题意,舍去),∴景灯灯罩的半径是12cm.(8分)25.(2007•白银)阳光经由过程窗口照耀到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.解答:解:∵AE∥BD,∴△ECA∽△DCB,∴.∵EC=8.7m,ED=2.7m,∴CD=6m.∵AB=1.8m,∴AC=BC+1.8m,∴,∴BC=4,即窗口底边离地面的高为4m.点评:此题根本上难度不大,应用类似比即可求出窗口底边离地面的高.26.如图,李华晚上在路灯下漫步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的程度距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请解释来由;(3)若李华在点A朝着影子(如图箭头)的偏向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.解答:解:(1)由已知:AB∥OP,∴△ABC∽△OPC.∵,∵OP=l,AB=h,OA=a,∴,∴解得:.(2)∵AB∥OP,∴△ABC∽△OPC,∴,即,即.∴.同理可得:,∴=是定值.(3)依据题意设李华由A到A',身高为A'B',A'C'代表其影长(如图).由(1)可知,即,∴,同理可得:,∴,由等比性质得:,当李华从A走到A'的时刻,他的影子也从C移到C',是以速度与旅程成正比∴,所以人影顶端在地面上移动的速度为.27.如图①,分离以直角三角形ABC三边为直径向外作三个半圆,其面积分离用S1,S2,S3暗示,则不难证实S1=S2+S3.(1)如图②,分离以直角三角形ABC三边为边向外作三个正方形,其面积分离用S1,S2,S3暗示,那么S1,S2,S3之间有什么关系;(不必证实)(2)如图③,分离以直角三角形ABC三边为边向外作三个正三角形,其面积分离用S1.S2.S3暗示,请你肯定S1,S2,S3之间的关系并加以证实;(3)若分离以直角三角形ABC三边为边向外作三个一般三角形,其面积分离用S1,S2,S3暗示,为使S1,S2,S3之间仍具有与(2)雷同的关系,所作三角形应知足什么前提证实你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.解:设直角三角形ABC的三边BC.CA.AB的长分离为a.b.c,则c2=a2+b2(1)S1=S2+S3;(2)S1=S2+S3.证实如下:显然,S1=,S2=,S3=∴S2+S3==S1;(3)当所作的三个三角形类似时,S1=S2+S3.证实如下:∵所作三个三角形类似∴∴=1∴S1=S2+S3;(4)分离以直角三角形ABC三边为一边向外作类似图形,其面积分离用S1.S2.S3暗示,则S1=S2+S3.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.解答:解:∵△ABC∽△ADE,∴AE:AC=AD:AB.∵AE:AC=(AB+BD):AB,∴AE:9=(15+5):15.∴AE=12.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD.CD的长;(2)过B作BE⊥DC于E,求BE的长.解答:解:(1)Rt△ABC中,依据勾股定理得:BC==5,∵Rt△ABC∽Rt△BDC,∴==,==,∴BD=,CD=;(2)在Rt△BDC中,S△BDC=BE•CD=BD•BC,∴BE===3.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两类似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.解:(1)设=k,那么x=2k,y=3k,z=5k,因为3x+4z﹣2y=40,∴6k+20k﹣6k=40,∴k=2,∴x=4,y=6,z=10.(2)设一个三角形周长为Ccm,则另一个三角形周长为(C+560)cm,则,∴C=240,C+560=800,即它们的周长分离为240cm,800cm。
初中数学经典相似三角形练习题(附参考答案)

经典演习题类似三角形【1 】一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延伸线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试解释:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,衔接BE,CD,M,N分离为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基本上,将△ADE绕点A按顺时针偏向扭转180°,其他前提不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的前提下,请你在图②中延伸ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延伸线上一点,衔接EC,交AD于点F.在不添加帮助线的情形下,请你写出图中所有的类似三角形,并任选一对类似三角形赐与证实.7.如图,在4×3的正方形方格中,△ABC和△DEF的极点都在边长为1的小正方形的极点上.(1)填空:∠ABC=_________°,BC=_________;(2)断定△ABC与△DEC是否类似,并证实你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点动身沿AB偏向以1cm/s的速度向B点匀速活动;同时,动点N从D点动身沿DA偏向以2cm/s的速度向A点匀速活动,问:(1)经由若干时光,△AMN的面积等于矩形ABCD面积的?(2)是否消失时刻t,使以A,M,N为极点的三角形与△ACD类似?若消失,求t的值;若不消失,请解释来由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD.AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情形,并求出拔取到的两个三角形是类似三角形的概率是若干;(留意:全等算作类似的特例)(2)请你任选一组类似三角形,并给出证实.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,衔接AE.(1)写出图中所有相等的线段,并加以证实;(2)图中有无类似三角形?如有,请写出一对;若没有,请解释来由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的随意率性一点,过点M分离作AB.AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对类似三角形(不需证实);(3)M位于BC的什么地位时,四边形AQMP为菱形并证实你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试解释:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B动身,以1cm/s的速度,沿B⇒A⇒D⇒C偏向,向点C活动;动点Q从点C动身,以1cm/s的速度,沿C⇒D⇒A偏向,向点A活动,过点Q作QE⊥BC于点E.若P.Q两点同时动身,当个中一点到达目标地时全部活动随之停止,设活动时光为t秒.问:①当点P在B⇒A上活动时,是否消失如许的t,使得直线PQ将梯形ABCD的周长等分?若消失,请求出t的值;若不消失,请解释来由;②在活动进程中,是否消失如许的t,使得以P.A.D为极点的三角形与△CQE类似?若消失,请求出所有相符前提的t的值;若不消失,请解释来由;③在活动进程中,是否消失如许的t,使得以P.D.Q为极点的三角形正好是以DQ为一腰的等腰三角形?若消失,请求出所有相符前提的t的值;若不消失,请解释来由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P.Q分离是AB.BC上活动的两点.若P自点A动身,以1cm/s 的速度沿AB偏向活动,同时,Q自点B动身以2cm/s的速度沿BC偏向活动,问经由几秒,以P.B.Q为极点的三角形与△BDC类似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开端沿AB边向B点以2cm/s的速度移动,点Q从点B 开端沿BC边向点C以4cm/s的速度移动,假如P.Q分离从A.B同时动身,问经由几秒钟,△PBQ与△ABC类似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为若干时,这两个直角三角形类似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,可否在边AB上找一点N(不含A.B),使得△CDM 与△MAN类似?若能,请给出证实,若不克不及,请解释来由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B动身,沿BC偏向以2cm/s的速度移动,点P从C动身,沿CA偏向以1cm/s的速度移动.若Q.P分离同时从B.C动身,试探讨经由若干秒后,以点C.P.Q为极点的三角形与△CBA类似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上肯定点P的地位,使得以P,A,D 为极点的三角形与以P,B,C为极点的三角形类似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的极点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E扭转,使得DE与BA的延伸线交于点M,EF与AC交于点N,于是,除(1)中的一对类似三角形外,可否再找出一对类似三角形并证实你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开端向B以2cm/s的速度移动;点Q沿DA边从点D开端向点A以1cm/s的速度移动.假如P.Q同时动身,用t(秒)暗示移动的时光,那么当t为何值时,以点Q.A.P为极点的三角形与△ABC类似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA地点的直线行走14米到B点时,身影的长度是变长了照样变短了?变长或变短了若干米?23.阳光亮媚的一天,数学兴致小组的同窗们去测量一棵树的高度(这棵树底部可以到达,顶部不轻易到达),他们带了以下测量对象:皮尺,标杆,一副三角尺,小平面镜.请你在他们供给的测量对象中选出所需对象,设计一种测量计划.(1)所需的测量对象是:_________;(2)请鄙人图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母暗示)求出x.24.问题布景在某次活动课中,甲.乙.丙三个进修小组于统一时刻在阳光下对校园中一些物体进行了测量.下面是他们经由过程测量得到的一些信息:甲组:如图1,测得一根竖立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得黉舍旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细疏忽不计)的高度为200cm,影长为156cm.义务请求:(1)请依据甲.乙两组得到的信息盘算出黉舍旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请依据甲.丙两组得到的信息,求景灯灯罩的半径.(友谊提醒:如图3,景灯的影长等于线段NG的影长;须要时可采取等式1562+2082=2602)25.阳光经由过程窗口照耀到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下漫步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的程度距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请解释来由;(3)若李华在点A朝着影子(如图箭头)的偏向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分离以直角三角形ABC三边为直径向外作三个半圆,其面积分离用S1,S2,S3暗示,则不难证实S1=S2+S3.(1)如图②,分离以直角三角形ABC三边为边向外作三个正方形,其面积分离用S1,S2,S3暗示,那么S1,S2,S3之间有什么关系;(不必证实)(2)如图③,分离以直角三角形ABC三边为边向外作三个正三角形,其面积分离用S1.S2.S3暗示,请你肯定S1,S2,S3之间的关系并加以证实;(3)若分离以直角三角形ABC三边为边向外作三个一般三角形,其面积分离用S1,S2,S3暗示,为使S1,S2,S3之间仍具有与(2)雷同的关系,所作三角形应知足什么前提证实你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD.CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两类似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点:类似三角形的剖断;平行线的性质.菁优网版权所有专题:证实题.剖析:依据平行线的性质可知∠AED=∠C,∠A=∠FEC,依据类似三角形的剖断定理可知△ADE∽△EFC.解答:证实:∵DE∥BC,∴DE∥FC,∴∠AED=∠C.又∵EF∥AB,∴EF∥AD,∴∠A=∠FEC.∴△ADE∽△EFC.点评:本题考核的是平行线的性质及类似三角形的剖断定理.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延伸线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.考点:类似三角形的剖断;三角形中位线定理;梯形.菁优网版权所有专题:几何分解题.剖析:(1)应用平行线的性质可证实△CDF∽△BGF.(2)依据点F是BC的中点这一已知前提,可得△CDF≌△BGF,则CD=BG,只请求出BG的长即可解题.解答:(1)证实:∵梯形ABCD,AB∥CD,∴∠CDF=∠FGB,∠DCF=∠GBF,(2分)∴△CDF∽△BGF.(3分)(2)解:由(1)△CDF∽△BGF,又F是BC的中点,BF=FC,∴△CDF≌△BGF,∴DF=GF,CD=BG,(6分)∵AB∥DC∥EF,F为BC中点,∴E为AD中点,∴EF是△DAG的中位线,∴2EF=AG=AB+BG.∴BG=2EF﹣AB=2×4﹣6=2,∴CD=BG=2cm.(8分)点评:本题重要考核了类似三角形的剖断定理及性质,全等三角形的剖断及线段的等量代换,比较庞杂.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.考点:类似三角形的剖断.菁优网版权所有专题:证实题.剖析:由FD∥AB,FE∥AC,可知∠B=∠FDE,∠C=∠FED,依据三角形类似的剖断定理可知:△ABC∽△FDE.解答:证实:∵FD∥AB,FE∥AC,∴∠B=∠FDE,∠C=∠FED,∴△ABC∽△FDE.点评:本题很简略,考核的是类似三角形的剖断定理:(1)假如两个三角形的两个角对应相等,那么这两个三角形类似;(2)假如一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形类似;(3)假如一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形类似.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试解释:△ABF∽△EAD.考点:类似三角形的剖断;矩形的性质.菁优网版权所有专题:证实题.剖析:依据两角对应相等的两个三角形类似可解.解答:证实:∵矩形ABCD中,AB∥CD,∠D=90°,(2分)∴∠BAF=∠AED.(4分)∵BF⊥AE,∴∠AFB=90°.∴∠AFB=∠D.(5分)∴△ABF∽△EAD.(6分)点评:考核类似三角形的剖断定理,症结是找准对应的角.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,衔接BE,CD,M,N分离为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基本上,将△ADE绕点A按顺时针偏向扭转180°,其他前提不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的前提下,请你在图②中延伸ED交线段BC于点P.求证:△PBD∽△AMN.考点:类似三角形的剖断;全等三角形的剖断;等腰三角形的剖断;扭转的性质.菁优网版权所有专题:几何分解题.剖析:(1)因为∠BAC=∠DAE,所以∠BAE=∠CAD,又因为AB=AC,AD=AE,应用SAS可证出△BAE≌△CAD,可知BE.CD是对应边,依据全等三角形对应边上的中线相等,可证△AMN是等腰三角形.(2)应用(1)中的证实办法仍然可以得出(1)中的结论,思绪不变.(3)先证出△ABM≌△ACN(SAS),可得出∠CAN=∠BAM,所以∠BAC=∠MAN(等角加等角和相等),又∵∠BAC=∠DAE,所以∠MAN=∠DAE=∠BAC,所以△AMN,△ADE和△ABC都是顶角相等的等腰三角形,所以∠PBD=∠AMN,所以△PBD∽△AMN(两个角对应相等,两三角形类似).6.如图,E是▱ABCD的边BA延伸线上一点,衔接EC,交AD于点F.在不添加帮助线的情形下,请你写出图中所有的类似三角形,并任选一对类似三角形赐与证实.考点:类似三角形的剖断;平行四边形的性质.菁优网版权所有专题:凋谢型.剖析:依据平行线的性质和两角对应相等的两个三角形类似这一剖断定理可证实图中类似三角形有:△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.解答:解:类似三角形有△AEF∽△BEC;△AEF∽△DCF;△BEC∽△DCF.(3分)如:△AEF∽△BEC.在▱ABCD中,AD∥BC,∴∠1=∠B,∠2=∠3.(6分)∴△AEF∽△BEC.(7分)点评:考核了平行线的性质及类似三角形的剖断定理.7.如图,在4×3的正方形方格中,△ABC和△DEF的极点都在边长为1的小正方形的极点上.(1)填空:∠ABC=135°°,BC=;(2)断定△ABC与△DEC是否类似,并证实你的结论.考点:类似三角形的剖断;正方形的性质.菁优网版权所有专题:证实题;网格型.剖析:(1)不雅察可得:BF=FC=2,故∠FBC=45°;则∠ABC=135°,BC==2;(2)不雅察可得:BC.EC的长为2.,可得,再依据其夹角相等;故△ABC∽△DEC.解答:解:(1)∠ABC=135°,BC=;(2)类似;∵BC=,EC==;∴,;∴;又∠ABC=∠CED=135°,∴△ABC∽△DEC.点评:解答本题要充分应用正方形的特别性质.留意在正方形中的特别三角形的应用,搞清晰矩形.菱形.正方形中的三角形的三边关系,可有助于进步解题速度和精确率.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点动身沿AB偏向以1cm/s的速度向B点匀速活动;同时,动点N从D点动身沿DA偏向以2cm/s的速度向A点匀速活动,问:(1)经由若干时光,△AMN的面积等于矩形ABCD面积的?(2)是否消失时刻t,使以A,M,N为极点的三角形与△ACD类似?若消失,求t的值;若不消失,请解释来由.考点:类似三角形的剖断;一元二次方程的应用;分式方程的应用;正方形的性质.菁优网版权所有专题:动点型.剖析:(1)关于动点问题,可设时光为x,依据速度暗示出所涉及到的线段的长度,找到相等关系,列方程求解即可,如本题中应用,△AMN的面积等于矩形ABCD面积的作为相等关系;(2)先假设类似,应用类似中的比例线段列出方程,有解的且相符题意的t值即可解释消失,反之则不消失.解答:解:(1)设经由x秒后,△AMN的面积等于矩形ABCD面积的,则有:(6﹣2x)x=×3×6,即x2﹣3x+2=0,(2分)解方程,得x1=1,x2=2,(3分)经磨练,可知x1=1,x2=2相符题意,所以经由1秒或2秒后,△AMN的面积等于矩形ABCD面积的.(4分)(2)假设经由t秒时,以A,M,N为极点的三角形与△ACD类似,由矩形ABCD,可得∠CDA=∠MAN=90°,是以有或(5分)即①,或②(6分)解①,得t=;解②,得t=(7分)经磨练,t=或t=都相符题意,所以动点M,N同时动身后,经由秒或秒时,以A,M,N为极点的三角形与△ACD类似.(8分)点评:重要考核了类似三角形的剖断,正方形的性质和一元二次方程的应用以及解分式方程.要控制正方形和类似三角形的性质,才会灵巧的应用.留意:一般关于动点问题,可设时光为x,依据速度暗示出所涉及到的线段的长度,找到相等关系,列方程求解即可.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD.AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情形,并求出拔取到的两个三角形是类似三角形的概率是若干;(留意:全等算作类似的特例)(2)请你任选一组类似三角形,并给出证实.考点:类似三角形的剖断;概率公式.菁优网版权所有专题:凋谢型.剖析:(1)采取列举法,列举出所有可能消失的情形,再找出类似三角形即可求得;①与③,②与④类似;(2)应用类似三角形的剖断定理即可证得.解答:解:(1)任选两个三角形的所有可能情形如下六种情形:①②,①③,①④,②③,②④,③④(2分)个中有两组(①③,②④)是类似的.∴拔取到的二个三角形是类似三角形的概率是P=(4分)证实:(2)选择①.③证实.在△AOB与△COD中,∵AB∥CD,∴∠CDB=∠DBA,∠DCA=∠CAB,∴△AOB∽△COD(8分)选择②.④证实.∵四边形ABCD是等腰梯形,∴∠DAB=∠CBA,∴在△DAB与△CBA中有AD=BC,∠DAB=∠CAB,AB=AB,∴△DAB≌△CBA,(6分)∴∠ADO=∠BCO.又∠DOA=∠COB,∴△DOA∽△COB(8分).点评:此题考核概率的求法:假如一个事宜有n种可能,并且这些事宜的可能性雷同,个中事宜A消失m种成果,那么事宜A的概率P(A)=,即类似三角形的证实.还考核了类似三角形的剖断.10.附加题:如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,衔接AE.(1)写出图中所有相等的线段,并加以证实;(2)图中有无类似三角形?如有,请写出一对;若没有,请解释来由;(3)求△BEC与△BEA的面积之比.考点:类似三角形的剖断;三角形的面积;含30度角的直角三角形.菁优网版权所有专题:分解题.剖析:(1)依据直角三角形中30度角所对的直角边是斜边的一半,可知CD=2ED,则可写出相等的线段;(2)两角对应相等的两个三角形类似则可断定△ADE∽△AEC;(3)请求△BEC与△BEA的面积之比,从图中可看出两三角形有一公共边可作为底边,若求得高之比可知面积之比,由此需作△BEA的边BE边上的高即可求解.解答:解:(1)AD=DE,AE=CE.∵CE⊥BD,∠BDC=60°,∴在Rt△CED中,∠ECD=30°.∴CD=2ED.∵CD=2DA,∴AD=DE,∴∠DAE=∠DEA=30°=∠ECD.∴AE=CE.(2)图中有三角形类似,△ADE∽△AEC;∵∠CAE=∠CAE,∠ADE=∠AEC,∴△ADE∽△AEC;(3)作AF⊥BD的延伸线于F,设AD=DE=x,在Rt△CED中,可得CE=,故AE=.∠ECD=30°.在Rt△AEF中,AE=,∠AED=∠DAE=30°,∴sin∠AEF=,∴AF=AE•sin∠AEF=.∴.点评:本题重要考核了直角三角形的性质,类似三角形的剖断及三角形面积的求法等,规模较广.11.如图,在△ABC中,AB=AC=a,M为底边BC上的随意率性一点,过点M分离作AB.AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对类似三角形(不需证实);(3)M位于BC的什么地位时,四边形AQMP为菱形并证实你的结论.考点:类似三角形的剖断;菱形的剖断.菁优网版权所有专题:分解题.剖析:(1)依据平行四边形的性质可得到对应角相等对应边相等,从而不难求得其周长;(2)因为∠B=∠C=∠PMC=∠QMB,所以△PMC∽△QMB∽△ABC;(3)依据中位线的性质及菱形的剖断不难求得四边形AQMP为菱形.解答:解:(1)∵AB∥MP,QM∥AC,∴四边形APMQ是平行四边形,∠B=∠PMC,∠C=∠QMB.∵AB=AC,∴∠B=∠C,∴∠PMC=∠QMB.∴BQ=QM,PM=PC.∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a.(2)∵PM∥AB,∴△PCM∽△ACB,∵QM∥AC,∴△BMQ∽△BCA;(3)当点M中BC的中点时,四边形APMQ是菱形,∵点M是BC的中点,AB∥MP,QM∥AC,∴QM,PM是三角形ABC的中位线.∵AB=AC,∴QM=PM=AB=AC.又由(1)知四边形APMQ是平行四边形,∴平行四边形APMQ是菱形.点评:此题重要考核了平行四边形的剖断和性质,中位线的性质,菱形的剖断等常识点的分解应用.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试解释:△ADM∽△MCP.考点:类似三角形的剖断;正方形的性质.菁优网版权所有专题:证实题.剖析:欲证△ADM∽△MCP,经由过程不雅察发明两个三角形已经具备一组角对应相等,即∠D=∠C,此时,再求夹此对应角的双方对应成比例即可.解答:证实:∵正方形ABCD,M为CD中点,∴CM=MD=AD.∵BP=3PC,∴PC=BC=AD=CM.∴.∵∠PCM=∠ADM=90°,∴△MCP∽△ADM.点评:本题考核类似三角形的剖断.辨认两三角形类似,除了要控制界说外,还要留意精确找出两三角形的对应边.对应角,可应用数形联合思惟依据图形供给的数据盘算对应角的度数.对应边的比.本题中把若干线段的长度用统一线段来暗示是求线段是否成比例时经常应用的办法.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B动身,以1cm/s的速度,沿B⇒A⇒D⇒C偏向,向点C活动;动点Q从点C动身,以1cm/s的速度,沿C⇒D⇒A偏向,向点A活动,过点Q作QE⊥BC于点E.若P.Q两点同时动身,当个中一点到达目标地时全部活动随之停止,设活动时光为t秒.问:①当点P在B⇒A上活动时,是否消失如许的t,使得直线PQ将梯形ABCD的周长等分?若消失,请求出t的值;若不消失,请解释来由;②在活动进程中,是否消失如许的t,使得以P.A.D为极点的三角形与△CQE类似?若消失,请求出所有相符前提的t的值;若不消失,请解释来由;③在活动进程中,是否消失如许的t,使得以P.D.Q为极点的三角形正好是以DQ为一腰的等腰三角形?若消失,请求出所有相符前提的t的值;若不消失,请解释来由.考点:类似三角形的剖断;三角形三边关系;等腰三角形的剖断;勾股定理;直角梯形.菁优网版权所有专题:动点型;凋谢型.剖析:(1)求面积要先求梯形的高,可依据两底的差和CD的长,在直角三角形顶用勾股定理进行求解,得出高后即可求出梯形的面积.(2)①PQ等分梯形的周长,那么AD+DQ+AP=BC+CQ+BP,已知了AD,BC的长,可以用t来暗示出AP,BP,CQ,QD的长,那么可依据上面的等量关系求出t的值.②本题要分三种情形进行评论辩论:一,当P在AB上时,即0<t≤8,假如两三角形类似,那么∠C=∠ADP,或∠C=∠APD,那么在△ADP中依据∠C的正切值,求出t的值.二,当P在AD上时,即8<t≤10,因为P,A,D在一条直线上,是以构不成三角形.三,当P在CD上时,即10<t≤12,因为∠ADC是个钝角,是以△ADP是个钝角三角形是以不成能和直角△CQE类似.分解三种情形即可得出相符前提的t的值.(3)和(2)雷同也要分三种情形进行评论辩论:一,当P在AB上时,即0<t≤8,等腰△PDQ以DQ为腰,是以DQ=DP或DQ=PQ,可以经由过程构建直角三角形来暗示出DP,PQ的长,然后依据得出的等量关系来求t的值.二,当P在AD上时,即8<t≤10,因为BA+AD=CD=10,是以DP=DQ=10﹣t,是以DP,DQ恒相等.三,当P在CD上时,即10<t≤12,情形同二.分解三种情形可得出等腰三角形以DQ为腰时,t的取值.点评:本题重要考核了梯形的性质以及类似三角形的剖断和性质等常识点,要留意(2)中要依据P,Q的不合地位,进行分类评论辩论,不要漏解.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P.Q分离是AB.BC上活动的两点.若P自点A动身,以1cm/s 的速度沿AB偏向活动,同时,Q自点B动身以2cm/s的速度沿BC偏向活动,问经由几秒,以P.B.Q为极点的三角形与△BDC类似?考点:类似三角形的剖断;矩形的性质.菁优网版权所有专题:几何动点问题;分类评论辩论.剖析:要使以P.B.Q为极点的三角形与△BDC类似,则要分两两种情形进行剖析.分离是△PBQ∽△BDC或△QBP∽△BDC,从而解得所需的时光.解答:解:设经x秒后,△PBQ∽△BCD,因为∠PBQ=∠BCD=90°,(1)当∠1=∠2时,有:,即;(2)当∠1=∠3时,有:,即,∴经由秒或2秒,△PBQ∽△BCD.点评:此题考核了类似三角形的剖断及矩形的性质等常识点的分解应用.15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开端沿AB边向B点以2cm/s的速度移动,点Q从点B 开端沿BC边向点C以4cm/s的速度移动,假如P.Q分离从A.B同时动身,问经由几秒钟,△PBQ与△ABC类似.考点:类似三角形的剖断;一元一次方程的应用.菁优网版权所有专题:动点型.剖析:设经由t秒后,△PBQ与△ABC类似,依据旅程公式可得AP=2t,BQ=4t,BP=10﹣2t,然后应用类似三角形的性质对应边的比相等列出方程求解即可.解答:解:设经由秒后t秒后,△PBQ与△ABC类似,则有AP=2t,BQ=4t,BP=10﹣2t,当△PBQ∽△ABC时,有BP:AB=BQ:BC,即(10﹣2t):10=4t:20,解得t=2.5(s)(6分)当△QBP∽△ABC时,有BQ:AB=BP:BC,即4t:10=(10﹣2t):20,解得t=1.所以,经由2.5s或1s时,△PBQ与△ABC类似(10分).解法二:设ts后,△PBQ与△ABC类似,则有,AP=2t,BQ=4t,BP=10﹣2t分两种情形:(1)当BP与AB对应时,有=,即=(2)当BP与BC对应时,有=,即=,解得t=1s所以经由1s或2.5s时,以P.B.Q三点为极点的三角形与△ABC类似.点评:本题分解了旅程问题和三角形的问题,所以学生日常平凡学过的常识要会融会起来.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为若干时,这两个直角三角形类似.考点:类似三角形的剖断.菁优网版权所有专题:分类评论辩论.剖析:假如一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形类似.在Rt△ABC和Rt△ACD,直角边的对应需分情形评论辩论.解答:解:∵AC=,AD=2,∴CD==.要使这两个直角三角形类似,有两种情形:(1)当Rt△ABC∽Rt△ACD时,有=,∴AB==3;(2)当Rt△ACB∽Rt△CDA时,有=,∴AB==3.故当AB的长为3或3时,这两个直角三角形类似.点评:本题考核类似三角形的剖断.辨认两三角形类似,除了要控制界说外,还要留意精确找出两三角形的对应边.对应角,可应用数形联合思惟依据图形供给的数据盘算对应角的度数.对应边的比.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,可否在边AB上找一点N(不含A.B),使得△CDM 与△MAN类似?若能,请给出证实,若不克不及,请解释来由.考点:类似三角形的剖断;正方形的性质.菁优网版权所有专题:探讨型;分类评论辩论.剖析:两个三角形都是直角三角形,还只需知足一对角对应相等或夹直角的双方对应成比例即可解释两个三角形类似.若DM与AM对应,则△CDM与△MAN全等,N与B重合,不合题意;若DM与AN对应,则CD:AM=DM:AN,得AN=a,从而肯定N的地位.解答:证实:分两种情形评论辩论:①若△CDM∽△MAN,则=.∵边长为a,M是AD的中点,∴AN=a.②若△CDM∽△NAM,则.∵边长为a,M是AD的中点,∴AN=a,即N点与B重合,不合题意.所以,能在边AB上找一点N(不含A.B),使得△CDM与△MAN类似.当AN=a时,N点的地位知足前提.点评:此题考核类似三角形的剖断.因不明白对应关系,所以需分类评论辩论.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B动身,沿BC偏向以2cm/s的速度移动,点P从C动身,沿CA偏向以1cm/s的速度移动.若Q.P分离同时从B.C动身,试探讨经由若干秒后,以点C.P.Q为极点的三角形与△CBA类似?考点:类似三角形的剖断.菁优网版权所有专题:分解题;动点型.。
初三最详细相似三角形解答题以及答案

一.解答题(共7小题)1.(2003•常德)如图1,D是△ABC的BC边上的中点,过点D的一条直线交AC于F,交BA的延长线于E,AG∥BC 交EF于G,我们可以证明EG•DC=ED•AG成立(不要求考生证明).(1)如图2,若将图1中的过点D的一条直线交AC于F,改为交CA的延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则EG•DC=ED•AG还成立吗?如果成立,请给出证明;如果不成立,请说出理由;(2)根据图2,请你找出EG、FD、ED、FG四条线段之间的关系,并给出证明;(3)如图3,若将图1中的过点D的一条直线交AC于F,改为交CA的反向延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则(2)得到的结论是否成立?2.(2003•厦门)如图,BD、BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,E、D为垂足.(1)求证:四边形AEBD是矩形;(2)若=3,F、G分别为AE、AD上的点,FG交AB于点H,且=3,求证:△AHG是等腰三角形.3.(2003•金华)如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.(1)当x为何值时,PQ∥BC;(2)当,求的值;(3)△APQ能否与△CQB相似?若能,求出AP的长;若不能,请说明理由.4.(2003•绍兴)已知∠AOB=90°,OM是∠AOB的平分线,按以下要求解答问题:(1)将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.①在图甲中,证明:PC=PD;②在图乙中,点G是CD与OP的交点,且PG=PD,求△POD与△PDG的面积之比;(2)将三角板的直角顶点P在射线OM上移动,一直角边与边OB交于点D,OD=1,另一直角边与直线OA,直线OB分别交于点C,E,使以P,D,E为顶点的三角形与△OCD相似,在图丙中作出图形,试求OP的长.5.(2002•盐城)已知:如图,在直角三角形ABC中,∠BAC=90°,AB=AC,D为BC的中点,E为AC上一点,点G在BE上,连接DG并延长交AE于F,若∠FGE=45°.(1)求证:BD•BC=BG•BE;(2)求证:AG⊥BE;(3)若E为AC的中点,求EF:FD的值.6.(2002•黄冈)已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明成立(不要求考生证明).若将图中的垂线改为斜交,如图,AB∥CD,AD,BC相交于点E,过点E作EF∥AB交BD于点F,则:(1)还成立吗?如果成立,请给出证明;如果不成立,请说明理由;(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.7.如图,已知直角梯形ABCD中,AB∥CD,∠D=90°,AB=AC,AE⊥AC且AE=AD,连BE交AC于F.(1)如图1,若CD=AD,试猜想BF与EF的数量关系;(2)如图2,若CD≠AD,问题(1)BF与EF的数量关系是否仍然成立?若成立,请证明.若不成立,请说明理由;(3)如图2,在第(2)问的条件下,取BC中点M,问线段MF与线段BD之间是否存在某种确定的数量关系?若存在,证明你的结论,若不存在,说明理由.答案与评分标准一.解答题(共7小题)1.(2003•常德)如图1,D是△ABC的BC边上的中点,过点D的一条直线交AC于F,交BA的延长线于E,AG∥BC 交EF于G,我们可以证明EG•DC=ED•AG成立(不要求考生证明).(1)如图2,若将图1中的过点D的一条直线交AC于F,改为交CA的延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则EG•DC=ED•AG还成立吗?如果成立,请给出证明;如果不成立,请说出理由;(2)根据图2,请你找出EG、FD、ED、FG四条线段之间的关系,并给出证明;(3)如图3,若将图1中的过点D的一条直线交AC于F,改为交CA的反向延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则(2)得到的结论是否成立?考点:相似三角形的判定与性质。
相似三角形难题集锦(含答_案)(精编文档).doc

【最新整理,下载后即可编辑】一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t 的值.2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ 为等腰三角形时,求出t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB 上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME 与△CNE相似?4.如图所示,在△ABC中,BA=BC =20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B 点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q 点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A 以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t <6)。
经典相似三角形练习题(附参考答案)

经典练习题相似三角形(附答案)一.解答题(共30 小题)1 .如图,在△ABC中,DE∥ BC, EF ∥ AB,求证:△ADE∽△EFC .2 .如图,梯形ABCD 中,AB∥ CD,点F 在 BC 上,连 DF 与 AB 的延长线交于点G.( 1 )求证:△CDF∽△BGF;( 2 )当点 F 是 BC 的中点时,过 F 作 EF ∥ CD交 AD 于点 E,若 AB=6cm , EF=4cm ,求 CD 的长.3.如图,点 D , E 在 BC 上,且 FD∥ AB, FE∥ AC.求证:△ABC∽△FDE .4 .如图,已知 E 是矩形 ABCD 的边 CD 上一点,BF ⊥ AE于 F,试说明:△ABF ∽△EAD.5 .已知:如图①所示,在△和△ABCADE中, AB=AC , AD=AE ,∠ BAC= ∠ DAE,且点B ,A ,D 在一条直线上,连接 BE ,CD , M , N 分别为 BE, CD 的中点.( 1)求证:①BE=CD ;②△AMN是等腰三角形;( 2)在图①的基础上,将△绕点ADE 按顺时针方向旋转 180 °,其他条件不变,得到图②所示的图形.请直接写出( 1)中的两个结论是否仍然成立;( 3)在( 2 )的条件下,请你在图②中延长ED 交线段 BC 于点 P.求证:△PBD∽△ AMN.6 .如图, E 是? ABCD 的边 BA 延长线上一点,连接EC,交 AD 于点 F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7 .如图,在 4 ×3的正方形方格中,△和ABC△ DEF的顶点都在边长为 1 的小正方形的顶点上.(1 )填空:∠ABC=_________ °,BC= _________ ;(2 )判断△ ABC与△ DEC是否相似,并证明你的结论.8 .如图,已知矩形 ABCD 的边长 AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB 方向以 1cm/s 的速度向 B 点匀速运动;同时,动点N 从 D 点出发沿 DA 方向以 2cm/s的速度向 A 点匀速运动,问:( 1)经过多少时间,△的AMN面积等于矩形 ABCD 面积的?( 2)是否存在时刻 t ,使以 A ,M , N 为顶点的三角形与△相ACD似?若存在,求t 的值;若不存在,请说明理由.9 .如图,在梯形ABCD 中,若 AB∥ DC,AD=BC ,对角线BD 、 AC 把梯形分成了四个小三角形.( 1 )列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)( 2 )请你任选一组相似三角形,并给出证明.10 .如图△ABC中, D 为 AC 上一点, CD=2DA,∠BAC=45 °,∠BDC=60 °,CE于⊥E,BD连接 AE.( 1 )写出图中所有相等的线段,并加以证明;( 2 )图中有无相似三角形?若有,请写出一对;若没有,请说明理由;( 3 )求△BEC与△BEA的面积之比.11 .如图,在△ABC中, AB=AC=a,M为底边BC上的任意一点,过点M 分别作 AB 、 AC 的平行线交AC于P,交 AB 于 Q.(1 )求四边形 AQMP 的周长;(2 )写出图中的两对相似三角形(不需证明);( 3 ) M 位于 BC 的什么位置时,四边形AQMP为菱形并证明你的结论.12 .已知: P 是正方形ABCD 的边 BC 上的点,且BP=3PC , M 是 CD 的中点,试说明:△ADM∽△MCP.13 .如图,已知梯形ABCD 中,AD∥ BC,AD=2 ,AB=BC=8,CD=10.( 1 )求梯形ABCD 的面积 S;( 2 )动点 P 从点 B 出发,以 1cm/s的速度,沿B? A ?D ? C方向,向点C运动;动点Q从点C出发,以1cm/s 的速度,沿C? D? A 方向,向点 A 运动,过点Q 作 QE⊥ BC 于点 E.若 P、Q 两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t 秒.问:①当点 P 在 B?A 上运动时,是否存在这样的t ,使得直线PQ 将梯形 ABCD 的周长平分?若存在,请求出t 的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t ,使得以 P、 A 、D 为顶点的三角形与△相CQE似?若存在,请求出所有符合条件的t 的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t ,使得以 P、D 、Q 为顶点的三角形恰好是以DQ 为一腰的等腰三角形?若存在,请求出所有符合条件的t 的值;若不存在,请说明理由.14 .已知矩形ABCD ,长 BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P 自点 A 出发,以 1cm/s的速度沿AB 方向运动,同时,Q 自点 B 出发以 2cm/s的速度沿BC 方向运动,问经过几秒,以 P 、B、 Q 为顶点的三角形与△相BDC似?15 .如图,在△ABC中, AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点 Q 从点 B 开始沿 BC 边向点 C 以 4cm/s的速度移动,如果P、 Q 分别从 A 、B 同时出发,问经过几秒钟,△PBQ与△ ABC相似.16 .如图,∠ACB= ∠ ADC=90 AC=°,,AD=2.问当AB的长为多少时,这两个直角三角形相似.17 .已知,如图,在边长为 a 的正方形ABCD 中,M 是 AD 的中点,能否在边AB 上找一点N(不含 A 、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.C=90°BC=8cm,, AC=6cm,点Q 从 B 出发,沿BC 方向以2cm/s的速度移动,18 .如图在△ABC中,∠点 P 从 C 出发,沿CA方向以1cm/s的速度移动.若Q 、P分别同时从B、C出发,试探究经过多少秒后,以点C、 P、Q为顶点的三角形与△相CBA似?19 .如图所示,梯形ABCD 中,AD∥ BC,∠A=90 °AB=7,, AD=2 , BC=3 ,试在腰AB 上确定点 P 的位置,使得以P ,A ,D 为顶点的三角形与以P, B,C 为顶点的三角形相似.20 .△ABC和△DEF是两个等腰直角三角形,∠A= ∠ D=90 °的,顶△点 DEF位于边 BC 的中点上.( 1)如图 1,设 DE 与 AB 交于点 M , EF 与 AC 交于点 N ,求证:△BEM∽△ CNE;( 2)如图 2,将△ DEF绕点 E 旋转,使得 DE 与 BA 的延长线交于点M ,EF 与 AC 交于点 N ,于是,除( 1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21 .如图,在矩形 ABCD 中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点 Q 沿 DA 边从点 D 开始向点 A 以 1cm/s的速度移动.如果P、Q 同时出发,用t(秒)表示移动的时间,那么当 t 为何值时,以点Q、 A 、P 为顶点的三角形与△相ABC似.22 .如图,路灯(P 点)距地面8 米,身高 1.6 米的小明从距路灯的底部(O 点) 20 米的 A 点,沿 OA 所在的直线行走14 米到 B 点时,身影的长度是变长了还是变短了?变长或变短了多少米?23 .阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1 )所需的测量工具是:_________ ;(2 )请在下图中画出测量示意图;( 3 )设树高AB 的长度为x,请用所测数据(用小写字母表示)求出x.24 .问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为 60cm .乙组:如图2,测得学校旗杆的影长为 900cm .丙组:如图 3 ,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm ,影长为156cm .任务要求:( 1 )请根据甲、乙两组得到的信息计算出学校旗杆的高度;( 2 )如图 3,设太阳光线NH 与⊙O 相切于点M .请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图 3 ,景灯的影长等于线段NG 的影长;需要时可采用等式156 2+2082=2602)25 .阳光通过窗口照射到室内,在地面上留下 2.7m 宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m ,窗口高AB=1.8m,求窗口底边离地面的高BC.26 .如图,李华晚上在路灯下散步.已知李华的身高AB=h ,灯柱的高 OP=O′ P′ =l两灯,柱之间的距离 OO′ =m.( 1)若李华距灯柱 OP 的水平距离 OA=a ,求他影子 AC 的长;( 2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC )是否是定值请说明理由;( 3)若李华在点 A 朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27 .如图①,分别以直角三角形ABC 三边为直径向外作三个半圆,其面积分别用S1, S2, S3表示,则不难证明 S1=S 2+S 3.( 1 )如图②,分别以直角三角形ABC 三边为边向外作三个正方形,其面积分别用S1, S2, S3表示,那么S1, S2, S3之间有什么关系;(不必证明)( 2 )如图③,分别以直角三角形ABC 三边为边向外作三个正三角形,其面积分别用S1、 S2、 S3表示,请你确定 S1,S2, S3之间的关系并加以证明;( 3 )若分别以直角三角形ABC 三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2, S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;( 4 )类比( 1 ),( 2 ),( 3 )的结论,请你总结出一个更具一般意义的结论.28 .已知:如图,△ABC∽△ AB=15ADE,, AC=9 , BD=5 .求 AE .29 .已知:如图Rt △ ABC∽ Rt △ BDC,AB=3若, AC=4 .(1)求 BD 、CD 的长;(2)过 B 作 BE⊥ DC于 E,求 BE 的长.30 .( 1 )已知,且3x+4z﹣2y=40,求x,y,z的值;( 2 )已知:两相似三角形对应高的比为3:10 ,且这两个三角形的周长差为560cm ,求它们的周长.参考答案与试题解析一.解答题(共30 小题)1 .如图,在△ABC中,DE∥ BC, EF ∥ AB,求证:△ADE∽△EFC .考点:相似三角形的判定;平行线的性质。
(完整版)相似三角形经典解答题难题含答案个人精心整理,推荐文档

一、相似三角形中的动点问题1.如图,在Rt △ABC 中,∠ACB=90°,AC=3,BC=4,过点B 作射线BB1∥AC .动点D 从点A 出发沿射线AC 方向以每秒5个单位的速度运动,同时动点E 从点C 沿射线AC 方向以每秒3个单位的速度运动.过点D 作DH ⊥AB 于H,过点E作EF⊥AC交射线BB1于F,G 是EF 中点,连接DG .设点D 运动的时间为t 秒.(1)当t 为何值时,AD=AB ,并求出此时DE 的长度;(2)当△DEG 与△ACB 相似时,求t 的值.2.如图,在△ABC 中,ABC =90°,AB=6m ,BC=8m ,动点P 以2m/s 的速度从A 点出发,沿AC 向点C 移动.同时,动点Q 以1m/s 的速度从C 点出发,沿CB 向点B 移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t 秒.(1)①当t=2.5s 时,求△CPQ 的面积;②求△CPQ 的面积S (平方米)关于时间t (秒)的函数解析式;(2)在P ,Q 移动的过程中,当△CPQ 为等腰三角形时,求出t 的值.3.如图1,在Rt △ABC 中,ACB =90°,AC =6,BC =8,点D 在边AB 上运动,DE 平分CDB 交边BC 于点E ,EM ⊥BD ,垂足为M ,EN ⊥CD ,垂足为N .(1)当AD =CD 时,求证:DE ∥AC ;(2)探究:AD 为何值时,△BME 与△CNE 相似?4.如图所示,在△ABC 中,BA =BC =20cm ,AC =30cm ,点P 从A 点出发,沿着AB 以每秒4cm 的速度向B 点运动;同时点Q 从C 点出发,沿CA 以每秒3cm 的速度向A 点运动,当P 点到达B 点时,Q 点随之停止运动.设运动的时间为x .(1)当x 为何值时,PQ ∥BC ?(2)△APQ 与△CQB 能否相似?若能,求出AP 的长;若不能说明理由.5.如图,在矩形ABCD 中,AB=12cm ,BC=6cm ,点P 沿AB 边从A 开始向点B 以2cm/s 的速度移动;点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P 、Q 同时出发,用t (s )表示移动的时间(0<t <6)。
初中数学相似三角形经典练习难题易错题(附详解)
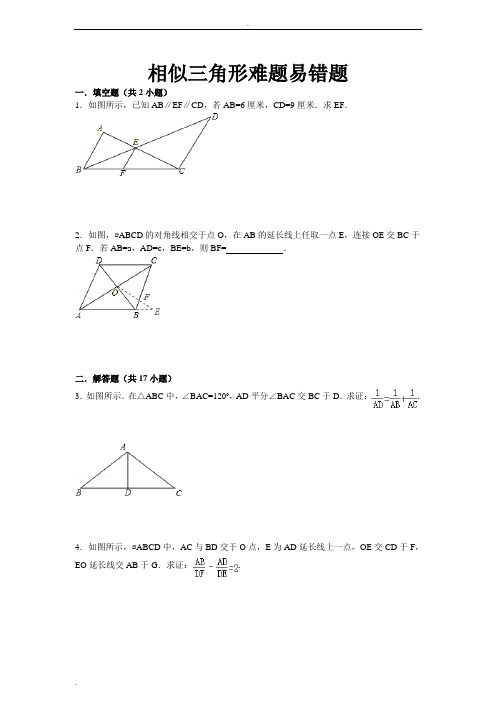
.相似三角形难题易错题一.填空题(共2小题)1.如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.2.如图,▱ABCD的对角线相交于点O,在AB的延长线上任取一点E,连接OE交BC于点F.若AB=a,AD=c,BE=b,则BF=_________.二.解答题(共17小题)3.如图所示.在△ABC中,∠BAC=120°,AD平分∠BAC交BC于D.求证:.4.如图所示,▱ABCD中,AC与BD交于O点,E为AD延长线上一点,OE交CD于F,EO延长线交AB于G.求证:.5.一条直线截△ABC的边BC、CA、AB(或它们的延长线)于点D、E、F.求证:.6.如图所示.P为△ABC内一点,过P点作线段DE,FG,HI分别平行于AB,BC和CA,且DE=FG=HI=d,AB=510,BC=450,CA=425.求d.7.如图所示.梯形ABCD中,AD∥BC,BD,AC交于O点,过O的直线分别交AB,CD 于E,F,且EF∥BC.AD=12厘米,BC=20厘米.求EF.8.已知:P为▱ABCD边BC上任意一点,DP交AB的延长线于Q点,求证:.9.如图所示,梯形ABCD中,AD∥BC,MN∥BC,且MN与对角线BD交于O.若AD=DO=a,BC=BO=b,求MN.10.P为△ABC内一点,过P点作DE,FG,IH分别平行于AB,BC,CA(如图所示).求证:.11.如图所示.在梯形ABCD中,AB∥CD,AB<CD.一条直线交BA延长线于E,交DC 延长线于J,交AD于F,交BD于G,交AC于H,交BC于I.已知EF=FG=GH=HI=IJ,求DC:AB.12.已知P为△ABC内任意一点,连AP,BP,CP并延长分别交对边于D,E,F.求证:(1)(2)三者中,至少有一个不大于2,也至少有一个不少于2.13.如图所示.在△ABC中,AM是BC边上的中线,AE平分∠BAC,BD⊥AE的延长线于D,且交AM延长线于F.求证:EF∥AB.14.如图所示.P,Q分别是正方形ABCD的边AB,BC上的点,且BP=BQ,BH⊥PC于H.求证:QH⊥DH.15.已知M是Rt△ABC中斜边BC的中点,P、Q分别在AB、AC上,且PM⊥QM.求证:PQ2=PB2+QC2.16.如图所示.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB,CF平分∠BCD.求证:EF∥BC.17.如图所示.在△ABC内有一点P,满足∠APB=∠BPC=∠CPA.若2∠B=∠A+∠C,求证:PB2=PA•PC.(提示:设法证明△PAB∽△PBC.)18.已知:如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1.求证:CE⊥AD.19.如图所示,△ABC中,M、N是边BC的三等分点,BE是AC边上的中线,连接AM、AN,分别交BE于F、G,求BF:FG:GE的值.20.在△ABC中,∠A∶∠B∶∠C=1∶2∶4.求证提示:要证明如几何题的常用方法:①比例法:将原等式变为,故构造成以a+b、b为边且与a、c所在三角形相似的三角形。
相似三角形试题及答案

相似三角形试题及答案一、选择题1. 在相似三角形中,对应角相等的条件是:A. 边长成比例B. 面积相等C. 周长相等D. 角相等答案:A2. 下列选项中,哪一项不是相似三角形的性质?A. 对应边成比例B. 对应角相等C. 面积比等于边长比的平方D. 周长比等于边长比答案:B二、填空题3. 若三角形ABC与三角形DEF相似,且AB:DE=2:3,则三角形ABC的面积与三角形DEF的面积之比是________。
答案:4:94. 若三角形ABC与三角形A'B'C'相似,且∠A=∠A'=60°,则∠B与∠B'的关系是________。
答案:相等三、简答题5. 解释为什么在相似三角形中,对应边长的比等于对应角的正弦值之比。
答案:在相似三角形中,由于对应角相等,根据正弦定理,对应边长的比等于对应角的正弦值之比。
这是因为正弦值与角的大小成正比,而相似三角形的对应角大小相同,因此它们的正弦值之比也相同。
四、计算题6. 在三角形ABC中,已知AB=5cm,AC=7cm,∠A=60°,求三角形ABC的面积。
答案:首先,利用余弦定理计算BC的长度。
根据余弦定理,BC²= AB² + AC² - 2AB*AC*cos∠A。
代入已知值,得到BC² = 5² +7² - 2*5*7*(1/2) = 25 + 49 - 35 = 39,所以BC = √39 cm。
然后,利用三角形的面积公式S = (1/2)AB*AC*sin∠A,代入已知值,得到S = (1/2)*5*7*(√3/2) = 17.5√3 cm²。
7. 若三角形ABC与三角形DEF相似,且AB:DE=3:5,求三角形ABC与三角形DEF的面积比。
答案:由于相似三角形的面积比等于边长比的平方,所以三角形ABC与三角形DEF的面积比为(3:5)² = 9:25。
相似三角形经典解答题难题含答案(个人精心整理)

一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC 方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.ﻭ(1)当t 为何值时,AD=AB,并求出此时DE的长度;ﻭ(2)当△DEG与△ACB相似时,求t的值.2.如图,在△A BC中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.ﻭ(1)①当t=2.5s时,求△CPQ的面积;ﻭ②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;ﻭ(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A 点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P 沿AB边从A开始向点B以2cm/s的速度移动;点Q 沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t<6)。
相似三角形难题及答案-精练版

相似三角形提高训练一.填空题(共2小题)1.如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.2.如图,▱ABCD的对角线相交于点O,在AB的延长线上任取一点E,连接OE交BC于点F.若AB=a,AD=c,BE=b,则BF=_________.二.解答题(共17小题)3.如图所示.在△ABC中,∠BAC=120°,AD平分∠BAC交BC于D.求证:.4.如图所示,▱ABCD中,AC与BD交于O点,E为AD延长线上一点,OE交CD于F,EO延长线交AB于G.求证:.5.一条直线截△ABC的边BC、CA、AB(或它们的延长线)于点D、E、F.求证:.6.如图所示.P为△ABC内一点,过P点作线段DE,FG,HI分别平行于AB,BC和CA,且DE=FG=HI=d,AB=510,BC=450,CA=425.求d.7.如图所示.梯形ABCD中,AD∥BC,BD,AC交于O点,过O的直线分别交AB,CD于E,F,且EF∥BC.AD=12厘米,BC=20厘米.求EF.8.已知:P为▱ABCD边BC上任意一点,DP交AB的延长线于Q点,求证:.9.如图所示,梯形ABCD中,AD∥BC,MN∥BC,且MN与对角线BD交于O.若AD=DO=a,BC=BO=b,求MN.10.P为△ABC内一点,过P点作DE,FG,IH分别平行于AB,BC,CA(如图所示).求证:.11.如图所示.在梯形ABCD中,AB∥CD,AB<CD.一条直线交BA延长线于E,交DC延长线于J,交AD于F,交BD于G,交AC于H,交BC于I.已知EF=FG=GH=HI=IJ,求DC:AB.12.已知P为△ABC内任意一点,连AP,BP,CP并延长分别交对边于D,E,F.求证:(1)(2)三者中,至少有一个不大于2,也至少有一个不少于2.13.如图所示.在△ABC中,AM是BC边上的中线,AE平分∠BAC,BD⊥AE的延长线于D,且交AM延长线于F.求证:EF∥AB.14.如图所示.P,Q分别是正方形ABCD的边AB,BC上的点,且BP=BQ,BH⊥PC于H.求证:QH⊥DH.15.已知M是Rt△ABC中斜边BC的中点,P、Q分别在AB、AC上,且PM⊥QM.求证:PQ2=PB2+QC2.16.如图所示.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB,CF平分∠BCD.求证:EF∥BC.17.如图所示.在△ABC内有一点P,满足∠APB=∠BPC=∠CPA.若2∠B=∠A+∠C,求证:PB2=PA•PC.(提示:设法证明△PAB∽△PBC.)18.已知:如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1.求证:CE⊥AD.19.如图所示,△ABC中,M、N是边BC的三等分点,BE是AC边上的中线,连接AM、AN,分别交BE于F、G,求BF:FG:GE的值.20.在△ABC中,∠A∶∠B∶∠C=1∶2∶4.求证提示:要证明如几何题的常用方法:①比例法:将原等式变为,故构造成以a+b、b为边且与a、c所在三角形相似的三角形。
相似三角形经典练习题及答案

相似三角形经典练习题及答案一、选择题1、若两个相似三角形的面积之比为 1∶4,则它们的周长之比为()A 1∶2B 1∶4C 1∶5D 1∶16答案:A解析:相似三角形面积的比等于相似比的平方,相似三角形周长的比等于相似比。
因为两个相似三角形的面积之比为 1∶4,所以相似比为 1∶2,那么它们的周长之比为 1∶2。
2、如图,在△ABC 中,点 D、E 分别在边 AB、AC 上,DE∥BC,若 AD∶DB = 1∶2,则下列结论中正确的是()A AE∶EC = 1∶2B AE∶EC = 1∶3 C DE∶BC = 1∶2 DDE∶BC = 1∶3答案:B解析:因为 DE∥BC,所以△ADE∽△ABC。
因为 AD∶DB =1∶2,所以 AD∶AB = 1∶3。
因为相似三角形对应边成比例,所以AE∶AC = AD∶AB = 1∶3,所以 AE∶EC = 1∶2。
3、已知△ABC∽△A'B'C',相似比为 3∶4,△ABC 的周长为 6,则△A'B'C'的周长为()A 8B 7C 9D 10答案:A解析:因为相似三角形周长的比等于相似比,所以△ABC 与△A'B'C'的周长之比为3∶4。
设△A'B'C'的周长为x,则6∶x =3∶4,解得 x = 8。
4、如图,在△ABC 中,D、E 分别是 AB、AC 上的点,且DE∥BC,如果 AD = 2cm,DB = 1cm,AE = 15cm,则 EC =()A 05cmB 1cmC 15cmD 3cm答案:B解析:因为 DE∥BC,所以△ADE∽△ABC,所以 AD∶AB =AE∶AC。
因为 AD = 2cm,DB = 1cm,所以 AB = 3cm。
所以 2∶3= 15∶(15 + EC),解得 EC = 1cm。
5、下列各组图形一定相似的是()A 两个直角三角形B 两个等边三角形C 两个菱形D 两个矩形答案:B解析:等边三角形的三个角都相等,都是 60°,所以两个等边三角形一定相似。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、相似三角形中的动点问题1.如图,在Rt△ ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D 从点A 出发沿射线AC方向以每秒5 个单位的速度运动,同时动点E 从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥ AC交射线BB1于F,G是EF中点,连接DG.设点D 运动的时间为t 秒.(1)当t 为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB 相似时,求t 的值.点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm 的速度向A点运动,当P点到达B点时,Q 点随之停止运动.设运动的时间为x.(1)当x 为何值时,PQ∥ BC?(2)△APQ 与△CQB能否相似?若能,求出AP的长;若不能说明理由.2.如图,在△ ABC中,ABC=90°,AB=6m,BC=8m,动点P 以2m/s 的速度从A 点出发,沿AC 向点C 移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t 秒.(1)① 当t=2.5s 时,求△ CPQ的面积;② 求△ CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q 移动的过程中,当△CPQ为等腰三角形时,求出t 的值.5.如图,在矩形ABCD 中,AB=12cm,BC=6cm,点P 沿AB 边从A 开始向点B 以2cm/s 的速度移动;点Q 沿DA边从点D开始向点A以1cm/s 的速度移动.如果P、Q 同时出发,用t(s)表示移动的时间(0< t <6)。
(1)当t 为何值时,△ QAP为等腰直角三角形?(2)当t 为何值时,以点Q、A、P 为顶点的三角形与△ABC相似?3.如图1,在Rt△ ABC中,ACB=90°,AC=6,BC=8,点D 在边AB 上运动,DE 平分CDB交边BC 于点E,EM⊥ BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD 时,求证:DE∥AC;(2)探究:AD 为何值时,△BME与△CNE相似?二、构造相似辅助线——双垂直模型6.在平面直角坐标系xOy 中,点A 的坐标为(2,1),正比例函数y=kx 的图象与线段OA 的夹角是45°,求这个正比例函数的表达式.7.在△ABC中,AB= ,AC=4,BC=2,以AB 为边在C点的异侧作△ABD,使△ABD为等腰直角三角形,4.如图所示,在△ ABC中,BA=BC=20cm,AC=30cm ,11.如图:△ABC中,D 是AB上一点,AD=AC,BC边上的中线AE交CD 于F。
12.四边形ABCD 中,AC 为AB、AD 的比例中项,且AC平分∠DAB。
求证:14.已知:如图,在△ABC中,M 是AC的中点,E、F求证:8.在△ ABC 中,AC=BC,9.如图,在直角坐标系中,矩形ABCO的边OA在x 轴上,边OC在y 轴上,点B 的坐标为(1,3),将矩形沿对角线AC翻折B 点落在D点的位置,且AD交y 轴于点E.那么D 点的坐标为()13.在梯形ABCD中,AB∥CD,AB=b,CD=a,E 为AD 边上的任意一点,EF∥ AB,且EF交BC于点F,某同学在研究这一问题时,发现如下事实:10..已知,如图,直线y=﹣2x +2 与坐标轴交于A、B 两点.以AB 为短边在第一象限EF= ;(2)当时,(1)当时,EF=(3)当时,EF= .当时,参照上述研a、b和k表示EF的一般结论,并究结论,请你猜想用给出证明.做一个矩形ABCD,使得矩形的两边之比为1﹕2。
求C、D 两点的坐标。
求线段CD 的长.∠ACB=90 ,°点M 是AC上的一点,点N是BC上的一点,沿着直线MN 折叠,使得点C恰好落在边AB上的P 点.求证:MC:NC=AP:PB.三、构造相似辅助线是 BC 上的两点,且 BE = EF =FC 。
求 BN : NQ :QM .五、 相似之共线线段的比例问题15.证明:(1)重心定理:三角形顶点到重心的距离等于 该顶点对边上中线长的 .(注:重心是三角形三条中线 的交点)(2)角平分线定理:三角形一个角的平分线分 对边所成的两条线段与这个角的两邻边对应成比18.如图,在 △ABC 中,已知 方形 EFGH 的四个顶点分别在 求证: .CD 为边 AB 上的高,正△ABC 上。
四、 相似类定值问题16.如图,在等边 △ ABC 中, M 、N 分别是边 AB ,AC 的中点,D 为 MN 上任意一点, BD 、CD 的延长线分别交 AC 、AB 于点 E 、 F .求证: .19. 已知,在 △ABC 中作内接菱形 CDEF ,设菱形的边长为 a .求证: .17.已知:如图,梯形 ABCD 中, AB//DC ,对角线 AC 、 BD交于 O ,过 O 作 EF//AB 分别交 AD 、BC 于 E 、F 。
求证: .20. (1)如图 1,点 在平行四边形 ABCD 的对角线 BD 上,一直线过点 P 分别交 BA ,BC 的延长线于点Q , S ,交于点 .求证:2)如图 2,图 3,当点 在平行四边形 ABCD 的对角线或 的延长线上时, 是否仍然成立?23.已知如图, P 为平行四边形 ABCD 的对角线 AC 上一点,过 P的直线与 AD 、BC 、 CD 的延长线、 AB 的延长线分别相交于点E 、F 、G 、H.求证:21. 已知:如图, △ ABC 中, AB = AC , AD 是中线, P 是 AD 上一点,过 C 作 CF ∥ AB ,延长 BP 交 AC 于 E ,交 CF 于 F .求证: BP 2=PE ·PF .若成立,试给出证明;若不成立,试说明理由(要求仅22.如图,已知ΔABC 中,AD , BF 分别为 BC ,AC 边上的高,过 D 作 AB 的垂线交 AB 于 E ,交 BF 于 G ,交 AC 延长线于 H 。
求证:DE 2=EG?EHE是AC的中点,ED 的延长线与CB 的延长线交于点F.(1)求证:.(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由.六、相似之等积式类型综合证:.26 如图,在Rt△ ABC中,CD 是斜边AB上的高,点M 在CD上,DH⊥ BM 且与AC的延长线交于点E.求证:(1)△AED∽ △CBM;(2)29.如图,BD、CE分别是△ABC 的两边上的高,过D 作DG⊥BC于G,分别交CE及BA 的延长线于F、H。
求证:(1)DG2=BG·CG;(2)BG·CG=GF·GH27.如图,△ABC是直角三角形,∠ ACB=90°,CD⊥AB于D,七、相似基本模型应用30.△ ABC 和△DEF 是两个等腰直角三角形,∠A=∠D=90 ,°△DEF的顶点E 位于边BC的中点上.(1)如图1,设DE与AB 交于点M,EF与AC交于点24.已知,如图,锐角△ABC中,AD⊥ BC于D,H 为垂心(三角形三条高线的交点);在AD 上有一点P,且∠BPC为直角.求证:PD2=AD·DH 。
25.已知如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED 的延长线交CA于F。
28.如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD 相交于点N.求求证:N,求证:△BEM∽△ CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.31.如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.(1)请写出图中各对相似三角形(相似比为 1 除外);(2)求BP:PQ:QR.1.答案:解:(1)∵∠ACB=90°,AC=3,BC=4∴AB=5又∵AD=AB,AD=5t∴t=1,此时CE=3,∴DE=3+3-5=132.如图,在△ABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F。
求证:∴∠CDE=∠ BDE∵∠CDB为△CDB的一个外角∴∠CDB=∠A+∠ACD=2∠ACD∵∠CDB=∠CDE+∠BDE=2∠CDE ∴∠ACD=∠ CDE∴DE∥AC(2)① ∠NCE=∠MBE ∵EM⊥BD,EN⊥CD,∴△BME∽△CNE,如图② △DEG∽△ BCA,此时,即:,求得:t= ;∵∠NCE=∠ MBE ∴BD=CD又∵∠NCE+∠ACD=∠MBE+∠A=90° ∴∠ ACD=∠ A∴AD=CD① △DEG∽△ ACB,此时,即:,求得:t=如图,当点D 在点E右侧,即:t> 时,DE=5t-(3t+3)=2t-3.若△DEG与△ACB相似,有两种情况:③ △DEG∽△ ACB,此时,即:,求得:t= ;④ △DEG∽△ BCA,此时,∴AD=BD= AB∵在Rt△ABC中,ACB=90 °,AC=6,BC=8 ∴AB=10∴AD=5② ∠NCE=∠ MEB∵EM⊥BD,EN⊥CD,∴△BME∽△ENC,如图即:,求得:t= .综上,t 的值为或或或.3.答案:解:(1)证明:∵ AD=CD ∴∠A=∠ACD∵DE 平分CDB交边BC于点E ∵∠NCE=∠ MEB∴EM∥CD∴CD⊥AB∵在Rt△ABC中,ACB=90 °,AC=6,BC=8 ∴AB=10∵∠A=∠A,∠ADC=∠ACB∴△ACD∽△ABC2)如图当点D在点E左侧,即:0≦t≦ 时,DE=3t+3-5t=3-2t .若△DEG与△ACB相似,有两种情况:综上:AD=5或时,△BME 与△CNE相似.4.答案:解(1)由题意:AP=4x,CQ=3x,AQ=30-3x,当PQ∥ BC 时,,即:解得:解得:(符合题意)此时:AP= cm故AP= cm 或20cm 时,△APQ 与△CQB能相似.5.答案:解:设运动时间为t ,则DQ=t,AQ=6-t,AP=2t,BP=12-2t.(1)若△QAP为等腰直角三角形,则AQ=AP,即:6-t=2t ,t=2(符合题意)∴t=2 时,△ QAP为等腰直角三角形.(2)∠ B=∠ QAP=9°0① 当△ QAP∽△ ABC时,,即:,解得:(符合题意);② 当△PAQ∽△ ABC时,,即:,解得:(符合题意).P 为顶点的三角① △APQ∽△ CBQ,则,即解得:或(舍)此时:AP= cm② △APQ∽△ CQB,则,即B,过点A 作平B作BD⊥ AC=90°当或时,以点Q、A、形与△ABC相似.6.答案:解:分两种情况第一种情况,图象经过第一、三象过点A 作AB⊥OA,交待求直线于点行于y 轴的直线交x 轴于点C,过点则由上可知:由双垂直模型知:△OCA∽ △ ADB∴∵A(2,1),=45 °∴OC=2,AC=1,AO=AB ∴AD=OC=2,BD=AC=1∴ D 点坐标为(2,3)∴B 点坐标为(1,3)∴此时正比例函数表达式为:y=3x 第二种情况,图象经过第二、四象限过点A 作AB⊥OA,交待求直线于点行于x 轴的直线交y 轴于点C,过点则由上可知:由双垂直模型知:△OCA∽ △ ADB∴B,过点A 作平B作BD⊥ AC=90°∵A(2,1),=45∴OC=1,AC=2,AO=AB2)能,AP= cm 或AP=20cm∴AD=OC=1,BD=AC=2∴D 点坐标为(3,1)∴B 点坐标为(3,﹣1)∴此时正比例函数表达式为:y=x7.答案:解:情形一:情形二:情形三:8.答案:证明:方法连接PC,过点P 作PD⊥AC于D,则PD//BC根据折叠可知MN ⊥CP∵∠2+∠PCN=90 ,°∠PCN+∠CNM=90 ∴∠2=∠CNM∵∠ CDP=∠ NCM=90 ° ∴△PDC∽MCN∴MC:CN=PD:DC ∵PD=DA ∴MC:CN=DA:DC ∵PD//BC ∴DA:DC=PA:PB ∴MC:CN=PA:PB方法二:如图,过M作MD⊥AB于D,过N作NE⊥AB于E由双垂直模型,可以推知△ PMD∽NPE ,则过点 C 作 x 轴的平行线交 y 轴于 G ,过点 D 作 y 轴的 平行线交 x 轴于 F ,交 GC 的延长线于 E 。
