安徽大学数学期末试卷汇编安徽大学自动控制原理期末考试试卷(三)
自动控制原理期末考试试卷(含答案)讲解学习

2017年自动控制原理期末考试卷与答案一、填空题(每空 1 分,共20分)1、对自动控制系统的基本要求可以概括为三个方面,即: 稳定性 、快速性和 准确性 。
2、控制系统的 输出拉氏变换与输入拉氏变换在零初始条件下的比值 称为传递函数。
3、在经典控制理论中,可采用 劳斯判据(或:时域分析法)、根轨迹法或奈奎斯特判据(或:频域分析法) 等方法判断线性控制系统稳定性。
4、控制系统的数学模型,取决于系统 结构 和 参数, 与外作用及初始条件无关。
5、线性系统的对数幅频特性,纵坐标取值为20lg ()A ω(或:()L ω),横坐标为lg ω 。
6、奈奎斯特稳定判据中,Z = P - R ,其中P 是指 开环传函中具有正实部的极点的个数,Z 是指 闭环传函中具有正实部的极点的个数,R 指 奈氏曲线逆时针方向包围 (-1, j0 )整圈数。
7、在二阶系统的单位阶跃响应图中,s t 定义为 调整时间 。
%σ是超调量 。
8、设系统的开环传递函数为12(1)(1)Ks T s T s ++频特性为01112()90()()tg T tg T ϕωωω--=---。
9、反馈控制又称偏差控制,其控制作用是通过 给定值 与反馈量的差值进行的。
10、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为1050.20.5s s s s+++。
11、自动控制系统有两种基本控制方式,当控制装置与受控对象之间只有顺向作用而无反向联系时,称为 开环控制系统;当控制装置与受控对象之间不但有顺向作用而且还有反向联系时,称为 闭环控制系统;含有测速发电机的电动机速度控制系统,属于 闭环控制系统。
12、根轨迹起始于开环极点,终止于开环零点。
13、稳定是对控制系统最基本的要求,若一个控制系统的响应曲线为衰减振荡,则该系统 稳定。
判断一个闭环线性控制系统是否稳定,在时域分析中采用劳斯判据;在频域分析中采用奈奎斯特判据。
安徽大学期末试卷09-10年度第一学期《自动控制原理》考卷B卷答案
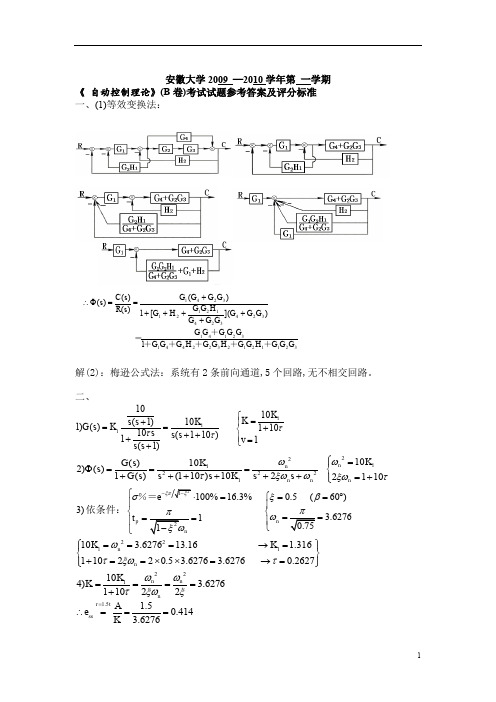
安徽大学2009 —2010学年第 一学期《 自动控制理论》(B 卷)考试试题参考答案及评分标准 一、(1)等效变换法:解(2):梅逊公式法:系统有2条前向通道,5个回路,无不相交回路。
二、111101010(1)1)() 11010(110)11(1)K K K s s G s K s s s v s s τττ⎧=+⎪==+⎨++⎪+=⎩+221122211010()2)() 1()(110)1022110n n n n n K K G s s G s s s K s s ωωτξωωξωτ⎧=⎪Φ===⎨++++++=+⎪⎩ 3)依条件:0.5 (60)100%16.3% 3.62761n p e t ξβσω-⎧==︒=⎧⎪⎪⎨⎨====⎪⎪⎩⎩%= 221110 3.627613.16 1.316110220.5 3.6276 3.6276 0.2627n n K K ωτξωτ⎧⎫===→=⎪⎪⎨⎬+==⨯⨯=→=⎪⎪⎩⎭221104) 3.627611022n n n K K ωωτξωξ====+1.5 1.50.4143.6276r t ss A e K =∴===3211212322441321413243241212132411)]([1)()()()(G G G H G G H G G H G G G G G G G G G G G G G G H G G H G G G G G s R s C s ++++++ =++++++==Φ∴三、(1)特征方程为()10(1)10(2)(1)10(2)(1)1(2)D s GH K s s s K s s s K s s s =+=-+=+-=+-=+换算成首一多项式,为:-根轨迹方程为: 由此可知,需要绘制零度根轨迹。
分离点的计算:12()()02.732,0.732dG sH s dss s ===- (2)由特征方程求取根轨迹与虚轴的交点,1,2s =±此时闭环系统临界稳定,出现等幅振荡,所对应的K =2。
安徽大学期末试卷MK09-10(1)高数A(三)答案.pdf

=λ
∑ 由此可知 λˆ
=
1 n
n i =1
xi 2
是λ
的无偏估计量。
五、证明题(本大题 8 分) 17. (本小题 8 分)证明:
(1)由 A2 + 2 AB − 2E = 0 得到
1 A( A + 2B) = E 2 故有 A + 2B 可逆。
(2)由(1)知 A + 2B 可逆,且逆矩阵为 1 A ,因而有 2
n i =1
xi 2
=0
得到 λ 的最大似然估计值为
∑ λˆ
=
1 n
n i =1
xi 2
∑ λ
的最大似然估计量为 λˆ
=
1 n
n i =1
Xi2
∫ (3)由于 EX 2 =
+∞
x2
i
2
−
xe
x2 λ
dx
=
λ
0
λ
∑ ∑ 因此 Eλˆ
=
E
⎛ ⎜⎝
1 n
n i =1
EX
i
2
⎞ ⎟⎠
=
1 n
n i =1
EX i2
0 0
−1 0
−2 0
−2 0
−6 0
−3⎟⎟ 0⎟
⎜ ⎝
0
0
0
0
0
0
⎟ ⎠
⎛1 0 −1 −1 −5 −2⎞
→
⎜ ⎜ ⎜
0 0
1 0
2 0
2 0
6 0
3⎟ ⎟Leabharlann 0⎟⎜ ⎝0
0
0
0
0
0
⎟ ⎠
对应的线性方程组为
安徽大学期末试卷离散数学期末试卷及答案.doc

一.判断题(共10小题,每题1分,共10分)在各题末尾的括号内画 表示正确,画 表示错误:1.设p、q为任意命题公式,则(p∧q)∨p ⇔ p ( )2.∀x(F(y)→G(x)) ⇔ F(y)→∃xG(x)。
( )3.初级回路一定是简单回路。
( )4.自然映射是双射。
( )5.对于给定的集合及其上的二元运算,可逆元素的逆元是唯一的。
( )6.群的运算是可交换的。
( )7.自然数集关于数的加法和乘法<N,+, >构成环。
( )8.若无向连通图G中有桥,则G的点连通度和边连通度皆为1。
( )9.设A={a,b,c},则A上的关系R={<a,b>,<a,c>}是传递的。
( )10.设A、B、C为任意集合,则A⨯(B⨯C)=(A⨯B)⨯C。
( )二、填空题(共10题,每题3分,共30分)11.设p:天气热。
q:他去游泳。
则命题“只有天气热,他才去游泳”可符号化为。
12.设M(x):x是人。
S(x):x到过月球。
则命题“有人到过月球”可符号化为。
13.p↔q的主合取范式是。
14.完全二部图K r,s(r < s)的边连通度等于。
15.设A={a,b},,则A上共有个不同的偏序关系。
16.模6加群<Z6,⊕>中,4是阶元。
17.设A={1,2,3,4,5}上的关系R={<1,3>,<1,5>,<2,5>,<3,3>,<4,5>},则R的传递闭包t(R) = 。
.18.已知有向图D的度数列为(2,3,2,3),出度列为(1,2,1,1),则有向图D的入度列为。
19.n阶无向简单连通图G的生成树有条边。
20.7阶圈的点色数是。
三、运算题(共5小题,每小题8分,共40分)21.求∃xF(x)→∃yG(x,y)的前束范式。
22.已知无向图G有11条边,2度和3度顶点各两个,其余为4度顶点,求G 的顶点数。
安徽大学期末试卷MKF学习学习文档高数09-10(1)高数A(三)试卷.pdf

答 题勿超装 订 线
------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------
专业
院/系
安徽大学期末试卷
二、填空题(每小题 2 分,共 10 分) 2 −3 1 5
6.方程 −4 6 x −10 = 0 的根为 1 24 7
x −1 −2 −4 −7
得分 。
7.设 3 阶矩阵 A 有 3 个特征值 1,2,3,且矩阵 B 与 A 相似,则| B + E |=
。
8. 设随机变量 X 的分布函数为
观察亩产量,得到 x = 500 kg,则总体均值 μ 的置信水平为 0.95 的置信区间为
。
( Φ(1.96) = 0.975, Φ(1.645) = 0.95 )
三、计算题(本大题 10 分) 11.计算下列行列式
an (a −1)n
(a − n)n
an−1 (a −1)n−1
(a − n)n−1
《高等数学 A(三) 》(A 卷) 第 4 页 共 7 页
安徽大学期末试卷
14.(本小题 10 分)设某人按如下原则决定某日的活动:如该天下雨则以 0.2 的概率外出 购物,以 0.8 的概率去探访朋友;如该天不下雨,则以 0.9 的概率外出购物,以 0.1 的概率 去探访朋友。已知该日下雨的概率为 0.3。 (1)试求那天他外出购物的概率; (2)若已知他那天外出购物,试求那天天下雨的概率。
自动控制原理期末试卷及答案
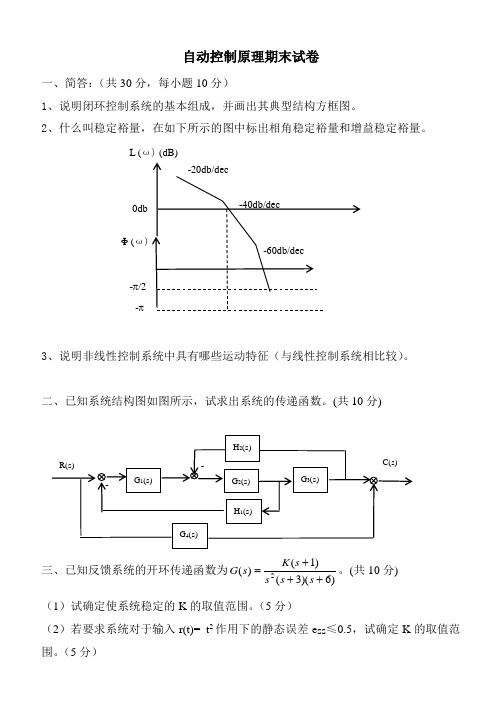
自动控制原理期末试卷一、简答:(共30分,每小题10分)1、说明闭环控制系统的基本组成,并画出其典型结构方框图。
2、什么叫稳定裕量,在如下所示的图中标出相角稳定裕量和增益稳定裕量。
3、说明非线性控制系统中具有哪些运动特征(与线性控制系统相比较)。
二、已知系统结构图如图所示,试求出系统的传递函数。
(共10分)三、已知反馈系统的开环传递函数为)6)(3()1()(2+++=s s s s K s G 。
(共10分) (1)试确定使系统稳定的K 的取值范围。
(5分)(2)若要求系统对于输入r(t)= t 2作用下的静态误差e SS ≤0.5,试确定K 的取值范围。
(5分)四、已知最小相位系统开环对数幅頻特性图如图所示,写出相应的传递函数。
(共10分)五、已知单位负反馈系统的开环传递函数为 )1)(1()(21++=s T s T s Ks G 。
(共10分)(1)试概略画出G (s )对应的Nyquist 图。
(5分) (2)由Nyquist 稳定判据给出闭环系统稳定的条件。
(5分) 六、已知系统的开环传递函数为)1()3(2)(+++=s s s s K s G )(绘制负反馈的根轨迹图,并确定使系统处于欠阻尼的K 值范围。
(共15分) 七、某采样控制系统的结构如图所示,已知τ=1,求: (1)求系统的脉冲传递函数。
(10分) (2)求系统稳定的K 值范围。
(5分)答案一、 简答:(共30分,每小题10分)1、答案:闭环控制系统的基本组成:检测元件、比较元件、放大元件、执行元件、给定元件、校正元件及被控对象。
(共6分,除被控对象外,每一个元件给1分)典型结构方框图(4分,可以没有局部反馈)2、答案:稳定裕量是系统距离稳定 的边界所具有的余量(5分)。
相角稳定裕量(3分)。
增益稳定裕量(2分)。
3、答案:与线性控制系统相比非线性控制系统表现出如下的特征: (1)非线性控制系统的运动不满足态的迭加原理。
自动控制原理期末考试试卷有答案

2017年自动控制原理期末考试卷与答案、填空题(每空 1 分,共20分)对自动控制系统的基本要求可以概括为三个方面,即: 稳定性 、快速性和 准确性 。
控制系统的 输出拉氏变换与输入拉氏变换在零初始条件下的比值 称为传递函数。
在经典控制理论中,可采用 劳斯判据(或:时域分析法)、根轨迹法或奈奎斯特判据(或:频域分析法) 等方法判断控制系统稳定性。
控制系统的数学模型,取决于系统 结构 和 参数, 与外作用及初始条件无关。
线性系统的对数幅频特性,纵坐标取值为20lg ()A ω(或:()L ω),横坐标为lg ω 。
奈奎斯特稳定判据中,Z = P - R ,其中P 是指 开环传函中具有正实部的极点的个数,Z 是指 闭环传函中具有正的极点的个数,R 指 奈氏曲线逆时针方向包围 (-1, j0 )整圈数。
在二阶系统的单位阶跃响应图中,s t 定义为 调整时间 。
%σ是超调量 。
设系统的开环传递函数为12(1)(1)K s T s T s ++,则其开环幅频特性为()A ω=,相频特性为01112)90()()tg T tg T ωω--=---。
反馈控制又称偏差控制,其控制作用是通过 给定值 与反馈量的差值进行的。
、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为1050.20.5s s s s +++。
、自动控制系统有两种基本控制方式,当控制装置与受控对象之间只有顺向作用而无反向联系时,称为 开环控制系统控制装置与受控对象之间不但有顺向作用而且还有反向联系时,称为 闭环控制系统;含有测速发电机的电动机速度系统,属于 闭环控制系统。
、根轨迹起始于开环极点,终止于开环零点。
、稳定是对控制系统最基本的要求,若一个控制系统的响应曲线为衰减振荡,则该系统 稳定。
判断一个闭环线性控统是否稳定,在时域分析中采用劳斯判据;在频域分析中采用奈奎斯特判据。
、频域性能指标与时域性能指标有着对应关系,开环频域性能指标中的幅值越频率c ω对应时域性能指标 调整时间们反映了系统动态过程的快速性、(8分)试建立如图3所示电路的动态微分方程,并求传递函数。
自动控制原理期末考试试卷六套+(答案详解)

自动控制原理1一、 单项选择题(每小题1分,共20分)1. 系统和输入已知,求输出并对动态特性进行研究,称为( c )C.系统分析2. 惯性环节和积分环节的频率特性在( d )上相等。
D.穿越频率3. 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为( d )D.放大元件4. ω从0变化到+∞时,延迟环节频率特性极坐标图为(a )A.圆5. 当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个( d )D.惯性环节6. 若系统的开环传 递函数为2)(5 10+s s ,则它的开环增益为(c ) C.57. 二阶系统的传递函数52 5)(2++=s s s G ,则该系统是(b ) B.欠阻尼系统8. 若保持二阶系统的ζ不变,提高ωn ,则可以(b )B.减少上升时间和峰值时间9. 一阶微分环节Ts s G +=1)(,当频率T1=ω时,则相频特性)(ωj G ∠为( a ) A.45°10.最小相位系统的开环增益越大,其( d )D.稳态误差越小11.设系统的特征方程为()0516178234=++++=s s s s s D ,则此系统 ( )A.稳定12.某单位反馈系统的开环传递函数为:())5)(1(++=s s s k s G ,当k =( )时,闭环系统临界稳定。
C.3013.设系统的特征方程为()025103234=++++=s s s s s D ,则此系统中包含正实部特征的个数有( )C.214.单位反馈系统开环传递函数为()ss s s G ++=652,当输入为单位阶跃时,则其位置误差为( )D.0.0515.若已知某串联校正装置的传递函数为1101)(++=s s s G c ,则它是一种( ) D.相位滞后校正16.稳态误差e ss 与误差信号E (s )的函数关系为( )B.)(lim 0s sE e s ss →=17.在对控制系统稳态精度无明确要求时,为提高系统的稳定性,最方便的是( )A.减小增益18.相位超前校正装置的奈氏曲线为( )B.上半圆19.开环传递函数为G (s )H (s )=)3(3+s s K ,则实轴上的根轨迹为( ) C.(-∞,-3)20.在直流电动机调速系统中,霍尔传感器是用作( )反馈的传感器。
安徽大学期末试卷离散数学期末试卷及答案.doc

安徽⼤学期末试卷离散数学期末试卷及答案.doc⼀.判断题(共10⼩题,每题1分,共10分)在各题末尾的括号内画表⽰正确,画表⽰错误:1.设p、q为任意命题公式,则(p∧q)∨p ? p ( )2.?x(F(y)→G(x)) ? F(y)→?xG(x)。
( )3.初级回路⼀定是简单回路。
( )4.⾃然映射是双射。
( )5.对于给定的集合及其上的⼆元运算,可逆元素的逆元是唯⼀的。
( )6.群的运算是可交换的。
( )7.⾃然数集关于数的加法和乘法构成环。
( )8.若⽆向连通图G中有桥,则G的点连通度和边连通度皆为1。
( )9.设A={a,b,c},则A上的关系R={,}是传递的。
( )10.设A、B、C为任意集合,则A?(B?C)=(A?B)?C。
( )⼆、填空题(共10题,每题3分,共30分)11.设p:天⽓热。
q:他去游泳。
则命题“只有天⽓热,他才去游泳”可符号化为。
12.设M(x):x是⼈。
S(x):x到过⽉球。
则命题“有⼈到过⽉球”可符号化为。
13.p?q的主合取范式是。
14.完全⼆部图K r,s(r < s)的边连通度等于。
15.设A={a,b},,则A上共有个不同的偏序关系。
16.模6加群中,4是阶元。
17.设A={1,2,3,4,5}上的关系R={<1,3>,<1,5>,<2,5>,<3,3>,<4,5>},则R的传递闭包t(R) = 。
.18.已知有向图D的度数列为(2,3,2,3),出度列为(1,2,1,1),则有向图D的⼊度列为。
19.n阶⽆向简单连通图G的⽣成树有条边。
20.7阶圈的点⾊数是。
三、运算题(共5⼩题,每⼩题8分,共40分)21.求?xF(x)→?yG(x,y)的前束范式。
22.已知⽆向图G有11条边,2度和3度顶点各两个,其余为4度顶点,求G 的顶点数。
23.设A={a,b,c,d,e,f},R=I A?{,},则R是A上的等价关系。
安徽大学期末试卷MK08-09(1)高数C(三)答案.pdf

<
⎫ 1⎬
⎭
=
P⎨⎧− 1 < ⎩
X
− 10 4
< 1⎬⎫ ⎭
= Φ(1) − Φ(−1)
= Φ(1) − (1 − Φ(1))
= 2Φ(1) − 1
= 2 × 0.8413 −1 = 0.6826
(2)解法 1:
由正态分布的对称性知 c = 10.
解法 2:
因为 P ( X > c) = P ( X ≤ c)
4
4
故 X ,Y 相关。
15.(本小题 14 分)
∫ 解:
pX
(x)
=
⎪⎧
1
4xydy,0
⎨0
⎪⎩0, 其它
≤
x
≤
1
=
⎧2x,0 ≤ x ⎩⎨0, 其它
≤
1
同理有
pY
(
y)
=
⎧2 y,0 ≤ ⎩⎨0, 其它
y
≤
1
∫ EX =
1
x ⋅ 2xdx
=
2
0
3
同理,
∫ ∫ ∫ EY =
1 y ⋅ 2 ydy = 2
解:设 B = {取到的产品为次品}
10. (19.8728,20.1472)
A1 = {取到的产品来自于甲车间} A2 = {取到的产品来自于乙车间} A3 = {取到的产品来自于丙车间}
(1) 由全概率公式有
P(B) = P( A1 )P(B | A1 ) + P( A2 )P(B | A2 ) + P( A3 )P(B | A3 )
σn
1.1 6
1 − α = 0.95 ,故 z0.025 = 1.96
期末考试试题集-自动控制原理(含完整答案)

期末考试—复习重点自动控制原理1一、单项选择题(每小题1分,共20分)1. 系统和输入已知,求输出并对动态特性进行研究,称为()A。
系统综合B。
系统辨识C。
系统分析 D.系统设计2。
惯性环节和积分环节的频率特性在( )上相等。
A。
幅频特性的斜率B。
最小幅值C。
相位变化率 D.穿越频率3。
通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为( )A.比较元件B.给定元件C.反馈元件D。
放大元件4。
ω从0变化到+∞时,延迟环节频率特性极坐标图为( )A.圆B。
半圆C。
椭圆D。
双曲线5. 当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个()A.比例环节B。
微分环节 C.积分环节D。
惯性环节6. 若系统的开环传递函数为,则它的开环增益为()A。
1 B。
2 C。
5 D.107. 二阶系统的传递函数,则该系统是()A。
临界阻尼系统B。
欠阻尼系统 C.过阻尼系统 D.零阻尼系统8。
若保持二阶系统的ζ不变,提高ωn,则可以( )A。
提高上升时间和峰值时间B。
减少上升时间和峰值时间C.提高上升时间和调整时间D。
减少上升时间和超调量9。
一阶微分环节,当频率时,则相频特性为()A。
45° B.—45°C。
90° D.—90°10.最小相位系统的开环增益越大,其()A。
振荡次数越多B。
稳定裕量越大C.相位变化越小D。
稳态误差越小11.设系统的特征方程为,则此系统()A.稳定B.临界稳定C。
不稳定 D.稳定性不确定。
12。
某单位反馈系统的开环传递函数为:,当k=()时,闭环系统临界稳定。
A。
10 B。
20 C.30 D.4013。
设系统的特征方程为,则此系统中包含正实部特征的个数有( )A。
0 B.1 C。
2 D。
314.单位反馈系统开环传递函数为,当输入为单位阶跃时,则其位置误差为()A。
2 B.0。
2 C。
0。
5 D。
0。
10-11年度第一学期《自动控制原理》考卷A卷答案

安徽大学20 10 —20 11 学年第 一 学期《 自动控制理论 》(A 卷)考试试题参考答案及评分标准一、 选择题(每小题2分,共10分)1、D2、D3、A4、B5、A二、填空题(每空1分,共10分)1、10,0.7072、s 左半平面3、5,104、主导极点1p =1L =1∆=∆=()()C s R s1、()t 时,则ssr e =()1()n t t =时,212lim ()()1ssn en s e sN s s k k →=Φ=-+(4分)故21211ss ssr ssn k e e e k k -=+=+(2分)2、解:(10分)(1)系统有三个开环极点,2p ,1p ,0p 321-=-==没有开环零点,根轨迹起于,2p ,1p ,0p 321-=-==点,终止于无穷远处,共有三条根轨迹。
(1分) (2)由法则4可知道,实轴上的根轨迹区间为:]0,1[],2,[---∞。
(1分)(3)根轨迹渐进线与正实轴的夹角:(1分)1,0,3)12(±=+=k k a πϕ 有︒︒±=180,60a ϕ(4)根轨迹渐进线与正实轴的交点(1分)1321331-=--==∑=iiapσ(5)分离点(1分)21111=++++ddd解得58.1,42.021-=-=dd,根据实轴上的根轨迹区间可以知道,2d并不在根轨迹上,故舍去,42.01-=d是分离点。
实轴上的分离点的分离角为︒±90。
(6)根轨迹与虚轴的交点令jws=带入特征方程,并令实部虚部为0,有:⎪⎩⎪⎨⎧=+-=+-253223Kwww解得:⎩⎨⎧=±===6,414.1w)(0,03,21KKw舍去(1分)根据以上条件,绘制根轨迹如下图:(4分)当60<<k时,系统稳定。
3、(15分)解:系统的开环频率特性为:1()(1)10jG jjjωωωω+=-(2分)(0),(0);2()0,(0);2A j jA j jπϕπϕ+++→∞→∞→→-(4分)其Nyquist曲线如图所示。
2011级2013-2014年度第一学期《自动控制原理》期末考试试卷A卷参考答案

安徽大学20 13 —20 14 学年第 一 学期 《 自动控制理论 》考试试卷参考答案(A 卷)(闭卷 时间120分钟)考场登记表序号一、填空题(每小题2分,共18分) 1. 已知某闭环系统的单位脉冲响应为2()()2t t k t t e e δ--=-+,则系统的传递函数为12()112G s s s =-+++ ;2. 欠阻尼二阶线性系统的阻尼比和阻尼角的关系是cos ζβ= ;3. 线性定常控制系统的根轨迹起始于 开环极点 ,终止于 开环零点或无穷远处。
4. 已知某单位负反馈系统的开环传递函数为)5(20)(+=s s s G ,则其为 I 型系统,当输入为单位斜坡信号时,系统的稳态误差为 0.25或者1/4 。
5. 已知系统的开环传递函数为()()()10.51KG s s s s =++,其根轨迹图如图1所示,则在单位阶跃信号作用下,K 的取值情况:A 系统等幅振荡,临界稳定; D 系统为衰减振荡过程; A. 3K = B. 3K >图1 C. 00.193K << D. 0.1933K <<6. 设某最小相位系统的相频特性为()()101()tan 90tan T ϕωτωω--=--,则该系统的开环传递函数为(1)(1)K s s Ts τ++;7. 在系统串联校正过程中,超前校正的实质是 利用超前相位角m ϕ增大被校正系统的幅频截止频率和相角裕度,滞后校正的实质是 牺牲系统快速性(或者幅频截止频率)获取系统的稳定裕度 ;8. 已知某最小相位系统的开环频率特性为()()()()215.012100++=ωωωωωj j j j H j G ,当频率ω从0到正无穷大(∞+)变化时,该系统相频变化范围为 -90°→-360° ,幅频的倍频变化范围为 -20db/de c →-80 db/dec ;9. PID 校正控制在工业控制系统中应用广泛,通常应使I 部分发生在系统频率特性的 低 (选择“低、中、高”)频段,以提高系统的稳态性能;使D 部分发生在系统频率特性的 中 (选择“低、中、高”)频段,以提高系统的动态性能。
安徽大学高等数学期末试卷和答案

安徽大学2011—2012学年第一学期《高等数学A (三)》考试试卷(A 卷)院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------(闭卷 时间120分钟)考场登记表序号题 号 一 二 三 四 五 总分 得 分阅卷人得分 一、选择题(每小题2分,共10分)1.设A 为阶可逆矩阵,则下列各式正确的是( )。
n (A); (B)1(2)2A −=1A −11(2)(2)T T A A −−=; (C); (D)。
1111(())(())T T A A −−−−=11(())(())T T T A A −−−=12.若向量组12,,,r αα α可由另一向量组12,,,s ββ β线性表示,则下列说法正确的是( )。
(A); (B)r ;r s ≤s ≥(C)秩(12,,,r ααα )≤秩(12,,,s ββ β); (D)秩(12,,,r ααα ≥)秩(12,,,s ββ β)。
3.设,A B 为阶矩阵,且n A 与B 相似,E 为阶单位矩阵,则下列说法正确的是( )。
n (A)E A E B λλ−=−;(B)A 与B 有相同的特征值和特征向量; (C)A 与B 都相似于一个对角矩阵;(D)对任意常数,与k kE A −kE B −相似。
4.设123,,ααα为3R 的一组基,则下列向量组中,( )可作为3R 的另一组基。
(A)11212,,3ααααα−−; (B)1212,,2αααα+; (C)12231,,3αααααα++−; (D)12231,,3αααααα+++。
安徽大学期末试卷MK10-11(1)高数C(三)答案.pdf

∫ ∫ fY
(
y)
=
+∞ −∞
f
(x,
y)dx
=
⎧ ⎪6 ⎨ ⎪⎩
y 0
xdx, 0,
0
<
y
< 1,
=
⎧3 y 2 , ⎨
其它 ⎩ 0,
0 < y < 1, . 其它
(4)因为在 0 ≤ x ≤ y ≤ 1 内, f (x, y) ≠ fX (x) fY ( y) ,所以, X ,Y 不相互独立。
16. (本小题 14 分)【解】(1) f (x) = ⎧⎪⎨θ1 , 0 < x < θ, ⎪⎩ 0, 其他.
15. (本小题 12 分)【解】
∫ ∫ ∫ ∫ ∫ (1)因为1 =
+∞ +∞
f
−∞ −∞
(x, y)dxdy
=
1
A
0
1
xdx dy
x
=
1
A
0
x(1 −
x)dx
=
A[ x2 2
−
x3 3
]
|10
=
A; 6
所以 A = 6 。
1
1
1
∫∫ ∫ ∫ ∫ (2)
P ⎛⎜⎝Y
≤
1⎞ 2 ⎟⎠
=
y
≤
1 2
f
( x,
= C22 ⋅ 4 + C31 ⋅ C21 ⋅ 5 + C32 ⋅ 6 = 13 C52 10 C52 10 C52 10 25
C31 ⋅ C21 ⋅ 5
(2) P(B1
|
A)
=
P( AB1) P( A)
=
安徽大学自动控制原理期末考试试卷(三)和答案

安徽大学20 07 —20 08学年第 一 学期 《 自动控制理论 》考试试卷(A 卷)一、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)。
二、(共10分)已知系统结构图如下所示。
若系统在输入r(t)=t 作用下的稳态误差0.1ss e ≤, 试确定1K 的取值范围。
误差定义为E(s)=R(s)-C(s)。
三(共15分)已知单位反馈控制系统的开环传递函数为:)102.0)(101.0()(++=s s s Ks G要求:(1)绘制系统根轨迹图。
(2)确定系统的临界稳定开环增益c K 。
四、(共15分)某最小相位控制系统其单位反馈系统的开环传递函数的对数幅频曲线如下图所示:试求:当系统的输入为)305sin(2)(ot t r +=时系统的稳态输出)(t C 。
五、(共15分)已知系统开环传递函数,试绘制奈氏图,并根据奈氏判据,判断系统的稳定性:)1()3()()(>-+=K S S S K s H s G六、(共15分)已知单位负反馈系统开环传递函数为)11.0(200)(+=s s s G o ,试设计串联校正装置,使系统的相角裕度045γ≥,截止频率不低于55 rad/s 。
七、(每小题5分,共15分)某含有零阶保持器的采样系统结构如图所示,试求: (1) 当采样周期s T 1=时系统的临界开环增益c K ; (2) 求1,1==K s T 时系统单位阶跃响应)(kT C ; (3) 求系统在阶跃输入信号作用下的稳态误差。
安徽大学20 07 —20 08 学年第 一 学期《 自动控制原理 》考试试题参考答案及评分标准(A 卷)一:解1131122111G L G L G G L -=-=-= (4分)12223141,,,1P G G P G P G P G ====-14321=∆=∆=∆=∆ (4分)1211121211G G G G G G G ++=+++=∆ (4分) 12122121)()(G G G G G G s R s C +++=(3分)二、解 闭环传递函数为:1150()()(1)(0.051)50K C s R s s s s K =+++ 特征方程为:3210.05 1.05500s s s K +++=列出劳斯表:3211101 0.05 1 1.05 50K 1.05-2.5K1.0550Ks s s s由劳斯判据得到,闭环系统稳定时1K 的范围:10<K <0.421(1)(0.051)()()()()(1)(0.051)50s s s E s R s C s R s s s s K ++=-=+++因为21()R s s=所以11lim ()0.150ss e sE s K ==≤ 故10.2K <0.42 ≤三、解(1)根轨迹绘制如下:① n=3,有3条根轨迹,且均趋于无穷远处; ② 实轴上的根轨迹: (]]0,50[,100,--∞-③渐近线: ⎪⎪⎩⎪⎪⎨⎧±=+=-=--=πππϕσ,33)12(50310050k a a④ 分离点:010015011=++++d d d , 8.78,3.2121-=-=d d (舍去) (2)与虚轴交点:闭环特征方程D(s)= s 3+150s 2+5000s +5000K=0把s=j ω代入上方程,整理,令实虚部分别为零得:⎪⎩⎪⎨⎧=+-==+-=05000))(Im(05000150))(Re(32ωωωωωj D K j D 解得: 71.702,1±=ω 150=c K四、 由开环对数幅频曲线可以设开环传递函数为)11()(1+=S W S K s G其低频段对数幅频 w k w L lg 20lg 20)(-=,可知W=10时,L(10)=0;则得到K=10;由方程20lgK-20lgW1=40(lg 10-lgW1) 可以得到W1=1;根轨迹图即系统的开环传递函数为 )1(10)(+=S S s G 则系统的闭环传递函数为: 10)1(10)(++=S S s φ其频率特性为: jww jw jw jw +-=++=2101010)1(10)(φ当输入为)305sin(2)(ot t r +=时 w=5; 则 5151055101010)15(510)5(2j j j j j +-=+-=++=φ51010210510250102522510|)5(|===+=j φ4.1986.161))3/1tan(180()3/1tan(180)155()5(1=-=--=+=--=∠-a a tg j φ-稳态输出为)6.1315sin(26.1)6.161305sin(26.1))5(305sin(5102)(-=-+=∠++=t t j t t C o φ五、当K>1时 N +=2,N -=1, N=N +-N -=1, P=1,则Z=P-N=0 稳定 当K<1时 N +=0,N -=1, N=N +-N -=-1, P=1,则Z=P-N=2 不稳定 K=1,临界稳定 六、解:设校正前系统的剪切频率为1c ω,相位裕量为1γ,则有 010lg 40110lg20200lg 201=--c ω,得111557.44--=<=s s c c ωω 0001001456.121.090180=<=--=γωγc arctg选用串联超前校正。
安徽大学历年高等数学期末试卷

安徽大学历年高等数学期末试卷安徽大学《高等数学A(一)》2011--2012学年第一学期一、填空题(本题共5小题, 每小题2分, 共10分)1. 若+∞→x lim (12+-x x -(ax+b )= 0, 则a =▁▁▁▁▁▁▁▁▁,b = ▁▁▁▁▁▁▁▁ . 2. 设函数y = y(x) 由方程 52arctan 2=+-=e ty y t x t 所确定,y = y(x) 关于x 的一阶导数为▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁.3.若f(x)= ,0,1sin x x a 00=≠x x 在x=0处右导数存在,则a 的取值区间为▁▁▁▁▁▁. 4.求lnx 在x 0=1处带有Lagrange 型余项的n 阶Taylor 展开式: ▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁.5. 微分方程y "+y '=x 的通解为▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁.二、选择题(本题共5小题, 每小题2分, 共10分)1. 已知数列{x n }、{y n }满足∞→n lim x n y n =0, 则下列断言正确的是( ). A. 若{x n }发散, 则{y n }不发散.B. 若{x n }无界, 则{y n }必有界C. 若{x n }有界, 则{y n }必为无穷小量.D. 若{nx 1}为无穷小量, 则{y n }必为无穷小量. 2. 设f(x)= ∞→n lim1sin )1(2+-nx x n ,则( ). A.f(0)不存在. B. f(0) 存在,且x=0为可去间断点.C.f(0)存在, 且x=0为无穷间断点.D.f(x)在x=0处连续. 3. 曲线y=x 4-2x 2+2的拐点个数为( ).A. 0.B. 1.C. 2 D . 3.4. 设f '(x) 存在且连续,则[?)(x df ]'= ( ).A. f '(x).B. f '(x)+C. C. f(x).D. f(x)+C.5. 设f(x) 连续, 则下列函数中, 必为偶函数的是( ).A.dt t f x ?02)(. B.dt t f t f t x-+0))()((. C. dt t f x ?02)(. D.dt t f t f t x--0))()((三、计算题(本题共8小题, 每小题7分, 共56分)1. ∞→n lim nn n n 22cos sin +2. 若0lim →x x x f cos 1)(- = 4, 求0lim →x (1+xx f )()x 1. 3. 设a>0, a 1>0, a 1+n =21(a n +na a ), n=1,2, …. 求极限∞→n lim a n 4. 0lim →x 21x ?xtt sin 02arctan dt . 5.?+++)1ln(1)1(1x x dx . (x>0) 6.?-112x x dx . (x>0)7. 设xx sin 是f(x) 的一个原函数, 求?103)('dx x f x . 8. 求曲线Γ: y = dt t x0sin (x ∈[0, π]) 的长 .四、综合分析题(本题共2小题, 每小题7分, 共14分)1.讨论函数y =(x+1)2-3|x |在[-3,3)上的最值.2. 讨论广义积分?∞++01n m xx dx (n ≥0)的敛散性。
安徽大学《高等数学》2020-2021第一学期期末试卷
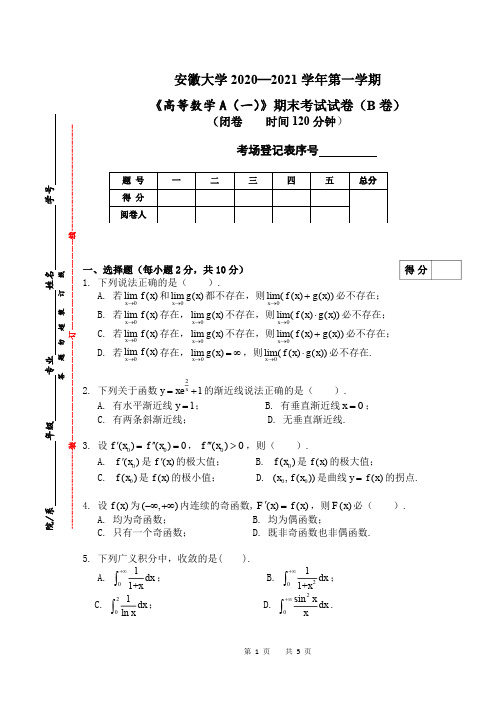
安徽大学2020—2021学年第一学期《高等数学A (一)》期末考试试卷(B 卷)(闭卷 时间120分钟)考场登记表序号一、选择题(每小题2分,共10分) 1. 下列说法正确的是( ).A. 若0lim ()x f x →和0lim ()x g x →都不存在,则0lim(()())x f x g x →+必不存在;B. 若0lim ()x f x →存在,0lim ()x g x →不存在,则0lim(()())x f x g x →⋅必不存在;C. 若0lim ()x f x →存在,0lim ()x g x →不存在,则0lim(()())x f x g x →+必不存在;D. 若0lim ()x f x →存在,0lim ()x g x →=∞,则0lim(()())x f x g x →⋅必不存在.2. 下列关于函数2e 1xy x =+的渐近线说法正确的是( ).A. 有水平渐近线1y =;B. 有垂直渐近线0x =;C. 有两条斜渐近线;D. 无垂直渐近线.3. 设00()()0f x f x '''==,0()0f x '''>,则( ).A. 0()f x '是()f x '的极大值;B. 0()f x 是()f x 的极大值;C. 0()f x 是()f x 的极小值;D. 00(,())x f x 是曲线()y f x =的拐点.4. 设()f x 为(,)-∞+∞内连续的奇函数,()()F x f x '=,则()F x 必( ). A. 均为奇函数; B. 均为偶函数;C. 只有一个奇函数;D. 既非奇函数也非偶函数.5. 下列广义积分中,收敛的是( ).A. 0l d 1+x x +∞⎰;B. 201d 1+x x +∞⎰; C. 201d ln x x ⎰; D. 20sin d xx x+∞⎰.院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------得分二、填空题(每小题2分,共10分)6.极限n →∞= .7.=y 是x 的函数,则d y = .8. e sin x y x =的10阶导数为 .9. 已知3 ()e x f x x '=且(1)0f =,则()f x = .10. 光滑曲线由极坐标()r r θ= ([,])θαβ∈表示,其弧长计算公式s = .三、计算题(每小题9分,共54分)11.求极限 1lim 2nn n n →∞+⎛⎫⎪+⎝⎭.12.求极限3limx x →.得分得分13.设11xy x ⎛⎫=+ ⎪⎝⎭,求导数y '.14. 计算 4d 1xx -⎰.15. 计算 12 0ln d x x ⎰.答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------16. 计算4422(sin 4cos )d x x x x ππ-+⎰.四、应用题(每小题8分,共16分)17. 求曲线 2e ,e ,t tx y -⎧=⎨=⎩在0t =相应的点处的切线方程和法线方程.得分18. 求由曲线36y x x =-与直线2y x =所围成的平面图形的面积.五、证明题(每小题10分,共10分)19. 设()f x 在(,)-∞+∞内连续,且()0f x >.证明00()d ()()d xx tf t tF x f t t=⎰⎰在(0,)+∞内单调增加.得分答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽大学20 07 —20 08学年第 一 学期 《 自动控制理论 》考试试卷(A 卷)
一、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)。
二、(共10分)已知系统结构图如下所示。
若系统在输入r(t)=t 作用下的稳态误差0.1ss e
≤, 试确定1K 的取值范围。
误差定义为E(s)=R(s)-C(s)。
三(共15分)
已知单位反馈控制系统的开环传递函数为:
)
102.0)(101.0()(++=
s s s K
s G
要求:(1)绘制系统根轨迹图。
(2)确定系统的临界稳定开环增益c K 。
四、
(共15分)
某最小相位控制系统其单位反馈系统的开环传递函数的对数
幅频曲线如下图所示:
试求:当系统的输入为
)305sin(2)(o
t t r +=时系统的稳态输出)(t C 。
五、(共15分)
已知系统开环传递函数,试绘制奈氏图,并根据奈氏判据,判断系统的稳定性:
)
1()
3()()(>-+=
K S S S K s H s G
六、(共15分)
已知单位负反馈系统开环传递函数为)
11.0(200
)(+=
s s s G o ,
试设计串联校正装置,使系统的相角裕度045γ≥,截止频率不低于55 rad/s 。
七、(每小题5分,共15分)
某含有零阶保持器的采样系统结构如图所示,试求: (1) 当采样周期s T 1=时系统的临界开环增益c K ; (2) 求1,1==K s T 时系统单位阶跃响应)(kT C ; (3) 求系统在阶跃输入信号作用下的稳态误差。
安徽大学20 07 —20 08 学年第 一 学期
《 自动控制原理 》考试试题参考答案及评分标准(A 卷)
一:解
1131122111G L G L G G L -=-=-= (4分)
12223141,,,1P G G P G P G P G ====-
14321=∆=∆=∆=∆ (4分)
1211121211G G G G G G G ++=+++=∆ (4分) 1
2122121)()
(G G G G G G s R s C +++=
(3分)
二、解 闭环传递函数为:
11
50()
()(1)(0.051)50K C s R s s s s K =+++ 特征方程为:
3210.05 1.05500s s s K +++=
列出劳斯表:
3211
1
01 0.05 1 1.05 50K 1.05-2.5K
1.05
50K
s s s s
由劳斯判据得到,闭环系统稳定时1K 的范围:
10<K <0.42
1
(1)(0.051)
()()()()(1)(0.051)50s s s E s R s C s R s s s s K ++=-=
+++
因为21()R s s
=
所以1
1
lim ()0.150ss e sE s K ==≤ 故10.2K <0.42 ≤
三、
解
(1)根轨迹绘制如下:
① n=3,有3条根轨迹,且均趋于无穷远处; ② 实轴上的根轨迹: (]]0,50[,100,--∞-
③渐近线: ⎪⎪⎩
⎪⎪⎨⎧±=+=-=--=πππϕσ,33)12(503
10050k a a
④ 分离点:
0100
1
5011=++++d d d , 8.78,3.2121-=-=d d (舍去) (2)
与虚轴交点:闭环特征方程
D(s)= s 3+150s 2+5000s +5000K=0
把s=j ω代入上方程,整理,令实虚部分别为零得:
⎪⎩⎪⎨⎧=+-==+-=0
5000))(Im(0
5000150))(Re(3
2
ωωωωωj D K j D 解得: 71.702,1±=ω 150=c K
四、 由开环对数幅频曲线可以设开环传递函数为
)11
()(1
+=
S W S K s G
其低频段对数幅频 w k w L lg 20lg 20)(-=,可知W=10时,L(10)=0;
则得到K=10;
由方程20lgK-20lgW1=40(lg 10-lgW1) 可以得到W1=1;
即系统的开环传递函数为 )1(10)(+=
S S s G 则系统的闭环传递函数为: 10)1(10
)(++=
S S s φ
其频率特性为: jw
w jw jw jw +-=
++=21010
10)1(10)(φ
当输入为
)305sin(2)(o
t t r +=时 w=5; 则 51510
55101010)15(510)5(2j j j j j +-=
+-=++=
φ
510
10
2
10510
25010
25
22510|)5(|=
==+=
j φ
4.1986.161))3/1tan(180()3/1tan(180)15
5
(
)5(1=-=--=+=--=∠-a a tg j φ-
稳态输出为)
6.1315sin(26.1)6.161305sin(26.1))5(305sin(510
2
)(-=-+=∠++=t t j t t C o φ
五、
当K>1时 N +=2,N -=1, N=N +-N -=1, P=1,则Z=P-N=0 稳定 当K<1时 N +=0,N -=1, N=N +-N -=-1, P=1,则Z=P-N=2 不稳定 K=1,临界稳定 六、
解:设校正前系统的剪切频率为1c ω,相位裕量为1γ,则有 010
lg 40110
lg
20200lg 201=--c ω,得111557.44--=<=s s c c ωω 0
001001456.121.090180=<=--=γωγc arctg
选用串联超前校正。
超前校正装置所需提供的最大超前角为:
000010455.125.1245=+-=+-=εγγϕm 则:8.5707
.01707
.01sin 1sin 1=-+=-+=
m m a ϕϕ 设校正后剪切频率为c ω且m c ωω=,令1
lg
40lg 10c c a ωω=,得14.69-=s c ω
则:121
18.28,1.167--==
==s a
s a c
c ωωωω
超前校正装置的传递函数为:1
006.01
035.0)(++=
s s s G c
校正后系统的传递函数为:)
11.0(200
1006.01035.0)()()(0+∙++==s s s s s G s G s G c
验证:
000455.510064.0034.01.090180>=-+--=c c c arctg arctg arctg ωωωγ
满足要求。
七、]
1[]1)[1(
)(T
T
T
e z e
K e z z
z z z z K z G -----=====----=
(1)
16
.20632.0632.0368.1368.0632.00
632.0*368.0)368.01()368.0()(0
)(1)(1<<<-<-+-==+-=-+-==+==K K K z K z K z z D z G z D T 时当
(2))
)264.0(1(5.0)()
264.0)(1(632.0)(264.0632
.0)(1)()(368.0632
.01)(1111
k k C z z z
z C z z G z G z z e z e z G T K --=+-=
+=+=-=
--=
==--φ时
和当
1
1)3(+=
k ee。
