平行四边形的图形变换

合集下载

人教版八年级数学下册《平行四边形的性质》平行四边形PPT优质教学课件

10 ●O
∴AC= AB2−BC2= 102−82=6
∵OA=OC，∴OA=12AC=3
B
C
∴S ABCD= BC×AC=8×6=48．
随堂检测
1．如图，在▱ABCD中，对角线AC、BD相交于点O，若 AC＝14，BD＝8，AB＝10，则△OAB的周长为 21 ．
2．如图，平行四边形ABCD中，AD＝5cm，AB⊥BD，点O是两条对角线的交点，OD＝2cm，则AB＝ 3 cm．
叫做这两条平行线之间的距离．
如图，直线a∥b，A是直线a上的任意
A
a
一点，AB ⊥b ，B是垂足，线段AB的
b
长就是a、b之间的距离．
B
随堂检测
1．如图，在 ABCD中，
A
D
A：基础知识：
B
C
若∠A=130°，则∠B=_5_0_°___ 、∠C=_1_3_0_°__ 、∠D=__5_0_°__．
B：变式训练：（1）若∠A+ ∠C= 200°，则∠A=__1_0_0_°_ 、∠B=__8_0_°__；（2）若∠A：∠B= 5：4，则∠C=__1_0_0_°_ 、∠D=___8_0_°_．
随堂检测
C:拓展延伸：
A
D
如图，在 ABCD中，
B
C
（1）∠A：∠B ： ∠C ： ∠D的度数可能是( B )
A． 1 ： 2 ： 3 ： 4
B．3 ： 2 ： 3 ： 2
C．2 ： 3 ： 3 ： 2
D．2 ： 2 ： 3 ： 3
（2）连接AC，若∠D=60°， ∠DAC=40°，则 ∠B=_6_0_°_，
一条直线的距离相等．
已知：如图，EF∥MN，A，D是直线

四边形与图形变换

五、四边形与图形变换1. 概念（1）四边形四边形有关知识① n 边形的内角和为．外角和为．② 如果一个多边形的边数增加一条，那么这个多边形的内角和增加，外角和增加．③ n 边形过每一个顶点的对角线有条，n 边形的对角线有条．（2）平面图形的镶嵌① 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个____________时，就拼成一个平面图形.② 只用一种正多边形铺满地面，请你写出这样的一种正多边形____________．（3）平面的密铺定义：把形状、大小完全相同的一种或几种平面图形拼接在一起，使得平面上不留空隙，不重叠，这就是平面图形的密铺，也叫平面图形的镶嵌．（4）对于限于用一种图形密铺的问题，有三角形、四边形和正六边形，如果能实现平面图形的密铺，密铺图的每个顶点都必须集中在几个多边形的顶角，于是在每个顶点集中的顶角刚好拼成一个周角．※易错知识辨析多边形的内角和随边数的增加而增加,但多边形的外角和随边数的增加没有变化，外角和恒为360 º．（5）平行四边形① 平行四边形的性质1) 平行四边形对边______，对角______；角平分线______；邻角______.2) 平行四边形两个邻角的平分线互相______，两个对角的平分线互相______．（填“平行”或“垂直”）3) 平行四边形的面积公式____________________.② 平行四边形的判定1) 定义法：两组对边的四边形是平行四边形.2) 边：两组对边的四边形是平行四边形；一组对边的四边形是平行四边形．3) 角：两组对角的四边形是平行四边形．4) 对角线：对角线的四边形是平行四边形．（6）特殊的平行四边形的之间的关系平行四边形矩形菱形正方形（7）特殊的平行四边形的判别条件成为矩形，需增加的条件是_______ _____ ；成为菱形，需增加的条件是_______ _____ ；要使矩形ABCD成为正方形，需增加的条件是______ ____ ；要使菱形ABCD成为正方形，需增加的条件是______ ____ .（9）梯形①梯形的面积公式是________________.②等腰梯形的性质：边 __________________________________.角 __________________________________.对角线 __________________________________.③等腰梯形的判别方法__________________________________.④梯形的中位线长等于__________________________.（10）轴对称及轴对称图形的意义①轴对称：两个图形沿着一条直线折叠后能够互相重合，我们就说这两个图形成轴对称，这条直线叫做对称轴，两个图形中的对应点叫做对称点，对应线段叫做对称线段．②如果一个图形沿某条直线对折后，直线两旁的部分能够互相重合，那么这个图形就叫做轴对称图形，这条直线叫做对称轴．③轴对称的性质：如果两个图形关于某广条直线对称，那以对应线段相等，对应角相等，对应点所连的线段被对称轴垂直平分．④简单的轴对称图形：线段：有两条对称轴：线段所在直线和线段中垂线．角：有一条对称轴：该角的平分线所在的直线．等腰(非等边）三角形：有一条对称轴，底边中垂线．等边三角形：有三条对称轴：每条边的中垂线．（11）中心对称图形①定义：在平面内，一个图形绕某个点旋转180○，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心．②性质：中心对称图形上的每一对对应点所连成的线段都被对称中心平分．③中心对称与旋转对称的关系：中心对称是旋转角是180o的旋转对称．④中心对称的判定：如果两个点的连线被某一点M平分，则这两个点关于点M成中心对称．（12）图形的平移①平移的概念：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移，平移不改变图形的形状和大小．注意:①平移是运动的一种形式，是图形变换的一种，本讲的平移是指平面图形在同一平面内的变换．②图形的平移有两个要素：一是图形平移的方向，二是图形平移的距离，这两个要素是图形平移的依据．③图形的平移是指图形整体的平移，经过平移后的图形，与原图形相比，只改变了位置，而不改变图形的大小，这个特征是得出图形平移的基本性质的依据．（13）平移的基本性质：由平移的基本概念知，经过平移，图形上的每一个点都沿同一个方向移动相同的距离，平移不改变图形的形状和大小，因此平移具有下列性质：经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．注意：①要正确找出“对应线段，对应角”，从而正确表达基本性质的特征．②“对应点所连的线段平行且相等”，这个基本性质既可作为平移图形之间的性质，又可作为平移作图的依据．（14）简单的平移作图平移作图：确定一个图形平移后的位置所需条件为：①图形原来的位置；②平移的方向；③平移的距离．（15）图形的旋转①旋转的概念：图形绕着某一点（固定）转动的过程，称为旋转，这一固定点叫做旋转中心。

教材分析之第十八章平行四边形

第十八章平行四边形一、地位与作用同三角形一样，四边形也是最基本的平面图形，是本学段“空间与图形”的主要研究对象．本章将在平行线、三角形的基础上进一步研究一些特殊四边形的知识，探索平行四边形、矩形、菱形、正方形的有关性质和常用判定方法，并对有关结论进行推理证明，进一步发展学生的逻辑思维能力和推理论证能力，对学生要求较高. 就本学期的教学内容来讲，本章是教学重点和难点之一. 就中考来讲，四边形的知识会以填空题、中档解答题、动手操作题、综合解答题等形式进行考察，2014年只有16题、20题涉及本章知识，分值为约3+4分，2015年只有20题、22题、23题涉及本章知识，分值为约4+4+1分，2016年只有14题、16题涉及本章知识，分值为3+3分，从近几年武汉的中考题看来，本章考试所占分值还是很重要的. 所以，学好这一章，既是对三角形知识的巩固，又是为后续的几何学习做好充分的知识和能力储备，更是为中考打下坚实的基础。

二、知识结构图从属关系:演变关系：三、课标要求及学习目标1、【课标要求】1、“理解平行四边形、矩形、菱形、正方形的概念，以及它们之间的关系”，这种“关系”是特殊与一般的关系，即图形越来越特殊，它的性质就越来越多，判定它需要的条件也越来越多，这对于研究平行四边形、矩形、菱形、正方形的性质和判定有着重要的作用。

这部分知识像链条一样环环紧扣，这条“知识链”不仅蕴涵着“一般和特殊”的思想，而且也是引导学生感悟“分类”思想的好素材。

2、四边形与三角形有着紧密的联系，研究四边形性质常常借助三角形的有关知识。

但是四边形与三角形有一个本质的差异：四边形不具有稳定性，三角形是具有稳定性。

如果不重视这种差异，就会给理解和掌握相关的知识带来困难。

比如，学生常常不能正确掌握正多边形的定义，其原因就是在于边数大于或等于4的多边形不具有稳定性，由各边相等不能推出各个角相等，所以必须定义“各边相等、各角相等的多边形叫做正多边形”；而三角形具有稳定性，由三边相等可以推出三个角相等，所以只需定义“各边相等的三角形叫做正三角形”。

探索平行四边形的特点

探索平行四边形的特点平行四边形是几何学中一种重要的图形，具有一些独特的性质和特点。

在本文中，我们将深入探讨平行四边形的定义、特征、性质和应用。

一、平行四边形的定义和特征平行四边形是由四条边组成的四边形，它的对边互相平行。

平行四边形具有以下特征：1. 对边平行特性：平行四边形的对边是互相平行的。

这意味着相邻两边的方向是平行的，永远不会相交。

2. 对角线交点连线平分特性：平行四边形的对角线相交于一个点，并且这个点将对角线等分。

也就是说，对角线的中点是平行四边形的顶点。

二、平行四边形的性质平行四边形除了上述定义和特征外，还具有一些重要的性质。

1. 边长性质：平行四边形的对边长度相等。

这意味着相对的两条边长度是相等的。

2. 角度性质：平行四边形的内角和为360度。

相邻两个内角以及对角的和都等于180度。

3. 直角性质：特殊情况下，平行四边形可以是矩形，其中每个角都是直角。

这意味着平行四边形可以包含正方形作为一种特例。

4. 对边比例性质：平行四边形两对对边的长度比例相等。

这意味着，如果一对对边的长度比例为a:b，那么另一对对边的长度比例也为a:b。

三、平行四边形的应用平行四边形的性质和特点在实际中有广泛的应用。

1.建筑设计：平行四边形的性质使得它在建筑设计中被广泛应用。

一些建筑物的地基、墙壁和天花板等常常设计为平行四边形，以增加结构的稳定性和美观性。

2.工程计算：平行四边形的对边比例性质在工程计算中起到重要作用。

例如，当计算桥梁或电线杆的倾斜度时，可以利用平行四边形的对边比例关系来确定相应的长度。

3.计算面积和周长：平行四边形的面积计算可以通过底边和对应的高来求解。

周长计算可以通过四边的边长之和来得到。

4.图形变换：平行四边形在平移、旋转和镜像等图形变换中有很多应用。

例如，在制作地图和计算机图像处理中，平行四边形的变换被广泛用于投影和坐标转换。

结论通过对平行四边形的定义、特征、性质和应用的深入探讨，我们可以更好地理解和应用这一几何图形。

专题特殊的平行四边形中的图形的折叠模型(学生版)

专题11特殊的平行四边形中的图形的折叠模型几何变换中的翻折（折叠、对称)问题是历年中考的热点问题，试题立意新颖，变幻巧妙，主要考查学生的识图能力及灵活运用数学知识解决问题的能力。

翻折以矩形对称最常见，变化形式多样。

无论如何变化，解题工具无非全等、相似、勾股以及三角函数，从条件出发，找到每种对称下隐藏的结论，往往是解题关键。

本专题以各类几个图形（菱形、矩形、正方形等）为背景进行梳理及对应试题分析，方便掌握。

【知识储备】折叠问题的解决,大都是以轴对称图形的性质作为切入点，而数形变化,是解决这类问题的突破口。

有了“折”就有了”形”--轴对称图形、全等形；有了“折”就有了“数”--线段之间、角与角之间的数量关系。

"折”就为“数”与“形”之间的转化搭起了桥梁。

特殊平行四边形中的折叠问题,还要考虑特殊平行四边形本身的性质,有时也需要用到计算工具：相似和勾股定理。

折叠的性质:重合部分是全等图形,对应边、对应角相等；对称点的连线被对称轴垂直平分。

【知识储备】（1）矩形的翻折模型【常见模型】BC A ．3.6B ．4.8例2．（2023春·河南商丘·八年级统考期末）如图，在长方形使得点D 落在BC 边上D ¢处，则DE 的长是（A ．3B ．4例3．（2023春·广东潮州·八年级统考期末）如图矩形交于点E ，若4,8AB AD ==．(1)求证：例4．（2023·贵州·八年级统考期末）如图，在矩形得到FBE ，EF 交BC 于点H ，延长A ．5B ．2ABA．35B．25例6．（2023春·江苏连云港·八年级统考期末）如图，矩形心，点E为边AB上的动点，连接EO例7．（2023春·河南南阳·八年级校考阶段练习）如图，将矩形EH=，EF=重叠的四边形EFGH，3cmA．18cm B．18.4cm（2）菱形的翻折模型【常见模型】A ∠结论I ：当'A N AD ∥时，四边形'ANA M 是菱形；结论Ⅱ：当点'A 在线段MC 上时，'AC 的长度为A ．I 对Ⅱ不对B ．I 不对Ⅱ对A ．①②④B ．①②③如图所示，点A ．90CEF ∠=︒B ．CE AG ∥C（3）正方形的翻折模型【常见模型】上取一点例4．（2023春·重庆·八年级专题练习）如图，在正方形翻折，使点D的对应点D¢恰好落在的垂直平分线分别交EF、A D''于点在边例6．（2023·广东深圳·统考中考模拟）如图在正方形对角线AC上，将AD沿AF翻折，使点例7．（2023春·江苏宿迁·八年级统考期末）问题情境：如图1，在正方形ABCD 中，6AB =，点F 是边AD 上一点（点F 不与,A D 重合），将CDF 沿直线CF 翻折，点D 落在点E 处．(1)如图2，当点E 落在对角线AC 上时，求DF 的长．(2)如图3，连接,,AC BD BD 分别交,CF AC 于点M ，点O ，连接OE 并延长交AD 于点G ，当M 为OD 中点时，试判断OG 与CF 的位置关系，并说明理由．(3)如图4，在线段CE 上取一点Q ，且使2CQ =，连接,AE BQ ，则在点F 从点A 运动到点D 的过程中，AE BQ +的值是否存在最小值？如果存在，请求出其值；若果不存在，请说明理由．课后专项训练A．23B．232-C．52．（2023春·江苏·八年级专题练习）如图，菱形ABCD的对角线相交于点所示的方式折叠，使点B与O重合，折痕为EF，则五边形A．14B．16C上，将A．3个B．2个C．0个边上，连接A ．230α-︒B ．30α+︒C ．1208．（2023春·重庆合川·八年级统考期末）如图，在矩形沿BE 所在直线翻折至四边形BCDE 所在平面内，得的面积为（）A ．63B ．83，将矩形纸片翻折，使点A．12B．1511．（2023·江苏苏州·校考二模）如图，正方形连接BE，将ABE沿BE翻折得到A．5510-B．512．（2023·陕西西安·八年级校考期末）如图，正方形A．107B．52C的对角线17．（2023·河南信阳·校考三模）如图，在矩形ABCD 中，6AB =，10BC =，将矩形翻折，使边18．（2023春·江苏无锡·八年级校考期中）如图，矩形得到AD C '，CD '与AB 交于点E ，再以CD19．（2023·江苏苏州·八年级统考期末）如图，在正方形ABCD 中，点E 是边AB 的中点，将BCE 沿CE 翻折得到GCE ．延长CG 交AD 于点H ，连接EH ．(1)求证：EAH EGH ≌△△；(2)若10AB =，求CH 的长．20．（2022秋·江西景德镇·九年级统考期中）【操作体验】如图，在正方形ABCD 中，点E 在AB 边上，点F 在CD 边上．将四边形EBCF 沿直线EF 翻折，得到四边形EHGF ，顶点B 落在AD 边上的点H （不与点A 、D 重合）处，点C 落在正方形右侧的点G 处，HG 与CD 相交于点P ．（1）在图1中，若4cm AE =，45AEH ∠=︒，则HD =_____cm ，EFG ∠的度数为_________【操作体验】（2）当2BE AE =时，如图2，求证：2PF CF =．【操作体验】（3）利用图3探究，当正方形边长不变时，随着折痕EF 的变化，DHP 的周长是否会发生变化？如果会，请说明变化规律；如果不会，请加以证明，并探究正方形周长与DHP 的周长的关系．，。

平行四边形恒等变换

平行四边形恒等变换
平行四边形是一种特殊的四边形，具有两对平行边。

平行四边形恒等变换是指通过变换操作保持平行四边形的形状和大小不变。

平行四边形恒等变换的基本操作有平移、旋转和对称变换。

1. 平移变换：
平移变换是将平行四边形沿着一定方向移动一段距离，同时保持平行四边形的形状和大小。

平行四边形的对应边保持平行，对应角保持相等。

平移变换可以使用向量来表示，其中向量的大小和方向表示平移的距离和方向。

2. 旋转变换：
旋转变换是将平行四边形按照某个旋转中心旋转一定角度，同时保持平行四边形的形状和大小。

旋转变换可以使用旋转矩阵来表示，其中旋转矩阵根据旋转角度来确定平行四边形的旋转方向。

3. 对称变换：
对称变换是将平行四边形按照一条直线或一个点进行对称，同
时保持平行四边形的形状和大小。

对称变换可以使用对称轴或对称
中心来表示，其中对称轴可以是平行四边形的边或对角线，对称中
心可以是平行四边形的重心或中点。

平行四边形恒等变换在几何学和图形变换中具有重要的作用。

通过平行四边形恒等变换，我们可以推导出平面上其他图形的变换
规律，并进行相关的几何证明和计算。

总结：平行四边形恒等变换包括平移、旋转和对称变换三种基
本操作，通过这些变换操作可以保持平行四边形的形状和大小不变。

平行四边形的特性

平行四边形的特性平行四边形是一种具有特殊几何性质的四边形，它拥有独特的性质和特点。

本文将详细介绍平行四边形的特性。

一、基本定义平行四边形是指具有两组对边分别平行的四边形。

根据这个定义，我们可以得出以下结论：1. 对边平行性：平行四边形的两组对边分别平行。

即，AB || CD，AD || BC。

2. 对角线关系：平行四边形的对角线互相平分，并且互相垂直。

即，AC和BD互相平分，同时AC ⊥ BD。

二、对边和角的特性1. 对边长度关系：平行四边形的对边长度相等。

即，AB = CD，AD = BC。

2. 对角线长度关系：平行四边形的对角线长度相等。

即，AC = BD。

3. 内角和：平行四边形的内角和为360度。

即，∠A + ∠B + ∠C +∠D = 360°。

三、角的特性1. 对角的特点：平行四边形的相对的内角是对等的。

即，∠A =∠C，∠B = ∠D。

2. 同位角关系：平行四边形的同位角（同位于两对顶点的角）是相等的。

即，∠A = ∠C，∠B = ∠D。

3. 内角关系：平行四边形的内角是对补的。

即，∠A + ∠D = 180°，∠B + ∠C = 180°。

四、边和角的特性1. 对边共线性：平行四边形的对边延长线会相交于一点，使得对边共线。

2. 相邻角关系：平行四边形的相邻角是补角。

即，∠A + ∠B = 180°，∠B + ∠C = 180°，∠C + ∠D = 180°，∠D + ∠A = 180°。

3. 交替角关系：平行四边形的交替角是相等的。

即，∠A = ∠C，∠B = ∠D。

四、平行四边形的判定1. 充分条件：如果一个四边形的两对边分别平行，则它是一个平行四边形。

2. 必要条件：如果一个四边形是平行四边形，则它的两对边分别平行。

五、平行四边形的应用平行四边形的性质在几何学和应用数学中有广泛的运用。

它们可以用于解决各种实际问题和证明几何命题，例如：1. 面积计算：平行四边形的面积可以通过底边长度和高的乘积来计算。

初中数学八年级下册第十八章《平行四边形》简介

初中数学八年级下册第十八章《平行四边形》简介平行四边形是特殊的四边形。

本章我们在平行线、三角形和四边形的基础上进一步研究平行四边形；并通过平行四边形角、边的特殊化，研究矩形、菱形和正方形等特殊的平行四边形，认识这些概念之间的联系与区别，明确它们的内涵与外延；探索并证明平行四边形、矩形、菱形、正方形的有关性质定理和判定定理，进一步明确命题及其逆命题的关系，不断发展学生的合情推理和演绎推理能力。

本章教学时间约需14课时，具体分配如下（仅供参考）：18.1 平行四边形6课时18.2 特殊的平行四边形6课时数学活动小结2课时一、教科书内容和本章学习目标（一）本章知识结构框图（二）教科书内容平行四边形是常见的几何图形，既有丰富的性质，又在现实生活中具有广泛的应用，尤其是矩形、菱形、正方形等特殊平行四边形的性质更加丰富、应用更加广泛。

学生在第一学段已经学习过平行四边形，本学段七年级下册“三角形”一章中研究了多边形及其内角和等内容，包括四边形及其内角和；八年级上册“全等三角形”一章又研究了三角形全等的判定及全等三角形的性质。

这些内容是学习本章的重要基础。

本章引言直接进入特殊的四边形——平行四边形：两组对边分别平行的四边形的学习，在平行四边形的基础上，学习矩形、菱形、正方形这些特殊平行四边形。

“18.1 平行四边形”主要研究平行四边形的概念、性质定理和判定定理；在平行四边形概念和性质的基础上，介绍两条平行线间距离的概念；作为性质定理和判定定理的一个应用，探究并证明三角形中位线定理。

“18.2 特殊的平行四边形”首先研究特殊的平行四边形：矩形和菱形，它们分别是有一个角是直角，或有一组邻边相等的特殊的平行四边形。

18.2.1和18.2.2分别研究矩形和菱形的概念、性质定理和判定定理，在矩形和菱形的基础上，再研究它们的特殊情况：同时具有两个特殊条件的平行四边形：正方形，它是有一个角是直角的特殊菱形，或者是有一组邻边相等的特殊矩形。

初中数学几何变换之平移

平移的性质：1．经过平移，对应点的连线平行且相等，对应边平行或在一条边上且相等，对应角度相等．2．平移前后，所对应的图形全等．1．平行四边形与平移变换由于在平移变换下，与平移方向不平行的线段变为与原线段平行且相等的线段，因此，对于已知条件中有平行四边形的平面几何问题，我们就可以考虑用平移变换处理．平移沿平行四边形的某条边进行．2．平行六边形和平移变换因为在平移变换下，平面上任意一点与其像点的连线总是平行于平移方向的，所以对于条件中有平行线（或平行线段）的平面几何问题当然也可以考虑用平移变换处理，平移方向平行于平行线（或平行线段），平移距离则要视具体情况（特别是所要证明的结论）而定．这种平移方式经常用来对分散图形进行集中．如图所示，P 为平行四边形ABCD 内一点，求证：以AP 、BP 、CP 、DP 为边可以构成一个四边形，并且所构成的四边形的对角线的长度恰好分别等于AB 和BC ．A CD BPA CD BPQ如图所示，将PAB △平移至QDC △的位置，易证DQ AP =，CQ BP =，则四边形DPCQ 恰好是一个以AP 、BP 、CP 、DP 为边的四边形，并且它的对角线恰好等于平行四边形ABCD 的两条邻边．模块一平行多边形和平移的构造如图2-1，四边形EFGH 中，若12∠=∠，则3∠必然等于4∠．请运用结论证明下述问题：如图2-2，在平行四边形ABCD 中取一点P ，使得56∠=∠，求证：78∠=∠．F GHE1423 B A D C 5867P图2-1 图2-2【分析】此题为信息题，难点在于如何理解已知条件，经观察我们发现，若1∠和2∠，位置为时，可得出3∠和4∠相等（本质为四点共圆），图（2）中，5∠与6∠关系并不像条件所示，因此，需要改变角位置，而这点可以通过构造平行四边形来解决．而构造平行四边形，恰可以达到改变角位置作用，为使5∠与6∠成形，我们可有如下四种方法．分别过点B 、P 作BK AP ∥，PK AB ∥，交于点K ，连接CK ．∵BK AP ∥，PK AB ∥，∴BK AP =，PK AB =，5BKP ∠=∠，7BPK ∠=∠ ∵AB CD =，AB CD ∥，∴PK CD ∥，PK CD =∴四边形PKCD 为平行四边形，∴PD CK =，∵AD BC = ∴ADP BCK △≌△，∴8BCK ∠=∠在四边形BKCP 中，56BKP ∠=∠=∠，∴BPK BCK ∠=∠，∴78∠=∠8765B DCA KPK8765PDCBA （6∠不动移5∠）（5∠不动移6∠）KA BCDP 5678K8765P D C BA （5∠，6∠均移动）（5∠，6∠均移动）【教师备课提示】老师们可以让学生自由发挥，体味构造平行四边形带来的快乐．如图，以ABC △的边AB 、AC 、BC 为一边，分别向三角形的外侧作正方形ABDE 、正方形ACGF 、正方形BCMN ．以EF 、DN 、GM 为边能否构成三角形？为什么？DE FGNMBCADE FGNMBCPA过点E 作PE DN ∥，过点N 作PN DE ∥，PE 与PN 交于点P ，连结PM 、PF ．∵PE DN ∥，DE PN ∥，∴DE PN =，PE DN =∵AB DE ∥，PN DE ∥，∴AB PN ∥，∵BC MN ∥，∴ABC PNM ∠=∠，∵AB DE PN ==，BC NM =，∴ABC PNM △≌△ ∴AC PM FG ==，ACB PMN ∠=∠，∴AC FG PM ∥∥， ∴四边形FGMP 是平行四边形， ∴MG PF =∴PEF △就是以EF 、DN 、GM 的长为边的三角形．【教师备课提示】这道题还可以给学生拓展PEF △的面积为ABC △的3倍.如图所示，一个六边形的六个内角都是120︒，连续四边的长依次是1、3、3、2，则该六边形的周长是多少？2133D F EC B AC 1E 12133A 1DF EC B A（方法1）：如图所示，由于六边形的内角都是120︒，易知CD AF ∥，AB ED ∥，BC FE ∥．把BC 、DE 、F A 分别平移至1AC 、1CE 、1EA ，可得等边111AC E △，其边长11111C E CE CC DE BA =-=-=．在此基础上可求得EF 、AF 的长，进而求得六边形的周长：11111312EF AA AC C A BC ==-=-=-=， 11111134AF A E A E E E CD ==+=+=+=，故六边形的周长是13322415+++++=．（方法2）：如图所示，将六边形补全为等边PQR △．易得PQR △的边长为1337++=，则7322EF =--=，7124FA =--=，故六边形的周长是13322415+++++=．在六边形ABCDEF 中，AB DE ∥，BC EF ∥，CD AF ∥，对边之差BC EF -= 0ED AB AF CD -=->．求证：六边形ABCDEF 的各内角均相等．FE DCBAPFE RQD CBA平移线段DE 到CR ，平移线段BC 到AQ ，平移线段F A 到EP ，如图所示，得到PQR △．易知PQ AQ AP BC EF =-=-， RQ RC QC ED AB =-=-，PR PE RE AF CD =-=-．由于BC EF ED AB AF CD -=-=-，∴PQ RQ PR ==，即PQR △是等边三角形， 60PQR QRP RPQ ∠=∠=∠=︒．故6060120DEF DER REF QRP RPQ ∠=∠+∠=∠+∠=︒+︒=︒． 180********CDE CRE QRP ∠=∠=︒-∠=︒-︒=︒．同理，120DCB CBA BAF AFE ∠=∠=∠=∠=︒， ∴六边形ABCDEF 的各内角均相等．如图所示，在六边形ABCDEF 中，AB ED ∥，AF CD ∥，BC FE ∥，AB ED =，AF CD =，BC FE =．又知对角线FD BD ⊥，24FD =厘米，18BD =厘米．请你回答：六边形ABCDEF 的面积是多少平方厘米？2133RQPD F EC B AACDBFEACDBFEG将DEF △平移到BAG △的位置；将BCD △平移到GAF △的位置，则长方形BDFG 的面积等于六边形ABCDEF 的面积．易知长方形BDFG 的面积等于2418432⨯=（平方厘米）， ∴六边形ABCDEF 的面积是432平方厘米．设凸六边形ABCDEF 的三组对边分别平行．求证：ACE △的面积与BDF △的面积相等．如图，将B 、D 、F 分别沿CD 、EF 、AB 平移至B '、D '、F '，则F '在BB '上，B '在DD '上，D '在FF '上，且D F AB DE ''=-，F B CD FA ''=-，B D EF BC ''=-．记六边形ABCDEF 的面积为S ，B D F '''△的面积为T ．因四边形FABF '、BCDB '、DEFD '均为平行四边形，于是，11()()22BDF S S T T S T =-+=+△．AB CDEFB'D'F'AB C DEFA'C'E'同样，如果我们作另外三个平移变换将六边形用类似的方式剖分为三个平行四边形与一个三角形A C E '''，则有||A C AB DE ''=-，||C E CD FA ''=-，||E A EF BC ''=-．因而A C E '''△的面积也为T ，于是也有1()2ACE S S T =+△，故BDF ACE S S =△△．AB CDEF如果两条相等线段既不平行也不共线，则其中一条线段不可能是另一条线段在某个平移变换下的像．但我们可以通过平移变换移动其中的一条线段，使两条线段有一个公共端点，然后通过等腰三角形的性质再加上其他相关条件使问题得到解决．如图所示，两条长度为1的线段AB 和CD 相交于O 点，且60AOC ∠=︒，求证：1AC BD +≥．CAOBDCAO'B DB考虑将AC 、BD 和AB 集中到同一个三角形中，以便运用三角形的不等关系．作CB AB '∥且CB AB '=，则四边形ABB C '是平行四边形，从而AC BB '=．在BB D '△中可得BB BD B D ''+≥，（当AC BD ∥时，BB BD B D ''+=），即AC BD B D '+≥．由于1CD AB CB '===，60B CD AOC '∠=∠=︒，所以B CD '△是等边三角形，故1B D '=，所以1AC BD +≥．如图，ABC △中，AB AC =，D 、E 是AB 、AC 上的点且AD CE =．求证：2DE BC ≥．EDCB AGHFEDC B AABC D EFHG H G HFEDC B A方法一：通过构造平行四边形把DE 和12BC 平移成共顶点的线段（如下图，作中位线利用斜边大于直角边）．模块二共端点的平移构造方法二：通过构造平行四边形平移DE ，使得DE 和BC 共顶点．下面写出方法二的解析：（如下图2）过点B 作BF DE ∥，且BF DE =，连接EF 、FC ． ∴DAE CEF =∠∠，AE BD EF ==又∵AD EC = ∴ADE ECF △≌△，∴DE CF = ∴BF CF BC +≥ 即2DE BC ≥，当且仅当DE 为ABC △的中位线时，取到等号．另外，此题还可以如图1，3，4那样平移，每次均产生一个平行四边形、一对全等三角形，和一个新的等腰三角形．图1图2图3图4ABCDE FABCDE F ABC DEFFE DC BA已知：ABC △．（1）如果AB AC =，D 、E 是AB 、AC 上的点，若AD AE =，请你写出此图中的另一组相等的线段；（2）如果AB AC >，D 、E 是AB 、AC 上的点，若BD CE =，请你确定DE 与BC 的数量关系，并证明你的结论．C AEBD NFEDC BA（1）DB EC =；（2）结论：BC DE >．过E 点作EF AB ∥，截取EF DB =，连结BF ，作CEF ∠的平分线EN 交BC 于N ，连结NF ．∵DB EF =，又∵DB EC =，∴EF EC =． ∵EN 平分CEF ∠，∴FEN CEN ∠=∠．在ENF △和ENC △中，EF EC =，FEN CEN ∠=∠，EN 为公共边，∴ENF ENC △≌△． ∴NF NC =．∵DB EF ∥，DB EF =，∴四边形BDEF 是平行四边形．∴DE BF =．在BFN △中，BN FN BF +>，即BN CN DE +>，所以BC DE >．已知：矩形ABCD内有定点M，试证：2222AM CM BM DM+=+．CABDM CABDMFE过点B、点M分别作AM、AB的平行线，交于点E，连接CE，ME，BC交ME于点F．∵AB EM∥，AM BE∥∴AM BE=，AB EM=∵AB CD=，AB CD∥∴EM CD∥，EM CD=∴ECDM为平行四边形，∴CE DM=∵EM BC⊥∴222BM BF FM=+，222CE EF CF=+，222CM CF FM=+，222BE BF EF=+∴2222AM CM BM DM+=+．如图所示，设ABCD是矩形，K为矩形所在平面上的一点，连接KA与KD均与BC相交．由点B向直线DK引垂线，由点C向直线AK引垂线，两垂线相交于M，求证MK AD⊥．AB CDEFMKKMFEDCBA AB CDEFMPK模块一平行多边形和平移的构造如图，过点K 作KP AB ∥，且KP AB =．连接PB ，PC ，KM ． ∵PK BA ∥，PK BA =∴四边形PKAB 为平行四边形 ∴BP KA ∥又CF AK ⊥，∴CF PB ⊥又在矩形ABCD 中，AB CD ∥，AB CD = ∴PK CD ∥，PK CD =∴四边形PKDC 为平行四边形 ∴PC KD ∥又BE KD ⊥，∴BE PC ⊥ ∴M 为PBC △的重心 ∴PM BC ⊥又AB BC ⊥，AB PK ∥，∴PK AB ⊥ ∴P ，K ，M 三点共线且KM BC ⊥又∵AD BC ∥，∴KM AD ⊥．如图A 、B 两地在一条河的两岸，现要在河上造一座桥MN 。

2020中考数学专题训练特殊平行四边形+尺规作图及图形变换

CE=BC(用尺规作图法，保留作图痕迹，不要求写作法); (2)在(1)的条件下，连结AE，交CD于点F，
求证:△AFD≌△EFC.
解：(1)如图所示,线段CE为所求; (2)证明:在□ABCD中， AD∥BC,AD=BC.∴∠CEF=∠DAF ∵CE=BC,∴AD=CE, 又∵∠CFE=∠DFA,∴△AFD≌△EFC.
珠海?2013年如图正方形abcd的边长为1顺次连接正方形abcd四边的中点得到第一个正方形a1b1c1d1又顺次连接正方形a1b1c1d1四边中点得到第二个正方形a2b2c2d2?以此类推则第六个正方形a6b6c6d6周长是
数学
第25课时特殊平行四边形
• 知识考点•对应精练
考点分类矩形、菱形、正方形的定义、性质和判定
提高题
6. （2013年广州市）如图，四边形ABCD是菱形，对角线 AC与BD相交于O，AB=5，AO=4，求BD的长.
解：∵四边形ABCD是菱形，对角线AC与BD相交于O，
∴AC⊥BD，DO=BO，
∵AB=5，AO=4，
∴BO=
=3，
∴BD=2BO=2×3=6．
7. (广东•2014年) 如图，在平行四边形ABCD中，E是AD 边上的中点，连接BE，并延长BE交CD的延长线于点F．（1）证明：FD=AB；（2）当平行四边形ABCD的面积为8时，求△FED的面积．
证明：（1）在□ABCD中,AB∥CD,∴∠CFE=∠ABF ∠A＝∠ADF ∵AE=ED,∴△ABE≌△EFD ∴FD=AB.
（2）∵平行四边形ABCD，∴AD=BC=2ED，
∵AD∥BC ∴△EFD∽△FBC
∴ S△EFD：S△FBC =1：4 ∴S△EFD =1.6
∴S△EFD：S四边形ABCD =1：5

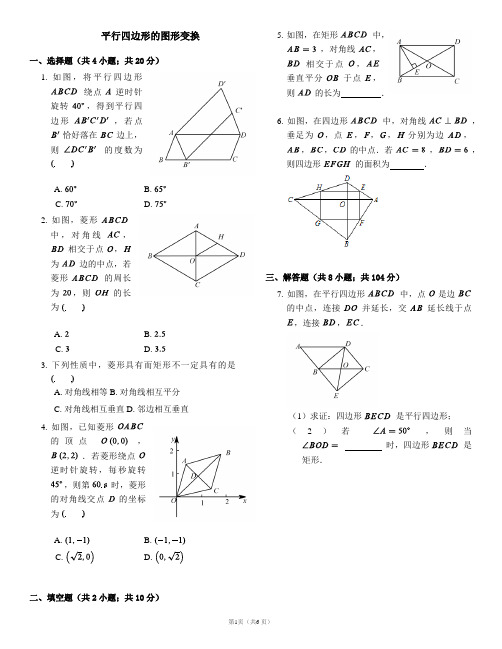
(完整版)平行四边形的图形变换

平行四边形的图形变换一、选择题（共4小题；共20分） 1. 如图，将平行四边形绕点逆时针旋转，得到平行四边形，若点恰好落在边上，则的度数为A. B.C.D.2. 如图，菱形中，对角线，相交于点，为边的中点，若菱形的周长为，则的长为A. B.C.D.3. 下列性质中，菱形具有而矩形不一定具有的是A. 对角线相等B. 对角线相互平分C. 对角线相互垂直D. 邻边相互垂直4. 如图，已知菱形的顶点，．若菱形绕点逆时针旋转，每秒旋转，则第时，菱形的对角线交点的坐标为A. B.C.D.二、填空题（共2小题；共10分）5. 如图，在矩形中，，对角线，相交于点，垂直平分于点，则的长为．6. 如图，在四边形中，对角线，垂足为，点，，，分别为边，，，的中点．若，，则四边形的面积为．三、解答题（共8小题；共104分） 7. 如图，在平行四边形中，点是边的中点，连接并延长，交延长线于点，连接，．（1）求证：四边形是平行四边形；（2）若，则当时，四边形是矩形．8. 已知：如图，四边形中，，，是对角线上一点，且．（1）求证：四边形是菱形；（2）如果，且，求证：四边形是正方形．9. 如图，在菱形中，对角线，相交于点，过点作对角线的垂线交的延长线于点．（1）求证：四边形是平行四边形；（2）若，，求的周长．10. 在一次课题学习中，老师让同学们合作编题．某学习小组受赵爽弦图的启发，编写了下面的这道题，请你来解一解．如图，将矩形的四边，，，分别延长至，，，，使得，，连接，，，．（1）求证：四边形为平行四边形；（2）若矩形是边长为的正方形，且，，求的长．11. 如图，将一张矩形纸片沿着对角线向上折叠，顶点落到点处，交于点．（1）求证：是等腰三角形；（2）如图，过点作，交于点，连接交于点，①判断四边形的形状，并说明理由；②若，，求的长．12. 准备一张矩形纸片，按如图操作：将沿翻折，使点落在对角线上的点，将沿翻折，使点落在对角线上的点．（1）求证：四边形是平行四边形；（2）若四边形是菱形，，求菱形的面积．13. 如图所示，，，，分别是四边形的边，，，的中点.（1）当四边形是矩形时，四边形是形，请说明理由；（2）当四边形满足什么条件时，四边形是正方形?并说明理由.14. 已知：在四边形中，，，，分别是，，，的中点.（1）求证：与互相平分；（2）当四边形的边满足条件时， .。

直角坐标系中平行四边形对角线法则

直角坐标系中平行四边形对角线法则
摘要：
一、引言
二、直角坐标系与平行四边形的概念
三、平行四边形对角线法则的定义与性质
四、平行四边形对角线法则的应用
五、结论
正文：
一、引言
在数学中，直角坐标系和平行四边形是两个重要的基本概念。

本文将介绍直角坐标系中平行四边形对角线法则的相关知识。

二、直角坐标系与平行四边形的概念
1.直角坐标系：在平面内，以横轴和纵轴建立直角坐标系，用有序实数对表示平面上的点。

2.平行四边形：在平面上，有两对平行的边的四边形称为平行四边形。

三、平行四边形对角线法则的定义与性质
1.定义：平行四边形的对角线法则是指，在直角坐标系中，平行四边形的两条对角线所代表的向量相等。

2.性质：对角线相交于中点，对角线长度相等，对角线互相平分。

四、平行四边形对角线法则的应用
1.向量计算：利用对角线法则，可以简化向量的计算过程。

2.图形变换：在计算机图形学中，可以利用对角线法则实现图形的平移、旋转等变换。

3.问题求解：在解决实际问题时，可以利用对角线法则快速求解。

五、结论
通过本文的介绍，相信大家对直角坐标系中平行四边形对角线法则有了更深入的了解。

3几种特殊的平行四边形和梯形

几种特殊的平行四边形和梯形一、几种特殊的平行四边形本节分为三部分，分别介绍了三种特殊的平行四边形：矩形、菱形、正方形。

关于矩形，我们要从平行四边形的内角的变化上认识其特殊性——一个内角是直角的平行四边形。

进一步研究其特有的性质——对角线相等、内角都为直角、是轴对称图形。

这里还要特别注意的是平行四边形的特征，矩形也都具有。

当然，识别矩形的方法也要从其特殊平行四边形的特殊性上去研究。

关于菱形，我们是通过折叠剪纸的趣味活动引入，当然也可以从平行四边形的边的变化上引入。

同矩形一样，同样注重对其特殊性进行研究，其特殊性表现在：四边都相等、对角线互相垂直且平分每一对对角、是轴对称图形。

正方形是矩形和菱形的混合体，既具有平行四边形的一般性质，又具有矩形和菱形的独特性质。

它本是大家早就熟悉的几何图形，因此在研究前面矩形和菱形的经验的基础上，对正方形特征性质的研究同学们也不难得出。

这里值得注意的是，要重视研究平行四边形、矩形、菱形和正方形各种图形之间的联系，并结合实际操作加深理解。

对于不同特殊平行四边形的不同特征与识别方式的区分与理解是本节的难点。

对于特征的理解都要通过边、角、对角线三方面进行分析：以上内容都能够通过图形自己观察出来，只要在研究时注重研究和记忆，就不至于混淆。

菱形的面积公式：S=(其中ab是菱形的两条对角线的长)（对角线将菱形分成的四个直角三角形，它们的面积和等于菱形的面积，由此很容易推出上面的公式。

）二、梯形梯形也是大家早已熟悉的几何图形，所以教材直接介绍梯形、等腰梯形、直角梯形的定义，这里要特别注意“只有”两个字的重要性，也就是说“一组对边平行，而另一组对边不平行的四边形是梯形”。

大家要认识等腰梯形的轴对称性，并由此推理得到等腰梯形的特征：“等腰梯形同一底上的两个内角相等”及“等腰梯形的对角线相等”通过将等腰梯形分割成平行四边形和等腰三角形来推理证明∠B=∠C的方法，应引起足够的重视，因为这是解决有关梯形问题的常用方法。

用图形变换思想引领学生有逻辑地思考——对“平行四边形的性质(1)

了相应的例题和习题. 执教教师在分析教材和学生学后面学生提出了“用不同折叠方法得到的对称中心是
情的基础上对平行四边形的内容进行了重组，先整体否重合”的问题后，执教教师引导学生用垂直平分线
研究平行四边形边、角、对角线的性质，并进行初步应用；再设置习题课巩固平行四边形的性质，解决综
的定义进行演绎证明. 在目标检测中，执教教师通过让学生应用平行四边形的性质进行推理证明，解决变
合性问题. 这样处理，可以让学生经历平行四边形性式问题，使学生体会平行四边形性质作为证明线段和
质的完整研究过程，让学生能自然、合理地发现和提出平行四边形的性质猜想，并用演绎推理证明猜想，使课堂教学顺着学生的思路进行，为学生探究中的自然生成设计了整体活动的平台.
角相等的工具作用，促进了学生逻辑推理能力的发展. 4. 开放探究，增强课堂教学的生成性在性质研究中，执教教师提出问题“平行四边形
收稿日期：2020-01-16 基金项目：人民教育出版社义务教育课标教材研究——《图形与几何》专题（KC2019-057）. 作者简介：吴增生（1962— ），男，正高级教师，浙江省特级教师，主要从事基于脑的数学教育研究 .
· 49 ·
中国数学教育·上半月（初中版） 2020 年第 5 期（总第 213 期）
关键词：平行四边形；课例点评；图形变换
变换是现代几何的核心思想. 1872 年，菲利克斯·克莱因用变换群的观点重新分类几何学，从此，变换作为重要的思想逐步进入到现代几何研究中. 2001年发布的《全日制义务教育数学课程标准（实验版）》第一次把图形变换纳入义务教育数学课程内容，《义务教育数学课程标准（2011年版）》则在“图形的变化”栏目下整合了图形变换的课程内容. 从2001年开始，各版本的初中数学教科书都把图形变换作为几何的重要内容组织课程资源. 这说明，从2001年开始，在几何内容中渗透变换思想，成为我国几何课程教学的重要价值取向. 几何内容的核心教育价值是发展学生的数学抽象、直观想象和逻辑推理能力. 几何作图和变换对直观想象能力的发展、几何推理对逻辑推理能力的发展分别具有举足轻重的作用. 因此，研究在几何教学实践中如何整合作图、变换和推理，设计合理的教学活动，是发展学生直观想象、逻辑推理等数学核心素养的需要.

特殊的平行四边形中的图形变换模型—2023-2024学年八年级数学下册常见几何模型(解析版)

特殊的平行四边形中的图形变换模型之旋转模型几何变换中的旋转问题是历年中考考查频率高且考查难度较高，综合性强，通常有线段、三角形、（特殊）平行四边形的旋转问题。

在解决此类问题时，要牢牢把握旋转的性质，即旋转前后的图形全等，对应角相等，对应边相等，再结合几何图形本身的性质，找到旋转过程中变化的量和不变的量，运用三角形全等或相似的有关知识，求解有关角、线段及面积问题。

近年来虽然关于（特殊）平行四边形旋转的考查频率高，由于之前的专题有总结过相关的旋转模型，故本专题就只对特殊的平行四边形旋转中的题型作全面的总结，方便大家学习掌握。

模型1.平行四边形中的旋转模型1）常规计算型例1．（2023·浙江八年级课时练习）如图，▱ABCD 绕点A 逆时针旋转30°，得到□AB′C′D′（点B′与点B 是对应点，点C′与点C 是对应点，点D′与点D 是对应点），点B′恰好落在BC 边上，则∠C=（）A ．155°B ．170°C ．105°D ．145° 【答案】C【详解】试题分析:先根据旋转的性质得到AB=AB′，∠BAB′=30°，再根据等腰三角形的性质和三角形内角和定理可得到∠B=∠AB′B=75°，然后根据平行四边形的性质得AB ∥CD ，再根据平行线的性质计算得∠C=180°﹣∠B=105°．解：∵▱ABCD 绕点A 逆时针旋转30°，得到□AB′C′D′′，∴AB=AB′，∠BAB′=30°，∴∠B=∠AB′B=12（180°﹣30°）=75°，∵四边形ABCD 为平行四边形，∴AB ∥CD ，∴∠B+∠C=180°，∴∠C=180°﹣75°=105°．故选C ．考点：旋转的性质；平行四边形的性质．例2．（2023·浙江·九年级期末）如图，在ABCD Y 中，=45ABC ∠︒，2AB =，将点B 绕点A 逆时针旋转120︒得到点E ，点E 落在线段BD 上，在线段BE 上取点F ，使BF DE =，连结AE ，CF ，则EF 的长为（）A ．2B ．2C ．2D ．3【答案】C【分析】根据已知条件利用勾股定理求得BG ，进而求得BE ，通过角度的计算可得EAD EDA ∠=∠，从而可求得DE ，根据EF BE BF BE ED =−=−即可求得【详解】过点A 作AG BD ⊥于点G ，120,BAE AB AE ∠=︒=190302ABG BAE ∴∠=︒−∠=︒2AB =112AG AB ∴==BG ∴=BE = =45ABC ∠︒∴453015DBC ABC ABD ∠=∠−∠=︒−︒=︒四边形ABCD 是平行四边形，, //AD BC ∴15ADE DBC ∴∠=∠=︒180********BAD ABC ∴∠=︒−∠=︒−︒=︒120BAE ∠=︒13512015EAD BAD EAB ∴∠=∠−∠=︒−︒=︒EAD EDA ∴∠=∠2ED EA AB ∴===∴EF BE BF BE ED =−=−2故选C【点睛】本题考查平行四边形的性质，勾股定理，等腰三角形的性质，熟悉几何图形的性质是解题的关键．2）最值（范围）型例1．（2023·广东·九年级阶段练习）如图，在平行四边形ABCD 中，AB =∠ABC ＝45°，点E 为射线AD 上一动点，连接BE ，将BE 绕点B 逆时针旋转60°得到BF ，连接AF ，则AF 的最小值是_____．【答案】【分析】以AB为边向下作等边△ABK，连接EK，在EK上取一点T，使得AT=TK．证明△ABF≌△KBE（SAS），推出AF=EK，根据垂线段最短可知，当KE⊥AD时，KE的值最小，解直角三角形求出EK即可解决问题．【详解】解：如图，以AB为边向下作等边△ABK，连接EK，在EK上取一点T，使得AT＝TK．∵BE＝BF，BK＝BA，∠EBF＝∠ABK＝60°，∴∠ABF＝∠KBE，∴△ABF≌△KBE（SAS），∴AF＝EK，根据垂线段最短可知，当KE⊥AD时，KE的值最小，∵四边形ABCD是平行四边形，∴AD∥BC，∵∠ABC＝45°，∴∠BAD＝180°﹣∠ABC＝135°，∵∠BAK＝60°，∴∠EAK＝75°，∵∠AEK＝90°，∴∠AKE＝15°，∵TA＝TK，∴∠TAK＝∠AKT＝15°，∴∠ATE＝∠TAK+∠AKT＝30°，设AE＝a，则AT＝TK＝2a，ET，在Rt△AEK中，∵AK2＝AE2+EK2，∴a2+（）2＝4，∴a＝，∴EK＝＝，∴AF的最小值为：．故答案为：．【点睛】本题考查旋转的性质，平行四边形的性质，等边三角形的性质，全等三角形的判定和性质，垂线段最短，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等的三角形解决问题，学会用转化的思想思考问题．例2．（2023·山东济南·九年级统考期末）如图，在□ABCD中，AB＝5，AD＝3，∠A＝60°，E是边AD上且AE＝2DE，F是射线AB上的一个动点，将线段EF绕点E逆时针旋转60°，得到EG，连接BG、DG，则BG －DG的最大值为________．【答案】1【分析】如图，在AB的一点N，使得AN=AE，连接EN，GN，可证明△AEN是等边三角形，∠AEN=∠FEG=60°，EA=EN，从而可证明△AEF≌△NEG得到∠ENG=∠A=60°，进而推出∠GNB=60°，则点G的运动轨迹是射线NG，过点B作BM⊥NG交CD延长线于M，连接MG，DG，先求出1322NK BN==，证明四边形ANTD是平行四边形，得到NT=AD=3，DT=AN=2，然后证明△MKT≌△BKN得到MK=BK，MT=BN=3，MD=1，NT垂直平分BM，进而推出当M、D、G三点共线时，MG-DG有最大值，DM，即BG-DG有最大值DM．【详解】解：如图，在AB的一点N，使得AN=AE，连接EN，GN，由旋转的性质可知EF=EG，∠FEG=60°，∵AE=2DE，AD=3∴AE=2，DE=1，∵AE=AN，∵∠A=60°，∴△AEN是等边三角形，∴∠AEN=∠FEG=60°，EA=EN，∴∠AEF=∠NEG，∵EA=EN，EF=EG，∴△AEF≌△NEG（SAS），∴∠ENG=∠A=60°，∵∠ANE=60°，∴∠GNB=180°-60°-60°=60°，∴点G的运动轨迹是射线NG，过点B作BM⊥NG交CD延长线于M，连接MG，DG，∴∠BKN=90°，∵∠BNK=60°，∴∠NBK=30°，∵AB=5，AN=AE=2，∴BN=3，∴1322NK BN==，∵∠BNK=∠A=60°，∴AD NK∥，∵四边形ABCD是平行四边形，∴CD AB∥，∴四边形ANTD是平行四边形，∠M=∠KBN，∴NT=AD=3，DT=AN=2，∴32TK NT NK=−=，∴NK=TK，又∵∠MKT=∠BKN，∴△MKT≌△BKN（AAS），∴MK=BK，MT=BN=3，∴MD=1，NT垂直平分BM，∴BG=MG，∵MG-DG≤MD，∴BG-DG≤MD，∴当M、D、G三点共线时，MG-DG有最大值，DM，即BG-DG有最大值DM，∴MG-DG的最大值为1，故答案为1．【点睛】本题主要考查了等边三角形的性质与判定，全等三角形的性质与判定，平行四边形的性质与判定，含30度角的直角三角形的性质，线段垂直平分线的性质与判定等等，正确作出辅助线构造全等三角形确定点G的运动轨迹是解题的关键．3）综合证明型【答案】(1)S△BCE=6；(2)①1＜BF＜5；②证明见解答；(3)BN的最小值为10-2，BN的最大值为．【分析】（1）如图1，过点E作EF⊥BC交CB的延长线于点F，根据题意求得∠EBF=180°-∠EBA-∠ABC=180°-90°-60°=30°，再根据特殊直角三角形的性质进而求得BC上的高EF=2，代入面积公式算出结果；（2）①如图，在线段FG上截取FK=BF，连接EK、CK，可证得四边形BCKE是平行四边形，得出：BE=CK=BE'=4，BC=6，再运用三角形三边关系即可求得答案；②可证△EKB≌△BGA（AAS），得出BK=AG，由AG=AD-DG，即可推出结论；（3）连接AE，取AE的中点P，PA的中点Q，连接BP、NP、NQ、BQ，可证△ABE是等腰直角三角形，得出：，再由点P是AE的中点，可得：BP⊥AE，且，当B、Q、N三点共线时，BN的最小值=BQ-S与点E重合时，EM=0，PN=0，此时，BN的最大值【详解】（1）解：如图1，过点E 作EH ⊥BC 交CB 的延长线于点H ，∴∠EHC=90°，∵∠ABC=60°，∠EBA=90°，∴∠EBH=180°-∠EBA -∠ABC=180°-90°-60°=30°，∵点E '在BC 边上且BE '=4，将B E '绕点B 逆时针旋转α°得到BE ，∴BE=B E '=4，∴EH=12BE=12×4=2，又∵BC=6，∴S △BCE=12BC•EH=12×6×2=6；（2）解：①如图，在线段FG 上截取FK=BF ，连接EK 、CK ，∵EF=FC ，BF=FK ，∴四边形BCKE 是平行四边形，∴BE=CK=BE '=4，BC=6，在△BCK 中，BC -CK ＜BK ＜BC+CK ，∴6-4＜BK ＜6+4，即2＜2BF ＜10，∴1＜BF ＜5；②证明：∵四边形ABCD 是平行四边形，且∠ABC=60°，AB=4，∴∠A=180°-∠ABC=180°-60°=120°，AD ∥BC ，AD=BC ，BE=AB ，∵∠EBF=120°，即∠EBK=120°，∴∠EBK=∠A ，∵EK ∥BC ，∴EK ∥AD ，∴∠EKB=∠BGA ，在△EKB 和△BGA 中，EKB BGA EBK A BE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EKB ≌△BGA （AAS ），∴BK=AG ，由①知：BK=2BF ，又∵AG=AD -DG ，∴2BF=BC -DG ；（3）解：连接AE ，取AE 的中点P ，PA 的中点Q ，连接BP 、NP 、NQ 、BQ ，∵∠ABE=90°，AB=BE=4，∴△ABE 是等腰直角三角形，∴∵点P 是AE 的中点，∴BP ⊥AE ，且，∵N 是AM 的中点，P 是AE 的中点，∴PN 是△AEM 的中位线，∴PN ∥EM ，∴∠ANP=∠AME=90°，∵点Q 是AP 的中点，∴QN=PQ=12Rt △BPQ 中，= 当B 、Q 、N 三点共线时，BN 的最小值=BQ -当点S 与点E 重合时，EM=0，PN=0，此时，BN 的最大值．【点睛】本题是几何变换综合题，主要考查了旋转的性质，平行四边形的性质，等腰直角三角形的性质，全等三角形的判定与性质，三角形中位线定理及勾股定理等知识，解题关键是灵活运用所学知识解决问题．模型2.菱形中的旋转模型1）常规计算型例1．（2023·江西九江·校考模拟预测）如图，在菱形ABCD 中，60BAD ∠︒＝．若将菱形ABCD 绕点A 逆时针旋转α（060α︒<<︒）得到四边形AEFG ，连接DE DG ，，则EDG ∠的度数为．【答案】150︒【分析】由旋转的性质得,60,AG AD AE EAD GAD αα==∠=−∠=，根据等腰三角形的性质可得出602ADE α=︒∠+，902ADG α=︒∠−，从而可得出结论．【详解】解：由题意可知AB=AD ，∠BAD=60°．由旋转知∠DAG=∠BAE=α，AE=AB ，AD=AG ，∴∠EAD=∠BAD －∠BAE=60°－α，AE=AD=AG ，∴1806022EAD ADE α−∠∠==+︒︒，1809022DAG ADG α−∠∠==−︒︒，∴∠EDG=∠ADE ＋∠ADG=150°．【点睛】本题考查了等腰三角形的性质，菱形的性质以及旋转的性质等知识，熟练掌握相关知识是解答本题的关键．A ．()2,3B ．【答案】C 【分析】首先根据菱形的性质及旋转的规律，可得第2023次旋转结束时，点C 在第三象限，过点A 作AE x⊥轴于点E ，延长OB 到'C 点，使'OC OA =，过点'C 作'C F x ⊥轴于点F ，再根据菱形的性质及全等三角形的性质，即可求得坐标.【详解】解：∵将菱形绕原点O 逆时针旋转，每次旋转90︒， 360904︒÷︒=，∴旋转4次后回到原来的位置，∵202345053÷=⋯⋯，∴第2023次旋转结束时，点C 在第三象限，如图：过点A 作AE x ⊥轴于点E ，延长OB 到'C 点，使'OC OA =，过点'C 作'C F x ⊥轴于点F ，∴'90AEO OFC ∠=∠=︒，∴90OAE AOE ∠+∠=︒，∵四边形ABCD 是菱形，∴'OA OC OC AC BD ==⊥，，∴'90C OF AOE ∠+∠=︒，∴'OAE C OF ∠=∠，∴'AAS OAE C OF ≌（），∴'AE OF OE C F ==，，∵()A −， ∴2OE AE ==，∴2'OF C F ==，∴('2,C −−，故第2023次旋转结束时，点C 的坐标为(2,−−，故选：C ．【点睛】本题主要考查菱形的性质和旋转的性质，全等三角形的判定及性质，以及坐标与图形的性质，直角三角形的性质，找出旋转规律是解题关键. 得到B O C ''，若A ．4B ．4【答案】C 【分析】利用菱形的性质求出OB 的长度，再利用勾股定理求出'AB 的长即可．【详解】解：∵菱形ABCD ，∴BD ⊥AC ，AB=BC ，AO=OC=1在Rt△OBC中，4OB=，∵旋转，∴OB O B''=，90O'∠=︒，在Rt△AO B''中，'5AB==，故选：C．【点睛】本题主要考查菱旋转和形的性质，能够利用勾股定理结合性质解三角形是解题关键．2）最值（范围）型例1．（2023·浙江·八年级假期作业）如图，菱形ABCD的边长为4，∠BAD＝120°，E是边CD的中点，F 是边AD上的一个动点，将线段EF绕着点E顺时针旋转60°得到线段EF'，连接AF'、BF'，则△ABF'的周长的最小值是___________．【答案】【分析】取AD中点G，连接EG，F'G，BE，作BH⊥DC的延长线于点H，利用全等三角形的性质证明∠F'GA ＝60°，点F'的轨迹为射线GF'，易得A、E关于GF'对称，推出AF'＝EF'，得到BF'+AF'＝BF'+EF'≥BE，求出BE 即可解决周长最小问题．【详解】解：取AD中点G，连接，F'G，BE，作BH⊥DC的延长线于点H，∵四边形ABCD为菱形，∴AB＝AD，∵∠BAD＝120°，∴∠CAD＝60°，∴△ACD为等边三角形，又∵DE＝DG，∴△DEG也为等边三角形．∴DE＝GE，∵∠DEG＝60°＝∠FEF'，∴∠DEG﹣∠FEG＝∠FEF'﹣∠FEG，即∠DEF＝∠GEF'，由线段EF绕着点E顺时针旋转60°得到线段EF'，所以EF＝EF'．在△DEF和△GEF'中DE GEDEF GEFEF EF'=⎧⎪∠=∠⎨='⎪⎩，∴△DEF≌△GEF'（SAS）．∴∠EGF'＝∠EDF＝60°，∴∠F'GA ＝180°﹣60°﹣60°＝60°，则点F'的运动轨迹为射线GF'．观察图形，可得A ，E 关于GF'对称，∴AF'＝EF'，∴BF'+AF'＝BF'+EF'≥BE ，在Rt △BCH 中，∵∠H ＝90°，BC ＝4，∠BCH ＝60°，∴12,2CH BC BH ===，在Rt △BEH 中，BE ，∴∴△ABF'的周长的最小值为AB+BF'+EF'＝．【点睛】本题考查旋转变换，菱形的性质，解直角三角形，全等三角形的判定与性质，勾股定理，等边三角形等知识，解题关键在于学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题．例2．（2023·山西·九年级专题练习）如图，菱形ABCD 中，AB ＝12，∠ABC ＝60°，点E 在AB 边上，且BE ＝2AE ，动点P 在BC 边上，连接PE ，将线段PE 绕点P 顺时针旋转60°至线段PF ，连接AF ，则线段AF 长的最小值为___．【答案】【分析】在BC 上取一点G ，使得BG BE =，连接,EG EF ，作直线FG 交AD 于T ，过点A 作AH GF ⊥于H ，先根据等边三角形的判定与性质、三角形全等的判定定理证出≌BEP GEF ，根据全等三角形的性质可得60EGF B ∠=∠=︒，从而可得120BGF ∠=︒，由此可得点F 在射线GF 上运动，再根据垂线段最短可得当点F 与点H 重合时，AF 的长最小，然后根据平行四边形的判定可得四边形ABGT 是平行四边形，根据平行四边形的性质可得860，AT BG BE ATH B ===∠=∠=︒，最后在Rt AHT 中，解直角三角形即可得．【详解】解：在BC 上取一点G ，使得BG BE =，连接，EG EF ，作直线FG 交AD 于T ，过点A 作AH GF ⊥于H ，60，B BE BG ∠=︒=，BEG ∴△是等边三角形，60，EB EG BEG BGE ∴=∠=∠=︒，60，PE PF EPF =∠=︒，EPF ∴△是等边三角形，60，PEF EF EP ∴∠=︒=，BEG PEF ∴∠=∠，BEG PEG PEF PEG ∴∠−∠=∠−∠，即BEP GEF ∠=∠，在BEP △和GEF △中，BE GE BEP GEFPE FE =⎧⎪∠=∠⎨⎪=⎩，()≌BEP GEF SAS ∴，60EGF B ∴∠=∠=︒，120BGF BGE EGF ∴∠=∠+∠=︒，∴点F 在射线GF 上运动，由垂线段最短可知，当点F 与点H 重合时，AF 的长最小，122，AB BE AE ==，84，BE AE ∴==，60BEG EGF ∠=∠=︒，//GT AB ∴，四边形ABCD 是菱形，BG AT ∴∥，∴四边形ABGT 是平行四边形，860，AT BG BE ATH B ∴===∠=∠=︒，sin 8AH AT ATH ∴=⋅∠==AF长的最小值为【点睛】本题考查了菱形的性质、平行四边形的判定与性质、等边三角形的判定与性质、解直角三角形等知识点，正确找出点F 的运动轨迹是解题关键．ADG S 等于（A ．2B ．3 【答案】D 【分析】当BE ⊥AE 时，∠ABE 的值最大，此时cos ∠BAE=A E A B，推出∠BAE=30°，过点G 作GT ⊥DA 交DA 延长线于点T ，求出GT ，可得结论．【详解】解：∵四边形ABCD ，四边形AEFG 都是菱形，∴AD=AB=2，，当BE ⊥AE 时，∠ABE 的值最大，此时cos ∠BAE=A E A B∴∠BAE=30°，∵∠DAB+∠EAG=180°，∴∠BAE+∠DAG=180°，∴∠DAG=150°，过点G 作GT ⊥DA 交DA 的延长线于点T ，如图，在Rt △AGT 中，，∠GAT=30°，∴GT=AG·sin30°= 11=··=222ADG S AD GT ⨯ 故选∶D ．【点睛】本题考查旋转变换，菱形的性质，三角形的面积等知识，解题的关键是理解题意，灵活运所学知识解决问题．3）分类讨论型的等边三角形ABC 和ACD 拼成菱形 A ．2或4B ．2或6C ．4或6 【答案】B【分析】过点A 作AG BC ⊥．根据等边三角形的性质可求出AG =结合AEC S=2CE =．又易证()ASA BAE CAF ≌，即得出BE CF =，从而即可得解．【详解】如图，过点A 作AG BC ⊥．∵ABC 为等边三角形，∴122CG BC ==，∴AG =∵12AEC S CE AG =⨯=12AEC S CE =⨯=∴2CE =，∴2BE BC CE =−=．∵三角尺的60︒角的顶点与点A 重合，∴BAC EAF ∠=∠，∴BAC EAC EAF EAC ∠−∠=∠−∠，即BAE CAF ∠=∠．又∵两个全等且边长为4的等边三角形ABC 和ACD 拼成菱形ABCD ，∴60B ACF ∠=∠=︒，AB AC =，∴()ASA BAE CAF ≌，∴2BE CF ==；如图，由（1）可知2CG =，∴12AEC S CE =⨯∴2CE =．∵BAC EAF ∠=∠，∴BAC EAC EAF EAC ∠+∠=∠+∠，即BAE CAF ∠=∠．又∵60B ACF ∠=∠=︒，AB AC =，∴()ASA BAE CAF ≌，∴6CF BE BC CE ==+=．∴CF 的长为2或6．故选B ．【点睛】本题主要考查等边三角形的性质，勾股定理，三角形全等的判定和性质等知识．利用数形结合的思想是解题关键．把ABC 分成面积相等两部分，于称为ABC 的“完美分割线，在钝角ABC 中，点是ABC 的“完美分割线【答案】[理解应用]见解析；[问题提升]（1）①CA ＝CE ＋CF ；②见解析；（2）t=15或45【分析】[理解应用]分别表示出ABE ACE ABC S S S V V V 、、，即可证得结论；[问题提升]（1）①如图，结论：CA ＝CE ＋CF ．只要证明△ADF ≌△ACE （SAS ）即可解决问题；②由题意易得△ADF ≌△ACE ，可得：,AE AF EAC FAD =∠=∠，可推得60EAF ∠=︒，进而问题可证；（2）分射线OM 是ABC ACD 、的“完美分割线”或射线ON 是ACD 的“完美分割线”，进行讨论即可得出答案．【详解】[理解应用]如图：过A 作AH ⊥BC 于H ，∵点E 是线段BC 的中点，∴12BE CE BC ==， ∵111,,222ABE ACE ABC S BE AH S CE AH S BC AH =⨯⨯=⨯⨯=⨯⨯V V V ，∴12ABE ACE ABC S S S ==△△△，故射线AD 是ABC 的“完美分割线”．[问题提升](1)①结论：CA ＝CE ＋CF ．理由：∵四边形ABCD 是菱形，∠BAD ＝120°，∴AB ＝AD ＝DC ＝BC ，∠BAC ＝∠DAC ＝60°，∴△ABC ，△ACD 都是等边三角形，∵∠DAC ＝∠EAF ＝60°，∴∠DAF ＝∠CAE ，∵CA ＝AD ，∠D ＝∠ACE ＝60°，∴△ADF ≌△ACE （SAS ），∴DF ＝CE ，∴CE ＋CF ＝CF ＋DF ＝CD ＝AC ，∴CA ＝CE ＋CF ；②∵△ADF ≌△ACE ，∴,AE AF EAC FAD =∠=∠，∴EAC CAF FAD CAF ∠+∠=∠+∠，∴60EAF CAD ∠=∠=︒，∵,60AE AF EAF =∠=︒,∴AEF △为等边三角形．(2)当OM 恰巧平分BC 时，此时ON 恰巧平分CD ，在等边ABC 中，OM 平分BC ，∴12ABE ACE ABC S S S ==△△△,1302BAE BAC ∠=∠=︒，故射线OM 是ABC 的“完美分割线”，∴302BAE t ∠=︒=︒，∴15t =（秒）；当ON 恰巧平分CD ，在等边ACD 中，ON 平分CD ， ∴12ACF ADF ACD S S S ==V V V ，130CAF CAD ∠==︒,∴603090BAF BAC CAF ∠=∠+∠=︒+︒=︒,故射线ON 是ACD 的“完美分割线”，∴90602BAE BAF MON t ∠=∠−∠=︒−︒=︒，∴15t =（秒）；当OM 恰巧平分CD 时，在等边ACD 中，OM 平分CD ，∴12ACQ ADQ ACD S S S ==V V V ,30CAQ ∠=︒，故射线OM 是ACD 的“完美分割线”，∴60302BAQ t ∠=︒+︒=︒，∴45t =（秒）．综上所述当t=15或45秒时，射线OM 或射线ON 是某个三角形的“完美分割线”．【点睛】本题属于四边形综合题，考查了全等三角形的判定和性质，等边三角形的性质，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．4）综合证明型【答案】①②③．【分析】过点B 作BH A D ''⊥于H ，BM AD ⊥于M ，BN CD ⊥于N ，利用角平分线的判定定理证明选项①、②是否正确，再利用全等三角形的性质证明DEF 的周长2DM =为定值，即可判断③ ；根据Rt △BEM ≌Rt △BEH ，Rt △BMA ≌Rt △BNC ，Rt △BFN ≌Rt △BFH ，得到S △BEM ＝S △BEH ，S △BMA ＝S △BNC ，S △BFN ＝S △BFH ，S △DEF+2S △BEF ＝S 四边形DMBN ，但是∠A 不一定为60°，即AM 不一定等于12AB ，由此判断④.【详解】如图，过点B 作BH ⊥A′D′于H ，BM ⊥AD 于M ，BN ⊥CD 于N ．∵菱形BA′D′C′是由菱形ABCD 旋转得到，菱形的每条边上的高相等，∴BM ＝BH ＝BN ，∵BH ⊥A′D′于H ，BM ⊥AD 于M ，BN ⊥CD 于N ，∴BE 平分∠AED′，BF 平分∠A′FC ，故选项①②正确，∵∠BME ＝∠NHE ＝90°，BE ＝BE ，BM ＝BH ，∴Rt △BEM ≌Rt △BEH （HL ），∴EH ＝EM ，同法可证，FH ＝FN ，∴△DEF 的周长＝DE+EF+DF ＝DE+EM+DF+FN ＝DM+DN ，∵∠BMA ＝∠BNC ＝90°，BM ＝BN ，BA ＝BC ，∴Rt △BMA ≌Rt △BNC （HL ），∴AM ＝CN ，∵DA ＝DC ，∴DM ＝DN ，∴△DEF 的周长＝2DM ＝定值，故③正确，∵Rt △BEM ≌Rt △BEH ，Rt △BMA ≌Rt △BNC ，Rt △BFN ≌Rt △BFH ，∴S △BEM ＝S △BEH ，S △BMA ＝S △BNC ，S △BFN ＝S △BFH ，∴S △DEF+2S △BEF ＝S 四边形DMBN ，∵∠A 不一定为60°，∴AM 不一定等于12AB ，∴S △DEF+2S △BEF≠12S 菱形ABCD ，故④错误；故答案：①②③ ．【点睛】旋转的性质、菱形的性质、全等三角形的判定与性质、三角形面积等知识，是重要考点，难度较易，掌握相关知识是解题关键．例2．（2023·湖北武汉·八年级统考期中）如图1，菱形AEFG 的两边AE 、AG 分别在菱形ABCD 的边AB 和AD 上，且∠BAD=60°，连接CF ；（1CF =；（2）如图2，将菱形AEFG 绕点A 进行顺时针旋转，在旋转过程中（1）中的结论是否发生变化？请说明理由．【答案】（1）见解析；（2），（1）中的结论不变．理由见解析．【分析】（1）延长EF 交CD 于M 点，证明三角形CMF 是等腰三角形，且∠EMC=120°，过点M 作MN ⊥CF ，垂足为N ，根据30°角所对直角边等于斜边的一半，和勾股定理，得FN=NC=2D G 即；（2）过D 做∠NDC=∠ADG,使DN=DG ，连接NC ，证明△DGN 为等腰三角形，四边形GFNC 为平行四边形即可．【详解】（1）如图１，延长EF 交CD 于M 点，∵四边形AEFG 和四边形ABCD 是菱形∴DC//GF//AB,DM//GF∴四边形GFMD 是平行四边形则∠D=∠EMC=120°，∴∠MFC=∠MCF=30°，过点M 作MN ⊥CF ，垂足为N ，∴MN=12M F ,根据勾股定理，得FN=D G ，∵MC=MF ，∴FN=NC ，∴；（2）如图2，过D 做∠NDC=∠ADG,使DN=DG ，连接NC ，∴△AGD ≌△DNC(SAS ）∴AG=NC ∠DNC=∠AGD ∴△DGN 为等腰三角形，则∠DGN=∠DNG ，∵∠NGF=360°-∠AGD -∠AGF -∠DGN=240°-∠DGA -∠DGN ∠GNC=∠DNC -∠DNG=∠DNC -∠DNG∴∠NGF+∠GNC=240°-∠DGN -∠DNG,∵∠DGN+∠DNG=180°-∠GDN=60°∴∠NGF+∠GNC=180°∴NC//GF ，∴四边形GFNC 为平行四边形∴CF=GN ，则GN=，∴，结论（1）不变．【点睛】本题考查了菱形的性质，平行四边形的判定，三角形的全等，等腰三角形的性质，灵活构造辅助线是解题的关键． ①CIJ 的周长是否变化？若不变，请求出CIJ 的周长；【答案】(1)BIE α∠=(2)见详解(3)①不变，CIJ 的周长为3，②6−【分析】（1）设BC 与AE 交于点H ，由旋转可知E B ∠=∠，再根据三角形的外角定理即可；（2）过点A 作AM EF ⊥于点M ，AN BC ⊥于点N ，证明AM AN =，由角平分线的判定定理即可得出结论；（3）①旋转前后的组合图形同样是轴对称图形，对称轴为直线AJ ，得到,CJ FJ =再证明(AAS)ABI AFI ≌，得到BI FI =即可；，②当0α=︒时AK 有最大值，当30α=︒时AK 有最小值，即可得出结果．【详解】（1）解：设BC 与AE 交于点H ，由旋转可知E B ∠=∠，再根据三角形的外角定理得：AHI E HIE B BAH ∠=∠+∠=∠+∠，BIE BAH α∠=∠=；（2）解：过点A 作AM EF ⊥于点M ，AN BC ⊥于点N ，90AME ANB ∴∠=∠=︒，由旋转可知E B ∠=∠，AE AB =，(AAS)AME ANB ∴≌，AM AN ∴=，AI ∴平分BIF ∠；（3）解：①不变，CIJ 的周长为3，理由如下：连接,,AJ AF AC ，根据菱形为轴对称图形，菱形对角线所在的直线为菱形的对称轴，旋转前后的组合图形同样是轴对称图形，对称轴为直线AJ ，,CJ FJ ∴=由第（2）问中AI 平分BIF ∠，AIB AIF ∴∠=∠，在菱形ABCD 中，3AB =，=60B ∠︒，ABC ∴和AEF △均为等边三角形，,60AB AE B E ∴=∠=∠=︒，(AAS)ABI AFI ∴≌，BI FI ∴=， CIJ 的周长为3CI IJ CJ FJ IJ CI BI CI BC ++=++=+==；②当0α=︒时AK 有最大值，3AK =；当30α=︒时AK 有最小值，AK =3AK ≤<．故点K 的运动路径长为236⎛=− ⎝ 【点睛】本题考查了旋转图形的性质，菱形的性质，等边三角形的性质和判定，全等三角形的性质和判定，综合运用旋转图形的性质、全等三角形的性质和判定是本题的关键．模型3.矩形中的旋转模型1）常规计算型例1．（2023上·成都市·九年级专题练习）如图，在矩形ABCD 中，1AB =，14CBD ∠=︒，将矩形ABCD 绕对角线BD 的中点O 旋转角度()090a α︒<<︒得到矩形A B C D ''''，当C '，D 的距离等于1时，α等于（）A ．28︒B ．42︒C ．48︒D ．56︒【答案】D 【分析】如图，连接OC C D ''，，由矩形性质可证OCB OBC ∠=∠，得28DOC ∠=︒，易知DOC DOC '≌，所以DOC DOC ∠=∠'，进而求得72C OC ∠'=︒，即旋转角度．【详解】如图，连接OC C D ''，，∵四边形ABCD 是矩形，∴1122AC BD OC AC OB OD BD ====，，，∴OB OC OD OC ==='，∴OCB OBC ∠=∠，∴228DOC OBC OCB CBD ∠=∠+∠=∠=︒．∵C '，D 的距离等于1，1AB CD ==，∴CD C D ='，∴()SSS DOC DOC '≌，∴DOC DOC ∠=∠'，∴256C OC DOC ∠'=∠=︒．故选D ．【点睛】本题考查矩形的性质、全等三角形的判定及性质、三角形外角的知识；由图形的旋转变换转化为全等三角形解决问题是求解的关键．例2．（2023·江西·统考三模）如图，矩形ABCD 中，4AB =，2BC =，将矩形ABCD 绕着点A 顺时针旋转得到矩形AFGE ，当点F 落在边CD 上时，连接BF 、DE ，则ADEABF SS =（）A ．12B ．13C ．14D ．23 【答案】C【分析】由题意作辅助线过点E 作EH AD ⊥于点H ，并利用旋转的性质以及三角函数进行分析求解.【详解】解：如解图，过点E 作EH AD ⊥于点H ，在矩形ABCD 中，4AB =，2BC =，2AD ∴=，90ADC DAB ∠=∠=︒.由旋转的性质可得4AF AB ==，2AE AD ==，90EAF DAB ∠=∠=︒，1sin 2AF AD AF D ==∴.30AFD ∴∠=︒，60DAF ∠=︒.30DAE ∴∠=︒.sin DAE 12AE EH AE =⋅∠==∴，1121122ADE E A H S D ==⨯⋅⨯=，1142422ABF A A D S B ==⨯⨯⋅=，14ADEABFS S ∴=.故选C【点睛】本题考查矩形相关，综合利用旋转的性质以及三角函数相关性质进行求解.例3．（2023·浙江·八年级假期作业）如图，矩形ABCD 中，8AB =，6AD =，将矩形ABCD 绕点B 顺时针方向旋转后得到矩形A BC D '''，若边A B '交线段CD 于H ，且BH DH =，则DH 的值是______．【答案】254【分析】设DH 的值是x ，那么CH=8x −，BH=x，在Rt△BCH 中根据勾股定理即可列出关于x 的方程，解方程就可以求出DH ．【详解】解：设DH 的值是x ， ∵AB=8，AD=6，且BH=DH ， 8,,CH x BH x ∴=−=6BC AD ==，在Rt △BCH 中，2222DH BH CH BC ==+， ()22836x x ∴=−+，25,4x ∴= 即254=DH ．故答案为：25.4 【点睛】此题考查了矩形的性质，勾股定理等知识，解题关键是利用勾股定理列出关于所求线段的方程．2）最值（范围）型例1．（2023·广东·八年级假期作业）如图，在矩形ABCD 中，AB ＝7，BC ＝P 在线段BC 上运动（含B 、C 两点），连接AP ，将线段AP 绕着点A 逆时针旋转60°得到AQ ，连接DQ ，则线段DQ 的最小值为 ___．【答案】3.5【分析】以AB 为边作等边△ABE ，D 作DH ⊥QE 于H ，利用SAS 证明△ABP ≌△AEQ ，得∠AEQ=∠ABP=90°，则点Q 在射线EQ 上运动，即求DH 的长度，再用含30°角的直角三角形性质进行解题．【详解】解：如图，以AB 为边作等边△ABE ，过点D 作DH ⊥QE 于H ，∴AB=AE ，∠BAE=60°，∵将线段AP 绕着点A 逆时针旋转60°得到AQ ，∴AP=AQ ，∠PAQ=60°，∴∠BAP=∠EAQ ，在△ABP 和△AEQ 中，AB AE BAP EAQ AP AQ =⎧⎪∠=∠⎨⎪=⎩，∴△ABP ≌△AEQ （SAS ），∴∠AEQ=∠ABP=90°，∴点Q 在射线EQ 上运动，当Q 与H 重合时，DQ 最小，在Rt △AEF 中，∠EAF=30°，∴EF=AE=，∴AF=2EF=，∴DF=AD -AF==，∴DH=DF=×=72，∴DQ 的最小值为72，故答案为：72．【点睛】本题主要考查了矩形的性质，等边三角形的性质，全等三角形的判定与性质，含30°角的直角三角形的性质，判断出点Q 的运动路径是解题的关键．，设EOF 的面积为【答案】 939s ≤≤【分析】（1）当点E 落在BC 上时，由勾股定理知（2）如图，由旋转知，EF=AD=8， EOF 的面积=12×EF×EF 边上的高，故找面积最值就转化成找EF 边上高的最值．当点E 落在BD 上时，EF 边上高的最小值为EO ，此时s 最小，当点D 落在BD 的反向延长线上时，EF 边上高的最大值为OE'，此时s 最大，分别算出最大值和最小值即可．【详解】（1）AB 6==，当点E 落在BC 上时，=答案：．（2）当点E 落在BD 上时，s 最小，此时，1()32OE BD BD AD =−−=，∴192s EO EF =⨯⋅=；当点D 落在BD 的反向延长线上时，s 最大，13E O OD DE ''=+=， ∴1392s E O E F '''=⨯⋅=，∴939s ≤≤．故答案为：939s ≤≤．【点睛】此题考查了图形的旋转和勾股定理，解题的关键是要有空间想象能力，正确作出辅助线求解．3）分类讨论型例1．（2023·江西南昌·九年级校联考阶段练习）在矩形ABCD 中，AB =3，AD =5，将边AD 绕它的端点旋转，当另一端点恰好落在边BC 所在直线的点E 处时，线段DE 的长为．5 【分析】分两种情形：绕A 旋转或绕D 旋转，利用勾股定理求解即可．【详解】解：如图，∵四边形∴AB=CD=3，AD=BC=5，∠ABC=∠DCB=90°，当AD 绕A 旋转，AD=12AE AE ==5时，124BE BE ===，∴C 1E =1，C 2E =9，∴1DE ===2DE ===，当AD 绕D 旋转时，345D DE DE A ===，综上所述，满足条件的DE 55．【点睛】本题考查旋转变换，矩形的性质，等腰三角形的性质，勾股定理等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．例2．（2023上·广东珠海·九年级校考期中）如图，在矩形ABCD 中，8AB =，6AD =，将矩形ABCD 绕点A 逆时针旋转（旋转角小于90度）得到矩形AEFG ．(1)如图①，若在旋转过程中，点E 落在对角线AC 上，AF EF 、分别交DC 于点M ，N ，①求证：MA MC =；②求MF 的长；(2)在旋转过程中，当旋转到如图②所示的情况，若直线AE 经过线段BG 的中点P ，连接BE ，求BEG 的面积．【答案】(1)①见解析；②154(2)BEG 的面积是48−48+【分析】（1）①根据矩形的性质和旋转的性质得到DCA FAE ∠=∠，证得MA MC =；②设MA MC x ==，则8DM x =−，根据勾股定理求出x 的值，即可求出MF 的值；（2）分情况讨论，第一种情况，过点B 作BH AE ⊥于点H ，证明()AAS HBP AGP ≌，用勾股定理求出AH 的长，从而得到AP 的长，再求出PE 的长，根据2BEG GPE S S =算出BEG 的面积；第二种情况，与第一种情况的区别在于PE 的长，求出PE 长之后，一样算出BEG 的面积．【详解】（1）解：①∵四边形ABCD 是矩形，∴AB CD ∥，∴DCA BAC ∠=∠，∵旋转，∴=FAE BAC ∠∠，∴DCA FAE ∠∠，∴MA MC =；②设MA MC x ==，则8DM x =−，在Rt ADM △中，()22268x x +−=，解得254x =，在Rt AEF 中，10AF ==，∴154MF AF AM =−=，（2）①如图，过点B 作BH AE ⊥于点H ，则90GAP BHP ∠=∠=︒，在HBP 和AGP 中，BHP GAP APG HPA GP BP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS HBP AGP ≌，∴AP HP =，6BH AG ==，在Rt ABH △中，AH =∴12AP AH == ∴8PE AE AP =−=∴(12268482BEG GPE S S ==⨯⨯⨯=−；②如图所示，同①得：AH =AP ∴8PE =∴(12268482BEG GPE S S ==⨯⨯⨯=+BEG 的面积是48−48+ 【点睛】本题考查的是四边形综合问题，解题的关键是掌握矩形的性质，旋转的性质，全等三角形的性质和判定，以及等腰三角形的判定，需要注意进行分类讨论．4）综合证明型例1．（2023·四川·眉山市东坡区模拟预测）如图，Rt △ABE 中，∠B=90°，AB=BE ，将△ABE 绕点A 逆时针旋转45°，得到△AHD ，过D 作DC ⊥BE 交BE 的延长线于点C ，连接BH 并延长交DC 于点F ，连接DE 交BF 于点O ．下列结论：①DE 平分∠HDC ；②DO=OE ；③H 是BF 的中点；④BC -CF=2CE ；⑤CD=HF ，其中正确的有（）A ．5个B ．4个C ．3个D ．2个【答案】B【分析】根据∠B=90°，AB=BE ，△ABE 绕点A 逆时针旋转45°，得到△AHD ，可得ABE AHD ≅，并且△ABE 和△AHD 都是等腰直角三角形，可证//AD BC ，根据DC BC ⊥，可得HDE CDE ∠=∠，根据三角形的内角和可得HDE CDE ∠=∠，即DE 平分∠HDC ，所以①正确；利用90DAB ABC BCD ∠=∠=∠=，得到四边形ABCD 是矩形，有90ADC ∠=︒，45HDC ∠=︒，由①有DE 平分∠HDC ，得22.5HDO ∠=︒，可得67.5AHB ∠=︒,22.5DHO ∠=，可证OD OH =，利用 AE AD =易证67.5AEB OHE HEO ∠=∠=∠=︒，则有OE OH =，OD OE =，所以②正确；过H 作HJ BC ⊥于J ，并延长HJ 交AD 于点I ，得IJ AD ⊥，I 是AD 的中点，J 是BC 的中点，H 是BF 的中点，所以③正确；根据ABE 是等腰直角三角形，JH JE ⊥，∵J 是BC 的中点，H 是BF 的中点，得到2JH CF =，2JC BC =，JC JE CE =+，易证2BC CF CE −=，所以④正确；利用AAS 证明DHE DCE ∆≅∆，则有DH DC =，22.5HDE CDE ∠=∠=︒，易的22.5DHF ∠=︒，112.5DFH ∠=︒，则DHF△不是直角三角形，并DH HF ≠ ，即有：CD HF ≠，所以⑤不正确；【详解】解：∵Rt △ABE 中，∠B=90°，AB=BE ，∴45BAE BEA ∠=∠=︒又∵将△ABE 绕点A 逆时针旋转45°，得到△AHD ，∴ABE AHD ≅，并且△ABE 和△AHD 都是等腰直角三角形，∴45EAD ∠=︒，AE AD = ，90AHD ∠=，∴ADE AED ∠=∠∴454590BAD BAE EAD ∠=∠+∠=+=，∴//AD BC ∴ADE DEC ∠=∠，∴AED DEC ∠=∠,又∵DC BC ⊥ ∴90DCE DHE ∠=∠=∴由三角形的内角和可得HDE CDE ∠=∠，即：DE 平分∠HDC ，所以①正确；∵90DAB ABC BCD ∠=∠=∠=∴四边形ABCD 是矩形，∴90ADC ∠=︒∴45HDC ∠=︒，由①有DE 平分∠HDC ，∴114522.522HDO HDC ∠=∠=⨯︒=︒ ∵45BAE ∠=︒，AB AH =∴()()111801804567.522AHB BAE ∠=︒−∠=⨯︒−︒=︒,∴9067.522.5DHO DHE FHE DHE AHB ∠=∠−∠=∠−∠=−=∴OD OH = 在AED △中，AE AD =∴()()111801804567.522AED EAD ∠=︒−∠=⨯︒−︒=︒∴67.5AEB OHE HEO ∠=∠=∠=︒∴OE ∴OD OE =，所以②正确；过H 作HJ BC ⊥于J ，并延长HJ 交AD 于点I ，∵//AD BC ∴IJ AD ⊥又∵AHD 是等腰直角三角形，∴I 是AD 的中点，∵四边形ABCD 是矩形，HJ BC ⊥∴J 是BC 的中点，∴H 是BF 的中点，所以③正确；∵ABE 是等腰直角三角形，JH JE ⊥∴JH JE =又∵J 是BC 的中点，H 是BF 的中点，∴2JH CF =，2JC BC =，JC JE CE =+，∴222222JC JE CE JH CE CF CE BC =+=+=+=即有：2BC CF CE −=，所以④正确；在DHE 和DCE △中，90DHE DCE HDE CDEDE DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴()DHE DCE AAS ∆≅∆，DH DC ∴=，14522.52HDE CDE ∠=∠=⨯︒=︒，∵OD OH =∴22.5DHF ∠=︒，∴1801804522.5112.5DFH HDF DHF ∠=︒−∠−∠=︒−︒−︒=︒∴DHF △不是直角三角形，并DH HF ≠ 即有：CD HF ≠，所以⑤不正确；综上所述，正确的有①②③④，故选：B ．【点睛】本题考查了全等三角形的判定与性质、旋转的性质、矩形的性质、角平分线的性质以及等腰直角三角形的判定与性质；证明三角形全等和等腰直角三角形是解决问题的关键．例2．（2023上·黑龙江哈尔滨·九年级统考期中）如图1，将矩形ABCD 绕着点C 按顺时针方向旋转得到矩形FECG ，点B 与点E 对应，点E 恰好落在AD 边上，BH CE ⊥交于点H ．(1)求证：CD BH =；(2)如图2，连接AH 并延长交CD 于点M ，交CG 于点N ，点K 在CD 的延长线上，连接EK ，若45EAH KED ∠+∠=︒，在不添加任何辅助线和字母的条件下，直接写出图中所有的等腰三角形．【答案】(1)见解析(2)AEH △、、CNM 、ECK【分析】（1）根据旋转的性质得出CE BC =，证明()AAS BHC CDE ≌，根据全等三角形的性质即可求解；（2）根据矩形FECG 是由矩形ABCD 绕着点C 按顺时针方向旋转得到的，直接可得AEH △、ABH 是等腰三角形，设EAH α∠=，根据三角形的外角的性质以及三角形内角和定理，得出,CMN CNM CEK K ∠=∠∠=∠，即可判断CNM 、ECK 是等腰三角形，即可求解．【详解】（1）证明：矩形FECG 是由矩形ABCD 绕着点C 按顺时针方向旋转得到的CE BC ∴= 四边形ABCD 是矩形AD BC ∴∥，90D Ð=° DEC BCH ∴∠=∠BH CE ⊥，90BHC \Ð=°BHC D ∴∠=∠，()AAS BHC CDE ∴≌ BH CD ∴=（2）。

初中数学单元整体复习的新视角——以“从图形变化的视角整体设计平行四边形”单元复习为例

教育部《关于加强初中学业水平考试命题工作的意见》指出：取消初中学业水平考试大纲，严格依据义务教育课程标准命题，不得超标命题.在此重大变革的机遇下，《义务教育数学课程标准（2011年版）》（以下简称《标准》）成为初中数学学业水平考试命题的根本依据.因此，遵从数学课程基本理念，实现数学课程目标，专注于发展学生的数学学科核心素养，是数学教学的根本任务.2020年4月20日，笔者有幸在“深化课堂教学改革提升数学育人水平行动研究”第一次主题教研活动中做了题为“从图形变化的视角整体设计平行四边形单元复习”的报告.笔者现将报告准备过程中的所思所想进行呈现，与大家共同探讨.一、复习教学的策略复习教学有别于新课教学，其意义不应止步于“温故”，而应积极探索如何“知新”.同时，复习教学不应否认新课教学的效果和作用，应在学生已有“四基”的基础上，寻找新的增长点.1.以课程标准为根本依据《标准》中的课程内容（第三学段）与平行四边形（包括平行四边形、矩形、菱形和正方形）有关的描述是“探索并证明平行四边形的性质定理；探索并证明平行四边形的判定定理”“探索并证明矩形、菱形、正方形的性质定理以及它们的判定定理”“探索矩形、菱形、正多边形的轴对称性质”“探索平行四边形、正多边形的中心对称性质”.其中，对平行四边形的性质定理和判定定理的要求均为“探索并证明”，对其轴对称性质与中心对称性质的要求均为“探索”.《标准》中将描述过程目标的行为动词“探索”定义为“独立或与他人合作参与特定的数学活动，理解或提出问题，寻求解决问题的思路，发现对象的特征及其与相关对象的区别和联系，获得一定的理性认识”，将描述结果目标的行为动词“证明”定义为“综合使用已掌握的对象，选择或创造适当的方法解决问题”.这两个行为动词体现出《标准》对平行四边形教学内容有很高的要求.因此，以平行四边形单元整体复习为例来谈复习教学的策略，可以为其他单元的复习提供借鉴与参考，具有一定的研究价值.在平行四边形单元整体复习设计中把上述目标具体分为以下四个方面.（1）能辨别平行四边形、矩形、菱形、正方形，理清它们之间的关系.（2）能运用平行四边形的性质定理与判定定理进行相关证明和计算.初中数学单元整体复习的新视角——以“从图形变化的视角整体设计平行四边形”单元复习为例李摘要：平行四边形内容是学生学习图形的变化的良好载体.在平行四边形的复习教学中，以课程标准为依据，以图形变化为主轴，用图形研究的一般观念引领单元整体复习教学，帮助学生建立知识之间的广泛联系.通过这些教学策略，旨在促进学生空间观念、几何直观和逻辑推理等能力的发展.关键词：课程标准；复习教学；整体教学；教学策略收稿日期：2021-01-16作者简介：李馨（1976—），男，高级教师，主要从事初中数学课堂教学与解题研究.··36（3）会利用图形的对称性对具体问题进行分析与推理.（4）经历以图形对称性的视角研究平行四边形的过程，寻求该视角下的研究思路、研究内容和研究方法.2.以图形变换为主轴，用图形研究的一般观念引领单元整体复习教学（1）以图形变换为主轴，开展单元整体复习教学.平行四边形单元整体复习教学设计的基本思路是以图形的对称性为主轴，串联平行四边形大单元的复习，共设置三个课时，分别为“平行四边形的中心对称性”“轴对称在矩形、菱形中的应用”“正方形的对称性”.每个课时均由具体活动引入，通过引导学生探究，感受图形对称性在平行四边形中的重要价值，并最终解释图形对称性之间的联系.图形的对称性包括轴对称、中心对称和旋转对称.轴对称的代表图形是等腰三角形，中心对称的代表图形是平行四边形，旋转对称的代表图形是圆.平行四边形具有中心对称性，将其特殊化后得到的矩形和菱形均为轴对称图形，再进一步特殊化后得到的正方形是旋转对称图形（正方形绕对角线的交点旋转90°后能与原正方形重合）.因此，以图形的对称性为主轴对平行四边形单元进行整体复习教学设计不但有利于用整体的视野，以平行四边形为载体，从研究思路、研究内容和研究方法上统一认识图形的对称性，而且可以实现以一个全新的视角对平行四边形进行再认识，发展学生的空间观念和几何直观.（2）以图形研究的一般观念引领单元整体教学.在新课教学中，学生已经掌握了研究几何图形的基本思路：概念—性质—判定—特例—应用.同时，在初学平行四边形时，学生已经掌握了通过对四边形的要素（边和角）特殊化（数量和位置）生成新的研究对象的方法.在本单元复习中，学生可以通过类似的研究方法，以新的视角，从相关要素（对角线）的特殊化（数量和位置）方向进行继续研究.这样的研究方法与之前的几何研究保持了内容结构的整体性和逻辑一致性，对研究其他几何图形同样具有示范性. 3.帮助学生建立知识之间的广泛联系单元整体教学设计强调学习内容的内部联系，强调活动设计的自然连贯，强调思想方法的良好承接，以帮助学生构建更全面的认知结构.本单元整体教学设计强调图形对称性与平行四边形的性质、判定之间的关系.图形的对称性是平行四边形性质的几何直观，平行四边形是图形对称性的载体，在学生的图形认知结构中，两者共同发挥着重要作用，相互依存、密不可分.二、复习教学设计核心流程教学设计不仅要围绕《标准》提出的教学目标、落实目标解析，还需要重视内容中蕴涵的数学思想和方法，实现数学教学的育人价值.本单元以深度学习理念设计复习教学活动，逐一突破难点，完成知识完整、思想一致、方法普适、思维系统和逻辑连贯的整体复习教学设计.1.分析教学内容，确定教学重点（1）分析知识内容的逻辑结构.平行四边形是中心对称图形，这是从整体上对平行四边形的认识，而平行四边形的两条对角线与一组对边所组成的两个三角形成中心对称，这是从局部看图形各部分之间的关系.在解决具体问题时，可以先对图形整体建立几何直观，再细化到局部，探索要素之间的关系.有时候也可以根据问题中对局部图形的描述，发现其具有对称性的本质，进而认识图形的整体.对称图形要素之间的关系需要从定性和定量两个方面进行研究.如何综合运用图形的对称性解决问题需要学生进行分析与推理.（2）分析思想方法和育人价值.平行四边形内容中蕴涵的基本思想是推理和图形变换思想，核心的育人价值是发展学生的空间观念、几何直观和逻辑推理能力.（3）确定单元教学重点.基于以上分析，确定平行四边形单元复习的教学重点是：通过图形的对称性，再认识平行四边形的性质和判定；以图形的对称性为主轴探究研究平行四边形的具体方法.2.诊断教学问题，明确教学难点，完善教学策略学生已经学习了图形的轴对称、中心对称和旋转··37具体课时的教学核心流程及解析如下.下面是三个课时教学的核心流程图、基本设计思路及深度学习活动设计.核心流程图主要体现复习教学组织的过程、内容之间的联系和蕴涵的思想方法等.在基本设计思路中简单介绍了各课时深度学习活动的组织方式及其意义和价值.深度学习活动设计在同一课时中是前后连贯的，在三个课时中是思路统一的，具有良好的承接性.（1）第1课时.①“平行四边形的中心对称性”一课的核心流程图如图1所示.一一一一整体→局部局部→整体过中心的直线中点→中线（1）（2）（3）图1②基本设计思路.第1课时的活动从整体到局部，根据平行四边形的中心对称性，以小见大.在探究“平行四边形与其过中心的直线组合后能获得哪些结论”的活动中，对问题进行分解，关注一边中点关于中心的对称点的位置，一边上的中线关于中心对称的线段的位置等.再从局部到整体引导学生认知，最终以中心对称的视角获得“过平行四边形两条对角线交点的任意一条直线把平行四边形分为两个全等图形”的结论，并结合图形的相关要素对问题进行各种拓展与变化.③深度学习活动设计.活动1：让学生通过两个三角形关于一点成中心对称获得平行四边形.利用中心对称图形的性质再次理解平行四边形的性质，帮助学生从静态到动态、从整体到局部，重新认识平行四边形.接下来，让学生在平行四边形中画出一边中点关于中心的对称点，通过一系列的追问，由点到线再到角，最后到形，引导学生关注图形的要素和相关要素，让学生再次从局部到整体认识平行四边形的性质与其中心对称性之间的联系.活动2：将平行四边形一边的中点变化为三等分点、四等分点，以及更一般的n等分点，让学生在这个一般化的变化过程中，寻找不变的关系，并以中心对称的视角获得“过平行四边形两条对角线交点的任意变化.在学习过程中，多次以图形的变化为工具解决数学问题和实际问题，具备了一定的基础.也已经通过要素之间的关系研究了平行四边形的性质和判定，并清楚平行四边形是中心对称图形，矩形、菱形和正方形都是轴对称图形.但是用整体视角，以图形的对称性为主轴，串联平行四边形的研究思路、研究内容和研究方法是学生没有经历过的.基于以上分析，确定平行四边形单元复习的教学难点是：利用图形的对称性解决与平行四边形相关问题的计算或证明.在复习教学中，教师要抓住平行四边形两条对角线之间的特殊数量关系和位置关系，引导学生建立图形对称性与平行四边形的性质及判定之间的关系，借助信息技术增强学生对平行四边形对称性的直观感受，帮助学生建立解决较为复杂问题的思路和方法，再进一步进行完整的推理和证明.3.在整体视野下设计单元教学的课时方案课时安排如下表所示.深度学习活动引入主要内容应用单元—课时第1课时平行四边形的中心对称性两个三角形成中心对称整体与局部的关系；静态到动态的视角平行四边形的中心对称性第2课时轴对称在矩形、菱形中的应用平行四边形对角线的特殊关系对角线的特殊关系；矩形、菱形的对称性平行四边形的轴对称性第3课时正方形的对称性寻找正方形中的相等线段正方形的对称性；旋转对称的根源正方形的对称性··38一条直线把平行四边形分为两个全等图形”的结论，最后再添加对角线，引导学生由整体到局部关注图形的要素与相关要素之间的关系.活动3：在前面活动获得的经验基础上，再增加一条过中心的直线，由学生判断这两条直线与平行四边形的交点顺次连接后所得四边形的形状，为下一课时研究矩形和菱形的轴对称性做铺垫.（2）第2课时.①“轴对称在矩形、菱形中的应用”一课的核心流程图如图2所示.一一一一一一整体局部整体图2②基本设计思路.第2课时延续第1课时的设计思路，从整体到局部，通过将局部小三角形两边（平行四边形对角线的一半）之间数量关系和位置关系特殊化，引导学生发现矩形和菱形既延续了平行四边形的中心对称性，又因为局部特殊化后产生的等腰三角形而拥有了轴对称性，再回到整体，因此矩形和菱形产生了一般平行四边形没有的新性质，这些性质的根源在于它们的轴对称性.最后，以轴对称结合中心对称，对矩形和菱形性质的进行应用.③深度学习活动设计.活动1：回顾新课学习中将平行四边形的要素（角）特殊化获得矩形和菱形，结合第1课时平行四边形的获得过程，从整体到局部，再将局部特殊化.分别通过局部小三角形的两边（平行四边形对角线的一半）数量的特殊化和位置的特殊化获得矩形和菱形.通过设置问题串及追问，引导学生发现矩形和菱形呈现的轴对称性与其局部中隐藏的等腰三角形的轴对称性有密切关系，从而将图形局部的轴对称性和整体的轴对称性进行了有机的统一.在此基础上，由矩形和菱形的中心对称性和轴对称性出发，整体复习矩形和菱形的性质，从而对其对称性及特殊性质形成整体认知.活动2：以矩形为背景，围绕其一条对称轴上点的不同位置展开探究，通过变式，借助图形对称性的视角解决系列问题，串联整个学习过程.（3）第3课时.①“正方形的对称性”一课的核心流程图如图3所示.一一一一一一一一一一一一图3②基本设计思路.第3课时对图形局部进一步特殊化，发现正方形不但延续了平行四边形的中心对称性，同时还延续了矩形和菱形的轴对称性，拥有四条对称轴，于是正方形有了其他四边形所没有的性质.而正方形所体现的旋转对称性，本质上正是因为它既有矩形的轴对称性，又有菱形的轴对称性.关于这两条对称轴各作一次轴对称就体现出了旋转对称性.③深度学习活动设计.活动1：延续前两个课时中对平行四边形、矩形和菱形的研究思路，继续特殊化矩形和菱形的对角线获得正方形，再次将局部的对称性和整体的对称性进行统一.从而发现正方形不仅延续了平行四边形的中心对称性，同时还延续了矩形和菱形的轴对称性，拥有四条对称轴，于是有了其他四边形所没有的性质.活动2：让学生在正方形中寻找和已知线段（连接正方形的一个顶点和与其不相邻的边上一点的线段）相等的线段，并对画出的各种图形根据与已知线段的不同位置进行分类，最终引导学生发现一切源于正方形的对称性——中心对称性、轴对称性和旋转对称性.然后通过两次轴对称解释正方形的旋转对称性，使学生构建对正方形所体现的图形对称性的统一认识.（下转第59页）··39用解直角三角形的条件，构造直角三角形；会进行图形的组合与拆解.从数学育人的出发点和归宿看，思维的教学就是培养学生的理性思维，发展学生的理性精神，实现它要依靠教学内容这一载体.“锐角三角函数”专题复习课不宜过度关注知识点和考点，这样会窄化教学视野，降低教育应有的内涵.必需在问题解决中培养学生的一般性观念：利用四边形、圆、相似等多个知识点综合解决问题时，等角及边的转化是解决问题的关键；解直角三角形中的确定性意识的形成等.虽然初中阶段对三角函数的要求较低，但是学生应该具有回归定义研究性质的能力.六、结束语专题复习课的功能主要是提升学生在知识、技能、思维层面上体现出来的数学素养.鉴于九年级学生现有的认知水平，专题复习课的内容必须为学生的能力发展和素养提升而设计.初中数学的核心素养虽然未作界定，但基于初中的十大核心概念和对核心素养观的理解，此专题复习中要发展的主要学科核心素养应该是数学运算、直观想象、逻辑推理.同时，专题复习课作为一种重要的课型，在教学设计时同样要进行教学背景的分析和教学目标的确定.新授课重在探究建构知识，专题复习课重在梳理、整合知识，感悟数学思想和方法；新授课关注学科知识本质、提升学生思维品质，专题复习课重在发展学生能力、提升核心素养.参考文献：［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.三、后续思考与展望1.复习教学建立在教师“四个理解”的基础上《标准》为复习教学指明了方向，同时也对教师本身的教学能力提出了更高要求.在进行复习教学设计前应做好“前测”工作，即充分了解学生知识和能力的起点，找准复习教学的提升点.教师要在理解数学、理解学生、理解技术、理解教学和评价“四个理解”上多下工夫，切勿把习题教学当成复习教学. 2.复习教学应以单元整体复习的思路进行设计在当前的教学改革形势下，加强“单元—课时”教学设计的研究是深化数学教育教学改革，提高数学教学质量的有力抓手，广大初中数学教师应给予充分重视.在复习教学中，教师应依据《标准》对单元整体学习内容进行解构、重构和建构，对复习教学整体设计的可行性进行科学论证，完成有“数学味”的单元整体复习教学设计.3.关注学生核心素养的教学才具有生命力教师通过全新的视角引导学生重新认识熟悉的数学对象，用相似的方法更系统地发现和提出问题，并进一步分析和解决问题.正所谓“研究对象在变，研究套路不变，思想方法不变”，这在培养学生的理性精神和科学态度的过程中起着积极作用.在复习教学中，教师要帮助学生建立知识之间的联系，促进学生对数学的理解，使学生能看得更高、走得更远.参考文献：［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.［2］章建跃，鲍建生.深化课程改革，提高数学教育教学质量：暨“第十一届初中青年数学教师优秀课展示与培训活动”总结［J］.中国数学教育（初中版），2020（4）：2-20.［3］章建跃.学会用数学的方式解读内容设计教学：以“相交线”为例［J］.数学通报，2019，58（1）：8-12，15.［4］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.（上接第39页）··59。

平行四边形的性质与判定(1)

还有一些其他的特殊四边形，如筝形（有一组对角相等且有一条对角线被另一条平分）等，它们与平行四边形之间也
存在一定的联系和区别。
对于这些特殊四边形，可以通过研究它们的性质、判定方法以及它们与平行四边形之间的关系来更深入地理解四边形
的性质和判定方法。
05
平行四边形在实际问题中应用
几何问题中求解边长、角度等
平行四边形的性质与判定
汇报人：XX 20XX-02-02
contents
目录
• 平行四边形基本概念 • 平行四边形性质探究 • 平行四边形判定方法 • 平行四边形与特殊四边形关系 • 平行四边形在实际问题中应用 • 总结回顾与拓展延伸
01
平行四边形基本概念
定义及表示方法
定义
平行四边形是一个四边形，其中一对相对边平行且相等。
1 2
矩形是特殊的平行四边形
矩形的对角线相等且互相平分，而且四个角都是直角。
菱形也是特殊的平行四边形
菱形的四条边都相等，对角线互相垂直且平分。
3
正方形是矩形和菱形的特例
正方形既具有矩形的性质（四个角都是直角），又具有菱形的性质（四条边都相等）。
梯形与平行四边形关系
梯形的一组对边平行而另一组对边不平行，而平行四边形两组对边都平行。
对于不规则四边形，虽然它们没有像平行四边形、矩形、菱形等那样具有明确的性质，但我们可以通过添加辅助线等方式来探究它们的性质和应用。例如，可以通过连接四边形的对角线来将其划分为两个三角形，从而利用三角形的性质来解决问题。
THANKS。
可以根据此性质证明两条线段相等。
这一性质在证明角度相等时非常有用。
可以利用平行四边形的对角相等性质来解决一些与角度有关的问

平行四边形的性质平行四边形的特征

已知对角线AC和BD相交于点O，△AOB的
周长等于14 ，AB=4，那么对角线AC与BD的
和是多少？
A
D
解：已知AO+BO+AB=14
又
AB=4
O
B
C
所以 AO+BO=14－4=10
因为平行四边形对角线互相平分
所以
AC+BD=2AO+2BO =2（AO+BO）
=2×10 =20
你能找出图中一些不变的量吗?
02
找一找
平行四边形是一个中心对称图形
A 邻边邻角对角
B
D
对边
C
读作：平行四边形ABCD
记作： ABCD
平行四边形的特征
对边
相等
对角线互相平分
对角相等,邻角互补
A
D
B
C
练一练
已知在
中，
∠A=100°, AB = 5，
BC = 8，求其余各内角
的度数及它的周长。
ABCD
一边为5cm的平行四
若D在BC边上移动
思考题:如图,已知等腰△ABC中AB=AC, D是BC边上任意一点,DE//AC,DF//A B
知识整理
1
利用平面图形的旋转变换探索平行四边形的特征
2
这节课我们学习平行四边形的概念和特征
202X
谢谢大家！
汇报人姓名汇报人日期
你能找出平行四边形吗？
01
平行四边形的对称中心在哪儿？
解：由于平行四边形的对角相等
所以 ∠ D =∠ B = 80
A
因为AD//BC
所以 ∠A+∠B= 180 B

认识平行四边形ppt课件

认识平行四边形
目录
• 平行四边形的定义 • 平行四边形的性质 • 平行四边形的判定 • 平行四边形的面积和周长 • 平行四边形的应用 • 总结与回顾
01
平行四边形的定义
定义
01
平行四边形是由两组相对边平行组成的四边形。
02
它是一种特殊的四边形，在几何学中具有重要地位。
特点
01
02
03
对边平行
面积计算方法
先确定平行四边形的底和高，然后使用面积公式进行计算。
注意事项
在计算面积时，要确保底和高的长度是有效的，即底不能为0，高不能为负数。
周长计算
周长公式
平行四边形的周长等于四条边的长度之和，用数学公式表示为 $P = text{边1} + text{边2} + text{
边3} + text{边4}$。
平行四边形的对边平行，这是平行四边形的基本性质。
对角相等
平行四边形的对角相等，即相邻的两个角的角度和为180度。
对角线互相平分
平行四边形的对角线互相平分，这是平行四边形的一个重要性质。
分类
按照角度分类
根据平行四边形内角的大小，可以分为锐角、直角、钝角和平角平行四边形。
按照边长分类
根据平行四边形的边长比例，可以分为等腰、不等腰和矩形等不同类型的平行四边形。
02
平行四边形的性质
对角线性质
对角线互相平分
平行四边形的对角线互相平分，将平行四边形分成两个面积相等的三角形。
对角线性质的应用
利用对角线互相平分的性质，可以证明平行四边形的相关性质，如平行四边形的相对两角相等。
对边性质

初三数学中考复习专题6_四边形(含变换).

初三数学中考复习专题6_四边形(含变换).京华中学初三数学辅导班资料6 四边形及平移旋转对称一、1、知识框图：矩形四边形平行四边形菱形梯形2、正方形一组对边平行四边形一组对边不平行3、有一个角是直角梯形两腰相等直角梯形等腰梯形图形之间的变换关系轴对称连结对应点的线段平行(或在同一直线上)且相等,对应线段平行(或在同一直线上)且相等对应点与旋转中心的距离不变;每一点都绕旋转中心旋转了同样大小的角度旋转对称中心对称平移旋转在轴对称、平移、旋转这些图形变换中,线段的长度不变,角的大小不变;图形的形状、大小不变二、例题分析1、四边形例1（1）凸五边形的内角和等于______度，外角和等于______度，（2）若一凸多边形的内角和等于它的外角和，则它的边数是_______．- 1 -2．平行四边形的运用例2 如图，∠1＝∠2，则下列结论一定成立的是（）A. AB∥CDB. AD∥BCC. ∠B＝∠DD. ∠3＝∠4 若ABCD是平行四边形，则上述四个结论中那些DA是正确？你还可以得到什么结论？41 23BC3．矩形的运用例3 如图1，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、则阴影部分的面积是矩形ABCD的面积的……………………………………………（）A、4．菱形的运用例4 1. 一个菱形的两条对角线的长的比是2 ：3 ，面积1113 B、C、D、54310AEBO图1DFC是12 cm2 ，则它的两条对角线的长分别为_____、____．2、已知菱形的周长为40cm，两条对角线之比为3：4，则菱形的面积为_______．5．等腰梯形的有关计算例5 已知：如图，等腰梯形ABCD中，AD∥BC，AD＝3，AB＝4，BC＝7.求∠B的度数.．AD BCE 6．轴对称的应用例6 如图，牧童在A处放牛，其家在B处，若牧童从A处出发牵牛到河岸CD边饮水后再回家，试问在何处饮水所走路程最短?_ B_ A_ C_ D- 2 -7．中心对称的运用例7 如图，作△ABC关于点O的中心对称图形△DEF AO BC8．平移作图例8 ．在5×5方格纸中将图（1）中的图形N平移后的位置如图（2）中所示，那么正确的平移方法是（）．（A）先向下移动1格，再向左移动1格（B）先向下移动1格，再向左移动2格（C）先向下移动2格，再向左移动1格（D）先向下移动2格，再向左移动2格NNM图(1)M(2)图1 图图2 （第1题）9．旋转的运用例9 如图，△ABC和△ADE都是等腰直角三角形，∠C和∠AED都是直角，点C在AD上，如果△ABC经旋转后能与△ADE重合，那么哪一点是旋转中心?旋转了多少度?解：_____是旋转中心，_______方向旋转了______．B基础达标一、选择题：ACDE1. 一个内角和是外角和的2倍的多边形是________边形．2. 有以下四个命题：（1）两条对角线互相平分的四边形是平行四边形．（2）两条对角线相等的四边形是菱形．（3）两条对角线互相垂直的四边形是正方形．（4）两条对角线相等且互相垂直的四边形是正方形，其中正确的个数为（） A.4 B.3 C.2 D.1- 3 -3．下面条件中，能判定四边形是平行四边形的条件是（）A．一组对角相等B．对角线互相平分C．一组对边相等D．对角线互相垂直4．在一个平面上有不在同一直线上的三点，则以这三点为顶点的平行四边形有（）A．1个B．2个C．3个D．4个5. 如图，□ABCD中，∠C＝108°，BE平分∠ABC，则∠ABE等于（） A.18° B.36° C.72°D.108° A6、下列说法中，正确的是（）A 、等腰梯形既是中心对称图形又是轴对称图形．BB 、正方形的对角线互相垂直平分且相等C 、矩形是轴对称图形且有四条对称轴D 、菱形的对角线相等7、如图，在平行四边形ABCD中，下列各式不一定正确的是（）A．?1??2?180 B．?2??3?180 C．?3??4?180 D．?2??4?1808、在平行四边形ABCD中，延长AD至F，延长CD至E，连接EF，则?E??F? ?B?110?，（）（A）110? （B）30? （C）50? （D）70? _ F_ E_ AD_ _ B_ C0000EDC9、如图7，直线l是四边形ABCD的对称轴，若AB＝CD，有下面的结论：①AB∥CD；②AC⊥BD；③AO＝OC；④AB⊥BC，其中正确的结论有_________．10.如图，观察下列图形，既是轴对称图形又是中心对称图形的个数是（）．A.3个B.4个C.5个D.6个- 4 -11．下列基本图形中，经过平移、旋转或轴对称变换后，不能得到右图的是（）．．A．B．C. D．12．右图可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是（）A．90o B．60o C．45o D．30o13．图2是我国古代数学赵爽所著的《勾股圆方图注》中所画的图形，它是由四个相同的直角三角形拼成的，下面关于此图形的说法正确的是（）A．它是轴对称图形，但不是中心对称图形B．它是中心对称图形，但不是轴对称图形C．它既是轴对称图形，又是中心对称图形(图2) D．它既不是轴对称图形，又不是中心对称图形14、下图可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是（）- 5 -A．90o B．60o C．45o D．30o14 图1515、如上图，O是正六边形ABCDE的中心，下列图形中可由△OBC平移得到的是（）A．△OCD B．△OAB C．△OAF D．OEF16.如图，D、E、F是△ABC三边的中点，且DE∥AB，DF∥AC，EF ∥BC，平移△AEF可以得到的三角形是（）A.△BDFB.△DEFC.△CDED.△BDF 和△CDE AFACEOBDBDC图16 图1717.将两块直角三角尺的直角顶点重合为如图17的位置，若∠AOD＝110°，则∠BOC＝____°18、如图将四个全等的矩形分别等分成四个全等的小矩形，其中阴影部分面积相等的是（）① ② ③ ④A．只有①和②相等B．只有③和④相等C．只有①和④相等D．①和②，③和④分别相等19.如图，已知△ABC，画出△ABC绕点C逆时针旋转90°后的图形．- 6 -ACB20、矩形纸片ABCD中，AD＝4cm ，AB＝10cm，按如图方式折叠，使点B与点D重合，折痕为EF，则DE＝______cm．E B A DF CC121、若四边形的两条对角线相等，则顺次连结该四边形各边中点所得的四边形是（）A.梯形B.矩形C.菱形D.正方形22．如图：已知在Rt△ABC中，∠ABC＝90°，∠C ＝60°，边AB＝6cm．（1）求边AC和BC的值；（2）求以直角边AB所在的直线l为轴旋转一周所得的几何体的侧面积．(结果用含π的代数式表示) 解：F分别在AB、AC、BC上，DE//BC，23、（2022常州市）如图，在?ABC中，点D、E、EF//AB，且F是BC的中点．求证：DE?CF- 7 -ADEBFC24．三月三，放风筝，小明制了一个风筝，如右图，且DE＝DF，EH＝FH，小明不用度量就知道∠DEH ＝∠DFH．请你用所学过的数学知识证明之．（提示：可连结DH，证明ΔDHE≌ΔDHF或连结EF，通过证明等腰三角形得证．）25.如图，E、F是□ABCD的对角线AC上两点，AE＝CF．求证：（1）△ABE≌△CDF.（2）BE∥DF．DEACFB- 8 -（B层）25、如图，在□ ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AC、BD分别交于E、F，求证：四边形AFCE是菱形．AE1DOB2FC26.(2022.上海)如图1，边长为3的正方形ABCD绕点C 按顺时针方向旋转30 °后得到正方形EFCG，EF交AD于点H，那么DH的长为________．- 9 -EAHDFBCG27．如图，已知正方形ABCD的边长为2.如果将线段BD 绕着点B旋转后，点D落在CB的延长线上的D′点处，那么tan?BAD′等于__________29、（2022广东省）如图，等腰梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，E、F分别是BM、CM的中点．（1）求证：四边形MENF是菱形；（2）若四边形MENF是正方形，请探索等腰梯形ABCD 的高和底边BC的数量关系，并证明你的结论．- 10 -四边形及平移旋转对称答案二、考题例析例1 (n －2)·180o ＝360o.解得n＝4. 例2 答案：B. 例3（ B ）例4_____4cm，6cm ___例5答案：∠B＝60°．例6．中心对称的运用例7 例8 ．（C）_____．AC BMM'D例9 点A是旋转中心，顺时针方向旋转了45．A'基础达标一、选择题：（D）9、（①AB∥CD；②AC⊥BD；③AO＝OC；10.( B ).11．C. 12．（C ）13．B．14 （C）15、D．16.(D ) 17.(_70°18、( D) 19．1.___6___2. D.3．（B ）4．（C）5 ( B )6、（B 7、（D8、20、DE＝___5．8___cm.21、C.菱形22．解：（1）AC＝43 cm，BC＝23cm （2）所求几何体的侧面积S＝23、∵DE//BC，EF//AB- 11 -1?(2??23)?43?24?（cm2）2∴四边形DBFE是平行四边形∴ DE＝BF，∵ F是BC的中点．∴BF＝CF ∴DE?CF24．：可连结DH，证明ΔDHE≌ΔDHF或连结EF，通过证明等腰三角形得证．25.（1）证明：∵在△ABC与△EFD中，AB＝EF，由EF∥AB得∠BAC＝∠FED.由AD＝CE得AC＝ED．∴△ABC≌△EFD．（2）四边形BDFC是平行四边形．证明：∵△ABC≌△EFD，∴BC＝FD，∠BCA＝∠EDF．∴BC∥FD∴四边形BDFC是平行四边形．26剖析：解题时，注意区分判定定理与性质定理的不同使用．∵□ ABCD中，AE∥CF，∴?1??2. 又?AOE??COF，AO?CO．AE1D∴△AOE≌△COF，∴EO?FO. ∴四边形AFCE是平行四边形．又EF?AC，∴□ AFCE是菱形．27. _3_______. 28___2_______ 29、BO2FC- 12 -第一章图形与证明（二）1.1等腰三角形的性质和判断定理：等腰三角形的两个底角相等（简称“等边对等角”）定理：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A. ﻩB. ﻩ
Ｃ． ﻩD．
二、填空题(共2小题；共1０分)
5．如图，在矩形中, ,对角线，相交于点 , 垂直平分于点 ,则的长为.
６.如图,在四边形中，对角线 ,垂足为，点， , ，分别为边 , ，，的中点.若，，则四边形的面积为.
三、解答题(共8小题；共104分)
7．如图，在平行四边形中，点是边的中点,连接并延长，交延长线于点，连接， .
【解析】因为垂直平分 ,
所以，， ,
．
６.
【解析】提示：利用中位线可知四边形是平行四边形，
再根据 ,可知平行四边形是矩形．
第三部分
7. (1）四边形为平行四边形，
, .
．
又为的中点，
.
在和中，
．
．
四边形是平行四边形．
（2）
８．（１)在和中，
，
.
，
，
,
.
又 ,
四边形是菱形.
（1）求证:四边形是平行四边形;
（2)若，则当时,四边形是矩形.
8.已知:如图,四边形中, , ，是对角线上一点,且 .
ﻩ
（1）求证：四边形是菱形；
（2)如果 ,且 ,求证:四边形是正方形.
9.如图,在菱形中，对角线 , 相交于点，过点作对角线的垂线交的延长线于点．
ﻩ
（1)求证：四边形是平行四边形；
（2)
【解析】当四边形的边满足条件时, .
当时,四边形是菱形,此时 .
因为 , , , ，
所以 .
所以当四边形的边满足条件时, ．
，
,
.
,
四边形为平行四边形.
(2) 四边形为菱形，
， ,
四边形是矩形,
, ,
.
, ,
, ，菱形的面积为 .
１3.（1)菱形；
理由：因为四边形是矩形，所以 .
因为 , ，分别是， , 的中点,
所以 , ,所以 .
同理可得 ,
所以四边形是菱形.
(2)当四边形满足且时,四边形是正方形．
ﻩ
（1）求证：四边形是平行四边形;
（２）若四边形是菱形， ,求菱形的面积．
1３．如图所示，，， , 分别是四边形的边 , , ，的中点.
ﻩ
（1）当四边形是矩形时，四边形是形,请说明理由；
（2）当四边形满足什么条件时，四边形是正方形?并说明理由.
14.已知:在四边形中， , , ，分别是 , , , 的中点.
理由:因为，分别是四边形的边，的中点，
所以 , ,
同理, , ，， .
因为，所以 ,
所以平行四边形是菱形.
因为，所以 ,所以四边形是正方形．
14.（1）连接 , , ， .
因为 , 分别是 , 的中点,
所以．
同理 , ， ,
所以 , .
所以四边形是平行四边形.
所以与互相平分.
11.如图，将一张矩形纸片沿着对角线向上折叠,顶点落到点处, 交于点．
(1）求证: 是等腰三角形；
(２)如图，过点作 ,交于点 ,连接交于点，
ﻩ①判断四边形的形状，并说明理由；
②若 , ，求的长．
12.准备一张矩形纸片，按如图操作:
将沿翻折,使点落在对角线上的点,将沿翻折,使点落在对角线上的点.
（2），
.
设， ,
则 ,
解得．
．
．
四边形是正方形.
9.（１）四边形是菱形，
, ，
, ，
，即，
，
，
四边形是平行四边形;
（2）四边形是菱形, , ，
, , ,
四边形是平行四边形，
，，
的周长为 .
10.（1）在矩形中， , .
，
，
.
即．
在中， .
在中, ．
,
．
同理得, .
四边形为平行四边形.
A. ﻩＢ. ﻩ
Ｃ. D.
2．如图，菱形中,对角线 , 相交于点，为边的中点，若菱形的周长为，则的长为
ﻩ
ﻩA. ﻩB.
C. ﻩD.
3.下列性质中，菱形具有而矩形不一定具有的是
A．对角线相等B.对角线相互平分
Ｃ.对角线相互垂直D.邻边相互垂直
4.如图,已知菱形的顶点 , ．若菱形绕点逆时针旋转，每秒旋转 ,则第时，菱形的对角线交点的坐标为
（2)在正方形中, .
设 ,则．
在中， .
.
,
.
.
在中, ，
.
．
．
即 .
11.（1)根据折叠， ,
又 ,
，
,
．
是等腰三角形.
(2)① ， ,
四边形为平行四边形,
,
四边形为菱Leabharlann ．② , , ,,
四边形为菱形，
， , ，
设 ,
，
在中, ,
,
, ,
，
．
12. (1) 四边形是矩形，
, ，，
平行四边形的图形变换
———————————————————————————————— 作者：
———————————————————————————————— 日期：
平行四边形的图形变换
一、选择题（共4小题；共20分)
1.如图，将平行四边形绕点逆时针旋转 ,得到平行四边形，若点恰好落在边上，则的度数为
(１)求证: 与互相平分；
（2)当四边形的边满足条件时, .
答案
第一部分
1. Cﻩ
2.Ｂﻩ
3．Cﻩ
４.Ｂ【解析】四边形是菱形，
点是的中点,
．
菱形绕点逆时针旋转，每秒旋转，
旋转的角度为 .
，
菱形终止的位置与原图形关于原点成中心对称,
第时，菱形的对角线交点的坐标为 .
第二部分
5.
(２）若， ,求的周长．
１0．在一次课题学习中，老师让同学们合作编题.某学习小组受赵爽弦图的启发，编写了下面的这道题，请你来解一解．
ﻩ如图，将矩形的四边，， , 分别延长至 , , ， ,使得， ,连接， , , .
（1）求证:四边形为平行四边形；
（2)若矩形是边长为的正方形，且，，求的长．