化工原理 第三章非均相物系分离 第一节重力沉降 课件
化工原理第三章 沉降

2 d p ( p ) g
1.86 10 Pa s
5
18
(40 106 )2 9.81 ( 2600 1.165) 18 1.86 10 5
0.12m s
校核:
Re dut 0.3 2
(正确)
6.非球形颗粒的沉降速度
同样条件下 因此
1 3
1 则:Re k 18
令
Rep 1
则
k 2.62
层流区:
k 2.6 2 采用斯托克斯公式
过渡区:
湍流区:
2.62 k 60.1
60.1 k 2364
采用阿伦公式
采用牛顿公式
试差法: 假设 流型 选择 公式
验算
计算
ut
计算
Re t
例:求直径40μm球形颗粒在30℃大气中的自由沉降 速度。已知ρ颗粒为2600kg/m3,大气压为0.1MPa。 解: 查30℃、0.1MPa空气: 1.165kg m3 设为层流,则:
ζ是流体相对于颗粒运动时的雷诺数的函数,
(Re) (d pu / )
层流区 过渡区 湍流区
10 4 Re 2
24 Re
2 Re 500
500 Re 2 10
5
10 0.5 Re 0.44
第二节 重力沉降
目的:流体与固体颗粒分离
上部易形成涡流 ——倾斜式、 旁路 尘粒易带走 ——扩散式
螺旋面进口:结构复杂,设计制造不方便。
蜗壳形进口:结构简单,减小阻力。
轴向进口:常用于多管式旋风分离器。
常用型式
标准型、CLT/A型、CLP型、扩散式等。
第三章 非均相物系分离

B B
含尘气体
用途:适用于含颗粒浓度为 0.01 ~ 500g/m3、粒度不小于5μm的气体净 化与颗粒回收操作,尤其是各种气固流态化装置的尾气处理。
排尘
结构和工作原理:含尘气体以较高的线速度切向进入器内, 在外筒与排气管之间形成旋转向下的外螺旋流场,到达锥底 后以相同的旋向折转向上形成内螺旋流场直至达到上部排气 管流出。颗粒在内、外旋转流场中均会受离心力作用向器壁 方向抛出,在重力作用下沿壁面下落到排灰口被排出。
2 gd p ( p )
18ut 0.153Pa s
9.81 (1.25103 ) 2 (7900 880) 18 0.039
校核雷诺数 R ep 上述计算有效
d put
1.25103 0.039 880 0.28 2 0.153
三、重力沉降设备-降尘室 降尘室:分离含尘气体中颗粒的重力沉降设备。
2 P
比表面积:单位体积颗粒所具有的表面积
S 6 a V dP
2、非球形颗粒
(1)当量直径 A:体积当量直径 B:面积当量直径:
d ev
3
6V
S
d es
C:比表面当量直径: d 6 6 ea a S /V (2)形状因数 常用球形度 Ψ 表示,即与颗粒等体积的一个球的表面积 与颗粒的表面积之比 2 2 d ev d ev 2 2 d es d es
CD为阻力系数,与颗粒的雷诺数Rep有关。对球形颗粒 24 d p u A:Rep<2,层流区 Rep 此时 CD Rep 2 gd p ( p ) 由此推出 u -斯托克斯公式 t 18
适用范围10-4<Rep<2
化工原理第三章1沉降解析

u0
d
2 s g
18
Re 0
du0
二、干扰沉降
颗粒之间距离很小的沉降称为干扰沉降。 • 干扰沉降的速度可用自由沉降速度的计算方法计
算,但要根据颗粒浓度对所用的流体密度及黏度 进行校正。 • 用上述方法计算干扰沉降的速度比自由沉降要小
二、重力沉降分离设备
一)降尘室 • 降尘室的生产能力
降尘室的生产能力是指降尘室所处理的含尘气体的体积流 量,用Vs表示,m3/s。 降尘室内的颗粒运动
以速度u
以速度u0
随气体流动 作沉降运动
颗粒在降尘室的停留时间 l u
颗粒沉降到室底所需的时间 0 H u0 为了满足除尘要求 0
l H ——降尘室使颗粒沉降的条件 u u0
0.44
u0 1.74
ds g
——牛顿公式
3)影响沉降速度的因素
①颗粒的体积浓度
在前面介绍的各种沉降速度关系式中,当颗粒的体积浓
度小于0.2%时,理论计算值的偏差在1%以内,但当颗粒浓
度较高时,由于颗粒间相互作用明显,便发生干扰沉降,
自由沉降的公式不再适用。
②器壁效应
当器壁尺寸远远大于颗粒尺寸时,(例如在100倍以上)
18VS
gs A底
• 说明
②最大的气体处理量还与降尘室底面积和颗粒的沉降速度 有关,底面积越大处理量越大,但处理量与高度无关。
为此,降尘室都做成扁平形;为提高气体处理量,室内 以水平隔板将降尘室分割若干层,称为多层降尘室。隔 板的间距应考虑出灰的方便。
• 降尘室的计算
设计型 已知气体处理量和除尘要求,求
化工原理第三章PPT
1 重力沉降
重力: 浮力: Fg Fb 6 6 4 d
2
d sg
3
阻力Fd 浮力Fb
d g
3
阻力:
Fd
u 2
2
6
d ( s )
3
4
d
2
u t 2
2
ut
4 d ( s )g 3
V2=KA2θ
q2=Kθ
• 例 拟在9.81kPa的恒定压强差下过滤悬浮于水中直径为 0.1mm的球形颗粒物质,悬浮液中固相体积分率为10%, 水的粘度为1×10-3Pa· s。过滤过程介质阻力不计,滤饼为 不可压缩滤饼,其空隙率为60%,过滤机过滤面积为10m2, 计算:(1)得到15m3滤液时需过滤时间;(2)若将过滤时间 延长一倍时,可得滤液共为若干? • 例 在100KPa的恒压下过滤某悬浮液,温度30℃,过滤 14 2 1 10 m 面积为40m2 ,并已知滤渣的比阻为 , υ值为 0.05m3/m-3。过滤介质的阻力忽略不计,滤渣为不可压 缩,试求:(1)要获得10m3滤液需要多少过滤时间?(2)若 仅将过滤时间延长一倍,又可以再获得多少滤液?(3)若 仅将过滤压差增加一倍,同样获得10m3滤液时又需要多 少过滤时间?
6.6 恒压过滤 (V+Ve)2=KA2(θ+θe)
(q+qe)2=K(θ+θe)
总结:恒压过滤方程式
以绝对滤液量为基准
(V+Ve)2=KA2(θ+θe) V2+2VeV =KA2θe
以相对滤液量为基准
(q+qe)2=K(θ+θe) q2+2qeq =Kθe qe=Kθe
化工原理课件第三章非均相物系的分离

第三章 非均相物系的分离一、填空题:1.⑴一球形石英颗粒,在空气中按斯托克斯定律沉降,若空气温度由20°C 升至50°C ,则其沉降速度将 。
⑵降尘室的生产能力只与降尘室的 和 有关,而与 无关。
解⑴下降 ⑵长度 宽度 高度2.①在除去某粒径的颗粒时,若降尘室的高度增加一倍,则沉降时间 ,气流速度 ,生产能力 。
②在滞流(层流)区,颗粒的沉降速度与颗粒直径的 次方成正比;在湍流区,颗粒的沉降速度与颗粒直径的 次方成正比。
解①增加一倍 , 减少一倍 , 不变 ②2 , 1/2沉降操作是指在某种 中利用分散相和连续相之间的 差异,使之发生相对运动而实现分离的操作过程。
沉降过程有 沉降和 沉降两种方式。
答案:力场;密度;重力;离心3.已知q 为单位过滤面积所得滤液体积V/S ,e e e S V q V /,为为过滤介质的当量滤液体积(滤液体积为e V 时所形成的滤饼层的阻力等于过滤介质的阻力),在恒定过滤时,测得2003740/+=∆∆q q τ,过滤常数K = ,e q = 。
解0.000535 , 0.05354.⑴间歇过滤机的生产能力可写为Q =V/∑τ,此外V 为 ,∑τ表示一个操作循环所需的 ,∑τ等于一个操作循环中 , 和 三项之和。
一个操作循环中得到的滤液体积 ,总时间 ,过滤时间τ ,洗涤时间τw , 辅助时间τ D⑵.一个过滤操作周期中,“过滤时间越长,生产能力越大”的看法是 ,“过滤时间越短,生产能力越大”的看法是 。
过滤时间有一个 值,此时过滤机生产能力为 。
不正确的 ,不正确的 , 最适宜 , 最大⑶.过滤机操作循环中,如辅助时间τ越长则最宜的过滤时间将 。
⑶ 越长(4). 实现过滤操作的外力可以是 、 或 。
答案:重力;压强差;惯性离心力5.⑴在过滤的大部分时间中, 起到了主要过滤介质的作用。
⑵最常见的间歇式过滤机有 和 连续式过滤机有 。
⑶在一套板框过滤机中,板有 种构造,框有 种构造。
化工原理下册第三章非均相物系分离

: 流-固之间的相对运动有三种情况
1).流体静止,固体颗粒作沉降 运动; 2).固体静止,流体对固体作绕 流; 3).流体和固体都运动,但二者 保持一定的相对速度。
20
制作者:黄德春
第一节 重力沉降
知识点:
重力沉降原理、沉降速度和 相关设备
《制作化者:工黄德原春 理》课件——第三章 非均相物系的分离
《制作化者:工黄德原春 理》课件——第三章 非均相物系的分离
自来水厂全貌
图中兰色粗管是来自黄浦江的原料水,条形池子是絮凝池,左侧池 是沉降池。
《制作化者:工黄德原春 理》课件——第三章 非均相物系的分离
自来水厂沉降池
这是沉降池。图为絮凝之后的水,是从沉降池底部流入,到池子上 部水已很清了。
《制作化者:工黄德原春 理》课件——第三章 非均相物系的分离
旋风分离
主要用于石油、化工、肥料、冶金、 煤炭及环保的尾气除尘和高炉烟气净化、 颗粒回收等,目前已成功应用于氮肥厂 造气炉的除尘及煤粉回收,也可用于石 油化工装置中如丙烯腈、苯酐、百菌清、 苯胺等作为流化床内旋风分离器用以回 收昂贵的细颗粒催化剂,以及钙镁磷肥 回转窑烘干、球磨系统的尾气除尘和高 炉烟气净化等。在正常工作状态下,气 固 分 离 效 率 不 小 于 99% , 阻 力 不 大 于 1000Pa。。
u ut 自由沉降速度
1 6
d
3s
g
1 6
d
3g
1 4
d
2 Leabharlann ut2 2ut 4gd(s ) m / s 3
自由沉降速度公式
制作者:黄德春
u金沉 u沙沉 金子
《制作化者:工黄德原春 理》课件——第三章 非均相物系的分离
化工原理第三章非均相物系的分离ppt课件

6 ds
精选ppt
5
2)非球形颗粒
(1) 描述颗粒形状
球形颗粒 非球形颗粒
① 颗粒的形状系数(球形度φ)
球 形 度 与 颗 粒 等 体 颗 积 粒 的 的 球 表 形 面 颗 积 粒 的 表 面 积
公式表示 : As A
1
表明:颗粒形状接近于球形的程度;φ↑,则颗粒
越接近于球形。球形颗粒:
1
精选ppt
ai — ………………………比表面积;
dai —混合颗粒中各种尺寸颗粒的等比
表面积当量直径。
精选ppt
13
3.2 沉 降
目的:流体与固体颗粒分离
原理:利用颗粒与流体之间的密度差,
将固体颗粒从流体中分离出来。
常用方法:
(1) 重力沉降(分离较大的颗粒),例:选矿
(2) 离心沉降 (分离尺寸小的颗粒),例:气体
• 对于非球形颗粒物,这种关非常复杂。
精选ppt
15
对于球形颗粒,流体阻力的计算方程:
牛顿阻力公式:
FD
d42
u02
2
FD
CDAP
u2
2
颗粒的投影面积
:阻力系数,通过因次分析法得知,ξ值是颗粒
与流体相对运动时的雷诺数的函数。
f(Roe)
Re0
duo
颗粒的雷诺数
精选ppt
16
层流区
过渡区
3. 非均相物系分离的目的
1)、回收分散物质,如从母液中分离出晶粒 (如海盐生产) ;从催化反应器出来的气体, 常带有催化剂颗粒,必须把这些有价值的颗粒 回收利用。
2)、劳动保护和环境卫生,对三废:废气、废 液、废渣的处理(环保),非均相物系分离的 目的是除害收益。
化工原理 第三章 非均项系分离

Re t
ut
d 2s
18
——斯托克斯公式
2020/10/5
2020/10/5
b) 过渡区或艾伦定律区(Allen)(1<Ret<103)
18.5
Re
0.6 t
ut 0.269
gd s Re t0.6
——艾伦公式
c) 滞流区或牛顿定律区(Nuton)(103<Ret < 2×105)
作用力
重力 惯性离心力
1、沉降速度
1)球形颗粒的自由沉降
重力 沉降 离心沉降
设颗粒的密度为ρs,直径为d,流体的密度为ρ,
2020/10/5
重力
Fg
6
d3sg
浮力
Fb
6
d 3g
而阻力随着颗粒与流体间的相对运动速度而变,可仿照
流体流动阻力的计算式写为 :
Fd
A u2
2
对球形颗粒A d 2
4
Fd
连续相 包围着分散相物质且处于连续 分散相介质 状态的流体
如:气态非均相物系中的气体 液态非均相物系中的连续液体
连续相与分散相 分离
不同的物理性质
机械 分离
分散相和连续相 发生相对运动的方式
2020/10/5
沉降 过滤
一、重力沉降
沉降 在某种力场中利用分散相和连续相之间的密度差异 ,使之发生相对运动而实现分离的操作过程。
第三章 非均相物系分离
第一节 重力沉降
一、沉降速度
1、球形颗粒的自由沉降 2、阻力系数 3、影响沉降速度的因素 4、沉降速度的计算 5、分级沉降
二、降尘室
1、降尘室的结构 2、降尘室的生产能力
2020/10/5
混合物
化工原理_11沉降分离原理及设备课件

二、重力沉降设备
对设置了n层水平隔板的降尘室,其生产能力为:
Vs n 1 blut
(3-30a)
动画14
33
二、重力沉降设备
降尘室结构简单,流动阻力小,但体积庞大, 分离效率低,通常只适用于分离粒度大于 50 m 的粗粒,一般作为预除尘使用。多层降尘室虽能 分离较细的颗粒且节省占地面积,但清灰比较麻 烦。
在实际沉降操作中,影响沉降速度的因素有:
1、颗粒的体积分数 2、器壁效应 3、颗粒形状的影响
21
第三章、非均相混合物 分离及固体流态化
3.1 沉降分离原理及设备 3.1.1 颗粒相对于流体的运动 3.1.2 重力沉降
22
一、 重力沉降速度的计算
1、试差法 假设沉降属 于某一流型 计算沉 降速度 核算 Ret
4 ( s ) g Re 3 2ut3
1 t
21 Re Re Re 查 t t t 曲线图,可求直径 d ,即
Ret d ut
26
一、 重力沉降速度的计算
量纲为一数群判别:
( s ) g K d3 2
K ≤2.62为斯托克斯定律区, 2.62< K <69.1为艾仑定律区,
6 da a
da s de
8
பைடு நூலகம்、颗粒的特性
非球形颗粒的特性,即 体积
Vp
6
de
3
表面积 比表面积
de Sp s
2
6 a s d e
9
二、 球形颗粒的自由沉降
图3-1
沉降颗粒的受力情况
10
二、 球形颗粒的自由沉降
颗粒受到三个力 重力 浮力 阻力
化工原理第三章概述、重力沉降ppt课件

(2〕过渡区:2<Re<500,Allen定律区
10
Re (3〕湍流区:500<Re<2×105,Newton定律区
0.44
【阐明】(1〕查ζ-Re关系曲线图,准确但复杂; (2〕经验公式计算简便,但是有误差。
2021/6/5
;
第二节 重力沉降
一、什么是沉降?
2021/6/5
【定义】在某种力场中利用分散相
有关说明
2021/6/5
;
【阻力系数ζ计算的经验公式】 【应用前提】球形颗粒。
根据不同的雷诺数范围〔区域〕内的阻力系数ζ 的变化情况,可用如下经验公式计算阻力系数ζ:
(1〕层流区:10-4<Re<2,Stokes定律区
24
Re
2021/6/5
;
层流区
过渡区
湍流区
2021/6/5
ζ-Re关系曲线图
;
何谓球形度
s
S Sp
S——与物体相同体积的球体的表面积; SP——物体的表面积。
【定义】与物体相同体积的球体的表面积和物体的 表面积之比。
2021/6/5
;
(1〕此处的雷诺数Re是指:
Re d Pu
计算Re时,dP应为足以表征颗粒大小的长度〔特 性尺寸),对球形颗粒而言,就是它的直径。
(2〕此处的区域〔如层流区〕范围与 流动型态的区域范围并不相同。
2021/6/5
;
【准数判别法】如果不能确定流动处在哪个区,亦 可采用以下方法先确定区域。通过实验整理数据可 得到:
其中:
Re
Ar
18 0.6 Ar
Ar
d
3 P
P
2
g
——阿基米德准数
2021/6/5
非均相物系分离第一节重力沉降

工业上处理的非均相混 合物颗粒小,加速段很 短,可以忽略不计。
第二章
13
ut =
4gd(s ) 3
试差法
是Ret的函数。
——重力沉降速度计算通式
Ret
ζ
ut
Ret
dut
103≤Ret<2×105 2< Ret<1000
10-4< Ret≤2
连续相
烟
气体
雾
分散相 固体
悬浮液 液体
液体 乳浊液
气体
泡沫
由于两相物理性质(如ρ、μ)不同,因此工业上常采用机 械的方法来分离(外界作用力)。
第二章
4
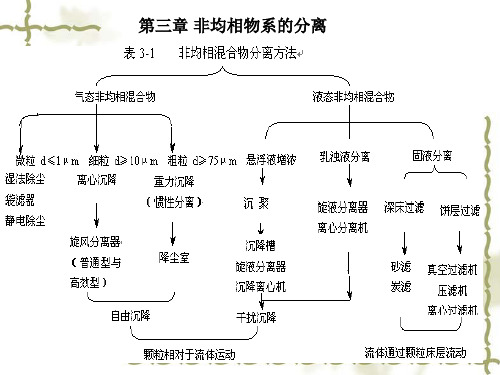
非均相物系分离方法
• 重力沉降
分散相颗粒在重力作用下,与周围流体发生相对运动实 现分离的过程。
• 离心沉降
颗粒在离心力的作用下沉降而实现分离的过程。
• 过滤
利用重力、离心力或人为造成的压差使悬浮液通过多孔性 过滤介质,固体颗粒被截留,滤液穿过介质流出,实现固 -液分离。
第二章
5
非均相物系分离在工业上的应用
• 回收分散物质 • 净化连续介质 • 环境保护
第二章
6
颗粒与颗粒群
• 颗粒形成的方式及原因不同,其形状与尺寸也不同。
球形颗粒的表面积 球形颗粒的体积 非球形颗粒的表面积 非球形颗粒的体积
假设成立。 ut =3.41×10-3m/s为所求。
第二章
17
(2)求d
设沉降属于层流区:
d 1u t 81 2 8 .3 1 3 0 0 .0 2 2 .4 1 2 4 m 0 (s) g ( 26 14 ) 2 9 0 .8 01 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
无因次数群K也可以判别流型
d ( ρs − ρ)g ut = 18µ
2
2011-11-9
d 3(ρs − ρ)ρg K3 Ret = = 2 18µ 18
当Ret=1时K=2.62,此值即为斯托克斯区的上限 牛顿定律区的下限K值为69.1 例:试计算直径为95µm,密度为3000kg/m3的固体颗粒分 别在20℃的空气和水中的自由沉降速度。 解:1)在20℃水中的沉降。 用试差法计算 先假设颗粒在滞流区内沉降 ,
2011-11-9
ξ=
4dg( ρs − ρ) 3ρut
2
QReet2 =
4d 3 ρ(ρs − ρ)g 3µ 2
2
令 k = d3 ρ( ρs − ρ)g 2
µ
4 3 ξ Re t = k 3
因ξ是Ret的已知函数,ξRet2必然也是Ret的已知函数, ξ~Ret曲线便可转化成 ξRet2~Ret曲线。 计算ut 时,先由已知数据算出ξRet2 的值,再由ξRet2~Ret 曲线查得Ret值,最后由Ret反算ut 。
——艾伦公式
c) 滞流区或牛顿定律区(Nuton)(103<Ret < 2×105) 滞流区或牛顿定律区( ) ×
ξ = 0.44
ut =1.74 d( ρs − ρ)g
ρ
——牛顿公式
2011-11-9
3、影响沉降速度的因素 、
1)颗粒的体积浓度 ) 在前面介绍的各种沉降速度关系式中,当颗粒的体积浓 度小于0.2%时,理论计算值的偏差在1%以内,但当颗粒浓 度较高时,由于颗粒间相互作用明显,便发生干扰沉降, 自由沉降的公式不再适用。 2)器壁效应 ) 当器壁尺寸远远大于颗粒尺寸时,(例如在100倍以上) 容器效应可忽略,否则需加以考虑。
µ
=
1.005×10
−3
= 0.9244< 1
原假设滞流区正确,求得的沉降速度有效。 2) 20℃的空气中的沉降速度 用摩擦数群法计算 20℃空气:ρ=⒈205 kg/m3,µ=⒈81×10-5 Pa.s 根据无因次数K值判别颗粒沉降的流型
2011-11-9
ρ(ρs − ρ)g −6 1.205(3000 −1.205) × 9.81 = 95×10 3 K = d3 2 −5 2 µ 1.81×10
d 2 (ρs − ρ)g ut = 18µ
附录查得,20℃时水的密度为998.2kg/m3,µ=1.005×10-3Pa.s
2011-11-9
(95×10 ) (3000 −998.2)×9.81 u =
−6 2 t
18×1.005×10
−3
= 9.797 ×10−3 m/ s
核算流型
Ret = dut ρ 95×10−6 ×9.797 ×10−3 ×998.2
2011-11-9
分散相 分散物质 非均相物系 连续相 分散相介质
处于分散状态的物质 如:分散于流体中的固体颗粒、 液滴或气泡 包围着分散相物质且处于连续 状态的流体 如:气态非均相物系中的气体 液态非均相物系中的连续液体
连续相与分散相 机械 分散相和连续相 分离 分离 不同的物理性质 发生相对运动的方式
φs=0.806,查图3-3的,Ret=60,则:
Ret µ 60×1.005×10−3 ut = = de ρ 998.2×8.685×10−4
= 0.0696m/ s
2011-11-9
2)纯方铅矿的尺寸范围 所得到的纯方铅矿粒尺寸最小的沉降速度应等于0.0696m/s 用摩擦数群法计算该粒子的当量直径。
2011-11-9
解:1)水的上升流速 为了得到纯方铅矿粒,应使全部石英粒子被溢流带出, 应按最大石英粒子的自由沉降速度决定水的上升流速。 对于正方体颗粒,先算出其当量直径和球形度。 设l代表棱长,Vp代表一个颗粒的体积。
de = 3
6
π
Vp
=3
6
π
l =3
3
6
π
(0.7×10−3) = 8.685×10−4 m
2011-11-9
4、沉降速度的计算 、
1)试差法 ) 方法: 假设沉降属于层流区
d 2 ( ρs − ρ) ut = 18µ
ut
Ret = duρ µ
Ret
ut为所求 公式适 用为止 2) 摩擦数群法 …… 判断 求ut 艾伦公式
Ret<1 Ret>1
4gd( ρs − ρ) 得 由 ut = 3ξρ
3 3
π
π
ρu2 2
2
=
π
6
d3ρsa
(a)
颗粒开始沉降的瞬间,速度u=0,因此阻力Fd=0,a→max 颗粒开始沉降后,u ↑ →Fd ↑;u →ut 时,a=0 。 等速阶段中颗粒相对与流体的运动速度ut 称为沉降速度。 当a=0时,u=ut,代入(a)式
π
d ρs g − d 3 ρg −ξ d 6 6 4
µ Ret ut = dρ
2011-11-9
2011-11-9
计算在一定介质中具有某一沉降速度ut的颗粒的直径, 令ξ与Ret-1相乘,
ξ Ret−1 = 4µ(ρs − ρ)g 3ρ2ut2
ξRet-1~Ret关系绘成曲线 ,由ξRet-1值查得Ret的值, 再根据沉降速度ut值计算d。
µ Ret d= ρut
Fg =
π
6
d3ρs g
F = b
π
6
d ρg
3
而阻力随着颗粒与流体间的相对运动速度而变,可仿照 流体流动阻力的计算式写为 :
Fd = ξA
ρu2
2
对球形颗粒A =
2
π
4
d2
∴Fd = ξ ⋅ d ⋅ 4 2
π
ρu2
Fg − Fb − Fd = ma
2011-11-9
π
d ρs g − d ρg −ξ d 6 6 4
2011-11-9
沉降 过滤
一、重力沉降
沉降 在某种力场中利用分散相和连续相之间的密度差异 ,使之发生相对运动而实现分离的操作过程。 重力 作用力 惯性离心力 离心沉降 重力 沉降
1、沉降速度 、
1)球形颗粒的自由沉降 ) 设颗粒的密度为ρs,直径为d,流体的密度为ρ,
2011-11-9
重力 浮力
与此当量直径相对应的正方体的棱长为:
de 3.182×10−4 l′ = = = 2.565×10−4 m 6 6 3 3
π
π
所得方铅矿的棱长范围为0.2565~0.7mm。
2011-11-9
3
π
ρut 2 π 2
2
=0
4dg(ρs − ρ) ut = 3ρξ
2011-11-9
——沉降速度表达式
2、阻力系数ξ 、阻力系数
通过因次分析法得知,ξ值是颗粒与流体相对运动时的 雷诺数Ret的函数。 对于球形颗粒的曲线,按Ret值大致分为三个区: a) 滞流区或托斯克斯 滞流区或托斯克斯(stokes)定律区(10 –4<Ret<1) 定律区( 定律区 )
沉降速度
第三章 非均相物系分离
第一节 重力沉降
1、球形颗粒的自由沉降 、 2、阻力系数 、 3、影响沉降速度的因素 、 4、沉降速度的计算 、 5、分级沉降 、
2011-11-9
均相混合物 物系内部各处物料性质均匀而且不 存在相界面的混合物。 混合物 例如:互溶溶液及混合气体 非均相混合物 物系内部有隔开两相的界面存在且 界面两侧的物料性质截然不同的混 合物。 固体颗粒和气体构成的含尘气体 例如 固体颗粒和液体构成的悬浮液 不互溶液体构成的乳浊液 液体颗粒和气体构成的含雾气体
2 S πde 8.685×10−4 φs = = 2= = 0.806 −3 2 Sp 6l 6×(0.7×10 )
2011-11-9
用摩擦数群法求最大石英粒子的沉降速度
2 4de (ρs2 − ρ)ρg ξ Ret2 = 3µ2
4(8.685×10−4 )3(2650 − 998.2) ×998.2×9.81 = =14000 −3 2 3(1.005×10 )
(
)
= 4.52
(
)
2.61<K<69.1,沉降在过渡区。用艾伦公式计算沉降速度。
ut =
1.6 1 1.4d 1.4 0.154g
(ρs − ρ)
1 1.4
ρ
0.4 1.4
µ
0.6 1.4
= 0.619m/ s
5、分级沉降 、
含有两种直径不同或密度不同的混合物,也可用沉降方法 加以分离。
2011-11-9
ξ
− Ret 1
4µ(ρs1 − ρ)g = 3ρ2ut3
4×1.005×10−3(7500 − 998.2) ×9.81 = = 0.2544 2 3 3×998.2 ×(0.0696)
φs=0.806,查图3-3的,Ret=22,则:
2011-11-9
Ret µ 22×1.005×10−3 de = = = 3.182×10−4 m ρut 998.2×0.0696
24 ξ= Ret
d ( ρs − ρ) ut = 18µ
2
2011-11-9
——斯托克斯公式
2011-11-9
b) 过渡区或艾伦定律区(Allen)(1<Ret<103) 过渡区或艾伦定律区( ) <
18.5 ξ = 0.6 Ret
ut = 0.269
gd( ρs − ρ) Re t 0.6
ρ
例:本题附图所示 为一双锥分级器,利 用它可将密度不同或 尺寸不同的粒子混合 物分开。混合粒子由 上部加入,水经可调 锥与外壁的环形间隙 向上流过。沉降速度大于水在环隙处上升流速的颗粒进 入底流,而沉降速度小于该流速的颗粒则被溢流带出。
