数据结构教程第三版第一章课后习题答案
数据结构1-3习题答案

试编写程序完成: 15个学生 个学生, 3.2 试编写程序完成:有15个学生,每个学生的 信息包括学号、姓名、性别、年龄、班级和3 信息包括学号、姓名、性别、年龄、班级和3 门课程成绩,从键盘输入15个学生的信息, 15个学生的信息 门课程成绩,从键盘输入15个学生的信息,要 求打印出3门课程的总平均成绩, 求打印出3门课程的总平均成绩,以及最高分 的学生的信息(包括学号、姓名、性别、年龄、 的学生的信息(包括学号、姓名、性别、年龄、 班级、 门课程成绩、平均分)。 班级、3门课程成绩、平均分)。
判断下述计算过程是否是一个算法: 2.4 判断下述计算过程是否是一个算法: Step1: 开始 Step2: n<=0; Step3: n=n+1; 重复步骤3; Step4: 重复步骤3; 结束; Step5: 结束; 该计算过程不是一个算法, 答:该计算过程不是一个算法,因为其不满足算法的 有穷性。 有穷性。
在下面两列中,左侧是算法(关于问题规模) 2.8 在下面两列中,左侧是算法(关于问题规模) 的执行时间,右侧是一些时间复杂度。 的执行时间,右侧是一些时间复杂度。请用连 线的方式表示每个算法的时间复杂度。 线的方式表示每个算法的时间复杂度。 100n3 6n2-12n+1 1024 n+2log2n n(n+1)(n+2)/6 2n+1+100n
线 性 表 存 储 方 式
顺序存储:初始化、插入、删除、 顺序存储:初始化、插入、删除、查找运算
: 存 插入、删除 插入、
存储:初始化、插入、删除、 存储:初始化、插入、 Nhomakorabea除、查找运算
:插入、删除 插入、 存储
存
重点:熟练掌握顺序表和单链表上实现的各种 重点: 基本算法及相关的时间性能分析 难点: 难点:能够使用本章所学到的基本知识设计有 效算法解决与线性表相关的应用问题。 效算法解决与线性表相关的应用问题。
数据结构第一章课后习题与答案

第 1 章 绪 论(2005-07-14) -第 1 章 绪 论课后习题讲解1. 填空⑴( )是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
【解答】数据元素⑵( )是数据的最小单位,( )是讨论数据结构时涉及的最小数据单位。
【解答】数据项,数据元素【分析】数据结构指的是数据元素以及数据元素之间的关系。
⑶ 从逻辑关系上讲,数据结构主要分为( )、( )、( )和( )。
【解答】集合,线性结构,树结构,图结构⑷ 数据的存储结构主要有( )和( )两种基本方法,不论哪种存储结构,都要存储两方面的内容:( )和()。
【解答】顺序存储结构,链接存储结构,数据元素,数据元素之间的关系⑸ 算法具有五个特性,分别是( )、( )、( )、( )、( )。
【解答】有零个或多个输入,有一个或多个输出,有穷性,确定性,可行性⑹ 算法的描述方法通常有( )、( )、( )和( )四种,其中,( )被称为算法语言。
【解答】自然语言,程序设计语言,流程图,伪代码,伪代码⑺ 在一般情况下,一个算法的时间复杂度是( )的函数。
【解答】问题规模⑻ 设待处理问题的规模为n,若一个算法的时间复杂度为一个常数,则表示成数量级的形式为( ),若为n*log25n,则表示成数量级的形式为( )。
【解答】Ο(1),Ο(nlog2n)【分析】用大O记号表示算法的时间复杂度,需要将低次幂去掉,将最高次幂的系数去掉。
2. 选择题⑴ 顺序存储结构中数据元素之间的逻辑关系是由( )表示的,链接存储结构中的数据元素之间的逻辑关系是由( )表示的。
A 线性结构B 非线性结构C 存储位置D 指针【解答】C,D【分析】顺序存储结构就是用一维数组存储数据结构中的数据元素,其逻辑关系由存储位置(即元素在数组中的下标)表示;链接存储结构中一个数据元素对应链表中的一个结点,元素之间的逻辑关系由结点中的指针表示。
⑵ 假设有如下遗产继承规则:丈夫和妻子可以相互继承遗产;子女可以继承父亲或母亲的遗产;子女间不能相互继承。
《数据结构基础教程》习题及解答

《数据结构基础教程》习题及解答数据结构基础教程习题及解答第一章:数据结构简介1.1 什么是数据结构?数据结构是指相互之间存在一种或多种特定关系的数据元素的集合,包括数据的逻辑结构、物理结构和数据元素之间的运算。
1.2 数据的逻辑结构有哪些?数据的逻辑结构包括线性结构、树形结构和图状结构。
1.3 数据的物理结构有哪些?数据的物理结构包括顺序存储结构和链式存储结构。
1.4 数据结构的主要目标是什么?数据结构的主要目标是提高数据的存储效率和运算效率。
第二章:线性表2.1 线性表的定义线性表是由n(≥0)个数据元素组成的有限序列。
线性表是一种常见的数据结构,常用的实现方式包括数组和链表。
2.2 线性表的顺序存储结构线性表的顺序存储结构是将线性表中的元素存储在连续的存储空间中,通过元素在内存中的物理位置来表示元素之间的关系。
2.3 线性表的链式存储结构线性表的链式存储结构是通过指针将线性表中的元素连接在一起,每个元素包括数据域和指针域。
2.4 线性表的基本操作包括初始化线性表、插入元素、删除元素、查找元素等。
第三章:栈与队列3.1 栈的定义与特性栈是一种具有后进先出特性的线性表,只允许在一端进行插入和删除操作,被称为栈顶。
3.2 栈的顺序存储结构和链式存储结构栈的顺序存储结构和链式存储结构与线性表的存储结构类似,不同之处在于栈只允许在一端进行插入和删除操作。
3.3 栈的应用栈在表达式求值、函数调用和递归等场景中有广泛应用。
3.4 队列的定义与特性队列是一种具有先进先出特性的线性表,允许在一端插入元素,在另一端删除元素。
3.5 队列的顺序存储结构和链式存储结构队列的顺序存储结构和链式存储结构与线性表的存储结构类似,不同之处在于队列允许在一端插入元素,在另一端删除元素。
3.6 队列的应用队列在模拟排队系统、操作系统进程调度等场景中有广泛应用。
第四章:树与二叉树4.1 树的基本概念树是由n(≥0)个节点组成的有限集合,其中有一个称为根节点,除了根节点之外的其余节点被分为m(m≥0)个互不相交的集合,每个集合本身又是一棵树。
数据结构实用教程(第三版)课后答案

数据结构实用教程( 第三版) 课后答案file:///D|/ ------------------ 上架商品---------------------- / 数据结构实用教程( 第三版)课后答案(徐孝凯著)清华大学/第一章绪论.txt第一章绪习题一一、单选题1. 一个数组元数a[i] 与( A ) 的表示等价。
A *(a+i)B a+iC *a+iD &a+i2. 对于两个函数,若函数名相同,但只是( C) 不同则不是重载函数。
A 参数类型B 参数个数C 函数类型3. 若需要利用形参直接访问实参,则应把形参变量说明为(B) 参数。
A 指针B 引用C 值4. 下面程序段的复杂度为(C ) 。
for(int i=0;i<m;i++)for(int j=0;j<n;j++)a[i][j]=i*j;A O(m2)B O(n2)C O(m*n)D O(m+n)5. 执行下面程序段时,执行S语句的次数为(D )。
for(int i=1;i<=n;i++)for(int j=1; j<=i;j++)S;A n2B n2/2C n(n+1)D n(n+1)/26. 下面算法的时间复杂度为( B) 。
int f(unsigned int n){if(n==0||n==1) return 1;Else return n*f(n-1);}A O(1)B O(n)C O(n2)D O(n!)二、填空题1. 数据的逻辑结构被除数分为集合结构、线性结构、树型结构和图形结构四种。
2. 数据的存储结构被分为顺序结构、结构、索引结构和散列结构四种。
3. 在线性结构、树型结构和图形结构中,前驱和后继结点之间分别存在着1 对1 、1 对N 和M对N的关系。
4. 一种抽象数据类型包括数据和操作两个部分。
5. 当一个形参类型的长度较大时,应最好说明为引用,以节省参数值的传输时间和存储参数的空间。
6. 当需要用一个形参访问对应的实参时,则该形参应说明为引用。
数据结构(第3版)习题答案

数据结构(第3版)习题答案⼗⼆五普通⾼等教育国家级本科规划教材第1章绪论⾼等学校精品资源共享课程1.1什么是数据结构?【答】:数据结构是指按⼀定的逻辑结构组成的⼀批数据,使⽤某种存储结构将这批数据存储于计算机中,并在这些数据上定义了⼀个运算集合。
1.2数据结构涉及哪⼏个⽅⾯?【答】:数据结构涉及三个⽅⾯的内容,即数据的逻辑结构、数据的存储结构和数据的运算集合。
1.3两个数据结构的逻辑结构和存储结构都相同,但是它们的运算集合中有⼀个运算的定义不⼀样,它们是否可以认作是同⼀个数据结构?为什么?【答】:不能,运算集合是数据结构的重要组成部分,不同的运算集合所确定的数据结构是不⼀样的,例如,栈与队列它们的逻辑结构与存储结构可以相同,但由于它们的运算集合不⼀样,所以它们是两种不同的数据结构。
1.4线性结构的特点是什么?⾮线性结构的特点是什么?【答】:线性结构元素之间的关系是⼀对⼀的,在线性结构中只有⼀个开始结点和⼀个终端结点,其他的每⼀个结点有且仅有⼀个前驱和⼀个后继结点。
⽽⾮线性结构则没有这个特点,元素之间的关系可以是⼀对多的或多对多的。
1.5数据结构的存储⽅式有哪⼏种?【答】:数据结构的存储⽅式有顺序存储、链式存储、散列存储和索引存储等四种⽅式。
1.6算法有哪些特点?它和程序的主要区别是什么?【答】:算法具有(1)有穷性(2)确定性(3)0个或多个输⼊(4)1个或多个输出(5)可⾏性等特征。
程序是算法的⼀种描述⽅式,通过程序可以在计算机上实现算法。
1.7抽象数据类型的是什么?它有什么特点?【答】:抽象数据类型是数据类型的进⼀步抽象,是⼤家熟知的基本数据类型的延伸和发展。
抽象数据类型是与表⽰⽆关的数据类型,是⼀个数据模型及定义在该模型上的⼀组运算。
对⼀个抽象数据类型进⾏定义时,必须给出它的名字及各运算的运算符名,即函数名,并且规定这些函数的参数性质。
⼀旦定义了⼀个抽象数据类型及具体实现,程序设计中就可以像使⽤基本数据类型那样,⼗分⽅便地使⽤抽象数据类型。
数据结构教程(含习题和答案)

第一章:概论(包括习题与答案及要点)本章的重点是了解数据结构的逻辑结构、存储结构、数据的运算三方面的概念及相互关系,难点是算法复杂度的分析方法。
需要达到<识记>层次的基本概念和术语有:数据、数据元素、数据项、数据结构。
特别是数据结构的逻辑结构、存储结构及数据运算的含义及其相互关系。
数据结构的两大类逻辑结构和四种常用的存储表示方法。
需要达到<领会>层次的内容有算法、算法的时间复杂度和空间复杂度、最坏的和平均时间复杂度等概念,算法描述和算法分析的方法、对一般的算法要能分析出时间复杂度。
--------------------------------------------------------------------------------对于基本概念,仔细看书就能够理解,这里简单提一下:数据就是指能够被计算机识别、存储和加工处理的信息的载体。
数据元素是数据的基本单位,有时一个数据元素可以由若干个数据项组成。
数据项是具有独立含义的最小标识单位。
如整数这个集合中,10这个数就可称是一个数据元素.又比如在一个数据库(关系式数据库)中,一个记录可称为一个数据元素,而这个元素中的某一字段就是一个数据项。
数据结构的定义虽然没有标准,但是它包括以下三方面内容:逻辑结构、存储结构、和对数据的操作。
这一段比较重要,我用自己的语言来说明一下,大家看看是不是这样。
比如一个表(数据库),我们就称它为一个数据结构,它由很多记录(数据元素)组成,每个元素又包括很多字段(数据项)组成。
那么这张表的逻辑结构是怎么样的呢? 我们分析数据结构都是从结点(其实也就是元素、记录、顶点,虽然在各种情况下所用名字不同,但说的是同一个东东)之间的关系来分析的,对于这个表中的任一个记录(结点),它只有一个直接前趋,只有一个直接后继(前趋后继就是前相邻后相邻的意思),整个表只有一个开始结点和一个终端结点,那我们知道了这些关系就能明白这个表的逻辑结构了。
数据结构第一章参考答案

习题11.填空题(1)(___________)是指数据之间的相互关系,即数据的组织形式。
通常人们认为它包含三个方面的内容,分别为数据的(___________)、(___________)及其运算。
答案:数据结构逻辑结构存储结构(2)(___________)是数据的基本单位,在计算机程序中通常作为一个整体进行处理。
答案:数据元素(3)数据元素之间的不同逻辑关系代表不同的逻辑结构,常见的逻辑结构有(___________)、(___________)、(___________)和(___________)。
答案:集合线形结构树结构图结构(4)数据的存储结构考虑的是如何在计算机中存储各个数据元素,并且同时兼顾数据元素间的逻辑关系。
基本的存储结构通常有两大类:(___________)和(___________)。
答案:顺序存储结构链式存储结构(5)通常一个问题可以有多种不同的算法,但每个算法必须满足5个准则:输入、输出、(___________)、(___________)和(___________)。
答案:有穷性确定性可行性(6)通常通过衡量算法的(___________)复杂度和(___________)复杂度来判定一个算法的好坏。
答案:时间空间(7)常见时间复杂性的量级有:常数阶O(___________)、对数阶O(___________)、线性阶O(___________)、线性对数阶O(___________)、平方阶O(___________)、和指数阶O(___________)。
通常认为,当问题规模较大时,具有(___________)量级的算法是不可计算的。
答案:1 log n n n log n n2 2n指数(8)STL提供的标准容器有顺序容器、(___________)和(___________)。
答案:排序容器哈希容器(9)算法可认为是STL的精髓,所有算法都是采用(___________)的形式提供的。
数据结构c语言版第三版习题解答

数据结构c语言版第三版习题解答数据结构 C 语言版第三版习题解答在学习计算机科学与技术的过程中,数据结构是一门非常重要的基础课程。
而《数据结构C 语言版第三版》更是众多教材中的经典之作。
其中的习题对于我们理解和掌握数据结构的概念、原理以及算法实现起着至关重要的作用。
接下来,我将为大家详细解答这本书中的一些典型习题。
首先,让我们来看一道关于线性表的习题。
题目是这样的:设计一个算法,从一个有序的线性表中删除所有其值重复的元素,使表中所有元素的值均不同。
对于这道题,我们可以采用双指针的方法来解决。
定义两个指针 p和 q,p 指向线性表的开头,q 从 p 的下一个位置开始。
当 q 所指向的元素与 p 所指向的元素相同时,我们就将 q 所指向的元素删除,并将 q 向后移动一位。
当 q 所指向的元素与 p 所指向的元素不同时,我们将 p 向后移动一位,并将 q 所指向的元素赋值给 p 所指向的位置,然后再将 q 向后移动一位。
当 q 超出线性表的范围时,算法结束。
下面是用 C 语言实现的代码:```cvoid removeDuplicates(int arr, int n) {int p = 0, q = 1;while (q < n) {if (arrp == arrq) {for (int i = q; i < n 1; i++){arri = arri + 1;}(n);} else {p++;arrp = arrq;}q++;}}```再来看一道关于栈的习题。
题目是:利用栈实现将一个十进制数转换为八进制数。
我们知道,将十进制数转换为八进制数可以通过不断除以 8 取余数的方法来实现。
而栈的特点是后进先出,正好适合存储这些余数。
以下是 C 语言实现的代码:```cinclude <stdioh>include <stdlibh>define MAX_SIZE 100typedef struct {int top;int dataMAX_SIZE;} Stack;//初始化栈void initStack(Stack s) {s>top =-1;}//判断栈是否为空int isEmpty(Stack s) {return s>top ==-1;}//判断栈是否已满int isFull(Stack s) {return s>top == MAX_SIZE 1;}//入栈操作void push(Stack s, int element) {if (isFull(s)){printf("Stack Overflow!\n");return;}s>data++s>top = element;}//出栈操作int pop(Stack s) {if (isEmpty(s)){printf("Stack Underflow!\n");return -1;}return s>datas>top;}//将十进制转换为八进制void decimalToOctal(int decimal) {Stack s;initStack(&s);while (decimal!= 0) {push(&s, decimal % 8);decimal /= 8;}while (!isEmpty(&s)){printf("%d", pop(&s));}printf("\n");}int main(){int decimal;printf("请输入一个十进制数: ");scanf("%d",&decimal);printf("转换后的八进制数为: ");decimalToOctal(decimal);return 0;}```接下来是一道关于队列的习题。
数据结构第一章答案

习题一1.1有下列几种用二元组表示的数据结构,试画出它们分别对应的图形表示(当出现多个关系时,对每个关系画出相应的结构图),并指出它们分别属于何种结构。
1.A=(K,R) 其中K={a1,a2,a3,…,a n}R={}2.B=(K,R),其中K={a,b,c,d,e,f,g,h}R={<a,b>,<b,c>,<c,d>,<d,e>,<e,f>,<f,g>,<g,h>}3.C=(K,R),其中K={a,b,c,d,e,f,g,h}R={<d,b>,<d,g>,<b,a>,<b,c>,<g,e>,<g,h>,<e,f>}4.D=(K,R),其中K={1,2,3,4,5,6}R={(1,2),(2,3),(2,4),(3,4),(3,5),(3,6),(4,5),(4,6)} 5.E=(K,R),其中K={48,25,64,57,82,36,75,43}R={r1,r2,r3}r1={<48,25>,<25,64>,<64,57>,<57,82>,<82,36>,<36,75>,<75,43>}r2={<48,25>,<48,64>,<64,57>,<64,82>,<25,36>,<82,75>,<36,43>}r3={<25,36>,<36,43>,<43,48>,<48,57>,<57,64>,<64,75>,<75,82>} 解:⑴是集合结构;⑵是线性结构;⑶⑷是树型结构;⑸散列结构1.2用C语言函数编写下列每一个算法,并分别求出它们的时间复杂度。
数据结构实用教程(第三版)课后答案

数据结构实用教程 (第三版) 课后答案file:///D|/-------------------上架商品---------------/数据结构实用教程 (第三版) 课后答案 (徐孝凯著) 清华大学出版社/第一章绪论.txt第一章绪习题一一、单选题1.一个数组元数a[i]与( A )的表示等价。
A *(a+i)B a+iC *a+iD &a+i2.对于两个函数,若函数名相同,但只是( C) 不同则不是重载函数。
A 参数类型B 参数个数C 函数类型3.若需要利用形参直接访问实参,则应把形参变量说明为 (B) 参数。
A 指针B 引用C 值4.下面程序段的复杂度为 (C )。
for(int i=0;i<m;i++)for(int j=0;j<n;j++)a[i][j]=i*j;A O(m2)B O(n2)C O(m*n)D O(m+n)5.执行下面程序段时,执行S语句的次数为 (D )。
for(int i=1;i<=n;i++)for(int j=1; j<=i;j++)S;A n2B n2/2C n(n+1)D n(n+1)/26.下面算法的时间复杂度为( B) 。
int f(unsigned int n){if(n==0||n==1) return 1;Else return n*f(n-1);}A O(1)B O(n)C O(n2)D O(n!)二、填空题1.数据的逻辑结构被除数分为集合结构、线性结构、树型结构和图形结构四种。
2.数据的存储结构被分为顺序结构、链接结构、索引结构和散列结构四种。
3.在线性结构、树型结构和图形结构中,前驱和后继结点之间分别存在着 1对1 、 1对N 和M对N 的关系。
4.一种抽象数据类型包括数据和操作两个部分。
5.当一个形参类型的长度较大时,应最好说明为引用,以节省参数值的传输时间和存储参数的空间。
6.当需要用一个形参访问对应的实参时,则该形参应说明为引用。
数据结构(c语言版)第三版清华大学出版社习题参考答案

不管怎样,生活还是要继续向前走去。
有的时候伤害和失败不见得是一件坏事,它会让你变得更好,孤单和失落亦是如此。
每件事到最后一定会变成一件好事,只要你能够走到最后。
附录习题参考答案习题1参考答案1.1.选择题(1). A. (2). A. (3). A. (4). B.C. (5). A. (6). A. (7). C. (8). A. (9). B. (10.) A.1.2.填空题(1). 数据关系(2). 逻辑结构物理结构(3). 线性数据结构树型结构图结构(4). 顺序存储链式存储索引存储散列表(Hash)存储(5). 变量的取值范围操作的类别(6). 数据元素间的逻辑关系数据元素存储方式或者数据元素的物理关系(7). 关系网状结构树结构(8). 空间复杂度和时间复杂度(9). 空间时间(10). Ο(n)1.3 名词解释如下:数据:数据是信息的载体是计算机程序加工和处理的对象包括数值数据和非数值数据数据项:数据项指不可分割的、具有独立意义的最小数据单位数据项有时也称为字段或域数据元素:数据元素是数据的基本单位在计算机程序中通常作为一个整体进行考虑和处理一个数据元素可由若干个数据项组成数据逻辑结构:数据的逻辑结构就是指数据元素间的关系数据存储结构:数据的物理结构表示数据元素的存储方式或者数据元素的物理关系数据类型:是指变量的取值范围和所能够进行的操作的总和算法:是对特定问题求解步骤的一种描述是指令的有限序列1.4 语句的时间复杂度为:(1) Ο(n2)(2) Ο(n2)(3) Ο(n2)(4) Ο(n-1)(5) Ο(n3) 1.5 参考程序:main(){int XYZ;scanf("%d %d%d"&X&YZ);if (X>=Y)if(X>=Z)if (Y>=Z) { printf("%d %d%d"XYZ);}else{ printf("%d %d%d"XZY);}else{ printf("%d %d%d"ZXY);}else if(Z>=X)if (Y>=Z) { printf("%d %d%d"YZX);}else{ printf("%d%d%d"ZYX);}else{ printf("%d%d%d"YXZ);}}1.6 参考程序:main(){int in;float xa[]p;printf("\nn=");scanf("%f"&n);printf("\nx=");scanf("%f"&x);for(i=0;i<=n;i++)scanf("%f "&a[i]);p=a[0];for(i=1;i<=n;i++){ p=p+a[i]*x;x=x*x;}printf("%f"p)'}习题2参考答案2.1选择题(1). C. (2). B. (3). B. (4). B. 5. D. 6. B. 7. B. 8. A. 9. A. 10. D.2.2.填空题(1). 有限序列(2). 顺序存储和链式存储(3). O(n) O(n)(4). n-i+1 n-i(5). 链式(6). 数据指针(7). 前驱后继(8). Ο(1) Ο(n)(9). s->next=p->next; p->next=s ;(10). s->next2.3. 解题思路:将顺序表A中的元素输入数组a若数组a中元素个数为n将下标为012...(n-1)/2的元素依次与下标为nn-1...(n-1)/2的元素交换输出数组a的元素参考程序如下:main(){int in;float ta[];printf("\nn=");scanf("%f"&n);for(i=0;i<=n-1;i++)scanf("%f "&a[i]);for(i=0;i<=(n-1)/2;i++){ t=a[i]; a[i] =a[n-1-i]; a[n-1-i]=t;} for(i=0;i<=n-1;i++)printf("%f"a[i]);}2.4 算法与程序:main(){int in;float ta[];printf("\nn=");scanf("%f"&n);for(i=0;i<n;i++)scanf("%f "&a[i]);for(i=1;i<n;i++)if(a[i]>a[0]{ t=a[i]; a[i] =a[0]; a[0]=t;} printf("%f"a[0]);for(i=2;i<n;i++)if(a[i]>a[1]{ t=a[i]; a[i] =a[1]; a[1]=t;} printf("%f"a[0]);}2.5 算法与程序:main(){int ijkn;float xta[];printf("\nx=");scanf("%f"&x);printf("\nn=");scanf("%f"&n);for(i=0;i<n;i++)scanf("%f "&a[i]); // 输入线性表中的元素for (i=0; i<n; i++) { // 对线性表中的元素递增排序 k=i;for (j=i+1; j<n; j++) if (a[j]<a[k]) k=j;if (k<>j) {t=a[i];a[i]=a[k];a[k]=t;}}for(i=0;i<n;i++) // 在线性表中找到合适的位置if(a[i]>x) break;for(k=n-1;k>=i;i--) // 移动线性表中元素然后插入元素xa[k+1]=a[k];a[i]=x;for(i=0;i<=n;i++) // 依次输出线性表中的元素printf("%f"a[i]);}2.6 算法思路:依次扫描A和B的元素比较A、B当前的元素的值将较小值的元素赋给C如此直到一个线性表扫描完毕最后将未扫描完顺序表中的余下部分赋给C即可C的容量要能够容纳A、B两个线性表相加的长度有序表的合并算法:void merge (SeqList ASeqList BSeqList *C){ int ijk;i=0;j=0;k=0;while ( i<=st && j<=st )if (A.data[i]<=B.data[j])C->data[k++]=A.data[i++];elseC->data[k++]=B.data[j++];while (i<=st )C->data[k++]= A.data[i++];while (j<=st )C->data[k++]=B.data[j++];C->last=k-1;}2.7 算法思路:依次将A中的元素和B的元素比较将值相等的元素赋给C如此直到线性表扫描完毕线性表C就是所求递增有序线性表算法:void merge (SeqList ASeqList BSeqList *C){ int ijk;i=0;j=0;k=0;while ( i<=st)while(j<=st )if (A.data[i]=B.data[j])C->data[k++]=A.data[i++];C->last=k-1;}习题3参考答案3.1.选择题(1). D (2). C (3). D (4). C (5). B (6). C (7). C (8). C (9). B (10).AB (11). D (12). B (13). D (14). C (15). C (16). D(17). D (18). C (19). C (20). C 3.2.填空题(1) FILOFIFO(2) -13 4 X * + 2 Y * 3 / -(3) stack.topstack.s[stack.top]=x(4) p>llink->rlink=p->rlinkp->rlink->llink=p->rlink(5) (R-F+M)%M(6) top1+1=top2(7) F==R(8) front==rear(9) front==(rear+1)%n(10) N-13.3 答:一般线性表使用数组来表示的线性表一般有插入、删除、读取等对于任意元素的操作而栈只是一种特殊的线性表栈只能在线性表的一端插入(称为入栈push)或者读取栈顶元素或者称为"弹出、出栈"(pop)3.4 答:相同点:栈和队列都是特殊的线性表只在端点处进行插入删除操作不同点:栈只在一端(栈顶)进行插入删除操作;队列在一端(top)删除一端(rear)插入3.5 答:可能序列有14种:ABCD; ACBD; ACDB; ABDC; ADCB; BACD; BADC; BCAD; BCDA; BDCA; CBAD; CBDA; CDBA; DCBA3.6 答:不能得到435612最先出栈的是4则按321的方式出不可能得到1在2前的序列可以得到135426按如下方式进行push(1)pop()push(2)push(3)pop()push(4)push(5)pop()pop()pop()push(6)pop()3.7 答:stack3.8 非递归:int vonvert (int noint a[]) //将十进制数转换为2进制存放在a[] 并返回位数{int r;SeStack s*p;P=&s;Init_stack(p);while(no){push(pno%2);no/=10;}r=0;while(!empty_stack(p)){pop(pa+r);r++;}return r;}递归算法:void convert(int no){if(no/2>0){Convert(no/2);Printf("%d"no%2);}elseprintf("%d"no);}3.9 参考程序:void view(SeStack s){SeStack *p; //假设栈元素为字符型char c;p=&s;while(!empty_stack(p)){c=pop(p);printf("%c"c);}printf("\n");}3.10 答:char3.11 参考程序:void out(linkqueue q){int e;while(q.rear !=q.front ){dequeue(qe);print(e); //打印}}习题4参考答案4.1 选择题:(1). A (2). D (3). C (4). C (5). B (6). B (7). D (8). A (9). B (10). D 4.2 填空题:(1)串长相等且对应位置字符相等(2)不含任何元素的串(3)所含字符均是空格所含空格数(4) 10(5) "hello boy"(6) 13(7) 1066(8)模式匹配(9)串中所含不同字符的个数(10) 364.3 StrLength (s)=14StrLength (t)=4SubStr( s87)=" STUDENT"SubStr(t21)="O"StrIndex(s"A")=3StrIndex (st)=0StrRep(s"STUDENT"q)=" I AM A WORKER"4.4 StrRep(s"Y""+");StrRep(s"+*""*Y");4.5 空串:不含任何字符;空格串:所含字符都是空格串变量和串常量:串常量在程序的执行过程中只能引用不能改变;串变量的值在程序执行过程中是可以改变和重新赋值的主串与子串:子串是主串的一个子集串变量的名字与串变量的值:串变量的名字表示串值的标识符4.6int EQUAl(ST){char *p*q;p=&S;q=&T;while(*p&&*q){if(*p!=*q)return *p-*q;p++;q++;}return *p-*q;}4.7(1)6*8*6=288(2)1000+47*6=1282(3)1000+(8+4)*8=1096(4)1000+(6*7+4)*8=13684.8习题5参考答案5.1 选择(1)C(2)B(3)C(4)B(5)C(6)D(7)C(8)C(9)B(10)C (11)B(12)C(13)C(14)C(15)C(16)B5.2 填空(1)1(2)1036;1040(3)2i(4) 1 ; n ; n-1 ; 2(5)2k-1;2k-1(6)ACDBGJKIHFE(7)p!=NULL(8)Huffman树(9)其第一个孩子; 下一个兄弟(10)先序遍历;中序遍历5.3叶子结点:C、F、G、L、I、M、K;非终端结点:A、B、D、E、J;各结点的度:结点: A B C D E F G L I J K M度: 4 3 0 1 2 0 0 0 0 1 0 0树深:45.4无序树形态如下:二叉树形态如下:5.5二叉链表如下:三叉链表如下:5.6先序遍历序列:ABDEHICFJG中序遍历序列:DBHEIAFJCG后序遍历序列:DHIEBJFGCA5.7(1) 先序序列和中序序列相同:空树或缺左子树的单支树;(2) 后序序列和中序序列相同:空树或缺右子树的单支树;(3) 先序序列和后序序列相同:空树或只有根结点的二叉树5.8这棵二叉树为:5.9先根遍历序列:ABFGLCDIEJMK后根遍历序列:FGLBCIDMJKEA层次遍历序列:ABCDEFGLIJKM5.10证明:设树中结点总数为n叶子结点数为n0则n=n0 + n1 + ...... + nm (1)再设树中分支数目为B则B=n1 + 2n2 + 3n3 + ...... + m nm (2)因为除根结点外每个结点均对应一个进入它的分支所以有n= B + 1 (3)将(1)和(2)代入(3)得n0 + n1 + ...... + nm = n1 + 2n2 + 3n3 + ...... + m nm + 1 从而可得叶子结点数为:n0 = n2 + 2n3 + ...... + (m-1)nm + 15.11由5.10结论得n0 = (k-1)nk + 1又由 n=n0 + nk得nk= n-n0代入上式得n0 = (k-1)(n-n0)+ 1叶子结点数为:n0 = n (k-1) / k5.12int NodeCount(BiTree T){ //计算结点总数if(T)if (T-> lchild==NULL )&&( T --> rchild==NULL )return 1;elsereturn NodeCount(T-> lchild ) +Node ( T --> rchild )+1; elsereturn 0;5.13void ExchangeLR(Bitree bt){/* 将bt所指二叉树中所有结点的左、右子树相互交换 */ if (bt && (bt->lchild || bt->rchild)) {bt->lchild<->bt->rchild;Exchange-lr(bt->lchild);Exchange-lr(bt->rchild);}}/* ExchangeLR */5.14int IsFullBitree(Bitree T){/* 是则返回1否则返回0*/Init_Queue(Q); /* 初始化队列*/flag=0;In_Queue(QT); /* 根指针入队列按层次遍历*/while(!Empty_Queue (Q)){Out_Queue(Qp);if(!p) flag=1; /* 若本次出队列的是空指针时则修改flag值为1若以后出队列的指针存在非空则可断定不是完全二叉树 */else if (flag) return 0; /*断定不是完全二叉树 */ else{In_Queue(Qp->lchild);In_Queue(Qp->rchild); /* 不管孩子是否为空都入队列*/}}/* while */return 1; /* 只有从某个孩子指针开始之后所有孩子指针都为空才可断定为完全二叉树*/}/* IsFullBitree */5.15转换的二叉树为:5.16对应的森林分别为:5.17typedef char elemtype;typedef struct{ elemtype data;int parent;} NodeType;(1) 求树中结点双亲的算法:int Parent(NodeType t[ ]elemtype x){/* x不存在时返回-2否则返回x双亲的下标(根的双亲为-1 */for(i=0;i<MAXNODE;i++)if(x==t[i].data) return t[i].parent; return -2;}/*Parent*/(2) 求树中结点孩子的算法:void Children(NodeType t[ ]elemtype x){for(i=0;i<MAXNODE;i++){if(x==t[i].data)break;/*找到x退出循环*/}/*for*/if(i>=MAXNODE) printf("x不存在\n"); else {flag=0;for(j=0;j<MAXNODE;j++)if(i==t[j].parent){ printf("x的孩子:%c\n"t[j].data);flag=1;}if(flag==0) printf("x无孩子\n");}}/*Children*/5.18typedef char elemtype;typedef struct ChildNode{ int childcode;struct ChildNode *nextchild;}typedef struct{ elemtype data;struct ChildNode *firstchild;} NodeType;(1) 求树中结点双亲的算法:int ParentCL(NodeType t[ ]elemtype x){/* x不存在时返回-2否则返回x双亲的下标 */for(i=0;i<MAXNODE;i++)if(x==t[i].data) {loc=i;/*记下x的下标*/break;}if(i>=MAXNODE) return -2; /* x不存在 *//*搜索x的双亲*/for(i=0;i<MAXNODE;i++)for(p=t[i].firstchild;p!=NULL;p=p->nextchild) if(loc==p->childcode)return i; /*返回x结点的双亲下标*/}/* ParentL */(2) 求树中结点孩子的算法:void ChildrenCL(NodeType t[ ]elemtype x){for(i=0;i<MAXNODE;i++)if(x==t[i].data) /*依次打印x的孩子*/{flag=0; /* x存在 */for(p=t[i].firstchild;p;p=p->nextchild){ printf("x的孩子:%c\n"t[p-> childcode].data);flag=1;}if(flag==0) printf("x无孩子\n");return;}/*if*/printf("x不存在\n");return;}/* ChildrenL */5.19typedef char elemtype;typedef struct TreeNode{ elemtype data;struct TreeNode *firstchild; struct TreeNode *nextsibling; } NodeType;void ChildrenCSL(NodeType *telemtype x){ /* 层次遍历方法 */Init_Queue(Q); /* 初始化队列 */In_Queue(Qt);count=0;while(!Empty_Queue (Q)){Out_Queue(Qp);if(p->data==x){ /*输出x的孩子*/p=p->firstchild;if(!p) printf("无孩子\n");else{ printf("x的第%i个孩子:%c\n"++countp->data);/*输出第一个孩子*/p=p->nextsibling; /*沿右分支*/while(p){printf("x的第%i个孩子:%c\n"++countp->data);p=p-> nextsibling;}}return;}if(p-> firstchild) In_Queue(Qp-> firstchild);if(p-> nextsibling) In_Queue(Qp-> nextsibling);}}/* ChildrenCSL */5.20(1) 哈夫曼树为:(2) 在上述哈夫曼树的每个左分支上标以1右分支上标以0并设这7个字母分别为A、B、C、D、E、F和H如下图所示:则它们的哈夫曼树为分别为:A:1100B:1101C:10D:011E:00F:010H:111习题6参考答案6.1 选择题(1)C (2)A (3)B(4)C(5)B______条边(6)B(7)A(8)A(9)B(10)A(11)A(12)A(13)B(14)A(15)B(16)A(17)C 6.2 填空(1) 4(2) 1对多 ; 多对多(3) n-1 ; n(4) 0_(5)有向图(6) 1(7)一半(8)一半(9)___第i个链表中边表结点数___(10)___第i个链表中边表结点数___(11)深度优先遍历;广度优先遍历(12)O(n2)(13)___无回路6.3(1)邻接矩阵:(2)邻接链表:(3)每个顶点的度:顶点度V1 3V2 3V3 2V4 3V5 36.4(1)邻接链表:(2)逆邻接链表:(3)顶点入度出度V1 3 0V2 2 2V3 1 2V4 1 3V5 2 1V6 2 36.5(1)深度优先查找遍历序列:V1 V2 V3 V4 V5; V1 V3 V5 V4 V2; V1 V4 V3 V5 V2 (1)广度优先查找遍历序列:V1 V2 V3 V4 V5; V1 V3 V2 V4 V5; V1 V4 V3 V2 V56.6有两个连通分量:6.7顶点(1)(2)(3)(4)(5)Low Close Cost VexLow CloseCost VexLow CloseCost VexLow CloseCost VexLow CloseCost VexV10 00 00 00 00 0V21 00 00 00 00 0V31 01 00 00 00 0V43 02 12 10 10 1V5∞ 05 13 22 30 3U{v1} {v1v2} {v1v2v3} {v1 v2 v3 v4} {v1 v2 v3 v4 v5} T {} { (v1 v2) } {(v1 v2) (v1 v3) } {(v1 v2) (v1 v3) (v2 v4) } {(v1 v2)(v1v3)(v2v4)(v4v5) }最小生成树的示意图如下:6.8拓扑排序结果: V3--> V1 --> V4 --> V5 --> V2 --> V66.9(1)建立无向图邻接矩阵算法:提示:参见算法6.1因为无向图的邻接矩阵是对称的所以有for (k=0; k<G ->e; k++) /*输入e条边建立无向图邻接矩阵*/{ scanf("\n%d%d"&i&j);G ->edges[i][j]= G ->edges[j][i]=1;}(2)建立无向网邻接矩阵算法:提示:参见算法6.1初始化邻接矩阵:#define INFINITY 32768 /* 表示极大值*/for(i=0;i<G->n;i++)for(j=0;j<G->n;j++) G->edges[i][j]= INFINITY;输入边的信息:不仅要输入边邻接的两个顶点序号还要输入边上的权值for (k=0; k<G ->e; k++) /*输入e条边建立无向网邻接矩阵*/{ scanf("\n%d%d%d"&i&j&cost); /*设权值为int型*/G ->edges[i][j]= G ->edges[j][i]=cost;/*对称矩阵*/}(3)建立有向图邻接矩阵算法:提示:参见算法6.16.10(1)建立无向图邻接链表算法:typedef VertexType char;int Create_NgAdjList(ALGraph *G){ /* 输入无向图的顶点数、边数、顶点信息和边的信息建立邻接表 */scanf("%d"&n); if(n<0) return -1; /* 顶点数不能为负 */G->n=n;scanf("%d"&e); if(e<0) return =1; /*边数不能为负 */G->e=e;for(m=0;m< G->n ;m++)G-> adjlist [m].firstedge=NULL; /*置每个单链表为空表*/for(m=0;m< G->n;m++)G->adjlist[m].vertex=getchar(); /*输入各顶点的符号*/for(m=1;m<= G->e; m++){scanf("\n%d%d"&i&j); /* 输入一对邻接顶点序号*/if((i<0 || j<0) return -1;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第i+1个链表中插入一个边表结点*/ p->adjvex=j;p->next= G-> adjlist [i].firstedge;G-> adjlist [i].firstedge=p;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第j+1个链表中插入一个边表结点*/ p->adjvex=i;p->next= G-> adjlist [j].firstedge;G-> adjlist [j].firstedge=p;} /* for*/return 0; /*成功*/}//Create_NgAdjList(2)建立有向图逆邻接链表算法:typedef VertexType char;int Create_AdjList(ALGraph *G){ /* 输入有向图的顶点数、边数、顶点信息和边的信息建立逆邻接链表 */scanf("%d"&n); if(n<0) return -1; /* 顶点数不能为负 */G->n=n;scanf("%d"&e); if(e<0) return =1; /*弧数不能为负 */G->e=e;for(m=0;m< G->n; m++)G-> adjlist [m].firstedge=NULL; /*置每个单链表为空表*/for(m=0;m< G->n;m++)G->adjlist[m].vertex=getchar(); /*输入各顶点的符号*/for(m=1;m<= G->e ; m++){scanf("\n%d%d"&t&h); /* 输入弧尾和弧头序号*/if((t<0 || h<0) return -1;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第h+1个链表中插入一个边表结点*/ p->adjvex=t;p->next= G-> adjlist [h].firstedge;G-> adjlist [h].firstedge=p;} /* for*/return 0; /*成功*/}//Create_AdjList6.11void Create_AdjM(ALGraph *G1MGraph *G2){ /*通过无向图的邻接链表G1生成无向图的邻接矩阵G2*/G2->n=G1->n; G2->e=G1->e;for(i=0;i<G2->n;i++) /* 置G2每个元素为0 */for(j=0;j<G2->n;j++) G2->edges[i][j]= 0;for(m=0;m< G1->n;m++)G2->vexs[m]=G1->adjlist[m].vertex; /*复制顶点信息*/num=(G1->n/2==0?G1->n/2:G1->n/2+1); /*只要搜索前n/2个单链表即可*/for(m=0;m< num;m++){ p=G1->adjlist[m].firstedge;while(p){ /* 无向图的存储具有对称性*/G2->edges[m][ p->adjvex ]= G2->edges[p->adjvex ] [m] =1;p==p->next;}}/* for */}/*Create_AdjM */6.12void Create_AdjL(ALGraph *G1MGraph *G2){ /*通过无向图的邻接矩阵G1生成无向图的邻接链表G2*/G2->n=G1->n; G2->e=G1->e;for(i=0;i<G1->n;i++) /* 建立每个单链表 */{ G2->vexs[i]=G1->adjlist[i].vertex;G2->adjlist[i].firstedge=NULL;for(j=i; j<G1->n; j++) /*对称矩阵只要搜索主对角以上的元素即可*/{ if(G1->edges[i][j]== 1){ p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第i+1个链表中插入一个边表结点*/p->adjvex=j;p->next= G-> adjlist [i].firstedge;G-> adjlist [i].firstedge=p;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第j+1个链表中插入一个边表结点*/p->adjvex=i;p->next= G-> adjlist [j].firstedge;G-> adjlist [j].firstedge=p;}/*if*/}/* for*/}/* for*/}/* Create_AdjL */6.13(1) 邻接矩阵中1的个数的一半;(2) 若位于[i-1j-1]或[j-1i-1]位置的元素值等于1则有边相连否则没有(3) 顶点i的度等于第i-1行中或第i-1列中1的个数6.14(1) 邻接链表中边表结点的个数的一半;(2) 若第i-1(或j-1)个单链表中存在adjvex域值等于j-1(或i-1)的边表结点则有边相连否则没有(3) 顶点i的度等于第i-1个单链表中边表结点的个数6.15提示:参见算法6.2 和6.3习题 7参考答案7.1 选择题(1)C (2)C (3) C (4)B (5) A (6)A (7) D (8)B (9)D (10) B(11)B (12)A (13)C (14)C (15)A (16)D (17)C (18)BC (19)B (20)A7.2 填空题(1) O(n)O(log2n)(2) 12485log2(n+1)-1(3)小于大于(4)增序序列(5)m-1(6) 70; 342055(7) n/m(8)开放地址法链地址法(9)产生冲突的可能性就越大产生冲突的可能性就越小(10)关键码直接(11)②①⑦(12) 1616821(13)直接定址法数字分析法平方取中法折叠法除留余数法随机数法(14)开放地址法再哈希法链地址法建立一个公共溢出区(15)装满程度(16)索引快(17)哈希函数装填因子(18)一个结点(19)中序(20)等于7.3 一棵二叉排序树(又称二叉查找树)或者是一棵空树或者是一棵同时满足下列条件的二叉树:(1)若它的左子树不空则左子树上所有结点的键值均小于它根结点键值(2)若它的右子树不空则右子树上所有结点的键值均大于它根结点键值(3)它的左、右子树也分别为二叉排序树7.4 对地址单元d=H(K)如发生冲突以d为中心在左右两边交替进行探测按照二次探测法键值K的散列地址序列为:do=H(K)d1=(d0+12)mod md2=(d0-12)mod md3=(d0+22)mod md4=(d0-12)mod m......7.5 衡量算法的标准有很多时间复杂度只是其中之一尽管有些算法时间性能很好但是其他方面可能就存在着不足比如散列查找的时间性能很优越但是需要关注如何合理地构造散列函数问题而且总存在着冲突等现象为了解决冲突还得采用其他方法二分查找也是有代价的因为事先必须对整个查找区间进行排序而排序也是费时的所以常应用于频繁查找的场合对于顺序查找尽管效率不高但却比较简单常用于查找范围较小或偶而进行查找的情况7.6此法要求设立多个散列函数Hii=1...k当给定值K与闭散列表中的某个键值是相对于某个散列函数Hi的同义词因而发生冲突时继续计算该给定值K在下一个散列函数Hi+1下的散列地址直到不再产生冲突为止7.7散列表由两个一维数组组成一个称为基本表另一个称为溢出表插入首先在基本表上进行;假如发生冲突则将同义词存人溢出表7.8 结点个数为n时高度最小的树的高度为1有两层它有n-1个叶结点1个分支结点;高度最大的树的高度为n-l有n层它有1个叶结点n-1个分支结点7.9 设顺序查找以h为表头指针的有序链表若查找成功则返回结点指针p查找失败则返回null值pointer sqesrearch(pointer hint xpointerp){p=null;while(h)if(x>h->key)h=h->link;else{if(x==h->key)p=h;return(p);}}虽然链表中的结点是按从小到大的顺序排列的但是其存储结构为单链表查找结点时只能从头指针开始逐步进行搜索故不能用折半(二分)查找7.10 分析:对二叉排序树来讲其中根遍历序列为一个递增有序序列因此对给定的二叉树进行中根遍历如果始终能保证前一个值比后一个值小则说明该二叉树是二叉排序树int bsbtr (bitreptr T) /*predt记录当前结点前趋值初值为-∞*/{ if (T==NULL) return(1);else{b1=bsbtr(T->lchild);/*判断左子树*/if (!b1|| (predt>=T->data)) return(0);*当前结点和前趋比较*/ predt=T->data;/*修改当前结点的前趋值*/return(bsbtr(T->rchild));/*判断右子树并返回最终结果*/}}7.11 (1)使用线性探查再散列法来构造散列表如表下所示散列表───────────────────────────────地址 0 1 2 3 4 5 6 7 8 9 10───────────────────────────────数据 33 1 13 12 34 38 27 22───────────────────────────────(2)使用链地址法来构造散列表如下图(3)装填因子a=8/11使用线性探查再散列法查找成功所需的平均查找次数为Snl=0.5(1+1/(1-a))=0.5*(1+1/(1-8/11))=7/3使用线性探查再散列法查找不成功所需的平均查找次数为:Unl=0.5(1+1/(1-a)2)=0.5*(1+1/(1-8/11)2)=65/9 使用链地址法查找成功所需的平均查找次数为:Snc=l+a/2=1+8/22=15/11使用链地址法查找不成功所需的平均查找次数为: 'Unl=a+e-a=8/1l+e-8/117.12 分析:在等查区间的上、下界处设两个指针由此计算出中间元素的序号当中间元素大于给定值X时接下来到其低端区间去查找;当中间元素小于给定值X时接下来到其高端区间去查找;当中间元素等于给定值X时表示查找成功输出其序号Int binlist(sqtable Aint stkeytype X) /*t、s分别为查找区间的上、下界*/{ if(s<t) return(0);/*查找失败*/else{ mid=(S+t)/2;switCh(mid){case x<A.item[midJ.key: return(binlist(Asmid-lX));/*在低端区间上递归*/case x==A.item[mid].key: return(mid);/+查找成功*/ case x>A.item[mid].key: return(amid+ltX));/*在高端区间上递归*/}}}7.13int sqsearch0 (sqtable Akeytype X) /*数组有元素n个*/{ i=l;A.item[n+1].key=X;/t设置哨兵*/while (A.item[n+1].key!=X) i++;return (i% (n/1));/*找不到返回0找到返回其下标*/}查找成功平均查找长度为:(1+2+3+...+n)/n:(1+n)/2查找不成功平均查找长度为:n+17.14散列函数:H(key)=100+(key个位数+key十位数) mod l0;形成的散列表:100 101 102 103 104 105 106 107 108 10998 75 63 46 49 79 61 53 17查找成功时的平均长度为:(1+2+1+1+5+1+1+5+5+3)/10=2.5次由于长度为10的哈希表已满因此在插人第11个记录时所需作的比较次数的期望值为10查找不成功时的平均长度为10习题 8参考答案8.1 选择题(1)B (2)A (3)D (4)C (5)B (6)A (7)B (8)C (9)A (10)C(11)D (12)C (13) C (14)D (15)C (16)B (17) D (18)C (19)B (20)D8.2填空题(1)快速归并(2) O(log2n)O(nlog2n)(3)归并(4)向上根结点(5) 1918163022(6)(7)4913275076386597(8)88(9)插入选择(每次选择最大的)(10)快速归并(11)O(1)O(nlog2n)(12)稳定(13)3(14)(15205040)(15)O(log2n)(16)O(n2)(17)冒泡排序快速排序(18)完全二叉树n/2(19)稳定不稳定(20)2(204015)8.3. 假定给定含有n个记录的文件(r1f2...rn)其相应的关键字为(k1k2...kn)则排序就是确定文件的一个序列rrr2...rn使得k1'≤k2'≤...≤kn'从而使得文件中n个记录按其对应关键字有序排列如果整个排序过程在内存中进行则排序叫内部排序假设在待排序的文件中存在两个或两个以上的记录具有相同的关键字若采用某种排序方法后使得这些具有相同关键字的记录在排序前后相对次序依然保持不变则认为该排序方法是稳定的否则就认为排序方法是不稳定的8.4.稳定的有:直接插入排序、二分法插入排序、起泡排序、归并排序和直接选择排序8.5.初始记录序列按关键字有序或基本有序时比较次数为最多8.6.设5个元素分别用abcde表示取a与b、c与d进行比较若a>bc>d(也可能是a<bc<d此时情况类似)显然此时进行了两次比较取b与d再比较若b>d则a>b>d若b<d则有c>d>b此时已进行了3次比较要使排序比较最多7次可把另外两个元素按折半检索排序插入到上面所得的有序序列中此时共需要4次比较从而可得算法共只需7次比较8.7.题目中所说的几种排序方法中其排序速度都很快但快速排序、归并排序、基数排序和Shell排序都是在排序结束后才能确定数据元素的全部序列而排序过程中无法知道部分连续位置上的最终元素而堆排序则是每次输出一个堆顶元素(即最大或最少值的元素)然后对堆进行再调整保证堆顶元素总是当前剩下元素的最大或最小的从而可知欲在一个大量数据的文件中如含有15000个元素的记录文件中选取前10个最大的元素可采用堆排序进行8.8.二分法排序8.9.void insertsort(seqlist r)  ;{ //对顺序表中记录R[0一N-1)按递增序进行插入排序&NBSP;int ij;  ;for(i=n-2;i>=0; i--) //在有序区中依次插入r[n-2]..r[0]  ;if(r[i].key>r[i+1].key) //若不是这样则r[i]原位不动 ;{  ;r[n]=r[i];j=i+l;//r[n]是哨兵 ;do{ //从左向右在有序区中查找插入位置 ;r[j-1]= r[j];//将关键字小于r[i].key的记录向右移 ;j++;  ;}whle(r[j].key r[j-1]=r[n];//将引i)插入到正确位置上 ;}//endif ;}//insertsort.  ;8.10.建立初始堆:[937 694 863 265 438 751 742129075 3011]&NBSP;&NBSP;第一次排序重建堆:[863 694 751 765 438 301 742 129 075]9378.11.在排序过程中每次比较会有两种情况出现若整个排序过程至少需作t次比较则显然会有2^t个情况由于n个结点总共有n!种不同的排列因而必须有n!种不同的比较路径于是: 2t≥n!即t≥log2n!因为log2nl=nlog2n-n/ln2+log2n/2+O(1)故有log2n!≈nlog2n从而t≧nlog2n得证8.12.依据堆定义可知:序列(1)、(2)、(4)是堆(3)不是堆从而可对其调整使之为如下的大根堆(1009580604095821020)8.13.第一趟:[265 301] [129 751] [863 937] [694 742] [076 438]&NBSP; &NBSP;第二趟:[129 265 301 751] [694 742 863 937] [076 438]&NBSP;&NBSP;第三趟:[129 265 301 694 742 751 863 937] [076 438]&NBSP;&NBSP;第四趟:[076 129 265 301 438 694 742 751 863 937]&NBSP;8.14.(1)归并排序:(1829) (2547) (1258) (1051)(18252947) (10125158)(1012182529475158)(2)快速排序:(1018251229585147)(1018251229475158)(1012182529475158)(3)堆排序:初始堆(大顶堆):(58 47512918122510)第一次调整:(51 472529181210)(58)第二次调整:(47 2925101812)(5158)第三次调整:(29 18251012)(475158)第四次调整:(25 181210)(29475158)第五次调整:(18 1012)(2529475158)第六次调整:(12 10) (182529475158)第七次调整:(1012182529475158)8.15.(1)直接插入排序序号 1 2 3 4 5 6 7 8 9 10 11 12 关键字 83 40 63 13 84 35 96 57 39 79 61 151=2 40 83 [63 13 84 35 96 57 39 79 61 15] 1=3 40 63 83 [13 84 35 96 57 39 79 61 15] 1=4 13 40 63 83 [84 3 5 96 57 39 79 61 15] I=5 13 40 63 83 84 [35 96 57 39 79 61 15] I=6 13 35 40 63 83 84 [96 57 39 79 61 15] 1=7 13 35 40 63 83 84 96 [57 39 79 61 15] 1=8 13 35 40 57 63 83 84 96 [ 39 79 61 15] 1=9 13 35 39 40 57 63 83 84 96 [79 61 15] I=10 13 35 39 40 57 63 79 83 84 96 [61 15] I=11 13 35 39 40 57 61 63 79 83 84 96 [15] 1=12 13 15 35 39 40 57 61 63 79 83 84 96 (2)直接选择排序序号 1 2 3 4 5 6 7 8 9 10 11 12 关键字 83 40 63 13 84 35 96 57 39 79 61 15i=1 13 [ 40 63 83 84 35 96 57 39 79 61 15] i=2 13 15 [63 83 84 35 96 57 39 79 61 40] i=3 13 15 35 [83 84 63 96 57 39 79 61 40] i=4 13 15 35 39 [84 63 96 57 83 79 61 40] i=5 13 15 35 39 40 [63 96 57 83 79 61 84] i=6 13 15 35 39 40 57 [96 63 83 79 61 84] i=7 13 15 35 39 40 57 61 [63 83 79 96 84] i=8 13 15 35 39 40 57 61 63 [83 79 96 84] i=9 13 15 35 39 40 57 61 63 79 183 96 84] i=10 13 15 35 39 40 57 61 63 79 83 [96 84] i=11 13 15 35 39 40 57 61 63 79 83 84 [96] (3)快速排序关键字 83 40 63 13 84 35 96 57 39 79 61 15 第一趟排序后 [15 40 63 13 61 35 79 57 39] 83 [96 84] 第二趟排序后 [13] 15 [63 40 61 35 79 57 39] 83 84 [96]第三趟排序后 13 15 [39 40 61 35 57] 63 [79] 83 84 96 第四趟排序后 13 15 [35] 39 [61 40 57] 63 79 83 84 96 第五趟排序后 13 15 35 39 [57 40] 61 63 79 83 84 96 第六趟排序后 13 15 35 39 40 [57] 61 63 79 83 84 96 第七趟排序后 13 15 35 39 40 57 61 63 79 83 84 96 (4)堆排序关键字 83 40 63 13 84 35 96 57 39 79 61 15排序成功的序列 96 84 83 79 63 61 57 40 39 35 15 13(5)归并排序关键字 83 40 63 13 84 35 96 57 39 79 61 15 第一趟排序后 [40 83] [13 63] [3584] [57 96] [39 79] [15 61]第二趟排序后 [13 40 63 83] [35 57 84 96] [15 39 61 79] 第三趟排序后 [13 35 40 57 63 83 84 96]] [15 39 61 79] 第四趟排序后 13 15 35 39 40 57 61 63 79 83 84 96。
数据结构(大专)第一章习题解答

数据结构(大专)第一章习题解答第一章绪论1.2 设计二次多项式ax2+bx+c的一种抽象数据类型,假定起名为QUAdratic,该类型的数据部分为三个系数项a、b和c,操作部分为:1.初始化数据成员a、b和c(假定用记录类型Quadratic定义数据成员),每个数据成员的默认值为0。
Qiadratic InitQuadratic(float aa=0, float bb=0, float cc=0);解:Quadratic InitQuadratic(float aa, float bb, float cc){Quadratic q;q·a=aa;q·b=bb;q·c=cc;return q;}2.做两个多项式加法,即使对应的系数相加,并返回相加结果。
解:Quadratic Add(Quadratic q1,Quadratic q2);{Quadratic q;q·a=q1·a+q2·a;q·b=q1·b+q2·b;q·c=q1·c+q2·c;retirn q;}3.据给定x的值计算多项式的值。
float Eval(Quadratic q,float x);解:float Eval(Quadratic q, float x){return(q·a*x*x+q·b*x+q·c);}4.计算方程ax2+bx+c=0的两个实数根,对于有实根、无实根和不是二次方程(即a= =0)这三种情况都要返回不同的整数值,以便调用函数做不同的处理。
int Root(Quadratic q, float& r1, float& r2);解:int Root (Quadratic q, float& r1, float& r2){if(q·a= =0) return –1;float x =q·b*q·b –4*q·a*q·c;if(x﹥=0){r1=(float) (-q·b+sqrt(x))/ (2*q·a);r2=(float) (-q·b-sqrt(x))/ (2*q·a);return 1;}elsereturn 0;}5.按照ax **2+bx+c的格式(x2用x **2表示)输出二次多项式,在输出时在注意去掉系数为0的项,并且当b和c的值为负时,其前不能出现加号。
数据库系统教程第三版课后答案

(1)教材P23的图1.24(四种逻辑数据模型的比较)。
(2)教材P25的图1.27(DB的体系结构)。
(3)教材P28的图1.29(DBMS的工作模式)。
(4)教材P33的图1.31(DBS的全局结构)。
1.2教材中习题1的解答
1.1 名词解释
·逻辑数据:指程序员或用户用以操作的数据形式。
第1章数据库概论
1.1基本内容分析
1.1.1本章的重要概念
(1)DB、DBMS和DBS的定义
(2)数据管理技术的发展阶段
人工管理阶段、文件系统阶段、数据库系统阶段和高级数据库技术阶段等各阶段的特点。
(3)数据描述
概念设计、逻辑设计和物理设计等各阶段中数据描述的术语,概念设计中实体间二元联系的描述(1:1,1:N,M:N)。
·物理数据:指存储设备上存储的数据。
·联系的元数:与一个联系有关的实体集个数,称为联系的元数。
·1:1联系:如果实体集E1中每个实体至多和实体集E2中的一个实体有联系,反之亦然,那么E1和E2的联系称为“1:1联系”。
·1:N联系:如果实体集E1中每个实体可以与实体集E2中任意个(零个或多个)实体有联系,而E2中每个实体至多和E1中一个实体有联系,那么E1和E2的联系是“1:N联系”。
·M:N联系:如果实体集E1中每个实体可以与实体集E2中任意个(零个或多个)实体有联系,反之亦然,那么E1和E2的联系称为“M:N联系”。
·数据模型:能表示实体类型及实体间联系的模型称为“数据模型”。
·概念数据模型:独立于计算机系统、完全不涉及信息在计算机中的表示、反映企业组织所关心的信息结构的数据模型。
1.8 什么是数据独立性?在数据库中有哪两级独立性?
算法数数据结构 第3版 绪论课后答案
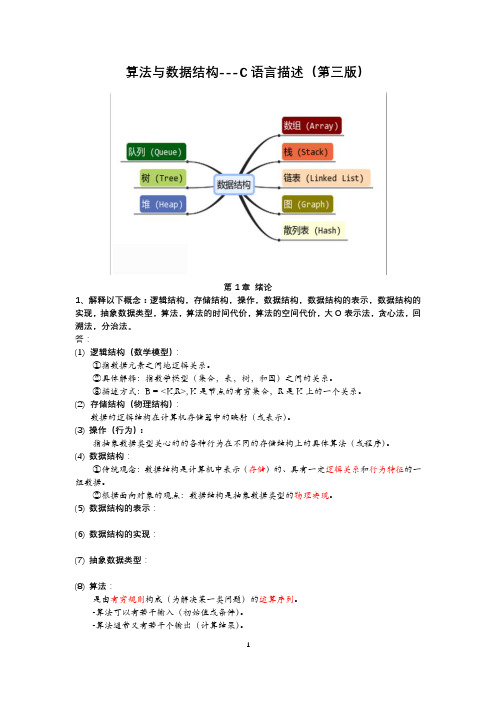
算法与数据结构---C语言描述(第三版)第1章绪论1、解释以下概念:逻辑结构,存储结构,操作,数据结构,数据结构的表示,数据结构的实现,抽象数据类型,算法,算法的时间代价,算法的空间代价,大O表示法,贪心法,回溯法,分治法。
答:(1)逻辑结构(数学模型):①指数据元素之间地逻辑关系。
②具体解释:指数学模型(集合,表,树,和图)之间的关系。
③描述方式:B = <K,R>, K是节点的有穷集合,R是K上的一个关系。
(2)存储结构(物理结构):数据的逻辑结构在计算机存储器中的映射(或表示)。
(3) 操作(行为):指抽象数据类型关心的的各种行为在不同的存储结构上的具体算法(或程序)。
(4) 数据结构:①传统观念:数据结构是计算机中表示(存储)的、具有一定逻辑关系和行为特征的一组数据。
②根据面向对象的观点:数据结构是抽象数据类型的物理实现。
(5) 数据结构的表示:(6) 数据结构的实现:(7) 抽象数据类型:(8) 算法:是由有穷规则构成(为解决某一类问题)的运算序列。
-算法可以有若干输入(初始值或条件)。
-算法通常又有若干个输出(计算结果)。
-算法应该具有有穷性。
一个算法必须在执行了有穷步之后结束。
-算法应该具有确定性。
算法的每一步,必须有确切的定义。
-算法应该有可行性。
算法中国的每个动作,原则上都是能够有机器或人准确完成的。
(9) 算法的时间代价:(10) 算法的空间代价:(11) 大O表示法:-更关注算法复杂性的量级。
-若存在正常数c和n0,当问题的规模n>=c*f(n), 则说改算法的时间(或空间)代价为O(f(n))(12) 贪心法:当追求的目标是一个问题的最优解是,设法把整个问题的求解工作分成若干步来完成。
在其中的每一个阶段都选择都选择从局部来看是最优的方案,以期望通过各个阶段的局部最有选择达到整体的最优。
例如:着色问题:先用一种颜色尽可能多的节点上色,然后用另一种颜色在为着色节点中尽可能多的节点上色,如此反复直到所有节点都着色为止;(13) 回溯法有一些问题,需要通过彻底搜索所有的情况寻找一个满足某些预定条件的最优解。
数据结构习题及答案-第1章 绪论

第1章绪论一、选择题1. 算法的计算量的大小称为计算的()。
【北京邮电大学2000 二、3 (20/8分)】A.效率 B. 复杂性 C. 现实性 D. 难度2. 算法的时间复杂度取决于()【中科院计算所 1998 二、1 (2分)】A.问题的规模 B. 待处理数据的初态 C. A和B3.计算机算法指的是(1),它必须具备(2)这三个特性。
(1) A.计算方法 B. 排序方法 C. 解决问题的步骤序列 D. 调度方法(2) A.可执行性、可移植性、可扩充性 B. 可执行性、确定性、有穷性C. 确定性、有穷性、稳定性D. 易读性、稳定性、安全性【南京理工大学 1999 一、1(2分)【武汉交通科技大学 1996 一、1( 4分)】4.一个算法应该是()。
【中山大学 1998 二、1(2分)】A.程序 B.问题求解步骤的描述 C.要满足五个基本特性 D.A和C.5. 下面关于算法说法错误的是()【南京理工大学 2000 一、1(1.5分)】A.算法最终必须由计算机程序实现B.为解决某问题的算法同为该问题编写的程序含义是相同的C. 算法的可行性是指指令不能有二义性D. 以上几个都是错误的6. 下面说法错误的是()【南京理工大学 2000 一、2 (1.5分)】(1)算法原地工作的含义是指不需要任何额外的辅助空间(2)在相同的规模n下,复杂度O(n)的算法在时间上总是优于复杂度O(2n)的算法(3)所谓时间复杂度是指最坏情况下,估算算法执行时间的一个上界(4)同一个算法,实现语言的级别越高,执行效率就越低A.(1) B.(1),(2) C.(1),(4) D.(3)7.从逻辑上可以把数据结构分为()两大类。
【武汉交通科技大学 1996 一、4(2分)】A.动态结构、静态结构 B.顺序结构、链式结构C.线性结构、非线性结构 D.初等结构、构造型结构8.以下与数据的存储结构无关的术语是()。
【北方交通大学 2000 二、1(2分)】A.循环队列 B. 链表 C. 哈希表 D. 栈9.以下数据结构中,哪一个是线性结构()?【北方交通大学 2001 一、1(2分)】A.广义表 B. 二叉树 C. 稀疏矩阵 D. 串10.以下那一个术语与数据的存储结构无关?()【北方交通大学 2001 一、2(2分)】A.栈 B. 哈希表 C. 线索树 D. 双向链表11.在下面的程序段中,对x的赋值语句的频度为()【北京工商大学 2001 一、10(3分)】FOR i:=1 TO n DOFOR j:=1 TO n DOx:=x+1;A. O(2n) B.O(n) C.O(n2) D.O(log2n)12.程序段 FOR i:=n-1 DOWNTO 1 DOFOR j:=1 TO i DOIF A[j]>A[j+1]THEN A[j]与A[j+1]对换;其中 n为正整数,则最后一行的语句频度在最坏情况下是()A. O(n)B. O(nlogn)C. O(n3)D. O(n2) 【南京理工大学1998一、1(2分)】13.以下哪个数据结构不是多型数据类型()【中山大学 1999 一、3(1分)】A.栈 B.广义表 C.有向图 D.字符串14.以下数据结构中,()是非线性数据结构【中山大学 1999 一、4】A.树 B.字符串 C.队 D.栈15. 下列数据中,()是非线性数据结构。
数据结构课后题答案(1-4章)

数据结构部分课后习题答案第一章1.1数据的逻辑结构是从具体问题中抽象出来的数学模型,体现了事物的组成和事物之间的逻辑关系。
数据的存储结构主要用来解决各种逻辑结构在计算机中物理存储表示的问题。
1.2事前分析和事后统计事前分析:优点,程序不必运行,所得结果只依赖于算法本身缺点,不够精确事后统计:优点,精确缺点,必须运行程序,所得结果依赖于硬件、环境等因素考虑赋值、运算操作执行的次数第3行赋值2次第6行赋值执行n次,加法执行n次所以,总共2n+2次操作,算法复杂度为O(n)1.4y= y + i * j 执行次数:1.5第二章2.9内存中一片连续空间(不妨假设地址从1到m)提供给两个栈S1和S2使用,怎样分配这部分存储空间,使得对任一个栈,仅当这部分空间全满时才发生上溢。
答:S1和S2共享内存中一片连续空间(地址1到m),可以将S1和S2的栈底设在两端,两栈顶向共享空间的中心延伸,仅当两栈顶指针相邻(两栈顶指针值之差的绝对值等于1)时,判断为栈满,当一个栈顶指针为0,另一个栈顶指针m+1时为两栈均空。
2.10线性表是数据项组成的一种有限且有序的序列,各元素之间呈线性关系。
从逻辑结构来说,栈和队列与线性表相同,都是典型的线性结构。
与线性表不同的是,栈和队列的操作特殊,受到一定的限制,仅允许在线性表的一端或两端进行。
栈是限定仅在一端进行插入删除的线性表,无论插入、删除还是读取都在一端进行,按后进先出的原则。
队列的元素只能从一端插入,从另一端删除,按先进先出的原则进行数据的存取。
2.11共有132种合法序列。
235641序列可以。
154623序列不可以。
对于每一个数来说,必须进栈一次、出栈一次。
我们把进栈设为状态‘1’,出栈设为状态‘0’。
n个数的所有状态对应n个1和n个0组成的2n位二进制数。
由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。
数据结构教程(第三版)课后答案

/*文件名:algo2-1.cpp*/#include <stdio.h>#include <malloc.h>#define MaxSize 50typedef char ElemType;typedef struct{ElemType elem[MaxSize];int length;} SqList;void InitList(SqList *&L){L=(SqList *)malloc(sizeof(SqList));L->length=0;}void DestroyList(SqList *L){free(L);}int ListEmpty(SqList *L){return(L->length==0);}int ListLength(SqList *L){return(L->length);}void DispList(SqList *L){int i;if (ListEmpty(L)) return;for (i=0;i<L->length;i++)printf("%c",L->elem[i]);printf("\n");}int GetElem(SqList *L,int i,ElemType &e) {if (i<1 || i>L->length)return 0;e=L->elem[i-1];return 1;}int LocateElem(SqList *L, ElemType e) {int i=0;while (i<L->length && L->elem[i]!=e) i++;if (i>=L->length)return 0;elsereturn i+1;}int ListInsert(SqList *&L,int i,ElemType e){int j;if (i<1 || i>L->length+1)return 0;i--; /*将顺序表位序转化为elem下标*/ for (j=L->length;j>i;j--) /*将elem[i]及后面元素后移一个位置*/ L->elem[j]=L->elem[j-1];L->elem[i]=e;L->length++; /*顺序表长度增1*/return 1;}int ListDelete(SqList *&L,int i,ElemType &e){int j;if (i<1 || i>L->length)return 0;i--; /*将顺序表位序转化为elem下标*/ e=L->elem[i];for (j=i;j<L->length-1;j++)L->elem[j]=L->elem[j+1];L->length--;return 1;}/*文件名:algo2-2.cpp*/#include <stdio.h>#include <malloc.h>typedef char ElemType;typedef struct LNode /*定义单链表结点类型*/{ElemType data;struct LNode *next;} LinkList;void InitList(LinkList *&L){L=(LinkList *)malloc(sizeof(LinkList)); /*创建头结点*/L->next=NULL;}void DestroyList(LinkList *&L){LinkList *p=L,*q=p->next;while (q!=NULL){free(p);p=q;q=p->next;}free(p);}int ListEmpty(LinkList *L){return(L->next==NULL);}int ListLength(LinkList *L){LinkList *p=L;int i=0;while (p->next!=NULL){i++;p=p->next;}return(i);}void DispList(LinkList *L){LinkList *p=L->next;while (p!=NULL){printf("%c",p->data);p=p->next;}printf("\n");}int GetElem(LinkList *L,int i,ElemType &e) {int j=0;LinkList *p=L;while (j<i && p!=NULL){j++;p=p->next;}if (p==NULL)return 0;else{e=p->data;return 1;}}int LocateElem(LinkList *L,ElemType e){LinkList *p=L->next;int n=1;while (p!=NULL && p->data!=e){p=p->next;n++;}if (p==NULL)return(0);elsereturn(n);}int ListInsert(LinkList *&L,int i,ElemType e){int j=0;LinkList *p=L,*s;while (j<i-1 && p!=NULL){j++;p=p->next;}if (p==NULL) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{s=(LinkList *)malloc(sizeof(LinkList)); /*创建新结点*s*/s->data=e;s->next=p->next; /*将*s插入到*p之后*/p->next=s;return 1;}}int ListDelete(LinkList *&L,int i,ElemType &e){int j=0;LinkList *p=L,*q;while (j<i-1 && p!=NULL){j++;p=p->next;}if (p==NULL) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{q=p->next; /*q指向要删除的结点*/p->next=q->next; /*从单链表中删除*q结点*/free(q); /*释放*q结点*/return 1;}}/*文件名:algo2-3.cpp*/#include <stdio.h>#include <malloc.h>typedef char ElemType;typedef struct DNode /*定义双链表结点类型*/{ElemType data;struct DNode *prior; /*指向前驱结点*/struct DNode *next; /*指向后继结点*/} DLinkList;void InitList(DLinkList *&L){L=(DLinkList *)malloc(sizeof(DLinkList)); /*创建头结点*/ L->prior=L->next=NULL;}void DestroyList(DLinkList *&L){DLinkList *p=L,*q=p->next;while (q!=NULL){free(p);p=q;q=p->next;}free(p);}int ListEmpty(DLinkList *L){return(L->next==NULL);}int ListLength(DLinkList *L){DLinkList *p=L;int i=0;while (p->next!=NULL){i++;p=p->next;}return(i);}void DispList(DLinkList *L){DLinkList *p=L->next;while (p!=NULL){printf("%c",p->data);p=p->next;}printf("\n");}int GetElem(DLinkList *L,int i,ElemType &e) {int j=0;DLinkList *p=L;while (j<i && p!=NULL){j++;p=p->next;}if (p==NULL)return 0;else{e=p->data;return 1;}}int LocateElem(DLinkList *L,ElemType e) {int n=1;DLinkList *p=L->next;while (p!=NULL && p->data!=e){n++;p=p->next;}if (p==NULL)return(0);elsereturn(n);}int ListInsert(DLinkList *&L,int i,ElemType e){int j=0;DLinkList *p=L,*s;while (j<i-1 && p!=NULL){j++;p=p->next;}if (p==NULL) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{s=(DLinkList *)malloc(sizeof(DLinkList)); /*创建新结点*s*/s->data=e;s->next=p->next; /*将*s插入到*p之后*/if (p->next!=NULL) p->next->prior=s;s->prior=p;p->next=s;return 1;}}int ListDelete(DLinkList *&L,int i,ElemType &e){int j=0;DLinkList *p=L,*q;while (j<i-1 && p!=NULL){j++;p=p->next;}if (p==NULL) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{q=p->next; /*q指向要删除的结点*/if (q==NULL) return 0; /*不存在第i个结点*/p->next=q->next; /*从单链表中删除*q结点*/if (p->next!=NULL) p->next->prior=p;free(q); /*释放*q结点*/return 1;}}void Sort(DLinkList *&head) /*双链表元素排序*/{DLinkList *p=head->next,*q,*r;if (p!=NULL) /*若原双链表中有一个或以上的数据结点*/{r=p->next; /*r保存*p结点后继结点的指针*/p->next=NULL; /*构造只含一个数据结点的有序表*/p=r;while (p!=NULL){r=p->next; /*r保存*p结点后继结点的指针*/q=head;while (q->next!=NULL && q->next->data<p->data) /*在有序表中找插入*p的前驱结点*q*/q=q->next;p->next=q->next; /*将*p插入到*q之后*/if (q->next!=NULL) q->next->prior=p;q->next=p;p->prior=q;p=r;}}}/*文件名:algo2-4.cpp*/#include <stdio.h>#include <malloc.h>typedef char ElemType;typedef struct LNode /*定义单链表结点类型*/{ElemType data;struct LNode *next;} LinkList;void InitList(LinkList *&L){L=(LinkList *)malloc(sizeof(LinkList)); /*创建头结点*/L->next=L;}void DestroyList(LinkList *&L){LinkList *p=L,*q=p->next;while (q!=L){free(p);p=q;q=p->next;}free(p);}int ListEmpty(LinkList *L){return(L->next==L);}int ListLength(LinkList *L){LinkList *p=L;int i=0;while (p->next!=L){i++;p=p->next;}return(i);}void DispList(LinkList *L){LinkList *p=L->next;while (p!=L){printf("%c",p->data);p=p->next;}printf("\n");}int GetElem(LinkList *L,int i,ElemType &e){int j=0;LinkList *p;if (L->next!=L) /*单链表不为空表时*/ {if (i==1){e=L->next->data;return 1;}else /*i不为1时*/{p=L->next;while (j<i-1 && p!=L){j++;p=p->next;}if (p==L)return 0;else{e=p->data;return 1;}}}else /*单链表为空表时*/return 0;}int LocateElem(LinkList *L,ElemType e){LinkList *p=L->next;int n=1;while (p!=L && p->data!=e){p=p->next;n++;}if (p==L)return(0);elsereturn(n);}int ListInsert(LinkList *&L,int i,ElemType e){int j=0;LinkList *p=L,*s;if (p->next==L || i==1) /*原单链表为空表或i==1时*/ {s=(LinkList *)malloc(sizeof(LinkList)); /*创建新结点*s*/s->data=e;s->next=p->next; /*将*s插入到*p之后*/p->next=s;return 1;}else{p=L->next;while (j<i-2 && p!=L){j++;p=p->next;}if (p==L) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{s=(LinkList *)malloc(sizeof(LinkList)); /*创建新结点*s*/s->data=e;s->next=p->next; /*将*s插入到*p之后*/p->next=s;return 1;}}}int ListDelete(LinkList *&L,int i,ElemType &e){int j=0;LinkList *p=L,*q;if (p->next!=L) /*原单链表不为空表时*/{if (i==1) /*i==1时*/{q=L->next; /*删除第1个结点*/L->next=q->next;free(q);return 1;}else /*i不为1时*/{p=L->next;while (j<i-2 && p!=L){j++;p=p->next;}if (p==L) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{q=p->next; /*q指向要删除的结点*/p->next=q->next; /*从单链表中删除*q结点*/free(q); /*释放*q结点*/return 1;}}}else return 0;}/*文件名:algo2-5.cpp*/#include <stdio.h>#include <malloc.h>typedef char ElemType;typedef struct DNode /*定义双链表结点类型*/{ElemType data;struct DNode *prior; /*指向前驱结点*/struct DNode *next; /*指向后继结点*/} DLinkList;void InitList(DLinkList *&L){L=(DLinkList *)malloc(sizeof(DLinkList)); /*创建头结点*/ L->prior=L->next=L;}void DestroyList(DLinkList *&L){DLinkList *p=L,*q=p->next;while (q!=L){free(p);p=q;q=p->next;}free(p);}int ListEmpty(DLinkList *L){return(L->next==L);}int ListLength(DLinkList *L){DLinkList *p=L;int i=0;while (p->next!=L){i++;p=p->next;}return(i);}void DispList(DLinkList *L){DLinkList *p=L->next;while (p!=L){printf("%c",p->data);p=p->next;}printf("\n");}int GetElem(DLinkList *L,int i,ElemType &e){int j=0;DLinkList *p;if (L->next!=L) /*双链表不为空表时*/ {if (i==1){e=L->next->data;return 1;}else /*i不为1时*/{p=L->next;while (j<i-1 && p!=L){j++;p=p->next;}if (p==L)return 0;else{e=p->data;return 1;}}else /*双链表为空表时*/return 0;}int LocateElem(DLinkList *L,ElemType e){int n=1;DLinkList *p=L->next;while (p!=NULL && p->data!=e){n++;p=p->next;}if (p==NULL)return(0);elsereturn(n);}int ListInsert(DLinkList *&L,int i,ElemType e){int j=0;DLinkList *p=L,*s;if (p->next==L) /*原双链表为空表时*/{s=(DLinkList *)malloc(sizeof(DLinkList)); /*创建新结点*s*/s->data=e;p->next=s;s->next=p;p->prior=s;s->prior=p;return 1;}else if (i==1) /*原双链表不为空表但i=1时*/ {s=(DLinkList *)malloc(sizeof(DLinkList)); /*创建新结点*s*/s->data=e;s->next=p->next;p->next=s; /*将*s插入到*p之后*/s->next->prior=s;s->prior=p;return 1;}else{p=L->next;while (j<i-2 && p!=L)p=p->next;}if (p==L) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{s=(DLinkList *)malloc(sizeof(DLinkList)); /*创建新结点*s*/s->data=e;s->next=p->next; /*将*s插入到*p之后*/if (p->next!=NULL) p->next->prior=s;s->prior=p;p->next=s;return 1;}}}int ListDelete(DLinkList *&L,int i,ElemType &e){int j=0;DLinkList *p=L,*q;if (p->next!=L) /*原双链表不为空表时*/{if (i==1) /*i==1时*/{q=L->next; /*删除第1个结点*/L->next=q->next;q->next->prior=L;free(q);return 1;}else /*i不为1时*/{p=L->next;while (j<i-2 && p!=NULL){j++;p=p->next;}if (p==NULL) /*未找到第i-1个结点*/return 0;else /*找到第i-1个结点*p*/{q=p->next; /*q指向要删除的结点*/if (q==NULL) return 0; /*不存在第i个结点*/p->next=q->next; /*从单链表中删除*q结点*/if (p->next!=NULL) p->next->prior=p;free(q); /*释放*q结点*/return 1;}}}else return 0; /*原双链表为空表时*/}/*文件名:algo3-1.cpp*/#include <stdio.h>#include <malloc.h>#define MaxSize 100typedef char ElemType;typedef struct{ElemType elem[MaxSize];int top; /*栈指针*/} SqStack;void InitStack(SqStack *&s){s=(SqStack *)malloc(sizeof(SqStack));s->top=-1;}void ClearStack(SqStack *&s){free(s);}int StackLength(SqStack *s){return(s->top+1);}int StackEmpty(SqStack *s){return(s->top==-1);}int Push(SqStack *&s,ElemType e){if (s->top==MaxSize-1)return 0;s->top++;s->elem[s->top]=e;return 1;}int Pop(SqStack *&s,ElemType &e){if (s->top==-1)return 0;e=s->elem[s->top];s->top--;return 1;}int GetTop(SqStack *s,ElemType &e){if (s->top==-1)return 0;e=s->elem[s->top];return 1;}void DispStack(SqStack *s){int i;for (i=s->top;i>=0;i--)printf("%c ",s->elem[i]);printf("\n");}/*文件名:algo3-2.cpp*/#include <stdio.h>#include <malloc.h>typedef char ElemType;typedef struct linknode{ElemType data; /*数据域*/ struct linknode *next; /*指针域*/} LiStack;void InitStack(LiStack *&s){s=(LiStack *)malloc(sizeof(LiStack));s->next=NULL;}void ClearStack(LiStack *&s){LiStack *p=s->next;while (p!=NULL){free(s);s=p;p=p->next;}int StackLength(LiStack *s){int i=0;LiStack *p;p=s->next;while (p!=NULL){i++;p=p->next;}return(i);}int StackEmpty(LiStack *s){return(s->next==NULL);}void Push(LiStack *&s,ElemType e){LiStack *p;p=(LiStack *)malloc(sizeof(LiStack));p->data=e;p->next=s->next; /*插入*p结点作为第一个数据结点*/ s->next=p;}int Pop(LiStack *&s,ElemType &e){LiStack *p;if (s->next==NULL) /*栈空的情况*/return 0;p=s->next; /*p指向第一个数据结点*/e=p->data;s->next=p->next;free(p);return 1;}int GetTop(LiStack *s,ElemType &e){if (s->next==NULL) /*栈空的情况*/return 0;e=s->next->data;return 1;}void DispStack(LiStack *s)LiStack *p=s->next;while (p!=NULL){printf("%c ",p->data);p=p->next;}printf("\n");}/*文件名:algo3-3.cpp*/#include <stdio.h>#include <malloc.h>#define MaxSize 5typedef char ElemType;typedef struct{ElemType elem[MaxSize];int front,rear; /*队首和队尾指针*/} SqQueue;void InitQueue(SqQueue *&q){q=(SqQueue *)malloc (sizeof(SqQueue));q->front=q->rear=0;}void ClearQueue(SqQueue *&q){free(q);}int QueueEmpty(SqQueue *q){return(q->front==q->rear);}int QueueLength(SqQueue *q){return (q->rear-q->front+MaxSize)%MaxSize; }int enQueue(SqQueue *&q,ElemType e){if ((q->rear+1)%MaxSize==q->front) /*队满*/ return 0;q->rear=(q->rear+1)%MaxSize;q->elem[q->rear]=e;return 1;}int deQueue(SqQueue *&q,ElemType &e)if (q->front==q->rear) /*队空*/return 0;q->front=(q->front+1)%MaxSize;e=q->elem[q->front];return 1;}/*文件名:algo3-4.cpp*/#include <stdio.h>#include <malloc.h>typedef char ElemType;typedef struct qnode{ElemType data;struct qnode *next;} QNode;typedef struct{QNode *front;QNode *rear;} LiQueue;void InitQueue(LiQueue *&q){q=(LiQueue *)malloc(sizeof(LiQueue));q->front=q->rear=NULL;}void ClearQueue(LiQueue *&q){QNode *p=q->front,*r;if (p!=NULL) /*释放数据结点占用空间*/ {r=p->next;while (r!=NULL){free(p);p=r;r=p->next;}}free(q); /*释放头结点占用空间*/ }int QueueLength(LiQueue *q){int n=0;QNode *p=q->front;while (p!=NULL){n++;p=p->next;}return(n);}int QueueEmpty(LiQueue *q){if (q->rear==NULL)return 1;elsereturn 0;}void enQueue(LiQueue *&q,ElemType e){QNode *s;s=(QNode *)malloc(sizeof(QNode));s->data=e;s->next=NULL;if (q->rear==NULL) /*若链队为空,则新结点是队首结点又是队尾结点*/ q->front=q->rear=s;else{q->rear->next=s; /*将*s结点链到队尾,rear指向它*/q->rear=s;}}int deQueue(LiQueue *&q,ElemType &e){QNode *t;if (q->rear==NULL) /*队列为空*/return 0;if (q->front==q->rear) /*队列中只有一个结点时*/{t=q->front;q->front=q->rear=NULL;}else /*队列中有多个结点时*/{t=q->front;q->front=q->front->next;}e=t->data;free(t);return 1;}/*文件名:algo4-1.cpp*/#include <stdio.h>#define MaxSize 100 /*最多的字符个数*/typedef struct{ char ch[MaxSize]; /*定义可容纳MaxSize个字符的空间*/ int len; /*标记当前实际串长*/} SqString;void StrAssign(SqString &str,char cstr[]) /*str为引用型参数*/{int i;for (i=0;cstr[i]!='\0';i++)str.ch[i]=cstr[i];str.len=i;}void StrCopy(SqString &s,SqString t) /*s为引用型参数*/{int i;for (i=0;i<t.len;i++)s.ch[i]=t.ch[i];s.len=t.len;}int StrEqual(SqString s,SqString t){int same=1,i;if (s.len!=t.len) /*长度不相等时返回0*/same=0;else{for (i=0;i<s.len;i++)if (s.ch[i]!=t.ch[i]) /*有一个对应字符不相同时返回0*/same=0;}return same;}int StrLength(SqString s){return s.len;}SqString Concat(SqString s,SqString t){SqString str;int i;str.len=s.len+t.len;for (i=0;i<s.len;i++) /*将s.ch[0]~s.ch[s.len-1]复制到str*/str.ch[i]=s.ch[i];for (i=0;i<t.len;i++) /*将t.ch[0]~t.ch[t.len-1]复制到str*/str.ch[s.len+i]=t.ch[i];return str;}SqString SubStr(SqString s,int i,int j){SqString str;int k;str.len=0;if (i<=0 || i>s.len || j<0 || i+j-1>s.len){printf("参数不正确\n");return str; /*参数不正确时返回空串*/ }for (k=i-1;k<i+j-1;k++) /*将s.ch[i]~s.ch[i+j]复制到str*/ str.ch[k-i+1]=s.ch[k];str.len=j;return str;}SqString InsStr(SqString s1,int i,SqString s2){int j;SqString str;str.len=0;if (i<=0 || i>s1.len+1) /*参数不正确时返回空串*/{printf("参数不正确\n");return s1;}for (j=0;j<i-1;j++) /*将s1.ch[0]~s1.ch[i-2]复制到str*/ str.ch[j]=s1.ch[j];for (j=0;j<s2.len;j++) /*将s2.ch[0]~s2.ch[s2.len-1]复制到str*/ str.ch[i+j-1]=s2.ch[j];for (j=i-1;j<s1.len;j++) /*将s1.ch[i-1]~s.ch[s1.len-1]复制到str*/ str.ch[s2.len+j]=s1.ch[j];str.len=s1.len+s2.len;return str;}SqString DelStr(SqString s,int i,int j){int k;SqString str;str.len=0;if (i<=0 || i>s.len || i+j>s.len+1) /*参数不正确时返回空串*/{printf("参数不正确\n");return str;}for (k=0;k<i-1;k++) /*将s.ch[0]~s.ch[i-2]复制到str*/str.ch[k]=s.ch[k];for (k=i+j-1;k<s.len;k++)/*将s.ch[i+j-1]~ch[s.len-1]复制到str*/ str.ch[k-j]=s.ch[k];str.len=s.len-j;return str;}SqString RepStr(SqString s,int i,int j,SqString t){int k;SqString str;str.len=0;if (i<=0 || i>s.len || i+j-1>s.len) /*参数不正确时返回空串*/{printf("参数不正确\n");return str;}for (k=0;k<i-1;k++) /*将s.ch[0]~s.ch[i-2]复制到str*/ str.ch[k]=s.ch[k];for (k=0;k<t.len;k++) /*将t.ch[0]~t.ch[t.len-1]复制到str*/ str.ch[i+k-1]=t.ch[k];for (k=i+j-1;k<s.len;k++) /*将s.ch[i+j-1]~ch[s.len-1]复制到str*/ str.ch[t.len+k-j]=s.ch[k];str.len=s.len-j+t.len;return str;}void DispStr(SqString str){int i;if (str.len>0){for (i=0;i<str.len;i++)printf("%c",str.ch[i]);printf("\n");}}/*文件名:algo4-2.cpp*/#include <stdio.h>#include <malloc.h>typedef struct snode{char data;struct snode *next;} LiString;void StrAssign(LiString *&s,char t[]){int i;LiString *r,*p;s=(LiString *)malloc(sizeof(LiString));s->next=NULL;r=s;for (i=0;t[i]!='\0';i++){p=(LiString *)malloc(sizeof(LiString));p->data=t[i];p->next=NULL;r->next=p;r=p;}}void StrCopy(LiString *&s,LiString *t){LiString *p=t->next,*q,*r;s=(LiString *)malloc(sizeof(LiString));s->next=NULL;s->next=NULL;r=s;while (p!=NULL) /*将t的所有结点复制到s*/ {q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}}int StrEqual(LiString *s,LiString *t){LiString *p=s->next,*q=t->next;while (p!=NULL && q!=NULL && p->data==q->data) {p=p->next;q=q->next;}if (p==NULL && q==NULL)return 1;elsereturn 0;}int StrLength(LiString *s){int i=0;LiString *p=s->next;while (p!=NULL){i++;p=p->next;}return i;}LiString *Concat(LiString *s,LiString *t){LiString *str,*p=s->next,*q,*r;str=(LiString *)malloc(sizeof(LiString));str->next=NULL;r=str;while (p!=NULL) /*将s的所有结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}p=t->next;while (p!=NULL) /*将t的所有结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}return str;}LiString *SubStr(LiString *s,int i,int j){int k;LiString *str,*p=s->next,*q,*r;str=(LiString *)malloc(sizeof(LiString));str->next=NULL;r=str;if (i<=0 || i>StrLength(s) || j<0 || i+j-1>StrLength(s)){printf("参数不正确\n");return str; /*参数不正确时返回空串*/ }for (k=0;k<i-1;k++)p=p->next;for (k=1;k<=j;k++) /*将s的第i个结点开始的j个结点复制到str*/ {q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}return str;}LiString *InsStr(LiString *s,int i,LiString *t){int k;LiString *str,*p=s->next,*p1=t->next,*q,*r;str=(LiString *)malloc(sizeof(LiString));str->next=NULL;r=str;if (i<=0 || i>StrLength(s)+1) /*参数不正确时返回空串*/{printf("参数不正确\n");return str;}for (k=1;k<i;k++) /*将s的前i个结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}while (p1!=NULL) /*将t的所有结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p1->data;q->next=NULL;r->next=q;r=q;p1=p1->next;}while (p!=NULL) /*将*p及其后的结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}return str;}LiString *DelStr(LiString *s,int i,int j){int k;LiString *str,*p=s->next,*q,*r;str=(LiString *)malloc(sizeof(LiString));str->next=NULL;r=str;if (i<=0 || i>StrLength(s) || j<0 || i+j-1>StrLength(s)){printf("参数不正确\n");return str; /*参数不正确时返回空串*/ }for (k=0;k<i-1;k++) /*将s的前i-1个结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}for (k=0;k<j;k++) /*让p沿next跳j个结点*/p=p->next;while (p!=NULL) /*将*p及其后的结点复制到str*/ {q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}return str;}LiString *RepStr(LiString *s,int i,int j,LiString *t){int k;LiString *str,*p=s->next,*p1=t->next,*q,*r;str=(LiString *)malloc(sizeof(LiString));str->next=NULL;r=str;if (i<=0 || i>StrLength(s) || j<0 || i+j-1>StrLength(s)){printf("参数不正确\n");return str; /*参数不正确时返回空串*/ }for (k=0;k<i-1;k++) /*将s的前i-1个结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}for (k=0;k<j;k++) /*让p沿next跳j个结点*/p=p->next;while (p1!=NULL) /*将t的所有结点复制到str*/{q=(LiString *)malloc(sizeof(LiString));q->data=p1->data;q->next=NULL;r->next=q;r=q;p1=p1->next;}while (p!=NULL) /*将*p及其后的结点复制到str*/ {q=(LiString *)malloc(sizeof(LiString));q->data=p->data;q->next=NULL;r->next=q;r=q;p=p->next;}return str;}void DispStr(LiString *s){LiString *p=s->next;while (p!=NULL){printf("%c",p->data);p=p->next;}printf("\n");}/*文件名:algo7-1.cpp*/#include <stdio.h>#include <malloc.h>#define MaxSize 100typedef char ElemType;typedef struct node{ElemType data; /*数据元素*/struct node *lchild; /*指向左孩子*/struct node *rchild; /*指向右孩子*/} BTNode;void CreateBTNode(BTNode *&b,char *str) /*由str串创建二叉链*/ {BTNode *St[MaxSize],*p=NULL;int top=-1,k,j=0;char ch;b=NULL; /*建立的二叉树初始时为空*/ch=str[j];while (ch!='\0') /*str未扫描完时循环*/{switch(ch){case '(':top++;St[top]=p;k=1; break; /*为左结点*/case ')':top--;break;case ',':k=2; break; /*为右结点*/default:p=(BTNode *)malloc(sizeof(BTNode));p->data=ch;p->lchild=p->rchild=NULL;if (b==NULL) /*p指向二叉树的根结点*/b=p;else /*已建立二叉树根结点*/{switch(k){case 1:St[top]->lchild=p;break;case 2:St[top]->rchild=p;break;}}}j++;ch=str[j];}}BTNode *FindNode(BTNode *b,ElemType x) /*返回data域为x的结点指针*/{BTNode *p;if (b==NULL)return NULL;else if (b->data==x)return b;else{p=FindNode(b->lchild,x);if (p!=NULL)return p;elsereturn FindNode(b->rchild,x);}}BTNode *LchildNode(BTNode *p) /*返回*p结点的左孩子结点指针*/{return p->lchild;}BTNode *RchildNode(BTNode *p) /*返回*p结点的右孩子结点指针*/{return p->rchild;}int BTNodeDepth(BTNode *b) /*求二叉树b的深度*/{int lchilddep,rchilddep;if (b==NULL)return(0); /*空树的高度为0*/ else{lchilddep=BTNodeDepth(b->lchild); /*求左子树的高度为lchilddep*/rchilddep=BTNodeDepth(b->rchild); /*求右子树的高度为rchilddep*/return (lchilddep>rchilddep)? (lchilddep+1):(rchilddep+1);}}void DispBTNode(BTNode *b) /*以括号表示法输出二叉树*/{if (b!=NULL){printf("%c",b->data);if (b->lchild!=NULL || b->rchild!=NULL){printf("(");DispBTNode(b->lchild);if (b->rchild!=NULL) printf(",");DispBTNode(b->rchild);printf(")");}}}int BTWidth(BTNode *b) /*求二叉树b的宽度*/{struct{int lno; /*结点的层次编号*/BTNode *p; /*结点指针*/} Qu[MaxSize]; /*定义顺序非循环队列*/int front,rear; /*定义队首和队尾指针*/int lnum,max,i,n;front=rear=0; /*置队列为空队*/if (b!=NULL){rear++;Qu[rear].p=b; /*根结点指针入队*/Qu[rear].lno=1; /*根结点的层次编号为1*/while (rear!=front) /*队列不为空*/{front++;b=Qu[front].p; /*队头出队*/lnum=Qu[front].lno;if (b->lchild!=NULL) /*左孩子入队*/{rear++;Qu[rear].p=b->lchild;Qu[rear].lno=lnum+1;}if (b->rchild!=NULL) /*右孩子入队*/{rear++;Qu[rear].p=b->rchild;Qu[rear].lno=lnum+1;}}max=0;lnum=1;i=1;while (i<=rear){n=0;while (i<=rear && Qu[i].lno==lnum){n++;i++;}lnum=Qu[i].lno;if (n>max) max=n;}return max;}elsereturn 0;}int Nodes(BTNode *b) /*求二叉树b的结点个数*/{int num1,num2;if (b==NULL)。
数据结构(1-2-3章)课后题答案解析

q=p; p=p->next; b->next=q; q->next=B; b=b->next; } else {//分出其他字符结点 q=p; p=p->next; c->next=q; q->next=C; c=c->next; } } }//结束
西北大学可视化技术研究所
A.双向链表
B.双向循环链表
C.单向循环链表 D.顺序表
(4)下列选项中, D 项是链表不具有的特点。
A.插入和删除运算不需要移动元素
B.所需要的存储空间与线性表的长度成正比
C.不必事先估计存储空间大小
D.可以随机访问表中的任意元素
西北大学可视化技术研究所
(5)在链表中最常用的操作是删除表中最后一个结点和 在最后一个结点之后插入元素,则采用 C 最 节省时间。
西北大学可视化技术研究所
8.假设两个按元素值递增有序排列的线性 表A和B,均以单链表作为存储结构,请 编写算法,将A表和B表归并成一个按元 素值递减有序排列的线性表C,并要求利 用原表(即A表和B表的)结点空间存放 表C。
西北大学可视化技术研究所
算法描述:要求利用现有的表A和B中的结 点空间来建立新表C,可通过更改结点的next 域来重新建立新的元素之间的线性关系。为保 证新表递减有序可以利用头插法建立单链表的 方法,只是新建表中的结点不用malloc,而只 需要从A和B中选择合适的点插入到新表C中即 可。
西北大学可视化技术研究所
1.3填空题: (1)变量的作用域是指 变量的有效范围 (2)抽象数据类型具有 数据抽象 、 信息隐 蔽 的特点。 (3)一种抽象类型包括 数据对象 、 结构 关系 和 基本操作 。
数据结构与算法第三版第1章参考答案

习题参考答案一.选择题1.从逻辑上可以把数据结构分为(C)两大类。
A.动态结构、静态结构B.顺序结构、链式结构C.线性结构、非线性结构D.初等结构、构造型结构2.在下面的程序段中,对x的斌值语句的频度为(C)。
for( t=1;k<=n;k++)for(j=1;j<=n; j++)x=x十1;A. O(2n)B. O (n)C. O (n2).D. O(1og2n)3.采用顺序存储结构表示数据时,相邻的数据元素的存储位置(A)。
A.一定连续B.一定不连续C.不一定连续D.部分连续,部分不连续4.下面关于算法说法正确的是(D)。
A.算法的时间复杂度一般与算法的空间复杂度成正比B.解决某问题的算法可能有多种,但肯定采用相同的数据结构C.算法的可行性是指算法的指令不能有二义性D.同一个算法,实现语言的级别越高,执行效率就越低5.在发生非法操作时,算法能够作出适当处理的特性称为(B)。
A.正确性B.健壮性C.可读性D.可移植性二、判断题1.数据的逻辑结构是指数据的各数据项之间的逻辑关系。
(√)2.顺序存储方式的优点是存储密度大,且插人、删除运算效率高。
(×)3.数据的逻辑结构说明数据元素之间的次序关系,它依赖于数据的存储结构。
(×)4.算法的优劣与描述算法的语言无关,但与所用计算机的性能有关。
(×)5.算法必须有输出,但可以没有输人。
(√)三、筒答题1.常见的逻辑结构有哪几种,各自的特点是什么?常用的存储结构有哪几种,各自的特点是什么?【答】常见的四种逻辑结构:①集合结构:数据元素之间是“属于同一个集合”②线性结构:数据元素之间存在着一对一的关系③树结构:数据元素之间存在着一对多的关系④结构:数据元素之间存在着多对多的关系。
常见的四种存储结构有:①顺序存储:把逻辑上相邻的元素存储在物理位置相邻的存储单元中。
顺序存储结构是一种最基本的存储表示方法,通常借助于程序设计语言中的数组来实现。
数据结构第一章习题答案

题1.7 实现输入和输出的三种方式:
(1) 直接和外部环境进行信息交换,复用性 较差,一般仅用在人机对话的用户界面中; (2) 和调用环境进行信息交换,安全性好, 使模块内部出现的错误不外传,进行模块测 试时,只要保证本模块从入口到出口的结果 正确即可。 (3) 交换方式同(2),但不安全,容易出现各 模块的错误滚动传递。
• 1.12 设有以下三个函数:
• f(n)=21n4+n2+1000,g(n)=15n4+500n3,h(n)=50 00n 3.5+nlogn
• 请判断以下断言正确与否: • (1) f(n)是O(g(n) ) 正确 • (2) h(n) 是O(f(n) ) 错误 • (3) g(n) 是O(h(n)) 错误 • (4) h(n) 是O(n 3.5) 正确 • (5) h(n) 是O(nlogn) 错误
• 数据:指能够被计算机识别、存储和加工处理的 信息载体。
• 数据元素:就是数据的基本单位,在某些情况下, 数据元素也称为元素、结点、顶点、记录。数据 元素有时可以由若干数据项组成。
• 数据类型:是一个值的集合以及在这些值上定义 的一组操作的总称。
• 数据结构:指的是数据之间的相互关系,即数据 的组织形式。一般包括三个方面的内容:数据的逻 辑结构、存储结构和数据的运算。
题1.8 学会系统分析的方法
(5) for( i=1; i<=n; i++)
for (j=1; j<=i; j++)
for (k=1; k<=j; k++)
语句频度
=
ni j
1
ni
j
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.4 e C/C++fgh述ij算法,klm算法的时间复杂
度。 n1o求一个 n p方q的所有元素之和。
n2o 对 rst 的 uv 三 个 w 数 , x 它 们 yz{|} 的 ~
sm
。
n3o对rst的uvn 个w数,sm€ 的‚}和‚{元素。
答:n1o算法ƒi:
int sum(int A[n][n],int n) { int i,j,s=0;
T(n)=2T( n )+cn=2(2T(
n )+ cn )+cn=22T(
n
n
)+2cn=23T( )+3cn
2
22 2
22
23
=“
=2kT( n )+kcn=2kO(1)+kcn
2k
n £¤
¢r 2k
r 1,‘ k=log2n。
所以 T(n)= 2log2n O(1)+cnlog2n=n+cnlog2n=O(nlog2n)。
1.1 简述数据与数据元素的关系与区别。
答:凡是能被计算机存储、加工的对象统称为数据,数据是一个集合。
数
据
元
素
是
数
据
的基本单位,是数据的一个元素。数据元素与数据之间的关系是元素与集
合之间的关系。
1.2 数据结构和数据类型有什么区别?
答:数据结构是相互之间存在一种或多种特定关系的数据元素的集合, 一般包括三个方 面的内容,即数据的逻辑结构、存储结构和数据的运算。 而数据类型是一个值的集合和定义 在这个值集上的一组运算的总称。
,merge(a,i,j,m)er˜个有 ™ j
a[m+1..j]的合k,是š”•函数,它的时间复杂度为 O(合k的元素个数)。
答:设mergesort(a,0,n-1)的Ž 数为T(n),分›œ|以i”•关系:
T(n)=
O(1) 2T( n )+O(n)
2
n=1 n>1
O(n)为 merge()所 的时间,设为 cnnc 为žŸo。 ¡ :
{ int i;
min=min=A[0];
for (i=1;i<n;i++)
{
if (A[i]>max) max=A[i];
if (A[i]<min) min=A[i];
}
}
本算法的时间复杂度为O(n)。
1.5 设 n 为‰w数,lmijŠ种算法关r n 的时间复杂
度。 n1o
void fun1(int n)
1.3 设 3 个表示算法频度的函数 f、g 和 h 分别 为: f(n)=100n3+n2+1000 g(n)=25n3+5000n2 h(n)=nl.5+5000nlog2n
求它们对应的时间复杂度。
答:f(n)=100n3+n2+1000=O(n3)
g(n)=25n3+5000n2=O(n3)
当n→∞时, n >log2n,所以 h(n)=nl.5+5000nlog2n=O(n1.5)。
} else { if (b>c)
{ if (a>c) printf("%d,%d,%d\n",c,a,b); else printf("%d,%d,%d\n",a,c,b);
}
else printf("%d,%d,%d\n",a,b,c);
}
}
本算法的时间复杂度为O(1)。 n3o算法ƒi:
void maxmin(int A[],int n,int &max,int &min)
∑n 1
2
T(n)= n2 1 = n (n i 1 )=
i0 ji 1 i
0
n(n 1 )
=O(n2)
2
数 T(n)为:
n3o设 while ‹Œf Ž 数为T(n),‘:
T (n ) 1 )
(n )(T
s=1+2+“+T(n)=
2
’n-数组 a[i..j]的元素– •k— :
}
}
n3o
void fun3(int n)
{ int i=0,s=0;
while (s<n)
{
i++;
s=s+i;
}
}
答:n1o设 for ‹Œf Ž 数为 T(n),‘:
i=2T(n)+1’n-1,即 T(n)’
n
- 1 =O(n)。
2
n2o算法 的基本运算f 是 if (b[k]>b[j]) k=j,€Ž
for (i=0;i<n;i++) for (j=0;j<n;j++) s=s+A[i][j];
return(s); } 本算法的时间复杂度为 „…†2‡ˆ
n2o算法ƒi:ˆ
void order(int a,int b,int c) { if (a>b)
{ if (b>c) printf("%d,%d,%d\n",c,b,a); else if (a>c) printf("%d,%d,%d\n",b,c,a); else printf("%d,%d,%d\n",b,a,c);
void mergesort(int a[],int i,int j)
{ int m;
if (i!=j)
{ m=(i+j)/2;
mergesort(a,i,m);
mergesort(a,m+1,j);
merge(a,i,j,m);
}
}
求 mergesort(a,0,n-1)的时间复杂度。€ a[i..m]和
{ i=1,k=100;
while (i<n)
{ k=k+1;
i+=2;
}
}
n2o
void fun2(int b[],int n)
{ int i,j,k,x;
for (i=0;i<n-1;i++)
{ k=i;
for (j=i+1;j<n;j++)
if (b[k]>b[j]) k=j;
x=b[i];b[i]=b[k];b[k]=x;
