多边形面积二等分问题
多边形的面积计算

多边形的面积计算多边形是几何学中常见的图形,它由多条直线段组成的封闭图形。
计算多边形的面积是一项基本的几何运算,有多种方法可供选择。
本文将介绍几种常见的计算多边形面积的方法,以及它们的应用范围和计算步骤。
一、三角形分割法计算多边形面积最常用的方法之一是三角形分割法。
这种方法将多边形划分为一系列三角形,然后计算每个三角形的面积,并将它们相加得到多边形的总面积。
步骤如下:1. 将多边形内部的一个点作为切割点,连接该点与多边形的各个顶点,形成一系列三角形。
2. 计算每个三角形的面积,可以使用海伦公式或直角三角形的半边长度乘以高来计算。
3. 将每个三角形的面积相加得到多边形的总面积。
需要注意的是,选择的切割点的位置可以影响计算结果的准确性和计算难度。
理想情况下,切割点应该在多边形的重心或对称中心,以避免计算过程中的复杂性。
二、边界点法边界点法是另一种计算多边形面积的常用方法。
它利用多边形的顶点坐标,通过计算边界点和原点(或其他已知点)的向量积之和来求得多边形的面积。
步骤如下:1. 将多边形的顶点坐标按照顺时针或逆时针的方向排序。
2. 以原点(或其他已知点)为基准点,依次计算相邻顶点与基准点构成的向量的向量积。
3. 将每个向量积求和,并取绝对值,即可得到多边形的面积。
需要注意的是,边界点法只适用于简单多边形(顶点没有重合或相交)。
对于存在自交或重叠的多边形,需要先进行适当的处理,确保顶点符合计算条件。
三、格林公式格林公式是一种用于计算任意多边形面积的公式,它基于平面图形的环量定义。
格林公式通过计算多边形边界上的线积分来确定其面积。
公式如下:A = 1/2 * ∫(x*dy - y*dx)其中,A表示多边形的面积,(x, y)为多边形边界上的点,dx和dy分别为该点在x和y方向上的微小变化量。
格林公式的计算过程较复杂,需要对多边形的边界进行参数化,并进行曲线积分的计算。
这种方法适用于各种复杂多边形,但计算过程相对繁琐。
多边形面积二等分问题

多边形面积二等分问题在初中阶段平面几何中,图形的等分问题比较多,常见的有以下几种:等分线段,等分角,等分圆,多边形面积二等分等。
线段和角的二等分比较简单,任意等分就稍显复杂;特别是角的任意等分,著名的“尺规作图不能问题”中就有角的三等分问题。
现在据说有人发明了一种工具叫做弧金规,这种工具不但可以任意等分任意角(包括三等分任意角),还能作一个正方形与已知圆的面积相等,即化圆为方问题;这样一来“尺规作图不能问题”中的三个就被其解决掉了两个,只还剩一个“立方倍积” 了。
非但如此,这种工具还能在圆弧上取黄金分割点及在任意曲线上任意取段;也就是说能任意等分圆周及任意曲线。
这项发明可以说是意义重大,但是,这种工具毕竟现在没有推广、普及,而且其操作也肯定不如传统中的直尺和圆规操作简单, 再说了,使用这种工具作图是否属于尺规作图还有待于进一步论证; 所以,本文还是想从传统的尺规作图的角度来论述一下初中数学中常见的有关几何图形特别是多边形的面积二等分问题。
无论是什么样的多边形,都可以用一条直线把它分成两部分;由于直线相对于多边形的方向与位置不同,被分出来的两部分面积可能相等,也可能不相等。
但无论直线开始时如何放置,只要放置好以后我们让它沿着与直线垂直的方向来回平移,在直线扫过整个多边形的过程中,总有一个位置是使被分出来的两部分面积相等,因此,对于任意多边形,都应该存在无数条直线能把它分成面积相等的两部分;或者换句话说,过多边形任意边上的任意一点也都应该存在一条直线能把多边形分成面积相等的两部分。
先说三角形的面积二等分问题。
对于三角形来说,由于等底等高的三角形面积相等,所以,三角形任意一边上的中线都可以把它分成面积相等的两部分,这个问题比较简单;下面说一下过任意边上的任意一点作直线平分三角形的问题。
如图,已知P为的边BC上的任意一点,求作直线戸(3,把厶ABC分成面积相等的两部分。
作法:1.连接AP; 2,取BC的中点D,作DQ〃AP,交AC于点Q;3,作直线PQ,如图0.则直线PQ就是所求作的直线。
等分图形面积

(2)若四边形ABCD是梯形. 点P在BC上什么位置?
A D
点P在线段CS上呢?
M B P S C N
T
P
设MC的中点为S. 点P在线段BS上时, 在线段CD上存在点Q,
设BN的中点为T. 点P在线段TC上时, 在线段AB上存在点Q, 直线PQ将△ABN面积 2等分.
直线PQ将△DMC面积 2等分.
经过边BC上的点P作直线将△ABC分割成 2个面积相等的图形.
A
(1)若点P与点B(或C)重合;
Q
取AC中点Q,连接PQ.
B
PA
C
(2)设BC边中点为M,点P与点M重合.
连接AP.
B
M P
C
(3)设BC中点为M,若点P与点B(C)、点M不重合. 如图,P在BM上.
A
Q
连接AP. 可能是AP吗?
满足条件的直线与三角形边的交 点Q可能在AB上吗?
等分图形面积
如何用直线将一个多边形分割成几个面积相等的图形? n边形 m个面积相等的图形
如何研究这个问题?
从最简单的开始研究. n=3,m=2.
活动1:将△ABC分割成2个面积相等的图形.
A
作法:(1)取BC边中点M; (2)作直线AM. 则直线AM即所求的分割线.
B
M
C
S△ABM= S△ACM(等底同高的三角形面积相等).
X
Y
S△XST= S△YST
T
数量关系
SE
F
XY∥ST
位置关系
过X作XE⊥ST,过Y作XF⊥ST ,垂足为E、F. 因为S△XST= S△YST,所以XE=YF. 所以XE∥YF.
反之,因为XE∥YF, 所以XE=YF.
教学案例:如何在幼儿园大班教授图形二等分

作为一名幼儿园大班的老师,我们需要教授孩子们一些基础的图形知识,其中之一就是图形二等分。
对于孩子们来说,学习如何将图形平均分成两份可能是很难的,我们需要使用一些方法来帮助孩子们轻松理解这一概念。
我们可以向孩子们展示不同形状的图形,并问他们这些形状是否可以平均分成两份。
我们可以用手指或针对形状的中心点来画一条线来表示平均分割线。
我们可以告诉孩子们,如果通过这条线将形状分成两半,每一半应该有同样的重量、面积、长度或角度,这就是二等分的意义。
我们可以通过一些有趣的游戏和活动来帮助孩子们更好地理解这一概念。
例如,我们可以准备一些图形模板,要求孩子们将模板二等分。
我们还可以分组让孩子们一起玩一些团队游戏,比如找到可以用直线二等分的物品,或者画出一个二等分的图形等等。
我们还可以使用一些故事和绘本来帮助孩子们理解这一概念。
例如,可以讲述关于一位漂亮的公主和她的一个经纪人的故事,经纪人必须将一块巨大的蛋糕二等分,以满足公主和她的姐妹们的需求。
而不幸的是,经纪人可能会犯一些错误,公主和她的姐妹必须帮助他找到正确的平分蛋糕的方式。
我们还可以为孩子们提供一些实践机会来巩固他们的学习成果。
我们可以使用一些简单的手工制作来培养孩子们的动手能力,如让孩子们用纸板制作一些简单的图形,并用剪纸或蜡笔将其分成两份。
在教学该主题时,我们需要明确以下几点:需要将知识点简化、明确,让孩子们易于理解。
需要提供生动有趣的游戏、活动和故事,来使孩子们更好地理解这一概念。
同时需要为孩子们提供足够的实践机会,让他们能够深入体验这一知识点。
教授孩子图形二等分这一知识点,需要使用多种方法和手段来帮助孩子深入理解这一概念。
通过简化知识点、提供趣味游戏、故事等丰富的教学资源,以及实践机会,可以有效促进孩子们的学习成果,并使其在学习过程中获得乐趣。
6用一直线将四边形的面积二等分

贝
里 二 一一 一 A卜
。M , K=
N] K M; K N3 K
r l sees L
・ M艺 K
・ N3 Ks i n Z N 2 K N 3 s i n Z M z K M 3 一 合 N 2 K CA B/ /D L
、 ! 卜 r !. j
a 2 十c 2 一了 b 2 +c 2二 a一 b . 为了
b , 则} A O} +} B O} +} ( 刀 } 十! O }) } D A C}+ I B D }其 中 ! A O I =
V a t +b 2 , I B O} =
厂 了 7 } -
下
入
) , C A二 C B, C I 〕为底 边A B上的高 , E为 C D 上的一点, 使得 口)二
同理可得 A D/ /B C
冷 =>
图( S )
图( 9 )
证明: 设梯形 A B C D高为 h .
万方数据
四边形 A B C D 为平行 四边形继而使用定理 2 可得定点 K为平行 四边形 A B C D 的对称中心.
初数 方 圆
犷 3 夕
三、 任意四边形面积的二等分
由定理 5 可知, 凸四边形中, 有且只有平行
B C : 相交于点 M 、 N.
的直线把梯形面积二等分的充要条件是: 这条 直线必过梯形中位线的中点. 通过对定理 1 到定理 4 的证明, 我们有下面
的重要定理 :
求证: 5 图 形 A B 1 V M=5 图 形 ”C D
A N 1 / 。 P , I " ' . u
, / a z +( b 一 1 ) 2 +, / ( a 一 1 ) 2 +( b 一 1 ) z > 2 在
小学五年级数学多边形的面积计算公式汇总附练习题

多边形面积计算公式1、长方形的面积=长×宽字母表示:S=ab长方形的长=面积÷宽 a=S÷b长方形的宽=面积÷长b=S÷a2、正方形的面积=边长×边长字母表示: S= a²3、平行四边形的面积=底×高字母表示:S=ah平行四边形的高=面积÷底 h=S÷a平行四边形的底=面积÷高 a=S÷h4、三角形的面积=底×高÷2字母表示:S=ah÷2三角形的高= 2×面积÷底h=2S÷a三角形的底= 2×面积÷高a=2S÷h5、梯形的面积=(上底+下底)×高÷2字母表示:S=(a+b)·h ÷2梯形的高=2×面积÷(上底+下底)h=2S÷(a+b)梯形的上底=2×面积÷高—下底a=2S÷h-b梯形的下底=2×面积÷高—上底b=2S÷h-a1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方米=10000平方厘米1米==10分米=100厘米多边形面积同步试题一、填空1.完成下表。
考查目的:平行四边形、三角形和梯形的面积计算及变式练习。
答案:解析:直接利用公式计算这三种图形的面积,对于学生来说完成的难度不大。
对于已知平行四边形的面积和高求底、已知三角形的面积和底求高这两个变式练习,可引导学生进行比较,理解并强化三角形和梯形的类似计算中需要先将“面积×2”这一知识点。
2.下图是一个平行四边形,它包含了三个三角形,其中两个空白三角形的面积分别是15平方厘米和25平方厘米。
中间涂色三角形的面积是()。
考查目的:等底等高的三角形和平行四边形的面积之间的关系。
五年级奥数专题二十:多边形的面积

五年级奥数专题二十:多边形的面积关键词:多边正方面积边长周长多边形奥数正方形之和厘米我们已经学习过三角形、正方形、长方形、平行四边形、梯形以及圆、扇形等基本图形的面积计算,图形及计算公式如下:正方形面积=边长×边长=a2,长方形面积=长×宽=ab,平行四边形面积=底×高=ah,圆面积=半径×半径×π=πr2,扇形面积=半径×半径×π×圆心角的度数÷360°在实际问题中,我们遇到的往往不是基本图形,而是由基本图形组合、拼凑成的组合图形,它们的面积不能直接用公式计算。
在本讲和后面的两讲中,我们将学习如何计算它们的面积。
例1小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
分析与解:组合图形的周长并不等于两个正方形的周长之和,因为CG部分重合了。
用组合图形的周长减去DG,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(52-4)÷3=16(厘米)。
又由两个正方形的边长之差是4厘米,可求出大正方形边长=(16+4)÷2=10(厘米),小正方形边长=(16-4)÷2=6(厘米)。
两个正方形的面积之和减去三角形ABD与三角形BEF的面积,就得到阴影部分的面积。
102+62-(10×10÷2)-(10+6)×6÷2=38(厘米2)。
例2如左下图所示,四边形ABCD与DEFG都是平行四边形,证明它们的面积相等。
分析与证明:这道题两个平行四边形的关系不太明了,似乎无从下手。
我们添加一条辅助线,即连结CE(见右上图),这时通过三角形DCE,就把两个平行四边形联系起来了。
在平行四边形ABCD中,三角形DCE的底是DC,高与平行四边形ABCD边DC上的高相等,所以平行四边形ABCD的面积是三角形DCE的两倍;同理,在平行四边形DEFG 中,三角形DCE的底是DE,高与平行四边形DEFG边DE上的高相等,所以平行四边形DEFG的面积也是三角形DCE的两倍。
利用分割法和填补法”计算多边形的面积课件

= 40 cm2 = 42 cm2
6cm
X 4cm
全圖面積 :
Y
24 + 40 + 42
10cm
Z
= 106 cm2
8cm 4cm
4cm
利用分割法和填补法”计算多边形的面积
下一題
9
請選擇以甚麼方法去計算左 圖的面積
16m 8m
分割法
6m 12m
填補法
利用分割法和填补法”计算多边形的面积
10
利用填補法似乎更合適! 試試填補法吧!
分割法
10cm
填補法
4cm
利用分割法和填补法”计算多边形的面积
5
填補法 大長方形的面積 : 正方形 C 的面積 : 三角形 D 的面積 :
6cm
C 4cm
4cm
14 x 10 4x4 6 x 6 2
= 140 cm2 = 16 cm2 = 18 cm2
全圖面積 :
140 - 16 - 18
= 106 cm2
4cm A
3cm
20 x 10 6x2 8x3
= 200 cm2 = 12 cm2 = 24 cm2
全圖面積 :
20cm
8cm
200 - 12 - 24
B
18cm
= 164 cm2
10cm
批 改 利用分割法和填补法”计算多边形的面积
下一題
4
請選擇以甚麼方法去計算左 圖的面積
6cm
8cm
4cm 4cm
A 4cm B
2cm C
全圖面積 :
12 + 12 + 30
= 54 cm2
3cm 3cm 4cm
多边形的面积公式的推导和应用

多边形的面积公式的推导和应用在几何学中,多边形是由直线段连接的一系列顶点组成的图形。
计算多边形的面积是几何学中的基本问题之一,对于不同形状的多边形,具有不同的公式来计算其面积。
本文将介绍一些常见的多边形形状的面积公式,并讨论其推导和应用。
一、三角形的面积公式三角形是最简单的多边形形状,其面积公式为:面积 = 0.5 * 底边长 * 高这个公式的推导可以使用以下方法:假设底边长为b,高为h,将三角形分为两个等腰三角形,然后计算两个等腰三角形的面积之和,即可得到整个三角形的面积。
三角形的面积公式在实际生活中有广泛的应用。
比如,在建筑设计中,计算房间的面积时常常会遇到三角形的情况,通过应用这个公式可以快速准确地计算出房间的面积。
二、正方形的面积公式正方形是一种特殊的矩形,其四条边都相等,且四个角都是直角。
正方形的面积公式为:面积 = 边长 * 边长这个公式的推导比较简单,可以通过将正方形分割为单位小正方形,并计算单位小正方形的个数来得到正方形的面积。
正方形的面积公式在日常生活中也有广泛的应用,比如计算正方形地板的面积、正方形花坛的面积等等。
三、矩形的面积公式矩形是一种具有四个直角的四边形,其相邻的两边长度相等。
矩形的面积公式为:面积 = 长 * 宽这个公式的推导和正方形的面积公式相似,也可以通过将矩形分割为单位小矩形,并计算单位小矩形的个数来得到矩形的面积。
矩形的面积公式在很多实际应用中都会遇到,比如计算房间的地板面积、计算矩形草坪的面积等等。
四、多边形的面积公式对于一般的多边形,没有特定的公式可以直接计算其面积。
然而,我们可以使用三角形的面积公式结合一些附加的几何性质来计算多边形的面积。
方法一:三角形分割法将多边形分割为若干个三角形,计算每个三角形的面积之和,即可得到整个多边形的面积。
这种方法的关键在于找到一种合适的分割方法,使得每个三角形的面积容易计算。
方法二:边界点连接法通过连接多边形的顶点和其中一个固定点,将多边形分割为若干个三角形和梯形,然后计算每个图形的面积之和,即可得到整个多边形的面积。
小学数学:多边形的面积常考知识点及易错题整理!

小学数学:多边形的面积常考知识点及易错题整理!在初步认识了长方形、正方形、三角形、梯形和平行四边形的基本特征后,同学们将进一步学习如何求多边形的面积。
在实际教学过程中,老师发现,不少同学只会背公式,不懂如何灵活运用公式解题,结果出现“一听就会,一做就废”的囧相。
首先老师带同学们回顾一下多边形的面积公式:1、公式(1)长方形周长=(长+宽)×2;字母公式:C=(a+b)×2面积=长×宽;字母公式:S=ab(2)正方形周长=边长×4;字母公式:C=4a面积=边长×边长;字母公式:S=a2(3)平行四边形:面积=底×高;字母公式:S=ah(4)三角形:面积=底×高÷2;字母公式:S=ah÷2底=面积×2÷高;高=面积×2÷底(5)梯形:面积= (上底+下底)×高÷2;字母公式:S= (a+b)h÷2上底=面积×2÷高-下底;下底=面积×2÷高-上底;高=面积×2÷(上底+下底)2、单位换算的方法大化小,乘进率;小化大,除以进率。
3、常用单位间的进率1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米4、图形之间的关系(1)平行四边形可以转化成一个长方形;两个完全相同的三角形可以拼成一个平行四边形;两个完全相同的梯形可以拼成一个平行四边形。
(2)等底等高的平行四边形面积相等;等底等高的三角形面积相等。
(3)等底等高的平行四边形面积是三角形面积的2倍。
如果一个三角形一个平行四边形等面积,等底,则三角形的高是平行四边形的2倍。
如果一个三角形和一个平行四边形等面积,等高,则三角形的底是平行四边形的2倍。
多边形面积应用题

多边形的面积应用题知识点梳理1、长方形:周长 = (长+宽)×2 字母公式:C=(a+b)×2面积 = 长×宽字母公式:S=ab2、正方形:周长 = 边长×4 字母公式:C=4a面积 = 边长×边长字母公式:S=a3、平行四边形:面积 = 底×高字母公式: S=ah4、三角形: 面积 = 底×高÷2 字母公式: S=ah÷2底 = 面积×2÷高高 = 面积×2÷底5、梯形: 面积 =(上底+下底)×高÷2字母公式: S=(a+b)h÷2上底 = 面积×2÷高-下底,下底 = 面积×2÷高-上底高 = 面积×2÷(上底+下底)6、等底等高的平行四边形面积相等;等底等高的三角形面积相等;等底等高的平行四边形面积是三角形面积的2倍。
7、长方形框架拉成平行四边形,周长不变,面积变小。
8、组合图形:转化成已学的简单图形,通过加、减进行计算。
例题讲解【例1】一个长方形长是18厘米宽是长的一半多2厘米求这个长方形面积和周长分别是多少?【例2】一个长方形是由两个大小相等的正方形拼成的正方形的边长是4厘米求这个长方形的面积是多少?【例3】一个正方形纸条周长是64厘米把这个正方形对折变成两个大小相同的长方形求这两个大小相同的长方形的面积是多少?【例4】用篱笆围成一个梯形养鸡场(如图),其中一边利用房屋墙壁。
已知篱笆长80m,求养鸡场的占地面积。
【例5】一个梯形的下底的长是上底的3倍,把上底延长8厘米,组成一个面积是288平方厘米的平行四边形。
原来梯形的面积是多少平方厘米?【例6】有一块青菜地,中间是有两个小池塘,如右图,平均每平方米菜地能生产出8千克的青菜,这块地的面积是多少平方米?这块地能产出多少千克的青菜?【例7】在上面的梯形中,剪去一最大的三角形,剩下的面积是多少,有几种剪法?巩固练习1、一个梯形,下底长14厘米,高12厘米,如果下底减少6厘米,它就成为一个平行四边形。
北师大版五年级上册 第四单元《多边形的面积》知识点和易错题总结
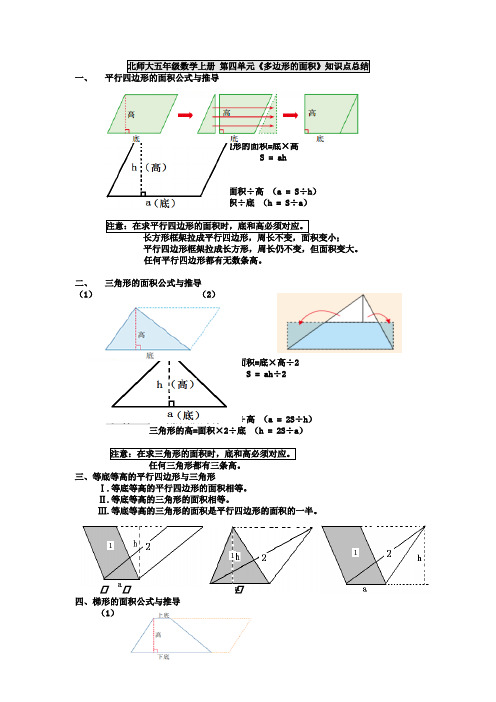
北师大五年级数学上册第四单元《多边形的面积》知识点总结一、平行四边形的面积=底×高S = ah逆运算公式:平行四边形的底=面积÷高(a = S÷h)平行四边形的高=面积÷底(h = S÷a)注意:在求平行四边形的面积时,底和高必须对应。
平行四边形框架拉成长方形,周长仍不变,但面积变大。
任何平行四边形都有无数条高。
二、三角形的面积公式与推导(1)(2)三角形的面积=底×高÷2S = ah÷2逆运算公式:三角形的底=面积×2÷高(a = 2S÷h)三角形的高=面积×2÷底(h = 2S÷a)注意:在求三角形的面积时,底和高必须对应。
三、等底等高的平行四边形与三角形Ⅰ.等底等高的平行四边形的面积相等。
Ⅱ.等底等高的三角形的面积相等。
Ⅲ.等底等高的三角形的面积是平行四边形的面积的一半。
Ⅰ.S 1 = S 2 Ⅱ.S△1 = S△2 Ⅲ.S 1÷2 = S△2四、梯形的面积公式与推导(1)(2)梯形的面积=(上底+下底)×高÷2S =(a +b )×h ÷2逆运算公式: 梯形的上底+下底的和=面积×2÷高 梯形的上底=面积×2÷高-下底 (a = 2S ÷h-b )梯形的下底=面积×2÷高-上底 (b = 2S ÷h-a )梯形的高=面积×2÷(上底+下底) h = 2S ÷(a +b )注意:任何梯形都有无数条高。
北师大五上 第四单元《多边形的面积》易错题总结一、 填空:1、(北师大第一附小学业考模拟)一个平行四边形和一个三角形底相等,面积也相等,如果平行四边形的高是4米,那么三角形的高是( )。
2、一个平行四边形的面积是36平方分米,与它等底等高的三角形面积是 ( )平方分米。
第二类面积分计算方法

第二类面积分计算方法
第二类面积分是研究曲面上的向量场与曲面元素相乘的积分,它在物理学、工程学和数学中都有广泛的应用。
计算第二类面积分的方法有多种,下面介绍其中的几种常见方法。
1. 参数化法
对于曲面上的某一点,可以用参数方程表示其坐标。
因此,可以将曲面上的向量场表示为参数方程的函数形式,进而求得曲面上的曲面元素并与向量场相乘,最终求出面积分的值。
2. 向量积法
向量积法是一种利用向量积计算面积分的方法。
首先,将曲面上的曲面元素表示为向量形式,然后计算向量场与曲面元素的向量积,最后对向量积进行积分即可得到面积分的值。
3. 散度定理法
散度定理是将曲面积分转化为对曲面内部的体积积分,从而简化计算的方法。
通过散度定理,将曲面上的向量场转化为它所围成的区域内的散度,进而求得区域内的体积积分,最终得到曲面积分的值。
4. 计算器算法
在现代计算机科学和数值计算中,有许多方法可以用计算机进行第二类面积分的计算。
其中一些算法利用数值积分或数值优化方法,将曲面分块并将积分计算转换为对这些块的积分,从而得到面积分的值。
综上所述,第二类面积分的计算方法有多种,选择不同的方法取决于具体的问题和计算需求。
利用平面图形二等分的数学教案

教学目标1.学生能够了解平面图形的特性,掌握分析平面图形的能力。
2.学生能够利用平面图形的特性进行二等分,掌握二等分的方法。
3.学生能够解决平面几何问题,增强数学思维。
教学内容一、“怎么二等分”——分析平面图形的特性1.四边形二等分①平行四边形的两个对角线相交,将其分为两个全等的三角形。
②长方形的对角线相交,将其分为两个全等的直角三角形。
③菱形的对角线相交,将其分为两个全等的直角三角形。
④梯形的对角线相交,将其分为两个全等的三角形。
2.三角形二等分①通过连接三角形的顶点和中心点,将三角形分为三个全等的小三角形。
②通过连接三角形的一边中点和相对顶点,将三角形分为两个全等的三角形。
3.多边形二等分①将任意一个多边形分解为若干个三角形,然后分别对这些三角形进行二等分。
二、“如何二等分”——二等分的方法1.分割法①将图形分解为多个简单的图形,然后对每个简单图形进行二等分。
②将图形中的某一条边作为分割线,将图形分为两个等面积的部分。
2.平移法①将图形沿着某条直线进行平移,使得平移后的图形与原图形面积相等。
②平移后的图形与原图形重合,这样就二等分了图形。
3.折叠法①根据图形的特性,可以将图形沿着某条对称轴对折,使得折叠后的图形与原图形重合。
②这样就二等分了图形。
三、“举一反三”——应用1.利用多边形二等分的方法,来解决多边形分割的问题。
2.利用平移法和折叠法,来解决平面图形摆放的问题。
3.利用图形的特性,来分析图形的性质和解决相关问题。
教学方法1.课堂讲授——教师以清晰的语言和透彻的解释,向学生介绍平面图形二等分的方法和应用。
2.实例演示——教师将具体的图形和问题呈现给学生,并进行详细的演示,帮助学生更好地理解和掌握相关知识和技能。
3.课前准备——老师对教学内容进行深入了解,搜集相关实例和资料,制定出有对性的教学计划。
教学评价1.考核方式——采用平时表现、小测验和期末考试等形式进行考核,检查学生对于平面图形特性和二等分方法的掌握程度。
人教版小学五年级数学上册多边形面积知识点归纳总结及参考题

五年级数学上册第五单元多边形面积知识点归纳总结一、基本图形(一)长方形1、长方形面积=长×宽字母公式:s=ab长方形周长=(长+宽)×2字母公式:c=(a+b)×2(长=周长÷2-宽;宽=周长÷2-长)2、★长方形中面积、周长与长和宽之间的变化关系:(1)长方形的长加宽等于长方形周长的一半。
即 a + b = c ÷ 2(2)当长方形的周长不变时,长与宽的差越大,这个长方形的面积就越小;反之,长与宽的差越小,这个长方形的面积就越大。
(3)当长方形的面积不变时,长与宽的差越大,这个长方形的周长就越长;长与宽的差越小,这个长方形的周长就越短。
(4)长方形框架拉成平行四边形,周长不变,面积变小。
(二)正方形1、正方形面积=边长×边长字母公式:s= a²或者s=a×a2、正方形周长=边长×4字母公式:c=4a 或者c= a×4(三)平行四边形1、平行四边形面积=底×高字母公式:s=ah2、★平行四边形面积公式的推导过程:剪拼、平移沿着平行四边形的任意一条高剪开,将其一部分平移与另一部分正好拼成一个长方形,这个长方形的长就是平行四边形的底,这个长方形的宽就是平行四边形的高。
因为长方形的面积=长×宽,所以平行四边形的面积=底×高,用字母表示S=a×h。
3、★等底等高的平行四边形面积相等。
(四)三角形1、三角形面积=底× 高÷2字母公式:s=ah÷2(底=面积×2÷高;高=面积×2÷底)2、★三角形面积公式的推导过程:旋转、平移将两个完全一样的三角形拼成一个平行四边形,拼成的平行四边形的底就是三角形的底,拼成的平行四边形的高就是三角形的高,拼成的平行四边形的面积是三角形面积的2倍。
一个三角形的面积是这个平行四边形的面积一半。
苏教版五年级数学上册第二单元《多边形的面积》答案

五年级数学上册第二单元《多边形的面积》答案一.选择题(共4小题,满分12分,每小题3分)1.(2020春•湘东区期末)从一个上底8cm,下底10cm,高6cm的梯形里剪去一个三角形,剪去部分的面积最大是()cm2.A.24B.48C.40D.30【分析】在梯形中减去三角形,三角形最大是以梯形的下底为底,梯形的高为高,由此根据三角形面积=底×高÷2进行计算即可.【解答】解:三角形的底是10厘米,高是6厘米10×6÷2=60÷2=30(平方厘米)答:剪去部分的面积最大是30cm2.故选:D.2.(2019秋•武川县期末)一个三角形与一个平行四边形的面积相等,底也相等.三角形的高是2分米,平行四边形的高是()分米.A.1B.2C.3D.4【分析】由题意可知:一个三角形和一个平行四边形的面积相等,底也相等,由两种图形的面积公式可得,平行四边形的高应是三角形高的一半,三角形的高是2分米,所以用三角形的高除以2即可解答.【解答】解:2÷2=1(分米)答:平行四边形的高是1分米.故选:A.3.如果一个平行四边形的面积比与它等底等高的三角形的面积大10平方厘米,那么这个平行四边形的面积是()平方厘米.A.5B.20C.15【分析】因为等底等高的平行四边形的面积是三角形面积的2倍,一个平行四边形的面积比与它等底等高的三角形的面积大10平方厘米,也就是与这个平行四边形等底等高的三角形的面积是10平方厘米,所以用这个三角形的面积乘2就是平行四边形的面积.【解答】解:10×2=20(平方厘米)答:这个平行四边形的面积是20平方厘米.故选:B.4.(2019秋•昌乐县期末)平行四边形面积是3.5m2,如果把它的底和高都扩大到原来的2倍,得到的平行四边形的面积是()m2.A.3.5B.7C.14D.28【分析】根据平行四边形的面积公式:S=ah,再根据因数与积的变化规律,积扩大的倍数等于因数扩大倍数的乘积,据此可知,如果平行四边形的底和高都扩大到原来的2倍,那么平行四边形的面积就扩大到原来的(2×2)倍,据此解答.【解答】解:3.5×2×2=14(平方米)答:得到的平行四边形的面积是14平方米.故选:C.二.填空题(共4小题,满分10分)5.(2分)(2020•十堰)甲木条长9厘米,乙木条长7厘米,用这两种长度的木条三根,围成一个等腰三角形,这个等腰三角形的周长是25或23厘米.【分析】因为根据题意不能确定腰和底的长度,所以分两种情况讨论:(1)当腰为9厘米,底为7厘米时,周长为9+9+7厘米;(2)当腰为7厘米,底为9厘米时,周长为7+7+9厘米.【解答】解:(1)当腰为9厘米,底为7厘米时周长为9+9+7=25(厘米)(2)当腰为7厘米,底为9厘米时周长为7+7+9=23(厘米)答:这个等腰三角形的周长是25或23厘米.故答案为:25或23.6.(2分)(2019秋•惠城区校级期末)一个平行四边形的面积是60dm2,底是5dm,这条底边对应的高是12dm.【分析】根据平行四边形的面积公式:S=ah,那么h=S÷a,把数据代入公式解答.【解答】解:60÷5=12(分米)答:这条底边对应的高是12分米.故答案为:12.7.(4分)(2019秋•铜官区期末)如图直角三角形的面积是6平方厘米,斜边上的高是 2.4厘米.【分析】根据三角形的面积公式:S=ah÷2,那么h=2S÷a,把数据代入公式解答.【解答】解:3×4÷2=6(平方厘米)6×2÷5=12÷5=2.4(厘米),答:这个三角形的面积是6平方厘米,斜边上的高是2.4厘米.故答案为:6平方厘米、2.4.8.(2分)(2019秋•濉溪县期末)一堆钢管,每相邻两层都相差1根,最上层2根,最下层8根,这堆钢管共35根.【分析】根据题意,这堆钢管共有(8﹣2+1)层,可利用梯形的面积公式计算这堆钢管的根数,列式解答即可.【解答】解:(2+8)×(8﹣2+1)÷2,=10×7÷2,=70÷2,=35(根);答:这堆钢管共有35根.故答案为:35.三.判断题(共4小题,满分12分,每小题3分)9.(2019秋•迎江区期末)一个平行四边形的面积是24cm2,将它的底增加2cm,高减少2cm,得到的平行四边形的面积一定仍是24cm2.×(判断对错)【分析】根据平行四边形的面积公式:S=ah,可以通过举例证明.假如原来平行四边形的底是3厘米,高是8厘米,底增加2厘米后是5厘米,高减少2厘米后是6厘米,分别求出原来和增加后的面积,然后进行比较即可.【解答】解:假如原来平行四边形的底是3厘米,高是8厘米,底增加2厘米后是5厘米,高减少2厘米后是6厘米,原来的面积:3×8=24(平方厘米);增加后的面积:(3+2)×(8﹣2)=5×6=30(平方厘米);24平方厘米<30平方厘米,答:所得到的平行四边行面积比原来平行四边形面积大.因此,所得到的平行四边行面积与原来平行四边形面积相等,这种说法是错误的.故答案为:×.10.(2019秋•武川县期末)两个等底等高的三角形,面积相等,并且一定能重合.×(判断对错)【分析】因为三角形的面积=底×高÷2,所以只要是等底等高的三角形,不管形状如何,面积一定相等.据此解答.【解答】解:由分析可知:两个等底等高的三角形,面积相等,但它们的形状不一定相同,不一定能重合.题干的说法是错误的.故答案为:×.11.(2018秋•黄冈期末)三角形的底和高都扩大4倍,它的面积就扩大8倍.×(判断对错)【分析】根据三角形的面积公式S=ah,知道底和高都扩大4倍,面积就扩大4×4倍;据此解答.【解答】解:因为三角形的面积S=ah,所以S′=×4a×4h=×16ah=16S,所以三角形的底和高都扩大4倍,它的面积扩大16倍,原题说法错误.故答案为:×.12.如图甲的面积是乙的面积的3倍√.(判断对错)【分析】由图可知,甲乙是两个不等底但是等高的三角形,设它们的高为2h,根据三角形的面积公式:三角形的面积=底×高÷2,求出两个三角形的面积即可判断.【解答】解:设甲和乙两三角形的高为2h,那么甲的面积是,4.5×2h÷2=4.5h;乙的面积是:1.5×2h÷2=1.5h;4.5h÷1.5h=3,所以甲部分的面积是乙部分的3倍,所以原题说法正确.故答案为:√.四.计算题(共3小题,满分15分)13.(4分)如图是一块长16m、宽10m的长方形草地,中间有两条小路,一条是长方形,一条是平行四边形.求草地(阴影部分)的面积.【分析】将阴影部分平移拼成一个长方形,长变成(16﹣2)米,宽变成(10﹣2)米,然后根据长方形的面积公式S=ab解答即可.【解答】解:(16﹣2)×(10﹣2)=14×8=112(平方米)答:草地的面积是112平方米.14.(6分)(2019秋•迎江区期末)求下面组合图形的面积.(单位:dm)【分析】(1)根据图示可知:该图形的面积等于长20分米、宽15分米的长方形的面积,减掉一个底12分米、高9分米的三角形面积.利用长方形和三角形面积公式计算即可.(2)根据图示可知:该图形的面积为一个上底6分米墩号下底8分米、高4分米的梯形面积,加上一个底6分米、高7﹣4=3(分米)的三角形的面积.利用三角形和梯形面积公式计算即可.【解答】解:(1)20×15﹣9×12÷2=300﹣54=246(平方分米)答:该图形的面积面积是246平方分米.(2)(6+8)×4÷2+6×(7﹣4)÷2=28+9=37(平方分米)答:该图形的面积是37平方分米.15.(5分)(2020•长白县)如图,小正方形ABCD的边长是5cm,大正方形CEFG的边长是10cm,求图中阴影部分的面积.【分析】通过观察图形可知,阴影部分的面积等于梯形ABEF的面积减去正方形ABCD 的面积再减去三角形CEF的面积,根据梯形的面积公式:S=(a+b)h÷2,正方形的面积公式:S=a2,三角形的面积公式:S=ah÷2,把数据代入公式解答.【解答】解:(10+5)×(10+5)÷2﹣5×5﹣10×10÷2=15×15÷2﹣25﹣50=112.5﹣25﹣50=37.5(平方厘米)答:阴影部分的面积是37.5平方厘米.五.应用题(共5小题,满分25分,每小题5分)16.(5分)(2019秋•丰台区期末)如图,一块平行四边形菜地,其中阴影部分种的是萝卜.这块菜地的面积是多少平方米?【分析】平行四边形面积=底×高,阴影部分种的是萝卜,用它的面积300平方米除以底15米求出平行四边形的高,再根据平行四边形的面积公式解答即可.【解答】解:300÷15×(25+15)=20×40=800(平方米)答:这块菜地的面积是800平方米.17.(5分)(2019秋•大兴区期末)有一块三角形的钢板,底是5米,高是4.4米.这种钢板每平方米重31.4千克.这块钢板重多少千克?【分析】根据三角形的面积公式:S=ah÷2,把数据代入公式求出这块钢板的面积是多少平方米,然后用钢板的面积乘每平方米钢板的质量即可.【解答】解:5×4.4÷2×31.4=11×31.4=345.4(千克)答:这块钢板重345.4千克.18.(5分)(2019秋•巩义市期末)华丰小学校园里有一块空地(如图).如果在这块空地上种草坪,每平方米草坪的价格是15元.需要多少钱?【分析】如图,,这块空地的面积=长方形的面积+三角形的面积,长方形的长是12m,宽是8.5m;三角形的底是18﹣12=6m,高是8.5﹣3.5=5m,根据长方形和三角形的面积公式,求出这块地的面积,然后再根据乘法的意义,乘上15即可.【解答】解:12×8.5+(18﹣12)×(8.5﹣3.5)÷2=102+15=117(平方米)15×117=1755(元)答:需要1755元钱.19.(5分)(2019秋•长垣县期末)一块近似平行四边形的桃园,被一条长方形的石子路分成了两块(如图).已知平行四边形的底是13.2米,高是10.4米,小路宽1米.如果平均每棵桃树占地5平方米,这个桃园大约有多少棵桃树?【分析】可以通过平移的方法把石子路两边的地转化为一个底是(13.2﹣1)米,高是10.4米的平行四边形,根据平行四边形的面积公式:S=ah,求出这个果园的面积,然后用果园的面积除以每棵桃树的占地面积即可.【解答】解:(13.2﹣1)×10.4÷5=12.2×10.4÷5=126.88÷5≈25(棵)答:这个桃园大约有125棵桃树.20.(5分)(2018秋•锦江区期末)粉刷一间教室的一面墙(如图),如果每平方米用涂料0.4千克,出去窗户,粉刷需多少涂料?如果每千克涂料10元,共需多少元?【分析】根据三角形的面积公式:S=ah÷2,长方形的面积公式:S=ab,把数据分别代入公式,求出三角形与长方形的面积和再减去窗户的面积就是粉刷的面积,用粉刷的面积乘每平方米用涂料的质量求出分数需要多少涂料;然后根据单价×数量=总价,据此列式解答.【解答】解:8×1.8÷2+8×6﹣2×1.2=7.2+48﹣2.4=55.2﹣2.4=52.8(平方米);52.8×0.4=21.12(千克);10×21.12=211.2(元);答:粉刷需21.12千克涂料,共需211.2元.六.解答题(共5小题,满分26分)21.(6分)(2018秋•点军区校级期末)妈妈在柜子里发现了一块花布(如图),想给莎莎做沙包.(1)你能求出这块花布的面积吗?(2)如果做一个沙包要用花布200cm2,这块花布够做一个沙包吗?【分析】(1)根据图形的特点,把这个不规则图形转化为一个梯形和一个三角形,利用梯形面积公式:S=(a+b)×h÷2和三角形面积公式:S=ah÷2,即可计算其面积.(2)根据(1)的分析,计算该花布的面积,并与做沙包的布料面积进行比较,即可得出结论.【解答】解:(1)如图:把这块花布分成一个上底7厘米、下底10厘米、高8厘米的梯形和一个底和高都是7厘米的三角形.(7+10)×8÷2+7×7÷2=68+24.5=92.5(平方厘米)答:这块花布的面积是92.5平方厘米.(2)92.5<200答:这块花布不够做一个沙包.22.(4分)(2019•永州模拟)梯形面积是96平方厘米.求下面图中阴影部分的面积.(单位:cm)【分析】已知梯形的面积是96平方厘米,根据图形的面积公式,用96×2除以上下底之和,即可得出梯形的高,再利用三角形的面积公式即可计算解答.【解答】解:96×2÷(10+6),=192÷16,=12(厘米),所以阴影部分的面积是:6×12÷2=36(平方厘米),答:阴影部分的面积是36平方厘米.23.(5分)(2019秋•会宁县期末)如图中阴影部分的面积是42分米2,求梯形的面积.(单位:分米)【分析】根据三角形的面积:S=ah÷2可知h=2s÷a,已知面积是42平方分米,底是15分米,据此可求出三角形的高,即是梯形的高,再根据梯形的面积公式:S=(a+b)h÷2可求出梯形的面积.据此解答.【解答】解:42×2÷15=84÷15=5.6(分米)(15+4.5)×5.6÷2=19.5×5.6÷2=54.6(平方厘米)答:梯形的面积是54.6平方厘米.24.(5分)(2020•盐城模拟)如图,两个相同的直角三角形部分重叠在一起,求阴影部分的面积.(单位:厘米)【分析】由图意可知:两个三角形都去掉公共部分(三角形DOC),则剩余部分的面积仍然相等,即阴影部分的面积=梯形OEFC的面积,先求出梯形的上底,进而利用梯形的面积公式即可求解.【解答】解:(9﹣3+9)×2÷2=15(平方厘米);答:阴影部分的面积是15平方厘米.25.(6分)(2019•南京)平行四边形ABCD周长为75厘米,以BC为底时高是14厘米(如图);以CD为底时高是16厘米.求:平行四边形ABCD的面积.【分析】用平行四边形的面积公式先求出邻边的关系,再由平行四边形的周长得到邻边的和,从而求得平行四边形的一条边长,进而求得其面积.【解答】解:由平行四边形面积公式知14×BC=16×CD,即14BC=16CD,则BC:CD=16:14=8:7,BC=CD,又2×(BC+CD)=75,则BC+CD=37.5(厘米),CD+CD=37.5(厘米),CD=17.5(厘米),因此,平行四边形ABCD的面积为:16×17.5=280(平方厘米);答:平行四边形ABCD的面积为280平方厘米.。
五年级上册数学试题-6《多边形的面积》专项培优 人教新课标含答案

《多边形的面积》专项培优专项一运用等分法巧求面积例1 如图是两个完全一样的等腰直角三角形,图①中正方形的面积是40平方分米,则图②中正方形的面积是多少平方分米?分析等分法,就是将整个图形平均分成若干份,再看所求图形的面积占多少份,从而求出所要求的图形面积。
本题中,根据图①中正方形的面积与大等腰直角三角形的面积关系,可求出大等腰直角三角形的面积;然后根据图②中正方形的面积与大等腰直角三角形的面积关系,求出图②中正方形的面积。
解答如图,运用等分法把图①平均分成9份,正方形的面积相当于这样的4份;把图②平均分成4份,正方形的面积相当于这样的2份。
等腰直角三角形的面积为40÷4×9=90(平方分米),图②中正方形的面积为90÷2=45(平方分米)。
反馈练习1.如图,七巧板拼成的正方形边长是20厘米,求图中阴影部分的面积2.如图,在一个面积是36平方分米的大正方形中,有两个带阴影的小正方形。
求阴影部分的面积和。
3.如图,将等腰直角三角形ABC与等腰直角三角形DEC重叠在一起,阴影部分是一个正方形。
已知三角形ABC的面积是72平方厘米,求三角形DEC的面积。
专项二运用等积变换巧求面积例2 如图,已知长方形ABCD的面积是1200平方厘米,阴影部分的面积是750平方厘米,求四边形EFGO的面积。
分析根据图形特点,由面积与面积之间的相等关系,进行一些转化,从而使间题得到简便解决。
本题根据题目中图形之间面积相等的关系可以将上图中的阴影部分三角形ABE移至三角形DFE中,从而求出四边形EFGO的面积。
解答在长方形ABCD中,三角形ABF与三角形DBF同底(即BF的长)、等高(即长方形的宽),所以三角形ABF与三角形DBF的面积相等。
若从这两个三角形中同时减去三角形BEF则剩下的图形面积相等,即:三角形ABE与三角形DFE 的面积相等。
这样阴影部分的面积就等于四边形EFCO加上三角形ACD的面积,要求四边形EFGO的面积,只要用阴影部分的面积减去三角形ACD的面积,列式为750-1200÷2=150(平方厘米)。
3第三讲 多边形的面积(等积变形)

第三讲多边形的面积(等积变形)【知识概述】三角形面积的公式是底×高÷2,两个三角形只要是底和高分别相等,它们的面积就相等,而这两个三角形的形状不一定完全相同,例如,下面的两个三角形面积就是相等的。
在解答一些平面图形的面积时,我们可以巧用等底等高两个三角形面积相等的方法来解答。
例题精学例1 四边形ABCD中,M为AB 的中点,N为CD 的中点,如果四边形ABCD 的面积是80 平方厘米,求阴影部分BNDM 的面积是多少平方厘米。
【思路点拨】图中阴影部分BNDM 是一个不规则的四边形,不能直接求出它的面积。
如果用一条对角线BD 将四边形ABCD 分成两个三角形。
(如右图所示)。
在△ABD和△BDC中,由于M,N 分别是AB,CD 的中点,根据等底等高三角形面积相等的道理,可知S△AMD=S△MBD,S△DNB=SΔcNB。
所以阴影部分的面积与空白部分的两个三角形的面积之和相等。
同步精练1. 如图,六边形ABCDEF 的面积是16 平方厘米,M,N,P,Q 分别是AB,CD,DE,AF 的中点。
求图中阴影部分的面积。
2. 如图,平行四边形的面积为50 平方厘米.P 是其中任意一点,求阴影部分面积3. 如图,正方形的边长是6 厘米,E,H 是所在边的二等分点,F,G,L,M 是所在边的三等分点,求阴影部分的面积和。
例2 如下图,三角形ABC 为等边三角形,D为AB 边上的中点。
已知三角形BDE 的面积为5 平方厘米。
求等边三角形ABC 的面积。
【思路点拨】我们在三角形ABC的AC 边上取中点F,BC 边上取中点G,然后连接DF,FG,GD(如右图)。
我们看到,三角形ADF,BDG,FGC,GFD 为四个完全一样的等边三角形。
因为DE为△DBG底BG上的高,所以S△DBE=S△DGE。
由此,我们可以想到三角形ABC 的面积是三角形DBE 面积的8倍。
同步精练1. 如图,平行四边形ABCD中,AE=EF=FB,AG=2CG,三角形GEF 的面积是6 平方厘米,平行四边形的面积是多少平方厘米?2.如图,已知长方形ABCD,三角形ABG 的面积为20 平方厘米,三角形CDQ 的面积为35 平方厘米,求阴影部分的面积是多少平方厘米。
多边形面积的求法及面积公式

多边形面积的求法及面积公式作为几何学中的重要概念,多边形的面积是我们经常需要计算的。
在实际应用中,我们经常需要确定不规则多边形的面积,或者计算规则多边形(如三角形、正方形、矩形等)的面积。
本文将介绍多边形面积的求法以及面积公式。
一、三角形面积的求法及面积公式三角形是最简单的多边形,其面积计算也是最基本的。
我们可以通过两种方法来计算三角形的面积:一种是通过底边和高的关系,另一种是通过三个顶点的坐标计算。
1. 底边和高的关系对于任意三角形,我们可以通过底边和高的关系来计算其面积。
假设三角形的底边长为b,高为h,则三角形的面积S等于底边长乘以高的一半,即S=1/2*b*h。
2. 三个顶点的坐标计算另一种计算三角形面积的方法是通过三个顶点的坐标计算。
假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3),则三角形的面积S可以通过以下公式计算得出:S=1/2*|x1(y2-y3)+x2(y3-y1)+x3(y1-y2)|二、正方形和矩形面积的求法及面积公式正方形和矩形是两种常见的规则多边形,其面积计算也十分简单。
1. 正方形正方形的面积计算非常简单,只需要知道正方形的边长a,就可以直接使用公式S=a^2来计算其面积。
2. 矩形矩形的面积计算也很简单,只需要知道矩形的长a和宽b,就可以使用公式S=a*b来计算其面积。
三、不规则多边形面积的求法对于不规则多边形,我们需要将其分割成若干个三角形或梯形,然后计算每个三角形或梯形的面积,最后将各个部分的面积相加,即可得到不规则多边形的面积。
1. 分割成三角形将不规则多边形分割成若干个三角形,然后分别计算每个三角形的面积,最后将各个三角形的面积相加,即可得到不规则多边形的面积。
2. 分割成梯形将不规则多边形分割成若干个梯形,然后分别计算每个梯形的面积,最后将各个梯形的面积相加,即可得到不规则多边形的面积。
需要注意的是,在分割不规则多边形时,我们可以选择不同的分割方式,尽量选择简单的形状(如三角形、梯形),以便计算其面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成面积相等的两部分。
作法:(1)连结AC、BD;(2)取AC的中点E,作EF∥BD交BC于点F;(3)连结DF.如图3.则直线DF把四边形ABCD分成面积相等的两部分。
证明:∵E为AC的中点,∴S四边形ADEB=S四边形DCBE∵EF∥BD,∴S△DEQ=S△BFQ,∴S四边形ADFB=S△DFC= S四边形ABCD.
由上述作图过程可知,不论是三角形,还是四边形,还是正五边形,对于它们的面积二等分,要不就是利用三角形的中线,要不就是利用梯形,目的都是为了得到面积相等的三角形,然后通过这样的两个三角形的互换,达到按照既定要求进行面积二等分的目的。实际上,面积相等的三角形并不一定等底等高,只要两个三角形底与高之积相等就可以,对于怎么样能够用尺规作图作三角形使之底与高之积等于已知常数,以后再单独讨论。最后以一个任意五边形的面积二等分来结束全文。
过四边形的顶点且二等分四边形面积的四条直线两两相交,把四边形的边分成了八条线段,如图5;很明显,其中的每一条线段都有另外一条线段与它是同两条面积等分线所截得的线段。为了叙述的方便,不妨称这两条线段为姊妹线段,如图5中的DN和BF。这八条线段中的任意一条线段上的任意一点都可以找一条面积等分线作对角线与之构造梯形,这个梯形的第四个顶点所在的线段必与这条线段是姊妹线段。所以,有了这四条过四边形顶点的面积等分线,就可以过四边形任意边上的任意点作直线把四边形面积二等分。对于四边形面积二等分来说这四条线的作用与三角形的中线的作用是一样的。
用这个方法,过四边形的每一个顶点都可以作出一条直线把四边形分成面积相等的两部分。再来说一下过任意边上的任一点如何作直线把四边形面积二等分。
如图4,已知任意四边形ABCD,P为DC上一点,求作一条直线PQ把四边形ABCD分成面积相等的两部分。
作法:(1)连结AC、BD;(2)取AC的中点E,作EF∥BD交BC于点F;(3)连结DF.如图3.则直线DF把四边形ABCD分成面积相等的两部分。(4)连接PF,作DQ∥PF交BC于点Q;(5)连接PQ。则PQ即为所求。
如图,已知P为正五边形ABCDE的边CD上的任意一点,求作直线PQ,把正五边形ABCDE分成面积相等的两部分。
作法①:1.连接AP;2,取CD的中点F,作FQ∥AP,交AE于点Q;3,作直线PQ,如图1.则直线PQ就是所求作的直线。
作法②:1.连接EP;2,取BC的中点F,作FQ∥EP,交AE于点Q;3,作直线PQ,如图2.则直线PQ就是所求作的直线。
证明:设AD、PQ的交点为O;∵D为BC的中点,∴S△ABD=S△ACD
= S△ABC,∵DQ∥AP,∴S△APQ=S△APD,∴S△AOQ=S△POD
∴S四边ABPQ=S△ABD-S△POD+S△AOQ=S△ABD= S△ABC。
∴直线PQ把△ABC分成面积相等的两部分。
为了作出直线PQ,先作出BC边上的中线AD,然后以这条中线为一条对角线,以A、P、D为顶点构造梯形,这个梯形的第四个顶点一定要在三角形的边上,则另一条对角线所在的直线PQ就是所求作的直线。这里除了利用了三角形的中线的性质以外,还用到了梯形的性质,实际上是利用了等底等高的三角形面积相等的性质。此例给出的是点P在A、D之间时的情形;不过,有了此例,相信大家都会作点P在B、D之间时的直线PQ.由此可以说明过三角形任意一边上的任意一点都可以作出一条直线把三角形分成面积相等的两部分。
多边形面积
在初中阶段平面几何中,图形的等分问题比较多,常见的有以下几种:等分线段,等分角,等分圆,多边形面积二等分等。线段和角的二等分比较简单,任意等分就稍显复杂;特别是角的任意等分,著名的“尺规作图不能问题”中就有角的三等分问题。现在据说有人发明了一种工具叫做弧金规,这种工具不但可以任意等分任意角(包括三等分任意角),还能作一个正方形与已知圆的面积相等,即化圆为方问题;这样一来“尺规作图不能问题”中的三个就被其解决掉了两个,只还剩一个“立方倍积”了。非但如此,这种工具还能在圆弧上取黄金分割点及在任意曲线上任意取段;也就是说能任意等分圆周及任意曲线。这项发明可以说是意义重大,但是,这种工具毕竟现在没有推广、普及,而且其操作也肯定不如传统中的直尺和圆规操作简单,再说了,使用这种工具作图是否属于尺规作图还有待于进一步论证;所以,本文还是想从传统的尺规作图的角度来论述一下初中数学中常见的有关几何图形特别是多边形的面积二等分问题。
先说三角形的面积二等分问题。
对于三角形来说,由于等底等高的三角形面积相等,所以,三角形任意一边上的中线都可以把它分成面积相等的两部分,这个问题比较简单;下面说一下过任意边上的任意一点作直线平分三角形的问题。如图,已知P为△ABC的边BC上的任意一点,求作直线PQ,把△ABC分成面积相等的两部分。
作法:1.连接AP;2,取BC的中点D,作DQ∥AP,交AC于点Q;3,作直线PQ,如图0.则直线PQ就是所求作的直线。
证明方法和三角形一样,就不重复了。
二.任意多边形。
任意多边形中,四边形的面积二等分最为简单;至于其他的多边形,随着边数的增加,面积二等分的难度会越来越大。由于那样的问题过于复杂,实用性不是太强,再加上初中阶段又不常见,所以就不一一说明了。接下来拟就四边形的面积二等分问题来详细说明一下,然后简单介绍一下任意五边形的面积二等分。
无论是什么样的多边形,都可以用一条直线把它分成两部分;由于直线相对于多边形的方向与位置不同,被分出来的两部分面积可能相等,也可能不相等。但无论直线开始时如何放置,只要放置好以后我们让它沿着与直线垂直的方向来回平移,在直线扫过整个多边形的过程中,总有一个位置是使被分出来的两部分面积相等,因此,对于任意多边形,都应该存在无数条直线能把它分成面积相等的两部分;或者换句话说,过多边形任意边上的任意一点也都应该存在一条直线能把多边形分成面积相等的两部分。
中心对称图形的面积二等分非常简单;过对称中心的任意一条直线都把图形分成面积相等的两部分。初中几何中常见的是两个中心对称图形的组合图形,这时,只要把每一个图形的对称中说一下非中心对称图形的多边形面积二等分问题。这样的问题常见的可以分为两大类别:
一、边数为奇数的正多边形。这类多边形都是轴对称图形,它们的每条对称轴都是各自的面积二等分线。除此之外,由于图形的对称性,过任意边上的任一点作面积的等分线也不是太难;现仅以正五边形为例说明一下这类图形的面积二等分方法。
如图6,已知任意五边形ABCDE;求作直线AF,把五边形ABCDE分成面积相等的两部分。
作法:(1)如图:取BE的中点O,连结AO;连结CE取CE的中点P,连结BD,取BD的中点Q,(2)过点P作RS∥BD交BE于R交DE于S;连结DR;(3)过点Q作MT∥CE交BC于M交BE于T,连结CT;(4)连结OD,作RH∥OD交CD于H,连结OH;(5)连结AH,作OF∥AH交CD于F,连结AF;则AF即为所求。(HN也把五边形面积二等分)
