第一轮复习—24圆的有关概念
人教版2020年中考数学一轮复习《与圆有关的证明和计算》大题专项练习含答案解析

中考专题——与圆有关的证明和计算纵观近几年全国各地中考题,圆的有关概念以及性质等一般以填空题,选择题的形式考查并占有一定的分值;圆的有关性质,如垂径定理,圆周角,切线的判定与性质等综合性问题的运用一般以计算证明的形式考查;一般在10分-15分左右,以后发展中利用圆的知识与其他知识点如函数,方程等相结合作为中考压轴题将会占有非常重要的地位。
考查的类型:(1)线段、角以及切线的证明;(2)利用勾股定理、相似以及锐角三角函数进行线段,比值和阴影面积的求解.例题精讲:1、如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC 交于点E,连接AD.(1)求证:AD平分∠BAC;(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).2、如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.(1)求证:△ABC是等边三角形;(2)若∠PAC=90°,AB=2,求PD的长.3、如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.4、如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.(1)求证:AC是⊙O的切线;(2)若BD=,BE=1.求阴影部分的面积.5、如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.(1)求证:CF是⊙O的切线.(2)若∠A=22.5°,求证:AC=DC.补充练习:1、如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC,AC于点D,E,过点D作DF⊥AC于点F.(1)求证:DF是⊙O的切线;(2)若∠C=60°,⊙O的半径为2,求由弧DE,线段DF,EF围成的阴影部分的面积(结果保留根号和π)2、如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;(2)若CD=1,求图中阴影部分的面积(结果保留π).3、如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.(1)求证:直线DF与⊙O相切;(2)若AE=7,BC=6,求AC的长.4、如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AB 的延长线于点F,连接DA.(1)求证:EF为半圆O的切线;(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)5、如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.(1)判断CE与⊙O的位置关系,并说明理由;(2)若∠DBA=30°,CG=8,求BE的长.6、如图,AB为⊙O的直径,C,E为⊙O上的两点,若AC平分∠EAB,CD⊥AE于点D.(1)求证:DC是⊙O的切线;3,求DE的长;(2)若AO=6,DC=33,求图中阴影部分面积.(3)过点C作CF⊥AB于F,如图2,若AD-OA=1.5,AC=3答案解析例题精讲:1、(1)证明:∵⊙O切BC于D,∴OD⊥BC,∵AC⊥BC,∴AC∥OD,∴∠CAD=∠ADO,∵OA=OD,∴∠OAD=∠ADO,∴∠OAD=∠CAD,即AD平分∠CAB;(2)设EO与AD交于点M,连接ED.∵∠BAC=60°,OA=OE,∴∠AEO是等边三角形,∴AE=OA,∠AOE=60°,∴AE=A0=OD,又由(1)知,AC∥OD即AE∥OD,∴四边形AEDO是菱形,则△AEM≌△DMO,∠EOD=60°,∴S△AEM=S△DMO,∴S阴影=S扇形EOD==.2、(1)证明:∵∵ABC=∵APC,∵BAC=∵BPC,∵APC=∵CPB=60°,∵∵ABC=∵BAC=60°,∵∵ABC是等边三角形.(2)解:∵∵ABC是等边三角形,AB=2,∵AC=BC=AB=2,∵ACB=60°.在Rt∵PAC中,∵PAC=90°,∵APC=60°,AC=2,∵AP=AC•cot∵APC=2.在Rt∵DAC中,∵DAC=90°,AC=2,∵ACD=60°,∵AD=AC•tan∵ACD=6.∵PD=AD﹣AP=6﹣2=4.3、(1)证明:∵BE平分∠BAC,AD平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,∴△ABC外接圆的半径=×4=2.4、(1)证明:连接OD,作OF⊥AC于F,如图,∵△ABC为等腰三角形,O是底边BC的中点,∴AO⊥BC,AO平分∠BAC,∵AB与⊙O相切于点D,∴OD⊥AB,∵OF⊥AC,∴OF=OD,∴AC是⊙O的切线;(2)解:在Rt△BOD中,设⊙O的半径为r,则OD=OE=r,∴r2+()2=(r+1)2,解得r=1,∴OD=1,OB=2,∴∠B=30°,∠BOD=60°,∴∠AOD=30°,在Rt△AOD中,AD=OD=,∴阴影部分的面积=2S△AOD﹣S扇形DOF=2××1×﹣=﹣.5、(1)证明:∵AB 是⊙O 的直径,∴∠ACB =∠ACD =90°,∵点F 是ED 的中点,∴CF =EF =DF ,∴∠AEO =∠FEC =∠FCE ,∵OA =OC ,∴∠OCA =∠OAC ,∵OD ⊥AB ,∴∠OAC+∠AEO =90°, ∴∠OCA+∠FCE =90°,即OC ⊥FC ,∴CF 与⊙O 相切;(2)解:∵OD ⊥AB ,AC ⊥BD ,∴∠AOE =∠ACD =90°,∵∠AEO =∠DEC ,∴∠OAE =∠CDE =22.5°, ∵AO =BO ,∴AD =BD ,∴∠ADO =∠BDO =22.5°,∴∠ADB =45°,∴∠CAD =∠ADC =45°,∴AC =CD .补充练习:1、(1)如图,连接OD ∵AB 为⊙O 的直径∴AD ⊥BC ∵AB=AC ∴BD=CD ,D 为BC 中点∵O 为AB 中点∴OD ∥AC ∵DF ⊥AC ∴DF ⊥OD ∴DF 为⊙O 的切线(2)如图,连接OE 、OD ∵AB=AC ,∠C=60°∴△ABC 为等边三角形∴∠B=∠A=60°,AB=AC=BC=2⨯2=4∵OA=OB=OD=OE ∴△OAE ,△OBD 都是等边三角形∴∠ODB=∠BOD=∠AOE -∠OEA=∠C=60° ∴∠DOE=180°-2⨯60°=60°,OD ∥AC ,OE ∥BC ∴四边形ODCE 是平行四边形∴OD=CE=BD=CD=2∴DF=CDsin60°=3232=⨯,CF=CDcos60°=1212=⨯ ∴ππ32-323360260-3121-32--2=⨯⨯⨯⨯==∆ODE CDF S S S S 扇形平行四边形阴影2、(1)证明:连接DE 、OD ∵BC 相切⊙O 于点D ∴∠CDA=∠AED ∵AE 为直径∴∠ADE=90°∵AC ⊥BC ∴∠ACD=90°∴∠DAO=∠CAD ∴AD 平分∠BAC(3)在Rt △ABC 中,∠C=90°,AC=BC ∴∠B=∠BAC=45°∵BC 相切⊙O 于点D ∴∠ODB=90°∴OD=BD ,∠BOD=45°设BD=x ,则OD=OA=x ,0B=3x ∴BC=AC=x+1∵AC 2+BC 2=AB 2∴22)2()12x x x +=+( 所以x=2∴BD=OD=2 ∴()4-1360245-22212ππ=⨯⨯=-∆=DOE S BOD S S 扇形阴影3、(1)证明:连接OD ,∵AB=AC ,∴∠B=∠C 。
中考第一轮复习数学人教版九年级上册第24章 圆 难题训练 附答案

2021年中考第一轮复习数学人教版九年级上册第24章圆难题训练一.选择题(共18小题)1.如图,已知弦AB与弦CD交于点P,且P为AB的中点,延长AC、DB交于点E,若AC=2,BD=3,则CE+BE=()A.9B.3+4C.10D.62.如图,半径为1的⊙O与直线l相切于点A,C为⊙O上的一点,CB⊥l于点B,则AB+BC 的最大值是()A.2B.C.D.3.如图,⊙O1的直径AB长度为12,⊙O2的直径为8,∠AO1O2=30°,⊙O2沿直线O1O2平移,当⊙O2平移到与⊙O1和AB所在直线都有公共点时,令圆心距O1O2=x,则x的取值范围是()A.2≤x≤10B.4≤x≤16C.4≤x≤4D.2≤x≤84.如图,AB是⊙O的直径,AB=AC且∠BAC=45°,⊙O交BC于点D,交AC于点E,F在AC上,DF与⊙O相切,OD与BE相交于点H.下列结论错误的是()A.BD=CD B.四边形DHEF为矩形C.=2D.BC=2CE5.如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是:①PB=PD;②的长为π;③∠DBE=45°;④当P为中点时,EC=EF;⑤∠DFB=∠CBP.其中正确的个数为()A.5B.4C.3D.26.如图,AB是⊙O的直径,CD为⊙O的弦,且CD⊥AB于点E,点F为圆上一点,若AE =BF,,OE=1,则BC的长为()A.2B.3C.4D.57.如图,是同一种蔬菜的两种栽植方法.甲:A、B、C、D四珠顺次连接成为一个菱形,且AB=BD.乙:A'、B'、C'、D'四株连接成一个正方形.其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距;设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积.设株距都为a,其它客观因素都相同.则对于下列说法:①甲的行距比乙的小;②甲的行距为;③甲、乙两种栽植方式,空隙地面积面积相同;④甲的空隙地面积比乙的空隙地面积少.其中正确的个数为()A.1B.2C.3D.48.如图,在平面直角坐标系中,将边长为1的正六边形OABCDE绕点O顺时针旋转i个45°,得到正六边形OA i B i∁i D i E i,则正六边形OA i B i∁i D i E i(i=2020)的顶点∁i的坐标是()A.(1,﹣)B.(1,)C.(1,﹣2)D.(2,1)9.如图,四边形ABCD内接于⊙O,AB=CB,∠BAC=30°,BD=,则AD+CD的值为()A.3B.2C.+1D.不能确定10.如图,⊙O的半径是5,点A是圆周上一定点,点B在⊙O上运动,且∠ABM=30°,AC⊥BM,垂足为点C,连接OC,则OC的最小值是()A.B.C.D.﹣11.如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为()A.3B.4C.5D.612.在⊙O中内接四边形ABCD,其中A,C为定点,AC=8,B在⊙O上运动,BD⊥AC,过O作AD的垂线,若⊙O的直径为10,则OE的最大值接近于()A.B.C.4D.513.如图,已知⊙O的半径为10,A、B是⊙O上的两点,∠AOB=90°,C是射线OB上一个动点,连接AC交⊙O于点D,过点D作DE⊥OD交OB的延长线于点E.当∠A 从30°增大到60°时,弦AD在圆内扫过的面积是()A.B.C.D.14.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE =1,EF=,则BF的长为()A.B.1C.D.15.已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为()A.1+B.1+2C.2+D.2﹣116.如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD=,BC=1,则⊙O 的半径为()A.B.C.D.17.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是()A.B.C.D.18.如图,AB是半圆O的直径,点D在半圆O上,AB=2,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是()A.5B.6C.7D.8二.填空题(共10小题)19.在△ABC中,AB=AC=10,BC=12,M,N是BC边上两个动点,若AB,AC边上分别存在点P,Q使得∠MPN=∠MQN=60°,则线段MN的最小值为.20.如图,正六边形ABCDEF中,G,H分别是边AF和DE上的点,GF=AB=2,∠GCH =60°,则线段EH长.21.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为弧AC上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为4,则PN+MN的长度的最大值是.22.如图,在平面直角坐标系xOy中,一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,点P在线段AB上,⊙P与x轴交于A、C两点,当⊙P与y轴相切时,AC的长度是.23.如图,在平面直角坐标系中,已知C(6,8),以点C为圆心的圆与y轴相切.点A、B 在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为.24.如图,平行四边形ABCD中,AC⊥BC,AB=5,BC=3,点P在边AB上运动,以P 为圆心,P A为半径作⊙P,若⊙P与平行四边形ABCD的边有四个公共点,则AP的长度的取值范围是.25.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM的最小值为.26.如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为.27.如图,直线y=﹣x+m(m>0)与x轴、y轴分别交于点A,B,C是AB的中点,点D 在直线y=﹣2上,以CD为直径的圆与直线AB的另一交点为E,交y轴于点F,G,已知CE+DE=6,FG=2,则CD的长是.28.如图,AB是半圆O的直径,点C在半圆上,AB=5,AC=4,D是上的一个动点,连接AD.过点C作CE⊥AD于E,连接BE,则BE的最小值是.三.解答题(共10小题)29.如图,在Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O交AB于点D,交AC于点E,点F在BC上,且BF=DF.(1)求证:DF是半圆O的切线;(2)若AC=4,BC=3,CF=1,求半圆O的半径长.30.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.(1)求证:AE=DE;(2)若CE=1,求四边形AECD的面积.31.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.(1)求证:BC是⊙O的切线;(2)若∠C=30°,且CD=3,试求阴影部分的面积.32.如图,四边形ABCD内接于⊙O,对角线BD是⊙O的直径,AC平分∠BAD,过点C 作CG∥BD交AD的延长线于点G.(1)求证:CG是⊙O的切线;(2)若AB=3,AD=5,求AC的长.33.如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.(1)求证:EB=EI;(2)若AB=4,AC=3,BE=2,求AI的长.34.如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,连接MB.(1)若BE=8,求⊙O的半径;(2)若∠DMB=∠D,求线段OE的长.35.如图在⊙O中,AB为直径,BP为⊙O的弦,AC与BP的延长线交于点C,且BP=PC,PE⊥AC于E.求证:PE是⊙O的切线.36.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.(1)求证:BD平分∠ABC;(2)若OE=3,AO=5,求AC的长.37.如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC 于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.(1)求证:EF是⊙O切线;(2)若AB=15,EF=10,求AE的长.38.如图,⊙O为△ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且∠EAC=∠ABC.(1)求证:直线AE是⊙O的切线.(2)若D为AB的中点,CD=6,AB=16①求⊙O的半径;②求△ABC的内心到点O的距离.2021年中考第一轮复习数学人教版九年级上册第24章圆难题训练参考答案与试题解析一.选择题(共18小题)1.如图,已知弦AB与弦CD交于点P,且P为AB的中点,延长AC、DB交于点E,若AC=2,BD=3,则CE+BE=()A.9B.3+4C.10D.6【分析】设EC=a,EB=b.证明△P AC∽△PDB,可得===,推出可以假设P A=PB=3k,则PC=2k,PD=k,再证明△EAB∽△EDC,可得==,构建方程组,求出a,b即可.【解答】解:设EC=a,EB=b.∵∠APC=∠DPB,∠A=∠D,∴△P AC∽△PDB,∴===,∴可以假设P A=PB=3k,则PC=2k,PD=k,∴CD=k,AB=6k,∵∠E=∠E,∠A=∠D,∴△EAB∽△EDC,∴==,∴==,可得a=,b=,∴EC+EB=a+b=10,故选:C.【点评】本题考查了圆周角定理,相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考选择题中的压轴题.2.如图,半径为1的⊙O与直线l相切于点A,C为⊙O上的一点,CB⊥l于点B,则AB+BC 的最大值是()A.2B.C.D.【分析】延长AB到点D,使BD=BC,则AB+BC=AD,当DC与⊙O相切于点C时,AD最大,则此时连接AO并延长交DC延长线于点E,则AE⊥AD,根据∠CDB=45°,可得OC=CE=1,根据勾股定理可得OE的长,进而可得结论.【解答】解:如图,延长AB到点D,使BD=BC,则AB+BC=AD,当DC与⊙O相切于点C时,AD最大,则此时连接AO并延长交DC延长线于点E,则AE⊥AD,∵CB⊥l,∴∠DBC=90°,∵BD=BC,∴∠CDB=45°,∵⊙O与直线l相切于点A,∴OA⊥l,∴∠OAD=90°,∴∠AED=45°,连接OC,则OC⊥DE,在Rt△OCE中,OC=CE=1,根据勾股定理,得OE==,∴AD=AE=AO+OE=1+.则AB+BC的最大值是+1.故选:C.【点评】本题考查了切线的性质,解决本题的关键是掌握切线的性质.3.如图,⊙O1的直径AB长度为12,⊙O2的直径为8,∠AO1O2=30°,⊙O2沿直线O1O2平移,当⊙O2平移到与⊙O1和AB所在直线都有公共点时,令圆心距O1O2=x,则x的取值范围是()A.2≤x≤10B.4≤x≤16C.4≤x≤4D.2≤x≤8【分析】由题意得出点O2在点O1的右侧,⊙O2与⊙O1和AB所在直线都有公共点时,O1O2的最大值和最小值,分别画出图形求解得出x的取值范围,根据对称性可得点O2在点O1的左侧时的结论.【解答】解:(1)当点O2在点O1的右侧时,当⊙O2向右移动到与直线AB相切时,如图1所示,设切点为M,则O2M=4,又∵∠AO2O1=30°,∴O1O2=2•O2M=8,当⊙O2继续向右移动到与⊙O1内切时,如图2所示,此时O1O2=6﹣4=2,所以当⊙O2平移到与⊙O1和AB所在直线都有公共点时,2≤x≤8;(2)当点O2在点O1的左侧时,根据圆的对称性可知,2≤x≤8,故选:D.【点评】本题考查直线与圆的位置关系、平移的性质,求出符合条件的x的最大值和最小值是解决问题的关键.4.如图,AB是⊙O的直径,AB=AC且∠BAC=45°,⊙O交BC于点D,交AC于点E,F在AC上,DF与⊙O相切,OD与BE相交于点H.下列结论错误的是()A.BD=CD B.四边形DHEF为矩形C.=2D.BC=2CE【分析】根据圆的切线、圆周角定理、垂径定理、矩形的判定等矩形逐一判断即可.【解答】解:如图,连接AD,∵AB是⊙O的直径,∴AD⊥BC,∵AB=AC,∴BD=CD,故A正确;∵DF与⊙O相切,∵AB是⊙O的直径,∴∠AEB=90°,∵AO=BO,BD=CD,∴OD∥AC,∴∠EHD=90°,∴四边形DHEF为矩形,故B正确;∵AB是⊙O的直径,∴∠AEB=90°,∵∠BAC=45°,∴∠ABE=45°,∴AE=BE,∵∠BAD=∠CAD,∴=,∵=,∴=2,故C正确;∵∠BAC=45°,AB=AC,∴∠ABC=∠ACB=67.5°,即∠BCE=67.5°,∴∠EBC=22.5°,∴sin∠EBC=sin22.5°=≠.故D错误.故选:D.【点评】本题考查了圆的切线、圆周角定理、垂径定理、矩形的判定,解决本题的关键是掌握圆的切线.5.如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B.点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则下列结论正确的是:①PB=PD;②的长为π;③∠DBE=45°;④当P为中点时,EC=EF;⑤∠DFB=∠CBP.其中正确的个数为()A.5B.4C.3D.2【分析】①连接AC,并延长AC,与BD的延长线交于点H,若PD=PB,得出P为的中点,与实际不符,即可判定正误.②先求出∠BOC,再由弧长公式求得的长度,进而判断正误.③由∠BOC=60°,得△OBC为等边三角形,再根据三线合一性质得∠OBE,再由角的和差关系得∠DBE,便可判断正误.④证明∠EFC=∠ECF=45°,可判断正误;⑤由∠CBF=∠CPB=30°,∠DFB=∠FBP+∠BPF,∠CBP=∠FBP+∠CBF推出∠DFB=∠CBP,可判断正误.【解答】解:①连接AC,并延长AC,与BD的延长线交于点H,如图,∵M,C是半圆上的三等分点,∴∠BAH=30°,∵BD与半圆O相切于点B.∴∠ABD=90°,∴∠H=60°,∵∠ACP=∠ABP,∠ACP=∠DCH,∴∠PDB=∠H+∠DCH=∠ABP+60°,∵∠PBD=90°﹣∠ABP,若∠PDB=∠PBD,则∠ABP+60°=90°﹣∠ABP,∴∠ABP=15°,∴P点为的中点,这与P为上的一动点不完全吻合,∴∠PDB不一定等于∠ABD,∴PB不一定等于PD,故①错误;②∵M,C是半圆上的三等分点,∴∠BOC=×180°=60°,∵直径AB=8,∴OB=OC=4,∴的长度==π,故②正确;③∵∠BOC=60°,OB=OC,∴∠ABC=60°,OB=OC=BC,∵BE⊥OC,∴∠OBE=∠CBE=30°,∵∠ABD=90°,∴∠DBE=60°,故③错误;④∵=,∴∠ABP=15°,∵∠ABD=90°,∠DBE=60°,∴∠PBF=15°,∵∠BPC=30°,∴∠CFE=∠FPb+∠FBP=45°,∵∠FEC=90°,∴∠EFC=∠ECF=45°,∴EC=EF,故④正确,⑤∵∠CBF=∠CPB=30°,∠DFB=∠FBP+∠BPF,∠CBP=∠FBP+∠CBF,∴∠DFB=∠CBP,故⑤正确,故选:C.【点评】本题主要考查了切线的性质,圆周角定理,直角三角形的性质,等边三角形的性质与判定,等腰三角形的性质,相似三角形的性质与判定,关键是熟练掌握这些性质,并能灵活应用.6.如图,AB是⊙O的直径,CD为⊙O的弦,且CD⊥AB于点E,点F为圆上一点,若AE =BF,,OE=1,则BC的长为()A.2B.3C.4D.5【分析】如图,连接OC交AF于J,设BC交AF于T,过点T作TH⊥AB于H.利用全等三角形的性质证明AE=CJ=BF=BH,CT=BH.EH=BH,再利用勾股定理求出EC,BC即可.【解答】解:如图,连接OC交AF于J,设BC交AF于T,过点T作TH⊥AB于H.∵AB⊥CD,∴=,∵=,∴=,∴OC⊥AF,∴∠AJO=∠CEO=90°,∵∠AOJ=∠COE,OA=OC,∴△AJO≌△CEO(AAS),∴OJ=OE,∴AE=CJ,∵AB是直径,∴∠F=∠CJT=90°,∵AE=BF,∴BF=CJ,∵∠CTJ=∠BTF,∴△CTJ≌△BTF(AAS),∴CT=BT,∵TH⊥AB,CD⊥AB,∴TH∥CE,∴EH=BH,∵=,∴∠TBF=∠TBH,∵∠F=∠THB=90°,BT=BT,∴△BTF≌△BTH(AAS),∴BF=BH,∵AE=BF,∴AE=BH,∵OA=OB,∴OE=OH=1,∴EH=BH=2,∴AE=BH=2,∴AB=6,OC=OB=3,∴EC===2,∴BC===2,故选:A.【点评】本题考查全等三角形的判定和性质,垂径定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.7.如图,是同一种蔬菜的两种栽植方法.甲:A、B、C、D四珠顺次连接成为一个菱形,且AB=BD.乙:A'、B'、C'、D'四株连接成一个正方形.其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距;设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积.设株距都为a,其它客观因素都相同.则对于下列说法:①甲的行距比乙的小;②甲的行距为;③甲、乙两种栽植方式,空隙地面积面积相同;④甲的空隙地面积比乙的空隙地面积少.其中正确的个数为()A.1B.2C.3D.4【分析】根据题意求出甲乙的行距,阴影部分的面积即可判断.【解答】解:∵甲的株距为a,行距为a,乙的行距为a,∴甲的行距比乙的小,故①②正确,∵甲阴影部分的面积=2×a2﹣π•()2=a2﹣,乙的阴影部分的面积=a2﹣π•()2=a2﹣,∴甲的空隙地面积比乙的空隙地面积少,故③错误,④正确.故选:C.【点评】本题考查圆与圆的位置关系,等边三角形的性质,正方形的性质,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考创新题型.8.如图,在平面直角坐标系中,将边长为1的正六边形OABCDE绕点O顺时针旋转i个45°,得到正六边形OA i B i∁i D i E i,则正六边形OA i B i∁i D i E i(i=2020)的顶点∁i的坐标是()A.(1,﹣)B.(1,)C.(1,﹣2)D.(2,1)【分析】由题意旋转8次应该循环,因为2020÷8=252…4,所以∁i的坐标与C4的坐标相同.【解答】解:由题意旋转8次应该循环,∵2020÷8=252…4,∴∁i的坐标与C4的坐标相同,∵C(﹣1,),点C与C4关于原点对称,∴C4(1,﹣),∴顶点∁i的坐标是(1,﹣),故选:A.【点评】本题考查正多边形与圆,坐标与图形变化﹣性质等知识,解题的关键是学会探究规律的方法,属于中考常考题型.9.如图,四边形ABCD内接于⊙O,AB=CB,∠BAC=30°,BD=,则AD+CD的值为()A.3B.2C.+1D.不能确定【分析】如图,过点B作BE⊥AD于E,BF⊥DC交DC的延长线于F.利用全等三角形的性质证明DE=DF,AE=CF,推出DA+DC=2DF,求出DF即可解决问题.【解答】解:如图,过点B作BE⊥AD于E,BF⊥DC交DC的延长线于F.∵AB=BC,∴=,∴∠BDE=∠BDF,∵∠DEB=∠DFB=90°,DB=DB,∴△BDE≌△BDF(AAS),∴BE=BF,DE=DF,∵∠AEB=∠F=90°,BA=BC,BE=BF,∴Rt△BEA≌Rt△BFC(HL),∴AE=CF,∴AD+DC=DE+AE+DF﹣CF=2DF,∵∠BDF=∠BAC=30°,BD=,∴BF=BD=,∴DF===,∴DA+DC=3,故选:A.【点评】本题考查全等三角形的判定和性质,圆周角定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.10.如图,⊙O的半径是5,点A是圆周上一定点,点B在⊙O上运动,且∠ABM=30°,AC⊥BM,垂足为点C,连接OC,则OC的最小值是()A.B.C.D.﹣【分析】如图,设BM交⊙O于T,连接OT,OA,过点O作OH⊥AT于H,连接CH.解直角三角形求出CH,OH,根据OC≥OH﹣CH求解即可.【解答】解:如图,设BM交⊙O于T,连接OT,OA,过点O作OH⊥AT于H,连接CH.∵∠B=30°,∴∠TOA=60°,∵OT=OA,∴△OTA是等边三角形,∴OT=OA=AT=5,∵OH⊥AT,∴TH=AH=,OH===,∵AC⊥BM,∴∠ACT=90°,∴CH=,∵OC≥OH﹣CH=﹣,∴OC的最小值为=﹣.故选:D.【点评】本题考查圆周角定理,等边三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造特殊三角形解决问题,属于中考选择题中的压轴题.11.如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为()A.3B.4C.5D.6【分析】设⊙O与AC相切于D,与BC相切于H,平移后的⊙O′与AB相切于F,与BC相切于E,连接OH,O′D,则点O在O′D上,连接O′F,EO′并延长交AB于G,根据正方形和矩形的性质得到OD=OH=O′E=O′F=CD=CH=1,OO′=HE,根据相似三角形的判定和性质定理即可得到结论.【解答】解:∵Rt△ACB中,∠C=90°,AC=6,BC=8,∴AB=10,设⊙O与AC相切于D,与BC相切于H,平移后的⊙O′与AB相切于F,与BC相切于E,连接OH,O′D,则点O在O′D上,连接O′F,EO′并延长交AB于G,∴四边形CDOH是正方形,四边形OHEO′是矩形,∴OD=OH=O′E=O′F=CD=CH=1,OO′=HE,∴EG⊥BC,∵∠C=90°,∴EG∥AC,∴∠FGE=∠A,∵∠GFO′=∠C=90°,∴△O′FG∽△BCA,∴,∴=,∴O′G=,∴EG=,∵GE∥AC,∴△BGE∽△BAC,∴=,∴=,∴BE=3,∴OO′=HE=BC﹣CH﹣BE=8﹣1﹣3=4,∴⊙O平移的距离为4,故选:B.【点评】本题考查了切线的性质,相似三角形的判定和性质,勾股定理,正方形的判定和性质,矩形的判定和性质,正确的作出辅助线是解题的关键.12.在⊙O中内接四边形ABCD,其中A,C为定点,AC=8,B在⊙O上运动,BD⊥AC,过O作AD的垂线,若⊙O的直径为10,则OE的最大值接近于()A.B.C.4D.5【分析】如图,当点B与A重合时,连接CD.证明OE=AC,此时OE的值最大.【解答】解:如图,当点B与A重合时,连接CD.∵BD⊥AC,∴∠DAC=90°,∴CD是直径,∵OE⊥AD,∴AE=ED,∵OC=OD,∴OE=AC=4,此时OE的值最大,最大值为4∴OE的最大值为4,故选:C.【点评】本题考查垂径定理,三角形的中位线定理等知识,解题的关键是学会利用特殊位置解决问题,属于中考常考题型.13.如图,已知⊙O的半径为10,A、B是⊙O上的两点,∠AOB=90°,C是射线OB上一个动点,连接AC交⊙O于点D,过点D作DE⊥OD交OB的延长线于点E.当∠A 从30°增大到60°时,弦AD在圆内扫过的面积是()A.B.C.D.【分析】过点D作AO的垂线,交AO的延长线于F,求两个弓形的面积之差即可;【解答】解:过点D作AO的垂线,交AO的延长线于F.当∠A=30°时,∠DOF=60°,DF=OD•sin60°=10×=5,S弓形ABD=﹣×10×5=π﹣25,当∠A=60°时,过点D'作D'F⊥OA于F',连接OD',∠D'OF'=60°,D'F'=5,S弓形AD′=﹣×10×5=π﹣25,∴S=π﹣25﹣(π﹣25)=π.故选:B.【点评】本题考查圆周角定理,圆心角,弧,弦之间的关系,弓形的面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.14.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE =1,EF=,则BF的长为()A.B.1C.D.【分析】如图,连接AC,BC,OC,过点B作BH⊥CF交CF的延长线于H,设OC交AD于J.利用全等三角形的性质证明CJ=BF,OJ=OF,设BF=CJ=x,OJ=OF=y,构建方程组解决问题即可.【解答】解:如图,连接AC,BC,OC,过点B作BH⊥CF交CF的延长线于H,设OC 交AD于J.∵=,∴AC=BC,OC⊥AB,∵AB是直径,∴ACB=90°,∴∠ACJ=∠CBF=45°,∵CF⊥AD,∴∠ACF+∠CAJ=90°,∠ACF+∠BCF=90°,∴∠CAJ=∠BCF,∴△CAJ≌△BCF(ASA),∴CJ=BF,AJ=CF=1+=,∵OC=OB,∴OJ=OF,设BF=CJ=x.OJ=OF=y,∵∠AEC=∠H=90°,∠CAE=∠BCH,CA=CB,∴△ACE≌△CBH(AAS),∴EC=BH=1,∵∠ECJ=∠FCO,∠CEJ=∠COF=90°,∴△CEJ∽△COF,∴==,∴==,∴EJ=,∵BF=CJ,∠H=∠CEJ,∠CJE=∠BFH,∴△BHF≌△CEJ(AAS),∴FH=EJ=,∵AE∥BH,∴=,∴=,整理得,10x2+7xy﹣6y2=0,解得x=y或x=﹣y(舍弃),∴y=2x,∴=,解得x=或﹣(舍弃).∴BF=,故选:A.【点评】本题考查垂径定理,圆周角定理,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,学会利用参数构建方程组解决问题,属于中考选择题中的压轴题.15.已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为()A.1+B.1+2C.2+D.2﹣1【分析】如图,将线段OA绕点O顺时针旋转120°得到线段OT,连接AT,GT,OP.则AO=OT=1,AT=,利用相似三角形的性质求出GT,再根据三角形的三边关系解决问题即可,【解答】解:如图,将线段OA绕点O顺时针旋转120°得到线段OT,连接AT,GT,OP.则AO=OT=1,AT=,∵△AOT,△APG都是顶角为120°的等腰三角形,∴∠OAT=∠P AG=30°,∴∠OAP=∠TAG,==∴=,∴△OAP∽△TAG,∴==,∵OP=2,∴TG=2,∵OG≤OT+GT,∴OG≤1+2,∴OG的最大值为1+2,故选:B.【点评】本题考查圆周角定理,相似三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考选择题中的压轴题.16.如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD=,BC=1,则⊙O 的半径为()A.B.C.D.【分析】如图延长DO交⊙O于E,作EF⊥CB交CB的延长线于F,连接BE、EC.只要证明△EFB是等腰直角三角形,即可推出EF=BF=1,再利用勾股定理求出EC即可解决问题;【解答】解:如图延长DO交⊙O于E,作EF⊥CB交CB的延长线于F,连接BE、EC.∵∠AOD=∠BOE,∴=,∴AD=BE=,∵∠DOC=∠COE=90°,OC=OB=OE,∴∠OCB=∠OBC,∠OBE=∠OEB,∴∠CBE=(360°﹣90°)=135°,∴∠EBF=45°,∴△EBF是等腰直角三角形,∴EF=BF=1,在Rt△ECF中,EC===,∵△OCE是等腰直角三角形,∴OC==.故选:C.【点评】本题考查圆周角定理、勾股定理、等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考选择题中的压轴题.17.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是()A.B.C.D.【分析】连接OC、OA、BD,作OH⊥AC于H.首先求出AC的长,利用三角形的中位线定理即可解决问题;【解答】解:连接OC、OA、BD,作OH⊥AC于H.∵∠AOC=2∠ABC=120°,∵OA=OC,OH⊥AC,∴∠COH=∠AOH=60°,CH=AH,∴CH=AH=OC•sin60°=,∴AC=2,∵CN=DN,DM=AM,∴MN=AC=,∵CP=PB,CN=DN,∴PN=BD,当BD是直径时,PN的值最大,最大值为2,∴PM+MN的最大值为2+.故选:D.【点评】本题考查圆周角定理、三角形的中位线的定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.18.如图,AB是半圆O的直径,点D在半圆O上,AB=2,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是()A.5B.6C.7D.8【分析】如图,取AD的中点M,连接BD,HM,BM.由题意点H在以M为圆心,MD 为半径的⊙M上,推出当M、H、B共线时,BH的值最小;【解答】解:如图,取AD的中点M,连接BD,HM,BM.∵DH⊥AC,∴∠AHD=90°,∴点H在以M为圆心,MD为半径的⊙M上,∴当M、H、B共线时,BH的值最小,∵AB是直径,∴∠ADB=90°,∴BD==12,BM===13,∴BH的最小值为BM﹣MH=13﹣5=8.故选:D.【点评】本题考查点与圆的位置关系、勾股定理、圆周角定理等知识,解题的关键是学会添加常用辅助线,利用辅助线圆解决问题,属于中考选择题中的压轴题.二.填空题(共10小题)19.在△ABC中,AB=AC=10,BC=12,M,N是BC边上两个动点,若AB,AC边上分别存在点P,Q使得∠MPN=∠MQN=60°,则线段MN的最小值为.【分析】如图1,在BC边上取点M、N,以MN为边作等边三角形△MNG,并作△MNG 外接圆⊙O,则所对圆周角=∠MGN=60°,⊙O交AB、AC于P、Q时,易知∠MPN =∠MQN=60°,则⊙O与△ABC有交点,且半径最小时MN可取得最小值,推出⊙O 与AB、AC相切时MN最小,如图2.【解答】解:如图1,在BC边上取点M、N,以MN为边作等边三角形△MNG,并作△MNG外接圆⊙O,则所对圆周角=∠MGN=60°,⊙O交AB、AC于P、Q时,易知∠MPN=∠MQN=60°,则⊙O与△ABC有交点,且半径最小时MN可取得最小值,∴⊙O与AB、AC相切时MN最小,如图2,此时OP⊥AB,OP=r,OQ⊥AC,OQ=r,∴圆心O在∠BAC角平分线上,即在△ABC底边上的高AD上,∴BD=CD=6,AD=8,连接MO,NO,PO,圆心角∠MON=2∠MPN=120°,MO=NO=OP=OQ,∴∠MOD=60°,设半径为r,则,,∵∠ADB=∠APO=90°,∠BAD=∠BAD,∴△APO∽△ADB,∴,即,解得,则.故答案为:.【点评】本题考查三角形的外接圆,等腰三角形的性质,圆周角定理等知识,解题的关键是学会用转化的思想思考问题,属于中考填空题中的压轴题.20.如图,正六边形ABCDEF中,G,H分别是边AF和DE上的点,GF=AB=2,∠GCH=60°,则线段EH长.【分析】作GP∥AB,交BC于点P,AN∥BC交GP于点N,可得四边形ABPN是平行四边形,根据六边形ABCDEF是正六边形,可得△ANG是等边三角形,然后证明△CPG ∽△HDC,对应边成比例即可解决问题.【解答】解:如图,作GP∥AB,交BC于点P,AN∥BC交GP于点N,∴四边形ABPN是平行四边形,∴PN=AB=6,∵六边形ABCDEF是正六边形,∴∠BAF=∠B=∠BCD=∠D=120°,AF=AB=BC=CD=6,∴∠BAN=∠NAG=∠AGN=60°,∠CPG=∠D=120°,∴△ANG是等边三角形,∴NG=AN=AG=6﹣2=4,∴PG=NG+PN=4+6=10,∵∠PCG+∠DCH=∠BCD﹣∠GCH=120°﹣60°=60°,∠DHC+∠DCH=180°﹣∠D=180°﹣120°=60°,∴∠PCG=∠DHC,∵∠CPG=∠D,∴△CPG∽△HDC,∴=,∵PC=BC﹣BP=6﹣4=2,PG=10,CD=6,∴EH=ED﹣DH=6﹣=.故答案为:.【点评】本题考查了正多边形和圆,解决本题的关键是综合运用正多边形和圆,平行四边形的判定与性质,等边三角形的判定与性质,相似三角形的判定与性质.21.如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为弧AC上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为4,则PN+MN的长度的最大值是4+2.【分析】连接OC、OA、BD,作OH⊥AC于H.首先求出AC的长,利用三角形的中位线定理即可解决问题.【解答】解:连接OC、OA、BD,作OH⊥AC于H.∵∠AOC=2∠ABC=120°,∵OA=OC,OH⊥AC,∴∠COH=∠AOH=60°,CH=AH,∴CH=AH=OC•sin60°=2,∴AC=4,∵CN=DN,DM=AM,∴MN=AC=2,∵CP=PB,CN=DN,当BD是直径时,PN的值最大,最大值为4,∴PM+MN的最大值为4+2.故答案为:4+2.【点评】本题考查圆周角定理、三角形的中位线的定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.22.如图,在平面直角坐标系xOy中,一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,点P在线段AB上,⊙P与x轴交于A、C两点,当⊙P与y轴相切时,AC的长度是﹣1.【分析】根据一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,求出OA和OB的长,设⊙P与y轴相切于点D,连接PD,根据平行线分线段成比例定理,设PD=PC=x,则BD=2x,作PE⊥OA于点E,可得四边形OEPD是矩形,PD=OE=x,PE =OD=x,4﹣2x,AE=CE=OA﹣OE=2﹣x,根据勾股定理可得x的值,再根据垂径定理可得AC的长.【解答】解:∵一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,∴A(2,0),B(0,4),∴OA=2,OB=4,如图,设⊙P与y轴相切于点D,连接PD,∴PD⊥OB,∵OA⊥OB,∴PD∥OA,∴==,设PD=PC=x,则BD=2x,∴OD=OB﹣BD=4﹣2x,作PE⊥OA于点E,∴四边形OEPD是矩形,∴PD=OE=x,PE=OD=4﹣2x,∴AE=CE=OA﹣OE=2﹣x,∴PC2=PE2+CE2,∴x2=(4﹣2x)2+(2﹣x)2,解得x=,∵>2,不符合题意舍去,∴x=,∵PE⊥AC,根据垂径定理,得AC=2AE=2(2﹣x)=4﹣(5﹣)=﹣1.故答案为:﹣1.【点评】本题考查了切线的判定与性质、一次函数图象上点的坐标特征、垂径定理、平行线分线段成比例定理、勾股定理,解决本题的关键是综合运用以上知识.23.如图,在平面直角坐标系中,已知C(6,8),以点C为圆心的圆与y轴相切.点A、B 在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为32.【分析】连接OC并延长,交⊙C上一点P,以O为圆心,以OP为半径作⊙O,交x轴于A、B,此时AB的长度最大,根据勾股定理和题意求得OP=16,则AB的最大长度为32.【解答】解:连接OC并延长,交⊙C上一点P,以O为圆心,以OP为半径作⊙O,交x轴于A、B,此时AB的长度最大,∵C(6,8),∴OC==10,∵以点C为圆心的圆与y轴相切.∴⊙C的半径为6,∴OP=OA=OB=16,∵AB是直径,∴∠APB=90°,∴AB长度的最大值为32,故答案为32.【点评】本题考查了切线的性质,坐标和图形的性质,圆周角定理,找到OP的最大值是解题的关键.24.如图,平行四边形ABCD中,AC⊥BC,AB=5,BC=3,点P在边AB上运动,以P 为圆心,P A为半径作⊙P,若⊙P与平行四边形ABCD的边有四个公共点,则AP的长度的取值范围是<AP<或AP=.【分析】求出⊙P与BC,CD相切时AP的长以及⊙P经过A,B,C三点时AP的长即可判断;【解答】解:如图1中,当⊙P与BC相切时,设切点为E,连接PE.在Rt△ABC中,由勾股定理得:AC==4,设AP=x,则BP=5﹣x,PE=x,∵⊙P与边BC相切于点E,∴PE⊥BC,∵AB⊥AC,∴AC⊥PE,∴AC∥PF,∴=,∴=,∴x=,AP=;如图2中,当⊙P与CD相切时,设切点为E,连接PE..S平行四边形ABCD=2××3×4=5PE,PE=,观察图象可知:<AP<时⊙P与平行四边形ABCD的边的公共点的个数为4,②⊙P过点A、B、C三点.,如图4,⊙P与平行四边形ABCD的边的公共点的个数为4,此时AP=,综上所述,AP的值的取值范围是:<AP<或AP=.故答案为:<AP<或AP=.【点评】本题考查平行四边形的性质,勾股定理,直线与圆的位置关系等知识,解题的关键是学会利用特殊位置解决问题,属于中考常考题型.25.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM 的最小值为5.【分析】如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.证明∠ACT=45°,求出AT即可解决问题.【解答】解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.。
数学中考一轮复习学案 第24节 圆的有关概念与性质(含解析)

第四章图形的性质第24节圆的有关概念与性质■知识点一:圆的有关概念(1)圆:平面上到定点的距离等于定长的所有点组成的图形叫做圆,其中定点为圆心,定长为半径.(2)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧称为优弧,小于半圆的弧称为劣弧.(3)弦:连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径.(4)相关概念:同心圆、弓形、等圆、等弧.(5)圆心角:顶点在圆心的角叫做圆心角.(6)圆周角:顶点在圆上,并且两边和圆相交的角是圆周角.(7)确定圆的条件:过已知一点可作无数个圆,过已知两点可作无数个圆,过不在同一条直线上的三点可作一个圆.(8)圆的对称性:圆是轴对称图形,其对称轴是直径所在的直线;圆是中对称图形,对称中心为圆心,并且圆具有旋转不变性.■知识点二:垂径定理及推论:①垂直于弦的直径平分弦,并且平分弦所对的两条弧.②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,③弦的垂直平分线经过圆心,并且平分弦所对的两条弧.④平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.⑤圆的两条平行弦所夹的弧相等.■知识点三:圆心角、弧、弦的关系(1)定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.说明:同一条弦对应两条弧,其中一条是优弧,一条是劣弧,而在本定理和推论中的“弧”是指同为优弧或劣弧.(3)正确理解和使用圆心角、弧、弦三者的关系三者关系可理解为:在同圆或等圆中,①圆心角相等,②所对的弧相等,③所对的弦相等,三项“知一推二”,一项相等,其余二项皆相等.这源于圆的旋转不变性,即:圆绕其圆心旋转任意角度,所得图形与原图形完全重合.(4)在具体应用上述定理解决问题时,可根据需要,选择其有关部分.■知识点四:圆周角定理及推论①圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等.推论2:直径所对的网周角是直角;90°的圆周角所对的弦是直径.推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.②圆内接四边形的任意一组对角互补.■考点1.圆的有关概念◇典例:(2017年黑龙江大庆)如图,点M,N在半圆的直径AB上,点P,Q在上,四边形MNPQ 为正方形.若半圆的半径为,则正方形的边长为.【考点】正方形的性质;勾股定理;圆的认识.【分析】连接OP,设正方形的边长为a,则ON=,PN=a,再由勾股定理求出a的值即可.解:连接OP,设正方形的边长为a,则ON=,PN=a,在Rt△OPN中,ON2+PN2=OP2,即()2+a2=()2,解得a=2.故答案为:2.【点评】本题考查的是正方形的性质,勾股定理;圆的认识,根据题意作出辅助线,构造出直角三角形是解答此题的关键.◆变式训练(2017•宁夏)如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 __________■考点2.垂径定理及其推论◇典例:(2018年黑龙江省龙东、七台河、佳木斯、鸡西、伊春、鹤岗、双鸭山)如图,AB为⊙O 的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为.【考点】垂径定理,勾股定理【分析】连接OC,由垂径定理知,点E是CD的中点,AE=CD,在直角△OCE中,利用勾股定理即可得到关于半径的方程,求得圆半径即可.解:连接OC,∵AB为⊙O的直径,AB⊥CD,∴CE=DE=CD=×6=3,设⊙O的半径为xcm,则OC=xcm,OE=OB﹣BE=x﹣1,在Rt△OCE中,OC2=OE2+CE2,∴x2=32+(x﹣1)2,解得:x=5,∴⊙O的半径为5,故答案为:5.【点评】本题利用了垂径定理和勾股定理求解,熟练掌握并应用定理是解题的关键.◆变式训练1.(2018年山东省烟台)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C 三点的圆的圆心坐标为.2.(2018年浙江省绍兴市)如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了步(假设1步为0.5米,结果保留整数).(参考数据:≈1.732,π取3.142)■考点3. 圆心角、弧、弦的关系◇典例(2017•牡丹江)如图,在⊙O中,=,CD⊥OA于D,CE⊥OB于E,求证:AD=BE.【考点】圆心角、弧、弦的关系;垂径定理.【分析】连接OC,先根据=得出∠AOC=∠BOC,再由已知条件根据AAS定理得出△COD ≌△COE,由此可得出结论.证明:连接OC,∵=,∴∠AOC=∠BOC.∵CD⊥OA于D,CE⊥OB于E,∴∠CDO=∠CEO=90°在△COD与△COE中,∵,∴△COD≌△COE(AAS),∴OD=OE,∵AO=BO,∴AD=BE.【点评】本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.◆变式训练(2017•宜昌)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A.AB=AD B.BC=CD C. D.∠BCA=∠DCA■考点4. 圆周角定理及其推论◇典例:1.(2018 年广西梧州市)如图,已知在⊙O 中,半径 OA=2,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO=__________度.【考点】圆周角定理,勾股定理的逆定理,等腰三角形的性质【分析】根据勾股定理的逆定理可以判断△AOB 的形状,由圆周角定理可以求得∠BOD 的度数,再根据三角形的外角和不相邻的内角的关系,即可求得∠AOC的度数.解:∵OA=2,OB=2,AB=2,∴OA 2+OB2=AB2,OA=OB,∴△AOB 是等腰直角三角形,∠AOB=90°,∴∠OBA=45°,∵∠BAD=18°,∴∠BOD=36°,∴∠ACO=∠OBA+∠BOD=45°+36°=81°,故答案为:81.【点评】本题考查圆周角定理、勾股定理的逆定理、等腰三角形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.◆变式训练1.(2018年四川省南充)如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B 的度数是()A.58° B.60° C.64° D.68°2.(2017•锦州)如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=80°,∠F=25°,则∠E的度数为()A.55°B.50°C.45°D.40°一、选择题1.(2018年广西柳州市)如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为()A.84°B.60°C.36°D.24°2.(2018年内蒙古赤峰市)如图,AB是⊙O的直线,C是⊙O上一点(A.B除外),∠AOD=130°,则∠C的度数是()A.50°B.60°C.25°D.30°3.(2018年浙江省衢州市)如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是()A.75°B.70°C.65°D.35°4.(2018年湖北省襄阳)如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为()A.4 B.2C. D.25.(2018年四川省甘孜州)如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是()A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD二、填空题6.(2018年广东省)同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是.7.(2018年青海省)如图,A.B、C是错误!未找到引用源。
2024年中考数学一轮复习考点精讲课件—圆的相关概念及性质

对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角.
考点二 圆的性质
题型01 由垂径定理及推论判断正误
【例1】(2023·浙江·模拟预测)如图,是⊙ 是直径,是弦且不是直径, ⊥ ,则下列结论不一定正
【详解】解:如图,连接,
∵线段是⊙ 的直径, ⊥ 于点E, = 16,
1
1
∴ = = 2 = 2 × 16 = 8,
∴在Rt △ 中,可有 = 2 + 2 = 62 + 82 = 10,
∴⊙ 半径是10.
故选:D.
考点二 圆的性质
题型03 根据垂径定理与全等三角形综合求解
直径)(4)平分弦所对的优弧(5)平分弦所对的劣弧,若已知五个条件中的两个,那么可推出其中三个,简
称“知二得三”,解题过程中应灵活运用该定理.
常见辅助线做法(考点):1)过圆心,作垂线,连半径,造Rt △,用勾股,求长度;
2)有弦中点,连中点和圆心,得垂直平分.
考点二 圆的性质
3. 弧、弦、圆心角的关系
即的最小值是8.故选:C.
考点二 圆的性质
1. 圆的对称性
内容
补充
圆的轴对称 经过圆心任意画一条直线,并沿此直线圆对折,直线两旁的部分能够 ①圆的旋转不变性是其他中心对称图形所
性
完全重合,因此圆是轴对称图形,每一条直径所在的直线都是它的 没有的性质.
对称轴,圆有无数条对称轴.
圆的中心对 将圆绕圆心旋转180°能与自身重合,因此它是中心对称图形,它
①圆心,它确定圆的位置.
②半径,它确定圆的大小.
的点组成的图形.
2024成都中考数学第一轮专题复习 圆的有关概念及性质 知识精练(含答案)

2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练基础题1. (2023江西)如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为()A. 3B. 4C. 5D. 6第1题图2. (2023广东省卷)如图,AB是⊙O的直径,∠BAC=50°,则∠D=()第2题图A. 20°B. 40°C. 50°D. 80°3. (2023广元)如图,AB是⊙O的直径,点C,D在⊙O上,连接CD,OD,A C.若∠BOD=124°,则∠ACD的度数是()A. 56°B. 33°C. 28°D. 23°第3题图4. (2023山西)如图,四边形ABCD内接于⊙O,AC,BD为对角线,BD经过圆心O.若∠BAC =40°,则∠DBC的度数为()第4题图A. 40°B. 50°C. 60°D. 70°5. (2023安徽)如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠BAE-∠COD=()A. 60°B. 54°C. 48°D. 36°第5题图6. (2023赤峰)如图,圆内接四边形ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC =2∠COD,则∠CBD的度数是()第6题图A. 25°B. 30°C. 35°D. 40°7. [新考法—数学文化](2023岳阳)我国古代数学名著《九章算术》中有这样一道题:“今有圆材,径二尺五寸.欲为方版,令厚七寸,问广几何?”结合下图,其大意是:今有圆形材质,直径BD为25寸,要做成方形板材,使其厚度CD达到7寸,则BC的长是() A. 674寸 B. 25寸C. 24寸D. 7寸第7题图8. (2023杭州)如图,在⊙O中,半径OA,OB互相垂直,点C在劣弧AB上.若∠ABC=19°,则∠BAC=()第8题图A. 23°B. 24°C. 25°D. 26°9. (2023广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为37 m,拱高约为7 m,则赵州桥主桥拱半径R约为()第9题图A. 20 mB. 28 mC. 35 mD. 40 m10. (2023凉山州)如图,在⊙O中,OA⊥BC,∠ADB=30°,BC=23,则OC=()A. 1B. 2C. 2 3D. 4第10题图11. 如图,点A,B,D在⊙O上,CD垂直平分AB于点C.现测得AB=CD=16,则圆形宣传图标的半径为()第11题图A. 12B. 10C. 8D. 612. 如图,在平面直角坐标系中,⊙O的半径为4,弦AB的长为3,过O作OC⊥AB于点C,则OC的长度是________;⊙O内一点D的坐标为(-2,1),当弦AB绕O点顺时针旋转时,点D到AB的距离的最小值是________.第12题图13. (2023武汉)如图,OA,OB,OC都是⊙O的半径,∠ACB=2∠BA C.(1)求证:∠AOB=2∠BOC;(2)若AB=4,BC=5,求⊙O的半径.第13题图拔高题14. (2023吉林省卷)如图,AB,AC是⊙O的弦,OB,OC是⊙O的半径,点P为OB上任意一点(点P不与点B重合),连接CP.若∠BAC=70°,则∠BPC的度数可能是()A. 70°B. 105°C. 125°D. 155°第14题图15. 如图,正方形ABCD 内接于⊙O ,点E 为弧AB 的中点,连接DE 与AB 交于点F .若AB=1,记△ADF 的面积为S 1,△AEF 的面积为S 2,则S 1S 2的值为________.第15题图16. 如图,以原点O 为圆心的圆交x 轴于A ,B 两点,交y 轴的正半轴于点C ,且点A 的坐标为(-2,0),D 为第一象限内⊙O 上的一点,若∠OCD =75°,则AD 的长为________.第16题图参考答案与解析1. D 【解析】本题考查了确定圆的条件及圆的有关定义及性质.∵过不在同一直线上的三个点一定能作一个圆,∴要经过题中所给的3个点画圆,除选定直线l 外的点P 外,再在直线l 上的A ,B ,C ,D 四个点中任选其中2个即可画圆.∵从A ,B ,C ,D 四个点中任选其中2个点的方法可以是AB ,AC ,AD ,BC ,BD ,CD ,共6种,∴最多可以画出圆的个数为6.2. B 【解析】∵AB 是⊙O 的直径,∠BAC =50°,∴∠ACB =90°,∠B =180°-50°-90°=40°.∵AC =AC ,∴∠D =∠B =40°.3. C 【解析】∵∠BOD =124°,∴∠AOD =180°-124°=56°,∴∠ACD =12∠AOD =28°. 4. B 【解析】∵BD 经过圆心O ,∴∠BCD =90°.∵∠BDC =∠BAC =40°,∴∠DBC =90°-∠BDC =50°.5. D 【解析】∵五边形ABCDE 是正五边形,∴∠BAE =(5-2)×180°5=108°,∠COD =360°5=72°,∴∠BAE -∠COD =108°-72°=36°. 6. A 【解析】∵∠BCD =105°,∴∠BAD =180°-105°=75°,∴∠BOD =150°.∵∠BOC=2∠COD ,∴∠COD =13 ∠BOD =50°,∴∠CBD =12∠COD =25°. 7. C 【解析】∵BD 是圆的直径,∴∠BCD =90°.∵BD =25,CD =7,∴在Rt △BCD 中,由勾股定理得,BC =252-72 =24(寸).8. D 【解析】如解图,连接OC ,∵∠ABC =19°,∴∠AOC =2∠ABC =38°.∵半径OA ,OB 互相垂直,∴∠AOB =90°,∴∠BOC =90°-38°=52°,∴∠BAC =12∠BOC =26°.第8题解图9. B 【解析】如解图,在Rt △OAB 中,由勾股定理,得AO 2+AB 2=OB 2,即(R -7)2+(372)2=R 2,解得R ≈28(m).第9题解图10. B 【解析】如解图,连接OB ,设OA 交BC 于点E ,∵∠ADB =30°,∴∠AOB =60°.∵OA ⊥BC ,BC =23 ,∴BE =12 BC =3 .在Rt △BOE 中,sin ∠AOB =BE OB,∴sin 60°=3OB =32,∴OB =2,∴OC =2.第10题解图11. B 【解析】如解图,连接OA ,设圆形宣传图标的半径为R ,∵CD 垂直平分AB ,AB=CD =16,∴CD 过点O ,AC =BC =12 AB =12×16=8,∠DCA =90°.∵AO =OD =R ,∴在Rt △AOC 中,由勾股定理,得OC 2+AC 2=OA 2,即(16-R )2+82=R 2,解得R =10,即圆形宣传图标的半径为10.第11题解图 12. 552 ;552 -5 【解析】如解图,连接OB ,∵OC ⊥AB ,∴BC =12 AB =32.由勾股定理,得OC =OB 2-BC 2 =552.当OD ⊥AB 时,点D 到AB 的距离最小,由勾股定理,得OD =22+12 =5 ,∴点D 到AB 的距离的最小值为552 -5 .第12题解图13. (1)证明:由圆周角定理,得∠ACB =12 ∠AOB ,∠BAC =12∠BOC . ∵∠ACB =2∠BAC ,∴∠AOB =2∠BOC ;(2)解:如解图,过点O 作半径OD ⊥AB 于点E ,连接BD .则∠DOB =12∠AOB ,AE =BE . ∵∠AOB =2∠BOC ,∴∠DOB =∠BOC .∴BD =BC .∵AB =4,BC =5 ,∴BE =2,DB =5 .在Rt △BDE 中,∵∠DEB =90°,∴DE =BD 2-BE 2 =1.在Rt △BOE 中,∵∠OEB =90°,∴OB 2=(OB -1)2+22,∴OB =52, 即⊙O 的半径是 52.第13题解图14. D 【解析】如解图,连接BC ,∵∠BAC =70°,∴∠BOC =2∠BAC =140°.∵OB =OC ,∴∠OBC =∠OCB =180°-140°2=20°.∵点P 为OB 上任意一点(点P 不与点B 重合),∴0°<∠OCP <20°.∵∠BPC =∠BOC +∠OCP =140°+∠OCP ,∴140°<∠BPC <160°,故选D.第14题解图15. 2(2 +1) 【解析】如解图,连接OE 交AB 于点G ,连接AC .根据垂径定理的推论,得OE ⊥AB ,AG =BG .由题意可得,AC 为⊙O 的直径,AC =2 ,则圆的半径是22.根据正方形的性质,得∠OAF =45°,∴OG =12 ,EG =2-12.∵OE ∥AD ,∴△ADF ∽△GEF ,∴FE FD =EG DA =2-12 .∵△ADF 与△AEF 等高,∴S 1S 2 =S △ADF S △AEF=DF EF =2(2 +1).第15题解图16. 23 【解析】如解图,连接OD ,BD .∵A (-2,0),∴OA =OB =2,∴AB =4.∵OC =OD ,∴∠OCD =∠ODC =75°,∴∠DOC =180°-2×75°=30°,∴∠DOB =90°-30°=60°,∴∠DAB =12∠DOB =30°.∵AB 是⊙O 的直径,∴∠ADB =90°,∴AD =AB ·cos 30°=23 .第16题解图。
2015连线中考数学一轮复习系列专题19_圆的基本性质

(3)有3对弧相等: , , .
(4)添加辅助线的方法:连接半径或作垂直于弦的直径,是两种重要的添线方法.
知识点五.圆周角定理
1.定义:
顶点在圆上,并且两边都与圆相交的角叫圆周角.
基础知识
知识点一、圆的有关概念
1.圆的定义①(动态定义)在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点叫做圆心,线段OA叫做半径.以点O为圆心的圆记做“⊙O”.
②(静态定义)圆是到定点的距离等于定长的点的集合.即:圆上各点到圆心的距离都等于定长(半径),反之到圆心距离等于半径的点一定在圆上;
11(邵阳)如图(八)所示,某窗户是由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出 所在圆O的半径r.
12. (武汉)如图,AB是⊙O的直径,C,P是上两点,AB=13,AC=5.
(1)如图(1),若点P是的中点,求PA的长;
(2)如图(2),若点P是的中点,求PA的长;
例7.如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
巩固练习
1.(湖州)如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是()
④等弧:能够完全重合的弧叫等弧.
知识点三、弧、弦、圆心角之间的关系
1.圆的旋转不变性
把圆绕着圆心旋转任意一个角度,都与原来的图形重合,我们把这种性质称为圆的旋转不变性.圆是中心对称图形,圆心是它的对称中心.
2014年中考数学一轮复习讲义:圆的有关性质圆与圆的位置关系

2014年中考数学一轮复习讲义:圆的有关性质圆与圆的位置关系【考纲要求】1.探索并了解圆与圆的位置关系,2. 结合相关图形性质的探索和证明,进一步培养合情推理能力,发展逻辑思维能力和推理论证的表达能力.【命题趋势】圆与圆位置关系的判定一般借助两圆公共点的个数或利用两圆半径与圆心距的关系来判定,通常出现在选择题、填空题中.【知识梳理】一、概念:①两圆外离:两个圆无公共点,并且一个圆上的点都在另一个圆的外部;②两圆外切:两个圆有一个公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的外部;③两圆相交:两个圆有两个公共点;④两圆内切:两个圆有一个公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部;⑤两圆内含:两个圆无公共点,并且一个圆上的点都在另一个圆的内部.二、圆与圆位置关系的判断:设的半径为,圆心距.(1)和没有公共点,且每一个圆上的所有点在另一个圆的外部外离.(2)和没有公共点,且的每一个点都在内部内含(3)和有唯一公共点,除这个点外,每个圆上的点都在另一个圆外部外切.(4)和有唯一公共点,除这个点外,的每个点都在内部内切.(5)和有两个公共点相交.题型分类、深度剖析:考点:圆与圆的位置关系:【例】在△ABC中,∠C=90°,AC=3 cm,BC=4 cm,若⊙A,⊙B的半径分别为1 cm,4 cm,则⊙A,⊙B的位置关系是( )A.外切 B.内切C.相交 D.外离解析:如图所示,由勾股定理可得AB=AC2+BC2=32+42=5(cm),∵⊙A,⊙B的半径分别为1 cm,4 cm,∴圆心距d=R+r,∴⊙A,⊙B的位置关系是外切.答案:A方法总结圆和圆的位置关系按公共点的个数可分为相离、相切和相交;两圆无公共点则相离,有一个公共点则相切;有两个公共点则相交.其中相离包括内含和外离,相切包括外切和内切,解答时,只要通过两圆的半径和或差与圆心距比较即可.触类旁通若两圆相切,圆心距是7,其中一个圆的半径为10,则另一个圆的半径为__________.。
高考数学一轮复习知识点:圆的方程

2019-2019 高考数学一轮复习知识点:圆的方程确立圆的方程主要方法是待定系数法,即列出对于a、b、r 的方程组,求 a、b、r,或直接求出圆心 (a,b)和半径 r。
下边是查词典数学网整理的2019-2019 高考数学一轮复习知识点,请考生仔细学习。
1、圆的定义:平面内到必定点的距离等于定长的点的会合叫圆,定点为圆心,定长为圆的半径。
2、圆的方程(1)标准方程,圆心,半径为r;(2)一般方程当时,方程表示圆,此时圆心为,半径为当时,表示一个点 ;当时,方程不表示任何图形。
(3)求圆方程的方法:一般都采纳待定系数法:先设后求。
确立一个圆需要三个独立条件,若利用圆的标准方程,需求出 a,b,r;若利用一般方程,需要求出 D,E,F;此外要注意多利用圆的几何性质:如弦的中垂线必经过原点,以此来确立圆心的地点。
3、直线与圆的地点关系:直线与圆的地点关系有相离,相切,订交三种状况,基本上由以下两种方法判断:(1)设直线,圆圆心到l 的距离为则有(2)设直线,圆,先将方程联立消元,获得一个一元二次方程以后,令此中的鉴别式为,则有 ;;注:如圆心的地点在原点,可使用公式去解直线与圆相切的问题,此中表示切点坐标, r 表示半径。
(3)过圆上一点的切线方程:①圆 x2+y2=r2,圆上一点为 (x0,y0),则过此点的切线方程为(课本命题 ).②圆 (x-a)2+(y-b)2=r2 ,圆上一点为 (x0,y0),则过此点的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2( 课本命题的推行 ).4、圆与圆的地点关系:经过两圆半径的和(差),与圆心距 (d)之间的大小比较来确立。
设圆,两圆的地点关系常经过两圆半径的和(差),与圆心距 (d)之间的大小比较来确立。
当时两圆外离,此时有公切线四条;要练说,得练听。
听是说的前提,听得正确,才有条件正确模拟,才能不停地掌握高一级水平的语言。
我在教课中,注意听闻联合,训练少儿听的能力,讲堂上,我特别重视教师的语言,我对少儿说话,注意声音清楚,高低起伏,抑扬有致,富裕吸引力,这样能惹起少儿的注意。
初三数学一轮复习课件 圆的基本概念和性质

H
训练慧
1 请完成随堂练习的必做题, 并填写座位表. 2 再完成选做题. (比比谁更棒!)
A
F
B C
A
F E O ·
B D
O ·
C
D
E
两平行弦在
两平行弦在
圆心两旁
圆心同旁
注意圆的对称性
深思促
我巩固了哪些知识 我还有哪些困惑 我还有哪些方面需要改进 同学中值得我学习的地方 自评得 ____分 (满分100分)
C O
A
B
A C
Eபைடு நூலகம்
B
O
D
垂径定理:
垂直于弦的直径平分这条弦以及 弦所对的两条弧. C
∵CD是直径, CD⊥AB
⌒ ⌒ ⌒ ⌒ ∴AP=BP, AD=BD, AC=BC
A D
O P
B
(课本43页第8题)如图,⊙O的直径 ⌒ AB=4,半径OC⊥AB,点D在BC上, DE⊥OC,DF⊥AB,垂足分别为E、 F .求EF的长.
中考一轮复习课
东台市三仓镇中学 郭敏
揭题明
一 学习目标:
1.梳理并理解圆的有关概念与性质, 能熟练运用解决问题. 2.通过互学、精讲、训练等数学活 动,感受小组互助互学的乐趣,培 养合作交流的意识.
展示互
1. 将学案上的课前练习在小组 内交流. 2. 组长将仍有疑问的题号或 想要展示的题号写到黑板上.
连接半径,是圆中常用的辅助线
例1 (课本42页 习题第4题) 如图,BD、
CE是△ABC的高,M是BC的中点.点B、 C、D、E是否在以点M为圆心的同一圆 上?为什么?
变式题1 ∠BDC在BC下方时,点B、C、
2025年甘肃中考数学一轮复习中考命题探究第6章 圆第24讲 与圆有关的位置关系

(2)当⊙O的半径为2,BC=3时,求tan∠AEB的值.
解:∵OB=2,
∴AB=2OB=4,
∴AC= AB 2-BC2= 42-32= 7,
AC
7
∴tan∠AEB=tan∠ABC= = .
BC 3
2.[2023省卷25题]如图,△ABC内接于⊙O,AB是⊙O的直径,D是⊙O上的一点,CO
2025年甘肃中考数学一轮复习中考命题探究
第24讲
与圆有关的位置关系
(省卷:5年5考;兰州:3年3考)
1 考点梳理
2 重难点突破
3 甘肃5年中考真题及拓展
考点梳理
2022年版课标重要变化
探索切线与过切点的半径的关系,会用三角尺过圆上一点画圆的切
线.(删除)
考点 1
点、直线与圆的位置关系
点与圆的位置关系
考点 41
三角形的外接圆与内切圆
三角形的外接圆
圆心
垂直平分线
外心:三角形三条边的⑧____________
内心:三角形三条
的交点
描述 经过三角形的三个顶点的圆
图示
三角形的内切圆
角平分线
⑨_________的交点
与三角形三边都相切的圆
性质
三角形的外心到三个顶点的
三角形的内心到三角形三边的
距离相等,即OA=OB=OC 距离相等,即OD=OE=OF
3
(2)当⊙O的半径为5,sinB= 5 时,求CE的长.
解:∵AB 是⊙O 的直径,∴∠ACB=90°.
AC 3
∵sin B= = ,AB=10,∴AC=6.
AB 5
∵∠OCE=∠ACB=90°,∴∠ACE=∠OCB=∠B,
中考数学一轮复习第二部分空间与图形第六章圆第24讲圆的基本性质课件

圆周角:顶点在圆上且角的两
边和圆相交的角叫做圆周角.
3.(1)如图,在☉O 中,
∠BOD=80°,则∠A= 40°,
∠C= 140°;
(2)圆周角定理
定理:一条弧所对的圆周角等于它
所对的圆心角的 一半 .
推论:
①同弧或等弧所对的圆周角相等.
②半圆(或直径)所对的圆周角
是 直角 ,90°的圆周角所对的弦
③平分弦所对的一条弧的直径,垂
直 平分 弦,并且 平分 弦所
对的另一条弧.
2.(1)如图,在☉O 中,
弦 AB 的长为 8 cm,
圆心 O 到 AB 的距离
为 3 cm,则☉O 的半
径为 5 cm ;
(3)推论 2:圆的两条平行弦
所夹的 弧 相等.
注意:轴对称Leabharlann 是圆的基本性质,垂径定理及其推论就
是根据圆的轴对称性总结
劣弧.
(6)连接圆上任意两点的线段叫做弦,经过
圆心的弦叫做直径.
(7)弧、弦、圆心角的关系
定理:在同圆或等圆中,相等的圆心角所对
的 弧 相等,所对的 弦 也相等.
推论:在同圆或等圆中,两个 圆心角 、两条
弧、两条 弦 中如果有一组量相等,则
它们所对应的其余各组量也分别相等.
(3)如果∠AOB=
∠COD,那么
材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,
锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径
是
26
寸.
圆心角和圆周角
4.(2020眉山)如图,四边形ABCD的外接圆为☉O,BC=CD,
∠DAC=35°,∠ACD=45°,则∠ADB的度数为( C )
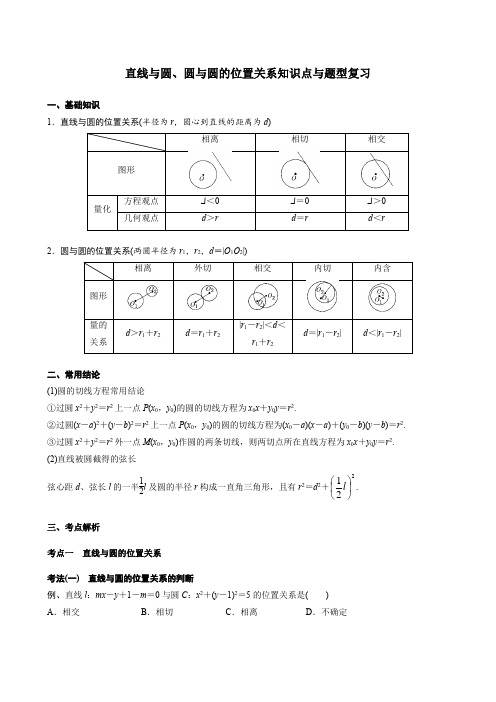
高考数学一轮复习---直线与圆、圆与圆的位置关系知识点与题型复习
直线与圆、圆与圆的位置关系知识点与题型复习一、基础知识1.直线与圆的位置关系(半径为r ,圆心到直线的距离为d )Δ<0 Δ=0 Δ>02.圆与圆的位置关系(两圆半径为r 1,r 2,d =|O 1O 2|)|r -r |<d <二、常用结论(1)圆的切线方程常用结论①过圆x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程为x 0x +y 0y =r 2.②过圆(x -a )2+(y -b )2=r 2上一点P (x 0,y 0)的圆的切线方程为(x 0-a )(x -a )+(y 0-b )(y -b )=r 2. ③过圆x 2+y 2=r 2外一点M (x 0,y 0)作圆的两条切线,则两切点所在直线方程为x 0x +y 0y =r 2. (2)直线被圆截得的弦长弦心距d 、弦长l 的一半12l 及圆的半径r 构成一直角三角形,且有r 2=d 2+221⎪⎭⎫⎝⎛l .三、考点解析考点一 直线与圆的位置关系 考法(一) 直线与圆的位置关系的判断例、直线l :mx -y +1-m =0与圆C :x 2+(y -1)2=5的位置关系是( ) A .相交 B .相切 C .相离 D .不确定[解题技法]判断直线与圆的位置关系的常见方法: (1)几何法:利用d 与r 的关系.(2)代数法:联立方程组,消元得一元二次方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.考法(二) 直线与圆相切的问题例、(1)过点P (2,4)作圆(x -1)2+(y -1)2=1的切线,则切线方程为( )A .3x +4y -4=0B .4x -3y +4=0C .x =2或4x -3y +4=0D .y =4或3x +4y -4=0 (2)已知圆C :x 2+y 2-2x -4y +1=0上存在两点关于直线l :x +my +1=0对称,经过点M (m ,m )作圆C 的切线,切点为P ,则|MP |=________.考法(三) 弦长问题例、(1)若a 2+b 2=2c 2(c ≠0),则直线ax +by +c =0被圆x 2+y 2=1所截得的弦长为( ) A.12 B .1 C.22D.2 (2)设直线y =x +2a 与圆C :x 2+y 2-2ay -2=0相交于A ,B 两点,若|AB |=23,则圆C 的面积为( ) A .4π B .2π C .9π D .22π跟踪练习:1.已知圆的方程是x 2+y 2=1,则经过圆上一点M ⎪⎪⎭⎫⎝⎛2222,的切线方程是________. 2.若直线kx -y +2=0与圆x 2+y 2-2x -3=0没有公共点,则实数k 的取值范围是________.3.设直线y =kx +1与圆x 2+y 2+2x -my =0相交于A ,B 两点,若点A ,B 关于直线l :x +y =0对称,则|AB |=________.考点二 圆与圆的位置关系例、已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( )A .内切B .相交C .外切D .相离变式练习:1.若圆C 1:x 2+y 2=1与圆C 2:x 2+y 2-6x -8y +m =0外切,则m =( )A .21B .19C .9D .-112.(变结论)若本例两圆的方程不变,则两圆的公共弦长为________.[解题技法]几何法判断圆与圆的位置关系的3步骤: (1)确定两圆的圆心坐标和半径长;(2)利用平面内两点间的距离公式求出圆心距d ,求r 1+r 2,|r 1-r 2|; (3)比较d ,r 1+r 2,|r 1-r 2|的大小,写出结论.课后作业1.若直线2x +y +a =0与圆x 2+y 2+2x -4y =0相切,则a 的值为( ) A .±5 B .±5 C .3 D .±32.与圆C 1:x 2+y 2-6x +4y +12=0,C 2:x 2+y 2-14x -2y +14=0都相切的直线有( ) A .1条 B .2条 C .3条 D .4条3.直线y =kx +3被圆(x -2)2+(y -3)2=4截得的弦长为23,则直线的倾斜角为( ) A.π6或5π6 B .-π3或π3 C .-π6或π6 D.π64.过点(3,1)作圆(x -1)2+y 2=r 2的切线有且只有一条,则该切线的方程为( ) A .2x +y -5=0 B .2x +y -7=0 C .x -2y -5=0 D .x -2y -7=05.若圆x 2+y 2+2x -6y +6=0上有且仅有三个点到直线x +ay +1=0的距离为1,则实数a 的值为( ) A .±1 B .±24 C .± 2 D .±326.过点P (1,-2)作圆C :(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则AB 所在直线的方程为( ) A .y =-34 B .y =-12 C .y =-32 D .y =-147.在平面直角坐标系xOy 中,直线x +2y -3=0被圆(x -2)2+(y +1)2=4截得的弦长为________. 8.若P (2,1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程为________. 9.过点P (-3,1),Q (a,0)的光线经x 轴反射后与圆x 2+y 2=1相切,则a 的值为________.10.点P 在圆C 1:x 2+y 2-8x -4y +11=0上,点Q 在圆C 2:x 2+y 2+4x +2y +1=0上,则|P Q |的最小值是________.11.已知圆C 1:x 2+y 2-2x -6y -1=0和圆C 2:x 2+y 2-10x -12y +45=0. (1)求证:圆C 1和圆C 2相交;(2)求圆C 1和圆C 2的公共弦所在直线的方程和公共弦长.12.已知圆C 经过点A (2,-1),和直线x +y =1相切,且圆心在直线y =-2x 上. (1)求圆C 的方程;(2)已知直线l 经过原点,并且被圆C 截得的弦长为2,求直线l 的方程.提高练习1.过圆x 2+y 2=1上一点作圆的切线,与x 轴、y 轴的正半轴相交于A ,B 两点,则|AB |的最小值为( ) A. 2 B.3 C .2 D .32.在平面直角坐标系xOy 中,A 为直线l :y =2x 上在第一象限内的点,B (5,0),以AB 为直径的圆C 与直线l 交于另一点D .若AB ―→·CD ―→=0,则点A 的横坐标为________. 3.已知圆C :x 2+(y -a )2=4,点A (1,0).(1)当过点A 的圆C 的切线存在时,求实数a 的取值范围; (2)设AM ,AN 为圆C 的两条切线,M ,N 为切点,当|MN |=455时,求MN 所在直线的方程.。
2023年高考数学(文科)一轮复习讲义——圆的方程

第3节圆的方程考试要求掌握确定圆的几何要素,掌握圆的标准方程与一般方程.1.圆的定义和圆的方程定义平面内到定点的距离等于定长的点的轨迹叫做圆方程标准(x-a)2+(y-b)2=r2(r>0)圆心C(a,b)半径为r一般x2+y2+Dx+Ey+F=0(D2+E2-4F>0)充要条件:D2+E2-4F>0圆心坐标:⎝⎛⎭⎪⎫-D2,-E2半径r=12D2+E2-4F2.点与圆的位置关系平面上的一点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2之间存在着下列关系:(1)|MC|>r⇔M在圆外,即(x0-a)2+(y0-b)2>r2⇔M在圆外;(2)|MC|=r⇔M在圆上,即(x0-a)2+(y0-b)2=r2⇔M在圆上;(3)|MC|<r⇔M在圆内,即(x0-a)2+(y0-b)2<r2⇔M在圆内.1.圆心在坐标原点,半径为r的圆的方程为x2+y2=r2.2.以A(x1,y1),B(x2,y2)为直径端点的圆的方程为(x-x1)·(x-x2)+(y-y1)(y-y2)=0.1.思考辨析(在括号内打“√”或“×”)(1)确定圆的几何要素是圆心与半径.()(2)方程x 2+y 2=a 2表示半径为a 的圆.( )(3)方程Ax 2+Bxy +Cy 2+Dx +Ey +F =0表示圆的充要条件是A =C ≠0,B =0,D 2+E 2-4AF >0.( )(4)若点M (x 0,y 0)在圆x 2+y 2+Dx +Ey +F =0外,则x 20+y 20+Dx 0+Ey 0+F >0.( )答案 (1)√ (2)× (3)√ (4)√解析 (2)当a =0时,x 2+y 2=a 2表示点(0,0);当a <0时,表示半径为|a |的圆. 2.圆x 2+y 2-4x +6y =0的圆心坐标和半径分别是( ) A.(2,3),3 B.(-2,3), 3 C.(-2,-3),13 D.(2,-3),13 答案 D解析 圆的方程可化为(x -2)2+(y +3)2=13,所以圆心坐标是(2,-3),半径r =13.3.(2021·合肥模拟)已知A (1,0),B (0,3)两点,则以AB 为直径的圆的方程是( ) A.⎝ ⎛⎭⎪⎫x -12 2+⎝ ⎛⎭⎪⎫y -322=104 B.⎝ ⎛⎭⎪⎫x +12 2+⎝ ⎛⎭⎪⎫y +322=104 C.⎝ ⎛⎭⎪⎫x +12 2+⎝ ⎛⎭⎪⎫y -322=104 D.⎝ ⎛⎭⎪⎫x -12 2+⎝ ⎛⎭⎪⎫y +322=104 答案 A 解析 |AB |=12+32=10,圆心为⎝ ⎛⎭⎪⎫12,32,半径r =102,∴圆的方程为⎝ ⎛⎭⎪⎫x -122+⎝ ⎛⎭⎪⎫y -322=104.4.(2022·银川模拟)若点(1,1)在圆(x -a )2+(y +a )2=4的内部,则实数a 的取值范围是( )A.(-1,1)B.(0,1)C.(-∞,-1)∪(1,+∞)D.{-4,4}答案 A解析因为点(1,1)在圆(x-a)2+(y+a)2=4的内部,所以表示点(1,1)到圆心(a,-a)的距离小于2,即(1-a)2+[1-(-a)]2<2,两边平方得:(1-a)2+(a+1)2<4,化简得a2<1,解得-1<a<1.5.(2020·北京卷)已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为()A.4B.5C.6D.7答案 A解析由平面几何知识知,当且仅当原点、圆心、点(3,4)共线时,圆心到原点的距离最小且最小值为d min=(3-0)2+(4-0)2-1=4.6.(易错题)若方程x2+y2+λxy+2kx+4y+5k+λ=0表示圆,则k的取值范围为________________.答案(-∞,1)∪(4,+∞)解析根据题意,若方程x2+y2+λxy+2kx+4y+5k+λ=0表示圆,则λ=0,方程为x2+y2+2kx+4y+5k=0,∴(2k)2+42-4×5k>0,即k2-5k+4>0,解得k<1或k>4,故k的取值范围为(-∞,1)∪(4,+∞).考点一圆的方程1.已知圆E 经过三点A (0,1),B (2,0),C (0,-1),则圆E 的标准方程为( ) A.⎝ ⎛⎭⎪⎫x -322+y 2=254 B.⎝ ⎛⎭⎪⎫x +342+y 2=2516 C.⎝ ⎛⎭⎪⎫x -342+y 2=2516 D.⎝ ⎛⎭⎪⎫x -342+y 2=254 答案 C解析 法一 (待定系数法)设圆E 的一般方程为x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0),则由题意得 ⎩⎪⎨⎪⎧1+E +F =0,4+2D +F =0,1-E +F =0,解得⎩⎪⎨⎪⎧D =-32,E =0,F =-1.所以圆E 的一般方程为x 2+y 2-32x -1=0,即⎝ ⎛⎭⎪⎫x -342+y 2=2516.法二 (几何法)因为圆E 经过点A (0,1),B (2,0),所以圆E 的圆心在线段AB 的垂直平分线y -12=2(x -1)上.又圆E 的圆心在x 轴的正半轴上, 所以圆E 的圆心坐标为⎝ ⎛⎭⎪⎫34,0.则圆E 的半径为 |EB |=⎝ ⎛⎭⎪⎫2-342+(0-0)2=54,所以圆E 的标准方程为⎝ ⎛⎭⎪⎫x -342+y 2=2516.2.在平面直角坐标系xOy 中,以点(0,1)为圆心且与直线x -by +2b +1=0相切的所有圆中,半径最大的圆的标准方程为( ) A.x 2+(y -1)2=4 B.x 2+(y -1)2=2 C.x 2+(y -1)2=8 D.x 2+(y -1)2=16答案 B解析 由直线x -by +2b +1=0可得该直线过定点A (-1,2),设圆心(0,1)为点B ,由题意可知要使所求圆的半径最大,则r max =|AB |=(-1-0)2+(2-1)2=2,所以半径最大的圆的标准方程为x 2+(y -1)2=2.3.已知圆C 的圆心在直线x +y =0上,圆C 与直线x -y =0相切,且截直线x -y -3=0所得的弦长为6,则圆C 的方程为________. 答案 (x -1)2+(y +1)2=2解析 法一 ∵所求圆的圆心在直线x +y =0上, ∴可设所求圆的圆心为(a ,-a ). ∵所求圆与直线x -y =0相切, ∴半径r =2|a |2=2|a |. 又所求圆截直线x -y -3=0所得的弦长为6,圆心(a ,-a )到直线x -y -3=0的距离d =|2a -3|2,∴d 2+⎝ ⎛⎭⎪⎫622=r 2,即(2a -3)22+32=2a 2,解得a =1,∴圆C 的方程为(x -1)2+(y +1)2=2.法二 设所求圆的方程为(x -a )2+(y -b )2=r 2(r >0), 则圆心(a ,b )到直线x -y -3=0的距离d =|a -b -3|2,∴r 2=(a -b -3)22+32,即2r 2=(a -b -3)2+3.① ∵所求圆与直线x -y =0相切, ∴|a -b |12+(-1)2=r .②又∵圆心在直线x +y =0上,∴a +b =0.③ 联立①②③,解得⎩⎪⎨⎪⎧a =1,b =-1,r =2,故圆C 的方程为(x -1)2+(y +1)2=2.感悟提升 求圆的方程时,应根据条件选用合适的圆的方程.一般来说,求圆的方程有两种方法:(1)几何法,通过研究圆的性质进而求出圆的基本量.确定圆的方程时,常用到的圆的三个性质:①圆心在过切点且垂直切线的直线上;②圆心在任一弦的中垂线上;③两圆内切或外切时,切点与两圆圆心三点共线; (2)代数法,即设出圆的方程,用待定系数法求解. 考点二 与圆有关的最值问题 角度1 利用几何意义求最值例1 已知实数x ,y 满足方程x 2+y 2-4x +1=0. (1)求yx 的最大值和最小值; (2)求y -x 的最大值和最小值; (3)求x 2+y 2的最大值和最小值.解 原方程可化为(x -2)2+y 2=3,表示以(2,0)为圆心,3为半径的圆. (1)y x 的几何意义是圆上一点与原点连线的斜率,所以设yx =k ,即y =kx . 当直线y =kx 与圆相切时,斜率k 取最大值或最小值,此时|2k -0|k 2+1=3,解得k=±3(如图1).所以yx的最大值为3,最小值为- 3.(2)y-x可看作是直线y=x+b在y轴上的截距,当直线y=x+b与圆相切时,纵截距b取得最大值或最小值,此时|2-0+b|2=3,解得b=-2±6(如图2).所以y-x的最大值为-2+6,最小值为-2- 6.(3)x2+y2表示圆上的一点与原点距离的平方,由平面几何知识知,在原点和圆心连线与圆的两个交点处取得最大值和最小值(如图3).又圆心到原点的距离为(2-0)2+(0-0)2=2,所以x2+y2的最大值是(2+3)2=7+43,x2+y2的最小值是(2-3)2=7-4 3. 感悟提升把有关式子进行转化或利用所给式子的几何意义解题,充分体现了数形结合以及转化的数学思想,其中以下几类转化较为常见:(1)形如m=y-bx-a的最值问题,可转化为动直线斜率的最值问题;(2)形如m=ax+by的最值问题,可转化为动直线截距的最值问题;(3)形如m=(x-a)2+(y-b)2的最值问题,可转化为两点间距离的平方的最值问题. 角度2利用对称性求最值例2 已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.52-4B.17-1C.6-2 2D.17答案 A解析 P 是x 轴上任意一点,则|PM |的最小值为|PC 1|-1,同理|PN |的最小值为|PC 2|-3,则|PM |+|PN |的最小值为|PC 1|+|PC 2|-4.作C 1关于x 轴的对称点C ′1(2,-3).所以|PC 1|+|PC 2|=|PC 1′|+|PC 2|≥|C 1′C 2|=52,即|PM |+|PN |=|PC 1|+|PC 2|-4≥52-4.感悟提升 求解形如|PM |+|PN |(其中M ,N 均为动点)且与圆C 有关的折线段的最值问题的基本思路:(1)“动化定”,把与圆上动点的距离转化为与圆心的距离;(2)“曲化直”,即将折线段之和转化为同一直线上的两线段之和,一般要通过对称性解决.角度3 建立函数关系求最值例3 (2022·衡水模拟)设点P (x ,y )是圆:x 2+(y -3)2=1上的动点,定点A (2,0),B (-2,0),则P A →·PB →的最大值为________. 答案 12解析 由题意,知P A →=(2-x ,-y ),PB →=(-2-x ,-y ),所以P A →·PB →=x 2+y 2-4,由于点P (x ,y )是圆上的点,故其坐标满足方程x 2+(y -3)2=1,故x 2=-(y -3)2+1,所以P A →·PB →=-(y -3)2+1+y 2-4=6y -12.由圆的方程x 2+(y -3)2=1,易知2≤y ≤4,所以,当y =4时,P A →·PB →的值最大,最大值为6×4-12=12. 感悟提升 根据题中条件列出相关的函数关系式,再根据函数知识或基本不等式求最值.训练1 已知M (x ,y )为圆C :x 2+y 2-4x -14y +45=0上任意一点,且点Q (-2,3).(1)求|MQ|的最大值和最小值;(2)求y-3x+2的最大值和最小值.解(1)由圆C:x2+y2-4x-14y+45=0,可得(x-2)2+(y-7)2=8,∴圆心C的坐标为(2,7),半径r=2 2. 又|QC|=(2+2)2+(7-3)2=42,∴|MQ|max=42+22=62,|MQ|min=42-22=2 2.(2)可知y-3x+2表示直线MQ的斜率k,设直线MQ的方程为y-3=k(x+2),即kx-y+2k+3=0.∵直线MQ与圆C有交点,∴|2k-7+2k+3|1+k2≤22,可得2-3≤k≤2+3,∴y-3x+2的最大值为2+3,最小值为2- 3. 考点三与圆有关的轨迹问题例4 已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.(1)求线段AP中点的轨迹方程;(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.解(1)设AP的中点为M(x,y),由中点坐标公式可知,P点坐标为(2x-2,2y).因为P 点在圆x 2+y 2=4上, 所以(2x -2)2+(2y )2=4.故线段AP 中点的轨迹方程为(x -1)2+y 2=1(x ≠2). (2)设PQ 的中点为N (x ,y ). 在Rt △PBQ 中,|PN |=|BN |.设O 为坐标原点,连接ON ,则ON ⊥PQ , 所以|OP |2=|ON |2+|PN |2=|ON |2+|BN |2, 所以x 2+y 2+(x -1)2+(y -1)2=4. 故线段PQ 中点的轨迹方程为 x 2+y 2-x -y -1=0.感悟提升 求与圆有关的轨迹问题时,根据题设条件的不同常采用以下方法: (1)直接法,直接根据题目提供的条件列出方程; (2)定义法,根据圆、直线等定义列方程; (3)几何法,利用圆的几何性质列方程;(4)代入法,找到要求点与已知点的关系,代入已知点满足的关系式等.训练2 设定点M (-3,4),动点N 在圆x 2+y 2=4上运动,以OM ,ON 为邻边作平行四边形MONP ,求点P 的轨迹方程. 解 如图,设P (x ,y ),N (x 0,y 0),则线段OP 的中点坐标为⎝ ⎛⎭⎪⎫x 2,y 2,线段MN 的中点坐标为⎝ ⎛⎭⎪⎫x 0-32,y 0+42. 因为平行四边形的对角线互相平分, 所以x 2=x 0-32,y 2=y 0+42, 整理得⎩⎪⎨⎪⎧x 0=x +3,y 0=y -4.又点N (x 0,y 0)在圆x 2+y 2=4上, 所以(x +3)2+(y -4)2=4,所以点P 的轨迹是以(-3,4)为圆心,2为半径的圆.直线OM 与轨迹相交于两点⎝ ⎛⎭⎪⎫-95,125和⎝ ⎛⎭⎪⎫-215,285,不符合题意,舍去,所以点P 的轨迹为(x +3)2+(y -4)2=4,除去两点⎝ ⎛⎭⎪⎫-95,125和⎝ ⎛⎭⎪⎫-215,285.1.圆x 2+y 2-6x +8y =0的圆心坐标和半径分别是( ) A.(3,4),5 B.(-3,4),5 C.(-3,-4),5 D.(3,-4),5答案 D解析 圆的方程可化为(x -3)2+(y +4)2=25,所以圆心坐标是(3,-4),半径r =5.2.过点A (1,-1),B (-1,1),且圆心在直线x +y -2=0上的圆的方程是( ) A.(x -3)2+(y +1)2=4 B.(x +3)2+(y -1)2=4 C.(x -1)2+(y -1)2=4 D.(x +1)2+(y +1)2=4 答案 C解析 设圆心C 的坐标为(a ,b ),半径为r . 因为圆心C 在直线x +y -2=0上, 所以b =2-a . 又|CA |2=|CB |2,所以(a -1)2+(2-a +1)2=(a +1)2+(2-a -1)2, 所以a =1,b =1,所以r =2, 所以方程为(x -1)2+(y -1)2=4.3.如果圆的方程为x 2+y 2+kx +2y +k 2=0,那么当圆面积最大时,圆心坐标为( ) A.(-1,1) B.(1,-1) C.(-1,0) D.(0,-1)答案 D 解析 r =12k 2+4-4k 2=124-3k 2,当k =0时,r 最大,此时圆心坐标为(0,-1). 4.(2022·太原期末)若k ∈⎩⎨⎧⎭⎬⎫-2,0,45,3,方程x 2+y 2+(k -1)x +2ky +k =0不表示圆,则k 的取值集合中元素的个数为( ) A.1 B.2 C.3 D.4 答案 A解析 方程x 2+y 2+(k -1)x +2ky +k =0表示圆的条件为(k -1)2+(2k )2-4k >0, 即5k 2-6k +1>0,解得k >1或k <15.又知该方程不表示圆,所以k 的取值范围为⎣⎢⎡⎦⎥⎤15,1.又因为k ∈⎩⎨⎧⎭⎬⎫-2,0,45,3,所以满足条件的k =45,即k 的取值集合为⎩⎨⎧⎭⎬⎫45. 5.(2022·昆明调研)已知圆C 经过P (-2,4),Q (3,-1)两点,且在x 轴上截得的弦长为6,则圆C 的方程为( )A.x 2+y 2-2x -4y -8=0B.x 2+y 2+2x -4y -8=0C.x 2+y 2-2x -4y -8=0或x 2+y 2-6x -8y =0D.x 2+y 2+2x -4y -8=0或x 2+y 2-6x -8y =0 答案 C解析 设圆的方程为x 2+y 2+Dx +Ey +F =0,D 2+E 2-4F >0, 将P ,Q 两点的坐标代入得 ⎩⎪⎨⎪⎧2D -4E -F =20, ①3D -E +F =-10. ②令y =0,得x 2+Dx +F =0, ③ 设x 1,x 2是方程③的两根, 由|x 1-x 2|=6得D 2-4F =36, ④ 由①②④得⎩⎪⎨⎪⎧D =-2,E =-4,F =-8或⎩⎪⎨⎪⎧D =-6,E =-8,F =0,故所求的圆的方程为x 2+y 2-2x -4y -8=0或x 2+y 2-6x -8y =0.6.已知两点A (-1,0),B (0,2),点P 是圆(x -1)2+y 2=1上任意一点,则△P AB 面积的最大值与最小值分别是( ) A.2,12(4-5) B.12(4+5),12(4-5) C.5,4- 5 D.12(5+2),12(5-2) 答案 B 解析 如图,圆心(1,0)到直线AB :2x -y +2=0的距离d =45,故圆上的点P 到直线AB 的距离的最大值是45+1,最小值是45-1.又|AB |=5,故△P AB 面积的最大值和最小值分别是2+52,2-52.7.(2021·郑州模拟)圆(x +2)2+(y -12)2=4关于直线x -y +8=0对称的圆的方程为________________. 答案 (x -4)2+(y -6)2=4 解析 设对称圆的圆心为(m ,n ), 则⎩⎪⎨⎪⎧n -12m +2=-1,m -22-n +122+8=0,解得⎩⎪⎨⎪⎧m =4,n =6,所以所求圆的圆心为(4,6), 故所求圆的方程为(x -4)2+(y -6)2=4.8.圆x 2+y 2-2x -2y +1=0上的点到直线x -y =2的距离的最大值是________. 答案2+1解析 将圆的方程化为(x -1)2+(y -1)2=1,圆心坐标为(1,1),半径为1,则圆心到直线x -y =2的距离d =|1-1-2|2=2,故圆上的点到直线x -y =2的距离的最大值为d +1=2+1.9.(2022·贵阳调研)已知A (0,2),点P 在直线x +y +2=0上,点Q 在圆C :x 2+y 2-4x -2y =0上,则|P A |+|PQ |的最小值是________. 答案 2 5解析 因为圆C :x 2+y 2-4x -2y =0,所以圆C 是以C (2,1)为圆心,半径r =5的圆.设点A (0,2)关于直线x +y +2=0的对称点为A ′(m ,n ),所以⎩⎪⎨⎪⎧m +02+n +22+2=0,n -2m -0=1,解得⎩⎪⎨⎪⎧m =-4,n =-2,故A ′(-4,-2).连接A ′C 交圆C 于Q (图略),此时,|P A |+|PQ |取得最小值,由对称性可知|P A |+|PQ |=|A ′P |+|PQ |≥|A ′Q |=|A ′C |-r =2 5.10.已知Rt △ABC 的斜边为AB ,且A (-1,0),B (3,0),求: (1)直角顶点C 的轨迹方程; (2)直角边BC 的中点M 的轨迹方程.解 (1)设AB 的中点为D ,由中点坐标公式得D (1,0),由直角三角形的性质知|CD |=12|AB |=2.由圆的定义知,动点C 的轨迹是以D (1,0)为圆心,2为半径的圆(由于A ,B ,C 三点不共线,所以应除去与x 轴的交点), 所以直角顶点C 的轨迹方程为(x -1)2+y 2=4(y ≠0).(2)设M (x ,y ),C (x 0,y 0),因为B (3,0),M 是线段BC 的中点,由中点坐标公式得x =x 0+32,y =y 0+02,所以x0=2x-3,y0=2y.由(1)知,点C的轨迹方程为(x-1)2+y2=4(y≠0),将x0=2x-3,y0=2y代入得(2x-4)2+(2y)2=4,即(x-2)2+y2=1.因此动点M的轨迹方程为(x-2)2+y2=1(y≠0). 11.已知点(x,y)在圆(x-2)2+(y+3)2=1上.(1)求yx的最大值和最小值;(2)求x+y的最大值和最小值;(3)求x2+y2+2x-4y+5的最大值和最小值.解(1)yx可视为点(x,y)与原点连线的斜率,yx的最大值和最小值就是与该圆有公共点的过原点的直线斜率的最大值和最小值,即直线与圆相切时的斜率.设过原点的直线的方程为y=kx,由直线与圆相切得圆心到直线的距离等于半径,即|2k+3|k2+1=1,解得k=-2+233或k=-2-233,∴yx的最大值为-2+233,最小值为-2-233.(2)设t=x+y,则y=-x+t,t可视为直线y=-x+t在y轴上的截距,∴x+y的最大值和最小值就是直线与圆有公共点时直线纵截距的最大值和最小值,即直线与圆相切时在y轴上的截距.由直线与圆相切得圆心到直线的距离等于半径,即|2+(-3)-t|2=1,解得t=2-1或t=-2-1.∴x+y的最大值为2-1,最小值为-2-1.(3)x2+y2+2x-4y+5=(x+1)2+(y-2)2,求它的最值可视为求点(x,y)到定点(-1,2)的距离的最值,可转化为求圆心(2,-3)到定点(-1,2)的距离与半径的和或差.又圆心到定点(-1,2)的距离为34, ∴x 2+y 2+2x -4y +5的最大值为34+1,最小值34-1.12.(2020·全国Ⅱ卷)若过点(2,1)的圆与两坐标轴都相切,则圆心到直线2x -y -3=0的距离为( ) A.55 B.255C.355D.455答案 B解析 设圆心为P (x 0,y 0),半径为r ,∵圆与x 轴,y 轴都相切, ∴|x 0|=|y 0|=r .又圆经过点(2,1),∴x 0=y 0=r 且(2-x 0)2+(1-y 0)2=r 2, ∴(r -2)2+(r -1)2=r 2,解得r =1或r =5.当r =1时,圆心坐标为(1,1),此时圆心到直线2x -y -3=0的距离 d =|2×1-1-3|22+(-1)2=255;当r =5时,圆心坐标为(5,5),此时圆心到直线2x -y -3=0的距离 d =|2×5-5-3|22+(-1)2=255.综上,圆心到直线2x -y -3=0的距离为255.13.(2022·郑州模拟)大约在2 000多年前,我国的墨子给出了圆的概念“一中同长也”,意思是说,圆有一个圆心,圆心到圆周上的点的长都相等.这个定义比古希腊数学家欧几里得给圆下定义要早100多年.现有动点P 满足|OP |=2,其中O 为坐标原点,若M ⎝ ⎛⎭⎪⎫12,-32,则|PM |的最小值为________.答案 1解析 由题意可得点P 在以O 为圆心,2为半径的圆上, 因为|OM |=⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫-322=1<2, 所以点M 在圆内,所以|PM |min =r -|OM |=2-1=1.14.设抛物线C :y 2=4x 的焦点为F ,过F 且斜率为k (k >0)的直线l 与C 交于A ,B 两点,|AB |=8. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程. 解 (1)由题意得F (1,0),l 的方程为 y =k (x -1)(k >0). 设A (x 1,y 1),B (x 2,y 2), 由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x得k 2x 2-(2k 2+4)x +k 2=0,Δ=16k 2+16>0,故x 1+x 2=2k 2+4k 2, 所以|AB |=|AF |+|BF | =(x 1+1)+(x 2+1)=4k 2+4k 2.由题设知4k 2+4k 2=8,解得k =-1(舍去),k =1, 因此l 的方程为y =x -1.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为y -2=-(x -3),即y =-x +5.设所求圆的圆心坐标为(x 0,y 0),则⎩⎪⎨⎪⎧y 0=-x 0+5,(x 0+1)2=(y 0-x 0+1)22+16, 解得⎩⎪⎨⎪⎧x 0=3,y 0=2或⎩⎪⎨⎪⎧x 0=11,y 0=-6.故圆的半径为x 0+p2=4或12,因此所求圆的方程为(x -3)2+(y -2)2=16或(x -11)2+(y +6)2=144.。
初三中考一轮复习(24)与圆有关的计算 题型分类 含答案(全面 非常好)

考点一:正多边形和圆例1 如图,正三角形的内切圆半径为1,那么这个正三角形的边长为() A. 2 B. 3 C.3D.32OD对应训练1.正六边形的边心距与边长之比为()A.3:3 B.3:2 C.1:2 D.2:21.B考点二:圆周长与弧长例2 如图,矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD沿直线l 作无滑动翻滚,当点A第一次翻滚到点A1位置时,则点A经过的路线长为6π.解:如图,∵四边形ABCD 是矩形,AB=4,BC=3,∴BC=AD=3,∠ADC=90°,对角线AC (BD )=5. ∵根据旋转的性质知,∠ADA ′=90°,AD=A ′D=BC=3, ∴点A 第一次翻滚到点A ′位置时,则点A ′经过的路线长为:90331802ππ⨯=. 同理,点A ′第一次翻滚到点A ″位置时,则点A ′经过的路线长为:904180π⨯=2π. 点″第一次翻滚到点A 1位置时,则点A ″经过的路线长为:90551802ππ⨯=. 则当点A 第一次翻滚到点A 1位置时,则点A 经过的路线长为:35222πππ++=6π. 故答案是:6π. 对应训练2.如图,将边长为1cm 的等边三角形ABC 沿直线l 向右翻动(不滑动),点B 从开始到结束,所经过路径的长度为( ) A .32πcmB .(2+32π)cm C .43πcmD .3cm2.C考点三:扇形面积与阴影部分面积π⨯,解得:r=1cm.2πr=1203180故选D.对应训练4.一个圆锥的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角等于()A.60°B.90°C.120°D.180°4.D考点五:圆的综合题例5如图,PA为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交与点C,连接AC,BF.(1)求证:PB与⊙O相切;(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;,求cos∠ACB的值.(3)若AC=12,tan∠F=12解答:(1)证明:连接OA,∵PA 与圆O 相切, ∴PA ⊥OA ,即∠OAP=90°, ∵OP ⊥AB ,∴D 为AB 中点,即OP 垂直平分AB , ∴PA=PB ,∵在△OAP 和△OBP 中,AP BP OP OP OA OB =⎧⎪=⎨⎪=⎩, ∴△OAP ≌△OBP (SSS ), ∴∠OAP=∠OBP=90°, ∴BP ⊥OB ,则直线PB 为圆O 的切线;(2)答:EF 2=4DO •PO .证明:∵∠OAP=∠ADO=90°,∠AOD=∠POA , ∴△OAD ∽△OPA , ∴OA ODOP OA=,即OA 2=OD •OP , ∵EF 为圆的直径,即EF=2OA ,【聚焦中考】1.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( ) A .6,32 B .3 2,3 C .6,3 D .62,321.B2.如图,正方形ABCD 中,分别以B 、D 为圆心,以正方形的边长a 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( ) A .πaB .2πaC .12πaD .3a2.A3.如图,扇形AOB 的半径为1,∠AOB=90°,以AB 为直径画半圆,则图中阴影部分的面积为( ) A .4πB .π-12C .12D .4π + 12.C4.将半径为3cm 的圆形纸片沿AB 折叠后,圆弧恰好能经过圆心O ,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )A .22B .2C .10D .32.A5.在半径为5的圆中,30°的圆心角所对的弧长为 (结果保留π). .56π6.已知一个扇形的半径为60cm ,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 cm . 257.如图,AB 是⊙O 的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 ..433π- 8.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( ) A .3π B .4π C .5π D .6π.B9.如果一个扇形的弧长是43π,半径是6,那么此扇形的圆心角为( )A.40°B.45°C.60°D.80°A10.已知圆锥的底面半径为6cm,高为8cm,则这个圆锥的母线长为()A.12cm B.10cm C.8cm D.6cm.B11.如图是某几何体的三视图,则该几何体的体积是()A.πB.2πC.3πD.4π.A12.用如图所示的扇形纸片制作一个圆锥的侧面,要求圆锥的高是4cm,底面周长是6πcm,则扇形的半径为()A.3cm B.5cm C.6cm D.8cm12.B,13.如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sinθ=13则该圆锥的侧面积是()A.242πB.24πC.16πD.12π.D14.如图,以AD 为直径的半圆O 经过Rt △ABC 斜边AB 的两个端点,交直角边AC 于点E 、B ,E 是半圆弧的三等分点,弧BE 的长为23π,则图中阴影部分的面积为( )A .9πB .39πC .33322π-D .33223π-D二、填空题1.已知扇形的圆心角为120°,弧长为10πcm ,则扇形的半径为 cm . .152.如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为(结果保留π) ..π-23.如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2,则正八边形的面积为 cm2..404.△OAB是以正多边形相邻的两个顶点A,B与它的中心O为顶点的三角形,若△OAB的一个内角为70°,则该正多边形的边数为..95.如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为 cm..4π6.如图,Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为.π6.2547.如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O 重合,点A在x轴上,点B在反比例函数k=位于第一象限的图象上,则k的值yx为..93三、解答题1.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.`.解:设圆锥的母线长为l,底面半径为r,则:πl=2πr,∴l=2r,∴母线与高的夹角的正弦值=12r l =,∴母线AB 与高AO 的夹角30°.2.如图,在矩形ABCD 中,AB=2DA ,以点A 为圆心,AB 为半径的圆弧交DC 于点E ,交AD 的延长线于点F ,设DA=2.(1)求线段EC 的长;(2)求图中阴影部分的面积.2.解;(1)∵在矩形ABCD 中,AB=2DA ,DA=2,∴AB=AE=4,∴DE=2223AE AD -=,∴EC=CD-DE=4-23;(2)∵sin ∠DEA=12AD AE =, ∴∠DEA=30°,∴∠EAB=30°,∴图中阴影部分的面积为:S 扇形FAB -S △DAE -S 扇形EAB=290413602π⨯-×2×23-2304360π⨯=83π-23.3.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.(1)求证:EF是⊙O的切线;(2)求证:AC2=AD•AB;(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.3.(1)证明:如图,连接OC,∵OA=OC,∴∠BAC=∠OCA,∵∠DAC=∠BAC,∴∠OCA=∠DAC,∴OC∥AD,∵AD⊥EF,∴OC⊥EF,∵OC为半径,∴EF是⊙O的切线.。
2015届九年级数学中考一轮复习教学案:第24课时圆的有关计算

第24课时圆的有关计算【课时目标】1.了解正多边形的概念及正多边形与圆的关系,能将正多边形问题转化为直角三角形问题.2.会计算圆的弧长、扇形的面积以及组合图形的周长与面积.3.理解圆柱、圆锥的侧面展开图,掌握圆柱、圆锥的侧面积和全面积的计算.【知识梳理】1.各边_______,各角_______的多边形叫做正多边形,正多边形的外接圆(或内切圆)的圆心叫做正多边形的_______.2.正多边形都是_______对称图形,一个正n边形共有_______条对称轴.如果正n边形的边数为偶数,它又是_______对称图形,那么它的中心就是_______中心.3.圆的有关计算公式(设半径为R,圆心角的度数为n°):(1)圆周长C=,弧长l=________.(2)圆面积S=________,S扇形=________=_______.4.圆锥:(1)连接圆锥的顶点和底面圆上任意一点的_______都叫做圆锥的母线,圆锥的母线长_______;连接顶点与_______的线段叫做圆锥的高.(2)圆锥的侧面展开图是一个________,这个扇形的_______是圆锥的母线长,_______是圆锥底面圆的周长.(3)设圆锥底面圆的半径为r,母线长为l,则S圆锥侧=________,S圆锥全=________.【考点例析】考点一与正多边形有关的运算例1正多边形的一个外角等于30°,则这个多边形的边数为( )A.6 B.9 C.12 D.15提示方法一:根据多边形内角和公式表示出内角和,另外根据正多边形的每个外角都相等也可以求出该多边形的内角和,从而列出方程求出方程的解即可;方法二:根据多边形的外角和为360°,正多边形的每个外角都相等,用360÷30即可求出边数.例2为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖.更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a ,则阴影部分的面积为 ( )A .2a 2B .3a 2C .4a 2D .5a 2提示 图中阴影部分的面积由一个正方形和四个等腰直角三角形组成,根据正八边形的边长相等知四个等腰直角三角形可拼接成边长为a 的正方形,从而得到阴影部分的面积等于2个边长为a 的正方形的面积.考点二 与弧长有关的运算例3如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连接BC .若∠ABC =120°,OC =3,则BC 的长为 ( )A .πB .2πC .3πD .5π 提示 连接OB ,由于AB 是切线,那么∠ABO =90°,而∠ABC =120°,易求∠OBC ,而OB =OC ,那么∠OBC =∠OCB ,进而求出∠BO C 的度数,再利用弧长公式即可求出BC 的长.例4如图,在由边长为1的正方形组成的网格中,△ABC 的顶点都在格点上,将△ABC 绕点C 顺时针旋转60°,则顶点A 所经过的路径长为 ( ) A .10πB .103C .103π D .π 提示 由题意得点A 所经过的路径是以C 为圆心,CA 长为半径,圆心角为60°的弧,而要求顶点A 所经过的路径长就是求该孤的长,利用弧长公式180n r l π=计算可得.考点三 与扇形面积有关的计算例5如图,四边形OABC 为菱形,点A ,B 在以O 为圆心的弧上.若OA =2,∠1=∠2,则扇形ODE的面积为 ( )A .43π B .53π C .2πD .3π提示 连接OB .根据等边三角形的性质可以求得∠AOC =120°,再结合∠1=∠2,即可求得扇形所在的圆心角的度数,从而根据扇形的面积公式进行求解.考点四 与圆锥的侧面展开图有关的运算例6 如图,在⊙O 中,半径OA =4,∠AOB =120°,用阴影部分的扇形围成的圆锥底面圆的半径长是 ( )A .1B .43C .53D .2提示 设出圆锥的底面圆的半径,利用圆锥底面圆的周长等于扇形的弧长列方程求解. 考点五 求阴影部分的面积例7如图,在△ABC 中,BC =4,以点A为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于点E ,交AC 于点F ,P 是⊙A 上的一点,且∠EPF =45°,则图中阴影部分的面积为 ( )A .4-πB .4-2πC .8+πD .8-2π提示 连接AD ,根据圆周角定理可以求得∠A 的度数,进而求得扇形EAF 的面积,根据阴影部分的面积=△ABC 的面积-扇形EAF 的面积即可求解.【反馈练习】1.已知正n 边形的一个内角为135°,则边数n 的值是 ( )A .6B .7C .8D .102.(2012.湛江)一个扇形的圆心角为60°,它所对的弧长为2πcm ,则这个扇形的半径为( )A .6 cmB .12 cmC .23 cmD .6cm3.如图,E 是BC 的中点,AB 是⊙O 的直径,AB =4,∠BED =120°,则图中阴影部分的面积之和为 ( ) A .1 B .32 C .3 D .234.(1)在半径为1 cm .的圆中,圆心角为120°的扇形的弧长是_______cm(结果保留π);(2)一个扇形的圆心角为120°,半径为3,则这个扇形的面积为_______(结果保留π).5.如图,SO 、SA 分别是圆锥的高和母线.若SA =12 cm ,∠ASO =30°,则这个圆锥的侧面积是_______cm 2(结果保留π).6.如图,在扇形OAB 中,∠AOB =90°,半径OA =6.将扇形OAB 沿过点B 的直线折叠,点O 恰好落在AB 上的点D 处,折痕交OA 于点C ,求整个阴影部分的周长和面积.。
最新中考数学-一轮复习:与圆有关的位置关系

与圆有关的位置关系基础知识知识点一、点与圆的位置关系1. 点和直线有三种位置关系:①点在圆外,即这个点到圆心的距离大于半径;②点在圆上,即这个点到圆心的距离等于半径;③点在圆内,即这个点到圆心的距离小于半径.2. 用数量关系表示位置关系:⊙O的半径为r,点P到圆心的距离OP=d,则有①点P在⊙O外d>r;②点P在⊙O上d=r;③点P在⊙O内d<r.知识点二、直线和圆的位置关系1.直线和圆的三种位置关系:(1)相离:直线和圆没有公共点,这时我们说这条直线和圆相离.(2)相切:直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.(3)相交:直线和圆有两个公共点,这时我们说这条直线和圆相交.2、直线和圆的位置关系的性质与判断:设圆的半径为r,圆心到直线的距离为d,则:①直线和圆相离 d < r②直线和圆相切 d = r③直线和圆相交 d > r.知识点三、切线的判定定理1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.在应用定理时,必须先弄清两个条件:一是经过半径的外端;二是垂直于这条半径,两者缺一不可.2. 切线的判定方法有以下几种:①可以直接应用定义:直线与圆有一个公共点时,直线是圆的切线.②圆心到直线的距离等于半径的直线是圆的切线.③切线的判定定理.当已知条件中没有指出圆与直线的公共点时,常运用方法②进行判定;当已知条件中明确指出圆与直线有公共点时,常运用判定定理进行判定.证题方法“有点连半径,无点作垂线”.知识点四、切线的性质定理与切线长定理1. 切线的性质定理:圆的切线垂直于过切点的半径.当已知圆的切线时,常常连接过切点的半径,得两线垂直关系. 2.切线长定理(1)切线长的定义:过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. (2)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等. 知识点五、三角形的外接圆与外心1. 三角形的外接圆:经过三角形的三个顶点的圆叫做三角形的外接圆.2. 三角形的外心:三角形外接圆的圆心,是三角形三条边垂直平分线的交点.这个点叫做三角形的外心.3. 三角形外心的性质:①三角形的外心是外接圆的圆心,它到三角形各顶点的距离相等;②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的;但一个圆的内接三角形却有无数个,这些三角形的外心重合.知识点六、三角形的内切圆与内心1.三角形的内切圆是指与三角形各边都相切的圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.任意一个三角形都有且只有一个内切圆.但一个圆的外切三角形有无数个.2. 三角形的内心:三角形内切圆的圆心,是三角形三条角平分线的交点,到三角形三边的距离相等. 常见结论:(1)Rt △ABC 的三条边分别为:a 、b 、c (c 为斜边),则它的内切圆的半径2ab cr ; (2)△ABC 的周长为l ,面积为S ,其内切圆的半径为r ,则12S lr . 知识点七、正多边形与圆的关系1. 正多边形的概念:各边相等,各角也相等的多边形叫做正多边形.2. 正多边形与圆的关系可以这样表述:把圆分成n (n≥3)等份,依次连接各分点所得的多边形就是这个圆的内接正n 边形.利用这一关系可以判定一个多边形是否是正多边形或作出一个正多边形.这个圆是这个正多边形的外接圆.正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做这个正多边形的半径.正多边形每一边所对的圆心角叫做正多边形的中心角.3. 对称性:①正多边形的轴对称性:正多边形都是轴对称图形,一个正n 边形共有n 条对称轴,每条对称轴都通过正n 边形的中心.②正多边形的中心对称性:边数为偶数的正多边形是中心对称图形,它的中心是对称中心. ③正多边形的旋转对称性:正多边形都是旋转对称图形,最小的旋转角等于中心角. 典型例题解析例1. 已知点P到⊙O上的点的最短距离为3cm,最长距离为5cm,则⊙O的半径为cm.例2. 已知⊙O的半径长为2cm,如果直线l上有一点P满足PO=2cm,那么直线l与⊙O的位置关系是()A.相切B.相交C.相离或相切D.相切或相交例3. Rt△ABC中,∠C=90°,AC=5,BC=12,如果以点C为圆心,r为半径,且⊙C与斜边AB仅有一个公共点,那么半径r的取值范围是.例4. (朝阳)如图,△MBC中,∠B=90°,∠C=60°,MB=23,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为()A.2B.3C.2 D.3例5. (葫芦岛)如图,边长为a的正六边形内有一边长为a的正三角形,则SS阴影空白()A.3 B.4 C.5 D.6例6. 如图:⊙I是Rt△ABC的内切圆,∠C=90°,AC=6,BC=8,则⊙I的半径是.例7. (锦州)已知,⊙O为∆ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE 的延长线上,且GA=GE.(1)求证:AG与⊙O相切.(2)若AC=6,AB=8,BE=3,求线段OE的长.(2)过点O作OH⊥AB,垂足为H,例8. (来宾)如图,AB为⊙O的直径,BF切⊙O于点B,AF交⊙O于点D,点C在DF上,BC交⊙O 于点E,且∠BAF=2∠CBF,CG⊥BF于点G.连接AE.(1) 直接写出AE与BC的位置关系;(2) 求证:△BCG∽△ACE ;(3) 若∠F=60°,GF=1,求⊙O得半径.巩固训练1. (青岛)直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是()A.r<6 B.r=6 C.r>6 D.r≥62. 在⊙O中,圆心O在坐标原点上,半径为210,点P的坐标为(4,5),那么点P与⊙O的位置关系是()A.点P在⊙O外B.点P在⊙O上C.点P在⊙O内D.不能确定3. 已知正三角形外接圆半径为3,这个正三角形的边长是()A.2 B.3 C.4 D.54. (天津)如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠B=25°,则∠C的大小等于()A.20°B.25°C.40°D.50°△放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个圆面5. 如下图,将ABC△,能够完全覆盖这个三角形的最小圆面的半径是________.去覆盖ABC6. (曲靖)如图,正六边形ABCDEF的边长为2,则对角线AE的长是.7. (莱芜)如图,正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是()A. △CDF的周长等于AD+CDB. FC平分∠BFDC. AC2+BF2=4CD2D. DE2=EF·CE8. (广安)如图,矩形ABCD的长为6,宽为3,点O1为矩形的中心,⊙O2的半径为1,O1O2⊥AB于点P,O1O2=6,若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边只有一个公共点的情况一共出现()A.3次B.4次C.5次D.6次9. (日照)如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数kyx(k≠0)的图象经过圆心P,则k= .10. (德州)如图,⊙O的直径AB为10cm,弦BC为6cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.(1)求AC,AD的长;(2)试判断直线PC与⊙O的位置关系,并说明理由.11. (河南)如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线P A、PB,切点分别为点A、B.(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;(2)填空:①当DP= cm时,四边形AOBD是菱形;②当DP=cm时,四边形AOBP是正方形.12. (抚州)如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A,B两点,连接AP 并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F,若点F的坐标为(0,1),点D的坐标为(6,-1).(1)求证:DC=FC.(2)判断⊙P与x轴的位置关系,并说明理由.(3)求直线AD的解析式.中考预测1. 在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是()A.当a=-1时,点B在圆A上B.当a<1时,点B在圆A内C.当a<-1时,点B在圆A外D.当-1<a<3时,点B在圆A内2. 如图,△ABC的边AC与⊙O相交于C,D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A =30°,则∠C的大小是( )A.30°B.45°C.60°D.40°3. 如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3, 0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为()A.1 B.1或5 C.3 D.54. 如图,P为⊙O的直径BA延长线上一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD. 已知PC=PD=BC. 下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°. 其中正确的个数为()A. 4个B. 3个C. 2个D. 1个5. ⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为.6. 直角三角形的两边长分别为16和12,则此三角形的外接圆半径是.7. 已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC只有一个公共点,那么x的取值范围是.8. 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是__________.(结果保留π)9. 如图,正方形ABCD的边长为2,⊙O的直径为AD,将正方形沿EC折叠,点B落在圆上的F点,则BE的长为.10. 如图,Rt△ABC中,∠ABC=90°.以AB的中点O为圆心、OA长为半径作半圆,交AC于点D.点E为BC的中点,连接DE.(1)求证:DE是该半圆的切线;(2)若∠BAC=30°,DE=2,求AD的长.11.如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE AC,垂足为E.(1)证明:DE为⊙O的切线;(2)连接OE,若BC=4,求△OEC的面积.12. 如图,AB 是⊙O 的直径,点C 在⊙O 上,与⊙O 相切, BD ∥AC . (1)图中∠OCD =_______°,理由是_____________________; (2)⊙O 的半径为3,AC =4,求OD 的长.13. 阅读材料:已知,如图(1),在面积为S 的△ABC 中, BC =a ,AC =b , AB =c ,内切圆O 的半径为r.连接OA 、OB 、OC ,△ABC 被划分为三个小三角形. ∵r c b a r AB r AC r BC S S S S OAB OAC OBC )(21212121++=⋅+⋅+⋅=++=△△△.. ∴cb a Sr ++=2.(1)类比推理:若面积为S 的四边形ABCD 存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB =a ,BC =b ,CD =c ,AD =d ,求四边形的内切圆半径r ;(2)理解应用:如图(3),在等腰梯形ABCD 中,AB ∥DC ,AB =21,CD =11,AD =13,⊙O 1与⊙O 2分别为△ABD 与△BCD 的内切圆,设它们的半径分别为r 1和r 2,求21r r 的值.参考答案:巩固训练∵∠ODE=∠DEA=90°,∴OD∥AC,∴11313222 OCES CE DE∆=⨯⨯=⨯=.13. 【解析】 (1)连接OA 、OB 、OC 、OD. ∵AOD COD BOC AOB S S S S S △△△△+++=dr cr br ar 21212121+++=r d c b a )(21+++=。
中考数学一轮复习专题解析—圆的证明与计算

中考数学一轮复习专题解析—圆的证明与计算复习目标1.了解圆的定义及点与圆的位置关系。
2.掌握圆的基本性质。
3.掌握圆中复杂证明及两圆位置关系中证明。
考点梳理一、圆的有关概念1. 圆的定义如图所示,有两种定义方式:①在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆.固定的端点O叫做圆心,以O为圆心的圆记作①O,线段OA叫做半径;①圆是到定点的距离等于定长的点的集合.2.与圆有关的概念①弦:连接圆上任意两点的线段叫做弦;如上图所示线段AB,BC,AC都是弦.①直径:经过圆心的弦叫做直径,如AC是①O的直径,直径是圆中最长的弦.①弧:圆上任意两点间的部分叫做圆弧,简称弧,如曲线BC、BAC都是①O中的弧,分别记作BC,BAC.①半圆:圆中任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆,如AC是半圆.①劣弧:像BC这样小于半圆周的圆弧叫做劣弧.①优弧:像BAC这样大于半圆周的圆弧叫做优弧.①同心圆:圆心相同,半径不相等的圆叫做同心圆.①弓形:由弦及其所对的弧组成的图形叫做弓形.①等圆:能够重合的两个圆叫做等圆.①等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.⑪圆心角:顶点在圆心的角叫做圆心角,如上图中①AOB,①BOC是圆心角.⑫圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角,如上图中①BAC、①ACB都是圆周角.例1.已知:如图所示,在①O中,弦AB的中点为C,过点C的半径为OD.(1)若AB=23,OC=1,求CD的长;(2)若半径OD=R,①AOB=120°,求CD的长.【答案】解:①半径OD经过弦AB的中点C,①半径OD①AB.(1)①AB=3AC=BC3①OC=1,由勾股定理得OA=2.①CD=OD-OC=OA-OC=1,即CD =1.(2)①OD①AB ,OA =OB , ①①AOD =①BOD .①①AOB =120°,①①AOC =60°. ①OC =OA·cos①AOC =OA·cos60°=12R , ①1122CD OD OC R R R =-=-=.二、圆的有关性质 1.圆的对称性圆是轴对称图形,经过圆心的直线都是它的对称轴,有无数条.圆是中心对称图形,圆心是对称中心,又是旋转对称图形,即旋转任意角度和自身重合. 2.垂径定理①垂直于弦的直径平分这条弦,且平分弦所对的两条弧.①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.如图所示:在图中(1)直径CD ,(2)CD①AB ,(3)AM =MB ,(4)C C A B =,(5)AD BD =.若上述5个条件有2个成立,则另外3个也成立.因此,垂径定理也称“五二三定理”.即知二推三.注意:(1)(3)作条件时,应限制AB 不能为直径. 3.弧、弦、圆心角之间的关系①在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;①在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.4.圆周角定理及推论①圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.①圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.例2.如图所示,AB=AC,O是BC的中点,①O与AB相切于点D,求证:AC与①O相切.【答案】证明:连接OD,作OE①AC,垂足为E,连结OA.①AB与①O相切于点D,①OD①AB.①AB=AC,OB=OC,①①1=①2,①OE=OD.①OD为①O半径,①AC与①O相切.三、与圆有关的位置关系1.点与圆的位置关系如图所示.d表示点到圆心的距离,r为圆的半径.点和圆的位置关系如下表:点与圆的位置关系d与r的大小关系点在圆内d<r点在圆上d=r点在圆外d>r(1)圆的确定:①过一点的圆有无数个,如图所示.①过两点A、B的圆有无数个,如图所示.①经过在同一直线上的三点不能作圆.①不在同一直线上的三点确定一个圆.如图所示.(2)三角形的外接圆经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆.三角形外接圆的圆心叫做这个三角形的外心.这个三角形叫做这个圆的内接三角形.三角形的外心就是三角形三条边的垂直平分线交点.它到三角形各顶点的距离相等,都等于三角形外接圆的半径.如图所示.2.直线与圆的位置关系①设r为圆的半径,d为圆心到直线的距离,直线与圆的位置关系如下表.①圆的切线.切线的定义:和圆有唯一公共点的直线叫做圆的切线.这个公共点叫切点.切线的判定定理:经过半径的外端.且垂直于这条半径的直线是圆的切线.友情提示:直线l是①O的切线,必须符合两个条件:①直线l经过①O上的一点A;①OA①l.切线的性质定理:圆的切线垂直于经过切点的半径.切线长定义:我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角.①三角形的内切圆:与三角形各边都相切的圆叫三角形的内切圆,三角形内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形,三角形的内心就是三角形三个内角平分线的交点.3.三角形外心、内心有关知识比较4.圆与圆的位置关系在同一平面内两圆作相对运动,可以得到下面5种位置关系,其中R、r为两圆半径(R≥r).d为圆心距.①相切包括内切和外切,相离包括外离和内舍.其中相切和相交是重点.①同心圆是内含的特殊情况.①圆与圆的位置关系可以从两个圆的相对运动来理解.①“r1-r2”时,要特别注意,r1>r2.四、正多边形和圆1.正多边形的有关概念正多边形的外接圆(或内切圆)的圆心叫正多边形的中心.外接圆的半径叫正多边形的半径,内切圆的半径叫正多边形的边心距,正多边形各边所对的外接圆的圆心角都相等,这个角叫正多边形的中心角,正多边形的每一个中心角都等于360 n °.要点诠释:通过中心角的度数将圆等分,进而画出内接正多边形,正六边形边长等于半径.2.正多边形的性质任何一个正多边形都有一个外接圆和一个内切圆,这两圆是同心圆.正多边形都是轴对称图形,偶数条边的正多边形也是中心对称图形,同边数的两个正多边形相似,其周长之比等于它们的边长(半径或边心距)之比. 3.正多边形的有关计算定理:正n 边形的半径和边心距把正n 边形分成2n 个全等的直角三角形. 正n 边形的边长a 、边心距r 、周长P 和面积S 的计算归结为直角三角形的计算.360n a n =°,1802sin n a R n =°,180cos n r R n=°, 2222n n a R r ⎛⎫=+ ⎪⎝⎭,n n P n a =,1122n nnn n S a r n P r ==.五、圆中的计算问题 1.弧长公式:180n Rl π=,其中l 为n°的圆心角所对弧的长,R 为圆的半径. 2.扇形面积公式:2360n R S π=扇,其中12S lR =扇.圆心角所对的扇形的面积,另外12S lR =扇.3.圆锥的侧面积和全面积:圆锥的侧面展开图是扇形,这个扇形的半径等于圆锥的母线长,弧长等于圆锥底面圆的周长.圆锥的全面积是它的侧面积与它的底面积的和.1.(2022·四川省宜宾市第二中学校九年级)如图,CD 为O 的直径,弦AB CD ⊥,垂足为E ,1CE =,6AB =,则O 的半径为( )A.3B.4C.5D.无法确定【答案】C【分析】连接OA,由垂径定理得AE=3,设OA=OC=x,根据勾股定理列出方程,进而即可求解.【详解】连接OA,①CD为O的直径,弦AB CD⊥,AB=3,①AE=12设OA=OC=x,则OE=x-1,①()222x x-+=,解得:x=5,13①O的半径为5.故选C.2.(2022·河南九年级期末)如图,AD为①O的直径,6cmAD=,DAC ABC∠=∠,则AC的长度为()A.2B.22C.32D.33【答案】C【分析】连接CD,由圆周角定理可知90∠=∠可知AC CD=,由∠=︒,再根据DAC ABCACD勾股定理即可得出AC的长.【详解】解:连接CD,AD是O的直径,∴∠=︒,ACD90∠=∠,DAC ABC∠=∠,ABC ADC∴∠=∠,DAC ADC∴CD AC=,∴=,AC CD又222AC CD AD+=,22∴=,2AC ADAD=,6∴=AC故选:C.3.(2022·全国九年级课时练习)O的半径为10cm,弦//AB CD.若==,则AB和CD的距离为()AB CD12cm,16cmA.2cm B.14cm C.2cm或14cm D.2cm或10cm 【答案】C【分析】分AB、CD在圆心的同侧和异侧两种情况求得AB与CD的距离.构造直角三角形利用勾股定理求出即可.【详解】当弦AB和CD在圆心异侧时,如图1,过点O作OE①AB于点E,反向延长OE交CD于点F,连接OA,OC,①AB①CD,①OF①CD,①AB=12cm,CD=16cm,①AE=6cm,CF=8cm,①OA=OC=10cm,①在Rt①AOE中,由勾股定理可得;8EO cm,在Rt①COF中,由勾股定理可得:6OF===cm,①EF=OF+OE=8+6=14cm.当弦AB和CD在圆心同侧时,如图2,过点O作OF①CD,垂足为F,交AB于点E,连接OA,OC,①AB①CD,①OE①AB,①AB=12cm,CD=16cm,①AE=6cm,CF=8cm,①OA=OC=5cm,在Rt①AOE中,由勾股定理可得:2222=-=-=cm,1068EO OA AE在Rt①COF中,由勾股定理可得:2222=-=-=cm,OF OC CF1086①EF=OE﹣OF=8﹣6=2cm;故选C.4.(2022·全国九年级课时练习)如图,在ABC中,10,8,6===,经过AB AC BC点C且与边AB相切的动圆与,CB CA分别相交于点E,F,则线段EF长度的最小值是()A.42B.4.75C.5D.4.8【答案】D【分析】设EF的中点为O,①O与AB的切点为D,连接OD,连接CO,CD,则有OD①AB,由勾股定理逆定理知,ABC是直角三角形,OC+OD=EF,而OC+OD≥CD,只有当点O在CD上时,OC+OD=EF有最小值为CD的长,即当点O在直角三角形ABC的斜边AB的高上CD时,EF=CD有最小值,由直角三角形的面积公式知求出CD的长即可.【详解】解:设EF的中点为O,①O与AB的切点为D,连接OD,连接CO,CD,①10,8,6===,AB AC BC①AC2+BC2=AB2,①ABC 是直角三角形,①ACB =90°, ①EF 是①O 的直径, ①OC +OD =EF , ①①O 与边AB 相切, ①OD ①AB , ①OC +OD ≥CD ,即当点O 在直角三角形ABC 的斜边AB 的高上时,OC +OD =EF 有最小值, 此时最小值为CD 的长, ①CD =864.810AC BC AB ⋅⨯==, ①EF 的最小值为4.8. 故选D .5.(2020·沭阳县怀文中学九年级月考)有下列说法:①直径是圆中最长的弦;①等弧所对的弦相等;①圆中90°的角所对的弦是直径;①相等的圆心角对的弧相等;①平分弦的直径垂直于弦;①任意三角形一定有一个外接圆.其中正确的有( ) A .2个 B .3个C .4个D .5个【答案】B 【分析】根据直径的定义对①进行判断;根据圆心角、弧、弦的关系对①①进行判断;根据圆周角定理对①进行判断;根据垂径定理对①进行判断;根据三角形外接圆的定义对①进行判断. 【详解】解:①直径是圆中最长的弦;故①正确,符合题意;①能够重合的弧叫做等弧,等弧所对的弦相等;故①正确,符合题意; ①圆中90°的圆周角所对的弦是直径;故①错误,不符合题意;①在同圆或等圆中,相等的圆心角所对的弧相等;故①错误,不符合题意; ①平分弦(弦不是直径)的直径垂直于弦;故①错误,不符合题意; ①任意三角形一定有一个外接圆;故①正确,符合题意; 其中正确的有①①①, 故选:B .6.(2022·厦门海沧实验中学九年级开学考试)四边形ABCD 中,ACD △是边长为6的等边三角形,ABC 是以AC 为斜边的直角三角形,则对角线BD 的长的取值范围是( ) A .33BD <≤+B .36BD << C .63BD <≤+D .3BD <≤【答案】C 【分析】由①ABC 是以AC 为斜边的直角三角形可知点B 在以AC 为直径的圆上,然后结合点到圆上点的距离求出对角线BD 长度的取值范围. 【详解】①①ABC 是以AC 为斜边的直角三角形, ①点B 在以AC 为直径的圆上,如图中①O ,连接OD 并延长,交①O 于点E 和点B ,①等边①ACD的边长为6,①AC=BE=6,OB=OE=OA=OC=3,OD①AC,①①COD=90°,①OD=2222CD OC-=-=,6333①BD=OD+OB=333+,△是边长为6的等边三角形,ACD当B与,A C重合时,BD最小6=①对角线BD的长度的取值范围为6<BD≤333+.故选:C.7.(2022·河南九年级期末)如图,在ABC∠=︒,30Rt△中,90ACB∠=︒,3ABCAB=,将ABCRt△绕直角顶点C顺时针旋转,当点A的对应点A'落在AB边上时,停止转动,则点B经过的路径长为__.3【分析】首先根据勾股定理计算出BC 长,再根据等边三角形的判定和性质计算出60ACA ∠'=,进而可得60BCB ∠'=,然后再根据弧长公式可得答案.【详解】解:30B ∠=,3AB =,①ACB=90° ①1322AC AB ==,60A ∠=,①22332BC AB AC =-=AC A C =',AA C ∴'是等边三角形, 60ACA ∴∠'=,60BCB ∴∠'=,∴弧长3360321802l ππ⋅⋅==, 故答案为:32π. 8.(2022·河南九年级期末)如图,在ABC 中,90ACB ∠=︒,60B ∠=︒,以AC 为直径做半圆交AB 于点D ,若1BC =,则图中阴影部分的面积为__.3π+【分析】连接OD ,CD ,根据圆周角定理得到90ADC ∠=︒,解直角三角形求得AC =CD OC OD =,32AD =,60COD ∠=︒,然后根据扇形的面积和三角形的面积公式即可得到结论. 【详解】解:连接OD ,CD ,在ABC 中,90ACB ∠=︒,60B ∠=︒, ①9030A B ∠=︒-∠=︒, 又①1BC =, ①22BA BC ==,①AC =AC 为O 的直径,90ADC ∴∠=︒,12OA AC =,又①30A ∠=︒,12CD AC ∴==①32AD , ①30A ∠=︒,260COD A ︒∴∠=∠=,∴阴影部分的面积()()ABC AOD AOD COD COD S S S S S S ∆∆=++--+△半圆扇形扇形 122ABC ACD COD S S S S ⎛⎫=+-+ ⎪⎝⎭△△半圆扇形22601111321222360222ππ⎛⋅ =⨯⋅-+⨯⨯⎪⎝⎭38π+=, 故答案为:38π+.9.(2022·河南九年级期末)如图,在ABC 中,AB BC =,以AB 为直径的①O 交BC 于点D ,交AC 于点F ,过点C 作//CE AB ,且CAD CAE ∠=∠. (1)求证:AE 是①O 的切线; (2)若5AB =,4=AD ,求CE 的长.【答案】(1)见解析;(2)2 【分析】(1)利用平行线的性质,圆的性质和等腰三角形的性质,证明AEC △和ADC 全等即可得到结论;(2)由勾股定理求出2CD =,根据全等三角形的性质可得出答案. 【详解】(1)证明:AB BC =,BAC BCA ∴∠=∠,//CE AB ,BAC ACE ∴∠=∠,ACB ACE ∴∠=∠,在AEC △和ADC 中,CAD CAE AC ACACB ACE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ADC AEC ASA ∴≅△△,ADC E ∴∠=∠, AB 是O 的直径,90ADB ADC ∴∠=∠=︒,90E ∴∠=︒,//AB CE ,180BAE E ∴∠+∠=︒,90BAE ∴∠=︒,AE ∴是O 的切线;(2)解:90ADB ∠=︒,5AB =,4=AD ,3BD ∴==,532CD BC BD ∴=-=-=,①ADC AEC ≅△△,2CE CD ∴==.10.(2022·安庆市第四中学九年级)如图,①O 是①ABC 的外接圆,FH 是①O 的切线,切点为F ,FH ①BC ,连结AF 交BC 于E ,①ABC 的平分线BD 交AF 于D ,连结BF .(1)求证:AF平分①BAC;(2)若EF=4,DE=3,求AD的长.【答案】(1)证明见详解;(2)AD =214.【分析】(1)连结OF,由FH是①O的切线,可得OF①FH,由FH∥BC,可得OF垂直平分BC,根据垂径定理可得BF FC=,根据圆周角性质可得①1=①2即可;(2)根据①ABC的平分线BD,可得①4=①3,可证①FDB=①FBD,可得BF=FD,再证①BFE①①AFB,根据性质可得BF AFFE BF=,再求BF=DF= 7,可求494FA=,即可求AD.【详解】(1)证明:连结OF,①FH是①O的切线,①OF①FH,①FH∥BC,①OF垂直平分BC,①BF FC=,①①1=①2,①AF平分①BAC,(2)解①①ABC 的平分线BD 交AF 于D , ①①4=①3,①1=①2,①①1+①4=①2+①3,①①5=①2,①①1+①4=①5+①3 ,①①FDB =①FBD ,①BF =FD ,在①BFE 和①AFB 中,①①5=①2=①1,①AFB =①EFB , ①①BFE ①①AFB , ①BF AF FE BF=, ①2BF FE FA =⋅, ①2BF FA FE= , ①BF =DF =EF +DE =7,①274944FA ==, ①AD=AF -DF =4974-=214.。
中考第一轮复习圆

中考第一轮复习圆第八单元Ⅰ.梳理知识1.圆的有关概念和基本性质(1)圆的有关概念(2)圆的基本性质①对称性②垂径定理及其逆定理③圆心角、弦、弧之间的关系④圆心角定理及其推论2.直线与圆的位置关系3.圆与圆的位置关系4.弧长、扇形的面积、圆锥的侧面积计算公式Ⅱ.典里例剖析例1、如图.PA和PB分别与⊙O相切于A,B两点,作直径AC,并延长交PB于点D.连结OP,CB.(1)求证:OP∥CB(2)若PA=12,DB:DC=2:1,求⊙O的半径.例2、现需测量一井盖(圆形)的直径,但只有一把角尺(尺的两边.互相垂直,一边有刻度,且两边长度都长于井盖半径).请配合图形、文字说明测量方案,写出测量的步骤(要求写出两种测量方案).例3、圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起,连结AC、BD.(1) 求证:△AOC≌△BOD;(2) 若OA=3cm,OC=1cm,求阴影部分的面积.例4、如图所示的曲边三角形可按下述方法作出:分别以正三角形的一个顶点为圆心,边长为半径,画弧使其经过另外两个顶点,然后檫去正三角形,三段圆弧所围成的图形就是一个曲边三角形。
如果一个曲边三角形的周长为π,求这个曲边三角形的面积.Ⅲ.同步测试一、选择题(每小题3分,共30分)1、在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( ) A.x 轴相交 B.y 轴相交 C.x 轴相切 D.y 轴相切2、如果两圆的半径分别为3和4,圆心距为7,那么这两个圆的位置关系是( ) A. 外切 B. 内切 C. 相交 D. 外离3、圆锥的侧面展开图是一个半圆,则这个圆锥的母线长与底面半径的比是( ) A. 2∶1 B.2π∶1 C.2∶1 D.3∶14、如图,扇子的圆心角为x °,余下扇形的圆心角为y °,x 与y 的比通常按黄金比来设计,这样的扇子外形较美观。
若取黄金比为0.6,则x 为( ) A .216 B .135 C .120 D .1085、如果圆锥的底面半径为3cm ,母线长为4cm ,那么它的侧面积等于( )A.24πcm 2B.12πcm 2C.12cm 2D.6πcm 2 6、一个圆锥的底面半径为23,母线长为6,则此圆锥侧面展开图的圆心角是( B ) A .180° B .150° C .120° D .90° 7、如图,正方形的变长为 a ,以各边为直径在正方形内画半圆,则阴影部分的面积为( ) A.4πa 2-21a 2 B.2πa 2-a 2 C.a 2-4πa 2 D.πa 2-a 2(第7题图) (第9题图) (第10题图)8、小华想用一个圆心角为120°、半径为6cm 的扇形做一个圆锥的侧面(接缝忽略不计),则做成的圆锥底面半径为( )A .4cm B.3cm C.2cm D.1cm 9、如图,A 、B 是⊙O 上的两点,AC 是⊙O 的切线,∠B =70°,则∠BAC 等于( ). A. 70° B. 35° C. 20° D. 10°10、如图,PA 、PB 是⊙O 的切线,切点分别为A 、B ,点C 在⊙O 上,如果∠P=50°, 那么∠ACB 等于( )OAB CBA ·OA.40°B.50°C.65°D.130°二、填空题(每小题3分,共24分)11、如图,AB 为⊙O 的直径,弦AC=4cm ,BC=3cm ,CD ⊥AB ,垂足为D ,那么CD 的长为____cm .(第10题图) (第12题图) (第16题图) 12、如图,A 、B 、C 是⊙O 上的三个点,当BC 平分∠ABO 时,能得出结论:(任写一个).13、已知⊙O 1和⊙O 2相外切,且圆心距为10c m ,若⊙O 1半径为3c m ,则⊙O 2的半径为__________c m.14、一圆锥的母线长为6cm ,它的侧面展开图的圆心角为120°,则这个圆锥的侧面积为________2cm .15、已知⊙O 1的半径为6cm ,⊙O 2的半径为2cm ,O 1O 2=8cm ,那么这两圆的位置关系是 . 16、如图,一把纸折扇完全打开后,外测两竹条AB 和AC 的夹角为120° ,AB 长为25cm ,贴纸部分....的宽BD 为17cm ,则贴纸部分的面积为 cm(结果用π表示) 17、某学校需修建一个圆心角为60°,半径为12米的扇形投掷场地,则该扇形场地的面积约为_____________米2(结果保留π).18、在△ABC 中,∠C=90°,AC=12,BC=5,现在AC 为轴旋转一周得到一个圆锥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
圆的有关概念
1. 圆上各点到圆心的距离都等于 .
2. 圆是 对称图形,任何一条直径所在的直线都是它的 ;圆又 是 对称图形, 是它的对称中心.
3. 垂直于弦的直径平分 ,并且平分 ;平分弦(不是直径)的 垂直于弦,并且平分 .
4. 在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量 ,那么它们所对应的其余各组量都分别 .
5. 同弧或等弧所对的圆周角 ,都等于它所对的圆心角的 .
6. 直径所对的圆周角是 ,90°所对的弦是 . 练习题 一、选择题
1.如图,A B 是⊙O 的直径,点D 在A B 的延长线上,D C 切⊙O 于C ,若
25A =
∠.
则D ∠等于( ) A . 20 B . 30 C . 40 D . 50
2.如图,⊙O 的半径OA =5,以A 为圆心,OA 为半径的弧交⊙O 于B 、C 两点,则BC 等于( ). A. 35 B. 25 C. 32
5 D. 8
3.AB 是⊙O 的直径,CD 为弦,AB CD ⊥于E ,则下列结论中不.成立的是( ) A.∠A ﹦∠D B.CE ﹦D E C.∠ACB ﹦90°
D .C
E ﹦BD
4.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,∠CDB =30°,⊙O 的半径为3cm ,则圆心O 到弦CD 的距离为( ) A .3
2 cm
B .3 cm
C .3 3 cm
D .6cm
二、填空题
1.如图,将半径为2cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕A B 的长为 __cm .
2.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为1cm 2
,则该半圆的直径为____
3.如图,AB 是⊙O 的直径, 点D 在⊙O 上,∠AOD =130°,BC
∥OD 交⊙O 于C ,则∠A = °.
A E
O
B
D
A
B
4.如图,四边形ABCD 是⊙O 的内接正方形,点P 是劣弧CD 上不同于点C 的任意一点,则∠BPC 的度数是 .
5.如图,AB 是⊙O 直径,且AB =4cm ,弦CD ⊥AB ,∠COB =45°,则CD 为 cm .
6.如图,△ABC 内接于⊙O ,AC 是⊙O 的直径,∠ACB =40°,点D 是弧BAC 上一点,则∠D 的度数是______.
7.如图,CD 是⊙O 的直径,弦AB ⊥CD 于点H ,若∠D =30°,CH =1cm ,则AB = cm .
A
C
D O
B
C
D。
