解三角形应用举例 (共33张PPT)
合集下载
解三角形的实际应用举例

AB sin CAB 15 sin15 BC sin120 sin ACB
6 2 sin15 4
5 6 BC ( 3 1) 4.48(海里) 2
(1)解决实际应用问题的关键思想方法是把实际问题转化为 数学问题,即数学建模思想。 (2)解决实际应用问题的步骤
(1)设A到P的距离为xkm,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离(结果精确到0.01km).
a
P B C
D A
分析
(1)PA,PB,PC长度之间的关系可以通过收到信号的先后时
间建立起来. (2)作PD⊥a,垂足为D,要求PD的长,只需要求出PA的长和cos∠APD, 即cos∠PAB的值.由题意,PA-PB,PC-PB都是定值,因此,只需分别在 △PAB和△PAC中,求出cos∠PAB, cos∠PAC的表达式,建立方程即 可.
=3.571 ∴BC≈1.89(m). 答:顶杆BC约长1.89m.
例2.如图,两点C,D与烟囱底部在同一水平直线上,在点C1,D1利
用高1.5m的测角仪器, 测得烟囱的仰角分别是 =450和 =600, CD间的距离是12m.求烟囱的高AB (结果精确到0.01m). B
C1 C
D1 D
(18 2 6)(m)
从而 A1 B 因此
2 BC1 18 3 19.732(m) 2 AB A1B AA1 19.732 1.5 21.23(m)
例3:如图是曲柄连杆机构的示意图,当曲柄CB绕点C旋转时,通
过连杆AB的传递,活塞作直线往复运动.当曲柄在CB0位置时,曲 柄和连杆成一条直线,连杆的端点A在A处.设连杆AB长为l mm,曲 柄CB长为r mm,l>r. (1)当曲柄自CB0按顺时针方向旋转角为θ时,其中0O≤θ<360O, 求活塞移动的距离(即连杆的端点A移动的距离A0A); (2)当l =340mm, r =85mm,θ=80O时,求A0A的长(结果精确到1mm).
解三角形的实际应用举例

第二章 解三角形
(2)由正弦定理得 AC=sin[180°20-sin((3405°°++4650°°+)60°)] =20ssiinn4150°5°=20sisnin4575°° =10(1+ 3)(米), BC=sin[180°-(206s0i°n 4+5°30°+45°)] =20sisnin4455°°=20(米).
栏目 导引
第二章 解三角形
测量高度问题 如图,一辆汽车在一条水平的公路上向 正西行驶,到 A 处时测得公路北侧一山顶 D 在 西偏北 30°的方向上,行驶 600 m 后到达 B 处, 测得此山顶在西偏北 75°的方向上,仰角为 30°,则此山的 高度 CD=________m.
栏目 导引
第二章 解三角形
栏目 导引
第二章 解三角形
若 P 在 Q 的北偏东 44°,则 Q 在 P 的( )
A.东偏北 46°
B.东偏北 44°
C.南偏西 44°
D.西偏南 44°
解析:选 C.如图,因为 P 在 Q 的北偏东 44°,则 Q 在 P 的南 偏西 44°.
栏目 导引
第二章 解三角形
A,B 两点间有一小山,选定能直接到达点 A,B 的点 C, 测得 AC=60 m,BC=160 m,∠ACB=60°,则 A,B 两点间 的距离为________m. 解析:在△ABC 中,由余弦定理得 AB2=AC2+BC2-2·AC·BC·cos 60° =602+1602-2×60×160cos 60°=196 00, 所以 AB=140 m,即 A、B 两点间的距离为 140 m. 答案:140
栏目 导引
第二章 解三角形
1.(1)在 200 m 高的山顶上,测得山下一塔顶
解三角形的实际应用举例ppt

A
(1) 已知三边 , 求三个角;
A
B
C
BCຫໍສະໝຸດ (2) 已知两边和它们的夹角,
(2) 已知两边和一边对角, 求其它元素。
A C
求其它元素。
A C
B
B
补充:我军有A、B两个小岛相距10海里, 敌军在C岛,从A岛望C岛和B岛成60°的视 角,从B岛望C岛和A岛成75°的视角,为 提高炮弹命中率,须计算B岛和C岛间的距 离,请你算算看。
0
A
6 2 0
0
D B
0
1 . 95 m
1 . 95
1 . 40
2
2 1 . 95 1 . 40 cos 66 2 0
=3.571 ∴BC≈1.89(m). 答:顶杆BC约长1.89m.
练1.如图,一艘船以32海里/时的 速度向正北航行,在A处看灯塔S 在船的北偏东200, 30分钟后航行 到B处,在B处看灯塔S在船的北 偏东650方向上,求灯塔S和B处的 距离.(保留到0.1) 解:AB=16,由正弦定理知:
数学结论 解三角形问题
谢谢
再见!
解三角形问题是三角学的基本问题之一。什 我国古代很早就有测量方面的知识,公元 解三角形的方法在度量工件、测量距离和高 么是三角学?三角学来自希腊文“三角形”和 一世纪的《周髀算经》里,已有关于平面测量 度及工程建筑等生产实际中,有广泛的应用, “测量”。最初的理解是解三角形的计算,后 的记载,公元三世纪, 我国数学家刘徽在计 在物理学中,有关向量的计算也要用到解三角 来,三角学才被看作包括三角函数和解三角形 算圆内接正六边形、正十二边形的边长时,就 形的方法。 两部分内容的一门数学分学科。 已经取得了某些特殊角的正弦……
(1) 已知三边 , 求三个角;
A
B
C
BCຫໍສະໝຸດ (2) 已知两边和它们的夹角,
(2) 已知两边和一边对角, 求其它元素。
A C
求其它元素。
A C
B
B
补充:我军有A、B两个小岛相距10海里, 敌军在C岛,从A岛望C岛和B岛成60°的视 角,从B岛望C岛和A岛成75°的视角,为 提高炮弹命中率,须计算B岛和C岛间的距 离,请你算算看。
0
A
6 2 0
0
D B
0
1 . 95 m
1 . 95
1 . 40
2
2 1 . 95 1 . 40 cos 66 2 0
=3.571 ∴BC≈1.89(m). 答:顶杆BC约长1.89m.
练1.如图,一艘船以32海里/时的 速度向正北航行,在A处看灯塔S 在船的北偏东200, 30分钟后航行 到B处,在B处看灯塔S在船的北 偏东650方向上,求灯塔S和B处的 距离.(保留到0.1) 解:AB=16,由正弦定理知:
数学结论 解三角形问题
谢谢
再见!
解三角形问题是三角学的基本问题之一。什 我国古代很早就有测量方面的知识,公元 解三角形的方法在度量工件、测量距离和高 么是三角学?三角学来自希腊文“三角形”和 一世纪的《周髀算经》里,已有关于平面测量 度及工程建筑等生产实际中,有广泛的应用, “测量”。最初的理解是解三角形的计算,后 的记载,公元三世纪, 我国数学家刘徽在计 在物理学中,有关向量的计算也要用到解三角 来,三角学才被看作包括三角函数和解三角形 算圆内接正六边形、正十二边形的边长时,就 形的方法。 两部分内容的一门数学分学科。 已经取得了某些特殊角的正弦……
解三角形的实际应用举例—高度、角度问题 课件

先在△ABC中, 根据正弦定理求得 AC.再在△ACD中求 CD即可.
【变式练习】 3.5 m长的木棒斜靠在石堤旁,棒的一端在离
堤足1.2 m的地面上,另一端在沿堤上2.8 m的地 方,求堤对地面的倾斜角α. (精确到0.01°)
解:棒、石堤及地面构成一钝角三角形,其钝角大小为 180°-α. 由余弦定理得, cos(180°-α)= 1.22 + 2.82 - 3.52
113.15,
根据正弦定理,
BC sinCAB
= AC , sinABC
sinCAB=
BC
sin ABC AC
=
54.0sin137° 113.15
0.325
5,
所以,∠CAB = 1.
答:此船应该沿北偏东56.0°的方向航行, 需要航行113.15n mile.
解:在△ABC中,∠A=15°, ∠C= 25°-15°=10°. 根据正弦定理,
BC = AB , sinA sinC
正确转化为 数学模型
BC=
AB sin sin C
A
=
5 sin 15 sin10
7.452
(4 km)
CD=BC×tan∠DBC≈BC×tan8°≈1 047(m).
答:山的高约为1 047米.
把测量数据代入上式,得
BD = 27.3cos501' sin 5440' sin(5440' 501')
.
=
27.3cos501' sin sin 439'
5440'
177.(4 m)
CD=BD-BC≈177.4-27.3≈150(m).
答:山的高度约为150米.
【变式练习】 3.5 m长的木棒斜靠在石堤旁,棒的一端在离
堤足1.2 m的地面上,另一端在沿堤上2.8 m的地 方,求堤对地面的倾斜角α. (精确到0.01°)
解:棒、石堤及地面构成一钝角三角形,其钝角大小为 180°-α. 由余弦定理得, cos(180°-α)= 1.22 + 2.82 - 3.52
113.15,
根据正弦定理,
BC sinCAB
= AC , sinABC
sinCAB=
BC
sin ABC AC
=
54.0sin137° 113.15
0.325
5,
所以,∠CAB = 1.
答:此船应该沿北偏东56.0°的方向航行, 需要航行113.15n mile.
解:在△ABC中,∠A=15°, ∠C= 25°-15°=10°. 根据正弦定理,
BC = AB , sinA sinC
正确转化为 数学模型
BC=
AB sin sin C
A
=
5 sin 15 sin10
7.452
(4 km)
CD=BC×tan∠DBC≈BC×tan8°≈1 047(m).
答:山的高约为1 047米.
把测量数据代入上式,得
BD = 27.3cos501' sin 5440' sin(5440' 501')
.
=
27.3cos501' sin sin 439'
5440'
177.(4 m)
CD=BD-BC≈177.4-27.3≈150(m).
答:山的高度约为150米.
北师大版九年级上册 4.6 利用相似三角形测高 (共33张PPT)-精品PPT

B
C
解:如图:过点 D 作 DE∥BC,交 AB 于点 E,
∴ DE = CB = 9.6 m,BE = CD = 2 m,
∵ 在同一时刻物高与影长成正比例,
∴ EA : ED=1 : 1.2,
∴ AE = 8 m,
∴ AB = AE + EB = 8 + 2 = 10 (m),
∴ 学校旗杆的高度为 10 m.
可在地面上竖一根竹竿 DE,
测量出 DE 的长以及 DE 和 AB
在同一时刻下地面上的影长即
可,则下面能用来求AB长的等
式是
(C)
A.A B E F DE BC
C.A B B C DE EF
B.A B D E EF BC
D.A B A C DE DF
2. 如图,九年级某班数学兴趣小组的同学想利用所学 数学知识测量学校旗杆的高度,当身高 1.6 米的楚 阳同学站在 C 处时,他头顶端的影子正好与旗杆 顶端的影子重合,同一时刻,其他成员测得 AC = 2 米,AB = 10 米,则旗杆的高度是___8___米.
试一试:
如图是小明设计用手电来测量某古城墙高度的
示意图,点 P 处放一水平的平面镜,光线从点 A出
发经平面镜反射后,刚好射到古城墙的顶端 C 处,
已知 AB = 2 米,且测得 BP = 3 米,DP = 12 米,那
么该古城墙的高度是
( B)
A. 6米 B. 8米 C. 18米 D. 24米
归纳总结
∴ BO?OA的O长A , EF FD
∴ BOOAEF2012 FD 3
=134 (m). 因此金字塔的高度为 134 m.
归纳:
测高方法一: 测量不能到达顶部的物体的高度,可以用“在
解直角三角形(共30张)PPT课件

比例性质应用
利用相似三角形中对应边 之间的比例关系进行计算。
实际应用举例
测量问题
利用相似三角形原理解决 测量中的实际问题,如测 量建筑物高度、河宽等。
航海问题
在航海中,利用相似三角 形原理解决船只定位、航 向确定等问题。
物理问题
在物理实验中,利用相似 三角形原理解决光学、力 学等问题,如光的折射、 力的合成与分解等。
利用相似三角形求边长
通过已知边长和相似比,可以求出未知边长。
利用相似三角形求角度
通过已知角度和相似关系,可以求出未知角度。
利用相似三角形求面积
通过已知面积和相似比,可以求出未知面积。
相似比计算方法和技巧
01
02
03
直接计算法
根据已知条件直接计算相 似比。
间接计算法
通过引入辅助线或构造特 殊图形来计算相似比。
解直角三角形(共30张)PPT课 件
目录
• 直角三角形基本概念与性质 • 解直角三角形方法论述 • 三角函数在解直角三角形中应用 • 相似三角形在解直角三角形中作用
目录
• 复杂图形中解直角三角形策略探讨 • 拓展延伸:非直角三角形解法探讨
01
直角三角形基本概念与性 质
直角三角形定义及特点
有一个角为90度的三角形称为直角三角形。
案例三
在三角形中解直角三角形问题。 通过作高线构造直角三角形,并
结合相似性质进行求解。
总结归纳与提高建议
总结归纳
在复杂图形中解直角三角形的关键在于构造直角三角形并利用 已知条件进行推理和计算。通过添加辅助线、利用相似性质和 三角函数关系等方法,可以有效地解决这类问题。
提高建议
为了更好地掌握解直角三角形的技巧和方法,建议多做相关练 习题并总结归纳经验。同时,也可以学习一些高级的数学知识 和技巧,如三角函数恒等式、极坐标等,以便更好地应对复杂 的数学问题。
高中数学解三角形ppt课件

证明几何定理
如勾股定理、正弦定理、余弦定理等 ,可以通过面积公式进行证明
计算三角形的内角和
利用面积公式和三角形内角和定理, 可以求出三角形的内角和
面积公式在物理问题中的应用
1 2
计算物体的受力面积
在物理学中,经常需要计算物体在某个方向上的 投影面积或受力面积,可以通过面积公式进行计 算
计算物体的体积和表面积
02 余弦定理
在任意三角形中,任何一边的平方等于其他两边 平方的和减去这两边与它们夹角的余弦的积的两 倍。
03 三角形的面积公式
S=1/2absinC,其中a、b为两边长,C为两边夹 角。
02
正弦定理及其应用
正弦定理的推导与证明
推导过程
通过三角形的外接圆和正弦函数的定义,推导出正弦定理的表达式。
一些几何性质。
最值问题
通过解三角形的方法,可以求解一 些与三角形相关的最值问题,如最 大面积、最小周长等。
存在性问题
在数学竞赛中,有时需要判断满足 某些条件的三角形是否存在,这可 以通过解三角形的方法来实现。
THANKS
感谢观看
对于一些规则或不规则的物体,可以通过计算其 各个面的面积,进而求出物体的体积和表面积
3
解决光学问题
在光学中,经常需要计算光线通过某个形状的面 积或光斑的大小,可以通过面积公式进行求解
05
解三角形综合应用举例
解直角三角形问题举例
已知两边求角度
通过正弦、余弦定理求解 直角三角形中的角度。
三角形的面积
解决三角形中的边长问题
利用正弦定理求出三角形中的未知边长。
正弦定理在物理问题中的应用
解决力学问题
在力学中,正弦定理可用于解决 涉及三角形的问题,如力的合成 与分解等。
解三角形应用举例
B
例4:如图,在山顶铁塔上B处测得地面上一 点A的俯角,在塔底C处测得A处的俯角.已 知铁塔BC部分的高为27.3米,求出山高 CD.
例5:一辆汽车在一条水平的公路上向正 东行驶,到A处时测得公路南侧远处一山 顶D在东偏南15°的方向上,行驶5KM后 到达B处,测得此山顶在东偏南25°的方 向上,仰角为8° ,求此山的高度CD.
(1)已知a=14.8cm,c=23.5cm,B=148.5° (2)已知B=62.7°C=65.8° ,b=3.16cm; (3)已知三边的长分别为 a=41.4cm,b=27.3cm,c=38.7cm.
例8:在某市进行城市环境建设中,要把 一个三角形的区域改造城市内公园,经 过测量得到这个三角形区域的三条边长 分别为68m,88m,127m,这个区域的面 积是多少? (精确到0.1cm2)
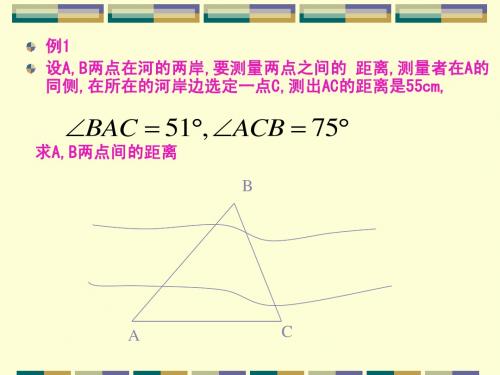
例1 设A,B两点在河的两岸,要测量两点之间的 距离,测量者在A的 同侧,在所在的河岸边选定一点C,测出AC的距离是55cm,
BAC 51, ACB 75
求A,B两点间的距离
B
A
C
例 2 如图A,B两点都在河的对岸(不可到达),设 计一种测量A,B两点距离的方法
A B
例3 : AB是底部B不可到达的一个建筑物,A 为建筑物的最高点,设计一种测量建筑物高 度AB的方法. A
例6:如图一艘海轮从A出发,沿北偏东75°的方 向航行67.5海里后到达海岛B,然后从B出发,沿 北偏东32°的方向航向54海里后到达海岛C. 如果下次航行直接从A出发到达C,此船应该沿 怎样的方向航行,需要航行多少距离?,根据下列条件,求三角 形的面积S(精确到0.1cm2)
解三角形应用举例

3:某人在塔的正东沿着南偏 600的方向前进40米后,看见 西 塔在东北方向,若沿途测得塔 300 ,求塔高为多 的最大仰角为 米?
4:已知在河的一侧可测有关 的距离,以及观测点及河对面 测量目标M和N的有关角度, 请设计测量对岸目标M和N之 间距离的方案,并用有关公式 给出计算步骤。
Hale Waihona Puke 本节小结: 1:对于平面图形,解三角形的关键在于确定三 角关系,选择恰当工具进行合理运算与转化。 2:对于空间图形,解三角形的关键在于确定空 间关系,建立空间的架构,进而确立已未知的 转化路径。 3:注意正余弦定理与均值定理等知识点的综合 运用。 4:注意生活中一些常见的角的表述及其意义。 5:注意建模类问题的训练,及其解答与表述。
解三角形应用举例
银川一中 蔡炜
1:为了竖一块广告牌,要制造三 角形支架,三角形支架如图所示: 0 60 要求∠ACB= BC的长度大于1 米,且AC比AB长0.5米,为了使 广告牌稳固,要求AC的长越短越 好,求AC最短为多少米?AC最 短时BC的长为多少米?
2:已知海军在海岸A处发现北偏东 0 45 方向距离A( 3 -1)Km的B处有一 0 艘敌舰,在A北偏西 75 方向距A 2Km 处有我军一驱逐舰奉命以 10 3 的 速度追截敌舰,此时敌舰以10的速度 0 从B处向北偏东30 方向逃窜,问驱逐 舰沿什么方向能最快追上敌舰?
解三角形(正弦定理余弦定理三角形面积公式)课件

反射定律
当光线遇到平面镜时,会产生反射现象。通过解三角形的方法可以计算入射角和反射角的关系,从而解释反射现 象。
建筑学中的角度计算
确定建筑物的角度
在建筑设计中,需要计算建筑物与水平面之间的角度,以确保建筑物的稳定性。利用解三角形的方法 可以计算出建筑物所需的倾斜角度。
测量建筑物的高度
通过观测建筑物与水平面之间的角度,利用解三角形的方法可以计算出建筑物的高度。
将三角形的三边长度转化为面积的表 达式,便于计算。
面积公式的应用
01
解决实际问题
利用三角形面积公式解决实际 问题,如土地测量、建筑规划
等。
02
数学竞赛解题
在数学竞赛中,三角形面积公 式是解决几何问题的重要工具
之一。
03
数学建模
在数学建模中,三角形面积公 式可以用于描述和解决现实生 活中的问题,如最优分割等。
详细描述
其中一种常见的证明方法是利用三角形的外接圆性质,通过相似三角形和勾股定 理进行推导。此外,还可以利用三角函数的加法定理、三角形的面积公式等其他 方法进行证明。掌握多种证明方法有助于加深对正弦定理的理解和应用。
02
余弦定理
定义与性质
总结词
余弦定理是三角形中一个重要的 定理,它描述了三角形各边与其 所对的角之间的关系。
应用场景
01
总结词
02
详细描述
正弦定理在解决三角形问题时非常有用,特别是在已知两边及夹角、 已知两角及夹边等情况下求解第三边。
通过正弦定理,我们可以解决各种与三角形相关的问题,如计算三角 形的面积、判断三角形的形状、解决几何作图问题等。它是三角函数 和几何学中非常重要的定理之一。
证明方法
总结词
当光线遇到平面镜时,会产生反射现象。通过解三角形的方法可以计算入射角和反射角的关系,从而解释反射现 象。
建筑学中的角度计算
确定建筑物的角度
在建筑设计中,需要计算建筑物与水平面之间的角度,以确保建筑物的稳定性。利用解三角形的方法 可以计算出建筑物所需的倾斜角度。
测量建筑物的高度
通过观测建筑物与水平面之间的角度,利用解三角形的方法可以计算出建筑物的高度。
将三角形的三边长度转化为面积的表 达式,便于计算。
面积公式的应用
01
解决实际问题
利用三角形面积公式解决实际 问题,如土地测量、建筑规划
等。
02
数学竞赛解题
在数学竞赛中,三角形面积公 式是解决几何问题的重要工具
之一。
03
数学建模
在数学建模中,三角形面积公 式可以用于描述和解决现实生 活中的问题,如最优分割等。
详细描述
其中一种常见的证明方法是利用三角形的外接圆性质,通过相似三角形和勾股定 理进行推导。此外,还可以利用三角函数的加法定理、三角形的面积公式等其他 方法进行证明。掌握多种证明方法有助于加深对正弦定理的理解和应用。
02
余弦定理
定义与性质
总结词
余弦定理是三角形中一个重要的 定理,它描述了三角形各边与其 所对的角之间的关系。
应用场景
01
总结词
02
详细描述
正弦定理在解决三角形问题时非常有用,特别是在已知两边及夹角、 已知两角及夹边等情况下求解第三边。
通过正弦定理,我们可以解决各种与三角形相关的问题,如计算三角 形的面积、判断三角形的形状、解决几何作图问题等。它是三角函数 和几何学中非常重要的定理之一。
证明方法
总结词
解三角形-PPT课件

2023最新整理收集 do something
本 章 优 化 总 结
本章优化总结
知识体系网络
专题探究精讲
知识体系网络
专题探究精讲
判断三角形形状 判断三角形的形状,一般有以下两种途径: (1)将已知条件统一化成边的关系,用代数方法 求解; (2)将已知条件统一化成角的关系,用三角方法 求解. 在解三角形时的常用结论有:
【解】 (1)依题意,PA-PB=1.5×8=12 (km), PC-PB=1.5×20=30 (km). 因此 PB=(x-12) km,PC=(18+x) km. 在△PAB 中,AB=20 km, cos∠PAB=PA2+2PAAB·A2-B PB2=x2+2022-x·20x-122 =3x+ 5x32.
(1)设A到P的距离为x km,用x表示B、C到P 的距离,并求x的值; (2)求静止目标P到海防警戒线a的距离.(结果 精确到0.01 km)
【思路点拨】 (1)PA、PB、PC长度之间的关 系可以通过收到信号的先后时间建立起来; (2)作PD⊥a,垂足为D,要求PD的长,只需要 求出PA的长和cos∠APD,即cos∠PAB的 值.由题意,PA-PB,PC-PB都是定值,因 此,只需要分别在△PAB和△PAC中,求出 cos∠PAB,cos∠PAC的表达式,建立方程即可.
例4 如图所示,a是海面上一条南北方向的 海防警戒线,在a上点A处有一个水声监测点, 另两个监测点B、C分别在A的正东方向20 km 处和54 km处,某时刻,监测点B收到发自静 止目标P的一个声波,8 s后监测点A、20 s后 监测点C相继收到这一信号,在当时的气象条 件下,声波在水中的传播速度是1.5 km/s.
(1) 在 △ ABC 中 , ∠ A> ∠ B⇔ a>b ⇔ sinA>sinB ⇔
本 章 优 化 总 结
本章优化总结
知识体系网络
专题探究精讲
知识体系网络
专题探究精讲
判断三角形形状 判断三角形的形状,一般有以下两种途径: (1)将已知条件统一化成边的关系,用代数方法 求解; (2)将已知条件统一化成角的关系,用三角方法 求解. 在解三角形时的常用结论有:
【解】 (1)依题意,PA-PB=1.5×8=12 (km), PC-PB=1.5×20=30 (km). 因此 PB=(x-12) km,PC=(18+x) km. 在△PAB 中,AB=20 km, cos∠PAB=PA2+2PAAB·A2-B PB2=x2+2022-x·20x-122 =3x+ 5x32.
(1)设A到P的距离为x km,用x表示B、C到P 的距离,并求x的值; (2)求静止目标P到海防警戒线a的距离.(结果 精确到0.01 km)
【思路点拨】 (1)PA、PB、PC长度之间的关 系可以通过收到信号的先后时间建立起来; (2)作PD⊥a,垂足为D,要求PD的长,只需要 求出PA的长和cos∠APD,即cos∠PAB的 值.由题意,PA-PB,PC-PB都是定值,因 此,只需要分别在△PAB和△PAC中,求出 cos∠PAB,cos∠PAC的表达式,建立方程即可.
例4 如图所示,a是海面上一条南北方向的 海防警戒线,在a上点A处有一个水声监测点, 另两个监测点B、C分别在A的正东方向20 km 处和54 km处,某时刻,监测点B收到发自静 止目标P的一个声波,8 s后监测点A、20 s后 监测点C相继收到这一信号,在当时的气象条 件下,声波在水中的传播速度是1.5 km/s.
(1) 在 △ ABC 中 , ∠ A> ∠ B⇔ a>b ⇔ sinA>sinB ⇔
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
—[通· 一类]—
2. (2017· 湖北省七市(州)协作体联考)如图, 为了估测某塔的 高度,在同一水平面的 A,B 两点处进行测量,在点 A 处测得塔 顶 C 在西偏北 20° 的方向上,仰角为 60° ;在点 B 处测得塔顶 C 在东偏北 40° 的方向上,仰角为 30° .若 A,B 两点相距 130 m,则 塔的高度 CD=________m.
二、必明 1●个易误点 易混淆方位角与方向角概念: 方位角是指北方向与目标方向 线按顺时针之间的夹角, 而方向角是正北或正南方向线与目标方 向线所成的锐角.
考向一 测量距离问题[自主练透型]
[例 1] 如图所示,A,B 两点在一条河的两岸,测量者在 A 的同侧,且 B 点不可到达,要测出 AB 的距离,其方法在 A 所在 的岸边选定一点 C,可以测出 AC 的距离 m,再借助仪器,测出 ∠ACB=α,∠CAB=β,在△ABC 中,运用正弦定理就可求出 AB.若测出 AC=60 m,∠BAC=75° ,∠BCA=45° ,则 A,B 两 点间的距离为________m.
—[通· 一类]—
3.如图,位于 A 处的信息中心获悉:在其正东方向相距 40 海里的 B 处有一艘渔船遇险, 在原地等待营救. 信息中心立即把 消息告知在其南偏西 30° 、相距 20 海里的 C 处的乙船,现乙船 朝北偏东 θ 的方向沿直线 CB 前往 B 处救援,求 cos θ 的值.
解析:在△ABC 中,AB=40,AC=20,∠BAC=120° ,由 余弦定理得,BC2=AB2+AC2-2AB· AC· cos 120° =2 800⇒BC= 20 7. AB BC AB 由正弦定理, 得 = ⇒sin∠ACB=BC· sin∠ sin∠ACB sin∠BAC 21 BAC= 7 . 2 7 由∠BAC=120° ,知∠ACB 为锐角,则 cos∠ACB= 7 . 由 θ=∠ACB+30° ,得 cos θ=cos(∠ACB+30° ) 21 =cos∠ACB cos 30° -sin∠ACBsin 30° = 14 .
解析:在△ABC 中,由余弦定理得 AB2=AC2+BC2-2AC· BCcos∠ACB, ∴AB2=4002+6002-2×400×600cos 60° =280 000. ∴AB=200 7(m). 即 A,B 两点间的距离为 200 7 m.
考向二 测量高度问题[互动讲练型] [例 2] (2015· 湖北卷)一辆汽车在一条水平的公路上向正西 行驶,到 A 处时测得公路北侧一山顶 D 在西偏北 30° 的方向上, 行驶 600 m 后到达 B 处,测得此山顶在西偏北 75° 的方向上,仰 角为 30° ,则此山的高度 CD=__________m.
解析:如图,设电视塔 AB 高为 x m,则在 Rt△ABC 中,由 ∠ACB=45° 得 BC=x.在 Rt△ABD 中, ∠ADB=30° , 则 BD= 3 x. 在△BDC 中,由余弦定理得, BD2=BC2+CD2-2BC· CD· cos 120° , 即( 3x)2=x2+402-2· x· 40· cos 120° , 即得 x=40,所以电视塔高为 40 m. 答案:40
[知识重温] 一、必记 4●个知识点 1.仰角和俯角
与目标视线同在一铅垂平面内的水平视线和目标视线的夹 角,目标视线在水平视线①______ 上方 时叫仰角,目标视线在水平视 线②______ 下方 时叫俯角.(如图所示)
2.方位角 一般指正北方向线顺时针到目标方向线的水平角, 如方位角 北偏东 45° 45° ,是指③__________ ,即东北方向. 3.坡角 坡面与④水平面 ______的夹角.(如图所示) 4.坡比 h 坡面的铅直高度与水平宽度之比,即 i= l =tanα(i 为坡比, α 为坡角).
—[通· 一类]— 1.
如图所示,要测量一水塘两侧 A,B 两点间的距离,其方法 先选定适当的位置 C,用经纬仪测出角 α,再分别测出 AC,BC 的 长 b , a , 则 可 求 出 A , B 两 点 间 的 距 离 . 即 AB = a2+b2-2abcos α.若测得 CA=400 m,CB=600 m,∠ACB= 60° ,试计算 AB 的长.
[解析] (1)依题意知,∠BAC=120° ,AB=12,AC=10×2 =20,∠BCA=α. 在△ABC 中,由余弦定理,得 BC2=AB2+AC2-2AB· AC· cos∠BAC =122+202-2×12×20×cos 120° =784, 解得 BC=28. BC 所以渔船甲的速度为 2 =14 海里/时.
解析:由已知∠ACB=180° -40° -60° =80° , 又 AC=BC,∴∠A=∠ABC=50° ,60° -50° =10° . ∴灯塔 A 位于灯塔 B 的北偏西 10° . 答案:北偏西 10°
6.要测量底部不能到达的电视塔 AB 的高度,在 C 点测得 塔顶 A 的仰角是 45° ,在 D 点测得塔顶 A 的仰角是 30° ,并测得 水平面上的∠ BCD = 120° , CD = 40 m ,则电视塔的高度为 ________ m.
(2)在△ABC 中,因为 AB=12,∠BAC=120° ,BC=28,∠ BCA=α, AB BC 由正弦定理,得sin α=sin 120° , 3 12× 2 ABsin 120° 3 3 即 sin α= = 28 = 14 . BC
—[悟· 技法]— 解决测量角度问题的注意事项 (1)明确方位角的含义. (2)分析题意,分清已知与所求,再根据题意正确画出示意 图,这是最关键、最重要的一步. (3)将实际问题转化为可用数学方法解决的问题后,注意正、 余弦定理的“联袂”使用.
—[悟· 技法]— 求解高度问题的注意事项 (1)在测量高度时,要理解仰角、俯角的概念,仰角和俯角 都是在同一铅垂面内,视线与水平线的夹角. (2)准确理解题意,分清已知条件与所求,画出示意图,转 化为解三角形问题. (3)运用正、余弦定理,有序地解相关的三角形,逐步求解 问题的答案,注意方程思想的运用.
2.如图,两座灯塔 A 和 B 与海岸观察站 C 的距离相等,灯 塔 A 在观察站南偏西 40° ,灯塔 B 在观察站南偏东 60° ,则灯塔 A 在灯塔 B 的( ) A.北偏东 10° B.北偏西 10° C.南偏东 80° D.南偏西 80°
解析:由条件及图可知,∠A=∠B=40° ,又∠BCD=60° , 所以∠CBD=30° ,所以∠DBA=10° ,因此灯塔 A 在灯塔 B 南偏 西 80° . 答案:D
[ 解析 ] 依题意,知∠ BAC = 30° ,∠ ABC = 105° . 在△ ABC 中,由∠ABC+∠BAC+∠ACB=180° ,所以∠ACB=45° .因为 AB BC AB=600 m,由正弦定理可得 sin 45° =sin 30° ,即 BC=300 2 m.在 Rt△BCD 中,因为∠CBD=30° ,BC=300 2 m,所以 tan CD 30° = BC ,所以 CD=100 6 m. [答案] 100 6
[解析] ∠ABC=180° -75° -45° =60° , AB AC 所以由正弦定理得,sin C=sin B, AC· sin C 60×sin 45° ∴AB= sin B = sin 60° =20 6(m). 即 A,B 两点间的距离为 20 6 m. [答案] 20 6
—[悟· 技法]— 测量问题中距离问题的解法 (1)选择合适的辅助测量点,构造三角形,将问题转化为求 某个三角形的边长问题. (2)根据已知条件,选择正弦定理或者余弦定理求解.
解析:在△BCD 中,∠CBD=180° -15° -30° =135° . 30 BC 由正弦定理得sin 30° =sin 135° ,解得 BC=15 2(m). 在 Rt△ABC 中, AB=BCtan∠ACB=15 2× 3=15 6(m). 答案:D
5.如图所示,已知两座灯塔 A 和 B 与 海洋观察站 C 的距离相等, 灯塔 A 在观察站 C 的北偏东 40° ,灯塔 B 在观察站 C 的南偏 东 60° , 则灯塔 A 在灯塔 B 的________方向.
3.一船向正北航行,看见正西方向相距 10 海里的两个灯塔 恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的 南偏西 60° ,另一灯塔在船的南偏西 75° ,则这艘船的速度是每 小时( ) A.5 海里 B.5 3海里 C.10 海里 D.10 3海里
解析:如图所示,依题意有∠BAC=60° ,∠BAD=75° ,所 以∠CAD=∠CDA=15° ,从而 CD=CA=10(海里), 在 Rt△ABC 中,得 AB=5(海里), 5 于是这艘船的速度是0.5=10(海里/时) 答案:C
4.如图,测量河对岸的塔高 AB 时可以选与塔底 B 在同一 水平面内的两个测点 C 与 D,测得∠BCD=15° ,∠BDC=30° , CD=30 m, 并在点 C 测得塔顶 A 的仰角为 60° , 则塔高 AB 等于 ( ) A.5 6 m B.15 3 m C.5 2 m D.15 6 m
h 解析:分析题意可知,设 CD=h,则 AD= ,BD= 3h, 3 在△ADB 中, ∠ADB=180° -20° -40° =120° , ∴由余弦定理 AB2 2 h = BD2 + AD2 - 2BD· AD· cos 120° ,可得 1302 = 3h2 + 3 - 2· 3 1 h h· · (-2),解得 h=10 39,故塔的高度为 10 39 m. 3 答案:10 39
[小题热身] 1.如图,设 A,B 两点在河的两岸,一测量者在 A 的同侧, 选定一点 C,测出 AC 的距离为 50 m,∠ACB=45° ,∠CAB= 105° ,则 A,B 两点的距离为( ) A.50 2 m B.50 3 m 25 2 C.25 2 m D. 2 m
解析:由正弦定理得 2 AC· sin∠ACB 50× 2 AB= = 1 =50Biblioteka 2(m). sin B 2 答案:A
