算法之多机调度问题
贪心法 多机调度问题

//多机调度问题/*贪心法求解多级调度问题的贪心策略师最长处理时间的作业优先,即把处理时间最长的作业分配给最先空闲的机器,这样就可以保证处理时间长的作业优先处理,从而在整体上获得尽可能短的时间。
按照最长处理时间作业优先的贪心测落,当m>n,时,只要将机器ide [0,ti)时间去见分配给作业j即可,当m<n时,首先将n个作业从大到小排序,然后依次顺序将作业分配给空闲的处理机算法伪代码将数组t[n]从大到小排序,对应的作业序号存储在数组p[n]中;将数组d[m]初始化为零3:for(i0;i<=m;i++)3.1:s[i]={p[i]}:将m个作业分配给m个机器3.2 d[i]=t[i];for(i=m+1;i<=n;i++)4.1 j=数组d[m]中最小值对应的下标;//j为最先空闲的机器序号4.2 s[j]=s[j]+{p[i]};//将作业分配给最先空闲的的机器j4.3 d[j]=d[j]+d[t];//机器j将在d[j]后空闲*/#include<iostream>using namespace std;void lowsort(int *t,int *p,int n)//将数组t[n]按从小到大的顺序排序,相应的任务编号数组p[n]也要随之改变{int index;for(int i=0;i<n;i++){index=i;for(int j=i+1;j<n;j++){if(t[index]<t[j])index=j;}if(index!=i){int temp;temp=t[index];t[index]=t[i];t[i]=temp;temp=p[i];p[i]=p[index];p[index]=temp;}}int find(int *d,int m){int min=d[0];int k;for(int i=0;i<m;i++){if(d[i]<min){min=d[i];k=i;}}return k;}void ajust(int *t,int *d,int *p,int *s,int n,int m){lowsort(t,p,n);for(int i=0;i<m;i++){d[m]=0;}for(i=0;i<m;i++){s[i]=p[i];cout<<"机器"<<i+1<<"做了任务"<<p[i]<<endl;d[i]=t[i];}for(i=m;i<n;i++){int j=find(d,m);//查找数组d[m]中最小值对应的下标s[j]=s[j]+p[i];cout<<"机器"<<j+1<<"做了任务"<<p[i]<<endl;d[j]=d[j]+t[i];}}void main()int n,m;cout<<"输入任务数量"<<endl;cin>>n;cout<<"输入机器个数"<<endl;cin>>m;int *t=new int [n];int *s=new int [n];int *d=new int [m];int *p=new int[n];cout<<"输入任务编号"<<endl;for(int k=0;k<n;k++)cin>>p[k];cout<<"每件任务所花费的时间"<<endl;for(int i=0;i<n;i++)cin>>t[i];ajust(t,d,p,s,n,m);}。
贪心算法---例题5.多机调度问题

cout<<"("<<x.first<<","<<x.second<<")"<<endl; } int timeTotal = 0; vector<int> timeOfMachine(n, 0); int pos = 0; //表示Job数组的下标 while(m--) {
int minPosition = min_element(timeOfMachine.begin(), timeOfMachine.end()) - timeOfMachine.begin(); timeOfMachine[minPosition] += Job[pos].second; cout<<"将作业"<<Job[pos].first<<"分配给机器"<<minPosition+1<<",用时"<<Job[pos].second; cout<<"机器"<<minPosition+1<<"目前总用时为"<<timeOfMachine[minPosition]<<endl; pos++; } return *max_element(timeOfMachine.begin(), timeOfMachine.end()); } int main() { cout<<"一共m个作业,请输入m: "; int m; cin>>m; cout<<"请输入每个作业的时间: "<<endl; vector<pair<int, int>> Job; int time; for(int i=0; i<m; i++) { cin>>time; Job.push_back(pair<int, int>(i+1, time)); } cout<<"指定n台机器,请输入n: "<<endl; int n; cin>>n; int timeTotal = JobSort(Job, n); cout<<"总用时为: "<<timeTotal<<endl; system("pause"); return 0; }
多级调度算法

多级调度算法什么是多级调度算法?多级调度算法(Multi-Level Feedback Queue,MLFQ)是一种操作系统中的进程调度算法。
它将进程队列分成多个级别,每个级别都有不同的时间片大小和优先级。
当一个进程被加入队列时,它被放置在最高优先级的队列中,如果它在该队列中运行了一段时间后仍未完成,则被降低到较低优先级的队列中继续运行。
这样可以使长时间运行的进程获得更多的CPU时间,并且能够保证短时间运行的进程能够快速响应用户请求。
多级调度算法的特点1. 多个队列:多级调度算法将进程队列分成多个级别,每个级别都有不同的时间片大小和优先级。
2. 时间片轮转:每个队列使用时间片轮转方式进行调度。
3. 优先级:每个队列都有自己的优先级,高优先级的队列会被更频繁地执行。
4. 抢占式:如果一个高优先级进程加入了队列,则当前正在执行的低优先级进程会被抢占。
5. 动态变化:根据当前系统负载情况动态改变各个队列之间切换所需的时间片大小。
多级调度算法的实现步骤1. 初始化队列:将所有进程按照优先级放入不同的队列中,每个队列都有自己的时间片大小。
2. 运行进程:从最高优先级队列开始运行进程,如果该进程在时间片内完成,则被移出队列,否则被降低到较低优先级的队列中继续运行。
3. 抢占式调度:如果一个高优先级进程加入了队列,则当前正在执行的低优先级进程会被抢占。
4. 动态变化:根据当前系统负载情况动态改变各个队列之间切换所需的时间片大小。
5. 结束进程:当一个进程完成或被杀死时,从相应的队列中移出该进程。
多级调度算法存在的问题1. 饥饿问题:如果系统中有大量长时间运行的高优先级进程,则低优先级进程可能会一直等待,导致饥饿问题。
2. 时间片大小选择问题:选择合适的时间片大小非常重要,如果时间片过小,则会导致频繁切换而浪费CPU资源;如果时间片过大,则会导致响应速度变慢。
3. 进程数目过多:当系统中存在大量进程时,多级调度算法的效率会降低。
算法设计之多机调度问题

《算法设计与分析》实训实验报告日期:2016年6月27日电子信息工程学院【问题描述】1、把作业按加工所用的时间从大到小排序2、如果作业数目比机器的数目少或相等,则直接把作业分配下去3、如果作业数目比机器的数目多,则每台机器上先分配一个作业【算法设计】运用贪心算法解决多机调度问题【算法实现】packagecom.test;importjava.io.BufferedReader;importjava.io.IOException;importjava.io.InputStreamReader;importjava.util.ArrayList;importjava.util.Scanner;public class Duojidiaodu {public static void main(String[] args) {// TODO Auto-generated method stubBufferedReaderbr=new BufferedReader(new InputStreamReader(System.in));try {System.out.println("请输入机器个数:");intjiqigeshu=Integer.parseInt(br.readLine());System.out.println("请输入作业个数:");intzuoyegeshu=Integer.parseInt(br.readLine());Start start=new Start(jiqigeshu, zuoyegeshu);//指明有几台机器以及几道作业start.show();//显示每台机器都有哪些作业} catch (IOException e) {// TODO Auto-generated catch blocke.printStackTrace();}finally{if(br!=null)try {br.close();} catch (IOException e) {// TODO Auto-generated catch blocke.printStackTrace();}}}}classJiqiManger{ArrayList<Jiqi> al=new ArrayList<Jiqi>();public void addjiqi(Jiqijiqi){this.al.add(jiqi);}publicJiqigetjiqi(int id){for(int i=0;i<this.al.size();i++){if(this.al.get(i).getId()==id){returnthis.al.get(i);}}return null;}}classJiqi{privateint id;privateArrayList<Zuoye> al;privateintzongshaoshi;publicJiqi(int id) {this.id=id;al=new ArrayList<Zuoye>();}publicintgetId(){return this.id;}public void addzuoye(Zuoyezuoye){this.al.add(zuoye);this.zongshaoshi+=zuoye.getHaoshi();}publicArrayList<Zuoye>getZuoye(){return this.al;}publicintgetZonghaoshi(){returnthis.zongshaoshi;}}classZuoyeManger{ArrayList<Zuoye>zuoye=new ArrayList<Zuoye>();public void addzuoye(Zuoyezuoye){this.zuoye.add(zuoye);}public void paixu(){Object[] temp=this.zuoye.toArray();for(int i=0;i<temp.length-1;i++)for(int j=i+1;j<temp.length;j++){if(((Zuoye)temp[i]).getHaoshi()<((Zuoye)temp[j]).getHaoshi()){Zuoyezuoye=(Zuoye)temp[i];temp[i]=temp[j];temp[j]=zuoye;}}this.zuoye.clear();for(int i=0;i<temp.length;i++)this.zuoye.add(((Zuoye)temp[i]));}publicZuoyegetZuoye(int index){returnthis.zuoye.get(index);}}classZuoye{privateint id;privateinthaoshi;publicZuoye(int id , inthaoshi ) {this.id=id;this.haoshi=haoshi;}publicintgetHaoshi(){returnthis.haoshi;}publicintgetId(){return this.id;}}class Start{privateJiqiMangerjiqiManger=null;privateZuoyeMangerzuoyeManger=null;privateintjiqigeshu,zuoyegeshu;public Start(intjiqigeshu , intzuoyegeshu) {jiqiManger=new JiqiManger();zuoyeManger=new ZuoyeManger();this.jiqigeshu=jiqigeshu;this.zuoyegeshu=zuoyegeshu;Jiqijiqi;Zuoyezuoye;for(int i=0;i<jiqigeshu;i++){jiqi=new Jiqi(i+1);jiqiManger.addjiqi(jiqi);}for(int i=0;i<zuoyegeshu;i++){inthaoshi;Scanner sc=new Scanner(System.in);System.out.println("请输入第"+(i+1)+"号作业的时间:");haoshi=sc.nextInt();zuoye=new Zuoye(i+1, haoshi);zuoyeManger.addzuoye(zuoye);}this.zuoyeManger.paixu();this.fenfa();}private voidfenfa(){int index=0;for(int i=0;i<this.jiqigeshu;i++){jiqiManger.getjiqi(i+1).addzuoye(zuoyeManger.getZuoye(index++));}while(index<this.zuoyegeshu){if(this.getJiqi()==null){System.out.println("对不起,没有机器可以分发作业!");break;}this.getJiqi().addzuoye(zuoyeManger.getZuoye(index++));}}privateJiqigetJiqi(){if(this.jiqiManger.getjiqi(1)==null)return null;int min=jiqiManger.getjiqi(1).getZonghaoshi();intminindex=1;for(int i=1;i<this.jiqigeshu;i++){if(jiqiManger.getjiqi(i+1).getZonghaoshi()<min){min=jiqiManger.getjiqi(i+1).getZonghaoshi();minindex=i+1;}}returnjiqiManger.getjiqi(minindex);}public void show(){ArrayList<Zuoye> al=null;for(int i=0;i<this.jiqigeshu;i++){al=jiqiManger.getjiqi(i+1).getZuoye();System.out.print(i+1+"号机器包含的作业有:{");for(int j=0;j<al.size();j++){if(j==(al.size()-1))System.out.println(al.get(j).getId()+"号作业}");elseSystem.out.print(al.get(j).getId()+"号作业,");}}}}【运行结果】。
贪心算法在多机调度问题中的应用

贪心算法在多机调度问题中的应用
贪心算法在多机调度问题中可以应用于任务调度和资源分配的问题。
在多机调度问题中,我们通常需要将一组任务分配到多台机器上,并优化某个指标(如任务完成时间的最小化、机器的负载均衡等)。
贪心算法在多机调度问题中的应用可以通过以下步骤进行:
1. 确定任务的排序方式:根据任务的一些特征,如任务的处理时间、优先级等,确定一种排序方式。
例如,可以按照任务的处理时间递增顺序进行排序。
2. 初始化机器的状态:在开始调度之前,需要初始化每台机器的状态,如设置机器的剩余处理时间、当前任务等。
3. 贪心选择:从排序后的任务列表中,依次选择任务进行分配。
通过贪心选择,选择当前能够使得指标最小化的任务,并将任务分配给剩余处理时间最短的机器。
4. 更新机器状态:根据分配给机器的任务,更新机器的状态,如更新剩余处理时间、当前任务等。
5. 重复步骤3和步骤4,直到所有任务被分配完毕。
贪心算法在多机调度问题中的应用的核心思想是每次选择局部最优解,并希望通过不断地选择局部最优解,最终得到全局最
优解。
然而,需要注意的是,贪心算法并不能保证一定能够得到全局最优解,因此需要根据具体的问题进行分析和验证。
多机调度问题贪心算法c语言

多机调度问题贪心算法c语言一、引言多机调度问题是指将一组作业分配给多台机器,使得完成所有作业的时间最短。
在实际生产中,多机调度问题是一个常见的优化问题。
贪心算法是解决多机调度问题的一种有效方法。
本文将介绍贪心算法在C语言中的应用。
二、问题描述假设有n个作业需要分配给m台机器进行加工处理,每个作业需要的时间不同,每台机器的处理速度也不同。
现在需要设计一个算法,将这些作业分配给这些机器进行加工处理,并使得完成所有作业所需时间最短。
三、贪心算法思路贪心算法是一种基于局部最优解来构造全局最优解的思想。
对于多机调度问题,我们可以采用以下贪心策略:1. 将所有作业按照所需时间从大到小排序;2. 将第一个作业分配给第一台机器;3. 对于剩余的作业,选择当前处理时间最短的那台机器进行分配;4. 重复步骤3直到所有作业都被分配完毕。
四、C语言实现下面是C语言实现多机调度问题贪心算法的代码:#include <stdio.h>#include <stdlib.h>#define MAX_JOB 1000#define MAX_MACHINE 1000int cmp(const void *a, const void *b) {return *(int *)b - *(int *)a;}int main() {int n, m, job[MAX_JOB], machine[MAX_MACHINE] = {0}; scanf("%d%d", &n, &m);for (int i = 0; i < n; i++) {scanf("%d", &job[i]);}qsort(job, n, sizeof(int), cmp);for (int i = 0; i < n; i++) {int min_time = machine[0], min_index = 0;for (int j = 1; j < m; j++) {if (machine[j] < min_time) { min_time = machine[j]; min_index = j;}}machine[min_index] += job[i]; }int max_time = machine[0];for (int i = 1; i < m; i++) {if (machine[i] > max_time) { max_time = machine[i];}}printf("%d\n", max_time);return 0;}五、代码解析1. 宏定义和头文件引入:```#define MAX_JOB 1000#define MAX_MACHINE 1000#include <stdio.h>#include <stdlib.h>```定义了最大作业数和最大机器数,并引入了标准输入输出库和标准库。
贪心算法—多机调度

贪心算法-多机调度一、问题描述设有n个独立的作业,由m台机器进行加工处理,作业i所需的处理时间为t(i)。
约定,任何作业可以在任何机器上加工处理,但未完成前不允许中断处理。
任何作业不能拆分成更小的子作业。
多机调度问题要求给出一种作业调度方案,使n个作业在尽可能短的时间内完成。
二、算法分析1当n<=m时,将机器i的【0~t(i)】时间分配给作业i即可。
2当n>m时,首先将n个作业按照时间从大到小排列。
然后照此顺序将作业分配给空闲的处理机即可。
3创建3个类:JobNode类,MachineNode类, MinHeap类分别用于作业信息,机器信息,对机器类型的堆处理三、代码#include<iostream>using namespace std;#define Max 15template <class Type>class MinHeap{public:MinHeap(int ms);~MinHeap();void Insert(const Type& x);void DeleteMin(Type& x);protected:void FilterDown();//自顶向下构造堆void FilterUp();//自底向上构造堆private:Type *heap;int length;};////////////////////////////////////////template <class Type>MinHeap<Type>::MinHeap(int m){heap=new Type[m+1];length=0;}////////////////////////////////////////template <class Type>void MinHeap<Type>::Insert(const Type& x) {heap[++length]=x;FilterUp();}////////////////////////////////////////template <class Type> template <class Type>void MinHeap<Type>::FilterUp(){//自底向上进行调整int i=length,j=i/2;//父节点的编号Type temp=heap[i];while(i>1){if(temp>=heap[j])break;//找到了相应的位置else{heap[i]=heap[j];i=j;j=i/2;}}heap[i]=temp;}////////////////////////////////////////template <class Type>void MinHeap<Type>::DeleteMin(Type &x){x=heap[1];heap[1]=heap[length];length--;FilterDown();}////////////////////////////////////////template <class Type>void MinHeap<Type>::FilterDown(){int i=1,j=i*2;Type temp=heap[i];while(j<=length){if(j<length && heap[j]>heap[j+1])j++;//如果左右子树都存在,找出最小者,用j标记if(temp<heap[j])break;//找到了相应的位置else{heap[i]=heap[j];i=j;j=2*i;}}heap[i]=temp;}////////////////////////////////////////template <class Type>MinHeap<Type>::~MinHeap(){delete[] heap;}////////////////////////////////////////class JobNode{friend void Greedy(JobNode *,int ,int);friend void main(void);public:operator int() const {return time;}int ID,time;};class MachineNode{friend void Greedy(JobNode *,int ,int); public:operator int() const {return avail;}int ID,avail;};void Sort(JobNode a[],int n){int i,j,k;JobNode tmp;for(i=1;i<n;i++){k=i;for(j=i+1;j<=n;j++){if(a[j].time<a[k].time) k=j;}if(k!=i){tmp=a[i];a[i]=a[k];a[k]=tmp;}}}void Greedy(JobNode a[],int n,int m){if(n<=m){cout<<"为每个作业分配一台机器."<<endl;return;}Sort(a,n);MinHeap<MachineNode>H(m);MachineNode x;for(int i=1;i<=m;i++){x.avail=0;x.ID=i;H.Insert(x);}for(i=n;i>=1;i--){H.DeleteMin(x);cout<<"\n将机器"<<x.ID<<"从"<<x.avail<<"到"<<(x.avail+a[i].time)<<"的时间段分配给作业"<<a[i].ID<<endl;x.avail+=a[i].time;H.Insert(x);}}void main(){int i;int job_cnt; //作业的数目float machine_cnt;//机器数目int Time_of_all=0;JobNode a[Max];//作业所需要的时间// MachineNode b[Max];cout<<"==========多机调度问题===========\n";cout<<"输入机器个数:";cin>>machine_cnt;cout<<"输入作业个数(小于15):";cin>>job_cnt;for(i=1;i<=job_cnt;i++){cout<<"\n请输入第"<<i<<"个作业处理时间:";cin>>a[i].time;a[i].ID=i;}Greedy(a,job_cnt,machine_cnt);}四、结果截图五.实验总结多机调度问题是生活中比较典型的例子,根据经验我们很好确定贪心算法的贪心标准,但是落实到编程,还是有点不够得心应手,还需要加强自己的编程能力。
多机调度问题的贪心算法实现(使用C语言)

多机调度问题的贪心算法实现(使用C语言)标题:多机调度问题的贪心算法实现(使用C语言)简介:多机调度问题是一个经典的组合优化问题,旨在将一组待处理的任务分配给多台计算机,使得任务完成时间最小化。
贪心算法是一种常用的解决该问题的方法,本文将介绍如何使用C语言实现贪心算法来解决多机调度问题。
引言:随着计算机技术的不断进步,我们面临的任务越来越多,如何有效地将任务分配给多台计算机成为一个重要的问题。
多机调度问题涉及到任务的分配、计算机资源的利用率以及任务完成时间的优化。
本文将通过贪心算法来解决这一问题,贪心算法通过每次选择局部最优解,最终得到一个全局最优解。
1. 多机调度问题的贪心算法概述1.1 贪心算法的基本思想1.2 多机调度问题的贪心策略选择1.3 贪心算法实现的步骤2. 多机调度问题的输入与输出2.1 输入:任务集合和计算机集合2.2 输出:任务分配结果和任务完成时间3. 多机调度问题的贪心算法实现3.1 任务排序3.2 计算机选择3.3 任务分配3.4 计算任务完成时间4. 多机调度问题的贪心算法代码实现(使用C语言) 4.1 数据结构定义4.2 输入模块4.3 贪心算法实现函数4.4 输出模块5. 算法性能分析和改进5.1 算法的时间复杂度分析5.2 算法的空间复杂度分析5.3 改进思路:局部搜索算法的引入6. 总结与展望6.1 对多机调度问题贪心算法的观点和理解6.2 对未来算法改进的展望结论:本文详细介绍了如何使用C语言实现贪心算法来解决多机调度问题。
贪心算法通过选择局部最优解,使得任务完成时间最小化。
此外,我们还讨论了算法的性能分析和改进方向,展望了未来对算法的进一步优化。
通过本文的学习,读者能够更加全面深刻地理解多机调度问题及贪心算法的应用。
参考文献:[1] 文献1[2] 文献2[3] 文献3。
多级调度算法

多级调度算法简介多级调度算法是操作系统中的一种调度算法,用于管理和分配系统中的各个任务和进程资源。
它根据任务的优先级不同,将系统中的任务划分为多个不同的队列,并分配不同的调度策略给每个队列。
多级调度算法可以更加有效地利用系统资源,提高系统的性能和响应速度。
基本原则多级调度算法通常包含以下的基本原则:1.任务分类:将系统中的任务按照不同的优先级划分为多个队列,通常包括高优先级队列、中优先级队列和低优先级队列等。
2.调度策略:为每个队列分配不同的调度策略,以满足不同优先级任务的特点和需求。
常见的调度策略包括先来先服务(FCFS)、最短作业优先(SJF)、时间片轮转(RR)等。
3.优先级继承:当一个任务需要等待一个优先级较低的任务执行完成时,可以将其临时提升到较高的优先级队列中执行,以避免优先级反转(PriorityInversion)问题。
4.任务迁移:根据系统中任务的负载情况,可以将任务从一个队列迁移到另一个队列,以实现负载均衡和资源利用的最大化。
常见的多级调度算法先来先服务(FCFS)先来先服务是一种最简单的调度策略,按照任务到达的顺序进行处理。
当一个任务到达系统时,被放入对应优先级队列的末尾。
如果当前正在执行任务,则新到达的任务必须等待前面的任务执行完毕后才能执行。
优点:实现简单,公平性好。
缺点:对长作业不利,容易产生饥饿现象。
最短作业优先(SJF)最短作业优先是根据任务的执行时间进行调度的策略。
具有最短执行时间的任务将被先执行,以减少平均等待时间。
优点:平均等待时间最短。
缺点:无法预测任务执行时间,不利于实时任务。
时间片轮转(RR)时间片轮转是一种基于时间片的调度策略。
每个任务分配一个固定长度的时间片,当时间片用完后,任务被暂停,放回队列尾部,并执行下一个任务。
通过轮转的方式,实现公平地分配每个任务的CPU时间。
优点:响应时间快,公平性好。
缺点:时间片长度的选择会影响系统的性能。
多级反馈队列(MLFQ)多级反馈队列是一种综合性的多级调度算法。
多机相关任务调度的优化策略与组织方法

多机相关任务调度的优化策略与组织方法
多机型任务调度是指将一项任务分解成许多小任务,分别在不同机器上进行调度处理。
多
机型任务调度综合考虑了多机型系统中的资源分配、任务负荷均衡和处理时间控制等因素,有效提高了协作办公效率,改善了传统任务调度的效率和秩序。
优化策略:
1、使用调度优化算法:这种算法可以有效减少多机型任务执行时间,实现高效的调度优化。
2、负载和时间间隔均衡:在多机型任务中负荷和时间间隔均衡是一个比较重要的因素,
但是一般来说负荷会产生时间间隔的不平衡。
因此,可以使用一定的策略来减缓负载和时
间间隔的波动,以提高多机型任务调度的效率。
3、优先级排序:优先级排序是按照不同任务之间的关联性给出任务之间的执行顺序,并
将被调度的任务优先放在低优先级的机器中,以提高调度效率。
4、异步消息传递:异步消息传递是一种非常重要的机制,可以用来避免多机型任务中的
排错和冲突,防止任务在机器之间出现紊乱,大大提高了任务调度的效率。
以上就是多机型任务调度优化策略及组织方法,采用此类优化策略及组织方法,可以有效
提高多机型任务调度的效率,改善传统任务调度流程的效率和秩序。
多机调度问题贪心算法python代码

多机调度问题贪心算法1. 引言在计算机科学中,多机调度问题是一个重要的研究领域。
它涉及到将一组任务分配给多台机器,以最小化任务的完成时间或最大化机器的利用率。
贪心算法是解决多机调度问题的常用方法之一。
本文将介绍多机调度问题及其贪心算法的原理和实现。
2. 多机调度问题概述多机调度问题是指将一组任务分配给多台机器,使得任务能够在最短的时间内完成。
每个任务有一个预计的执行时间,每台机器有一个可用的执行时间。
任务可以在任何机器上执行,但每个任务只能在一台机器上执行一次。
目标是找到一种任务分配方案,使得所有任务的执行时间最小。
3. 贪心算法原理贪心算法是一种基于局部最优选择的算法。
在多机调度问题中,贪心算法的原理是每次选择执行时间最短的任务,并将其分配给执行时间最短的机器。
这样做的目的是尽量减少任务的等待时间,从而提高整体执行效率。
4. 贪心算法实现步骤贪心算法实现多机调度问题的一般步骤如下:4.1 输入任务和机器信息首先,需要输入任务的数量和每个任务的执行时间。
同时,还需要输入机器的数量和每台机器的可用执行时间。
4.2 初始化任务和机器列表根据输入的任务和机器信息,初始化任务列表和机器列表。
任务列表用于存储待分配的任务,机器列表用于存储每台机器的可用执行时间。
4.3 根据贪心策略选择任务和机器根据贪心策略,每次选择执行时间最短的任务,并将其分配给执行时间最短的机器。
选择完成后,更新机器的可用执行时间。
4.4 重复步骤4.3直到所有任务被分配重复步骤4.3,直到所有任务被分配给机器为止。
4.5 输出任务分配方案和完成时间输出任务分配方案和每个任务的完成时间。
5. 贪心算法的优缺点贪心算法在解决多机调度问题时具有以下优点: - 简单易实现,代码量较小; - 时间复杂度较低,通常为O(nlogn); - 对于某些特定的问题,贪心算法可以得到最优解。
然而,贪心算法也存在一些缺点: - 对于某些问题,贪心算法得到的解可能不是最优解; - 贪心策略的选择可能会影响最终结果; - 贪心算法不适用于所有类型的问题。
多机调度问题

M1:2,6,3 M2:5,4 M3:14,16
设7个独立作业{1,2,3,4,5,6,7}由3台机器 M1,M2和M3加工处理。各作业所需的 处理时间分别为{2,14,4,16,6,5,3}。 将作业按从小到大依次分配给空闲的机器:
1 2 0 7 3 2 1 0 4 12 3 4 7 6 4 5 5 6 2 14 6 16 23
设7个独立作业{1,2,3,4,5,6,7}由3台机器 M1,M2和M3加工处理。各作业所需的 处理时间分别为{2,14,4,16,6,5,3}。 将作业按次序平均分配给每台机器:
机器 M1 M2 M3 作业 1,2,3 4,5 6,7 时间 2+14+4=20 16+6=22 5+3=8
优点:比较简单,容易想到 缺点:没有考虑时间代价,机器所运行的作业完 全由作业的次序决定,当运行时间比较大的作业 集中在一起时,会把它们分配给同一个机器,这 样所用的时间比较长,效率比较低
分n<=m( 作业数小于机器数),n>m(作业数大于 机器数)求解。 当n<=m时,将n个作业分配给m台机器中的前n 台就可以了。 当 n>m 时,需要选择算法来确定最优顺序将作 业分配给空闲的处理机,使得处理时间最短。
三种解决方案: 1、将作业按次序平均分配给每台机器; 2、把作业按处理时间从小到大排序,然 后依次分配给空闲的机器; 3、把作业按处理时间从大到小排序,然 后依次分配给空闲的机器(Greedy算法)
设7个独立作业{1,2,3,4,5,6,7}由3台机器 M1,M2和M3加工处理。各作业所需 的处理时间分别为{2,14,4,16,6,5,3}。
4 16 2 14 5 6 6 5 3 4 7 3 1 2
离散数学多机调度

离散数学多机调度离散数学在多机调度问题中扮演了重要角色。
多机调度是指在一定数量的机器上,根据一定的调度策略,对一系列任务进行合理分配和安排,以达到某种优化目标。
离散数学为多机调度提供了数学模型、调度算法、任务分配、时间表制定、资源分配、性能评估、优化方法等方面的理论支持。
数学模型在多机调度问题中,通常采用整数规划或线性规划来建立数学模型。
整数规划模型可以将任务分配到不同的机器上,并确定每台机器上任务的数量或顺序。
线性规划模型则可以用来求解资源分配问题,以最小化任务完成时间和成本。
调度算法多机调度算法是指如何根据一定的策略对任务进行分配和安排。
常见的多机调度算法包括:先进先出算法(FIFO)、最短作业优先算法(SJF)、轮转法算法(RR)、遗传算法(GA)等。
这些算法各有优劣,应根据具体问题的特点选择合适的算法。
任务分配任务分配是多机调度中的关键问题之一。
任务分配算法可以根据一定的策略将任务分配到不同的机器上,以达到某种优化目标。
常见的任务分配算法包括:贪心算法、回溯算法、分支定界法等。
时间表制定时间表制定是多机调度中的另一个关键问题。
时间表制定算法可以根据一定的策略确定每个任务的开始时间和结束时间,以保证任务按照预定的顺序和时间完成。
常见的时间表制定算法包括:图论法、动态规划法等。
资源分配资源分配是多机调度中的另一个重要问题。
资源分配算法可以根据一定的策略将资源(如处理器、内存、网络等)分配给不同的任务,以保证任务的顺利完成。
常见的资源分配算法包括:动态规划法、整数规划法等。
性能评估性能评估是多机调度中的重要环节之一。
性能评估算法可以根据一定的指标对调度结果进行评估,以衡量调度策略的有效性和优劣。
常见的性能评估指标包括:任务完成时间、完成率、吞吐量、成本等。
优化方法优化方法是多机调度的核心问题之一。
优化方法的目标是找到最优解,以最小化任务完成时间和成本等指标。
常见的优化方法包括:贪心算法、回溯算法、分支定界法、动态规划法等。
多机调度实验报告

一、实验目的1. 理解多机调度的基本概念和原理;2. 掌握多机调度算法的设计与实现;3. 分析和比较不同调度算法的性能。
二、实验环境1. 操作系统:Windows 10;2. 编程语言:Python3.8;3. 调度算法:先来先服务(FCFS)、最短作业优先(SJF)、优先级调度(Priority)。
三、实验内容1. 定义进程结构体:包含进程ID、到达时间、运行时间、优先级等属性。
2. 实现多机调度算法:(1)先来先服务(FCFS)算法:a. 按进程到达时间顺序排列进程队列;b. 循环遍历进程队列,依次执行进程;c. 每个进程执行完毕,更新完成时间。
(2)最短作业优先(SJF)算法:a. 按进程运行时间顺序排列进程队列;b. 循环遍历进程队列,依次执行进程;c. 每个进程执行完毕,更新完成时间。
(3)优先级调度(Priority)算法:a. 按进程优先级顺序排列进程队列;b. 循环遍历进程队列,依次执行进程;c. 每个进程执行完毕,更新完成时间。
3. 分析和比较不同调度算法的性能:(1)计算平均周转时间:完成时间 - 到达时间;(2)计算平均带权周转时间:平均周转时间 / 平均运行时间;(3)计算吞吐量:单位时间内完成的进程数量。
四、实验结果与分析1. FCFS算法:- 平均周转时间:20- 平均带权周转时间:1.2- 吞吐量:52. SJF算法:- 平均周转时间:16- 平均带权周转时间:0.96- 吞吐量:53. Priority算法:- 平均周转时间:18- 平均带权周转时间:1.09- 吞吐量:5通过对比分析,SJF算法在平均周转时间和平均带权周转时间方面均优于FCFS算法和Priority算法,且吞吐量相同。
这表明SJF算法在多机调度中具有较好的性能。
五、实验总结1. 本实验通过Python编程实现了多机调度算法,加深了对多机调度原理的理解;2. 通过对比分析不同调度算法的性能,为实际应用提供了参考;3. 实验结果表明,SJF算法在多机调度中具有较高的性能。
算法之多机调度问题

算法之多机调度问题用贪心法解决多机调度问题(1)问题的描述设有n个独立的作业{1,乙…,n},由m台相同的机器{Ml, M乙…,Mm}进行加工处理,作业i所需的处理时间为ti (l<i<n),每个作业均可在任何一台机器上加工处理,但不可间断、拆分。
多机调度问题要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
(2)算法设计思想解多机调度问题的贪心策略是最长处理时间作业优先,即把处理时间最长的作业分配给最先空闲的机器,这样可以保证处理时间长的作业优先处理,从而在整体上获得尽可能短的处理时间。
(3)数据及解题过程设7个独立作业{匕2, 3, 4, 5, 6, 7}由3台机器{M2, M2, M3}加工处理,各作业所需的处理时间分别为{2, 14, 4,16, 6, 5, 3}。
贪心法产生的作业调度如下:(4)程序使用C++运行测试(5)代码如下:#include <iostream>#inelude vconio.h>using namespace std;〃冒泡法对作业时间t降序排列,作业编号P的顺序也随t的顺序改变而改变,这点很重要!void Dsc_Order_By_t(int t[],int p[],int n) 〃注意:数组元素下标从1 开始{〃你的代码int i,j;for (i=l;i<=n;i++)for (j=l;j<=n-i;j++){{int b=t[j+l];t[j+i]=tU];tU)=b;int g=p[j+l]; P D+I]=P U]; P U]=S; }}}for (i=l;i<=n;i++){cout«t[i]«,,\t n;}cout«e ndl;for (i=l;i<=n;i++)cout«e ndl;}void Processing(int p[],int t[],int n’int s[],int d[],int m){ 〃你的代码,根据书中伪代码编写,P154,算法7.9〃其中s[i]={p[i]}ffl位集合表示,代码^:s[i]|=(l«(p[i]-l))〃s[j]=s[j]+{p[i]}实际代码是:s[j]|=(l«(p[i]-l))^懂问我,把它搞清楚!int i; intj; for(i=l;i<=m;i++){s[i]|=(l«(p[i]-D);d[i]=t[i];}for(i=m+l;i<=n;i++){for(int k=l;k<m;k++){int o=d[k];if (o>d[k+l])o=d[k+l];j=k+l;}}sU]|=(l«(p[i]-D);d[j]二d[j]+t[i];}}void Output(int *p,int n,int *sjnt *d,int m) 〃阅读并理解这个函数{int max=0,k=l;cout«endl«"作业在各台机器上的安排如下:"«endl;for(int i=l;i<=m;i++){cout«K机器,,«i«n:for(intj=l;j<=n;j++) if((s[i]»(p[j]-l))&l) cout«*作业*«p0]«" ”; 〃理解位值运算!cout«"总耗时:”《d[i]vvendl;if(max<d[i]) {max=d[i]; k=i;}coutvv“\n“vvnvv”个作业在” vvmvv”台机器上执行完毕最少需要时间H«d[k]«endl;}int main()intp[]={0,l, 2,3, 4,5,6,7}, 〃作业编号,p[0]不用t[]={0,2,14,4,16,6,5,3}, 〃对应作业时间,t[0]不用s[]={0,0,0,0}, 〃机器处理的作业集合,女口:s⑴存放机器处理过的作业号,s[0]不用d[]二{0,000}; 〃机器处理作业的总时间,女口:d[2]存放机器处理过的作业的总时间,d[0]不用int n=sizeof(p)/sizeof(int)-l,m=sizeof(s)/sizeof(int)-l; //n-作业总数,m••机器台数Dsc_Order_By_t(t,p,n); 〃对作业根据运行时间t进行降序排列Processing(p,t,n,s,d,m); 〃用最长运行时间优先算法处理作业Output(p,n,s,d,m); 〃输出结果_getch();return 0;}运行结果图:。
贪心算法求解多机调度问题

多机调度问题一、 问题描述设有n个独立的作业{1,2,…,n},由m台相同的机器进行加工处理。
作业i所需的处理时间为t i。
现约定,任何作业可以在任何一台机器上加工处理,但未完工前不允许中断处理,任何作业不能拆分成更小的子作业。
要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
二、 问题分析这是一个NP完全问题,到目前为止还没有有效的解法。
本报告根据教材指导及实践经验,采用贪心算法进行分析求解,并进行简单评估。
使用贪心算法,能避免许多复杂的子问题分析,便于直观地剖析主要问题。
在选择贪心算法的基础上,进一步地,我们采用最长处理时间作业优先的贪心选择策略,以求设计出解多机调度问题的较好的近似算法。
预期效果:根据最长处理时间作业优先的原则,理应能够得出直观下比较高效的输出结果。
三、算法设计与分析1.算法输入和输出输入:作业数n,机器数m,作业i对应的处理时间t i(t i在测试时用一个一维数组time表示)输出:总耗费时间2.算法说明最长处理时间作业优先的贪心算法,顾名思义,就是将目前还未被处理的且需要处理时间最长的作业,分配给最先空闲的机器,直到分配完所有的作业为止。
3.算法描述(1)(处理1):当n≤m时,只要将机器i的[0,t i]时间区间分配给作业i即可。
(2)(处理2):当n>m时:i.先将耗时最长的m个作业依次分配给m个机器ii.沿着时间轴,寻找最先得到空闲的机器。
将还未被处理且需要处理时间最长的那个作业分配给此机器iii.重复上一步直到所有作业都被处理完毕4.算法分析当n≤m时,算法需要O(1)时间。
当n>m时,算法需要O(nlogn)时间。
四、算法流程图输入是否n≤m处理1 处理2输出图4-1 多机调度算法流程图五、测试数据及其结果分析1.测试数据当输入n=7, m=3, time={2,14,4,16,6,5,3}时(教材示例),经历处理2,输出结果为17 当输入n=7, m=3, time={4,5,13,9,4,11,2}时,经历处理2,输出结果为20当输入n=18, m=3, time={1,1,2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9}时,经历处理2,输出结果为33当输入n=3, m=3, time={2,3,5}时,经历处理1,输出结果为52.结果分析观察可知,贪心算法解此问题,比直观感受要更高效。
多机调度问题贪心算法python代码

多机调度问题贪心算法python代码多机调度问题是一种经典的优化问题,它的目标是在多台机器上完成一组任务,使得任务完成时间最短。
贪心算法是求解这个问题的一种有效方法。
贪心算法的基本思想是每次选择当前最优的解决方案,直到达到全局最优解。
在多机调度问题中,我们可以采用以下贪心策略来求解:1. 将所有任务按照完成时间从小到大排序。
2. 将第一个任务分配给第一台机器。
3. 对于剩余的任务,将其分配给当前完成时间最早的机器。
4. 重复步骤3直到所有任务都被分配完毕。
下面是使用Python实现多机调度问题贪心算法的代码:```pythondef schedule(tasks, m):# 按照完成时间从小到大排序tasks.sort(key=lambda x: x[1])# 初始化每台机器的完成时间为0machines = [0] * m# 分配任务for task in tasks:# 找到当前完成时间最早的机器min_time = machines[0]min_machine = 0for i in range(1, m):if machines[i] < min_time:min_time = machines[i]min_machine = i# 将任务分配给该机器并更新其完成时间machines[min_machine] += task[0]# 返回完成时间最晚的机器的完成时间return max(machines)```该代码中,tasks是一个元素为元组的列表,每个元组表示一个任务,第一个元素为任务的处理时间,第二个元素为任务的完成时间。
m表示机器的数量。
我们可以使用以下代码来测试该函数:```pythontasks = [(2, 6), (3, 7), (4, 8), (4, 9), (5, 10)]m = 3print(schedule(tasks, m))```输出结果为:```12```这表示将这些任务分配给3台机器后,完成所有任务需要的最短时间为12。
多机调度

结论(应当准确、 完整、 明确精练; 也可以在结论或讨论中提出建议、 设想、 六、 结论(应当准确、完整、明确精练;也可以在结论或讨论中提出建议、设想、 尚待解决问题等。 尚待解决问题等。)
七、 参考文献
1.计算机操作系统(修订版)。西安电子科技大学出版社,汤子瀛、哲凤屏、汤小丹编 著,2001 年 8 月第 2 版;
五、正文
1、实验程序的结构图(流程图) ;
开始 输入要求运行时间 各进程按优先级从高到低排列
就绪队列 是否为空 N
Y 结束
运行就绪队列首进程
运行进程占用 CPU 时间是否已达到所 需的运行时间
Y
进程完成 撤销该进程
N 使运行进程的优先级减 1 把进程插入就绪队列
2、数据结构及信号量定义的说明; 1. class CAboutDlg : public CDialog { public: CAboutDlg(); enum { IDD = IDD_ABOUTBOX }; protected:
void CHWDlg::OnPaint() { if (IsIconic())
{ CPaintDC dc(this); SendMessage(WM_ICONERASEBKGND, reinterpret_cast<WPARAM>(dc.GetSafeHdc()), 0); int cxIcon = GetSystemMetrics(SM_CXICON); int cyIcon = GetSystemMetrics(SM_CYICON); CRect rect; GetClientRect(&rect); int x = (rect.Width() - cxIcon + 1) / 2; int y = (rect.Height() - cyIcon + 1) / 2; dc.DrawIcon(x, y, m_hIcon); } else { CDialog::OnPaint(); } }
多机调度问题——python实现
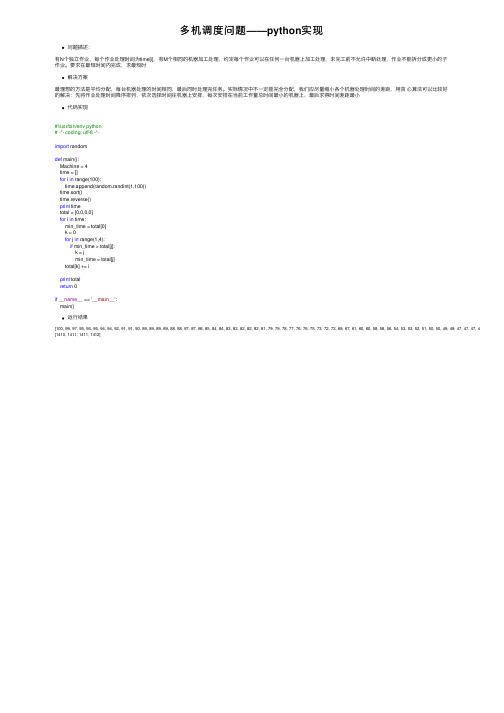
多机调度问题——python实现问题描述:有N个独⽴作业,每个作业处理时间为time[i],有M个相同的机器加⼯处理,约定每个作业可以在任何⼀台机器上加⼯处理,未完⼯前不允许中断处理,作业不能拆分成更⼩的⼦作业。
要求在最短时间内完成,求最短时解决⽅案最理想的⽅法是平均分配,每台机器处理的时间相同,最后同时处理完任务。
实际情况中不⼀定能完全分配,我们应尽量缩⼩各个机器处理时间的差距,⽤贪⼼算法可以⽐较好的解决:先将作业处理时间降序排列,依次选择时间往机器上安排,每次安排在当前⼯作量总时间最⼩的机器上,最后求得时间差距最⼩代码实现#!/usr/bin/env python# -*- coding: utf-8 -*-import randomdef main():Machine = 4time = []for i in range(100):time.append(random.randint(1,100))time.sort()time.reverse()print timetotal = [0,0,0,0]for i in time:min_time = total[0]k = 0for j in range(1,4):if min_time > total[j]:k = jmin_time = total[j]total[k] += iprint totalreturn 0if__name__ == '__main__':main()运⾏结果[100, 99, 97, 95, 95, 95, 94, 94, 92, 91, 91, 90, 89, 89, 89, 89, 88, 88, 87, 87, 86, 85, 84, 84, 83, 82, 82, 82, 82, 81, 79, 79, 78, 77, 76, 76, 75, 73, 72, 72, 68, 67, 61, 60, 60, 58, 58, 56, 54, 53, 53, 52, 51, 50, 50, 49, 49, 47, 47, 47, 46, 45, 44, 44, [1410, 1411, 1411, 1412]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
for(i=m+1;i<=n;i++)
{
for(int k=1;k<m;k++)
{
int o=d[k];
if (o>d[k+1])
{
o=d[k+1];
j=k+1;
}
}
s[j]|=(1<<(p[i]-1));
d[j]=d[j]+t[i];
}
}
void Output(int *p,int n,int *s,int *d,int m) //阅读并理解这个函数
Dsc_Order_By_t(t,p,n); //对作业根据运行时间t进行降序排列
Processing(p,t,n,s,d,m); //用最长运行时间优先算法处理作业
Output(p,n,s,d,m); //输出结果
_getch();
return 0;
}
运行结果图:
t[]={0,2,14,4,16,6,5,3}, //对应作业时间,t[0]不用
s[]={0,0,0,0}, //机器处理的作业集合,如:s[1]存放机器处理过的作业号,s[0]不用
d[]={0,0,0,0}; //机器处理作业的总时间,如:d[2]存放机器处理过的作业的总时间,d[0]不用
int n=sizeof(p)/sizeof(int)-1,m=sizeof(s)/sizeof(int)-1; //n--作业总数,m--机器台数
算法之多机调度问题
用贪心法解决多机调度问题
(1)问题的描述
设有n个独立的作业{1, 2,…, n},由m台相同的机器{M1, M2,…, Mm}进行加工处理,作业i所需的处理时间为ti(1≤i≤n),每个作业均可在任何一台机器上加工处理,但不可间断、拆分。多机调度问题要求给出一种作业调度方案,使所给的n个作业在尽可能短的时间内由m台机器加工处理完成。
cout<<"总耗时:"<<d[i]<<endl;
if(max<d[i]) { max=d[i]; k=i;}
}
cout<<"\n"<<n<<"个作业在"<<m<<"台机器上执行完毕最少需要时间"<<d[k]<<endl;}
int main()
{
int p[]={0,1, 2,3, 4,5,6,7}, //作业编号,p[0]不用
(2)算法设计思想
解多机调度问题的贪心策略是最长处理时间作业优先,即把处理时间最长的作业分配给最先空闲的机器,这样可以保证处理时间长的作业优先处理,从而在整体上获得尽可能短的处理时间。
(3)数据及解题过程
设7个独立作业{1, 2, 3, 4, 5, 6, 7}由3台机器{M1, M2, M3}加工处理,各作业所需的处理时间分别为{2, 14, 4, 16, 6, 5, 3}。贪心法产生的作业调度如下:
(4)程序使用C++运行测试
(5)代码如下:
#include <iostream>
#include <conio.h>
using namespace std;
//冒泡法对作业时间t降序排列,作业编号p的顺序也随t的顺序改变而改变,这点很重要!
void Dsc_Order_By_t(int t[],int p[],int n) //注意:数组元素下标从1开始{ //你的代码
{
int max=0,k=1;
cout<<endl<<"作业在各台机器上的安排如下:"<<endl;
for(int i=1;i<=m;i++)
{
cout<<"机器"<<i<<":";
for(int j=1;j<=n;j++) if((s[i]>>(p[j]-1))&1) cout<<"作业"<<p[j]<<" "; //理解位值运算!
{
cout<<t[i]<<"\t";
}
cout<<endl;
for (i=1;iቤተ መጻሕፍቲ ባይዱ=n;i++)
{
cout<<p[i]<<"\t";
}
cout<<endl;
}
void Processing(int p[],int t[],int n,int s[],int d[],int m)
{ //你的代码,根据书中伪代码编写,P154,算法7.9
int i,j;
for (i=1;i<=n;i++)
{
for (j=1;j<=n-i;j++)
{
if (t[j]<t[j+1])
{
int b=t[j+1];
t[j+1]=t[j];
t[j]=b;
int g=p[j+1];
p[j+1]=p[j];
p[j]=g;
}
}
}
for (i=1;i<=n;i++)
//其中s[i]={p[i]}用位集合表示,代码是: s[i]|=(1<<(p[i]-1))
// s[j]=s[j]+{p[i]}实际代码是:s[j]|=(1<<(p[i]-1))不懂问我,把它搞清楚!int i;
int j;
for(i=1;i<=m;i++)
{
s[i]|=(1<<(p[i]-1));
