matlab中希腊字母表示方法
Matlab中常用希腊字母表查询

Matlab中常用希腊字母表查询————————————————————————————————作者:————————————————————————————————日期:Matlab中常用希腊字母表查询Matlab的text中经常需要用到希腊字母表,我现在将所有的都总结了下比如在坐标轴的[0.5 0.5]位置上要显示δ字符,那么可以直接输入text(0.5,0.5,'\delta')如果需要显示大写希腊字符的话,那直接将首字母改为大写就可以了注意必须使用“\”引导,如果需要显示“\”,那么必须输入“\\”;类似的在字符串组合的时候如果要输入“'”则必须如下输入“''”另外text字符可以重叠显示,这样就可以构造出一些有趣的效果,比如将某个字符上添加一个斜杠或者画一个叉等序号大写小写英文注音国际音标注音中文读音意义1Ααalpha a:lf阿尔法角度;系数2Ββbeta bet贝塔磁通系数;角度;系数3Γγgamma ga:m伽马电导系数4Δδdelta delt德尔塔变动;密度;屈光度5Εεepsilon ep`silon 伊普西龙对数之基数6Ζζzeta zat截塔阻抗;相对粘度;原子序数7Ηηeta eit艾塔磁滞系数;效率8Θθthetθit西塔温度;相位角9Ιιiot aiot约塔微小,一点儿10Κκkappa kap卡帕介质常数11Λλlambda lambd兰布达波长;体积12Μμmu mju缪磁导系数;放大因子13Ννnu nju纽磁阻系数14Ξξxi ksi克西15Οοomicron omik`ron 奥密克戎16Ππpi pai派圆周率17Ρρrho rou肉电阻系数18Σσsigma`sigma西格马求和,表面密度;跨导19Ττtau tau套时间常数20Υυupsilon jup`silon 宇普西龙位移21Φφphi fai佛爱磁通;角度22Χχchi phai西开平方分布23Ψψpsi psai普西介质电通量24Ωωomega o`miga欧米伽欧姆;角速;角。
matlab中legend希腊字母的输入

matlab中legend希腊字母的输入(最新版)目录1.MATLAB 中 legend 的作用2.如何在 MATLAB 中输入希腊字母3.在 MATLAB 中使用 legend 的注意事项正文在 MATLAB 中,legend 函数的作用是用于创建图例,以便在绘制图形时,帮助用户区分不同线条或数据系列。
有时候,我们需要在图例中使用希腊字母,那么如何在 MATLAB 中输入希腊字母呢?首先,要了解 MATLAB 中的希腊字母是作为特殊字符处理的,它们在ASCII 码表中的位置是固定的。
例如,希腊字母 alpha 的 ASCII 码是975,beta 的 ASCII 码是 976,以此类推。
在 MATLAB 中,可以直接使用这些 ASCII 码来输入希腊字母。
为了方便输入,可以先在命令窗口中输入"希腊字母的 ASCII 码",例如"alpha 975",这样在输入时,只需输入数字 975,MATLAB 会自动将其转换为希腊字母 alpha。
在创建图例时,如果使用了希腊字母,还需要注意以下几点:1.在调用 legend 函数时,需要确保图例中使用的希腊字母与实际数据系列中的符号一致。
否则,图例将无法正确显示。
2.如果需要在图例中使用多个希腊字母,可以在 legend 函数中使用多个参数。
例如,"legend("alpha", "beta", "gamma"),这将在图例中显示三个希腊字母。
3.若要设置图例的样式,可以使用 legend 函数的选项。
例如,"legend("fontname", "times new roman", "fontsize", 12) 将设置图例字体为 Times New Roman,字号为 12。
关于matlab的一些画图技巧及希腊字母下标

matlab中如何在指定一点画一个填充颜色的小圆plot(1,1,'r.','markersize',50)二维作图绘图命令plot绘制x-y坐标图;loglog命令绘制对数坐标图;semilogx和semilogy命令绘制半对数坐标图;polor命令绘制极坐标图.基本形式如果y是一个向量,那么plot(y)绘制一个y中元素的线性图.假设我们希望画出y=[0., 0.48, 0.84, 1., 0.91, 6.14 ]则用命令:plot(y)它相当于命令:plot(x, y),其中x=[1,2,…,n]或x=[1;2;…;n],即向量y的下标编号, n为向量y的长度Matlab会产生一个图形窗口,显示如下图形,请注意:坐标x和y是由计算机自动绘出的.图4.1.1.1 plot([0.,0.48,0.84,1.,0.91,6.14])上面的图形没有加上x轴和y轴的标注,也没有标题.用xlabel,ylabel,title 命令可以加上.如果x,y是同样长度的向量,plot(x,y)命令可画出相应的x元素与y元素的x-y坐标图.例:x=0:0.05:4*pi; y=sin(x); plot(x,y)grid on, title(' y=sin( x )曲线图' )xlabel(' x = 0 : 0.05 : 4Pi ')结果见下图.图4.1.1.2 y=sin(x)的图形title图形标题xlabel x坐标轴标注ylabel y坐标轴标注text标注数据点grid给图形加上网格hold保持图形窗口的图形表4.1.1.1 Matlab图形命令多重线在一个单线图上,绘制多重线有三种办法.第一种方法是利用plot的多变量方式绘制:plot(x1,y1,x2,y2,...,xn,yn)x1,y1,x2,y2,...,xn,yn是成对的向量,每一对x, y在图上产生如上方式的单线.多变量方式绘图是允许不同长度的向量显示在同一图形上.第二种方法也是利用plot绘制,但加上hold on/off命令的配合:plot(x1,y1)hold onplot(x2,y2)hold off第三种方法还是利用plot绘制,但代入矩阵:如果plot用于两个变量plot(x,y),并且x,y是矩阵,则有以下情况:(1)如果y是矩阵,x是向量,plot(x,y)用不同的画线形式绘出y的行或列及相应的x向量,y的行或列的方向与x向量元素的值选择是相同的.(2)如果x是矩阵,y是向量,则除了x向量的线族及相应的y向量外,以上的规则也适用.(3)如果x,y是同样大小的矩阵,plot(x,y)绘制x的列及y相应的列.还有其它一些情况,请参见Matlab的帮助系统.线型和颜色的控制如果不指定划线方式和颜色,Matlab会自动为您选择点的表示方式及颜色.您也可以用不同的符号指定不同的曲线绘制方式.例如:plot(x,y,'*') 用'*'作为点绘制的图形.plot(x1,y1,':',x2,y2,'+') 用':'画第一条线,用'+'画第二条线.线型、点标记和颜色的取值有以下几种:线型点标记颜色-实线.点y黄:虚线o小圆圈m棕色-.点划线x叉子符c青色--间断线+加号r红色*星号g绿色s方格b蓝色d菱形w白色^朝上三角k黑色v朝下三角> 朝右三角< 朝左三角p五角星h六角星表4.1.3.1线型和颜色控制符如果你的计算机系统不支持彩色显示,Matlab将把颜色符号解释为线型符号,用不同的线型表示不同的颜色.颜色与线型也可以一起给出,即同时指定曲线的颜色和线型.例如:t=-3.14:0.2:3.14;x=sin(t); y=cos(t);plot(t,x, '+r',t,y, '-b')图4.1.3.1不同线型、颜色的sin,cos图形对数图、极坐标图及条形图loglog、semilogx、semilogy和polar的用法和plot相似.这些命令允许数据在不同的graph paper上绘制,例如不同的坐标系统.先介绍的fplot是扩展来的可用于符号作图的函数.●fplot(fname,lims)绘制fname指定的函数的图形.●polar( theta, rho)使用相角theta为极坐标形式绘图,相应半径为rho,其次可使用grid命令画出极坐标网格.●loglog 用log10-log10标度绘图.●semilogx用半对数坐标绘图,x轴是log10,y是线性的.●semilogy用半对数坐标绘图,y轴是log10,x是线性的.●bar(x)显示x向量元素的条形图,bar不接受多变量.●hist绘制统计频率直方图.●histfit(data,nbins)绘制统计直方图与其正态分布拟合曲线.fplot函数的绘制区域为lims=[xmin,xmax],也可以用lims=[xmin,xmax,ymin,ymax]指定y轴的区域.函数表达式可以是一个函数名,如sin,tan等;也可以是带上参数x的函数表达式,如sin(x),diric(x,10);也可以是一个用方括号括起的函数组,如[sin, cos].例1:fplot('sin',[0 4*pi])例2:fplot('sin(1 ./ x)', [0.01 0.1])例3:fplot('abs(exp(-j*x*(0:9))*ones(10,1))',[0 2*pi],'-o')例4:fplot('[sin(x), cos(x) , tan(x)]',[-2*pi 2*pi -2*pi 2*pi]) %%(图4.1.4.1)图4.1.4.1 sin,cos,tan函数图形图4.1.4.2半对数图下面介绍的是其它几个作图函数的应用.例5:半对数坐标绘图t=0.001:0.002:20;y=5 + log(t) + t;semilogx(t,y, 'b')hold onsemilogx(t,t+5, 'r') %% (图4.1.4.2)例6:极坐标绘图t=0:0.01:2*pi;polar(t,sin(6*t)) %% (图4.1.4.3)图4.1.4.3极坐标绘图图4.1.4.4正态分布的统计直方图与其正态分布拟合曲线例7:正态分布图我们可以用命令normrnd生成符合正态分布的随机数.normrnd(u,v,m,n)其中,u表示生成随机数的期望,v代表随机数的方差.运行:a=normrnd(10,2,10000,1);histfit(a) %% (图4.1.4.4)我们可以得到正态分布的统计直方图与其正态分布拟合曲线.例8:比较正态分布(图4.1.4.5(1))与平均分布(图4.1.4.5(2))的分布图:yn=randn(30000,1); %%正态分布x=min(yn) : 0.2 : max(yn);subplot(121)hist(yn, x)yu=rand(30000,1); %%平均分布subplot(122)hist(yu, 25)4.1.4.5(1) 4.1.4.5(2)图4.1.4.5正态分布与平均分布的分布图在绘图过程中,经常要把几个图形在同一个图形窗口中表现出来,而不是简单地叠加(例如上面的例8).这就用到函数subplot.其调用格式如下:subplot(m,n,p)subplot函数把一个图形窗口分割成m×n个子区域,用户可以通过参数p 调用个各子绘图区域进行操作.子绘图区域的编号为按行从左至右编号.例9:绘制子图x=0:0.1*pi:2*pi;subplot(2,2,1)plot(x,sin(x),'-*');title('sin(x)');subplot(2,2,2)plot(x,cos(x),'--o');title('cos(x)');subplot(2,2,3)plot(x,sin(2*x),'-.*');title('sin(2x)');subplot(2,2,4);plot(x,cos(3*x),':d')title('cos(3x)')得到图形如下:图4.1.5.1子图利用二维绘图函数patch,我们可绘制填充图.绘制填充图的另一个函数为fill.下面的例子绘出了函数humps(一个Matlab演示函数)在指定区域内的函数图形.例10:用函数patch绘制填充图fplot('humps',[0,2],'b')patch([0.5 0.5:0.02:1 1],[0 humps(0.5:0.02:1) 0],'r');hold offtitle('A region under an interesting function.')grid图4.1.6.1填充图我们还可以用函数fill来绘制类似的填充图.例11:用函数fill绘制填充图x=0:pi/60:2*pi;y=sin(x);x1=0:pi/60:1;y1=sin(x1);plot(x,y,'r');fill([x1 1],[y1 0],'g')图4.1.6.2填充图三维作图mesh(Z)语句可以给出矩阵Z元素的三维消隐图,网络表面由Z坐标点定义,与前面叙述的x-y平面的线格相同,图形由邻近的点连接而成.它可用来显示用其它方式难以输出的包含大量数据的大型矩阵,也可用来绘制Z变量函数.显示两变量的函数Z=f(x,y),第一步需产生特定的行和列的x-y矩阵.然后计算函数在各网格点上的值.最后用mesh函数输出.下面我们绘制sin(r)/r函数的图形.建立图形用以下方法:x=-8:.5:8;y=x';x=ones(size(y))*x;y=y*ones(size(y))';R=sqrt(x.^2+y.^2)+eps;z=sin(R)./R;mesh(z) %% 试运行mesh(x,y,z),看看与mesh(z)有什么不同之处?各语句的意义是:首先建立行向量x,列向量y;然后按向量的长度建立1-矩阵;用向量乘以产生的1-矩阵,生成网格矩阵,它们的值对应于x-y坐标平面;接下来计算各网格点的半径;最后计算函数值矩阵Z.用mesh函数即可以得到图形.图4.2.1三维消隐图第一条语句x的赋值为定义域,在其上估计函数;第三条语句建立一个重复行的x矩阵,第四条语句产生y的响应,第五条语句产生矩阵R(其元素为各网格点到原点的距离).用mesh方法结果如上.另外,上述命令系列中的前4行可用以下一条命令替代:[x, y]=meshgrid(-8:0.5:8)(1) meshc与函数mesh的调用方式相同,只是该函数在mesh的基础上又增加了绘制相应等高线的功能.下面来看一个meshc的例子:[x,y]=meshgrid([-4:.5:4]);z=sqrt(x.^2+y.^2);meshc(z) %% 试运行meshc(x,y,z),看看与meshc(z)有什么不同之处?我们可以得到图形:图4.2.2.1 meshc 图地面上的圆圈就是上面图形的等高线.(2)函数meshz与mesh的调用方式也相同,不同的是该函数在mesh函数的作用之上增加了屏蔽作用,即增加了边界面屏蔽.例如:[x,y]=meshgrid([-4:.5:4]);z=sqrt(x.^2+y.^2);meshz(z) %% 试运行meshz(x,y,z),看看与meshz(z)有什么不同之处?我们得到图形:图4.2.2.2 meshz 图(1)在Matlab中有一个专门绘制圆球体的函数sphere,其调用格式如下:[x,y,z]=sphere(n)此函数生成三个(n+1)×(n+1)阶的矩阵,再利用函数surf(x,y,z)可生成单位球面.[x,y,z]=sphere 此形式使用了默认值n=20sphere(n) 只绘制球面图,不返回值.运行下面程序:sphere(30);axis square;我们得到球体图形:图4.2.3.1 球面图若只输入sphere画图,则是默认了n=20的情况.(2) surf函数也是Matlab中常用的三维绘图函数.其调用格式如下:surf(x,y,z,c)输入参数的设置与mesh相同,不同的是mesh函数绘制的是一网格图,而surf绘制的是着色的三维表面.Matlab语言对表面进行着色的方法是,在得到相应网格后,对每一网格依据该网格所代表的节点的色值(由变量c控制),来定义这一网格的颜色.若不输入c,则默认为c=z.我们看下面的例子:%绘制地球表面的气温分布示意图.[a,b,c]=sphere(40);t=abs(c); %求绝对值surf(a,b,c,t);axis equalcolormap('hot')我们可以得到图形如下:图4.2.3.2 等温线示意图(1)坐标轴的控制函数axis,调用格式如下:axis([xmin,xmax,ymin,ymax,zmin,zmax])用此命令可以控制坐标轴的范围.与axis相关的几条常用命令还有:axis auto 自动模式,使得图形的坐标范围满足图中一切图元素axis equal 严格控制各坐标的分度使其相等axis square 使绘图区为正方形axis on 恢复对坐标轴的一切设置axis off 取消对坐标轴的一切设置axis manual 以当前的坐标限制图形的绘制(2)grid on 在图形中绘制坐标网格.grid off 取消坐标网格.(3)xlabel, ylabel, zlabel分别为x轴, y轴, z轴添加标注.title为图形添加标题.以上函数的调用格式大同小异,我们以xlabel为例进行介绍:xlabel('标注文本','属性1','属性值1','属性2','属性值2',…)这里的属性是标注文本的属性,包括字体大小、字体名、字体粗细等.例如:[x, y]=meshgrid(-4:.2:4);R=sqrt(x.^2+y.^2);z=-cos(R);mesh(x,y,z)xlabel('x\in[-4,4]','fontweight','bold');ylabel('y\in[-4,4]','fontweight','bold');zlabel('z=-cos(sqrt(x^2+y^2))','fontweight','bold');title('旋转曲面','fontsize',15,'fontweight','bold','fontname','隶书');图4.2.4.1添加标注以上各种绘图方法的详细用法,请看联机信息.对平面上n个点:在平面直线族{为实数}中寻求一条直线,使得散点到与散点相对应的在直线上的点之间的纵坐标的误差的平方和最小,用微积分的方法可得:所求得的这条直线:称为回归直线.例:已知如下点列,求其回归直线,并计算最小误差平方和.x0.10.11.12.13.14.15.16.17.18.2.21.23y4243.54545.54547.5495350555560参考的程序如下:x=[0.1 0.11 .12 .13 .14 .15 .16 .17 .18 .2 .21 .23]; y=[42 43.5 45 45.5 45 47.5 49 53 50 55 55 60]; n=length(x);xb=mean(x);yb=mean(y);x2b=sum(x.^2)/n;xyb=x*y'/n;b=(xb*yb-xyb)/(xb^2-x2b);a=yb-b*xb;y1=a+b.*x;plot(x,y,'*',x,y1);serror=sum((y-y1).^2)Matlab中下标及希腊字母很多时候都要在matlab画图的时候添加一些公式符号之类的,有一些特殊的字符并不能直接从键盘上输入,比如希腊字母等等。
Matlab中下标,斜体,及希腊字母的使用方法
Symbol
û ⊥ ∧ ù ∨ ∠
Character Sequence
cdot neg times surd varpi rangle
Symbol
· ¬ x √
∠
Character Sequence
ldots prime
mid copyright
Symbol
... ´ ∅ | ©
下面给出 Matlab 中下标及希腊字母的使用方法,还有更多的使用方法可以参考 matlab 帮助 文档中的 Text Properties: 下标用 _(下划线) 上标用^ (尖号) 斜体 it 黑体 bf << ll >> gg 正负 pm 左箭头 leftarrow 右箭头 rightarrow 上箭头 uparrow 上圆圈(度数) circ 例: text(2,3,'\alpha_2^\beta')
rightarrow
→
Σ
downarrow
↓
ϒ
circ
º
Φ
pm
±
Ψ
geq
≥
Ω
propto
∝
∀
partial
∂
∃
bullet
•
∍
div
÷
≅
neq
≠
≈
alephℵຫໍສະໝຸດ ℜwp℘⊕
oslash
∅
∪
supseteq
⊇
⊆
subset
⊂
∈
o
ο
é
nabla
∇
Character Sequence
lfloor perp wedge rceil vee langle
matlab中legend希腊字母的输入

在MATLAB中,图例(legend)是一种用于在图表中标识不同曲线或数据系列的重要元素。
而在某些情况下,我们可能希望在图例中使用希腊字母来表示特定的变量或参数。
在本文中,我将重点探讨在MATLAB中如何输入希腊字母到图例中,并对其进行全面评估。
1. 基本方法:使用希腊字母的转义序列MATLAB允许用户在字符串中使用希腊字母的转义序列来表示相应的希腊字母。
要在图例中使用希腊字母α,可以在字符串中输入'\alpha'来表示。
这种方法简单易行,但对于不熟悉希腊字母的用户来说,可能需要花费一些时间去了解转义序列的对应关系。
2. 自定义图例:使用文本对象除了基本方法外,MATLAB还提供了更加灵活的自定义图例的方式。
可以使用文本对象来创建希腊字母表示的图例。
通过创建文本对象,并设置其字符串属性为希腊字母的转义序列,就可以在图例中显示相应的希腊字母。
这种方法不仅方便了用户在图例中使用希腊字母,而且还使得图例的样式和位置更加灵活,可以满足不同需求的定制化。
3. 使用 TeX 解析器MATLAB的图形绘制功能内置了TeX解析器,允许用户在图例中使用TeX语法来实现复杂的数学表达式和符号表示。
通过在字符串中使用'$'符号包裹希腊字母的TeX命令,就可以在图例中直接显示希腊字母,而无需使用转义序列。
这种方法对于熟悉TeX语法的用户来说非常便利,可以实现更加复杂和美观的图例表示。
4. 结合使用不同方法在实际应用中,可以根据具体情况结合不同的方法来实现图例中的希腊字母表示。
可以使用转义序列表示简单的希腊字母,而对于复杂的数学表达式,则使用TeX解析器来实现。
这种灵活的组合方式可以使得图例的表示更加清晰和美观。
总结回顾通过本文的全面评估,我们可以得出结论:在MATLAB中使用希腊字母表示图例是非常灵活和便利的。
无论是简单的转义序列还是复杂的TeX解析器,都可以满足用户对图例样式和内容的个性化需求。
matlab_希腊字母

>> \gg
正负 \pm
左箭头 \leftarrow
右箭头 \rightarrow
上箭头 \uparrow
上圆圈(度数) \circ
例 text(2,3,’\alpha_2^\beta’)
注: 可用{}把须放在一起的括起来
�
很多时候都要在matlab画图的时候添加一些公式符号之类的,有一些特殊的字符并不能直接从键盘上输入,比如希腊字母等等。但是有想用,因为这样使图看起来漂亮而且容易理解。
例如:我想输入摄氏度的符号,怎么办咧?
也许你突然想到,摄氏度不就是一个小圆圈加一个大写的C么。
于是就用’T=25^oC’来表示了,一看,多少还算是那么回事,但怎么看怎么有点别扭。
λ \lamda
Λ \Lamda
π \pi Π \Pi σ \siga Σ \Sigma
φ \phi
Φ \Phi
ψ \psi
Ψ \Psi
χ \chi
ω \ommiga
Ω \Ommiga
< \leq
> \geq
不等于 \neq
β \beta
γ \gamma
θ \theta
Θ \Theta
Г \Gamma
δ \delta
Δ \Delta
ξ \xi
Ξ \Xi
η \elta
ε \epsilong
ζ \zeta
μ \miu
υ \nu
τ \tau
因为o作为上标的时候它不是一个正真的圆圈,最多是个椭圆,并且它体积太大了。
好吧,既然如此,那就用中文输入法打个句号“。”上去,即’T=25^。C’
MATLAB中希腊字母

2009年10月27日星期二07:16 P.M.
文档中的Text Properties:
下标用_(下划线) 上标用^ (尖号)斜体\it 黑体\bf
比如在坐标轴的[0.5 0.5]位置上要显示δ字符,那么可以直接输入text(0.5,0.5,'\delta')
如果需要显示大写希腊字符的话,那直接将首字母改为大写就可以了
注意必须使用“\”引导,如果需要显示“\”,那么必须输入“\\”;类似的在字符串组合的时候如果要输入“'”则必须如下输入“''”
另外text字符可以重叠显示,这样就可以构造出一些有趣的效果,比如将某个字符上添加
例 text(2,3,'\alpha_2^\beta')
注:可用{}把须放在一起的括起来
/redirect.php?fid=9&tid=2118&goto=nextoldset
(From:/%BA%EC%C8%D5%D4%C6%C6%AE/blog/item/652cdc06 59dd60c47b89475d.html)
另外,可以直接在Matlab帮助里Search"Text Properties"和“Annotation Textarrow Properties”,即可以看到此表,而且还可以看到如下表:。
在Matlab图片里输入数学公式、符号和希腊字母和字体设置,线条等设置

在Matlab图片里输入数学公式、符号和希腊字母的方法在所有的Matlab Figure里都可以使用大量的Tex代码来输入公式、数学符号等。
而且,与Word2007类似,都能够写完立马显示,不对的话可以迅速更正。
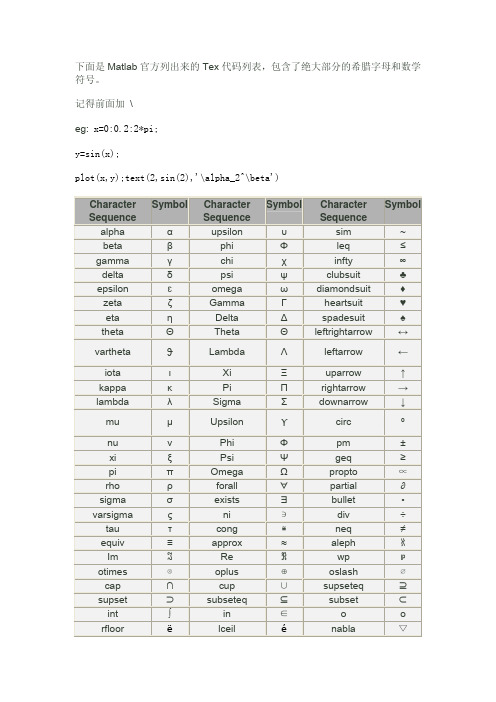
很好!下面是Matlab官方列出来的Tex代码列表,包含了绝大部分的希腊字母和数学符号。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%常用选项和小技巧%%%%%%画等值线[cc hh]=contour(peaks(30),'LINESPEC','b-')clabel(cc,hh,'manual')%写文本text(5,10,'\bf math \sl math \it math \rm math \alpha','color',[0.1 0.1 0.9],'fontsize',24)%设置线宽set(gca,'linewidth',2)%写标题并设置字体的大小ti=title('Title of My Figure','color','blue')set(ti,'fontsize',24)drawnow%输出文件print -dpsc plotE.psprint -append -dpsc plotE.psprint -djpeg100 plotE.jpg%给定图窗口标题figure('Name','My Figure1')%设置使用调色板map=hsv(32);colormap(map)%设定等值线的范围caxis([-6 6])%设定colorbar的方向和位置hc=colorbar('hori');po=get(hc,'position');%set(hc,'position',[po(1) po(2)+0.14 po(3) po(4)-0.01]);%set(hc,'XLim',[0 300]);%设置绘图的缺省值set(0,'DefaultLineLineWidth',2)set(0,'DefaultAxesFontSize',18)set(0,'DefaultAxesLineWidth',2)set(0,'DefaultAxesTickLength',[0.01 0.025])set(0,'DefaultPatchLineWidth',2)set(0,'DefaultSurfaceLineWidth',2)set(0,'DefaultRectangleLineWidth',2)set(0,'DefaultLineLineWidth','remove')set(0,'DefaultAxesFontSize','remove')set(0,'DefaultAxesLineWidth','remove')set(0,'DefaultAxesTickLength','remove')set(0,'DefaultPatchLineWidth','remove')set(0,'DefaultSurfaceLineWidth','remove')set(0,'DefaultRectangleLineWidth','remove')%%set(0,'DefaultLineLineWidth','factory')%%get(0,'factory')%设置坐标轴的间隔和显示set(gca,'XTick',[0:1:25],'YTick',[0:300:6000])set(gca,'XTickLabelMode','manual')set(gca,'XTickLabel','0|||||5|||||10|||||15|||||20|||||25|')%分别设置等值线和等值线标注的间隔[cc hh]=contour(peaks(30),[-6:2:8])c(cc,hh,[-6:4:8],'fontsize',15,'color','r','rotation',0,'labelspacing',200)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%几个实例%%%%%%给定月份名字name='JanFebMarAprMayJunJulAugSepOctNovDec'%给定每层深度depth=[5 15 25 35 45 55 65 75 85 95 110 130 155 185 220 260 305 365 450 575 755 1115 1735 2615 3645 4830]%给定经纬度x=31:1:288;y=-61:1:61。
matplotlib 希腊字符

[文章标题]一、引言本文将探讨matplotlib中的希腊字符的使用和应用,通过深入分析不同希腊字符的特点和用法,帮助读者更好地理解和掌握这一方面的知识。
二、希腊字符在matplotlib中的应用在matplotlib中,希腊字符被广泛应用于数学公式、图表标注等方面。
它们以其独特的符号形式,常常用于表示特定的数学常量、变量或函数名称。
在图表中,使用希腊字符可以增强图表的专业性和美观度,也有利于准确传达数学信息。
三、常见的希腊字符及其特点1. α(alpha):希腊字母表的第一个字母,常用于表示角度、系数等。
2. β(beta):希腊字母表的第二个字母,用于表示比例、角标、系数等。
3. γ(gamma):希腊字母表的第三个字母,常用于表示角度、系数等。
4. θ(theta):表示角度、温度等,常用于数学公式中。
5. π(pi):表示圆周率,是数学中的重要常数。
在matplotlib中,经常使用π来表示圆周率。
四、希腊字符的使用技巧1. 在matplotlib中,通过LaTeX语法可以很方便地插入希腊字符,例如可以使用r'$\alpha$'来表示α。
2. 希腊字符的大小和样式可以根据具体需求进行设置和调整,以符合整体图表的风格要求。
五、结语本文简要介绍了matplotlib中希腊字符的应用和使用技巧,希望可以帮助读者更好地应用希腊字符,提升图表的表达能力和美观度。
理解和掌握希腊字符在matplotlib中的使用,对于深入学习数据可视化和数学建模都具有重要意义。
希望读者能通过本文对希腊字符有更加全面、深刻的认识,从而在实际的工作和学习中运用自如。
建议读者在实际操作中多加练习,并灵活运用希腊字符,从而更好地适应不同的需求和场景。
个人观点:在实际的数据可视化和科学研究工作中,对希腊字符的熟练运用可以提升图表的专业性和准确性,也有助于提升学术论文和报告的质量。
我鼓励每一位研究者和科学工作者都要深入学习和灵活运用希腊字符,从而更好地表达数学和科学的精髓。
matlab sigma用法 -回复

matlab sigma用法-回复Matlab是一种功能强大的数值计算环境和编程语言,广泛应用于科学、工程和应用数学。
其中的sigma函数是Matlab中的一个重要函数,它在数学和统计分析中起着重要的作用。
本文将详细介绍Matlab中sigma函数的用法,从基本概念开始逐步解释,帮助读者深入了解和使用这一函数。
首先,我们需要明确sigma函数的定义和用途。
在数学中,sigma表示求和操作,通常用希腊字母“Σ”表示。
在Matlab中,sigma函数用于计算一系列数值的和。
它的用法很灵活,可以用于向量、矩阵和多维数组等不同的数据类型。
在Matlab中,sigma函数的基本语法如下:sum(A)其中,A表示待求和的向量、矩阵或数组。
这意味着我们可以使用sigma 函数对不同类型的数据进行求和操作。
如果使用sigma函数求解向量的和,可以直接传入一个向量作为参数。
例如,我们可以创建一个简单的向量并使用sigma函数计算其和,代码如下:matlabA = [1, 2, 3, 4, 5];result = sum(A);disp(result);上述代码中,我们创建了一个向量A,包含了从1到5的整数。
然后,我们调用sigma函数对向量A进行求和,并将结果保存在result变量中。
最后,通过disp函数将结果输出到命令窗口。
运行以上代码,将得到结果15,即向量A的元素之和。
除了向量,sigma函数还适用于矩阵和多维数组。
对于矩阵来说,sigma 函数可以沿着指定的维度对矩阵的元素进行求和。
例如,我们可以创建一个简单的2x3矩阵并使用sigma函数分别对行和列进行求和,代码如下:matlabB = [1, 2, 3; 4, 5, 6];row_sum = sum(B, 1); 对列求和col_sum = sum(B, 2); 对行求和disp(row_sum);disp(col_sum);上述代码中,我们创建了一个2x3矩阵B,然后使用sigma函数分别对列和行进行求和。
