经验分布函数图形R语言实现
经验分布函数及其应用

经验分布函数及其应用经验分布函数定义定义:设12n x x x ⋯,,,是总体(离散型、或连续型,分布函数F(x)未知)的n 个独立观测值,按大小顺序可排成12***n x x x ≤≤⋯≤ 。
若1**k k x x x +<< ,则不超过x 的观测值的频率为函数,就等于在n 次重复独立试验中事件{}x ξ≤的频率。
()110,=,,1,2,,11,k k nn x x k x x x k n nx x x F ***+*⎧≤⎪⎪<≤=-⎨⎪>⎩*⎪…… 我们称此函数()n F x 为总体的经验分布函数或样本分布函数。
简单性质:1.对于每一组观测值1,2,i i x i ξ*=*=,……,n ,()n F x *单调,非降,左连续且在1,2,i x x i =*=,……,n 点有间断点,在每个点的跳跃值都是1n 。
2.显然()01n F x ≤≤,具有分布函数的其他性质。
3.()n F x *为样本12n x x x ⋯,,,的函数,是一统计量,即为一随机变量,由于12n x x x ⋯,,,相互独立且有相同的分布函数()F x ,因而它等价于n 次独立重复试验的伯努利概型中事件{}x ξ≤发生k 次其余n k - 次不发生的额概率,即有:{}{}()()1()k n k k k n n k P F x C F x F x n -⎧⎫==-⎨⎬⎩⎭4.格列汶科定理设总体ξ 的分布函数为()F x ,经验分布函数为()n F x *,对于任何实数x ,记 ()()sup n x n F x F x D -∞<<*+∞=-则有lim 01n n P D →∞⎧⎫⎪⎪==⎨⎬⎪⎪⎩⎭ 其中n D 也为一统计量用来衡量()n F x *与()F x 之间在所有的x 的值上的最大差异程度,格列汶科定理证明了统计量n D 以概率为1地收敛于0,也就是如下所要说的经验分布函数的收敛性问题。
R语言画图简介

条形图
•若height是一个向量,则它的值就确定了各条形的高 度,并将绘制一幅垂直的条形图。使用选项 horiz=TRUE则生成水平条形图。 例. 使用”vcd”包中的数据集Arthritis(关于一项探索类 风湿性关节炎新疗法的研究结果)画条形图: install.packages(“vcd”) library(vcd) counts <- table(Arthritis$Improved) #提取变量Improved 中各类的频数 barplot(counts,main=“Simple Bar Plot”,xlab=“Improvement”,ylab=“Frequency”,horiz=TRUE)
画图
•案例(可以用boxplot()作两个样本的均值检 验,考察两个样本的均值是否相同) •A<c(79.98,80.04,80.02,80.04,80.03,80.03,80.0 4,79.97,80.05,80.03,80.02,80.00,80.02) B<c(80.02,79.94,79.98,9.97,79.97,80.03,79.95, 79.97)#比较他们的均值是否相同 •boxplot(A,B,notch=T,names=c("A","B"),col=c( 2,3),ylim=c(79.94,80.1))
条形图
•条形图通过垂直的或水平的条形展示了分类变量的频 数。 •条形图用barplot()这个函数,形式如下 •barplot(height, ...)#height是table类型的向量或者矩阵 •barplot(height, width = 1, space = NULL, names.arg = NULL, legend.text = NULL, beside = FALSE, horiz = FALSE, density = NULL, angle = 45, col = NULL, border = par("fg"), main = NULL, sub = NULL, xlab = NULL, ylab = NULL, xlim = NULL, ylim = NULL, xpd = TRUE, log = "", axes = TRUE, axisnames = TRUE, cex.axis = par("cex.axis"), s = par("cex.axis"), inside = TRUE, plot = TRUE, axis.lty = 0, offset = 0, add = FALSE, args.legend = NULL, ...)
r语言正态分布函数

r语言正态分布函数正态分布(Normal Distribution)是应用最广泛的概率分布之一,在统计学与概率论中具有重要的地位。
它也被称为高斯分布(Gaussian Distribution),由于其形状像一个钟形曲线,因此也常被称为钟形曲线。
正态分布的概率密度函数(Probability Density Function, PDF)如下:\[ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]其中,\( \mu \) 表示均值(mean),\( \sigma \) 表示标准差(standard deviation),\( \pi \) 是圆周率。
正态分布函数的特征:1.它是单峰的且呈对称分布,左右两侧的概率密度相等。
2. 均值 \( \mu \) 决定着正态分布的中心位置,标准差 \( \sigma \) 决定着曲线的陡峭程度。
当 \( \sigma \) 较小时,曲线较陡峭;当\( \sigma \) 较大时,曲线较平缓。
3. 标准正态分布是均值 \( \mu = 0 \) ,标准差 \( \sigma = 1 \) 的正态分布。
在R语言中,可以使用以下函数进行正态分布相关的计算。
(1)dnorm(:计算给定取值的概率密度函数值。
具体用法如下:\[ dnorm(x, mean = \mu, sd = \sigma) \]其中,x 表示指定的取值,mean 表示均值,sd 表示标准差。
示例代码:```#计算x=2的概率密度dnorm(2, mean = 0, sd = 1)```(2)pnorm(:计算给定取值的累积分布函数值。
具体用法如下:\[ pnorm(x, mean = \mu, sd = \sigma) \]其中,x 表示指定的取值,mean 表示均值,sd 表示标准差。
示例代码:```#计算x≤2的累积概率pnorm(2, mean = 0, sd = 1)```(3)qnorm(:给定一个概率值,计算对应的分位点。
也能做精算actuar 包学习笔记一

用R也能做精算—actuar包学习笔记(一)李皞(中国人民大学统计学院风险管理与精算)本文是对R中精算学专用包actuar使用的一个简单教程。
actuar项目开始于2005年,在2006年2月首次提供公开下载,其目的就是将一些常用的精算功能引入R系统。
actuar是一个集成化的精算函数系统,虽然其他R包中的很多函数可以供精算师使用,但是为了达到某个目的而寻找某个包的某个函数是一个费时费力的过程,因此,actuar将精算建模中常用的函数汇集到一个包中,方便了人们的使用。
目前,该包提供的函数主要涉及风险理论,损失分布和信度理论,特别是为非寿险研究提供了很多方便的工具。
如题所示,本文是我在学习actuar包过程中的学习笔记,主要涉及这个包中一些函数的使用方法和细节,对一些方法的结论也有稍许探讨,因此能简略的地方简略,而讨论的地方可能讲的会比较详细。
文章主要是针对R语言的初学者,因此每种函数或数据的结构进行了尽可能直白的描述,以便于理解,如有描述不清或者错漏之处,敬请各位指正。
闲话少提,下面就正式开始咯!1 数据描述本节介绍描述数据的基本方法,数据类型主要分为分组数据和非分组数据。
对于非分组数据的描述方法大家会比较熟悉,无论是数量上,还是图形上的,比如均值、方差、直方图、柱形图还有核密度估计等。
因此下文的某些部分只介绍如何处理分组数据。
1.1 构造分组数据对象分组数据是精算研究中经常见到的数据类型,虽然原始的损失数据比分组数据包含有更多的信息,但是某些情况下受条件所限,只能获得某个损失所在的范围。
与此同时,将数据分组也是处理原始数据的基本方法,通过将数据分到不同的组中,我们可以看到各组中数据的相对频数,有助于对数据形成直观的印象(比如我们对连续变量绘制直方图);而且在生存函数的估计中,数据量经常成千上万,一种处理方法是选定合适的时间或损失额度间隔,对数据进行分组,然后再使用分组数据进行生存函数的估计,这样可以有效减小计算量。
r语言plot基本函数

r语言plot基本函数1.引言1.1 概述R语言是一种流行的统计分析和数据可视化工具,它提供了丰富而强大的plot基本函数,用于创建各种图形和图表。
这些函数可以用于绘制散点图、折线图、柱状图、箱线图等各种常见或定制的图形。
本文将介绍R语言中plot基本函数的使用方法和特点。
我们将详细讨论这些函数的参数设置、数据输入方式、图形样式定制等方面的内容,以帮助读者快速掌握基本函数的使用技巧。
在本文的第二节,我们将重点介绍plot函数的常用技巧和注意事项。
通过这些技巧,读者将能够灵活运用plot函数,绘制出符合需求的图形,并对数据进行准确的分析和展示。
在第三节中,我们将对文章进行总结,并给出一些结论。
通过本文的学习,读者将能够熟练使用R语言中的plot基本函数,提高自己的数据分析和可视化能力。
总的来说,本文将围绕R语言的plot基本函数展开论述,从概述到具体实例,帮助读者全面了解和掌握这些函数的使用方法和技巧。
希望本文能够对读者在数据分析和可视化方面有所帮助,进一步提升读者的工作能力和水平。
1.2文章结构文章结构部分的内容可以如下所示:1.2 文章结构本文主要介绍R语言中的plot基本函数,通过对这些函数的详细讲解和示例,帮助读者快速掌握如何使用R语言进行数据可视化和图形绘制。
文章的结构如下:2.1 R语言中的plot基本函数:本节将介绍R语言中常用的plot基本函数,包括plot()、hist()、boxplot()等,在讲解函数的使用方法的同时,还会通过实例演示如何绘制不同类型的图形和如何进行相关设置。
2.2 第一个要点:在本节中,将重点介绍plot()函数,该函数是R语言中最基础、最常用的绘图函数之一。
我们将详细介绍plot()函数的参数用法,包括如何设置图形的标题、坐标轴标签、图例等,并通过示例展示不同数据类型的绘制方法,如散点图、折线图、柱状图等。
2.3 第二个要点:本节将着重介绍hist()和boxplot()函数,在实际的数据分析中,这两个函数经常被用于绘制直方图和箱线图。
R语言常用统计方法实现

变异系数、平方和
• 对于变异系数、校正平方和、未校正平方和等指 标,需要编写简单的程序. • 变异系数CV计算: cv<-100*sd(x)/mean(x);cv • 校正平方和CSS: css<-sum((x-mean(x))^2);css • 未校正平方和USS: uss<-sum(x^2);uss
quantile(x,probs=seq(0,1,0.25),na.rm=FALSE)
分散程度的度量
• 表示数据分散(或变异)程度的特征量有方差、标准 差、极差、四分位极差、变异系数和标准误等. • 在R软件中,用var()和sd()计算方差、标准差: var(x, na.rm=FALSE,) sd(x,na.rm=FALSE)
求解程序
• blood<data.frame( X1=c(76.0,91.5,85.5,82.5,79.0,80.5,74.5,79.0,85.0, 76.5,82.0,95.0,92.5),X2=c(50,20,20,30,30,50,60,50,40,55,40,40, 20),Y=c(120,141,124,126,117,125,123,125,132,123,132,155,147 ) ) #建立数据框 • lm.sol<-lm(Y~X1+X2,data=blood) #进行回归分析 • summary(lm.sol) #汇总分析结果 • Y=-62.96+2.136X1+0.4002X2. • 预测:X=(80, 40)时,相应Y的概率为0. 95的预测区间. • new<-data.frame(X1=c(80,75),X2=c(40,38)) • lm.pred<-predict(lm.sol,new,interval="prediction",level=0.95) • lm.pred
第六篇:R语言数据可视化之数据分布图(直方图、密度曲线、箱线图、等高线、2D密度图)
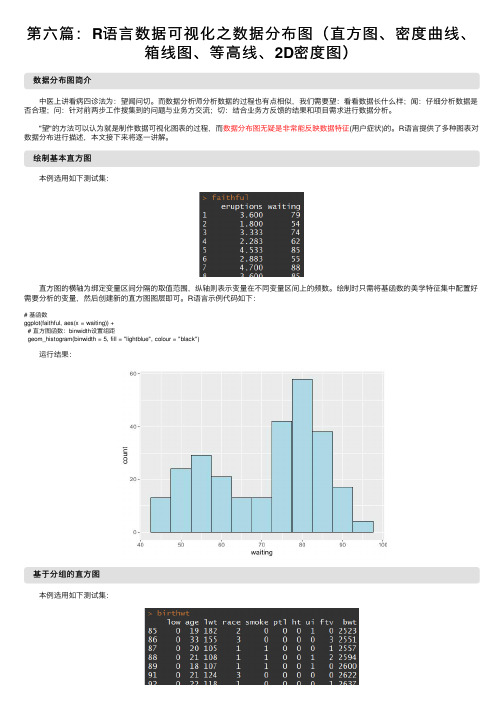
第六篇:R语⾔数据可视化之数据分布图(直⽅图、密度曲线、箱线图、等⾼线、2D密度图)数据分布图简介中医上讲看病四诊法为:望闻问切。
⽽数据分析师分析数据的过程也有点相似,我们需要望:看看数据长什么样;闻:仔细分析数据是否合理;问:针对前两步⼯作搜集到的问题与业务⽅交流;切:结合业务⽅反馈的结果和项⽬需求进⾏数据分析。
"望"的⽅法可以认为就是制作数据可视化图表的过程,⽽数据分布图⽆疑是⾮常能反映数据特征(⽤户症状)的。
R语⾔提供了多种图表对数据分布进⾏描述,本⽂接下来将逐⼀讲解。
绘制基本直⽅图本例选⽤如下测试集:直⽅图的横轴为绑定变量区间分隔的取值范围,纵轴则表⽰变量在不同变量区间上的频数。
绘制时只需将基函数的美学特征集中配置好需要分析的变量,然后创建新的直⽅图图层即可。
R语⾔⽰例代码如下:# 基函数ggplot(faithful, aes(x = waiting)) +# 直⽅图函数:binwidth设置组距geom_histogram(binwidth = 5, fill = "lightblue", colour = "black")运⾏结果:基于分组的直⽅图本例选⽤如下测试集:直⽅图的分组图和本系列前⾯⼀些博⽂中讲的⼀些分组图不同,它不能进⾏⽔平⽅向的堆积 - 这样看不出频数变化趋势;也不能进⾏垂直⽅向的堆积 - 这样同样看不出趋势。
这⾥采⽤⼀种新的堆积⽅法:重叠堆积,R语⾔实现代码如下:# 预处理:将smoke变量转换为因⼦类型birthwt$smoke = factor(birthwt$smoke)# 基函数:x设置⽬标变量ggplot(birthwt, aes(x = bwt, fill = smoke)) +# 直⽅图函数:position设置堆积模式为重叠geom_histogram(position = "identity", alpha = 0.4)运⾏结果:也可以采⽤分⾯的⽅法,R语⾔实现代码如下:# 预处理1:将smoke变量转换为因⼦类型birthwt$smoke = factor(birthwt$smoke)# 预处理2:改变因⼦⽔平名称birthwt$smoke = revalue(birthwt$smoke, c("0" = "No Smoke", "1" = "Smoke"))# 基函数ggplot(birthwt, aes(x = bwt)) +# 直⽅图函数geom_histogram(fill = "lightblue", colour = "black") +# 分⾯函数:纵向分⾯facet_grid(smoke ~ .)运⾏结果:绘制密度曲线本例选⽤如下测试集:密度曲线表达的意思和直⽅图很相似,因此密度曲线的绘制⽅法和直⽅图也⼏乎是相同的。
mape r语言实现方法

mape r语言实现方法R语言是一种用于统计分析和图形绘制的编程语言,它在数据科学领域非常流行。
Mape R语言实现方法指的是使用R语言来实现平均绝对百分比误差(Mean Absolute Percentage Error,简称MAPE)的计算和分析方法。
本文将介绍如何使用R语言来实现MAPE方法。
首先,我们需要明确MAPE的定义和计算方法。
MAPE用于衡量预测值与实际值之间的误差大小。
其计算公式如下:MAPE = (1/n) * ∑(|(A - F)/A|) * 100其中,A代表实际值,F代表预测值,n代表数据点的个数。
MAPE的值越小,表示预测结果与真实情况的误差越小。
接下来,我们可以使用R语言来实现MAPE方法。
首先,需要加载R中的相关包,比如"data.table"包和"dplyr"包。
可以使用以下代码进行加载:```Rlibrary(data.table)library(dplyr)```然后,我们需要将实际值和预测值存储在R语言中的数据结构中,比如数据框(data frame)或数据表(data table)。
假设我们的实际值存储在一个名为"actual"的列中,预测值存储在一个名为"forecast"的列中,可以使用以下代码创建一个数据框:```Rdata <- data.frame(actual = c(10, 15, 20, 25), forecast = c(12, 14, 18, 24))```接下来,我们可以使用R语言中的内置函数和操作符来计算MAPE。
可以使用以下代码计算MAPE值:```Rn <- nrow(data) # 获取数据点的个数mape <- (1/n) * sum(abs((data$actual - data$forecast) / data$actual)) * 100 # 计算MAPE值```在计算MAPE值之后,我们可以对其进行分析和可视化。
5-R语言统计绘图基础

条形图、箱线图和饼图
进一步 如果height是一个矩阵而不是一个向量,则绘图结果将是一幅堆砌条形图或分组条形图 (1)若beside=FALSE(默认值),则矩阵中的每一列都将生成图中的一个条形,各列中的值将给 出堆砌的“子条”的高度。 (2)若beside=TRUE,则矩阵中的每一列都表示一个分组 ,各列中的值将并列而不是堆砌。
● x:是数据向量. ● scale:控制绘出茎叶图的长度. ● Width:绘图的宽度
应用举例如右图:
核密度图
■核密度图 :用来估计随机变量概率密度函数
的一种非参数法,核密度图是一种用来观察连续 型变量分布的有效办法。
其绘图函数为:
Plot(density(x),col,main,…)
x :为一个数值型向量
● x: 数值矩阵或数据框; ● full:为图形形状,TRUE为圆形 ,FALSE为半 圆; ●draw.segments:为分支形状:TRUE为圆形,False为半圆
应用举例:
直方图、星相图、茎叶图
■茎叶图: 茎叶图包含原始数据的所有信息, 很直观的展现数据,其函数为:
stem(x, scale,width)
■应用举例:正太随机数排序连线
> x<-c(1:10) > y<-sort(rnorm(10)) > par(mfrow=c(1:2)) > plot(x,y,col=4,pch=11) > i<-c(1:10) > segments(x[i],y[i],x[i+1],y[i+1],col=1:3,lwd=2) > plot(x,y,col=4,pch=11) > arrows(x[i],y[i],x[i+1],y[i+1],col=1:3,lwd=2) >
数据分析技巧使用R语言和RStudio进行数据分析的基本操作

数据分析技巧使用R语言和RStudio进行数据分析的基本操作在当今信息爆炸的时代,大量的数据产生和存储成为了常态。
对这些数据进行有效的分析和解读成为了各行业追求的目标。
在数据分析方面,R语言和RStudio成为了广泛使用的工具。
本文将介绍使用R语言和RStudio进行数据分析的基本操作,帮助读者快速上手。
一、R语言和RStudio简介R语言是一种自由、开放源代码的编程语言,主要用于统计计算和绘图。
它拥有丰富的数据处理和分析函数库,可以满足各种复杂的数据分析需求。
RStudio是一个集成开发环境(IDE),为R语言提供了图形化界面和一系列便捷的工具,使得数据分析更加高效。
二、数据导入与清洗在进行数据分析之前,首先需要将数据导入RStudio,并进行必要的数据清洗。
导入数据可以通过读取本地文件、从数据库中获取数据以及通过API接口获取数据等方式实现。
数据清洗包括处理缺失值、处理异常值、去除重复数据、转换数据类型等操作。
R语言提供了丰富的函数和包来支持数据导入和清洗,例如read.csv、na.omit、duplicated等函数。
三、数据探索与可视化数据分析的第一步是对数据进行探索性分析,了解数据的基本情况、变量之间的关系等。
R语言提供了丰富的统计计算和可视化函数库,如summary、cor、hist等,可以帮助我们进行数据探索。
通过绘制直方图、散点图、箱线图等图形,可以更直观地观察数据的分布和变化趋势。
四、数据预处理在进行进一步的分析之前,通常需要对数据进行预处理,包括特征选择、特征缩放、数据标准化等操作。
R语言提供了多种数据处理的函数和包,如caret、dplyr、tidyr等,可以轻松实现数据预处理的各种需求。
例如,可以使用scale函数对数据进行标准化,使用select函数选择需要的特征变量。
五、数据建模与评估在数据分析的最核心部分是建立统计模型,并对模型进行评估。
R语言提供了丰富的建模工具和函数库,如lm、glm、randomForest等,可以满足各种常见的统计建模需求。
基于R语言数据可视化-分布特征可视化

9
数据可视化
12/15/2019
4.1
直方图与核密度图
直方图——堆叠直方图——例题分析
【例4-1】
堆叠直方图 ( stacked histogram) 是将按因子 水平分类的 直方图堆叠 在一起的一 种图形。比 如,我们按 “质 量 等 级 ” 这一因子来 绘 制 AQI的 直 方图并堆叠 在一起
数绘制的按质 量等级分类来 绘制点图
37
数据可视化
12/15/2019
4.3
点图和带状图
带状图 l 带 状 图 ( stripchart) 又 称 平 行 散 点 图 ( parallel
scatterplot) l 它与点图类似,用于产生一维(one dimensional)
散点图 l 当样本数据较少时,可作为直方图和箱线图的替
25
数据可视化
12/15/2019
4.2
箱线图和小提琴图
箱线图——例题分析
【例4-1】 graphics包 中 的 boxplot函 数绘制的6项 空气污染指 标的箱线图
26
数据可视化
12/15/2019
4.2
箱线图和小提琴图
箱线图——例题分析
【例4-1】 对数变换和 标准化变换 后的6项空气 污染指标的 箱线图
【 例 4-1】 ( 数 据 : data4_1.csv) 。 空 气 质 量 指 数 ( Air Quality Index,AQI)用来描述空气质量状况,指数的数值 越大说明空气污染状况越严重。参与空气质量评价的主要 污染物有细颗粒物(PM 2.5)、可吸入颗粒物(PM10)、 二氧化硫(SO2)、一氧化碳(CO)、二氧化氮(NO2)、 臭氧浓度(O3)等6项。根据空气质量指数将空气质量分 为6级:优(0-50),良(51-100),轻度污染(101-150), 中度污染(151-200),重度污染(201-300),严重污染 (300以上);分别用绿色、黄色、橙色、红色、紫色、褐 红色表示。表4-1是2018年1月1日~12月31日北京市的空气 质量数据
数理统计14:什么是假设检验,拟合优度检验(1),经验分布函数

数理统计14:什么是假设检验,拟合优度检验(1),经验分布函数在之前的内容中,我们完成了参数估计的步骤,今天起我们将进⼊假设检验部分,这部分内容可参照《数理统计学教程》(陈希孺、倪国熙)。
由于本系列为我独⾃完成的,缺少审阅,如果有任何错误,欢迎在评论区中指出,谢谢!⽬录Part 1:什么是假设检验假设检验是⼀种统计推断⽅法,⽤来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的。
其步骤,其实就是提出⼀个假设,然后⽤抽样作为证据,判断这个假设是正确的或是错误的,这⾥判断的依据就称为该假设的⼀个检验。
假设检验在数理统计中有重要的⽤途,⽐如:橙⼦的平均重量是80⽄,这就是⼀个假设。
我们怎么才能知道它是对的还是错的?这需要我们对橙⼦总体进⾏抽样,然后对样本进⾏⼀定的处理,⽐如计算总体均值的区间估计,如果区间估计不包含80⽄,就认为原假设不成⽴,便拒绝原假设。
当然,由于样本具有随机性,因此我们只是对该假设进⾏检验⽽不是证明,也就是说不论假设检验的结果是接受假设还是拒绝假设,都不能认为假设本⾝是正确的或是错误的。
同时,假设的检验也不是唯⼀确定的,对任何假设都可以有⽆数种⽅案进⾏检验,⽐如上⾯的例⼦,95%的区间估计是⼀种检验,99%的区间估计也可以作为检验,90%的当然也可以,只要事先确定了即可。
总之,要将实⽤问题转化为统计假设检验问题处理,⼀般需要经历以下⼏个步骤:明确所要处理的问题,将其转化为⼆元问题,只能⽤“是”和“否”来回答。
设计适当的检验,规定假设的拒绝域,即拒绝假设时样本X 会落⼊的区域范围(当然也可以是统计量会落⼊的范围,这两个意思是⼀致的)。
抽取样本X 进⾏观测,计算需要的统计量的值。
根据样本的具体值作出接受假设或者否定假设的决定。
以下是假设检验问题的⼀些常⽤概念:零假设即原假设,指的是进⾏统计检验时预先建⽴的假设,⼀般是希望证明其错误的假设,⽤字母H 0表⽰。
这种区分⽅式⽐较⽞乎。
r语言rug函数

R语言rug函数解释1. 函数定义rug()是R语言中的一个用于绘制轴刻度标记的函数。
它可以在指定轴上绘制一条短线段,表示数据分布的位置。
2. 函数用途rug()函数主要用于辅助数据可视化,通过在坐标轴上添加短线段,帮助观察者更直观地了解数据的分布情况。
它通常与其他绘图函数(如plot()或hist())一起使用,将数据分布与图形结合展示。
3. 函数工作方式rug()函数可以在x轴或y轴上绘制短线段。
其工作方式如下:•rug(x, side = "both", ticksize = NULL, lineheight = NULL, col = par("fg"), lwd = par("lwd"))•x: 待绘制刻度标记的向量。
•side: 指定刻度标记绘制在哪一侧的轴上,默认为”both”,即两侧都有刻度标记;还可以选择”bottom”(底部)或”top”(顶部)。
•ticksize: 刻度标记的长度,默认为NULL,即由系统自动确定。
•lineheight: 刻度标记距离坐标轴线的垂直距离,默认为NULL,即由系统自动确定。
•col: 刻度标记的颜色,默认为当前绘图设备的前景色。
•lwd: 刻度标记的线宽,默认为当前绘图设备的线宽。
rug()函数根据提供的向量x,在指定的轴上绘制短线段。
短线段的位置由向量x中的元素确定,每个元素对应一个刻度标记。
如果x是数值型向量,则刻度标记将在数值对应的位置上;如果x是逻辑型向量,则TRUE对应1,FALSE对应0。
刻度标记可以同时绘制在底部和顶部,也可以只绘制在其中一侧。
刻度标记的长度和距离坐标轴线的垂直距离可以通过ticksize和lineheight参数进行调整。
默认情况下,这两个参数由系统自动确定。
4. 示例下面通过一个示例来演示如何使用rug()函数:# 创建一个随机数向量set.seed(123)data <- rnorm(100)# 绘制直方图,并添加刻度标记hist(data)rug(data, col = "red")运行以上代码,将会生成一个包含100个随机数数据分布情况的直方图,并在底部添加了红色刻度标记。
R语言-统计分布和模拟

R语⾔-统计分布和模拟R语⾔中统计分布和模拟前⾔ 很多应⽤都需要随机数。
像interlink connection,密码系统、视频游戏、⼈⼯智能、优化、问题的初始条件,⾦融等都需要⽣成随机数。
但实际上⽬前我们并没有“真正”的随机数⽣成器,尽管有⼀些伪随机数⽣成器也是⾮常有效的。
⽬录 1. 概率统计分布概述 2. 随机函数模拟介绍 3. 密度函数模拟介绍 4. 分布函数模拟介绍 5. 分位数函数模拟介绍 6. 函数模拟举例1. 概率统计分布概述 各种统计分布在R中的名称,这张表取⾃《An Introduction to R》中概率分布⼀章,基本涵盖了R中所有的概率函数。
R给出了详尽的统计表。
R 还提供了相关函数来计算累计概率分布函数 X <= x),概率密度函数和分位数函数(给定 q,符合 P(X <= x) > q的最⼩x就是对应的分位数),和基于概率分布的计算机模拟。
R中的各种概率统计分布汉⽂名称英⽂名称R对应的名字附加参数β分布beta beta shape1, shape2, ncp⼆项式分布binomial binom size, prob柯西分布Cauchy cauchy location, scale卡⽅分布chi-squared chisq df, ncp指数分布exponential exp rateF分布F f df1, df1, ncpGamma(γ)分布gamma gamma shape, scale⼏何分布geometric geom prob超⼏何分布hypergeometric hyper m, n, k对数正态分布log-normal lnorm meanlog, sdlogLogistic分布logistic logis location, scale负⼆项式分布negative binomial nbinom size, prob正态分布normal norm mean, sd泊松分布Poisson pois lambdaWilcoxon分布signed rank signrank nt分布Student's t t df, ncp均匀分布uniform unif min, max韦伯分布Weibull weibull shape, scale秩和分布Wilcoxon wilcox m, n 概率函数介绍 在R中各种概率函数都有统⼀的形式,即⼀套统⼀的前缀+分布函数名: d 表⽰密度函数(density); p 表⽰分布函数(⽣成相应分布的累积概率密度函数); q 表⽰分位数函数,能够返回特定分布的分位数(quantile); r 表⽰随机函数,⽣成特定分布的随机数(random)。
pnorm函数 r语言

pnorm函数r语言
pnorm函数是一个R语言中用来计算标准正态分布的累积分布函数的函数。
它的作用是给出随机变量X 的分布函数值小于或等于给定的数值的概率。
pnorm 函数的基本语法如下:
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
其中,
- q:表示要计算分布函数值的某个值。
- mean:表示分布的均值,默认为0。
- sd:表示分布的标准差,默认为1。
- lower.tail:如果为TRUE,则计算P(X <= q);如果为FALSE,则计算P(X > q)。
默认为TRUE。
- log.p:如果为TRUE,则返回概率的自然对数。
例如,如果要计算X ~ N(0,1) 的分布函数值小于等于1 的概率,可以使用以下代码:
pnorm(1)
输出结果为:
[1] 0.8413447
这表示X ~ N(0,1) 分布函数值小于等于1 的概率为0.8413。
r语言densityplot函数

R语言是一种统计分析和数据可视化的编程语言,具有强大的功能和灵活性。
在数据可视化领域,R语言提供了丰富的绘图函数,其中densityplot函数是用于绘制密度图的一种重要函数。
本文将介绍R语言densityplot函数的基本用法和实际案例,帮助读者更好地理解并应用这一函数进行数据可视化。
一、densityplot函数概述1.1 densityplot函数作用densityplot函数是R语言中lattice包提供的一个函数,用于绘制变量的概率密度图。
通过密度图,可以直观地展现数据的分布情况,帮助我们了解数据的集中趋势和离散程度。
1.2 densityplot函数参数densityplot函数包含多个参数,常用的参数包括x(需要绘制密度图的变量)、data(数据框)、m本人n(图表标题)、xlab(x轴标签)、ylab(y轴标签)等。
在实际使用中,可以根据需要调整参数的取值,以满足不同的绘图需求。
二、densityplot函数基本用法2.1 导入lattice包在使用densityplot函数之前,需要先导入lattice包,可以使用以下代码实现导入:```Rlibrary(lattice)```2.2 绘制简单的密度图接下来,我们以R语言自带的iris数据集为例,演示如何使用densityplot函数绘制简单的密度图。
假设我们需要绘制iris数据集中花瓣长度(Petal.Length)的概率密度图,可以使用以下代码实现:```Rdata(iris)densityplot(~ Petal.Length, data = iris, m本人n = "Petal Length Density Plot", xlab = "Petal Length", ylab = "Density")```在上述代码中,使用了densityplot函数绘制了Petal.Length的概率密度图,图表标题为“Petal Length Density Plot”,x轴标签为“Petal Length”,y轴标签为“Density”。
r语言coplot函数

R语言coplot函数引言在数据分析和可视化中,R语言是一种非常强大的工具。
其中,coplot函数是一个用于绘制多变量数据的图形的函数。
本文将详细介绍coplot函数的用法、参数和实例,并探讨其在数据分析中的应用。
coplot函数概述coplot函数是R语言中的一个可视化函数,用于绘制条件作图(condition plot)。
它可以用于观察多个变量之间的关系,并帮助我们理解数据的分布、趋势和异常值。
coplot函数的语法如下:coplot(formula, data, panel = ..., rows = ..., columns = ..., show.given = ..., show.missing = ..., type = ..., ...)其中,参数的含义如下: - formula:指定变量之间的关系,通常是一个公式,如y ~ x1 + x2,表示y与x1和x2之间的关系。
- data:指定数据集。
- panel:指定面板函数,用于绘制每个面板中的图形。
- rows:指定行数。
- columns:指定列数。
- show.given:是否显示给定的值。
- show.missing:是否显示缺失值。
- type:指定图形的类型。
coplot函数实例为了更好地理解coplot函数的用法,我们将通过一个实例来演示。
假设我们有一个数据集,包含了一些汽车的相关信息,如品牌、价格和里程等。
我们想要观察汽车品牌与价格和里程之间的关系。
首先,我们需要加载相关的R包,并读取数据集。
library(ggplot2)data <- read.csv("cars.csv")接下来,我们可以使用coplot函数来绘制条件作图。
我们将品牌作为条件变量,价格和里程作为响应变量。
coplot(price ~ brand | mileage, data = data, panel = panel.smooth, rows = 2, c olumns = 2)在这个例子中,我们使用了panel.smooth函数作为面板函数,它可以绘制出每个面板中的平滑曲线。
r语言计算特定值的对数正态分布函数的数值代码

r语言计算特定值的对数正态分布函数的数值代码在统计学中,对数正态分布是一种常见的概率分布,特别是在生物、医学、经济等领域中经常被使用。
在对数正态分布中,如果一个随机变量X的对数取值与正态分布相同,那么这个X就是对数正态分布的。
这种分布在对数尺度上具有广泛的应用,因为它能够更好地处理那些数据变化范围大的问题。
在R语言中,我们可以使用内置的函数来计算特定值的对数正态分布。
下面是一段简单的代码,展示了如何使用R语言来计算特定值的对数正态分布。
```r#引入必要的库library(ggplot2)#设定对数正态分布的参数mu<-0#对数的均值sigma<-1#对数的标准差x_value<-5#我们想要计算的特定值#使用rpois函数生成对应的对数值y_values<-rpois(1,lambda=sigma*log(x_value))#计算对数正态分布的概率密度函数(PDF)log_normal_pdf<-dlogis(y_values,mu=mu,sigma=sigma)#打印结果print(log_normal_pdf)```这段代码首先引入了ggplot2库,这是一个非常强大的图形绘制库。
然后,我们设定了对数正态分布的均值和标准差。
接着,我们使用rpois函数生成了对数值,这个函数会生成一个泊松分布的对数值。
最后,我们使用dlogis函数计算了对数正态分布的概率密度函数(PDF)。
这个函数会返回一个向量,包含了对应于给定对数值的概率密度值。
这段代码只是一个基本的示例,实际应用中可能需要根据具体需求进行调整。
例如,你可能需要调整均值和标准差的值,或者可能需要处理大量的数据。
此外,如果你需要更复杂的对数正态分布的计算(例如,需要计算累积分布函数(CDF)或逆变换等),你可能需要使用更专门的库或函数。
请注意,这段代码只是一个基础的示例,它并没有考虑到所有的错误处理和边界情况。
r语言正态分布曲线

R语言正态分布曲线1. 什么是正态分布曲线?正态分布(Normal Distribution),又称高斯分布(Gaussian Distribution),是统计学中最为重要和常见的概率分布之一。
它的特点是呈钟形曲线,两侧尾部逐渐趋于无穷远,中间部分较高且集中。
正态分布曲线在自然界和社会科学中广泛应用,被认为是随机变量的理想模型。
正态分布曲线由两个参数决定:均值(μ)和标准差(σ)。
均值决定了曲线的位置,标准差决定了曲线的形状。
2. R语言中绘制正态分布曲线的方法在R语言中,我们可以使用dnorm()函数来生成正态分布的概率密度函数(Probability Density Function, PDF)。
dnorm()函数有三个参数:x表示要计算概率密度函数的数值向量;mean表示均值;sd表示标准差。
首先,我们需要安装并加载ggplot2包,用于绘图:install.packages("ggplot2")library(ggplot2)接下来,我们可以使用以下代码绘制一个标准正态分布曲线:x <- seq(-4, 4, length.out = 1000) # 生成从-4到4的等间距数值向量y <- dnorm(x, mean = 0, sd = 1) # 计算标准正态分布曲线的概率密度函数data <- data.frame(x = x, y = y) # 创建数据框ggplot(data, aes(x = x, y = y)) +geom_line() +labs(title = "Standard Normal Distribution Curve",x = "x",y = "Probability Density") +theme_minimal()上述代码中,我们使用seq()函数生成了一个从-4到4的等间距数值向量。
